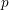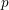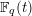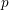1 Introduction
We fix an odd prime
![]() $p$
throughout the paper. The Cohen–Lenstra heuristics [Reference Cohen and LenstraCL84] predict the distribution of abelian
$p$
throughout the paper. The Cohen–Lenstra heuristics [Reference Cohen and LenstraCL84] predict the distribution of abelian
![]() $p$
-groups that show up as the
$p$
-groups that show up as the
![]() $p$
-primary part of the class group of an imaginary quadratic number field as we vary the field. In particular, there is a measure
$p$
-primary part of the class group of an imaginary quadratic number field as we vary the field. In particular, there is a measure
![]() $\unicode[STIX]{x1D707}_{\text{CL}}$
on finite abelian
$\unicode[STIX]{x1D707}_{\text{CL}}$
on finite abelian
![]() $p$
-groups, such that
$p$
-groups, such that
 $\unicode[STIX]{x1D707}_{\text{CL}}(G)>0$
for every finite abelian
$\unicode[STIX]{x1D707}_{\text{CL}}(G)>0$
for every finite abelian
![]() $p$
-group
$p$
-group
![]() $G$
, that is uniquely characterized by the fact that for any
$G$
, that is uniquely characterized by the fact that for any
![]() $G_{1},G_{2}$
finite abelian
$G_{1},G_{2}$
finite abelian
![]() $p$
-groups
$p$
-groups
 $\unicode[STIX]{x1D707}_{\text{CL}}(G_{1})/\unicode[STIX]{x1D707}_{\text{CL}}(G_{2})=|\!\operatorname{Aut}(G_{2})|/|\!\operatorname{Aut}(G_{1})|$
. We let
$\unicode[STIX]{x1D707}_{\text{CL}}(G_{1})/\unicode[STIX]{x1D707}_{\text{CL}}(G_{2})=|\!\operatorname{Aut}(G_{2})|/|\!\operatorname{Aut}(G_{1})|$
. We let
![]() $D_{X}$
denote the set of imaginary quadratic fields of absolute discriminant less than
$D_{X}$
denote the set of imaginary quadratic fields of absolute discriminant less than
![]() $X$
, and let
$X$
, and let
![]() $C_{K}$
denote the
$C_{K}$
denote the
![]() $p$
-primary part of the class group of a field
$p$
-primary part of the class group of a field
![]() $K$
, called the
$K$
, called the
![]() $p$
-class group of
$p$
-class group of
![]() $K$
. Cohen and Lenstra then conjecture the following.
$K$
. Cohen and Lenstra then conjecture the following.
Conjecture 1.1 (Cohen–Lenstra, [Reference Cohen and LenstraCL84, 8.1]).
For any ‘reasonable’ function
![]() $f$
on isomorphism classes of finite abelian
$f$
on isomorphism classes of finite abelian
![]() $p$
-groups, we have
$p$
-groups, we have
 $$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}f(C_{K})}{\#D_{X}}=\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{CL}}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}f(C_{K})}{\#D_{X}}=\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{CL}}.\end{eqnarray}$$
By class field theory, the
![]() $p$
-class group of a number field
$p$
-class group of a number field
![]() $K$
is isomorphic to the Galois group
$K$
is isomorphic to the Galois group
![]() $A_{K}$
of the maximal abelian unramified
$A_{K}$
of the maximal abelian unramified
![]() $p$
-extension of
$p$
-extension of
![]() $K$
. We use this perspective in which Cohen–Lenstra predicts the distribution of Galois groups of such extensions to consider a generalization of the above conjecture to non-abelian unramified extensions of imaginary quadratic fields
$K$
. We use this perspective in which Cohen–Lenstra predicts the distribution of Galois groups of such extensions to consider a generalization of the above conjecture to non-abelian unramified extensions of imaginary quadratic fields
![]() $K$
, as follows.
$K$
, as follows.
Let
![]() $G_{K}$
be the Galois group of the maximal unramified pro-
$G_{K}$
be the Galois group of the maximal unramified pro-
![]() $p$
extension of
$p$
extension of
![]() $K$
, also called its
$K$
, also called its
![]() $p$
-class tower group. Boston et al. [Reference Boston, Bush and HajirBBH16] have made predictions about how often one should expect a given group to appear as
$p$
-class tower group. Boston et al. [Reference Boston, Bush and HajirBBH16] have made predictions about how often one should expect a given group to appear as
![]() $G_{K}$
. Unlike
$G_{K}$
. Unlike
![]() $A_{K}$
, it turns out that
$A_{K}$
, it turns out that
![]() $G_{K}$
can be infinite and this introduces new features in the non-abelian case, for example, the measure on candidate groups is no longer discrete. We put a measure
$G_{K}$
can be infinite and this introduces new features in the non-abelian case, for example, the measure on candidate groups is no longer discrete. We put a measure
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
on the set of finitely generated pro-
$\unicode[STIX]{x1D707}_{\text{BBH}}$
on the set of finitely generated pro-
![]() $p$
groups (see § 3 for the precise definition), so that the conjecture of Boston, Bush and Hajir is the following.
$p$
groups (see § 3 for the precise definition), so that the conjecture of Boston, Bush and Hajir is the following.
Conjecture 1.2 (Boston–Bush–Hajir, cf. [Reference Boston, Bush and HajirBBH16]).
For any ‘reasonable’ function
![]() $f$
on isomorphism classes of pro-
$f$
on isomorphism classes of pro-
![]() $p$
groups, we have
$p$
groups, we have
 $$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}f(G_{K})}{\#D_{X}}=\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{BBH}}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}f(G_{K})}{\#D_{X}}=\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{BBH}}.\end{eqnarray}$$
Of such reasonable
![]() $f$
, certain are particularly interesting, and their averages
$f$
, certain are particularly interesting, and their averages
 $\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{BBH}}$
we call the moments of the measure
$\int _{G}f(G)\,d\unicode[STIX]{x1D707}_{\text{BBH}}$
we call the moments of the measure
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
. To define these
$\unicode[STIX]{x1D707}_{\text{BBH}}$
. To define these
![]() $f$
, first note that the
$f$
, first note that the
![]() $p$
-class tower group
$p$
-class tower group
![]() $G_{K}$
has a generator-inverting automorphism
$G_{K}$
has a generator-inverting automorphism
![]() $\unicode[STIX]{x1D70E}$
coming from the action of
$\unicode[STIX]{x1D70E}$
coming from the action of
 $\operatorname{Gal}(K/\mathbb{Q})$
. If
$\operatorname{Gal}(K/\mathbb{Q})$
. If
![]() $G$
and
$G$
and
![]() $H$
are both profinite groups for which we have a chosen automorphism (we call both automorphisms
$H$
are both profinite groups for which we have a chosen automorphism (we call both automorphisms
![]() $\unicode[STIX]{x1D70E}$
), then we write
$\unicode[STIX]{x1D70E}$
), then we write
 $\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)$
for the continuous ‘
$\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)$
for the continuous ‘
![]() $\unicode[STIX]{x1D70E}$
-equivariant’ surjections from
$\unicode[STIX]{x1D70E}$
-equivariant’ surjections from
![]() $G$
to
$G$
to
![]() $H$
. The measure
$H$
. The measure
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
is supported on groups
$\unicode[STIX]{x1D707}_{\text{BBH}}$
is supported on groups
![]() $G$
with a unique, up to conjugation, generator-inverting automorphism, which we also denote as
$G$
with a unique, up to conjugation, generator-inverting automorphism, which we also denote as
![]() $\unicode[STIX]{x1D70E}$
. The average
$\unicode[STIX]{x1D70E}$
. The average
 $\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}$
is called the
$\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}$
is called the
![]() $H$
-moment of the measure
$H$
-moment of the measure
![]() $d\unicode[STIX]{x1D707}_{\text{BBH}}$
, and we determine these moments. (See § 7 for the simple relationship between these moments and the analog without the
$d\unicode[STIX]{x1D707}_{\text{BBH}}$
, and we determine these moments. (See § 7 for the simple relationship between these moments and the analog without the
![]() $\unicode[STIX]{x1D70E}$
-equivariant condition.)
$\unicode[STIX]{x1D70E}$
-equivariant condition.)
Theorem 1.3 (Moments of
 $\unicode[STIX]{x1D707}_{\text{BBH}}$
).
$\unicode[STIX]{x1D707}_{\text{BBH}}$
).
For every finite
![]() $p$
-group
$p$
-group
![]() $H$
with a generator-inverting automorphism
$H$
with a generator-inverting automorphism
![]() $\unicode[STIX]{x1D70E}$
, we have
$\unicode[STIX]{x1D70E}$
, we have
 $$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}=1.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}=1.\end{eqnarray}$$
Theorem 1.3 will be proven as part of Theorem 4.1 below. Further, we show that these moments characterize the measure
![]() $d\unicode[STIX]{x1D707}_{\text{BBH}}$
.
$d\unicode[STIX]{x1D707}_{\text{BBH}}$
.
Theorem 1.4 (Moments characterize
 $\unicode[STIX]{x1D707}_{\text{BBH}}$
).
$\unicode[STIX]{x1D707}_{\text{BBH}}$
).
If
![]() $\unicode[STIX]{x1D708}$
is a measure (for the
$\unicode[STIX]{x1D708}$
is a measure (for the
![]() $\unicode[STIX]{x1D70E}$
-algebra
$\unicode[STIX]{x1D70E}$
-algebra
![]() $\unicode[STIX]{x1D6FA}$
generated by groups with a fixed
$\unicode[STIX]{x1D6FA}$
generated by groups with a fixed
![]() $p$
-class
$p$
-class
![]() $c$
quotient; these terms will be defined in § 3) on the set of isomorphism classes of finitely generated pro-
$c$
quotient; these terms will be defined in § 3) on the set of isomorphism classes of finitely generated pro-
![]() $p$
groups such that
$p$
groups such that
 $$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D708}=1\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D708}=1\end{eqnarray}$$
for every finite
![]() $p$
-group
$p$
-group
![]() $H$
with a generator-inverting automorphism
$H$
with a generator-inverting automorphism
![]() $\unicode[STIX]{x1D70E}$
, then
$\unicode[STIX]{x1D70E}$
, then
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}_{\text{BBH}}$
.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}_{\text{BBH}}$
.
In fact, in Theorem 4.9 we prove a slightly stronger version of Theorem 1.4 in which we only use some of the moments. If we take
![]() $H$
in (1) to be abelian and note that under abelianization
$H$
in (1) to be abelian and note that under abelianization
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
pushes forward to
$\unicode[STIX]{x1D707}_{\text{BBH}}$
pushes forward to
![]() $\unicode[STIX]{x1D707}_{\text{CL}}$
, then we recover the observation of Ellenberg et al. [Reference Ellenberg, Venkatesh and WesterlandEVW16, § 8.1] that the
$\unicode[STIX]{x1D707}_{\text{CL}}$
, then we recover the observation of Ellenberg et al. [Reference Ellenberg, Venkatesh and WesterlandEVW16, § 8.1] that the
![]() $A$
-moments of
$A$
-moments of
![]() $\unicode[STIX]{x1D707}_{\text{CL}}$
are 1 for every abelian
$\unicode[STIX]{x1D707}_{\text{CL}}$
are 1 for every abelian
![]() $p$
-group
$p$
-group
![]() $A$
. They have also shown that these
$A$
. They have also shown that these
![]() $A$
-moments characterize
$A$
-moments characterize
![]() $\unicode[STIX]{x1D707}_{\text{CL}}$
[Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2]. The collection of moments given by averaging
$\unicode[STIX]{x1D707}_{\text{CL}}$
[Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2]. The collection of moments given by averaging
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(-,H)|$
is a fixed upper triangular transformation from the averages of
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(-,H)|$
is a fixed upper triangular transformation from the averages of
 $|\!\operatorname{Hom}_{\unicode[STIX]{x1D70E}}(-,H)|$
. For finite abelian groups, these latter averages are the mixed moments (of the standard invariants of the group) in the usual sense (see [Reference Clancy, Kaplan, Leake, Payne and WoodCKLPW15, § 3.3]).
$|\!\operatorname{Hom}_{\unicode[STIX]{x1D70E}}(-,H)|$
. For finite abelian groups, these latter averages are the mixed moments (of the standard invariants of the group) in the usual sense (see [Reference Clancy, Kaplan, Leake, Payne and WoodCKLPW15, § 3.3]).
In this paper, we prove a theorem towards the function field analog of Conjecture 1.2. We consider the function field
![]() $\mathbb{F}_{q}(t)$
, where
$\mathbb{F}_{q}(t)$
, where
![]() $q$
is a prime power. We say
$q$
is a prime power. We say
 $K/\mathbb{F}_{q}(t)$
is imaginary quadratic if
$K/\mathbb{F}_{q}(t)$
is imaginary quadratic if
![]() $K$
is a degree-2 extension of
$K$
is a degree-2 extension of
![]() $\mathbb{F}_{q}(t)$
that is ramified at the place corresponding to
$\mathbb{F}_{q}(t)$
that is ramified at the place corresponding to
![]() $1/t$
, or equivalently, the smooth, projective hyperelliptic curve corresponding to
$1/t$
, or equivalently, the smooth, projective hyperelliptic curve corresponding to
![]() $K$
is ramified over
$K$
is ramified over
![]() $\infty$
. For a quadratic extension
$\infty$
. For a quadratic extension
 $K/\mathbb{F}_{q}(t)$
, we let
$K/\mathbb{F}_{q}(t)$
, we let
![]() $K^{\operatorname{un},\infty }$
be the maximal unramified extension of
$K^{\operatorname{un},\infty }$
be the maximal unramified extension of
![]() $K$
that is split completely over every place of
$K$
that is split completely over every place of
![]() $K$
that lies over the place
$K$
that lies over the place
![]() $\infty$
in
$\infty$
in
![]() $\mathbb{F}_{q}(t)$
, and let
$\mathbb{F}_{q}(t)$
, and let
 $G_{K}^{\operatorname{un},\infty }=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
, with a generator-inverting automorphism
$G_{K}^{\operatorname{un},\infty }=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
, with a generator-inverting automorphism
![]() $\unicode[STIX]{x1D70E}$
coming from the action of
$\unicode[STIX]{x1D70E}$
coming from the action of
 $\operatorname{Gal}(K/\mathbb{F}_{q}(t))$
(see § 2).
$\operatorname{Gal}(K/\mathbb{F}_{q}(t))$
(see § 2).
Theorem 1.5. Let
![]() $H$
be a finite odd-order group with a generator-inverting automorphism such that the center of
$H$
be a finite odd-order group with a generator-inverting automorphism such that the center of
![]() $H$
contains no elements fixed by
$H$
contains no elements fixed by
![]() $\unicode[STIX]{x1D70E}$
except the identity. Let
$\unicode[STIX]{x1D70E}$
except the identity. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q}^{+}:=\limsup _{m\rightarrow \infty }\frac{\mathop{\sum }_{K\in E_{m}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#E_{m}}\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{q}^{-}:=\liminf _{m\rightarrow \infty }\frac{\mathop{\sum }_{K\in E_{m}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#E_{m}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q}^{+}:=\limsup _{m\rightarrow \infty }\frac{\mathop{\sum }_{K\in E_{m}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#E_{m}}\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{q}^{-}:=\liminf _{m\rightarrow \infty }\frac{\mathop{\sum }_{K\in E_{m}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#E_{m}},\end{eqnarray}$$
where
![]() $E_{m}$
denotes the set of imaginary quadratic extensions
$E_{m}$
denotes the set of imaginary quadratic extensions
![]() $\mathbb{F}_{q}(t)$
with discriminant of norm
$\mathbb{F}_{q}(t)$
with discriminant of norm
![]() $q^{2m+2}$
. Then as
$q^{2m+2}$
. Then as
![]() $q\rightarrow \infty$
among prime powers relatively prime to
$q\rightarrow \infty$
among prime powers relatively prime to
![]() $2|H|$
and with
$2|H|$
and with
 $(q-1,|H|)=1$
, we have
$(q-1,|H|)=1$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q}^{+},\quad \unicode[STIX]{x1D6FF}_{q}^{-}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q}^{+},\quad \unicode[STIX]{x1D6FF}_{q}^{-}\rightarrow 1.\end{eqnarray}$$
In light of Theorems 1.3 and 1.4, this is good evidence for Conjecture 1.2. When
![]() $H$
is a
$H$
is a
![]() $p$
-group, the surjections in Theorem 1.5 factor through the maximal pro-
$p$
-group, the surjections in Theorem 1.5 factor through the maximal pro-
![]() $p$
quotient of
$p$
quotient of
![]() $G_{K}^{\operatorname{un},\infty }$
, which is analogous to the
$G_{K}^{\operatorname{un},\infty }$
, which is analogous to the
![]() $G_{K}$
defined above. If we have an analogy between
$G_{K}$
defined above. If we have an analogy between
![]() $\mathbb{F}_{q}(t)$
and
$\mathbb{F}_{q}(t)$
and
![]() $\mathbb{Q}$
for any
$\mathbb{Q}$
for any
![]() $q$
, then the
$q$
, then the
![]() $q$
limits in Theorem 1.5 should not matter, and after that limit we get agreement with the
$q$
limits in Theorem 1.5 should not matter, and after that limit we get agreement with the
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
moments by Theorem 1.3. Since these moments determine a unique measure by Theorem 1.4, that suggests Conjecture 1.2 for general
$\unicode[STIX]{x1D707}_{\text{BBH}}$
moments by Theorem 1.3. Since these moments determine a unique measure by Theorem 1.4, that suggests Conjecture 1.2 for general
![]() $f$
, though technically the
$f$
, though technically the
![]() $G_{K}$
do not have to be distributed according to a measure, but only a limit of measures.
$G_{K}$
do not have to be distributed according to a measure, but only a limit of measures.
Further, if we assume a vanishing conjecture on the homology of Hurwitz spaces, then under the hypotheses of Theorem 1.5 we would in fact obtain that for
 $q\geqslant N(H)$
we have
$q\geqslant N(H)$
we have
 $\unicode[STIX]{x1D6FF}_{q}^{+}=\unicode[STIX]{x1D6FF}_{q}^{-}=1$
(see Theorem 6.6). Theorem 1.5 suggests the following conjecture, extending Conjecture 1.2 from pro-
$\unicode[STIX]{x1D6FF}_{q}^{+}=\unicode[STIX]{x1D6FF}_{q}^{-}=1$
(see Theorem 6.6). Theorem 1.5 suggests the following conjecture, extending Conjecture 1.2 from pro-
![]() $p$
groups to pro-odd groups, at least in the case of the moments.
$p$
groups to pro-odd groups, at least in the case of the moments.
Conjecture 1.6. For any imaginary quadratic number field
![]() $K$
, let
$K$
, let
![]() ${\mathcal{G}}_{K}$
be the maximal pro-odd quotient of the Galois group of the maximal unramified extension of
${\mathcal{G}}_{K}$
be the maximal pro-odd quotient of the Galois group of the maximal unramified extension of
![]() $K$
. Then for every finite odd group
$K$
. Then for every finite odd group
![]() $H$
with a generating-inverting automorphism
$H$
with a generating-inverting automorphism
 $$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}\operatorname{Sur}_{\unicode[STIX]{x1D70E}}({\mathcal{G}}_{K},H)}{\#D_{X}}=1.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{K\in D_{X}}\operatorname{Sur}_{\unicode[STIX]{x1D70E}}({\mathcal{G}}_{K},H)}{\#D_{X}}=1.\end{eqnarray}$$
Bhargava [Reference BhargavaBha14, § 1.2] has asked what we should expect for the average number of
![]() $H$
quotients of
$H$
quotients of
![]() $G_{K}^{\operatorname{un},\infty }$
, for any
$G_{K}^{\operatorname{un},\infty }$
, for any
![]() $H$
. Conjecture 1.6 suggests the answer for odd
$H$
. Conjecture 1.6 suggests the answer for odd
![]() $H$
. (See § 7 for the translation from our conjecture for
$H$
. (See § 7 for the translation from our conjecture for
![]() $\unicode[STIX]{x1D70E}$
-equivariant quotients to the consequence for more general quotients.) Bhargava [Reference BhargavaBha14, § 1.2] has proven some intriguing moments for
$\unicode[STIX]{x1D70E}$
-equivariant quotients to the consequence for more general quotients.) Bhargava [Reference BhargavaBha14, § 1.2] has proven some intriguing moments for
 $H=A_{3},A_{4},A_{5},S_{3},S_{4},S_{5}$
.
$H=A_{3},A_{4},A_{5},S_{3},S_{4},S_{5}$
.
It would be interesting to have a concrete description of an underlying measure on pro-odd groups that gives the moments on Conjecture 1.6, as
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
does in the pro-
$\unicode[STIX]{x1D707}_{\text{BBH}}$
does in the pro-
![]() $p$
case. However, before making a conjectural analog of Conjecture 1.2, one should note it is an open question whether
$p$
case. However, before making a conjectural analog of Conjecture 1.2, one should note it is an open question whether
![]() ${\mathcal{G}}_{K}$
is (topologically) finitely generated or not, let alone finitely presented.
${\mathcal{G}}_{K}$
is (topologically) finitely generated or not, let alone finitely presented.
In order to prove Theorem 1.5, in § 5, we translate the sum of counts of surjections to a count of extensions of
![]() $\mathbb{F}_{q}(t)$
with certain properties. We then, in § 6, apply the recent powerful results of Ellenberg et al. [Reference Ellenberg, Venkatesh and WesterlandEVW16, Reference Ellenberg, Venkatesh and WesterlandEVW12] on homological stability of Hurwitz spaces and the components of Hurwitz spaces along with their Galois action over
$\mathbb{F}_{q}(t)$
with certain properties. We then, in § 6, apply the recent powerful results of Ellenberg et al. [Reference Ellenberg, Venkatesh and WesterlandEVW16, Reference Ellenberg, Venkatesh and WesterlandEVW12] on homological stability of Hurwitz spaces and the components of Hurwitz spaces along with their Galois action over
![]() $\mathbb{F}_{q}$
in order to count the extensions. A main motivation for the work of Ellenberg, Venkatesh and Westerland is to prove function field analogs of Conjecture 1.1. In particular, [Reference Ellenberg, Venkatesh and WesterlandEVW16, Theorem 8.8] gives the case of Theorem 1.5 when
$\mathbb{F}_{q}$
in order to count the extensions. A main motivation for the work of Ellenberg, Venkatesh and Westerland is to prove function field analogs of Conjecture 1.1. In particular, [Reference Ellenberg, Venkatesh and WesterlandEVW16, Theorem 8.8] gives the case of Theorem 1.5 when
![]() $H$
is an abelian
$H$
is an abelian
![]() $p$
-group. The analysis of components of Hurwitz spaces in [Reference Ellenberg, Venkatesh and WesterlandEVW12] gives the number of components in terms of certain group-theoretically defined quantities, which we compute in the cases necessary for our application. We apply results on Hurwitz spaces from [Reference Ellenberg, Venkatesh and WesterlandEVW16, Reference Ellenberg, Venkatesh and WesterlandEVW12], the Grothendieck–Lefschetz trace formula, and our group theory computation to count
$p$
-group. The analysis of components of Hurwitz spaces in [Reference Ellenberg, Venkatesh and WesterlandEVW12] gives the number of components in terms of certain group-theoretically defined quantities, which we compute in the cases necessary for our application. We apply results on Hurwitz spaces from [Reference Ellenberg, Venkatesh and WesterlandEVW16, Reference Ellenberg, Venkatesh and WesterlandEVW12], the Grothendieck–Lefschetz trace formula, and our group theory computation to count
![]() $\mathbb{F}_{q}$
points of a moduli space that parametrize the relevant extensions of
$\mathbb{F}_{q}$
points of a moduli space that parametrize the relevant extensions of
![]() $\mathbb{F}_{q}(t)$
.
$\mathbb{F}_{q}(t)$
.
Finally, we make some remarks on the hypotheses in Theorem 1.5. The condition on the center of
![]() $H$
comes from a technical limitation of [Reference Ellenberg, Venkatesh and WesterlandEVW12]. The requirement that
$H$
comes from a technical limitation of [Reference Ellenberg, Venkatesh and WesterlandEVW12]. The requirement that
 $(q-1,|H|)=1$
ensures that the base field does not have ‘extra roots of unity.’ The case of extra roots of unity is one in which even the Cohen–Lenstra heuristics are expected to be wrong [Reference MalleMal08] and new heuristics have been proposed by Garton [Reference GartonGar15] and Adam and Malle [Reference Adam and MalleAM15] for that case. To the authors’ knowledge, there is no work on even the Cohen–Lenstra heuristics in the function field setting when
$(q-1,|H|)=1$
ensures that the base field does not have ‘extra roots of unity.’ The case of extra roots of unity is one in which even the Cohen–Lenstra heuristics are expected to be wrong [Reference MalleMal08] and new heuristics have been proposed by Garton [Reference GartonGar15] and Adam and Malle [Reference Adam and MalleAM15] for that case. To the authors’ knowledge, there is no work on even the Cohen–Lenstra heuristics in the function field setting when
 $(q,|H|)>1$
or
$(q,|H|)>1$
or
![]() $2\mid q$
.
$2\mid q$
.
2 Background on non-abelian analogs of class groups
Let
![]() $Q$
be a global field and
$Q$
be a global field and
![]() $\infty$
a place of
$\infty$
a place of
![]() $Q$
. In this paper, we are interested in the cases
$Q$
. In this paper, we are interested in the cases
![]() $Q=\mathbb{Q}$
or
$Q=\mathbb{Q}$
or
![]() $\mathbb{F}_{q}(t)$
with the usual infinite place. For a separable, quadratic extension
$\mathbb{F}_{q}(t)$
with the usual infinite place. For a separable, quadratic extension
![]() $K/Q$
, we let
$K/Q$
, we let
![]() $K^{\operatorname{un},\infty }$
be the maximal unramified extension of
$K^{\operatorname{un},\infty }$
be the maximal unramified extension of
![]() $K$
that is split completely over all places of
$K$
that is split completely over all places of
![]() $K$
over
$K$
over
![]() $\infty$
, and let
$\infty$
, and let
 $G_{K}^{\operatorname{un},\infty }=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
. We let
$G_{K}^{\operatorname{un},\infty }=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
. We let
![]() $G_{K}$
be the maximal pro-
$G_{K}$
be the maximal pro-
![]() $p$
quotient of
$p$
quotient of
![]() $G_{K}^{\operatorname{un},\infty }$
.
$G_{K}^{\operatorname{un},\infty }$
.
Remark 2.1. While it looks like we have added the condition at
![]() $\infty$
compared with the definition of
$\infty$
compared with the definition of
![]() $G_{K}$
for number fields in the introduction, we could in fact add this condition to the definition of
$G_{K}$
for number fields in the introduction, we could in fact add this condition to the definition of
![]() $G_{K}$
for a quadratic number field
$G_{K}$
for a quadratic number field
![]() $K$
without effect because, for an archimedean place, unramified is the same as split completely. Also, if
$K$
without effect because, for an archimedean place, unramified is the same as split completely. Also, if
 $Q=\mathbb{F}_{q}(t)$
and
$Q=\mathbb{F}_{q}(t)$
and
![]() ${\mathcal{O}}_{K}$
is the integral closure of
${\mathcal{O}}_{K}$
is the integral closure of
![]() $\mathbb{F}_{q}[t]$
in
$\mathbb{F}_{q}[t]$
in
![]() $K$
, then class field theory gives that the abelianization
$K$
, then class field theory gives that the abelianization
 $(G_{K}^{\operatorname{un},\infty })^{\text{ab}}$
is isomorphic to the class group
$(G_{K}^{\operatorname{un},\infty })^{\text{ab}}$
is isomorphic to the class group
 $Cl({\mathcal{O}}_{K})$
of ideals modulo principal ideals, so
$Cl({\mathcal{O}}_{K})$
of ideals modulo principal ideals, so
![]() $G_{K}^{\operatorname{un},\infty }$
is the natural function field analog of a ‘non-abelian class group’.
$G_{K}^{\operatorname{un},\infty }$
is the natural function field analog of a ‘non-abelian class group’.
Lemma 2.2. If
![]() $K/Q$
is a separable, quadratic extension, then all inertia subgroups of
$K/Q$
is a separable, quadratic extension, then all inertia subgroups of
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
and the decomposition group at infinity are contained in
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
and the decomposition group at infinity are contained in
 $$\begin{eqnarray}\{1\}\cup \{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}.\end{eqnarray}$$
$$\begin{eqnarray}\{1\}\cup \{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}.\end{eqnarray}$$
Proof. The intersection with
![]() $G_{K}^{\operatorname{un},\infty }$
of any inertia subgroup or the decomposition group at infinity is trivial by the definition of
$G_{K}^{\operatorname{un},\infty }$
of any inertia subgroup or the decomposition group at infinity is trivial by the definition of
![]() $K^{\operatorname{un},\infty }$
, which also implies they have order at most
$K^{\operatorname{un},\infty }$
, which also implies they have order at most
![]() $2$
.◻
$2$
.◻
If
![]() $Q$
is a global field and
$Q$
is a global field and
![]() $\infty$
is a place of
$\infty$
is a place of
![]() $Q$
such that
$Q$
such that
![]() $Q$
has no non-trivial finite extensions unramified everywhere and split completely over
$Q$
has no non-trivial finite extensions unramified everywhere and split completely over
![]() $\infty$
(such as in our cases of interest
$\infty$
(such as in our cases of interest
![]() $Q=\mathbb{Q}$
or
$Q=\mathbb{Q}$
or
![]() $\mathbb{F}_{q}(t)$
), we call
$\mathbb{F}_{q}(t)$
), we call
![]() $Q,\infty$
rational-like. Then we have that
$Q,\infty$
rational-like. Then we have that
 $\{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}$
is non-empty. So the exact sequence
$\{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}$
is non-empty. So the exact sequence
 $$\begin{eqnarray}1\rightarrow G_{K}^{\operatorname{un},\infty }\rightarrow \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\rightarrow \operatorname{Gal}(K/Q)\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G_{K}^{\operatorname{un},\infty }\rightarrow \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\rightarrow \operatorname{Gal}(K/Q)\rightarrow 1\end{eqnarray}$$
splits. Any lift of the generator of
 $\operatorname{Gal}(K/Q)$
gives an order-
$\operatorname{Gal}(K/Q)$
gives an order-
![]() $2$
automorphism of
$2$
automorphism of
![]() $G_{K}^{\operatorname{un},\infty }$
by conjugation.
$G_{K}^{\operatorname{un},\infty }$
by conjugation.
Proposition 2.3. Let
![]() $Q,\infty$
be rational-like and
$Q,\infty$
be rational-like and
![]() $K/Q$
a separable, quadratic extension. The action of an element
$K/Q$
a separable, quadratic extension. The action of an element
 $\unicode[STIX]{x1D70F}\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }$
of order
$\unicode[STIX]{x1D70F}\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }$
of order
![]() $2$
on
$2$
on
![]() $G_{K}^{\operatorname{un},\infty }$
by conjugation inverts a set of (topological) generators of
$G_{K}^{\operatorname{un},\infty }$
by conjugation inverts a set of (topological) generators of
![]() $G_{K}^{\operatorname{un},\infty }$
.
$G_{K}^{\operatorname{un},\infty }$
.
Proof. We write
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)=G_{K}^{\operatorname{un},\infty }\rtimes \langle \unicode[STIX]{x1D70F}\rangle$
. Let
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)=G_{K}^{\operatorname{un},\infty }\rtimes \langle \unicode[STIX]{x1D70F}\rangle$
. Let
![]() $R$
be the closed subgroup of
$R$
be the closed subgroup of
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
generated by
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
generated by
 $\{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}$
. From the definition, it follows that
$\{r\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }\mid r^{2}=1\}$
. From the definition, it follows that
![]() $R$
is normal. So
$R$
is normal. So
![]() $R$
corresponds to a subfield
$R$
corresponds to a subfield
![]() $M$
of
$M$
of
![]() $K^{\operatorname{un},\infty },$
which is Galois over
$K^{\operatorname{un},\infty },$
which is Galois over
![]() $Q$
, and such that in
$Q$
, and such that in
 $\operatorname{Gal}(M/Q)$
all inertia groups are trivial and the decomposition group at infinity is trivial by Lemma 2.2. It follows that
$\operatorname{Gal}(M/Q)$
all inertia groups are trivial and the decomposition group at infinity is trivial by Lemma 2.2. It follows that
![]() $M=Q$
. The order-
$M=Q$
. The order-
![]() $2$
elements of
$2$
elements of
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }$
are the
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)\setminus G_{K}^{\operatorname{un},\infty }$
are the
![]() $(g_{i},\unicode[STIX]{x1D70F})$
, for
$(g_{i},\unicode[STIX]{x1D70F})$
, for
 $g_{i}\in G_{K}^{\operatorname{un},\infty }$
such that
$g_{i}\in G_{K}^{\operatorname{un},\infty }$
such that
 $g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}$
. So the words in
$g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}$
. So the words in
 $\{(g_{i},\unicode[STIX]{x1D70F})\mid g_{i}\in G_{K}^{\operatorname{un},\infty },g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
are dense in
$\{(g_{i},\unicode[STIX]{x1D70F})\mid g_{i}\in G_{K}^{\operatorname{un},\infty },g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
are dense in
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
. An element of
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
. An element of
![]() $G_{K}^{\operatorname{un},\infty }$
equivalent to one of these words is a word in the symbols
$G_{K}^{\operatorname{un},\infty }$
equivalent to one of these words is a word in the symbols
 $\{g_{i}\in G_{K}^{\operatorname{un},\infty }\mid g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
, and such elements are a dense subgroup of
$\{g_{i}\in G_{K}^{\operatorname{un},\infty }\mid g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
, and such elements are a dense subgroup of
![]() $G_{K}^{\operatorname{un},\infty }$
. Thus the set
$G_{K}^{\operatorname{un},\infty }$
. Thus the set
 $\{g_{i}\in G_{K}^{\operatorname{un},\infty }\mid g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
topologically generates
$\{g_{i}\in G_{K}^{\operatorname{un},\infty }\mid g_{i}^{\unicode[STIX]{x1D70F}}=g_{i}^{-1}\}$
topologically generates
![]() $G_{K}^{\operatorname{un},\infty }$
.◻
$G_{K}^{\operatorname{un},\infty }$
.◻
In light of Proposition 2.3, we pick a lift
![]() $\unicode[STIX]{x1D70F}$
of the generator of
$\unicode[STIX]{x1D70F}$
of the generator of
 $\operatorname{Gal}(K/Q)$
to
$\operatorname{Gal}(K/Q)$
to
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
and let conjugation by
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
and let conjugation by
![]() $\unicode[STIX]{x1D70F}$
be our chosen generator-inverting automorphism
$\unicode[STIX]{x1D70F}$
be our chosen generator-inverting automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $G_{K}^{\operatorname{un},\infty }$
. Further, the Schur–Zassenhaus theorem [Reference WilsonWil98, Proposition 2.3.3] guarantees that all the lifts of the generator of
$G_{K}^{\operatorname{un},\infty }$
. Further, the Schur–Zassenhaus theorem [Reference WilsonWil98, Proposition 2.3.3] guarantees that all the lifts of the generator of
 $\operatorname{Gal}(K/Q)$
to the pro-
$\operatorname{Gal}(K/Q)$
to the pro-
![]() $p$
quotient
$p$
quotient
![]() $G_{K}$
of
$G_{K}$
of
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
(or the pro-odd quotient) are conjugate. Thus for an odd finite group
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
(or the pro-odd quotient) are conjugate. Thus for an odd finite group
![]() $H$
with automorphism
$H$
with automorphism
![]() $\unicode[STIX]{x1D70E}$
, we then have that
$\unicode[STIX]{x1D70E}$
, we then have that
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|$
does not depend on the choice of
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|$
does not depend on the choice of
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
3 Boston–Bush–Hajir heuristics: background and notation
Koch and Venkov [Reference Koch and VenkovKV75] have shown that for an imaginary quadratic extension
![]() $K/\mathbb{Q}$
, the group
$K/\mathbb{Q}$
, the group
![]() $G_{K}$
satisfies certain properties we will now outline. For a pro-
$G_{K}$
satisfies certain properties we will now outline. For a pro-
![]() $p$
group
$p$
group
![]() $G$
, let
$G$
, let
 $d(G):=\dim _{\mathbb{Z}/p\mathbb{Z}}H^{1}(G,\mathbb{Z}/p\mathbb{Z})$
and
$d(G):=\dim _{\mathbb{Z}/p\mathbb{Z}}H^{1}(G,\mathbb{Z}/p\mathbb{Z})$
and
 $r(G):=\dim _{\mathbb{Z}/p\mathbb{Z}}H^{2}(G,\mathbb{Z}/p\mathbb{Z})$
. These are, respectively, the generator rank and the relation rank of
$r(G):=\dim _{\mathbb{Z}/p\mathbb{Z}}H^{2}(G,\mathbb{Z}/p\mathbb{Z})$
. These are, respectively, the generator rank and the relation rank of
![]() $G$
as a pro-
$G$
as a pro-
![]() $p$
group. For a pro-finite group
$p$
group. For a pro-finite group
![]() $G$
, we define a GI-automorphism of
$G$
, we define a GI-automorphism of
![]() $G$
to be a
$G$
to be a
 $\unicode[STIX]{x1D70E}\in \operatorname{Aut}(G)$
such that
$\unicode[STIX]{x1D70E}\in \operatorname{Aut}(G)$
such that
![]() $\unicode[STIX]{x1D70E}$
acts as inversion on a set of (topological) generators. For a pro-
$\unicode[STIX]{x1D70E}$
acts as inversion on a set of (topological) generators. For a pro-
![]() $p$
group, this is equivalent to requiring that
$p$
group, this is equivalent to requiring that
![]() $\unicode[STIX]{x1D70E}^{2}=1$
, which
$\unicode[STIX]{x1D70E}^{2}=1$
, which
![]() $\unicode[STIX]{x1D70E}$
are called involutions, and
$\unicode[STIX]{x1D70E}$
are called involutions, and
![]() $\unicode[STIX]{x1D70E}$
acts as inversion on the abelianization of
$\unicode[STIX]{x1D70E}$
acts as inversion on the abelianization of
![]() $G$
[Reference BostonBos91].
$G$
[Reference BostonBos91].
Definition.
A Schur-
![]() $\unicode[STIX]{x1D70E}$
group is a finitely generated pro-
$\unicode[STIX]{x1D70E}$
group is a finitely generated pro-
![]() $p$
group
$p$
group
![]() $G$
with finite abelianization such that:
$G$
with finite abelianization such that:
-
(a)
 $d(G)=r(G)$
(then called just the rank of
$d(G)=r(G)$
(then called just the rank of
 $G$
);
$G$
); -
(b)
 $G$
admits a GI-automorphism.
$G$
admits a GI-automorphism.
Koch and Venkov [Reference Koch and VenkovKV75] have shown that for an imaginary quadratic extension
![]() $K/\mathbb{Q}$
, the group
$K/\mathbb{Q}$
, the group
![]() $G_{K}$
is a Schur-
$G_{K}$
is a Schur-
![]() $\unicode[STIX]{x1D70E}$
group. The groups
$\unicode[STIX]{x1D70E}$
group. The groups
![]() $G_{K}$
we are considering in the function field case are also Schur-
$G_{K}$
we are considering in the function field case are also Schur-
![]() $\unicode[STIX]{x1D70E}$
groups when
$\unicode[STIX]{x1D70E}$
groups when
 $p\nmid q-1$
. This follows by class field theory, Proposition 2.3 above, and the upper bound on
$p\nmid q-1$
. This follows by class field theory, Proposition 2.3 above, and the upper bound on
 $r(G_{K})-d(G_{K})$
, namely
$r(G_{K})-d(G_{K})$
, namely
![]() $0$
, due to Shafarevich, given as [Reference Hajir, Maire and CasacubertaHM01, Theorem 2.2]. Note that
$0$
, due to Shafarevich, given as [Reference Hajir, Maire and CasacubertaHM01, Theorem 2.2]. Note that
 $r(G_{K})-d(G_{K})\geqslant 0$
since
$r(G_{K})-d(G_{K})\geqslant 0$
since
![]() $G_{K}^{\text{ab}}$
is finite and so the upper bound of 0 yields
$G_{K}^{\text{ab}}$
is finite and so the upper bound of 0 yields
 $r(G_{K})-d(G_{K})=0$
.
$r(G_{K})-d(G_{K})=0$
.
We will put a measure on the set of isomorphism classes of Schur
![]() $\unicode[STIX]{x1D70E}$
-groups in order to state the Boston–Bush–Hajir heuristics. For this, we first need to define a
$\unicode[STIX]{x1D70E}$
-groups in order to state the Boston–Bush–Hajir heuristics. For this, we first need to define a
![]() $\unicode[STIX]{x1D70E}$
-algebra (in the sense of measure theory – not our automorphism
$\unicode[STIX]{x1D70E}$
-algebra (in the sense of measure theory – not our automorphism
![]() $\unicode[STIX]{x1D70E}$
) on this set. Since many infinite Schur
$\unicode[STIX]{x1D70E}$
) on this set. Since many infinite Schur
![]() $\unicode[STIX]{x1D70E}$
-groups are expected to occur as
$\unicode[STIX]{x1D70E}$
-groups are expected to occur as
![]() $G_{K}$
with density 0, it makes sense to focus on certain finite quotients of these groups.
$G_{K}$
with density 0, it makes sense to focus on certain finite quotients of these groups.
Any pro-
![]() $p$
group
$p$
group
![]() $G$
has a lower
$G$
has a lower
![]() $p$
-central series defined as
$p$
-central series defined as
 $P_{0}(G):=G$
and for
$P_{0}(G):=G$
and for
![]() $n\geqslant 0$
, we let
$n\geqslant 0$
, we let
 $P_{n+1}(G)$
be the closed subgroup generated by
$P_{n+1}(G)$
be the closed subgroup generated by
 $[G,P_{n}(G)]$
and
$[G,P_{n}(G)]$
and
![]() $P_{n}(G)^{p}$
. The groups
$P_{n}(G)^{p}$
. The groups
 $P_{0}(G)\geqslant P_{1}(G)\geqslant P_{2}(G)\geqslant \cdots$
form a descending chain of characteristic subgroups of
$P_{0}(G)\geqslant P_{1}(G)\geqslant P_{2}(G)\geqslant \cdots$
form a descending chain of characteristic subgroups of
![]() $G$
called the lower
$G$
called the lower
![]() $p$
-central series. The
$p$
-central series. The
![]() $p$
-class of a finite
$p$
-class of a finite
![]() $p$
-group
$p$
-group
![]() $G$
is the smallest
$G$
is the smallest
![]() $c\geqslant 0$
for which
$c\geqslant 0$
for which
 $P_{c}(G)=\{1\}$
. Note that for a finitely generated pro-
$P_{c}(G)=\{1\}$
. Note that for a finitely generated pro-
![]() $p$
group
$p$
group
![]() $G$
, the successive quotients
$G$
, the successive quotients
 $P_{n}(G)/P_{n+1}(G)$
are finite abelian groups of exponent
$P_{n}(G)/P_{n+1}(G)$
are finite abelian groups of exponent
![]() $p$
, and so, in particular, if
$p$
, and so, in particular, if
 $P_{c}(G)=\{1\}$
, then
$P_{c}(G)=\{1\}$
, then
![]() $G$
must be finite. The lower
$G$
must be finite. The lower
![]() $p$
-central series and
$p$
-central series and
![]() $p$
-class can be thought of as analogous to the lower central series and nilpotency class, respectively. Note that
$p$
-class can be thought of as analogous to the lower central series and nilpotency class, respectively. Note that
![]() $P_{1}(G)$
is also the Frattini subgroup
$P_{1}(G)$
is also the Frattini subgroup
![]() $\unicode[STIX]{x1D6F7}(G)$
.
$\unicode[STIX]{x1D6F7}(G)$
.
For a pro-
![]() $p$
group
$p$
group
![]() $G$
, we define
$G$
, we define
 $Q_{c}(G):=G/P_{c}(G)$
, the maximal quotient of
$Q_{c}(G):=G/P_{c}(G)$
, the maximal quotient of
![]() $G$
with
$G$
with
![]() $p$
-class at most
$p$
-class at most
![]() $c$
. So
$c$
. So
 $Q_{c}(G_{K})$
is the Galois group of the maximal unramified
$Q_{c}(G_{K})$
is the Galois group of the maximal unramified
![]() $p$
-extension of
$p$
-extension of
![]() $K$
among extensions of Galois group with
$K$
among extensions of Galois group with
![]() $p$
-class at most
$p$
-class at most
![]() $c$
. Note that since a Schur
$c$
. Note that since a Schur
![]() $\unicode[STIX]{x1D70E}$
-group
$\unicode[STIX]{x1D70E}$
-group
![]() $G$
(such as
$G$
(such as
![]() $G_{K}$
) is finitely generated, we have that
$G_{K}$
) is finitely generated, we have that
![]() $Q_{c}(G)$
is finite. It may be that
$Q_{c}(G)$
is finite. It may be that
![]() $Q_{c}(G)$
has
$Q_{c}(G)$
has
![]() $p$
-class strictly less than
$p$
-class strictly less than
![]() $c$
: certainly when
$c$
: certainly when
![]() $G$
itself has
$G$
itself has
![]() $p$
-class strictly less than
$p$
-class strictly less than
![]() $c$
, this happens, but in fact since the subquotients of the lower
$c$
, this happens, but in fact since the subquotients of the lower
![]() $p$
-central series for
$p$
-central series for
![]() $G$
and for
$G$
and for
![]() $Q_{c}(G)$
are the same up to index
$Q_{c}(G)$
are the same up to index
![]() $c$
, this is the only way it can happen.
$c$
, this is the only way it can happen.
Let
![]() $\unicode[STIX]{x1D6FA}$
be the
$\unicode[STIX]{x1D6FA}$
be the
![]() $\unicode[STIX]{x1D70E}$
-algebra on the set of isomorphism classes of Schur
$\unicode[STIX]{x1D70E}$
-algebra on the set of isomorphism classes of Schur
![]() $\unicode[STIX]{x1D70E}$
-groups generated by the sets
$\unicode[STIX]{x1D70E}$
-groups generated by the sets
 $$\begin{eqnarray}\{G\mid Q_{c}(G)\simeq P\}\end{eqnarray}$$
$$\begin{eqnarray}\{G\mid Q_{c}(G)\simeq P\}\end{eqnarray}$$
for each finite
![]() $p$
-group
$p$
-group
![]() $P$
and fixed
$P$
and fixed
![]() $c$
. For example, we can fix a Schur
$c$
. For example, we can fix a Schur
![]() $\unicode[STIX]{x1D70E}$
-group
$\unicode[STIX]{x1D70E}$
-group
![]() $G_{0}$
and take the intersection over all
$G_{0}$
and take the intersection over all
![]() $c$
of
$c$
of
 $\{G\mid Q_{c}(G)\simeq Q_{c}(G_{0})\}$
to see that
$\{G\mid Q_{c}(G)\simeq Q_{c}(G_{0})\}$
to see that
![]() $\unicode[STIX]{x1D6FA}$
contains the singleton set containing the class of
$\unicode[STIX]{x1D6FA}$
contains the singleton set containing the class of
![]() $G_{0}$
.
$G_{0}$
.
We will next define a measure on the set of isomorphism classes of Schur
![]() $\unicode[STIX]{x1D70E}$
-groups for a
$\unicode[STIX]{x1D70E}$
-groups for a
![]() $\unicode[STIX]{x1D70E}$
-algebra containing
$\unicode[STIX]{x1D70E}$
-algebra containing
![]() $\unicode[STIX]{x1D6FA}$
. Any Schur
$\unicode[STIX]{x1D6FA}$
. Any Schur
![]() $\unicode[STIX]{x1D70E}$
-group of rank
$\unicode[STIX]{x1D70E}$
-group of rank
![]() $g$
can be presented as a quotient of the free pro-
$g$
can be presented as a quotient of the free pro-
![]() $p$
group
$p$
group
![]() $F_{g}$
on
$F_{g}$
on
![]() $g$
generators
$g$
generators
 $x_{1},\ldots ,x_{g}$
(with GI-automorphism
$x_{1},\ldots ,x_{g}$
(with GI-automorphism
 $\unicode[STIX]{x1D70E}(x_{i})=x_{i}^{-1}$
) by
$\unicode[STIX]{x1D70E}(x_{i})=x_{i}^{-1}$
) by
![]() $g$
relations chosen from
$g$
relations chosen from
 $X=\{s\in \unicode[STIX]{x1D6F7}(F_{g})\mid \unicode[STIX]{x1D70E}(s)=s^{-1}\}$
. Since
$X=\{s\in \unicode[STIX]{x1D6F7}(F_{g})\mid \unicode[STIX]{x1D70E}(s)=s^{-1}\}$
. Since
![]() $X$
is a closed subset of the profinite group
$X$
is a closed subset of the profinite group
![]() $F_{g}$
, we have a natural profinite probability measure
$F_{g}$
, we have a natural profinite probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $X$
from the limit of the uniform measures on finite quotients of
$X$
from the limit of the uniform measures on finite quotients of
![]() $F_{g}$
, on the
$F_{g}$
, on the
![]() $\unicode[STIX]{x1D70E}$
-algebra generated by fibers of these quotients.
$\unicode[STIX]{x1D70E}$
-algebra generated by fibers of these quotients.
The Boston–Bush–Hajir probability measure
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
will be given by randomly selecting such relations. However, this only gives a measure for a fixed rank
$\unicode[STIX]{x1D707}_{\text{BBH}}$
will be given by randomly selecting such relations. However, this only gives a measure for a fixed rank
![]() $g$
of Schur
$g$
of Schur
![]() $\unicode[STIX]{x1D70E}$
-groups. Since, however, the rank of a Schur
$\unicode[STIX]{x1D70E}$
-groups. Since, however, the rank of a Schur
![]() $\unicode[STIX]{x1D70E}$
-group is the rank of its abelianization (in fact, of the quotient of the abelianization
$\unicode[STIX]{x1D70E}$
-group is the rank of its abelianization (in fact, of the quotient of the abelianization
 $G/\unicode[STIX]{x1D6F7}(G)$
, by the Burnside basis theorem), we can use the Cohen–Lenstra heuristics to predict how often each rank
$G/\unicode[STIX]{x1D6F7}(G)$
, by the Burnside basis theorem), we can use the Cohen–Lenstra heuristics to predict how often each rank
![]() $g$
occurs. Let
$g$
occurs. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{CL}}(g):=\mathop{\sum }_{G~\text{fin. ab.},~\text{rk}~g~p\text{-}\text{gp}}\unicode[STIX]{x1D707}_{\text{CL}}(G)=p^{-g^{2}}\mathop{\prod }_{k=1}^{g}(1-p^{-k})^{-2}\mathop{\prod }_{i=1}^{\infty }(1-p^{-i}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{CL}}(g):=\mathop{\sum }_{G~\text{fin. ab.},~\text{rk}~g~p\text{-}\text{gp}}\unicode[STIX]{x1D707}_{\text{CL}}(G)=p^{-g^{2}}\mathop{\prod }_{k=1}^{g}(1-p^{-k})^{-2}\mathop{\prod }_{i=1}^{\infty }(1-p^{-i}).\end{eqnarray}$$
The above formula is from [Reference Cohen and LenstraCL84, Theorem 6.3]. Let
![]() $A$
be a set of isomorphism classes of rank
$A$
be a set of isomorphism classes of rank
![]() $g$
Schur
$g$
Schur
![]() $\unicode[STIX]{x1D70E}$
-groups. Then we define
$\unicode[STIX]{x1D70E}$
-groups. Then we define
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH}}(A):=\unicode[STIX]{x1D707}_{\text{CL}}(g)\unicode[STIX]{x1D707}(\{(r_{1},\ldots ,r_{g})\in X^{g}\mid F_{g}/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \in A\}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH}}(A):=\unicode[STIX]{x1D707}_{\text{CL}}(g)\unicode[STIX]{x1D707}(\{(r_{1},\ldots ,r_{g})\in X^{g}\mid F_{g}/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \in A\}),\end{eqnarray}$$
whenever
 $\{(r_{1},\ldots ,r_{g})\in X^{g}\mid F_{g}/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \in A\}$
is measurable, where the double angle brackets denote the closed normal subgroup generated by the elements. We can think of this measure as generating a random group by picking a rank
$\{(r_{1},\ldots ,r_{g})\in X^{g}\mid F_{g}/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \in A\}$
is measurable, where the double angle brackets denote the closed normal subgroup generated by the elements. We can think of this measure as generating a random group by picking a rank
![]() $g$
according to the Cohen–Lenstra measure and then independently creating a random Schur
$g$
according to the Cohen–Lenstra measure and then independently creating a random Schur
![]() $\unicode[STIX]{x1D70E}$
-group of rank
$\unicode[STIX]{x1D70E}$
-group of rank
![]() $g$
by taking the quotient of the free pro-
$g$
by taking the quotient of the free pro-
![]() $p$
group
$p$
group
![]() $F_{g}$
on
$F_{g}$
on
![]() $g$
generators by
$g$
generators by
![]() $g$
randomly chosen relations in
$g$
randomly chosen relations in
![]() $X$
. Note that this process does not necessarily produce a Schur
$X$
. Note that this process does not necessarily produce a Schur
![]() $\unicode[STIX]{x1D70E}$
-group, as there may be redundancy among the relations and so the resulting group may not have relation rank
$\unicode[STIX]{x1D70E}$
-group, as there may be redundancy among the relations and so the resulting group may not have relation rank
![]() $g$
. However, such redundancy happens with probability 0 (the abelianization would be infinite, and, as noted by Friedman and Washington [Reference Friedman and WashingtonFW89], this occurs with zero probability under
$g$
. However, such redundancy happens with probability 0 (the abelianization would be infinite, and, as noted by Friedman and Washington [Reference Friedman and WashingtonFW89], this occurs with zero probability under
![]() $\unicode[STIX]{x1D707}_{\text{CL}}$
, which is induced on abelianizations from
$\unicode[STIX]{x1D707}_{\text{CL}}$
, which is induced on abelianizations from
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
[Reference Boston, Bush and HajirBBH16, Theorem 2.20]).
$\unicode[STIX]{x1D707}_{\text{BBH}}$
[Reference Boston, Bush and HajirBBH16, Theorem 2.20]).
Let
 $X_{c}=\{s\in \unicode[STIX]{x1D6F7}(Q_{c}(F_{g}))\mid \unicode[STIX]{x1D70E}(s)=s^{-1}\}$
. Note that
$X_{c}=\{s\in \unicode[STIX]{x1D6F7}(Q_{c}(F_{g}))\mid \unicode[STIX]{x1D70E}(s)=s^{-1}\}$
. Note that
![]() $X_{c}$
is a finite set and has a uniform discrete probability measure
$X_{c}$
is a finite set and has a uniform discrete probability measure
![]() $\unicode[STIX]{x1D707}_{c}$
that pulls back to
$\unicode[STIX]{x1D707}_{c}$
that pulls back to
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $X$
. If
$X$
. If
![]() $P$
is a fixed finite
$P$
is a fixed finite
![]() $p$
-group with
$p$
-group with
 $d(P)=g$
, we define
$d(P)=g$
, we define
 $\unicode[STIX]{x1D707}_{\text{BBH},c}(P):=\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})$
, and then
$\unicode[STIX]{x1D707}_{\text{BBH},c}(P):=\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})$
, and then
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH},c}(P)=\unicode[STIX]{x1D707}_{\text{CL}}(g)\unicode[STIX]{x1D707}_{c}(\{(r_{1},\ldots ,r_{g})\in X_{c}^{g}\mid Q_{c}(F_{g})/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \simeq P\}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH},c}(P)=\unicode[STIX]{x1D707}_{\text{CL}}(g)\unicode[STIX]{x1D707}_{c}(\{(r_{1},\ldots ,r_{g})\in X_{c}^{g}\mid Q_{c}(F_{g})/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle \simeq P\}).\end{eqnarray}$$
In particular
 $\{G\mid Q_{c}(G)\simeq P\}$
is measurable for
$\{G\mid Q_{c}(G)\simeq P\}$
is measurable for
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
.
$\unicode[STIX]{x1D707}_{\text{BBH}}$
.
If
 $P\simeq Q_{c}(G)$
for some Schur
$P\simeq Q_{c}(G)$
for some Schur
![]() $\unicode[STIX]{x1D70E}$
-group
$\unicode[STIX]{x1D70E}$
-group
![]() $G$
, we call
$G$
, we call
![]() $P$
a Schur
$P$
a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group. Note that a Schur
$\unicode[STIX]{x1D70E}$
-ancestor group. Note that a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group is necessarily a finite
$\unicode[STIX]{x1D70E}$
-ancestor group is necessarily a finite
![]() $p$
-group with a GI-automorphism (though these conditions are not sufficient). The Schur
$p$
-group with a GI-automorphism (though these conditions are not sufficient). The Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor groups are exactly those presented as
$\unicode[STIX]{x1D70E}$
-ancestor groups are exactly those presented as
 $Q_{c}(F_{g})/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle$
for some
$Q_{c}(F_{g})/\langle \langle r_{1},\ldots ,r_{g}\rangle \rangle$
for some
 $r_{1},\ldots ,r_{g}\in X_{c}$
. This is because one can choose an irredundant lift of the relations from
$r_{1},\ldots ,r_{g}\in X_{c}$
. This is because one can choose an irredundant lift of the relations from
![]() $X_{c}$
to
$X_{c}$
to
![]() $X$
to give a Schur
$X$
to give a Schur
![]() $\unicode[STIX]{x1D70E}$
-group [Reference Boston, Bush and HajirBBH16]. In particular, for any Schur
$\unicode[STIX]{x1D70E}$
-group [Reference Boston, Bush and HajirBBH16]. In particular, for any Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group
$\unicode[STIX]{x1D70E}$
-ancestor group
![]() $G$
of
$G$
of
![]() $p$
-class
$p$
-class
![]() $c$
, we have that
$c$
, we have that
 $\unicode[STIX]{x1D707}_{\text{BBH},c}(G)>0.$
$\unicode[STIX]{x1D707}_{\text{BBH},c}(G)>0.$
3.1 Choice of GI-automorphisms
It might seem strange at first that we do not include the choice of GI-automorphism with our data of a Schur
![]() $\unicode[STIX]{x1D70E}$
-group or Schur
$\unicode[STIX]{x1D70E}$
-group or Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group. However, we have the following proposition.
$\unicode[STIX]{x1D70E}$
-ancestor group. However, we have the following proposition.
Proposition 3.1 [Reference HallHal34, § 1.3].
Any two GI-automorphisms of a finitely generated pro-
![]() $p$
group
$p$
group
![]() $G$
are conjugate in
$G$
are conjugate in
![]() $\operatorname{Aut}(G)$
.
$\operatorname{Aut}(G)$
.
If
![]() $G$
and
$G$
and
![]() $H$
are finitely generated pro-
$H$
are finitely generated pro-
![]() $p$
groups, we define
$p$
groups, we define
 $\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)$
to be the continuous surjections from
$\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)$
to be the continuous surjections from
![]() $G$
to
$G$
to
![]() $H$
that take some particular choice of GI-automorphism for
$H$
that take some particular choice of GI-automorphism for
![]() $G$
to some particular choice of GI-automorphism for
$G$
to some particular choice of GI-automorphism for
![]() $H$
. We define
$H$
. We define
 $\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)$
similarly. These definitions of course depend on the particular choice of GI-automorphisms, but in this paper we will be concerned mostly with the size of these sets, and by Proposition 3.1 their sizes do not depend on these choices.
$\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)$
similarly. These definitions of course depend on the particular choice of GI-automorphisms, but in this paper we will be concerned mostly with the size of these sets, and by Proposition 3.1 their sizes do not depend on these choices.
3.2 Choice of generators
The description of
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
above actually gives a finer measure on the set of isomorphism classes of Schur
$\unicode[STIX]{x1D707}_{\text{BBH}}$
above actually gives a finer measure on the set of isomorphism classes of Schur
![]() $\unicode[STIX]{x1D70E}$
-groups with a choice of GI-automorphism and minimal generating set inverted by that automorphism. We will later take advantage of this generating set, though for simplicity we do not introduce notation for this finer measure.
$\unicode[STIX]{x1D70E}$
-groups with a choice of GI-automorphism and minimal generating set inverted by that automorphism. We will later take advantage of this generating set, though for simplicity we do not introduce notation for this finer measure.
4 Boston–Bush–Hajir moments
We now determine the moments of the measure
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
as stated in Theorem 1.3.
$\unicode[STIX]{x1D707}_{\text{BBH}}$
as stated in Theorem 1.3.
Theorem 4.1 (Moments of
 $\unicode[STIX]{x1D707}_{\text{BBH}}$
).
$\unicode[STIX]{x1D707}_{\text{BBH}}$
).
Let
![]() $H$
be a finite
$H$
be a finite
![]() $p$
-group of
$p$
-group of
![]() $p$
-class
$p$
-class
![]() $c$
with a GI-automorphism
$c$
with a GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70E}$
. Then
 $$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}=\mathop{\sum }_{G~\mathit{Schur}~\unicode[STIX]{x1D70E}\text{-}\mathit{ancestor~of}~p\text{-}\mathit{class}~c}\unicode[STIX]{x1D707}_{\text{BBH},c}(G)|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|=1.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D707}_{\text{BBH}}=\mathop{\sum }_{G~\mathit{Schur}~\unicode[STIX]{x1D70E}\text{-}\mathit{ancestor~of}~p\text{-}\mathit{class}~c}\unicode[STIX]{x1D707}_{\text{BBH},c}(G)|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|=1.\end{eqnarray}$$
Note the hypothesis that
![]() $\unicode[STIX]{x1D70E}$
is
$\unicode[STIX]{x1D70E}$
is
![]() $GI$
on
$GI$
on
![]() $H$
does not place any real restriction, because if we have a surjection
$H$
does not place any real restriction, because if we have a surjection
 $G\rightarrow H$
that takes a GI-automorphism
$G\rightarrow H$
that takes a GI-automorphism
![]() $\unicode[STIX]{x1D70E}_{G}$
on
$\unicode[STIX]{x1D70E}_{G}$
on
![]() $G$
to any automorphism
$G$
to any automorphism
![]() $\unicode[STIX]{x1D70E}_{H}$
on
$\unicode[STIX]{x1D70E}_{H}$
on
![]() $H$
, then
$H$
, then
![]() $\unicode[STIX]{x1D70E}_{H}$
must also be GI.
$\unicode[STIX]{x1D70E}_{H}$
must also be GI.
Let
![]() $H$
be a finite
$H$
be a finite
![]() $p$
group with an order-
$p$
group with an order-
![]() $2$
automorphism
$2$
automorphism
![]() $\unicode[STIX]{x1D70E}$
. We write
$\unicode[STIX]{x1D70E}$
. We write
 $$\begin{eqnarray}Z(H)=\{g\in H\mid \unicode[STIX]{x1D70E}(g)=g\}\end{eqnarray}$$
$$\begin{eqnarray}Z(H)=\{g\in H\mid \unicode[STIX]{x1D70E}(g)=g\}\end{eqnarray}$$
and
 $Y(H)=\{g\in H\mid \unicode[STIX]{x1D70E}(g)=g^{-1}\}$
. This notation implicitly depends on
$Y(H)=\{g\in H\mid \unicode[STIX]{x1D70E}(g)=g^{-1}\}$
. This notation implicitly depends on
![]() $\unicode[STIX]{x1D70E}$
. We now prove several lemmas that will be used in the proof of Theorem 4.1.
$\unicode[STIX]{x1D70E}$
. We now prove several lemmas that will be used in the proof of Theorem 4.1.
Lemma 4.2. Let
![]() $G$
be a finite
$G$
be a finite
![]() $p$
-group with an order-
$p$
-group with an order-
![]() $2$
automorphism
$2$
automorphism
![]() $\unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70E}$
. Then
 $|G|=|Y(G)|\,|Z(G)|$
.
$|G|=|Y(G)|\,|Z(G)|$
.
Proof. This is [Reference GorensteinGor07, Theorem 3.5 (p. 180) of ch. 5]. ◻
Lemma 4.3. Let
![]() $G$
and
$G$
and
![]() $H$
be finite
$H$
be finite
![]() $p$
-groups, each with an order-
$p$
-groups, each with an order-
![]() $2$
automorphism
$2$
automorphism
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
 $\unicode[STIX]{x1D719}:G\rightarrow H$
be a
$\unicode[STIX]{x1D719}:G\rightarrow H$
be a
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjection. Then
$\unicode[STIX]{x1D70E}$
-equivariant surjection. Then
 $\unicode[STIX]{x1D719}:Z(G)\rightarrow Z(H)$
is a surjection.
$\unicode[STIX]{x1D719}:Z(G)\rightarrow Z(H)$
is a surjection.
Proof. Associated to the exact sequence
 $1\rightarrow \ker (\unicode[STIX]{x1D719})\rightarrow G\rightarrow H\rightarrow 1$
is the exact sequence
$1\rightarrow \ker (\unicode[STIX]{x1D719})\rightarrow G\rightarrow H\rightarrow 1$
is the exact sequence
 $$\begin{eqnarray}\cdots \rightarrow H^{0}(\langle \unicode[STIX]{x1D70E}\rangle ,G)\rightarrow H^{0}(\langle \unicode[STIX]{x1D70E}\rangle ,H)\rightarrow H^{1}(\langle \unicode[STIX]{x1D70E}\rangle ,\ker (\unicode[STIX]{x1D719}))\rightarrow \cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}\cdots \rightarrow H^{0}(\langle \unicode[STIX]{x1D70E}\rangle ,G)\rightarrow H^{0}(\langle \unicode[STIX]{x1D70E}\rangle ,H)\rightarrow H^{1}(\langle \unicode[STIX]{x1D70E}\rangle ,\ker (\unicode[STIX]{x1D719}))\rightarrow \cdots \,.\end{eqnarray}$$
The first and second terms are
![]() $Z(G)$
and
$Z(G)$
and
![]() $Z(H)$
respectively. The last term is
$Z(H)$
respectively. The last term is
 $H^{1}(\langle \unicode[STIX]{x1D70E}\rangle ,\ker (\unicode[STIX]{x1D719}))$
, which vanishes by the Schur–Zassenhaus theorem since
$H^{1}(\langle \unicode[STIX]{x1D70E}\rangle ,\ker (\unicode[STIX]{x1D719}))$
, which vanishes by the Schur–Zassenhaus theorem since
![]() $p$
is odd.◻
$p$
is odd.◻
Lemma 4.4. Let
![]() $G$
and
$G$
and
![]() $H$
be finite
$H$
be finite
![]() $p$
-groups, each with an order-
$p$
-groups, each with an order-
![]() $2$
automorphism
$2$
automorphism
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
 $\unicode[STIX]{x1D719}:G\rightarrow H$
be a
$\unicode[STIX]{x1D719}:G\rightarrow H$
be a
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjection with kernel
$\unicode[STIX]{x1D70E}$
-equivariant surjection with kernel
![]() $K$
. Then
$K$
. Then
 $Z(K)=K\cap Z(G)$
and
$Z(K)=K\cap Z(G)$
and
 $Y(K)=K\cap Y(G)$
, and
$Y(K)=K\cap Y(G)$
, and
 $|Y(K)|=|Y(G)|/|Y(H)|$
.
$|Y(K)|=|Y(G)|/|Y(H)|$
.
Proof. The first two claims are clear. Using the above two lemmas, we then observe
 $$\begin{eqnarray}|Y(K)|=\frac{|K|}{|Z(K)|}=\frac{|G|/|H|}{|Z(G)|/|Z(H)|}=\frac{|Y(G)|}{|Y(H)|},\end{eqnarray}$$
$$\begin{eqnarray}|Y(K)|=\frac{|K|}{|Z(K)|}=\frac{|G|/|H|}{|Z(G)|/|Z(H)|}=\frac{|Y(G)|}{|Y(H)|},\end{eqnarray}$$
which proves the final claim. ◻
Lemma 4.5. Let
![]() $H$
be a finite
$H$
be a finite
![]() $p$
-group with GI-automorphism
$p$
-group with GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
. Then the elements of
$\unicode[STIX]{x1D70E}$
. Then the elements of
![]() $Y(H)$
are equidistributed in
$Y(H)$
are equidistributed in
 $H/\unicode[STIX]{x1D6F7}(H)$
. That is, any two cosets in
$H/\unicode[STIX]{x1D6F7}(H)$
. That is, any two cosets in
![]() $H$
of
$H$
of
![]() $\unicode[STIX]{x1D6F7}(H)$
, when intersected with
$\unicode[STIX]{x1D6F7}(H)$
, when intersected with
![]() $Y(H)$
have the same number of elements.
$Y(H)$
have the same number of elements.
Proof. We consider the maps of sets
 $f:H\rightarrow Y(H)$
given by
$f:H\rightarrow Y(H)$
given by
 $f(g)=g^{-1}\unicode[STIX]{x1D70E}(g)$
and
$f(g)=g^{-1}\unicode[STIX]{x1D70E}(g)$
and
 $\unicode[STIX]{x1D70B}:Y(H)\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
the composition of the inclusion and quotient maps
$\unicode[STIX]{x1D70B}:Y(H)\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
the composition of the inclusion and quotient maps
 $Y(H)\rightarrow H\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
.
$Y(H)\rightarrow H\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
.
Then the composition
 $\unicode[STIX]{x1D70B}f:H\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
sends
$\unicode[STIX]{x1D70B}f:H\rightarrow H/\unicode[STIX]{x1D6F7}(H)$
sends
 $g\mapsto g^{-2}$
since
$g\mapsto g^{-2}$
since
![]() $\unicode[STIX]{x1D70E}$
acts by inversion on
$\unicode[STIX]{x1D70E}$
acts by inversion on
 $H/\unicode[STIX]{x1D6F7}(H)$
. This is a homomorphism since
$H/\unicode[STIX]{x1D6F7}(H)$
. This is a homomorphism since
 $H/\unicode[STIX]{x1D6F7}(H)$
is abelian, and a surjection since
$H/\unicode[STIX]{x1D6F7}(H)$
is abelian, and a surjection since
 $H/\unicode[STIX]{x1D6F7}(H)$
has odd order. Thus the fibers of
$H/\unicode[STIX]{x1D6F7}(H)$
has odd order. Thus the fibers of
![]() $\unicode[STIX]{x1D70B}f$
are of equal size. Further, the fibers of
$\unicode[STIX]{x1D70B}f$
are of equal size. Further, the fibers of
![]() $f$
are cosets of
$f$
are cosets of
![]() $Z(H)$
and thus are also of equal size. Also, since for any
$Z(H)$
and thus are also of equal size. Also, since for any
![]() $g\in H$
,
$g\in H$
,
 $g\unicode[STIX]{x1D6F7}(H)\cap Y(H)=\unicode[STIX]{x1D70B}^{-1}(g)$
, it suffices to show the fibres of
$g\unicode[STIX]{x1D6F7}(H)\cap Y(H)=\unicode[STIX]{x1D70B}^{-1}(g)$
, it suffices to show the fibres of
![]() $\unicode[STIX]{x1D70B}$
have equal sizes, which now follows.◻
$\unicode[STIX]{x1D70B}$
have equal sizes, which now follows.◻
Lemma 4.6. Let
![]() $H$
be a finite
$H$
be a finite
![]() $p$
-group of generator rank
$p$
-group of generator rank
![]() $r$
with a GI-automorphism
$r$
with a GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
. Then
$\unicode[STIX]{x1D70E}$
. Then
 $$\begin{eqnarray}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{d},H)|=\frac{|Y(H)|^{d}(p^{d}-p^{r-1})\cdots (p^{d}-1)}{p^{dr}}.\end{eqnarray}$$
$$\begin{eqnarray}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{d},H)|=\frac{|Y(H)|^{d}(p^{d}-p^{r-1})\cdots (p^{d}-1)}{p^{dr}}.\end{eqnarray}$$
Proof. A homomorphism
 $F_{d}\rightarrow H$
is
$F_{d}\rightarrow H$
is
![]() $\unicode[STIX]{x1D70E}$
-equivariant if and only if it sends each of the
$\unicode[STIX]{x1D70E}$
-equivariant if and only if it sends each of the
![]() $d$
generators of
$d$
generators of
![]() $F_{d}$
to an element of
$F_{d}$
to an element of
![]() $Y(H)$
, and so there are
$Y(H)$
, and so there are
 $|Y(H)|^{d}$
such maps. By the Burnside basis theorem, such a homomorphism is surjective if and only if its composition with the quotient map is surjective to
$|Y(H)|^{d}$
such maps. By the Burnside basis theorem, such a homomorphism is surjective if and only if its composition with the quotient map is surjective to
 $H/\unicode[STIX]{x1D6F7}(H)$
. Since the elements of
$H/\unicode[STIX]{x1D6F7}(H)$
. Since the elements of
![]() $Y(H)$
are equidistributed in
$Y(H)$
are equidistributed in
 $H/\unicode[STIX]{x1D6F7}(H)$
, the proportion of
$H/\unicode[STIX]{x1D6F7}(H)$
, the proportion of
![]() $\unicode[STIX]{x1D70E}$
-equivariant homomorphisms
$\unicode[STIX]{x1D70E}$
-equivariant homomorphisms
 $F_{d}\rightarrow H$
that are surjective is the same as the proportion of
$F_{d}\rightarrow H$
that are surjective is the same as the proportion of
![]() $d$
-tuples from
$d$
-tuples from
 $H/\unicode[STIX]{x1D6F7}(H)\simeq (\mathbb{Z}/p\mathbb{Z})^{r}$
that span this
$H/\unicode[STIX]{x1D6F7}(H)\simeq (\mathbb{Z}/p\mathbb{Z})^{r}$
that span this
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space, which is easily computed to be
$\mathbb{Z}/p\mathbb{Z}$
-vector space, which is easily computed to be
 $(p^{d}-p^{r-1})\cdots (p^{d}-1)/p^{dr}$
.◻
$(p^{d}-p^{r-1})\cdots (p^{d}-1)/p^{dr}$
.◻
Proof of Theorem 4.1.
Since a surjection from
![]() $G$
to
$G$
to
![]() $H$
factors through
$H$
factors through
![]() $Q_{c}(G)$
, we see that
$Q_{c}(G)$
, we see that
 $f(G)=|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|$
is in fact a measurable function and that the first equality is by definition of the two measures.
$f(G)=|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|$
is in fact a measurable function and that the first equality is by definition of the two measures.
Let
![]() $H$
have generator rank
$H$
have generator rank
![]() $r$
. The random group
$r$
. The random group
![]() $G$
is constructed first by picking a random generator rank
$G$
is constructed first by picking a random generator rank
![]() $d$
for
$d$
for
![]() $G$
according to the Cohen–Lenstra measure, and then taking a random quotient of
$G$
according to the Cohen–Lenstra measure, and then taking a random quotient of
![]() $F_{d}$
. Certainly, any surjection
$F_{d}$
. Certainly, any surjection
 $G\rightarrow H$
lifts uniquely to a surjection
$G\rightarrow H$
lifts uniquely to a surjection
 $F_{d}\rightarrow H$
. From Lemma 4.6 we see there are
$F_{d}\rightarrow H$
. From Lemma 4.6 we see there are
 $|Y(H)|^{d}(p^{d}-p^{r-1})\cdots (p^{d}-1)/p^{dr}$
$|Y(H)|^{d}(p^{d}-p^{r-1})\cdots (p^{d}-1)/p^{dr}$
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjections
$\unicode[STIX]{x1D70E}$
-equivariant surjections
 $F_{d}\rightarrow H$
. A surjection
$F_{d}\rightarrow H$
. A surjection
 $\unicode[STIX]{x1D719}:F_{d}\rightarrow H$
factors through
$\unicode[STIX]{x1D719}:F_{d}\rightarrow H$
factors through
![]() $G$
if and only if the
$G$
if and only if the
![]() $d$
random relations in
$d$
random relations in
 $Y(\unicode[STIX]{x1D6F7}(F_{d}))$
that present
$Y(\unicode[STIX]{x1D6F7}(F_{d}))$
that present
![]() $G$
are in
$G$
are in
![]() $\ker (\unicode[STIX]{x1D719})$
, the probability of which we now compute. Since
$\ker (\unicode[STIX]{x1D719})$
, the probability of which we now compute. Since
![]() $H$
is
$H$
is
![]() $p$
-class
$p$
-class
![]() $c$
, we may equivalently take the random relations in
$c$
, we may equivalently take the random relations in
 $Y(\unicode[STIX]{x1D6F7}(F_{d})/P_{c}(F_{d}))$
.
$Y(\unicode[STIX]{x1D6F7}(F_{d})/P_{c}(F_{d}))$
.
Let
 $F:=F_{d}/P_{c}(F_{d})$
. The probability that a random relation in
$F:=F_{d}/P_{c}(F_{d})$
. The probability that a random relation in
 $X_{c}=Y(\unicode[STIX]{x1D6F7}(F))$
is in
$X_{c}=Y(\unicode[STIX]{x1D6F7}(F))$
is in
![]() $\ker (\unicode[STIX]{x1D719})$
is
$\ker (\unicode[STIX]{x1D719})$
is
 $|\text{ker}(\unicode[STIX]{x1D719})\cap Y(\unicode[STIX]{x1D6F7}(F))|/|Y(\unicode[STIX]{x1D6F7}(F))|$
. Applying Lemma 4.4 to the surjection
$|\text{ker}(\unicode[STIX]{x1D719})\cap Y(\unicode[STIX]{x1D6F7}(F))|/|Y(\unicode[STIX]{x1D6F7}(F))|$
. Applying Lemma 4.4 to the surjection
 $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6F7}(F)\rightarrow \unicode[STIX]{x1D6F7}(G)$
, we see that
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6F7}(F)\rightarrow \unicode[STIX]{x1D6F7}(G)$
, we see that
 $|\text{ker}(\unicode[STIX]{x1D719})\cap Y(\unicode[STIX]{x1D6F7}(F))|/|Y(\unicode[STIX]{x1D6F7}(F))|=|Y(\unicode[STIX]{x1D6F7}(G))|^{-1}$
. Also, applying Lemma 4.4 to the quotient
$|\text{ker}(\unicode[STIX]{x1D719})\cap Y(\unicode[STIX]{x1D6F7}(F))|/|Y(\unicode[STIX]{x1D6F7}(F))|=|Y(\unicode[STIX]{x1D6F7}(G))|^{-1}$
. Also, applying Lemma 4.4 to the quotient
 $G\rightarrow G/\unicode[STIX]{x1D6F7}(G)$
, we have that
$G\rightarrow G/\unicode[STIX]{x1D6F7}(G)$
, we have that
 $|Y(\unicode[STIX]{x1D6F7}(G))|=|Y(G)|/p^{r}$
, since
$|Y(\unicode[STIX]{x1D6F7}(G))|=|Y(G)|/p^{r}$
, since
![]() $\unicode[STIX]{x1D70E}$
acts on all of
$\unicode[STIX]{x1D70E}$
acts on all of
 $G/\unicode[STIX]{x1D6F7}(G)$
by inversion. Thus, the probability that
$G/\unicode[STIX]{x1D6F7}(G)$
by inversion. Thus, the probability that
![]() $d$
random relations are in
$d$
random relations are in
![]() $\ker (\unicode[STIX]{x1D719})$
, and so the map
$\ker (\unicode[STIX]{x1D719})$
, and so the map
![]() $\unicode[STIX]{x1D719}$
factors through the random
$\unicode[STIX]{x1D719}$
factors through the random
![]() $G$
, is
$G$
, is
 $p^{dr}/|Y(H)|^{d}$
.
$p^{dr}/|Y(H)|^{d}$
.
Multiplying by the number of
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjections
$\unicode[STIX]{x1D70E}$
-equivariant surjections
 $F_{d}\rightarrow H$
, we find that among generator rank
$F_{d}\rightarrow H$
, we find that among generator rank
![]() $d$
groups
$d$
groups
![]() $G$
, the expected number of
$G$
, the expected number of
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjections to
$\unicode[STIX]{x1D70E}$
-equivariant surjections to
![]() $H$
is
$H$
is
 $(p^{d}-p^{r-1})\cdots (p^{d}-1)$
, which is the number of surjections from a rank
$(p^{d}-p^{r-1})\cdots (p^{d}-1)$
, which is the number of surjections from a rank
![]() $d$
abelian
$d$
abelian
![]() $p$
-group to
$p$
-group to
 $(\mathbb{Z}/p\mathbb{Z})^{r}$
. Thus the expected number of
$(\mathbb{Z}/p\mathbb{Z})^{r}$
. Thus the expected number of
![]() $\unicode[STIX]{x1D70E}$
-equivariant surjections is
$\unicode[STIX]{x1D70E}$
-equivariant surjections is
 $$\begin{eqnarray}\mathop{\sum }_{d\geqslant 0}\unicode[STIX]{x1D707}_{\text{CL}}(d)(p^{d}-p^{r-1})\cdots (p^{d}-1)=\mathop{\sum }_{A}\unicode[STIX]{x1D707}_{\text{CL}}(A)|\!\operatorname{Sur}(A,(\mathbb{Z}/p\mathbb{Z})^{r})|=1,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{d\geqslant 0}\unicode[STIX]{x1D707}_{\text{CL}}(d)(p^{d}-p^{r-1})\cdots (p^{d}-1)=\mathop{\sum }_{A}\unicode[STIX]{x1D707}_{\text{CL}}(A)|\!\operatorname{Sur}(A,(\mathbb{Z}/p\mathbb{Z})^{r})|=1,\end{eqnarray}$$
by the moments formula for the Cohen–Lenstra measure. ◻
In fact, we will see in Theorem 4.9 that the moments where
![]() $H$
is a Schur
$H$
is a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group characterize
$\unicode[STIX]{x1D70E}$
-ancestor group characterize
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
as a measure on
$\unicode[STIX]{x1D707}_{\text{BBH}}$
as a measure on
![]() $\unicode[STIX]{x1D6FA}$
. At each
$\unicode[STIX]{x1D6FA}$
. At each
![]() $p$
-class, showing the moments characterize the measure amounts to inverting an infinite-dimensional matrix. Our method to invert this matrix can be seen as a generalization of the method of [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2], which proves that the moments characterize the Cohen–Lenstra measure on finite abelian
$p$
-class, showing the moments characterize the measure amounts to inverting an infinite-dimensional matrix. Our method to invert this matrix can be seen as a generalization of the method of [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2], which proves that the moments characterize the Cohen–Lenstra measure on finite abelian
![]() $p$
-groups. First we need an infinite-dimensional linear algebra lemma, since our infinite matrices are not quite as simple as those in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2].
$p$
-groups. First we need an infinite-dimensional linear algebra lemma, since our infinite matrices are not quite as simple as those in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 8.2].
Lemma 4.7. Let
![]() $a_{i,j}$
be non-negative real numbers indexed by pairs of natural numbers
$a_{i,j}$
be non-negative real numbers indexed by pairs of natural numbers
![]() $i,j$
, such that for all
$i,j$
, such that for all
![]() $i$
we have
$i$
we have
![]() $a_{i,i}=1$
, and also
$a_{i,i}=1$
, and also
 $\sup _{i}\sum _{j}a_{ij}<2$
. Let
$\sup _{i}\sum _{j}a_{ij}<2$
. Let
![]() $x_{j},y_{j}$
be non-negative reals indexed by natural numbers
$x_{j},y_{j}$
be non-negative reals indexed by natural numbers
![]() $j$
. If for all
$j$
. If for all
![]() $i$
,
$i$
,
 $$\begin{eqnarray}\mathop{\sum }_{j}a_{i,j}x_{j}=\mathop{\sum }_{j}a_{i,j}y_{j}=1,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j}a_{i,j}x_{j}=\mathop{\sum }_{j}a_{i,j}y_{j}=1,\end{eqnarray}$$
then
![]() $x_{j}=y_{j}$
for all
$x_{j}=y_{j}$
for all
![]() $j$
.
$j$
.
Proof. Note that
 $x_{i}=a_{ii}x_{i}\leqslant \sum _{j}a_{i,j}x_{j}\leqslant 1$
. Similarly
$x_{i}=a_{ii}x_{i}\leqslant \sum _{j}a_{i,j}x_{j}\leqslant 1$
. Similarly
 $0\leqslant y_{i}\leqslant 1$
. Let
$0\leqslant y_{i}\leqslant 1$
. Let
 $d_{i}=x_{i}-y_{i}$
. Let
$d_{i}=x_{i}-y_{i}$
. Let
 $a=\sup _{i}\sum _{j}a_{ij}<2$
. Let
$a=\sup _{i}\sum _{j}a_{ij}<2$
. Let
 $s=\sup _{i}|d_{i}|$
, so
$s=\sup _{i}|d_{i}|$
, so
 $0\leqslant s\leqslant 1$
. For each
$0\leqslant s\leqslant 1$
. For each
![]() $i$
, we have
$i$
, we have
 $\sum a_{ij}d_{j}=0$
, so
$\sum a_{ij}d_{j}=0$
, so
 $d_{i}=-\!\sum _{j\neq i}a_{ij}d_{j}$
. So,
$d_{i}=-\!\sum _{j\neq i}a_{ij}d_{j}$
. So,
 $|d_{i}|\leqslant \sum _{j\neq i}a_{ij}|d_{j}|$
. Taking the supremum over
$|d_{i}|\leqslant \sum _{j\neq i}a_{ij}|d_{j}|$
. Taking the supremum over
![]() $i$
yields
$i$
yields
 $s\leqslant (a-1)s$
. Since
$s\leqslant (a-1)s$
. Since
 $a-1<1$
, so
$a-1<1$
, so
![]() $s=0$
. Thus
$s=0$
. Thus
![]() $x_{i}=y_{i}$
for all
$x_{i}=y_{i}$
for all
![]() $i$
.◻
$i$
.◻
Next, we will prove a formula for
 $\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})$
for a given Schur
$\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})$
for a given Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group
$\unicode[STIX]{x1D70E}$
-ancestor group
![]() $P$
. The formula combines [Reference Boston, Bush and HajirBBH16, Theorems 2.25 and 2.29], which are subject to a further conjecture called KIP, but we prove below that the combined formula is not conjectural. For the formula, we will need one further invariant of
$P$
. The formula combines [Reference Boston, Bush and HajirBBH16, Theorems 2.25 and 2.29], which are subject to a further conjecture called KIP, but we prove below that the combined formula is not conjectural. For the formula, we will need one further invariant of
![]() $p$
-groups. For a finite
$p$
-groups. For a finite
![]() $p$
-group
$p$
-group
![]() $G$
of
$G$
of
![]() $p$
-class
$p$
-class
![]() $c$
presented as
$c$
presented as
![]() $F/R$
, where
$F/R$
, where
![]() $F$
is a free group of
$F$
is a free group of
![]() $d(G)$
generators, then
$d(G)$
generators, then
![]() $h(G)$
is defined to be the dimension of the quotient of
$h(G)$
is defined to be the dimension of the quotient of
![]() $R$
by the topological closure of the subgroup
$R$
by the topological closure of the subgroup
 $R^{p}[F,R]P_{c}(F)$
(by [Reference O’BrienO’B90] and [Reference Boston, Bush and HajirBBH16, Remark 2.4] the quantity does not depend on the choice of presentation).
$R^{p}[F,R]P_{c}(F)$
(by [Reference O’BrienO’B90] and [Reference Boston, Bush and HajirBBH16, Remark 2.4] the quantity does not depend on the choice of presentation).
Alternatively, the
![]() $p$
-groups of
$p$
-groups of
![]() $p$
-class
$p$
-class
![]() ${\leqslant}c$
form a variety of groups whose free objects are precisely the groups
${\leqslant}c$
form a variety of groups whose free objects are precisely the groups
![]() $Q_{c}(F_{d})$
. For a group
$Q_{c}(F_{d})$
. For a group
![]() $G$
in this variety, we can let
$G$
in this variety, we can let
![]() $h_{c}(G)$
be the number of relators required to present
$h_{c}(G)$
be the number of relators required to present
![]() $G$
in this variety. If
$G$
in this variety. If
![]() $G$
is
$G$
is
![]() $p$
-class
$p$
-class
![]() $c$
, then
$c$
, then
 $h_{c}(G)=h(G)$
and if
$h_{c}(G)=h(G)$
and if
![]() $G$
is
$G$
is
![]() $p$
-class smaller than
$p$
-class smaller than
![]() $c$
, then
$c$
, then
 $h_{c}(G)=r(G)$
.
$h_{c}(G)=r(G)$
.
Lemma 4.8. Fix a
![]() $c$
. Let
$c$
. Let
 $g=d(G)$
and
$g=d(G)$
and
 $h=h_{c}(G)$
. We have
$h=h_{c}(G)$
. We have
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})}{\unicode[STIX]{x1D707}_{\text{CL}}(g)}=\frac{p^{g^{2}}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|}\mathop{\prod }_{k=1}^{g}(1-p^{-k})\mathop{\prod }_{k=1+g-h}^{g}(1-p^{-k}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq P\})}{\unicode[STIX]{x1D707}_{\text{CL}}(g)}=\frac{p^{g^{2}}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|}\mathop{\prod }_{k=1}^{g}(1-p^{-k})\mathop{\prod }_{k=1+g-h}^{g}(1-p^{-k}).\end{eqnarray}$$
Proof. Let
 $F_{c}=Q_{c}(F_{g})$
. We need to compute the sum of the probabilities that a given
$F_{c}=Q_{c}(F_{g})$
. We need to compute the sum of the probabilities that a given
![]() $g$
-tuple of relations
$g$
-tuple of relations
![]() $v\in X_{c}^{g}$
generates
$v\in X_{c}^{g}$
generates
![]() $\overline{R}$
as a normal subgroup of
$\overline{R}$
as a normal subgroup of
![]() $F_{c}$
, where
$F_{c}$
, where
![]() $\overline{R}$
runs over all normal subgroups of
$\overline{R}$
runs over all normal subgroups of
![]() $F_{c}$
with quotient
$F_{c}$
with quotient
![]() $G$
. The key thing to note here is that since each element of
$G$
. The key thing to note here is that since each element of
![]() $X_{c}$
is inverted by
$X_{c}$
is inverted by
![]() $\unicode[STIX]{x1D70E}$
, any subgroup generated by elements of
$\unicode[STIX]{x1D70E}$
, any subgroup generated by elements of
![]() $X_{c}$
is
$X_{c}$
is
![]() $\unicode[STIX]{x1D70E}$
-invariant, as is the normal closure of such a subgroup. Thus if
$\unicode[STIX]{x1D70E}$
-invariant, as is the normal closure of such a subgroup. Thus if
![]() $\overline{R}$
is a normal subgroup of
$\overline{R}$
is a normal subgroup of
![]() $F_{c}$
that is not
$F_{c}$
that is not
![]() $\unicode[STIX]{x1D70E}$
-invariant, then the probability that is generated as a normal subgroup by relations from
$\unicode[STIX]{x1D70E}$
-invariant, then the probability that is generated as a normal subgroup by relations from
![]() $X_{c}$
is
$X_{c}$
is
![]() $0$
. In [Reference Boston, Bush and HajirBBH16], the conjectural property KIP (kernel invariance property) was assumed to ensure that every normal subgroup with quotient
$0$
. In [Reference Boston, Bush and HajirBBH16], the conjectural property KIP (kernel invariance property) was assumed to ensure that every normal subgroup with quotient
![]() $G$
is
$G$
is
![]() $\unicode[STIX]{x1D70E}$
-invariant. We do not assume this, since by the above remark we can restrict our attention to the set of
$\unicode[STIX]{x1D70E}$
-invariant. We do not assume this, since by the above remark we can restrict our attention to the set of
![]() $\unicode[STIX]{x1D70E}$
-invariant normal subgroups with quotient
$\unicode[STIX]{x1D70E}$
-invariant normal subgroups with quotient
![]() $G$
.
$G$
.
The number of
![]() $\unicode[STIX]{x1D70E}$
-invariant normal subgroups of
$\unicode[STIX]{x1D70E}$
-invariant normal subgroups of
![]() $F_{c}$
with quotient
$F_{c}$
with quotient
![]() $G$
is
$G$
is
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{c},G)|/|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|$
, by counting the quotient maps and dividing by how often maps give isomorphic quotients. (There are similarly
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{c},G)|/|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|$
, by counting the quotient maps and dividing by how often maps give isomorphic quotients. (There are similarly
 $|\!\operatorname{Sur}(F_{c},G)|/|\!\operatorname{Aut}(G)|$
normal subgroups with quotient
$|\!\operatorname{Sur}(F_{c},G)|/|\!\operatorname{Aut}(G)|$
normal subgroups with quotient
![]() $G$
, but if there are any that are not
$G$
, but if there are any that are not
![]() $\unicode[STIX]{x1D70E}$
-invariant we have already seen they have
$\unicode[STIX]{x1D70E}$
-invariant we have already seen they have
![]() $0$
probability of being generated by our relations in
$0$
probability of being generated by our relations in
![]() $X_{g}$
.) The probability that a
$X_{g}$
.) The probability that a
![]() $g$
-tuple of relations
$g$
-tuple of relations
![]() $v\in X_{c}^{g}$
generates a
$v\in X_{c}^{g}$
generates a
![]() $\unicode[STIX]{x1D70E}$
-invariant
$\unicode[STIX]{x1D70E}$
-invariant
![]() $\overline{R}$
as a normal subgroup can be computed by the earlier methods of [Reference Boston, Bush and HajirBBH16]. We give a slightly alternative treatment here.
$\overline{R}$
as a normal subgroup can be computed by the earlier methods of [Reference Boston, Bush and HajirBBH16]. We give a slightly alternative treatment here.
First note that by Lemma 4.6,
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{c},G)|=|Y(G)|^{g}\prod _{k=1}^{g}(1-p^{-k})$
, since every such surjection from the free pro-
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(F_{c},G)|=|Y(G)|^{g}\prod _{k=1}^{g}(1-p^{-k})$
, since every such surjection from the free pro-
![]() $p$
group
$p$
group
![]() $F_{g}$
on
$F_{g}$
on
![]() $g$
generators factors through
$g$
generators factors through
![]() $F_{c}$
. As for the probability that
$F_{c}$
. As for the probability that
![]() $v\in X_{c}^{g}$
normally generates
$v\in X_{c}^{g}$
normally generates
![]() $\overline{R}$
, this happens if and only if its image generates the
$\overline{R}$
, this happens if and only if its image generates the
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
 $V=\overline{R}/\overline{R}^{\ast }$
, where
$V=\overline{R}/\overline{R}^{\ast }$
, where
![]() $R$
is the preimage of
$R$
is the preimage of
![]() $\overline{R}$
in
$\overline{R}$
in
![]() $F_{g}$
,
$F_{g}$
,
![]() $R^{\ast }$
is the topological closure of
$R^{\ast }$
is the topological closure of
 $R^{p}[F_{g},R]$
, and
$R^{p}[F_{g},R]$
, and
 $\overline{R}^{\ast }=P_{c}(F_{g})R^{\ast }/P_{c}(F_{g})$
[Reference GruenbergGru76, Proposition 2.8]. When
$\overline{R}^{\ast }=P_{c}(F_{g})R^{\ast }/P_{c}(F_{g})$
[Reference GruenbergGru76, Proposition 2.8]. When
![]() $G$
is
$G$
is
![]() $p$
-class
$p$
-class
![]() $c$
, the dimension of
$c$
, the dimension of
![]() $V$
is
$V$
is
![]() $h$
(by definition of
$h$
(by definition of
![]() $h$
). When
$h$
). When
![]() $G$
is
$G$
is
![]() $p$
-class
$p$
-class
![]() ${<}c$
, we have
${<}c$
, we have
 $P_{c-1}(F_{g})\subset R$
and so
$P_{c-1}(F_{g})\subset R$
and so
![]() $P_{c}(F_{g})$
is a subgroup of
$P_{c}(F_{g})$
is a subgroup of
![]() $R^{\ast }$
. Then
$R^{\ast }$
. Then
 $V=R/R^{\ast }$
, which has dimension
$V=R/R^{\ast }$
, which has dimension
![]() $r(G)$
. Let
$r(G)$
. Let
 $s=\dim V$
, which we have just determined in each case. The number of
$s=\dim V$
, which we have just determined in each case. The number of
![]() $g$
-tuples generating
$g$
-tuples generating
![]() $V$
is
$V$
is
 $\prod _{k=1}^{s}(p^{g}-p^{s-k})$
and so we just need the size of the intersection of
$\prod _{k=1}^{s}(p^{g}-p^{s-k})$
and so we just need the size of the intersection of
![]() $X_{c}$
with a fiber of the quotient map
$X_{c}$
with a fiber of the quotient map
 $r:\overline{R}\rightarrow V$
.
$r:\overline{R}\rightarrow V$
.
We claim each of these has
 $|\overline{R}^{\ast }|/|Z(\overline{R})|$
elements. This follows by considering the map
$|\overline{R}^{\ast }|/|Z(\overline{R})|$
elements. This follows by considering the map
![]() $f$
of Lemma 4.5, defined by
$f$
of Lemma 4.5, defined by
 $f(g)=g^{-1}\unicode[STIX]{x1D70E}(g)$
. Since
$f(g)=g^{-1}\unicode[STIX]{x1D70E}(g)$
. Since
![]() $V$
is abelian,
$V$
is abelian,
 $f\circ r=-2r$
, whose fibers have the same size as those of
$f\circ r=-2r$
, whose fibers have the same size as those of
![]() $r$
, namely
$r$
, namely
![]() $|\overline{R}^{\ast }|$
, since
$|\overline{R}^{\ast }|$
, since
![]() $p$
is odd. On the other hand,
$p$
is odd. On the other hand,
 $f\circ r=r\circ f$
, the size of the fibers of which are the size of those of
$f\circ r=r\circ f$
, the size of the fibers of which are the size of those of
![]() $r$
times those of
$r$
times those of
![]() $f$
. This latter term is
$f$
. This latter term is
![]() $|Z(\overline{R})|$
by Lemma 4.2. Putting these facts together establishes the claim.
$|Z(\overline{R})|$
by Lemma 4.2. Putting these facts together establishes the claim.
To recap, the desired measure is the sum over
 $|Y(G)|^{g}\prod _{k=1}^{g}(1-p^{-k})/|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|$
terms of the number of
$|Y(G)|^{g}\prod _{k=1}^{g}(1-p^{-k})/|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|$
terms of the number of
![]() $v$
in
$v$
in
![]() $X_{c}^{g}$
normally generating each
$X_{c}^{g}$
normally generating each
![]() $\overline{R}$
, which we just found to be
$\overline{R}$
, which we just found to be
 $\prod _{k=1}^{s}(p^{g}-p^{s-k})(|\overline{R}^{\ast }|/|Z(\overline{R})|)^{g}$
, divided by the total number of
$\prod _{k=1}^{s}(p^{g}-p^{s-k})(|\overline{R}^{\ast }|/|Z(\overline{R})|)^{g}$
, divided by the total number of
![]() $v$
, namely
$v$
, namely
![]() $|X_{c}|^{g}$
. In other words,
$|X_{c}|^{g}$
. In other words,
 $$\begin{eqnarray}\mathop{\prod }_{k=1}^{s}(p^{g}-p^{s-k})\mathop{\prod }_{k=1}^{g}(1-p^{-k})\frac{(|\overline{R}^{\ast }|/|Z(\overline{R})|)^{g}|Y(G)|^{g}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|\,|X_{c}|^{g}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{k=1}^{s}(p^{g}-p^{s-k})\mathop{\prod }_{k=1}^{g}(1-p^{-k})\frac{(|\overline{R}^{\ast }|/|Z(\overline{R})|)^{g}|Y(G)|^{g}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(G)|\,|X_{c}|^{g}}.\end{eqnarray}$$
It remains to show that
 $|Y(G)|\,|\overline{R}^{\ast }|/(|Z(\overline{R})|\,|X_{c}|)=p^{g-s}$
. This follows from Lemma 4.4, which says that
$|Y(G)|\,|\overline{R}^{\ast }|/(|Z(\overline{R})|\,|X_{c}|)=p^{g-s}$
. This follows from Lemma 4.4, which says that
 $|Y(F_{c})|=|Y(G)|\,|Y(\overline{R})|$
and
$|Y(F_{c})|=|Y(G)|\,|Y(\overline{R})|$
and
 $|Y(F_{c})|=|Y(\unicode[STIX]{x1D6F7}(F_{c}))|\,|Y(F_{c}/\unicode[STIX]{x1D6F7}(F_{c}))|=|X_{c}|p^{g}$
. Thus,
$|Y(F_{c})|=|Y(\unicode[STIX]{x1D6F7}(F_{c}))|\,|Y(F_{c}/\unicode[STIX]{x1D6F7}(F_{c}))|=|X_{c}|p^{g}$
. Thus,
 $|X_{c}|=|Y(G)|\,|Y(\overline{R})|p^{-g}$
. Combining this with
$|X_{c}|=|Y(G)|\,|Y(\overline{R})|p^{-g}$
. Combining this with
 $|Y(\overline{R})|\,|Z(\overline{R})|=|\overline{R}|$
(Lemma 4.2) and
$|Y(\overline{R})|\,|Z(\overline{R})|=|\overline{R}|$
(Lemma 4.2) and
 $|\overline{R}|/|\overline{R}^{\ast }|=p^{s}$
gives the result.◻
$|\overline{R}|/|\overline{R}^{\ast }|=p^{s}$
gives the result.◻
Theorem 4.9 (Moments characterize
 $\unicode[STIX]{x1D707}_{\text{BBH}}$
).
$\unicode[STIX]{x1D707}_{\text{BBH}}$
).
Let
![]() $\unicode[STIX]{x1D708}$
be a measure on
$\unicode[STIX]{x1D708}$
be a measure on
![]() $\unicode[STIX]{x1D6FA}$
such that for every Schur
$\unicode[STIX]{x1D6FA}$
such that for every Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group
$\unicode[STIX]{x1D70E}$
-ancestor group
![]() $H$
,
$H$
,
 $$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D708}=1.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,H)|\,d\unicode[STIX]{x1D708}=1.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}_{\text{BBH}}$
.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}_{\text{BBH}}$
.
Note that Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor groups are a proper subset of finite
$\unicode[STIX]{x1D70E}$
-ancestor groups are a proper subset of finite
![]() $p$
-groups with GI-automorphisms, so this theorem does not require all of the moments determined in Theorem 4.1.
$p$
-groups with GI-automorphisms, so this theorem does not require all of the moments determined in Theorem 4.1.
Proof. By Carathéodory’s theorem, a measure
![]() $\unicode[STIX]{x1D708}$
on
$\unicode[STIX]{x1D708}$
on
![]() $\unicode[STIX]{x1D6FA}$
is determined by the measures
$\unicode[STIX]{x1D6FA}$
is determined by the measures
 $\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S\})$
for all Schur
$\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S\})$
for all Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor groups
$\unicode[STIX]{x1D70E}$
-ancestor groups
![]() $S$
. If
$S$
. If
![]() $G$
is a Schur
$G$
is a Schur
![]() $\unicode[STIX]{x1D70E}$
-group, then
$\unicode[STIX]{x1D70E}$
-group, then
![]() $Q_{c}(G)$
is either a Schur
$Q_{c}(G)$
is either a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group of
$\unicode[STIX]{x1D70E}$
-ancestor group of
![]() $p$
-class
$p$
-class
![]() $c$
or a Schur
$c$
or a Schur
![]() $\unicode[STIX]{x1D70E}$
-group of
$\unicode[STIX]{x1D70E}$
-group of
![]() $p$
-class
$p$
-class
![]() ${<}c$
. (This is because if
${<}c$
. (This is because if
![]() $Q_{c}(G)$
is
$Q_{c}(G)$
is
![]() $p$
-class
$p$
-class
![]() ${<}c$
then
${<}c$
then
 $Q_{c}(G)=G$
.) Let
$Q_{c}(G)=G$
.) Let
![]() ${\mathcal{S}}$
be the set of isomorphism classes of groups that are either a Schur
${\mathcal{S}}$
be the set of isomorphism classes of groups that are either a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group of
$\unicode[STIX]{x1D70E}$
-ancestor group of
![]() $p$
-class
$p$
-class
![]() $c$
or a Schur
$c$
or a Schur
![]() $\unicode[STIX]{x1D70E}$
-group of
$\unicode[STIX]{x1D70E}$
-group of
![]() $p$
-class
$p$
-class
![]() ${<}c$
.
${<}c$
.
For
![]() $H$
a Schur
$H$
a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor group of
$\unicode[STIX]{x1D70E}$
-ancestor group of
![]() $p$
-class
$p$
-class
![]() $c$
, we have that
$c$
, we have that
 $$\begin{eqnarray}\mathop{\sum }_{S\in {\mathcal{S}}}\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S,H)|=1\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{S\in {\mathcal{S}}}\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S,H)|=1\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathop{\sum }_{S\in {\mathcal{S}}}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S,H)|=1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{S\in {\mathcal{S}}}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S,H)|=1.\end{eqnarray}$$
We can index
![]() ${\mathcal{S}}$
by natural numbers
${\mathcal{S}}$
by natural numbers
 $S_{1},S_{2},\ldots \,$
. We then apply Lemma 4.7 with
$S_{1},S_{2},\ldots \,$
. We then apply Lemma 4.7 with
 $$\begin{eqnarray}a_{i,j}=\frac{|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\end{eqnarray}$$
$$\begin{eqnarray}a_{i,j}=\frac{|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\end{eqnarray}$$
and
 $x_{j}=\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|$
and
$x_{j}=\unicode[STIX]{x1D708}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|$
and
 $y_{j}=\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|$
, which will prove the proposition. We must verify that
$y_{j}=\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|$
, which will prove the proposition. We must verify that
 $\sum _{j}a_{i,j}<2$
.
$\sum _{j}a_{i,j}<2$
.
Using the explicit formulae for
![]() $\unicode[STIX]{x1D707}_{\text{CL}}(d)$
(from [Reference Cohen and LenstraCL84]) and for
$\unicode[STIX]{x1D707}_{\text{CL}}(d)$
(from [Reference Cohen and LenstraCL84]) and for
![]() $\unicode[STIX]{x1D707}_{\text{BBH}}$
(from Lemma 4.8), we have that
$\unicode[STIX]{x1D707}_{\text{BBH}}$
(from Lemma 4.8), we have that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D707}_{\text{CL}}(d(S_{j}))p^{d(S_{j})^{2}}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\mathop{\prod }_{k\geqslant 1}(1-p^{-k})\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})^{-2}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k\geqslant 1}(1-p^{-k})\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})^{-1}\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D707}_{\text{CL}}(d(S_{j}))p^{d(S_{j})^{2}}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\mathop{\prod }_{k\geqslant 1}(1-p^{-k})\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})^{-2}}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k\geqslant 1}(1-p^{-k})\mathop{\prod }_{k=1}^{d(S_{j})}(1-p^{-k})^{-1}\mathop{\prod }_{k=1+d(S_{j})-h_{c}(S_{j})}^{d(S_{j})}(1-p^{-k}).\nonumber\end{eqnarray}$$
When
![]() $S_{j}$
is
$S_{j}$
is
![]() $p$
-class
$p$
-class
![]() $c$
, we have that
$c$
, we have that
 $h_{c}(S_{j})=h(S_{j})$
, and since
$h_{c}(S_{j})=h(S_{j})$
, and since
![]() $S_{j}$
is a Schur
$S_{j}$
is a Schur
![]() $\unicode[STIX]{x1D70E}$
-ancestor, it is
$\unicode[STIX]{x1D70E}$
-ancestor, it is
![]() $Q_{c}(G)$
for some Schur
$Q_{c}(G)$
for some Schur
![]() $\unicode[STIX]{x1D70E}$
-group
$\unicode[STIX]{x1D70E}$
-group
![]() $G$
. Since
$G$
. Since
 $r(G)=d(G)=d(S_{j})$
, and
$r(G)=d(G)=d(S_{j})$
, and
 $r(G)\geqslant h(S_{j})$
[Reference Boston and NoverBN06, Proposition 2], we have
$r(G)\geqslant h(S_{j})$
[Reference Boston and NoverBN06, Proposition 2], we have
 $d(S_{j})\geqslant h_{c}(S_{j}).$
When
$d(S_{j})\geqslant h_{c}(S_{j}).$
When
![]() $S_{j}$
is a Schur
$S_{j}$
is a Schur
![]() $\unicode[STIX]{x1D70E}$
-group, we have that
$\unicode[STIX]{x1D70E}$
-group, we have that
 $h_{c}(S_{j})=r(S_{j})=d(S_{j})$
. In either case, we conclude that
$h_{c}(S_{j})=r(S_{j})=d(S_{j})$
. In either case, we conclude that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})\geqslant \frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k\geqslant 1}(1-p^{-k}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})\geqslant \frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\mathop{\prod }_{k\geqslant 1}(1-p^{-k}).\end{eqnarray}$$
For all
![]() $p\geqslant 3$
, we have that
$p\geqslant 3$
, we have that
 $\prod _{k\geqslant 1}(1-p^{-k})>0.53$
and so
$\prod _{k\geqslant 1}(1-p^{-k})>0.53$
and so
 $$\begin{eqnarray}\frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}<1.9\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}<1.9\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\}).\end{eqnarray}$$
Thus,
 $$\begin{eqnarray}\displaystyle \sup _{i}\mathop{\sum }_{j}a_{i,j} & = & \displaystyle \sup _{i}\mathop{\sum }_{j}\frac{|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1.9\sup _{i}\mathop{\sum }_{j}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|\leqslant 1.9.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sup _{i}\mathop{\sum }_{j}a_{i,j} & = & \displaystyle \sup _{i}\mathop{\sum }_{j}\frac{|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|}{|\!\operatorname{Aut}_{\unicode[STIX]{x1D70E}}(S_{j})|}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 1.9\sup _{i}\mathop{\sum }_{j}\unicode[STIX]{x1D707}_{\text{BBH}}(\{G\mid Q_{c}(G)\simeq S_{j}\})|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(S_{j},S_{i})|\leqslant 1.9.\Box \nonumber\end{eqnarray}$$
5 Moments as an extension counting problem
Let
![]() $Q$
be a global field with a choice of place
$Q$
be a global field with a choice of place
![]() $\infty$
. (We are mainly interested in
$\infty$
. (We are mainly interested in
![]() $Q=\mathbb{Q}$
or
$Q=\mathbb{Q}$
or
![]() $\mathbb{F}_{q}(t)$
with the usual infinite place.) We fix a separable closure
$\mathbb{F}_{q}(t)$
with the usual infinite place.) We fix a separable closure
![]() $\bar{Q}_{\infty }$
of the completion
$\bar{Q}_{\infty }$
of the completion
![]() $Q_{\infty }$
. Then, inside
$Q_{\infty }$
. Then, inside
![]() $\bar{Q}_{\infty }$
we have the separable closure
$\bar{Q}_{\infty }$
we have the separable closure
![]() $\bar{Q}$
of
$\bar{Q}$
of
![]() $Q$
. This gives a map
$Q$
. This gives a map
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(\bar{Q}/Q)$
, and in particular distinguished decomposition and inertia groups in
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(\bar{Q}/Q)$
, and in particular distinguished decomposition and inertia groups in
 $\operatorname{Gal}(\bar{Q}/Q)$
at
$\operatorname{Gal}(\bar{Q}/Q)$
at
![]() $\infty$
(as opposed to just a conjugacy classes of subgroups).
$\infty$
(as opposed to just a conjugacy classes of subgroups).
As in § 2, when
![]() $K\subset \bar{Q}$
with
$K\subset \bar{Q}$
with
![]() $K/Q$
a separable, quadratic extension, we let
$K/Q$
a separable, quadratic extension, we let
 $K^{\operatorname{un},\infty }\subset \bar{Q}$
be the maximal extension of
$K^{\operatorname{un},\infty }\subset \bar{Q}$
be the maximal extension of
![]() $K$
that is unramified everywhere and split completely at
$K$
that is unramified everywhere and split completely at
![]() $\infty$
. We let
$\infty$
. We let
 $G_{K}^{\operatorname{un},\infty }:=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
. We note that in
$G_{K}^{\operatorname{un},\infty }:=\operatorname{Gal}(K^{\operatorname{un},\infty }/K)$
. We note that in
 $\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
the inertia group at
$\operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
the inertia group at
![]() $\infty$
has order dividing
$\infty$
has order dividing
![]() $2$
by Lemma 2.2. Thus if
$2$
by Lemma 2.2. Thus if
![]() $K$
is ramified at
$K$
is ramified at
![]() $\infty$
, we have a distinguished non-trivial inertia element
$\infty$
, we have a distinguished non-trivial inertia element
 $i_{K,\infty }\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
. As noted earlier, an automorphism that has order dividing
$i_{K,\infty }\in \operatorname{Gal}(K^{\operatorname{un},\infty }/Q)$
. As noted earlier, an automorphism that has order dividing
![]() $2$
is called an involution. Conjugation by
$2$
is called an involution. Conjugation by
![]() $i_{K,\infty }$
gives an involution of
$i_{K,\infty }$
gives an involution of
![]() $G_{K}^{\operatorname{un},\infty }$
, and we let this conjugation be our chosen automorphism
$G_{K}^{\operatorname{un},\infty }$
, and we let this conjugation be our chosen automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $G_{K}^{\operatorname{un},\infty }$
. (Note this is a more specific choice than we made in § 2 under different hypotheses.)
$G_{K}^{\operatorname{un},\infty }$
. (Note this is a more specific choice than we made in § 2 under different hypotheses.)
Recall, for any finite group
![]() $H$
with an involution
$H$
with an involution
![]() $\unicode[STIX]{x1D70E}$
, we write
$\unicode[STIX]{x1D70E}$
, we write
 $\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)$
for the continuous surjections taking conjugation by
$\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)$
for the continuous surjections taking conjugation by
![]() $i_{K,\infty }$
to
$i_{K,\infty }$
to
![]() $\unicode[STIX]{x1D70E}$
. We let
$\unicode[STIX]{x1D70E}$
. We let
 $G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
, and we denote the generator of
$G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
, and we denote the generator of
![]() $C_{2}$
by
$C_{2}$
by
![]() $\unicode[STIX]{x1D70E}$
(a convenient overloading of notation). Let
$\unicode[STIX]{x1D70E}$
(a convenient overloading of notation). Let
![]() $c$
be the set of elements of
$c$
be the set of elements of
![]() $G\setminus H$
of order
$G\setminus H$
of order
![]() $2$
.
$2$
.
We define (as in [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 10.2]) a marked
![]() $(G,c)$
extension of
$(G,c)$
extension of
![]() $Q$
to be
$Q$
to be
 $(L,\unicode[STIX]{x1D70B},m)$
such that
$(L,\unicode[STIX]{x1D70B},m)$
such that
![]() $L/Q$
is a Galois extension of fields,
$L/Q$
is a Galois extension of fields,
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism
$\unicode[STIX]{x1D70B}$
is an isomorphism
 $\unicode[STIX]{x1D70B}:\operatorname{Gal}(L/Q)\simeq G$
such that all inertia groups in
$\unicode[STIX]{x1D70B}:\operatorname{Gal}(L/Q)\simeq G$
such that all inertia groups in
 $\operatorname{Gal}(L/Q)$
(except for possibly the one at
$\operatorname{Gal}(L/Q)$
(except for possibly the one at
![]() $\infty$
) have image in
$\infty$
) have image in
![]() $\{1\}\cup c$
, and
$\{1\}\cup c$
, and
![]() $m$
, the marking, is a homomorphism
$m$
, the marking, is a homomorphism
 $L_{\infty }:=L\otimes _{Q}Q_{\infty }\rightarrow \bar{Q}_{\infty }$
. Note that restriction to
$L_{\infty }:=L\otimes _{Q}Q_{\infty }\rightarrow \bar{Q}_{\infty }$
. Note that restriction to
![]() $L$
gives a bijection between homomorphisms
$L$
gives a bijection between homomorphisms
 $L_{\infty }\rightarrow \bar{Q}_{\infty }$
and homomorphisms
$L_{\infty }\rightarrow \bar{Q}_{\infty }$
and homomorphisms
![]() $L\rightarrow \bar{Q}$
. Also, note that the condition that an inertia group in
$L\rightarrow \bar{Q}$
. Also, note that the condition that an inertia group in
 $\operatorname{Gal}(L/Q)$
has image in
$\operatorname{Gal}(L/Q)$
has image in
![]() $\{1\}\cup c$
is equivalent to requiring that it has trivial intersection with
$\{1\}\cup c$
is equivalent to requiring that it has trivial intersection with
 $\unicode[STIX]{x1D70B}^{-1}(H)$
because any element in
$\unicode[STIX]{x1D70B}^{-1}(H)$
because any element in
 $G\setminus (\{1\}\cup c)$
is either in
$G\setminus (\{1\}\cup c)$
is either in
![]() $H$
or has square non-trivial in
$H$
or has square non-trivial in
![]() $H$
. Two marked
$H$
. Two marked
![]() $(G,c)$
extensions
$(G,c)$
extensions
 $(L_{1},\unicode[STIX]{x1D70B}_{1},m_{1})$
and
$(L_{1},\unicode[STIX]{x1D70B}_{1},m_{1})$
and
 $(L_{2},\unicode[STIX]{x1D70B}_{2},m_{2})$
are isomorphic when there is an isomorphism
$(L_{2},\unicode[STIX]{x1D70B}_{2},m_{2})$
are isomorphic when there is an isomorphism
 $L_{1}\rightarrow L_{2}$
taking
$L_{1}\rightarrow L_{2}$
taking
![]() $\unicode[STIX]{x1D70B}_{1}$
to
$\unicode[STIX]{x1D70B}_{1}$
to
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $m_{1}$
to
$m_{1}$
to
![]() $m_{2}$
. The marking
$m_{2}$
. The marking
![]() $m$
in a marked
$m$
in a marked
![]() $(G,c)$
extension
$(G,c)$
extension
 $(L,\unicode[STIX]{x1D70B},m)$
gives a map
$(L,\unicode[STIX]{x1D70B},m)$
gives a map
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(L/Q)$
. Composing with
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(L/Q)$
. Composing with
![]() $\unicode[STIX]{x1D70B}$
we get an infinity type
$\unicode[STIX]{x1D70B}$
we get an infinity type
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
. Such a homomorphism is called ramified if the image of inertia is non-trivial.
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
. Such a homomorphism is called ramified if the image of inertia is non-trivial.
Note that in each isomorphism class of marked
![]() $(G,c)$
extensions of
$(G,c)$
extensions of
![]() $Q$
, there is a distinguished element such that
$Q$
, there is a distinguished element such that
![]() $L\subset \bar{Q}$
and
$L\subset \bar{Q}$
and
![]() $m|_{L}$
is the inclusion map.
$m|_{L}$
is the inclusion map.
Theorem 5.1. Let
![]() $Q$
be a global field with a choice of place
$Q$
be a global field with a choice of place
![]() $\infty$
. Let
$\infty$
. Let
![]() $H$
be a finite group with involution
$H$
be a finite group with involution
![]() $\unicode[STIX]{x1D70E}$
, let
$\unicode[STIX]{x1D70E}$
, let
 $G:=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
, and let
$G:=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
, and let
![]() $c$
be the set of order-
$c$
be the set of order-
![]() $2$
elements of
$2$
elements of
![]() $G\setminus H$
. Let
$G\setminus H$
. Let
 $\unicode[STIX]{x1D719}:\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
be a ramified homomorphism with image
$\unicode[STIX]{x1D719}:\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
be a ramified homomorphism with image
![]() $\langle (1,\unicode[STIX]{x1D70E})\rangle$
. There is a bijection between
$\langle (1,\unicode[STIX]{x1D70E})\rangle$
. There is a bijection between
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{(K,f)|K\subset \bar{Q},[K:Q]\nonumber\\ \displaystyle & & \displaystyle \quad =2,K_{\infty }/Q_{\infty }~\text{the quadratic extension given by}~\ker (\unicode[STIX]{x1D719}),f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{(K,f)|K\subset \bar{Q},[K:Q]\nonumber\\ \displaystyle & & \displaystyle \quad =2,K_{\infty }/Q_{\infty }~\text{the quadratic extension given by}~\ker (\unicode[STIX]{x1D719}),f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)\}\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\{\text{isomorphism classes of marked}~(G,c)~\text{extensions}~(L,\unicode[STIX]{x1D70B},m)~\text{of}~Q~\text{with infinity type}~\unicode[STIX]{x1D719}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{\text{isomorphism classes of marked}~(G,c)~\text{extensions}~(L,\unicode[STIX]{x1D70B},m)~\text{of}~Q~\text{with infinity type}~\unicode[STIX]{x1D719}\}.\end{eqnarray}$$
In this bijection, we have
 $\operatorname{Disc}(L)=\operatorname{Disc}(K)^{|H|}$
.
$\operatorname{Disc}(L)=\operatorname{Disc}(K)^{|H|}$
.
Proof. Given a
![]() $(K,f)$
, we have that
$(K,f)$
, we have that
![]() $\ker (f)$
gives a subfield of
$\ker (f)$
gives a subfield of
 $L\subset K^{\operatorname{un},v}\subset \bar{Q}$
and we have
$L\subset K^{\operatorname{un},v}\subset \bar{Q}$
and we have
 $f:\operatorname{Gal}(L/K)\simeq H$
. We see that
$f:\operatorname{Gal}(L/K)\simeq H$
. We see that
 $\operatorname{Gal}(L/K)$
is an index
$\operatorname{Gal}(L/K)$
is an index
![]() $2$
subgroup of
$2$
subgroup of
 $\operatorname{Gal}(L/Q)$
, and
$\operatorname{Gal}(L/Q)$
, and
![]() $i_{K,\infty }$
is an order-
$i_{K,\infty }$
is an order-
![]() $2$
element of
$2$
element of
 $\operatorname{Gal}(L/Q)\setminus \operatorname{Gal}(L/K)$
. From the condition on the surjection
$\operatorname{Gal}(L/Q)\setminus \operatorname{Gal}(L/K)$
. From the condition on the surjection
![]() $f$
, we have that
$f$
, we have that
![]() $f$
takes the conjugation action of
$f$
takes the conjugation action of
![]() $i_{K,\infty }$
on
$i_{K,\infty }$
on
 $\operatorname{Gal}(L/K)$
to the involution
$\operatorname{Gal}(L/K)$
to the involution
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $H$
. Thus we can lift
$H$
. Thus we can lift
![]() $f$
to
$f$
to
 $\unicode[STIX]{x1D70B}:\operatorname{Gal}(L/Q)\simeq G$
with
$\unicode[STIX]{x1D70B}:\operatorname{Gal}(L/Q)\simeq G$
with
 $i_{K,\infty }\mapsto (1,\unicode[STIX]{x1D70E})$
. We let the marking
$i_{K,\infty }\mapsto (1,\unicode[STIX]{x1D70E})$
. We let the marking
![]() $m$
be the map
$m$
be the map
 $L_{\infty }\rightarrow \bar{Q}_{\infty }$
induced by the identity on
$L_{\infty }\rightarrow \bar{Q}_{\infty }$
induced by the identity on
 $L\subset \bar{Q}\subset \bar{Q}_{\infty }$
. Since
$L\subset \bar{Q}\subset \bar{Q}_{\infty }$
. Since
 $L\subset K^{\operatorname{un},\infty }$
, all inertia subgroups of
$L\subset K^{\operatorname{un},\infty }$
, all inertia subgroups of
 $\operatorname{Gal}(L/Q)$
have image under
$\operatorname{Gal}(L/Q)$
have image under
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $\{1\}\cup c$
. The infinity type
$\{1\}\cup c$
. The infinity type
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
factors through the map
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
factors through the map
![]() $\unicode[STIX]{x1D70B}$
. Since the index
$\unicode[STIX]{x1D70B}$
. Since the index
![]() $2$
subgroup
$2$
subgroup
 $\operatorname{Gal}(\bar{Q}_{\infty }/K_{\infty })$
has trivial image (it factors through
$\operatorname{Gal}(\bar{Q}_{\infty }/K_{\infty })$
has trivial image (it factors through
 $\operatorname{Gal}(L/K)$
, and
$\operatorname{Gal}(L/K)$
, and
![]() $L/K$
is split completely at
$L/K$
is split completely at
![]() $\infty$
), the infinity type of
$\infty$
), the infinity type of
![]() $m$
factors through the order-
$m$
factors through the order-
![]() $2$
group
$2$
group
 $\operatorname{Gal}(K_{\infty }/Q_{\infty })$
. Since, by construction of
$\operatorname{Gal}(K_{\infty }/Q_{\infty })$
. Since, by construction of
![]() $\unicode[STIX]{x1D70B}$
, the inertia group
$\unicode[STIX]{x1D70B}$
, the inertia group
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })$
has image
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })$
has image
![]() $\langle (1,\unicode[STIX]{x1D70E})\rangle$
, it follows that the infinity type is
$\langle (1,\unicode[STIX]{x1D70E})\rangle$
, it follows that the infinity type is
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(K_{\infty }/Q_{\infty })\simeq \langle (1,\unicode[STIX]{x1D70E})\rangle$
, which is
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow \operatorname{Gal}(K_{\infty }/Q_{\infty })\simeq \langle (1,\unicode[STIX]{x1D70E})\rangle$
, which is
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Given an isomorphism class of marked
![]() $(G,c)$
extensions
$(G,c)$
extensions
 $(L,\unicode[STIX]{x1D70B},m)$
of
$(L,\unicode[STIX]{x1D70B},m)$
of
![]() $Q$
with infinity type
$Q$
with infinity type
![]() $\unicode[STIX]{x1D719}$
, we take the representative for which
$\unicode[STIX]{x1D719}$
, we take the representative for which
![]() $L\subset \bar{Q}$
and
$L\subset \bar{Q}$
and
![]() $m|_{L}$
is the identity map. Then we let
$m|_{L}$
is the identity map. Then we let
![]() $K\subset \bar{Q}$
be the fixed field of
$K\subset \bar{Q}$
be the fixed field of
 $\unicode[STIX]{x1D70B}^{-1}(H)$
. From the infinity type, we see that
$\unicode[STIX]{x1D70B}^{-1}(H)$
. From the infinity type, we see that
![]() $L/K$
is split completely at
$L/K$
is split completely at
![]() $\infty$
, and that
$\infty$
, and that
![]() $K/Q$
is ramified at
$K/Q$
is ramified at
![]() $\infty$
such that
$\infty$
such that
![]() $K_{\infty }$
corresponds to
$K_{\infty }$
corresponds to
![]() $\ker (\unicode[STIX]{x1D719})$
. By the fact that
$\ker (\unicode[STIX]{x1D719})$
. By the fact that
 $(L,\unicode[STIX]{x1D70B},m)$
is a
$(L,\unicode[STIX]{x1D70B},m)$
is a
![]() $(G,c)$
extension of infinity type
$(G,c)$
extension of infinity type
![]() $\unicode[STIX]{x1D719}$
, it follows that
$\unicode[STIX]{x1D719}$
, it follows that
 $L\subset K^{\operatorname{un},\infty }$
, so we get a surjection
$L\subset K^{\operatorname{un},\infty }$
, so we get a surjection
 $f:G_{K}^{\operatorname{un},\infty }\rightarrow \operatorname{Gal}(L/K)\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }H$
. From the infinity type, we see that
$f:G_{K}^{\operatorname{un},\infty }\rightarrow \operatorname{Gal}(L/K)\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }H$
. From the infinity type, we see that
![]() $\unicode[STIX]{x1D70B}$
takes
$\unicode[STIX]{x1D70B}$
takes
 $i_{K,\infty }\mapsto (1,\unicode[STIX]{x1D70E})$
, so we get that
$i_{K,\infty }\mapsto (1,\unicode[STIX]{x1D70E})$
, so we get that
 $f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)$
.
$f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)$
.
If we start with
![]() $(K,f)$
, then by construction the fixed field of the
$(K,f)$
, then by construction the fixed field of the
 $\unicode[STIX]{x1D70B}^{-1}(H)$
from our constructed
$\unicode[STIX]{x1D70B}^{-1}(H)$
from our constructed
![]() $(L,\unicode[STIX]{x1D70B})$
is
$(L,\unicode[STIX]{x1D70B})$
is
![]() $K$
, and the restriction of
$K$
, and the restriction of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
 $\operatorname{Gal}(L/K)$
is
$\operatorname{Gal}(L/K)$
is
![]() $f$
. So if we apply both these constructions we return to the same
$f$
. So if we apply both these constructions we return to the same
![]() $(K,f)$
. On the other hand, if we start with
$(K,f)$
. On the other hand, if we start with
 $(L,\unicode[STIX]{x1D70B},m)$
(such that
$(L,\unicode[STIX]{x1D70B},m)$
(such that
![]() $m$
is the identity),
$m$
is the identity),
![]() $L$
is the fixed field of the constructed morphism
$L$
is the fixed field of the constructed morphism
![]() $f$
, and
$f$
, and
![]() $\unicode[STIX]{x1D70B}$
is determined by the constructed
$\unicode[STIX]{x1D70B}$
is determined by the constructed
![]() $f$
and the image of
$f$
and the image of
![]() $i_{K,\infty }$
, and so if we apply both these constructions we return to
$i_{K,\infty }$
, and so if we apply both these constructions we return to
 $(L,\unicode[STIX]{x1D70B},m)$
.◻
$(L,\unicode[STIX]{x1D70B},m)$
.◻
6 Applying methods of Ellenberg–Venkatesh–Westerland to the extension counting problem
Theorem 1.5 will follow from Corollary 6.5 in this section. We will prove this result using a method and many results due to Ellenberg, Venkatesh and Westerland in papers [Reference Ellenberg, Venkatesh and WesterlandEVW16, Reference Ellenberg, Venkatesh and WesterlandEVW12]. The method counts extensions of function fields by considering this as a problem of counting
![]() $\mathbb{F}_{q}$
points on a moduli space of curves with maps to
$\mathbb{F}_{q}$
points on a moduli space of curves with maps to
![]() $\mathbb{P}^{1}$
, applying the Grothendieck–Lefschetz trace formula to count these points, and using results from topology to bound the dimensions of the cohomology groups.
$\mathbb{P}^{1}$
, applying the Grothendieck–Lefschetz trace formula to count these points, and using results from topology to bound the dimensions of the cohomology groups.
6.1 Group theory computation
In this section, we will prove a lemma in group theory that will be central to proving Theorem 1.5. This lemma will count
![]() $\mathbb{F}_{q}$
-rational components in a moduli space on which we will eventually count points.
$\mathbb{F}_{q}$
-rational components in a moduli space on which we will eventually count points.
First we will define the universal marked central extension
![]() $\tilde{G}$
of a finite group
$\tilde{G}$
of a finite group
![]() $G$
for a union
$G$
for a union
![]() $c$
of conjugacy classes of
$c$
of conjugacy classes of
![]() $G$
, following [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 7]. Let
$G$
, following [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 7]. Let
![]() $C$
be a Schur cover of
$C$
be a Schur cover of
![]() $G$
so we have an exact sequence
$G$
so we have an exact sequence
 $$\begin{eqnarray}1\rightarrow H_{2}(G,\mathbb{Z})\rightarrow C\rightarrow G\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow H_{2}(G,\mathbb{Z})\rightarrow C\rightarrow G\rightarrow 1\end{eqnarray}$$
by the Schur covering map. For
 $x,y\in G$
that commute, let
$x,y\in G$
that commute, let
![]() $\hat{x}$
and
$\hat{x}$
and
![]() ${\hat{y}}$
be arbitrary lifts to
${\hat{y}}$
be arbitrary lifts to
![]() $C$
, and let
$C$
, and let
![]() $\langle x,y\rangle$
be the commutator
$\langle x,y\rangle$
be the commutator
 $[\hat{x},{\hat{y}}]\in C$
, which actually lies in
$[\hat{x},{\hat{y}}]\in C$
, which actually lies in
 $H_{2}(G,\mathbb{Z})$
since
$H_{2}(G,\mathbb{Z})$
since
![]() $x$
and
$x$
and
![]() $y$
commute. It we take the quotient of the above exact sequence by all
$y$
commute. It we take the quotient of the above exact sequence by all
![]() $\langle x,y\rangle$
for
$\langle x,y\rangle$
for
![]() $x\in c$
and
$x\in c$
and
![]() $y$
commuting with
$y$
commuting with
![]() $x$
, we obtain an exact sequence
$x$
, we obtain an exact sequence
 $$\begin{eqnarray}1\rightarrow H_{2}(G,c)\rightarrow \tilde{G}_{c}\rightarrow G\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow H_{2}(G,c)\rightarrow \tilde{G}_{c}\rightarrow G\rightarrow 1,\end{eqnarray}$$
which is still a central extension. Let
![]() $G^{\text{ab}}$
denote the abelianization of
$G^{\text{ab}}$
denote the abelianization of
![]() $H$
. The universal marked central extension is
$H$
. The universal marked central extension is
 $\tilde{G}=\tilde{G}_{c}\times _{G^{\text{ab}}}\mathbb{Z}^{c/G}$
, where
$\tilde{G}=\tilde{G}_{c}\times _{G^{\text{ab}}}\mathbb{Z}^{c/G}$
, where
![]() $c/G$
denotes the set of conjugacy classes in
$c/G$
denotes the set of conjugacy classes in
![]() $c$
and the map
$c$
and the map
 $\mathbb{Z}^{c/G}\rightarrow G^{\text{ab}}$
sends each standard generator to an element of the associated conjugacy class. We have a map
$\mathbb{Z}^{c/G}\rightarrow G^{\text{ab}}$
sends each standard generator to an element of the associated conjugacy class. We have a map
![]() $\tilde{G}\rightarrow G$
, given through projecting to the first factor. (See [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 7] for why this is called a universal marked central extension.)
$\tilde{G}\rightarrow G$
, given through projecting to the first factor. (See [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 7] for why this is called a universal marked central extension.)
Lemma 6.1. Let
![]() $H$
be an odd finite group with a GI-automorphism
$H$
be an odd finite group with a GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
, and
$\unicode[STIX]{x1D70E}$
, and
 $G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
. Let
$G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
. Let
![]() $c$
be the (single) conjugacy class of order-
$c$
be the (single) conjugacy class of order-
![]() $2$
elements. Let
$2$
elements. Let
![]() $q$
be a power of a prime and
$q$
be a power of a prime and
![]() $n$
be an odd integer. If
$n$
be an odd integer. If
 $(q,2|H|)=1$
and
$(q,2|H|)=1$
and
 $(q-1,|H|)=1$
, then for each
$(q-1,|H|)=1$
, then for each
![]() $y\in c$
, there is exactly
$y\in c$
, there is exactly
![]() $1$
element
$1$
element
![]() $x\in \tilde{G}_{c}$
such that
$x\in \tilde{G}_{c}$
such that
 $(x,n)\in \tilde{G}$
, and
$(x,n)\in \tilde{G}$
, and
![]() $x$
has image
$x$
has image
![]() $y$
in
$y$
in
![]() $G$
, and
$G$
, and
![]() $x^{q}=x$
.
$x^{q}=x$
.
Proof. We have that
 $|\tilde{G}_{c}|=2|H||H_{2}(G,c)|$
and that
$|\tilde{G}_{c}|=2|H||H_{2}(G,c)|$
and that
 $H_{2}(G,\mathbb{Z})$
is a quotient of
$H_{2}(G,\mathbb{Z})$
is a quotient of
 $H_{2}(H,\mathbb{Z})$
by [Reference Ellenberg, Venkatesh and WesterlandEVW12, Example 9.3.2]. Thus since
$H_{2}(H,\mathbb{Z})$
by [Reference Ellenberg, Venkatesh and WesterlandEVW12, Example 9.3.2]. Thus since
![]() $|H|$
is relatively prime to
$|H|$
is relatively prime to
 $2(q-1)$
, we have that
$2(q-1)$
, we have that
 $|H_{2}(G,\mathbb{Z})|$
is as well and thus
$|H_{2}(G,\mathbb{Z})|$
is as well and thus
 $|H_{2}(G,c)|$
is as well. Since
$|H_{2}(G,c)|$
is as well. Since
![]() $|\tilde{G}_{c}|/2$
is relatively prime to
$|\tilde{G}_{c}|/2$
is relatively prime to
![]() $q-1$
, we have that for
$q-1$
, we have that for
![]() $x\in \tilde{G}_{c}$
,
$x\in \tilde{G}_{c}$
,
![]() $x^{q}=x$
if and only if
$x^{q}=x$
if and only if
![]() $x^{2}=1$
.
$x^{2}=1$
.
Let
![]() $w\in \tilde{G}_{c}$
be in the inverse image of
$w\in \tilde{G}_{c}$
be in the inverse image of
![]() $y$
. Then we ask for which
$y$
. Then we ask for which
 $k\in H_{2}(G,c)$
is
$k\in H_{2}(G,c)$
is
![]() $wk$
of order
$wk$
of order
![]() $2$
. Since
$2$
. Since
 $H_{2}(G,c)\rightarrow \tilde{G}_{c}$
is central, we have
$H_{2}(G,c)\rightarrow \tilde{G}_{c}$
is central, we have
 $(wk)^{2}=w^{2}k^{2}$
, and note
$(wk)^{2}=w^{2}k^{2}$
, and note
 $w^{2}\in H_{2}(G,c)$
since
$w^{2}\in H_{2}(G,c)$
since
![]() $y^{2}=1$
. Since
$y^{2}=1$
. Since
 $H_{2}(G,c)$
is an odd abelian group, there is exactly one
$H_{2}(G,c)$
is an odd abelian group, there is exactly one
 $k\in H_{2}(G,c)$
such that
$k\in H_{2}(G,c)$
such that
 $w^{2}k^{2}=1$
. Let
$w^{2}k^{2}=1$
. Let
![]() $x=wk$
for this
$x=wk$
for this
![]() $k$
, which is the only possible
$k$
, which is the only possible
![]() $x$
satisfying the conditions of the lemma. Also, note that
$x$
satisfying the conditions of the lemma. Also, note that
 $(x,n)\in \tilde{G}$
since
$(x,n)\in \tilde{G}$
since
![]() $x$
and
$x$
and
![]() $n$
have image of the class of
$n$
have image of the class of
![]() $y$
in
$y$
in
![]() $G^{\text{ab}}$
, proving the lemma.◻
$G^{\text{ab}}$
, proving the lemma.◻
6.2 Properties of the Hurwitz scheme constructed by Ellenberg, Venkatesh and Westerland
In this theorem, we recall the Hurwitz scheme constructed by Ellenberg, Venkatesh and Westerland to study extensions of
![]() $\mathbb{F}_{q}(t)$
and its properties.
$\mathbb{F}_{q}(t)$
and its properties.
Theorem 6.2 (Ellenberg, Venkatesh and Westerland).
Let
![]() $H$
be an odd finite group with GI-automorphism
$H$
be an odd finite group with GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
 $G:=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
. Let
$G:=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
. Let
![]() $c$
be the elements of
$c$
be the elements of
![]() $G$
of order
$G$
of order
![]() $2$
. Let
$2$
. Let
![]() $\mathbb{F}_{q}$
be a finite field with
$\mathbb{F}_{q}$
be a finite field with
![]() $q$
relatively prime to
$q$
relatively prime to
![]() $|G|$
. When
$|G|$
. When
![]() $G$
is center-free, there is a Hurwitz scheme
$G$
is center-free, there is a Hurwitz scheme
 $\mathsf{CHur}_{G,n}$
over
$\mathsf{CHur}_{G,n}$
over
 $\mathbb{Z}[|G|^{-1}]$
constructed in [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 8.6.2]Footnote
1
with the following properties.
$\mathbb{Z}[|G|^{-1}]$
constructed in [Reference Ellenberg, Venkatesh and WesterlandEVW12, § 8.6.2]Footnote
1
with the following properties.
-
(i) We have
 $\mathsf{CHur}_{G,n}$
is a finite étale cover of the relatively smooth
$\mathsf{CHur}_{G,n}$
is a finite étale cover of the relatively smooth
 $n$
-dimensional configuration space
$n$
-dimensional configuration space
 $\operatorname{Conf}^{n}$
of
$\operatorname{Conf}^{n}$
of
 $n$
distinct unlabeled points in
$n$
distinct unlabeled points in
 $\mathbb{A}^{1}$
over
$\mathbb{A}^{1}$
over
 $\operatorname{Spec}\mathbb{Z}[|G|^{-1}]$
.
$\operatorname{Spec}\mathbb{Z}[|G|^{-1}]$
. -
(ii) The scheme
 $\mathsf{CHur}_{G,n}$
has an open and closed subscheme
$\mathsf{CHur}_{G,n}$
has an open and closed subscheme
 $\mathsf{CHur}_{G,n}^{c,c}$
such that there is a bijection between:
$\mathsf{CHur}_{G,n}^{c,c}$
such that there is a bijection between:-
(a) isomorphism classes of marked
 $(G,c)$
-extensions
$(G,c)$
-extensions
 $L$
of
$L$
of
 $\mathbb{F}_{q}(t)$
of
$\mathbb{F}_{q}(t)$
of
 $\operatorname{Nm}\operatorname{Disc}(L)=q^{(n+1)|H|}$
and an infinity type
$\operatorname{Nm}\operatorname{Disc}(L)=q^{(n+1)|H|}$
and an infinity type
 $\unicode[STIX]{x1D719}$
such that
$\unicode[STIX]{x1D719}$
such that
 $\unicode[STIX]{x1D719}(F_{\unicode[STIX]{x1D6E5}})=1$
and
$\unicode[STIX]{x1D719}(F_{\unicode[STIX]{x1D6E5}})=1$
and
 $\operatorname{im}\unicode[STIX]{x1D719}$
is of order
$\operatorname{im}\unicode[STIX]{x1D719}$
is of order
 $2$
and in
$2$
and in
 $c\,\cup \,\{1\}$
(where
$c\,\cup \,\{1\}$
(where
 $F_{\unicode[STIX]{x1D6E5}}$
is a lift of the Frobenius automorphism to
$F_{\unicode[STIX]{x1D6E5}}$
is a lift of the Frobenius automorphism to
 $\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })$
that acts trivially on
$\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })$
that acts trivially on
 $\mathbb{F}_{q}((t^{-1/\infty }))$
);
$\mathbb{F}_{q}((t^{-1/\infty }))$
); -
(b) points of
 $\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 10.4].
$\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 10.4].
-
-
(iii) We have
 $\mathsf{CHur}_{G,n}(\mathbb{C})$
is homotopy equivalent to a topological space
$\mathsf{CHur}_{G,n}(\mathbb{C})$
is homotopy equivalent to a topological space
 $\operatorname{CHur}_{G,n}$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 8.6.2], such that for any field
$\operatorname{CHur}_{G,n}$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 8.6.2], such that for any field
 $k$
of characteristic relatively prime to
$k$
of characteristic relatively prime to
 $|G|$
, there is a constant
$|G|$
, there is a constant
 $C$
such that for all
$C$
such that for all
 $i\geqslant 1$
and for all
$i\geqslant 1$
and for all
 $n$
we have
$n$
we have
 $\dim H^{i}(\operatorname{CHur}_{G,n},k)\leqslant C^{i}$
[Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 2.5 and Theorem 6.1].
$\dim H^{i}(\operatorname{CHur}_{G,n},k)\leqslant C^{i}$
[Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 2.5 and Theorem 6.1]. -
(iv) Given
 $G$
, for
$G$
, for
 $n$
sufficiently large and all
$n$
sufficiently large and all
 $q$
with
$q$
with
 $(q,G)=1$
, the
$(q,G)=1$
, the
 $\operatorname{Frob}$
fixed components of
$\operatorname{Frob}$
fixed components of
 $\mathsf{CHur}_{G,n}^{c,c}\otimes _{\mathbb{Z}[|G|^{-1}]}\bar{\mathbb{F}}_{q}$
are in bijection with elements
$\mathsf{CHur}_{G,n}^{c,c}\otimes _{\mathbb{Z}[|G|^{-1}]}\bar{\mathbb{F}}_{q}$
are in bijection with elements
 $(x,n)\in \tilde{G}$
such that
$(x,n)\in \tilde{G}$
such that
 $x^{q}=x$
and
$x^{q}=x$
and
 $x$
has image of order
$x$
has image of order
 $2$
in
$2$
in
 $G$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 8.7.3]. (The requirement that
$G$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 8.7.3]. (The requirement that
 $x$
has image of order
$x$
has image of order
 $2$
in
$2$
in
 $G$
ensures the monodromy at
$G$
ensures the monodromy at
 $\infty$
is in
$\infty$
is in
 $c$
.)
$c$
.)
Remark 6.3. The scheme
 $\mathsf{CHur}_{G,n}^{c,c}\subset \mathsf{CHur}_{G,n}$
comes from restricting to the parametrization of covers of
$\mathsf{CHur}_{G,n}^{c,c}\subset \mathsf{CHur}_{G,n}$
comes from restricting to the parametrization of covers of
![]() $\mathbb{P}^{1}$
all of whose local inertia groups have image in
$\mathbb{P}^{1}$
all of whose local inertia groups have image in
![]() $c\cup \{1\}$
. We use two
$c\cup \{1\}$
. We use two
![]() $c$
superscripts because [Reference Ellenberg, Venkatesh and WesterlandEVW12] uses a single
$c$
superscripts because [Reference Ellenberg, Venkatesh and WesterlandEVW12] uses a single
![]() $c$
superscript to denote when this restriction is made only over points in
$c$
superscript to denote when this restriction is made only over points in
 $\mathbb{A}^{1}\subset \mathbb{P}^{1}$
. The argument that
$\mathbb{A}^{1}\subset \mathbb{P}^{1}$
. The argument that
 $\mathsf{CHur}_{G,n}^{c,c}\subset \mathsf{CHur}_{G,n}$
is an open and closed subscheme is as in [Reference Ellenberg, Venkatesh and WesterlandEVW16, § 7.3]. Our description of the components requires a bit of translation from that in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 8.7.3]. They biject the components with
$\mathsf{CHur}_{G,n}^{c,c}\subset \mathsf{CHur}_{G,n}$
is an open and closed subscheme is as in [Reference Ellenberg, Venkatesh and WesterlandEVW16, § 7.3]. Our description of the components requires a bit of translation from that in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 8.7.3]. They biject the components with
![]() $\hat{\mathbb{Z}}^{\times }$
equivariant functions from topological generators of
$\hat{\mathbb{Z}}^{\times }$
equivariant functions from topological generators of
![]() $\varprojlim \unicode[STIX]{x1D707}_{n}$
(taken over
$\varprojlim \unicode[STIX]{x1D707}_{n}$
(taken over
![]() $n$
relatively prime to
$n$
relatively prime to
![]() $q$
) to the preimage of
$q$
) to the preimage of
![]() $c$
in
$c$
in
![]() $\tilde{G}$
that are fixed by the discrete action of
$\tilde{G}$
that are fixed by the discrete action of
![]() $\operatorname{Frob}$
. By choosing any topological generator of
$\operatorname{Frob}$
. By choosing any topological generator of
![]() $\varprojlim \unicode[STIX]{x1D707}_{n}$
, its image under a function to
$\varprojlim \unicode[STIX]{x1D707}_{n}$
, its image under a function to
![]() $\tilde{G}$
gives us a corresponding element of
$\tilde{G}$
gives us a corresponding element of
![]() $\tilde{G}$
. Using the definition of the discrete action and [Reference Ellenberg, Venkatesh and WesterlandEVW12, (9.4.1) and 9.3.2], we can see that under this correspondence
$\tilde{G}$
. Using the definition of the discrete action and [Reference Ellenberg, Venkatesh and WesterlandEVW12, (9.4.1) and 9.3.2], we can see that under this correspondence
 $(x,n)\mapsto (x^{q},n)$
describes the inverse of
$(x,n)\mapsto (x^{q},n)$
describes the inverse of
![]() $\operatorname{Frob}$
.
$\operatorname{Frob}$
.
6.3 Counting
 $\mathbb{F}_{q}$
points
$\mathbb{F}_{q}$
points
In this section, we will count the
![]() $\mathbb{F}_{q}$
points of
$\mathbb{F}_{q}$
points of
![]() $\mathsf{CHur}^{c,c}$
in Theorem 6.4, and then use our Theorem 5.1 to translate that into a result about surjections from Galois groups
$\mathsf{CHur}^{c,c}$
in Theorem 6.4, and then use our Theorem 5.1 to translate that into a result about surjections from Galois groups
![]() $G_{K}$
in Corollary 6.5, which will finally prove Theorem 1.5.
$G_{K}$
in Corollary 6.5, which will finally prove Theorem 1.5.
Theorem 6.4. Given
![]() $G$
and
$G$
and
![]() $c$
as in Theorem 6.2, we have a constant
$c$
as in Theorem 6.2, we have a constant
![]() $C$
and a constant
$C$
and a constant
![]() $n_{G}$
such that for
$n_{G}$
such that for
![]() $q>C^{2}$
, with
$q>C^{2}$
, with
 $(q,|G|)=1$
and
$(q,|G|)=1$
and
 $(q-1,|G|/2)=1$
, and odd
$(q-1,|G|/2)=1$
, and odd
![]() $n\geqslant n_{G}$
,
$n\geqslant n_{G}$
,
 $$\begin{eqnarray}|\#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})-q^{n}\cdot \#c|\leqslant \frac{q^{n}}{\sqrt{q}/C-1}.\end{eqnarray}$$
$$\begin{eqnarray}|\#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})-q^{n}\cdot \#c|\leqslant \frac{q^{n}}{\sqrt{q}/C-1}.\end{eqnarray}$$
Proof. Our theorem will follow by applying the Grothendieck–Lefschetz trace formula to
 $X:=\mathsf{CHur}_{G,n}^{c,c}\otimes _{\mathbb{Z}[|G|^{-1}]}\mathbb{F}_{q}$
. By Theorem 6.2(i), we have that
$X:=\mathsf{CHur}_{G,n}^{c,c}\otimes _{\mathbb{Z}[|G|^{-1}]}\mathbb{F}_{q}$
. By Theorem 6.2(i), we have that
![]() $X$
is smooth of dimension
$X$
is smooth of dimension
![]() $n$
. We have that
$n$
. We have that
 $\dim H_{\text{c},\acute{\text{e}}\text{t}}^{i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{2n-i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
by Poincaré duality.
$\dim H_{\text{c},\acute{\text{e}}\text{t}}^{i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{2n-i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
by Poincaré duality.
Next, we will relate
 $\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
to
$\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
to
 $\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })$
for some
$\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })$
for some
![]() $\ell >n$
. To compare étale cohomology between characteristic 0 and positive characteristic, we will use [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7]. The result [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] gives an isomorphism between étale cohomology between characteristic 0 and positive characteristic in the case of a finite cover of a complement of a reduced normal crossing divisor in a smooth proper scheme. Though [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] is only stated for étale cohomology with coefficients in
$\ell >n$
. To compare étale cohomology between characteristic 0 and positive characteristic, we will use [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7]. The result [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] gives an isomorphism between étale cohomology between characteristic 0 and positive characteristic in the case of a finite cover of a complement of a reduced normal crossing divisor in a smooth proper scheme. Though [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] is only stated for étale cohomology with coefficients in
![]() $\mathbb{Z}/\ell \mathbb{Z}$
, the argument goes through identically for coefficients in
$\mathbb{Z}/\ell \mathbb{Z}$
, the argument goes through identically for coefficients in
![]() $\mathbb{Z}/\ell ^{k}\mathbb{Z}$
, and then we can take the indirect limit and tensor with
$\mathbb{Z}/\ell ^{k}\mathbb{Z}$
, and then we can take the indirect limit and tensor with
![]() $\mathbb{Q}_{\ell }$
to obtain the result of [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] with
$\mathbb{Q}_{\ell }$
to obtain the result of [Reference Ellenberg, Venkatesh and WesterlandEVW16, Proposition 7.7] with
![]() $\mathbb{Z}/\ell \mathbb{Z}$
coefficients replaced by
$\mathbb{Z}/\ell \mathbb{Z}$
coefficients replaced by
![]() $\mathbb{Q}_{\ell }$
coefficients. So we apply this strengthened version to conclude that
$\mathbb{Q}_{\ell }$
coefficients. So we apply this strengthened version to conclude that
 $\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{j}((\mathsf{CHur}_{G,n}^{c,c})_{\mathbb{C}},\mathbb{Q}_{\ell })$
. (As in [Reference Ellenberg, Venkatesh and WesterlandEVW16, proof of Proposition 7.8], we apply comparison to
$\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{j}((\mathsf{CHur}_{G,n}^{c,c})_{\mathbb{C}},\mathbb{Q}_{\ell })$
. (As in [Reference Ellenberg, Venkatesh and WesterlandEVW16, proof of Proposition 7.8], we apply comparison to
 $\mathsf{CHur}_{G,n}^{c,c}\times _{\operatorname{Conf}^{n}}\text{PConf}_{n}$
, where
$\mathsf{CHur}_{G,n}^{c,c}\times _{\operatorname{Conf}^{n}}\text{PConf}_{n}$
, where
 $\text{PConf}_{n}$
is the moduli space of
$\text{PConf}_{n}$
is the moduli space of
![]() $n$
labeled points on
$n$
labeled points on
![]() $\mathbb{A}^{1}$
and is the complement of a relative normal crossings divisor in a smooth proper scheme [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 7.6]. Then we take
$\mathbb{A}^{1}$
and is the complement of a relative normal crossings divisor in a smooth proper scheme [Reference Ellenberg, Venkatesh and WesterlandEVW16, Lemma 7.6]. Then we take
![]() $S_{n}$
invariants to compare the étale cohomology of
$S_{n}$
invariants to compare the étale cohomology of
 $\mathsf{CHur}_{G,n}^{c,c}$
across characteristics.) By the comparison of étale and analytic cohomology [Reference Artin, Grothendieck and VerdierSGA4(3), Exposé XI, Theorem 4.4]
$\mathsf{CHur}_{G,n}^{c,c}$
across characteristics.) By the comparison of étale and analytic cohomology [Reference Artin, Grothendieck and VerdierSGA4(3), Exposé XI, Theorem 4.4]
 $\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{j}((\mathsf{CHur}_{G,n}^{c,c})_{\mathbb{C}},\mathbb{Q}_{\ell })$
.
$\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })=\dim H_{\acute{\text{e}}\text{t}}^{j}((\mathsf{CHur}_{G,n}^{c,c})_{\mathbb{C}},\mathbb{Q}_{\ell })$
.
By Theorem 6.2(iii), there is a constant
![]() $C$
such that for all
$C$
such that for all
![]() $j\geqslant 1$
and for all
$j\geqslant 1$
and for all
![]() $n$
, we have
$n$
, we have
 $\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })\leqslant C^{j}$
. Thus
$\dim H^{j}(\mathsf{CHur}_{G,n}^{c,c}(\mathbb{C}),\mathbb{Q}_{\ell })\leqslant C^{j}$
. Thus
 $\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })\leqslant C^{j}$
for all
$\dim H_{\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })\leqslant C^{j}$
for all
![]() $j\geqslant 1$
. Thus using Poincaré duality,
$j\geqslant 1$
. Thus using Poincaré duality,
 $\dim H_{\acute{\text{e}}\text{t},c}^{i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })\leqslant C^{2n-i}$
for all
$\dim H_{\acute{\text{e}}\text{t},c}^{i}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })\leqslant C^{2n-i}$
for all
![]() $i<2n$
. By Theorem 6.2(iv) and Lemma 6.1, we have that
$i<2n$
. By Theorem 6.2(iv) and Lemma 6.1, we have that
![]() $X$
has
$X$
has
![]() $\#c$
components fixed by
$\#c$
components fixed by
![]() $\operatorname{Frob}$
for odd
$\operatorname{Frob}$
for odd
![]() $n\geqslant n_{G}$
for some fixed
$n\geqslant n_{G}$
for some fixed
![]() $n_{G}$
.
$n_{G}$
.
Then by the Grothendieck–Lefschetz trace formula we have
 $$\begin{eqnarray}\#X(\mathbb{F}_{q})=\mathop{\sum }_{j\geqslant 0}(-1)^{j}\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})\end{eqnarray}$$
$$\begin{eqnarray}\#X(\mathbb{F}_{q})=\mathop{\sum }_{j\geqslant 0}(-1)^{j}\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})\end{eqnarray}$$
and also we know
 $\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{2n}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})$
is
$\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{2n}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})$
is
![]() $q^{n}$
times the number of components of
$q^{n}$
times the number of components of
![]() $X$
fixed by
$X$
fixed by
![]() $\operatorname{Frob}$
. Since
$\operatorname{Frob}$
. Since
![]() $X$
is smooth, we have that the absolute value of any eigenvalue of
$X$
is smooth, we have that the absolute value of any eigenvalue of
![]() $\operatorname{Frob}$
on
$\operatorname{Frob}$
on
 $H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
is at most
$H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })$
is at most
![]() $q^{j/2}$
. Thus, for odd
$q^{j/2}$
. Thus, for odd
![]() $n\geqslant n_{G}$
,
$n\geqslant n_{G}$
,
 $$\begin{eqnarray}\displaystyle |\#X(\mathbb{F}_{q})-q^{n}\times \#c| & = & \displaystyle \biggl|\mathop{\sum }_{0\leqslant j<2\dim X}(-1)^{j}\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{0\leqslant j<2\dim X}q^{j/2}C^{2n-j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle q^{n}\mathop{\sum }_{1\leqslant i}(\sqrt{q}/C)^{-i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\#X(\mathbb{F}_{q})-q^{n}\times \#c| & = & \displaystyle \biggl|\mathop{\sum }_{0\leqslant j<2\dim X}(-1)^{j}\operatorname{Tr}(\operatorname{Frob}\!|_{H_{\text{c},\acute{\text{e}}\text{t}}^{j}(X_{\bar{\mathbb{F}}_{q}},\mathbb{Q}_{\ell })})\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{0\leqslant j<2\dim X}q^{j/2}C^{2n-j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle q^{n}\mathop{\sum }_{1\leqslant i}(\sqrt{q}/C)^{-i}.\nonumber\end{eqnarray}$$
The theorem follows. ◻
We have
 $Q=\mathbb{F}_{q}(t)$
and
$Q=\mathbb{F}_{q}(t)$
and
 $Q_{\infty }=\mathbb{F}_{q}((t^{-1}))$
, for
$Q_{\infty }=\mathbb{F}_{q}((t^{-1}))$
, for
![]() $q$
odd. Unlike in the number field case, in which there is only one possible ramified quadratic extension of
$q$
odd. Unlike in the number field case, in which there is only one possible ramified quadratic extension of
 $\mathbb{Q}_{\infty }=\mathbb{R}$
, here there are two ramified quadratic extensions of
$\mathbb{Q}_{\infty }=\mathbb{R}$
, here there are two ramified quadratic extensions of
 $Q_{\infty }=\mathbb{F}_{q}((t^{-1}))$
. If
$Q_{\infty }=\mathbb{F}_{q}((t^{-1}))$
. If
 $K/\mathbb{F}_{q}(t)$
is a quadratic extension, we say it is imaginary quadratic of type I if
$K/\mathbb{F}_{q}(t)$
is a quadratic extension, we say it is imaginary quadratic of type I if
 $K_{\infty }\simeq \mathbb{F}_{q}((t^{-1/2}))$
and of type II if
$K_{\infty }\simeq \mathbb{F}_{q}((t^{-1/2}))$
and of type II if
 $K_{\infty }\simeq \mathbb{F}_{q}(((\unicode[STIX]{x1D6FC}t)^{-1/2}))$
for an
$K_{\infty }\simeq \mathbb{F}_{q}(((\unicode[STIX]{x1D6FC}t)^{-1/2}))$
for an
 $\unicode[STIX]{x1D6FC}\in \mathbb{F}_{q}\setminus \mathbb{F}_{q}^{2}$
. Let
$\unicode[STIX]{x1D6FC}\in \mathbb{F}_{q}\setminus \mathbb{F}_{q}^{2}$
. Let
![]() $IQ_{n}$
be the set of
$IQ_{n}$
be the set of
![]() $K\subset \bar{Q}$
such that
$K\subset \bar{Q}$
such that
![]() $K$
is imaginary quadratic of type I and
$K$
is imaginary quadratic of type I and
 $\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}$
. Let
$\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}$
. Let
![]() $IQ_{n}^{\prime }$
be the set of
$IQ_{n}^{\prime }$
be the set of
![]() $K\subset \bar{Q}$
such that
$K\subset \bar{Q}$
such that
![]() $K$
is imaginary quadratic of type II and
$K$
is imaginary quadratic of type II and
 $\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}$
.
$\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}$
.
Corollary 6.5. Let
![]() $H$
be an odd finite group with GI-automorphism
$H$
be an odd finite group with GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
such that
$\unicode[STIX]{x1D70E}$
such that
 $H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free. As
$H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free. As
![]() $q$
ranges through powers of primes such that
$q$
ranges through powers of primes such that
 $(q,2|H|)=1$
and
$(q,2|H|)=1$
and
 $(q-1,|H|)=1$
, we have
$(q-1,|H|)=1$
, we have
 $$\begin{eqnarray}\lim _{q\rightarrow \infty }\limsup _{\substack{ n\rightarrow \infty \\ n~\text{odd}}}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=1.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{q\rightarrow \infty }\limsup _{\substack{ n\rightarrow \infty \\ n~\text{odd}}}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=1.\end{eqnarray}$$
The same result holds if we replace
![]() $\limsup$
by
$\limsup$
by
![]() $\liminf$
and/or replace
$\liminf$
and/or replace
![]() $IQ_{n}$
by
$IQ_{n}$
by
![]() $IQ_{n}^{\prime }$
.
$IQ_{n}^{\prime }$
.
Theorem 1.5 then follows from Corollary 6.5 after noting that
 $H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free if and only if the center of
$H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free if and only if the center of
![]() $H$
contains no elements fixed by
$H$
contains no elements fixed by
![]() $\unicode[STIX]{x1D70E}$
except the identity.
$\unicode[STIX]{x1D70E}$
except the identity.
Proof. By Theorem 6.2(ii) the points
 $\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})$
are in bijection with isomorphism classes of marked
$\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q})$
are in bijection with isomorphism classes of marked
![]() $(G,c)$
extensions
$(G,c)$
extensions
 $(L,\unicode[STIX]{x1D70B},m)$
of
$(L,\unicode[STIX]{x1D70B},m)$
of
![]() $Q$
with certain infinity types
$Q$
with certain infinity types
![]() $\unicode[STIX]{x1D719}$
. These infinity types are all
$\unicode[STIX]{x1D719}$
. These infinity types are all
![]() $G$
-conjugate, and there are
$G$
-conjugate, and there are
![]() $\#c$
of them. Let
$\#c$
of them. Let
![]() $\unicode[STIX]{x1D719}_{0}$
be the infinity type such that
$\unicode[STIX]{x1D719}_{0}$
be the infinity type such that
 $\unicode[STIX]{x1D719}(F_{\unicode[STIX]{x1D6E5}})=1$
and
$\unicode[STIX]{x1D719}(F_{\unicode[STIX]{x1D6E5}})=1$
and
 $\operatorname{im}\unicode[STIX]{x1D719}=\langle (1,\unicode[STIX]{x1D70E})\rangle$
. Note that
$\operatorname{im}\unicode[STIX]{x1D719}=\langle (1,\unicode[STIX]{x1D70E})\rangle$
. Note that
 $\mathbb{F}_{q}((t^{-1/2}))$
is the imaginary quadratic extension given by
$\mathbb{F}_{q}((t^{-1/2}))$
is the imaginary quadratic extension given by
![]() $\ker (\unicode[STIX]{x1D719}_{0})$
.
$\ker (\unicode[STIX]{x1D719}_{0})$
.
Let
 $\unicode[STIX]{x1D719}:\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
be a ramified homomorphism with image
$\unicode[STIX]{x1D719}:\operatorname{Gal}(\bar{Q}_{\infty }/Q_{\infty })\rightarrow G$
be a ramified homomorphism with image
![]() $\langle (1,\unicode[STIX]{x1D70E})\rangle$
, let
$\langle (1,\unicode[STIX]{x1D70E})\rangle$
, let
![]() $g\in G$
, and let
$g\in G$
, and let
![]() $\unicode[STIX]{x1D719}^{g}$
denote the conjugation. Then isomorphism classes of marked
$\unicode[STIX]{x1D719}^{g}$
denote the conjugation. Then isomorphism classes of marked
![]() $(G,c)$
extensions
$(G,c)$
extensions
 $(L,\unicode[STIX]{x1D70B},m)$
of
$(L,\unicode[STIX]{x1D70B},m)$
of
![]() $Q$
with infinity type
$Q$
with infinity type
![]() $\unicode[STIX]{x1D719}$
of a given discriminant are in bijection with isomorphism classes of marked
$\unicode[STIX]{x1D719}$
of a given discriminant are in bijection with isomorphism classes of marked
![]() $(G,c)$
extensions
$(G,c)$
extensions
 $(L,\unicode[STIX]{x1D70B},m)$
of
$(L,\unicode[STIX]{x1D70B},m)$
of
![]() $Q$
with infinity type
$Q$
with infinity type
![]() $\unicode[STIX]{x1D719}^{g}$
and that discriminant by sending
$\unicode[STIX]{x1D719}^{g}$
and that discriminant by sending
 $(L,\unicode[STIX]{x1D70B},m)$
to
$(L,\unicode[STIX]{x1D70B},m)$
to
 $(L,\unicode[STIX]{x1D70B}^{g},m)$
. So, we have that
$(L,\unicode[STIX]{x1D70B}^{g},m)$
. So, we have that
 $$\begin{eqnarray}\displaystyle \#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q}) & = & \displaystyle \#c\cdot \#\{\text{isomorphism classes of marked}~(G,c)\text{-}\text{extensions}~L/\mathbb{F}_{q}(t)~\text{of infinity}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \hspace{5.0pt}\text{type}~\unicode[STIX]{x1D719}_{0}\text{ and }\operatorname{Nm}\operatorname{Disc}(L)=q^{(n+1)|H|}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q}) & = & \displaystyle \#c\cdot \#\{\text{isomorphism classes of marked}~(G,c)\text{-}\text{extensions}~L/\mathbb{F}_{q}(t)~\text{of infinity}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \hspace{5.0pt}\text{type}~\unicode[STIX]{x1D719}_{0}\text{ and }\operatorname{Nm}\operatorname{Disc}(L)=q^{(n+1)|H|}\}.\nonumber\end{eqnarray}$$
Further, by Theorem 5.1, we then conclude that
 $$\begin{eqnarray}\displaystyle \#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q}) & = & \displaystyle \#c\cdot \{(K,f)\mid K\subset \bar{Q},K~\text{imaginary quadratic type I},\nonumber\\ \displaystyle & & \displaystyle \qquad \hspace{6.00006pt}f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H),\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \#\mathsf{CHur}_{G,n}^{c,c}(\mathbb{F}_{q}) & = & \displaystyle \#c\cdot \{(K,f)\mid K\subset \bar{Q},K~\text{imaginary quadratic type I},\nonumber\\ \displaystyle & & \displaystyle \qquad \hspace{6.00006pt}f\in \operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H),\operatorname{Nm}\operatorname{Disc}(K)=q^{n+1}\}.\nonumber\end{eqnarray}$$
So by Theorem 6.4, we have a constant
![]() $C$
, only depending on
$C$
, only depending on
![]() $H$
, such that for
$H$
, such that for
 $q\geqslant 4C^{2}$
and odd
$q\geqslant 4C^{2}$
and odd
![]() $n\geqslant n_{G}$
$n\geqslant n_{G}$
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|-q^{n}\biggr|\leqslant 2Cq^{n-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|-q^{n}\biggr|\leqslant 2Cq^{n-1/2}.\end{eqnarray}$$
Thus, for
 $q\geqslant 4C^{2}$
and all odd
$q\geqslant 4C^{2}$
and all odd
![]() $n\geqslant n_{G}$
$n\geqslant n_{G}$
 $$\begin{eqnarray}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=\frac{q^{n}+O(q^{n-1/2})}{q^{n}-q^{n-1}}=1+O(q^{-1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=\frac{q^{n}+O(q^{n-1/2})}{q^{n}-q^{n-1}}=1+O(q^{-1/2}).\end{eqnarray}$$
It follows that the limit as
![]() $q\rightarrow \infty$
, of the of
$q\rightarrow \infty$
, of the of
![]() $\limsup$
or
$\limsup$
or
![]() $\liminf$
, in odd
$\liminf$
, in odd
![]() $n$
, of the lefthand side are both 1. For the case of
$n$
, of the lefthand side are both 1. For the case of
![]() $IQ_{n}^{\prime }$
, we have a bijection
$IQ_{n}^{\prime }$
, we have a bijection
 $K\mapsto K\otimes _{\mathbb{F}_{q}(t)}\mathbb{F}_{q}(t)$
(where the map
$K\mapsto K\otimes _{\mathbb{F}_{q}(t)}\mathbb{F}_{q}(t)$
(where the map
 $\mathbb{F}_{q}(t)\rightarrow \mathbb{F}_{q}(t)$
is given by
$\mathbb{F}_{q}(t)\rightarrow \mathbb{F}_{q}(t)$
is given by
![]() $t\mapsto \unicode[STIX]{x1D6FC}t$
, for some
$t\mapsto \unicode[STIX]{x1D6FC}t$
, for some
 $\unicode[STIX]{x1D6FC}\in \mathbb{F}_{q}\setminus \mathbb{F}_{q}^{2}$
) between
$\unicode[STIX]{x1D6FC}\in \mathbb{F}_{q}\setminus \mathbb{F}_{q}^{2}$
) between
![]() $IQ_{n}$
and
$IQ_{n}$
and
![]() $IQ_{n}^{\prime }$
that preserves
$IQ_{n}^{\prime }$
that preserves
![]() $G_{K}^{\operatorname{un},\infty }$
.◻
$G_{K}^{\operatorname{un},\infty }$
.◻
6.4 Further results assuming a conjecture on the homology of Hurwitz spaces
The program developed by Ellenberg, Venkatesh and Westerland in [Reference Ellenberg, Venkatesh and WesterlandEVW12] aims to prove stronger results on the topology of Hurwitz spaces, from which corresponding stronger results on the point counts would follow. For example,
![]() $\text{HS}_{\unicode[STIX]{x1D6FC}}$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 11.1] is a conjecture on the homology of Hurwitz spaces for a given group
$\text{HS}_{\unicode[STIX]{x1D6FC}}$
[Reference Ellenberg, Venkatesh and WesterlandEVW12, § 11.1] is a conjecture on the homology of Hurwitz spaces for a given group
![]() $G$
and conjugacy invariant subset
$G$
and conjugacy invariant subset
![]() $c$
.
$c$
.
Theorem 6.6. Let
![]() $H$
be an odd finite group with GI-automorphism
$H$
be an odd finite group with GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
such that
$\unicode[STIX]{x1D70E}$
such that
 $H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free. If
$H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
is center-free. If
![]() $\text{HS}_{\unicode[STIX]{x1D6FC}}$
holds for
$\text{HS}_{\unicode[STIX]{x1D6FC}}$
holds for
 $G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
and
$G=H\rtimes _{\unicode[STIX]{x1D70E}}C_{2}$
and
![]() $c$
the order-
$c$
the order-
![]() $2$
elements of
$2$
elements of
![]() $G$
, then there is a
$G$
, then there is a
![]() $q_{0}$
such that for
$q_{0}$
such that for
![]() $q\geqslant q_{0}$
, with
$q\geqslant q_{0}$
, with
 $(q,2|H|)=1$
and
$(q,2|H|)=1$
and
 $(q-1,|H|)=1$
, we have
$(q-1,|H|)=1$
, we have
 $$\begin{eqnarray}\limsup _{\substack{ n\rightarrow \infty \\ n~\text{odd}}}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=1.\end{eqnarray}$$
$$\begin{eqnarray}\limsup _{\substack{ n\rightarrow \infty \\ n~\text{odd}}}\frac{\mathop{\sum }_{K\in IQ_{n}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|}{\#IQ_{n}}=1.\end{eqnarray}$$
The same result holds if we replace
![]() $IQ_{n}$
by
$IQ_{n}$
by
![]() $IQ_{n}^{\prime }$
.
$IQ_{n}^{\prime }$
.
Proof. We apply Theorem 5.1 and [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 11.1.1]. Lemma 6.1 shows that the quantity
 $B(L_{\infty },\mathfrak{m})$
appearing in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 11.1.1] is 1. Finally, we use that an étale
$B(L_{\infty },\mathfrak{m})$
appearing in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 11.1.1] is 1. Finally, we use that an étale
![]() $G$
-extension
$G$
-extension
![]() $L_{\infty }$
has
$L_{\infty }$
has
 $|G|/|\!\operatorname{Aut}_{G}(L_{\infty })|$
corresponding infinity types and a
$|G|/|\!\operatorname{Aut}_{G}(L_{\infty })|$
corresponding infinity types and a
![]() $G$
-extension has
$G$
-extension has
![]() $|G|$
markings.◻
$|G|$
markings.◻
7 Non-equivariant moments
While in this paper, we have asked about the equivariant moments, or averages of
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|$
, one could naturally ask about non-equivariant moments, or averages of
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G_{K}^{\operatorname{un},\infty },H)|$
, one could naturally ask about non-equivariant moments, or averages of
 $|\!\operatorname{Sur}(G_{K}^{\operatorname{un},\infty },H)|$
. It turns out these non-equivariant moments reduce in a simple way to equivariant moments.
$|\!\operatorname{Sur}(G_{K}^{\operatorname{un},\infty },H)|$
. It turns out these non-equivariant moments reduce in a simple way to equivariant moments.
Let
![]() $G$
be a group with a GI-automorphism
$G$
be a group with a GI-automorphism
![]() $\unicode[STIX]{x1D70E}$
. Then we have an injection
$\unicode[STIX]{x1D70E}$
. Then we have an injection
 $$\begin{eqnarray}\displaystyle \operatorname{Sur}(G,H) & \rightarrow & \displaystyle \operatorname{Hom}_{\unicode[STIX]{x1D70E}}(G,H\times H)\nonumber\\ \displaystyle f & \mapsto & \displaystyle f\times f\unicode[STIX]{x1D70E},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sur}(G,H) & \rightarrow & \displaystyle \operatorname{Hom}_{\unicode[STIX]{x1D70E}}(G,H\times H)\nonumber\\ \displaystyle f & \mapsto & \displaystyle f\times f\unicode[STIX]{x1D70E},\nonumber\end{eqnarray}$$
where the automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $H\times H$
is switching the factors. In fact, this is a bijection onto the subset of
$H\times H$
is switching the factors. In fact, this is a bijection onto the subset of
 $\operatorname{Hom}_{\unicode[STIX]{x1D70E}}(G,H\times H)$
that surject onto the first factor. Let
$\operatorname{Hom}_{\unicode[STIX]{x1D70E}}(G,H\times H)$
that surject onto the first factor. Let
![]() ${\mathcal{F}}$
be the set of
${\mathcal{F}}$
be the set of
![]() $\unicode[STIX]{x1D70E}$
-invariant subgroups of
$\unicode[STIX]{x1D70E}$
-invariant subgroups of
![]() $H\times H$
that surject onto the first factor. Then
$H\times H$
that surject onto the first factor. Then
 $$\begin{eqnarray}|\!\operatorname{Sur}(G,H)|=\mathop{\sum }_{F\in {\mathcal{F}}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,F)|.\end{eqnarray}$$
$$\begin{eqnarray}|\!\operatorname{Sur}(G,H)|=\mathop{\sum }_{F\in {\mathcal{F}}}|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,F)|.\end{eqnarray}$$
Note since
![]() $\unicode[STIX]{x1D70E}$
is GI on
$\unicode[STIX]{x1D70E}$
is GI on
![]() $G$
, if it is not
$G$
, if it is not
![]() $GI$
on
$GI$
on
![]() $F$
, then
$F$
, then
 $|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,F)|=0$
. Thus (3) would still hold if we restrict the sum on the right to
$|\!\operatorname{Sur}_{\unicode[STIX]{x1D70E}}(G,F)|=0$
. Thus (3) would still hold if we restrict the sum on the right to
![]() $F$
such that switching factors in
$F$
such that switching factors in
![]() $H\times H$
is
$H\times H$
is
![]() $GI$
on
$GI$
on
![]() $F$
(i.e.
$F$
(i.e.
![]() $F$
generated by elements of the form
$F$
generated by elements of the form
 $(h,h^{-1})$
for
$(h,h^{-1})$
for
![]() $h\in H$
).
$h\in H$
).
Acknowledgements
The authors thank Jordan Ellenberg, Daniel Ross and Akshay Venkatesh for helpful conversations. We thank Bjorn Poonen for pointing out a mistake in an earlier version of Lemma 4.7 as well as providing a quicker proof of the lemma. The first author was supported by Simons Foundation Award MSN-179747. The second author was supported by an American Institute of Mathematics Five-Year Fellowship, a Packard Fellowship for Science and Engineering, a Sloan Research Fellowship, and National Science Foundation grants DMS-1147782 and DMS-1301690.