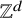MacMahon’s statistics on higher-dimensional partitions

Abstract

We study some combinatorial properties of higher-dimensional partitions which generalize plane partitions. We present a natural bijection between d-dimensional partitions and d-dimensional arrays of nonnegative integers. This bijection has a number of important applications. We introduce a statistic on d-dimensional partitions, called the corner-hook volume, whose generating function has the formula of MacMahon’s conjecture. We obtain multivariable formulas whose specializations give analogues of various formulas known for plane partitions. We also introduce higher-dimensional analogues of dual stable Grothendieck polynomials which are quasisymmetric functions and whose specializations enumerate higher-dimensional partitions of a given shape. Finally, we show probabilistic connections with a directed last passage percolation model in $\mathbb {Z}^d$.

1 Introduction

Higher-dimensional partitions are classical combinatorial objects introduced by MacMahon over a century ago. While the concept itself is a straightforward generalization of the usual (1-dimensional) integer partitions, the problems related to it are very challenging. For (2-dimensional) plane partitions, MacMahon obtained his celebrated enumerative formulas [Mac16] (cf. [Sta99, Ch. 7]). For general d-dimensional partitions, he only conjectured a formula of the volume generating function, which was later computed to be incorrect [ABMM67].

Despite long interest and many connections to various fields including algebra, combinatorics, geometry, probability and statistical physics, the subject remains rather mysterious – very little is known about d-dimensional partitions for $d \ge 3$ (e.g., according to Stanley [Sta99, Ch. 7.20], ‘almost nothing significant is known’). See [ABMM67, Knu70, Gov13] on some computational and enumerative aspects; [MR03, BGP12, DG15] on asymptotic data and connections to physics; [BBS13, Nek17, CK18] on further aspects particularly related to the theory of Donaldson–Thomas invariants. A few more remarks and some early references can also be found in [Sta71].

At the same time, the theory of plane partitions has greatly developed; see [And98, Sta99, Krat16] and many references therein. Its success mainly comes from the theory of symmetric functions, especially by using the Robinson–Schensted–Knuth (RSK) correspondence and Schur polynomials. The lack of tools for higher-dimensional generalizations makes it difficult to approach them, and here, one can try to develop analogous methods. This paper is in this direction.

Let us summarize our results.

1.1 Higher-dimensional partitions and hypermatrices

First, we present a natural bijection between d-dimensional arrays of nonnegative integers and d-dimensional partitions; see Section 3. Roughly speaking, any d-dimensional partition can be viewed as a hypermatrix of largest paths for some source weight hypermatrix. The bijection has nice properties which relate natural statistics for both objects. We then give a number of applications.

1.2 Corner-hook volume and interpretation of MacMahon’s numbers

One of the main consequences of this bijection is the multivariable generating series presented in Theorem 4.1 whose specializations allow to explicitly compute generating functions for certain statistics on d-dimensional partitions. In particular, we introduce two statistics on d-dimensional partitions: corners $\mathrm {cor}(\cdot )$ and corner-hook volume $|\cdot |_{ch}$ (see Sections 3.3 and 5 for definitions) with generating functions shown below.

Theorem 1.1 (Corner-hook generating function, cf. Corollary 5.4).

We have the following generating function:

$$ \begin{align*}\sum_{\pi} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^{\infty} {(1 - t q^n)^{-\binom{n + d - 2}{d-1}}}, \end{align*} $$

where the sum runs over d-dimensional partitions $\pi $ .

For $d = 2$ , this formula is equidistributed with Stanley’s trace generating function [Sta99, Thm. 7.20.1], but the statistics are not identical. MacMahon conjectured [Mac16] that the generating function defined as

$$ \begin{align*} \sum_{n = 0}^{\infty} m_d(n)\, q^n := \prod_{n = 1}^{\infty} {(1 - q^n)^{-\binom{n + d - 2}{d-1}}} \end{align*} $$

gives the volume generating function $\sum _{\pi } q^{|\pi |}$ for d-dimensional partitions. This was shown to be incorrect for $d \ge 3$ [ABMM67]. However, from Theorem 1.1, we obtain the following interpretation of MacMahon’s numbers $m_d(n)$ , thus showing that (instead of the volume) they count d-dimensional partitions via the corner-hook volume statistic so that

$$ \begin{align*}m_d(n) = |\{d\text{-dimensional partitions } \pi : |\pi|_{ch} = n\}|.\end{align*} $$

More generally, we also prove results for generating functions over partitions with fixed shape.

Theorem 1.2 (Corner-hook generating function with fixed shape, cf. Theorem 5.2).

Let $\rho \subset \mathbb {Z}^d_+$ be a fixed shape of a d-dimensional partition. We have the following generating function:

$$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - t q^{i_1 + \ldots + i_d - d + 1}\right)^{-1}}, \end{align*} $$

where the sum runs over d-dimensional partitions $\pi $ whose shape is contained in $\rho $ .

1.3 d-dimensional Grothendieck polynomials

To develop tools for studying d-dimensional partitions, one might be looking for analogues of Schur polynomials whose specializations allow to enumerate them. We work in a slightly different direction. In Section 6, we define higher-dimensional analogues of dual stable Grothendieck polynomials. These new functions are indexed by shapes of d-dimensional partitions, and in specializations they compute the number of such partitions. For $d = 2$ , they turn into the dual stable Grothendieck polynomials (indexed by partitions) known as K-theoretic analogues of Schur polynomials introduced in [LP07] (see also [Yel17, Yel19] for more on these functions).

Let us illustrate our results in the special case for (3-dimensional) solid partitions. We define the polynomials (see Equation (8)) $g_{\pi }(\mathbf {x}; \mathbf {y}; \mathbf {z})$ in three sets of variables indexed by plane partitions $\{\pi \}$ . These polynomials enumerate solid partitions within a given shape. For example, we have

$$ \begin{align*}g_{[b] \times [c] \times [d]}(1^{a+1}; 1^{b}; 1^c) = \text{number of solid partitions inside the box }[a] \times [b] \times [c] \times [d]. \end{align*} $$

We show that the following generating series identity holds.

Theorem 1.3 (Cauchy–Littlewood-type identity for 3d Grothendieck polynomials, cf. Corollary 6.5).

We have

$$ \begin{align*}\sum_{\pi} g_{\pi}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{a} \prod_{j = 1}^{b} \prod_{k = 1}^{c} \frac{1}{1 - x_i y_j z_k}, \end{align*} $$

where the sum runs over plane partitions $\pi $ with shape inside the rectangle $b \times c$ and $\mathbf {x} = (x_1,\ldots , x_a), \mathbf {y} = (y_1,\ldots , y_b), \mathbf {z} = (z_1,\ldots , z_c).$

It is known that dual stable Grothendieck polynomials (for $d = 2$ ) are symmetric (in $\mathbf {x}$ ). As we show, this is no longer the case for $d \ge 3$ . However, we prove that these new functions are quasisymmetric (cf. Proposition 6.9), the next known class containing symmetric functions (see, for example, [Sta99, Ch. 7.19]).

1.4 Last passage percolation in $\mathbb {Z}^{d}$

It turns out that these problems are closely related to the directed last passage percolation model with geometric weights in $\mathbb {Z}^d$ (see [Mar06] for a survey on this probabilistic model). We prove that d-dimensional Grothendieck polynomials naturally compute distribution formulas for this model (see Theorem 7.1). See Section 7 for details.

2 Preliminary definitions

We use the following basic notation: $\mathbb {N}$ is the set of nonnegative integers; $\mathbb {Z}_+$ is the set of positive integers; $\{\mathbf {e}_1, \ldots , \mathbf {e}_d\}$ is the standard basis of $\mathbb {Z}^d$ ; and $[n] := \{1, \ldots , n \}$ .

A d-dimensional $\mathbb {N}$ -hypermatrix is an array $\left (a_{i_1, \ldots , i_d}\right )_{i_1, \ldots , i_d \ge 1}$ of nonnegative integers with only finitely many nonzero elements. A d-dimensional partition is a d-dimensional $\mathbb {N}$ -hypermatrix $\left (\pi _{i_1, \ldots , i_d} \right )$ such that

$$ \begin{align*}\pi_{i_1, \ldots, i_d} \ge \pi_{j_1, \ldots, j_d} ~\text{ for }~ i_1 \le j_1, \ldots, i_d \le j_d. \end{align*} $$

Let $\mathcal {M}^{(d)}$ be the set of d-dimensional $\mathbb {N}$ -hypermatrices and $\mathcal {P}^{(d)}$ be the set of d-dimensional partitions. For $\pi = (\pi _{i_1, \ldots , i_d}) \in \mathcal {P}^{(d)}$ , the volume (or size) of $\pi $ denoted by $|\pi |$ is defined as

$$ \begin{align*}|\pi| = \sum_{i_1, \ldots, i_d} \pi_{i_1, \ldots, i_d}. \end{align*} $$

Any partition $\pi $ is uniquely determined by its diagram $D(\pi )$ which is the set

$$ \begin{align*}D(\pi) := \{(i_1, \ldots, i_d, i) \in \mathbb{Z}^{d+1}_+: 1 \le i \le \pi_{i_1, \ldots, i_d} \}. \end{align*} $$

The shape of $\pi $ denoted by $\mathrm {sh}(\pi )$ is the set

$$ \begin{align*}\mathrm{sh}(\pi) := \{(i_1, \ldots, i_d) \in \mathbb{Z}^d_+ : \pi_{i_1, \ldots, i_d}> 0\}.\end{align*} $$

Note that $\mathrm {sh}(\pi )$ is a diagram of some $(d-1)$ -dimensional partition. Let

$$ \begin{align*}\mathcal{M}(n_1,\ldots, n_d) = \{ (a_{\mathbf{i}})_{} : a_{\mathbf{i}} \in \mathbb{N}, \mathbf{i} \in [n_1] \times \cdots \times [n_d] \}\end{align*} $$

be the set of $[n_1] \times \cdots \times [n_d]\ \mathbb {N}$ -hypermatrices and

$$ \begin{align*}\mathcal{P}(n_1,\ldots, n_{d+1}) := \{ \pi \in \mathcal{P}^{(d)} : D(\pi) \subseteq [n_1] \times \cdots \times [n_{d+1}]\}\end{align*} $$

be the set of boxed d-dimensional partitions.

For $d = 2,3$ , partitions are called plane partitions and solid partitions. ¹

Let us note that for a set $\rho \subset \mathbb {Z}^d_+$ , the following three conditions are equivalent:

1. (1) The set $\rho $ is the shape of some d-dimensional partition.

2. (2) The set $\rho $ is the diagram of some $(d-1)$ -dimensional partition.

3. (3) The set $\rho $ is finite and has the property that if $\mathbf {i} \in \mathbb {Z}^d_+$ and $\ell \in [d]$ satisfy $\mathbf {i} + \mathbf {e}_{\ell } \in \rho $ , then $\mathbf {i} \in \rho $ .

Sometimes we will identify a partition with its diagram (but never with its shape).

3 A bijection between d-dimensional $\mathbb {N}$ -hypermatrices and partitions

3.1 Last passage hypermatrix

A lattice path in $\mathbb {Z}^d$ is called directed if it uses only steps of the form $\mathbf {i} \to \mathbf {i} + \mathbf {e}_\ell $ for $\mathbf {i} \in \mathbb {Z}^d$ and $\ell \in [d]$ . Given a d-dimensional $\mathbb {N}$ -hypermatrix $A = (a_{i_1, \ldots , i_d})$ , define the last passage times ²

$$ \begin{align*} G_{i_1, \ldots, i_d} := \max_{\Pi\, :\, (i_1, \ldots, i_d) \to (\infty,\ldots,\infty)} \sum_{(j_1, \ldots, j_d) \in \Pi} a_{j_1, \ldots, j_d}, \end{align*} $$

where the maximum is over directed lattice paths $\Pi $ which start at $(i_1, \ldots , i_d) \in \mathbb {Z}^d_+$ . It is easy to see that the following recurrence relation holds:

(1) $$ \begin{align} G_{\mathbf{i}} = a_{\mathbf{i}} + \max_{\ell \in [d]} G_{\mathbf{i} + \mathbf{e}_\ell}, \quad \mathbf{i} \in \mathbb{Z}^d_+. \end{align} $$

Notice that the hypermatrix $G = (G_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+} \in \mathcal {P}^{(d)}$ is a d-dimensional partition.

3.2 The bijection

Define the map $\Phi : \mathcal {M}^{(d)} \to \mathcal {P}^{(d)}$ as follows:

(2) $$ \begin{align} \Phi : A \longmapsto G \end{align} $$

Let $\rho \subset \mathbb {Z}^d_+$ be a shape of some d-dimensional partition (or a diagram of a $(d-1)$ -dimensional partition). Let

$$ \begin{align*} \mathcal{P}(\rho, n) := \left \{ \pi \in \mathcal{P}^{(d)} : \mathrm{sh}(\pi) \subseteq \rho,\, \pi_{1, \ldots, 1} \le n \right \} \end{align*} $$

be the set of d-dimensional partitions whose shape is a subset of $\rho $ and the largest entry is at most n. Let

$$ \begin{align*} \mathcal{M}(\rho, n) := \left \{A = (a_{\mathbf{i}}) \in \mathcal{M}^{(d)} : a_{\mathbf{i}}> 0 \implies \mathbf{i} \in \rho,\, G_{1,\ldots, 1} \le n \right \} \end{align*} $$

be the set of d-dimensional $\mathbb {N}$ -hypermatrices whose support (i.e., the set of indices corresponding to positive entries) lies inside $\rho $ and whose largest last passage time is at most n.

Theorem 3.1. The map $\Phi $ defines a bijection between the sets $\mathcal {M}(\rho , n)$ and $\mathcal {P}(\rho , n)$ .

Proof. Let $A = (a_{\mathbf {i}}) \in \mathcal {M}(\rho , n)$ . By construction of the map, it is not difficult to see that $\pi = \Phi (A) \in \mathcal {P}(\rho , n)$ . Indeed, we have the largest last passage time $\pi _{1,\ldots , 1} \le n$ , and $\mathrm {sh}(\pi ) \subseteq \rho $ since if $a_{\mathbf {i}}> 0$ , then $\mathbf {i} \in \rho $ .

Conversely, given $\pi \in \mathcal {P}(\rho , n)$ , to reconstruct the inverse map $\Phi ^{-1}$ , using the recurrence (1) we define the hypermatrix $A = (a_{\mathbf {i}})$ given by

(3) $$ \begin{align} a_{\mathbf{i}} = \pi_{\mathbf{i}} - \max_{\ell \in [d]} \pi_{\mathbf{i} + \mathbf{e}_\ell} \ge 0, \quad \mathbf{i} \in \mathbb{Z}^d_+. \end{align} $$

Let $G = (G_{\mathbf {i}}) = \Phi (A)$ . Let us check that $G = \pi $ and $A \in \mathcal {M}(\rho , n)$ . Since $\mathrm {sh}(\pi ) \subseteq \rho $ , we have $a_{\mathbf {i}} = 0$ for all $\mathbf {i} \not \in \rho $ (in particular, $A \in \mathcal {M}(\rho , \infty )$ ). Hence, $G_{\mathbf {i}} = \pi _{\mathbf {i}} = 0$ for all $\mathbf {i} \not \in \rho $ . Consider the directed graph $\Gamma $ on the vertex set $\rho $ and edges $\mathbf {i} \to \mathbf {i} + \mathbf {e}_{\ell }$ (when $\mathbf {i} + \mathbf {e}_{\ell } \in \rho $ ) for $\ell \in [d]$ . Then $\Gamma $ is acyclic (i.e., has no directed cycles). Notice that $a_{\mathbf {i}} = \pi _{\mathbf {i}} = G_{\mathbf {i}}$ if a vertex $\mathbf {i} \in \Gamma $ has no outgoing edges. Since $\Gamma $ is acyclic, we can sort its vertices in linear order $(\mathbf {i}^{(1)}, \ldots , \mathbf {i}^{(m)})$ so that the edges go only in one direction $\mathbf {i}^{(\ell )} \to \mathbf {i}^{(k)}$ for $\ell < k$ . We already noticed that $\pi _{\mathbf {i}^{(m)}} = G_{\mathbf {i}^{(m)}}$ . Then inductively on $\ell = m-1,\ldots , 1$ , we have

$$ \begin{align*}\pi_{\mathbf{i}^{(\ell)}} = a_{\mathbf{i}^{(\ell)}} + \max_{\mathbf{i}^{(\ell)} \to \mathbf{i}^{(k)}} \pi_{\mathbf{i}^{(k)}} = a_{\mathbf{i}^{(\ell)}} + \max_{\mathbf{i}^{(\ell)} \to \mathbf{i}^{(k)}} G_{\mathbf{i}^{(k)}} = G_{\mathbf{i}^{(\ell)}}. \end{align*} $$

Therefore, $\pi = G$ . In particular, $G_{1,\ldots , 1} \le n$ and hence, $A \in \mathcal {M}(\rho , n)$ .

Corollary 3.2. The map $\Phi $ defines a bijection between each of the following pairs of sets:

1. (i) $\mathcal {M}([n_1]\times \cdots \times [n_d], n_{d+1})$ and $\mathcal {P}(n_1,\ldots , n_{d+1})$

2. (ii) $\mathcal {M}(n_1, \ldots , n_d)$ and $\mathcal {P}(n_1,\ldots , n_{d}, \infty )$

3. (iii) $\mathcal {M}(\rho , \infty )$ and $\mathcal {P}(\rho , \infty )$

4. (iv) $\mathcal {M}^{(d)}$ and $\mathcal {P}^{(d)}$ .

Remark 1. The item (i) above states that the number of boxed d-dimensional partitions with diagrams inside the box $[n_1] \times \cdots \times [n_{d+1}]$ is equal to the number of $[n_1]\times \cdots \times [n_d]\ \mathbb {N}$ -hypermatrices whose largest last passage time is at most $n_{d+1}$ .

Remark 2. The map $\Phi ^{-1}$ is essentially Stanley’s ‘transfer map’ between order and chain poset polytopes [Sta86a], specific to d-dimensional partitions. For $d = 2$ , the map $\Phi $ gives a bijection between $\mathbb {N}$ -hypermatrices and plane partitions. This bijection is essentially equivalent (up to diagram rotations) to the one studied in [Yel21a, Yel21b]. Note that one can construct d-dimensional partitions G dynamically using an insertion type procedure as in RSK, similarly as in [Yel21a, Yel21b] for $d = 2$ ; we plan to address this in more detail in [AY23+]. Note also that similar largest path (last passage time) properties hold for RSK as well; see [Pak01, Sag01].

3.3 Corners and the inverse map $\Phi ^{-1}$

Now we are going to describe the inverse map $\Phi ^{-1}$ more concretely using a structure of d-dimensional partitions.

Given a partition $\pi \in \mathcal {P}^{(d)}$ , define the set of corners as follows:

$$ \begin{align*}\mathrm{Cor}(\pi) := \left\{\mathbf{i} \in \mathbb{Z}^{d+1}_+ : \mathbf{i} \in D(\pi),\, \mathbf{i} + \mathbf{e}_{\ell} \not\in D(\pi) \text{ for all } \ell \in [d] \right\} \subseteq D(\pi). \end{align*} $$

(Here $\{\mathbf {e}_{\ell }\}$ is the standard basis in $\mathbb {Z}^{d+1}$ .) Let $\mathrm {cor}(\pi ) := |\mathrm {Cor}(\pi )|$ be the number of corners of $\pi $ . Define also the set of top corners as follows:

$$ \begin{align*}\mathrm{Cr}(\pi) := \left\{\mathbf{i} \in \mathbb{Z}^{d+1}_+ : \mathbf{i} \in D(\pi),\, \mathbf{i} + \mathbf{e}_{\ell} \not\in D(\pi) \text{ for all } \ell \in [d + 1] \right \}\, \subseteq\, \mathrm{Cor}(\pi). \end{align*} $$

Let $\mathrm {cr}(\pi ) := |\mathrm {Cr}(\pi )|$ be the number of top corners of $\pi $ . More intuitively, a top corner (resp. corner) of $\pi $ is an element removable from the diagram of (resp. the shape of) $\pi $ . Note that the set of top corners $\mathrm {Cr}(\pi )$ uniquely determines the partition $\pi $ .

Example 3.3. Let $d = 2$ and $\pi $ be the plane partition given in Figure 1. We then have

$$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}\\ \mathrm{Cr}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k),(i,j,k+1) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,2), (2,2,3)\}, \end{align*} $$

where corners in Figure 1 correspond to local configurations and top corners correspond to the configurations .

Figure 1 A plane partition $\pi \in \mathcal {P}^{(2)}$ whose $\mathrm {sh}(\pi )$ is the diagram of the partition $(3,2)$ ; its boxed diagram presentation as a pile of cubes in $\mathbb {R}^3$ ; and boxes of this diagram which correspond to corners.

Consider the corner projection map $\varphi : \mathcal {P}^{(d)} \to \mathcal {M}^{(d)}$ given by $\pi \mapsto (a_{\mathbf {i}})$ , where

$$ \begin{align*} a_{\mathbf{i}} = |\{i_{d+1} : (\mathbf{i}, i_{d+1}) \in \mathrm{Cor}(\pi) \}|, \quad \mathbf{i} \in \mathbb{Z}^{d}_+. \end{align*} $$

Lemma 3.4. We have: $\varphi = \Phi ^{-1}$ .

Proof. The key observation is that $(\mathbf {i}, i_{d+1}) \in \mathrm {Cor}(\pi )$ if and only if $\pi _{\mathbf {i}} \ge i_{d+1}> \pi _{\mathbf {i} + \mathbf {e}_\ell }$ for all $\ell \in [d]$ . Hence,

$$ \begin{align*}a_{\mathbf{i}} = |\{i_{d+1} : (\mathbf{i}, i_{d+1}) \in \mathrm{Cor}(\pi) \}| = \pi_{\mathbf{i}} - \max_{\ell \in [d]} \pi_{\mathbf{i} + \mathbf{e}_{\ell}}, \quad \mathbf{i} \in \mathbb{Z}^{d}_+, \end{align*} $$

which gives $\Phi ^{-1} : \pi \mapsto (a_{\mathbf {i}})$ .

We will also use the following properties relating shapes of partitions and top corners.

Lemma 3.5. Let $\rho \subset \mathbb {Z}^d_+$ be a shape of a d-dimensional partition, $A = (a_{\mathbf {i}}) \in \mathcal {M}^{}(\rho , \infty )$ and $\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{}(\rho ,\infty )$ . The following are equivalent:

1. (a) $a_{\mathbf {i}}> 0$ for all $(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$

2. (b) $\mathrm {sh}(\pi ) = \rho $ .

Proof. Let $(\mathbf {i},\cdot ) \in \mathrm {Cr}(\rho )$ . Assume (a) holds. Since $A \in \mathcal {M}^{}(\rho , \infty )$ , we have $a_{\mathbf {i} + \mathbf {e}_{\ell }} = 0$ for all $\ell \in [d]$ . Therefore, $\pi _{\mathbf {i}} = a_{\mathbf {i}}> 0$ and $\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$ . Hence, $\mathrm {sh}(\pi ) = \rho $ .

Assume (b) holds. Then we have $\pi _{\mathbf {i} + \mathbf {e}_{\ell }} = 0$ for all $\ell \in [d]$ . Therefore, $a_{\mathbf {i}} = \pi _{\mathbf {i}}> 0$ .

4 Multivariate identities

4.1 Main formulas

Let $(x_{i_1,\ldots , i_d})$ be indeterminate variables.

Theorem 4.1. Let $\rho \subset \mathbb {Z}^d_+$ be a fixed shape of a d-dimensional partition. We have the following multivariate generating function identities:

(4) $$ \begin{align} \sum_{{\pi \in \mathcal{P}^{(d)}, \atop \, \mathrm{sh}(\pi) \subseteq \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}} ,\qquad\qquad\qquad\ \ \qquad \end{align} $$

(5) $$ \begin{align} \sum_{ {\pi \in \mathcal{P}^{(d)},\atop \, \mathrm{sh}(\pi) = \rho} }\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots, i_d) \in \rho} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}, \end{align} $$

where $\mathrm {Cr}(\rho ) := \mathrm {Cr}(\text {the partition whose diagram is } \rho )$ .

It is convenient to define weights of hypermatrices and partitions as follows. Given a hypermatrix $A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{(d)}$ , we associate to it a multivariable monomial weight

$$ \begin{align*}w_A := \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}}.\end{align*} $$

Given a partition $\pi \in \mathcal {P}^{(d)}$ , we associate to it a multivariable monomial weight

$$ \begin{align*}w(\pi) := \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d}. \end{align*} $$

The following lemma shows that the bijection $\Phi $ is weight-preserving.

Lemma 4.2. Let $A = (a_{\mathbf {i}}) \in \mathcal {M}^{(d)}$ and $\pi = (\pi _{\mathbf {i}}) = \Phi (A) \in \mathcal {P}^{(d)}$ . Then $w_A = w(\pi )$ .

Proof. Using the corner projection map $\varphi = \Phi ^{-1}$ , by Lemma 3.4, we have

$$ \begin{align*} w_A &= \prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &=\prod_{(i_1,\ldots,i_d) \in \mathbb{Z}^d_+} \left(x_{i_1,\ldots, i_d} \right)^{|\{i_{d+1} : (i_1,\ldots,i_d, i_{d+1}) \in \mathrm{Cor}(\pi) \}|} \\ &=\prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \\ &= w(\pi), \end{align*} $$

which gives what is needed.

Proof of Theorem 4.1.

First, note that

$$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots,i_d) \in \rho} \left( x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$

On the other hand, using Corollary 3.2 (iii) and Lemma 4.2, we have

$$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty)} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$

and hence the identity (4) follows.

Let $\overline {\mathcal {M}}(\rho , \infty ) = \{A \in \mathcal {M}(\rho , \infty ) : \mathbf {i} \in \mathrm {Cr}(\rho ) \implies a_{\mathbf {i}}> 0\}$ . Similarly, note that

$$ \begin{align*} \sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A &= \sum_{A = (a_{\mathbf{i}}) \in \mathcal{M}(\rho, \infty)} \, \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(x_{i_1,\ldots, i_d} \right)^{a_{i_1,\ldots,i_d}} \\ &= \prod_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} x_{i_1,\ldots, i_d} \prod_{(i_1,\ldots,i_d) \in \rho} \left(1 - x_{i_1,\ldots, i_d} \right)^{-1}. \end{align*} $$

On the other hand, using Lemma 3.5 we have

$$ \begin{align*}\sum_{A = (a_{\mathbf{i}}) \in \overline{\mathcal{M}}(\rho, \infty)} w_A = \sum_{\pi \in \mathcal{P}(\rho, \infty), \mathrm{sh}(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} \, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} \end{align*} $$

and hence, the identity (5) follows.

4.2 Some special cases

Let us list a few immediate special cases of the above formulas.

Corollary 4.3 (Boxed case).

For any $n_1,\ldots , n_d \ge 0$ , we have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots,n_d, \infty)}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x_{i_1,\ldots, i_d} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left(1 - x_{i_1,\ldots, i_d} \right)^{-1}}. \end{align*} $$

Corollary 4.4 (Solid partitions, $d = 3$ ).

Let $\rho $ be a plane partition. We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)}\, \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x^{}_{i j k} &= \prod_{(i,j,k) \in D(\rho)} {\left(1 - x^{}_{i j k} \right)^{-1}} \prod_{(i, j, k) \in \mathrm{Cr}(\rho)} x^{}_{i j k}. \end{align*} $$

For $d = 2$ we obtain the following new identity for plane partitions.

Corollary 4.5 (Plane partitions, $d = 2$ ).

Let $\lambda $ be a partition. We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}}\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi)= D(\lambda)}\, \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x^{}_{i j} &= \prod_{(i,j) \in D(\lambda)} {\left(1 - x^{}_{i j} \right)^{-1}} \prod_{(i, j) \in \mathrm{Cr}(\lambda)} x^{}_{i j}. \end{align*} $$

Remark 3. For $d = 2$ , the formula in the special rectangular case (with $x_{ij} = x_{i} y_j$ up to rotation of diagrams of plane partitions) was proved in [Yel21b].

5 MacMahon’s numbers and statistics

5.1 Corner-hook volume

Let $\pi \in \mathcal {P}^{(d)}$ be a d-dimensional partition. For each point $(i_1,\ldots ,i_d)$ , define the cohook length

$$ \begin{align*}\mathrm{ch}(i_1,\ldots,i_d) := i_1 + \ldots + i_d - d + 1. \end{align*} $$

Define now the corner-hook volume statistic $|\cdot |_{ch} : \mathcal {P}^{(d)} \to \mathbb {N}$ , computed as follows:

$$ \begin{align*}|\pi|_{ch} := \sum_{(\mathbf{i}, i_{d+1})\, \in\, \mathrm{Cor}(\pi)} \mathrm{ch}(\mathbf{i}). \end{align*} $$

Example 5.1. Let $d = 2$ and $\pi $ be the plane partition given in Figure 1. Recall that

$$ \begin{align*} \mathrm{Cor}(\pi) &= \{(i,j,k) \in D(\pi) : (i+1,j,k), (i,j+1,k) \not\in D(\pi) \} \\ &= \{(1,1,4), (1,3,1), (1,3,2), (2,2,1), (2,2,2), (2,2,3) \}, \end{align*} $$

and hence, we have

$$ \begin{align*}|\pi|_{ch} = (1 + 1 - 1) + (1 + 3 - 1) + (1 + 3 - 1) + (2 + 2 - 1) + (2 + 2 - 1) + (2 + 2 - 1) = 16. \end{align*} $$

Theorem 5.2. Let $\rho \subset \mathbb {Z}^d_+$ be a fixed shape of a d-dimensional partition. We have the following generating functions:

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i_1,\ldots,i_d) \in \rho} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}, \end{align*} $$

where

$$ \begin{align*}|\rho|_{cr} := \sum_{(i_1,\ldots, i_d) \in \mathrm{Cr}(\rho)} \mathrm{ch}(i_1,\ldots,i_d). \end{align*} $$

Proof. In Theorem 4.1 set $x_{i_1,\ldots , i_d} = t q^{i_1 + \ldots + i_d - d + 1}$ .

Corollary 5.3 (Boxed version).

We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_d, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} {\left( 1 - t q^{i_1 + \cdots + i_d - d + 1} \right)^{-1}}. \end{align*} $$

Corollary 5.4 (Full generating function).

We have

$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$

Corollary 5.5 (Interpretation of MacMahon’s numbers).

We have

$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_{ch}} = \prod_{n \ge 1} (1 - q^{n})^{-\binom{n + d - 2}{d - 1}} = \sum_{n = 0}^{\infty} m_d(n) q^n, \end{align*} $$

and hence,

$$ \begin{align*}m_d(n) = |\{ \pi \in \mathcal{P}^{(d)} : |\pi|_{ch} = n \}|\end{align*} $$

(i.e., $m_d(n)$ is the number of d-dimensional partitions whose corner-hook volume is n).

Corollary 5.6 (Pyramid partitions).

Let $\Delta _d({m})$ be a d-dimensional partition whose diagram is $D(\Delta _{d}({m})) = \{(i_1,\ldots , i_{d+1}) : \mathbb {Z}^{d+1}_+ : i_1 + \cdots + i_{d+1} - d \le m\}$ . We have

$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{}(D(\Delta_{d-1}({m})), \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \prod_{n = 1}^m (1 - t q^{n})^{-\binom{n + d - 2}{d - 1}}. \end{align*} $$

Corollary 5.7 ( $q = 1$ specialization).

We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) \subseteq \rho} t^{\mathrm{cor}(\pi)} &= {\left( 1 - t \right)^{-|\rho|}},\\ \sum_{\pi \in \mathcal{P}^{(d)},\, \mathrm{sh}(\pi) = \rho} t^{\mathrm{cor}(\pi)} &= t^{\mathrm{cr}(\rho)} {\left( 1 - t \right)^{-|\rho|}}. \end{align*} $$

Then the number of $\pi \in \mathcal {P}^{(d)}$ of shape $\rho $ with k corners is equal to $\binom {k - \mathrm {cr}(\rho ) + |\rho | - 1}{|\rho | - 1}$ .

5.2 Solid partitions, $d = 3$

Let us restate some of these results for solid partitions. Let $\pi \in \mathcal {P}^{(3)}$ be a solid partition. We then have

$$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k,\ell)\in \mathrm{Cor}(\pi)} (i + j + k - 2). \end{align*} $$

Corollary 5.8. Let $\rho $ be a fixed plane partition. We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) \subseteq D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(3)},\, \mathrm{sh}(\pi) = D(\rho)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\rho)} q^{|\rho|_{cr}} \prod_{(i, j, k) \in D(\rho)} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}, \end{align*} $$

and, in particular, the boxed version

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, n_3, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} {\left( 1 - t q^{i + j + k - 2} \right)^{-1}}. \end{align*} $$

5.3 Plane partitions, $d = 2$

Similarly, let us restate some of these results for plane partitions. Let $\pi \in \mathcal {P}^{(2)}$ be a plane partition. We then have

$$ \begin{align*}|\pi|_{ch} = \sum_{(i,j,k)\in \mathrm{Cor}(\pi)} (i + j - 1). \end{align*} $$

Corollary 5.9. Let $\lambda $ be a fixed partition. We have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) \subseteq D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}},\\ \sum_{\pi \in \mathcal{P}^{(2)},\, \mathrm{sh}(\pi) = D(\lambda)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= t^{\mathrm{cr}(\lambda)} q^{|\lambda|_{cr}} \prod_{(i, j) \in D(\lambda)} {\left( 1 - t q^{i + j - 1} \right)^{-1}}, \end{align*} $$

and, in particular, the boxed version

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} &= \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}}. \end{align*} $$

Let us compare the last boxed formula with known results. The following trace generating function is known for plane partitions (see, for example, [Sta99, Thm 7.20.1]):

$$ \begin{align*}\prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} {\left( 1 - t q^{i + j - 1} \right)^{-1}} = \sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{tr}(\pi)} q^{|\pi|}, \end{align*} $$

where $\mathrm {tr}(\pi ) := \sum _{i} \pi _{i,i}$ is the trace of a plane partition. Therefore, in this case, we actually have the following equidistribution result.

Theorem 5.10 (Equidistribution of (tr, vol) and (cor, ch-vol) for plane partitions).

We have

$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{}(n_1,n_2, \infty)} t^{\mathrm{cor}(\pi)} q^{|\pi|_{ch}} = \sum_{\pi \in \mathcal{P}^{}(n_1,n_2,\infty)} t^{\mathrm{tr}(\pi)} q^{|\pi|}. \end{align*} $$

Remark 4. Up to a rotation of coordinates, this equidistribution result was proved by the second author in [Yel21b]. We also have a direct bijective argument for (a stronger version of) this identity which is somewhat long and will be addressed elsewhere.

Remark 5. The formulas in Theorem 5.2 can be viewed as higher-dimensional analogues of the well-known formula

$$ \begin{align*}\sum_{\mathrm{sh}(\pi) = \lambda} q^{|\pi|} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$

where $\lambda $ is a (usual) partition, $h_{\lambda }(i,j) := \lambda _i - i + \lambda ^{\prime }_j - j + 1$ are hook lengths and the sum runs over weak reverse plane partitions $\pi $ ; see [Sta99, Ch. 7.22]. Its combinatorial proof is known as the Hillman–Grassl correspondence [HG76]. Now, setting $x_{i j} = q^{h_{\lambda }(i,j)}$ in Corollary 4.5 gives

$$ \begin{align*}\sum_{\mathrm{sh}(\pi) \subseteq \lambda} q^{|\pi|_h} = \prod_{(i,j) \in D(\lambda)} \left(1 - q^{h_{\lambda}(i,j)} \right)^{-1}, \end{align*} $$

where the sum runs over plane partitions $\pi $ and

$$ \begin{align*}|\pi|_h := \sum_{(i,j,k) \in \mathrm{Cor}(\pi)} h_{\lambda}(i,j). \end{align*} $$

These formulas give another interesting equidistribution result.

Remark 6. There are various enumeration and generating function formulas known for classes of symmetric plane partitions; see [Sta86b]. Similarly, one can define classes of symmetries of diagrams for d-dimensional partitions. Are there any explicit corner-hook generating functions over symmetric d-dimensional partitions as in Theorem 5.2?

5.4 Other statistics

Theorem 4.1 is a source for many statistics over d-dimensional partitions, whose generating functions can be computed explicitly by taking appropriate specializations. For instance, another interesting statistic $|\cdot |_{c} : \mathcal {P}^{(d)} \to \mathbb {N}$ is given by

$$ \begin{align*}|\pi|_c := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} i_1, \quad \pi \in \mathcal{P}^{(d)}. \end{align*} $$

Then via the substitution $x_{i_1,\ldots , i_d} = q^{i_1}$ we obtain the following generating function:

$$ \begin{align*} \sum_{\pi \in \mathcal{P}^{}(n_1,\ldots, n_{d}, \infty)} q^{|\pi|_c} = \prod_{i = 1}^{n_1} (1 - q^{i})^{-n_2\cdots n_d}. \end{align*} $$

Another curious statistic is given by

$$ \begin{align*}|\pi|_p := \sum_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} (i_1 + 2 \, i_2 + \ldots + d \, i_d), \quad \pi \in \mathcal{P}^{(d)} \end{align*} $$

for which via the substitution $x_{i_1,\ldots , i_d} = q^{i_1 + 2 i_2 + \ldots + d i_d}$ we obtain the following generating function:

$$ \begin{align*}\sum_{\pi \in \mathcal{P}^{(d)}} q^{|\pi|_p} = \prod_{n = 1}^{\infty} (1 - q^{n})^{-p(n, d)}, \end{align*} $$

where $p(n, d)$ is the number of integer partitions of n into d distinct parts.

6 d-dimensional Grothendieck polynomials

From now on, we specialize $x_{i_1,\ldots , i_d} = x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}$ .

6.1 Definitions

Let $\pi $ be a d-dimensional partition. Define the set

$$ \begin{align*}\mathrm{sh}_1(\pi) := \{(i_2,\ldots, i_{d+1}) : (i_1,\ldots, i_{d+1}) \in D(\pi) \} = \{(i_2,\ldots, i_{d+1}) : (1, i_2, \ldots, i_{d+1}) \in D(\pi) \}, \end{align*} $$

which can be viewed as a shape of $\pi $ with respect to the first coordinate. Note that if $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$ , then $\mathrm {sh}_1(\pi )$ is a diagram of $(d-1)$ -dimensional partition from $\mathcal {P}(n_2,\ldots , n_{d+1}).$ Concretely, $\mathrm {sh}_1(\pi )$ is the diagram of the partition $(\pi _{1,i_2,\ldots ,i_d})$ . For example, if $\pi $ is the plane partition in Figure 1, then $\mathrm {sh}_1(\pi )$ corresponds to the partition $(4,3,2)$ , which is the first row of $\pi $ .

Throughout this section, let us assume that $n_1, \ldots , n_d$ are fixed and we have the sets of variables

$$ \begin{align*}\mathbf{x}^{(i)} := (x^{(i)}_1,\ldots, x^{(i)}_{n_i}), \quad i \in [d].\end{align*} $$

Definition 6.1. Let $\rho $ be a $(d-1)$ -dimensional partition from the set $\mathcal {P}(n_2,\ldots ,n_{d+1})$ . Define the d-dimensional Grothendieck polynomials in d sets of variables as follows:

(6) $$ \begin{align} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align} $$

where the sum runs over d-dimensional partitions $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$ with $\mathrm {sh}_1(\pi ) = \rho $ (here $\rho $ is identified with its diagram).

In the specialization $x^{(k)}_{i} = 1$ for all $k \ge 2$ , we simply denote these polynomials by $g_{\rho }(\mathbf {x}) = g_{\rho }(x_1,x_2,\ldots )$ in one set of variables $\mathbf {x}^{(1)} = \mathbf {x} = (x_1,\ldots , x_{n_1})$ so that

(7) $$ \begin{align} g_{\rho}(\mathbf{x}^{}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho}\, \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) := |\{\mathbf{i} : (i, \mathbf{i}) \in \mathrm{Cor}(\pi) \}| \end{align} $$

and the sum runs over $\pi \in \mathcal {P}(n_1,\ldots , n_{d+1})$ .

6.2 Examples

Example 6.2. Consider the case $d = 2$ . Let $\lambda \in \mathcal {P}(n_2, n_3)$ be a partition and $\mathbf {x}^{(1)} = \mathbf {x}, \mathbf {x}^{(2)} = \mathbf {y}$ . Then (7) becomes

$$ \begin{align*}g_{\lambda}(\mathbf{x}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{i = 1}^{n_1} x_i^{c_i(\pi)}, \text{ where } c_i(\pi) = |\{(j,k) : (i, j, k) \in \mathrm{Cor}(\pi) \}|, \end{align*} $$

and the sum runs over plane partitions $\pi \in \mathcal {P}(n_1,n_2,n_3)$ . Let us transpose $\pi $ to $\pi '$ via cyclic shift of the diagram so that $(i,j,k) \in D(\pi ) \iff (j,k, i) \in D(\pi ')$ . Note that $\mathrm {sh}_1(\pi ) = \mathrm {sh}(\pi ') = \lambda $ and $c_i(\pi )$ is equal to the number of columns of $\pi '$ (viewed as a 2d array) containing the entry $i \in [n_1]$ ; see Figure 2. This shows that $\{g_{\lambda }(\mathbf {x})\}$ are the dual stable Grothendieck polynomials introduced ³ in [LP07], but phrased in a slightly different yet equivalent form.

Figure 2 A plane partition $\pi $ and its transpose $\pi '$ of the shape $\lambda = (432)$ with the corresponding diagrams in which the corner boxes of $\pi $ are highlighted.

More generally, (6) becomes

$$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) = \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$

which by rescaling $\tilde g_{\lambda }(\mathbf {x}; \mathbf {y}) = \mathbf {y}^{\lambda } g_{\lambda }(\mathbf {x}; \mathbf {y}^{-1})$ gives the refined version of dual stable Grothendieck polynomials introduced in [GGL16], where it was shown that these polynomials are symmetric in the variables $\mathbf {x}$ .

Example 6.3. Let $d = 3$ , $(n_1,n_2,n_3,n_4) = (3,2,2,2)$ and $\mathbf {x}^{(1)} = \mathbf {x} = (x_1,x_2,x_3)$ , $\mathbf {x}^{(2)} = \mathbf {y} = (y_1,y_2)$ , $\mathbf {x}^{(3)} = \mathbf {z} = (z_1,z_2)$ . Note that in this case, $3$ -dimensional Grothendieck polynomials are indexed by plane partitions and defined as sums over solid partitions. Consider a few examples.

(a) Let . Then we have

$$ \begin{align*} g_\rho(\mathbf{x};\mathbf{y};\mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{1}x_{2}^{2} + x_{1}x_{3}^{2} + x_{2}^{2}x_{3} + x_{2}x_{3}^{2} + 2 x_{1}x_{2}x_{3}) \cdot y_{1}^{3}z_{1}^{2}z_{2}\\ &+ (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{1}x_{2} + x_{1}x_{3} + x_{2}x_{3}) \cdot y_{1}^{2}z_{1}z_{2}, \end{align*} $$

which coincides with the ordinary dual stable Grothendieck polynomial indexed by the partition $\lambda = (2,1)$ (i.e., in this case, we have $g_{\lambda }(\mathbf {x}) = g_\rho (\mathbf {x}, \mathbf {1}, \mathbf {1})$ ).

(b) Let . Then we have

$$ \begin{align*} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) = (x_{1}^{2}x_{2} &+ x_{1}^{2}x_{3} + x_{2}^{2}x_{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} + 2 x_{1}x_{2}x_{3} \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2} \\ & + (x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + 2 x_{1}x_{2} + 2 x_{1}x_{3} + 2 x_{2}x_{3}) \cdot y_{1}y_{2}z_{1}z_{2}, \end{align*} $$

and in particular,

$$ \begin{align*} g_{\rho}(\mathbf{x}) = x_{1}^{2}x_{2} + x_{1}^{2}x_{3} + x_{2}^{2}x_{3} + 2 x_{1}x_{2}x_{3} + x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + 2 (x_{1}x_{2} + x_{1}x_{3} + x_{2}x_{3}). \end{align*} $$

(c) Let . Then we have

$$ \begin{align*} g_{\rho}(\mathbf{x},\mathbf{y},\mathbf{z}) &= (3 x_{1}^{2}x_{2}x_{3} + 3 x_{1}x_{2}^{2}x_{3} + 2 x_{1}x_{2}x_{3}^{2} + x_{1}^{2}x_{2}^{2} + x_{1}^{2}x_{3}^{2} + x_{2}^{2}x_{3}^{2} + x_{1}^{3}x_{2} + x_{1}^{3}x_{3} + x_{2}^{3}x_{3})\cdot y_{1}^{3}y_{2}z_{1}^{3}z_{2}\\ &+ (4 x_{1}x_{2}x_{3} + 2 x_{1}^{2}x_{2} + 2 x_{1}^{2}x_{3} + 2 x_{2}^{2}x_{3} + 3 x_{1}x_{2}^{2} + 3 x_{1}x_{3}^{2} + 3 x_{2}x_{3}^{2} + x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) \cdot y_{1}^{2}y_{2}z_{1}^{2}z_{2}. \end{align*} $$

Figure 3 illustrates a few examples of solid partitions contributing to the last expansion.

Figure 3 Each picture here represents a solid partition as a filling of a diagram of some plane partition with numbers written on top of each box (to make entries of inner boxes visible, some facets are removed). On the left, we have $\mathrm {sh}_{1}\!(\pi ) = \rho $ . The next two are solid partitions $\pi ^{(1)}$ and $\pi ^{(2)}$ represented as fillings of diagrams of plane partitions and ; each has the weight $w(\pi ^{(i)}) = x_2^2x_3 \cdot y_1^2 y_2 z_1^2 z_2$ ; and both have the same $\mathrm {sh}_1(\pi ^{(i)}) =\rho $ ( $i = 1,2$ ) displayed on the left.

6.3 Properties

We now prove some properties of d-dimensional Grothendieck polynomials.

Theorem 6.4 (Cauchy–Littlewood-type identity).

Let $\eta \in \mathcal {P}(n_2,\ldots , n_d)$ be a $(d-2)$ -dimensional partition. Let $n \times \eta $ be a $(d-1)$ -dimensional partition with the diagram $D(n \times \eta ) = \{(i, \mathbf {i}) : i \in [n], \mathbf {i} \in D(\eta ) \}$ . Then we have the following generating series:

$$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$

Proof. Notice that we have

$$ \begin{align*}\sum_{\rho \in \mathcal{P}(\eta, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(\eta, \infty)} \sum_{\mathrm{sh}_1(\pi) = \rho} w(\pi) = \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi). \end{align*} $$

On the other hand, from Theorem 4.1, we have

$$ \begin{align*} \sum_{\pi \in \mathcal{P}(n_1 \times \eta, \infty)} w(\pi) = \prod_{(i_1,\ldots, i_d) \in D(n_1 \times \eta)} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1} \end{align*} $$

which gives the result.

Corollary 6.5. We have

$$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2,\ldots, n_d, \infty)} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$

Lemma 6.6 (Simple branching rule).

We have

$$ \begin{align*}g_{\pi}(1, x_1,\ldots, x_n) = \sum_{\rho \subseteq \pi} g_{\rho}(x_1,\ldots, x_n). \end{align*} $$

Proof. Given a d-dimensional partition $\tau $ with $\mathrm {sh}_1(\tau ) = \pi $ , it contributes to the l.h.s. the weight $\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )}$ (see Equation (7)). Let us form the new partition $\eta \subseteq \pi $ with the diagram

$$ \begin{align*}\{(i, \mathbf{i}) : (i+1, \mathbf{i}) \in D(\tau) \}\end{align*} $$

so that $\prod _{i = 1}^{n} x_i^{c_{i+1}(\tau )} = \prod _{i = 1}^{n} x_i^{c_{i}(\eta )}$ , which contributes to the r.h.s. In other words, remove from $D(\tau )$ the points with the first coordinate $1$ , then decrease by $1$ the first coordinates for the remaining points. It is not difficult to see that this defines a proper weight-preserving bijection between both sides of the equation.

Denote $1^k = (1,\ldots , 1)$ with k ones.

Proposition 6.7 (Boxed specialization).

We have

$$ \begin{align*}g_{[n_2] \times \cdots \times [n_{d+1}]}(1^{n_1 + 1}) = g_{[n_2] \times \cdots \times [n_{d+1}]}(1^{n_1 + 1}; 1^{n_2}; \ldots; 1^{n_d}) = |\mathcal{P}(n_1,\ldots, n_{d+1})|. \end{align*} $$

Proof. Denote $B = [n_2] \times \cdots \times [n_{d+1}]$ . Let $\rho $ be a partition diagram inside B. From the definition of g, we immediately obtain that

$$ \begin{align*}g_{\rho}(1^{n_1}; \ldots; 1^{n_d}) = |\{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})\, :\, \mathrm{sh}_1(\pi) = \rho \}|.\end{align*} $$

Therefore, using the branching formula above, we get

$$ \begin{align*} g_{B}(1^{n_1 + 1}; 1^{n_2}; \ldots; 1^{n_d}) &= \sum_{\rho \subseteq B} g_{\rho}(1^{n_1}; 1^{n_2}; \ldots; 1^{n_d}) \\ &= \sum_{\rho \subseteq B} |\{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})\, :\, \mathrm{sh}_1(\pi) = \rho \}| \\ &=|\mathcal{P}(n_1,\ldots, n_{d+1})|, \end{align*} $$

which gives what is needed.

6.4 Quasisymmetry

It is known that the dual stable Grothendieck polynomials $g_{\lambda }(\mathbf {x})$ are symmetric in $\mathbf {x}$ (in the case $d = 2$ ). As Example 6.3 shows, the generalized polynomials $g_{\rho }$ are not necessarily symmetric for $d \ge 3$ . However, as we show in this subsection, these polynomials are always quasisymmetric.

Definition 6.8. A polynomial $f \in \mathbb {Z}[x_1,\ldots , x_n]$ is called quasisymmetric if for all $1 \le \ell _1 < \cdots < \ell _k \le n$ , $1 \le j_1 < \cdots < j_k \le n$ , and $a_1,\ldots , a_k \in \mathbb {Z}_+$ , we have

$$ \begin{align*}[x^{a_1}_{\ell_1} \cdots x^{a_{k}}_{\ell_k}]\, f = [x^{a_1}_{j_1} \cdots x^{a_{k}}_{j_k}]\, f, \end{align*} $$

where $[\mathbf {x}^{\alpha }] f$ denotes the coefficient of the monomial $\mathbf {x}^{\alpha }$ in f.

Proposition 6.9. We have: $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$ is quasisymmetric in the variables $\mathbf {x}^{(1)}$ .

Proof. To simplify notation, let us denote $\mathbf {x}^{(1)} = \mathbf {x} = (x_1, x_2,\ldots )$ . We need to show that for all $a_1,\ldots , a_k \in \mathbb {Z}_+$ , $1 \le \ell _1 < \cdots < \ell _k \le n_1$ , $1 \le j_1 < \cdots < j_k \le n_1$ , we have

$$ \begin{align*}[x^{a_1}_{\ell_1} \cdots x^{a_{k}}_{\ell_k}]\, g_{\rho} = [x^{a_1}_{j_1} \cdots x^{a_{k}}_{j_k}]\, g_{\rho} \end{align*} $$

(where the indeterminates $\mathbf {x}^{(2)}, \ldots , \mathbf {x}^{(d)}$ are regarded as constants). Let L and R be the sets of d-dimensional partitions which contribute to the l.h.s. and r.h.s., respectively. We are going to construct a weight-preserving bijection $\phi : L \to R$ .

Let $\pi \in L$ for which we have $\pi \in \mathcal {P}(n_1,\ldots ,n_{d+1})$ with $\mathrm {sh}_1(\pi ) = D(\rho )$ and $w(\pi ) = x^{a_1}_{\ell _1} \cdots x^{a_{k}}_{\ell _k} \times w'$ , where $w'$ is the remaining product which does not contain the variables $\mathbf {x}$ .

For a hypermatrix $X = ({x}_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d}_+}$ , define the slices $X^{(\ell )} = (x_{\ell ,\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^{d-1}_+}$ . Let $|X|$ denote the sum of the entries of X.

Let $A = (a_{\mathbf {i}}) = \Phi ^{-1}(\pi ) \in \mathcal {M}(n_1,\ldots , n_d)$ . Note that $A^{(\ell )} \in \mathcal {M}(n_2,\ldots , n_d)$ for $\ell \in [n_1]$ . Since $\Phi $ preserves weights (i.e., $w_A = w(\pi )$ ; see Lemma 4.2), we must have $A^{(\ell )} \ne \mathbf {0}$ iff $\ell \in \{\ell _1,\ldots , \ell _k \}$ . We then have

$$ \begin{align*}w(\pi) = w_A = \prod_{i = 1}^{n_1} x_i^{|A^{(i)}|} \prod_{\mathbf{i} = (i_2,\ldots, i_d)} (x^{(2)}_{i_2} \cdots x^{(d)}_{i_d})^{a_{i,\mathbf{i}}} = \prod_{i = 1}^{k} x_{\ell_i}^{a_i} \times w'. \end{align*} $$

Let us now construct another hypermatrix $B = (b_{\mathbf {i}}) \in \mathcal {M}(n_1,\ldots , n_d)$ so that $B^{(j)} \ne \mathbf {0}$ iff ${j \in \{j_1,\ldots ,j_k\}}$ and $B^{(j_i)} = A^{(\ell _i)}$ for all $i \in [k]$ . Let $\pi ' = \Phi (B)$ . We then clearly have

$$ \begin{align*}w(\pi') = w_B = \prod_{i = 1}^{k} x_{j_i}^{a_i} \times w'. \end{align*} $$

Let us show that $\mathrm {sh}_1(\pi ') = D(\rho ) = \mathrm {sh}_1(\pi )$ . Recall that $\mathrm {sh}_1(\pi ')$ is the diagram of the partition $(\pi ^{\prime }_{1,i_2,\ldots ,i_d})$ . By definition of $\Phi $ , each entry $\pi ^{\prime }_{1,i_2,\ldots ,i_d} $ is the largest weight of a directed path from $(1,i_2,\ldots , i_d)$ to $(n_1,\ldots , n_d)$ through the hypermatrix B. This holds as the maximum of $\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$ among all paths $\Pi : (1,i_2,\ldots , i_d) \to \infty ^d$ is achieved for some path that passes through $(n_1,\ldots , n_d)$ , as any other path could be redirected to $(n_1,\ldots , n_d)$ from the point where it first leaves the box $[n_1] \times \cdots \times [n_d]$ without lowering $\sum _{\mathbf {j} \in \Pi } b_{\mathbf {j}}$ . Similarly, each entry $\pi _{1,i_2,\ldots ,i_d} $ is the largest weight of a directed path from $(1,i_2,\ldots , i_d)$ to $(n_1,\ldots , n_d)$ through the hypermatrix A. In addition, note that when taking the maximum over lattice paths, we can ‘skip’ zero slices $A^{(\ell )} = \mathbf {0}$ . We then have

$$ \begin{align*} \pi_{1,i_2,\ldots,i_d} &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(\ell,\mathbf{i}) \in \Pi, \, \ell \in \{\ell_1,\ldots, \ell_k \}} a_{(\ell, \mathbf{i}) } \\ &= \max_{\Pi : (1,i_2,\ldots, i_d) \to (n_1,\ldots, n_d)} \sum_{(j,\mathbf{i}) \in \Pi, \, j \in \{j_1,\ldots, j_k \}} b_{(j, \mathbf{i}) } \\ &= \pi^{\prime}_{1,i_2,\ldots,i_d}. \end{align*} $$

Hence $\pi ' \in R$ , we can set $\phi : \pi \mapsto \pi '$ and it is a well-defined bijection between L and R.

Note also that d-dimensional Grothendieck polynomials satisfy the stability: $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$ does not change for $n_1 \to n_1 + 1$ and $x^{(1)}_{n_1+1} = 0$ (i.e., if we add an extra $0$ at the end of $\mathbf {x}^{(1)}$ ). Therefore, $g_{\rho }(\mathbf {x}^{(1)}; \ldots ;\mathbf {x}^{(d)})$ can be treated as a quasisymmetric function in infinitely many variables $\mathbf {x}^{(1)}$ (The stability is just the projective limit of quasisymmetric functions).

Let us define the boxed polynomials

$$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) := \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} \prod_{(i_1,\ldots, i_{d+1}) \in \mathrm{Cor}(\pi)} x^{(1)}_{i_1} \cdots x^{(d)}_{i_d}, \end{align*} $$

which are bounded versions of the Cauchy product as by Corollary 4.3; we have

$$ \begin{align*}\lim_{n_{d+1} \to \infty} F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \prod_{i_1 = 1}^{n_1} \cdots \prod_{i_d = 1}^{n_d} \left(1 - x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \right)^{-1}. \end{align*} $$

These polynomials can also be expanded as follows:

$$ \begin{align*}F_{(n_1,\ldots, n_{d+ 1})}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} \sum_{\mathrm{sh}_{1}(\pi) = \rho} w(\pi) = \sum_{\rho \in \mathcal{P}(n_2,\ldots,n_{d+1})} g_{\rho}(\mathbf{x}^{(1)}; \ldots; \mathbf{x}^{(d)}). \end{align*} $$

Corollary 6.10 (Full quasisymmetry of boxed polynomials).

We have: $ F_{(n_1,\ldots , n_{d+ 1})} $ is quasisymmetric in each set of the variables $\mathbf {x}^{(1)}, \ldots , \mathbf {x}^{(d)}$ independently.

Proof. The quasisymmetry in $\mathbf {x}^{(1)}$ is immediate from the previous proposition. The same holds for any other set of variables by noting that the definitions of $\mathrm {Cor}(\pi )$ and weights $w(\pi )$ are symmetric in the first d coordinates, and hence we may repeat the proof by ‘rotation’ (i.e., moving any coordinate to the position of the first one).

Definition 6.11. Let $A = (a_{i_1,\ldots ,i_d})\in \mathcal {M}^{}(n_1,\ldots , n_d)$ . For each $\ell \in [d]$ , consider the hypermatrices $B^{(\ell )}_{i} = (a_{i_1,\ldots ,i_d})_{i_{\ell } = i}$ (i.e., slices of A with fixed $\ell $ -th coordinate). Define the vectors

$$ \begin{align*}s_{\ell}(A) := (|B^{(\ell)}_1|, |B^{(\ell)}_2|, \ldots),\end{align*} $$

where $|B|$ denotes the sum of entries of B. For example, if $d = 2$ , then $s_{1}(A)$ is the vector of row sums of A, and $s_{2}(A)$ is the column sums of A. Let us also say that A is a packed hypermatrix if for each $\ell \in [d]$ , the sequence $s_{\ell }(A)$ does not contain zeros between its positive entries. Denote by $\mathrm {pack}(A)$ the packed hypermatrix formed from A by removing its zero slices $B^{(\ell )}_i = \mathbf {0}$ .

Note that for any $A \in \mathcal {M}(n_1,\ldots , n_d)$ , we have

$$ \begin{align*}w_A = \prod_{\ell = 1}^d \left(\mathbf{x}^{(\ell)} \right)^{s_{\ell}(A)}, \end{align*} $$

where for a set of variables $\mathbf {x} = (x_1,x_2,\ldots )$ and a vector $s = (s_1, s_2,\ldots )$ , we use the notation ${\mathbf {x}^{s} = x_1^{s_1} x_2^{s_2} \cdots }$ .

For a composition $\alpha = (\alpha _1,\ldots , \alpha _k) \in \mathbb {Z}^k_+$ , recall the monomial quasisymmetric functions

$$ \begin{align*}M_{\alpha}(\mathbf{x}) := \sum_{i_1 < \ldots < i_k} x^{\alpha_1}_{i_1} \cdots x^{\alpha_k}_{i_k}. \end{align*} $$

Note that they form a basis of the algebra of quasisymmetric functions.

It is easy to see that

$$ \begin{align*}F_{(n_1,\ldots,n_d, \infty)} = \sum_{A \in \mathcal{M}(n_1,\ldots,n_d)} w_A = \sum_{{\alpha^{(1)}, \ldots, \alpha^{(d)} \atop \text{compositions}} } m^{}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, (\mathbf{x}^{(1)})^{\alpha^{(1)}} \cdots (\mathbf{x}^{(d)})^{\alpha^{(d)}}, \end{align*} $$

where $m^{}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$ is the number of $A \in \mathcal {M}(n_1,\ldots , n_d)$ with $s_{\ell }(A) = \alpha ^{(\ell )} \in \mathbb {N}^{n_{\ell }}$ . The following result is a finite boxed version of this expansion.

Theorem 6.12 (Monomial basis expansion of boxed polynomials).

We have

$$ \begin{align*}F_{(n_1,\ldots,n_{d+1})} = \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}), \end{align*} $$

where the sum runs over compositions $\alpha ^{(1)}, \ldots , \alpha ^{(d)}$ such that $|\alpha ^{(i)}| = |\alpha ^{(j)}|$ for all $i,j$ , and the coefficient $m^{(n_{d+1})}_{\alpha ^{(1)},\ldots ,\alpha ^{(d)}}$ is equal to the number of packed hypermatrices $A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$ such that $s_{\ell }(A) = \alpha ^{(\ell )}$ for all $\ell \in [d]$ .

Proof. Note that replacing a hypermatrix A by $\mathrm {pack}(A)$ does not change its last passage time $G_{1,\ldots , 1}$ . Let $P \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$ be a packed hypermatrix and let $M(P)$ be the set of hypermatrices $A \in \mathcal {M}([n_1] \times \cdots \times [n_d], n_{d+1})$ such that $\mathrm {pack}(A) = P$ . Let $s_{\ell }(P) = \alpha ^{(\ell )}$ . Then (by an argument as in Proposition 6.9) it is not difficult to obtain that we have

$$ \begin{align*}\sum_{A \in M(P)} w_A = M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}). \end{align*} $$

Therefore, we obtain

$$ \begin{align*} F_{(n_1,\ldots,n_{d+1})} &= \sum_{\pi \in \mathcal{P}(n_1,\ldots, n_{d+1})} w(\pi) \\ &= \sum_{A \in \mathcal{M}([n_1] \times \cdots \times [n_d], n_{d+1})} w_A \\ &= \sum_{P \text{ packed}} \sum_{A \in M(P)} w_A \\ &= \sum_{\alpha^{(1)}, \ldots, \alpha^{(d)}} m^{(n_{d+1})}_{\alpha^{(1)},\ldots,\alpha^{(d)}}\, M_{\alpha^{(1)}}(\mathbf{x}^{(1)}) \cdots M_{\alpha^{(d)}}(\mathbf{x}^{(d)}) \end{align*} $$

as needed.

Remark 7. For $d = 2$ , packed matrices appear in the algebra of matrix quasisymmetric functions; see [DHT02].

6.5 Some remarks

Remark 8 (Dual stable Grothendieck polynomials, $d = 2$ ).

Recall that in this case (see Example 6.2), we get the following definition of polynomials $g_{\lambda }(\mathbf {x}; \mathbf {y})$ indexed by partitions $\lambda $ . We define

$$ \begin{align*}g_{\lambda}(\mathbf{x}; \mathbf{y}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \lambda} \prod_{(i,j,k) \in \mathrm{Cor}(\pi)} x_i y_j, \end{align*} $$

where the sum runs over plane partitions $\pi $ . The polynomials $g_{\lambda }(\mathbf {x}; \mathbf {y})$ are generalizations of dual stable Grothendieck polynomials which correspond to the specialization $g_{\lambda }(\mathbf {x}) = g_{\lambda }(\mathbf {x}; \mathbf {1})$ . In fact, $g_{\lambda }(\mathbf {x}; \mathbf {y})$ is symmetric in $\mathbf {x}$ . The Cauchy–Littlewood-type identity in Corollary 6.5 becomes

$$ \begin{align*}\sum_{\lambda \in \mathcal{P}(n_2, \infty)} g_{\lambda}(\mathbf{x}; \mathbf{y}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \frac{1}{1 - x_i y_j}, \end{align*} $$

which was proved in [Yel21a, Yel21b]. The boxed specialization formula in Proposition 6.7 becomes the following:

$$ \begin{align*}g_{[n_2] \times [n_3]}(1^{n_1 + 1}) = |\mathcal{P}(n_1, n_2, n_3)|, \end{align*} $$

the number of plane partitions inside the box $[n_1] \times [n_2] \times [n_3]$ , for which there is also the famous MacMahon boxed product formula

$$ \begin{align*}|\mathcal{P}(n_1, n_2, n_3)| = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \frac{i + j + k - 1}{i + j + k - 2}. \end{align*} $$

Using determinantal formulas for dual stable Grothendieck polynomials [Yel17], we also have the following ‘coincidence’ formula (see [Yel21a, Lemma 3.4], [Yel21b, Lemma 6.9]) connecting them with the Schur polynomials $\{s_{\lambda } \}$ as follows:

$$ \begin{align*}g_{[n_2] \times [n_3]}(\mathbf{x}) = s_{[n_2] \times [n_3]}(\mathbf{x}, 1^{n_2 - 1}). \end{align*} $$

Remark 9 (3d Grothendieck polynomials, $d = 3$ ).

In this case, we get the following definition of polynomials $g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$ indexed by plane partitions $\rho $ . We define

(8) $$ \begin{align} g_{\rho}(\mathbf{x}; \mathbf{y}; \mathbf{z}) := \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \prod_{(i,j,k,\ell) \in \mathrm{Cor}(\pi)} x_{i} y_{j} z_{k}, \end{align} $$

where the sum runs over solid partitions $\pi \in \mathcal {P}(n_1,n_2,n_3,n_4)$ . Note also that if $\rho $ satisfies $D(\rho ) = \{(1,i,j) : (i,j) \in D(\lambda )\}$ where $\lambda $ is a partition, we then have $g_{\rho }(\mathbf {x}; \mathbf {1}; \mathbf {z}) = g_{\lambda }(\mathbf {x}; \mathbf {z})$ reduces to the 2d case discussed above. The polynomials $g_{\rho }(\mathbf {x}; \mathbf {y}; \mathbf {z})$ are quasisymmetric in $\mathbf {x}$ . The Cauchy–Littlewood-type identity in Corollary 6.5 becomes

$$ \begin{align*}\sum_{\rho \in \mathcal{P}(n_2, n_3, \infty)} g_{\rho}(\mathbf{x}^{}; \mathbf{y}; \mathbf{z}) = \prod_{i = 1}^{n_1} \prod_{j = 1}^{n_2} \prod_{k = 1}^{n_3} \left(1 - x^{}_{i} y_j z_k \right)^{-1}. \end{align*} $$

The boxed specialization formula becomes the following:

$$ \begin{align*}g_{[n_2] \times [n_3] \times [n_4]}(1^{n_1 + 1}) = |\mathcal{P}(n_1, n_2, n_3, n_4)|, \end{align*} $$

the number of solid partitions inside the box $[n_1] \times [n_2] \times [n_3] \times [n_4]$ .

Remark 10 (On higher-dimensional Schur polynomials and SSYT).

Note that the d-dimensional Grothendieck polynomials $g_{\rho }(\mathbf {x})$ are inhomogeneous. It is well known that for $d = 2$ , we have $g_{\lambda } = s_{\lambda } + \text {lower degree terms}$ . By analogy, the top degree homogeneous component of $g_{\rho }(\mathbf {x})$ denoted by $s_{\rho }(\mathbf {x})$ can be viewed as a higher-dimensional analogue of Schur polynomials. It sums over a subset of d-dimensional partitions which are analogous to semistandard Young tableaux (SSYT) for the case $d = 2$ . By Proposition 6.9, $\{s_{\rho }\}$ are also quasisymmetric polynomials. Are there any interesting properties of these functions and tableaux?

7 Last passage percolation in $\mathbb {Z}^{d}$

In this section, we consider a directed last passage percolation model with geometric weights and show its connections with d-dimensional Grothendieck polynomials studied in the previous section.

Let $W = (w_{\mathbf {i}})_{\mathbf {i} \in \mathbb {Z}^d_+}$ be a random hypermatrix with i.i.d. entries $w_{\mathbf {i}}$ which have geometric distribution with parameter $q \in (0,1)$ ; that is,

$$ \begin{align*}\mathrm{Prob}(w_{\mathbf{i}} = k) = (1 - q)\, q^k, \quad k \in \mathbb{N}. \end{align*} $$

Define the last passage times as follows:

$$ \begin{align*}G(\mathbf{i}) = G(\mathbf{1} \to \mathbf{i}) = \max_{\Pi : \mathbf{1} \to \mathbf{i}}\, \sum_{\mathbf{j} \in \Pi} w_{\mathbf{j}}, \quad \mathbf{i} \in \mathbb{Z}^d_+, \end{align*} $$

where the maximum is over directed lattice paths $\Pi $ from $(1,\ldots , 1)$ to $\mathbf {i}$ .

Now we are going to show that d-dimensional Grothendieck polynomials naturally appear in distribution formulas for this model.

Theorem 7.1. Let $n_1,\ldots , n_d \in \mathbb {Z}_+$ and $\rho \in \mathcal {P}(n_2,\ldots , n_{d}, \infty )$ be a $(d-1)$ -dimensional partition. Denote $\mathbf {n} = (n_2 + 1,\ldots , n_{d} + 1)$ and $N = n_1 \cdots n_{d}$ . We have the following joint distribution formula:

$$ \begin{align*} \mathrm{Prob}\left( G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) = (1 - q)^{N}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$

Proof. Let us flip and truncate the hypermatrix W to get $W' =(w^{\prime }_{\mathbf {i}}) = (w_{(n_1 + 1,\mathbf {n}) - \mathbf {i}} )_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$ .

Let $\pi = (\pi _{\mathbf {i}}) \in \mathcal {P}(n_1,\ldots , n_d, \infty )$ and $(a_{\mathbf {i}}) = \Phi ^{-1}(\pi )$ . We obtain

$$ \begin{align*}\mathrm{Prob}(W' = \Phi^{-1}(\pi)) = \prod_{\mathbf{i} \in [n_1] \times \cdots \times [n_{d}]} \mathrm{Prob}(w^{\prime}_{\mathbf{i}} = a_{\mathbf{i}}) = (1-q)^{N} q^{S(\pi)}, \end{align*} $$

where $S(\pi ) = \sum _{\mathbf {i}} a_{\mathbf {i}}$ . Note that

$$ \begin{align*}S(\pi) = \# \text{ corners of }D(\pi) = c_1(\pi) + \ldots + c_{n_1}(\pi), \end{align*} $$

where we defined $c_{i}(\pi ) = |\{ \mathbf {i} : (i, \mathbf {i}) \in \mathrm {Cor}(\pi ) \}|$ . Then from (7), we have

$$ \begin{align*} (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}) &= (1 - q)^{N} \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} q^{c_1(\pi) + \ldots + c_{n_1}(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} (1 - q)^{N} q^{S(\pi)} \\ &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(W' = \Phi^{-1}(\pi)), \end{align*} $$

where the sum runs over $\pi \in \mathcal {P}(n_1,\ldots , n_d, \infty )$ .

Note that we have $\Phi (W') = (G((n_1 + 1, \mathbf {n}) - \mathbf {i}))_{\mathbf {i} \in [n_1] \times \cdots \times [n_d]}$ since the maximum of $\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$ among all paths $\Pi : \mathbf {j} \to \infty ^d$ is achieved for some path that passes through $(n_1 + 1, \mathbf {n})$ and therefore equals the maximum of $\sum _{\mathbf {j} \in \Pi } W^{\prime }_{\mathbf {j}}$ among all paths $\Pi : \mathbf {j} \to (n_1 + 1, \mathbf {n})$ . Therefore, now we get

$$ \begin{align*} \mathrm{Prob}\left(G(n_1, \mathbf{n} - \mathbf{i}) = \rho_{\mathbf{i}}\, :\, \mathbf{i} \in [n_2] \times \cdots \times [n_{d}] \right) &= \sum_{\pi\, :\, \mathrm{sh}_1(\pi) = \rho} \mathrm{Prob}(\Phi(W') = \pi) \\ &= (1 - q)^{N} g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \end{align*} $$

as needed.

Remark 11. The same proof (with slight modifications) works in a more general case if $(w_{\mathbf {i}})$ are independent geometric random variables with different parameters $x^{(1)}_{i_1} \cdots x^{(d)}_{i_d} \in (0,1)$ . Then the corresponding probability will be proportional to the d-dimensional Grothendieck polynomial $g_{\rho }$ of variables $x^{(\ell )}_{i}$ . As it was pointed out by one of the referees, a proof can also be given using an analogue of Gelfand–Tsetlin patterns and conditioning as in [MS20] for $d = 2$ .

Corollary 7.2 (Single point distribution formula).

We have

$$ \begin{align*}\mathrm{Prob}(G(n_1,\ldots, n_d) \le n) = (1 - q)^{N}\, g_{[n_2] \times \cdots \times [n_d] \times [n]}(1,\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$

Proof. Follows by combining the theorem with Lemma 6.6.

Corollary 7.3 (The case $d = 2$ ).

Let $\lambda \in \mathcal {P}(n_2, \infty )$ be a partition. We have

$$ \begin{align*} \mathrm{Prob}\left(G(n_1, n_2 + 1 - i) = \lambda_i \, :\, i \in [n_2] \right) = (1 - q)^{n_1 n_2}\, g_{\lambda}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}). \end{align*} $$

Remark 12. This formula (which shows that dual stable Grothendieck polynomials arise naturally in the last passage percolation model) was proved in [Yel21a] and in a more general case with different parameters in [Yel20]. Note that in this case we can obtain many determinantal formulas.

Remark 13. Theorem 7.1 suggests a probability distribution on the set $\mathcal {P}(n_2,\ldots , n_{d}, \infty )$ of $(d-1)$ -dimensional partitions defined as follows:

$$ \begin{align*}\mathrm{Prob}_{g}(\rho) := (1 - q)^{n_1 \cdots n_d}\, g_{\rho}(\underbrace{q,\ldots, q}_{n_1 \text{ times}}), \qquad \rho \in \mathcal{P}(n_2,\ldots, n_{d}, \infty). \end{align*} $$

Remark 14. Using Kingman’s subadditivity theorem, one can show that there is a deterministic limit shape $\psi : \mathbb {R}^{d}_{\ge 0} \to \mathbb {R}_{\ge 0}$ (see [Mar06]) such that as $n \to \infty $ , we have a.s. convergence

$$ \begin{align*}\frac{1}{n} G(\lfloor n\mathbf{x} \rfloor) \to \psi(\mathbf{x}), \quad \mathbf{x} \in \mathbb{R}^d_{\ge 0}. \end{align*} $$

The case $d = 2$ is exactly solvable and $\psi (x,y) = (x + y + 2\sqrt {qxy})/(1 - q)$ ; moreover, the point fluctuations around the shape are of order $n^{1/3}$ and tend to the Tracy-Widom distribution [Joh00]. However, much less is known for $d \ge 3$ .

8 Concluding remarks and open questions

8.1 Asymptotics

MacMahon’s numbers $m_d(n)$ have the following asymptotics [BGP12]:

$$ \begin{align*}\lim_{n \to \infty} n^{-d/(1 + d)}\log m_d(n) = \frac{1 + d}{d} \left(d\, \zeta(1 + d) \right)^{1/(1 + d)}, \end{align*} $$

where $\zeta $ is the Riemann zeta function (which is computed based on the explicit formula for the generating function). Let $p_d(n)$ be the number of d-dimensional partitions of volume n. Supported by numerical experiments for solid partitions, it was conjectured in [MR03] that $p_3(n)$ has the same asymptotics as $m_3(n)$ . However, later computations reported in [DG15] suggest that this is not the case and that $p_3(n)$ is asymptotically larger than $m_3(n)$ , despite the fact that $m_3(n) = p_3(n)$ for $n \le 5$ and $m_3(n)> p_3(n)$ for the next many values of n [ABMM67, DG15]; cf. the sequences A000293, A000294 in [OEIS]). See also [Ekh12] and a useful resource [Gov] for more related data. Using our interpretation for $m_d(n)$ (Corollary 5.5) and bounds on the corner-hook volume, it was shown in [Yel23] that $p_d(n) < dn \cdot m_d(dn)$ , and obtaining a more accurate comparison between these sequences (e.g., by showing that $\log p_d(n) \sim \log m_d(\alpha n)$ for some $\alpha $ ) will be important for understanding the asymptotics of $p_d(n)$ .

8.2 d-dimensional Grothendieck polynomials

Are there any (algebraic, determinantal) formulas for d-dimensional Grothendieck polynomials? They will be important for at least two applications: enumeration of boxed higher-dimensional partitions and computing distribution formulas (or performing asymptotic analysis) for the last passage percolation problem discussed above. Note that for $d = 2$ , there are several determinantal formulas (Jacobi-Trudi, bialternant types) known; see, for example, [Yel17, AY22, Iwa20, Kim22, HJKSS21, Iwa21].