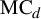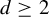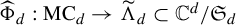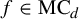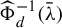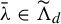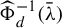1 Introduction
This paper is a continuation of the author’s previous work [Reference Sugiyama14].
We first remind our setting from [Reference Sugiyama14]. Let
![]() $\mathrm {MP}_d$
be the family of affine conjugacy classes of polynomial maps of one complex variable with degree
$\mathrm {MP}_d$
be the family of affine conjugacy classes of polynomial maps of one complex variable with degree
![]() $d \geq 2$
, and
$d \geq 2$
, and
![]() $\mathbb {C}^d / \mathfrak {S}_d$
the set of unordered collections of d complex numbers, where
$\mathbb {C}^d / \mathfrak {S}_d$
the set of unordered collections of d complex numbers, where
![]() ${\mathfrak S}_{d}$
denotes the dth symmetric group. We denote by
${\mathfrak S}_{d}$
denotes the dth symmetric group. We denote by
![]() $\Phi _d$
the map
$\Phi _d$
the map
which maps each
![]() $f \in \mathrm {MP}_d$
to its unordered collection of fixed-point multipliers. Here, fixed-point multipliers of
$f \in \mathrm {MP}_d$
to its unordered collection of fixed-point multipliers. Here, fixed-point multipliers of
![]() $f \in \mathrm {MP}_d$
always satisfy a certain relation by the fixed point theorem for polynomial maps (see §12 in [Reference Milnor11]), which implies that the image of
$f \in \mathrm {MP}_d$
always satisfy a certain relation by the fixed point theorem for polynomial maps (see §12 in [Reference Milnor11]), which implies that the image of
![]() $\Phi _d$
is contained in a certain hyperplane
$\Phi _d$
is contained in a certain hyperplane
![]() $\widetilde {\Lambda }_d$
in
$\widetilde {\Lambda }_d$
in
![]() $\mathbb {C}^d / \mathfrak {S}_d$
.
$\mathbb {C}^d / \mathfrak {S}_d$
.
As mentioned in [Reference Sugiyama14], it is well known that the map
![]() $\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
is bijective for
$\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
is bijective for
![]() $d=2$
and also for
$d=2$
and also for
![]() $d=3$
(see [Reference Milnor9]). For
$d=3$
(see [Reference Milnor9]). For
![]() $d \geq 4$
, Fujimura and Nishizawa have done some preliminary works in finding
$d \geq 4$
, Fujimura and Nishizawa have done some preliminary works in finding
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
for
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
for
![]() $\bar {\unicode{x3bb} } \in \widetilde {\Lambda }_d$
in their series of papers such as [Reference Fujimura2, Reference Fujimura3, Reference Nishizawa and Fujimura12]. Hereafter,
$\bar {\unicode{x3bb} } \in \widetilde {\Lambda }_d$
in their series of papers such as [Reference Fujimura2, Reference Fujimura3, Reference Nishizawa and Fujimura12]. Hereafter,
![]() $\#(X)$
, or simply
$\#(X)$
, or simply
![]() $\# X$
, denotes the cardinality of a set X. Fujimura and Taniguchi [Reference Fujimura and Taniguchi4] also constructed a compactification of
$\# X$
, denotes the cardinality of a set X. Fujimura and Taniguchi [Reference Fujimura and Taniguchi4] also constructed a compactification of
![]() $\mathrm {MP}_d$
, which gave us a strong geometric insight on the fiber structure of
$\mathrm {MP}_d$
, which gave us a strong geometric insight on the fiber structure of
![]() $\Phi _d$
. Other compactifications of
$\Phi _d$
. Other compactifications of
![]() $\mathrm {MP}_d$
were also constructed independently by Silverman [Reference Silverman13] and by DeMarco and McMullen [Reference DeMarco and McMullen1]. For rational maps and their periodic-point multipliers, McMullen [Reference McMullen8] gave a general important result. In a special case of [Reference McMullen8], there is a famous result by Milnor [Reference Milnor10] for rational maps of degree two and their fixed-point multipliers. There is also a result by Hutz and Tepper [Reference Hutz and Tepper7] for rational maps of degree three and their periodic-point multipliers of period less than or equal to two. There are some other results [Reference Gorbovickis5, Reference Gorbovickis6] concerning polynomial or rational maps and their periodic-point multipliers. (See [Reference Sugiyama14] for more details.)
$\mathrm {MP}_d$
were also constructed independently by Silverman [Reference Silverman13] and by DeMarco and McMullen [Reference DeMarco and McMullen1]. For rational maps and their periodic-point multipliers, McMullen [Reference McMullen8] gave a general important result. In a special case of [Reference McMullen8], there is a famous result by Milnor [Reference Milnor10] for rational maps of degree two and their fixed-point multipliers. There is also a result by Hutz and Tepper [Reference Hutz and Tepper7] for rational maps of degree three and their periodic-point multipliers of period less than or equal to two. There are some other results [Reference Gorbovickis5, Reference Gorbovickis6] concerning polynomial or rational maps and their periodic-point multipliers. (See [Reference Sugiyama14] for more details.)
Following the results above, in [Reference Sugiyama14], we succeeded in giving, for every
![]() $\bar {\unicode{x3bb} } = \{ \unicode{x3bb} _1,\ldots , \unicode{x3bb} _d \} \in \widetilde {\Lambda }_d$
, an algorithm for counting the number of elements of
$\bar {\unicode{x3bb} } = \{ \unicode{x3bb} _1,\ldots , \unicode{x3bb} _d \} \in \widetilde {\Lambda }_d$
, an algorithm for counting the number of elements of
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
except when
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
except when
![]() $\unicode{x3bb} _i = 1$
for some i. However, the algorithm was rather long and complicated. In this paper, we make a drastic improvement to its algorithm; we no longer need induction processes to find
$\unicode{x3bb} _i = 1$
for some i. However, the algorithm was rather long and complicated. In this paper, we make a drastic improvement to its algorithm; we no longer need induction processes to find
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
if we consider
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
if we consider
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity (see Theorem I). Moreover, if we consider the family
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity (see Theorem I). Moreover, if we consider the family
![]() $\mathrm {MC}_d$
of monic centered polynomials of degree d and the map
$\mathrm {MC}_d$
of monic centered polynomials of degree d and the map
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, instead of
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, instead of
![]() $\mathrm {MP}_d$
and
$\mathrm {MP}_d$
and
![]() $\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
, we can always give an explicit expression of
$\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
, we can always give an explicit expression of
![]() $\#(\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} }))$
even when its multiplicity is ignored (see Theorem II and Corollary III). Here,
$\#(\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} }))$
even when its multiplicity is ignored (see Theorem II and Corollary III). Here,
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is defined to be the composite mapping of the natural projection
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is defined to be the composite mapping of the natural projection
![]() $\mathrm {MC}_d \to \mathrm {MP}_d$
and
$\mathrm {MC}_d \to \mathrm {MP}_d$
and
![]() $\Phi _d$
. Interestingly, the formula for finding
$\Phi _d$
. Interestingly, the formula for finding
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
in Theorem I has the form of the inclusion-exclusion formula.
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
in Theorem I has the form of the inclusion-exclusion formula.
There are five sections in this paper. In §§2 and 3, we shall review the results in [Reference Sugiyama14] more precisely and state Theorems I, II, and Corollary III, which are the main results in this paper. Section 4 is devoted to the proof of Theorem I and §5 is devoted to the proof of Theorem II. The main part in this paper is the proof of Theorem I in §4, which consists of a good deal of combinatorial argument. Compared with the proof of Theorem I, the proof of Theorem II in §5 is relatively easy under the assumption of [Reference Sugiyama14]. However, by combining Theorems I and II, we directly have Corollary III, which is, in some sense, a monumental achievement of our study.
2 Main result 1
In this section, we always consider
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity and deal with improvements to the algorithm for finding
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity and deal with improvements to the algorithm for finding
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
. We first fix our notation.
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
. We first fix our notation.
For
![]() $d \ge 2$
, we put
$d \ge 2$
, we put
Since
![]() $\gamma \in \mathrm {Aut}(\mathbb {C})$
naturally acts on
$\gamma \in \mathrm {Aut}(\mathbb {C})$
naturally acts on
![]() $f \in \mathrm {Poly}_d$
by
$f \in \mathrm {Poly}_d$
by
![]() $\gamma \cdot f := \gamma \circ f \circ \gamma ^{-1}$
, we can define its quotient
$\gamma \cdot f := \gamma \circ f \circ \gamma ^{-1}$
, we can define its quotient
![]() $\mathrm {MP}_d := \mathrm {Poly}_d / \mathrm {Aut}(\mathbb {C})$
, which we usually call the moduli space of polynomial maps of degree d. We put
$\mathrm {MP}_d := \mathrm {Poly}_d / \mathrm {Aut}(\mathbb {C})$
, which we usually call the moduli space of polynomial maps of degree d. We put
![]() $\mathrm {Fix}(f) := \{ z \in \mathbb {C} \mid f(z)=z\}$
for
$\mathrm {Fix}(f) := \{ z \in \mathbb {C} \mid f(z)=z\}$
for
![]() $f \in \mathrm {Poly}_d$
, where
$f \in \mathrm {Poly}_d$
, where
![]() $\mathrm {Fix}(f)$
is considered counted with multiplicity. Hence, we always have
$\mathrm {Fix}(f)$
is considered counted with multiplicity. Hence, we always have
![]() $\# (\mathrm {Fix}(f)) = d$
. Since the unordered collection of fixed-point multipliers
$\# (\mathrm {Fix}(f)) = d$
. Since the unordered collection of fixed-point multipliers
![]() $(f'(\zeta ))_{\zeta \in \mathrm {Fix}(f)}$
of
$(f'(\zeta ))_{\zeta \in \mathrm {Fix}(f)}$
of
![]() $f \in \mathrm {Poly}_d$
is invariant under the action of
$f \in \mathrm {Poly}_d$
is invariant under the action of
![]() $\mathrm {Aut}(\mathbb {C})$
, we can naturally define the map
$\mathrm {Aut}(\mathbb {C})$
, we can naturally define the map
![]() $\Phi _d:\mathrm {MP}_d \to \mathbb {C}^{d}/\mathfrak {S}_{d}$
by
$\Phi _d:\mathrm {MP}_d \to \mathbb {C}^{d}/\mathfrak {S}_{d}$
by
![]() $\Phi _d(f):=(f'(\zeta ))_{\zeta \in \mathrm {Fix}(f)}$
. Here,
$\Phi _d(f):=(f'(\zeta ))_{\zeta \in \mathrm {Fix}(f)}$
. Here,
![]() $\mathfrak {S}_{d}$
denotes the dth symmetric group which acts on
$\mathfrak {S}_{d}$
denotes the dth symmetric group which acts on
![]() $\mathbb {C}^{d}$
by the permutation of coordinates. Note that a fixed point
$\mathbb {C}^{d}$
by the permutation of coordinates. Note that a fixed point
![]() $\zeta \in \mathrm {Fix}(f)$
is multiple if and only if
$\zeta \in \mathrm {Fix}(f)$
is multiple if and only if
![]() $f'(\zeta )=1$
.
$f'(\zeta )=1$
.
By the fixed point theorem for polynomial maps, we always have
![]() $\sum _{\zeta \in \mathrm {Fix}(f)} {1}/({1-f'(\zeta )}) = 0$
for
$\sum _{\zeta \in \mathrm {Fix}(f)} {1}/({1-f'(\zeta )}) = 0$
for
![]() $f \in \mathrm {Poly}_d$
if f has no multiple fixed point. (See §12 in [Reference Milnor11] or Proposition 1.1 in [Reference Sugiyama14] for more details.) Hence, putting
$f \in \mathrm {Poly}_d$
if f has no multiple fixed point. (See §12 in [Reference Milnor11] or Proposition 1.1 in [Reference Sugiyama14] for more details.) Hence, putting
![]() $\Lambda _d :=\{(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d)\in \mathbb {C}^d \mid \sum _{i=1}^d \prod _{j\ne i} ( 1- \unicode{x3bb} _j ) = 0 \}$
and
$\Lambda _d :=\{(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d)\in \mathbb {C}^d \mid \sum _{i=1}^d \prod _{j\ne i} ( 1- \unicode{x3bb} _j ) = 0 \}$
and
![]() $\widetilde {\Lambda }_d := \Lambda _d / \mathfrak {S}_d$
, we have the inclusion relation
$\widetilde {\Lambda }_d := \Lambda _d / \mathfrak {S}_d$
, we have the inclusion relation
![]() $\Phi _d(\mathrm {MP}_d) \subseteq \widetilde {\Lambda }_d \subseteq \mathbb {C}^{d}/\mathfrak {S}_{d}$
. We therefore have the map
$\Phi _d(\mathrm {MP}_d) \subseteq \widetilde {\Lambda }_d \subseteq \mathbb {C}^{d}/\mathfrak {S}_{d}$
. We therefore have the map
by
![]() $f \mapsto (f'(\zeta ) )_{\zeta \in \mathrm {Fix}(f)}$
, which is the main object of our study.
$f \mapsto (f'(\zeta ) )_{\zeta \in \mathrm {Fix}(f)}$
, which is the main object of our study.
In this paper, we again restrict our attention to the map
![]() $\Phi _d$
on the domain where polynomial maps have no multiple fixed points, that is, on the domains
$\Phi _d$
on the domain where polynomial maps have no multiple fixed points, that is, on the domains
which are Zariski open subsets of
![]() $\Lambda _d$
and
$\Lambda _d$
and
![]() $\widetilde {\Lambda }_d$
, respectively. Here, note that we also have
$\widetilde {\Lambda }_d$
, respectively. Here, note that we also have
 $$ \begin{align*} V_d = \bigg\{ (\unicode{x3bb}_1,\ldots ,\unicode{x3bb}_d) \in \mathbb{C}^d\, \bigg|\, \unicode{x3bb}_i \ne 1 \textrm{ for every } 1\le i\le d, \sum_{i=1}^d \frac{1}{1-\unicode{x3bb}_i} = 0 \bigg\}. \end{align*} $$
$$ \begin{align*} V_d = \bigg\{ (\unicode{x3bb}_1,\ldots ,\unicode{x3bb}_d) \in \mathbb{C}^d\, \bigg|\, \unicode{x3bb}_i \ne 1 \textrm{ for every } 1\le i\le d, \sum_{i=1}^d \frac{1}{1-\unicode{x3bb}_i} = 0 \bigg\}. \end{align*} $$
Throughout this paper, we always denote by
![]() $\bar {\unicode{x3bb} }$
the equivalence class of
$\bar {\unicode{x3bb} }$
the equivalence class of
![]() $\unicode{x3bb} \in \Lambda _d$
in
$\unicode{x3bb} \in \Lambda _d$
in
![]() $\widetilde {\Lambda }_d$
, that is,
$\widetilde {\Lambda }_d$
, that is,
![]() $\bar {\unicode{x3bb} }=\textit {pr}(\unicode{x3bb} )$
, where
$\bar {\unicode{x3bb} }=\textit {pr}(\unicode{x3bb} )$
, where
![]() $\textit {pr}: \Lambda _d \to \widetilde {\Lambda }_d$
denotes the canonical projection. Hence, for
$\textit {pr}: \Lambda _d \to \widetilde {\Lambda }_d$
denotes the canonical projection. Hence, for
![]() $\unicode{x3bb} = (\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in \Lambda _d$
, we sometimes express
$\unicode{x3bb} = (\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in \Lambda _d$
, we sometimes express
![]() $\bar {\unicode{x3bb} } = \{ \unicode{x3bb} _1,\ldots , \unicode{x3bb} _d \} \in \widetilde {\Lambda }_d$
. We never denote by
$\bar {\unicode{x3bb} } = \{ \unicode{x3bb} _1,\ldots , \unicode{x3bb} _d \} \in \widetilde {\Lambda }_d$
. We never denote by
![]() $\bar {\unicode{x3bb} }$
the complex conjugate of
$\bar {\unicode{x3bb} }$
the complex conjugate of
![]() $\unicode{x3bb} $
in this paper.
$\unicode{x3bb} $
in this paper.
The objects defined in the following definition play a central roll in [Reference Sugiyama14] and also in this paper.
Definition 2.1. For
![]() $\unicode{x3bb} = (\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, we put
$\unicode{x3bb} = (\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, we put
 $$ \begin{align*} \mathfrak{I}(\unicode{x3bb}) := \left\{ \{I_1,\ldots,I_l\}\ \left| \ \begin{matrix} l \ge 2,\ \ I_1 \amalg \cdots \amalg I_l = \{1,\ldots,d \},\\ I_u \ne \emptyset \textrm{ for every } 1\le u\le l,\\ \sum_{i \in I_u} 1/(1-\unicode{x3bb}_i)=0 \textrm{ for every } 1\le u\le l \end{matrix} \right.\right\}\hspace{-2.5pt}, \end{align*} $$
$$ \begin{align*} \mathfrak{I}(\unicode{x3bb}) := \left\{ \{I_1,\ldots,I_l\}\ \left| \ \begin{matrix} l \ge 2,\ \ I_1 \amalg \cdots \amalg I_l = \{1,\ldots,d \},\\ I_u \ne \emptyset \textrm{ for every } 1\le u\le l,\\ \sum_{i \in I_u} 1/(1-\unicode{x3bb}_i)=0 \textrm{ for every } 1\le u\le l \end{matrix} \right.\right\}\hspace{-2.5pt}, \end{align*} $$
where
![]() $I_1 \amalg \cdots \amalg I_l$
denotes the disjoint union of
$I_1 \amalg \cdots \amalg I_l$
denotes the disjoint union of
![]() $I_1,\ldots ,I_l$
. By definition, each element of
$I_1,\ldots ,I_l$
. By definition, each element of
![]() $\mathfrak {I}(\unicode{x3bb} )$
is considered to be a partition of
$\mathfrak {I}(\unicode{x3bb} )$
is considered to be a partition of
![]() $\{1,\ldots ,d \}$
. The partial order
$\{1,\ldots ,d \}$
. The partial order
![]() $\prec $
in
$\prec $
in
![]() $\mathfrak {I}(\unicode{x3bb} )$
is defined by the refinement of partitions, namely, for
$\mathfrak {I}(\unicode{x3bb} )$
is defined by the refinement of partitions, namely, for
![]() $\mathbb {I}, \mathbb {I}'\in \mathfrak {I}(\unicode{x3bb} )$
, the relation
$\mathbb {I}, \mathbb {I}'\in \mathfrak {I}(\unicode{x3bb} )$
, the relation
![]() $\mathbb {I} \prec \mathbb {I}'$
holds if and only if
$\mathbb {I} \prec \mathbb {I}'$
holds if and only if
![]() $\mathbb {I}'$
is a refinement of
$\mathbb {I}'$
is a refinement of
![]() $\mathbb {I}$
as partitions of
$\mathbb {I}$
as partitions of
![]() $\{1,\ldots ,d \}$
.
$\{1,\ldots ,d \}$
.
For
![]() $\unicode{x3bb} \in V_d$
and for
$\unicode{x3bb} \in V_d$
and for
![]() $I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, we put
$I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, we put
![]() $\unicode{x3bb} _I := (\unicode{x3bb} _i)_{i \in I}$
.
$\unicode{x3bb} _I := (\unicode{x3bb} _i)_{i \in I}$
.
In the above definition, note that the condition
![]() $I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
for I is equivalent to the conditions
$I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
for I is equivalent to the conditions
![]() $\emptyset \subsetneq I \subsetneq \{1,\ldots ,d \}$
and
$\emptyset \subsetneq I \subsetneq \{1,\ldots ,d \}$
and
![]() $\sum _{i \in I} 1/(1-\unicode{x3bb} _i)=0$
. Hence, we always have
$\sum _{i \in I} 1/(1-\unicode{x3bb} _i)=0$
. Hence, we always have
![]() $\unicode{x3bb} _I \in V_{\# I}$
for
$\unicode{x3bb} _I \in V_{\# I}$
for
![]() $\unicode{x3bb} \in V_d$
and
$\unicode{x3bb} \in V_d$
and
![]() $I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
by definition. Also note that
$I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
by definition. Also note that
![]() $\# I \geq 2$
holds for every
$\# I \geq 2$
holds for every
![]() $I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
.
$I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
.
The following object is also very important in this paper.
Definition 2.2. For
![]() $\unicode{x3bb} \in V_d$
, we put
$\unicode{x3bb} \in V_d$
, we put
The partial order
![]() $\prec $
in
$\prec $
in
![]() $\mathfrak {I}(\unicode{x3bb} )$
is naturally extended to the partial order
$\mathfrak {I}(\unicode{x3bb} )$
is naturally extended to the partial order
![]() $\prec $
in
$\prec $
in
![]() $\mathfrak {I}'(\unicode{x3bb} )$
.
$\mathfrak {I}'(\unicode{x3bb} )$
.
By definition,
![]() $\mathfrak {I}'(\unicode{x3bb} )$
is obtained from
$\mathfrak {I}'(\unicode{x3bb} )$
is obtained from
![]() $\mathfrak {I}(\unicode{x3bb} )$
by adding exactly one element
$\mathfrak {I}(\unicode{x3bb} )$
by adding exactly one element
![]() $\mathbb {I}_0 := \{\{ 1, \ldots , d\}\}$
. Here,
$\mathbb {I}_0 := \{\{ 1, \ldots , d\}\}$
. Here,
![]() $\mathbb {I}_0$
is the unique minimum element of
$\mathbb {I}_0$
is the unique minimum element of
![]() $\mathfrak {I}'(\unicode{x3bb} )$
with respect to the partial order
$\mathfrak {I}'(\unicode{x3bb} )$
with respect to the partial order
![]() $\prec $
. Moreover,
$\prec $
. Moreover,
![]() $\mathbb {I}_0$
is considered to be a partition of
$\mathbb {I}_0$
is considered to be a partition of
![]() $\{ 1, \ldots , d \}$
which, in practice, does not partition
$\{ 1, \ldots , d \}$
which, in practice, does not partition
![]() $\{ 1, \ldots , d \}$
. We also have the equality
$\{ 1, \ldots , d \}$
. We also have the equality
 $$ \begin{align*} \mathfrak{I}'(\unicode{x3bb}) = \left\{ \{I_1,\ldots,I_l\}\ \left| \ \begin{matrix} l \ge 1, I_1 \amalg \cdots \amalg I_l = \{1,\ldots,d \},\\ I_u \ne \emptyset \textrm{ for every } 1\le u\le l,\\ \sum_{i \in I_u} 1/(1-\unicode{x3bb}_i)=0 \textrm{ for every } 1\le u\le l \end{matrix} \right.\right\}\hspace{-2.5pt}. \end{align*} $$
$$ \begin{align*} \mathfrak{I}'(\unicode{x3bb}) = \left\{ \{I_1,\ldots,I_l\}\ \left| \ \begin{matrix} l \ge 1, I_1 \amalg \cdots \amalg I_l = \{1,\ldots,d \},\\ I_u \ne \emptyset \textrm{ for every } 1\le u\le l,\\ \sum_{i \in I_u} 1/(1-\unicode{x3bb}_i)=0 \textrm{ for every } 1\le u\le l \end{matrix} \right.\right\}\hspace{-2.5pt}. \end{align*} $$
We already have the following theorem by Main Theorem III and Remark 1.8 in [Reference Sugiyama14] and by Theorem B and Proposition C in §6 in [Reference Sugiyama14].
Theorem 2.3. We can define the non-negative integer
![]() $e_{\mathbb {I}}(\unicode{x3bb} )$
for each
$e_{\mathbb {I}}(\unicode{x3bb} )$
for each
![]() $d \geq 4$
,
$d \geq 4$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, and can also define the non-negative integer
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, and can also define the non-negative integer
![]() $s_d(\unicode{x3bb} )$
for each
$s_d(\unicode{x3bb} )$
for each
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
inductively by the equalities
$\unicode{x3bb} \in V_d$
inductively by the equalities
 $$ \begin{align} s_d(\unicode{x3bb}) = (d-2)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-2}k \bigg) \end{align} $$
$$ \begin{align} s_d(\unicode{x3bb}) = (d-2)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-2}k \bigg) \end{align} $$
for
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
for
![]() $d \geq 4$
,
$d \geq 4$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
. Here, in the case
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
. Here, in the case
![]() $\# \mathbb {I} = 2$
, we put
$\# \mathbb {I} = 2$
, we put
![]() $\prod _{k=d-\# \mathbb {I} +1}^{d-2}k = \prod _{k=d-1}^{d-2}k = 1$
.
$\prod _{k=d-\# \mathbb {I} +1}^{d-2}k = \prod _{k=d-1}^{d-2}k = 1$
.
If we consider
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
‘counted with multiplicity’ for
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
‘counted with multiplicity’ for
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
, then we have
$\unicode{x3bb} \in V_d$
, then we have
Remark 2.4. For
![]() $d=2$
or
$d=2$
or
![]() $3$
, we always have
$3$
, we always have
![]() $\mathfrak {I}(\unicode{x3bb} ) = \emptyset $
for every
$\mathfrak {I}(\unicode{x3bb} ) = \emptyset $
for every
![]() $\unicode{x3bb} \in V_d$
by definition. Hence, by equation (2.1), we have
$\unicode{x3bb} \in V_d$
by definition. Hence, by equation (2.1), we have
![]() $s_2(\unicode{x3bb} ) = (2-2)!=1$
for every
$s_2(\unicode{x3bb} ) = (2-2)!=1$
for every
![]() $\unicode{x3bb} \in V_2$
and
$\unicode{x3bb} \in V_2$
and
![]() $s_3(\unicode{x3bb} ) = (3-2)!=1$
for every
$s_3(\unicode{x3bb} ) = (3-2)!=1$
for every
![]() $\unicode{x3bb} \in V_3$
. For
$\unicode{x3bb} \in V_3$
. For
![]() $d \geq 4$
, every
$d \geq 4$
, every
![]() $e_{\mathbb {I}}(\unicode{x3bb} )$
and
$e_{\mathbb {I}}(\unicode{x3bb} )$
and
![]() $s_d(\unicode{x3bb} )$
are determined uniquely and can actually be found by equations (2.1) and (2.2) by induction on d, since
$s_d(\unicode{x3bb} )$
are determined uniquely and can actually be found by equations (2.1) and (2.2) by induction on d, since
![]() $2 \leq \# I < d$
holds for
$2 \leq \# I < d$
holds for
![]() $I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
with
$I \in \mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\unicode{x3bb} \in V_d$
.
$\unicode{x3bb} \in V_d$
.
In the rest of this paper, we always assume that
![]() $e_{\mathbb {I}}(\unicode{x3bb} )$
and
$e_{\mathbb {I}}(\unicode{x3bb} )$
and
![]() $s_d(\unicode{x3bb} )$
are the non-negative integers defined in Theorem 2.3.
$s_d(\unicode{x3bb} )$
are the non-negative integers defined in Theorem 2.3.
We already made a minor improvement to the above algorithm by Main Theorem III in [Reference Sugiyama14] and by Proposition D in §6 in [Reference Sugiyama14], as in the following.
Theorem 2.5. The non-negative integer
![]() $e_{\mathbb {I}}(\unicode{x3bb} )$
for
$e_{\mathbb {I}}(\unicode{x3bb} )$
for
![]() $\unicode{x3bb} \in V_d$
and
$\unicode{x3bb} \in V_d$
and
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
defined in Theorem 2.3 also satisfies the equality
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
defined in Theorem 2.3 also satisfies the equality
 $$ \begin{align} e_{\mathbb{I}}(\unicode{x3bb}) = \bigg(\prod_{I \in \mathbb{I}} ( \# I -1 )! \bigg) - \sum_{{{\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I}, \; \mathbb{I}' \ne \mathbb{I} \end{matrix}}}} \bigg( e_{\mathbb{I}'}(\unicode{x3bb}) \cdot \prod_{I \in \mathbb{I}} \bigg( \prod_{k=\# I - \chi_I(\mathbb{I}')+1 }^{\# I -1}k \bigg) \bigg), \end{align} $$
$$ \begin{align} e_{\mathbb{I}}(\unicode{x3bb}) = \bigg(\prod_{I \in \mathbb{I}} ( \# I -1 )! \bigg) - \sum_{{{\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I}, \; \mathbb{I}' \ne \mathbb{I} \end{matrix}}}} \bigg( e_{\mathbb{I}'}(\unicode{x3bb}) \cdot \prod_{I \in \mathbb{I}} \bigg( \prod_{k=\# I - \chi_I(\mathbb{I}')+1 }^{\# I -1}k \bigg) \bigg), \end{align} $$
where we put
![]() $\chi _I(\mathbb {I}'):=\#(\{ I'\in \mathbb {I}' \mid I' \subseteq I \})$
for
$\chi _I(\mathbb {I}'):=\#(\{ I'\in \mathbb {I}' \mid I' \subseteq I \})$
for
![]() $\mathbb {I}' \succ \mathbb {I}$
and
$\mathbb {I}' \succ \mathbb {I}$
and
![]() $I \in \mathbb {I}$
. Here, in the case
$I \in \mathbb {I}$
. Here, in the case
![]() $\chi _I(\mathbb {I}') = 1$
, we put
$\chi _I(\mathbb {I}') = 1$
, we put
![]() $\prod _{k=\# I - \chi _I(\mathbb {I}')+1 }^{\# I -1}k = \prod _{k=\# I}^{\# I -1}k = 1$
.
$\prod _{k=\# I - \chi _I(\mathbb {I}')+1 }^{\# I -1}k = \prod _{k=\# I}^{\# I -1}k = 1$
.
Remark 2.6. By definition, we always have
![]() $\sum _{I \in \mathbb {I}} \chi _I(\mathbb {I}') = \# \mathbb {I}'$
for
$\sum _{I \in \mathbb {I}} \chi _I(\mathbb {I}') = \# \mathbb {I}'$
for
![]() $\mathbb {I}' \succ \mathbb {I}$
.
$\mathbb {I}' \succ \mathbb {I}$
.
Remark 2.7. We can also find
![]() $s_d(\unicode{x3bb} )$
only by using equations (2.1) and (2.3). The algorithm using equations (2.1) and (2.3) is a little simpler than the algorithm in Theorem 2.3.
$s_d(\unicode{x3bb} )$
only by using equations (2.1) and (2.3). The algorithm using equations (2.1) and (2.3) is a little simpler than the algorithm in Theorem 2.3.
Remark 2.8. We present a rough outline of the proof of Theorem 2.5 in this remark, since the proof can be an easy exercise for the proof of Theorem I in this paper. (See ‘Proof of Proposition D’ on pp. 175–177 in [Reference Sugiyama14] for details.) In the case where
![]() $d = \# I$
and
$d = \# I$
and
![]() $\unicode{x3bb} = \unicode{x3bb} _I$
, equation (2.1) is equivalent to the following:
$\unicode{x3bb} = \unicode{x3bb} _I$
, equation (2.1) is equivalent to the following:
 $$ \begin{align} ( \# I - 1 )! = ( \# I - 1 ) s_{\# I}(\unicode{x3bb}_I) + \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb}_I)} \bigg( e_{\mathbb{I}}(\unicode{x3bb}_I)\cdot \prod_{k=\#I -\# \mathbb{I}+1}^{\#I - 1}k \bigg). \end{align} $$
$$ \begin{align} ( \# I - 1 )! = ( \# I - 1 ) s_{\# I}(\unicode{x3bb}_I) + \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb}_I)} \bigg( e_{\mathbb{I}}(\unicode{x3bb}_I)\cdot \prod_{k=\#I -\# \mathbb{I}+1}^{\#I - 1}k \bigg). \end{align} $$
Plugging equation (2.4) into
![]() $\prod _{I \in \mathbb {I}} ( \# I -1 )!$
and using equation (2.2) carefully, we have equation (2.3).
$\prod _{I \in \mathbb {I}} ( \# I -1 )!$
and using equation (2.2) carefully, we have equation (2.3).
In this paper, we make a drastic improvement to the above algorithm as in the following.
Theorem I. The non-negative integer
![]() $s_d(\unicode{x3bb} )$
for
$s_d(\unicode{x3bb} )$
for
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
defined in Theorem 2.3 is expressed in the form
$\unicode{x3bb} \in V_d$
defined in Theorem 2.3 is expressed in the form
 $$ \begin{align} (d-1)s_d(\unicode{x3bb}) = \sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align} $$
$$ \begin{align} (d-1)s_d(\unicode{x3bb}) = \sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align} $$
Hence, if we consider
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
‘counted with multiplicity’ for
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
‘counted with multiplicity’ for
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
, then we have
$\unicode{x3bb} \in V_d$
, then we have
 $$ \begin{align} \#(\Phi_d^{-1}(\bar{\unicode{x3bb}})) = -\sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 2} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align} $$
$$ \begin{align} \#(\Phi_d^{-1}(\bar{\unicode{x3bb}})) = -\sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 2} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align} $$
Remark 2.9. By Theorem I, we no longer need induction processes to find
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
if we consider
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
if we consider
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity. We only need to find
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
counted with multiplicity. We only need to find
![]() $\mathfrak {I}'(\unicode{x3bb} )$
and to compute straightforward the right-hand side of equation (2.6).
$\mathfrak {I}'(\unicode{x3bb} )$
and to compute straightforward the right-hand side of equation (2.6).
However, there are some minor defects in the form of equation (2.6) comparing with equation (2.1). By equation (2.1), we can easily see the inequality
![]() $s_d(\unicode{x3bb} ) \leq (d-2)!$
; however, it cannot be easily seen by equation (2.6). The sum of the absolute value
$s_d(\unicode{x3bb} ) \leq (d-2)!$
; however, it cannot be easily seen by equation (2.6). The sum of the absolute value
![]() $\sum _{\mathbb {I}\in \mathfrak {I}'(\unicode{x3bb} )} ( (d-1)^{\#\mathbb {I} - 2} \cdot \prod _{I \in \mathbb {I}}( \#I - 1 )! )$
in the right-hand side of equation (2.6) can be much greater than
$\sum _{\mathbb {I}\in \mathfrak {I}'(\unicode{x3bb} )} ( (d-1)^{\#\mathbb {I} - 2} \cdot \prod _{I \in \mathbb {I}}( \#I - 1 )! )$
in the right-hand side of equation (2.6) can be much greater than
![]() $(d-2)!$
.
$(d-2)!$
.
Remark 2.10. Each term in the right-hand side of equation (2.5)
![]() $\{ -(d-1) \}^{\#\mathbb {I} - 1} \cdot \prod _{I \in \mathbb {I}}( \#I - 1 )!$
is positive or negative, according to whether
$\{ -(d-1) \}^{\#\mathbb {I} - 1} \cdot \prod _{I \in \mathbb {I}}( \#I - 1 )!$
is positive or negative, according to whether
![]() $\#\mathbb {I}$
is odd or even. Moreover, if
$\#\mathbb {I}$
is odd or even. Moreover, if
![]() $\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} )$
and
$\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} )$
and
![]() $\mathbb {I}' \prec \mathbb {I}$
, then we automatically have
$\mathbb {I}' \prec \mathbb {I}$
, then we automatically have
![]() $\mathbb {I}' \in \mathfrak {I}'(\unicode{x3bb} )$
. Hence, equation (2.5) is considered to be a kind of inclusion-exclusion formula.
$\mathbb {I}' \in \mathfrak {I}'(\unicode{x3bb} )$
. Hence, equation (2.5) is considered to be a kind of inclusion-exclusion formula.
3 Main result 2
In this section, we proceed to the next step, in which we discuss the possibility of improving the algorithm for counting the number of discrete elements of
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
. Therefore, in this section,
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
. Therefore, in this section,
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity;
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity;
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is considered to be a set. In this setting, we have already obtained an algorithm for counting the number of discrete elements of
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is considered to be a set. In this setting, we have already obtained an algorithm for counting the number of discrete elements of
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
by using
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
by using
![]() $\{s_{d'}(\unicode{x3bb} ') \mid 2 \leq d' \leq d,\ \unicode{x3bb} ' \in V_{d'} \}$
in the third and fourth steps in Main Theorem III in [Reference Sugiyama14]. To review the result more precisely and to discuss further properties, we first fix our notation.
$\{s_{d'}(\unicode{x3bb} ') \mid 2 \leq d' \leq d,\ \unicode{x3bb} ' \in V_{d'} \}$
in the third and fourth steps in Main Theorem III in [Reference Sugiyama14]. To review the result more precisely and to discuss further properties, we first fix our notation.
The following objects are important in this section.
Definition 3.1. For
![]() $\unicode{x3bb} = (\unicode{x3bb} _1, \ldots , \unicode{x3bb} _d) \in V_d$
, we put
$\unicode{x3bb} = (\unicode{x3bb} _1, \ldots , \unicode{x3bb} _d) \in V_d$
, we put
 $$ \begin{align*} \mathfrak{K}(\unicode{x3bb}) := \left\{K \ \left| \ \begin{matrix} \emptyset \subsetneq K \subseteq \{1,\ldots,d \},\\ i,j \in K \Rightarrow \unicode{x3bb}_i = \unicode{x3bb}_j,\\ i\in K,\ j\in\{1,\ldots,d\}\setminus K\Longrightarrow\unicode{x3bb}_i\ne\unicode{x3bb}_j \end{matrix} \right.\right\}\hspace{-2.5pt}. \end{align*} $$
$$ \begin{align*} \mathfrak{K}(\unicode{x3bb}) := \left\{K \ \left| \ \begin{matrix} \emptyset \subsetneq K \subseteq \{1,\ldots,d \},\\ i,j \in K \Rightarrow \unicode{x3bb}_i = \unicode{x3bb}_j,\\ i\in K,\ j\in\{1,\ldots,d\}\setminus K\Longrightarrow\unicode{x3bb}_i\ne\unicode{x3bb}_j \end{matrix} \right.\right\}\hspace{-2.5pt}. \end{align*} $$
Note that if we put
![]() $\mathfrak {K}(\unicode{x3bb} ) =: \{ K_1,\ldots , K_q \}$
, then
$\mathfrak {K}(\unicode{x3bb} ) =: \{ K_1,\ldots , K_q \}$
, then
![]() $K_1,\ldots , K_q$
are mutually disjoint, and the equality
$K_1,\ldots , K_q$
are mutually disjoint, and the equality
![]() $K_1 \amalg \cdots \amalg K_q = \{1,\ldots ,d\}$
holds by definition; and hence
$K_1 \amalg \cdots \amalg K_q = \{1,\ldots ,d\}$
holds by definition; and hence
![]() $\mathfrak {K}(\unicode{x3bb} )$
is a partition of
$\mathfrak {K}(\unicode{x3bb} )$
is a partition of
![]() $\{1,\ldots ,d\}$
.
$\{1,\ldots ,d\}$
.
Definition 3.2. We denote the family of monic centered polynomials of degree d by
 $$ \begin{align*} \mathrm{MC}_d := \bigg\{ f(z) = z^d + \sum_{k=0}^{d-2}a_kz^k \ \bigg| \ a_k \in \mathbb{C} \text{ for } 0 \leq k \leq d-2 \bigg\}, \end{align*} $$
$$ \begin{align*} \mathrm{MC}_d := \bigg\{ f(z) = z^d + \sum_{k=0}^{d-2}a_kz^k \ \bigg| \ a_k \in \mathbb{C} \text{ for } 0 \leq k \leq d-2 \bigg\}, \end{align*} $$
denote the composite mapping of
![]() $\mathrm {MC}_d \subset \mathrm {Poly}_d \twoheadrightarrow \mathrm {Poly}_d / \mathrm {Aut}(\mathbb {C}) = \mathrm {MP}_d$
by
$\mathrm {MC}_d \subset \mathrm {Poly}_d \twoheadrightarrow \mathrm {Poly}_d / \mathrm {Aut}(\mathbb {C}) = \mathrm {MP}_d$
by
![]() $p : \mathrm {MC}_d \to \mathrm {MP}_d$
, and also denote the composite mapping of
$p : \mathrm {MC}_d \to \mathrm {MP}_d$
, and also denote the composite mapping of
![]() $p: \mathrm {MC}_d \to \mathrm {MP}_d$
and
$p: \mathrm {MC}_d \to \mathrm {MP}_d$
and
![]() $\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
by
$\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
by
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, that is,
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, that is,
![]() $\widehat {\Phi }_d := \Phi _d \circ p$
.
$\widehat {\Phi }_d := \Phi _d \circ p$
.
In the above definition, the map p is surjective since every affine conjugacy class of polynomial maps contains monic centered polynomials. Moreover, two monic centered polynomials
![]() $f, g \in \mathrm {MC}_d$
are affinely conjugate if and only if there exists a
$f, g \in \mathrm {MC}_d$
are affinely conjugate if and only if there exists a
![]() $(d-1)$
th radical root a of
$(d-1)$
th radical root a of
![]() $1$
such that the equality
$1$
such that the equality
![]() $g(z) = a f(a^{-1}z)$
holds. Hence, the group
$g(z) = a f(a^{-1}z)$
holds. Hence, the group
![]() $\{ a \in \mathbb {C} \mid a^{d-1} = 1 \} \cong \mathbb {Z} /(d-1)\mathbb {Z}$
naturally acts on
$\{ a \in \mathbb {C} \mid a^{d-1} = 1 \} \cong \mathbb {Z} /(d-1)\mathbb {Z}$
naturally acts on
![]() $\mathrm {MC}_d$
, and the induced mapping
$\mathrm {MC}_d$
, and the induced mapping
![]() $\overline {p} : \mathrm {MC}_d / ( \mathbb {Z} /(d-1)\mathbb {Z} ) \to \mathrm {MP}_d$
is an isomorphism. Since
$\overline {p} : \mathrm {MC}_d / ( \mathbb {Z} /(d-1)\mathbb {Z} ) \to \mathrm {MP}_d$
is an isomorphism. Since
![]() $\mathrm {MC}_d \cong \mathbb {C}^{d-1}$
, we also have
$\mathrm {MC}_d \cong \mathbb {C}^{d-1}$
, we also have
![]() $\mathrm {MP}_d \cong \mathbb {C}^{d-1} / ( \mathbb {Z} /(d-1)\mathbb {Z} )$
. Here, the action of
$\mathrm {MP}_d \cong \mathbb {C}^{d-1} / ( \mathbb {Z} /(d-1)\mathbb {Z} )$
. Here, the action of
![]() $\mathbb {Z} /(d-1)\mathbb {Z}$
on
$\mathbb {Z} /(d-1)\mathbb {Z}$
on
![]() $\mathrm {MC}_d$
is not free for
$\mathrm {MC}_d$
is not free for
![]() $d \geq 3$
, and
$d \geq 3$
, and
![]() $\mathrm {MP}_d$
has the set of singular points
$\mathrm {MP}_d$
has the set of singular points
![]() $\mathrm {Sing}(\mathrm {MP}_d)$
for
$\mathrm {Sing}(\mathrm {MP}_d)$
for
![]() $d \geq 4$
. Hence, in some sense, the map
$d \geq 4$
. Hence, in some sense, the map
![]() $p : \mathrm {MC}_d \to \mathrm {MP}_d$
can be considered to be a ‘desingularization’ of
$p : \mathrm {MC}_d \to \mathrm {MP}_d$
can be considered to be a ‘desingularization’ of
![]() $\mathrm {MP}_d$
for
$\mathrm {MP}_d$
for
![]() $d \geq 4$
.
$d \geq 4$
.
We already have the following theorem by Remark 1.9 in [Reference Sugiyama14].
Theorem 3.3. For
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} \in V_d$
, we put
$\unicode{x3bb} \in V_d$
, we put
![]() $\mathfrak {K}(\unicode{x3bb} ) =: \{ K_1,\ldots , K_q \}$
and denote by
$\mathfrak {K}(\unicode{x3bb} ) =: \{ K_1,\ldots , K_q \}$
and denote by
![]() $g_w$
the greatest common divisor of
$g_w$
the greatest common divisor of
![]() $\#K_1,\ldots ,\#K_{(w-1)},(\#K_w)-1,\#K_{(w+1)},\ldots ,\#K_q$
for each
$\#K_1,\ldots ,\#K_{(w-1)},(\#K_w)-1,\#K_{(w+1)},\ldots ,\#K_q$
for each
![]() $1\le w\le q$
. If
$1\le w\le q$
. If
![]() $g_w=1$
holds for every
$g_w=1$
holds for every
![]() $1 \leq w \leq q$
, then we have
$1 \leq w \leq q$
, then we have
 $$ \begin{align} \#(\Phi_d^{-1}(\bar{\unicode{x3bb}})) = \frac{s_d(\unicode{x3bb})}{(\#K_1)!\cdots(\#K_q)!} = \frac{s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align} $$
$$ \begin{align} \#(\Phi_d^{-1}(\bar{\unicode{x3bb}})) = \frac{s_d(\unicode{x3bb})}{(\#K_1)!\cdots(\#K_q)!} = \frac{s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align} $$
where
![]() $s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3 and rewritten in Theorem I. Here, note that
$s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3 and rewritten in Theorem I. Here, note that
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity, and hence
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity, and hence
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
denotes the number of discrete elements of
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
denotes the number of discrete elements of
![]() $\Phi _d^{-1}(\bar {\unicode{x3bb} })$
.
$\Phi _d^{-1}(\bar {\unicode{x3bb} })$
.
In the case of
![]() $g_w \geq 2$
for some w, we also have an algorithm for finding
$g_w \geq 2$
for some w, we also have an algorithm for finding
![]() $\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
in the third and fourth steps in Main Theorem III in [Reference Sugiyama14]. However, it contains induction processes and is much more complicated than equation (3.1); and hence we omit to describe it again in this paper.
$\#(\Phi _d^{-1}(\bar {\unicode{x3bb} }))$
in the third and fourth steps in Main Theorem III in [Reference Sugiyama14]. However, it contains induction processes and is much more complicated than equation (3.1); and hence we omit to describe it again in this paper.
As we already mentioned in Remark 1.9 in [Reference Sugiyama14], we find that for
![]() $d \geq 4$
and for
$d \geq 4$
and for
![]() $\unicode{x3bb} \in V_d$
, the inequality
$\unicode{x3bb} \in V_d$
, the inequality
![]() $g_w \geq 2$
holds for some w only if
$g_w \geq 2$
holds for some w only if
![]() $\bar {\unicode{x3bb} } \in \Phi _d(\mathrm {Sing}(\mathrm {MP}_d))$
. Since
$\bar {\unicode{x3bb} } \in \Phi _d(\mathrm {Sing}(\mathrm {MP}_d))$
. Since
![]() $\mathrm {MC}_d$
is a ‘desingularization’ of
$\mathrm {MC}_d$
is a ‘desingularization’ of
![]() $\mathrm {MP}_d$
, it is natural to expect that the map
$\mathrm {MP}_d$
, it is natural to expect that the map
![]() $\widehat {\Phi }_d = \Phi _d\circ p : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is simpler than the map
$\widehat {\Phi }_d = \Phi _d\circ p : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is simpler than the map
![]() $\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
itself. In the following, we consider
$\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
itself. In the following, we consider
![]() $\mathrm {MC}_d$
instead of
$\mathrm {MC}_d$
instead of
![]() $\mathrm {MP}_d$
, and also consider
$\mathrm {MP}_d$
, and also consider
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
instead of
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
instead of
![]() $\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
.
$\Phi _d : \mathrm {MP}_d \to \widetilde {\Lambda }_d$
.
We now state the second main theorem in this paper.
Theorem II. For
![]() $d \geq 2$
,
$d \geq 2$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, we have
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, we have
 $$ \begin{align} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{(d-1)s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align} $$
$$ \begin{align} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{(d-1)s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align} $$
where
![]() $s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3 and rewritten in Theorem I. Here, note that
$s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3 and rewritten in Theorem I. Here, note that
![]() $\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity, and hence
$\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
is not considered counted with multiplicity, and hence
![]() $\#(\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} }))$
denotes the number of discrete elements of
$\#(\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} }))$
denotes the number of discrete elements of
![]() $\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
.
$\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
.
Remark 3.4. Theorem II holds for every
![]() $\unicode{x3bb} \in V_d$
with no exception, and has no induction process. Hence, we can say that the fiber structure of the map
$\unicode{x3bb} \in V_d$
with no exception, and has no induction process. Hence, we can say that the fiber structure of the map
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is simpler than the fiber structure of the map
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
is simpler than the fiber structure of the map
![]() $\Phi _d: \mathrm {MP}_d \to \widetilde {\Lambda }_d$
, or moreover we can also say that the complexity of the map
$\Phi _d: \mathrm {MP}_d \to \widetilde {\Lambda }_d$
, or moreover we can also say that the complexity of the map
![]() $\Phi _d: \mathrm {MP}_d \to \widetilde {\Lambda }_d$
is composed of the two complexities: one of them is the complexity of the map
$\Phi _d: \mathrm {MP}_d \to \widetilde {\Lambda }_d$
is composed of the two complexities: one of them is the complexity of the map
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
and the other is the complexity of the map
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
and the other is the complexity of the map
![]() $p: \mathrm {MC}_d \to \mathrm {MP}_d$
. Therefore, in some sense, consideration of the map
$p: \mathrm {MC}_d \to \mathrm {MP}_d$
. Therefore, in some sense, consideration of the map
![]() $\widehat {\Phi }_d$
is more essential than that of the map
$\widehat {\Phi }_d$
is more essential than that of the map
![]() $\Phi _d$
in the study of fixed-point multipliers for polynomial maps.
$\Phi _d$
in the study of fixed-point multipliers for polynomial maps.
Remark 3.5. Theorem II is proved by a closer look at Propositions 4.3 and 9.1 in [Reference Sugiyama14].
Combining Theorems I and II, we have the following.
Corollary III. For
![]() $d \geq 2$
,
$d \geq 2$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, we have
$\widehat {\Phi }_d : \mathrm {MC}_d \to \widetilde {\Lambda }_d$
, we have
 $$ \begin{align*} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{\sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} ( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )! )}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}. \end{align*} $$
$$ \begin{align*} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{\sum_{\mathbb{I}\in \mathfrak{I}'(\unicode{x3bb})} ( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )! )}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}. \end{align*} $$
4 Proof of Theorem I
In this section, we prove Theorem I. We assume
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, and denote by
$\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, and denote by
![]() $\mathbb {I}_0 = \{\{ 1,\ldots ,d \}\}$
the minimum element of
$\mathbb {I}_0 = \{\{ 1,\ldots ,d \}\}$
the minimum element of
![]() $\mathfrak {I}'(\unicode{x3bb} )$
, which are fixed throughout this section.
$\mathfrak {I}'(\unicode{x3bb} )$
, which are fixed throughout this section.
First we put
for
![]() $\mathbb {I}_0 = \{\{ 1,\ldots ,d \}\} \in \mathfrak {I}'(\unicode{x3bb} )$
. Then, equation (2.2) for
$\mathbb {I}_0 = \{\{ 1,\ldots ,d \}\} \in \mathfrak {I}'(\unicode{x3bb} )$
. Then, equation (2.2) for
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
is rewritten in the form
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
is rewritten in the form
Here,
![]() $\{I\}$
denotes the minimum element of
$\{I\}$
denotes the minimum element of
![]() $\mathfrak {I}'(\unicode{x3bb} _I)$
. Moreover, equation (2.1) is rewritten in the form
$\mathfrak {I}'(\unicode{x3bb} _I)$
. Moreover, equation (2.1) is rewritten in the form
 $$ \begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg), \end{align} $$
$$ \begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg), \end{align} $$
which is also equivalent to the equality
 $$ \begin{align*} (d-1)! = \sum_{\mathbb{I} \in \mathfrak{I}'(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \end{align*} $$
$$ \begin{align*} (d-1)! = \sum_{\mathbb{I} \in \mathfrak{I}'(\unicode{x3bb})} \bigg( e_{\mathbb{I}}(\unicode{x3bb})\cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \end{align*} $$
since for
![]() $\mathbb {I}_0 \in \mathfrak {I}'(\unicode{x3bb} )$
, we have
$\mathbb {I}_0 \in \mathfrak {I}'(\unicode{x3bb} )$
, we have
![]() $e_{\mathbb {I}_0}(\unicode{x3bb} )\cdot \prod _{k=d-\# \mathbb {I}_0 +1}^{d-1}k = e_{\mathbb {I}_0}(\unicode{x3bb} )\cdot \prod _{k=d}^{d-1}k = e_{\mathbb {I}_0}(\unicode{x3bb} )$
. Equation (2.5), which we would like to prove in this section, is also rewritten in the form
$e_{\mathbb {I}_0}(\unicode{x3bb} )\cdot \prod _{k=d-\# \mathbb {I}_0 +1}^{d-1}k = e_{\mathbb {I}_0}(\unicode{x3bb} )\cdot \prod _{k=d}^{d-1}k = e_{\mathbb {I}_0}(\unicode{x3bb} )$
. Equation (2.5), which we would like to prove in this section, is also rewritten in the form
 $$\begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = \sum_{\mathbb{I} \in \mathfrak{I}'(\unicode{x3bb}) } \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align}$$
$$\begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = \sum_{\mathbb{I} \in \mathfrak{I}'(\unicode{x3bb}) } \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg). \end{align}$$
Hence, to prove Theorem I, it suffices to derive equation (4.3) d from equations (4.1) and (4.2).
In the following, we show equation (4.3) d by induction on d.
For
![]() $d=2$
or
$d=2$
or
![]() $3$
, we have
$3$
, we have
![]() $s_d(\unicode{x3bb} )=1$
and
$s_d(\unicode{x3bb} )=1$
and
![]() $\mathfrak {I}'(\unicode{x3bb} ) = \{ \mathbb {I}_0 \}$
for every
$\mathfrak {I}'(\unicode{x3bb} ) = \{ \mathbb {I}_0 \}$
for every
![]() $\unicode{x3bb} \in V_d$
. Hence, for
$\unicode{x3bb} \in V_d$
. Hence, for
![]() $\unicode{x3bb} \in V_d$
, we always have
$\unicode{x3bb} \in V_d$
, we always have
and also have
 $$ \begin{align*} \sum\limits_{{\mathbb{I}\in \mathfrak{I}'}(\unicode{x3bb}) } \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg) &= \{ -(d-1) \}^{\#\mathbb{I}_0 - 1} \cdot \prod_{I \in \mathbb{I}_0}( \#I - 1 )!\\ &= \{ -(d-1) \}^{1 - 1} \cdot ( d - 1 )! = (d-1)!. \end{align*} $$
$$ \begin{align*} \sum\limits_{{\mathbb{I}\in \mathfrak{I}'}(\unicode{x3bb}) } \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg) &= \{ -(d-1) \}^{\#\mathbb{I}_0 - 1} \cdot \prod_{I \in \mathbb{I}_0}( \#I - 1 )!\\ &= \{ -(d-1) \}^{1 - 1} \cdot ( d - 1 )! = (d-1)!. \end{align*} $$
Since
![]() $d-1 = (d-1)!$
for
$d-1 = (d-1)!$
for
![]() $d=2$
or
$d=2$
or
![]() $3$
, we have equations
$3$
, we have equations
![]() $(4.3)_2$
and
$(4.3)_2$
and
![]() $(4.3)_3$
.
$(4.3)_3$
.
In the following, we assume
![]() $d \geq 4$
and show equation (4.3)
d
by the assumption of equations
$d \geq 4$
and show equation (4.3)
d
by the assumption of equations
![]() $(4.3)_2, (4.3)_3, \ldots , (4.3)_{d-1}$
, (4.1), and (4.2).
$(4.3)_2, (4.3)_3, \ldots , (4.3)_{d-1}$
, (4.1), and (4.2).
For each
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\unicode{x3bb} \in V_d$
, we put
$\unicode{x3bb} \in V_d$
, we put
![]() $\mathbb {I}=:\{ I_1,\ldots ,I_l \}$
. Then, by using equations (4.1) and
$\mathbb {I}=:\{ I_1,\ldots ,I_l \}$
. Then, by using equations (4.1) and
![]() $(4.3)_{d'}$
for
$(4.3)_{d'}$
for
![]() $2 \leq d' < d$
, we have the following equalities:
$2 \leq d' < d$
, we have the following equalities:
 $$ \begin{align}\begin{aligned} e_{\mathbb{I}}(\unicode{x3bb}) &= \prod_{I \in \mathbb{I}} e_{\{I\}}(\unicode{x3bb}_I) = \prod_{u=1}^l e_{\{I_u\}}(\unicode{x3bb}_{I_u}) \\ &= \prod_{u=1}^l \bigg( \sum_{\mathbb{I}^{\prime}_u\in \mathfrak{I}'(\unicode{x3bb}_{I_u})} \bigg[ \{ -(\#I_u-1) \}^{\#\mathbb{I}^{\prime}_u - 1} \cdot \prod_{I^{\prime}_u \in \mathbb{I}^{\prime}_u}( \#I^{\prime}_u - 1 )! \bigg] \bigg) \\ &= \sum_{\mathbb{I}^{\prime}_1\in \mathfrak{I}'(\unicode{x3bb}_{I_1})} \cdots \sum_{\mathbb{I}^{\prime}_l\in \mathfrak{I}'(\unicode{x3bb}_{I_l})} \prod_{u=1}^l \bigg[ \{ -(\#I_u-1) \}^{\#\mathbb{I}^{\prime}_u - 1} \cdot \prod_{I^{\prime}_u \in \mathbb{I}^{\prime}_u}( \#I^{\prime}_u - 1 )! \bigg] \\ &= \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I} \end{matrix}}}} \bigg[ \bigg( \prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg) \cdot \bigg( \prod_{u=1}^l \{ -(\#I_u-1) \}^{\chi_{I_u}( \mathbb{I}' ) - 1} \bigg) \bigg] \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} e_{\mathbb{I}}(\unicode{x3bb}) &= \prod_{I \in \mathbb{I}} e_{\{I\}}(\unicode{x3bb}_I) = \prod_{u=1}^l e_{\{I_u\}}(\unicode{x3bb}_{I_u}) \\ &= \prod_{u=1}^l \bigg( \sum_{\mathbb{I}^{\prime}_u\in \mathfrak{I}'(\unicode{x3bb}_{I_u})} \bigg[ \{ -(\#I_u-1) \}^{\#\mathbb{I}^{\prime}_u - 1} \cdot \prod_{I^{\prime}_u \in \mathbb{I}^{\prime}_u}( \#I^{\prime}_u - 1 )! \bigg] \bigg) \\ &= \sum_{\mathbb{I}^{\prime}_1\in \mathfrak{I}'(\unicode{x3bb}_{I_1})} \cdots \sum_{\mathbb{I}^{\prime}_l\in \mathfrak{I}'(\unicode{x3bb}_{I_l})} \prod_{u=1}^l \bigg[ \{ -(\#I_u-1) \}^{\#\mathbb{I}^{\prime}_u - 1} \cdot \prod_{I^{\prime}_u \in \mathbb{I}^{\prime}_u}( \#I^{\prime}_u - 1 )! \bigg] \\ &= \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I} \end{matrix}}}} \bigg[ \bigg( \prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg) \cdot \bigg( \prod_{u=1}^l \{ -(\#I_u-1) \}^{\chi_{I_u}( \mathbb{I}' ) - 1} \bigg) \bigg] \end{aligned}\end{align} $$
since we have the equality
by definition. Here, since
![]() $\mathbb {I} \succ \mathbb {I}$
holds for
$\mathbb {I} \succ \mathbb {I}$
holds for
![]() $\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, we have
$\mathbb {I} \in \mathfrak {I}(\unicode{x3bb} )$
, we have
![]() $\mathbb {I} \in \{ \mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} ) \mid \mathbb {I}' \succ \mathbb {I} \}$
. Note that in equation (4.4),
$\mathbb {I} \in \{ \mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} ) \mid \mathbb {I}' \succ \mathbb {I} \}$
. Note that in equation (4.4),
![]() $\chi _{I_u}( \mathbb {I}' ) = \#( \{ I' \in \mathbb {I}' \mid I' \subseteq I_u \} )$
is the function defined in Theorem 2.5.
$\chi _{I_u}( \mathbb {I}' ) = \#( \{ I' \in \mathbb {I}' \mid I' \subseteq I_u \} )$
is the function defined in Theorem 2.5.
Substituting equation (4.4) into equation (4.2), we have
 $$ \begin{align}\begin{aligned} &e_{\mathbb{I}_0}(\unicode{x3bb}) \\ &= (d-1)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg\{ \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I} \end{matrix}}}} \bigg(\prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \bigg\} \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \\ &= (d-1)! - \sum_{\mathbb{I}' \in \mathfrak{I}(\unicode{x3bb})} \bigg\{ \prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg\} \cdot \bigg\{ \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg\}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &e_{\mathbb{I}_0}(\unicode{x3bb}) \\ &= (d-1)! - \sum_{\mathbb{I} \in \mathfrak{I}(\unicode{x3bb})} \bigg\{ \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I}' \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I}' \succ \mathbb{I} \end{matrix}}}} \bigg(\prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \bigg\} \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \\ &= (d-1)! - \sum_{\mathbb{I}' \in \mathfrak{I}(\unicode{x3bb})} \bigg\{ \prod_{I' \in \mathbb{I}'}( \#I' - 1 )! \bigg\} \cdot \bigg\{ \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg\}. \end{aligned}\end{align} $$
Here, equation (4.3) d , which we would like to prove in this section, is equivalent to the equality
 $$ \begin{align*} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! + \sum_{\mathbb{I}\in \mathfrak{I}(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg), \end{align*} $$
$$ \begin{align*} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! + \sum_{\mathbb{I}\in \mathfrak{I}(\unicode{x3bb})} \bigg( \{ -(d-1) \}^{\#\mathbb{I} - 1} \cdot \prod_{I \in \mathbb{I}}( \#I - 1 )!\!\bigg), \end{align*} $$
which is also equivalent to
 $$ \begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! + \sum_{\mathbb{I}'\in \mathfrak{I}(\unicode{x3bb})} \bigg[ \bigg\{\prod_{I' \in \mathbb{I}'}( \#I' - 1 )!\bigg\} \cdot \{ -(d-1) \}^{\#\mathbb{I}' - 1} \bigg]. \end{align} $$
$$ \begin{align} e_{\mathbb{I}_0}(\unicode{x3bb}) = (d-1)! + \sum_{\mathbb{I}'\in \mathfrak{I}(\unicode{x3bb})} \bigg[ \bigg\{\prod_{I' \in \mathbb{I}'}( \#I' - 1 )!\bigg\} \cdot \{ -(d-1) \}^{\#\mathbb{I}' - 1} \bigg]. \end{align} $$
Hence, comparing equations (4.5) and (4.6), we find that to prove equation (4.3)
d
, we only need to show the following equality for each
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
:
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
:
 $$ \begin{align} \{ -(d-1) \}^{\#\mathbb{I}' - 1} = - \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k. \end{align} $$
$$ \begin{align} \{ -(d-1) \}^{\#\mathbb{I}' - 1} = - \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) \cdot \prod_{k=d-\# \mathbb{I} +1}^{d-1}k. \end{align} $$
Here, equation (4.7) is equivalent to the equality
 $$ \begin{align} \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}'(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) = 0 \end{align} $$
$$ \begin{align} \sum_{\mathrm{\scriptsize {\begin{matrix} \mathbb{I} \in \mathfrak{I}'(\unicode{x3bb}) \\ \mathbb{I} \prec \mathbb{I}' \end{matrix}}}} \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg) = 0 \end{align} $$
since for
![]() $\mathbb {I}_0 \in \mathfrak {I}'(\unicode{x3bb} )$
and
$\mathbb {I}_0 \in \mathfrak {I}'(\unicode{x3bb} )$
and
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, we have
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, we have
![]() $\mathbb {I}_0 \prec \mathbb {I}'$
and
$\mathbb {I}_0 \prec \mathbb {I}'$
and
 $$ \begin{align*} \bigg( \prod_{k=d-\# \mathbb{I}_0 +1}^{d-1}k \bigg) \cdot \prod_{I \in \mathbb{I}_0} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \bigg( \prod_{k=d}^{d-1}k \bigg) \cdot \{ -(d-1) \}^{\#\mathbb{I}' - 1} = \{ -(d-1) \}^{\#\mathbb{I}' - 1}. \end{align*} $$
$$ \begin{align*} \bigg( \prod_{k=d-\# \mathbb{I}_0 +1}^{d-1}k \bigg) \cdot \prod_{I \in \mathbb{I}_0} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \bigg( \prod_{k=d}^{d-1}k \bigg) \cdot \{ -(d-1) \}^{\#\mathbb{I}' - 1} = \{ -(d-1) \}^{\#\mathbb{I}' - 1}. \end{align*} $$
Hence, to prove Theorem I, we only need to show equation (4.8) for every
![]() $d \geq 4$
,
$d \geq 4$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
. In the following, instead of expressing
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
. In the following, instead of expressing
![]() $\sum _{\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} ),\, \mathbb {I} \prec \mathbb {I}'}$
for
$\sum _{\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} ),\, \mathbb {I} \prec \mathbb {I}'}$
for
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, we simply express
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, we simply express
![]() $\sum _{\mathbb {I} \prec \mathbb {I}'}$
, because if
$\sum _{\mathbb {I} \prec \mathbb {I}'}$
, because if
![]() $\mathbb {I}$
is a partition of
$\mathbb {I}$
is a partition of
![]() $\{1,\ldots ,d\}$
and
$\{1,\ldots ,d\}$
and
![]() $\mathbb {I} \prec \mathbb {I}'$
for
$\mathbb {I} \prec \mathbb {I}'$
for
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, then we automatically have
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, then we automatically have
![]() $\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} )$
.
$\mathbb {I} \in \mathfrak {I}'(\unicode{x3bb} )$
.
To prove equation (4.8), we make use of the following.
Definition 4.1. For
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\#\mathbb {I}'=l$
and for
$\#\mathbb {I}'=l$
and for
![]() $k \in \mathbb {Z}$
, we put
$k \in \mathbb {Z}$
, we put
 $$ \begin{align*} f_{l, k} := \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1}. \end{align*} $$
$$ \begin{align*} f_{l, k} := \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1}. \end{align*} $$
Remark 4.2. For
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\#\mathbb {I}'=l$
and for
$\#\mathbb {I}'=l$
and for
![]() $\mathbb {I} \prec \mathbb {I}'$
, we always have
$\mathbb {I} \prec \mathbb {I}'$
, we always have
![]() $1 \leq \#\mathbb {I} \leq l$
. Hence, if
$1 \leq \#\mathbb {I} \leq l$
. Hence, if
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
, then we have
$k \geq l+1$
, then we have
![]() $f_{l, k}=0$
by definition.
$f_{l, k}=0$
by definition.
Example 4.3. Let us find
![]() $f_{l,l}$
and
$f_{l,l}$
and
![]() $f_{l,1}$
for
$f_{l,1}$
for
![]() $l \geq 2$
in this example.
$l \geq 2$
in this example.
Since
![]() $\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=l \} = \{ \mathbb {I}' \}$
, we have
$\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=l \} = \{ \mathbb {I}' \}$
, we have
Let us consider
![]() $f_{l,1}$
next. Since
$f_{l,1}$
next. Since
![]() $\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=1 \} = \{ \mathbb {I}_0 \}$
, we have
$\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=1 \} = \{ \mathbb {I}_0 \}$
, we have
 $$ \begin{align*} f_{l,1} = \prod_{I \in \mathbb{I}_0} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(d-1) \}^{l - 1}. \end{align*} $$
$$ \begin{align*} f_{l,1} = \prod_{I \in \mathbb{I}_0} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(d-1) \}^{l - 1}. \end{align*} $$
Example 4.4. Let us also find
![]() $f_{4,2}$
in this example. For
$f_{4,2}$
in this example. For
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\#\mathbb {I}'=4$
, we can put
$\#\mathbb {I}'=4$
, we can put
![]() $\mathbb {I}'=\{ I_1, I_2, I_3, I_4 \}$
, and in this expression, we have
$\mathbb {I}'=\{ I_1, I_2, I_3, I_4 \}$
, and in this expression, we have
![]() $\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=2 \} = \{ \mathbb {I}_1,\ldots , \mathbb {I}_7 \}$
, where
$\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=2 \} = \{ \mathbb {I}_1,\ldots , \mathbb {I}_7 \}$
, where
 $$ \begin{align*} &\mathbb{I}_1=\{ I_1,\ I_2\amalg I_3\amalg I_4 \},\quad \mathbb{I}_2=\{ I_2,\ I_1\amalg I_3\amalg I_4 \},\\ &\mathbb{I}_3=\{ I_3,\ I_1\amalg I_2\amalg I_4 \},\quad \mathbb{I}_4=\{ I_4,\ I_1\amalg I_2\amalg I_3 \},\\ &\mathbb{I}_5=\{ I_1\amalg I_2,\ I_3\amalg I_4 \},\quad \mathbb{I}_6=\{ I_1\amalg I_3,\ I_2\amalg I_4 \},\quad \text{and} \quad \mathbb{I}_7=\{ I_1\amalg I_4,\ I_2\amalg I_3 \}. \end{align*} $$
$$ \begin{align*} &\mathbb{I}_1=\{ I_1,\ I_2\amalg I_3\amalg I_4 \},\quad \mathbb{I}_2=\{ I_2,\ I_1\amalg I_3\amalg I_4 \},\\ &\mathbb{I}_3=\{ I_3,\ I_1\amalg I_2\amalg I_4 \},\quad \mathbb{I}_4=\{ I_4,\ I_1\amalg I_2\amalg I_3 \},\\ &\mathbb{I}_5=\{ I_1\amalg I_2,\ I_3\amalg I_4 \},\quad \mathbb{I}_6=\{ I_1\amalg I_3,\ I_2\amalg I_4 \},\quad \text{and} \quad \mathbb{I}_7=\{ I_1\amalg I_4,\ I_2\amalg I_3 \}. \end{align*} $$
We put
![]() $\#I_u=:i_u$
for
$\#I_u=:i_u$
for
![]() $1 \leq u \leq 4$
. Note that the equality
$1 \leq u \leq 4$
. Note that the equality
![]() $i_1 + i_2 + i_3 + i_4 = d$
holds. We have
$i_1 + i_2 + i_3 + i_4 = d$
holds. We have
 $$ \begin{align*} &\prod_{I \in \mathbb{I}_1} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(i_1-1) \}^{1-1} \cdot \{ -(i_2+i_3+i_4-1) \}^{3-1},\\ &\prod_{I \in \mathbb{I}_5} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(i_1+i_2-1) \}^{2-1} \cdot \{ -(i_3+i_4-1) \}^{2-1}, \end{align*} $$
$$ \begin{align*} &\prod_{I \in \mathbb{I}_1} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(i_1-1) \}^{1-1} \cdot \{ -(i_2+i_3+i_4-1) \}^{3-1},\\ &\prod_{I \in \mathbb{I}_5} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \{ -(i_1+i_2-1) \}^{2-1} \cdot \{ -(i_3+i_4-1) \}^{2-1}, \end{align*} $$
for instance, which implies
 $$ \begin{align*} \sum_{u=1}^4 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} &= \sum_{u=1}^4 (i_1+i_2+i_3+i_4 - i_u-1)^2 = \sum_{u=1}^4 (d - i_u-1)^2\\ &= 4(d-1)^2 - 2(d-1)d + \sum_{u=1}^4 i_u^2,\\ \sum_{u=5}^7 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} &= (i_1+i_2-1)(i_3+i_4-1) + (i_1+i_3-1)(i_2+i_4-1) \\ & \quad + (i_1+i_4-1)(i_2+i_3-1) = 2\sum_{1 \leq u <v \leq 4}i_ui_v - 3d + 3. \end{align*} $$
$$ \begin{align*} \sum_{u=1}^4 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} &= \sum_{u=1}^4 (i_1+i_2+i_3+i_4 - i_u-1)^2 = \sum_{u=1}^4 (d - i_u-1)^2\\ &= 4(d-1)^2 - 2(d-1)d + \sum_{u=1}^4 i_u^2,\\ \sum_{u=5}^7 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} &= (i_1+i_2-1)(i_3+i_4-1) + (i_1+i_3-1)(i_2+i_4-1) \\ & \quad + (i_1+i_4-1)(i_2+i_3-1) = 2\sum_{1 \leq u <v \leq 4}i_ui_v - 3d + 3. \end{align*} $$
Hence, we have
 $$ \begin{align*} f_{4, 2} &= \sum_{u=1}^7 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1}\\ &= 4(d-1)^2 - 2(d-1)d + \sum_{u=1}^4 i_u^2 + 2\sum_{1 \leq u <v \leq 4}i_ui_v - 3d + 3\\ &= 2d^2 - 9d + 7 + \bigg(\sum_{u=1}^4 i_u \bigg)^2 = 3d^2 - 9d + 7. \end{align*} $$
$$ \begin{align*} f_{4, 2} &= \sum_{u=1}^7 \prod_{I \in \mathbb{I}_u} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1}\\ &= 4(d-1)^2 - 2(d-1)d + \sum_{u=1}^4 i_u^2 + 2\sum_{1 \leq u <v \leq 4}i_ui_v - 3d + 3\\ &= 2d^2 - 9d + 7 + \bigg(\sum_{u=1}^4 i_u \bigg)^2 = 3d^2 - 9d + 7. \end{align*} $$
Example 4.5. By a similar computation to Example 4.4, we have the following for
![]() $l \leq 5$
:
$l \leq 5$
:
 $$ \begin{align*} f_{2,1} &= -d+1, & f_{3,1} &= (d-1)^2, & f_{4,1} &= \{-(d-1)\}^3, & f_{5,1} &= \{-(d-1)\}^4,\\f_{2,2} &= 1, & f_{3,2} &= -2d+3, & f_{4,2} &= 3d^2-9d+7, & f_{5,2} &= -4d^3+18d^2-28d+15,\\& & f_{3,3} &= 1, & f_{4,3} &= -3d+6, & f_{5,3} &= 6d^2-24d+25,\\& & & & f_{4,4} &= 1, & f_{5,4} &= -4d+10,\\& & & & & & f_{5,5} &= 1. \end{align*} $$
$$ \begin{align*} f_{2,1} &= -d+1, & f_{3,1} &= (d-1)^2, & f_{4,1} &= \{-(d-1)\}^3, & f_{5,1} &= \{-(d-1)\}^4,\\f_{2,2} &= 1, & f_{3,2} &= -2d+3, & f_{4,2} &= 3d^2-9d+7, & f_{5,2} &= -4d^3+18d^2-28d+15,\\& & f_{3,3} &= 1, & f_{4,3} &= -3d+6, & f_{5,3} &= 6d^2-24d+25,\\& & & & f_{4,4} &= 1, & f_{5,4} &= -4d+10,\\& & & & & & f_{5,5} &= 1. \end{align*} $$
The following is the key proposition to prove equation (4.8).
Proposition 4.6. The number
![]() $f_{l, k}$
defined in Definition 4.1 is a function of
$f_{l, k}$
defined in Definition 4.1 is a function of
![]() $l, k$
, and d, and does not depend on the choice of
$l, k$
, and d, and does not depend on the choice of
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\#\mathbb {I}'=l$
. Moreover, for
$\#\mathbb {I}'=l$
. Moreover, for
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, we have the equality
$l \geq 2$
, we have the equality
Proposition 4.7. Admitting Proposition 4.6, we have equation (4.8) for every
![]() $d \geq 4$
,
$d \geq 4$
,
![]() $\unicode{x3bb} \in V_d$
, and
$\unicode{x3bb} \in V_d$
, and
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
. Hence, Proposition 4.6 implies Theorem I.
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
. Hence, Proposition 4.6 implies Theorem I.
Proof of Proposition 4.7
If
![]() $\#\mathbb {I}'=2$
, then we can put
$\#\mathbb {I}'=2$
, then we can put
![]() $\mathbb {I}'=\{I_1, I_2\}$
and have
$\mathbb {I}'=\{I_1, I_2\}$
and have
![]() $\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}' \} = \{\mathbb {I}_0, \mathbb {I}'\}$
. Hence, we have
$\{ \mathbb {I} \mid \mathbb {I} \prec \mathbb {I}' \} = \{\mathbb {I}_0, \mathbb {I}'\}$
. Hence, we have
 $$ \begin{align*} \sum_{\mathbb{I} \prec \mathbb{I}'}& \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg)\\[3pt] &= 1\cdot \{ -(d-1) \}^{2-1} + (d-1) \cdot \{ -(\#I_1-1) \}^{1-1} \cdot \{ -(\#I_2-1) \}^{1-1}\\[3pt] &= -(d-1) + (d-1) = 0. \end{align*} $$
$$ \begin{align*} \sum_{\mathbb{I} \prec \mathbb{I}'}& \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg)\\[3pt] &= 1\cdot \{ -(d-1) \}^{2-1} + (d-1) \cdot \{ -(\#I_1-1) \}^{1-1} \cdot \{ -(\#I_2-1) \}^{1-1}\\[3pt] &= -(d-1) + (d-1) = 0. \end{align*} $$
In the case where
![]() $\#\mathbb {I}' \geq 3$
, we put
$\#\mathbb {I}' \geq 3$
, we put
![]() $\#\mathbb {I}' =:l+1$
. Then we have
$\#\mathbb {I}' =:l+1$
. Then we have
![]() $l \geq 2$
and have the following equalities by Proposition 4.6:
$l \geq 2$
and have the following equalities by Proposition 4.6:
 $$ \begin{align*} \sum_{\mathbb{I} \prec \mathbb{I}'}& \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg)\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot f_{l+1, k}\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot ( f_{l, k-1} - (d-k)f_{l,k} )\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot f_{l, k-1} - \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot (d-k)f_{l,k}\\ &= \sum_{k=0}^{l} \bigg( \prod_{k'=d-k}^{d-1}k' \bigg) \cdot f_{l, k} - \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k}^{d-1}k' \bigg) \cdot f_{l,k}\\ &= \bigg( \prod_{k'=d}^{d-1}k' \bigg) \cdot f_{l, 0} - \bigg( \prod_{k'=d-(l+1)}^{d-1}k' \bigg) \cdot f_{l,l+1} = 0, \end{align*} $$
$$ \begin{align*} \sum_{\mathbb{I} \prec \mathbb{I}'}& \bigg( \prod_{k=d-\# \mathbb{I} +1}^{d-1}k \bigg) \cdot \bigg( \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} \bigg)\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot f_{l+1, k}\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot ( f_{l, k-1} - (d-k)f_{l,k} )\\ &= \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot f_{l, k-1} - \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k +1}^{d-1}k' \bigg) \cdot (d-k)f_{l,k}\\ &= \sum_{k=0}^{l} \bigg( \prod_{k'=d-k}^{d-1}k' \bigg) \cdot f_{l, k} - \sum_{k=1}^{l+1} \bigg( \prod_{k'=d-k}^{d-1}k' \bigg) \cdot f_{l,k}\\ &= \bigg( \prod_{k'=d}^{d-1}k' \bigg) \cdot f_{l, 0} - \bigg( \prod_{k'=d-(l+1)}^{d-1}k' \bigg) \cdot f_{l,l+1} = 0, \end{align*} $$
which completes the proof of Proposition 4.7.
In the rest of this section, we shall prove Proposition 4.6. We make use of the following polynomial to prove Proposition 4.6.
Definition 4.8. For
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, we define
$l \geq 2$
, we define
![]() $\mathfrak {J}_l(k)$
as follows: if
$\mathfrak {J}_l(k)$
as follows: if
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
, then we put
$k \geq l+1$
, then we put
![]() $\mathfrak {J}_l(k) = \emptyset $
; if
$\mathfrak {J}_l(k) = \emptyset $
; if
![]() $1 \leq k \leq l$
, then we put
$1 \leq k \leq l$
, then we put
 $$ \begin{align*} \mathfrak{J}_l(k) := \left\{ \{J_1,\ldots,J_k\}\ \left| \ \begin{matrix} J_1 \amalg \cdots \amalg J_k = \{1,\ldots,l \},\\ J_v \ne \emptyset \textrm{ for every } 1\le v\le k \end{matrix} \right.\right\}, \end{align*} $$
$$ \begin{align*} \mathfrak{J}_l(k) := \left\{ \{J_1,\ldots,J_k\}\ \left| \ \begin{matrix} J_1 \amalg \cdots \amalg J_k = \{1,\ldots,l \},\\ J_v \ne \emptyset \textrm{ for every } 1\le v\le k \end{matrix} \right.\right\}, \end{align*} $$
where
![]() $J_1 \amalg \cdots \amalg J_k$
denotes the disjoint union of
$J_1 \amalg \cdots \amalg J_k$
denotes the disjoint union of
![]() $J_1,\ldots , J_k$
. Moreover, for
$J_1,\ldots , J_k$
. Moreover, for
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, we put
$l \geq 2$
, we put
 $$ \begin{align*} g_{l,k}(X_1,\ldots,X_l) := \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}. \end{align*} $$
$$ \begin{align*} g_{l,k}(X_1,\ldots,X_l) := \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}. \end{align*} $$
By definition,
![]() $\mathfrak {J}_l(k)$
is the set of all the partitions of
$\mathfrak {J}_l(k)$
is the set of all the partitions of
![]() $\{1, \ldots ,l\}$
into k pieces. Note that the equality
$\{1, \ldots ,l\}$
into k pieces. Note that the equality
![]() $g_{l,k}(X_1,\ldots ,X_l)=0$
trivially holds for
$g_{l,k}(X_1,\ldots ,X_l)=0$
trivially holds for
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
.
$k \geq l+1$
.
Lemma 4.9. For
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
with
![]() $\#\mathbb {I}'=l$
and for every
$\#\mathbb {I}'=l$
and for every
![]() $k \in \mathbb {Z}$
, putting
$k \in \mathbb {Z}$
, putting
![]() $\mathbb {I}' =: \{ I_1, \ldots , I_l \}$
and
$\mathbb {I}' =: \{ I_1, \ldots , I_l \}$
and
![]() $\# I_u =: i_u$
for
$\# I_u =: i_u$
for
![]() $1 \leq u \leq l$
, we have
$1 \leq u \leq l$
, we have
Proof. If
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
, then equation (4.9) trivially holds since both sides of equation (4.9) are equal to zero. In the following, we assume
$k \geq l+1$
, then equation (4.9) trivially holds since both sides of equation (4.9) are equal to zero. In the following, we assume
![]() $1 \leq k \leq l$
.
$1 \leq k \leq l$
.
By definition, we have
 $$ \begin{align*} f_{l,k} =\! \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \!\sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \bigg\{\! -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I}\! i_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}. \end{align*} $$
$$ \begin{align*} f_{l,k} =\! \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \prod_{I \in \mathbb{I}} \{ -(\#I-1) \}^{\chi_{I}( \mathbb{I}' ) - 1} = \!\sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \bigg\{\! -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I}\! i_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}. \end{align*} $$
Hence, putting
 $$ \begin{align*} \tilde{g}_{l,k}(X_1,\ldots,X_l) := \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I} X_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}, \end{align*} $$
$$ \begin{align*} \tilde{g}_{l,k}(X_1,\ldots,X_l) := \sum_{\mathbb{I} \prec \mathbb{I}',\, \#\mathbb{I}=k} \, \prod_{I \in \mathbb{I}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I} X_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}, \end{align*} $$
we obviously have
![]() $\tilde {g}_{l,k}(i_1,\ldots ,i_l) = f_{l,k}$
.
$\tilde {g}_{l,k}(i_1,\ldots ,i_l) = f_{l,k}$
.
Here, we can make a bijection
![]() $\mathfrak {J}_l(k) \to \{\mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=k \}$
by
$\mathfrak {J}_l(k) \to \{\mathbb {I} \mid \mathbb {I} \prec \mathbb {I}',\, \#\mathbb {I}=k \}$
by
which implies that
 $$ \begin{align*} \tilde{g}_{l,k}(X_1,\ldots,X_l) &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{I \in \{ \amalg_{u \in J} I_u \mid \ J \in \mathbb{J} \}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I} X_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset \amalg_{u' \in J} I_{u'}} X_u - 1 \bigg) \bigg\}^{\chi_{(\amalg_{u' \in J} I_{u'})}( \mathbb{I}' ) - 1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1} = g_{l,k}(X_1,\ldots,X_l). \end{align*} $$
$$ \begin{align*} \tilde{g}_{l,k}(X_1,\ldots,X_l) &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{I \in \{ \amalg_{u \in J} I_u \mid \ J \in \mathbb{J} \}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset I} X_u-1 \bigg) \bigg\}^{\chi_{I}( \mathbb{I}' ) - 1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{1 \leq u \leq l,\ I_u \subset \amalg_{u' \in J} I_{u'}} X_u - 1 \bigg) \bigg\}^{\chi_{(\amalg_{u' \in J} I_{u'})}( \mathbb{I}' ) - 1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \, \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1} = g_{l,k}(X_1,\ldots,X_l). \end{align*} $$
Hence, we have equation (4.9).
Lemma 4.10. The polynomial
![]() $g_{l,k}(X_1,\ldots ,X_l)$
defined in Definition 4.8 is determined only by l and k, belongs to the polynomial ring
$g_{l,k}(X_1,\ldots ,X_l)$
defined in Definition 4.8 is determined only by l and k, belongs to the polynomial ring
![]() $\mathbb {Z}[X_1,\ldots ,X_l]$
, and is symmetric in l variables
$\mathbb {Z}[X_1,\ldots ,X_l]$
, and is symmetric in l variables
![]() $X_1,\ldots ,X_l$
. Moreover, the equality
$X_1,\ldots ,X_l$
. Moreover, the equality
![]() $\deg g_{l,k} = l-k$
holds for
$\deg g_{l,k} = l-k$
holds for
![]() $l \geq 2$
and
$l \geq 2$
and
![]() $1 \leq k \leq ~l$
.
$1 \leq k \leq ~l$
.
Proof. The former two assertions are obvious by definition.
The action of
![]() $\mathfrak {S}_l$
on
$\mathfrak {S}_l$
on
![]() $\{1,\ldots ,l\}$
naturally induces the action of
$\{1,\ldots ,l\}$
naturally induces the action of
![]() $\mathfrak {S}_l$
on
$\mathfrak {S}_l$
on
![]() $\mathfrak {J}_l(k)$
for each k, which implies that for every
$\mathfrak {J}_l(k)$
for each k, which implies that for every
![]() $\tau \in \mathfrak {S}_l$
, we have
$\tau \in \mathfrak {S}_l$
, we have
![]() $g_{l,k}(X_{\tau (1)},\ldots ,X_{\tau (l)}) = g_{l,k}(X_1,\ldots ,X_l)$
. Hence,
$g_{l,k}(X_{\tau (1)},\ldots ,X_{\tau (l)}) = g_{l,k}(X_1,\ldots ,X_l)$
. Hence,
![]() $g_{l,k}(X_1,\ldots ,X_l)$
is a symmetric polynomial in l variables
$g_{l,k}(X_1,\ldots ,X_l)$
is a symmetric polynomial in l variables
![]() $X_1,\ldots ,X_l$
.
$X_1,\ldots ,X_l$
.
Since
![]() $\sum _{J \in \mathbb {J}} ( \#J-1 ) = l-\#\mathbb {J} = l-k$
for every
$\sum _{J \in \mathbb {J}} ( \#J-1 ) = l-\#\mathbb {J} = l-k$
for every
![]() $\mathbb {J} \in \mathfrak {J}_l(k)$
, we have
$\mathbb {J} \in \mathfrak {J}_l(k)$
, we have
![]() $\deg g_{l,k} \leq l-k$
. Moreover, for
$\deg g_{l,k} \leq l-k$
. Moreover, for
![]() $\mathbb {J} \in \mathfrak {J}_l(k)$
with
$\mathbb {J} \in \mathfrak {J}_l(k)$
with
![]() $1 \leq k \leq l$
, the coefficient of each term of
$1 \leq k \leq l$
, the coefficient of each term of
![]() $\prod _{J\in \mathbb {J}} \{ - ( \sum _{u\in J} X_u - 1 ) \}^{\#J-1}$
with degree
$\prod _{J\in \mathbb {J}} \{ - ( \sum _{u\in J} X_u - 1 ) \}^{\#J-1}$
with degree
![]() $l-k$
is positive or negative according to whether
$l-k$
is positive or negative according to whether
![]() $l-k$
is even or odd. Hence, the terms with degree
$l-k$
is even or odd. Hence, the terms with degree
![]() $l-k$
in
$l-k$
in
![]() $g_{l,k}(X_1,\ldots ,X_l)$
are not canceled, which implies that the degree of
$g_{l,k}(X_1,\ldots ,X_l)$
are not canceled, which implies that the degree of
![]() $g_{l,k}(X_1,\ldots ,X_l)$
is exactly equal to
$g_{l,k}(X_1,\ldots ,X_l)$
is exactly equal to
![]() $l-k$
if
$l-k$
if
![]() $1 \leq k \leq l$
.
$1 \leq k \leq l$
.
Proposition 4.11. For
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, we have
$l \geq 2$
, we have
Proof. First, we put
for
![]() $l \geq 2$
. Then we have
$l \geq 2$
. Then we have
![]() $\mathfrak {J}_{l+1}^1(k) \, \amalg \, \mathfrak {J}_{l+1}^2(k) = \mathfrak {J}_{l+1}(k)$
for every k. Moreover, we have
$\mathfrak {J}_{l+1}^1(k) \, \amalg \, \mathfrak {J}_{l+1}^2(k) = \mathfrak {J}_{l+1}(k)$
for every k. Moreover, we have
![]() $\mathfrak {J}_{l+1}^1(k)= \emptyset $
for
$\mathfrak {J}_{l+1}^1(k)= \emptyset $
for
![]() $k \leq 1$
or
$k \leq 1$
or
![]() $k \geq l+2$
, and
$k \geq l+2$
, and
![]() $\mathfrak {J}_{l+1}^2(k)= \emptyset $
for
$\mathfrak {J}_{l+1}^2(k)= \emptyset $
for
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
.
$k \geq l+1$
.
For
![]() $\mathbb {J} \in \mathfrak {J}_{l+1}^1(k)$
, we can express
$\mathbb {J} \in \mathfrak {J}_{l+1}^1(k)$
, we can express
![]() $\mathbb {J} = \{J_1,\ldots ,J_{k-1}, \{l+1\}\}$
, where
$\mathbb {J} = \{J_1,\ldots ,J_{k-1}, \{l+1\}\}$
, where
![]() $J_1 \amalg \cdots \amalg J_{k-1} = \{1,\ldots ,l\}$
. Hence, we can make a bijection
$J_1 \amalg \cdots \amalg J_{k-1} = \{1,\ldots ,l\}$
. Hence, we can make a bijection
![]() $\pi _1: \mathfrak {J}_{l+1}^1(k) \to \mathfrak {J}_{l}(k-1)$
by
$\pi _1: \mathfrak {J}_{l+1}^1(k) \to \mathfrak {J}_{l}(k-1)$
by
![]() $\mathbb {J} \mapsto \mathbb {J} \setminus \{\{l+1\}\}$
. Moreover, for
$\mathbb {J} \mapsto \mathbb {J} \setminus \{\{l+1\}\}$
. Moreover, for
![]() $J=\{l+1\} \in \mathbb {J} \in \mathfrak {J}_{l+1}^1(k)$
, we have
$J=\{l+1\} \in \mathbb {J} \in \mathfrak {J}_{l+1}^1(k)$
, we have
 $$ \begin{align*} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} = \bigg\{ - \bigg( X_{l+1} - 1 \bigg) \bigg\}^{1-1} = 1. \end{align*} $$
$$ \begin{align*} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} = \bigg\{ - \bigg( X_{l+1} - 1 \bigg) \bigg\}^{1-1} = 1. \end{align*} $$
Hence, we have
 $$ \begin{align}\begin{aligned} \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} &= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \pi_1(\mathbb{J})} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_{l}(k-1)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\ &= g_{l,k-1}(X_1,\ldots,X_l). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} &= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \pi_1(\mathbb{J})} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_{l}(k-1)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\ &= g_{l,k-1}(X_1,\ldots,X_l). \end{aligned}\end{align} $$
For
![]() $\mathbb {J}' \in \mathfrak {J}_{l+1}^2(k)$
, we can express
$\mathbb {J}' \in \mathfrak {J}_{l+1}^2(k)$
, we can express
![]() $\mathbb {J}' = \{J_1,\ldots ,J_k\}$
with
$\mathbb {J}' = \{J_1,\ldots ,J_k\}$
with
![]() $\{l+1\} \subsetneq J_k$
, and in this expression, we have
$\{l+1\} \subsetneq J_k$
, and in this expression, we have
![]() $\{J_1,\ldots ,J_{k-1}, (J_k\setminus \{l+1\}) \} \in \mathfrak {J}_{l}(k)$
. Hence, we can make a surjection
$\{J_1,\ldots ,J_{k-1}, (J_k\setminus \{l+1\}) \} \in \mathfrak {J}_{l}(k)$
. Hence, we can make a surjection
![]() $\pi _2: \mathfrak {J}_{l+1}^2(k) \to \mathfrak {J}_{l}(k)$
by
$\pi _2: \mathfrak {J}_{l+1}^2(k) \to \mathfrak {J}_{l}(k)$
by
![]() $\mathbb {J}' \mapsto \{ J \setminus \{l+1\} \mid J \in \mathbb {J}' \}$
. For each
$\mathbb {J}' \mapsto \{ J \setminus \{l+1\} \mid J \in \mathbb {J}' \}$
. For each
![]() $\mathbb {J} = \{J_1,\ldots ,J_k\} \in \mathfrak {J}_{l}(k)$
, its fiber
$\mathbb {J} = \{J_1,\ldots ,J_k\} \in \mathfrak {J}_{l}(k)$
, its fiber
![]() $\pi _2^{-1}( \mathbb {J} )$
consists of k elements, which are
$\pi _2^{-1}( \mathbb {J} )$
consists of k elements, which are
![]() $\{J_v \mid 1 \leq v \leq k,\ v \ne v' \} \cup \{ J_{v'}\amalg \{l+1\} \}$
for
$\{J_v \mid 1 \leq v \leq k,\ v \ne v' \} \cup \{ J_{v'}\amalg \{l+1\} \}$
for
![]() $1 \leq v' \leq k$
. Hence, for each
$1 \leq v' \leq k$
. Hence, for each
![]() $\mathbb {J} = \{J_1,\ldots ,J_k\} \in \mathfrak {J}_{l}(k)$
, we have
$\mathbb {J} = \{J_1,\ldots ,J_k\} \in \mathfrak {J}_{l}(k)$
, we have
 $$ \begin{align*} \sum_{\mathbb{J}' \in \pi_2^{-1}( \mathbb{J} )}& \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}\amalg\{l+1\}} X_u -1 \bigg) \bigg\}^{\#( J_{v'}\amalg \{l+1\} ) - 1} \\ &\quad\times \prod_{1 \leq v \leq k,\ v \ne v'} \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg] \bigg|_{X_{l+1}=0}\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\}^{\# J_{v'}} \cdot \prod_{1 \leq v \leq k,\ v \ne v'} \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg]\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\} \cdot \prod_{v=1}^k \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg]\\ &= \bigg[ \sum_{v'=1}^k \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\} \bigg] \cdot \prod_{v=1}^k \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1}\\ &= - \bigg( \sum_{u=1}^l X_u - k \bigg) \cdot \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1}. \end{align*} $$
$$ \begin{align*} \sum_{\mathbb{J}' \in \pi_2^{-1}( \mathbb{J} )}& \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}\amalg\{l+1\}} X_u -1 \bigg) \bigg\}^{\#( J_{v'}\amalg \{l+1\} ) - 1} \\ &\quad\times \prod_{1 \leq v \leq k,\ v \ne v'} \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg] \bigg|_{X_{l+1}=0}\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\}^{\# J_{v'}} \cdot \prod_{1 \leq v \leq k,\ v \ne v'} \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg]\\ &= \sum_{v'=1}^k \bigg[ \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\} \cdot \prod_{v=1}^k \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1} \bigg]\\ &= \bigg[ \sum_{v'=1}^k \bigg\{ -\bigg( \sum_{u \in J_{v'}} X_u -1 \bigg) \bigg\} \bigg] \cdot \prod_{v=1}^k \bigg\{ -\bigg( \sum_{u \in J_v} X_u - 1 \bigg) \bigg\}^{\#J_v - 1}\\ &= - \bigg( \sum_{u=1}^l X_u - k \bigg) \cdot \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1}. \end{align*} $$
We therefore have
 $$ \begin{align}\begin{aligned} \sum_{\mathbb{J}' \in \mathfrak{J}_{l+1}^2(k)}& \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \sum_{\mathbb{J}' \in \pi_2^{-1}( \mathbb{J} )} \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \bigg[ - \bigg( \sum_{u=1}^l X_u - k \bigg) \cdot \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1} \bigg]\\ &= - \bigg( \sum_{u=1}^l X_u - k \bigg) \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1}\\ &= - (X_1+\cdots+X_l-k)g_{l,k}(X_1,\ldots,X_l). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{\mathbb{J}' \in \mathfrak{J}_{l+1}^2(k)}& \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \sum_{\mathbb{J}' \in \pi_2^{-1}( \mathbb{J} )} \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\ &= \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \bigg[ - \bigg( \sum_{u=1}^l X_u - k \bigg) \cdot \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1} \bigg]\\ &= - \bigg( \sum_{u=1}^l X_u - k \bigg) \sum_{\mathbb{J} \in \mathfrak{J}_l(k)} \prod_{J \in \mathbb{J}} \bigg\{ -\bigg( \sum_{u \in J} X_u - 1 \bigg) \bigg\}^{\#J - 1}\\ &= - (X_1+\cdots+X_l-k)g_{l,k}(X_1,\ldots,X_l). \end{aligned}\end{align} $$
By equations (4.10) and (4.11), we have
 $$ \begin{align*} g_{l+1,k}(X_1,\ldots,X_l,0) &= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\&= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\& \quad + \sum_{\mathbb{J}' \in \mathfrak{J}_{l+1}^2(k)} \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\&= g_{l,k-1}(X_1,\ldots,X_l) - (X_1+\cdots+X_l-k)g_{l,k}(X_1,\ldots,X_l), \end{align*} $$
$$ \begin{align*} g_{l+1,k}(X_1,\ldots,X_l,0) &= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\&= \sum_{\mathbb{J} \in \mathfrak{J}_{l+1}^1(k)} \prod_{J\in \mathbb{J}} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1}\\& \quad + \sum_{\mathbb{J}' \in \mathfrak{J}_{l+1}^2(k)} \prod_{J\in \mathbb{J}'} \bigg\{ - \bigg( \sum_{u\in J} X_u - 1 \bigg) \bigg\}^{\#J-1} \bigg|_{X_{l+1}=0}\\&= g_{l,k-1}(X_1,\ldots,X_l) - (X_1+\cdots+X_l-k)g_{l,k}(X_1,\ldots,X_l), \end{align*} $$
which completes the proof of Proposition 4.11.
Lemma 4.12. For every
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, there exists a polynomial
$l \geq 2$
, there exists a polynomial
![]() $h_{l,k}(Y) \in \mathbb {Z}[Y]$
such that the equality
$h_{l,k}(Y) \in \mathbb {Z}[Y]$
such that the equality
holds. Moreover, for every
![]() $l, k \in \mathbb {Z}$
with
$l, k \in \mathbb {Z}$
with
![]() $l \geq 2$
, the equality
$l \geq 2$
, the equality
holds.
Proof. In the case where
![]() $l=2$
, we have
$l=2$
, we have
![]() $g_{2,1}(X_1, X_2) = -(X_1 + X_2 - 1)$
and
$g_{2,1}(X_1, X_2) = -(X_1 + X_2 - 1)$
and
![]() $g_{2,2}(X_1, X_2) = 1$
by a direct calculation. Hence, putting
$g_{2,2}(X_1, X_2) = 1$
by a direct calculation. Hence, putting
![]() $h_{2,1}(Y) \kern1.3pt{=}\kern1.3pt -(Y-1)$
,
$h_{2,1}(Y) \kern1.3pt{=}\kern1.3pt -(Y-1)$
,
![]() $h_{2,2}(Y) \kern1.3pt{=}\kern1.3pt 1$
, and
$h_{2,2}(Y) \kern1.3pt{=}\kern1.3pt 1$
, and
![]() $h_{2,k}(Y) = 0$
for
$h_{2,k}(Y) = 0$
for
![]() $k \ne 1, 2$
, we have
$k \ne 1, 2$
, we have
![]() $g_{2,k}(X_1, X_2) = h_{2, k}(X_1+X_2)$
for every
$g_{2,k}(X_1, X_2) = h_{2, k}(X_1+X_2)$
for every
![]() $k \in \mathbb {Z}$
.
$k \in \mathbb {Z}$
.
For
![]() $l \geq 3$
and for every
$l \geq 3$
and for every
![]() $k\in \mathbb {Z}$
, we define the polynomials
$k\in \mathbb {Z}$
, we define the polynomials
![]() $h_{l,k}(Y)$
inductively by equation (4.13). Then we obviously have
$h_{l,k}(Y)$
inductively by equation (4.13). Then we obviously have
![]() $h_{l,k}(Y)=0$
for
$h_{l,k}(Y)=0$
for
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
. Hence, equation (4.12) holds for
$k \geq l+1$
. Hence, equation (4.12) holds for
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $k \geq l+1$
. In the following, we show equation (4.12) for
$k \geq l+1$
. In the following, we show equation (4.12) for
![]() $l\geq 3$
and
$l\geq 3$
and
![]() $1 \leq k \leq l$
by induction on l. Hence, we suppose equation (4.12) for every
$1 \leq k \leq l$
by induction on l. Hence, we suppose equation (4.12) for every
![]() $k \in \mathbb {Z}$
, and show the equality
$k \in \mathbb {Z}$
, and show the equality
![]() $g_{l+1,k}(X_1,\ldots ,X_{l+1})= h_{l+1,k}(X_1 + \cdots + X_{l+1})$
for
$g_{l+1,k}(X_1,\ldots ,X_{l+1})= h_{l+1,k}(X_1 + \cdots + X_{l+1})$
for
![]() $1 \leq k \leq l+1$
.
$1 \leq k \leq l+1$
.
By the assumption and Proposition 4.11, we have
 $$ \begin{align*} g_{l+1, k}(X_1, \ldots, X_l, 0) &= g_{l, k-1}(X_1,\ldots, X_l) - (X_1+\cdots+X_l - k) g_{l,k}(X_1,\ldots, X_l)\\ &= h_{l, k-1}(X_1+\cdots+X_l) - (X_1+\cdots+X_l - k) h_{l,k}(X_1+\cdots+X_l)\\ &= h_{l+1,k}(X_1+\cdots+X_l). \end{align*} $$
$$ \begin{align*} g_{l+1, k}(X_1, \ldots, X_l, 0) &= g_{l, k-1}(X_1,\ldots, X_l) - (X_1+\cdots+X_l - k) g_{l,k}(X_1,\ldots, X_l)\\ &= h_{l, k-1}(X_1+\cdots+X_l) - (X_1+\cdots+X_l - k) h_{l,k}(X_1+\cdots+X_l)\\ &= h_{l+1,k}(X_1+\cdots+X_l). \end{align*} $$
Hence, putting
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1}) := g_{l+1, k}(X_1, \ldots , X_{l+1}) - h_{l+1,k}(X_1+\cdots +X_{l+1})$
, we have
$P_{l+1,k}(X_1,\ldots ,X_{l+1}) := g_{l+1, k}(X_1, \ldots , X_{l+1}) - h_{l+1,k}(X_1+\cdots +X_{l+1})$
, we have
![]() $P_{l+1,k}(X_1,\ldots ,X_l,0)=0$
. Moreover, by Lemma 4.10, the polynomial
$P_{l+1,k}(X_1,\ldots ,X_l,0)=0$
. Moreover, by Lemma 4.10, the polynomial
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1})$
is symmetric in
$P_{l+1,k}(X_1,\ldots ,X_{l+1})$
is symmetric in
![]() $l+1$
variables
$l+1$
variables
![]() $X_1,\ldots ,X_{l+1}$
.
$X_1,\ldots ,X_{l+1}$
.
We denote by
![]() $\sigma _{l+1, m}=\sigma _{l+1,m}(X_1,\ldots ,X_{l+1})$
the elementary symmetric polynomial of degree m in
$\sigma _{l+1, m}=\sigma _{l+1,m}(X_1,\ldots ,X_{l+1})$
the elementary symmetric polynomial of degree m in
![]() $l+1$
variables
$l+1$
variables
![]() $X_1,\ldots ,X_{l+1}$
. Since
$X_1,\ldots ,X_{l+1}$
. Since
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1})$
is a symmetric polynomial with coefficients in
$P_{l+1,k}(X_1,\ldots ,X_{l+1})$
is a symmetric polynomial with coefficients in
![]() $\mathbb {Z}$
, we have
$\mathbb {Z}$
, we have
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1}) \in \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l+1} ]$
. Moreover, since
$P_{l+1,k}(X_1,\ldots ,X_{l+1}) \in \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l+1} ]$
. Moreover, since
![]() $\deg g_{l+1,k} = \deg h_{l+1,k} = l+1-k \leq l$
, we have
$\deg g_{l+1,k} = \deg h_{l+1,k} = l+1-k \leq l$
, we have
![]() $\deg P_{l+1,k} \leq l$
, which implies that
$\deg P_{l+1,k} \leq l$
, which implies that
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1}) \in \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l} ]$
.
$P_{l+1,k}(X_1,\ldots ,X_{l+1}) \in \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l} ]$
.
Since
![]() $\sigma _{l+1,m}(X_1,\ldots ,X_l,0) = \sigma _{l,m}(X_1,\ldots ,X_l)$
for
$\sigma _{l+1,m}(X_1,\ldots ,X_l,0) = \sigma _{l,m}(X_1,\ldots ,X_l)$
for
![]() $1 \leq m \leq l$
, we have a ring isomorphism
$1 \leq m \leq l$
, we have a ring isomorphism
![]() $\varphi : \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l} ] \to \mathbb {Z}[ \sigma _{l,1},\ldots ,\sigma _{l,l} ]$
by substituting
$\varphi : \mathbb {Z}[ \sigma _{l+1,1},\ldots ,\sigma _{l+1,l} ] \to \mathbb {Z}[ \sigma _{l,1},\ldots ,\sigma _{l,l} ]$
by substituting
![]() $X_{l+1}=0$
, and under the map
$X_{l+1}=0$
, and under the map
![]() $\varphi $
, we have
$\varphi $
, we have
![]() $\varphi ( P_{l+1,k} ) = P_{l+1,k}(X_1,\ldots ,X_l,0)=0$
. Hence, injectivity of
$\varphi ( P_{l+1,k} ) = P_{l+1,k}(X_1,\ldots ,X_l,0)=0$
. Hence, injectivity of
![]() $\varphi $
implies
$\varphi $
implies
![]() $P_{l+1,k}(X_1,\ldots ,X_{l+1})=0$
. We therefore have
$P_{l+1,k}(X_1,\ldots ,X_{l+1})=0$
. We therefore have
![]() $g_{l+1,k}(X_1,\ldots ,X_{l+1})= h_{l+1,k}(X_1 + \cdots + X_{l+1})$
, which completes the proof of Lemma 4.12 by induction on l.
$g_{l+1,k}(X_1,\ldots ,X_{l+1})= h_{l+1,k}(X_1 + \cdots + X_{l+1})$
, which completes the proof of Lemma 4.12 by induction on l.
Proof of Proposition 4.6
By Definition 4.1,
![]() $f_{l,k}$
is originally a function of
$f_{l,k}$
is originally a function of
![]() $d \geq 4$
,
$d \geq 4$
,
![]() $\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, and
$\mathbb {I}' \in \mathfrak {I}(\unicode{x3bb} )$
, and
![]() $k \in \mathbb {Z}$
. However, putting
$k \in \mathbb {Z}$
. However, putting
![]() $\#\mathbb {I}'=l$
,
$\#\mathbb {I}'=l$
,
![]() $\mathbb {I}' =: \{ I_1, \ldots , I_l \}$
, and
$\mathbb {I}' =: \{ I_1, \ldots , I_l \}$
, and
![]() $\# I_u =: i_u$
for
$\# I_u =: i_u$
for
![]() $1 \leq u \leq l$
, we have by Lemmas 4.9 and 4.12 the equality
$1 \leq u \leq l$
, we have by Lemmas 4.9 and 4.12 the equality
Hence,
![]() $f_{l,k}$
is in practice a function of
$f_{l,k}$
is in practice a function of
![]() $l, k$
, and d since the polynomial
$l, k$
, and d since the polynomial
![]() $h_{l,k}(Y)$
depends only on l and k.
$h_{l,k}(Y)$
depends only on l and k.
Moreover, by equation (4.14) and Lemma 4.12, we have
for every
![]() $l,k\in \mathbb {Z}$
with
$l,k\in \mathbb {Z}$
with
![]() $l \geq 2$
, which completes the proof of Proposition 4.6.
$l \geq 2$
, which completes the proof of Proposition 4.6.
To summarize the above mentioned, we have completed the proof of Theorem I.
5 Proof of Theorem II
In this section, we prove Theorem II. Throughout this section, we always assume
![]() $\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, and moreover assume that
$\unicode{x3bb} =(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _d) \in V_d$
, and moreover assume that
![]() $s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3.
$s_d(\unicode{x3bb} )$
is the non-negative integer defined in Theorem 2.3.
First, we consider the case where
![]() $d=2$
. If
$d=2$
. If
![]() $d=2$
, then the maps
$d=2$
, then the maps
![]() $p: \mathrm {MC}_2 \to \mathrm {MP}_2$
and
$p: \mathrm {MC}_2 \to \mathrm {MP}_2$
and
![]() $\Phi _2: \mathrm {MP}_2 \to \widetilde {\Lambda }_2$
are bijective. Hence, we have
$\Phi _2: \mathrm {MP}_2 \to \widetilde {\Lambda }_2$
are bijective. Hence, we have
![]() $\#( \widehat {\Phi }_2^{-1} ( \bar {\unicode{x3bb} } ) ) = 1$
for every
$\#( \widehat {\Phi }_2^{-1} ( \bar {\unicode{x3bb} } ) ) = 1$
for every
![]() $\unicode{x3bb} \in V_2$
. Regarding the right-hand side of equation (3.2), since
$\unicode{x3bb} \in V_2$
. Regarding the right-hand side of equation (3.2), since
![]() $s_2(\unicode{x3bb} )= 1$
and
$s_2(\unicode{x3bb} )= 1$
and
![]() $\mathfrak {K}(\unicode{x3bb} ) = \{ \{1\}, \{2\} \}$
for every
$\mathfrak {K}(\unicode{x3bb} ) = \{ \{1\}, \{2\} \}$
for every
![]() $\unicode{x3bb} \in V_2$
, we always have
$\unicode{x3bb} \in V_2$
, we always have
 $$ \begin{align*} \frac{(d-1)s_d(\unicode{x3bb})}{ \prod_{K\in\mathfrak{K}(\unicode{x3bb})}(\#K)!} = \frac{(2-1)s_2(\unicode{x3bb})}{ 1!\cdot 1!} = 1. \end{align*} $$
$$ \begin{align*} \frac{(d-1)s_d(\unicode{x3bb})}{ \prod_{K\in\mathfrak{K}(\unicode{x3bb})}(\#K)!} = \frac{(2-1)s_2(\unicode{x3bb})}{ 1!\cdot 1!} = 1. \end{align*} $$
Hence, equation (3.2) holds for every
![]() $\unicode{x3bb} \in V_2$
.
$\unicode{x3bb} \in V_2$
.
In the rest of this section, we consider the case
![]() $d \geq 3$
. We denote by
$d \geq 3$
. We denote by
![]() $\mathbb {P}^{d-1}$
the complex projective space of dimension
$\mathbb {P}^{d-1}$
the complex projective space of dimension
![]() $d-1$
, and put
$d-1$
, and put
 $$ \begin{align*} \Sigma_d(\unicode{x3bb}) := \left\{(\zeta_1:\cdots:\zeta_d) \in \mathbb{P}^{d-1} \ \left|\ \begin{matrix} \sum\limits_{i=1}^d \zeta_i = 0 \\ \sum\limits_{i=1}^d (1/(1-\lambda_i))\zeta_i^{k} = 0 \quad \textrm{for} \quad 1 \le k \le d-2 \\ \zeta_1,\ldots,\zeta_d \textrm{ are mutually distinct} \end{matrix} \right. \right\}. \end{align*} $$
$$ \begin{align*} \Sigma_d(\unicode{x3bb}) := \left\{(\zeta_1:\cdots:\zeta_d) \in \mathbb{P}^{d-1} \ \left|\ \begin{matrix} \sum\limits_{i=1}^d \zeta_i = 0 \\ \sum\limits_{i=1}^d (1/(1-\lambda_i))\zeta_i^{k} = 0 \quad \textrm{for} \quad 1 \le k \le d-2 \\ \zeta_1,\ldots,\zeta_d \textrm{ are mutually distinct} \end{matrix} \right. \right\}. \end{align*} $$
We already have the following proposition by Propositions 4.3 and 9.1 in [Reference Sugiyama14].
Proposition 5.1. The equality
![]() $\#( \Sigma _d(\unicode{x3bb} ) ) = s_d(\unicode{x3bb} )$
holds. Moreover, we can define the surjection
$\#( \Sigma _d(\unicode{x3bb} ) ) = s_d(\unicode{x3bb} )$
holds. Moreover, we can define the surjection
![]() $\pi (\unicode{x3bb} ) : \Sigma _d(\unicode{x3bb} ) \to \Phi _d^{-1}(\bar {\unicode{x3bb} })$
by
$\pi (\unicode{x3bb} ) : \Sigma _d(\unicode{x3bb} ) \to \Phi _d^{-1}(\bar {\unicode{x3bb} })$
by
where
![]() $-{1}/{\rho }= \sum _{i=1}^d (1/(1-\lambda_i))\zeta_i^{d-1}$
.
$-{1}/{\rho }= \sum _{i=1}^d (1/(1-\lambda_i))\zeta_i^{d-1}$
.
We put
 $$ \begin{align*} \widetilde{\Sigma}_d(\unicode{x3bb}) := \left\{(\zeta_1,\ldots,\zeta_d) \in \mathbb{C}^{d} \ \left|\ \begin{matrix} \sum\limits_{i=1}^d \zeta_i = 0 \\ \sum\limits_{i=1}^d ({1}/{(1-\unicode{x3bb}_i)})\zeta_i^k = \begin{cases} 0 & \textrm{for } 1 \le k \le d-2 \\ -1 & \textrm{for } k = d-1 \end{cases}\\ \zeta_1,\ldots,\zeta_d \textrm{ are mutually distinct} \end{matrix} \right. \right\}\hspace{-2.5pt}. \end{align*} $$
$$ \begin{align*} \widetilde{\Sigma}_d(\unicode{x3bb}) := \left\{(\zeta_1,\ldots,\zeta_d) \in \mathbb{C}^{d} \ \left|\ \begin{matrix} \sum\limits_{i=1}^d \zeta_i = 0 \\ \sum\limits_{i=1}^d ({1}/{(1-\unicode{x3bb}_i)})\zeta_i^k = \begin{cases} 0 & \textrm{for } 1 \le k \le d-2 \\ -1 & \textrm{for } k = d-1 \end{cases}\\ \zeta_1,\ldots,\zeta_d \textrm{ are mutually distinct} \end{matrix} \right. \right\}\hspace{-2.5pt}. \end{align*} $$
Then the natural projection
![]() $\widetilde {\Sigma }_d(\unicode{x3bb} ) \to \Sigma _d(\unicode{x3bb} )$
defined by
$\widetilde {\Sigma }_d(\unicode{x3bb} ) \to \Sigma _d(\unicode{x3bb} )$
defined by
![]() $(\zeta _1,\ldots ,\zeta _d) \mapsto (\zeta _1:\cdots :\zeta _d)$
is a
$(\zeta _1,\ldots ,\zeta _d) \mapsto (\zeta _1:\cdots :\zeta _d)$
is a
![]() $(d-1)$
-to-one map because for every
$(d-1)$
-to-one map because for every
![]() $(\zeta _1:\cdots :\zeta _d) \in \Sigma _d(\unicode{x3bb} )$
, we have
$(\zeta _1:\cdots :\zeta _d) \in \Sigma _d(\unicode{x3bb} )$
, we have
![]() $\sum _{i=1}^d ({1}/({1-\unicode{x3bb} _i}))\zeta _i^{d-1} \ne 0$
by Proposition 5.1. Hence, we have
$\sum _{i=1}^d ({1}/({1-\unicode{x3bb} _i}))\zeta _i^{d-1} \ne 0$
by Proposition 5.1. Hence, we have
We consider next the relation between
![]() $\widetilde{\Sigma}_d(\unicode{x3bb})$
and
$\widetilde{\Sigma}_d(\unicode{x3bb})$
and
![]() $\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
. We can define the surjection
$\widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
. We can define the surjection
![]() $\widehat {\pi }(\unicode{x3bb} ) : \widetilde {\Sigma }_d(\unicode{x3bb} ) \to \widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
by
$\widehat {\pi }(\unicode{x3bb} ) : \widetilde {\Sigma }_d(\unicode{x3bb} ) \to \widehat {\Phi }_d^{-1}(\bar {\unicode{x3bb} })$
by
by lifting up the map
![]() $\pi (\unicode{x3bb} ) : \Sigma _d(\unicode{x3bb} ) \to \Phi _d^{-1}(\bar {\unicode{x3bb} })$
in Proposition 5.1. Here, since
$\pi (\unicode{x3bb} ) : \Sigma _d(\unicode{x3bb} ) \to \Phi _d^{-1}(\bar {\unicode{x3bb} })$
in Proposition 5.1. Here, since
![]() $d \geq 3$
, every polynomial
$d \geq 3$
, every polynomial
![]() $f(z)=z+(z - \zeta _1)\cdots (z-\zeta _d)$
for
$f(z)=z+(z - \zeta _1)\cdots (z-\zeta _d)$
for
![]() $(\zeta _1,\ldots ,\zeta _d) \in \widetilde {\Sigma }_d(\unicode{x3bb} )$
is monic and centered.
$(\zeta _1,\ldots ,\zeta _d) \in \widetilde {\Sigma }_d(\unicode{x3bb} )$
is monic and centered.
We put
Here, note that we also have
![]() $\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) ) = \{ \sigma \in \mathfrak {S}_d \mid \unicode{x3bb} _{\sigma (i)} = \unicode{x3bb} _i \text { for every } 1 \leq i \leq d \}$
. Moreover,
$\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) ) = \{ \sigma \in \mathfrak {S}_d \mid \unicode{x3bb} _{\sigma (i)} = \unicode{x3bb} _i \text { for every } 1 \leq i \leq d \}$
. Moreover,
![]() $\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
is a subgroup of
$\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
is a subgroup of
![]() $\mathfrak {S}_d$
and is isomorphic to
$\mathfrak {S}_d$
and is isomorphic to
![]() $\prod _{K \in \mathfrak {K}(\unicode{x3bb} )} \mathrm {Aut}(K) \cong \prod _{K \in \mathfrak {K}(\unicode{x3bb} )} \mathfrak {S}_{\#K}$
.
$\prod _{K \in \mathfrak {K}(\unicode{x3bb} )} \mathrm {Aut}(K) \cong \prod _{K \in \mathfrak {K}(\unicode{x3bb} )} \mathfrak {S}_{\#K}$
.
The group
![]() $\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
naturally acts on
$\mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
naturally acts on
![]() $\widetilde {\Sigma }_d(\unicode{x3bb} )$
by the permutation of coordinates, and its action is free. Moreover, for
$\widetilde {\Sigma }_d(\unicode{x3bb} )$
by the permutation of coordinates, and its action is free. Moreover, for
![]() $\zeta , \zeta ' \in \widetilde {\Sigma }_d(\unicode{x3bb} )$
, the equality
$\zeta , \zeta ' \in \widetilde {\Sigma }_d(\unicode{x3bb} )$
, the equality
![]() $\widehat {\pi }(\unicode{x3bb} )(\zeta ) = \widehat {\pi }(\unicode{x3bb} )(\zeta ')$
holds if and only if the equality
$\widehat {\pi }(\unicode{x3bb} )(\zeta ) = \widehat {\pi }(\unicode{x3bb} )(\zeta ')$
holds if and only if the equality
![]() $\zeta ' = \sigma \cdot \zeta $
holds for some
$\zeta ' = \sigma \cdot \zeta $
holds for some
![]() $\sigma \in \mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
, which can be verified by a similar argument to the proof of Lemma 4.5(6) in [Reference Sugiyama14]. We therefore have the bijection
$\sigma \in \mathfrak {S}( \mathfrak {K}(\unicode{x3bb} ) )$
, which can be verified by a similar argument to the proof of Lemma 4.5(6) in [Reference Sugiyama14]. We therefore have the bijection
which implies the equality
 $$ \begin{align} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{\#( \widetilde{\Sigma}_d(\unicode{x3bb}) )}{\#( \mathfrak{S}( \mathfrak{K}(\unicode{x3bb}) ) )} = \frac{\#( \widetilde{\Sigma}_d(\unicode{x3bb}) )}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}. \end{align} $$
$$ \begin{align} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{\#( \widetilde{\Sigma}_d(\unicode{x3bb}) )}{\#( \mathfrak{S}( \mathfrak{K}(\unicode{x3bb}) ) )} = \frac{\#( \widetilde{\Sigma}_d(\unicode{x3bb}) )}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}. \end{align} $$
Combining equations (5.1) and (5.2), we have
 $$ \begin{align*} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{(d-1)s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align*} $$
$$ \begin{align*} \#( \widehat{\Phi}_d^{-1}(\bar{\unicode{x3bb}}) ) = \frac{(d-1)s_d(\unicode{x3bb})}{\prod_{K \in \mathfrak{K}(\unicode{x3bb})}(\#K)!}, \end{align*} $$
which completes the proof of Theorem II.
Acknowledgements
The author would like to express his thanks to Professor Hiroki Sumi for valuable advice on this paper. This work was supported by JSPS KAKENHI grant number JP19K14557.