Introduction
Hybrid pixel array detectors (PADs) have advanced scientific X-ray imaging at synchrotron light sources by offering low noise direct detection of photons coupled to custom signal processing electronics (Graafsma et al., Reference Graafsma, Becker, Gruner, Jaeschke, Khan, Schneider and Hastings2020). Using this platform for electron imaging in scanning transmission electron microscopy (STEM) has enabled a major jump in data collection fidelity and speed (Mir et al., Reference Mir, Clough, MacInnes, Gough, Plackett, Shipsey, Sawada, MacLaren, Ballabriga, Maneuski, O'Shea, McGrouther and Kirkland2016; Tate et al., Reference Tate, Purohit, Chamberlain, Nguyen, Hovden, Chang, Deb, Turgut, Heron, Schlom, Ralph, Fuchs, Shanks, Philipp, Muller and Gruner2016; Jiang et al., Reference Jiang, Chen, Han, Deb, Gao, Xie, Purohit, Tate, Park, Gruner, Elser and Muller2018; Plotkin-Swing et al., Reference Plotkin-Swing, Corbin, De Carlo, Dellby, Hoermann, Hoffman, Lovejoy, Meyer, Mittelberger, Pantelic, Piazza and Krivaneka2020). At the heart of the technology is a hybrid PAD that uses a pixelated silicon sensor to directly absorb and perform extremely low noise detection of incident energetic electrons. The resulting electrical signal is collected and processed at the pixel level using customized CMOS electronics. The flexibility of analog and digital CMOS electronics offers many design choices and optimizations for different types of measurements. As a result, there are different types of PADs and detector performance depends on the specific design choices and optimizations that are reviewed elsewhere (Faruqi & Henderson, Reference Faruqi and Henderson2007; Levin, Reference Levin2021).
One of the necessary design choices is how the pixel circuitry processes charge collected from the sensor. Two broad and fundamentally different approaches dominate PAD design. The first is counting of events, that is, the detection of current pulses caused by discrete absorption of incident X-rays or electrons. This method relies on pulse shaping, thresholding of signal, and digital tallying of the total number of quanta detected. The second method is the integration of current in the pixel. This second method relies upon charge creation in the sensor that is proportional to absorbed energy. In integrating detectors, the pixel output is proportional to the total charge collected by the pixel. Both methods can have advantages and disadvantages, depending on the specifics of the experiment and what data are of interest. A key requirement for charge integration is that the sensor must be thick enough to collect all the deposited energy from the incident electron. If this condition is not met, the energy straggle follows a Landau distribution which for thin detectors becomes as large as the mean energy deposited (Bichsel, Reference Bichsel1988). The Landau distribution leads to large noise fluctuations that cannot be effectively suppressed even by summing multiple measurements. This problem is particularly noticeable in the analog output of thin monolithic active pixel sensor (MAPS) detectors (Bichsel, Reference Bichsel1988). At low count rates, this problem can be overcome by using pulse counters set to trigger if the deposited energy is above the thermal noise level. This is an effective strategy for low-dose imaging sensors, such as used in cryo-transmission electron microscopy. For the higher beam currents per pixel used in electron diffraction, electron energy loss spectroscopy and STEM imaging, pulse counting cannot reliably count all electrons that arrive at high rates, and the detector efficiency and noise performance degrade rapidly with increasing beam current. For high speed, or high beam current experiments, the integration of current by the pixel is favored because of difficulties of reliably counting quanta that arrive at high rates. Of course, for the charge integration strategy to work, the sensor must be thicker than the range of the electron, which at 300 keV is 452 μm in silicon. This is the strategy we have taken and described in this paper.
The prototype imager described in this paper, the second-generation Electron Microscope Pixel Array Detector (EMPAD-G2), uses current-integrating pixel circuitry and builds on the technology of an earlier generation EMPAD (Tate et al., Reference Tate, Purohit, Chamberlain, Nguyen, Hovden, Chang, Deb, Turgut, Heron, Schlom, Ralph, Fuchs, Shanks, Philipp, Muller and Gruner2016). This earlier generation EMPAD (first generation) demonstrated collection and processing of 4D-STEM datasets to provide center of mass (CoM), bright field, dark field, differential phase contrast, and full diffraction analysis. Applying advanced techniques like ptychography has yielded record-breaking microscopic resolution (Jiang et al., Reference Jiang, Chen, Han, Deb, Gao, Xie, Purohit, Tate, Park, Gruner, Elser and Muller2018; Chen et al., Reference Chen, Jiang, Shao, Holtz, Odstrčil, Guizar-Sicairos, Hanke, Ganschow, Schlom and Muller2021). EMPAD data has been analyzed for high-resolution strain mapping over extended sample areas (Han et al., Reference Han, Nguyen, Cao, Cueva, Xie, Tate, Purohit, Gruner, Park and Muller2018) and to reconstruct magnetic and electric field distributions in samples (Nguyen et al., Reference Nguyen, Purohit, Hovden, Turgut, Tate, Kourkoutis, Fuchs, Gruner and Muller2016a, Reference Nguyen, Purohit, Yadav, Tate, Chang, Ramesh, Gruner and Muller2016b). The first-generation EMPAD was developed at Cornell and is available from Thermo Fisher. Like the EMPAD-G2 described in this paper, it is also a high-fidelity STEM imager. It is, however, limited to frame rates of 1.1 kHz and has a data-acquisition duty cycle that falls sharply above 1 kHz because the readout requires 860 μs to complete and the EMPAD is not designed to acquire new signal during readout.
The EMPAD-G2 prototype increases framing speeds to 10 kHz, extends the dynamic range, and allows for acquisition of signal during readout for a near-unity duty cycle even at 10 kHz. These capabilities allow for fast electron imaging of signals that vary by orders of magnitude across the face of the detector with almost no detector dead time. In practical terms, this allows for efficient high-speed, high-resolution raster imaging of extended areas. The speed of data acquisition and the dynamic range of the detector mitigate problems associated with sample stability by allowing high-quality, information-rich data to be collected quickly. The extension of critical performance metrics is expected to impact many types of STEM measurements. For many STEM applications, from ptychography (Chen et al., Reference Chen, Jiang, Shao, Holtz, Odstrčil, Guizar-Sicairos, Hanke, Ganschow, Schlom and Muller2021) to strain (Padgett et al., Reference Padgett, Holtz, Cueva, Shao, Langenberg, Schlom and Muller2020) and magnetic field (Xu et al., Reference Xu, Chen, Zhou, Wang, Dong, Aballe, Foerster, Gargiani, Valvidares, Bracher, Savchenko, Kleibert, Tomasello, Finocchio, Je, Im, Muller and Jiang2021) mapping, we find 128 × 128 pixels sufficient for high-resolution, high precision work. As noted previously for magnetic and strain mapping, and discussed in the section on the MUIS, the ability to deliver a high dose per pixel is more important than the number of pixels on the detector (Nguyen et al., Reference Nguyen, Turgut, Cao, Glaser, Chen, Stolt, Jin, Fuchs and Muller2020). Nevertheless, there are applications such as spectroscopy and continuous-rotation 3D electron diffraction where a larger pixel count is desirable. Our basic detector element has readout wiring along only one edge to allow for future stacking into tiled designs when larger pixel formats are needed.
This paper describes the design of the EMPAD-G2, the measured performance of the prototype, and examples of data acquired using the detector. These examples all demonstrate the need to work with higher beam currents when operating at higher speeds so as not leave the detector electron-starved. For atomic-resolution imaging, we want to record data as fast as possible to outrun environmental noise, but the faster we run the detector, the fewer electrons/pixel we will be able to record unless the counting or dose rate of the detector can be increased as well, as we have done so here. In mapping strains and fields, the ultimate precision depends on counting statistics and hence the dose delivered. Here, by increasing the maximum usable beam current on the detector, we show strain and polarization maps recorded at 100 μs/pixel instead of the more typical 10–100 ms needed to reach comparable precision. The resulting speed up reduces the acquisition time for typical 128 × 128 maps from 5–30 min down to under 2 s.
We also introduce a measure that describes the rate at which the detector can collect information—the maximum usable imaging speed (MUIS) at which the detector can reach a desired signal-to-noise ratio (SNR). We have found this helpful in thinking about detector design strategies and addressing questions such as how many pixels can be usefully illuminated. Usually, detector performance as a function of dose is described in terms of dynamic range, but this gives no indication of how long it will take to deliver sufficient electrons to fill the dynamic range. This can sometimes be as long as 20–30 s dwell time per frame, which is a far cry from the millisecond operating times expected for 4D-STEM mapping. Reporting the saturation current per pixel can be helpful to ameliorate this problem and should be done. However, when there is a soft roll-off in linearity, as, for instance, with pulse counting detectors, there can be an order-of-magnitude difference in where to define the saturation level. The ambiguity can be resolved by properly accounting for the loss of detective quantum efficiency when the output signal becomes sublinear. The MUIS can capture these details, making it simple to trade-off pixel count for SNR when the detector is electron-starved, or increasing the pixel count if individual pixels are saturating, with an end goal of reaching the desired SNR in shortest possible time. The EMPAD-G2 retains a high MUIS across a wide range of SNRs, allowing very high precision field measurements to be performed at speeds more typically associated with imaging (0.1 ms per pixel) than traditional quantitative mapping (10–100 ms per pixel). Qualitative information, such as visual recognition of features in an image requires a signal to noise ratio of at least 5:1 using the Rose criterion. Quantitative mapping, usually of details such as composition, strain, polarity, electric or magnetic fields, implies a higher precision and accordingly a higher SNR such as 100:1 to ensure 1% precision. Reaching the higher signals has traditionally required longer acquisition times, so quantitative maps historically have had fewer pixels than qualitative images.
Materials and Methods
Detector Description
The EMPAD-G2, like all hybrid PADs, comprises two functional layers. The first layer is a sensor layer that absorbs incident radiation, converting the absorbed energy to electron–hole pairs. The second layer is a custom CMOS integrated circuit (IC) that collects the charge generated in the sensor layer and converts it into readable information that can be used to construct quantitative images. To ensure complete energy transfer and minimum energy straggle, the sensor layer is chosen to be thicker than the 452 μm range of a 300 keV electron. This can be done without compromising the lateral point spread function because the incident beam's maximum spread occurs at about half the range. The sensor layer is a 500-μm thick, high-resistivity, silicon diode that is pixelated on one side. The pixelated side mates to the signal processing CMOS, which is also pixelated. The pixel size is 150 × 150 μm. In operation, the silicon diode (i.e., sensor) is kept fully depleted by reverse biasing the diode with high voltage applied to the detector face. Typical reverse bias voltages are between 150 and 200 V. The sensor is fabricated to specification by SINTEF (Trondheim, Norway). A pixel pitch of 150 μm is well matched the lateral spread of charge deposited by high energy (300 keV) electrons in the silicon sensor (see Spatial resolution section). Because of this, reducing pixel size would have limited advantages at higher incident electron energies and this has motivated us to remain with a 150 μm pixel pitch, similar to the first-generation EMPAD.
The CMOS Application Specific Integrated Circuit (ASIC) layer of the electronics is fabricated by Taiwan Semiconductor Manufacturing Corporation (TSMC) using a 0.18 μm mixed-mode process. The full monolithic CMOS die has 128 × 128 pixels, matching the pixel-by-pixel format of the Si sensor.
The sensor and the CMOS layers are mated to one another, pixel-by-pixel, using an array of solder bump bonds. The bumps are lithographically fabricated on the fully fabricated TSMC CMOS wafer by Micross Advanced Interconnect Technology LLC (Research Triangle Park, NC). Micross also processes the sensor wafer to apply a pixel-level metallization that is compatible with the bumps on the CMOS wafer. After processing, the wafers are singulated to make compatible CMOS and sensor dies. The dies are mated using a flip-chip process, and the resulting hybrid detector module is mounted on a heatsink and wire bonded to a printed circuit board that conveys the signals necessary for operating the chip and reading data. Signals supplied to the ASIC include voltage and current biases for analog and digital components; and digital waveforms for chip operation that allow for the synchronization of image acquisition with external systems (e.g., electron microscope scanning). Output signals from the ASIC include 16 differential analog and 16 LVDS digital data outputs; and two additional LVDS clocking outputs for synchronizing the 200 MHz digital data from the LVDS data outputs.
The detector module is actively cooled by a miniature thermoelectric cooler. The cooler is attached underneath the module and held to −20 ± 0.1 C via a tuned thermal feedback loop. An external chilled water circulator is used to remove heat from the thermoelectric unit. The detector module assembly, shown in Figure 1, is attached to a pneumatic actuator that allows for in-vacuum insertion into the microscope or retraction into a radiation-shielded shroud.

Fig. 1. Picture of the detector module showing the active imaging area and wire bonds along one edge. The single-edge connection simplifies future tiled detector designs, allowing for a 2 × n tiling of modules without wire bonds interfering with the active imaging area. The block diagram shows functional components of the system that includes the hybrid detector module, an in-vacuum PC board, a vacuum feedthrough board, and a PC board external to the vacuum that has a module-controlling FPGA. Data are collected through a fiberoptic link that connects to frame grabber card.
Pixel Operation
The design of the EMPAD-G2 CMOS pixel offers several advances over the previous EMPAD, including a higher frame rate that reduces scan time; extended dynamic range that allows use of higher EM beam currents; and the ability to acquire data during readout, greatly reducing detector deadtime and speeding up STEM dataset collection. This is important because many applications require sample stability at the sub-Angstrom level over the dataset collection time, thus depending on rapid data acquisition. The dynamic range metric that is relevant to these types of high-speed measurements is defined by incident power on the detector, not simply a statement of well-depth or number of bits in a digital counter.
The high-level pixel diagram shown in Figure 2 indicates how some new detector capabilities are accomplished. The easiest way to describe pixel operation is by tracking the processing of collected charge through the schematic. The charge enters the pixel from the sensor diode through a bump bond and is collected by an analog integrator that has one capacitor (40 fF) actively in the feedback loop and another that is primed to be switched into the feedback circuit. Both capacitors are cleared of charge before acquisition. If the output of the integrator passes a threshold voltage, Vth, during acquisition, the second capacitor (840 fF) is switched into the feedback of the front-end integrator, lowering the gain of the front-end integrator and extending the dynamic range of the analog front-end. This scheme is similar to that used by the X-ray adaptive gain integrating pixel detector (AGIPD; Trunk et al., Reference Trunk, Allahgholi, Becker, Delfs, Dinapoli, Göttlicher, Graafsma, Greiffenberg, Hirsemann, Jack, Klyuev, Kruger, Lange, Laurus, Marras, Mezza, Mozzanica, Poehlsen, Rah, Schmitt, Schwandt, Sheviakov, Shi, Xia, Zhang and Zimmer2017). If the front-end is in low gain and the Vth is passed again, a switched capacitor charge dump circuit is triggered that extracts a bolus of charge from the front-end without breaking the feedback loop of the integration stage, so that integration continues uninterrupted. Every subsequent passing of Vth also triggers the charge dump circuit. Each time a charge dump occurs, an in-pixel counter is incremented. Charge dumping can happen at rates up to 108 dumps per second, a hundred times faster than in the original EMPAD, resulting in a significant extension of the dynamic range of incident electron current. The output of the pixel is the combination of the remaining signal in the integrator at the end of the frame (conveyed as a residual voltage from the pixel differentially referenced to a reference voltage), a digital gain bit (that conveys what gain state the pixel is in), and a 16-bit word that encodes how many charge dumps have happened during acquisition. These data are merged using calibration constants to yield a smooth, linear, monotonic signal proportional to the incident electron energy deposited in the sensor.

Fig. 2. High-level pixel diagram. The bump bond and sensor diode are shown schematically on the left. The charge integrating front-end actively adapts during integration if a threshold is crossed, first reducing the gain by adding a feedback capacitor, then removing charge in fixed increments.
In addition to the basic signal processing, additional features allow for acquisition of signal during readout. First, two 16-bit counters are alternately used in successive frames so that the value of one is being read out while the other is actively counting charge dumps of the next image. Second, the analog voltage is sampled onto one of two in-pixel track-and-hold circuits at the end of any given frame. While one of the track-and-hold circuits is tracking the output of the front-end integrating stage, the other is holding the value of the previous frame and is read out. This in-pixel double buffering of both digital and analog values allows for very high duty cycle active detection of more up to 99% even while framing at 10,000 frames per second. The gain bit is latched into one of two additional pixel status bits and shifted out with the counter data. As a result, the pixel produces 18 bits of digital data. Since the analog data is digitized to 14-bits using a pipelined off-chip ADC, each pixel yields a 32-bit data value for each frame.
Readout Structure
Readout of the CMOS ASIC requires both analog and digital readout. These are performed in parallel and independently, meaning that waveforms for each readout have no predetermined phase with respect to one another, other than that imposed by the acquisition of frames. The ASIC is composed of 128 × 128 pixels organized into 16 separate banks with 8 × 128 pixels each. The banks are read out in parallel with one digital LVDS pair and one analog differential pair for each bank.
The analog readout structure, shown in Figure 3, consists of the dual track-and-hold circuits (discussed in the pixel description above), a dual track-and-hold multiplexer at the top of a bank, and a differential output amplifier. The in-pixel dual track-and-hold circuits alternate with each frame, so that during the readout of a single frame the selection is static, that is, a single analog value is ready to be read. Addressing of pixels to be read out is done by a row-select signal that is fanned out to all pixels in the row, with a row defined as the shorter dimension in an 8 × 128 pixel bank. The addressing of the column is accomplished with the dual 8 × 1 mux. The reason for dual track and hold at the column level is to allow pre-charging of the analog lines before sampling while previously sampled values are being read out. This mitigates the effects of parasitic time constants and produces a clean sample-and-hold signal that is fed into a differential amplifier. Both the signal from the pixel and the reference voltage from the pixel are sampled in parallel. Analog values are converted to digital values off-chip at a 10 MHz rate.

Fig. 3. A high-level schematic analog output—column level.
The digital readout scheme, diagrammed in Figure 4, consists of two in-pixel counters that are read out as shift registers on alternate frames. Each of these, arbitrarily designated as data streams A and B, are daisy-chained with all pixels in the same column during readout. On the edge of the chip a pixel worth of bits (i.e., 18 bits) are shifted into a shift register at the column edge. This shift register is then daisy-chained with all similar shift registers in the bank and read out at approximately 200 MHz. While these bits are shifted out, a clock running at approximately 1/8th the speed shifts data from the array into another set of shift registers. These shift registers follow the same process and are multiplexed into a daisy-chain for 200 MHz readout. This scheme has the advantages of feeding a slower clock signal (200 MHz/8 = 25 MHz) through the array, and keeping bits associated with a particular pixel grouped together. This second advantage reduces the need to re-order bits in the readout FPGA and simplifies trouble shooting, if needed, because pixel outputs are easily isolated on an oscilloscope.
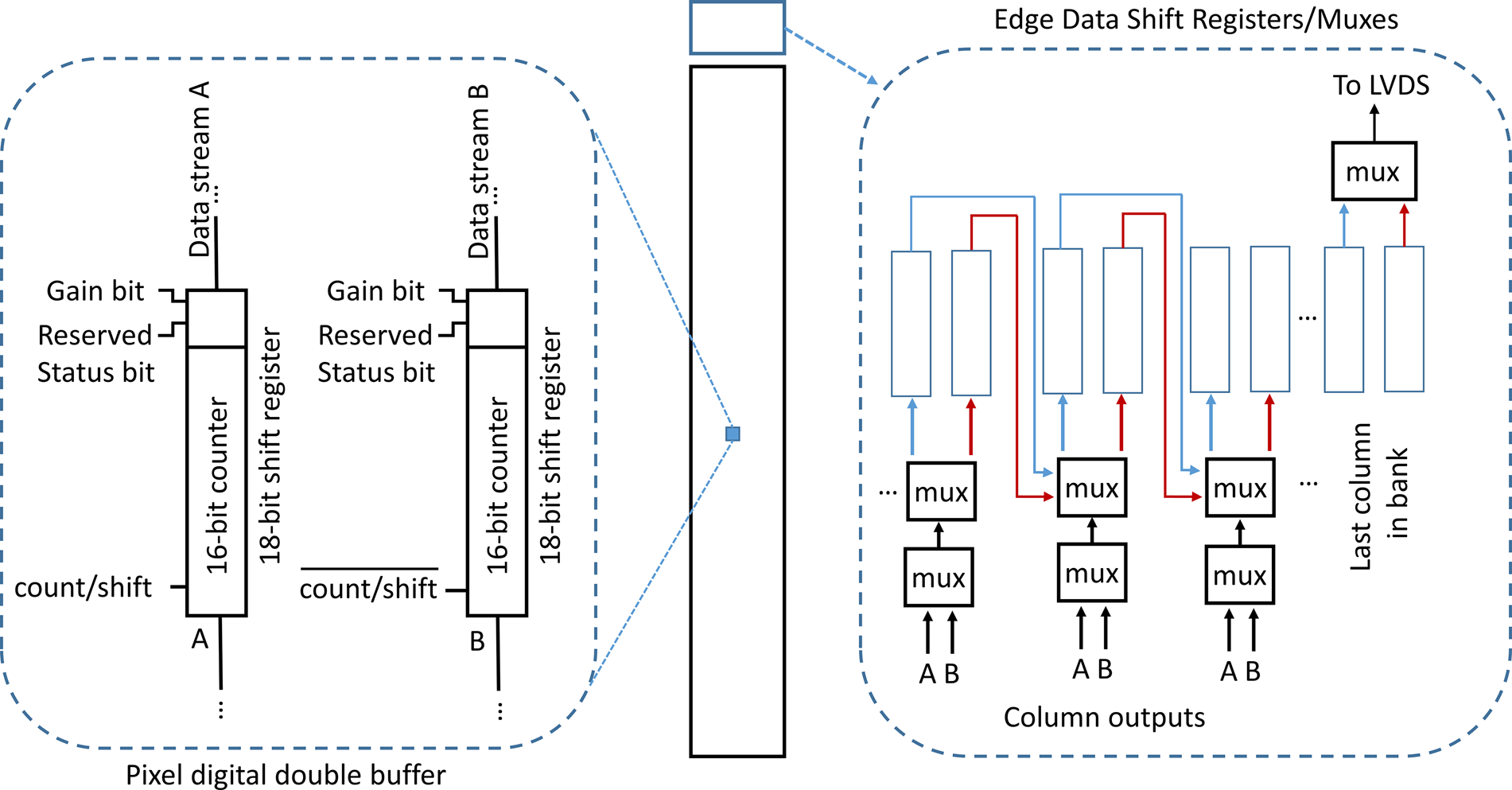
Fig. 4. A high-level schematic digital readout—column level.
Support Electronics
The wire bonds of the ASIC that connect to the signal processing electronics are all on the same side of the detector module, allowing for potential three-side tiling of modules. All power, biases, digital control, and signal outputs from the chip are wire-bonded from this single edge of the module to a PC board that has appropriate buffers, digital-to-analog converters (DACs), and power biases for the chip. This board resides in the vacuum and connects to a feedthrough board that provides electrical connections through a vacuum flange to the PC board with analog-to-digital converters, voltage regulators, and an FPGA that manages the low-level waveform operation. A fiber optical link from this board provides a GenICam, Generic Interface for Cameras standard (“GenICam – EMVA” n.d.), compliant control interface for the detector. Data are captured using a frame grabber board.
Results and Discussion
Data Combination and Calibration
Raw data from the array is comprised of the analog signal from the amplifier, the gain bit, and the output from the digital counter that indicates the number of times a charge removal operation was performed (a 16-bit word). To calibrate the scaling factors needed to combine the raw data into a linear response, a dataset is taken with constant illumination and increasing integration time (Fig. 5). The data shown were obtained using an optical LED array (Bridgelux, BXRC-50C1001-D-74-SE), run at a constant current. This optical flood field is not completely uniform because of variations in the entrance window metallization, but uniformity in this calibration step is not needed. A source that is stable in time is required. Optical photons have the added benefit of providing a signal with much less Poisson shot noise than an equivalent illumination with high-energy electrons, reducing the number of frames needed to average to obtain the scaling factors to high precision.
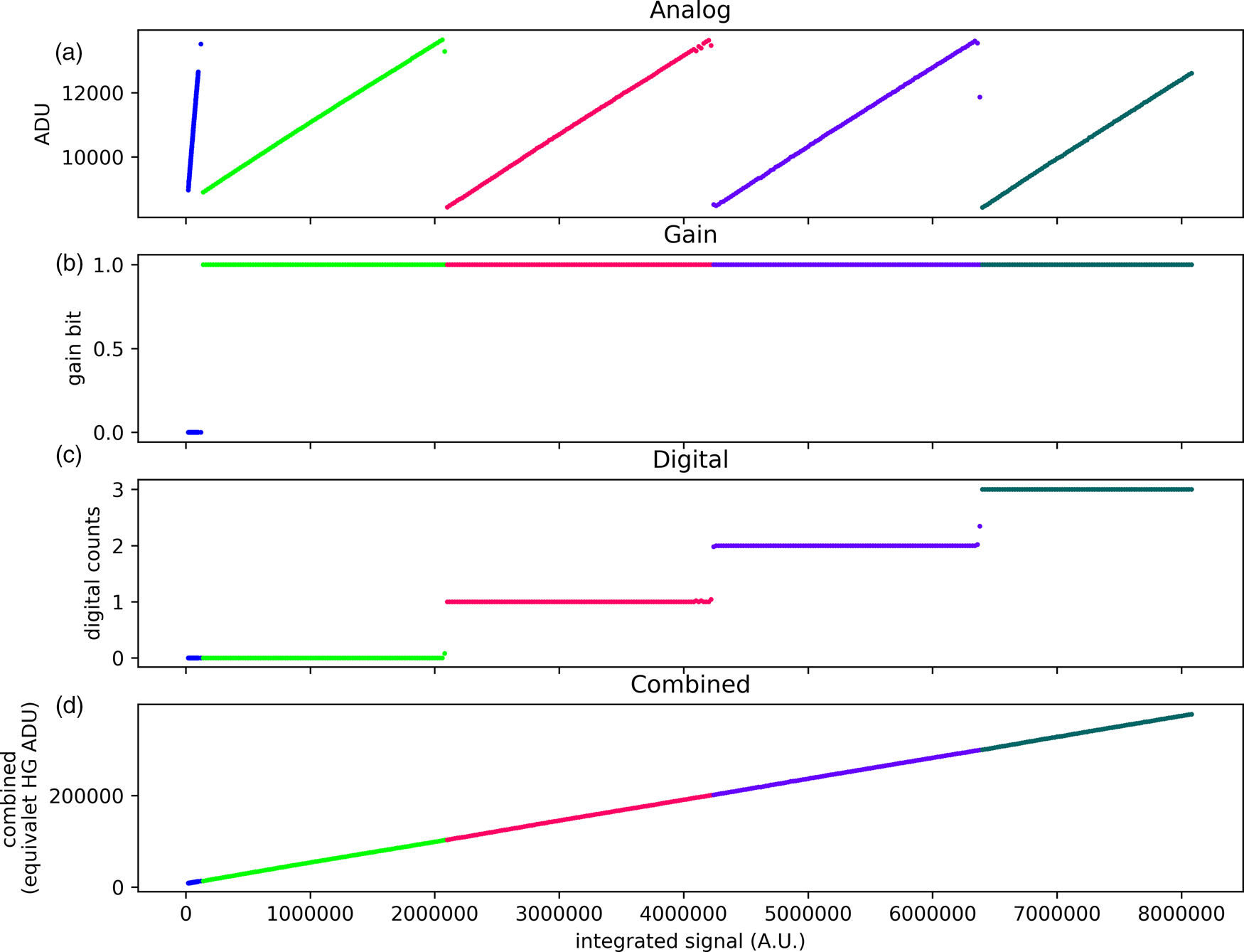
Fig. 5. Data recorded in a single pixel under uniform illumination with increasing integration time. The raw data includes an analog value (a) from the voltage remaining on the integration capacitor, a gain bit (b), and a 16-bit digital number (c) corresponding to the number of charge dump cycles. These data are scaled together (d) to obtain calibration constants which provide a continuous linear measurement of charge carriers produced in the sensor diode. The data shown were obtained using an optical LED array (Bridgelux, BXRC-50C1001-D-74-SE), run at a constant current, providing an optical flood field. Each point is an average of 50 readings and accounts for non-digital integer counts. The blue traces at left are acquired in high gain, before the pixel is triggered to flip the gain bit. The light green trace is after the pixel has adaptively switched to a lower gain. The red trace is the first digital count. Colors to the right of the red traces represent subsequent increments of the pixel's digital counter.
Linear regression is applied to the three different signal domains: high-gain analog (analog when the gain bit equals 0), low-gain analog (analog when the gain bit equals 1), and digital. With these regressions, all signals are scaled to equivalent high gain analog-to-digital units to produce a continuous linear output (Fig. 5d). Each pixel has unique scaling coefficients arising from fabrication process variations (e.g., variations in capacitor sizes). Also, double buffering leads to two unique sets of analog sampling circuitry, so each pixel requires two sets of calibration coefficients.
The above procedure produces a linear output for each pixel, scaled to the output voltage of that pixel. The relative gain between pixels can vary, so a final scaling factor is needed to normalize all pixels to the same scale. This calibration can be obtained using histograms of the response of each pixel to single electrons, as shown in the next section. The position of the single electron peak is directly proportional to the absolute gain of each pixel. It was found in practice that the pixel normalization coefficients could be determined to higher precision using the optical flat field illumination rather than a defocused source of electrons (3% precision for coefficients determined by electron histograms versus <0.1% precision by using LED flood field calibration).
Low-Fluence Electron Microscopy Measurements
Figure 6 shows low fluence measurements made with a wide aperture in the Thermo Fisher Themis CryoS/TEM electron microscope. The aperture was chosen such that a roughly uniform illumination was incident on the detector. Signal levels less than 0.1 electrons/pixel/frame on average are needed to avoid substantial overlap of the desired individual electron events. Three electron energies were used: 300, 120, and 80 keV. Figure 6a shows histograms of single pixel outputs gathered from the full array over 50,000 frames. Background pedestal subtraction was applied to this dataset, with the pedestal measured by taking frames with no incident electrons present (i.e., a dark frame). Pixel calibrations described in the previous sections were also applied. There is a zero-electron peak on the left corresponding to no detected charge from incident radiation and, for the different energies, an integer number of peaks to the right. The positioning of the peaks is determined by the energy of the detected electrons, meaning 300 keV electrons deposit proportionately more energy and produce a proportionately higher signal than 80 or 120 keV electrons.

Fig. 6. Low-fluence histograms. (a) Histograms of raw pixel values across the array for three incident electron energies (80, 120, and 300 keV) showing the zero-signal peak and discrete energy peaks. (b) Histograms of signal from identified connected clusters of pixels that detected electron events. Histograms of connected pixels that recombine charge that was split between pixels. (c) A subsection of a single low-fluence image of 300 keV electrons, showing the splitting of charge between multiple pixels.
The distinctness of the peaks is also a function of energy because the charge produced in the silicon sensor can spread over adjacent pixels. The area over which charge is likely to spread increases with electron energy and only a few events at 300 keV will be contained within a single pixel. The histograms are a mapping of these stochastic processes projected onto many thousands of measurements. In other words, the charge resulting from single incident electrons can spread over multiple pixels. For energetic electrons, this spread depends primarily on the random paths that the resultant secondary electrons take through the silicon as they lose energy and produce collectable charge. Over a large number of frames, the sum of these random walks can be viewed as producing a probabilistic distribution of deposited charge. Figure 6c shows single-electron events at 300 keV for a single frame and a small subsection of the imaging area.
A cluster analysis can be performed on these images to provide a histogram of the total energy deposited per electron event (Fig. 6b). Individual events are detected, a local area around each is defined and the signal from each event is summed using the OpenCV (Culjak et al., Reference Culjak, Abram, Pribanic, Dzapo and Cifrek2012) connected components algorithms (Bolelli et al., Reference Bolelli, Cancilla, Grana, Battiato, Gallo, Schettini and Stanco2017). This recombines the charge deposited from single electrons that has been split between pixels. The single electron peak is much more distinct and symmetric than in Figure 6a. In this plot, electrons that fully deposit their energy within the sensor contribute to the peak, whereas electrons that lose energy due to other processes (e.g., fluorescence or backscatter) contribute to the low energy tail. The peak position is found to be 3,661 ADU for 300 keV, 1,453 for 120 keV and 960 for 80 keV. Using the shape of the tail in the distributions, the mean signal per recorded electron is 3,262 ADU for 300 keV, 1,258 ADU for 120 keV, and 832 ADU for 80 keV.
Linearity of Response at High Flux
To measure the linearity of response to increasing beam current, a small (<4 pixels FWHM) focused spot of 300 keV electrons was imaged at beam current settings that varied over three orders of magnitude. A cross-section of the spot is shown in Figure 7 (left). As the beam intensity increases, the signal within a pixel continues to increase up to a maximum rate determined by the speed of the charge dump circuitry in each pixel. At beam currents above this rate, the pixel response will saturate. An independent measure of the beam current was obtained by recording the current flowing from the sensor power supply (Keithley 2400 source meter). This supply shows a linear response well beyond the limit set by the pixel circuitry. The sensor current will have a gain of 8.33 × 104 with respect to the beam current since an electron–hole pair is created in the sensor for every 3.6 eV of incident electron energy. At each beam current, 1,000 frames were averaged, with each frame having a 100 μs exposure. The intensity in the brightest pixel was converted to a primary electron current over this time using the gain factor for 1 electron obtained from single-electron histograms shown in Figure 6. Figure 7 (right) shows the current in the brightest pixel as a function of total sensor current. Response is nearly linear up to 175 pA/pixel of 300 keV incident electron beam current, at which point the response saturates.

Fig. 7. (Left) Cross-section of a small focused spot of 300 keV electrons used in linearity measurements. Data taken from the average of 1,000 images with 100 us exposure time at 182 uA sensor current and a maximum incident 300 keV electron current of 144 pA/pixel. Intensity in the peak was >60,000 electrons/pixel/frame, whereas the tail regions had <0.03 electrons/pixel/frame on average. (Right) Intensity in the brightest pixel as a function of varying beam current. Intensity has been converted to incident electron current per pixel. The pixel shows nearly linear response up to 175 pA/pixel of incident beam current at 300 keV.
Pixel saturation is a function of biasing levels supplied to the signal processing electronics of the ASIC. These measurements were made at nominal settings and it should be noted that adjusting biases can affect (both increase and decrease) the saturation level. In-pixel bias settings do affect other properties (e.g., uniformity and pixel gain) with these nominal settings chosen for good overall performance. All characterizations in this paper were taken with the same bias settings. The maximum usable primary beam current also scales inversely with the incident electron beam's energy, so at 60 keV the saturation beam current would be around 875 pA/pixel. Written explicitly, the integrated signal incident on a single pixel at the maximum measurable beam current and full frame rate is:
 $$\eqalign{S_{{\rm max}}& = {\rm \;}\left({175 \times {10}^{{-}12}\displaystyle{{{\rm \;coulomb\;}} \over {{\rm s}\,{\rm pixel}}}} \right)\left({\displaystyle{{{10}^{{-}4}{\rm \;s}} \over {{\rm frame}}}} \right)\cr &\quad\times \left({\displaystyle{{1{\rm \;}{\rm e}^ {-} } \over {1.6{\rm \;} \times {10}^{{-}19}{\rm \;coulomb\;}}}} \right)\left({\displaystyle{{300\,{\rm keV}} \over {1{\rm \;}{\rm e}^-}}} \right)\cr {\rm \;}& = 3.3 \times 10^7\,{\rm keV/pixel/frame.}}$$
$$\eqalign{S_{{\rm max}}& = {\rm \;}\left({175 \times {10}^{{-}12}\displaystyle{{{\rm \;coulomb\;}} \over {{\rm s}\,{\rm pixel}}}} \right)\left({\displaystyle{{{10}^{{-}4}{\rm \;s}} \over {{\rm frame}}}} \right)\cr &\quad\times \left({\displaystyle{{1{\rm \;}{\rm e}^ {-} } \over {1.6{\rm \;} \times {10}^{{-}19}{\rm \;coulomb\;}}}} \right)\left({\displaystyle{{300\,{\rm keV}} \over {1{\rm \;}{\rm e}^-}}} \right)\cr {\rm \;}& = 3.3 \times 10^7\,{\rm keV/pixel/frame.}}$$Detecting individual electrons allows for high fidelity measurements, but the real strength of a high dynamic range detector is combining low fluence (i.e., single electron) detection with the ability to quantify high intensity signals in the same frame. Looking again at Figure 7 (left), we see the profile of the spot is measured over six orders of magnitude. The tails show a fairly uniform floor at <0.03 electrons/pixel (i.e., an electron strikes a pixel in this region only once in every 30 images on average). Importantly, the dynamic range shown in Figure 7 is realizable at a 10 kHz frame rate (100 μs frame time). As noted in Table 1, the dynamic range of the pixels at a 10 kHz frame rate is 1.3 × 107, calculated by taking the ratio of the highest measurable signal (175 pA incident current) and noise of a detector pixel in equivalent keV (2.6 keV).
Table 1. EMPAD-G2 performance specifications.

Spatial Resolution
The spatial resolution of the EMPAD-G2 is a function of both the pixel size and the spread of charge when incident electrons interact with the 500-μm thick silicon sensor. Each incident electron yields secondary electrons that undergo random paths through the sensor. When taken as an ensemble, the r.m.s. width of the charge spread increases with increasing incident electron energy. The spatial resolution was measured by imaging a sharp-edged, nominally circular aperture at three energies (80, 120, and 300 keV; Fig. 8a). The aperture edge was fit to a circle and the one-dimensional (1D) edge spread function (ESF) was found by plotting the intensity of a pixel in the image versus the distance of that pixel from the fit circle (Fig. 8b). This method allows the ESF to be sampled much more finely than the size of the pixel. The ESF was fit to the convolution of a linear ramp (ramping from 1 to 0 over the width of one pixel) and a Gaussian function. The widths of the Gaussian function in these fits show a charge spread (full width at half maximum) of 201, 67, and 44 μm for 300, 120, and 80 keV, respectively.

Fig. 8. Measurements of the spatial response at the different energies. (Upper left, a) An image of an aperture projected onto the detector face. (Upper right, b) The edge response the detector at 300, 120, and 80 keV, as a function of the distance from the imaged aperture edge. The best fit circular arc was used to define the edge of the aperture. The ideal pixel response corresponds to an ideal pixel, that is, no charge spread. (Lower left, c) The line spread function (LSF) at 300, 120, and 80 keV found by differentiating the fitted function to the edge response. (Lower right, d) The modulation transfer function (MTF), derived from the FFT of the LSF, plotted up to the Nyquist frequency.
The line spread function (LSF) can be computed by differentiating the ESF. Here, we differentiate the fitted function as a method to smooth the sampling noise of the data (Fig. 8c). For high dynamic range imaging, the low-level tails to the LSF are important quantities as they determine how far a weak signal must be from a strong signal before it can be seen. One can measure the full width at 1/100 maximum (FWCM) and the full width at 1/1,000 maximum (FWKM). For 300 keV electrons, the FWCM is 4.4 pixels and the FWKM is 5.6 pixels. These are reduced to 1.8 and 2.1 pixels for 120 keV and 1.6 and 1.8 pixels for 80 keV.
The modulation transfer function (MTF) was computed by taking the Fourier transform of the LSF (Fig. 8d).
Detective Quantum Efficiency
The precision of any measurement is Poisson limited by the number of primary quanta in the signal. For M incident electrons, the shot noise scales as ![]() $\sqrt M$. How well a detector achieves this ideal performance is quantified by measuring the detective quantum efficiency (DQE), defined by
$\sqrt M$. How well a detector achieves this ideal performance is quantified by measuring the detective quantum efficiency (DQE), defined by
where S/N output is the signal-to-noise ratio as recorded by the detector, and S/N input is the signal-to-noise ratio of the incident signal. With a Poisson distribution for the incident electrons, this reduces to
In general, DQE will be a function of electron energy, spatial frequency and total dose recorded. DQE as a function of spatial frequency, ω, is usually computed by
where DQE(0) is the DQE at zero spatial frequency, NPS(ω) is the normalized noise power spectrum, and MTF(ω) is the modulation transfer function.
The noise power spectrum was calculated by taking the 2D-Fast Fourier Transform (FFT) of the difference of two nominally uniform illuminations. This was averaged from the FFTs of 200 to 5,000 difference pairs at each energy. The 1D NPS was found by taking the azimuthal average of the 2D FFT.
DQE(0) is found by applying equation (1) above to the uniform illumination dataset. DQE is calculated with regions of interest spanning 1 × 1 pixels to 50 × 50 pixels. DQE(0) is taken as the asymptotic value found as the size of the region becomes larger to avoid smoothing effects in the noise due to the point spread function. Images are taken pairwise, with the signal found from the sum of the pair, and the noise computed from the difference. Taking the difference will eliminate systematic variations within the flood illumination. The incident signal in each region of interest is found from the average signal in each region, normalized by the average signal per incident electron found from single-electron event histograms. DQE(0) is found to be 0.94 for 300 keV, 0.9 for 120 keV, and 0.9 for 80 keV. DQE(ω) is shown in Figure 9 for each of these energies.

Fig. 9. DQE(ω) for 300, 120, and 80 keV. Also shown is the ideal response for a detector with 150 um pixilation. The DQE(0) for the 300, 120, and 80 keV are 0.94, 0.90, and 0.90, respectively.
Maximum Usable Imaging Speed
An important criterion in designing and operating a detector is how many electrons we can deliver to a given pixel in a given frame exposure time—if too many electrons arrive in the given interval, then the detector will saturate, and if too few electrons are delivered, we are wasting readout bandwidth, storage memory and risking adding additional and unnecessary noise. Dynamic range, when defined as the ratio of largest to smallest detectable signal in a frame with indeterminate frame rate, is not sufficient to capture this effect—for instance, if a counting detector saturates at a count rate of 1 MHz but has a dynamic range of 24 bits, then it will take over 16 s to fill the dynamic range. We also need a detector that can tolerate a high beam current so that a reasonable frame rate can be achieved. Here, we introduce a metric that captures both of these requirements, which can be helpful for matching source and detector to reach the desired information quality needed for a particular experiment. This is the MUIS at which a particular signal-to-noise ratio can be reached.
The S/N output will depend on the number of electrons collected and the DQE of the detector. For pulse-counting detectors, the DQE is often quoted for the very-low-fluence limit because it degrades as a function of fluence (Li et al., Reference Li, Zheng, Egami, Agard and Cheng2013). Equation (2) can be modified to capture this trend by noting that if some counts are missed and the dead times are uncorrelated, then if only a fraction η of electrons are counted, then ![]() $S/N_{{\rm output}}( \eta ) = $
$S/N_{{\rm output}}( \eta ) = $ ![]() $( {\eta M} ) /\sqrt {\eta M} = \sqrt {\eta M}$ instead of
$( {\eta M} ) /\sqrt {\eta M} = \sqrt {\eta M}$ instead of ![]() $\sqrt M$. Substituting into equation (2), the DQE at a collection efficiency η, due to dead-time limitations, is related to the DQE at low fluence. DQElow (the low-count limit where there are no dead time losses and hence η = 1) as
$\sqrt M$. Substituting into equation (2), the DQE at a collection efficiency η, due to dead-time limitations, is related to the DQE at low fluence. DQElow (the low-count limit where there are no dead time losses and hence η = 1) as
This expression holds for low to moderate dead times, that is, high collection efficiencies (![]() $\eta {\rm >rsim }0.7)$, but once the signal becomes noticeably nonlinear the DQE degrades exponentially, reflecting the exponential sensitivity to noise in attempting to correct nonlinearities (Li et al., Reference Li, Zheng, Egami, Agard and Cheng2013).
$\eta {\rm >rsim }0.7)$, but once the signal becomes noticeably nonlinear the DQE degrades exponentially, reflecting the exponential sensitivity to noise in attempting to correct nonlinearities (Li et al., Reference Li, Zheng, Egami, Agard and Cheng2013).
The question of what is the maximum speed we can operate at to reach a desired S/N output now becomes the question of what is the maximum speed at which M e- can be delivered to the pixel?
That is to reach a signal/noise ratio of SNR, the number of incident electrons needed is
The shortest frame time in which M electrons/pixel can be captured gives the MUIS:
where I is the incident beam current/pixel in Amps. For instance, the Rose criterion for imaging requires a SNR = 5. If we had an ideal detector that operated at 100 kHz but only counted at most 1 electron/pixel/frame for a saturation current of 16 fA/pixel, it would take 25 frames to reach Rose criterion, and the Rose speed or MUIS(SNR = 5) would be only 4 kHz. Note that the analysis so far has assumed readout noise is negligible, which is generally the case for direct electron detectors. When readout noise is present, such as for scintillator-based detectors, the DQE must be modified in a dose-dependent manner. This can be done by replacing the DQE = η DQElow term in equation (6) by equation (5) of ref (Krivanek et al., Reference Krivanek, Ahn and Keeney1987). The Landau noise in analog MAPS detectors can accounted for if the mean, μ, and standard deviation, σ, of the Landau straggle is known—the DQE can be written as DQE = μ 2/(μ 2 + σ 2). Often σ > μ for thin sensors such as the MAPS architecture, leading to a typical DQE below 0.4 (McMullan et al., Reference McMullan, Faruqi, Clare and Henderson2014). The formula also holds for general charge integration modes, including the EMPADs, but for thick sensors, σ ≪ μ, so can be neglected. For instance, for the EMPAD2, σ = 2.6 keV, so when μ is in the range of 60 . . 300 keV the respective correction to DQE is 0.9998 . . 0.9999.
One strategy to increase the MUIS is to reduce the pixel count, though potentially at the sacrifice of momentum resolution. For a total beam current, I tot, and n x n pixels in the detector, the beam current per pixel can be written as I = I tot/n 2. Substituting into equation (6), we see that reducing n increases the MUIS quadratically, so long as each individual pixel can handle the increased beam current without saturation:
To put it another way, doubling the number of pixels in each direction will reduce the MUIS by a factor of 4 if the incident beam current is unchanged. This substitution also gives the MUIS in a form that explicitly depends on pixel count.
The EMPAD-G2, operating at 10 kHz frame rate, has a saturation current/pixel of 175 pA at 300 keV allowing for a signal-to-noise ratio per pixel of over 300, that is, MUIS(SNR = 300) would be 10 kHz. Only when a signal-to-noise ratio/pixel greater than 300 was needed would the imaging speed drop below 10 kHz. For instance, if we were trying to resolve the diffuse scattering in a diffraction pattern simultaneously with the details of the central disk, we might require a SNR of 1,000, and the MUIS(SNR = 1,000) would now be a little over 1 kHz as shown in Figure 10a.

Fig. 10. Maximum usable imaging speed (MUIS): (a) MUIS as a function of SNR for the different detector strategies discussed in the text. 8-bit pulse models a modern pulse counting PAD, MAPS models a large-pixel format MAPS detector optimized for cryoelectron microscopy and 1-bit MAPS models a high-speed detector designed to operate at an 87 kHz frame rate but with only a 1-bit readout. (b) A summary of achievable MUIS for different detector designs, represented by a high-speed but noisy imaging mode at SNR = 5 in all pixels intended to reflect TEM usage or basic atomic-resolution STEM imaging, and a quantitative mapping mode at SNR = 300 in a few pixels (see text) such as for strain and diffraction measurements. Here, a range of dead-times, readout, and data-transfer schemes are explored for the different pulse counting options. Deliverable beam currents limits set by the source performance are also shown for thermal-field and cold-field emitters. Currently, system performance is still limited by the detectors and not the sources. In both panels, these are not a direct pixel-to-pixel comparisons, but instead assumes that the other designs, which typically have smaller pixels, have been binned down to match the EMPAD pixel count. Without re-binning, their MUIS performance would drop 4–16 × compared to what is plotted here.
In Figure 10, we explore the MUIS attainable for different detector strategies, including the EMPAD and EMPAD-G2. We also consider:
• A state-of-the-art pulse counting detector operating with 8-bit collection for high-speed sampling and with DQE = 0.8 and η=0.55 at 1 pA input current/pixel, that is, at 1 pA, 55% of incident electrons are counted. We re-bin over 16 pixels to compare to the 128 × 128 EMPAD. This is labeled “8-bit pulse” in Figure 10.
• A MAPS detector pulse counting at 1 e−/pixel/frame sampled at 87 kHz, and re-binned by 16 as well. This is labeled “1-bit MAPS” in Figure 10.
• A large-pixel format MAPS detector, such as that typically used in cryo-electron microscopy with a maximum count rate of 30 e−/pixel/frame, a frame rate of 1.5 kHz and re-binned by 256. This is labeled “MAPS” in Figure 10.
There are many more permutations of designs to consider. For instance, if the readout speed is limited by the data transfer bandwidth, doubling the bit-depth of the signal and halving the frame rate can lead to a significantly larger MUIS at large SNR. To capture different design choices on a single plot, we summarize the performance of each combination by its MUIS at SNR = 5 versus SNR = 300 in Figure 10b. This reflects two extreme limits of possible use cases: SNR = 5 for high-speed but noisy readout for TEM imaging or simple STEM imaging modes like atomic-resolution, center of mass (CoM) where the signal will be integrated over the detector plane, and SNR = 300 for quantitative measurements of strain and magnetic fields where high doses are needed for high precision. For quantitative work, the EMPAD-G2 can reach the needed SNR roughly two orders of magnitude faster than the other designs.
Again, it is worth noting that when the SNR per pixel drops well below the Rose criterion of SNR = 5, then the detector is too electron starved to make effective use of such small pixels, and either a larger pixel size should be chosen, or a sparser readout scheme employed to increase the frame rate. Currently, detector frame rates are limited by the data transfer bandwidth, so the fastest detectors are currently quadrant detectors, that is, 2 × 2 pixels, with discrete readout electronics, and these can reach readout speeds of ~20 MHz with a nanoamp of beam current. This would give a MUISquad(SNR = 5) of 20 MHz, and a MUISquad(SNR = 300) of 55 kHz. Given that the differential phase contrast (DPC) output of the quadrant detector is visually almost indistinguishable from the CoM analysis from a pixelated detector at low to moderate signals, MUISquad serves as a useful guideline as when to use a quadrant detector, and when to use a multi-pixel direct detector. For present detector technologies, using a quadrant detector for high-speed, low-dose DPC imaging outperforms a PAD using CoM (as the PAD MUIS(SNR = 5) would only reach 20 kHz), especially since live frame averaging and data storage becomes much simpler to manage. However, low-dose, widefield ptychography where the large-pixel-number format is exploited to avoid sampling at every spatial point will outperform the quadrant detector in required dose and collection speed (Chen et al., Reference Chen, Odstrcil, Jiang, Han, Chiu, Li and Muller2020).
The source performance can also be captured on this type of plot for different imaging modes. SNR = 5 can be used to evaluate the maximum frame rate that can be delivered to a uniformly illuminated detector with 128 × 128 pixels, while SNR = 300 is useful for diffraction experiments when the incident beam is focused into a few pixels—here assumed to be 4 pixels. The expected performance limits for a cold-field emission source (4 nA for diffraction and 10 nA for imaging) are shown as the bounds for Figure 10b. From this we can see that there is considerable room for improvement in detector technology, both in frame rate and saturation current, before performance becomes source limited. Pixel count can be traded for speed, provided the necessary current/pixel can be maintained as discussed above.
Experimental Data
As a demonstration of the detector sensitivity and dynamic range, Figure 11 shows the convergent beam electron diffraction (CEBD) patterns of [101]O TbScO3 recorded with 300 keV electrons and a beam current of 1 nA so high-quality patterns can be recorded with a short dwell time, taking advantage of the good MUIS metric for the detector. Figures 11a and 11b show the CBED pattern recorded in 100 μs and displayed in a logarithmic scale, and in units of number of electrons. Even at 100 μs, the CBED pattern shows both the unsaturated central beam and intensity variations in the Bragg reflections (Fig. 11a), as well as the details of Kikuchi bands and high-order Laue zone (HOLZ) rings, while still retaining an unsaturated central beam (Fig. 11b). In particular, Figure 11b shows an unsaturated, undistorted central peak with 50 × 106 e−/s/pixel, well beyond the possible linear or correctable count rate for a pulse-counting detector. In addition, it is not even close to the saturation limit for the EMPAD-G2, which is 109 e−/s/pixel at 300 kV—we would get closer to this limit for the beam in vacuum, or in a 2D material. The high SNR and dynamic range are essential for resolving both these strong and weak features, spanning more than 4 orders of magnitude. Because of the detector's high SNR for high-energy electrons and quality of the pedestal subtraction, multiple frames can be summed without a significant impact from systematic noise. This has been demonstrated with integrating pixel array detectors used for X-ray imaging (Philipp et al., Reference Philipp, Tate and Gruner2011) and the same principle applies to electron microscopy data. Figures 11c and 11d show the accumulation of data over 10 frames, where the details of the unsaturated central beams and Kikuchi bands are much clearer. Even after summing over 100 frames (Figs. 11e, 11f), there is no noticeable systematic fixed pattern noise. In practice, millions of frames can be summed without significant addition of systematic noise, where the systematic noise in low-fluence (i.e., single-electron) regions in each frame can be suppressed by thresholding without deteriorating the quality of the summed frames. This is important for imaging radiation-sensitive materials, especially for building up quantitative signals by averaging many low-dose exposures.
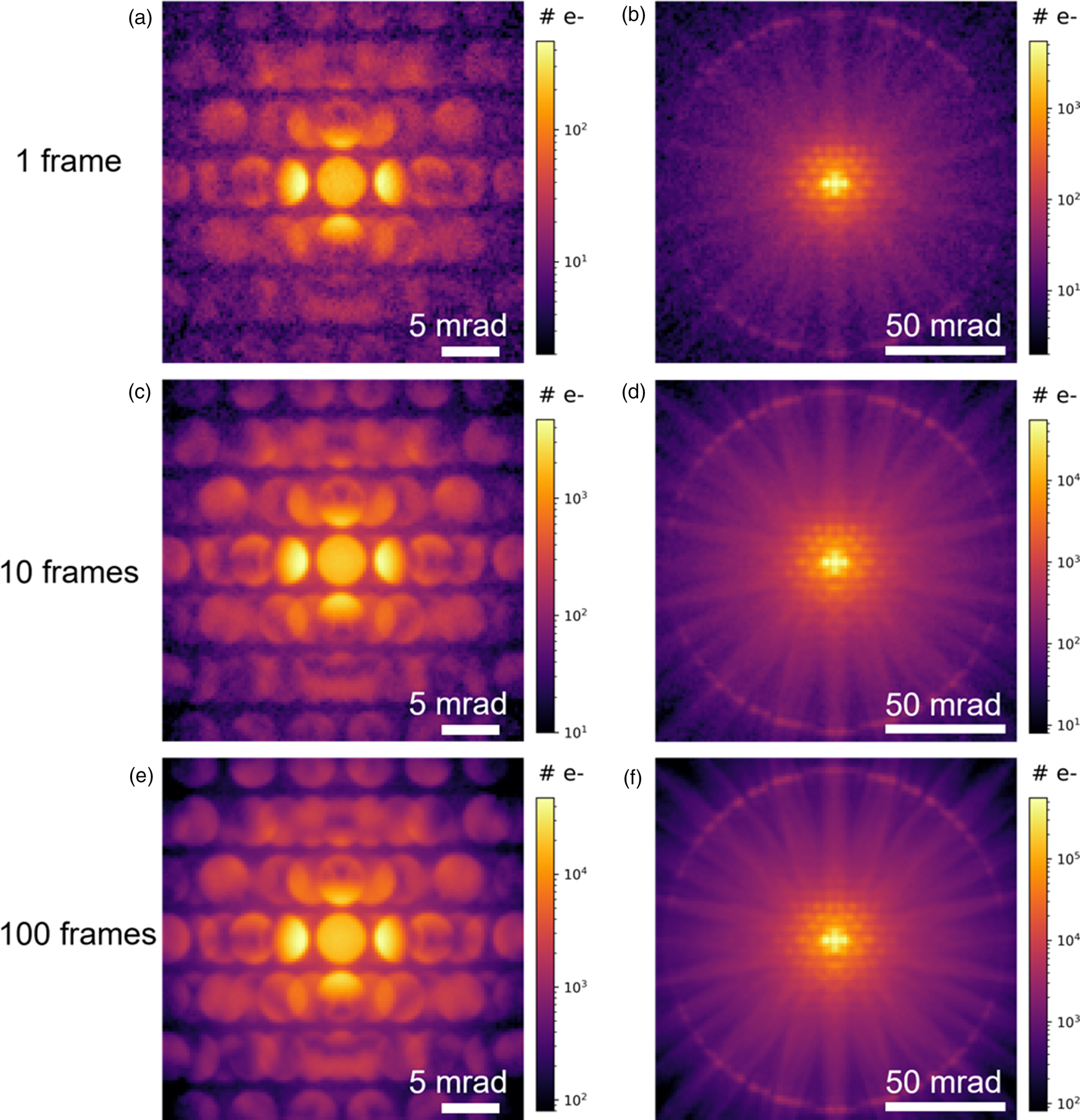
Fig. 11. High-current, high-dynamic range imaging: CBED patterns of TbScO3 recorded using the EMPAD-G2 at 300 keV with 1 nA of beam current, 100 μs dwell time and summed over (a,b) 1 frame, (c,d) 10 frames, and (e,f) 100 frames for two different camera lengths, and total acquisition times of 0.1, 1, and 10 ms, respectively. All CBED images show the number of electrons detected on the G2-EMPAD, showing quantitative electron counting.
Figure 12 shows the high-angle annular dark-field (HAADF), annular bright-field (ABF), and ptychographic phase image of BaFe12O19 along the [100] zone axis reconstructed from four-dimensional (4D) datasets recorded with 300 keV electrons and beam current of 15 pA. The HAADF and ABF images were synthesized from the same 4D dataset with a focused probe, and the ptychographic reconstruction used a second dataset with a 20 nm defocused probe (crossover before sample). Both datasets were acquired using a 512 × 512 scan with a dwell time of 100 μs per pixel, spanning a total acquisition time of 38 s. BaFe12O19 is a highly insulating material that charges easily under the electron beam, hence the need to keep the beam current low in this instance. Nevertheless, no obvious distortions appeared in the HAADF (Fig. 12a) and ABF (Fig. 12b) images, indicating the detector speed outrunning the large sample drift that was visible with the 1 ms dwell time of the old EMPAD. Multislice ptychography, along with position correction algorithms, is used to retrieve the atomic coordinates of both light and heavy elements with high precision (Chen et al., Reference Chen, Odstrcil, Jiang, Han, Chiu, Li and Muller2020, Reference Chen, Jiang, Shao, Holtz, Odstrčil, Guizar-Sicairos, Hanke, Ganschow, Schlom and Muller2021). However, it may not be able to accurately correct large sample drifts using ptychographic algorithms, which can reduce the reconstruction quality. To circumvent the drift issue when using slower detectors, such as the old EMPAD, datasets with a small number of scan points are usually chosen, which limits the field of view. With a faster detector like EMPAD-2G, high-quality ptychographic reconstruction is achieved, shown in Figure 12c, even using a dataset with such a large amount of scan points. In particular, we can identify the Fe–Fe off-mirror-plane displacement with a distance of ~0.35 Å (Cao et al., Reference Cao, Zhao, Lee, Choi, McGuire, Sales, Zhou, Yan and Mandrus2015) from the elongated contrast in the ptychographic reconstruction (illustrated as a red ellipse in Fig. 12c), whereas such structural features cannot be observed in HAADF or ABF images due to the limited resolution (0.78 Å information limit in normal operation with conventional detectors). Figure 12c shows a reconstruction using a part of the dataset containing only 64 × 64 diffraction patterns, but the whole 512 × 512 scan data is ready for ptychography when the computational resources are available.

Fig. 12. Comparing atomic resolution images of BaFe12O19. (a) Atomic-resolution high-angle annular dark-field (HAADF) and (b) annular bright-field (ABF) images of highly insulating BaFe12O19 acquired using the EMPAD-G2 with 300 keV electron beam and current of 15 pA to reduce sample charging. The four-dimensional dataset was acquired using a 512 × 512 scan with a 100 μs dwell time per pixel, spanning a total acquisition time of 38 s. (c) Phase image from the multislice ptychography reconstruction from the 4D dataset using a defocused probe. The sample thickness is about 14 nm estimated from ptychography. To show the same field of view as the ptychography, (a,b) were cropped to 210 × 210 pixels from the 512 × 512 scan—an equivalent of 4.5 s acquisition time. Scale bars, 5 Å. The red elliptical circle illustrates the Fe–Fe off-mirror-plane displacement.
As a final example, we show the imaging of order parameters in ferroelectric thin films using the EMPAD-G2. Figure 13 shows the imaging of a PbTiO3 film epitaxially grown on a DyScO3 substrate recorded using a 300 keV electron probe with a semi-convergence angle of 2.2 mrad and 2 nA of beam current—a dose rate of 12.5 × 109 e−/s. The PbTiO3 film exhibits periodic a/c domains due to the −0.25% epitaxial strain imposed by the DyScO3 substrate (Langenberg et al., Reference Langenberg, Saha, Holtz, Wang, Bugallo, Ferreiro-Vila, Paik, Hanke, Ganschow, Muller, Chen, Catalan, Domingo, Malen, Schlom and Rivadulla2019). Figure 13a shows the ADF image of the film reconstructed from the 4D dataset acquired using a 512 × 512 scan and dwell time of 100 μs per pixel. Inherent from the Poisson statistics, for which the SNR scales with the square root of the number of electrons recorded in the detector, the large electron beam current was essential for a precise determination of strain and polarization fields. With a maximum of a little over 1.25 million electrons per frame in this experiment, the best achievable precision is about 0.1% of a disk width. It will always be worse than this as the dose is distributed among multiple beams, but it provides a bound and shows the need to record large doses in a short time for high-speed mapping. For example, Figure 13b shows the well-defined HOLZ ring, zero-order Laue zone (ZOLZ) reflections, and the Kikuchi bands all captured simultaneously in 100 μs. The principle of determining polarization using CBED patterns is based on dynamical diffraction effects in which the charge redistribution associated with ferroelectric polarization leads to the intensity asymmetry of Friedel pairs (Zuo & Spence, Reference Zuo and Spence2017; Deb et al., Reference Deb, Cao, Han, Holtz, Xie, Park, Hovden and Muller2020). However, this intensity asymmetry in Bragg reflections may be subject to, or dominated by artifacts such as disinclination strain or crystal mis-tilts, which are inevitable in ferroic perovskites (MacLaren et al., Reference MacLaren, Wang, McGrouther, Craven, McVitie, Schierholz, Kovács, Barthel and Dunin-Borkowski2015; Shao & Zuo, Reference Shao and Zuo2017). To extract the polarization information (Figs. 13c, 13d), we employ the polarity-sensitive Kikuchi bands which are more robust against crystal mis-tilt artifacts (Shao et al., Reference Shao, Das, Hong, Xu, Chandrika, Gómez-Ortiz, García-Fernández, Chen, Hwang, Junquera and Martin2021) and exclude the Bragg spots from the Kikuchi analysis. Instead, we use the Bragg reflections for a simultaneous strain analysis where a precision of close to 0.1% was obtained (Figs. 13e–13g) with the exit-wave power Cepstrum (EWPC) analysis of the 4D dataset. EWPC quantitatively measures the changes in projected interatomic distances at each probe position (Padgett et al., Reference Padgett, Holtz, Cueva, Shao, Langenberg, Schlom and Muller2020; Harikrishnan et al., Reference Harikrishnan, Yoon, Shao, Mele, Mitterbauer and Muller2021). The EWPC method was chosen for its relative robustness against thickness and crystal mis-tilt artifacts, as the TEM specimen thickness varies from 35 to 60 nm within the PbTiO3 layer estimated by CBED analysis.

Fig. 13. Large field of view, high-speed simultaneous mapping of ferroelectric polarization and strain fields in an epitaxial PbTiO3 film grown on a DyScO3 substrate. The four-dimensional dataset is acquired using the EMPAD-G2 with a 512 × 512 scan, a 100 μs dwell time per pixel, and a large beam current of 2 nA. (a) HAADF-STEM image reconstructed from the 4D dataset. (b) Experimental diffraction pattern of DyScO3 [101] recorded within 100 μs showing the HOLZ ring, Kikuchi bands and unsaturated central beam. (c,d) Polarization maps extracted from the intensity asymmetry in the Kikuchi bands of PTO layer. For clarity, (c) shows the enlarged region of 50 × 26 pixels (0.13 s total dwell time), while (d) shows the 512 × 26 pixels (1.33 s total dwell time) for the polarization map. Strain maps obtained from the same dataset by employing Cepstral transform strain analysis, showing (e) ε11, (f) ε22, and (g) in-plane rotation θ, respectively. Scale bars in (e–g): 50 nm.
Conclusion
The EMPAD-G2 allows for rapid acquisition of high dynamic range images, resulting in extremely flexible data analysis, including dark field, bright field, differential phase contrast, and multislice ptychography. The advantages offered by this detector are fast acquisition (i.e., a 10 kHz frame rate), almost no dead times because signal continues to be acquired while the detector is read out, and a high dynamic range even when operated at full speed. These advantages stem from the technology chosen, that is, direct detection of electrons in a silicon diode coupled to signal processing electronics, and the specific design of the signal processing. One of the design specifics is a charge integrating front-end that allows for high-flux measurements without the drawbacks of counting detectors (e.g., coincidence loss) that put strict limits on the quality of data that can be collected at high speeds with counting detectors. With an integrating front-end, there is no specific signal processing time required for identifying single-electron events or losses at high currents. Additionally, the extension of the dynamic range with adaptive gain and incremental (and quantitative) charge removal from the front-end node allows for information to be collected quickly. The importance of these capabilities is clear: high fidelity data from high current probing of a sample can be collected at 10 kHz with minimal deadtime and a high SNR, meaning that the impact of sample instabilities is markedly reduced. We have demonstrated strain and polarization mapping at these speeds and introduced an information content metric, the MUIS, that describes the maximum speed a detector can be operated at to obtain a desired SNR. Comparing the MUIS for different design strategies, it becomes clear that pulse counting results in lower frame rates than charge integration for quantitative work that requires high doses, like measuring magnetic and strain fields with high precision. Ultrafast electron diffraction and microscopy, where many electrons can arrive in short bunches, will be another area where this charge integration strategy will be essential for efficient operation. We hope that both this detector and the additional metric to guide the design of future detectors will significantly improve the chances of new scientific observations for electron microscopists.
Acknowledgments
Support for detector development at Cornell includes:
• Thermo Fisher Scientific, Inc.
• The Kavli Foundation
• The W.M. Keck Foundation
• U.S. DOE grants DE-FG02-10ER46693, DE-SC0016035, DE-SC0004079, and DE-SC0017631
• Cornell microscope facilities are supported by the U.S. NSF grants DMR-1719875 and DMR-2039380
This project has received funding from the ECSEL Joint Undertaking (JU) under grant agreement No 783247. The JU receives support from the European Union's Horizon 2020 research and innovation program and the Netherlands, Belgium, Germany, France, Austria, United Kingdom, Israel, and Switzerland.
The oxide test samples were provided by Darrell Schlom and Evan Y. Li, with specimen prep help from Harikrishan K. P. We thank Dr Mariena Sylvestry Ramos for assistance with the Thermo Fisher Scientific Themis, and Bert Freitag for helpful comments. We thank Prafull Purohit for the partial schematic entry of digital edge readout structures.
Conflict of interest
Funding sources for the detector development, including Thermo Fisher Scientific, are described in the acknowledgements. Thermo Fisher Scientific employees involved in the project are identified by their authorship bylines. We have no other competing interests.


















