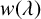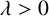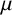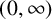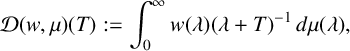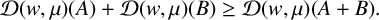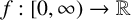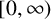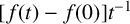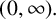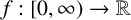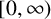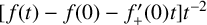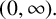1 Introduction
Consider a complex Hilbert space
![]() $( H,\langle \cdot \, ,\cdot \rangle ) $
. An operator T is said to be positive (denoted by
$( H,\langle \cdot \, ,\cdot \rangle ) $
. An operator T is said to be positive (denoted by
![]() $ T\geq 0$
) if
$ T\geq 0$
) if
![]() $\langle Tx,x\rangle \geq 0$
for all
$\langle Tx,x\rangle \geq 0$
for all
![]() $x\in H$
and strictly positive (denoted by
$x\in H$
and strictly positive (denoted by
![]() $T>0$
) if T is positive and invertible. A real valued continuous function
$T>0$
) if T is positive and invertible. A real valued continuous function
![]() $ f $
on
$ f $
on
![]() $(0,\infty )$
is said to be operator monotone if
$(0,\infty )$
is said to be operator monotone if
![]() $f(A)\geq f(B)$
holds for any
$f(A)\geq f(B)$
holds for any
![]() $A\geq B>0.$
As usual, by
$A\geq B>0.$
As usual, by
![]() $A\geq B$
, we understand that
$A\geq B$
, we understand that
![]() $A-B\geq 0.$
$A-B\geq 0.$
We have the following representation of operator monotone functions (see for instance [Reference Bhatia1, pages 144–145]).
Theorem 1.1 (Löwner, [Reference Löwner5]).
A function
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is operator monotone in
$f:[0,\infty )\rightarrow \mathbb {R}$
is operator monotone in
![]() $[0,\infty )$
if and only if it has the representation
$[0,\infty )$
if and only if it has the representation
 $$ \begin{align} f( t) =f( 0) +bt+\int_{0}^{\infty }\frac{t\lambda }{t+\lambda }\,d\mu ( \lambda ) , \end{align} $$
$$ \begin{align} f( t) =f( 0) +bt+\int_{0}^{\infty }\frac{t\lambda }{t+\lambda }\,d\mu ( \lambda ) , \end{align} $$
where
![]() $b\geq 0$
and
$b\geq 0$
and
![]() $\mu $
is a positive measure on
$\mu $
is a positive measure on
![]() $(0,\infty )$
such that
$(0,\infty )$
such that
 $$ \begin{align} \int_{0}^{\infty }\frac{\lambda }{1+\lambda }\,d\mu ( \lambda ) <\infty. \end{align} $$
$$ \begin{align} \int_{0}^{\infty }\frac{\lambda }{1+\lambda }\,d\mu ( \lambda ) <\infty. \end{align} $$
A real valued continuous function f on an interval I is said to be operator convex (operator concave) on I if
in the operator order, for all
![]() $\lambda \in [ 0,1] $
and for all selfadjoint operators A and B on a Hilbert space H whose spectra are contained in
$\lambda \in [ 0,1] $
and for all selfadjoint operators A and B on a Hilbert space H whose spectra are contained in
![]() $I.$
Notice that a function f is operator concave if
$I.$
Notice that a function f is operator concave if
![]() $-f$
is operator convex.
$-f$
is operator convex.
We have the following representation of operator convex functions [Reference Bhatia1, page 147].
Theorem 1.2. A function
![]() $f:(0,\infty )\rightarrow \mathbb {R}$
is operator convex in
$f:(0,\infty )\rightarrow \mathbb {R}$
is operator convex in
![]() $(0,\infty )$
with
$(0,\infty )$
with
![]() $f_{+}^{\prime }( 0) \in \mathbb {R}$
if and only if it has the representation
$f_{+}^{\prime }( 0) \in \mathbb {R}$
if and only if it has the representation
 $$ \begin{align} f( t) =f( 0) +f_{+}^{\prime }( 0) t+ct^{2}+\int_{0}^{\infty }\frac{t^{2}\lambda }{t+\lambda }\,d\mu (\lambda ) , \end{align} $$
$$ \begin{align} f( t) =f( 0) +f_{+}^{\prime }( 0) t+ct^{2}+\int_{0}^{\infty }\frac{t^{2}\lambda }{t+\lambda }\,d\mu (\lambda ) , \end{align} $$
where
![]() $c\geq 0$
and
$c\geq 0$
and
![]() $\mu $
is a positive measure on
$\mu $
is a positive measure on
![]() $(0,\infty )$
such that (1.2) holds.
$(0,\infty )$
such that (1.2) holds.
Assume that A,
![]() $B\geq 0$
. Moslehian and Najafi [Reference Moslehian and Najafi6] showed that
$B\geq 0$
. Moslehian and Najafi [Reference Moslehian and Najafi6] showed that
![]() $AB+BA$
is positive if and only if the operator subadditivity property holds, that is,
$AB+BA$
is positive if and only if the operator subadditivity property holds, that is,
for all nonnegative operator monotone functions f on
![]() $[0,\infty ).$
For some interesting consequences of this result, see [Reference Moslehian and Najafi6].
$[0,\infty ).$
For some interesting consequences of this result, see [Reference Moslehian and Najafi6].
We have the following integral representation for the power function when
![]() $ t>0$
,
$ t>0$
,
![]() $r\in (0,1]$
(see for instance [Reference Bhatia1, page 145]),
$r\in (0,1]$
(see for instance [Reference Bhatia1, page 145]),
 $$ \begin{align*} t^{r-1}=\frac{\sin ( r\pi ) }{\pi }\int_{0}^{\infty }\frac{\lambda ^{r-1}}{\lambda +t}\,d\lambda. \end{align*} $$
$$ \begin{align*} t^{r-1}=\frac{\sin ( r\pi ) }{\pi }\int_{0}^{\infty }\frac{\lambda ^{r-1}}{\lambda +t}\,d\lambda. \end{align*} $$
Motivated by these representations, we introduce, for a continuous and positive function
![]() $w( \lambda ) $
,
$w( \lambda ) $
,
![]() $\lambda>0$
, the integral transform
$\lambda>0$
, the integral transform
 $$ \begin{align} \mathcal{D}( w,\mu ) ( t) :=\int_{0}^{\infty }\frac{w( \lambda ) }{\lambda +t}\,d\mu ( \lambda ) , \quad t>0, \end{align} $$
$$ \begin{align} \mathcal{D}( w,\mu ) ( t) :=\int_{0}^{\infty }\frac{w( \lambda ) }{\lambda +t}\,d\mu ( \lambda ) , \quad t>0, \end{align} $$
where
![]() $\mu $
is a positive measure on
$\mu $
is a positive measure on
![]() $(0,\infty )$
and the integral (1.4) exists for all
$(0,\infty )$
and the integral (1.4) exists for all
![]() $t>0.$
For
$t>0.$
For
![]() $\mu $
, the usual Lebesgue measure, we put
$\mu $
, the usual Lebesgue measure, we put
 $$ \begin{align*} \mathcal{D}( w) ( t) :=\int_{0}^{\infty }\frac{w(\lambda ) }{\lambda +t}\,d\lambda , \quad t>0. \end{align*} $$
$$ \begin{align*} \mathcal{D}( w) ( t) :=\int_{0}^{\infty }\frac{w(\lambda ) }{\lambda +t}\,d\lambda , \quad t>0. \end{align*} $$
Now, assume that
![]() $T>0$
. By the continuous functional calculus for selfadjoint operators, we can define the positive operator
$T>0$
. By the continuous functional calculus for selfadjoint operators, we can define the positive operator
 $$ \begin{align*} \mathcal{D}( w,\mu ) ( T) :=\int_{0}^{\infty }w(\lambda ) ( \lambda +T) ^{-1}\,d\mu ( \lambda ) , \end{align*} $$
$$ \begin{align*} \mathcal{D}( w,\mu ) ( T) :=\int_{0}^{\infty }w(\lambda ) ( \lambda +T) ^{-1}\,d\mu ( \lambda ) , \end{align*} $$
where w and
![]() $\mu $
are as above. When
$\mu $
are as above. When
![]() $\mu $
is the usual Lebesgue measure, for
$\mu $
is the usual Lebesgue measure, for
![]() $T>0$
,
$T>0$
,
 $$ \begin{align*} \mathcal{D}( w) ( T) :=\int_{0}^{\infty }w(\lambda ) ( \lambda +T) ^{-1}\,d\lambda. \end{align*} $$
$$ \begin{align*} \mathcal{D}( w) ( T) :=\int_{0}^{\infty }w(\lambda ) ( \lambda +T) ^{-1}\,d\lambda. \end{align*} $$
If we take
![]() $\mu $
to be the usual Lebesgue measure and the kernel
$\mu $
to be the usual Lebesgue measure and the kernel
![]() $w_{r}( \lambda ) =\lambda ^{r-1}$
,
$w_{r}( \lambda ) =\lambda ^{r-1}$
,
![]() $r\in (0,1],$
then
$r\in (0,1],$
then
Motivated by these results, we show among other things that if B,
![]() $A>0,$
then
$A>0,$
then
that is,
![]() $\mathcal {D}( w,\mu ) $
is operator subadditive on
$\mathcal {D}( w,\mu ) $
is operator subadditive on
![]() $( 0,\infty ) .$
From this, if
$( 0,\infty ) .$
From this, if
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
![]() $[0,\infty )$
, we show that the function
$[0,\infty )$
, we show that the function
![]() $[ f( t) -f( 0) ] t^{-1}$
is operator subadditive on
$[ f( t) -f( 0) ] t^{-1}$
is operator subadditive on
![]() $( 0,\infty ) .$
Also, if
$( 0,\infty ) .$
Also, if
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
![]() $[0,\infty )$
, then the function
$[0,\infty )$
, then the function
![]() $[ f( t) -f( 0) -f_{+}^{\prime }( 0) t] t^{-2}$
is operator subadditive on
$[ f( t) -f( 0) -f_{+}^{\prime }( 0) t] t^{-2}$
is operator subadditive on
![]() $( 0,\infty ) .$
Some examples for integral transforms
$( 0,\infty ) .$
Some examples for integral transforms
![]() $\mathcal {D}( \cdot \, ,\cdot ) $
related to the exponential and logarithmic functions are also provided.
$\mathcal {D}( \cdot \, ,\cdot ) $
related to the exponential and logarithmic functions are also provided.
2 Subadditivity property
Theorem 2.1. For all A,
![]() $B>0$
,
$B>0$
,
namely,
![]() $D(w,\mu )$
is operator subadditive.
$D(w,\mu )$
is operator subadditive.
Proof. For all A,
![]() $B>0,$
by using the representation of
$B>0,$
by using the representation of
![]() $D(w,\mu ),$
$D(w,\mu ),$
 $$ \begin{align} D(w,\mu )( A) & +D(w,\mu )( B) -D(w,\mu )(A+B) \notag \\ & =\int_{0}^{\infty }w( \lambda ) [ ( A+\lambda )^{-1}+( B+\lambda ) ^{-1}-( A+B+\lambda ) ^{-1}] \,d\mu ( \lambda ). \end{align} $$
$$ \begin{align} D(w,\mu )( A) & +D(w,\mu )( B) -D(w,\mu )(A+B) \notag \\ & =\int_{0}^{\infty }w( \lambda ) [ ( A+\lambda )^{-1}+( B+\lambda ) ^{-1}-( A+B+\lambda ) ^{-1}] \,d\mu ( \lambda ). \end{align} $$
For
![]() $\lambda \geq 0,$
define the operator
$\lambda \geq 0,$
define the operator
If we multiply both sides of
![]() $K_{\lambda }$
by
$K_{\lambda }$
by
![]() $A+B+\lambda ,$
then we obtain successively
$A+B+\lambda ,$
then we obtain successively
 $$ \begin{align} \hspace{-7pt}( A+B+\lambda ) K_{\lambda }( A+B+\lambda ) & =( A+B+\lambda ) ( A+\lambda ) ^{-1}(A+B+\lambda ) \notag \\ &\quad +( A+B+\lambda ) ( B+\lambda ) ^{-1}(A+B+\lambda ) -A-B-\lambda \notag \\ & =( 1+B( A+\lambda ) ^{-1}) ( A+\lambda +B)\notag \\ &\quad +( A( B+\lambda ) ^{-1}+1) ( A+B+\lambda ) -A-B-\lambda \notag \\ & =A+\lambda +B+B+B( A+\lambda ) ^{-1}B \notag \\ &\quad +A( B+\lambda ) ^{-1}A+A+A+B+\lambda -A-B-\lambda \notag \\ & =B( A+\lambda ) ^{-1}B+A( B+\lambda ) ^{-1}A+2(A+B) +\lambda =:L_{\lambda }.\ \end{align} $$
$$ \begin{align} \hspace{-7pt}( A+B+\lambda ) K_{\lambda }( A+B+\lambda ) & =( A+B+\lambda ) ( A+\lambda ) ^{-1}(A+B+\lambda ) \notag \\ &\quad +( A+B+\lambda ) ( B+\lambda ) ^{-1}(A+B+\lambda ) -A-B-\lambda \notag \\ & =( 1+B( A+\lambda ) ^{-1}) ( A+\lambda +B)\notag \\ &\quad +( A( B+\lambda ) ^{-1}+1) ( A+B+\lambda ) -A-B-\lambda \notag \\ & =A+\lambda +B+B+B( A+\lambda ) ^{-1}B \notag \\ &\quad +A( B+\lambda ) ^{-1}A+A+A+B+\lambda -A-B-\lambda \notag \\ & =B( A+\lambda ) ^{-1}B+A( B+\lambda ) ^{-1}A+2(A+B) +\lambda =:L_{\lambda }.\ \end{align} $$
By multiplying both sides of (2.3) by
![]() $( A+B+\lambda ) ^{-1}$
,
$( A+B+\lambda ) ^{-1}$
,
We then have the representation
 $$ \begin{align*} & D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B)\\ & =\int_{0}^{\infty }w( \lambda ) K_{\lambda }\,d\mu ( \lambda) =\int_{0}^{\infty }w( \lambda ) ( A+B+\lambda ) ^{-1}L_{\lambda }( A+B+\lambda ) ^{-1}\,d\mu ( \lambda ) \end{align*} $$
$$ \begin{align*} & D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B)\\ & =\int_{0}^{\infty }w( \lambda ) K_{\lambda }\,d\mu ( \lambda) =\int_{0}^{\infty }w( \lambda ) ( A+B+\lambda ) ^{-1}L_{\lambda }( A+B+\lambda ) ^{-1}\,d\mu ( \lambda ) \end{align*} $$
for all A,
![]() $B>0.$
$B>0.$
Since A,
![]() $B>0$
and
$B>0$
and
![]() $\lambda \geq 0,$
we obtain
$\lambda \geq 0,$
we obtain
![]() $L_{\lambda }\geq 0$
from (2.3). By (2.4),
$L_{\lambda }\geq 0$
from (2.3). By (2.4),
![]() $K_{\lambda }\geq 0$
, and multiplying by
$K_{\lambda }\geq 0$
, and multiplying by
![]() $w( \lambda ) \geq 0$
and integrating over the measure
$w( \lambda ) \geq 0$
and integrating over the measure
![]() $\mu $
gives (2.1).
$\mu $
gives (2.1).
Corollary 2.2. Assume that
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
![]() $[0,\infty )$
. If A,
$[0,\infty )$
. If A,
![]() $B>0$
, then
$B>0$
, then
that is, the function
![]() $[ f( t) -f( 0) ] t^{-1}$
is operator subadditive on
$[ f( t) -f( 0) ] t^{-1}$
is operator subadditive on
![]() $( 0,\infty ) .$
In particular, if
$( 0,\infty ) .$
In particular, if
![]() $f( 0) =0,$
then
$f( 0) =0,$
then
Proof. If
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is operator monotone, then by (1.1),
$f:[0,\infty )\rightarrow \mathbb {R}$
is operator monotone, then by (1.1),
for some positive measure
![]() $\mu ,$
where
$\mu ,$
where
![]() $\ell ( \lambda ) =\lambda $
,
$\ell ( \lambda ) =\lambda $
,
![]() $\lambda>0.$
By applying Theorem 2.1 for
$\lambda>0.$
By applying Theorem 2.1 for
![]() $\mathcal {D}( \ell ,\mu ) $
and performing the required calculations, we deduce
$\mathcal {D}( \ell ,\mu ) $
and performing the required calculations, we deduce
 $$ \begin{align*} 0& \leq D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B) \\ & =[ f( A) -f( 0) ] A^{-1}-b+[ f( B) -f( 0) ] B^{-1}-b -[ f( A+B) -f( 0) ] ( A+B) ^{-1}+b \\ & =f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} -f( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] -b \end{align*} $$
$$ \begin{align*} 0& \leq D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B) \\ & =[ f( A) -f( 0) ] A^{-1}-b+[ f( B) -f( 0) ] B^{-1}-b -[ f( A+B) -f( 0) ] ( A+B) ^{-1}+b \\ & =f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} -f( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] -b \end{align*} $$
for all A,
![]() $B>0,$
which gives
$B>0,$
which gives
 $$ \begin{align*} f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} & \geq f( 0) ( A^{-1}+B^{-1}-( A+B) ^{-1}) +b \\ & \geq f( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] \end{align*} $$
$$ \begin{align*} f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} & \geq f( 0) ( A^{-1}+B^{-1}-( A+B) ^{-1}) +b \\ & \geq f( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] \end{align*} $$
for all A,
![]() $B>0$
and (2.5) is obtained.
$B>0$
and (2.5) is obtained.
Remark 2.3. If we take
![]() $f( t) =t^{r}$
,
$f( t) =t^{r}$
,
![]() $r\in (0,1]$
, in (2.6), then we get the power inequality
$r\in (0,1]$
, in (2.6), then we get the power inequality
for all A,
![]() $B>0.$
$B>0.$
If we take
![]() $f( t) =\ln ( t+1) $
in (2.6), then we get the logarithmic inequality
$f( t) =\ln ( t+1) $
in (2.6), then we get the logarithmic inequality
Similar inequalities can be obtained by using the examples of operator monotone functions from [Reference Fujii and Seo2, Reference Furuta3] and the references therein.
Corollary 2.4. Assume that
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
![]() $[0,\infty )$
. If A,
$[0,\infty )$
. If A,
![]() $B>0,$
then
$B>0,$
then
 $$ \begin{align*} &f( A) A^{-2} +f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ & \quad\geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] , \end{align*} $$
$$ \begin{align*} &f( A) A^{-2} +f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ & \quad\geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] , \end{align*} $$
that is, the function
![]() $[ f( t) -f( 0) -f_{+}^{\prime }( 0) t] t^{-2}$
is operator subadditive on
$[ f( t) -f( 0) -f_{+}^{\prime }( 0) t] t^{-2}$
is operator subadditive on
![]() $ ( 0,\infty ) .$
$ ( 0,\infty ) .$
If
![]() $f( 0) =0,$
then
$f( 0) =0,$
then
Proof. If
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
![]() $ [0,\infty ),$
then by (1.3),
$ [0,\infty ),$
then by (1.3),
for some positive measure
![]() $\mu ,$
where
$\mu ,$
where
![]() $\ell ( \lambda ) =\lambda $
,
$\ell ( \lambda ) =\lambda $
,
![]() $\lambda>0.$
$\lambda>0.$
By applying Theorem 2.1 for
![]() $\mathcal {D}( \ell ,\mu ) $
and performing the required calculations, we deduce
$\mathcal {D}( \ell ,\mu ) $
and performing the required calculations, we deduce
 $$ \begin{align*} &0 \leq D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B) \\ &\quad =f( A) A^{-2}-f( 0) A^{-2}-f_{+}^{\prime }( 0) A^{-1}-c +f( B) B^{-2}-f( 0) B^{-2}-f_{+}^{\prime }( 0) B^{-1}-c \\ &\qquad -f( A+B) ( A+B) ^{-2}+f( 0) ( A+B) ^{-2}+f_{+}^{\prime }( 0) ( A+B) ^{-1}+c \\ &\quad =f( A) A^{-2}+f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ &\qquad -f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] -f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] -c \end{align*} $$
$$ \begin{align*} &0 \leq D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )( A+B) \\ &\quad =f( A) A^{-2}-f( 0) A^{-2}-f_{+}^{\prime }( 0) A^{-1}-c +f( B) B^{-2}-f( 0) B^{-2}-f_{+}^{\prime }( 0) B^{-1}-c \\ &\qquad -f( A+B) ( A+B) ^{-2}+f( 0) ( A+B) ^{-2}+f_{+}^{\prime }( 0) ( A+B) ^{-1}+c \\ &\quad =f( A) A^{-2}+f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ &\qquad -f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] -f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] -c \end{align*} $$
for all A,
![]() $B>0.$
From this,
$B>0.$
From this,
 $$ \begin{align*} & f( A) A^{-2} +f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ &\quad \geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] +c \\ &\quad \geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] , \end{align*} $$
$$ \begin{align*} & f( A) A^{-2} +f( B) B^{-2}-f( A+B) ( A+B) ^{-2} \\ &\quad \geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] +c \\ &\quad \geq f( 0) [ A^{-2}+B^{-2}-( A+B) ^{-2}] +f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1} ] , \end{align*} $$
which proves (2.7).
Remark 2.5. Let
![]() $a>0$
and
$a>0$
and
![]() $p\in \lbrack -1,0)\cup \lbrack 1,2].$
Then for all A,
$p\in \lbrack -1,0)\cup \lbrack 1,2].$
Then for all A,
![]() $B>0$
, we have the power inequality
$B>0$
, we have the power inequality
 $$ \begin{align*} ( A & +a) ^{p}A^{-2}+( B+a) ^{p}B^{-2}-( A+B+a) ^{p}( A+B) ^{-2} \\ & \geq a^{p}[ A^{-2}+B^{-2}-( A+B) ^{-2}] +pa^{p-1} [ A^{-1}+B^{-1}-( A+B) ^{-1}]. \end{align*} $$
$$ \begin{align*} ( A & +a) ^{p}A^{-2}+( B+a) ^{p}B^{-2}-( A+B+a) ^{p}( A+B) ^{-2} \\ & \geq a^{p}[ A^{-2}+B^{-2}-( A+B) ^{-2}] +pa^{p-1} [ A^{-1}+B^{-1}-( A+B) ^{-1}]. \end{align*} $$
We also have the logarithmic inequality
 $$ \begin{align*} ( A & +B) ^{-2}\ln ( A+B+1) -A^{-2}\ln ( A+1) -B^{-2}\ln ( B+1) \\ & \geq ( A+B) ^{-1}-B^{-1}-A^{-1} \end{align*} $$
$$ \begin{align*} ( A & +B) ^{-2}\ln ( A+B+1) -A^{-2}\ln ( A+1) -B^{-2}\ln ( B+1) \\ & \geq ( A+B) ^{-1}-B^{-1}-A^{-1} \end{align*} $$
for all A,
![]() $B>0.$
$B>0.$
3 Reverse inequalities
We define the difference
![]() $\mathcal {D}( w,\mu ) ( \cdot \, ,\cdot ) $
for positive numbers t, s by
$\mathcal {D}( w,\mu ) ( \cdot \, ,\cdot ) $
for positive numbers t, s by
and the difference for positive operators A,
![]() $B,$
$B,$
for a continuous and positive function
![]() $w( \lambda ) $
,
$w( \lambda ) $
,
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $\mu $
a positive measure on
$\mu $
a positive measure on
![]() $(0,\infty )$
such that the integral (1.4) exists for all
$(0,\infty )$
such that the integral (1.4) exists for all
![]() $t\geq 0.$
We prove the following reverse inequality.
$t\geq 0.$
We prove the following reverse inequality.
Theorem 3.1. Assume that there exists positive constants
![]() $\alpha $
,
$\alpha $
,
![]() $\beta ,$
$\beta ,$
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
such that
$\delta $
such that
Then,
Proof. Observe that
and
that is,
which gives
and so
 $$ \begin{align*} ( A & +\lambda ) ^{-1}+( B+\lambda ) ^{-1}-( A+B+\lambda ) ^{-1} \\ & \leq ( \alpha +\lambda ) ^{-1}+( \gamma +\lambda ) ^{-1}-( \alpha +\gamma +\lambda ) ^{-1}+( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1} \end{align*} $$
$$ \begin{align*} ( A & +\lambda ) ^{-1}+( B+\lambda ) ^{-1}-( A+B+\lambda ) ^{-1} \\ & \leq ( \alpha +\lambda ) ^{-1}+( \gamma +\lambda ) ^{-1}-( \alpha +\gamma +\lambda ) ^{-1}+( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1} \end{align*} $$
for all
![]() $\lambda \geq 0.$
If we multiply by
$\lambda \geq 0.$
If we multiply by
![]() $w( \lambda ) \geq 0$
and integrate, then by (2.2),
$w( \lambda ) \geq 0$
and integrate, then by (2.2),
 $$ \begin{align*} & D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )(A+B) \\ &\quad \leq D(w,\mu )( \alpha ) +D(w,\mu )( \gamma ) -D(w,\mu )( \alpha +\gamma ) \\ &\qquad +\int_{0}^{\infty }w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) , \end{align*} $$
$$ \begin{align*} & D(w,\mu )( A) +D(w,\mu )( B) -D(w,\mu )(A+B) \\ &\quad \leq D(w,\mu )( \alpha ) +D(w,\mu )( \gamma ) -D(w,\mu )( \alpha +\gamma ) \\ &\qquad +\int_{0}^{\infty }w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) , \end{align*} $$
which gives
 $$ \begin{align}&\mathcal{D}(w,\mu)(A,B)\nonumber \\&\quad \le \mathcal{D}(w,\mu)(\alpha,\gamma) + \int_0^\infty w(\lambda)[(\alpha+\gamma+\lambda)^{-1} - (\beta+\delta+\lambda)^{-1}] \,d\mu(\lambda).\end{align} $$
$$ \begin{align}&\mathcal{D}(w,\mu)(A,B)\nonumber \\&\quad \le \mathcal{D}(w,\mu)(\alpha,\gamma) + \int_0^\infty w(\lambda)[(\alpha+\gamma+\lambda)^{-1} - (\beta+\delta+\lambda)^{-1}] \,d\mu(\lambda).\end{align} $$
Observe that
 $$ \begin{align*} \int_{0}^{\infty } & w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) \\ & =\int_{0}^{\infty }w( \lambda ) \bigg[ \frac{\beta +\delta -\alpha -\gamma }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) }\bigg] \,d\mu ( \lambda ) \\ & =(\, \beta +\delta -\alpha -\gamma ) \int_{0}^{\infty }\frac{ w( \lambda ) }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) }\,d\mu ( \lambda ) \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty } & w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) \\ & =\int_{0}^{\infty }w( \lambda ) \bigg[ \frac{\beta +\delta -\alpha -\gamma }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) }\bigg] \,d\mu ( \lambda ) \\ & =(\, \beta +\delta -\alpha -\gamma ) \int_{0}^{\infty }\frac{ w( \lambda ) }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) }\,d\mu ( \lambda ) \end{align*} $$
and
 $$ \begin{align*} \frac{1}{\alpha +\gamma +\lambda }\leq \frac{1}{\alpha +\gamma }\quad \text{for } \lambda \geq 0, \end{align*} $$
$$ \begin{align*} \frac{1}{\alpha +\gamma +\lambda }\leq \frac{1}{\alpha +\gamma }\quad \text{for } \lambda \geq 0, \end{align*} $$
which implies that
 $$ \begin{align*} \int_{0}^{\infty }\frac{w( \lambda ) }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) \,}\,d\mu ( \lambda) & \leq \frac{1}{\alpha +\gamma }\int_{0}^{\infty }\frac{w( \lambda ) }{\beta +\delta +\lambda }\,d\mu ( \lambda ) \\ & =\frac{1}{\alpha +\gamma }D(w,\mu )(\, \beta +\delta ). \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty }\frac{w( \lambda ) }{( \alpha +\gamma +\lambda ) (\, \beta +\delta +\lambda ) \,}\,d\mu ( \lambda) & \leq \frac{1}{\alpha +\gamma }\int_{0}^{\infty }\frac{w( \lambda ) }{\beta +\delta +\lambda }\,d\mu ( \lambda ) \\ & =\frac{1}{\alpha +\gamma }D(w,\mu )(\, \beta +\delta ). \end{align*} $$
Therefore,
 $$ \begin{align} \int_{0}^{\infty }w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) \leq \bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) D(w,\mu )(\, \beta +\delta ). \end{align} $$
$$ \begin{align} \int_{0}^{\infty }w( \lambda ) [ ( \alpha +\gamma +\lambda ) ^{-1}-(\, \beta +\delta +\lambda ) ^{-1}] \,d\mu ( \lambda ) \leq \bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) D(w,\mu )(\, \beta +\delta ). \end{align} $$
The case of operator monotone functions is the following corollary.
Corollary 3.2. Assume that
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator monotone function on
![]() $[0,\infty )$
with
$[0,\infty )$
with
![]() $f( 0) =0.$
If
$f( 0) =0.$
If
![]() $ A$
,
$ A$
,
![]() $B>0$
satisfy the condition (3.1), then
$B>0$
satisfy the condition (3.1), then
 $$ \begin{align} 0& \leq f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} \notag \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) f(\, \beta +\delta ) (\, \beta +\delta ) ^{-1}. \end{align} $$
$$ \begin{align} 0& \leq f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} \notag \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) f(\, \beta +\delta ) (\, \beta +\delta ) ^{-1}. \end{align} $$
Proof. Write
for some positive measure
![]() $\mu ,$
where
$\mu ,$
where
![]() $\ell ( \lambda ) =\lambda $
,
$\ell ( \lambda ) =\lambda $
,
![]() $\lambda>0$
. From (3.2),
$\lambda>0$
. From (3.2),
 $$ \begin{align*} 0& \leq f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma ^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \bigg( \frac{ f(\, \beta +\delta ) }{\beta +\delta }-b\bigg) \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma ^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{f(\, \beta +\delta ) }{\beta +\delta }, \end{align*} $$
$$ \begin{align*} 0& \leq f( A) A^{-1}+f( B) B^{-1}-f( A+B) ( A+B) ^{-1} \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma ^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \bigg( \frac{ f(\, \beta +\delta ) }{\beta +\delta }-b\bigg) \\ & \leq f( \alpha ) \alpha ^{-1}+f( \gamma ) \gamma ^{-1}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-1} +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{f(\, \beta +\delta ) }{\beta +\delta }, \end{align*} $$
which proves the desired result (3.5).
Remark 3.3. If A,
![]() $B>0$
satisfy the condition (3.1) and
$B>0$
satisfy the condition (3.1) and
![]() $r\in (0,1],$
then we have the reverse power inequality
$r\in (0,1],$
then we have the reverse power inequality
The case of operator convex functions is the following corollary.
Corollary 3.4. Assume that
![]() $f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
$f:[0,\infty )\rightarrow \mathbb {R}$
is an operator convex function on
![]() $[0,\infty )$
with
$[0,\infty )$
with
![]() $f( 0) =0.$
If A,
$f( 0) =0.$
If A,
![]() $B>0$
satisfy the condition (3.1), then
$B>0$
satisfy the condition (3.1), then
 $$ \begin{align} 0 & \leq f( A) A^{-2}+f( B) B^{-2}-f( A+B) ( A+B) ^{-2} -f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] \notag \\ & \leq f( \alpha ) \alpha ^{-2}+f( \gamma ) \gamma ^{-2}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-2} -f_{+}^{\prime }( 0) [ \alpha ^{-1}+\gamma ^{-1}-( \alpha +\gamma ) ^{-1}] \notag \\ &\quad +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{f(\, \beta +\delta ) -f_{+}^{\prime }( 0) (\, \beta +\delta ) }{(\, \beta +\delta ) ^{2}}. \end{align} $$
$$ \begin{align} 0 & \leq f( A) A^{-2}+f( B) B^{-2}-f( A+B) ( A+B) ^{-2} -f_{+}^{\prime }( 0) [ A^{-1}+B^{-1}-( A+B) ^{-1}] \notag \\ & \leq f( \alpha ) \alpha ^{-2}+f( \gamma ) \gamma ^{-2}-f( \alpha +\gamma ) ( \alpha +\gamma ) ^{-2} -f_{+}^{\prime }( 0) [ \alpha ^{-1}+\gamma ^{-1}-( \alpha +\gamma ) ^{-1}] \notag \\ &\quad +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{f(\, \beta +\delta ) -f_{+}^{\prime }( 0) (\, \beta +\delta ) }{(\, \beta +\delta ) ^{2}}. \end{align} $$
Proof. The result follows from (3.2) observing, by (1.3), that
for some positive measure
![]() $\mu ,$
where
$\mu ,$
where
![]() $\ell ( \lambda ) =\lambda $
,
$\ell ( \lambda ) =\lambda $
,
![]() $\lambda>0.$
$\lambda>0.$
Remark 3.5. If A,
![]() $B>0$
satisfy the condition (3.1), then by taking
$B>0$
satisfy the condition (3.1), then by taking
![]() $f( t) =-\ln ( t+1)$
in (3.6), we obtain
$f( t) =-\ln ( t+1)$
in (3.6), we obtain
 $$ \begin{align*} 0& \leq ( A+B) ^{-2}\ln ( A+B+1) -A^{-2}\ln ( A+1) -B^{-2}\ln ( B+1) -( A+B) ^{-1}+A^{-1}+B^{-1} \notag \\ & \leq ( \alpha +\gamma ) ^{-2}\ln ( \alpha +\gamma +1) -\alpha ^{-2}\ln ( \alpha +1) -\gamma ^{-2}\ln ( \gamma +1) -( \alpha +\gamma ) ^{-1}+\alpha ^{-1}+\gamma ^{-1} \notag \\ &\quad +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{(\, \beta +\delta ) -\ln (\, \beta +\delta +1) }{(\, \beta +\delta ) ^{2}}. \end{align*} $$
$$ \begin{align*} 0& \leq ( A+B) ^{-2}\ln ( A+B+1) -A^{-2}\ln ( A+1) -B^{-2}\ln ( B+1) -( A+B) ^{-1}+A^{-1}+B^{-1} \notag \\ & \leq ( \alpha +\gamma ) ^{-2}\ln ( \alpha +\gamma +1) -\alpha ^{-2}\ln ( \alpha +1) -\gamma ^{-2}\ln ( \gamma +1) -( \alpha +\gamma ) ^{-1}+\alpha ^{-1}+\gamma ^{-1} \notag \\ &\quad +\bigg( \frac{\beta +\delta }{\alpha +\gamma }-1\bigg) \frac{(\, \beta +\delta ) -\ln (\, \beta +\delta +1) }{(\, \beta +\delta ) ^{2}}. \end{align*} $$
4 Some examples
We define the upper incomplete Gamma function
 $$ \begin{align*} \Gamma (a,z):=\int_{z}^{\infty }t^{a-1}e^{-t}\,dt, \end{align*} $$
$$ \begin{align*} \Gamma (a,z):=\int_{z}^{\infty }t^{a-1}e^{-t}\,dt, \end{align*} $$
which for
![]() $z=0$
, gives the Gamma function
$z=0$
, gives the Gamma function
 $$ \begin{align*} \Gamma (a):=\int_{0}^{\infty }t^{a-1}e^{-t}\,dt \quad \text{for }\mbox{Re}\, a>0. \end{align*} $$
$$ \begin{align*} \Gamma (a):=\int_{0}^{\infty }t^{a-1}e^{-t}\,dt \quad \text{for }\mbox{Re}\, a>0. \end{align*} $$
We have the integral representation [Reference Paris8]
 $$ \begin{align} \Gamma (a,z)=\frac{z^{a}e^{-z}}{\Gamma (1-a)}\int_{0}^{\infty }\frac{ t^{-a}e^{-t}}{z+t}\,dt \end{align} $$
$$ \begin{align} \Gamma (a,z)=\frac{z^{a}e^{-z}}{\Gamma (1-a)}\int_{0}^{\infty }\frac{ t^{-a}e^{-t}}{z+t}\,dt \end{align} $$
for
![]() $\mbox {Re\,}a<1$
and
$\mbox {Re\,}a<1$
and
![]() $\vert \mbox {arg\,}z\vert <\pi .$
$\vert \mbox {arg\,}z\vert <\pi .$
Now, we consider the weight
![]() $w_{\cdot ^{-a}e^{-\cdot }}( \lambda ) :=\lambda ^{-a}e^{-\lambda }$
for
$w_{\cdot ^{-a}e^{-\cdot }}( \lambda ) :=\lambda ^{-a}e^{-\lambda }$
for
![]() $\lambda>0.$
Then by (4.1),
$\lambda>0.$
Then by (4.1),
 $$ \begin{align} \mathcal{D}( w_{\cdot ^{-a}e^{-\cdot }}) ( t) =\int_{0}^{\infty }\frac{\lambda ^{-a}e^{-\lambda }}{t+\lambda }\,d\lambda =\Gamma (1-a)t^{-a}e^{t}\Gamma (a,t) \end{align} $$
$$ \begin{align} \mathcal{D}( w_{\cdot ^{-a}e^{-\cdot }}) ( t) =\int_{0}^{\infty }\frac{\lambda ^{-a}e^{-\lambda }}{t+\lambda }\,d\lambda =\Gamma (1-a)t^{-a}e^{t}\Gamma (a,t) \end{align} $$
for
![]() $a<1$
and
$a<1$
and
![]() $t>0.$
For
$t>0.$
For
![]() $a=0$
in (4.2),
$a=0$
in (4.2),
 $$ \begin{align*} \mathcal{D}( w_{e^{-\cdot }}) ( t) =\int_{0}^{\infty } \frac{e^{-\lambda }}{t+\lambda }\,d\lambda =\Gamma (1)e^{t}\Gamma (0,t)=e^{t}E_{1}( t) \end{align*} $$
$$ \begin{align*} \mathcal{D}( w_{e^{-\cdot }}) ( t) =\int_{0}^{\infty } \frac{e^{-\lambda }}{t+\lambda }\,d\lambda =\Gamma (1)e^{t}\Gamma (0,t)=e^{t}E_{1}( t) \end{align*} $$
for
![]() $t>0,$
where
$t>0,$
where
 $$ \begin{align*} E_{1}( t) :=\int_{t}^{\infty }\frac{e^{-u}}{u}\,du. \end{align*} $$
$$ \begin{align*} E_{1}( t) :=\int_{t}^{\infty }\frac{e^{-u}}{u}\,du. \end{align*} $$
From Theorem 2.1, we conclude that
![]() $\mathcal {D}( w_{\cdot ^{-a}e^{-\cdot }}) $
and, in particular,
$\mathcal {D}( w_{\cdot ^{-a}e^{-\cdot }}) $
and, in particular,
![]() $\mathcal {D}( w_{e^{-\cdot }}) $
are operator subadditive on
$\mathcal {D}( w_{e^{-\cdot }}) $
are operator subadditive on
![]() $( 0,\infty ) .$
$( 0,\infty ) .$
We can also consider the weight
![]() $w_{( \cdot ^{2}+a^{2}) ^{-1}}( \lambda ) :={1}/{(\lambda ^{2}+a^{2})}$
for
$w_{( \cdot ^{2}+a^{2}) ^{-1}}( \lambda ) :={1}/{(\lambda ^{2}+a^{2})}$
for
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $a>0.$
Then, by simple calculations,
$a>0.$
Then, by simple calculations,
 $$ \begin{align*} \mathcal{D}( w_{( \cdot ^{2}+a^{2}) ^{-1}}) (t) & :=\int_{0}^{\infty }\frac{1}{( \lambda +t) (\lambda ^{2}+a^{2}) }\,d\lambda =\frac{\pi t}{2a( t^{2}+a^{2}) }-\frac{\ln t-\ln a}{t^{2}+a^{2}} \end{align*} $$
$$ \begin{align*} \mathcal{D}( w_{( \cdot ^{2}+a^{2}) ^{-1}}) (t) & :=\int_{0}^{\infty }\frac{1}{( \lambda +t) (\lambda ^{2}+a^{2}) }\,d\lambda =\frac{\pi t}{2a( t^{2}+a^{2}) }-\frac{\ln t-\ln a}{t^{2}+a^{2}} \end{align*} $$
for
![]() $t>0$
and
$t>0$
and
![]() $a>0.$
For
$a>0.$
For
![]() $a=1$
, we also have
$a=1$
, we also have
 $$ \begin{align*} \mathcal{D}( w_{( \cdot ^{2}+1) ^{-1}}) ( t) :=\int_{0}^{\infty }\frac{1}{( \lambda +t) ( \lambda ^{2}+1) }\,d\lambda =\frac{\pi t}{2( t^{2}+1) }-\frac{ \ln t}{t^{2}+1} \end{align*} $$
$$ \begin{align*} \mathcal{D}( w_{( \cdot ^{2}+1) ^{-1}}) ( t) :=\int_{0}^{\infty }\frac{1}{( \lambda +t) ( \lambda ^{2}+1) }\,d\lambda =\frac{\pi t}{2( t^{2}+1) }-\frac{ \ln t}{t^{2}+1} \end{align*} $$
for
![]() $t>0.$
If
$t>0.$
If
![]() $T>0$
and
$T>0$
and
![]() $a>0,$
then
$a>0,$
then
 $$ \begin{align*} ( T^{2}+a^{2}) ^{-1}\bigg( \frac{\pi }{2a}T-\ln T+\ln a\bigg) =\int_{0}^{\infty }\frac{1}{( \lambda ^{2}+a^{2}) }( \lambda +T) ^{-1}\,d\lambda \end{align*} $$
$$ \begin{align*} ( T^{2}+a^{2}) ^{-1}\bigg( \frac{\pi }{2a}T-\ln T+\ln a\bigg) =\int_{0}^{\infty }\frac{1}{( \lambda ^{2}+a^{2}) }( \lambda +T) ^{-1}\,d\lambda \end{align*} $$
and, in particular,
 $$ \begin{align*} ( T^{2}+1) ^{-1}\bigg( \frac{\pi }{2}T-\ln T\bigg) =\int_{0}^{\infty }\frac{1}{( \lambda ^{2}+1) }( \lambda +T) ^{-1}\,d\lambda. \end{align*} $$
$$ \begin{align*} ( T^{2}+1) ^{-1}\bigg( \frac{\pi }{2}T-\ln T\bigg) =\int_{0}^{\infty }\frac{1}{( \lambda ^{2}+1) }( \lambda +T) ^{-1}\,d\lambda. \end{align*} $$
From Theorem 2.1, we conclude that
![]() $\mathcal {D}( w_{( \cdot ^{2}+a^{2}) ^{-1}}) $
and, in particular,
$\mathcal {D}( w_{( \cdot ^{2}+a^{2}) ^{-1}}) $
and, in particular,
![]() $\mathcal {D} ( w_{( \cdot ^{2}+1) ^{-1}}) $
are operator subadditive on
$\mathcal {D} ( w_{( \cdot ^{2}+1) ^{-1}}) $
are operator subadditive on
![]() $( 0,\infty ) .$
$( 0,\infty ) .$
Other similar inequalities can be obtained by using the examples of operator monotone functions provided in [Reference Fujii and Seo2–Reference Furuta4, Reference Moslehian and Najafi6, Reference Moslehian and Najafi7].