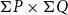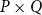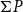1. Introduction
Sobriety is one of the earliest studied major properties of
![]() $T_0$
topological spaces. It has been used in the characterization of spectra spaces of commutative rings (Hochster Reference Hochster1969). In recent years, this property and some of its weaker forms have been extensively investigated from various different perspectives. The Scott topology is the most important topology in domain theory which bridges a strong link between topological and order structures. Lawson (Reference Lawson1979) and Hoffmann (Reference Hoffmann1981) proved independently that the Scott space of every domain (continuous directed complete poset) is sober. At the early time, it was an open problem whether the Scott space of every directed complete poset (dcpo, for short) is sober. Johnstone constructed the first counterexample to give a negative answer (Johnstone Reference Johnstone1981). Soon, Isbell (Reference Isbell1982) came up with a complete lattice whose Scott space is non-sober. However, Isbell’s complete lattice is neither distributive nor countable.
$T_0$
topological spaces. It has been used in the characterization of spectra spaces of commutative rings (Hochster Reference Hochster1969). In recent years, this property and some of its weaker forms have been extensively investigated from various different perspectives. The Scott topology is the most important topology in domain theory which bridges a strong link between topological and order structures. Lawson (Reference Lawson1979) and Hoffmann (Reference Hoffmann1981) proved independently that the Scott space of every domain (continuous directed complete poset) is sober. At the early time, it was an open problem whether the Scott space of every directed complete poset (dcpo, for short) is sober. Johnstone constructed the first counterexample to give a negative answer (Johnstone Reference Johnstone1981). Soon, Isbell (Reference Isbell1982) came up with a complete lattice whose Scott space is non-sober. However, Isbell’s complete lattice is neither distributive nor countable.
A poset P will be called sober if its Scott space
![]() $\Sigma P$
is sober. In Jung (Reference Jung2018), Achim Jung posed two problems. One of them is whether every distributive complete lattice is sober.
$\Sigma P$
is sober. In Jung (Reference Jung2018), Achim Jung posed two problems. One of them is whether every distributive complete lattice is sober.
Using Isbell’s complete lattice, Xu, Xi, and Zhao gave a negative answer to this problem (Xu et al. Reference Xu, Xi and Zhao2021).
The second problem by Jung (also mentioned by Xu and Zhao in 2020) is the following one:
Problem 1.1 Is there a non-sober countable complete lattice?
In the current paper, we will give an answer to this problem. The main structure we are going to use is the poset
![]() $\mathbb{N}^{<\mathbb{N}}$
of all words (or, nonempty finite sequences) in the set
$\mathbb{N}^{<\mathbb{N}}$
of all words (or, nonempty finite sequences) in the set
![]() $\mathbb{N}$
of all positive integers. In Section 2, we shall list some properties of
$\mathbb{N}$
of all positive integers. In Section 2, we shall list some properties of
![]() $\mathbb{N}^{<\mathbb{N}}$
to be used. In Section 3, we construct a countable complete distributive lattice whose Scott space is non-sober; thus, we give an answer to Problem 1.1.
$\mathbb{N}^{<\mathbb{N}}$
to be used. In Section 3, we construct a countable complete distributive lattice whose Scott space is non-sober; thus, we give an answer to Problem 1.1.
In Section 4, we prove some positive results on the sobriety of Scott spaces. First, we prove that the topology of the product space
![]() $\Sigma P\times \Sigma Q$
coincides with the Scott topology on the product poset
$\Sigma P\times \Sigma Q$
coincides with the Scott topology on the product poset
![]() $P\times Q$
if the set Id(P) and Id(Q) of all incremental ideals of posets P and Q are both countable. Based on this result, we deduce that a directed complete poset P is sober if Id(P) is countable and the space
$P\times Q$
if the set Id(P) and Id(Q) of all incremental ideals of posets P and Q are both countable. Based on this result, we deduce that a directed complete poset P is sober if Id(P) is countable and the space
![]() $\Sigma P$
is coherent and well filtered. In particular, every complete lattice L with Id(L) countable is sober.
$\Sigma P$
is coherent and well filtered. In particular, every complete lattice L with Id(L) countable is sober.
2. Preliminaries
In this section, we recall some basic definitions and results to be used later. For more details on them, we refer the reader to Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003) and Goubault-Larrecq (Reference Goubault-Larrecq2013).
Let P be a poset. A nonempty subset D of P is directed if every two elements of D have an upper bound in D. If D is also a lower set (
![]() $D={\downarrow} D=\{x\in P: x\le d \mbox{ for some } d\in D\}$
), then D is called an ideal. A poset is called a directed complete poset (dcpo, for short) if its every directed subset has a supremum. A complete lattice is a poset in which every subset has a supremum and an infimum. A subset U of a poset P is Scott open if (i) it is an upper set (
$D={\downarrow} D=\{x\in P: x\le d \mbox{ for some } d\in D\}$
), then D is called an ideal. A poset is called a directed complete poset (dcpo, for short) if its every directed subset has a supremum. A complete lattice is a poset in which every subset has a supremum and an infimum. A subset U of a poset P is Scott open if (i) it is an upper set (
![]() $U=\mathord{\uparrow} U=\{x\in P: u\le x \mbox{ for some } u\in U\}$
) and (ii) for every directed subset D of P with
$U=\mathord{\uparrow} U=\{x\in P: u\le x \mbox{ for some } u\in U\}$
) and (ii) for every directed subset D of P with
![]() $\sup D$
existing and
$\sup D$
existing and
![]() $\sup D\in U$
, it follows that
$\sup D\in U$
, it follows that
![]() $D\cap U\not=\emptyset$
. The complements of Scott open sets are called Scott closed sets. The collection of all Scott open subsets of P forms a topology on P, called the Scott topology of P, and is denoted by
$D\cap U\not=\emptyset$
. The complements of Scott open sets are called Scott closed sets. The collection of all Scott open subsets of P forms a topology on P, called the Scott topology of P, and is denoted by
![]() $\sigma(P)$
. The collection of all Scott closed subsets of P is denoted by
$\sigma(P)$
. The collection of all Scott closed subsets of P is denoted by
![]() $\Gamma (P)$
. The space
$\Gamma (P)$
. The space
![]() $(P,\sigma(P))$
called the Scott space of P is written as
$(P,\sigma(P))$
called the Scott space of P is written as
![]() $\Sigma P$
.
$\Sigma P$
.
For two elements x, y in a poset P, x is way-below y, denoted by
![]() $x \ll y$
, if for any directed subset D of P for which
$x \ll y$
, if for any directed subset D of P for which
![]() $\sup D$
exists,
$\sup D$
exists,
![]() $y \leq \sup D$
implies
$y \leq \sup D$
implies
![]() $D \cap \mathord{\uparrow} x \neq \emptyset$
. A poset P is continuous if for each
$D \cap \mathord{\uparrow} x \neq \emptyset$
. A poset P is continuous if for each
![]() is directed and
is directed and
![]() A continuous dcpo is usually called a domain.
A continuous dcpo is usually called a domain.
An element x of P is compact if
![]() $x\ll x$
. The set of all compact elements of P is denoted by
$x\ll x$
. The set of all compact elements of P is denoted by
![]() $\textit{K}(P)$
. A poset P is algebraic if for every
$\textit{K}(P)$
. A poset P is algebraic if for every
![]() $x\in P$
, the set
$x\in P$
, the set
![]() $\textit{K}(P)\cap \mathord{\downarrow} x$
is directed and
$\textit{K}(P)\cap \mathord{\downarrow} x$
is directed and
![]() $x=\sup (\mbox{K}(P)\cap \mathord{\downarrow} x).$
For any compact element
$x=\sup (\mbox{K}(P)\cap \mathord{\downarrow} x).$
For any compact element
![]() $x\in P$
,
$x\in P$
,
![]() $\mathord{\uparrow} x\in \sigma(P)$
. Every algebraic poset is continuous. If L is a complete lattice such that
$\mathord{\uparrow} x\in \sigma(P)$
. Every algebraic poset is continuous. If L is a complete lattice such that
![]() $\mbox{K}(L)=L$
(all elements are compact), then L is algebraic.
$\mbox{K}(L)=L$
(all elements are compact), then L is algebraic.
A subset K of a topological space X is compact if every open cover of K has a finite subcover. A set K of a topological space is called saturated if it is the intersection of its open neighborhood (
![]() $K=\mathord{\uparrow} K$
in its specialization order). The saturation satA of a set A is the intersection of all its open neighborhoods.
$K=\mathord{\uparrow} K$
in its specialization order). The saturation satA of a set A is the intersection of all its open neighborhoods.
Definition 2.1. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003)
-
(1) A topological space X is sober if it is
 $T_{0}$
and every irreducible closed subset of X is the closure of a (unique) point.
$T_{0}$
and every irreducible closed subset of X is the closure of a (unique) point. -
(2) A
 $T_{0}$
space X is well filtered if for each filter base
$T_{0}$
space X is well filtered if for each filter base
 $\mathcal{C}$
of compact saturated sets and each open set U with
$\mathcal{C}$
of compact saturated sets and each open set U with
 $\bigcap \mathcal{C} \subseteq U$
, there is a
$\bigcap \mathcal{C} \subseteq U$
, there is a
 $K\in \mathcal{C}$
with
$K\in \mathcal{C}$
with
 $K\subseteq U$
.
$K\subseteq U$
. -
(3) A space X is coherent if the intersection of any two compact saturated sets is again compact.
Remark 2.2.
-
(1) The Scott space of every continuous dcpo is sober.
-
(2) Every sober space is well filtered. A retraction of a sober space is sober.
-
(3) If X is well filtered and
 $\{F_i: i\in I\}$
is a filtered family of compact saturated subsets of X, then
$\{F_i: i\in I\}$
is a filtered family of compact saturated subsets of X, then
 $\bigcap\{F_i: i\in I\}$
is a compact saturated set.
$\bigcap\{F_i: i\in I\}$
is a compact saturated set.
Lemma 2.3.
Assume that L is a complete lattice such that
![]() $\mbox{K}(L)=L$
. Let
$\mbox{K}(L)=L$
. Let
Then
![]() $(L^{*}, \subseteq)$
is a distributive complete lattice.
$(L^{*}, \subseteq)$
is a distributive complete lattice.
Proof. Since L is a complete lattice with
![]() $\mbox{K}(L)=L$
, L is an algebraic lattice. Thus,
$\mbox{K}(L)=L$
, L is an algebraic lattice. Thus,
![]() $\Sigma L$
is sober; hence, it is well filtered.
$\Sigma L$
is sober; hence, it is well filtered.
For any
![]() $\mathord{\uparrow} F, \mathord{\uparrow} G\in L^{*}$
, it is easy to verify that in
$\mathord{\uparrow} F, \mathord{\uparrow} G\in L^{*}$
, it is easy to verify that in
![]() $L^*$
,
$L^*$
,
Thus,
![]() $L^{*}$
is a lattice.
$L^{*}$
is a lattice.
-
(1)
 $L^{*}$
is a distributive lattice. For any two elements
$L^{*}$
is a distributive lattice. For any two elements
 $\mathord{\uparrow} F, \mathord{\uparrow} G $
in
$\mathord{\uparrow} F, \mathord{\uparrow} G $
in
 $L^{*}$
, it is easy to see that
$L^{*}$
, it is easy to see that
 $\inf\{\mathord{\uparrow} F, \mathord{\uparrow} G\}=\mathord{\uparrow} F\cap \mathord{\uparrow} G$
and
$\inf\{\mathord{\uparrow} F, \mathord{\uparrow} G\}=\mathord{\uparrow} F\cap \mathord{\uparrow} G$
and
 $\sup\{\mathord{\uparrow} F,\mathord{\uparrow} G\}=\mathord{\uparrow} F\cup \mathord{\uparrow} G$
. Hence, the finite sup (inf) in
$\sup\{\mathord{\uparrow} F,\mathord{\uparrow} G\}=\mathord{\uparrow} F\cup \mathord{\uparrow} G$
. Hence, the finite sup (inf) in
 $L^{*}$
is the set union (intersection), which means that
$L^{*}$
is the set union (intersection), which means that
 $L^{*}$
is a sublattice of the distributive powerset lattice
$L^{*}$
is a sublattice of the distributive powerset lattice
 $\mathcal{P}(L)$
; thus,
$\mathcal{P}(L)$
; thus,
 $L^{*}$
is distributive.
$L^{*}$
is distributive. -
(2)
 $L^{*}$
is a complete lattice
$L^{*}$
is a complete lattice
Since
![]() $L^{*}$
is a lattice and has a top element
$L^{*}$
is a lattice and has a top element
![]() $\mathord{\uparrow} 0_{L}$
, in order to prove
$\mathord{\uparrow} 0_{L}$
, in order to prove
![]() $L^{*}$
is a complete lattice, it remains to show that every filtered subset of
$L^{*}$
is a complete lattice, it remains to show that every filtered subset of
![]() $L^{*}$
has an infimum. Let
$L^{*}$
has an infimum. Let
![]() $\mathcal{D}=\{\mathord{\uparrow} F_i: i\in I\}$
be a filtered subset of
$\mathcal{D}=\{\mathord{\uparrow} F_i: i\in I\}$
be a filtered subset of
![]() $L^{*}$
. Then each
$L^{*}$
. Then each
![]() $\mathord{\uparrow} F_{i}$
is a compact saturated subset of
$\mathord{\uparrow} F_{i}$
is a compact saturated subset of
![]() $\Sigma L$
. Hence, by Remarks
2.2(3), the intersection
$\Sigma L$
. Hence, by Remarks
2.2(3), the intersection
![]() $A=\bigcap \{\mathord{\uparrow} F_i: i\in I\}$
is a compact saturated subset of
$A=\bigcap \{\mathord{\uparrow} F_i: i\in I\}$
is a compact saturated subset of
![]() $\Sigma L$
. For each
$\Sigma L$
. For each
![]() $x\in A$
, x is compact, so
$x\in A$
, x is compact, so
![]() $\mathord{\uparrow} x\in\sigma(L)$
.
$\mathord{\uparrow} x\in\sigma(L)$
.
Now
![]() $A=\bigcup\{\mathord{\uparrow} x: x\in A\}$
(note that A is an upper set). As A is compact, there is a finite subset
$A=\bigcup\{\mathord{\uparrow} x: x\in A\}$
(note that A is an upper set). As A is compact, there is a finite subset
![]() $G\subseteq A$
, such that
$G\subseteq A$
, such that
![]() $A=\bigcup\{\mathord{\uparrow} y: y\in G\}=\mathord{\uparrow} G$
, which is in
$A=\bigcup\{\mathord{\uparrow} y: y\in G\}=\mathord{\uparrow} G$
, which is in
![]() $L^{*}$
. Clearly
$L^{*}$
. Clearly
![]() $\inf \mathcal{D}=\mathord{\uparrow} G$
.
$\inf \mathcal{D}=\mathord{\uparrow} G$
.
It follows that
![]() $(L^{*}, \subseteq)$
is a complete lattice.
$(L^{*}, \subseteq)$
is a complete lattice.
An ideal I of a poset P is incremental if I is not a principal ideal (
![]() $I\neq \mathord{\downarrow} x$
for any
$I\neq \mathord{\downarrow} x$
for any
![]() $x\in P$
). We use Id(P) to denote the set of all incremental ideals of a poset P.
$x\in P$
). We use Id(P) to denote the set of all incremental ideals of a poset P.
Proposition 2.4. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Corollary II-1.12) If L is a dcpo and a sup semilattice such that the sup operation is jointly Scott continuous, then
![]() $\Sigma L$
is sober.
$\Sigma L$
is sober.
Let
![]() $\mathbb{N}$
be the set of all nonnegative integers. Then,
$\mathbb{N}$
be the set of all nonnegative integers. Then,
![]() $\mathbb{N}$
is a poset with the ordinary order
$\mathbb{N}$
is a poset with the ordinary order
![]() $\le$
of numbers. Let
$\le$
of numbers. Let
![]() $\mathbb{N}^{<\mathbb{N}}$
be the set of all nonempty finite words (or, finite strings) over
$\mathbb{N}^{<\mathbb{N}}$
be the set of all nonempty finite words (or, finite strings) over
![]() $\mathbb{N}$
. The prefix order “
$\mathbb{N}$
. The prefix order “
![]() $\le$
” on
$\le$
” on
![]() $\mathbb{N}^{<\mathbb{N}}$
is defined as follows:
$\mathbb{N}^{<\mathbb{N}}$
is defined as follows:
For any
![]() $x=a_1a_2\cdots a_n, y= b_1b_2\cdots b_m$
in
$x=a_1a_2\cdots a_n, y= b_1b_2\cdots b_m$
in
![]() $\mathbb{N}^{<\mathbb{N}}$
,
$\mathbb{N}^{<\mathbb{N}}$
,
The poset
![]() $\mathbb{N}^{<\mathbb{N}}$
is countable and does not have infinite decreasing sequences. One can arrange all the elements from
$\mathbb{N}^{<\mathbb{N}}$
is countable and does not have infinite decreasing sequences. One can arrange all the elements from
![]() $\mathbb{N}^{<\mathbb{N}}$
in a sequence such that larger elements appear later. Thus, we can define a monotone injective function from
$\mathbb{N}^{<\mathbb{N}}$
in a sequence such that larger elements appear later. Thus, we can define a monotone injective function from
![]() $\mathbb{N}^{<\mathbb{N}}$
to
$\mathbb{N}^{<\mathbb{N}}$
to
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
We shall make use of the following result, for its proof, see Remark 6.1.
Proposition 2.5. There is a monotone bijective function
![]() $f: \mathbb{N}^{<\mathbb{N}}\rightarrow\mathbb{N}$
.
$f: \mathbb{N}^{<\mathbb{N}}\rightarrow\mathbb{N}$
.
Remark 2.6. Consider the set
![]() $\mathbb{N}$
. There exists a sequence
$\mathbb{N}$
. There exists a sequence
![]() $\{E_{k}\}_{k\in\mathbb{N}}$
of disjoint infinite subsets of
$\{E_{k}\}_{k\in\mathbb{N}}$
of disjoint infinite subsets of
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
For example, let
![]() $E_{1}=\{2m: m\in \mathbb{N}\}$
. Assume that we have defined disjoint subsets
$E_{1}=\{2m: m\in \mathbb{N}\}$
. Assume that we have defined disjoint subsets
![]() $E_{k} (k=1, 2, \cdots, m)$
such that each
$E_{k} (k=1, 2, \cdots, m)$
such that each
![]() $E_{i}$
is an infinite subset of
$E_{i}$
is an infinite subset of
![]() $\mathbb{N} - \bigcup\{E_j: j\le i-1\}$
and
$\mathbb{N} - \bigcup\{E_j: j\le i-1\}$
and
![]() $\mathbb{N} - \bigcup\{E_j: j\le i\}$
is infinite. Then choose
$\mathbb{N} - \bigcup\{E_j: j\le i\}$
is infinite. Then choose
![]() $E_{m+1}$
to be an infinite subset of
$E_{m+1}$
to be an infinite subset of
![]() $\mathbb{N} - \bigcup\{E_i: i\le m\}$
such that
$\mathbb{N} - \bigcup\{E_i: i\le m\}$
such that
![]() $\mathbb{N} - \bigcup\{E_i: i\le m+1\}$
is infinite.
$\mathbb{N} - \bigcup\{E_i: i\le m+1\}$
is infinite.
By induction, we can have a sequence
![]() $\{E_k\}_{k\in\mathbb{N}}$
of disjoint infinite subsets of
$\{E_k\}_{k\in\mathbb{N}}$
of disjoint infinite subsets of
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
Since
![]() $\mathbb{N}\times \mathbb{N}$
is a countable set, there exists a bijection
$\mathbb{N}\times \mathbb{N}$
is a countable set, there exists a bijection
![]() $h: \mathbb{N}\times \mathbb{N}\rightarrow \mathbb{N}$
. Using h and the above remarks, we see that there is an injective function
$h: \mathbb{N}\times \mathbb{N}\rightarrow \mathbb{N}$
. Using h and the above remarks, we see that there is an injective function
![]() $i: \mathbb{N}\times \mathbb{N}\rightarrow \mathcal{P}(\mathbb{N})$
such that each i(m, n) is an infinite set and
$i: \mathbb{N}\times \mathbb{N}\rightarrow \mathcal{P}(\mathbb{N})$
such that each i(m, n) is an infinite set and
![]() $i(m_1, n_1)\cap i(m_2, n_2)=\emptyset$
whenever
$i(m_1, n_1)\cap i(m_2, n_2)=\emptyset$
whenever
![]() $(m_1, n_1)\not=(m_2, n_2)$
. In addition, by subtracting
$(m_1, n_1)\not=(m_2, n_2)$
. In addition, by subtracting
![]() $\{1, 2, \cdots, m\}$
from i(m, n), we can guarantee that all numbers in i(m, n) are strictly greater than m.
$\{1, 2, \cdots, m\}$
from i(m, n), we can guarantee that all numbers in i(m, n) are strictly greater than m.
Now for each
![]() $(m, n)\in \mathbb{N}\times\mathbb{N}$
, there is a monotone injection
$(m, n)\in \mathbb{N}\times\mathbb{N}$
, there is a monotone injection
![]() $h_{m, n}: \mathbb{N}\rightarrow i(m, n)$
. Let
$h_{m, n}: \mathbb{N}\rightarrow i(m, n)$
. Let
![]() $f_{m,n}=h_{m,n}\circ f$
. Then,
$f_{m,n}=h_{m,n}\circ f$
. Then,
![]() $f_{m,n}$
is a monotone injective function from
$f_{m,n}$
is a monotone injective function from
![]() $\mathbb{N}^{<\mathbb{N}}$
into i(m, n).
$\mathbb{N}^{<\mathbb{N}}$
into i(m, n).
3. A Countable Complete Distributive Lattice Whose Scott Space is Non-sober
We now construct a countable complete distributive lattice whose Scott space is non-sober.
Let
![]() $L=\mathbb{N}\cup \mathbb{N}^{<\mathbb{N}}\cup \{\top\}$
with the order
$L=\mathbb{N}\cup \mathbb{N}^{<\mathbb{N}}\cup \{\top\}$
with the order
![]() $\leq $
such that both
$\leq $
such that both
![]() $\mathbb{N}^{<\mathbb{N}}$
and
$\mathbb{N}^{<\mathbb{N}}$
and
![]() $\mathbb{N}$
are sub posets and T is the top element.
$\mathbb{N}$
are sub posets and T is the top element.
The poset L can be depicted as Fig. 1.

Figure 1. The basic gadget of P.
Next, let
![]() $P=\mathbb{N}\times L$
.
$P=\mathbb{N}\times L$
.
Let
![]() $L_{n}=\{(n, x)\in P: x\in L\}$
. In this section, for
$L_{n}=\{(n, x)\in P: x\in L\}$
. In this section, for
![]() $s\in \mathbb{N}^{<\mathbb{N}}$
with length equaling 1 sometimes is considered as a natural number s. We first define the relations
$s\in \mathbb{N}^{<\mathbb{N}}$
with length equaling 1 sometimes is considered as a natural number s. We first define the relations
![]() $<_{1}, <_{2}, <_{3}$
and
$<_{1}, <_{2}, <_{3}$
and
![]() $<_{4}$
on P as follows:
$<_{4}$
on P as follows:
-
 $(n, x)<_{1}(m,y)$
if
$(n, x)<_{1}(m,y)$
if
 $n=m$
and
$n=m$
and
 $x< y$
holds in L;
$x< y$
holds in L; -
 $(n, x)<_{2}(m,y)$
if
$(n, x)<_{2}(m,y)$
if
 $y=\top$
,
$y=\top$
,
 $x\in \mathbb{N}^{<\mathbb{N}}$
and there exists
$x\in \mathbb{N}^{<\mathbb{N}}$
and there exists
 $k\in \mathbb{N}$
with
$k\in \mathbb{N}$
with
 $k>n$
such that
$k>n$
such that
 $m\in i(n,k)$
and
$m\in i(n,k)$
and
 $m=f_{n,k}(x)$
. (In other words,
$m=f_{n,k}(x)$
. (In other words,
 $(n, x)<_{2}(f_{n,k}(x),\top)$
for all
$(n, x)<_{2}(f_{n,k}(x),\top)$
for all
 $n<k$
).
$n<k$
). -
 $(n, x)<_{3}(m,y)$
if
$(n, x)<_{3}(m,y)$
if
 $y=\top$
,
$y=\top$
,
 $x\in \mathbb{N}$
and there exists
$x\in \mathbb{N}$
and there exists
 $d\in \mathbb{N}$
with
$d\in \mathbb{N}$
with
 $d<n$
such that
$d<n$
such that
 $m\in i(d, n)$
and
$m\in i(d, n)$
and
 $m=f_{d,n}(x)$
. (In other words,
$m=f_{d,n}(x)$
. (In other words,
 $(n, x)<_{3}(f_{d, n}(x),\top)$
for all
$(n, x)<_{3}(f_{d, n}(x),\top)$
for all
 $d<n$
).
$d<n$
).
Here
![]() $(n, x)\in \mathbb{N}\times\mathbb{N}$
, and in the definition of
$(n, x)\in \mathbb{N}\times\mathbb{N}$
, and in the definition of
![]() $f_{d, n}(x)$
,
$f_{d, n}(x)$
,
![]() $x\in\mathbb{N}$
is taken as an element of
$x\in\mathbb{N}$
is taken as an element of
![]() $\mathbb{N}^{<\mathbb{N}}$
with length equaling 1.
$\mathbb{N}^{<\mathbb{N}}$
with length equaling 1.
-
 $(n,x)<_{4}(m,y)$
if
$(n,x)<_{4}(m,y)$
if
 $y=\top$
,
$y=\top$
,
 $x\in \mathbb{N}$
and there exists
$x\in \mathbb{N}$
and there exists
 $a,b\in \mathbb{N}$
,
$a,b\in \mathbb{N}$
,
 $s\in\mathbb{N}$
with
$s\in\mathbb{N}$
with
 $a<b$
such that
$a<b$
such that
 $f_{a,b}(s)=n$
and
$f_{a,b}(s)=n$
and
 $f_{a,b}(s.x)=m$
. (In other words,
$f_{a,b}(s.x)=m$
. (In other words,
 $(f_{a,b}(s),x)<_{4}(f_{a,b}(s.x),\top)$
for all
$(f_{a,b}(s),x)<_{4}(f_{a,b}(s.x),\top)$
for all
 $(a,b)\in \mathbb{N}\times \mathbb{N}$
with
$(a,b)\in \mathbb{N}\times \mathbb{N}$
with
 $a<b$
).
$a<b$
).
By the above definitions, it is clear that as subsets of
![]() $P\times P$
,
$P\times P$
,
![]() $<_1$
,
$<_1$
,
![]() $<_2$
,
$<_2$
,
![]() $<_3$
and
$<_3$
and
![]() $<_4$
are disjoint. Here we explain, in particular, why
$<_4$
are disjoint. Here we explain, in particular, why
![]() $<_3$
and
$<_3$
and
![]() $<_4$
are disjoint. In fact, suppose that
$<_4$
are disjoint. In fact, suppose that
![]() $((f_{a,b}(s),x),(f_{a,b}(s.x), \top))$
is in
$((f_{a,b}(s),x),(f_{a,b}(s.x), \top))$
is in
![]() $<_4$
. Let
$<_4$
. Let
![]() $n=f_{a,b}(s)$
. Then by the definition of
$n=f_{a,b}(s)$
. Then by the definition of
![]() $f_{a,b}$
,
$f_{a,b}$
,
![]() $n>b$
, hence,
$n>b$
, hence,
![]() $f_{a,b}(s.x)\neq f_{d,n}(x)$
for any
$f_{a,b}(s.x)\neq f_{d,n}(x)$
for any
![]() $d \in \mathbb{N}$
with
$d \in \mathbb{N}$
with
![]() $d<n$
. Hence,
$d<n$
. Hence,
![]() $((f_{a,b}(s),x),(f_{a,b}(s.x), \top))$
is not in
$((f_{a,b}(s),x),(f_{a,b}(s.x), \top))$
is not in
![]() $<_3$
.
$<_3$
.
Example 3.1. The following are some concrete examples illustrating the strict orders
![]() $ <_{i} (i=1, 2, 3, 4)$
.
$ <_{i} (i=1, 2, 3, 4)$
.
-
(1)
 $(2, 3) <_{1} (2, 3\cdot 1)$
.
$(2, 3) <_{1} (2, 3\cdot 1)$
. -
(2)
 $(3, 12\cdot 4) <_{2} (f_{3, k}(12\cdot 4), \top)$
for all
$(3, 12\cdot 4) <_{2} (f_{3, k}(12\cdot 4), \top)$
for all
 $k > 3$
.
$k > 3$
. -
(3)
 $(3, 5) <_{3}(f_{d, 3}(5), \top)$
for all
$(3, 5) <_{3}(f_{d, 3}(5), \top)$
for all
 $ d < 3$
. Here, the 5 in
$ d < 3$
. Here, the 5 in
 $f_{d, 3}(5)$
is a member of
$f_{d, 3}(5)$
is a member of
 $\mathbb{N}^{<\mathbb{N}}$
with length equaling 1.
$\mathbb{N}^{<\mathbb{N}}$
with length equaling 1. -
(4)
 $(f_{2, 3}(2\cdot 6), 7) <_{4} (f_{2, 3}(2\cdot 6\cdot 7), \top)$
.
$(f_{2, 3}(2\cdot 6), 7) <_{4} (f_{2, 3}(2\cdot 6\cdot 7), \top)$
.
Now let
![]() $\le$
be the partial order on P generated by
$\le$
be the partial order on P generated by
![]() $<_1\cup <_2\cup <_3\cup <_4$
(the smallest partial order relation containing all
$<_1\cup <_2\cup <_3\cup <_4$
(the smallest partial order relation containing all
![]() $<_i (i=1, 2, 3, 4)$
). Note that the partial order
$<_i (i=1, 2, 3, 4)$
). Note that the partial order
![]() $\leq $
coincides with
$\leq $
coincides with
![]() $\leq_{1}\cup (\leq_{1}; <_{2})\cup (\leq _{1}; <_{3})\cup (\leq_{1}; <_4)$
, where
$\leq_{1}\cup (\leq_{1}; <_{2})\cup (\leq _{1}; <_{3})\cup (\leq_{1}; <_4)$
, where
![]() $\leq_{1}$
is the reflexive closure of
$\leq_{1}$
is the reflexive closure of
![]() $<_{1}$
and
$<_{1}$
and
![]() $(R; S)$
denotes the composition of two relations R and S, defined by
$(R; S)$
denotes the composition of two relations R and S, defined by
![]() $x(R; S)y$
iff
$x(R; S)y$
iff
![]() $\exists z : xRzSy$
.
$\exists z : xRzSy$
.
If
![]() $n=m$
, then the strict order
$n=m$
, then the strict order
![]() $<_1$
is depicted as in Fig. 1. For
$<_1$
is depicted as in Fig. 1. For
![]() $n\neq m$
, the strict orders
$n\neq m$
, the strict orders
![]() $<_2, <_3, <_4$
of P are depicted in the following figures, respectively.
$<_2, <_3, <_4$
of P are depicted in the following figures, respectively.
When
![]() $k \gt n$
, the red lines in Fig. 2 illustrate three specific cases:
$k \gt n$
, the red lines in Fig. 2 illustrate three specific cases:
![]() $(n,1)<_{2}(f_{n,k}(1),\top)$
,
$(n,1)<_{2}(f_{n,k}(1),\top)$
,
![]() $(n,2)<_{2}(f_{n,k}(2),\top)$
and
$(n,2)<_{2}(f_{n,k}(2),\top)$
and
![]() $(n,x)<_{2}(f_{n,k}(x),\top)$
.
$(n,x)<_{2}(f_{n,k}(x),\top)$
.

Figure 2. The strict order
![]() $<_{3}$
.
$<_{3}$
.
The red lines in Fig. 3 illustrate the cases:
![]() $(n,1)<_{3}(f_{d,n}(1),\top)$
,
$(n,1)<_{3}(f_{d,n}(1),\top)$
,
![]() $(n,2)<_{3}(f_{d,n}(2),\top)$
, and
$(n,2)<_{3}(f_{d,n}(2),\top)$
, and
![]() $(n,x)<_{3}(f_{d,n}(x),\top)$
.
$(n,x)<_{3}(f_{d,n}(x),\top)$
.

Figure 3. The strict order
![]() $<_{3}$
.
$<_{3}$
.
The red lines in Fig. 4 illustrate the cases:
![]() $(f_{a,b}(1),1)<_{4}(f_{a,b}(1.1),\top)$
and
$(f_{a,b}(1),1)<_{4}(f_{a,b}(1.1),\top)$
and
![]() $(f_{a,b}(1),x)<_{4}(f_{a,b}(1.x),\top)$
.
$(f_{a,b}(1),x)<_{4}(f_{a,b}(1.x),\top)$
.

Figure 4. The strict order
![]() $<_{4}$
.
$<_{4}$
.
The red lines in Fig. 5 illustrate the cases:
![]() $(f_{a,b}(1),x)<_{4}(f_{a,b}(1.x),\top)$
and
$(f_{a,b}(1),x)<_{4}(f_{a,b}(1.x),\top)$
and
![]() $(f_{a,b}(1.x),y)<_{4}(f_{a,b}(1.x.y),\top)$
.
$(f_{a,b}(1.x),y)<_{4}(f_{a,b}(1.x.y),\top)$
.

Figure 5. The strict order
![]() $<_{4}$
.
$<_{4}$
.
The red lines in Fig. 6 illustrate the cases:
![]() $(b,y)<_{3}(f_{a,b}(y),\top)$
;
$(b,y)<_{3}(f_{a,b}(y),\top)$
;
![]() $(f_{a,b}(y),z)<_{4}(f_{a,b}(y.z),\top)$
;
$(f_{a,b}(y),z)<_{4}(f_{a,b}(y.z),\top)$
;
![]() $(f_{a,b}(y.z),u)<_{4}(f_{a,b}(y.z.u),\top)$
.
$(f_{a,b}(y.z),u)<_{4}(f_{a,b}(y.z.u),\top)$
.

Figure 6. Assembling the strict orders
![]() $<_{3}$
and
$<_{3}$
and
![]() $<_{4}$
.
$<_{4}$
.
In Fig. 7, the red lines are the same as Fig. 6 and the blue lines add the cases of
![]() $<_{2}$
:
$<_{2}$
:
![]() $(a,y)<_{2}(f_{a,b}(y),\top)$
,
$(a,y)<_{2}(f_{a,b}(y),\top)$
,
![]() $(a,y.z)<_{2}(f_{a,b}(y.z),\top)$
, and
$(a,y.z)<_{2}(f_{a,b}(y.z),\top)$
, and
![]() $(a,y.z.u)<_{2}(f_{a,b}(y.z.u),\top)$
.
$(a,y.z.u)<_{2}(f_{a,b}(y.z.u),\top)$
.

Figure 7. Assembling the strict orders
![]() $<_{2}$
,
$<_{2}$
,
![]() $<_{3}$
and
$<_{3}$
and
![]() $<_{4}$
.
$<_{4}$
.
Lemma 3.2. P is an irreducible subset of
![]() $\Sigma P$
.
$\Sigma P$
.
Proof. By the definition of irreducibility, it suffices to prove that
![]() $U\cap V\neq \emptyset$
for any two nonempty Scott open sets U,V of P.
$U\cap V\neq \emptyset$
for any two nonempty Scott open sets U,V of P.
Since U and V are nonempty Scott open sets, there exist
![]() $(n_{0}, \top)\in U$
and
$(n_{0}, \top)\in U$
and
![]() $(m_{0}, \top)\in V$
.
$(m_{0}, \top)\in V$
.
If
![]() $n_{0}=m_{0}$
, then
$n_{0}=m_{0}$
, then
![]() $(n_{0},\top)\in U\cap V$
.
$(n_{0},\top)\in U\cap V$
.
Next, assume that
![]() $n_{0} \not= m_{0}$
. Without loss of generality, we just consider the case
$n_{0} \not= m_{0}$
. Without loss of generality, we just consider the case
![]() $n_{0}<m_{0}$
.
$n_{0}<m_{0}$
.
Since V is Scott open and
![]() $\bigvee\{(m_0, k): k\in\mathbb{N}\}=(m_0, \top)\in V$
, there exists
$\bigvee\{(m_0, k): k\in\mathbb{N}\}=(m_0, \top)\in V$
, there exists
![]() $a_{1}\in \mathbb{N}$
such that
$a_{1}\in \mathbb{N}$
such that
![]() $(m_{0}, a_{1})\in V$
.
$(m_{0}, a_{1})\in V$
.
From the definition of
![]() $<_{3}$
, it follows that
$<_{3}$
, it follows that
![]() $(m_{0},a_{1})<_{3}(f_{n_{0}, m_{0}}(a_{1}),\top)$
. Whence,
$(m_{0},a_{1})<_{3}(f_{n_{0}, m_{0}}(a_{1}),\top)$
. Whence,
![]() $(f_{n_{0},m_{0}}(a_{1}),\top)\in V$
. By the similar reason for the existence of
$(f_{n_{0},m_{0}}(a_{1}),\top)\in V$
. By the similar reason for the existence of
![]() $a_1$
, there is
$a_1$
, there is
![]() $a_2\in \mathbb{N}$
such that
$a_2\in \mathbb{N}$
such that
![]() $(f_{n_{0},m_{0}}(a_{1}), a_{2})\in V$
.
$(f_{n_{0},m_{0}}(a_{1}), a_{2})\in V$
.
By the definition of
![]() $<_{4}$
, we have that
$<_{4}$
, we have that
![]() $(f_{n_{0}, m_{0}}(a_{1}), a_{2})<_{4}(f_{n_{0}, m_{0}}(a_{1}.a_{2}),\top)$
. It follows that
$(f_{n_{0}, m_{0}}(a_{1}), a_{2})<_{4}(f_{n_{0}, m_{0}}(a_{1}.a_{2}),\top)$
. It follows that
![]() $(f_{n_{0},m_{0}}(a_{1}.a_{2}),\top)\in V$
.
$(f_{n_{0},m_{0}}(a_{1}.a_{2}),\top)\in V$
.
By induction on
![]() $\mathbb{N}$
, for any
$\mathbb{N}$
, for any
![]() $n\in \mathbb{N}$
, there exists
$n\in \mathbb{N}$
, there exists
![]() $(f_{n_{0},m_{0}}(a_{1}.a_{2}.\cdots .a_{n}),\top)\in V$
. Note that
$(f_{n_{0},m_{0}}(a_{1}.a_{2}.\cdots .a_{n}),\top)\in V$
. Note that
![]() $\{(n_0, a_{1}.a_{2}.\cdots .a_{k})): k\in\mathbb{N}\}$
is an increasing sequence in P and
$\{(n_0, a_{1}.a_{2}.\cdots .a_{k})): k\in\mathbb{N}\}$
is an increasing sequence in P and
Thus, there exists
![]() $k\in \mathbb{N}$
such that
$k\in \mathbb{N}$
such that
![]() $(n_{0}, a_{1}.\cdots.a_{k})\in U$
. By the definition of
$(n_{0}, a_{1}.\cdots.a_{k})\in U$
. By the definition of
![]() $<_{2}$
, we have that
$<_{2}$
, we have that
![]() $(n_{0}, a_{1}.\cdots.a_{k}) <_{2} (f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)$
(see Fig. 8 for the process of the proof).
$(n_{0}, a_{1}.\cdots.a_{k}) <_{2} (f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)$
(see Fig. 8 for the process of the proof).

Figure 8. The proof of Lemma 3.2 (
![]() $n<m$
).
$n<m$
).
Hence,
![]() $(f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)\in U$
, implying that
$(f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)\in U$
, implying that
![]() $(f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)\in U\cap V$
.
$(f_{n_{0},m_{0}}(a_{1}.\cdots.a_{k}),\top)\in U\cap V$
.
Lemma 3.3. Let
![]() $M=\{\bigcap_{x\in E}\mathord{\downarrow} x:\emptyset \neq E\subseteq P\}$
. Then
$M=\{\bigcap_{x\in E}\mathord{\downarrow} x:\emptyset \neq E\subseteq P\}$
. Then
![]() $(M,\subseteq)$
is a bounded complete dcpo.
$(M,\subseteq)$
is a bounded complete dcpo.
Proof. If
![]() $\{A_{i}: i\in I\}\subseteq M$
has an upper bound in M, where
$\{A_{i}: i\in I\}\subseteq M$
has an upper bound in M, where
![]() $A_i=\bigcap_{x\in E_i}\mathord{\downarrow} x ~(i\in I)$
with
$A_i=\bigcap_{x\in E_i}\mathord{\downarrow} x ~(i\in I)$
with
![]() $E_i\subseteq P$
, then there is
$E_i\subseteq P$
, then there is
![]() $y_0\in P$
such that
$y_0\in P$
such that
![]() $\bigcup\{A_i: i\in I\}\subseteq \mathord{\downarrow} y_0$
. Hence,
$\bigcup\{A_i: i\in I\}\subseteq \mathord{\downarrow} y_0$
. Hence,
![]() $\bigcap\{\mathord{\downarrow} y: \bigcup\{A_i: i\in I\}\subseteq \mathord{\downarrow} y\}$
is the supremum of
$\bigcap\{\mathord{\downarrow} y: \bigcup\{A_i: i\in I\}\subseteq \mathord{\downarrow} y\}$
is the supremum of
![]() $\{A_i: i\in I\}$
in M. It follows that M is bounded complete.
$\{A_i: i\in I\}$
in M. It follows that M is bounded complete.
now show that M is a dcpo. Let
![]() $B=\{(n,m)\in \mathbb{N}\times \mathbb{N}: n<m\}$
. In order to determine what the intersections of two principal[-350pt][0pt]Figures 8–15 have not been mentioned in the text. Please cite the figure in the relevant place in the text. ideals of P are, we first list all types of principal ideals
$B=\{(n,m)\in \mathbb{N}\times \mathbb{N}: n<m\}$
. In order to determine what the intersections of two principal[-350pt][0pt]Figures 8–15 have not been mentioned in the text. Please cite the figure in the relevant place in the text. ideals of P are, we first list all types of principal ideals
![]() $\mathord{\downarrow} x$
of P.
$\mathord{\downarrow} x$
of P.

Figure 9. The Type I ideals.

Figure 10. The Type II ideals.

Figure 11. The Type III ideals.

Figure 12. The Type IV ideals.

Figure 13. The Type V ideals.

Figure 14. The Type
![]() $\mathrm{I}\cup \mathrm{II}^{1}$
sets.
$\mathrm{I}\cup \mathrm{II}^{1}$
sets.

Figure 15. The Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
sets.
$\mathrm{I}\cup \mathrm{II}^{2}$
sets.
Types I :
![]() $\mathord{\downarrow} (m_{0}, s_0)=\{(m_{0}, s): s\leq s_{0}\}$
for some
$\mathord{\downarrow} (m_{0}, s_0)=\{(m_{0}, s): s\leq s_{0}\}$
for some
![]() $m_{0}\in \mathbb{N},s_{0}\in \mathbb{N}^{<\mathbb{N}}$
(see Fig. 9 for Type I ideals).
$m_{0}\in \mathbb{N},s_{0}\in \mathbb{N}^{<\mathbb{N}}$
(see Fig. 9 for Type I ideals).
Types II :
![]() $\mathord{\downarrow} (m_{0}, n_0)=\{(m_{0}, n): n\leq n_{0}\}$
for some
$\mathord{\downarrow} (m_{0}, n_0)=\{(m_{0}, n): n\leq n_{0}\}$
for some
![]() $m_{0}, n_{0}\in \mathbb{N}$
(see Fig. 10 for Type II ideals).
$m_{0}, n_{0}\in \mathbb{N}$
(see Fig. 10 for Type II ideals).
Types III. :
![]() $\mathord{\downarrow} (n_0, \top)=L_{n_{0}}$
for some
$\mathord{\downarrow} (n_0, \top)=L_{n_{0}}$
for some
![]() $n_{0}\in \mathbb{N}\backslash \bigcup_{(n,m)\in B}i(n,m)$
(see Fig. 11 for Type III ideals).
$n_{0}\in \mathbb{N}\backslash \bigcup_{(n,m)\in B}i(n,m)$
(see Fig. 11 for Type III ideals).
Types IV :
![]() $\mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)=L_{f_{m_{0},n_{0}}(s_{0})}\cup \{(m_{0},s_{0})\}\cup\{(n_{0},n): n\leq s_{0}\}$
for some
$\mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)=L_{f_{m_{0},n_{0}}(s_{0})}\cup \{(m_{0},s_{0})\}\cup\{(n_{0},n): n\leq s_{0}\}$
for some
![]() $(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{0}{\mid}=1$
(see Fig. 12 for Type IV ideals).
$ {\mid}s_{0}{\mid}=1$
(see Fig. 12 for Type IV ideals).
Types V :
![]() $\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)=L_{f_{m_{0},n_{0}}(s_{0})}\cup \{(m_{0},s): s\leq s_{0}\}\cup\{(f_{m_{0},n_{0}}(s_{0}^{*}),n): n\leq n_{0}^{*}\}$
for some
$\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)=L_{f_{m_{0},n_{0}}(s_{0})}\cup \{(m_{0},s): s\leq s_{0}\}\cup\{(f_{m_{0},n_{0}}(s_{0}^{*}),n): n\leq n_{0}^{*}\}$
for some
![]() $(m_{0},n_{0})\in B, s_{0}=s_{0}^{*}.n_{0}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{0},n_{0})\in B, s_{0}=s_{0}^{*}.n_{0}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{0}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{0}^{*}\in \mathbb{N}$
(see Fig. 13 for Type V ideals).
$s_{0}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{0}^{*}\in \mathbb{N}$
(see Fig. 13 for Type V ideals).
The Types I, II, and III are easily understood.
For the Type IV principle ideal
![]() $\mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)$
, clearly it contains the whole
$\mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)$
, clearly it contains the whole
![]() $L_{f_{m_{0},n_{0}}(s_{0})}$
. Also
$L_{f_{m_{0},n_{0}}(s_{0})}$
. Also
![]() $(m_0, s_0) <_{2} (f_{m_{0}, n_{0}}(s_{0}),\top)$
, where
$(m_0, s_0) <_{2} (f_{m_{0}, n_{0}}(s_{0}),\top)$
, where
![]() $(m_0, s_0)$
is taken as an element in
$(m_0, s_0)$
is taken as an element in
![]() $\mathbb{N}\times \mathbb{N}^{<\mathbb{N}}$
. Thus,
$\mathbb{N}\times \mathbb{N}^{<\mathbb{N}}$
. Thus,
![]() $(m_0, s_0)\in \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. Note that this
$(m_0, s_0)\in \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. Note that this
![]() $(m_0, s_0)$
is a minimal element of P. Next,
$(m_0, s_0)$
is a minimal element of P. Next,
![]() $(n_0, s_0) <_{3} (f_{m_{0}, n_{0}}(s_{0}),\top)$
where the
$(n_0, s_0) <_{3} (f_{m_{0}, n_{0}}(s_{0}),\top)$
where the
![]() $s_0$
in
$s_0$
in
![]() $(n_0, s_0)$
is a member of
$(n_0, s_0)$
is a member of
![]() $\mathbb{N}$
, thus we have
$\mathbb{N}$
, thus we have
![]() $\mathord{\downarrow} (n_0, s_0)= \{(n_{0},n): n\leq s_{0}\}\subseteq \mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)$
.
$\mathord{\downarrow} (n_0, s_0)= \{(n_{0},n): n\leq s_{0}\}\subseteq \mathord{\downarrow}(f_{m_{0}, n_{0}}(s_{0}),\top)$
.
Now consider the Type V principle ideal
![]() $\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
, where
$\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
, where
![]() $s_0\in \mathbb{N}^{<\mathbb{N}}$
. Trivially, it contains the whole
$s_0\in \mathbb{N}^{<\mathbb{N}}$
. Trivially, it contains the whole
![]() $L_{f_{m_{0}, n_{0}}(s_{0})}$
. Next,
$L_{f_{m_{0}, n_{0}}(s_{0})}$
. Next,
![]() $(m_0, s_0) <_{2} (f_{m_{0},n_{0}}(s_{0}),\top)$
, thus
$(m_0, s_0) <_{2} (f_{m_{0},n_{0}}(s_{0}),\top)$
, thus
![]() $\mathord{\downarrow} (m_0, s_0)=\{(m_{0},s): s\leq s_{0}\}\subseteq \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. Furthermore, if
$\mathord{\downarrow} (m_0, s_0)=\{(m_{0},s): s\leq s_{0}\}\subseteq \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. Furthermore, if
![]() $s_0=s_{0}^{*}.n_{0}^{*}$
with
$s_0=s_{0}^{*}.n_{0}^{*}$
with
![]() $n_{0}^{*}\in\mathbb{N}$
, then
$n_{0}^{*}\in\mathbb{N}$
, then
![]() $(f_{m_{0},n_{0}}(s_{0}^{*}),n_{0}^{*}) <_{4} (f_{m_{0},n_{0}}(s_{0}^{*}. n_{0}^{*}), \top)=(f_{m_{0},n_{0}}(s_{0}), \top)$
, hence
$(f_{m_{0},n_{0}}(s_{0}^{*}),n_{0}^{*}) <_{4} (f_{m_{0},n_{0}}(s_{0}^{*}. n_{0}^{*}), \top)=(f_{m_{0},n_{0}}(s_{0}), \top)$
, hence
![]() $\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}^{*}),n_{0}^{*})=\{(f_{m_{0},n_{0}}(s_{0}^{*}),n): n\leq n_{0}^{*}\}\subseteq \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. And these are all the elements in
$\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}^{*}),n_{0}^{*})=\{(f_{m_{0},n_{0}}(s_{0}^{*}),n): n\leq n_{0}^{*}\}\subseteq \mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
. And these are all the elements in
![]() $\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
.
$\mathord{\downarrow}(f_{m_{0},n_{0}}(s_{0}),\top)$
.
These types of principle ideas are depicted as below (as the blue regions).
We now list all the subsets of P which are the intersections of two principal ideals in the following table.

In the aforementioned table, Type I
![]() $\cup \mathrm{II}^{1}$
sets are of the form
$\cup \mathrm{II}^{1}$
sets are of the form
![]() $\{(m_{0},s_{0})\}\cup\{(n_{0},n): n\leq k_{0}\}$
for some
$\{(m_{0},s_{0})\}\cup\{(n_{0},n): n\leq k_{0}\}$
for some
![]() $(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}},k_{0}\in \mathbb{N}$
with
$(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}},k_{0}\in \mathbb{N}$
with
![]() $ {\mid}s_{0}{\mid}=1$
,
$ {\mid}s_{0}{\mid}=1$
,
![]() $k_{0}\leq s_{0}$
(see Fig. 14 for Type I
$k_{0}\leq s_{0}$
(see Fig. 14 for Type I
![]() $\cup \mathrm{II}^{1}$
ideals).
$\cup \mathrm{II}^{1}$
ideals).
Type I
![]() $\cup \mathrm{II}^{2}$
sets are of the form
$\cup \mathrm{II}^{2}$
sets are of the form
![]() $\{(m_{0},s)\mid s\leq s_{0}\}\cup\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{0}\}$
for some
$\{(m_{0},s)\mid s\leq s_{0}\}\cup\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{0}\}$
for some
![]() $(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}},k_{0}\in \mathbb{N}$
(see Fig. 15 for Type I
$(m_{0},n_{0})\in B, s_{0}\in \mathbb{N}^{<\mathbb{N}},k_{0}\in \mathbb{N}$
(see Fig. 15 for Type I
![]() $\cup \mathrm{II}^{2}$
ideals).
$\cup \mathrm{II}^{2}$
ideals).
The two new types of subsets are depicted in Fig. 14, as the blue regions.
For the intersections with Type I, Type II, and Type III principle ideals, the results are easily seen. We now explain the intersections of two Type IV principle ideas, one Type IV and one Type V principle ideals and two Type V principle ideals.
Intersections of two Type IV principle ideals
The corresponding cell for intersections of two Type IV ideals is indicated as
![]() $\mathrm{I}/\mathrm{II}/\mathrm{IV}/\mathrm{I} \cup \mathrm{II}^{1}$
,
$\mathrm{I}/\mathrm{II}/\mathrm{IV}/\mathrm{I} \cup \mathrm{II}^{1}$
,
![]() $\emptyset$
, meaning that intersection can be a Type I ideal, a Type II ideal, a Type IV ideal, a Type
$\emptyset$
, meaning that intersection can be a Type I ideal, a Type II ideal, a Type IV ideal, a Type
![]() $\mathrm{I}\cup \mathrm{II}^{1}$
set, or the empty set.
$\mathrm{I}\cup \mathrm{II}^{1}$
set, or the empty set.
Let
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
be two Type IV principle ideals, where
$I_{2}$
be two Type IV principle ideals, where
![]() $I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq s_{1}\}$
for some
$I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq s_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{1}{\mid}=1$
, and
$ {\mid}s_{1}{\mid}=1$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{2}{\mid}=1$
.
$ {\mid}s_{2}{\mid}=1$
.
We prove this by considering the following different cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2}, n_{2}}(s_{2}) < m_{1}$
.In this case, as
$f_{m_{2}, n_{2}}(s_{2}) < m_{1}$
.In this case, as
 $m_{2}<n_{2}<f_{m_{2},n_{2}}(s_{2})<m_{1}<n_{1} < f_{m_{1},n_{1}}(s_{1})$
, it follows that
$m_{2}<n_{2}<f_{m_{2},n_{2}}(s_{2})<m_{1}<n_{1} < f_{m_{1},n_{1}}(s_{1})$
, it follows that
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
.Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
.Then
 $m_2 < n_2 < f_{m_{2},n_{2}}(s_{2})=m_{1} < n_1 < f_{{m_1}, n_{1}}$
, so
$m_2 < n_2 < f_{m_{2},n_{2}}(s_{2})=m_{1} < n_1 < f_{{m_1}, n_{1}}$
, so
 $\{(m_{1}, s_{1})\}\subseteq I_{2}$
and
$\{(m_{1}, s_{1})\}\subseteq I_{2}$
and
 $I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal.
 $m_{1}<f_{m_{2}, n_{2}}(s_{2}) < n_{1}$
.
$m_{1}<f_{m_{2}, n_{2}}(s_{2}) < n_{1}$
. -
(3) Let
 $m_{2}\neq m_{1}$
. Then
$m_{2}\neq m_{1}$
. Then
 $I_{1}\cap I_{2}=\emptyset$
.Let
$I_{1}\cap I_{2}=\emptyset$
.Let
 $m_{2}=m_{1}$
.If
$m_{2}=m_{1}$
.If
 $s_{1}\neq s_{2}$
, then
$s_{1}\neq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
. Otherwise,
$I_{1}\cap I_{2}=\emptyset$
. Otherwise,
 $I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}=\{(m_{2}, s_{2})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}=\{(m_{2}, s_{2})\}$
, which is a Type I ideal. -
(4)
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
.Then, as
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
.Then, as
 $m_2 < n_2 <f_{m_{2},n_{2}}(s_{2})=n_{1}$
, we have
$m_2 < n_2 <f_{m_{2},n_{2}}(s_{2})=n_{1}$
, we have
 $m_{2} < n_{2} <n_{1}<f_{m_{1},n_{1}}(s_{1})$
.If
$m_{2} < n_{2} <n_{1}<f_{m_{1},n_{1}}(s_{1})$
.If
 $m_2\not=m_1$
, then
$m_2\not=m_1$
, then
 $I_{1}\cap I_{2}=\{(n_{1}, n): n\leq s_{1}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(n_{1}, n): n\leq s_{1}\}$
, which is a Type II ideal. If
 $m_2=m_1$
and
$m_2=m_1$
and
 $s_1=s_2$
, then
$s_1=s_2$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},n): n\leq s_{1}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},n): n\leq s_{1}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set. -
(5) If
 $m_{2}=m_{1}$
and
$m_{2}=m_{1}$
and
 $s_{1}\neq s_{2}$
, then
$s_{1}\neq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(n_{1}, n): n\leq s_{1}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1}, n): n\leq s_{1}\}$
, which is a Type II ideal.
 $n_{1}<f_{m_{2}, n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
.If
$n_{1}<f_{m_{2}, n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
.If
 $m_{1}\neq m_{2}, n_{1}\neq n_{2}$
, then
$m_{1}\neq m_{2}, n_{1}\neq n_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{1}=m_{2}, n_{1}\neq n_{2}$
and
$m_{1}=m_{2}, n_{1}\neq n_{2}$
and
 $s_{1}\neq s_{2}$
.Then
$s_{1}\neq s_{2}$
.Then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{1}=m_{2}, n_{1}\neq n_{2}$
and
$m_{1}=m_{2}, n_{1}\neq n_{2}$
and
 $s_{1} = s_{2}$
, then
$s_{1} = s_{2}$
, then
 $ I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal. Now consider the case
$ I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal. Now consider the case
 $m_{1}=m_{2}, n_{1}= n_{2}$
.By
$m_{1}=m_{2}, n_{1}= n_{2}$
.By
 $f_{m_{2}, n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
, we have
$f_{m_{2}, n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
, we have
 $s_1\not=s_2$
. Hence,
$s_1\not=s_2$
. Hence,
 $I_1\cap I_2=\{(n_1, n): n\le min\{s_1, s_2\}\}$
.For the case
$I_1\cap I_2=\{(n_1, n): n\le min\{s_1, s_2\}\}$
.For the case
 $m_{1}\neq m_{2}$
,
$m_{1}\neq m_{2}$
,
 $n_{1}=n_{2}$
, we have
$n_{1}=n_{2}$
, we have
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},s_{2}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},s_{2}\}\}$
, which is a Type II ideal. -
(6)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
$(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
, thus
$f_{m_{1},n_{1}}$
, thus
 $I_{1}\cap I_{2}=I_{1}$
, which is a type IV ideal.
$I_{1}\cap I_{2}=I_{1}$
, which is a type IV ideal. -
(7)
 $f_{m_{1},n_{1}}(s_{1}) < f_{m_{2},n_{2}}(s_{2})$
By interchanging
$f_{m_{1},n_{1}}(s_{1}) < f_{m_{2},n_{2}}(s_{2})$
By interchanging
 $m_1$
and
$m_1$
and
 $m_2$
,
$m_2$
,
 $n_1$
and
$n_1$
and
 $m_2$
in the cases (1)–(5), we deduce again that
$m_2$
in the cases (1)–(5), we deduce again that
 $I_1\cap I_2$
is of Type
$I_1\cap I_2$
is of Type
 $\mathrm{I}/\mathrm{II}/\mathrm{IV}/\mathrm{I}\cup\mathrm{II}^{1}/\emptyset$
.
$\mathrm{I}/\mathrm{II}/\mathrm{IV}/\mathrm{I}\cup\mathrm{II}^{1}/\emptyset$
.
Intersections of one Type IV and one Type V principle ideals
Let
![]() $I_{1}$
be a Type IV ideal and
$I_{1}$
be a Type IV ideal and
![]() $I_{2}$
a Type V ideal.
$I_{2}$
a Type V ideal.
Specifically,
![]() $I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq s_{1}\}$
for some
$I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq s_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{1}{\mid}=1$
, and
$ {\mid}s_{1}{\mid}=1$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
$s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
Note that in this case,
![]() $s_1\not=s_2$
.
$s_1\not=s_2$
.
We prove this by considering the following cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
.Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
.Then
 $m_2 < n_2 < f_{m_{2},n_{2}}(s_{2}) <m_1 <n_1 < f_{m_{1},n_{1}}(s_{1})$
and
$m_2 < n_2 < f_{m_{2},n_{2}}(s_{2}) <m_1 <n_1 < f_{m_{1},n_{1}}(s_{1})$
and
 $f_{m_{2},n_{2}}(s_{2}^{*}) < f_{m_{2},n_{2}}(s_{2}).$
Hence,
$f_{m_{2},n_{2}}(s_{2}^{*}) < f_{m_{2},n_{2}}(s_{2}).$
Hence,
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
.Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
.Then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2}, n_{2}}(s_{2})<n_{1}$
$m_{1}<f_{m_{2}, n_{2}}(s_{2})<n_{1}$
-
(3.1)
 $m_{2}\neq m_{1}$
$m_{2}\neq m_{1}$
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
-
(4.1)
 $m_{2}\neq m_{1}$
$m_{2}\neq m_{1}$
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq s_{1}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq s_{1}\}$
, which is a Type II ideal. -
(4.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $s_{1}\nleq s_{2}$
, then we have the same result as in case
$s_{1}\nleq s_{2}$
, then we have the same result as in case
 $m_{2}\neq m_{1}$
.If
$m_{2}\neq m_{1}$
.If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},s): s\leq s_{1}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},s): s\leq s_{1}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
-
(5)
 $n_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
$n_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
-
(5.1)
 $m_{1}\neq m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
$m_{1}\neq m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(5.2)
 $m_{1}=m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
$m_{1}=m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
 $s_{1}\nleq s_{2}$
,
$s_{1}\nleq s_{2}$
,
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $s_{1}\leq s_{2}$
,
$s_{1}\leq s_{2}$
,
 $ I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$ I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(5.3)
 $m_{1}=m_{2},n_{1}= f_{m_{2},n_{2}}(s_{2}^{*})$
If
$m_{1}=m_{2},n_{1}= f_{m_{2},n_{2}}(s_{2}^{*})$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. Otherwise If
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. Otherwise If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}\cup \{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type
$I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}\cup \{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type
 $\mathrm{I}\cup \mathrm{II}^{1}$
set.
$\mathrm{I}\cup \mathrm{II}^{1}$
set. -
(5.4)
 $m_{1}\neq m_{2}$
,
$m_{1}\neq m_{2}$
,
 $n_{1}=f_{m_{2},n_{2}}(s_{2}^{*})$
$n_{1}=f_{m_{2},n_{2}}(s_{2}^{*})$
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal.
-
-
(6)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
$(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
, which contradicts the assumption that
$f_{m_{1},n_{1}}$
, which contradicts the assumption that
 $s_{1}\neq s_{2}$
. Thus, this case does not exist.
$s_{1}\neq s_{2}$
. Thus, this case does not exist. -
(7)
 $f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
$f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
-
(7.1)
 $f_{m_{1},n_{1}}(s_{1})<m_{2}$
Then
$f_{m_{1},n_{1}}(s_{1})<m_{2}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(7.2)
 $f_{m_{1},n_{1}}(s_{1})=m_{2}$
Then
$f_{m_{1},n_{1}}(s_{1})=m_{2}$
Then
 $I_{1}\cap I_{2}=\{(m_{2},s):s\leq s_{2}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{2},s):s\leq s_{2}\}$
, which is a Type I ideal. -
(7.3)
 $m_{2}<f_{m_{1},n_{1}}(s_{1})<f_{m_{2},n_{2}}(s_{2}^{*})$
If
$m_{2}<f_{m_{1},n_{1}}(s_{1})<f_{m_{2},n_{2}}(s_{2}^{*})$
If
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{2}=m_{1}$
and
$m_{2}=m_{1}$
and
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{2}=m_{1}$
and
$m_{2}=m_{1}$
and
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal. -
(7.4)
 $f_{m_{1},n_{1}}(s_{1})=f_{m_{2},n_{2}}(s_{2}^{*})$
Then
$f_{m_{1},n_{1}}(s_{1})=f_{m_{2},n_{2}}(s_{2}^{*})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}), s_{2}^{*}=s_{1}$
by the property of functions i and
$(m_{1},n_{1})=(m_{2},n_{2}), s_{2}^{*}=s_{1}$
by the property of functions i and
 $f_{m_{1},n_{1}}$
. This implies that
$f_{m_{1},n_{1}}$
. This implies that
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq n_{2}^{*}\}$
which is a Type
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq n_{2}^{*}\}$
which is a Type
 $\mathrm{I}\cup \mathrm{II}^{2}$
set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set. -
(7.5)
 $f_{m_{2},n_{2}}(s_{2}^{*})<f_{m_{1},n_{1}}(s_{1})<f_{m_{2},n_{2}}(s_{2})$
$f_{m_{2},n_{2}}(s_{2}^{*})<f_{m_{1},n_{1}}(s_{1})<f_{m_{2},n_{2}}(s_{2})$
-
(7.5.1)
 $m_{1}\neq m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
, then
$m_{1}\neq m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
, then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(7.5.2)
 $m_{1}=m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
$m_{1}=m_{2},n_{1}\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $s_{1}\leq s_{2}$
,
$s_{1}\leq s_{2}$
,
 $ I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$ I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(7.5.3)
 $m_{1}=m_{2},n_{1}= f_{m_{2},n_{2}}(s_{2}^{*})$
.If
$m_{1}=m_{2},n_{1}= f_{m_{2},n_{2}}(s_{2}^{*})$
.If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{1})\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}), n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type
$I_{1}\cap I_{2}=\{(m_{2},s_{1})\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}), n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type
 $\mathrm{I}\cup \mathrm{II}^{1}$
set.
$\mathrm{I}\cup \mathrm{II}^{1}$
set. -
(7.5.4)
 $m_{1}\neq m_{2}$
,
$m_{1}\neq m_{2}$
,
 $n_{1}=f_{m_{2},n_{2}}(s_{2}^{*})$
$n_{1}=f_{m_{2},n_{2}}(s_{2}^{*})$
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq \min\{s_{1},n_{2}^{*}\}\}$
, which is a Type II ideal.
-
-
These cover all possible cases and we are done.
Intersections of two Type V principle ideals
Next, we show that the intersection of two Type V ideals has the form I/II/V/I
![]() $\cup$
$\cup$
![]() $ \mathrm{II}^{2}$
/
$ \mathrm{II}^{2}$
/
![]() $\emptyset$
, that is, either a Type I ideal, a Type II ideal, a Type V ideal, and a Type
$\emptyset$
, that is, either a Type I ideal, a Type II ideal, a Type V ideal, and a Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
set or the empty set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set or the empty set.
Let
![]() $I_{1}, I_{2}$
be two Type V ideals, where
$I_{1}, I_{2}$
be two Type V ideals, where
![]() $I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s): s\leq s_{1}\}\cup\{(f_{m_{1},n_{1}}(s_{1}^{*}),n): n\leq n_{1}^{*}\}$
for some
$I_{1}=\mathord{\downarrow}(f_{m_{1},n_{1}}(s_{1}),\top)=L_{f_{m_{1},n_{1}}(s_{1})}\cup \{(m_{1},s): s\leq s_{1}\}\cup\{(f_{m_{1},n_{1}}(s_{1}^{*}),n): n\leq n_{1}^{*}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}=s_{1}^{*}.n_{1}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}=s_{1}^{*}.n_{1}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{1}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{1}^{*}\in \mathbb{N}$
, and
$s_{1}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{1}^{*}\in \mathbb{N}$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
$s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
We prove for the case
![]() $f_{m_{2},n_{2}}(s_{2})\le f_{m_{1},n_{1}}(s_{1})$
. The proof for the case
$f_{m_{2},n_{2}}(s_{2})\le f_{m_{1},n_{1}}(s_{1})$
. The proof for the case
![]() $f_{m_{1},n_{1}}(s_{1})\le f_{m_{2},n_{2}}(s_{2})$
is similar.
$f_{m_{1},n_{1}}(s_{1})\le f_{m_{2},n_{2}}(s_{2})$
is similar.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1}^{*})$
$m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1}^{*})$
-
(3.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
 $I_{1}\cap I_{2}=\{(m_{1}, s): s\leq\inf\{s_{1},s_{2}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1}, s): s\leq\inf\{s_{1},s_{2}\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1}^{*})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1}^{*})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}), s_{1}^{*}=s_{2}$
by the property of i and
$(m_{1},n_{1})=(m_{2},n_{2}), s_{1}^{*}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
. Note that
$f_{m_{1},n_{1}}$
. Note that
 $s_2 < s_{1}$
in this case. We have which is a Type
$s_2 < s_{1}$
in this case. We have which is a Type $$I_{1}\cap I_{2}=\{(m_{2},s): s\leq s_{2})\}\cup\{(f_{m_{2},n_{2}}(s_{2}), n): n\leq n_{1}^{*}\}$$
$$I_{1}\cap I_{2}=\{(m_{2},s): s\leq s_{2})\}\cup\{(f_{m_{2},n_{2}}(s_{2}), n): n\leq n_{1}^{*}\}$$
 $\mathrm{I}\cup \mathrm{II}^{2}$
set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set.
-
(5)
 $f_{m_{1},n_{1}}(s_{1}^{*})<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
$f_{m_{1},n_{1}}(s_{1}^{*})<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
-
(5.1)
 $m_{1}\neq m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})\neq f_{m_{2},n_{2}}(s_{2}^{*})$
Then
$m_{1}\neq m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})\neq f_{m_{2},n_{2}}(s_{2}^{*})$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(5.2)
 $m_{1}=m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
$m_{1}=m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})\neq f_{m_{2},n_{2}}(s_{2}^{*})$
If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
 $ I_{1}\cap I_{2}=\{(m_{1}, s): s\leq \inf\{s_{1}, s_{2}\}\}$
, which is a Type I ideal.
$ I_{1}\cap I_{2}=\{(m_{1}, s): s\leq \inf\{s_{1}, s_{2}\}\}$
, which is a Type I ideal. -
(5.3)
 $m_{1}=m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})= f_{m_{2},n_{2}}(s_{2}^{*})$
Then
$m_{1}=m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})= f_{m_{2},n_{2}}(s_{2}^{*})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}), s_{1}^{*}=s_{2}^{*}$
by the property of i and
$(m_{1},n_{1})=(m_{2},n_{2}), s_{1}^{*}=s_{2}^{*}$
by the property of i and
 $f_{m_{1},n_{1}}$
. Thus,
$f_{m_{1},n_{1}}$
. Thus,
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}^{*})\}\cup\{(f_{m_{1},n_{1}}(s_{1}^{*}),n): n\leq \min\{n_{1}^{*},n_{2}^{*}\}\}$
, which is a Type
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}^{*})\}\cup\{(f_{m_{1},n_{1}}(s_{1}^{*}),n): n\leq \min\{n_{1}^{*},n_{2}^{*}\}\}$
, which is a Type
 $\mathrm{I}\cup \mathrm{II}^{2}$
set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set. -
(5.4)
 $m_{1}\neq m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})= f_{m_{2},n_{2}}(s_{2}^{*})$
The second equality implies
$m_{1}\neq m_{2}, f_{m_{1},n_{1}}(s_{1}^{*})= f_{m_{2},n_{2}}(s_{2}^{*})$
The second equality implies
 $m_{1}=m_{2}$
, contradicting the first inequality
$m_{1}=m_{2}$
, contradicting the first inequality
 $m_{1}\neq m_{2}$
. Thus, this case does not exist.
$m_{1}\neq m_{2}$
. Thus, this case does not exist.
-
-
(6)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1}, n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1}, n_{1}}(s_{1})$
Then
 $(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
$(m_{1},n_{1})=(m_{2},n_{2}),s_{1}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
. This reveals that
$f_{m_{1},n_{1}}$
. This reveals that
 $I_{1}\cap I_{2}=I_{1}$
, which is a type V ideal.
$I_{1}\cap I_{2}=I_{1}$
, which is a type V ideal.
This covers all possible cases, and we have confirmed that the intersections of two Type V ideals can be a Type I ideal, a Type II ideal, a Type V ideal, Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
set, or the empty set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set, or the empty set.
Next, we consider the intersections of Type I
![]() $\cup$
$\cup$
![]() $ \mathrm{II}^{1}$
(Type I
$ \mathrm{II}^{1}$
(Type I
![]() $\cup$
$\cup$
![]() $ \mathrm{II}^{2}$
, resp.) sets with Type I
$ \mathrm{II}^{2}$
, resp.) sets with Type I
![]() $\cup$
$\cup$
![]() $ \mathrm{II}^{1}$
, I
$ \mathrm{II}^{1}$
, I
![]() $\cup$
$\cup$
![]() $ \mathrm{II}^{2}$
sets, Type I, Type II, Type III, Type IV, and Type V ideals.
$ \mathrm{II}^{2}$
sets, Type I, Type II, Type III, Type IV, and Type V ideals.
The results are shown in the following table.

We now explain the aforementioned table.
We only consider the following nontrivial cases.
Intersections of a Type IV ideal and a Type I
 $\cup \mathrm{II}^{1}$
set
$\cup \mathrm{II}^{1}$
set
Let
![]() $I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
![]() $ {\mid}s_{1}{\mid}=1$
,
$ {\mid}s_{1}{\mid}=1$
,
![]() $k_{1}\leq s_{1}$
, and
$k_{1}\leq s_{1}$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{2}{\mid}=1$
.
$ {\mid}s_{2}{\mid}=1$
.
Then
![]() $I_{1}$
is a Type I
$I_{1}$
is a Type I
![]() $\cup \mathrm{II}^{1}$
set and
$\cup \mathrm{II}^{1}$
set and
![]() $I_{2}$
is a type IV ideal.
$I_{2}$
is a type IV ideal.
We prove this by considering the following cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2},n_{2}}(s_{2})<n_{1}$
$m_{1}<f_{m_{2},n_{2}}(s_{2})<n_{1}$
-
(3.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}= m_{1}$
If
$m_{2}= m_{1}$
If
 $s_{2}\neq s_{1}$
, then
$s_{2}\neq s_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $s_{2}=s_{1}$
, then
$s_{2}=s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
-
(4.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq k_{1}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq k_{1}\}$
, which is a Type II ideal. -
(4.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $s_{2}\neq s_{1}$
, then we have the same result as in case
$s_{2}\neq s_{1}$
, then we have the same result as in case
 $m_{2}\neq m_{1}$
.If
$m_{2}\neq m_{1}$
.If
 $s_{2}=s_{1}$
, then
$s_{2}=s_{1}$
, then
 $I_{1}\cap I_{2}=I_{1}$
, which is a Type I
$I_{1}\cap I_{2}=I_{1}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
-
(5)
 $f_{m_{2},n_{2}}(s_{2})>n_{1}$
If
$f_{m_{2},n_{2}}(s_{2})>n_{1}$
If
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $n_{2}\neq n_{1}$
, then
$n_{2}\neq n_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $n_{2}=n_{1}$
, then
$n_{2}=n_{1}$
, then
 $I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}\neq n_{1}$
, and
$n_{2}\neq n_{1}$
, and
 $s_{2}\neq s_{1}$
, then
$s_{2}\neq s_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}\neq n_{1}$
, and
$n_{2}\neq n_{1}$
, and
 $s_{2}= s_{1}$
, then
$s_{2}= s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal. If
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal. If
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}=n_{1}$
, and
$n_{2}=n_{1}$
, and
 $s_{2}\neq s_{1}$
, then
$s_{2}\neq s_{1}$
, then
 $I_{1}\cap I_{2}=\{(n_{2},n):n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(n_{2},n):n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}=n_{1}$
, and
$n_{2}=n_{1}$
, and
 $s_{2}= s_{1}$
, then
$s_{2}= s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
These cover all possible cases and we are done.
Intersections of a Type V ideal and a Type I
![]() $\cup \mathrm{II}^{1}$
set
$\cup \mathrm{II}^{1}$
set
Let
![]() $I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
![]() $ {\mid}s_{1}{\mid}=1$
,
$ {\mid}s_{1}{\mid}=1$
,
![]() $k_{1}\leq s_{1}$
, and
$k_{1}\leq s_{1}$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
$s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
Then
![]() $I_{1}$
is a Type I
$I_{1}$
is a Type I
![]() $\cup \mathrm{II}^{1}$
set and
$\cup \mathrm{II}^{1}$
set and
![]() $I_{2}$
is a type V ideal.
$I_{2}$
is a type V ideal.
Note that in this case,
![]() $s_{1}\neq s_{2}$
because
$s_{1}\neq s_{2}$
because
![]() $|s_1|=1$
and
$|s_1|=1$
and
![]() $|s_2| >1$
.
$|s_2| >1$
.
We prove this by considering the following cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2},n_{2}}(s_{2})<n_{1}$
$m_{1}<f_{m_{2},n_{2}}(s_{2})<n_{1}$
-
(3.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}= m_{1}$
If
$m_{2}= m_{1}$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1}, s_{1})\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
-
(4.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\{(n_{1},n): n\leq k_{1}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{1},n): n\leq k_{1}\}$
, which is a Type II ideal. -
(4.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $s_{1}\nleq s_{2}$
, then we have the same result as in case
$s_{1}\nleq s_{2}$
, then we have the same result as in case
 $m_{2}\neq m_{1}$
. If
$m_{2}\neq m_{1}$
. If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=I_{1}$
, which is a Type I
$I_{1}\cap I_{2}=I_{1}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
-
(5)
 $f_{m_{2},n_{2}}(s_{2})>n_{1}$
$f_{m_{2},n_{2}}(s_{2})>n_{1}$
-
(5.1)
 $m_{2}\neq m_{1}$
If
$m_{2}\neq m_{1}$
If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
, then
$f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
, then
$f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
, then
 $I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. -
(5.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
and
$f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
and
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
and
$f_{m_{2},n_{2}}(s_{2}^{*})\neq n_{1}$
and
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
 $f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
and
$f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
and
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type II ideal. If
 $f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
and
$f_{m_{2},n_{2}}(s_{2}^{*})=n_{1}$
and
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
These cover all possible cases and we are done.
Intersections of two Type I
![]() $\cup \mathrm{II}^{1}$
sets
$\cup \mathrm{II}^{1}$
sets
Let
![]() $I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
![]() $ {\mid}s_{1}{\mid}=1$
,
$ {\mid}s_{1}{\mid}=1$
,
![]() $k_{1}\leq s_{1}$
, and
$k_{1}\leq s_{1}$
, and
![]() $I_{2}=\{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq k_{2}\}$
for some
$I_{2}=\{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq k_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}},k_{2}\in \mathbb{N}$
with
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}},k_{2}\in \mathbb{N}$
with
![]() $ {\mid}s_{2}{\mid}=1$
,
$ {\mid}s_{2}{\mid}=1$
,
![]() $k_{2}\leq s_{2}$
.
$k_{2}\leq s_{2}$
.
Then
![]() $I_{1}, I_{2}$
are both Type I
$I_{1}, I_{2}$
are both Type I
![]() $\cup \mathrm{II}^{1}$
sets.
$\cup \mathrm{II}^{1}$
sets.
We prove this by considering the following cases.
-
(1)
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $n_{2}\neq n_{1}$
Then
$n_{2}\neq n_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $n_{2}=n_{1}$
Then
$n_{2}=n_{1}$
Then
 $I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal. -
(3)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}\neq n_{1}$
, and
$n_{2}\neq n_{1}$
, and
 $s_{2}\neq s_{1}$
Then
$s_{2}\neq s_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(4)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}\neq n_{1}$
, and
$n_{2}\neq n_{1}$
, and
 $s_{2}= s_{1}$
Then
$s_{2}= s_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal. -
(5)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}=n_{1}$
, and
$n_{2}=n_{1}$
, and
 $s_{2}\neq s_{1}$
then
$s_{2}\neq s_{1}$
then
 $I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal. -
(6)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $n_{2}=n_{1}$
, and
$n_{2}=n_{1}$
, and
 $s_{2}= s_{1}$
then
$s_{2}= s_{1}$
then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
These cover all possible cases and we are done.
Intersections of a Type I
![]() $\cup \mathrm{II}^{1}$
set and a I
$\cup \mathrm{II}^{1}$
set and a I
![]() $\cup \mathrm{II}^{2}$
set
$\cup \mathrm{II}^{2}$
set
Let
![]() $I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s_{1})\}\cup\{(n_{1},n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}},k_{1}\in \mathbb{N}$
with
![]() $ {\mid}s_{1}{\mid}=1$
,
$ {\mid}s_{1}{\mid}=1$
,
![]() $k_{1}\leq s_{1}$
, and
$k_{1}\leq s_{1}$
, and
![]() $I_{2}=\{(m_{2},s):s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq k_{2}\}$
for some
$I_{2}=\{(m_{2},s):s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq k_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}},k_{2}\in \mathbb{N}$
.
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}},k_{2}\in \mathbb{N}$
.
Then
![]() $I_{1}$
is a Type I
$I_{1}$
is a Type I
![]() $\cup \mathrm{II}^{1}$
set and
$\cup \mathrm{II}^{1}$
set and
![]() $I_{2}$
is a Type I
$I_{2}$
is a Type I
![]() $\cup \mathrm{II}^{2}$
set.
$\cup \mathrm{II}^{2}$
set.
We prove this by considering the following cases.
-
(1)
 $m_{2}\neq m_{1}$
If
$m_{2}\neq m_{1}$
If
 $f_{m_{2},n_{2}}(s_{2})\neq n_{1}$
, then
$f_{m_{2},n_{2}}(s_{2})\neq n_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
, then
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
, then
 $I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal. -
(2)
 $m_{2}=m_{1}$
$m_{2}=m_{1}$
-
(2.1)
 $f_{m_{2},n_{2}}(s_{2})\neq n_{1}$
If
$f_{m_{2},n_{2}}(s_{2})\neq n_{1}$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}$
, which is a Type I ideal. -
(2.2)
 $f_{m_{2},n_{2}}(s_{2})=n_{1}$
If
$f_{m_{2},n_{2}}(s_{2})=n_{1}$
If
 $s_{1}\nleq s_{2}$
, then
$s_{1}\nleq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type II ideal. If
 $s_{1}\leq s_{2}$
, then
$s_{1}\leq s_{2}$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{1},s_{1})\}\cup \{(n_{1},n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
These cover all possible cases and we are done.
Intersections of a Type IV ideal and a Type I
![]() $\cup \mathrm{II}^{2}$
set
$\cup \mathrm{II}^{2}$
set
Let
![]() $I_{1}=\{(m_{1},s): s\leq s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s): s\leq s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $k_{1}\in \mathbb{N}$
, and
$k_{1}\in \mathbb{N}$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s_{2})\}\cup\{(n_{2},n): n\leq s_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $ {\mid}s_{2}{\mid}=1$
.
$ {\mid}s_{2}{\mid}=1$
.
Then
![]() $I_{1}$
is a Type I
$I_{1}$
is a Type I
![]() $\cup \mathrm{II}^{2}$
set and
$\cup \mathrm{II}^{2}$
set and
![]() $I_{2}$
is a Type IV ideal.
$I_{2}$
is a Type IV ideal.
We prove this by considering the following cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{1},s):s\leq s_{1}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s):s\leq s_{1}\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
$m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
-
(3.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}= m_{1}$
If
$m_{2}= m_{1}$
If
 $s_{2}\nleq s_{1}$
, then
$s_{2}\nleq s_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $s_{2}\leq s_{1}$
, then
$s_{2}\leq s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{1}=s_{2}$
by the property of i and
$s_{1}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
.So
$f_{m_{1},n_{1}}$
.So
 $I_{1}\cap I_{2}=I_{1}$
, which is a Type I
$I_{1}\cap I_{2}=I_{1}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{2}$
set.
$\mathrm{II}^{2}$
set. -
(5)
 $f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
$f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
-
(5.1)
 $m_{2}\neq m_{1}$
If
$m_{2}\neq m_{1}$
If
 $n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
, then
$n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
, then
 $I_{1}\cap I_{2}=\emptyset$
. If
$I_{1}\cap I_{2}=\emptyset$
. If
 $n_{2}=f_{m_{1},n_{1}}(s_{1})$
, then
$n_{2}=f_{m_{1},n_{1}}(s_{1})$
, then
 $I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal.
$I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. -
(5.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
and
$n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
and
 $s_{2}\nleq s_{1}$
, then
$s_{2}\nleq s_{1}$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
and
$n_{2}\neq f_{m_{1},n_{1}}(s_{1})$
and
 $s_{2}\leq s_{1}$
, then
$s_{2}\leq s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal. If
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}$
, which is a Type I ideal. If
 $n_{2}=f_{m_{1},n_{1}}(s_{1})$
and
$n_{2}=f_{m_{1},n_{1}}(s_{1})$
and
 $s_{2}\nleq s_{1}$
, then
$s_{2}\nleq s_{1}$
, then
 $I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
$I_{1}\cap I_{2}=\{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type II ideal. If
 $n_{2}=f_{m_{1},n_{1}}(s_{1})$
, and
$n_{2}=f_{m_{1},n_{1}}(s_{1})$
, and
 $s_{2}\leq s_{1}$
, then
$s_{2}\leq s_{1}$
, then
 $I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{2},s_{2})\}\cup \{(n_{2},n): n\leq \min\{k_{1},s_{2}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{1}$
set.
$\mathrm{II}^{1}$
set.
-
These cover all possible cases and we are done.
Intersections of a Type V ideal and a Type I
![]() $\cup \mathrm{II}^{2}$
set
$\cup \mathrm{II}^{2}$
set
Let
![]() $I_{1}=\{(m_{1},s): s\leq s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s): s\leq s_{1})\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $k_{1}\in \mathbb{N}$
, and
$k_{1}\in \mathbb{N}$
, and
![]() $I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
$I_{2}=\mathord{\downarrow}(f_{m_{2},n_{2}}(s_{2}),\top)=L_{f_{m_{2},n_{2}}(s_{2})}\cup \{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq n_{2}^{*}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}=s_{2}^{*}.n_{2}^{*}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
$s_{2}^{*}\in \mathbb{N}^{<\mathbb{N}},n_{2}^{*}\in \mathbb{N}$
.
Then
![]() $I_{1}$
is a Type I
$I_{1}$
is a Type I
![]() $\cup \mathrm{II}^{2}$
set and
$\cup \mathrm{II}^{2}$
set and
![]() $I_{2}$
is a Type V ideal.
$I_{2}$
is a Type V ideal.
We prove this by considering the following cases for
![]() $f_{m_{2},n_{2}}(s_{2})$
.
$f_{m_{2},n_{2}}(s_{2})$
.
-
(1)
 $f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})<m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
$f_{m_{2},n_{2}}(s_{2})=m_{1}$
Then
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{1}\}$
, which is a Type I ideal. -
(3)
 $m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
$m_{1}<f_{m_{2},n_{2}}(s_{2})<f_{m_{1},n_{1}}(s_{1})$
-
(3.1)
 $m_{2}\neq m_{1}$
Then
$m_{2}\neq m_{1}$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(3.2)
 $m_{2}= m_{1}$
If
$m_{2}= m_{1}$
If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq \inf\{s_{1},s_{2}\}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq \inf\{s_{1},s_{2}\}\}$
, which is a Type I ideal.
-
-
(4)
 $f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})=f_{m_{1},n_{1}}(s_{1})$
Then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{1}=s_{2}$
by the property of i and
$s_{1}=s_{2}$
by the property of i and
 $f_{m_{1},n_{1}}$
. Thus
$f_{m_{1},n_{1}}$
. Thus
 $I_{1}\cap I_{2}=I_{1}$
, which is a Type I
$I_{1}\cap I_{2}=I_{1}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{2}$
set.
$\mathrm{II}^{2}$
set. -
(5)
 $f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
$f_{m_{2},n_{2}}(s_{2})>f_{m_{1},n_{1}}(s_{1})$
-
(5.1)
 $m_{2}\neq m_{1}$
If
$m_{2}\neq m_{1}$
If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
, then
$f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $f_{m_{2},n_{2}}(s_{2}^{*})=f_{m_{1},n_{1}}(s_{1})$
, then
$f_{m_{2},n_{2}}(s_{2}^{*})=f_{m_{1},n_{1}}(s_{1})$
, then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{2}^{*}=s_{1}$
by the property of i and
$s_{2}^{*}=s_{1}$
by the property of i and
 $f_{m_{1},n_{1}}$
, which contradicts
$f_{m_{1},n_{1}}$
, which contradicts
 $m_{2}\neq m_{1}$
. Thus, this case does not occur.
$m_{2}\neq m_{1}$
. Thus, this case does not occur. -
(5.2)
 $m_{2}=m_{1}$
If
$m_{2}=m_{1}$
If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
and
$f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
and
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}=\emptyset$
, then
 $I_{1}\cap I_{2}=\emptyset$
.If
$I_{1}\cap I_{2}=\emptyset$
.If
 $f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
and
$f_{m_{2},n_{2}}(s_{2}^{*})\neq f_{m_{1},n_{1}}(s_{1})$
and
 $\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
$\mathord{\downarrow} s_{1}\cap \mathord{\downarrow} s_{2}\neq \emptyset$
, then
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq \inf\{s_{1},s_{2}\}\}$
, which is a Type I ideal. If
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq \inf\{s_{1},s_{2}\}\}$
, which is a Type I ideal. If
 $f_{m_{2},n_{2}}(s_{2}^{*})=f_{m_{1},n_{1}}(s_{1})$
, then
$f_{m_{2},n_{2}}(s_{2}^{*})=f_{m_{1},n_{1}}(s_{1})$
, then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{2}^{*}=s_{1}$
. It follows that
$s_{2}^{*}=s_{1}$
. It follows that
 $I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{2}^{*}\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{1},s): s\leq s_{2}^{*}\}\cup \{(f_{m_{2},n_{2}}(s_{2}^{*}),n): n\leq \min\{k_{1},n_{2}^{*}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{2}$
set.
$\mathrm{II}^{2}$
set.
-
These cover all possible cases and we are done.
Intersections of two Type I
![]() $\cup \mathrm{II}^{2}$
sets
$\cup \mathrm{II}^{2}$
sets
Let
![]() $I_{1}=\{(m_{1},s): s\leq s_{1}\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
$I_{1}=\{(m_{1},s): s\leq s_{1}\}\cup\{(f_{m_{1},n_{1}}(s_{1}),n): n\leq k_{1}\}$
for some
![]() $(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{1},n_{1})\in B, s_{1}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $k_{1}\in \mathbb{N}$
, and
$k_{1}\in \mathbb{N}$
, and
![]() $I_{2}=\{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq k_{2}\}$
for some
$I_{2}=\{(m_{2},s): s\leq s_{2}\}\cup\{(f_{m_{2},n_{2}}(s_{2}),n): n\leq k_{2}\}$
for some
![]() $(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
$(m_{2},n_{2})\in B, s_{2}\in \mathbb{N}^{<\mathbb{N}}$
with
![]() $k_{2}\in \mathbb{N}$
.
$k_{2}\in \mathbb{N}$
.
Then
![]() $I_{1}, I_{2}$
are both Type I
$I_{1}, I_{2}$
are both Type I
![]() $\cup \mathrm{II}^{2}$
sets. We prove this by considering the following cases.
$\cup \mathrm{II}^{2}$
sets. We prove this by considering the following cases.
-
(1)
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(2)
 $m_{2}\neq m_{1}$
,
$m_{2}\neq m_{1}$
,
 $f_{m_{2},n_{2}}(s_{2})= f_{m_{1},n_{1}}(s_{1})$
Then
$f_{m_{2},n_{2}}(s_{2})= f_{m_{1},n_{1}}(s_{1})$
Then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{2}=s_{1}$
, which contradicts the assumption that
$s_{2}=s_{1}$
, which contradicts the assumption that
 $m_{2}\neq m_{1}$
. Hence, this case does not occur.
$m_{2}\neq m_{1}$
. Hence, this case does not occur. -
(3)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
, and
$f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
, and
 $\mathord{\downarrow} s_{2}\cap \mathord{\downarrow} s_{1}= \emptyset$
Then
$\mathord{\downarrow} s_{2}\cap \mathord{\downarrow} s_{1}= \emptyset$
Then
 $I_{1}\cap I_{2}=\emptyset$
.
$I_{1}\cap I_{2}=\emptyset$
. -
(4)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
, and
$f_{m_{2},n_{2}}(s_{2})\neq f_{m_{1},n_{1}}(s_{1})$
, and
 $\mathord{\downarrow} s_{2}\cap \mathord{\downarrow} s_{1}\neq \emptyset$
Then
$\mathord{\downarrow} s_{2}\cap \mathord{\downarrow} s_{1}\neq \emptyset$
Then
 $I_{1}\cap I_{2}=\{(m_{2},s):s\leq \min\{s_{1},s_{2}\}\}$
, which is a Type I ideal.
$I_{1}\cap I_{2}=\{(m_{2},s):s\leq \min\{s_{1},s_{2}\}\}$
, which is a Type I ideal. -
(5)
 $m_{2}=m_{1}$
,
$m_{2}=m_{1}$
,
 $f_{m_{2},n_{2}}(s_{2})= f_{m_{1},n_{1}}(s_{1})$
, then
$f_{m_{2},n_{2}}(s_{2})= f_{m_{1},n_{1}}(s_{1})$
, then
 $(m_{2},n_{2})=(m_{1},n_{1})$
,
$(m_{2},n_{2})=(m_{1},n_{1})$
,
 $s_{2}=s_{1}$
. It follows that
$s_{2}=s_{1}$
. It follows that
 $I_{1}\cap I_{2}=\{(m_{2},s): s\leq s_{2}\}\cup \{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
$I_{1}\cap I_{2}=\{(m_{2},s): s\leq s_{2}\}\cup \{(f_{m_{2},n_{2}}(s_{2}),n): n\leq \min\{k_{1},k_{2}\}\}$
, which is a Type I
 $\cup$
$\cup$
 $\mathrm{II}^{2}$
set.
$\mathrm{II}^{2}$
set.
These cover all possible cases and we are done.
It follows that the intersection of finite number of principle ideals of P is either a principle ideal, or a Type I
![]() $\cup \mathrm{II}^{1}$
set, or a Type I
$\cup \mathrm{II}^{1}$
set, or a Type I
![]() $\cup \mathrm{II}^{2}$
set, or the empty set.
$\cup \mathrm{II}^{2}$
set, or the empty set.
Let
By the above arguments, we deduce that
![]() $\Psi$
is closed under finite non-nullary intersections. In addition, since all elements of
$\Psi$
is closed under finite non-nullary intersections. In addition, since all elements of
![]() $\Psi$
are principal ideals or finite subsets of P, and P has no infinite decreasing chains, we have that
$\Psi$
are principal ideals or finite subsets of P, and P has no infinite decreasing chains, we have that
![]() $\Psi$
does not contain an infinite decreasing chain.
$\Psi$
does not contain an infinite decreasing chain.
For any nonempty
![]() $E\subseteq P$
,
$E\subseteq P$
,
Each
![]() $\bigcap\{\mathord{\downarrow} x: x\in F\}$
is a member of
$\bigcap\{\mathord{\downarrow} x: x\in F\}$
is a member of
![]() $\Psi$
, so
$\Psi$
, so
![]() $\{\bigcap\{\mathord{\downarrow} x: x\in F\}: F \mbox{ is a finite subset of } E\}$
is a filter of members of
$\{\bigcap\{\mathord{\downarrow} x: x\in F\}: F \mbox{ is a finite subset of } E\}$
is a filter of members of
![]() $\Psi$
. Since
$\Psi$
. Since
![]() $\Psi$
does not have infinite decreasing chains, this family must have a smallest member, which equals
$\Psi$
does not have infinite decreasing chains, this family must have a smallest member, which equals
![]() $\bigcap\{\mathord{\downarrow} x: x\in E\}$
and is in
$\bigcap\{\mathord{\downarrow} x: x\in E\}$
and is in
![]() $\Psi$
. Therefore,
$\Psi$
. Therefore,
![]() $M=\Psi$
.
$M=\Psi$
.
We now show that every directed subset of M has a supremum in M.
Let
![]() $\mathcal{D}=\{I_{i}:i\in I\}$
be a directed subset of M. If
$\mathcal{D}=\{I_{i}:i\in I\}$
be a directed subset of M. If
![]() $\mathcal{D}$
has a largest member, then its supremum exists and equals the largest member. Now we assume that
$\mathcal{D}$
has a largest member, then its supremum exists and equals the largest member. Now we assume that
![]() $\mathcal{D}$
does not have a largest member. Then
$\mathcal{D}$
does not have a largest member. Then
![]() $\mathcal{D}$
contains an infinite chain. Since Type III ideals, Type IV ideals and Type V ideals are maximal elements of M, we deduce that none of the
$\mathcal{D}$
contains an infinite chain. Since Type III ideals, Type IV ideals and Type V ideals are maximal elements of M, we deduce that none of the
![]() $I_i$
is a Type III ideal, Type IV ideal, and Type V ideal.
$I_i$
is a Type III ideal, Type IV ideal, and Type V ideal.
We consider the following two remaining cases.
Case 1: All members of
![]() $\{I_{i}: i\in I\}$
are Type I ideals or Type II ideals.
$\{I_{i}: i\in I\}$
are Type I ideals or Type II ideals.
Then, as a Type I ideal and a Type II ideal are not comparable, it follows that either all
![]() $I_{i}$
are Type I ideals or they are all Type II ideals. Thus,
$I_{i}$
are Type I ideals or they are all Type II ideals. Thus,
![]() $\sup_{i\in I}I_{i}$
exists because P is a dcpo.
$\sup_{i\in I}I_{i}$
exists because P is a dcpo.
Case 2: There exists
![]() $i_{0}\in I$
such that
$i_{0}\in I$
such that
![]() $I_{i_{0}}$
is a Type
$I_{i_{0}}$
is a Type
![]() $\mathrm{I}\cup \mathrm{II}^{1}$
set or a Type
$\mathrm{I}\cup \mathrm{II}^{1}$
set or a Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
set.
$\mathrm{I}\cup \mathrm{II}^{2}$
set.
Then all members of
![]() $\{I_{i}:I_{i}\geq I_{i_{0}}\}$
are either Type
$\{I_{i}:I_{i}\geq I_{i_{0}}\}$
are either Type
![]() $\mathrm{I}\cup \mathrm{II}^{1}$
sets or Type
$\mathrm{I}\cup \mathrm{II}^{1}$
sets or Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
sets. Note that there exist no infinite increasing chains consisting of Type
$\mathrm{I}\cup \mathrm{II}^{2}$
sets. Note that there exist no infinite increasing chains consisting of Type
![]() $\mathrm{I}\cup \mathrm{II}^{1}$
sets. Hence, there exists
$\mathrm{I}\cup \mathrm{II}^{1}$
sets. Hence, there exists
![]() $i_{1}$
such that
$i_{1}$
such that
![]() $\mathcal{D}_{1}=\{I_{i}: I_{i}\ge I_{i_{1}}\}$
consists of only Type
$\mathcal{D}_{1}=\{I_{i}: I_{i}\ge I_{i_{1}}\}$
consists of only Type
![]() $\mathrm{I}\cup \mathrm{II}^{2}$
sets. In order to prove
$\mathrm{I}\cup \mathrm{II}^{2}$
sets. In order to prove
![]() $\sup\mathcal{D}$
exists, it is enough to prove
$\sup\mathcal{D}$
exists, it is enough to prove
![]() $\sup\mathcal{D}_1$
exists.
$\sup\mathcal{D}_1$
exists.
Let
![]() $\mathcal{D}_{1}=\{I_{j}: j\in J\}$
, where J is a subset of I.
$\mathcal{D}_{1}=\{I_{j}: j\in J\}$
, where J is a subset of I.
For each
![]() $j\in J$
, let
$j\in J$
, let
![]() $I_{j}=\{(m_{j}, s): s\leq s_{j}\}\cup\{(f_{m_{j},n_{j}}(s_{j}),n): n\leq k_{j}\}$
for some
$I_{j}=\{(m_{j}, s): s\leq s_{j}\}\cup\{(f_{m_{j},n_{j}}(s_{j}),n): n\leq k_{j}\}$
for some
![]() $(m_{j},n_{j})\in B, s_{j}\in \mathbb{N}^{<\mathbb{N}},k_{j}\in \mathbb{N}$
.
$(m_{j},n_{j})\in B, s_{j}\in \mathbb{N}^{<\mathbb{N}},k_{j}\in \mathbb{N}$
.
Then
![]() $f_{m_{i}, n_{i}}(s_{i})=f_{m_{j},n_{j}}(s_{j})$
for all
$f_{m_{i}, n_{i}}(s_{i})=f_{m_{j},n_{j}}(s_{j})$
for all
![]() $i, j\in J$
, which implies that
$i, j\in J$
, which implies that
![]() $(m_{i}, n_{i})=(m_{j}, n_{j})$
and
$(m_{i}, n_{i})=(m_{j}, n_{j})$
and
![]() $ s_{i}=s_{j}$
. Let
$ s_{i}=s_{j}$
. Let
![]() $m_{j}=m_{0}$
,
$m_{j}=m_{0}$
,
![]() $n_{j}=n_{0}$
and
$n_{j}=n_{0}$
and
![]() $s_{j}=s_{0} ~(j\in J)$
. Then,
$s_{j}=s_{0} ~(j\in J)$
. Then,
![]() $I_{j}=\{(m_{0}, s): s\leq s_{0}\}\cup\{(f_{m_{0}, n_{0}}(s_{0}),n): n\leq k_{j}\}$
. Since
$I_{j}=\{(m_{0}, s): s\leq s_{0}\}\cup\{(f_{m_{0}, n_{0}}(s_{0}),n): n\leq k_{j}\}$
. Since
![]() $\mathcal{D}$
does not have a largest member,
$\mathcal{D}$
does not have a largest member,
![]() $\mathcal{D}_{1}$
has no a largest member either. It follows that the set
$\mathcal{D}_{1}$
has no a largest member either. It follows that the set
![]() $\{k_j: j\in J\}$
does not have a largest element.
$\{k_j: j\in J\}$
does not have a largest element.
We claim that
![]() $\sup \mathcal{D}_1=\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
.
$\sup \mathcal{D}_1=\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
.
Clearly,
![]() $\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
is an upper bound of
$\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
is an upper bound of
![]() $\mathcal{D}_1$
. For any upper bound I of
$\mathcal{D}_1$
. For any upper bound I of
![]() $\mathcal{D}_1$
in M, we have that
$\mathcal{D}_1$
in M, we have that
![]() $\bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}\subseteq I$
. Note that I is a Scott closed set of P, and
$\bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}\subseteq I$
. Note that I is a Scott closed set of P, and
![]() $\bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}$
is a directed subset of P. Therefore,
$\bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}$
is a directed subset of P. Therefore,
![]() $\sup \bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}=(f_{m_{0},n_{0}}(s_{0}),\top)\in I$
.
$\sup \bigcup\{\{(f_{m_{0},n_{0}}(s_{0}),n): n\leq k_{j}\}: j\in J\}=(f_{m_{0},n_{0}}(s_{0}),\top)\in I$
.
All the above together show that
![]() $\sup \mathcal{D}=\sup\mathcal{D}_1=\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
. Thus, M is a dcpo.
$\sup \mathcal{D}=\sup\mathcal{D}_1=\mathord{\downarrow} (f_{m_{0},n_{0}}(s_{0}),\top)$
. Thus, M is a dcpo.
Remark 3.4. From the structure of M, it is easy to see that the dcpo M does not contain an infinite decreasing chain. Thus, in the dual poset
![]() $M^{op}$
of M, every element is compact.
$M^{op}$
of M, every element is compact.
Theorem 3.5. M is a countable bounded complete dcpo whose Scott space
![]() $\Sigma M$
is not sober.
$\Sigma M$
is not sober.
Proof. Because every element of M is a finite intersection of principal downsets of P, and P is countable, M is countable. By Lemma 3.3, it remains to verify that
![]() $\Sigma M$
is not sober.
$\Sigma M$
is not sober.
Define the mapping
![]() $g: P\rightarrow M$
by
$g: P\rightarrow M$
by
![]() $g(x)=\mathord{\downarrow} x$
for all
$g(x)=\mathord{\downarrow} x$
for all
![]() $x\in P$
. By the last part of the proof of Lemma 3.3, we see easily that g is Scott continuous. By Lemma 3.2, P is irreducible; thus, g(P) is irreducible. Clearly, the closure of g(P) equals M, so M is irreducible (with respect to the Scott topology). As M does not have a top element, it is not the closure of a singleton set. It follows that
$x\in P$
. By the last part of the proof of Lemma 3.3, we see easily that g is Scott continuous. By Lemma 3.2, P is irreducible; thus, g(P) is irreducible. Clearly, the closure of g(P) equals M, so M is irreducible (with respect to the Scott topology). As M does not have a top element, it is not the closure of a singleton set. It follows that
![]() $\Sigma M$
is not sober.
$\Sigma M$
is not sober.
Let
![]() $\hat{M}=M\cup\{\mbox{T}\}$
be the poset obtained by adding a top element
$\hat{M}=M\cup\{\mbox{T}\}$
be the poset obtained by adding a top element
![]() $\mbox{T}$
to M. Then
$\mbox{T}$
to M. Then
![]() $\hat{M}$
is a countable non-sober complete lattice.
$\hat{M}$
is a countable non-sober complete lattice.
Corollary 3.6. There exists a countable non-sober complete lattice.
Note that the non-sober complete lattice
![]() $\hat{M}$
constructed above is not distributive. Thus, it remains to know whether there is a distributive countable non-sober complete lattice.
$\hat{M}$
constructed above is not distributive. Thus, it remains to know whether there is a distributive countable non-sober complete lattice.
By applying the Lemma 2.3, we give a negative answer to the above problem.
Theorem 3.7. Let
![]() $\mathcal{F}=\{\mathord{\downarrow} F: F\subseteq_{fin} \hat{M}\}$
. Then,
$\mathcal{F}=\{\mathord{\downarrow} F: F\subseteq_{fin} \hat{M}\}$
. Then,
![]() $(\mathcal{F},\subseteq)$
is a countable non-sober distributive complete lattice.
$(\mathcal{F},\subseteq)$
is a countable non-sober distributive complete lattice.
Proof. First, every element in the dual
![]() $\hat{M}^{op}$
of the complete lattice
$\hat{M}^{op}$
of the complete lattice
![]() $\hat{M}$
is compact. Now apply Lemma 2.3 to
$\hat{M}$
is compact. Now apply Lemma 2.3 to
![]() $\hat{M}^{op}$
, we deduce that
$\hat{M}^{op}$
, we deduce that
![]() $\mathcal{F}=\{\mathord{\downarrow} F: F\subseteq_{fin} \hat{M}\}$
is a distributive complete lattice. It is countable because
$\mathcal{F}=\{\mathord{\downarrow} F: F\subseteq_{fin} \hat{M}\}$
is a distributive complete lattice. It is countable because
![]() $\hat{M}$
is countable.
$\hat{M}$
is countable.
Define
![]() $g: \hat{M} \rightarrow \mathcal{F}$
by
$g: \hat{M} \rightarrow \mathcal{F}$
by
![]() $g(x) = \mathord{\downarrow} x$
and
$g(x) = \mathord{\downarrow} x$
and
![]() $f : \mathcal{F} \rightarrow \hat{M}$
by
$f : \mathcal{F} \rightarrow \hat{M}$
by
![]() $f(A) = \sup A$
for any
$f(A) = \sup A$
for any
![]() $A \in \mathcal{F}$
. Clearly, both f and g are monotone. In addition, for any
$A \in \mathcal{F}$
. Clearly, both f and g are monotone. In addition, for any
![]() $x\in \hat{M}$
and
$x\in \hat{M}$
and
![]() $\mathord{\downarrow} F\in\mathcal{F}$
, we have
$\mathord{\downarrow} F\in\mathcal{F}$
, we have
Hence, f is the left adjoint of g. Then f preserves all suprema, in particular the suprema of directed subsets. Hence, it is Scott continuous. Also by the structure of
![]() $\hat{M}$
and
$\hat{M}$
and
![]() $\mathcal{F}$
, we easily see that g also preserves the suprema of directed subsets; hence, it is also Scott continuous. Note that
$\mathcal{F}$
, we easily see that g also preserves the suprema of directed subsets; hence, it is also Scott continuous. Note that
![]() $f\circ g=id_{\hat{M}}$
. It thus follows that
$f\circ g=id_{\hat{M}}$
. It thus follows that
![]() $\Sigma \hat{M}$
is a retraction of
$\Sigma \hat{M}$
is a retraction of
![]() $\Sigma \mathcal{F}$
. Since
$\Sigma \mathcal{F}$
. Since
![]() $\Sigma \hat{M}$
is non-sober, thus
$\Sigma \hat{M}$
is non-sober, thus
![]() $\Sigma \mathcal{F}$
is non-sober.
$\Sigma \mathcal{F}$
is non-sober.
4. A Sufficient Condition for Complete Lattices to be Sober
In this section, we prove some positive results on the sobriety of Scott spaces of dcpos. One immediate corollary is that every complete lattice L with Id(L) countable has a sober Scott space.
From the above section, we know that a countable complete lattice may not be sober in the Scott topology. In this section, we show that the Scott space of a complete lattice with Id(P) countable is sober.
The following lemma is critical for our later discussions.
Lemma 4.1.
Let P,Q be two posets. If
![]() ${\mid}Id(P){\mid},{\mid}Id(Q){\mid}$
are both countable, then
${\mid}Id(P){\mid},{\mid}Id(Q){\mid}$
are both countable, then
![]() $\Sigma(P\times Q)=\Sigma P\times \Sigma Q$
.
$\Sigma(P\times Q)=\Sigma P\times \Sigma Q$
.
Proof. Obviously,
![]() $\sigma(P)\times \sigma(Q)\subseteq \sigma(P\times Q)$
. It remains to prove that
$\sigma(P)\times \sigma(Q)\subseteq \sigma(P\times Q)$
. It remains to prove that
![]() $\sigma(P\times Q)\subseteq \sigma(P)\times \sigma(Q)$
. Let U be a nonempty Scott open set and
$\sigma(P\times Q)\subseteq \sigma(P)\times \sigma(Q)$
. Let U be a nonempty Scott open set and
![]() $(a_{1},b_{1})\in U$
. We denote Id(P) and Id(Q) by
$(a_{1},b_{1})\in U$
. We denote Id(P) and Id(Q) by
![]() $\{I_{n}^{P}\mid n\in \mathbb{N}\}$
and
$\{I_{n}^{P}\mid n\in \mathbb{N}\}$
and
![]() $\{I_{n}^{Q}\mid n\in \mathbb{N}\}$
, respectively.
$\{I_{n}^{Q}\mid n\in \mathbb{N}\}$
, respectively.
For
![]() $n=1$
,
$n=1$
,
![]() $A_{1}=\{a_{1}\},B_{1}=\{b_{1}\}$
.
$A_{1}=\{a_{1}\},B_{1}=\{b_{1}\}$
.
For
![]() $n=2$
, we define
$n=2$
, we define
![]() $A_{2}$
and
$A_{2}$
and
![]() $B_{2}$
below:
$B_{2}$
below:
If
![]() $\sup I_{1}^{P}\in \mathord{\uparrow} A_{1}$
, then
$\sup I_{1}^{P}\in \mathord{\uparrow} A_{1}$
, then
![]() $(\sup I_{1}^{P},b_{1})\in U$
. It follows that there exists
$(\sup I_{1}^{P},b_{1})\in U$
. It follows that there exists
![]() $d_{1}^{P}\in I_{1}^{P}$
such that
$d_{1}^{P}\in I_{1}^{P}$
such that
![]() $(d_{1}^{P},b_{1})\in U$
by the Scott openness of U. Let
$(d_{1}^{P},b_{1})\in U$
by the Scott openness of U. Let
![]() $A_{2}=\{d_{1}^{P}\}$
in this case, and
$A_{2}=\{d_{1}^{P}\}$
in this case, and
![]() $A_{2}=\emptyset$
otherwise. Note that
$A_{2}=\emptyset$
otherwise. Note that
![]() $(A_{1}\cup A_{2})\times B_{1}\subseteq U$
.
$(A_{1}\cup A_{2})\times B_{1}\subseteq U$
.
If
![]() $\sup I_{1}^{Q}\in \mathord{\uparrow} B_{1}$
, we have
$\sup I_{1}^{Q}\in \mathord{\uparrow} B_{1}$
, we have
![]() $(A_{1}\cup A_{2})\times \{\sup I_{1}^{Q}\}\subseteq U$
. For each
$(A_{1}\cup A_{2})\times \{\sup I_{1}^{Q}\}\subseteq U$
. For each
![]() $a\in A_{1}\cup A_{2}$
, we can choose a
$a\in A_{1}\cup A_{2}$
, we can choose a
![]() $d_a$
form
$d_a$
form
![]() $I_1^Q$
satisfying
$I_1^Q$
satisfying
![]() $(a,d_a)\in U$
by the Scott openness of U. Since
$(a,d_a)\in U$
by the Scott openness of U. Since
![]() $A_1\cup A_2$
is finite and
$A_1\cup A_2$
is finite and
![]() $I_1^Q$
is directed, there exists
$I_1^Q$
is directed, there exists
![]() $d_{1}^{Q}\in I_{1}^{Q}$
such that
$d_{1}^{Q}\in I_{1}^{Q}$
such that
![]() $(A_{1}\cup A_{2})\times \{d_{1}^{Q}\}\subseteq U$
. Let
$(A_{1}\cup A_{2})\times \{d_{1}^{Q}\}\subseteq U$
. Let
![]() $B_{2}=\{d_{1}^{Q}\}$
in this case, and
$B_{2}=\{d_{1}^{Q}\}$
in this case, and
![]() $B_{2}=\emptyset$
otherwise. We conclude that
$B_{2}=\emptyset$
otherwise. We conclude that
![]() $(A_{1}\cup A_{2})\times (B_{1}\cup B_{2})\subseteq U$
.
$(A_{1}\cup A_{2})\times (B_{1}\cup B_{2})\subseteq U$
.
For
![]() $n=3$
, we first consider the two index sets:
$n=3$
, we first consider the two index sets:
 \begin{align*} E_{1} & =\Big\{i\in\{1\}\mid \sup I_{i}^{P}\notin \mathord{\uparrow} A_{1} ~ {\rm and}~ \sup I_{i}^{P}\in \mathord{\uparrow} A_{2}\Big\}\cup\Big\{i\in \{2\}\mid \sup I_{i}^{P}\in \mathord{\uparrow} (A_{1}\cup A_{2})\Big\}~ {\rm and} \\F_{1} & =\Big\{i\in\{1\}\mid \sup I_{i}^{Q} \notin \mathord{\uparrow} B_{1} ~ {\rm and}~ \sup I_{i}^{Q}\in \mathord{\uparrow} B_{2}\Big\}\cup\Big\{i\in \{2\}\mid \sup I_{i}^{Q}\in \mathord{\uparrow} (B_{1}\cup B_{2})\Big\}.\end{align*}
\begin{align*} E_{1} & =\Big\{i\in\{1\}\mid \sup I_{i}^{P}\notin \mathord{\uparrow} A_{1} ~ {\rm and}~ \sup I_{i}^{P}\in \mathord{\uparrow} A_{2}\Big\}\cup\Big\{i\in \{2\}\mid \sup I_{i}^{P}\in \mathord{\uparrow} (A_{1}\cup A_{2})\Big\}~ {\rm and} \\F_{1} & =\Big\{i\in\{1\}\mid \sup I_{i}^{Q} \notin \mathord{\uparrow} B_{1} ~ {\rm and}~ \sup I_{i}^{Q}\in \mathord{\uparrow} B_{2}\Big\}\cup\Big\{i\in \{2\}\mid \sup I_{i}^{Q}\in \mathord{\uparrow} (B_{1}\cup B_{2})\Big\}.\end{align*}
However, if
![]() $\sup I_{1}^{P} \notin \mathord{\uparrow} A_{1}$
and
$\sup I_{1}^{P} \notin \mathord{\uparrow} A_{1}$
and
![]() $\sup I_{1}^{Q} \notin \mathord{\uparrow} B_{1}$
, then
$\sup I_{1}^{Q} \notin \mathord{\uparrow} B_{1}$
, then
![]() $A_2=\emptyset$
and
$A_2=\emptyset$
and
![]() $B_2=\emptyset$
from the above step. In this way,
$B_2=\emptyset$
from the above step. In this way,
![]() $\Big\{i\in\{1\}\mid \sup I_{i}^{P} \notin \mathord{\uparrow} A_{1} $
and
$\Big\{i\in\{1\}\mid \sup I_{i}^{P} \notin \mathord{\uparrow} A_{1} $
and
![]() $ \sup I_{i}^{P}\in \mathord{\uparrow} A_{2}\Big\}$
and
$ \sup I_{i}^{P}\in \mathord{\uparrow} A_{2}\Big\}$
and
![]() $\Big\{i\in\{1\}\mid \sup I_{i}^{Q} \notin \mathord{\uparrow} B_{1} $
and
$\Big\{i\in\{1\}\mid \sup I_{i}^{Q} \notin \mathord{\uparrow} B_{1} $
and
![]() $\sup I_{i}^{Q}\in \mathord{\uparrow} B_{2}\Big\}$
must be empty.
$\sup I_{i}^{Q}\in \mathord{\uparrow} B_{2}\Big\}$
must be empty.
Next, we define
![]() $A_{3}$
and
$A_{3}$
and
![]() $B_{3}$
in the similar way as before.
$B_{3}$
in the similar way as before.
If
![]() $E_1\neq \emptyset$
, then
$E_1\neq \emptyset$
, then
![]() $E_1=\{2\}$
. We have
$E_1=\{2\}$
. We have
![]() $\{\sup I_{2}^{P}\}\times (B_{1}\cup B_{2})\subseteq U$
. Through the similar discussion process, we can deduce that there exists
$\{\sup I_{2}^{P}\}\times (B_{1}\cup B_{2})\subseteq U$
. Through the similar discussion process, we can deduce that there exists
![]() $d_{2}^{P}\in I_{2}^{P}$
such that
$d_{2}^{P}\in I_{2}^{P}$
such that
![]() $\{d_{2}^{P}\}\times (B_{1}\cup B_{2})\subseteq U$
because
$\{d_{2}^{P}\}\times (B_{1}\cup B_{2})\subseteq U$
because
![]() $B_{1}\cup B_{2}$
is finite and
$B_{1}\cup B_{2}$
is finite and
![]() $I_{2}^{P}$
is directed. Let
$I_{2}^{P}$
is directed. Let
![]() $A_{3}=\{d_{2}^{P}\}$
in this case, and
$A_{3}=\{d_{2}^{P}\}$
in this case, and
![]() $A_{3}=\emptyset$
otherwise. Note that
$A_{3}=\emptyset$
otherwise. Note that
![]() $(A_{1}\cup A_{2}\cup A_{3})\times (B_{1}\cup B_{2})\subseteq U$
.
$(A_{1}\cup A_{2}\cup A_{3})\times (B_{1}\cup B_{2})\subseteq U$
.
If
![]() $F_{1}\neq \emptyset$
, then
$F_{1}\neq \emptyset$
, then
![]() $F_{1}=\{2\}$
. Thus,
$F_{1}=\{2\}$
. Thus,
![]() $(A_{1}\cup A_{2}\cup A_{3})\times \{\sup I_{2}^{Q}\}\subseteq U$
. Note that
$(A_{1}\cup A_{2}\cup A_{3})\times \{\sup I_{2}^{Q}\}\subseteq U$
. Note that
![]() $A_{1}\cup A_{2}\cup A_{3}$
is a finite set. It follows that there exists
$A_{1}\cup A_{2}\cup A_{3}$
is a finite set. It follows that there exists
![]() $d_{2}^{Q}\in I_{2}^{Q}$
such that
$d_{2}^{Q}\in I_{2}^{Q}$
such that
![]() $(A_{1}\cup A_{2}\cup A_{3})\times \{d_{2}^{Q}\}\subseteq U$
. Let
$(A_{1}\cup A_{2}\cup A_{3})\times \{d_{2}^{Q}\}\subseteq U$
. Let
![]() $B_{3}=\{d_{2}^{Q}\}$
in this case, and
$B_{3}=\{d_{2}^{Q}\}$
in this case, and
![]() $B_{3}=\emptyset$
otherwise. We conclude that
$B_{3}=\emptyset$
otherwise. We conclude that
![]() $(A_{1}\cup A_{2}\cup A_{3})\times (B_{1}\cup B_{2}\cup B_{3})\subseteq U$
.
$(A_{1}\cup A_{2}\cup A_{3})\times (B_{1}\cup B_{2}\cup B_{3})\subseteq U$
.
For
![]() $n=4$
, we also consider the two index sets:
$n=4$
, we also consider the two index sets:
 \begin{align*} E_{2} & =\Big\{i\in\{1,2\}\mid \sup I_{i}^{P}\notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~ {\rm and}~ \sup I_{i}^{P}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} A_{k}\Big\}\cup\Big\{i\in \{3\}\mid \sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}\Big\}, \\ F_{2} & =\Big\{i\in\{1,2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} B_{k}~ {\rm and}~ \sup I_{i}^{Q}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} B_{k}\Big\}\cup\Big\{i\in \{3\}\mid \sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}\Big\}. \end{align*}
\begin{align*} E_{2} & =\Big\{i\in\{1,2\}\mid \sup I_{i}^{P}\notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~ {\rm and}~ \sup I_{i}^{P}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} A_{k}\Big\}\cup\Big\{i\in \{3\}\mid \sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}\Big\}, \\ F_{2} & =\Big\{i\in\{1,2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} B_{k}~ {\rm and}~ \sup I_{i}^{Q}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} B_{k}\Big\}\cup\Big\{i\in \{3\}\mid \sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}\Big\}. \end{align*}
Next, we define
![]() $A_{4}$
and
$A_{4}$
and
![]() $B_{4}$
in the following:
$B_{4}$
in the following:
If
![]() $E_2\neq \emptyset$
, then
$E_2\neq \emptyset$
, then
![]() $i\in \{1,2\}$
implies
$i\in \{1,2\}$
implies
![]() $\sup I_{i}^{P}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} A_{k}\subseteq \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
, and
$\sup I_{i}^{P}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} A_{k}\subseteq \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
, and
![]() $i=3$
implies
$i=3$
implies
![]() $\sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
. Thus,
$\sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
. Thus,
![]() $\sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
for all
$\sup I_{i}^{P}\in \bigcup_{k=1}^{3}\mathord{\uparrow} A_{k}$
for all
![]() $i\in E_2$
. So for each
$i\in E_2$
. So for each
![]() $i\in E_2$
,
$i\in E_2$
,
![]() $\{\sup I_{i}^{P}\}\times (B_{1}\cup B_{2}\cup B_3)\subseteq U$
implies that there exists
$\{\sup I_{i}^{P}\}\times (B_{1}\cup B_{2}\cup B_3)\subseteq U$
implies that there exists
![]() $d_{i}^{P}\in I_{i}^{P}$
such that
$d_{i}^{P}\in I_{i}^{P}$
such that
![]() $\{d_{i}^{P}\}\times (B_{1}\cup B_{2}\cup B_3)\subseteq U$
because
$\{d_{i}^{P}\}\times (B_{1}\cup B_{2}\cup B_3)\subseteq U$
because
![]() $B_{1}\cup B_{2}\cup B_3$
is finite and
$B_{1}\cup B_{2}\cup B_3$
is finite and
![]() $I_{i}^{P}$
is directed. Let
$I_{i}^{P}$
is directed. Let
![]() $A_{4}=\{d_{i}^{P}\mid i\in E_2\}$
in this case, and
$A_{4}=\{d_{i}^{P}\mid i\in E_2\}$
in this case, and
![]() $A_{4}=\emptyset$
otherwise. Note that
$A_{4}=\emptyset$
otherwise. Note that
 $$\Big(\bigcup_{k=1}^{4}\mathord{\uparrow} A_k\Big)\times \Big(\bigcup_{k=1}^{3}\mathord{\uparrow} B_k\Big)\subseteq U.$$
$$\Big(\bigcup_{k=1}^{4}\mathord{\uparrow} A_k\Big)\times \Big(\bigcup_{k=1}^{3}\mathord{\uparrow} B_k\Big)\subseteq U.$$
If
![]() $F_{2}\neq \emptyset$
, then
$F_{2}\neq \emptyset$
, then
![]() $i\in \{1,2\}$
implies
$i\in \{1,2\}$
implies
![]() $\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} B_{k}\subseteq \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
, and
$\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{3}\mathord{\uparrow} B_{k}\subseteq \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
, and
![]() $i=3$
implies
$i=3$
implies
![]() $\sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
. Thus,
$\sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
. Thus,
![]() $\sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
for all
$\sup I_{i}^{Q}\in \bigcup_{k=1}^{3}\mathord{\uparrow} B_{k}$
for all
![]() $i\in F_2$
. So for each
$i\in F_2$
. So for each
![]() $i\in F_2$
,
$i\in F_2$
,
![]() $(\bigcup_{k=1}^{4}A_{k})\times \{\sup I_{i}^{Q}\}\subseteq U$
implies that there exists
$(\bigcup_{k=1}^{4}A_{k})\times \{\sup I_{i}^{Q}\}\subseteq U$
implies that there exists
![]() $d_{i}^{Q}\in I_{i}^{Q}$
such that
$d_{i}^{Q}\in I_{i}^{Q}$
such that
![]() $(\bigcup_{k=1}^{4}A_{k})\times \{d_{i}^{Q}\}\subseteq U$
since
$(\bigcup_{k=1}^{4}A_{k})\times \{d_{i}^{Q}\}\subseteq U$
since
![]() $\bigcup_{k=1}^{4}A_{k}$
is a finite set and
$\bigcup_{k=1}^{4}A_{k}$
is a finite set and
![]() $I_{i}^{Q}$
is directed. Let
$I_{i}^{Q}$
is directed. Let
![]() $B_{4}=\{d_{i}^{Q}\mid i\in F_2\}$
in this case, and
$B_{4}=\{d_{i}^{Q}\mid i\in F_2\}$
in this case, and
![]() $B_{4}=\emptyset$
otherwise. We conclude that
$B_{4}=\emptyset$
otherwise. We conclude that
 $$\Big(\bigcup_{k=1}^{4}A_{k}\Big)\times \Big(\bigcup_{k=1}^{4}B_{k}\Big)\subseteq U.$$
$$\Big(\bigcup_{k=1}^{4}A_{k}\Big)\times \Big(\bigcup_{k=1}^{4}B_{k}\Big)\subseteq U.$$
For
![]() $n\geq 4$
, we assume that
$n\geq 4$
, we assume that
 $$\Big(\bigcup_{k=1}^{n-1}A_k \Big)\times \Big(\bigcup_{k=1}^{n-1} B_k \Big)\subseteq U.$$
$$\Big(\bigcup_{k=1}^{n-1}A_k \Big)\times \Big(\bigcup_{k=1}^{n-1} B_k \Big)\subseteq U.$$
Then, we define
![]() $A_{n}$
and
$A_{n}$
and
![]() $B_{n}$
inductively.
$B_{n}$
inductively.
We first consider the following two index sets:
 \begin{align*} E_{n-2} = &\Big\{i\in\{1,\ldots, n-2\}\mid \sup I_{i}^{P} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~{\rm and}~\sup I_{i}^{P}\in \bigcup_{k=i+1}^{n-1}\mathord{\uparrow} A_{k}\Big\}\\ &\cup\Big\{i\in \{n-1\}\mid \sup I_{i}^{P}\in \bigcup_{k=1}^{n-1}\mathord{\uparrow} A_{k}\Big\},\\ F_{n-2} =& \Big\{i \in \{1,\ldots, n-2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i} \mathord{\uparrow} B_{k}~{\rm and}~\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{n-1} \mathord{\uparrow} B_{k}\Big\}\\ &\cup\Big\{i\in \{n-1\}\mid \sup I_{i}^{Q}\in \bigcup_{k=1}^{n-1} \mathord{\uparrow} B_{k}\Big\}. \end{align*}
\begin{align*} E_{n-2} = &\Big\{i\in\{1,\ldots, n-2\}\mid \sup I_{i}^{P} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~{\rm and}~\sup I_{i}^{P}\in \bigcup_{k=i+1}^{n-1}\mathord{\uparrow} A_{k}\Big\}\\ &\cup\Big\{i\in \{n-1\}\mid \sup I_{i}^{P}\in \bigcup_{k=1}^{n-1}\mathord{\uparrow} A_{k}\Big\},\\ F_{n-2} =& \Big\{i \in \{1,\ldots, n-2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i} \mathord{\uparrow} B_{k}~{\rm and}~\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{n-1} \mathord{\uparrow} B_{k}\Big\}\\ &\cup\Big\{i\in \{n-1\}\mid \sup I_{i}^{Q}\in \bigcup_{k=1}^{n-1} \mathord{\uparrow} B_{k}\Big\}. \end{align*}
Note that
![]() $\Big\{i\in\{1,\ldots, n-2\}\mid \sup I_{i}^{P} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~{\rm and}~\sup I_{i}^{P}\in \bigcup_{k=i+1}^{n-1}\mathord{\uparrow} A_{k}\Big\}$
and
$\Big\{i\in\{1,\ldots, n-2\}\mid \sup I_{i}^{P} \notin \bigcup_{k=1}^{i}\mathord{\uparrow} A_{k} ~{\rm and}~\sup I_{i}^{P}\in \bigcup_{k=i+1}^{n-1}\mathord{\uparrow} A_{k}\Big\}$
and
![]() $\Big\{i \in \{1,\ldots, n-2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i} \mathord{\uparrow} B_{k}~{\rm and}~\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{n-1} \mathord{\uparrow} B_{k}\Big\}$
may not be empty.
$\Big\{i \in \{1,\ldots, n-2\}\mid \sup I_{i}^{Q} \notin \bigcup_{k=1}^{i} \mathord{\uparrow} B_{k}~{\rm and}~\sup I_{i}^{Q}\in \bigcup_{k=i+1}^{n-1} \mathord{\uparrow} B_{k}\Big\}$
may not be empty.
If
![]() $E_{n-2}\neq \emptyset$
, similarly, we can deduce {
$E_{n-2}\neq \emptyset$
, similarly, we can deduce {
![]() $\sup I_{i}^{P}\}\times \big(\bigcup_{k=1}^{n-1} B_{k}\big)\subseteq U$
for any
$\sup I_{i}^{P}\}\times \big(\bigcup_{k=1}^{n-1} B_{k}\big)\subseteq U$
for any
![]() $i\in E_{n-2}$
. Note that
$i\in E_{n-2}$
. Note that
![]() $\bigcup_{k=1}^{n-1} B_{k}$
is a finite set and each
$\bigcup_{k=1}^{n-1} B_{k}$
is a finite set and each
![]() $I_{i}^{P}$
is directed. Thus, there exists
$I_{i}^{P}$
is directed. Thus, there exists
![]() $d_{i}^{P}\in I_{i}^{P}$
such that
$d_{i}^{P}\in I_{i}^{P}$
such that
![]() $\{d_{i}^{P}\}\times \big(\bigcup_{k=1}^{n-1} B_{k}\big)\subseteq U$
for any
$\{d_{i}^{P}\}\times \big(\bigcup_{k=1}^{n-1} B_{k}\big)\subseteq U$
for any
![]() $i\in E_{n-2}$
. Let
$i\in E_{n-2}$
. Let
![]() $A_{n}=\{d_{i}^{P}{\mid} i\in E_{n-2}\}$
in this case, and
$A_{n}=\{d_{i}^{P}{\mid} i\in E_{n-2}\}$
in this case, and
![]() $A_{n}=\emptyset$
otherwise. It follows that
$A_{n}=\emptyset$
otherwise. It follows that
 $$\Big(\bigcup_{k=1}^{n} A_{k}\Big)\times \Big(\bigcup_{k=1}^{n-1} B_{k}\Big)\subseteq U.$$
$$\Big(\bigcup_{k=1}^{n} A_{k}\Big)\times \Big(\bigcup_{k=1}^{n-1} B_{k}\Big)\subseteq U.$$
If
![]() $F_{n-2}\neq \emptyset$
, then
$F_{n-2}\neq \emptyset$
, then
![]() $\big(\bigcup_{k=1}^{n} A_{k}\big)\times \{\sup I_{i}^{Q}\}\subseteq U$
for any
$\big(\bigcup_{k=1}^{n} A_{k}\big)\times \{\sup I_{i}^{Q}\}\subseteq U$
for any
![]() $i\in F_{n-2}$
. Note that
$i\in F_{n-2}$
. Note that
![]() $\bigcup_{k=1}^{n} A_{k}$
is a finite set. This means that there exists
$\bigcup_{k=1}^{n} A_{k}$
is a finite set. This means that there exists
![]() $d_{i}^{Q}\in I_{i}^{Q}$
such that
$d_{i}^{Q}\in I_{i}^{Q}$
such that
![]() $\big(\bigcup_{k=1}^{n} A_{k}\big)\times \{d_{i}^{Q}\}\subseteq U$
for any
$\big(\bigcup_{k=1}^{n} A_{k}\big)\times \{d_{i}^{Q}\}\subseteq U$
for any
![]() $i\in F_{n-2}$
. Let
$i\in F_{n-2}$
. Let
![]() $B_{n}=\{d_{i}^{Q}\mid i\in F_{n-2}\}$
in this case, and
$B_{n}=\{d_{i}^{Q}\mid i\in F_{n-2}\}$
in this case, and
![]() $B_{n}=\emptyset$
otherwise. We conclude that
$B_{n}=\emptyset$
otherwise. We conclude that
Let
![]() $A=\bigcup_{n\in \mathbb{N}}A_{n}$
and
$A=\bigcup_{n\in \mathbb{N}}A_{n}$
and
![]() $B=\bigcup_{n\in \mathbb{N}}B_{n}$
. It is easy to see that
$B=\bigcup_{n\in \mathbb{N}}B_{n}$
. It is easy to see that
![]() $(a_{1},b_{1})\in A_1\times B_1 \subseteq\mathord{\uparrow} A\times \mathord{\uparrow} B \subseteq U$
. It suffices to prove that
$(a_{1},b_{1})\in A_1\times B_1 \subseteq\mathord{\uparrow} A\times \mathord{\uparrow} B \subseteq U$
. It suffices to prove that
![]() $\mathord{\uparrow} A,\mathord{\uparrow} B$
are both Scott open.
$\mathord{\uparrow} A,\mathord{\uparrow} B$
are both Scott open.
Let D be a directed subset of P with
![]() $\sup D\in \mathord{\uparrow} A$
. If
$\sup D\in \mathord{\uparrow} A$
. If
![]() $\sup D \in D$
, then
$\sup D \in D$
, then
![]() $D\cap \mathord{\uparrow} A\neq \emptyset$
. If
$D\cap \mathord{\uparrow} A\neq \emptyset$
. If
![]() $\sup D \notin D$
, i.e., D contains no maximal element, then
$\sup D \notin D$
, i.e., D contains no maximal element, then
![]() $\mathord{\downarrow} D \in Id(P)$
. Thus, there exists
$\mathord{\downarrow} D \in Id(P)$
. Thus, there exists
![]() $n_0\in \mathbb{N}$
such that
$n_0\in \mathbb{N}$
such that
![]() $\mathord{\downarrow} D=I_{n_{0}}^{P}$
.
$\mathord{\downarrow} D=I_{n_{0}}^{P}$
.
Therefore,
![]() $\sup D\in \mathord{\uparrow} A$
can imply that
$\sup D\in \mathord{\uparrow} A$
can imply that
![]() $\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A$
. Let
$\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A$
. Let
![]() $n_{1}=\inf\{n\in \mathbb{N}\mid \sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n}\}$
. Then
$n_{1}=\inf\{n\in \mathbb{N}\mid \sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n}\}$
. Then
![]() $\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n_{1}}$
. Now we need to distinguish between the following two cases for
$\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n_{1}}$
. Now we need to distinguish between the following two cases for
![]() $n_{0},n_{1}$
.
$n_{0},n_{1}$
.
Case 1,
![]() $n_{0}<n_{1}$
. If
$n_{0}<n_{1}$
. If
![]() $n_0=1,n_1=2$
, then
$n_0=1,n_1=2$
, then
![]() $\sup I_1^P \notin \mathord{\uparrow} A_1$
implies
$\sup I_1^P \notin \mathord{\uparrow} A_1$
implies
![]() $A_2= \emptyset$
, which contradicts the condition
$A_2= \emptyset$
, which contradicts the condition
![]() $\sup I_1^P \in \mathord{\uparrow} A_2$
. So
$\sup I_1^P \in \mathord{\uparrow} A_2$
. So
![]() $n_1 \geqslant 3$
. The fact that
$n_1 \geqslant 3$
. The fact that
![]() $\sup I_{n_{0}}^{P}\notin \bigcup_{k=1}^{n_{0}}\mathord{\uparrow} A_{k}$
and
$\sup I_{n_{0}}^{P}\notin \bigcup_{k=1}^{n_{0}}\mathord{\uparrow} A_{k}$
and
![]() $\sup I_{n_{0}}^{P}\in \bigcup_{k=n_{0}+1}^{n_{1}}\mathord{\uparrow} A_{k}$
can imply
$\sup I_{n_{0}}^{P}\in \bigcup_{k=n_{0}+1}^{n_{1}}\mathord{\uparrow} A_{k}$
can imply
![]() $n_0 \in E_{n_1-1}$
. This means that
$n_0 \in E_{n_1-1}$
. This means that
![]() $I_{n_{0}}^{P}\cap A_{n_{1}+1}\neq \emptyset$
. Hence,
$I_{n_{0}}^{P}\cap A_{n_{1}+1}\neq \emptyset$
. Hence,
![]() $D\cap \mathord{\uparrow} A\neq \emptyset$
.
$D\cap \mathord{\uparrow} A\neq \emptyset$
.
Case 2,
![]() $n_{0}\geq n_{1}$
. If
$n_{0}\geq n_{1}$
. If
![]() $n_0=n_1=1$
, then
$n_0=n_1=1$
, then
![]() $\sup I_1^P \in \mathord{\uparrow} A_1$
implies
$\sup I_1^P \in \mathord{\uparrow} A_1$
implies
![]() $I_1^P \cap A_2 \neq \emptyset$
. If
$I_1^P \cap A_2 \neq \emptyset$
. If
![]() $n_0 \geqslant 2$
, then
$n_0 \geqslant 2$
, then
![]() $\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n_1}\subseteq \bigcup_{k=1}^{n_{0}}\mathord{\uparrow} A_{k}$
, which implies
$\sup I_{n_{0}}^{P}\in \mathord{\uparrow} A_{n_1}\subseteq \bigcup_{k=1}^{n_{0}}\mathord{\uparrow} A_{k}$
, which implies
![]() $n_0 \in E_{n_0-1}$
. It follows that
$n_0 \in E_{n_0-1}$
. It follows that
![]() $I_{n_{0}}^{P}\cap A_{n_{0}+1}\neq \emptyset$
. Therefore,
$I_{n_{0}}^{P}\cap A_{n_{0}+1}\neq \emptyset$
. Therefore,
![]() $D\cap \mathord{\uparrow} A\neq \emptyset$
.
$D\cap \mathord{\uparrow} A\neq \emptyset$
.
Hence,
![]() $\mathord{\uparrow} A$
is Scott open, and
$\mathord{\uparrow} A$
is Scott open, and
![]() $\mathord{\uparrow} B$
is Scott open by the similar proof.
$\mathord{\uparrow} B$
is Scott open by the similar proof.
Theorem 4.2. Let L be a dcpo with Id(L) countable. If
![]() $\Sigma L$
is coherent and well filtered, then
$\Sigma L$
is coherent and well filtered, then
![]() $\Sigma L$
is sober.
$\Sigma L$
is sober.
Proof. Let A be an irreducible closed subset of
![]() $\Sigma L$
. It suffices to prove that A is directed, which means that
$\Sigma L$
. It suffices to prove that A is directed, which means that
![]() $\mathord{\uparrow} x\cap \mathord{\uparrow} y\cap A\neq \emptyset$
for any
$\mathord{\uparrow} x\cap \mathord{\uparrow} y\cap A\neq \emptyset$
for any
![]() $x,y\in A$
.
$x,y\in A$
.
Write
![]() $B=\{(a,b)\in L\times L\mid \mathord{\uparrow} a\cap \mathord{\uparrow} b\subseteq L\backslash A\}$
. We claim that B is Scott open in
$B=\{(a,b)\in L\times L\mid \mathord{\uparrow} a\cap \mathord{\uparrow} b\subseteq L\backslash A\}$
. We claim that B is Scott open in
![]() $L\times L$
. Obviously, B is an upper set. Let
$L\times L$
. Obviously, B is an upper set. Let
![]() $(x_{i},y_{i})_{i\in I}$
be a directed subset of
$(x_{i},y_{i})_{i\in I}$
be a directed subset of
![]() $L\times L$
with
$L\times L$
with
![]() $\sup_{i\in I}(x_{i},y_{i})\in B$
. Then
$\sup_{i\in I}(x_{i},y_{i})\in B$
. Then
![]() $(\sup_{i\in I}x_{i},\sup_{i\in I}y_{i})\in B$
, which is equivalent to saying that
$(\sup_{i\in I}x_{i},\sup_{i\in I}y_{i})\in B$
, which is equivalent to saying that
![]() $\mathord{\uparrow} \sup_{i\in I}x_{i}\cap \mathord{\uparrow} \sup_{i\in I}y_{i}\subseteq L\backslash A$
. It follows that
$\mathord{\uparrow} \sup_{i\in I}x_{i}\cap \mathord{\uparrow} \sup_{i\in I}y_{i}\subseteq L\backslash A$
. It follows that
![]() $\bigcap_{i\in I} (\mathord{\uparrow} x_{i}\cap \mathord{\uparrow} y_{i})\subseteq L\backslash A$
. Since
$\bigcap_{i\in I} (\mathord{\uparrow} x_{i}\cap \mathord{\uparrow} y_{i})\subseteq L\backslash A$
. Since
![]() $\Sigma L$
is coherent and well filtered, we can find some index
$\Sigma L$
is coherent and well filtered, we can find some index
![]() $i\in I$
such that
$i\in I$
such that
![]() $\mathord{\uparrow} x_{i}\cap \mathord{\uparrow} y_{i}\subseteq L\backslash A$
. This implies that
$\mathord{\uparrow} x_{i}\cap \mathord{\uparrow} y_{i}\subseteq L\backslash A$
. This implies that
![]() $(x_{i},y_{i})\in B$
. Thus, B is Scott open.
$(x_{i},y_{i})\in B$
. Thus, B is Scott open.
It is worth noting that Id(L) is countable.
![]() $\Sigma(L\times L)=\Sigma L\times \Sigma L$
from Lemma 4.1. For the sake of contradiction, we assume that there are
$\Sigma(L\times L)=\Sigma L\times \Sigma L$
from Lemma 4.1. For the sake of contradiction, we assume that there are
![]() $x,y\in A$
such that
$x,y\in A$
such that
![]() $\mathord{\uparrow} x\cap \mathord{\uparrow} y\cap A=\emptyset$
. The fact that
$\mathord{\uparrow} x\cap \mathord{\uparrow} y\cap A=\emptyset$
. The fact that
![]() $(x,y)\in B\subseteq \sigma(L\times L)$
implies that we can find
$(x,y)\in B\subseteq \sigma(L\times L)$
implies that we can find
![]() $U_{x},U_{y}\in \sigma (L)$
such that
$U_{x},U_{y}\in \sigma (L)$
such that
![]() $(x,y)\in U_{x}\times U_{y}\subseteq B$
. Note that
$(x,y)\in U_{x}\times U_{y}\subseteq B$
. Note that
![]() $x\in U_{x}\cap A$
and
$x\in U_{x}\cap A$
and
![]() $y\in U_{y}\cap A$
. By the irreducibility of A, we have
$y\in U_{y}\cap A$
. By the irreducibility of A, we have
![]() $A\cap U_{x}\cap U_{y}\neq \emptyset$
. Pick
$A\cap U_{x}\cap U_{y}\neq \emptyset$
. Pick
![]() $a\in A\cap U_{x}\cap U_{y}$
. Then
$a\in A\cap U_{x}\cap U_{y}$
. Then
![]() $(a,a)\in U_{x}\times U_{y}\subseteq B$
, that is,
$(a,a)\in U_{x}\times U_{y}\subseteq B$
, that is,
![]() $a\in \mathord{\uparrow} a \cap \mathord{\uparrow} a\subseteq L\backslash A$
. It contradicts the assumption that
$a\in \mathord{\uparrow} a \cap \mathord{\uparrow} a\subseteq L\backslash A$
. It contradicts the assumption that
![]() $a\in A$
. Hence, A is directed and
$a\in A$
. Hence, A is directed and
![]() $\sup A\in A$
. So
$\sup A\in A$
. So
![]() $A=\mathord{\downarrow} \sup A$
.
$A=\mathord{\downarrow} \sup A$
.
Corollary 4.3. Let L be a complete lattice. If Id(L) is countable, then
![]() $\Sigma L$
is sober.
$\Sigma L$
is sober.
Proof. From Jia et al. (Reference Jia, Jung and Li2016) and Xi and Lawson (Reference Xi and Lawson2017), we deduce that
![]() $\Sigma L$
is well filtered and coherent. The result is evident by Theorem 4.2.
$\Sigma L$
is well filtered and coherent. The result is evident by Theorem 4.2.
5. Conclusions
In this paper, we constructed a countable complete lattice whose Scott space is non-sober, thus answering a problem posed by Achim Jung. Based on this complete lattice, we further obtained a countable distributive complete lattice whose Scott space is not sober.
The countable complete lattice constructed here is not a frame (or complete Heyting algebra). Thus, the following problem is still open.
Problem
Is there a countable frame whose Scott space is non-sober?
Funding statement
This work is supported by the National Natural Science Foundation of China (No.12231007 and 12071188) and by Hunan Provincial Innovation Foundation For Postgraduate (CX20200419).
Competing interests
The authors declare that there is no conflict of interest.
Data availability
The authors confirm that no data were collected for this work.
Author contribution
Xiaoyong Xi gives the main idea of the counterexample. Hualin Miao and Qingguo Li make up the details of the counterexample and give a sufficient condition for the open problem posed by Achim Jung. Dongsheng Zhao writes the main manuscript text, and all authors reviewed the manuscript.
Appendix
Remark 6.1. There exists a monotone bijection
![]() $f: \mathbb{N}^{<\mathbb{N}}\rightarrow \mathbb{N}$
.
$f: \mathbb{N}^{<\mathbb{N}}\rightarrow \mathbb{N}$
.
In fact, consider the set of prime numbers
![]() $\mathbf{P}=\{p_{1}, p_{2},\cdots p_{n},\cdots\}$
, where
$\mathbf{P}=\{p_{1}, p_{2},\cdots p_{n},\cdots\}$
, where
![]() $p_{i}<p_{i+1}$
for all
$p_{i}<p_{i+1}$
for all
![]() $i\geq 1$
. For any element
$i\geq 1$
. For any element
![]() $a = n_{1}.n_{2}.\cdots.n_{k} \in \mathbb{N}^{<\mathbb{N}}$
, we set
$a = n_{1}.n_{2}.\cdots.n_{k} \in \mathbb{N}^{<\mathbb{N}}$
, we set
![]() $f(a)=p_{1}^{n_{1}}\cdot p_{2}^{n_{2}}\cdots p_{k}^{n_{k}}$
. Then f is monotone and injective. Notice that image of f is orderly isomorphic to
$f(a)=p_{1}^{n_{1}}\cdot p_{2}^{n_{2}}\cdots p_{k}^{n_{k}}$
. Then f is monotone and injective. Notice that image of f is orderly isomorphic to
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
The above explanation was suggested by one of the referees.