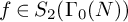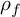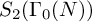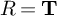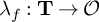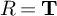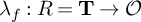1 Introduction
In the work on modularity of elliptic curves, Wiles pioneered methods to prove
![]() ${R={\mathbf T}}$
theorems where R is a deformation ring and
${R={\mathbf T}}$
theorems where R is a deformation ring and
![]() ${\mathbf T}$
a Hecke algebra, thus proving an equality of moduli spaces of Galois representations to pro-p Artinian rings arising from modular forms with the a priori larger moduli space of corresponding abstract Galois representations, both with certain prescribed local (ramification) behavior.
${\mathbf T}$
a Hecke algebra, thus proving an equality of moduli spaces of Galois representations to pro-p Artinian rings arising from modular forms with the a priori larger moduli space of corresponding abstract Galois representations, both with certain prescribed local (ramification) behavior.
The injectivity of the a priori surjective map
![]() $R \twoheadrightarrow {\mathbf T}$
was proven by using two different types of criteria/methods:
$R \twoheadrightarrow {\mathbf T}$
was proven by using two different types of criteria/methods:
-
(i) the numerical criterion of [Reference WilesWil95, Proposition 2 of Appendix];
-
(ii) the patching method of [Reference Taylor and WilesTW95].
In [Reference Taylor and WilesTW95], the local conditions imposed on the deformations were smooth. Kisin [Reference KisinKis09] later generalized the patching method to allow local conditions on the deformations that were not necessarily smooth. The generic fiber of the local deformation rings in question was smooth and Kisin proved a
![]() $R[1/p]={\mathbf T}[1/p]$
theorem, thus proving a coarser equality of moduli spaces of p-adic Galois representations arising from modular forms with the a priori larger moduli space of corresponding abstract Galois representations, both with certain prescribed local behavior. When the local conditions are Cohen–Macaulay, one sees a posteriori that R has no p-torsion (see [Reference Khare and WintenbergerKW09, paragraph before Corollary 4.7], [Reference SnowdenSno18, §5] or [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] for instance) and thus as
$R[1/p]={\mathbf T}[1/p]$
theorem, thus proving a coarser equality of moduli spaces of p-adic Galois representations arising from modular forms with the a priori larger moduli space of corresponding abstract Galois representations, both with certain prescribed local behavior. When the local conditions are Cohen–Macaulay, one sees a posteriori that R has no p-torsion (see [Reference Khare and WintenbergerKW09, paragraph before Corollary 4.7], [Reference SnowdenSno18, §5] or [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] for instance) and thus as
![]() ${\mathbf T}$
is also torsion-free one can promote an
${\mathbf T}$
is also torsion-free one can promote an
![]() $R[1/p]={\mathbf T}[1/p]$
theorem to an integral
$R[1/p]={\mathbf T}[1/p]$
theorem to an integral
![]() $R={\mathbf T}$
theorem, without the rings in question turning out to be complete intersections.
$R={\mathbf T}$
theorem, without the rings in question turning out to be complete intersections.
Wiles used his numerical criterion for maps between rings to be isomorphisms of complete intersections to deduce
![]() $R={\mathbf T}$
theorems in the nonminimal case from
$R={\mathbf T}$
theorems in the nonminimal case from
![]() $R={\mathbf T}$
theorems in the minimal case (see [Reference WilesWil95, Theorem 2.17 of §2]). The minimal case was proved via the patching method of [Reference Taylor and WilesTW95]. The numerical criterion has been used subsequently in [Reference KhareKha03] to prove
$R={\mathbf T}$
theorems in the minimal case (see [Reference WilesWil95, Theorem 2.17 of §2]). The minimal case was proved via the patching method of [Reference Taylor and WilesTW95]. The numerical criterion has been used subsequently in [Reference KhareKha03] to prove
![]() $R={\mathbf T}$
theorems without any reliance on patching. The numerical criterion of Wiles has not as yet been generalized to give a criterion for maps between rings to be an isomorphism when the rings are known to not be complete intersections.
$R={\mathbf T}$
theorems without any reliance on patching. The numerical criterion of Wiles has not as yet been generalized to give a criterion for maps between rings to be an isomorphism when the rings are known to not be complete intersections.
The work of this paper, like that of the previous paper [Reference Böckle, Khare and ManningBKM21] of this series, arises when considering situations when we have
![]() $R={\mathbf T}$
theorems proved by patching, but R and
$R={\mathbf T}$
theorems proved by patching, but R and
![]() ${\mathbf T}$
fail to be complete intersections. In [Reference Böckle, Khare and ManningBKM21] and the present paper, we seek to study the failure (quantified in a numerical quantity called the Wiles defect introduced in [Reference Tilouine and UrbanTU22], see also [Reference Böckle, Khare and ManningBKM21, Definition 3.10]) of the numerical criterion for being a complete intersection locally at an augmentation
${\mathbf T}$
fail to be complete intersections. In [Reference Böckle, Khare and ManningBKM21] and the present paper, we seek to study the failure (quantified in a numerical quantity called the Wiles defect introduced in [Reference Tilouine and UrbanTU22], see also [Reference Böckle, Khare and ManningBKM21, Definition 3.10]) of the numerical criterion for being a complete intersection locally at an augmentation
![]() $\lambda _f:{\mathbf T} \to {\mathcal O}$
induced by a newform f. The term defect is justified since, as we shall explain in Proposition 3.28, for a complete Noetherian
$\lambda _f:{\mathbf T} \to {\mathcal O}$
induced by a newform f. The term defect is justified since, as we shall explain in Proposition 3.28, for a complete Noetherian
![]() ${\mathcal O}$
-algebra R with an augmentation
${\mathcal O}$
-algebra R with an augmentation
![]() $\lambda :R\to {\mathcal O}$
, the Wiles defect
$\lambda :R\to {\mathcal O}$
, the Wiles defect
![]() $\delta _\lambda (R)$
vanishes if and only if R is a complete intersection ring.
$\delta _\lambda (R)$
vanishes if and only if R is a complete intersection ring.
In [Reference Böckle, Khare and ManningBKM21] we studied the Wiles defect (at
![]() $\lambda _f$
of a certain Hecke ring
$\lambda _f$
of a certain Hecke ring
![]() ${\mathbf T}$
acting on the cohomology of a Shimura curve) using a combination of patching and level lowering results of Ribet–Takahashi [Reference Ribet and TakahashiRT97]. In the present paper, we combine the new results in commutative algebra that we prove here with patching to determine the Wiles defect. The patching method allows one to show that the Wiles defect of a global deformation ring at an augmentation
${\mathbf T}$
acting on the cohomology of a Shimura curve) using a combination of patching and level lowering results of Ribet–Takahashi [Reference Ribet and TakahashiRT97]. In the present paper, we combine the new results in commutative algebra that we prove here with patching to determine the Wiles defect. The patching method allows one to show that the Wiles defect of a global deformation ring at an augmentation
![]() $\lambda _f$
depends only on the induced augmentations of the corresponding local deformation rings. This gives yet another illustration of the versatility of the patching method and its ability to reduce proving properties of global deformation rings to proving properties of the corresponding local deformation rings.
$\lambda _f$
depends only on the induced augmentations of the corresponding local deformation rings. This gives yet another illustration of the versatility of the patching method and its ability to reduce proving properties of global deformation rings to proving properties of the corresponding local deformation rings.
As a curious consequence, we derive and strengthen the results of Ribet–Takahashi in [Reference Ribet and TakahashiRT97] on degrees of optimal parametrizations of elliptic curves over
![]() ${\mathbf Q}$
by Shimura curves, via a new argument. The methods of Ribet–Takahashi use arithmetic geometry, while the method here uses patching. Our strengthening of their results is not accessible using only the methods of their paper as we explain below in the introduction.
${\mathbf Q}$
by Shimura curves, via a new argument. The methods of Ribet–Takahashi use arithmetic geometry, while the method here uses patching. Our strengthening of their results is not accessible using only the methods of their paper as we explain below in the introduction.
1.1 A particular case of our main theorem
In [Reference Böckle, Khare and ManningBKM21, Theorem 10.1], we determined the Wiles defect associated to a newform
![]() ${f \in S_2(\Gamma _0(NQ))}$
of squarefree level
${f \in S_2(\Gamma _0(NQ))}$
of squarefree level
![]() $NQ$
that arises by the Jacquet–Langlands correspondence from a newform in
$NQ$
that arises by the Jacquet–Langlands correspondence from a newform in
![]() $S_2(\Gamma ^Q_0(N))$
. Here,
$S_2(\Gamma ^Q_0(N))$
. Here,
![]() $\Gamma ^Q_0(N)$
is the congruence subgroup of a quaternion algebra that is ramified at the set of primes dividing Q, of level
$\Gamma ^Q_0(N)$
is the congruence subgroup of a quaternion algebra that is ramified at the set of primes dividing Q, of level
![]() $\Gamma _0(N)$
and the maximal compact subgroup at the primes in Q.
$\Gamma _0(N)$
and the maximal compact subgroup at the primes in Q.
We state an improvement of [Reference Böckle, Khare and ManningBKM21, Theorem 10.1] referring to it for any of the unexplained notation in the statement below (we do recall the definition of the Wiles defect below). The proof relies on the Taylor–Wiles–Kisin patching method, but not on [Reference Ribet and TakahashiRT97], and also explains en passant why the Wiles defect computed below is a sum of local defects in a sense we make precise later in the introduction.
Theorem 1.1. Let N and Q be relatively prime squarefree integers. Let
![]() $p>2$
be a prime not dividing
$p>2$
be a prime not dividing
![]() $NQ$
, and let
$NQ$
, and let
![]() $E/{\mathbf Q}_p$
be a finite extension with ring of integers
$E/{\mathbf Q}_p$
be a finite extension with ring of integers
![]() ${\mathcal O}$
, uniformizer
${\mathcal O}$
, uniformizer
![]() $\varpi $
and residue field k. Let
$\varpi $
and residue field k. Let
![]() $\rho _f:G_{{\mathbf Q}}\to {\mathrm {GL}}_2({\mathcal O})$
be a Galois representation arising from a newform
$\rho _f:G_{{\mathbf Q}}\to {\mathrm {GL}}_2({\mathcal O})$
be a Galois representation arising from a newform
![]() $f\in S_2(\Gamma _0(NQ))$
, and let
$f\in S_2(\Gamma _0(NQ))$
, and let
![]() $\overline {\rho }_f:G_{{\mathbf Q}}\to {\mathrm {GL}}_2(k)$
be the residual representation. Assume that
$\overline {\rho }_f:G_{{\mathbf Q}}\to {\mathrm {GL}}_2(k)$
be the residual representation. Assume that
![]() $\overline {\rho }_f$
is irreducible and
$\overline {\rho }_f$
is irreducible and
![]() $N|N(\overline {\rho }_f)$
.
$N|N(\overline {\rho }_f)$
.
Let
![]() $R^{{\mathrm {st}}}$
be the Galois deformation ring of
$R^{{\mathrm {st}}}$
be the Galois deformation ring of
![]() $\overline {\rho }_f$
parameterizing lifts of
$\overline {\rho }_f$
parameterizing lifts of
![]() $\overline {\rho }_f$
of fixed determinant which are Steinberg at each prime dividing Q, finite flat at p and minimal at all other primes.
$\overline {\rho }_f$
of fixed determinant which are Steinberg at each prime dividing Q, finite flat at p and minimal at all other primes.
Let D be the quaternion algebra with discriminant Q, and let
![]() $\Gamma _0^Q(N)$
be the level N congruence subgroup for D. Let
$\Gamma _0^Q(N)$
be the level N congruence subgroup for D. Let
![]() ${\mathbf T}^Q(N)$
and
${\mathbf T}^Q(N)$
and
![]() $S^Q(\Gamma _0^Q(N))$
be the Hecke algebra and cohomological Hecke module at level
$S^Q(\Gamma _0^Q(N))$
be the Hecke algebra and cohomological Hecke module at level
![]() $\Gamma ^Q_0(N)$
, and let
$\Gamma ^Q_0(N)$
, and let
![]() ${\mathfrak m}\subseteq {\mathbf T}^Q(N)$
be the maximal ideal corresponding to
${\mathfrak m}\subseteq {\mathbf T}^Q(N)$
be the maximal ideal corresponding to
![]() $ f$
. Let
$ f$
. Let
![]() ${\mathbf T}^{{\mathrm {st}}} = {\mathbf T}^Q(N)_{\mathfrak m}$
, and let
${\mathbf T}^{{\mathrm {st}}} = {\mathbf T}^Q(N)_{\mathfrak m}$
, and let
![]() $\lambda :{\mathbf T}^{{\mathrm {st}}}\to {\mathcal O}$
be the augmentation corresponding to f.
$\lambda :{\mathbf T}^{{\mathrm {st}}}\to {\mathcal O}$
be the augmentation corresponding to f.
Then the Wiles defects of
![]() ${\mathbf T}^{{\mathrm {st}}}$
and
${\mathbf T}^{{\mathrm {st}}}$
and
![]() $S^Q(\Gamma _0^Q(N))$
with respect to the map
$S^Q(\Gamma _0^Q(N))$
with respect to the map
![]() $R^{{\mathrm {st}}}\twoheadrightarrow {\mathbf T}^{{\mathrm {st}}}$
and the augmentation
$R^{{\mathrm {st}}}\twoheadrightarrow {\mathbf T}^{{\mathrm {st}}}$
and the augmentation
![]() $\lambda $
are
$\lambda $
are
 $$\begin{align*}\delta_\lambda(R^{\mathrm{st}})=\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e}, \end{align*}$$
$$\begin{align*}\delta_\lambda(R^{\mathrm{st}})=\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e}, \end{align*}$$
where e is the ramification index of
![]() ${\mathcal O}$
and for each
${\mathcal O}$
and for each
![]() $q|Q$
,
$q|Q$
,
![]() $n_q$
is the largest integer for which
$n_q$
is the largest integer for which
![]() $\rho _f|_{G_{{\mathbf Q}_q}} \ \pmod {\varpi ^{n_q}}$
is unramified and
$\rho _f|_{G_{{\mathbf Q}_q}} \ \pmod {\varpi ^{n_q}}$
is unramified and
![]() $\rho _f(\operatorname {\mathrm {Frob}}_q)\equiv \pm \mathrm {Id}\ \pmod {\varpi ^{n_q}}$
.
$\rho _f(\operatorname {\mathrm {Frob}}_q)\equiv \pm \mathrm {Id}\ \pmod {\varpi ^{n_q}}$
.
The improvement as far as the statement of the theorem is concerned, if one compares to [Reference Böckle, Khare and ManningBKM21, Theorem 10.1], is that the assumptions needed there on Q:
-
1. Q is a product of an even number of primes (i.e., D is indefinite), and
 $(N(\overline {\rho }),Q)>1$
;
$(N(\overline {\rho }),Q)>1$
; -
2. Q is a product of an odd number of primes (i.e., D is definite), and
 $N>1$
;
$N>1$
; -
3.
 $N(\overline {\rho })$
is divisible by at least two primes,
$N(\overline {\rho })$
is divisible by at least two primes,
which arose from our relying on delicate results in [Reference Ribet and TakahashiRT97], are no longer needed because of the innovations introduced in this paper. We prove a much more general theorem below; see Theorem 6.5, that works with more general local conditions than being Steinberg at trivial primes (see [Reference Böckle, Khare and ManningBKM21, §2]) and with the field
![]() ${\mathbf Q}$
replaced by any totally real field F, but focus on this special case for the purposes of the introduction to more easily explain the novelty of our methods in comparison to [Reference Böckle, Khare and ManningBKM21].
${\mathbf Q}$
replaced by any totally real field F, but focus on this special case for the purposes of the introduction to more easily explain the novelty of our methods in comparison to [Reference Böckle, Khare and ManningBKM21].
If we look at the shape of the formula
 $$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e} \end{align*}$$
$$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e} \end{align*}$$
we see that the Wiles defect
![]() $\delta _\lambda ({\mathbf T}^{{\mathrm {st}}}), $
that is defined as a global quantity arising from the augmentation
$\delta _\lambda ({\mathbf T}^{{\mathrm {st}}}), $
that is defined as a global quantity arising from the augmentation
![]() $\lambda _f:{\mathbf T}^{\mathrm {st}} \to {\mathcal O}$
is expressed as a sum over the primes dividing
$\lambda _f:{\mathbf T}^{\mathrm {st}} \to {\mathcal O}$
is expressed as a sum over the primes dividing
![]() $ Q$
of terms
$ Q$
of terms
![]() $2n_q/e$
. Furthermore, each of the integers
$2n_q/e$
. Furthermore, each of the integers
![]() $n_q$
depends only on
$n_q$
depends only on
![]() $\rho _f|_{G_{{\mathbf Q}_q}}$
. In [Reference Böckle, Khare and ManningBKM21], it is only after having proved the theorem that one observes that the formula depends only on
$\rho _f|_{G_{{\mathbf Q}_q}}$
. In [Reference Böckle, Khare and ManningBKM21], it is only after having proved the theorem that one observes that the formula depends only on
![]() $(\rho _f|_{G_{{\mathbf Q}_q}})_{q \in Q}$
. In this paper, we show that the Wiles defect
$(\rho _f|_{G_{{\mathbf Q}_q}})_{q \in Q}$
. In this paper, we show that the Wiles defect
![]() $\delta _\lambda (R^{\mathrm {st}}) $
is a priori local, and in fact is a sum of the defects of local deformation rings (equivalently, local defects) at primes in Q that we define below. The proof of [Reference Böckle, Khare and ManningBKM21, Theorem 10.1] did not shed light on the local-global aspect of the statement of the theorem.
$\delta _\lambda (R^{\mathrm {st}}) $
is a priori local, and in fact is a sum of the defects of local deformation rings (equivalently, local defects) at primes in Q that we define below. The proof of [Reference Böckle, Khare and ManningBKM21, Theorem 10.1] did not shed light on the local-global aspect of the statement of the theorem.
Further, the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 10.1] computed the Wiles defect using a combination of patching and arguments related to level lowering results of [Reference Ribet and TakahashiRT97]. The latter was used to first show that
 $$\begin{align*}\delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e}. \end{align*}$$
$$\begin{align*}\delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) = \sum_{q|Q}\frac{2n_q}{e}. \end{align*}$$
Then delicate results from [Reference ManningMan21] were used to prove [Reference Böckle, Khare and ManningBKM21, Theorem 3.10, Theorem 8.1, Corollary 8.3] that
(As the referee has remarked, the inequality
![]() $\delta _\lambda ({\mathbf T}^{{\mathrm {st}}}) \leq \delta _\lambda (S^Q(\Gamma _0^Q(N))_{{\mathfrak m}})$
is easier and follows from [Reference Böckle, Khare and ManningBKM21, Theorem 3.12].) One deduces that
$\delta _\lambda ({\mathbf T}^{{\mathrm {st}}}) \leq \delta _\lambda (S^Q(\Gamma _0^Q(N))_{{\mathfrak m}})$
is easier and follows from [Reference Böckle, Khare and ManningBKM21, Theorem 3.12].) One deduces that
 $$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \sum_{q|Q}\frac{2n_q}{e}.\end{align*}$$
$$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}}}) = \sum_{q|Q}\frac{2n_q}{e}.\end{align*}$$
Here, we reverse the logic of the proof in [Reference Böckle, Khare and ManningBKM21] and show using patching and the new commutative algebra results about the Wiles defect that are proven here (see Theorem 6.5) that
 $$\begin{align*}\delta_\lambda(R^{\mathrm{st}})=\delta_\lambda({\mathbf T}^{{\mathrm{st}}})= \sum_{q|Q}\frac{2n_q}{e}\end{align*}$$
$$\begin{align*}\delta_\lambda(R^{\mathrm{st}})=\delta_\lambda({\mathbf T}^{{\mathrm{st}}})= \sum_{q|Q}\frac{2n_q}{e}\end{align*}$$
and deduce from this (see Theorem 7.5 (ii) and Proposition 7.7) that
 $$\begin{align*}\delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) =\sum_{q|Q}\frac{2n_q}{e}. \end{align*}$$
$$\begin{align*}\delta_\lambda(S^Q(\Gamma_0^Q(N))_{{\mathfrak m}}) =\sum_{q|Q}\frac{2n_q}{e}. \end{align*}$$
Thus, our determination of
![]() $\delta _\lambda ({\mathbf T}^{\mathrm {st}})$
no longer relies on [Reference Ribet and TakahashiRT97]. Indeed, we show how to use defects of Hecke rings to compute the defects of their ‘cohomological’ modules (arising from the first cohomology of modular curves and Shimura curves that they act on). Besides the intrinsic interest in having methods that work for modules over rings rather than just for rings, the computations of defects
$\delta _\lambda ({\mathbf T}^{\mathrm {st}})$
no longer relies on [Reference Ribet and TakahashiRT97]. Indeed, we show how to use defects of Hecke rings to compute the defects of their ‘cohomological’ modules (arising from the first cohomology of modular curves and Shimura curves that they act on). Besides the intrinsic interest in having methods that work for modules over rings rather than just for rings, the computations of defects
![]() $ \delta _\lambda (S^Q(\Gamma _0^Q(N))_{{\mathfrak m}}) $
of modules such as
$ \delta _\lambda (S^Q(\Gamma _0^Q(N))_{{\mathfrak m}}) $
of modules such as
![]() $ S^Q(\Gamma _0^Q(N))$
, turns out to be key to the next application that we outline below. It relies on exact computations of changes of lengths of congruence modules that arise from cohomology groups of modular curves and Shimura curves.
$ S^Q(\Gamma _0^Q(N))$
, turns out to be key to the next application that we outline below. It relies on exact computations of changes of lengths of congruence modules that arise from cohomology groups of modular curves and Shimura curves.
1.2 Application to change of degree formula of parametrizations of elliptic curves by Shimura curves
Our results and methods allow one to give a more robust approach (see Theorem 7.5(ii), Corollary 7.9 and Corollary 7.10 below and the remarks that follow) to the main result proved by Ribet and Takahashi [Reference Ribet and TakahashiRT97, Theorem 1] that computes changes of p-parts of degrees of optimal parametrizations of semistable elliptic curves E over
![]() ${\mathbf Q}$
by Shimura curves as one varies the Shimura curve for a prime p such that
${\mathbf Q}$
by Shimura curves as one varies the Shimura curve for a prime p such that
![]() $E[p]$
is irreducible as a
$E[p]$
is irreducible as a
![]() $G_{\mathbf Q}$
-module. The methods of [Reference Ribet and TakahashiRT97, Theorem1] rely at a crucial point (see proof of second assertion of [Reference Ribet and TakahashiRT97, Theorem 1]) on the following consequence of E being defined over
$G_{\mathbf Q}$
-module. The methods of [Reference Ribet and TakahashiRT97, Theorem1] rely at a crucial point (see proof of second assertion of [Reference Ribet and TakahashiRT97, Theorem 1]) on the following consequence of E being defined over
![]() ${\mathbf Q}$
and semistable:
${\mathbf Q}$
and semistable:
-
• (*) There is a prime q dividing the conductor of E (of semistable bad reduction) at which the order of the group of components at q is not divisible by p. Equivalently, the mod p representation
 $\overline {\rho }$
arising from E is such that
$\overline {\rho }$
arising from E is such that
 $\overline {\rho }({I_q})$
is either not finite flat (in the case
$\overline {\rho }({I_q})$
is either not finite flat (in the case
 $q =p$
), and ramified (in the case
$q =p$
), and ramified (in the case
 $q \neq p$
), with
$q \neq p$
), with
 $I_q$
an inertia group at q.
$I_q$
an inertia group at q.
This is used to show that certain maps on the p-primary parts of components groups are surjective (by a clever trick of permuting primes around, see [Reference Ribet and TakahashiRT97, pg. 11113]) which is the key to computing change of degrees of parametrizations in [Reference Ribet and TakahashiRT97, Theorem 1]. We generalize the results of [Reference Ribet and TakahashiRT97] (Corollary 7.9 and Corollary 7.10 below) to elliptic curves over
![]() ${\mathbf Q}$
which need not be semistable and for which (*) may not necessarily hold. Our methods should also extend to situations where we replace
${\mathbf Q}$
which need not be semistable and for which (*) may not necessarily hold. Our methods should also extend to situations where we replace
![]() ${\mathbf Q}$
by a totally real number field F, and E is an elliptic curve over F which need not be semistable (outside the set of primes at which the quaternion algebra giving rise to the Shimura X curve that parametrizes E is ramified and at which both X and E have multiplicative reduction at these primes), provided that the mod p representation
${\mathbf Q}$
by a totally real number field F, and E is an elliptic curve over F which need not be semistable (outside the set of primes at which the quaternion algebra giving rise to the Shimura X curve that parametrizes E is ramified and at which both X and E have multiplicative reduction at these primes), provided that the mod p representation
![]() $\overline {\rho }$
arising from E is irreducible when restricted to
$\overline {\rho }$
arising from E is irreducible when restricted to
![]() $G_{F(\zeta _p)}$
.
$G_{F(\zeta _p)}$
.
Our very indirect method to compute change of degrees, that is arithmetic and global in nature, seems necessary to get results of [Reference Ribet and TakahashiRT97] in general situations. We note that the surjectivity of maps on component groups arising from optimal quotients of abelian varieties with multiplicative reduction defined over a finite extension K of
![]() ${\mathbf Q}_q$
is not generally true. More precisely, there are
${\mathbf Q}_q$
is not generally true. More precisely, there are
![]() $A,A^\prime {}$
be abelian varieties defined over a finite extension K of
$A,A^\prime {}$
be abelian varieties defined over a finite extension K of
![]() ${\mathbf Q}_q$
that have multiplicative reduction at q, and
${\mathbf Q}_q$
that have multiplicative reduction at q, and
![]() $f: A \to A^\prime {}$
is an optimal quotient over K (i.e.,
$f: A \to A^\prime {}$
is an optimal quotient over K (i.e.,
![]() $\ker (f)$
is connected) such that the induced map
$\ker (f)$
is connected) such that the induced map
![]() $\phi (A) \to \phi (A^\prime {})$
on component groups is not surjective on the p-primary parts for a prime p. (K. Ribet showed us an example due to Raynaud.) It is easy to show that the map is surjective when the pth roots of unity are not in K. Our global methods show that the surjectivity holds even when K contains pth roots of unity in the situations we consider; namely, when A arises from Jacobian of Shimura curves over F and K is a completion of F,
$\phi (A) \to \phi (A^\prime {})$
on component groups is not surjective on the p-primary parts for a prime p. (K. Ribet showed us an example due to Raynaud.) It is easy to show that the map is surjective when the pth roots of unity are not in K. Our global methods show that the surjectivity holds even when K contains pth roots of unity in the situations we consider; namely, when A arises from Jacobian of Shimura curves over F and K is a completion of F,
![]() $A^\prime {}$
is an optimal
$A^\prime {}$
is an optimal
![]() ${\mathrm {GL}}_2$
-abelian variety quotient, and with p a prime so that that the residual characteristic p representations
${\mathrm {GL}}_2$
-abelian variety quotient, and with p a prime so that that the residual characteristic p representations
![]() $\overline {\rho }_\lambda $
arising from
$\overline {\rho }_\lambda $
arising from
![]() $A^\prime {}$
satisfy the Taylor–Wiles hypothesis that
$A^\prime {}$
satisfy the Taylor–Wiles hypothesis that
![]() $\overline {\rho }_\lambda |_{F(\zeta _p)}$
is irreducible.
$\overline {\rho }_\lambda |_{F(\zeta _p)}$
is irreducible.
1.3 Main ideas of proof of Theorem 1.1
We consider in this paper the category
![]() $C_{\mathcal O}$
of tuples
$C_{\mathcal O}$
of tuples
![]() $(R, \lambda )$
, with
$(R, \lambda )$
, with
![]() $R \in {\mathrm {CNL}}_{\mathcal O}$
(with
$R \in {\mathrm {CNL}}_{\mathcal O}$
(with
![]() ${\mathrm {CNL}}_{\mathcal O}$
the usual category; see §1.6) that is flat over
${\mathrm {CNL}}_{\mathcal O}$
the usual category; see §1.6) that is flat over
![]() ${\mathcal O}$
and Cohen–Macaulay, together with an augmentation
${\mathcal O}$
and Cohen–Macaulay, together with an augmentation
![]() $\lambda : R \to {\mathcal O}$
(that is by definition a continuous surjective
$\lambda : R \to {\mathcal O}$
(that is by definition a continuous surjective
![]() ${\mathcal O}$
-algebra homomorphism) that is formally smooth over the generic fiber.
${\mathcal O}$
-algebra homomorphism) that is formally smooth over the generic fiber.
We take a cue from a formula discovered by Venkatesh [Reference VenkateshVen16, Reference VenkateshVen20] (see Proposition A.6 of the appendix) and define in §2 the Wiles defect
![]() $\delta _\lambda (R)$
for
$\delta _\lambda (R)$
for
![]() $ (R,\lambda ) \in C_{\mathcal O}$
. The defect
$ (R,\lambda ) \in C_{\mathcal O}$
. The defect
![]() $\delta _\lambda (R)$
is expressed in terms of two invariants first introduced by Venkatesh (for rings R finite over
$\delta _\lambda (R)$
is expressed in terms of two invariants first introduced by Venkatesh (for rings R finite over
![]() ${\mathcal O}$
):
${\mathcal O}$
):
-
(i) the length of the
 ${\mathcal O}$
-module
${\mathcal O}$
-module
 $\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
which can be directly defined using a continuous version of the André–Quillen cohomology of rings (cf. §3.3), (which will agree with the standard André–Quillen cohomology module
$\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
which can be directly defined using a continuous version of the André–Quillen cohomology of rings (cf. §3.3), (which will agree with the standard André–Quillen cohomology module
 $\operatorname {\mathrm {Der}}_{\mathcal O}^1(R, E/{\mathcal O})$
in the case when R has dimension
$\operatorname {\mathrm {Der}}_{\mathcal O}^1(R, E/{\mathcal O})$
in the case when R has dimension
 $1$
) and
$1$
) and -
(ii) the length of the
 ${\mathcal O}$
-module
${\mathcal O}$
-module
 $C_{1,\lambda }(R)$
(cf. §3.2, in particular Corollary 3.12).
$C_{1,\lambda }(R)$
(cf. §3.2, in particular Corollary 3.12).
The Wiles defect
![]() $\delta _\lambda (R)$
is then defined (cf. Definition 3.24) to be
$\delta _\lambda (R)$
is then defined (cf. Definition 3.24) to be
 $$\begin{align*}\displaystyle \delta_\lambda(R) = \frac{\log|\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log|C_{1,\lambda}(R)|}{\log|{\mathcal O}/p|}=\frac{\ell_{\mathcal O}(\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O}))-\ell_{\mathcal O}(C_{1,\lambda}(R))}{\ell_{\mathcal O}({\mathcal O}/p)}.\end{align*}$$
$$\begin{align*}\displaystyle \delta_\lambda(R) = \frac{\log|\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log|C_{1,\lambda}(R)|}{\log|{\mathcal O}/p|}=\frac{\ell_{\mathcal O}(\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O}))-\ell_{\mathcal O}(C_{1,\lambda}(R))}{\ell_{\mathcal O}({\mathcal O}/p)}.\end{align*}$$
This definition of the defect we give for
![]() $R \in C_{\mathcal O}$
agrees, by Proposition A.6 and Proposition 3.27, in the case when
$R \in C_{\mathcal O}$
agrees, by Proposition A.6 and Proposition 3.27, in the case when
![]() $R \in C_{\mathcal O}$
is of dimension one with the definition of the Wiles defect given in [Reference Böckle, Khare and ManningBKM21] as
$R \in C_{\mathcal O}$
is of dimension one with the definition of the Wiles defect given in [Reference Böckle, Khare and ManningBKM21] as
 $$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
$$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
We note that this latter definition makes sense only for rings
![]() $R \in C_{\mathcal O}$
of dimension one as only then are the modules
$R \in C_{\mathcal O}$
of dimension one as only then are the modules
![]() $\Phi _\lambda (R), \Psi _\lambda (R)$
of finite cardinality (see Lemma 2.4).
$\Phi _\lambda (R), \Psi _\lambda (R)$
of finite cardinality (see Lemma 2.4).
Our main technique for the proof of Theorem 1.1 is the Taylor–Wiles–Kisin patching method. Specifically, under some mild global hypotheses, one can write
![]() $R^{\mathrm {st}}$
as a quotient
$R^{\mathrm {st}}$
as a quotient
![]() $ R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}[[x_1,\ldots ,x_g]]/(y_1,\ldots ,y_d)$
(see Theorem 6.4 and Theorem 6.5), where
$ R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}[[x_1,\ldots ,x_g]]/(y_1,\ldots ,y_d)$
(see Theorem 6.4 and Theorem 6.5), where
![]() $R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
is a completed tensor product of local Galois deformation rings and is thus determined by local Galois theoretic information. In the case when
$R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
is a completed tensor product of local Galois deformation rings and is thus determined by local Galois theoretic information. In the case when
![]() $R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
is Cohen–MacaulayFootnote
1
we prove general results (see Theorem 3.9 and Theorem 3.20) that imply that
$R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
is Cohen–MacaulayFootnote
1
we prove general results (see Theorem 3.9 and Theorem 3.20) that imply that
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
and
![]() $C_{1,\lambda }(R)$
are independent of the choice of ideal
$C_{1,\lambda }(R)$
are independent of the choice of ideal
![]() $(y_1,\ldots ,y_d)$
and thus depend only on the ring
$(y_1,\ldots ,y_d)$
and thus depend only on the ring
![]() $R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
and the induced composite map
$R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}}$
and the induced composite map
![]() $R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}} \to R^{{\mathrm {st}}} \xrightarrow {\lambda }{\mathcal O}$
, which shows that
$R_{\operatorname {\mathrm {loc}}}^{{\mathrm {st}}} \to R^{{\mathrm {st}}} \xrightarrow {\lambda }{\mathcal O}$
, which shows that
 $$\begin{align*}\delta_\lambda(R^{{\mathrm{st}}}) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^{{\mathrm{st}}})=\sum_{q|Q} \delta_\lambda(R_q^{\mathrm{st}}), \end{align*}$$
$$\begin{align*}\delta_\lambda(R^{{\mathrm{st}}}) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^{{\mathrm{st}}})=\sum_{q|Q} \delta_\lambda(R_q^{\mathrm{st}}), \end{align*}$$
where
![]() $\delta (R_q^{\mathrm {st}})$
is the defect of the local deformation ring
$\delta (R_q^{\mathrm {st}})$
is the defect of the local deformation ring
![]() $R_q^{\mathrm {st}} \in C_{\mathcal O}$
. Thus, to determine
$R_q^{\mathrm {st}} \in C_{\mathcal O}$
. Thus, to determine
![]() $\delta _\lambda (R^{\mathrm {st}})$
, we have to compute the defects
$\delta _\lambda (R^{\mathrm {st}})$
, we have to compute the defects
![]() $\delta _\lambda (R_q^{\mathrm {st}})$
of the local deformation rings
$\delta _\lambda (R_q^{\mathrm {st}})$
of the local deformation rings
![]() $R_q^{\mathrm {st}}$
. These computations are quite elaborate and are done in Theorem 5.18 of §5 (Theorems 5.26 and 5.33 do analogous computations for local deformation rings defined by conditions of being unipotent and unipotent together with a choice of Frobenius eigenvalue). One of the contributions of this paper is to show that these subtle invariants
$R_q^{\mathrm {st}}$
. These computations are quite elaborate and are done in Theorem 5.18 of §5 (Theorems 5.26 and 5.33 do analogous computations for local deformation rings defined by conditions of being unipotent and unipotent together with a choice of Frobenius eigenvalue). One of the contributions of this paper is to show that these subtle invariants
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
and
![]() $C_{1,\lambda }(R)$
are computable for fairly complicated rings: The local deformation rings
$C_{1,\lambda }(R)$
are computable for fairly complicated rings: The local deformation rings
![]() $R \in C_{\mathcal O}$
that we consider below at trivial primes are not Gorenstein (for the Steinberg and unipotent local conditions) and Gorenstein but not complete intersections (for the unipotent condition with choice of Frobenius eigenvalue). The computations are delicate.
$R \in C_{\mathcal O}$
that we consider below at trivial primes are not Gorenstein (for the Steinberg and unipotent local conditions) and Gorenstein but not complete intersections (for the unipotent condition with choice of Frobenius eigenvalue). The computations are delicate.
1.4 Broader context
We make some more informal remarks about the broader context of our work and further questions to pursue in this context.
Our work is in the general context of understanding deformation rings R when they are ‘obstructed’ and are thus not expected to be complete intersections. The Wiles defect is a measure of the obstructedness of R at a given augmentation
![]() $\lambda : R \to {\mathcal O}$
. In the context of the present paper, the obstructions are local in nature. The Wiles defect is a global quantity which in our case turns out to be a sum of local defects. This is proved by patching and showing that that the invariants
$\lambda : R \to {\mathcal O}$
. In the context of the present paper, the obstructions are local in nature. The Wiles defect is a global quantity which in our case turns out to be a sum of local defects. This is proved by patching and showing that that the invariants
![]() $\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
and
![]() $C_{1,\lambda }(R)$
remain invariant under going modulo regular sequences. In other situations (as in [Reference Tilouine and UrbanTU22]), the obstructedness of deformation rings R is because of global reasons, in that one is in a situation of positive defect
$C_{1,\lambda }(R)$
remain invariant under going modulo regular sequences. In other situations (as in [Reference Tilouine and UrbanTU22]), the obstructedness of deformation rings R is because of global reasons, in that one is in a situation of positive defect
![]() $\ell _0>0$
, and the natural ‘automorphic cohomology’ to consider lives in more than one degree. The work in [Reference Galatius and VenkateshGV18] gives a framework to understand this more deeply via considering derived deformation rings
$\ell _0>0$
, and the natural ‘automorphic cohomology’ to consider lives in more than one degree. The work in [Reference Galatius and VenkateshGV18] gives a framework to understand this more deeply via considering derived deformation rings
![]() $\cal R$
such that
$\cal R$
such that
![]() $R=\pi _0(\cal R)$
, and
$R=\pi _0(\cal R)$
, and
![]() $\pi _*(\cal R)$
acts as a graded ring on the ‘automorphic cohomology’. It seems interesting to explore these ideas in the context of the paper, and for instance ‘derive’ the local deformation rings at trivial primes. One of the points of our work both here and in [Reference Böckle, Khare and ManningBKM21] is that in the cases which we study, the Wiles defect of Hecke algebras can be calculated unconditionally and one can determine it explicitly.
$\pi _*(\cal R)$
acts as a graded ring on the ‘automorphic cohomology’. It seems interesting to explore these ideas in the context of the paper, and for instance ‘derive’ the local deformation rings at trivial primes. One of the points of our work both here and in [Reference Böckle, Khare and ManningBKM21] is that in the cases which we study, the Wiles defect of Hecke algebras can be calculated unconditionally and one can determine it explicitly.
We have not dealt with cases when the local deformation ring at p is not a complete intersection in this paper, but our results will still be applicable provided that the local deformation rings are Cohen–Macaulay. For example, [Reference SnowdenSno18] considers a fixed weight ordinary deformation ring when the residual representation is trivial at p and shows that this ring is Cohen–Macaulay but not a complete intersection (or even Gorenstein). Our methods show that the global Wiles defect is again a sum of local defects in this case. However, we have not been able to determine the local defect at p in this case (due largely to the fact that [Reference SnowdenSno18] only computes the special fiber of the ring, while computing the local defect would require the integral version of the ring).
In the tame cases we have considered here and in [Reference Böckle, Khare and ManningBKM21, §11], the local defect at q is related to tame regulators (in the sense of Mazur–Tate) of the q-adic Mumford–Raynaud–Tate periods of the corresponding abelian variety
![]() $A_f$
which has multiplicative reduction at q. In the wild case, one imagines that the local defect will be related to p-adic regulators.
$A_f$
which has multiplicative reduction at q. In the wild case, one imagines that the local defect will be related to p-adic regulators.
Our work should also help in formulating and proving Bloch–Kato conjectures for newforms
![]() $f \in S_2(\Gamma _0(N))$
(say N squarefree) and the p-part of special value of the
$f \in S_2(\Gamma _0(N))$
(say N squarefree) and the p-part of special value of the
![]() $L(1,\operatorname {\mathrm {Ad}})$
for the adjoint L-function of f for suitable primes p. The algebraic part of the L-value is traditionally related to congruence modules of f by the work of Hida [Reference HidaHid81]. The Selmer group for the adjoint motive of f can be related to the cotangent space at the augmentation
$L(1,\operatorname {\mathrm {Ad}})$
for the adjoint L-function of f for suitable primes p. The algebraic part of the L-value is traditionally related to congruence modules of f by the work of Hida [Reference HidaHid81]. The Selmer group for the adjoint motive of f can be related to the cotangent space at the augmentation
![]() $\lambda _f: R \to {\mathcal O}$
where the local deformation problem at primes dividing N is the unipotent condition. The Wiles defect here by Theorem 6.5 is
$\lambda _f: R \to {\mathcal O}$
where the local deformation problem at primes dividing N is the unipotent condition. The Wiles defect here by Theorem 6.5 is
![]() $\sum _{q|N} n_q$
and is the discrepancy between the length of the congruence module for f and the Selmer group for the adjoint motive of f. It will be interesting to see this defect emerge from automorphic considerations. We believe that the Selmer group we are alluding to here is the natural (primitive) Selmer group to consider for the adjoint motive of f, reflecting nature of
$\sum _{q|N} n_q$
and is the discrepancy between the length of the congruence module for f and the Selmer group for the adjoint motive of f. It will be interesting to see this defect emerge from automorphic considerations. We believe that the Selmer group we are alluding to here is the natural (primitive) Selmer group to consider for the adjoint motive of f, reflecting nature of
![]() $\pi _f$
locally at primes dividing N. (See [Reference Tilouine and UrbanTU22, Theorem 5.20] that relates the ratio of different integral normalizations of periods (cohomological and motivic) of the adjoint motive of a Bianchi form to the Wiles defect, and to Bloch–Kato conjectures.) Note that if we relax the Selmer conditions at primes dividing N to be unrestricted of fixed determinant and consider the corresponding imprimitive Selmer group, then the Wiles defect becomes 0 and one is in a setting where Wiles-type methods prove the Bloch–Kato conjecture for this imprimitive Selmer group.
$\pi _f$
locally at primes dividing N. (See [Reference Tilouine and UrbanTU22, Theorem 5.20] that relates the ratio of different integral normalizations of periods (cohomological and motivic) of the adjoint motive of a Bianchi form to the Wiles defect, and to Bloch–Kato conjectures.) Note that if we relax the Selmer conditions at primes dividing N to be unrestricted of fixed determinant and consider the corresponding imprimitive Selmer group, then the Wiles defect becomes 0 and one is in a setting where Wiles-type methods prove the Bloch–Kato conjecture for this imprimitive Selmer group.
We could also consider a Bloch–Kato conjectures in this context with the local condition at primes dividing N to be Steinberg. The Wiles defect in this case by Theorem 6.5 is
![]() $\sum _{q|N} 2n_q$
, and the automorphic cohomology to consider here is
$\sum _{q|N} 2n_q$
, and the automorphic cohomology to consider here is
![]() $H^1(X^Q,{\mathcal O})$
, where
$H^1(X^Q,{\mathcal O})$
, where
![]() $X^Q$
is a Shimura curve over
$X^Q$
is a Shimura curve over
![]() ${\mathbf Q}$
arising from the quaternion algebra
${\mathbf Q}$
arising from the quaternion algebra
![]() $D_Q$
ramified at places Q dividing N (which we assume here is a set of even cardinality). If we consider the Jacquet–Langlands correspondent g of f on
$D_Q$
ramified at places Q dividing N (which we assume here is a set of even cardinality). If we consider the Jacquet–Langlands correspondent g of f on
![]() $D_Q$
, normalized (as in [Reference PrasannaPra06]) using the schematic structure over
$D_Q$
, normalized (as in [Reference PrasannaPra06]) using the schematic structure over
![]() ${\mathbf Z}_p$
of the corresponding Shimura curve
${\mathbf Z}_p$
of the corresponding Shimura curve
![]() $X^Q$
over
$X^Q$
over
![]() ${\mathbf Q}$
, with p a prime such that
${\mathbf Q}$
, with p a prime such that
![]() $(p,N)=1$
, then one sees easily that the ratio of Petersson inner products
$(p,N)=1$
, then one sees easily that the ratio of Petersson inner products
 $$\begin{align*}\frac{(f,f)}{(g,g)}=\frac{\deg(\phi)}{\deg(\phi^\prime{})},\end{align*}$$
$$\begin{align*}\frac{(f,f)}{(g,g)}=\frac{\deg(\phi)}{\deg(\phi^\prime{})},\end{align*}$$
where
![]() $\phi ,\phi ^\prime {}$
are optimal parametrizations of abelian varieties in the isogeny class
$\phi ,\phi ^\prime {}$
are optimal parametrizations of abelian varieties in the isogeny class
![]() ${\cal A}_f$
over
${\cal A}_f$
over
![]() ${\mathbf Q}$
associated to
${\mathbf Q}$
associated to
![]() $A_f$
. We could ask for a different ‘natural’ normalization
$A_f$
. We could ask for a different ‘natural’ normalization
![]() $g^\prime {}$
such that
$g^\prime {}$
such that
 $$\begin{align*}\frac{(f,f)}{(g^\prime{},g^\prime{})}=\frac{\deg(\phi)}{\deg(\phi^\prime{})} \Pi_{q \in Q} \omega^{-2n_q}\end{align*}$$
$$\begin{align*}\frac{(f,f)}{(g^\prime{},g^\prime{})}=\frac{\deg(\phi)}{\deg(\phi^\prime{})} \Pi_{q \in Q} \omega^{-2n_q}\end{align*}$$
would be the change of the corresponding Selmer groups (when we change the local conditions at primes in Q from Steinberg to unrestricted with fixed determinant) and thus would incorporate the Wiles defect
![]() $\sum _{q \in Q} \frac {2n_q}{e}$
.
$\sum _{q \in Q} \frac {2n_q}{e}$
.
Our method to compute p-parts of change of degrees of parametrizations of elliptic curves over
![]() ${\mathbf Q}$
by Shimura curves gives results that are stronger than the ones which can be obtained using the arithmetic-geometric methods of [Reference Ribet and TakahashiRT97]. To have these results in the fullest possible generality should be important for applications (see [Reference PastenPas24] for Diophantine applications of [Reference Ribet and TakahashiRT97]).
${\mathbf Q}$
by Shimura curves gives results that are stronger than the ones which can be obtained using the arithmetic-geometric methods of [Reference Ribet and TakahashiRT97]. To have these results in the fullest possible generality should be important for applications (see [Reference PastenPas24] for Diophantine applications of [Reference Ribet and TakahashiRT97]).
1.5 Structure of this paper
We begin by developing the commutative algebra tools that are needed for our main theorem Theorem 6.5. In §2, we state a formula for Wiles defects of rings of dimension one that is proved in Appendix A. In the key §3, we define and prove properties of the invariants
![]() $\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R, E/{\mathcal O})$
and
![]() $C_{1,\lambda }(R)$
for rings
$C_{1,\lambda }(R)$
for rings
![]() $R \in C_{\mathcal O}$
. In §4, we summarize information about local and global deformation rings. In §5, we compute the invariants defined in §3 for the local deformation rings we consider. This is a key input in computing the Wiles defect of global deformation rings in Theorem 6.5. In §6, we use patching and the work in §3 to show that the Wiles defect of global deformation rings and Hecke rings we consider is the sum of local defects. As the local defects have been computed in §5, this allows us to complete the proof of our main Theorem 6.5. In §7, we apply Theorem 6.5 to compute the Wiles defect for modules over Hecke algebras that arise from their action on the cohomology of modular and Shimura curves. This also leads to a new approach to, and strengthening of, the results in [Reference Ribet and TakahashiRT97] about change of degrees of optimal parametrizations of elliptic curves by Shimura curves as one changes the Shimura curve.
$R \in C_{\mathcal O}$
. In §4, we summarize information about local and global deformation rings. In §5, we compute the invariants defined in §3 for the local deformation rings we consider. This is a key input in computing the Wiles defect of global deformation rings in Theorem 6.5. In §6, we use patching and the work in §3 to show that the Wiles defect of global deformation rings and Hecke rings we consider is the sum of local defects. As the local defects have been computed in §5, this allows us to complete the proof of our main Theorem 6.5. In §7, we apply Theorem 6.5 to compute the Wiles defect for modules over Hecke algebras that arise from their action on the cohomology of modular and Shimura curves. This also leads to a new approach to, and strengthening of, the results in [Reference Ribet and TakahashiRT97] about change of degrees of optimal parametrizations of elliptic curves by Shimura curves as one changes the Shimura curve.
In Appendix A (written by Najmuddin Fakhruddin and CBK), a formula stated in a particular case by Venkatesh is proven; it was previously proved in a special case in [Reference Tilouine and UrbanTU22, Proposition 4].
1.6 Notation
By F we denote a totally real number field, our base field, by
![]() $F_v$
its completion at any place v of F, and we choose algebraic closures
$F_v$
its completion at any place v of F, and we choose algebraic closures
![]() $\overline F$
of F and
$\overline F$
of F and
![]() $\overline F_v$
if
$\overline F_v$
if
![]() $F_v$
for all places v. These choices define the absolute Galois groups
$F_v$
for all places v. These choices define the absolute Galois groups
![]() $G_F=\operatorname {\mathrm {Gal}}(\overline F/F)$
and
$G_F=\operatorname {\mathrm {Gal}}(\overline F/F)$
and
![]() $G_{F_v}=\operatorname {\mathrm {Gal}}(\overline F_v/F_v)$
. We write
$G_{F_v}=\operatorname {\mathrm {Gal}}(\overline F_v/F_v)$
. We write
![]() $I_v\subset G_{F_v}$
for the inertia subgroup. We also fix embeddings
$I_v\subset G_{F_v}$
for the inertia subgroup. We also fix embeddings
![]() $\overline F\to \overline F_v$
, extending the canonical embeddings
$\overline F\to \overline F_v$
, extending the canonical embeddings
![]() $F\to F_v$
. This determines for each place v of F an embedding
$F\to F_v$
. This determines for each place v of F an embedding
![]() $G_{F_v}\to G_F$
. By
$G_{F_v}\to G_F$
. By
![]() $\operatorname {\mathrm {Frob}}_v$
we denote a Frobenius automorphism in
$\operatorname {\mathrm {Frob}}_v$
we denote a Frobenius automorphism in
![]() $G_{F_v}$
, that is unique up to
$G_{F_v}$
, that is unique up to
![]() $I_v$
, and we also write
$I_v$
, and we also write
![]() $\operatorname {\mathrm {Frob}}_v$
for its image in
$\operatorname {\mathrm {Frob}}_v$
for its image in
![]() $G_F$
. All representations of
$G_F$
. All representations of
![]() $G_F$
or of
$G_F$
or of
![]() $G_{F_v}$
will be assumed to be continuous. If v is a finite place of F, then we write
$G_{F_v}$
will be assumed to be continuous. If v is a finite place of F, then we write
![]() $q_v$
for the cardinality of its residue field.
$q_v$
for the cardinality of its residue field.
Throughout the paper, we fix a prime
![]() $p>2$
, and we denote by
$p>2$
, and we denote by
![]() $\overline {\mathbf Q}_p$
an algebraic closure of
$\overline {\mathbf Q}_p$
an algebraic closure of
![]() ${\mathbf Q}_p$
. We will call a finite extension E of
${\mathbf Q}_p$
. We will call a finite extension E of
![]() ${\mathbf Q}_p$
inside
${\mathbf Q}_p$
inside
![]() $\overline {\mathbf Q}_p$
a coefficient field. For a coefficient field E, we let
$\overline {\mathbf Q}_p$
a coefficient field. For a coefficient field E, we let
![]() ${\mathcal O}$
be its ring of integers, k its residue field and
${\mathcal O}$
be its ring of integers, k its residue field and
![]() $\varpi \in {\mathcal O}$
a uniformizer. We write
$\varpi \in {\mathcal O}$
a uniformizer. We write
![]() $\Sigma _p$
for the set of places of F above p, and we assume throughout the paper that F over
$\Sigma _p$
for the set of places of F above p, and we assume throughout the paper that F over
![]() ${\mathbf Q}$
is unramified at all places above p. It is likely that this hypothesis could be weakened.
${\mathbf Q}$
is unramified at all places above p. It is likely that this hypothesis could be weakened.
The category of complete Noetherian local
![]() ${\mathcal O}$
-algebras with residue field k is denoted by
${\mathcal O}$
-algebras with residue field k is denoted by
![]() ${\mathrm {CNL}}_{\mathcal O}$
, and for any object R in
${\mathrm {CNL}}_{\mathcal O}$
, and for any object R in
![]() ${\mathrm {CNL}}_{\mathcal O}$
, we write
${\mathrm {CNL}}_{\mathcal O}$
, we write
![]() ${\mathfrak m}_R\subset R$
for its maximal ideal. Each object
${\mathfrak m}_R\subset R$
for its maximal ideal. Each object
![]() $R\in {\mathrm {CNL}}_{\mathcal O}$
will be endowed with its profinite (
$R\in {\mathrm {CNL}}_{\mathcal O}$
will be endowed with its profinite (
![]() ${\mathfrak m}_R$
-adic) topology. By a complete Noetherian local
${\mathfrak m}_R$
-adic) topology. By a complete Noetherian local
![]() ${\mathcal O}$
-algebra, we implicitly mean that its residue field is equal to k; we feel justified because our rings typically have an augmentation to
${\mathcal O}$
-algebra, we implicitly mean that its residue field is equal to k; we feel justified because our rings typically have an augmentation to
![]() ${\mathcal O}$
.
${\mathcal O}$
.
We denote by
![]() $\varepsilon _p$
the p-adic cyclotomic character
$\varepsilon _p$
the p-adic cyclotomic character
![]() $\varepsilon _p:G_F \to {\mathbf Z}_p^\times $
; if we compose
$\varepsilon _p:G_F \to {\mathbf Z}_p^\times $
; if we compose
![]() $\varepsilon _p$
on the right with any map
$\varepsilon _p$
on the right with any map
![]() $G_{F_v}\to G_F$
or on the left with
$G_{F_v}\to G_F$
or on the left with
![]() ${\mathbf Z}_p^\times \to R^\times $
, induced from any morphism
${\mathbf Z}_p^\times \to R^\times $
, induced from any morphism
![]() ${\mathbf Z}_p\to R$
in
${\mathbf Z}_p\to R$
in
![]() ${\mathrm {CNL}}_{{\mathbf Z}_p}$
, then we also write
${\mathrm {CNL}}_{{\mathbf Z}_p}$
, then we also write
![]() $\varepsilon _p$
by slight abuse of notation.
$\varepsilon _p$
by slight abuse of notation.
For an
![]() ${\mathcal O}$
-algebra R, an augmentation
${\mathcal O}$
-algebra R, an augmentation
![]() $\lambda $
of R will always mean a surjective
$\lambda $
of R will always mean a surjective
![]() ${\mathcal O}$
-algebra homomorphism
${\mathcal O}$
-algebra homomorphism
![]() $\lambda :R\to {\mathcal O}'$
, where
$\lambda :R\to {\mathcal O}'$
, where
![]() ${\mathcal O}'$
is the ring of integers in a finite extension of E (we will almost always take
${\mathcal O}'$
is the ring of integers in a finite extension of E (we will almost always take
![]() ${\mathcal O}={\mathcal O}'$
). For an
${\mathcal O}={\mathcal O}'$
). For an
![]() ${\mathcal O}$
-module M that is a finite abelian group, we denote by
${\mathcal O}$
-module M that is a finite abelian group, we denote by
![]() $\ell _{\mathcal O}(M)$
the length of M as an
$\ell _{\mathcal O}(M)$
the length of M as an
![]() ${\mathcal O}$
-module. For
${\mathcal O}$
-module. For
![]() $\alpha \in {\mathcal O}$
, we denote by
$\alpha \in {\mathcal O}$
, we denote by
![]() $\operatorname {\mathrm {ord}}_{\mathcal O}(\alpha )=\ell _{\mathcal O}({\mathcal O}/(\alpha ))$
.
$\operatorname {\mathrm {ord}}_{\mathcal O}(\alpha )=\ell _{\mathcal O}({\mathcal O}/(\alpha ))$
.
For a Galois representation
![]() $\overline {\rho }:G_{F}\to {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
which is finite flat at p, we will let
$\overline {\rho }:G_{F}\to {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
which is finite flat at p, we will let
![]() $N(\overline {\rho })$
represent its Artin conductor.
$N(\overline {\rho })$
represent its Artin conductor.
2 Wiles defect for rings of dimension one
In this section, we state results from the Appendix A in the form in which they are used in the paper, and also with a view to generalizing these results to higher-dimensional rings in §3.
For any ring R, any ideal
![]() $I\subseteq R$
and any R-module M, we will always use
$I\subseteq R$
and any R-module M, we will always use
![]() $M[I]\subseteq M$
for the submodule of I-torsion elements of M. In particular,
$M[I]\subseteq M$
for the submodule of I-torsion elements of M. In particular,
![]() $R[I]=\operatorname {\mathrm {Ann}}_R(I)\subseteq R$
is the annihilator of the ideal I.
$R[I]=\operatorname {\mathrm {Ann}}_R(I)\subseteq R$
is the annihilator of the ideal I.
If M is a finitely generated R-module, with generating set
![]() $m_1,\ldots ,m_n$
inducing a surjection
$m_1,\ldots ,m_n$
inducing a surjection
![]() $R^n\twoheadrightarrow M$
, then we will let
$R^n\twoheadrightarrow M$
, then we will let
![]() $\operatorname {\mathrm {Fitt}}_R(M)\subseteq R$
(called the
$\operatorname {\mathrm {Fitt}}_R(M)\subseteq R$
(called the
![]() $0^{\mathrm {th}}$
fitting ideal) denote the ideal generated by all elements of the form
$0^{\mathrm {th}}$
fitting ideal) denote the ideal generated by all elements of the form
![]() $\det (v_1,\ldots ,v_n)\in R$
for
$\det (v_1,\ldots ,v_n)\in R$
for
![]() $v_1,\ldots ,v_n\in \ker (R^n\twoheadrightarrow M)$
. It is well known that this is independent of the choice of generating set
$v_1,\ldots ,v_n\in \ker (R^n\twoheadrightarrow M)$
. It is well known that this is independent of the choice of generating set
![]() $m_1,\ldots ,m_n$
and moreover that
$m_1,\ldots ,m_n$
and moreover that
![]() $\operatorname {\mathrm {Fitt}}_R(M)\subseteq \operatorname {\mathrm {Ann}}_R(M)$
. When the ring R is clear from context, we will sometimes write
$\operatorname {\mathrm {Fitt}}_R(M)\subseteq \operatorname {\mathrm {Ann}}_R(M)$
. When the ring R is clear from context, we will sometimes write
![]() $\operatorname {\mathrm {Fitt}}(M)$
in place of
$\operatorname {\mathrm {Fitt}}(M)$
in place of
![]() $\operatorname {\mathrm {Fitt}}_R(M)$
.
$\operatorname {\mathrm {Fitt}}_R(M)$
.
Let R be a complete, local Noetherian
![]() ${\mathcal O}$
-algebra with
${\mathcal O}$
-algebra with
![]() $\dim (R) = 1$
and assume that R is finite over
$\dim (R) = 1$
and assume that R is finite over
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\lambda :R\twoheadrightarrow {\mathcal O}$
be any augmentation (i.e., surjective
$\lambda :R\twoheadrightarrow {\mathcal O}$
be any augmentation (i.e., surjective
![]() ${\mathcal O}$
-algebra homomorphism). Let
${\mathcal O}$
-algebra homomorphism). Let
![]() $R^{\mathrm {tf}}$
be the maximal
$R^{\mathrm {tf}}$
be the maximal
![]() $\varpi $
-torsion free quotient of R, which is automatically finite free over
$\varpi $
-torsion free quotient of R, which is automatically finite free over
![]() ${\mathcal O}$
.Footnote
2
Also, use
${\mathcal O}$
.Footnote
2
Also, use
![]() $\lambda $
to denote the augmentation
$\lambda $
to denote the augmentation
![]() $R^{\mathrm {tf}} \twoheadrightarrow {\mathcal O}$
induced by
$R^{\mathrm {tf}} \twoheadrightarrow {\mathcal O}$
induced by
![]() $\lambda $
. Define
$\lambda $
. Define
and
which we will call the cotangent space and congruence module of R (with respect to
![]() $\lambda $
). From now on, we will assume that
$\lambda $
). From now on, we will assume that
![]() $\Phi _\lambda (R)$
is finite, which geometrically means that
$\Phi _\lambda (R)$
is finite, which geometrically means that
![]() $\lambda $
is smooth on the generic fiber of R.
$\lambda $
is smooth on the generic fiber of R.
In [Reference Böckle, Khare and ManningBKM21], we define the Wiles defect of R with respect to
![]() $\lambda $
to be
$\lambda $
to be
 $$ \begin{align} \delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}= \frac{\ell_{\mathcal O}(\Phi_\lambda(R))-\ell_{\mathcal O}(\Psi_\lambda(R))}{\ell_{\mathcal O}({\mathcal O}/p)}, \end{align} $$
$$ \begin{align} \delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}= \frac{\ell_{\mathcal O}(\Phi_\lambda(R))-\ell_{\mathcal O}(\Psi_\lambda(R))}{\ell_{\mathcal O}({\mathcal O}/p)}, \end{align} $$
which is known to be a nonnegative rational number. The reason for the normalization factor of
![]() $\log |{\mathcal O}/p|$
is to ensure that
$\log |{\mathcal O}/p|$
is to ensure that
![]() $\delta _\lambda (R)$
is invariant under expanding the coefficient ring
$\delta _\lambda (R)$
is invariant under expanding the coefficient ring
![]() ${\mathcal O}$
. Moreover, we have the following standard result (cf. [Reference WilesWil95, Reference LenstraLen95]):
${\mathcal O}$
. Moreover, we have the following standard result (cf. [Reference WilesWil95, Reference LenstraLen95]):
Lemma 2.1. For R as above, we have
![]() $\delta _\lambda (R) = 0$
if and only if
$\delta _\lambda (R) = 0$
if and only if
![]() $R=R^{\mathrm {tf}}$
and R is a complete intersection
$R=R^{\mathrm {tf}}$
and R is a complete intersection
Proof. From
![]() $\delta _\lambda (R)=0$
, we see by [Reference Fakhruddin, Khare and RamakrishnaFKR21, Proposition A.6] that the map
$\delta _\lambda (R)=0$
, we see by [Reference Fakhruddin, Khare and RamakrishnaFKR21, Proposition A.6] that the map
![]() $R \to R^{\mathrm {tf}}$
is an isomorphism of complete intersections.
$R \to R^{\mathrm {tf}}$
is an isomorphism of complete intersections.
Venkatesh, in an unpublished note [Reference VenkateshVen16], observed that
![]() $\delta _\lambda (R)$
can be expressed in terms of two other invariants of R (see Appendix A of this paper for a detailed proof of a more general version of Venkatesh’s observation).
$\delta _\lambda (R)$
can be expressed in terms of two other invariants of R (see Appendix A of this paper for a detailed proof of a more general version of Venkatesh’s observation).
First, let R act on
![]() $E/{\mathcal O}$
through its quotient
$E/{\mathcal O}$
through its quotient
![]() $R\xrightarrow {\lambda } {\mathcal O}$
. Venkatesh’s first invariant is simply the first André–Quillen cohomology group
$R\xrightarrow {\lambda } {\mathcal O}$
. Venkatesh’s first invariant is simply the first André–Quillen cohomology group
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
To define Venkatesh’s second invariant, we will fix an
![]() ${\mathcal O}$
-algebra
${\mathcal O}$
-algebra
![]() $\widetilde {R}$
and a surjection
$\widetilde {R}$
and a surjection
![]() $\varphi :\widetilde {R}\twoheadrightarrow R$
with the properties that
$\varphi :\widetilde {R}\twoheadrightarrow R$
with the properties that
-
•
 $\widetilde {R}$
is a complete intersection of dimension
$\widetilde {R}$
is a complete intersection of dimension
 $1$
, finite free over
$1$
, finite free over
 ${\mathcal O}$
.
${\mathcal O}$
. -
•
 $\Phi _{\lambda \circ \varphi }(\widetilde {R})$
is finite.
$\Phi _{\lambda \circ \varphi }(\widetilde {R})$
is finite.
(such a ring always exists, as explained in Appendix A). When there is no chance of confusion we will also use
![]() $\lambda $
to denote the induced map
$\lambda $
to denote the induced map
![]() $\lambda \circ \varphi :\widetilde {R}\twoheadrightarrow R\twoheadrightarrow {\mathcal O}$
.
$\lambda \circ \varphi :\widetilde {R}\twoheadrightarrow R\twoheadrightarrow {\mathcal O}$
.
Now, write
![]() $I=\ker \varphi $
so that
$I=\ker \varphi $
so that
![]() $\lambda (I) = 0$
. As
$\lambda (I) = 0$
. As
![]() $\widetilde {R}$
-modules, we have that
$\widetilde {R}$
-modules, we have that
![]() $\operatorname {\mathrm {Fitt}}(I)\subseteq \widetilde {R}[I]$
, and hence
$\operatorname {\mathrm {Fitt}}(I)\subseteq \widetilde {R}[I]$
, and hence
![]() $\lambda (\operatorname {\mathrm {Fitt}}(I))\subseteq \lambda (\widetilde {R}[I])$
as ideals of
$\lambda (\operatorname {\mathrm {Fitt}}(I))\subseteq \lambda (\widetilde {R}[I])$
as ideals of
![]() ${\mathcal O}$
(and in fact, both of these ideals are nonzero as explained in Appendix A). We then define Venkatesh’s second invariant to be the cyclic
${\mathcal O}$
(and in fact, both of these ideals are nonzero as explained in Appendix A). We then define Venkatesh’s second invariant to be the cyclic
![]() ${\mathcal O}$
-module
${\mathcal O}$
-module
A priori, this looks like it will depend on the choice of complete intersection
![]() $\widetilde {R}$
, but the work of Appendix A shows that it in fact depends only on R and
$\widetilde {R}$
, but the work of Appendix A shows that it in fact depends only on R and
![]() $\lambda $
. The main result Proposition A.6 of Appendix A is the following formula for the Wiles defect
$\lambda $
. The main result Proposition A.6 of Appendix A is the following formula for the Wiles defect
![]() $\delta _\lambda (R)$
. We recall as noted earlier that [Reference Tilouine and UrbanTU22, Proposition 4] proves a particular case (when
$\delta _\lambda (R)$
. We recall as noted earlier that [Reference Tilouine and UrbanTU22, Proposition 4] proves a particular case (when
![]() $C_{1,\lambda }(R)$
is trivial) of this formula.
$C_{1,\lambda }(R)$
is trivial) of this formula.
Theorem 2.2 (see A.6).
If R and
![]() $\lambda :R\twoheadrightarrow {\mathcal O}$
are as described above, and
$\lambda :R\twoheadrightarrow {\mathcal O}$
are as described above, and
![]() $\Phi _\lambda (R)$
is finite, then
$\Phi _\lambda (R)$
is finite, then
 $$\begin{align*}\frac{|\operatorname{\mathrm{Der}}^1_{\mathcal O}(R,E/{\mathcal O})|}{|C_{1,\lambda}(R)|} = \frac{|\Phi_\lambda(R)|}{|\Psi_\lambda(R)|}. \end{align*}$$
$$\begin{align*}\frac{|\operatorname{\mathrm{Der}}^1_{\mathcal O}(R,E/{\mathcal O})|}{|C_{1,\lambda}(R)|} = \frac{|\Phi_\lambda(R)|}{|\Psi_\lambda(R)|}. \end{align*}$$
In particular,
 $\displaystyle \delta _\lambda (R) = \frac {\log |\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log |C_{1,\lambda }(R)|}{\log |{\mathcal O}/p|}$
.
$\displaystyle \delta _\lambda (R) = \frac {\log |\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log |C_{1,\lambda }(R)|}{\log |{\mathcal O}/p|}$
.
Remark 2.3. In practice, one is often interested in the Wiles defect
![]() $\delta _\lambda (M)$
(as defined in [Reference Böckle, Khare and ManningBKM21, Section 3]) of a particular module M over R, as well as, or instead of
$\delta _\lambda (M)$
(as defined in [Reference Böckle, Khare and ManningBKM21, Section 3]) of a particular module M over R, as well as, or instead of
![]() $\delta _\lambda (R)$
. However, in many cases relevant to us, the results of [Reference Böckle, Khare and ManningBKM21] imply that
$\delta _\lambda (R)$
. However, in many cases relevant to us, the results of [Reference Böckle, Khare and ManningBKM21] imply that
![]() $\delta _\lambda (R) = \delta _\lambda (M)$
, so we will focus mainly on
$\delta _\lambda (R) = \delta _\lambda (M)$
, so we will focus mainly on
![]() $\delta _\lambda (R)$
in this paper, except in §7 in which we apply Theorem 6.5 which determines defects of Hecke rings to detect the defect of modules that they act on.
$\delta _\lambda (R)$
in this paper, except in §7 in which we apply Theorem 6.5 which determines defects of Hecke rings to detect the defect of modules that they act on.
We do suspect that there may exist some generalization of Theorem 2.2 which would directly express
![]() $\delta _\lambda (M)$
in terms of similar invariants. Such a generalization would allow us to directly study
$\delta _\lambda (M)$
in terms of similar invariants. Such a generalization would allow us to directly study
![]() $\delta _\lambda (M)$
in cases when we can not prove it is equal to
$\delta _\lambda (M)$
in cases when we can not prove it is equal to
![]() $\delta _\lambda (R)$
, and could possibly work in cases when the results of this paper do not apply. The results of [Reference Brochard, Iyengar and KhareBIK23, Theorem 1.2] support such a suspicion.
$\delta _\lambda (R)$
, and could possibly work in cases when the results of this paper do not apply. The results of [Reference Brochard, Iyengar and KhareBIK23, Theorem 1.2] support such a suspicion.
We end this section by remarking that the definition of the Wiles defect
![]() $\delta _\lambda (R)$
in [Reference Böckle, Khare and ManningBKM21], which depends on finiteness of
$\delta _\lambda (R)$
in [Reference Böckle, Khare and ManningBKM21], which depends on finiteness of
![]() $\Phi _\lambda (R)$
, makes sense for a complete Noetherian, Cohen–Macaulay local
$\Phi _\lambda (R)$
, makes sense for a complete Noetherian, Cohen–Macaulay local
![]() ${\mathcal O}$
-algebra R only when R is of dimension one.
${\mathcal O}$
-algebra R only when R is of dimension one.
Lemma 2.4. Let R be a complete Noetherian local
![]() ${\mathcal O}$
-algebra together with an augmentation
${\mathcal O}$
-algebra together with an augmentation
![]() $\lambda : R \to {\mathcal O}$
such that
$\lambda : R \to {\mathcal O}$
such that
![]() $\Phi _\lambda (R)$
is a finite abelian group then
$\Phi _\lambda (R)$
is a finite abelian group then
![]() $\ker (\lambda )$
is a minimal prime ideal. If we further assume that R is Cohen–Macaulay then R is of dimension one.
$\ker (\lambda )$
is a minimal prime ideal. If we further assume that R is Cohen–Macaulay then R is of dimension one.
Proof. Let
![]() $\ker (\lambda )={\mathfrak p}$
, and we observe that the localization
$\ker (\lambda )={\mathfrak p}$
, and we observe that the localization
![]() $R_{{\mathfrak p}}$
is a local ring with maximal ideal
$R_{{\mathfrak p}}$
is a local ring with maximal ideal
![]() $m={\mathfrak p}R_{{\mathfrak p}}$
and infinite residue field E, and by our assumption that
$m={\mathfrak p}R_{{\mathfrak p}}$
and infinite residue field E, and by our assumption that
![]() $\ker (\lambda )/\ker (\lambda )^2$
is finite we deduce that
$\ker (\lambda )/\ker (\lambda )^2$
is finite we deduce that
![]() $m=m^2$
and thus
$m=m^2$
and thus
![]() $m=0$
. This implies that
$m=0$
. This implies that
![]() $R_{\mathfrak p}$
is a field, and thus
$R_{\mathfrak p}$
is a field, and thus
![]() ${\mathfrak p}$
is a minimal prime ideal of R. As Cohen–Macaulay rings are equidimensional, we deduce the last statement of the lemma.
${\mathfrak p}$
is a minimal prime ideal of R. As Cohen–Macaulay rings are equidimensional, we deduce the last statement of the lemma.
3 Wiles defect for higher-dimensional Cohen–Macaulay rings
We define and prove properties of the Wiles defect for (higher-dimensional) rings in the category
![]() $C_{\mathcal O}$
. The category
$C_{\mathcal O}$
. The category
![]() $C_{\mathcal O}$
was alluded to in the introduction.
$C_{\mathcal O}$
was alluded to in the introduction.
Definition 3.1. The category
![]() $C_{\mathcal O}$
consists of tuples
$C_{\mathcal O}$
consists of tuples
![]() $(R, \lambda _R)$
such that:
$(R, \lambda _R)$
such that:
-
• R a complete, Noetherian local
 ${\mathcal O}$
-algebra, with maximal ideal
${\mathcal O}$
-algebra, with maximal ideal
 ${\mathfrak m}$
and residue field
${\mathfrak m}$
and residue field
 $k={\mathcal O}/ \varpi$
, which is flat over
$k={\mathcal O}/ \varpi$
, which is flat over
 ${\mathcal O}$
and Cohen–Macaulay;
${\mathcal O}$
and Cohen–Macaulay; -
•
 $\lambda _R: R \to {\mathcal O}$
is an augmentation (that is, a continuous surjective
$\lambda _R: R \to {\mathcal O}$
is an augmentation (that is, a continuous surjective
 ${\mathcal O}$
-algebra homomorphism) such that
${\mathcal O}$
-algebra homomorphism) such that
 $\operatorname {\mathrm {Spec}} R[1/\varpi ]$
is formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R[1/\varpi ]$
is formally smooth at the point corresponding to
 $\lambda $
.
$\lambda $
.
The morphisms in the category
![]() $C_{\mathcal O}$
are local homomorphisms of
$C_{\mathcal O}$
are local homomorphisms of
![]() ${\mathcal O}$
-algebras compatible with the augmentation, namely local
${\mathcal O}$
-algebras compatible with the augmentation, namely local
![]() ${\mathcal O}$
-algebra maps
${\mathcal O}$
-algebra maps
![]() $f \colon R\to S$
such that
$f \colon R\to S$
such that
![]() $\lambda _S\circ f=\lambda _R$
. (As the augmentation considered will be clear from the context, we will often denote
$\lambda _S\circ f=\lambda _R$
. (As the augmentation considered will be clear from the context, we will often denote
![]() $\lambda _R$
by just
$\lambda _R$
by just
![]() $\lambda $
and also given a pair
$\lambda $
and also given a pair
![]() $(R,\lambda ) \in C_{\mathcal O}$
we will sometimes write
$(R,\lambda ) \in C_{\mathcal O}$
we will sometimes write
![]() $R \in C_{\mathcal O}$
.)
$R \in C_{\mathcal O}$
.)
In light of Lemma 2.4, the definition of the Wiles defect as given in [Reference Böckle, Khare and ManningBKM21] can be applied to
![]() $R \in C_{\mathcal O}$
only when R is of dimension 1. Thus, we define the Wiles defect
$R \in C_{\mathcal O}$
only when R is of dimension 1. Thus, we define the Wiles defect
![]() $\delta _\lambda (R)$
for
$\delta _\lambda (R)$
for
![]() $R \in C_{\mathcal O}$
(cf. Definition 3.24) motivated by the Venkatesh formula of the defect
$R \in C_{\mathcal O}$
(cf. Definition 3.24) motivated by the Venkatesh formula of the defect
![]() $\delta _\lambda (R)$
for
$\delta _\lambda (R)$
for
![]() $R \in C_{\mathcal O}$
when R is one-dimensional. This requires some preliminary work that we undertake first. To orient the reader, we indicate the main steps towards the definition.
$R \in C_{\mathcal O}$
when R is one-dimensional. This requires some preliminary work that we undertake first. To orient the reader, we indicate the main steps towards the definition.
The Wiles defect is expressed in terms of:
-
(i) the invariant
 $\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R,E/{\mathcal O})$
which can be directly defined using a continuous version of the André–Quillen cohomology of rings (cf. §3.3, in particular Theorem 3.20);
$\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R,E/{\mathcal O})$
which can be directly defined using a continuous version of the André–Quillen cohomology of rings (cf. §3.3, in particular Theorem 3.20); -
(ii) the invariant
 $C_{1,\lambda }(R)$
that is defined in terms of an auxiliary complete intersection
$C_{1,\lambda }(R)$
that is defined in terms of an auxiliary complete intersection
 $\widetilde {R}$
surjecting onto R (cf. §3.2, in particular Corollary 3.12, which shows that this does not depend on the choice of
$\widetilde {R}$
surjecting onto R (cf. §3.2, in particular Corollary 3.12, which shows that this does not depend on the choice of
 $\widetilde {R}$
).
$\widetilde {R}$
).
The Wiles defect
![]() $\delta _\lambda (R)$
is then defined (cf. Definition 3.24) via the formula
$\delta _\lambda (R)$
is then defined (cf. Definition 3.24) via the formula
 $$\begin{align*}\displaystyle \delta_\lambda(R) = \frac{\log|\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log|C_{1,\lambda}(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
$$\begin{align*}\displaystyle \delta_\lambda(R) = \frac{\log|\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|-\log|C_{1,\lambda}(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
We show below the key property of independence of the invariants we define under forming quotients by regular sequences (see §3.2 and 3.3). We also provide formulas for the invariants in terms of certain complete intersection rings that surject onto
![]() $ R \in C_{\mathcal O}$
, similar to the treatment in the appendix, but in higher dimensions.
$ R \in C_{\mathcal O}$
, similar to the treatment in the appendix, but in higher dimensions.
In the case when R is of dimension 1, this definition of the defect for
![]() $R \in C_{\mathcal O}$
agrees, by Theorem 2.2 and Proposition 3.27, with the definition of the Wiles defect defined in [Reference Böckle, Khare and ManningBKM21] as
$R \in C_{\mathcal O}$
agrees, by Theorem 2.2 and Proposition 3.27, with the definition of the Wiles defect defined in [Reference Böckle, Khare and ManningBKM21] as
 $$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
$$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}.\end{align*}$$
(Note that when R is of dimension one, the finiteness of
![]() $|\Phi _\lambda (R)|$
is equivalent to saying that
$|\Phi _\lambda (R)|$
is equivalent to saying that
![]() $\lambda : R \to {\mathcal O}$
has formally smooth generic fiber.)
$\lambda : R \to {\mathcal O}$
has formally smooth generic fiber.)
For the remainder of this section, we will fix
![]() $(R,\lambda _R)\in C_{\mathcal O}$
, and let
$(R,\lambda _R)\in C_{\mathcal O}$
, and let
![]() $\lambda = \lambda _R:R\to {\mathcal O}$
denote the augmentation. Recall that by the definition of
$\lambda = \lambda _R:R\to {\mathcal O}$
denote the augmentation. Recall that by the definition of
![]() $C_{\mathcal O}$
, R is Cohen–Macaulay. We will let
$C_{\mathcal O}$
, R is Cohen–Macaulay. We will let
![]() $d = \dim _{\mathcal O} R$
, and consider the power series ring
$d = \dim _{\mathcal O} R$
, and consider the power series ring
![]() $S = {\mathcal O}[[y_1,\ldots ,y_d]]$
.
$S = {\mathcal O}[[y_1,\ldots ,y_d]]$
.
We will introduce a number of other auxiliary rings and morphisms which will be used to define the invariants
![]() $\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R,E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}_{\mathcal O}^1(R,E/{\mathcal O})$
and
![]() $C_{1,\lambda }(R)$
and to prove the key property of invariance under regular sequences. For ease of reading, we will summarize all of this in the following commutative diagram:
$C_{1,\lambda }(R)$
and to prove the key property of invariance under regular sequences. For ease of reading, we will summarize all of this in the following commutative diagram:

Here:
-
•
 $\theta $
is an injective map
$\theta $
is an injective map
 ${\mathcal O}$
-algebra map, satisfying Property (P);
${\mathcal O}$
-algebra map, satisfying Property (P); -
•
 $\widetilde {R}$
is a complete intersection with
$\widetilde {R}$
is a complete intersection with
 $\dim _{\mathcal O} \widetilde {R} = \dim _{\mathcal O} R = d$
and
$\dim _{\mathcal O} \widetilde {R} = \dim _{\mathcal O} R = d$
and
 $\varphi :\widetilde {R}\to R$
is a continuous surjective map with kernel
$\varphi :\widetilde {R}\to R$
is a continuous surjective map with kernel
 $I\subseteq \widetilde {R}$
(the precise properties satisfied by
$I\subseteq \widetilde {R}$
(the precise properties satisfied by
 $(\widetilde {R},I,\varphi )$
are outlined in Property (CI));
$(\widetilde {R},I,\varphi )$
are outlined in Property (CI)); -
•
 ${\widetilde {\theta }}:S\hookrightarrow \widetilde {R}$
is a lift of
${\widetilde {\theta }}:S\hookrightarrow \widetilde {R}$
is a lift of
 $\theta $
along
$\theta $
along
 $\varphi $
, satisfying certain properties, which is proven to exist in Lemma 3.7;
$\varphi $
, satisfying certain properties, which is proven to exist in Lemma 3.7; -
• We will usually identify S with its images in R and
 $\widetilde {R}$
so that in particular
$\widetilde {R}$
so that in particular
 $y_1,\ldots ,y_d\in R$
and
$y_1,\ldots ,y_d\in R$
and
 $y_1,\ldots ,y_d\in \widetilde {R}$
;
$y_1,\ldots ,y_d\in \widetilde {R}$
; -
• Treating R and
 $\widetilde {R}$
as S-modules via
$\widetilde {R}$
as S-modules via
 $\theta $
and
$\theta $
and
 ${\widetilde {\theta }}$
, we have
${\widetilde {\theta }}$
, we have
 $R_\theta = R\otimes _S{\mathcal O}$
and
$R_\theta = R\otimes _S{\mathcal O}$
and
 $\widetilde {R}_\theta = \widetilde {R}\otimes _S{\mathcal O}$
. Equivalently,
$\widetilde {R}_\theta = \widetilde {R}\otimes _S{\mathcal O}$
. Equivalently,
 $R_\theta = R/(\theta (y_1),\ldots ,\theta (y_d))$
and
$R_\theta = R/(\theta (y_1),\ldots ,\theta (y_d))$
and
 $\widetilde {R}_\theta = \widetilde {R}/({\widetilde {\theta }}(y_1),\ldots ,{\widetilde {\theta }}(y_d))$
;
$\widetilde {R}_\theta = \widetilde {R}/({\widetilde {\theta }}(y_1),\ldots ,{\widetilde {\theta }}(y_d))$
; -
•
 $\varphi _\theta :\widetilde {R}_\theta \to R_\theta $
is the map induced by
$\varphi _\theta :\widetilde {R}_\theta \to R_\theta $
is the map induced by
 $\varphi $
;
$\varphi $
; -
•
 $\lambda _\theta :R_\theta \to {\mathcal O}$
is the augmentation induced by
$\lambda _\theta :R_\theta \to {\mathcal O}$
is the augmentation induced by
 $\lambda $
;
$\lambda $
; -
•
 $\pi _\theta :\widetilde {R}\twoheadrightarrow \widetilde {R}_\theta $
is the quotient map;
$\pi _\theta :\widetilde {R}\twoheadrightarrow \widetilde {R}_\theta $
is the quotient map; -
•
 $I_\theta = \ker \varphi _\theta $
. From the surjectivity of
$I_\theta = \ker \varphi _\theta $
. From the surjectivity of
 $\pi _\theta $
, it also follows that
$\pi _\theta $
, it also follows that
 $I_\theta = \pi _\theta (I)$
;
$I_\theta = \pi _\theta (I)$
; -
•
 $\widetilde {\lambda }:\widetilde {R}\twoheadrightarrow {\mathcal O}$
and
$\widetilde {\lambda }:\widetilde {R}\twoheadrightarrow {\mathcal O}$
and
 $\widetilde {\lambda }_\theta :\widetilde {R}_\theta \twoheadrightarrow {\mathcal O}$
are simply the induced augmentations
$\widetilde {\lambda }_\theta :\widetilde {R}_\theta \twoheadrightarrow {\mathcal O}$
are simply the induced augmentations
 $\widetilde {\lambda } = \lambda \circ \varphi $
and
$\widetilde {\lambda } = \lambda \circ \varphi $
and
 $\widetilde {\lambda }_\theta = \lambda _\theta \circ \varphi _\theta $
.
$\widetilde {\lambda }_\theta = \lambda _\theta \circ \varphi _\theta $
.
We say that the inclusion
![]() $\theta :S \hookrightarrow R$
satisfies (P) if the following conditions hold:
$\theta :S \hookrightarrow R$
satisfies (P) if the following conditions hold:
Property (P).
-
•
 $\theta :S \hookrightarrow R$
is a continuous
$\theta :S \hookrightarrow R$
is a continuous
 ${\mathcal O}$
-algebra homomorphism.
${\mathcal O}$
-algebra homomorphism. -
•
 $\theta $
makes R into a finite free S-module (so that
$\theta $
makes R into a finite free S-module (so that
 $(\theta (y_1),\ldots ,\theta (y_d),\varpi )$
is a regular sequence for R).
$(\theta (y_1),\ldots ,\theta (y_d),\varpi )$
is a regular sequence for R). -
•
 $(\theta (y_1),\ldots ,\theta (y_d))\subseteq \ker \lambda $
.
$(\theta (y_1),\ldots ,\theta (y_d))\subseteq \ker \lambda $
. -
• If
 $R_\theta = R/(\theta (y_1),\ldots ,\theta (y_d)) = R \otimes _{S}{\mathcal O}$
and
$R_\theta = R/(\theta (y_1),\ldots ,\theta (y_d)) = R \otimes _{S}{\mathcal O}$
and
 $\lambda _\theta :R_\theta \twoheadrightarrow {\mathcal O}$
is the map induced by
$\lambda _\theta :R_\theta \twoheadrightarrow {\mathcal O}$
is the map induced by
 $\lambda $
, then
$\lambda $
, then
 $\Phi _{\lambda _\theta }(R_\theta )$
is finite.
$\Phi _{\lambda _\theta }(R_\theta )$
is finite.
We will say that the triple
![]() $(\widetilde {R}, I, \varphi )$
satisfies (CI) if:
$(\widetilde {R}, I, \varphi )$
satisfies (CI) if:
Property (CI).
-
•
 $\widetilde {R}$
is a complete, Noetherian local
$\widetilde {R}$
is a complete, Noetherian local
 ${\mathcal O}$
-algebra, flat and equidimensional over
${\mathcal O}$
-algebra, flat and equidimensional over
 ${\mathcal O}$
of relative dimension d.
${\mathcal O}$
of relative dimension d. -
•
 $\widetilde {R}$
is a complete intersection.
$\widetilde {R}$
is a complete intersection. -
•
 $\varphi :\widetilde {R}\to R$
is a continuous surjection of
$\varphi :\widetilde {R}\to R$
is a continuous surjection of
 ${\mathcal O}$
-algebras with
${\mathcal O}$
-algebras with
 $I=\ker \varphi $
.
$I=\ker \varphi $
. -
• The point corresponding to
 $\lambda \circ \varphi $
in
$\lambda \circ \varphi $
in
 $\operatorname {\mathrm {Spec}} \widetilde {R}[1/\varpi ]$
is a formally smooth point.
$\operatorname {\mathrm {Spec}} \widetilde {R}[1/\varpi ]$
is a formally smooth point.
We note the following two results, which will be proved in Section 3.1:
Proposition 3.2. For any
![]() $(R,\lambda )\in C_{\mathcal O}$
with
$(R,\lambda )\in C_{\mathcal O}$
with
![]() $\dim _{\mathcal O} R = d$
, a map
$\dim _{\mathcal O} R = d$
, a map
![]() $\theta $
satisfying property (P) exists.
$\theta $
satisfying property (P) exists.
Proposition 3.3. For any
![]() $(R,\lambda )\in C_{\mathcal O}$
with
$(R,\lambda )\in C_{\mathcal O}$
with
![]() $\dim _{\mathcal O} R = d$
, there exists a triple
$\dim _{\mathcal O} R = d$
, there exists a triple
![]() $(\widetilde {R},I,\varphi )$
satisfying Property (CI).
$(\widetilde {R},I,\varphi )$
satisfying Property (CI).
We will give the proof of Proposition 3.2 in Section 3.1, after the proof of Lemma 3.6. Proposition 3.3 will be a direct consequence of Lemma 3.6.
Note that Property (P) implies that
![]() $R_\theta $
is finite free over
$R_\theta $
is finite free over
![]() ${\mathcal O}$
and that
${\mathcal O}$
and that
![]() $\Phi _{\lambda _\theta }(R_\theta )$
is finite. Thus, it satisfies the conditions of Section 2, and so we may consider the Wiles defect
$\Phi _{\lambda _\theta }(R_\theta )$
is finite. Thus, it satisfies the conditions of Section 2, and so we may consider the Wiles defect
![]() $\delta _{\lambda _\theta }(R_\theta )$
and the Venkatesh invariants
$\delta _{\lambda _\theta }(R_\theta )$
and the Venkatesh invariants
![]() $\operatorname {\mathrm {Der}}^1_{{\mathcal O}}(R_\theta ,E/{\mathcal O})$
and
$\operatorname {\mathrm {Der}}^1_{{\mathcal O}}(R_\theta ,E/{\mathcal O})$
and
![]() $C_{1,\lambda _\theta }(R_\theta )$
. The main result of this section is Theorem 3.25, which shows that all three of these quantities depend only on R and
$C_{1,\lambda _\theta }(R_\theta )$
. The main result of this section is Theorem 3.25, which shows that all three of these quantities depend only on R and
![]() $\lambda $
and not on the choice of
$\lambda $
and not on the choice of
![]() $\theta $
.
$\theta $
.
This section is structured as follows: In Section 3.1, we prove Propositions 3.2 and 3.3 and establish the basic properties of all of the auxiliary rings we are considering; Section 3.2 proves the invariance of
![]() $C_{1,\lambda _\theta }(R_\theta )$
; Section 3.3 proves the invariance of
$C_{1,\lambda _\theta }(R_\theta )$
; Section 3.3 proves the invariance of
![]() $\operatorname {\mathrm {Der}}^1_{{\mathcal O}}(R_\theta ,E/{\mathcal O})$
; Section 3.4 uses the prior work to give a definition the invariants
$\operatorname {\mathrm {Der}}^1_{{\mathcal O}}(R_\theta ,E/{\mathcal O})$
; Section 3.4 uses the prior work to give a definition the invariants
![]() $D_{1,\lambda }(R)$
and
$D_{1,\lambda }(R)$
and
![]() $c_{1,\lambda }(R)$
and of the Wiles defect
$c_{1,\lambda }(R)$
and of the Wiles defect
![]() $\delta _\lambda (R)$
, for any
$\delta _\lambda (R)$
, for any
![]() $(R,\lambda )\in C_{\mathcal O}$
; lastly, Section 3.5 proves a key property of these invariants – that they are compatible with completed tensor products (see Proposition 3.32).
$(R,\lambda )\in C_{\mathcal O}$
; lastly, Section 3.5 proves a key property of these invariants – that they are compatible with completed tensor products (see Proposition 3.32).
Remark 3.4. In our main number theoretic applications in Section 6, the rings R and S will typically be the rings
![]() $R_\infty $
(or
$R_\infty $
(or
![]() $R_\infty ^\tau $
in our notation) and
$R_\infty ^\tau $
in our notation) and
![]() $S_\infty $
appearing the classical in the Taylor–Wiles–Kisin patching method – see Theorem 6.4 for specifics. The ring
$S_\infty $
appearing the classical in the Taylor–Wiles–Kisin patching method – see Theorem 6.4 for specifics. The ring
![]() $R_\theta $
will be a global Galois deformation ring, denoted
$R_\theta $
will be a global Galois deformation ring, denoted
![]() $R_0^\tau $
, and the augmentation
$R_0^\tau $
, and the augmentation
![]() $\lambda _\theta :R_\theta \to {\mathcal O}$
will be induced by a Galois representation
$\lambda _\theta :R_\theta \to {\mathcal O}$
will be induced by a Galois representation
![]() $\rho _\lambda :G_F\to {\mathrm {GL}}_2({\mathcal O})$
, where F is a (totally real) number field. The augmentation
$\rho _\lambda :G_F\to {\mathrm {GL}}_2({\mathcal O})$
, where F is a (totally real) number field. The augmentation
![]() $\lambda :R\to {\mathcal O}$
will simply be the pullback of
$\lambda :R\to {\mathcal O}$
will simply be the pullback of
![]() $\lambda _\theta $
.
$\lambda _\theta $
.
The map
![]() $\theta :S\to R$
, and hence the ring
$\theta :S\to R$
, and hence the ring
![]() $R_\theta $
and the augmentation
$R_\theta $
and the augmentation
![]() $\lambda _\theta :R_\theta \to {\mathcal O}$
, will depend on subtle global Galois theoretic information involving the representation
$\lambda _\theta :R_\theta \to {\mathcal O}$
, will depend on subtle global Galois theoretic information involving the representation
![]() $\rho _\lambda $
. However, the ring R and the augmentation
$\rho _\lambda $
. However, the ring R and the augmentation
![]() $\lambda :R\to {\mathcal O}$
will depend only on the restrictions
$\lambda :R\to {\mathcal O}$
will depend only on the restrictions
![]() $\rho _\lambda |_{G_{F_v}}$
for a finite collection of places v of F – that is, only on local information. Thus, Theorem 3.25 will imply the the Wiles defect
$\rho _\lambda |_{G_{F_v}}$
for a finite collection of places v of F – that is, only on local information. Thus, Theorem 3.25 will imply the the Wiles defect
![]() $\delta _{\lambda _\theta }(R_\theta )$
, a priori a global invariant, will depend only on local information. See Theorem 6.5 for a precise result.
$\delta _{\lambda _\theta }(R_\theta )$
, a priori a global invariant, will depend only on local information. See Theorem 6.5 for a precise result.
The ring
![]() $\widetilde {R}$
will have no particular number theoretic significance. It will be chosen in Section 5 in order to facilitate computations of the Wiles defects of various local deformation rings.
$\widetilde {R}$
will have no particular number theoretic significance. It will be chosen in Section 5 in order to facilitate computations of the Wiles defects of various local deformation rings.
3.1 Complete intersection (CI) covers
We begin with the following lemma:
Lemma 3.5. Let S be a complete, Noetherian local
![]() ${\mathcal O}$
-algebra with an augmentation
${\mathcal O}$
-algebra with an augmentation
![]() $\lambda \colon S\to {\mathcal O}$
, and let
$\lambda \colon S\to {\mathcal O}$
, and let
![]() $d>0$
. Suppose that
$d>0$
. Suppose that
![]() $S[1/\varpi ]$
is formally smooth at
$S[1/\varpi ]$
is formally smooth at
![]() $\lambda $
of dimension
$\lambda $
of dimension
![]() $n\ge d$
and that there are elements
$n\ge d$
and that there are elements
![]() $f_1,\ldots ,f_d\in \operatorname {\mathrm {ker}} \lambda $
such that
$f_1,\ldots ,f_d\in \operatorname {\mathrm {ker}} \lambda $
such that
![]() $f_1,\ldots ,f_d,\varpi $
is a regular sequence in S. Then there exist
$f_1,\ldots ,f_d,\varpi $
is a regular sequence in S. Then there exist
![]() $h_1,\ldots ,h_d\in (\operatorname {\mathrm {ker}} \lambda \cap (f_1,\ldots ,f_d,\varpi ))$
such that
$h_1,\ldots ,h_d\in (\operatorname {\mathrm {ker}} \lambda \cap (f_1,\ldots ,f_d,\varpi ))$
such that
![]() $h_1,\ldots ,h_d,\varpi $
is a regular sequence in S and such that for
$h_1,\ldots ,h_d,\varpi $
is a regular sequence in S and such that for
![]() $A=S/(h_1,\ldots ,h_d)$
and the induced augmentation
$A=S/(h_1,\ldots ,h_d)$
and the induced augmentation
![]() $\lambda _A\colon A\to {\mathcal O}$
, the ring
$\lambda _A\colon A\to {\mathcal O}$
, the ring
![]() $A[1/\varpi ]$
is formally smooth at
$A[1/\varpi ]$
is formally smooth at
![]() $\lambda _A$
of dimension
$\lambda _A$
of dimension
![]() $n-d$
.
$n-d$
.
Proof. By replacing
![]() $(f_1,\ldots ,f_d)$
by
$(f_1,\ldots ,f_d)$
by
![]() $(f_1^2,\ldots ,f_d^2)$
, we may assume that
$(f_1^2,\ldots ,f_d^2)$
, we may assume that
![]() $(f_1,\ldots ,f_d)\subset \operatorname {\mathrm {ker}}\lambda ^2$
; see [Reference MatsumuraMat80, 15.A, Theorem 26]. Write
$(f_1,\ldots ,f_d)\subset \operatorname {\mathrm {ker}}\lambda ^2$
; see [Reference MatsumuraMat80, 15.A, Theorem 26]. Write
![]() $S[1/\varpi ]$
for the localization of S at
$S[1/\varpi ]$
for the localization of S at
![]() $\varpi $
and
$\varpi $
and
![]() $\widehat {S[1/\varpi ]}$
for the completion of the latter at the point corresponding to
$\widehat {S[1/\varpi ]}$
for the completion of the latter at the point corresponding to
![]() $\lambda $
. By our hypothesis, the ring
$\lambda $
. By our hypothesis, the ring
![]() $\widehat {S[1/\varpi ]}$
is a power series ring over E in
$\widehat {S[1/\varpi ]}$
is a power series ring over E in
![]() $n\ge d$
indeterminates. Let
$n\ge d$
indeterminates. Let
![]() $\widehat I$
denote its maximal ideal. Choose
$\widehat I$
denote its maximal ideal. Choose
![]() $g_1,\ldots ,g_d$
in
$g_1,\ldots ,g_d$
in
![]() $\ker \lambda $
whose images in
$\ker \lambda $
whose images in
![]() $\widehat I/\widehat I^2$
are linearly independent over E. Then
$\widehat I/\widehat I^2$
are linearly independent over E. Then
![]() $(h_1,\ldots ,h_d)$
with
$(h_1,\ldots ,h_d)$
with
![]() $h_i=f_i+\varpi g_i$
has all properties required.
$h_i=f_i+\varpi g_i$
has all properties required.
Lemma 3.6. Suppose B is a complete, Noetherian local
![]() ${\mathcal O}$
-algebra with
${\mathcal O}$
-algebra with
![]() $\dim B=d+1$
and
$\dim B=d+1$
and
![]() $\dim B/\varpi =d$
and
$\dim B/\varpi =d$
and
![]() $\lambda :B\to {\mathcal O}$
is an augmentation such that
$\lambda :B\to {\mathcal O}$
is an augmentation such that
![]() $\operatorname {\mathrm {Spec}} B[1/\varpi ]$
is formally smooth at
$\operatorname {\mathrm {Spec}} B[1/\varpi ]$
is formally smooth at
![]() $\lambda $
of dimension d. Then there exists a Noetherian
$\lambda $
of dimension d. Then there exists a Noetherian
![]() ${\mathcal O}$
-algebra A and a surjective homomorphism
${\mathcal O}$
-algebra A and a surjective homomorphism
![]() $\pi \colon A\to B$
such that the following holds:
$\pi \colon A\to B$
such that the following holds:
-
1. The ring A is local and complete, a complete intersection, flat over
 ${\mathcal O}$
and of relative dimension d.
${\mathcal O}$
and of relative dimension d. -
2. The map
 $\pi [1/\varpi ]\colon A[1/\varpi ]\to B[1/\varpi ]$
, obtained from
$\pi [1/\varpi ]\colon A[1/\varpi ]\to B[1/\varpi ]$
, obtained from
 $\pi $
by inverting
$\pi $
by inverting
 $\varpi $
, induces an isomorphism after completion at the points corresponding to the augmentations
$\varpi $
, induces an isomorphism after completion at the points corresponding to the augmentations
 $\lambda $
and
$\lambda $
and
 $\mu =\lambda \circ \pi \colon A\to {\mathcal O}$
, respectively. In particular,
$\mu =\lambda \circ \pi \colon A\to {\mathcal O}$
, respectively. In particular,
 $\operatorname {\mathrm {Spec}} A[1/\varpi ]$
is formally smooth at
$\operatorname {\mathrm {Spec}} A[1/\varpi ]$
is formally smooth at
 $\mu $
of dimension d.
$\mu $
of dimension d.
Proof. Let
![]() $\Pi \colon S={\mathcal O}[[z_1,\ldots ,z_n]]\to B$
be a surjective ring homomorphism. Let
$\Pi \colon S={\mathcal O}[[z_1,\ldots ,z_n]]\to B$
be a surjective ring homomorphism. Let
![]() ${{\mathfrak p}}_\lambda \subset {\mathfrak m}_B$
be the prime ideal
${{\mathfrak p}}_\lambda \subset {\mathfrak m}_B$
be the prime ideal
![]() $\ker \lambda $
, and denote by
$\ker \lambda $
, and denote by
![]() ${\mathfrak q}_\lambda \subset {\mathfrak m}_S$
its inverse image under
${\mathfrak q}_\lambda \subset {\mathfrak m}_S$
its inverse image under
![]() $\Pi $
, that is,
$\Pi $
, that is,
![]() ${\mathfrak q}_\lambda =\ker \lambda \circ \Pi $
. Let
${\mathfrak q}_\lambda =\ker \lambda \circ \Pi $
. Let
![]() $m=n-d\ge 0$
.
$m=n-d\ge 0$
.
By hypothesis
![]() $B/\varpi $
has dimension d. Because S is
$B/\varpi $
has dimension d. Because S is
![]() $\varpi $
-torsion free and
$\varpi $
-torsion free and
![]() $S/\varpi $
is regular, we can find a regular sequence
$S/\varpi $
is regular, we can find a regular sequence
![]() $(f_1,\ldots ,f_m)$
in
$(f_1,\ldots ,f_m)$
in
![]() $\ker \Pi \subset S$
such that
$\ker \Pi \subset S$
such that
![]() $(f_1,\ldots ,f_m,\varpi )$
is a regular sequence. Because
$(f_1,\ldots ,f_m,\varpi )$
is a regular sequence. Because
![]() $S[1/\varpi ]$
is regular of dimension n and
$S[1/\varpi ]$
is regular of dimension n and
![]() ${\mathfrak q}_\lambda [1/\varpi ]$
is a maximal ideal of that ring, the ring
${\mathfrak q}_\lambda [1/\varpi ]$
is a maximal ideal of that ring, the ring
![]() $S[1/\varpi ]$
is formally smooth at
$S[1/\varpi ]$
is formally smooth at
![]() ${\mathfrak q}_\lambda [1/\varpi ]$
of dimension n.
${\mathfrak q}_\lambda [1/\varpi ]$
of dimension n.
It follows from Lemma 3.5 that there exist
![]() $h_1,\ldots ,h_m\in \operatorname {\mathrm {ker}} \Pi +\varpi S$
such that
$h_1,\ldots ,h_m\in \operatorname {\mathrm {ker}} \Pi +\varpi S$
such that
![]() $h_1,\ldots ,h_m,\varpi $
is a regular sequence in S and such that for
$h_1,\ldots ,h_m,\varpi $
is a regular sequence in S and such that for
![]() $A=S/(h_1,\ldots ,h_m)$
and induced augmentation
$A=S/(h_1,\ldots ,h_m)$
and induced augmentation
![]() $\lambda _A\colon A\to {\mathcal O}$
the ring
$\lambda _A\colon A\to {\mathcal O}$
the ring
![]() $A[1/\varpi ]$
is formally smooth at
$A[1/\varpi ]$
is formally smooth at
![]() $\lambda _A$
of dimension
$\lambda _A$
of dimension
![]() $n-m=d$
. It follows that one has an induced surjection
$n-m=d$
. It follows that one has an induced surjection
![]() $A\to B$
, where A is a local complete, complete intersection
$A\to B$
, where A is a local complete, complete intersection
![]() ${\mathcal O}$
-algebra, flat over
${\mathcal O}$
-algebra, flat over
![]() ${\mathcal O}$
of relative dimension d and that the induced surjection
${\mathcal O}$
of relative dimension d and that the induced surjection
![]() $A[1/\varpi ]\to B[1/\varpi ]$
becomes an isomorphism after completion at
$A[1/\varpi ]\to B[1/\varpi ]$
becomes an isomorphism after completion at
![]() ${\mathfrak q}_\lambda [1/\varpi ]$
.
${\mathfrak q}_\lambda [1/\varpi ]$
.
Proof of Proposition 3.2.
Because R is Cohen–Macaulay and flat over
![]() ${\mathcal O}$
of relative dimension d, we can find a regular sequence
${\mathcal O}$
of relative dimension d, we can find a regular sequence
![]() $\varpi ,f_1,\ldots ,f_d$
in R. If we replace each
$\varpi ,f_1,\ldots ,f_d$
in R. If we replace each
![]() $f_i$
by an element in
$f_i$
by an element in
![]() $f_i+\varpi R$
the resulting sequence is again regular. Now, using that
$f_i+\varpi R$
the resulting sequence is again regular. Now, using that
![]() $\operatorname {\mathrm {ker}} \lambda $
together with
$\operatorname {\mathrm {ker}} \lambda $
together with
![]() $\varpi $
generate the maximal ideal of R, we may assume that
$\varpi $
generate the maximal ideal of R, we may assume that
![]() $f_1,\ldots ,f_d$
lie in
$f_1,\ldots ,f_d$
lie in
![]() $\operatorname {\mathrm {ker}} \lambda $
. Again by hypothesis
$\operatorname {\mathrm {ker}} \lambda $
. Again by hypothesis
![]() $R[1/\varpi ]$
is Cohen–Macaulay of dimension d and formally smooth at
$R[1/\varpi ]$
is Cohen–Macaulay of dimension d and formally smooth at
![]() $\lambda $
, and hence it is formally smooth at
$\lambda $
, and hence it is formally smooth at
![]() $\lambda $
of dimension d.
$\lambda $
of dimension d.
Then by Lemma 3.5, there exist
![]() $h_1,\ldots ,h_d\in \operatorname {\mathrm {ker}} \lambda $
such that
$h_1,\ldots ,h_d\in \operatorname {\mathrm {ker}} \lambda $
such that
![]() $h_1,\ldots ,h_d,\varpi $
is a regular sequence in R and such that for
$h_1,\ldots ,h_d,\varpi $
is a regular sequence in R and such that for
![]() $B=R/(h_1,\ldots ,h_d)$
and the induced augmentation
$B=R/(h_1,\ldots ,h_d)$
and the induced augmentation
![]() $\lambda _B\colon B\to {\mathcal O}$
the ring
$\lambda _B\colon B\to {\mathcal O}$
the ring
![]() $B[1/\varpi ]$
is formally smooth at
$B[1/\varpi ]$
is formally smooth at
![]() $\lambda _B$
of dimension
$\lambda _B$
of dimension
![]() $0$
. It follows that the continuous
$0$
. It follows that the continuous
![]() ${\mathcal O}$
-algebra map
${\mathcal O}$
-algebra map
![]() $\theta \colon S={\mathcal O}[[y_1,\ldots ,y_d]]\to R$
with
$\theta \colon S={\mathcal O}[[y_1,\ldots ,y_d]]\to R$
with
![]() $y_i\mapsto f_i$
makes R into a finite free S-module such that in the notation of (P), we have
$y_i\mapsto f_i$
makes R into a finite free S-module such that in the notation of (P), we have
![]() $B=R_\theta $
and
$B=R_\theta $
and
![]() $\lambda _B=\lambda _\theta $
, and moreover
$\lambda _B=\lambda _\theta $
, and moreover
![]() $R_\theta $
is finite free over
$R_\theta $
is finite free over
![]() ${\mathcal O}$
. Hence,
${\mathcal O}$
. Hence,
![]() $R_\theta [1/\varpi ]$
is a product of Artin E-algebras, and the smoothness at
$R_\theta [1/\varpi ]$
is a product of Artin E-algebras, and the smoothness at
![]() $\lambda _\theta $
shows that the component corresponding to
$\lambda _\theta $
shows that the component corresponding to
![]() $\lambda _\theta $
is equal to E. From this, it follows that
$\lambda _\theta $
is equal to E. From this, it follows that
![]() $\Phi _{\lambda _\theta }(R_\theta ) =\operatorname {\mathrm {ker}} \lambda _\theta /(\operatorname {\mathrm {ker}}\lambda _\theta )^2$
is of finite
$\Phi _{\lambda _\theta }(R_\theta ) =\operatorname {\mathrm {ker}} \lambda _\theta /(\operatorname {\mathrm {ker}}\lambda _\theta )^2$
is of finite
![]() ${\mathcal O}$
-length, as it is finitely generated over
${\mathcal O}$
-length, as it is finitely generated over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() ${\mathcal O}$
-torsion.
${\mathcal O}$
-torsion.
Next, we observe that we can lift regular sequences of R along
![]() $\widetilde {R} \to R$
.
$\widetilde {R} \to R$
.
Lemma 3.7. Assume that
![]() $\theta :S \hookrightarrow R$
satisfies (P) and
$\theta :S \hookrightarrow R$
satisfies (P) and
![]() $(\widetilde {R},I,\varphi )$
satisfies (CI). Then
$(\widetilde {R},I,\varphi )$
satisfies (CI). Then
![]() $\theta $
lifts to a morphism
$\theta $
lifts to a morphism
![]() ${\widetilde {\theta }}:S \to \widetilde {R}$
(making
${\widetilde {\theta }}:S \to \widetilde {R}$
(making
![]() $\varphi $
into a S-algebra homomorphism) which makes
$\varphi $
into a S-algebra homomorphism) which makes
![]() $\widetilde {R}$
into a finite free S-module. That is, identifying S with its image in
$\widetilde {R}$
into a finite free S-module. That is, identifying S with its image in
![]() $\widetilde {R}$
, that
$\widetilde {R}$
, that
![]() $(y_1,\ldots ,y_d,\varpi )$
is a regular sequence for both
$(y_1,\ldots ,y_d,\varpi )$
is a regular sequence for both
![]() $\widetilde {R}$
and R.
$\widetilde {R}$
and R.
Moreover, if
![]() $\widetilde {R}_\theta = \widetilde {R}/(y_1,\ldots ,y_d)$
and
$\widetilde {R}_\theta = \widetilde {R}/(y_1,\ldots ,y_d)$
and
![]() $\widetilde {\lambda }_\theta :\widetilde {R}_\theta \twoheadrightarrow {\mathcal O}$
is the map induced by
$\widetilde {\lambda }_\theta :\widetilde {R}_\theta \twoheadrightarrow {\mathcal O}$
is the map induced by
![]() $\widetilde {\lambda }$
, then
$\widetilde {\lambda }$
, then
![]() $\widetilde {R}_\theta $
is a complete intersection of dimension
$\widetilde {R}_\theta $
is a complete intersection of dimension
![]() $1$
, finite free over
$1$
, finite free over
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\Phi _{\widetilde {\lambda }_\theta }(\widetilde {R}_\theta )$
is finite.
$\Phi _{\widetilde {\lambda }_\theta }(\widetilde {R}_\theta )$
is finite.
This will follow from the following lemma:
Lemma 3.8. Let A be a Noetherian local ring, and let
![]() $B = A/I$
for some ideal I of A. Let
$B = A/I$
for some ideal I of A. Let
![]() $x\in {\mathfrak m}_B$
be an element not contained in any minimal prime of B. Then x lifts to an element
$x\in {\mathfrak m}_B$
be an element not contained in any minimal prime of B. Then x lifts to an element
![]() $\widetilde {x}\in {\mathfrak m}_A$
which is not contained in any minimal primes of A.
$\widetilde {x}\in {\mathfrak m}_A$
which is not contained in any minimal primes of A.
Proof. Pick any lift
![]() $\widetilde {x}_0\in {\mathfrak m}_A$
of x. Let the set of minimal primes of A be
$\widetilde {x}_0\in {\mathfrak m}_A$
of x. Let the set of minimal primes of A be
![]() $\{P_1,\ldots ,P_n\}$
, labeled so that there is some
$\{P_1,\ldots ,P_n\}$
, labeled so that there is some
![]() $0\le a\le n$
for which
$0\le a\le n$
for which
![]() $\widetilde {x}_0\not \in P_1,P_2,\ldots ,P_a$
, and
$\widetilde {x}_0\not \in P_1,P_2,\ldots ,P_a$
, and
![]() $\widetilde {x}_0\in P_{a+1},\ldots ,P_n$
.
$\widetilde {x}_0\in P_{a+1},\ldots ,P_n$
.
Now, fix any
![]() $i>a$
, so that
$i>a$
, so that
![]() $\widetilde {x}_0\in P_i$
. Note that if
$\widetilde {x}_0\in P_i$
. Note that if
![]() $I\subseteq P_i$
then
$I\subseteq P_i$
then
![]() $P_i/I$
would be a minimal prime of B containing x, contradicting our assumption. Hence,
$P_i/I$
would be a minimal prime of B containing x, contradicting our assumption. Hence,
![]() $I\not \subseteq P_i$
, and so there is some
$I\not \subseteq P_i$
, and so there is some
![]() $r_i\in I\smallsetminus P_i$
.
$r_i\in I\smallsetminus P_i$
.
Also, for any
![]() $j\ne i$
,
$j\ne i$
,
![]() $P_j\not \subseteq P_i$
, and so there is some
$P_j\not \subseteq P_i$
, and so there is some
![]() $s_{ij}\in P_j\smallsetminus P_i$
. Now, define
$s_{ij}\in P_j\smallsetminus P_i$
. Now, define
so that
![]() $y_i\in I$
,
$y_i\in I$
,
![]() $y_i\in P_j$
for
$y_i\in P_j$
for
![]() $j\ne i$
and
$j\ne i$
and
![]() $y_i\not \in P_i$
. Finally, let
$y_i\not \in P_i$
. Finally, let
Then we have
![]() $\widetilde {x}\equiv \widetilde {x}_0\equiv x{\operatorname {mod}}{I}$
,
$\widetilde {x}\equiv \widetilde {x}_0\equiv x{\operatorname {mod}}{I}$
,
![]() $\widetilde {x}\equiv \widetilde {x}_0\not \equiv 0\, {\operatorname {mod}}\, {P_i}$
for
$\widetilde {x}\equiv \widetilde {x}_0\not \equiv 0\, {\operatorname {mod}}\, {P_i}$
for
![]() $i\le a$
and
$i\le a$
and
![]() $\widetilde {x}\equiv y_i\not \equiv 0\, {\operatorname {mod}}\, {P_i}$
for
$\widetilde {x}\equiv y_i\not \equiv 0\, {\operatorname {mod}}\, {P_i}$
for
![]() $i>a$
. So
$i>a$
. So
![]() $\widetilde {x}$
is our desired lift.
$\widetilde {x}$
is our desired lift.
Proof of Lemma 3.7.
Identifying S with its image in R, we get that
![]() $(y_1,\ldots ,y_d,\varpi )$
, and thus
$(y_1,\ldots ,y_d,\varpi )$
, and thus
![]() $(\varpi ,y_1,\ldots ,y_d)$
, is a regular sequence for R. We claim that we can inductively construct a sequence
$(\varpi ,y_1,\ldots ,y_d)$
, is a regular sequence for R. We claim that we can inductively construct a sequence
![]() $\widetilde {y}_1,\widetilde {y}_2,\ldots ,\widetilde {y}_d\in \widetilde {R}$
such that
$\widetilde {y}_1,\widetilde {y}_2,\ldots ,\widetilde {y}_d\in \widetilde {R}$
such that
![]() $\varphi _\infty (\widetilde {y}_i) = y_i$
for all i and
$\varphi _\infty (\widetilde {y}_i) = y_i$
for all i and
![]() $\dim \widetilde {R}/(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_j) = d-j = \dim R/(\varpi ,y_1,\ldots ,y_j)$
for all
$\dim \widetilde {R}/(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_j) = d-j = \dim R/(\varpi ,y_1,\ldots ,y_j)$
for all
![]() $0\le j\le d$
.
$0\le j\le d$
.
As
![]() $\widetilde {R}$
and R are both flat over
$\widetilde {R}$
and R are both flat over
![]() ${\mathcal O}$
of relative dimension d, we have
${\mathcal O}$
of relative dimension d, we have
![]() $\dim \widetilde {R}/(\varpi ) = d = \dim R/(\varpi )$
. Now, assume that
$\dim \widetilde {R}/(\varpi ) = d = \dim R/(\varpi )$
. Now, assume that
![]() $\widetilde {y}_1,\ldots ,\widetilde {y}_j$
have been constructed for some
$\widetilde {y}_1,\ldots ,\widetilde {y}_j$
have been constructed for some
![]() $j<d$
. Let
$j<d$
. Let
![]() $A_j = \widetilde {R}/(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_j)$
and
$A_j = \widetilde {R}/(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_j)$
and
![]() $B_j = R/(\varpi ,y_1,\ldots ,y_j)$
so that
$B_j = R/(\varpi ,y_1,\ldots ,y_j)$
so that
![]() $\varphi _\infty :\widetilde {R}\to R$
induces a map
$\varphi _\infty :\widetilde {R}\to R$
induces a map
![]() $\varphi _j:A_j\to B_j$
. As
$\varphi _j:A_j\to B_j$
. As
![]() $(\varpi ,y_1,\ldots ,y_d)$
is a regular sequence for R,
$(\varpi ,y_1,\ldots ,y_d)$
is a regular sequence for R,
![]() $y_{j+1}$
is by definition not a zero divisor in
$y_{j+1}$
is by definition not a zero divisor in
![]() $B_j$
, and so in particular cannot be contained in any minimal primes of
$B_j$
, and so in particular cannot be contained in any minimal primes of
![]() $B_j$
. By Lemma 3.8 it follows there is some
$B_j$
. By Lemma 3.8 it follows there is some
![]() $y_{j+1}'\in A_j$
with
$y_{j+1}'\in A_j$
with
![]() $\varphi _j(y_{j+1}') = y_{j+1}$
which is not contained in any minimal prime of
$\varphi _j(y_{j+1}') = y_{j+1}$
which is not contained in any minimal prime of
![]() $A_j$
. Let
$A_j$
. Let
![]() $\widetilde {y}_{j+1}\in \widetilde {R}$
be any lift of
$\widetilde {y}_{j+1}\in \widetilde {R}$
be any lift of
![]() $y_{j+1}'$
. But now
$y_{j+1}'$
. But now
which has dimension
![]() $\dim A_j - 1 = d-(j+1)$
, by the assumption that
$\dim A_j - 1 = d-(j+1)$
, by the assumption that
![]() $y_{j+1}'$
is not contained in any minimal prime of
$y_{j+1}'$
is not contained in any minimal prime of
![]() $A_j$
. This completes the induction.
$A_j$
. This completes the induction.
Now,
![]() $(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_d)$
is a system of parameters for
$(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_d)$
is a system of parameters for
![]() $\widetilde {R}$
. As
$\widetilde {R}$
. As
![]() $\widetilde {R}$
is a complete intersection and thus Cohen–Macaulay, it follows that
$\widetilde {R}$
is a complete intersection and thus Cohen–Macaulay, it follows that
![]() $(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_d)$
, and thus
$(\varpi ,\widetilde {y}_1,\ldots ,\widetilde {y}_d)$
, and thus
![]() $(y_1,\ldots ,y_d,\varpi )$
, is a regular sequence for
$(y_1,\ldots ,y_d,\varpi )$
, is a regular sequence for
![]() $\widetilde {R}$
.
$\widetilde {R}$
.
So now defining
![]() ${\widetilde {\theta }}:S\to \widetilde {R}$
by
${\widetilde {\theta }}:S\to \widetilde {R}$
by
![]() ${\widetilde {\theta }}(y_i)=\widetilde {y}_i$
makes
${\widetilde {\theta }}(y_i)=\widetilde {y}_i$
makes
![]() $\widetilde {R}$
into a finite free S module, as desired.
$\widetilde {R}$
into a finite free S module, as desired.
The fact that
![]() $\widetilde {R}_\theta $
is a complete intersection of dimension
$\widetilde {R}_\theta $
is a complete intersection of dimension
![]() $1$
, and finite free over
$1$
, and finite free over
![]() ${\mathcal O}$
, now follows immediately from the fact that
${\mathcal O}$
, now follows immediately from the fact that
![]() $\widetilde {R}$
is a complete intersection. For the last assertion, the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 7.16] gives rise to a commutative diagram with exact rows:
$\widetilde {R}$
is a complete intersection. For the last assertion, the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 7.16] gives rise to a commutative diagram with exact rows:

where
![]() $\Phi _{\lambda }(R) = (\ker \lambda )/(\ker \lambda )^2 = {\widehat {\Omega }}_{R/{\mathcal O}}\otimes _\lambda {\mathcal O}$
and
$\Phi _{\lambda }(R) = (\ker \lambda )/(\ker \lambda )^2 = {\widehat {\Omega }}_{R/{\mathcal O}}\otimes _\lambda {\mathcal O}$
and
![]() $\Phi _{\widetilde {\lambda }}(\widetilde {R}) = (\ker \widetilde {\lambda })/(\ker \widetilde {\lambda })^2 = {\widehat {\Omega }}_{\widetilde {R}/{\mathcal O}}\otimes _{\widetilde {\lambda }}{\mathcal O}$
, and the maps
$\Phi _{\widetilde {\lambda }}(\widetilde {R}) = (\ker \widetilde {\lambda })/(\ker \widetilde {\lambda })^2 = {\widehat {\Omega }}_{\widetilde {R}/{\mathcal O}}\otimes _{\widetilde {\lambda }}{\mathcal O}$
, and the maps
![]() $\Theta $
and
$\Theta $
and
![]() ${\widetilde {\Theta }}$
are given in terms of differentials by
${\widetilde {\Theta }}$
are given in terms of differentials by
![]() $e_i\mapsto dy_i$
.
$e_i\mapsto dy_i$
.
Now, as in [Reference Böckle, Khare and ManningBKM21, Theorem 7.16], the fact that
![]() $\operatorname {\mathrm {Spec}} R[1/\varpi ]$
and
$\operatorname {\mathrm {Spec}} R[1/\varpi ]$
and
![]() $\operatorname {\mathrm {Spec}}\widetilde {R}[1/\varpi ]$
are both equidimensional of dimension d and
$\operatorname {\mathrm {Spec}}\widetilde {R}[1/\varpi ]$
are both equidimensional of dimension d and
![]() $\lambda $
and
$\lambda $
and
![]() $\widetilde {\lambda }$
, respectively, correspond to formally smooth points on these schemes, implies that
$\widetilde {\lambda }$
, respectively, correspond to formally smooth points on these schemes, implies that
![]() $\Phi _{\lambda }(R)$
and
$\Phi _{\lambda }(R)$
and
![]() $\Phi _{\widetilde {\lambda }}(\widetilde {R})$
both have rank d as
$\Phi _{\widetilde {\lambda }}(\widetilde {R})$
both have rank d as
![]() ${\mathcal O}$
-modules.
${\mathcal O}$
-modules.
But now the fact that
![]() $\Phi _{\lambda _\theta }(R_\theta )$
is finite implies that
$\Phi _{\lambda _\theta }(R_\theta )$
is finite implies that
![]() $\Theta $
must be injective. By commutativity, this implies that
$\Theta $
must be injective. By commutativity, this implies that
![]() ${\widetilde {\Theta }}$
is also injective, which in turn implies that
${\widetilde {\Theta }}$
is also injective, which in turn implies that
![]() $\Phi _{\widetilde {\lambda }_\theta }(\widetilde {R}_\theta )$
is also finite.
$\Phi _{\widetilde {\lambda }_\theta }(\widetilde {R}_\theta )$
is also finite.
3.2 Invariance of
 $C_{1,\lambda _\theta }(R_\theta )$
of
$C_{1,\lambda _\theta }(R_\theta )$
of
 $\theta $
$\theta $
For this section, we will fix
![]() $\theta $
satisfying (P) and
$\theta $
satisfying (P) and
![]() $(\widetilde {R}, I,\varphi )$
satisfying (CI). We will let
$(\widetilde {R}, I,\varphi )$
satisfying (CI). We will let
![]() ${\widetilde {\theta }}:S \hookrightarrow \widetilde {R}$
be a lift of
${\widetilde {\theta }}:S \hookrightarrow \widetilde {R}$
be a lift of
![]() $\theta $
satisfying the conclusion of Lemma 3.7, and we will identify S with its images in R and
$\theta $
satisfying the conclusion of Lemma 3.7, and we will identify S with its images in R and
![]() $\widetilde {R}$
.
$\widetilde {R}$
.
Let
![]() $\widetilde {R}_\theta $
and
$\widetilde {R}_\theta $
and
![]() $\widetilde {\lambda }_\theta $
be as in Lemma 3.7, and let
$\widetilde {\lambda }_\theta $
be as in Lemma 3.7, and let
![]() $\varphi _\theta = \varphi \otimes _{S}{\mathcal O}:\widetilde {R}_\theta \twoheadrightarrow R_\theta $
(so that
$\varphi _\theta = \varphi \otimes _{S}{\mathcal O}:\widetilde {R}_\theta \twoheadrightarrow R_\theta $
(so that
![]() $\widetilde {\lambda } = \lambda \circ \varphi $
), and let
$\widetilde {\lambda } = \lambda \circ \varphi $
), and let
![]() $I_\theta = \ker \varphi _\theta \subseteq \widetilde {R}_\theta $
. Also, let
$I_\theta = \ker \varphi _\theta \subseteq \widetilde {R}_\theta $
. Also, let
![]() $\pi _\theta :\widetilde {R} \to \widetilde {R}_\theta $
be the quotient map so that
$\pi _\theta :\widetilde {R} \to \widetilde {R}_\theta $
be the quotient map so that
![]() $\widetilde {\lambda } = \widetilde {\lambda }_\theta \circ \pi _\theta $
and
$\widetilde {\lambda } = \widetilde {\lambda }_\theta \circ \pi _\theta $
and
![]() $I_\theta = \pi _\theta (I)$
.
$I_\theta = \pi _\theta (I)$
.
The ring
![]() $\widetilde {R}_\theta $
now satisfies the conditions from Section 2, so we have
$\widetilde {R}_\theta $
now satisfies the conditions from Section 2, so we have
The main result of this subsection is the following:
Theorem 3.9. We have the following:
-
1.
 $\widetilde {R}_\theta [I_\theta ] = \pi _\theta (\widetilde {R}[I])$
$\widetilde {R}_\theta [I_\theta ] = \pi _\theta (\widetilde {R}[I])$
-
2.
 $\operatorname {\mathrm {Fitt}}(I_\theta ) = \pi _\theta (\operatorname {\mathrm {Fitt}}(I))$
$\operatorname {\mathrm {Fitt}}(I_\theta ) = \pi _\theta (\operatorname {\mathrm {Fitt}}(I))$
So in particular,
which depends only on
![]() $\widetilde {R}$
, R and
$\widetilde {R}$
, R and
![]() $\widetilde {\lambda }:R \to {\mathcal O}$
, all of which are independent of
$\widetilde {\lambda }:R \to {\mathcal O}$
, all of which are independent of
![]() $\theta $
.
$\theta $
.
Thus, if we define
![]() $C_{1,\widetilde {\lambda }}(\widetilde {R})=\widetilde {\lambda }\left (\widetilde {R}[I]\right )/\widetilde {\lambda }\left (\operatorname {\mathrm {Fitt}}(I)\right )$
, then we have
$C_{1,\widetilde {\lambda }}(\widetilde {R})=\widetilde {\lambda }\left (\widetilde {R}[I]\right )/\widetilde {\lambda }\left (\operatorname {\mathrm {Fitt}}(I)\right )$
, then we have
Proof of Theorem 3.9(1).
Clearly, we have
![]() $\pi _\theta (\widetilde {R}[I]) \subseteq \widetilde {R}_\theta [I_\theta ]$
(since
$\pi _\theta (\widetilde {R}[I]) \subseteq \widetilde {R}_\theta [I_\theta ]$
(since
![]() $I_\theta = \pi _\theta (I)$
and so
$I_\theta = \pi _\theta (I)$
and so
![]() $\widetilde {R}_\theta [I_\theta ] = \widetilde {R}[I]$
), so it suffices to prove that
$\widetilde {R}_\theta [I_\theta ] = \widetilde {R}[I]$
), so it suffices to prove that
![]() $\pi _\theta |_{\widetilde {R}[I]}:\widetilde {R}[I]\to \widetilde {R}_\theta [I_\theta ]$
is surjective.
$\pi _\theta |_{\widetilde {R}[I]}:\widetilde {R}[I]\to \widetilde {R}_\theta [I_\theta ]$
is surjective.
We first note that as
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\widetilde {R}_\theta $
are complete intersections, and thus are Gorenstein, we get the following:
$\widetilde {R}_\theta $
are complete intersections, and thus are Gorenstein, we get the following:
Lemma 3.10. There are isomorphisms
![]() $\Psi :\widetilde {R}\xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
and
$\Psi :\widetilde {R}\xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
and
![]() $\Psi _\theta :\widetilde {R}_\theta \xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R}_\theta ,{\mathcal O})$
of
$\Psi _\theta :\widetilde {R}_\theta \xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R}_\theta ,{\mathcal O})$
of
![]() $\widetilde {R}$
-modules, fitting into a commutative diagram:
$\widetilde {R}$
-modules, fitting into a commutative diagram:

where the vertical map
![]() $\sigma :\operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)\to \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},{\mathcal O}) = \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R}_\theta ,{\mathcal O})$
is just composition with the map
$\sigma :\operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)\to \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},{\mathcal O}) = \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R}_\theta ,{\mathcal O})$
is just composition with the map
![]() $S \to S/(y_1,\ldots ,y_d)={\mathcal O}$
.
$S \to S/(y_1,\ldots ,y_d)={\mathcal O}$
.
Proof. As
![]() $\widetilde {R}$
is Cohen–Macaulay and free of finite rank over S, we have
$\widetilde {R}$
is Cohen–Macaulay and free of finite rank over S, we have
![]() $\omega _{\widetilde {R}} \cong \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
. But as
$\omega _{\widetilde {R}} \cong \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
. But as
![]() $\widetilde {R}$
is a complete intersection, it is Gorenstein, and so
$\widetilde {R}$
is a complete intersection, it is Gorenstein, and so
![]() $\omega _{\widetilde {R}}\cong \widetilde {R}$
. Composing these isomorphisms gives the desired isomorphism
$\omega _{\widetilde {R}}\cong \widetilde {R}$
. Composing these isomorphisms gives the desired isomorphism
![]() $\Psi :\widetilde {R} \xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
.
$\Psi :\widetilde {R} \xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
.
Now, note that (as
![]() $\widetilde {R}$
is a free S-module):
$\widetilde {R}$
is a free S-module):
 $$ \begin{align*} \Psi(\ker \pi_\theta) &= \Psi(y_1\widetilde{R}+\cdots+y_d\widetilde{R}) = y_1\Psi(\widetilde{R})+\cdots+y_d\Psi(\widetilde{R})\\ &= y_1\operatorname{\mathrm{Hom}}_{S}(\widetilde{R},S)+\cdots+y_d\operatorname{\mathrm{Hom}}_{S}(\widetilde{R},S) = \operatorname{\mathrm{Hom}}_{S}(\widetilde{R},y_1S+\cdots +y_dS)\\ &= \ker \sigma, \end{align*} $$
$$ \begin{align*} \Psi(\ker \pi_\theta) &= \Psi(y_1\widetilde{R}+\cdots+y_d\widetilde{R}) = y_1\Psi(\widetilde{R})+\cdots+y_d\Psi(\widetilde{R})\\ &= y_1\operatorname{\mathrm{Hom}}_{S}(\widetilde{R},S)+\cdots+y_d\operatorname{\mathrm{Hom}}_{S}(\widetilde{R},S) = \operatorname{\mathrm{Hom}}_{S}(\widetilde{R},y_1S+\cdots +y_dS)\\ &= \ker \sigma, \end{align*} $$
which implies that there is an injection
![]() $\Psi _\theta :\widetilde {R}\xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R},{\mathcal O})$
making the above diagram commute. As
$\Psi _\theta :\widetilde {R}\xrightarrow {\sim } \operatorname {\mathrm {Hom}}_{{\mathcal O}}(\widetilde {R},{\mathcal O})$
making the above diagram commute. As
![]() $\sigma $
is clearly surjective (since
$\sigma $
is clearly surjective (since
![]() $\widetilde {R}$
is a projective S-module), it follows that
$\widetilde {R}$
is a projective S-module), it follows that
![]() $\Psi _\theta $
is also surjective.
$\Psi _\theta $
is also surjective.
Lemma 3.11. We have
and
Proof. As
![]() $\Psi $
is an isomorphism of
$\Psi $
is an isomorphism of
![]() $\widetilde {R}$
-modules, we have
$\widetilde {R}$
-modules, we have
![]() $\Psi (\widetilde {R}[I]) = \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)[I]$
and thus
$\Psi (\widetilde {R}[I]) = \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)[I]$
and thus
 $$ \begin{align*} \Psi(\widetilde{R}[I]) &= \{f:\widetilde{R}\to S|rf=0 \text{ for all }r\in I\}\\ &= \{f:\widetilde{R}\to S|(rf)(x)=0 \text{ for all }r\in I\text{ and } x\in \widetilde{R}\}\\ &= \{f:\widetilde{R}\to S|f(rx)=0 \text{ for all }r\in I\text{ and } x\in \widetilde{R}\}\\ &= \{f:\widetilde{R}\to S|f(I) = 0\}\\ &=\operatorname{\mathrm{Hom}}_{S}(\widetilde{R}/I,S). \end{align*} $$
$$ \begin{align*} \Psi(\widetilde{R}[I]) &= \{f:\widetilde{R}\to S|rf=0 \text{ for all }r\in I\}\\ &= \{f:\widetilde{R}\to S|(rf)(x)=0 \text{ for all }r\in I\text{ and } x\in \widetilde{R}\}\\ &= \{f:\widetilde{R}\to S|f(rx)=0 \text{ for all }r\in I\text{ and } x\in \widetilde{R}\}\\ &= \{f:\widetilde{R}\to S|f(I) = 0\}\\ &=\operatorname{\mathrm{Hom}}_{S}(\widetilde{R}/I,S). \end{align*} $$
The proof for
![]() $\Psi _\theta (\widetilde {R}_\theta [I_\theta ])$
is identical.
$\Psi _\theta (\widetilde {R}_\theta [I_\theta ])$
is identical.
Now, since
![]() $\widetilde {R}/I\cong R$
is a projective S-module,
$\widetilde {R}/I\cong R$
is a projective S-module,
![]() $\sigma $
induces a surjective map
$\sigma $
induces a surjective map
![]() $\operatorname {\mathrm {Hom}}_{S}(\widetilde {R}/I,S)\to \operatorname {\mathrm {Hom}}_{S}(\widetilde {R}/I,{\mathcal O})$
. By Lemma 3.11, this is a surjective map
$\operatorname {\mathrm {Hom}}_{S}(\widetilde {R}/I,S)\to \operatorname {\mathrm {Hom}}_{S}(\widetilde {R}/I,{\mathcal O})$
. By Lemma 3.11, this is a surjective map
![]() $\sigma |_{\Psi (\widetilde {R}[I])}:\Psi (\widetilde {R}[I])\to \Psi _\theta (\widetilde {R}_\theta [I_\theta ])$
, so the commutative diagram from Lemma 3.10 gives that
$\sigma |_{\Psi (\widetilde {R}[I])}:\Psi (\widetilde {R}[I])\to \Psi _\theta (\widetilde {R}_\theta [I_\theta ])$
, so the commutative diagram from Lemma 3.10 gives that
![]() $\pi _\theta |_{\widetilde {R}[I]}:\widetilde {R}[I]\to \widetilde {R}_\theta [I_\theta ]$
is surjective. This completes the proof of (1).
$\pi _\theta |_{\widetilde {R}[I]}:\widetilde {R}[I]\to \widetilde {R}_\theta [I_\theta ]$
is surjective. This completes the proof of (1).
Proof of Theorem 3.9(2).
By the definition of I, we have a short exact sequence of S-modules
Applying
![]() $-\otimes _{S}{\mathcal O}$
to this gives an exact sequence
$-\otimes _{S}{\mathcal O}$
to this gives an exact sequence
and so as
![]() $I_\theta = \ker \varphi _\theta $
, this gives as exact sequence
$I_\theta = \ker \varphi _\theta $
, this gives as exact sequence
But now as R is a finite free S-module,
![]() $\operatorname {\mathrm {Tor}}_1^{S}(R,{\mathcal O}) = 0$
and so we have an isomorphism
$\operatorname {\mathrm {Tor}}_1^{S}(R,{\mathcal O}) = 0$
and so we have an isomorphism
![]() $I\otimes _{S}{\mathcal O}\cong I_\theta $
of
$I\otimes _{S}{\mathcal O}\cong I_\theta $
of
![]() $\widetilde {R}_\theta $
-modules.
$\widetilde {R}_\theta $
-modules.
Now, by [Sta19, Lemma 07ZA] we indeed have:
as desired. This completes the proof of (2) and hence of Theorem 3.9.
We note the following corollary.
Corollary 3.12. With notation as above
depends only on its quotient
![]() $\widetilde {R}/I \simeq R$
and we define
$\widetilde {R}/I \simeq R$
and we define
Proof. This follows from Theorem 3.9 which shows that
and the results of Appendix A which show that
![]() $C_{1,\lambda _\theta }(R_\theta )$
is well defined and independent of
$C_{1,\lambda _\theta }(R_\theta )$
is well defined and independent of
![]() $\widetilde {R}_\theta $
.
$\widetilde {R}_\theta $
.
Remark 3.13. The above Corollary 3.12 can also be proved directly by using the proof of Lemma A.5 instead of reducing to the statement of Lemma A.5.
For later use, we also state the following result.
Lemma 3.14. As R-modules one has
![]() $\widetilde {R}[I]\cong \omega _{R}$
.
$\widetilde {R}[I]\cong \omega _{R}$
.
Proof. As R is Cohen–Macaulay and
![]() $\widetilde {R}$
is Gorenstein, we have that
$\widetilde {R}$
is Gorenstein, we have that
![]() $\omega _{R}\cong \operatorname {\mathrm {Hom}}_{S}(R,S)$
and
$\omega _{R}\cong \operatorname {\mathrm {Hom}}_{S}(R,S)$
and
![]() $\widetilde {R}\cong \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
as
$\widetilde {R}\cong \operatorname {\mathrm {Hom}}_{S}(\widetilde {R},S)$
as
![]() $\widetilde {R}$
-modules. Now, by [Sta19, Lemma 08YP]:
$\widetilde {R}$
-modules. Now, by [Sta19, Lemma 08YP]:
as R-modules.
3.3 Invariance of
 $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
In this section, we will let
![]() $R\in C_{\mathcal O}$
and
$R\in C_{\mathcal O}$
and
![]() $S = {\mathcal O}[[y_1,\ldots ,y_d]]$
be as above. We shall show that for any inclusion
$S = {\mathcal O}[[y_1,\ldots ,y_d]]$
be as above. We shall show that for any inclusion
![]() $\theta :S\hookrightarrow R$
satisfying (P), the André–Quillen cohomology group
$\theta :S\hookrightarrow R$
satisfying (P), the André–Quillen cohomology group
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
does not depend on the choice of
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
does not depend on the choice of
![]() $\theta $
.
$\theta $
.
In order to do this, we will need to make use of a continuous version of André–Quillen cohomology, as the classical version does not behave well for rings that are not of finite type but only topologically of finite type over the base. We will define this in terms of the analytic cotangent complex defined in [Reference Gabber and RameroGR03, Chapter 7].
For any ring A, we will let
![]() $\operatorname {\mathrm {Mod}}_A$
denote the category of A-modules,
$\operatorname {\mathrm {Mod}}_A$
denote the category of A-modules,
![]() $D(\operatorname {\mathrm {Mod}}_A)$
its derived category, and
$D(\operatorname {\mathrm {Mod}}_A)$
its derived category, and
![]() $D^-(\operatorname {\mathrm {Mod}}_A)\subseteq D(\operatorname {\mathrm {Mod}}_A)$
the subcategory of bounded above complexes.
$D^-(\operatorname {\mathrm {Mod}}_A)\subseteq D(\operatorname {\mathrm {Mod}}_A)$
the subcategory of bounded above complexes.
For any map of rings
![]() $A\to B$
, let
$A\to B$
, let
![]() $L_{B/A}\in D^-(\operatorname {\mathrm {Mod}}_B)$
denote the relative cotangent complex.
$L_{B/A}\in D^-(\operatorname {\mathrm {Mod}}_B)$
denote the relative cotangent complex.
Now, consider any
![]() $A\in {\mathrm {CNL}_{\mathcal O}}$
and let
$A\in {\mathrm {CNL}_{\mathcal O}}$
and let
![]() $\wedge :\operatorname {\mathrm {Mod}}_A\to \operatorname {\mathrm {Mod}}_A$
denote the
$\wedge :\operatorname {\mathrm {Mod}}_A\to \operatorname {\mathrm {Mod}}_A$
denote the
![]() ${\mathfrak m}_A$
-adic completion functor. As in [Reference Gabber and RameroGR03, Chapter 7.1], let
${\mathfrak m}_A$
-adic completion functor. As in [Reference Gabber and RameroGR03, Chapter 7.1], let
![]() $\wedge :D^-(\operatorname {\mathrm {Mod}}_A)\to D^-(\operatorname {\mathrm {Mod}}_A)$
denote its left-derived functor.
$\wedge :D^-(\operatorname {\mathrm {Mod}}_A)\to D^-(\operatorname {\mathrm {Mod}}_A)$
denote its left-derived functor.
If
![]() $A\to B$
is a continuous map of rings in
$A\to B$
is a continuous map of rings in
![]() ${\mathrm {CNL}_{\mathcal O}}$
, then define the analytic relative cotangent complex to be
${\mathrm {CNL}_{\mathcal O}}$
, then define the analytic relative cotangent complex to be
![]() $L^{\operatorname {\mathrm {an}}}_{B/A} = (L_{B/A})^{\wedge }$
. For any B-module M and any
$L^{\operatorname {\mathrm {an}}}_{B/A} = (L_{B/A})^{\wedge }$
. For any B-module M and any
![]() $i\ge 0$
we may then define the
$i\ge 0$
we may then define the
![]() $i^{th}$
continuous André–Quillen cohomology group to be
$i^{th}$
continuous André–Quillen cohomology group to be
Similarly, if
![]() $A\to B$
is any ring map and M is any B-module, the
$A\to B$
is any ring map and M is any B-module, the
![]() $i^{th}$
André–Quillen cohomology group is just
$i^{th}$
André–Quillen cohomology group is just
We will begin by recording the basic properties of continuous André–Quillen cohomology we will need in our arguments.
Proposition 3.15. Given any
![]() $A,B,C\in {\mathrm {CNL}_{\mathcal O}}$
, and continuous ring homomorphisms
$A,B,C\in {\mathrm {CNL}_{\mathcal O}}$
, and continuous ring homomorphisms
![]() $A\to B\to C$
and any C-module M, there is a long exact sequence:
$A\to B\to C$
and any C-module M, there is a long exact sequence:
Proof. This follows from the distinguished triangle
from [Reference Gabber and RameroGR03, Theorem 7.1.33].
Proposition 3.16. If
![]() $A\to B$
is a continuous map of rings in
$A\to B$
is a continuous map of rings in
![]() ${\mathrm {CNL}_{\mathcal O}}$
which makes B into a finite A-module, then
${\mathrm {CNL}_{\mathcal O}}$
which makes B into a finite A-module, then
![]() $L_{B/A}^{\operatorname {\mathrm {an}}}\cong L_{B/A}$
, and so
$L_{B/A}^{\operatorname {\mathrm {an}}}\cong L_{B/A}$
, and so
![]() $\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)\cong \operatorname {\mathrm {Der}}^i_A(B,M)$
for all
$\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)\cong \operatorname {\mathrm {Der}}^i_A(B,M)$
for all
![]() $i\ge 0$
and all
$i\ge 0$
and all
![]() $M\in \operatorname {\mathrm {Mod}}_B$
.
$M\in \operatorname {\mathrm {Mod}}_B$
.
Proof. As the map
![]() $A\to B$
is finite, it is finite type (and not merely topologically finite type). By [Reference IyengarIye07, 6.11],
$A\to B$
is finite, it is finite type (and not merely topologically finite type). By [Reference IyengarIye07, 6.11],
![]() $L_{B/A}$
is quasi-isomorphic to a bounded above complex of finite free B-modules
$L_{B/A}$
is quasi-isomorphic to a bounded above complex of finite free B-modules
![]() ${\mathcal L}^\bullet $
. Using
${\mathcal L}^\bullet $
. Using
![]() ${\mathcal L}^\bullet $
to compute
${\mathcal L}^\bullet $
to compute
![]() $(L_{B/A})^\wedge $
, we get
$(L_{B/A})^\wedge $
, we get
as finitely generated B-modules are already
![]() ${\mathfrak m}_B$
-adically complete. The last claim now follows from the definition of
${\mathfrak m}_B$
-adically complete. The last claim now follows from the definition of
![]() $\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)$
and
$\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)$
and
![]() $\operatorname {\mathrm {Der}}^i_A(B,M)$
.
$\operatorname {\mathrm {Der}}^i_A(B,M)$
.
Proposition 3.17. If
![]() $A\to B$
is a continuous map of rings in
$A\to B$
is a continuous map of rings in
![]() ${\mathrm {CNL}_{\mathcal O}}$
, then the module
${\mathrm {CNL}_{\mathcal O}}$
, then the module
![]() ${\widehat {\Omega }}_{B/A} \hspace {-.5pt}= \varprojlim \Omega _{(B/{\mathfrak m}_B^n)/A}$
of continuous Kähler differentials defined in [Reference Böckle, Khare and ManningBKM21, Section 7.1] is the
${\widehat {\Omega }}_{B/A} \hspace {-.5pt}= \varprojlim \Omega _{(B/{\mathfrak m}_B^n)/A}$
of continuous Kähler differentials defined in [Reference Böckle, Khare and ManningBKM21, Section 7.1] is the
![]() ${\mathfrak m}_B$
-adic completion of
${\mathfrak m}_B$
-adic completion of
![]() $\Omega _{B/A}$
and we have
$\Omega _{B/A}$
and we have
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_A(B,M)\cong \operatorname {\mathrm {Hom}}_A({\widehat {\Omega }}_{B/A},M)$
for any B-module M.
$\widehat {\operatorname {\mathrm {Der}}}^0_A(B,M)\cong \operatorname {\mathrm {Hom}}_A({\widehat {\Omega }}_{B/A},M)$
for any B-module M.
Proof. For the first claim, we argue as in [Reference Böckle, Khare and ManningBKM21, Lemma 7.1] (and note that the assumption that
![]() ${\mathcal R}$
is finitely generated over A in that lemma was used only in the last step, to conclude that
${\mathcal R}$
is finitely generated over A in that lemma was used only in the last step, to conclude that
![]() $\Omega _{{\mathcal R}/A}$
was finitely generated over A). Specifically, for any
$\Omega _{{\mathcal R}/A}$
was finitely generated over A). Specifically, for any
![]() $n>k$
we have
$n>k$
we have
![]() $\Omega _{B/A}/{\mathfrak m}_B^k\Omega _{B/A} = \Omega _{B/A}\otimes _B B/{\mathfrak m}_B^k\cong \Omega _{(B/{\mathfrak m}_B^n)/A}\otimes B/{\mathfrak m}_B^k$
and so taking inverse limits gives
$\Omega _{B/A}/{\mathfrak m}_B^k\Omega _{B/A} = \Omega _{B/A}\otimes _B B/{\mathfrak m}_B^k\cong \Omega _{(B/{\mathfrak m}_B^n)/A}\otimes B/{\mathfrak m}_B^k$
and so taking inverse limits gives
Taking inverse limits again and using the fact that
![]() ${\widehat {\Omega }}_{B/A}$
is finite over B, and hence
${\widehat {\Omega }}_{B/A}$
is finite over B, and hence
![]() ${\mathfrak m}_B$
-adically complete gives
${\mathfrak m}_B$
-adically complete gives
as desired.
In particular, this shows that the module
![]() ${\widehat {\Omega }}_{B/A}$
is simply the module
${\widehat {\Omega }}_{B/A}$
is simply the module
![]() $\Omega _{B/A}^{\operatorname {\mathrm {an}}} = (\Omega _{B/A})^{\wedge }$
from [Reference Gabber and RameroGR03], and so the second claim follows from [Reference Gabber and RameroGR03, Lemma 7.1.27(iii)] and the definition of
$\Omega _{B/A}^{\operatorname {\mathrm {an}}} = (\Omega _{B/A})^{\wedge }$
from [Reference Gabber and RameroGR03], and so the second claim follows from [Reference Gabber and RameroGR03, Lemma 7.1.27(iii)] and the definition of
![]() $\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)$
.
$\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M)$
.
We will also need the following specific computations of continuous André–Quillen cohomology:
Lemma 3.18. For any
![]() $n\ge 0$
and any
$n\ge 0$
and any
![]() ${\mathcal O}[[x_1,\ldots ,x_n]]$
-module M, we have
${\mathcal O}[[x_1,\ldots ,x_n]]$
-module M, we have
 $$\begin{align*}\widehat{\operatorname{\mathrm{Der}}}^i_{\mathcal O}({\mathcal O}[[x_1,\ldots,x_n]],M) = \begin{cases} M^n & i=0\\ 0 & i\ge 1. \end{cases} \end{align*}$$
$$\begin{align*}\widehat{\operatorname{\mathrm{Der}}}^i_{\mathcal O}({\mathcal O}[[x_1,\ldots,x_n]],M) = \begin{cases} M^n & i=0\\ 0 & i\ge 1. \end{cases} \end{align*}$$
Proof. By [Reference Gabber and RameroGR03, Proposition 7.1.29], we have
![]() $L^{\operatorname {\mathrm {an}}}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}} = {\widehat {\Omega }}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}}[0] = {\mathcal O}[[x_1,\ldots ,x_n]]^n[0]$
and so
$L^{\operatorname {\mathrm {an}}}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}} = {\widehat {\Omega }}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}}[0] = {\mathcal O}[[x_1,\ldots ,x_n]]^n[0]$
and so
so the claim follows.
Lemma 3.19. If A is a ring and
![]() $B= A/I$
for some ideal
$B= A/I$
for some ideal
![]() $I\subseteq A$
, then for any B-module M,
$I\subseteq A$
, then for any B-module M,
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_A(B,M) = 0$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_A(B,M) = 0$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_A(B,M) = \operatorname {\mathrm {Hom}}_B(I/I^2,M)$
.
$\widehat {\operatorname {\mathrm {Der}}}^1_A(B,M) = \operatorname {\mathrm {Hom}}_B(I/I^2,M)$
.
Proof. As
![]() $B=A/I$
is clearly finite over A, Proposition 3.16 gives
$B=A/I$
is clearly finite over A, Proposition 3.16 gives
![]() $\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M) = \operatorname {\mathrm {Der}}^i(B,M)$
for all
$\widehat {\operatorname {\mathrm {Der}}}^i_A(B,M) = \operatorname {\mathrm {Der}}^i(B,M)$
for all
![]() $i\ge 0$
and all M. The claim now follows from [Reference IyengarIye07, 6.12].
$i\ge 0$
and all M. The claim now follows from [Reference IyengarIye07, 6.12].
For the remainder of this section, we always treat
![]() $E/{\mathcal O}$
as an
$E/{\mathcal O}$
as an
![]() $R_\theta $
-module (and hence as an R-module) via
$R_\theta $
-module (and hence as an R-module) via
![]() $\lambda _\theta :R_\theta \to {\mathcal O}$
. Our main result is the following:
$\lambda _\theta :R_\theta \to {\mathcal O}$
. Our main result is the following:
Theorem 3.20. We have
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})\cong \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})\cong \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
This implies that
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
depends only on R and the R-module structure on
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R_\theta ,E/{\mathcal O})$
depends only on R and the R-module structure on
![]() $E/{\mathcal O}$
, which is induced by
$E/{\mathcal O}$
, which is induced by
![]() $\lambda :R\to {\mathcal O}$
, and not on
$\lambda :R\to {\mathcal O}$
, and not on
![]() $\theta $
. This will thus complete the proof of Theorem 3.25.
$\theta $
. This will thus complete the proof of Theorem 3.25.
We first observe the following:
Lemma 3.21. For any
![]() $i\ge 0$
and any
$i\ge 0$
and any
![]() $R_\theta $
-module M, we have
$R_\theta $
-module M, we have
Proof. The first and last isomorphisms follow from Proposition 3.16, as R is finite over S and
![]() $R_\theta $
is finite over
$R_\theta $
is finite over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
For the second isomorphism, first note that as R is a finite free S-module, it is a projective resolution for itself in
![]() $D(S)$
, and so we have
$D(S)$
, and so we have
![]() $R\otimes ^{\mathbf {L}}_{S}{\mathcal O} = R\otimes _{S}{\mathcal O} \cong R_\theta $
. By [Sta19, Lemma 08QQ], this implies that
$R\otimes ^{\mathbf {L}}_{S}{\mathcal O} = R\otimes _{S}{\mathcal O} \cong R_\theta $
. By [Sta19, Lemma 08QQ], this implies that
![]() $L_{R/S}\otimes ^{\mathbf {L}}_{R}R_\theta \cong L_{R_\theta /{\mathcal O}}$
. But now [Sta19, Lemma 0E1W] gives that
$L_{R/S}\otimes ^{\mathbf {L}}_{R}R_\theta \cong L_{R_\theta /{\mathcal O}}$
. But now [Sta19, Lemma 0E1W] gives that
so the claim follows by definition.
So to prove Theorem 3.20, it will suffice to prove the following:
Proposition 3.22.
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{S}(R,E/{\mathcal O})\cong \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
$\widehat {\operatorname {\mathrm {Der}}}^1_{S}(R,E/{\mathcal O})\cong \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
.
Proof. Applying Proposition 3.15 to the ring maps
![]() ${\mathcal O}\to S\to R$
gives an exact sequence:
${\mathcal O}\to S\to R$
gives an exact sequence:
 $$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{S}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(S,E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{S}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(S,E/{\mathcal O}). \end{align*} $$
$$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{S}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(S,E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{S}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(S,E/{\mathcal O}). \end{align*} $$
By Lemma 3.18,
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(S,E/{\mathcal O}) = (E/{\mathcal O})^d$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(S,E/{\mathcal O}) = (E/{\mathcal O})^d$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(S,E/{\mathcal O}) = 0$
.
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(S,E/{\mathcal O}) = 0$
.
But now by the assumption that
![]() $\lambda :R \to {\mathcal O}$
represents a smooth point of
$\lambda :R \to {\mathcal O}$
represents a smooth point of
![]() $\operatorname {\mathrm {Spec}} R[1/\varpi ]$
we get that
$\operatorname {\mathrm {Spec}} R[1/\varpi ]$
we get that
![]() ${\widehat {\Omega }}_{R/{\mathcal O}}\otimes _\lambda {\mathcal O}$
has rank d as an
${\widehat {\Omega }}_{R/{\mathcal O}}\otimes _\lambda {\mathcal O}$
has rank d as an
![]() ${\mathcal O}$
-module (as in [Reference Böckle, Khare and ManningBKM21, Theorem 7.16]), and so
${\mathcal O}$
-module (as in [Reference Böckle, Khare and ManningBKM21, Theorem 7.16]), and so
for some finite group G. Also as
![]() $\Phi _{\lambda _\theta }(R_\theta )={\widehat {\Omega }}_{R^\theta /{\mathcal O}}\otimes _{\lambda _\theta }{\mathcal O}$
is finite (as
$\Phi _{\lambda _\theta }(R_\theta )={\widehat {\Omega }}_{R^\theta /{\mathcal O}}\otimes _{\lambda _\theta }{\mathcal O}$
is finite (as
![]() $\theta $
satisfies (P)),
$\theta $
satisfies (P)),
is finite as well. Now, the exact sequence simplifies to
But comparing coranks in the sequence
![]() $0\to \widehat {\operatorname {\mathrm {Der}}}^0_{S}(R,E/{\mathcal O}) \to (E/{\mathcal O})^d\oplus G\to (E/{\mathcal O})^d$
implies that
$0\to \widehat {\operatorname {\mathrm {Der}}}^0_{S}(R,E/{\mathcal O}) \to (E/{\mathcal O})^d\oplus G\to (E/{\mathcal O})^d$
implies that
![]() $(E/{\mathcal O})^d\oplus G\to (E/{\mathcal O})^d$
has finite cokernel and hence must be surjective, as
$(E/{\mathcal O})^d\oplus G\to (E/{\mathcal O})^d$
has finite cokernel and hence must be surjective, as
![]() $E/{\mathcal O}$
does not have any nontrivial finite quotients. This implies that the map
$E/{\mathcal O}$
does not have any nontrivial finite quotients. This implies that the map
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{S}(R, E/{\mathcal O})\to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
is indeed an isomorphism. This completes the proof of Theorem 3.20.
$\widehat {\operatorname {\mathrm {Der}}}^1_{S}(R, E/{\mathcal O})\to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
is indeed an isomorphism. This completes the proof of Theorem 3.20.
We note that in Theorem 3.20 and Corollary 3.12, we have proved that
In order to actually compute
![]() $\delta _{\lambda _\theta }(R_\theta )$
, we will need a method for computing
$\delta _{\lambda _\theta }(R_\theta )$
, we will need a method for computing
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
. For this, take any triple
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
. For this, take any triple
![]() $(\widetilde {R},I,\varphi )$
satisfying (CI). Then we now have the following generalization of Equation (A.3):
$(\widetilde {R},I,\varphi )$
satisfying (CI). Then we now have the following generalization of Equation (A.3):
Theorem 3.23. There is a four-term exact sequence:
Proof. Applying Proposition 3.15 to the ring maps
![]() ${\mathcal O}\to \widetilde {R} \to R$
gives an exact sequence:
${\mathcal O}\to \widetilde {R} \to R$
gives an exact sequence:
 $$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{\widetilde{R}}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(\widetilde{R},E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{\widetilde{R}}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(\widetilde{R},E/{\mathcal O}), \end{align*} $$
$$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{\widetilde{R}}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(\widetilde{R},E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{\widetilde{R}}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(\widetilde{R},E/{\mathcal O}), \end{align*} $$
and Lemma 3.19 implies that
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\widetilde {R}}(R,E/{\mathcal O}) = 0$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_{\widetilde {R}}(R,E/{\mathcal O}) = 0$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\widetilde {R}}(R,E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{R}(I/I^2,E/{\mathcal O})$
, so it’s enough to prove that
$\widehat {\operatorname {\mathrm {Der}}}^1_{\widetilde {R}}(R,E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{R}(I/I^2,E/{\mathcal O})$
, so it’s enough to prove that
![]() $ \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(\widetilde {R},E/{\mathcal O}) = 0$
(since by Proposition 3.17,
$ \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(\widetilde {R},E/{\mathcal O}) = 0$
(since by Proposition 3.17,
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(R,E/{\mathcal O})=\operatorname {\mathrm {Hom}}_{R}({\widehat {\Omega }}_{R},E/{\mathcal O})$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(R,E/{\mathcal O})=\operatorname {\mathrm {Hom}}_{R}({\widehat {\Omega }}_{R},E/{\mathcal O})$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(\widetilde {R},E/{\mathcal O})=\operatorname {\mathrm {Hom}}_{\widetilde {R}}({\widehat {\Omega }}_{\widetilde {R}},E/{\mathcal O})$
).
$\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(\widetilde {R},E/{\mathcal O})=\operatorname {\mathrm {Hom}}_{\widetilde {R}}({\widehat {\Omega }}_{\widetilde {R}},E/{\mathcal O})$
).
Since
![]() $\widetilde {R}$
is a complete intersection, we can write
$\widetilde {R}$
is a complete intersection, we can write
![]() $\widetilde {R} = P/J$
, where
$\widetilde {R} = P/J$
, where
![]() $P = {\mathcal O}[[x_1,\ldots ,x_{d+n}]]$
and
$P = {\mathcal O}[[x_1,\ldots ,x_{d+n}]]$
and
![]() $J=(f_1,\ldots ,f_n)$
is generated by a regular sequence. Applying Proposition 3.15 to the ring maps
$J=(f_1,\ldots ,f_n)$
is generated by a regular sequence. Applying Proposition 3.15 to the ring maps
![]() ${\mathcal O}\to P\to \widetilde {R}$
gives an exact sequence:
${\mathcal O}\to P\to \widetilde {R}$
gives an exact sequence:
 $$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{P}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(P,E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{P}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(P,E/{\mathcal O}). \end{align*} $$
$$ \begin{align*} 0 &\to \widehat{\operatorname{\mathrm{Der}}}^0_{P}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^0_{\mathcal O}(P,E/{\mathcal O})\\ &\to \widehat{\operatorname{\mathrm{Der}}}^1_{P}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(\widetilde{R},E/{\mathcal O})\to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(P,E/{\mathcal O}). \end{align*} $$
Now, Lemma 3.18 gives the identification
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(P,E/{\mathcal O}) = (E/{\mathcal O})^{d+n}$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(P,E/{\mathcal O}) = (E/{\mathcal O})^{d+n}$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(P,E/{\mathcal O}) = 0$
and Lemma 3.19 gives
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(P,E/{\mathcal O}) = 0$
and Lemma 3.19 gives
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{P}(\widetilde {R},E/{\mathcal O}) = 0$
and
$\widehat {\operatorname {\mathrm {Der}}}^0_{P}(\widetilde {R},E/{\mathcal O}) = 0$
and
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{P}(\widetilde {R},E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{\widetilde {R}}(J/J^2,E/{\mathcal O})$
. Moreover, as J is generated by a regular sequence of length n, it follows that
$\widehat {\operatorname {\mathrm {Der}}}^1_{P}(\widetilde {R},E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{\widetilde {R}}(J/J^2,E/{\mathcal O})$
. Moreover, as J is generated by a regular sequence of length n, it follows that
![]() $J/J^2\cong (\widetilde {R})^n$
as
$J/J^2\cong (\widetilde {R})^n$
as
![]() $\widetilde {R}$
-modules, and so
$\widetilde {R}$
-modules, and so
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{P}(\widetilde {R},E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{\widetilde {R}}(J/J^2,E/{\mathcal O})\cong (E/{\mathcal O})^n$
. Thus, the above exact sequence simplifies to
$\widehat {\operatorname {\mathrm {Der}}}^1_{P}(\widetilde {R},E/{\mathcal O}) = \operatorname {\mathrm {Hom}}_{\widetilde {R}}(J/J^2,E/{\mathcal O})\cong (E/{\mathcal O})^n$
. Thus, the above exact sequence simplifies to
But now, just as in the proof of Proposition 3.22 above, the fact that
![]() $\operatorname {\mathrm {Spec}} \widetilde {R}[1/\varpi ]$
is smooth of dimension d at
$\operatorname {\mathrm {Spec}} \widetilde {R}[1/\varpi ]$
is smooth of dimension d at
![]() $\widetilde {\lambda }$
implies that
$\widetilde {\lambda }$
implies that
![]() $\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(\widetilde {R},E/{\mathcal O}) \cong (E/{\mathcal O})^d\oplus H$
for some finite group H, and so comparing ranks gives that
$\widehat {\operatorname {\mathrm {Der}}}^0_{\mathcal O}(\widetilde {R},E/{\mathcal O}) \cong (E/{\mathcal O})^d\oplus H$
for some finite group H, and so comparing ranks gives that
![]() $(E/{\mathcal O})^{n+d} \to (E/{\mathcal O})^n$
has finite cokernel, and hence is surjective. Thus,
$(E/{\mathcal O})^{n+d} \to (E/{\mathcal O})^n$
has finite cokernel, and hence is surjective. Thus,
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(\widetilde {R},E/{\mathcal O})=0$
, and so the claim follows.
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(\widetilde {R},E/{\mathcal O})=0$
, and so the claim follows.
3.4 Wiles defect for augmented rings
 $(R,\lambda ) \in C_{\mathcal O}$
$(R,\lambda ) \in C_{\mathcal O}$
We make the following definitions and in particular define the Wiles defect for tuples
![]() $(R,\lambda ) \in C_{\mathcal O}$
. Recall that by definition all such R are Cohen–Macaulay and flat over
$(R,\lambda ) \in C_{\mathcal O}$
. Recall that by definition all such R are Cohen–Macaulay and flat over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Definition 3.24. Let R be a complete, Noetherian local
![]() ${\mathcal O}$
-algebra which is Cohen–Macaulay and flat over
${\mathcal O}$
-algebra which is Cohen–Macaulay and flat over
![]() ${\mathcal O}$
of relative dimension d and with an augmentation
${\mathcal O}$
of relative dimension d and with an augmentation
![]() $\lambda :R \to {\mathcal O}$
such that
$\lambda :R \to {\mathcal O}$
such that
![]() $\operatorname {\mathrm {Spec}} R[1/\varpi ]$
is formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R[1/\varpi ]$
is formally smooth at the point corresponding to
![]() $\lambda $
.
$\lambda $
.
-
• Define
(see Theorem 3.20). $$\begin{align*}D_{1,\lambda}(R) = \frac{\log |\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|}{\log|{\mathcal O}/p|}\end{align*}$$
$$\begin{align*}D_{1,\lambda}(R) = \frac{\log |\widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R,E/{\mathcal O})|}{\log|{\mathcal O}/p|}\end{align*}$$
-
• Define
for any triple $$\begin{align*}c_{1,\lambda}(R) = \frac{\log\left| C_{1,\lambda}(R)\right|}{\log|{\mathcal O}/p|} =\frac{\log\left|\widetilde{\lambda}(\widetilde{R}[I])/\widetilde{\lambda}(\operatorname{\mathrm{Fitt}}(I))\right|}{\log|{\mathcal O}/p|},\end{align*}$$
$$\begin{align*}c_{1,\lambda}(R) = \frac{\log\left| C_{1,\lambda}(R)\right|}{\log|{\mathcal O}/p|} =\frac{\log\left|\widetilde{\lambda}(\widetilde{R}[I])/\widetilde{\lambda}(\operatorname{\mathrm{Fitt}}(I))\right|}{\log|{\mathcal O}/p|},\end{align*}$$
 $(\widetilde {R},I,\varphi )$
satisfying (CI).
$(\widetilde {R},I,\varphi )$
satisfying (CI).
-
• The Wiles defect
 $ \delta _\lambda (R)$
of R at
$ \delta _\lambda (R)$
of R at
 $\lambda $
is defined to be
$\lambda $
is defined to be  $$\begin{align*}\delta_\lambda(R) = D_{1,\lambda}(R)-c_{1,\lambda}(R).\end{align*}$$
$$\begin{align*}\delta_\lambda(R) = D_{1,\lambda}(R)-c_{1,\lambda}(R).\end{align*}$$
Here is the main theorem of this section which uses all the work we have done here.
Theorem 3.25. Let R and
![]() $\lambda :R \twoheadrightarrow {\mathcal O}$
be as above, and let
$\lambda :R \twoheadrightarrow {\mathcal O}$
be as above, and let
![]() $\theta :S\hookrightarrow R$
be a map satisfying (P). Then the invariants
$\theta :S\hookrightarrow R$
be a map satisfying (P). Then the invariants
![]() $C_{1,\lambda _\theta }(R_\theta )$
,
$C_{1,\lambda _\theta }(R_\theta )$
,
![]() $\operatorname {\mathrm {Der}}_{\mathcal O}^1(R_\theta ,E/{\mathcal O})$
and
$\operatorname {\mathrm {Der}}_{\mathcal O}^1(R_\theta ,E/{\mathcal O})$
and
![]() $\delta _{\lambda _\theta }(R_\theta )$
are independent of the choice of
$\delta _{\lambda _\theta }(R_\theta )$
are independent of the choice of
![]() $\theta $
.
$\theta $
.
Proof. The proofs of the independence statements for
![]() $C_{1,\lambda _\theta }(R_\theta )$
and
$C_{1,\lambda _\theta }(R_\theta )$
and
![]() $\operatorname {\mathrm {Der}}_{\mathcal O}^1(R_\theta ,E/{\mathcal O})$
follow from Theorems 3.9 and 3.20, respectively. The assertion for the Wiles defect
$\operatorname {\mathrm {Der}}_{\mathcal O}^1(R_\theta ,E/{\mathcal O})$
follow from Theorems 3.9 and 3.20, respectively. The assertion for the Wiles defect
![]() $\delta _{\lambda _\theta }(R_\theta )$
is then immediate from Theorem 2.2.
$\delta _{\lambda _\theta }(R_\theta )$
is then immediate from Theorem 2.2.
Corollary 3.26. The numbers
are all nonnegative rational numbers depending only on R and
![]() $\lambda $
. Moreover, if
$\lambda $
. Moreover, if
![]() $E'/E$
is any finite extension and
$E'/E$
is any finite extension and
![]() ${\mathcal O}'$
is the ring of integers of
${\mathcal O}'$
is the ring of integers of
![]() $E'$
, then we have
$E'$
, then we have
That is,
![]() $D_{1,\lambda }(R), c_{1,\lambda }(R), \delta _\lambda (R)$
are all unaffected by changing the coefficient ring.
$D_{1,\lambda }(R), c_{1,\lambda }(R), \delta _\lambda (R)$
are all unaffected by changing the coefficient ring.
Proof. This is a consequence of Theorem 3.25, Theorem 3.9, Corollary 3.12 and Theorem 3.20, combined with Remark A.7 which confirms the finiteness of length of the terms involved in the one-dimensional case.
The final claim about changing the coefficient ring is easy to verify in the case when R is finite free over
![]() ${\mathcal O}$
(this fact was already noted in [Reference Böckle, Khare and ManningBKM21, Section 3] for
${\mathcal O}$
(this fact was already noted in [Reference Böckle, Khare and ManningBKM21, Section 3] for
![]() $\delta _{\lambda }(R)$
), and the general claim follows from this.
$\delta _{\lambda }(R)$
), and the general claim follows from this.
We note the consistency of this definition with the definition of Wiles defect for tuples
![]() $(R,\lambda ) \in C_{\mathcal O}$
when R is of dimension one.
$(R,\lambda ) \in C_{\mathcal O}$
when R is of dimension one.
Proposition 3.27. In the case when
![]() $(R,\lambda ) \in C_{\mathcal O}$
and R is of dimension one, then
$(R,\lambda ) \in C_{\mathcal O}$
and R is of dimension one, then
 $$\begin{align*}\delta_\lambda(R) = D_{1,\lambda}(R)-c_{1,\lambda}(R)=\frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|} .\end{align*}$$
$$\begin{align*}\delta_\lambda(R) = D_{1,\lambda}(R)-c_{1,\lambda}(R)=\frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|} .\end{align*}$$
Proposition 3.28. For
![]() $(R,\lambda ) \in C_{\mathcal O}$
,
$(R,\lambda ) \in C_{\mathcal O}$
,
![]() $\delta _\lambda (R)=0$
if and only if R is a complete intersection. In particular,
$\delta _\lambda (R)=0$
if and only if R is a complete intersection. In particular,
![]() $\delta _\lambda ({\mathcal O}[[x_1,\ldots ,x_n]])=0$
for any
$\delta _\lambda ({\mathcal O}[[x_1,\ldots ,x_n]])=0$
for any
![]() $n\ge 1$
and any
$n\ge 1$
and any
![]() $\lambda :{\mathcal O}[[x_1,\ldots ,x_n]]\twoheadrightarrow {\mathcal O}$
.
$\lambda :{\mathcal O}[[x_1,\ldots ,x_n]]\twoheadrightarrow {\mathcal O}$
.
Proof. If R is a complete intersection, then
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})=0$
by the argument given in the proof of Theorem 3.23. Further
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})=0$
by the argument given in the proof of Theorem 3.23. Further
![]() $C_{1,\lambda }(R)=0$
(as we can take the CI cover
$C_{1,\lambda }(R)=0$
(as we can take the CI cover
![]() $\widetilde R=R$
). This gives that
$\widetilde R=R$
). This gives that
![]() $\delta _\lambda (R)=0$
.
$\delta _\lambda (R)=0$
.
Conversely, assume
![]() $\delta _\lambda (R)=0$
. Then by our results we have a quotient
$\delta _\lambda (R)=0$
. Then by our results we have a quotient
![]() $(R_\theta ,\lambda _\theta ) \in C_{\mathcal O}$
of
$(R_\theta ,\lambda _\theta ) \in C_{\mathcal O}$
of
![]() $(R,\lambda ) \in C_{\mathcal O}$
by a regular sequence
$(R,\lambda ) \in C_{\mathcal O}$
by a regular sequence
![]() $(y_1,\ldots , y_d)$
, namely
$(y_1,\ldots , y_d)$
, namely
![]() $R_\theta =R/(y_1,\ldots , y_d)$
and
$R_\theta =R/(y_1,\ldots , y_d)$
and
![]() $\lambda _\theta : R \to R_\theta \to {\mathcal O}$
(the last map being
$\lambda _\theta : R \to R_\theta \to {\mathcal O}$
(the last map being
![]() $\lambda $
) with
$\lambda $
) with
![]() $R_\theta $
of dimension one. Further,
$R_\theta $
of dimension one. Further,
![]() $\delta _{\lambda _\theta }(R_\theta )=\delta _\lambda (R)=0$
. Thus, by Lemma 2.1,
$\delta _{\lambda _\theta }(R_\theta )=\delta _\lambda (R)=0$
. Thus, by Lemma 2.1,
![]() $R_\theta $
is a complete intersection, which implies that R is a complete intersection.
$R_\theta $
is a complete intersection, which implies that R is a complete intersection.
Remark 3.29. For
![]() $(R,\lambda ) \in C_{\mathcal O}$
and R of dimension
$(R,\lambda ) \in C_{\mathcal O}$
and R of dimension
![]() $1$
, by Lemma 2.1 note that the vanishing of
$1$
, by Lemma 2.1 note that the vanishing of
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})$
implies that R is a complete intersection because of the inequality
$\operatorname {\mathrm {Der}}^1_{\mathcal O}(R,E/{\mathcal O})$
implies that R is a complete intersection because of the inequality
![]() $|\Phi _\lambda (R)| \geq |\Psi _\lambda (R)|$
which follows from the usual Fitting ideals argument (cf. [Reference LenstraLen95]). From this, we again deduce, by invariance of
$|\Phi _\lambda (R)| \geq |\Psi _\lambda (R)|$
which follows from the usual Fitting ideals argument (cf. [Reference LenstraLen95]). From this, we again deduce, by invariance of
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
quotienting by regular sequences, that in general for
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
quotienting by regular sequences, that in general for
![]() $(R,\lambda ) \in C_{\mathcal O}$
, the vanishing of
$(R,\lambda ) \in C_{\mathcal O}$
, the vanishing of
![]() $\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
implies that R is a complete intersection.
$\widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
implies that R is a complete intersection.
Example 3.30. At the suggestion of the referee, we now compute the Wiles defect for a simple example of a pair
![]() $(R,\lambda )\in {\mathcal C}_{{\mathbf Z}_p}$
with R a non-CI ring. Much more elaborate computations will be done in Section 5. We consider
$(R,\lambda )\in {\mathcal C}_{{\mathbf Z}_p}$
with R a non-CI ring. Much more elaborate computations will be done in Section 5. We consider
As a
![]() ${\mathbf Z}_p$
-module R is free of rank
${\mathbf Z}_p$
-module R is free of rank
![]() $3$
, and possible bases are
$3$
, and possible bases are
![]() $\{1,X,Y\}$
and
$\{1,X,Y\}$
and
![]() $\{1,X-p,Y-p\}$
. In particular, R is of Krull dimension
$\{1,X-p,Y-p\}$
. In particular, R is of Krull dimension
![]() $1$
and we have
$1$
and we have
![]() $R=R^{\mathrm {tf}}$
. The most direct way to compute the Wiles defect
$R=R^{\mathrm {tf}}$
. The most direct way to compute the Wiles defect
![]() $\delta _\lambda (R)$
is via formula (2.1): We have
$\delta _\lambda (R)$
is via formula (2.1): We have
![]() $\operatorname {\mathrm {ker}}(\lambda )=(X,Y)={\mathbf Z}_p X\oplus {\mathbf Z}_p Y$
,
$\operatorname {\mathrm {ker}}(\lambda )=(X,Y)={\mathbf Z}_p X\oplus {\mathbf Z}_p Y$
,
![]() $R[\operatorname {\mathrm {ker}}(\lambda )]={\mathbf Z}_p (X+Y-p)$
, and hence
$R[\operatorname {\mathrm {ker}}(\lambda )]={\mathbf Z}_p (X+Y-p)$
, and hence
Moreover
![]() $\Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p=({\mathbf Z}_p\mathrm {d}X\oplus {\mathbf Z}_p\mathrm {d}Y)/\langle \frac {\partial f_i}{\partial X}(0,0) \mathrm {d}X+\frac {\partial f_i}{\partial Y}(0,0) \mathrm {d}Y :i=1,2,3\rangle _{{\mathbf Z}_p}$
for
$\Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p=({\mathbf Z}_p\mathrm {d}X\oplus {\mathbf Z}_p\mathrm {d}Y)/\langle \frac {\partial f_i}{\partial X}(0,0) \mathrm {d}X+\frac {\partial f_i}{\partial Y}(0,0) \mathrm {d}Y :i=1,2,3\rangle _{{\mathbf Z}_p}$
for
![]() $f_1=X(X-p)$
,
$f_1=X(X-p)$
,
![]() $f_2=Y(Y-p)$
,
$f_2=Y(Y-p)$
,
![]() $f_3=XY$
, and computing the Jacobian of the
$f_3=XY$
, and computing the Jacobian of the
![]() $f_i$
relative to X and Y at
$f_i$
relative to X and Y at
![]() $(0,0)$
shows that
$(0,0)$
shows that
This gives
 $$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}=\frac{2-1}1=1. \end{align*}$$
$$\begin{align*}\delta_\lambda(R) = \frac{\log|\Phi_\lambda(R)|-\log|\Psi_\lambda(R)|}{\log|{\mathcal O}/p|}=\frac{2-1}1=1. \end{align*}$$
Alternatively, one may compute
![]() $\delta _\lambda (R) $
via Definition 3.24: A possible choice of CI-cover is the quotient map
$\delta _\lambda (R) $
via Definition 3.24: A possible choice of CI-cover is the quotient map
with kernel
![]() $I={\mathbf Z}_p XY$
. Then
$I={\mathbf Z}_p XY$
. Then
![]() $\widetilde {R}[I]={\mathbf Z}_p(X-p)\oplus {\mathbf Z}_p(Y-p)\oplus {\mathbf Z}_p(X-p)(Y-p)$
. To obtain the fitting ideal of I, we consider the right exact sequence
$\widetilde {R}[I]={\mathbf Z}_p(X-p)\oplus {\mathbf Z}_p(Y-p)\oplus {\mathbf Z}_p(X-p)(Y-p)$
. To obtain the fitting ideal of I, we consider the right exact sequence
The fitting ideal is the ideal generated by the
![]() $1\times 1$
-minors of the matrix describing the map on the left, that is,
$1\times 1$
-minors of the matrix describing the map on the left, that is,
![]() $\operatorname {\mathrm {Fitt}}(I)=(X-p,Y-p)$
. One deduces that
$\operatorname {\mathrm {Fitt}}(I)=(X-p,Y-p)$
. One deduces that
 $$\begin{align*}c_{1,\lambda}(R) =\frac{\log\left|\widetilde{\lambda}(\widetilde{R}[I])/\widetilde{\lambda}(\operatorname{\mathrm{Fitt}}(I))\right|}{\log|{\mathbf Z}_p/p|}= \frac{\log (1)}{\log(p)}=0.\end{align*}$$
$$\begin{align*}c_{1,\lambda}(R) =\frac{\log\left|\widetilde{\lambda}(\widetilde{R}[I])/\widetilde{\lambda}(\operatorname{\mathrm{Fitt}}(I))\right|}{\log|{\mathbf Z}_p/p|}= \frac{\log (1)}{\log(p)}=0.\end{align*}$$
To compute
![]() $D_{1,\lambda }(R) $
, we rely on the exact sequence from Theorem 3.23. An expression for
$D_{1,\lambda }(R) $
, we rely on the exact sequence from Theorem 3.23. An expression for
![]() $\Omega _{\widetilde {R}/ {\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
is obtained in the same way as above for
$\Omega _{\widetilde {R}/ {\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
is obtained in the same way as above for
![]() $\Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
, and in fact one finds an isomorphism
$\Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
, and in fact one finds an isomorphism
![]() $ \Omega _{\widetilde {R}/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p\to \Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
. Theorem 3.23 now gives the isomorphism
$ \Omega _{\widetilde {R}/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p\to \Omega _{R/{\mathbf Z}_p}\otimes _\lambda {\mathbf Z}_p$
. Theorem 3.23 now gives the isomorphism
![]() $\operatorname {\mathrm {Hom}}_{R}(I/I^2,{\mathbf Q}_p/{\mathbf Z}_p) \stackrel \simeq \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
. We compute
$\operatorname {\mathrm {Hom}}_{R}(I/I^2,{\mathbf Q}_p/{\mathbf Z}_p) \stackrel \simeq \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R,E/{\mathcal O})$
. We compute
so that
![]() $\operatorname {\mathrm {Hom}}_{R}(I/I^2,E/{\mathcal O}) \cong {\mathbf Z}_p/p$
. In turn this gives
$\operatorname {\mathrm {Hom}}_{R}(I/I^2,E/{\mathcal O}) \cong {\mathbf Z}_p/p$
. In turn this gives
 $$\begin{align*}D_{1,\lambda}(R) = \frac{\log |\widehat{\operatorname{\mathrm{Der}}}^1_{{\mathbf Z}_p}(R,{\mathbf Q}_p/{\mathbf Z}_p)|}{\log|{\mathbf Z}_p/p|}=\frac{\log |\operatorname{\mathrm{Hom}}_{R}(I/I^2,E/{\mathcal O})|}{1}=\frac11=1,\end{align*}$$
$$\begin{align*}D_{1,\lambda}(R) = \frac{\log |\widehat{\operatorname{\mathrm{Der}}}^1_{{\mathbf Z}_p}(R,{\mathbf Q}_p/{\mathbf Z}_p)|}{\log|{\mathbf Z}_p/p|}=\frac{\log |\operatorname{\mathrm{Hom}}_{R}(I/I^2,E/{\mathcal O})|}{1}=\frac11=1,\end{align*}$$
and we conclude (again)
3.5 Properties of the Wiles defect
Theorem 3.25 can be restated as:
Theorem 3.31. If
![]() $(y_1,\ldots ,y_d,\varpi )$
is a regular sequence for R with
$(y_1,\ldots ,y_d,\varpi )$
is a regular sequence for R with
![]() $y_1,\ldots ,y_d\in \ker \lambda $
, where we will also use
$y_1,\ldots ,y_d\in \ker \lambda $
, where we will also use
![]() $\lambda $
to denote the induced map
$\lambda $
to denote the induced map
![]() $R/(y_1,\ldots ,y_d)\twoheadrightarrow {\mathcal O}$
, then
$R/(y_1,\ldots ,y_d)\twoheadrightarrow {\mathcal O}$
, then
![]() $\delta _\lambda (R) = \delta _\lambda (R/(y_1,\ldots ,y_d))$
. In particular,
$\delta _\lambda (R) = \delta _\lambda (R/(y_1,\ldots ,y_d))$
. In particular,
![]() $\delta _\lambda (R/(y_1,\ldots ,y_d))$
is independent of the choice of regular sequence.
$\delta _\lambda (R/(y_1,\ldots ,y_d))$
is independent of the choice of regular sequence.
We now deduce some additivity properties of
![]() $\delta _\lambda (R)$
that we use later.
$\delta _\lambda (R)$
that we use later.
Proposition 3.32. Let
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
be complete, Noetherian, Cohen–Macaulay, reduced
$R_{2}$
be complete, Noetherian, Cohen–Macaulay, reduced
![]() ${\mathcal O}$
-algebras, which are flat over
${\mathcal O}$
-algebras, which are flat over
![]() ${\mathcal O}$
of relative dimensions
${\mathcal O}$
of relative dimensions
![]() $d_1$
and
$d_1$
and
![]() $d_2$
. Pick augmentations
$d_2$
. Pick augmentations
![]() $\lambda _i:R_{i}\to {\mathcal O}$
such that
$\lambda _i:R_{i}\to {\mathcal O}$
such that
![]() $\operatorname {\mathrm {Spec}} R_{i}[1/\varpi ]$
is formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R_{i}[1/\varpi ]$
is formally smooth at the point corresponding to
![]() $\lambda _i$
. Let
$\lambda _i$
. Let
![]() $R= R_1 {\widehat {\otimes }}_{{\mathcal O}} R_{2}$
and
$R= R_1 {\widehat {\otimes }}_{{\mathcal O}} R_{2}$
and
![]() $\lambda = \lambda _1{\widehat {\otimes }} \lambda _2:R\to {\mathcal O}$
.
$\lambda = \lambda _1{\widehat {\otimes }} \lambda _2:R\to {\mathcal O}$
.
Then
-
1.
 $D_{1,\lambda }(R) = D_{1,\lambda _1}(R_{1})+D_{1,\lambda _2}(R_{2})$
$D_{1,\lambda }(R) = D_{1,\lambda _1}(R_{1})+D_{1,\lambda _2}(R_{2})$
-
2.
 $c_{1,\lambda }(R) = c_{1,\lambda _1}(R_{1})+c_{1,\lambda _2}(R_{2})$
$c_{1,\lambda }(R) = c_{1,\lambda _1}(R_{1})+c_{1,\lambda _2}(R_{2})$
-
3.
 $\delta _{\lambda }(R) = \delta _{\lambda _1}(R_{1})+\delta _{\lambda _2}(R_{2})$
.
$\delta _{\lambda }(R) = \delta _{\lambda _1}(R_{1})+\delta _{\lambda _2}(R_{2})$
.
Proof. By definition, (3) will follow from (1) and (2).
For (1), we will first reduce to dimension
![]() $1$
. Let
$1$
. Let
![]() $S_1 = {\mathcal O}[[x_1,\ldots ,x_{d_1}]]$
and
$S_1 = {\mathcal O}[[x_1,\ldots ,x_{d_1}]]$
and
![]() $S_2 = {\mathcal O}[[y_1,\ldots ,y_{d_2}]]$
. By Proposition 3.2, we may find maps
$S_2 = {\mathcal O}[[y_1,\ldots ,y_{d_2}]]$
. By Proposition 3.2, we may find maps
![]() $\theta _1:S_1\hookrightarrow R_1$
and
$\theta _1:S_1\hookrightarrow R_1$
and
![]() $\theta _2:S_2\hookrightarrow R_2$
satisfying (P). Then the map
$\theta _2:S_2\hookrightarrow R_2$
satisfying (P). Then the map
![]() $\theta = \theta _1{\widehat {\otimes }}_{{\mathcal O}}\theta _2:S_1{\widehat {\otimes }}_{{\mathcal O}}S_2\hookrightarrow R$
satisfies (P) as well. So consider the rings
$\theta = \theta _1{\widehat {\otimes }}_{{\mathcal O}}\theta _2:S_1{\widehat {\otimes }}_{{\mathcal O}}S_2\hookrightarrow R$
satisfies (P) as well. So consider the rings
and note that these are all finite free over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
By Theorem 3.20, we now have that
 $$ \begin{align*} \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_1,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{1,\theta_1},E/{\mathcal O}),\\ \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_2,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{2,\theta_2},E/{\mathcal O}),\\ \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{\theta},E/{\mathcal O}). \end{align*} $$
$$ \begin{align*} \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_1,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{1,\theta_1},E/{\mathcal O}),\\ \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_2,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{2,\theta_2},E/{\mathcal O}),\\ \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R,E/{\mathcal O}) &= \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{\theta},E/{\mathcal O}). \end{align*} $$
But now by [Sta19, Lemma 09DA], as
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are both free over
$R_2$
are both free over
![]() ${\mathcal O}$
, and hence Tor-independent, we have
${\mathcal O}$
, and hence Tor-independent, we have
Thus,
 $$ \begin{align*} &\widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R,E/{\mathcal O})\\& \quad \cong \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{\theta},E/{\mathcal O}) = H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R/{\mathcal O}},E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{1,\theta_1}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{1,\theta_1}}R_\theta\oplus L_{R_{2,\theta_2}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{2,\theta_1}}R_\theta,E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{1,\theta_1}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{1,\theta_1}}R_\theta,E/{\mathcal O}))\oplus H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{2,\theta_2}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{2,\theta_1}}R_\theta,E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_{1,\theta_1}}(L_{R_{1,\theta_1}/{\mathcal O}},E/{\mathcal O}))\oplus H^1(\operatorname{\mathrm{RHom}}_{R_{2,\theta_2}}(L_{R_{2,\theta_2}/{\mathcal O}},E/{\mathcal O}))\\& \quad = \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{1,\theta_1},E/{\mathcal O})\oplus \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{2,\theta_2},E/{\mathcal O}) = \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_1,E/{\mathcal O})\oplus \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_2,E/{\mathcal O}) \end{align*} $$
$$ \begin{align*} &\widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R,E/{\mathcal O})\\& \quad \cong \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{\theta},E/{\mathcal O}) = H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R/{\mathcal O}},E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{1,\theta_1}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{1,\theta_1}}R_\theta\oplus L_{R_{2,\theta_2}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{2,\theta_1}}R_\theta,E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{1,\theta_1}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{1,\theta_1}}R_\theta,E/{\mathcal O}))\oplus H^1(\operatorname{\mathrm{RHom}}_{R_\theta}(L_{R_{2,\theta_2}/{\mathcal O}}\otimes^{\mathbf{L}}_{R_{2,\theta_1}}R_\theta,E/{\mathcal O}))\\& \quad \cong H^1(\operatorname{\mathrm{RHom}}_{R_{1,\theta_1}}(L_{R_{1,\theta_1}/{\mathcal O}},E/{\mathcal O}))\oplus H^1(\operatorname{\mathrm{RHom}}_{R_{2,\theta_2}}(L_{R_{2,\theta_2}/{\mathcal O}},E/{\mathcal O}))\\& \quad = \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{1,\theta_1},E/{\mathcal O})\oplus \operatorname{\mathrm{Der}}^1_{{\mathcal O}}(R_{2,\theta_2},E/{\mathcal O}) = \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_1,E/{\mathcal O})\oplus \widehat{\operatorname{\mathrm{Der}}}^1_{{\mathcal O}}(R_2,E/{\mathcal O}) \end{align*} $$
and so (1) follows.
It remains to prove (2). Consider triples
![]() $(\widetilde {R}_{1},I_{1},\varphi _{1})$
and
$(\widetilde {R}_{1},I_{1},\varphi _{1})$
and
![]() $(\widetilde {R}_{2},I_{2},\varphi _{2})$
satisfying (CI) (with
$(\widetilde {R}_{2},I_{2},\varphi _{2})$
satisfying (CI) (with
![]() $(R_1,\lambda _1)$
and
$(R_1,\lambda _1)$
and
![]() $(R_{2},\lambda _2)$
, respectively, in place of
$(R_{2},\lambda _2)$
, respectively, in place of
![]() $(R,\lambda )$
).
$(R,\lambda )$
).
Define
![]() $\widetilde {R}= \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
, and note that
$\widetilde {R}= \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
, and note that
![]() $I_{1}{\widehat {\otimes }}_{{\mathcal O}} \widetilde {R}_{2}$
and
$I_{1}{\widehat {\otimes }}_{{\mathcal O}} \widetilde {R}_{2}$
and
![]() $\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
are both ideals of
$\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
are both ideals of
![]() $\widetilde {R}$
. Let
$\widetilde {R}$
. Let
![]() $\varphi =\varphi _{1}\otimes \varphi _{2}:\widetilde {R}= \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\twoheadrightarrow R_{1}{\widehat {\otimes }}_{{\mathcal O}} R_{2} = R$
, and note that
$\varphi =\varphi _{1}\otimes \varphi _{2}:\widetilde {R}= \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\twoheadrightarrow R_{1}{\widehat {\otimes }}_{{\mathcal O}} R_{2} = R$
, and note that
![]() $\ker \varphi = \left (I_{1}{\widehat {\otimes }}_{{\mathcal O}} \widetilde {R}_{2}\right )+\left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}\right )$
. Denoting this ideal
$\ker \varphi = \left (I_{1}{\widehat {\otimes }}_{{\mathcal O}} \widetilde {R}_{2}\right )+\left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}\right )$
. Denoting this ideal
![]() $I \subseteq \widetilde {R}$
, the triple
$I \subseteq \widetilde {R}$
, the triple
![]() $(\widetilde {R},I,\varphi )$
satisfies (CI). So by the definition of
$(\widetilde {R},I,\varphi )$
satisfies (CI). So by the definition of
![]() $c_{1,\lambda }$
,
$c_{1,\lambda }$
,
 $$ \begin{align*} c_{1,\lambda_1}(R_{1})\log|{\mathcal O}/p| &= \log\left|\lambda_1(\widetilde{R}_{1}[I_{1}])/\lambda_1(\operatorname{\mathrm{Fitt}}(I_{1}))\right|\\ c_{1,\lambda_2}(R_{1})\log|{\mathcal O}/p| &= \log\left|\lambda_2(\widetilde{R}_{2}[I_{2}])/\lambda_2(\operatorname{\mathrm{Fitt}}(I_{2}))\right|\\ c_{1,\lambda}(R)\log|{\mathcal O}/p| &= \log\left|\lambda(\widetilde{R}[I_{}])/\lambda(\operatorname{\mathrm{Fitt}}(I))\right|. \end{align*} $$
$$ \begin{align*} c_{1,\lambda_1}(R_{1})\log|{\mathcal O}/p| &= \log\left|\lambda_1(\widetilde{R}_{1}[I_{1}])/\lambda_1(\operatorname{\mathrm{Fitt}}(I_{1}))\right|\\ c_{1,\lambda_2}(R_{1})\log|{\mathcal O}/p| &= \log\left|\lambda_2(\widetilde{R}_{2}[I_{2}])/\lambda_2(\operatorname{\mathrm{Fitt}}(I_{2}))\right|\\ c_{1,\lambda}(R)\log|{\mathcal O}/p| &= \log\left|\lambda(\widetilde{R}[I_{}])/\lambda(\operatorname{\mathrm{Fitt}}(I))\right|. \end{align*} $$
The desired equality will now follow from Lemma 3.33.
Lemma 3.33. If
![]() $\widetilde {R}_1,\widetilde {R}_2,\widetilde {R}$
,
$\widetilde {R}_1,\widetilde {R}_2,\widetilde {R}$
,
![]() $I_1,I_2,I$
,
$I_1,I_2,I$
,
![]() $\lambda _1,\lambda _2$
and
$\lambda _1,\lambda _2$
and
![]() $\lambda $
are as in the proof of Proposition 3.32, then we have
$\lambda $
are as in the proof of Proposition 3.32, then we have
as ideals of
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Proof. For the first claim, standard properties of annihilators imply that
 $$ \begin{align*} \widetilde{R}[I] & = \widetilde{R}\left[\left(I_{1}{\widehat{\otimes}}_{{\mathcal O}} \widetilde{R}_{2}\right)+\left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}I_{2}\right)\right] = \widetilde{R}_{}\left[\left(I_{1}{\widehat{\otimes}}_{{\mathcal O}} \widetilde{R}_{2}\right)\right]\cap \widetilde{R}_{}\left[\left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}I_{2}\right)\right]\\ &= \left(\widetilde{R}_{1}\left[I_{1}\right]{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\right)\cap \left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\left[I_{2}\right]\right) = \widetilde{R}_{1}\left[I_{1}\right]{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\left[I_{2}\right] \end{align*} $$
$$ \begin{align*} \widetilde{R}[I] & = \widetilde{R}\left[\left(I_{1}{\widehat{\otimes}}_{{\mathcal O}} \widetilde{R}_{2}\right)+\left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}I_{2}\right)\right] = \widetilde{R}_{}\left[\left(I_{1}{\widehat{\otimes}}_{{\mathcal O}} \widetilde{R}_{2}\right)\right]\cap \widetilde{R}_{}\left[\left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}I_{2}\right)\right]\\ &= \left(\widetilde{R}_{1}\left[I_{1}\right]{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\right)\cap \left(\widetilde{R}_{1}{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\left[I_{2}\right]\right) = \widetilde{R}_{1}\left[I_{1}\right]{\widehat{\otimes}}_{{\mathcal O}}\widetilde{R}_{2}\left[I_{2}\right] \end{align*} $$
(where we’ve used that fact that
![]() $\left (A{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\right )\cap \left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}B\right ) = \left (A{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\right ) \left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}B\right ) = A{\widehat {\otimes }}_{{\mathcal O}}B$
for any ideals
$\left (A{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\right )\cap \left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}B\right ) = \left (A{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\right ) \left (\widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}B\right ) = A{\widehat {\otimes }}_{{\mathcal O}}B$
for any ideals
![]() $A\subseteq \widetilde {R}_{1}$
and
$A\subseteq \widetilde {R}_{1}$
and
![]() $B\subseteq \widetilde {R}_{2}$
). Thus,
$B\subseteq \widetilde {R}_{2}$
). Thus,
For the statement about fitting ideals, fix presentations
 $$ \begin{align*} 0&\to K_1\to \widetilde{R}_{1}^{m} \xrightarrow{A} I_{1}\to 0\\ 0&\to K_2\to \widetilde{R}_{2}^{n} \xrightarrow{B} I_{2}\to 0, \end{align*} $$
$$ \begin{align*} 0&\to K_1\to \widetilde{R}_{1}^{m} \xrightarrow{A} I_{1}\to 0\\ 0&\to K_2\to \widetilde{R}_{2}^{n} \xrightarrow{B} I_{2}\to 0, \end{align*} $$
where
![]() $K_i$
is a finitely generated
$K_i$
is a finitely generated
![]() $\widetilde {R}_{i}$
-module. Then A and B induce surjective maps
$\widetilde {R}_{i}$
-module. Then A and B induce surjective maps
![]() $A\otimes \operatorname {\mathrm {Id}}:\widetilde {R}_{}^{m} = \widetilde {R}_{1}^{m}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\to I_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
and
$A\otimes \operatorname {\mathrm {Id}}:\widetilde {R}_{}^{m} = \widetilde {R}_{1}^{m}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}\to I_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
and
![]() $\operatorname {\mathrm {Id}}\otimes B:\widetilde {R}_{}^{n} = \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}^n\to \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
, and so we may combine them to produce a surjective map
$\operatorname {\mathrm {Id}}\otimes B:\widetilde {R}_{}^{n} = \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}^n\to \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
, and so we may combine them to produce a surjective map
Write
![]() $K \subseteq \widetilde {R}_{}^{m+n}$
for the kernel of C.
$K \subseteq \widetilde {R}_{}^{m+n}$
for the kernel of C.
By definition:
![]() $\operatorname {\mathrm {Fitt}}(I_{1})$
is the ideal of
$\operatorname {\mathrm {Fitt}}(I_{1})$
is the ideal of
![]() $\widetilde {R}_{1}$
generated by all elements of the form
$\widetilde {R}_{1}$
generated by all elements of the form
![]() $\det \left (u_1,\ldots ,u_m\right )\in \widetilde {R}_{1}$
for
$\det \left (u_1,\ldots ,u_m\right )\in \widetilde {R}_{1}$
for
![]() $u_1,\ldots ,u_m\in K_1\subseteq \widetilde {R}_{1}^m$
;
$u_1,\ldots ,u_m\in K_1\subseteq \widetilde {R}_{1}^m$
;
![]() $\operatorname {\mathrm {Fitt}}(I_{2})$
is the ideal of
$\operatorname {\mathrm {Fitt}}(I_{2})$
is the ideal of
![]() $\widetilde {R}_{2}$
generated by all elements of the form
$\widetilde {R}_{2}$
generated by all elements of the form
![]() $\det \left (v_1,\ldots ,v_n\right )\in \widetilde {R}_{1}$
for
$\det \left (v_1,\ldots ,v_n\right )\in \widetilde {R}_{1}$
for
![]() $v_1,\ldots ,v_n\in K_2\subseteq \widetilde {R}_{2}^n$
; and lastly
$v_1,\ldots ,v_n\in K_2\subseteq \widetilde {R}_{2}^n$
; and lastly
![]() $\operatorname {\mathrm {Fitt}}(I)$
is the ideal of
$\operatorname {\mathrm {Fitt}}(I)$
is the ideal of
![]() $\widetilde {R}$
generated by all elements of the form
$\widetilde {R}$
generated by all elements of the form
![]() $\det \left (w_1,\ldots ,w_{m+n}\right )\in \widetilde {R}$
for
$\det \left (w_1,\ldots ,w_{m+n}\right )\in \widetilde {R}$
for
![]() $w_1,\ldots ,w_{m+n}\in K\subseteq \widetilde {R}^{m+n}$
.
$w_1,\ldots ,w_{m+n}\in K\subseteq \widetilde {R}^{m+n}$
.
Now, given any
![]() $u_1,\ldots ,u_m\in K_1$
and
$u_1,\ldots ,u_m\in K_1$
and
![]() $v_1,\ldots ,v_n\in K_2$
it’s easy to see that
$v_1,\ldots ,v_n\in K_2$
it’s easy to see that
 $\displaystyle \binom {u_i\otimes 1}{0}, \binom {0}{1\otimes v_j}\in K$
for all i and j, and so
$\displaystyle \binom {u_i\otimes 1}{0}, \binom {0}{1\otimes v_j}\in K$
for all i and j, and so
![]() $\operatorname {\mathrm {Fitt}}(I_{})$
contains the element
$\operatorname {\mathrm {Fitt}}(I_{})$
contains the element
 $$\begin{align*}\det\begin{pmatrix} u_1\otimes 1&\cdots & u_m\otimes 1&0&\cdots&0\\ 0&\cdots&0&1\otimes v_1&\otimes&1\otimes v_n \end{pmatrix} =\det(u_1,\ldots,u_m)\otimes\det(v_1,\ldots,v_m). \end{align*}$$
$$\begin{align*}\det\begin{pmatrix} u_1\otimes 1&\cdots & u_m\otimes 1&0&\cdots&0\\ 0&\cdots&0&1\otimes v_1&\otimes&1\otimes v_n \end{pmatrix} =\det(u_1,\ldots,u_m)\otimes\det(v_1,\ldots,v_m). \end{align*}$$
It follows that
![]() $\operatorname {\mathrm {Fitt}}(I_{1}){\widehat {\otimes }}_{{\mathcal O}}\operatorname {\mathrm {Fitt}}(I_{2})\subseteq \operatorname {\mathrm {Fitt}}(I_{})$
and so
$\operatorname {\mathrm {Fitt}}(I_{1}){\widehat {\otimes }}_{{\mathcal O}}\operatorname {\mathrm {Fitt}}(I_{2})\subseteq \operatorname {\mathrm {Fitt}}(I_{})$
and so
![]() $\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )\subseteq \lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )$
.
$\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )\subseteq \lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )$
.
For the reverse inclusion, we will use the following simple lemma:
Lemma 3.34. For any
 $\displaystyle w = \binom {w_1}{w_2}\in K$
, for
$\displaystyle w = \binom {w_1}{w_2}\in K$
, for
![]() $w_1 \in \widetilde {R}^m$
and
$w_1 \in \widetilde {R}^m$
and
![]() $w_2\in \widetilde {R}^n$
, there exist
$w_2\in \widetilde {R}^n$
, there exist
![]() $u\in K_1$
and
$u\in K_1$
and
![]() $v\in K_2$
for which
$v\in K_2$
for which
![]() $\lambda (w_1) = \lambda _1(u)$
and
$\lambda (w_1) = \lambda _1(u)$
and
![]() $\lambda (w_2) = \lambda _2(v)$
.
$\lambda (w_2) = \lambda _2(v)$
.
Proof. As
![]() $w\in K$
, we have
$w\in K$
, we have
![]() $(A\otimes \operatorname {\mathrm {Id}})(w_1)-(\operatorname {\mathrm {Id}}\otimes B)(w_2) = C(w) = 0$
so let
$(A\otimes \operatorname {\mathrm {Id}})(w_1)-(\operatorname {\mathrm {Id}}\otimes B)(w_2) = C(w) = 0$
so let
![]() $r = (A\otimes \operatorname {\mathrm {Id}})(w_1) = (\operatorname {\mathrm {Id}}\otimes B)(w_2) \in \widetilde {R}$
. By the definitions of A and B, we have
$r = (A\otimes \operatorname {\mathrm {Id}})(w_1) = (\operatorname {\mathrm {Id}}\otimes B)(w_2) \in \widetilde {R}$
. By the definitions of A and B, we have
![]() $r = (A\otimes \operatorname {\mathrm {Id}})(w_1) \in I_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
and
$r = (A\otimes \operatorname {\mathrm {Id}})(w_1) \in I_{1}{\widehat {\otimes }}_{{\mathcal O}}\widetilde {R}_{2}$
and
![]() $r = (\operatorname {\mathrm {Id}}\otimes B)(w_2) \in \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
and so
$r = (\operatorname {\mathrm {Id}}\otimes B)(w_2) \in \widetilde {R}_{1}{\widehat {\otimes }}_{{\mathcal O}}I_{2}$
and so
Now, as
![]() $\lambda _1(I_{1}) = \lambda _2(I_{2})=0$
by assumption, we get that
$\lambda _1(I_{1}) = \lambda _2(I_{2})=0$
by assumption, we get that
![]() $(\lambda _1\otimes \operatorname {\mathrm {Id}})(r) = (\operatorname {\mathrm {Id}}\otimes \lambda _2)(r) = 0$
. Now, let
$(\lambda _1\otimes \operatorname {\mathrm {Id}})(r) = (\operatorname {\mathrm {Id}}\otimes \lambda _2)(r) = 0$
. Now, let
![]() $u = (\operatorname {\mathrm {Id}}\otimes \lambda _2)(w_1)\in \widetilde {R}_{1}^m$
and
$u = (\operatorname {\mathrm {Id}}\otimes \lambda _2)(w_1)\in \widetilde {R}_{1}^m$
and
![]() $v = (\lambda _1\otimes \operatorname {\mathrm {Id}})(w_2)\in \widetilde {R}_{2}^n$
so that
$v = (\lambda _1\otimes \operatorname {\mathrm {Id}})(w_2)\in \widetilde {R}_{2}^n$
so that
 $$ \begin{align*} \lambda_1(u) &= \lambda_1((\operatorname{\mathrm{Id}}\otimes\lambda_2)(w_1)) = (\lambda_1\otimes\lambda_2)(w_1) = \lambda(w_1)\\ \lambda_2(v) &= \lambda_2((\lambda_1\otimes\operatorname{\mathrm{Id}})(w_2)) = (\lambda_1\otimes\lambda_2)(w_2) = \lambda(w_2) \end{align*} $$
$$ \begin{align*} \lambda_1(u) &= \lambda_1((\operatorname{\mathrm{Id}}\otimes\lambda_2)(w_1)) = (\lambda_1\otimes\lambda_2)(w_1) = \lambda(w_1)\\ \lambda_2(v) &= \lambda_2((\lambda_1\otimes\operatorname{\mathrm{Id}})(w_2)) = (\lambda_1\otimes\lambda_2)(w_2) = \lambda(w_2) \end{align*} $$
and
 $$ \begin{align*} A(u) &= (A\otimes\operatorname{\mathrm{Id}})(\operatorname{\mathrm{Id}}\otimes\lambda_2)(w_1) = (\operatorname{\mathrm{Id}}\otimes\lambda_2)(A\otimes\operatorname{\mathrm{Id}})(w_1) = (\operatorname{\mathrm{Id}}\otimes\lambda_2)(r) = 0\\ B(v) &= (\operatorname{\mathrm{Id}}\otimes B)(\lambda_1\otimes\operatorname{\mathrm{Id}})(w_2) = (\lambda_1\otimes\operatorname{\mathrm{Id}})(\operatorname{\mathrm{Id}}\otimes B)(w_2) = (\lambda_1\otimes\operatorname{\mathrm{Id}})(r) = 0. \end{align*} $$
$$ \begin{align*} A(u) &= (A\otimes\operatorname{\mathrm{Id}})(\operatorname{\mathrm{Id}}\otimes\lambda_2)(w_1) = (\operatorname{\mathrm{Id}}\otimes\lambda_2)(A\otimes\operatorname{\mathrm{Id}})(w_1) = (\operatorname{\mathrm{Id}}\otimes\lambda_2)(r) = 0\\ B(v) &= (\operatorname{\mathrm{Id}}\otimes B)(\lambda_1\otimes\operatorname{\mathrm{Id}})(w_2) = (\lambda_1\otimes\operatorname{\mathrm{Id}})(\operatorname{\mathrm{Id}}\otimes B)(w_2) = (\lambda_1\otimes\operatorname{\mathrm{Id}})(r) = 0. \end{align*} $$
So now
![]() $w_1\in \ker A = K_1$
and
$w_1\in \ker A = K_1$
and
![]() $w_2 \in \ker B = K_2$
, as desired.
$w_2 \in \ker B = K_2$
, as desired.
So now take any
![]() $w_1,\ldots ,w_{m+n}\in K$
. The lemma allows us to write
$w_1,\ldots ,w_{m+n}\in K$
. The lemma allows us to write
 $\displaystyle \lambda (w_i) = \binom {\lambda _1(u_i)}{\lambda _2(v_1)}$
for
$\displaystyle \lambda (w_i) = \binom {\lambda _1(u_i)}{\lambda _2(v_1)}$
for
![]() $u_i\in K_1$
and
$u_i\in K_1$
and
![]() $v_i\in K_2$
, which gives
$v_i\in K_2$
, which gives
 $$\begin{align*}\lambda(\det(w_1,\ldots,w_{m+n})) = \det \begin{pmatrix} \lambda_1(u_1)&\cdots&\lambda_1(u_{m+n})\\ \lambda_2(v_1)&\cdots&\lambda_2(v_{m+n}) \end{pmatrix}. \end{align*}$$
$$\begin{align*}\lambda(\det(w_1,\ldots,w_{m+n})) = \det \begin{pmatrix} \lambda_1(u_1)&\cdots&\lambda_1(u_{m+n})\\ \lambda_2(v_1)&\cdots&\lambda_2(v_{m+n}) \end{pmatrix}. \end{align*}$$
But now by standard properties of determinants, the determinant of this
![]() $(m+n)\times (m+n)$
matrix may be written as an alternating sum in the form
$(m+n)\times (m+n)$
matrix may be written as an alternating sum in the form
(where the sum is taken over partitions
![]() $X\sqcup Y = \{1,\ldots ,m+n\}$
with
$X\sqcup Y = \{1,\ldots ,m+n\}$
with
![]() $|X|=m$
and
$|X|=m$
and
![]() $|Y|=n$
). As this sum is in
$|Y|=n$
). As this sum is in
![]() $\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, it follows that
$\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, it follows that
![]() $\lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )\subseteq \lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right ) \lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, giving the desired equality
$\lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )\subseteq \lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right ) \lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, giving the desired equality
![]() $\lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )=\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, and completing the proof.
$\lambda \left (\operatorname {\mathrm {Fitt}}(I_{})\right )=\lambda _1\left (\operatorname {\mathrm {Fitt}}(I_{1})\right )\lambda _2\left (\operatorname {\mathrm {Fitt}}(I_{2})\right )$
, and completing the proof.
4 Galois deformation theory
This section recalls basic results on Galois deformation theory and fixes some notation for the remainder of this work. Our main references are [Reference ThorneTho16, § 5] and [Reference Böckle, Khare and ManningBKM21, § 4].
Recall the notation from the end of Section 1. We fix a continuous, absolutely irreducible residual representation
with
![]() $\det \overline {\rho }=\varepsilon _p$
, for simplicity. We will assume that k contains the eigenvalues of all elements in the image of
$\det \overline {\rho }=\varepsilon _p$
, for simplicity. We will assume that k contains the eigenvalues of all elements in the image of
![]() $\overline {\rho }$
. We also fix a finite set
$\overline {\rho }$
. We also fix a finite set
![]() $\Sigma $
of finite places v of F disjoint from
$\Sigma $
of finite places v of F disjoint from
![]() $\Sigma _p$
that contains all places
$\Sigma _p$
that contains all places
![]() $v\notin \Sigma _p$
at which
$v\notin \Sigma _p$
at which
![]() $\overline {\rho }$
is ramified and possibly further places of F.
$\overline {\rho }$
is ramified and possibly further places of F.
Local deformation rings
Let
![]() $v \in \Sigma $
. We write
$v \in \Sigma $
. We write
![]() ${\mathcal D}_v^\square : {\mathrm {CNL}}_{{\mathcal O}} \to \mathrm {Sets}$
for the functor that associates to
${\mathcal D}_v^\square : {\mathrm {CNL}}_{{\mathcal O}} \to \mathrm {Sets}$
for the functor that associates to
![]() $R \in \mathrm {CNL}_{{\mathcal O}}$
the set of all continuous homomorphisms
$R \in \mathrm {CNL}_{{\mathcal O}}$
the set of all continuous homomorphisms
![]() $r : G_{F_v} \to {\mathrm {GL}}_2(R)$
such that
$r : G_{F_v} \to {\mathrm {GL}}_2(R)$
such that
![]() $r \ \pmod {{\mathfrak m}_R} = \overline {\rho }|_{G_{F_v}}$
and
$r \ \pmod {{\mathfrak m}_R} = \overline {\rho }|_{G_{F_v}}$
and
![]() $\det r=\varepsilon _p$
. The functor
$\det r=\varepsilon _p$
. The functor
![]() ${\mathcal D}_v^\square $
is representable by an object
${\mathcal D}_v^\square $
is representable by an object
![]() $R_v^{\square } \in {\mathrm {CNL}}_{{\mathcal O}}$
, a framed deformation ring. We will write
$R_v^{\square } \in {\mathrm {CNL}}_{{\mathcal O}}$
, a framed deformation ring. We will write
![]() $\rho _v^\square : G_{F_v} \to {\mathrm {GL}}_2(R_v^\square )$
for the universal framed deformation.
$\rho _v^\square : G_{F_v} \to {\mathrm {GL}}_2(R_v^\square )$
for the universal framed deformation.
A local deformation problem for
![]() $\overline {\rho }|_{G_{F_v}}$
is a subfunctor
$\overline {\rho }|_{G_{F_v}}$
is a subfunctor
![]() ${\mathcal D}_v \subset {\mathcal D}_v^\square $
satisfying the following conditions:
${\mathcal D}_v \subset {\mathcal D}_v^\square $
satisfying the following conditions:
-
1. The functor
 ${\mathcal D}_v$
is represented by a quotient
${\mathcal D}_v$
is represented by a quotient
 $R_v$
of
$R_v$
of
 $R_v^\square $
.
$R_v^\square $
. -
2. For all
 $R \in {\mathrm {CNL}}_{{\mathcal O}}$
,
$R \in {\mathrm {CNL}}_{{\mathcal O}}$
,
 $g \in \ker ({\mathrm {GL}}_2(R) \to {\mathrm {GL}}_2(k))$
and
$g \in \ker ({\mathrm {GL}}_2(R) \to {\mathrm {GL}}_2(k))$
and
 $r \in {\mathcal D}_v(R)$
, we have
$r \in {\mathcal D}_v(R)$
, we have
 $g r g^{-1} \in {\mathcal D}_v(R)$
.
$g r g^{-1} \in {\mathcal D}_v(R)$
.
The ring
![]() $R_v$
will be called the local deformation ring representing
$R_v$
will be called the local deformation ring representing
![]() ${\mathcal D}_v$
.
${\mathcal D}_v$
.
If a quotient
![]() $R_v$
of
$R_v$
of
![]() $R_v^\square $
corresponding to a local deformation problem
$R_v^\square $
corresponding to a local deformation problem
![]() ${\mathcal D}_v$
has been fixed, we will write
${\mathcal D}_v$
has been fixed, we will write
![]() $\rho _v : G_{F_v} \to {\mathrm {GL}}_2(R_v)$
for the universal framed deformation of type
$\rho _v : G_{F_v} \to {\mathrm {GL}}_2(R_v)$
for the universal framed deformation of type
![]() ${\mathcal D}_v$
. A sufficient condition for a quotient
${\mathcal D}_v$
. A sufficient condition for a quotient
![]() $R_v$
of
$R_v$
of
![]() $R_v^\square $
to be a local deformation ring is the following; see [Reference ThorneTho16, Lemma 5.12].
$R_v^\square $
to be a local deformation ring is the following; see [Reference ThorneTho16, Lemma 5.12].
Lemma 4.1. Let
![]() $\pi \colon R_v^\square \to R_v$
be a surjective morphism in
$\pi \colon R_v^\square \to R_v$
be a surjective morphism in
![]() $\mathrm {CNL}_{{\mathcal O}}$
with specialization
$\mathrm {CNL}_{{\mathcal O}}$
with specialization
![]() ${r : G_{F_v} \to {\mathrm {GL}}_2(R_v)}$
induced from the universal framed deformation, and assume the following conditions:
${r : G_{F_v} \to {\mathrm {GL}}_2(R_v)}$
induced from the universal framed deformation, and assume the following conditions:
-
1. The ring
 $R_v$
is reduced, and not isomorphic to k.
$R_v$
is reduced, and not isomorphic to k. -
2. For all
 $g \in \ker ({\mathrm {GL}}_2(R_v) \to {\mathrm {GL}}_2(k))$
, the homomorphism
$g \in \ker ({\mathrm {GL}}_2(R_v) \to {\mathrm {GL}}_2(k))$
, the homomorphism
 $R_v^\square \to R_v$
associated to the representation
$R_v^\square \to R_v$
associated to the representation
 $g r g^{-1}$
by universality factors through
$g r g^{-1}$
by universality factors through
 $\pi $
.
$\pi $
.
Then the subfunctor of
![]() ${\mathcal D}_ v^\square $
defined by
${\mathcal D}_ v^\square $
defined by
![]() $R_v$
is a local deformation problem.
$R_v$
is a local deformation problem.
Below, we consider quotients of
![]() $R_v^\square $
which are defined as in [Reference KisinKis09] as reduced,
$R_v^\square $
which are defined as in [Reference KisinKis09] as reduced,
![]() ${\mathcal O}$
-flat quotients
${\mathcal O}$
-flat quotients
![]() $R_v$
of
$R_v$
of
![]() $R_v^\square $
, that are the Zariski closure of a set of
$R_v^\square $
, that are the Zariski closure of a set of
![]() $\overline {\mathbf Q}_p$
-valued points of
$\overline {\mathbf Q}_p$
-valued points of
![]() $R_v^\square $
; in each case the set forms the closed points of a Zariski closed subset of the generic fiber Jacobson ring
$R_v^\square $
; in each case the set forms the closed points of a Zariski closed subset of the generic fiber Jacobson ring
![]() $R_v^\square [1/p]$
and thus the generic fiber
$R_v^\square [1/p]$
and thus the generic fiber
![]() $R_v[1/p]$
has this set as its
$R_v[1/p]$
has this set as its
![]() $\overline {\mathbf Q}_p$
-points; in particular, these
$\overline {\mathbf Q}_p$
-points; in particular, these
![]() $R_v$
satisfy Lemma 4.1 and thus give rise to a local deformation problem. [Reference KisinKis09] computes the dimension of generic fibers of the quotients we consider and proves that they are regular.
$R_v$
satisfy Lemma 4.1 and thus give rise to a local deformation problem. [Reference KisinKis09] computes the dimension of generic fibers of the quotients we consider and proves that they are regular.
Modified local deformation rings
We shall also consider modified deformation problems as introduced in [Reference CalegariCal18]. For this, one fixes an eigenvalue
![]() $\alpha _v$
of
$\alpha _v$
of
![]() $\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
. Note that
$\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
. Note that
![]() $\alpha _v\in k$
by our hypothesis that the eigenvalues of all matrices in the image
$\alpha _v\in k$
by our hypothesis that the eigenvalues of all matrices in the image
![]() $\overline {\rho }(G_F)\subset {\mathrm {GL}}_2(k)$
lie in k.
$\overline {\rho }(G_F)\subset {\mathrm {GL}}_2(k)$
lie in k.
Definition 4.2. The functor
![]() ${\widetilde {{\mathcal D}}}\!{}_v^\square : {\mathrm {CNL}}_{{\mathcal O}} \to \mathrm {Sets}$
of modified framed deformations associates to
${\widetilde {{\mathcal D}}}\!{}_v^\square : {\mathrm {CNL}}_{{\mathcal O}} \to \mathrm {Sets}$
of modified framed deformations associates to
![]() $R \in \mathrm {CNL}_{{\mathcal O}}$
a pair
$R \in \mathrm {CNL}_{{\mathcal O}}$
a pair
![]() $(r,a)$
with
$(r,a)$
with
![]() $r\in {\mathcal D}_v^\square (R)$
and
$r\in {\mathcal D}_v^\square (R)$
and
![]() $a\in R$
a root of the characteristic polynomial of
$a\in R$
a root of the characteristic polynomial of
![]() $r(\operatorname {\mathrm {Frob}}_v)$
such that
$r(\operatorname {\mathrm {Frob}}_v)$
such that
![]() $a\equiv \alpha _v{\operatorname {mod}} {{\mathfrak m}_R}$
.
$a\equiv \alpha _v{\operatorname {mod}} {{\mathfrak m}_R}$
.
There is an obvious natural transformation
![]() $u_v\colon {\widetilde {{\mathcal D}}}\!{}_v^\square \Rightarrow {\mathcal D}\!{}_v^\square $
, and
$u_v\colon {\widetilde {{\mathcal D}}}\!{}_v^\square \Rightarrow {\mathcal D}\!{}_v^\square $
, and
![]() ${\widetilde {{\mathcal D}}}\!{}_v^\square $
is representable by the localization
${\widetilde {{\mathcal D}}}\!{}_v^\square $
is representable by the localization
![]() ${\widetilde R}{}_v^\square $
of the ring
${\widetilde R}{}_v^\square $
of the ring
![]() $R_v^\square [x]/(x^2-x\operatorname {\mathrm {tr}} \rho _v^\square (\operatorname {\mathrm {Frob}}_v)+\det \rho _v^\square (\operatorname {\mathrm {Frob}}_v))$
at the maximal ideal generated by
$R_v^\square [x]/(x^2-x\operatorname {\mathrm {tr}} \rho _v^\square (\operatorname {\mathrm {Frob}}_v)+\det \rho _v^\square (\operatorname {\mathrm {Frob}}_v))$
at the maximal ideal generated by
![]() ${\mathfrak m}_{R_v^\square }$
and
${\mathfrak m}_{R_v^\square }$
and
![]() $(x-\alpha _v)$
. If
$(x-\alpha _v)$
. If
![]() $\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
has a multiple eigenvalue, the ring
$\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
has a multiple eigenvalue, the ring
![]() $R_v^\square [x]/(x^2-x\operatorname {\mathrm {tr}} \rho _v^\square (\operatorname {\mathrm {Frob}}_v)+\det \rho _v^\square (\operatorname {\mathrm {Frob}}_v))$
is local and hence isomorphic to
$R_v^\square [x]/(x^2-x\operatorname {\mathrm {tr}} \rho _v^\square (\operatorname {\mathrm {Frob}}_v)+\det \rho _v^\square (\operatorname {\mathrm {Frob}}_v))$
is local and hence isomorphic to
![]() ${\widetilde R}{}_v^\square $
. This proves the following result; see [Reference CalegariCal18, Lemma 2.1].
${\widetilde R}{}_v^\square $
. This proves the following result; see [Reference CalegariCal18, Lemma 2.1].
Lemma 4.3. If
![]() $\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
has distinct eigenvalues, the canonical map
$\overline {\rho }(\operatorname {\mathrm {Frob}}_v)$
has distinct eigenvalues, the canonical map
![]() $R{}_v^\square \to {\widetilde R}{}_v^\square $
is an isomorphism. Otherwise, the extension
$R{}_v^\square \to {\widetilde R}{}_v^\square $
is an isomorphism. Otherwise, the extension
![]() $R{}_v^\square \to {\widetilde R}{}_v^\square $
is a finite flat extension of degree two.
$R{}_v^\square \to {\widetilde R}{}_v^\square $
is a finite flat extension of degree two.
The following definition is extracted from [Reference CalegariCal18, § 2].
Definition 4.4. A modified local deformation problem for
![]() $\overline {\rho }|_{G_{F_v}}$
is a subfunctor
$\overline {\rho }|_{G_{F_v}}$
is a subfunctor
![]() ${\widetilde {{\mathcal D}}}_v \subset {\widetilde {{\mathcal D}}}\!{}_v^\square $
satisfying the following conditions:
${\widetilde {{\mathcal D}}}_v \subset {\widetilde {{\mathcal D}}}\!{}_v^\square $
satisfying the following conditions:
-
1. The functor
 ${\widetilde {{\mathcal D}}}_v$
is represented by a quotient
${\widetilde {{\mathcal D}}}_v$
is represented by a quotient
 ${\widetilde R}_v$
of
${\widetilde R}_v$
of
 ${\widetilde R}{}_v^\square $
.
${\widetilde R}{}_v^\square $
. -
2. For all
 $R \in {\mathrm {CNL}}_{{\mathcal O}}$
,
$R \in {\mathrm {CNL}}_{{\mathcal O}}$
,
 $g \in \ker ({\mathrm {GL}}_2(R) \to {\mathrm {GL}}_2(k))$
and
$g \in \ker ({\mathrm {GL}}_2(R) \to {\mathrm {GL}}_2(k))$
and
 $(r,a) \in {\widetilde {\mathcal D}}_v(R)$
, we have
$(r,a) \in {\widetilde {\mathcal D}}_v(R)$
, we have
 ${(g r g^{-1},a) \in {\widetilde {\mathcal D}}_v(R)}$
.
${(g r g^{-1},a) \in {\widetilde {\mathcal D}}_v(R)}$
.
One has the following analog of Lemma 4.1.
Lemma 4.5. Let
![]() ${\widetilde {\pi }}\colon {\widetilde R}_v^\square \to {\widetilde R}_v$
be a surjective morphism in
${\widetilde {\pi }}\colon {\widetilde R}_v^\square \to {\widetilde R}_v$
be a surjective morphism in
![]() $\mathrm {CNL}_{{\mathcal O}}$
, with specialization
$\mathrm {CNL}_{{\mathcal O}}$
, with specialization
![]() $(r, a) \in {\widetilde {\mathcal D}}({\widetilde {\mathcal R}}_v) $
induced from the universal pair via
$(r, a) \in {\widetilde {\mathcal D}}({\widetilde {\mathcal R}}_v) $
induced from the universal pair via
![]() ${\widetilde {\pi}}$
. Suppose that
${\widetilde {\pi}}$
. Suppose that
-
1. The ring
 ${\widetilde R}_v$
is reduced, and not isomorphic to k.
${\widetilde R}_v$
is reduced, and not isomorphic to k. -
2. The surjection
 ${\widetilde {\pi}} $
satisfies condition 2 of Lemma 4.1 with
${\widetilde {\pi}} $
satisfies condition 2 of Lemma 4.1 with
 ${\widetilde R}_v$
and
${\widetilde R}_v$
and
 ${\widetilde R}_v^{\square}$
replacing
${\widetilde R}_v^{\square}$
replacing
 $R_v$
and
$R_v$
and
 $R_v^{\square}$
, respectively.
$R_v^{\square}$
, respectively.
Then the subfunctor
![]() ${\widetilde {{\mathcal D}}}_v$
of
${\widetilde {{\mathcal D}}}_v$
of
![]() ${\widetilde {{\mathcal D}}}\!{}_ v^\square $
defined by
${\widetilde {{\mathcal D}}}\!{}_ v^\square $
defined by
![]() ${\widetilde R}_v$
is a modified local deformation problem.
${\widetilde R}_v$
is a modified local deformation problem.
Proof. The proof follows from the aruguments given in the proof of [Lemma 3.2, Reference Barnet-Lamb, Geraghty, Harris and TaylorBLGHT11] which contains a proof of Lemma 4.1.
Local deformation conditions
We now define the local deformation conditions relevant to this work; the resulting framed deformation rings will be denoted by
![]() $R_v^{\tau _v}$
, where the superscripts
$R_v^{\tau _v}$
, where the superscripts
![]() ${\tau _v\in \{\operatorname {\mathrm {fl}},\ {\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {un}},\ {\operatorname {\varphi -uni}},\ \square \}}$
indicate the type of condition used to define
${\tau _v\in \{\operatorname {\mathrm {fl}},\ {\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {un}},\ {\operatorname {\varphi -uni}},\ \square \}}$
indicate the type of condition used to define
![]() $R_v$
, and the corresponding universal framed deformation by
$R_v$
, and the corresponding universal framed deformation by
![]() $\rho _v^{\tau _v}$
. Our conditions for framed deformations r of
$\rho _v^{\tau _v}$
. Our conditions for framed deformations r of
![]() $\overline {\rho }|_{G_v}$
will always include the condition
$\overline {\rho }|_{G_v}$
will always include the condition
![]() $\det r=\varepsilon _p$
; we shall not repeat this below. We shall be brief, as we closely follow [Reference Böckle, Khare and ManningBKM21, § 4].
$\det r=\varepsilon _p$
; we shall not repeat this below. We shall be brief, as we closely follow [Reference Böckle, Khare and ManningBKM21, § 4].
For all
![]() $v\in \Sigma _p$
the extension
$v\in \Sigma _p$
the extension
![]() $F_v/{\mathbf Q}_p$
is unramified by the hypotheses from Subsection 1.6 and we moreover assume that that
$F_v/{\mathbf Q}_p$
is unramified by the hypotheses from Subsection 1.6 and we moreover assume that that
![]() $\overline {\rho }|_{G_v}$
is finite flat, so that Fontaine–Laffaille theory applies, and we let
$\overline {\rho }|_{G_v}$
is finite flat, so that Fontaine–Laffaille theory applies, and we let
-
•
 $R_v^{\operatorname {\mathrm {fl}}}$
be the quotient of
$R_v^{\operatorname {\mathrm {fl}}}$
be the quotient of
 $R_v^{\square }$
parameterizing flat framed deformations of
$R_v^{\square }$
parameterizing flat framed deformations of
 $\overline {\rho }|_{G_v}$
.
$\overline {\rho }|_{G_v}$
.
For
![]() $v\in \Sigma $
, we let
$v\in \Sigma $
, we let
-
•
 $R_v^{{\operatorname {min}}}$
be the quotient of
$R_v^{{\operatorname {min}}}$
be the quotient of
 $R_v^\square $
parametrizing minimally ramified framed deformations of
$R_v^\square $
parametrizing minimally ramified framed deformations of
 $\overline {\rho }|_{G_v}$
. Concretely, a framed deformation
$\overline {\rho }|_{G_v}$
. Concretely, a framed deformation
 $\rho _v$
of
$\rho _v$
of
 $\overline {\rho }|_{G_v}$
parameterized by
$\overline {\rho }|_{G_v}$
parameterized by
 $R_v^{{\operatorname {min}}}$
is required to satisfy one of the following two conditions depending on
$R_v^{{\operatorname {min}}}$
is required to satisfy one of the following two conditions depending on
 $\overline {\rho }|_{I_v}$
:
$\overline {\rho }|_{I_v}$
:-
(i) if
 $\overline {\rho }|_{I_v}$
is semisimple, then the restriction
$\overline {\rho }|_{I_v}$
is semisimple, then the restriction
 $\rho _v(I_v)\to \overline {\rho }(I_v)$
is an isomorphism,
$\rho _v(I_v)\to \overline {\rho }(I_v)$
is an isomorphism, -
(ii) if
 $\overline {\rho }|_{I_v}$
is a nontrivial extension of a character
$\overline {\rho }|_{I_v}$
is a nontrivial extension of a character
 $\xi $
of
$\xi $
of
 $I_v$
by itself, then
$I_v$
by itself, then
 $\rho _v|_{I_v}$
is an extension of
$\rho _v|_{I_v}$
is an extension of
 $\widetilde \xi $
by itself, for
$\widetilde \xi $
by itself, for
 $\widetilde \xi $
the Teichmüller lift of
$\widetilde \xi $
the Teichmüller lift of
 $\xi $
.
$\xi $
.
In particular, if
 $\overline {\rho }$
is unramified at v, then
$\overline {\rho }$
is unramified at v, then
 $R_v^{{\operatorname {min}}}$
parameterizes unramified framed deformations, and then, occasionally we write
$R_v^{{\operatorname {min}}}$
parameterizes unramified framed deformations, and then, occasionally we write
 $R^{{\mathrm {unr}}}_v$
for
$R^{{\mathrm {unr}}}_v$
for
 $R^{{\operatorname {min}}}_v$
.
$R^{{\operatorname {min}}}_v$
. -
Let
![]() $Q\subset \Sigma $
be the subset of those v such that the representation
$Q\subset \Sigma $
be the subset of those v such that the representation
![]() $\overline {\rho }|_{G_{F_v}}$
is of the form
$\overline {\rho }|_{G_{F_v}}$
is of the form
 $$ \begin{align} \left( \begin{array}{cc} \varepsilon_p {\overline{\chi}}& *\\ 0 & {\overline{\chi}} \end{array} \right) \end{align} $$
$$ \begin{align} \left( \begin{array}{cc} \varepsilon_p {\overline{\chi}}& *\\ 0 & {\overline{\chi}} \end{array} \right) \end{align} $$
with respect to some basis
![]() $e_1,e_2$
of
$e_1,e_2$
of
![]() $k^2$
and where the character
$k^2$
and where the character
![]() ${\overline {\chi }}$
is unramified;Footnote
3
we further assume that the basis is chosen so that
${\overline {\chi }}$
is unramified;Footnote
3
we further assume that the basis is chosen so that
![]() $*$
is trivial whenever
$*$
is trivial whenever
![]() $\overline {\rho }|_{G_{F_v}}$
is split, which holds if
$\overline {\rho }|_{G_{F_v}}$
is split, which holds if
![]() $\overline {\rho }$
is unramified and
$\overline {\rho }$
is unramified and
![]() $\varepsilon _p$
is nontrivial. Also,
$\varepsilon _p$
is nontrivial. Also,
![]() ${\overline {\chi }}$
has to be quadratic and we let
${\overline {\chi }}$
has to be quadratic and we let
![]() $\chi $
be its unique (quadratic) lift to
$\chi $
be its unique (quadratic) lift to
![]() ${\mathcal O}$
. Let
${\mathcal O}$
. Let
![]() $\beta _v=\chi (\operatorname {\mathrm {Frob}}_v)\in \{\pm 1\}$
.
$\beta _v=\chi (\operatorname {\mathrm {Frob}}_v)\in \{\pm 1\}$
.
For
![]() $v\in Q$
, we define the Steinberg quotient
$v\in Q$
, we define the Steinberg quotient
![]() $R_v^{\mathrm {st}}$
of
$R_v^{\mathrm {st}}$
of
![]() $R_v^\square $
as follows:
$R_v^\square $
as follows:
-
• If
 $\overline {\rho }$
is ramified at v, then
$\overline {\rho }$
is ramified at v, then
 $R_v^{\mathrm {st}}$
is defined to be
$R_v^{\mathrm {st}}$
is defined to be
 $R^{{\operatorname {min}}}_v$
.
$R^{{\operatorname {min}}}_v$
. -
• If
 $\overline {\rho }$
is unramified at v, we define
$\overline {\rho }$
is unramified at v, we define
 $R_v^{{\mathrm {st}}}$
as the unique reduced quotient of
$R_v^{{\mathrm {st}}}$
as the unique reduced quotient of
 $R_v^\square $
characterized by the fact that the L-valued points of its generic fiber, for any finite extension
$R_v^\square $
characterized by the fact that the L-valued points of its generic fiber, for any finite extension
 $L/E$
, correspond to representations of the form and with the additional condition
$L/E$
, correspond to representations of the form and with the additional condition $$\begin{align*}\left( \begin{array}{cc} \varepsilon_p \chi& \ast \\ 0 & \chi\end{array} \right),\end{align*}$$
$$\begin{align*}\left( \begin{array}{cc} \varepsilon_p \chi& \ast \\ 0 & \chi\end{array} \right),\end{align*}$$
 $\chi (\operatorname {\mathrm {Frob}}_v)=\beta _v$
in the case
$\chi (\operatorname {\mathrm {Frob}}_v)=\beta _v$
in the case
 $q_v\equiv -1\ {\operatorname {mod}}\ p$
. In the case
$q_v\equiv -1\ {\operatorname {mod}}\ p$
. In the case
 $q_v\equiv -1\ {\operatorname {mod}}\ p$
, without fixing
$q_v\equiv -1\ {\operatorname {mod}}\ p$
, without fixing
 $\beta _v$
,
$\beta _v$
,
 $\operatorname {\mathrm {Spec}} R_v^{{\mathrm {st}}}$
would have two irreducible components because here
$\operatorname {\mathrm {Spec}} R_v^{{\mathrm {st}}}$
would have two irreducible components because here
 $\varepsilon _p$
is quadratic and unramified; see also [Reference Böckle, Khare and ManningBKM21, § 4].
$\varepsilon _p$
is quadratic and unramified; see also [Reference Böckle, Khare and ManningBKM21, § 4].
For
![]() $v\in Q$
such that
$v\in Q$
such that
![]() $\overline {\rho }|_{G_{F_v}}$
is unramified, we also define:
$\overline {\rho }|_{G_{F_v}}$
is unramified, we also define:
-
• The unipotent quotient
 $R_v^{\mathrm {uni}}$
of
$R_v^{\mathrm {uni}}$
of
 $R_v^\square $
is the unique reduced quotient such that
$R_v^\square $
is the unique reduced quotient such that
 $\operatorname {\mathrm {Spec}} R_v^{\mathrm {uni}}=\operatorname {\mathrm {Spec}} R_v^{\mathrm {st}}\cup \operatorname {\mathrm {Spec}} R_v^{{\mathrm {unr}}}$
inside
$\operatorname {\mathrm {Spec}} R_v^{\mathrm {uni}}=\operatorname {\mathrm {Spec}} R_v^{\mathrm {st}}\cup \operatorname {\mathrm {Spec}} R_v^{{\mathrm {unr}}}$
inside
 $\operatorname {\mathrm {Spec}} R_v^\square $
. If
$\operatorname {\mathrm {Spec}} R_v^\square $
. If
 $q_v\equiv -1\ {\operatorname {mod}}\ p$
, then note that
$q_v\equiv -1\ {\operatorname {mod}}\ p$
, then note that
 $R_v^{\mathrm {st}}$
depends on
$R_v^{\mathrm {st}}$
depends on
 $\beta _v$
.
$\beta _v$
.
-
• The modified unipotent quotient
 ${\widetilde R}_v^{\mathrm {uni}}$
of
${\widetilde R}_v^{\mathrm {uni}}$
of
 ${\widetilde R}{}_v^\square $
is the unique reduced quotient of
${\widetilde R}{}_v^\square $
is the unique reduced quotient of
 ${\widetilde R}{}_v^\square $
characterized by the fact that the L-valued points of its generic fiber, for any finite extension
${\widetilde R}{}_v^\square $
characterized by the fact that the L-valued points of its generic fiber, for any finite extension
 $L/E$
, correspond to pairs
$L/E$
, correspond to pairs
 $(r,a)$
, where r is a representation of the form with
$(r,a)$
, where r is a representation of the form with $$\begin{align*}\begin{pmatrix} \varepsilon_p\chi &*\\0& \chi\end{pmatrix}\end{align*}$$
$$\begin{align*}\begin{pmatrix} \varepsilon_p\chi &*\\0& \chi\end{pmatrix}\end{align*}$$
 $\chi $
unramified, and such that
$\chi $
unramified, and such that
 $\chi (\operatorname {\mathrm {Frob}}_v)=a$
, and such that
$\chi (\operatorname {\mathrm {Frob}}_v)=a$
, and such that
 $\alpha _v=\beta _v\ {\operatorname {mod}}\ p$
in the case
$\alpha _v=\beta _v\ {\operatorname {mod}}\ p$
in the case
 $q_v\equiv -1\ {\operatorname {mod}}\ p$
.
$q_v\equiv -1\ {\operatorname {mod}}\ p$
.
It is clear from the definitions that the natural map
![]() $R_v^\square \to {\widetilde R}{}_v^{\mathrm {uni}}$
factors via
$R_v^\square \to {\widetilde R}{}_v^{\mathrm {uni}}$
factors via
![]() $R^\square _v\to R_v^{\mathrm {uni}}\to {\widetilde R}{}_v^{\mathrm {uni}}$
, and by Lemma 4.3, the map
$R^\square _v\to R_v^{\mathrm {uni}}\to {\widetilde R}{}_v^{\mathrm {uni}}$
, and by Lemma 4.3, the map
![]() $R_v^{\mathrm {uni}}\to {\widetilde R}{}_v^{\mathrm {uni}}$
is an isomorphism, unless
$R_v^{\mathrm {uni}}\to {\widetilde R}{}_v^{\mathrm {uni}}$
is an isomorphism, unless
![]() $q_v\equiv 1\ {\operatorname {mod}}\ p$
.
$q_v\equiv 1\ {\operatorname {mod}}\ p$
.
For a more uniform notation, from now on we write
![]() $R_v^{\operatorname {\varphi -uni}}$
instead of
$R_v^{\operatorname {\varphi -uni}}$
instead of
![]() ${\widetilde R}{}_v^{\mathrm {uni}}$
.
${\widetilde R}{}_v^{\mathrm {uni}}$
.
The following result summarizes basic ring theoretic properties of the
![]() $R_v^{\tau _v}$
.
$R_v^{\tau _v}$
.
Proposition 4.6. The following hold:
-
1. We have
 $R^{\operatorname {\mathrm {fl}}}_v \cong {\mathcal O}[[x_1,\ldots ,x_{3+[F_v:{\mathbf Q}_p]}]]$
for
$R^{\operatorname {\mathrm {fl}}}_v \cong {\mathcal O}[[x_1,\ldots ,x_{3+[F_v:{\mathbf Q}_p]}]]$
for
 $v\in \Sigma _p$
and
$v\in \Sigma _p$
and
 $R^{{\operatorname {min}}}_v \cong {\mathcal O}[[x_1,x_2,x_3]]$
for
$R^{{\operatorname {min}}}_v \cong {\mathcal O}[[x_1,x_2,x_3]]$
for
 $v\in \Sigma $
.
$v\in \Sigma $
. -
2. For
 $v\in \Sigma $
, the ring
$v\in \Sigma $
, the ring
 $R_v^\square $
is a complete intersection, reduced and flat over
$R_v^\square $
is a complete intersection, reduced and flat over
 ${\mathcal O}$
of relative dimension
${\mathcal O}$
of relative dimension
 $3$
.
$3$
. -
3. For
 $v\in Q$
, the ring
$v\in Q$
, the ring
 $R_v^{{\mathrm {st}}}$
is Cohen–Macaulay, flat of relative dimension
$R_v^{{\mathrm {st}}}$
is Cohen–Macaulay, flat of relative dimension
 $3$
over
$3$
over
 ${\mathcal O}$
and geometrically integral and if v is not a trivial prime for
${\mathcal O}$
and geometrically integral and if v is not a trivial prime for
 $\overline {\rho }$
, we in fact have
$\overline {\rho }$
, we in fact have
 $R^{{\mathrm {st}}}_v\cong {\mathcal O}[[x_1,x_2,x_3]]$
.
$R^{{\mathrm {st}}}_v\cong {\mathcal O}[[x_1,x_2,x_3]]$
. -
4. For each
 $v\in Q$
and each minimal prime
$v\in Q$
and each minimal prime
 ${{\mathfrak p}}$
of
${{\mathfrak p}}$
of
 $R_v^\square $
,
$R_v^\square $
,
 $R_v^\square /{{\mathfrak p}}$
is flat over
$R_v^\square /{{\mathfrak p}}$
is flat over
 ${\mathcal O}$
and geometrically integral.
${\mathcal O}$
and geometrically integral. -
5. For
 $v\in Q$
such that in addition
$v\in Q$
such that in addition
 $\overline {\rho }$
is unramified at v, the rings
$\overline {\rho }$
is unramified at v, the rings
 $R_v^{\mathrm {uni}}$
and
$R_v^{\mathrm {uni}}$
and
 $R_v^{\operatorname {\varphi -uni}}$
are Gorenstein, reduced and flat over
$R_v^{\operatorname {\varphi -uni}}$
are Gorenstein, reduced and flat over
 ${\mathcal O}$
of relative dimension
${\mathcal O}$
of relative dimension
 $3$
.
$3$
.
Moreover, the rings
![]() $R_v^{\tau _v}$
in 1.–5. are the completion of a finite type
$R_v^{\tau _v}$
in 1.–5. are the completion of a finite type
![]() ${\mathcal O}$
-algebra at a maximal ideal.
${\mathcal O}$
-algebra at a maximal ideal.
Proof. For all but 5, we refer to [Reference Böckle, Khare and ManningBKM21, Prop. 4.3] and the references given in its proof. The proof of 5 is given in Lemmas 5.4 and 5.3 below.
For each
![]() $v\in \Sigma $
, fix a
$v\in \Sigma $
, fix a
![]() $\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {un}},\ {\operatorname {\varphi -uni}},\ \square \}$
, and let
$\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {un}},\ {\operatorname {\varphi -uni}},\ \square \}$
, and let
![]() $\tau = (\tau _v)_{v\in \Sigma }$
, and defineFootnote
4
$\tau = (\tau _v)_{v\in \Sigma }$
, and defineFootnote
4
 $$ \begin{align*} R_{\operatorname{\mathrm{loc}}}^\tau &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}} \, R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}} \,R_v^{\operatorname{\mathrm{fl}}}\right). \end{align*} $$
$$ \begin{align*} R_{\operatorname{\mathrm{loc}}}^\tau &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}} \, R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}} \,R_v^{\operatorname{\mathrm{fl}}}\right). \end{align*} $$
We simply write
![]() $R_{\operatorname {\mathrm {loc}}}$
for
$R_{\operatorname {\mathrm {loc}}}$
for
![]() $R^\tau _{\operatorname {\mathrm {loc}}}$
, if
$R^\tau _{\operatorname {\mathrm {loc}}}$
, if
![]() $\tau _v=\square $
for all v. Note in particular, that for any
$\tau _v=\square $
for all v. Note in particular, that for any
![]() $\tau $
there is a natural morphism
$\tau $
there is a natural morphism
![]() $R_{\operatorname {\mathrm {loc}}}\to R^\tau _{\operatorname {\mathrm {loc}}}$
and that it factors via
$R_{\operatorname {\mathrm {loc}}}\to R^\tau _{\operatorname {\mathrm {loc}}}$
and that it factors via
![]() $R^{\tau '}_{\operatorname {\mathrm {loc}}}$
, where
$R^{\tau '}_{\operatorname {\mathrm {loc}}}$
, where
![]() $\tau '$
is obtained from
$\tau '$
is obtained from
![]() $\tau $
be replacing all
$\tau $
be replacing all
![]() ${\operatorname {\varphi -uni}}$
by
${\operatorname {\varphi -uni}}$
by
![]() ${\mathrm {uni}}$
.
${\mathrm {uni}}$
.
Proposition 4.6 and [Reference Böckle, Khare and ManningBKM21, Lemma 4.4] yield:
Proposition 4.7. The ring
![]() $R_{\operatorname {\mathrm {loc}}}$
is a complete intersection, the ring
$R_{\operatorname {\mathrm {loc}}}$
is a complete intersection, the ring
![]() $R^\tau _{\operatorname {\mathrm {loc}}}$
is Cohen–Macaulay, and both are reduced and flat over
$R^\tau _{\operatorname {\mathrm {loc}}}$
is Cohen–Macaulay, and both are reduced and flat over
![]() ${\mathcal O}$
. If
${\mathcal O}$
. If
![]() $R_v^{\tau _v}$
is Gorenstein for all
$R_v^{\tau _v}$
is Gorenstein for all
![]() $v\in \Sigma $
, then so is
$v\in \Sigma $
, then so is
![]() $R^\tau _{\operatorname {\mathrm {loc}}}$
.
$R^\tau _{\operatorname {\mathrm {loc}}}$
.
Moreover, each irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_{\operatorname {\mathrm {loc}}}$
is of the form
$\operatorname {\mathrm {Spec}} R_{\operatorname {\mathrm {loc}}}$
is of the form
 $$\begin{align*}\operatorname{\mathrm{Spec}} \left[\widehat{\bigotimes_{v\in\Sigma}} \, R_v^\square/{{\mathfrak p}}^{(v)}\right] \widehat{\otimes} \, R^{\operatorname{\mathrm{fl}}}_p,\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spec}} \left[\widehat{\bigotimes_{v\in\Sigma}} \, R_v^\square/{{\mathfrak p}}^{(v)}\right] \widehat{\otimes} \, R^{\operatorname{\mathrm{fl}}}_p,\end{align*}$$
where each
![]() $\operatorname {\mathrm {Spec}} R^\square _v/{{\mathfrak p}}^{(v)}$
is an irreducible component of
$\operatorname {\mathrm {Spec}} R^\square _v/{{\mathfrak p}}^{(v)}$
is an irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_v^\square $
, that is, each
$\operatorname {\mathrm {Spec}} R_v^\square $
, that is, each
![]() ${{\mathfrak p}}^{(v)}$
is a minimal prime of
${{\mathfrak p}}^{(v)}$
is a minimal prime of
![]() $R_v^\square $
.
$R_v^\square $
.
Global deformation rings
Now, we set up the notation for the corresponding global deformation rings, following [Reference Böckle, Khare and ManningBKM21, Section 4.3], where further details can be found.
Let R (resp.
![]() $R^\square $
) denote the global unframed (resp. framed) deformation ring parameterizing lifts of
$R^\square $
) denote the global unframed (resp. framed) deformation ring parameterizing lifts of
![]() $\overline {\rho }$
with determinant
$\overline {\rho }$
with determinant
![]() $\varepsilon _p$
which are unramified outside
$\varepsilon _p$
which are unramified outside
![]() $\Sigma \cup \Sigma _p$
(together with a choice of basis at every
$\Sigma \cup \Sigma _p$
(together with a choice of basis at every
![]() $v\in \Sigma \cup \Sigma _p$
), One may noncanonically fix an isomorphism
$v\in \Sigma \cup \Sigma _p$
), One may noncanonically fix an isomorphism
![]() $R^\square = R[[X_1,\ldots ,X_{4\#(\Sigma \cup \Sigma _p)-1}]]$
so that we may treat the subring R of
$R^\square = R[[X_1,\ldots ,X_{4\#(\Sigma \cup \Sigma _p)-1}]]$
so that we may treat the subring R of
![]() $R^\square $
also as a quotient of
$R^\square $
also as a quotient of
![]() $R^\square $
. One also has a natural map
$R^\square $
. One also has a natural map
![]() $R_{\operatorname {\mathrm {loc}}}\to R^\square $
(and thus a map
$R_{\operatorname {\mathrm {loc}}}\to R^\square $
(and thus a map
![]() $R_{\operatorname {\mathrm {loc}}}\to R$
), by restricting the global framed deformation and performing locally a base change.
$R_{\operatorname {\mathrm {loc}}}\to R$
), by restricting the global framed deformation and performing locally a base change.
Let
![]() $\tau = (\tau _v)_{v\in \Sigma }$
be as in the previous subsection. Then we define
$\tau = (\tau _v)_{v\in \Sigma }$
be as in the previous subsection. Then we define
5 The Wiles defect for some local framed deformation rings
In this section, R will denote a ring
![]() $R_v^{\tau _v}$
as defined in Section 4 for a residual representation
$R_v^{\tau _v}$
as defined in Section 4 for a residual representation
![]() $\overline {\rho }_v=\overline {\rho }|_{G_{F_v}}:G_{F_v}\to {\mathrm {GL}}_2(k)$
as described in the displayed matrix (4.1) at a place
$\overline {\rho }_v=\overline {\rho }|_{G_{F_v}}:G_{F_v}\to {\mathrm {GL}}_2(k)$
as described in the displayed matrix (4.1) at a place
![]() $v\in Q$
of F, and a deformation condition
$v\in Q$
of F, and a deformation condition
![]() $\tau _v\in \{{\mathrm {st}},{\operatorname {\varphi -uni}},{\mathrm {uni}}\}$
. We let
$\tau _v\in \{{\mathrm {st}},{\operatorname {\varphi -uni}},{\mathrm {uni}}\}$
. We let
![]() $q=q_v$
be the cardinality of the residue field of
$q=q_v$
be the cardinality of the residue field of
![]() $F_v$
and e the ramification index of
$F_v$
and e the ramification index of
![]() ${\mathcal O}$
over
${\mathcal O}$
over
![]() $W(k)$
. We also fix an augmentation
$W(k)$
. We also fix an augmentation
![]() $\lambda :R\twoheadrightarrow {\mathcal O}$
.
$\lambda :R\twoheadrightarrow {\mathcal O}$
.
Throughout this section, we assume, in fact, that
![]() $q\equiv 1\ {\operatorname {mod}}\ p$
and that
$q\equiv 1\ {\operatorname {mod}}\ p$
and that
![]() $\overline {\rho }_v$
is trivial.
$\overline {\rho }_v$
is trivial.
Definition 5.1. Let
![]() $\rho _\lambda :G_{F_v}\to {\mathrm {GL}}_2({\mathcal O})$
be the representation at v induced from the augmentation
$\rho _\lambda :G_{F_v}\to {\mathrm {GL}}_2({\mathcal O})$
be the representation at v induced from the augmentation
![]() $\lambda $
. We define the local monodromy invariant
$\lambda $
. We define the local monodromy invariant
![]() $n_v$
of
$n_v$
of
![]() $\lambda $
to be the largest integers n such that
$\lambda $
to be the largest integers n such that
![]() $\rho _\lambda (G_{F_v})$
mod
$\rho _\lambda (G_{F_v})$
mod
![]() $\varpi ^n$
has trivial projective image.Footnote
5
$\varpi ^n$
has trivial projective image.Footnote
5
The aim of this section is to compute the invariants
![]() $D_{1,\lambda }(R)$
and
$D_{1,\lambda }(R)$
and
![]() $c_{1,\lambda }(R)$
of Venkatesh and the Wiles defect
$c_{1,\lambda }(R)$
of Venkatesh and the Wiles defect
![]() $\delta _\lambda (R)$
as attached in Definition 3.24 to the pair
$\delta _\lambda (R)$
as attached in Definition 3.24 to the pair
![]() $(R,\lambda )$
for certain types of
$(R,\lambda )$
for certain types of
![]() $\overline {\rho }_v$
and
$\overline {\rho }_v$
and
![]() $\tau _v$
. The three types of deformation conditions that we shall investigate are weight
$\tau _v$
. The three types of deformation conditions that we shall investigate are weight
![]() $2$
Steinberg representations, weight
$2$
Steinberg representations, weight
![]() $2$
unipotent representations and weight
$2$
unipotent representations and weight
![]() $2$
unipotent representations with an additional choice of Frobenius eigenvalue; we call the corresponding cases
$2$
unipotent representations with an additional choice of Frobenius eigenvalue; we call the corresponding cases
![]() $({\mathrm {st}})$
,
$({\mathrm {st}})$
,
![]() $({\mathrm {un}})$
and
$({\mathrm {un}})$
and
![]() $({\operatorname {\varphi -uni}})$
, respectively. We shall see that the invariants will only depend on the monodromy invariant
$({\operatorname {\varphi -uni}})$
, respectively. We shall see that the invariants will only depend on the monodromy invariant
![]() $n_v$
and on the type of deformation condition.
$n_v$
and on the type of deformation condition.
The overall strategy in each case is the same. The actual computations between case
![]() $({\mathrm {st}})$
and cases
$({\mathrm {st}})$
and cases
![]() $({\mathrm {un}})$
and
$({\mathrm {un}})$
and
![]() $({\operatorname {\varphi -uni}})$
differ greatly. In each case, we first give (or recall) an explicit description of R, as a quotient of a power series ring over
$({\operatorname {\varphi -uni}})$
differ greatly. In each case, we first give (or recall) an explicit description of R, as a quotient of a power series ring over
![]() ${\mathcal O}$
modulo some ideal given by explicit relations. Then we need to find a ring
${\mathcal O}$
modulo some ideal given by explicit relations. Then we need to find a ring
![]() $\widetilde {R}$
and a morphism
$\widetilde {R}$
and a morphism
![]() $\varphi :\widetilde {R}\twoheadrightarrow R$
that satisfy property (CI). In the unipotent cases, we also need a morphism
$\varphi :\widetilde {R}\twoheadrightarrow R$
that satisfy property (CI). In the unipotent cases, we also need a morphism
![]() ${\widetilde {\theta }}:S\to \widetilde {R}$
as in Lemma 3.7. We greatly benefit from the freedom in choosing
${\widetilde {\theta }}:S\to \widetilde {R}$
as in Lemma 3.7. We greatly benefit from the freedom in choosing
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\varphi $
. Venkatesh’s invariants do not depend on this choice. So we do this in a way amenable to computation. Our choices are not ‘natural’, but they ‘work’.Footnote
6
They allow us to explicitly compute at least the following objects that by Theorem 3.9 and Theorem 3.23 give Venkatesh’s invariants:
$\varphi $
. Venkatesh’s invariants do not depend on this choice. So we do this in a way amenable to computation. Our choices are not ‘natural’, but they ‘work’.Footnote
6
They allow us to explicitly compute at least the following objects that by Theorem 3.9 and Theorem 3.23 give Venkatesh’s invariants:
-
(a) the first two steps in a finite free
 $\widetilde {R}$
-resolution of
$\widetilde {R}$
-resolution of
 $I=\operatorname {\mathrm {ker}} \varphi $
,
$I=\operatorname {\mathrm {ker}} \varphi $
, -
(b) the
 $\widetilde {R}$
-annihilator
$\widetilde {R}$
-annihilator
 $\widetilde {R}[I]$
of I and
$\widetilde {R}[I]$
of I and -
(c) the modules of formal differentials
 ${\widehat {\Omega }}_{R}$
and
${\widehat {\Omega }}_{R}$
and
 ${\widehat {\Omega }}_{\widetilde {R}}$
.
${\widehat {\Omega }}_{\widetilde {R}}$
.
The computation of the quantities in (c) is done as in [Reference Böckle, Khare and ManningBKM21]. They can be related to
![]() ${\mathcal O}$
-linear subspaces of
${\mathcal O}$
-linear subspaces of
![]() ${\widehat {\Omega }}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}}$
formed by differentials in the kernel ideal of a surjective presentation
${\widehat {\Omega }}_{{\mathcal O}[[x_1,\ldots ,x_n]]/{\mathcal O}}$
formed by differentials in the kernel ideal of a surjective presentation
![]() ${\mathcal O}[[x_1,\ldots ,x_n]]\to \widetilde {R}$
and are not difficult to compute. The resolutions needed for (a) turned out to be manageable, even by hand calculation. The most difficult quantity to compute was (b). In case
${\mathcal O}[[x_1,\ldots ,x_n]]\to \widetilde {R}$
and are not difficult to compute. The resolutions needed for (a) turned out to be manageable, even by hand calculation. The most difficult quantity to compute was (b). In case
![]() $({\mathrm {st}})$
, we can rely on the rich theory of determinantal rings. In the other cases, we needed explicit bases of
$({\mathrm {st}})$
, we can rely on the rich theory of determinantal rings. In the other cases, we needed explicit bases of
![]() $\widetilde {R}$
and R as free modules over S, and we need to understand the socle of the mod p fiber of the latter rings modulo the standard regular sequence of S and the chain of isomorphisms in the proof of Lemma 3.14.
$\widetilde {R}$
and R as free modules over S, and we need to understand the socle of the mod p fiber of the latter rings modulo the standard regular sequence of S and the chain of isomorphisms in the proof of Lemma 3.14.
In the Steinberg case, we were able to perform all computations by hand. For (a) we made use of a standard resolution from commutative algebra, the Eagon–Northcott complex; see the proof of Lemma 5.8. Also, (b) and (c) turned out to be directly computable. The reason is that the ring we consider is the completion of a certain determinantal variety of
![]() $2\times 2$
-minors of a
$2\times 2$
-minors of a
![]() $4\times 2$
-matrix. The equations defining such varieties possess many symmetries and have been much studied in commutative algebra.
$4\times 2$
-matrix. The equations defining such varieties possess many symmetries and have been much studied in commutative algebra.
In the unipotent cases, the defining equations had no structure that we could link to well-studied classical varieties. In these two cases, we employed for nearly all computations the computer algebra system Macaulay2.Footnote
7
To do so, we modeled the sequence of maps
![]() $S\to \widetilde {R}\to R$
by a sequence of rings
$S\to \widetilde {R}\to R$
by a sequence of rings
![]() $ S_{\mathbf Z}\to \widetilde {R}_{\mathbf Z} \to R_{\mathbf Z}$
of finite type over
$ S_{\mathbf Z}\to \widetilde {R}_{\mathbf Z} \to R_{\mathbf Z}$
of finite type over
![]() ${\mathbf Z}$
, that obviously depend on the case
${\mathbf Z}$
, that obviously depend on the case
![]() $({\mathrm {un}})$
or
$({\mathrm {un}})$
or
![]() $({\operatorname {\varphi -uni}})$
. With the help of Macaulay2 and suitable choices of integral models, that we found by experiment, we were able to work out (a)–(c) in fact over
$({\operatorname {\varphi -uni}})$
. With the help of Macaulay2 and suitable choices of integral models, that we found by experiment, we were able to work out (a)–(c) in fact over
![]() ${\mathbf Z}$
(or over
${\mathbf Z}$
(or over
![]() ${\mathbf Q}$
when this was sufficient). Using base change and completion, we convert these computations to answers to (a)–(c) for
${\mathbf Q}$
when this was sufficient). Using base change and completion, we convert these computations to answers to (a)–(c) for
![]() $S\to \widetilde {R}\to R$
. Our models in fact work for all primes p simultaneously. The models we find satisfy in particular, that
$S\to \widetilde {R}\to R$
. Our models in fact work for all primes p simultaneously. The models we find satisfy in particular, that
![]() $\widetilde {R}_{\mathbf Z}$
and
$\widetilde {R}_{\mathbf Z}$
and
![]() $R_{\mathbf Z}$
are finite free over
$R_{\mathbf Z}$
are finite free over
![]() $S_{\mathbf Z}$
and that certain related models for the mod p fibers of
$S_{\mathbf Z}$
and that certain related models for the mod p fibers of
![]() $S\to \widetilde {R}\to R$
have the analogous property with the same rank. Finding models that are in addition smooth at the augmentation point in the generic fiber of
$S\to \widetilde {R}\to R$
have the analogous property with the same rank. Finding models that are in addition smooth at the augmentation point in the generic fiber of
![]() $\widetilde {R}_{\mathbf Z}$
posed an additional challenge. The code that performs our calculation can be found the the GitHub repository of the first author; see [Reference BöckleBöc23].
$\widetilde {R}_{\mathbf Z}$
posed an additional challenge. The code that performs our calculation can be found the the GitHub repository of the first author; see [Reference BöckleBöc23].
Let us also mention here that in Subsection 5.5, at the end of this section, we gather some results on Cohen–Macaulay and Gorenstein rings that we use repeatedly. It also contains some elementary results on generating sets on dual modules that were useful in explicit computations in Subsections 5.3 and 5.4.
5.1 Presentations of and basic results on the rings R
Case
 $({\mathrm {st}})$
$({\mathrm {st}})$
In case
![]() $({\mathrm {st}})$
, the ring R is the Steinberg quotient
$({\mathrm {st}})$
, the ring R is the Steinberg quotient
![]() $R^{\mathrm {st}}_v$
defined in Section 4. The setup is as in [Reference Böckle, Khare and ManningBKM21, § 7.2] except for two minor differences: In [Reference Böckle, Khare and ManningBKM21] the coordinates used for
$R^{\mathrm {st}}_v$
defined in Section 4. The setup is as in [Reference Böckle, Khare and ManningBKM21, § 7.2] except for two minor differences: In [Reference Böckle, Khare and ManningBKM21] the coordinates used for
![]() $R^{\mathrm {st}}_v$
were adapted to the augmentation, while here we chose the coordinates to better fit standard results on the Eagon–Northcott complex. Moreover, here
$R^{\mathrm {st}}_v$
were adapted to the augmentation, while here we chose the coordinates to better fit standard results on the Eagon–Northcott complex. Moreover, here
![]() $F_v$
is an arbitrary l-adic field, there it was
$F_v$
is an arbitrary l-adic field, there it was
![]() ${\mathbf Q}_l$
, where l the prime divisor of q. As recalled in Proposition 4.6, the ring
${\mathbf Q}_l$
, where l the prime divisor of q. As recalled in Proposition 4.6, the ring
![]() $R_v^{\mathrm {st}}$
is a reduced Cohen–Macaulay domain (but non-Gorenstein), and it is flat over
$R_v^{\mathrm {st}}$
is a reduced Cohen–Macaulay domain (but non-Gorenstein), and it is flat over
![]() ${\mathcal O}$
of relative dimension
${\mathcal O}$
of relative dimension
![]() $3$
. From [Reference Böckle, Khare and ManningBKM21, § 7.3], we have the explicit presentation
$3$
. From [Reference Böckle, Khare and ManningBKM21, § 7.3], we have the explicit presentation
![]() $R_v^{\mathrm {st}}={\mathcal R}/J_{\mathrm {st}}$
where
$R_v^{\mathrm {st}}={\mathcal R}/J_{\mathrm {st}}$
where
![]() ${\mathcal R}={\mathcal O}[[a,b,c,\alpha ,\beta ,\gamma ]]$
and
${\mathcal R}={\mathcal O}[[a,b,c,\alpha ,\beta ,\gamma ]]$
and
![]() $J_{\mathrm {st}}$
is the ideal of
$J_{\mathrm {st}}$
is the ideal of
![]() ${\mathcal R}$
generated by the
${\mathcal R}$
generated by the
![]() $2\times 2$
-minors of the matrix
$2\times 2$
-minors of the matrix
 $$ \begin{align} \left( \begin{array}{cccc} \alpha & \beta & (q\!-\!1\!+\!a) & b \\ \gamma & -\alpha & c & -a \end{array} \right). \end{align} $$
$$ \begin{align} \left( \begin{array}{cccc} \alpha & \beta & (q\!-\!1\!+\!a) & b \\ \gamma & -\alpha & c & -a \end{array} \right). \end{align} $$
To describe various explicit calculations to be given below, we denote by
![]() $t_{i,j}$
the
$t_{i,j}$
the
![]() $2\times 2$
-minor for columns
$2\times 2$
-minor for columns
![]() $i<j$
, and we set
$i<j$
, and we set
so that
![]() $J_{\mathrm {st}}=(r^{\mathrm {st}}_1,\ldots ,r^{\mathrm {st}}_6)$
.
$J_{\mathrm {st}}=(r^{\mathrm {st}}_1,\ldots ,r^{\mathrm {st}}_6)$
.
As in [Reference Böckle, Khare and ManningBKM21, § 7.2], we consider the augmentation
![]() $\lambda \colon R_v^{{\mathrm {st}}}\to {\mathcal O}$
given by
$\lambda \colon R_v^{{\mathrm {st}}}\to {\mathcal O}$
given by
![]() $\lambda (a)=\lambda (\alpha )=\lambda (c)=\lambda (\gamma )=0$
and
$\lambda (a)=\lambda (\alpha )=\lambda (c)=\lambda (\gamma )=0$
and
![]() $\lambda (b)=s$
,
$\lambda (b)=s$
,
![]() $\lambda (\beta )=t$
, with
$\lambda (\beta )=t$
, with
![]() $t\in {\mathfrak m}_{\mathcal O}$
nonzero.
$t\in {\mathfrak m}_{\mathcal O}$
nonzero.
Case
 $({\operatorname {\varphi -uni}})$
$({\operatorname {\varphi -uni}})$
Fix a lift
![]() $\sigma \in G_{F_v}$
of Frobenius. In case
$\sigma \in G_{F_v}$
of Frobenius. In case
![]() $({\operatorname {\varphi -uni}})$
, the ring R is the universal framed deformation ring
$({\operatorname {\varphi -uni}})$
, the ring R is the universal framed deformation ring
![]() $R^{\operatorname {\varphi -uni}}_v$
defined in [Reference CalegariCal18, § 2.1; called there
$R^{\operatorname {\varphi -uni}}_v$
defined in [Reference CalegariCal18, § 2.1; called there
![]() ${R}_{\ell}^{\mathrm{mod}}$
] for framed deformations
${R}_{\ell}^{\mathrm{mod}}$
] for framed deformations
![]() $\rho $
of
$\rho $
of
![]() $\overline {\rho }_v$
of trivial inertia type together with a choice of eigenvalue
$\overline {\rho }_v$
of trivial inertia type together with a choice of eigenvalue
![]() $(1+X)$
of
$(1+X)$
of
![]() $\rho (\sigma )$
, and with
$\rho (\sigma )$
, and with
![]() $\det \rho (\sigma )=q$
. In other words, the p-adic framed deformations parameterized by
$\det \rho (\sigma )=q$
. In other words, the p-adic framed deformations parameterized by
![]() $R^{\operatorname {\varphi -uni}}_v$
are those that can be made upper-triangular with unipotent inertia and with
$R^{\operatorname {\varphi -uni}}_v$
are those that can be made upper-triangular with unipotent inertia and with
![]() $q(1+X)^{-1}$
and
$q(1+X)^{-1}$
and
![]() $(1+X)$
as diagonal entries of
$(1+X)$
as diagonal entries of
![]() $\rho (\sigma )$
for some X. It is shown in [Reference CalegariCal18, Lem. 2.4 and its proof] that we have
$\rho (\sigma )$
for some X. It is shown in [Reference CalegariCal18, Lem. 2.4 and its proof] that we have
where
![]() ${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,X,a,b,c]]$
and
${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,X,a,b,c]]$
and
![]() ${\mathcal I}\subset {\mathcal R}$
is the ideal generated by the entries of the matrices
${\mathcal I}\subset {\mathcal R}$
is the ideal generated by the entries of the matrices
The corresponding universal framed deformation factors through the tame quotient
![]() $G^t_q$
of
$G^t_q$
of
![]() $G_{F_v}$
, and if
$G_{F_v}$
, and if
![]() $\tau $
is a topological generator of the inertia subgroup of
$\tau $
is a topological generator of the inertia subgroup of
![]() $G^t_q$
such that
$G^t_q$
such that
![]() $\sigma \tau \sigma ^{-1}=\tau ^q$
, then this framed deformation is given by
$\sigma \tau \sigma ^{-1}=\tau ^q$
, then this framed deformation is given by
![]() $\sigma \mapsto A$
and
$\sigma \mapsto A$
and
![]() $\tau \mapsto I+N$
.
$\tau \mapsto I+N$
.
Lemma 5.2. We have
![]() ${\mathcal I}=(r^{\operatorname {\varphi -uni}}_1\ldots ,r^{\operatorname {\varphi -uni}}_9)$
for
${\mathcal I}=(r^{\operatorname {\varphi -uni}}_1\ldots ,r^{\operatorname {\varphi -uni}}_9)$
for
Proof. We claim that
![]() ${\mathcal I}$
is generated by the elements
${\mathcal I}$
is generated by the elements
![]() $\alpha X,\beta X,\gamma X$
,
$\alpha X,\beta X,\gamma X$
,
![]() $\det A-q$
,
$\det A-q$
,
![]() $\det N$
together with the entries of the
$\det N$
together with the entries of the
![]() $2\times 2$
-matrix
$2\times 2$
-matrix
![]() $N(A-(1+X )I)$
with X specialized to zero. From the claim and in particular
$N(A-(1+X )I)$
with X specialized to zero. From the claim and in particular
![]() $\alpha X,\beta X,\gamma X\in {\mathcal I}$
, it is straightforward to see that the
$\alpha X,\beta X,\gamma X\in {\mathcal I}$
, it is straightforward to see that the
![]() $r^{\operatorname {\varphi -uni}}_i$
,
$r^{\operatorname {\varphi -uni}}_i$
,
![]() $i=1,\ldots ,9$
generate
$i=1,\ldots ,9$
generate
![]() ${\mathcal I}$
.
${\mathcal I}$
.
To show the claim, denote for a
![]() $2\times 2$
-matrix D over a ring R by
$2\times 2$
-matrix D over a ring R by
![]() $D^\iota $
the main involution applied to D as in the proof of [Reference Böckle, Khare and ManningBKM21, Lem. 7.2]; recall that the map
$D^\iota $
the main involution applied to D as in the proof of [Reference Böckle, Khare and ManningBKM21, Lem. 7.2]; recall that the map
![]() $D\mapsto D^\iota $
is R-linear and satisfies
$D\mapsto D^\iota $
is R-linear and satisfies
![]() $ D+D^\iota =\operatorname {\mathrm {tr}} D\cdot I$
, and that, up to sign, the set of entries of D and
$ D+D^\iota =\operatorname {\mathrm {tr}} D\cdot I$
, and that, up to sign, the set of entries of D and
![]() $D^\iota $
are the same.
$D^\iota $
are the same.
It follows that
![]() $N^\iota =-N$
and
$N^\iota =-N$
and
![]() $A^\iota =-A+(q(1+X)^{-1}+(1+X))I$
, and from this one deduces that
$A^\iota =-A+(q(1+X)^{-1}+(1+X))I$
, and from this one deduces that
Hence, either the entries of
![]() $N(A-(1+X)I) $
or those of
$N(A-(1+X)I) $
or those of
![]() $(A-q(1+X)^{-1})N$
can be omitted when generating
$(A-q(1+X)^{-1})N$
can be omitted when generating
![]() ${\mathcal I}$
.
${\mathcal I}$
.
The vanishing of
![]() $N^2$
is easily be seen equivalent to that of
$N^2$
is easily be seen equivalent to that of
![]() $\det N$
. It remains to show that assuming
$\det N$
. It remains to show that assuming
![]() $N(A-(1+X)I)=0$
, we have
$N(A-(1+X)I)=0$
, we have
![]() $AN=qNA \Longleftrightarrow \alpha X=\beta X=\gamma X=0$
: To see ‘
$AN=qNA \Longleftrightarrow \alpha X=\beta X=\gamma X=0$
: To see ‘
![]() $\Rightarrow $
’, we compute
$\Rightarrow $
’, we compute
Subtracting the latter from
![]() $(A-q(1+X)^{-1})N=0$
yields
$(A-q(1+X)^{-1})N=0$
yields
![]() $ q (1+X-(1+X)^{-1})N=0$
, and from this and our hypothesis
$ q (1+X-(1+X)^{-1})N=0$
, and from this and our hypothesis
![]() $p>2$
it is straightforward to see that
$p>2$
it is straightforward to see that
![]() $XN=0$
, i.a., that
$XN=0$
, i.a., that
![]() $\alpha X=\beta X=\gamma X=0$
. For ‘
$\alpha X=\beta X=\gamma X=0$
. For ‘
![]() $\Leftarrow $
’, observe that the steps can be reverted.
$\Leftarrow $
’, observe that the steps can be reverted.
Lemma 5.3. The ring
![]() $R^{\operatorname {\varphi -uni}}_v$
has the following properties:
$R^{\operatorname {\varphi -uni}}_v$
has the following properties:
-
1. It is reduced, flat over
 ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
 $3$
.
$3$
. -
2. Its two minimal primes
 $I_1$
and
$I_1$
and
 $I_2$
can be labeled so that
$I_2$
can be labeled so that
 $R^{\operatorname {\varphi -uni}}_v/I_1$
parameterizes unramified framed deformations of
$R^{\operatorname {\varphi -uni}}_v/I_1$
parameterizes unramified framed deformations of
 $\overline {\rho }$
with a choice of Frobenius eigenvalue, and
$\overline {\rho }$
with a choice of Frobenius eigenvalue, and
 $R^{\operatorname {\varphi -uni}}_v/I_2$
is the Steinberg framed deformation ring
$R^{\operatorname {\varphi -uni}}_v/I_2$
is the Steinberg framed deformation ring
 $R_v^{\mathrm {st}}$
from case
$R_v^{\mathrm {st}}$
from case
 $({\mathrm {st}})$
.
$({\mathrm {st}})$
. -
3. The elements
 $\varpi , b-c,b-\beta ,X-\gamma $
form a regular system of parameters and
$\varpi , b-c,b-\beta ,X-\gamma $
form a regular system of parameters and
 $R^{\operatorname {\varphi -uni}}$
is Gorenstein.
$R^{\operatorname {\varphi -uni}}$
is Gorenstein.
Proof. Part 1 is [Reference CalegariCal18, Lem. 2.2]. To see 2, set
![]() ${\mathcal I}_1={\mathcal I}+(\alpha ,\beta ,\gamma )$
and
${\mathcal I}_1={\mathcal I}+(\alpha ,\beta ,\gamma )$
and
![]() ${\mathcal I}_2={\mathcal I}+(X)$
. From the description of
${\mathcal I}_2={\mathcal I}+(X)$
. From the description of
![]() $R^{\operatorname {\varphi -uni}}_v$
and its universal framed deformation, it follows that the rings
$R^{\operatorname {\varphi -uni}}_v$
and its universal framed deformation, it follows that the rings
![]() $R^{\operatorname {\varphi -uni}}_1/{\mathcal I}_j$
have the moduli interpretation we claim in 2. It remains to show
$R^{\operatorname {\varphi -uni}}_1/{\mathcal I}_j$
have the moduli interpretation we claim in 2. It remains to show
![]() ${\mathcal I}\supseteq {\mathcal I}_1\cap {\mathcal I}_2$
. Observe first that
${\mathcal I}\supseteq {\mathcal I}_1\cap {\mathcal I}_2$
. Observe first that
is a domain because
![]() $aq+(a^2+bc)(1+X)-a(1+X)^2 $
cannot be factored in the regular ring
$aq+(a^2+bc)(1+X)-a(1+X)^2 $
cannot be factored in the regular ring
![]() $ {\mathcal O}[[a,b,c,X]]$
. Hence, X is a nonzero divisor in the quotient
$ {\mathcal O}[[a,b,c,X]]$
. Hence, X is a nonzero divisor in the quotient
![]() ${\mathcal R}/{\mathcal I}_1$
. Suppose now that we are given
${\mathcal R}/{\mathcal I}_1$
. Suppose now that we are given
![]() $r+r'X\in {\mathcal I}_1\cap {\mathcal I}_2$
with
$r+r'X\in {\mathcal I}_1\cap {\mathcal I}_2$
with
![]() $r\in {\mathcal I}$
and
$r\in {\mathcal I}$
and
![]() $r'\in {\mathcal R}$
. Reducing modulo
$r'\in {\mathcal R}$
. Reducing modulo
![]() ${\mathcal I}_1$
yields
${\mathcal I}_1$
yields
![]() $r'\in {\mathcal I}_1$
and hence
$r'\in {\mathcal I}_1$
and hence
![]() $r'X\in {\mathcal I}_1\cdot {\mathcal I}_2\subset {\mathcal I}$
. This concludes 2.
$r'X\in {\mathcal I}_1\cdot {\mathcal I}_2\subset {\mathcal I}$
. This concludes 2.
We prove 3. The ring
![]() ${\mathcal R}/{\mathcal I}_2$
is isomorphic to
${\mathcal R}/{\mathcal I}_2$
is isomorphic to
![]() $R_v^{\mathrm {st}}$
and hence Cohen–Macaulay of dimension
$R_v^{\mathrm {st}}$
and hence Cohen–Macaulay of dimension
![]() $4$
. The ring
$4$
. The ring
![]() ${\mathcal R}/{\mathcal I}_1$
, given explicitly above, and its quotient by X, that is, the ring
${\mathcal R}/{\mathcal I}_1$
, given explicitly above, and its quotient by X, that is, the ring
![]() ${\mathcal R}/({\mathcal I}_1+{\mathcal I}_2)$
, are Cohen–Macaulay of dimension
${\mathcal R}/({\mathcal I}_1+{\mathcal I}_2)$
, are Cohen–Macaulay of dimension
![]() $4$
and
$4$
and
![]() $3$
, respectively, by Proposition 5.35.3. Hence,
$3$
, respectively, by Proposition 5.35.3. Hence,
![]() $R_v^{\operatorname {\varphi -uni}}={\mathcal R}/({\mathcal I}_1\cap {\mathcal I}_2)$
is Cohen–Macaulay of dimension
$R_v^{\operatorname {\varphi -uni}}={\mathcal R}/({\mathcal I}_1\cap {\mathcal I}_2)$
is Cohen–Macaulay of dimension
![]() $4$
by [Reference EisenbudEis95, Exerc. 18.13]. In particular systems of parameters of
$4$
by [Reference EisenbudEis95, Exerc. 18.13]. In particular systems of parameters of
![]() $R_v^{\operatorname {\varphi -uni}}$
are regular sequences by Proposition 5.35.
$R_v^{\operatorname {\varphi -uni}}$
are regular sequences by Proposition 5.35.
Let now A be the quotient of
![]() $R_v^{\operatorname {\varphi -uni}}$
modulo the sequence
$R_v^{\operatorname {\varphi -uni}}$
modulo the sequence
![]() $\varpi ,b-c,b-\beta ,X-\gamma $
. The relations allow one to eliminate the variables
$\varpi ,b-c,b-\beta ,X-\gamma $
. The relations allow one to eliminate the variables
![]() $c,\beta ,\gamma $
, and after some simple manipulations one finds
$c,\beta ,\gamma $
, and after some simple manipulations one finds
It is a k-vector space of dimension
![]() $6$
with basis
$6$
with basis
![]() $1,a,b,X,\alpha ,a^2$
and one computes
$1,a,b,X,\alpha ,a^2$
and one computes
![]() $\operatorname {{{\mathrm {socle}}}} (A)=ka^2$
. Hence, the sequence
$\operatorname {{{\mathrm {socle}}}} (A)=ka^2$
. Hence, the sequence
![]() $\varpi ,b-c,b-\beta ,X-\gamma $
is regular and it follows from Proposition 5.35 that
$\varpi ,b-c,b-\beta ,X-\gamma $
is regular and it follows from Proposition 5.35 that
![]() $R_v^{\operatorname {\varphi -uni}}$
is Gorenstein.
$R_v^{\operatorname {\varphi -uni}}$
is Gorenstein.
We consider the ‘same’ augmentation as in case
![]() $({\mathrm {st}})$
, namely the
$({\mathrm {st}})$
, namely the
![]() ${\mathcal O}$
-algebra map
${\mathcal O}$
-algebra map
![]() $R_v^{\operatorname {\varphi -uni}}\to {\mathcal O}$
that is the projection
$R_v^{\operatorname {\varphi -uni}}\to {\mathcal O}$
that is the projection
![]() $R^{\operatorname {\varphi -uni}}_v\to R^{\operatorname {\varphi -uni}}_v/I_2=R_v^{\mathrm {st}}$
from Lemma 5.3.2. composed with the augmentation
$R^{\operatorname {\varphi -uni}}_v\to R^{\operatorname {\varphi -uni}}_v/I_2=R_v^{\mathrm {st}}$
from Lemma 5.3.2. composed with the augmentation
![]() $R^{\mathrm {st}}_v\to {\mathcal O}$
from case
$R^{\mathrm {st}}_v\to {\mathcal O}$
from case
![]() $({\mathrm {st}})$
. Concretely,
$({\mathrm {st}})$
. Concretely,
![]() $\lambda $
is given by
$\lambda $
is given by
for some
![]() $s,t\in {\mathfrak m}_{\mathcal O}$
with t nonzero.
$s,t\in {\mathfrak m}_{\mathcal O}$
with t nonzero.
Case
 $({\mathrm {un}})$
$({\mathrm {un}})$
One has natural surjections
![]() $R^\square _v\to R_v^{\mathrm {st}}$
and
$R^\square _v\to R_v^{\mathrm {st}}$
and
![]() $R^\square _v\to R_v^{\mathrm {unr}}$
. Denote by
$R^\square _v\to R_v^{\mathrm {unr}}$
. Denote by
![]() $I^{\mathrm {st}}$
and
$I^{\mathrm {st}}$
and
![]() $I^{\mathrm {unr}}$
the corresponding ideals of
$I^{\mathrm {unr}}$
the corresponding ideals of
![]() $R^\square _v$
. Then in the case
$R^\square _v$
. Then in the case
![]() $({\mathrm {un}})$
, we define R as the quotient
$({\mathrm {un}})$
, we define R as the quotient
cf. [Reference ShottonSho16, Rem. 5.7] for a comparable definition. In other words,
![]() $R_v^{\mathrm {uni}}$
is the reduced quotient of
$R_v^{\mathrm {uni}}$
is the reduced quotient of
![]() $R_v^\square $
such that
$R_v^\square $
such that
![]() $\operatorname {\mathrm {Spec}} R^{\mathrm {uni}}=\operatorname {\mathrm {Spec}} R_v^{\mathrm {st}}\cup \operatorname {\mathrm {Spec}} R_v^{\mathrm {unr}}\subset \operatorname {\mathrm {Spec}} R_v^\square $
; see Lemma 5.4.
$\operatorname {\mathrm {Spec}} R^{\mathrm {uni}}=\operatorname {\mathrm {Spec}} R_v^{\mathrm {st}}\cup \operatorname {\mathrm {Spec}} R_v^{\mathrm {unr}}\subset \operatorname {\mathrm {Spec}} R_v^\square $
; see Lemma 5.4.
The ring
![]() $R_v^\square $
is can be realized as the quotient
$R_v^\square $
is can be realized as the quotient
![]() ${\mathcal R}'/{\mathcal I}'$
for
${\mathcal R}'/{\mathcal I}'$
for
![]() ${\mathcal R}'={\mathcal O}[[\alpha ,\beta ,\gamma ,\delta ,a,b,c,X]]$
and
${\mathcal R}'={\mathcal O}[[\alpha ,\beta ,\gamma ,\delta ,a,b,c,X]]$
and
![]() ${\mathcal I}'\subset {\mathcal R}'$
as the ideal generated by the entries of the (
${\mathcal I}'\subset {\mathcal R}'$
as the ideal generated by the entries of the (
![]() $2\times 2$
- and
$2\times 2$
- and
![]() $1\times 1$
-) matrices
$1\times 1$
-) matrices
The ideals
![]() $I^{\mathrm {unr}}$
and
$I^{\mathrm {unr}}$
and
![]() $I^{\mathrm {st}}$
both contain
$I^{\mathrm {st}}$
both contain
![]() $\alpha +\delta $
since these quotient describe situations where either
$\alpha +\delta $
since these quotient describe situations where either
![]() $N=B-I$
is zero, or N is of trace and determinant zero. Therefore,
$N=B-I$
is zero, or N is of trace and determinant zero. Therefore,
![]() $R_v^{\mathrm {uni}}$
can be written as a quotient of
$R_v^{\mathrm {uni}}$
can be written as a quotient of
![]() ${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,a,b,c,X]]$
by an ideal
${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,a,b,c,X]]$
by an ideal
![]() ${\mathcal I}^{\mathrm {uni}}\subset {\mathcal R}$
; with
${\mathcal I}^{\mathrm {uni}}\subset {\mathcal R}$
; with
![]() $\delta =-\alpha $
.
$\delta =-\alpha $
.
We computed in Macaulay2 generators of
![]() $I^{\mathrm {unr}}$
and
$I^{\mathrm {unr}}$
and
![]() $I^{\mathrm {st}}$
by working inside the polynomial ring
$I^{\mathrm {st}}$
by working inside the polynomial ring
![]() ${\mathcal R}_{\mathbf Z}={\mathbf Z}[{\underline {q}},a,b,c,X,\alpha ,\beta ,\gamma ]$
, where we represent the prime power q in
${\mathcal R}_{\mathbf Z}={\mathbf Z}[{\underline {q}},a,b,c,X,\alpha ,\beta ,\gamma ]$
, where we represent the prime power q in
![]() ${\mathbf Z}$
by the indeterminate
${\mathbf Z}$
by the indeterminate
![]() ${\underline {q}}+1$
in the polynomial ring.Footnote
8
Let
${\underline {q}}+1$
in the polynomial ring.Footnote
8
Let
![]() $I_{\mathbf Z}^{\mathrm {unr}}$
and
$I_{\mathbf Z}^{\mathrm {unr}}$
and
![]() $I^{\mathrm {st}}_{\mathbf Z}$
denote the corresponding ideals of
$I^{\mathrm {st}}_{\mathbf Z}$
denote the corresponding ideals of
![]() ${\mathcal R}_{\mathbf Z}$
. Then we let Macaulay2 also compute the intersection
${\mathcal R}_{\mathbf Z}$
. Then we let Macaulay2 also compute the intersection
![]() $I_{\mathbf Z}^{\mathrm {uni}}=I_{\mathbf Z}^{\mathrm {unr}}\cap I_{\mathbf Z}^{\mathrm {st}}$
. The ideal
$I_{\mathbf Z}^{\mathrm {uni}}=I_{\mathbf Z}^{\mathrm {unr}}\cap I_{\mathbf Z}^{\mathrm {st}}$
. The ideal
![]() $I_{\mathbf Z}^{\mathrm {uni}}$
is generated by the elements
$I_{\mathbf Z}^{\mathrm {uni}}$
is generated by the elements
We also have
![]() $I^{\mathrm {unr}}_{\mathbf Z}=( \alpha ,\beta ,\gamma )$
and
$I^{\mathrm {unr}}_{\mathbf Z}=( \alpha ,\beta ,\gamma )$
and
![]() $I^{\mathrm {st}}_{\mathbf Z}=(X,r_4^{\mathrm {uni}},\ldots ,r_9^{\mathrm {uni}})$
. We shall use the same names
$I^{\mathrm {st}}_{\mathbf Z}=(X,r_4^{\mathrm {uni}},\ldots ,r_9^{\mathrm {uni}})$
. We shall use the same names
![]() $r^{\mathrm {uni}}_i$
for the corresponding elements in
$r^{\mathrm {uni}}_i$
for the corresponding elements in
![]() ${\mathcal R}$
, with the silent assumption that in
${\mathcal R}$
, with the silent assumption that in
![]() ${\mathcal R}$
we replace
${\mathcal R}$
we replace
![]() ${\underline {q}}$
by q.
${\underline {q}}$
by q.
Lemma 5.4. The ring
![]() $R^{\mathrm {uni}}_v={\mathcal R}/{\mathcal I}^{\mathrm {uni}}$
with
$R^{\mathrm {uni}}_v={\mathcal R}/{\mathcal I}^{\mathrm {uni}}$
with
![]() ${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,X,a,b,c]]$
and
${\mathcal R}={\mathcal O}[[\alpha ,\beta ,\gamma ,X,a,b,c]]$
and
![]() ${\mathcal I}^{\mathrm {uni}}=(r^{\mathrm {uni}}_1,\ldots ,r^{\mathrm {uni}}_9)$
has the following properties:
${\mathcal I}^{\mathrm {uni}}=(r^{\mathrm {uni}}_1,\ldots ,r^{\mathrm {uni}}_9)$
has the following properties:
-
1. We have
 ${\mathcal I}^{\mathrm {uni}}={\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
for
${\mathcal I}^{\mathrm {uni}}={\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
for
 ${\mathcal I}^{\mathrm {unr}}={\mathcal I}+(\alpha ,\beta ,\gamma )$
and
${\mathcal I}^{\mathrm {unr}}={\mathcal I}+(\alpha ,\beta ,\gamma )$
and
 ${\mathcal I}^{\mathrm {st}}={\mathcal I}+(X)$
so that
${\mathcal I}^{\mathrm {st}}={\mathcal I}+(X)$
so that
 ${\mathcal R}/{\mathcal I}^{\mathrm {unr}}$
and
${\mathcal R}/{\mathcal I}^{\mathrm {unr}}$
and
 ${\mathcal R}/{\mathcal I}^{\mathrm {st}}$
are identified with the unramified and the Steinberg quotient of
${\mathcal R}/{\mathcal I}^{\mathrm {st}}$
are identified with the unramified and the Steinberg quotient of
 $R_v^{\mathrm {uni}}$
, respectively.
$R_v^{\mathrm {uni}}$
, respectively. -
2. The ring
 $R_v^{\mathrm {uni}}$
is Cohen–Macaulay, flat over
$R_v^{\mathrm {uni}}$
is Cohen–Macaulay, flat over
 ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
 $3$
and reduced.
$3$
and reduced. -
3. The elements
 $\varpi , b-c,b-\beta ,X-\gamma $
form a regular system of parameters and
$\varpi , b-c,b-\beta ,X-\gamma $
form a regular system of parameters and
 $R_v^{\mathrm {uni}}$
is Gorenstein.
$R_v^{\mathrm {uni}}$
is Gorenstein.
Proof. Part 1 is clear, except for the containment
![]() ${\mathcal I}^{\mathrm {uni}}\supset {\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
. Similar to Lemma 5.3, the quotient
${\mathcal I}^{\mathrm {uni}}\supset {\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
. Similar to Lemma 5.3, the quotient
![]() ${\mathcal R}/{\mathcal I}^{\mathrm {unr}}\cong {\mathcal O}[[X,a,b,c]]/(r_9^{\mathrm {uni}})$
is a Cohen–Macaulay domain of dimension
${\mathcal R}/{\mathcal I}^{\mathrm {unr}}\cong {\mathcal O}[[X,a,b,c]]/(r_9^{\mathrm {uni}})$
is a Cohen–Macaulay domain of dimension
![]() $4$
. The inclusion
$4$
. The inclusion
![]() ${\mathcal I}^{\mathrm {uni}}\supset {\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
now follows as in the proof of Lemma 5.3, and this completes part 1. Because of part 1, the central factors in the short exact sequence of
${\mathcal I}^{\mathrm {uni}}\supset {\mathcal I}^{\mathrm {unr}}\cap {\mathcal I}^{\mathrm {st}}$
now follows as in the proof of Lemma 5.3, and this completes part 1. Because of part 1, the central factors in the short exact sequence of
![]() ${\mathcal R}$
-modules
${\mathcal R}$
-modules
are domains, and so
![]() $R_v^{\mathrm {uni}}$
is reduced. The two central factors and also
$R_v^{\mathrm {uni}}$
is reduced. The two central factors and also
![]() ${\mathcal R}/({\mathcal I}^{\mathrm {unr}}+{\mathcal I}^{\mathrm {st}})\cong {\mathcal O}[[a,b,c]]/(r_3^{\mathrm {st}})$
are Cohen–Macaulay of dimensions
${\mathcal R}/({\mathcal I}^{\mathrm {unr}}+{\mathcal I}^{\mathrm {st}})\cong {\mathcal O}[[a,b,c]]/(r_3^{\mathrm {st}})$
are Cohen–Macaulay of dimensions
![]() $4$
,
$4$
,
![]() $4$
and
$4$
and
![]() $3$
, respectively. As before we find that
$3$
, respectively. As before we find that
![]() $R_v^{\mathrm {uni}}$
is Cohen–Macaulay of dimension
$R_v^{\mathrm {uni}}$
is Cohen–Macaulay of dimension
![]() $4$
by [Reference EisenbudEis95, Exerc. 18.13].
$4$
by [Reference EisenbudEis95, Exerc. 18.13].
Finally, one verifies, by hand or via Macaulay2, that
![]() ${\mathcal R}_{\mathbf Z}/({\mathcal I}_{\mathbf Z}^{\mathrm {uni}}+({\underline {q}}, b-c,b-\beta ,X-\gamma ))$
is a free
${\mathcal R}_{\mathbf Z}/({\mathcal I}_{\mathbf Z}^{\mathrm {uni}}+({\underline {q}}, b-c,b-\beta ,X-\gamma ))$
is a free
![]() ${\mathbf Z}$
-module of rank
${\mathbf Z}$
-module of rank
![]() $6$
with basis
$6$
with basis
![]() $1,a,b,b\alpha ,X,\alpha $
and socle
$1,a,b,b\alpha ,X,\alpha $
and socle
![]() $b\alpha $
. By reduction modulo any prime number p, one deduces that
$b\alpha $
. By reduction modulo any prime number p, one deduces that
![]() $R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
is a zero-dimensional ring. It follows that
$R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
is a zero-dimensional ring. It follows that
![]() $\varpi , b-c,b-\beta ,X-\gamma $
form a system of parameters, and hence a regular system of parameters by Proposition 5.35.3. In particular,
$\varpi , b-c,b-\beta ,X-\gamma $
form a system of parameters, and hence a regular system of parameters by Proposition 5.35.3. In particular,
![]() $R_v^{\mathrm {uni}}$
is
$R_v^{\mathrm {uni}}$
is
![]() ${\mathcal O}$
-flat. By computing the socle of
${\mathcal O}$
-flat. By computing the socle of
![]() $R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
, which turns out to be of length
$R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
, which turns out to be of length
![]() $1$
, one deduces from Proposition 5.35.1 and Proposition 5.35.2 that
$1$
, one deduces from Proposition 5.35.1 and Proposition 5.35.2 that
![]() $R_v^{\mathrm {uni}}$
is Gorenstein.
$R_v^{\mathrm {uni}}$
is Gorenstein.
Let us indicate the relevant computation for
![]() $A:=R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
. Using the relations given by
$A:=R_v^{\mathrm {uni}}/(\varpi ,b-c,b-\beta ,X-\gamma )$
. Using the relations given by
![]() $\varpi , b-c,b-\beta ,X-\gamma $
to eliminate
$\varpi , b-c,b-\beta ,X-\gamma $
to eliminate
![]() $c,\beta ,\gamma $
, one finds
$c,\beta ,\gamma $
, one finds
The last relation gives
![]() $X(1+a)=-a^2$
, from the first it follows that
$X(1+a)=-a^2$
, from the first it follows that
![]() $X^2=0$
and hence
$X^2=0$
and hence
![]() $a^4=0$
so that
$a^4=0$
so that
![]() $1+a$
has inverse
$1+a$
has inverse
![]() $1-a-a^2-a^3$
, and with it
$1-a-a^2-a^3$
, and with it
![]() $X=-a^2+a^3$
. This allows one to eliminate X and after elementary simplifications one finds:
$X=-a^2+a^3$
. This allows one to eliminate X and after elementary simplifications one finds:
![]() $A=k[a,b,\alpha ]/(a^2,\alpha ^2,b(a-\alpha ),a\alpha ,b^2,ba+a^3)$
. Then a simple computation shows that a k-basis is given by
$A=k[a,b,\alpha ]/(a^2,\alpha ^2,b(a-\alpha ),a\alpha ,b^2,ba+a^3)$
. Then a simple computation shows that a k-basis is given by
![]() $1,a,b,\alpha ,a^2,ab$
. To find the socle one computes the solution set of the equations
$1,a,b,\alpha ,a^2,ab$
. To find the socle one computes the solution set of the equations
![]() $a x=bx=\alpha x=0$
for x a general k-linear combination of the above k-basis of A. This gives
$a x=bx=\alpha x=0$
for x a general k-linear combination of the above k-basis of A. This gives
![]() $x\in k ab$
, and since
$x\in k ab$
, and since
![]() $ab=b\alpha $
and
$ab=b\alpha $
and
![]() $X=-a^2-ab$
in A, this is a direct proof of the first sentence of the previous paragraph.
$X=-a^2-ab$
in A, this is a direct proof of the first sentence of the previous paragraph.
Remark 5.5. One can also work out the above argument by first working out properties for
![]() ${\mathcal R}_{\mathbf Z}$
,
${\mathcal R}_{\mathbf Z}$
,
![]() ${\mathcal I}^{\mathrm {st}}$
,
${\mathcal I}^{\mathrm {st}}$
,
![]() ${\mathcal I}^{\mathrm {unr}}$
and
${\mathcal I}^{\mathrm {unr}}$
and
![]() ${\mathcal I}^{\mathrm {uni}}$
and then completing at
${\mathcal I}^{\mathrm {uni}}$
and then completing at
![]() ${\mathfrak m}_Z=(p,{\underline {q}},\alpha ,\beta ,\gamma ,X,a,b,c)$
and then passing to the quotient modulo
${\mathfrak m}_Z=(p,{\underline {q}},\alpha ,\beta ,\gamma ,X,a,b,c)$
and then passing to the quotient modulo
![]() ${\underline {q}}-(q-1)$
. The above direct argument is shorter.
${\underline {q}}-(q-1)$
. The above direct argument is shorter.
5.2 Steinberg deformations at trivial primes
Lemma 5.6.
-
1. The elements
 $r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3,\gamma -\beta ,c+b,\beta +b,\varpi $
of
$r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3,\gamma -\beta ,c+b,\beta +b,\varpi $
of
 ${\mathcal R}={\mathcal O}[[a,b,c,\alpha ,\beta ,\gamma ]]$
form a regular sequence.
${\mathcal R}={\mathcal O}[[a,b,c,\alpha ,\beta ,\gamma ]]$
form a regular sequence. -
2. The complete intersection
 $\widetilde {R}:={\mathcal R}/(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3)$
is flat over
$\widetilde {R}:={\mathcal R}/(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3)$
is flat over
 ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
 $3$
.
$3$
. -
3. The point in
 $\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
corresponding to the augmentation
$\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
corresponding to the augmentation
 $\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by the same prescription as
$\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by the same prescription as
 $\lambda $
is formally smooth.
$\lambda $
is formally smooth.
Proof. 1. It suffices to show that
![]() ${\mathcal R}$
modulo the ideal generated by the given sequence is finite. Modding out
${\mathcal R}$
modulo the ideal generated by the given sequence is finite. Modding out
![]() $\gamma -\beta ,c+b,\beta +b,\varpi $
from
$\gamma -\beta ,c+b,\beta +b,\varpi $
from
![]() ${\mathcal R}$
, we need to show that
${\mathcal R}$
, we need to show that
![]() $k[[a,b,\alpha ]]$
modulo the
$k[[a,b,\alpha ]]$
modulo the
![]() $2\times 2$
-minors
$2\times 2$
-minors
![]() $t_{1,2}, t_{2,3}, t_{3,4}$
of the matrix
$t_{1,2}, t_{2,3}, t_{3,4}$
of the matrix
 $$\begin{align*}\left( \begin{array}{cccc} \alpha & -b & a & b \\ -b & -\alpha & -b & -a \end{array} \right) \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccc} \alpha & -b & a & b \\ -b & -\alpha & -b & -a \end{array} \right) \end{align*}$$
is finite. Using the relation
![]() $\alpha a+b^2$
as a relation for b, it follows that the quotient ring is a degree
$\alpha a+b^2$
as a relation for b, it follows that the quotient ring is a degree
![]() $2$
extension of
$2$
extension of
![]() $k[[a,\alpha ]]/(\alpha ^2-a\alpha ,a^2+a\alpha )$
, and the latter ring is finite, as
$k[[a,\alpha ]]/(\alpha ^2-a\alpha ,a^2+a\alpha )$
, and the latter ring is finite, as
![]() $p>2$
; a k-basis is
$p>2$
; a k-basis is
![]() $1,a,\alpha ,a\alpha $
.
$1,a,\alpha ,a\alpha $
.
2. The regular sequence in 1. remains a regular sequence under any reordering and after any truncation. This shows that
![]() $\widetilde {R}$
is flat over
$\widetilde {R}$
is flat over
![]() ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
![]() $3$
over
$3$
over
![]() ${\mathcal O}$
.
${\mathcal O}$
.
3. To see the formal smoothness, we form the Jacobian matrix of
![]() $r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3$
relative to the variables of
$r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3$
relative to the variables of
![]() ${\mathcal R}[\frac 1\varpi ]$
and evaluate at the augmentation. This gives
${\mathcal R}[\frac 1\varpi ]$
and evaluate at the augmentation. This gives
 $$\begin{align*}\left( \begin{array}{cccccc} 0 & 0 & 0 & 2\alpha & \gamma & \beta \\ \alpha & \gamma &0 & q-1+a & 0 & b\\ 2a +q-1& c &b & 0 &0 & 0 \end{array} \right) \stackrel{\mathrm{eval.\, at\,}\widetilde{\lambda}}\longrightarrow \left( \begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & t \\ 0 & 0 &0 & q-1 & 0 & s\\ q-1& 0 &s & 0 &0 & 0 \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccc} 0 & 0 & 0 & 2\alpha & \gamma & \beta \\ \alpha & \gamma &0 & q-1+a & 0 & b\\ 2a +q-1& c &b & 0 &0 & 0 \end{array} \right) \stackrel{\mathrm{eval.\, at\,}\widetilde{\lambda}}\longrightarrow \left( \begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & t \\ 0 & 0 &0 & q-1 & 0 & s\\ q-1& 0 &s & 0 &0 & 0 \end{array} \right). \end{align*}$$
Columns
![]() $1,4,6$
witness the formal smoothness asserted for
$1,4,6$
witness the formal smoothness asserted for
![]() $\widetilde {\lambda }$
.
$\widetilde {\lambda }$
.
Remark 5.7. From the proof of Lemma 5.6.1, one deduces that as an
![]() ${\mathcal O}$
-algebra map
${\mathcal O}$
-algebra map
![]() $S={\mathcal O}[[y_1,y_1,y_3]]\to \widetilde {R}$
one can take
$S={\mathcal O}[[y_1,y_1,y_3]]\to \widetilde {R}$
one can take
Similar to the proof of Lemma 5.6.1, one can show that
![]() $R_v^{\mathrm {st}}/(\varpi ,y_1,y_2,y_3)\cong k[a,\alpha ,\gamma ]/(a,\alpha ,\gamma )^2$
. Its socle is obviously spanned by
$R_v^{\mathrm {st}}/(\varpi ,y_1,y_2,y_3)\cong k[a,\alpha ,\gamma ]/(a,\alpha ,\gamma )^2$
. Its socle is obviously spanned by
![]() $\{a,\alpha ,\gamma \}$
and has thus k-dimension
$\{a,\alpha ,\gamma \}$
and has thus k-dimension
![]() $3$
. Using that
$3$
. Using that
![]() $R^{\mathrm {st}}_v$
is local Cohen–Macaulay of dimension
$R^{\mathrm {st}}_v$
is local Cohen–Macaulay of dimension
![]() $4$
, by combining parts 3, 2 and 1 of Proposition 5.35 one deduces that
$4$
, by combining parts 3, 2 and 1 of Proposition 5.35 one deduces that
![]() $R_v^{\mathrm {st}}$
is not Gorenstein.
$R_v^{\mathrm {st}}$
is not Gorenstein.
In the following, let
![]() $\widetilde {R}={\mathcal R}/(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3)$
and
$\widetilde {R}={\mathcal R}/(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,r^{\mathrm {st}}_3)$
and
![]() $I=\ker (\widetilde {R} \to R_v^{\mathrm {st}})$
. We need some preparations to give a presentation of I as an
$I=\ker (\widetilde {R} \to R_v^{\mathrm {st}})$
. We need some preparations to give a presentation of I as an
![]() $\widetilde {R}$
-module. Recall that
$\widetilde {R}$
-module. Recall that
![]() $J_{\mathrm {st}}$
was defined before formula (5.1).
$J_{\mathrm {st}}$
was defined before formula (5.1).
Lemma 5.8. The sequence of
![]() ${\mathcal R}$
-modules
${\mathcal R}$
-modules
![]() ${\mathcal R}^8\stackrel {A}\to {\mathcal R}^6\stackrel {B}\to J_{\mathrm {st}}\to 0$
is exact, where B is the
${\mathcal R}^8\stackrel {A}\to {\mathcal R}^6\stackrel {B}\to J_{\mathrm {st}}\to 0$
is exact, where B is the
![]() $1\times 6$
-matrix
$1\times 6$
-matrix
![]() $(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,\ldots ,r^{\mathrm {st}}_6)$
and A is the
$(r^{\mathrm {st}}_1,r^{\mathrm {st}}_2,\ldots ,r^{\mathrm {st}}_6)$
and A is the
![]() $8\times 6$
-matrix
$8\times 6$
-matrix
 $$\begin{align*}\left( \begin{array}{cccccccc} b& q-1+a &0&0& -a&c&0&0 \\ 0&-\alpha &-b&0 &0&-\gamma &a&0 \\ 0&0&\beta&\alpha&0 &0 & -\alpha &\gamma\\ 0&\beta&0&-b&0 & -\alpha &0&a \\ \beta&0&0& q-1+a & -\alpha &0&0&c \\ -\alpha&0& q-1+a &0& -\gamma &0&c&0 \\ \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} b& q-1+a &0&0& -a&c&0&0 \\ 0&-\alpha &-b&0 &0&-\gamma &a&0 \\ 0&0&\beta&\alpha&0 &0 & -\alpha &\gamma\\ 0&\beta&0&-b&0 & -\alpha &0&a \\ \beta&0&0& q-1+a & -\alpha &0&0&c \\ -\alpha&0& q-1+a &0& -\gamma &0&c&0 \\ \end{array} \right). \end{align*}$$
Proof. The displayed presentation is part of the Eagon–Northcott complex attached to the
![]() $4\times 2$
-matrix from Equation (5.1), considered as an
$4\times 2$
-matrix from Equation (5.1), considered as an
![]() ${\mathcal R}$
-linear map
${\mathcal R}$
-linear map
![]() $\nu \colon {\mathcal R}^4\to {\mathcal R}^2$
, and in the present case, this complex is exact: The Eagon–Northcott complex is described in detail in [Reference EisenbudEis05, § 11H], which we now recall in parts. We follow the notation of [Reference EisenbudEis05] and set
$\nu \colon {\mathcal R}^4\to {\mathcal R}^2$
, and in the present case, this complex is exact: The Eagon–Northcott complex is described in detail in [Reference EisenbudEis05, § 11H], which we now recall in parts. We follow the notation of [Reference EisenbudEis05] and set
![]() $G={\mathcal R}^2$
and
$G={\mathcal R}^2$
and
![]() $F={\mathcal R}^4$
, so that
$F={\mathcal R}^4$
, so that
![]() $\nu ^*\colon F^*\to G^*$
. Then in the case at hand, the Eagon–Northcott complex is the complex
$\nu ^*\colon F^*\to G^*$
. Then in the case at hand, the Eagon–Northcott complex is the complex
choosing bases
![]() $f_1,\ldots ,f_4$
of F and
$f_1,\ldots ,f_4$
of F and
![]() $g_1,g_2$
of G, the complex is seen to be of the form
$g_1,g_2$
of G, the complex is seen to be of the form
![]() $0\to {\mathcal R}^3\to {\mathcal R}^8\to {\mathcal R}^6\to {\mathcal R}$
; the right most map of the complex sends the basis element
$0\to {\mathcal R}^3\to {\mathcal R}^8\to {\mathcal R}^6\to {\mathcal R}$
; the right most map of the complex sends the basis element
![]() $f_i\wedge f_j$
,
$f_i\wedge f_j$
,
![]() $i<j$
, to the minor
$i<j$
, to the minor
![]() $t_{i,j}$
of Equation (5.1) formed by column i and column j, and thus its image is the ideal
$t_{i,j}$
of Equation (5.1) formed by column i and column j, and thus its image is the ideal
![]() $J_{\mathrm {st}}$
.
$J_{\mathrm {st}}$
.
To describe the maps
![]() $d_i$
, let
$d_i$
, let
be the map dual to the multiplication map
![]() $ G\otimes \operatorname {\mathrm {Sym}}^{j-1} G \to \operatorname {\mathrm {Sym}}^j G$
, and write
$ G\otimes \operatorname {\mathrm {Sym}}^{j-1} G \to \operatorname {\mathrm {Sym}}^j G$
, and write
![]() $\Gamma _j(u)=\sum _l u^{\prime }_l\otimes u^{\prime \prime }_l $
for
$\Gamma _j(u)=\sum _l u^{\prime }_l\otimes u^{\prime \prime }_l $
for
![]() $u\in (\operatorname {\mathrm {Sym}}^j G)^*$
. Let furthermore
$u\in (\operatorname {\mathrm {Sym}}^j G)^*$
. Let furthermore
be the
![]() ${\mathcal R}$
-linear map given on basis elements by
${\mathcal R}$
-linear map given on basis elements by
 $$\begin{align*}f_{i_1}\wedge\ldots \wedge f_{i_k}\mapsto \sum_{j=1}^k (-1)^{j-1} f_{i_j} \otimes f_{i_1}\wedge\ldots\wedge \widehat{f_{i_j}} \wedge \ldots \wedge f_{i_k},\end{align*}$$
$$\begin{align*}f_{i_1}\wedge\ldots \wedge f_{i_k}\mapsto \sum_{j=1}^k (-1)^{j-1} f_{i_j} \otimes f_{i_1}\wedge\ldots\wedge \widehat{f_{i_j}} \wedge \ldots \wedge f_{i_k},\end{align*}$$
and write
![]() $\Phi _{k}(v)=\sum _m v^{\prime }_m\otimes v^{\prime \prime }_m$
for
$\Phi _{k}(v)=\sum _m v^{\prime }_m\otimes v^{\prime \prime }_m$
for
![]() $v\in \bigwedge ^k F$
. Then for a pure tensor
$v\in \bigwedge ^k F$
. Then for a pure tensor
![]() $u\otimes v$
in
$u\otimes v$
in
![]() $ (\operatorname {\mathrm {Sym}}^j G)^*\otimes \bigwedge F^{j+2}$
, and
$ (\operatorname {\mathrm {Sym}}^j G)^*\otimes \bigwedge F^{j+2}$
, and
![]() $k=j+2$
, one has
$k=j+2$
, one has
This procedure can be applied to the basis
![]() $g_l\otimes f_{i_1}\wedge f_{i_2}\wedge f_{i_3}$
,
$g_l\otimes f_{i_1}\wedge f_{i_2}\wedge f_{i_3}$
,
![]() $1\le i_1 < i_2 < i_3 \le 4$
, of
$1\le i_1 < i_2 < i_3 \le 4$
, of
![]() $(\operatorname {\mathrm {Sym}}^1 G)^*\otimes \bigwedge ^3F$
to obtain the matrix A.
$(\operatorname {\mathrm {Sym}}^1 G)^*\otimes \bigwedge ^3F$
to obtain the matrix A.
To complete the proof, it remains to show exactness of the Eagon–Northcott complex in the case at hand. By [Reference EisenbudEis05, Thm. 11.35], this holds if and only if the grade of the ideal
![]() $J_{\mathrm {st}}$
attains the maximal value possible, namely the height of
$J_{\mathrm {st}}$
attains the maximal value possible, namely the height of
![]() $J_{\mathrm {st}}$
; see [Reference MatsumuraMat80, p. 103]. Because
$J_{\mathrm {st}}$
; see [Reference MatsumuraMat80, p. 103]. Because
![]() ${\mathcal R}/J_{\mathrm {st}}=R_v^{{\mathrm {st}}}$
has Krull dimension
${\mathcal R}/J_{\mathrm {st}}=R_v^{{\mathrm {st}}}$
has Krull dimension
![]() $4$
, the height of
$4$
, the height of
![]() $J_{\mathrm {st}}$
is
$J_{\mathrm {st}}$
is
![]() $3$
. The grade of
$3$
. The grade of
![]() $J_{\mathrm {st}}$
is the maximal length of a regular sequence of
$J_{\mathrm {st}}$
is the maximal length of a regular sequence of
![]() ${\mathcal R}$
contained in
${\mathcal R}$
contained in
![]() $J_{\mathrm {st}}$
; see [Reference MatsumuraMat80, p. 103], and because of Lemma 5.6 this number is at least
$J_{\mathrm {st}}$
; see [Reference MatsumuraMat80, p. 103], and because of Lemma 5.6 this number is at least
![]() $3$
.
$3$
.
Lemma 5.9. Let
![]() ${\mathcal R}^m\stackrel {A}\to {\mathcal R}^n\stackrel {B}\to J\to 0$
be a right exact sequence of
${\mathcal R}^m\stackrel {A}\to {\mathcal R}^n\stackrel {B}\to J\to 0$
be a right exact sequence of
![]() ${\mathcal R}$
-modules for J an ideal of
${\mathcal R}$
-modules for J an ideal of
![]() ${\mathcal R}$
. We consider A as an
${\mathcal R}$
. We consider A as an
![]() $n\times m$
-matrix and B as a
$n\times m$
-matrix and B as a
![]() $1\times n$
-matrix over
$1\times n$
-matrix over
![]() ${\mathcal R}$
. Decompose
${\mathcal R}$
. Decompose
![]() $n=n'+n"$
with
$n=n'+n"$
with
![]() $n',n">0$
, and decompose correspondingly the matrix A into
$n',n">0$
, and decompose correspondingly the matrix A into
![]() $A'$
and
$A'$
and
![]() $A"$
of size
$A"$
of size
![]() $n'\times m$
and
$n'\times m$
and
![]() $n"\times m$
, and the matrix B into matrices
$n"\times m$
, and the matrix B into matrices
![]() $B'$
of size
$B'$
of size
![]() $1\times n'$
and
$1\times n'$
and
![]() $B"$
of size
$B"$
of size
![]() $1\times n"$
, respectively. Let
$1\times n"$
, respectively. Let
![]() $J'\subset J$
be the image of
$J'\subset J$
be the image of
![]() ${\mathcal R}^{n'}$
under
${\mathcal R}^{n'}$
under
![]() $B'$
. Then the induced sequence of
$B'$
. Then the induced sequence of
![]() ${\mathcal R}/J'$
-modules
${\mathcal R}/J'$
-modules
is right exact.
Proof. By the definition of
![]() $J'$
, the map defined by
$J'$
, the map defined by
![]() $B"\ \pmod {J'}$
is clearly surjective. Also,
$B"\ \pmod {J'}$
is clearly surjective. Also,
![]() $BA=0$
implies
$BA=0$
implies
![]() $B'A'=-B"A"$
as maps on
$B'A'=-B"A"$
as maps on
![]() ${\mathcal R}^m$
. But
${\mathcal R}^m$
. But
![]() $B'\ \pmod {J'}$
is the zero map, and hence
$B'\ \pmod {J'}$
is the zero map, and hence
It remains to show that
![]() $\ker (B"\ \pmod {J'})\subset \operatorname {\mathrm {im}}(A"\ \pmod {J'})$
. For this, let
$\ker (B"\ \pmod {J'})\subset \operatorname {\mathrm {im}}(A"\ \pmod {J'})$
. For this, let
![]() $x"\ \pmod {J'} \in \ker (B"\ \pmod {J'})$
with
$x"\ \pmod {J'} \in \ker (B"\ \pmod {J'})$
with
![]() $x"\in {\mathcal R}^{n"}$
. Then
$x"\in {\mathcal R}^{n"}$
. Then
![]() $B"x"$
lies in
$B"x"$
lies in
![]() $J'$
and hence we can find
$J'$
and hence we can find
![]() $x'\in {\mathcal R}^{n'}$
such that
$x'\in {\mathcal R}^{n'}$
such that
![]() $B"x"=B'x'$
. We let
$B"x"=B'x'$
. We let
![]() $x=(-x',x")\in {\mathcal R}^n$
so that
$x=(-x',x")\in {\mathcal R}^n$
so that
![]() $Bx=0$
. By the exactness of the given complex, we can find
$Bx=0$
. By the exactness of the given complex, we can find
![]() $y\in {\mathcal R}^m$
such that
$y\in {\mathcal R}^m$
such that
![]() $Ay=x$
. But then
$Ay=x$
. But then
![]() $A"y=x"$
and this implies
$A"y=x"$
and this implies
![]() $x"\ \pmod {J'}\in \operatorname {\mathrm {im}}(A"\ \pmod {J'})$
.
$x"\ \pmod {J'}\in \operatorname {\mathrm {im}}(A"\ \pmod {J'})$
.
By combining the previous two lemmas, we find.
Corollary 5.10. As a module over
![]() $\widetilde {R}$
the ideal I has a presentation
$\widetilde {R}$
the ideal I has a presentation
where
![]() $A'$
is the matrix
$A'$
is the matrix
 $$\begin{align*}\left( \begin{array}{cccccccc} 0&\beta&0&-b&0 & -\alpha &0&a \\ \beta&0&0& q-1+a & -\alpha &0&0&c \\ -\alpha&0& q-1+a &0& -\gamma &0&c&0 \\ \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} 0&\beta&0&-b&0 & -\alpha &0&a \\ \beta&0&0& q-1+a & -\alpha &0&0&c \\ -\alpha&0& q-1+a &0& -\gamma &0&c&0 \\ \end{array} \right). \end{align*}$$
Corollary 5.11. We have
![]() $\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )=(q-1)t(s,t,q-1)\subset {\mathcal O}$
.
$\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )=(q-1)t(s,t,q-1)\subset {\mathcal O}$
.
Proof. The ideal
![]() $\operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I)$
is the ideal generated by the
$\operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I)$
is the ideal generated by the
![]() $3\times 3$
-minors of the matrix
$3\times 3$
-minors of the matrix
![]() $A'$
from Corollary 5.10. Hence, its image under
$A'$
from Corollary 5.10. Hence, its image under
![]() $\widetilde {\lambda }$
is the ideal of
$\widetilde {\lambda }$
is the ideal of
![]() ${\mathcal O}$
generated by the
${\mathcal O}$
generated by the
![]() $3\times 3$
-minors of
$3\times 3$
-minors of
 $$ \begin{align} \widetilde{\lambda}(A')=\left( \begin{array}{cccccccc} 0&t&0&-s&0 & 0&0&0 \\ t&0&0& q-1 & 0&0&0&0 \\ 0&0& q-1 &0& 0 &0&0&0 \\ \end{array} \right). \end{align} $$
$$ \begin{align} \widetilde{\lambda}(A')=\left( \begin{array}{cccccccc} 0&t&0&-s&0 & 0&0&0 \\ t&0&0& q-1 & 0&0&0&0 \\ 0&0& q-1 &0& 0 &0&0&0 \\ \end{array} \right). \end{align} $$
This is the ideal
![]() $(t^2(q-1),t(q-1)^2,ts(q-1))=t(q-1)(s,t,q-1)$
.
$(t^2(q-1),t(q-1)^2,ts(q-1))=t(q-1)(s,t,q-1)$
.
Remark 5.12. Using the matrix
![]() $A'$
, a Macaulay2 computation shows that
$A'$
, a Macaulay2 computation shows that
![]() $\operatorname {\mathrm {Fitt}}^{\widetilde {R}}_0(I)$
equals
$\operatorname {\mathrm {Fitt}}^{\widetilde {R}}_0(I)$
equals
Corollary 5.13. We have
![]() $\operatorname {\mathrm {Hom}}_{R^{\mathrm {st}}_v}(I/I^2,E/{\mathcal O})\cong {\mathcal O}/(s,t,q-1) \times {\mathcal O}/(t,q-1) \times (t,q-1))/ (t(q-1))$
.
$\operatorname {\mathrm {Hom}}_{R^{\mathrm {st}}_v}(I/I^2,E/{\mathcal O})\cong {\mathcal O}/(s,t,q-1) \times {\mathcal O}/(t,q-1) \times (t,q-1))/ (t(q-1))$
.
Proof. Note first that
where in the second isomorphism, we use that E is regarded as a
![]() $R^{\mathrm {st}}_v$
-module via the augmentation
$R^{\mathrm {st}}_v$
-module via the augmentation
![]() $\lambda $
. Tensoring now the presentation of I in subsection 5.10 with
$\lambda $
. Tensoring now the presentation of I in subsection 5.10 with
![]() ${\mathcal O}$
over
${\mathcal O}$
over
![]() $\widetilde {R}$
(via
$\widetilde {R}$
(via
![]() $\widetilde {\lambda }$
) gives the right exact sequence of
$\widetilde {\lambda }$
) gives the right exact sequence of
![]() ${\mathcal O}$
-modules
${\mathcal O}$
-modules
Using the theory of invariant factors and elementary divisors of matrices over principal ideal domains, for example, [Reference JacobsonJac85, Thm. 3.9], the cokernel of this sequence is seen to be isomorphic to
![]() $\prod _{i=1}^3 {\mathcal O}/d_i{\mathcal O}$
where
$\prod _{i=1}^3 {\mathcal O}/d_i{\mathcal O}$
where
![]() $d_1$
,
$d_1$
,
![]() $d_1d_2$
and
$d_1d_2$
and
![]() $d_1d_2d_3$
are the gcds of the
$d_1d_2d_3$
are the gcds of the
![]() $i\times i$
-minors of
$i\times i$
-minors of
![]() $\widetilde {\lambda }(A')$
displayed in Equation (5.2) for
$\widetilde {\lambda }(A')$
displayed in Equation (5.2) for
![]() $i=1,2,3$
. One readily computes
$i=1,2,3$
. One readily computes
 $$\begin{align*}d_1&=\gcd(s,t,q-1),\\d_2&=\gcd(t^2,t(q-1),t(q-1),ts,(q-1)s,(q-1)^2)=\gcd(s,t,q-1)\gcd(t,q-1),\\d_3&=\gcd(t^2(q-1),t(q-1)s,t(q-1)^2)=t(q-1)\gcd(s,t,q-1), \end{align*}$$
$$\begin{align*}d_1&=\gcd(s,t,q-1),\\d_2&=\gcd(t^2,t(q-1),t(q-1),ts,(q-1)s,(q-1)^2)=\gcd(s,t,q-1)\gcd(t,q-1),\\d_3&=\gcd(t^2(q-1),t(q-1)s,t(q-1)^2)=t(q-1)\gcd(s,t,q-1), \end{align*}$$
and this implies the assertion of the corollary.
Lemma 5.14. For the ideals
![]() $P=(\alpha ,\beta )$
,
$P=(\alpha ,\beta )$
,
![]() $Q=(q-1+a,c)$
and
$Q=(q-1+a,c)$
and
![]() $I'=((q-1+a)\alpha , (q-1+a)\beta ,c\alpha ,c\beta )$
of
$I'=((q-1+a)\alpha , (q-1+a)\beta ,c\alpha ,c\beta )$
of
![]() $\widetilde {R}$
the following hold.
$\widetilde {R}$
the following hold.
-
1. P is a prime ideal and
 $P=\{x\in \widetilde {R} \mid x r^{\mathrm {st}}_4=0\}$
.
$P=\{x\in \widetilde {R} \mid x r^{\mathrm {st}}_4=0\}$
. -
2. Q is a prime ideal and
 $Q=\{x\in \widetilde {R} \mid x r^{\mathrm {st}}_6=0\}$
.
$Q=\{x\in \widetilde {R} \mid x r^{\mathrm {st}}_6=0\}$
. -
3. One has (a)
 $P\cap Q=\widetilde {R}[I]$
and (b)
$P\cap Q=\widetilde {R}[I]$
and (b)
 $P\cap Q=I'$
.
$P\cap Q=I'$
.
Proof. 1. Note first that
![]() $\widetilde {R}/P$
is isomorphic to
$\widetilde {R}/P$
is isomorphic to
![]() ${\mathcal O}[[a,b,c,\beta ]]/((q-1+a)a+bc)$
. Since this is a domain, P is a prime ideal. Next, observe that
${\mathcal O}[[a,b,c,\beta ]]/((q-1+a)a+bc)$
. Since this is a domain, P is a prime ideal. Next, observe that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
annihilate
$\beta $
annihilate
![]() $r^{\mathrm {st}}_4$
as follows by considering columns
$r^{\mathrm {st}}_4$
as follows by considering columns
![]() $2$
and
$2$
and
![]() $6$
in the relation matrix
$6$
in the relation matrix
![]() $A'$
in Corollary 5.10. It remains to show that
$A'$
in Corollary 5.10. It remains to show that
![]() $P=(\alpha ,\beta )$
contains
$P=(\alpha ,\beta )$
contains
![]() $\{x\in \widetilde {R}\mid xr^{\mathrm {st}}_4=0\}$
. So suppose that
$\{x\in \widetilde {R}\mid xr^{\mathrm {st}}_4=0\}$
. So suppose that
![]() $xr^{\mathrm {st}}_4=0$
in
$xr^{\mathrm {st}}_4=0$
in
![]() $\widetilde {R}$
. The main observation is that
$\widetilde {R}$
. The main observation is that
![]() $r^{\mathrm {st}}_4\ {\operatorname {mod}}\ P=(q-1+a)\gamma $
is a nonzero element in the domain
$r^{\mathrm {st}}_4\ {\operatorname {mod}}\ P=(q-1+a)\gamma $
is a nonzero element in the domain
![]() $\widetilde {R}/P$
. Therefore,
$\widetilde {R}/P$
. Therefore,
![]() $x\ {\operatorname {mod}}\ P$
is zero and thus
$x\ {\operatorname {mod}}\ P$
is zero and thus
![]() $x\in P$
, as had to be shown. The proof of 2. is completely parallel to that of 1. and left to the reader.
$x\in P$
, as had to be shown. The proof of 2. is completely parallel to that of 1. and left to the reader.
From the definition of P, Q and
![]() $I'$
it is clear that
$I'$
it is clear that
![]() $I'\subset P\cap Q$
. It is also straight forward to see from the columns of
$I'\subset P\cap Q$
. It is also straight forward to see from the columns of
![]() $A'$
that
$A'$
that
![]() $I'$
annihilates
$I'$
annihilates
![]() $r^{\mathrm {st}}_5$
(multiply the first column and the fifth column by c or by
$r^{\mathrm {st}}_5$
(multiply the first column and the fifth column by c or by
![]() $(q-1+a)$
, and use 1.; alternatively, multiply the forth and the eighth column by
$(q-1+a)$
, and use 1.; alternatively, multiply the forth and the eighth column by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, and use 2.). We shall now prove 3(b), and from this and what we already proved, 3(a) will follow.
$\beta $
, and use 2.). We shall now prove 3(b), and from this and what we already proved, 3(a) will follow.
To see 3(b), let x be in
![]() $P\cap Q$
. Write
$P\cap Q$
. Write
![]() $x=f_1\alpha +f_2\beta $
. To show that x lies in
$x=f_1\alpha +f_2\beta $
. To show that x lies in
![]() $I'\subset P\cap Q$
, we may subtract from x arbitrary elements in
$I'\subset P\cap Q$
, we may subtract from x arbitrary elements in
![]() $I'$
. Writing elements in
$I'$
. Writing elements in
![]() ${\mathcal R}$
as power series over
${\mathcal R}$
as power series over
![]() ${\mathcal O}$
in
${\mathcal O}$
in
![]() $q-1+a,b,c,\alpha ,\beta ,\gamma $
, we may thus assume
$q-1+a,b,c,\alpha ,\beta ,\gamma $
, we may thus assume
![]() $f_1,f_2\in (\alpha ,\beta ,\gamma ,b)$
. Shifting multiples of
$f_1,f_2\in (\alpha ,\beta ,\gamma ,b)$
. Shifting multiples of
![]() $\alpha $
in
$\alpha $
in
![]() $f_2$
to
$f_2$
to
![]() $\alpha f_1$
, we may further assume
$\alpha f_1$
, we may further assume
![]() $f_2\in (\beta ,\gamma ,b)$
and using
$f_2\in (\beta ,\gamma ,b)$
and using
![]() $r^{\mathrm {st}}_1$
, we can replace
$r^{\mathrm {st}}_1$
, we can replace
![]() $\beta \gamma $
by
$\beta \gamma $
by
![]() $\alpha ^2$
, and this finally allows us to assume that
$\alpha ^2$
, and this finally allows us to assume that
![]() $f_2$
lies in
$f_2$
lies in
![]() $(b,\beta )$
. We now reduce
$(b,\beta )$
. We now reduce
![]() $x\in P\cap Q$
modulo Q. This yields
$x\in P\cap Q$
modulo Q. This yields
![]() $f_1\alpha +f_2\beta =0$
in
$f_1\alpha +f_2\beta =0$
in
![]() ${\mathcal O}[[\alpha ,\beta ,\gamma ,b]]/(\alpha ^2+\beta \gamma )$
. In other words, we can find
${\mathcal O}[[\alpha ,\beta ,\gamma ,b]]/(\alpha ^2+\beta \gamma )$
. In other words, we can find
![]() $f_3\in {\mathcal R}':={\mathcal O}[[\alpha ,\beta ,\gamma ,b]]$
such that
$f_3\in {\mathcal R}':={\mathcal O}[[\alpha ,\beta ,\gamma ,b]]$
such that
Reducing modulo
![]() $\alpha $
and using
$\alpha $
and using
![]() $f_2\in (b,\beta )$
it follows that
$f_2\in (b,\beta )$
it follows that
![]() $\gamma $
had to divide
$\gamma $
had to divide
![]() $f_2$
and hence that
$f_2$
and hence that
![]() $f_2=0$
. Since
$f_2=0$
. Since
![]() ${\mathcal R}'$
is a UFD it follows that
${\mathcal R}'$
is a UFD it follows that
![]() $r^{\mathrm {st}}_1=\alpha ^2+\beta \gamma $
divides
$r^{\mathrm {st}}_1=\alpha ^2+\beta \gamma $
divides
![]() $f_1$
and hence that
$f_1$
and hence that
![]() $f_1=0$
in
$f_1=0$
in
![]() $\widetilde {R}$
. Hence, we proved that x lies in
$\widetilde {R}$
. Hence, we proved that x lies in
![]() $I'$
.
$I'$
.
Corollary 5.15. Let e be the ramification index of E over
![]() ${\mathbf Q}_l$
. Then
${\mathbf Q}_l$
. Then
![]() $\widetilde {\lambda }( \widetilde {R}[I])=(q-1)t \subset {\mathcal O}$
and
$\widetilde {\lambda }( \widetilde {R}[I])=(q-1)t \subset {\mathcal O}$
and
![]() $c_{1,\lambda }(R^{\mathrm {st}}_v)=\frac 1e\log _p({\mathcal O}/(s,t,q-1))=\frac {n_v}e$
.
$c_{1,\lambda }(R^{\mathrm {st}}_v)=\frac 1e\log _p({\mathcal O}/(s,t,q-1))=\frac {n_v}e$
.
Proof. In Lemma 5.14, we identified
![]() $\widetilde {R}[I]$
with
$\widetilde {R}[I]$
with
![]() $I'$
. The image of
$I'$
. The image of
![]() $I'$
under
$I'$
under
![]() $\lambda $
is simply
$\lambda $
is simply
![]() $((q-1)t)$
. Invoking also Corollary 5.11, we deduce
$((q-1)t)$
. Invoking also Corollary 5.11, we deduce
To complete the computation of
![]() $D_{1,\lambda }(R_v^{\mathrm {st}})$
, we still have to compute the size of the cokernel of
$D_{1,\lambda }(R_v^{\mathrm {st}})$
, we still have to compute the size of the cokernel of
![]() $\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {st}}}({\widehat {\Omega }}_{R_v^{\mathrm {st}}},E/{\mathcal O})\to \operatorname {\mathrm {Hom}}_{\widetilde {R}}({\widehat {\Omega }}_{\widetilde {R}},E/{\mathcal O}) $
. Using the methods of [Reference Böckle, Khare and ManningBKM21, § 7.2] and its terminology, we need to compute the lattice
$\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {st}}}({\widehat {\Omega }}_{R_v^{\mathrm {st}}},E/{\mathcal O})\to \operatorname {\mathrm {Hom}}_{\widetilde {R}}({\widehat {\Omega }}_{\widetilde {R}},E/{\mathcal O}) $
. Using the methods of [Reference Böckle, Khare and ManningBKM21, § 7.2] and its terminology, we need to compute the lattice
![]() $\widetilde {\Lambda }\subset {\mathcal O}^8$
that is the kernel of the natural surjection
$\widetilde {\Lambda }\subset {\mathcal O}^8$
that is the kernel of the natural surjection
![]() ${\mathcal O}^8\cong {\widehat {\Omega }}_{{\mathcal R}/{\mathcal O}}\otimes _{{\mathcal R}}^{\widetilde {\lambda }}{\mathcal O}\to {\widehat {\Omega }}_{\widetilde {R}/{\mathcal O}}\otimes _{\widetilde {R}}^{\widetilde {\lambda }}{\mathcal O}$
. The lattice
${\mathcal O}^8\cong {\widehat {\Omega }}_{{\mathcal R}/{\mathcal O}}\otimes _{{\mathcal R}}^{\widetilde {\lambda }}{\mathcal O}\to {\widehat {\Omega }}_{\widetilde {R}/{\mathcal O}}\otimes _{\widetilde {R}}^{\widetilde {\lambda }}{\mathcal O}$
. The lattice
![]() $\widetilde {\Lambda }$
is contained in
$\widetilde {\Lambda }$
is contained in
![]() $\Lambda ^{{\mathrm {st}}}$
, and the cardinality wanted is
$\Lambda ^{{\mathrm {st}}}$
, and the cardinality wanted is
![]() $\#(\Lambda ^{{\mathrm {st}}}/\widetilde {\Lambda })$
.
$\#(\Lambda ^{{\mathrm {st}}}/\widetilde {\Lambda })$
.
Lemma 5.16. The lattice
![]() $\widetilde {\Lambda }\subset {\mathcal O}^8$
is spanned by the rows of the matrix
$\widetilde {\Lambda }\subset {\mathcal O}^8$
is spanned by the rows of the matrix
 $$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&0&0&t&0\\ 0&0&s&q-1&0&0&0&0\\ 0&0&t&0&q-1&0&0&0\\ \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&0&0&t&0\\ 0&0&s&q-1&0&0&0&0\\ 0&0&t&0&q-1&0&0&0\\ \end{array} \right). \end{align*}$$
and the quotient
![]() $\Lambda ^{{\mathrm {st}}}/\widetilde {\Lambda }$
as an
$\Lambda ^{{\mathrm {st}}}/\widetilde {\Lambda }$
as an
![]() ${\mathcal O}$
-module is isomorphic to
${\mathcal O}$
-module is isomorphic to
![]() $(s,t,q-1)/(t) \times (s,t,q-1)/(q-1)$
.
$(s,t,q-1)/(t) \times (s,t,q-1)/(q-1)$
.
Proof. In the notation of [Reference Böckle, Khare and ManningBKM21, § 7.3], the ring
![]() $\widetilde {R}$
is given as
$\widetilde {R}$
is given as
![]() ${\mathcal O}[[a,b,c,e,\alpha ,\beta ,\gamma ,\delta ]]$
modulo the relations
${\mathcal O}[[a,b,c,e,\alpha ,\beta ,\gamma ,\delta ]]$
modulo the relations
![]() $a-e,\alpha +\delta ,\alpha \delta -\beta \gamma , (q-1+a)e+bc,(q-1+a)\delta -c\beta $
. The spanning vectors of
$a-e,\alpha +\delta ,\alpha \delta -\beta \gamma , (q-1+a)e+bc,(q-1+a)\delta -c\beta $
. The spanning vectors of
![]() $\widetilde {\Lambda }$
are then the image of the Jacobian matrix
$\widetilde {\Lambda }$
are then the image of the Jacobian matrix
 $$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&\delta&-\gamma&-\beta&\alpha\\ e&c&b&q-1+a&0&0&0&0\\ \delta&0&-\beta&0&0&-c&0&q-1+a\\ \end{array} \right) \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&\delta&-\gamma&-\beta&\alpha\\ e&c&b&q-1+a&0&0&0&0\\ \delta&0&-\beta&0&0&-c&0&q-1+a\\ \end{array} \right) \end{align*}$$
under the augmentation
![]() $\widetilde {\lambda }$
. The matrix displayed in the assertion of the lemma is obtained from this image after some simple row operations. By [Reference Böckle, Khare and ManningBKM21, § 7.2], the lattice
$\widetilde {\lambda }$
. The matrix displayed in the assertion of the lemma is obtained from this image after some simple row operations. By [Reference Böckle, Khare and ManningBKM21, § 7.2], the lattice
![]() $\Lambda ^{{\mathrm {st}}}$
is spanned by the rows of
$\Lambda ^{{\mathrm {st}}}$
is spanned by the rows of
 $$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&0&0&(s,t,q-1)&0\\ 0&0&t&0&q-1&0&0&0\\ 0&0&0&(t,q-1)&{\textstyle \frac st}(t,q-1)&0&0&0\\ \end{array} \right) \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} 1&0&0&-1&0&0&0&0\\ 0&0&0&0&1&0&0&1\\ 0&0&0&0&0&0&(s,t,q-1)&0\\ 0&0&t&0&q-1&0&0&0\\ 0&0&0&(t,q-1)&{\textstyle \frac st}(t,q-1)&0&0&0\\ \end{array} \right) \end{align*}$$
if
![]() $ \mathrm {ord}_\varpi (s)\ge \mathrm {ord}_\varpi (t)$
; and in the other case, the last two rows have to be replaced by
$ \mathrm {ord}_\varpi (s)\ge \mathrm {ord}_\varpi (t)$
; and in the other case, the last two rows have to be replaced by
 $$\begin{align*}\left( \begin{array}{cccccccc} 0&0&-s&q-1&0&0&0&0\\ 0&0&0&{\textstyle \frac ts} (s,q-1)&(s,q-1)&0&0&0\\ \end{array} \right). \end{align*}$$
$$\begin{align*}\left( \begin{array}{cccccccc} 0&0&-s&q-1&0&0&0&0\\ 0&0&0&{\textstyle \frac ts} (s,q-1)&(s,q-1)&0&0&0\\ \end{array} \right). \end{align*}$$
In both cases, it is easy to express the basis spanning
![]() $\widetilde {\Lambda }$
in terms of the basis spanning
$\widetilde {\Lambda }$
in terms of the basis spanning
![]() $\Lambda ^{{\mathrm {st}}}$
, by an upper triangular transition matrix over
$\Lambda ^{{\mathrm {st}}}$
, by an upper triangular transition matrix over
![]() ${\mathcal O}$
diagonal entries
${\mathcal O}$
diagonal entries
![]() $1,1,1,\frac {t}{(s,t,q-1)},\frac {(q-1)}{(s,t,q-1)}$
. The assertions of the lemma are now clear.
$1,1,1,\frac {t}{(s,t,q-1)},\frac {(q-1)}{(s,t,q-1)}$
. The assertions of the lemma are now clear.
Corollary 5.17. We have
![]() $D_{1,\lambda }(R_v^{\mathrm {st}})=\frac 1e \cdot \log _p \#( {\mathcal O}/(s,t,q-1))^3 =3\frac {n_v}e$
.
$D_{1,\lambda }(R_v^{\mathrm {st}})=\frac 1e \cdot \log _p \#( {\mathcal O}/(s,t,q-1))^3 =3\frac {n_v}e$
.
Proof. From Lemma 5.16, the observations preceding it and from Theorem 3.23, we have
In Corollary 5.13 we computed
![]() $\#\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {st}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/(t(q-1)(s,t,q-1))$
. Forming the quotient, the result follows from Theorem 3.23.
$\#\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {st}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/(t(q-1)(s,t,q-1))$
. Forming the quotient, the result follows from Theorem 3.23.
From
![]() $\delta _\lambda (R_v^{\mathrm {st}}) = D_{1,\lambda }(R_v^{\mathrm {st}})-c_{1,\lambda }(R_v^{\mathrm {st}})$
and Corollaries 5.15 and 5.17, we deduce.
$\delta _\lambda (R_v^{\mathrm {st}}) = D_{1,\lambda }(R_v^{\mathrm {st}})-c_{1,\lambda }(R_v^{\mathrm {st}})$
and Corollaries 5.15 and 5.17, we deduce.
Theorem 5.18. We have
![]() $\delta _\lambda (R_v^{{\mathrm {st}}}) = 2\frac {n_v}e$
.
$\delta _\lambda (R_v^{{\mathrm {st}}}) = 2\frac {n_v}e$
.
5.3 Unipotent deformations with a choice of Frobenius at trivial primes
In the following,
![]() ${\underline {s}}$
and
${\underline {s}}$
and
![]() ${\underline {t}}$
will denote indeterminates that we shall specialize to s and t, respectively, whenever we pass to
${\underline {t}}$
will denote indeterminates that we shall specialize to s and t, respectively, whenever we pass to
![]() ${\mathcal O}$
-algebras. Recall the expressions
${\mathcal O}$
-algebras. Recall the expressions
![]() $r_i^{\operatorname {\varphi -uni}}$
from Lemma 5.2, and observe that in the following we regard them as elements in the ring
$r_i^{\operatorname {\varphi -uni}}$
from Lemma 5.2, and observe that in the following we regard them as elements in the ring
![]() ${\mathcal R}_{\mathbf Z}={\mathbf Z}[{\underline {q}},a,b,c,X,\alpha ,\beta ,\gamma ]\subset {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]$
, replacing any occurrence of q by the indeterminate
${\mathcal R}_{\mathbf Z}={\mathbf Z}[{\underline {q}},a,b,c,X,\alpha ,\beta ,\gamma ]\subset {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]$
, replacing any occurrence of q by the indeterminate
![]() ${\underline {q}}+1$
. Set
${\underline {q}}+1$
. Set
 $$ \begin{align*} s_1^{\operatorname{\varphi-uni}}&= r_9^{\operatorname{\varphi-uni}}+r_6^{\operatorname{\varphi-uni}},\\ s_2^{\operatorname{\varphi-uni}}&= r_8^{\operatorname{\varphi-uni}}-r_7^{\operatorname{\varphi-uni}} +r_2^{\operatorname{\varphi-uni}},\\ s_3^{\operatorname{\varphi-uni}}&= r_5^{\operatorname{\varphi-uni}},\\ s_4^{\operatorname{\varphi-uni}}&= r_2^{\operatorname{\varphi-uni}}+a r_3^{\operatorname{\varphi-uni}} +r_4^{\operatorname{\varphi-uni}}+ar_6^{\operatorname{\varphi-uni}}-br_7^{\operatorname{\varphi-uni}} -r_3^{\operatorname{\varphi-uni}}, \\ s_4^{\prime\,{\operatorname{\varphi-uni}}}&= a r_3^{\operatorname{\varphi-uni}} +r_4^{\operatorname{\varphi-uni}}+ar_6^{\operatorname{\varphi-uni}}-br_7^{\operatorname{\varphi-uni}} -r_3^{\operatorname{\varphi-uni}}, \end{align*} $$
$$ \begin{align*} s_1^{\operatorname{\varphi-uni}}&= r_9^{\operatorname{\varphi-uni}}+r_6^{\operatorname{\varphi-uni}},\\ s_2^{\operatorname{\varphi-uni}}&= r_8^{\operatorname{\varphi-uni}}-r_7^{\operatorname{\varphi-uni}} +r_2^{\operatorname{\varphi-uni}},\\ s_3^{\operatorname{\varphi-uni}}&= r_5^{\operatorname{\varphi-uni}},\\ s_4^{\operatorname{\varphi-uni}}&= r_2^{\operatorname{\varphi-uni}}+a r_3^{\operatorname{\varphi-uni}} +r_4^{\operatorname{\varphi-uni}}+ar_6^{\operatorname{\varphi-uni}}-br_7^{\operatorname{\varphi-uni}} -r_3^{\operatorname{\varphi-uni}}, \\ s_4^{\prime\,{\operatorname{\varphi-uni}}}&= a r_3^{\operatorname{\varphi-uni}} +r_4^{\operatorname{\varphi-uni}}+ar_6^{\operatorname{\varphi-uni}}-br_7^{\operatorname{\varphi-uni}} -r_3^{\operatorname{\varphi-uni}}, \end{align*} $$
and also
The next result summarizes some explicit computations done via Macaulay2.
Lemma 5.19.
-
1. The ring
is free over $$\begin{align*} {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/({\underline {q}},{\underline {s}},{\underline {t}},b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X, s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4) \end{align*}$$
$$\begin{align*} {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/({\underline {q}},{\underline {s}},{\underline {t}},b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X, s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4) \end{align*}$$
 ${\mathbf Z}$
of rank
${\mathbf Z}$
of rank
 $16$
. The same holds if we replace
$16$
. The same holds if we replace
 $s_4^{\operatorname {\varphi -uni}}$
by
$s_4^{\operatorname {\varphi -uni}}$
by
 $s_4^{\prime \,{\operatorname {\varphi -uni}}}$
. A basis is
$s_4^{\prime \,{\operatorname {\varphi -uni}}}$
. A basis is
 $1,a,aX,aX\alpha ,a\alpha , b,b\alpha , X, X^2,X^2\alpha ,X\alpha ,X\alpha ^2,X\alpha ^3,\alpha ,\alpha ^2,\alpha ^3$
. A basis of the socle of the ring modulo any prime is
$1,a,aX,aX\alpha ,a\alpha , b,b\alpha , X, X^2,X^2\alpha ,X\alpha ,X\alpha ^2,X\alpha ^3,\alpha ,\alpha ^2,\alpha ^3$
. A basis of the socle of the ring modulo any prime is
 $X\alpha ^3$
.
$X\alpha ^3$
.
-
2. The ring
 ${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/(({\underline {q}},{\underline {s}},{\underline {t}},b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X)+{\mathcal I}^{\operatorname {\varphi -uni}}_{\mathbf Z})$
is free over
${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/(({\underline {q}},{\underline {s}},{\underline {t}},b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X)+{\mathcal I}^{\operatorname {\varphi -uni}}_{\mathbf Z})$
is free over
 ${\mathbf Z}$
of rank
${\mathbf Z}$
of rank
 $6$
. A basis is
$6$
. A basis is
 $1,a,b,bX,X,\alpha $
. A basis of the socle of the ring modulo any prime is
$1,a,b,bX,X,\alpha $
. A basis of the socle of the ring modulo any prime is
 $X\alpha $
.
$X\alpha $
. -
3. Write
 $x_1,\ldots ,x_7$
for
$x_1,\ldots ,x_7$
for
 $a,b,c,X,\alpha ,\beta ,\gamma $
. Then the ideal in
$a,b,c,X,\alpha ,\beta ,\gamma $
. Then the ideal in
 ${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
generated by the
${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
generated by the
 $4\times 4$
-minors of the Jacobian
$4\times 4$
-minors of the Jacobian
 $(\partial s_i^{\operatorname {\varphi -uni}}/\partial x_j)_{i=1,\ldots ,4; j=1,\ldots ,7}$
evaluated at
$(\partial s_i^{\operatorname {\varphi -uni}}/\partial x_j)_{i=1,\ldots ,4; j=1,\ldots ,7}$
evaluated at
 $(x_1,\ldots ,x_7)=(0,{\underline {s}},0,0,0,{\underline {t}},0)$
is
$(x_1,\ldots ,x_7)=(0,{\underline {s}},0,0,0,{\underline {t}},0)$
is
 $({\underline {s}}-{\underline {t}}){\underline {t}}^2({\underline {q}},{\underline {s}}, {\underline {t}})$
. If one replaces
$({\underline {s}}-{\underline {t}}){\underline {t}}^2({\underline {q}},{\underline {s}}, {\underline {t}})$
. If one replaces
 $s_4^{\operatorname {\varphi -uni}}$
by
$s_4^{\operatorname {\varphi -uni}}$
by
 $s_4^{\prime \,{\operatorname {\varphi -uni}}}$
, the resulting ideal is
$s_4^{\prime \,{\operatorname {\varphi -uni}}}$
, the resulting ideal is
 ${\underline {s}}{\underline {t}}^2({\underline {q}},{\underline {s}}, {\underline {t}})$
.
${\underline {s}}{\underline {t}}^2({\underline {q}},{\underline {s}}, {\underline {t}})$
.
Remark 5.20. We note that the number 16 in part 1 is optimal. After reducing the number of variables by those relations that are linear, the
![]() $s_i^{\operatorname {\varphi -uni}}$
are quadratic relations of a polynomial ring over
$s_i^{\operatorname {\varphi -uni}}$
are quadratic relations of a polynomial ring over
![]() ${\mathbf Z}$
in
${\mathbf Z}$
in
![]() $4$
variables. Now, the intersection of four quadrics in general position consists of
$4$
variables. Now, the intersection of four quadrics in general position consists of
![]() $16$
points. Therefore, dimension
$16$
points. Therefore, dimension
![]() $16$
for the coordinate ring of the corresponding scheme is optimal.
$16$
for the coordinate ring of the corresponding scheme is optimal.
Let
![]() $s,t\in {\mathfrak m}$
with
$s,t\in {\mathfrak m}$
with
![]() $t\neq 0$
.
$t\neq 0$
.
Corollary 5.21.
-
1. The ring
 $\widetilde {R}={\mathcal O}[[a,b,c,X,\alpha ,\beta ,\gamma ]]/(s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)$
is a complete intersection, flat over
$\widetilde {R}={\mathcal O}[[a,b,c,X,\alpha ,\beta ,\gamma ]]/(s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)$
is a complete intersection, flat over
 ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
 $3$
, and this also holds with
$3$
, and this also holds with
 $s_4^{\operatorname {\varphi -uni}}$
replaced by
$s_4^{\operatorname {\varphi -uni}}$
replaced by
 $s_4^{\prime \,{\operatorname {\varphi -uni}}}$
. One has a natural surjection
$s_4^{\prime \,{\operatorname {\varphi -uni}}}$
. One has a natural surjection
 $\widetilde {R}\to R^{\operatorname {\varphi -uni}}_v$
induced from the inclusion of ideals
$\widetilde {R}\to R^{\operatorname {\varphi -uni}}_v$
induced from the inclusion of ideals
 $(s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)\subset (r_j^{\operatorname {\varphi -uni}},j=1,\ldots ,9)$
.
$(s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)\subset (r_j^{\operatorname {\varphi -uni}},j=1,\ldots ,9)$
. -
2. Via the ring map
 $S={\mathcal O}[[y_1,y_2,y_3]]\to \widetilde {R}$
given by
$S={\mathcal O}[[y_1,y_2,y_3]]\to \widetilde {R}$
given by
 $y_1\mapsto b-s-c, y_2\mapsto \beta -t-c, y_3\mapsto \gamma -X$
, the rings
$y_1\mapsto b-s-c, y_2\mapsto \beta -t-c, y_3\mapsto \gamma -X$
, the rings
 $\widetilde {R}$
and
$\widetilde {R}$
and
 $R^{\operatorname {\varphi -uni}}_v$
are free S-modules of rank
$R^{\operatorname {\varphi -uni}}_v$
are free S-modules of rank
 $16$
and
$16$
and
 $6$
, respectively (for either choice of
$6$
, respectively (for either choice of
 $\widetilde {R}$
).
$\widetilde {R}$
). -
3. The augmentation
 $\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by
$\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by
 $a,c,X,\alpha ,\gamma \mapsto 0$
,
$a,c,X,\alpha ,\gamma \mapsto 0$
,
 $b\mapsto s$
and
$b\mapsto s$
and
 $\beta \mapsto t$
defines a formally smooth point of
$\beta \mapsto t$
defines a formally smooth point of
 $\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
, for at least one of the two choices of
$\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
, for at least one of the two choices of
 $\widetilde {R}$
from 1, provided that
$\widetilde {R}$
from 1, provided that
 $t\in {\mathcal O}\setminus \{0\}$
.
$t\in {\mathcal O}\setminus \{0\}$
.
Proof. The quotient
![]() $\widetilde {R}/(\varpi , b-s-c, \beta -t-c, \gamma -X)$
is isomorphic to the ring from Lemma 5.19.1 tensored with k over
$\widetilde {R}/(\varpi , b-s-c, \beta -t-c, \gamma -X)$
is isomorphic to the ring from Lemma 5.19.1 tensored with k over
![]() ${\mathbf Z}$
– since the latter ring is free of rank 16 over
${\mathbf Z}$
– since the latter ring is free of rank 16 over
![]() ${\mathbf Z}$
, no completion is necessary. This implies that
${\mathbf Z}$
, no completion is necessary. This implies that
![]() $(\varpi , b-s-c, \beta -t-c, \gamma -X,s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)$
is a regular sequence in
$(\varpi , b-s-c, \beta -t-c, \gamma -X,s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4)$
is a regular sequence in
![]() ${\mathcal R}$
with quotient a k-algebra of k-dimension
${\mathcal R}$
with quotient a k-algebra of k-dimension
![]() $16$
. We deduce part 1 and the first half of part 2. The second half of part 2 uses Lemma 5.19.2 in an analogous way.
$16$
. We deduce part 1 and the first half of part 2. The second half of part 2 uses Lemma 5.19.2 in an analogous way.
To prove part 3, observe that not both, s and
![]() $s+t$
can be zero since otherwise
$s+t$
can be zero since otherwise
![]() $t=0$
which is ruled out. So we choose
$t=0$
which is ruled out. So we choose
![]() $s_4^{\operatorname {\varphi -uni}}$
or
$s_4^{\operatorname {\varphi -uni}}$
or
![]() $s_4^{\prime \,{\operatorname {\varphi -uni}}}$
accordingly. Then we evaluate the ideal in Lemma 5.19.3 at the made choice. This gives either the nonzero value
$s_4^{\prime \,{\operatorname {\varphi -uni}}}$
accordingly. Then we evaluate the ideal in Lemma 5.19.3 at the made choice. This gives either the nonzero value
![]() $(s-t)t^2\gcd (t,s,q-1)$
or
$(s-t)t^2\gcd (t,s,q-1)$
or
![]() $st^2\gcd (t,s,q-1)$
for a generator of the corresponding ideal over
$st^2\gcd (t,s,q-1)$
for a generator of the corresponding ideal over
![]() ${\mathcal O}$
. This implies the stated formal smoothness.
${\mathcal O}$
. This implies the stated formal smoothness.
Our aim is to compute
![]() $D_{1,\lambda }(R_v^{\operatorname {\varphi -uni}})$
and
$D_{1,\lambda }(R_v^{\operatorname {\varphi -uni}})$
and
![]() $c_{1,\lambda }(R_v^{\operatorname {\varphi -uni}})$
. Instead, we shall compute these invariants for the ring
$c_{1,\lambda }(R_v^{\operatorname {\varphi -uni}})$
. Instead, we shall compute these invariants for the ring
![]() $R_v^{\operatorname {\varphi -uni}}\otimes _{S}{\mathcal O}$
, where S is the ring from Corollary 5.21 and where the map
$R_v^{\operatorname {\varphi -uni}}\otimes _{S}{\mathcal O}$
, where S is the ring from Corollary 5.21 and where the map
![]() $S\to {\mathcal O}$
is the augmentation
$S\to {\mathcal O}$
is the augmentation
![]() $\widetilde {\lambda }$
composed with
$\widetilde {\lambda }$
composed with
![]() $S\to \widetilde {R}$
. This is allowed due to Theorems 3.9 and 3.20.Footnote
9
It is probably not strictly necessary to perform this base change. However, it seems easier to work with Gorenstein and complete intersection rings that are finite flat over
$S\to \widetilde {R}$
. This is allowed due to Theorems 3.9 and 3.20.Footnote
9
It is probably not strictly necessary to perform this base change. However, it seems easier to work with Gorenstein and complete intersection rings that are finite flat over
![]() ${\mathcal O}$
. In particular, this will allow us to (have Macaulay2) compute structural constants of these rings, namely their multiplication tables in a given
${\mathcal O}$
. In particular, this will allow us to (have Macaulay2) compute structural constants of these rings, namely their multiplication tables in a given
![]() ${\mathcal O}$
-bases. In the remainder of this subsection, we consider the rings
${\mathcal O}$
-bases. In the remainder of this subsection, we consider the rings
and we let
![]() $\overline {I}$
be the kernel of
$\overline {I}$
be the kernel of
![]() $\overline {\pi }:\overline {R}\to \overline {R}^{\operatorname {\varphi -uni}}_v$
.
$\overline {\pi }:\overline {R}\to \overline {R}^{\operatorname {\varphi -uni}}_v$
.
We first explain the part that for us was the most difficult one, namely the computation of
![]() $\overline {R}[\overline {I}]$
. Let
$\overline {R}[\overline {I}]$
. Let
![]() $(b_i)_{i=1,\ldots ,16}$
be an
$(b_i)_{i=1,\ldots ,16}$
be an
![]() ${\mathcal O}$
-basis of
${\mathcal O}$
-basis of
![]() $\overline {R}$
such that
$\overline {R}$
such that
![]() $(b_i)_{i=7,\ldots ,16}$
is a basis of the kernel of
$(b_i)_{i=7,\ldots ,16}$
is a basis of the kernel of
![]() $\overline {R}\to \overline {R}_v^{\operatorname {\varphi -uni}}$
. Suppose further that
$\overline {R}\to \overline {R}_v^{\operatorname {\varphi -uni}}$
. Suppose further that
![]() $b_6$
and
$b_6$
and
![]() $b_{16}$
are chosen so that they reduce to a generators of the socle of the finite Gorenstein rings
$b_{16}$
are chosen so that they reduce to a generators of the socle of the finite Gorenstein rings
![]() $\overline {R}_v^{\operatorname {\varphi -uni}}/(\varpi )$
and
$\overline {R}_v^{\operatorname {\varphi -uni}}/(\varpi )$
and
![]() $\overline {R}/(\varpi )$
, respectively; this is always possible. Denote by
$\overline {R}/(\varpi )$
, respectively; this is always possible. Denote by
![]() $(b_i^*)_{i=1,\ldots ,16}$
the dual basis. It follows from Proposition 5.39 that
$(b_i^*)_{i=1,\ldots ,16}$
the dual basis. It follows from Proposition 5.39 that
![]() $b_6^*$
is a generator of
$b_6^*$
is a generator of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal O}(\overline {R}_v^{\operatorname {\varphi -uni}},{\mathcal O})$
as a free
$\operatorname {\mathrm {Hom}}_{\mathcal O}(\overline {R}_v^{\operatorname {\varphi -uni}},{\mathcal O})$
as a free
![]() $\overline {R}_v^{\operatorname {\varphi -uni}}$
-module, and
$\overline {R}_v^{\operatorname {\varphi -uni}}$
-module, and
![]() $b_{16}^*$
of
$b_{16}^*$
of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal O}(\overline {R},{\mathcal O})$
as a free
$\operatorname {\mathrm {Hom}}_{\mathcal O}(\overline {R},{\mathcal O})$
as a free
![]() $\overline {R}$
-module. Denote by
$\overline {R}$
-module. Denote by
![]() $\Theta $
the isomorphism
$\Theta $
the isomorphism
and consider the chain of isomorphisms
from Lemma 3.14. The generator
![]() $b_6^*$
on the right is successively mapped to, first
$b_6^*$
on the right is successively mapped to, first
![]() $h_1\otimes h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)) $
, second
$h_1\otimes h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)) $
, second
![]() $(h_1\mapsto (h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)))$
, third
$(h_1\mapsto (h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)))$
, third
![]() $(h_1\mapsto \Theta ^{-1}(h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)))$
, lastly to
$(h_1\mapsto \Theta ^{-1}(h_2\mapsto b_6^*(h_1\cdot \overline {\pi }(h_2)))$
, lastly to
Now, write
![]() $ \Theta ^{-1}\circ b_6^*=\sum _i \mu _i b_i$
with
$ \Theta ^{-1}\circ b_6^*=\sum _i \mu _i b_i$
with
![]() $\mu _i\in {\mathcal O}$
. By the definition of
$\mu _i\in {\mathcal O}$
. By the definition of
![]() $\Theta $
, this is equivalent to
$\Theta $
, this is equivalent to
![]() $b_6^*(f)=b_{16}^*( \sum _i \mu _i b_i f)$
for all
$b_6^*(f)=b_{16}^*( \sum _i \mu _i b_i f)$
for all
![]() $f\in \overline {R}$
. Let
$f\in \overline {R}$
. Let
![]() $c_{ijk}\in {\mathcal O}$
be the structural constants for multiplication in
$c_{ijk}\in {\mathcal O}$
be the structural constants for multiplication in
![]() $\overline {R}$
over
$\overline {R}$
over
![]() ${\mathcal O}$
with respect to the basis
${\mathcal O}$
with respect to the basis
![]() $(b_j)$
so that
$(b_j)$
so that
![]() $b_ib_j=\sum _k c_{ijk} b_k$
. Then substituting for f all basis elements of
$b_ib_j=\sum _k c_{ijk} b_k$
. Then substituting for f all basis elements of
![]() $\overline {R}$
over
$\overline {R}$
over
![]() ${\mathcal O}$
gives
${\mathcal O}$
gives
Let C be the matrix
![]() $ (c_{ij16})_{i,j=1,\ldots ,16}$
. Then the row vector
$ (c_{ij16})_{i,j=1,\ldots ,16}$
. Then the row vector
![]() $(\mu _i)$
is given as the product
$(\mu _i)$
is given as the product
![]() $e_6C^{-1}$
for
$e_6C^{-1}$
for
![]() $e_6$
the
$e_6$
the
![]() $6$
-th standard basis vector of the column vector space
$6$
-th standard basis vector of the column vector space
![]() ${\mathcal O}^{16}$
. To obtain C, consider the following commutative diagram
${\mathcal O}^{16}$
. To obtain C, consider the following commutative diagram

Applying Nakayama’s lemma to the right column, we see that the basis in Lemma 5.19 is an
![]() ${\mathcal O}$
-basis of
${\mathcal O}$
-basis of
![]() $\overline {R}$
, and thus an E-basis of
$\overline {R}$
, and thus an E-basis of
![]() $\overline {R}[\frac 1\varpi ] $
. The analogous diagram holds for
$\overline {R}[\frac 1\varpi ] $
. The analogous diagram holds for
![]() $\overline {R}^{\operatorname {\varphi -uni}}_v$
in place of
$\overline {R}^{\operatorname {\varphi -uni}}_v$
in place of
![]() $\overline {R}$
. Macaulay2 computations give us the following lemma:
$\overline {R}$
. Macaulay2 computations give us the following lemma:
Lemma 5.22.
-
1. The ring
is free over $$\begin{align*} R_1={\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/(b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X, s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4) \end{align*}$$
$$\begin{align*} R_1={\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]/(b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X, s_i^{\operatorname {\varphi -uni}}, i=1,\ldots ,4) \end{align*}$$
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $16$
with the same basis as that given in Lemma 5.19.1. The same holds if we replace
$16$
with the same basis as that given in Lemma 5.19.1. The same holds if we replace
 $s_4^{\operatorname {\varphi -uni}}$
by
$s_4^{\operatorname {\varphi -uni}}$
by
 $s_4^{\prime \,{\operatorname {\varphi -uni}}}$
.
$s_4^{\prime \,{\operatorname {\varphi -uni}}}$
.
-
2. The ring
 $R_2={\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}},,a,b,c,X,\alpha ,\beta ,\gamma ]/((b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X)+{\mathcal I}^{\operatorname {\varphi -uni}}_{\mathbf Z})$
is free over
$R_2={\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}},,a,b,c,X,\alpha ,\beta ,\gamma ]/((b-{\underline {s}}-c, \beta -{\underline {t}}-c, \gamma -X)+{\mathcal I}^{\operatorname {\varphi -uni}}_{\mathbf Z})$
is free over
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $6$
with the same basis as that given in Lemma 5.19.2.
$6$
with the same basis as that given in Lemma 5.19.2. -
3. The kernel of the surjective ring homomorphism
 $R_1\to R_2$
is free over
$R_1\to R_2$
is free over
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $10$
.
$10$
.
Thus, we can compute C as a matrix with entries in
![]() ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
, that is, before specialization. For this, we computed new basis elements
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
, that is, before specialization. For this, we computed new basis elements
![]() $b_7,\ldots ,b_{16}$
that span
$b_7,\ldots ,b_{16}$
that span
![]() $\operatorname {\mathrm {ker}} (R_1\to R_2)$
. To our surprise, we found
$\operatorname {\mathrm {ker}} (R_1\to R_2)$
. To our surprise, we found
![]() $\det C=1$
, and inverting C posed no problem. This allowed us to compute the tuples of
$\det C=1$
, and inverting C posed no problem. This allowed us to compute the tuples of
![]() $\mu _i$
and then the
$\mu _i$
and then the
![]() $\overline {R}$
-generator
$\overline {R}$
-generator
![]() $\Theta ^{-1}(b_6^*)$
of
$\Theta ^{-1}(b_6^*)$
of
![]() $\overline {R}[\overline {I}]$
. Under our augmentation, Macaulay2 evaluated it to
$\overline {R}[\overline {I}]$
. Under our augmentation, Macaulay2 evaluated it to
![]() $({\underline {s}}-{\underline {t}}) {\underline {t}}$
in
$({\underline {s}}-{\underline {t}}) {\underline {t}}$
in
![]() ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
. This shows:
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
. This shows:
Corollary 5.23. We have
 $$\begin{align*}\overline\lambda( \overline{R}[\overline{I}])= \left\{ \begin{array}{cc}((s-t)t) \subset {\mathcal O},&\text{if we work with }s_4^{\operatorname{\varphi-uni}}\text{, and}\\ (st) \subset {\mathcal O},&\text{if we work with }s_4^{\prime\,{\operatorname{\varphi-uni}}}. \end{array} \right.\end{align*}$$
$$\begin{align*}\overline\lambda( \overline{R}[\overline{I}])= \left\{ \begin{array}{cc}((s-t)t) \subset {\mathcal O},&\text{if we work with }s_4^{\operatorname{\varphi-uni}}\text{, and}\\ (st) \subset {\mathcal O},&\text{if we work with }s_4^{\prime\,{\operatorname{\varphi-uni}}}. \end{array} \right.\end{align*}$$
The next steps are the computation of
![]() $\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )$
and of
$\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )$
and of
![]() $\operatorname {\mathrm {Hom}}_{R_v^{\operatorname {\varphi -uni}}}(I/I^2,E/{\mathcal O})$
. For this, we proceed essentially as in the Steinberg case, cf. Corollaries 5.11 and 5.13, except that we rely on Macaulay2. Namely, we compute the first two steps of a resolution of
$\operatorname {\mathrm {Hom}}_{R_v^{\operatorname {\varphi -uni}}}(I/I^2,E/{\mathcal O})$
. For this, we proceed essentially as in the Steinberg case, cf. Corollaries 5.11 and 5.13, except that we rely on Macaulay2. Namely, we compute the first two steps of a resolution of
![]() ${\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}}$
, considered as an ideal of
${\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}}$
, considered as an ideal of
![]() ${\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}]={\mathbf Z}[ {\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]$
. This results in a right exact sequence
${\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}]={\mathbf Z}[ {\underline {q}},{\underline {s}},{\underline {t}},a,b,c,X,\alpha ,\beta ,\gamma ]$
. This results in a right exact sequence
for some matrix A in
![]() $M_{9\times 26}({\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}])$
(with rather simple entries). We tensor the sequence over
$M_{9\times 26}({\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}])$
(with rather simple entries). We tensor the sequence over
![]() ${\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]$
with
${\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]$
with
![]() $R_3={\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]/\widetilde {\mathcal I}$
, where
$R_3={\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]/\widetilde {\mathcal I}$
, where
![]() $\widetilde {\mathcal I}$
(as well as
$\widetilde {\mathcal I}$
(as well as
![]() $\widetilde {\mathcal I}'$
) is defined in Equation (5.4). Now, observe that over
$\widetilde {\mathcal I}'$
) is defined in Equation (5.4). Now, observe that over
![]() $R_3$
, the ideal
$R_3$
, the ideal
![]() $I_3={\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}} \otimes _{{\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]} R_3$
is generated by the elements
$I_3={\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}} \otimes _{{\mathcal R}_{\mathbf Z}[{\underline {q}},{\underline {s}}]} R_3$
is generated by the elements
![]() $r_1^{\operatorname {\varphi -uni}},r_2^{\operatorname {\varphi -uni}},r_3^{\operatorname {\varphi -uni}},r_6^{\operatorname {\varphi -uni}},r_7^{\operatorname {\varphi -uni}}$
; because these five elements together with our generators of
$r_1^{\operatorname {\varphi -uni}},r_2^{\operatorname {\varphi -uni}},r_3^{\operatorname {\varphi -uni}},r_6^{\operatorname {\varphi -uni}},r_7^{\operatorname {\varphi -uni}}$
; because these five elements together with our generators of
![]() $\widetilde {\mathcal I}$
generate
$\widetilde {\mathcal I}$
generate
![]() ${\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}}$
. So we extract a matrix
${\mathcal I}_{\mathbf Z}^{\operatorname {\varphi -uni}}$
. So we extract a matrix
![]() $A'\in M_{5\times 26}(R_3)$
, from the specialization of A under
$A'\in M_{5\times 26}(R_3)$
, from the specialization of A under
![]() ${\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}]\to R_3$
, that gives a short exact sequence
${\mathcal R}_{\mathbf Z}[{\underline {s}},{\underline {t}}]\to R_3$
, that gives a short exact sequence
Specializing under
![]() $R_3\to {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
via
$R_3\to {\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
via
![]() $a,c,\alpha ,\gamma ,X\mapsto 0$
,
$a,c,\alpha ,\gamma ,X\mapsto 0$
,
![]() $b\mapsto {\underline {s}}$
,
$b\mapsto {\underline {s}}$
,
![]() $\beta \mapsto {\underline {t}}$
, and computing the ideal of the resulting
$\beta \mapsto {\underline {t}}$
, and computing the ideal of the resulting
![]() $5\times 5$
-minors gives the ideal
$5\times 5$
-minors gives the ideal
![]() $({\underline {s}},{\underline {t}},{\underline {q}})^3\cdot ( {\underline {s}}-{\underline {t}}) {\underline {t}} $
. If we work with
$({\underline {s}},{\underline {t}},{\underline {q}})^3\cdot ( {\underline {s}}-{\underline {t}}) {\underline {t}} $
. If we work with
![]() $\widetilde {\mathcal I}'$
in place of
$\widetilde {\mathcal I}'$
in place of
![]() $\widetilde {\mathcal I}$
, the answer is
$\widetilde {\mathcal I}$
, the answer is
![]() $ ({\underline {s}},{\underline {t}},{\underline {q}})^3\cdot {\underline {s}}{\underline {t}} $
. Continuing with the natural map
$ ({\underline {s}},{\underline {t}},{\underline {q}})^3\cdot {\underline {s}}{\underline {t}} $
. Continuing with the natural map
![]() ${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]\to {\mathcal O}$
, and observing the computations in Corollaries 5.11 and 5.13, we find:
${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]\to {\mathcal O}$
, and observing the computations in Corollaries 5.11 and 5.13, we find:
Corollary 5.24. We have
 $$\begin{align*}&\#{\mathcal O}/\widetilde{\lambda}( \operatorname{\mathrm{Fitt}}_0^{\widetilde{R}}(I) )\\ & \quad = \# \operatorname{\mathrm{Hom}}_{R_v^{\operatorname{\varphi-uni}}}(I/I^2,E/{\mathcal O})=\left\{ \begin{array}{cc} \#{\mathcal O}/((s-t) t (s,t,q-1)^3),&\text{if we work with }\widetilde{\mathcal I}\text{, and}\\ \#{\mathcal O}/(st (s,t,q-1)^3),&\text{if we work with }\widetilde{\mathcal I}'. \end{array} \right.\end{align*}$$
$$\begin{align*}&\#{\mathcal O}/\widetilde{\lambda}( \operatorname{\mathrm{Fitt}}_0^{\widetilde{R}}(I) )\\ & \quad = \# \operatorname{\mathrm{Hom}}_{R_v^{\operatorname{\varphi-uni}}}(I/I^2,E/{\mathcal O})=\left\{ \begin{array}{cc} \#{\mathcal O}/((s-t) t (s,t,q-1)^3),&\text{if we work with }\widetilde{\mathcal I}\text{, and}\\ \#{\mathcal O}/(st (s,t,q-1)^3),&\text{if we work with }\widetilde{\mathcal I}'. \end{array} \right.\end{align*}$$
Finally, we had Macaulay2 work out the analog of Lemma 5.16 to determine the lattice
![]() $\Lambda ^{\operatorname {\varphi -uni}}$
, which, as to be expected, is rather easy. Following the proof of Corollary 5.17, one finds.
$\Lambda ^{\operatorname {\varphi -uni}}$
, which, as to be expected, is rather easy. Following the proof of Corollary 5.17, one finds.
Corollary 5.25. We have
 $$ \begin{align*} &\#\operatorname{\mathrm{ker}}(\operatorname{\mathrm{Hom}}_{R_v^{\operatorname{\varphi-uni}}}(I/I^2,E/{\mathcal O}) \to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R_v^{\operatorname{\varphi-uni}},E/{\mathcal O}))=\# \Lambda^{{\operatorname{\varphi-uni}}}/\widetilde{\Lambda}\\& \quad= \left\{ \begin{array}{cc} \!\!\!\#(s,t,q-1)^3/((s-t)t),&\!\!\!\text{if we work with }\widetilde{\mathcal I},\\ \!\!\!\#(s,t,q-1)^3/(st),&\!\!\!\text{if we work with }\widetilde{\mathcal I}'. \end{array} \right. \end{align*} $$
$$ \begin{align*} &\#\operatorname{\mathrm{ker}}(\operatorname{\mathrm{Hom}}_{R_v^{\operatorname{\varphi-uni}}}(I/I^2,E/{\mathcal O}) \to \widehat{\operatorname{\mathrm{Der}}}^1_{\mathcal O}(R_v^{\operatorname{\varphi-uni}},E/{\mathcal O}))=\# \Lambda^{{\operatorname{\varphi-uni}}}/\widetilde{\Lambda}\\& \quad= \left\{ \begin{array}{cc} \!\!\!\#(s,t,q-1)^3/((s-t)t),&\!\!\!\text{if we work with }\widetilde{\mathcal I},\\ \!\!\!\#(s,t,q-1)^3/(st),&\!\!\!\text{if we work with }\widetilde{\mathcal I}'. \end{array} \right. \end{align*} $$
As in the Steinberg case, the following result is now an immediate consequence. It is independent of whether we use
![]() $\widetilde {\mathcal I}$
or
$\widetilde {\mathcal I}$
or
![]() $\widetilde {\mathcal I}'$
.
$\widetilde {\mathcal I}'$
.
Theorem 5.26. Let e be the ramification index of E over
![]() ${\mathbf Q}_l$
. Then we have
${\mathbf Q}_l$
. Then we have
-
1.
 $D_{1,\lambda }(R_v^{{\operatorname {\varphi -uni}}})=6\frac {n_v}e$
.
$D_{1,\lambda }(R_v^{{\operatorname {\varphi -uni}}})=6\frac {n_v}e$
. -
2.
 $c_{1,\lambda }(R_v^{{\operatorname {\varphi -uni}}})=3\frac {n_v}e$
.
$c_{1,\lambda }(R_v^{{\operatorname {\varphi -uni}}})=3\frac {n_v}e$
. -
3.
 $\delta _\lambda (R_v^{{\operatorname {\varphi -uni}}}) = 3\frac {n_v}e$
.
$\delta _\lambda (R_v^{{\operatorname {\varphi -uni}}}) = 3\frac {n_v}e$
.
5.4 Unipotent deformations
This case we handled in the same way as the previous one via the use of Macaulay2 code. For this, we found a model over
![]() ${\mathbf Z}$
of a complete intersection cover of the (model of the) Gorenstein ring that we are interested in. We only indicate outcomes of some intermediate steps but give no further details. The steps are completely parallel to those in Subsection 5.3. We define
${\mathbf Z}$
of a complete intersection cover of the (model of the) Gorenstein ring that we are interested in. We only indicate outcomes of some intermediate steps but give no further details. The steps are completely parallel to those in Subsection 5.3. We define
![]() $\widetilde {\mathcal I}=(s_1^{\mathrm {uni}},s_2^{\mathrm {uni}},s_3^{\mathrm {uni}},s_4^{\mathrm {uni}})$
, where
$\widetilde {\mathcal I}=(s_1^{\mathrm {uni}},s_2^{\mathrm {uni}},s_3^{\mathrm {uni}},s_4^{\mathrm {uni}})$
, where
Note that these elements of
![]() ${\mathcal I}^{\mathrm {uni}}$
have simple expressions modulo
${\mathcal I}^{\mathrm {uni}}$
have simple expressions modulo
![]() $\varpi , b-c,b-\beta ,X-\gamma $
, namely
$\varpi , b-c,b-\beta ,X-\gamma $
, namely
![]() $(s_1^{\mathrm {uni}},\ldots ,s_4^{\mathrm {uni}})\equiv (b^2,\alpha ^2,X^2+a\alpha ,X(1+a)+a^2)$
. We chose them as lifts of reductions that are well understood if, for instance, one follows the proof of Lemma 5.4. The challenge is to find lifts so that in particular the properties stated in Lemma 5.27 and 5.30 hold. Once suitable candidates for the lifts are guessed, we use Macaulay2 to verify these properties and to compute the quantities collected in Proposition 5.31.
$(s_1^{\mathrm {uni}},\ldots ,s_4^{\mathrm {uni}})\equiv (b^2,\alpha ^2,X^2+a\alpha ,X(1+a)+a^2)$
. We chose them as lifts of reductions that are well understood if, for instance, one follows the proof of Lemma 5.4. The challenge is to find lifts so that in particular the properties stated in Lemma 5.27 and 5.30 hold. Once suitable candidates for the lifts are guessed, we use Macaulay2 to verify these properties and to compute the quantities collected in Proposition 5.31.
Lemma 5.27.
-
1. The ring
is free over $$ \begin{align*}{\mathbf Z}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/({\underline{q}},{\underline{s}},{\underline{t}}, b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c , s_i^{\mathrm{uni}}, i=1,\ldots,4)\end{align*} $$
$$ \begin{align*}{\mathbf Z}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/({\underline{q}},{\underline{s}},{\underline{t}}, b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c , s_i^{\mathrm{uni}}, i=1,\ldots,4)\end{align*} $$
 ${\mathbf Z}$
of rank
${\mathbf Z}$
of rank
 $16$
. A basis is
$16$
. A basis is
 $1, a, ab, abX, abX\alpha , ab\alpha , aX, aX\alpha , a\alpha , b, bX, bX\alpha , b\alpha , X, X\alpha , \alpha $
. A basis of its socle over
$1, a, ab, abX, abX\alpha , ab\alpha , aX, aX\alpha , a\alpha , b, bX, bX\alpha , b\alpha , X, X\alpha , \alpha $
. A basis of its socle over
 ${\mathbf Z}$
is
${\mathbf Z}$
is
 $abX\alpha $
.
$abX\alpha $
.
-
2. The ring
is free over $$ \begin{align*}{\mathbf Z}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/(({\underline{q}},{\underline{s}},{\underline{t}}, b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c )+{\mathcal I}^{\mathrm{uni}}_{\mathbf Z})\end{align*} $$
$$ \begin{align*}{\mathbf Z}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/(({\underline{q}},{\underline{s}},{\underline{t}}, b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c )+{\mathcal I}^{\mathrm{uni}}_{\mathbf Z})\end{align*} $$
 ${\mathbf Z}$
of rank
${\mathbf Z}$
of rank
 $6$
. A basis is
$6$
. A basis is
 $1,a,b,b\alpha ,X,\alpha $
. A basis of its socle over
$1,a,b,b\alpha ,X,\alpha $
. A basis of its socle over
 ${\mathbf Z}$
is
${\mathbf Z}$
is
 $b\alpha $
.
$b\alpha $
.
-
3. Write
 $x_1,\ldots ,x_7$
for
$x_1,\ldots ,x_7$
for
 $a,b,c,X,\alpha ,\beta ,\gamma $
. Then the ideal in
$a,b,c,X,\alpha ,\beta ,\gamma $
. Then the ideal in
 ${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
generated by the
${\mathbf Z}[{\underline {q}},{\underline {s}},{\underline {t}}]$
generated by the
 $4\times 4$
-minors of the Jacobian
$4\times 4$
-minors of the Jacobian
 $(\partial s_i^{\mathrm {uni}}/\partial x_j)_{i=1,\ldots ,4; j=1,\ldots ,7}$
evaluated at
$(\partial s_i^{\mathrm {uni}}/\partial x_j)_{i=1,\ldots ,4; j=1,\ldots ,7}$
evaluated at
 $(x_1,\ldots ,x_7)=(0,{\underline {s}},0,0,0,{\underline {t}},0)$
is
$(x_1,\ldots ,x_7)=(0,{\underline {s}},0,0,0,{\underline {t}},0)$
is
 ${\underline {q}}^2({\underline {s}}-{\underline {t}}){\underline {t}}({\underline {q}},{\underline {s}}, {\underline {t}})$
.
${\underline {q}}^2({\underline {s}}-{\underline {t}}){\underline {t}}({\underline {q}},{\underline {s}}, {\underline {t}})$
.
Remark 5.28. As the observant reader will have noted, the evaluation in Lemma 5.27.3 may lead to zero if
![]() $s=t$
under our standard hypothesis
$s=t$
under our standard hypothesis
![]() $t\neq 0$
. We will explain in Remark 5.32 on how to modify
$t\neq 0$
. We will explain in Remark 5.32 on how to modify
![]() $\widetilde {\mathcal I}$
(by changing
$\widetilde {\mathcal I}$
(by changing
![]() $s_3^{\mathrm {uni}}$
) so that our computations are also valid in the case
$s_3^{\mathrm {uni}}$
) so that our computations are also valid in the case
![]() $s=t$
.
$s=t$
.
Let
![]() $s,t\in {\mathfrak m}$
with
$s,t\in {\mathfrak m}$
with
![]() $t\neq 0$
and
$t\neq 0$
and
![]() $s\neq t$
.
$s\neq t$
.
Corollary 5.29.
-
1. The ring
 $\widetilde {R}={\mathcal O}[[a,b,c,X,\alpha ,\beta ,\gamma ]]/(s_i^{\mathrm {uni}}, i=1,\ldots ,4)$
is a complete intersection, flat over
$\widetilde {R}={\mathcal O}[[a,b,c,X,\alpha ,\beta ,\gamma ]]/(s_i^{\mathrm {uni}}, i=1,\ldots ,4)$
is a complete intersection, flat over
 ${\mathcal O}$
and of relative dimension
${\mathcal O}$
and of relative dimension
 $3$
. One has a natural surjection
$3$
. One has a natural surjection
 $\widetilde {R}\to R^{\mathrm {uni}}_v$
induced from
$\widetilde {R}\to R^{\mathrm {uni}}_v$
induced from
 $(s_i^{\mathrm {uni}}, i=1,\ldots ,4)\subset (r_j^{\mathrm {uni}},j=1,\ldots ,9)$
.
$(s_i^{\mathrm {uni}}, i=1,\ldots ,4)\subset (r_j^{\mathrm {uni}},j=1,\ldots ,9)$
. -
2. Via the ring map
 $S={\mathcal O}[[y_1,y_2,y_3]]\to \widetilde {R}$
given by
$S={\mathcal O}[[y_1,y_2,y_3]]\to \widetilde {R}$
given by
 $y_1\mapsto b-{\underline {s}}-\beta +{\underline {t}}$
,
$y_1\mapsto b-{\underline {s}}-\beta +{\underline {t}}$
,
 $y_2\mapsto X-\gamma $
,
$y_2\mapsto X-\gamma $
,
 $y_3\mapsto b-{\underline {s}}-c$
, the rings
$y_3\mapsto b-{\underline {s}}-c$
, the rings
 $\widetilde {R}$
and
$\widetilde {R}$
and
 $R^{\mathrm {uni}}_v$
are free S-modules of rank
$R^{\mathrm {uni}}_v$
are free S-modules of rank
 $16$
and
$16$
and
 $6$
, respectively.
$6$
, respectively. -
3. The augmentation
 $\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by
$\widetilde {\lambda }\colon \widetilde {R}\to {\mathcal O}$
given by
 $a,c,X,\alpha ,\gamma \mapsto 0$
,
$a,c,X,\alpha ,\gamma \mapsto 0$
,
 $b\mapsto s$
and
$b\mapsto s$
and
 $\beta \mapsto t$
defines a formally smooth point of
$\beta \mapsto t$
defines a formally smooth point of
 $\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
.
$\operatorname {\mathrm {Spec}} \widetilde {R}[\frac 1\varpi ]$
.
A further Macaulay2 shows the following:
Lemma 5.30.
-
1. The ring
is free over $$\begin{align*}R_1={\mathbf Q}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/(b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c , s_i^{\mathrm{uni}}, i=1,\ldots,4)\end{align*}$$
$$\begin{align*}R_1={\mathbf Q}[{\underline{q}},{\underline{s}},{\underline{t}},a,b,c,X,\alpha,\beta,\gamma]/(b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c , s_i^{\mathrm{uni}}, i=1,\ldots,4)\end{align*}$$
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $16$
with the same basis as that given in Lemma 5.27.1.
$16$
with the same basis as that given in Lemma 5.27.1.
-
2. The ring
is free over $$\begin{align*}R_2={\mathbf Q}[{\underline{q}},{\underline{s}},{\underline{t}},,a,b,c,X,\alpha,\beta,\gamma]/((b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c )+{\mathcal I}^{\mathrm{uni}}_{\mathbf Z})\end{align*}$$
$$\begin{align*}R_2={\mathbf Q}[{\underline{q}},{\underline{s}},{\underline{t}},,a,b,c,X,\alpha,\beta,\gamma]/((b-{\underline{s}}-\beta+{\underline{t}},X-\gamma,b-{\underline{s}}-c )+{\mathcal I}^{\mathrm{uni}}_{\mathbf Z})\end{align*}$$
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $6$
with the same basis as that given in Lemma 5.27.2.
$6$
with the same basis as that given in Lemma 5.27.2.
-
3. The kernel of the surjective ring homomorphism
 $R_1\to R_2$
is free over
$R_1\to R_2$
is free over
 ${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
${\mathbf Q}[{\underline {q}},{\underline {s}},{\underline {t}}]$
of rank
 $10$
.
$10$
.
Computations as for Corollaries 5.23, 5.24 and 5.25 give the following result:
Proposition 5.31. We have
-
1.
 $\widetilde {\lambda }( \widetilde {R}[\widetilde {I}])= (s-t)(q-1)^2$
.
$\widetilde {\lambda }( \widetilde {R}[\widetilde {I}])= (s-t)(q-1)^2$
. -
2.
 $\#{\mathcal O}/\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )= \# \operatorname {\mathrm {Hom}}_{R_v^{\mathrm {un}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/((q-1)^2(s-t)\gcd (s,t,q-1))$
.
$\#{\mathcal O}/\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )= \# \operatorname {\mathrm {Hom}}_{R_v^{\mathrm {un}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/((q-1)^2(s-t)\gcd (s,t,q-1))$
. -
3.
 $\#\operatorname {\mathrm {ker}}(\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {uni}}}(I/I^2,E/{\mathcal O}) \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R_v^{\mathrm {uni}},E/{\mathcal O}))=\# \Lambda ^{{\mathrm {uni}}}/\widetilde {\Lambda }=\#(\gcd (s,t,q-1) /(s-t)(q-1)^2)$
.
$\#\operatorname {\mathrm {ker}}(\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {uni}}}(I/I^2,E/{\mathcal O}) \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R_v^{\mathrm {uni}},E/{\mathcal O}))=\# \Lambda ^{{\mathrm {uni}}}/\widetilde {\Lambda }=\#(\gcd (s,t,q-1) /(s-t)(q-1)^2)$
.
Remark 5.32. In the case
![]() $s=t$
(but
$s=t$
(but
![]() $t\neq 0$
), one can replace
$t\neq 0$
), one can replace
![]() $s_3^{\mathrm {uni}}$
by
$s_3^{\mathrm {uni}}$
by
![]() $s_3^{\mathrm {uni}} +r_2^{\mathrm {uni}}$
and work with the modified ideal
$s_3^{\mathrm {uni}} +r_2^{\mathrm {uni}}$
and work with the modified ideal
![]() $\widetilde {\mathcal I}$
. Then the results in Subsection 5.4 hold with the following modifications (where in all calculations we used
$\widetilde {\mathcal I}$
. Then the results in Subsection 5.4 hold with the following modifications (where in all calculations we used
![]() $s=t$
and the modified
$s=t$
and the modified
![]() $\widetilde {\mathcal I}$
):
$\widetilde {\mathcal I}$
):
-
1. In Lemma 5.27, in part 1, the basis is
 $1,a,ab,ab\alpha ,aX,aX^2,aX^2\alpha , aX\alpha , a\alpha , b,b\alpha ,X,X^2, X^2\alpha ,X\alpha ,\alpha $
and the socle is
$1,a,ab,ab\alpha ,aX,aX^2,aX^2\alpha , aX\alpha , a\alpha , b,b\alpha ,X,X^2, X^2\alpha ,X\alpha ,\alpha $
and the socle is
 $aX^2\alpha $
, and in part 3, the evaluation gives the value
$aX^2\alpha $
, and in part 3, the evaluation gives the value
 $(q-1)t^2\gcd (q-1,t)$
.
$(q-1)t^2\gcd (q-1,t)$
. -
2. In Proposition 5.31, one has
-
(a)
 $\widetilde {\lambda }( \widetilde {R}[\widetilde {I}])= (t(q-1))$
.
$\widetilde {\lambda }( \widetilde {R}[\widetilde {I}])= (t(q-1))$
. -
(b)
 $\#{\mathcal O}/\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )= \# \operatorname {\mathrm {Hom}}_{R_v^{\mathrm {un}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/((q-1)t \gcd (t,q-1))$
.
$\#{\mathcal O}/\widetilde {\lambda }( \operatorname {\mathrm {Fitt}}_0^{\widetilde {R}}(I) )= \# \operatorname {\mathrm {Hom}}_{R_v^{\mathrm {un}}}(I/I^2,E/{\mathcal O})=\#{\mathcal O}/((q-1)t \gcd (t,q-1))$
. -
(c)
 $\#\operatorname {\mathrm {ker}}(\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {uni}}}(I/I^2,E/{\mathcal O}) \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R_v^{\mathrm {uni}},E/{\mathcal O}))=\# \Lambda ^{{\mathrm {uni}}}/\widetilde {\Lambda }=\#(\gcd (t,q-1) /(t(q-1))$
.
$\#\operatorname {\mathrm {ker}}(\operatorname {\mathrm {Hom}}_{R_v^{\mathrm {uni}}}(I/I^2,E/{\mathcal O}) \to \widehat {\operatorname {\mathrm {Der}}}^1_{\mathcal O}(R_v^{\mathrm {uni}},E/{\mathcal O}))=\# \Lambda ^{{\mathrm {uni}}}/\widetilde {\Lambda }=\#(\gcd (t,q-1) /(t(q-1))$
.
-
Theorem 5.33. Let e be the ramification index of E over
![]() ${\mathbf Q}_l$
, and let
${\mathbf Q}_l$
, and let
![]() $t\in {\mathfrak m}\setminus \{0\}$
. Then we have
$t\in {\mathfrak m}\setminus \{0\}$
. Then we have
-
1.
 $D_{1,\lambda }(R_v^{^{\mathrm {uni}}})=2\frac {n_v}e$
.
$D_{1,\lambda }(R_v^{^{\mathrm {uni}}})=2\frac {n_v}e$
. -
2.
 $c_{1,\lambda }(R_v^{^{\mathrm {uni}}})=\frac {n_v}e$
.
$c_{1,\lambda }(R_v^{^{\mathrm {uni}}})=\frac {n_v}e$
. -
3.
 $\delta _\lambda (R_v^{^{\mathrm {uni}}}) = \frac {n_v}e$
.
$\delta _\lambda (R_v^{^{\mathrm {uni}}}) = \frac {n_v}e$
.
5.5 Recollections about Cohen–Macaulay and Gorenstein rings
Let R be a Noetherian local ring with maximal ideal
![]() ${\mathfrak m}$
and residue field k. In this subsection, we want to briefly recall some results on Cohen–Macaulay and Gorenstein rings that occur repeatedly in our arguments or, more importantly, in our computations. We also present a result on generating sets of dual modules that was useful in our computations. For basic notions such as
${\mathfrak m}$
and residue field k. In this subsection, we want to briefly recall some results on Cohen–Macaulay and Gorenstein rings that occur repeatedly in our arguments or, more importantly, in our computations. We also present a result on generating sets of dual modules that was useful in our computations. For basic notions such as
![]() $\operatorname {\mathrm {depth}}$
, R-sequence, Cohen–Macaulay and Gorenstein rings, we refer to [Reference Bruns and HerzogBH93, §§ 1.2, 2.1, 3.1],
$\operatorname {\mathrm {depth}}$
, R-sequence, Cohen–Macaulay and Gorenstein rings, we refer to [Reference Bruns and HerzogBH93, §§ 1.2, 2.1, 3.1],
Definition 5.34. The socle of R is defined as
![]() $\operatorname {{{\mathrm {socle}}}} R=R[{\mathfrak m}]=\{x\in R\mid {\mathfrak m} x =0\}$
.
$\operatorname {{{\mathrm {socle}}}} R=R[{\mathfrak m}]=\{x\in R\mid {\mathfrak m} x =0\}$
.
Proposition 5.35 [Reference MatsumuraMat80, Thm. 17.4 and p. 136], [Reference Bruns and HerzogBH93, 2.1.3, 2.1.8, 3.1.19].
-
1. Any local Artin ring R is Cohen–Macaulay. It is Gorenstein if in addition it satisfies
 $\operatorname {{{\mathrm {socle}}}} R\cong k$
.
$\operatorname {{{\mathrm {socle}}}} R\cong k$
. -
2. If R is Noetherian local, and if
 $(x_1\ldots ,x_n)$
is an R-sequence in
$(x_1\ldots ,x_n)$
is an R-sequence in
 ${\mathfrak m}$
, then R is Cohen–Macaulay or Gorenstein, respectively, if and only if
${\mathfrak m}$
, then R is Cohen–Macaulay or Gorenstein, respectively, if and only if
 $R/(x_1,\ldots ,x_n)$
has this property. In particular, if
$R/(x_1,\ldots ,x_n)$
has this property. In particular, if
 $R/(x_1\ldots ,x_n)$
is Artinian, then R is Cohen–Macaulay, and if moreover
$R/(x_1\ldots ,x_n)$
is Artinian, then R is Cohen–Macaulay, and if moreover
 $\operatorname {{{\mathrm {socle}}}} R/(x_1\ldots ,x_n)\cong k$
, then R is Gorenstein.
$\operatorname {{{\mathrm {socle}}}} R/(x_1\ldots ,x_n)\cong k$
, then R is Gorenstein. -
3. If R is a local Cohen–Macaulay ring, then any system of parameters is a regular R-sequence.
Let now
![]() $(A,{\mathfrak m})$
be a local Artin ring. In this case,
$(A,{\mathfrak m})$
be a local Artin ring. In this case,
![]() $I\cap \operatorname {{{\mathrm {socle}}}} A\supsetneq 0$
for any nonzero ideal I of A: To see this, consider
$I\cap \operatorname {{{\mathrm {socle}}}} A\supsetneq 0$
for any nonzero ideal I of A: To see this, consider
![]() $n\in {\mathbf Z}_{\ge 0}$
such that
$n\in {\mathbf Z}_{\ge 0}$
such that
![]() ${\mathfrak m}^{n-1}I\neq 0$
and
${\mathfrak m}^{n-1}I\neq 0$
and
![]() ${\mathfrak m}^nI=0$
. Then
${\mathfrak m}^nI=0$
. Then
![]() ${\mathfrak m}^{n -1}I\subset I\cap \operatorname {{{\mathrm {socle}}}} A$
.
${\mathfrak m}^{n -1}I\subset I\cap \operatorname {{{\mathrm {socle}}}} A$
.
Lemma 5.36. Let
![]() $(\bar \psi _i)_{i\in B}$
be a finite tuple in
$(\bar \psi _i)_{i\in B}$
be a finite tuple in
![]() $\operatorname {\mathrm {Hom}}_k(A,k)$
such that
$\operatorname {\mathrm {Hom}}_k(A,k)$
such that
![]() $(\bar \psi _i)_{i\in B}\colon \operatorname {{{\mathrm {socle}}}}(A)\to k^{B}$
is injective. Then
$(\bar \psi _i)_{i\in B}\colon \operatorname {{{\mathrm {socle}}}}(A)\to k^{B}$
is injective. Then
![]() $(\bar \psi _i)_{i\in B}$
is a set of generators of
$(\bar \psi _i)_{i\in B}$
is a set of generators of
![]() $\operatorname {\mathrm {Hom}}_k(A,k)$
as an A-module. In particular, if A is Gorenstein and if
$\operatorname {\mathrm {Hom}}_k(A,k)$
as an A-module. In particular, if A is Gorenstein and if
![]() $B=\{0\}$
is a singleton, then
$B=\{0\}$
is a singleton, then
![]() $\bar \psi _0$
is an A-basis of
$\bar \psi _0$
is an A-basis of
![]() $\operatorname {\mathrm {Hom}}_k(A,k)$
.
$\operatorname {\mathrm {Hom}}_k(A,k)$
.
The proof relies on the following result from linear algebra.
Lemma 5.37. Let V be a finite-dimensional k-vector space. Let
![]() $(V_j)_{j\in J}$
be a finite tuple of sub vector spaces such that
$(V_j)_{j\in J}$
be a finite tuple of sub vector spaces such that
![]() $\bigcap _{j\in J} V_j=0$
. Then for any
$\bigcap _{j\in J} V_j=0$
. Then for any
![]() $\bar \psi \in \operatorname {\mathrm {Hom}}_k(V,k)$
, there exist
$\bar \psi \in \operatorname {\mathrm {Hom}}_k(V,k)$
, there exist
![]() $\bar \psi _j\in \operatorname {\mathrm {Hom}}_k(V,k)$
with
$\bar \psi _j\in \operatorname {\mathrm {Hom}}_k(V,k)$
with
![]() $V_j\subset \operatorname {\mathrm {ker}} \bar \psi _j$
for
$V_j\subset \operatorname {\mathrm {ker}} \bar \psi _j$
for
![]() $j\in J$
such that
$j\in J$
such that
![]() $\bar \psi =\sum _{j\in J} \bar \psi _j$
.
$\bar \psi =\sum _{j\in J} \bar \psi _j$
.
Proof. We may assume
![]() $J=\{1,\ldots ,t\}$
for some
$J=\{1,\ldots ,t\}$
for some
![]() $t\in {\mathbf Z}_{\ge 1}$
. We induct over t, noting that the case
$t\in {\mathbf Z}_{\ge 1}$
. We induct over t, noting that the case
![]() $t=1$
is trivial, since then
$t=1$
is trivial, since then
![]() $V_1=0$
. For the induction step suppose
$V_1=0$
. For the induction step suppose
![]() $t\ge 2$
, and let
$t\ge 2$
, and let
![]() $W=\bigcap _{j=2}^t V_j$
. Then
$W=\bigcap _{j=2}^t V_j$
. Then
![]() $V_1\cap W=0$
, and so we can choose a basis for W and one for
$V_1\cap W=0$
, and so we can choose a basis for W and one for
![]() $V_1$
and then extend the one for
$V_1$
and then extend the one for
![]() $V_1$
to a complementary basis to that of W. Then one can find
$V_1$
to a complementary basis to that of W. Then one can find
![]() $\bar \psi _1$
and
$\bar \psi _1$
and
![]() $\bar \phi $
in
$\bar \phi $
in
![]() $\operatorname {\mathrm {Hom}}_k(V,k)$
such that
$\operatorname {\mathrm {Hom}}_k(V,k)$
such that
![]() $\operatorname {\mathrm {ker}} \bar \psi _1\supseteq V_1$
and
$\operatorname {\mathrm {ker}} \bar \psi _1\supseteq V_1$
and
![]() $\operatorname {\mathrm {ker}}\bar \phi \supseteq W$
, and
$\operatorname {\mathrm {ker}}\bar \phi \supseteq W$
, and
![]() $\bar \psi =\bar \psi _1+\bar \phi $
. Now, apply the induction hypothesis to
$\bar \psi =\bar \psi _1+\bar \phi $
. Now, apply the induction hypothesis to
![]() $V/V_1$
and
$V/V_1$
and
![]() $(V_j/V_1)_{j=2,\ldots ,t}$
and
$(V_j/V_1)_{j=2,\ldots ,t}$
and
![]() $\bar \psi _1$
considered as a map in
$\bar \psi _1$
considered as a map in
![]() $\operatorname {\mathrm {Hom}}_k(V/V_1,k)$
.
$\operatorname {\mathrm {Hom}}_k(V/V_1,k)$
.
Proof of Lemma 5.36.
Let
![]() $N=\sum _{i\in B} A\bar \psi _i$
. We shall show that
$N=\sum _{i\in B} A\bar \psi _i$
. We shall show that
![]() $\operatorname {\mathrm {Hom}}_k(A,k)\subseteq N+{\mathfrak m} \operatorname {\mathrm {Hom}}_k(A,k)$
. Then the lemma will follow from Nakayama’s lemma.
$\operatorname {\mathrm {Hom}}_k(A,k)\subseteq N+{\mathfrak m} \operatorname {\mathrm {Hom}}_k(A,k)$
. Then the lemma will follow from Nakayama’s lemma.
Let
![]() $\bar \psi $
be in
$\bar \psi $
be in
![]() $\operatorname {\mathrm {Hom}}_k(A,k)$
. By our hypothesis, there is a k-linear map
$\operatorname {\mathrm {Hom}}_k(A,k)$
. By our hypothesis, there is a k-linear map
![]() $\alpha \colon k^{B}\to k$
such that the restriction
$\alpha \colon k^{B}\to k$
such that the restriction
![]() $\bar \psi |_{\operatorname {{{\mathrm {socle}}}} A}$
agree with
$\bar \psi |_{\operatorname {{{\mathrm {socle}}}} A}$
agree with
![]() $\alpha \circ (\bar \psi _i)_{i\in B}$
. In other words, the map
$\alpha \circ (\bar \psi _i)_{i\in B}$
. In other words, the map
vanishes on
![]() $\operatorname {{{\mathrm {socle}}}} A$
.
$\operatorname {{{\mathrm {socle}}}} A$
.
Next, let
![]() $x_1,\ldots ,x_t$
be a set of A-module generators of
$x_1,\ldots ,x_t$
be a set of A-module generators of
![]() ${\mathfrak m}$
, and let
${\mathfrak m}$
, and let
![]() $V_i=\{r\in A\mid x_ir=0\}$
. Then
$V_i=\{r\in A\mid x_ir=0\}$
. Then
By Lemma 5.37 applied to
![]() $A/\operatorname {{{\mathrm {socle}}}} A$
, there exist
$A/\operatorname {{{\mathrm {socle}}}} A$
, there exist
![]() $\bar \phi _i\in \operatorname {\mathrm {Hom}}_k(A,k)$
with
$\bar \phi _i\in \operatorname {\mathrm {Hom}}_k(A,k)$
with
![]() $\operatorname {\mathrm {ker}}\bar \phi _i\supset V_i$
, and
$\operatorname {\mathrm {ker}}\bar \phi _i\supset V_i$
, and
![]() $\bar \phi =\sum _{i\in B}\bar \phi _i$
.
$\bar \phi =\sum _{i\in B}\bar \phi _i$
.
Now, consider the short exact sequence
![]() $0\to V_i \to A \stackrel {x_i\cdot }\to x_iA \to 0$
. Then the
$0\to V_i \to A \stackrel {x_i\cdot }\to x_iA \to 0$
. Then the
![]() $\bar \psi _i$
induce k-linear maps
$\bar \psi _i$
induce k-linear maps
![]() $x_i A\to k$
. The latter can be extended to k-linear maps
$x_i A\to k$
. The latter can be extended to k-linear maps
![]() $\bar \xi _i\colon A\to k$
under
$\bar \xi _i\colon A\to k$
under
![]() $x_iA\subset A$
. In other words
$x_iA\subset A$
. In other words
![]() $\bar \phi _i=x_i \bar \xi _i$
, and this gives
$\bar \phi _i=x_i \bar \xi _i$
, and this gives
proving the claim from the first line and hence the lemma.
Let now
![]() $(R,{\mathfrak m})$
be a local complete Noetherian Cohen–Macaulay ring that is an
$(R,{\mathfrak m})$
be a local complete Noetherian Cohen–Macaulay ring that is an
![]() ${\mathcal O}$
-algebra, and suppose that
${\mathcal O}$
-algebra, and suppose that
![]() $\mathbf {r}=(\varpi , r_1,\ldots ,r_n)$
is a system of parameters. Let
$\mathbf {r}=(\varpi , r_1,\ldots ,r_n)$
is a system of parameters. Let
![]() $(\bar e_i)_{i\in B}$
be a k-basis of
$(\bar e_i)_{i\in B}$
be a k-basis of
![]() $A=R/\mathbf {r} R$
, let
$A=R/\mathbf {r} R$
, let
![]() $(e_i)_{i\in B}$
be a tuple of preimages in R, and consider the
$(e_i)_{i\in B}$
be a tuple of preimages in R, and consider the
![]() ${\mathcal O}$
-algebra homomorphism
${\mathcal O}$
-algebra homomorphism
![]() $S={\mathcal O}[[x_1,\ldots ,x_n]]\to R, x_i\mapsto e_i$
.
$S={\mathcal O}[[x_1,\ldots ,x_n]]\to R, x_i\mapsto e_i$
.
Lemma 5.38. As an S-module, R is free with basis
![]() $(e_i)_{i=1,\ldots ,n}$
.
$(e_i)_{i=1,\ldots ,n}$
.
Proof. The ring S is regular local and thus of finite global dimension. Hence, R has finite projective dimension over S. By Nakayama’s lemma R is also finitely generated as an S-module because
![]() $\dim _k R/\mathbf {r}R$
is finite for the system of parameters
$\dim _k R/\mathbf {r}R$
is finite for the system of parameters
![]() $\mathbf {r}$
. The sequence
$\mathbf {r}$
. The sequence
![]() $\mathbf {r}$
is in fact regular as R is Cohen–Macaulay. It follows that
$\mathbf {r}$
is in fact regular as R is Cohen–Macaulay. It follows that
![]() $\operatorname {\mathrm {depth}}_SR=1+n=\dim S$
, so that by the Auslander–Buchsbaum theorem R is a finite free S-module. One finds that
$\operatorname {\mathrm {depth}}_SR=1+n=\dim S$
, so that by the Auslander–Buchsbaum theorem R is a finite free S-module. One finds that
![]() $\psi \colon S^B\to R, (s_i)_{i\in B}\mapsto \sum _i s_i e_i$
is an isomorphism because S is local and
$\psi \colon S^B\to R, (s_i)_{i\in B}\mapsto \sum _i s_i e_i$
is an isomorphism because S is local and
![]() $\psi\ {\operatorname {mod}}\ {\mathbf {r}}$
is bijective.
$\psi\ {\operatorname {mod}}\ {\mathbf {r}}$
is bijective.
The following result gives a generating set (or a basis) over R of the free S-module
![]() $\operatorname {\mathrm {Hom}}_S(R,S)$
.
$\operatorname {\mathrm {Hom}}_S(R,S)$
.
Proposition 5.39. Let
![]() $\psi _i\in \operatorname {\mathrm {Hom}}_S(R,S)$
,
$\psi _i\in \operatorname {\mathrm {Hom}}_S(R,S)$
,
![]() $i\in B$
, be a tuple of elements such that the elements
$i\in B$
, be a tuple of elements such that the elements
![]() $\bar \psi _i:=\psi _i\otimes _RA\colon A\to k$
satisfy the condition of Lemma 5.36. Then
$\bar \psi _i:=\psi _i\otimes _RA\colon A\to k$
satisfy the condition of Lemma 5.36. Then
![]() $(\psi _i)_{i\in B}$
is a set of R-module generators of
$(\psi _i)_{i\in B}$
is a set of R-module generators of
![]() $\operatorname {\mathrm {Hom}}_S(R,S)$
. If moreover R is Gorenstein and
$\operatorname {\mathrm {Hom}}_S(R,S)$
. If moreover R is Gorenstein and
![]() $B=\{0\}$
is a singleton, then
$B=\{0\}$
is a singleton, then
![]() $\psi _0$
is an R-basis of
$\psi _0$
is an R-basis of
![]() $\operatorname {\mathrm {Hom}}_S(R,S)$
.
$\operatorname {\mathrm {Hom}}_S(R,S)$
.
Proof. This is immediate from Nakayama’s lemma and Lemma 5.36.
6 Wiles defect of Hecke algebras and global deformation rings
In this section, we’ll describe how the commutative algebra results from Sections 4 and 5 can be applied to Galois deformation rings, in the setup of Taylor–Wiles–Kisin patching. For ease of exposition we’ll restrict our attention to the case of two-dimensional Galois representations over a totally real number field, and moreover ones that are modular of parallel weight
![]() $2$
, as all of the computations and applications we give in this paper will be concerned with this case. This is not a fundamental limitation on our methods, and indeed everything we describe in this section will generalize automatically to any ‘
$2$
, as all of the computations and applications we give in this paper will be concerned with this case. This is not a fundamental limitation on our methods, and indeed everything we describe in this section will generalize automatically to any ‘
![]() $\ell _0=0$
’ patching setup (such as the definite unitary groups considered by [Reference Clozel, Harris and TaylorCHT08] and others).
$\ell _0=0$
’ patching setup (such as the definite unitary groups considered by [Reference Clozel, Harris and TaylorCHT08] and others).
Let F be a totally real number field. Fix a finite set
![]() $\Sigma $
of finite places of F. For each
$\Sigma $
of finite places of F. For each
![]() $v\in \Sigma $
, fix a
$v\in \Sigma $
, fix a
![]() $\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
, let
$\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
, let
![]() $\tau = (\tau _v)_{v\in \Sigma }$
and for
$\tau = (\tau _v)_{v\in \Sigma }$
and for
![]() $\sigma \in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
write
$\sigma \in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
write
![]() $\Sigma ^\sigma = \{v\in \Sigma |\tau _v=\sigma \}$
.
$\Sigma ^\sigma = \{v\in \Sigma |\tau _v=\sigma \}$
.
Pick a prime
![]() $p>2$
which is not ramified in F and is not divisible by any prime in
$p>2$
which is not ramified in F and is not divisible by any prime in
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $E/{\mathbf Q}_p$
be a finite extension with ring of integers
$E/{\mathbf Q}_p$
be a finite extension with ring of integers
![]() ${\mathcal O}$
, uniformizer
${\mathcal O}$
, uniformizer
![]() $\varpi $
and residue field k. Let
$\varpi $
and residue field k. Let
![]() $\varepsilon _p:G_F\to {\mathcal O}^\times $
be the cyclotomic character. Let
$\varepsilon _p:G_F\to {\mathcal O}^\times $
be the cyclotomic character. Let
![]() $\rho :G_F\to {\mathrm {GL}}_2({\mathcal O})$
be a Galois representation for which:
$\rho :G_F\to {\mathrm {GL}}_2({\mathcal O})$
be a Galois representation for which:
-
•
 $\rho $
corresponds to a Hilbert modular form of parallel weight 2;
$\rho $
corresponds to a Hilbert modular form of parallel weight 2; -
•
 $\det \rho = \varepsilon _p$
;
$\det \rho = \varepsilon _p$
; -
• For every
 $v\not \in \Sigma $
and
$v\not \in \Sigma $
and
 $v\nmid p$
,
$v\nmid p$
,
 $\rho $
is unramified at v;
$\rho $
is unramified at v; -
• For every
 $v|p$
,
$v|p$
,
 $\overline {\rho }|_{G_v}$
is finite flat;
$\overline {\rho }|_{G_v}$
is finite flat; -
• If
 $v\in \Sigma ^{{\operatorname {min}}}$
, then either
$v\in \Sigma ^{{\operatorname {min}}}$
, then either
 $|{\mathcal O}/v|\not \equiv -1\ \pmod {\ell }$
,
$|{\mathcal O}/v|\not \equiv -1\ \pmod {\ell }$
,
 $\overline {\rho }|_{I_v}$
is irreducible or
$\overline {\rho }|_{I_v}$
is irreducible or
 $\overline {\rho }|_{G_v}$
is absolutely reducible;
$\overline {\rho }|_{G_v}$
is absolutely reducible; -
• If
 $v\in \Sigma ^{{\mathrm {st}}}\cup \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
, then
$v\in \Sigma ^{{\mathrm {st}}}\cup \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
, then
 $\rho |_{G_v}$
is Steinberg (i.e.,
$\rho |_{G_v}$
is Steinberg (i.e.,
 $\rho |_{G_v}\sim \begin {pmatrix} \chi \,\varepsilon _p&*\\ 0 & \chi \end {pmatrix}$
for some unramified quadratic character);
$\rho |_{G_v}\sim \begin {pmatrix} \chi \,\varepsilon _p&*\\ 0 & \chi \end {pmatrix}$
for some unramified quadratic character); -
• The residual representation
 $\overline {\rho }:G_F\to {\mathrm {GL}}_2(k)$
is absolutely irreducible, and moreover that it satisfies the Taylor–Wiles conditions:
$\overline {\rho }:G_F\to {\mathrm {GL}}_2(k)$
is absolutely irreducible, and moreover that it satisfies the Taylor–Wiles conditions:
 $\overline {\rho }|_{G_{F(\zeta _p)}}$
is still absolutely irreducible, and in the case when
$\overline {\rho }|_{G_{F(\zeta _p)}}$
is still absolutely irreducible, and in the case when
 $p=5$
,
$p=5$
,
 $\sqrt {5}\in F$
and the projective image
$\sqrt {5}\in F$
and the projective image
 $\operatorname {\mathrm {proj}} \overline {\rho }:G_{F}\to {\mathrm {PGL}}_2({\overline {{\mathbf F}}}_5)$
is isomorphic to
$\operatorname {\mathrm {proj}} \overline {\rho }:G_{F}\to {\mathrm {PGL}}_2({\overline {{\mathbf F}}}_5)$
is isomorphic to
 ${\mathrm {PGL}}_2({\mathbb F}_5)$
, that
${\mathrm {PGL}}_2({\mathbb F}_5)$
, that
 $\ker \operatorname {\mathrm {proj}}\overline {\rho }\not \subseteq G_{F(\zeta _5)}$
.
$\ker \operatorname {\mathrm {proj}}\overline {\rho }\not \subseteq G_{F(\zeta _5)}$
.
Let
![]() $Q = \Sigma ^{{\mathrm {st}}}$
, and let D be a quaternion algebra over F ramified at the primes in Q (and no other finite primes) and at either all, or all but one infinite place of F (depending on whether
$Q = \Sigma ^{{\mathrm {st}}}$
, and let D be a quaternion algebra over F ramified at the primes in Q (and no other finite primes) and at either all, or all but one infinite place of F (depending on whether
![]() $|Q|+[F:{\mathbf Q}]$
is even or odd). Define a compact open subgroup
$|Q|+[F:{\mathbf Q}]$
is even or odd). Define a compact open subgroup
![]() $K^\tau = \prod _v K_v^\tau \subset (D \otimes {\mathbf A}_{F,f})^\times $
by:
$K^\tau = \prod _v K_v^\tau \subset (D \otimes {\mathbf A}_{F,f})^\times $
by:
-
•
 $K_v^\tau = {\mathrm {GL}}_2({\mathcal O}_{F,v})$
if
$K_v^\tau = {\mathrm {GL}}_2({\mathcal O}_{F,v})$
if
 $v\not \in \Sigma $
;
$v\not \in \Sigma $
; -
•
 $K_v^\tau $
is a maximal compact subgroup of
$K_v^\tau $
is a maximal compact subgroup of
 $(D\otimes F_v)^\times $
if
$(D\otimes F_v)^\times $
if
 $v\in \Sigma ^{{\mathrm {st}}} = Q$
;
$v\in \Sigma ^{{\mathrm {st}}} = Q$
; -
•
 $K_v^\tau = U_0(v)$
if
$K_v^\tau = U_0(v)$
if
 $v\in \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
;
$v\in \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
; -
•
 $K_v^\tau = U_0(v^{a_v})$
if
$K_v^\tau = U_0(v^{a_v})$
if
 $v\in \Sigma ^{{\operatorname {min}}}$
, where
$v\in \Sigma ^{{\operatorname {min}}}$
, where
 $a_v$
is the Artin conductor of
$a_v$
is the Artin conductor of
 $\overline {\rho }|_{G_v}$
;
$\overline {\rho }|_{G_v}$
; -
•
 $K_v^\tau = U_0(v^{a_v+2})$
if
$K_v^\tau = U_0(v^{a_v+2})$
if
 $v\in \Sigma ^{\square }$
.
$v\in \Sigma ^{\square }$
.
For convenience, we will simply write
![]() $K = K^\tau $
and
$K = K^\tau $
and
![]() $K_v = K_v^\tau $
.
$K_v = K_v^\tau $
.
When D is ramified at all but one infinite places (resp. all infinite places) let
![]() $X_K$
be the Shimura curve (resp. Shimura set) associated to K. Let
$X_K$
be the Shimura curve (resp. Shimura set) associated to K. Let
![]() ${\mathbf T}^D(K)$
be the Hecke algebra acting on
${\mathbf T}^D(K)$
be the Hecke algebra acting on
![]() $H^1(X_K,{\mathcal O})$
in the Shimura curve case and on
$H^1(X_K,{\mathcal O})$
in the Shimura curve case and on
![]() $H^0(X_K,{\mathcal O})$
in the Shimura set case, generated (as an
$H^0(X_K,{\mathcal O})$
in the Shimura set case, generated (as an
![]() ${\mathcal O}$
-algebra) by the Hecke operators
${\mathcal O}$
-algebra) by the Hecke operators
![]() $T_v$
and
$T_v$
and
![]() $S_v$
for all finite primes
$S_v$
for all finite primes
![]() $v\not \in \Sigma $
, and let
$v\not \in \Sigma $
, and let
![]() ${\overline {{\mathbf T}}}^{D}(K) = {\mathbf T}^D(K)[U_v|v\in \Sigma ^{{\operatorname {\varphi -uni}}}]$
. Note that
${\overline {{\mathbf T}}}^{D}(K) = {\mathbf T}^D(K)[U_v|v\in \Sigma ^{{\operatorname {\varphi -uni}}}]$
. Note that
![]() ${\mathbf T}^D(K)$
and
${\mathbf T}^D(K)$
and
![]() ${\overline {{\mathbf T}}}^D(K)$
are finite
${\overline {{\mathbf T}}}^D(K)$
are finite
![]() ${\mathcal O}$
-algebras.
${\mathcal O}$
-algebras.
Let
![]() ${\mathbf T}^D(K)^\varepsilon = {\mathbf T}^D(K)/\left (S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v)\middle |v\not \in \Sigma \right )$
and
${\mathbf T}^D(K)^\varepsilon = {\mathbf T}^D(K)/\left (S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v)\middle |v\not \in \Sigma \right )$
and
![]() ${\overline {{\mathbf T}}}^D(K)^\varepsilon = {\overline {{\mathbf T}}}^D(K)/(S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v) | v\not \in \Sigma )$
be the fixed determinant Hecke algebras.
${\overline {{\mathbf T}}}^D(K)^\varepsilon = {\overline {{\mathbf T}}}^D(K)/(S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v) | v\not \in \Sigma )$
be the fixed determinant Hecke algebras.
The assumption that
![]() $\rho $
corresponds to a Hilbert modular form of parallel weight
$\rho $
corresponds to a Hilbert modular form of parallel weight
![]() $2$
gives the following:
$2$
gives the following:
Proposition 6.1. There is an augmentation
![]() $\lambda :{\overline {{\mathbf T}}}^D(K)^\varepsilon \twoheadrightarrow {\mathcal O}$
with the property that for any
$\lambda :{\overline {{\mathbf T}}}^D(K)^\varepsilon \twoheadrightarrow {\mathcal O}$
with the property that for any
![]() $v\not \in \Sigma \cup \Sigma _p$
,
$v\not \in \Sigma \cup \Sigma _p$
,
![]() $\rho (\operatorname {\mathrm {Frob}}_v)$
has characteristic polynomial
$\rho (\operatorname {\mathrm {Frob}}_v)$
has characteristic polynomial
![]() $x^2-\lambda (T_v)x+\lambda (S_v)$
. Moreover,
$x^2-\lambda (T_v)x+\lambda (S_v)$
. Moreover,
![]() $\Phi _{\lambda }({\overline {{\mathbf T}}}^D(K)^\varepsilon )$
is finite.
$\Phi _{\lambda }({\overline {{\mathbf T}}}^D(K)^\varepsilon )$
is finite.
Let
![]() ${\mathfrak m} = \lambda ^{-1}(\varpi {\mathcal O})\subseteq {\overline {{\mathbf T}}}^D(K)^\varepsilon $
be the maximal ideal of
${\mathfrak m} = \lambda ^{-1}(\varpi {\mathcal O})\subseteq {\overline {{\mathbf T}}}^D(K)^\varepsilon $
be the maximal ideal of
![]() ${\overline {{\mathbf T}}}^D(K)^\varepsilon $
corresponding to
${\overline {{\mathbf T}}}^D(K)^\varepsilon $
corresponding to
![]() $\overline {\rho }$
. By slight abuse of notation, also write
$\overline {\rho }$
. By slight abuse of notation, also write
![]() ${\mathfrak m} = {\mathfrak m}\cap {\mathbf T}^D(K)$
for the maximal ideal of
${\mathfrak m} = {\mathfrak m}\cap {\mathbf T}^D(K)$
for the maximal ideal of
![]() ${\mathbf T}^D(K)$
corresponding to
${\mathbf T}^D(K)$
corresponding to
![]() $\overline {\rho }$
.
$\overline {\rho }$
.
Write
![]() ${\mathbf T}^\tau = {\mathbf T}^D(K)^\varepsilon _{{\mathfrak m}}$
and
${\mathbf T}^\tau = {\mathbf T}^D(K)^\varepsilon _{{\mathfrak m}}$
and
![]() ${\overline {{\mathbf T}}}^\tau = {\overline {{\mathbf T}}}^D(K)^\varepsilon _{{\mathfrak m}}$
for the localizations at
${\overline {{\mathbf T}}}^\tau = {\overline {{\mathbf T}}}^D(K)^\varepsilon _{{\mathfrak m}}$
for the localizations at
![]() ${\mathfrak m}$
(and note that we are suppressing
${\mathfrak m}$
(and note that we are suppressing
![]() $\varepsilon $
from our notation).
$\varepsilon $
from our notation).
Note that any
![]() $x:{\overline {{\mathbf T}}}^\tau \to {\overline {{\mathbf Q}}_p}$
corresponds to a Galois representation
$x:{\overline {{\mathbf T}}}^\tau \to {\overline {{\mathbf Q}}_p}$
corresponds to a Galois representation
![]() $\rho _x:G_F\to {\mathrm {GL}}_2({\overline {{\mathbf Q}}_p})$
lifting
$\rho _x:G_F\to {\mathrm {GL}}_2({\overline {{\mathbf Q}}_p})$
lifting
![]() $\overline {\rho }$
with
$\overline {\rho }$
with
![]() $\det \rho _x = \varepsilon _p = \det \rho $
and
$\det \rho _x = \varepsilon _p = \det \rho $
and
![]() $\operatorname {\mathrm {tr}}\rho _x(\operatorname {\mathrm {Frob}}_v) = x(T_v)$
for all
$\operatorname {\mathrm {tr}}\rho _x(\operatorname {\mathrm {Frob}}_v) = x(T_v)$
for all
![]() $v\not \in \Sigma $
(so that
$v\not \in \Sigma $
(so that
![]() $\rho = \rho _{\lambda }$
).
$\rho = \rho _{\lambda }$
).
Define
![]() $H^\tau = H^1(X_K,{\mathcal O})^*$
if D is indefinite and
$H^\tau = H^1(X_K,{\mathcal O})^*$
if D is indefinite and
![]() $H^\tau = H^0(X_K,{\mathcal O})^*$
if D is definite (where for any
$H^\tau = H^0(X_K,{\mathcal O})^*$
if D is definite (where for any
![]() ${\mathcal O}$
-module M,
${\mathcal O}$
-module M,
![]() $M^* = \operatorname {\mathrm {Hom}}_{{\mathcal O}}(M,{\mathcal O})$
), viewed as a
$M^* = \operatorname {\mathrm {Hom}}_{{\mathcal O}}(M,{\mathcal O})$
), viewed as a
![]() ${\overline {{\mathbf T}}}^D(K)$
-module, and hence as a
${\overline {{\mathbf T}}}^D(K)$
-module, and hence as a
![]() ${\mathbf T}^D(K)$
-module. Define
${\mathbf T}^D(K)$
-module. Define
For the convenience of the reader, we recall some notation and results from Sections 4 and 5. For each prime v of F, the universal (fixed determinant) ring, parameterizing framed deformations of
![]() $\overline {\rho }|_{G_{F_v}}$
with determinant
$\overline {\rho }|_{G_{F_v}}$
with determinant
![]() $\varepsilon _p$
is
$\varepsilon _p$
is
![]() $R_v^{\square }$
. For
$R_v^{\square }$
. For
![]() $v\nmid p$
and
$v\nmid p$
and
![]() $\tau _v \in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
, let
$\tau _v \in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ {\operatorname {\varphi -uni}},\ \square \}$
, let
![]() $R_v^{\tau _v}$
be the deformation ring defined in Section 5, provided it exists (which is does for
$R_v^{\tau _v}$
be the deformation ring defined in Section 5, provided it exists (which is does for
![]() $v\in \Sigma $
and
$v\in \Sigma $
and
![]() $\tau = \tau _v$
, by assumption). The ring
$\tau = \tau _v$
, by assumption). The ring
![]() $R_v^{\tau _v}$
is naturally an
$R_v^{\tau _v}$
is naturally an
![]() $R_v^\square $
-algebra, and unless
$R_v^\square $
-algebra, and unless
![]() $\tau _v = {\operatorname {\varphi -uni}}$
it is a quotient of
$\tau _v = {\operatorname {\varphi -uni}}$
it is a quotient of
![]() $R_v^{\square }$
. Summarizing the results of Proposition 4.6 we have:
$R_v^{\square }$
. Summarizing the results of Proposition 4.6 we have:
Proposition 6.2. For each
![]() $v\in \Sigma $
, the ring
$v\in \Sigma $
, the ring
![]() $R_v^{\tau _v}$
is a complete, Noetherian
$R_v^{\tau _v}$
is a complete, Noetherian
![]() ${\mathcal O}$
-algebra which is flat and equidimensional over
${\mathcal O}$
-algebra which is flat and equidimensional over
![]() ${\mathcal O}$
of relative dimension
${\mathcal O}$
of relative dimension
![]() $3$
. Moreover,
$3$
. Moreover,
![]() $R_v^{\tau _v}$
is Cohen–Macaulay and is a complete intersection whenever
$R_v^{\tau _v}$
is Cohen–Macaulay and is a complete intersection whenever
![]() $\tau _v={\operatorname {min}}$
or
$\tau _v={\operatorname {min}}$
or
![]() $\square $
or whenever
$\square $
or whenever
![]() $\overline {\rho }|_{G_v}$
is not a scalar.
$\overline {\rho }|_{G_v}$
is not a scalar.
As in Section 4, let:
 $$ \begin{align*} R_{\operatorname{\mathrm{loc}}} &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}} \,R_v^{\square}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}}\,R_v^{\operatorname{\mathrm{fl}}}\right),& &\text{and}& R_{\operatorname{\mathrm{loc}}}^\tau &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}}\,R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}}\,R_v^{\operatorname{\mathrm{fl}}}\right) \end{align*} $$
$$ \begin{align*} R_{\operatorname{\mathrm{loc}}} &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}} \,R_v^{\square}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}}\,R_v^{\operatorname{\mathrm{fl}}}\right),& &\text{and}& R_{\operatorname{\mathrm{loc}}}^\tau &= \left({\widehat{\bigotimes_{{v\in \Sigma}}}}\,R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}}\,R_v^{\operatorname{\mathrm{fl}}}\right) \end{align*} $$
so that
![]() $R^\tau _{\operatorname {\mathrm {loc}}}$
is naturally a
$R^\tau _{\operatorname {\mathrm {loc}}}$
is naturally a
![]() $R_{\operatorname {\mathrm {loc}}}$
-algebra. By Propositions 4.6 and 4.7,
$R_{\operatorname {\mathrm {loc}}}$
-algebra. By Propositions 4.6 and 4.7,
![]() $R_{\operatorname {\mathrm {loc}}}$
is flat over
$R_{\operatorname {\mathrm {loc}}}$
is flat over
![]() ${\mathcal O}$
and Cohen–Macaulay.
${\mathcal O}$
and Cohen–Macaulay.
By R (resp.
![]() $R^\square $
), we denote the (global) unframed (resp. framed) deformation ring parameterizing lifts of
$R^\square $
), we denote the (global) unframed (resp. framed) deformation ring parameterizing lifts of
![]() $\overline {\rho }$
with determinant
$\overline {\rho }$
with determinant
![]() $\varepsilon _p$
which are flat at every prime
$\varepsilon _p$
which are flat at every prime
![]() $v|p$
. One may noncanonically fix an isomorphism
$v|p$
. One may noncanonically fix an isomorphism
![]() $R^\square = R[[X_1,\ldots ,X_{4j-1}]]$
for some j, and thereby treat R as a quotient of
$R^\square = R[[X_1,\ldots ,X_{4j-1}]]$
for some j, and thereby treat R as a quotient of
![]() $R^\square $
. Using the natural map
$R^\square $
. Using the natural map
![]() $R_{\operatorname {\mathrm {loc}}}\to R^\square $
(and
$R_{\operatorname {\mathrm {loc}}}\to R^\square $
(and
![]() $R_{\operatorname {\mathrm {loc}}}\to R$
), one defines
$R_{\operatorname {\mathrm {loc}}}\to R$
), one defines
![]() $R^{\square ,\tau } = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}}R^\square $
and
$R^{\square ,\tau } = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}}R^\square $
and
![]() $R^{\tau } = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}}R$
.
$R^{\tau } = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}}R$
.
Lemma 6.3. There is a surjective map
![]() $R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
inducing a representation
$R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
inducing a representation
![]() $\rho ^\tau :G_F\to {\mathrm {GL}}_2(R^\tau )\twoheadrightarrow {\mathrm {GL}}_2({\mathbf T}^\tau )$
such that for all
$\rho ^\tau :G_F\to {\mathrm {GL}}_2(R^\tau )\twoheadrightarrow {\mathrm {GL}}_2({\mathbf T}^\tau )$
such that for all
![]() $v\not \in \Sigma \cup \Sigma _p$
,
$v\not \in \Sigma \cup \Sigma _p$
,
![]() $\rho ^\tau (\operatorname {\mathrm {Frob}}_v)$
has characteristic polynomial
$\rho ^\tau (\operatorname {\mathrm {Frob}}_v)$
has characteristic polynomial
![]() $t^2-T_vt+S_v$
, and for all
$t^2-T_vt+S_v$
, and for all
![]() $v\in \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
,
$v\in \Sigma ^{{\mathrm {un}}}\cup \Sigma ^{{\operatorname {\varphi -uni}}}$
,
![]() $\rho ^\tau |_{G_{F_v}}$
is unipotent and if
$\rho ^\tau |_{G_{F_v}}$
is unipotent and if
![]() $\operatorname {\mathrm {Frob}}_v\in G_{F_v}$
is any lift of Frobenius, then
$\operatorname {\mathrm {Frob}}_v\in G_{F_v}$
is any lift of Frobenius, then
![]() $\rho ^\tau (\operatorname {\mathrm {Frob}}_v)$
again has characteristic polynomial
$\rho ^\tau (\operatorname {\mathrm {Frob}}_v)$
again has characteristic polynomial
![]() $t^2-T_vt+S_v$
.
$t^2-T_vt+S_v$
.
Proof. If
![]() $\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, this is just [Reference ManningMan21, Lemma 2.4].
$\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, this is just [Reference ManningMan21, Lemma 2.4].
In general, for each for each
![]() $v\in \Sigma $
, set
$v\in \Sigma $
, set
![]() $\sigma _v = \tau _v$
if
$\sigma _v = \tau _v$
if
![]() $\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ \square \}$
and
$\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ \square \}$
and
![]() $\sigma _v = {\mathrm {uni}}$
if
$\sigma _v = {\mathrm {uni}}$
if
![]() $\tau _v = {\operatorname {\varphi -uni}}$
. Note that under this definition,
$\tau _v = {\operatorname {\varphi -uni}}$
. Note that under this definition,
![]() $K^\sigma = K^\tau = K$
and
$K^\sigma = K^\tau = K$
and
![]() ${\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
.
${\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
.
It follows that there is a surjection
![]() $R^\sigma \twoheadrightarrow {\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
satisfying the desired conditions on
$R^\sigma \twoheadrightarrow {\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
satisfying the desired conditions on
![]() $\rho ^\sigma $
. By definition,
$\rho ^\sigma $
. By definition,
![]() ${\overline {{\mathbf T}}}^\tau = {\mathbf T}^\tau [U_v|v\in \Sigma ^{{\operatorname {\varphi -uni}}}]$
. From the identity
${\overline {{\mathbf T}}}^\tau = {\mathbf T}^\tau [U_v|v\in \Sigma ^{{\operatorname {\varphi -uni}}}]$
. From the identity
![]() $U_v^2-T_vU_v+S_v=0$
in
$U_v^2-T_vU_v+S_v=0$
in
![]() ${\overline {{\mathbf T}}}^D(K)$
and the definition of modified global deformation rings given in Section 4, it follows that
${\overline {{\mathbf T}}}^D(K)$
and the definition of modified global deformation rings given in Section 4, it follows that
![]() $R^\sigma \twoheadrightarrow {\mathbf T}^\tau \to {\overline {{\mathbf T}}}^\tau $
induces a map
$R^\sigma \twoheadrightarrow {\mathbf T}^\tau \to {\overline {{\mathbf T}}}^\tau $
induces a map
![]() $R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
sending
$R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
sending
![]() $\alpha _v$
to
$\alpha _v$
to
![]() $U_v$
for
$U_v$
for
![]() $v\in \Sigma ^{{\operatorname {\varphi -uni}}}$
, which is therefore surjective, and hence is the desired map.
$v\in \Sigma ^{{\operatorname {\varphi -uni}}}$
, which is therefore surjective, and hence is the desired map.
Now, similarly to [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], the Taylor–Wiles–Kisin patching method gives the following:
Theorem 6.4. There exist integers
![]() $g,d\ge 0$
and rings
$g,d\ge 0$
and rings
 $$ \begin{align*} R_\infty^{\tau} &= R_{\operatorname{\mathrm{loc}}}^{\tau}[[x_1,\ldots,x_g]]\\ S_\infty &= {\mathcal O}[[y_1,\ldots,y_d]] \end{align*} $$
$$ \begin{align*} R_\infty^{\tau} &= R_{\operatorname{\mathrm{loc}}}^{\tau}[[x_1,\ldots,x_g]]\\ S_\infty &= {\mathcal O}[[y_1,\ldots,y_d]] \end{align*} $$
satisfying the following:
-
1.
 $\dim S_\infty = \dim R_\infty ^{\tau }$
.
$\dim S_\infty = \dim R_\infty ^{\tau }$
. -
2. There exists a continuous
 ${\mathcal O}$
-algebra morphism
${\mathcal O}$
-algebra morphism
 $i:S_\infty \to R_\infty ^\tau $
making
$i:S_\infty \to R_\infty ^\tau $
making
 $R_\infty ^\tau $
into a finite free
$R_\infty ^\tau $
into a finite free
 $S_\infty $
-module.
$S_\infty $
-module. -
3. There is an isomorphism
 $R_\infty ^{\tau }\otimes _{S_\infty } {\mathcal O} \cong R^{\tau }$
of
$R_\infty ^{\tau }\otimes _{S_\infty } {\mathcal O} \cong R^{\tau }$
of
 $R^\tau _{\operatorname {\mathrm {loc}}}$
-algebras, and
$R^\tau _{\operatorname {\mathrm {loc}}}$
-algebras, and
 $R^\tau $
is finite free over
$R^\tau $
is finite free over
 ${\mathcal O}$
.
${\mathcal O}$
. -
4. The map
 $R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
from Lemma 6.3 is an isomorphism. These rings are reduced if
$R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
from Lemma 6.3 is an isomorphism. These rings are reduced if
 $\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
.
$\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
. -
5. If
 $\lambda $
is the induced map
$\lambda $
is the induced map
 $R_\infty ^\tau \twoheadrightarrow R^\tau \xrightarrow {\sim } {\overline {{\mathbf T}}}^\tau \xrightarrow {\lambda }{\mathcal O}$
, then
$R_\infty ^\tau \twoheadrightarrow R^\tau \xrightarrow {\sim } {\overline {{\mathbf T}}}^\tau \xrightarrow {\lambda }{\mathcal O}$
, then
 $\operatorname {\mathrm {Spec}} R_\infty ^\tau [1/\varpi ]$
is formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R_\infty ^\tau [1/\varpi ]$
is formally smooth at the point corresponding to
 $\lambda $
.
$\lambda $
.
Proof. This is proved similarly to Theorem 6.3 in [Reference Böckle, Khare and ManningBKM21].
First, we will consider the case when
![]() $\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, and so
$\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, and so
![]() ${\overline {{\mathbf T}}}^D(K) = {\mathbf T}^D(K)$
. More precisely, as in the proof of Lemma 6.3, for each
${\overline {{\mathbf T}}}^D(K) = {\mathbf T}^D(K)$
. More precisely, as in the proof of Lemma 6.3, for each
![]() $v\in \Sigma $
, define
$v\in \Sigma $
, define
![]() $\sigma _v = \tau _v$
if
$\sigma _v = \tau _v$
if
![]() $\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ \square \}$
and define
$\tau _v\in \{{\operatorname {min}},\ {\mathrm {st}},\ {\mathrm {uni}},\ \square \}$
and define
![]() $\sigma _v = {\mathrm {uni}}$
if
$\sigma _v = {\mathrm {uni}}$
if
![]() $\tau _v = {\operatorname {\varphi -uni}}$
. Note that under this definition,
$\tau _v = {\operatorname {\varphi -uni}}$
. Note that under this definition,
![]() $K^\sigma = K^\tau = K$
,
$K^\sigma = K^\tau = K$
,
![]() $M^\sigma = M^\tau $
and
$M^\sigma = M^\tau $
and
![]() ${\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
.
${\overline {{\mathbf T}}}^\sigma = {\mathbf T}^\sigma = {\mathbf T}^\tau $
.
By assumption,
![]() $\overline {\rho }$
satisfies the Taylor–Wiles conditions, and so we may apply the Taylor–Wiles–Kisin patching method (as summarized in [Reference ManningMan21, Section 4]) to the rings
$\overline {\rho }$
satisfies the Taylor–Wiles conditions, and so we may apply the Taylor–Wiles–Kisin patching method (as summarized in [Reference ManningMan21, Section 4]) to the rings
![]() $R^\sigma $
and
$R^\sigma $
and
![]() ${\mathbf T}^\sigma $
and the module
${\mathbf T}^\sigma $
and the module
![]() $M^\sigma $
.
$M^\sigma $
.
First, as in [Reference ManningMan21, Section 4.2], we may add auxiliary level structure at a carefully chosen prime not in
![]() $\Sigma $
to remove any isotropy issues, without affecting any of the objects considered considered in this theorem.
$\Sigma $
to remove any isotropy issues, without affecting any of the objects considered considered in this theorem.
Now, exactly as in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] (and the method outlined in [Reference ManningMan21, Section 4.3]), there exist integers
![]() $g,d\ge 0$
, satisfying
$g,d\ge 0$
, satisfying
![]() $d+1 = \dim R_{\operatorname {\mathrm {loc}}}+g = \dim R_{\operatorname {\mathrm {loc}}}^{\sigma }+g$
(see [Reference ManningMan21, Lemma 2.5] and [Reference KisinKis09, Proposition (3.2.5)]) such that for each
$d+1 = \dim R_{\operatorname {\mathrm {loc}}}+g = \dim R_{\operatorname {\mathrm {loc}}}^{\sigma }+g$
(see [Reference ManningMan21, Lemma 2.5] and [Reference KisinKis09, Proposition (3.2.5)]) such that for each
![]() $n\ge 1$
, there is a unframed global deformation ring
$n\ge 1$
, there is a unframed global deformation ring
![]() $R_n^\sigma $
and a framed global deformation ring
$R_n^\sigma $
and a framed global deformation ring
![]() $R_n^{\sigma ,\square }$
(with fixed determinant, the same deformation conditions as
$R_n^{\sigma ,\square }$
(with fixed determinant, the same deformation conditions as
![]() $R^\sigma $
at each
$R^\sigma $
at each
![]() $v\in \Sigma $
, and relaxed deformation conditions at a carefully selected set
$v\in \Sigma $
, and relaxed deformation conditions at a carefully selected set
![]() $Q_n$
of ‘Taylor–Wiles’ primes) such that
$Q_n$
of ‘Taylor–Wiles’ primes) such that
![]() $R_n^{\sigma ,\square }$
has the structure of a
$R_n^{\sigma ,\square }$
has the structure of a
![]() $S_\infty $
-algebra and there is a surjective map
$S_\infty $
-algebra and there is a surjective map
![]() $R_\infty \twoheadrightarrow R_n^{\sigma ,\square }$
and an isomorphism
$R_\infty \twoheadrightarrow R_n^{\sigma ,\square }$
and an isomorphism
![]() $R_n^{\sigma ,\square } \otimes _{S_\infty } {\mathcal O} \cong R^\sigma $
, where
$R_n^{\sigma ,\square } \otimes _{S_\infty } {\mathcal O} \cong R^\sigma $
, where
![]() $S_\infty $
is as in the theorem statement, and
$S_\infty $
is as in the theorem statement, and
![]() $R_\infty ^\sigma $
satisfies the properties of
$R_\infty ^\sigma $
satisfies the properties of
![]() $R_\infty ^\tau $
from the theorem statement.
$R_\infty ^\tau $
from the theorem statement.
Moreover, for each
![]() $n\ge 1$
the construction in [Reference ManningMan21, Section 4.2] also constructs a compact open subgroup
$n\ge 1$
the construction in [Reference ManningMan21, Section 4.2] also constructs a compact open subgroup
![]() $K_n = \prod _v K_{n,v}\subseteq (D\otimes {\mathbf A}_{F,f})^\times $
(with
$K_n = \prod _v K_{n,v}\subseteq (D\otimes {\mathbf A}_{F,f})^\times $
(with
![]() $K_{n,v} = K_v$
for all
$K_{n,v} = K_v$
for all
![]() $v\not \in Q_n$
), and a Hecke algebra
$v\not \in Q_n$
), and a Hecke algebra
![]() ${\mathbf T}^\sigma _n$
and Hecke module
${\mathbf T}^\sigma _n$
and Hecke module
![]() $M^\sigma _n$
at level
$M^\sigma _n$
at level
![]() $K_n$
(defined analogously to
$K_n$
(defined analogously to
![]() ${\mathbf T}^\sigma $
and
${\mathbf T}^\sigma $
and
![]() $M^\sigma $
above, by localizing at a particular maximal ideal, and fixing determinants by taking a quotient). One then has a surjection
$M^\sigma $
above, by localizing at a particular maximal ideal, and fixing determinants by taking a quotient). One then has a surjection
![]() $R^\sigma _n\twoheadrightarrow {\mathbf T}^\sigma _n$
, making
$R^\sigma _n\twoheadrightarrow {\mathbf T}^\sigma _n$
, making
![]() $M^\sigma _n$
into a
$M^\sigma _n$
into a
![]() $R^\sigma _n$
-module. Using this surjection, we may define framed versions of these objects:
$R^\sigma _n$
-module. Using this surjection, we may define framed versions of these objects:
![]() ${\mathbf T}^{\sigma ,\square }_n= {\mathbf T}^\sigma _n\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
and
${\mathbf T}^{\sigma ,\square }_n= {\mathbf T}^\sigma _n\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
and
![]() $M^{\sigma ,\square }_n= M^\sigma _n\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
.
$M^{\sigma ,\square }_n= M^\sigma _n\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
.
Applying the ‘ultrapatching’ construction described in [Reference ManningMan21, Section 4.1] (as well as in the proof of Lemma 4.8) then produces an
![]() $S_\infty $
-algebra
$S_\infty $
-algebra
![]() ${\mathcal R}_\infty ^\sigma $
as well as an
${\mathcal R}_\infty ^\sigma $
as well as an
![]() ${\mathcal R}_\infty $
-module
${\mathcal R}_\infty $
-module
![]() $M_\infty ^\sigma $
(which would be called
$M_\infty ^\sigma $
(which would be called
![]() $\mathscr {P}(\{R^{\sigma ,\square }_n\})$
and
$\mathscr {P}(\{R^{\sigma ,\square }_n\})$
and
![]() $\mathscr {P}(\{M^{\sigma ,\square }_n\})$
in the notation of that paper), for which:
$\mathscr {P}(\{M^{\sigma ,\square }_n\})$
in the notation of that paper), for which:
-
•
 $M_\infty ^\sigma $
is finite free over
$M_\infty ^\sigma $
is finite free over
 $S_\infty $
;
$S_\infty $
; -
•
 ${\mathcal R}_\infty ^\sigma \otimes _{S_\infty }{\mathcal O} \cong R^\sigma $
and
${\mathcal R}_\infty ^\sigma \otimes _{S_\infty }{\mathcal O} \cong R^\sigma $
and
 $M_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}\cong M^\sigma $
;
$M_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}\cong M^\sigma $
; -
• There is a surjection
 $R_\infty ^\sigma \twoheadrightarrow {\mathcal R}_\infty ^\sigma $
such that the composition is the map
$R_\infty ^\sigma \twoheadrightarrow {\mathcal R}_\infty ^\sigma $
such that the composition is the map $$\begin{align*}R_{\operatorname{\mathrm{loc}}}^\sigma\hookrightarrow R_\infty^\sigma\twoheadrightarrow {\mathcal R}_\infty^\sigma\twoheadrightarrow R^\sigma\end{align*}$$
$$\begin{align*}R_{\operatorname{\mathrm{loc}}}^\sigma\hookrightarrow R_\infty^\sigma\twoheadrightarrow {\mathcal R}_\infty^\sigma\twoheadrightarrow R^\sigma\end{align*}$$
 $R_{\operatorname {\mathrm {loc}}}^\sigma \to R^\sigma $
from above.
$R_{\operatorname {\mathrm {loc}}}^\sigma \to R^\sigma $
from above.
Just as in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], we may lift the structure map
![]() $S_\infty \to {\mathcal R}_\infty ^\sigma $
to a map
$S_\infty \to {\mathcal R}_\infty ^\sigma $
to a map
![]() $i:S_\infty \to R_\infty ^\sigma $
making
$i:S_\infty \to R_\infty ^\sigma $
making
![]() $\pi _\infty :R_\infty ^\sigma \to {\mathcal R}^\sigma _\infty $
into an
$\pi _\infty :R_\infty ^\sigma \to {\mathcal R}^\sigma _\infty $
into an
![]() $S_\infty $
-module surjection, and so it follows that
$S_\infty $
-module surjection, and so it follows that
![]() $M_\infty ^\sigma $
is a maximal Cohen–Macaulay
$M_\infty ^\sigma $
is a maximal Cohen–Macaulay
![]() $R_\infty ^\sigma $
-module.
$R_\infty ^\sigma $
-module.
But now by standard properties of maximal Cohen–Macaulay modules, the support of
![]() $M_\infty ^{\sigma }$
is a union of irreducible components of
$M_\infty ^{\sigma }$
is a union of irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
. As
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
. As
![]() $R_\infty ^\sigma = R_{\operatorname {\mathrm {loc}}}^\sigma [[x_1,\ldots ,x_g]]$
, the irreducible components of
$R_\infty ^\sigma = R_{\operatorname {\mathrm {loc}}}^\sigma [[x_1,\ldots ,x_g]]$
, the irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
are in bijection with those of
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
are in bijection with those of
![]() $\operatorname {\mathrm {Spec}} R_{\operatorname {\mathrm {loc}}}^\sigma $
.
$\operatorname {\mathrm {Spec}} R_{\operatorname {\mathrm {loc}}}^\sigma $
.
By an analogous result to Lemma 6.2 from [Reference Böckle, Khare and ManningBKM21] (using Corollary 3.1.7 of [Reference GeeGee11] instead of the results of [Reference Diamond and TaylorDT94] that are used there), it follows that each irreducible component of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
contains a point in the support of
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
contains a point in the support of
![]() $M_\infty ^\sigma /(i(y_1),\ldots ,i(y_d))\otimes _{\mathcal O} E = M^\sigma \otimes _{\mathcal O} E$
, which is not contained in any other component. Then as in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], as
$M_\infty ^\sigma /(i(y_1),\ldots ,i(y_d))\otimes _{\mathcal O} E = M^\sigma \otimes _{\mathcal O} E$
, which is not contained in any other component. Then as in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], as
![]() $R_\infty ^\sigma $
is reduced, it follows that
$R_\infty ^\sigma $
is reduced, it follows that
![]() $R_\infty ^\sigma $
acts faithfully on
$R_\infty ^\sigma $
acts faithfully on
![]() $M_\infty $
and so
$M_\infty $
and so
![]() ${\mathcal R}^\sigma _\infty = R^\sigma _\infty $
, and so we indeed have an isomorphism
${\mathcal R}^\sigma _\infty = R^\sigma _\infty $
, and so we indeed have an isomorphism
![]() $R_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}\cong R^\sigma $
, proving the first part of (3).
$R_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}\cong R^\sigma $
, proving the first part of (3).
By Proposition 6.2,
![]() $R_\infty ^\tau $
is Cohen–Macaulay. As in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] this, combined with the fact that
$R_\infty ^\tau $
is Cohen–Macaulay. As in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] this, combined with the fact that
![]() $M_\infty ^\sigma $
is free over
$M_\infty ^\sigma $
is free over
![]() $S_\infty $
, implies that
$S_\infty $
, implies that
![]() $R_\infty ^\tau $
is free over
$R_\infty ^\tau $
is free over
![]() $S_\infty $
, proving (2). As in [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], this also implies that
$S_\infty $
, proving (2). As in [Reference Böckle, Khare and ManningBKM21, Theorem 6.3], this also implies that
![]() $R^\sigma =R_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}$
is finite free over
$R^\sigma =R_\infty ^\sigma \otimes _{S_\infty }{\mathcal O}$
is finite free over
![]() ${\mathcal O}$
, proving the second part of (3). In particular (as
${\mathcal O}$
, proving the second part of (3). In particular (as
![]() ${\mathbf T}^\sigma $
is finite free over
${\mathbf T}^\sigma $
is finite free over
![]() ${\mathcal O}$
by definition) to show that
${\mathcal O}$
by definition) to show that
![]() $R^\sigma \twoheadrightarrow {\mathbf T}^\sigma $
is an isomorphism, it will suffice to show that the induced map
$R^\sigma \twoheadrightarrow {\mathbf T}^\sigma $
is an isomorphism, it will suffice to show that the induced map
![]() $R^\sigma [1/\varpi ]\twoheadrightarrow {\mathbf T}^\sigma [1/\varpi ]$
is.
$R^\sigma [1/\varpi ]\twoheadrightarrow {\mathbf T}^\sigma [1/\varpi ]$
is.
Now, as in the proof of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3],
![]() $\operatorname {\mathrm {Spec}} R_\infty ^{\sigma }[1/\varpi ]$
is formally smooth at every point in the support of
$\operatorname {\mathrm {Spec}} R_\infty ^{\sigma }[1/\varpi ]$
is formally smooth at every point in the support of
![]() $\operatorname {\mathrm {Spec}} M^\sigma \otimes _{\mathcal O} E$
, and so in particular at the point corresponding to
$\operatorname {\mathrm {Spec}} M^\sigma \otimes _{\mathcal O} E$
, and so in particular at the point corresponding to
![]() $\lambda :R_\infty ^\sigma \twoheadrightarrow {\mathcal O}$
, proving (5). This is proved as in [Reference Böckle, Khare and ManningBKM21, Lemma 6.1] by using the fact that Galois representations arising from cohomological Hilbert modular forms are known to be generic in the sense of [Reference AllenAll16, Lemma 1.1.5], which follows from the genericity of the corresponding automorphic representation of
$\lambda :R_\infty ^\sigma \twoheadrightarrow {\mathcal O}$
, proving (5). This is proved as in [Reference Böckle, Khare and ManningBKM21, Lemma 6.1] by using the fact that Galois representations arising from cohomological Hilbert modular forms are known to be generic in the sense of [Reference AllenAll16, Lemma 1.1.5], which follows from the genericity of the corresponding automorphic representation of
![]() ${\mathrm {GL}}_2({\mathbf A}_F)$
at all finite places and local-global compatibility as recorded in [Reference AllenAll16, Theorem 2.1.2].
${\mathrm {GL}}_2({\mathbf A}_F)$
at all finite places and local-global compatibility as recorded in [Reference AllenAll16, Theorem 2.1.2].
The argument of [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] now proves that
![]() $R^\sigma [1/\varphi ]\twoheadrightarrow {\mathbf T}^\sigma [1/\varpi ]$
is an isomorphism, and hence
$R^\sigma [1/\varphi ]\twoheadrightarrow {\mathbf T}^\sigma [1/\varpi ]$
is an isomorphism, and hence
![]() $R^\sigma \twoheadrightarrow {\mathbf T}^\sigma $
is an isomorphism. This proves (4) in the case when
$R^\sigma \twoheadrightarrow {\mathbf T}^\sigma $
is an isomorphism. This proves (4) in the case when
![]() $\Sigma ^{{\operatorname {\varphi -uni}}}=\varnothing $
(the last claim in (4), that the rings are reduced, is a consequence of the standard fact that the Hecke operators
$\Sigma ^{{\operatorname {\varphi -uni}}}=\varnothing $
(the last claim in (4), that the rings are reduced, is a consequence of the standard fact that the Hecke operators
![]() $T_v$
and
$T_v$
and
![]() $S_v$
for
$S_v$
for
![]() $v\not \in \Sigma $
are all simultaneously diagonalizable as operators on
$v\not \in \Sigma $
are all simultaneously diagonalizable as operators on
![]() $H^\sigma $
).
$H^\sigma $
).
In the case when
![]() $\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, and hence
$\Sigma ^{{\operatorname {\varphi -uni}}} = \varnothing $
, and hence
![]() $\sigma =\tau $
, this completes the proof. In the case when
$\sigma =\tau $
, this completes the proof. In the case when
![]() $\Sigma ^{{\operatorname {\varphi -uni}}}\ne \varnothing $
and so
$\Sigma ^{{\operatorname {\varphi -uni}}}\ne \varnothing $
and so
![]() $\sigma \ne \tau $
, it remains to deduce the statement of the theorem for
$\sigma \ne \tau $
, it remains to deduce the statement of the theorem for
![]() $\tau $
from the one for
$\tau $
from the one for
![]() $\sigma $
.
$\sigma $
.
First, by the definition of modified global deformation rings given in Equation 4.2, we have that
and similarly
![]() $R^\tau _n = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_n^\sigma $
and
$R^\tau _n = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_n^\sigma $
and
![]() $R^{\tau ,\square }_n = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_n^{\sigma ,\square }$
for all
$R^{\tau ,\square }_n = R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_n^{\sigma ,\square }$
for all
![]() $n\ge 1$
. The
$n\ge 1$
. The
![]() $S_\infty $
-algebra structure on
$S_\infty $
-algebra structure on
![]() $R_n^{\sigma ,\square }$
then induces an
$R_n^{\sigma ,\square }$
then induces an
![]() $S_\infty $
-algebra structure on
$S_\infty $
-algebra structure on
![]() $R_n^{\sigma ,\square }$
, and we have
$R_n^{\sigma ,\square }$
, and we have
Also, as
![]() $R_n^{\sigma ,\square }$
is a quotient of
$R_n^{\sigma ,\square }$
is a quotient of
![]() $R_\infty ^\sigma $
(as a
$R_\infty ^\sigma $
(as a
![]() $R_{\operatorname {\mathrm {loc}}}^\sigma $
-algebra), if we let
$R_{\operatorname {\mathrm {loc}}}^\sigma $
-algebra), if we let
then
![]() $R_n^{\tau ,\square }$
is a quotient of
$R_n^{\tau ,\square }$
is a quotient of
![]() $R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_\infty ^\sigma =R_\infty ^\tau $
(as a
$R_{\operatorname {\mathrm {loc}}}^\tau \otimes _{R_{\operatorname {\mathrm {loc}}}^\sigma }R_\infty ^\sigma =R_\infty ^\tau $
(as a
![]() $R_{\operatorname {\mathrm {loc}}}^\tau $
-algebra).
$R_{\operatorname {\mathrm {loc}}}^\tau $
-algebra).
Now, just as in the proof of Lemma 6.3, the map
![]() $R_n^{\sigma }\twoheadrightarrow {\mathbf T}^\sigma _n$
induces a map
$R_n^{\sigma }\twoheadrightarrow {\mathbf T}^\sigma _n$
induces a map
![]() $R_n^{\tau }\twoheadrightarrow {\overline {{\mathbf T}}}^\tau _n$
making the diagram
$R_n^{\tau }\twoheadrightarrow {\overline {{\mathbf T}}}^\tau _n$
making the diagram

commute. As the
![]() ${\mathbf T}^\sigma _n$
-action on
${\mathbf T}^\sigma _n$
-action on
![]() $M^\sigma _n$
extends to a
$M^\sigma _n$
extends to a
![]() ${\overline {{\mathbf T}}}^\tau _n$
-action (since the
${\overline {{\mathbf T}}}^\tau _n$
-action (since the
![]() $U_v$
operators naturally act on
$U_v$
operators naturally act on
![]() $M^\sigma $
), the
$M^\sigma $
), the
![]() $R^\sigma _n$
-action on
$R^\sigma _n$
-action on
![]() $M^\sigma _n$
also extends to a
$M^\sigma _n$
also extends to a
![]() $R^\tau _n$
-action on
$R^\tau _n$
-action on
![]() $M^\sigma _n$
. Passing to the framed versions (by applying
$M^\sigma _n$
. Passing to the framed versions (by applying
![]() $-\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
), it follows that the action of
$-\otimes _{R^\sigma _n}R^{\sigma ,\square }_n$
), it follows that the action of
![]() $R^{\sigma ,\square }_n$
on
$R^{\sigma ,\square }_n$
on
![]() $M^{\sigma ,\square }_n$
extends to an action of
$M^{\sigma ,\square }_n$
extends to an action of
![]() $R^{\tau ,\square }_n$
. Moreover, it’s easy to check that the isomorphism
$R^{\tau ,\square }_n$
. Moreover, it’s easy to check that the isomorphism
![]() $M^{\sigma ,\square }_n\otimes _{S_\infty }{\mathcal O}\cong M^\sigma $
is compatible with the action of the
$M^{\sigma ,\square }_n\otimes _{S_\infty }{\mathcal O}\cong M^\sigma $
is compatible with the action of the
![]() $U_v$
-operators, and so it is an isomorphism of
$U_v$
-operators, and so it is an isomorphism of
![]() ${\overline {{\mathbf T}}}^\tau $
-modules and hence of
${\overline {{\mathbf T}}}^\tau $
-modules and hence of
![]() $R^\tau $
-modules.
$R^\tau $
-modules.
Combining all of this, we can again use the ‘ultrapatching’ construction of [Reference ManningMan21, Section 4.1], with
![]() $\{R^{\tau ,\square }_n\}$
in place of
$\{R^{\tau ,\square }_n\}$
in place of
![]() $\{R^{\sigma ,\square }_n\}$
and
$\{R^{\sigma ,\square }_n\}$
and
![]() $R_\infty ^\tau $
in place of
$R_\infty ^\tau $
in place of
![]() $R_\infty ^\sigma $
. This produces a
$R_\infty ^\sigma $
. This produces a
![]() $S_\infty $
-algebra
$S_\infty $
-algebra
![]() ${\mathcal R}^\tau _\infty $
together with a surjection
${\mathcal R}^\tau _\infty $
together with a surjection
![]() $R_\infty ^\tau \twoheadrightarrow {\mathcal R}^\tau _\infty $
and an isomorphism
$R_\infty ^\tau \twoheadrightarrow {\mathcal R}^\tau _\infty $
and an isomorphism
![]() ${\mathcal R}_\infty ^\tau \otimes _{S_\infty }{\mathcal O}\cong R^\tau $
such that the composition
${\mathcal R}_\infty ^\tau \otimes _{S_\infty }{\mathcal O}\cong R^\tau $
such that the composition
is the map
![]() $R_{\operatorname {\mathrm {loc}}}^\tau \to R^\tau $
.
$R_{\operatorname {\mathrm {loc}}}^\tau \to R^\tau $
.
By the functorality of the ultrapatching construction, the maps
![]() $R_n^{\sigma ,\square }\to R_n^{\tau ,\square }$
induce an
$R_n^{\sigma ,\square }\to R_n^{\tau ,\square }$
induce an
![]() $S_\infty $
-algebra homomorphism
$S_\infty $
-algebra homomorphism
![]() $R_\infty ^\sigma = {\mathcal R}_\infty ^\sigma \to {\mathcal R}_\infty ^\tau $
. Moreover, the action of
$R_\infty ^\sigma = {\mathcal R}_\infty ^\sigma \to {\mathcal R}_\infty ^\tau $
. Moreover, the action of
![]() $R_n^{\tau ,\square }$
on
$R_n^{\tau ,\square }$
on
![]() $M^{\sigma ,\square }_n$
induces an action of
$M^{\sigma ,\square }_n$
induces an action of
![]() ${\mathcal R}_\infty ^\tau $
on
${\mathcal R}_\infty ^\tau $
on
![]() $M_\infty ^\sigma $
, extending the action of
$M_\infty ^\sigma $
, extending the action of
![]() ${\mathcal R}_\infty ^\sigma $
. In particular, we may treat
${\mathcal R}_\infty ^\sigma $
. In particular, we may treat
![]() $M_\infty ^\sigma $
as a
$M_\infty ^\sigma $
as a
![]() $R_\infty ^\tau $
-module.
$R_\infty ^\tau $
-module.
We can now finish the proof. First, we have
![]() $R_v^\sigma = R_v^\tau $
for
$R_v^\sigma = R_v^\tau $
for
![]() $v\not \in \Sigma ^{\operatorname {\varphi -uni}}$
and
$v\not \in \Sigma ^{\operatorname {\varphi -uni}}$
and
![]() $\dim R_v^\sigma = \dim R_v^\tau = 3+1$
for
$\dim R_v^\sigma = \dim R_v^\tau = 3+1$
for
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}$
, so
$v\in \Sigma ^{\operatorname {\varphi -uni}}$
, so
![]() $\dim R_\infty ^\tau = \dim R_\infty ^\sigma = \dim S_\infty $
, proving (1).
$\dim R_\infty ^\tau = \dim R_\infty ^\sigma = \dim S_\infty $
, proving (1).
We shall now show (5). First, for
![]() $v\in \Sigma \smallsetminus \Sigma ^{\operatorname {\varphi -uni}}$
, we have
$v\in \Sigma \smallsetminus \Sigma ^{\operatorname {\varphi -uni}}$
, we have
![]() $R_v^{\tau _v} = R_v^{\sigma _v}$
and
$R_v^{\tau _v} = R_v^{\sigma _v}$
and
![]() $\operatorname {\mathrm {Spec}} R_v^{\sigma _v}[1/\varpi ]$
is formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R_v^{\sigma _v}[1/\varpi ]$
is formally smooth at the point corresponding to
![]() $\lambda :R_v^{\sigma _v}\hookrightarrow R_\infty ^\sigma \xrightarrow {\lambda }{\mathcal O}$
by the above. Thus, to show (5), it suffices to show that for each
$\lambda :R_v^{\sigma _v}\hookrightarrow R_\infty ^\sigma \xrightarrow {\lambda }{\mathcal O}$
by the above. Thus, to show (5), it suffices to show that for each
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}$
,
$v\in \Sigma ^{\operatorname {\varphi -uni}}$
,
![]() $\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
is also formally smooth at the point corresponding to
$\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
is also formally smooth at the point corresponding to
![]() $\lambda :R_v^{\operatorname {\varphi -uni}}\hookrightarrow R_\infty ^\tau \xrightarrow {\lambda }{\mathcal O}$
.
$\lambda :R_v^{\operatorname {\varphi -uni}}\hookrightarrow R_\infty ^\tau \xrightarrow {\lambda }{\mathcal O}$
.
Take any such
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}$
. Recall that by assumption the representation
$v\in \Sigma ^{\operatorname {\varphi -uni}}$
. Recall that by assumption the representation
![]() $\rho |_{G_v}$
is Steinberg. Thus, the point of
$\rho |_{G_v}$
is Steinberg. Thus, the point of
![]() $\operatorname {\mathrm {Spec}} R_v^{\mathrm {un}}[1/\varpi ]$
corresponding to
$\operatorname {\mathrm {Spec}} R_v^{\mathrm {un}}[1/\varpi ]$
corresponding to
![]() $\lambda :R_v^{\mathrm {un}}\hookrightarrow R_\infty ^\sigma \xrightarrow {\lambda }{\mathcal O}$
is in the Steinberg component and not in the unramified component (it can’t lie on both components, as it corresponds to a formally smooth point of
$\lambda :R_v^{\mathrm {un}}\hookrightarrow R_\infty ^\sigma \xrightarrow {\lambda }{\mathcal O}$
is in the Steinberg component and not in the unramified component (it can’t lie on both components, as it corresponds to a formally smooth point of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma [1/\varpi ]$
, by the above argument). But now by the explicit descriptions of the rings
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma [1/\varpi ]$
, by the above argument). But now by the explicit descriptions of the rings
![]() $R_v^{\mathrm {un}}$
and
$R_v^{\mathrm {un}}$
and
![]() $R_v^{\operatorname {\varphi -uni}}$
given in Lemmas 5.3 and 5.4, it follows that the natural map
$R_v^{\operatorname {\varphi -uni}}$
given in Lemmas 5.3 and 5.4, it follows that the natural map
![]() $R_v^{\mathrm {un}}\to R_v^{\operatorname {\varphi -uni}}$
induces an isomorphism
$R_v^{\mathrm {un}}\to R_v^{\operatorname {\varphi -uni}}$
induces an isomorphism
![]() $R_v^{\mathrm {un}}/{\mathcal I}^{{\mathrm {st}}}\cong R_v^{{\operatorname {\varphi -uni}}}/I_2$
between the Steinberg quotients constructed in Lemmas 5.3 and 5.4. It follows that the point of
$R_v^{\mathrm {un}}/{\mathcal I}^{{\mathrm {st}}}\cong R_v^{{\operatorname {\varphi -uni}}}/I_2$
between the Steinberg quotients constructed in Lemmas 5.3 and 5.4. It follows that the point of
![]() $\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
corresponding to
$\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
corresponding to
![]() $\lambda :R_v^{\operatorname {\varphi -uni}}\hookrightarrow R_\infty ^\tau \xrightarrow {\lambda }{\mathcal O}$
is also contained in the Steinberg component and that
$\lambda :R_v^{\operatorname {\varphi -uni}}\hookrightarrow R_\infty ^\tau \xrightarrow {\lambda }{\mathcal O}$
is also contained in the Steinberg component and that
![]() $\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
is formally smooth at this point (which again implies that this point does not lie on any other components). This proves (5).
$\operatorname {\mathrm {Spec}} R_v^{\operatorname {\varphi -uni}}[1/\varpi ]$
is formally smooth at this point (which again implies that this point does not lie on any other components). This proves (5).
As
![]() $M_\infty ^\sigma $
is maximal Cohen–Macaulay over
$M_\infty ^\sigma $
is maximal Cohen–Macaulay over
![]() $R_\infty ^\sigma $
, it follows that it is also maximal Cohen–Macaulay over
$R_\infty ^\sigma $
, it follows that it is also maximal Cohen–Macaulay over
![]() $R_\infty ^\tau $
, and so the support of
$R_\infty ^\tau $
, and so the support of
![]() $M_\infty ^\sigma $
as an
$M_\infty ^\sigma $
as an
![]() $R_\infty ^\tau $
-module is again a union of irreducible components of
$R_\infty ^\tau $
-module is again a union of irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\tau $
. But now for each
$\operatorname {\mathrm {Spec}} R_\infty ^\tau $
. But now for each
![]() $v\in \Sigma $
, the irreducible components of
$v\in \Sigma $
, the irreducible components of
![]() $R_v^\sigma $
are in bijection with those of
$R_v^\sigma $
are in bijection with those of
![]() $R_v^\tau $
(this is trivial for
$R_v^\tau $
(this is trivial for
![]() $v\not \in \Sigma ^{\operatorname {\varphi -uni}}$
and for
$v\not \in \Sigma ^{\operatorname {\varphi -uni}}$
and for
![]() $v\in \Sigma ^{{\operatorname {\varphi -uni}}}$
follows from the description of the minimal primes of
$v\in \Sigma ^{{\operatorname {\varphi -uni}}}$
follows from the description of the minimal primes of
![]() $R^{\mathrm {un}}_v$
and
$R^{\mathrm {un}}_v$
and
![]() $R^{\operatorname {\varphi -uni}}_v$
given in Lemmas 5.3 and 5.4). By Proposition 4.7, it follows that the irreducible components of
$R^{\operatorname {\varphi -uni}}_v$
given in Lemmas 5.3 and 5.4). By Proposition 4.7, it follows that the irreducible components of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
are in bijection with those of
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
are in bijection with those of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\tau $
. Since
$\operatorname {\mathrm {Spec}} R_\infty ^\tau $
. Since
![]() $M_\infty ^\sigma $
is supported on all of
$M_\infty ^\sigma $
is supported on all of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
, it follows that
$\operatorname {\mathrm {Spec}} R_\infty ^\sigma $
, it follows that
![]() $M_\infty ^\sigma $
is supported on all of
$M_\infty ^\sigma $
is supported on all of
![]() $\operatorname {\mathrm {Spec}} R_\infty ^\tau $
as well. Since
$\operatorname {\mathrm {Spec}} R_\infty ^\tau $
as well. Since
![]() $R_\infty ^\tau $
is reduced, it follows that
$R_\infty ^\tau $
is reduced, it follows that
![]() $R_\infty ^\tau $
acts faithfully on
$R_\infty ^\tau $
acts faithfully on
![]() $M_\infty ^\sigma $
. Since the action of
$M_\infty ^\sigma $
. Since the action of
![]() $R_\infty ^\tau $
on
$R_\infty ^\tau $
on
![]() $M_\infty ^\sigma $
factors through
$M_\infty ^\sigma $
factors through
![]() $R_\infty ^\tau \twoheadrightarrow {\mathcal R}_\infty ^\tau $
, it follows that
$R_\infty ^\tau \twoheadrightarrow {\mathcal R}_\infty ^\tau $
, it follows that
![]() $R_\infty ^\tau \cong {\mathcal R}_\infty ^\tau $
.
$R_\infty ^\tau \cong {\mathcal R}_\infty ^\tau $
.
Just as before, (2) and (3) follow from this, and again, the second part of (3) implies that to show that
![]() $R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
is an isomorphism, it will suffice to show that the induced map
$R^\tau \twoheadrightarrow {\overline {{\mathbf T}}}^\tau $
is an isomorphism, it will suffice to show that the induced map
![]() $R^\tau [1/\varpi ]\twoheadrightarrow {\overline {{\mathbf T}}}^\tau [1/\varpi ]$
is.
$R^\tau [1/\varpi ]\twoheadrightarrow {\overline {{\mathbf T}}}^\tau [1/\varpi ]$
is.
To prove (4), consider the commutative diagram

As the bottom map is an isomorphism of finite free reduced E-algebras, to show that the top map is an isomorphism, it will suffice to show that for any
![]() ${\overline {{\mathbf Q}}}_p$
point
${\overline {{\mathbf Q}}}_p$
point
![]() $\eta :{\mathbf T}^\sigma [1/\varpi ]\to {\overline {{\mathbf Q}}}_p$
of
$\eta :{\mathbf T}^\sigma [1/\varpi ]\to {\overline {{\mathbf Q}}}_p$
of
![]() $\operatorname {\mathrm {Spec}} {\mathbf T}^\sigma \cong \operatorname {\mathrm {Spec}} R^\sigma $
the induced map
$\operatorname {\mathrm {Spec}} {\mathbf T}^\sigma \cong \operatorname {\mathrm {Spec}} R^\sigma $
the induced map
![]() $R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\twoheadrightarrow {\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is an isomorphism.
$R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\twoheadrightarrow {\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is an isomorphism.
Fix any such
![]() $\eta :{\mathbf T}^\sigma [1/\varpi ]\to {\overline {{\mathbf Q}}}_p$
. Then
$\eta :{\mathbf T}^\sigma [1/\varpi ]\to {\overline {{\mathbf Q}}}_p$
. Then
![]() $\eta $
corresponds to a modular Galois representation
$\eta $
corresponds to a modular Galois representation
![]() $\rho _\eta :G_F\to {\mathrm {GL}}_2({\overline {{\mathbf Q}}}_p)$
lifting
$\rho _\eta :G_F\to {\mathrm {GL}}_2({\overline {{\mathbf Q}}}_p)$
lifting
![]() $\overline {\rho }$
. For each
$\overline {\rho }$
. For each
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}$
,
$v\in \Sigma ^{\operatorname {\varphi -uni}}$
,
![]() $\overline {\rho }|_{G_{F_v}}$
must be either Steinberg or unramified. Let
$\overline {\rho }|_{G_{F_v}}$
must be either Steinberg or unramified. Let
![]() $S_\eta \subseteq \Sigma ^{\operatorname {\varphi -uni}}$
be the set of
$S_\eta \subseteq \Sigma ^{\operatorname {\varphi -uni}}$
be the set of
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}$
for which
$v\in \Sigma ^{\operatorname {\varphi -uni}}$
for which
![]() $\rho _\eta |_{G_{F_v}}$
is unramified.
$\rho _\eta |_{G_{F_v}}$
is unramified.
By Equation 4.2 and Definition 4.2, we have
![]() $R^\tau = R^\sigma \left [a_v\middle |v\in \Sigma ^{\operatorname {\varphi -uni}}\right ]$
as subrings of
$R^\tau = R^\sigma \left [a_v\middle |v\in \Sigma ^{\operatorname {\varphi -uni}}\right ]$
as subrings of
![]() $R^\tau $
, where for each
$R^\tau $
, where for each
![]() $v\in \Sigma $
,
$v\in \Sigma $
,
![]() $a_v$
is the chosen root of the characteristic polynomial of
$a_v$
is the chosen root of the characteristic polynomial of
![]() $\rho _{\eta }(\operatorname {\mathrm {Frob}}_v)$
. Hence,
$\rho _{\eta }(\operatorname {\mathrm {Frob}}_v)$
. Hence,
For
![]() $v\in \Sigma ^{\operatorname {\varphi -uni}}\smallsetminus S_\eta $
(so that
$v\in \Sigma ^{\operatorname {\varphi -uni}}\smallsetminus S_\eta $
(so that
![]() $\rho _\eta |_{G_{F_v}}$
is Steinberg) the definition of
$\rho _\eta |_{G_{F_v}}$
is Steinberg) the definition of
![]() $R_v^{\operatorname {\varphi -uni}}$
implies that
$R_v^{\operatorname {\varphi -uni}}$
implies that
![]() $a_v=\pm 1\in {\overline {{\mathbf Q}}}_p$
, so in fact,
$a_v=\pm 1\in {\overline {{\mathbf Q}}}_p$
, so in fact,
![]() $R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p = {\overline {{\mathbf Q}}}_p\left [a_v\middle |v\in S_\eta \right ]$
, and so
$R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p = {\overline {{\mathbf Q}}}_p\left [a_v\middle |v\in S_\eta \right ]$
, and so
![]() $R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is a quotient of
$R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is a quotient of
In particular, we have
![]() $\dim _{{\overline {{\mathbf Q}}}_p}R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\le 2^{|S_\eta |}$
.
$\dim _{{\overline {{\mathbf Q}}}_p}R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\le 2^{|S_\eta |}$
.
On the other hand,
![]() ${\overline {{\mathbf T}}}^\tau = {\mathbf T}^\sigma \left [U_v\middle |v\in \Sigma ^{\operatorname {\varphi -uni}}\right ]$
is a subalgebra of
${\overline {{\mathbf T}}}^\tau = {\mathbf T}^\sigma \left [U_v\middle |v\in \Sigma ^{\operatorname {\varphi -uni}}\right ]$
is a subalgebra of
![]() $\operatorname {\mathrm {End}}_{{\mathcal O}}(M^\tau )$
, and so
$\operatorname {\mathrm {End}}_{{\mathcal O}}(M^\tau )$
, and so
is a subalgebra of
![]() $\operatorname {\mathrm {End}}_{{\overline {{\mathbf Q}}}_p}(M^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p)$
(where the last inequality comes from the fact that
$\operatorname {\mathrm {End}}_{{\overline {{\mathbf Q}}}_p}(M^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p)$
(where the last inequality comes from the fact that
![]() $U_v$
acts as a scalar on
$U_v$
acts as a scalar on
![]() $M^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
if
$M^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
if
![]() $\rho _\eta |_{G_{F_v}}$
is Steinberg). But now as
$\rho _\eta |_{G_{F_v}}$
is Steinberg). But now as
![]() $\rho _\eta $
is unramified at each
$\rho _\eta $
is unramified at each
![]() $v\in S_\eta $
, it corresponds to a Hilbert modular form
$v\in S_\eta $
, it corresponds to a Hilbert modular form
![]() $f_\eta $
of level not divisible by any
$f_\eta $
of level not divisible by any
![]() $v\in S_\eta $
. Standard properties of Hilbert modular forms now imply that
$v\in S_\eta $
. Standard properties of Hilbert modular forms now imply that
![]() $\dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p = \dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf Q}}}_p\left [U_v\middle |v\in S_\eta \right ] = 2^{|S_\eta |}$
; we are using here that the
$\dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p = \dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf Q}}}_p\left [U_v\middle |v\in S_\eta \right ] = 2^{|S_\eta |}$
; we are using here that the
![]() $U_v$
for
$U_v$
for
![]() $v \in S_\eta $
act as independent nonscalar endomorphisms on the
$v \in S_\eta $
act as independent nonscalar endomorphisms on the
![]() $2^{|S_\eta |}$
dimensional (
$2^{|S_\eta |}$
dimensional (
![]() ${\overline {{\mathbf Q}}}_p$
-) vector space generated by the image of
${\overline {{\mathbf Q}}}_p$
-) vector space generated by the image of
![]() $f_\eta $
under the standard degeneracy maps arising from the places
$f_\eta $
under the standard degeneracy maps arising from the places
![]() $v \in S_\eta $
. Thus,
$v \in S_\eta $
. Thus,
![]() $\dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p= 2^{|S_\eta |} \ge \dim _{{\overline {{\mathbf Q}}}_p}R^\tau \otimes _\eta $
, and so as the map
$\dim _{{\overline {{\mathbf Q}}}_p}{\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p= 2^{|S_\eta |} \ge \dim _{{\overline {{\mathbf Q}}}_p}R^\tau \otimes _\eta $
, and so as the map
![]() $R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\twoheadrightarrow {\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is surjective, it must be an isomorphism. This completes the proof of (4), and thus of the theorem.
$R^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p\twoheadrightarrow {\overline {{\mathbf T}}}^\tau \otimes _\eta {\overline {{\mathbf Q}}}_p$
is surjective, it must be an isomorphism. This completes the proof of (4), and thus of the theorem.
Combining this with Proposition 3.32 and the computations in Section 5 gives the following generalization of [Reference Böckle, Khare and ManningBKM21, Theorem 10.1]:
Theorem 6.5. In setting described in this section, we have:
 $$\begin{align*}\delta(R^\tau) = \delta({\mathbf T}^\tau) = \sum_{v\in\Sigma^{{\mathrm{st}}}}\frac{2n_v}{e}+\sum_{v\in\Sigma^{{\operatorname{\varphi-uni}}}}\frac{3n_v}{e}+\sum_{v\in\Sigma^{{\mathrm{uni}}}}\frac{n_v}{e}, \end{align*}$$
$$\begin{align*}\delta(R^\tau) = \delta({\mathbf T}^\tau) = \sum_{v\in\Sigma^{{\mathrm{st}}}}\frac{2n_v}{e}+\sum_{v\in\Sigma^{{\operatorname{\varphi-uni}}}}\frac{3n_v}{e}+\sum_{v\in\Sigma^{{\mathrm{uni}}}}\frac{n_v}{e}, \end{align*}$$
where
![]() $n_v$
is as above, and e is the ramification index of
$n_v$
is as above, and e is the ramification index of
![]() $E/{\mathbf Q}_p$
.
$E/{\mathbf Q}_p$
.
Proof. Theorem 6.4 implies that the map
![]() $\theta :S_\infty \to R_\infty ^\tau $
satisfies property (P), and so Theorem 3.25 implies that implies that
$\theta :S_\infty \to R_\infty ^\tau $
satisfies property (P), and so Theorem 3.25 implies that implies that
Now, by Proposition 3.32 and Proposition 3.28 we get
 $$ \begin{align*} \delta_\lambda(R_\infty^\tau) &= \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau[[x_1,\ldots,x_g]]) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau)+\delta_\lambda({\mathcal O}[[x_1,\ldots,x_g]]) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau)\\ &= \delta_\lambda\left(\left({\widehat{\bigotimes_{{v\in \Sigma}}}}R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}} R_v^{\operatorname{\mathrm{fl}}}\right)\right) = \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})+\sum_{v|p}\delta_\lambda(R_v^{\operatorname{\mathrm{fl}}})\\ &= \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})+\sum_{v|p}\delta_\lambda({\mathcal O}[[x_1,\ldots,x_{3+[F_v:{\mathbf Q}_p]}]]) = \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})\\ &= \sum_{v\in \Sigma^{{\operatorname{min}}}}\delta_\lambda(R_v^{{\operatorname{min}}}) +\sum_{v\in \Sigma^{{\mathrm{st}}}}\delta_\lambda(R_v^{{\mathrm{st}}}) +\sum_{v\in \Sigma^{{\operatorname{\varphi-uni}}}}\delta_\lambda(R_v^{{\operatorname{\varphi-uni}}}) +\sum_{v\in \Sigma^{{\mathrm{uni}}}}\delta_\lambda(R_v^{{\mathrm{uni}}}) +\sum_{v\in \Sigma^{\square}}\delta_\lambda(R_v^{\square}). \end{align*} $$
$$ \begin{align*} \delta_\lambda(R_\infty^\tau) &= \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau[[x_1,\ldots,x_g]]) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau)+\delta_\lambda({\mathcal O}[[x_1,\ldots,x_g]]) = \delta_\lambda(R_{\operatorname{\mathrm{loc}}}^\tau)\\ &= \delta_\lambda\left(\left({\widehat{\bigotimes_{{v\in \Sigma}}}}R_v^{\tau_v}\right){\widehat{\otimes}}_{\mathcal O}\left( {\widehat{\bigotimes_{{v|p}}}} R_v^{\operatorname{\mathrm{fl}}}\right)\right) = \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})+\sum_{v|p}\delta_\lambda(R_v^{\operatorname{\mathrm{fl}}})\\ &= \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})+\sum_{v|p}\delta_\lambda({\mathcal O}[[x_1,\ldots,x_{3+[F_v:{\mathbf Q}_p]}]]) = \sum_{v\in \Sigma}\delta_\lambda(R_v^{\tau_v})\\ &= \sum_{v\in \Sigma^{{\operatorname{min}}}}\delta_\lambda(R_v^{{\operatorname{min}}}) +\sum_{v\in \Sigma^{{\mathrm{st}}}}\delta_\lambda(R_v^{{\mathrm{st}}}) +\sum_{v\in \Sigma^{{\operatorname{\varphi-uni}}}}\delta_\lambda(R_v^{{\operatorname{\varphi-uni}}}) +\sum_{v\in \Sigma^{{\mathrm{uni}}}}\delta_\lambda(R_v^{{\mathrm{uni}}}) +\sum_{v\in \Sigma^{\square}}\delta_\lambda(R_v^{\square}). \end{align*} $$
Now, Proposition 4.6 implies that
![]() $R_v^{{\operatorname {min}}}$
and
$R_v^{{\operatorname {min}}}$
and
![]() $R_v^{\square }$
are complete intersections, and so Proposition 3.28 gives
$R_v^{\square }$
are complete intersections, and so Proposition 3.28 gives
![]() $\delta _\lambda (R_v^{{\operatorname {min}}}) = 0=\delta _\lambda (R_v^{\square })$
. Thus, the claim follows by the computations in Theorems 5.18, 5.26 and 5.33.
$\delta _\lambda (R_v^{{\operatorname {min}}}) = 0=\delta _\lambda (R_v^{\square })$
. Thus, the claim follows by the computations in Theorems 5.18, 5.26 and 5.33.
Remark 6.6. While Theorem 6.5 only computes the ‘noncohomological’ Wiles defect, and [Reference Böckle, Khare and ManningBKM21, Theorem 10.1] computes both the cohomological and noncohomological defects, we still have these defects are equal in the minimal level case (i.e.,
![]() $\Sigma ^{{\mathrm {un}}}=\Sigma ^{{\operatorname {\varphi -uni}}}=\Sigma ^\square = \varnothing $
) by [Reference ManningMan21, Theorem 1.2] and [Reference Böckle, Khare and ManningBKM21, Theorem 3.12].
$\Sigma ^{{\mathrm {un}}}=\Sigma ^{{\operatorname {\varphi -uni}}}=\Sigma ^\square = \varnothing $
) by [Reference ManningMan21, Theorem 1.2] and [Reference Böckle, Khare and ManningBKM21, Theorem 3.12].
In the next section, we show that in fact our work here, which determines the defect of Hecke algebras and deformation rings, can be used to show an equality of cohomological and noncohomological defects in many situations.
7 Cohomological Wiles defects and degrees of parametrizations by Shimura curves
The main theorem of this paper, Theorem 6.5, that we have proven above computes Wiles defects of Hecke algebras acting on the cohomology of modular curves and Shimura curves. We use this to compute in the present section the Wiles defect of the modules of the Hecke algebras of Theorem 6.5 that are given by the cohomology of the Shimura curve on which the respective Hecke algebras acts faithfully; Theorem 7.5 and Proposition 7.7 below.
Our methods here also allow us to improve on the results of [Reference Ribet and TakahashiRT97] about degrees of optimal parametrizations of elliptic curves over
![]() ${\mathbf Q}$
by Shimura curves: See Corollaries 7.9 and 7.10 below. (By optimal we mean as usual that the induced maps on the Jacobian of the Shimura curve has connected kernel.) Our approach diverges considerably from the one of [Reference Ribet and TakahashiRT97]. Our proofs are rather indirect but fill in a lacuna caused by the basic problem that one does not know in generality surjectivity of maps on p-parts of component groups at primes q (of multiplicative reduction), induced by optimal parametrization of an elliptic curve E over
${\mathbf Q}$
by Shimura curves: See Corollaries 7.9 and 7.10 below. (By optimal we mean as usual that the induced maps on the Jacobian of the Shimura curve has connected kernel.) Our approach diverges considerably from the one of [Reference Ribet and TakahashiRT97]. Our proofs are rather indirect but fill in a lacuna caused by the basic problem that one does not know in generality surjectivity of maps on p-parts of component groups at primes q (of multiplicative reduction), induced by optimal parametrization of an elliptic curve E over
![]() ${\mathbf Q}$
by a Shimura curve which has multiplicative reduction at q (the prime q divides the discriminant of the quaternion algebra from which the Shimura curve arises). The difficulty of proving the surjectivity alluded to above is specially vexing when considering component groups at a prime q that is trivial for
${\mathbf Q}$
by a Shimura curve which has multiplicative reduction at q (the prime q divides the discriminant of the quaternion algebra from which the Shimura curve arises). The difficulty of proving the surjectivity alluded to above is specially vexing when considering component groups at a prime q that is trivial for
![]() $E[p]$
(and thus in particular q is not 1 mod p). Both corollaries are deduced from Theorem 7.5 and Proposition 7.7. We only consider non-Eisenstein primes, namely primes p such that
$E[p]$
(and thus in particular q is not 1 mod p). Both corollaries are deduced from Theorem 7.5 and Proposition 7.7. We only consider non-Eisenstein primes, namely primes p such that
![]() $E[p]$
is irreducible. The arguments in [Reference Ribet and TakahashiRT97, page 11113] rely on auxiliary hypotheses: for instance, that there is a prime q such that the image of an inertia group
$E[p]$
is irreducible. The arguments in [Reference Ribet and TakahashiRT97, page 11113] rely on auxiliary hypotheses: for instance, that there is a prime q such that the image of an inertia group
![]() $I_q$
at q acting on
$I_q$
at q acting on
![]() $E[p]$
has image of order p. This hypothesis is fulfilled when E is a semistable elliptic curve over
$E[p]$
has image of order p. This hypothesis is fulfilled when E is a semistable elliptic curve over
![]() ${\mathbf Q}$
and
${\mathbf Q}$
and
![]() $E[p]$
is irreducible, our methods allow one to consider all elliptic curves over
$E[p]$
is irreducible, our methods allow one to consider all elliptic curves over
![]() ${\mathbf Q}$
provided
${\mathbf Q}$
provided
![]() $E[p]$
is irreducible as a
$E[p]$
is irreducible as a
![]() $G_{{\mathbf Q}(\zeta _p)}$
-module. We work with the setup in [Reference Böckle, Khare and ManningBKM21, Section 5] and thus operate (mainly for simplicity) at less generality than the work in the previous sections (for instance, we will assume
$G_{{\mathbf Q}(\zeta _p)}$
-module. We work with the setup in [Reference Böckle, Khare and ManningBKM21, Section 5] and thus operate (mainly for simplicity) at less generality than the work in the previous sections (for instance, we will assume
![]() $F={\mathbf Q}$
.) There are slight differences between the setup here and that of [Reference Böckle, Khare and ManningBKM21, Section 5] that we begin by highlighting.
$F={\mathbf Q}$
.) There are slight differences between the setup here and that of [Reference Böckle, Khare and ManningBKM21, Section 5] that we begin by highlighting.
7.1 Cohomological Wiles defects
Fix Q a finite set of primes, and let
![]() $D_Q$
be the quaternion algebra over
$D_Q$
be the quaternion algebra over
![]() ${\mathbf Q}$
considered in [Reference Böckle, Khare and ManningBKM21, §5]: It is definite if Q has odd cardinality and indefinite if Q is of even cardinality. (By abuse of notation, we will also frequently use Q to denote the product of all the primes in the set Q. The context will make clear which meaning is intended.) We assume here that Q has even cardinality and thus
${\mathbf Q}$
considered in [Reference Böckle, Khare and ManningBKM21, §5]: It is definite if Q has odd cardinality and indefinite if Q is of even cardinality. (By abuse of notation, we will also frequently use Q to denote the product of all the primes in the set Q. The context will make clear which meaning is intended.) We assume here that Q has even cardinality and thus
![]() $D_Q$
is an indefinite quaternion algebra. For a positive integer N with
$D_Q$
is an indefinite quaternion algebra. For a positive integer N with
![]() $(N,Q)=1$
let
$(N,Q)=1$
let
![]() $\Gamma _0^{Q}(N)$
be the congruence subgroup for
$\Gamma _0^{Q}(N)$
be the congruence subgroup for
![]() $D_{Q}^\times $
, which is maximal compact at primes in Q, and upper triangular mod
$D_{Q}^\times $
, which is maximal compact at primes in Q, and upper triangular mod
![]() $\ell $
for all
$\ell $
for all
![]() $\ell |N$
. We consider also the usual congruence subgroups
$\ell |N$
. We consider also the usual congruence subgroups
![]() $\Gamma _0(NQ)$
and
$\Gamma _0(NQ)$
and
![]() $\Gamma _0(N^2Q^2)$
of
$\Gamma _0(N^2Q^2)$
of
![]() ${\mathrm {SL}}_2({\mathbf Z})$
. Let
${\mathrm {SL}}_2({\mathbf Z})$
. Let
![]() $K_0(N^2Q^2)\subseteq {\mathrm {GL}}_2({\mathbf A}_{{\mathbf Q},f})$
and
$K_0(N^2Q^2)\subseteq {\mathrm {GL}}_2({\mathbf A}_{{\mathbf Q},f})$
and
![]() $K_0^{Q}(NQ)\subseteq D_{Q}^\times ({\mathbf A}_{{\mathbf Q},f})$
be the corresponding compact open subgroups. Let
$K_0^{Q}(NQ)\subseteq D_{Q}^\times ({\mathbf A}_{{\mathbf Q},f})$
be the corresponding compact open subgroups. Let
![]() $N^\prime $
be the squarefree part of N.
$N^\prime $
be the squarefree part of N.
We consider
![]() $X^{Q}_0(N)$
the (compact) Riemann surface
$X^{Q}_0(N)$
the (compact) Riemann surface
(where
![]() ${\mathcal {H}}$
is the complex upper half plane). Give
${\mathcal {H}}$
is the complex upper half plane). Give
![]() $X^{Q}_0(N)$
its canonical structure as an algebraic curve over
$X^{Q}_0(N)$
its canonical structure as an algebraic curve over
![]() ${\mathbf Q}$
. Let as before p be a prime not dividing
${\mathbf Q}$
. Let as before p be a prime not dividing
![]() $2NQ$
, and we fix a finite extension
$2NQ$
, and we fix a finite extension
![]() $E/{\mathbf Q}_p$
, with
$E/{\mathbf Q}_p$
, with
![]() ${\mathcal O}$
the ring of integers in E,
${\mathcal O}$
the ring of integers in E,
![]() $\varpi $
a uniformizer,
$\varpi $
a uniformizer,
![]() $k={\mathcal O}/\varpi $
the residue field, and e the ramification index of
$k={\mathcal O}/\varpi $
the residue field, and e the ramification index of
![]() $E/{\mathbf Q}_p$
. We will assume below that E is sufficiently large so that
$E/{\mathbf Q}_p$
. We will assume below that E is sufficiently large so that
![]() ${\mathcal O}$
contains the Fourier coefficients of all newforms in
${\mathcal O}$
contains the Fourier coefficients of all newforms in
![]() $S_2(\Gamma _0(N^2Q^2))$
. Consider the finite free
$S_2(\Gamma _0(N^2Q^2))$
. Consider the finite free
![]() ${\mathcal O}$
-modules
${\mathcal O}$
-modules
![]() $S^{Q}(\Gamma _0^{Q}(N))=H^1(X^{Q}_0(N),{\mathcal O})$
,
$S^{Q}(\Gamma _0^{Q}(N))=H^1(X^{Q}_0(N),{\mathcal O})$
,
![]() $S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})$
and
$S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})$
and
![]() $S(NQ)=H^1(X_0(NQ),{\mathcal O})$
. Let
$S(NQ)=H^1(X_0(NQ),{\mathcal O})$
. Let
![]() ${\mathbf T}(N^2Q^2)$
,
${\mathbf T}(N^2Q^2)$
,
![]() ${\mathbf T}(NQ)$
and
${\mathbf T}(NQ)$
and
![]() ${\mathbf T}^{Q}(N)$
be the
${\mathbf T}^{Q}(N)$
be the
![]() ${\mathcal O}$
-algebras at level
${\mathcal O}$
-algebras at level
![]() $\Gamma _0(NQ^2)$
,
$\Gamma _0(NQ^2)$
,
![]() $\Gamma _0(NQ)$
and
$\Gamma _0(NQ)$
and
![]() $\Gamma _0^{Q}(N)$
, respectively, generated by the Hecke operators
$\Gamma _0^{Q}(N)$
, respectively, generated by the Hecke operators
![]() $T_r$
for primes r coprime to
$T_r$
for primes r coprime to
![]() $NQ$
acting on
$NQ$
acting on
![]() $S(N^2Q^2)$
,
$S(N^2Q^2)$
,
![]() $S(NQ)$
and
$S(NQ)$
and
![]() $S^{Q}(\Gamma _0^{Q}(N))$
. (We call such Hecke algebras deprived of operators
$S^{Q}(\Gamma _0^{Q}(N))$
. (We call such Hecke algebras deprived of operators
![]() $U_r$
for dividing the level anemic Hecke algebras.) Note that by the Jacquet–Langlands correspondence,
$U_r$
for dividing the level anemic Hecke algebras.) Note that by the Jacquet–Langlands correspondence,
![]() ${\mathbf T}^{Q}(N)$
is a quotient of
${\mathbf T}^{Q}(N)$
is a quotient of
![]() ${\mathbf T}(N^2Q^2)$
, and this quotient factors through
${\mathbf T}(N^2Q^2)$
, and this quotient factors through
![]() ${\mathbf T}(NQ)$
.
${\mathbf T}(NQ)$
.
Let
![]() $f \in S_2(\Gamma _0(NQ))$
be a newform of level
$f \in S_2(\Gamma _0(NQ))$
be a newform of level
![]() $NQ$
such that all its Fourier coefficients lie in E, and consider the corresponding
$NQ$
such that all its Fourier coefficients lie in E, and consider the corresponding
![]() ${\mathcal O}$
-algebra homomorphisms
${\mathcal O}$
-algebra homomorphisms
![]() $\lambda _f:{\mathbf T}(N^2Q^2) \to {\mathcal O}$
and (abusing notation slightly)
$\lambda _f:{\mathbf T}(N^2Q^2) \to {\mathcal O}$
and (abusing notation slightly)
![]() $\lambda _f:{\mathbf T}(NQ) \to {\mathcal O}$
. We will fix this newform and our main results will be in relation to f. By the Jacquet–Langlands correspondence, this also gives a related homomorphism
$\lambda _f:{\mathbf T}(NQ) \to {\mathcal O}$
. We will fix this newform and our main results will be in relation to f. By the Jacquet–Langlands correspondence, this also gives a related homomorphism
![]() ${\mathbf T}^{Q}(N) \to {\mathcal O}$
that we again denote by the same symbol
${\mathbf T}^{Q}(N) \to {\mathcal O}$
that we again denote by the same symbol
![]() $\lambda _f$
. We denote the corresponding maximal ideals which contain the prime ideal
$\lambda _f$
. We denote the corresponding maximal ideals which contain the prime ideal
![]() $\ker (\lambda _f)$
by the same symbol
$\ker (\lambda _f)$
by the same symbol
![]() ${\mathfrak m}$
. Let
${\mathfrak m}$
. Let
![]() $\rho _f : G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathcal O})$
be the Galois representation associated by Eichler and Shimura to f and assume that the corresponding residual Galois representation
$\rho _f : G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathcal O})$
be the Galois representation associated by Eichler and Shimura to f and assume that the corresponding residual Galois representation
![]() $\overline {\rho }_f=\overline {\rho } :G_{\mathbf Q}\to {\mathrm {GL}}_2(k)$
is absolutely irreducible. By enlarging
$\overline {\rho }_f=\overline {\rho } :G_{\mathbf Q}\to {\mathrm {GL}}_2(k)$
is absolutely irreducible. By enlarging
![]() ${\mathcal O}$
if necessary, we may assume that k contains all eigenvalues of
${\mathcal O}$
if necessary, we may assume that k contains all eigenvalues of
![]() $\overline {\rho }(\sigma )$
for all
$\overline {\rho }(\sigma )$
for all
![]() $\sigma \in G_{\mathbf Q}$
. The Galois representation
$\sigma \in G_{\mathbf Q}$
. The Galois representation
![]() $\rho _f:G_{\mathbf Q} \to {\mathrm {GL}}_2(E)$
, with irreducible residual representation
$\rho _f:G_{\mathbf Q} \to {\mathrm {GL}}_2(E)$
, with irreducible residual representation
![]() $\overline {\rho }$
, is locally at primes
$\overline {\rho }$
, is locally at primes
![]() $q\in Q$
of the form
$q\in Q$
of the form
 $$\begin{align*}\left( \begin{array}{cc} \varepsilon_p& \ast \\ 0 & 1 \end{array} \right),\end{align*}$$
$$\begin{align*}\left( \begin{array}{cc} \varepsilon_p& \ast \\ 0 & 1 \end{array} \right),\end{align*}$$
up to twist by an unramified character
![]() $\chi $
of order dividing 2. The
$\chi $
of order dividing 2. The
![]() $\beta _q \in \{\pm 1\}$
of Section 4 (see discussion after Equation (4.1)) will be chosen so that
$\beta _q \in \{\pm 1\}$
of Section 4 (see discussion after Equation (4.1)) will be chosen so that
![]() $\rho _f|_{G_q}$
gives rise to a point of
$\rho _f|_{G_q}$
gives rise to a point of
![]() $\operatorname {\mathrm {Spec}} R_q^{{\mathrm {st}}}$
in what follows (and thus depends on whether
$\operatorname {\mathrm {Spec}} R_q^{{\mathrm {st}}}$
in what follows (and thus depends on whether
![]() $\chi $
is trivial or not). Let
$\chi $
is trivial or not). Let
![]() ${\mathcal A}_f$
stand for the isogeny class of the abelian variety
${\mathcal A}_f$
stand for the isogeny class of the abelian variety
![]() $A_f$
(which is an optimal quotient of
$A_f$
(which is an optimal quotient of
![]() $J_0(NQ)$
). The residual representations arising from the class
$J_0(NQ)$
). The residual representations arising from the class
![]() ${\mathcal A}_f$
with respect to the fixed embedding
${\mathcal A}_f$
with respect to the fixed embedding
![]() $K_f \hookrightarrow \overline {\mathbf Q}_p$
are all isomorphic to our fixed absolutely irreducible
$K_f \hookrightarrow \overline {\mathbf Q}_p$
are all isomorphic to our fixed absolutely irreducible
![]() $\overline {\rho }$
. Consider the representation
$\overline {\rho }$
. Consider the representation
![]() $\rho _f:G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathcal O})$
arising from
$\rho _f:G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathcal O})$
arising from
![]() $A_f$
. As in [Reference Böckle, Khare and ManningBKM21, Definition 7.7], we define the invariants
$A_f$
. As in [Reference Böckle, Khare and ManningBKM21, Definition 7.7], we define the invariants
![]() $m_q,n_q$
for
$m_q,n_q$
for
![]() $q \in Q$
as follows. The representation
$q \in Q$
as follows. The representation
![]() $\rho _f|_{G_q}:G_q \rightarrow {\mathrm {GL}}_2({\mathcal O})$
is of the form
$\rho _f|_{G_q}:G_q \rightarrow {\mathrm {GL}}_2({\mathcal O})$
is of the form
 $$\begin{align*}\left( \begin{array}{cc} \varepsilon_p & \ast \\ 0 & 1 \end{array} \right)\end{align*}$$
$$\begin{align*}\left( \begin{array}{cc} \varepsilon_p & \ast \\ 0 & 1 \end{array} \right)\end{align*}$$
up to twist by an unramified character of order dividing 2 and is ramified (i.e., generic). We define the local invariants
![]() $m_q$
(respectively,
$m_q$
(respectively,
![]() $n_q$
) to be the largest integer n such that
$n_q$
) to be the largest integer n such that
![]() $\rho _\lambda (I_q)$
(respectively,
$\rho _\lambda (I_q)$
(respectively,
![]() $\rho _\lambda (G_q)$
) mod
$\rho _\lambda (G_q)$
) mod
![]() $\varpi ^n$
has trivial projective image.
$\varpi ^n$
has trivial projective image.
There is an oldform
![]() $f^{NQ}$
in
$f^{NQ}$
in
![]() $S_2(\Gamma _0(N^2Q^2))$
with corresponding newform f which is characterized by the property that it is an eigenform for the Hecke operators
$S_2(\Gamma _0(N^2Q^2))$
with corresponding newform f which is characterized by the property that it is an eigenform for the Hecke operators
![]() $T_\ell $
for
$T_\ell $
for
![]() $\ell $
prime with
$\ell $
prime with
![]() $(\ell ,NQ)=1$
and
$(\ell ,NQ)=1$
and
![]() $U_\ell $
for
$U_\ell $
for
![]() $\ell |NQ$
and such that
$\ell |NQ$
and such that
![]() $a_\ell (f^{NQ})=0$
, that is,
$a_\ell (f^{NQ})=0$
, that is,
![]() $f^Q|U_\ell =0$
, for
$f^Q|U_\ell =0$
, for
![]() $\ell |NQ$
. Let
$\ell |NQ$
. Let
![]() $\lambda _{f^{NQ}}: {\mathbf T}^{\mathrm {full}}(N^2Q^2) \to {\mathcal O}$
be the induced homomorphism of the full Hecke algebra
$\lambda _{f^{NQ}}: {\mathbf T}^{\mathrm {full}}(N^2Q^2) \to {\mathcal O}$
be the induced homomorphism of the full Hecke algebra
![]() ${\mathbf T}^{\mathrm {full}}(N^2Q^2)$
acting on
${\mathbf T}^{\mathrm {full}}(N^2Q^2)$
acting on
![]() $H^1(X_0(N^2Q^2),{\mathcal O})$
which is generated as an
$H^1(X_0(N^2Q^2),{\mathcal O})$
which is generated as an
![]() ${\mathcal O}$
-algebra by the action of the Hecke operators
${\mathcal O}$
-algebra by the action of the Hecke operators
![]() $T_\ell $
for
$T_\ell $
for
![]() $(\ell ,NQ^2)=1$
and
$(\ell ,NQ^2)=1$
and
![]() $U_\ell $
for
$U_\ell $
for
![]() $\ell |NQ$
on
$\ell |NQ$
on
![]() $S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})$
. We denote by
$S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})$
. We denote by
![]() ${\mathfrak m}_{Q}$
the maximal ideal of
${\mathfrak m}_{Q}$
the maximal ideal of
![]() ${\mathbf T}^{\mathrm {full}}(N^2Q^2)$
that contains the kernel of
${\mathbf T}^{\mathrm {full}}(N^2Q^2)$
that contains the kernel of
![]() $\lambda _{f^{NQ}}$
.
$\lambda _{f^{NQ}}$
.
The homomorphism
![]() $\lambda _f: {\mathbf T}^{Q}(N) \to {\mathcal O}$
extends to the full Hecke algebra
$\lambda _f: {\mathbf T}^{Q}(N) \to {\mathcal O}$
extends to the full Hecke algebra
![]() ${\mathbf T}^Q(N)^{\mathrm {full}}$
(which has operators
${\mathbf T}^Q(N)^{\mathrm {full}}$
(which has operators
![]() $U_r$
for r dividing
$U_r$
for r dividing
![]() $NQ$
) acting on
$NQ$
) acting on
![]() $S^Q(\Gamma _0^{Q}(N))$
, and we denote by
$S^Q(\Gamma _0^{Q}(N))$
, and we denote by
![]() ${\mathfrak m}_{Q}$
again the maximal ideal of
${\mathfrak m}_{Q}$
again the maximal ideal of
![]() ${\mathbf T}^Q(N)^{\mathrm {full}}$
which contains the kernel of the extended homomorphism. We define
${\mathbf T}^Q(N)^{\mathrm {full}}$
which contains the kernel of the extended homomorphism. We define
![]() ${\mathbf T}$
,
${\mathbf T}$
,
![]() ${\mathbf T}^{{\mathrm {uni}}}$
(resp.
${\mathbf T}^{{\mathrm {uni}}}$
(resp.
![]() ${\mathbf T}^{{\mathrm {st}},{Q}} $
) to be the image of
${\mathbf T}^{{\mathrm {st}},{Q}} $
) to be the image of
![]() ${\mathbf T}(NQ^2)$
(resp.
${\mathbf T}(NQ^2)$
(resp.
![]() ${\mathbf T}^{Q}(N)$
) in the endomorphisms of the finitely generated
${\mathbf T}^{Q}(N)$
) in the endomorphisms of the finitely generated
![]() ${\mathcal O}$
-modules
${\mathcal O}$
-modules
![]() $S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})_{{\mathfrak m}_Q}$
,
$S(N^2Q^2)=H^1(X_0(N^2Q^2),{\mathcal O})_{{\mathfrak m}_Q}$
,
![]() $S(NQ)=H^1(X_0(NQ),{\mathcal O})_{{\mathfrak m}}$
(resp.
$S(NQ)=H^1(X_0(NQ),{\mathcal O})_{{\mathfrak m}}$
(resp.
![]() $S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}$
).
$S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}$
).
We denote by
![]() $R, R^{{\mathrm {uni}}}, R^{{\mathrm {st}},Q}$
the corresponding universal deformation rings and thus we have surjective maps
$R, R^{{\mathrm {uni}}}, R^{{\mathrm {st}},Q}$
the corresponding universal deformation rings and thus we have surjective maps
![]() $R \twoheadrightarrow {\mathbf T}$
,
$R \twoheadrightarrow {\mathbf T}$
,
![]() $R^{\mathrm {uni}} \twoheadrightarrow {\mathbf T}^{{\mathrm {uni}}}$
and
$R^{\mathrm {uni}} \twoheadrightarrow {\mathbf T}^{{\mathrm {uni}}}$
and
![]() $R^{{\mathrm {st}},Q} \twoheadrightarrow {\mathbf T}^{{\mathrm {st}}, Q}$
of
$R^{{\mathrm {st}},Q} \twoheadrightarrow {\mathbf T}^{{\mathrm {st}}, Q}$
of
![]() ${\mathcal O}$
-algebras. (Thus, in each of these cases the type
${\mathcal O}$
-algebras. (Thus, in each of these cases the type
![]() $\tau =(\tau _v)$
for
$\tau =(\tau _v)$
for
![]() $v|N^\prime {}Q$
is such that
$v|N^\prime {}Q$
is such that
![]() $\tau _v$
is unrestricted, or unipotent, or unipotent at
$\tau _v$
is unrestricted, or unipotent, or unipotent at
![]() $v|N$
and Steinberg at
$v|N$
and Steinberg at
![]() $v|Q$
.) We have the corresponding universal modular deformation
$v|Q$
.) We have the corresponding universal modular deformation
![]() $\rho ^{{\operatorname {mod}}}:G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathbf T})$
by results of Carayol [Reference CarayolCar94] which is a specialization of a universal representation
$\rho ^{{\operatorname {mod}}}:G_{\mathbf Q} \to {\mathrm {GL}}_2({\mathbf T})$
by results of Carayol [Reference CarayolCar94] which is a specialization of a universal representation
![]() $G_{\mathbf Q} \to {\mathrm {GL}}_2(R)$
.
$G_{\mathbf Q} \to {\mathrm {GL}}_2(R)$
.
Define
 $$\begin{align*}M(N^2Q^2)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S(N^2Q^2)_{{\mathfrak m}_Q}^*),\\M(NQ)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S(NQ)_{{\mathfrak m}}^*),\\M^{{\mathrm{st}},{Q}}(N)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S^{Q}(\Gamma_0^{Q}(N))_{{\mathfrak m}_{Q}}^*).\end{align*}$$
$$\begin{align*}M(N^2Q^2)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S(N^2Q^2)_{{\mathfrak m}_Q}^*),\\M(NQ)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S(NQ)_{{\mathfrak m}}^*),\\M^{{\mathrm{st}},{Q}}(N)&= \operatorname{\mathrm{Hom}}_{{\mathbf T}[G_{\mathbf Q}]}(\rho^{{\operatorname{mod}}},S^{Q}(\Gamma_0^{Q}(N))_{{\mathfrak m}_{Q}}^*).\end{align*}$$
As in Lemma 5.1 of [Reference Böckle, Khare and ManningBKM21], we have using [Reference CarayolCar94] that the evaluation map
![]() $M(N^2Q^2)\otimes _{\mathbf T} \rho ^{{\operatorname {mod}}}\to S(N^2Q^2)_{{\mathfrak m}_Q}^*$
is an isomorphism, as is
$M(N^2Q^2)\otimes _{\mathbf T} \rho ^{{\operatorname {mod}}}\to S(N^2Q^2)_{{\mathfrak m}_Q}^*$
is an isomorphism, as is
![]() $M^{{\mathrm {st}},{Q}}(N)\otimes _{\mathbf T} \rho ^{{\operatorname {mod}}}\to S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}^*$
. In particular, as
$M^{{\mathrm {st}},{Q}}(N)\otimes _{\mathbf T} \rho ^{{\operatorname {mod}}}\to S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}^*$
. In particular, as
![]() ${\mathbf T}$
-modules we have
${\mathbf T}$
-modules we have
![]() $S(N^2Q^2)_{{\mathfrak m}_Q}^* = M(N^2Q^2)^{\oplus 2}$
and
$S(N^2Q^2)_{{\mathfrak m}_Q}^* = M(N^2Q^2)^{\oplus 2}$
and
![]() $S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}^* = M^{{\mathrm {st}},{Q}}(N)^{\oplus 2}$
.
$S^{Q}(\Gamma _0^{Q}(N))_{{\mathfrak m}_{Q}}^* = M^{{\mathrm {st}},{Q}}(N)^{\oplus 2}$
.
We have the following lemma proved using Proposition 4.7 of [Reference Darmon, Diamond and TaylorDDT97] (see proof of Theorem 5.2 of [Reference Böckle, Khare and ManningBKM21]).
Lemma 7.1.
-
(i) The Hecke module
 $M(N^2Q^2)[{\frac 1p}]$
is free of rank one over
$M(N^2Q^2)[{\frac 1p}]$
is free of rank one over
 ${\mathbf T}[{\frac 1p}]$
.
${\mathbf T}[{\frac 1p}]$
. -
(ii) The
 ${\mathbf T}$
-modules are self-dual.
${\mathbf T}$
-modules are self-dual. $$\begin{align*}M(N^2Q^2), M(NQ), M^{{\mathrm{st}},{Q}}(N)\end{align*}$$
$$\begin{align*}M(N^2Q^2), M(NQ), M^{{\mathrm{st}},{Q}}(N)\end{align*}$$
-
(iii) The
 ${\mathcal O}$
-modules are each free of rank 1 over
${\mathcal O}$
-modules are each free of rank 1 over $$\begin{align*}M(N^2Q^2)[\ker(\lambda_{f^{NQ}})], M(NQ)[\ker(\lambda_f)], M^{{\mathrm{st}},{Q}}(N)[\ker(\lambda_f)]\end{align*}$$
$$\begin{align*}M(N^2Q^2)[\ker(\lambda_{f^{NQ}})], M(NQ)[\ker(\lambda_f)], M^{{\mathrm{st}},{Q}}(N)[\ker(\lambda_f)]\end{align*}$$
 ${\mathcal O}$
.
${\mathcal O}$
.
Proof. The first part follows from the arguments in Proposition 4.7 of [Reference Darmon, Diamond and TaylorDDT97] (see proof of Theorem 5.2 of [Reference Böckle, Khare and ManningBKM21]). For the second part, we use that f is a newform of level
![]() $NQ$
and the explicit description of
$NQ$
and the explicit description of
![]() $f^{NQ}$
and the corresponding maximal ideal
$f^{NQ}$
and the corresponding maximal ideal
![]() ${\mathfrak m}_Q$
that is used to define
${\mathfrak m}_Q$
that is used to define
![]() $M(N^2Q^2)$
.
$M(N^2Q^2)$
.
Remark 7.2. In general the modules
![]() $M(NQ), M^{{\mathrm {st}},{Q}}(N)$
, because of the presence of oldforms, are not generically free over the anemic Hecke algebras acting on them that do not have the operators
$M(NQ), M^{{\mathrm {st}},{Q}}(N)$
, because of the presence of oldforms, are not generically free over the anemic Hecke algebras acting on them that do not have the operators
![]() $U_v$
for
$U_v$
for
![]() $v|NQ$
in them. This generic freeness holds for
$v|NQ$
in them. This generic freeness holds for
![]() $M^{{\mathrm {st}},{Q}}(N)$
if
$M^{{\mathrm {st}},{Q}}(N)$
if
![]() $N|N(\overline {\rho })$
which was the assumption in [Reference Böckle, Khare and ManningBKM21]. They are generically free over the full Hecke algebras acting on them that have the operators
$N|N(\overline {\rho })$
which was the assumption in [Reference Böckle, Khare and ManningBKM21]. They are generically free over the full Hecke algebras acting on them that have the operators
![]() $U_v$
for
$U_v$
for
![]() $v|NQ$
in them.
$v|NQ$
in them.
Remark 7.3. The definition of the modules
![]() $M(N^2Q^2)$
,
$M(N^2Q^2)$
,
![]() $M(NQ)$
and
$M(NQ)$
and
![]() $M^{{\mathrm {st}},{Q}}(N)$
differs slightly from the definition of the modules
$M^{{\mathrm {st}},{Q}}(N)$
differs slightly from the definition of the modules
![]() $M^\tau $
; see (6.1) from Section 6. In particular, we do not quotient by the elements
$M^\tau $
; see (6.1) from Section 6. In particular, we do not quotient by the elements
![]() $S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v)$
(or even explicitly use the Hecke operators
$S_v-\varepsilon _p(\operatorname {\mathrm {Frob}}_v)$
(or even explicitly use the Hecke operators
![]() $S_v$
). The definition of
$S_v$
). The definition of
![]() $M^\tau $
from Section 6 is needed when
$M^\tau $
from Section 6 is needed when
![]() $F\ne {\mathbf Q}$
in order to make the patching argument work (for subtle reasons involving the unit group
$F\ne {\mathbf Q}$
in order to make the patching argument work (for subtle reasons involving the unit group
![]() ${\mathcal O}_F^\times $
). In this section, we are only considering the case
${\mathcal O}_F^\times $
). In this section, we are only considering the case
![]() $F={\mathbf Q}$
for convenience, and so we are still able to use patching arguments with the simpler definitions of the modules given in this section.
$F={\mathbf Q}$
for convenience, and so we are still able to use patching arguments with the simpler definitions of the modules given in this section.
Also, here we ‘factor out’ the Galois representation
![]() $\rho ^{{\operatorname {mod}}}$
as above, while we do not do so in Section 6. This also does not significantly affect the patching argument. See [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] or [Reference ManningMan21, Section 4] for more details on patching arguments in which the Galois representation is factored out.
$\rho ^{{\operatorname {mod}}}$
as above, while we do not do so in Section 6. This also does not significantly affect the patching argument. See [Reference Böckle, Khare and ManningBKM21, Theorem 6.3] or [Reference ManningMan21, Section 4] for more details on patching arguments in which the Galois representation is factored out.
One can prove completely analogous versions of Theorems 6.4 and 6.5 for the modules defined in this section by applying the patching arguments applied there to the modules
![]() $M^\tau $
instead to the modules
$M^\tau $
instead to the modules
![]() $M(N^2Q^2)$
,
$M(N^2Q^2)$
,
![]() $M(NQ)$
and
$M(NQ)$
and
![]() $M^{{\mathrm {st}},{Q}}(N)$
. We will leave the details of this to the interested reader, and for the remainder of the section we will simply cite the results of Section 6 as if they literally applied to the modules considered in this section.
$M^{{\mathrm {st}},{Q}}(N)$
. We will leave the details of this to the interested reader, and for the remainder of the section we will simply cite the results of Section 6 as if they literally applied to the modules considered in this section.
We denote by
![]() $\langle \ , \ \rangle $
certain
$\langle \ , \ \rangle $
certain
![]() ${\mathcal O}$
-valued, perfect
${\mathcal O}$
-valued, perfect
![]() ${\mathbf T}$
-equivariant pairings on the
${\mathbf T}$
-equivariant pairings on the
![]() ${\mathbf T}$
-modules
${\mathbf T}$
-modules
that are induced by Poincare duality (see [Reference Böckle, Khare and ManningBKM21, §9]). We then recall from [Reference Böckle, Khare and ManningBKM21, §3, Lemma 3.5], that if
![]() $X,Y,Z$
are generators of the rank one
$X,Y,Z$
are generators of the rank one
![]() ${\mathcal O}$
-modules
${\mathcal O}$
-modules
we have the following relationship:
Here, we are abbreviating all the augmentations arising from the newform f to
![]() $\lambda $
.
$\lambda $
.
We recall the definition of the Wiles defect for modules from [Reference Böckle, Khare and ManningBKM21]. (As we did not consider defects of modules till now we have deferred the definition till this section.)
Definition 7.4. Let R denote a finite, local
![]() ${\mathcal O}$
-algebra, which is
${\mathcal O}$
-algebra, which is
![]() $\varpi $
-torsion free and reduced. Let M be a R-module, that is finite free over
$\varpi $
-torsion free and reduced. Let M be a R-module, that is finite free over
![]() ${\mathcal O}$
and with
${\mathcal O}$
and with
![]() $\operatorname {\mathrm {rank}}_\lambda M = d>0$
.
$\operatorname {\mathrm {rank}}_\lambda M = d>0$
.
The Wiles defect of M is the quantity
 $$\begin{align*}\delta_{\lambda,R}(M) = \frac{d\log{|{\Phi_{\lambda,R}}|}-\log{|{{\Psi_\lambda}(M)}|}}{d \log{|{{\mathcal O}/p}|}},\end{align*}$$
$$\begin{align*}\delta_{\lambda,R}(M) = \frac{d\log{|{\Phi_{\lambda,R}}|}-\log{|{{\Psi_\lambda}(M)}|}}{d \log{|{{\mathcal O}/p}|}},\end{align*}$$
which we will denote by
![]() $\delta _\lambda (M)$
when R is clear from context.
$\delta _\lambda (M)$
when R is clear from context.
Recall from [Reference Böckle, Khare and ManningBKM21, Definition 3.3] that the congruence module
![]() ${\Psi _\lambda }(M)$
is the cokernel of the composition
${\Psi _\lambda }(M)$
is the cokernel of the composition
We should remark that the Wiles defect is normalized differently in [Reference Brochard, Iyengar and KhareBIK23]; the definitions differ by a factor of
![]() $d \log {|{{\mathcal O}/p}|}$
. The interest of studying defects of the modules considered in Theorem 7.5 is that, besides the intrinsic interest, this is directly responsible for our improvements to the result of Ribet–Takahashi about changes of degrees of optimal parametrizations when we switch between Shimura curves. We have recalled above the definition [Reference Böckle, Khare and ManningBKM21, Definition 7.7] of the inertial invariants
$d \log {|{{\mathcal O}/p}|}$
. The interest of studying defects of the modules considered in Theorem 7.5 is that, besides the intrinsic interest, this is directly responsible for our improvements to the result of Ribet–Takahashi about changes of degrees of optimal parametrizations when we switch between Shimura curves. We have recalled above the definition [Reference Böckle, Khare and ManningBKM21, Definition 7.7] of the inertial invariants
![]() $m_q$
for
$m_q$
for
![]() $q \in Q$
.
$q \in Q$
.
Theorem 7.5. Let
![]() $N^\prime {}$
be the squarefree part of N. We have the equality of lengths of
$N^\prime {}$
be the squarefree part of N. We have the equality of lengths of
![]() ${\mathcal O}$
-modules:
${\mathcal O}$
-modules:
 $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1)+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)), \end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1)+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)), \end{align*}$$
and
We have equality of defects
![]() $\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}}(M^{{\mathrm {st}},Q}(N)) =\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}}({\mathbf T}^{{\mathrm {st}},Q})=\sum _{\ell |N^\prime {}} \frac {n_\ell }{e}+\sum _{q \in Q} \frac {2n_q}{e}$
.
$\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}}(M^{{\mathrm {st}},Q}(N)) =\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}}({\mathbf T}^{{\mathrm {st}},Q})=\sum _{\ell |N^\prime {}} \frac {n_\ell }{e}+\sum _{q \in Q} \frac {2n_q}{e}$
.
Proof. The proof follows from the following facts:
-
1. We use the exact computation of the length of a relative cotangent space, namely
by a slight variant of the arguments in the proof of [Reference Böckle, Khare and ManningBKM21, Corollary 7.15] using as key input Theorem 6.4 (there the level considered when we relax ramification conditions is $$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{{\mathrm{st}},Q}})= \ell_{\mathcal O}(\Phi_{{\mathbf T}/{\mathbf T}^{{\mathrm{st}},Q}})=\sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) +\sum_{q \in Q}(m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)-2n_q)\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{{\mathrm{st}},Q}})= \ell_{\mathcal O}(\Phi_{{\mathbf T}/{\mathbf T}^{{\mathrm{st}},Q}})=\sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) +\sum_{q \in Q}(m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)-2n_q)\end{align*}$$
 $NQ^2$
rather than
$NQ^2$
rather than
 $N^2Q^2$
, and it is assumed that
$N^2Q^2$
, and it is assumed that
 $N|N(\overline {\rho })$
, but the arguments carry over to our slightly different situation mutatis mutandis);
$N|N(\overline {\rho })$
, but the arguments carry over to our slightly different situation mutatis mutandis);
-
2.
 $\delta _{\lambda , {\mathbf T}}({\mathbf T})=\delta _{\lambda , {\mathbf T}}(M(N^2Q^2))=0$
. This follows from the arguments in [Reference Böckle, Khare and ManningBKM21, Theorem 5.2] (see also [Reference Böckle, Khare and ManningBKM21, Remark 5.3, 5.4]) which is proved using the arguments of [Reference DiamondDia97, Theorem 3.4].
$\delta _{\lambda , {\mathbf T}}({\mathbf T})=\delta _{\lambda , {\mathbf T}}(M(N^2Q^2))=0$
. This follows from the arguments in [Reference Böckle, Khare and ManningBKM21, Theorem 5.2] (see also [Reference Böckle, Khare and ManningBKM21, Remark 5.3, 5.4]) which is proved using the arguments of [Reference DiamondDia97, Theorem 3.4]. -
3. The inequality
that follows from the following two inequalities: $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) )+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1))\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) )+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1))\end{align*}$$
-
•
which follows from [Reference Ribet and TakahashiRT97, Theorem 2]. To justify this, as noted above as a consequence of [Reference Böckle, Khare and ManningBKM21, §3, Lemma 3.5], we have $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{q \in Q} m_q\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{q \in Q} m_q\end{align*}$$
 $\ell _{\mathcal O}(\Psi _\lambda (M(NQ)))=\operatorname {\mathrm {ord}}_{\mathcal O}(\langle Y, Y \rangle )$
and
$\ell _{\mathcal O}(\Psi _\lambda (M(NQ)))=\operatorname {\mathrm {ord}}_{\mathcal O}(\langle Y, Y \rangle )$
and
 $\ell _{\mathcal O}(\Psi _\lambda (M^{{\mathrm {st}},Q}(N)))=\operatorname {\mathrm {ord}}_{\mathcal O}(\langle Z, Z \rangle )$
. Further, the ideals generated by the inner products
$\ell _{\mathcal O}(\Psi _\lambda (M^{{\mathrm {st}},Q}(N)))=\operatorname {\mathrm {ord}}_{\mathcal O}(\langle Z, Z \rangle )$
. Further, the ideals generated by the inner products
 $(\langle Y, Y \rangle )$
and
$(\langle Y, Y \rangle )$
and
 $(\langle Z, Z \rangle )$
can be read off from the optimal quotients
$(\langle Z, Z \rangle )$
can be read off from the optimal quotients
 $\xi $
and
$\xi $
and
 $\xi ^\prime {}$
of the isogeny class of abelian varieties
$\xi ^\prime {}$
of the isogeny class of abelian varieties
 ${\cal A}_f$
by the Jacobians of
${\cal A}_f$
by the Jacobians of
 $X_0(NQ)$
and
$X_0(NQ)$
and
 $X^Q_0(N)$
as follows. The composition
$X^Q_0(N)$
as follows. The composition
 $\xi _* \xi ^*$
of the pullback
$\xi _* \xi ^*$
of the pullback
 $\xi ^*$
and pushforward of the maps induced by
$\xi ^*$
and pushforward of the maps induced by
 $\xi $
on the
$\xi $
on the
 $\mathrm {Ta}_\wp (A)_{{\mathfrak m}}={\mathcal O}^2$
is identified with multiplication by a scalar in
$\mathrm {Ta}_\wp (A)_{{\mathfrak m}}={\mathcal O}^2$
is identified with multiplication by a scalar in
 ${\mathcal O}$
. We denote the ideal of
${\mathcal O}$
. We denote the ideal of
 ${\mathcal O}$
generated by this scalar by
${\mathcal O}$
generated by this scalar by
 $(\xi _* \xi ^*)$
. Then
$(\xi _* \xi ^*)$
. Then
 $(\langle Y, Y \rangle )=(\xi _* \xi ^*)$
. Similarly,
$(\langle Y, Y \rangle )=(\xi _* \xi ^*)$
. Similarly,
 $(\langle Z, Z \rangle )=(\xi ^\prime _* {\xi ^\prime {}} ^*)$
. Then using [Reference Ribet and TakahashiRT97, Theorem 2] in the case when
$(\langle Z, Z \rangle )=(\xi ^\prime _* {\xi ^\prime {}} ^*)$
. Then using [Reference Ribet and TakahashiRT97, Theorem 2] in the case when
 ${\cal A}_f$
is an isogeny class of elliptic curves, and its generalization to optimal abelian variety quotients in [Reference KhareKha03] we deduce that the ideal
${\cal A}_f$
is an isogeny class of elliptic curves, and its generalization to optimal abelian variety quotients in [Reference KhareKha03] we deduce that the ideal
 $(\xi _* \xi ^*)(\xi ^\prime _* {\xi ^\prime {}} ^*)^{-1}$
divides the ideal
$(\xi _* \xi ^*)(\xi ^\prime _* {\xi ^\prime {}} ^*)^{-1}$
divides the ideal
 $(\Pi _{q \in Q}\omega ^{m_q})$
of
$(\Pi _{q \in Q}\omega ^{m_q})$
of
 ${\mathcal O}$
which justifies our claim.
${\mathcal O}$
which justifies our claim.
-
•
This statement, in the stronger form of an equality follows easily from the arguments in Step 2 of proof of [Reference Böckle, Khare and ManningBKM21, Proposition 9.1]. $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) \leq \ell_{\mathcal O}(\Psi_\lambda(M(NQ))) + \sum_{\ell|N^\prime{}Q} \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1)\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) \leq \ell_{\mathcal O}(\Psi_\lambda(M(NQ))) + \sum_{\ell|N^\prime{}Q} \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1)\end{align*}$$
-
-
4. The inequality
which is equivalent to the inequality $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q})) \leq \ell_{\mathcal O}(\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q})),\end{align*}$$
This follows from [Reference Böckle, Khare and ManningBKM21, Theorem 3.12].
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q})) \leq \ell_{\mathcal O}(\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q})),\end{align*}$$
This follows from [Reference Böckle, Khare and ManningBKM21, Theorem 3.12]. $$\begin{align*}\delta_\lambda(M^{{\mathrm{st}},Q}(N)) \geq \delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}).\end{align*}$$
$$\begin{align*}\delta_\lambda(M^{{\mathrm{st}},Q}(N)) \geq \delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}).\end{align*}$$
-
5. The equality
 $\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}} = \sum _{\ell |N^\prime {}} \frac {n_\ell }{e} + \sum _{q|Q} \frac {2n_q}{e}$
which is a consequence of our main theorem, Theorem 6.5. (To deduce this from our main theorem, we use for
$\delta _{\lambda ,{\mathbf T}^{{\mathrm {st}},Q}} = \sum _{\ell |N^\prime {}} \frac {n_\ell }{e} + \sum _{q|Q} \frac {2n_q}{e}$
which is a consequence of our main theorem, Theorem 6.5. (To deduce this from our main theorem, we use for
 $\ell |N^\prime {}$
the local deformation condition described by
$\ell |N^\prime {}$
the local deformation condition described by
 $R_\ell ^{{\mathrm {uni}}}$
and for
$R_\ell ^{{\mathrm {uni}}}$
and for
 $q \in Q$
that described by
$q \in Q$
that described by
 $R_q^{{\mathrm {st}}}$
.)
$R_q^{{\mathrm {st}}}$
.)
Using the first three points (1), (2) and (3), we conclude that
![]() $\delta _\lambda (M^{{\mathrm {st}},Q}(N)) \leq \sum _{\ell |N^\prime {}} \frac {n_\ell }{e} + \sum _{q|Q} \frac {2n_q}{e}$
. Using (4) and (5) we deduce the series of (in)equalities
$\delta _\lambda (M^{{\mathrm {st}},Q}(N)) \leq \sum _{\ell |N^\prime {}} \frac {n_\ell }{e} + \sum _{q|Q} \frac {2n_q}{e}$
. Using (4) and (5) we deduce the series of (in)equalities
 $$\begin{align*}\sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}= \delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}} ({\mathbf T}^{{\mathrm{st}},Q}) \leq \delta_\lambda(M^{{\mathrm{st}},Q}(N)) \leq \sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}\end{align*}$$
$$\begin{align*}\sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}= \delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}} ({\mathbf T}^{{\mathrm{st}},Q}) \leq \delta_\lambda(M^{{\mathrm{st}},Q}(N)) \leq \sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}\end{align*}$$
and hence
 $$\begin{align*}\delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}}(M^{{\mathrm{st}},Q}(N)) =\delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}}({\mathbf T}^{{\mathrm{st}},Q})=\sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}.\end{align*}$$
$$\begin{align*}\delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}}(M^{{\mathrm{st}},Q}(N)) =\delta_{\lambda,{\mathbf T}^{{\mathrm{st}},Q}}({\mathbf T}^{{\mathrm{st}},Q})=\sum_{\ell|N^\prime{}} \frac{n_\ell}{e}+\sum_{q \in Q} \frac{2n_q}{e}.\end{align*}$$
From this, using (1) and (2) we conclude that
 $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1))+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)).\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1))+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)).\end{align*}$$
Finally, using the two inequalities that occurred in proof of (3) above we deduce that
finishing the proof of all parts of the theorem.
Remark 7.6.
-
• The first part of Theorem 7.5 was proved in [Reference Böckle, Khare and ManningBKM21, Proposition 9.1], using the methods of [Reference Ribet and TakahashiRT97], in particular [Reference Ribet and TakahashiRT97, Theorem 1]. We have reverse engineered the arguments of [Reference Böckle, Khare and ManningBKM21, Proposition 9.1] and are able to deduce [Reference Ribet and TakahashiRT97, Theorem 1] below by a different method which is more robust. We still use [Reference Ribet and TakahashiRT97, Theorem 2] to prove upper bounds on change of congruence modules (or equivalently degrees of parametrizations)
but not the less robust and delicate methods of the proof of the second part of [Reference Ribet and TakahashiRT97, Theorem 1, see also page 11113], which show that these upper bounds in fact give exactly the change of lengths of the congruence modules. We view the correct upper bounds on change of congruence modules, when we relax deformation conditions at primes in Q (from Steinberg to unrestricted with fixed determinant) as ‘easier’ than the corresponding correct lower bounds (correctness lying in the fact that the bounds are expected to turn into equalities). In the analogous case of lengths of relative cotangent spaces, the inequality $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{q \in Q} m_q\end{align*}$$
follows purely from local arguments: See [Reference Böckle, Khare and ManningBKM21, Proposition 7.9] for the local computation, and also note that the surjectivity of the map
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ))) \leq \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{q \in Q} m_q\end{align*}$$
follows purely from local arguments: See [Reference Böckle, Khare and ManningBKM21, Proposition 7.9] for the local computation, and also note that the surjectivity of the map $$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{\mathrm{st}}}) \leq \sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) +\sum_{q \in Q}(m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)-2n_q)\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{\mathrm{st}}}) \leq \sum_{\ell|N^\prime{}} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) +\sum_{q \in Q}(m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)-2n_q)\end{align*}$$
 $\Phi _{\lambda ,R_\infty /R_\infty ^{{\mathrm {st}}} } \rightarrow \Phi _{\lambda ,R/R^{{\mathrm {st}}}}$
of [Reference Böckle, Khare and ManningBKM21, Theorem 7.14] is elementary. The injectivity of this map which is proved in [Reference Böckle, Khare and ManningBKM21, Theorem 7.14] lies deeper and uses patching arguments. Thus, the heuristic that we justify by our work here is that (correct) upper bounds on change of congruence modules, or change of cotangent spaces, are ‘easy’ and our methods allow one to convert these upper bounds to equalities using the methods of this paper.
$\Phi _{\lambda ,R_\infty /R_\infty ^{{\mathrm {st}}} } \rightarrow \Phi _{\lambda ,R/R^{{\mathrm {st}}}}$
of [Reference Böckle, Khare and ManningBKM21, Theorem 7.14] is elementary. The injectivity of this map which is proved in [Reference Böckle, Khare and ManningBKM21, Theorem 7.14] lies deeper and uses patching arguments. Thus, the heuristic that we justify by our work here is that (correct) upper bounds on change of congruence modules, or change of cotangent spaces, are ‘easy’ and our methods allow one to convert these upper bounds to equalities using the methods of this paper.
-
• Using (a straightforward modification) of [Reference Böckle, Khare and ManningBKM21, Theorem 5.2] and [Reference Böckle, Khare and ManningBKM21, Theorem 8.1, Cor. 8.3] (which considered
 $M(NQ^2)$
rather than
$M(NQ^2)$
rather than
 $M(N^2Q^2)$
), and under the assumption that
$M(N^2Q^2)$
), and under the assumption that
 $N|N(\overline {\rho })$
of [Reference Böckle, Khare and ManningBKM21, §2] we know from [Reference Böckle, Khare and ManningBKM21] that On the other hand using Theorem 6.5, together with [Reference Böckle, Khare and ManningBKM21, Proposition 7.9, Corollary 7.15] we know that
$N|N(\overline {\rho })$
of [Reference Böckle, Khare and ManningBKM21, §2] we know from [Reference Böckle, Khare and ManningBKM21] that On the other hand using Theorem 6.5, together with [Reference Böckle, Khare and ManningBKM21, Proposition 7.9, Corollary 7.15] we know that $$\begin{align*}\Psi_\lambda(M(N^2Q^2))=\Psi_\lambda({\mathbf T}), \Psi_\lambda(M^{{\mathrm{st}},Q}(N))=\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q}).\end{align*}$$
Combining this we can deduce the first part
$$\begin{align*}\Psi_\lambda(M(N^2Q^2))=\Psi_\lambda({\mathbf T}), \Psi_\lambda(M^{{\mathrm{st}},Q}(N))=\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q}).\end{align*}$$
Combining this we can deduce the first part $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda({\mathbf T}))= \ell_{\mathcal O}(\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q})) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1)+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)).\end{align*}$$
of the theorem above. The arguments given in Theorem 7.5 use Theorem 6.5 to deduce numerically the equality of cohomological and ring theoretic defects or equivalently of lengths as
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda({\mathbf T}))= \ell_{\mathcal O}(\Psi_\lambda({\mathbf T}^{{\mathrm{st}},Q})) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1)+ \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1)).\end{align*}$$
of the theorem above. The arguments given in Theorem 7.5 use Theorem 6.5 to deduce numerically the equality of cohomological and ring theoretic defects or equivalently of lengths as $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1) + \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1))\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(NQ^2)))= \ell_{\mathcal O}(\Psi_\lambda(M^{{\mathrm{st}},Q}(N))) + \sum_{\ell|N^\prime{}} \operatorname{\mathrm{ord}}_{\mathcal O}(\ell^2-1) + \sum_{q \in Q} (m_q+\operatorname{\mathrm{ord}}_{\mathcal O}(q^2-1))\end{align*}$$
 ${\mathcal O}$
-modules of ring theoretic and cohomological congruence modules seem more versatile and apply in cases where the arguments of [Reference Böckle, Khare and ManningBKM21, Corollary 8.3] do not apply and do not use the assumption that
${\mathcal O}$
-modules of ring theoretic and cohomological congruence modules seem more versatile and apply in cases where the arguments of [Reference Böckle, Khare and ManningBKM21, Corollary 8.3] do not apply and do not use the assumption that
 $N|N(\overline {\rho })$
.
$N|N(\overline {\rho })$
.
-
• We assumed in this section that f was a newform of level
 $NQ$
, and so in particular
$NQ$
, and so in particular
 $\rho _f$
ramifies at each prime dividing N. It it possible to prove the equality of cohomological and ring theoretic defects somewhat more generally by using the arguments of [Reference DiamondDia97].
$\rho _f$
ramifies at each prime dividing N. It it possible to prove the equality of cohomological and ring theoretic defects somewhat more generally by using the arguments of [Reference DiamondDia97].Specifically, assume that f is a newform of level
 $N_\varnothing Q$
for some integer
$N_\varnothing Q$
for some integer
 $N_\varnothing $
. Then Theorem 7.5 gives an equality
$N_\varnothing $
. Then Theorem 7.5 gives an equality
 $\delta _{\lambda }(M^{{\mathrm {st}},Q}(N_\varnothing )) = \delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\varnothing ))$
.
$\delta _{\lambda }(M^{{\mathrm {st}},Q}(N_\varnothing )) = \delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\varnothing ))$
.Now, let
 $\Sigma $
be a finite set of primes not containing any primes dividing
$\Sigma $
be a finite set of primes not containing any primes dividing
 $N_\varnothing Q$
, and let
$N_\varnothing Q$
, and let
 $N_\Sigma $
be the level considered in [Reference DiamondDia97, Section 3.2]. The inequalities given in the proof of [Reference DiamondDia97, Theorem 3.4] (which in our case rely on Ihara’s Lemma for the Shimura curves
$N_\Sigma $
be the level considered in [Reference DiamondDia97, Section 3.2]. The inequalities given in the proof of [Reference DiamondDia97, Theorem 3.4] (which in our case rely on Ihara’s Lemma for the Shimura curves
 $X^Q_0(N)$
) then show that
$X^Q_0(N)$
) then show that
 $\delta _\lambda (M^{{\mathrm {st}},Q}(N_\Sigma ))\le \delta _\lambda (M^{{\mathrm {st}},Q}(N_\varnothing ))$
.
$\delta _\lambda (M^{{\mathrm {st}},Q}(N_\Sigma ))\le \delta _\lambda (M^{{\mathrm {st}},Q}(N_\varnothing ))$
.But now for each prime
 $q\in \Sigma $
, one has that
$q\in \Sigma $
, one has that
 $R_q^{{\operatorname {min}}}$
and
$R_q^{{\operatorname {min}}}$
and
 $R_q^{\square }$
are both complete intersections. Theorems 6.4 and 6.5 of Section 6 (that express defects of global deformation rings as sums of local defects) give that
$R_q^{\square }$
are both complete intersections. Theorems 6.4 and 6.5 of Section 6 (that express defects of global deformation rings as sums of local defects) give that
 $\delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\varnothing )) = \delta _{\lambda }({\mathbf T}^{{\mathrm {st}},Q}(N_\Sigma ))$
. One then deduces that and so
$\delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\varnothing )) = \delta _{\lambda }({\mathbf T}^{{\mathrm {st}},Q}(N_\Sigma ))$
. One then deduces that and so $$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}(N_\Sigma))\le\delta_\lambda(M^{{\mathrm{st}},Q}(N_\Sigma))\le \delta_\lambda(M^{{\mathrm{st}},Q}(N_\varnothing)) = \delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}(N_\varnothing)) = \delta_{\lambda}({\mathbf T}^{{\mathrm{st}},Q}(N_\Sigma)) \end{align*}$$
$$\begin{align*}\delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}(N_\Sigma))\le\delta_\lambda(M^{{\mathrm{st}},Q}(N_\Sigma))\le \delta_\lambda(M^{{\mathrm{st}},Q}(N_\varnothing)) = \delta_\lambda({\mathbf T}^{{\mathrm{st}},Q}(N_\varnothing)) = \delta_{\lambda}({\mathbf T}^{{\mathrm{st}},Q}(N_\Sigma)) \end{align*}$$
 $\delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\Sigma ))=\delta _\lambda (M^{{\mathrm {st}},Q}(N_\Sigma ))$
for all
$\delta _\lambda ({\mathbf T}^{{\mathrm {st}},Q}(N_\Sigma ))=\delta _\lambda (M^{{\mathrm {st}},Q}(N_\Sigma ))$
for all
 $\Sigma $
, generalizing Theorem 7.5. By a similar argument, one can also generalize Proposition 7.7.
$\Sigma $
, generalizing Theorem 7.5. By a similar argument, one can also generalize Proposition 7.7.
We note a variant of the result above which computes defects for the module
![]() $M(NQ)$
when considered as a module for an anemic Hecke algebra and a full Hecke algebra. (We assume for simplicity for the result below that
$M(NQ)$
when considered as a module for an anemic Hecke algebra and a full Hecke algebra. (We assume for simplicity for the result below that
![]() $N^\prime {}=1$
.) The module
$N^\prime {}=1$
.) The module
![]() $M(NQ)$
is a module for the (anemic) Hecke algebra
$M(NQ)$
is a module for the (anemic) Hecke algebra
![]() ${\mathbf T}^{\mathrm {uni}}$
, and it is also a module for the (full) Hecke algebra
${\mathbf T}^{\mathrm {uni}}$
, and it is also a module for the (full) Hecke algebra
![]() $\overline {{\mathbf T}^{\mathrm {uni}}}$
(and thus
$\overline {{\mathbf T}^{\mathrm {uni}}}$
(and thus
![]() $U_v \in \overline {\mathbf T}^{\mathrm {uni}}$
for all primes v dividing
$U_v \in \overline {\mathbf T}^{\mathrm {uni}}$
for all primes v dividing
![]() $NQ$
) that acts faithfully on
$NQ$
) that acts faithfully on
![]() $M(NQ)$
. The augmentation
$M(NQ)$
. The augmentation
![]() $\lambda :{\mathbf T}^{\mathrm {uni}} \to {\mathcal O}$
extends uniquely to
$\lambda :{\mathbf T}^{\mathrm {uni}} \to {\mathcal O}$
extends uniquely to
![]() $\lambda ^\prime {}:\overline {\mathbf T}^{\mathrm {uni}} \to {\mathcal O}$
, and
$\lambda ^\prime {}:\overline {\mathbf T}^{\mathrm {uni}} \to {\mathcal O}$
, and
![]() $\lambda ^\prime {}(U_v)=\pm 1$
for
$\lambda ^\prime {}(U_v)=\pm 1$
for
![]() $v|NQ$
. We determine next the defects
$v|NQ$
. We determine next the defects
![]() $\delta _{\lambda ^\prime {},\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))$
and
$\delta _{\lambda ^\prime {},\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))$
and
![]() $\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))$
.
$\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))$
.
Proposition 7.7. Assume that
![]() $N^\prime {}=1$
.
$N^\prime {}=1$
.
-
(i)
 $\delta _{\lambda ,\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {3n_v}{e}$
.
$\delta _{\lambda ,\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {3n_v}{e}$
. -
(ii)
 $\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}({\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
.
$\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}({\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
.
Proof. (i) By Theorem 6.5,
![]() $\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {3n_v}{e}$
. Using arguments pioneered by Mazur to prove mod p multiplicity one statements (see, for instance, [Reference WilesWil95, Theorem 2.1] for an example of this type of argument, note that under our hypothesis
$\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {3n_v}{e}$
. Using arguments pioneered by Mazur to prove mod p multiplicity one statements (see, for instance, [Reference WilesWil95, Theorem 2.1] for an example of this type of argument, note that under our hypothesis
![]() $(p,NQ)=1$
), one sees that
$(p,NQ)=1$
), one sees that
![]() $M(NQ)$
is a free
$M(NQ)$
is a free
![]() $\overline {\mathbf T}^{\mathrm {uni}}$
-module, and thus
$\overline {\mathbf T}^{\mathrm {uni}}$
-module, and thus
![]() $\delta _{\lambda , \overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})$
.
$\delta _{\lambda , \overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _\lambda (\overline {\mathbf T}^{\mathrm {uni}})$
.
(ii) In this case, we argue as in the proof of Theorem 7.5 except that the proof is easier. Namely, we first observe that
 $$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{\mathrm{uni}}})=\sum_{\ell|N^\prime{}Q} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) \end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Phi_{R/R^{\mathrm{uni}}})=\sum_{\ell|N^\prime{}Q} ( \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1) -n_{\ell}) \end{align*}$$
by a slight variant of the arguments in the proof of [Reference Böckle, Khare and ManningBKM21, Corollary 7.15]. Further,
 $$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) = \ell_{\mathcal O}(\Psi_\lambda(M(NQ))) + \sum_{\ell|N^\prime{}Q} \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1).\end{align*}$$
$$\begin{align*}\ell_{\mathcal O}(\Psi_\lambda(M(N^2Q^2))) = \ell_{\mathcal O}(\Psi_\lambda(M(NQ))) + \sum_{\ell|N^\prime{}Q} \operatorname{\mathrm{ord}}_{\mathcal O} (\ell^2-1).\end{align*}$$
This together with
![]() $\delta _{\lambda , {\mathbf T}}(M(N^2Q^2))=0$
, proves that
$\delta _{\lambda , {\mathbf T}}(M(N^2Q^2))=0$
, proves that
![]() $\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
. Theorem 6.5 gives that
$\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
. Theorem 6.5 gives that
![]() $\delta _\lambda ({\mathbf T})=\sum _{v|N^\prime {}Q}\frac {n_v}{e}$
, and thus altogether we get that
$\delta _\lambda ({\mathbf T})=\sum _{v|N^\prime {}Q}\frac {n_v}{e}$
, and thus altogether we get that
![]() $\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}({\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
.
$\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}(M(NQ))=\delta _{\lambda ,{\mathbf T}^{\mathrm {uni}}}({\mathbf T}^{\mathrm {uni}})=\sum _{v|N^\prime {}Q} \frac {n_v}{e}$
.
Remark 7.8. We could prove Proposition 7.7(i) by a different method that exploits the equality of congruence modules
![]() $\Psi _{\lambda ,\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\Psi _{\lambda , {\mathbf T}^{\mathrm {uni}}}(M(NQ))$
. This should follow from [Reference Böckle, Khare and ManningBKM21, Lemma 3.4] (see also [Reference Brochard, Iyengar and KhareBIK23, Lemma 3.7]) on using the fact that
$\Psi _{\lambda ,\overline {\mathbf T}^{\mathrm {uni}}}(M(NQ))=\Psi _{\lambda , {\mathbf T}^{\mathrm {uni}}}(M(NQ))$
. This should follow from [Reference Böckle, Khare and ManningBKM21, Lemma 3.4] (see also [Reference Brochard, Iyengar and KhareBIK23, Lemma 3.7]) on using the fact that
![]() $M(NQ)[\ker (\lambda )]=M(NQ)[\ker (\lambda ^\prime {})]={\mathcal O}$
. Then we have to compute the change of the local cotangent space at v when we consider the induced augmentations of the map of local deformation rings
$M(NQ)[\ker (\lambda )]=M(NQ)[\ker (\lambda ^\prime {})]={\mathcal O}$
. Then we have to compute the change of the local cotangent space at v when we consider the induced augmentations of the map of local deformation rings
![]() $R_v^{\mathrm {uni}} \to \overline R_v^{\mathrm {uni}}$
. We have not done this computation, but one can make the educated guess that the difference of the lengths of the respective cotangent spaces is
$R_v^{\mathrm {uni}} \to \overline R_v^{\mathrm {uni}}$
. We have not done this computation, but one can make the educated guess that the difference of the lengths of the respective cotangent spaces is
![]() $2n_v$
. This would also compute the defects when we consider
$2n_v$
. This would also compute the defects when we consider
![]() $M(NQ)$
as a module for Hecke algebras that have
$M(NQ)$
as a module for Hecke algebras that have
![]() $U_v$
in them for only a subset
$U_v$
in them for only a subset
![]() $\Sigma $
of places that divide
$\Sigma $
of places that divide
![]() $N^\prime {}Q$
, and our educated guess for this defect is
$N^\prime {}Q$
, and our educated guess for this defect is
 $$\begin{align*}\sum_{v \in \Sigma} \frac{3n_v}{e} + \sum_{v|N^\prime{}Q, v \notin \Sigma} \frac{n_v}{e}.\end{align*}$$
$$\begin{align*}\sum_{v \in \Sigma} \frac{3n_v}{e} + \sum_{v|N^\prime{}Q, v \notin \Sigma} \frac{n_v}{e}.\end{align*}$$
7.2 Change of degrees of parametrizations by Shimura curves
From Theorem 7.5, it is easy to deduce the formula for the change of degrees of optimal parametrizations of elliptic curves by Shimura curves which may be summarized in the following formula (compare to [Reference Ribet and TakahashiRT97, Theorem 1]).
Corollary 7.9. Let
![]() $\cal E$
be an isogeny class of elliptic curves over
$\cal E$
be an isogeny class of elliptic curves over
![]() ${\mathbf Q}$
of conductor N and p be a prime such that the mod p representation arising from
${\mathbf Q}$
of conductor N and p be a prime such that the mod p representation arising from
![]() $\cal E$
is irreducible as a
$\cal E$
is irreducible as a
![]() $G_{{\mathbf Q}(\zeta _p)}$
-module. We also assume that p is prime to N. Consider a factorisation
$G_{{\mathbf Q}(\zeta _p)}$
-module. We also assume that p is prime to N. Consider a factorisation
![]() $N=D\cdot (N/D)$
with D a positive squarefree integer with an an even number of prime factors, and an optimal parametrization
$N=D\cdot (N/D)$
with D a positive squarefree integer with an an even number of prime factors, and an optimal parametrization
![]() $X_0^D(N/D) \to E$
with
$X_0^D(N/D) \to E$
with
![]() $ E \in \cal E$
, and let
$ E \in \cal E$
, and let
![]() $\delta _D$
be its degree. Then for primes
$\delta _D$
be its degree. Then for primes
![]() $q,r$
such that
$q,r$
such that
![]() $qr|D$
, the p-part of
$qr|D$
, the p-part of
and the p-part of
![]() $c_qc_r$
are equal where
$c_qc_r$
are equal where
![]() $c_q,c_r$
are the orders of the component groups of any
$c_q,c_r$
are the orders of the component groups of any
![]() $E \in \cal E$
at the primes q and r.
$E \in \cal E$
at the primes q and r.
Proof. The result follows from the first part of Theorem 7.5 and the well-known relation between congruence modules and degrees. For instance,
![]() $\operatorname {\mathrm {ord}}_p(\delta _D)$
is the same as
$\operatorname {\mathrm {ord}}_p(\delta _D)$
is the same as
![]() $\operatorname {\mathrm {ord}}_p(\langle X,Y\rangle )$
, where
$\operatorname {\mathrm {ord}}_p(\langle X,Y\rangle )$
, where
![]() $X,Y$
is a
$X,Y$
is a
![]() ${\mathcal O}$
-basis of
${\mathcal O}$
-basis of
![]() $H^1(X_0^D(N/D),{\mathcal O})[\ker \lambda ]$
, where
$H^1(X_0^D(N/D),{\mathcal O})[\ker \lambda ]$
, where
![]() $\lambda $
is the augmentation of the Hecke algebra acting on
$\lambda $
is the augmentation of the Hecke algebra acting on
![]() $H^1(X_0^D(N/D),{\mathcal O})$
arising from E. We leave the details to the interested reader.
$H^1(X_0^D(N/D),{\mathcal O})$
arising from E. We leave the details to the interested reader.
We get results about the surjectivity of maps on component groups at primes q of multiplicative reduction of elliptic curves E that are induced by parametrizations of E by Shimura curves whose Jacobians have purely toric reduction at q (compare to the the arguments on [Reference Ribet and TakahashiRT97, page 11113]).
Corollary 7.10. With the notation of the previous corollary, for a prime
![]() $q|D$
, the map induced by an optimal parametrization
$q|D$
, the map induced by an optimal parametrization
![]() $X_0^D(N/D) \to E$
on the p-parts of the component groups
$X_0^D(N/D) \to E$
on the p-parts of the component groups
![]() $\phi _q(J_0^D(N/D)) \to \phi _q(E)$
is surjective.
$\phi _q(J_0^D(N/D)) \to \phi _q(E)$
is surjective.
Proof. This follows from the corollary above and [Reference Ribet and TakahashiRT97, Proposition 2].
Remark 7.11.
-
• The proof of [Reference Ribet and TakahashiRT97, Theorem 1, part 2] on page 11113 depends on the hypothesis that
 $N/D$
is not prime (that is used to ‘permute’ primes around there) and uses the hypothesis that E is semistable to ensure the hypothesis:
$N/D$
is not prime (that is used to ‘permute’ primes around there) and uses the hypothesis that E is semistable to ensure the hypothesis:(*): There is a prime q dividing the conductor of E (of semistable bad reduction) at which the order of the group of components at q is not divisible by p. Equivalently the mod p representation
 $\overline {\rho }$
arising from E is such that
$\overline {\rho }$
arising from E is such that
 $\overline {\rho }({I_q})$
is either not finite flat (in the case
$\overline {\rho }({I_q})$
is either not finite flat (in the case
 $q =p$
), and ramified (in the case
$q =p$
), and ramified (in the case
 $q \neq p$
), with
$q \neq p$
), with
 $I_q$
an inertia group at q.
$I_q$
an inertia group at q.We can dispense with these hypotheses in Corollary 7.9.
-
• The results of this section should in principle generalize to the cases of totally real fields F. (The main theorems of this paper, for instance Theorem 6.5, on which our results depend are written in the setting of such F.)
Theorem 7.5 should generalize without too much difficulty to the case of newforms of weight
 $k> 2$
. There are some related results in [Reference Kim and OtaKO23]; they only consider situations where the Hecke algebras are complete intersections and hence of defect 0. The results given here are more illustrative than exhaustive.
$k> 2$
. There are some related results in [Reference Kim and OtaKO23]; they only consider situations where the Hecke algebras are complete intersections and hence of defect 0. The results given here are more illustrative than exhaustive.
Appendix. A formula of Venkatesh
By N. Fakhruddin and C. Khare
The results of this section are inspired by unpublished notes of A. Venkatesh [Reference VenkateshVen16]. Venkatesh’s formula was stated (as a conjecture, but it was checked in many cases) for certain derived commutative rings, but we prove a version in the context of ordinary commutative algebra; we briefly explain the connection in Section A.1. The invariants
![]() $c_0$
and
$c_0$
and
![]() $c_1$
are essentially the same as those defined in [Reference VenkateshVen16], but our method of proof is different from the approach taken there. The main result is Proposition A.6. This is used in the main text to compute the Wiles defect for certain Hecke algebras that are not complete intersections.
$c_1$
are essentially the same as those defined in [Reference VenkateshVen16], but our method of proof is different from the approach taken there. The main result is Proposition A.6. This is used in the main text to compute the Wiles defect for certain Hecke algebras that are not complete intersections.
Let
![]() $\mathcal {O}$
be a complete discrete valvation ring (DVR), and let B be a complete local Noetherian
$\mathcal {O}$
be a complete discrete valvation ring (DVR), and let B be a complete local Noetherian
![]() $\mathcal {O}$
-algebra with
$\mathcal {O}$
-algebra with
![]() $\dim (B) = 1$
with an augmentation
$\dim (B) = 1$
with an augmentation
![]() $\pi _B: B \to {\mathcal {O}}$
. Let E be the quotient field of
$\pi _B: B \to {\mathcal {O}}$
. Let E be the quotient field of
![]() $\mathcal {O}$
which we view as a module over any augmented ring using the augmentation. We assume that the augmentation has a finite cotangent space, by which we mean that
$\mathcal {O}$
which we view as a module over any augmented ring using the augmentation. We assume that the augmentation has a finite cotangent space, by which we mean that
![]() $\ker (\pi _B)/\ker (\pi _B)^2$
is a finite length
$\ker (\pi _B)/\ker (\pi _B)^2$
is a finite length
![]() $\mathcal {O}$
-module. Let C be the largest Cohen–Macaulay quotient of B – if B is finite over
$\mathcal {O}$
-module. Let C be the largest Cohen–Macaulay quotient of B – if B is finite over
![]() $\mathcal {O}$
, then this is simply the quotient of B by its
$\mathcal {O}$
, then this is simply the quotient of B by its
![]() $\mathcal {O}$
-torsion (which is an ideal) – and let
$\mathcal {O}$
-torsion (which is an ideal) – and let
![]() $\pi _C: C \to {\mathcal {O}}$
be the augmentation of C induced by
$\pi _C: C \to {\mathcal {O}}$
be the augmentation of C induced by
![]() $\pi _B$
.
$\pi _B$
.
Definition A.1.
![]() $c_0(B) := \ell ({\mathcal {O}}/\pi _C(\operatorname {\mathrm {Ann}}(\ker (\pi _C))))$
.
$c_0(B) := \ell ({\mathcal {O}}/\pi _C(\operatorname {\mathrm {Ann}}(\ker (\pi _C))))$
.
Since B is complete, we may write it as a quotient of
![]() $S = {\mathcal {O}}[[x_1,x_2,\dots ,x_n]]$
for some
$S = {\mathcal {O}}[[x_1,x_2,\dots ,x_n]]$
for some
![]() $n \geq 0$
. Then by the prime avoidance lemma ([Reference Bruns and HerzogBH93, Lemma 1.2.2]), we may find a quotient A of S through which the map to B factors and such that A is a complete intersection ring with
$n \geq 0$
. Then by the prime avoidance lemma ([Reference Bruns and HerzogBH93, Lemma 1.2.2]), we may find a quotient A of S through which the map to B factors and such that A is a complete intersection ring with
![]() $\dim (A) = 1$
. Denote this map
$\dim (A) = 1$
. Denote this map
![]() $A \to B$
by
$A \to B$
by
![]() $\phi _B$
and the induced map
$\phi _B$
and the induced map
![]() $A \to {\mathcal {O}}$
by
$A \to {\mathcal {O}}$
by
![]() $\pi _A$
. We may (and do) choose A such that
$\pi _A$
. We may (and do) choose A such that
![]() $\ker (\pi _A)/\ker (\pi _A)^2$
is a finite length
$\ker (\pi _A)/\ker (\pi _A)^2$
is a finite length
![]() $\mathcal {O}$
-module. Furthermore, if B is finite over
$\mathcal {O}$
-module. Furthermore, if B is finite over
![]() $\mathcal {O}$
the lemma also allows us to choose A finite over
$\mathcal {O}$
the lemma also allows us to choose A finite over
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Let
![]() $\mathbf {x}$
be a sequence of generators of
$\mathbf {x}$
be a sequence of generators of
![]() $\ker (\phi _B)$
of length
$\ker (\phi _B)$
of length
![]() $\delta $
and consider the Koszul complexFootnote
10
$\delta $
and consider the Koszul complexFootnote
10
![]() $K_A(\mathbf {x})$
. It is a graded-commutative differential graded A-algebra whose homology modules are B-modules. Let
$K_A(\mathbf {x})$
. It is a graded-commutative differential graded A-algebra whose homology modules are B-modules. Let
![]() $H_{\delta }(K_A(\mathbf {x}))_1$
be the submodule of
$H_{\delta }(K_A(\mathbf {x}))_1$
be the submodule of
![]() $H_{\delta }(K_A(\mathbf {x}))$
generated by products of elements of
$H_{\delta }(K_A(\mathbf {x}))$
generated by products of elements of
![]() $H_1(K_A(\mathbf {x}))$
. The Koszul complex is functorial for ring homomorphisms, so we have a map
$H_1(K_A(\mathbf {x}))$
. The Koszul complex is functorial for ring homomorphisms, so we have a map
where
![]() $\overline {\mathbf {x}}$
denotes the image of the sequence
$\overline {\mathbf {x}}$
denotes the image of the sequence
![]() $\mathbf {x}$
in
$\mathbf {x}$
in
![]() $\mathcal {O}$
. However, all terms of this sequence are
$\mathcal {O}$
. However, all terms of this sequence are
![]() $0$
, so
$0$
, so
![]() $H_*(K_{\mathcal {O}}(\overline {\mathbf {x}}))$
is the exterior algebra in
$H_*(K_{\mathcal {O}}(\overline {\mathbf {x}}))$
is the exterior algebra in
![]() $\delta $
generators (in homological degree
$\delta $
generators (in homological degree
![]() $1$
). In particular,
$1$
). In particular,
![]() $H_{\delta }(K_{\mathcal {O}}(\overline {\mathbf {x}})) \cong {\mathcal {O}}$
.
$H_{\delta }(K_{\mathcal {O}}(\overline {\mathbf {x}})) \cong {\mathcal {O}}$
.
Definition A.2.
![]() $c_1(B) := \ell (\pi _{A,*}(H_{\delta }(K_A(\mathbf {x})))/ \pi _{A,*}(H_{\delta }(K_A(\mathbf {x}))_1))$
.
$c_1(B) := \ell (\pi _{A,*}(H_{\delta }(K_A(\mathbf {x})))/ \pi _{A,*}(H_{\delta }(K_A(\mathbf {x}))_1))$
.
We see that this is finite by localizing at the prime ideal corresponding to the kernel of
![]() $\pi _A$
and observing that this localization map factors through
$\pi _A$
and observing that this localization map factors through
![]() $\pi _A$
.
$\pi _A$
.
From the definition of the Koszul complex, it follows that
![]() $H_{\delta }(K_A(\mathbf {x}))$
is the annihilator of the ideal I generated by the sequence
$H_{\delta }(K_A(\mathbf {x}))$
is the annihilator of the ideal I generated by the sequence
![]() $\mathbf {x}$
. The A-submodule of
$\mathbf {x}$
. The A-submodule of
![]() $H_{\delta }(K_A(\mathbf {x}))$
generated by products of elements of
$H_{\delta }(K_A(\mathbf {x}))$
generated by products of elements of
![]() $H_1(K_A(\mathbf {x}))$
is precisely the Fitting ideal of I (sitting inside its annihilator). It follows that
$H_1(K_A(\mathbf {x}))$
is precisely the Fitting ideal of I (sitting inside its annihilator). It follows that
We show below in Lemma A.5 that
![]() $c_1(B)$
is independent of all choices. For a fixed A as above, the Koszul complex only depends on the minimal number of generators of the kernel. Moreover, adding more elements in the kernel to the sequence of generators has the effect of tensoring the Koszul complex with an exterior algebra ([Reference Bruns and HerzogBH93, Proposition 1.6.21]) in which case it is easy to see that
$c_1(B)$
is independent of all choices. For a fixed A as above, the Koszul complex only depends on the minimal number of generators of the kernel. Moreover, adding more elements in the kernel to the sequence of generators has the effect of tensoring the Koszul complex with an exterior algebra ([Reference Bruns and HerzogBH93, Proposition 1.6.21]) in which case it is easy to see that
![]() $c_1$
does not change.
$c_1$
does not change.
To show that it is independent of the choice of
![]() $\phi _B: A \to B$
, we will need the following elementary lemma.
$\phi _B: A \to B$
, we will need the following elementary lemma.
Lemma A.3. Let
![]() $\mathcal {O}$
be any commutative ring,
$\mathcal {O}$
be any commutative ring,
![]() $A_1,A_2, B$
be local Noetherian
$A_1,A_2, B$
be local Noetherian
![]() $\mathcal {O}$
-algebras and
$\mathcal {O}$
-algebras and
![]() $\phi _i:A_i \to B$
,
$\phi _i:A_i \to B$
,
![]() $i=1,2$
surjections of
$i=1,2$
surjections of
![]() $\mathcal {O}$
-algebras. Then
$\mathcal {O}$
-algebras. Then
-
1.
 $A :=A_1 \times _B A_2$
is also a local Noetherian
$A :=A_1 \times _B A_2$
is also a local Noetherian
 $\mathcal {O}$
-algebra and
$\mathcal {O}$
-algebra and
 $\dim (A) = \max \{\dim (A_1), \dim (A_2)\}$
.
$\dim (A) = \max \{\dim (A_1), \dim (A_2)\}$
. -
2. If
 $A_1$
and
$A_1$
and
 $A_2$
are complete, then so is A.
$A_2$
are complete, then so is A. -
3. Let P be any prime ideal in B,
 $P_i = \phi _i^{-1}(P)$
the corresponding prime ideals of
$P_i = \phi _i^{-1}(P)$
the corresponding prime ideals of
 $A_i$
and
$A_i$
and
 $P_A = \phi ^{-1}(P)$
that of A (where
$P_A = \phi ^{-1}(P)$
that of A (where
 $\phi :A \to B$
is the surjection induced by
$\phi :A \to B$
is the surjection induced by
 $\phi _i$
). Then
$\phi _i$
). Then
 $A_{P_A} = (A_1)_{P_1} \times _{B_P} (A_1)_{P_2}$
.
$A_{P_A} = (A_1)_{P_1} \times _{B_P} (A_1)_{P_2}$
.
Proof. We have
![]() $A = \{ (a_1,a_2) \in A_1 \times A_2: \phi _1(a_1) = \phi _2(a_2) \}$
. The ideal
$A = \{ (a_1,a_2) \in A_1 \times A_2: \phi _1(a_1) = \phi _2(a_2) \}$
. The ideal
![]() $m_A$
of A consisting of all pairs
$m_A$
of A consisting of all pairs
![]() $(a_1,a_2)$
with
$(a_1,a_2)$
with
![]() $a_i \in m_{A_i}$
is the unique maximal ideal of A since the surjectivity of
$a_i \in m_{A_i}$
is the unique maximal ideal of A since the surjectivity of
![]() $\phi _1, \phi _2$
implies that the complement consists of invertible elements, so A is local. The two projections induce surjections
$\phi _1, \phi _2$
implies that the complement consists of invertible elements, so A is local. The two projections induce surjections
![]() $p_i:A \to A_i$
. If I is an ideal of A, then
$p_i:A \to A_i$
. If I is an ideal of A, then
![]() $p_1(I)$
is an ideal of
$p_1(I)$
is an ideal of
![]() $A_1$
. The kernel of the map
$A_1$
. The kernel of the map
![]() $I \to p_1(I)$
is naturally an ideal of
$I \to p_1(I)$
is naturally an ideal of
![]() $A_2$
. Since
$A_2$
. Since
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are Noetherian, this implies that A is Noetherian.
$A_2$
are Noetherian, this implies that A is Noetherian.
Now, since A is a subring of
![]() $A_1 \times A_2$
which is finite as an A-module (it is generated by
$A_1 \times A_2$
which is finite as an A-module (it is generated by
![]() $(1,0)$
and
$(1,0)$
and
![]() $(0,1)$
), it follows from the going-up theorem [Reference MatsumuraMat80, Theorem 5, (i), (ii) and (iii)] that
$(0,1)$
), it follows from the going-up theorem [Reference MatsumuraMat80, Theorem 5, (i), (ii) and (iii)] that
![]() $\dim (A)= \dim (A_1 \times A_2) = \max \{\dim (A_1), \dim (A_2)\}$
.
$\dim (A)= \dim (A_1 \times A_2) = \max \{\dim (A_1), \dim (A_2)\}$
.
Suppose
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are complete. To show that A is complete it suffices to prove that the
$A_2$
are complete. To show that A is complete it suffices to prove that the
![]() $m_A$
-adic topology on A is the same as the topology induced from the inclusion of A in
$m_A$
-adic topology on A is the same as the topology induced from the inclusion of A in
![]() $A_1 \times A_2$
. Since
$A_1 \times A_2$
. Since
![]() $m_A^n \subset m_{A_1}^n \times m_{A_2}^n$
for all
$m_A^n \subset m_{A_1}^n \times m_{A_2}^n$
for all
![]() $n>0$
, we only need to show that given any
$n>0$
, we only need to show that given any
![]() $n'>0$
,
$n'>0$
,
This follows immediately by applying the Artin–Rees lemma [Reference MatsumuraMat80, Theorem 15], with
![]() $I = m_A$
,
$I = m_A$
,
![]() $M = A_1 \times A_2$
and
$M = A_1 \times A_2$
and
![]() $N = A$
since
$N = A$
since
![]() $I^nM = m_{A_1}^n \times m_{A_2}^n$
.
$I^nM = m_{A_1}^n \times m_{A_2}^n$
.
We will use the following elementary fact whose simple proof we skip: If A is any commutative ring, S any multiplicative subset of A,
![]() $M_1$
,
$M_1$
,
![]() $M_2$
and N any A-modules with maps
$M_2$
and N any A-modules with maps
![]() $M_i \to N$
,
$M_i \to N$
,
![]() $i=1,2$
, then the natural map
$i=1,2$
, then the natural map
![]() $M_1 \times _N M_2 \to (M_2)_S \times _{N_{S}} (M_2)_S$
of A-modules induces an isomorphism
$M_1 \times _N M_2 \to (M_2)_S \times _{N_{S}} (M_2)_S$
of A-modules induces an isomorphism
![]() $(M_1 \times _N M_2)_S \to (M_1)_S \times _{N_{S}} (M_2)_S$
. The statement (3) follows from this by taking
$(M_1 \times _N M_2)_S \to (M_1)_S \times _{N_{S}} (M_2)_S$
. The statement (3) follows from this by taking
![]() $M_i$
to be
$M_i$
to be
![]() $A_i$
, N to be B and
$A_i$
, N to be B and
![]() $S = A \setminus P_A$
and by observing that
$S = A \setminus P_A$
and by observing that
![]() $A_i \otimes _A A_{P_A} = (A_i)_{P_i}$
,
$A_i \otimes _A A_{P_A} = (A_i)_{P_i}$
,
![]() $i=1,2$
and
$i=1,2$
and
![]() $B \otimes _A A_{P_A} = B_P$
.
$B \otimes _A A_{P_A} = B_P$
.
It follows from Lemma A.3 and the prime avoidance lemma already used earlier, that if
![]() $A_i$
are complete intersections of the same dimension with surjections to B, then both of them may be dominated by a complete intersection
$A_i$
are complete intersections of the same dimension with surjections to B, then both of them may be dominated by a complete intersection
![]() $A'$
of the same dimension. The condition on the finiteness of the cotangent space can also be preserved by (3) of Lemma A.3. For the independence of the choice of A in the definition of
$A'$
of the same dimension. The condition on the finiteness of the cotangent space can also be preserved by (3) of Lemma A.3. For the independence of the choice of A in the definition of
![]() $c_1(B)$
we will also need:
$c_1(B)$
we will also need:
Lemma A.4. Let
![]() $f:A' \to A$
be a surjection of (complete) complete intersection local rings and let
$f:A' \to A$
be a surjection of (complete) complete intersection local rings and let
![]() $\phi _B:A \to B$
be any surjection of rings. Let
$\phi _B:A \to B$
be any surjection of rings. Let
![]() $\mathbf {z}$
be any finite sequence of generators of
$\mathbf {z}$
be any finite sequence of generators of
![]() $\ker (f)$
,
$\ker (f)$
,
![]() $\mathbf {x}$
any sequence of generators of
$\mathbf {x}$
any sequence of generators of
![]() $\ker (\phi _B)$
, and
$\ker (\phi _B)$
, and
![]() $\mathbf {x}'$
a lift of
$\mathbf {x}'$
a lift of
![]() $\mathbf {x}$
to
$\mathbf {x}$
to
![]() $A'$
. Then
$A'$
. Then
![]() $H_*(K_{A'}((\mathbf {z}, \mathbf {x}')))$
is isomorphic to
$H_*(K_{A'}((\mathbf {z}, \mathbf {x}')))$
is isomorphic to
![]() $H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra over A with
$H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra over A with
![]() $|\mathbf {z}| + \dim (A) - \dim (A')$
free generators.
$|\mathbf {z}| + \dim (A) - \dim (A')$
free generators.
Proof. Let
![]() $g: S \to A'$
be a surjection from a regular local ring S (which exists because
$g: S \to A'$
be a surjection from a regular local ring S (which exists because
![]() $A'$
is complete), so both
$A'$
is complete), so both
![]() $\ker (g)$
and
$\ker (g)$
and
![]() $\ker (fg)$
are generated by regular sequences. Choose a sequence of generators
$\ker (fg)$
are generated by regular sequences. Choose a sequence of generators
![]() ${\mathbf {y}}$
of
${\mathbf {y}}$
of
![]() $\ker (\phi _Bfg)$
by first choosing a regular sequence of generators
$\ker (\phi _Bfg)$
by first choosing a regular sequence of generators
![]() $\mathbf {w}$
of
$\mathbf {w}$
of
![]() $\ker (g)$
and then adding lifts
$\ker (g)$
and then adding lifts
![]() $\tilde {\mathbf {z}}$
of elements of
$\tilde {\mathbf {z}}$
of elements of
![]() $\mathbf {z}$
and lifts
$\mathbf {z}$
and lifts
![]() $\tilde {\mathbf {x}}'$
of lifts
$\tilde {\mathbf {x}}'$
of lifts
![]() $\mathbf {x}'$
in
$\mathbf {x}'$
in
![]() $A'$
of elements of
$A'$
of elements of
![]() $\mathbf {x}$
. We then set
$\mathbf {x}$
. We then set
![]() $\mathbf {y} = (\mathbf {w}, \tilde {\mathbf {x}}', \tilde {\mathbf {z}})$
and consider
$\mathbf {y} = (\mathbf {w}, \tilde {\mathbf {x}}', \tilde {\mathbf {z}})$
and consider
![]() $K_S(\mathbf {y})$
. Since the Koszul complex of a regular sequence is a resolution of the corresponding quotient ring by applying this to
$K_S(\mathbf {y})$
. Since the Koszul complex of a regular sequence is a resolution of the corresponding quotient ring by applying this to
![]() $\mathbf {w}$
we see that
$\mathbf {w}$
we see that
![]() $K_S(\mathbf {y})$
is quasi-isomorphic (as a differential graded S-algebra) to
$K_S(\mathbf {y})$
is quasi-isomorphic (as a differential graded S-algebra) to
![]() $K_S((\tilde {\mathbf {z}}, \tilde {\mathbf {x}}')) \otimes _S A'$
, that is,
$K_S((\tilde {\mathbf {z}}, \tilde {\mathbf {x}}')) \otimes _S A'$
, that is,
![]() $K_{A'}((\mathbf {z},\mathbf {x}'))$
. On the other hand, since A is also a complete intersection ring, by choosing a minimal generating set of
$K_{A'}((\mathbf {z},\mathbf {x}'))$
. On the other hand, since A is also a complete intersection ring, by choosing a minimal generating set of
![]() $\ker (fg)$
from among the elements of
$\ker (fg)$
from among the elements of
![]() $(\mathbf {w}, \tilde {\mathbf {z}})$
, one sees that
$(\mathbf {w}, \tilde {\mathbf {z}})$
, one sees that
![]() $K_S(\mathbf {y})$
is quasi-isomorphic to
$K_S(\mathbf {y})$
is quasi-isomorphic to
![]() $K_A(\mathbf {x})$
tensored with an exterior algebra (since
$K_A(\mathbf {x})$
tensored with an exterior algebra (since
![]() $gf(\tilde {\mathbf {x}}') = \mathbf {x}$
and the remaining elements of
$gf(\tilde {\mathbf {x}}') = \mathbf {x}$
and the remaining elements of
![]() $(\mathbf {w}, \tilde {\mathbf {z}})$
become
$(\mathbf {w}, \tilde {\mathbf {z}})$
become
![]() $0$
in A). On taking homology, we see that
$0$
in A). On taking homology, we see that
![]() $H_*(K_{A'}((\mathbf {z},\mathbf {x}')))$
is isomorphic to
$H_*(K_{A'}((\mathbf {z},\mathbf {x}')))$
is isomorphic to
![]() $H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra. The minimal number of generators of this exterior algebra is easily seen to be
$H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra. The minimal number of generators of this exterior algebra is easily seen to be
![]() $|\mathbf {z}| + \dim (A) - \dim (A')$
since
$|\mathbf {z}| + \dim (A) - \dim (A')$
since
![]() $|\mathbf {w}| = \dim (S) - \dim (A')$
.
$|\mathbf {w}| = \dim (S) - \dim (A')$
.
Lemma A.5. The invariant
![]() $c_1(B)$
is well defined.
$c_1(B)$
is well defined.
Proof. By Lemma A.3 and the remarks following it, it suffices to show that if
![]() $\phi _B:A \to B$
is as above and we have a surjection
$\phi _B:A \to B$
is as above and we have a surjection
![]() $f:A' \to A$
such that
$f:A' \to A$
such that
![]() $\phi _B' := \phi _B f$
also satisfies the conditions analogous to those imposed on
$\phi _B' := \phi _B f$
also satisfies the conditions analogous to those imposed on
![]() $\phi _B$
, then the number
$\phi _B$
, then the number
![]() $c_1(B)$
defined using
$c_1(B)$
defined using
![]() $\phi _B$
is equal to the one defined using
$\phi _B$
is equal to the one defined using
![]() $\phi _B'$
.
$\phi _B'$
.
Let
![]() $\mathbf {x}$
be a sequence of generators of
$\mathbf {x}$
be a sequence of generators of
![]() $\ker (\phi _B)$
,
$\ker (\phi _B)$
,
![]() $\mathbf {x}'$
a lift of this sequence to
$\mathbf {x}'$
a lift of this sequence to
![]() $A'$
and
$A'$
and
![]() $\mathbf {z}$
a sequence of generators of
$\mathbf {z}$
a sequence of generators of
![]() $\ker (f)$
. Let
$\ker (f)$
. Let
![]() $\mathbf {w} = (\mathbf {z}, \mathbf {x}')$
, so
$\mathbf {w} = (\mathbf {z}, \mathbf {x}')$
, so
![]() $\mathbf {w}$
is a sequence of generators of
$\mathbf {w}$
is a sequence of generators of
![]() $\ker (\phi _B')$
. Thus,
$\ker (\phi _B')$
. Thus,
![]() $\delta = |\mathbf {x}|$
and
$\delta = |\mathbf {x}|$
and
![]() $\delta '$
, the corresponding number of generators for
$\delta '$
, the corresponding number of generators for
![]() $\ker (\phi _B')$
, equals
$\ker (\phi _B')$
, equals
![]() $|\mathbf {w}| = \delta + |\mathbf {z}|$
. Note that
$|\mathbf {w}| = \delta + |\mathbf {z}|$
. Note that
![]() $H_{\delta '}(K_{A'}((\mathbf {z}, \mathbf {x}^\prime {})))$
is canonically isomorphic to
$H_{\delta '}(K_{A'}((\mathbf {z}, \mathbf {x}^\prime {})))$
is canonically isomorphic to
![]() $\operatorname {\mathrm {Ann}}(\ker (\phi _B'))$
and
$\operatorname {\mathrm {Ann}}(\ker (\phi _B'))$
and
![]() $H_{\delta }(K_A(\mathbf {x}))$
is canonically isomorphic to
$H_{\delta }(K_A(\mathbf {x}))$
is canonically isomorphic to
![]() $\operatorname {\mathrm {Ann}}(\ker (\phi _B))$
. From the result of Lemma A.4 (specialized to the case
$\operatorname {\mathrm {Ann}}(\ker (\phi _B))$
. From the result of Lemma A.4 (specialized to the case
![]() $\dim (A) = \dim (A')$
) that
$\dim (A) = \dim (A')$
) that
![]() $H_*(K_{A'}((\mathbf {z}, \mathbf {x}^\prime {})))$
is isomorphic to
$H_*(K_{A'}((\mathbf {z}, \mathbf {x}^\prime {})))$
is isomorphic to
![]() $H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra over A with
$H_*(K_A(\mathbf {x}))$
tensored with an exterior algebra over A with
![]() $|\mathbf {z}|$
free generators, it follows that there is an isomorphism of A-modules
$|\mathbf {z}|$
free generators, it follows that there is an isomorphism of A-modules
![]() $\alpha : \operatorname {\mathrm {Ann}}(\ker (\phi _B')) \to \operatorname {\mathrm {Ann}}(\ker (\phi _B))$
such that
$\alpha : \operatorname {\mathrm {Ann}}(\ker (\phi _B')) \to \operatorname {\mathrm {Ann}}(\ker (\phi _B))$
such that
![]() $\alpha (\operatorname {\mathrm {Fitt}}(\ker (\phi _B'))) = \operatorname {\mathrm {Fitt}}(\ker (\phi _B))$
.
$\alpha (\operatorname {\mathrm {Fitt}}(\ker (\phi _B'))) = \operatorname {\mathrm {Fitt}}(\ker (\phi _B))$
.
Now, we use the finite cotangent space assumption on A and
![]() $A'$
. This implies that the ideal
$A'$
. This implies that the ideal
![]() $\pi _A(\operatorname {\mathrm {Ann}}(\ker (\phi _B))) \subset \mathcal {O}$
is nonzero and equal to the image of
$\pi _A(\operatorname {\mathrm {Ann}}(\ker (\phi _B))) \subset \mathcal {O}$
is nonzero and equal to the image of
![]() $\operatorname {\mathrm {Ann}}(\ker (\phi _B)) \otimes _A \mathcal {O}$
in
$\operatorname {\mathrm {Ann}}(\ker (\phi _B)) \otimes _A \mathcal {O}$
in
![]() $A \otimes _A \mathcal {O} = \mathcal {O}$
(and similarly for
$A \otimes _A \mathcal {O} = \mathcal {O}$
(and similarly for
![]() $A'$
and also for the fitting ideals). The
$A'$
and also for the fitting ideals). The
![]() $\mathcal {O}$
-module
$\mathcal {O}$
-module
![]() $\operatorname {\mathrm {Ann}}(\ker (\phi _B)) \otimes _A \mathcal {O}$
modulo its torsion is free of rank one (and similarly for
$\operatorname {\mathrm {Ann}}(\ker (\phi _B)) \otimes _A \mathcal {O}$
modulo its torsion is free of rank one (and similarly for
![]() $A'$
) so the lemma follows from Equation (A.1) and the above by using the isomorphism
$A'$
) so the lemma follows from Equation (A.1) and the above by using the isomorphism
![]() $\alpha \otimes _A \mathcal {O}$
.
$\alpha \otimes _A \mathcal {O}$
.
For any map of rings
![]() $R_1 \to R_2$
, an
$R_1 \to R_2$
, an
![]() $R_2$
-module M and
$R_2$
-module M and
![]() $ i \geq 0$
, we denote by
$ i \geq 0$
, we denote by
![]() $\operatorname {\mathrm {Der}}^i_{R_1}(R_2,M)$
the i-th André–Quillen cohomology group ([Reference IyengarIye07, Def. 5.8] or [Reference AndréAnd74, III a), Def. 11 and 12]) of
$\operatorname {\mathrm {Der}}^i_{R_1}(R_2,M)$
the i-th André–Quillen cohomology group ([Reference IyengarIye07, Def. 5.8] or [Reference AndréAnd74, III a), Def. 11 and 12]) of
![]() $R_2$
with coefficients in M. Let E denote the quotient field of
$R_2$
with coefficients in M. Let E denote the quotient field of
![]() $\mathcal {O}$
viewed as a B-module via
$\mathcal {O}$
viewed as a B-module via
![]() $\pi _B$
.
$\pi _B$
.
The invariants
![]() $c_0(B)$
and
$c_0(B)$
and
![]() $c_1(B)$
defined above are linked by the following proposition, which may be viewed as a derived version of Wiles’s formula for complete intersections [Reference WilesWil95], [Reference LenstraLen95], [Reference Fakhruddin, Khare and RamakrishnaFKR21, §A]; a variant of this formula was first discovered by A. Venkatesh [Reference VenkateshVen16].
$c_1(B)$
defined above are linked by the following proposition, which may be viewed as a derived version of Wiles’s formula for complete intersections [Reference WilesWil95], [Reference LenstraLen95], [Reference Fakhruddin, Khare and RamakrishnaFKR21, §A]; a variant of this formula was first discovered by A. Venkatesh [Reference VenkateshVen16].
Proposition A.6. Let
![]() $\mathcal {O}$
, E and
$\mathcal {O}$
, E and
![]() $\pi _B:B \to \mathcal {O}$
be as in the beginning of Appendix A, and let
$\pi _B:B \to \mathcal {O}$
be as in the beginning of Appendix A, and let
![]() $c_0(B)$
(resp.
$c_0(B)$
(resp.
![]() $c_1(B)$
) be the invariant of B defined in Definition A.1 (resp. A.2). Then
$c_1(B)$
) be the invariant of B defined in Definition A.1 (resp. A.2). Then
Proof. We denote by J the ideal
![]() $\ker (\phi _B)$
with
$\ker (\phi _B)$
with
![]() $\phi _B:A \to B$
as above. The sequence of maps
$\phi _B:A \to B$
as above. The sequence of maps
![]() ${\mathcal {O}} \to A \to B$
gives rise to an exact sequence of André–Quillen cohomology
${\mathcal {O}} \to A \to B$
gives rise to an exact sequence of André–Quillen cohomology
The
![]() $0$
on the left comes from the fact that
$0$
on the left comes from the fact that
![]() $\operatorname {\mathrm {Der}}^0_A(B,E/{\mathcal {O}}) = 0$
since
$\operatorname {\mathrm {Der}}^0_A(B,E/{\mathcal {O}}) = 0$
since
![]() $\phi _B$
is surjective (which also gives that
$\phi _B$
is surjective (which also gives that
![]() $\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})$
is equal to
$\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})$
is equal to
![]() $\operatorname {\mathrm {Der}}^1_A(B, E/{\mathcal {O}})$
). The
$\operatorname {\mathrm {Der}}^1_A(B, E/{\mathcal {O}})$
). The
![]() $0$
on the right comes from the fact that
$0$
on the right comes from the fact that
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal {O}}(A,E/{\mathcal {O}}) = \operatorname {\mathrm {Der}}^2_{\mathcal {O}}(A, {\mathcal {O}}) = 0$
, where the first equality is because
$\operatorname {\mathrm {Der}}^1_{\mathcal {O}}(A,E/{\mathcal {O}}) = \operatorname {\mathrm {Der}}^2_{\mathcal {O}}(A, {\mathcal {O}}) = 0$
, where the first equality is because
![]() $\operatorname {\mathrm {Der}}^i_{\mathcal {O}}(A,E) = 0$
for all i (a consequence of the finite tangent space condition on
$\operatorname {\mathrm {Der}}^i_{\mathcal {O}}(A,E) = 0$
for all i (a consequence of the finite tangent space condition on
![]() $\pi _A$
) and the second follows from [Reference AvramovAvr99, (1.2) Theorem] because A is a complete intersection,
$\pi _A$
) and the second follows from [Reference AvramovAvr99, (1.2) Theorem] because A is a complete intersection,
![]() $\mathcal {O}$
is regular and we have a surjection from S onto A.
$\mathcal {O}$
is regular and we have a surjection from S onto A.
We claim that
![]() $\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})$
and
$\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})$
and
![]() $\operatorname {\mathrm {Der}}^0_{\mathcal {O}}(A,E/{\mathcal {O}})$
are finite length
$\operatorname {\mathrm {Der}}^0_{\mathcal {O}}(A,E/{\mathcal {O}})$
are finite length
![]() ${\mathcal O}$
-modules and that we have equalities
${\mathcal O}$
-modules and that we have equalities
![]() $\ell (\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})) = \ell ({\mathcal {O}}/\pi _A(\operatorname {\mathrm {Fitt}}(J)))$
and
$\ell (\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})) = \ell ({\mathcal {O}}/\pi _A(\operatorname {\mathrm {Fitt}}(J)))$
and
![]() $\ell (\operatorname {\mathrm {Der}}^0_{\mathcal {O}}(A,E/{\mathcal {O}})) = \ell ({\mathcal {O}}/\pi _A(\operatorname {\mathrm {Fitt}}(\ker (\pi _A))))$
. Assuming the claim, from sequence (A.3) we deduce
$\ell (\operatorname {\mathrm {Der}}^0_{\mathcal {O}}(A,E/{\mathcal {O}})) = \ell ({\mathcal {O}}/\pi _A(\operatorname {\mathrm {Fitt}}(\ker (\pi _A))))$
. Assuming the claim, from sequence (A.3) we deduce
By definition
![]() $c_0(B) = \ell ({\mathcal {O}}/\pi _C(\operatorname {\mathrm {Ann}}(\ker (\pi _C))))$
,
$c_0(B) = \ell ({\mathcal {O}}/\pi _C(\operatorname {\mathrm {Ann}}(\ker (\pi _C))))$
,
![]() $c_1(B) = \ell (\pi _A (\operatorname {\mathrm {Ann}}(\ker (\phi _B)))/\pi _A (\operatorname {\mathrm {Fitt}}(\ker (\phi _B))))$
by Equation (A.1), and Lemma A.9 below implies that
$c_1(B) = \ell (\pi _A (\operatorname {\mathrm {Ann}}(\ker (\phi _B)))/\pi _A (\operatorname {\mathrm {Fitt}}(\ker (\phi _B))))$
by Equation (A.1), and Lemma A.9 below implies that
Recalling that
![]() $J = \ker (\phi _B)$
and
$J = \ker (\phi _B)$
and
![]() $\operatorname {\mathrm {Fitt}}(\ker (\pi _A)) = \operatorname {\mathrm {Ann}}_A(\ker (\pi _A))$
(since A is a complete intersection), the proposition follows by inserting these three equalities in Equation (A.4).
$\operatorname {\mathrm {Fitt}}(\ker (\pi _A)) = \operatorname {\mathrm {Ann}}_A(\ker (\pi _A))$
(since A is a complete intersection), the proposition follows by inserting these three equalities in Equation (A.4).
We now prove the claim made above: For the first part, note that
![]() $E/{\mathcal O}$
is an A-module via
$E/{\mathcal O}$
is an A-module via
![]() $\pi _A$
, so that
$\pi _A$
, so that
![]() $\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})\cong \operatorname {\mathrm {Hom}}_{\mathcal O}(J/J^2\otimes _A{\mathcal O},E/{\mathcal O})$
, where
$\mathrm {Hom}_A(J/J^2, E/{\mathcal {O}})\cong \operatorname {\mathrm {Hom}}_{\mathcal O}(J/J^2\otimes _A{\mathcal O},E/{\mathcal O})$
, where
![]() ${\mathcal O}$
is an A-module via
${\mathcal O}$
is an A-module via
![]() $\pi _A$
, and it suffices to show that
$\pi _A$
, and it suffices to show that
![]() $J/J^2\otimes _A{\mathcal O}$
is a finite length
$J/J^2\otimes _A{\mathcal O}$
is a finite length
![]() ${\mathcal O}$
-module. The module
${\mathcal O}$
-module. The module
![]() $J/J^2\otimes _A{\mathcal O}$
is of finite type over
$J/J^2\otimes _A{\mathcal O}$
is of finite type over
![]() ${\mathcal O}$
because
${\mathcal O}$
because
![]() $J/J^2$
is of finite type over A, and so we need to show that
$J/J^2$
is of finite type over A, and so we need to show that
![]() $J/J^2[1/\varpi ]\otimes _{A[1/\varpi ]}E$
vanishes. Now, the map
$J/J^2[1/\varpi ]\otimes _{A[1/\varpi ]}E$
vanishes. Now, the map
![]() $\phi [1/\varpi ]:A[1/\varpi ]\to B[1/\varpi ]$
is a map of finite-dimensional E-algebras and the (compatible) augmentations to
$\phi [1/\varpi ]:A[1/\varpi ]\to B[1/\varpi ]$
is a map of finite-dimensional E-algebras and the (compatible) augmentations to
![]() $\pi _A[1/\varpi ]$
and
$\pi _A[1/\varpi ]$
and
![]() $\pi _B[1/\varpi ]$
give rise to isomorphisms of a single factor with E, that is,
$\pi _B[1/\varpi ]$
give rise to isomorphisms of a single factor with E, that is,
![]() $\pi _A[1/\varpi ]\otimes _{A[1/\varpi ]} E$
is an isomorphism and
$\pi _A[1/\varpi ]\otimes _{A[1/\varpi ]} E$
is an isomorphism and
![]() $J[1/\varpi ]\otimes _{A[1/\varpi ]}E=0$
because
$J[1/\varpi ]\otimes _{A[1/\varpi ]}E=0$
because
![]() $J[1/\varpi ]$
must then be supported on the other factors, and hence
$J[1/\varpi ]$
must then be supported on the other factors, and hence
![]() $J/J^2[1/\varpi ]\otimes _{A[1/\varpi ]}E=0$
. For the second part, we apply the conormal sequence to
$J/J^2[1/\varpi ]\otimes _{A[1/\varpi ]}E=0$
. For the second part, we apply the conormal sequence to
![]() ${\mathcal O}\to A\to {\mathcal O}$
which gives the isomorphism
${\mathcal O}\to A\to {\mathcal O}$
which gives the isomorphism
![]() $\ker (\pi _A)/\ker (\pi _A)^2\cong \Omega _{A/{\mathcal O}}\otimes _A{\mathcal O}$
due to the splitting of
$\ker (\pi _A)/\ker (\pi _A)^2\cong \Omega _{A/{\mathcal O}}\otimes _A{\mathcal O}$
due to the splitting of
![]() $A\to {\mathcal O}$
. By construction the right-hand term in the isomorphism is of finite
$A\to {\mathcal O}$
. By construction the right-hand term in the isomorphism is of finite
![]() ${\mathcal O}$
-length, and the second part now follows from
${\mathcal O}$
-length, and the second part now follows from
For the first assertion on lengths, we need to show that
![]() $J/J^2\otimes _A{\mathcal O}$
and
$J/J^2\otimes _A{\mathcal O}$
and
![]() ${\mathcal O}/\pi _A(\operatorname {\mathrm {Fitt}}(J))$
have the same lengths. Because
${\mathcal O}/\pi _A(\operatorname {\mathrm {Fitt}}(J))$
have the same lengths. Because
![]() $\pi _A(J)=0$
, the image of
$\pi _A(J)=0$
, the image of
![]() $J^2\otimes _A{\mathcal O}$
in
$J^2\otimes _A{\mathcal O}$
in
![]() $J\otimes _A{\mathcal O}$
is zero, and hence
$J\otimes _A{\mathcal O}$
is zero, and hence
![]() $J/J^2\otimes _A{\mathcal O}\cong J \otimes _A{\mathcal O}$
. Next, observe that
$J/J^2\otimes _A{\mathcal O}\cong J \otimes _A{\mathcal O}$
. Next, observe that
![]() $\pi _A(\operatorname {\mathrm {Fitt}}(J))=\operatorname {\mathrm {Fitt}}(J\otimes _A{\mathcal O})$
, as follows from the definition of the fitting ideal. The equality of length now follows because for a finite length
$\pi _A(\operatorname {\mathrm {Fitt}}(J))=\operatorname {\mathrm {Fitt}}(J\otimes _A{\mathcal O})$
, as follows from the definition of the fitting ideal. The equality of length now follows because for a finite length
![]() ${\mathcal O}$
-module over the DVR
${\mathcal O}$
-module over the DVR
![]() ${\mathcal O}$
the theory of elementary divisors gives
${\mathcal O}$
the theory of elementary divisors gives
![]() $\ell (M)=\ell ({\mathcal O}/\operatorname {\mathrm {Fitt}}(M))$
. The argument for the second length equality proceeds in the same way. One reduces the equality to showing that
$\ell (M)=\ell ({\mathcal O}/\operatorname {\mathrm {Fitt}}(M))$
. The argument for the second length equality proceeds in the same way. One reduces the equality to showing that
![]() $ \ker (\pi _A)/\ker (\pi _A)^2\cong \ker (\pi _A)\otimes _A{\mathcal O}$
and
$ \ker (\pi _A)/\ker (\pi _A)^2\cong \ker (\pi _A)\otimes _A{\mathcal O}$
and
![]() ${\mathcal O}/\operatorname {\mathrm {Fitt}}(\ker (\pi _A)\otimes _A{\mathcal O})$
have the same length.
${\mathcal O}/\operatorname {\mathrm {Fitt}}(\ker (\pi _A)\otimes _A{\mathcal O})$
have the same length.
Remark A.7. The above proof shows in particular that the terms
![]() $\operatorname {\mathrm {Der}}^1_{\mathcal {O}}(B,E/{\mathcal {O}})$
and
$\operatorname {\mathrm {Der}}^1_{\mathcal {O}}(B,E/{\mathcal {O}})$
and
![]() ${\mathcal O}/\pi _A(\operatorname {\mathrm {Fitt}}(J))$
are of finite
${\mathcal O}/\pi _A(\operatorname {\mathrm {Fitt}}(J))$
are of finite
![]() ${\mathcal O}$
-length.
${\mathcal O}$
-length.
Remark A.8. If B is a complete intersection in Proposition A.6, we may take
![]() $A=B$
, so
$A=B$
, so
![]() $c_1(B) = 0$
,
$c_1(B) = 0$
,
![]() $c_0(B) = \ell ({\mathcal {O}}/\eta _B)$
and Equation (A.4) shows that Proposition A.6 reduces to Wiles’s formula. The proposition shows once again that
$c_0(B) = \ell ({\mathcal {O}}/\eta _B)$
and Equation (A.4) shows that Proposition A.6 reduces to Wiles’s formula. The proposition shows once again that
![]() $c_1(B)$
is independent of all choices since all the other terms in the formula are clearly so.
$c_1(B)$
is independent of all choices since all the other terms in the formula are clearly so.
The following lemma was used in the proof of Proposition A.6.
Lemma A.9. Let A be a Gorenstein local ring with an augmentation
![]() $\pi _A:A \to \mathcal {O}$
such that the length of
$\pi _A:A \to \mathcal {O}$
such that the length of
![]() $\ker (\pi _A)/\ker (\pi _A)^2$
is finite. Assume that
$\ker (\pi _A)/\ker (\pi _A)^2$
is finite. Assume that
![]() $\pi _A$
factors through a surjective ring homomorphism
$\pi _A$
factors through a surjective ring homomorphism
![]() $\phi _B: A \to B$
, and let C be the largest quotient of B which is Cohen–Macaulay, so there are surjections
$\phi _B: A \to B$
, and let C be the largest quotient of B which is Cohen–Macaulay, so there are surjections
![]() $\phi _C:A \to C$
,
$\phi _C:A \to C$
,
![]() $\pi _B: B \to \mathcal {O}$
and
$\pi _B: B \to \mathcal {O}$
and
![]() $\pi _C: C \to \mathcal {O}$
. Then
$\pi _C: C \to \mathcal {O}$
. Then
Proof. We may apply Lemma A.10 of [Reference Fakhruddin, Khare and RamakrishnaFKR21] to the map
![]() $\phi _C$
since C is Cohen–Macaulay, to deduce that
$\phi _C$
since C is Cohen–Macaulay, to deduce that
so it suffices to to prove that
![]() $\operatorname {\mathrm {Ann}}_A(\ker (\phi _C)) = \operatorname {\mathrm {Ann}}_A(\ker (\phi _B))$
. We have
$\operatorname {\mathrm {Ann}}_A(\ker (\phi _C)) = \operatorname {\mathrm {Ann}}_A(\ker (\phi _B))$
. We have
![]() $\ker (\phi _B) \subset \ker (\phi _C)$
and the quotient is a finite length A-module by the definition of C. The quotient map
$\ker (\phi _B) \subset \ker (\phi _C)$
and the quotient is a finite length A-module by the definition of C. The quotient map
is an isomorphism since
![]() $\operatorname {\mathrm {Ann}}_A(\ker (\phi _B))\ker (\phi _B) = (0)$
, so
$\operatorname {\mathrm {Ann}}_A(\ker (\phi _B))\ker (\phi _B) = (0)$
, so
![]() $\operatorname {\mathrm {Ann}}_A(\ker (\phi _B)) \ker (\phi _C)$
, being a submodule of a finite length A-module, is also of finite length. On the other hand, it is a submodule of A and
$\operatorname {\mathrm {Ann}}_A(\ker (\phi _B)) \ker (\phi _C)$
, being a submodule of a finite length A-module, is also of finite length. On the other hand, it is a submodule of A and
![]() $\mathrm {depth}(A) = 1$
, so it must be
$\mathrm {depth}(A) = 1$
, so it must be
![]() $(0)$
. Thus,
$(0)$
. Thus,
![]() $\operatorname {\mathrm {Ann}}_A(\ker (\phi _C)) = \operatorname {\mathrm {Ann}}_A(\ker (\phi _B))$
.
$\operatorname {\mathrm {Ann}}_A(\ker (\phi _C)) = \operatorname {\mathrm {Ann}}_A(\ker (\phi _B))$
.
A.1
We briefly explain how the formula (A.2) can be viewed as a derived version of Wiles’s formula:
Suppose we have a presentation
![]() $B = \mathcal {O}[[x_1,x_2,\dots , x_n]]/(f_1,f_2,\dots , f_{n+\delta })$
with
$B = \mathcal {O}[[x_1,x_2,\dots , x_n]]/(f_1,f_2,\dots , f_{n+\delta })$
with
![]() $\delta \geq 0$
. We may use this to construct a ‘derived’ ring
$\delta \geq 0$
. We may use this to construct a ‘derived’ ring
where the tensor product is defined as in [Reference Galatius and VenkateshGV18, Definition 3.3]. Here, the
![]() $x_i, y_j$
are in ‘degree 0’ and the map from
$x_i, y_j$
are in ‘degree 0’ and the map from
![]() $\mathcal {O}[[y_1,y_2,\dots ,y_n,\dots , y_{n+\delta }]]$
to
$\mathcal {O}[[y_1,y_2,\dots ,y_n,\dots , y_{n+\delta }]]$
to
![]() $\mathcal {O}[[x_1,x_2,\dots ,x_n]]$
is given by
$\mathcal {O}[[x_1,x_2,\dots ,x_n]]$
is given by
![]() $y_j \mapsto f_j$
and to
$y_j \mapsto f_j$
and to
![]() $\mathcal {O}$
by
$\mathcal {O}$
by
![]() $y_j \mapsto 0$
.
$y_j \mapsto 0$
.
If we assume that
![]() $A = \mathcal {O}[[x_1,\dots ,x_n]]/(f_1,f_2,\dots , f_{n})$
is a one-dimensional complete intersection, then the derived ring has ‘defect’ equal to
$A = \mathcal {O}[[x_1,\dots ,x_n]]/(f_1,f_2,\dots , f_{n})$
is a one-dimensional complete intersection, then the derived ring has ‘defect’ equal to
![]() $\delta $
. The invariant
$\delta $
. The invariant
![]() $c_1(B)$
may then be viewed as coming from
$c_1(B)$
may then be viewed as coming from
![]() $\pi _*(\mathcal {B})$
, since this may be computed in terms of a Koszul complex. Venkatesh views Equation (A.2) as an analogue of Wiles’s formula for the derived ring
$\pi _*(\mathcal {B})$
, since this may be computed in terms of a Koszul complex. Venkatesh views Equation (A.2) as an analogue of Wiles’s formula for the derived ring
![]() $\mathcal {B}$
, which is a ‘derived complete intersection’. (However, as we have shown, all the terms in the formula only depend on
$\mathcal {B}$
, which is a ‘derived complete intersection’. (However, as we have shown, all the terms in the formula only depend on
![]() $B =\pi _0(\mathcal {B})$
, so it may also be viewed as a generalization of Wiles’s formula to rings which are not necessarily complete intersections.)
$B =\pi _0(\mathcal {B})$
, so it may also be viewed as a generalization of Wiles’s formula to rings which are not necessarily complete intersections.)
Acknowledgements.
We would like to thank Najmuddin Fakhruddin, Tony Feng, Michael Harris, Srikanth Iyengar and Akshay Venkatesh for helpful discussions related to this paper. G.B. acknowledges support by Deutsche Forschungsgemeinschaft (DFG) through CRC-TR 326 ‘Geometry and Arithmetic of Uniformized Structures’, project number 444845124. We thank the referee for a careful reading of the paper and many helpful suggestions.
Competing interests
The authors have no competing interest to declare.