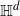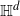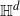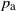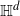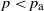1. Introduction
Consider an infinite, connected, locally finite graph G. Fix
![]() $p\in[0,1]$
and for each edge, mark it as ‘open’ with probability p, independently for all edges of G. We mark as ‘closed’ the edges which are not declared open. The state of an edge is the information of whether it is open or closed. The (random) set
$p\in[0,1]$
and for each edge, mark it as ‘open’ with probability p, independently for all edges of G. We mark as ‘closed’ the edges which are not declared open. The state of an edge is the information of whether it is open or closed. The (random) set
![]() $\omega$
of open edges of G forms, together with all the vertices of G, a random subgraph of G. We will often identify the latter with the set
$\omega$
of open edges of G forms, together with all the vertices of G, a random subgraph of G. We will often identify the latter with the set
![]() $\omega$
. This is a model of percolation, which we call Bernoulli bond percolation on G with parameter p. We will denote the corresponding probability measure by
$\omega$
. This is a model of percolation, which we call Bernoulli bond percolation on G with parameter p. We will denote the corresponding probability measure by
![]() ${\mathbb{P}}_p$
to indicate the parameter p.
${\mathbb{P}}_p$
to indicate the parameter p.
Among the main objects of interest in percolation theory are the connected components of the random subgraph
![]() $\omega$
, called clusters, and their ‘sizes’. Here, ‘size’ can mean the number of vertices, the diameter, or some other property of a cluster which measures how ‘large’ it is. For example, one may ask whether there is a cluster containing infinitely many vertices in the random subgraph, with positive probability.
$\omega$
, called clusters, and their ‘sizes’. Here, ‘size’ can mean the number of vertices, the diameter, or some other property of a cluster which measures how ‘large’ it is. For example, one may ask whether there is a cluster containing infinitely many vertices in the random subgraph, with positive probability.
In this paper, all the graphs are connected, infinite, and locally finite.
Definition 1.1. We define the critical probability for the above percolation model on G as
It follows from the Kolmogorov 0–1 law that if the graph G is connected and locally finite, then the probability
![]() ${\mathbb{P}}_p(\omega\textrm{ has some infinite cluster})$
always equals 0 or 1. Since this event is an increasing event (see Definition 5.3), its probability is an increasing function of p. Thus, it is 0 for
${\mathbb{P}}_p(\omega\textrm{ has some infinite cluster})$
always equals 0 or 1. Since this event is an increasing event (see Definition 5.3), its probability is an increasing function of p. Thus, it is 0 for
![]() $p<{{p_{\text{c}}}}(G)$
and 1 for
$p<{{p_{\text{c}}}}(G)$
and 1 for
![]() $p>{{p_{\text{c}}}}(G)$
.
$p>{{p_{\text{c}}}}(G)$
.
Definition 1.2. A graph G is transitive if its automorphism group acts transitively on the set of vertices of G. It is quasi-transitive if there are finitely many orbits of vertices of G under the action of its automorphism group.
If G is connected, locally finite, and quasi-transitive, then it is known from [Reference Newman and Schulman18, Theorem 1] that the number of infinite clusters in
![]() $\omega$
is almost surely (a.s.) constant and equal to 0, 1, or
$\omega$
is almost surely (a.s.) constant and equal to 0, 1, or
![]() $\infty$
(see also [Reference Lyons and Peres16, Theorem 7.5]). Let us focus on the question of determining when this number is
$\infty$
(see also [Reference Lyons and Peres16, Theorem 7.5]). Let us focus on the question of determining when this number is
![]() $\infty$
.
$\infty$
.
Definition 1.3. The unification probability for the above percolation model on any graph G is the number
Definition 1.4. A locally finite graph G is non-amenable if there is a constant
![]() $\Phi>0$
such that for every non-empty finite set K of vertices of G,
$\Phi>0$
such that for every non-empty finite set K of vertices of G,
![]() $|\text{bd}\, K|\ge\Phi|K|$
, where
$|\text{bd}\, K|\ge\Phi|K|$
, where
![]() $\text{bd}\, K$
is the set of edges of G with exactly one vertex in K (a kind of boundary of K). Otherwise, G is amenable.
$\text{bd}\, K$
is the set of edges of G with exactly one vertex in K (a kind of boundary of K). Otherwise, G is amenable.
It turns out that if a connected, transitive, locally finite graph G is amenable, then there is at most one infinite cluster a.s. for bond and site Bernoulli percolation; see [Reference Lyons and Peres16, Theorem 7.6]. So if
![]() ${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
, then the graph G must be non-amenable. It is an interesting question whether the converse is true.
${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
, then the graph G must be non-amenable. It is an interesting question whether the converse is true.
Conjecture 1.1. ([Reference Benjamini and Schramm4]) If G is non-amenable and quasi-transitive, then
![]() ${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
.
${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
.
There are several classes of non-amenable graphs for which the above conjecture has been established. Let us mention a few of them here. For an infinite regular tree it is actually folklore. It was shown for bond percolation on the Cartesian product of
![]() $\mathbb{Z}^d$
with an infinite regular tree of sufficiently high degree in [Reference Grimmett and Newman10]. Later, it was shown for site percolation on Cayley graphs of a wide class of Fuchsian groups in [Reference Lalley15], and for site and bond percolation on transitive, non-amenable, planar graphs with one end in [Reference Benjamini and Schramm5]. (A graph has one end if after throwing out any finite set of vertices, exactly one of its connected components is infinite.) These two results concern the hyperbolic plane
$\mathbb{Z}^d$
with an infinite regular tree of sufficiently high degree in [Reference Grimmett and Newman10]. Later, it was shown for site percolation on Cayley graphs of a wide class of Fuchsian groups in [Reference Lalley15], and for site and bond percolation on transitive, non-amenable, planar graphs with one end in [Reference Benjamini and Schramm5]. (A graph has one end if after throwing out any finite set of vertices, exactly one of its connected components is infinite.) These two results concern the hyperbolic plane
![]() ${{\mathbb{H}^2}}$
. Similarly, the conjecture is obtained in [Reference Czajkowski7] for many tiling graphs in
${{\mathbb{H}^2}}$
. Similarly, the conjecture is obtained in [Reference Czajkowski7] for many tiling graphs in
![]() ${{\mathbb{H}^3}}$
. There is also a rather general result in [Reference Pak and Smirnova-Nagnibeda19] saying that any finitely generated non-amenable group has a Cayley graph G with
${{\mathbb{H}^3}}$
. There is also a rather general result in [Reference Pak and Smirnova-Nagnibeda19] saying that any finitely generated non-amenable group has a Cayley graph G with
![]() ${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
for bond percolation. Recently a general result [Reference Hutchcroft12] was published which says that
${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
for bond percolation. Recently a general result [Reference Hutchcroft12] was published which says that
![]() ${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
for any hyperbolic non-amenable quasi-transitive graph.
${{p_{\text{c}}}}(G)<{{p_{\text{u}}}}(G)$
for any hyperbolic non-amenable quasi-transitive graph.
The interested reader may consult e.g. [Reference Grimmett9] and [Reference Lyons and Peres16], which give quite wide introductions to percolation theory.
1.1. Boundaries of ends
In this paper, we consider percolation clusters on graphs ‘naturally’ embedded in
![]() $\mathbb{H}^d$
with
$\mathbb{H}^d$
with
![]() $d\ge 2$
. We define the boundaries of ends of a cluster in
$d\ge 2$
. We define the boundaries of ends of a cluster in
![]() $\mathbb{H}^d$
as follows.
$\mathbb{H}^d$
as follows.
Definition 1.5. For any topological space X, by
![]() $\text{int}\,_X$
and
$\text{int}\,_X$
and ![]() we mean the operations of taking the interior and the closure, respectively, in the space X.
we mean the operations of taking the interior and the closure, respectively, in the space X.
Definition 1.6. Let X be a locally compact completely regular Hausdorff
![]() $\Big(\text{T}_{3\frac{1}{2}}\Big)$
space.
$\Big(\text{T}_{3\frac{1}{2}}\Big)$
space.
-
An end of a subset
 $C\subseteq X$
is a function e from the family of all compact subsets of X to the family of subsets of C that satisfies the following conditions:
$C\subseteq X$
is a function e from the family of all compact subsets of X to the family of subsets of C that satisfies the following conditions:-
For any compact
 $K\subseteq X$
, the set e(K) is one of the connected components of
$K\subseteq X$
, the set e(K) is one of the connected components of
 $C\setminus K$
.
$C\setminus K$
. -
For
 $K\subseteq K^{\prime}\subseteq X$
—both compact—we have
$K\subseteq K^{\prime}\subseteq X$
—both compact—we have  \begin{equation*}e(K)\supseteq e(K^{\prime}).\end{equation*}
\begin{equation*}e(K)\supseteq e(K^{\prime}).\end{equation*}
-
One can think of an end of a given set
![]() $C\subseteq X$
as a ‘direction’ in C when escaping any compact subset of X.
$C\subseteq X$
as a ‘direction’ in C when escaping any compact subset of X.
Now let
![]() $\hat{X}$
be an arbitrary compactification of X. Then we make the following definitions:
$\hat{X}$
be an arbitrary compactification of X. Then we make the following definitions:
-
The boundary of
 $C\subseteq X$
(not to be confused with the usual topological notion of boundary) is given by
$C\subseteq X$
(not to be confused with the usual topological notion of boundary) is given by  \begin{equation*}\partial C = \overline{C}^{\hat{X}}\setminus {X}.\end{equation*}
\begin{equation*}\partial C = \overline{C}^{\hat{X}}\setminus {X}.\end{equation*}
-
Finally, the boundary of an end e of
 $C\subseteq X$
is
$C\subseteq X$
is \begin{equation*}\partial e= \displaystyle{\bigcap_{\substack{K\subseteq X\\ K\text{ compact}}}} \partial e(K).\end{equation*}
\begin{equation*}\partial e= \displaystyle{\bigcap_{\substack{K\subseteq X\\ K\text{ compact}}}} \partial e(K).\end{equation*}
We also put
![]() $\hat{C} = \overline{C}^{\hat{X}}$
. Whenever we use the usual notion of boundary (taken in
$\hat{C} = \overline{C}^{\hat{X}}$
. Whenever we use the usual notion of boundary (taken in
![]() $\mathbb{H}^d$
by default), we denote it by
$\mathbb{H}^d$
by default), we denote it by
![]() $\text{bd}\,$
to distinguish it from
$\text{bd}\,$
to distinguish it from
![]() $\partial$
(and we do not call it the ‘boundary’).
$\partial$
(and we do not call it the ‘boundary’).
We use these notions in the context of the hyperbolic space
![]() $\mathbb{H}^d$
, where the underlying compactification is the compactification
$\mathbb{H}^d$
, where the underlying compactification is the compactification
![]() $\hat{\mathbb{H}}^d$
of
$\hat{\mathbb{H}}^d$
of
![]() $\mathbb{H}^d$
by its set of points at infinity (it is the same as the Gromov boundary of
$\mathbb{H}^d$
by its set of points at infinity (it is the same as the Gromov boundary of
![]() $\mathbb{H}^d$
; see [Reference Bridson and Haefliger2, Definition II.8.1] and [Reference Bridson and Haefliger2, Section III.H.3]). The role of C above will be played by percolation clusters in
$\mathbb{H}^d$
; see [Reference Bridson and Haefliger2, Definition II.8.1] and [Reference Bridson and Haefliger2, Section III.H.3]). The role of C above will be played by percolation clusters in
![]() $\mathbb{H}^d$
.
$\mathbb{H}^d$
.
Thus,
![]() $\partial\mathbb{H}^d =\hat{\mathbb{H}}^d{\setminus}\mathbb{H}^d$
is the set of points at infinity. If
$\partial\mathbb{H}^d =\hat{\mathbb{H}}^d{\setminus}\mathbb{H}^d$
is the set of points at infinity. If
![]() $\mathbb{H}^d$
is considered in its Poincaré disc (also called ball) model,
$\mathbb{H}^d$
is considered in its Poincaré disc (also called ball) model,
![]() $\partial\mathbb{H}^d$
is naturally identified with the boundary sphere of the Poincaré disc.
$\partial\mathbb{H}^d$
is naturally identified with the boundary sphere of the Poincaré disc.
Remark 1.1. In this paper, whenever we consider a subset of
![]() $\mathbb{H}^{d}$
denoted by a longer formula e.g. of the form ‘
$\mathbb{H}^{d}$
denoted by a longer formula e.g. of the form ‘
![]() $C(\ldots)$
’, we use the notation
$C(\ldots)$
’, we use the notation
![]() $\hat{C}({\ldots})$
for its closure in
$\hat{C}({\ldots})$
for its closure in
![]() $\hat{\mathbb{H}}^{d}$
, instead of
$\hat{\mathbb{H}}^{d}$
, instead of
![]() $\widehat{C(\ldots)}$
, for aesthetic reasons.
$\widehat{C(\ldots)}$
, for aesthetic reasons.
Let us define a percolation threshold
![]() $p_{\text{e}}$
as the supremum of percolation parameters p such that a.s. for every infinite cluster, the boundary of each of its ends is a singleton. (We say that such a cluster has one-point boundaries of ends or is thin-ended for short.) The question is whether
$p_{\text{e}}$
as the supremum of percolation parameters p such that a.s. for every infinite cluster, the boundary of each of its ends is a singleton. (We say that such a cluster has one-point boundaries of ends or is thin-ended for short.) The question is whether
![]() $p_{\text{c}}<p_{\text{e}}<p_{\text{u}}$
, e.g., for some natural tiling graphs in
$p_{\text{c}}<p_{\text{e}}<p_{\text{u}}$
, e.g., for some natural tiling graphs in
![]() $\mathbb{H}^{d}$
for
$\mathbb{H}^{d}$
for
![]() $d\ge 3$
. In such a case one will have an additional percolation threshold in the non-uniqueness phase. In this paper, we give a sufficient condition for p-Bernoulli bond percolation to have only thin-ended infinite clusters, for a large class of transitive graphs embedded in
$d\ge 3$
. In such a case one will have an additional percolation threshold in the non-uniqueness phase. In this paper, we give a sufficient condition for p-Bernoulli bond percolation to have only thin-ended infinite clusters, for a large class of transitive graphs embedded in
![]() $\mathbb{H}^{d}$
. That sufficient condition is ‘
$\mathbb{H}^{d}$
. That sufficient condition is ‘
![]() $p<p_{\text{a}}$
’, where
$p<p_{\text{a}}$
’, where
![]() $p_{\text{a}}$
is a threshold defined in Definition 1.8. (In Section 1.3 we will make a few remarks about how
$p_{\text{a}}$
is a threshold defined in Definition 1.8. (In Section 1.3 we will make a few remarks about how
![]() $p_{\text{a}}$
may be related to the other percolation thresholds.) The key part of the proof is an adaptation of the proof of Theorem (5.4) from [Reference Grimmett9], which in turn is based on [Reference Menshikov17].
$p_{\text{a}}$
may be related to the other percolation thresholds.) The key part of the proof is an adaptation of the proof of Theorem (5.4) from [Reference Grimmett9], which in turn is based on [Reference Menshikov17].
In the next section, we formulate the assumptions on the graph and the main theorem.
1.2. The graph, the sufficient condition, and the main theorem
Definition 1.7. For any graph G, let
![]() $V(G)$
denote its set of vertices and
$V(G)$
denote its set of vertices and
![]() $E(G)$
its set of edges. In this paper, we often think of an
$E(G)$
its set of edges. In this paper, we often think of an
![]() $\omega\subseteq E(G)$
as a sample, called a percolation configuration. Accordingly, the power set
$\omega\subseteq E(G)$
as a sample, called a percolation configuration. Accordingly, the power set
![]() $2^{E(G)}$
is the sample space for modelling Bernoulli bond percolation. The accompanying measure
$2^{E(G)}$
is the sample space for modelling Bernoulli bond percolation. The accompanying measure
![]() ${\mathbb{P}}_p$
on it is induced by the product measure
${\mathbb{P}}_p$
on it is induced by the product measure
![]() $\prod_{e\in E(G)}\!(p{\delta}_1+(1-p){\delta}_0)$
on
$\prod_{e\in E(G)}\!(p{\delta}_1+(1-p){\delta}_0)$
on
![]() $\{0,1\}^{E(G)}$
, so
$\{0,1\}^{E(G)}$
, so
![]() ${\mathbb{P}}_p(\omega\ni e)=p$
for any
${\mathbb{P}}_p(\omega\ni e)=p$
for any
![]() $e\in E(G)$
. In this way one can define formally the configuration
$e\in E(G)$
. In this way one can define formally the configuration
![]() $\omega$
as a set-valued random variable. For any graph G embedded in an arbitrary metric space, we call this embedded graph transitive under isometries if some group of isometries of the space acts on G by graph automorphisms transitively on its set of vertices.
$\omega$
as a set-valued random variable. For any graph G embedded in an arbitrary metric space, we call this embedded graph transitive under isometries if some group of isometries of the space acts on G by graph automorphisms transitively on its set of vertices.
A graph embedding in a topological space is locally finite if every point has a neighbourhood intersecting only finitely many vertices and edges of the embedded graph.
By a simple graph we mean a graph without loops or multiple edges.
Assumption 1.1. Throughout this paper we assume that G is an infinite, connected (simple) graph embedded in
![]() $\mathbb{H}^d$
, such that
$\mathbb{H}^d$
, such that
-
its edges are geodesic segments;
-
the embedding is locally finite; and
-
it is transitive under isometries.
Let us also pick a vertex o (for ‘origin’) of G and fix it once and for all.
Note that by these assumptions, V(G) is countable, every vertex of G has finite degree, and G is a closed subset of
![]() $\mathbb{H}^d$
.
$\mathbb{H}^d$
.
Definition 1.8. For
![]() $v\in V(G)$
, by
$v\in V(G)$
, by
![]() $C(v)$
we mean the percolation cluster of v in G. Let
$C(v)$
we mean the percolation cluster of v in G. Let
![]() ${{\mathcal{N}}}(G)$
(for ‘null’), or
${{\mathcal{N}}}(G)$
(for ‘null’), or
![]() ${{\mathcal{N}}}$
for short, be defined by
${{\mathcal{N}}}$
for short, be defined by
and put
Here the subscript ‘a’ stands for ‘accumulation point’.
Remark 1.2. In words,
![]() ${{\mathcal{N}}}$
is the set of parameters p of Bernoulli bond percolation on G such that no point of
${{\mathcal{N}}}$
is the set of parameters p of Bernoulli bond percolation on G such that no point of
![]() $\partial\mathbb{H}^d$
lies in the boundary of the cluster of o with positive probability. Note that
$\partial\mathbb{H}^d$
lies in the boundary of the cluster of o with positive probability. Note that
![]() ${{\mathcal{N}}}$
is an interval (the author does not know whether it is right-open or right-closed), because the events
${{\mathcal{N}}}$
is an interval (the author does not know whether it is right-open or right-closed), because the events
![]() $\{x\in\partial C(o)\}$
for
$\{x\in\partial C(o)\}$
for
![]() $x\in\partial\mathbb{H}^d$
are all increasing, so
$x\in\partial\mathbb{H}^d$
are all increasing, so
![]() ${\mathbb{P}}_p(x\in\partial C(o))$
is a non-decreasing function of p (see [Reference Grimmett9, Theorem (2.1)]). That allows us to think of
${\mathbb{P}}_p(x\in\partial C(o))$
is a non-decreasing function of p (see [Reference Grimmett9, Theorem (2.1)]). That allows us to think of
![]() $p_{\text{a}}$
as the point of a phase transition.
$p_{\text{a}}$
as the point of a phase transition.
We now formulate the main theorem.
Theorem 1.1. Let G satisfy Assumption 1.1. Then, for any
![]() $0\le p<p_{\text{a}}$
, a.s. every cluster in p-Bernoulli bond percolation on G is thin-ended, i.e. has only one-point boundaries of ends.
$0\le p<p_{\text{a}}$
, a.s. every cluster in p-Bernoulli bond percolation on G is thin-ended, i.e. has only one-point boundaries of ends.
This theorem was already known in dimension
![]() $d=2$
, when the group of the isometries preserving the graph acts cocompactly on
$d=2$
, when the group of the isometries preserving the graph acts cocompactly on
![]() ${{\mathbb{H}^2}}$
, i.e. for vertex-transitive graphs of tilings of
${{\mathbb{H}^2}}$
, i.e. for vertex-transitive graphs of tilings of
![]() ${{\mathbb{H}^2}}$
by bounded hyperbolic polygons. It is proved in that generality in [Reference Czajkowski6] (based on [Reference Benjamini and Schramm5]), but is also easily seen in a much earlier paper, [Reference Lalley15], for Cayley graphs of a wide class of Fuchsian groups.
${{\mathbb{H}^2}}$
by bounded hyperbolic polygons. It is proved in that generality in [Reference Czajkowski6] (based on [Reference Benjamini and Schramm5]), but is also easily seen in a much earlier paper, [Reference Lalley15], for Cayley graphs of a wide class of Fuchsian groups.
The key ingredient of the proof of Theorem 1.1 is Lemma 3.1, which is a corollary of Theorem 3.2. The latter is quite interesting in its own right. These results are presented (along with a proof of Lemma 3.1) in Section 3. The elaborate proof of Theorem 3.2, rewritten from the proof of Theorem (5.4) in [Reference Grimmett9], is deferred to Section 5. The proof of the main theorem, Theorem 1.1, is presented in Section 4.
1.3. Remarks on the sufficient condition
In this section, we give some remarks on the threshold
![]() $p_{\text{a}}$
and on the events
$p_{\text{a}}$
and on the events
![]() $\{x\in\partial C(o)\}$
(used to define
$\{x\in\partial C(o)\}$
(used to define
![]() ${{\mathcal{N}}}$
).
${{\mathcal{N}}}$
).
Definition 1.9. For
![]() $A,B\subseteq\mathbb{H}^d$
, let
$A,B\subseteq\mathbb{H}^d$
, let
![]() $A\leftrightarrow B$
be the event that there is an open path in the percolation process (given by the context) intersecting both A and B. We also say that such a path joins A and B. If any of the sets is of the form
$A\leftrightarrow B$
be the event that there is an open path in the percolation process (given by the context) intersecting both A and B. We also say that such a path joins A and B. If any of the sets is of the form
![]() $\{x\}$
, we write x instead of
$\{x\}$
, we write x instead of
![]() $\{x\}$
in that formula and those phrases.
$\{x\}$
in that formula and those phrases.
Remark 1.3. The threshold
![]() $p_{\text{a}}$
is bounded as follows:
$p_{\text{a}}$
is bounded as follows:
The inequality
![]() ${{p_{\text{c}}}}\le p_{\text{a}}$
is obvious, and the inequality
${{p_{\text{c}}}}\le p_{\text{a}}$
is obvious, and the inequality
![]() $p_{\text{a}}\le{{p_{\text{u}}}}$
can be shown as follows: if p is such that
$p_{\text{a}}\le{{p_{\text{u}}}}$
can be shown as follows: if p is such that
![]() ${\mathbb{P}}_p$
-a.s. there is a unique infinite cluster in G, then with some probability
${\mathbb{P}}_p$
-a.s. there is a unique infinite cluster in G, then with some probability
![]() $a>0$
, o belongs to the infinite cluster, and by the Harris–FKG inequality, for any
$a>0$
, o belongs to the infinite cluster, and by the Harris–FKG inequality, for any
![]() $v\in V(G)$
,
$v\in V(G)$
,
Take
![]() $x\in\partial G$
. Choose a decreasing (in the sense of set inclusion) sequence
$x\in\partial G$
. Choose a decreasing (in the sense of set inclusion) sequence
![]() $(H_n)_n$
of half-spaces such that
$(H_n)_n$
of half-spaces such that
![]() $\bigcap_{n=1}^\infty \text{int}\,_{\partial\mathbb{H}^d}\partial H_n=\{x\}$
. Since
$\bigcap_{n=1}^\infty \text{int}\,_{\partial\mathbb{H}^d}\partial H_n=\{x\}$
. Since
![]() $x\in\partial G$
, we have
$x\in\partial G$
, we have
![]() $V(G)\cap H_n \neq \emptyset$
for all n. Therefore
$V(G)\cap H_n \neq \emptyset$
for all n. Therefore
 \begin{align*}{\mathbb{P}}_p(x\in\partial C(o)) &= {\mathbb{P}}_p\!\left(\bigcap_{n\in{\mathbb{N}}}\{(\exists v\in V(G)\cap H_n)(o\leftrightarrow v)\}\right) \\&= \lim_{n\to\infty} {\mathbb{P}}_p((\exists v\in V(G)\cap H_n)(o\leftrightarrow v)) \ge a^2.\end{align*}
\begin{align*}{\mathbb{P}}_p(x\in\partial C(o)) &= {\mathbb{P}}_p\!\left(\bigcap_{n\in{\mathbb{N}}}\{(\exists v\in V(G)\cap H_n)(o\leftrightarrow v)\}\right) \\&= \lim_{n\to\infty} {\mathbb{P}}_p((\exists v\in V(G)\cap H_n)(o\leftrightarrow v)) \ge a^2.\end{align*}
Hence,
![]() $p\notin{{\mathcal{N}}}$
, so
$p\notin{{\mathcal{N}}}$
, so
![]() $p\ge p_{\text{a}}$
, as desired.
$p\ge p_{\text{a}}$
, as desired.
The main theorem (Theorem 1.1) is interesting when
![]() ${{p_{\text{c}}}}<p_{\text{a}}$
. The author does not know what the class of embedded graphs G (even among those arising from Coxeter reflection groups as in [Reference Czajkowski7]) satisfying
${{p_{\text{c}}}}<p_{\text{a}}$
. The author does not know what the class of embedded graphs G (even among those arising from Coxeter reflection groups as in [Reference Czajkowski7]) satisfying
![]() ${{p_{\text{c}}}}(G)<p_{\text{a}}(G)$
is. The author suspects that
${{p_{\text{c}}}}(G)<p_{\text{a}}(G)$
is. The author suspects that
![]() $p_{\text{a}}={{p_{\text{u}}}}$
for such graphs as in [Reference Czajkowski7] in the cocompact case (see Remark 1.5; in such a case, most often we would have
$p_{\text{a}}={{p_{\text{u}}}}$
for such graphs as in [Reference Czajkowski7] in the cocompact case (see Remark 1.5; in such a case, most often we would have
![]() $p_{\text{a}}>{{p_{\text{c}}}}$
). In dimension
$p_{\text{a}}>{{p_{\text{c}}}}$
). In dimension
![]() $d=2$
the equality
$d=2$
the equality
![]() $p_{\text{a}}={{p_{\text{u}}}}$
follows easily from the following fact. If such a graph embedded in
$p_{\text{a}}={{p_{\text{u}}}}$
follows easily from the following fact. If such a graph embedded in
![]() ${{\mathbb{H}^2}}$
has one end, then in the middle phase of Bernoulli percolation on it we have many bi-infinite curves disjoint from the percolation subgraph and dividing
${{\mathbb{H}^2}}$
has one end, then in the middle phase of Bernoulli percolation on it we have many bi-infinite curves disjoint from the percolation subgraph and dividing
![]() ${{\mathbb{H}^2}}$
into pieces (see e.g. Subsection 2.7 in [Reference Lalley14]). This implies exponential decay of the probability of joining o to a distant hyperbolic half-plane, which gives
${{\mathbb{H}^2}}$
into pieces (see e.g. Subsection 2.7 in [Reference Lalley14]). This implies exponential decay of the probability of joining o to a distant hyperbolic half-plane, which gives
![]() ${\mathbb{P}}_p(x\in\partial C(o))=0$
for any
${\mathbb{P}}_p(x\in\partial C(o))=0$
for any
![]() $x\in\partial\mathbb{H}^d$
.
$x\in\partial\mathbb{H}^d$
.
On the other hand, there are examples where
![]() $p_{\text{a}}<{{p_{\text{u}}}}$
(see Example 1.1 below).
$p_{\text{a}}<{{p_{\text{u}}}}$
(see Example 1.1 below).
Remark 1.4. In the assumptions of Theorem 1.1,
![]() $p_{\text{a}}$
can be replaced by
$p_{\text{a}}$
can be replaced by
with
![]() $g_p(r)$
from Definition 3.1, because only the fact that for
$g_p(r)$
from Definition 3.1, because only the fact that for
![]() $p<p_{\text{a}}$
,
$p<p_{\text{a}}$
,
![]() $g_p(r)\xrightarrow[r\to\infty]{}0$
(Proposition 5.1) is used. Accordingly,
$g_p(r)\xrightarrow[r\to\infty]{}0$
(Proposition 5.1) is used. Accordingly,
![]() $p^{\prime}_{\text{a}}\ge p_{\text{a}}$
. Nevertheless, the author does not know whether it is possible that
$p^{\prime}_{\text{a}}\ge p_{\text{a}}$
. Nevertheless, the author does not know whether it is possible that
![]() $p^{\prime}_{\text{a}}>p_{\text{a}}$
.
$p^{\prime}_{\text{a}}>p_{\text{a}}$
.
Example 1.1. Let
![]() $\Pi$
be an ‘unbounded polyhedron’ with six faces in
$\Pi$
be an ‘unbounded polyhedron’ with six faces in
![]() ${{\mathbb{H}^3}}$
, five of which are cyclically perpendicular, with the sixth one disjoint from them (see Figure 1). Then the group
${{\mathbb{H}^3}}$
, five of which are cyclically perpendicular, with the sixth one disjoint from them (see Figure 1). Then the group
![]() ${\Gamma}$
generated by the (hyperbolic) reflections in the faces of
${\Gamma}$
generated by the (hyperbolic) reflections in the faces of
![]() $\Pi$
is isomorphic to the free product of
$\Pi$
is isomorphic to the free product of
![]() $\mathbb Z_2$
and the Coxeter group
$\mathbb Z_2$
and the Coxeter group
![]() ${\Gamma}_5 < \text{Isom}({{\mathbb{H}^2}})$
generated by the reflections in the sides of a right-angled pentagon in
${\Gamma}_5 < \text{Isom}({{\mathbb{H}^2}})$
generated by the reflections in the sides of a right-angled pentagon in
![]() ${{\mathbb{H}^2}}$
. Let G and
${{\mathbb{H}^2}}$
. Let G and
![]() $G_5$
be the Cayley graphs of
$G_5$
be the Cayley graphs of
![]() ${\Gamma}$
and
${\Gamma}$
and
![]() ${\Gamma}_5$
, respectively. Then G has infinitely many ends, so from [Reference Lyons and Peres16, Exercise 7.12(b)]
${\Gamma}_5$
, respectively. Then G has infinitely many ends, so from [Reference Lyons and Peres16, Exercise 7.12(b)]
![]() ${{p_{\text{u}}}}(G)=1$
. Next, if
${{p_{\text{u}}}}(G)=1$
. Next, if
![]() $p>{{p_{\text{u}}}}(G_5)$
, then with positive probability
$p>{{p_{\text{u}}}}(G_5)$
, then with positive probability
![]() $\partial C(o)$
contains the whole circle
$\partial C(o)$
contains the whole circle
![]() $\partial({\Gamma}_5\cdot o)$
. (This is implied by Theorem 4.1 and Lemma 4.3 from [Reference Benjamini and Schramm5].) Hence,
$\partial({\Gamma}_5\cdot o)$
. (This is implied by Theorem 4.1 and Lemma 4.3 from [Reference Benjamini and Schramm5].) Hence,
![]() $p_{\text{a}}(G)\le{{p_{\text{u}}}}(G_5)<{{p_{\text{u}}}}(G)$
, as
$p_{\text{a}}(G)\le{{p_{\text{u}}}}(G_5)<{{p_{\text{u}}}}(G)$
, as
![]() ${{p_{\text{u}}}}(G_5)<1$
by [Reference Babson and Benjamini1, Theorem 10] (because
${{p_{\text{u}}}}(G_5)<1$
by [Reference Babson and Benjamini1, Theorem 10] (because
![]() $G_5$
is one-ended). Moreover, the conclusion of the main theorem (Theorem 1.1) fails for any
$G_5$
is one-ended). Moreover, the conclusion of the main theorem (Theorem 1.1) fails for any
![]() $p>{{p_{\text{u}}}}(G_5)$
.
$p>{{p_{\text{u}}}}(G_5)$
.

Figure 1. Polyhedron in Example 1.1 (shown in Poincaré disc model of
![]() ${{\mathbb{H}^3}}$
).
${{\mathbb{H}^3}}$
).
Remark 1.5. This remark is hoped to somewhat explain the suspicion that for the Cayley graph of a cocompact Coxeter reflection group in
![]() $\mathbb{H}^d$
, we have
$\mathbb{H}^d$
, we have
![]() $p_{\text{a}}={{p_{\text{u}}}}$
(Remark 1.3). It was based on another suspicion: that for
$p_{\text{a}}={{p_{\text{u}}}}$
(Remark 1.3). It was based on another suspicion: that for
![]() $p<{{p_{\text{u}}}}$
in the same setting,
$p<{{p_{\text{u}}}}$
in the same setting,
where
![]() $|{\cdot}|$
is the Lebesgue measure on
$|{\cdot}|$
is the Lebesgue measure on
![]() $\partial\mathbb{H}^d={{\mathbb{S}}}^{d-1}$
.
$\partial\mathbb{H}^d={{\mathbb{S}}}^{d-1}$
.
During the preparation of this article, the author was able to verify (1.2) for some
![]() $p>{{p_{\text{c}}}}$
in the case when the group in Assumption 1.1 is a reflection group of a bounded right-angled polyhedron in
$p>{{p_{\text{c}}}}$
in the case when the group in Assumption 1.1 is a reflection group of a bounded right-angled polyhedron in
![]() ${{\mathbb{H}^3}}$
with at least 16 faces, acting faithfully on the vertex set of G. It seems that this can easily be generalized to many cocompact groups in higher dimensions. This is based on recent work by Sidoravicius, Wang, and Xiang concerning the boundary of the trace of a branching random walk on a hyperbolic group; see [Reference Sidoravicius, Wang and Xiang20, Theorem 1.2, Remark 1.3(iii)].
${{\mathbb{H}^3}}$
with at least 16 faces, acting faithfully on the vertex set of G. It seems that this can easily be generalized to many cocompact groups in higher dimensions. This is based on recent work by Sidoravicius, Wang, and Xiang concerning the boundary of the trace of a branching random walk on a hyperbolic group; see [Reference Sidoravicius, Wang and Xiang20, Theorem 1.2, Remark 1.3(iii)].
If one proves (1.2), then the probability vanishing in (1.1) follows for
![]() $|{\cdot}|$
-almost every point
$|{\cdot}|$
-almost every point
![]() $x\in\partial\mathbb{H}^d$
. In addition, because the induced action of such a cocompact group on
$x\in\partial\mathbb{H}^d$
. In addition, because the induced action of such a cocompact group on
![]() $\partial\mathbb{H}^d$
has only dense orbits (see e.g. [Reference Kapovich and Benakli13, Proposition 4.2]), one might suspect that in such a situation as above,
$\partial\mathbb{H}^d$
has only dense orbits (see e.g. [Reference Kapovich and Benakli13, Proposition 4.2]), one might suspect that in such a situation as above,
![]() ${\mathbb{P}}_p(x\in\partial C(o))=0$
holds for all
${\mathbb{P}}_p(x\in\partial C(o))=0$
holds for all
![]() $x\in\partial\mathbb{H}^d$
.
$x\in\partial\mathbb{H}^d$
.
2. Definitions: percolation on a subset of
 $\mathbb{H}^d$
$\mathbb{H}^d$
Here we are going to introduce some notions and notation used in Theorem 3.2 and Lemma 3.1 and in the proof of the main theorem.
Definition 2.1. Let us adopt the convention that the natural numbers include 0. We denote the set of all positive natural numbers by
![]() ${\mathbb{N}}_+$
.
${\mathbb{N}}_+$
.
Definition 2.2. For the rest of this paper, consider
![]() $\mathbb{H}^d$
in its fixed half-space Poincaré model (being the upper half-space
$\mathbb{H}^d$
in its fixed half-space Poincaré model (being the upper half-space
![]() ${\mathbb{R}}^{d-1}\times(0,\infty)$
), in which the point o (the distinguished vertex of G) is represented by
${\mathbb{R}}^{d-1}\times(0,\infty)$
), in which the point o (the distinguished vertex of G) is represented by
![]() $(0,\ldots,0,1)$
. (This point will play the role of the origin of both
$(0,\ldots,0,1)$
. (This point will play the role of the origin of both
![]() $\mathbb{H}^d$
and G.) The half-space model of
$\mathbb{H}^d$
and G.) The half-space model of
![]() $\mathbb{H}^d$
and its relation to the Poincaré ball model are explained in [Reference Bridson and Haefliger2, Chapter I.6, p. 90]. Note that the inversion of
$\mathbb{H}^d$
and its relation to the Poincaré ball model are explained in [Reference Bridson and Haefliger2, Chapter I.6, p. 90]. Note that the inversion of
![]() ${\mathbb{R}}^d$
mapping the Poincaré ball model
${\mathbb{R}}^d$
mapping the Poincaré ball model
![]() $\mathbb{B}^d$
to our fixed half-space model sends one point of the sphere
$\mathbb{B}^d$
to our fixed half-space model sends one point of the sphere
![]() $\text{bd}\,\mathbb{B}^d$
to infinity. In the context of the half-space model, we treat that ‘infinity’ as an abstract point (outside
$\text{bd}\,\mathbb{B}^d$
to infinity. In the context of the half-space model, we treat that ‘infinity’ as an abstract point (outside
![]() ${\mathbb{R}}^d$
) compactifying
${\mathbb{R}}^d$
) compactifying
![]() ${\mathbb{R}}^d$
. We call it the point at infinity and denote it by
${\mathbb{R}}^d$
. We call it the point at infinity and denote it by
![]() $\infty$
.
$\infty$
.
Let ![]() be the closure of
be the closure of
![]() $\mathbb{H}^d$
in
$\mathbb{H}^d$
in
![]() ${\mathbb{R}}^d$
, and let
${\mathbb{R}}^d$
, and let ![]() (so here
(so here ![]() and
and
![]() $\eth\mathbb{H}^d={\mathbb{R}}^{d-1}\times\{0\}$
). We identify
$\eth\mathbb{H}^d={\mathbb{R}}^{d-1}\times\{0\}$
). We identify ![]() with
with
![]() $\hat{\mathbb{H}}^d{\setminus}\{\infty\}$
and
$\hat{\mathbb{H}}^d{\setminus}\{\infty\}$
and
![]() $\eth\mathbb{H}^d$
with
$\eth\mathbb{H}^d$
with
![]() $\partial\mathbb{H}^d{\setminus}\{\infty\}$
in a natural way. Also, for any closed
$\partial\mathbb{H}^d{\setminus}\{\infty\}$
in a natural way. Also, for any closed
![]() $A\subseteq\mathbb{H}^d$
, let
$A\subseteq\mathbb{H}^d$
, let ![]() and
and ![]() . (Here, for complex notation for a subset of
. (Here, for complex notation for a subset of
![]() $\mathbb{H}^d$
(of the form e.g.
$\mathbb{H}^d$
(of the form e.g.
![]() $A_x^y(z)$
), we use the same notational convention for
$A_x^y(z)$
), we use the same notational convention for ![]() as for
as for
![]() $\,\hat{\cdot}\,$
—see Remark 1.1.)
$\,\hat{\cdot}\,$
—see Remark 1.1.)
Although sometimes we use the linear and Euclidean structure of
![]() ${\mathbb{R}}^d$
in
${\mathbb{R}}^d$
in
![]() $\mathbb{H}^d$
, the default geometry on
$\mathbb{H}^d$
, the default geometry on
![]() $\mathbb{H}^d$
is the hyperbolic one, unless indicated otherwise. On the other hand, by the Euclidean metric of the disc model we mean the metric on
$\mathbb{H}^d$
is the hyperbolic one, unless indicated otherwise. On the other hand, by the Euclidean metric of the disc model we mean the metric on
![]() $\hat{\mathbb{H}}^d$
induced by the embedding of
$\hat{\mathbb{H}}^d$
induced by the embedding of
![]() $\hat{\mathbb{H}}^d$
in
$\hat{\mathbb{H}}^d$
in
![]() ${\mathbb{R}}^d$
(as a unit disc) arising from the Poincaré disc model of
${\mathbb{R}}^d$
(as a unit disc) arising from the Poincaré disc model of
![]() $\mathbb{H}^d$
. Nevertheless, we are going to treat that metric as a metric on the set
$\mathbb{H}^d$
. Nevertheless, we are going to treat that metric as a metric on the set ![]() , never really considering
, never really considering
![]() $\mathbb{H}^d$
in the disc model.
$\mathbb{H}^d$
in the disc model.
Definition 2.3. For
![]() $k>0$
and
$k>0$
and
![]() $x\in{\mathbb{R}}^{d-1}\times\{0\}$
, by
$x\in{\mathbb{R}}^{d-1}\times\{0\}$
, by
![]() $y\mapsto k\cdot y$
and
$y\mapsto k\cdot y$
and
![]() $y\mapsto y+x$
(or
$y\mapsto y+x$
(or
![]() $k\cdot$
,
$k\cdot$
,
![]() $\cdot+x$
, respectively, for short) we mean always just a scaling and a translation of
$\cdot+x$
, respectively, for short) we mean always just a scaling and a translation of
![]() ${\mathbb{R}}^d$
, respectively, often as isometries of
${\mathbb{R}}^d$
, respectively, often as isometries of
![]() $\mathbb{H}^d$
. (Note that restricted to
$\mathbb{H}^d$
. (Note that restricted to
![]() $\mathbb{H}^d$
they are indeed hyperbolic isometries.)
$\mathbb{H}^d$
they are indeed hyperbolic isometries.)
Definition 2.4. Let
![]() $\text{Isom}\big(\mathbb{H}^d\big)$
denote the isometry group of
$\text{Isom}\big(\mathbb{H}^d\big)$
denote the isometry group of
![]() $\mathbb{H}^d$
.
$\mathbb{H}^d$
.
For any
![]() $h\in(0,1]$
and
$h\in(0,1]$
and
![]() $R\in O(d)$
(the orthogonal linear group of
$R\in O(d)$
(the orthogonal linear group of
![]() ${\mathbb{R}}^d$
) the pair (h, R) uniquely determines an isometry of
${\mathbb{R}}^d$
) the pair (h, R) uniquely determines an isometry of
![]() $\mathbb{H}^d$
, denoted by
$\mathbb{H}^d$
, denoted by
![]() $\Phi^{(h,R)}$
, such that
$\Phi^{(h,R)}$
, such that
![]() $\Phi^{(h,R)}(o)=(0,\ldots,0,h)$
and
$\Phi^{(h,R)}(o)=(0,\ldots,0,h)$
and
![]() $D\Phi^{(h,R)}(o)=hR$
(as an ordinary derivative of a function
$D\Phi^{(h,R)}(o)=hR$
(as an ordinary derivative of a function
![]() ${\mathbb{R}}^{d-1}\times(0,\infty)\to{\mathbb{R}}^d$
).
${\mathbb{R}}^{d-1}\times(0,\infty)\to{\mathbb{R}}^d$
).
Let
![]() $G^{(h,R)}$
denote
$G^{(h,R)}$
denote
![]() $\Phi^{(h,R)}[G]$
. Similarly, for any
$\Phi^{(h,R)}[G]$
. Similarly, for any
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
let
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
let
![]() $G^\Phi=\Phi[G]$
. Furthermore, in the same fashion, let
$G^\Phi=\Phi[G]$
. Furthermore, in the same fashion, let
![]() $o^{(h,R)}=\Phi^{(h,R)}(o)$
(which is
$o^{(h,R)}=\Phi^{(h,R)}(o)$
(which is
![]() $h\cdot o$
) and
$h\cdot o$
) and
![]() $o^\Phi=\Phi(o)$
.
$o^\Phi=\Phi(o)$
.
Definition 2.5. For any
![]() $p\in[0,1]$
, whenever we consider p-Bernoulli bond percolation on
$p\in[0,1]$
, whenever we consider p-Bernoulli bond percolation on
![]() $G^\Phi$
for
$G^\Phi$
for
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
, we just take
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
, we just take
![]() $\Phi[\omega]$
, where
$\Phi[\omega]$
, where
![]() $\omega$
denotes the random configuration in p-Bernoulli bond percolation on G.
$\omega$
denotes the random configuration in p-Bernoulli bond percolation on G.
Remark 2.1. One can say that this is a way of coupling the Bernoulli bond percolation processes on
![]() $G^\Phi$
for
$G^\Phi$
for
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
.
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
.
Formally, the notion of ‘p-Bernoulli bond percolation on
![]() $G^\Phi$
’ is not well-defined, because for different isometries
$G^\Phi$
’ is not well-defined, because for different isometries
![]() $\Phi_1$
,
$\Phi_1$
,
![]() $\Phi_2$
of
$\Phi_2$
of
![]() $\mathbb{H}^d$
such that
$\mathbb{H}^d$
such that
![]() $G^{\Phi_1}=G^{\Phi_2}$
, the processes
$G^{\Phi_1}=G^{\Phi_2}$
, the processes
![]() $\Phi_1[\omega]$
and
$\Phi_1[\omega]$
and
![]() $\Phi_2[\omega]$
are still different. Thus, we are going to use the convention that the isometry
$\Phi_2[\omega]$
are still different. Thus, we are going to use the convention that the isometry
![]() $\Phi$
used to determine the process
$\Phi$
used to determine the process
![]() $\Phi[\omega]$
is the same as used in the notation
$\Phi[\omega]$
is the same as used in the notation
![]() $G^\Phi$
determining the underlying graph.
$G^\Phi$
determining the underlying graph.
Definition 2.6. Let
![]() $L^h={\mathbb{R}}^{d-1}\times(0,h]\subseteq\mathbb{H}^d$
and put
$L^h={\mathbb{R}}^{d-1}\times(0,h]\subseteq\mathbb{H}^d$
and put
![]() $L=L^1$
. (In other words,
$L=L^1$
. (In other words,
![]() $L^h$
is the complement of some open horoball in
$L^h$
is the complement of some open horoball in
![]() $\mathbb{H}^d$
, which viewed in the Poincaré disc model
$\mathbb{H}^d$
, which viewed in the Poincaré disc model
![]() $\mathbb{B}^d$
is tangent to
$\mathbb{B}^d$
is tangent to
![]() $\partial\mathbb{B}^d$
at the point corresponding to
$\partial\mathbb{B}^d$
at the point corresponding to
![]() $\infty$
.)
$\infty$
.)
Definition 2.7. Consider any closed set
![]() $A\subseteq\mathbb{H}^d$
intersecting each geodesic line only in finitely many intervals and half-lines of that line (every set from the algebra of sets generated by convex sets satisfies this condition, e.g.
$A\subseteq\mathbb{H}^d$
intersecting each geodesic line only in finitely many intervals and half-lines of that line (every set from the algebra of sets generated by convex sets satisfies this condition, e.g.
![]() $A=L^h$
). Then by
$A=L^h$
). Then by
![]() $G^\Phi\cap A$
we mean an embedded graph in A with the set of vertices consisting of
$G^\Phi\cap A$
we mean an embedded graph in A with the set of vertices consisting of
![]() $V\big(G^\Phi\big)\cap A$
and the points of intersection of the edges of
$V\big(G^\Phi\big)\cap A$
and the points of intersection of the edges of
![]() $G^\Phi$
with
$G^\Phi$
with
![]() $\text{bd}\, A$
, and with the edges being all the non-degenerate connected components of intersections of edges of
$\text{bd}\, A$
, and with the edges being all the non-degenerate connected components of intersections of edges of
![]() $G^\Phi$
with A. The percolation process on
$G^\Phi$
with A. The percolation process on
![]() $G^\Phi\cap A$
considered in this paper is, by default, the process
$G^\Phi\cap A$
considered in this paper is, by default, the process
![]() $\Phi[\omega]\cap A$
. The same convention as in Remark 2.1 is used for these processes.
$\Phi[\omega]\cap A$
. The same convention as in Remark 2.1 is used for these processes.
Remark 2.2. To prove the main theorem, we use the process
![]() $\Phi^{(h,R)}[\omega]\cap L^H$
for
$\Phi^{(h,R)}[\omega]\cap L^H$
for
![]() $p\in[0,1]$
and for different H. In some sense, it is p-Bernoulli bond percolation on
$p\in[0,1]$
and for different H. In some sense, it is p-Bernoulli bond percolation on
![]() $G^{(h,R)}\cap L^H$
: on one hand, this process is defined in terms of the independent random states of the edges of
$G^{(h,R)}\cap L^H$
: on one hand, this process is defined in terms of the independent random states of the edges of
![]() $G^{(h,R)}$
, but on the other hand, sometimes different edges of the graph
$G^{(h,R)}$
, but on the other hand, sometimes different edges of the graph
![]() $G^{(h,R)}\cap L^H$
are obtained from the same edge of
$G^{(h,R)}\cap L^H$
are obtained from the same edge of
![]() $G^{(h,R)}$
, so their states are stochastically dependent. Nevertheless, we are going to use some facts about Bernoulli percolation for the percolation process on
$G^{(h,R)}$
, so their states are stochastically dependent. Nevertheless, we are going to use some facts about Bernoulli percolation for the percolation process on
![]() $G^{(h,R)}\cap L^H$
. In such a situation, we consider the edges of
$G^{(h,R)}\cap L^H$
. In such a situation, we consider the edges of
![]() $G^{(h,R)}$
intersecting
$G^{(h,R)}$
intersecting
![]() $L^H$
instead of their fragments obtained in the intersection with
$L^H$
instead of their fragments obtained in the intersection with
![]() $L^H$
.
$L^H$
.
3. Exponential decay of the cluster radius distribution
We are going to treat the percolation process
![]() $\Phi^{(h,R)}[\omega]\cap L^H$
roughly as a Bernoulli percolation process on the standard lattice
$\Phi^{(h,R)}[\omega]\cap L^H$
roughly as a Bernoulli percolation process on the standard lattice
![]() $\mathbb{Z}^{d-1}$
(given a graph structure by joining every pair of vertices from
$\mathbb{Z}^{d-1}$
(given a graph structure by joining every pair of vertices from
![]() $\mathbb{Z}^{d-1}$
with distance 1 by an edge). This is motivated by the fact that
$\mathbb{Z}^{d-1}$
with distance 1 by an edge). This is motivated by the fact that
![]() $\mathbb{Z}^{d-1}$
with the graph metric is quasi-isometric to
$\mathbb{Z}^{d-1}$
with the graph metric is quasi-isometric to
![]() $\eth\mathbb{H}^d$
or
$\eth\mathbb{H}^d$
or
![]() $L^H$
with the Euclidean metric. (Two metric spaces are quasi-isometric if, loosely speaking, there are mappings in both directions between them which are bi-Lipschitz up to an additive constant. For a strict definition, see [Reference Bridson and Haefliger2, Definition I.8.14]; cf. also Exercise 8.16(1) there.)
$L^H$
with the Euclidean metric. (Two metric spaces are quasi-isometric if, loosely speaking, there are mappings in both directions between them which are bi-Lipschitz up to an additive constant. For a strict definition, see [Reference Bridson and Haefliger2, Definition I.8.14]; cf. also Exercise 8.16(1) there.)
In the setting of
![]() $\mathbb{Z}^{d-1}$
, we have a theorem on exponential decay of the cluster radius distribution, below the critical threshold of percolation.
$\mathbb{Z}^{d-1}$
, we have a theorem on exponential decay of the cluster radius distribution, below the critical threshold of percolation.
Theorem 3.1. ([Reference Grimmett9, Theorem (5.4)].) For any
![]() $p<{{p_{\text{c}}}}\big(\mathbb{Z}^d\big)$
there exists
$p<{{p_{\text{c}}}}\big(\mathbb{Z}^d\big)$
there exists
![]() $\psi(p)>0$
such that in p-Bernoulli bond percolation on
$\psi(p)>0$
such that in p-Bernoulli bond percolation on
![]() $\mathbb{Z}^d$
$\mathbb{Z}^d$
for all n, where the spheres are considered in the graph metric on
![]() $\mathbb{Z}^d$
.
$\mathbb{Z}^d$
.
The idea (of a slightly more general theorem) comes from [Reference Menshikov17], where a sketch of the proof is given, and a detailed proof of the above statement is presented in [Reference Grimmett9].
We adapt the idea of this theorem to the percolation process on
![]() $G^{(h,R)}\cap L$
in Theorem 3.2 and Lemma 3.1, appropriately rewriting the proof in [Reference Grimmett9], which is going to be the key part of the proof of the main theorem. In order to consider such a counterpart of the above theorem, we define a kind of tail of all the distributions of the cluster radius in
$G^{(h,R)}\cap L$
in Theorem 3.2 and Lemma 3.1, appropriately rewriting the proof in [Reference Grimmett9], which is going to be the key part of the proof of the main theorem. In order to consider such a counterpart of the above theorem, we define a kind of tail of all the distributions of the cluster radius in
![]() $G^{(h,R)}\cap L$
for
$G^{(h,R)}\cap L$
for
![]() $(h,R)\in(0,1]\times O(d)$
, as follows.
$(h,R)\in(0,1]\times O(d)$
, as follows.
Definition 3.1. Let
![]() $\pi$
be the Euclidean orthogonal projection from
$\pi$
be the Euclidean orthogonal projection from
![]() $\mathbb{H}^d$
onto
$\mathbb{H}^d$
onto
![]() $\eth\mathbb{H}^d$
, and for any
$\eth\mathbb{H}^d$
, and for any
![]() $x,y\in\mathbb{H}^d$
, let
$x,y\in\mathbb{H}^d$
, let
where
![]() $\|\cdot\|_\infty$
is the maximum (i.e.
$\|\cdot\|_\infty$
is the maximum (i.e.
![]() $l^\infty$
) norm on
$l^\infty$
) norm on
![]() $\eth\mathbb{H}^d={\mathbb{R}}^{d-1}\times\{0\}$
. Then, for
$\eth\mathbb{H}^d={\mathbb{R}}^{d-1}\times\{0\}$
. Then, for
![]() $r>0$
and
$r>0$
and
![]() $x\in\mathbb{H}^d$
, let
$x\in\mathbb{H}^d$
, let
and for
![]() $h>0$
, put
$h>0$
, put
If
![]() $x=o$
(or, more generally, if
$x=o$
(or, more generally, if
![]() $\pi(x)=\pi(o)$
), then we omit ‘(x)’. Finally, for
$\pi(x)=\pi(o)$
), then we omit ‘(x)’. Finally, for
![]() $p\in[0,1]$
and
$p\in[0,1]$
and
![]() $r>0$
, let
$r>0$
, let
This can be thought of as the distribution function of the ‘size’ (projection radius) of the cluster at the origin in the percolation process restricted to L, ‘made invariant’ under all isometries
![]() $\Phi^{(h,R)}$
.
$\Phi^{(h,R)}$
.
Remark 3.1. In the Euclidean geometry,
![]() $B_r(x)$
and
$B_r(x)$
and
![]() $B_r^h(x)$
are just cuboids of dimensions
$B_r^h(x)$
are just cuboids of dimensions
![]() $r\times\ldots\times r\times\infty$
(unbounded in the direction of the dth axis) and
$r\times\ldots\times r\times\infty$
(unbounded in the direction of the dth axis) and
![]() $r\times\ldots\times r\times h$
, respectively (up to removal of the face lying in
$r\times\ldots\times r\times h$
, respectively (up to removal of the face lying in
![]() $\eth\mathbb{H}^d$
).
$\eth\mathbb{H}^d$
).
The condition ‘
![]() $p<p_c\big(\mathbb{Z}^d\big)$
’ in Theorem 3.1 will be replaced by ‘
$p<p_c\big(\mathbb{Z}^d\big)$
’ in Theorem 3.1 will be replaced by ‘
![]() $p<p_{\text{a}}$
’, which is natural because of the remark below. Before stating the remark, we introduce some notation concerning the percolation clusters.
$p<p_{\text{a}}$
’, which is natural because of the remark below. Before stating the remark, we introduce some notation concerning the percolation clusters.
Definition 3.2. For
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
and
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
and
![]() $v\in V\big(G^\Phi\big)$
and a set
$v\in V\big(G^\Phi\big)$
and a set
![]() $A\subseteq\mathbb{H}^d$
from the algebra generated by the convex sets, let
$A\subseteq\mathbb{H}^d$
from the algebra generated by the convex sets, let
![]() $C^\Phi(v)$
and
$C^\Phi(v)$
and
![]() $C_A^\Phi(v)$
be the clusters of v in
$C_A^\Phi(v)$
be the clusters of v in
![]() $G^\Phi$
and
$G^\Phi$
and
![]() $G^\Phi\cap A$
, respectively, in the percolation configuration. Similarly, for
$G^\Phi\cap A$
, respectively, in the percolation configuration. Similarly, for
![]() $(h,R)\in(0,1]\times O(d)$
and
$(h,R)\in(0,1]\times O(d)$
and
![]() $\Phi=\Phi^{(h,R)}$
, we use the notation
$\Phi=\Phi^{(h,R)}$
, we use the notation
![]() $C^{(h,R)}(v)$
and
$C^{(h,R)}(v)$
and
![]() $C^{(h,R)}_A(v)$
, respectively.
$C^{(h,R)}_A(v)$
, respectively.
If
![]() $v=\Phi(o)$
, we omit ‘(v)’ for brevity, and if
$v=\Phi(o)$
, we omit ‘(v)’ for brevity, and if
![]() $\Phi={\text{Id}}$
, we omit ‘
$\Phi={\text{Id}}$
, we omit ‘
![]() $\Phi$
’.
$\Phi$
’.
Remark 3.2. If
![]() $p\in{{\mathcal{N}}}$
, then for any
$p\in{{\mathcal{N}}}$
, then for any
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
, the cluster
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
, the cluster
![]() $C^\Phi$
is
$C^\Phi$
is
![]() ${\mathbb{P}}_p$
-a.s. bounded in the Euclidean metric. The reason is as follows. Take any
${\mathbb{P}}_p$
-a.s. bounded in the Euclidean metric. The reason is as follows. Take any
![]() $p\in{{\mathcal{N}}}$
and
$p\in{{\mathcal{N}}}$
and
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Then, for any
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Then, for any
![]() $x\in\partial\mathbb{H}^d$
, we have
$x\in\partial\mathbb{H}^d$
, we have
![]() $x\notin \hat{C}(o)$
$x\notin \hat{C}(o)$
![]() ${\mathbb{P}}_p$
-a.s. as well as
${\mathbb{P}}_p$
-a.s. as well as
![]() $x\notin \hat{C}^\Phi$
$x\notin \hat{C}^\Phi$
![]() ${\mathbb{P}}_p$
-a.s. If we choose
${\mathbb{P}}_p$
-a.s. If we choose
![]() $x=\infty$
(for our half-space model of
$x=\infty$
(for our half-space model of
![]() $\mathbb{H}^d$
), then
$\mathbb{H}^d$
), then
![]() $\hat{C}^\Phi$
is
$\hat{C}^\Phi$
is
![]() ${\mathbb{P}}_p$
-a.s. a compact set in
${\mathbb{P}}_p$
-a.s. a compact set in ![]() , so
, so
![]() $C^\Phi$
is bounded in the Euclidean metric.
$C^\Phi$
is bounded in the Euclidean metric.
Now we formulate the aforementioned counterpart of Theorem 3.1. Its proof (based on that of [Reference Grimmett9, Theorem (5.4)]) is deferred to Section 5.
Theorem 3.2. (Exponential decay of
![]() $g_p({\cdot})$
) Let a graph G embedded in
$g_p({\cdot})$
) Let a graph G embedded in
![]() $\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Then, for any
$\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Then, for any
![]() $p<p_{\text{a}}$
, there exists
$p<p_{\text{a}}$
, there exists
![]() $\psi=\psi(p)>0$
such that for any
$\psi=\psi(p)>0$
such that for any
![]() $r>0$
,
$r>0$
,
The next lemma is a stronger version of the above theorem, where we take the union of all the clusters meeting some
![]() ${B^1_{r_0}}$
instead of the cluster of
${B^1_{r_0}}$
instead of the cluster of
![]() $o^{(h,R)}$
in
$o^{(h,R)}$
in
![]() $G^{(h,R)}\cap L$
. In other words, here the role played by
$G^{(h,R)}\cap L$
. In other words, here the role played by
![]() $o^{(h,R)}$
in Theorem 3.2 is taken over by its thickened version
$o^{(h,R)}$
in Theorem 3.2 is taken over by its thickened version
![]() ${B^1_{r_0}}\cap V\big(G^\Phi\big)$
for any
${B^1_{r_0}}\cap V\big(G^\Phi\big)$
for any
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. That leads to the following notation.
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. That leads to the following notation.
Definition 3.3. For any
![]() $C\subseteq\mathbb{H}^d$
, we define its projection radius by
$C\subseteq\mathbb{H}^d$
, we define its projection radius by
Lemma 3.1. Let a graph G embedded in
![]() $\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Fix an arbitrary
$\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Fix an arbitrary
![]() $r_0>0$
and let
$r_0>0$
and let
![]() ${\textbf{o}}_\Phi={B^1_{r_0}}\cap V\big(G^\Phi\big)$
for
${\textbf{o}}_\Phi={B^1_{r_0}}\cap V\big(G^\Phi\big)$
for
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Then, for any p such that the conclusion of Theorem 3.2 holds (in particular, for
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Then, for any p such that the conclusion of Theorem 3.2 holds (in particular, for
![]() $p<p_{\text{a}}$
), there exist
$p<p_{\text{a}}$
), there exist
![]() ${\alpha}={\alpha}(p,r_0)$
,
${\alpha}={\alpha}(p,r_0)$
,
![]() ${\varphi}={\varphi}(p,r_0)>0$
such that for any
${\varphi}={\varphi}(p,r_0)>0$
such that for any
![]() $r > 0$
and
$r > 0$
and
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
,
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
,
which is to say that for any
![]() $r>0$
$r>0$
 \begin{equation}\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} {\mathbb{P}}_p\bigg(r_\eth\bigg(\bigcup_{v\in{\textbf{o}}_\Phi} C_L^\Phi(v)\bigg)\ge r\bigg) \le {\alpha} e^{-{\varphi} r}.\end{equation}
\begin{equation}\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} {\mathbb{P}}_p\bigg(r_\eth\bigg(\bigcup_{v\in{\textbf{o}}_\Phi} C_L^\Phi(v)\bigg)\ge r\bigg) \le {\alpha} e^{-{\varphi} r}.\end{equation}
Remark 3.3. The version of the conclusion of the lemma with the inequality (3.2) is equivalent to the version with the inequality (3.1), though the probabilities involved are not necessarily equal. Still,
for any
![]() $r>\varepsilon>0$
, so if the continuous function
$r>\varepsilon>0$
, so if the continuous function
![]() ${\alpha} e^{-{\varphi} r}$
bounds one of these probabilities, then it also bounds the other.
${\alpha} e^{-{\varphi} r}$
bounds one of these probabilities, then it also bounds the other.
Before we prove the lemma, let us outline the proof. The first step is the following observation.
Definition 3.4. Put
![]() ${\textbf{o}}={\textbf{o}}_\Phi$
. For
${\textbf{o}}={\textbf{o}}_\Phi$
. For
![]() $x\in\mathbb{H}^d\subseteq{\mathbb{R}}^d$
, let h(x) denote the dth coordinate of x (or the Euclidean distance from x to
$x\in\mathbb{H}^d\subseteq{\mathbb{R}}^d$
, let h(x) denote the dth coordinate of x (or the Euclidean distance from x to
![]() $\eth\mathbb{H}^d$
), which we call the height of x.
$\eth\mathbb{H}^d$
), which we call the height of x.
Observation 3.1. There exists
![]() $H\ge 1$
such that a.s. if
$H\ge 1$
such that a.s. if
![]() ${\textbf{o}}\leftrightarrow S_r$
in
${\textbf{o}}\leftrightarrow S_r$
in
![]() $G^\Phi\cap L$
, then there exists
$G^\Phi\cap L$
, then there exists
![]() ${v_{\text{h}}}\in V\big(G^\Phi\big)\cap B_r^1$
such that
${v_{\text{h}}}\in V\big(G^\Phi\big)\cap B_r^1$
such that
![]() ${v_{\text{h}}} \leftrightarrow S_\frac{r-r_0}{2}({v_{\text{h}}})$
in
${v_{\text{h}}} \leftrightarrow S_\frac{r-r_0}{2}({v_{\text{h}}})$
in
![]() $G^\Phi\cap L^{Hh({v_{\text{h}}})}$
(not only in
$G^\Phi\cap L^{Hh({v_{\text{h}}})}$
(not only in
![]() $G^\Phi\cap L$
).
$G^\Phi\cap L$
).
Then we derive the inequality
 \begin{equation*}{\mathbb{P}}_p\big({\textbf{o}} \leftrightarrow S_r\textrm{ in }G^\Phi\cap L\big) \le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} g_p\!\left(\frac{r-r_0}{2Hh(v)}\right),\end{equation*}
\begin{equation*}{\mathbb{P}}_p\big({\textbf{o}} \leftrightarrow S_r\textrm{ in }G^\Phi\cap L\big) \le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} g_p\!\left(\frac{r-r_0}{2Hh(v)}\right),\end{equation*}
and we estimate the right-hand side using Theorem 3.2, obtaining (3.1).
We now prove the observation, then turn to proving the lemma.
Proof of the observation. Assume that
![]() ${\textbf{o}}\leftrightarrow S_r$
in
${\textbf{o}}\leftrightarrow S_r$
in
![]() $G^\Phi\cap L$
(note that this event may have probability 0, e.g. when
$G^\Phi\cap L$
(note that this event may have probability 0, e.g. when
![]() ${\textbf{o}}=\emptyset$
). Consider all open paths in
${\textbf{o}}=\emptyset$
). Consider all open paths in
![]() $G^\Phi\cap L$
joining
$G^\Phi\cap L$
joining
![]() ${\textbf{o}}$
to
${\textbf{o}}$
to
![]() $S_r$
, and consider all the vertices of
$S_r$
, and consider all the vertices of
![]() $G^\Phi$
visited by those paths before they reach
$G^\Phi$
visited by those paths before they reach
![]() $S_r$
starting from
$S_r$
starting from
![]() ${\textbf{o}}$
. There is a non-zero finite number of vertices of maximal height among them, because the embedding of
${\textbf{o}}$
. There is a non-zero finite number of vertices of maximal height among them, because the embedding of
![]() $G^\Phi$
is locally finite. Choose one of these vertices and call it
$G^\Phi$
is locally finite. Choose one of these vertices and call it
![]() ${v_{\text{h}}}$
. We prove that
${v_{\text{h}}}$
. We prove that
![]() ${v_{\text{h}}}$
satisfies the condition in the observation. Take an open path P in
${v_{\text{h}}}$
satisfies the condition in the observation. Take an open path P in
![]() $G^\Phi\cap L$
joining
$G^\Phi\cap L$
joining
![]() ${\textbf{o}}$
to
${\textbf{o}}$
to
![]() $S_r$
passing through
$S_r$
passing through
![]() ${v_{\text{h}}}$
which ends once it reaches
${v_{\text{h}}}$
which ends once it reaches
![]() $S_r$
. In fact, all the vertices of P (except the last one) lie in
$S_r$
. In fact, all the vertices of P (except the last one) lie in
![]() $B_r^{h({v_{\text{h}}})}$
.
$B_r^{h({v_{\text{h}}})}$
.
Hyperbolic lengths of edges in
![]() $G^\Phi$
are bounded from above (by the transitivity of
$G^\Phi$
are bounded from above (by the transitivity of
![]() $G^\Phi$
under isometries). That implies that for any edge of
$G^\Phi$
under isometries). That implies that for any edge of
![]() $G^\Phi$
the ratio between the heights of any two of its points is also bounded from above by some constant
$G^\Phi$
the ratio between the heights of any two of its points is also bounded from above by some constant
![]() $H\ge 1$
(this is going to be the H in the observation). The reasons for that are the following two basic properties of the half-space model of
$H\ge 1$
(this is going to be the H in the observation). The reasons for that are the following two basic properties of the half-space model of
![]() $\mathbb{H}^d$
:
$\mathbb{H}^d$
:
-
The heights of points of any fixed hyperbolic ball (of finite radius) are bounded from above and from below by some positive constants.
-
Any hyperbolic ball can be mapped onto any other hyperbolic ball of the same radius by a translation by a vector from
 ${\mathbb{R}}^{d-1}\times\{0\}$
composed with a linear scaling of
${\mathbb{R}}^{d-1}\times\{0\}$
composed with a linear scaling of
 ${\mathbb{R}}^d$
.
${\mathbb{R}}^d$
.
That implies that the path
![]() $P\subseteq L^{Hh({v_{\text{h}}})}$
.
$P\subseteq L^{Hh({v_{\text{h}}})}$
.
Now, because P contains some points
![]() $x\in{B^1_{r_0}}$
and
$x\in{B^1_{r_0}}$
and
![]() $y\in S_r$
, and because, by the triangle inequality,
$y\in S_r$
, and because, by the triangle inequality,
![]() $d_\eth(x,y)\ge r-r_0$
, it follows that
$d_\eth(x,y)\ge r-r_0$
, it follows that
![]() $d_\eth({v_{\text{h}}},x)$
or
$d_\eth({v_{\text{h}}},x)$
or
![]() $d_\eth({v_{\text{h}}},y)$
is at least
$d_\eth({v_{\text{h}}},y)$
is at least
![]() $\frac{r-r_0}{2}$
(again by the triangle inequality). Hence, P intersects
$\frac{r-r_0}{2}$
(again by the triangle inequality). Hence, P intersects
![]() $S_\frac{r-r_0}{2}({v_{\text{h}}})$
, which finishes the proof.
$S_\frac{r-r_0}{2}({v_{\text{h}}})$
, which finishes the proof.
Proof of Lemma 3.1. Note that, thanks to Remark 3.3, it is sufficient to prove inequality (3.1),
for any
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
and
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
and
![]() $r>0$
, and for some
$r>0$
, and for some
![]() ${\alpha}$
and
${\alpha}$
and
![]() ${\varphi}$
independent of r and
${\varphi}$
independent of r and
![]() $\Phi$
.
$\Phi$
.
Let
![]() $r>r_0$
and
$r>r_0$
and
![]() $\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Using Observation 3.1 with an appropriate H, we estimate
$\Phi\in\text{Isom}\big(\mathbb{H}^d\big)$
. Using Observation 3.1 with an appropriate H, we estimate
 \begin{align}{\mathbb{P}}_p&\big({\textbf{o}}\leftrightarrow S_r\textrm{ in }G^\Phi\cap L\big) \\&\le \sum\limits_{v\in V\big(G^\Phi\big)\cap B_r^1}\quad {\mathbb{P}}_p\big(v\leftrightarrow S_\frac{r-r_0}{2}(v)\textrm{ in }G^\Phi\cap L^{Hh(v)}\big) \notag \\&= \sum\limits_{v\in V\big(G^\Phi\big)\cap B_r^1}\quad {\mathbb{P}}_p\Bigl(\textstyle\frac{1}{H}\cdot o\leftrightarrow S_\frac{r-r_0}{2Hh(v)}\left(\frac{1}{H}\cdot o\right)\textrm{ in }\frac{1}{Hh(v)}\big(G^{\Phi} - \pi(v)\big)\cap L^1\Bigr), \notag \end{align}
\begin{align}{\mathbb{P}}_p&\big({\textbf{o}}\leftrightarrow S_r\textrm{ in }G^\Phi\cap L\big) \\&\le \sum\limits_{v\in V\big(G^\Phi\big)\cap B_r^1}\quad {\mathbb{P}}_p\big(v\leftrightarrow S_\frac{r-r_0}{2}(v)\textrm{ in }G^\Phi\cap L^{Hh(v)}\big) \notag \\&= \sum\limits_{v\in V\big(G^\Phi\big)\cap B_r^1}\quad {\mathbb{P}}_p\Bigl(\textstyle\frac{1}{H}\cdot o\leftrightarrow S_\frac{r-r_0}{2Hh(v)}\left(\frac{1}{H}\cdot o\right)\textrm{ in }\frac{1}{Hh(v)}\big(G^{\Phi} - \pi(v)\big)\cap L^1\Bigr), \notag \end{align}
by mapping the situation via the (hyperbolic) isometry
![]() $\frac{1}{Hh(v)}({\cdot} - \pi(v))$
for each v. Note that because for
$\frac{1}{Hh(v)}({\cdot} - \pi(v))$
for each v. Note that because for
![]() $v\in V\big(G^\Phi\big)\cap B_r^1$
,
$v\in V\big(G^\Phi\big)\cap B_r^1$
,
![]() $\frac{1}{H}\cdot o$
indeed is a vertex of
$\frac{1}{H}\cdot o$
indeed is a vertex of
![]() $\frac{1}{Hh(v)}\big(G^{\Phi} - \pi(v)\big)$
, by the transitivity of G under isometries, we can replace the isometry
$\frac{1}{Hh(v)}\big(G^{\Phi} - \pi(v)\big)$
, by the transitivity of G under isometries, we can replace the isometry
![]() $\frac{1}{Hh(v)}\left({\cdot}-\pi(v)\right)$
with an isometry giving the same image of G and mapping o to
$\frac{1}{Hh(v)}\left({\cdot}-\pi(v)\right)$
with an isometry giving the same image of G and mapping o to
![]() $\frac{1}{H}\cdot o$
, hence of the form
$\frac{1}{H}\cdot o$
, hence of the form
![]() $\Phi^{(1/H,R)}$
. That, combined with the assumption on p (the conclusion of Theorem 3.2), gives
$\Phi^{(1/H,R)}$
. That, combined with the assumption on p (the conclusion of Theorem 3.2), gives
 \begin{equation}({*}) \le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} g_p\!\left(\frac{r-r_0}{2Hh(v)}\right)\le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} e^{-\psi\frac{r-r_0}{2Hh(v)}},\end{equation}
\begin{equation}({*}) \le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} g_p\!\left(\frac{r-r_0}{2Hh(v)}\right)\le \sum_{v\in V\big(G^\Phi\big)\cap B_r^1} e^{-\psi\frac{r-r_0}{2Hh(v)}},\end{equation}
where
![]() $\psi$
is as in Theorem 3.2.
$\psi$
is as in Theorem 3.2.
Because
![]() $B_r^1 = [{-}r,r]^{d-1}\times(0,1]$
, one can cover it by
$B_r^1 = [{-}r,r]^{d-1}\times(0,1]$
, one can cover it by
![]() $\left\lceil\frac{r}{r_0}\right\rceil^{d-1}$
translations of
$\left\lceil\frac{r}{r_0}\right\rceil^{d-1}$
translations of
![]() ${B^1_{r_0}}$
by vectors from
${B^1_{r_0}}$
by vectors from
![]() ${\mathbb{R}}^{d-1}\times\{0\}$
. So, let
${\mathbb{R}}^{d-1}\times\{0\}$
. So, let
 \begin{equation*}\left\{{B^1_{r_0}}(x_i)\,:\,i=1,\ldots,\left\lceil\frac{r}{r_0}\right\rceil^{d-1}\right\}\end{equation*}
\begin{equation*}\left\{{B^1_{r_0}}(x_i)\,:\,i=1,\ldots,\left\lceil\frac{r}{r_0}\right\rceil^{d-1}\right\}\end{equation*}
be such a covering. Moreover, each
![]() ${B^1_{r_0}}(x_i)$
can be tessellated by infinitely many isometric (in the hyperbolic sense) copies of
${B^1_{r_0}}(x_i)$
can be tessellated by infinitely many isometric (in the hyperbolic sense) copies of
![]() $K={B^1_{r_0}}{\setminus} L^{\frac{1}{2}}$
—more precisely, by a translation of K,
$K={B^1_{r_0}}{\setminus} L^{\frac{1}{2}}$
—more precisely, by a translation of K,
![]() $2^{d-1}$
translations of
$2^{d-1}$
translations of
![]() $\frac{1}{2}K$
,
$\frac{1}{2}K$
,
![]() $\big(2^{d-1}\big)^2$
translations of
$\big(2^{d-1}\big)^2$
translations of
![]() $\frac{1}{2^2}K$
, etc., all along
$\frac{1}{2^2}K$
, etc., all along
![]() ${\mathbb{R}}^{d-1}\times\{0\}$
. Let
${\mathbb{R}}^{d-1}\times\{0\}$
. Let
![]() $U=\sup_{{\varphi}\in\text{Isom}\big(\mathbb{H}^d\big)}\#(V\big(G^\Phi\big)\cap{\varphi}[K])$
(we have
$U=\sup_{{\varphi}\in\text{Isom}\big(\mathbb{H}^d\big)}\#(V\big(G^\Phi\big)\cap{\varphi}[K])$
(we have
![]() $U<\infty$
by Assumption 1.1). Then, splitting the sum from (3.3) according to those tessellations,
$U<\infty$
by Assumption 1.1). Then, splitting the sum from (3.3) according to those tessellations,
 \begin{align}({*}) &\le \sum_{i=1}^{\left\lceil\frac{r}{r_0}\right\rceil^{d-1}} \sum_{v\in V\big(G^\Phi\big)\cap B_{r_0}^1(x_i)} e^{-\psi\frac{r-r_0}{2Hh(v)}} \notag \\&\le \left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty \big(2^{d-1}\big)^k U\sup_{h\in\big[\frac{1}{2^{k+1}},\frac{1}{2^k}\big]} e^{-\psi\frac{r-r_0}{2Hh}} \notag \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty \big(2^{d-1}\big)^k e^{-\frac{\psi}{H}2^{k-1}(r-r_0)} \end{align}
\begin{align}({*}) &\le \sum_{i=1}^{\left\lceil\frac{r}{r_0}\right\rceil^{d-1}} \sum_{v\in V\big(G^\Phi\big)\cap B_{r_0}^1(x_i)} e^{-\psi\frac{r-r_0}{2Hh(v)}} \notag \\&\le \left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty \big(2^{d-1}\big)^k U\sup_{h\in\big[\frac{1}{2^{k+1}},\frac{1}{2^k}\big]} e^{-\psi\frac{r-r_0}{2Hh}} \notag \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty \big(2^{d-1}\big)^k e^{-\frac{\psi}{H}2^{k-1}(r-r_0)} \end{align}
 \begin{align}&= U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty e^{\ln 2\cdot k(d-1) - \frac{\psi}{H}2^{k-1}(r-r_0)}.\notag\end{align}
\begin{align}&= U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \sum_{k=0}^\infty e^{\ln 2\cdot k(d-1) - \frac{\psi}{H}2^{k-1}(r-r_0)}.\notag\end{align}
Now we are going to show that the above bound is finite and tends to 0 at an exponential rate as
![]() $r\to\infty$
. First, we claim that there exists
$r\to\infty$
. First, we claim that there exists
![]() $k_0\in{\mathbb{N}}$
such that
$k_0\in{\mathbb{N}}$
such that
Indeed, for sufficiently large k we have
![]() $2^{k-1}\frac{\psi}{H}-k>0$
, so for
$2^{k-1}\frac{\psi}{H}-k>0$
, so for
![]() $r\ge 2r_0$
,
$r\ge 2r_0$
,
and
for sufficiently large k. So, let
![]() $k_0$
satisfy (3.5). Then, for
$k_0$
satisfy (3.5). Then, for
![]() $r\ge 2r_0$
,
$r\ge 2r_0$
,
 \begin{align*}({*}) &\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \left(\sum_{k=0}^{k_0-1} \big(2^{d-1}\big)^k e^{-2^{k-1} \frac{\psi}{H}(r-r_0)} + \sum_{k=k_0}^\infty e^{-kr}\right) \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \biggl(k_0\big(2^{d-1}\big)^{k_0-1} e^{-\frac{\psi}{2H}(r-r_0)} + e^{-k_0r}\underbrace{\frac{1}{1-e^{-r}}}_{\le \frac{1}{1-e^{-2r_0}}}\biggr) \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \big(De^{-Er}\big)\end{align*}
\begin{align*}({*}) &\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \left(\sum_{k=0}^{k_0-1} \big(2^{d-1}\big)^k e^{-2^{k-1} \frac{\psi}{H}(r-r_0)} + \sum_{k=k_0}^\infty e^{-kr}\right) \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \biggl(k_0\big(2^{d-1}\big)^{k_0-1} e^{-\frac{\psi}{2H}(r-r_0)} + e^{-k_0r}\underbrace{\frac{1}{1-e^{-r}}}_{\le \frac{1}{1-e^{-2r_0}}}\biggr) \\&\le U\!\left\lceil\frac{r}{r_0}\right\rceil^{d-1} \big(De^{-Er}\big)\end{align*}
for some constants
![]() $D,E>0$
. If we choose
$D,E>0$
. If we choose
![]() $r_1\ge 2r_0$
such that
$r_1\ge 2r_0$
such that
 \begin{equation*}(\forall r\ge r_1)\left( \left\lceil\frac{r}{r_0}\right\rceil^{d-1} \le e^\frac{Er}{2}\right)\end{equation*}
\begin{equation*}(\forall r\ge r_1)\left( \left\lceil\frac{r}{r_0}\right\rceil^{d-1} \le e^\frac{Er}{2}\right)\end{equation*}
(which is possible), then
For
![]() $r<r_1$
we have simply
$r<r_1$
we have simply
![]() $({*}) \le 1$
, so picking
$({*}) \le 1$
, so picking
![]() ${\varphi}=-\frac{E}{2}$
and sufficiently large
${\varphi}=-\frac{E}{2}$
and sufficiently large
![]() ${\alpha}$
, we complete the proof of the lemma.
${\alpha}$
, we complete the proof of the lemma.
4. Scaling—proof of the main theorem
Now we complete the proof of the main theorem.
Theorem 4.1. (Recalled from Theorem 1.1) Let G satisfy Assumption 1.1. Then, for any
![]() $0\le p<p_{\text{a}}$
, a.s. every cluster in p-Bernoulli bond percolation on G is thin-ended, i.e. has only one-point boundaries of ends.
$0\le p<p_{\text{a}}$
, a.s. every cluster in p-Bernoulli bond percolation on G is thin-ended, i.e. has only one-point boundaries of ends.
Proof of Theorem
1.1. Fix
![]() $p\in[0,p_{\text{a}})$
and suppose towards a contradiction that with some positive probability there is some cluster with some end with a non-one-point boundary. Note that by Remark 3.2 and by the transitivity of G under isometries, for any
$p\in[0,p_{\text{a}})$
and suppose towards a contradiction that with some positive probability there is some cluster with some end with a non-one-point boundary. Note that by Remark 3.2 and by the transitivity of G under isometries, for any
![]() $v\in V(G)$
a.s. C(v) is bounded in the Euclidean metric, so a.s. all the percolation clusters in G are bounded in the Euclidean metric. Then, for some
$v\in V(G)$
a.s. C(v) is bounded in the Euclidean metric, so a.s. all the percolation clusters in G are bounded in the Euclidean metric. Then, for some
![]() ${\delta}>0$
and
${\delta}>0$
and
![]() $r>0$
, there exists with probability
$r>0$
, there exists with probability
![]() $a>0$
a cluster, bounded in the Euclidean metric, with the boundary of some end having Euclidean diameter greater than or equal to
$a>0$
a cluster, bounded in the Euclidean metric, with the boundary of some end having Euclidean diameter greater than or equal to
![]() ${\delta}$
and intersecting the open disc
${\delta}$
and intersecting the open disc
![]() $\text{int}\,_{\eth\mathbb{H}^d}\eth B_r$
. Let C and e be such a cluster and its end, respectively. For
$\text{int}\,_{\eth\mathbb{H}^d}\eth B_r$
. Let C and e be such a cluster and its end, respectively. For
![]() $A\subseteq\mathbb{H}^d$
, let the projection diameter of A be the Euclidean diameter of
$A\subseteq\mathbb{H}^d$
, let the projection diameter of A be the Euclidean diameter of
![]() $\pi(A)$
. Then for
$\pi(A)$
. Then for
![]() $h>0$
,
$h>0$
,
-
the set
 $\overline{C{\setminus} L^h}$
is compact;
$\overline{C{\setminus} L^h}$
is compact; -
 $e(\overline{C{\setminus} L^h})$
is a cluster in the percolation configuration on
$e(\overline{C{\setminus} L^h})$
is a cluster in the percolation configuration on
 $G\cap L^h$
;
$G\cap L^h$
; -
 $e(\overline{C{\setminus} L^h})$
has projection diameter at least
$e(\overline{C{\setminus} L^h})$
has projection diameter at least
 ${\delta}$
and intersects
${\delta}$
and intersects
 $B_r\cap V(G)$
.
$B_r\cap V(G)$
.
All of the above implies that for any
![]() $k\in{\mathbb{N}}$
,
$k\in{\mathbb{N}}$
,
so, by scaling by
![]() $2^k$
in
$2^k$
in
![]() ${\mathbb{R}}^d$
(which is a hyperbolic isometry), we obtain
${\mathbb{R}}^d$
(which is a hyperbolic isometry), we obtain
(where we take the cluster in the intersection of L and
![]() $G^{2^k\cdot}$
, the image of G under the scaling). The set
$G^{2^k\cdot}$
, the image of G under the scaling). The set
![]() $B_{2^kr}\cap L$
is a union of
$B_{2^kr}\cap L$
is a union of
![]() $\big(2^k\big)^{d-1}$
isometric copies of
$\big(2^k\big)^{d-1}$
isometric copies of
![]() $B_r\cap L$
, so the left-hand side of the above inequality is bounded from above by
$B_r\cap L$
, so the left-hand side of the above inequality is bounded from above by
 \begin{align}\big(2^k\big)^{d-1}\!\!\!\!\!\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} \!\!\!{\mathbb{P}}_p\Big(\exists\ C_L^\Phi(v)\textrm{ of proj. diam. $\ge2^k{\delta}$ intersecting $B_{r}\cap V\big(G^\Phi\big)$}\Big) \\ \le \big(2^k\big)^{d-1}\!\!\!\!\!\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} \!\!\!{\mathbb{P}}_p\!\left(r_\eth\left(\bigcup_{v\in B_r^1\cap V\big(G^\Phi\big)} C_L^\Phi(v)\right)\ge \frac{2^k{\delta}}{2}\right)\end{align}
\begin{align}\big(2^k\big)^{d-1}\!\!\!\!\!\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} \!\!\!{\mathbb{P}}_p\Big(\exists\ C_L^\Phi(v)\textrm{ of proj. diam. $\ge2^k{\delta}$ intersecting $B_{r}\cap V\big(G^\Phi\big)$}\Big) \\ \le \big(2^k\big)^{d-1}\!\!\!\!\!\sup_{\Phi\in\text{Isom}\big(\mathbb{H}^d\big)} \!\!\!{\mathbb{P}}_p\!\left(r_\eth\left(\bigcup_{v\in B_r^1\cap V\big(G^\Phi\big)} C_L^\Phi(v)\right)\ge \frac{2^k{\delta}}{2}\right)\end{align}
(because the projection radius of a cluster is at least half its projection diameter). Therefore, by Lemma 3.1, for any
![]() $k\in{\mathbb{N}}$
,
$k\in{\mathbb{N}}$
,
where
![]() ${\alpha},{\varphi}>0$
are constants (as well as
${\alpha},{\varphi}>0$
are constants (as well as
![]() ${\delta}$
, a, and r). But the right-hand side of this inequality tends to 0 as
${\delta}$
, a, and r). But the right-hand side of this inequality tends to 0 as
![]() $k\to \infty$
, which yields a contradiction.
$k\to \infty$
, which yields a contradiction.
5. Proof of the exponential decay
In this section, we prove Theorem 3.2.
Theorem 5.1. (Recalled from Theorem 3.2) Let a graph G embedded in
![]() $\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Then, for any
$\mathbb{H}^d$
satisfy the conditions in Assumption 1.1. Then, for any
![]() $p<p_{\text{a}}$
, there exists
$p<p_{\text{a}}$
, there exists
![]() $\psi=\psi(p)>0$
such that for any
$\psi=\psi(p)>0$
such that for any
![]() $r>0$
,
$r>0$
,
Before giving the proof, we present a rough outline of it with some preliminaries. As mentioned earlier, the proof is an adaptation of the proof of Theorem (5.4) in [Reference Grimmett9], based on the work [Reference Menshikov17]. Its structure and most of its notation are also borrowed from [Reference Grimmett9], so it is quite easy to compare both proofs. (The differences are technical; they are summarized in Remark 5.2.)
We consider the following events depending only on a finite fragment of the percolation configuration; cf. Remark 5.1.
Definition 5.1. Fix an arbitrary
![]() $(h,R)\in(0,1]\times O(d)$
. Let
$(h,R)\in(0,1]\times O(d)$
. Let
![]() $p\in[0,1]$
,
$p\in[0,1]$
,
![]() $r>0$
, and
$r>0$
, and
![]() ${\delta}\in(0,h]$
, and define
${\delta}\in(0,h]$
, and define
![]() $L_{\delta}={\mathbb{R}}^{d-1}\times[{\delta},1]\subseteq\mathbb{H}^d$
(not to be confused with
$L_{\delta}={\mathbb{R}}^{d-1}\times[{\delta},1]\subseteq\mathbb{H}^d$
(not to be confused with
![]() $L^{\delta}$
). Let the event
$L^{\delta}$
). Let the event
and let
We will use Russo’s formula for the events
![]() $A^{\delta}(r)$
. Before we formulate it, we provide a couple of definitions needed there.
$A^{\delta}(r)$
. Before we formulate it, we provide a couple of definitions needed there.
Definition 5.2. For an event A in the percolation on any graph G, call an edge pivotal for a given configuration if and only if changing the state of that edge (and preserving the states of the other edges) causes A to change its state as well (from occurring to not occurring, or vice versa). Then let N(A) be the (random) number of all edges that are pivotal for A.
Definition 5.3. We say that an event A (being a set of configurations) is increasing if and only if for any configurations
![]() $\omega\subseteq\omega^{\prime}$
, if
$\omega\subseteq\omega^{\prime}$
, if
![]() $\omega\in A$
, then
$\omega\in A$
, then
![]() $\omega^{\prime}\in A$
.
$\omega^{\prime}\in A$
.
Theorem 5.2. (Russo’s formula) Consider Bernoulli bond percolation on any graph G, and let A be an increasing event defined in terms of the states of only finitely many edges of G. Then
This formula is proved as Theorem (2.25) in [Reference Grimmett9] for G being the classical lattice
![]() $\mathbb{Z}^d$
, but the proof applies for any graph G.
$\mathbb{Z}^d$
, but the proof applies for any graph G.
We will use Russo’s formula to derive a functional inequality for
![]() $f_p^{\delta}(r)$
involving
$f_p^{\delta}(r)$
involving
![]() ${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
(see (5.3)). Then we will estimate
${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
(see (5.3)). Then we will estimate
![]() ${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
from below (Lemma 5.2), looking at the cluster in
${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
from below (Lemma 5.2), looking at the cluster in
![]() $G^{(h,R)}\cap L_{\delta}$
joining
$G^{(h,R)}\cap L_{\delta}$
joining
![]() $o^{(h,R)}$
to
$o^{(h,R)}$
to
![]() $S_r$
as a ‘chain of sausages’ separated from each other by the pivotal edges for
$S_r$
as a ‘chain of sausages’ separated from each other by the pivotal edges for
![]() $A^{\delta}(r)$
. We will compare that ‘chain of sausages’ to a renewal process with inter-renewal times distributed roughly as the projection radius of the cluster at the origin. For this, we would like to use random variables with left-continuous distribution function
$A^{\delta}(r)$
. We will compare that ‘chain of sausages’ to a renewal process with inter-renewal times distributed roughly as the projection radius of the cluster at the origin. For this, we would like to use random variables with left-continuous distribution function
![]() $1-g_p$
. (By the left-continuous distribution function of a probability distribution (measure)
$1-g_p$
. (By the left-continuous distribution function of a probability distribution (measure)
![]() $\mu$
on
$\mu$
on
![]() ${\mathbb{R}}$
, we mean the function
${\mathbb{R}}$
, we mean the function
![]() ${\mathbb{R}}\ni x\mapsto\mu(({-}\infty,x))$
.) Because
${\mathbb{R}}\ni x\mapsto\mu(({-}\infty,x))$
.) Because
![]() $g_p$
does not need to be left-continuous, we replace it, when needed, by its left-continuous version
$g_p$
does not need to be left-continuous, we replace it, when needed, by its left-continuous version
![]() ${\tilde{g}}_p$
, defined as follows.
${\tilde{g}}_p$
, defined as follows.
Definition 5.4. Put
![]() ${\tilde{g}}_p(r)=\lim_{\varrho\to r^-} g_p(\varrho)$
for
${\tilde{g}}_p(r)=\lim_{\varrho\to r^-} g_p(\varrho)$
for
![]() $r>0$
.
$r>0$
.
In this way we will derive the following functional inequality:
 \begin{equation}f_{\alpha}^{\delta}(r)\le f_{\beta}^{\delta}(r)\exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m} - 1\right)\right)\end{equation}
\begin{equation}f_{\alpha}^{\delta}(r)\le f_{\beta}^{\delta}(r)\exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m} - 1\right)\right)\end{equation}
for any
![]() $0\le{\alpha}<{\beta}\le 1$
,
$0\le{\alpha}<{\beta}\le 1$
,
![]() $r>0$
and for
$r>0$
and for
![]() ${\delta}\in(0,h)$
, where a is a positive constant depending only on G. Then we will pass to some limits and to the supremum over (h, R), obtaining a functional inequality for
${\delta}\in(0,h)$
, where a is a positive constant depending only on G. Then we will pass to some limits and to the supremum over (h, R), obtaining a functional inequality for
![]() ${\tilde{g}}_\cdot({\cdot})$
: for any
${\tilde{g}}_\cdot({\cdot})$
: for any
![]() ${\alpha},{\beta}$
s.t.
${\alpha},{\beta}$
s.t.
![]() $0\le{\alpha}<{\beta}\le 1$
and for
$0\le{\alpha}<{\beta}\le 1$
and for
![]() $r>0$
,
$r>0$
,
 \begin{equation}{\tilde{g}}_{\alpha}(r) \le {\tilde{g}}_{\beta}(r)\exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m} - 1\right)\right).\end{equation}
\begin{equation}{\tilde{g}}_{\alpha}(r) \le {\tilde{g}}_{\beta}(r)\exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m} - 1\right)\right).\end{equation}
Note that this implies Theorem 3.2, provided that the integral in the denominator is a bounded function of r.
Then we arrive at a mild asymptotic estimate,
![]() ${\tilde{g}}_p(r)\le {\delta}(p)/\sqrt{r}$
(Lemma 5.3), whose proof uses the above functional inequality. That asymptotic estimate is then sharpened to that desired in Theorem 3.2, by repeatedly using the inequality (5.2).
${\tilde{g}}_p(r)\le {\delta}(p)/\sqrt{r}$
(Lemma 5.3), whose proof uses the above functional inequality. That asymptotic estimate is then sharpened to that desired in Theorem 3.2, by repeatedly using the inequality (5.2).
Proof of the theorem. Let
![]() $p>0$
,
$p>0$
,
![]() $(h,R)\in(0,1]\times O(d)$
,
$(h,R)\in(0,1]\times O(d)$
,
![]() $r>0$
, and
$r>0$
, and
![]() ${\delta}\in(0,h]$
be fixed.
${\delta}\in(0,h]$
be fixed.
Note that if there is no path joining
![]() $o^{(h,R)}$
to
$o^{(h,R)}$
to
![]() $S_r$
in
$S_r$
in
![]() $G^{(h,R)}\cap L_{\delta}$
at all, then for any
$G^{(h,R)}\cap L_{\delta}$
at all, then for any
![]() $p\in[0,1]$
,
$p\in[0,1]$
,
![]() $f_p^{\delta}(r)=0$
and the inequality (5.1) is obvious. The same happens when
$f_p^{\delta}(r)=0$
and the inequality (5.1) is obvious. The same happens when
![]() ${\alpha}=0$
. Because in the proof of that inequality we need
${\alpha}=0$
. Because in the proof of that inequality we need
![]() $f_p^{\delta}(r)>0$
and
$f_p^{\delta}(r)>0$
and
![]() ${\alpha}>0$
, we now make the following assumption (without loss of generality).
${\alpha}>0$
, we now make the following assumption (without loss of generality).
Assumption 5.1. We assume that there is a path joining
![]() $o^{(h,R)}$
to
$o^{(h,R)}$
to
![]() $S_r$
in
$S_r$
in
![]() $G^{(h,R)}\cap L_{\delta}$
and that
$G^{(h,R)}\cap L_{\delta}$
and that
![]() ${\alpha}>0$
.
${\alpha}>0$
.
![]() $($
Then for
$($
Then for
![]() $p>0$
,
$p>0$
,
![]() $f_p^{\delta}(r)>0.)$
$f_p^{\delta}(r)>0.)$
The events
![]() $A^{\delta}(r)$
depend on the states of only finitely many edges of
$A^{\delta}(r)$
depend on the states of only finitely many edges of
![]() $G^{(h,R)}$
(namely, those intersecting
$G^{(h,R)}$
(namely, those intersecting
![]() $L_{\delta}\cap B_r$
), so we are able to use Russo’s formula for them, obtaining
$L_{\delta}\cap B_r$
), so we are able to use Russo’s formula for them, obtaining
Now,
![]() $A^{\delta}(r)$
is increasing, and for
$A^{\delta}(r)$
is increasing, and for
![]() $e\in E\big(G^{(h,R)}\big)$
, the event
$e\in E\big(G^{(h,R)}\big)$
, the event
![]() $\big\{e\textrm{ pivotal for }A^{\delta}(r)\big\}$
is independent of the state of e (which is easily seen; it is the rule for any event), so
$\big\{e\textrm{ pivotal for }A^{\delta}(r)\big\}$
is independent of the state of e (which is easily seen; it is the rule for any event), so
 \begin{align*}{\mathbb{P}}_p\big(A^{\delta}(r)\land e\textrm{ is pivotal for }A^{\delta}(r)\big) &= {\mathbb{P}}_p\big(e\textrm{ is open and pivotal for }A^{\delta}(r)\big) \\&= p{\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)\big);\end{align*}
\begin{align*}{\mathbb{P}}_p\big(A^{\delta}(r)\land e\textrm{ is pivotal for }A^{\delta}(r)\big) &= {\mathbb{P}}_p\big(e\textrm{ is open and pivotal for }A^{\delta}(r)\big) \\&= p{\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)\big);\end{align*}
hence
 \begin{align*}\frac{{\text{d}}}{{\text{d}} p} f_p^{\delta}(r) &=\, \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)\big) \\&=\, \frac 1p \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(A^{\delta}(r)\land e\textrm{ is pivotal for }A^{\delta}(r)\big) \\&=\,\frac{f_p^{\delta}(r)}{p} \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)|A^{\delta}(r)\big) \\&=\, \frac{f_p^{\delta}(r)}{p} {\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big),\end{align*}
\begin{align*}\frac{{\text{d}}}{{\text{d}} p} f_p^{\delta}(r) &=\, \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)\big) \\&=\, \frac 1p \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(A^{\delta}(r)\land e\textrm{ is pivotal for }A^{\delta}(r)\big) \\&=\,\frac{f_p^{\delta}(r)}{p} \sum_{e\in E\big(G^{(h,R)}\big)} {\mathbb{P}}_p\big(e\textrm{ is pivotal for }A^{\delta}(r)|A^{\delta}(r)\big) \\&=\, \frac{f_p^{\delta}(r)}{p} {\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big),\end{align*}
which can be written as
For any
![]() $0<{\alpha}<{\beta}\le 1$
, integrating over
$0<{\alpha}<{\beta}\le 1$
, integrating over
![]() $[{\alpha},{\beta}]$
and exponentiating the above equality gives
$[{\alpha},{\beta}]$
and exponentiating the above equality gives
which implies
At this point, our aim is to bound
![]() ${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
from below. Fix any
${\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)$
from below. Fix any
![]() $r>0$
and
$r>0$
and
![]() ${\delta}\in(0,h]$
and assume for now that
${\delta}\in(0,h]$
and assume for now that
![]() $A^{\delta}(r)$
occurs. Let us look at the structure of the cluster of
$A^{\delta}(r)$
occurs. Let us look at the structure of the cluster of
![]() $o^{(h,R)}$
in
$o^{(h,R)}$
in
![]() $G^{(h,R)}\cap L_{\delta}$
in the context of the pivotal edges for
$G^{(h,R)}\cap L_{\delta}$
in the context of the pivotal edges for
![]() $A^{\delta}(r)$
(following [Reference Grimmett9] and [Reference Menshikov17]). If
$A^{\delta}(r)$
(following [Reference Grimmett9] and [Reference Menshikov17]). If
![]() $e\in E\big(G^{(h,R)}\big)$
is pivotal for
$e\in E\big(G^{(h,R)}\big)$
is pivotal for
![]() $A^{\delta}(r)$
, then if we change the percolation configuration by closing e, we cause the cluster of
$A^{\delta}(r)$
, then if we change the percolation configuration by closing e, we cause the cluster of
![]() $C^{(h,R)}_{L_{\delta}}\big(o^{(h,R)}\big)$
to be disjoint from
$C^{(h,R)}_{L_{\delta}}\big(o^{(h,R)}\big)$
to be disjoint from
![]() $S_r$
. So, in our situation, all the pivotal edges lie on any open path in
$S_r$
. So, in our situation, all the pivotal edges lie on any open path in
![]() $G^{(h,R)}\cap L_{\delta}$
joining
$G^{(h,R)}\cap L_{\delta}$
joining
![]() $o^{(h,R)}$
to
$o^{(h,R)}$
to
![]() $S_r$
, and they are visited by the path in the same order and direction (regardless of the choice of the path).
$S_r$
, and they are visited by the path in the same order and direction (regardless of the choice of the path).
Definition 5.5. Assume that
![]() $A^{\delta}(r)$
occurs. Let
$A^{\delta}(r)$
occurs. Let
![]() $N=N\big(A^{\delta}(r)\big)$
, and let
$N=N\big(A^{\delta}(r)\big)$
, and let
![]() $e_1$
,…,
$e_1$
,…,
![]() $e_N$
be the above ordering of the pivotal edges. Denote by
$e_N$
be the above ordering of the pivotal edges. Denote by
![]() $x_i,y_i$
the end vertices of
$x_i,y_i$
the end vertices of
![]() $e_i$
,
$e_i$
,
![]() $x_i$
being the one closer to
$x_i$
being the one closer to
![]() $o^{(h,R)}$
along a path as above. Also, let
$o^{(h,R)}$
along a path as above. Also, let
![]() $y_0=o^{(h,R)}$
. By convention, whenever we mention
$y_0=o^{(h,R)}$
. By convention, whenever we mention
![]() $e_i$
, we assume that
$e_i$
, we assume that
![]() $i\le N\big(A^{\delta}(r)\big)$
.
$i\le N\big(A^{\delta}(r)\big)$
.
Note that because there is no edge separating
![]() $y_{i-1}$
from
$y_{i-1}$
from
![]() $x_i$
in the open cluster in
$x_i$
in the open cluster in
![]() $G^{(h,R)}\cap L_{\delta}$
for
$G^{(h,R)}\cap L_{\delta}$
for
![]() $i=1,\ldots,N$
, by Menger’s theorem (see e.g. [Reference Diestel8, Theorem 3.3.1, Corollary 3.3.5(ii)]), there exist two edge-disjoint open paths in that cluster joining
$i=1,\ldots,N$
, by Menger’s theorem (see e.g. [Reference Diestel8, Theorem 3.3.1, Corollary 3.3.5(ii)]), there exist two edge-disjoint open paths in that cluster joining
![]() $y_{i-1}$
to
$y_{i-1}$
to
![]() $x_i$
. (One can say, following the discoverer of this proof idea, that that open cluster resembles a chain of sausages.)
$x_i$
. (One can say, following the discoverer of this proof idea, that that open cluster resembles a chain of sausages.)
Now, for
![]() $i=1,\ldots,N$
, let
$i=1,\ldots,N$
, let
![]() $\varrho_i=d_\eth(y_{i-1},x_i)$
(this way of defining
$\varrho_i=d_\eth(y_{i-1},x_i)$
(this way of defining
![]() $\varrho_i$
, which one can view as the ‘projection length’ of the ith ‘sausage’, is an adaptation of the definition of
$\varrho_i$
, which one can view as the ‘projection length’ of the ith ‘sausage’, is an adaptation of the definition of
![]() $\rho_i$
in [Reference Grimmett9]). We use the convention that for
$\rho_i$
in [Reference Grimmett9]). We use the convention that for
![]() $i\in{\mathbb{N}}$
such that
$i\in{\mathbb{N}}$
such that
![]() $i>N\big(A^{\delta}(r)\big)$
(i.e.
$i>N\big(A^{\delta}(r)\big)$
(i.e.
![]() $e_i$
,
$e_i$
,
![]() $\varrho_i$
are undefined),
$\varrho_i$
are undefined),
![]() $\varrho_i=+\infty$
(being greater than any real number).
$\varrho_i=+\infty$
(being greater than any real number).
The next lemma is used to compare
![]() $(\varrho_1,\ldots,\varrho_N)$
to some renewal process with inter-renewal times of roughly the same distribution as the projection radius of
$(\varrho_1,\ldots,\varrho_N)$
to some renewal process with inter-renewal times of roughly the same distribution as the projection radius of
![]() $C_L^{(h,R)}\big(o^{(h,R)}\big)$
. Its proof is deferred to Subsection 5.1.
$C_L^{(h,R)}\big(o^{(h,R)}\big)$
. Its proof is deferred to Subsection 5.1.
Definition 5.6. Let a denote the supremum of the projection distance (in the sense of
![]() $d_\eth$
) between the endpoints of an edge, taken over all
$d_\eth$
) between the endpoints of an edge, taken over all
![]() $(h,R)\in(0,1]\times O(d)$
and all the edges of
$(h,R)\in(0,1]\times O(d)$
and all the edges of
![]() $G^{(h,R)}$
intersecting L.
$G^{(h,R)}$
intersecting L.
Lemma 5.1. (Cf. [Reference Grimmett9, Lemma (5.12)]) Let
![]() $k\in{\mathbb{N}}_+$
and let
$k\in{\mathbb{N}}_+$
and let
![]() $r_1,\ldots,r_k\ge 0$
be such that
$r_1,\ldots,r_k\ge 0$
be such that
![]() $\sum_{i=1}^k r_i \le r - (k-1)a$
. Then for
$\sum_{i=1}^k r_i \le r - (k-1)a$
. Then for
![]() $0<p<1$
,
$0<p<1$
,
 \begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k,\ \bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) \ge (1-g_p(r_k)){\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg).\end{equation*}
\begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k,\ \bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) \ge (1-g_p(r_k)){\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg).\end{equation*}
Now we want to do some probabilistic reasoning using random variables with the left-continuous distribution function
![]() $1-{\tilde{g}}_p$
. The function
$1-{\tilde{g}}_p$
. The function
![]() $1-{\tilde{g}}_p$
is non-decreasing (because for
$1-{\tilde{g}}_p$
is non-decreasing (because for
![]() $(h,R)\in(0,1]\times O(d)$
,
$(h,R)\in(0,1]\times O(d)$
,
![]() ${\mathbb{P}}_p\big(o^{(h,R)} \leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\big)$
is non-increasing with respect to r, so
${\mathbb{P}}_p\big(o^{(h,R)} \leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\big)$
is non-increasing with respect to r, so
![]() $g_p$
and
$g_p$
and
![]() ${\tilde{g}}_p$
are non-increasing as well), left-continuous, with values in [0, 1], and such that
${\tilde{g}}_p$
are non-increasing as well), left-continuous, with values in [0, 1], and such that
![]() $1-{\tilde{g}}_p(0)=0$
, so it is the left-continuous distribution function of a random variable with values in
$1-{\tilde{g}}_p(0)=0$
, so it is the left-continuous distribution function of a random variable with values in
![]() $[0,\infty]$
. So let
$[0,\infty]$
. So let
![]() $M_1, M_2,\ldots$
be an infinite sequence of independent random variables all distributed according to
$M_1, M_2,\ldots$
be an infinite sequence of independent random variables all distributed according to
![]() $1-{\tilde{g}}_p$
and all independent of the whole percolation process. Because their distribution depends on p, we will also denote them by
$1-{\tilde{g}}_p$
and all independent of the whole percolation process. Because their distribution depends on p, we will also denote them by
![]() $M_1^{(p)},M_2^{(p)},\ldots$
. (Here, an abuse of notation is going to happen, as we are still writing
$M_1^{(p)},M_2^{(p)},\ldots$
. (Here, an abuse of notation is going to happen, as we are still writing
![]() ${\mathbb{P}}_p$
for the whole probability measure used also for defining the variables
${\mathbb{P}}_p$
for the whole probability measure used also for defining the variables
![]() $M_1, M_2,\ldots$
.)
$M_1, M_2,\ldots$
.)
We can now state the following corollary of Lemma 5.1.
Corollary 5.1. For any
![]() $r>0$
, positive integer k, and
$r>0$
, positive integer k, and
![]() $0<p<1$
,
$0<p<1$
,
This corollary is proved in Subsection 5.2 and is used to prove the following lemma in Subsection 5.3.
Lemma 5.2. (Cf. [Reference Grimmett9, Lemma (5.17)]) For
![]() $0<p<1$
,
$0<p<1$
,
![]() $r>0$
,
$r>0$
,
Now, combining Lemma 5.2 above with the inequality (5.3) for
![]() $0<{\alpha}<{\beta}\le 1$
, we have
$0<{\alpha}<{\beta}\le 1$
, we have
 \begin{align}f_{\alpha}^{\delta}(r) &\le f_{\beta}^{\delta}(r) \exp\!\left({-}\int_{\alpha}^{\beta} {\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)\,{\text{d}} p\right) \notag \\&\le f_{\beta}^{\delta}(r) \exp\!\left({-}\int_{\alpha}^{\beta} \left(\frac{r}{a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m}-1\right)\,{\text{d}} p\right) \notag \\&\le f_{\beta}^{\delta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right)\end{align}
\begin{align}f_{\alpha}^{\delta}(r) &\le f_{\beta}^{\delta}(r) \exp\!\left({-}\int_{\alpha}^{\beta} {\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big)\,{\text{d}} p\right) \notag \\&\le f_{\beta}^{\delta}(r) \exp\!\left({-}\int_{\alpha}^{\beta} \left(\frac{r}{a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m}-1\right)\,{\text{d}} p\right) \notag \\&\le f_{\beta}^{\delta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^r {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right)\end{align}
(because
![]() ${\tilde{g}}_p\le {\tilde{g}}_{\beta}$
for
${\tilde{g}}_p\le {\tilde{g}}_{\beta}$
for
![]() $p\le{\beta}$
), which completes the proof of the inequality (5.1). (Let us now drop Assumption 5.1.)
$p\le{\beta}$
), which completes the proof of the inequality (5.1). (Let us now drop Assumption 5.1.)
Now, note that for any
![]() $r>0$
and
$r>0$
and
![]() $p\in[0,1]$
, the event
$p\in[0,1]$
, the event
![]() $A^{\delta}(r)$
increases as
$A^{\delta}(r)$
increases as
![]() ${\delta}$
decreases. Thus, taking the limit with
${\delta}$
decreases. Thus, taking the limit with
![]() ${\delta}\to 0$
, we have
${\delta}\to 0$
, we have
 \begin{equation*}\lim_{{\delta}\to 0^+} f_p^{\delta}(r) = {\mathbb{P}}_p\Bigg(\bigcup_{{\delta}> 0} A^{\delta}(r)\Bigg) = {\mathbb{P}}_p\Big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\Big).\end{equation*}
\begin{equation*}\lim_{{\delta}\to 0^+} f_p^{\delta}(r) = {\mathbb{P}}_p\Bigg(\bigcup_{{\delta}> 0} A^{\delta}(r)\Bigg) = {\mathbb{P}}_p\Big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\Big).\end{equation*}
So for any
![]() $r>0$
and
$r>0$
and
![]() $0\le{\alpha}<{\beta}\le 1$
, using this for the inequality (5.1) gives
$0\le{\alpha}<{\beta}\le 1$
, using this for the inequality (5.1) gives
 $$\eqalign{
& {\mathbb{P}}_{\alpha }({o^{(h,R)}} \leftrightarrow {S_r}{\rm{in}}{G^{(h,R)}} \cap L) \cr
& \quad \quad \quad \quad \quad \le {\mathbb{P}}_{\beta }({o^{(h,R)}} \leftrightarrow {S_r}{\rm{in}}{G^{(h,R)}} \cap L)\exp \left( { - (\beta - \alpha )\left( {{r \over {a + \int_0^r {{{\tilde g}_\beta }} (m){\mkern 1mu} {\rm{d}}m}} - 1} \right)} \right). \cr} $$
$$\eqalign{
& {\mathbb{P}}_{\alpha }({o^{(h,R)}} \leftrightarrow {S_r}{\rm{in}}{G^{(h,R)}} \cap L) \cr
& \quad \quad \quad \quad \quad \le {\mathbb{P}}_{\beta }({o^{(h,R)}} \leftrightarrow {S_r}{\rm{in}}{G^{(h,R)}} \cap L)\exp \left( { - (\beta - \alpha )\left( {{r \over {a + \int_0^r {{{\tilde g}_\beta }} (m){\mkern 1mu} {\rm{d}}m}} - 1} \right)} \right). \cr} $$
Further, we take the supremum over
![]() $(h,R)\in(0,1]\times O(d)$
, obtaining
$(h,R)\in(0,1]\times O(d)$
, obtaining
 \begin{equation*}g_{\alpha}(r) \le g_{\beta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right).\end{equation*}
\begin{equation*}g_{\alpha}(r) \le g_{\beta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right).\end{equation*}
Finally, taking the limits with r from the left, we get the functional inequality (5.2) involving only
![]() ${\tilde{g}}_\cdot({\cdot})$
:
${\tilde{g}}_\cdot({\cdot})$
:
 \begin{equation}{\tilde{g}}_{\alpha}(r) \le {\tilde{g}}_{\beta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right).\end{equation}
\begin{equation}{\tilde{g}}_{\alpha}(r) \le {\tilde{g}}_{\beta}(r) \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right).\end{equation}
(Note that the exponent remains unchanged throughout, from (5.4) until now.)
Recall that once we have
we then obtain Theorem 3.2 for
![]() ${\tilde{g}}_{\alpha}(r)$
, for
${\tilde{g}}_{\alpha}(r)$
, for
![]() ${\alpha}<{\beta}$
. This bound is going to be established by showing the rapid decay of
${\alpha}<{\beta}$
. This bound is going to be established by showing the rapid decay of
![]() ${\tilde{g}}_p$
, using (5.5) repeatedly. The next lemma is the first step of this procedure.
${\tilde{g}}_p$
, using (5.5) repeatedly. The next lemma is the first step of this procedure.
Lemma 5.3. (Cf. [Reference Grimmett9, Lemma (5.24)]) For any
![]() $p<p_{\text{a}}$
, there exists
$p<p_{\text{a}}$
, there exists
![]() ${\delta}(p)$
such that
${\delta}(p)$
such that
We defer the proof of the above lemma to Subsection 5.4.
It is relatively easy to obtain Theorem 3.2 (which is being proved) from Lemma 5.3. First, we deduce that for
![]() $r>0$
and
$r>0$
and
![]() $p<p_{\text{a}}$
,
$p<p_{\text{a}}$
,
so if
![]() $r\ge a^2$
, then
$r\ge a^2$
, then
Then, using (5.5), for
![]() $0\le{\alpha}<{\beta}<p_{\text{a}}$
we have
$0\le{\alpha}<{\beta}<p_{\text{a}}$
we have
 \begin{align*}\int_{a^2}^{\infty} {\tilde{g}}_{\alpha}(r)\,{\text{d}} r &\le \int_{a^2}^{\infty} \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right) \,{\text{d}} r \\&\le e \int_{a^2}^{\infty} \exp\left({-}\underbrace{\frac{{\beta}-{\alpha}}{2{\delta}({\beta})+1}}_{=C>0} \sqrt{r}\right) \,{\text{d}} r \\&= e \int_{a}^{\infty} e^{-Cx}\cdot 2x \,{\text{d}} x,\end{align*}
\begin{align*}\int_{a^2}^{\infty} {\tilde{g}}_{\alpha}(r)\,{\text{d}} r &\le \int_{a^2}^{\infty} \exp\!\left({-}({\beta}-{\alpha}) \left(\frac{r}{a+\int_0^{r} {\tilde{g}}_{\beta}(m)\,{\text{d}} m}-1\right)\right) \,{\text{d}} r \\&\le e \int_{a^2}^{\infty} \exp\left({-}\underbrace{\frac{{\beta}-{\alpha}}{2{\delta}({\beta})+1}}_{=C>0} \sqrt{r}\right) \,{\text{d}} r \\&= e \int_{a}^{\infty} e^{-Cx}\cdot 2x \,{\text{d}} x,\end{align*}
so
as desired. Finally, we use the finiteness of
![]() ${\mathbb{E}}\Big(M_1^{({\alpha})}\Big)$
as promised: for
${\mathbb{E}}\Big(M_1^{({\alpha})}\Big)$
as promised: for
![]() $r>0$
and
$r>0$
and
![]() $0\le{\alpha}<p_{\text{a}}$
, if we take
$0\le{\alpha}<p_{\text{a}}$
, if we take
![]() ${\alpha}<{\beta}<p_{\text{a}}$
, then, using (5.5) again,
${\alpha}<{\beta}<p_{\text{a}}$
, then, using (5.5) again,
 \begin{align*}g_{\alpha}(r) \le {\tilde{g}}_{\alpha}(r) \le \exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+{\mathbb{E}}\Big(M_1^{({\beta})}\Big)} -1\right)\right) \le e^{-{\varphi}({\alpha},{\beta})r+{\gamma}({\alpha},{\beta})},\end{align*}
\begin{align*}g_{\alpha}(r) \le {\tilde{g}}_{\alpha}(r) \le \exp\!\left({-}({\beta}-{\alpha})\left(\frac{r}{a+{\mathbb{E}}\Big(M_1^{({\beta})}\Big)} -1\right)\right) \le e^{-{\varphi}({\alpha},{\beta})r+{\gamma}({\alpha},{\beta})},\end{align*}
for some constants
![]() ${\varphi}({\alpha},{\beta}),{\gamma}({\alpha},{\beta})>0$
.
${\varphi}({\alpha},{\beta}),{\gamma}({\alpha},{\beta})>0$
.
Now we perform a standard estimation, aiming to rule out the additive constant
![]() ${\gamma}({\alpha},{\beta})$
. For any
${\gamma}({\alpha},{\beta})$
. For any
![]() $0<\psi_1<{\varphi}({\alpha},{\beta})$
, there exists
$0<\psi_1<{\varphi}({\alpha},{\beta})$
, there exists
![]() $r_0>0$
such that for
$r_0>0$
such that for
![]() $r\ge r_0$
,
$r\ge r_0$
,
so
On the other hand, for any
![]() $r>0$
,
$r>0$
,
![]() $g_p(r)$
is no greater than the probability of opening at least one edge adjacent to o, so
$g_p(r)$
is no greater than the probability of opening at least one edge adjacent to o, so
![]() $g_{\alpha}(r) \le 1-(1-{\alpha})^{\deg\!(o)}<1$
, where
$g_{\alpha}(r) \le 1-(1-{\alpha})^{\deg\!(o)}<1$
, where
![]() $\deg\!(o)$
is the degree of o in the graph G. Hence,
$\deg\!(o)$
is the degree of o in the graph G. Hence,
for
![]() $r\le r_0$
, for some sufficiently small
$r\le r_0$
, for some sufficiently small
![]() $\psi_2({\alpha})>0$
. Taking
$\psi_2({\alpha})>0$
. Taking
![]() $\psi = \min\!(\psi_1,\psi_2({\alpha}))$
gives
$\psi = \min\!(\psi_1,\psi_2({\alpha}))$
gives
for any
![]() $r>0$
, completing the proof of Theorem 3.2.
$r>0$
, completing the proof of Theorem 3.2.
Remark 5.1. In order to prove Theorem 3.2, one could try to consider the percolation processes on the whole graph
![]() $G^{(h,R)}\cap L$
(without restricting it to
$G^{(h,R)}\cap L$
(without restricting it to
![]() $L_{\delta}$
) in order to obtain a functional inequality similar to (5.2), involving only one function. However, that approach caused the author many difficulties, some of which have not been overcome. Restricting the situation to
$L_{\delta}$
) in order to obtain a functional inequality similar to (5.2), involving only one function. However, that approach caused the author many difficulties, some of which have not been overcome. Restricting the situation to
![]() $L_{\delta}$
makes the event
$L_{\delta}$
makes the event
![]() $A^{\delta}$
depend on the states of only finitely many edges. This allows one e.g. to condition the event
$A^{\delta}$
depend on the states of only finitely many edges. This allows one e.g. to condition the event
![]() $A^{\delta}(r)\cap B$
on the family of events
$A^{\delta}(r)\cap B$
on the family of events
![]() $\{\Gamma\textrm{ a witness for }B\}$
in the proof of Lemma 5.1, where
$\{\Gamma\textrm{ a witness for }B\}$
in the proof of Lemma 5.1, where
![]() $\Gamma$
runs over a countable set, or to use the BK inequality and Russo’s formula.
$\Gamma$
runs over a countable set, or to use the BK inequality and Russo’s formula.
5.1. Proof of Lemma 5.1—the chain of sausages
Definition 5.7.
(Recalled from Definition 5.6) Let a denote the supremum of the projection distance (in the sense of
![]() $d_\eth$
) between the endpoints of an edge, taken over all
$d_\eth$
) between the endpoints of an edge, taken over all
![]() $(h,R)\in(0,1]\times O(d)$
and all the edges of
$(h,R)\in(0,1]\times O(d)$
and all the edges of
![]() $G^{(h,R)}$
intersecting L.
$G^{(h,R)}$
intersecting L.
Lemma 5.4. (Recalled from Lemma 5.1; cf. [Reference Grimmett9, Lemma (5.12)]) Let
![]() $k\in{\mathbb{N}}_+$
, and let
$k\in{\mathbb{N}}_+$
, and let
![]() $r_1,\ldots,r_k\ge 0$
be such that
$r_1,\ldots,r_k\ge 0$
be such that
![]() $\sum_{i=1}^k r_i \le r - (k-1)a$
. Then for
$\sum_{i=1}^k r_i \le r - (k-1)a$
. Then for
![]() $0<p<1$
,
$0<p<1$
,
 \begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k,\ \bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) \ge (1-g_p(r_k)){\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg).\end{equation*}
\begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k,\ \bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) \ge (1-g_p(r_k)){\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg).\end{equation*}
Before we start the proof, we state a few preliminaries.
Definition 5.8. For increasing events A and B in a percolation on any graph G, the event
![]() $A\circ B$
means that ‘A and B occur on disjoint sets of edges’. Formally,
$A\circ B$
means that ‘A and B occur on disjoint sets of edges’. Formally,
that is,
![]() $A\circ B$
is the set of configurations containing two disjoint sets of open edges (
$A\circ B$
is the set of configurations containing two disjoint sets of open edges (
![]() $\omega_A, \omega_B$
above) which guarantee the occurrence of the events A and B, respectively.
$\omega_A, \omega_B$
above) which guarantee the occurrence of the events A and B, respectively.
Theorem 5.3. (BK inequality, [Reference Grimmett9, Theorems (2.12) and (2.15)]) For any graph G and increasing events A and B depending on the states of only finitely many edges in p-Bernoulli bond percolation on G, we have
Recall that in the setting of the lemma to be proved we have fixed
![]() $(h,R)\in(0,1]\times O(d)$
,
$(h,R)\in(0,1]\times O(d)$
,
![]() $p\in[0,1]$
,
$p\in[0,1]$
,
![]() $r>0$
, and
$r>0$
, and
![]() ${\delta}\in(0,h]$
. We will use the following notation.
${\delta}\in(0,h]$
. We will use the following notation.
Definition 5.9. Let
![]() $\eta$
denote the percolation configuration in
$\eta$
denote the percolation configuration in
![]() $G^{(h,R)}\cap L_{\delta}$
, i.e.
$G^{(h,R)}\cap L_{\delta}$
, i.e.
Proof of the lemma. This proof mimics that of [Reference Grimmett9, Lemma (5.12)]. Let
![]() $k\ge 2$
(we defer the case of
$k\ge 2$
(we defer the case of
![]() $k=1$
to the end of the proof).
$k=1$
to the end of the proof).
For
![]() $e\in E\big(G^{(h,R)}\cap L_{\delta}\big)$
, let
$e\in E\big(G^{(h,R)}\cap L_{\delta}\big)$
, let
![]() $D_e$
be the connected component of
$D_e$
be the connected component of
![]() $o^{(h,R)}$
in
$o^{(h,R)}$
in
![]() $\eta{\setminus}\{e\}$
. Let
$\eta{\setminus}\{e\}$
. Let
![]() $B_e$
denote the event that the following conditions are satisfied:
$B_e$
denote the event that the following conditions are satisfied:
-
e is open;
-
exactly one end vertex of e lies in
 $D_e$
—call it x(e) and call the other y(e);
$D_e$
—call it x(e) and call the other y(e); -
 $D_e$
is disjoint from
$D_e$
is disjoint from
 $S_r$
;
$S_r$
; -
there are exactly
 $k-1$
pivotal edges for the event
$k-1$
pivotal edges for the event
 $\big\{o^{(h,R)}\leftrightarrow y(e)\textrm{ in }\eta\big\}$
(i.e. the edges each of which separates
$\big\{o^{(h,R)}\leftrightarrow y(e)\textrm{ in }\eta\big\}$
(i.e. the edges each of which separates
 $o^{(h,R)}$
from y(e) in
$o^{(h,R)}$
from y(e) in
 $D_e\cup\{e\}$
)—call them
$D_e\cup\{e\}$
)—call them
 $e^{\prime}_1=\big\{x^{\prime}_1,y^{\prime}_1\big\}$
, …,
$e^{\prime}_1=\big\{x^{\prime}_1,y^{\prime}_1\big\}$
, …,
 $e^{\prime}_{k-1}=\big\{x^{\prime}_{k-1},y^{\prime}_{k-1}\big\}=e$
, where
$e^{\prime}_{k-1}=\big\{x^{\prime}_{k-1},y^{\prime}_{k-1}\big\}=e$
, where
 $x^{\prime}_i$
is closer to
$x^{\prime}_i$
is closer to
 $o^{(h,R)}$
than
$o^{(h,R)}$
than
 $y^{\prime}_i$
, in the order from
$y^{\prime}_i$
, in the order from
 $o^{(h,R)}$
to y(e) (as in Definition 5.5);
$o^{(h,R)}$
to y(e) (as in Definition 5.5); -
 $d_\eth\big(y^{\prime}_{i-1},x^{\prime}_i\big)=r_i$
for
$d_\eth\big(y^{\prime}_{i-1},x^{\prime}_i\big)=r_i$
for
 $i<k$
, where
$i<k$
, where
 $y^{\prime}_0 =o^{(h,R)}$
.
$y^{\prime}_0 =o^{(h,R)}$
.
Let
![]() $B=\bigcup_{e\in E\big(G^{(h,R)}\cap L_{\delta}\big)} B_e$
. When
$B=\bigcup_{e\in E\big(G^{(h,R)}\cap L_{\delta}\big)} B_e$
. When
![]() $B_e$
occurs, we say that
$B_e$
occurs, we say that
![]() $D_e\cup\{e\}$
with y(e) marked, as a graph with distinguished vertex, is a witness for B.
$D_e\cup\{e\}$
with y(e) marked, as a graph with distinguished vertex, is a witness for B.
Note that it may happen that there is more than one such witness (which means that
![]() $B_e$
occurs for many different e). On the other hand, if
$B_e$
occurs for many different e). On the other hand, if
![]() $A^{\delta}(r)$
occurs, then
$A^{\delta}(r)$
occurs, then
![]() $B_e$
occurs for only one edge e, namely
$B_e$
occurs for only one edge e, namely
![]() $e=e_{k-1}$
(in other words,
$e=e_{k-1}$
(in other words, ![]() , and there is only one witness for B. Hence,
, and there is only one witness for B. Hence,
where the sum is always over all
![]() $\Gamma$
that are finite subgraphs of
$\Gamma$
that are finite subgraphs of
![]() $G^{(h,R)}\cap L_{\delta}$
with distinguished vertices such that
$G^{(h,R)}\cap L_{\delta}$
with distinguished vertices such that
![]() ${\mathbb{P}}_p(\Gamma\textrm{ a witness for }B)>0$
.
${\mathbb{P}}_p(\Gamma\textrm{ a witness for }B)>0$
.
For
![]() $\Gamma$
a graph with a distinguished vertex, let
$\Gamma$
a graph with a distinguished vertex, let
![]() $y(\Gamma)$
denote that vertex. Under the condition that
$y(\Gamma)$
denote that vertex. Under the condition that
![]() $\Gamma$
is a witness for B,
$\Gamma$
is a witness for B,
![]() $A^{\delta}(r)$
is equivalent to the event that
$A^{\delta}(r)$
is equivalent to the event that
![]() $y(\Gamma)$
is joined to
$y(\Gamma)$
is joined to
![]() $S_r$
by an open path in
$S_r$
by an open path in
![]() $\eta$
which is disjoint from
$\eta$
which is disjoint from
![]() $V(\Gamma){\setminus} \{y(\Gamma)\}$
. For brevity, we write the latter event as
$V(\Gamma){\setminus} \{y(\Gamma)\}$
. For brevity, we write the latter event as
![]() $\{y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma\}$
. Now, the event
$\{y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma\}$
. Now, the event
![]() $\{\Gamma\textrm{ a witness for }B\}$
depends only on the states of edges incident to vertices from
$\{\Gamma\textrm{ a witness for }B\}$
depends only on the states of edges incident to vertices from
![]() $V(\Gamma){\setminus}\{y(\Gamma)\}$
, so it is independent of the event
$V(\Gamma){\setminus}\{y(\Gamma)\}$
, so it is independent of the event
![]() $\{y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma\}$
. Hence,
$\{y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma\}$
. Hence,
A similar argument, carried out below, gives us the estimate of
![]() ${\mathbb{P}}_p(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B)$
. Here we also use the following fact: conditioned on the event
${\mathbb{P}}_p(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B)$
. Here we also use the following fact: conditioned on the event
![]() $\{\Gamma\textrm{ a witness for }B\}$
, the event
$\{\Gamma\textrm{ a witness for }B\}$
, the event
![]() $A^{\delta}(r)\cap\{\varrho_k\ge r_k\}$
implies each of the following:
$A^{\delta}(r)\cap\{\varrho_k\ge r_k\}$
implies each of the following:
 \begin{align*}&\big(A^{\delta}(r)\land e_k\textrm{ does not exist}\big) \lor \big(A^{\delta}(r)\land e_k\textrm{ exists }\land\varrho_k\ge r_k\big) \\\Longrightarrow &(\exists\textrm{ two edge-disjoint paths joining $y(\Gamma)$ to $S_r$ in $\eta$ off }\Gamma) \lor\\&\begin{aligned}\lor (\exists\ &\textrm{two edge-disjoint paths in $\eta$ off $\Gamma$,}\\&\textrm{joining $y(\Gamma)$ to $S_r$ and to $S_{r_k}(y(\Gamma))$, respectively})\end{aligned}\\\iff &\begin{aligned}[t](\exists\ &\textrm{two edge-disjoint paths in $\eta$ off $\Gamma$,}\\&\textrm{joining $y(\Gamma)$ to $S_r$ and to $S_{r_k}(y(\Gamma))$, respectively}),\end{aligned}\end{align*}
\begin{align*}&\big(A^{\delta}(r)\land e_k\textrm{ does not exist}\big) \lor \big(A^{\delta}(r)\land e_k\textrm{ exists }\land\varrho_k\ge r_k\big) \\\Longrightarrow &(\exists\textrm{ two edge-disjoint paths joining $y(\Gamma)$ to $S_r$ in $\eta$ off }\Gamma) \lor\\&\begin{aligned}\lor (\exists\ &\textrm{two edge-disjoint paths in $\eta$ off $\Gamma$,}\\&\textrm{joining $y(\Gamma)$ to $S_r$ and to $S_{r_k}(y(\Gamma))$, respectively})\end{aligned}\\\iff &\begin{aligned}[t](\exists\ &\textrm{two edge-disjoint paths in $\eta$ off $\Gamma$,}\\&\textrm{joining $y(\Gamma)$ to $S_r$ and to $S_{r_k}(y(\Gamma))$, respectively}),\end{aligned}\end{align*}
because
![]() $S_{r_k}(y(\Gamma))\subseteq B_r$
from the assumption on
$S_{r_k}(y(\Gamma))\subseteq B_r$
from the assumption on
![]() $\sum_{i=1}^k r_i$
. So we estimate
$\sum_{i=1}^k r_i$
. So we estimate
 \begin{align}& {\mathbb{P}}_p\big(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B\big)\nonumber\\& \qquad = \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witn. for }B) {\mathbb{P}}_p\big(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\big|\Gamma\textrm{ a witn. for }B\big) \nonumber\\& \qquad\le \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witn. for }B) \,{\mathbb{P}}_p((y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\nonumber\\&\qquad\qquad\circ (y(\Gamma)\leftrightarrow S_{r_k}(y(\Gamma))\textrm{ in $\eta$ off }\Gamma)). \end{align}
\begin{align}& {\mathbb{P}}_p\big(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B\big)\nonumber\\& \qquad = \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witn. for }B) {\mathbb{P}}_p\big(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\big|\Gamma\textrm{ a witn. for }B\big) \nonumber\\& \qquad\le \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witn. for }B) \,{\mathbb{P}}_p((y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\nonumber\\&\qquad\qquad\circ (y(\Gamma)\leftrightarrow S_{r_k}(y(\Gamma))\textrm{ in $\eta$ off }\Gamma)). \end{align}
Now we use the BK inequality for the last term
![]() $\big($
as the events involved are increasing and defined in terms of only the edges from
$\big($
as the events involved are increasing and defined in terms of only the edges from
![]() $E\big(G^{(h,R)}\cap(L_{\delta}\cap B_r)\big)\big)$
, obtaining
$E\big(G^{(h,R)}\cap(L_{\delta}\cap B_r)\big)\big)$
, obtaining
 \begin{align*} &{\mathbb{P}}_p(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B) \\&\qquad\le \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witness for }B) \cdot {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\\&\qquad\qquad\cdot {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_{r_k}(y(\Gamma))\textrm{ in $\eta$ off }\Gamma) \\& \qquad\le \left(\sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witness for }B) {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\right)g_p(r_k) \\&\qquad=\, {\mathbb{P}}_p\big(A^{\delta}(r)\cap B\big) g_p(r_k)\end{align*}
\begin{align*} &{\mathbb{P}}_p(\{\varrho_k\ge r_k\}\cap A^{\delta}(r)\cap B) \\&\qquad\le \sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witness for }B) \cdot {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\\&\qquad\qquad\cdot {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_{r_k}(y(\Gamma))\textrm{ in $\eta$ off }\Gamma) \\& \qquad\le \left(\sum_{\Gamma} {\mathbb{P}}_p(\Gamma\textrm{ a witness for }B) {\mathbb{P}}_p(y(\Gamma)\leftrightarrow S_r\textrm{ in $\eta$ off }\Gamma)\right)g_p(r_k) \\&\qquad=\, {\mathbb{P}}_p\big(A^{\delta}(r)\cap B\big) g_p(r_k)\end{align*}
(by (5.6)). Dividing by
![]() ${\mathbb{P}}_p\big(A^{\delta}(r)\big)$
(which is positive by Assumption 5.1) gives
${\mathbb{P}}_p\big(A^{\delta}(r)\big)$
(which is positive by Assumption 5.1) gives
and subtracting both sides of the inequality from
![]() ${\mathbb{P}}_p\big(B|A^{\delta}(r)\big)$
gives
${\mathbb{P}}_p\big(B|A^{\delta}(r)\big)$
gives
Note that, conditioned on
![]() $A^{\delta}(r)$
, B is equivalent to the event
$A^{\delta}(r)$
, B is equivalent to the event
![]() $\{\varrho_i=r_i\textrm{ for }i<k\}$
, so the above amounts to
$\{\varrho_i=r_i\textrm{ for }i<k\}$
, so the above amounts to
 \begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k, \bigwedge_{i<k}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg) \ge {\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) (1-g_p(r_k)),\end{equation*}
\begin{equation*}{\mathbb{P}}_p\Bigg(\varrho_k<r_k, \bigwedge_{i<k}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg) \ge {\mathbb{P}}_p\Bigg(\bigwedge_{i<k}\varrho_i=r_i\Big|A^{\delta}(r)\Bigg) (1-g_p(r_k)),\end{equation*}
which is the desired conclusion.
Now consider the case of
![]() $k=1$
. In this case, similarly to (5.7) and thanks to the assumption
$k=1$
. In this case, similarly to (5.7) and thanks to the assumption
![]() $r_1\le r$
,
$r_1\le r$
,
 \begin{align*}{\mathbb{P}}_p\big(\{\varrho_1\ge r_1\}\cap A^{\delta}(r)\big) &\le {\mathbb{P}}_p\big(\big(o^{(h,R)}\leftrightarrow S_{r_1}\textrm{ in }\eta\big)\circ\big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }\eta\big)\big)\\&\le g_p(r_1) {\mathbb{P}}_p\big(A^{\delta}(r)\big).\end{align*}
\begin{align*}{\mathbb{P}}_p\big(\{\varrho_1\ge r_1\}\cap A^{\delta}(r)\big) &\le {\mathbb{P}}_p\big(\big(o^{(h,R)}\leftrightarrow S_{r_1}\textrm{ in }\eta\big)\circ\big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }\eta\big)\big)\\&\le g_p(r_1) {\mathbb{P}}_p\big(A^{\delta}(r)\big).\end{align*}
Further, similarly to (5.8),
which is the lemma’s conclusion for
![]() $k=1$
.
$k=1$
.
5.2. Proof of Corollary 5.1
Corollary 5.2. (Recalled from Corollary 5.1) For any
![]() $r>0$
, positive integer k, and
$r>0$
, positive integer k, and
![]() $0<p<1$
,
$0<p<1$
,
Proof. We compose the proof of the intermediate inequalities
 \begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_k < r-(k-1)a |A^{\delta}(r)\big) \\&\ge {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{k-1}+M_k < r-(k-1)a |A^{\delta}(r)\big)\\&\cdots\\&\ge {\mathbb{P}}_p\big(\varrho_1+M_2+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\&\ge {\mathbb{P}}_p\big(M_1+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big)\\&= {\mathbb{P}}_p\big(M_1+\cdots+M_k < r-(k-1)a\big)\end{align*}
\begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_k < r-(k-1)a |A^{\delta}(r)\big) \\&\ge {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{k-1}+M_k < r-(k-1)a |A^{\delta}(r)\big)\\&\cdots\\&\ge {\mathbb{P}}_p\big(\varrho_1+M_2+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\&\ge {\mathbb{P}}_p\big(M_1+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big)\\&= {\mathbb{P}}_p\big(M_1+\cdots+M_k < r-(k-1)a\big)\end{align*}
using the step
 \begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\\ge\ &{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big),\end{align*}
\begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\\ge\ &{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big),\end{align*}
for
![]() $j=k,k-1,\ldots,2,1$
. Now we prove this step: let
$j=k,k-1,\ldots,2,1$
. Now we prove this step: let
![]() $j\in\{1,2,\ldots k\}$
. Put
$j\in\{1,2,\ldots k\}$
. Put
Note that this is a countable set of all possible values of
![]() $\varrho_i$
for
$\varrho_i$
for
![]() $i=1,\ldots,N$
.
$i=1,\ldots,N$
.
We express the probability under consideration as an integral, thinking of the whole probability space as the Cartesian product of the space on which the percolation processes are defined and the space used for defining
![]() $M_1,M_2,\ldots$
, and using a version of Fubini’s theorem for events:
$M_1,M_2,\ldots$
, and using a version of Fubini’s theorem for events:
 \begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\= &\int {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + S_M < r-(k-1)a |A^{\delta}(r)\big)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M),\end{align*}
\begin{align*}&{\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big) \\= &\int {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_j + S_M < r-(k-1)a |A^{\delta}(r)\big)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M),\end{align*}
where
![]() ${\mathcal{L}}_{j+1}^k$
denotes the distribution of the random variable
${\mathcal{L}}_{j+1}^k$
denotes the distribution of the random variable
![]() $M_{j+1}+\cdots+M_k$
,
$M_{j+1}+\cdots+M_k$
,
 \begin{align*}= \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)} {\mathbb{P}}_p\Bigg(\bigwedge_{i<j}\varrho_i=r_i\land \varrho_j < r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M),\end{align*}
\begin{align*}= \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)} {\mathbb{P}}_p\Bigg(\bigwedge_{i<j}\varrho_i=r_i\land \varrho_j < r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M),\end{align*}
where the sum is taken over all
![]() $\big(r_1,\ldots,r_{j-1}\big)\in\big({\mathcal{R}^{(h,R)}}\big)^{j-1}\;\text{such that}\;r_1+\cdots+r_{j-1}<r-(k-1)a-S_M$
,
$\big(r_1,\ldots,r_{j-1}\big)\in\big({\mathcal{R}^{(h,R)}}\big)^{j-1}\;\text{such that}\;r_1+\cdots+r_{j-1}<r-(k-1)a-S_M$
,
 \begin{align*}\ge \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)}\Bigg(1-{\tilde{g}}_p\Bigg(r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M\Bigg)\Bigg) \cdot{\mathbb{P}}_p\Bigg(\bigwedge_{i<j}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M)\end{align*}
\begin{align*}\ge \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)}\Bigg(1-{\tilde{g}}_p\Bigg(r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M\Bigg)\Bigg) \cdot{\mathbb{P}}_p\Bigg(\bigwedge_{i<j}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M)\end{align*}
from Lemma 5.1
![]() $\Big($
with
$\Big($
with
![]() $k=j$
and
$k=j$
and
![]() $r_j=r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M\Big)$
and because
$r_j=r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M\Big)$
and because
![]() $g_p\le{\tilde{g}}_p$
,
$g_p\le{\tilde{g}}_p$
,
 \begin{align*}& = \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)} {\mathbb{P}}_p \Bigg(M_j < r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M \land \bigwedge_{i<j}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M) \\& = \int {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+S_M < r-(k-1)a |A^{\delta}(r)\big)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M) \\& = {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big).\end{align*}
\begin{align*}& = \int \sum\limits_{\big(r_1,\ldots,r_{j-1}\big)} {\mathbb{P}}_p \Bigg(M_j < r-(k-1)a - \sum_{i=1}^{j-1} r_i - S_M \land \bigwedge_{i<j}\varrho_i=r_i \Big|A^{\delta}(r)\Bigg)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M) \\& = \int {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+S_M < r-(k-1)a |A^{\delta}(r)\big)\,{\text{d}}{\mathcal{L}}_{j+1}^k(S_M) \\& = {\mathbb{P}}_p\big(\varrho_1+\cdots+\varrho_{j-1} + M_j+M_{j+1}+\cdots+M_k < r-(k-1)a |A^{\delta}(r)\big).\end{align*}
That completes the proof.
5.3. Proof of Lemma 5.2
Lemma 5.5. (Recalled from Lemma 5.2; cf. [Reference Grimmett9, Lemma (5.17)]) For
![]() $0<p<1$
,
$0<p<1$
,
![]() $r>0$
,
$r>0$
,
Proof. For any
![]() $k\in{\mathbb{N}}_+$
, if
$k\in{\mathbb{N}}_+$
, if
![]() $\varrho_1+\cdots+\varrho_k < r-(k-1)a$
, then
$\varrho_1+\cdots+\varrho_k < r-(k-1)a$
, then
![]() $e_1,\ldots,e_k$
exist and
$e_1,\ldots,e_k$
exist and
![]() $N\big(A^{\delta}(r)\big)\ge k$
. So, from Corollary 5.1,
$N\big(A^{\delta}(r)\big)\ge k$
. So, from Corollary 5.1,
 \begin{align}{\mathbb{P}}_p\big(N\big(A^{\delta}(r)\big)\ge k|A^{\delta}(r)\big) &\ge {\mathbb{P}}_p\Bigg(\sum_{i=1}^k \varrho_i < r-(k-1)a\Bigg)\notag\\&\ge {\mathbb{P}}_p \Bigg(\sum_{i=1}^k M_i < r-(k-1)a\Bigg).\end{align}
\begin{align}{\mathbb{P}}_p\big(N\big(A^{\delta}(r)\big)\ge k|A^{\delta}(r)\big) &\ge {\mathbb{P}}_p\Bigg(\sum_{i=1}^k \varrho_i < r-(k-1)a\Bigg)\notag\\&\ge {\mathbb{P}}_p \Bigg(\sum_{i=1}^k M_i < r-(k-1)a\Bigg).\end{align}
Now we use a calculation which relates
![]() $a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m$
to the distribution of
$a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m$
to the distribution of
![]() $M_1$
. Namely, we replace the variables
$M_1$
. Namely, we replace the variables
![]() $M_i$
by
$M_i$
by
for
![]() $i=1,2,\ldots$
(a kind of truncated version of
$i=1,2,\ldots$
(a kind of truncated version of
![]() $M_i$
). In this setting,
$M_i$
). In this setting,
 \begin{align*}\sum_{i=1}^k M_i < r-(k-1)a \iff\sum_{i=1}^k M^{\prime}_i < r+a.\end{align*}
\begin{align*}\sum_{i=1}^k M_i < r-(k-1)a \iff\sum_{i=1}^k M^{\prime}_i < r+a.\end{align*}
For the ‘
![]() $\Leftarrow$
’ implication, note that the right-hand side implies
$\Leftarrow$
’ implication, note that the right-hand side implies
 \begin{equation*}r-(k-1)a > \sum_{i=1}^k \big(M^{\prime}_i-a\big) = \sum_{i=1}^k \min\!(M_i,r)\end{equation*}
\begin{equation*}r-(k-1)a > \sum_{i=1}^k \big(M^{\prime}_i-a\big) = \sum_{i=1}^k \min\!(M_i,r)\end{equation*}
and then each
![]() $M_i<r$
; hence
$M_i<r$
; hence
![]() $M_i=\min\!(M_i,r)$
. So from (5.11),
$M_i=\min\!(M_i,r)$
. So from (5.11),
 \begin{align*}{\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big) &= \sum_{k=1}^\infty {\mathbb{P}}_p\big(N\big(A^{\delta}(r)\big)\ge k |A^{\delta}(r)\big) \\&\ge \sum_{k=1}^\infty {\mathbb{P}}_p\Bigg(\sum_{i=1}^k M^{\prime}_i < r+a\Bigg) = \sum_{k=1}^\infty {\mathbb{P}}_p(K\ge k+1) \\&= {\mathbb{E}}_p(K)-1,\end{align*}
\begin{align*}{\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big) &= \sum_{k=1}^\infty {\mathbb{P}}_p\big(N\big(A^{\delta}(r)\big)\ge k |A^{\delta}(r)\big) \\&\ge \sum_{k=1}^\infty {\mathbb{P}}_p\Bigg(\sum_{i=1}^k M^{\prime}_i < r+a\Bigg) = \sum_{k=1}^\infty {\mathbb{P}}_p(K\ge k+1) \\&= {\mathbb{E}}_p(K)-1,\end{align*}
where
For
![]() $k\in{\mathbb{N}}$
, let
$k\in{\mathbb{N}}$
, let
By Wald’s equation (see e.g. [Reference Grimmett and Stirzaker11, p. 396]) for the random variable
![]() $S_K$
,
$S_K$
,
For Wald’s equation to be valid for
![]() $S_K$
, the random variable K has to satisfy
$S_K$
, the random variable K has to satisfy
![]() ${\mathbb{E}}_p\big(M^{\prime}_i|K\ge i\big) = {\mathbb{E}}_p\big(M^{\prime}_i\big)$
for
${\mathbb{E}}_p\big(M^{\prime}_i|K\ge i\big) = {\mathbb{E}}_p\big(M^{\prime}_i\big)$
for
![]() $i\in{\mathbb{N}}_+$
. But we have
$i\in{\mathbb{N}}_+$
. But we have
so
![]() $M^{\prime}_i$
is independent of the event
$M^{\prime}_i$
is independent of the event
![]() $\{K\ge i\}$
for
$\{K\ge i\}$
for
![]() $i\in{\mathbb{N}}_+$
, which allows us to use Wald’s equation.
$i\in{\mathbb{N}}_+$
, which allows us to use Wald’s equation.
![]() $\big($
In fact, K is a stopping time for the sequence
$\big($
In fact, K is a stopping time for the sequence
![]() $\big(M^{\prime}_i\big)_{i=1}^\infty$
.
$\big(M^{\prime}_i\big)_{i=1}^\infty$
.
![]() $\big)$
Hence,
$\big)$
Hence,
 \begin{align*}{\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big) &\ge {\mathbb{E}}_p(K)-1 \ge \frac{r+a}{{\mathbb{E}}_p\big(M^{\prime}_1\big)}-1 \\&= \frac{r+a}{a+\int_0^\infty {\mathbb{P}}_p(\!\min\!(M_1,r)\ge m)\,{\text{d}} m} -1\\&\ge \frac{r}{a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m}-1,\end{align*}
\begin{align*}{\mathbb{E}}_p\big(N\big(A^{\delta}(r)\big)|A^{\delta}(r)\big) &\ge {\mathbb{E}}_p(K)-1 \ge \frac{r+a}{{\mathbb{E}}_p\big(M^{\prime}_1\big)}-1 \\&= \frac{r+a}{a+\int_0^\infty {\mathbb{P}}_p(\!\min\!(M_1,r)\ge m)\,{\text{d}} m} -1\\&\ge \frac{r}{a+\int_0^r {\tilde{g}}_p(m)\,{\text{d}} m}-1,\end{align*}
which finishes the proof.
5.4. Proof of Lemma 5.3
Lemma 5.6. (Recalled from Lemma 5.3; cf. [Reference Grimmett9, Lemma (5.24)]) For any
![]() $p<p_{\text{a}}$
, there exists
$p<p_{\text{a}}$
, there exists
![]() ${\delta}(p)$
such that
${\delta}(p)$
such that
One fact about
![]() ${\tilde{g}}_p(r)$
that we will use in the proof is that it just converges to
${\tilde{g}}_p(r)$
that we will use in the proof is that it just converges to
![]() $0$
with
$0$
with
![]() $r\to\infty$
.
$r\to\infty$
.
Proposition 5.1. For any
![]() $p\in{{\mathcal{N}}}$
,
$p\in{{\mathcal{N}}}$
,
Proof of the proposition. Put
for
![]() $(h,R)\in(0,1]\times O(d)$
. Note that it is sufficient to prove
$(h,R)\in(0,1]\times O(d)$
. Note that it is sufficient to prove
because
 \begin{align*}g_p(r) &= \sup_{(h,R)\in(0,1]\times O(d)} {\mathbb{P}}_p\big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\big) \\&\le \sup_{(h,R)\in(0,1]\times O(d)} {\mathbb{P}}_p\big(o^{(h,R)}\leftrightarrow S_{hr}\textrm{ in }G^{(h,R)}\big) &&\textrm{(because $hr\le r$)}\\&= \sup_{R\in O(d)} {\mathbb{P}}_p\big(o\leftrightarrow S_r\textrm{ in }G^{(1,R)}\big) &&\textrm{(by scaling the situation)}\\&\le \sup_{R\in O(d)} {\mathbb{P}}_p\big(M^{(1,R)}\ge r\big),\end{align*}
\begin{align*}g_p(r) &= \sup_{(h,R)\in(0,1]\times O(d)} {\mathbb{P}}_p\big(o^{(h,R)}\leftrightarrow S_r\textrm{ in }G^{(h,R)}\cap L\big) \\&\le \sup_{(h,R)\in(0,1]\times O(d)} {\mathbb{P}}_p\big(o^{(h,R)}\leftrightarrow S_{hr}\textrm{ in }G^{(h,R)}\big) &&\textrm{(because $hr\le r$)}\\&= \sup_{R\in O(d)} {\mathbb{P}}_p\big(o\leftrightarrow S_r\textrm{ in }G^{(1,R)}\big) &&\textrm{(by scaling the situation)}\\&\le \sup_{R\in O(d)} {\mathbb{P}}_p\big(M^{(1,R)}\ge r\big),\end{align*}
so
![]() $g_p(r)\xrightarrow[r\to\infty]{}0$
and, equivalently,
$g_p(r)\xrightarrow[r\to\infty]{}0$
and, equivalently,
![]() ${\tilde{g}}_p(r){\xrightarrow[r\to\infty]{}}0$
will be implied. To prove (5.11), we use the upper semi-continuity of the function
${\tilde{g}}_p(r){\xrightarrow[r\to\infty]{}}0$
will be implied. To prove (5.11), we use the upper semi-continuity of the function
for any
![]() $p\in{{\mathcal{N}}}$
and
$p\in{{\mathcal{N}}}$
and
![]() $r>0$
. In order to verify the latter, let us fix such p and r and let
$r>0$
. In order to verify the latter, let us fix such p and r and let
![]() $(R_n)_n$
be a sequence of elements of O(d) convergent to some R. Assume without loss of generality that the cluster
$(R_n)_n$
be a sequence of elements of O(d) convergent to some R. Assume without loss of generality that the cluster
![]() $C^{(1,R)}$
is bounded in the Euclidean metric, and throughout this proof, condition on it for all the events by default. We are going to show that
$C^{(1,R)}$
is bounded in the Euclidean metric, and throughout this proof, condition on it for all the events by default. We are going to show that
For any isometry
![]() $\Phi$
of
$\Phi$
of
![]() $\mathbb{H}^d$
, let
$\mathbb{H}^d$
, let
![]() $\hat{\Phi}$
denote the unique continuous extension of
$\hat{\Phi}$
denote the unique continuous extension of
![]() $\Phi$
to
$\Phi$
to
![]() $\hat{\mathbb{H}}^d$
(which is a homeomorphism of
$\hat{\mathbb{H}}^d$
(which is a homeomorphism of
![]() $\hat{\mathbb{H}}^d$
—see [Reference Bridson and Haefliger2, Corollary II.8.9]). Put
$\hat{\mathbb{H}}^d$
—see [Reference Bridson and Haefliger2, Corollary II.8.9]). Put
![]() $\Phi_n=\Phi^{(1,R)}\circ\big(\Phi^{(1,R_n)}\big)^{-1}$
and assume that the event
$\Phi_n=\Phi^{(1,R)}\circ\big(\Phi^{(1,R_n)}\big)^{-1}$
and assume that the event
![]() $\limsup_{n\to\infty}\big\{M^{(1,R_n)}\ge r\big\}$
occurs. Then, for infinitely many values of n, all the following occur:
$\limsup_{n\to\infty}\big\{M^{(1,R_n)}\ge r\big\}$
occurs. Then, for infinitely many values of n, all the following occur:
and, by applying
![]() $\hat{\Phi}_n$
,
$\hat{\Phi}_n$
,
For any such n, let
![]() $x_n$
be chosen from the set
$x_n$
be chosen from the set ![]() . Because
. Because ![]() is compact, the sequence
is compact, the sequence
![]() $(x_n)_n$
(indexed by a subset of
$(x_n)_n$
(indexed by a subset of
![]() ${\mathbb{N}}_+$
) has an (infinite) subsequence
${\mathbb{N}}_+$
) has an (infinite) subsequence
![]() $(x_{n_k})_{k=1}^\infty$
convergent to some point in
$(x_{n_k})_{k=1}^\infty$
convergent to some point in ![]() . On the other hand, note that
. On the other hand, note that
![]() $\hat{\Phi}_n\xrightarrow[n\to\infty]{}{\text{Id}}_{\hat{\mathbb{H}}^d}$
uniformly in the Euclidean metric of the disc model (see Definition 2.2). Hence, the distance in that metric between
$\hat{\Phi}_n\xrightarrow[n\to\infty]{}{\text{Id}}_{\hat{\mathbb{H}}^d}$
uniformly in the Euclidean metric of the disc model (see Definition 2.2). Hence, the distance in that metric between
![]() $x_{n_k}\in\hat{\Phi}_{n_k}(\hat{S}_r)$
and
$x_{n_k}\in\hat{\Phi}_{n_k}(\hat{S}_r)$
and
![]() $\hat{S}_r$
tends to 0 as
$\hat{S}_r$
tends to 0 as
![]() $k\to\infty$
, so
$k\to\infty$
, so
which shows that
![]() $ M^{(1,R)}\ge r$
, as desired in (5.12). Now,
$ M^{(1,R)}\ge r$
, as desired in (5.12). Now,
 \begin{align*}\limsup_{n\to\infty} {\mathbb{P}}_p\big(M^{(1,R_n)}\ge r\big) &\le {\mathbb{P}}_p\big(\limsup_{n\to\infty}\big\{M^{(1,R_n)}\ge r\big\}\big) \\&\le {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big),\end{align*}
\begin{align*}\limsup_{n\to\infty} {\mathbb{P}}_p\big(M^{(1,R_n)}\ge r\big) &\le {\mathbb{P}}_p\big(\limsup_{n\to\infty}\big\{M^{(1,R_n)}\ge r\big\}\big) \\&\le {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big),\end{align*}
which means exactly the upper semi-continuity of
![]() $R\mapsto {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big)$
.
$R\mapsto {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big)$
.
Next, note that for
![]() $p\in{{\mathcal{N}}}$
and
$p\in{{\mathcal{N}}}$
and
![]() $R\in O(d)$
$R\in O(d)$
because
![]() ${\mathbb{P}}_p$
-a.s.
${\mathbb{P}}_p$
-a.s.
![]() $M^{(1,R)}<\infty$
by Remark 3.2. Hence, if for
$M^{(1,R)}<\infty$
by Remark 3.2. Hence, if for
![]() $r>0$
and
$r>0$
and
![]() $\varepsilon>0$
we put
$\varepsilon>0$
we put
then for any fixed
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $U_\varepsilon(r)$
is always an open subset of O(d) by the upper semi-continuity of
$U_\varepsilon(r)$
is always an open subset of O(d) by the upper semi-continuity of
![]() $R\mapsto {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big)$
, so by the compactness of O(d), the union (5.13) is indeed finite. Moreover, because
$R\mapsto {\mathbb{P}}_p\big( M^{(1,R)}\ge r\big)$
, so by the compactness of O(d), the union (5.13) is indeed finite. Moreover, because
![]() $U_\varepsilon(r)$
increases as r increases, it equals O(d) for some
$U_\varepsilon(r)$
increases as r increases, it equals O(d) for some
![]() $r>0$
. This means that
$r>0$
. This means that
![]() $\sup_{R\in O(d)}{\mathbb{P}}_p\big(M^{(1,R)}\ge r\big)\le\varepsilon$
, whence
$\sup_{R\in O(d)}{\mathbb{P}}_p\big(M^{(1,R)}\ge r\big)\le\varepsilon$
, whence
![]() $\sup_{R\in O(d)}{\mathbb{P}}_p\big(M^{(1,R)}\ge r\big)\xrightarrow[r\to\infty]{} 0$
, as desired.
$\sup_{R\in O(d)}{\mathbb{P}}_p\big(M^{(1,R)}\ge r\big)\xrightarrow[r\to\infty]{} 0$
, as desired.
Proof of the lemma. Assume without loss of generality that
![]() ${\tilde{g}}_p(r)>0$
for
${\tilde{g}}_p(r)>0$
for
![]() $r>0$
. We are going to construct sequences
$r>0$
. We are going to construct sequences
![]() $(p_i)_{i=1}^\infty$
and
$(p_i)_{i=1}^\infty$
and
![]() $(r_i)_{i=1}^\infty$
such that
$(r_i)_{i=1}^\infty$
such that
and such that the sequence
![]() $\big({\tilde{g}}_{p_i}(r_i)\big)_{i=1}^\infty$
decays rapidly. The construction is by recursion: for
$\big({\tilde{g}}_{p_i}(r_i)\big)_{i=1}^\infty$
decays rapidly. The construction is by recursion: for
![]() $i\ge 1$
, having constructed
$i\ge 1$
, having constructed
![]() $p_1,\ldots,p_i$
and
$p_1,\ldots,p_i$
and
![]() $r_1,\ldots,r_i$
, we put
$r_1,\ldots,r_i$
, we put
where
![]() $g_i = {\tilde{g}}_{p_i}(r_i)$
. (Note that, indeed,
$g_i = {\tilde{g}}_{p_i}(r_i)$
. (Note that, indeed,
![]() $r_{i+1}\le r_i$
and
$r_{i+1}\le r_i$
and
![]() $p_{i+1}<p_i$
.) The above formula may give an incorrect value of
$p_{i+1}<p_i$
.) The above formula may give an incorrect value of
![]() $p_{i+1}$
, i.e. a value not satisfying
$p_{i+1}$
, i.e. a value not satisfying
![]() $p_{i+1}>p$
(this condition is needed because we want to bound values of
$p_{i+1}>p$
(this condition is needed because we want to bound values of
![]() ${\tilde{g}}_p$
). In order to prevent that, we use the following inequality and choose appropriate values of
${\tilde{g}}_p$
). In order to prevent that, we use the following inequality and choose appropriate values of
![]() $p_1,r_1$
.
$p_1,r_1$
.
Fix
![]() $i\ge1$
and assume that
$i\ge1$
and assume that
![]() $r_1\ge a$
and
$r_1\ge a$
and
![]() $p_1,\ldots,p_i>p$
are defined by (5.14). Let
$p_1,\ldots,p_i>p$
are defined by (5.14). Let
![]() $j\in\{1,\ldots,i-1\}$
. Then
$j\in\{1,\ldots,i-1\}$
. Then
We now prove this inequality. From (5.5),
 \begin{align*}g_{j+1} &\le {\tilde{g}}_{p_j}(r_{j+1})\exp\!\left({-}(p_j-p_{j+1})\left(\frac{r_{j+1}}{a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m} -1\right)\right) \\&\le g_j \exp\!\left(1 - (p_j-p_{j+1}) \frac{r_{j+1}}{a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m} \right).\end{align*}
\begin{align*}g_{j+1} &\le {\tilde{g}}_{p_j}(r_{j+1})\exp\!\left({-}(p_j-p_{j+1})\left(\frac{r_{j+1}}{a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m} -1\right)\right) \\&\le g_j \exp\!\left(1 - (p_j-p_{j+1}) \frac{r_{j+1}}{a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m} \right).\end{align*}
The inverse of the fraction above is estimated as follows:
 \begin{align*}\frac{1}{r_{j+1}} \left(a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m\right) &\le \frac{a}{r_{j+1}} + \frac{r_j}{r_{j+1}} + \frac{1}{r_{j+1}} \int_{r_j}^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m \\&\le \frac{a}{r_{j+1}} + g_j + \frac{r_{j+1}-r_j}{r_{j+1}} {\tilde{g}}_{p_j}(r_j), \\ \text{using $r_{j+1} = r_j/g_j$ and the monotonicity of ${\tilde{g}}_{p_j}({\cdot})$,} \\&\le \frac{a}{r_{j+1}} + 2g_j.\end{align*}
\begin{align*}\frac{1}{r_{j+1}} \left(a+\int_0^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m\right) &\le \frac{a}{r_{j+1}} + \frac{r_j}{r_{j+1}} + \frac{1}{r_{j+1}} \int_{r_j}^{r_{j+1}} {\tilde{g}}_{p_j}(m)\,{\text{d}} m \\&\le \frac{a}{r_{j+1}} + g_j + \frac{r_{j+1}-r_j}{r_{j+1}} {\tilde{g}}_{p_j}(r_j), \\ \text{using $r_{j+1} = r_j/g_j$ and the monotonicity of ${\tilde{g}}_{p_j}({\cdot})$,} \\&\le \frac{a}{r_{j+1}} + 2g_j.\end{align*}
Now, by the assumption,
![]() $r_j\ge r_1\ge a$
, so
$r_j\ge r_1\ge a$
, so
![]() $r_{j+1} = r_j/g_j \ge a/g_j$
and
$r_{j+1} = r_j/g_j \ge a/g_j$
and
That gives
by the definition of
![]() $p_{j+1}$
.
$p_{j+1}$
.
We define a sequence
![]() $(x_i)_{i=1}^\infty$
by
$(x_i)_{i=1}^\infty$
by
![]() $x_{i+1}=x_i^2$
for
$x_{i+1}=x_i^2$
for
![]() $i\ge 1$
$i\ge 1$
![]() $\Big($
i.e.
$\Big($
i.e.
![]() $x_i=x_1^{2^{i-1}}\Big)$
, where
$x_i=x_1^{2^{i-1}}\Big)$
, where
![]() $0<x_1<1$
. It is an exercise to prove that for such a sequence,
$0<x_1<1$
. It is an exercise to prove that for such a sequence,
is finite and
![]() $s(x_1)\xrightarrow[x_1\to 0]{}0$
. (The idea of the proof of this fact is similar to that of estimating the sum in (3.4).)
$s(x_1)\xrightarrow[x_1\to 0]{}0$
. (The idea of the proof of this fact is similar to that of estimating the sum in (3.4).)
Now, taking any
![]() $p_1\in(p,p_{\text{a}})$
and
$p_1\in(p,p_{\text{a}})$
and
![]() $1>x_1>0$
in (5.16) such that
$1>x_1>0$
in (5.16) such that
![]() $s(x_1) \le p_1-p$
, and taking
$s(x_1) \le p_1-p$
, and taking
![]() $r_1\ge a$
so large that
$r_1\ge a$
so large that
![]() ${\tilde{g}}_{p_1}(r_1)<x_1$
(thanks to Proposition 5.1), we obtain
${\tilde{g}}_{p_1}(r_1)<x_1$
(thanks to Proposition 5.1), we obtain
![]() $g_i<x_i$
for
$g_i<x_i$
for
![]() $j\in\{1,\ldots,i\}$
(by induction). Then, in the setting of (5.14),
$j\in\{1,\ldots,i\}$
(by induction). Then, in the setting of (5.14),
 \begin{align*}p_{i+1} &= p_1 - \sum_{j=1}^i 3g_i(1-\ln g_i) > p_1 - \sum_{j=1}^i 3x_i(1-\ln x_i)\end{align*}
\begin{align*}p_{i+1} &= p_1 - \sum_{j=1}^i 3g_i(1-\ln g_i) > p_1 - \sum_{j=1}^i 3x_i(1-\ln x_i)\end{align*}
because
![]() $x\mapsto 3x(1-\ln x)$
is increasing for
$x\mapsto 3x(1-\ln x)$
is increasing for
![]() $x\in(0,1]$
,
$x\in(0,1]$
,
Now we know that the recursion (5.14) is well-defined, and we can use the constructed sequences to prove the lemma. First, note that for
![]() $k\ge 1$
,
$k\ge 1$
,
Furthermore, (5.15) implies
where
![]() ${\delta}=\sqrt{r_1 g_1}$
. Now, let
${\delta}=\sqrt{r_1 g_1}$
. Now, let
![]() $r\ge r_1$
. We have
$r\ge r_1$
. We have
![]() $r_k\xrightarrow[k\to\infty]{}\infty$
because
$r_k\xrightarrow[k\to\infty]{}\infty$
because
![]() $\frac{r_k}{r_{k+1}}=g_k \xrightarrow[k\to\infty]{}0$
, so for some k,
$\frac{r_k}{r_{k+1}}=g_k \xrightarrow[k\to\infty]{}0$
, so for some k,
![]() $r_{k-1}\le r<r_k$
. Then
$r_{k-1}\le r<r_k$
. Then
(from (5.17) and the monotonicity of
![]() ${\tilde{g}}_p(r)$
with respect to each of p and r), which finishes the proof.
${\tilde{g}}_p(r)$
with respect to each of p and r), which finishes the proof.
Remark 5.2. As promised in Section 5, in this remark we summarize the differences between the proof of Theorem 3.2 and the proof of Theorem (5.4) in [Reference Grimmett9]:
-
1. First of all, the skeleton structure and most of the notation of the proof here is borrowed from [Reference Grimmett9]. The major difference in notation here is the use of
 $A^{\delta}(r)$
and
$A^{\delta}(r)$
and
 $S_r$
(corresponding respectively to
$S_r$
(corresponding respectively to
 $A_n$
and
$A_n$
and
 $\partial S(s)$
in [Reference Grimmett9]).
$\partial S(s)$
in [Reference Grimmett9]). -
2. Strictly speaking, the proper line of the proof borrowed from [Reference Grimmett9] starts by considering the functions
 $f_p$
instead of
$f_p$
instead of
 $g_p$
or
$g_p$
or
 ${\tilde{g}}_p$
, although the functional inequality (5.1) involves both functions
${\tilde{g}}_p$
, although the functional inequality (5.1) involves both functions
 $f_\cdot({\cdot})$
and
$f_\cdot({\cdot})$
and
 ${\tilde{g}}_\cdot({\cdot})$
. In fact, each of the functions
${\tilde{g}}_\cdot({\cdot})$
. In fact, each of the functions
 $f_\cdot({\cdot})$
,
$f_\cdot({\cdot})$
,
 ${\tilde{g}}_\cdot({\cdot})$
, and
${\tilde{g}}_\cdot({\cdot})$
, and
 $g_\cdot({\cdot})$
is a counterpart of the function
$g_\cdot({\cdot})$
is a counterpart of the function
 $g_\cdot({\cdot})$
from [Reference Grimmett9] at some stage of the proof. After proving the inequality (5.1), we pass to a couple of limits with it in order to obtain the inequality (5.2), which involves only
$g_\cdot({\cdot})$
from [Reference Grimmett9] at some stage of the proof. After proving the inequality (5.1), we pass to a couple of limits with it in order to obtain the inequality (5.2), which involves only
 ${\tilde{g}}_\cdot({\cdot})$
(the step not present in [Reference Grimmett9]). This is necessary to enable the repeated use of the inequality (5.2) at the end of the proof of Theorem 3.2.
${\tilde{g}}_\cdot({\cdot})$
(the step not present in [Reference Grimmett9]). This is necessary to enable the repeated use of the inequality (5.2) at the end of the proof of Theorem 3.2. -
3. Obviously, the geometry used here is much different from that in [Reference Grimmett9]. In fact, we analyse the percolation cluster in
 $G^{(h,R)}\cap L_{\delta}$
using the pseudometric
$G^{(h,R)}\cap L_{\delta}$
using the pseudometric
 $d_\eth$
(in place of the graph metric
$d_\eth$
(in place of the graph metric
 ${\delta}$
in [Reference Grimmett9]). Consequently, the set
${\delta}$
in [Reference Grimmett9]). Consequently, the set
 ${\mathcal{R}^{(h,R)}}$
of possible values of the random variables
${\mathcal{R}^{(h,R)}}$
of possible values of the random variables
 $\varrho$
in Lemma 5.1 is much richer than
$\varrho$
in Lemma 5.1 is much richer than
 ${\mathbb{N}}$
, the respective set for the graph
${\mathbb{N}}$
, the respective set for the graph
 ${\mathbb{Z}}^d$
. Moreover, the functions
${\mathbb{Z}}^d$
. Moreover, the functions
 ${\tilde{g}}_p$
arise from the percolation process on the whole
${\tilde{g}}_p$
arise from the percolation process on the whole
 $G^{(h,R)}\cap L$
, so the distribution of the random variables
$G^{(h,R)}\cap L$
, so the distribution of the random variables
 $M_i$
is not necessarily discrete. That necessitates the use of integrals instead of sums to handle those random variables, especially in the proof of Corollary 5.1. All of this also leads to a few other minor technical differences between the proof here and the proof in [Reference Grimmett9].
$M_i$
is not necessarily discrete. That necessitates the use of integrals instead of sums to handle those random variables, especially in the proof of Corollary 5.1. All of this also leads to a few other minor technical differences between the proof here and the proof in [Reference Grimmett9]. -
4. The author has tried to clarify the use of the assumption on
 $\sum_{i=1}^k r_i$
in Lemma 5.1 and to explain why Wald’s equation can be used in the proof of Lemma 5.2, a consideration that is somewhat hidden in [Reference Grimmett9].
$\sum_{i=1}^k r_i$
in Lemma 5.1 and to explain why Wald’s equation can be used in the proof of Lemma 5.2, a consideration that is somewhat hidden in [Reference Grimmett9]. -
5. The proof of Lemma 5.3 has been reorganized a little (compared to the proof of Lemma (5.24) in [Reference Grimmett9]) and contains a proof of the convergence
 ${\tilde{g}}_p(r)\xrightarrow[r]{}0$
(Proposition 5.1).
${\tilde{g}}_p(r)\xrightarrow[r]{}0$
(Proposition 5.1).
Acknowledgement
This paper is essentially the second part of my doctoral thesis. I express my gratitude to my advisor, Jan Dymara, for his supervision and words of advice.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.