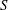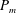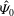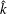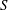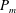1. Introduction
Magnetic reconnection is a process whereby the magnetic field line connectivity (Newcomb Reference Newcomb1958; Pegoraro Reference Pegoraro2012; Asenjo & Comisso Reference Asenjo and Comisso2015) is modified due to the presence of a localized diffusion region. This gives rise to a change in magnetic field line topology and a release of magnetic energy into kinetic and thermal energy. Reconnection of magnetic field lines is ubiquitous in laboratory, space and astrophysical plasmas, where it is believed to play a key role in many of the most striking and energetic phenomena. The most notable examples of such phenomena include sawtooth crashes (Yamada et al. Reference Yamada, Levinton, Pomphrey, Budny, Manickam and Nagayama1994; Nicolas et al. Reference Nicolas, Sabot, Garbet, Lütjens, Luciani, Guimaraes-Filho, Decker and Merle2012) and major disruptions in tokamak experiments (Waddell et al. Reference Waddell, Carreras, Hicks, Holmes and Lee1978; Boozer Reference Boozer2012), solar and stellar flares (Masuda et al. Reference Masuda, Kosugi, Hara, Tsuneta and Ogawara1994; Su et al. Reference Su, Veronig, Holman, Dennis, Wang, Temmer and Gan2013), coronal mass ejections (Lin & Forbes Reference Lin and Forbes2000; Murphy et al. Reference Murphy, Miralles, Pope, Raymond, Winter, Reeves, Seaton, van Ballegooijen and Lin2012), magnetospheric substorms (Øieroset et al. Reference Øieroset, Phan, Fujimoto, Lin and Lepping2001; Eastwood et al. Reference Eastwood, Phan, Mozer, Shay, Fujimoto, Retinò, Hesse, Balogh, Lucek and Dandouras2007), coronal heating (Priest et al. Reference Priest, Foley, Heyvaerts, Arber, Culhane and Acton1998; Cassak et al. Reference Cassak, Mullan and Shay2008), and high-energy emissions in pulsar wind nebulae, gamma-ray bursts and jets from active galactic nuclei (Guo et al. Reference Guo, Liu, Daughton and Li2015; Kagan et al. Reference Kagan, Sironi, Cerutti and Giannios2015; Sironi et al. Reference Sironi, Petropoulou and Giannios2015). An exhaustive understanding of how magnetic reconnection proceeds in various regimes is therefore essential in order to shed light on these phenomena.
In recent years, for the purpose of organizing the current knowledge of the reconnection dynamics that is expected in a system with given plasma parameters, a particular type of phase diagrams has been developed (Huang et al. Reference Huang, Bhattacharjee and Sullivan2011; Ji & Daughton Reference Ji and Daughton2011; Daughton & Roytershteyn Reference Daughton and Roytershteyn2012; Cassak & Drake Reference Cassak and Drake2013; Huang & Bhattacharjee Reference Huang and Bhattacharjee2013; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013). These diagrams classify what ‘phase’ of magnetic reconnection should occur in a particular system, which is identified by two dimensionless plasma parameters, the Lundquist number
and the macroscopic system size
Here,
![]() $L_{s}$
indicates the system size in the direction of the reconnecting current sheet,
$L_{s}$
indicates the system size in the direction of the reconnecting current sheet,
![]() $v_{A,u}$
is the Alfvén speed based on the reconnecting component of the magnetic field upstream of the diffusion region,
$v_{A,u}$
is the Alfvén speed based on the reconnecting component of the magnetic field upstream of the diffusion region,
![]() $D_{{\it\eta}}={\it\eta}c^{2}/4{\rm\pi}$
is the magnetic diffusivity, and
$D_{{\it\eta}}={\it\eta}c^{2}/4{\rm\pi}$
is the magnetic diffusivity, and
![]() $l_{k}$
is the relevant kinetic length scale. This length scale corresponds to (see e.g. Simakov & Chacón Reference Simakov and Chacón2008; Comisso et al.
Reference Comisso, Grasso, Waelbroeck and Borgogno2013)
$l_{k}$
is the relevant kinetic length scale. This length scale corresponds to (see e.g. Simakov & Chacón Reference Simakov and Chacón2008; Comisso et al.
Reference Comisso, Grasso, Waelbroeck and Borgogno2013)
Of course,
![]() ${\it\omega}_{pi}$
is the ion plasma frequency,
${\it\omega}_{pi}$
is the ion plasma frequency,
![]() ${\it\omega}_{ci}$
is the ion cyclotron frequency,
${\it\omega}_{ci}$
is the ion cyclotron frequency,
![]() $c$
is the speed of light, and
$c$
is the speed of light, and
![]() $c_{s}$
is the sound speed based on both the electron and ion temperatures.
$c_{s}$
is the sound speed based on both the electron and ion temperatures.
All the proposed phase diagrams (Huang et al.
Reference Huang, Bhattacharjee and Sullivan2011; Ji & Daughton Reference Ji and Daughton2011; Daughton & Roytershteyn Reference Daughton and Roytershteyn2012; Cassak & Drake Reference Cassak and Drake2013; Huang & Bhattacharjee Reference Huang and Bhattacharjee2013; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013) exhibit strong similarity and only a few minor differences. They are useful for summarizing some of the current knowledge of the magnetic reconnection dynamics, but they lack fundamental aspects that can greatly affect the reconnection process (some caveats in the use of these diagrams have been discussed by Cassak & Drake Reference Cassak and Drake2013). For example, they do not take into account the dependence of the reconnection process on the external drive or on the magnetic free energy available in the system. An attempt to include these effects has been discussed by Ji & Daughton (Reference Ji and Daughton2011), who proposed incorporating them by adjusting the definition of the Lundquist number (1.1), but this solution should be viewed only as a rough way to circumnavigate the problem. A further issue is that these diagrams do not consider the evolution of the reconnection process, and predict reconnection rates which are always fast (the estimated reconnection inflow is always a significant fraction of
![]() $v_{A,u}$
). This, however, is not what is commonly observed in laboratory, space, and astrophysical plasmas, where magnetic reconnection exhibits disparate time scales and is often characterized by an impulsive behaviour, i.e. a sudden increase in the time derivative of the reconnection rate (see e.g. Bhattacharjee Reference Bhattacharjee2004; Yamada Reference Yamada2011).
$v_{A,u}$
). This, however, is not what is commonly observed in laboratory, space, and astrophysical plasmas, where magnetic reconnection exhibits disparate time scales and is often characterized by an impulsive behaviour, i.e. a sudden increase in the time derivative of the reconnection rate (see e.g. Bhattacharjee Reference Bhattacharjee2004; Yamada Reference Yamada2011).
Here we propose a different point of view in which we include explicitly the effects of the external drive and the plasma viscosity (neglected in all previous diagrams) on the magnetic reconnection process by considering a four-dimensional parameter space. Then, in this four-dimensional diagram we identify specific domains of parameters where the reconnection process exhibits distinct dynamical evolutions. In other words, in each of these domains the reconnection process goes through diverse phases characterized by different reconnection rates. This analysis leads us to evaluate in greater detail the dynamical evolution of a forced magnetic reconnection process, while collisionless effects have not been taken into account in the present work. We introduce the considered model of forced magnetic reconnection in § 2, whereas § 3 is devoted to the presentation of the possible evolutions of the system and the conditions under which these different evolutions occur. In § 4 we construct the parameter space diagrams that show which reconnection evolution is expected in a system with given characteristic parameters. Finally, open issues are discussed in § 5.
2. Forced magnetic reconnection in Taylor’s model
Magnetic reconnection in a given system is conventionally categorized as spontaneous or forced. Spontaneous magnetic reconnection refers to the case in which the reconnection arises by some internal instability of the system or loss of equilibrium, with the most typical example being the tearing mode. Forced magnetic reconnection instead refers to the cases in which the reconnection is driven by some externally imposed flow or magnetic perturbation. In this case, one of the most important paradigms is the so-called ‘Taylor problem’, which consists in the study of the evolution of the magnetic reconnection process in a tearing-stable slab plasma equilibrium which is subject to a small amplitude boundary perturbation. This situation is depicted in figure 1, where the shared equilibrium magnetic field has the form
with
![]() $B_{z}$
,
$B_{z}$
,
![]() $B_{0}$
and
$B_{0}$
and
![]() $L$
as constants, and the perfectly conducting walls which bound the plasma are located at
$L$
as constants, and the perfectly conducting walls which bound the plasma are located at
![]() $x=\pm L$
. Magnetic reconnection is driven at the resonant surface
$x=\pm L$
. Magnetic reconnection is driven at the resonant surface
![]() $x=0$
by a deformation of the conducting walls such that
$x=0$
by a deformation of the conducting walls such that
where
![]() $k=2{\rm\pi}/L_{y}$
is the perturbation wave number and
$k=2{\rm\pi}/L_{y}$
is the perturbation wave number and
![]() ${\it\Xi}_{0}$
is a small (
${\it\Xi}_{0}$
is a small (
![]() $\ll L$
) displacement amplitude. The boundary perturbation is assumed to be set up in a time scale that is long compared to the Alfvén time
$\ll L$
) displacement amplitude. The boundary perturbation is assumed to be set up in a time scale that is long compared to the Alfvén time
![]() ${\it\tau}_{A}=L/v_{A}$
, with
${\it\tau}_{A}=L/v_{A}$
, with
![]() $v_{A}=B_{0}/\sqrt{4{\rm\pi}{\it\rho}}$
, but short compared to any characteristic reconnection time scale. Hence, the plasma can be considered in magnetostatic equilibrium everywhere except near the resonant surface at
$v_{A}=B_{0}/\sqrt{4{\rm\pi}{\it\rho}}$
, but short compared to any characteristic reconnection time scale. Hence, the plasma can be considered in magnetostatic equilibrium everywhere except near the resonant surface at
![]() $x=0$
.
$x=0$
.
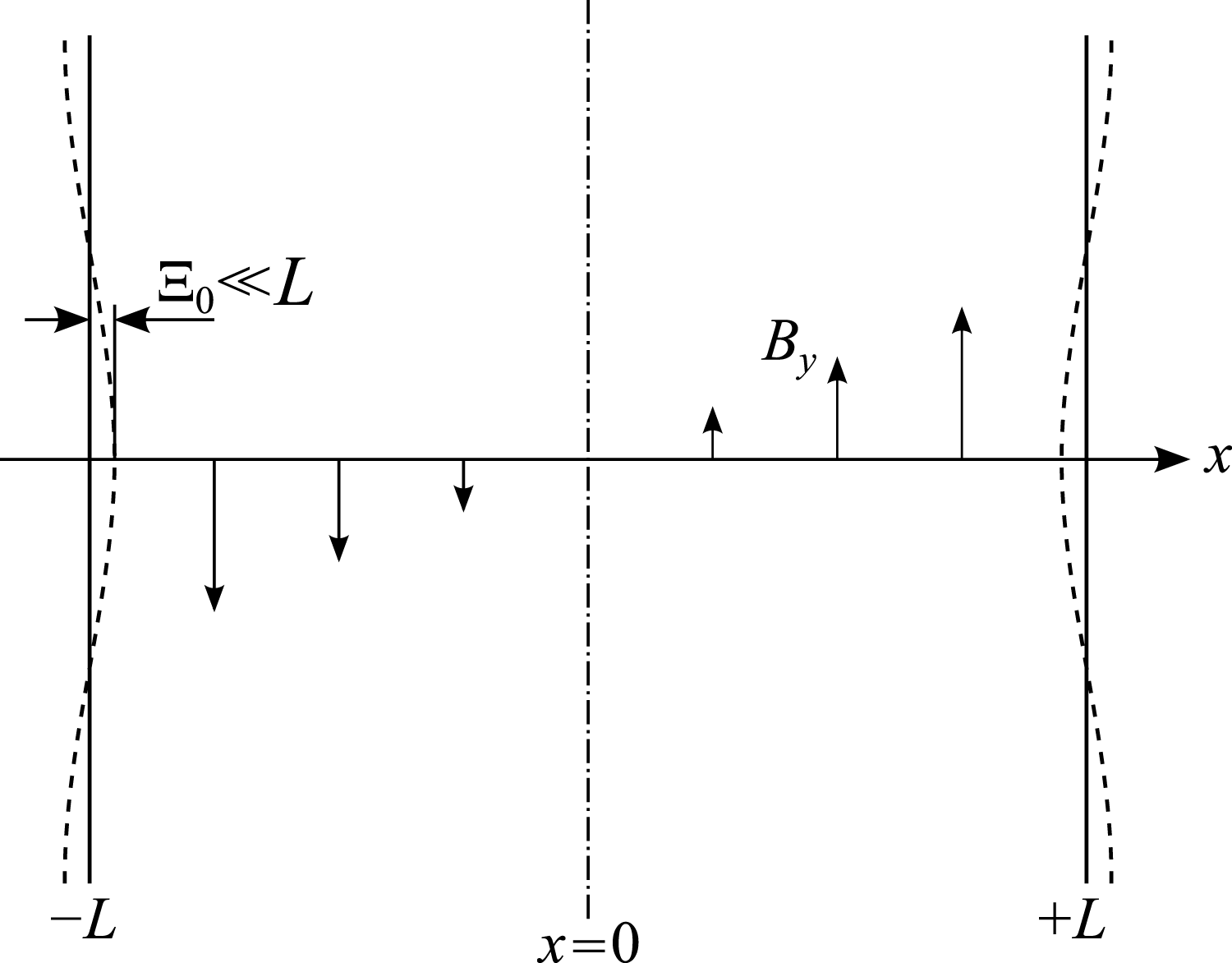
Figure 1. Geometry of the Taylor model. The equilibrium magnetic field component
![]() $B_{y}$
is sheared in the
$B_{y}$
is sheared in the
![]() $x$
direction, being null at
$x$
direction, being null at
![]() $x=0$
. The plasma is bounded by perfectly conducting walls at
$x=0$
. The plasma is bounded by perfectly conducting walls at
![]() $x=\pm L$
, while it is periodic in the
$x=\pm L$
, while it is periodic in the
![]() $y$
direction. Magnetic reconnection is driven at
$y$
direction. Magnetic reconnection is driven at
![]() $x=0$
by the perturbation
$x=0$
by the perturbation
![]() ${\it\Xi}_{0}\cos (ky)$
at the perfectly conducting walls.
${\it\Xi}_{0}\cos (ky)$
at the perfectly conducting walls.
The first and probably most important contribution to unveiling the behaviour of forced magnetic reconnection in Taylor’s model is due to Hahm & Kulsrud (Reference Hahm and Kulsrud1985), who showed that very small amplitude boundary perturbations cause an initial linear phase in which a current sheet builds up at the resonant surface, and successive phases in which the reconnection process evolves according to a linear resistive regime and a nonlinear Rutherford regime (Rutherford Reference Rutherford1973). The scenario discussed by Hahm & Kulsrud (Reference Hahm and Kulsrud1985), which is characterized by a very slow evolution of the reconnection process, was complemented some years later by Wang & Bhattacharjee (Reference Wang and Bhattacharjee1992a ), who showed that larger perturbations may foster reconnection to proceed through the nonlinear regime according to a Sweet–Parker-like evolution (Waelbroeck Reference Waelbroeck1989), which gives way to a Rutherford evolution only on the long time scale of resistive diffusion. The scenario outlined by Wang & Bhattacharjee (Reference Wang and Bhattacharjee1992a ) is characterized by a reconnection evolution faster than that presented by Hahm & Kulsrud (Reference Hahm and Kulsrud1985), but it could still be slow for very small values of plasma resistivity, since in both the Sweet–Parker-like (Waelbroeck Reference Waelbroeck1989) and Rutherford (Rutherford Reference Rutherford1973) regimes, the reconnection rate is strongly dependent on the resistivity, which is known to be extremely small in many laboratory fusion plasmas and space/astrophysical plasmas. However, recent works (Comisso et al. Reference Comisso, Grasso and Waelbroeck2014, Reference Comisso, Grasso and Waelbroeck2015) have shown that relatively large boundary perturbations lead to a different reconnection evolution in plasmas with small resistivity and viscosity. In these cases, after a linear inertial phase and an initial nonlinear regime characterized by a gradually evolving current sheet, the reconnection suddenly enters into a fast reconnection regime distinguished by the disruption of the current sheet due to the development of secondary magnetic islands (usually called plasmoids: see Biskamp Reference Biskamp2000 or Loureiro et al. Reference Loureiro, Schekochihin and Cowley2007).
In addition to the works discussed above, which adopt a magnetohydrodynamic (MHD) description of the plasma, we emphasize that many other efforts have been devoted to investigating the Taylor problem assuming MHD, two-fluid and kinetic descriptions (see Wang & Bhattacharjee Reference Wang and Bhattacharjee1992b ; Ma et al. Reference Ma, Wang and Bhattacharjee1996; Avinash et al. Reference Avinash, Bulanov, Esirkepov, Kaw, Pegoraro, Sasorov and Sen1998; Rem & Schep Reference Rem and Schep1998; Valori et al. Reference Valori, Grasso and de Blank2000; Fitzpatrick Reference Fitzpatrick2003; Fitzpatrick Reference Fitzpatrick2004a ,Reference Fitzpatrick b , Reference Fitzpatrick2008; Fitzpatrick et al. Reference Fitzpatrick, Bhattacharjee, Ma and Linde2003; Cole & Fitzpatrick Reference Cole and Fitzpatrick2004; Bian & Vekstein Reference Bian and Vekstein2005; Birn et al. Reference Birn, Galsgaard, Hesse, Hoshino, Huba, Lapenta, Pritchett, Schindler, Yin, Büchner, Neukirch and Priest2005; Vekstein & Bian Reference Vekstein and Bian2006; Birn & Hesse Reference Birn and Hesse2007; Hosseinpour & Vekstein Reference Hosseinpour and Vekstein2008; Gordovskyy et al. Reference Gordovskyy, Browning and Vekstein2010a ,Reference Gordovskyy, Browning and Vekstein b ; Lazzaro & Comisso Reference Lazzaro and Comisso2011; Dewar et al. Reference Dewar, Bhattacharjee, Kulsrud and Wright2013; Hosseinpour Reference Hosseinpour2013). Indeed, the Taylor problem has important applications besides being interesting from the point of view of basic physics. For instance, in laboratory fusion plasmas the Taylor model represents a convenient way to study magnetic reconnection processes driven by resonant magnetic perturbations, while in astrophysical plasmas this model can be adopted to the study of magnetic reconnection forced by the motions of photospheric flux tubes.
3. Evolution of the reconnection process in Taylor’s model
In this section we review the present understanding of the forced magnetic reconnection dynamics in Taylor’s model focusing on a visco-resistive plasma with
![]() $P_{m}$
greater than 1. As shown by Hahm & Kulsrud (Reference Hahm and Kulsrud1985), this dynamics always starts with a linear inertial phase in which a current sheet builds up at the resonant surface and shrinks inversely in time. Concurrently, the current density at the
$P_{m}$
greater than 1. As shown by Hahm & Kulsrud (Reference Hahm and Kulsrud1985), this dynamics always starts with a linear inertial phase in which a current sheet builds up at the resonant surface and shrinks inversely in time. Concurrently, the current density at the
![]() $X$
-point increases linearly in time. The reconnection rate during this phase can be evaluated by recalling that the current density is proportional to the out-of-plane electric field at the
$X$
-point increases linearly in time. The reconnection rate during this phase can be evaluated by recalling that the current density is proportional to the out-of-plane electric field at the
![]() $X$
-point, which is equal to
$X$
-point, which is equal to
for
![]() $t\ll {\it\tau}_{{\it\nu}}^{1/3}({\it\tau}_{A}/kL)^{2/3}$
(Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015). Here,
$t\ll {\it\tau}_{{\it\nu}}^{1/3}({\it\tau}_{A}/kL)^{2/3}$
(Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015). Here,
![]() ${\it\psi}$
stands for the magnetic flux function of the perturbed magnetic field in the reconnection plane (
${\it\psi}$
stands for the magnetic flux function of the perturbed magnetic field in the reconnection plane (
![]() ${\it\delta}\boldsymbol{B}_{\bot }=\boldsymbol{{\rm\nabla}}{\it\psi}\times \boldsymbol{e}_{z}$
),
${\it\delta}\boldsymbol{B}_{\bot }=\boldsymbol{{\rm\nabla}}{\it\psi}\times \boldsymbol{e}_{z}$
),
![]() ${\it\tau}_{{\it\nu}}=L^{2}/{\it\nu}$
and
${\it\tau}_{{\it\nu}}=L^{2}/{\it\nu}$
and
![]() ${\it\tau}_{{\it\eta}}=L^{2}/D_{{\it\eta}}$
indicate the characteristic time for viscous and resistive diffusion, respectively, while
${\it\tau}_{{\it\eta}}=L^{2}/D_{{\it\eta}}$
indicate the characteristic time for viscous and resistive diffusion, respectively, while
![]() ${\it\Delta}_{s}^{\prime }=2k/\sinh \,(kL)$
parametrizes the contribution of the external source perturbation to the gradient discontinuity of the magnetic flux function at the resonant surface. It is important to point out that this phase is characterized by a non-constant-
${\it\Delta}_{s}^{\prime }=2k/\sinh \,(kL)$
parametrizes the contribution of the external source perturbation to the gradient discontinuity of the magnetic flux function at the resonant surface. It is important to point out that this phase is characterized by a non-constant-
![]() ${\it\psi}$
behaviour of the magnetic flux function across the island. Depending on whether or not this property persists until the beginning of the nonlinear regime, different scenarios may occur.
${\it\psi}$
behaviour of the magnetic flux function across the island. Depending on whether or not this property persists until the beginning of the nonlinear regime, different scenarios may occur.
3.1. Hahm–Kulsrud scenario
If the boundary perturbation is such that (Fitzpatrick Reference Fitzpatrick2003; Comisso et al. Reference Comisso, Grasso and Waelbroeck2015)
after the inertial phase the reconnection process evolves through a visco-resistive phase, which is a linear regime characterized by a constant-
![]() ${\it\psi}$
behaviour, i.e. the perturbed magnetic flux function can be treated as a constant in
${\it\psi}$
behaviour, i.e. the perturbed magnetic flux function can be treated as a constant in
![]() $x$
over the width of the reconnection layer. During this phase the reconnection rate is given by
$x$
over the width of the reconnection layer. During this phase the reconnection rate is given by
where
![]() ${\it\Delta}_{0}^{\prime }=2k/\tanh \,(kL)$
is the standard tearing stability parameter and
${\it\Delta}_{0}^{\prime }=2k/\tanh \,(kL)$
is the standard tearing stability parameter and
![]() ${\it\tau}_{\ast }$
is a characteristic time defined as (Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
${\it\tau}_{\ast }$
is a characteristic time defined as (Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
with
![]() ${\it\Gamma}$
indicating the Gamma function. Equation (3.3) is valid for
${\it\Gamma}$
indicating the Gamma function. Equation (3.3) is valid for
![]() $t\gg {\it\tau}_{{\it\nu}}^{-1/3}{\it\tau}_{{\it\eta}}^{2/3}$
$t\gg {\it\tau}_{{\it\nu}}^{-1/3}{\it\tau}_{{\it\eta}}^{2/3}$
![]() $({\it\tau}_{A}/kL)^{2/3}$
(Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015) and a magnetic island width much smaller than the linear layer width, i.e.
$({\it\tau}_{A}/kL)^{2/3}$
(Fitzpatrick Reference Fitzpatrick2003; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015) and a magnetic island width much smaller than the linear layer width, i.e.
![]() $w\ll {\it\delta}_{{\it\nu}{\it\eta}}\sim ({\it\tau}_{{\it\nu}}{\it\tau}_{{\it\eta}})^{-1/6}({\it\tau}_{A}/kL)^{1/3}L$
(Porcelli Reference Porcelli1987; Fitzpatrick Reference Fitzpatrick1993). If the perturbation is sufficient to drive the magnetic island into the nonlinear regime (
$w\ll {\it\delta}_{{\it\nu}{\it\eta}}\sim ({\it\tau}_{{\it\nu}}{\it\tau}_{{\it\eta}})^{-1/6}({\it\tau}_{A}/kL)^{1/3}L$
(Porcelli Reference Porcelli1987; Fitzpatrick Reference Fitzpatrick1993). If the perturbation is sufficient to drive the magnetic island into the nonlinear regime (
![]() $w\gtrsim {\it\delta}_{{\it\nu}{\it\eta}}$
), the visco-resistive phase ends up in a Rutherford evolution, whose island width growth is governed by the Rutherford equation
$w\gtrsim {\it\delta}_{{\it\nu}{\it\eta}}$
), the visco-resistive phase ends up in a Rutherford evolution, whose island width growth is governed by the Rutherford equation
where
![]() ${\mathcal{I}}=0.823$
(Rutherford Reference Rutherford1973; Fitzpatrick Reference Fitzpatrick1993). This is a very slow reconnection evolution in which the reconnection rate can be evaluated analytically in the two limits (Hahm & Kulsrud Reference Hahm and Kulsrud1985; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
${\mathcal{I}}=0.823$
(Rutherford Reference Rutherford1973; Fitzpatrick Reference Fitzpatrick1993). This is a very slow reconnection evolution in which the reconnection rate can be evaluated analytically in the two limits (Hahm & Kulsrud Reference Hahm and Kulsrud1985; Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
3.2. Wang–Bhattacharjee scenario
If the boundary perturbation is such that (Fitzpatrick Reference Fitzpatrick2003; Comisso et al. Reference Comisso, Grasso and Waelbroeck2015)
the non-constant-
![]() ${\it\psi}$
behaviour characteristic of the inertial phase lingers until the nonlinear regime is entered. Therefore, since in this case the magnetic island grows faster than the current can diffuse out of the reconnecting layer, the evolution of the reconnection process is distinguished by a strong current sheet at the resonant surface (Waelbroeck Reference Waelbroeck1989). The reconnecting current sheet turns out to be stable if the boundary perturbation is such that (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
${\it\psi}$
behaviour characteristic of the inertial phase lingers until the nonlinear regime is entered. Therefore, since in this case the magnetic island grows faster than the current can diffuse out of the reconnecting layer, the evolution of the reconnection process is distinguished by a strong current sheet at the resonant surface (Waelbroeck Reference Waelbroeck1989). The reconnecting current sheet turns out to be stable if the boundary perturbation is such that (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
where the multiplicative constant
![]() $C\sim 2{\it\epsilon}_{c}^{-2}$
depends on the critical inverse aspect ratio of the reconnecting current sheet (specified later). In this case, the reconnection process follows a Sweet–Parker evolution (modified by plasma viscosity: Park et al.
Reference Park, Monticello and White1984), whose reconnection rate in Taylor’s model is (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
$C\sim 2{\it\epsilon}_{c}^{-2}$
depends on the critical inverse aspect ratio of the reconnecting current sheet (specified later). In this case, the reconnection process follows a Sweet–Parker evolution (modified by plasma viscosity: Park et al.
Reference Park, Monticello and White1984), whose reconnection rate in Taylor’s model is (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015)
Finally, the Sweet–Parker type of evolution gives way to a Rutherford evolution on the time scale of resistive diffusion.
3.3. Our scenario
If the boundary perturbation satisfies (Fitzpatrick Reference Fitzpatrick2003; Comisso et al. Reference Comisso, Grasso and Waelbroeck2015)
and also the condition (Comisso et al. Reference Comisso, Grasso and Waelbroeck2015)
the reconnection process does not reach a stable Sweet–Parker regime, but a different situation occurs. A gradually thinning current sheet evolves until its aspect ratio reaches the limit that allows the plasmoid instability to develop. The growth of the plasmoids leads to the disruption of the current sheet, and therefore to a dramatic increase in the reconnection rate. The reconnection rate during this plasmoid-dominated phase has been evaluated in a statistical steady state as (Comisso et al. Reference Comisso, Grasso and Waelbroeck2015)
where
![]() ${\it\epsilon}_{c}={\it\delta}_{c}/L_{c}$
is the critical inverse aspect ratio of the reconnecting current sheet. This quantity, whose value has been found to lie in the range
${\it\epsilon}_{c}={\it\delta}_{c}/L_{c}$
is the critical inverse aspect ratio of the reconnecting current sheet. This quantity, whose value has been found to lie in the range
![]() $1/100$
–
$1/100$
–
![]() $1/200$
by means of numerical simulations (Bhattacharjee et al.
Reference Bhattacharjee, Huang, Yang and Rogers2009; Cassak et al.
Reference Cassak, Shay and Drake2009; Samtaney et al.
Reference Samtaney, Loureiro, Uzdensky, Schekochihin and Cowley2009; Huang & Bhattacharjee Reference Huang and Bhattacharjee2010; Skender & Lapenta Reference Skender and Lapenta2010), represents the threshold below which the reconnecting current sheet becomes unstable to the plasmoid instability (Loureiro et al.
Reference Loureiro, Schekochihin and Cowley2007). This threshold condition as a function of the Lundquist and magnetic Prandtl numbers has been recently discussed by Loureiro et al. (Reference Loureiro, Schekochihin and Uzdensky2013), Comisso et al. (Reference Comisso, Grasso and Waelbroeck2015) and Tenerani et al. (Reference Tenerani, Rappazzo, Velli and Pucci2015). In particular, it has been shown (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015) that a reconnecting current sheet becomes unstable when the Lundquist number based on its length exceeds the critical value
$1/200$
by means of numerical simulations (Bhattacharjee et al.
Reference Bhattacharjee, Huang, Yang and Rogers2009; Cassak et al.
Reference Cassak, Shay and Drake2009; Samtaney et al.
Reference Samtaney, Loureiro, Uzdensky, Schekochihin and Cowley2009; Huang & Bhattacharjee Reference Huang and Bhattacharjee2010; Skender & Lapenta Reference Skender and Lapenta2010), represents the threshold below which the reconnecting current sheet becomes unstable to the plasmoid instability (Loureiro et al.
Reference Loureiro, Schekochihin and Cowley2007). This threshold condition as a function of the Lundquist and magnetic Prandtl numbers has been recently discussed by Loureiro et al. (Reference Loureiro, Schekochihin and Uzdensky2013), Comisso et al. (Reference Comisso, Grasso and Waelbroeck2015) and Tenerani et al. (Reference Tenerani, Rappazzo, Velli and Pucci2015). In particular, it has been shown (Comisso et al.
Reference Comisso, Grasso and Waelbroeck2015) that a reconnecting current sheet becomes unstable when the Lundquist number based on its length exceeds the critical value
![]() $S_{c}\approx {\it\epsilon}_{c}^{-2}\left(1+{\it\tau}_{{\it\nu}}/{\it\tau}_{{\it\eta}}\right)^{1/2}$
.
$S_{c}\approx {\it\epsilon}_{c}^{-2}\left(1+{\it\tau}_{{\it\nu}}/{\it\tau}_{{\it\eta}}\right)^{1/2}$
.
4. Phase diagrams
In this section we illustrate the domain of existence of the three different scenarios described above, with the help of appropriate parameter space maps. For the sake of clarity we restate the three types of reconnection evolutions we are referring to:
-
(1) the Hahm–Kulsrud scenario (Hahm & Kulsrud Reference Hahm and Kulsrud1985; Fitzpatrick Reference Fitzpatrick2003);
-
(2) the Wang–Bhattacharjee scenario (Wang & Bhattacharjee Reference Wang and Bhattacharjee1992a ; Fitzpatrick Reference Fitzpatrick2003);
-
(3) our scenario (Comisso et al. Reference Comisso, Grasso and Waelbroeck2015).
Since each of these scenarios includes different phases/regimes of reconnection, the concept of ‘phase diagrams’ is intended here in a broader sense. Due to this fact, they could also be defined in a more general way as ‘scenario diagrams’. This type of diagrams can be constructed from the conditions summarized in the previous section. Therefore, the possible evolutions of the reconnection process may be organized in a four-dimensional parameter space map with
![]() $\hat{{\it\Psi}}_{0}={\it\Psi}_{0}/B_{0}L$
,
$\hat{{\it\Psi}}_{0}={\it\Psi}_{0}/B_{0}L$
,
![]() $\hat{k}=kL$
,
$\hat{k}=kL$
,
![]() $S=Lv_{A}/D_{{\it\eta}}$
, and
$S=Lv_{A}/D_{{\it\eta}}$
, and
![]() $P_{m}={\it\nu}/D_{{\it\eta}}$
on the four axes. However, due to the difficulty in visualizing such a four-dimensional diagram, it is convenient to consider two-dimensional slices for fixed values of two of the four parameters.
$P_{m}={\it\nu}/D_{{\it\eta}}$
on the four axes. However, due to the difficulty in visualizing such a four-dimensional diagram, it is convenient to consider two-dimensional slices for fixed values of two of the four parameters.
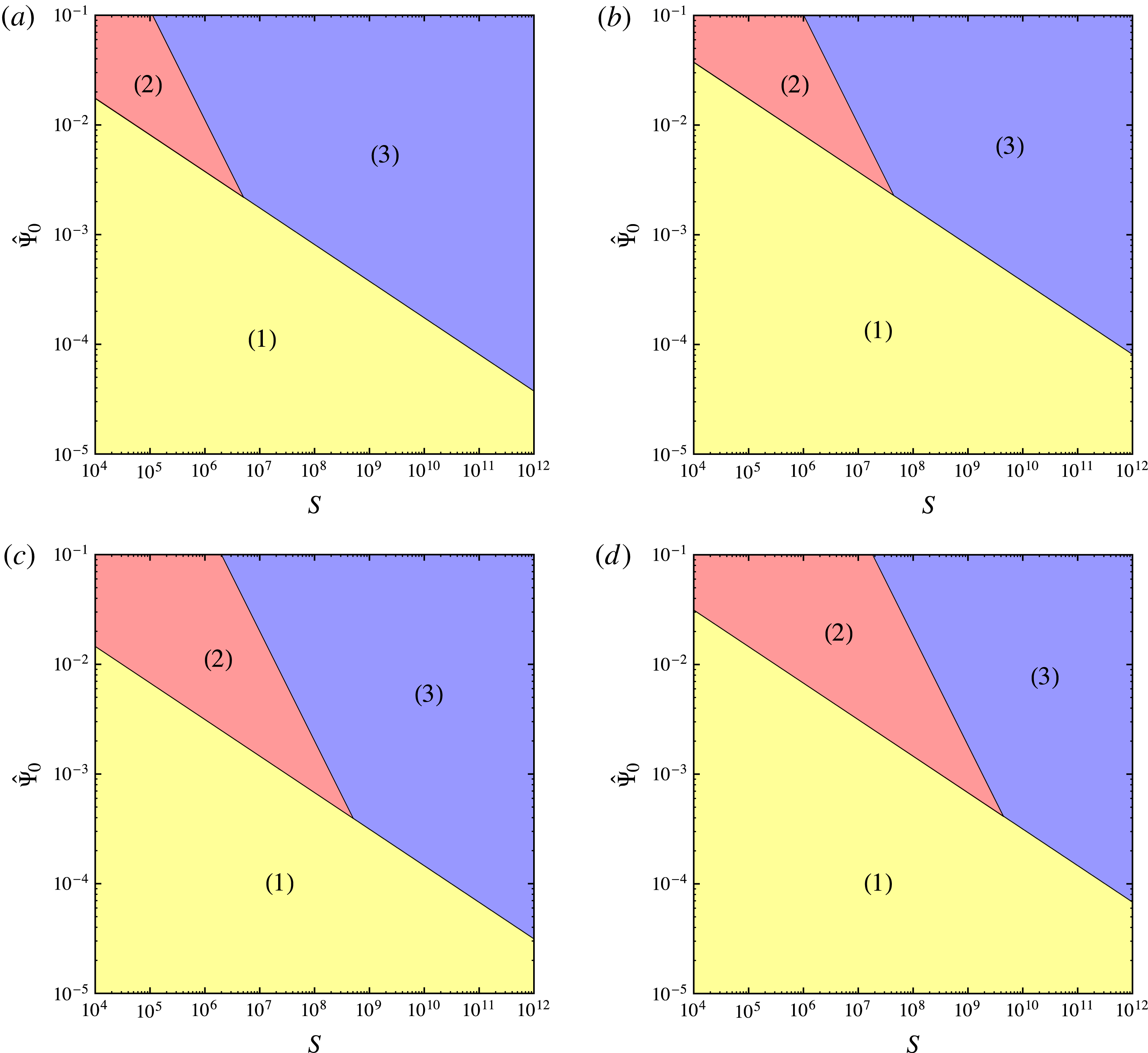
Figure 2. Two-dimensional slices of a phase/scenario diagram for forced magnetic reconnection in the magnetohydrodynamical Taylor model. Fixed parameters are (a)
![]() $\hat{k}=1/8$
,
$\hat{k}=1/8$
,
![]() $P_{m}=5$
, (b)
$P_{m}=5$
, (b)
![]() $\hat{k}=1/8$
,
$\hat{k}=1/8$
,
![]() $P_{m}=500$
, (c)
$P_{m}=500$
, (c)
![]() $\hat{k}=2$
,
$\hat{k}=2$
,
![]() $P_{m}=5$
, and (d)
$P_{m}=5$
, and (d)
![]() $\hat{k}=2$
,
$\hat{k}=2$
,
![]() $P_{m}=500$
. The numerical labels indicate (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario. The boundaries between the different scenarios are identified by the functions
$P_{m}=500$
. The numerical labels indicate (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario. The boundaries between the different scenarios are identified by the functions
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
![]() $\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
.
$\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
.

Figure 3. (a) Thresholds
![]() $\hat{{\it\Psi}}_{W}/3$
(red line) and
$\hat{{\it\Psi}}_{W}/3$
(red line) and
![]() $\hat{{\it\Psi}}_{c}$
(blue line) as a function of the magnetic Prandtl number
$\hat{{\it\Psi}}_{c}$
(blue line) as a function of the magnetic Prandtl number
![]() $P_{m}$
for
$P_{m}$
for
![]() $S=10^{8}$
,
$S=10^{8}$
,
![]() $\hat{k}=0.5$
and
$\hat{k}=0.5$
and
![]() $C=2(150)^{2}$
. (b) Corresponding two-dimensional slice of the phase/scenario diagram identifying (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario.
$C=2(150)^{2}$
. (b) Corresponding two-dimensional slice of the phase/scenario diagram identifying (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario.

Figure 4. Boundaries (identified by the functions
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
![]() $\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
) of the different possible evolutions of the reconnection process for
$\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
) of the different possible evolutions of the reconnection process for
![]() $\hat{k}=0.5$
and various values of the magnetic Prandtl number.
$\hat{k}=0.5$
and various values of the magnetic Prandtl number.
Let us first consider four two-dimensional slices with fixed values of the magnetic Prandtl number and perturbation wave number. Assuming that the Hahm–Kulsrud scenario (which occurs if
![]() ${\it\Psi}_{0}\ll {\it\Psi}_{W}$
) holds until
${\it\Psi}_{0}\ll {\it\Psi}_{W}$
) holds until
![]() ${\it\Psi}_{0}={\it\Psi}_{W}/3$
, the corresponding diagrams for (a)
${\it\Psi}_{0}={\it\Psi}_{W}/3$
, the corresponding diagrams for (a)
![]() $\hat{k}=1/8$
,
$\hat{k}=1/8$
,
![]() $P_{m}=5$
, (b)
$P_{m}=5$
, (b)
![]() $\hat{k}=1/8$
,
$\hat{k}=1/8$
,
![]() $P_{m}=500$
, (c)
$P_{m}=500$
, (c)
![]() $\hat{k}=2$
,
$\hat{k}=2$
,
![]() $P_{m}=5$
, and (d)
$P_{m}=5$
, and (d)
![]() $\hat{k}=2$
,
$\hat{k}=2$
,
![]() $P_{m}=500$
are shown in figure 2(a–d). From these plots it is clear that the Wang–Bhattacharjee scenario is limited to a small range of values of the Lundquist number and the source perturbation amplitude. Increasing values of the magnetic Prandtl number and perturbation wave number extend the domain of existence of this possible type of evolution of the system. However, after a threshold value of the Lundquist number (identified by the intersection of the two black lines representing
$P_{m}=500$
are shown in figure 2(a–d). From these plots it is clear that the Wang–Bhattacharjee scenario is limited to a small range of values of the Lundquist number and the source perturbation amplitude. Increasing values of the magnetic Prandtl number and perturbation wave number extend the domain of existence of this possible type of evolution of the system. However, after a threshold value of the Lundquist number (identified by the intersection of the two black lines representing
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
), the Wang–Bhattacharjee scenario cannot occur because it is not possible to obtain a stable Sweet–Parker-type evolution. In these cases the Hahm–Kulsrud scenario is facilitated by very small perturbation amplitudes, whereas larger perturbations lead the system to a fast reconnection regime as described in § 3.3. Note that while previously proposed phase diagrams always predict fast reconnection (Huang et al.
Reference Huang, Bhattacharjee and Sullivan2011; Ji & Daughton Reference Ji and Daughton2011; Daughton & Roytershteyn Reference Daughton and Roytershteyn2012; Cassak & Drake Reference Cassak and Drake2013; Huang & Bhattacharjee Reference Huang and Bhattacharjee2013; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013), in clear contrast to what happens in nature, our diagrams show that reconnection proceeds very slowly (region (1)) if the source perturbation is not sufficiently large.
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
), the Wang–Bhattacharjee scenario cannot occur because it is not possible to obtain a stable Sweet–Parker-type evolution. In these cases the Hahm–Kulsrud scenario is facilitated by very small perturbation amplitudes, whereas larger perturbations lead the system to a fast reconnection regime as described in § 3.3. Note that while previously proposed phase diagrams always predict fast reconnection (Huang et al.
Reference Huang, Bhattacharjee and Sullivan2011; Ji & Daughton Reference Ji and Daughton2011; Daughton & Roytershteyn Reference Daughton and Roytershteyn2012; Cassak & Drake Reference Cassak and Drake2013; Huang & Bhattacharjee Reference Huang and Bhattacharjee2013; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013), in clear contrast to what happens in nature, our diagrams show that reconnection proceeds very slowly (region (1)) if the source perturbation is not sufficiently large.
Let us now examine the effect of the plasma viscosity by considering the domain of existence of the different scenarios as a function of the parameters
![]() $\hat{{\it\Psi}}_{0}$
and
$\hat{{\it\Psi}}_{0}$
and
![]() $P_{m}$
. Figure 3(a) shows the functions
$P_{m}$
. Figure 3(a) shows the functions
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
![]() $S=10^{8}$
and
$S=10^{8}$
and
![]() $\hat{k}=0.5$
. For
$\hat{k}=0.5$
. For
![]() $\hat{{\it\Psi}}_{c}<\hat{{\it\Psi}}_{W}/3$
the threshold for plasmoid formation coincides with that for the nonlinear evolution characterized by a strong reconnecting current sheet. Therefore, for
$\hat{{\it\Psi}}_{c}<\hat{{\it\Psi}}_{W}/3$
the threshold for plasmoid formation coincides with that for the nonlinear evolution characterized by a strong reconnecting current sheet. Therefore, for
![]() $\hat{{\it\Psi}}_{c}<\hat{{\it\Psi}}_{W}/3$
an increase in the amplitude perturbation
$\hat{{\it\Psi}}_{c}<\hat{{\it\Psi}}_{W}/3$
an increase in the amplitude perturbation
![]() $\hat{{\it\Psi}}_{0}$
drives the system directly from scenario (1) to scenario (3). This situation is depicted in figure 3(b), where it is clearly shown that the increase of the magnetic Prandtl number has the effect of making possible or extending the domain of existence of scenario (2), as recently pointed out in Tenerani et al. (Reference Tenerani, Rappazzo, Velli and Pucci2015) and Comisso et al. (Reference Comisso, Grasso and Waelbroeck2015).
$\hat{{\it\Psi}}_{0}$
drives the system directly from scenario (1) to scenario (3). This situation is depicted in figure 3(b), where it is clearly shown that the increase of the magnetic Prandtl number has the effect of making possible or extending the domain of existence of scenario (2), as recently pointed out in Tenerani et al. (Reference Tenerani, Rappazzo, Velli and Pucci2015) and Comisso et al. (Reference Comisso, Grasso and Waelbroeck2015).
To clarify the effect of the plasma viscosity we also delineate the boundaries of the diverse evolutions (1)–(3) in a parameter space map
![]() $(\hat{{\it\Psi}}_{0},S)$
(as in figure 2) for fixed
$(\hat{{\it\Psi}}_{0},S)$
(as in figure 2) for fixed
![]() $\hat{k}=0.5$
but different values of
$\hat{k}=0.5$
but different values of
![]() $P_{m}$
. This is shown in figure 4 for
$P_{m}$
. This is shown in figure 4 for
![]() $P_{m}=5-5\times 10^{5}$
. The increase of the magnetic Prandtl number extends the domain of existence of the slow reconnection scenario (1) at the expense of the fast reconnection scenario (3). The area of existence of scenario (2) remains almost unchanged, but shifted towards higher values of the Lundquist number.
$P_{m}=5-5\times 10^{5}$
. The increase of the magnetic Prandtl number extends the domain of existence of the slow reconnection scenario (1) at the expense of the fast reconnection scenario (3). The area of existence of scenario (2) remains almost unchanged, but shifted towards higher values of the Lundquist number.

Figure 5. (a) Thresholds
![]() $\hat{{\it\Psi}}_{W}/3$
(red line) and
$\hat{{\it\Psi}}_{W}/3$
(red line) and
![]() $\hat{{\it\Psi}}_{c}$
(blue line) as a function of the perturbation wave number
$\hat{{\it\Psi}}_{c}$
(blue line) as a function of the perturbation wave number
![]() $\hat{k}$
for
$\hat{k}$
for
![]() $S=10^{8}$
,
$S=10^{8}$
,
![]() $P_{m}=5$
and
$P_{m}=5$
and
![]() $C=2(150)^{2}$
. (b) Corresponding two-dimensional slice of the phase/scenario diagram identifying (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario.
$C=2(150)^{2}$
. (b) Corresponding two-dimensional slice of the phase/scenario diagram identifying (1) the Hahm–Kulsrud scenario, (2) the Wang–Bhattacharjee scenario, and (3) our scenario.

Figure 6. Boundaries (identified by the functions
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
for
![]() $\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
) of the different possible evolutions of the reconnection process for
$\hat{{\it\Psi}}_{c}>\hat{{\it\Psi}}_{W}/3$
) of the different possible evolutions of the reconnection process for
![]() $P_{m}=5$
and various values of the perturbation wave number.
$P_{m}=5$
and various values of the perturbation wave number.
We now examine in more detail how the possible evolutions of the forced magnetic reconnection process depend on the wave number of the boundary perturbation. Figure 5(a) shows the thresholds
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{W}/3$
and
![]() $\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
as a function of
$\hat{{\it\Psi}}_{0}=\hat{{\it\Psi}}_{c}$
as a function of
![]() $\hat{k}$
for fixed values of
$\hat{k}$
for fixed values of
![]() $S=10^{8}$
and
$S=10^{8}$
and
![]() $P_{m}=5$
. Below a critical perturbation wave number
$P_{m}=5$
. Below a critical perturbation wave number
![]() $\hat{k}^{\ast }$
(corresponding to
$\hat{k}^{\ast }$
(corresponding to
![]() $\hat{k}^{\ast }\approx 1$
for the fixed parameters used in figure 5
a), every time the non-constant-
$\hat{k}^{\ast }\approx 1$
for the fixed parameters used in figure 5
a), every time the non-constant-
![]() ${\it\psi}$
magnetic island passes into the nonlinear regime, the evolution of the system leads to the plasmoid-dominated phase predicted in scenario (3). The domains of existence of the possible evolutions (1)–(3) are illustrated in figure 5(b). The scenario discussed by Wang and Bhattacharjee happens only for a small range of (
${\it\psi}$
magnetic island passes into the nonlinear regime, the evolution of the system leads to the plasmoid-dominated phase predicted in scenario (3). The domains of existence of the possible evolutions (1)–(3) are illustrated in figure 5(b). The scenario discussed by Wang and Bhattacharjee happens only for a small range of (
![]() $\hat{{\it\Psi}}_{0},\hat{k}$
) parameters. Note also that scenario (3) is facilitated for
$\hat{{\it\Psi}}_{0},\hat{k}$
) parameters. Note also that scenario (3) is facilitated for
![]() $\hat{k}\lesssim \hat{k}^{\ast }$
, while scenario (1) may occur for large amplitude boundary perturbations if
$\hat{k}\lesssim \hat{k}^{\ast }$
, while scenario (1) may occur for large amplitude boundary perturbations if
![]() $\hat{k}\gg \hat{k}^{\ast }$
.
$\hat{k}\gg \hat{k}^{\ast }$
.
To better evaluate the effects of
![]() $\hat{k}$
on the possible evolutions of the reconnection process, we plot in figure 6 the boundaries between scenarios (1)–(3) in a parameter space map
$\hat{k}$
on the possible evolutions of the reconnection process, we plot in figure 6 the boundaries between scenarios (1)–(3) in a parameter space map
![]() $(\hat{{\it\Psi}}_{0},S)$
(as in figures 2 and 4) for fixed
$(\hat{{\it\Psi}}_{0},S)$
(as in figures 2 and 4) for fixed
![]() $P_{m}=5$
but different values of
$P_{m}=5$
but different values of
![]() $\hat{k}$
. The maximum area of existence of scenario (2) occurs for
$\hat{k}$
. The maximum area of existence of scenario (2) occurs for
![]() $\hat{k}\sim 1$
, while for
$\hat{k}\sim 1$
, while for
![]() $\hat{k}\ll 1$
and
$\hat{k}\ll 1$
and
![]() $\hat{k}\gg 1$
, scenario (2) appears for a very limited range of (
$\hat{k}\gg 1$
, scenario (2) appears for a very limited range of (
![]() $\hat{{\it\Psi}}_{0},\hat{k}$
) parameters. Note also that scenario (1) is greatly facilitated in the case of very large perturbation wave numbers (
$\hat{{\it\Psi}}_{0},\hat{k}$
) parameters. Note also that scenario (1) is greatly facilitated in the case of very large perturbation wave numbers (
![]() $\hat{k}\gg 1$
), while scenario (3) is facilitated by relatively large amplitude perturbations with
$\hat{k}\gg 1$
), while scenario (3) is facilitated by relatively large amplitude perturbations with
![]() $\hat{k}\lesssim 1$
.
$\hat{k}\lesssim 1$
.
5. Discussion
The introduction of a new type of phase/scenario diagram that explicitly includes the effects of the external drive has allowed us to graphically organize in detail the possible evolutions of forced magnetic reconnection processes in collisional plasmas. In contrast to previous versions of the phase diagrams (Huang et al.
Reference Huang, Bhattacharjee and Sullivan2011; Ji & Daughton Reference Ji and Daughton2011; Daughton & Roytershteyn Reference Daughton and Roytershteyn2012; Cassak & Drake Reference Cassak and Drake2013; Huang & Bhattacharjee Reference Huang and Bhattacharjee2013; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013), this new representation highlights regions of the parameter space (
![]() $\hat{{\it\Psi}}_{0},\hat{k}$
,
$\hat{{\it\Psi}}_{0},\hat{k}$
,
![]() $S$
,
$S$
,
![]() $P_{m}$
) in which reconnection is a slow diffusive process (§ 3.1), in addition to regions where reconnection can be fast (§§ 3.2 and 3.3). We recall that by fast we mean that the out-of-plane inductive electric field at the
$P_{m}$
) in which reconnection is a slow diffusive process (§ 3.1), in addition to regions where reconnection can be fast (§§ 3.2 and 3.3). We recall that by fast we mean that the out-of-plane inductive electric field at the
![]() $X$
-point is a significant fraction of the one evaluated upstream of the reconnection layer. We also emphasize that this type of diagram responds to the criticism made by Cassak & Drake (Reference Cassak and Drake2013), concerning the fact that the previously proposed diagrams are not able to take into account the dynamical evolution of the reconnection process from a slow to a fast regime inside a given region of the parameter space. Indeed, scenarios (1)–(3) describe the forced magnetic reconnection process from the current sheet formation all the way to their specific nonlinear evolution.
$X$
-point is a significant fraction of the one evaluated upstream of the reconnection layer. We also emphasize that this type of diagram responds to the criticism made by Cassak & Drake (Reference Cassak and Drake2013), concerning the fact that the previously proposed diagrams are not able to take into account the dynamical evolution of the reconnection process from a slow to a fast regime inside a given region of the parameter space. Indeed, scenarios (1)–(3) describe the forced magnetic reconnection process from the current sheet formation all the way to their specific nonlinear evolution.
We would like to remark that while the proposed parameter space diagrams represent a valid way to summarize the current knowledge of the forced magnetic reconnection dynamics in a collisional plasma, there are a number of conditions that may significantly affect the reconnection process but which have not been addressed in this paper. For instance, two-fluid/kinetic effects should be considered if the length scale associated with the width of the reconnecting current sheet becomes of the order of, or smaller than, the characteristic length scales of these effects. In fact, effects associated with finite electron inertia (Ottaviani & Porcelli Reference Ottaviani and Porcelli1993; Comisso & Asenjo Reference Comisso and Asenjo2014) are known to enhance the reconnection rate, as well as Hall effects (Birn et al. Reference Birn, Drake, Shay, Rogers, Denton, Hesse, Kuznetsova, Ma, Bhattacharjee, Otto and Pritchett2001; Simakov & Chacón Reference Simakov and Chacón2008) in antiparallel reconnection (i.e. in the absence of a guide magnetic field) and electron pressure (Kleva et al. Reference Kleva, Drake and Waelbroeck1995; Grasso et al. Reference Grasso, Califano, Pegoraro and Porcelli1999) and ion gyration effects (Comisso et al. Reference Comisso, Grasso, Waelbroeck and Borgogno2013) in the case of reconnection with a strong guide field. We would also like to remark that a common condition in many physical systems is the presence of velocity flows, which are known to suppress the reconnection (Fitzpatrick Reference Fitzpatrick1993; Waelbroeck et al. Reference Waelbroeck, Joseph, Nardon, Bécoulet and Fitzpatrick2012) or to alter the reconnection rate (Cassak Reference Cassak2011; Tassi et al. Reference Tassi, Grasso and Comisso2014). In this case our analysis should be extended by considering the effects of a plasma flow on the reconnection dynamics. Similarly, the effects of turbulence should also be considered (Servidio et al. Reference Servidio, Matthaeus, Shay, Cassak and Dmitruk2009; Karimabadi & Lazarian Reference Karimabadi and Lazarian2013) in order to obtain a more complete description of the magnetic reconnection dynamics.
Finally, it is important to recall that all the presented diagrams of magnetic reconnection are based on two-dimensional models and simulations. At present, the knowledge of how magnetic reconnection evolves in large three-dimensional systems is still far behind our understanding of what happens in two-dimensional systems. Therefore, despite the great progress achieved in recent years (Borgogno et al. Reference Borgogno, Grasso, Porcelli, Califano, Pegoraro and Farina2005; Yin et al. Reference Yin, Daughton, Karimabadi, Albright, Bowers and Margulies2008; Daughton et al. Reference Daughton, Roytershteyn, Karimabadi, Yin, Albright, Bergen and Bowers2011; Wyper & Pontin Reference Wyper and Pontin2014), other work is needed in this direction before we can implement a phase diagram description of three-dimensional magnetic reconnection.
Acknowledgements
The authors would like to acknowledge fruitful conversations with R. Fitzpatrick and E. Lazzaro. This work was carried out under the Contract of Association Euratom-ENEA and was also supported by the US Department of Energy under Contract DE-FG02-04ER-54742.