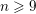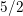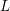1 Introduction
In this paper, we prove that most monic even hyperelliptic curves have exactly two rational points. Consider the family of monic even hyperelliptic curves over
![]() $\mathbb{Q}$
, namely complete genus-
$\mathbb{Q}$
, namely complete genus-
![]() $n$
curves given by the affine equation
$n$
curves given by the affine equation
 $$\begin{eqnarray}C_{f}:=y^{2}=f(x)=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2},\end{eqnarray}$$
$$\begin{eqnarray}C_{f}:=y^{2}=f(x)=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2},\end{eqnarray}$$
where
![]() $n\geqslant 2$
and the
$n\geqslant 2$
and the
![]() $c_{i}$
are elements of
$c_{i}$
are elements of
![]() $\mathbb{Q}$
such that the polynomial
$\mathbb{Q}$
such that the polynomial
![]() $f(x)$
has distinct roots, or equivalently the discriminant
$f(x)$
has distinct roots, or equivalently the discriminant
![]() $\unicode[STIX]{x1D6E5}(f)$
of
$\unicode[STIX]{x1D6E5}(f)$
of
![]() $f$
is non-zero. We can realize
$f$
is non-zero. We can realize
![]() $C_{f}$
as a smooth curve in the weighted projective space
$C_{f}$
as a smooth curve in the weighted projective space
![]() $\mathbb{P}_{1,n+1,1}$
by homogenizing
$\mathbb{P}_{1,n+1,1}$
by homogenizing
![]() $f$
to obtain
$f$
to obtain
![]() $F(x,z)$
, where
$F(x,z)$
, where
 $F(x,1)=f(x)$
, and considering the projective curve given by
$F(x,1)=f(x)$
, and considering the projective curve given by
 $y^{2}=F(x,z)$
. Every curve in this family has a pair of non-Weierstrass points at infinity, denoted by
$y^{2}=F(x,z)$
. Every curve in this family has a pair of non-Weierstrass points at infinity, denoted by
 $\infty =[1:1:0]$
and
$\infty =[1:1:0]$
and
 $\infty ^{\prime }=[1:-1:0]$
, which are conjugate to each other by the hyperelliptic involution sending
$\infty ^{\prime }=[1:-1:0]$
, which are conjugate to each other by the hyperelliptic involution sending
 $[x:y:z]$
to
$[x:y:z]$
to
 $[x:-y:z]$
. Scaling each
$[x:-y:z]$
. Scaling each
![]() $c_{i}$
by
$c_{i}$
by
![]() $\unicode[STIX]{x1D706}^{2i}$
for
$\unicode[STIX]{x1D706}^{2i}$
for
![]() $\unicode[STIX]{x1D706}\in \mathbb{Q}^{\times }$
gives isomorphic curves. We then define a height on this family by setting
$\unicode[STIX]{x1D706}\in \mathbb{Q}^{\times }$
gives isomorphic curves. We then define a height on this family by setting
 $$\begin{eqnarray}h(C_{f})=\max _{i}\{|c_{i}|^{1/i}\},\end{eqnarray}$$
$$\begin{eqnarray}h(C_{f})=\max _{i}\{|c_{i}|^{1/i}\},\end{eqnarray}$$
where the
![]() $c_{i}$
have been appropriately scaled so that
$c_{i}$
have been appropriately scaled so that
![]() $c_{i}\in \mathbb{Z}$
and there is no prime
$c_{i}\in \mathbb{Z}$
and there is no prime
![]() $p$
such that
$p$
such that
![]() $p^{2i}\mid c_{i}$
for all
$p^{2i}\mid c_{i}$
for all
![]() $i$
. Throughout this paper, we order curves in our family by this height. The main result of our paper is the following theorem.
$i$
. Throughout this paper, we order curves in our family by this height. The main result of our paper is the following theorem.
Theorem 1. As
![]() $n$
tends to infinity, a proportion approaching
$n$
tends to infinity, a proportion approaching
![]() $100\%$
of monic even hyperelliptic curves have exactly two rational points, namely
$100\%$
of monic even hyperelliptic curves have exactly two rational points, namely
![]() $\infty$
and
$\infty$
and
![]() $\infty ^{\prime }$
. More precisely, the proportion of monic even hyperelliptic curves having genus
$\infty ^{\prime }$
. More precisely, the proportion of monic even hyperelliptic curves having genus
![]() $n$
that have exactly two rational points is at least
$n$
that have exactly two rational points is at least
 $1-(24n+60)2^{-n}$
.
$1-(24n+60)2^{-n}$
.
Note that the lower bound
 $1-(24n\,+\,60)2^{-n}$
is positive when
$1-(24n\,+\,60)2^{-n}$
is positive when
![]() $n\geqslant 9$
. Theorem 1 adds to recent works on the study of rational points on curves as they vary across families. Bhargava [Reference BhargavaBha13] uses geometry-of-numbers techniques to prove that most hyperelliptic curves have no rational points. Using Chabauty’s method in conjunction with the results and techniques of [Reference Bhargava and GrossBG13], Poonen and Stoll [Reference Poonen and StollPS14] prove that most odd hyperelliptic curves have exactly one rational point. Our result adds evidence to the minimalist belief that when curves vary over a family, most of them have only the rational points that are forced on them. See [Reference Bektemirov, Mazur, Stein and WatkinsBMSW07] for a beautiful exposition on the implications of this belief for the distribution of ranks of elliptic curves.
$n\geqslant 9$
. Theorem 1 adds to recent works on the study of rational points on curves as they vary across families. Bhargava [Reference BhargavaBha13] uses geometry-of-numbers techniques to prove that most hyperelliptic curves have no rational points. Using Chabauty’s method in conjunction with the results and techniques of [Reference Bhargava and GrossBG13], Poonen and Stoll [Reference Poonen and StollPS14] prove that most odd hyperelliptic curves have exactly one rational point. Our result adds evidence to the minimalist belief that when curves vary over a family, most of them have only the rational points that are forced on them. See [Reference Bektemirov, Mazur, Stein and WatkinsBMSW07] for a beautiful exposition on the implications of this belief for the distribution of ranks of elliptic curves.
There are three main steps in our proof of Theorem 1. First, we determine an upper bound on the average size of the 2-Selmer groups of Jacobians of curves in our family. More precisely, we prove the following theorem.
Theorem 2. When all hyperelliptic curves of fixed genus
![]() $n\geqslant 2$
over
$n\geqslant 2$
over
![]() $\mathbb{Q}$
having a marked rational non-Weierstrass point are ordered by height, the average size of the
$\mathbb{Q}$
having a marked rational non-Weierstrass point are ordered by height, the average size of the
![]() $2$
-Selmer groups of their Jacobians is at most
$2$
-Selmer groups of their Jacobians is at most
![]() $6$
.
$6$
.
Theorem 2 is proved by constructing and counting locally soluble
![]() $2$
-covers of these Jacobians. Our proof naturally yields an equidistribution result (Theorem 34), which is important to our applications to rational points on these curves.
$2$
-covers of these Jacobians. Our proof naturally yields an equidistribution result (Theorem 34), which is important to our applications to rational points on these curves.
Next, we use these counting and equidistribution results in conjunction with Chabauty’s method [Reference ChabautyCha41, Reference ColemanCol85], as refined by Poonen and Stoll [Reference Poonen and StollPS14], to prove that a positive proportion (the same proportion as in Theorem 1) of curves
![]() $C$
in our family satisfy the following property: if
$C$
in our family satisfy the following property: if
 $P\in C(\mathbb{Q})$
, then
$P\in C(\mathbb{Q})$
, then
 $(P)-(\infty )$
is a rational multiple of
$(P)-(\infty )$
is a rational multiple of
 $(\infty ^{\prime })-(\infty )$
. Since our global results concern the 2-Selmer group, we need to work 2-adically in this step.
$(\infty ^{\prime })-(\infty )$
. Since our global results concern the 2-Selmer group, we need to work 2-adically in this step.
Finally, we use elimination theory over
![]() $\mathbb{Z}_{p}$
, especially the theory of
$\mathbb{Z}_{p}$
, especially the theory of
![]() $p$
-adic subanalytic sets, to prove that 0% of curves
$p$
-adic subanalytic sets, to prove that 0% of curves
![]() $C$
in our family have rational points
$C$
in our family have rational points
![]() $P$
such that
$P$
such that
 $(P)\,-\,(\infty )$
is a rational multiple of
$(P)\,-\,(\infty )$
is a rational multiple of
 $(\infty ^{\prime })\,-\,(\infty )$
. This step is entirely local, and we work over large primes
$(\infty ^{\prime })\,-\,(\infty )$
. This step is entirely local, and we work over large primes
![]() $p$
.
$p$
.
In [Reference Bhargava and GrossBG13], Bhargava and Gross study odd hyperelliptic curves over
![]() $\mathbb{Q}$
, and prove that the average size of the 2-Selmer groups of their Jacobians is bounded above by 3. We will show in Proposition 30 that the class
$\mathbb{Q}$
, and prove that the average size of the 2-Selmer groups of their Jacobians is bounded above by 3. We will show in Proposition 30 that the class
 $(\infty ^{\prime })-(\infty )$
is not divisible by 2 in
$(\infty ^{\prime })-(\infty )$
is not divisible by 2 in
![]() $J(\mathbb{Q})$
for 100% of monic even hyperelliptic curves. Hence we expect the 2-Selmer groups of these Jacobians to have, on average, one extra generator compared to the Jacobians of monic odd hyperelliptic curves. This gives a heuristic reason for the ratio of these average values to be 2. In fact, we expect that these average values are indeed equal to 6 and 3.
$J(\mathbb{Q})$
for 100% of monic even hyperelliptic curves. Hence we expect the 2-Selmer groups of these Jacobians to have, on average, one extra generator compared to the Jacobians of monic odd hyperelliptic curves. This gives a heuristic reason for the ratio of these average values to be 2. In fact, we expect that these average values are indeed equal to 6 and 3.
For the 100% of curves where
 $(\infty ^{\prime })-(\infty )$
is not divisible by 2 in
$(\infty ^{\prime })-(\infty )$
is not divisible by 2 in
![]() $J(\mathbb{Q})$
, the average 2-rank of the 2-Selmer group minus 1 is at most
$J(\mathbb{Q})$
, the average 2-rank of the 2-Selmer group minus 1 is at most
![]() $3/2$
. This is because
$3/2$
. This is because
 $|\text{Sel}_{2}(J)|/2$
is at least 1 and its average is at most 3. Therefore, we obtain the following immediate corollary to Theorem 2.
$|\text{Sel}_{2}(J)|/2$
is at least 1 and its average is at most 3. Therefore, we obtain the following immediate corollary to Theorem 2.
Corollary 3. When all hyperelliptic curves of fixed genus
![]() $n\geqslant 2$
over
$n\geqslant 2$
over
![]() $\mathbb{Q}$
having a marked rational non-Weierstrass point are ordered by height, the average rank of the
$\mathbb{Q}$
having a marked rational non-Weierstrass point are ordered by height, the average rank of the
![]() $2$
-Selmer group of their Jacobians is at most
$2$
-Selmer group of their Jacobians is at most
![]() $5/2$
. Thus the average rank of the Mordell–Weil groups of their Jacobians is at most
$5/2$
. Thus the average rank of the Mordell–Weil groups of their Jacobians is at most
![]() $5/2$
.
$5/2$
.
To prove Theorem 2, we follow the same strategy as [Reference Bhargava and ShankarBS15] and [Reference Bhargava and GrossBG13]: obtain first a bijection between Selmer elements and certain rational orbits of a representation
![]() $V$
of a reductive group
$V$
of a reductive group
![]() $G$
; and then count these orbits using geometry-of-numbers methods. Let
$G$
; and then count these orbits using geometry-of-numbers methods. Let
![]() $(U,Q)$
denote the split quadratic space of dimension
$(U,Q)$
denote the split quadratic space of dimension
![]() $2n+2$
over
$2n+2$
over
![]() $\mathbb{Q}$
and let
$\mathbb{Q}$
and let
![]() $V$
denote the space of operators
$V$
denote the space of operators
![]() $T$
on
$T$
on
![]() $U$
self-adjoint with respect to
$U$
self-adjoint with respect to
![]() $Q$
. For any monic separable polynomial
$Q$
. For any monic separable polynomial
![]() $f(x)$
of degree
$f(x)$
of degree
![]() $2n+2$
, let
$2n+2$
, let
![]() $J_{f}$
denote the Jacobian of the hyperelliptic curve defined by the affine equation
$J_{f}$
denote the Jacobian of the hyperelliptic curve defined by the affine equation
 $y^{2}=f(x)$
, and let
$y^{2}=f(x)$
, and let
![]() $V_{f}$
denote the subscheme of
$V_{f}$
denote the subscheme of
![]() $V$
consisting of self-adjoint operators
$V$
consisting of self-adjoint operators
![]() $T$
with characteristic polynomial
$T$
with characteristic polynomial
![]() $f(x)$
. In § 2, we obtain a bijection between
$f(x)$
. In § 2, we obtain a bijection between
 $\operatorname{Sel}_{2}(J_{f})$
and locally soluble orbits of the conjugation action of
$\operatorname{Sel}_{2}(J_{f})$
and locally soluble orbits of the conjugation action of
 $\operatorname{PSO}(U)(\mathbb{Q})$
on
$\operatorname{PSO}(U)(\mathbb{Q})$
on
![]() $V_{f}(\mathbb{Q})$
. This parameterization step can be viewed as an example of arithmetic invariant theory. The various cohomological calculations are more complicated than in [Reference Bhargava and GrossBG13]. Although not strictly needed, we give in § 3 a very nice geometric interpretation of solubility using the arithmetic theory of pencils of quadrics as developed in [Reference WangWan13b]. More precisely, a self-adjoint operator
$V_{f}(\mathbb{Q})$
. This parameterization step can be viewed as an example of arithmetic invariant theory. The various cohomological calculations are more complicated than in [Reference Bhargava and GrossBG13]. Although not strictly needed, we give in § 3 a very nice geometric interpretation of solubility using the arithmetic theory of pencils of quadrics as developed in [Reference WangWan13b]. More precisely, a self-adjoint operator
 $T\in V_{f}(\mathbb{Q})$
is soluble if and only if there exists a rational
$T\in V_{f}(\mathbb{Q})$
is soluble if and only if there exists a rational
![]() $n$
-plane
$n$
-plane
![]() $X$
that is isotropic with respect to the following two quadrics:
$X$
that is isotropic with respect to the following two quadrics:
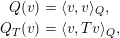 $$\begin{eqnarray}\displaystyle Q(v) & = & \displaystyle \langle v,v\rangle _{Q},\nonumber\\ \displaystyle Q_{T}(v) & = & \displaystyle \langle v,Tv\rangle _{Q},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(v) & = & \displaystyle \langle v,v\rangle _{Q},\nonumber\\ \displaystyle Q_{T}(v) & = & \displaystyle \langle v,Tv\rangle _{Q},\nonumber\end{eqnarray}$$
where
![]() $\langle \,,\,\rangle _{Q}$
is the bilinear form associated to
$\langle \,,\,\rangle _{Q}$
is the bilinear form associated to
![]() $Q$
. A self-adjoint operator
$Q$
. A self-adjoint operator
 $T\in V_{f}(\mathbb{Q})$
is locally soluble if for every completion
$T\in V_{f}(\mathbb{Q})$
is locally soluble if for every completion
![]() $\mathbb{Q}_{v}$
of
$\mathbb{Q}_{v}$
of
![]() $\mathbb{Q}$
, there exists an
$\mathbb{Q}$
, there exists an
![]() $n$
-plane
$n$
-plane
![]() $X$
defined over
$X$
defined over
![]() $\mathbb{Q}_{v}$
that is isotropic with respect to the quadrics
$\mathbb{Q}_{v}$
that is isotropic with respect to the quadrics
![]() $Q$
and
$Q$
and
![]() $Q_{T}$
.
$Q_{T}$
.
In § 4, we count the number of locally soluble orbits using techniques of Bhargava developed in [Reference BhargavaBha05] and prove Theorem 2. We count first the number of integral orbits soluble at
![]() $\mathbb{R}$
by counting the number of integral points inside a fundamental domain for the action of
$\mathbb{R}$
by counting the number of integral points inside a fundamental domain for the action of
 $\operatorname{PSO}(U)(\mathbb{Z})$
on
$\operatorname{PSO}(U)(\mathbb{Z})$
on
![]() $V(\mathbb{R})$
. We break up this fundamental domain into a compact part and a cusp region where separate estimations are required. The compact part of the fundamental domain will contribute to, on average, four Selmer elements. The cusp region corresponds to the two ‘obvious’ classes: 0 and
$V(\mathbb{R})$
. We break up this fundamental domain into a compact part and a cusp region where separate estimations are required. The compact part of the fundamental domain will contribute to, on average, four Selmer elements. The cusp region corresponds to the two ‘obvious’ classes: 0 and
 $(\infty ^{\prime })-(\infty )$
. We then apply a sieve to the locally soluble orbits by imposing infinitely many congruence conditions. This gives an upper bound for the average size of the 2-Selmer groups. To show that the average size is in fact equal to 6, we would need a uniformity estimate on the number of
$(\infty ^{\prime })-(\infty )$
. We then apply a sieve to the locally soluble orbits by imposing infinitely many congruence conditions. This gives an upper bound for the average size of the 2-Selmer groups. To show that the average size is in fact equal to 6, we would need a uniformity estimate on the number of
 $\operatorname{PSO}(U)(\mathbb{Z})$
-orbits on
$\operatorname{PSO}(U)(\mathbb{Z})$
-orbits on
![]() $V(\mathbb{Z})$
analogous to Proposition 25.
$V(\mathbb{Z})$
analogous to Proposition 25.
In § 5, we apply a refinement of Chabauty’s method to study rational points on monic even hyperelliptic curves following the strategy of Poonen and Stoll [Reference Poonen and StollPS14]. The curve
![]() $C$
embeds into its Jacobian
$C$
embeds into its Jacobian
![]() $J$
via the map sending a point
$J$
via the map sending a point
![]() $P$
to the divisor class of
$P$
to the divisor class of
 $(P)-(\infty )$
. The image of
$(P)-(\infty )$
. The image of
![]() $C(\mathbb{Q}_{2})$
is a one-dimensional 2-adic manifold in
$C(\mathbb{Q}_{2})$
is a one-dimensional 2-adic manifold in
![]() $J(\mathbb{Q}_{2})$
. On the other hand,
$J(\mathbb{Q}_{2})$
. On the other hand,
![]() $C(\mathbb{Q})$
also maps to the 2-Selmer group of its Jacobian which admits a natural map to
$C(\mathbb{Q})$
also maps to the 2-Selmer group of its Jacobian which admits a natural map to
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
. The image of
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
. The image of
![]() $C(\mathbb{Q}_{2})$
in
$C(\mathbb{Q}_{2})$
in
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
is on average quite small compared to the size
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
is on average quite small compared to the size
 $2^{n}\#J(\mathbb{Q}_{2})[2]$
of
$2^{n}\#J(\mathbb{Q}_{2})[2]$
of
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
, once the genus
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
, once the genus
![]() $n$
is large enough. Furthermore, the Selmer group has on average very few elements which, with the exception of 0 and the class of
$n$
is large enough. Furthermore, the Selmer group has on average very few elements which, with the exception of 0 and the class of
 $(\infty ^{\prime })-(\infty )$
, equidistribute onto
$(\infty ^{\prime })-(\infty )$
, equidistribute onto
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
. However, these two sets, the image of
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
. However, these two sets, the image of
![]() $C(\mathbb{Q}_{2})$
and the image of the 2-Selmer group in
$C(\mathbb{Q}_{2})$
and the image of the 2-Selmer group in
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
, do always intersect at two points, namely the image of 0 and
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
, do always intersect at two points, namely the image of 0 and
 $(\infty ^{\prime })-(\infty )$
. We thus modify the
$(\infty ^{\prime })-(\infty )$
. We thus modify the
![]() $n$
-dimensional
$n$
-dimensional
![]() $\mathbb{F}_{2}$
-vector space
$\mathbb{F}_{2}$
-vector space
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
as follows: we mod out by the line spanned by the (primitive part of the) image of
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
as follows: we mod out by the line spanned by the (primitive part of the) image of
 $(\infty ^{\prime })-(\infty )$
and replace the remaining
$(\infty ^{\prime })-(\infty )$
and replace the remaining
![]() $(n-1)$
-dimensional
$(n-1)$
-dimensional
![]() $\mathbb{F}_{2}$
-vector space by its projectivization. We then prove that for a proportion at least
$\mathbb{F}_{2}$
-vector space by its projectivization. We then prove that for a proportion at least
 $1-O(n2^{-n})$
of curves
$1-O(n2^{-n})$
of curves
![]() $C$
, these two sets do not intersect and that every rational point
$C$
, these two sets do not intersect and that every rational point
![]() $P$
of
$P$
of
![]() $C$
is bad, that is,
$C$
is bad, that is,
 $(P)-(\infty )$
is a rational multiple of
$(P)-(\infty )$
is a rational multiple of
 $(\infty ^{\prime })-(\infty )$
.
$(\infty ^{\prime })-(\infty )$
.
Finally, in § 6, we use the theory of
![]() $p$
-adic subanalytic sets to prove that the
$p$
-adic subanalytic sets to prove that the
![]() $p$
-adic closure of the set of curves
$p$
-adic closure of the set of curves
![]() $C$
over
$C$
over
![]() $\mathbb{Q}_{p}$
such that
$\mathbb{Q}_{p}$
such that
 $C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains a bad point has measure 0 in the corresponding moduli space. Combining this result with results from previous sections, we prove Theorem 1.
$C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains a bad point has measure 0 in the corresponding moduli space. Combining this result with results from previous sections, we prove Theorem 1.
2 Orbit parameterization
Let
![]() $k$
be a field of characteristic not equal to 2 and let
$k$
be a field of characteristic not equal to 2 and let
![]() $(U,Q)$
be the (unique) split quadratic space over
$(U,Q)$
be the (unique) split quadratic space over
![]() $k$
of dimension
$k$
of dimension
![]() $2n+2$
and discriminant 1. Recall that a
$2n+2$
and discriminant 1. Recall that a
 $(2n+2)$
-dimensional quadratic space over
$(2n+2)$
-dimensional quadratic space over
![]() $k$
is split if and only if there exists an isotropic subspace of dimension
$k$
is split if and only if there exists an isotropic subspace of dimension
![]() $n+1$
defined over
$n+1$
defined over
![]() $k$
. Let
$k$
. Let
![]() $f(x)$
be a monic polynomial of degree
$f(x)$
be a monic polynomial of degree
![]() $2n+2$
with no repeated roots and splitting completely over
$2n+2$
with no repeated roots and splitting completely over
![]() $k^{s}$
, the separable closure of
$k^{s}$
, the separable closure of
![]() $k$
. In this section, we study the action of
$k$
. In this section, we study the action of
 $\operatorname{PSO}(U)$
on self-adjoint operators on
$\operatorname{PSO}(U)$
on self-adjoint operators on
![]() $U$
with characteristic polynomial
$U$
with characteristic polynomial
![]() $f(x)$
via conjugation. More precisely, let
$f(x)$
via conjugation. More precisely, let
 $\langle v,w\rangle _{Q}=Q(v+w)-Q(v)-Q(w)$
denote the bilinear form associated to
$\langle v,w\rangle _{Q}=Q(v+w)-Q(v)-Q(w)$
denote the bilinear form associated to
![]() $Q$
. For any linear operator
$Q$
. For any linear operator
 $T:U\rightarrow U$
, its adjoint
$T:U\rightarrow U$
, its adjoint
![]() $T^{\ast }$
is defined via the following equation:
$T^{\ast }$
is defined via the following equation:
 $$\begin{eqnarray}\langle Tv,w\rangle _{Q}=\langle v,T^{\ast }w\rangle _{Q},\quad \forall v,w\in U.\end{eqnarray}$$
$$\begin{eqnarray}\langle Tv,w\rangle _{Q}=\langle v,T^{\ast }w\rangle _{Q},\quad \forall v,w\in U.\end{eqnarray}$$
Let
![]() $V$
denote the
$V$
denote the
![]() $k$
-scheme
$k$
-scheme
 $$\begin{eqnarray}V=\{T:U\rightarrow U\mid T=T^{\ast }\},\end{eqnarray}$$
$$\begin{eqnarray}V=\{T:U\rightarrow U\mid T=T^{\ast }\},\end{eqnarray}$$
and
![]() $V_{f}$
the
$V_{f}$
the
![]() $k$
-scheme
$k$
-scheme
 $$\begin{eqnarray}V_{f}=\{T:U\rightarrow U\mid T=T^{\ast },\det (xI-T)=f(x)\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{f}=\{T:U\rightarrow U\mid T=T^{\ast },\det (xI-T)=f(x)\}.\end{eqnarray}$$
The group scheme
 $$\begin{eqnarray}\operatorname{SO}(U):=\{g\in \text{GL}(U)\mid g^{\ast }g=I,\det (g)=1\}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{SO}(U):=\{g\in \text{GL}(U)\mid g^{\ast }g=I,\det (g)=1\}\end{eqnarray}$$
acts on
![]() $V_{f}$
via
$V_{f}$
via
 $g\cdot T=gTg^{-1}$
. The center
$g\cdot T=gTg^{-1}$
. The center
 $\unicode[STIX]{x1D707}_{2}\leqslant \operatorname{SO}(U)$
acts trivially. Hence we obtain a faithful action of
$\unicode[STIX]{x1D707}_{2}\leqslant \operatorname{SO}(U)$
acts trivially. Hence we obtain a faithful action of
 $$\begin{eqnarray}G=\operatorname{PSO}_{2n+2}:=\operatorname{PSO}(U)=\operatorname{SO}(U)/\unicode[STIX]{x1D707}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}G=\operatorname{PSO}_{2n+2}:=\operatorname{PSO}(U)=\operatorname{SO}(U)/\unicode[STIX]{x1D707}_{2}.\end{eqnarray}$$
To study the orbits of these actions, we first work over the separable closure
![]() $k^{s}$
of
$k^{s}$
of
![]() $k$
in § 2.1 and show that
$k$
in § 2.1 and show that
![]() $G(k^{s})$
acts transitively on
$G(k^{s})$
acts transitively on
![]() $V_{f}(k^{s})$
for separable polynomials
$V_{f}(k^{s})$
for separable polynomials
![]() $f$
. In § 2.2, we work over
$f$
. In § 2.2, we work over
![]() $k$
and classify the
$k$
and classify the
![]() $G(k)$
-orbits on
$G(k)$
-orbits on
![]() $V_{f}(k)$
using Galois cohomology. In § 2.3, we consider the Jacobian
$V_{f}(k)$
using Galois cohomology. In § 2.3, we consider the Jacobian
![]() $J$
of the hyperelliptic curve given by the equation
$J$
of the hyperelliptic curve given by the equation
 $y^{2}=f(x)$
and obtain a bijection between the set
$y^{2}=f(x)$
and obtain a bijection between the set
 $G(k)\backslash V_{f}(k)$
of
$G(k)\backslash V_{f}(k)$
of
![]() $k$
-rational orbits with characteristic polynomial
$k$
-rational orbits with characteristic polynomial
![]() $f(x)$
and a subset of
$f(x)$
and a subset of
 $H^{1}(k,J[2])$
. The most difficult part of this section will be to show that this subset contains the image of
$H^{1}(k,J[2])$
. The most difficult part of this section will be to show that this subset contains the image of
 $J(k)/2J(k)$
in
$J(k)/2J(k)$
in
 $H^{1}(k,J[2])$
. Finally, in § 2.4, we work over
$H^{1}(k,J[2])$
. Finally, in § 2.4, we work over
![]() $\mathbb{Z}_{p}$
and describe the set
$\mathbb{Z}_{p}$
and describe the set
 $G(\mathbb{Z}_{p})\backslash V(\mathbb{Z}_{p})$
of integral orbits with characteristic polynomial
$G(\mathbb{Z}_{p})\backslash V(\mathbb{Z}_{p})$
of integral orbits with characteristic polynomial
![]() $f(x)$
.
$f(x)$
.
2.1 Geometric orbits
Proposition 4. Let
 $f(x)\in k[x]$
be a monic separable polynomial of degree
$f(x)\in k[x]$
be a monic separable polynomial of degree
![]() $2n+2$
splitting completely over
$2n+2$
splitting completely over
![]() $k^{s}$
. Then the group
$k^{s}$
. Then the group
![]() $G(k^{s})$
acts transitively on
$G(k^{s})$
acts transitively on
![]() $V_{f}(k^{s})$
. For any
$V_{f}(k^{s})$
. For any
 $T\in V_{f}(k)$
, the stabilizer subscheme
$T\in V_{f}(k)$
, the stabilizer subscheme
 $\operatorname{Stab}_{G}(T)$
is isomorphic to
$\operatorname{Stab}_{G}(T)$
is isomorphic to
 $(\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2},$
where
$(\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2},$
where
 $L=k[x]/f(x)$
is an étale
$L=k[x]/f(x)$
is an étale
![]() $k$
-algebra of dimension
$k$
-algebra of dimension
![]() $2n+2$
.
$2n+2$
.
Proof. Fix any
![]() $T$
in
$T$
in
![]() $V_{f}(k)$
. Since
$V_{f}(k)$
. Since
![]() $T$
has distinct eigenvalues, its stabilizer scheme in
$T$
has distinct eigenvalues, its stabilizer scheme in
![]() $\operatorname{GL}(U)$
is a maximal torus. It contains and hence is equal to the maximal torus
$\operatorname{GL}(U)$
is a maximal torus. It contains and hence is equal to the maximal torus
 $\operatorname{Res}_{L/k}\mathbb{G}_{m}$
. For any
$\operatorname{Res}_{L/k}\mathbb{G}_{m}$
. For any
![]() $k$
-algebra
$k$
-algebra
![]() $K$
, we have
$K$
, we have
 $$\begin{eqnarray}\operatorname{Stab}_{\text{O}(U)}(T)(K)=\{g\in (K[T]/f(T))^{\times }\mid g^{\ast }g=1\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Stab}_{\text{O}(U)}(T)(K)=\{g\in (K[T]/f(T))^{\times }\mid g^{\ast }g=1\}.\end{eqnarray}$$
Since
![]() $T=T^{\ast }$
and
$T=T^{\ast }$
and
![]() $g$
is a polynomial in
$g$
is a polynomial in
![]() $T$
, we have
$T$
, we have
![]() $g=g^{\ast }$
. Thus,
$g=g^{\ast }$
. Thus,
 $$\begin{eqnarray}\displaystyle \operatorname{Stab}_{\text{O}(U)}(T) & \simeq & \displaystyle \operatorname{Stab}_{\operatorname{GL}(U)}(T)[2]\simeq \operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2},\nonumber\\ \displaystyle \operatorname{Stab}_{\text{SO}(U)}(T) & \simeq & \displaystyle (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1},\nonumber\\ \displaystyle \operatorname{Stab}_{\text{PSO}(U)}(T) & \simeq & \displaystyle (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Stab}_{\text{O}(U)}(T) & \simeq & \displaystyle \operatorname{Stab}_{\operatorname{GL}(U)}(T)[2]\simeq \operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2},\nonumber\\ \displaystyle \operatorname{Stab}_{\text{SO}(U)}(T) & \simeq & \displaystyle (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1},\nonumber\\ \displaystyle \operatorname{Stab}_{\text{PSO}(U)}(T) & \simeq & \displaystyle (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}.\nonumber\end{eqnarray}$$
Since
![]() $T$
is self-adjoint, there is an orthonormal basis
$T$
is self-adjoint, there is an orthonormal basis
 $\{u_{1},\ldots ,u_{2n+2}\}$
for
$\{u_{1},\ldots ,u_{2n+2}\}$
for
![]() $U$
consisting of eigenvectors of
$U$
consisting of eigenvectors of
![]() $T$
with eigenvalues
$T$
with eigenvalues
 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{2n+2}$
. If
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{2n+2}$
. If
![]() $T^{\prime }$
is another element of
$T^{\prime }$
is another element of
![]() $V_{f}(k^{s}),$
then there is an orthonormal basis
$V_{f}(k^{s}),$
then there is an orthonormal basis
 $\{u_{1}^{\prime },\ldots ,u_{2n+2}^{\prime }\}$
of
$\{u_{1}^{\prime },\ldots ,u_{2n+2}^{\prime }\}$
of
![]() $U$
consisting of eigenvectors of
$U$
consisting of eigenvectors of
![]() $T^{\prime }$
with eigenvalues
$T^{\prime }$
with eigenvalues
 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{2n+2}$
. Let
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{2n+2}$
. Let
 $g\in \operatorname{GL}(U)(k^{s})$
be an operator sending
$g\in \operatorname{GL}(U)(k^{s})$
be an operator sending
![]() $u_{i}$
to
$u_{i}$
to
![]() $\pm u_{i}^{\prime }$
, where the signs are chosen so that
$\pm u_{i}^{\prime }$
, where the signs are chosen so that
 $g\in \operatorname{SL}(U)(k^{s})$
. Then
$g\in \operatorname{SL}(U)(k^{s})$
. Then
 $g\in \operatorname{SO}(U)(k^{s})$
and the image of
$g\in \operatorname{SO}(U)(k^{s})$
and the image of
![]() $g$
in
$g$
in
 $\operatorname{PSO}(U)(k^{s})$
sends
$\operatorname{PSO}(U)(k^{s})$
sends
![]() $T$
to
$T$
to
![]() $T^{\prime }$
.◻
$T^{\prime }$
.◻
2.2 Rational orbits via Galois cohomology
Our first aim is to show that
![]() $V_{f}(k)$
is non-empty. Indeed, one can view
$V_{f}(k)$
is non-empty. Indeed, one can view
 $L=k[x]/(f(x))$
as a (
$L=k[x]/(f(x))$
as a (
![]() $2n+2$
)-dimensional
$2n+2$
)-dimensional
![]() $k$
-vector space with a power basis
$k$
-vector space with a power basis
 $\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{2n+1}\}$
where
$\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{2n+1}\}$
where
 $\unicode[STIX]{x1D6FD}\in k[x]/(f(x))$
is the image of
$\unicode[STIX]{x1D6FD}\in k[x]/(f(x))$
is the image of
![]() $x$
. We define the bilinear form
$x$
. We define the bilinear form
![]() $\langle \,,\,\rangle$
on
$\langle \,,\,\rangle$
on
![]() $L$
as follows:
$L$
as follows:
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle :=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle :=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
This form is split since the
![]() $(n+1)$
-plane
$(n+1)$
-plane
 $Y=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n}\}$
is isotropic. Its discriminant is 1, as one can readily compute using the above power basis. By the uniqueness of split quadratic spaces of fixed dimension and discriminant 1, there exists an isometry between
$Y=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n}\}$
is isotropic. Its discriminant is 1, as one can readily compute using the above power basis. By the uniqueness of split quadratic spaces of fixed dimension and discriminant 1, there exists an isometry between
![]() $(L,\langle \,,\,\rangle )$
and
$(L,\langle \,,\,\rangle )$
and
 $(U,\langle \,,\,\rangle _{Q})$
, well defined up to post-composition by elements in
$(U,\langle \,,\,\rangle _{Q})$
, well defined up to post-composition by elements in
 $\text{O}(U)(k)$
. Let
$\text{O}(U)(k)$
. Let
 $\cdot \unicode[STIX]{x1D6FD}:L\rightarrow L$
denote the linear map on
$\cdot \unicode[STIX]{x1D6FD}:L\rightarrow L$
denote the linear map on
![]() $L$
given by multiplication by
$L$
given by multiplication by
![]() $\unicode[STIX]{x1D6FD}$
. Then
$\unicode[STIX]{x1D6FD}$
. Then
![]() $\cdot \unicode[STIX]{x1D6FD}$
is self-adjoint with characteristic polynomial
$\cdot \unicode[STIX]{x1D6FD}$
is self-adjoint with characteristic polynomial
![]() $f(x)$
, and hence yields an element in
$f(x)$
, and hence yields an element in
![]() $V_{f}(k)$
well defined up to
$V_{f}(k)$
well defined up to
 $\text{O}(U)(k)$
conjugation. In what follows, we fix an isometry
$\text{O}(U)(k)$
conjugation. In what follows, we fix an isometry
 $\unicode[STIX]{x1D704}:L\rightarrow U$
, thus yielding a fixed element
$\unicode[STIX]{x1D704}:L\rightarrow U$
, thus yielding a fixed element
 $T_{f}\in V_{f}(k)$
.
$T_{f}\in V_{f}(k)$
.
Given
 $T\in V_{f}(k)$
, there exists
$T\in V_{f}(k)$
, there exists
 $g\in G(k^{s})$
such that
$g\in G(k^{s})$
such that
 $T=gT_{f}g^{-1}$
, since there is a unique geometric orbit by Proposition 4. For any
$T=gT_{f}g^{-1}$
, since there is a unique geometric orbit by Proposition 4. For any
 $\unicode[STIX]{x1D70E}\in \operatorname{Gal}(k^{s}/k)$
, the element
$\unicode[STIX]{x1D70E}\in \operatorname{Gal}(k^{s}/k)$
, the element
![]() $\text{}^{\unicode[STIX]{x1D70E}\!}g$
also conjugates
$\text{}^{\unicode[STIX]{x1D70E}\!}g$
also conjugates
![]() $T_{f}$
to
$T_{f}$
to
![]() $T$
and hence
$T$
and hence
 $g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g\in \operatorname{Stab}_{G}(T_{f})(k^{s})$
. The 1-cochain
$g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g\in \operatorname{Stab}_{G}(T_{f})(k^{s})$
. The 1-cochain
![]() $c_{T}$
given by
$c_{T}$
given by
 $(c_{T})_{\unicode[STIX]{x1D70E}}=g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g$
is a 1-cocycle whose image in
$(c_{T})_{\unicode[STIX]{x1D70E}}=g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g$
is a 1-cocycle whose image in
 $H^{1}(k,G)$
is trivial. This defines a bijection
$H^{1}(k,G)$
is trivial. This defines a bijection
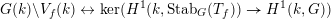 $$\begin{eqnarray}\displaystyle G(k)\backslash V_{f}(k) & \leftrightarrow & \displaystyle \ker (H^{1}(k,\operatorname{Stab}_{G}(T_{f}))\rightarrow H^{1}(k,G))\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G(k)\backslash V_{f}(k) & \leftrightarrow & \displaystyle \ker (H^{1}(k,\operatorname{Stab}_{G}(T_{f}))\rightarrow H^{1}(k,G))\end{eqnarray}$$
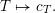 $$\begin{eqnarray}\displaystyle T & \mapsto & \displaystyle c_{T}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T & \mapsto & \displaystyle c_{T}.\end{eqnarray}$$
See [Reference Bhargava and GrossBG14, Proposition 1] for more details.
2.2.1 Distinguished orbits
We call a self-adjoint operator
 $T\in V_{f}(k)$
distinguished if it is
$T\in V_{f}(k)$
distinguished if it is
 $\operatorname{PO}(U)(k)$
-equivalent to
$\operatorname{PO}(U)(k)$
-equivalent to
![]() $T_{f}$
. Since the
$T_{f}$
. Since the
 $\operatorname{PO}(U)(k)$
-orbit of
$\operatorname{PO}(U)(k)$
-orbit of
![]() $T_{f}$
might break up into two
$T_{f}$
might break up into two
 $\operatorname{PSO}(U)(k)$
-orbits, there might exist two distinguished
$\operatorname{PSO}(U)(k)$
-orbits, there might exist two distinguished
 $\operatorname{PSO}(U)(k)$
-orbits in contrast to the odd hyperelliptic case. As
$\operatorname{PSO}(U)(k)$
-orbits in contrast to the odd hyperelliptic case. As
 $\operatorname{Stab}_{\text{PO}(U)}(T_{f})\simeq \operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}$
, we have the following diagram of exact rows.
$\operatorname{Stab}_{\text{PO}(U)}(T_{f})\simeq \operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}$
, we have the following diagram of exact rows.

Note that the second row consists of maps between pointed sets where the trivial classes in
 $H^{1}(k,\operatorname{PSO}(U))$
and
$H^{1}(k,\operatorname{PSO}(U))$
and
 $H^{1}(k,\operatorname{PO}(U))$
correspond to the split quadratic form
$H^{1}(k,\operatorname{PO}(U))$
correspond to the split quadratic form
![]() $(U,Q)$
; and where exactness means that the preimages of the trivial classes equal the images of the previous maps. A self-adjoint operator
$(U,Q)$
; and where exactness means that the preimages of the trivial classes equal the images of the previous maps. A self-adjoint operator
 $T\in V_{f}(k)$
is distinguished if and only if
$T\in V_{f}(k)$
is distinguished if and only if
 $$\begin{eqnarray}c_{T}\in \ker (H^{1}(k,\operatorname{Stab}_{\text{PSO}(U)}(T_{f}))\rightarrow H^{1}(k,\operatorname{Stab}_{\text{PO}(U)}(T_{f}))).\end{eqnarray}$$
$$\begin{eqnarray}c_{T}\in \ker (H^{1}(k,\operatorname{Stab}_{\text{PSO}(U)}(T_{f}))\rightarrow H^{1}(k,\operatorname{Stab}_{\text{PO}(U)}(T_{f}))).\end{eqnarray}$$
Since
 $H^{1}(k,\operatorname{PSO}(U))\rightarrow H^{1}(k,\operatorname{PO}(U))$
is injective, every class in the above kernel corresponds to a
$H^{1}(k,\operatorname{PSO}(U))\rightarrow H^{1}(k,\operatorname{PO}(U))$
is injective, every class in the above kernel corresponds to a
 $\operatorname{PSO}(U)(k)$
-orbit.
$\operatorname{PSO}(U)(k)$
-orbit.
Distinguished
 $\operatorname{PSO}(U)(k)$
-orbits in
$\operatorname{PSO}(U)(k)$
-orbits in
![]() $V_{f}(k)$
are unique if and only if the norm map
$V_{f}(k)$
are unique if and only if the norm map
 $N:\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective. Therefore, [Reference Poonen and SchaeferPS97, Lemma 11.2] immediately implies the following result.
$N:\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective. Therefore, [Reference Poonen and SchaeferPS97, Lemma 11.2] immediately implies the following result.
Proposition 5. Let
![]() $f(x)$
be as in Proposition 4. Then the set of distinguished elements in
$f(x)$
be as in Proposition 4. Then the set of distinguished elements in
![]() $V_{f}(k)$
consists of a single
$V_{f}(k)$
consists of a single
 $\operatorname{PSO}(U)(k)$
-orbit if and only if one of the following conditions is satisfied:
$\operatorname{PSO}(U)(k)$
-orbit if and only if one of the following conditions is satisfied:
-
(i)
 $f(x)$
has a factor of odd degree in
$f(x)$
has a factor of odd degree in
 $k[x]$
;
$k[x]$
; -
(ii)
 $n$
is even and
$n$
is even and
 $f(x)$
factors over some quadratic extension
$f(x)$
factors over some quadratic extension
 $K$
of
$K$
of
 $k$
as
$k$
as
 $h(x)\bar{h}(x)$
, where
$h(x)\bar{h}(x)$
, where
 $h(x)\in K[x]$
and
$h(x)\in K[x]$
and
 $\bar{h}(x)$
is the
$\bar{h}(x)$
is the
 $\operatorname{Gal}(K/k)$
-conjugate of
$\operatorname{Gal}(K/k)$
-conjugate of
 $h(x)$
.
$h(x)$
.
Otherwise, the set of distinguished elements in
![]() $V_{f}(k)$
consists of two
$V_{f}(k)$
consists of two
 $\operatorname{PSO}(U)(k)$
-orbits. Condition
$\operatorname{PSO}(U)(k)$
-orbits. Condition
![]() $(\text{ii})$
is equivalent to saying that
$(\text{ii})$
is equivalent to saying that
![]() $n$
is even, and
$n$
is even, and
![]() $L$
contains a quadratic extension
$L$
contains a quadratic extension
![]() $K$
of
$K$
of
![]() $k$
.
$k$
.
To give a more explicit description of distinguished orbits, we have the following result, the proof of which is deferred to § 3.
Proposition 6. Let
![]() $f(x)$
be as in Proposition 4. Then a self-adjoint operator
$f(x)$
be as in Proposition 4. Then a self-adjoint operator
 $T\in V_{f}(k)$
is distinguished if and only if there exists a
$T\in V_{f}(k)$
is distinguished if and only if there exists a
![]() $k$
-rational
$k$
-rational
![]() $n$
-plane
$n$
-plane
![]() $X\subset U$
such that
$X\subset U$
such that
 $\operatorname{Span}\{X,TX\}$
is an isotropic
$\operatorname{Span}\{X,TX\}$
is an isotropic
![]() $(n+1)$
-plane.
$(n+1)$
-plane.
After a change of basis, we may take the matrix
![]() $A$
with 1s on the anti-diagonal and 0s elsewhere as a Gram matrix for
$A$
with 1s on the anti-diagonal and 0s elsewhere as a Gram matrix for
![]() $Q$
. We express this basis as
$Q$
. We express this basis as
 $$\begin{eqnarray}\{e_{1},\ldots ,e_{n+1},f_{n+1},\ldots ,f_{1}\}\end{eqnarray}$$
$$\begin{eqnarray}\{e_{1},\ldots ,e_{n+1},f_{n+1},\ldots ,f_{1}\}\end{eqnarray}$$
where
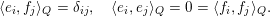 $$\begin{eqnarray}\langle e_{i},f_{j}\rangle _{Q}=\unicode[STIX]{x1D6FF}_{ij},\quad \langle e_{i},e_{j}\rangle _{Q}=0=\langle f_{i},f_{j}\rangle _{Q}.\end{eqnarray}$$
$$\begin{eqnarray}\langle e_{i},f_{j}\rangle _{Q}=\unicode[STIX]{x1D6FF}_{ij},\quad \langle e_{i},e_{j}\rangle _{Q}=0=\langle f_{i},f_{j}\rangle _{Q}.\end{eqnarray}$$
We call this the standard basis. Then the above proposition yields the following explicit description of distinguished elements which will be useful in § 4.
Proposition 7. A self-adjoint operator in
![]() $V_{f}(k)$
is distinguished if and only if its
$V_{f}(k)$
is distinguished if and only if its
 $\operatorname{PSO}(U)(k)$
-orbit contains an element
$\operatorname{PSO}(U)(k)$
-orbit contains an element
![]() $T$
whose matrix
$T$
whose matrix
![]() $M$
, with respect to the standard basis, satisfies
$M$
, with respect to the standard basis, satisfies
 $$\begin{eqnarray}AM=\left(\begin{array}{@{}ccccccc@{}}0 & 0 & \cdots \, & 0 & 0 & \ast & \ast \\ 0 & 0 & \cdots \, & 0 & \ast & \ast & \ast \\ \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \ddots & \cdots \, & \vdots & \vdots & \vdots \\ 0 & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \\ \ast & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \\ \ast & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}AM=\left(\begin{array}{@{}ccccccc@{}}0 & 0 & \cdots \, & 0 & 0 & \ast & \ast \\ 0 & 0 & \cdots \, & 0 & \ast & \ast & \ast \\ \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \ddots & \cdots \, & \vdots & \vdots & \vdots \\ 0 & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \\ \ast & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \\ \ast & \ast & \cdots \, & \cdots \, & \ast & \ast & \ast \end{array}\right).\end{eqnarray}$$
Proof. The forward direction follows from an argument identical to the proof of [Reference Bhargava and GrossBG13, Proposition 4.4]. For the backward direction, suppose
![]() $AM$
has the form in (5). Then
$AM$
has the form in (5). Then
 $$\begin{eqnarray}Te_{i}\in \operatorname{Span}\{e_{1},\ldots ,e_{n+1}\}^{\bot }=\operatorname{Span}\{e_{1},\ldots ,e_{n+1}\},\quad \text{for}~i=1,\ldots ,n.\end{eqnarray}$$
$$\begin{eqnarray}Te_{i}\in \operatorname{Span}\{e_{1},\ldots ,e_{n+1}\}^{\bot }=\operatorname{Span}\{e_{1},\ldots ,e_{n+1}\},\quad \text{for}~i=1,\ldots ,n.\end{eqnarray}$$
Let
![]() $X$
be the
$X$
be the
![]() $n$
-plane
$n$
-plane
 $\operatorname{Span}\{e_{1},\ldots ,e_{n}\}$
. Since
$\operatorname{Span}\{e_{1},\ldots ,e_{n}\}$
. Since
![]() $T$
is self-adjoint, its eigenspaces are pairwise orthogonal. Since
$T$
is self-adjoint, its eigenspaces are pairwise orthogonal. Since
![]() $Q$
is non-degenerate, none of the eigenvectors of
$Q$
is non-degenerate, none of the eigenvectors of
![]() $T$
is isotropic. As a result, no isotropic linear space is
$T$
is isotropic. As a result, no isotropic linear space is
![]() $T$
-stable. Hence by (6),
$T$
-stable. Hence by (6),
 $$\begin{eqnarray}\operatorname{Span}\{X,TX\}=\operatorname{Span}\{e_{1},\ldots ,e_{n+1}\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Span}\{X,TX\}=\operatorname{Span}\{e_{1},\ldots ,e_{n+1}\}.\end{eqnarray}$$
By Proposition 6,
![]() $T$
is distinguished.◻
$T$
is distinguished.◻
2.2.2 Remaining orbits
We start by describing the set of
 $\text{O}(U)(k)$
-orbits on
$\text{O}(U)(k)$
-orbits on
![]() $V_{f}(k)$
. Recall that
$V_{f}(k)$
. Recall that
 $\operatorname{Stab}_{\text{O}(U)}(T_{f})\simeq \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}$
. The set
$\operatorname{Stab}_{\text{O}(U)}(T_{f})\simeq \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}$
. The set
 $$\begin{eqnarray}\ker (H^{1}(k,\operatorname{Stab}_{\text{O}(U)}(T_{f}))\rightarrow H^{1}(k,O(U)))\end{eqnarray}$$
$$\begin{eqnarray}\ker (H^{1}(k,\operatorname{Stab}_{\text{O}(U)}(T_{f}))\rightarrow H^{1}(k,O(U)))\end{eqnarray}$$
consists of elements
 $\unicode[STIX]{x1D6FC}\in H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})\simeq L^{\times }/L^{\times 2}$
whose image in
$\unicode[STIX]{x1D6FC}\in H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})\simeq L^{\times }/L^{\times 2}$
whose image in
 $H^{1}(k,O(U))$
is trivial. For any
$H^{1}(k,O(U))$
is trivial. For any
 $\unicode[STIX]{x1D6FC}\in L^{\times }/L^{\times 2}$
, lift it arbitrarily to
$\unicode[STIX]{x1D6FC}\in L^{\times }/L^{\times 2}$
, lift it arbitrarily to
![]() $L^{\times }$
and consider the following bilinear form on
$L^{\times }$
and consider the following bilinear form on
![]() $L$
:
$L$
:
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle _{\unicode[STIX]{x1D6FC}}=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle _{\unicode[STIX]{x1D6FC}}=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
We claim that
![]() $\unicode[STIX]{x1D6FC}$
maps to 0 in
$\unicode[STIX]{x1D6FC}$
maps to 0 in
 $H^{1}(k,\text{O}(U))$
if and only if
$H^{1}(k,\text{O}(U))$
if and only if
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split with discriminant 1. Indeed, let
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split with discriminant 1. Indeed, let
 $\unicode[STIX]{x1D704}:(L,\langle \,,\,\rangle )\rightarrow (U,\langle \,,\,\rangle _{Q})$
denote the isometry used to define
$\unicode[STIX]{x1D704}:(L,\langle \,,\,\rangle )\rightarrow (U,\langle \,,\,\rangle _{Q})$
denote the isometry used to define
![]() $T_{f}$
. Now
$T_{f}$
. Now
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split with discriminant 1 if and only if there exists
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split with discriminant 1 if and only if there exists
 $g\in O(U)(k^{s})$
such that the following composite map is defined over
$g\in O(U)(k^{s})$
such that the following composite map is defined over
![]() $k$
:
$k$
:
 $$\begin{eqnarray}(L,\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}})\mathop{\xrightarrow[{}]{\sqrt{\unicode[STIX]{x1D6FC}}}}\nolimits_{k^{s}}(L,\langle \,,\,\rangle )\mathop{\xrightarrow[{}]{\unicode[STIX]{x1D704}}}\nolimits_{k}(U,\langle \,,\,\rangle _{Q})\mathop{\xrightarrow[{}]{g}}\nolimits_{k^{s}}(U,\langle \,,\,\rangle _{Q}),\end{eqnarray}$$
$$\begin{eqnarray}(L,\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}})\mathop{\xrightarrow[{}]{\sqrt{\unicode[STIX]{x1D6FC}}}}\nolimits_{k^{s}}(L,\langle \,,\,\rangle )\mathop{\xrightarrow[{}]{\unicode[STIX]{x1D704}}}\nolimits_{k}(U,\langle \,,\,\rangle _{Q})\mathop{\xrightarrow[{}]{g}}\nolimits_{k^{s}}(U,\langle \,,\,\rangle _{Q}),\end{eqnarray}$$
where the subscripts below the arrows indicate the fields of definition and where the last map is the standard action of
 $g\in \text{O}(U)(k^{s})$
. Unwinding the definitions [Reference WangWan13b, Proposition 2.13], we see that this is equivalent to the image of
$g\in \text{O}(U)(k^{s})$
. Unwinding the definitions [Reference WangWan13b, Proposition 2.13], we see that this is equivalent to the image of
![]() $\unicode[STIX]{x1D6FC}$
mapping to 0 in
$\unicode[STIX]{x1D6FC}$
mapping to 0 in
 $H^{1}(k,\text{O}(U))$
. We have therefore shown the following result.
$H^{1}(k,\text{O}(U))$
. We have therefore shown the following result.
Theorem 8. Let
![]() $f(x)$
be as in Proposition 4. Then there is a bijection between
$f(x)$
be as in Proposition 4. Then there is a bijection between
 $\text{O}(U)(k)$
-orbits on
$\text{O}(U)(k)$
-orbits on
![]() $V_{f}(k)$
and classes
$V_{f}(k)$
and classes
 $\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2})_{N=1}$
such that
$\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2})_{N=1}$
such that
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split.
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split.
To study
 $\operatorname{SO}(U)(k)$
- and
$\operatorname{SO}(U)(k)$
- and
 $\operatorname{PO}(U)(k)$
-orbits, we note that all the maps in the following diagram are injections.
$\operatorname{PO}(U)(k)$
-orbits, we note that all the maps in the following diagram are injections.

The horizontal maps are injective because the determinant map from
 $\text{O}(U)(k)$
to
$\text{O}(U)(k)$
to
![]() $\unicode[STIX]{x1D707}_{2}(k)$
is surjective. The vertical maps are injective because the connecting homomorphism
$\unicode[STIX]{x1D707}_{2}(k)$
is surjective. The vertical maps are injective because the connecting homomorphism
 $\operatorname{PSO}(U)(k)\rightarrow k^{\times }/k^{\times 2}$
is surjective. Indeed, for any
$\operatorname{PSO}(U)(k)\rightarrow k^{\times }/k^{\times 2}$
is surjective. Indeed, for any
![]() $c\in k^{\times }$
, the element in
$c\in k^{\times }$
, the element in
 $\operatorname{PSO}(U)(k)$
mapping to
$\operatorname{PSO}(U)(k)$
mapping to
![]() $c$
is the operator
$c$
is the operator
 $$\begin{eqnarray}e_{i}\mapsto \sqrt{c}\,e_{i},\quad f_{i}\mapsto \sqrt{c}^{-1}f_{i},\quad \forall i=1,\ldots ,n+1.\end{eqnarray}$$
$$\begin{eqnarray}e_{i}\mapsto \sqrt{c}\,e_{i},\quad f_{i}\mapsto \sqrt{c}^{-1}f_{i},\quad \forall i=1,\ldots ,n+1.\end{eqnarray}$$
Recall that
 $\operatorname{Stab}_{\operatorname{SO}(U)}(T_{f})\simeq (\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}$
. From the exact sequence
$\operatorname{Stab}_{\operatorname{SO}(U)}(T_{f})\simeq (\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}$
. From the exact sequence
 $$\begin{eqnarray}1\rightarrow (\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}\rightarrow \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow (\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}\rightarrow \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}\rightarrow 1,\end{eqnarray}$$
we obtain the isomorphism
 $$\begin{eqnarray}\ker (H^{1}(k,(\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1})\rightarrow H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}))\simeq \text{coker}(\unicode[STIX]{x1D707}_{2}(L)\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}(k)).\end{eqnarray}$$
$$\begin{eqnarray}\ker (H^{1}(k,(\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1})\rightarrow H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}))\simeq \text{coker}(\unicode[STIX]{x1D707}_{2}(L)\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}(k)).\end{eqnarray}$$
We see that each
 $O(U)(k)$
-orbit breaks up into one or two
$O(U)(k)$
-orbit breaks up into one or two
 $\operatorname{SO}(U)(k)$
-orbits depending on whether
$\operatorname{SO}(U)(k)$
-orbits depending on whether
![]() $f(x)$
has an odd degree factor or not, respectively.
$f(x)$
has an odd degree factor or not, respectively.
We next describe the set of
 $\operatorname{PO}(U)(k)$
-orbits on
$\operatorname{PO}(U)(k)$
-orbits on
![]() $V_{f}(k)$
. Each such orbit breaks up into either one or two
$V_{f}(k)$
. Each such orbit breaks up into either one or two
 $\operatorname{PSO}(U)(k)$
-orbits depending on whether the norm map
$\operatorname{PSO}(U)(k)$
-orbits depending on whether the norm map
 $N:(\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective or not, respectively (see Proposition 5 for a more descriptive criterion). As the stabilizer subscheme of
$N:(\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective or not, respectively (see Proposition 5 for a more descriptive criterion). As the stabilizer subscheme of
![]() $T_{f}$
in
$T_{f}$
in
![]() $\operatorname{PO}(U)$
is
$\operatorname{PO}(U)$
is
 $\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}$
, we have the following diagram of exact rows:
$\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}$
, we have the following diagram of exact rows:

Suppose
 $$\begin{eqnarray}c_{T}^{\prime }\in \ker (H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})\rightarrow H^{1}(k,\operatorname{PO}(U))).\end{eqnarray}$$
$$\begin{eqnarray}c_{T}^{\prime }\in \ker (H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})\rightarrow H^{1}(k,\operatorname{PO}(U))).\end{eqnarray}$$
Since
![]() $c_{T}^{\prime }$
maps to 0 in
$c_{T}^{\prime }$
maps to 0 in
 $H^{2}(k,\unicode[STIX]{x1D707}_{2})$
, it is the image of some
$H^{2}(k,\unicode[STIX]{x1D707}_{2})$
, it is the image of some
 $\unicode[STIX]{x1D6FC}\in L^{\times }/L^{\times 2}$
well defined up to
$\unicode[STIX]{x1D6FC}\in L^{\times }/L^{\times 2}$
well defined up to
 $k^{\times }/k^{\times 2}$
. Since the map
$k^{\times }/k^{\times 2}$
. Since the map
 $H^{1}(k,\text{O}(U))\rightarrow H^{1}(k,\operatorname{PO}(U))$
is injective, the image of
$H^{1}(k,\text{O}(U))\rightarrow H^{1}(k,\operatorname{PO}(U))$
is injective, the image of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
 $H^{1}(k,\text{O}(U))$
is trivial. By Theorem 8, this is equivalent to the form
$H^{1}(k,\text{O}(U))$
is trivial. By Theorem 8, this is equivalent to the form
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
being split with discriminant 1. Therefore, we have the following characterization of
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
being split with discriminant 1. Therefore, we have the following characterization of
 $\operatorname{PO}(U)(k)$
-orbits.
$\operatorname{PO}(U)(k)$
-orbits.
Theorem 9. There is a bijection between
 $\operatorname{PO}(U)(k)$
-orbits and classes
$\operatorname{PO}(U)(k)$
-orbits and classes
 $\unicode[STIX]{x1D6FC}\in (L^{\times }/(L^{\times 2}k^{\times }))_{N=1}$
such that
$\unicode[STIX]{x1D6FC}\in (L^{\times }/(L^{\times 2}k^{\times }))_{N=1}$
such that
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. The distinguished orbit corresponds to
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. The distinguished orbit corresponds to
![]() $\unicode[STIX]{x1D6FC}=1$
. Two
$\unicode[STIX]{x1D6FC}=1$
. Two
 $\text{O}(U)(k)$
-orbits corresponding to
$\text{O}(U)(k)$
-orbits corresponding to
 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in (L^{\times }/L^{\times 2})_{N=1}$
are
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in (L^{\times }/L^{\times 2})_{N=1}$
are
 $\operatorname{PO}(U)(k)$
-equivalent if and only if
$\operatorname{PO}(U)(k)$
-equivalent if and only if
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FC}_{2}$
have the same image in
$\unicode[STIX]{x1D6FC}_{2}$
have the same image in
 $(L^{\times }/L^{\times 2}k^{\times })_{N=1}$
.
$(L^{\times }/L^{\times 2}k^{\times })_{N=1}$
.
2.3 Connection to hyperelliptic curves
Let
![]() $C$
be the monic even hyperelliptic curve of genus
$C$
be the monic even hyperelliptic curve of genus
![]() $n$
given by the affine equation
$n$
given by the affine equation
 $y^{2}=f(x)$
, and let
$y^{2}=f(x)$
, and let
![]() $J$
denote its Jacobian. The curve
$J$
denote its Jacobian. The curve
![]() $C$
has two rational points above infinity, denoted by
$C$
has two rational points above infinity, denoted by
![]() $\infty$
and
$\infty$
and
![]() $\infty ^{\prime }$
. Let
$\infty ^{\prime }$
. Let
 $P_{1},\ldots ,P_{2n+2}$
denote the Weierstrass points of
$P_{1},\ldots ,P_{2n+2}$
denote the Weierstrass points of
![]() $C$
over
$C$
over
![]() $k^{s}$
. These form the ramification locus of the map
$k^{s}$
. These form the ramification locus of the map
 $x:C\rightarrow \mathbb{P}^{1}$
. Let
$x:C\rightarrow \mathbb{P}^{1}$
. Let
![]() $D_{0}$
denote the hyperelliptic class obtained as the pullback of
$D_{0}$
denote the hyperelliptic class obtained as the pullback of
![]() ${\mathcal{O}}_{\mathbb{P}^{1}}(1)$
. Then the group
${\mathcal{O}}_{\mathbb{P}^{1}}(1)$
. Then the group
 $J[2](k^{s})$
is generated by the divisor classes
$J[2](k^{s})$
is generated by the divisor classes
 $(P_{i})+(P_{j})-D_{0}$
for
$(P_{i})+(P_{j})-D_{0}$
for
![]() $i\neq j$
subject only to the condition that
$i\neq j$
subject only to the condition that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{2n+2}(P_{i})-(n+1)D_{0}\sim 0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{2n+2}(P_{i})-(n+1)D_{0}\sim 0.\end{eqnarray}$$
We have the following isomorphisms of group schemes over
![]() $k$
:
$k$
:
 $$\begin{eqnarray}J[2]\simeq (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}\simeq \operatorname{Stab}_{G}(T_{f}).\end{eqnarray}$$
$$\begin{eqnarray}J[2]\simeq (\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}\simeq \operatorname{Stab}_{G}(T_{f}).\end{eqnarray}$$
An explicit formula for this identification is given in [Reference WangWan13a, Remark 2.6].
In conjunction with (2), this identification yields a bijection
 $$\begin{eqnarray}G(k)\backslash V_{f}(k)\longrightarrow \ker (H^{1}(k,J[2])\rightarrow H^{1}(k,G)).\end{eqnarray}$$
$$\begin{eqnarray}G(k)\backslash V_{f}(k)\longrightarrow \ker (H^{1}(k,J[2])\rightarrow H^{1}(k,G)).\end{eqnarray}$$
Hence
![]() $G(k)$
-orbits on
$G(k)$
-orbits on
![]() $V_{f}(k)$
can be identified with a subset of
$V_{f}(k)$
can be identified with a subset of
 $H^{1}(k,J[2])$
. Recall that we have the following descent exact sequence:
$H^{1}(k,J[2])$
. Recall that we have the following descent exact sequence:
 $$\begin{eqnarray}1\rightarrow J(k)/2J(k)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,J)[2]\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow J(k)/2J(k)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,J)[2]\rightarrow 1.\end{eqnarray}$$
A
![]() $G(k)$
-orbit in
$G(k)$
-orbit in
![]() $V_{f}(k)$
is said to be soluble if it corresponds to a class in
$V_{f}(k)$
is said to be soluble if it corresponds to a class in
 $H^{1}(k,J[2])$
which is in the image of the map from
$H^{1}(k,J[2])$
which is in the image of the map from
 $J(k)/2J(k)$
. The following theorem states that there is a bijection between soluble
$J(k)/2J(k)$
. The following theorem states that there is a bijection between soluble
![]() $G(k)$
-orbits in
$G(k)$
-orbits in
![]() $V_{f}(k)$
and elements of
$V_{f}(k)$
and elements of
 $J(k)/2J(k)$
.
$J(k)/2J(k)$
.
Theorem 10. The following composite map is trivial:
 $$\begin{eqnarray}J(k)/2J(k)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,G).\end{eqnarray}$$
$$\begin{eqnarray}J(k)/2J(k)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,G).\end{eqnarray}$$
Therefore, there is a bijection between soluble
![]() $G(k)$
-orbits in
$G(k)$
-orbits in
![]() $V_{f}(k)$
and elements of
$V_{f}(k)$
and elements of
 $J(k)/2J(k)$
.
$J(k)/2J(k)$
.
Proof. We prove Theorem 10 in the case when
![]() $k$
is a local field. For a complete proof, see § 3. Combining the descent sequence (9) and the long exact sequence obtained by taking Galois cohomology of the short exact sequence
$k$
is a local field. For a complete proof, see § 3. Combining the descent sequence (9) and the long exact sequence obtained by taking Galois cohomology of the short exact sequence
 $$\begin{eqnarray}1\rightarrow J[2]\rightarrow \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow J[2]\rightarrow \text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}\xrightarrow[{}]{N}\unicode[STIX]{x1D707}_{2}\rightarrow 1,\end{eqnarray}$$
we get the following commutative diagram.

The map
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
is defined in [Reference Poonen and SchaeferPS97] by evaluating
$\unicode[STIX]{x1D6FF}^{\prime }$
is defined in [Reference Poonen and SchaeferPS97] by evaluating
![]() $(x-\unicode[STIX]{x1D6FD})$
on a given divisor class. As shown in [Reference Poonen and SchaeferPS97], the first row is not exact: the map
$(x-\unicode[STIX]{x1D6FD})$
on a given divisor class. As shown in [Reference Poonen and SchaeferPS97], the first row is not exact: the map
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
lands inside, generally not onto,
$\unicode[STIX]{x1D6FF}^{\prime }$
lands inside, generally not onto,
 $(L^{\times }/L^{\times 2}k^{\times })_{N=1}$
with kernel the subgroup generated by the class
$(L^{\times }/L^{\times 2}k^{\times })_{N=1}$
with kernel the subgroup generated by the class
 $(\infty ^{\prime })-(\infty )$
. Note that
$(\infty ^{\prime })-(\infty )$
. Note that
 $(\infty ^{\prime })-(\infty )\in 2J(k)$
if and only if the norm map
$(\infty ^{\prime })-(\infty )\in 2J(k)$
if and only if the norm map
 $N:\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective if and only if there is a unique distinguished orbit.
$N:\operatorname{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2}(k)\rightarrow \unicode[STIX]{x1D707}_{2}(k)$
is surjective if and only if there is a unique distinguished orbit.
To prove Theorem 10, it suffices to show that if
 $\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}k^{\times })_{N=1}$
lies in the image of
$\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}k^{\times })_{N=1}$
lies in the image of
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
, then
$\unicode[STIX]{x1D6FF}^{\prime }$
, then
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. We will prove this by explicitly writing down a
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. We will prove this by explicitly writing down a
![]() $k$
-rational (
$k$
-rational (
![]() $n+1$
)-dimensional isotropic subspace in the special case when
$n+1$
)-dimensional isotropic subspace in the special case when
![]() $k$
is a local field. For a complete and more conceptual proof using pencils of quadrics, see § 3. Suppose
$k$
is a local field. For a complete and more conceptual proof using pencils of quadrics, see § 3. Suppose
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}^{\prime }([D])$
for some
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}^{\prime }([D])$
for some
 $[D]\in J(k)/2J(k)$
of the form
$[D]\in J(k)/2J(k)$
of the form
 $$\begin{eqnarray}[D]=(Q_{1})+\cdots +(Q_{m})-m(\infty )\hspace{0.6em}{\rm mod}\hspace{0.2em}2J(k)\cdot \langle (\infty ^{\prime })-(\infty )\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}[D]=(Q_{1})+\cdots +(Q_{m})-m(\infty )\hspace{0.6em}{\rm mod}\hspace{0.2em}2J(k)\cdot \langle (\infty ^{\prime })-(\infty )\rangle ,\end{eqnarray}$$
where
 $Q_{1},\ldots ,Q_{m}\in C(k^{s})$
are non-Weierstrass non-infinity points and
$Q_{1},\ldots ,Q_{m}\in C(k^{s})$
are non-Weierstrass non-infinity points and
 $m\leqslant n+1$
. When
$m\leqslant n+1$
. When
![]() $k$
is a local field, every
$k$
is a local field, every
 $[D]\in J(k)/2J(k)$
can be written in this form [Reference WangWan13b, Lemma 3.8]. If we write
$[D]\in J(k)/2J(k)$
can be written in this form [Reference WangWan13b, Lemma 3.8]. If we write
 $Q_{i}=(x_{i},y_{i})$
, then
$Q_{i}=(x_{i},y_{i})$
, then
 $\unicode[STIX]{x1D6FC}=(x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})$
and
$\unicode[STIX]{x1D6FC}=(x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})$
and
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle _{\unicode[STIX]{x1D6FC}}=\operatorname{Tr}_{L/k}((x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle _{\unicode[STIX]{x1D6FC}}=\operatorname{Tr}_{L/k}((x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
We may also assume that the
![]() $x_{i}$
are all distinct since the sum of all the
$x_{i}$
are all distinct since the sum of all the
![]() $Q_{i}$
whose
$Q_{i}$
whose
![]() $x$
-coordinates appear more than once lies in
$x$
-coordinates appear more than once lies in
 $2J(k)\cdot \langle (\infty ^{\prime })-(\infty )\rangle$
. Write
$2J(k)\cdot \langle (\infty ^{\prime })-(\infty )\rangle$
. Write
 $$\begin{eqnarray}\widetilde{V}=\mathop{\prod }_{1\leqslant i<j\leqslant m}(x_{i}-x_{j})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{V}=\mathop{\prod }_{1\leqslant i<j\leqslant m}(x_{i}-x_{j})\end{eqnarray}$$
for the Vandermonde polynomial, and, for each
 $i=1,\ldots ,m$
, define
$i=1,\ldots ,m$
, define
 $$\begin{eqnarray}q_{i}:=\mathop{\prod }_{1\leqslant j\leqslant m,j\neq i}(x_{j}-x_{i}),\quad a_{i}:=\widetilde{V}/q_{i},\quad h_{i}(t):=\frac{f(t)-f(x_{i})}{t-x_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}q_{i}:=\mathop{\prod }_{1\leqslant j\leqslant m,j\neq i}(x_{j}-x_{i}),\quad a_{i}:=\widetilde{V}/q_{i},\quad h_{i}(t):=\frac{f(t)-f(x_{i})}{t-x_{i}}.\end{eqnarray}$$
For any
![]() $j\geqslant 0,$
we define
$j\geqslant 0,$
we define
 $$\begin{eqnarray}g_{j}(t)=\mathop{\sum }_{i=1}^{m}x_{i}^{j}a_{i}\frac{h_{i}(t)}{y_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}g_{j}(t)=\mathop{\sum }_{i=1}^{m}x_{i}^{j}a_{i}\frac{h_{i}(t)}{y_{i}}.\end{eqnarray}$$
Then the
![]() $(n+1)$
-plane
$(n+1)$
-plane
![]() $Y$
defined below is
$Y$
defined below is
![]() $k$
-rational and isotropic [Reference WangWan13b, Lemma 2.44]:
$k$
-rational and isotropic [Reference WangWan13b, Lemma 2.44]:
 $$\begin{eqnarray}Y:=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n-m^{\prime }},g_{0}(\unicode[STIX]{x1D6FD}),\ldots ,g_{m^{\prime }-1}(\unicode[STIX]{x1D6FD})\}\quad \text{if}~m=2m^{\prime }~\text{or}~m=2m^{\prime }+1.\end{eqnarray}$$
$$\begin{eqnarray}Y:=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n-m^{\prime }},g_{0}(\unicode[STIX]{x1D6FD}),\ldots ,g_{m^{\prime }-1}(\unicode[STIX]{x1D6FD})\}\quad \text{if}~m=2m^{\prime }~\text{or}~m=2m^{\prime }+1.\end{eqnarray}$$
This completes the proof of Theorem 10 when
![]() $k$
is a local field.◻
$k$
is a local field.◻
Suppose that
![]() $k$
is a number field. Then the 2-Selmer group
$k$
is a number field. Then the 2-Selmer group
 $\operatorname{Sel}_{2}(k,J)$
is the subgroup of
$\operatorname{Sel}_{2}(k,J)$
is the subgroup of
 $H^{1}(k,J[2])$
consisting of elements whose images in
$H^{1}(k,J[2])$
consisting of elements whose images in
 $H^{1}(k_{\unicode[STIX]{x1D708}},J[2])$
lie in the images of
$H^{1}(k_{\unicode[STIX]{x1D708}},J[2])$
lie in the images of
 $J(k_{\unicode[STIX]{x1D708}})/2J(k_{\unicode[STIX]{x1D708}})$
for all the local completions
$J(k_{\unicode[STIX]{x1D708}})/2J(k_{\unicode[STIX]{x1D708}})$
for all the local completions
![]() $k_{\unicode[STIX]{x1D708}}$
of
$k_{\unicode[STIX]{x1D708}}$
of
![]() $k$
. Since the group
$k$
. Since the group
 $G=\operatorname{PSO}_{2n+2}$
is an adjoint group, it satisfies the Hasse principle (see [Reference Platonov and RapinchukPR94, Theorem 6.22]), that is, the map
$G=\operatorname{PSO}_{2n+2}$
is an adjoint group, it satisfies the Hasse principle (see [Reference Platonov and RapinchukPR94, Theorem 6.22]), that is, the map
 $$\begin{eqnarray}H^{1}(k,G)\rightarrow \mathop{\prod }_{v}H^{1}(k_{v},G)\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(k,G)\rightarrow \mathop{\prod }_{v}H^{1}(k_{v},G)\end{eqnarray}$$
is injective, where the product is over all places
![]() $v$
of
$v$
of
![]() $k$
. Hence, Theorem 10 implies that the following composite is also trivial:
$k$
. Hence, Theorem 10 implies that the following composite is also trivial:
 $$\begin{eqnarray}\operatorname{Sel}_{2}(k,J)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,G).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sel}_{2}(k,J)\rightarrow H^{1}(k,J[2])\rightarrow H^{1}(k,G).\end{eqnarray}$$
A self-adjoint operator
 $T\in V_{f}(k)$
is said to be locally soluble if
$T\in V_{f}(k)$
is said to be locally soluble if
![]() $T$
is soluble in
$T$
is soluble in
![]() $V_{f}(k_{\unicode[STIX]{x1D708}})$
for all the local completions
$V_{f}(k_{\unicode[STIX]{x1D708}})$
for all the local completions
![]() $k_{\unicode[STIX]{x1D708}}$
of
$k_{\unicode[STIX]{x1D708}}$
of
![]() $k$
. Equivalently,
$k$
. Equivalently,
![]() $T$
is locally soluble if and only if
$T$
is locally soluble if and only if
![]() $c_{T}$
lies in
$c_{T}$
lies in
 $\operatorname{Sel}_{2}(k,J)$
. We have thus proven the following theorem.
$\operatorname{Sel}_{2}(k,J)$
. We have thus proven the following theorem.
Theorem 11. Let
![]() $k$
be a number field. Let
$k$
be a number field. Let
![]() $f(x)$
be a monic separable polynomial of degree
$f(x)$
be a monic separable polynomial of degree
![]() $2n+2$
over
$2n+2$
over
![]() $k$
. Then there is a bijection between locally soluble
$k$
. Then there is a bijection between locally soluble
![]() $G(k)$
-orbits on
$G(k)$
-orbits on
![]() $V_{f}(k)$
and elements in
$V_{f}(k)$
and elements in
 $\operatorname{Sel}_{2}(k,J)$
, where
$\operatorname{Sel}_{2}(k,J)$
, where
![]() $J$
is the Jacobian of the hyperelliptic curve given by the equation
$J$
is the Jacobian of the hyperelliptic curve given by the equation
 $y^{2}=f(x)$
.
$y^{2}=f(x)$
.
2.4 Integral orbits
Let
 $f(x)\in \mathbb{Q}[x]$
be a monic separable polynomial of degree
$f(x)\in \mathbb{Q}[x]$
be a monic separable polynomial of degree
![]() $2n+2$
. Let
$2n+2$
. Let
![]() $C$
be the hyperelliptic curve defined by
$C$
be the hyperelliptic curve defined by
 $y^{2}=f(x)$
, and let
$y^{2}=f(x)$
, and let
![]() $J$
be its Jacobian. We have seen that elements in the 2-Selmer group of
$J$
be its Jacobian. We have seen that elements in the 2-Selmer group of
![]() $J$
are in bijection with locally soluble
$J$
are in bijection with locally soluble
![]() $G(\mathbb{Q})$
-orbits in
$G(\mathbb{Q})$
-orbits in
![]() $V_{f}(\mathbb{Q})$
. In this section, our aim is to show that when
$V_{f}(\mathbb{Q})$
. In this section, our aim is to show that when
![]() $f$
has integral coefficients, every locally soluble
$f$
has integral coefficients, every locally soluble
![]() $G(\mathbb{Q})$
-orbit in
$G(\mathbb{Q})$
-orbit in
![]() $V_{f}(\mathbb{Q})$
contains an integral representative.
$V_{f}(\mathbb{Q})$
contains an integral representative.
We do this by working over the field
![]() $\mathbb{Q}_{p}$
and the ring
$\mathbb{Q}_{p}$
and the ring
![]() $\mathbb{Z}_{p}$
. Specifically, we prove the following result.
$\mathbb{Z}_{p}$
. Specifically, we prove the following result.
Proposition 12. Let
![]() $p$
be a prime and let
$p$
be a prime and let
 $f(x)=x^{2n+2}+c_{1}x^{2n+1}+\cdots +c_{2n+2}$
be a monic separable polynomial in
$f(x)=x^{2n+2}+c_{1}x^{2n+1}+\cdots +c_{2n+2}$
be a monic separable polynomial in
![]() $\mathbb{Z}_{p}[x]$
such that
$\mathbb{Z}_{p}[x]$
such that
![]() $2^{4i}|c_{i}$
in
$2^{4i}|c_{i}$
in
![]() $\mathbb{Z}_{p}$
for
$\mathbb{Z}_{p}$
for
 $i=1,\ldots ,2n+2$
. Then every soluble
$i=1,\ldots ,2n+2$
. Then every soluble
![]() $G(\mathbb{Q}_{p})$
-orbit in
$G(\mathbb{Q}_{p})$
-orbit in
![]() $V_{f}(\mathbb{Q}_{p})$
contains an integral representative.
$V_{f}(\mathbb{Q}_{p})$
contains an integral representative.
Recall that the class number of
![]() $G$
over
$G$
over
![]() $\mathbb{Q}$
is the number of double cosets
$\mathbb{Q}$
is the number of double cosets
 $G(\mathbb{A}(\infty ))xG(\mathbb{Q})$
of the group
$G(\mathbb{A}(\infty ))xG(\mathbb{Q})$
of the group
![]() $G(\mathbb{A})$
, where
$G(\mathbb{A})$
, where
![]() $\mathbb{A}$
is the ring of adeles of
$\mathbb{A}$
is the ring of adeles of
![]() $\mathbb{Q}$
and
$\mathbb{Q}$
and
![]() $\mathbb{A}(\infty )$
denotes the ring of integral adeles, that is, the product of
$\mathbb{A}(\infty )$
denotes the ring of integral adeles, that is, the product of
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $\mathbb{Z}_{p}$
over all primes
$\mathbb{Z}_{p}$
over all primes
![]() $p$
. For a quadratic space
$p$
. For a quadratic space
![]() $U$
, it is known (see [Reference Platonov and RapinchukPR94, Proposition 8.4]) that the class number of
$U$
, it is known (see [Reference Platonov and RapinchukPR94, Proposition 8.4]) that the class number of
![]() $\text{O}(U)$
over
$\text{O}(U)$
over
![]() $\mathbb{Q}$
is the same as the number of classes in the genus of
$\mathbb{Q}$
is the same as the number of classes in the genus of
![]() $U$
. The number of classes in the genus of any space having determinant
$U$
. The number of classes in the genus of any space having determinant
![]() $\pm 1$
is 1 [Reference SerreSer73, ch. V, Theorem 6]. It then easily follows that the class number of
$\pm 1$
is 1 [Reference SerreSer73, ch. V, Theorem 6]. It then easily follows that the class number of
![]() $G$
over
$G$
over
![]() $\mathbb{Q}$
is 1. We therefore immediately obtain the following corollary.
$\mathbb{Q}$
is 1. We therefore immediately obtain the following corollary.
Corollary 13. Let
 $f(x)=x^{2n+2}+c_{1}x^{2n+1}+\cdots +c_{2n+2}$
be a monic separable polynomial in
$f(x)=x^{2n+2}+c_{1}x^{2n+1}+\cdots +c_{2n+2}$
be a monic separable polynomial in
![]() $\mathbb{Z}[x]$
such that
$\mathbb{Z}[x]$
such that
![]() $2^{4i}|c_{i}$
for
$2^{4i}|c_{i}$
for
 $i=1,\ldots ,2n+2$
. Then every locally soluble
$i=1,\ldots ,2n+2$
. Then every locally soluble
![]() $G(\mathbb{Q})$
-orbit in
$G(\mathbb{Q})$
-orbit in
![]() $V_{f}(\mathbb{Q})$
contains an integral representative.
$V_{f}(\mathbb{Q})$
contains an integral representative.
We will also prove the following result.
Proposition 14. Let
![]() $p$
be any odd prime, and let
$p$
be any odd prime, and let
 $f(x)\in \mathbb{Z}_{p}[x]$
be a monic separable polynomial of degree
$f(x)\in \mathbb{Z}_{p}[x]$
be a monic separable polynomial of degree
![]() $2n+2$
such that
$2n+2$
such that
 $p^{2}\nmid \unicode[STIX]{x1D6E5}(f)$
. Then the
$p^{2}\nmid \unicode[STIX]{x1D6E5}(f)$
. Then the
![]() $G(\mathbb{Z}_{p})$
-orbits in
$G(\mathbb{Z}_{p})$
-orbits in
![]() $V_{f}(\mathbb{Z}_{p})$
are in bijection with soluble
$V_{f}(\mathbb{Z}_{p})$
are in bijection with soluble
![]() $G(\mathbb{Q}_{p})$
-orbits in
$G(\mathbb{Q}_{p})$
-orbits in
![]() $V_{f}(\mathbb{Q}_{p})$
. Furthermore, if
$V_{f}(\mathbb{Q}_{p})$
. Furthermore, if
 $T\in V_{f}(\mathbb{Z}_{p})$
, then
$T\in V_{f}(\mathbb{Z}_{p})$
, then
 $\operatorname{Stab}_{G(\mathbb{Z}_{p})}(T)=\operatorname{Stab}_{G(\mathbb{Q}_{p})}(T)$
.
$\operatorname{Stab}_{G(\mathbb{Z}_{p})}(T)=\operatorname{Stab}_{G(\mathbb{Q}_{p})}(T)$
.
Let
![]() $p$
be a fixed prime. We start by considering the
$p$
be a fixed prime. We start by considering the
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbits. A self-adjoint operator
$\text{O}(U)(\mathbb{Z}_{p})$
-orbits. A self-adjoint operator
 $T\in V_{f}(\mathbb{Q}_{p})$
is integral if it stabilizes the self-dual lattice
$T\in V_{f}(\mathbb{Q}_{p})$
is integral if it stabilizes the self-dual lattice
 $$\begin{eqnarray}M_{0}=\operatorname{Span}_{\mathbb{Z}_{p}}\{e_{1},\ldots ,e_{n+1},f_{n+1},\ldots ,f_{1}\}.\end{eqnarray}$$
$$\begin{eqnarray}M_{0}=\operatorname{Span}_{\mathbb{Z}_{p}}\{e_{1},\ldots ,e_{n+1},f_{n+1},\ldots ,f_{1}\}.\end{eqnarray}$$
In other words,
![]() $T$
is integral if and only if, when expressed in the standard basis (4), its entries are in
$T$
is integral if and only if, when expressed in the standard basis (4), its entries are in
![]() $\mathbb{Z}_{p}$
. In general, a lattice
$\mathbb{Z}_{p}$
. In general, a lattice
![]() $M$
is self-dual if the bilinear form restricts to a non-degenerate bilinear form:
$M$
is self-dual if the bilinear form restricts to a non-degenerate bilinear form:
 $M\times M\rightarrow \mathbb{Z}_{p}$
. Since genus theory implies that any two self-dual lattices are
$M\times M\rightarrow \mathbb{Z}_{p}$
. Since genus theory implies that any two self-dual lattices are
 $\text{O}(U)(\mathbb{Q}_{p})$
-conjugate, the rational orbit of
$\text{O}(U)(\mathbb{Q}_{p})$
-conjugate, the rational orbit of
![]() $T$
contains an integral representative if and only if
$T$
contains an integral representative if and only if
![]() $T$
stabilizes a self-dual lattice.
$T$
stabilizes a self-dual lattice.
The action of
![]() $T$
on
$T$
on
![]() $U$
gives
$U$
gives
![]() $U$
the structure of a
$U$
the structure of a
![]() $\mathbb{Q}_{p}[x]$
-module, where
$\mathbb{Q}_{p}[x]$
-module, where
![]() $x$
acts via
$x$
acts via
![]() $T$
. Since
$T$
. Since
![]() $T$
is regular, we have an isomorphism of
$T$
is regular, we have an isomorphism of
![]() $\mathbb{Q}_{p}[x]$
-modules:
$\mathbb{Q}_{p}[x]$
-modules:
 $U\simeq \mathbb{Q}_{p}[x]/(f(x))=L$
. Suppose
$U\simeq \mathbb{Q}_{p}[x]/(f(x))=L$
. Suppose
![]() $T$
is integral, stabilizing the self-dual lattice
$T$
is integral, stabilizing the self-dual lattice
![]() $M_{0}$
. The action of
$M_{0}$
. The action of
![]() $T$
on
$T$
on
![]() $M_{0}$
realizes
$M_{0}$
realizes
![]() $M_{0}$
as a
$M_{0}$
as a
 $\mathbb{Z}_{p}[x]/(f(x))$
-module. Write
$\mathbb{Z}_{p}[x]/(f(x))$
-module. Write
![]() $R$
for
$R$
for
 $\mathbb{Z}_{p}[x]/f(x)$
. Since
$\mathbb{Z}_{p}[x]/f(x)$
. Since
![]() $M_{0}$
is a lattice, we see that after the identification
$M_{0}$
is a lattice, we see that after the identification
![]() $U\simeq L$
,
$U\simeq L$
,
![]() $M_{0}$
becomes a fractional ideal
$M_{0}$
becomes a fractional ideal
![]() $I$
for the order
$I$
for the order
![]() $R$
. The split form
$R$
. The split form
![]() $Q$
on
$Q$
on
![]() $U$
gives a split form of discriminant 1 on
$U$
gives a split form of discriminant 1 on
![]() $L$
for which multiplication by
$L$
for which multiplication by
![]() $\unicode[STIX]{x1D6FD}$
is self-adjoint. Any such form on
$\unicode[STIX]{x1D6FD}$
is self-adjoint. Any such form on
![]() $L$
is of the form
$L$
is of the form
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
for some
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
for some
![]() $\unicode[STIX]{x1D6FC}\in L^{\times }$
with
$\unicode[STIX]{x1D6FC}\in L^{\times }$
with
 $N_{L/k}(\unicode[STIX]{x1D6FC})\in k^{\times 2}$
. The condition that
$N_{L/k}(\unicode[STIX]{x1D6FC})\in k^{\times 2}$
. The condition that
![]() $M_{0}$
is self-dual translates to saying
$M_{0}$
is self-dual translates to saying
 $\unicode[STIX]{x1D6FC}\cdot I^{2}\subset R$
and
$\unicode[STIX]{x1D6FC}\cdot I^{2}\subset R$
and
 $N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
.
$N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
.
The identification
![]() $U\simeq L$
is unique up to multiplication by some element
$U\simeq L$
is unique up to multiplication by some element
![]() $c\in L^{\times }$
, which transforms the data
$c\in L^{\times }$
, which transforms the data
![]() $(I,\unicode[STIX]{x1D6FC})$
to
$(I,\unicode[STIX]{x1D6FC})$
to
 $(c\cdot I,c^{-2}\unicode[STIX]{x1D6FC})$
. We call two pairs
$(c\cdot I,c^{-2}\unicode[STIX]{x1D6FC})$
. We call two pairs
![]() $(I,\unicode[STIX]{x1D6FC})$
,
$(I,\unicode[STIX]{x1D6FC})$
,
![]() $(I^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
equivalent if there exists
$(I^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
equivalent if there exists
![]() $c\in L^{\times }$
such that
$c\in L^{\times }$
such that
 $I^{\prime }=c\cdot I$
and
$I^{\prime }=c\cdot I$
and
 $\unicode[STIX]{x1D6FC}^{\prime }=c^{-2}\unicode[STIX]{x1D6FC}$
. Choosing a different integral representative
$\unicode[STIX]{x1D6FC}^{\prime }=c^{-2}\unicode[STIX]{x1D6FC}$
. Choosing a different integral representative
![]() $T$
in an integral orbit amounts to pre-composing the map
$T$
in an integral orbit amounts to pre-composing the map
![]() $U\simeq L$
by an element of
$U\simeq L$
by an element of
 $\text{O}(U)(\mathbb{Z}_{p})$
which does not change the equivalence class of the pair
$\text{O}(U)(\mathbb{Z}_{p})$
which does not change the equivalence class of the pair
![]() $(I,\unicode[STIX]{x1D6FC})$
. Hence we have a well-defined map
$(I,\unicode[STIX]{x1D6FC})$
. Hence we have a well-defined map
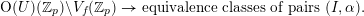 $$\begin{eqnarray}\text{O}(U)(\mathbb{Z}_{p})\backslash V_{f}(\mathbb{Z}_{p})\rightarrow \text{equivalence classes of pairs}~(I,\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
$$\begin{eqnarray}\text{O}(U)(\mathbb{Z}_{p})\backslash V_{f}(\mathbb{Z}_{p})\rightarrow \text{equivalence classes of pairs}~(I,\unicode[STIX]{x1D6FC}).\end{eqnarray}$$
Theorem 15. There is a bijection between
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbits and equivalence classes of pairs
$\text{O}(U)(\mathbb{Z}_{p})$
-orbits and equivalence classes of pairs
![]() $(I,\unicode[STIX]{x1D6FC})$
such that
$(I,\unicode[STIX]{x1D6FC})$
such that
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split,
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split,
 $\unicode[STIX]{x1D6FC}\cdot I^{2}\subset R$
, and
$\unicode[STIX]{x1D6FC}\cdot I^{2}\subset R$
, and
 $N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
. The image of
$N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
. The image of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
 $(L^{\times }/L^{\times 2})_{N=1}$
determines the rational orbit.
$(L^{\times }/L^{\times 2})_{N=1}$
determines the rational orbit.
Proof. Given a pair
![]() $(I,\unicode[STIX]{x1D6FC})$
such that
$(I,\unicode[STIX]{x1D6FC})$
such that
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split,
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split,
 $\unicode[STIX]{x1D6FC}I^{2}\subset R$
and
$\unicode[STIX]{x1D6FC}I^{2}\subset R$
and
 $N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
, there exists an isometry over
$N(I)^{2}=N(\unicode[STIX]{x1D6FC}^{-1})$
, there exists an isometry over
![]() $\mathbb{Q}_{p}$
from
$\mathbb{Q}_{p}$
from
 $(L,\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}})$
to
$(L,\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}})$
to
 $(U,\langle \,,\,\rangle _{Q})$
that sends
$(U,\langle \,,\,\rangle _{Q})$
that sends
![]() $I$
to the self-dual lattice
$I$
to the self-dual lattice
![]() $M_{0}$
. The image of the multiplication by
$M_{0}$
. The image of the multiplication by
![]() $\unicode[STIX]{x1D6FD}$
operator lies in
$\unicode[STIX]{x1D6FD}$
operator lies in
![]() $V_{f}(\mathbb{Z}_{p})$
. Any two such isometries differ by an element in
$V_{f}(\mathbb{Z}_{p})$
. Any two such isometries differ by an element in
 $\text{O}(U)(\mathbb{Z}_{p})$
. Hence we get a well-defined
$\text{O}(U)(\mathbb{Z}_{p})$
. Hence we get a well-defined
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbit in
$\text{O}(U)(\mathbb{Z}_{p})$
-orbit in
![]() $V_{f}(\mathbb{Z}_{p})$
. Along with (12), we have proved the first statement.
$V_{f}(\mathbb{Z}_{p})$
. Along with (12), we have proved the first statement.
For the second statement, from the sequence of isometries (7), we see that since
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split, there exists
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split, there exists
 $g\in \text{O}(U)(\mathbb{Q}_{p}^{s})$
such that
$g\in \text{O}(U)(\mathbb{Q}_{p}^{s})$
such that
 $$\begin{eqnarray}\text{}^{\unicode[STIX]{x1D70E}\!}\sqrt{\unicode[STIX]{x1D6FC}}/\sqrt{\unicode[STIX]{x1D6FC}}=g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g\quad \forall \unicode[STIX]{x1D70E}\in \operatorname{Gal}(k^{s}/k).\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\unicode[STIX]{x1D70E}\!}\sqrt{\unicode[STIX]{x1D6FC}}/\sqrt{\unicode[STIX]{x1D6FC}}=g^{-1}\,\text{}^{\unicode[STIX]{x1D70E}\!}g\quad \forall \unicode[STIX]{x1D70E}\in \operatorname{Gal}(k^{s}/k).\end{eqnarray}$$
Here, the left-hand side is viewed as an element of
 $\operatorname{Stab}_{\text{O}(U)}(T_{f})(k^{s})$
. The rational orbit corresponding the pair
$\operatorname{Stab}_{\text{O}(U)}(T_{f})(k^{s})$
. The rational orbit corresponding the pair
![]() $(I,\unicode[STIX]{x1D6FC})$
is the rational orbit of
$(I,\unicode[STIX]{x1D6FC})$
is the rational orbit of
 $T=gT_{f}g^{-1}$
. The rest follows formally from unwinding definitions.◻
$T=gT_{f}g^{-1}$
. The rest follows formally from unwinding definitions.◻
Suppose the
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbit of some
$\text{O}(U)(\mathbb{Z}_{p})$
-orbit of some
 $T\in V_{f}(\mathbb{Z}_{p})$
corresponds to the equivalence class of the pair
$T\in V_{f}(\mathbb{Z}_{p})$
corresponds to the equivalence class of the pair
![]() $(I,\unicode[STIX]{x1D6FC})$
. Upon identifying
$(I,\unicode[STIX]{x1D6FC})$
. Upon identifying
![]() $R$
with
$R$
with
![]() $\mathbb{Z}_{p}[T]$
, the stabilizer of
$\mathbb{Z}_{p}[T]$
, the stabilizer of
![]() $T$
in
$T$
in
 $\operatorname{GL}(U)(\mathbb{Z}_{p})$
is
$\operatorname{GL}(U)(\mathbb{Z}_{p})$
is
 $\operatorname{End}_{R}(I)^{\times }$
. Moreover, as in the proof of Proposition 4, we have
$\operatorname{End}_{R}(I)^{\times }$
. Moreover, as in the proof of Proposition 4, we have
 $$\begin{eqnarray}\displaystyle \operatorname{Stab}_{\text{O}(U)}(T)(\mathbb{Z}_{p}) & = & \displaystyle \operatorname{End}_{R}(I)^{\times }[2],\nonumber\\ \displaystyle \operatorname{Stab}_{\operatorname{SO}(U)}(T)(\mathbb{Z}_{p}) & = & \displaystyle (\operatorname{End}_{R}(I)^{\times }[2])_{N=1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Stab}_{\text{O}(U)}(T)(\mathbb{Z}_{p}) & = & \displaystyle \operatorname{End}_{R}(I)^{\times }[2],\nonumber\\ \displaystyle \operatorname{Stab}_{\operatorname{SO}(U)}(T)(\mathbb{Z}_{p}) & = & \displaystyle (\operatorname{End}_{R}(I)^{\times }[2])_{N=1}.\nonumber\end{eqnarray}$$
The stabilizer of
![]() $T$
in the group
$T$
in the group
 $\operatorname{PO}(U)(\mathbb{Z}_{p})$
(and
$\operatorname{PO}(U)(\mathbb{Z}_{p})$
(and
 $\operatorname{PSO}(U)(\mathbb{Z}_{p})$
) is slightly complicated because
$\operatorname{PSO}(U)(\mathbb{Z}_{p})$
) is slightly complicated because
 $\operatorname{PO}(U)(\mathbb{Z}_{p})$
contains
$\operatorname{PO}(U)(\mathbb{Z}_{p})$
contains
 $\text{O}(U)(\mathbb{Z}_{p})/\unicode[STIX]{x1D707}_{2}$
as a subgroup with quotient
$\text{O}(U)(\mathbb{Z}_{p})/\unicode[STIX]{x1D707}_{2}$
as a subgroup with quotient
 $\mathbb{Z}_{p}^{\times }/\mathbb{Z}_{p}^{\times 2}$
. We have the following exact sequences:
$\mathbb{Z}_{p}^{\times }/\mathbb{Z}_{p}^{\times 2}$
. We have the following exact sequences:
 $$\begin{eqnarray}1\rightarrow \operatorname{End}_{R}(I)^{\times }[2]/\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{Stab}_{\operatorname{PO}(U)}(T)(\mathbb{Z}_{p})\rightarrow (R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \operatorname{End}_{R}(I)^{\times }[2]/\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{Stab}_{\operatorname{PO}(U)}(T)(\mathbb{Z}_{p})\rightarrow (R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}\rightarrow 1,\end{eqnarray}$$
 $$\begin{eqnarray}1\rightarrow (\operatorname{End}_{R}(I)^{\times }[2])_{N=1}/\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{Stab}_{\operatorname{PSO}(U)}(T)(\mathbb{Z}_{p})\rightarrow (R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow (\operatorname{End}_{R}(I)^{\times }[2])_{N=1}/\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{Stab}_{\operatorname{PSO}(U)}(T)(\mathbb{Z}_{p})\rightarrow (R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}\rightarrow 1.\end{eqnarray}$$
Proof of Proposition 12.
First note that it suffices to show that the
 $\operatorname{PO}(U)(\mathbb{Q}_{p})$
-orbit of
$\operatorname{PO}(U)(\mathbb{Q}_{p})$
-orbit of
![]() $T$
contains an integral representative. Since
$T$
contains an integral representative. Since
![]() $T$
is soluble, there exists some
$T$
is soluble, there exists some
 $[D]\in J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p})$
such that
$[D]\in J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p})$
such that
 $\widetilde{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FF}^{\prime }([D])\in (L^{\times }/L^{\times 2}\mathbb{Q}_{p}^{\times })_{N=1}$
corresponds to the
$\widetilde{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FF}^{\prime }([D])\in (L^{\times }/L^{\times 2}\mathbb{Q}_{p}^{\times })_{N=1}$
corresponds to the
 $\operatorname{PO}(U)(\mathbb{Q}_{p})$
-orbit of
$\operatorname{PO}(U)(\mathbb{Q}_{p})$
-orbit of
![]() $T$
. By [Reference WangWan13b, Lemma 3.8], there exist non-Weierstrass non-infinity points
$T$
. By [Reference WangWan13b, Lemma 3.8], there exist non-Weierstrass non-infinity points
 $Q_{1},\ldots ,Q_{m}\in C(\mathbb{Q}_{p}^{s})$
, with
$Q_{1},\ldots ,Q_{m}\in C(\mathbb{Q}_{p}^{s})$
, with
 $m\leqslant n+1$
, such that
$m\leqslant n+1$
, such that
 $$\begin{eqnarray}[D]=(Q_{1})+\cdots +(Q_{m})-m(\infty )\hspace{0.6em}{\rm mod}\hspace{0.2em}2J(\mathbb{Q}_{p})\cdot \langle (\infty ^{\prime })-(\infty )\rangle .\end{eqnarray}$$
$$\begin{eqnarray}[D]=(Q_{1})+\cdots +(Q_{m})-m(\infty )\hspace{0.6em}{\rm mod}\hspace{0.2em}2J(\mathbb{Q}_{p})\cdot \langle (\infty ^{\prime })-(\infty )\rangle .\end{eqnarray}$$
Write each
 $Q_{i}=(x_{i},y_{i})\in C({\mathcal{O}}_{\mathbb{Q}_{p}^{s}})$
. Then
$Q_{i}=(x_{i},y_{i})\in C({\mathcal{O}}_{\mathbb{Q}_{p}^{s}})$
. Then
 $\unicode[STIX]{x1D6FC}=(x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})$
is a lift of
$\unicode[STIX]{x1D6FC}=(x_{1}-\unicode[STIX]{x1D6FD})\cdots (x_{m}-\unicode[STIX]{x1D6FD})$
is a lift of
![]() $\widetilde{\unicode[STIX]{x1D6FC}}$
to
$\widetilde{\unicode[STIX]{x1D6FC}}$
to
![]() $L^{\times }$
. We claim that either the
$L^{\times }$
. We claim that either the
 $\text{O}(U)(\mathbb{Q}_{p})$
-orbit of
$\text{O}(U)(\mathbb{Q}_{p})$
-orbit of
![]() $T$
corresponding to the image of
$T$
corresponding to the image of
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
 $L^{\times }/L^{\times 2}$
has an integral representative, or
$L^{\times }/L^{\times 2}$
has an integral representative, or
![]() $[D]$
can be expressed in the form (14) with
$[D]$
can be expressed in the form (14) with
![]() $m$
replaced by
$m$
replaced by
![]() $m-2$
. Applying induction on
$m-2$
. Applying induction on
![]() $m$
completes the proof.
$m$
completes the proof.
The claim follows verbatim from the proof of [Reference Bhargava and GrossBG13, Proposition 8.5]. We give a quick sketch here. Let
 $r(x)\in \mathbb{Q}_{p}[x]$
be a polynomial of degree at most
$r(x)\in \mathbb{Q}_{p}[x]$
be a polynomial of degree at most
![]() $m-1$
such that, for all
$m-1$
such that, for all
![]() $i$
,
$i$
,
 $r(x_{i})=y_{i}$
, and let
$r(x_{i})=y_{i}$
, and let
 $$\begin{eqnarray}p(x)=(x-x_{1})\cdots (x-x_{m})\in \mathbb{Z}_{p}[x].\end{eqnarray}$$
$$\begin{eqnarray}p(x)=(x-x_{1})\cdots (x-x_{m})\in \mathbb{Z}_{p}[x].\end{eqnarray}$$
Now
![]() $p(x)$
divides
$p(x)$
divides
 $r(x)^{2}-f(x)$
in
$r(x)^{2}-f(x)$
in
![]() $\mathbb{Q}_{p}[x]$
and we denote the quotient by
$\mathbb{Q}_{p}[x]$
and we denote the quotient by
![]() $q(x)$
. By definition,
$q(x)$
. By definition,
 $\unicode[STIX]{x1D6FC}=(-1)^{m}P(\unicode[STIX]{x1D6FD})$
. If the polynomial
$\unicode[STIX]{x1D6FC}=(-1)^{m}P(\unicode[STIX]{x1D6FD})$
. If the polynomial
 $r(x)\in \mathbb{Z}_{p}[x]$
, then the ideal
$r(x)\in \mathbb{Z}_{p}[x]$
, then the ideal
 $I=(1,r(\unicode[STIX]{x1D6FD})/\unicode[STIX]{x1D6FC})$
does the job. Note that
$I=(1,r(\unicode[STIX]{x1D6FD})/\unicode[STIX]{x1D6FC})$
does the job. Note that
 $\unicode[STIX]{x1D6FC}I^{2}=(\unicode[STIX]{x1D6FC},r(\unicode[STIX]{x1D6FD}),q(\unicode[STIX]{x1D6FD}))$
. The integrality assumption of
$\unicode[STIX]{x1D6FC}I^{2}=(\unicode[STIX]{x1D6FC},r(\unicode[STIX]{x1D6FD}),q(\unicode[STIX]{x1D6FD}))$
. The integrality assumption of
![]() $r(x)$
is used to show that
$r(x)$
is used to show that
 $r(\unicode[STIX]{x1D6FD}),q(\unicode[STIX]{x1D6FD})\in R$
. A computation of ideal norms shows that
$r(\unicode[STIX]{x1D6FD}),q(\unicode[STIX]{x1D6FD})\in R$
. A computation of ideal norms shows that
 $N(I)^{2}=N(\unicode[STIX]{x1D6FC})^{-1}$
.
$N(I)^{2}=N(\unicode[STIX]{x1D6FC})^{-1}$
.
When
![]() $r(x)$
is not integral, a Newton polygon analysis on
$r(x)$
is not integral, a Newton polygon analysis on
 $f(x)-r(x)^{2}$
shows that
$f(x)-r(x)^{2}$
shows that
 $\operatorname{div}(y-r(x))-[D]$
has the form
$\operatorname{div}(y-r(x))-[D]$
has the form
 $D^{\ast }+E$
with
$D^{\ast }+E$
with
![]() $D^{\ast }$
,
$D^{\ast }$
,
 $E\in J(\mathbb{Q}_{p})$
, where
$E\in J(\mathbb{Q}_{p})$
, where
![]() $D^{\ast }$
can be expressed in (14) with
$D^{\ast }$
can be expressed in (14) with
![]() $m$
replaced by
$m$
replaced by
![]() $m-2$
and the
$m-2$
and the
![]() $x$
-coordinates of the non-infinity points in
$x$
-coordinates of the non-infinity points in
![]() $E$
have negative valuation. The condition of divisibility on the coefficients of
$E$
have negative valuation. The condition of divisibility on the coefficients of
![]() $f(x)$
ensures that
$f(x)$
ensures that
 $E\in 2J(\mathbb{Q}_{p})\cdot ((\infty ^{\prime })-(\infty ))$
, or equivalently
$E\in 2J(\mathbb{Q}_{p})\cdot ((\infty ^{\prime })-(\infty ))$
, or equivalently
 $(x-\unicode[STIX]{x1D6FD})(E)\in L^{\times 2}\mathbb{Q}_{p}^{\times }$
.◻
$(x-\unicode[STIX]{x1D6FD})(E)\in L^{\times 2}\mathbb{Q}_{p}^{\times }$
.◻
Proof of Proposition 14.
Once again, it suffices to work with
![]() $\operatorname{PO}(U)$
-orbits instead of
$\operatorname{PO}(U)$
-orbits instead of
 $\operatorname{PSO}(U)$
-orbits directly. The assumption on
$\operatorname{PSO}(U)$
-orbits directly. The assumption on
![]() $\unicode[STIX]{x1D6E5}(f)$
implies that
$\unicode[STIX]{x1D6E5}(f)$
implies that
![]() $R$
is the maximal order. Hence there is a bijection between
$R$
is the maximal order. Hence there is a bijection between
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbits and
$\text{O}(U)(\mathbb{Z}_{p})$
-orbits and
 $(R^{\times }/R^{\times 2})_{N=1}$
. Note that over non-archimedean local fields, the splitness of the quadratic form is automatic from the existence of a self-dual lattice. Taking flat cohomology over
$(R^{\times }/R^{\times 2})_{N=1}$
. Note that over non-archimedean local fields, the splitness of the quadratic form is automatic from the existence of a self-dual lattice. Taking flat cohomology over
 $\text{Spec}(\mathbb{Z}_{p})$
of the sequence
$\text{Spec}(\mathbb{Z}_{p})$
of the sequence
 $$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D707}_{2}\rightarrow \text{O}(U)\rightarrow \operatorname{PO}(U)\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D707}_{2}\rightarrow \text{O}(U)\rightarrow \operatorname{PO}(U)\rightarrow 1\end{eqnarray}$$
gives:
 $$\begin{eqnarray}1\rightarrow \text{O}(U)(\mathbb{Z}_{p})/\pm 1\rightarrow \operatorname{PO}(U)(\mathbb{Z}_{p})\rightarrow \mathbb{Z}_{p}^{\times }/\mathbb{Z}_{p}^{\times 2}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{O}(U)(\mathbb{Z}_{p})/\pm 1\rightarrow \operatorname{PO}(U)(\mathbb{Z}_{p})\rightarrow \mathbb{Z}_{p}^{\times }/\mathbb{Z}_{p}^{\times 2}\rightarrow 1.\end{eqnarray}$$
Hence
 $\operatorname{PO}(U)(\mathbb{Z}_{p})$
-orbits correspond bijectively to
$\operatorname{PO}(U)(\mathbb{Z}_{p})$
-orbits correspond bijectively to
 $(R^{\times }/R^{\times 2}\mathbb{Z}_{p}^{\times })_{N=1}$
.
$(R^{\times }/R^{\times 2}\mathbb{Z}_{p}^{\times })_{N=1}$
.
On the other hand, the assumption on
![]() $\unicode[STIX]{x1D6E5}(f)$
implies that the projective closure
$\unicode[STIX]{x1D6E5}(f)$
implies that the projective closure
![]() ${\mathcal{C}}$
(in weighted projective space) of the hyperelliptic curve
${\mathcal{C}}$
(in weighted projective space) of the hyperelliptic curve
![]() $C$
defined by affine equation
$C$
defined by affine equation
 $y^{2}=f(x)$
over
$y^{2}=f(x)$
over
 $\operatorname{Spec}(\mathbb{Z}_{p})$
is regular. Since the special fiber of
$\operatorname{Spec}(\mathbb{Z}_{p})$
is regular. Since the special fiber of
![]() ${\mathcal{C}}$
is geometrically reduced and irreducible, the Neron model
${\mathcal{C}}$
is geometrically reduced and irreducible, the Neron model
![]() ${\mathcal{J}}$
of its Jacobian
${\mathcal{J}}$
of its Jacobian
![]() $J_{\mathbb{Q}_{p}}$
is fiberwise connected [Reference Bosch, Lutkebohmert and RaynaudBLR90, § 9.5, Theorem 1] and its 2-torsion
$J_{\mathbb{Q}_{p}}$
is fiberwise connected [Reference Bosch, Lutkebohmert and RaynaudBLR90, § 9.5, Theorem 1] and its 2-torsion
![]() ${\mathcal{J}}[2]$
is isomorphic to
${\mathcal{J}}[2]$
is isomorphic to
 $(\operatorname{Res}_{R/\mathbb{Z}_{p}}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}$
. Using diagram (11) after replacing
$(\operatorname{Res}_{R/\mathbb{Z}_{p}}\unicode[STIX]{x1D707}_{2})_{N=1}/\unicode[STIX]{x1D707}_{2}$
. Using diagram (11) after replacing
![]() $L,k,J$
by
$L,k,J$
by
 $R,\mathbb{Z}_{p},{\mathcal{J}}$
, we see that the vertical maps are all isomorphisms and
$R,\mathbb{Z}_{p},{\mathcal{J}}$
, we see that the vertical maps are all isomorphisms and
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
maps
$\unicode[STIX]{x1D6FF}^{\prime }$
maps
 ${\mathcal{J}}(\mathbb{Z}_{p})/2{\mathcal{J}}(\mathbb{Z}_{p})$
surjectively to
${\mathcal{J}}(\mathbb{Z}_{p})/2{\mathcal{J}}(\mathbb{Z}_{p})$
surjectively to
 $(R^{\times }/R^{\times 2}\mathbb{Z}_{p}^{\times })_{N=1}$
. The Neron mapping property implies that
$(R^{\times }/R^{\times 2}\mathbb{Z}_{p}^{\times })_{N=1}$
. The Neron mapping property implies that
 ${\mathcal{J}}(\mathbb{Z}_{p})/2{\mathcal{J}}(\mathbb{Z}_{p})=J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p})$
.
${\mathcal{J}}(\mathbb{Z}_{p})/2{\mathcal{J}}(\mathbb{Z}_{p})=J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p})$
.
Suppose the
 $\text{O}(U)(\mathbb{Z}_{p})$
-orbit of some
$\text{O}(U)(\mathbb{Z}_{p})$
-orbit of some
 $T\in V_{f}(\mathbb{Z}_{p})$
corresponds to an equivalence class of pair
$T\in V_{f}(\mathbb{Z}_{p})$
corresponds to an equivalence class of pair
![]() $(I,\unicode[STIX]{x1D6FC})$
. Since
$(I,\unicode[STIX]{x1D6FC})$
. Since
![]() $R$
is maximal, we have
$R$
is maximal, we have
 $\operatorname{End}_{R}(I)=R$
. Since
$\operatorname{End}_{R}(I)=R$
. Since
 $R^{\times }[2]=L^{\times }[2]$
, we see from (13) that it remains to compare
$R^{\times }[2]=L^{\times }[2]$
, we see from (13) that it remains to compare
 $(R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}$
with
$(R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}$
with
 $(L^{\times 2}\cap \mathbb{Q}_{p}^{\times })/\mathbb{Q}_{p}^{\times 2}$
. These two groups are only non-trivial when
$(L^{\times 2}\cap \mathbb{Q}_{p}^{\times })/\mathbb{Q}_{p}^{\times 2}$
. These two groups are only non-trivial when
![]() $L$
contains a quadratic extension
$L$
contains a quadratic extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $\mathbb{Q}_{p}$
. The condition
$\mathbb{Q}_{p}$
. The condition
 $p^{2}\nmid \unicode[STIX]{x1D6E5}(f)$
implies that
$p^{2}\nmid \unicode[STIX]{x1D6E5}(f)$
implies that
 $K^{\prime }=\mathbb{Q}_{p}(\sqrt{u})$
can only be the unramified quadratic extension of
$K^{\prime }=\mathbb{Q}_{p}(\sqrt{u})$
can only be the unramified quadratic extension of
![]() $\mathbb{Q}_{p}$
. In other words,
$\mathbb{Q}_{p}$
. In other words,
![]() $u$
can be chosen to be a unit in
$u$
can be chosen to be a unit in
![]() $\mathbb{Z}_{p}^{\times }$
. Hence in this case
$\mathbb{Z}_{p}^{\times }$
. Hence in this case
 $(L^{\times 2}\cap \mathbb{Q}_{p}^{\times })/\mathbb{Q}_{p}^{\times 2}$
and
$(L^{\times 2}\cap \mathbb{Q}_{p}^{\times })/\mathbb{Q}_{p}^{\times 2}$
and
 $(R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}$
are both equal to the group of order 2 generated by the class of
$(R^{\times 2}\cap \mathbb{Z}_{p}^{\times })/\mathbb{Z}_{p}^{\times 2}$
are both equal to the group of order 2 generated by the class of
![]() $u$
.◻
$u$
.◻
3 Interpretation using pencils of quadrics
In this section, we give geometric meanings to the notions of distinguished and soluble. For the proof of all the statements below, see [Reference WangWan13a, § 2.2]. These geometric interpretations are not necessary if one wants only the average size of the 2-Selmer groups.
Let
![]() $k$
be a field of characteristic not equal to 2 and let
$k$
be a field of characteristic not equal to 2 and let
![]() $f(x)$
be a monic separable polynomial of degree
$f(x)$
be a monic separable polynomial of degree
![]() $2n+2$
. Let
$2n+2$
. Let
![]() $C$
denote the monic even hyperelliptic curve defined by
$C$
denote the monic even hyperelliptic curve defined by
 $y^{2}=f(x)$
and let
$y^{2}=f(x)$
and let
![]() $\infty$
and
$\infty$
and
![]() $\infty ^{\prime }$
denote the two points above infinity. Let
$\infty ^{\prime }$
denote the two points above infinity. Let
![]() $T$
be a self-adjoint operator in
$T$
be a self-adjoint operator in
![]() $V_{f}(k)$
. One has a pencil of quadrics in
$V_{f}(k)$
. One has a pencil of quadrics in
![]() $U$
spanned by the following two quadrics:
$U$
spanned by the following two quadrics:
 $$\begin{eqnarray}\displaystyle Q(v) & = & \displaystyle \langle v,v\rangle _{Q},\nonumber\\ \displaystyle Q_{T}(v) & = & \displaystyle \langle v,Tv\rangle _{Q}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q(v) & = & \displaystyle \langle v,v\rangle _{Q},\nonumber\\ \displaystyle Q_{T}(v) & = & \displaystyle \langle v,Tv\rangle _{Q}.\nonumber\end{eqnarray}$$
This pencil is generic in the sense that there are precisely
![]() $2n+2$
singular quadrics among
$2n+2$
singular quadrics among
 $x_{1}Q-x_{2}Q_{T}$
for
$x_{1}Q-x_{2}Q_{T}$
for
 $[x_{1},x_{2}]\in \mathbb{P}^{1}$
, and that they are all simple cones. Its associated hyperelliptic curve
$[x_{1},x_{2}]\in \mathbb{P}^{1}$
, and that they are all simple cones. Its associated hyperelliptic curve
![]() $C^{\prime }$
is the curve parameterizing the rulings of the quadrics in the pencil. A ruling of a quadric
$C^{\prime }$
is the curve parameterizing the rulings of the quadrics in the pencil. A ruling of a quadric
![]() $Q_{0}$
is a connected component of the Lagrangian variety of maximal isotropic subspaces. When
$Q_{0}$
is a connected component of the Lagrangian variety of maximal isotropic subspaces. When
![]() $Q_{0}$
is a simple cone, there is only one ruling. When
$Q_{0}$
is a simple cone, there is only one ruling. When
![]() $Q_{0}$
is non-degenerate, there are two rulings defined over
$Q_{0}$
is non-degenerate, there are two rulings defined over
 $k(\sqrt{\operatorname{disc}(Q_{0})})$
. To give a point on
$k(\sqrt{\operatorname{disc}(Q_{0})})$
. To give a point on
![]() $C^{\prime }$
is the same as giving a quadric in the pencil along with a choice of ruling. Therefore, the curve
$C^{\prime }$
is the same as giving a quadric in the pencil along with a choice of ruling. Therefore, the curve
![]() $C^{\prime }$
is isomorphic over
$C^{\prime }$
is isomorphic over
![]() $k$
to the hyperelliptic curve
$k$
to the hyperelliptic curve
 $$\begin{eqnarray}y^{2}=\operatorname{disc}(xQ-Q_{T})=\operatorname{disc}(Q)\det (xI-T)=f(x),\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=\operatorname{disc}(xQ-Q_{T})=\operatorname{disc}(Q)\det (xI-T)=f(x),\end{eqnarray}$$
canonical up to the hyperelliptic involution.
We fix an isomorphism between
![]() $C^{\prime }$
and
$C^{\prime }$
and
![]() $C$
as follows. Recall the model space
$C$
as follows. Recall the model space
![]() $(L,\langle \,,\,\rangle )$
defined in § 2.2 where
$(L,\langle \,,\,\rangle )$
defined in § 2.2 where
 $L=k[x]/(f(x))=k[\unicode[STIX]{x1D6FD}]$
and
$L=k[x]/(f(x))=k[\unicode[STIX]{x1D6FD}]$
and
![]() $\langle \,,\,\rangle$
is the bilinear form on
$\langle \,,\,\rangle$
is the bilinear form on
![]() $L$
defined by
$L$
defined by
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle :=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\rangle :=\text{coefficient of}~\unicode[STIX]{x1D6FD}^{2n+1}\quad \text{in}~\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}=\operatorname{Tr}_{L/k}(\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}/f^{\prime }(\unicode[STIX]{x1D6FD})).\end{eqnarray}$$
This form is split since the
![]() $(n+1)$
-plane
$(n+1)$
-plane
 $Y=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n}\}$
is isotropic. We fix an isometry
$Y=\operatorname{Span}\{1,\unicode[STIX]{x1D6FD},\ldots ,\unicode[STIX]{x1D6FD}^{n}\}$
is isotropic. We fix an isometry
 $\unicode[STIX]{x1D704}:(L,\langle \,,\,\rangle )\rightarrow (U,\langle \,,\,\rangle _{Q})$
. Let
$\unicode[STIX]{x1D704}:(L,\langle \,,\,\rangle )\rightarrow (U,\langle \,,\,\rangle _{Q})$
. Let
![]() $Y_{0}$
denote ruling on
$Y_{0}$
denote ruling on
![]() $Q$
containing the isotropic
$Q$
containing the isotropic
![]() $(n+1)$
-plane
$(n+1)$
-plane
![]() $\unicode[STIX]{x1D704}(Y)$
. We fix an isomorphism
$\unicode[STIX]{x1D704}(Y)$
. We fix an isomorphism
![]() $C^{\prime }\simeq C$
so that the ruling
$C^{\prime }\simeq C$
so that the ruling
![]() $Y_{0}$
corresponds to
$Y_{0}$
corresponds to
 $\infty \in C(k)$
.
$\infty \in C(k)$
.
Since
![]() $C$
has a rational point, the Fano variety
$C$
has a rational point, the Fano variety
![]() $F_{T}$
of
$F_{T}$
of
![]() $n$
-planes isotropic with respect to both quadrics is a torsor of
$n$
-planes isotropic with respect to both quadrics is a torsor of
![]() $J$
of order dividing 2. In fact, it fits inside a disconnected algebraic group
$J$
of order dividing 2. In fact, it fits inside a disconnected algebraic group
 $$\begin{eqnarray}J\,\dot{\cup }\,F_{T}\,\dot{\cup }\,\text{Pic}^{1}(C)\,\dot{\cup }\,F_{T}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}J\,\dot{\cup }\,F_{T}\,\dot{\cup }\,\text{Pic}^{1}(C)\,\dot{\cup }\,F_{T}^{\prime }\end{eqnarray}$$
where
 $F_{T}^{\prime }\simeq F_{T}$
as varieties. Using the point
$F_{T}^{\prime }\simeq F_{T}$
as varieties. Using the point
![]() $\infty$
, one obtains a lift of
$\infty$
, one obtains a lift of
![]() $F_{T}$
to a torsor of
$F_{T}$
to a torsor of
![]() $J[2]$
by taking
$J[2]$
by taking
 $$\begin{eqnarray}\displaystyle F_{T}[2]_{\infty } & = & \displaystyle \{X\in F_{T}\mid X+X=(\infty )\}\nonumber\\ \displaystyle & = & \displaystyle \{X~n\text{-}\text{plane}\mid \operatorname{Span}\{X,TX\}~\text{is an isotropic}~(n+1)\text{-}\text{plane in the ruling}~Y_{0}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{T}[2]_{\infty } & = & \displaystyle \{X\in F_{T}\mid X+X=(\infty )\}\nonumber\\ \displaystyle & = & \displaystyle \{X~n\text{-}\text{plane}\mid \operatorname{Span}\{X,TX\}~\text{is an isotropic}~(n+1)\text{-}\text{plane in the ruling}~Y_{0}\}.\nonumber\end{eqnarray}$$
The second equality is [Reference WangWan13a, Proposition 2.32].
The group scheme
 $G=\operatorname{PSO}(U)$
acts on the
$G=\operatorname{PSO}(U)$
acts on the
![]() $k$
-scheme
$k$
-scheme
 $$\begin{eqnarray}W_{f}=\{(T,X)\mid T\in V_{f},X\in F_{T}[2]_{\infty }\}\end{eqnarray}$$
$$\begin{eqnarray}W_{f}=\{(T,X)\mid T\in V_{f},X\in F_{T}[2]_{\infty }\}\end{eqnarray}$$
via
 $g\cdot (T,X)=(gTg^{-1},gX)$
. Let
$g\cdot (T,X)=(gTg^{-1},gX)$
. Let
![]() $W_{T}$
denote the fiber above any fixed
$W_{T}$
denote the fiber above any fixed
 $T\in V_{f}(k)$
. This action is simply transitive on
$T\in V_{f}(k)$
. This action is simply transitive on
![]() $k$
-points [Reference WangWan13a, Corollary 2.36]. Hence for any
$k$
-points [Reference WangWan13a, Corollary 2.36]. Hence for any
 $T\in V_{f}(k)$
, the above action induces a simply transitive action of
$T\in V_{f}(k)$
, the above action induces a simply transitive action of
 $J[2]\simeq \operatorname{Stab}_{G}(T)$
on the fiber
$J[2]\simeq \operatorname{Stab}_{G}(T)$
on the fiber
 $W_{T}=F_{T}[2]_{\infty }$
.
$W_{T}=F_{T}[2]_{\infty }$
.
Theorem 16 ([Reference WangWan13a, Proposition 2.38], [Reference WangWan13b, Lemma 2.19]).
These two actions of
![]() $J[2]$
coincide, and as elements of
$J[2]$
coincide, and as elements of
 $H^{1}(k,J[2])$
,
$H^{1}(k,J[2])$
,
 $$\begin{eqnarray}[F_{T}[2]_{\infty }]=[W_{T}]=c_{T},\end{eqnarray}$$
$$\begin{eqnarray}[F_{T}[2]_{\infty }]=[W_{T}]=c_{T},\end{eqnarray}$$
where
 $c_{T}\in H^{1}(k,J[2])$
is defined in (2).
$c_{T}\in H^{1}(k,J[2])$
is defined in (2).
Theorem 16 gives a geometric realization of torsors of
![]() $J[2]$
using pencils of quadrics. For hyperelliptic curves with a rational Weierstrass point, one can obtain all torsors of
$J[2]$
using pencils of quadrics. For hyperelliptic curves with a rational Weierstrass point, one can obtain all torsors of
![]() $J[2]$
using pencils of quadrics [Reference WangWan13b, Proposition 2.11]. For hyperelliptic curves with no rational Weierstrass point but with a rational non-Weierstrass point, not all torsors of
$J[2]$
using pencils of quadrics [Reference WangWan13b, Proposition 2.11]. For hyperelliptic curves with no rational Weierstrass point but with a rational non-Weierstrass point, not all torsors of
![]() $J[2]$
arise as some
$J[2]$
arise as some
![]() $F_{T}[2]_{\infty }$
coming from a pencil of quadrics, but all of them that correspond to
$F_{T}[2]_{\infty }$
coming from a pencil of quadrics, but all of them that correspond to
 $\operatorname{PSO}(U)(k)$
-orbits do.
$\operatorname{PSO}(U)(k)$
-orbits do.
Suppose
 $T\in V_{f}(k)$
. From (15), we see that there exists a
$T\in V_{f}(k)$
. From (15), we see that there exists a
![]() $k$
-rational
$k$
-rational
![]() $n$
-plane
$n$
-plane
![]() $X$
such that
$X$
such that
 $\operatorname{Span}\{X,TX\}$
is an isotropic
$\operatorname{Span}\{X,TX\}$
is an isotropic
![]() $(n+1)$
-plane if and only if at least one of
$(n+1)$
-plane if and only if at least one of
 $[F_{T}[2]_{\infty }]$
and
$[F_{T}[2]_{\infty }]$
and
 $[F_{T}[2]_{\infty ^{\prime }}]$
is trivial. Again by (15), this is equivalent to
$[F_{T}[2]_{\infty ^{\prime }}]$
is trivial. Again by (15), this is equivalent to
![]() $c_{T}$
being in the image of the subgroup generated by
$c_{T}$
being in the image of the subgroup generated by
 $(\infty ^{\prime })-(\infty )\in J(k)/2J(k)$
under the Kummer map
$(\infty ^{\prime })-(\infty )\in J(k)/2J(k)$
under the Kummer map
 $J(k)/2J(k){\hookrightarrow}H^{1}(k,J[2])$
. Commutativity of the top left square in (11) implies that this is in turn equivalent to
$J(k)/2J(k){\hookrightarrow}H^{1}(k,J[2])$
. Commutativity of the top left square in (11) implies that this is in turn equivalent to
![]() $c_{T}$
mapping to 0 in
$c_{T}$
mapping to 0 in
 $H^{1}(k,\operatorname{Stab}_{\operatorname{PO}(U)}(T))$
. Finally, this is equivalent to
$H^{1}(k,\operatorname{Stab}_{\operatorname{PO}(U)}(T))$
. Finally, this is equivalent to
![]() $T$
being distinguished. We have therefore proved Proposition 6.
$T$
being distinguished. We have therefore proved Proposition 6.
Since
 $[F_{T}[2]_{\infty }]$
maps to
$[F_{T}[2]_{\infty }]$
maps to
![]() $[F_{T}]$
under the canonical map
$[F_{T}]$
under the canonical map
 $H^{1}(k,J[2])\rightarrow H^{1}(k,J)[2]$
, we see that
$H^{1}(k,J[2])\rightarrow H^{1}(k,J)[2]$
, we see that
![]() $T$
is soluble if and only if
$T$
is soluble if and only if
 $F_{T}(k)\neq \emptyset$
. This equivalence of solubility and the existence of rational points is the main reason why the name ‘soluble’ is used. Likewise,
$F_{T}(k)\neq \emptyset$
. This equivalence of solubility and the existence of rational points is the main reason why the name ‘soluble’ is used. Likewise,
![]() $T$
is locally soluble if and only if
$T$
is locally soluble if and only if
 $F_{T}(k_{\unicode[STIX]{x1D708}})\neq \emptyset$
at all places
$F_{T}(k_{\unicode[STIX]{x1D708}})\neq \emptyset$
at all places
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
We now give a complete proof for the claim that if
 $\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}k^{\times })_{N=1}$
lies in the image of
$\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}k^{\times })_{N=1}$
lies in the image of
![]() $\unicode[STIX]{x1D6FF}^{\prime }$
, then
$\unicode[STIX]{x1D6FF}^{\prime }$
, then
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. Consider the pencil of quadrics in
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split. Consider the pencil of quadrics in
![]() $L$
spanned by the following two quadrics:
$L$
spanned by the following two quadrics:
 $$\begin{eqnarray}\displaystyle Q_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D706}) & = & \displaystyle \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle _{\unicode[STIX]{x1D6FC}},\nonumber\\ \displaystyle Q_{\unicode[STIX]{x1D6FC}}^{\prime }(\unicode[STIX]{x1D706}) & = & \displaystyle \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}\rangle _{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D706}) & = & \displaystyle \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D706}\rangle _{\unicode[STIX]{x1D6FC}},\nonumber\\ \displaystyle Q_{\unicode[STIX]{x1D6FC}}^{\prime }(\unicode[STIX]{x1D706}) & = & \displaystyle \langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}\rangle _{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
This pencil is once again generic, its associated hyperelliptic curve
![]() $C_{\unicode[STIX]{x1D6FC}}$
is smooth of genus
$C_{\unicode[STIX]{x1D6FC}}$
is smooth of genus
![]() $n$
isomorphic non-canonically to the hyperelliptic curve defined by affine equation
$n$
isomorphic non-canonically to the hyperelliptic curve defined by affine equation
 $$\begin{eqnarray}y^{2}=\operatorname{disc}(xQ_{\unicode[STIX]{x1D6FC}}-Q_{\unicode[STIX]{x1D6FC}}^{\prime })=N_{L/k}(\unicode[STIX]{x1D6FC})f(x).\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=\operatorname{disc}(xQ_{\unicode[STIX]{x1D6FC}}-Q_{\unicode[STIX]{x1D6FC}}^{\prime })=N_{L/k}(\unicode[STIX]{x1D6FC})f(x).\end{eqnarray}$$
Since
 $N_{L/k}(\unicode[STIX]{x1D6FC})\in k^{\times 2}$
, the curve
$N_{L/k}(\unicode[STIX]{x1D6FC})\in k^{\times 2}$
, the curve
![]() $C_{\unicode[STIX]{x1D6FC}}$
is isomorphic to
$C_{\unicode[STIX]{x1D6FC}}$
is isomorphic to
![]() $C$
over
$C$
over
![]() $k$
. Fix any isomorphism
$k$
. Fix any isomorphism
 $C_{\unicode[STIX]{x1D6FC}}^{\prime }\simeq C$
. The Fano variety
$C_{\unicode[STIX]{x1D6FC}}^{\prime }\simeq C$
. The Fano variety
![]() $F_{\unicode[STIX]{x1D6FC}}$
of
$F_{\unicode[STIX]{x1D6FC}}$
of
![]() $n$
-planes isotropic with respect to both quadrics is a torsor of
$n$
-planes isotropic with respect to both quadrics is a torsor of
![]() $J$
of order dividing 2. There are two natural lifts of
$J$
of order dividing 2. There are two natural lifts of
![]() $F_{\unicode[STIX]{x1D6FC}}$
to torsors of
$F_{\unicode[STIX]{x1D6FC}}$
to torsors of
![]() $J[2]$
by taking
$J[2]$
by taking
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6FC}}[2]_{\infty }=\{X\in F\mid X+X=(\infty )\}\quad \text{or}\quad F_{\unicode[STIX]{x1D6FC}}[2]_{\infty ^{\prime }}=\{X\in F\mid X+X=(\infty ^{\prime })\}.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6FC}}[2]_{\infty }=\{X\in F\mid X+X=(\infty )\}\quad \text{or}\quad F_{\unicode[STIX]{x1D6FC}}[2]_{\infty ^{\prime }}=\{X\in F\mid X+X=(\infty ^{\prime })\}.\end{eqnarray}$$
As elements of
 $H^{1}(k,J[2])$
, these two lifts map to the same class in
$H^{1}(k,J[2])$
, these two lifts map to the same class in
 $H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})$
. The class
$H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})$
. The class
![]() $\unicode[STIX]{x1D6FC}$
also maps to a class in
$\unicode[STIX]{x1D6FC}$
also maps to a class in
 $H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})$
as in (11). By [Reference WangWan13b, Proposition 2.27], these two classes coincide. Suppose
$H^{1}(k,\text{Res}_{L/k}\unicode[STIX]{x1D707}_{2}/\unicode[STIX]{x1D707}_{2})$
as in (11). By [Reference WangWan13b, Proposition 2.27], these two classes coincide. Suppose
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}^{\prime }([D])$
comes from
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}^{\prime }([D])$
comes from
 $J(k)/2J(k)$
. Then one of these two lifts recovers
$J(k)/2J(k)$
. Then one of these two lifts recovers
![]() $[D]$
and hence
$[D]$
and hence
 $F_{\unicode[STIX]{x1D6FC}}(k)\neq \emptyset$
. Pick any
$F_{\unicode[STIX]{x1D6FC}}(k)\neq \emptyset$
. Pick any
 $X\in F_{\unicode[STIX]{x1D6FC}}(k)$
. If
$X\in F_{\unicode[STIX]{x1D6FC}}(k)$
. If
 $X+X=(\infty )$
, then
$X+X=(\infty )$
, then
![]() $[D]=0$
,
$[D]=0$
,
![]() $\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FC}=1$
and
![]() $\langle \,,\,\rangle$
is split. Otherwise,
$\langle \,,\,\rangle$
is split. Otherwise,
 $\operatorname{Span}\{X,(\infty )-X\}$
is a
$\operatorname{Span}\{X,(\infty )-X\}$
is a
![]() $k$
-rational
$k$
-rational
![]() $(n+1)$
-plane isotropic with respect to
$(n+1)$
-plane isotropic with respect to
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
implying again that
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
implying again that
![]() $\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split.
$\langle \,,\,\rangle _{\unicode[STIX]{x1D6FC}}$
is split.
4 Orbit counting
In this section, we let the polynomial
![]() $f(x)$
vary in the family of monic polynomials of degree
$f(x)$
vary in the family of monic polynomials of degree
![]() $2n+2$
over
$2n+2$
over
![]() $\mathbb{Z}$
whose
$\mathbb{Z}$
whose
![]() $x^{2n+1}$
-coefficient is 0 and count the average number of locally soluble orbits of the action of
$x^{2n+1}$
-coefficient is 0 and count the average number of locally soluble orbits of the action of
![]() $G(\mathbb{Q})$
on
$G(\mathbb{Q})$
on
![]() $V_{f}(\mathbb{Q})$
. We redefine
$V_{f}(\mathbb{Q})$
. We redefine
![]() $V$
to be the following scheme over
$V$
to be the following scheme over
![]() $\mathbb{Z}$
:
$\mathbb{Z}$
:
 $$\begin{eqnarray}V=\{B\in M_{(2n+2)\times (2n+2)}\mid B=B^{t},B~\text{has anti}\text{-}\text{trace}~0\}\simeq \mathbb{A}_{\mathbb{ Z}}^{2n^{2}+5n+2},\end{eqnarray}$$
$$\begin{eqnarray}V=\{B\in M_{(2n+2)\times (2n+2)}\mid B=B^{t},B~\text{has anti}\text{-}\text{trace}~0\}\simeq \mathbb{A}_{\mathbb{ Z}}^{2n^{2}+5n+2},\end{eqnarray}$$
consisting of symmetric
 $(2n+2)\times (2n+2)$
matrices with anti-trace
$(2n+2)\times (2n+2)$
matrices with anti-trace
![]() $0$
. Recall that the anti-trace is the sum of the entries on the anti-diagonal. We impose the extra condition on the anti-trace since the
$0$
. Recall that the anti-trace is the sum of the entries on the anti-diagonal. We impose the extra condition on the anti-trace since the
![]() $x^{2n+1}$
-coefficients of our polynomials are 0. One passes between self-adjoint operators
$x^{2n+1}$
-coefficients of our polynomials are 0. One passes between self-adjoint operators
![]() $T$
and symmetric matrices
$T$
and symmetric matrices
![]() $B$
via the relation
$B$
via the relation
 $B=AT$
. This change of perspective is only to simplify notation in what follows. We view elements of the group
$B=AT$
. This change of perspective is only to simplify notation in what follows. We view elements of the group
![]() $\operatorname{SO}_{2n+2}$
also as
$\operatorname{SO}_{2n+2}$
also as
 $(2n+2)\times (2n+2)$
matrices using the standard basis defined in (4). The group
$(2n+2)\times (2n+2)$
matrices using the standard basis defined in (4). The group
 $G=\operatorname{PSO}_{2n+2}$
acts on
$G=\operatorname{PSO}_{2n+2}$
acts on
![]() $V$
by
$V$
by
 $g\cdot B:=gBg^{t}$
. The ring of polynomial invariants for this action is freely generated by the coefficients
$g\cdot B:=gBg^{t}$
. The ring of polynomial invariants for this action is freely generated by the coefficients
 $c_{2},\ldots ,c_{2n+2}$
of the invariant polynomial
$c_{2},\ldots ,c_{2n+2}$
of the invariant polynomial
 $\det (Ax-By)$
. Indeed, Proposition 4 implies that there are no other independent polynomial invariants, and the existence of a self-adjoint operator
$\det (Ax-By)$
. Indeed, Proposition 4 implies that there are no other independent polynomial invariants, and the existence of a self-adjoint operator
![]() $T_{f}$
with any given characteristic polynomial
$T_{f}$
with any given characteristic polynomial
![]() $f(x)$
obtained in § 2.2 shows that there are no relations among these invariants. We define the scheme
$f(x)$
obtained in § 2.2 shows that there are no relations among these invariants. We define the scheme
![]() $S$
to be
$S$
to be
 $$\begin{eqnarray}S=\operatorname{Spec}\mathbb{Z}[c_{2},\ldots ,c_{2n+2}].\end{eqnarray}$$
$$\begin{eqnarray}S=\operatorname{Spec}\mathbb{Z}[c_{2},\ldots ,c_{2n+2}].\end{eqnarray}$$
The map
 $\unicode[STIX]{x1D70B}:V\rightarrow S$
is given by the coefficients of the invariant polynomial; we call
$\unicode[STIX]{x1D70B}:V\rightarrow S$
is given by the coefficients of the invariant polynomial; we call
![]() $\unicode[STIX]{x1D70B}(B)$
the invariant of
$\unicode[STIX]{x1D70B}(B)$
the invariant of
![]() $B$
.
$B$
.
A point
 $c=(c_{2},\ldots ,c_{2n+2})\in S(\mathbb{R})$
corresponds to a monic polynomial
$c=(c_{2},\ldots ,c_{2n+2})\in S(\mathbb{R})$
corresponds to a monic polynomial
 $$\begin{eqnarray}f_{c}(x):=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2}.\end{eqnarray}$$
$$\begin{eqnarray}f_{c}(x):=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2}.\end{eqnarray}$$
We define its height
![]() $H(f_{c})$
by
$H(f_{c})$
by
 $$\begin{eqnarray}H(f_{c}):=H(c):=\max \{|c_{k}|^{1/k}\}_{k=2}^{2n+2}.\end{eqnarray}$$
$$\begin{eqnarray}H(f_{c}):=H(c):=\max \{|c_{k}|^{1/k}\}_{k=2}^{2n+2}.\end{eqnarray}$$
The height of
 $B\in V(\mathbb{R})$
is defined to be the height of
$B\in V(\mathbb{R})$
is defined to be the height of
![]() $\unicode[STIX]{x1D70B}(B)$
, and the height of the hyperelliptic curve
$\unicode[STIX]{x1D70B}(B)$
, and the height of the hyperelliptic curve
![]() $C(c)$
given by
$C(c)$
given by
 $y^{2}=f_{c}(x)$
is defined to be
$y^{2}=f_{c}(x)$
is defined to be
![]() $H(c)$
.
$H(c)$
.
For each prime
![]() $p$
, let
$p$
, let
![]() $\unicode[STIX]{x1D6F4}_{p}$
be a closed subset of
$\unicode[STIX]{x1D6F4}_{p}$
be a closed subset of
 $S(\mathbb{Z}_{p})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
whose boundary has measure 0. Let
$S(\mathbb{Z}_{p})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
whose boundary has measure 0. Let
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
be the set of all
$\unicode[STIX]{x1D6F4}_{\infty }$
be the set of all
 $c\in S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that the corresponding polynomial
$c\in S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that the corresponding polynomial
![]() $f_{c}$
has
$f_{c}$
has
![]() $m$
distinct pairs of complex conjugate roots, where
$m$
distinct pairs of complex conjugate roots, where
![]() $m$
belongs to a fixed subset of
$m$
belongs to a fixed subset of
 $\{0,\ldots ,n+1\}$
. To such a collection
$\{0,\ldots ,n+1\}$
. To such a collection
![]() $(\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D708}})_{\unicode[STIX]{x1D708}}$
we associate the family
$(\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D708}})_{\unicode[STIX]{x1D708}}$
we associate the family
 $F=F_{\unicode[STIX]{x1D6F4}}$
of monic even hyperelliptic curves, where
$F=F_{\unicode[STIX]{x1D6F4}}$
of monic even hyperelliptic curves, where
 $C(c)\in F$
if and only if
$C(c)\in F$
if and only if
![]() $c\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D708}}$
for all places
$c\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D708}}$
for all places
![]() $\unicode[STIX]{x1D708}$
. Such a family is said to be defined by congruence conditions.
$\unicode[STIX]{x1D708}$
. Such a family is said to be defined by congruence conditions.
Given a family
![]() $F$
of monic even hyperelliptic curves defined by congruence conditions, let
$F$
of monic even hyperelliptic curves defined by congruence conditions, let
 $\operatorname{Inv}(F)\subset S(\mathbb{Z})$
denote the set of coefficients of the defining affine equations. We denote the
$\operatorname{Inv}(F)\subset S(\mathbb{Z})$
denote the set of coefficients of the defining affine equations. We denote the
![]() $p$
-adic closure of
$p$
-adic closure of
![]() $\operatorname{Inv}(F)$
in
$\operatorname{Inv}(F)$
in
 $S(\mathbb{Z}_{p})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
by
$S(\mathbb{Z}_{p})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
by
 $\operatorname{Inv}_{p}(F)$
. We say that a family
$\operatorname{Inv}_{p}(F)$
. We say that a family
![]() $F$
defined by congruence conditions is large at
$F$
defined by congruence conditions is large at
![]() $p$
if
$p$
if
 $\operatorname{Inv}_{p}(F)$
contains every element
$\operatorname{Inv}_{p}(F)$
contains every element
 $c\in S(\mathbb{Z}_{p})$
such that
$c\in S(\mathbb{Z}_{p})$
such that
 $p^{2}\nmid \unicode[STIX]{x1D6E5}(c)$
. Finally, we say that
$p^{2}\nmid \unicode[STIX]{x1D6E5}(c)$
. Finally, we say that
![]() $F$
and
$F$
and
![]() $\operatorname{Inv}(F)$
are large if
$\operatorname{Inv}(F)$
are large if
![]() $F$
is large at all but finitely many primes. An example of a large subset of
$F$
is large at all but finitely many primes. An example of a large subset of
![]() $S(\mathbb{Z})$
is the set
$S(\mathbb{Z})$
is the set
 $$\begin{eqnarray}F_{0}=\{(c_{2},\ldots ,c_{2n+2})\in S(\mathbb{Z})\mid p^{2k}\nmid c_{k},\forall k=2,\ldots ,2n+2,\forall p,\text{prime}\}.\end{eqnarray}$$
$$\begin{eqnarray}F_{0}=\{(c_{2},\ldots ,c_{2n+2})\in S(\mathbb{Z})\mid p^{2k}\nmid c_{k},\forall k=2,\ldots ,2n+2,\forall p,\text{prime}\}.\end{eqnarray}$$
Another example is the set of elements in
![]() $S(\mathbb{Z})$
having squarefree discriminant.
$S(\mathbb{Z})$
having squarefree discriminant.
In this section, our goal is to prove the following strengthening of Theorem 2.
Theorem 17. When all hyperelliptic curves over
![]() $\mathbb{Q}$
of genus
$\mathbb{Q}$
of genus
![]() $n$
with a marked rational non-Weierstrass point in any large family are ordered by height, the average size of the
$n$
with a marked rational non-Weierstrass point in any large family are ordered by height, the average size of the
![]() $2$
-Selmer groups of their Jacobians is at most
$2$
-Selmer groups of their Jacobians is at most
![]() $6$
.
$6$
.
In view of the correspondence (Theorem 11) between locally soluble orbits and 2-Selmer elements, the above result is an immediate consequence of the following theorem.
Theorem 18. The average number of locally soluble orbits for the action of
![]() $G(\mathbb{Q})$
on
$G(\mathbb{Q})$
on
![]() $V_{f}(\mathbb{Q})$
as
$V_{f}(\mathbb{Q})$
as
![]() $f$
runs through any large subset of
$f$
runs through any large subset of
![]() $S(\mathbb{Z})$
, when ordered by height, is at most
$S(\mathbb{Z})$
, when ordered by height, is at most
![]() $6$
.
$6$
.
This section is organized as follows. First, in § 4.1, we construct fundamental domains for the action of
![]() $G(\mathbb{Z})$
on the set of
$G(\mathbb{Z})$
on the set of
![]() $\mathbb{R}$
-soluble elements in
$\mathbb{R}$
-soluble elements in
![]() $V(\mathbb{R})$
. In § 4.2, we then use geometry-of-numbers techniques developed by Bhargava to determine the asymptotics for the number of
$V(\mathbb{R})$
. In § 4.2, we then use geometry-of-numbers techniques developed by Bhargava to determine the asymptotics for the number of
![]() $\mathbb{R}$
-soluble
$\mathbb{R}$
-soluble
![]() $G(\mathbb{Z})$
-orbits on non-distinguished elements in
$G(\mathbb{Z})$
-orbits on non-distinguished elements in
![]() $V(\mathbb{Z})$
having non-zero discriminant and bounded height. In § 4.3, we bound the number of weighted
$V(\mathbb{Z})$
having non-zero discriminant and bounded height. In § 4.3, we bound the number of weighted
![]() $G(\mathbb{Z})$
-orbits, where the weights are products of
$G(\mathbb{Z})$
-orbits, where the weights are products of
![]() $p$
-adic weights over all
$p$
-adic weights over all
![]() $p$
. We also determine the number of monic even hyperelliptic curves having bounded height in any large family. Finally, in § 4.4, we deduce Theorem 18.
$p$
. We also determine the number of monic even hyperelliptic curves having bounded height in any large family. Finally, in § 4.4, we deduce Theorem 18.
4.1 Construction of fundamental domains
Let
![]() $V(\mathbb{R})^{\text{sol}}$
denote the set of
$V(\mathbb{R})^{\text{sol}}$
denote the set of
![]() $\mathbb{R}$
-soluble elements in
$\mathbb{R}$
-soluble elements in
![]() $V(\mathbb{R})$
having non-zero discriminant. We partition
$V(\mathbb{R})$
having non-zero discriminant. We partition
 $V(\mathbb{R})^{\text{sol}}$
into
$V(\mathbb{R})^{\text{sol}}$
into
![]() $n+2$
sets,
$n+2$
sets,
 $$\begin{eqnarray}V(\mathbb{R})^{\text{sol}}=\mathop{\bigcup }_{m=0}^{n+1}V(\mathbb{R})^{(m)},\end{eqnarray}$$
$$\begin{eqnarray}V(\mathbb{R})^{\text{sol}}=\mathop{\bigcup }_{m=0}^{n+1}V(\mathbb{R})^{(m)},\end{eqnarray}$$
where
 $V(\mathbb{R})^{(m)}$
consists of elements
$V(\mathbb{R})^{(m)}$
consists of elements
 $B\in V(\mathbb{R})^{\text{sol}}$
such that the polynomial corresponding to
$B\in V(\mathbb{R})^{\text{sol}}$
such that the polynomial corresponding to
![]() $\unicode[STIX]{x1D70B}(B)$
has
$\unicode[STIX]{x1D70B}(B)$
has
![]() $m$
pairs of complex conjugate roots (and
$m$
pairs of complex conjugate roots (and
 $2n+2-2m$
real roots). In this subsection, our goal is to describe convenient fundamental domains for the action of
$2n+2-2m$
real roots). In this subsection, our goal is to describe convenient fundamental domains for the action of
![]() $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
 $V(\mathbb{R})^{(m)}$
for
$V(\mathbb{R})^{(m)}$
for
 $m\in \{0,\ldots ,n+1\}$
.
$m\in \{0,\ldots ,n+1\}$
.
4.1.1 Fundamental sets for the action of
 $G(\mathbb{R})$
on
$G(\mathbb{R})$
on
 $V(\mathbb{R})^{\text{sol}}$
$V(\mathbb{R})^{\text{sol}}$
First, we construct convenient fundamental sets for the action of
![]() $G(\mathbb{R})$
on
$G(\mathbb{R})$
on
 $V(\mathbb{R})^{(m)}$
. Let
$V(\mathbb{R})^{(m)}$
. Let
 $S(\mathbb{R})^{(m)}$
denote the set of elements
$S(\mathbb{R})^{(m)}$
denote the set of elements
 $c\in S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that the corresponding polynomial has
$c\in S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that the corresponding polynomial has
![]() $m$
pairs of complex conjugate roots. There exists an algebraic section
$m$
pairs of complex conjugate roots. There exists an algebraic section
 $\unicode[STIX]{x1D705}:S\rightarrow V$
defined over
$\unicode[STIX]{x1D705}:S\rightarrow V$
defined over
![]() $\mathbb{Z}[1/2]$
such that every element in the image of
$\mathbb{Z}[1/2]$
such that every element in the image of
 $S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
under
$S(\mathbb{R})\backslash \{\unicode[STIX]{x1D6E5}=0\}$
under
![]() $\unicode[STIX]{x1D705}$
is distinguished [Reference WangWan13b, § 3.1]. The number of
$\unicode[STIX]{x1D705}$
is distinguished [Reference WangWan13b, § 3.1]. The number of
![]() $\mathbb{R}$
-soluble
$\mathbb{R}$
-soluble
![]() $G(\mathbb{R})$
-orbits in
$G(\mathbb{R})$
-orbits in
![]() $V_{f_{c}}(\mathbb{R})$
, for
$V_{f_{c}}(\mathbb{R})$
, for
 $c\in S(\mathbb{R})^{(m)}$
, depends only on
$c\in S(\mathbb{R})^{(m)}$
, depends only on
![]() $m$
. We denote it by
$m$
. We denote it by
![]() $\unicode[STIX]{x1D70F}_{m}$
. There exist elements
$\unicode[STIX]{x1D70F}_{m}$
. There exist elements
 $g_{1},\ldots ,g_{\unicode[STIX]{x1D70F}_{m}}\in \operatorname{GL}(U)(\mathbb{R})$
such that the set
$g_{1},\ldots ,g_{\unicode[STIX]{x1D70F}_{m}}\in \operatorname{GL}(U)(\mathbb{R})$
such that the set
 $$\begin{eqnarray}R^{\prime (m)}:=\mathop{\bigcup }_{i}g_{i}\unicode[STIX]{x1D705}(S(\mathbb{R})^{(m)})g_{i}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}R^{\prime (m)}:=\mathop{\bigcup }_{i}g_{i}\unicode[STIX]{x1D705}(S(\mathbb{R})^{(m)})g_{i}^{-1}\end{eqnarray}$$
is a fundamental set for
 $G(\mathbb{R})\backslash V(\mathbb{R})^{(m)}$
. Indeed, since
$G(\mathbb{R})\backslash V(\mathbb{R})^{(m)}$
. Indeed, since
 $L:=\mathbb{R}[x]/(f_{c}(x))$
is independent of
$L:=\mathbb{R}[x]/(f_{c}(x))$
is independent of
 $c\in S(\mathbb{R})^{(m)}$
, an element
$c\in S(\mathbb{R})^{(m)}$
, an element
 $g\in \operatorname{GL}(U)(\mathbb{R})$
that conjugates
$g\in \operatorname{GL}(U)(\mathbb{R})$
that conjugates
![]() $\unicode[STIX]{x1D705}(c_{0})$
, for any fixed
$\unicode[STIX]{x1D705}(c_{0})$
, for any fixed
 $c_{0}\in S(\mathbb{Q})^{(m)}$
, to a
$c_{0}\in S(\mathbb{Q})^{(m)}$
, to a
![]() $G(\mathbb{R})$
-orbit corresponding to a class
$G(\mathbb{R})$
-orbit corresponding to a class
 $\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}\mathbb{R}^{\times })_{N=1}$
does so for every
$\unicode[STIX]{x1D6FC}\in (L^{\times }/L^{\times 2}\mathbb{R}^{\times })_{N=1}$
does so for every
 $c\in S(\mathbb{R})^{(m)}$
.
$c\in S(\mathbb{R})^{(m)}$
.
We now construct our fundamental set
![]() $R^{(m)}$
for
$R^{(m)}$
for
 $G(\mathbb{R})\backslash V(\mathbb{R})^{(m)}$
to be
$G(\mathbb{R})\backslash V(\mathbb{R})^{(m)}$
to be
 $$\begin{eqnarray}R^{(m)}:=\mathbb{R}_{{>}0}\cdot \{B\in R^{\prime (m)}:H(B)=1\}.\end{eqnarray}$$
$$\begin{eqnarray}R^{(m)}:=\mathbb{R}_{{>}0}\cdot \{B\in R^{\prime (m)}:H(B)=1\}.\end{eqnarray}$$
The reason why we use the set
![]() $R^{(m)}$
instead of
$R^{(m)}$
instead of
![]() $R^{\prime (m)}$
is that the sizes of the coefficients of elements in
$R^{\prime (m)}$
is that the sizes of the coefficients of elements in
![]() $R^{(m)}$
having height
$R^{(m)}$
having height
![]() $X$
are bounded by
$X$
are bounded by
 $O(X^{1/d})$
, where
$O(X^{1/d})$
, where
 $d=(2n+2)(2n+1)$
is the degree of the height function. This follows because the elements in
$d=(2n+2)(2n+1)$
is the degree of the height function. This follows because the elements in
![]() $R^{\prime (m)}$
having height 1 lie in a bounded subset of
$R^{\prime (m)}$
having height 1 lie in a bounded subset of
![]() $V(\mathbb{R})$
.
$V(\mathbb{R})$
.
4.1.2 Fundamental domains for the action of
 $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
 $G(\mathbb{R})$
$G(\mathbb{R})$
We now describe Borel’s construction [Reference BorelBor62] of a fundamental domain
![]() ${\mathcal{F}}$
for the left action of
${\mathcal{F}}$
for the left action of
![]() $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
![]() $G(\mathbb{R})$
. Since
$G(\mathbb{R})$
. Since
 $G(\mathbb{R})=\operatorname{SO}(U)(\mathbb{R})/\{\pm 1\}$
, and
$G(\mathbb{R})=\operatorname{SO}(U)(\mathbb{R})/\{\pm 1\}$
, and
 $\{\pm 1\}\subset \operatorname{SO}(U)(\mathbb{Z})$
, the image in
$\{\pm 1\}\subset \operatorname{SO}(U)(\mathbb{Z})$
, the image in
![]() $G(\mathbb{R})$
of a fundamental domain for
$G(\mathbb{R})$
of a fundamental domain for
 $\operatorname{SO}(U)(\mathbb{Z})\backslash \operatorname{SO}(U)(\mathbb{R})$
will map bijectively onto a fundamental domain for
$\operatorname{SO}(U)(\mathbb{Z})\backslash \operatorname{SO}(U)(\mathbb{R})$
will map bijectively onto a fundamental domain for
 $G(\mathbb{Z})\backslash G(\mathbb{R})$
. We will abuse notation and refer to both fundamental domains by
$G(\mathbb{Z})\backslash G(\mathbb{R})$
. We will abuse notation and refer to both fundamental domains by
![]() ${\mathcal{F}}$
. Let
${\mathcal{F}}$
. Let
 $\operatorname{SO}(U)(\mathbb{R})=NTK$
be the Iwasawa decomposition of
$\operatorname{SO}(U)(\mathbb{R})=NTK$
be the Iwasawa decomposition of
 $\operatorname{SO}(U)(\mathbb{R})$
. Here,
$\operatorname{SO}(U)(\mathbb{R})$
. Here,
![]() $N$
denotes the set of unipotent lower triangular matrices,
$N$
denotes the set of unipotent lower triangular matrices,
![]() $T$
denotes the set of diagonal matrices, and
$T$
denotes the set of diagonal matrices, and
![]() $K$
is a maximal compact subgroup. Then the fundamental domain
$K$
is a maximal compact subgroup. Then the fundamental domain
![]() ${\mathcal{F}}$
may be expressed in the form
${\mathcal{F}}$
may be expressed in the form
 $$\begin{eqnarray}{\mathcal{F}}:=\{utk\mid u\in N^{\prime }(t),t\in T^{\prime },k\in K\}\subset N^{\prime }T^{\prime }K,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}:=\{utk\mid u\in N^{\prime }(t),t\in T^{\prime },k\in K\}\subset N^{\prime }T^{\prime }K,\end{eqnarray}$$
where
 $N^{\prime }\subset N$
is a bounded set,
$N^{\prime }\subset N$
is a bounded set,
 $N^{\prime }(t)\subset N^{\prime }$
is a measurable set depending on
$N^{\prime }(t)\subset N^{\prime }$
is a measurable set depending on
![]() $t\in T^{\prime }$
, and
$t\in T^{\prime }$
, and
![]() $T^{\prime }\subset T$
is given by
$T^{\prime }\subset T$
is given by
 $$\begin{eqnarray}T^{\prime }:=\{\text{diag}(t_{1}^{-1},t_{2}^{-1},\ldots ,t_{n+1}^{-1},t_{n+1},\ldots ,t_{1})\mid t_{1}/t_{2}>c,\ldots ,t_{n}/t_{n+1}>c,t_{n}t_{n+1}>c\},\end{eqnarray}$$
$$\begin{eqnarray}T^{\prime }:=\{\text{diag}(t_{1}^{-1},t_{2}^{-1},\ldots ,t_{n+1}^{-1},t_{n+1},\ldots ,t_{1})\mid t_{1}/t_{2}>c,\ldots ,t_{n}/t_{n+1}>c,t_{n}t_{n+1}>c\},\end{eqnarray}$$
for some constant
![]() $c>0$
.
$c>0$
.
4.1.3 Fundamental domains for the action of
 $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
 $V(\mathbb{R})^{\text{sol}}$
$V(\mathbb{R})^{\text{sol}}$
For
 $h\in G(\mathbb{R})$
, we regard
$h\in G(\mathbb{R})$
, we regard
 ${\mathcal{F}}h\cdot R^{(m)}$
as a multiset, where the multiplicity of
${\mathcal{F}}h\cdot R^{(m)}$
as a multiset, where the multiplicity of
![]() $B$
in
$B$
in
 ${\mathcal{F}}h\cdot R^{(m)}$
is given by
${\mathcal{F}}h\cdot R^{(m)}$
is given by
 $\#\{g\in {\mathcal{F}}\mid B\in gh\cdot R^{(m)}\}$
. The
$\#\{g\in {\mathcal{F}}\mid B\in gh\cdot R^{(m)}\}$
. The
![]() $G(\mathbb{Z})$
-orbit of any
$G(\mathbb{Z})$
-orbit of any
 $B\in V(\mathbb{R})$
is represented
$B\in V(\mathbb{R})$
is represented
 $\#\text{Stab}_{G(\mathbb{R})}(B)/\#\text{Stab}_{G(\mathbb{Z})}(B)$
times in this multiset
$\#\text{Stab}_{G(\mathbb{R})}(B)/\#\text{Stab}_{G(\mathbb{Z})}(B)$
times in this multiset
 ${\mathcal{F}}h\cdot R^{(m)}$
.
${\mathcal{F}}h\cdot R^{(m)}$
.
The group
 $\operatorname{Stab}_{G(\mathbb{Z})}(B)$
is non-trivial only for a set of measure 0 in
$\operatorname{Stab}_{G(\mathbb{Z})}(B)$
is non-trivial only for a set of measure 0 in
 $V(\mathbb{R})^{(m)}$
. Indeed,
$V(\mathbb{R})^{(m)}$
. Indeed,
![]() $G(\mathbb{Z})$
is countable and every non-trivial element
$G(\mathbb{Z})$
is countable and every non-trivial element
 $g\in G(\mathbb{Z})$
only fixes a set of measure 0 in
$g\in G(\mathbb{Z})$
only fixes a set of measure 0 in
![]() $V(\mathbb{R})$
. (Later on, in Proposition 23, we will show that the number of
$V(\mathbb{R})$
. (Later on, in Proposition 23, we will show that the number of
![]() $G(\mathbb{Z})$
-orbits on
$G(\mathbb{Z})$
-orbits on
![]() $V(\mathbb{Z})$
having a non-trivial stabilizer in
$V(\mathbb{Z})$
having a non-trivial stabilizer in
![]() $G(\mathbb{Z})$
is negligible.) The size
$G(\mathbb{Z})$
is negligible.) The size
 $\#\text{Stab}_{G(\mathbb{R})}(B)$
is constant over
$\#\text{Stab}_{G(\mathbb{R})}(B)$
is constant over
 $B\in V(\mathbb{R})^{(m)}$
. We denote it by
$B\in V(\mathbb{R})^{(m)}$
. We denote it by
 $\#J^{(m)}[2](\mathbb{R})$
. Therefore, the multiset
$\#J^{(m)}[2](\mathbb{R})$
. Therefore, the multiset
 ${\mathcal{F}}h\cdot R^{(m)}$
is a cover of a fundamental domain for
${\mathcal{F}}h\cdot R^{(m)}$
is a cover of a fundamental domain for
![]() $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
 $V(\mathbb{R})^{(m)}$
(aside from a set of measure 0) of degree
$V(\mathbb{R})^{(m)}$
(aside from a set of measure 0) of degree
 $\#J^{(m)}[2](\mathbb{R})$
.
$\#J^{(m)}[2](\mathbb{R})$
.
4.2 Averaging, cutting off the cusp, and estimation in the main body
An element
 $B\in V(\mathbb{Q})$
is said to be irreducible if it has non-zero discriminant and it is not distinguished. For any
$B\in V(\mathbb{Q})$
is said to be irreducible if it has non-zero discriminant and it is not distinguished. For any
![]() $G(\mathbb{Z})$
-invariant set
$G(\mathbb{Z})$
-invariant set
 ${\mathcal{L}}\subset V(\mathbb{Z})^{(m)}:=V(\mathbb{R})^{(m)}\cap V(\mathbb{Z})$
, let
${\mathcal{L}}\subset V(\mathbb{Z})^{(m)}:=V(\mathbb{R})^{(m)}\cap V(\mathbb{Z})$
, let
 $N({\mathcal{L}};X)$
denote the number of irreducible
$N({\mathcal{L}};X)$
denote the number of irreducible
![]() $G(\mathbb{Z})$
-orbits of
$G(\mathbb{Z})$
-orbits of
![]() ${\mathcal{L}}$
that have height bounded by
${\mathcal{L}}$
that have height bounded by
![]() $X$
, where each orbit
$X$
, where each orbit
 $G(\mathbb{Z})\cdot B$
is weighted by
$G(\mathbb{Z})\cdot B$
is weighted by
 $1/\#\text{Stab}_{G(\mathbb{Z})}(B)$
. The result of the previous section shows that we have
$1/\#\text{Stab}_{G(\mathbb{Z})}(B)$
. The result of the previous section shows that we have
 $$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\#\{{\mathcal{F}}hR^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\end{eqnarray}$$
$$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\#\{{\mathcal{F}}hR^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\end{eqnarray}$$
for any
![]() $h$
in
$h$
in
![]() $G(\mathbb{R})$
, where
$G(\mathbb{R})$
, where
 $R^{(m)}(X)$
denotes the elements in
$R^{(m)}(X)$
denotes the elements in
![]() $R^{(m)}$
having height bounded by
$R^{(m)}$
having height bounded by
![]() $X$
and
$X$
and
![]() ${\mathcal{L}}^{\text{irr}}$
denotes the set of irreducible elements in
${\mathcal{L}}^{\text{irr}}$
denotes the set of irreducible elements in
![]() ${\mathcal{L}}$
. Let
${\mathcal{L}}$
. Let
![]() $G_{0}$
be a bounded open
$G_{0}$
be a bounded open
![]() $K$
-invariant non-empty semialgebraic set in
$K$
-invariant non-empty semialgebraic set in
![]() $G(\mathbb{R})$
. Averaging the above equation over
$G(\mathbb{R})$
. Averaging the above equation over
![]() $h\in G_{0}$
, we obtain
$h\in G_{0}$
, we obtain
 $$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\#\{{\mathcal{F}}hR^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\,dh,\end{eqnarray}$$
$$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\#\{{\mathcal{F}}hR^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\,dh,\end{eqnarray}$$
for any Haar measure
![]() $dh$
on
$dh$
on
![]() $G(\mathbb{R})$
, and where the volume of
$G(\mathbb{R})$
, and where the volume of
![]() $G_{0}$
is computed with respect to
$G_{0}$
is computed with respect to
![]() $dh$
. Note that since
$dh$
. Note that since
![]() $G$
is reductive, every Haar measure is both left- and right-invariant. We may use (18) to define
$G$
is reductive, every Haar measure is both left- and right-invariant. We may use (18) to define
 $N({\mathcal{L}};X)$
when
$N({\mathcal{L}};X)$
when
![]() ${\mathcal{L}}$
is not
${\mathcal{L}}$
is not
![]() $G(\mathbb{Z})$
-invariant. This could be useful to estimate the number of
$G(\mathbb{Z})$
-invariant. This could be useful to estimate the number of
![]() $G(\mathbb{Z})$
-orbits having bounded height on a
$G(\mathbb{Z})$
-orbits having bounded height on a
![]() $G(\mathbb{Z})$
-invariant set which is not a lattice, but which can be partitioned into a union of lattices each of which is not necessarily
$G(\mathbb{Z})$
-invariant set which is not a lattice, but which can be partitioned into a union of lattices each of which is not necessarily
![]() $G(\mathbb{Z})$
-invariant. Note that if
$G(\mathbb{Z})$
-invariant. Note that if
![]() ${\mathcal{L}}$
is not
${\mathcal{L}}$
is not
![]() $G(\mathbb{Z})$
-invariant, then our definition of
$G(\mathbb{Z})$
-invariant, then our definition of
 $N({\mathcal{L}};X)$
depends on
$N({\mathcal{L}};X)$
depends on
![]() $G_{0}$
and on the choice of the fundamental domain
$G_{0}$
and on the choice of the fundamental domain
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
By an argument identical to the proof of [Reference Bhargava and ShankarBS15, Theorem 2.5], we obtain
 $$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\,dh.\end{eqnarray}$$
$$\begin{eqnarray}N({\mathcal{L}};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap {\mathcal{L}}^{\text{irr}}\}\,dh.\end{eqnarray}$$
To estimate the number of integral points in the bounded region
 $hG_{0}R^{(m)}(X)$
, we use the following result of Davenport [Reference DavenportDav51].
$hG_{0}R^{(m)}(X)$
, we use the following result of Davenport [Reference DavenportDav51].
Proposition 19. Let
![]() ${\mathcal{R}}$
be a bounded, semi-algebraic multiset in
${\mathcal{R}}$
be a bounded, semi-algebraic multiset in
![]() $\mathbb{R}^{n}$
having maximum multiplicity
$\mathbb{R}^{n}$
having maximum multiplicity
![]() $m$
and defined by at most
$m$
and defined by at most
![]() $k$
polynomial inequalities each having degree at most
$k$
polynomial inequalities each having degree at most
![]() $\ell$
. Then the number of integral lattice points (counted with multiplicity) contained in the region
$\ell$
. Then the number of integral lattice points (counted with multiplicity) contained in the region
![]() ${\mathcal{R}}$
is
${\mathcal{R}}$
is
 $$\begin{eqnarray}\operatorname{Vol}({\mathcal{R}})+O(\max \{\operatorname{Vol}(\bar{{\mathcal{R}}}),1\}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}({\mathcal{R}})+O(\max \{\operatorname{Vol}(\bar{{\mathcal{R}}}),1\}),\end{eqnarray}$$
where
![]() $\operatorname{Vol}(\bar{{\mathcal{R}}})$
denotes the greatest
$\operatorname{Vol}(\bar{{\mathcal{R}}})$
denotes the greatest
![]() $d$
-dimensional volume of any projection of
$d$
-dimensional volume of any projection of
![]() ${\mathcal{R}}$
onto a coordinate subspace obtained by equating
${\mathcal{R}}$
onto a coordinate subspace obtained by equating
![]() $n-d$
coordinates to zero, where
$n-d$
coordinates to zero, where
![]() $d$
takes all values from
$d$
takes all values from
![]() $1$
to
$1$
to
![]() $n-1$
. The implied constant in the second summand depends only on
$n-1$
. The implied constant in the second summand depends only on
![]() $n$
,
$n$
,
![]() $m$
,
$m$
,
![]() $k$
, and
$k$
, and
![]() $\ell$
.
$\ell$
.
The set
 $hG_{0}R^{(m)}(X)$
is a bounded region on which Proposition 19 may be applied. We can express any
$hG_{0}R^{(m)}(X)$
is a bounded region on which Proposition 19 may be applied. We can express any
![]() $h\in {\mathcal{F}}$
as
$h\in {\mathcal{F}}$
as
 $h=utk$
, where
$h=utk$
, where
![]() $u\in N^{\prime }$
,
$u\in N^{\prime }$
,
![]() $t\in T^{\prime }$
, and
$t\in T^{\prime }$
, and
![]() $k\in K$
. As
$k\in K$
. As
![]() $t$
grows in
$t$
grows in
![]() $T^{\prime }$
, the estimates on the number of integral points in
$T^{\prime }$
, the estimates on the number of integral points in
 $hG_{0}R^{(m)}(X)$
obtained from Proposition 19 get worse and worse. Indeed, when
$hG_{0}R^{(m)}(X)$
obtained from Proposition 19 get worse and worse. Indeed, when
![]() $t$
gets high enough (in the cusp of
$t$
gets high enough (in the cusp of
![]() $T^{\prime }$
), the top left entry
$T^{\prime }$
), the top left entry
![]() $b_{11}$
of every element in
$b_{11}$
of every element in
 $hG_{0}R^{(m)}(X)$
will be less than 1 in absolute value, at which point the error term in Proposition 19 dominates the main term. As
$hG_{0}R^{(m)}(X)$
will be less than 1 in absolute value, at which point the error term in Proposition 19 dominates the main term. As
![]() $t$
gets bigger, other entries start becoming less than 1 in absolute value and we get even worse estimates. To deal with this problem, we break
$t$
gets bigger, other entries start becoming less than 1 in absolute value and we get even worse estimates. To deal with this problem, we break
![]() $V(\mathbb{R})$
up into two pieces: the main body, which contains all elements
$V(\mathbb{R})$
up into two pieces: the main body, which contains all elements
 $B\in V(\mathbb{R})$
with
$B\in V(\mathbb{R})$
with
 $|b_{11}|\geqslant 1$
; and the cusp region, which contains all elements
$|b_{11}|\geqslant 1$
; and the cusp region, which contains all elements
 $B\in V(\mathbb{R})$
with
$B\in V(\mathbb{R})$
with
 $|b_{11}|<1$
. As
$|b_{11}|<1$
. As
![]() $t$
gets bigger, more and more coefficients of the integral elements of
$t$
gets bigger, more and more coefficients of the integral elements of
 $hG_{0}R^{(m)}(X)$
will become 0. Using Proposition 7, we know that once enough entries of
$hG_{0}R^{(m)}(X)$
will become 0. Using Proposition 7, we know that once enough entries of
![]() $B$
are 0, it will become distinguished and thus reducible. In Proposition 21 we compute the number of irreducible integral points in the cusp region, and in Proposition 23 we compute the number of reducible integral points in the main body. They are both negligible when compared to the number of integral points in the main region, and as a result we will prove the following theorem.
$B$
are 0, it will become distinguished and thus reducible. In Proposition 21 we compute the number of irreducible integral points in the cusp region, and in Proposition 23 we compute the number of reducible integral points in the main body. They are both negligible when compared to the number of integral points in the main region, and as a result we will prove the following theorem.
Theorem 20. We have for any
 $m=0,\ldots ,n+1$
,
$m=0,\ldots ,n+1$
,
 $$\begin{eqnarray}N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))+o(X^{(\dim V)/d}).\end{eqnarray}$$
$$\begin{eqnarray}N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))+o(X^{(\dim V)/d}).\end{eqnarray}$$
In § 4.4, we show that
 $\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
grows on the order of
$\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
grows on the order of
 $X^{(\dim V)/d}$
so the error term is indeed smaller than the main term.
$X^{(\dim V)/d}$
so the error term is indeed smaller than the main term.
Let
 $V(\mathbb{Z})(b_{11}=0)$
denote the set of points
$V(\mathbb{Z})(b_{11}=0)$
denote the set of points
 $B\in V(\mathbb{Z})$
such that
$B\in V(\mathbb{Z})$
such that
![]() $b_{11}=0$
. Then we have the following proposition.
$b_{11}=0$
. Then we have the following proposition.
Proposition 21. With notation as above, we have
 $N(V(\mathbb{Z})(b_{11}=0);X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V-1)/d+\unicode[STIX]{x1D716}})$
.
$N(V(\mathbb{Z})(b_{11}=0);X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V-1)/d+\unicode[STIX]{x1D716}})$
.
Proof. It will be convenient to use the following parameters for
![]() $T$
:
$T$
:
 $$\begin{eqnarray}\displaystyle s_{i} & = & \displaystyle t_{i}/t_{i+1}\quad \text{for}~i=1,\ldots ,n;\nonumber\\ \displaystyle s_{n+1} & = & \displaystyle t_{n}t_{n+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{i} & = & \displaystyle t_{i}/t_{i+1}\quad \text{for}~i=1,\ldots ,n;\nonumber\\ \displaystyle s_{n+1} & = & \displaystyle t_{n}t_{n+1}.\nonumber\end{eqnarray}$$
The condition for
![]() $t\in T^{\prime }$
translates to
$t\in T^{\prime }$
translates to
![]() $s_{i}>c$
for all
$s_{i}>c$
for all
![]() $i$
. We pick the following Haar measure
$i$
. We pick the following Haar measure
![]() $dh$
on
$dh$
on
 $G(\mathbb{R})=NTK$
:
$G(\mathbb{R})=NTK$
:
 $$\begin{eqnarray}\displaystyle dh & = & \displaystyle du\mathop{\prod }_{j=1}^{n-1}s_{j}^{j(j-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}d^{\times }s_{j}\,dk\nonumber\\ \displaystyle & = & \displaystyle du\unicode[STIX]{x1D6FF}(s)d^{\times }s\,dk,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle dh & = & \displaystyle du\mathop{\prod }_{j=1}^{n-1}s_{j}^{j(j-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}d^{\times }s_{j}\,dk\nonumber\\ \displaystyle & = & \displaystyle du\unicode[STIX]{x1D6FF}(s)d^{\times }s\,dk,\end{eqnarray}$$
where
![]() $du$
is a Haar measure on the unipotent group
$du$
is a Haar measure on the unipotent group
![]() $N$
,
$N$
,
![]() $dk$
is the Haar measure on
$dk$
is the Haar measure on
![]() $K$
normalized so that
$K$
normalized so that
![]() $K$
has volume 1,
$K$
has volume 1,
![]() $\unicode[STIX]{x1D6FF}(s)$
denotes
$\unicode[STIX]{x1D6FF}(s)$
denotes
 $\prod _{j=1}^{n-1}s_{j}^{j(j-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}$
, and
$\prod _{j=1}^{n-1}s_{j}^{j(j-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}$
, and
![]() $d^{\times }s$
denotes
$d^{\times }s$
denotes
 $\prod _{j=1}^{n+1}d^{\times }s_{j}$
in which each
$\prod _{j=1}^{n+1}d^{\times }s_{j}$
in which each
 $d^{\times }s_{j}=ds_{j}/s_{j}$
is the standard Haar measure on
$d^{\times }s_{j}=ds_{j}/s_{j}$
is the standard Haar measure on
![]() $\mathbb{R}^{\times }$
. The conjugation action of
$\mathbb{R}^{\times }$
. The conjugation action of
![]() $T$
on
$T$
on
![]() $N$
breaks up into a direct sum of characters of
$N$
breaks up into a direct sum of characters of
![]() $T$
. The Haar measure character
$T$
. The Haar measure character
![]() $\unicode[STIX]{x1D6FF}(s)$
is the product of the inverses of all the characters of
$\unicode[STIX]{x1D6FF}(s)$
is the product of the inverses of all the characters of
![]() $T$
arising in this decomposition, in order for the measure
$T$
arising in this decomposition, in order for the measure
![]() $dh$
above to be left-invariant.
$dh$
above to be left-invariant.
Then, since
![]() $G_{0}$
is
$G_{0}$
is
![]() $K$
-invariant, (19) implies that
$K$
-invariant, (19) implies that
 $$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})(b_{11}=0);X) & = & \displaystyle O\biggl(\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,dh\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\int _{u\in N^{\prime }}\int _{t\in T^{\prime }}\#\{utG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\,du\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\int _{t\in T^{\prime }}\#\{tG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})(b_{11}=0);X) & = & \displaystyle O\biggl(\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,dh\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\int _{u\in N^{\prime }}\int _{t\in T^{\prime }}\#\{utG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\,du\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(\int _{t\in T^{\prime }}\#\{tG_{0}R^{(m)}(X)\cap V(\mathbb{Z})(b_{11}=0)\}\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr),\end{eqnarray}$$
where the final equality follows because
![]() $N^{\prime }$
has finite measure,
$N^{\prime }$
has finite measure,
 $$\begin{eqnarray}utG_{0}R^{(m)}(X)=t(t^{-1}ut)G_{0}R^{(m)}(X),\end{eqnarray}$$
$$\begin{eqnarray}utG_{0}R^{(m)}(X)=t(t^{-1}ut)G_{0}R^{(m)}(X),\end{eqnarray}$$
and the coefficients of
![]() $t^{-1}ut$
are bounded independent of
$t^{-1}ut$
are bounded independent of
![]() $t\in T^{\prime }$
and
$t\in T^{\prime }$
and
![]() $u\in N^{\prime }$
.
$u\in N^{\prime }$
.
Let
![]() $b_{ij}$
, with
$b_{ij}$
, with
![]() $i\leqslant j$
and
$i\leqslant j$
and
 $(i,j)\neq (n+1,n+2)$
, be the system of coordinates on
$(i,j)\neq (n+1,n+2)$
, be the system of coordinates on
![]() $V(\mathbb{R})$
, where
$V(\mathbb{R})$
, where
![]() $b_{ij}$
is the
$b_{ij}$
is the
![]() $(i,j)$
th entry of the symmetric matrix
$(i,j)$
th entry of the symmetric matrix
![]() $B$
. To each coordinate
$B$
. To each coordinate
![]() $b_{ij}$
we associate the weight
$b_{ij}$
we associate the weight
![]() $w(i,j)$
, which records how an element
$w(i,j)$
, which records how an element
![]() $s\in T$
scales
$s\in T$
scales
![]() $b_{ij}$
. For example,
$b_{ij}$
. For example,
 $$\begin{eqnarray}\displaystyle w(1,1) & = & \displaystyle s_{1}^{-2}\cdots s_{n-1}^{-2}s_{n}^{-1}s_{n+1}^{-1}\nonumber\\ \displaystyle w(i,2n+3-i) & = & \displaystyle 1,\quad i=1,\ldots ,2n+2,\quad \text{coordinates on the anti}\text{-}\text{diagonal}\nonumber\\ \displaystyle w(i,2n+2-i) & = & \displaystyle s_{i}^{-1},\quad i=1,\ldots ,2n+1,\quad \text{coordinates above the anti}\text{-}\text{diagonal}\nonumber\\ \displaystyle w(n+1,n+1) & = & \displaystyle s_{n}s_{n+1}^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w(1,1) & = & \displaystyle s_{1}^{-2}\cdots s_{n-1}^{-2}s_{n}^{-1}s_{n+1}^{-1}\nonumber\\ \displaystyle w(i,2n+3-i) & = & \displaystyle 1,\quad i=1,\ldots ,2n+2,\quad \text{coordinates on the anti}\text{-}\text{diagonal}\nonumber\\ \displaystyle w(i,2n+2-i) & = & \displaystyle s_{i}^{-1},\quad i=1,\ldots ,2n+1,\quad \text{coordinates above the anti}\text{-}\text{diagonal}\nonumber\\ \displaystyle w(n+1,n+1) & = & \displaystyle s_{n}s_{n+1}^{-1}.\nonumber\end{eqnarray}$$
Let
![]() $C$
be an absolute constant such that
$C$
be an absolute constant such that
![]() $CX^{1/d}$
bounds the absolute value of all the coordinates of elements
$CX^{1/d}$
bounds the absolute value of all the coordinates of elements
 $B\in G_{0}R^{(m)}(X)$
. If, for
$B\in G_{0}R^{(m)}(X)$
. If, for
 $(s_{1},\ldots ,s_{n+1})\in T^{\prime }$
, we have
$(s_{1},\ldots ,s_{n+1})\in T^{\prime }$
, we have
 $CX^{1/d}\,w(i_{0},2n+2-i_{0})<1$
for some
$CX^{1/d}\,w(i_{0},2n+2-i_{0})<1$
for some
 $i_{0}\in \{1,\ldots ,n+1\}$
, then
$i_{0}\in \{1,\ldots ,n+1\}$
, then
 $CX^{1/d}\,w(i,j)<1$
for all
$CX^{1/d}\,w(i,j)<1$
for all
 $i\leqslant i_{0},j\leqslant 2n+2-i_{0}$
. Hence the top left
$i\leqslant i_{0},j\leqslant 2n+2-i_{0}$
. Hence the top left
 $i_{0}\times (2n+2-i_{0})$
block of any integral
$i_{0}\times (2n+2-i_{0})$
block of any integral
 $B\in tG_{0}R^{(m)}(X)$
is 0. Just as [Reference Bhargava and GrossBG13, Lemma 10.3] shows, any such
$B\in tG_{0}R^{(m)}(X)$
is 0. Just as [Reference Bhargava and GrossBG13, Lemma 10.3] shows, any such
![]() $B$
has zero discriminant. Hence, to prove Proposition 21, we may assume
$B$
has zero discriminant. Hence, to prove Proposition 21, we may assume
 $$\begin{eqnarray}s_{i}\leqslant CX^{1/d},~i=1,\ldots ,n;\quad s_{n+1}\leqslant C^{2}X^{2/d}.\end{eqnarray}$$
$$\begin{eqnarray}s_{i}\leqslant CX^{1/d},~i=1,\ldots ,n;\quad s_{n+1}\leqslant C^{2}X^{2/d}.\end{eqnarray}$$
We use
![]() $T_{X}$
to denote the set of
$T_{X}$
to denote the set of
 $t=(s_{1},\ldots ,s_{n+1})\in T^{\prime }$
satisfying these bounds.
$t=(s_{1},\ldots ,s_{n+1})\in T^{\prime }$
satisfying these bounds.
Let
![]() $U$
denote the set of pairs of integers
$U$
denote the set of pairs of integers
![]() $(i,j)$
with
$(i,j)$
with
 $1\leqslant i,j,\leqslant 2n+2$
and
$1\leqslant i,j,\leqslant 2n+2$
and
![]() $i\leqslant j$
. For any subset
$i\leqslant j$
. For any subset
![]() $U_{1}$
of
$U_{1}$
of
![]() $U$
, let
$U$
, let
 $V(\mathbb{R})(U_{1})$
denote the subset of
$V(\mathbb{R})(U_{1})$
denote the subset of
![]() $V(\mathbb{R})$
consisting of elements
$V(\mathbb{R})$
consisting of elements
![]() $B$
whose
$B$
whose
![]() $(i,j)$
th entry is less than 1 in absolute value when
$(i,j)$
th entry is less than 1 in absolute value when
 $(i,j)\in U_{1}$
and at least 1 in absolute value when
$(i,j)\in U_{1}$
and at least 1 in absolute value when
 $(i,j)\notin U_{1}$
. Let
$(i,j)\notin U_{1}$
. Let
 $V(\mathbb{Z})(U_{1})$
denote the set of integral points in
$V(\mathbb{Z})(U_{1})$
denote the set of integral points in
 $V(\mathbb{R})(U_{1})$
. Then to prove Proposition 21, it suffices to show that
$V(\mathbb{R})(U_{1})$
. Then to prove Proposition 21, it suffices to show that
 $$\begin{eqnarray}N(V(\mathbb{Z})(U_{1});X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V-1)/d+\unicode[STIX]{x1D716}}),\end{eqnarray}$$
$$\begin{eqnarray}N(V(\mathbb{Z})(U_{1});X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V-1)/d+\unicode[STIX]{x1D716}}),\end{eqnarray}$$
for every set
![]() $U_{1}$
containing
$U_{1}$
containing
![]() $(1,1)$
.
$(1,1)$
.
Proposition 19, in conjunction with the argument used to justify (21), implies
 $$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})(U_{1});X) & = & \displaystyle O\biggl(\int _{t\in T_{X}}\operatorname{Vol}(tG_{0}R^{(m)}(X)\cap V(\mathbb{R})(U_{1}))\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(X^{(\dim V-\#U_{1})/d}\int _{t\in T_{X}}\mathop{\prod }_{(i,j)\not \in U_{1}}w(i,j)\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})(U_{1});X) & = & \displaystyle O\biggl(\int _{t\in T_{X}}\operatorname{Vol}(tG_{0}R^{(m)}(X)\cap V(\mathbb{R})(U_{1}))\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr)\nonumber\\ \displaystyle & = & \displaystyle O\biggl(X^{(\dim V-\#U_{1})/d}\int _{t\in T_{X}}\mathop{\prod }_{(i,j)\not \in U_{1}}w(i,j)\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s\biggr).\nonumber\end{eqnarray}$$
Hence, to prove (23), we need to bound
 $$\begin{eqnarray}\widetilde{I}(U_{1},X):=X^{(\dim V-\#U_{1})/d}\int _{t\in T_{X}}\mathop{\prod }_{(i,j)\not \in U_{1}}w(i,j)\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s,\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{I}(U_{1},X):=X^{(\dim V-\#U_{1})/d}\int _{t\in T_{X}}\mathop{\prod }_{(i,j)\not \in U_{1}}w(i,j)\,\unicode[STIX]{x1D6FF}(s)\,d^{\times }s,\end{eqnarray}$$
for every set
![]() $U_{1}$
containing
$U_{1}$
containing
![]() $(1,1)$
.
$(1,1)$
.
Note that if
![]() $i^{\prime }\leqslant i$
and
$i^{\prime }\leqslant i$
and
![]() $j^{\prime }\leqslant j$
, then
$j^{\prime }\leqslant j$
, then
![]() $w(i^{\prime },j^{\prime })$
has smaller exponents in all the
$w(i^{\prime },j^{\prime })$
has smaller exponents in all the
![]() $s_{k}$
than
$s_{k}$
than
![]() $w(i,j)$
. Thus, if a set
$w(i,j)$
. Thus, if a set
![]() $U_{1}$
contains
$U_{1}$
contains
![]() $(i,j)$
but not
$(i,j)$
but not
![]() $(i^{\prime },j^{\prime })$
, then
$(i^{\prime },j^{\prime })$
, then
 $$\begin{eqnarray}\widetilde{I}(U_{1}\backslash \{(i,j)\}\cup \{(i^{\prime },j^{\prime })\},X)\geqslant \widetilde{I}(U_{1},X).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{I}(U_{1}\backslash \{(i,j)\}\cup \{(i^{\prime },j^{\prime })\},X)\geqslant \widetilde{I}(U_{1},X).\end{eqnarray}$$
Hence, for the purpose of obtaining an upper bound for
 $\widetilde{I}(U_{1},X)$
, we may assume that if
$\widetilde{I}(U_{1},X)$
, we may assume that if
 $(i,j)\in U_{1}$
, then
$(i,j)\in U_{1}$
, then
 $(i^{\prime },j^{\prime })\in U_{1}$
for all
$(i^{\prime },j^{\prime })\in U_{1}$
for all
![]() $i^{\prime }\leqslant i$
and
$i^{\prime }\leqslant i$
and
![]() $j^{\prime }\leqslant j$
. We say that such a set
$j^{\prime }\leqslant j$
. We say that such a set
![]() $U_{1}$
is closed. If a closed set
$U_{1}$
is closed. If a closed set
![]() $U_{1}$
contains any element on, or to the right of, the off-anti-diagonal, then every element in
$U_{1}$
contains any element on, or to the right of, the off-anti-diagonal, then every element in
 $V(\mathbb{Z})(U_{1})$
has discriminant 0 and, by definition,
$V(\mathbb{Z})(U_{1})$
has discriminant 0 and, by definition,
 $N(V(\mathbb{Z})(U_{1});X)=0$
. Let
$N(V(\mathbb{Z})(U_{1});X)=0$
. Let
![]() $U_{0}$
denote the set of coordinates
$U_{0}$
denote the set of coordinates
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $i\leqslant j$
and
$i\leqslant j$
and
 $i+j\leqslant 2n+1$
. In other words,
$i+j\leqslant 2n+1$
. In other words,
![]() $U_{0}$
contains every coordinate to the left of the off-anti-diagonal. Since every element in
$U_{0}$
contains every coordinate to the left of the off-anti-diagonal. Since every element in
 $V(\mathbb{Z})(U_{0})$
is distinguished (by Proposition 7), hence reducible, it suffices to consider
$V(\mathbb{Z})(U_{0})$
is distinguished (by Proposition 7), hence reducible, it suffices to consider
 $\widetilde{I}(U_{1},X)$
for all
$\widetilde{I}(U_{1},X)$
for all
 $U_{1}\subsetneq U_{0}$
.
$U_{1}\subsetneq U_{0}$
.
To this end, as the product of the weights over all coordinates is 1, we define
 $$\begin{eqnarray}I(U_{1},X)=X^{-\#U_{1}/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\!\mathop{\prod }_{(i,j)\in U_{1}}w(i,j)^{-1}\,\mathop{\prod }_{k=1}^{n-1}s_{k}^{k(k-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}\,d^{\times }s.\end{eqnarray}$$
$$\begin{eqnarray}I(U_{1},X)=X^{-\#U_{1}/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\!\mathop{\prod }_{(i,j)\in U_{1}}w(i,j)^{-1}\,\mathop{\prod }_{k=1}^{n-1}s_{k}^{k(k-2n-1)}\cdot (s_{n}s_{n+1})^{-n(n+1)/2}\,d^{\times }s.\end{eqnarray}$$
To complete the proof of Proposition 21, it suffices to prove the following lemma.
Lemma 22. Let
![]() $U_{1}$
be non-empty proper closed subset of
$U_{1}$
be non-empty proper closed subset of
![]() $U_{0}$
. Then
$U_{0}$
. Then
 $$\begin{eqnarray}I(U_{1},X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}).\end{eqnarray}$$
$$\begin{eqnarray}I(U_{1},X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}).\end{eqnarray}$$
If
 $U_{1}=U_{0}$
or
$U_{1}=U_{0}$
or
![]() $U_{1}=\emptyset$
, then
$U_{1}=\emptyset$
, then
 $I(U_{1},X)=O(1)$
.
$I(U_{1},X)=O(1)$
.
Proof. The proof of this lemma is a combinatorial argument using induction on
![]() $n\geqslant 2$
. We first compute
$n\geqslant 2$
. We first compute
 $$\begin{eqnarray}I(U_{0},X)=X^{-n(n+1)/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}s_{1}s_{2}^{3}\cdots s_{n-1}^{2n-3}s_{n}^{n-1}s_{n+1}^{n}\,d^{\times }s=O(1).\end{eqnarray}$$
$$\begin{eqnarray}I(U_{0},X)=X^{-n(n+1)/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}s_{1}s_{2}^{3}\cdots s_{n-1}^{2n-3}s_{n}^{n-1}s_{n+1}^{n}\,d^{\times }s=O(1).\end{eqnarray}$$
This is expected since
 $V(\mathbb{Z})(U_{0})$
contains all but negligibly few distinguished orbits (see Proposition 23). It is also easy to see that
$V(\mathbb{Z})(U_{0})$
contains all but negligibly few distinguished orbits (see Proposition 23). It is also easy to see that
 $I(\emptyset ,X)=O(1)$
. Let
$I(\emptyset ,X)=O(1)$
. Let
![]() $U_{1}^{\prime }$
denote
$U_{1}^{\prime }$
denote
![]() $U_{0}\backslash U_{1}$
, and define
$U_{0}\backslash U_{1}$
, and define
 $I_{n}^{\prime }(U_{1}^{\prime },X)$
to equal
$I_{n}^{\prime }(U_{1}^{\prime },X)$
to equal
 $I(U_{1},X)$
. Combining (25) with (26), we obtain
$I(U_{1},X)$
. Combining (25) with (26), we obtain
 $$\begin{eqnarray}\displaystyle I_{n}^{\prime }(U_{1}^{\prime },X) & = & \displaystyle I(U_{1},X)\nonumber\\ \displaystyle & = & \displaystyle X^{(\#U_{1}^{\prime }-n(n+1))/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(i,j)\in U_{1}^{\prime }}w(i,j)\cdot s_{1}s_{2}^{3}\cdots s_{n-1}^{2n-3}s_{n}^{n-1}s_{n+1}^{n}\,d^{\times }s.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{n}^{\prime }(U_{1}^{\prime },X) & = & \displaystyle I(U_{1},X)\nonumber\\ \displaystyle & = & \displaystyle X^{(\#U_{1}^{\prime }-n(n+1))/d}\int _{s_{1},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(i,j)\in U_{1}^{\prime }}w(i,j)\cdot s_{1}s_{2}^{3}\cdots s_{n-1}^{2n-3}s_{n}^{n-1}s_{n+1}^{n}\,d^{\times }s.\nonumber\end{eqnarray}$$
Even though we only need the result when
![]() $n\geqslant 2$
, for the purpose of the induction it is also necessary to work out the case
$n\geqslant 2$
, for the purpose of the induction it is also necessary to work out the case
![]() $n=1$
. When
$n=1$
. When
![]() $n=1$
, we have
$n=1$
, we have
 $U_{0}=\{(1,1),(1,2)\}$
and
$U_{0}=\{(1,1),(1,2)\}$
and
 $$\begin{eqnarray}\displaystyle I_{1}(\emptyset ,X) & = & \displaystyle O(1),\nonumber\\ \displaystyle I_{1}(\{(1,1)\},X) & = & \displaystyle O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}),\nonumber\\ \displaystyle I_{1}(U_{0},X) & = & \displaystyle O_{\unicode[STIX]{x1D716}}(X^{\unicode[STIX]{x1D716}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1}(\emptyset ,X) & = & \displaystyle O(1),\nonumber\\ \displaystyle I_{1}(\{(1,1)\},X) & = & \displaystyle O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}),\nonumber\\ \displaystyle I_{1}(U_{0},X) & = & \displaystyle O_{\unicode[STIX]{x1D716}}(X^{\unicode[STIX]{x1D716}}).\nonumber\end{eqnarray}$$
To establish the inductive step, we write
 $U_{1}^{\prime }=U_{2}^{\prime }\cup U_{3}^{\prime }$
where
$U_{1}^{\prime }=U_{2}^{\prime }\cup U_{3}^{\prime }$
where
![]() $U_{2}^{\prime }$
is the set of coordinates
$U_{2}^{\prime }$
is the set of coordinates
![]() $(1,j)$
in
$(1,j)$
in
![]() $U_{1}^{\prime }$
and
$U_{1}^{\prime }$
and
 $U_{3}^{\prime }=U_{1}^{\prime }\backslash U_{2}^{\prime }$
. Since we have
$U_{3}^{\prime }=U_{1}^{\prime }\backslash U_{2}^{\prime }$
. Since we have
 $$\begin{eqnarray}\int _{c}^{CX^{1/d}}s^{k}\,d^{\times }s\ll _{c,C}\int _{c}^{CX^{1/d}}s^{k_{1}}\,d^{\times }s\int _{c}^{CX^{1/d}}s^{k_{2}}\,d^{\times }s\end{eqnarray}$$
$$\begin{eqnarray}\int _{c}^{CX^{1/d}}s^{k}\,d^{\times }s\ll _{c,C}\int _{c}^{CX^{1/d}}s^{k_{1}}\,d^{\times }s\int _{c}^{CX^{1/d}}s^{k_{2}}\,d^{\times }s\end{eqnarray}$$
for every
 $k_{1}+k_{2}=k$
, it follows that we may bound
$k_{1}+k_{2}=k$
, it follows that we may bound
 $I_{n}^{\prime }(U_{1}^{\prime },X)$
by the product
$I_{n}^{\prime }(U_{1}^{\prime },X)$
by the product
 $$\begin{eqnarray}I_{n}^{\prime }(U_{1}^{\prime },X)\ll _{c,C}J_{n}(U_{2}^{\prime },X)K_{n}(U_{3}^{\prime },X),\end{eqnarray}$$
$$\begin{eqnarray}I_{n}^{\prime }(U_{1}^{\prime },X)\ll _{c,C}J_{n}(U_{2}^{\prime },X)K_{n}(U_{3}^{\prime },X),\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle J_{n}(U_{2}^{\prime },X) & := & \displaystyle X^{(\#U_{2}^{\prime }-2n)/d}\int _{s_{1}=c}^{CX^{1/d}}\int _{s_{2},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(1,j)\in U_{2}^{\prime }}w(1,j)\,s_{1}s_{2}^{2}\cdots s_{n-1}^{2}s_{n}s_{n+1}\,d^{\times }s,\nonumber\\ \displaystyle K_{n}(U_{3}^{\prime },X) & := & \displaystyle X^{(\#U_{3}^{\prime }-(n-1)n)/d}\int _{s_{2},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(i,j)\in U_{3}^{\prime }}w(i,j)\,s_{2}s_{3}^{3}\cdots s_{n-1}^{2n-5}s_{n}^{n-2}s_{n+1}^{n-1}\,d^{\times }s.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{n}(U_{2}^{\prime },X) & := & \displaystyle X^{(\#U_{2}^{\prime }-2n)/d}\int _{s_{1}=c}^{CX^{1/d}}\int _{s_{2},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(1,j)\in U_{2}^{\prime }}w(1,j)\,s_{1}s_{2}^{2}\cdots s_{n-1}^{2}s_{n}s_{n+1}\,d^{\times }s,\nonumber\\ \displaystyle K_{n}(U_{3}^{\prime },X) & := & \displaystyle X^{(\#U_{3}^{\prime }-(n-1)n)/d}\int _{s_{2},\ldots ,s_{n}=c}^{CX^{1/d}}\int _{s_{n+1}=c}^{C^{2}X^{2/d}}\mathop{\prod }_{(i,j)\in U_{3}^{\prime }}w(i,j)\,s_{2}s_{3}^{3}\cdots s_{n-1}^{2n-5}s_{n}^{n-2}s_{n+1}^{n-1}\,d^{\times }s.\nonumber\end{eqnarray}$$
Note that
 $K_{n}(U_{3}^{\prime },X)=I_{n-1}^{\prime }(\{(i,j):(i+1,j+1)\in U_{3}^{\prime }\},X)$
(which we denote by
$K_{n}(U_{3}^{\prime },X)=I_{n-1}^{\prime }(\{(i,j):(i+1,j+1)\in U_{3}^{\prime }\},X)$
(which we denote by
 $I_{n-1}^{\prime }(U_{3}^{\prime },X)$
) and we may estimate it using induction. Since
$I_{n-1}^{\prime }(U_{3}^{\prime },X)$
) and we may estimate it using induction. Since
![]() $U_{1}$
is closed and non-empty, the subset
$U_{1}$
is closed and non-empty, the subset
![]() $U_{2}^{\prime }$
is either empty or of the form
$U_{2}^{\prime }$
is either empty or of the form
 $\{(1,k),(1,k+1),\ldots ,(1,2n)\}$
with
$\{(1,k),(1,k+1),\ldots ,(1,2n)\}$
with
![]() $k\geqslant 2$
. A direct calculation gives
$k\geqslant 2$
. A direct calculation gives
 $$\begin{eqnarray}J_{n}(U_{2}^{\prime },X)=\left\{\begin{array}{@{}ll@{}}O(1)\quad & \text{if}~U_{2}^{\prime }=\emptyset ,\\ O_{\unicode[STIX]{x1D716}}(X^{(-k+1)/d+\unicode[STIX]{x1D716}})\quad & \text{if}~2\leqslant k\leqslant n+1,\\ O_{\unicode[STIX]{x1D716}}(X^{(k-2n-1)/d+\unicode[STIX]{x1D716}})\quad & \text{if}~n+2\leqslant k\leqslant 2n.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}J_{n}(U_{2}^{\prime },X)=\left\{\begin{array}{@{}ll@{}}O(1)\quad & \text{if}~U_{2}^{\prime }=\emptyset ,\\ O_{\unicode[STIX]{x1D716}}(X^{(-k+1)/d+\unicode[STIX]{x1D716}})\quad & \text{if}~2\leqslant k\leqslant n+1,\\ O_{\unicode[STIX]{x1D716}}(X^{(k-2n-1)/d+\unicode[STIX]{x1D716}})\quad & \text{if}~n+2\leqslant k\leqslant 2n.\end{array}\right.\end{eqnarray}$$
Hence we have
 $$\begin{eqnarray}J_{n}(U_{2}^{\prime },X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}),\end{eqnarray}$$
$$\begin{eqnarray}J_{n}(U_{2}^{\prime },X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}}),\end{eqnarray}$$
unless
![]() $U_{2}^{\prime }=\emptyset$
, in which case it is
$U_{2}^{\prime }=\emptyset$
, in which case it is
![]() $O(1)$
.
$O(1)$
.
Hence, if
![]() $U_{2}^{\prime }$
is not empty, then the lemma follows by induction on
$U_{2}^{\prime }$
is not empty, then the lemma follows by induction on
![]() $n$
(used to bound
$n$
(used to bound
 $I_{n-1}^{\prime }(U_{3}^{\prime },X)$
by
$I_{n-1}^{\prime }(U_{3}^{\prime },X)$
by
![]() $O_{\unicode[STIX]{x1D716}}(X^{\unicode[STIX]{x1D716}})$
). If
$O_{\unicode[STIX]{x1D716}}(X^{\unicode[STIX]{x1D716}})$
). If
![]() $U_{2}^{\prime }$
is empty, then
$U_{2}^{\prime }$
is empty, then
![]() $U_{3}^{\prime }$
must be non-empty since
$U_{3}^{\prime }$
must be non-empty since
![]() $U_{1}^{\prime }$
is non-empty. If, further,
$U_{1}^{\prime }$
is non-empty. If, further,
 $U_{3}^{\prime }\neq U_{0}\backslash \{(1,1),\ldots ,(1,2n)\}$
, then by induction we have
$U_{3}^{\prime }\neq U_{0}\backslash \{(1,1),\ldots ,(1,2n)\}$
, then by induction we have
 $I_{n-1}^{\prime }(U_{3}^{\prime },X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}})$
. The only remaining case is when
$I_{n-1}^{\prime }(U_{3}^{\prime },X)=O_{\unicode[STIX]{x1D716}}(X^{-1/d+\unicode[STIX]{x1D716}})$
. The only remaining case is when
 $U_{1}=\{(1,1),\ldots ,(1,2n)\}$
, for which a direct computation yields the result.◻
$U_{1}=\{(1,1),\ldots ,(1,2n)\}$
, for which a direct computation yields the result.◻
This concludes the proof of Proposition 21. ◻
We now have the following proposition, whose proof follows that of [Reference BhargavaBha10, Lemma 14].
Proposition 23. Let
 $V(\mathbb{Z})(\emptyset )^{\text{red}}$
denote the set of elements in
$V(\mathbb{Z})(\emptyset )^{\text{red}}$
denote the set of elements in
![]() $V(\mathbb{Z})$
with
$V(\mathbb{Z})$
with
![]() $b_{11}\neq 0$
that are not irreducible, and let
$b_{11}\neq 0$
that are not irreducible, and let
 $V(\mathbb{Z})^{\text{bigstab}}$
denote the set of elements in
$V(\mathbb{Z})^{\text{bigstab}}$
denote the set of elements in
![]() $V(\mathbb{Z})$
which have a non-trivial stabilizer in
$V(\mathbb{Z})$
which have a non-trivial stabilizer in
![]() $G(\mathbb{Z})$
. Then
$G(\mathbb{Z})$
. Then
 $$\begin{eqnarray}\displaystyle \int _{G_{0}}\#\{V(\mathbb{Z})(\emptyset )^{\text{red}}\cap {\mathcal{F}}g\cdot R^{(m)}(X)\}\,dg & = & \displaystyle o(X^{(\dim V)/d}),\nonumber\\ \displaystyle N(V(\mathbb{Z})^{\text{bigstab}};X) & = & \displaystyle o(X^{(\dim V)/d}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{G_{0}}\#\{V(\mathbb{Z})(\emptyset )^{\text{red}}\cap {\mathcal{F}}g\cdot R^{(m)}(X)\}\,dg & = & \displaystyle o(X^{(\dim V)/d}),\nonumber\\ \displaystyle N(V(\mathbb{Z})^{\text{bigstab}};X) & = & \displaystyle o(X^{(\dim V)/d}).\nonumber\end{eqnarray}$$
Proof. Observe that if
 $B\in V(\mathbb{Z})$
is reducible over
$B\in V(\mathbb{Z})$
is reducible over
![]() $\mathbb{Z}$
, then the image of
$\mathbb{Z}$
, then the image of
![]() $B$
in
$B$
in
![]() $V(\mathbb{F}_{p})$
is reducible for all
$V(\mathbb{F}_{p})$
is reducible for all
![]() $p$
. For any prime
$p$
. For any prime
![]() $p$
, let
$p$
, let
![]() $\unicode[STIX]{x1D719}_{p}$
denote the
$\unicode[STIX]{x1D719}_{p}$
denote the
![]() $p$
-adic density of the set of elements of
$p$
-adic density of the set of elements of
![]() $V(\mathbb{Z}_{p})$
that are reducible mod
$V(\mathbb{Z}_{p})$
that are reducible mod
![]() $p$
. Then, to prove Proposition 23, it suffices to show
$p$
. Then, to prove Proposition 23, it suffices to show
 $$\begin{eqnarray}\mathop{\prod }_{p}\unicode[STIX]{x1D719}_{p}=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{p}\unicode[STIX]{x1D719}_{p}=0.\end{eqnarray}$$
We show this by proving that
![]() $\unicode[STIX]{x1D719}_{p}$
is bounded above by some constant less than 1 when
$\unicode[STIX]{x1D719}_{p}$
is bounded above by some constant less than 1 when
![]() $p$
is large enough. For large enough
$p$
is large enough. For large enough
![]() $p$
, there is a positive proportion
$p$
, there is a positive proportion
![]() $r_{n}$
(depending only on
$r_{n}$
(depending only on
![]() $n$
) of polynomials of degree
$n$
) of polynomials of degree
![]() $2n+2$
over
$2n+2$
over
![]() $\mathbb{F}_{p}$
that factor into two linear terms and an irreducible polynomial of degree
$\mathbb{F}_{p}$
that factor into two linear terms and an irreducible polynomial of degree
![]() $2n$
. Suppose
$2n$
. Suppose
 $f(x)\in \mathbb{Z}_{p}[x]$
with this reduction type over
$f(x)\in \mathbb{Z}_{p}[x]$
with this reduction type over
![]() $\mathbb{F}_{p}$
. Since it has a linear factor, Proposition 5 implies that there is one distinguished orbit. Since
$\mathbb{F}_{p}$
. Since it has a linear factor, Proposition 5 implies that there is one distinguished orbit. Since
 $H^{1}(\mathbb{F}_{p},J)=0$
by Lang’s theorem, every orbit is soluble. The number of orbits
$H^{1}(\mathbb{F}_{p},J)=0$
by Lang’s theorem, every orbit is soluble. The number of orbits
 $\#J(\mathbb{F}_{p})/2J(\mathbb{F}_{p})$
is equal to the size of the stabilizer
$\#J(\mathbb{F}_{p})/2J(\mathbb{F}_{p})$
is equal to the size of the stabilizer
 $\#J[2](\mathbb{F}_{p})$
. Since
$\#J[2](\mathbb{F}_{p})$
. Since
![]() $f(x)$
has a factor of degree 2,
$f(x)$
has a factor of degree 2,
 $\#J[2](\mathbb{F}_{p})\geqslant 2$
. Therefore at least half of the elements in
$\#J[2](\mathbb{F}_{p})\geqslant 2$
. Therefore at least half of the elements in
![]() $V_{f}(\mathbb{F}_{p})$
are not distinguished. Hence, for
$V_{f}(\mathbb{F}_{p})$
are not distinguished. Hence, for
![]() $p$
large enough,
$p$
large enough,
 $\unicode[STIX]{x1D719}_{p}\leqslant 1-\frac{1}{2}r_{n}<1$
.
$\unicode[STIX]{x1D719}_{p}\leqslant 1-\frac{1}{2}r_{n}<1$
.
We use the same technique to prove the second claim in Proposition 23. For
![]() $p$
large enough, there is a positive proportion
$p$
large enough, there is a positive proportion
![]() $r_{n}^{\prime }$
(depending only on
$r_{n}^{\prime }$
(depending only on
![]() $n$
) of polynomials of degree
$n$
) of polynomials of degree
![]() $2n+2$
over
$2n+2$
over
![]() $\mathbb{F}_{p}$
that factors into a linear term and an irreducible polynomial of degree
$\mathbb{F}_{p}$
that factors into a linear term and an irreducible polynomial of degree
![]() $2n+1$
. If
$2n+1$
. If
 $B\in V_{f}(\mathbb{Z}_{p})$
where
$B\in V_{f}(\mathbb{Z}_{p})$
where
![]() $f(x)$
has this reduction type mod
$f(x)$
has this reduction type mod
![]() $p$
, then
$p$
, then
![]() $p$
does not divide the discriminant of
$p$
does not divide the discriminant of
![]() $f(x)$
. As a consequence, the hyperelliptic curve
$f(x)$
. As a consequence, the hyperelliptic curve
 $y^{2}=f(x)$
is smooth over
$y^{2}=f(x)$
is smooth over
 $\operatorname{Spec}(\mathbb{Z}_{p})$
and the 2-torsion of its Jacobian
$\operatorname{Spec}(\mathbb{Z}_{p})$
and the 2-torsion of its Jacobian
![]() $J[2]$
is a finite étale group scheme over
$J[2]$
is a finite étale group scheme over
 $\operatorname{Spec}(\mathbb{Z}_{p})$
. From the reduction type of
$\operatorname{Spec}(\mathbb{Z}_{p})$
. From the reduction type of
![]() $f(x)$
over
$f(x)$
over
![]() $p$
, we see that
$p$
, we see that
 $\#J[2](\mathbb{Q}_{p})=\#J[2](\mathbb{F}_{p})=1$
. Denote by
$\#J[2](\mathbb{Q}_{p})=\#J[2](\mathbb{F}_{p})=1$
. Denote by
![]() $\unicode[STIX]{x1D719}_{p}$
the
$\unicode[STIX]{x1D719}_{p}$
the
![]() $p$
-adic density of the set of elements of
$p$
-adic density of the set of elements of
![]() $V(\mathbb{Z}_{p})$
with non-trivial stabilizer in
$V(\mathbb{Z}_{p})$
with non-trivial stabilizer in
![]() $G(\mathbb{Q}_{p})$
. Then we have shown that
$G(\mathbb{Q}_{p})$
. Then we have shown that
 $\unicode[STIX]{x1D719}_{p}\leqslant 1-r_{n}^{\prime }<1$
for
$\unicode[STIX]{x1D719}_{p}\leqslant 1-r_{n}^{\prime }<1$
for
![]() $p$
sufficiently large. This completes the proof.◻
$p$
sufficiently large. This completes the proof.◻
We may now prove the main result of this section, which we state again for the convenience of the reader.
Theorem 24. We have, for any
 $m=0,\ldots ,n+1$
,
$m=0,\ldots ,n+1$
,
 $$\begin{eqnarray}N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))+o(X^{(\dim V)/d}).\end{eqnarray}$$
$$\begin{eqnarray}N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))+o(X^{(\dim V)/d}).\end{eqnarray}$$
Proof. Let
 ${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
be the set consisting of
${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
be the set consisting of
![]() $h\in {\mathcal{F}}$
such that the
$h\in {\mathcal{F}}$
such that the
![]() $b_{11}$
-coefficient of any
$b_{11}$
-coefficient of any
 $B\in hG_{0}R^{(m)}(X)$
is less than 1 in absolute value. From (19), we see that
$B\in hG_{0}R^{(m)}(X)$
is less than 1 in absolute value. From (19), we see that
 $N(V(\mathbb{Z})^{(m)};X)$
is equal to
$N(V(\mathbb{Z})^{(m)};X)$
is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\nonumber\\ \displaystyle & & \displaystyle \quad =\displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\biggl(\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{h\in {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\nonumber\\ \displaystyle & & \displaystyle \quad =\displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\biggl(\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{h\in {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})^{\text{irr}}\}\,dh\biggr).\nonumber\end{eqnarray}$$
From Propositions 21 and 23, we obtain
 $$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})\}\,dh+o(X^{(\dim V)/d}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\#\{hG_{0}R^{(m)}(X)\cap V(\mathbb{Z})\}\,dh+o(X^{(\dim V)/d}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Note that
![]() $b_{11}$
has minimal weight among all the
$b_{11}$
has minimal weight among all the
![]() $b_{ij}$
, that is, the powers of the
$b_{ij}$
, that is, the powers of the
![]() $s_{k}$
in
$s_{k}$
in
 $w(1,1)/w(i,j)$
are non-negative for each
$w(1,1)/w(i,j)$
are non-negative for each
![]() $i,j,k$
. Furthermore, the length of the projection of
$i,j,k$
. Furthermore, the length of the projection of
 $hG_{0}R^{(m)}(X)$
onto the
$hG_{0}R^{(m)}(X)$
onto the
![]() $b_{11}$
-line is greater than 1 for any
$b_{11}$
-line is greater than 1 for any
 $h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }$
(by the definition of
$h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }$
(by the definition of
![]() ${\mathcal{F}}^{\prime }$
). Hence, for
${\mathcal{F}}^{\prime }$
). Hence, for
 $h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }$
, the volumes of all smaller-dimensional projections of
$h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }$
, the volumes of all smaller-dimensional projections of
 $hG_{0}R^{(m)}(X)$
are bounded by a constant times the volume of its projection onto the
$hG_{0}R^{(m)}(X)$
are bounded by a constant times the volume of its projection onto the
![]() $b_{11}=0$
hyperplane. Proposition 19 then implies that
$b_{11}=0$
hyperplane. Proposition 19 then implies that
 $$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X) & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\operatorname{Vol}(hG_{0}R^{(m)}(X))\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(\frac{\operatorname{Vol}(hG_{0}R^{(m)}(X))}{X^{1/d}w(1,1)}\biggr)\,dh+o(X^{(\dim V)/d}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X) & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}\operatorname{Vol}(hG_{0}R^{(m)}(X))\nonumber\\ \displaystyle & & \displaystyle +\,O\biggl(\frac{\operatorname{Vol}(hG_{0}R^{(m)}(X))}{X^{1/d}w(1,1)}\biggr)\,dh+o(X^{(\dim V)/d}).\nonumber\end{eqnarray}$$
Recall that
![]() ${\mathcal{F}}^{\prime }$
is defined by the condition
${\mathcal{F}}^{\prime }$
is defined by the condition
 $CX^{1/d}w(1,1)<1$
. Hence, to be in
$CX^{1/d}w(1,1)<1$
. Hence, to be in
![]() ${\mathcal{F}}^{\prime }$
, one of the
${\mathcal{F}}^{\prime }$
, one of the
![]() $s_{i}$
must be at least
$s_{i}$
must be at least
 $C^{1/2n}X^{1/2nd}$
, which implies that the volume of
$C^{1/2n}X^{1/2nd}$
, which implies that the volume of
![]() ${\mathcal{F}}^{\prime }$
is bounded by
${\mathcal{F}}^{\prime }$
is bounded by
![]() $o(1)$
. Moreover, since
$o(1)$
. Moreover, since
 $\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}1/w(1,1)\,dh=O(1)$
, we obtain
$\int _{h\in {\mathcal{F}}\backslash {\mathcal{F}}^{\prime }}1/w(1,1)\,dh=O(1)$
, we obtain
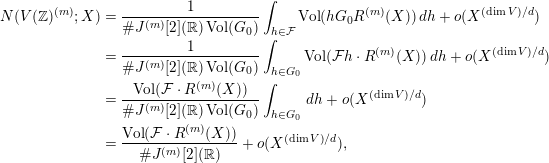 $$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X) & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\operatorname{Vol}(hG_{0}R^{(m)}(X))\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\operatorname{Vol}({\mathcal{F}}h\cdot R^{(m)}(X))\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))}{\#J^{(m)}[2](\mathbb{R})}+o(X^{(\dim V)/d}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(V(\mathbb{Z})^{(m)};X) & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in {\mathcal{F}}}\operatorname{Vol}(hG_{0}R^{(m)}(X))\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\operatorname{Vol}({\mathcal{F}}h\cdot R^{(m)}(X))\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))}{\#J^{(m)}[2](\mathbb{R})\operatorname{Vol}(G_{0})}\int _{h\in G_{0}}\,dh+o(X^{(\dim V)/d})\nonumber\\ \displaystyle & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))}{\#J^{(m)}[2](\mathbb{R})}+o(X^{(\dim V)/d}),\end{eqnarray}$$
where the third equality follows because the volume of
 ${\mathcal{F}}h\cdot R^{(m)}(X)$
is independent of
${\mathcal{F}}h\cdot R^{(m)}(X)$
is independent of
![]() $h$
. This concludes the proof of Theorem 24.◻
$h$
. This concludes the proof of Theorem 24.◻
4.3 A squarefree sieve
For any subset
![]() $U$
of
$U$
of
![]() $S(\mathbb{Z})$
, let
$S(\mathbb{Z})$
, let
 $N(U;X)$
denote the number of elements in
$N(U;X)$
denote the number of elements in
![]() $U$
having height bounded by
$U$
having height bounded by
![]() $X$
. Let
$X$
. Let
 $F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions. We assume without loss of generality that
$F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions. We assume without loss of generality that
 $\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
$\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
 $m\in \{0,\ldots ,n+1\}$
. We first determine asymptotics for
$m\in \{0,\ldots ,n+1\}$
. We first determine asymptotics for
 $N(\operatorname{Inv}(F);X)$
as
$N(\operatorname{Inv}(F);X)$
as
![]() $X$
goes to infinity. To this end, we have the following uniformity estimate, proved in [Reference Bhargava, Shankar and WangBSW16].
$X$
goes to infinity. To this end, we have the following uniformity estimate, proved in [Reference Bhargava, Shankar and WangBSW16].
Proposition 25. For each prime
![]() $p$
, let
$p$
, let
![]() $U_{p}$
denote the set of elements
$U_{p}$
denote the set of elements
 $c\in S(\mathbb{Z})$
such that
$c\in S(\mathbb{Z})$
such that
 $p^{2}\mid \unicode[STIX]{x1D6E5}(c)$
. Then for any
$p^{2}\mid \unicode[STIX]{x1D6E5}(c)$
. Then for any
![]() $M>0$
, we have
$M>0$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{p>M}N(U_{p};X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V)/d}/M^{1-\unicode[STIX]{x1D716}})+o(X^{(\dim V)/d}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{p>M}N(U_{p};X)=O_{\unicode[STIX]{x1D716}}(X^{(\dim V)/d}/M^{1-\unicode[STIX]{x1D716}})+o(X^{(\dim V)/d}),\end{eqnarray}$$
where the implied constant is independent of
![]() $X$
and
$X$
and
![]() $M$
.
$M$
.
Then we have the following theorem which follows from Propositions 19 and 25 just as [Reference Bhargava and ShankarBS15, Theorem 2.21] followed from [Reference Bhargava and ShankarBS15, Theorems 2.12 and 2.13].
Theorem 26. Let
 $F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions such that
$F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions such that
 $\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some
$\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some
 $m=0,\ldots ,n+1$
. Then the number of hyperelliptic curves in
$m=0,\ldots ,n+1$
. Then the number of hyperelliptic curves in
![]() $F$
having height bounded by
$F$
having height bounded by
![]() $X$
is
$X$
is
 $$\begin{eqnarray}\operatorname{Vol}(S(\mathbb{R})_{H<X}^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/d}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}(S(\mathbb{R})_{H<X}^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/d}).\end{eqnarray}$$
The following weighted version of Theorem 20 follows immediately from the proof of Theorem 20.
Theorem 27. Fix some
 $m=0,\ldots ,n+1$
. Let
$m=0,\ldots ,n+1$
. Let
 $p_{1},\ldots ,p_{k}$
be distinct prime numbers. For
$p_{1},\ldots ,p_{k}$
be distinct prime numbers. For
 $j=1,\ldots ,k$
, let
$j=1,\ldots ,k$
, let
 $\unicode[STIX]{x1D719}_{p_{j}}:V(\mathbb{Z})\rightarrow \mathbb{R}$
be
$\unicode[STIX]{x1D719}_{p_{j}}:V(\mathbb{Z})\rightarrow \mathbb{R}$
be
![]() $G(\mathbb{Z})$
-invariant functions on
$G(\mathbb{Z})$
-invariant functions on
![]() $V(\mathbb{Z})$
such that
$V(\mathbb{Z})$
such that
![]() $\unicode[STIX]{x1D719}_{p_{j}}(B)$
depends only on the congruence class of
$\unicode[STIX]{x1D719}_{p_{j}}(B)$
depends only on the congruence class of
![]() $B$
modulo some power
$B$
modulo some power
![]() $p_{j}^{a_{j}}$
of
$p_{j}^{a_{j}}$
of
![]() $p_{j}$
. Let
$p_{j}$
. Let
 $N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)$
denote the number of irreducible
$N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)$
denote the number of irreducible
![]() $G(\mathbb{Z})$
-orbits of
$G(\mathbb{Z})$
-orbits of
 $V^{(m)}(\mathbb{Z})$
having height bounded by
$V^{(m)}(\mathbb{Z})$
having height bounded by
![]() $X$
, where each orbit
$X$
, where each orbit
 $G(\mathbb{Z})\cdot B$
is counted with weight
$G(\mathbb{Z})\cdot B$
is counted with weight
 $\unicode[STIX]{x1D719}(B)/\#\text{Stab}_{G(\mathbb{Z})}(B)$
; here
$\unicode[STIX]{x1D719}(B)/\#\text{Stab}_{G(\mathbb{Z})}(B)$
; here
![]() $\unicode[STIX]{x1D719}$
is defined by
$\unicode[STIX]{x1D719}$
is defined by
 $\unicode[STIX]{x1D719}(B):=\prod _{j=1}^{k}\unicode[STIX]{x1D719}_{p_{j}}(B)$
. Then we have
$\unicode[STIX]{x1D719}(B):=\prod _{j=1}^{k}\unicode[STIX]{x1D719}_{p_{j}}(B)$
. Then we have
 $$\begin{eqnarray}N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)=N(V^{(m)}(\mathbb{Z});X)\mathop{\prod }_{j=1}^{k}\int _{B\in V(\mathbb{Z}_{p_{j}})}\tilde{\unicode[STIX]{x1D719}}_{p_{j}}(B)\,dB+o(X^{(\dim V)/d}),\end{eqnarray}$$
$$\begin{eqnarray}N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)=N(V^{(m)}(\mathbb{Z});X)\mathop{\prod }_{j=1}^{k}\int _{B\in V(\mathbb{Z}_{p_{j}})}\tilde{\unicode[STIX]{x1D719}}_{p_{j}}(B)\,dB+o(X^{(\dim V)/d}),\end{eqnarray}$$
where
![]() $\tilde{\unicode[STIX]{x1D719}}_{p_{j}}$
is the natural extension of
$\tilde{\unicode[STIX]{x1D719}}_{p_{j}}$
is the natural extension of
![]() $\unicode[STIX]{x1D719}_{p_{j}}$
to
$\unicode[STIX]{x1D719}_{p_{j}}$
to
![]() $V(\mathbb{Z}_{p_{j}})$
and
$V(\mathbb{Z}_{p_{j}})$
and
![]() $dB$
denotes the additive measure on
$dB$
denotes the additive measure on
![]() $V(\mathbb{Z}_{p_{j}})$
normalized so that
$V(\mathbb{Z}_{p_{j}})$
normalized so that
 $\int _{B\in V(\mathbb{Z}_{p_{j}})}\,dB=1$
.
$\int _{B\in V(\mathbb{Z}_{p_{j}})}\,dB=1$
.
However, in order to prove Theorem 18, we shall need weights that are defined by certain infinite sets of congruence conditions. To describe which weight functions on
![]() $V(\mathbb{Z})$
are allowed, we need the following definition.
$V(\mathbb{Z})$
are allowed, we need the following definition.
Definition 28. A function
 $\unicode[STIX]{x1D719}:V(\mathbb{Z})\rightarrow [0,1]$
is said to be defined by congruence conditions if there exist local functions
$\unicode[STIX]{x1D719}:V(\mathbb{Z})\rightarrow [0,1]$
is said to be defined by congruence conditions if there exist local functions
 $\unicode[STIX]{x1D719}_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
satisfying the following conditions:
$\unicode[STIX]{x1D719}_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
satisfying the following conditions:
-
(i) for all
 $B\in V(\mathbb{Z})$
, the product
$B\in V(\mathbb{Z})$
, the product
 $\prod _{p}\unicode[STIX]{x1D719}_{p}(B)$
converges to
$\prod _{p}\unicode[STIX]{x1D719}_{p}(B)$
converges to
 $\unicode[STIX]{x1D719}(B)$
;
$\unicode[STIX]{x1D719}(B)$
; -
(ii) for each prime
 $p$
, the function
$p$
, the function
 $\unicode[STIX]{x1D719}_{p}$
is locally constant outside some closed set
$\unicode[STIX]{x1D719}_{p}$
is locally constant outside some closed set
 $S_{p}$
of measure 0.
$S_{p}$
of measure 0.
Then we have the following theorem.
Theorem 29. Let
 $\unicode[STIX]{x1D719}:V(\mathbb{Z})\rightarrow [0,1]$
be a function defined by congruence conditions via local functions
$\unicode[STIX]{x1D719}:V(\mathbb{Z})\rightarrow [0,1]$
be a function defined by congruence conditions via local functions
 $\unicode[STIX]{x1D719}_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
. Then, with notation as in Theorem 27, we have
$\unicode[STIX]{x1D719}_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
. Then, with notation as in Theorem 27, we have
 $$\begin{eqnarray}N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)\leqslant N(V^{(m)};X)\mathop{\prod }_{p}\int _{B\in V(\mathbb{Z}_{p})}\unicode[STIX]{x1D719}_{p}(B)\,dB+o(X^{(\dim V)/d}).\end{eqnarray}$$
$$\begin{eqnarray}N_{\unicode[STIX]{x1D719}}(V^{(m)}(\mathbb{Z});X)\leqslant N(V^{(m)};X)\mathop{\prod }_{p}\int _{B\in V(\mathbb{Z}_{p})}\unicode[STIX]{x1D719}_{p}(B)\,dB+o(X^{(\dim V)/d}).\end{eqnarray}$$
Theorem 29 follows from Theorem 27. The proof is identical to the first half of the proof of [Reference Bhargava and ShankarBS15, Theorem 2.21].
4.4 Compatibility of measures and local computations
Let
 $F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions. We assume without loss of generality that
$F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions. We assume without loss of generality that
 $\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
$\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
 $m\in \{0,\ldots ,n+1\}$
. To prove Theorem 18 we need to weight each locally soluble element
$m\in \{0,\ldots ,n+1\}$
. To prove Theorem 18 we need to weight each locally soluble element
 $B\in V(\mathbb{Z})$
(having invariant
$B\in V(\mathbb{Z})$
(having invariant
![]() $\unicode[STIX]{x1D70B}(B)$
in
$\unicode[STIX]{x1D70B}(B)$
in
![]() $\operatorname{Inv}(F)$
) by the reciprocal of the number of
$\operatorname{Inv}(F)$
) by the reciprocal of the number of
![]() $G(\mathbb{Z})$
-orbits in
$G(\mathbb{Z})$
-orbits in
 $G(\mathbb{Q})\cdot B\cap V(\mathbb{Z})$
. However, in order for our weight function to be defined by congruence conditions, we use instead the following weight function
$G(\mathbb{Q})\cdot B\cap V(\mathbb{Z})$
. However, in order for our weight function to be defined by congruence conditions, we use instead the following weight function
 $w:V(\mathbb{Z})\rightarrow [0,1]$
:
$w:V(\mathbb{Z})\rightarrow [0,1]$
:
 $$\begin{eqnarray}w(B):=\left\{\begin{array}{@{}ll@{}}\biggl(\displaystyle \mathop{\sum }_{B^{\prime }}\frac{\#\text{Stab}_{G(\mathbb{Q})}(B^{\prime })}{\#\text{Stab}_{G(\mathbb{Z})}(B^{\prime })}\biggr)^{-1}\quad & \text{if}~B~\text{is locally soluble and}~\unicode[STIX]{x1D70B}(B)\in \operatorname{Inv}(F),\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}w(B):=\left\{\begin{array}{@{}ll@{}}\biggl(\displaystyle \mathop{\sum }_{B^{\prime }}\frac{\#\text{Stab}_{G(\mathbb{Q})}(B^{\prime })}{\#\text{Stab}_{G(\mathbb{Z})}(B^{\prime })}\biggr)^{-1}\quad & \text{if}~B~\text{is locally soluble and}~\unicode[STIX]{x1D70B}(B)\in \operatorname{Inv}(F),\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
where the sum is over a complete set of representatives for the action of
![]() $G(\mathbb{Z})$
on
$G(\mathbb{Z})$
on
 $G(\mathbb{Q})\cdot B\cap V(\mathbb{Z})$
.
$G(\mathbb{Q})\cdot B\cap V(\mathbb{Z})$
.
We start with the following proposition proving that the class
 $(\infty ^{\prime })-(\infty )$
is not divisible by 2 in the Jacobians of most hyperelliptic curves in our family.
$(\infty ^{\prime })-(\infty )$
is not divisible by 2 in the Jacobians of most hyperelliptic curves in our family.
Proposition 30. Let
![]() $F$
be a large family of hyperelliptic curves. Then for
$F$
be a large family of hyperelliptic curves. Then for
![]() $100\%$
of elements
$100\%$
of elements
![]() $C\in F$
, the class
$C\in F$
, the class
 $(\infty ^{\prime })-(\infty )$
is not divisible by
$(\infty ^{\prime })-(\infty )$
is not divisible by
![]() $2$
in
$2$
in
![]() $J(\mathbb{Q})$
.
$J(\mathbb{Q})$
.
Proof. By the proof of Theorem 10 and Proposition 5, for a monic even hyperelliptic curve
![]() $C$
over
$C$
over
![]() $\mathbb{Q}$
defined by
$\mathbb{Q}$
defined by
 $y^{2}=f(x)$
, the element
$y^{2}=f(x)$
, the element
 $(\infty ^{\prime })-(\infty )$
is divisible by 2 in
$(\infty ^{\prime })-(\infty )$
is divisible by 2 in
![]() $J(\mathbb{Q})$
if and only if the étale algebra
$J(\mathbb{Q})$
if and only if the étale algebra
 $L=\mathbb{Q}[x]/(f(x))$
contains a quadratic extension of
$L=\mathbb{Q}[x]/(f(x))$
contains a quadratic extension of
![]() $\mathbb{Q}$
. Proposition 30 then follows since for
$\mathbb{Q}$
. Proposition 30 then follows since for
![]() $100\%$
of monic integral polynomials of degree
$100\%$
of monic integral polynomials of degree
![]() $2n+2$
, when ordered by height, the Galois group of the normal closure of
$2n+2$
, when ordered by height, the Galois group of the normal closure of
 $\mathbb{Q}[x]/(f(x))$
is
$\mathbb{Q}[x]/(f(x))$
is
![]() $S_{n}$
.◻
$S_{n}$
.◻
We now have the following theorem.
Theorem 31. Let
 $F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions with
$F=F_{\unicode[STIX]{x1D6F4}}$
be a large family of monic even hyperelliptic curves defined by congruence conditions with
 $\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
$\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
for some fixed integer
 $m\in \{0,\ldots ,n+1\}$
.
$m\in \{0,\ldots ,n+1\}$
.
![]() $L$
Then
$L$
Then
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ C\in F \\ H(C)\leqslant X}}(\#\text{Sel}_{2}(J(C))-2)=N_{w}(V(\mathbb{Z})^{(m)};X)+o(X^{(\dim V)/d}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ C\in F \\ H(C)\leqslant X}}(\#\text{Sel}_{2}(J(C))-2)=N_{w}(V(\mathbb{Z})^{(m)};X)+o(X^{(\dim V)/d}),\end{eqnarray}$$
where
 $V(\mathbb{Z})^{(m)}$
is the set of all elements in
$V(\mathbb{Z})^{(m)}$
is the set of all elements in
![]() $V(\mathbb{Z})$
whose invariants belong to
$V(\mathbb{Z})$
whose invariants belong to
 $\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
.
$\unicode[STIX]{x1D6F4}_{\infty }=S(\mathbb{R})^{(m)}$
.
Proof. It follows from Proposition 30 that for 100% of hyperelliptic curves
 $C(c)\in F$
, the set
$C(c)\in F$
, the set
![]() $V_{f_{c}}(\mathbb{Q})$
has two distinguished orbits. Hence, Theorem 11 and Corollary 13 show that, up to an error of
$V_{f_{c}}(\mathbb{Q})$
has two distinguished orbits. Hence, Theorem 11 and Corollary 13 show that, up to an error of
 $o(X^{(\dim V)/d})$
, the left-hand side of (32) is equal to the number of
$o(X^{(\dim V)/d})$
, the left-hand side of (32) is equal to the number of
![]() $G(\mathbb{Q})$
-equivalence classes of elements in
$G(\mathbb{Q})$
-equivalence classes of elements in
![]() $V(\mathbb{Z})$
that are locally soluble, have invariants in
$V(\mathbb{Z})$
that are locally soluble, have invariants in
![]() $\operatorname{Inv}(F)$
, and have height bounded by
$\operatorname{Inv}(F)$
, and have height bounded by
![]() $X$
.
$X$
.
Given a locally soluble element
 $B\in V(\mathbb{Z})$
such that
$B\in V(\mathbb{Z})$
such that
 $\unicode[STIX]{x1D70B}(B)\in F$
, let
$\unicode[STIX]{x1D70B}(B)\in F$
, let
 $B_{1}\ldots B_{k}$
denote a complete set of representatives for the action of
$B_{1}\ldots B_{k}$
denote a complete set of representatives for the action of
![]() $G(\mathbb{Z})$
on the
$G(\mathbb{Z})$
on the
![]() $G(\mathbb{Q})$
-equivalence class of
$G(\mathbb{Q})$
-equivalence class of
![]() $B$
in
$B$
in
![]() $V(\mathbb{Z})$
. Then
$V(\mathbb{Z})$
. Then
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{k}\frac{w(B_{i})}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})} & = & \displaystyle \frac{1}{\#\text{Stab}_{G(\mathbb{Q})}(B)}\biggl(\mathop{\sum }_{i=1}^{k}\frac{1}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})}\biggr)^{-1}\mathop{\sum }_{i=1}^{k}\frac{1}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\#\text{Stab}_{G(\mathbb{Q})}(B)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{k}\frac{w(B_{i})}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})} & = & \displaystyle \frac{1}{\#\text{Stab}_{G(\mathbb{Q})}(B)}\biggl(\mathop{\sum }_{i=1}^{k}\frac{1}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})}\biggr)^{-1}\mathop{\sum }_{i=1}^{k}\frac{1}{\#\text{Stab}_{G(\mathbb{Z})}(B_{i})}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\#\text{Stab}_{G(\mathbb{Q})}(B)}.\end{eqnarray}$$
Hence the right-hand side of (32) counts the number of
![]() $G(\mathbb{Q})$
-equivalence classes of elements in
$G(\mathbb{Q})$
-equivalence classes of elements in
![]() $V(\mathbb{Z})$
that are locally soluble, have invariants in
$V(\mathbb{Z})$
that are locally soluble, have invariants in
![]() $F$
, and have height bounded by
$F$
, and have height bounded by
![]() $X$
, such that the
$X$
, such that the
![]() $G(\mathbb{Q})$
-orbit of
$G(\mathbb{Q})$
-orbit of
![]() $B$
is weighted with
$B$
is weighted with
 $1/\#\text{Stab}_{G(\mathbb{Q})}(B)$
for all orbits. The theorem now follows since
$1/\#\text{Stab}_{G(\mathbb{Q})}(B)$
for all orbits. The theorem now follows since
 $\operatorname{Stab}_{G(\mathbb{Q})}(B)=1$
for all but negligibly few
$\operatorname{Stab}_{G(\mathbb{Q})}(B)=1$
for all but negligibly few
 $B\in V(\mathbb{Z})$
by Proposition 23.◻
$B\in V(\mathbb{Z})$
by Proposition 23.◻
In order to demonstrate that
![]() $w$
is defined by congruence conditions, we need to express it as a local product of weight functions on
$w$
is defined by congruence conditions, we need to express it as a local product of weight functions on
![]() $V(\mathbb{Z}_{p})$
. To this end, we define
$V(\mathbb{Z}_{p})$
. To this end, we define
 $w_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
:
$w_{p}:V(\mathbb{Z}_{p})\rightarrow [0,1]$
:
 $$\begin{eqnarray}w_{p}(B):=\left\{\begin{array}{@{}ll@{}}\biggl(\displaystyle \mathop{\sum }_{B^{\prime }}\frac{\#\text{Stab}_{G(\mathbb{Q}_{p})}(B^{\prime })}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B^{\prime })}\biggr)^{-1}\quad & \text{if}~B~\text{is}~\mathbb{Q}_{p}\text{-}\text{soluble and}~\unicode[STIX]{x1D70B}(B)\in \operatorname{Inv}_{p}(F),\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}w_{p}(B):=\left\{\begin{array}{@{}ll@{}}\biggl(\displaystyle \mathop{\sum }_{B^{\prime }}\frac{\#\text{Stab}_{G(\mathbb{Q}_{p})}(B^{\prime })}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B^{\prime })}\biggr)^{-1}\quad & \text{if}~B~\text{is}~\mathbb{Q}_{p}\text{-}\text{soluble and}~\unicode[STIX]{x1D70B}(B)\in \operatorname{Inv}_{p}(F),\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
where the sum is over a set of representatives for the action of
![]() $G(\mathbb{Z}_{p})$
on the
$G(\mathbb{Z}_{p})$
on the
![]() $G(\mathbb{Q}_{p})$
-equivalence class of
$G(\mathbb{Q}_{p})$
-equivalence class of
![]() $B$
in
$B$
in
![]() $V(\mathbb{Z})$
. We have the following result whose proof is identical to that of [Reference Bhargava and ShankarBS15, Proposition 3.6], using the fact that
$V(\mathbb{Z})$
. We have the following result whose proof is identical to that of [Reference Bhargava and ShankarBS15, Proposition 3.6], using the fact that
![]() $G$
has class number 1 over
$G$
has class number 1 over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Proposition 32. If
 $B\in V(\mathbb{Z})$
has non-zero discriminant, then
$B\in V(\mathbb{Z})$
has non-zero discriminant, then
 $w(B)=\prod _{p}w_{p}(B)$
.
$w(B)=\prod _{p}w_{p}(B)$
.
From Theorems 20 and 29, we have the equality
 $$\begin{eqnarray}N_{w}(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))\mathop{\prod }_{p}\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB+o(X^{(\dim V)/d}).\end{eqnarray}$$
$$\begin{eqnarray}N_{w}(V(\mathbb{Z})^{(m)};X)=\frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))\mathop{\prod }_{p}\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB+o(X^{(\dim V)/d}).\end{eqnarray}$$
For the rest of the section, our aim is to express
 $\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
and
$\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
and
 $\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB$
in more convenient forms. To this end, we introduce the following notation. Recall that
$\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB$
in more convenient forms. To this end, we introduce the following notation. Recall that
![]() $dB$
is Haar measure on
$dB$
is Haar measure on
![]() $V$
normalized so that
$V$
normalized so that
![]() $V(\mathbb{Z}_{p})$
has volume 1 for each prime
$V(\mathbb{Z}_{p})$
has volume 1 for each prime
![]() $p$
, and such that
$p$
, and such that
![]() $V(\mathbb{Z})$
has covolume 1 in
$V(\mathbb{Z})$
has covolume 1 in
![]() $V(\mathbb{R})$
. Let
$V(\mathbb{R})$
. Let
![]() $d\unicode[STIX]{x1D707}(c)$
denote similarly normalized Euclidean measure on
$d\unicode[STIX]{x1D707}(c)$
denote similarly normalized Euclidean measure on
![]() $S$
. Finally, let
$S$
. Finally, let
![]() $\unicode[STIX]{x1D714}$
be a differential which generates the rank-1 module of top-degree differentials of
$\unicode[STIX]{x1D714}$
be a differential which generates the rank-1 module of top-degree differentials of
![]() $G$
over
$G$
over
![]() $\mathbb{Z}$
. We denote the measure associated with
$\mathbb{Z}$
. We denote the measure associated with
![]() $\unicode[STIX]{x1D714}$
by
$\unicode[STIX]{x1D714}$
by
![]() $d\unicode[STIX]{x1D70F}(g)$
. We now have the following result that allows us to compute volumes of multisets in
$d\unicode[STIX]{x1D70F}(g)$
. We now have the following result that allows us to compute volumes of multisets in
![]() $V(K)$
, for
$V(K)$
, for
![]() $K=\mathbb{R}$
and
$K=\mathbb{R}$
and
![]() $\mathbb{Z}_{p}$
. This result follows from [Reference Bhargava and ShankarBS15, Propositions 3.11 and 3.12].
$\mathbb{Z}_{p}$
. This result follows from [Reference Bhargava and ShankarBS15, Propositions 3.11 and 3.12].
Proposition 33. Let
![]() $K$
be
$K$
be
![]() $\mathbb{R}$
or
$\mathbb{R}$
or
![]() $\mathbb{Z}_{p}$
for some prime
$\mathbb{Z}_{p}$
for some prime
![]() $p$
, let
$p$
, let
![]() $|\cdot |$
denote the usual valuation on
$|\cdot |$
denote the usual valuation on
![]() $K$
, and let
$K$
, and let
 $s:S(K)\rightarrow V(K)$
be a continuous section. Then there exists a rational non-zero constant
$s:S(K)\rightarrow V(K)$
be a continuous section. Then there exists a rational non-zero constant
![]() ${\mathcal{J}}$
, independent of
${\mathcal{J}}$
, independent of
![]() $K$
and
$K$
and
![]() $s$
, such that for any measurable function
$s$
, such that for any measurable function
![]() $\unicode[STIX]{x1D719}$
on
$\unicode[STIX]{x1D719}$
on
![]() $V(K)$
, we have
$V(K)$
, we have
 $$\begin{eqnarray}\displaystyle \int _{G(K)\cdot s(S(K))}\unicode[STIX]{x1D719}(B)\,dB & = & \displaystyle |{\mathcal{J}}|\displaystyle \int _{c\in S(K)}\displaystyle \int _{g\in G(K)}\unicode[STIX]{x1D719}(g\cdot s(c))\,d\unicode[STIX]{x1D70F}(g)\,d\unicode[STIX]{x1D707}(c),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{G(K)\cdot s(S(K))}\unicode[STIX]{x1D719}(B)\,dB & = & \displaystyle |{\mathcal{J}}|\displaystyle \int _{c\in S(K)}\displaystyle \int _{g\in G(K)}\unicode[STIX]{x1D719}(g\cdot s(c))\,d\unicode[STIX]{x1D70F}(g)\,d\unicode[STIX]{x1D707}(c),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{V(K)}\unicode[STIX]{x1D719}(B)\,dB\nonumber\\ \displaystyle & & \displaystyle \quad =|{\mathcal{J}}|\displaystyle \int _{\substack{ c\in S(K) \\ \unicode[STIX]{x1D6E5}(c)\neq 0}}\biggl(\displaystyle \mathop{\sum }_{B\in (V_{f_{c}}(K)/G(K))}\frac{1}{\#\text{Stab}_{G(K)}(B)}\int _{g\in G(K)}\unicode[STIX]{x1D719}(g\cdot B)\,d\unicode[STIX]{x1D70F}(g)\!\biggr)\,d\unicode[STIX]{x1D707}(c),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{V(K)}\unicode[STIX]{x1D719}(B)\,dB\nonumber\\ \displaystyle & & \displaystyle \quad =|{\mathcal{J}}|\displaystyle \int _{\substack{ c\in S(K) \\ \unicode[STIX]{x1D6E5}(c)\neq 0}}\biggl(\displaystyle \mathop{\sum }_{B\in (V_{f_{c}}(K)/G(K))}\frac{1}{\#\text{Stab}_{G(K)}(B)}\int _{g\in G(K)}\unicode[STIX]{x1D719}(g\cdot B)\,d\unicode[STIX]{x1D70F}(g)\!\biggr)\,d\unicode[STIX]{x1D707}(c),\qquad\end{eqnarray}$$
where we regard
 $G(K)\cdot s(R)$
as a multiset, and
$G(K)\cdot s(R)$
as a multiset, and
 $V_{f_{c}}(K)/G(K)$
denotes a set of representatives for the action of
$V_{f_{c}}(K)/G(K)$
denotes a set of representatives for the action of
![]() $G(K)$
on
$G(K)$
on
![]() $V_{f_{c}}(K)$
.
$V_{f_{c}}(K)$
.
We use Proposition 33 to compute
 $\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
. If
$\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X))$
. If
 $c\in R^{(m)}$
and
$c\in R^{(m)}$
and
![]() $J$
denotes the Jacobian of the corresponding hyperelliptic curve, then the number of
$J$
denotes the Jacobian of the corresponding hyperelliptic curve, then the number of
![]() $\mathbb{R}$
-soluble
$\mathbb{R}$
-soluble
![]() $G(\mathbb{R})$
-orbits of
$G(\mathbb{R})$
-orbits of
![]() $V_{f_{c}}(\mathbb{R})$
is
$V_{f_{c}}(\mathbb{R})$
is
 $\#(J(\mathbb{R})/2J(\mathbb{R}))$
. This number is independent of
$\#(J(\mathbb{R})/2J(\mathbb{R}))$
. This number is independent of
 $c\in V(\mathbb{R})^{(m)}$
, and we denote it by
$c\in V(\mathbb{R})^{(m)}$
, and we denote it by
 $\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))$
. Hence, by (36), we have
$\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))$
. Hence, by (36), we have
 $$\begin{eqnarray}\displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X)) & = & \displaystyle |{\mathcal{J}}|\displaystyle \frac{\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\nonumber\\ \displaystyle & = & \displaystyle |{\mathcal{J}}|a_{\infty }\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}}\cdot R^{(m)}(X)) & = & \displaystyle |{\mathcal{J}}|\displaystyle \frac{\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))}{\#J^{(m)}[2](\mathbb{R})}\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\nonumber\\ \displaystyle & = & \displaystyle |{\mathcal{J}}|a_{\infty }\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)}),\end{eqnarray}$$
where
 $$\begin{eqnarray}a_{\infty }=\frac{\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))}{\#J^{(m)}[2](\mathbb{R})}=2^{-n},\end{eqnarray}$$
$$\begin{eqnarray}a_{\infty }=\frac{\#(J^{(m)}(\mathbb{R})/2J^{(m)}(\mathbb{R}))}{\#J^{(m)}[2](\mathbb{R})}=2^{-n},\end{eqnarray}$$
by [Reference StollSto01, Lemma 5.14].
Next we compute
 $\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB$
. Note that since
$\int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB$
. Note that since
![]() $w_{p}$
is
$w_{p}$
is
![]() $G(\mathbb{Z}_{p})$
-invariant, we have
$G(\mathbb{Z}_{p})$
-invariant, we have
 $$\begin{eqnarray}\displaystyle \int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB & = & \displaystyle |{\mathcal{J}}|_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\int _{c\in \operatorname{Inv}_{p}(F)}\biggl(\mathop{\sum }_{B\in (V_{c}(\mathbb{Z}_{p})/G(\mathbb{Z}_{p}))}\frac{w_{p}(B)}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B)}\biggr)\,d\unicode[STIX]{x1D707}(c)\nonumber\\ \displaystyle & = & \displaystyle |{\mathcal{J}}|_{p}\,a_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{V(\mathbb{Z}_{p})}w_{p}(B)\,dB & = & \displaystyle |{\mathcal{J}}|_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\int _{c\in \operatorname{Inv}_{p}(F)}\biggl(\mathop{\sum }_{B\in (V_{c}(\mathbb{Z}_{p})/G(\mathbb{Z}_{p}))}\frac{w_{p}(B)}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B)}\biggr)\,d\unicode[STIX]{x1D707}(c)\nonumber\\ \displaystyle & = & \displaystyle |{\mathcal{J}}|_{p}\,a_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F)).\end{eqnarray}$$
The final equality follows from a computation similar to (33); namely, if
![]() $J$
is the Jacobian of the monic even hyperelliptic curve
$J$
is the Jacobian of the monic even hyperelliptic curve
![]() $c$
and
$c$
and
![]() $B_{c}$
is any element in
$B_{c}$
is any element in
 $V_{f_{c}}(\mathbb{Q}_{p})$
, we have by Proposition 12,
$V_{f_{c}}(\mathbb{Q}_{p})$
, we have by Proposition 12,
 $$\begin{eqnarray}\mathop{\sum }_{B\in (V_{f_{c}}(\mathbb{Z}_{p})/G(\mathbb{Z}_{p}))}\frac{w_{p}(B)}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B)}=\frac{\#(G(\mathbb{Q}_{p})\backslash V_{f_{c}}^{\text{sol}}(\mathbb{Q}_{p}))}{\#\text{Stab}_{G(\mathbb{Q}_{p})}(B_{c})}=\frac{\#(J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p}))}{\#J[2](\mathbb{Q}_{p})}=:a_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{B\in (V_{f_{c}}(\mathbb{Z}_{p})/G(\mathbb{Z}_{p}))}\frac{w_{p}(B)}{\#\text{Stab}_{G(\mathbb{Z}_{p})}(B)}=\frac{\#(G(\mathbb{Q}_{p})\backslash V_{f_{c}}^{\text{sol}}(\mathbb{Q}_{p}))}{\#\text{Stab}_{G(\mathbb{Q}_{p})}(B_{c})}=\frac{\#(J(\mathbb{Q}_{p})/2J(\mathbb{Q}_{p}))}{\#J[2](\mathbb{Q}_{p})}=:a_{p}.\end{eqnarray}$$
Note that
![]() $a_{p}=1$
if
$a_{p}=1$
if
![]() $p\neq 2$
and
$p\neq 2$
and
 $a_{2}=2^{n}$
, by [Reference StollSto01, Lemma 5.7].
$a_{2}=2^{n}$
, by [Reference StollSto01, Lemma 5.7].
Combining Theorem 31 with (35), (38), and (39), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ C\in F \\ H(C)\leqslant X}}(\#\text{Sel}_{2}(J(C))-2)\nonumber\\ \displaystyle & & \displaystyle \quad =|{\mathcal{J}}|\,a_{\infty }\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}|{\mathcal{J}}|_{p}\,a_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/(\deg H)})\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/(\deg H)}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ C\in F \\ H(C)\leqslant X}}(\#\text{Sel}_{2}(J(C))-2)\nonumber\\ \displaystyle & & \displaystyle \quad =|{\mathcal{J}}|\,a_{\infty }\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}|{\mathcal{J}}|_{p}\,a_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/(\deg H)})\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F))+o(X^{(\dim V)/(\deg H)}),\end{eqnarray}$$
since
 $a_{\infty }\prod _{p}a_{p}=1$
and
$a_{\infty }\prod _{p}a_{p}=1$
and
 $|{\mathcal{J}}|\prod _{p}|{\mathcal{J}}|_{p}=1$
.
$|{\mathcal{J}}|\prod _{p}|{\mathcal{J}}|_{p}=1$
.
Theorem 26, Proposition 30 and (40) imply that
 $$\begin{eqnarray}\displaystyle \lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{\substack{ C\in F \\ H(C)<X}}(\#\text{Sel}_{2}(J(C))-2)}{\mathop{\sum }_{\substack{ C\in F \\ H(C)<X}}1} & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}(\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F)))}{\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(\operatorname{Inv}_{p}(F))}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70F}_{G},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{X\rightarrow \infty }\frac{\mathop{\sum }_{\substack{ C\in F \\ H(C)<X}}(\#\text{Sel}_{2}(J(C))-2)}{\mathop{\sum }_{\substack{ C\in F \\ H(C)<X}}1} & = & \displaystyle \frac{\operatorname{Vol}({\mathcal{F}})\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}(\operatorname{Vol}(G(\mathbb{Z}_{p}))\operatorname{Vol}(\operatorname{Inv}_{p}(F)))}{\operatorname{Vol}(S(\mathbb{R})^{(m)})\mathop{\prod }_{p}\operatorname{Vol}(\operatorname{Inv}_{p}(F))}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70F}_{G},\end{eqnarray}$$
the Tamagawa number of
![]() $G$
. Since the Tamagawa number of
$G$
. Since the Tamagawa number of
![]() $\operatorname{PSO}$
is 4 [Reference LanglandsLan66], Theorem 18 follows.
$\operatorname{PSO}$
is 4 [Reference LanglandsLan66], Theorem 18 follows.
Finally, as a by-product of our proof of Theorem 18, we have the following analogue of [Reference Bhargava and GrossBG13, Theorem 12.4]; the proof is identical.
Theorem 34. Fix a place
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $\mathbb{Q}$
. Let
$\mathbb{Q}$
. Let
![]() $F$
be a large family of hyperelliptic curves
$F$
be a large family of hyperelliptic curves
![]() $C$
over
$C$
over
![]() $\mathbb{Q}$
with a marked non-Weierstrass point such that:
$\mathbb{Q}$
with a marked non-Weierstrass point such that:
-
(a) the cardinality of
 $J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
is a constant
$J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
is a constant
 $k$
for all
$k$
for all
 $C\in F$
; and
$C\in F$
; and -
(b) the set
 $U_{\unicode[STIX]{x1D708}}(F)\subset V(\mathbb{Z}_{\unicode[STIX]{x1D708}})$
, defined to be the set of soluble elements in
$U_{\unicode[STIX]{x1D708}}(F)\subset V(\mathbb{Z}_{\unicode[STIX]{x1D708}})$
, defined to be the set of soluble elements in
 $V(\mathbb{Z}_{\unicode[STIX]{x1D708}})$
having invariants in
$V(\mathbb{Z}_{\unicode[STIX]{x1D708}})$
having invariants in
 $\operatorname{Inv}_{\unicode[STIX]{x1D708}}(F)$
, can be partitioned into
$\operatorname{Inv}_{\unicode[STIX]{x1D708}}(F)$
, can be partitioned into
 $k$
open sets
$k$
open sets
 $\unicode[STIX]{x1D6FA}_{i}$
such that:
$\unicode[STIX]{x1D6FA}_{i}$
such that:-
(i) for all
 $i$
, if two elements in
$i$
, if two elements in
 $\unicode[STIX]{x1D6FA}_{i}$
have the same invariants, then they are
$\unicode[STIX]{x1D6FA}_{i}$
have the same invariants, then they are
 $G(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
-equivalent; and
$G(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
-equivalent; and -
(ii) for all
 $i\neq j$
, we have
$i\neq j$
, we have
 $G(\mathbb{Q}_{\unicode[STIX]{x1D708}})\unicode[STIX]{x1D6FA}_{i}\cap G(\mathbb{Q}_{\unicode[STIX]{x1D708}})\unicode[STIX]{x1D6FA}_{j}=\emptyset$
.
$G(\mathbb{Q}_{\unicode[STIX]{x1D708}})\unicode[STIX]{x1D6FA}_{i}\cap G(\mathbb{Q}_{\unicode[STIX]{x1D708}})\unicode[STIX]{x1D6FA}_{j}=\emptyset$
.
-
(In particular, the groups
 $J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
are naturally identified for all
$J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})$
are naturally identified for all
![]() $C\in F$
.) Then when elements
$C\in F$
.) Then when elements
![]() $C\in F$
are ordered by height, the images of the non-distinguished elements (i.e., elements that do not correspond to either the identity or the class of
$C\in F$
are ordered by height, the images of the non-distinguished elements (i.e., elements that do not correspond to either the identity or the class of
 $(\infty ^{\prime })-(\infty )$
in
$(\infty ^{\prime })-(\infty )$
in
 $J(C)(\mathbb{Q})$
) under the map
$J(C)(\mathbb{Q})$
) under the map
 $$\begin{eqnarray}\operatorname{Sel}_{2}(J(C))\rightarrow J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sel}_{2}(J(C))\rightarrow J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})/2J(C)(\mathbb{Q}_{\unicode[STIX]{x1D708}})\end{eqnarray}$$
are equidistributed.
5 An application of Chabauty’s method
In this section, we apply Chabauty’s method as refined by Poonen and Stoll [Reference Poonen and StollPS14]. Let
![]() $C$
be a monic even hyperelliptic curve over
$C$
be a monic even hyperelliptic curve over
![]() $\mathbb{Q}$
with Jacobian
$\mathbb{Q}$
with Jacobian
![]() $J$
and two rational points, denoted by
$J$
and two rational points, denoted by
![]() $\infty$
and
$\infty$
and
![]() $\infty ^{\prime }$
, at infinity. We embed
$\infty ^{\prime }$
, at infinity. We embed
![]() $C(\mathbb{Q})$
and
$C(\mathbb{Q})$
and
![]() $C(\mathbb{Q}_{2})$
into
$C(\mathbb{Q}_{2})$
into
![]() $J(\mathbb{Q})$
and
$J(\mathbb{Q})$
and
![]() $J(\mathbb{Q}_{2})$
via the map
$J(\mathbb{Q}_{2})$
via the map
 $P\mapsto (P)-(\infty )$
. Normalize the log map from
$P\mapsto (P)-(\infty )$
. Normalize the log map from
![]() $J(\mathbb{Q}_{2})$
to
$J(\mathbb{Q}_{2})$
to
![]() $\mathbb{Z}_{2}^{n}$
to be surjective as in [Reference Poonen and StollPS14]. Let
$\mathbb{Z}_{2}^{n}$
to be surjective as in [Reference Poonen and StollPS14]. Let
 $v_{0}\in \mathbb{Z}_{2}^{n}$
denote the primitive part of
$v_{0}\in \mathbb{Z}_{2}^{n}$
denote the primitive part of
 $\log ((\infty )-(\infty ^{\prime }))$
and let
$\log ((\infty )-(\infty ^{\prime }))$
and let
![]() $\overline{v_{0}}$
denote the reduction modulo 2 of
$\overline{v_{0}}$
denote the reduction modulo 2 of
![]() $v_{0}$
in
$v_{0}$
in
![]() $\mathbb{F}_{2}^{n}$
. For any
$\mathbb{F}_{2}^{n}$
. For any
 $v\in \mathbb{Z}_{2}^{n}/(\mathbb{Z}_{2}\cdot v_{0})\simeq \mathbb{Z}_{2}^{n-1}$
,
$v\in \mathbb{Z}_{2}^{n}/(\mathbb{Z}_{2}\cdot v_{0})\simeq \mathbb{Z}_{2}^{n-1}$
,
![]() $\unicode[STIX]{x1D70C}(v)$
is defined by taking the reduction modulo 2 of the primitive part of
$\unicode[STIX]{x1D70C}(v)$
is defined by taking the reduction modulo 2 of the primitive part of
![]() $v$
and then taking its image under
$v$
and then taking its image under
![]() $\mathbb{P}$
, which takes a non-zero element in
$\mathbb{P}$
, which takes a non-zero element in
![]() $\mathbb{F}_{2}^{n-1}$
and sends it to its projectivization in
$\mathbb{F}_{2}^{n-1}$
and sends it to its projectivization in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
. Note that the maps
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
. Note that the maps
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\mathbb{P}$
are only partially defined, since
$\mathbb{P}$
are only partially defined, since
![]() $\mathbb{P}$
is undefined on 0. Consider now the following diagram, which is commutative on elements where all the maps are defined:
$\mathbb{P}$
is undefined on 0. Consider now the following diagram, which is commutative on elements where all the maps are defined:

A similar diagram is used in [Reference Poonen and StollPS14] to study rational points on hyperelliptic curves with a rational Weierstrass point. One major difference in our case is the extra generator
 $(\infty )^{\prime }-(\infty )$
of
$(\infty )^{\prime }-(\infty )$
of
![]() $J(\mathbb{Q})$
. Its class in
$J(\mathbb{Q})$
. Its class in
![]() $\operatorname{Sel}_{2}(J)$
does not equidistribute in
$\operatorname{Sel}_{2}(J)$
does not equidistribute in
 $J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
.
$J(\mathbb{Q}_{2})/2J(\mathbb{Q}_{2})$
.
As in [Reference Poonen and StollPS14, Proposition 8.4], 100% of monic even hyperelliptic curves over
![]() $\mathbb{Q}$
have trivial torsion in their Jacobians. Hence in what follows, we consider only monic even hyperelliptic curves
$\mathbb{Q}$
have trivial torsion in their Jacobians. Hence in what follows, we consider only monic even hyperelliptic curves
![]() $C$
such that
$C$
such that
 $J(\mathbb{Q})_{\text{tors}}=\{0\}$
.
$J(\mathbb{Q})_{\text{tors}}=\{0\}$
.
5.1 The image of
 $C(\mathbb{Q}_{2})$
in
$C(\mathbb{Q}_{2})$
in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is locally constant and small on average
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is locally constant and small on average
Break up the set of monic even hyperelliptic curves over
![]() $\mathbb{Q}$
of genus
$\mathbb{Q}$
of genus
![]() $n$
with trivial torsion in their Jacobians into large families such that over each such large family
$n$
with trivial torsion in their Jacobians into large families such that over each such large family
![]() $F$
, the log map is normalized so that the image of
$F$
, the log map is normalized so that the image of
 $(\infty ^{\prime })-(\infty )$
in
$(\infty ^{\prime })-(\infty )$
in
![]() $\mathbb{Z}_{2}^{n}$
is locally constant and, as
$\mathbb{Z}_{2}^{n}$
is locally constant and, as
![]() $C$
varies in
$C$
varies in
![]() $F$
, the image of
$F$
, the image of
![]() $C(\mathbb{Q}_{2})$
in
$C(\mathbb{Q}_{2})$
in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is constant. The analogous statement for odd hyperelliptic curves is proved in [Reference Poonen and StollPS14, §§ 8.1 and 8.2]. The same proofs carry through verbatim for monic even hyperelliptic curves.
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is constant. The analogous statement for odd hyperelliptic curves is proved in [Reference Poonen and StollPS14, §§ 8.1 and 8.2]. The same proofs carry through verbatim for monic even hyperelliptic curves.
Write
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
for the image of
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
for the image of
![]() $C(\mathbb{Q}_{2})$
in
$C(\mathbb{Q}_{2})$
in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
(ignoring the points where
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
(ignoring the points where
![]() $\unicode[STIX]{x1D70C}$
is not defined). For any prime
$\unicode[STIX]{x1D70C}$
is not defined). For any prime
![]() $p$
, associated to any
$p$
, associated to any
 $(2n+1)$
-tuple
$(2n+1)$
-tuple
 $(c_{2},\ldots ,c_{2n+2})\in \mathbb{Z}_{p}^{2n+1}$
with
$(c_{2},\ldots ,c_{2n+2})\in \mathbb{Z}_{p}^{2n+1}$
with
 $\unicode[STIX]{x1D6E5}(x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2})\neq 0$
is a monic even hyperelliptic curve over
$\unicode[STIX]{x1D6E5}(x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2})\neq 0$
is a monic even hyperelliptic curve over
![]() $\mathbb{Q}_{p}$
defined by
$\mathbb{Q}_{p}$
defined by
 $y^{2}=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2}$
. We write
$y^{2}=x^{2n+2}+c_{2}x^{2n}+\cdots +c_{2n+2}$
. We write
 $\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
for this set of monic even hyperelliptic curves over
$\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
for this set of monic even hyperelliptic curves over
![]() $\mathbb{Q}_{p}$
of genus
$\mathbb{Q}_{p}$
of genus
![]() $n$
. Then we have the following proposition.
$n$
. Then we have the following proposition.
Proposition 35. Let
![]() $C$
range over monic even hyperelliptic curves corresponding to elements in
$C$
range over monic even hyperelliptic curves corresponding to elements in
 $\mathbb{Z}_{2}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
$\mathbb{Z}_{2}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
 $(\infty )-(\infty ^{\prime })\notin J(\mathbb{Q}_{2})_{\text{tors}}$
. Then the average size of
$(\infty )-(\infty ^{\prime })\notin J(\mathbb{Q}_{2})_{\text{tors}}$
. Then the average size of
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
is at most
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
is at most
![]() $6n+9$
.
$6n+9$
.
Proof. This result follows immediately from the proofs of [Reference Poonen and StollPS14, Proposition 5.4, Theorem 9.1] by breaking up
![]() $C(\mathbb{Q}_{2})$
into residue disks in accordance with
$C(\mathbb{Q}_{2})$
into residue disks in accordance with
 ${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{2})$
where
${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{2})$
where
![]() ${\mathcal{C}}$
denotes the minimal proper regular model of
${\mathcal{C}}$
denotes the minimal proper regular model of
![]() $C$
and then counting the number of images coming from each residue disk. Denote by
$C$
and then counting the number of images coming from each residue disk. Denote by
![]() $\unicode[STIX]{x1D70C}^{\prime }$
the scale and reduce map from
$\unicode[STIX]{x1D70C}^{\prime }$
the scale and reduce map from
![]() $\mathbb{Z}_{2}^{n}$
to
$\mathbb{Z}_{2}^{n}$
to
 $\mathbb{P}^{n-1}(\mathbb{F}_{2})$
. Then we see that the average size of
$\mathbb{P}^{n-1}(\mathbb{F}_{2})$
. Then we see that the average size of
 $\unicode[STIX]{x1D70C}^{\prime }\log (C(\mathbb{Q}_{2}))$
is at most
$\unicode[STIX]{x1D70C}^{\prime }\log (C(\mathbb{Q}_{2}))$
is at most
 $6n+14$
using the upper bound of 4 for the average size of
$6n+14$
using the upper bound of 4 for the average size of
 ${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{2})$
. Note that the definition of
${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{2})$
. Note that the definition of
![]() $\unicode[STIX]{x1D70C}\log$
involves quotienting out by the
$\unicode[STIX]{x1D70C}\log$
involves quotienting out by the
![]() $\mathbb{Z}_{2}$
-line spanned by
$\mathbb{Z}_{2}$
-line spanned by
![]() $v_{0}$
. Hence the residue disk at
$v_{0}$
. Hence the residue disk at
![]() $\infty$
and the residue disk at
$\infty$
and the residue disk at
![]() $\infty ^{\prime }$
give the same image under
$\infty ^{\prime }$
give the same image under
![]() $\unicode[STIX]{x1D70C}\log$
. Thus, following the proof of [Reference Poonen and StollPS14, Proposition 5.4], we obtain a bound of
$\unicode[STIX]{x1D70C}\log$
. Thus, following the proof of [Reference Poonen and StollPS14, Proposition 5.4], we obtain a bound of
![]() $6n+9$
for the average size of
$6n+9$
for the average size of
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
.◻
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
.◻
5.2 The image of
 $J(\mathbb{Q})$
in
$J(\mathbb{Q})$
in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is contained in the image of
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is contained in the image of
 $\operatorname{Sel}_{2}(J)/\langle (\infty ^{\prime })-(\infty )\rangle$
$\operatorname{Sel}_{2}(J)/\langle (\infty ^{\prime })-(\infty )\rangle$
Lemma 36. Suppose
![]() $C$
is a monic even-degree hyperelliptic curve over
$C$
is a monic even-degree hyperelliptic curve over
![]() $\mathbb{Q}$
with
$\mathbb{Q}$
with
 $J(\mathbb{Q})_{\text{tors}}=\{0\}$
. Write
$J(\mathbb{Q})_{\text{tors}}=\{0\}$
. Write
 $d_{0}=(\infty ^{\prime })-(\infty )$
. Suppose the map
$d_{0}=(\infty ^{\prime })-(\infty )$
. Suppose the map
![]() $\unicode[STIX]{x1D70E}^{\prime }$
is injective. Then
$\unicode[STIX]{x1D70E}^{\prime }$
is injective. Then
 $\unicode[STIX]{x1D70C}\log (\overline{J(\mathbb{Q})})\subset \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )$
where
$\unicode[STIX]{x1D70C}\log (\overline{J(\mathbb{Q})})\subset \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )$
where
![]() $\overline{J(\mathbb{Q})}$
denotes the
$\overline{J(\mathbb{Q})}$
denotes the
![]() $p$
-adic closure of
$p$
-adic closure of
![]() $J(\mathbb{Q})$
in
$J(\mathbb{Q})$
in
![]() $J(\mathbb{Q}_{p})$
. Furthermore, if
$J(\mathbb{Q}_{p})$
. Furthermore, if
 $g\in J(\mathbb{Q})$
has no image under
$g\in J(\mathbb{Q})$
has no image under
![]() $\unicode[STIX]{x1D70C}\log$
, then there exist integers
$\unicode[STIX]{x1D70C}\log$
, then there exist integers
![]() $m$
and
$m$
and
![]() $k$
such that
$k$
such that
 $mg=kd_{0}$
.
$mg=kd_{0}$
.
Proof. Since
![]() $\unicode[STIX]{x1D70C}\log$
is continuous and
$\unicode[STIX]{x1D70C}\log$
is continuous and
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is discrete,
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is discrete,
 $\unicode[STIX]{x1D70C}\log (\overline{J(\mathbb{Q})})=\unicode[STIX]{x1D70C}\log (J(\mathbb{Q}))$
. Since
$\unicode[STIX]{x1D70C}\log (\overline{J(\mathbb{Q})})=\unicode[STIX]{x1D70C}\log (J(\mathbb{Q}))$
. Since
 $J(\mathbb{Q})_{\text{tors}}=0$
, we have
$J(\mathbb{Q})_{\text{tors}}=0$
, we have
 $J(\mathbb{Q})/\mathbb{Z}d_{0}\simeq F\oplus \mathbb{Z}^{r^{\prime }}$
, where
$J(\mathbb{Q})/\mathbb{Z}d_{0}\simeq F\oplus \mathbb{Z}^{r^{\prime }}$
, where
![]() $r^{\prime }$
is the rank of
$r^{\prime }$
is the rank of
 $J(\mathbb{Q})/\mathbb{Z}d_{0}$
and
$J(\mathbb{Q})/\mathbb{Z}d_{0}$
and
![]() $F$
is a finite abelian group such that any lift
$F$
is a finite abelian group such that any lift
![]() $g$
to
$g$
to
![]() $J(\mathbb{Q})$
of an element in
$J(\mathbb{Q})$
of an element in
![]() $F$
satisfies
$F$
satisfies
 $mg=kd_{0}$
for some integers
$mg=kd_{0}$
for some integers
![]() $m$
and
$m$
and
![]() $k$
. This implies that such a
$k$
. This implies that such a
![]() $g$
has no image under the partially defined map
$g$
has no image under the partially defined map
![]() $\unicode[STIX]{x1D70C}^{\prime }\log$
.
$\unicode[STIX]{x1D70C}^{\prime }\log$
.
Let
 $h\in J(\mathbb{Q})$
be an element that does have an image under
$h\in J(\mathbb{Q})$
be an element that does have an image under
![]() $\unicode[STIX]{x1D70C}\log$
. Write the image of
$\unicode[STIX]{x1D70C}\log$
. Write the image of
![]() $h$
in
$h$
in
![]() $F\oplus \mathbb{Z}^{r^{\prime }}$
as
$F\oplus \mathbb{Z}^{r^{\prime }}$
as
![]() $(t,h^{\prime })$
with
$(t,h^{\prime })$
with
![]() $t\in F$
and
$t\in F$
and
 $h^{\prime }\in \mathbb{Z}^{r^{\prime }}$
. Let
$h^{\prime }\in \mathbb{Z}^{r^{\prime }}$
. Let
![]() $h_{0}$
denote the primitive part of
$h_{0}$
denote the primitive part of
![]() $h^{\prime }$
. Then, viewing
$h^{\prime }$
. Then, viewing
![]() $h_{0}$
as an element of
$h_{0}$
as an element of
![]() $J(\mathbb{Q})$
, we have
$J(\mathbb{Q})$
, we have
 $\unicode[STIX]{x1D70C}\log (h)=\unicode[STIX]{x1D70C}\log (h_{0})$
. Since
$\unicode[STIX]{x1D70C}\log (h)=\unicode[STIX]{x1D70C}\log (h_{0})$
. Since
![]() $\unicode[STIX]{x1D70E}^{\prime }$
is injective, the element
$\unicode[STIX]{x1D70E}^{\prime }$
is injective, the element
![]() $h_{0}$
has non-zero image under
$h_{0}$
has non-zero image under
![]() $\unicode[STIX]{x1D70E}^{\prime }$
. Therefore, we obtain
$\unicode[STIX]{x1D70E}^{\prime }$
. Therefore, we obtain
 $\unicode[STIX]{x1D70C}\log (h)=\mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(h_{0}+\langle d_{0}\rangle )$
, which proves the first assertion of the lemma.
$\unicode[STIX]{x1D70C}\log (h)=\mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(h_{0}+\langle d_{0}\rangle )$
, which proves the first assertion of the lemma.
For the second statement, let
 $h\in J(\mathbb{Q})$
be an element that does not have an image under
$h\in J(\mathbb{Q})$
be an element that does not have an image under
![]() $\unicode[STIX]{x1D70C}\log$
. Let the image of
$\unicode[STIX]{x1D70C}\log$
. Let the image of
![]() $h$
in
$h$
in
![]() $F\oplus \mathbb{Z}^{r^{\prime }}$
be
$F\oplus \mathbb{Z}^{r^{\prime }}$
be
![]() $(t,h^{\prime })$
, where
$(t,h^{\prime })$
, where
![]() $t\in F$
and
$t\in F$
and
 $h^{\prime }\in \mathbb{Z}^{r^{\prime }}$
. If
$h^{\prime }\in \mathbb{Z}^{r^{\prime }}$
. If
![]() $h^{\prime }=0$
, then we are done. Suppose for a contradiction that
$h^{\prime }=0$
, then we are done. Suppose for a contradiction that
![]() $h^{\prime }$
is non-zero. Let
$h^{\prime }$
is non-zero. Let
![]() $h_{0}$
denote the primitive part of
$h_{0}$
denote the primitive part of
![]() $h^{\prime }$
. Since
$h^{\prime }$
. Since
![]() $h$
has no image under
$h$
has no image under
![]() $\unicode[STIX]{x1D70C}\log$
, neither does
$\unicode[STIX]{x1D70C}\log$
, neither does
![]() $h_{0}$
, and we have
$h_{0}$
, and we have
 $\log (h_{0})\in \mathbb{Z}_{2}\cdot v_{0}$
. This implies that the class of
$\log (h_{0})\in \mathbb{Z}_{2}\cdot v_{0}$
. This implies that the class of
![]() $h_{0}$
in
$h_{0}$
in
 $\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
maps to 0 under
$\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
maps to 0 under
![]() $\unicode[STIX]{x1D70E}^{\prime }$
, contradicting the injectivity of
$\unicode[STIX]{x1D70E}^{\prime }$
, contradicting the injectivity of
![]() $\unicode[STIX]{x1D70E}^{\prime }$
.◻
$\unicode[STIX]{x1D70E}^{\prime }$
.◻
5.3 The equidistributed sets
 $\mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle (\infty ^{\prime })-(\infty )\rangle )$
rarely intersect the small sets
$\mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle (\infty ^{\prime })-(\infty )\rangle )$
rarely intersect the small sets
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
Let
![]() $F$
be a large family of monic even hyperelliptic curves over
$F$
be a large family of monic even hyperelliptic curves over
![]() $\mathbb{Q}$
satisfying the hypothesis of Theorem 34 such that the image of
$\mathbb{Q}$
satisfying the hypothesis of Theorem 34 such that the image of
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
in
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))$
in
 $\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is constant for
$\mathbb{P}^{n-2}(\mathbb{F}_{2})$
is constant for
![]() $C\in F$
. (We assume also that the log maps are normalized such that the image of
$C\in F$
. (We assume also that the log maps are normalized such that the image of
 $d_{0}=(\infty ^{\prime })-(\infty )$
is constant throughout this family.) Denote this image by
$d_{0}=(\infty ^{\prime })-(\infty )$
is constant throughout this family.) Denote this image by
![]() $I$
.
$I$
.
On average over the curves in
![]() $F$
, there are at most four non-distinguished elements in
$F$
, there are at most four non-distinguished elements in
![]() $\operatorname{Sel}_{2}(J)$
by Theorem 18, and the images of these elements under
$\operatorname{Sel}_{2}(J)$
by Theorem 18, and the images of these elements under
![]() $\unicode[STIX]{x1D70E}$
equidistribute in
$\unicode[STIX]{x1D70E}$
equidistribute in
![]() $\mathbb{F}_{2}^{n}$
by Theorem 34. By Proposition 30, the class
$\mathbb{F}_{2}^{n}$
by Theorem 34. By Proposition 30, the class
![]() $d_{0}$
is not a multiple of 2 in the Jacobian for 100% of the curves in
$d_{0}$
is not a multiple of 2 in the Jacobian for 100% of the curves in
![]() $F$
. Hence, on average over
$F$
. Hence, on average over
![]() $F$
, there are at most two non-identity elements in
$F$
, there are at most two non-identity elements in
 $\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
and their images under
$\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
and their images under
![]() $\unicode[STIX]{x1D70E}^{\prime }$
equidistribute in
$\unicode[STIX]{x1D70E}^{\prime }$
equidistribute in
 $\mathbb{F}_{2}^{n}/(\mathbb{F}_{2}\cdot \overline{v_{0}})$
. Hence a proportion of at least
$\mathbb{F}_{2}^{n}/(\mathbb{F}_{2}\cdot \overline{v_{0}})$
. Hence a proportion of at least
 $1-(\#I)2^{2-n}$
curves
$1-(\#I)2^{2-n}$
curves
![]() $C$
in
$C$
in
![]() $F$
satisfy
$F$
satisfy
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))\cap \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )=\emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))\cap \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )=\emptyset .\end{eqnarray}$$
Furthermore, a proportion of at most
![]() $2^{2-n}$
curves in
$2^{2-n}$
curves in
![]() $F$
fail to satisfy the conditions of Lemma 36 (corresponding to those curves
$F$
fail to satisfy the conditions of Lemma 36 (corresponding to those curves
![]() $C$
such that a non-identity element of
$C$
such that a non-identity element of
 $\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
maps to 0 under
$\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle$
maps to 0 under
![]() $\unicode[STIX]{x1D70E}^{\prime }$
). A point
$\unicode[STIX]{x1D70E}^{\prime }$
). A point
 $P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is said to be bad if there exist integers
$P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is said to be bad if there exist integers
![]() $m$
and
$m$
and
![]() $k$
, not both zero, such that
$k$
, not both zero, such that
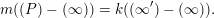 $$\begin{eqnarray}m((P)-(\infty ))=k((\infty ^{\prime })-(\infty )).\end{eqnarray}$$
$$\begin{eqnarray}m((P)-(\infty ))=k((\infty ^{\prime })-(\infty )).\end{eqnarray}$$
Hence aside from a set of density at most
 $(1+\#I)2^{2-n}$
, all curves
$(1+\#I)2^{2-n}$
, all curves
![]() $C\in F$
are such that every point
$C\in F$
are such that every point
 $P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is bad.
$P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is bad.
We summarize the above discussion in the following theorem.
Theorem 37. Suppose
![]() $C$
is a monic even hyperelliptic curve of genus
$C$
is a monic even hyperelliptic curve of genus
![]() $n$
over
$n$
over
![]() $\mathbb{Q}$
satisfying the following three conditions:
$\mathbb{Q}$
satisfying the following three conditions:
-
(i)
 $J(\mathbb{Q})_{\text{tors}}=\{0\}$
;
$J(\mathbb{Q})_{\text{tors}}=\{0\}$
; -
(ii)
 $\ker \unicode[STIX]{x1D70E}^{\prime }=\{0\}$
;
$\ker \unicode[STIX]{x1D70E}^{\prime }=\{0\}$
; -
(iii)
 $\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))\cap \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )=\emptyset$
.
$\unicode[STIX]{x1D70C}\log (C(\mathbb{Q}_{2}))\cap \mathbb{P}\unicode[STIX]{x1D70E}^{\prime }(\operatorname{Sel}_{2}(J)/\langle d_{0}\rangle )=\emptyset$
.
Then every point
 $P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is bad, that is, there exist integers
$P\in C(\mathbb{Q})\backslash \{\infty ,\infty ^{\prime }\}$
is bad, that is, there exist integers
![]() $m$
and
$m$
and
![]() $k$
, not both
$k$
, not both
![]() $0$
, such that
$0$
, such that
 $$\begin{eqnarray}m((P)-(\infty ))=k((\infty ^{\prime })-(\infty )).\end{eqnarray}$$
$$\begin{eqnarray}m((P)-(\infty ))=k((\infty ^{\prime })-(\infty )).\end{eqnarray}$$
Moreover, the proportion of monic even hyperelliptic curves of genus
![]() $n$
over
$n$
over
![]() $\mathbb{Q}$
satisfying the above three conditions is at least
$\mathbb{Q}$
satisfying the above three conditions is at least
 $1-(24n+40)2^{-n}$
.
$1-(24n+40)2^{-n}$
.
6 Most monic even hyperelliptic curves have only two rational points
We say that a monic even hyperelliptic curve
![]() $C$
over
$C$
over
![]() $\mathbb{Q}$
is good if
$\mathbb{Q}$
is good if
![]() $C(\mathbb{Q})$
has no bad points. Then, to prove Theorem 1, it remains to prove the following result.
$C(\mathbb{Q})$
has no bad points. Then, to prove Theorem 1, it remains to prove the following result.
Theorem 38. All but
![]() $0\%$
of monic even hyperelliptic curves over
$0\%$
of monic even hyperelliptic curves over
![]() $\mathbb{Q}$
having fixed genus
$\mathbb{Q}$
having fixed genus
![]() $n\geqslant 4$
are good.
$n\geqslant 4$
are good.
We work
![]() $p$
-adically for some fixed prime
$p$
-adically for some fixed prime
![]() $p$
not dividing
$p$
not dividing
![]() $2n+2$
. Suppose
$2n+2$
. Suppose
![]() $C$
is a monic even-degree hyperelliptic curve with coefficients in
$C$
is a monic even-degree hyperelliptic curve with coefficients in
![]() $\mathbb{Z}_{p}$
. Let
$\mathbb{Z}_{p}$
. Let
 $\ell :C(\mathbb{Q}_{p})\rightarrow \mathbb{Z}_{p}^{n}$
denote the map sending
$\ell :C(\mathbb{Q}_{p})\rightarrow \mathbb{Z}_{p}^{n}$
denote the map sending
 $P\in C(\mathbb{Q}_{p})$
to
$P\in C(\mathbb{Q}_{p})$
to
 $\log ((P)-(P^{\unicode[STIX]{x1D70F}}))$
where
$\log ((P)-(P^{\unicode[STIX]{x1D70F}}))$
where
![]() $\unicode[STIX]{x1D70F}$
denotes the hyperelliptic involution and
$\unicode[STIX]{x1D70F}$
denotes the hyperelliptic involution and
![]() $\log$
is computed with respect to the differentials
$\log$
is computed with respect to the differentials
 $$\begin{eqnarray}\{dx/y,x\,dx/y,\ldots ,x^{n-1}\,dx/y\}.\end{eqnarray}$$
$$\begin{eqnarray}\{dx/y,x\,dx/y,\ldots ,x^{n-1}\,dx/y\}.\end{eqnarray}$$
We say that a point
 $P\in C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
is bad if the
$P\in C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
is bad if the
![]() $\mathbb{Z}_{p}$
-lines spanned by
$\mathbb{Z}_{p}$
-lines spanned by
![]() $\ell (P)$
and
$\ell (P)$
and
![]() $\ell (\infty )$
have non-zero intersections. Note that if
$\ell (\infty )$
have non-zero intersections. Note that if
 $P\in C(\mathbb{Q})$
is bad, that is, satisfies (42), then
$P\in C(\mathbb{Q})$
is bad, that is, satisfies (42), then
![]() $P$
considered as a point in
$P$
considered as a point in
![]() $C(\mathbb{Q}_{p})$
is bad since we have
$C(\mathbb{Q}_{p})$
is bad since we have
 $$\begin{eqnarray}m((P)-(P^{\unicode[STIX]{x1D70F}}))=(m-2k)((\infty )-(\infty ^{\prime })).\end{eqnarray}$$
$$\begin{eqnarray}m((P)-(P^{\unicode[STIX]{x1D70F}}))=(m-2k)((\infty )-(\infty ^{\prime })).\end{eqnarray}$$
We thank Jacob Tsimerman for several conversations which led to the proof of the following theorem, from which Theorem 38 will be shown to follow.
Theorem 39. Suppose
![]() $n\geqslant 4$
. The set
$n\geqslant 4$
. The set
![]() $U$
of elements in
$U$
of elements in
 $\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
corresponding to monic even hyperelliptic curves
$\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
corresponding to monic even hyperelliptic curves
![]() $C$
of genus
$C$
of genus
![]() $n$
such that
$n$
such that
 $C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains no bad points is dense. Furthermore, the
$C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains no bad points is dense. Furthermore, the
![]() $p$
-adic closure of its complement has measure
$p$
-adic closure of its complement has measure
![]() $0$
.
$0$
.
Proof. Let
![]() $C$
be a monic even hyperelliptic curve over
$C$
be a monic even hyperelliptic curve over
![]() $\mathbb{Q}_{p}$
corresponding to an element
$\mathbb{Q}_{p}$
corresponding to an element
 $v\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
. Let
$v\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
. Let
 $P\in C(\mathbb{Q}_{p})$
be a non-Weierstrass point such that
$P\in C(\mathbb{Q}_{p})$
be a non-Weierstrass point such that
 $P\notin \{\infty ,\infty ^{\prime }\}$
. Given such a point, we obtain elements
$P\notin \{\infty ,\infty ^{\prime }\}$
. Given such a point, we obtain elements
 $v^{\prime }\in \mathbb{Z}_{p}^{2n+1}$
such that the curves
$v^{\prime }\in \mathbb{Z}_{p}^{2n+1}$
such that the curves
![]() $C^{\prime }$
corresponding to
$C^{\prime }$
corresponding to
![]() $v^{\prime }$
are isomorphic to
$v^{\prime }$
are isomorphic to
![]() $C$
but the point
$C$
but the point
 $\infty \in C^{\prime }(\mathbb{Q}_{p})$
is
$\infty \in C^{\prime }(\mathbb{Q}_{p})$
is
![]() $P$
. Clearly it is possible to construct a sequence of points
$P$
. Clearly it is possible to construct a sequence of points
![]() $P_{i}$
tending to
$P_{i}$
tending to
 $\infty \in C(\mathbb{Q}_{p})$
along with a corresponding sequence
$\infty \in C(\mathbb{Q}_{p})$
along with a corresponding sequence
 $v_{i}\in \mathbb{Z}_{p}^{2n+1}$
such that
$v_{i}\in \mathbb{Z}_{p}^{2n+1}$
such that
![]() $v_{i}$
tends to
$v_{i}$
tends to
![]() $v$
. We say that a pair of points
$v$
. We say that a pair of points
 $(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is a bad pair if
$(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is a bad pair if
 $P\notin \{Q,Q^{\unicode[STIX]{x1D70F}}\}$
, and the
$P\notin \{Q,Q^{\unicode[STIX]{x1D70F}}\}$
, and the
![]() $\mathbb{Z}_{p}$
-lines spanned by
$\mathbb{Z}_{p}$
-lines spanned by
![]() $\ell (P)$
and
$\ell (P)$
and
![]() $\ell (Q)$
have a non-zero intersection. Note that even though the definition of
$\ell (Q)$
have a non-zero intersection. Note that even though the definition of
![]() $\ell$
depends on a choice of the marked point
$\ell$
depends on a choice of the marked point
![]() $\infty$
through the chosen basis of the differentials, the property of being a bad pair is independent of the choice of
$\infty$
through the chosen basis of the differentials, the property of being a bad pair is independent of the choice of
![]() $\infty$
. We will show in Lemma 40 below that the number of bad pairs
$\infty$
. We will show in Lemma 40 below that the number of bad pairs
 $(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is finite for any monic even-degree hyperelliptic curve over
$(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is finite for any monic even-degree hyperelliptic curve over
![]() $\mathbb{Q}_{p}$
. From this it follows that, given
$\mathbb{Q}_{p}$
. From this it follows that, given
![]() $(C,\infty )$
corresponding to
$(C,\infty )$
corresponding to
 $v\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
, there exist points
$v\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
, there exist points
![]() $P$
arbitrarily close to
$P$
arbitrarily close to
![]() $\infty$
such that
$\infty$
such that
![]() $P$
is not part of any bad pair. It then follows that there exist points
$P$
is not part of any bad pair. It then follows that there exist points
 $v^{\prime }\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
(corresponding to
$v^{\prime }\in \mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
(corresponding to
![]() $(C,P)$
), arbitrarily close to
$(C,P)$
), arbitrarily close to
![]() $v$
, that correspond to hyperelliptic curves containing no bad points. Hence
$v$
, that correspond to hyperelliptic curves containing no bad points. Hence
![]() $U$
is dense.
$U$
is dense.
Let
![]() $V$
denote the complement of
$V$
denote the complement of
![]() $U$
in
$U$
in
 $M=\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
. We claim that
$M=\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
. We claim that
![]() $V$
is a
$V$
is a
![]() $p$
-adic subanalytic subset of
$p$
-adic subanalytic subset of
![]() $M$
. The theory of subanalytic sets is studied in great detail in [Reference Denef and van den DriesDD88]. We do not repeat the definition of subanalytic sets and instead remark that subanalytic sets are stable under projections onto coordinate hyperplanes and that sets defined by the vanishing and non-vanishing of analytic functions are subanalytic. Moreover, being subanalytic is a (
$M$
. The theory of subanalytic sets is studied in great detail in [Reference Denef and van den DriesDD88]. We do not repeat the definition of subanalytic sets and instead remark that subanalytic sets are stable under projections onto coordinate hyperplanes and that sets defined by the vanishing and non-vanishing of analytic functions are subanalytic. Moreover, being subanalytic is a (
![]() $p$
-adic) local property. The dimension of a subanalytic set is defined to be the maximal dimension of a
$p$
-adic) local property. The dimension of a subanalytic set is defined to be the maximal dimension of a
![]() $p$
-adic manifold contained in it [Reference Denef and van den DriesDD88, 3.15]. This notion of dimension behaves as expected: a zero-dimensional subanalytic set is finite; the dimension of the boundary
$p$
-adic manifold contained in it [Reference Denef and van den DriesDD88, 3.15]. This notion of dimension behaves as expected: a zero-dimensional subanalytic set is finite; the dimension of the boundary
![]() $\bar{A}\backslash A$
of a subanalytic set
$\bar{A}\backslash A$
of a subanalytic set
![]() $A$
is less than the dimension of
$A$
is less than the dimension of
![]() $A$
[Reference Denef and van den DriesDD88, 3.26].
$A$
[Reference Denef and van den DriesDD88, 3.26].
We now show that
![]() $V$
is a
$V$
is a
![]() $p$
-adic subanalytic subset of
$p$
-adic subanalytic subset of
![]() $M$
. It suffices to check this locally. Restrict to an open subset
$M$
. It suffices to check this locally. Restrict to an open subset
![]() $W$
of
$W$
of
 $\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
$\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
 ${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})$
is constant for curves
${\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})$
is constant for curves
![]() $C$
corresponding to elements in
$C$
corresponding to elements in
![]() $W$
where
$W$
where
![]() ${\mathcal{C}}$
denotes the minimal proper regular model of
${\mathcal{C}}$
denotes the minimal proper regular model of
![]() $C$
. Then the moduli space of pairs
$C$
. Then the moduli space of pairs
![]() $(C,P)$
, where
$(C,P)$
, where
![]() $C$
is a curve corresponding to an element in
$C$
is a curve corresponding to an element in
![]() $W$
and
$W$
and
![]() $P$
is a point in
$P$
is a point in
![]() $C(\mathbb{Q}_{p})$
, is isomorphic to
$C(\mathbb{Q}_{p})$
, is isomorphic to
 $W\times {\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})\times \mathbb{Z}_{p}$
. The set of pairs
$W\times {\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})\times \mathbb{Z}_{p}$
. The set of pairs
![]() $(C,P)$
corresponding to elements in this moduli space such that
$(C,P)$
corresponding to elements in this moduli space such that
![]() $P$
is a bad point of
$P$
is a bad point of
![]() $C(\mathbb{Q}_{p})$
is a subanalytic set of
$C(\mathbb{Q}_{p})$
is a subanalytic set of
 $W\times {\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})\times \mathbb{Z}_{p}$
defined by
$W\times {\mathcal{C}}^{\text{smooth}}(\mathbb{F}_{p})\times \mathbb{Z}_{p}$
defined by
 $\ell (P)\neq 0$
,
$\ell (P)\neq 0$
,
 $\ell (\infty )\neq 0$
, and
$\ell (\infty )\neq 0$
, and
 $\unicode[STIX]{x1D706}_{1}\ell (P)=\unicode[STIX]{x1D706}_{2}\ell (\infty )$
for some
$\unicode[STIX]{x1D706}_{1}\ell (P)=\unicode[STIX]{x1D706}_{2}\ell (\infty )$
for some
 $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbb{Z}_{p}-\{0\}$
(a condition easily handled by projections). Since subanalytic sets are preserved by projections, this implies that
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbb{Z}_{p}-\{0\}$
(a condition easily handled by projections). Since subanalytic sets are preserved by projections, this implies that
![]() $V\cap W$
is subanalytic in
$V\cap W$
is subanalytic in
![]() $W$
, as desired. We have already proven that
$W$
, as desired. We have already proven that
![]() $V$
does not contain any
$V$
does not contain any
![]() $p$
-adic open ball of dimension
$p$
-adic open ball of dimension
![]() $2n+1$
since its complement is dense. Hence its dimension as a subanalytic set [Reference Denef and van den DriesDD88, 3.15] is less than
$2n+1$
since its complement is dense. Hence its dimension as a subanalytic set [Reference Denef and van den DriesDD88, 3.15] is less than
 $\dim (\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\})=2n+1$
. Moreover, the dimension of
$\dim (\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\})=2n+1$
. Moreover, the dimension of
![]() $\bar{V}\backslash V$
is less than the dimension of
$\bar{V}\backslash V$
is less than the dimension of
![]() $V$
[Reference Denef and van den DriesDD88, 3.26], where
$V$
[Reference Denef and van den DriesDD88, 3.26], where
![]() $\bar{V}$
denotes the
$\bar{V}$
denotes the
![]() $p$
-adic closure of
$p$
-adic closure of
![]() $V$
. Therefore, the
$V$
. Therefore, the
![]() $p$
-adic closure of
$p$
-adic closure of
![]() $V$
has measure 0 as desired.◻
$V$
has measure 0 as desired.◻
We now prove the following result which was assumed in the proof of Theorem 39.
Lemma 40. Let
![]() $C$
be a monic even-degree hyperelliptic curve with coefficients in
$C$
be a monic even-degree hyperelliptic curve with coefficients in
![]() $\mathbb{Z}_{p}$
, having genus
$\mathbb{Z}_{p}$
, having genus
![]() $n\geqslant 4$
. Then the set of bad pairs
$n\geqslant 4$
. Then the set of bad pairs
 $(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is finite.
$(P,Q)\in C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
is finite.
Proof. Let
![]() $\unicode[STIX]{x1D6F4}$
denote the subset of
$\unicode[STIX]{x1D6F4}$
denote the subset of
 $C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
consisting of bad pairs
$C(\mathbb{Q}_{p})\times C(\mathbb{Q}_{p})$
consisting of bad pairs
![]() $(P,Q)$
. Then
$(P,Q)$
. Then
![]() $\unicode[STIX]{x1D6F4}$
is subanalytic as it is defined by
$\unicode[STIX]{x1D6F4}$
is subanalytic as it is defined by
 $x(P)\neq x(Q)$
,
$x(P)\neq x(Q)$
,
 $\ell (P)\neq 0$
,
$\ell (P)\neq 0$
,
 $\ell (Q)\neq 0$
, and
$\ell (Q)\neq 0$
, and
 $\unicode[STIX]{x1D706}_{1}\ell (P)=\unicode[STIX]{x1D706}_{2}\ell (Q)$
for some
$\unicode[STIX]{x1D706}_{1}\ell (P)=\unicode[STIX]{x1D706}_{2}\ell (Q)$
for some
 $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbb{Z}_{p}-\{0\}$
. We will show that the dimension of
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbb{Z}_{p}-\{0\}$
. We will show that the dimension of
![]() $\unicode[STIX]{x1D6F4}$
as a subanalytic set is zero, which implies that
$\unicode[STIX]{x1D6F4}$
as a subanalytic set is zero, which implies that
![]() $\unicode[STIX]{x1D6F4}$
is finite by [Reference Denef and van den DriesDD88, 3.26].
$\unicode[STIX]{x1D6F4}$
is finite by [Reference Denef and van den DriesDD88, 3.26].
Let
 $P\in C(\mathbb{Q}_{p})$
be any point. The main difficulty in proving Lemma 40 is that it is difficult to explicitly compute the function
$P\in C(\mathbb{Q}_{p})$
be any point. The main difficulty in proving Lemma 40 is that it is difficult to explicitly compute the function
![]() $\ell$
. However, for any
$\ell$
. However, for any
![]() $P^{\prime }$
in a small enough residue disk around
$P^{\prime }$
in a small enough residue disk around
![]() $P$
,
$P$
,
![]() $\ell (P^{\prime })$
is the sum of
$\ell (P^{\prime })$
is the sum of
![]() $\ell (P)$
and a
$\ell (P)$
and a
![]() $p$
-adic integral (multiplied by 2). Hence we can compute the derivative of
$p$
-adic integral (multiplied by 2). Hence we can compute the derivative of
![]() $\ell$
with respect to
$\ell$
with respect to
![]() $x$
and obtain
$x$
and obtain
 $$\begin{eqnarray}\ell ^{\prime }(P^{\prime })=\biggl(\frac{2}{y(P^{\prime })},\frac{2x(P^{\prime })}{y(P^{\prime })},\ldots ,\frac{2x(P^{\prime })^{n-1}}{y(P^{\prime })}\biggr)\quad \text{if}~P^{\prime }\not \in \{\infty ,\infty ^{\prime }\}.\end{eqnarray}$$
$$\begin{eqnarray}\ell ^{\prime }(P^{\prime })=\biggl(\frac{2}{y(P^{\prime })},\frac{2x(P^{\prime })}{y(P^{\prime })},\ldots ,\frac{2x(P^{\prime })^{n-1}}{y(P^{\prime })}\biggr)\quad \text{if}~P^{\prime }\not \in \{\infty ,\infty ^{\prime }\}.\end{eqnarray}$$
One key fact to note is that two vectors
![]() $\ell ^{\prime }(P^{\prime })$
and
$\ell ^{\prime }(P^{\prime })$
and
![]() $\ell ^{\prime }(Q^{\prime })$
are
$\ell ^{\prime }(Q^{\prime })$
are
![]() $\mathbb{Q}_{p}$
-parallel if and only if
$\mathbb{Q}_{p}$
-parallel if and only if
 $x(P^{\prime })=x(Q^{\prime })$
. This observation is crucial in what follows.
$x(P^{\prime })=x(Q^{\prime })$
. This observation is crucial in what follows.
Lemma 41. For a fixed point
 $P\in C(\mathbb{Q}_{p})$
, the set of points
$P\in C(\mathbb{Q}_{p})$
, the set of points
 $Q\in C(\mathbb{Q}_{p})$
such that
$Q\in C(\mathbb{Q}_{p})$
such that
![]() $(P,Q)$
is a bad pair is finite.
$(P,Q)$
is a bad pair is finite.
Proof. Indeed, the intersection of
 $\mathbb{Q}_{p}\cdot \ell (P)$
and
$\mathbb{Q}_{p}\cdot \ell (P)$
and
 $\ell (C(\mathbb{Z}_{p}))$
is a subanalytic set of dimension at most 1. Hence it either is finite or contains an open ball
$\ell (C(\mathbb{Z}_{p}))$
is a subanalytic set of dimension at most 1. Hence it either is finite or contains an open ball
![]() $B$
. If it is finite, then we are done. Otherwise, the derivatives
$B$
. If it is finite, then we are done. Otherwise, the derivatives
![]() $\ell ^{\prime }(Q)$
are all parallel (to
$\ell ^{\prime }(Q)$
are all parallel (to
![]() $\ell (P)$
) for every
$\ell (P)$
) for every
![]() $Q\in B$
, which is a contradiction.◻
$Q\in B$
, which is a contradiction.◻
We return to the proof of Lemma 40. Suppose for a contradiction that
 $\dim (\unicode[STIX]{x1D6F4})\geqslant 1$
. Then it contains a subset
$\dim (\unicode[STIX]{x1D6F4})\geqslant 1$
. Then it contains a subset
![]() $\unicode[STIX]{x1D6F4}_{1}$
diffeomorphic to
$\unicode[STIX]{x1D6F4}_{1}$
diffeomorphic to
![]() $\mathbb{Z}_{p}$
. By shrinking
$\mathbb{Z}_{p}$
. By shrinking
![]() $\unicode[STIX]{x1D6F4}_{1}$
if necessary, we may assume that
$\unicode[STIX]{x1D6F4}_{1}$
if necessary, we may assume that
![]() $\unicode[STIX]{x1D6F4}_{1}$
is diffeomorphic to its images under the two coordinate projections by Lemma 41. That is, there exist an open subset
$\unicode[STIX]{x1D6F4}_{1}$
is diffeomorphic to its images under the two coordinate projections by Lemma 41. That is, there exist an open subset
![]() $W$
of
$W$
of
![]() $C(\mathbb{Q}_{p})$
and an analytic map
$C(\mathbb{Q}_{p})$
and an analytic map
 $s:W\rightarrow C(\mathbb{Q}_{p})$
such that
$s:W\rightarrow C(\mathbb{Q}_{p})$
such that
 $(R,s(R))\in \unicode[STIX]{x1D6F4}$
for any
$(R,s(R))\in \unicode[STIX]{x1D6F4}$
for any
![]() $R\in W$
. Let
$R\in W$
. Let
 $\unicode[STIX]{x1D6FC}:W\rightarrow \mathbb{Q}_{p}^{\times }$
denote the analytic function such that
$\unicode[STIX]{x1D6FC}:W\rightarrow \mathbb{Q}_{p}^{\times }$
denote the analytic function such that
 $$\begin{eqnarray}\ell (s(R))=\unicode[STIX]{x1D6FC}(R)\ell (R),\end{eqnarray}$$
$$\begin{eqnarray}\ell (s(R))=\unicode[STIX]{x1D6FC}(R)\ell (R),\end{eqnarray}$$
for any
![]() $R\in W$
. The vanishing set of the derivative
$R\in W$
. The vanishing set of the derivative
![]() $s^{\prime }$
of
$s^{\prime }$
of
![]() $s$
is analytic and hence either is finite or contains an open ball. In the latter case,
$s$
is analytic and hence either is finite or contains an open ball. In the latter case,
![]() $s$
is constant on this open ball, which contradicts Lemma 41. By replacing
$s$
is constant on this open ball, which contradicts Lemma 41. By replacing
![]() $W$
by an open ball inside it, we may assume that
$W$
by an open ball inside it, we may assume that
 $s^{\prime }(R)\neq 0$
for any
$s^{\prime }(R)\neq 0$
for any
![]() $R\in W$
. Differentiating (44) gives
$R\in W$
. Differentiating (44) gives
 $$\begin{eqnarray}\ell ^{\prime }(s(R))=\unicode[STIX]{x1D6FC}_{1}(R)\ell (R)+\unicode[STIX]{x1D6FC}_{2}(R)\ell ^{\prime }(R),\end{eqnarray}$$
$$\begin{eqnarray}\ell ^{\prime }(s(R))=\unicode[STIX]{x1D6FC}_{1}(R)\ell (R)+\unicode[STIX]{x1D6FC}_{2}(R)\ell ^{\prime }(R),\end{eqnarray}$$
with
 $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}^{\prime }/s^{\prime }$
and
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}^{\prime }/s^{\prime }$
and
 $\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}/s^{\prime }$
. Differentiating (45) again shows that the vectors
$\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}/s^{\prime }$
. Differentiating (45) again shows that the vectors
 $\ell ^{\prime \prime }(s(R))$
,
$\ell ^{\prime \prime }(s(R))$
,
![]() $\ell ^{\prime \prime }(R)$
,
$\ell ^{\prime \prime }(R)$
,
![]() $\ell ^{\prime }(R)$
,
$\ell ^{\prime }(R)$
,
![]() $\ell (R)$
are linearly dependent over
$\ell (R)$
are linearly dependent over
![]() $\mathbb{Q}_{p}$
for any
$\mathbb{Q}_{p}$
for any
![]() $R\in W$
. By the definition of bad pairs, we see that
$R\in W$
. By the definition of bad pairs, we see that
 $x(R)\neq x(s(R))$
for any
$x(R)\neq x(s(R))$
for any
![]() $R\in W$
. Hence, for such
$R\in W$
. Hence, for such
![]() $R$
, the lines
$R$
, the lines
 $\ell ^{\prime }(s(R))$
and
$\ell ^{\prime }(s(R))$
and
![]() $\ell ^{\prime }(R)$
are not parallel, which implies that
$\ell ^{\prime }(R)$
are not parallel, which implies that
![]() $\ell (R)$
can be written as a linear combination of
$\ell (R)$
can be written as a linear combination of
 $\ell ^{\prime }(s(R))$
and
$\ell ^{\prime }(s(R))$
and
![]() $\ell ^{\prime }(R)$
by (45). It follows that the vectors
$\ell ^{\prime }(R)$
by (45). It follows that the vectors
 $\ell ^{\prime \prime }(s(R))$
,
$\ell ^{\prime \prime }(s(R))$
,
 $\ell ^{\prime }(s(R))$
,
$\ell ^{\prime }(s(R))$
,
![]() $\ell ^{\prime \prime }(R)$
,
$\ell ^{\prime \prime }(R)$
,
![]() $\ell ^{\prime }(R)$
are linearly dependent over
$\ell ^{\prime }(R)$
are linearly dependent over
![]() $\mathbb{Q}_{p}$
for every
$\mathbb{Q}_{p}$
for every
![]() $R\in W$
. An elementary determinant computation (using the first four coordinates, which requires
$R\in W$
. An elementary determinant computation (using the first four coordinates, which requires
![]() $n\geqslant 4$
) shows that if
$n\geqslant 4$
) shows that if
 $R,T\in C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
, then the vectors
$R,T\in C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
, then the vectors
![]() $\ell ^{\prime \prime }(T)$
,
$\ell ^{\prime \prime }(T)$
,
![]() $\ell ^{\prime }(T)$
,
$\ell ^{\prime }(T)$
,
![]() $\ell ^{\prime \prime }(R)$
,
$\ell ^{\prime \prime }(R)$
,
![]() $\ell ^{\prime }(R)$
are linearly dependent if and only if
$\ell ^{\prime }(R)$
are linearly dependent if and only if
 $x(R)=x(T)$
. This never happens if
$x(R)=x(T)$
. This never happens if
![]() $R\in W$
and
$R\in W$
and
 $T=s(R)$
. We have obtained the desired contradiction, thus completing the proof of Lemma 40.◻
$T=s(R)$
. We have obtained the desired contradiction, thus completing the proof of Lemma 40.◻
Proof of Theorem 38.
Let
![]() $\unicode[STIX]{x1D6FA}$
denote the set of elements in
$\unicode[STIX]{x1D6FA}$
denote the set of elements in
 $\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
corresponding to monic even hyperelliptic curves
$\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
corresponding to monic even hyperelliptic curves
![]() $C$
such that
$C$
such that
 $C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains bad points. Let
$C(\mathbb{Q}_{p})\backslash \{\infty ,\infty ^{\prime }\}$
contains bad points. Let
![]() $\overline{\unicode[STIX]{x1D6FA}}$
denote the closure of
$\overline{\unicode[STIX]{x1D6FA}}$
denote the closure of
![]() $\unicode[STIX]{x1D6FA}$
, which by Theorem 39 has measure 0 in
$\unicode[STIX]{x1D6FA}$
, which by Theorem 39 has measure 0 in
![]() $\mathbb{Z}_{p}^{2n+1}$
. Therefore, for every
$\mathbb{Z}_{p}^{2n+1}$
. Therefore, for every
![]() $\unicode[STIX]{x1D716}>0$
there exists a subset
$\unicode[STIX]{x1D716}>0$
there exists a subset
![]() $U(\unicode[STIX]{x1D716})$
of
$U(\unicode[STIX]{x1D716})$
of
 $\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
$\mathbb{Z}_{p}^{2n+1}\backslash \{\unicode[STIX]{x1D6E5}=0\}$
such that
![]() $U(\unicode[STIX]{x1D716})$
is defined by congruence conditions modulo some fixed power of
$U(\unicode[STIX]{x1D716})$
is defined by congruence conditions modulo some fixed power of
![]() $p$
, the measure of
$p$
, the measure of
![]() $U(\unicode[STIX]{x1D716})$
is at least
$U(\unicode[STIX]{x1D716})$
is at least
![]() $1-\unicode[STIX]{x1D716}$
, and every curve corresponding to a point in
$1-\unicode[STIX]{x1D716}$
, and every curve corresponding to a point in
![]() $U(\unicode[STIX]{x1D716})$
has no bad points over
$U(\unicode[STIX]{x1D716})$
has no bad points over
![]() $\mathbb{Q}_{p}$
apart from
$\mathbb{Q}_{p}$
apart from
![]() $\infty$
and
$\infty$
and
![]() $\infty ^{\prime }$
. Therefore the proportion of hyperelliptic curves
$\infty ^{\prime }$
. Therefore the proportion of hyperelliptic curves
![]() $C$
over
$C$
over
![]() $\mathbb{Q}$
that are good is at least
$\mathbb{Q}$
that are good is at least
![]() $1-\unicode[STIX]{x1D716}$
. Letting
$1-\unicode[STIX]{x1D716}$
. Letting
![]() $\unicode[STIX]{x1D716}$
tend to 0, we obtain Theorem 38.◻
$\unicode[STIX]{x1D716}$
tend to 0, we obtain Theorem 38.◻
Acknowledgements
We are very grateful to Manjul Bhargava and Benedict Gross for suggesting this problem to us and for many helpful conversations. We are also very grateful to Bjorn Poonen for explaining Chabauty’s method to us and for helpful comments on earlier versions of the argument. We are extremely grateful to Cheng-Chiang Tsai, Jacob Tsimerman, and Ila Varma for several helpful conversations. We are also very grateful for detailed and helpful comments from the annonymous referee. The first author is grateful for support from NSF grant DMS-1128155. The second author is grateful for support from a Simons Investigator Grant and NSF grant DMS-1001828.