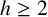1 Introduction
Let
![]() $\mathbb {N}$
be the set of all nonnegative integers. For
$\mathbb {N}$
be the set of all nonnegative integers. For
![]() $A\subseteq \mathbb {N} $
,
$A\subseteq \mathbb {N} $
,
![]() $h\geq 2$
, the h-fold sum of A, denoted
$h\geq 2$
, the h-fold sum of A, denoted
![]() $hA$
, is the set of sums of h not necessarily distinct elements of A and
$hA$
, is the set of sums of h not necessarily distinct elements of A and
![]() $h^{\wedge }A$
is the set of sums of h distinct elements of A. Let W be a nonempty subset of
$h^{\wedge }A$
is the set of sums of h distinct elements of A. Let W be a nonempty subset of
![]() $\mathbb {N}$
. Denote by
$\mathbb {N}$
. Denote by
![]() ${F}^{\ast }(W)$
the set of all finite, nonempty subsets of W. Given positive integers
${F}^{\ast }(W)$
the set of all finite, nonempty subsets of W. Given positive integers
![]() $g,h \geq 2$
, denote
$g,h \geq 2$
, denote
 $$ \begin{align*} A_g(W)=\bigg\{\sum_{f\in F}a_fg^f: 1\leq a_f \leq g-1,F \in {F}^{\ast}(W)\bigg\}. \end{align*} $$
$$ \begin{align*} A_g(W)=\bigg\{\sum_{f\in F}a_fg^f: 1\leq a_f \leq g-1,F \in {F}^{\ast}(W)\bigg\}. \end{align*} $$
For
![]() $i = 0,1,\ldots ,h-1$
, let
$i = 0,1,\ldots ,h-1$
, let
![]() $W_i^{(h)}=\{n\in \mathbb {N}: n\equiv i\pmod h\}$
and let
$W_i^{(h)}=\{n\in \mathbb {N}: n\equiv i\pmod h\}$
and let
The set A is an asymptotic basis of order h if
![]() $hA$
contains all sufficiently large integers. An asymptotic basis A of order h is minimal if
$hA$
contains all sufficiently large integers. An asymptotic basis A of order h is minimal if
![]() $A\setminus \{a\}$
is not an asymptotic basis of order h for every nonnegative integer
$A\setminus \{a\}$
is not an asymptotic basis of order h for every nonnegative integer
![]() $a\in A$
. In 1974, Nathanson [Reference Nathanson4] first gave an explicit construction of a minimal asymptotic basis of order
$a\in A$
. In 1974, Nathanson [Reference Nathanson4] first gave an explicit construction of a minimal asymptotic basis of order
![]() $2$
by using properties of binary representations. In 2010, Jańczak and Schoen [Reference Jańczak and Schoen3] constructed a dense minimal asymptotic basis of order two. Nathanson’s method has been widely used in the construction of minimal asymptotic bases. For related problems concerning minimal asymptotic bases, see [Reference Chen and Tang2, Reference Nathanson6, Reference Sun7]. The study of asymptotic bases and minimal asymptotic bases is closely related to the famous Erdős–Turán conjecture in additive number theory (see [Reference Alladi and Krantz1, Reference Nathanson, Chudnovsky and Chudnovsky5]).
$2$
by using properties of binary representations. In 2010, Jańczak and Schoen [Reference Jańczak and Schoen3] constructed a dense minimal asymptotic basis of order two. Nathanson’s method has been widely used in the construction of minimal asymptotic bases. For related problems concerning minimal asymptotic bases, see [Reference Chen and Tang2, Reference Nathanson6, Reference Sun7]. The study of asymptotic bases and minimal asymptotic bases is closely related to the famous Erdős–Turán conjecture in additive number theory (see [Reference Alladi and Krantz1, Reference Nathanson, Chudnovsky and Chudnovsky5]).
It is natural to introduce a parallel concept of minimal restricted asymptotic bases. We call A a restricted asymptotic basis of order h if
![]() $h^{\wedge }A$
contains all sufficiently large integers. A restricted asymptotic basis A of order h is minimal if
$h^{\wedge }A$
contains all sufficiently large integers. A restricted asymptotic basis A of order h is minimal if
![]() $A\setminus \{a\}$
is not a restricted asymptotic basis of order h for every nonnegative integer
$A\setminus \{a\}$
is not a restricted asymptotic basis of order h for every nonnegative integer
![]() $a\in A$
. Does there exist a minimal restricted asymptotic basis of order h?
$a\in A$
. Does there exist a minimal restricted asymptotic basis of order h?
Our study begins with a result of Sun and Tao on minimal asymptotic bases.
Theorem 1.1 [Reference Sun and Tao8]
Let
![]() $h \geq 2$
. Then for any
$h \geq 2$
. Then for any
![]() $g \geq h$
, the set
$g \geq h$
, the set
![]() $\mathcal {A}_{g,h}$
is a minimal asymptotic basis of order h.
$\mathcal {A}_{g,h}$
is a minimal asymptotic basis of order h.
We obtain the following results.
Proposition 1.2. For
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $g\geq 2$
:
$g\geq 2$
:
-
(1)
 $2g^{2k+1}\notin 2^{\wedge }\mathcal {A}_{g,2}$
;
$2g^{2k+1}\notin 2^{\wedge }\mathcal {A}_{g,2}$
; -
(2)
 $2g^{3k+2}+1\notin 3^{\wedge }\mathcal {A}_{g,3}$
;
$2g^{3k+2}+1\notin 3^{\wedge }\mathcal {A}_{g,3}$
; -
(3)
 $2\cdot 4^{4k+3}+5\notin 4^{\wedge }\mathcal {A}_{4,4}$
.
$2\cdot 4^{4k+3}+5\notin 4^{\wedge }\mathcal {A}_{4,4}$
.
Theorem 1.3. Let
![]() $h\geq 4$
. Then for any
$h\geq 4$
. Then for any
![]() $g\geq \max \{h,5\}$
, the set
$g\geq \max \{h,5\}$
, the set
![]() $\mathcal {A}_{g,h}$
is a minimal restricted asymptotic basis of order h.
$\mathcal {A}_{g,h}$
is a minimal restricted asymptotic basis of order h.
2 A preliminary lemma
Lemma 2.1. Given positive integers
![]() $h\geq 2$
,
$h\geq 2$
,
![]() $g\geq 5$
and
$g\geq 5$
and
![]() $u\geq 2$
, let the g-adic representation of n be
$u\geq 2$
, let the g-adic representation of n be
where
![]() $0 \leq i_1<\cdots <i_{u}$
and
$0 \leq i_1<\cdots <i_{u}$
and
![]() $1\leq e_j\leq g-1$
for
$1\leq e_j\leq g-1$
for
![]() $j=1,\ldots ,u-1$
. Then
$j=1,\ldots ,u-1$
. Then
![]() $n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
$n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
Proof. If
![]() $i_{u-1}<i_{u}-1$
, or if
$i_{u-1}<i_{u}-1$
, or if
![]() $i_{u-1}= i_{u}-1$
,
$i_{u-1}= i_{u}-1$
,
![]() $e_{u-1}\notin \{1,g-1\}$
, then because
$e_{u-1}\notin \{1,g-1\}$
, then because
![]() $g\geq 5$
and
$g\geq 5$
and
we see that
![]() $n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
$n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
If
![]() $i_{u-1}= i_{u}-1$
and
$i_{u-1}= i_{u}-1$
and
![]() $e_{u-1}=1 $
, then because
$e_{u-1}=1 $
, then because
![]() $g\geq 5$
and
$g\geq 5$
and
we see that
![]() $n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
$n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
If
![]() $i_{u-1}= i_{u}-1$
and
$i_{u-1}= i_{u}-1$
and
![]() $e_{u-1}=g-1 $
, then because
$e_{u-1}=g-1 $
, then because
![]() $g\geq 5$
and
$g\geq 5$
and
again
![]() $n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
$n\in (u+1)^{\wedge }\mathcal {A}_{g,h}$
.
This completes the proof of Lemma 2.1.
3 Proof of Proposition 1.2
(1) Assume that
![]() $2g^{2k+1}=a_0+a_1\in 2^{\wedge }\mathcal {A}_{g,2}$
with
$2g^{2k+1}=a_0+a_1\in 2^{\wedge }\mathcal {A}_{g,2}$
with
![]() $0<a_0<a_1$
. Then
$0<a_0<a_1$
. Then
![]() $a_0<g^{2k+1}$
and
$a_0<g^{2k+1}$
and
![]() $a_1<2g^{2k+1}$
. Since
$a_1<2g^{2k+1}$
. Since
![]() $a_0,a_1\in \mathcal {A}_{g,2}$
,
$a_0,a_1\in \mathcal {A}_{g,2}$
,
 $$ \begin{align*} a_0+a_1 &\leq (g-1)(g^0+\cdots+g^{2k-2}+g^{2k})+(g-1)(g^1+\cdots+g^{2k-3}+g^{2k-1})+g^{2k+1}\\ &<2g^{2k+1}, \end{align*} $$
$$ \begin{align*} a_0+a_1 &\leq (g-1)(g^0+\cdots+g^{2k-2}+g^{2k})+(g-1)(g^1+\cdots+g^{2k-3}+g^{2k-1})+g^{2k+1}\\ &<2g^{2k+1}, \end{align*} $$
which is a contradiction. Hence,
![]() $2g^{2k+1}\notin 2^{\wedge }\mathcal {A}_{g,2}\ \text{for all } g\geq 2$
.
$2g^{2k+1}\notin 2^{\wedge }\mathcal {A}_{g,2}\ \text{for all } g\geq 2$
.
(2) Assume that
![]() $2g^{3k+2}+1\in 3^{\wedge }\mathcal {A}_{g,3}$
. Write
$2g^{3k+2}+1\in 3^{\wedge }\mathcal {A}_{g,3}$
. Write
Then
![]() $a_1<g^{3k+2}$
and
$a_1<g^{3k+2}$
and
![]() $a_2<2g^{3k+2}$
. By (3.1), there exists at least one
$a_2<2g^{3k+2}$
. By (3.1), there exists at least one
![]() $a_i\in A_g(W_0^{(3)})$
.
$a_i\in A_g(W_0^{(3)})$
.
If
![]() $a_2\notin A_g(W_{2}^{(3)})$
, then
$a_2\notin A_g(W_{2}^{(3)})$
, then
![]() $a_2\leq (g-1)(g^1+g^4+\cdots +g^{3k+1}).$
Thus,
$a_2\leq (g-1)(g^1+g^4+\cdots +g^{3k+1}).$
Thus,
 $$ \begin{align*} a_0+a_1+a_2&<(g-1)(g^0+g^3+\cdots+g^{3k})+ 2(g-1)(g^1+g^4+\cdots+g^{3k+1})\\ &< 2g^{3k+2}+1, \end{align*} $$
$$ \begin{align*} a_0+a_1+a_2&<(g-1)(g^0+g^3+\cdots+g^{3k})+ 2(g-1)(g^1+g^4+\cdots+g^{3k+1})\\ &< 2g^{3k+2}+1, \end{align*} $$
which is a contradiction.
If
![]() $a_2\in A_g(W_{2}^{(3)})$
, then
$a_2\in A_g(W_{2}^{(3)})$
, then
![]() $a_2\leq (g-1)(g^2+g^5+\cdots +g^{3k-1})+g^{3k+2}.$
Thus,
$a_2\leq (g-1)(g^2+g^5+\cdots +g^{3k-1})+g^{3k+2}.$
Thus,
 $$ \begin{align*} a_0+a_1+a_2 &\leq(g-1)(g^0+g^3+\cdots+g^{3k})+(g-1)(g^1+g^4+\cdots+g^{3k+1})\\ &\quad +(g-1)(g^2+g^5+\cdots+g^{3k-1})+g^{3k+2}\\ &<2g^{3k+2}+1, \end{align*} $$
$$ \begin{align*} a_0+a_1+a_2 &\leq(g-1)(g^0+g^3+\cdots+g^{3k})+(g-1)(g^1+g^4+\cdots+g^{3k+1})\\ &\quad +(g-1)(g^2+g^5+\cdots+g^{3k-1})+g^{3k+2}\\ &<2g^{3k+2}+1, \end{align*} $$
which is a contradiction.
Hence,
![]() $2g^{3k+2}+1\notin 3^{\wedge }\mathcal {A}_{g,3}$
for all
$2g^{3k+2}+1\notin 3^{\wedge }\mathcal {A}_{g,3}$
for all
![]() $g\geq 2$
.
$g\geq 2$
.
(3) Assume that
![]() $2\cdot 4^{4k+3}+5\in 4^{\wedge }\mathcal {A}_{4,4}$
. Write
$2\cdot 4^{4k+3}+5\in 4^{\wedge }\mathcal {A}_{4,4}$
. Write
Then
![]() $a_{3}<2\cdot 4^{4k+3}$
.
$a_{3}<2\cdot 4^{4k+3}$
.
If
![]() $a_3\notin A_4(W_{3}^{(4)})$
, then
$a_3\notin A_4(W_{3}^{(4)})$
, then
![]() $a_3\leq 3(4^2+4^6+\cdots +4^{4k+2})$
. Since
$a_3\leq 3(4^2+4^6+\cdots +4^{4k+2})$
. Since
![]() $2\cdot 4^{4k+3}+5\equiv 5 \pmod {16},$
it follows from (3.2) that
$2\cdot 4^{4k+3}+5\equiv 5 \pmod {16},$
it follows from (3.2) that
 $$ \begin{align*}a_0+a_1+a_2+a_3 &< 4^0+3\times(4^4+\cdots+4^{4k})+4^1+3\times(4^5+\cdots+4^{4k+1})\\ &\quad + 2\times3\times(4^2+4^6+\cdots+4^{4k+2})\\ &<2\cdot 4^{4k+3}+5, \end{align*} $$
$$ \begin{align*}a_0+a_1+a_2+a_3 &< 4^0+3\times(4^4+\cdots+4^{4k})+4^1+3\times(4^5+\cdots+4^{4k+1})\\ &\quad + 2\times3\times(4^2+4^6+\cdots+4^{4k+2})\\ &<2\cdot 4^{4k+3}+5, \end{align*} $$
which is a contradiction.
If
![]() $a_3\in A_4(W_{3}^{(4)})$
, then
$a_3\in A_4(W_{3}^{(4)})$
, then
![]() $a_3\leq 3(4^3+4^7+\cdots +4^{4k-1})+4^{4k+3}$
. If
$a_3\leq 3(4^3+4^7+\cdots +4^{4k-1})+4^{4k+3}$
. If
![]() $a_2\geq 4^{4k+3}$
, then we have
$a_2\geq 4^{4k+3}$
, then we have
![]() $a_2+a_3>2\cdot 4^{4k+3}+5$
, which is a contradiction. It follows that
$a_2+a_3>2\cdot 4^{4k+3}+5$
, which is a contradiction. It follows that
![]() $a_2<4^{4k+3}$
. Again by (3.2) and
$a_2<4^{4k+3}$
. Again by (3.2) and
![]() $2\cdot 4^{4k+3}+5\equiv 5 \pmod {16},$
$2\cdot 4^{4k+3}+5\equiv 5 \pmod {16},$
 $$ \begin{align*}a_0+a_1+a_2+a_3 &\leq 4^0+3\times(4^4+\cdots+4^{4k})+4^1+3\times(4^5+\cdots+4^{4k+1})\\ &\quad + 3(4^2+4^6+\cdots+4^{4k+2})+3(4^3+4^7+\cdots+4^{4k-1})+4^{4k+3} \\ &< 2\cdot 4^{4k+3}+5, \end{align*} $$
$$ \begin{align*}a_0+a_1+a_2+a_3 &\leq 4^0+3\times(4^4+\cdots+4^{4k})+4^1+3\times(4^5+\cdots+4^{4k+1})\\ &\quad + 3(4^2+4^6+\cdots+4^{4k+2})+3(4^3+4^7+\cdots+4^{4k-1})+4^{4k+3} \\ &< 2\cdot 4^{4k+3}+5, \end{align*} $$
which is a contradiction.
Hence,
![]() $2\cdot 4^{4k+3}+5\notin 4^{\wedge }\mathcal {A}_{4,4}$
.
$2\cdot 4^{4k+3}+5\notin 4^{\wedge }\mathcal {A}_{4,4}$
.
This completes the proof of Proposition 1.2.
4 Proof of Theorem 1.3
By Theorem 1.1,
![]() $\mathcal {A}_{g,h}$
is a minimal asymptotic basis of order h. Thus, we only need to prove that
$\mathcal {A}_{g,h}$
is a minimal asymptotic basis of order h. Thus, we only need to prove that
![]() $\mathcal {A}_{g,h}$
is a restricted asymptotic basis of order h.
$\mathcal {A}_{g,h}$
is a restricted asymptotic basis of order h.
Let
![]() $n\geq g^{(h-2)^2+1}$
and let the g-adic representation of n be
$n\geq g^{(h-2)^2+1}$
and let the g-adic representation of n be
where
![]() $0 \leq i_1<\cdots <i_{t}$
and
$0 \leq i_1<\cdots <i_{t}$
and
![]() $1\leq e_j\leq g-1$
for
$1\leq e_j\leq g-1$
for
![]() $j=1,\ldots ,t$
.
$j=1,\ldots ,t$
.
Case 1:
![]() $t=1$
. Then
$t=1$
. Then
![]() $i_1\geq h$
. Note that
$i_1\geq h$
. Note that
where
![]() $\delta =0$
if
$\delta =0$
if
![]() $e_1=1$
and otherwise
$e_1=1$
and otherwise
![]() $\delta =1$
. Hence,
$\delta =1$
. Hence,
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
Case 2:
![]() $2 \leq t \leq h-2$
. If there exists a
$2 \leq t \leq h-2$
. If there exists a
![]() $k\in \{2,\ldots ,t\}$
such that
$k\in \{2,\ldots ,t\}$
such that
![]() $i_{k}-i_{k-1}>h-t$
, then
$i_{k}-i_{k-1}>h-t$
, then
 $$ \begin{align*} n=(e_k-1)g^{i_k}+(g-1)g^{i_{k}-1} + \cdots + (g-1)g^{i_{k}-(h-t-\delta)}+g^{i_{k}-(h-t-\delta)} + \sum_{j\in\{1,\ldots,t\} \setminus\{k\}}e_jg^{i_{j}}, \end{align*} $$
$$ \begin{align*} n=(e_k-1)g^{i_k}+(g-1)g^{i_{k}-1} + \cdots + (g-1)g^{i_{k}-(h-t-\delta)}+g^{i_{k}-(h-t-\delta)} + \sum_{j\in\{1,\ldots,t\} \setminus\{k\}}e_jg^{i_{j}}, \end{align*} $$
where
![]() $\delta =0$
if
$\delta =0$
if
![]() $e_k=1$
and otherwise
$e_k=1$
and otherwise
![]() $\delta =1$
. Hence,
$\delta =1$
. Hence,
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
If
![]() $i_{k}-i_{k-1}\leq h-t$
for all
$i_{k}-i_{k-1}\leq h-t$
for all
![]() $k\in \{2,\ldots ,t\}$
, then by
$k\in \{2,\ldots ,t\}$
, then by
![]() $n\geq g^{(h-2)^2+1}$
, we have
$n\geq g^{(h-2)^2+1}$
, we have
![]() $i_1\geq h-t$
. Otherwise, if
$i_1\geq h-t$
. Otherwise, if
![]() $i_1<h-t$
, then
$i_1<h-t$
, then
![]() $i_t<t(h-t)$
, so that
$i_t<t(h-t)$
, so that
which is a contradiction. Thus,
 $$ \begin{align*} n=(e_1-1)g^{i_1} + ( g-1)g^{i_{1}-1} + \cdots + (g-1)g^{i_{1} - (h-t-\delta)} + g^{i_{1}-(h-t-\delta)} +\sum_{j\in\{2,\ldots,t\}}e_jg^{i_{j}}, \end{align*} $$
$$ \begin{align*} n=(e_1-1)g^{i_1} + ( g-1)g^{i_{1}-1} + \cdots + (g-1)g^{i_{1} - (h-t-\delta)} + g^{i_{1}-(h-t-\delta)} +\sum_{j\in\{2,\ldots,t\}}e_jg^{i_{j}}, \end{align*} $$
where
![]() $\delta =0$
if
$\delta =0$
if
![]() $e_1=1$
and otherwise
$e_1=1$
and otherwise
![]() $\delta =1$
. Hence,
$\delta =1$
. Hence,
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
Case 3:
![]() $t = h-1$
. Then
$t = h-1$
. Then
where
![]() $0 \leq i_1<\cdots <i_{h-1}$
,
$0 \leq i_1<\cdots <i_{h-1}$
,
![]() $1\leq e_j\leq g-1$
for
$1\leq e_j\leq g-1$
for
![]() $j=1,\ldots ,h-1$
.
$j=1,\ldots ,h-1$
.
If there exists a
![]() $k\in \{1,\ldots ,h-1\}$
such that
$k\in \{1,\ldots ,h-1\}$
such that
![]() $3 \leq e_k \leq g-1$
, then
$3 \leq e_k \leq g-1$
, then
 $$ \begin{align*} n =\sum_{j\in I\backslash\{k\}}e_jg^{i_j}+g^{i_{k}} +(e_{k}-1) g^{i_{k}}, \end{align*} $$
$$ \begin{align*} n =\sum_{j\in I\backslash\{k\}}e_jg^{i_j}+g^{i_{k}} +(e_{k}-1) g^{i_{k}}, \end{align*} $$
where
![]() $I=\{1,\ldots ,h-1\}$
, and thus
$I=\{1,\ldots ,h-1\}$
, and thus
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
Now we consider what happens if
![]() $1\leq e_j\leq 2$
for
$1\leq e_j\leq 2$
for
![]() $j=1,\ldots ,h-1$
.
$j=1,\ldots ,h-1$
.
(a) Suppose
![]() $e_{h-1}=1$
. Then by Lemma 2.1,
$e_{h-1}=1$
. Then by Lemma 2.1,
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
(b) Suppose
![]() $e_1=e_2=\cdots =e_{h-2}=e_{h-1}=2$
.
$e_1=e_2=\cdots =e_{h-2}=e_{h-1}=2$
.
If there exist
![]() $i_u<i_v $
with
$i_u<i_v $
with
![]() $1\leq u,v\leq h-1$
such that
$1\leq u,v\leq h-1$
such that
![]() $i_u \equiv i_v \pmod h$
, then because
$i_u \equiv i_v \pmod h$
, then because
and
![]() $i_v \geq h$
, we have
$i_v \geq h$
, we have
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
If
![]() $i_s\not \equiv i_t\pmod h$
for
$i_s\not \equiv i_t\pmod h$
for
![]() $1\leq s\neq t\leq h-1$
, then because
$1\leq s\neq t\leq h-1$
, then because
![]() $h\geq 4$
, there exist
$h\geq 4$
, there exist
![]() $i_v\ (\geq 1)$
,
$i_v\ (\geq 1)$
,
![]() $i_u$
with
$i_u$
with
![]() $u,v \in \{1,2,\ldots ,h-1\}$
such that
$u,v \in \{1,2,\ldots ,h-1\}$
such that
![]() $i_v \equiv i_u+1 \pmod h$
. Since
$i_v \equiv i_u+1 \pmod h$
. Since
![]() $g\geq 5$
and
$g\geq 5$
and
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
(c) Suppose
![]() $e_{h-1}=2$
,
$e_{h-1}=2$
,
![]() $e_{k}=1$
for some
$e_{k}=1$
for some
![]() $k\in \{2,\ldots ,h-2\}$
. Then
$k\in \{2,\ldots ,h-2\}$
. Then
 $$ \begin{align*} n=\sum_{j\in K}e_jg^{i_{j}}+g^{i_k}+\sum_{j\in I}e_jg^{i_{j}}, \end{align*} $$
$$ \begin{align*} n=\sum_{j\in K}e_jg^{i_{j}}+g^{i_k}+\sum_{j\in I}e_jg^{i_{j}}, \end{align*} $$
where
![]() $K=\{1,\ldots ,k-1\}$
and
$K=\{1,\ldots ,k-1\}$
and
![]() $I=\{k+1,\ldots ,h-1\}$
. By Lemma 2.1,
$I=\{k+1,\ldots ,h-1\}$
. By Lemma 2.1,
 $$ \begin{align*} \sum\limits_{j\in K}e_jg^{i_{j}}+g^{i_k}\in (k+1)^{\wedge}\mathcal{A}_{g,h} \end{align*} $$
$$ \begin{align*} \sum\limits_{j\in K}e_jg^{i_{j}}+g^{i_k}\in (k+1)^{\wedge}\mathcal{A}_{g,h} \end{align*} $$
and so
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
(d) Suppose
![]() $e_{h-1}=e_{h-2}=\cdots =e_2=2$
,
$e_{h-1}=e_{h-2}=\cdots =e_2=2$
,
![]() $e_1=1$
. If
$e_1=1$
. If
![]() $i_1>0$
, then
$i_1>0$
, then
 $$ \begin{align*} n=g^{i_1-1}+(g-1)g^{i_1-1}+\sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}} \end{align*} $$
$$ \begin{align*} n=g^{i_1-1}+(g-1)g^{i_1-1}+\sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}} \end{align*} $$
and so
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
If
![]() $i_1=0$
, then
$i_1=0$
, then
 $$ \begin{align*} n=1+\sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}. \end{align*} $$
$$ \begin{align*} n=1+\sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}. \end{align*} $$
(d1) There exists a
![]() $k\in \{2,\ldots ,h-1\}$
such that
$k\in \{2,\ldots ,h-1\}$
such that
![]() $i_{k}\equiv 0\pmod h$
. Then
$i_{k}\equiv 0\pmod h$
. Then
 $$ \begin{align*} n=(1+g^{i_{k}})+g^{i_{k}-1}+(g-1)g^{i_{k}-1}+\sum_{j\in\{2,\ldots,h-1\}\setminus\{k\}}2g^{i_{j}}. \end{align*} $$
$$ \begin{align*} n=(1+g^{i_{k}})+g^{i_{k}-1}+(g-1)g^{i_{k}-1}+\sum_{j\in\{2,\ldots,h-1\}\setminus\{k\}}2g^{i_{j}}. \end{align*} $$
Thus,
![]() $n\in h^{\wedge }\mathcal {A}_{g,h}$
.
$n\in h^{\wedge }\mathcal {A}_{g,h}$
.
(d2) Suppose
![]() $i_{k}\not \equiv 0\pmod h$
for all
$i_{k}\not \equiv 0\pmod h$
for all
![]() $k\in \{2,\ldots ,h-1\}$
.
$k\in \{2,\ldots ,h-1\}$
.
If
![]() $h\geq 5$
, then one of the following two cases must occur.
$h\geq 5$
, then one of the following two cases must occur.
Case (i): There exist
![]() $i_u<i_v $
with
$i_u<i_v $
with
![]() $2\leq u,v\leq h-1$
such that
$2\leq u,v\leq h-1$
such that
![]() $i_u \equiv i_v \pmod h$
. Since
$i_u \equiv i_v \pmod h$
. Since
and
![]() $i_v>h$
, we have
$i_v>h$
, we have
 $$ \begin{align*} \sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}\in (h-1)^{\wedge}(\mathcal{A}_{g,h}\backslash \{1\}). \end{align*} $$
$$ \begin{align*} \sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}\in (h-1)^{\wedge}(\mathcal{A}_{g,h}\backslash \{1\}). \end{align*} $$
Thus,
![]() $n \in h^{\wedge }\mathcal {A}_{g,h}$
.
$n \in h^{\wedge }\mathcal {A}_{g,h}$
.
Case (ii):
![]() $i_s\not \equiv i_t\pmod h$
for
$i_s\not \equiv i_t\pmod h$
for
![]() $2\leq s\neq t\leq h-1$
. Then there exist
$2\leq s\neq t\leq h-1$
. Then there exist
![]() $i_v\ (\geq 1)$
,
$i_v\ (\geq 1)$
,
![]() $i_u$
for some
$i_u$
for some
![]() $u,v \in \{2,\ldots ,h-1\}$
such that
$u,v \in \{2,\ldots ,h-1\}$
such that
![]() $i_v \equiv i_u+1 \pmod h$
. Because
$i_v \equiv i_u+1 \pmod h$
. Because
![]() $g\geq 5$
and
$g\geq 5$
and
we have
 $$ \begin{align*} \sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}\in (h-1)^{\wedge}(\mathcal{A}_{g,h}\backslash \{1\}). \end{align*} $$
$$ \begin{align*} \sum\limits_{j\in\{2,\ldots,h-1\}}2g^{i_{j}}\in (h-1)^{\wedge}(\mathcal{A}_{g,h}\backslash \{1\}). \end{align*} $$
Thus,
![]() $n \in h^{\wedge }\mathcal {A}_{g,h}$
.
$n \in h^{\wedge }\mathcal {A}_{g,h}$
.
Now suppose
![]() $h=4$
. Since
$h=4$
. Since
![]() $i_2,i_3\not \equiv 0\pmod 4$
, there is one further case in addition to (i) and (ii), namely,
$i_2,i_3\not \equiv 0\pmod 4$
, there is one further case in addition to (i) and (ii), namely,
![]() $\{i_2\pmod 4, i_3\pmod 4\}=\{1\pmod 4, 3\pmod 4\}$
. We may assume that
$\{i_2\pmod 4, i_3\pmod 4\}=\{1\pmod 4, 3\pmod 4\}$
. We may assume that
![]() $i_{2}\equiv 1\pmod 4$
. Because
$i_{2}\equiv 1\pmod 4$
. Because
![]() $g\geq 5$
and
$g\geq 5$
and
we have
![]() $n\in 4^{\wedge }\mathcal {A}_{g,4}$
.
$n\in 4^{\wedge }\mathcal {A}_{g,4}$
.
Case 4:
![]() $t \geq h$
.
$t \geq h$
.
Write
![]() $I=\{i_{1},\ldots ,i_{t}\}$
. Since
$I=\{i_{1},\ldots ,i_{t}\}$
. Since
![]() $\lvert I\rvert \geq h$
, it is possible to write I as a union of h nonempty sets
$\lvert I\rvert \geq h$
, it is possible to write I as a union of h nonempty sets
![]() $I_{1},\ldots ,I_{h}$
, where each
$I_{1},\ldots ,I_{h}$
, where each
![]() $I_{j}$
is a subset of some
$I_{j}$
is a subset of some
![]() $W^{(h)}_{k}$
. It follows that
$W^{(h)}_{k}$
. It follows that
![]() $n \in h^{\wedge }\mathcal {A}_{g,h}$
.
$n \in h^{\wedge }\mathcal {A}_{g,h}$
.
This completes the proof of Theorem 1.3.