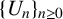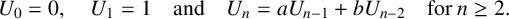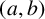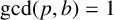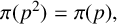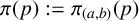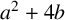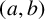A NOTE ON GENERALISED WALL–SUN–SUN PRIMES

Abstract

Let a and b be positive integers and let $\{U_n\}_{n\ge 0}$ be the Lucas sequence of the first kind defined by

$$ \begin{align*}U_0=0,\quad U_1=1\quad \mbox{and} \quad U_n=aU_{n-1}+bU_{n-2} \quad \mbox{for }n\ge 2.\end{align*} $$

We define an $(a,b)$-Wall–Sun–Sun prime to be a prime p such that $\gcd (p,b)=1$ and $\pi (p^2)=\pi (p),$ where $\pi (p):=\pi _{(a,b)}(p)$ is the length of the period of $\{U_n\}_{n\ge 0}$ modulo p. When $(a,b)=(1,1)$, such primes are known in the literature simply as Wall–Sun–Sun primes. In this note, we provide necessary and sufficient conditions such that a prime p dividing $a^2+4b$ is an $(a,b)$-Wall–Sun–Sun prime.

1 Introduction

Throughout this note, for positive integers a and b, we let $\{U_n\}_{n\ge 0}$ be the Lucas sequence of the first kind [6] defined by

(1.1) $$ \begin{align} U_0=0,\quad U_1=1\quad \mbox{and} \quad U_n=aU_{n-1}+bU_{n-2} \quad \mbox{for }n\ge 2. \end{align} $$

The sequence $\{U_n\}_{n\ge 0}$ is periodic modulo any prime p with $\gcd (p,b)=1$ , and we denote by $\pi (p):=\pi _{(a,b)}(p)$ the length of the period of $\{U_n\}_{n\ge 0}$ modulo p.

We define an $(a,b)$ -Wall–Sun–Sun prime to be a prime p such that

(1.2) $$ \begin{align} \pi(p^2)=\pi(p). \end{align} $$

An $(a,1)$ -Wall–Sun–Sun prime is also known in the literature as an a-Wall–Sun–Sun prime [10] or an a-Fibonacci–Wieferich prime. Note that when $(a,b)=(1,1)$ , the sequence $\{U_n\}_{n\ge 0}$ is the well-known Fibonacci sequence. In this case, such primes are referred to simply as Wall–Sun–Sun primes [3, 10] or Fibonacci–Wieferich primes [11]. However, at the time this note was written, no Wall–Sun–Sun primes were known to exist. The existence of Wall–Sun–Sun primes was first investigated by Wall [9] in 1960, and subsequently studied by the Sun brothers [8], who showed that the first case of Fermat’s last theorem is false for exponent p only if p is a Wall–Sun–Sun prime.

For an a-Wall–Sun–Sun prime p, it can be shown [4, 5] that the following conditions are equivalent:

1. (1) $\pi (p^2)=\pi (p)$ ;

2. (2) $U_{\pi (p)}\equiv 0 \pmod {p^2}$ ;

3. (3) $U_{p-\delta _p}\equiv 0 \pmod {p^2}$ , where $\delta _p$ is the Legendre symbol $\big(\frac{a^2\, {+}\ 4}{p}\big)$ .

Because of this equivalence, various authors have chosen to use either item (2) or item (3) for the definition of an a-Wall–Sun–Sun prime. However, for the more general $(a,b)$ -Wall–Sun–Sun prime p, it turns out that, while item (1) implies the still-equivalent items (2) and (3), the converse is false in general. For example, with $(a,b)=(5,8)$ and $p=7$ , an easy calculation shows that items (2) and (3) are true, but item (1) is false since $\pi (49)=42$ and $\pi (7)=6$ . Because of this phenomenon, and the fact that Wall [9] was originally concerned with the impossibility of item (1) in the Wall–Sun–Sun situation, we have chosen to adopt (1.2) as our definition of an $(a,b)$ -Wall–Sun–Sun prime.

This note is motivated in part by recent results of Bouazzaoui [1, 2] which show, under certain restrictions on a, b and p, that an odd prime p is an $(a,b)$ -Wall–Sun–Sun prime if and only if ${\mathbb Q}(\sqrt {a^2+4b})$ is not p-rational. We recall that a number field K is p-rational if the Galois group of the maximal pro-p-extension of K which is unramified outside p is a free pro-p-group of rank $r_2 + 1$ , where $r_2$ is the number of pairs of complex embeddings of K.

A second motivation for this note is recent work of the second author which, again under certain restrictions on a and p, establishes a connection between $(a,1)$ -Wall–Sun–Sun primes p and the monogenicity of certain power-compositional trinomials [5].

One restriction imposed on p in the work of these motivational articles is that $a^2+4b\not \equiv 0\pmod {p}$ . In this note, our focus is on primes p that divide $a^2+4b$ , and in this case, we provide necessary and sufficient conditions so that p is an $(a,b)$ -Wall–Sun–Sun prime. More precisely, we prove the following result.

Theorem 1.1. Let a and b be positive integers and let p be a prime divisor of $a^2+4b$ such that $\gcd (p,b)=1$ . Let $(a,b)_{m}:=(a \ \mathrm {mod}\ m,b \ \mathrm {mod}\ m)$ . Then

• • $p=2$ is an $(a,b)$ -Wall–Sun–Sun prime if and only if $(a,b)_4=(0,1)$ ;

• • $p=3$ is an $(a,b)$ -Wall–Sun–Sun prime if and only if

  $$ \begin{align*}(a,b)_9\in \{(1,8),(2,5),(4,2),(5,2),(7,5),(8,8)\};\end{align*} $$

• • $p\ge 5$ is never an $(a,b)$ -Wall–Sun–Sun prime.

2 Proof of Theorem 1.1

Note that the sequence $\{U_n\}_{n\ge 0}$ from (1.1) is explicitly

(2.1) $$ \begin{align} \{U_n\}=[0, 1, a, a^2+b, a^3+2ab, a^4+3a^2b+b^2, a^5+4a^3b+3ab^2, \ldots]. \end{align} $$

We let $\{U_n\}_p$ denote the sequence (2.1) modulo the prime p.

We first address the prime $p=2$ . Since $a^2+4b\equiv 0 \pmod {2}$ , it follows that ${a\equiv 0 \pmod {2}}$ . Then, since $\gcd (p,b)=1$ , we see from (2.1) that

$$ \begin{align*} \{U_n\}_2=[0,1,0,1,\ldots] \quad \mbox{and} \quad \{U_n\}_4=[0,1,a,b,0,b^2\ldots]. \end{align*} $$

Thus, $\pi (2)=2$ and $\pi (4)=2$ if and only if $(a,b)_4=(0,1)$ , which finishes the case ${p=2}$ .

Next, let $p=3$ . Since $a^2+4b\equiv 0 \pmod {3}$ , we see that $a^2\equiv -b \pmod {3}$ . Since $\gcd (3,b)=1$ , we deduce that $b\equiv 2 \pmod {3}$ and $a^2\equiv 1 \pmod {3}$ . Hence, from (2.1),

$$ \begin{align*} \{U_n\}_3=[0, 1, a, 0, 2a, 2, 0,1, \ldots], \end{align*} $$

where $a\equiv 1,2 \pmod {3}$ . We conclude that

$$ \begin{align*}\pi(3)=\begin{cases} 6&\mbox{if }a\equiv 1 \pmod{3},\\ 3&\mbox{if }a\equiv 2 \pmod{3}. \end{cases}\end{align*} $$

Observe that $\pi (9)=3$ if and only if

$$ \begin{align*}U_3=a^2+b\equiv 0 \pmod{9} \quad \mbox{and}\quad U_4=aU_3+bU_2\equiv ba\equiv 1 \pmod{9}.\end{align*} $$

Since $b \ \mathrm {mod}\ 9\in \{2,5,8\}$ , it follows that

$$ \begin{align*}\pi(9)=3 \quad\mbox{if and only if } (a,b)_9\in \{(2,5),(5,2),(8,8)\}.\end{align*} $$

If $\pi (9)=6$ , then

$$ \begin{align*}U_6=a^5+4a^3b+3ab^2=a(a^2+b)(a^2+3b)\equiv 0 \pmod{9},\end{align*} $$

which implies that $a^2+b\equiv 0\pmod {9}$ , since $a^2+b\equiv 0 \pmod {3}$ and $\gcd (3,b)=1$ . Hence, from (2.1), we have that

$$ \begin{align*} \{U_n\}_9=[0, 1, a, 0, ab, a^2b, 0,a^2b^2,\ldots], \end{align*} $$

where $a^2b^2\equiv 1 \pmod {9}$ . Thus,

(2.2) $$ \begin{align} ab\equiv -1\pmod{9}, \end{align} $$

since we are assuming that $\pi (9)\ne 3$ . Consequently,

$$ \begin{align*} \{U_n\}_9=[0, 1, a, 0, -1, -a, 0,1,\ldots]. \end{align*} $$

Recall that $b\equiv 2 \pmod {3}$ . Then, for each $b\ \mathrm {mod}\ 9\in \{2,5,8\}$ , solving (2.2) for a yields

$$ \begin{align*}\pi(9)=6 \quad\mbox{if and only if } (a,b)_9\in \{(1,8),(4,2),(7,5)\},\end{align*} $$

which completes the proof when $p=3$ .

Finally, suppose that $p\ge 5$ . Since

$$ \begin{align*}\pi(p^2)=\pi(p) \quad\mbox{implies } U_{\pi(p^2)}=U_{\pi(p)}\equiv 0 \pmod{p^2},\end{align*} $$

we show that $U_{\pi (p)}\not \equiv 0 \pmod {p^2}$ to establish that p is not an $(a,b)$ -Wall–Sun–Sun prime.

We claim that, for $n\ge 0$ ,

(2.3) $$ \begin{align} U_n\equiv\begin{cases} \dfrac{(-1)^{n/2}ab^{(n-4)/2}n(a^2(n^2-4)+4b(n^2-10))}{48} \pmod{p^2} &\mbox{if }n\mbox{ is even},\\[2ex] \dfrac{(-1)^{(n+1)/2}b^{(n-3)/2}n(a^2(n^2-1)+4b(n^2-7))}{24} \pmod{p^2} &\mbox{if }n\mbox{ is odd.} \end{cases} \end{align} $$

The proof is by induction on n. The claim is easily verified when $n\in \{0,1,2\}$ . Since p divides $a^2+4b$ , we see that $p^2$ divides $(a^2+4b)^2=a^4+8a^2b+16b^2$ . It follows that

(2.4) $$ \begin{align} a^4\equiv -8a^2b-16b^2\pmod{p^2}. \end{align} $$

Suppose that the claim holds for all $n\leq t$ for some even integer t. Then, modulo $p^2$ ,

$$ \begin{align*} U_{t+1} & \equiv aU_{t}+bU_{t-1}\\ & \equiv a\dfrac{(-1)^{t/2}ab^{(t-4)/2}t(a^2(t^2-4)+4b(t^2-10))}{48}\\ & \quad +b\dfrac{(-1)^{t/2}b^{(t-4)/2}(t-1)(a^2(t^2-2t)+4b(t^2-2t-6))}{24}\\ & \equiv(-1)^{t/2}b^{(t-4)/2}\dfrac{a^4(t^3-4t)+6(t+2)(t-3)tba^2+8(t-1)(t^2-2t-6)b^2}{48}\\ & \equiv\dfrac{(-1)^{(t+2)/2}b^{(t-2)/2}(t+1)(a^2t(t+2)+4b(t^2+2t-6))}{24}\quad (\mbox{by}\ (2.4))\\ & \equiv\dfrac{(-1)^{((t+1)+1)/2}b^{((t+1)-3)/2}(t+1)(a^2((t+1)^2-1)+4b((t+1)^2-7))}{24} \end{align*} $$

and

$$ \begin{align*} U_{t+2} & \equiv aU_{t+1}+bU_{t}\\ & \equiv a\dfrac{(-1)^{((t+1)+1)/2}b^{((t+1)-3)/2}(t+1)(a^2((t+1)^2-1)+4b((t+1)^2-7))}{24}\\ & \quad +b\dfrac{(-1)^{t/2}ab^{(t-4)/2}t(a^2(t^2-4)+4b(t^2-10))}{48}\\ & \equiv (-1)^{t/2}\dfrac{-ab^{(t-2)/2}(a^2(t+2)(t^2+4t)+4b(t+2)(t^2+t-6))}{48}\\ & \equiv \dfrac{(-1)^{(t+2)/2}ab^{((t+2)-4)/2}(t+2)(a^2((t+2)^2-4)+4b((t+2)^2-10))}{48}, \end{align*} $$

which establishes the claim.

For brevity of notation, we let $\lambda $ denote the order of $2^{-1}a$ modulo p. Then, since $\gcd (p,b)=1$ , it follows that $\pi (p)=p\lambda $ [7, Theorem 3(c)]. Since $\lambda $ divides $p-1$ , it follows that $\gcd (p,\lambda )=1$ . To finish the proof, we must show that $U_{\pi (p)}\not \equiv 0 \pmod {p^2}$ . We use (2.3).

If $\lambda \equiv 0 \pmod {2}$ , then modulo $p^2$ ,

$$ \begin{align*} U_{p\lambda} &\equiv \dfrac{(-1)^{p\lambda/2}ab^{(p\lambda-4)/2}p\lambda(a^2((p\lambda)^2-4)+4b((p\lambda)^2-10))}{48}\\ &\equiv\dfrac{(-1)^{p\lambda/2}ab^{(p\lambda-4)/2}p\lambda(a^2(-4)+4b(-10))}{48}\\ &\equiv\dfrac{(-1)^{\lambda (p+2)/2}4ab^{(p\lambda-4)/2}p\lambda(a^2+10b)}{48}. \end{align*} $$

Since $p\not \in \{2,3\}$ and does not divide a, b or $\lambda $ , if $U_{p\lambda }\equiv 0\pmod {p^2}$ , then p divides $a^2+10b$ . However, since p divides $a^2+4b$ , it follows that

$$ \begin{align*}a^2+10b\equiv 6b\not\equiv 0\pmod{p},\end{align*} $$

completing the proof in this case.

Suppose now that $\lambda \equiv 1 \pmod {2}$ . Then, modulo $p^2$ ,

$$ \begin{align*} U_{p\lambda} &\equiv \dfrac{(-1)^{(p\lambda+1)/2}b^{(p\lambda-3)/2}p\lambda(a^2((p\lambda)^2-1)+4b((p\lambda)^2-7))}{24}\\ &\equiv\dfrac{(-1)^{(p\lambda+1)/2}b^{(p\lambda-3)/2}p\lambda(a^2(-1)+4b(-7))}{24}\\ &\equiv\dfrac{(-1)^{(p\lambda+3)/2}b^{(p\lambda-3)/2}p\lambda(a^2+28b)}{24}. \end{align*} $$

Reasoning as in the previous case, we see that $U_{p\lambda }\equiv 0 \pmod {p^2}$ if and only if ${a^2+28b\equiv 0 \pmod {p}}$ . However, since $a^2+4b\equiv 0\pmod {p}$ , it follows that

$$ \begin{align*}a^2+28b\equiv 24b \not \equiv 0 \pmod{p},\end{align*} $$

which completes the proof of the theorem.