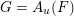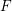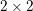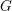Introduction
The study of harmonic functions on trees has a long history. In the early 1960s Dynkin and Malyutov [Reference Dynkin and MalyutovDM61] considered nearest-neighbor random walks on free groups and obtained an analogue of the Poisson formula for them by identifying the Martin boundary of such a group with the space of ends of its Cayley graph. This result was then generalized by a number of authors, among others by Cartier [Reference CartierCar72], who considered nearest-neighbor, but not necessarily homogeneous, random walks on trees. Finite-range random walks were subsequently studied by Derriennic [Reference DerriennicDer75] in the homogeneous case and by Picardello and Woess [Reference Picardello and WoessPW87] in general. In both cases the result was the same as before: the Martin boundary of a tree coincides with its space of ends. This was later generalized to hyperbolic graphs by Ancona [Reference AnconaAnc88] who considered finite-range random walks on such graphs and showed that (under mild assumptions) the corresponding Martin boundaries coincide with the Gromov boundaries. A related result was also obtained by Kaimanovich [Reference KaimanovichKai00] who studied only bounded harmonic functions on hyperbolic groups but went beyond finite-range random walks.
The natural quantum analogues of free groups are the duals of free quantum groups of Van Daele and Wang [Reference Van Daele and WangVDW96]. An interpretation of these duals as vertices of some quantum trees was proposed by Vergnioux [Reference VergniouxVer05], and an analogue of the end compactification was defined by Vaes and Vergnioux [Reference Vaes and VergniouxVV07] in the free orthogonal case and by Vaes and Vander Vennet in the free unitary case [Reference Vaes and Vander VennetVVV10]. The duals of free orthogonal quantum groups behave in many respects like the group
![]() $\mathbb{Z}$
, so the corresponding tree has valency
$\mathbb{Z}$
, so the corresponding tree has valency
![]() $2$
, but the quantum boundary is less trivial than this analogy might suggest; for example, for the dual of
$2$
, but the quantum boundary is less trivial than this analogy might suggest; for example, for the dual of
![]() $\text{SU}_{q}(2)$
(
$\text{SU}_{q}(2)$
(
![]() $q\neq \pm 1$
) it is the Podleś quantum sphere
$q\neq \pm 1$
) it is the Podleś quantum sphere
![]() $S_{q}^{2}$
. An identification of the quantum Poisson and Martin boundaries with the quantum spaces of ends was obtained in [Reference IzumiIzu02, Reference Neshveyev and TusetNT04, Reference Vaes and VergniouxVV07]; see also the earlier paper by Biane [Reference BianeBia94] on the dual of
$S_{q}^{2}$
. An identification of the quantum Poisson and Martin boundaries with the quantum spaces of ends was obtained in [Reference IzumiIzu02, Reference Neshveyev and TusetNT04, Reference Vaes and VergniouxVV07]; see also the earlier paper by Biane [Reference BianeBia94] on the dual of
![]() $\text{SU}(2)$
, which to a great extent motivated the development of the quantum theory.
$\text{SU}(2)$
, which to a great extent motivated the development of the quantum theory.
The duals of free unitary quantum groups behave more like the free group with two generators. In this case Vaes and Vander Vennet showed [Reference Vaes and Vander VennetVVV10] that the Poisson boundary is isomorphic to the quantum boundary they defined, or more precisely, that the von Neumann algebra of bounded harmonic functions is isomorphic to the von Neumann algebra generated by the C
![]() $^{\ast }$
-algebra of continuous functions on the boundary in the GNS-representation defined by a particular state. Classically this would mean a computation of the Martin boundary as a measure space rather than as a topological space, where the measure is defined as the hitting distribution of the random walk. The goal of the present paper is to show that the Martin boundary of the dual of a free unitary quantum group does coincide with the boundary defined in [Reference Vaes and Vander VennetVVV10] topologically, that is, we have an equality of C
$^{\ast }$
-algebra of continuous functions on the boundary in the GNS-representation defined by a particular state. Classically this would mean a computation of the Martin boundary as a measure space rather than as a topological space, where the measure is defined as the hitting distribution of the random walk. The goal of the present paper is to show that the Martin boundary of the dual of a free unitary quantum group does coincide with the boundary defined in [Reference Vaes and Vander VennetVVV10] topologically, that is, we have an equality of C
![]() $^{\ast }$
-algebras.
$^{\ast }$
-algebras.
It should be added that a precise relation between quantum Poisson and Martin boundaries has not been established. It was shown in [Reference Neshveyev and TusetNT04] that for the dual of
![]() $\text{SU}_{q}(2)$
the computation of the Martin boundary allows one to easily identify the Poisson boundary as well. This was also recently confirmed in [Reference JordansJor17] by a different argument, and the same is true for the duals of free orthogonal quantum groups. But a general result of this sort is not available yet, so we cannot claim that our result automatically covers the computation of the Poisson boundary in [Reference Vaes and Vander VennetVVV10].
$\text{SU}_{q}(2)$
the computation of the Martin boundary allows one to easily identify the Poisson boundary as well. This was also recently confirmed in [Reference JordansJor17] by a different argument, and the same is true for the duals of free orthogonal quantum groups. But a general result of this sort is not available yet, so we cannot claim that our result automatically covers the computation of the Poisson boundary in [Reference Vaes and Vander VennetVVV10].
If one wants to compute the Martin boundary of the dual a free unitary quantum group
![]() $G=A_{u}(F)$
, it is natural to try to follow the strategy used in [Reference Vaes and VergniouxVV07] in the free orthogonal case. However, this requires more precise information on the Green functions of particular classical random walks on trees than seems to be available. We propose a different approach, which also reduces the computation to a classical problem (and works equally well in the free orthogonal case). The idea is that by considering the spectral subspaces of
$G=A_{u}(F)$
, it is natural to try to follow the strategy used in [Reference Vaes and VergniouxVV07] in the free orthogonal case. However, this requires more precise information on the Green functions of particular classical random walks on trees than seems to be available. We propose a different approach, which also reduces the computation to a classical problem (and works equally well in the free orthogonal case). The idea is that by considering the spectral subspaces of
![]() $\ell ^{\infty }({\hat{G}})$
with respect to the adjoint action of
$\ell ^{\infty }({\hat{G}})$
with respect to the adjoint action of
![]() $G$
, we see that a quantum random walk is determined by a collection of operators on the
$G$
, we see that a quantum random walk is determined by a collection of operators on the
![]() $\ell ^{2}$
-spaces of branches of the classical tree
$\ell ^{2}$
-spaces of branches of the classical tree
![]() $\operatorname{Irr}(G)$
. It turns out that the matrix coefficients of any two such operators corresponding to the common branch of definition are exponentially small perturbations of each other (with respect to the distance to the root of
$\operatorname{Irr}(G)$
. It turns out that the matrix coefficients of any two such operators corresponding to the common branch of definition are exponentially small perturbations of each other (with respect to the distance to the root of
![]() $\operatorname{Irr}(G)$
). Our main technical result roughly says that the corresponding classical Green functions all have the same asymptotics at infinity. While this is probably not surprising, we point out that the tree
$\operatorname{Irr}(G)$
). Our main technical result roughly says that the corresponding classical Green functions all have the same asymptotics at infinity. While this is probably not surprising, we point out that the tree
![]() $\operatorname{Irr}(G)$
has exponential growth, so it is not immediately obvious that even an exponentially small perturbation is enough to compensate for this growth.
$\operatorname{Irr}(G)$
has exponential growth, so it is not immediately obvious that even an exponentially small perturbation is enough to compensate for this growth.
1 Preliminaries
1.1 Compact and discrete quantum groups
In this section we recall the basic notions related to compact and discrete quantum groups; see, for example, [Reference Neshveyev and TusetNT13] for more details.
A compact quantum group
![]() $G$
is given by a unital C
$G$
is given by a unital C
![]() $^{\ast }$
-algebra
$^{\ast }$
-algebra
![]() $C(G)$
and a unital
$C(G)$
and a unital
![]() $\ast$
-homomorphism
$\ast$
-homomorphism
such that
![]() $(\unicode[STIX]{x1D6E5}\otimes \unicode[STIX]{x1D704})\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6E5}$
and the spaces
$(\unicode[STIX]{x1D6E5}\otimes \unicode[STIX]{x1D704})\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6E5}$
and the spaces
![]() $(C(G)\otimes 1)\unicode[STIX]{x1D6E5}(C(G))$
and
$(C(G)\otimes 1)\unicode[STIX]{x1D6E5}(C(G))$
and
![]() $(1\otimes C(G))\unicode[STIX]{x1D6E5}(C(G))$
are dense in
$(1\otimes C(G))\unicode[STIX]{x1D6E5}(C(G))$
are dense in
![]() $C(G)\otimes C(G)$
.
$C(G)\otimes C(G)$
.
A finite-dimensional unitary representation of
![]() $G$
is a pair
$G$
is a pair
![]() $(U,H_{U})$
consisting of a finite-dimensional Hilbert space
$(U,H_{U})$
consisting of a finite-dimensional Hilbert space
![]() $H_{U}$
and a unitary element
$H_{U}$
and a unitary element
![]() $U\in B(H_{U})\otimes C(G)$
such that
$U\in B(H_{U})\otimes C(G)$
such that
![]() $\unicode[STIX]{x1D6E5}(U)=U_{12}U_{13}$
. The tensor product of two representations
$\unicode[STIX]{x1D6E5}(U)=U_{12}U_{13}$
. The tensor product of two representations
![]() $U$
and
$U$
and
![]() $V$
is defined by
$V$
is defined by
With this tensor product, the finite-dimensional unitary representations of
![]() $G$
form a C
$G$
form a C
![]() $^{\ast }$
-tensor category
$^{\ast }$
-tensor category
![]() $\operatorname{Rep}G$
.
$\operatorname{Rep}G$
.
The space
![]() $\mathbb{C}[G]$
of matrix coefficients of all finite-dimensional unitary representations of
$\mathbb{C}[G]$
of matrix coefficients of all finite-dimensional unitary representations of
![]() $G$
is a Hopf
$G$
is a Hopf
![]() $\ast$
-algebra with comultiplication
$\ast$
-algebra with comultiplication
![]() $\unicode[STIX]{x1D6E5}$
and antipode
$\unicode[STIX]{x1D6E5}$
and antipode
![]() $S$
such that
$S$
such that
![]() $(\unicode[STIX]{x1D704}\otimes S)(U)=U^{\ast }$
for all
$(\unicode[STIX]{x1D704}\otimes S)(U)=U^{\ast }$
for all
![]() $U\in \operatorname{Rep}G$
. The dual space
$U\in \operatorname{Rep}G$
. The dual space
![]() ${\mathcal{U}}(G)=\mathbb{C}[G]^{\ast }$
is a
${\mathcal{U}}(G)=\mathbb{C}[G]^{\ast }$
is a
![]() $\ast$
-algebra with multiplication dual to
$\ast$
-algebra with multiplication dual to
![]() $\unicode[STIX]{x1D6E5}$
, so that
$\unicode[STIX]{x1D6E5}$
, so that
![]() $\unicode[STIX]{x1D714}\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D702})\unicode[STIX]{x1D6E5}$
, and involution
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D702})\unicode[STIX]{x1D6E5}$
, and involution
![]() $\unicode[STIX]{x1D714}^{\ast }=\bar{\unicode[STIX]{x1D714}}S$
, where
$\unicode[STIX]{x1D714}^{\ast }=\bar{\unicode[STIX]{x1D714}}S$
, where
![]() $\bar{\unicode[STIX]{x1D714}}(a)=\overline{\unicode[STIX]{x1D714}(a^{\ast })}$
. This is by definition the algebra of all (unbounded) functions on the dual discrete quantum group
$\bar{\unicode[STIX]{x1D714}}(a)=\overline{\unicode[STIX]{x1D714}(a^{\ast })}$
. This is by definition the algebra of all (unbounded) functions on the dual discrete quantum group
![]() $\unicode[STIX]{x1D6E4}={\hat{G}}$
.
$\unicode[STIX]{x1D6E4}={\hat{G}}$
.
More concretely,
![]() ${\mathcal{U}}(G)$
can be described as follows. For every
${\mathcal{U}}(G)$
can be described as follows. For every
![]() $U\in \operatorname{Rep}G$
we have a
$U\in \operatorname{Rep}G$
we have a
![]() $\ast$
-representation
$\ast$
-representation
![]() $\unicode[STIX]{x1D70B}_{U}:{\mathcal{U}}(G)\rightarrow B(H_{U})$
defined by
$\unicode[STIX]{x1D70B}_{U}:{\mathcal{U}}(G)\rightarrow B(H_{U})$
defined by
![]() $\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(U)$
. Consider the set
$\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(U)$
. Consider the set
![]() $I=\operatorname{Irr}(G)$
of isomorphism classes of irreducible unitary representations of
$I=\operatorname{Irr}(G)$
of isomorphism classes of irreducible unitary representations of
![]() $G$
. For every
$G$
. For every
![]() $s\in I$
choose a representative
$s\in I$
choose a representative
![]() $U_{s}$
. We write
$U_{s}$
. We write
![]() $\unicode[STIX]{x1D70B}_{s}$
,
$\unicode[STIX]{x1D70B}_{s}$
,
![]() $H_{s}$
, etc., instead of
$H_{s}$
, etc., instead of
![]() $\unicode[STIX]{x1D70B}_{U_{s}}$
,
$\unicode[STIX]{x1D70B}_{U_{s}}$
,
![]() $H_{U_{s}}$
. Then the collection of representations
$H_{U_{s}}$
. Then the collection of representations
![]() $(\unicode[STIX]{x1D70B}_{s})_{s\in I}$
defines a
$(\unicode[STIX]{x1D70B}_{s})_{s\in I}$
defines a
![]() $\ast$
-isomorphism
$\ast$
-isomorphism
![]() ${\mathcal{U}}(G)\cong \prod _{s\in I}B(H_{s})$
. The subalgebra
${\mathcal{U}}(G)\cong \prod _{s\in I}B(H_{s})$
. The subalgebra
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})\subset {\mathcal{U}}(G)$
corresponding to
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})\subset {\mathcal{U}}(G)$
corresponding to
![]() $\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
under this isomorphism is, by definition, the algebra of bounded functions on
$\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
under this isomorphism is, by definition, the algebra of bounded functions on
![]() $\unicode[STIX]{x1D6E4}$
. We will not distinguish between the algebras
$\unicode[STIX]{x1D6E4}$
. We will not distinguish between the algebras
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
and
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
and
![]() $\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
. We will also consider the subalgebras
$\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
. We will also consider the subalgebras
of functions vanishing at infinity and of finitely supported functions, respectively.
By duality the product on
![]() $\mathbb{C}[G]$
defines a comultiplication
$\mathbb{C}[G]$
defines a comultiplication
By restriction it gives a map
![]() $\hat{\unicode[STIX]{x1D6E5}}:\ell ^{\infty }(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})\,\bar{\otimes }\,\ell ^{\infty }(\unicode[STIX]{x1D6E4}).$
$\hat{\unicode[STIX]{x1D6E5}}:\ell ^{\infty }(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})\,\bar{\otimes }\,\ell ^{\infty }(\unicode[STIX]{x1D6E4}).$
The antipode
![]() $S$
on
$S$
on
![]() $\mathbb{C}[G]$
defines an antipode
$\mathbb{C}[G]$
defines an antipode
![]() ${\hat{S}}$
on
${\hat{S}}$
on
![]() ${\mathcal{U}}(G)$
by
${\mathcal{U}}(G)$
by
![]() ${\hat{S}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}S$
. There exists a unique element
${\hat{S}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}S$
. There exists a unique element
![]() $\unicode[STIX]{x1D70C}\in {\mathcal{U}}(G)$
, called the Woronowicz character, such that
$\unicode[STIX]{x1D70C}\in {\mathcal{U}}(G)$
, called the Woronowicz character, such that
![]() $\unicode[STIX]{x1D70C}$
is positive, invertible,
$\unicode[STIX]{x1D70C}$
is positive, invertible,
![]() ${\hat{S}}^{2}=\operatorname{Ad}\unicode[STIX]{x1D70C}$
and
${\hat{S}}^{2}=\operatorname{Ad}\unicode[STIX]{x1D70C}$
and
![]() $\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))=\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{-1}))$
for all
$\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))=\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{-1}))$
for all
![]() $U\in \operatorname{Rep}G$
. It also has the property
$U\in \operatorname{Rep}G$
. It also has the property
![]() $\hat{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D70C}$
justifying the name ‘character’. The number
$\hat{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D70C}$
justifying the name ‘character’. The number
![]() $\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))$
is called the quantum dimension of
$\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))$
is called the quantum dimension of
![]() $U$
and denoted by
$U$
and denoted by
![]() $\dim _{q}(U)$
. We will write
$\dim _{q}(U)$
. We will write
![]() $\dim _{q}(s)$
instead of
$\dim _{q}(s)$
instead of
![]() $\dim _{q}(U_{s})$
.
$\dim _{q}(U_{s})$
.
The element
![]() $\unicode[STIX]{x1D70C}$
allows one to define a canonical duality functor on
$\unicode[STIX]{x1D70C}$
allows one to define a canonical duality functor on
![]() $\operatorname{Rep}G$
. Namely, given a finite-dimensional unitary representation
$\operatorname{Rep}G$
. Namely, given a finite-dimensional unitary representation
![]() $U$
of
$U$
of
![]() $G$
, the conjugate representation is defined by
$G$
, the conjugate representation is defined by
where
![]() $\bar{H}_{U}$
is the complex conjugate Hilbert space to
$\bar{H}_{U}$
is the complex conjugate Hilbert space to
![]() $H_{U}$
and
$H_{U}$
and
![]() $j$
is the canonical
$j$
is the canonical
![]() $\ast$
-anti-isomorphism
$\ast$
-anti-isomorphism
![]() $B(H_{U})\rightarrow B(\bar{H}_{U})$
,
$B(H_{U})\rightarrow B(\bar{H}_{U})$
,
![]() $j(T)\bar{\unicode[STIX]{x1D709}}=\overline{T^{\ast }\unicode[STIX]{x1D709}}$
. Note that the element
$j(T)\bar{\unicode[STIX]{x1D709}}=\overline{T^{\ast }\unicode[STIX]{x1D709}}$
. Note that the element
![]() $U^{c}=(j\otimes \unicode[STIX]{x1D704})(U^{\ast })$
already satisfies
$U^{c}=(j\otimes \unicode[STIX]{x1D704})(U^{\ast })$
already satisfies
![]() $(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})(U^{c})=U_{12}^{c}U_{13}^{c}$
, and the additional conjugation by
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})(U^{c})=U_{12}^{c}U_{13}^{c}$
, and the additional conjugation by
![]() $j(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{1/2}))\otimes 1$
is needed only to make this element unitary.
$j(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{1/2}))\otimes 1$
is needed only to make this element unitary.
The object
![]() $\bar{U}$
is conjugate to
$\bar{U}$
is conjugate to
![]() $U$
in
$U$
in
![]() $\operatorname{Rep}G$
, meaning that there exist morphisms
$\operatorname{Rep}G$
, meaning that there exist morphisms
![]() $R_{U}:\unicode[STIX]{x1D7D9}\rightarrow \bar{U}\otimes U$
and
$R_{U}:\unicode[STIX]{x1D7D9}\rightarrow \bar{U}\otimes U$
and
![]() $\bar{R}_{U}:\unicode[STIX]{x1D7D9}\rightarrow U\otimes \bar{U}$
, where
$\bar{R}_{U}:\unicode[STIX]{x1D7D9}\rightarrow U\otimes \bar{U}$
, where
![]() $\unicode[STIX]{x1D7D9}$
is the trivial representation of
$\unicode[STIX]{x1D7D9}$
is the trivial representation of
![]() $G$
on the one-dimensional space
$G$
on the one-dimensional space
![]() $\mathbb{C}$
, solving the conjugate equations: the compositions
$\mathbb{C}$
, solving the conjugate equations: the compositions
are the identity morphisms. Using the Woronowicz character
![]() $\unicode[STIX]{x1D70C}$
, we can define such morphisms by
$\unicode[STIX]{x1D70C}$
, we can define such morphisms by
where
![]() $\{{\unicode[STIX]{x1D709}_{i}\}}_{i}$
is an orthonormal basis in
$\{{\unicode[STIX]{x1D709}_{i}\}}_{i}$
is an orthonormal basis in
![]() $H_{U}$
. The pair
$H_{U}$
. The pair
![]() $(R_{U},\bar{R}_{U})$
is standard, meaning that
$(R_{U},\bar{R}_{U})$
is standard, meaning that
![]() $\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert$
and the product
$\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert$
and the product
![]() $\Vert R_{U}\Vert \,\Vert \bar{R}_{U}\Vert$
is minimal among all possible solutions of the conjugate equations for
$\Vert R_{U}\Vert \,\Vert \bar{R}_{U}\Vert$
is minimal among all possible solutions of the conjugate equations for
![]() $U$
and
$U$
and
![]() $\bar{U}$
. Note that
$\bar{U}$
. Note that
![]() $\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert =\dim _{q}(U)^{1/2}$
.
$\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert =\dim _{q}(U)^{1/2}$
.
1.2 Quantum random walks
We now recall the main concepts of the boundary theory of quantum random walks; see [Reference IzumiIzu02, Reference Neshveyev and TusetNT04].
For every
![]() $s\in I=\operatorname{Irr}(G)$
, consider the state
$s\in I=\operatorname{Irr}(G)$
, consider the state
![]() $\unicode[STIX]{x1D719}_{s}$
on
$\unicode[STIX]{x1D719}_{s}$
on
![]() $B(H_{s})$
defined by
$B(H_{s})$
defined by
This is a unique state invariant under the left action of
![]() $G$
on
$G$
on
![]() $B(H_{s})$
given by
$B(H_{s})$
given by
Taken together, these actions define the left adjoint action of
![]() $G$
on
$G$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
Consider now a probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $I$
and define a normal state
$I$
and define a normal state
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
by
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
by
Consider the corresponding convolution Markov operator
![]() $P_{\unicode[STIX]{x1D707}}$
on
$P_{\unicode[STIX]{x1D707}}$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
:
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
:
This operator commutes with the left adjoint action of
![]() $G$
and the right action by translations of
$G$
and the right action by translations of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, which is defined by
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, which is defined by
![]() $\hat{\unicode[STIX]{x1D6E5}}$
. We therefore say that
$\hat{\unicode[STIX]{x1D6E5}}$
. We therefore say that
![]() $P_{\unicode[STIX]{x1D707}}$
defines a
$P_{\unicode[STIX]{x1D707}}$
defines a
![]() $G$
-
$G$
-
![]() $\unicode[STIX]{x1D6E4}$
-invariant quantum random walk on
$\unicode[STIX]{x1D6E4}$
-invariant quantum random walk on
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
By the
![]() $G$
-equivariance, the operator
$G$
-equivariance, the operator
![]() $P_{\unicode[STIX]{x1D707}}$
preserves the center
$P_{\unicode[STIX]{x1D707}}$
preserves the center
![]() $\ell ^{\infty }(I)$
of
$\ell ^{\infty }(I)$
of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, hence it defines a classical random walk on the set
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, hence it defines a classical random walk on the set
![]() $I$
with transition probabilities
$I$
with transition probabilities
![]() $p_{\unicode[STIX]{x1D707}}(s,t)$
such that
$p_{\unicode[STIX]{x1D707}}(s,t)$
such that
where
![]() $I_{s}$
denotes the unit of
$I_{s}$
denotes the unit of
![]() $B(H_{s})\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Explicitly, the transition probabilities are given by
$B(H_{s})\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Explicitly, the transition probabilities are given by
where
![]() $m_{rs}^{t}$
is the multiplicity of
$m_{rs}^{t}$
is the multiplicity of
![]() $U_{t}$
in
$U_{t}$
in
![]() $U_{r}\otimes U_{s}$
. We will only be interested in the case where this classical random walk is irreducible and transient. The irreducibility assumption means that, given
$U_{r}\otimes U_{s}$
. We will only be interested in the case where this classical random walk is irreducible and transient. The irreducibility assumption means that, given
![]() $s,t$
, there exist
$s,t$
, there exist
![]() $s_{0}=s,s_{1},\ldots ,s_{n}=t$
such that
$s_{0}=s,s_{1},\ldots ,s_{n}=t$
such that
![]() $p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})>0$
. Equivalently, every representation
$p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})>0$
. Equivalently, every representation
![]() $U_{t}$
is a subrepresentation of
$U_{t}$
is a subrepresentation of
![]() $U_{r_{1}}\otimes \cdots \otimes U_{r_{n}}$
for some
$U_{r_{1}}\otimes \cdots \otimes U_{r_{n}}$
for some
![]() $r_{1},\ldots ,r_{n}\in \operatorname{supp}\unicode[STIX]{x1D707}$
. In this case we also say that the measure
$r_{1},\ldots ,r_{n}\in \operatorname{supp}\unicode[STIX]{x1D707}$
. In this case we also say that the measure
![]() $\unicode[STIX]{x1D707}$
and the state
$\unicode[STIX]{x1D707}$
and the state
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
are generating. The assumption of transience means that the sum of all such products
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
are generating. The assumption of transience means that the sum of all such products
![]() $p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})$
(with
$p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})$
(with
![]() $s_{0}=s$
and
$s_{0}=s$
and
![]() $s_{n}=t$
) is finite for all
$s_{n}=t$
) is finite for all
![]() $s,t\in I$
. In this case we also say that
$s,t\in I$
. In this case we also say that
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
and
![]() $\unicode[STIX]{x1D707}$
are transient. Similarly to [Reference Derriennic and Guivarc’hDG73], it can be shown that, assuming irreducibility, the random walk is transient if the quantum dimension function is non-amenable; in particular, when
$\unicode[STIX]{x1D707}$
are transient. Similarly to [Reference Derriennic and Guivarc’hDG73], it can be shown that, assuming irreducibility, the random walk is transient if the quantum dimension function is non-amenable; in particular, when
![]() $\unicode[STIX]{x1D6E4}$
is either non-amenable or non-Kac (recall that the latter means that
$\unicode[STIX]{x1D6E4}$
is either non-amenable or non-Kac (recall that the latter means that
![]() $\unicode[STIX]{x1D70C}\neq 1$
). We will prove a related result more useful for our purposes in Lemma 4.1 below.
$\unicode[STIX]{x1D70C}\neq 1$
). We will prove a related result more useful for our purposes in Lemma 4.1 below.
Assuming irreducibility and transience, the Green kernel is defined as the completely positive map
and then the Martin kernel is defined as the map
where
![]() $e\in I$
is the point corresponding to the trivial representation
$e\in I$
is the point corresponding to the trivial representation
![]() $\unicode[STIX]{x1D7D9}$
. We remark that the element
$\unicode[STIX]{x1D7D9}$
. We remark that the element
![]() $G_{\unicode[STIX]{x1D707}}(I_{e})$
is a strictly positive scalar in every matrix block
$G_{\unicode[STIX]{x1D707}}(I_{e})$
is a strictly positive scalar in every matrix block
![]() $B(H_{s})$
, so
$B(H_{s})$
, so
![]() $G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}$
is a well-defined, but possibly unbounded, function on
$G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}$
is a well-defined, but possibly unbounded, function on
![]() $I$
. The elements
$I$
. The elements
![]() $K_{\unicode[STIX]{x1D707}}(a)=G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}G_{\unicode[STIX]{x1D707}}(a)$
are, however, bounded. Furthermore, if
$K_{\unicode[STIX]{x1D707}}(a)=G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}G_{\unicode[STIX]{x1D707}}(a)$
are, however, bounded. Furthermore, if
![]() $a\in c_{c}(\unicode[STIX]{x1D6E4})$
is positive and non-zero, then
$a\in c_{c}(\unicode[STIX]{x1D6E4})$
is positive and non-zero, then
![]() $K_{\unicode[STIX]{x1D707}}(a)$
is a positive invertible element of
$K_{\unicode[STIX]{x1D707}}(a)$
is a positive invertible element of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
We have an involution
![]() $s\mapsto \bar{s}$
on
$s\mapsto \bar{s}$
on
![]() $I$
defined by
$I$
defined by
![]() $\bar{U}_{s}\cong U_{\bar{s}}$
. For every probability measure
$\bar{U}_{s}\cong U_{\bar{s}}$
. For every probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $I$
, we define a new probability measure
$I$
, we define a new probability measure
![]() $\check{\unicode[STIX]{x1D707}}$
on
$\check{\unicode[STIX]{x1D707}}$
on
![]() $I$
by
$I$
by
![]() $\check{\unicode[STIX]{x1D707}}(s)=\unicode[STIX]{x1D707}(\bar{s})$
. The corresponding transition probabilities satisfy
$\check{\unicode[STIX]{x1D707}}(s)=\unicode[STIX]{x1D707}(\bar{s})$
. The corresponding transition probabilities satisfy
It follows that
![]() $\check{\unicode[STIX]{x1D707}}$
is generating and transient if and only if
$\check{\unicode[STIX]{x1D707}}$
is generating and transient if and only if
![]() $\unicode[STIX]{x1D707}$
has the same properties.
$\unicode[STIX]{x1D707}$
has the same properties.
Finally, given a generating transient probability measure
![]() $\unicode[STIX]{x1D707}$
, the Martin compactification of
$\unicode[STIX]{x1D707}$
, the Martin compactification of
![]() $\unicode[STIX]{x1D6E4}$
is defined as the C
$\unicode[STIX]{x1D6E4}$
is defined as the C
![]() $^{\ast }$
-subalgebra
$^{\ast }$
-subalgebra
![]() $C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
generated by
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
generated by
![]() $K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))$
and
$K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))$
and
![]() $c_{c}(\unicode[STIX]{x1D6E4})$
. This C
$c_{c}(\unicode[STIX]{x1D6E4})$
. This C
![]() $^{\ast }$
-algebra is invariant under the left adjoint action of
$^{\ast }$
-algebra is invariant under the left adjoint action of
![]() $G$
and the right action of
$G$
and the right action of
![]() $\unicode[STIX]{x1D6E4}$
by translations. The Martin boundary is defined by
$\unicode[STIX]{x1D6E4}$
by translations. The Martin boundary is defined by
![]() $C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})/c_{0}(\unicode[STIX]{x1D6E4})$
.
$C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})/c_{0}(\unicode[STIX]{x1D6E4})$
.
1.3 Module categories and categorical random walks
To every C
![]() $^{\ast }$
-algebra
$^{\ast }$
-algebra
![]() $A$
equipped with a left action of
$A$
equipped with a left action of
![]() $G$
one can associate the category of equivariant finitely generated Hilbert modules. We will need this only for unital C
$G$
one can associate the category of equivariant finitely generated Hilbert modules. We will need this only for unital C
![]() $^{\ast }$
-subalgebras
$^{\ast }$
-subalgebras
![]() $A\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, equipped with the action given by the restriction of the adjoint action, in which case this category has the following concrete description [Reference Neshveyev and YamashitaNY14, § 4].
$A\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, equipped with the action given by the restriction of the adjoint action, in which case this category has the following concrete description [Reference Neshveyev and YamashitaNY14, § 4].
For
![]() $U,V\in \operatorname{Rep}G$
, consider the subspace
$U,V\in \operatorname{Rep}G$
, consider the subspace
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V) & := & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}\operatorname{Hom}_{G}(H_{s}\otimes H_{U},H_{s}\otimes H_{V})\nonumber\\ \displaystyle & \subset & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s}\otimes H_{U},H_{s}\otimes H_{V})=\ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V) & := & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}\operatorname{Hom}_{G}(H_{s}\otimes H_{U},H_{s}\otimes H_{V})\nonumber\\ \displaystyle & \subset & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s}\otimes H_{U},H_{s}\otimes H_{V})=\ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V}),\nonumber\end{eqnarray}$$
and define
![]() ${\mathcal{D}}_{A}(U,V)$
as the intersection of this space with
${\mathcal{D}}_{A}(U,V)$
as the intersection of this space with
![]() $A\otimes B(H_{U},H_{V})$
. We can then define a new category
$A\otimes B(H_{U},H_{V})$
. We can then define a new category
![]() ${\mathcal{D}}_{A}$
with the same objects as in
${\mathcal{D}}_{A}$
with the same objects as in
![]() $\operatorname{Rep}G$
, but with the morphism spaces
$\operatorname{Rep}G$
, but with the morphism spaces
![]() ${\mathcal{D}}_{A}(U,V)$
. (To be more precise, we also need to complete
${\mathcal{D}}_{A}(U,V)$
. (To be more precise, we also need to complete
![]() ${\mathcal{D}}_{A}$
with respect to subobjects, but whether we do this or not is not going to play any role in this paper.) The category
${\mathcal{D}}_{A}$
with respect to subobjects, but whether we do this or not is not going to play any role in this paper.) The category
![]() $\operatorname{Rep}G$
can be considered as a (non-full) subcategory of
$\operatorname{Rep}G$
can be considered as a (non-full) subcategory of
![]() ${\mathcal{D}}_{A}$
, if we identify a morphism
${\mathcal{D}}_{A}$
, if we identify a morphism
![]() $T:H_{U}\rightarrow H_{V}$
in
$T:H_{U}\rightarrow H_{V}$
in
![]() $\operatorname{Rep}G$
with the collection of morphisms
$\operatorname{Rep}G$
with the collection of morphisms
![]() $\unicode[STIX]{x1D704}_{s}\otimes T:H_{s}\otimes H_{U}\rightarrow H_{s}\otimes H_{V}$
. Furthermore, the functors of tensoring on the right by objects of
$\unicode[STIX]{x1D704}_{s}\otimes T:H_{s}\otimes H_{U}\rightarrow H_{s}\otimes H_{V}$
. Furthermore, the functors of tensoring on the right by objects of
![]() $\operatorname{Rep}G$
define on
$\operatorname{Rep}G$
define on
![]() ${\mathcal{D}}_{A}$
the structure of a right
${\mathcal{D}}_{A}$
the structure of a right
![]() $(\operatorname{Rep}G)$
-module category.
$(\operatorname{Rep}G)$
-module category.
The morphism spaces
![]() ${\mathcal{D}}_{A}(U,V)$
are completely determined by the spaces of the form
${\mathcal{D}}_{A}(U,V)$
are completely determined by the spaces of the form
![]() ${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U)$
thanks to the Frobenius reciprocity isomorphisms
${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U)$
thanks to the Frobenius reciprocity isomorphisms
By decomposing
![]() $V\otimes \bar{U}$
into irreducibles we see that
$V\otimes \bar{U}$
into irreducibles we see that
![]() ${\mathcal{D}}_{A}$
is completely determined already by the spaces
${\mathcal{D}}_{A}$
is completely determined already by the spaces
![]() ${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
![]() $s\in I$
.
$s\in I$
.
The
![]() $G$
-C
$G$
-C
![]() $^{\ast }$
-algebra
$^{\ast }$
-algebra
![]() $A$
can be easily reconstructed from the morphism spaces
$A$
can be easily reconstructed from the morphism spaces
![]() ${\mathcal{D}}_{A}(U,V)$
: the elements of the form
${\mathcal{D}}_{A}(U,V)$
: the elements of the form
![]() $(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, where
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, where
![]() $T\in {\mathcal{D}}_{A}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
and
$T\in {\mathcal{D}}_{A}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
and
![]() $\unicode[STIX]{x1D714}\in B(H_{U},H_{V})^{\ast }$
, span a dense
$\unicode[STIX]{x1D714}\in B(H_{U},H_{V})^{\ast }$
, span a dense
![]() $\ast$
-subalgebra of
$\ast$
-subalgebra of
![]() $A$
. By the previous paragraph it is clear that it suffices to take
$A$
. By the previous paragraph it is clear that it suffices to take
![]() $T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
$T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
![]() $s\in I$
. For each
$s\in I$
. For each
![]() $s\in I$
, the linear span of elements of the form
$s\in I$
, the linear span of elements of the form
![]() $(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, with
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, with
![]() $T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
and
$T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
and
![]() $\unicode[STIX]{x1D714}\in B(H_{e},H_{e}\otimes H_{s})^{\ast }=H_{s}^{\ast }$
, is nothing other than the spectral subspace of
$\unicode[STIX]{x1D714}\in B(H_{e},H_{e}\otimes H_{s})^{\ast }=H_{s}^{\ast }$
, is nothing other than the spectral subspace of
![]() $A$
corresponding to
$A$
corresponding to
![]() $\bar{U}_{s}$
.
$\bar{U}_{s}$
.
Assume now that we are given a probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $I$
and consider the corresponding Markov operator
$I$
and consider the corresponding Markov operator
![]() $P_{\unicode[STIX]{x1D707}}$
on
$P_{\unicode[STIX]{x1D707}}$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Since
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Since
![]() $P_{\unicode[STIX]{x1D707}}$
commutes with left adjoint action of
$P_{\unicode[STIX]{x1D707}}$
commutes with left adjoint action of
![]() $G$
, the operator
$G$
, the operator
![]() $P_{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D704}$
is well defined on
$P_{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D704}$
is well defined on
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
. We will denote this operator by
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
. We will denote this operator by
![]() $P_{\unicode[STIX]{x1D707}}$
again. This operator can be described in purely categorical terms as follows.
$P_{\unicode[STIX]{x1D707}}$
again. This operator can be described in purely categorical terms as follows.
The space
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)$
can be identified with the space
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)$
can be identified with the space
![]() $\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
of bounded natural transformations between the functors
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
of bounded natural transformations between the functors
![]() $\unicode[STIX]{x1D704}\otimes U$
and
$\unicode[STIX]{x1D704}\otimes U$
and
![]() $\unicode[STIX]{x1D704}\otimes V$
on
$\unicode[STIX]{x1D704}\otimes V$
on
![]() $\operatorname{Rep}G$
, that is, uniformly bounded collections
$\operatorname{Rep}G$
, that is, uniformly bounded collections
![]() $(\unicode[STIX]{x1D702}_{W})_{W}$
of morphisms
$(\unicode[STIX]{x1D702}_{W})_{W}$
of morphisms
![]() $\unicode[STIX]{x1D702}_{W}:W\otimes U\rightarrow W\otimes V$
that are natural in
$\unicode[STIX]{x1D702}_{W}:W\otimes U\rightarrow W\otimes V$
that are natural in
![]() $W$
, since any such collection is completely determined by the morphisms
$W$
, since any such collection is completely determined by the morphisms
![]() $\unicode[STIX]{x1D702}_{s}=\unicode[STIX]{x1D702}_{U_{s}}$
. For every
$\unicode[STIX]{x1D702}_{s}=\unicode[STIX]{x1D702}_{U_{s}}$
. For every
![]() $s\in I$
, we have a contraction
$s\in I$
, we have a contraction
![]() $P_{s}$
on
$P_{s}$
on
![]() $\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
defined by
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
defined by
where
![]() $\text{tr}_{s}\,\otimes \,\unicode[STIX]{x1D704}$
denotes the normalized categorical partial trace
$\text{tr}_{s}\,\otimes \,\unicode[STIX]{x1D704}$
denotes the normalized categorical partial trace
![]() $\operatorname{Mor}(U_{s}\otimes X,U_{s}\otimes Y)\rightarrow \operatorname{Mor}(X,Y)$
defined by
$\operatorname{Mor}(U_{s}\otimes X,U_{s}\otimes Y)\rightarrow \operatorname{Mor}(X,Y)$
defined by
and where
![]() $(R_{s},\bar{R}_{s})$
is a standard solution of the conjugate equations for
$(R_{s},\bar{R}_{s})$
is a standard solution of the conjugate equations for
![]() $U_{s}$
and
$U_{s}$
and
![]() $U_{\bar{s}}$
. Then
$U_{\bar{s}}$
. Then
This leads to the following categorical description of the Martin compactification
![]() $C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
in [Reference JordansJor17]; see also [Reference Neshveyev and YamashitaNY17] for the initial motivation and [Reference De Rijdt and Vander VennetDRVV10] for a precursor of this picture.
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
in [Reference JordansJor17]; see also [Reference Neshveyev and YamashitaNY17] for the initial motivation and [Reference De Rijdt and Vander VennetDRVV10] for a precursor of this picture.
Consider the subspace
![]() $\operatorname{Nat}_{c}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)\subset \operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
consisting of all natural transformations
$\operatorname{Nat}_{c}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)\subset \operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
consisting of all natural transformations
![]() $\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}$
such that
![]() $\unicode[STIX]{x1D702}_{s}=0$
for all but finitely many
$\unicode[STIX]{x1D702}_{s}=0$
for all but finitely many
![]() $s$
. In other words, we consider the subspace
$s$
. In other words, we consider the subspace
We have well-defined maps
where
![]() $G_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D702})=\sum _{n=0}^{\infty }P_{\unicode[STIX]{x1D707}}^{n}(\unicode[STIX]{x1D702})$
. Then
$G_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D702})=\sum _{n=0}^{\infty }P_{\unicode[STIX]{x1D707}}^{n}(\unicode[STIX]{x1D702})$
. Then
![]() ${\mathcal{D}}_{C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})}$
is the smallest C
${\mathcal{D}}_{C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})}$
is the smallest C
![]() $^{\ast }$
-subcategory of
$^{\ast }$
-subcategory of
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}$
containing
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}$
containing
![]() $\operatorname{Rep}G$
,
$\operatorname{Rep}G$
,
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
and all morphisms of the form
${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
and all morphisms of the form
![]() $K_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702})$
, where
$K_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702})$
, where
![]() $\unicode[STIX]{x1D702}$
is a morphism in
$\unicode[STIX]{x1D702}$
is a morphism in
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
. Again using (4), we see that it suffices to take
${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
. Again using (4), we see that it suffices to take
![]() $\unicode[STIX]{x1D702}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(\unicode[STIX]{x1D7D9},U_{s})$
,
$\unicode[STIX]{x1D702}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(\unicode[STIX]{x1D7D9},U_{s})$
,
![]() $s\in I$
.
$s\in I$
.
Note that the previous paragraph does not really add any new information on
![]() $C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
. What we are basically saying is that in computing
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
. What we are basically saying is that in computing
![]() $K_{\check{\unicode[STIX]{x1D707}}}:c_{c}(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
it suffices to consider elements
$K_{\check{\unicode[STIX]{x1D707}}}:c_{c}(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
it suffices to consider elements
![]() $a$
lying in spectral subspaces of
$a$
lying in spectral subspaces of
![]() $c_{c}(\unicode[STIX]{x1D6E4})$
(with respect to the left adjoint action of
$c_{c}(\unicode[STIX]{x1D6E4})$
(with respect to the left adjoint action of
![]() $G$
) corresponding to
$G$
) corresponding to
![]() $U_{s}$
, and then
$U_{s}$
, and then
![]() $K_{\check{\unicode[STIX]{x1D707}}}(a)$
is again an element of the spectral subspace of
$K_{\check{\unicode[STIX]{x1D707}}}(a)$
is again an element of the spectral subspace of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
corresponding to
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
corresponding to
![]() $U_{s}$
. But this is clear, since
$U_{s}$
. But this is clear, since
![]() $c_{c}(\unicode[STIX]{x1D6E4})$
is the direct sum of its spectral subspaces and the operator
$c_{c}(\unicode[STIX]{x1D6E4})$
is the direct sum of its spectral subspaces and the operator
![]() $P_{\unicode[STIX]{x1D707}}$
is
$P_{\unicode[STIX]{x1D707}}$
is
![]() $G$
-equivariant. Nevertheless, working with the spaces
$G$
-equivariant. Nevertheless, working with the spaces
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
is more convenient than with the spectral subspaces, and the interpretation of elements of
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
is more convenient than with the spectral subspaces, and the interpretation of elements of
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
as natural transformations between certain functors makes some computations more transparent.
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
as natural transformations between certain functors makes some computations more transparent.
1.4 Free unitary quantum groups
In this section we recall some properties of free unitary quantum groups introduced in [Reference Van Daele and WangVDW96] and studied in detail in [Reference BanicaBan97].
Fix a natural number
![]() $n\geqslant 2$
and a matrix
$n\geqslant 2$
and a matrix
![]() $F\in \operatorname{GL}_{n}(\mathbb{C})$
such that
$F\in \operatorname{GL}_{n}(\mathbb{C})$
such that
![]() $\operatorname{Tr}(F^{\ast }F)=\operatorname{Tr}((F^{\ast }F)^{-1})$
. The compact free unitary quantum group
$\operatorname{Tr}(F^{\ast }F)=\operatorname{Tr}((F^{\ast }F)^{-1})$
. The compact free unitary quantum group
![]() $A_{u}(F)$
is defined as the universal unital C
$A_{u}(F)$
is defined as the universal unital C
![]() $^{\ast }$
-algebra with generators
$^{\ast }$
-algebra with generators
![]() $u_{ij}$
,
$u_{ij}$
,
![]() $1\leqslant i,j\leqslant n$
, such that the matrices
$1\leqslant i,j\leqslant n$
, such that the matrices
![]() $U=(u_{ij})_{i,j}$
and
$U=(u_{ij})_{i,j}$
and
![]() $FU^{c}F^{-1}$
are unitary, where
$FU^{c}F^{-1}$
are unitary, where
![]() $U^{c}=(u_{ij}^{\ast })_{i,j}$
, equipped with the comultiplication
$U^{c}=(u_{ij}^{\ast })_{i,j}$
, equipped with the comultiplication
Therefore
![]() $U$
defines a unitary representation of the quantum group
$U$
defines a unitary representation of the quantum group
![]() $A_{u}(F)$
on the
$A_{u}(F)$
on the
![]() $n$
-dimensional Hilbert space, called the fundamental representation.
$n$
-dimensional Hilbert space, called the fundamental representation.
The set
![]() $I$
of isomorphism classes of irreducible representations of
$I$
of isomorphism classes of irreducible representations of
![]() $A_{u}(F)$
is the free monoid on letters
$A_{u}(F)$
is the free monoid on letters
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
, with
$\unicode[STIX]{x1D6FD}$
, with
![]() $\unicode[STIX]{x1D6FC}$
corresponding to
$\unicode[STIX]{x1D6FC}$
corresponding to
![]() $U$
. The involution
$U$
. The involution
![]() $s\mapsto \bar{s}$
is the anti-automorphism of the monoid defined by
$s\mapsto \bar{s}$
is the anti-automorphism of the monoid defined by
![]() $\bar{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FD}$
and
$\bar{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FD}$
and
![]() $\bar{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}$
.
$\bar{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}$
.
From now on we will use the conventions of [Reference Vaes and Vander VennetVVV10] in that we write
![]() $x$
instead of
$x$
instead of
![]() $U_{x}$
for
$U_{x}$
for
![]() $x\in I$
whenever convenient. The fusion rules for the representations of
$x\in I$
whenever convenient. The fusion rules for the representations of
![]() $A_{u}(F)$
are given by
$A_{u}(F)$
are given by
Therefore if the last letter of
![]() $x$
is the same as the first letter of
$x$
is the same as the first letter of
![]() $y$
, then
$y$
, then
![]() $U_{x}\otimes U_{y}$
is irreducible and isomorphic to
$U_{x}\otimes U_{y}$
is irreducible and isomorphic to
![]() $U_{xy}$
. In this case we write
$U_{xy}$
. In this case we write
![]() $xy=x\otimes y$
.
$xy=x\otimes y$
.
The Woronowicz character
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $A_{u}(F)$
is determined by the property
$A_{u}(F)$
is determined by the property
Clearly,
![]() $\dim _{q}(\unicode[STIX]{x1D6FC})=\operatorname{Tr}(F^{\ast }F)\geqslant n$
, and the equality holds if and only if
$\dim _{q}(\unicode[STIX]{x1D6FC})=\operatorname{Tr}(F^{\ast }F)\geqslant n$
, and the equality holds if and only if
![]() $F$
is unitary. Let
$F$
is unitary. Let
![]() $q\in (0,1]$
be such that
$q\in (0,1]$
be such that
Then
![]() $q=1$
if and only if
$q=1$
if and only if
![]() $F$
is a unitary
$F$
is a unitary
![]() $2\times 2$
matrix.
$2\times 2$
matrix.
An element
![]() $x\in I$
is said to be indecomposable if there are only trivial decompositions
$x\in I$
is said to be indecomposable if there are only trivial decompositions
![]() $x=y\otimes z$
, that is, we must have
$x=y\otimes z$
, that is, we must have
![]() $y=e$
or
$y=e$
or
![]() $z=e$
. Equivalently,
$z=e$
. Equivalently,
![]() $x$
is an alternating product of
$x$
is an alternating product of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Every word
$\unicode[STIX]{x1D6FD}$
. Every word
![]() $x\in I$
can be written as
$x\in I$
can be written as
![]() $x_{1}\otimes \cdots \otimes x_{n}$
, where
$x_{1}\otimes \cdots \otimes x_{n}$
, where
![]() $x_{1},\ldots ,x_{n}$
are indecomposable. Then
$x_{1},\ldots ,x_{n}$
are indecomposable. Then
where
![]() $|x_{i}|$
denotes the length of
$|x_{i}|$
denotes the length of
![]() $x_{i}$
and
$x_{i}$
and
![]() $\displaystyle [n]_{q}=(q^{n}-q^{-n})/(q-q^{-1})$
.
$\displaystyle [n]_{q}=(q^{n}-q^{-n})/(q-q^{-1})$
.
2 Topological boundary of the dual of
 $A_{u}(F)$
$A_{u}(F)$
Consider a free unitary quantum group
![]() $G=A_{u}(F)$
, with
$G=A_{u}(F)$
, with
![]() $F$
not a unitary
$F$
not a unitary
![]() $2\times 2$
matrix. Recall that this assumption means that the number
$2\times 2$
matrix. Recall that this assumption means that the number
![]() $q\in (0,1]$
defined by (5) is strictly less than
$q\in (0,1]$
defined by (5) is strictly less than
![]() $1$
. Denote by
$1$
. Denote by
![]() $\unicode[STIX]{x1D6E4}$
the dual discrete quantum group.
$\unicode[STIX]{x1D6E4}$
the dual discrete quantum group.
As we discussed in § 1.4, the set
![]() $I$
of isomorphism classes of irreducible representations of
$I$
of isomorphism classes of irreducible representations of
![]() $G$
is a free monoid on letters
$G$
is a free monoid on letters
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. The empty word is denoted by
$\unicode[STIX]{x1D6FD}$
. The empty word is denoted by
![]() $e$
. Consider the tree with vertex set
$e$
. Consider the tree with vertex set
![]() $I$
such that different elements
$I$
such that different elements
![]() $x$
and
$x$
and
![]() $y$
of
$y$
of
![]() $I$
are connected by an edge if and only if one of them is obtained from the other by adding (or removing) one letter on the left. Denote by
$I$
are connected by an edge if and only if one of them is obtained from the other by adding (or removing) one letter on the left. Denote by
![]() $\bar{I}$
the corresponding end compactification of
$\bar{I}$
the corresponding end compactification of
![]() $I$
. The elements of
$I$
. The elements of
![]() $\bar{I}$
are words in
$\bar{I}$
are words in
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
that are either finite or infinite on the left, and the boundary
$\unicode[STIX]{x1D6FD}$
that are either finite or infinite on the left, and the boundary
![]() $\unicode[STIX]{x2202}I=\bar{I}\setminus I$
is the set of infinite words. The algebra
$\unicode[STIX]{x2202}I=\bar{I}\setminus I$
is the set of infinite words. The algebra
![]() $C(\bar{I})$
of continuous functions on
$C(\bar{I})$
of continuous functions on
![]() $\bar{I}$
can be identified with the algebra of functions
$\bar{I}$
can be identified with the algebra of functions
![]() $f\in \ell ^{\infty }(I)$
such that
$f\in \ell ^{\infty }(I)$
such that
In [Reference Vaes and Vander VennetVVV10], Vaes and Vander Vennet extended this construction to
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
as follows. (More precisely, they consider words infinite on the right, while in order to be consistent with our conventions, we consider words infinite on the left.)
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
as follows. (More precisely, they consider words infinite on the right, while in order to be consistent with our conventions, we consider words infinite on the left.)
For all
![]() $x,y\in I$
, fix an isometry
$x,y\in I$
, fix an isometry
![]() $V(xy,x\otimes y)\in \operatorname{Mor}(xy,x\otimes y)$
. Define ucp maps
$V(xy,x\otimes y)\in \operatorname{Mor}(xy,x\otimes y)$
. Define ucp maps
They do not depend on any choices. Define
By [Reference Vaes and Vander VennetVVV10, Theorem 3.2], this is a unital C
![]() $^{\ast }$
-subalgebra of
$^{\ast }$
-subalgebra of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
containing
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
containing
![]() $c_{0}(\unicode[STIX]{x1D6E4})$
. It can therefore be considered as the algebra of continuous functions on a compactification of
$c_{0}(\unicode[STIX]{x1D6E4})$
. It can therefore be considered as the algebra of continuous functions on a compactification of
![]() $\unicode[STIX]{x1D6E4}$
. The (non-commutative) algebra of continuous functions on the corresponding boundary is defined by
$\unicode[STIX]{x1D6E4}$
. The (non-commutative) algebra of continuous functions on the corresponding boundary is defined by
![]() ${\mathcal{B}}_{\infty }={\mathcal{B}}/c_{0}(\unicode[STIX]{x1D6E4})$
. The left adjoint action of
${\mathcal{B}}_{\infty }={\mathcal{B}}/c_{0}(\unicode[STIX]{x1D6E4})$
. The left adjoint action of
![]() $G$
and the right action by translations of
$G$
and the right action by translations of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
define actions of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
define actions of
![]() $G$
and
$G$
and
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() ${\mathcal{B}}$
and
${\mathcal{B}}$
and
![]() ${\mathcal{B}}_{\infty }$
.
${\mathcal{B}}_{\infty }$
.
If we view
![]() ${\mathcal{B}}$
only as a
${\mathcal{B}}$
only as a
![]() $G$
-C
$G$
-C
![]() $^{\ast }$
-algebra, then from our discussion in § 1.3 we immediately get the following result.
$^{\ast }$
-algebra, then from our discussion in § 1.3 we immediately get the following result.
Proposition 2.1. Consider the module category
![]() ${\mathcal{D}}_{{\mathcal{B}}}$
associated with the left action of
${\mathcal{D}}_{{\mathcal{B}}}$
associated with the left action of
![]() $G$
on
$G$
on
![]() ${\mathcal{B}}$
. Then, for all
${\mathcal{B}}$
. Then, for all
![]() $U,V\in \operatorname{Rep}G$
, the morphism space
$U,V\in \operatorname{Rep}G$
, the morphism space
![]() ${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
consists of all elements
${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
consists of all elements
such that
![]() $\Vert T_{yx}-(V(yx,y\otimes x)^{\ast }\otimes \unicode[STIX]{x1D704}_{V})(\unicode[STIX]{x1D704}_{y}\otimes T_{x})(V(yx,y\otimes x)\otimes \unicode[STIX]{x1D704}_{U})\Vert \rightarrow 0$
as
$\Vert T_{yx}-(V(yx,y\otimes x)^{\ast }\otimes \unicode[STIX]{x1D704}_{V})(\unicode[STIX]{x1D704}_{y}\otimes T_{x})(V(yx,y\otimes x)\otimes \unicode[STIX]{x1D704}_{U})\Vert \rightarrow 0$
as
![]() $x\rightarrow \infty$
, uniformly in
$x\rightarrow \infty$
, uniformly in
![]() $y\in I$
.
$y\in I$
.
In order to get a better understanding of the morphism spaces
![]() ${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
we will now make a particular choice of representations
${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
we will now make a particular choice of representations
![]() $U_{x}$
and isometries
$U_{x}$
and isometries
![]() $V(z,x\otimes y)\in \operatorname{Mor}(z,x\otimes y)$
for all
$V(z,x\otimes y)\in \operatorname{Mor}(z,x\otimes y)$
for all
![]() $z\prec x\otimes y$
; cf. [Reference Vaes and VergniouxVV07, Appendix].
$z\prec x\otimes y$
; cf. [Reference Vaes and VergniouxVV07, Appendix].
Fix representatives
![]() $U_{\unicode[STIX]{x1D6FC}}$
and
$U_{\unicode[STIX]{x1D6FC}}$
and
![]() $U_{\unicode[STIX]{x1D6FD}}$
of
$U_{\unicode[STIX]{x1D6FD}}$
of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. All other representatives
$\unicode[STIX]{x1D6FD}$
. All other representatives
![]() $U_{x}$
we construct as follows. If
$U_{x}$
we construct as follows. If
![]() $x=x_{1}\cdots x_{n}\in I$
, with
$x=x_{1}\cdots x_{n}\in I$
, with
![]() $x_{i}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
$x_{i}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
![]() $i$
, then, since
$i$
, then, since
![]() $\operatorname{Mor}(x,x_{1}\otimes \cdots \otimes x_{n})$
is one-dimensional,
$\operatorname{Mor}(x,x_{1}\otimes \cdots \otimes x_{n})$
is one-dimensional,
![]() $H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
contains a unique invariant subspace on which
$H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
contains a unique invariant subspace on which
![]() $U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
is irreducible of class
$U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
is irreducible of class
![]() $x$
. We take this subspace as
$x$
. We take this subspace as
![]() $H_{x}$
and define
$H_{x}$
and define
![]() $U_{x}$
as the restriction of
$U_{x}$
as the restriction of
![]() $U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
to
$U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
to
![]() $H_{x}$
. Denote by
$H_{x}$
. Denote by
![]() $p_{x}$
the projection in
$p_{x}$
the projection in
![]() $B(H_{x_{1}}\otimes \cdots \otimes H_{x_{n}})$
with image
$B(H_{x_{1}}\otimes \cdots \otimes H_{x_{n}})$
with image
![]() $H_{x}$
.
$H_{x}$
.
Note that the fusion rules and our choice of representatives imply that
![]() $H_{xy}$
is a subspace of
$H_{xy}$
is a subspace of
![]() $H_{x}\otimes H_{y}$
. We take the embedding map
$H_{x}\otimes H_{y}$
. We take the embedding map
![]() $H_{xy}\rightarrow H_{x}\otimes H_{y}$
as
$H_{xy}\rightarrow H_{x}\otimes H_{y}$
as
![]() $V(xy,x\otimes y)$
. Then
$V(xy,x\otimes y)$
. Then
![]() $V(xy,x\otimes y)^{\ast }$
coincides with the projection
$V(xy,x\otimes y)^{\ast }$
coincides with the projection
![]() $p_{xy}^{x\otimes y}:=p_{xy}|_{H_{x}\otimes H_{y}}$
.
$p_{xy}^{x\otimes y}:=p_{xy}|_{H_{x}\otimes H_{y}}$
.
Next, viewing
![]() $U_{\unicode[STIX]{x1D6FD}}$
as the dual of
$U_{\unicode[STIX]{x1D6FD}}$
as the dual of
![]() $U_{\unicode[STIX]{x1D6FC}}$
, fix a standard solution
$U_{\unicode[STIX]{x1D6FC}}$
, fix a standard solution
![]() $(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations for
$(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations for
![]() $U_{\unicode[STIX]{x1D6FC}}$
. Put
$U_{\unicode[STIX]{x1D6FC}}$
. Put
![]() $R_{\unicode[STIX]{x1D6FD}}=\bar{R}_{\unicode[STIX]{x1D6FC}}$
and
$R_{\unicode[STIX]{x1D6FD}}=\bar{R}_{\unicode[STIX]{x1D6FC}}$
and
![]() $\bar{R}_{\unicode[STIX]{x1D6FD}}=R_{\unicode[STIX]{x1D6FC}}$
. Assume now that
$\bar{R}_{\unicode[STIX]{x1D6FD}}=R_{\unicode[STIX]{x1D6FC}}$
. Assume now that
![]() $x=x_{1}\cdots x_{n}$
and
$x=x_{1}\cdots x_{n}$
and
![]() $y=y_{1}\cdots y_{m}$
, with
$y=y_{1}\cdots y_{m}$
, with
![]() $x_{i},y_{j}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
$x_{i},y_{j}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
![]() $i$
and
$i$
and
![]() $j$
, and assume that
$j$
, and assume that
![]() $z$
is a subrepresentation of
$z$
is a subrepresentation of
![]() $x\otimes y$
, so
$x\otimes y$
, so
![]() $z=x_{1}\cdots x_{n-k}\,y_{k+1}\cdots y_{m}$
for some
$z=x_{1}\cdots x_{n-k}\,y_{k+1}\cdots y_{m}$
for some
![]() $k$
and
$k$
and
![]() $x_{n-i}=\bar{y}_{i+1}$
for
$x_{n-i}=\bar{y}_{i+1}$
for
![]() $i=0,\ldots ,k-1$
. We then define an operator
$i=0,\ldots ,k-1$
. We then define an operator
![]() $\tilde{V}(z,x\otimes y):H_{z}\rightarrow H_{x}\otimes H_{y}$
by
$\tilde{V}(z,x\otimes y):H_{z}\rightarrow H_{x}\otimes H_{y}$
by
This can also be described as follows. Our fixed standard solutions
![]() $(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
and
$(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
and
![]() $(R_{\unicode[STIX]{x1D6FD}},\bar{R}_{\unicode[STIX]{x1D6FD}})=(\bar{R}_{\unicode[STIX]{x1D6FC}},R_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations allow us to construct standard solutions of the conjugate equations for tensor products of
$(R_{\unicode[STIX]{x1D6FD}},\bar{R}_{\unicode[STIX]{x1D6FD}})=(\bar{R}_{\unicode[STIX]{x1D6FC}},R_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations allow us to construct standard solutions of the conjugate equations for tensor products of
![]() $U_{\unicode[STIX]{x1D6FC}}$
and
$U_{\unicode[STIX]{x1D6FC}}$
and
![]() $U_{\unicode[STIX]{x1D6FD}}$
. By restriction we then get standard solutions
$U_{\unicode[STIX]{x1D6FD}}$
. By restriction we then get standard solutions
![]() $(R_{x},\bar{R}_{x})$
of the conjugate equations for all
$(R_{x},\bar{R}_{x})$
of the conjugate equations for all
![]() $x\in I$
. By construction, we have
$x\in I$
. By construction, we have
![]() $(R_{\bar{x}},\bar{R}_{\bar{x}})=(\bar{R}_{x},R_{x})$
and
$(R_{\bar{x}},\bar{R}_{\bar{x}})=(\bar{R}_{x},R_{x})$
and
Then the morphism
![]() $\tilde{V}(z,x\otimes y)$
for
$\tilde{V}(z,x\otimes y)$
for
![]() $x=sv$
,
$x=sv$
,
![]() $y=\bar{v}t$
and
$y=\bar{v}t$
and
![]() $z=st$
is given by
$z=st$
is given by
Since
![]() $\tilde{V}(st,sv\otimes \bar{v}t)$
is an element of
$\tilde{V}(st,sv\otimes \bar{v}t)$
is an element of
![]() $\operatorname{Mor}(st,sv\otimes \bar{v}t)$
, it must be isometric up to a scalar factor.
$\operatorname{Mor}(st,sv\otimes \bar{v}t)$
, it must be isometric up to a scalar factor.
Lemma 2.2. There is a constant
![]() $c>0$
depending only on
$c>0$
depending only on
![]() $q$
such that
$q$
such that
for all
![]() $v,s,t\in I$
.
$v,s,t\in I$
.
Proof. The first inequality is an immediate consequence of (9), since
![]() $\Vert \bar{R}_{v}\Vert =\dim _{q}(v)^{1/2}$
.
$\Vert \bar{R}_{v}\Vert =\dim _{q}(v)^{1/2}$
.
The second inequality can be deduced from an analogous result for
![]() $\text{SU}_{-q}(2)$
using arguments similar to those in [Reference Vaes and Vander VennetVVV10, Reference Vander VennetVan08]. Namely, we proceed as follows.
$\text{SU}_{-q}(2)$
using arguments similar to those in [Reference Vaes and Vander VennetVVV10, Reference Vander VennetVan08]. Namely, we proceed as follows.
We first reduce the proof to a particular case. If
![]() $v=v_{1}\otimes v_{2}$
, then, using that
$v=v_{1}\otimes v_{2}$
, then, using that
![]() $\bar{R}_{v}=(\unicode[STIX]{x1D704}_{v_{1}}\otimes \bar{R}_{v_{2}}\otimes \unicode[STIX]{x1D704}_{\bar{v}_{1}})\bar{R}_{v_{1}}$
by (8) and that
$\bar{R}_{v}=(\unicode[STIX]{x1D704}_{v_{1}}\otimes \bar{R}_{v_{2}}\otimes \unicode[STIX]{x1D704}_{\bar{v}_{1}})\bar{R}_{v_{1}}$
by (8) and that
![]() $p_{sv}^{s\otimes v}=p_{sv_{1}}^{s\otimes v_{1}}\otimes \unicode[STIX]{x1D704}_{v_{2}}$
,
$p_{sv}^{s\otimes v}=p_{sv_{1}}^{s\otimes v_{1}}\otimes \unicode[STIX]{x1D704}_{v_{2}}$
,
![]() $p_{\bar{v}t}^{\bar{v}\otimes t}=\unicode[STIX]{x1D704}_{\bar{v}_{2}}\otimes p_{\bar{v}_{1}t}^{\bar{v}_{1}\otimes t}$
, we see that
$p_{\bar{v}t}^{\bar{v}\otimes t}=\unicode[STIX]{x1D704}_{\bar{v}_{2}}\otimes p_{\bar{v}_{1}t}^{\bar{v}_{1}\otimes t}$
, we see that
We may therefore assume that
![]() $v$
is indecomposable. We also assume that
$v$
is indecomposable. We also assume that
![]() $v\neq e$
, since
$v\neq e$
, since
![]() $\tilde{V}(st,s\otimes t)=V(st,s\otimes t)$
is isometric by definition.
$\tilde{V}(st,s\otimes t)=V(st,s\otimes t)$
is isometric by definition.
Next, write
![]() $sv$
as
$sv$
as
![]() $s_{1}\otimes s_{2}v$
, with
$s_{1}\otimes s_{2}v$
, with
![]() $s_{2}v$
indecomposable. Assume first that
$s_{2}v$
indecomposable. Assume first that
![]() $s_{2}=e$
. Then
$s_{2}=e$
. Then
hence
where
![]() $\operatorname{Tr}_{\bar{v}}$
denotes the categorical trace. The morphism
$\operatorname{Tr}_{\bar{v}}$
denotes the categorical trace. The morphism
![]() $(\operatorname{Tr}_{\bar{v}}\otimes \unicode[STIX]{x1D704})(p_{\bar{v}t}^{\bar{v}\otimes t})$
is a scalar multiple of
$(\operatorname{Tr}_{\bar{v}}\otimes \unicode[STIX]{x1D704})(p_{\bar{v}t}^{\bar{v}\otimes t})$
is a scalar multiple of
![]() $\unicode[STIX]{x1D704}_{t}$
, and, applying
$\unicode[STIX]{x1D704}_{t}$
, and, applying
![]() $\operatorname{Tr}_{t}$
, we see that this scalar is
$\operatorname{Tr}_{t}$
, we see that this scalar is
![]() $\dim _{q}(\bar{v}t)/\text{dim}_{q}(t)$
. It follows that
$\dim _{q}(\bar{v}t)/\text{dim}_{q}(t)$
. It follows that
From (6) it is easy to see that this quantity is not smaller than
![]() $c\dim _{q}(v)^{1/2}$
for a constant
$c\dim _{q}(v)^{1/2}$
for a constant
![]() $c$
depending only on
$c$
depending only on
![]() $q$
; cf. [Reference Vaes and VergniouxVV07, (5)].
$q$
; cf. [Reference Vaes and VergniouxVV07, (5)].
Assume now that
![]() $s_{2}\neq e$
. Then
$s_{2}\neq e$
. Then
![]() $st=s_{1}\otimes s_{2}t$
and
$st=s_{1}\otimes s_{2}t$
and
![]() $\tilde{V}(st,sv\otimes \bar{v}t)=\unicode[STIX]{x1D704}_{s_{1}}\otimes \tilde{V}(s_{2}t,s_{2}v\otimes \bar{v}t)$
. We see that in this case the computation reduces to the case where
$\tilde{V}(st,sv\otimes \bar{v}t)=\unicode[STIX]{x1D704}_{s_{1}}\otimes \tilde{V}(s_{2}t,s_{2}v\otimes \bar{v}t)$
. We see that in this case the computation reduces to the case where
![]() $s_{1}=e$
, that is, we may assume that
$s_{1}=e$
, that is, we may assume that
![]() $sv$
is indecomposable. In a similar way we reduce the computation to the case where
$sv$
is indecomposable. In a similar way we reduce the computation to the case where
![]() $\bar{v}t$
is indecomposable as well, so we assume that all three elements
$\bar{v}t$
is indecomposable as well, so we assume that all three elements
![]() $sv$
,
$sv$
,
![]() $v\bar{v}$
and
$v\bar{v}$
and
![]() $\bar{v}t$
are indecomposable (and
$\bar{v}t$
are indecomposable (and
![]() $v\neq e$
). In other words,
$v\neq e$
). In other words,
![]() $sv\bar{v}t$
equals
$sv\bar{v}t$
equals
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\cdots \,$
or
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\cdots \,$
or
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cdots \,$
. But in this case the computation of the norm of
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cdots \,$
. But in this case the computation of the norm of
![]() $\tilde{V}(st,sv\otimes \bar{v}t)$
is equivalent to a similar computation for
$\tilde{V}(st,sv\otimes \bar{v}t)$
is equivalent to a similar computation for
![]() $\text{SU}_{-q}(2)$
(see [Reference Vander VennetVan08, Lemma 8.7.2]), which gives
$\text{SU}_{-q}(2)$
(see [Reference Vander VennetVan08, Lemma 8.7.2]), which gives
(see [Reference Vaes and VergniouxVV07, (7.3)]), where
![]() $[\begin{smallmatrix}n\\ k\end{smallmatrix}]_{q}$
denote the
$[\begin{smallmatrix}n\\ k\end{smallmatrix}]_{q}$
denote the
![]() $q$
-binomial coefficients. Using that
$q$
-binomial coefficients. Using that
we easily deduce that
![]() $\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert \geqslant c[|v|+1]_{q}^{1/2}=c\dim _{q}(v)^{1/2}$
for a constant
$\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert \geqslant c[|v|+1]_{q}^{1/2}=c\dim _{q}(v)^{1/2}$
for a constant
![]() $c>0$
depending only on
$c>0$
depending only on
![]() $q$
; cf. [Reference Vaes and VergniouxVV07, Lemma 8.5].◻
$q$
; cf. [Reference Vaes and VergniouxVV07, Lemma 8.5].◻
In particular, the morphisms
![]() $\tilde{V}(z,x\otimes y)$
are non-zero, so we can define isometries
$\tilde{V}(z,x\otimes y)$
are non-zero, so we can define isometries
The following result will play a crucial role in our computations. Note that it does not depend on the particular choice of isometries
![]() $V(z,x\otimes y)$
.
$V(z,x\otimes y)$
.
Proposition 2.3 ([Reference Vaes and Vander VennetVVV10, Lemma A.1], [Reference Vander VennetVan08, Lemma 8.7.3]).
There is a constant
![]() $C$
depending only on
$C$
depending only on
![]() $q$
such that
$q$
such that
for all
![]() $u,x,y,z\in I$
such that
$u,x,y,z\in I$
such that
![]() $z\prec x\otimes y$
.
$z\prec x\otimes y$
.
For our particular choice of
![]() $V(z,x\otimes y)$
this implies the following estimates. (In fact, it is not difficult to see that these estimates are equivalent to the ones above, but with different constants.)
$V(z,x\otimes y)$
this implies the following estimates. (In fact, it is not difficult to see that these estimates are equivalent to the ones above, but with different constants.)
Corollary 2.4. There is a constant
![]() $C$
depending only on
$C$
depending only on
![]() $q$
such that
$q$
such that
for all
![]() $u,x,y,z\in I$
such that
$u,x,y,z\in I$
such that
![]() $z\prec x\otimes y$
.
$z\prec x\otimes y$
.
Proof. By construction we have
hence
so in particular
Therefore in order to prove the first inequality in the formulation it suffices to show that the last norm is close to
![]() $1$
up to
$1$
up to
![]() $C^{\prime }q^{(|z|+|x|-|y|)/2}$
for some constant
$C^{\prime }q^{(|z|+|x|-|y|)/2}$
for some constant
![]() $C^{\prime }$
, and that
$C^{\prime }$
, and that
is close to
![]() $(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))$
up to
$(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))$
up to
![]() $C^{\prime }q^{(|z|+|x|-|y|)/2}$
. But this is indeed the case by the previous proposition, since
$C^{\prime }q^{(|z|+|x|-|y|)/2}$
. But this is indeed the case by the previous proposition, since
![]() $(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}$
is an isometry on
$(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}$
is an isometry on
![]() $H_{uz}$
. The second inequality is proved in a similar way.◻
$H_{uz}$
. The second inequality is proved in a similar way.◻
We can now get a description of the morphism spaces
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,y)$
. If
${\mathcal{D}}_{{\mathcal{B}}}(e,y)$
. If
![]() $y$
is not of the form
$y$
is not of the form
![]() $\bar{z}z$
,
$\bar{z}z$
,
![]() $z\in I$
, then
$z\in I$
, then
![]() $\operatorname{Mor}(x,x\otimes y)=0$
for all
$\operatorname{Mor}(x,x\otimes y)=0$
for all
![]() $x$
, so
$x$
, so
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,y)=0$
. If
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=0$
. If
![]() $y=\bar{z}z$
, then
$y=\bar{z}z$
, then
![]() $x\prec x\otimes y$
precisely for
$x\prec x\otimes y$
precisely for
![]() $x$
of the form
$x$
of the form
![]() $uz$
,
$uz$
,
![]() $u\in I$
. Denote by
$u\in I$
. Denote by
![]() $\unicode[STIX]{x1D6FA}_{y}$
the set of all such
$\unicode[STIX]{x1D6FA}_{y}$
the set of all such
![]() $x$
. It forms a branch of the tree
$x$
. It forms a branch of the tree
![]() $I$
and its closure
$I$
and its closure
![]() $\bar{\unicode[STIX]{x1D6FA}}_{y}$
in
$\bar{\unicode[STIX]{x1D6FA}}_{y}$
in
![]() $\bar{I}$
is a clopen subset.
$\bar{I}$
is a clopen subset.
Corollary 2.5. Fix
![]() $y\in I$
of the form
$y\in I$
of the form
![]() $\bar{z}z$
. Define an element
$\bar{z}z$
. Define an element
![]() $T=(T_{x})_{x}\in \ell ^{\infty }\text{-}\bigoplus _{x\in I}\operatorname{Mor}(x,x\otimes y)$
by
$T=(T_{x})_{x}\in \ell ^{\infty }\text{-}\bigoplus _{x\in I}\operatorname{Mor}(x,x\otimes y)$
by
Then
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
.
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
.
Proof. By Proposition 2.1, in order to show that
![]() $T\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
we have to prove that
$T\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
we have to prove that
as
![]() $x\rightarrow \infty$
, uniformly in
$x\rightarrow \infty$
, uniformly in
![]() $u\in I$
. But this is true by the previous corollary. Next, if
$u\in I$
. But this is true by the previous corollary. Next, if
![]() $S\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
, then
$S\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
, then
![]() $S=fT$
for a function
$S=fT$
for a function
![]() $f\in \ell ^{\infty }(\unicode[STIX]{x1D6FA}_{y})$
such that
$f\in \ell ^{\infty }(\unicode[STIX]{x1D6FA}_{y})$
such that
![]() $|f(ux)-f(x)|\rightarrow 0$
as
$|f(ux)-f(x)|\rightarrow 0$
as
![]() $x\rightarrow \infty$
in
$x\rightarrow \infty$
in
![]() $\unicode[STIX]{x1D6FA}_{y}$
, uniformly in
$\unicode[STIX]{x1D6FA}_{y}$
, uniformly in
![]() $u\in I$
. But this means precisely that
$u\in I$
. But this means precisely that
![]() $f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
.◻
$f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
.◻
Later we will also need the following estimate.
Corollary 2.6. There is a constant
![]() $C$
depending only on
$C$
depending only on
![]() $q$
such that
$q$
such that
for all
![]() $u,v,x,y\in I$
such that
$u,v,x,y\in I$
such that
![]() $x\prec x\otimes y$
.
$x\prec x\otimes y$
.
Proof. Using Corollary 2.4, we see that up to an operator of norm
![]() ${\leqslant}Cq^{|x|-|y|/2}$
the morphism
${\leqslant}Cq^{|x|-|y|/2}$
the morphism
equals
![]() $(V(ux,uv\otimes \bar{v}x)\otimes \unicode[STIX]{x1D704}_{y})(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}$
. By (9), the latter operator equals
$(V(ux,uv\otimes \bar{v}x)\otimes \unicode[STIX]{x1D704}_{y})(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}$
. By (9), the latter operator equals
By Proposition 2.3, this, in turn, equals
up to an operator of norm not greater than
The last quantity is not greater than
![]() $Cc^{-1}q^{|x|-|y|/2}$
, where
$Cc^{-1}q^{|x|-|y|/2}$
, where
![]() $c$
is the constant from Lemma 2.2.
$c$
is the constant from Lemma 2.2.
In a similar way one checks that the right-hand side of (10) equals
up to an operator of norm not greater than
![]() $Cq^{|x|-|y|/2}+Cc^{-1}q^{|x|-|y|/2}$
, where
$Cq^{|x|-|y|/2}+Cc^{-1}q^{|x|-|y|/2}$
, where
![]() $C$
is from Proposition 2.3 and
$C$
is from Proposition 2.3 and
![]() $c$
is from Lemma 2.2.◻
$c$
is from Lemma 2.2.◻
3 Identification of the Martin boundary
The following theorem is our main result.
Theorem 3.1. Consider a free unitary quantum group
![]() $G=A_{u}(F)$
, with
$G=A_{u}(F)$
, with
![]() $F$
not a unitary
$F$
not a unitary
![]() $2\times 2$
matrix, and a generating finitely supported probability measure
$2\times 2$
matrix, and a generating finitely supported probability measure
![]() $\unicode[STIX]{x1D707}$
on
$\unicode[STIX]{x1D707}$
on
![]() $I=\operatorname{Irr}(G)$
. Then the Martin compactification
$I=\operatorname{Irr}(G)$
. Then the Martin compactification
![]() $C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of the discrete quantum group
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of the discrete quantum group
![]() $\unicode[STIX]{x1D6E4}={\hat{G}}$
with respect to the quantum random walk defined by
$\unicode[STIX]{x1D6E4}={\hat{G}}$
with respect to the quantum random walk defined by
![]() $\unicode[STIX]{x1D707}$
coincides with the compactification
$\unicode[STIX]{x1D707}$
coincides with the compactification
![]() ${\mathcal{B}}$
defined in (7). It follows that the Martin boundary
${\mathcal{B}}$
defined in (7). It follows that the Martin boundary
![]() $C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})$
coincides with
$C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})$
coincides with
![]() ${\mathcal{B}}_{\infty }$
.
${\mathcal{B}}_{\infty }$
.
In order to simplify the notation, let us denote the Martin compactification
![]() $C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
by
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
by
![]() ${\mathcal{M}}$
. Since both
${\mathcal{M}}$
. Since both
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
![]() ${\mathcal{B}}$
are
${\mathcal{B}}$
are
![]() $G$
-C
$G$
-C
![]() $^{\ast }$
-subalgebras of
$^{\ast }$
-subalgebras of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, with the actions of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, with the actions of
![]() $G$
coming from the left adjoint action of
$G$
coming from the left adjoint action of
![]() $G$
on
$G$
on
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, by the discussion in § 1.3 in order to show that they coincide it suffices to check that
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, by the discussion in § 1.3 in order to show that they coincide it suffices to check that
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,y)={\mathcal{D}}_{{\mathcal{B}}}(e,y)$
for all
${\mathcal{D}}_{{\mathcal{M}}}(e,y)={\mathcal{D}}_{{\mathcal{B}}}(e,y)$
for all
![]() $y\in I$
.
$y\in I$
.
Consider first
![]() $y=e$
. Then, by definition,
$y=e$
. Then, by definition,
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,e)$
coincides with
${\mathcal{D}}_{{\mathcal{B}}}(e,e)$
coincides with
![]() $C(\bar{I})$
considered as a subalgebra of the center
$C(\bar{I})$
considered as a subalgebra of the center
![]() $\ell ^{\infty }(I)$
of
$\ell ^{\infty }(I)$
of
![]() $\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. On the other hand,
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. On the other hand,
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
contains the algebra of continuous functions on the Martin compactification of
${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
contains the algebra of continuous functions on the Martin compactification of
![]() $I$
defined by the Markov operator with transition probabilities
$I$
defined by the Markov operator with transition probabilities
![]() $p_{\unicode[STIX]{x1D707}}(s,t)$
defined by (1). More precisely, denoting by
$p_{\unicode[STIX]{x1D707}}(s,t)$
defined by (1). More precisely, denoting by
![]() $P$
this Markov operator and by
$P$
this Markov operator and by
![]() $G_{P}$
the corresponding classical Green kernel,
$G_{P}$
the corresponding classical Green kernel,
in view of (3) we have
Therefore, denoting by
![]() $K_{P}$
the classical Martin kernel,
$K_{P}$
the classical Martin kernel,
![]() $\displaystyle K_{P}(s,t)=G_{P}(s,t)/G_{P}(e,t)$
, we see that the function
$\displaystyle K_{P}(s,t)=G_{P}(s,t)/G_{P}(e,t)$
, we see that the function
![]() $K_{P}(s,\cdot )\in \ell ^{\infty }(I)$
differs from
$K_{P}(s,\cdot )\in \ell ^{\infty }(I)$
differs from
![]() $K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
only by a scalar factor:
$K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
only by a scalar factor:
Hence the C
![]() $^{\ast }$
-algebra generated by
$^{\ast }$
-algebra generated by
![]() $c_{c}(I)\subset c_{c}(\unicode[STIX]{x1D6E4})$
and the elements
$c_{c}(I)\subset c_{c}(\unicode[STIX]{x1D6E4})$
and the elements
![]() $K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
,
$K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
,
![]() $s\in I$
, coincides with the algebra of continuous functions on the Martin compactification of
$s\in I$
, coincides with the algebra of continuous functions on the Martin compactification of
![]() $I$
. (Note that this does not yet exclude the possibility that
$I$
. (Note that this does not yet exclude the possibility that
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,e)={\mathcal{M}}\cap \ell ^{\infty }(I)$
is a strictly larger algebra.) By a result of Picardello and Woess [Reference Picardello and WoessPW87] (see also [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1]), the Martin compactification of
${\mathcal{D}}_{{\mathcal{M}}}(e,e)={\mathcal{M}}\cap \ell ^{\infty }(I)$
is a strictly larger algebra.) By a result of Picardello and Woess [Reference Picardello and WoessPW87] (see also [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1]), the Martin compactification of
![]() $I$
coincides with the end compactification
$I$
coincides with the end compactification
![]() $\bar{I}$
. It is checked in [Reference Vaes and Vander VennetVVV10, § 2] that this result can indeed be applied in our case, since the transition probabilities
$\bar{I}$
. It is checked in [Reference Vaes and Vander VennetVVV10, § 2] that this result can indeed be applied in our case, since the transition probabilities
![]() $p_{\unicode[STIX]{x1D707}}(s,t)$
satisfy the following properties.
$p_{\unicode[STIX]{x1D707}}(s,t)$
satisfy the following properties.
– The spectral radius
 $\lim _{n}p_{\unicode[STIX]{x1D707}}^{(n)}(s,s)^{1/n}$
of the random walk is strictly less than
$\lim _{n}p_{\unicode[STIX]{x1D707}}^{(n)}(s,s)^{1/n}$
of the random walk is strictly less than
 $1$
(see also Remark 4.2 below).
$1$
(see also Remark 4.2 below).– The random walk has bounded range: there is
 $S\in \mathbb{N}$
such that
$S\in \mathbb{N}$
such that
 $p_{\unicode[STIX]{x1D707}}(s,t)=0$
whenever
$p_{\unicode[STIX]{x1D707}}(s,t)=0$
whenever
 $d(s,t)>S$
,
$d(s,t)>S$
,– The random walk is uniformly irreducible (in the sense used in [Reference WoessWoe00]): there are
 $\unicode[STIX]{x1D700}_{0}>0$
and
$\unicode[STIX]{x1D700}_{0}>0$
and
 $K\in \mathbb{N}$
such that for any
$K\in \mathbb{N}$
such that for any
 $s,t\in I$
with
$s,t\in I$
with
 $d(s,t)=1$
we have
$d(s,t)=1$
we have
 $p_{\unicode[STIX]{x1D707}}^{(k)}(s,t)\geqslant \unicode[STIX]{x1D700}_{0}$
for some
$p_{\unicode[STIX]{x1D707}}^{(k)}(s,t)\geqslant \unicode[STIX]{x1D700}_{0}$
for some
 $k\leqslant K$
.
$k\leqslant K$
.
We thus have
Assume next
![]() $y=\bar{z}z$
for some
$y=\bar{z}z$
for some
![]() $z\neq e$
. Then, by Corollary 2.5, we have
$z\neq e$
. Then, by Corollary 2.5, we have
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
, where
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
, where
![]() $T_{x}=V(x,x\otimes y)$
for
$T_{x}=V(x,x\otimes y)$
for
![]() $x\in \unicode[STIX]{x1D6FA}_{y}$
. For every
$x\in \unicode[STIX]{x1D6FA}_{y}$
. For every
![]() $t\in \unicode[STIX]{x1D6FA}_{y}$
define
$t\in \unicode[STIX]{x1D6FA}_{y}$
define
![]() $\unicode[STIX]{x1D702}^{(t)}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(e,y)=\operatorname{Nat}_{c}(\unicode[STIX]{x1D704},\unicode[STIX]{x1D704}\otimes y)$
by
$\unicode[STIX]{x1D702}^{(t)}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(e,y)=\operatorname{Nat}_{c}(\unicode[STIX]{x1D704},\unicode[STIX]{x1D704}\otimes y)$
by
Define numbers
![]() $\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
for
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
for
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
by
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
by
Motivated by (3), we then put
Lemma 3.2. The numbers
![]() $q_{\unicode[STIX]{x1D707}}(s,t)$
are real and
$q_{\unicode[STIX]{x1D707}}(s,t)$
are real and
![]() $|q_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\unicode[STIX]{x1D707}}(s,t)$
for all
$|q_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\unicode[STIX]{x1D707}}(s,t)$
for all
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
Proof. Equivalently, we have to show that the numbers
![]() $\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
are real and
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
are real and
![]() $|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.
Since
![]() $\check{\unicode[STIX]{x1D707}}$
is a convex combination of point masses, it suffices to consider
$\check{\unicode[STIX]{x1D707}}$
is a convex combination of point masses, it suffices to consider
![]() $\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
. Fix
$\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
. Fix
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
. We may assume that
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
. We may assume that
![]() $t\prec u\otimes s$
, as otherwise
$t\prec u\otimes s$
, as otherwise
![]() $\check{q}_{\unicode[STIX]{x1D707}}(s,t)=p_{\check{\unicode[STIX]{x1D707}}}(s,t)=0$
. Then, with
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)=p_{\check{\unicode[STIX]{x1D707}}}(s,t)=0$
. Then, with
![]() $\unicode[STIX]{x1D702}^{(t)}$
given by (12),
$\unicode[STIX]{x1D702}^{(t)}$
given by (12),
and hence
Somewhat informally, the statement that
![]() $\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
is real follows now from the fact that in order to compute the above trace we need only to use that
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
is real follows now from the fact that in order to compute the above trace we need only to use that
![]() $R_{\unicode[STIX]{x1D6FC}}$
and
$R_{\unicode[STIX]{x1D6FC}}$
and
![]() $\bar{R}_{\unicode[STIX]{x1D6FC}}$
solve the conjugate equations and satisfy
$\bar{R}_{\unicode[STIX]{x1D6FC}}$
solve the conjugate equations and satisfy
![]() $R_{\unicode[STIX]{x1D6FC}}^{\ast }R_{\unicode[STIX]{x1D6FC}}=q+q^{-1}=\bar{R}_{\unicode[STIX]{x1D6FC}}^{\ast }\bar{R}_{\unicode[STIX]{x1D6FC}}$
, and all these relations involve only real numbers. This can be formalized, for example, as follows. We can choose orthonormal bases
$R_{\unicode[STIX]{x1D6FC}}^{\ast }R_{\unicode[STIX]{x1D6FC}}=q+q^{-1}=\bar{R}_{\unicode[STIX]{x1D6FC}}^{\ast }\bar{R}_{\unicode[STIX]{x1D6FC}}$
, and all these relations involve only real numbers. This can be formalized, for example, as follows. We can choose orthonormal bases
![]() $(e_{i})_{i}$
of
$(e_{i})_{i}$
of
![]() $H_{\unicode[STIX]{x1D6FC}}$
and
$H_{\unicode[STIX]{x1D6FC}}$
and
![]() $(f_{i})_{i}$
of
$(f_{i})_{i}$
of
![]() $H_{\unicode[STIX]{x1D6FD}}$
such that
$H_{\unicode[STIX]{x1D6FD}}$
such that
for some
![]() $\unicode[STIX]{x1D706}_{i}>0$
(with
$\unicode[STIX]{x1D706}_{i}>0$
(with
![]() $\sum _{i}\unicode[STIX]{x1D706}_{i}^{2}=\sum _{i}\unicode[STIX]{x1D706}_{i}^{-2}=q+q^{-1}$
). Then the real linear spans of these bases define real forms of
$\sum _{i}\unicode[STIX]{x1D706}_{i}^{2}=\sum _{i}\unicode[STIX]{x1D706}_{i}^{-2}=q+q^{-1}$
). Then the real linear spans of these bases define real forms of
![]() $H_{\unicode[STIX]{x1D6FC}}$
and
$H_{\unicode[STIX]{x1D6FC}}$
and
![]() $H_{\unicode[STIX]{x1D6FD}}$
. Taking tensor products of these forms, we get a real form of
$H_{\unicode[STIX]{x1D6FD}}$
. Taking tensor products of these forms, we get a real form of
![]() $H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
for every word
$H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
for every word
![]() $x=x_{1}\cdots x_{n}$
in
$x=x_{1}\cdots x_{n}$
in
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Since
$\unicode[STIX]{x1D6FD}$
. Since
![]() $H_{x}$
is the orthogonal complement of the images of operators of the form
$H_{x}$
is the orthogonal complement of the images of operators of the form
![]() $\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes R_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes R_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
and
![]() $\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes \bar{R}_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
, which respect the real forms of the tensor products, we then also get a real form of
$\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes \bar{R}_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
, which respect the real forms of the tensor products, we then also get a real form of
![]() $H_{x}$
. Now, in computing the right-hand side of (13) we may work only with the real forms of all the spaces involved, hence the result must be real.
$H_{x}$
. Now, in computing the right-hand side of (13) we may work only with the real forms of all the spaces involved, hence the result must be real.
In order to prove the second statement of the lemma, note that we also have
![]() $|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|=\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert$
. Consider the map
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|=\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert$
. Consider the map
![]() $P_{\check{\unicode[STIX]{x1D707}}}$
on
$P_{\check{\unicode[STIX]{x1D707}}}$
on
![]() $\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes (e\oplus y),\unicode[STIX]{x1D704}\otimes (e\oplus y))\cong \ell ^{\infty }\text{-}\bigoplus _{x}\operatorname{End}(x\otimes (e\oplus y))$
. Then, by restricting it to the block corresponding to
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes (e\oplus y),\unicode[STIX]{x1D704}\otimes (e\oplus y))\cong \ell ^{\infty }\text{-}\bigoplus _{x}\operatorname{End}(x\otimes (e\oplus y))$
. Then, by restricting it to the block corresponding to
![]() $t$
and by projecting the image onto the block corresponding to
$t$
and by projecting the image onto the block corresponding to
![]() $s$
, we get a completely positive map
$s$
, we get a completely positive map
![]() $P_{st}:\operatorname{End}(t\otimes (e\oplus y))\rightarrow \operatorname{End}(s\otimes (e\oplus y))$
. By definition, this map, being divided by
$P_{st}:\operatorname{End}(t\otimes (e\oplus y))\rightarrow \operatorname{End}(s\otimes (e\oplus y))$
. By definition, this map, being divided by
![]() $p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
, becomes unital. Hence
$p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
, becomes unital. Hence
![]() $\Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
. Viewing
$\Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
. Viewing
![]() $V(t,t\otimes y)$
as the element
$V(t,t\otimes y)$
as the element
we conclude that
![]() $\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert \leqslant \Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
$\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert \leqslant \Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
Denote by
![]() $Q$
the matrix
$Q$
the matrix
![]() $(q_{\unicode[STIX]{x1D707}}(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
. We can define the ‘Green kernel’
$(q_{\unicode[STIX]{x1D707}}(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
. We can define the ‘Green kernel’
Then
Therefore if we let
![]() $\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
, then
$\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
, then
with
![]() $T$
as in Corollary 2.5. We thus need to understand the behavior of the functions
$T$
as in Corollary 2.5. We thus need to understand the behavior of the functions
![]() $K_{Q}(s,\cdot )$
at infinity. As we will see, this behavior is not that different from that of
$K_{Q}(s,\cdot )$
at infinity. As we will see, this behavior is not that different from that of
![]() $K_{P}(s,\cdot )$
. The starting point is the following estimate.
$K_{P}(s,\cdot )$
. The starting point is the following estimate.
Lemma 3.3. There is a constant
![]() $C$
(depending on
$C$
(depending on
![]() $q$
,
$q$
,
![]() $|y|$
and the support of
$|y|$
and the support of
![]() $\unicode[STIX]{x1D707}$
) such that
$\unicode[STIX]{x1D707}$
) such that
for all
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
Proof. Recall that
![]() $p_{\unicode[STIX]{x1D707}}(s,t)=0$
if
$p_{\unicode[STIX]{x1D707}}(s,t)=0$
if
![]() $d(s,t)>S$
, and then
$d(s,t)>S$
, and then
![]() $q_{\unicode[STIX]{x1D707}}(s,t)=0$
as well, so we could equally well use
$q_{\unicode[STIX]{x1D707}}(s,t)=0$
as well, so we could equally well use
![]() $q^{|t|}$
instead of
$q^{|t|}$
instead of
![]() $q^{|s|}$
in the formulation. Using (6), it is also easy to see that the ratios
$q^{|s|}$
in the formulation. Using (6), it is also easy to see that the ratios
![]() $\dim _{q}(s)/\text{dim}_{q}(t)$
are bounded when
$\dim _{q}(s)/\text{dim}_{q}(t)$
are bounded when
![]() $d(s,t)\leqslant S$
. It follows that the statement of the lemma is equivalent to the existence of
$d(s,t)\leqslant S$
. It follows that the statement of the lemma is equivalent to the existence of
![]() $C^{\prime }$
such that
$C^{\prime }$
such that
![]() $|\check{q}_{\unicode[STIX]{x1D707}}(s,t)-p_{\check{\unicode[STIX]{x1D707}}}(s,t)|\leqslant C^{\prime }q^{|s|}$
.
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)-p_{\check{\unicode[STIX]{x1D707}}}(s,t)|\leqslant C^{\prime }q^{|s|}$
.
Similarly to the proof of the previous lemma, we may assume that
![]() $\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
and consider
$\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
and consider
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
such that
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
such that
![]() $t\prec u\otimes s$
. We may also assume that
$t\prec u\otimes s$
. We may also assume that
![]() $|s|-|u|\geqslant |y|/2$
, as there are only finitely many pairs
$|s|-|u|\geqslant |y|/2$
, as there are only finitely many pairs
![]() $(s,t)$
as above not satisfying this condition. Then
$(s,t)$
as above not satisfying this condition. Then
![]() $u=u_{0}v$
,
$u=u_{0}v$
,
![]() $s=\bar{v}s_{0}$
and
$s=\bar{v}s_{0}$
and
![]() $t=u_{0}s_{0}$
for some
$t=u_{0}s_{0}$
for some
![]() $s_{0},u_{0},v\in I$
. Since
$s_{0},u_{0},v\in I$
. Since
![]() $|s_{0}|=|s|-|v|\geqslant |s|-|u|\geqslant |y|/2$
, we have
$|s_{0}|=|s|-|v|\geqslant |s|-|u|\geqslant |y|/2$
, we have
![]() $s_{0}\prec s_{0}\otimes y$
. By (13) we have
$s_{0}\prec s_{0}\otimes y$
. By (13) we have
By Corollary 2.6 the last expression is close to
up to
![]() $Cq^{|s_{0}|-|y|/2}\leqslant Cq^{|s|-|u|-|y|/2}$
. By (2), the quantity on the right is exactly
$Cq^{|s_{0}|-|y|/2}\leqslant Cq^{|s|-|u|-|y|/2}$
. By (2), the quantity on the right is exactly
![]() $p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
$p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
From this we will deduce in the next section the following result.
Proposition 3.4. For every
![]() $s\in \unicode[STIX]{x1D6FA}_{y}$
, the function
$s\in \unicode[STIX]{x1D6FA}_{y}$
, the function
![]() $\displaystyle K_{Q}(s,\cdot )=G_{Q}(s,\cdot )/G_{P}(e,\cdot )$
on
$\displaystyle K_{Q}(s,\cdot )=G_{Q}(s,\cdot )/G_{P}(e,\cdot )$
on
![]() $\unicode[STIX]{x1D6FA}_{y}$
extends to a continuous function on
$\unicode[STIX]{x1D6FA}_{y}$
extends to a continuous function on
![]() $\bar{\unicode[STIX]{x1D6FA}}_{y}\subset \bar{I}$
.
$\bar{\unicode[STIX]{x1D6FA}}_{y}\subset \bar{I}$
.
By (14), this already shows that
As opposed to the functions
![]() $K_{P}(s,\cdot )$
, it may happen that the functions
$K_{P}(s,\cdot )$
, it may happen that the functions
![]() $K_{Q}(s,\cdot )$
vanish at some points of the boundary of
$K_{Q}(s,\cdot )$
vanish at some points of the boundary of
![]() $\unicode[STIX]{x1D6FA}_{y}$
. Nevertheless we have the following result, whose proof we also postpone till the next section.
$\unicode[STIX]{x1D6FA}_{y}$
. Nevertheless we have the following result, whose proof we also postpone till the next section.
Proposition 3.5. For every point
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
, we have
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
, we have
![]() $K_{Q}(s,t_{\infty })>0$
for all
$K_{Q}(s,t_{\infty })>0$
for all
![]() $s$
sufficiently close to
$s$
sufficiently close to
![]() $t_{\infty }$
.
$t_{\infty }$
.
It is now easy to complete the proof of the equality
![]() ${\mathcal{M}}={\mathcal{B}}$
.
${\mathcal{M}}={\mathcal{B}}$
.
Proof of Theorem 3.1.
By (11), (15) and our discussion at the end of § 1.3, we can already conclude that
![]() $K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))\subset {\mathcal{B}}$
. Hence
$K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))\subset {\mathcal{B}}$
. Hence
![]() ${\mathcal{M}}\subset {\mathcal{B}}$
, since we also have
${\mathcal{M}}\subset {\mathcal{B}}$
, since we also have
![]() $c_{0}(\unicode[STIX]{x1D6E4})\subset {\mathcal{B}}$
.
$c_{0}(\unicode[STIX]{x1D6E4})\subset {\mathcal{B}}$
.
Furthermore,
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,y)$
is a bimodule over
${\mathcal{D}}_{{\mathcal{M}}}(e,y)$
is a bimodule over
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
and by (11) we know that
${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
and by (11) we know that
![]() ${\mathcal{D}}_{{\mathcal{M}}}(e,e)\supset C(\bar{I})$
. Using Proposition 3.5, for every function
${\mathcal{D}}_{{\mathcal{M}}}(e,e)\supset C(\bar{I})$
. Using Proposition 3.5, for every function
![]() $f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
we can find
$f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
we can find
![]() $s_{1},\ldots ,s_{n}\in \unicode[STIX]{x1D6FA}_{y}$
and
$s_{1},\ldots ,s_{n}\in \unicode[STIX]{x1D6FA}_{y}$
and
![]() $g_{1},\ldots ,g_{n}\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
such that
$g_{1},\ldots ,g_{n}\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
such that
![]() $f(t_{\infty })=\sum _{i}g_{i}(t_{\infty })K_{Q}(s_{i},t_{\infty })$
for all
$f(t_{\infty })=\sum _{i}g_{i}(t_{\infty })K_{Q}(s_{i},t_{\infty })$
for all
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. In view of (14) this shows that, with
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. In view of (14) this shows that, with
![]() $T$
as in Corollary 2.5, we have
$T$
as in Corollary 2.5, we have
Hence
![]() ${\mathcal{D}}_{{\mathcal{B}}}(e,y)\subset {\mathcal{D}}_{{\mathcal{M}}}(e,y)$
and therefore
${\mathcal{D}}_{{\mathcal{B}}}(e,y)\subset {\mathcal{D}}_{{\mathcal{M}}}(e,y)$
and therefore
![]() ${\mathcal{B}}\subset {\mathcal{M}}$
.◻
${\mathcal{B}}\subset {\mathcal{M}}$
.◻
Remark 3.6. The equality
![]() ${\mathcal{M}}={\mathcal{B}}$
and (16) imply that the space
${\mathcal{M}}={\mathcal{B}}$
and (16) imply that the space
![]() $C(\bar{I})K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))+c_{0}(\unicode[STIX]{x1D6E4})$
is dense in
$C(\bar{I})K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))+c_{0}(\unicode[STIX]{x1D6E4})$
is dense in
![]() ${\mathcal{B}}=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
.
${\mathcal{B}}=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
.
4 Estimates of the Green kernels
In this section we will prove Propositions 3.4 and 3.5. We thus fix a generating probability measure
![]() $\unicode[STIX]{x1D707}$
, a point
$\unicode[STIX]{x1D707}$
, a point
![]() $y\in I$
of the form
$y\in I$
of the form
![]() $\bar{z}z$
,
$\bar{z}z$
,
![]() $z\neq e$
, and consider the set
$z\neq e$
, and consider the set
![]() $\unicode[STIX]{x1D6FA}_{y}\subset I$
of words of the form
$\unicode[STIX]{x1D6FA}_{y}\subset I$
of words of the form
![]() $uz$
. In order to simplify the notation we denote the transition probabilities
$uz$
. In order to simplify the notation we denote the transition probabilities
![]() $p_{\unicode[STIX]{x1D707}}(s,t)$
by
$p_{\unicode[STIX]{x1D707}}(s,t)$
by
![]() $p(s,t)$
.
$p(s,t)$
.
In the previous section we introduced the numbers
![]() $q_{\unicode[STIX]{x1D707}}(s,t)$
,
$q_{\unicode[STIX]{x1D707}}(s,t)$
,
![]() $s,t\in \unicode[STIX]{x1D6FA}_{y}$
, which we now denote simply by
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
, which we now denote simply by
![]() $q(s,t)$
. The only information we will need about them is that, by Lemmas 3.2 and 3.3, they are real and
$q(s,t)$
. The only information we will need about them is that, by Lemmas 3.2 and 3.3, they are real and
Denote by
![]() $P$
and
$P$
and
![]() $Q$
the matrices
$Q$
the matrices
![]() $(p(s,t))_{s,t\in I}$
and
$(p(s,t))_{s,t\in I}$
and
![]() $(q(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
.
$(q(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
.
The space
![]() $c_{c}(I)$
can be completed to two different Hilbert spaces, depending on the inner product we choose. Denote by
$c_{c}(I)$
can be completed to two different Hilbert spaces, depending on the inner product we choose. Denote by
![]() $\ell ^{2}(I)$
the completion of
$\ell ^{2}(I)$
the completion of
![]() $c_{c}(I)$
with respect to the inner product
$c_{c}(I)$
with respect to the inner product
![]() $(\cdot ,\cdot )$
corresponding to the counting measure:
$(\cdot ,\cdot )$
corresponding to the counting measure:
![]() $(f,g)=\sum _{x\in I}f(x)\overline{g(x)}$
. Denote by
$(f,g)=\sum _{x\in I}f(x)\overline{g(x)}$
. Denote by
![]() $\ell ^{2}(I,m)$
the completion of
$\ell ^{2}(I,m)$
the completion of
![]() $c_{c}(I)$
with respect to the inner product corresponding to the ‘Haar measure’
$c_{c}(I)$
with respect to the inner product corresponding to the ‘Haar measure’
![]() $m$
given by
$m$
given by
![]() $m(x)=\dim _{q}(x)^{2}$
:
$m(x)=\dim _{q}(x)^{2}$
:
![]() $(f,g)_{m}=\sum _{x\in I}\,m(x)\,f(x)\overline{g(x)}$
. For any
$(f,g)_{m}=\sum _{x\in I}\,m(x)\,f(x)\overline{g(x)}$
. For any
![]() $f\in c_{c}(I)$
and
$f\in c_{c}(I)$
and
![]() $s\in I$
, we have
$s\in I$
, we have
Lemma 4.1. The operator
![]() $P$
on
$P$
on
![]() $c_{c}(I)$
extends to a bounded operator on
$c_{c}(I)$
extends to a bounded operator on
![]() $\ell ^{2}(I,m)$
of norm
$\ell ^{2}(I,m)$
of norm
![]() $\unicode[STIX]{x1D706}<1$
. The operator
$\unicode[STIX]{x1D706}<1$
. The operator
![]() $Q$
on
$Q$
on
![]() $c_{c}(\unicode[STIX]{x1D6FA}_{y})$
extends to a bounded operator on
$c_{c}(\unicode[STIX]{x1D6FA}_{y})$
extends to a bounded operator on
![]() $\ell ^{2}(\unicode[STIX]{x1D6FA}_{y},m)$
of norm not greater than
$\ell ^{2}(\unicode[STIX]{x1D6FA}_{y},m)$
of norm not greater than
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Proof. Denote by
![]() $\dim _{\text{min}}$
the dimension function on the finite-dimensional representations of our quantum group
$\dim _{\text{min}}$
the dimension function on the finite-dimensional representations of our quantum group
![]() $G=A_{u}(F)$
obtained by letting
$G=A_{u}(F)$
obtained by letting
![]() $q=1$
in formula (6).
$q=1$
in formula (6).
As can be easily seen from (2), the unitary operator
![]() $\ell ^{2}(I,m)\rightarrow \ell ^{2}(I)$
,
$\ell ^{2}(I,m)\rightarrow \ell ^{2}(I)$
,
![]() $\unicode[STIX]{x1D6FF}_{s}\mapsto \dim _{q}(s)\unicode[STIX]{x1D6FF}_{s}$
, transforms the operator
$\unicode[STIX]{x1D6FF}_{s}\mapsto \dim _{q}(s)\unicode[STIX]{x1D6FF}_{s}$
, transforms the operator
![]() $P$
into the operator
$P$
into the operator
where
![]() $\unicode[STIX]{x1D706}_{r}$
is the operator of multiplication by
$\unicode[STIX]{x1D706}_{r}$
is the operator of multiplication by
![]() $r$
on the fusion algebra
$r$
on the fusion algebra
![]() $\mathbb{C}[I]$
of
$\mathbb{C}[I]$
of
![]() $G$
(which we identify with
$G$
(which we identify with
![]() $c_{c}(I)$
as a space). By [Reference Neshveyev and TusetNT13, Lemma 2.7.3], the operator
$c_{c}(I)$
as a space). By [Reference Neshveyev and TusetNT13, Lemma 2.7.3], the operator
![]() $\unicode[STIX]{x1D706}_{r}$
on
$\unicode[STIX]{x1D706}_{r}$
on
![]() $\ell ^{2}(I)$
is bounded, of norm not greater than
$\ell ^{2}(I)$
is bounded, of norm not greater than
![]() $\dim _{\text{min}}(r)$
. Therefore
$\dim _{\text{min}}(r)$
. Therefore
since
![]() $\dim _{\text{min}}(r)<\dim _{q}(r)$
for all
$\dim _{\text{min}}(r)<\dim _{q}(r)$
for all
![]() $r\neq e$
.
$r\neq e$
.
The second statement of the lemma follows from (17), since we get
for all
![]() $f,g\in c_{c}(\unicode[STIX]{x1D6FA}_{y})$
.◻
$f,g\in c_{c}(\unicode[STIX]{x1D6FA}_{y})$
.◻
Remark 4.2. Note that by (18) we have
From this we see that the spectral radius of the random walk defined by
![]() $P$
is not greater than
$P$
is not greater than
![]() $\unicode[STIX]{x1D706}$
. This (already mentioned) fact that the spectral radius of the random walk is strictly less than one is actually enough for the results below, but since the inequality
$\unicode[STIX]{x1D706}$
. This (already mentioned) fact that the spectral radius of the random walk is strictly less than one is actually enough for the results below, but since the inequality
![]() $\Vert P\Vert <1$
slightly simplifies the arguments, we will use it.
$\Vert P\Vert <1$
slightly simplifies the arguments, we will use it.
For
![]() $x\in I$
, let us introduce the following subset of
$x\in I$
, let us introduce the following subset of
![]() $I$
:
$I$
:
We will have to consider the substochastic matrices
![]() $P_{\unicode[STIX]{x1D6E5}_{x}}=(p(s,t))_{s,t\in \unicode[STIX]{x1D6E5}_{x}}$
and the corresponding Green kernels, which we denote by
$P_{\unicode[STIX]{x1D6E5}_{x}}=(p(s,t))_{s,t\in \unicode[STIX]{x1D6E5}_{x}}$
and the corresponding Green kernels, which we denote by
![]() $G_{P,\unicode[STIX]{x1D6E5}_{x}}$
. For
$G_{P,\unicode[STIX]{x1D6E5}_{x}}$
. For
![]() $x\in \unicode[STIX]{x1D6FA}_{y}$
, we similarly define
$x\in \unicode[STIX]{x1D6FA}_{y}$
, we similarly define
![]() $Q_{\unicode[STIX]{x1D6E5}_{x}}$
and
$Q_{\unicode[STIX]{x1D6E5}_{x}}$
and
![]() $G_{Q,\unicode[STIX]{x1D6E5}_{x}}$
.
$G_{Q,\unicode[STIX]{x1D6E5}_{x}}$
.
The Green kernels
![]() $G_{P,\unicode[STIX]{x1D6E5}_{x}}$
satisfy the following uniform version of Harnack’s inequality.
$G_{P,\unicode[STIX]{x1D6E5}_{x}}$
satisfy the following uniform version of Harnack’s inequality.
Lemma 4.3. There exists
![]() $\unicode[STIX]{x1D6FF}\in (0,1)$
such that
$\unicode[STIX]{x1D6FF}\in (0,1)$
such that
for all
![]() $x\in I$
and
$x\in I$
and
![]() $v,s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
$v,s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
Proof. As we already mentioned in the previous section, the random walk defined by
![]() $P$
is uniformly irreducible. In fact, the following slightly stronger property (also called uniform irreducibility in [Reference Picardello and WoessPW87]) is shown in [Reference Vaes and Vander VennetVVV10, § 2]. There exist
$P$
is uniformly irreducible. In fact, the following slightly stronger property (also called uniform irreducibility in [Reference Picardello and WoessPW87]) is shown in [Reference Vaes and Vander VennetVVV10, § 2]. There exist
![]() $K\in \mathbb{N}$
and
$K\in \mathbb{N}$
and
![]() $\unicode[STIX]{x1D6FF}_{0}>0$
such that:
$\unicode[STIX]{x1D6FF}_{0}>0$
such that:
–
 $p(s,t)\geqslant \unicode[STIX]{x1D6FF}_{0}$
whenever
$p(s,t)\geqslant \unicode[STIX]{x1D6FF}_{0}$
whenever
 $p(s,t)>0$
;
$p(s,t)>0$
;– for any
 $s,t\in I$
with
$s,t\in I$
with
 $d(s,t)=1$
we have
$d(s,t)=1$
we have
 $p^{(k)}(s,t)>0$
for some
$p^{(k)}(s,t)>0$
for some
 $k\leqslant K$
.
$k\leqslant K$
.
In particular, given
![]() $s,t\in I$
with
$s,t\in I$
with
![]() $d(s,t)=1$
, there are points
$d(s,t)=1$
, there are points
![]() $x_{0}=s,x_{1},\ldots ,x_{k}=t$
,
$x_{0}=s,x_{1},\ldots ,x_{k}=t$
,
![]() $k\leqslant K$
, such that
$k\leqslant K$
, such that
![]() $p(x_{i},x_{i+1})\geqslant \unicode[STIX]{x1D6FF}_{0}$
for all
$p(x_{i},x_{i+1})\geqslant \unicode[STIX]{x1D6FF}_{0}$
for all
![]() $i=0,\ldots ,k-1$
. But then we also have
$i=0,\ldots ,k-1$
. But then we also have
![]() $p(x_{i}x,x_{i+1}x)\geqslant \unicode[STIX]{x1D6FF}_{0}$
for any
$p(x_{i}x,x_{i+1}x)\geqslant \unicode[STIX]{x1D6FF}_{0}$
for any
![]() $x\in I$
. That is, the same constants
$x\in I$
. That is, the same constants
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6FF}_{0}$
work for
$\unicode[STIX]{x1D6FF}_{0}$
work for
![]() $P_{\unicode[STIX]{x1D6E5}_{x}}$
. This implies the lemma; specifically, we can take
$P_{\unicode[STIX]{x1D6E5}_{x}}$
. This implies the lemma; specifically, we can take
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{0}^{K}$
.◻
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{0}^{K}$
.◻
The most important property of the Green kernels of random walks on trees (shared also by random walks on hyperbolic graphs, where it is much more difficult to prove [Reference AnconaAnc88]) is their almost multiplicativity along geodesics. We will need the following uniform version of this property, cf. [Reference Izumi, Neshveyev and OkayasuINO08, Proposition 2.1].
For
![]() $s,t\in I$
, we denote by
$s,t\in I$
, we denote by
![]() $[s,t]$
the unique geodesic segment between
$[s,t]$
the unique geodesic segment between
![]() $s$
and
$s$
and
![]() $t$
.
$t$
.
Lemma 4.4. There exists a constant
![]() $C_{1}>0$
such that
$C_{1}>0$
such that
for all
![]() $x\in I$
,
$x\in I$
,
![]() $s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
![]() $v\in [s,t]$
.
$v\in [s,t]$
.
Proof. The first inequality is true, with
![]() $C_{1}=(1-\unicode[STIX]{x1D70C})^{-1}$
, for any irreducible random walk with spectral radius
$C_{1}=(1-\unicode[STIX]{x1D70C})^{-1}$
, for any irreducible random walk with spectral radius
![]() $\unicode[STIX]{x1D70C}<1$
. Namely, we have
$\unicode[STIX]{x1D70C}<1$
. Namely, we have
since the expression on the left is the sum of
![]() $p(s_{0},s_{1})\cdots p(s_{n-1},s_{n})$
over all paths
$p(s_{0},s_{1})\cdots p(s_{n-1},s_{n})$
over all paths
![]() $(s=s_{0},s_{1},\ldots ,s_{n}=t)$
in
$(s=s_{0},s_{1},\ldots ,s_{n}=t)$
in
![]() $\unicode[STIX]{x1D6E5}_{x}$
that pass through
$\unicode[STIX]{x1D6E5}_{x}$
that pass through
![]() $v$
. As
$v$
. As
![]() $G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,v)\leqslant G_{P}(v,v)\leqslant (1-\unicode[STIX]{x1D706})^{-1}$
by Remark 4.2, we can take
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,v)\leqslant G_{P}(v,v)\leqslant (1-\unicode[STIX]{x1D706})^{-1}$
by Remark 4.2, we can take
![]() $C_{1}=(1-\unicode[STIX]{x1D706})^{-1}$
.
$C_{1}=(1-\unicode[STIX]{x1D706})^{-1}$
.
For the second inequality, take
![]() $x\in I$
,
$x\in I$
,
![]() $s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
![]() $v\in [s,t]$
. Then any path from
$v\in [s,t]$
. Then any path from
![]() $s$
to
$s$
to
![]() $t$
in
$t$
in
![]() $\unicode[STIX]{x1D6E5}_{x}$
contributing to
$\unicode[STIX]{x1D6E5}_{x}$
contributing to
![]() $G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
![]() $A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(v)$
, where
$A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(v)$
, where
![]() $B_{S}(v)$
is the open ball of radius
$B_{S}(v)$
is the open ball of radius
![]() $S$
with center
$S$
with center
![]() $v$
. (Recall that
$v$
. (Recall that
![]() $S\in \mathbb{N}$
is such that
$S\in \mathbb{N}$
is such that
![]() $p(u,w)=0$
whenever
$p(u,w)=0$
whenever
![]() $d(u,w)>S$
.) It follows that
$d(u,w)>S$
.) It follows that
By Lemma 4.3, for every
![]() $u\in A$
, we have
$u\in A$
, we have
Since the number of vertices in
![]() $B_{S}(v)$
is not greater than
$B_{S}(v)$
is not greater than
![]() $3\cdot 2^{S-1}-2$
, we thus see that for the second inequality in the formulation of the lemma we can take
$3\cdot 2^{S-1}-2$
, we thus see that for the second inequality in the formulation of the lemma we can take
![]() $C_{1}=3(2/\unicode[STIX]{x1D6FF}^{2})^{S-1}$
.◻
$C_{1}=3(2/\unicode[STIX]{x1D6FF}^{2})^{S-1}$
.◻
We are now ready to prove the following key estimate.
Lemma 4.5. There is a constant
![]() $C_{2}$
such that
$C_{2}$
such that
for all
![]() $x\in \unicode[STIX]{x1D6FA}_{y}$
and
$x\in \unicode[STIX]{x1D6FA}_{y}$
and
![]() $s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
Proof. By (19) we have
![]() $G_{P}(s,t)=m(s)^{-1}((1-P)^{-1}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}$
. Similarly,
$G_{P}(s,t)=m(s)^{-1}((1-P)^{-1}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}$
. Similarly,
Define functions
![]() $\tilde{\unicode[STIX]{x1D6FF}}_{u}=\unicode[STIX]{x1D6FF}_{u}/\sqrt{m(u)}$
for
$\tilde{\unicode[STIX]{x1D6FF}}_{u}=\unicode[STIX]{x1D6FF}_{u}/\sqrt{m(u)}$
for
![]() $u\in I$
. Then we can write
$u\in I$
. Then we can write
From this we get
Since
![]() $\{{\tilde{\unicode[STIX]{x1D6FF}}_{u}\}}_{u\in \unicode[STIX]{x1D6E5}_{x}}$
is an orthonormal basis in
$\{{\tilde{\unicode[STIX]{x1D6FF}}_{u}\}}_{u\in \unicode[STIX]{x1D6E5}_{x}}$
is an orthonormal basis in
![]() $\ell ^{2}(\unicode[STIX]{x1D6E5}_{x},m)$
, the scalar product in the expression above equals
$\ell ^{2}(\unicode[STIX]{x1D6E5}_{x},m)$
, the scalar product in the expression above equals
It follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant \frac{\sqrt{m(t)}}{\sqrt{m(s)}}\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}|((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{v})_{m}((Q_{\unicode[STIX]{x1D6E5}_{x}}-P_{\unicode[STIX]{x1D6E5}_{x}})\tilde{\unicode[STIX]{x1D6FF}}_{v},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}|\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\,|q(u,v)-p(u,v)|\,|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant \frac{\sqrt{m(t)}}{\sqrt{m(s)}}\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}|((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{v})_{m}((Q_{\unicode[STIX]{x1D6E5}_{x}}-P_{\unicode[STIX]{x1D6E5}_{x}})\tilde{\unicode[STIX]{x1D6FF}}_{v},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}|\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\,|q(u,v)-p(u,v)|\,|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|.\nonumber\end{eqnarray}$$
By (17) we have
![]() $|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|\leqslant G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)$
and
$|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|\leqslant G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)$
and
![]() $|q(u,v)-p(u,v)|\leqslant Cq^{|u|}$
. Since we also have
$|q(u,v)-p(u,v)|\leqslant Cq^{|u|}$
. Since we also have
![]() $q(u,v)=p(u,v)=0$
if
$q(u,v)=p(u,v)=0$
if
![]() $d(u,v)>S$
, we conclude that
$d(u,v)>S$
, we conclude that
Applying Lemma 4.3, we then get
where we used again that every closed ball of radius
![]() $S$
contains not more than
$S$
contains not more than
![]() $3\cdot 2^{S}-2$
vertices.
$3\cdot 2^{S}-2$
vertices.
In order to estimate the above expression, for every
![]() $u\in \unicode[STIX]{x1D6E5}_{x}$
denote by
$u\in \unicode[STIX]{x1D6E5}_{x}$
denote by
![]() $u^{\prime }$
the point on the geodesic
$u^{\prime }$
the point on the geodesic
![]() $[s,t]$
closest to
$[s,t]$
closest to
![]() $u$
. Then
$u$
. Then
![]() $u^{\prime }\in [u,s]\cap [u,t]$
, so by Lemma 4.4 we have
$u^{\prime }\in [u,s]\cap [u,t]$
, so by Lemma 4.4 we have
and hence
It remains to estimate the sum in the above expression on the right. Observe that if
![]() $u^{\prime }\neq x^{\prime }$
(where
$u^{\prime }\neq x^{\prime }$
(where
![]() $x^{\prime }\in [s,t]$
is the vertex closest to
$x^{\prime }\in [s,t]$
is the vertex closest to
![]() $x$
), then
$x$
), then
If
![]() $u^{\prime }=x^{\prime }$
, then the inequality
$u^{\prime }=x^{\prime }$
, then the inequality
![]() $|u|\geqslant |x|+d(u^{\prime },x^{\prime })$
is obvious. See Figure 1 illustrating these two cases.
$|u|\geqslant |x|+d(u^{\prime },x^{\prime })$
is obvious. See Figure 1 illustrating these two cases.

Figure 1. Possible positions of the closest point on the geodesic.
It follows that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime }) & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{d(u^{\prime },x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime })\nonumber\\ \displaystyle & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}\mathop{\sum }_{w\in [s,t]}q^{d(w,x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime }) & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{d(u^{\prime },x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime })\nonumber\\ \displaystyle & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}\mathop{\sum }_{w\in [s,t]}q^{d(w,x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w).\end{eqnarray}$$
Next, for every
![]() $w\in [s,t]$
, we have
$w\in [s,t]$
, we have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w) & = & \displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{w}}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}\nonumber\\ \displaystyle & = & \displaystyle ((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-2}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}\leqslant (1-\unicode[STIX]{x1D706})^{-2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w) & = & \displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{w}}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}\nonumber\\ \displaystyle & = & \displaystyle ((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-2}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}\leqslant (1-\unicode[STIX]{x1D706})^{-2}.\end{eqnarray}$$
We also have
Combining (22)–(24), we get from (21) that
and we are done.◻
Proof of Proposition 3.4.
Fix
![]() $s\in \unicode[STIX]{x1D6FA}_{y}$
and
$s\in \unicode[STIX]{x1D6FA}_{y}$
and
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. We have to show that as
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. We have to show that as
![]() $t\rightarrow t_{\infty }$
the numbers
$t\rightarrow t_{\infty }$
the numbers
![]() $\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
converge to a finite limit.
$\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
converge to a finite limit.
Fix
![]() $\unicode[STIX]{x1D700}>0$
. By Lemma 4.5 there exists
$\unicode[STIX]{x1D700}>0$
. By Lemma 4.5 there exists
![]() $x\in \unicode[STIX]{x1D6FA}_{y}$
such that
$x\in \unicode[STIX]{x1D6FA}_{y}$
such that
![]() $s\not \in \unicode[STIX]{x1D6E5}_{x}$
,
$s\not \in \unicode[STIX]{x1D6E5}_{x}$
,
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}\cap \unicode[STIX]{x2202}I$
and
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}\cap \unicode[STIX]{x2202}I$
and
Take
![]() $t\in \unicode[STIX]{x1D6E5}_{x}$
. Then
$t\in \unicode[STIX]{x1D6E5}_{x}$
. Then
![]() $x\in [s,t]$
, so, similarly to the proof of Lemma 4.4, every path from
$x\in [s,t]$
, so, similarly to the proof of Lemma 4.4, every path from
![]() $s$
to
$s$
to
![]() $t$
in
$t$
in
![]() $I$
contributing to
$I$
contributing to
![]() $G_{P}(s,t)$
must pass through the set
$G_{P}(s,t)$
must pass through the set
![]() $A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(x)$
and there is a well-defined moment when it leaves
$A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(x)$
and there is a well-defined moment when it leaves
![]() $I\setminus \unicode[STIX]{x1D6E5}_{x}$
and enters
$I\setminus \unicode[STIX]{x1D6E5}_{x}$
and enters
![]() $A$
for the last time. It follows that if for
$A$
for the last time. It follows that if for
![]() $u\in A$
we put
$u\in A$
we put
 $$\begin{eqnarray}M_{P}(s,u)=\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{\substack{ s=s_{0},s_{1},\ldots ,s_{n}=u: \\ s_{n-1\not \in \unicode[STIX]{x1D6E5}_{x}}}}p(s_{0},s_{1})\cdots p(s_{n-1},s_{n}),\end{eqnarray}$$
$$\begin{eqnarray}M_{P}(s,u)=\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{\substack{ s=s_{0},s_{1},\ldots ,s_{n}=u: \\ s_{n-1\not \in \unicode[STIX]{x1D6E5}_{x}}}}p(s_{0},s_{1})\cdots p(s_{n-1},s_{n}),\end{eqnarray}$$
then
We can similarly define
![]() $M_{Q}(s,u)$
and get a decomposition of
$M_{Q}(s,u)$
and get a decomposition of
![]() $G_{Q}(s,t)$
. Then, for any
$G_{Q}(s,t)$
. Then, for any
![]() $t,t^{\prime }\in \unicode[STIX]{x1D6E5}_{x}$
, we have
$t,t^{\prime }\in \unicode[STIX]{x1D6E5}_{x}$
, we have
 $$\begin{eqnarray}\displaystyle |K_{Q}(s,t)-K_{Q}(s,t^{\prime })| & = & \displaystyle \biggl|\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}+\unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}(K_{P}(s,t)+K_{P}(s,t^{\prime }))+\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |K_{Q}(s,t)-K_{Q}(s,t^{\prime })| & = & \displaystyle \biggl|\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}+\unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}(K_{P}(s,t)+K_{P}(s,t^{\prime }))+\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|,\nonumber\end{eqnarray}$$
where we used that
![]() $|M_{Q}(s,u)|\leqslant M_{P}(s,u)$
by (17). If we could prove that the sum above converges to zero as
$|M_{Q}(s,u)|\leqslant M_{P}(s,u)$
by (17). If we could prove that the sum above converges to zero as
![]() $t,t^{\prime }\rightarrow t_{\infty }$
, then we would get
$t,t^{\prime }\rightarrow t_{\infty }$
, then we would get
and since
![]() $\unicode[STIX]{x1D700}$
could be taken arbitrarily small, we would be able to conclude that the numbers
$\unicode[STIX]{x1D700}$
could be taken arbitrarily small, we would be able to conclude that the numbers
![]() $K_{Q}(s,t)$
converge to a finite limit as
$K_{Q}(s,t)$
converge to a finite limit as
![]() $t\rightarrow t_{\infty }$
.
$t\rightarrow t_{\infty }$
.
Therefore it remains to show that for every
![]() $u\in A$
we have
$u\in A$
we have
Again using (25), but now applied to
![]() $G_{P}(e,t)$
, we can rewrite this as
$G_{P}(e,t)$
, we can rewrite this as
In order to prove this, it suffices to show that for all
![]() $u,v\in A$
the function
$u,v\in A$
the function
![]() $G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,\cdot )/G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,\cdot )$
on
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,\cdot )/G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,\cdot )$
on
![]() $\unicode[STIX]{x1D6E5}_{x}$
extends to a non-vanishing continuous function on
$\unicode[STIX]{x1D6E5}_{x}$
extends to a non-vanishing continuous function on
![]() $\bar{\unicode[STIX]{x1D6E5}}_{x}\subset \bar{I}$
. But this is indeed true, since this function is nothing else than the Martin kernel of the random walk on the tree
$\bar{\unicode[STIX]{x1D6E5}}_{x}\subset \bar{I}$
. But this is indeed true, since this function is nothing else than the Martin kernel of the random walk on the tree
![]() $\unicode[STIX]{x1D6E5}_{x}$
defined by the matrix
$\unicode[STIX]{x1D6E5}_{x}$
defined by the matrix
![]() $P_{\unicode[STIX]{x1D6E5}_{x}}$
. Although this matrix is only substochastic, it still satisfies the assumptions of [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1], as we essentially discussed in the proof of Lemma 4.3. So the same arguments as in [Reference WoessWoe00] show that the Martin compactification of
$P_{\unicode[STIX]{x1D6E5}_{x}}$
. Although this matrix is only substochastic, it still satisfies the assumptions of [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1], as we essentially discussed in the proof of Lemma 4.3. So the same arguments as in [Reference WoessWoe00] show that the Martin compactification of
![]() $\unicode[STIX]{x1D6E5}_{x}$
with respect to
$\unicode[STIX]{x1D6E5}_{x}$
with respect to
![]() $P_{\unicode[STIX]{x1D6E5}_{x}}$
coincides with the end compactification, which is
$P_{\unicode[STIX]{x1D6E5}_{x}}$
coincides with the end compactification, which is
![]() $\bar{\unicode[STIX]{x1D6E5}}_{x}$
.◻
$\bar{\unicode[STIX]{x1D6E5}}_{x}$
.◻
Proof of Proposition 3.5.
Fix
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. By Lemma 4.5 we can find
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. By Lemma 4.5 we can find
![]() $x\in \unicode[STIX]{x1D6FA}_{y}$
such that
$x\in \unicode[STIX]{x1D6FA}_{y}$
such that
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}$
and
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}$
and
Suppose next that we can find
![]() $u\in \unicode[STIX]{x1D6E5}_{x}$
such that
$u\in \unicode[STIX]{x1D6E5}_{x}$
such that
![]() $t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{u}$
and
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{u}$
and
Then, by (17),
whence
and therefore
Therefore it remains to find
![]() $u$
such that (26) is satisfied.
$u$
such that (26) is satisfied.
For
![]() $s,t\in \unicode[STIX]{x1D6E5}_{x}$
, similarly to the proof of Lemma 4.4, the paths from
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
, similarly to the proof of Lemma 4.4, the paths from
![]() $s$
to
$s$
to
![]() $t$
contributing to
$t$
contributing to
![]() $G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
$G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
![]() $A=B_{S}(x)\cap \unicode[STIX]{x1D6E5}_{x}$
of cardinality
$A=B_{S}(x)\cap \unicode[STIX]{x1D6E5}_{x}$
of cardinality
![]() $2^{S}-1$
. It follows that
$2^{S}-1$
. It follows that
and, using Lemma 4.3, we get
Now take any
![]() $u\in \unicode[STIX]{x1D6E5}_{x}$
and assume that
$u\in \unicode[STIX]{x1D6E5}_{x}$
and assume that
![]() $s,t\in \unicode[STIX]{x1D6E5}_{u}$
. Let
$s,t\in \unicode[STIX]{x1D6E5}_{u}$
. Let
![]() $v$
be the point on
$v$
be the point on
![]() $[s,t]$
closest to
$[s,t]$
closest to
![]() $u$
, or equivalently, to
$u$
, or equivalently, to
![]() $x$
. Then
$x$
. Then
![]() $v\in [s,x]\cap [t,x]$
, so, similarly to (20), we have
$v\in [s,x]\cap [t,x]$
, so, similarly to (20), we have
Hence
Therefore for (26) to be satisfied it suffices to have
for all
![]() $v\in \unicode[STIX]{x1D6E5}_{u}$
. But, similarly to (23),
$v\in \unicode[STIX]{x1D6E5}_{u}$
. But, similarly to (23),
so (27) is true for all but finitely many
![]() $v$
in
$v$
in
![]() $I$
.◻
$I$
.◻
Remark 4.6. Essentially the same proof shows that actually
![]() $K_{Q}(s,t_{\infty })/K_{P}(s,t_{\infty })\rightarrow 1$
as
$K_{Q}(s,t_{\infty })/K_{P}(s,t_{\infty })\rightarrow 1$
as
![]() $s\rightarrow t_{\infty }$
.
$s\rightarrow t_{\infty }$
.
Acknowledgements
Part of the research leading to this article was carried out during the authors’ visit to the Texas A&M University. The authors are grateful to Michael Brannan, Ken Dykema, Guoliang Yu and the staff of the university for their hospitality.