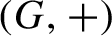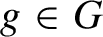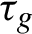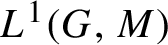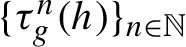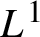Ergodic theorem in CAT(0) spaces in terms of inductive means

Abstract

Let $(G,+)$ be a compact, abelian, and metrizable topological group. In this group we take $g\in G$ such that the corresponding automorphism $\tau _g$ is ergodic. The main result of this paper is a new ergodic theorem for functions in $L^1(G,M)$ , where M is a Hadamard space. The novelty of our result is that we use inductive means to average the elements of the orbit $\{\tau _g^n(h)\}_{n\in \mathbb {N}}$ . The advantage of inductive means is that they can be explicitly computed in many important examples. The proof of the ergodic theorem is done firstly for continuous functions, and then it is extended to $L^1$ functions. The extension is based on a new construction of mollifiers in Hadamard spaces. This construction has the advantage that it only uses the metric structure and the existence of barycenters, and does not require the existence of an underlying vector space. For this reason, it can be used in any Hadamard space, in contrast to those results that need to use the tangent space or some chart to define the mollifier.

1 Introduction

One of the classical results in ergodic theory is the Birkhoff ergodic theorem.

Theorem 1.1. (Birkhoff)

Let $(X,\mathfrak {X},m)$ be a probability space, $\tau :X\to X$ an ergodic map, and $f\in L^1(X,\mathbb {C})$ . Then, for m-almost every $x\in X$ ,

(1.1) $$ \begin{align} \frac{1}{n}\sum_{k=0}^{n-1} f(\tau^k(x))\xrightarrow[n\rightarrow\infty]{} \int_{X} f(t)\,d{\kern-0.6pt}m(t). \end{align} $$

The aim of this work is to study this result in the context of CAT(0) spaces. The traditional extensions of the Birkhoff theorem to this setting replace the arithmetic means by the so-called barycenters. In particular, the barycenters are used to average the function along the ergodic orbit. Our motivation to consider variants of these traditional extensions is that usually the barycenters cannot be computed explicitly. Moreover, in many important cases, the usual ways to approximate the barycenters using convex optimization methods are not useful for applications (see Example 2.3). A similar situation can be found in the extensions of other well-known theorems to CAT(0) spaces. This is the case for the law of large numbers. In [30] Sturm introduced the so-called inductive means, which can be computed easily in those spaces where the geodesics are known. Using these means to average the independent copies of the random variable, he obtained in [30] a new version of the law of large numbers in CAT(0) spaces. Motivated by this result, we studied a version of the classical Birkhoff ergodic theorem using the inductive means defined by Sturm to average the functions along the ergodic orbit. As a consequence, we get new ways to approximate a barycenter of integrable function with values in a CAT(0) space.

1.1 Framework and related results

Recall that a CAT(0) space, also called a Hadamard space, is a complete metric space $(M,\delta )$ whose metric satisfies the following semiparallelogram law: given $x, y \in M$ , there exists $m \in M$ satisfying

(1.2) $$ \begin{align} \delta^2(m, z) \leq \tfrac{1}{2}\delta^2(x, z) + \tfrac{1}{2}\delta^2(y, z) - \tfrac{1}{4}\delta^2(x, y), \end{align} $$

for all $z \in M$ . The point m is unique, and it is called the midpoint between x and y, because, taking $z=x$ and $z=y$ the following identities hold:

$$ \begin{align*}\delta(x,m)=\delta(m,y)=\tfrac12 \delta(x,y). \end{align*} $$

The existence and uniqueness of midpoints give rise to a unique (continuous) geodesic which we will denote by $\gamma :[0,1]\to M$ (see §2 for more details). We will denote this curve by $x \#_t y$ instead of $\gamma (t)$ . Typical examples of CAT(0) spaces are the Riemannian manifolds with non-positive sectional curvature, and certain types of graphs such as trees or spiders. The systematic study of these spaces started with work by Alexandrov [1] and Reshetnyak [28], and the subject was strongly influenced by the works of Gromov [13, 14]. Nowadays there exists a huge bibliography on the subject. The interested reader is referred to the monographs [4, 5, 10, 15].

The convexity properties of the metric allow us to define a notion of barycenter in CAT(0) spaces. Endowed with this barycenter, Hadamard spaces play an important role in the theory of integrations (random variables, expectations and variances), law of large numbers, ergodic theory, Jensen’s inequality (see [9, 12, 18, 24, 30]), stochastic generalization of Lipschitz retractions and extension problems of Lipschitz and Hölder maps (see [19, 22, 25]), optimal transport theory on Riemannian manifolds (see [26, 27]), and so on.

Roughly speaking, the barycenter constitutes a way to average points in M, taking into account the metric properties of the space. More precisely, the barycenter is defined for some measures with separable support (see §2 for the formal definition). Given n points in the space M, let $\beta (x_1,\ldots ,x_n)$ denote the barycenter of the points $x_1,\ldots ,x_n$ (more precisely, the barycenter of the point measure $\mu =\delta _{x_1}+\cdots +\delta _{x_n}$ ). On the other hand, if $(X,\mathfrak {X},\mu )$ is a measure space and $f:X\to M$ is a measurable function such that for some $y\in M$ (and therefore for any $y\in M$ )

(1.3) $$ \begin{align} \int_X \delta(f(x),y)\,d{\kern-0.7pt}\mu(x)<\infty, \end{align} $$

then $\beta _f$ denotes the barycenter of the pushforward measure $f_*(\mu )$ .

Any Hilbert space $\mathcal {H}$ , and in particular $\mathbb {C}$ , is a CAT(0) space with the metric induced by the norm, and the barycenter in $\mathcal {H}$ is precisely the arithmetic mean. Therefore, the natural extension of the Birkhoff theorem for a function f satisfying (1.3) is obtained by replacing the arithmetic means by the barycenters

(1.4) $$ \begin{align} \beta(f(x),\ldots,f(\tau^{n-1}(x))) \xrightarrow[n\rightarrow\infty]{} \beta_f. \end{align} $$

This result was proved by Austin in [2] for functions satisfying the integrability condition

(1.5) $$ \begin{align} \int_X \delta(f(x),y)^2\,d{\kern-0.7pt}\mu(x)<\infty, \end{align} $$

instead of (1.3). Later on, in [24] Navas proved it for functions satisfying (1.3). In both cases, the authors considered not only $\mathbb {Z}$ -actions but also much more general actions given by amenable groups. Moreover, Navas’s theorem holds not only in CAT(0) spaces but also in metric spaces of non-positive curvature in the sense of Busemann.

However, the barycenters $\beta (f(x),\ldots ,f(\tau ^{n-1}(x)))$ in (1.4) may be very difficult to compute for $n\geq 4$ . Hence, it is natural to look for an alternative way to average the points $f(x),\ldots ,f(\tau ^{n-1}(x))$ . This leads to the definition of inductive means. To motivate their definition, note that, given a sequence $\{a_n\}_{n\in \mathbb {N}}$ of complex numbers,

$$ \begin{align*} \frac{a_1+a_2+a_3}{3}&=\displaystyle\frac{2}{3}\bigg(\frac{a_1+a_2}{2}\bigg)+\frac13\, a_3,\\ \vdots&\\ \frac{a_1+\cdots+a_n}{n}&=\displaystyle\frac{n-1}{n}\bigg(\frac{a_1+\cdots+a_{n-1}}{n-1}\bigg)+\frac1n\, a_n. \end{align*} $$

Let $\gamma _{a,b}(t)=t\,b+(1-t)a$ , and for a moment let us use the notation $a\,\sharp _t\, b=\gamma _{a,b}(t)$ . Then

$$ \begin{align*} \frac{a_1+a_2+a_3}{3}&=(a_1\,\sharp_{\frac12}\, a_2)\,\sharp_{\frac13}\,a_3,\\[3pt] \frac{a_1+a_2+a_3+a_4}{4}&=((a_1\,\sharp_{\frac12}\, a_2)\,\sharp_{\frac13}\,a_3)\,\sharp_{\frac14}\,a_4, \end{align*} $$

and so on and so forth. The segments are the geodesics in the euclidean space. Thus, in our setting, we can replace the segments by the geodesic associated to the Hadamard space. This is the idea that leads to the definition of the inductive means. Given a sequence $\{a_n\}_{n\in \mathbb {N}}$ whose elements belong to a CAT(0) space M, the inductive means are defined as follows:

$$ \begin{align*} S_1(a) & = a_1,\\ S_{n}(a) & = S_{n-1}(a) \#_{\frac{1}{n}} a_n \quad (n \geq 2). \end{align*} $$

These means were introduced by Sturm in [30], where he proved the following version of the law of the large numbers.

Theorem 1.2. (Sturm)

Let $(X,\mathfrak {X},\mu )$ be a probability space, and let $A=\{A_j\}_{j\in \mathbb {N}}$ be a sequences of independent and identically distributed bounded random variables satisfying (1.5). Then, almost surely,

$$ \begin{align*}S_n(A)\xrightarrow[n\rightarrow\infty]{} \beta_{A_1}. \end{align*} $$

This result suggests the possibility of finding extensions of the Birkhoff ergodic theorem using inductive means to average the values of the function on the ergodic orbit. Note that, if we want to use inductive means, then we are compelled to consider only $\mathbb {Z}$ -actions.

1.2 Main results

Let $(G,+)$ be a compact and metrizable topological group. In this group we fix a Haar measure m, a shift-invariant metric ${d}_{G}$ , and we take an ergodic automorphism $\tau (h)=h+g$ for some $g\in G$ . Note that the existence of such an ergodic automorphism implies that the group must be abelian (see [32, Theorem 1.9])

On the other hand, let $(M,\delta )$ be a fixed CAT(0) space. Given a function $A: G \rightarrow M$ , we define $a^{\tau } : G \rightarrow M^{\mathbb {N}}$ by

(1.6) $$ \begin{align} a^{\tau}(x) :=\{a^{\tau}_j(x)\}_{j\in\mathbb{N}} \quad\text{where } a^{\tau}_j(x)=A(\tau^j(x)). \end{align} $$

Our first main theorem is the following continuous version of the ergodic theorem.

Theorem 1.3. Let M be a Hadamard space and $A:G\to M$ a continuous function. Then

(1.7) $$ \begin{align} \lim_{n\to\infty} S_{n}(a^{\tau}(g)) = {\beta}_{{{{A}}}}, \end{align} $$

uniformly in $g\in G$ .

To extend this result to $L^1(G,M)$ functions, we need to find ‘good $L^1$ -approximations by continuous functions’. These approximations are obtained in §3.3, where we study mollifiers in general Hadamard spaces. The results on mollifiers obtained in this subsection are of interest in their own right, since they generalize some results proved by Karcher in [16] for Riemannian manifolds. Using this $L^1$ -approximation we get the following $L^1$ version of the ergodic theorem.

Theorem 1.4. Given $A\in L^1(G, M)$ , for almost every $g\in G$ ,

(1.8) $$ \begin{align} \lim_{n\to\infty }S_{n}(a^{\tau}(g))={\beta}_{\mbox{A}}. \end{align} $$

From this result, using standard techniques we get the following $L^p$ versions.

Theorem 1.5. Let $1 \leq p < \infty $ and $A\in L^p(G, M)$ . Then

(1.9) $$ \begin{align} \lim_{n\to\infty } \int_{G} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) = 0. \end{align} $$

Recall that a topological dynamical system $(\Omega ,\tau )$ is called a Kronecker system if it is isomorphic to a group dynamical system $(G,\tau )$ like the one described above. Also recall that any equicontinuous dynamical system becomes an isometric system by changing the metric, and any minimal isometric dynamical system is a Kronecker system (see, for example, [31, §2.6]). Therefore, using standard arguments, all the main results of this work can be extended to equicontinuous systems. In order to go further and consider more general dynamical systems we think that a different approach is required.

1.3 Organization of the paper

The paper is organized as follows. Section 2 is devoted to gathering together some preliminaries on Hadamard spaces, barycenters and inductive means that will be used throughout the paper. Section 3 is devoted to the proofs of our main results. In this section we also prove those results related to approximation by continuous functions in general Hadamard spaces.

2 Preliminaries

In this section we recall some results on CAT(0) spaces, barycenters, as well as proving some results on inductive means that we will need later. The interested reader is referred to the monographs [3–5, 10, 15] for more information.

2.1 CAT(0) spaces

Recall that a CAT(0) space, also known as Hadamard space, is a complete metric space $(M,\delta )$ that satisfies the following semiparallelogram law: given $x, y \in M$ , there exists $m \in M$ satisfying

(2.1) $$ \begin{align} \delta^2(m, z) \leq \displaystyle\tfrac{1}{2}\delta^2(x, z) + \displaystyle\tfrac{1}{2}\delta^2(y, z) - \displaystyle\tfrac{1}{4}\delta^2(x, y) \end{align} $$

for all $z \in M$ . The point m is unique, and it is called midpoint between x and y, since $ \delta (x,m)=\delta (m,y)=\tfrac 12 \delta (x,y)$ . Recall that, given a continuous curve $\gamma :[a,b]\to M$ , its length is computed as

$$ \begin{align*}\inf \sum_{n=1}^N \delta(\gamma(t_{n+1}),\gamma(t_n)) \end{align*} $$

where the infimum is taken over all the partitions $\{t_1,\ldots ,t_N\}$ of the interval $[a,b]$ . The existence and uniqueness of midpoints give rise to a unique (continuous) geodesic $\gamma _{x,y} : [0, 1] \rightarrow M$ connecting any given two points x and y. Indeed, we first define $\gamma _{x,y}(1/2)$ to be the midpoint of x and y. Then, using an inductive argument, we define the geodesic for all dyadic rational numbers in $[0, 1]$ . Finally, by completeness, it can be extended to all $t \in [0, 1]$ . It can be proved that this curve is the shortest path connecting x and y. As we mentioned in the introduction, we will use the notation $x \#_t y$ instead of $\gamma _{x,y}(t)$ . It is not difficult to see that the points of this geodesic satisfy the following generalized semiparallelogram inequality:

(2.2) $$ \begin{align} \delta^2(x \#_t y, z) \leq (1-t)\delta^2(x, z) + t\delta^2(y, z) - t(1-t)\delta^2(x, y). \end{align} $$

As consequence of this inequality the next result on the convexity of the metric is obtained (see, for example, [30, Corollary 2.5]).

Proposition 2.1. Given four points $a, a^{\prime }, b, b^{\prime } \in M$ , let

$$ \begin{align*}f(t) = \delta(a \#_t a^{\prime}, b \#_t b^{\prime}). \end{align*} $$

Then f is convex on $[0, 1]$ ; that is,

(2.3) $$ \begin{align} \delta(a \#_t a^{\prime}, b \#_t b^{\prime}) \leq (1-t)\delta(a, b) + t\delta(a^{\prime}, b^{\prime}). \end{align} $$

Another very important result in CAT(0) spaces is the so-called Reshetnyak quadruple comparison theorem (see, for example, [30, Proposition 2.4]).

Theorem 2.2. Let $(M, \delta )$ be a Hadamard space. For all $x_1, x_2, x_3, x_4 \in M$ ,

(2.4) $$ \begin{align} \delta^2(x_1, x_3) + \delta^2(x_2, x_4) \leq \delta^2(x_2, x_3) + \delta^2(x_1, x_4) + 2\delta(x_1, x_2)\delta(x_3, x_4). \end{align} $$

2.2 Barycenters in CAT(0) spaces

Let $\mathcal {B}(M)$ be the $\sigma $ -algebra of Borel sets (that is, the smallest $\sigma $ -algebra that contains the open sets). Denote by $\mathcal {P}(M)$ the set of all probability measures on $\mathcal {B}(M)$ with separable support, and for $1 \leq \theta < \infty $ , let $\mathcal {P}^{\theta }(M)$ be the set of those measures $\mu \in \mathcal {P}(M)$ such that

$$ \begin{align*}\int_M \delta^{\theta}(x, y)\,d{\kern-0.7pt}\mu(y) < \infty, \end{align*} $$

for some (and hence for all) $x \in M$ . By means of $\mathcal {P}^{\infty }(M)$ we will denote the set of all measures in $\mathcal {P}(M)$ with bounded support. Finally, given a measure space $(X,\mathfrak {X},\mu )$ and a measurable function $f:X\to M$ , we say that f belongs to $L^p(X,M)$ if the pushforward of $\mu $ by f belongs to $\mathcal {P}^p(M)$ ( $1\leq p\leq \infty $ ).

If $\mu \in \mathcal {P}^2(M)$ , then the usual Cartan definition of barycenter $\beta _\mu $ can be extrapolated to this setting:

$$ \begin{align*}\beta_\mu=\arg\!\min_{z \in M} \int_M \delta^2(z, x)\,d{\kern-0.7pt}\mu(x). \end{align*} $$

The existence of a unique minimizer is guaranteed by the convexity properties of the metric. This definition can be extended to measures in $\mathcal {P}^1(M)$ . Following the ideas of Sturm in [30], given any point $y\in M$ , the barycenter of a measure $\mu \in \mathcal {P}^1(M)$ is defined as the unique minimizer of the functional

$$ \begin{align*}z \mapsto \int_M [\delta^2(z, x) - \delta^2(y, x)]\,d{\kern-0.7pt}\mu(x). \end{align*} $$

Although the functional depends on the point y, it is easy to see that the minimizer is independent of it. Hence, the barycenter is well defined. Moreover, if $\mu \in \mathcal {P}^2(M)$ this definition coincides with Cartan’s definition. Note that in this case the quantity

$$ \begin{align*}\int_M \delta^2(z, x)\,d{\kern-0.7pt}\mu(x) \end{align*} $$

can be thought as a variance. Moreover, the barycenters in this case also satisfy the following inequality known as the variance inequality:

(2.5) $$ \begin{align} \int_{M} [\delta^2(z, x) - \delta^2({\beta}_{\mu}, x)]\,d{\kern-0.7pt}\mu(x) \geq \delta^2(z, {\beta}_{\mu}). \end{align} $$

Therefore, sometimes the barycenter is considered as a nonlinear version of the expectations. For instance, this idea was used by Sturm to extend different result from probability theory to this nonlinear setting (see [30, 29] and the references therein).

Special notation

As we mentioned in the introduction, we will use a special notation in the following two cases. On the one hand, let $(X,\mathfrak {X},\mu )$ be a measure space and let $f:X\to M$ be a measurable function in $L^1(X,M)$ . By means of $\beta _f$ we will denote the barycenter of the pushforward measure $f_*(\mu )$ . On the other hand, given n points $x_1,\ldots ,x_n\in M$ , by means of $\beta (x_1,\ldots ,x_n)$ we will denote the barycenter of the point measure $\mu =\delta _{x_1}+\cdots +\delta _{x_n}$ .

The main issue dealing with barycenters is that they are difficult to compute. The computation of the barycenter of three or more points may be difficult. Although there exists a very rich convex theory in Hadamard space (see, for instance, [3]), sometimes the approximation of the barycenter using convex optimization is not satisfactory. A good example of this situation is as follows.

Example 2.3. (Positive matrices)

Recall that the set of positive invertible matrices $\mathcal {M}_n(\mathbb {C})^+$ is an open cone in the real vector space of self-adjoint matrices $\mathcal {H}(n)$ . In particular, it is a differentiable manifold and the tangent spaces can be identified for simplicity with $\mathcal {H}(n)$ . The manifold $\mathcal {M}_n(\mathbb {C})^+$ can be endowed with a natural Riemannian structure. With respect to this metric structure, if $\alpha :[a,b]\to \mathcal {M}_n(\mathbb {C})^+$ is a piecewise smooth path, its length is defined by

$$ \begin{align*}L(\alpha)=\int_a^b \|\alpha^{-1/2}(t)\alpha'(t)\alpha^{-1/2}(t)\|_2 \,dt, \end{align*} $$

where $\|\cdot \|_2$ denotes the Frobenius or Hilbert–Schmidt norm. In this way, $\mathcal {M}_n(\mathbb {C})^+$ becomes a Riemannian manifold with non-positive curvature, and in particular a CAT(0) space. The geodesic connecting two positive matrices A and B has the following simple expression:

$$ \begin{align*}\gamma_{AB}(t)=A^{1/2}(A^{-1/2}BA^{-1/2})^{t}A^{1/2}\,. \end{align*} $$

So, the barycenter of the measure $\mu =\tfrac 12(\delta _{A}+\delta _{B})$ is given by

$$ \begin{align*}A^{1/2}(A^{-1/2}BA^{-1/2})^{1/2}A^{1/2}. \end{align*} $$

However, if we add an atom to $\mu $ , there is no longer a closed formula for the barycenter (also called the geometric mean in this setting). As a consequence, simple questions such as the monotonicity of the barycenter with respect to the usual order of matrices become difficult. Using convex optimization, it is possible to construct a sequence that approximates the barycenter of a measure. However, that sequence does not contain enough information in order to prove that the barycenter is monotone. This issue, for instance, motivated intensive research with the aim of finding good ways to approximate the barycenters of more than two matrices [7, 17, 20]. The barycenters in this setting have attracted much attention in recent years because of their interesting applications in signal processing (see [6] and the references therein), and gradient or Newton-like optimization methods (see [8, 23]).

2.3 The inductive means

Recall that, given $a \in M^{\mathbb {N}}$ , the inductive means are define as:

$$ \begin{align*} S_1(a) & = a_1, \\ S_{n}(a) & = S_{n-1}(a) \#_{{1}/{n}} a_{n} \quad (n \geq 2). \end{align*} $$

As a consequence of (2.3), we directly get the following result.

Corollary 2.4. Given $a,b \in M^{\mathbb {N}}$ , then

(2.6) $$ \begin{align} \delta(S_n(a), S_n(b)) \leq \frac{1}{n}\sum_{i=1}^{n} \delta(a_i, b_i). \end{align} $$

The next lemma follows from (2.2), and it is a special case of a weighted inequality considered by Lim and Pálfia in [21].

Lemma 2.5. Given $a \in M^{\mathbb {N}}$ and $z\in M$ , for every $k,m \in \mathbb {N}$ ,

$$ \begin{align*} \delta^2(S_{k+m}(a), z) &\leq \ \frac{k}{k+m}\ \delta^2(S_{k}(a), z) + \displaystyle\frac{1}{k+m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(a_{k+j+1}, z)\\ &\quad - \displaystyle\frac{k}{(k+m)^2}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(S_{k+j}(a), a_{k+j+1}). \end{align*} $$

Proof. By the inequality (2.2) applied to $S_{n+1}(a)=S_n(a)\,\#_{n+1}\,(a_{n+1})$ we obtain

$$ \begin{align*} (n+1)\ \delta^2(S_{n+1}(a), z) - n\ \delta^2(S_{n}(a), z) & \leq \delta^2(a_{n+1}, z) - \displaystyle\frac{n}{(n + 1)}\delta^2(S_{n}(a), a_{n+1}). \end{align*} $$

Summing these inequalities from $n=k$ to $n=k+m-1$ , we get that the difference

$$ \begin{align*} (k+m)\ \delta^2(S_{k+m}(a), z) - k\ \delta^2(S_{k}(a), z), \end{align*} $$

obtained from the telescopic sum of the left-hand side, is less than or equal to

$$ \begin{align*} \sum_{j=0}^{m-1}\bigg(\delta^2(a_{k+j+1}, z) - \displaystyle\frac{k+j}{(k+j+1)}\delta^2(S_{k+j}(a), a_{k+j+1})\bigg). \end{align*} $$

Finally, using that $({k+j})/({k+j+1})\geq {k}/({k+m})$ for every $j\in \{0,\ldots ,m-1\}$ , this sum is bounded from above by

$$ \begin{align*} \sum_{j=0}^{m-1}\bigg(\delta^2(a_{k+j+1}, z) - \displaystyle\frac{k}{(k+m)}\delta^2(S_{k+j}(a), a_{k+j+1})\bigg), \end{align*} $$

which completes the proof.

Given a sequence $a \in M^{\mathbb {N}}$ , let $\Delta (a)$ denote the diameter of its image, that is,

$$ \begin{align*}\Delta(a) := \sup_{n,m\in\mathbb{N}} \delta(a_n, a_m). \end{align*} $$

Note that, also by (2.2), $\delta (S_n(a), a_k) \leq \Delta (a)$ for all $n, k \in \mathbb {N}$ .

Lemma 2.6. Given $a\in M^{\mathbb {N}}$ such that $\Delta (a) < \infty $ , we have for all $k,m \in \mathbb {N}$ that

$$ \begin{align*} \frac{1}{m} \sum_{j = 0}^{m-1} \delta^2(S_{k}(a), a_{k+j+1}) \leq \tilde{R}_{m,k} + \frac{1}{m} \sum_{j = 0}^{m-1}\delta^2(S_{k+j}(a), a_{k+j+1}), \end{align*} $$

where $\tilde {R}_{m,k}=(({m^2}/{(k+1)^2}) + 2({m}/({k+1}))) \Delta ^2(a)$ .

Proof. Note that by (2.6) and for all k,

$$ \begin{align*}\delta(S_{k+j}(a), S_{k+j+1}(a)) \leq \frac{1}{k+j+1}\Delta(a). \end{align*} $$

Hence

$$ \begin{align*} \delta(S_{k}(a), a_{k+j+1}) & \leq \delta(S_{k}(a), S_{k+j}(a)) + \delta(S_{k+j}(a), a_{k+j+1}) \\[3pt] & \leq \displaystyle\sum_{h=1}^{j} \displaystyle\frac{1}{k+h} \Delta(a) + \delta(S_{k+j}(a), a_{k+j+1}) \\[3pt] & \leq \displaystyle\frac{j}{k+1} \Delta(a) + \delta(S_{k+j}(a), a_{k+j+1}). \end{align*} $$

Therefore, for every $j\leq m$ ,

$$ \begin{align*} \delta^2(S_{k}(a), a_{k+j+1}) & \leq \bigg(\displaystyle\frac{m^2}{(k+1)^2} + 2\displaystyle\frac{m}{k+1}\bigg) \Delta^2(a) + \delta^2(S_{k+j}(a), a_{k+j+1}), \end{align*} $$

where we have used that $\delta (S_{k+j}(a), a_{k+j+1}) \leq \Delta (a)$ for every $k,j\in \mathbb {N}$ . Summing up these inequalities and dividing by m, we get the desired result.

3 Proof of the main results

3.1 Continuous case

In this section we will prove Theorem 1.3. Recall that, given a function $A: G \rightarrow M$ , we define $a^{\tau } : G \rightarrow M^{\mathbb {N}}$ by

$$ \begin{align*}a^{\tau}(x) :=\{a^{\tau}_j(x)\}_{n\in\mathbb{N}}\quad \textrm{where } a^{\tau}_j(x)=A(\tau^j(x)). \end{align*} $$

The proof is rather long and technical, so we split it into several lemmas and a technical result, which will be combined at the end of the section to provide the proof of Theorem 1.3.

Lemma 3.1. Let $A: G\rightarrow M$ be a continuous function, and let K be any compact subset of M. For each $n\in \mathbb {N}$ , define $F_n :G \times K \rightarrow \mathbb {R}$ by

$$ \begin{align*}F_n(g, x) = \frac{1}{n} \sum_{j = 0}^{n-1} \delta^{2}(a_j^{\tau}(g), x). \end{align*} $$

Then the family $\{F_n\}_{n \in \mathbb {N}}$ is equicontinuous.

Proof. By the triangular inequality, the map $y\mapsto \delta ^2(A(\cdot ),y)$ is continuous from $(K,\delta )$ into the set of real-valued continuous functions defined on G endowed with the uniform norm. Since K is compact, the family $\{\delta ^2(A(\cdot ),x)\}_{x\in K}$ is (uniformly) equicontinuous. Hence, given $\varepsilon>0$ , there exists $\delta>0$ such that if $d_G(g_1,g_2) < \delta $ then

$$ \begin{align*}|\delta^2(A(g_1),x)-\delta^2(A(g_2),x)|<\frac{\varepsilon}{2}, \end{align*} $$

for every $x\in K$ . Since $\tau $ is isometric and $d_G(g_1,g_2) < \delta $ , we get that

$$ \begin{align*}|F_n(g_1, x)-F_n(g_2, x)| = \bigg|\frac{1}{n} \sum_{j = 0}^{n-1} \delta^{2}(a_j^{\tau}(g_1), x)-\delta^{2}(a_j^{\tau}(g_2), x)\bigg|<\frac{\varepsilon}{2}. \end{align*} $$

Let $\Delta $ be the diameter of the set $\,(\mbox {Image}(A)\times K)$ in $M^2$ . Since both sets are compact, $\Delta <\infty $ . So, take $(g_1,x_1)$ and $(g_2,x_2)$ such that $d_G(g_1,g_2)<\delta $ and $\delta (x_1,x_2)<{\varepsilon }/{4\Delta }$ . Then

$$ \begin{align*} |F_n(g_1, x_1)-F_n(g_2, x_2)|&\leq |F_n(g_1, x_1)-F_n(g_1, x_2)|+|F_n(g_1, x_2)-F_n(g_2, x_2)|\\[3pt] &\leq \frac{2\Delta}{n}\sum_{k=0}^{n-1} \delta(x_1,x_2) \ +\ \frac{\varepsilon}{2}<\varepsilon.\\[-3.8pc] \end{align*} $$

Now, as a consequence of the Arzelà–Ascoli and Birkhoff theorems, we get the following proposition.

Proposition 3.2. Let $A:G\to M$ be a continuous function, and K a compact subset of M. Then

$$ \begin{align*}\lim_{n \rightarrow \infty} \frac{1}{n} \sum_{j = 0}^{n-1} \delta^{2}(a_j^{\tau}(g), x) = \int_{G} \delta^2(A(\gamma), x)\,d{\kern-0.6pt}m(\gamma), \end{align*} $$

and the convergence is uniform in $(g, x) \in G \times K$ .

From now on we will fix the continuous function $A:G\to M$ . Let

$$ \begin{align*}\alpha := \min_{x\in M} \int_{G} \delta^2(A(g), x)\,d{\kern-0.6pt}m(g), \end{align*} $$

and ${\beta }_{\mbox{A}}$ is the point where this minimum is attained, that is, ${\beta }_{\mbox{A}}$ is the barycenter of the pushforward by A of the Haar measure in G. Then we obtain the following upper estimate.

Lemma 3.3. For every $\varepsilon> 0$ , there exists $m_0 \in \mathbb {N}$ such that, for all $m \geq m_0$ and for all $k \in \mathbb {N}$ ,

$$ \begin{align*} \delta^2(S_{k+m}(a^{\tau}(g)), {\beta}_{\mbox{A}}) & \leq \frac{k}{k+m}\delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{m}{k+m}(\alpha+\varepsilon) \\[3pt] &\quad - \displaystyle\frac{km}{(k+m)^2}\bigg(\frac{1}{m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(S_{k+j}(a^{\tau}(g)), a^{\tau}_{k+j+1}(g))\bigg). \end{align*} $$

Proof. For every $\varepsilon> 0$ , there exists $m_0 \in \mathbb {N}$ such that for all $m \geq m_0$ ,

$$ \begin{align*}\bigg|\frac{1}{m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(a_{k+j+1}^{\tau}(g), {\beta}_{\mbox{A}}) - \alpha\bigg| < \varepsilon. \end{align*} $$

Note that $m_0$ is independent of k by Proposition 3.2. Now, by Lemma 2.5,

$$ \begin{align*} \delta^2(S_{k+m}(a^{\tau}(g)),{\beta}_{\mbox{A}}) &\leq \frac{k}{k+m}\ \delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{1}{k+m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(a_{k+j+1}^{\tau}(g), {\beta}_{\mbox{A}})\\ & \quad - \displaystyle\frac{k}{(k+m)^2}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(S_{k+j}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g)) \nonumber\\& = \frac{k}{k+m} \ \delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{m}{k+m}\bigg(\frac{1}{m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(a_{k+j+1}^{\tau}(g), {\beta}_{\mbox{A}})\bigg) \\ & \quad - \displaystyle\frac{km}{(k+m)^2}\bigg(\frac{1}{m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(S_{k+j}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g))\bigg) \\ & \leq \frac{k}{k+m}\ \delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{m}{k+m}(\alpha+\varepsilon) \\ & \quad - \displaystyle\frac{km}{(k+m)^2}\bigg(\frac{1}{m}\displaystyle\sum_{j = 0}^{m - 1}\delta^2(S_{k+j}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g))\bigg).\\[-3.8pc] \end{align*} $$

Since $A:G\to M$ is continuous, note that

$$ \begin{align*}C_a:= \sup_{g\in G} \Delta(a^{\tau}(g))<\infty, \end{align*} $$

where, as we have defined before Lemma 2.6, $\Delta (a^{\tau }(g))$ denotes the diameter of the image of the sequence $a^{\tau }(g)$ .

Lemma 3.4. For every $\varepsilon> 0$ , there exists $m_0 \in \mathbb {N}$ such that for all $m \geq m_0$ and for all $k \in \mathbb {N}$ ,

$$ \begin{align*}\delta^2(S_k(a^{\tau}(g)), {\beta}_{\mbox{A}}) - \varepsilon + \alpha - R_{m,k} \leq \frac{1}{m} \sum_{j = 0}^{m-1}\delta^2(S_{k+j}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g)), \end{align*} $$

where $\displaystyle R_{m,k}= ({m^2}/{(k+1)^2}) + 2({m}/({k+1})) C_a^2$ .

Proof. Consider the compact set

$$ \begin{align*}K := \overline{cc\{S_k(a^{\tau}(x)) : k \in \mathbb{N}\}}, \end{align*} $$

where the convex hull is in the geodesic sense. For every $\varepsilon> 0$ , there exists $m_0 \in \mathbb {N}$ such that, for all $m \geq m_0$ , by the variance inequality (2.5) and Proposition 3.2,

$$ \begin{align*} \delta^2(S_k(a^{\tau}(x)), {\beta}_{\mbox{A}}) & \leq \int_G \delta^2(S_k(a^{\tau}(g)), A(\gamma))\,d{\kern-0.6pt}m(\gamma)\ -\ \alpha \\[3pt] &\leq \varepsilon+ \frac{1}{m} \sum_{j = 0}^{m-1} \delta^2(S_{k}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g)) - \alpha. \end{align*} $$

Finally, by Lemma 2.6,

$$ \begin{align*} \delta^2(S_k(a^{\tau}(x)), {\beta}_{\mbox{A}}) & \leq \varepsilon + \frac{1}{m} \sum_{j = 0}^{m-1}\delta^2(S_{k+j}(a^{\tau}(x)), a_{k+j+1}^{\tau}(x))+R_{m,k}- \alpha, \end{align*} $$

where $\displaystyle R_{m,k}=(({m^2}/{(k+1)^2}) + 2({m}/({k+1}))) C_a$ .

Lemma 3.5. Given $\varepsilon> 0$ , there exists $m_0\geq 1$ such that for every $\ell \in \mathbb {N}$ ,

$$ \begin{align*}\delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) \leq \frac{L}{\ell} + \varepsilon, \end{align*} $$

uniformly in $g\in G$ , where $L = \alpha + 3 C_a^2$ .

Proof. Fix $\varepsilon> 0$ . By Lemmas 3.3 and 3.4, there exists $m_0 \geq 1$ such that for all $k \in \mathbb {N}$ ,

$$ \begin{align*} \delta^2(S_{k+m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) & \leq \frac{k}{k+m_0}\delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{m_0}{k+m_0}(\alpha+\varepsilon) \\[3pt] &\quad - \displaystyle\frac{km_0}{(k+m_0)^2}\bigg(\frac{1}{m_0}\displaystyle\sum_{j = 0}^{m_0 - 1}\delta^2(S_{k+j}(a^{\tau}(x)), a_{k+j+1}^{\tau}(x))\bigg) \end{align*} $$

and

$$ \begin{align*} \frac{1}{m_0} \sum_{j = 0}^{m_0-1}\delta^2(S_{k+j}(a^{\tau}(g)), a_{k+j+1}^{\tau}(g)) \geq \delta^2(S_k(a^{\tau}(g)), {\beta}_{\mbox{A}}) - \varepsilon+ \alpha - R_{m_0,k}. \end{align*} $$

Therefore, combining these two inequalities, we obtain

$$ \begin{align*} \delta^2(S_{k+m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) & \leq \frac{k}{k+m_0}\delta^2(S_{k}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{m_0}{k+m_0}(\alpha+\varepsilon) \\[3pt] & \quad - \displaystyle\frac{km_0}{(k+m_0)^2}(\delta^2(S_k(a^{\tau}(g)), {\beta}_{\mbox{A}}) - \varepsilon + \alpha - R_{m_0,k}). \end{align*} $$

Consider now the particular case where $k=\ell m_0$ . Since $\displaystyle R_{m_0,\ell m_0} \leq ({3}/{\ell }) C_a^2$ , we get

(3.1) $$ \begin{align} \delta^2(S_{(\ell+1)m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) & \leq \frac{\ell}{\ell+1}\delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) + \displaystyle\frac{1}{l+1}(\alpha+\varepsilon)\nonumber \\[3pt] & \quad -\frac{\ell}{(\ell+1)^2}(\delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) - \varepsilon + \alpha - R_{m_0,\ell m_0})\nonumber\\[3pt] &\leq \frac{\ell^2\ \delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) +(2\ell+1)\varepsilon+\alpha+3C_a^2}{(\ell+1)^2}. \end{align} $$

Using this recursive inequality, the result follows by induction on $\ell $ . Indeed, if $\ell =1$ then

$$ \begin{align*}\delta^2(S_{m_0}(a^{\tau}(g)),{\beta}_{\mbox{A}})\leq C_a^2 \leq L. \end{align*} $$

On the other hand, if we assume that the result holds for some $\ell \geq 1$ , that is,

$$ \begin{align*}\delta^2(S_{\ell m_0}(a^{\tau}(x)), g) \leq \frac{L}{\ell} + \varepsilon, \end{align*} $$

then, combining this inequality with (3.1), we have that

$$ \begin{align*} \delta^2(S_{(\ell+1)m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) &\leq \frac{\ell L+ \ell^2\varepsilon +(2\ell+1)\varepsilon+\alpha+3C_a^2}{(\ell+1)^2}=\frac{L}{\ell+1}+\varepsilon.\\[-3pc] \end{align*} $$

Now we are ready to prove the ergodic formula for continuous functions.

Proof of Theorem 1.3

Given $\varepsilon> 0$ , by Lemma 3.5, there exists $m_0 \in \mathbb {N}$ such that

$$ \begin{align*}\delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) \leq \frac{L}{\ell} + \frac{\varepsilon^2}{8}, \end{align*} $$

for every $\ell \in \mathbb {N}$ . Take $\ell _0 \in \mathbb {N}$ such that for all $\ell \geq \ell _0$ ,

(3.2) $$ \begin{align} \delta^2(S_{\ell m_0}(a^{\tau}(g)), {\beta}_{\mbox{A}}) \leq \frac{\varepsilon^2}{4}. \end{align} $$

Let $n=\ell m_0+d$ such that $\ell \geq \ell _0$ and $d\in \{1,\ldots , m_0-1\}$ . Since $x \#_{t} x = x$ for all $x \in M$ , using Corollary 2.4 with the sequences

$$ \begin{align*} &(\ a^\tau_1(g),\ldots,a^\tau_{\ell m_0}(g), \underbrace{S_{\ell m_0}(a^{\tau}(g)),\ldots, S_{\ell m_0}(a^{\tau}(g))}_{\mbox{d times}}\ )\\ \text{and}\\ &(\ a^\tau_1(g),\ldots,a^\tau_{\ell m_0}(g), \ a^\tau_{\ell m_0+1}(g)\ ,\ \ldots\ ,\ a^\tau_{\ell m_0+d}(g)\ ) \end{align*} $$

we get

$$ \begin{align*} \delta(S_{\ell m_0}(a^{\tau}(g)), S_{\ell m_0+d}(a^{\tau}(g))) & \leq \frac{1}{\ell m_0 + d}\sum_{j = 1}^{d} \delta(S_{\ell m_0}(a^{\tau}(g)),a^\tau_{\ell m_0+j}(g)). \end{align*} $$

Now, taking into account that $\delta(S_{\ell m_0}(a^{\tau}(g)),a^\tau_{\ell m_0+j}(g))\leq C_a$ for every $j\in\{1,\ldots, m_0-1\}$ , we obtain that

$$ \begin{align*} \delta(S_{\ell m_0}(a^{\tau}(g)), S_{\ell m_0+d}(a^{\tau}(g))) & \leq \frac{d}{\ell m_0 + d} C_a \leq\frac{1}{\ell} C_a\xrightarrow[k \rightarrow \infty]{} 0. \end{align*} $$

Combining this with (3.2) we conclude that, for n big enough, $\delta(S_{n}(a^{\tau}(g)), {\beta }_{\mbox{A}})<\varepsilon$ .

3.2 Preparation for the $L^{1}$ case

The natural framework for the ergodic theorem is $L^1$ . In this section we will firstly prove Theorem 1.4, which is the main result of this paper.

The strategy of the proof involves constructing good approximations by continuous functions, and obtaining the result for $L^1$ functions as a consequence of the theorem for continuous functions (Theorem 1.3 above). So, the first questions that arise are: what does good approximation mean and what should we require of the approximation in order to get the $L^1$ case as a limit of the continuous case? The next two lemmas contain the clues to answer these two questions. The first lemma can be found as [30, Theorem 6.3], and it is often called fundamental contraction property. For the sake of completeness we include a simple proof of this fact.

Lemma 3.6. Let $(\Omega ,\mathcal {B}, P)$ be a probability space, and $A, B \in L^1(X, M)$ . If

$$ \begin{align*} {\beta}_{\mbox{A}} & = \arg\!\min_{z \in M} \int_{\Omega} [\delta^2(A(\omega), z) - \delta^2(A(\omega), y)]\,d{\kern-1pt}P(\omega), \\[3pt] {\beta}_{\mbox {B}} & = \arg\!\min_{z \in M} \int_{\Omega} [\delta^2(B(\omega), z) - \delta^2(B(\omega), y)]\,d{\kern-1pt}P(\omega), \end{align*} $$

then

(3.3) $$ \begin{align} \delta({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}}) \leq \int_\Omega \delta(A(\omega), B(\omega))\,d{\kern-1pt}P(\omega). \end{align} $$

Remark 3.7. Recall that the definition of ${\beta }_{\mbox{A}}$ (respectively, ${\beta }_{\mbox {B}}$ ) does not depend on the chosen $y \in M$ .

Proof. By the variance inequality (2.5) we get

$$ \begin{align*} \delta^2({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}}) & \leq \int_\Omega \delta^2({\beta}_{\mbox{A}}, B(\omega)) - \delta^2({\beta}_{\mbox {B}}, B(\omega))\,d{\kern-1pt}P(\omega), \\[3pt] \delta^2({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}}) & \leq \int_\Omega \delta^2({\beta}_{\mbox {B}}, A(\omega)) - \delta^2({\beta}_{\mbox{A}}, A(\omega))\,d{\kern-1pt}P(\omega), \end{align*} $$

and the combination of these two inequalities leads to

$$ \begin{align*} 2\delta^2({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}}) & \leq \int_\Omega \delta^2({\beta}_{\mbox{A}}, B(\omega)) + \delta^2({\beta}_{\mbox {B}}, A(\omega))\\[3pt] & \quad - \delta^2({\beta}_{\mbox {B}}, B(\omega)) - \delta^2({\beta}_{\mbox{A}}, A(\omega))\,d{\kern-1pt}P(\omega). \end{align*} $$

Finally, using the Reshetnyak quadruple comparison theorem (Theorem 2.2), we obtain

$$ \begin{align*} 2\delta^2({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}}) & \leq 2\delta({\beta}_{\mbox{A}}, {\beta}_{\mbox {B}})\ \int_\Omega \delta(A(\omega), B(\omega))\,d{\kern-1pt}P(\omega), \end{align*} $$

which is, after some algebraic simplification, the desired result.

Lemma 3.8. Let $A, B \in L^1(G, M)$ . Given $\varepsilon>0$ , for almost every $g\in G$ there exists $n_0$ , which may depend on g, such that

(3.4) $$ \begin{align} \delta(S_{n}(a^{\tau}(g)), S_{n}(b^{\tau}(g))) \leq \varepsilon + \int_{G} \delta(A(g), B(g))\,d{\kern-0.6pt}m(g), \end{align} $$

provided $n\geq n_0$ .

Proof. Indeed, by Corollary 2.4,

$$ \begin{align*}\delta(S_n(a^{\tau}(g)), S_n(b^{\tau}(g))) \leq \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta(a_k^{\tau}(g), b_k^{\tau}(g)) = \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta(A(\tau^k(g)), B(\tau^k(g))), \end{align*} $$

and therefore, the lemma follows from the Birkhoff ergodic theorem.

3.3 Good approximation by continuous functions

The previous two lemmas indicate that we need a kind of $L^1$ approximation. More precisely, given $A\in L^1(G,M)$ and $\varepsilon>0$ , we are looking for a continuous function $A_\varepsilon :G\to M$ such that

$$ \begin{align*}\int_G \delta(A(g),A_\varepsilon(g))\,d{\kern-0.6pt}m(g)<\varepsilon. \end{align*} $$

In some cases there exists an underlying finite-dimensional vector space. This is the case, for instance, when M is the set of (strictly) positive matrices, or more generally, when M is a Riemannian manifold with non-positive curvature. In these cases, the function $A_\varepsilon $ can be constructed by using mollifiers. This idea was used by Karcher in [16]. In the general case, we can use a similar idea.

Given $\eta>0$ , let $U_\eta $ be a neighborhood of the identity of G so that $m(U_\eta )<\eta $ , whose diameter is also less than $\eta $ . Fix any $y\in M$ , and define

(3.5) $$ \begin{align} A_\eta(g_0)=\arg\!\min_{z\in M} \int_{U_\eta} [\delta^2(z, A(g+g_0)) - \delta^2(y, A(g+g_0)) ]\,d{\kern-0.6pt}m(g). \end{align} $$

Equivalently, $A_\eta (g_0)$ is the barycenter of the pushforward by A of the Haar measure restricted to $g_0+U_\eta $ . This definition follows the idea of mollifiers, replacing the arithmetic mean by the average induced by barycenters. We will prove that, as in the case of usual mollifiers, these continuous functions provide good approximation in $L^1$ (Theorem 3.12 below). With this aim, we first prove the following lemma.

Lemma 3.9. Let $A \in L^p(G, M)$ where $1 \leq p < \infty $ . The function defined by $\varphi : G \rightarrow [0,+\infty )$ by

$$ \begin{align*}\varphi(h) = \int_{G} \delta^p(A(g), A(g + h))\,d{\kern-0.6pt}m(g) \end{align*} $$

is a continuous function.

Proof. Fix $z_0 \in M$ , and define the measure

$$ \begin{align*}\nu(B) := \int_{B} \delta^p(A(g), z_0)\,d{\kern-0.6pt}m(g) \end{align*} $$

on the Borel sets of G. By definition, $\nu $ is absolutely continuous with respect to the Haar measure m. In consequence, given $\varepsilon> 0$ , there exists $\eta> 0$ , such that, whenever a Borel set B satisfies

$$ \begin{align*}\int_{B} \,d{\kern-0.6pt}m(g) < \eta, \end{align*} $$

the inequality

(3.6) $$ \begin{align} \nu(B) = \int_{B} \delta^p(A(g), z_0)\,d{\kern-0.6pt}m(g) < \frac{\varepsilon}{2^{p+1}} \end{align} $$

holds. By the Lusin theorem [11, Theorem 7.5.2], there is a compact set $C_{\eta } \subset G$ such that $m(C_{\eta }) \geq 1 - \eta /2$ and the restriction of A to $C_{\eta }$ is (uniformly) continuous.

Since m is a Haar measure, it is enough to prove the continuity of $\varphi $ at the identity. With this aim in mind, take a neighborhood of the identity U so that whenever $g_1,g_2\in C_\eta $ satisfy that $g_1-g_2\in U$ , we have

$$ \begin{align*}\delta^p(A(g_1), A(g_2)) \leq \frac{\varepsilon}{2}. \end{align*} $$

Given $h\in U$ , define $\Omega := C_{\eta } \cap (C_{\eta } + h)$ , and $\Omega ^c :=G \setminus \Omega $ . Then

$$ \begin{align*} \int_G \delta^p(A(g), A(g+ h))\,d{\kern-0.6pt}m(g) & \leq \int_{\Omega}\frac{\varepsilon}{2}\,d{\kern-0.6pt}m(g) +\int_{\Omega^c} \delta^p(A(g), A(g + h))\,d{\kern-0.6pt}m(g) \\[3pt] & \leq \frac{\varepsilon}{2}+ \int_{\Omega^c} \delta^p(A(g), A(g+h))\,d{\kern-0.6pt}m(g) \nonumber\\& \leq \frac{\varepsilon}{2} + \int_{\Omega^c} [\delta(A(g), z_0) + \delta(A(g + h), z_0)]^p\, d{\kern-0.6pt}m(g) \\[3pt] & \leq \frac{\varepsilon}{2} + 2^{p} \int_{\Omega^c} \delta^p(A(g), z_0)\,d{\kern-0.6pt}m(g), \end{align*} $$

where in the last identity we have used that m is shift invariant. Since $|\Omega ^c|<\eta $ we obtain that

$$ \begin{align*} \int_G \delta^p(A(g), A(g+ h))\,d{\kern-0.6pt}m(g) & \leq \frac{\varepsilon}{2}+ \frac{\varepsilon}{2}=\varepsilon.\\[-3.4pc] \end{align*} $$

Corollary 3.10. For every $\eta>0$ , the functions $A_\eta $ are continuous.

Proof. Indeed, by Lemma 3.6

$$ \begin{align*} \delta(A_\eta(h_1),A_\eta(h_2))&\leq\frac{1}{m(U_\eta)}\int_{U_\eta} \delta(A(g+h_1),A(g+h_2))\,d{\kern-0.6pt}m(g)\\[2pt] &\leq\frac{1}{m(U_\eta)}\int_G \delta(A(g+h_1),A(g+h_2))\,d{\kern-0.6pt}m(g)\\[2pt] &\leq\frac{1}{m(U_\eta)}\int_G \delta[\,A(g),A(g+(h_2-h_1))\,]\,d{\kern-0.6pt}m(g). \end{align*} $$

So the continuity of $A_\eta $ is a consequence of the continuity of $\varphi $ at the identity.

The map $A\mapsto A_\varepsilon $ has the following useful continuity property.

Lemma 3.11. Let $A, B \in L^1(G, M)$ , and $\eta> 0$ . For every $\varepsilon>0$ , there exists $\rho>0$ such that if

$$ \begin{align*}\int_G \delta(A(g), B(g))\,d{\kern-0.6pt}m(g) \leq \rho, \end{align*} $$

then the corresponding continuous functions $A_\eta $ and $B_\eta $ satisfy that

$$ \begin{align*}\max_{g \in G} \, \delta(A_{\eta}(g), B_{\eta}(g)) \leq \varepsilon. \end{align*} $$

Proof. Indeed, given $\varepsilon>0$ , take $\rho =m(U_{\eta })\varepsilon $ . Then, by Lemma 3.6,

$$ \begin{align*} \delta(A_{\eta}(g), B_{\eta}(g)) & \leq \frac{1}{| U_{\eta} | }\int_{U_{\eta}} \delta(A(g + h), B(g + h))\,d{\kern-0.6pt}m(h)\\[2pt] & \leq \frac{1}{| U_{\eta} | }\int_{G} \delta(A(h), B(h))\,d{\kern-0.6pt}m(h) \leq \varepsilon, \end{align*} $$

for all $g \in G$ .

We arrive at the main result on approximation.

Proposition 3.12. Given a function $A\in L^1(G,M)$ , if $A_\eta $ are the continuous functions defined by (3.5) then

$$ \begin{align*}\lim_{\eta\to0^+}\int_G\delta(A(g),A_\eta(g))\,d{\kern-0.6pt}m(g) = 0. \end{align*} $$

Proof. First, assume that $A\in L^2(G,M)$ . In this case, by the variance inequality, the inequality

$$ \begin{align*}\delta^2(A(g), A_{\eta}(g)) \leq \frac{1}{| U_{\eta} | }\int_{U_{\eta}} \delta^2(A(g), A(g + h))\,d{\kern-0.6pt}m(h) \end{align*} $$

holds. So, using Fubini’s theorem, we obtain

$$ \begin{align*} \int_G\delta^2(A(g),A_\eta(g))\,d{\kern-0.6pt}m(g) &\leq \frac{1}{| U_{\eta} | }\int_{U_{\eta}} \int_G \delta^2(A(g), A(g + h))\,d{\kern-0.6pt}m(g)\,d{\kern-0.6pt}m(h)\\[3pt] &= \frac{1}{| U_{\eta} | }\int_{U_{\eta}} \varphi (h) \,d{\kern-0.6pt}m(h). \end{align*} $$

By Lemma 3.9, the function $\varphi $ is continuous. In consequence, if e denotes the identity of G, then

$$ \begin{align*}\lim_{\eta\to 0^+} \frac{1}{| U_{\eta} | }\int_{U_{\eta}} \varphi (h) \,d{\kern-0.6pt}m(h) = \varphi (e)=0. \end{align*} $$

This proves the result for functions in $L^2(G,M)$ since, by Jensen’s inequality,

$$ \begin{align*}\ \ \int_G\delta(A(g),A_\eta(g))\,d{\kern-0.6pt}m(g)\leq \bigg( \int_G\delta^2(A(g),A_\eta(g))\,d{\kern-0.6pt}m(g) \bigg)^{1/2}. \end{align*} $$

Now consider a general $A \in L^1(G, M)$ . Fix $z_0\in M$ , and for each natural number N define the truncations

$$ \begin{align*}A^{(N)}(g) := \begin{cases} A(g) & \mbox{if }\delta(A(g), z_0) < N, \\ z_0 & \mbox{if }\delta(A(g), z_0) \geq N. \end{cases} \end{align*} $$

For each N we have that $A^{(N)}\in L^1(G,M)\cap L^\infty (G,M)$ , and therefore it also belongs to $L^2(G,M)$ . On the other hand, since the function defined on G by $g\mapsto \delta (A(g),z_0)$ is integrable, we have that

(3.7) $$ \begin{align} \int_G \delta(A(g),A^{(N)}(g))\,d{\kern-0.6pt}m(g)= \int_{\{g:\,\delta(A(g), z_0) \geq N\}} \delta(A(g),z_0)\,d{\kern-0.6pt}m(g) \xrightarrow[N\to \infty]{}0. \end{align} $$

So, if $A_\eta $ and $A^{(N)}_\eta $ are the continuous functions associated to A and $A^{(N)}$ respectively, then

$$ \begin{align*} \int_G \delta(A(g),A_\eta(g))\,d{\kern-0.6pt}m(g) &\leq \int_G \delta(A(g),A^{(N)}(g))\,d{\kern-0.6pt}m(g) \\[3pt] &\quad + \int_G \delta(A^{(N)}(g),A^{(N)}_\eta(g))\,d{\kern-0.6pt}m(g) \\[3pt] &\quad + \int_G \delta(A^{(N)}_\eta(g),A_\eta(g))\,d{\kern-0.6pt}m(g). \end{align*} $$

Note that each term of the right-hand side tends to zero: the first by (3.7), the second by the $L^2$ case done in the first part, and the last by Lemma 3.11.

3.4 The $L^{1}$ case and almost everywhere convergence

Let $\varepsilon>0$ . For each $k\in \mathbb {N}$ , let $A_k$ be a continuous function such that

$$ \begin{align*}\int_G \delta(A(g),A_k(g))\,d{\kern-0.6pt}m(g)\leq\frac{1}{k}. \end{align*} $$

By Lemma 3.8, we can take a set of measure zero $N\subseteq G$ such that if we take $g\in G\setminus N$ and $k\in \mathbb {N}$ , there exists $n_0$ , which may depend on g and k, such that

$$ \begin{align*}\delta(S_{n}(a^{\tau}(g)), S_{n}(a^{\tau}_{(k)}(g))) \leq \frac{\varepsilon}{4} + \int_{G} \delta(A(g), A_k(g))\,d{\kern-0.6pt}m(g), \end{align*} $$

provided $n\geq n_0$ . In this expression, $a_{(k)}^{\tau }$ is the sequence defined in terms of $A_k$ and $\tau $ as in (1.6). Fix $g\in G\setminus N$ . Taking k so that $1/k<\varepsilon /4$ , we get that

$$ \begin{align*}\delta(S_{n}(a^{\tau}(g)), S_{n}(a^{\tau}_{(k)}(g))) \leq \frac{\varepsilon}{2}, \end{align*} $$

for every $n\geq n_0$ . By Lemma 3.6, we also have that $ \delta ({\beta }_{\mbox{A}}, {\beta }_{\mbox {A_k}}) \leq {\varepsilon }/{4}, $ where

$$ \begin{align*} {\beta}_{\mbox{A}} & = \arg\!\min_{z \in M} \int_G [\delta^2(A(g), z) - \delta^2(A(g), y)]\,d{\kern-0.6pt}m(g), \\ {\beta}_{\mbox{A_k}} & = \arg\!\min_{z \in M} \int_G [\delta^2(A_k(g), z) - \delta^2(A_k(g), y)]\,d{\kern-0.6pt}m(g). \end{align*} $$

Finally, by Theorem 1.3, there exists $n_1\geq 1$ such that, for every $n\geq n_1$ ,

$$ \begin{align*}\delta(S_{n}(a_{(k)}^{\tau}(g),{\beta}_{\mbox{A_k}})\leq\frac{\varepsilon}{4}. \end{align*} $$

Combining all these inequalities, we obtain that

$$ \begin{align*} \delta(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})&\leq \delta(S_{n}(a^{\tau}(g)), S_{n}(a^{\tau}_{(k)}(g)))\\[3pt] &\quad +\delta(S_{n}(a^{\tau}_{(k)}(g)),{\beta}_{\mbox{A_k}})+\delta({\beta}_{\mbox{A_k}}, {\beta}_{\mbox{A}})\leq\varepsilon, \end{align*} $$

which concludes the proof.

3.5 The $L^p$ results

We conclude this section by proving the $L^p$ ergodic theorems.

Theorem 3.13. Let $1 \leq p < \infty $ and $A\in L^p(G, M)$ . Then

(3.8) $$ \begin{align} \lim_{n\to\infty } \int_{G} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) = 0. \end{align} $$

Proof. Let us define the following measure on the Borel sets of G:

$$ \begin{align*}\nu(B) := \int_{B} \delta^p(A(g), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g). \end{align*} $$

By definition, $\nu $ is absolutely continuous with respect to the Haar measure m. In consequence, given $\varepsilon> 0$ , there exists $\eta> 0$ such that, whenever a Borel set B satisfies

$$ \begin{align*}\int_{B} \,d{\kern-0.6pt}m(g) < \eta, \end{align*} $$

we have that

(3.9) $$ \begin{align} \nu(B) = \int_{B} \delta^p(A(g), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) < \frac{\varepsilon}{2}. \end{align} $$

By Egoroff’s theorem, as

$$ \begin{align*}\delta^p(S_n(a^{\tau}(g)), {\beta}_{\mbox{A}}) \xrightarrow[n \rightarrow \infty]{} 0\end{align*} $$

converge almost everywhere on a finite measure space, there exists a set $C_{\eta } \subset G$ with $m(C_{\eta }) < \eta $ such that

(3.10) $$ \begin{align} \delta^p(S_n(a^{\tau}(g)), {\beta}_{\mbox{A}}) \xrightarrow[n \rightarrow \infty]{} 0 \end{align} $$

uniformly on $G \setminus C_\eta .$

On the other hand,

$$ \begin{align*}\delta(S_n(a^{\tau}(g)), {\beta}_{\mbox{A}}) \leq \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta(a_k^{\tau}(g), {\beta}_{\mbox{A}}) = \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta(A(\tau^k(g)), {\beta}_{\mbox{A}}), \end{align*} $$

Therefore, by Jensen’s inequality,

(3.11) $$ \begin{align} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}}) & \leq \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta^p(A(\tau^k(g)), {\beta}_{\mbox{A}}). \end{align} $$

Now, there exists $n_0 \in \mathbb {N}$ such that, for all $n \geq n_0$ ,

$$ \begin{align*}\int_{G \setminus C_\eta} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) < \frac{\varepsilon}{2}, \end{align*} $$

as a consequence of (3.10). Therefore

$$ \begin{align*} \int_{G} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) & = \int_{G \setminus C_\eta} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g)\\[3pt] &\quad + \int_{C_\eta} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) \\[3pt] &= \frac{\varepsilon}{2} + \int_{C_\eta} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g). \end{align*} $$

On the other hand, taking integral over $C_\eta $ in (3.11), we obtain

$$ \begin{align*} \int_{C_\eta} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) &\leq \int_{C_\eta} \displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n-1} \delta^p(A(\tau^k(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) \\[3pt] & = \sum_{k = 0}^{n-1}\displaystyle\frac{1}{n} \int_{C_\eta} \delta^p(A(\tau^k(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g). \end{align*} $$

Since $\displaystyle \int _{C_{\eta }} \,d{\kern-0.6pt}m(g) < \eta , $ by (3.9),

$$ \begin{align*}\nu(C_{\eta}) = \int_{C_{\eta}} \delta^p(A(g), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) < \frac{\varepsilon}{2}. \end{align*} $$

So, for all $n \in \mathbb {N}$ ,

$$ \begin{align*}\displaystyle\sum_{k = 0}^{n-1}\displaystyle\frac{1}{n} \int_{C_\eta} \delta^p(A(\tau^k(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) < \frac{\varepsilon}{2}. \end{align*} $$

Finally, combining this two bounds, given $\varepsilon $ , there exists $n_0 \in \mathbb {N}$ such that, for all $n \geq n_0$ ,

$$ \begin{align*}\int_{G} \delta^p(S_{n}(a^{\tau}(g)), {\beta}_{\mbox{A}})\,d{\kern-0.6pt}m(g) < \varepsilon, \end{align*} $$

which concludes the proof.