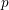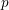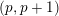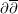1 Introduction
Local stabilities of complex structures are important topics in deformation theory of complex structures. We will prove local stabilities of
![]() $p$
-Kähler structures with the
$p$
-Kähler structures with the
![]() $(p,p+1)$
th mild
$(p,p+1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma by the power series method, initiated by Kodaira–Nirenberg–Spencer [Reference Kodaira, Nirenberg and SpencerKNS58] and Kuranishi [Reference KuranishiKur64].
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma by the power series method, initiated by Kodaira–Nirenberg–Spencer [Reference Kodaira, Nirenberg and SpencerKNS58] and Kuranishi [Reference KuranishiKur64].
Theorem 1.1. For any positive integer
![]() $p\leqslant n-1$
, any small differentiable deformation
$p\leqslant n-1$
, any small differentiable deformation
![]() $X_{t}$
of an
$X_{t}$
of an
![]() $n$
-dimensional
$n$
-dimensional
![]() $p$
-Kähler manifold
$p$
-Kähler manifold
![]() $X_{0}$
satisfying the
$X_{0}$
satisfying the
![]() $(p,p\,+\,1)$
th mild
$(p,p\,+\,1)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is still
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is still
![]() $p$
-Kählerian.
$p$
-Kählerian.
Here the
![]() $(p,p\,+\,1)th$
mild
$(p,p\,+\,1)th$
mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma for a complex manifold means that each
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma for a complex manifold means that each
![]() $\overline{\unicode[STIX]{x2202}}$
-closed
$\overline{\unicode[STIX]{x2202}}$
-closed
![]() $\unicode[STIX]{x2202}$
-exact
$\unicode[STIX]{x2202}$
-exact
![]() $(p,p+1)$
-form on this manifold is
$(p,p+1)$
-form on this manifold is
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact, which is a new notion generalizing the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact, which is a new notion generalizing the
![]() $(n-1,n)$
th one first introduced in [Reference Rao, Wan and ZhaoRWZ16]. A complex manifold is
$(n-1,n)$
th one first introduced in [Reference Rao, Wan and ZhaoRWZ16]. A complex manifold is
![]() $p$
-Kählerian if it admits a
$p$
-Kählerian if it admits a
![]() $p$
-Kähler form, i.e., a
$p$
-Kähler form, i.e., a
![]() $d$
-closed transverse
$d$
-closed transverse
![]() $(p,p)$
-form as in Definition 2.5.
$(p,p)$
-form as in Definition 2.5.
Recall the fact that each
![]() $n$
-dimensional complex manifold is
$n$
-dimensional complex manifold is
![]() $n$
-Kählerian and the following two basic properties of
$n$
-Kählerian and the following two basic properties of
![]() $p$
-Kählerian structures.
$p$
-Kählerian structures.
Lemma 1.2 ([Reference Alessandrini and AndreattaAA87, Proposition 1.15] and also [Reference Rao, Wan and ZhaoRWZ16, Corollary 4.6]).
A complex manifold
![]() $M$
is
$M$
is
![]() $1$
-Kähler if and only if
$1$
-Kähler if and only if
![]() $M$
is Kähler; an
$M$
is Kähler; an
![]() $n$
-dimensional complex manifold
$n$
-dimensional complex manifold
![]() $M$
is
$M$
is
![]() $(n-1)$
-Kähler if and only if
$(n-1)$
-Kähler if and only if
![]() $M$
is balanced, i.e., it admits a real positive
$M$
is balanced, i.e., it admits a real positive
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\unicode[STIX]{x1D714}$
, satisfying
$\unicode[STIX]{x1D714}$
, satisfying
Thus, we obtain the following as a direct corollary of Theorem 1.1.
Corollary 1.3. Let
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
be a differentiable family of compact complex manifolds.
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
be a differentiable family of compact complex manifolds.
(i) [Reference Kodaira and SpencerKS60, Theorem 15] If a fiber
 $X_{0}:=\unicode[STIX]{x1D70B}^{-1}(t_{0})$
admits a Kähler metric, then, for a sufficiently small neighborhood
$X_{0}:=\unicode[STIX]{x1D70B}^{-1}(t_{0})$
admits a Kähler metric, then, for a sufficiently small neighborhood
 $U$
of
$U$
of
 $t_{0}$
on
$t_{0}$
on
 $B$
, the fiber
$B$
, the fiber
 $X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
over any point
$X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
over any point
 $t\in U$
still admits a Kähler metric, which depends smoothly on
$t\in U$
still admits a Kähler metric, which depends smoothly on
 $t$
and coincides for
$t$
and coincides for
 $t=t_{0}$
with the given Kähler metric on
$t=t_{0}$
with the given Kähler metric on
 $X_{0}$
.
$X_{0}$
.(ii) [Reference Rao, Wan and ZhaoRWZ16, Theorem 1.5] Let
 $X_{0}$
be a balanced manifold of complex dimension
$X_{0}$
be a balanced manifold of complex dimension
 $n$
, satisfying the
$n$
, satisfying the
 $(n-1,n)$
th mild
$(n-1,n)$
th mild
 $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Then
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Then
 $X_{t}$
also admits a balanced metric for
$X_{t}$
also admits a balanced metric for
 $t$
small.
$t$
small.
The first assertion of Corollary 1.3 is the fundamental Kodaira–Spencer’s local stability theorem of Kähler structure, and motivates the second assertion of Corollary 1.3 and many other related works on local stabilities of complex structures in [Reference Fu and YauFY11, Reference VoisinVoi02, Reference WuWu06, Reference Angella and UgarteAU17, Reference Angella and UgarteAU16]. The counter-example of Alessandrini and Bassanelli [Reference Alessandrini and BassanelliAB90] tells us that the result in the second assertion of Corollary 1.3 does not necessarily hold without the
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma assumption.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma assumption.
In § 2, we will study the difference between the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and other versions of
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and other versions of
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata in the roles of Theorem 1.1, and the modification stability of the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata in the roles of Theorem 1.1, and the modification stability of the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by Proposition 3.14, which provides us with more classes of complex manifolds to admit the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by Proposition 3.14, which provides us with more classes of complex manifolds to admit the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Here the (standard)
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Here the (standard)
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma refers to: for every pure-type
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma refers to: for every pure-type
![]() $d$
-closed form on a complex manifold, the properties of
$d$
-closed form on a complex manifold, the properties of
![]() $d$
-exactness,
$d$
-exactness,
![]() $\unicode[STIX]{x2202}$
-exactness,
$\unicode[STIX]{x2202}$
-exactness,
![]() $\bar{\unicode[STIX]{x2202}}$
-exactness and
$\bar{\unicode[STIX]{x2202}}$
-exactness and
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-exactness are equivalent, while its variants are described by § 3.1. Obviously, one has the implication hierarchy on a complex
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-exactness are equivalent, while its variants are described by § 3.1. Obviously, one has the implication hierarchy on a complex
![]() $n$
-dimensional manifold for any positive integer
$n$
-dimensional manifold for any positive integer
![]() $p\leqslant n-1$
:
$p\leqslant n-1$
:
For
![]() $p=n-1$
, the implication hierarchy is strict: [Reference Angella and UgarteAU17, Example 4.10] is one example satisfying the strong
$p=n-1$
, the implication hierarchy is strict: [Reference Angella and UgarteAU17, Example 4.10] is one example satisfying the strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but not the standard one; the nilmanifold endowed with a left-invariant abelian complex structure of dimension
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but not the standard one; the nilmanifold endowed with a left-invariant abelian complex structure of dimension
![]() $2n$
or a left-invariant non-nilpotent balanced complex structure of complex dimension
$2n$
or a left-invariant non-nilpotent balanced complex structure of complex dimension
![]() $3$
by [Reference Rao, Wan and ZhaoRWZ16, Proposition 3.8 and Corollary 3.4] and [Reference Angella and UgarteAU16, Proposition 2.9] distinguishes the mild and strong
$3$
by [Reference Rao, Wan and ZhaoRWZ16, Proposition 3.8 and Corollary 3.4] and [Reference Angella and UgarteAU16, Proposition 2.9] distinguishes the mild and strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata; and the weak
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata; and the weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds on the complex three-dimensional Iwasawa manifold [Reference Rao, Wan and ZhaoRWZ16, Example 3.7] but the mild one fails. Moreover, we construct a new ten-dimensional balanced nilmanifold in Example 3.8 for the strictness of implication 2, which satisfies the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds on the complex three-dimensional Iwasawa manifold [Reference Rao, Wan and ZhaoRWZ16, Example 3.7] but the mild one fails. Moreover, we construct a new ten-dimensional balanced nilmanifold in Example 3.8 for the strictness of implication 2, which satisfies the
![]() $(4,5)$
th mild but not strong
$(4,5)$
th mild but not strong
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma and also the deformation variance of the
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma and also the deformation variance of the
![]() $(4,4)$
th Bott–Chern numbers. Motivated by these, it is natural to ask the following question.
$(4,4)$
th Bott–Chern numbers. Motivated by these, it is natural to ask the following question.
Question 1.4. Find an
![]() $n$
-dimensional complex manifold or in particular a
$n$
-dimensional complex manifold or in particular a
![]() $p$
-Kähler manifold such that one of implications (1), (2), (3) is strict for each positive integer
$p$
-Kähler manifold such that one of implications (1), (2), (3) is strict for each positive integer
![]() $p<n-1$
.
$p<n-1$
.
Now let us describe our approach to proving local stability of
![]() $p$
-Kähler structures. An application of Kuranishi’s completeness theorem [Reference KuranishiKur64] reduces our power series proof to the Kuranishi family
$p$
-Kähler structures. An application of Kuranishi’s completeness theorem [Reference KuranishiKur64] reduces our power series proof to the Kuranishi family
![]() $\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
, that is, we will construct a natural
$\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
, that is, we will construct a natural
![]() $p$
-Kähler extension
$p$
-Kähler extension
![]() $\tilde{\unicode[STIX]{x1D714}}_{t}$
of the
$\tilde{\unicode[STIX]{x1D714}}_{t}$
of the
![]() $p$
-Kähler form
$p$
-Kähler form
![]() $\unicode[STIX]{x1D714}_{0}$
on
$\unicode[STIX]{x1D714}_{0}$
on
![]() $X_{0}$
, such that
$X_{0}$
, such that
![]() $\tilde{\unicode[STIX]{x1D714}}_{t}$
is a
$\tilde{\unicode[STIX]{x1D714}}_{t}$
is a
![]() $p$
-Kähler form on the general fiber
$p$
-Kähler form on the general fiber
![]() $\unicode[STIX]{x1D71B}^{-1}(t)=X_{t}$
. More precisely, the extension is given by
$\unicode[STIX]{x1D71B}^{-1}(t)=X_{t}$
. More precisely, the extension is given by
where
![]() $\unicode[STIX]{x1D714}(t)$
is a family of smooth
$\unicode[STIX]{x1D714}(t)$
is a family of smooth
![]() $(p,p)$
-forms to be constructed on
$(p,p)$
-forms to be constructed on
![]() $X_{0}$
, depending smoothly on
$X_{0}$
, depending smoothly on
![]() $t$
, and
$t$
, and
![]() $\unicode[STIX]{x1D714}(0)=\unicode[STIX]{x1D714}_{0}$
. Here
$\unicode[STIX]{x1D714}(0)=\unicode[STIX]{x1D714}_{0}$
. Here
![]() $\unicode[STIX]{x1D711}$
is the family of Beltrami differentials induced by the Kuranishi family. The extension map
$\unicode[STIX]{x1D711}$
is the family of Beltrami differentials induced by the Kuranishi family. The extension map
![]() $e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}$
is first introduced in [Reference Zhao and RaoZR15, Reference Rao and ZhaoRZ18] and given in Definition 2.2.
$e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}$
is first introduced in [Reference Zhao and RaoZR15, Reference Rao and ZhaoRZ18] and given in Definition 2.2.
This method is developed in [Reference Liu, Sun and YauLSY09, Reference SunSun12, Reference Sun and YauSY11, Reference Liu, Rao and YangLRY15, Reference Zhao and RaoZR13, Reference Zhao and RaoZR15, Reference Rao and ZhaoRZ18, Reference Rao, Wan and ZhaoRWZ16, Reference Liu, Rao and WanLRW17]. However, we have to solve many more equations in system (11) here than in the balanced case [Reference Rao, Wan and ZhaoRWZ16]; those in system (11) are much more difficult in essence. Fortunately, we are able to reduce this complicated system to that with only two equations as in (15) by comparing the types of the forms in the system and the orders in the induction simultaneously. This crucial consideration is also important in the solution of this system.
In this approach, we will use the following observation crucially.
Proposition 1.5 [Reference Rao, Wan and ZhaoRWZ16, Proposition 4.12].
Let
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
be a differentiable family of compact complex
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
be a differentiable family of compact complex
![]() $n$
-dimensional manifolds and
$n$
-dimensional manifolds and
![]() $\unicode[STIX]{x1D6FA}_{t}$
a family of real
$\unicode[STIX]{x1D6FA}_{t}$
a family of real
![]() $(p,p)$
-forms with
$(p,p)$
-forms with
![]() $p<n$
, depending smoothly on
$p<n$
, depending smoothly on
![]() $t$
. Assume that
$t$
. Assume that
![]() $\unicode[STIX]{x1D6FA}_{0}$
is a transverse
$\unicode[STIX]{x1D6FA}_{0}$
is a transverse
![]() $(p,p)$
-form on
$(p,p)$
-form on
![]() $X_{0}$
. Then
$X_{0}$
. Then
![]() $\unicode[STIX]{x1D6FA}_{t}$
is also transverse on
$\unicode[STIX]{x1D6FA}_{t}$
is also transverse on
![]() $X_{t}$
for small
$X_{t}$
for small
![]() $t$
.
$t$
.
This proposition actually shows that any smooth real extension of a transverse
![]() $(p,p)$
-form is still transverse. So the obstruction to extend a
$(p,p)$
-form is still transverse. So the obstruction to extend a
![]() $d$
-closed transverse
$d$
-closed transverse
![]() $(p,p)$
-form on a compact complex manifold lies in the
$(p,p)$
-form on a compact complex manifold lies in the
![]() $d$
-closedness, to be resolved in Theorem 1.6 in a more general setting. The detailed proof of main Theorem 1.1 is given in § 4.
$d$
-closedness, to be resolved in Theorem 1.6 in a more general setting. The detailed proof of main Theorem 1.1 is given in § 4.
Theorem 1.6 (= Theorem 4.1).
If
![]() $X_{0}$
satisfies the
$X_{0}$
satisfies the
![]() $(p,q\,+\,1)$
th and
$(p,q\,+\,1)$
th and
![]() $(q,p\,+\,1)$
th mild
$(q,p\,+\,1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, then there is a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, then there is a
![]() $d$
-closed
$d$
-closed
![]() $(p,q)$
-form
$(p,q)$
-form
![]() $\unicode[STIX]{x1D6FA}(t)$
on
$\unicode[STIX]{x1D6FA}(t)$
on
![]() $X_{t}$
depending smoothly on
$X_{t}$
depending smoothly on
![]() $t$
with
$t$
with
![]() $\unicode[STIX]{x1D6FA}(0)=\unicode[STIX]{x1D6FA}_{0}$
for any
$\unicode[STIX]{x1D6FA}(0)=\unicode[STIX]{x1D6FA}_{0}$
for any
![]() $d$
-closed
$d$
-closed
![]() $\unicode[STIX]{x1D6FA}_{0}\in A^{p,q}(X_{0})$
.
$\unicode[STIX]{x1D6FA}_{0}\in A^{p,q}(X_{0})$
.
Remark 1.7. The case
![]() $p=q=n-1$
of Theorem 1.6 implies that the dimension of the space of
$p=q=n-1$
of Theorem 1.6 implies that the dimension of the space of
![]() $d$
-closed left-invariant
$d$
-closed left-invariant
![]() $(n-1,n-1)$
-forms on a
$(n-1,n-1)$
-forms on a
![]() $2n$
-dimensional nilmanifold endowed with a left-invariant abelian complex structure is deformation invariant, where the
$2n$
-dimensional nilmanifold endowed with a left-invariant abelian complex structure is deformation invariant, where the
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma holds from [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.4].
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma holds from [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.4].
In § 5, inspired by [Reference Rao and ZhaoRZ18], we will use Theorem 1.6 to prove a result on deformation invariance of Bott–Chern numbers in Theorem 5.1.
This paper will follow the notation in [Reference Liu, Rao and YangLRY15, Reference Rao and ZhaoRZ18, Reference Rao, Wan and ZhaoRWZ16]. All manifolds in this paper are assumed to be compact complex
![]() $n$
-dimensional manifolds. The symbol
$n$
-dimensional manifolds. The symbol
![]() $A^{p,q}(X,E)$
stands for the space of the holomorphic vector bundle
$A^{p,q}(X,E)$
stands for the space of the holomorphic vector bundle
![]() $E$
-valued
$E$
-valued
![]() $(p,q)$
-forms on a complex manifold
$(p,q)$
-forms on a complex manifold
![]() $X$
. We will always consider the differentiable family
$X$
. We will always consider the differentiable family
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of compact complex
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of compact complex
![]() $n$
-dimensional manifolds over a sufficiently small domain in
$n$
-dimensional manifolds over a sufficiently small domain in
![]() $\mathbb{R}^{k}$
with the reference fiber
$\mathbb{R}^{k}$
with the reference fiber
![]() $X_{0}:=\unicode[STIX]{x1D70B}^{-1}(0)$
for the reference point
$X_{0}:=\unicode[STIX]{x1D70B}^{-1}(0)$
for the reference point
![]() $0$
and the general fibers
$0$
and the general fibers
![]() $X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
.
$X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
.
2 Deformation and
 $p$
-Kähler structure
$p$
-Kähler structure
This section is to state some basics of analytic deformation theory of complex structures and the notion of
![]() $p$
-Kähler structure.
$p$
-Kähler structure.
2.1 Deformation theory
For the holomorphic family of compact complex manifolds, we adopt the definition [Reference KodairaKod86, Definition 2.8]; while for the differentiable one, we adopt the following definition.
Definition 2.1 [Reference KodairaKod86, Definition 4.1].
Let
![]() ${\mathcal{X}}$
be a differentiable manifold,
${\mathcal{X}}$
be a differentiable manifold,
![]() $B$
a domain of
$B$
a domain of
![]() $\mathbb{R}^{k}$
and
$\mathbb{R}^{k}$
and
![]() $\unicode[STIX]{x1D70B}$
a smooth map of
$\unicode[STIX]{x1D70B}$
a smooth map of
![]() ${\mathcal{X}}$
onto
${\mathcal{X}}$
onto
![]() $B$
. By a differentiable family of
$B$
. By a differentiable family of
![]() $n$
-dimensional compact complex manifolds we mean the triple
$n$
-dimensional compact complex manifolds we mean the triple
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
satisfying the following conditions.
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
satisfying the following conditions.
(i) The rank of the Jacobian matrix of
 $\unicode[STIX]{x1D70B}$
is equal to
$\unicode[STIX]{x1D70B}$
is equal to
 $k$
at every point of
$k$
at every point of
 ${\mathcal{X}}$
.
${\mathcal{X}}$
.(ii) For each point
 $t\in B$
,
$t\in B$
,
 $\unicode[STIX]{x1D70B}^{-1}(t)$
is a compact connected subset of
$\unicode[STIX]{x1D70B}^{-1}(t)$
is a compact connected subset of
 ${\mathcal{X}}$
.
${\mathcal{X}}$
.(iii) The fiber
 $\unicode[STIX]{x1D70B}^{-1}(t)$
is the underlying differentiable manifold of the
$\unicode[STIX]{x1D70B}^{-1}(t)$
is the underlying differentiable manifold of the
 $n$
-dimensional compact complex manifold
$n$
-dimensional compact complex manifold
 $X_{t}$
associated to each
$X_{t}$
associated to each
 $t\in B$
.
$t\in B$
.(iv) There is a locally finite open covering
 $\{{\mathcal{U}}_{j}\mid j=1,2,\ldots \}$
of
$\{{\mathcal{U}}_{j}\mid j=1,2,\ldots \}$
of
 ${\mathcal{X}}$
and complex-valued smooth functions
${\mathcal{X}}$
and complex-valued smooth functions
 $\unicode[STIX]{x1D701}_{j}^{1}(p),\ldots ,\unicode[STIX]{x1D701}_{j}^{n}(p)$
, defined on
$\unicode[STIX]{x1D701}_{j}^{1}(p),\ldots ,\unicode[STIX]{x1D701}_{j}^{n}(p)$
, defined on
 ${\mathcal{U}}_{j}$
such that for each
${\mathcal{U}}_{j}$
such that for each
 $t$
, form a system of local holomorphic coordinates of
$t$
, form a system of local holomorphic coordinates of $$\begin{eqnarray}\{p\rightarrow (\unicode[STIX]{x1D701}_{j}^{1}(p),\ldots ,\unicode[STIX]{x1D701}_{j}^{n}(p))\mid {\mathcal{U}}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(t)\neq \emptyset \}\end{eqnarray}$$
$$\begin{eqnarray}\{p\rightarrow (\unicode[STIX]{x1D701}_{j}^{1}(p),\ldots ,\unicode[STIX]{x1D701}_{j}^{n}(p))\mid {\mathcal{U}}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(t)\neq \emptyset \}\end{eqnarray}$$
 $X_{t}$
.
$X_{t}$
.
Beltrami differentials play an important role in deformation theory. A Beltrami differential on
![]() $X$
, generally denoted by
$X$
, generally denoted by
![]() $\unicode[STIX]{x1D719}$
, is an element in
$\unicode[STIX]{x1D719}$
, is an element in
![]() $A^{0,1}(X,T_{X}^{1,0})$
, where
$A^{0,1}(X,T_{X}^{1,0})$
, where
![]() $T_{X}^{1,0}$
is the holomorphic tangent bundle of
$T_{X}^{1,0}$
is the holomorphic tangent bundle of
![]() $X$
. Then
$X$
. Then
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D719}}$
or
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D719}}$
or
![]() $\unicode[STIX]{x1D719}\lrcorner$
denotes the contraction operator with respect to
$\unicode[STIX]{x1D719}\lrcorner$
denotes the contraction operator with respect to
![]() $\unicode[STIX]{x1D719}\in A^{0,1}(X,T_{X}^{1,0})$
or other analogous vector-valued complex differential forms alternatively if there is no confusion. We also use the convention
$\unicode[STIX]{x1D719}\in A^{0,1}(X,T_{X}^{1,0})$
or other analogous vector-valued complex differential forms alternatively if there is no confusion. We also use the convention
where
![]() $\spadesuit ^{k}$
denotes
$\spadesuit ^{k}$
denotes
![]() $k$
-time action of the operator
$k$
-time action of the operator
![]() $\spadesuit$
. As the dimension of
$\spadesuit$
. As the dimension of
![]() $X$
is finite, the summation in the above formulation is always finite.
$X$
is finite, the summation in the above formulation is always finite.
We will always consider the differentiable family
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of compact complex
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of compact complex
![]() $n$
-dimensional manifolds over a sufficiently small domain in
$n$
-dimensional manifolds over a sufficiently small domain in
![]() $\mathbb{R}^{k}$
with the reference fiber
$\mathbb{R}^{k}$
with the reference fiber
![]() $X_{0}:=\unicode[STIX]{x1D70B}^{-1}(0)$
and the general fibers
$X_{0}:=\unicode[STIX]{x1D70B}^{-1}(0)$
and the general fibers
![]() $X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
. For simplicity we set
$X_{t}:=\unicode[STIX]{x1D70B}^{-1}(t)$
. For simplicity we set
![]() $k=1$
. Denote by
$k=1$
. Denote by
![]() $\unicode[STIX]{x1D701}:=(\unicode[STIX]{x1D701}_{j}^{\unicode[STIX]{x1D6FC}}(z,t))$
the holomorphic coordinates of
$\unicode[STIX]{x1D701}:=(\unicode[STIX]{x1D701}_{j}^{\unicode[STIX]{x1D6FC}}(z,t))$
the holomorphic coordinates of
![]() $X_{t}$
induced by the family with the holomorphic coordinates
$X_{t}$
induced by the family with the holomorphic coordinates
![]() $z:=(z^{i})$
of
$z:=(z^{i})$
of
![]() $X_{0}$
, under a coordinate covering
$X_{0}$
, under a coordinate covering
![]() $\{{\mathcal{U}}_{j}\}$
of
$\{{\mathcal{U}}_{j}\}$
of
![]() ${\mathcal{X}}$
, when
${\mathcal{X}}$
, when
![]() $t$
is assumed to be fixed, as the standard notions in deformation theory described at the beginning of [Reference Morrow and KodairaMK71, ch. 4]. This family induces a canonical differentiable family of integrable Beltrami differentials on
$t$
is assumed to be fixed, as the standard notions in deformation theory described at the beginning of [Reference Morrow and KodairaMK71, ch. 4]. This family induces a canonical differentiable family of integrable Beltrami differentials on
![]() $X_{0}$
, denoted by
$X_{0}$
, denoted by
![]() $\unicode[STIX]{x1D711}(z,t)$
,
$\unicode[STIX]{x1D711}(z,t)$
,
![]() $\unicode[STIX]{x1D711}(t)$
and
$\unicode[STIX]{x1D711}(t)$
and
![]() $\unicode[STIX]{x1D711}$
interchangeably.
$\unicode[STIX]{x1D711}$
interchangeably.
In [Reference Zhao and RaoZR15, Reference Zhao and RaoZR13], the first and third authors introduced an extension map
to play an important role in this paper.
Definition 2.2. For
![]() $s\in A^{p,q}(X_{0})$
, we define
$s\in A^{p,q}(X_{0})$
, we define
where
![]() $s$
is locally written as
$s$
is locally written as
and the operators
![]() $e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}}$
,
$e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}}$
,
![]() $e^{\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}$
follow convention (4). It is easy to check that this map is a real linear isomorphism as in [Reference Rao and ZhaoRZ18, Lemma 2.8].
$e^{\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}$
follow convention (4). It is easy to check that this map is a real linear isomorphism as in [Reference Rao and ZhaoRZ18, Lemma 2.8].
The following proposition is crucial in this paper.
Proposition 2.3 [Reference Liu, Rao and YangLRY15, Theorem 3.4], [Reference Rao and ZhaoRZ18, Proposition 2.2].
Let
![]() $\unicode[STIX]{x1D719}\in A^{0,1}(X,T_{X}^{1,0})$
on a complex manifold
$\unicode[STIX]{x1D719}\in A^{0,1}(X,T_{X}^{1,0})$
on a complex manifold
![]() $X$
. Then on the space
$X$
. Then on the space
![]() $A^{\ast ,\ast }(X)$
,
$A^{\ast ,\ast }(X)$
,
From the proof of Proposition 2.3, we see that (5) is a natural generalization of the Tian–Todorov lemma [Reference TianTia87, Reference TodorovTod89], whose variants appeared in [Reference FriedmanFri91, Reference Barannikov and KontsevichBK98, Reference LiLi05, Reference Liu, Sun and YauLSY09, Reference ClemensCle05] and also [Reference Liu and RaoLR12, Reference Liu, Rao and YangLRY15] for vector bundle valued forms.
Lemma 2.4. For
![]() $\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}\in A^{0,1}(X,T_{X}^{1,0})$
and
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}\in A^{0,1}(X,T_{X}^{1,0})$
and
![]() $\unicode[STIX]{x1D6FC}\in A^{\ast ,\ast }(X)$
on an
$\unicode[STIX]{x1D6FC}\in A^{\ast ,\ast }(X)$
on an
![]() $n$
-dimensional complex manifold
$n$
-dimensional complex manifold
![]() $X$
,
$X$
,
where
for
![]() $\unicode[STIX]{x1D711}=\sum _{i}\unicode[STIX]{x1D711}^{i}\otimes \unicode[STIX]{x2202}_{i}$
and
$\unicode[STIX]{x1D711}=\sum _{i}\unicode[STIX]{x1D711}^{i}\otimes \unicode[STIX]{x2202}_{i}$
and
![]() $\unicode[STIX]{x1D713}=\sum _{i}\unicode[STIX]{x1D713}^{i}\otimes \unicode[STIX]{x2202}_{i}$
.
$\unicode[STIX]{x1D713}=\sum _{i}\unicode[STIX]{x1D713}^{i}\otimes \unicode[STIX]{x2202}_{i}$
.
2.2 The
 $p$
-Kähler structures
$p$
-Kähler structures
Let
![]() $V$
be a complex
$V$
be a complex
![]() $n$
-dimensional vector space with its dual space
$n$
-dimensional vector space with its dual space
![]() $V^{\ast }$
, i.e., the space of complex linear functionals over
$V^{\ast }$
, i.e., the space of complex linear functionals over
![]() $V$
. Denote the complexified space of the exterior
$V$
. Denote the complexified space of the exterior
![]() $m$
-vectors of
$m$
-vectors of
![]() $V^{\ast }$
by
$V^{\ast }$
by
![]() $\bigwedge _{\mathbb{C}}^{m}V^{\ast }$
, which admits a natural direct sum decomposition
$\bigwedge _{\mathbb{C}}^{m}V^{\ast }$
, which admits a natural direct sum decomposition
where
![]() $\bigwedge ^{r,s}V^{\ast }$
denotes the complex vector space of
$\bigwedge ^{r,s}V^{\ast }$
denotes the complex vector space of
![]() $(r,s)$
-forms on
$(r,s)$
-forms on
![]() $V^{\ast }$
. The case
$V^{\ast }$
. The case
![]() $m=1$
exactly reads
$m=1$
exactly reads
where the natural isomorphism
![]() $V^{\ast }\cong \bigwedge ^{1,0}V^{\ast }$
is used. Let
$V^{\ast }\cong \bigwedge ^{1,0}V^{\ast }$
is used. Let
![]() $q\in \{1,\ldots ,n\}$
and
$q\in \{1,\ldots ,n\}$
and
![]() $p=n-q$
. Clearly, the complex dimension
$p=n-q$
. Clearly, the complex dimension
![]() $N$
of
$N$
of
![]() $\bigwedge ^{q,0}V^{\ast }$
is equal to the combination number
$\bigwedge ^{q,0}V^{\ast }$
is equal to the combination number
![]() $C_{n}^{q}$
. After a basis
$C_{n}^{q}$
. After a basis
![]() $\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
of the complex vector space
$\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
of the complex vector space
![]() $\bigwedge ^{q,0}V^{\ast }$
is fixed, the canonical Plücker embedding as in [Reference Griffiths and HarrisGH78, p. 209] is given by
$\bigwedge ^{q,0}V^{\ast }$
is fixed, the canonical Plücker embedding as in [Reference Griffiths and HarrisGH78, p. 209] is given by
 $$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D70C}: & G(q,n) & {\hookrightarrow} & \displaystyle \mathbb{P}\biggl(\bigwedge ^{q,0}V^{\ast }\biggr)\\ & \unicode[STIX]{x1D6EC} & \mapsto & [\ldots ,\unicode[STIX]{x1D6EC}_{i},\ldots ].\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D70C}: & G(q,n) & {\hookrightarrow} & \displaystyle \mathbb{P}\biggl(\bigwedge ^{q,0}V^{\ast }\biggr)\\ & \unicode[STIX]{x1D6EC} & \mapsto & [\ldots ,\unicode[STIX]{x1D6EC}_{i},\ldots ].\end{array}\end{eqnarray}$$
Here
![]() $G(q,n)$
denotes the Grassmannian of
$G(q,n)$
denotes the Grassmannian of
![]() $q$
-planes in the vector space
$q$
-planes in the vector space
![]() $V^{\ast }$
and
$V^{\ast }$
and
![]() $\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
is the projectivization of
$\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
is the projectivization of
![]() $\bigwedge ^{q,0}V^{\ast }$
. A
$\bigwedge ^{q,0}V^{\ast }$
. A
![]() $q$
-plane in
$q$
-plane in
![]() $V^{\ast }$
can be represented by a decomposable
$V^{\ast }$
can be represented by a decomposable
![]() $(q,0)$
-form
$(q,0)$
-form
![]() $\unicode[STIX]{x1D6EC}\in \bigwedge ^{q,0}V^{\ast }$
up to a nonzero complex number, and
$\unicode[STIX]{x1D6EC}\in \bigwedge ^{q,0}V^{\ast }$
up to a nonzero complex number, and
![]() $\{\unicode[STIX]{x1D6EC}_{i}\}_{i=1}^{N}$
are exactly the coordinates of
$\{\unicode[STIX]{x1D6EC}_{i}\}_{i=1}^{N}$
are exactly the coordinates of
![]() $\unicode[STIX]{x1D6EC}$
under the fixed basis
$\unicode[STIX]{x1D6EC}$
under the fixed basis
![]() $\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
. Decomposable
$\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
. Decomposable
![]() $(q,0)$
-forms are those forms in
$(q,0)$
-forms are those forms in
![]() $\bigwedge ^{q,0}V^{\ast }$
that can be expressed as
$\bigwedge ^{q,0}V^{\ast }$
that can be expressed as
![]() $\unicode[STIX]{x1D6FE}_{1}\bigwedge \cdots \bigwedge \unicode[STIX]{x1D6FE}_{q}$
with
$\unicode[STIX]{x1D6FE}_{1}\bigwedge \cdots \bigwedge \unicode[STIX]{x1D6FE}_{q}$
with
![]() $\unicode[STIX]{x1D6FE}_{i}\in V^{\ast }\cong \bigwedge ^{1,0}V^{\ast }$
for
$\unicode[STIX]{x1D6FE}_{i}\in V^{\ast }\cong \bigwedge ^{1,0}V^{\ast }$
for
![]() $1\leqslant i\leqslant q$
. Set
$1\leqslant i\leqslant q$
. Set
to be the codimension of
![]() $\unicode[STIX]{x1D70C}(G(q,n))$
in
$\unicode[STIX]{x1D70C}(G(q,n))$
in
![]() $\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
, whose locus characterizes the decomposable
$\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
, whose locus characterizes the decomposable
![]() $(q,0)$
-forms in
$(q,0)$
-forms in
![]() $\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
.
$\mathbb{P}(\bigwedge ^{q,0}V^{\ast })$
.
Now we list notation for several types of positivity and refer the readers to [Reference Harvey and KnappHK74, Reference HarveyHar75, Reference DemaillyDem12] for more details. A
![]() $(q,q)$
-form
$(q,q)$
-form
![]() $\unicode[STIX]{x1D6E9}$
in
$\unicode[STIX]{x1D6E9}$
in
![]() $\bigwedge ^{q,q}V^{\ast }$
is defined to be strictly positive (respectively, positive) if
$\bigwedge ^{q,q}V^{\ast }$
is defined to be strictly positive (respectively, positive) if
where
![]() $\unicode[STIX]{x1D6E9}_{ij}$
is a positive (respectively, semi-positive) hermitian matrix of size
$\unicode[STIX]{x1D6E9}_{ij}$
is a positive (respectively, semi-positive) hermitian matrix of size
![]() $N\times N$
with
$N\times N$
with
![]() $N=C_{n}^{q}$
under the basis
$N=C_{n}^{q}$
under the basis
![]() $\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
of the complex vector space
$\{\unicode[STIX]{x1D6FD}_{i}\}_{i=1}^{N}$
of the complex vector space
![]() $\bigwedge ^{q,0}V^{\ast }$
and
$\bigwedge ^{q,0}V^{\ast }$
and
![]() $\unicode[STIX]{x1D70E}_{q}$
is defined to be the constant
$\unicode[STIX]{x1D70E}_{q}$
is defined to be the constant
![]() $2^{-q}(\sqrt{-1})^{q^{2}}$
. According to this definition, the fundamental form of a hermitian metric on a complex manifold is actually a strictly positive
$2^{-q}(\sqrt{-1})^{q^{2}}$
. According to this definition, the fundamental form of a hermitian metric on a complex manifold is actually a strictly positive
![]() $(1,1)$
-form everywhere. A
$(1,1)$
-form everywhere. A
![]() $(p,p)$
-form
$(p,p)$
-form
![]() $\unicode[STIX]{x1D6E4}\in \bigwedge ^{p,p}V^{\ast }$
is called weakly positive if the volume form
$\unicode[STIX]{x1D6E4}\in \bigwedge ^{p,p}V^{\ast }$
is called weakly positive if the volume form
is positive for every nonzero decomposable
![]() $(q,0)$
-form
$(q,0)$
-form
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $V^{\ast }$
, while a
$V^{\ast }$
, while a
![]() $(q,q)$
-form
$(q,q)$
-form
![]() $\unicode[STIX]{x1D6F6}\in \bigwedge ^{q,q}V^{\ast }$
is said to be strongly positive if
$\unicode[STIX]{x1D6F6}\in \bigwedge ^{q,q}V^{\ast }$
is said to be strongly positive if
![]() $\unicode[STIX]{x1D6F6}$
is a convex combination
$\unicode[STIX]{x1D6F6}$
is a convex combination
where
![]() $\unicode[STIX]{x1D6FC}_{s,i}\in V^{\ast }$
and
$\unicode[STIX]{x1D6FC}_{s,i}\in V^{\ast }$
and
![]() $\unicode[STIX]{x1D6FE}_{s}\geqslant 0$
. As shown in [Reference DemaillyDem12, ch. III.§ 1.A], the sets of weakly positive and strongly positive forms are closed convex cones, and by definition, the weakly positive cone is dual to the strongly positive cone via the pairing
$\unicode[STIX]{x1D6FE}_{s}\geqslant 0$
. As shown in [Reference DemaillyDem12, ch. III.§ 1.A], the sets of weakly positive and strongly positive forms are closed convex cones, and by definition, the weakly positive cone is dual to the strongly positive cone via the pairing
Then all weakly positive forms are real. An element
![]() $\unicode[STIX]{x1D6EF}$
in
$\unicode[STIX]{x1D6EF}$
in
![]() $\bigwedge ^{p,p}V^{\ast }$
is called transverse, if the volume form
$\bigwedge ^{p,p}V^{\ast }$
is called transverse, if the volume form
is strictly positive for every nonzero decomposable
![]() $(q,0)$
-form
$(q,0)$
-form
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $V^{\ast }$
. There exist many names for this terminology and we refer to [Reference Alessandrini and BassanelliAB91, Appendix] for a list.
$V^{\ast }$
. There exist many names for this terminology and we refer to [Reference Alessandrini and BassanelliAB91, Appendix] for a list.
This positivity notation on complex vector spaces can be extended pointwise to complex differential forms on a complex manifold. Let
![]() $M$
be an
$M$
be an
![]() $n$
-dimensional complex manifold. Then we have the following definition.
$n$
-dimensional complex manifold. Then we have the following definition.
Definition 2.5 ([Reference Alessandrini and AndreattaAA87, Definition 1.11], for example).
Let
![]() $p$
be an integer,
$p$
be an integer,
![]() $1\leqslant p\leqslant n$
. Then
$1\leqslant p\leqslant n$
. Then
![]() $M$
is called a
$M$
is called a
![]() $p$
-Kähler manifold if there exists a
$p$
-Kähler manifold if there exists a
![]() $p$
-Kähler form, that is a
$p$
-Kähler form, that is a
![]() $d$
-closed transverse
$d$
-closed transverse
![]() $(p,p)$
-form on
$(p,p)$
-form on
![]() $M$
.
$M$
.
The readers are referred to [Reference SullivanSul76] for more related concepts (such as differential form transversal to the cone structure on a real differentiable manifold) to
![]() $p$
-Kähler structures.
$p$
-Kähler structures.
3 Relevance to mild
 $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and modification
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and modification
We will introduce the so-called
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma and its relevance, and also present its modification stability on compact complex manifolds.
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma and its relevance, and also present its modification stability on compact complex manifolds.
3.1 The
 $(p,q)$
th mild
$(p,q)$
th mild
 $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and its relevance
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and its relevance
This subsection is to study various
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata related to local stabilities of complex structures, their properties, differences and roles there in some special case. More details can be found in [Reference Rao, Wan and ZhaoRWZ16, §3.1] and the references therein.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata related to local stabilities of complex structures, their properties, differences and roles there in some special case. More details can be found in [Reference Rao, Wan and ZhaoRWZ16, §3.1] and the references therein.
Now we introduce a new notion.
Definition 3.1. We say a complex manifold
![]() $X$
satisfies the
$X$
satisfies the
![]() $(p,q)th$
mild
$(p,q)th$
mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma if for any complex differential
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma if for any complex differential
![]() $(p-1,q)$
-form
$(p-1,q)$
-form
![]() $\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D709}$
with
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D709}=0$
on
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D709}=0$
on
![]() $X$
, there exists a
$X$
, there exists a
![]() $(p-1,q-1)$
-form
$(p-1,q-1)$
-form
![]() $\unicode[STIX]{x1D703}$
such that
$\unicode[STIX]{x1D703}$
such that
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}=\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D703}=\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
.
So we can state our main theorem.
Theorem 3.2. For any positive integer
![]() $p\leqslant n-1$
, any small differentiable deformation
$p\leqslant n-1$
, any small differentiable deformation
![]() $X_{t}$
of a
$X_{t}$
of a
![]() $p$
-Kähler manifold
$p$
-Kähler manifold
![]() $X_{0}$
satisfying the
$X_{0}$
satisfying the
![]() $(p,p+1)$
th mild
$(p,p+1)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is still
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is still
![]() $p$
-Kählerian.
$p$
-Kählerian.
According to Lemma 1.2, Theorem 3.2 unifies the local stabilities of Kähler structures [Reference Kodaira and SpencerKS60, Theorem 15] and balanced structures under the
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma [Reference Rao, Wan and ZhaoRWZ16, Theorem 1.5], which is an obvious generalization of Wu’s result [Reference WuWu06, Theorem 5.13] that the balanced structure is stable under small deformation when the
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma [Reference Rao, Wan and ZhaoRWZ16, Theorem 1.5], which is an obvious generalization of Wu’s result [Reference WuWu06, Theorem 5.13] that the balanced structure is stable under small deformation when the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds, to
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds, to
![]() $p$
-Kähler mild
$p$
-Kähler mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-structures for
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-structures for
![]() $1\leqslant p\leqslant n-1$
.
$1\leqslant p\leqslant n-1$
.
Let
![]() $X$
be a compact complex manifold of complex dimension
$X$
be a compact complex manifold of complex dimension
![]() $n$
with the following commutative diagram.
$n$
with the following commutative diagram.

Recall that Dolbeault cohomology groups
![]() $H_{\overline{\unicode[STIX]{x2202}}}^{\bullet ,\bullet }(X)$
of
$H_{\overline{\unicode[STIX]{x2202}}}^{\bullet ,\bullet }(X)$
of
![]() $X$
are defined by
$X$
are defined by
with
![]() $H_{\unicode[STIX]{x2202}}^{\bullet ,\bullet }(X)$
similarly defined, while Bott–Chern and Aeppli cohomology groups are defined as
$H_{\unicode[STIX]{x2202}}^{\bullet ,\bullet }(X)$
similarly defined, while Bott–Chern and Aeppli cohomology groups are defined as
respectively. The dimensions of
![]() $H_{dR}^{p+q}(X)$
,
$H_{dR}^{p+q}(X)$
,
![]() $H_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
,
$H_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
,
![]() $H_{\text{BC}}^{p,q}(X)$
,
$H_{\text{BC}}^{p,q}(X)$
,
![]() $H_{\text{A}}^{p,q}(X)$
and
$H_{\text{A}}^{p,q}(X)$
and
![]() $H_{\unicode[STIX]{x2202}}^{p,q}(X)$
over
$H_{\unicode[STIX]{x2202}}^{p,q}(X)$
over
![]() $\mathbb{C}$
are denoted by
$\mathbb{C}$
are denoted by
![]() $b_{p+q}(X)$
,
$b_{p+q}(X)$
,
![]() $h_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
,
$h_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
,
![]() $h_{\text{BC}}^{p,q}(X)$
,
$h_{\text{BC}}^{p,q}(X)$
,
![]() $h_{\text{A}}^{p,q}(X)$
and
$h_{\text{A}}^{p,q}(X)$
and
![]() $h_{\unicode[STIX]{x2202}}^{p,q}(X)$
, respectively, and the first four of them are usually called
$h_{\unicode[STIX]{x2202}}^{p,q}(X)$
, respectively, and the first four of them are usually called
![]() $(p\,+\,q)$
th Betti numbers,
$(p\,+\,q)$
th Betti numbers,
![]() $(p,q)$
-Hodge numbers, Bott–Chern numbers and Aeppli numbers, respectively. So the (standard)
$(p,q)$
-Hodge numbers, Bott–Chern numbers and Aeppli numbers, respectively. So the (standard)
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is equivalent to the injectivities of the mappings
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is equivalent to the injectivities of the mappings
for all
![]() $p,q$
, or to the isomorphisms of all the maps in diagram (6) by [Reference Deligne, Griffiths, Morgan and SullivanDGMS75, Remark 5.16].
$p,q$
, or to the isomorphisms of all the maps in diagram (6) by [Reference Deligne, Griffiths, Morgan and SullivanDGMS75, Remark 5.16].
Notice that the
![]() $(1,2)$
th mild
$(1,2)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is different from the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma is different from the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a complex manifold. It is easy to see that the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a complex manifold. It is easy to see that the
![]() $(1,2)$
th mild
$(1,2)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma amounts to the injectivity of the mapping
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma amounts to the injectivity of the mapping
Then by [Reference Angella and KasuyaAK17, Tables 5 and 6 in Appendix A] and [Reference KasuyaKas13, the case
![]() $B$
in Example 1], we have the following example.
$B$
in Example 1], we have the following example.
Example 3.3 [Reference Rao, Wan and ZhaoRWZ16, Example 1.7].
Let
![]() $X$
be the manifold in case (ii) of the completely-solvable Nakamura manifold as given in [Reference Angella and KasuyaAK17, Example 3.1]. Then the manifold
$X$
be the manifold in case (ii) of the completely-solvable Nakamura manifold as given in [Reference Angella and KasuyaAK17, Example 3.1]. Then the manifold
![]() $X$
satisfies the
$X$
satisfies the
![]() $(1,2)$
th mild
$(1,2)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, but not the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, but not the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
There are another three similar conditions relating to the local stabilities of complex structures. The
![]() $(p,p+1)th$
weak
$(p,p+1)th$
weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a compact complex manifold
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a compact complex manifold
![]() $X$
, first introduced by Fu and Yau [Reference Fu and YauFY11] for
$X$
, first introduced by Fu and Yau [Reference Fu and YauFY11] for
![]() $(p,p+1)=(n-1,n)$
, says that for any real
$(p,p+1)=(n-1,n)$
, says that for any real
![]() $(p,p)$
-form
$(p,p)$
-form
![]() $\unicode[STIX]{x1D713}$
such that
$\unicode[STIX]{x1D713}$
such that
![]() $\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D713}$
is
$\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D713}$
is
![]() $\unicode[STIX]{x2202}$
-exact, there is a
$\unicode[STIX]{x2202}$
-exact, there is a
![]() $(p-1,p)$
-form
$(p-1,p)$
-form
![]() $\unicode[STIX]{x1D703}$
, satisfying
$\unicode[STIX]{x1D703}$
, satisfying
And the
![]() $(p,q)th$
strong
$(p,q)th$
strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on
![]() $X$
, first proposed by Angella–Ugarte [Reference Angella and UgarteAU17] in the case
$X$
, first proposed by Angella–Ugarte [Reference Angella and UgarteAU17] in the case
![]() $(p,q)=(n-1,n)$
, states that the induced mapping
$(p,q)=(n-1,n)$
, states that the induced mapping
![]() $\unicode[STIX]{x1D704}_{\text{BC},\text{A}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\text{A}}^{p,q}(X)$
by the identity map is injective, which is equivalent to the statement that for any
$\unicode[STIX]{x1D704}_{\text{BC},\text{A}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\text{A}}^{p,q}(X)$
by the identity map is injective, which is equivalent to the statement that for any
![]() $d$
-closed
$d$
-closed
![]() $(p,q)$
-form
$(p,q)$
-form
![]() $\unicode[STIX]{x1D6E4}$
of the type
$\unicode[STIX]{x1D6E4}$
of the type
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x2202}\unicode[STIX]{x1D709}\,+\,\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D713}$
, there exists a
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x2202}\unicode[STIX]{x1D709}\,+\,\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D713}$
, there exists a
![]() $(p-1,q-1)$
-form
$(p-1,q-1)$
-form
![]() $\unicode[STIX]{x1D703}$
such that
$\unicode[STIX]{x1D703}$
such that
Angella–Ugarte [Reference Angella and UgarteAU17, Proposition 4.8] showed the deformation openness of the
![]() $(n-1,n)$
th strong
$(n-1,n)$
th strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Besides, the condition that the induced mapping
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. Besides, the condition that the induced mapping
![]() $\unicode[STIX]{x1D704}_{\text{BC},\overline{\unicode[STIX]{x2202}}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
by the identity map is injective, is first presented by Angella–Ugarte [Reference Angella and UgarteAU16] in the case
$\unicode[STIX]{x1D704}_{\text{BC},\overline{\unicode[STIX]{x2202}}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\overline{\unicode[STIX]{x2202}}}^{p,q}(X)$
by the identity map is injective, is first presented by Angella–Ugarte [Reference Angella and UgarteAU16] in the case
![]() $(p,q)=(n-1,n)$
to study local conformal balanced structures and global ones, which we may call the
$(p,q)=(n-1,n)$
to study local conformal balanced structures and global ones, which we may call the
![]() $(p,q)th$
dual mild
$(p,q)th$
dual mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
After a simple check, we have the following observation.
Observation 3.4. The compact complex manifold
![]() $X$
satisfies the
$X$
satisfies the
![]() $(p,q)$
th strong
$(p,q)$
th strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma if and only if both of the mild and dual mild ones hold on
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma if and only if both of the mild and dual mild ones hold on
![]() $X$
.
$X$
.
All these four ‘
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata’ hold if the compact complex manifold
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata’ hold if the compact complex manifold
![]() $X$
satisfies the standard
$X$
satisfies the standard
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. And either the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. And either the
![]() $(p,p+1)$
th mild or dual mild
$(p,p+1)$
th mild or dual mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma implies the weak one, while [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.9] implies that the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma implies the weak one, while [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.9] implies that the
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and the dual mild one are unrelated.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and the dual mild one are unrelated.
By [Reference Alessandrini and BassanelliAB90], a small deformation of the Iwasawa manifold, which satisfies the
![]() $(2,3)$
th weak
$(2,3)$
th weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but does not satisfy the mild one from Example 3.5, may not be balanced. Thus, the condition ‘
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but does not satisfy the mild one from Example 3.5, may not be balanced. Thus, the condition ‘
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma’ in Corollary 1.3(ii) cannot be replaced by the weak one.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma’ in Corollary 1.3(ii) cannot be replaced by the weak one.
Example 3.5 [Reference Rao, Wan and ZhaoRWZ16, Example 3.7].
The complex structure in category
![]() $(i)$
of [Reference Ugarte and VillacampaUV15, Proposition 2.3], i.e., the complex parallelizable case of complex dimension
$(i)$
of [Reference Ugarte and VillacampaUV15, Proposition 2.3], i.e., the complex parallelizable case of complex dimension
![]() $3$
, satisfies the
$3$
, satisfies the
![]() $(2,3)$
th weak
$(2,3)$
th weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and the dual mild one, but does not satisfy the mild one. The Iwasawa manifold belongs to category
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma and the dual mild one, but does not satisfy the mild one. The Iwasawa manifold belongs to category
![]() $(i)$
.
$(i)$
.
The next example shows that neither the
![]() $(n-1,n)$
th weak
$(n-1,n)$
th weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma nor the mild one is deformation open. And it shows that the condition in [Reference Fu and YauFY11, Theorem 6] is not a necessary one for the deformation openness of balanced structures as mentioned in [Reference Ugarte and VillacampaUV15, the discussion ahead of Example 3.7]. Recall that [Reference Fu and YauFY11, Theorem 6] says that the balanced structure is deformation open, if the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma nor the mild one is deformation open. And it shows that the condition in [Reference Fu and YauFY11, Theorem 6] is not a necessary one for the deformation openness of balanced structures as mentioned in [Reference Ugarte and VillacampaUV15, the discussion ahead of Example 3.7]. Recall that [Reference Fu and YauFY11, Theorem 6] says that the balanced structure is deformation open, if the
![]() $(n-1,n)$
th weak
$(n-1,n)$
th weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds on the general fibers
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma holds on the general fibers
![]() $X_{t}$
for
$X_{t}$
for
![]() $t\neq 0$
. Fortunately, Corollary 1.3(ii) can be applied to this example. See also [Reference Angella and UgarteAU17, Remark 4.7], where Corollary 1.3(ii) can also be applied.
$t\neq 0$
. Fortunately, Corollary 1.3(ii) can be applied to this example. See also [Reference Angella and UgarteAU17, Remark 4.7], where Corollary 1.3(ii) can also be applied.
Example 3.6 [Reference Ugarte and VillacampaUV15, Example 3.7].
Ugarte–Villacampa constructed an explicit family of nilmanifolds with left-invariant complex structures
![]() $I_{\unicode[STIX]{x1D706}}$
for
$I_{\unicode[STIX]{x1D706}}$
for
![]() $\unicode[STIX]{x1D706}\in [0,1)$
(of complex dimension
$\unicode[STIX]{x1D706}\in [0,1)$
(of complex dimension
![]() $3$
), with the fixed underlying manifold the Iwasawa manifold. The complex structure of the reference fiber
$3$
), with the fixed underlying manifold the Iwasawa manifold. The complex structure of the reference fiber
![]() $I_{0}$
is abelian and admits a left-invariant balanced metric, satisfying the
$I_{0}$
is abelian and admits a left-invariant balanced metric, satisfying the
![]() $(2,3)$
th mild
$(2,3)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by [Reference Rao, Wan and ZhaoRWZ16, Proposition 3.8]. The complex structures of
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by [Reference Rao, Wan and ZhaoRWZ16, Proposition 3.8]. The complex structures of
![]() $I_{\unicode[STIX]{x1D706}}$
for
$I_{\unicode[STIX]{x1D706}}$
for
![]() $\unicode[STIX]{x1D706}\neq 0$
are nilpotent from [Reference Console, Fino and PoonCFP06, Corollary 2], but neither complex-parallelizable nor abelian. Thus, they do not satisfy the
$\unicode[STIX]{x1D706}\neq 0$
are nilpotent from [Reference Console, Fino and PoonCFP06, Corollary 2], but neither complex-parallelizable nor abelian. Thus, they do not satisfy the
![]() $(2,3)$
th weak
$(2,3)$
th weak
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by [Reference Ugarte and VillacampaUV15, Proposition 3.6]. However, the nilmanifolds
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma by [Reference Ugarte and VillacampaUV15, Proposition 3.6]. However, the nilmanifolds
![]() $I_{\unicode[STIX]{x1D706}}$
for
$I_{\unicode[STIX]{x1D706}}$
for
![]() $\unicode[STIX]{x1D706}\neq 0$
admit balanced metrics.
$\unicode[STIX]{x1D706}\neq 0$
admit balanced metrics.
Meanwhile, a
![]() $2n$
-dimensional nilmanifold endowed with a left-invariant abelian complex structure satisfies the
$2n$
-dimensional nilmanifold endowed with a left-invariant abelian complex structure satisfies the
![]() $(n-1,n)$
th mild
$(n-1,n)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but never satisfies the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma but never satisfies the
![]() $(n-1,n)$
th dual mild
$(n-1,n)$
th dual mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. It shows that the deformation openness of balanced structures with the reference fiber a nilmanifold endowed with a left-invariant abelian balanced Hermitian structure is easily obtained by Corollary 1.3(ii), but not from [Reference Angella and UgarteAU17, Theorem 4.9], which says that if
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma. It shows that the deformation openness of balanced structures with the reference fiber a nilmanifold endowed with a left-invariant abelian balanced Hermitian structure is easily obtained by Corollary 1.3(ii), but not from [Reference Angella and UgarteAU17, Theorem 4.9], which says that if
![]() $X_{0}$
admits a locally conformal balanced metric and satisfies the
$X_{0}$
admits a locally conformal balanced metric and satisfies the
![]() $(n-1,n)$
th strong
$(n-1,n)$
th strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, then
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, then
![]() $X_{t}$
is balanced for small
$X_{t}$
is balanced for small
![]() $t$
.
$t$
.
Moreover, the deformation invariance of the
![]() $(n-1,n-1)$
th Bott–Chern numbers
$(n-1,n-1)$
th Bott–Chern numbers
![]() $h_{\text{BC}}^{n\,-\,1,n\,-\,1}(X_{t})$
can assure the deformation openness of balanced structures as shown in [Reference Angella and UgarteAU17, Proposition 4.1]. Inspired by Wu’s result [Reference WuWu06, Theorem 5.13], we have the following generalization.
$h_{\text{BC}}^{n\,-\,1,n\,-\,1}(X_{t})$
can assure the deformation openness of balanced structures as shown in [Reference Angella and UgarteAU17, Proposition 4.1]. Inspired by Wu’s result [Reference WuWu06, Theorem 5.13], we have the following generalization.
Theorem 3.7 [Reference Rao, Wan and ZhaoRWZ16, Theorem 1.9].
For any positive integer
![]() $p\leqslant n\,-\,1$
, any small differentiable deformation
$p\leqslant n\,-\,1$
, any small differentiable deformation
![]() $X_{t}$
of a
$X_{t}$
of a
![]() $p$
-Kähler manifold
$p$
-Kähler manifold
![]() $X_{0}$
satisfying the deformation invariance of
$X_{0}$
satisfying the deformation invariance of
![]() $(p,p)$
-Bott–Chern numbers is still
$(p,p)$
-Bott–Chern numbers is still
![]() $p$
-Kählerian.
$p$
-Kählerian.
Nevertheless, Corollary 1.3(ii) may be applied to some cases with deformation variance of the
![]() $(n-1,n-1)$
th Bott–Chern numbers. The newly constructed example that follows is one case among nilmanifolds, while the manifold in [Reference Angella and UgarteAU17, Example 4.10], satisfying the
$(n-1,n-1)$
th Bott–Chern numbers. The newly constructed example that follows is one case among nilmanifolds, while the manifold in [Reference Angella and UgarteAU17, Example 4.10], satisfying the
![]() $(2,3)$
th strong
$(2,3)$
th strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, is a solvable manifold but not a nilmanifold by [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.9].
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, is a solvable manifold but not a nilmanifold by [Reference Rao, Wan and ZhaoRWZ16, Corollary 3.9].
Example 3.8. Let
![]() $G$
be the simply connected nilpotent Lie group determined by a ten-dimensional
$G$
be the simply connected nilpotent Lie group determined by a ten-dimensional
![]() $3$
-step nilpotent Lie algebra
$3$
-step nilpotent Lie algebra
![]() $\mathfrak{g}$
endowed with a left-invariant abelian complex structure
$\mathfrak{g}$
endowed with a left-invariant abelian complex structure
![]() $J$
, satisfying the structure equation
$J$
, satisfying the structure equation
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}d\unicode[STIX]{x1D6FE}^{1}=d\unicode[STIX]{x1D6FE}^{2}=d\unicode[STIX]{x1D6FE}^{3}=0,\quad \\ d\unicode[STIX]{x1D6FE}^{4}=\unicode[STIX]{x1D6FE}^{1\bar{3}},\quad \\ d\unicode[STIX]{x1D6FE}^{5}=\unicode[STIX]{x1D6FE}^{3\bar{4}},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}d\unicode[STIX]{x1D6FE}^{1}=d\unicode[STIX]{x1D6FE}^{2}=d\unicode[STIX]{x1D6FE}^{3}=0,\quad \\ d\unicode[STIX]{x1D6FE}^{4}=\unicode[STIX]{x1D6FE}^{1\bar{3}},\quad \\ d\unicode[STIX]{x1D6FE}^{5}=\unicode[STIX]{x1D6FE}^{3\bar{4}},\quad \end{array}\right.\end{eqnarray}$$
where the natural decomposition with respect to
![]() $J$
yields
$J$
yields
![]() $\{\unicode[STIX]{x1D6FE}^{i}\}_{i=1}^{5}$
is the basis of
$\{\unicode[STIX]{x1D6FE}^{i}\}_{i=1}^{5}$
is the basis of
![]() $\mathfrak{g}^{\ast (1,0)}$
and the convention
$\mathfrak{g}^{\ast (1,0)}$
and the convention
![]() $\unicode[STIX]{x1D6FE}^{1\bar{3}}=\unicode[STIX]{x1D6FE}^{1}\wedge \overline{\unicode[STIX]{x1D6FE}^{3}}$
is used here and afterwards. Define a lattice
$\unicode[STIX]{x1D6FE}^{1\bar{3}}=\unicode[STIX]{x1D6FE}^{1}\wedge \overline{\unicode[STIX]{x1D6FE}^{3}}$
is used here and afterwards. Define a lattice
![]() $\unicode[STIX]{x1D6E4}$
in
$\unicode[STIX]{x1D6E4}$
in
![]() $G$
, determined by the rational span of
$G$
, determined by the rational span of
![]() $\{\unicode[STIX]{x1D6FE}^{i},\bar{\unicode[STIX]{x1D6FE}}^{i}\}_{i=1}^{5}$
. Then
$\{\unicode[STIX]{x1D6FE}^{i},\bar{\unicode[STIX]{x1D6FE}}^{i}\}_{i=1}^{5}$
. Then
![]() $M:=\unicode[STIX]{x1D6E4}\backslash G$
is a compact nilmanifold with the abelian complex structure
$M:=\unicode[STIX]{x1D6E4}\backslash G$
is a compact nilmanifold with the abelian complex structure
![]() $J$
given above. It is easy to check that
$J$
given above. It is easy to check that
is a left-invariant balanced metric on
![]() $(\mathfrak{g},J)$
, descending to
$(\mathfrak{g},J)$
, descending to
![]() $M$
. Denote the basis of
$M$
. Denote the basis of
![]() $\mathfrak{g}^{1,0}$
dual to
$\mathfrak{g}^{1,0}$
dual to
![]() $\{\unicode[STIX]{x1D6FE}^{i}\}_{i=1}^{5}$
by
$\{\unicode[STIX]{x1D6FE}^{i}\}_{i=1}^{5}$
by
![]() $\{\unicode[STIX]{x1D703}_{i}\}_{i=1}^{5}$
. The equation
$\{\unicode[STIX]{x1D703}_{i}\}_{i=1}^{5}$
. The equation
![]() $d\unicode[STIX]{x1D714}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })=-\unicode[STIX]{x1D714}([\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }])$
for
$d\unicode[STIX]{x1D714}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime })=-\unicode[STIX]{x1D714}([\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }])$
for
![]() $\unicode[STIX]{x1D714}\in \mathfrak{g}_{\mathbb{C}}^{\ast }$
and
$\unicode[STIX]{x1D714}\in \mathfrak{g}_{\mathbb{C}}^{\ast }$
and
![]() $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \mathfrak{g}_{\mathbb{C}}$
, establishes the equalities
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \mathfrak{g}_{\mathbb{C}}$
, establishes the equalities
According to [Reference Console, Fino and PoonCFP06, Theorem 3.6], the linear operator
![]() $\overline{\unicode[STIX]{x2202}}$
on
$\overline{\unicode[STIX]{x2202}}$
on
![]() $\mathfrak{g}^{1,0}$
, defined in [Reference Console, Fino and PoonCFP06, §3.2], amounts to
$\mathfrak{g}^{1,0}$
, defined in [Reference Console, Fino and PoonCFP06, §3.2], amounts to
which induces an isomorphism
![]() $H^{1}(M,T_{M}^{1,0})\cong H_{\overline{\unicode[STIX]{x2202}}}^{1}(\mathfrak{g}^{1,0})$
. Therefore, from Kodaira–Spencer’s deformation theory, an analytic deformation
$H^{1}(M,T_{M}^{1,0})\cong H_{\overline{\unicode[STIX]{x2202}}}^{1}(\mathfrak{g}^{1,0})$
. Therefore, from Kodaira–Spencer’s deformation theory, an analytic deformation
![]() $M_{t}$
of
$M_{t}$
of
![]() $M$
can be constructed by use of the integrable left-invariant Beltrami differential
$M$
can be constructed by use of the integrable left-invariant Beltrami differential
for
![]() $t=(t_{1},t_{2},t_{3},t_{4})$
and
$t=(t_{1},t_{2},t_{3},t_{4})$
and
![]() $|t_{4}|<1$
, which satisfies
$|t_{4}|<1$
, which satisfies
![]() $\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}(t)=\frac{1}{2}[\unicode[STIX]{x1D711}(t),\unicode[STIX]{x1D711}(t)]$
and the so-called Schouten-Nijenhuis bracket
$\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D711}(t)=\frac{1}{2}[\unicode[STIX]{x1D711}(t),\unicode[STIX]{x1D711}(t)]$
and the so-called Schouten-Nijenhuis bracket
![]() $[\cdot ,\cdot ]$
(cf. [Reference Console, Fino and PoonCFP06, Formula (4.1)]) works as
$[\cdot ,\cdot ]$
(cf. [Reference Console, Fino and PoonCFP06, Formula (4.1)]) works as
Then the general fibers
![]() $M_{t}$
are still nilmanifolds, determined by the Lie algebra
$M_{t}$
are still nilmanifolds, determined by the Lie algebra
![]() $\mathfrak{g}$
with respect to the decompositions
$\mathfrak{g}$
with respect to the decompositions
where the basis of
![]() $\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (1,0)}$
is given by
$\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (1,0)}$
is given by
![]() $\unicode[STIX]{x1D6FE}^{i}(t)=e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}}(\unicode[STIX]{x1D6FE}^{i})=(\unicode[STIX]{x1D7D9}+\unicode[STIX]{x1D711}(t))\lrcorner \unicode[STIX]{x1D6FE}^{i}$
for
$\unicode[STIX]{x1D6FE}^{i}(t)=e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}}(\unicode[STIX]{x1D6FE}^{i})=(\unicode[STIX]{x1D7D9}+\unicode[STIX]{x1D711}(t))\lrcorner \unicode[STIX]{x1D6FE}^{i}$
for
![]() $1\leqslant i\leqslant 5$
. Hence, the structure equation of
$1\leqslant i\leqslant 5$
. Hence, the structure equation of
![]() $\{\unicode[STIX]{x1D6FE}^{i}(t)\}_{i=1}^{5}$
is
$\{\unicode[STIX]{x1D6FE}^{i}(t)\}_{i=1}^{5}$
is
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}d\unicode[STIX]{x1D6FE}^{1}(t)=d\unicode[STIX]{x1D6FE}^{3}(t)=0,\quad \\ d\unicode[STIX]{x1D6FE}^{2}(t)=-t_{1}\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)-t_{2}\unicode[STIX]{x1D6FE}^{4\bar{3}}(t),\quad \\ d\unicode[STIX]{x1D6FE}^{4}(t)=\unicode[STIX]{x1D6FE}^{1\bar{3}}(t),\quad \\ d\unicode[STIX]{x1D6FE}^{5}(t)=\unicode[STIX]{x1D6FE}^{3\bar{4}}(t)-t_{3}\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)-t_{4}\unicode[STIX]{x1D6FE}^{4\bar{3}}(t),\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}d\unicode[STIX]{x1D6FE}^{1}(t)=d\unicode[STIX]{x1D6FE}^{3}(t)=0,\quad \\ d\unicode[STIX]{x1D6FE}^{2}(t)=-t_{1}\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)-t_{2}\unicode[STIX]{x1D6FE}^{4\bar{3}}(t),\quad \\ d\unicode[STIX]{x1D6FE}^{4}(t)=\unicode[STIX]{x1D6FE}^{1\bar{3}}(t),\quad \\ d\unicode[STIX]{x1D6FE}^{5}(t)=\unicode[STIX]{x1D6FE}^{3\bar{4}}(t)-t_{3}\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)-t_{4}\unicode[STIX]{x1D6FE}^{4\bar{3}}(t),\quad \end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)$
denotes
$\unicode[STIX]{x1D6FE}^{3\bar{1}}(t)$
denotes
![]() $\unicode[STIX]{x1D6FE}^{3}(t)\wedge \overline{\unicode[STIX]{x1D6FE}^{1}(t)}$
, similarly for others. It is well known from [Reference Console and FinoCF01, Reference RollenskeRol09, Reference AngellaAng13] that the Bott–Chern cohomologies of nilmanifolds with abelian complex structures and their small deformation can be calculated via left-invariant differential forms. Remark 1.7 tells us that the dimension of the space of the
$\unicode[STIX]{x1D6FE}^{3}(t)\wedge \overline{\unicode[STIX]{x1D6FE}^{1}(t)}$
, similarly for others. It is well known from [Reference Console and FinoCF01, Reference RollenskeRol09, Reference AngellaAng13] that the Bott–Chern cohomologies of nilmanifolds with abelian complex structures and their small deformation can be calculated via left-invariant differential forms. Remark 1.7 tells us that the dimension of the space of the
![]() $d$
-closed left-invariant
$d$
-closed left-invariant
![]() $(4,4)$
-forms is invariant along the deformation
$(4,4)$
-forms is invariant along the deformation
![]() $M_{t}$
, which is equal to
$M_{t}$
, which is equal to
![]() $21$
. And one can calculate the
$21$
. And one can calculate the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact terms directly by use of the structure equation
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact terms directly by use of the structure equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (3,3)})\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \!-(1+|t_{4}|^{2})\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-|t_{2}|^{2}\unicode[STIX]{x1D6FE}^{1345\overline{1345}}+t_{2}\overline{t}_{4}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{4}\overline{t}_{2}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\unicode[STIX]{x1D6FE}^{1235\overline{1235}}(t)-|t_{1}|^{2}\unicode[STIX]{x1D6FE}^{1345\overline{1345}}(t)-|t_{3}|^{2}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)+t_{1}\overline{t}_{3}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{3}\overline{t}_{1}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,t_{1}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{2}\unicode[STIX]{x1D6FE}^{1345\overline{1235}}(t)+t_{3}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-t_{4}\unicode[STIX]{x1D6FE}^{1234\overline{1235}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\overline{t}_{1}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t)+\overline{t}_{2}\unicode[STIX]{x1D6FE}^{1235\overline{1345}}(t)+\overline{t}_{3}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-\overline{t}_{4}\unicode[STIX]{x1D6FE}^{1235\overline{1234}}(t)\!\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (3,3)})\nonumber\\ \displaystyle & & \displaystyle \quad =\langle \!-(1+|t_{4}|^{2})\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-|t_{2}|^{2}\unicode[STIX]{x1D6FE}^{1345\overline{1345}}+t_{2}\overline{t}_{4}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{4}\overline{t}_{2}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\unicode[STIX]{x1D6FE}^{1235\overline{1235}}(t)-|t_{1}|^{2}\unicode[STIX]{x1D6FE}^{1345\overline{1345}}(t)-|t_{3}|^{2}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)+t_{1}\overline{t}_{3}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{3}\overline{t}_{1}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,t_{1}\unicode[STIX]{x1D6FE}^{1345\overline{1234}}(t)+t_{2}\unicode[STIX]{x1D6FE}^{1345\overline{1235}}(t)+t_{3}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-t_{4}\unicode[STIX]{x1D6FE}^{1234\overline{1235}}(t),\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\overline{t}_{1}\unicode[STIX]{x1D6FE}^{1234\overline{1345}}(t)+\overline{t}_{2}\unicode[STIX]{x1D6FE}^{1235\overline{1345}}(t)+\overline{t}_{3}\unicode[STIX]{x1D6FE}^{1234\overline{1234}}(t)-\overline{t}_{4}\unicode[STIX]{x1D6FE}^{1235\overline{1234}}(t)\!\rangle .\nonumber\end{eqnarray}$$
It is clear that
![]() $\dim \unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\mathfrak{g}_{J}^{\ast (3,3)})=2$
and
$\dim \unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\mathfrak{g}_{J}^{\ast (3,3)})=2$
and
![]() $\dim \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (3,3)})=4$
for general
$\dim \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\mathfrak{g}_{\unicode[STIX]{x1D711}(t)}^{\ast (3,3)})=4$
for general
![]() $t$
. Therefore, the Bott–Chern number
$t$
. Therefore, the Bott–Chern number
![]() $h_{\text{BC}}^{4,4}(M_{t})$
varies from
$h_{\text{BC}}^{4,4}(M_{t})$
varies from
![]() $19$
to
$19$
to
![]() $17$
along the deformation
$17$
along the deformation
![]() $M_{t}$
.
$M_{t}$
.
It may not be difficult to find an example of a non-Kähler
![]() $p$
-Kähler manifold in the Fujiki class for
$p$
-Kähler manifold in the Fujiki class for
![]() $1<p<n-1$
in the literature, and thus it satisfies the
$1<p<n-1$
in the literature, and thus it satisfies the
![]() $(p,p\,+\,1)$
th mild
$(p,p\,+\,1)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, for example [Reference Alessandrini and BassanelliAB92, §4]. However, motivated by Example 3.8, we ask the following question.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, for example [Reference Alessandrini and BassanelliAB92, §4]. However, motivated by Example 3.8, we ask the following question.
Question 3.9. Is it possible to find an
![]() $n$
-dimensional nilmanifold with a left-invariant complex structure of complex dimension
$n$
-dimensional nilmanifold with a left-invariant complex structure of complex dimension
![]() $n$
, which admits a left-invariant
$n$
, which admits a left-invariant
![]() $p$
-Kähler metric for
$p$
-Kähler metric for
![]() $1<p<n-1$
and satisfies the
$1<p<n-1$
and satisfies the
![]() $(p,p+1)$
th mild
$(p,p+1)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, but the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, but the
![]() $(p,p)$
-Bott–Chern number varies along some deformation? This example would not satisfy the standard
$(p,p)$
-Bott–Chern number varies along some deformation? This example would not satisfy the standard
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma.
Finally, from the perspective of Corollary 1.3(ii), we may have a clear picture of Angella–Ugarte’s result [Reference Angella and UgarteAU17, Theorem 4.9]. Actually, Observation 3.4 tells us that the
![]() $(n\,-\,1,n)$
th strong
$(n\,-\,1,n)$
th strong
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma decomposes into the mild one and the dual mild one. A locally conformal balanced metric can be transformed into a balanced one by the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma decomposes into the mild one and the dual mild one. A locally conformal balanced metric can be transformed into a balanced one by the
![]() $(n-1,n)$
th dual mild
$(n-1,n)$
th dual mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, from [Reference Angella and UgarteAU16, Theorem 2.5]. Then the
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma, from [Reference Angella and UgarteAU16, Theorem 2.5]. Then the
![]() $(n\,-\,1,n)$
th mild
$(n\,-\,1,n)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma assures the deformation openness of balanced structures originally from the transformed balanced metric on the reference fiber, thanks to Corollary 1.3(ii).
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma assures the deformation openness of balanced structures originally from the transformed balanced metric on the reference fiber, thanks to Corollary 1.3(ii).
3.2 Modification stabilities
We consider the modification on a compact complex manifold defined as follows and refer the reader to [Reference UenoUen75, §2] for its general definition on complex spaces.
Definition 3.10. A modification of an
![]() $n$
-dimensional compact complex manifold
$n$
-dimensional compact complex manifold
![]() $M$
is a holomorphic map
$M$
is a holomorphic map
so that:
(i)
 $\tilde{M}$
is also an
$\tilde{M}$
is also an
 $n$
-dimensional compact complex manifold;
$n$
-dimensional compact complex manifold;(ii) there exists an analytic subset
 $S\subseteq M$
of codimension greater than or equal to
$S\subseteq M$
of codimension greater than or equal to
 $1$
such that
$1$
such that
 $\unicode[STIX]{x1D707}\mid _{\tilde{M}\setminus \unicode[STIX]{x1D707}^{-1}(S)}:\tilde{M}\setminus \unicode[STIX]{x1D707}^{-1}(S)\rightarrow M\setminus S$
is a biholomorphism.
$\unicode[STIX]{x1D707}\mid _{\tilde{M}\setminus \unicode[STIX]{x1D707}^{-1}(S)}:\tilde{M}\setminus \unicode[STIX]{x1D707}^{-1}(S)\rightarrow M\setminus S$
is a biholomorphism.
It is a classical result, [Reference ParshinPar66] or [Reference Deligne, Griffiths, Morgan and SullivanDGMS75, Theorem 5.22], that if the modification of a complex manifold is a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold, then so is this manifold. Therefore, each compact complex manifold in the Fujiki class
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold, then so is this manifold. Therefore, each compact complex manifold in the Fujiki class
![]() ${\mathcal{C}}$
(i.e. admitting a Kähler modification) is a
${\mathcal{C}}$
(i.e. admitting a Kähler modification) is a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold. The converse is an open question as in [Reference AlessandriniAle17, Introduction]: Is the modification of a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold. The converse is an open question as in [Reference AlessandriniAle17, Introduction]: Is the modification of a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold still a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold still a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold? A recent result [Reference Yang and YangYY17, Theorem 1.3] of S. Yang and X. Yang, by means of a blow-up formula for Bott–Chern cohomologies and the characterizations by Angella and Tomassini [Reference Angella and TomassiniAT13] and Angella and Tardini [Reference Angella and TardiniAT17] of
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifold? A recent result [Reference Yang and YangYY17, Theorem 1.3] of S. Yang and X. Yang, by means of a blow-up formula for Bott–Chern cohomologies and the characterizations by Angella and Tomassini [Reference Angella and TomassiniAT13] and Angella and Tardini [Reference Angella and TardiniAT17] of
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifolds, and also [Reference Rao, Yang and YangRYY17, Main Theorem 1.1] by S. Yang, X. Yang and the first author confirm this question in dimension three, that is, the modification of a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-manifolds, and also [Reference Rao, Yang and YangRYY17, Main Theorem 1.1] by S. Yang, X. Yang and the first author confirm this question in dimension three, that is, the modification of a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-threefold is still a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-threefold is still a
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-threefold. See also, more recently, [Reference Angella, Suwa, Tardini and TomassiniASTT17, Theorem 2.1]. These results provide us with more classes of complex manifolds satisfying mild
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-threefold. See also, more recently, [Reference Angella, Suwa, Tardini and TomassiniASTT17, Theorem 2.1]. These results provide us with more classes of complex manifolds satisfying mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata. Moreover, it is natural to ask the following analogous question.
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata. Moreover, it is natural to ask the following analogous question.
Question 3.11. Does the modification of a complex manifold satisfying the mild
![]() $(p,q)$
th
$(p,q)$
th
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma still satisfy the mild
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma still satisfy the mild
![]() $(p,q)$
th
$(p,q)$
th
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma for each
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma for each
![]() $p,q$
?
$p,q$
?
Now we present a modification stability of
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a compact complex manifold. Let
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma on a compact complex manifold. Let
![]() $M$
be a complex manifold. One has the
$M$
be a complex manifold. One has the
![]() $\mathbb{K}$
-valued de Rham complex
$\mathbb{K}$
-valued de Rham complex
![]() $(A^{\bullet }(M)_{\mathbb{K}},d)$
for
$(A^{\bullet }(M)_{\mathbb{K}},d)$
for
![]() $\mathbb{K}\in \{\mathbb{R},\mathbb{C}\}$
. Fixing a
$\mathbb{K}\in \{\mathbb{R},\mathbb{C}\}$
. Fixing a
![]() $d$
-closed
$d$
-closed
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D719}\in A^{1}(M)_{\mathbb{K}}$
, we consider another complex. Namely, define
$\unicode[STIX]{x1D719}\in A^{1}(M)_{\mathbb{K}}$
, we consider another complex. Namely, define
where
![]() $L_{\unicode[STIX]{x1D719}}:=\unicode[STIX]{x1D719}\wedge \bullet$
. The cochain complex
$L_{\unicode[STIX]{x1D719}}:=\unicode[STIX]{x1D719}\wedge \bullet$
. The cochain complex
can be regarded as the de Rham complex with values in the topologically trivial flat bundle
![]() $M\times \mathbb{K}$
with the connection form
$M\times \mathbb{K}$
with the connection form
![]() $\unicode[STIX]{x1D719}$
. We study cohomologies and Hodge theory for general complex manifolds with twisted differentials. More precisely, for
$\unicode[STIX]{x1D719}$
. We study cohomologies and Hodge theory for general complex manifolds with twisted differentials. More precisely, for
![]() $\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2}\in H_{\text{BC}}^{1,0}(M)$
, consider the bi-differential
$\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2}\in H_{\text{BC}}^{1,0}(M)$
, consider the bi-differential
![]() $\mathbb{Z}$
-graded complex
$\mathbb{Z}$
-graded complex
where
It is easy to check that
Angella and Kasuya [Reference Angella and KasuyaAK14] investigated cohomological properties of this bi-differential complex and considered (more than) two cohomologies:
and
which are simply denoted by
![]() $H_{\text{BC}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
and
$H_{\text{BC}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
and
![]() $H_{\unicode[STIX]{x2202}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
, respectively. If one sets
$H_{\unicode[STIX]{x2202}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
, respectively. If one sets
![]() $\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}=0$
,
$\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}=0$
,
![]() $H_{\text{BC}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
and
$H_{\text{BC}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
and
![]() $H_{\unicode[STIX]{x2202}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
are just the ordinary Bott–Chern cohomology
$H_{\unicode[STIX]{x2202}}^{\bullet }(M,\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
are just the ordinary Bott–Chern cohomology
![]() $H_{\text{BC}}^{\bullet ,\bullet }(M)$
and
$H_{\text{BC}}^{\bullet ,\bullet }(M)$
and
![]() $H_{\unicode[STIX]{x2202}}^{\bullet ,\bullet }(M)$
of
$H_{\unicode[STIX]{x2202}}^{\bullet ,\bullet }(M)$
of
![]() $M$
, respectively.
$M$
, respectively.
Following Wells in [Reference WellsWel74, Theorem 3.1], Angella and Kasuya proved the following proposition.
Proposition 3.12 [Reference Angella and KasuyaAK14, Theorem 2.4].
Let
![]() $\unicode[STIX]{x1D707}:\tilde{M}\rightarrow M$
be a modification of a compact complex manifold
$\unicode[STIX]{x1D707}:\tilde{M}\rightarrow M$
be a modification of a compact complex manifold
![]() $M$
. Then the induced maps
$M$
. Then the induced maps
are injective.
We reformulate Definition 3.1 for the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma as follows.
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma as follows.
Definition 3.13. For any positive integers
![]() $p,q\leqslant n$
, an
$p,q\leqslant n$
, an
![]() $n$
-dimensional complex manifold
$n$
-dimensional complex manifold
![]() $X$
satisfies the
$X$
satisfies the
![]() $(p,q)th$
mild
$(p,q)th$
mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma if the induced map
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma if the induced map
![]() $\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\unicode[STIX]{x2202}}^{p,q}(X)$
by the identity map is injective.
$\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}:H_{\text{BC}}^{p,q}(X)\rightarrow H_{\unicode[STIX]{x2202}}^{p,q}(X)$
by the identity map is injective.
Proposition 3.14. With the notation in Proposition 3.12, if
![]() $\tilde{M}$
satisfies the
$\tilde{M}$
satisfies the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma, then so does
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma, then so does
![]() $M$
.
$M$
.
Proof. Taking
![]() $\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}=0$
, we have the following commutative diagram.
$\unicode[STIX]{x1D703}_{1}=\unicode[STIX]{x1D703}_{2}=0$
, we have the following commutative diagram.

By the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma assumption on
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma assumption on
![]() $\tilde{M}$
, the map
$\tilde{M}$
, the map
![]() $\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}$
for
$\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}$
for
![]() $\tilde{M}$
is injective and so are
$\tilde{M}$
is injective and so are
![]() $\unicode[STIX]{x1D707}_{\text{BC}}^{\ast },\unicode[STIX]{x1D707}_{\unicode[STIX]{x2202}}^{\ast }$
by Proposition 3.12. So the map
$\unicode[STIX]{x1D707}_{\text{BC}}^{\ast },\unicode[STIX]{x1D707}_{\unicode[STIX]{x2202}}^{\ast }$
by Proposition 3.12. So the map
![]() $\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}$
for
$\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{p,q}$
for
![]() $M$
is injective, i.e.,
$M$
is injective, i.e.,
![]() $M$
satisfies the
$M$
satisfies the
![]() $(p,q)$
th mild
$(p,q)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma.◻
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma.◻
4 Power series proof of main result
This section is used to prove main Theorem 3.2. Let us sketch Kodaira–Spencer’s proof of the local stability theorem [Reference Kodaira and SpencerKS60]. Let
![]() $F_{t}$
be the orthogonal projection to the kernel
$F_{t}$
be the orthogonal projection to the kernel
![]() $\unicode[STIX]{x1D53D}_{t}$
of the first 4th order Kodaira–Spencer operator (also often called Bott–Chern Laplacian)
$\unicode[STIX]{x1D53D}_{t}$
of the first 4th order Kodaira–Spencer operator (also often called Bott–Chern Laplacian)
and
![]() $\mathbb{G}_{t}$
the corresponding Green’s operator with respect to
$\mathbb{G}_{t}$
the corresponding Green’s operator with respect to
![]() $\unicode[STIX]{x1D6FC}_{t}$
on
$\unicode[STIX]{x1D6FC}_{t}$
on
![]() $X_{t}$
. Here
$X_{t}$
. Here
is a hermitian metric on
![]() $X_{t}$
depending differentiably on
$X_{t}$
depending differentiably on
![]() $t$
with
$t$
with
![]() $\unicode[STIX]{x1D6FC}_{0}$
being a Kähler metric on
$\unicode[STIX]{x1D6FC}_{0}$
being a Kähler metric on
![]() $X_{0}$
, and
$X_{0}$
, and
![]() $\overline{\unicode[STIX]{x2202}}_{t}^{\ast }$
(respectively,
$\overline{\unicode[STIX]{x2202}}_{t}^{\ast }$
(respectively,
![]() $\unicode[STIX]{x2202}_{t}^{\ast }$
) is the dual of
$\unicode[STIX]{x2202}_{t}^{\ast }$
) is the dual of
![]() $\overline{\unicode[STIX]{x2202}}_{t}$
(respectively,
$\overline{\unicode[STIX]{x2202}}_{t}$
(respectively,
![]() $\unicode[STIX]{x2202}_{t}$
) with respect to
$\unicode[STIX]{x2202}_{t}$
) with respect to
![]() $\unicode[STIX]{x1D6FC}_{t}$
. By a cohomological argument with the upper semi-continuity theorem, they prove that
$\unicode[STIX]{x1D6FC}_{t}$
. By a cohomological argument with the upper semi-continuity theorem, they prove that
![]() $F_{t}$
and
$F_{t}$
and
![]() $\mathbb{G}_{t}$
depend differentiably on
$\mathbb{G}_{t}$
depend differentiably on
![]() $t$
. Then they can construct the desired Kähler metric on
$t$
. Then they can construct the desired Kähler metric on
![]() $X_{t}$
as
$X_{t}$
as
See also [Reference VoisinVoi02, §9.3].
Our proof is quite different. As explained in § 1, to prove Theorem 3.2, it suffices to prove the special case
![]() $p=q$
of the following theorem.
$p=q$
of the following theorem.
Theorem 4.1. If
![]() $X_{0}$
satisfies the
$X_{0}$
satisfies the
![]() $(p,q+1)$
th and
$(p,q+1)$
th and
![]() $(q,p+1)$
th mild
$(q,p+1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, then there is a
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, then there is a
![]() $d$
-closed
$d$
-closed
![]() $(p,q)$
-form
$(p,q)$
-form
![]() $\unicode[STIX]{x1D6FA}(t)$
on
$\unicode[STIX]{x1D6FA}(t)$
on
![]() $X_{t}$
depending smoothly on
$X_{t}$
depending smoothly on
![]() $t$
with
$t$
with
![]() $\unicode[STIX]{x1D6FA}(0)=\unicode[STIX]{x1D6FA}_{0}$
for any
$\unicode[STIX]{x1D6FA}(0)=\unicode[STIX]{x1D6FA}_{0}$
for any
![]() $d$
-closed
$d$
-closed
![]() $\unicode[STIX]{x1D6FA}_{0}\in A^{p,q}(X_{0})$
.
$\unicode[STIX]{x1D6FA}_{0}\in A^{p,q}(X_{0})$
.
We first reduce the local stability Theorem 4.1 to the Kuranishi family since the family of Beltrami differentials induced by this Kuranishi family plays an important role in the construction of the family of
![]() $d$
-closed
$d$
-closed
![]() $(p,q)$
-forms
$(p,q)$
-forms
![]() $\unicode[STIX]{x1D6FA}(t)$
.
$\unicode[STIX]{x1D6FA}(t)$
.
4.1 Kuranishi family and Beltrami differentials
We introduce some basics on the Kuranishi family of complex structures in this subsection, which is extracted from [Reference Rao and ZhaoRZ18, Reference Rao, Wan and ZhaoRWZ16] and obviously originally from [Reference KuranishiKur64].
By (the proof of) Kuranishi’s completeness theorem [Reference KuranishiKur64], for any compact complex manifold
![]() $X_{0}$
, there exists a complete holomorphic family
$X_{0}$
, there exists a complete holomorphic family
![]() $\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
of complex manifolds at the reference point
$\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
of complex manifolds at the reference point
![]() $0\in T$
in the sense that for any differentiable family
$0\in T$
in the sense that for any differentiable family
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
with
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
with
![]() $\unicode[STIX]{x1D70B}^{-1}(s_{0})=\unicode[STIX]{x1D71B}^{-1}(0)=X_{0}$
, there exist a sufficiently small neighborhood
$\unicode[STIX]{x1D70B}^{-1}(s_{0})=\unicode[STIX]{x1D71B}^{-1}(0)=X_{0}$
, there exist a sufficiently small neighborhood
![]() $E\subseteq B$
of
$E\subseteq B$
of
![]() $s_{0}$
, and smooth maps
$s_{0}$
, and smooth maps
![]() $\unicode[STIX]{x1D6F7}:{\mathcal{X}}_{E}\rightarrow {\mathcal{K}}$
,
$\unicode[STIX]{x1D6F7}:{\mathcal{X}}_{E}\rightarrow {\mathcal{K}}$
,
![]() $\unicode[STIX]{x1D70F}:E\rightarrow T$
with
$\unicode[STIX]{x1D70F}:E\rightarrow T$
with
![]() $\unicode[STIX]{x1D70F}(s_{0})=0$
such that the diagram
$\unicode[STIX]{x1D70F}(s_{0})=0$
such that the diagram

commutes,
![]() $\unicode[STIX]{x1D6F7}$
maps
$\unicode[STIX]{x1D6F7}$
maps
![]() $\unicode[STIX]{x1D70B}^{-1}(s)$
biholomorphically onto
$\unicode[STIX]{x1D70B}^{-1}(s)$
biholomorphically onto
![]() $\unicode[STIX]{x1D71B}^{-1}(\unicode[STIX]{x1D70F}(s))$
for each
$\unicode[STIX]{x1D71B}^{-1}(\unicode[STIX]{x1D70F}(s))$
for each
![]() $s\in E$
, and
$s\in E$
, and
is the identity map. This family is called Kuranishi family and is constructed as follows. Let
![]() $\{\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D708}}\}_{\unicode[STIX]{x1D708}=1}^{m}$
be a base for
$\{\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D708}}\}_{\unicode[STIX]{x1D708}=1}^{m}$
be a base for
![]() $\mathbb{H}^{0,1}(X_{0},T_{X_{0}}^{1,0})$
, where some suitable hermitian metric is fixed on
$\mathbb{H}^{0,1}(X_{0},T_{X_{0}}^{1,0})$
, where some suitable hermitian metric is fixed on
![]() $X_{0}$
and
$X_{0}$
and
![]() $m\geqslant 1$
. Otherwise the complex manifold
$m\geqslant 1$
. Otherwise the complex manifold
![]() $X_{0}$
would be rigid, i.e., for any differentiable family
$X_{0}$
would be rigid, i.e., for any differentiable family
![]() $\unicode[STIX]{x1D705}:{\mathcal{M}}\rightarrow P$
with
$\unicode[STIX]{x1D705}:{\mathcal{M}}\rightarrow P$
with
![]() $s_{0}\in P$
and
$s_{0}\in P$
and
![]() $\unicode[STIX]{x1D705}^{-1}(s_{0})=X_{0}$
, there is a neighborhood
$\unicode[STIX]{x1D705}^{-1}(s_{0})=X_{0}$
, there is a neighborhood
![]() $V\subseteq P$
of
$V\subseteq P$
of
![]() $s_{0}$
such that
$s_{0}$
such that
![]() $\unicode[STIX]{x1D705}:\unicode[STIX]{x1D705}^{-1}(V)\rightarrow V$
is trivial. Then one can construct a holomorphic family
$\unicode[STIX]{x1D705}:\unicode[STIX]{x1D705}^{-1}(V)\rightarrow V$
is trivial. Then one can construct a holomorphic family
for
![]() $|t|<\unicode[STIX]{x1D70C}$
a small positive constant, of Beltrami differentials as follows:
$|t|<\unicode[STIX]{x1D70C}$
a small positive constant, of Beltrami differentials as follows:
and for
![]() $|I|\geqslant 2$
,
$|I|\geqslant 2$
,
It is clear that
![]() $\unicode[STIX]{x1D711}(t)$
satisfies the equation
$\unicode[STIX]{x1D711}(t)$
satisfies the equation
Let
So for each
![]() $t\in T$
,
$t\in T$
,
![]() $\unicode[STIX]{x1D711}(t)$
satisfies
$\unicode[STIX]{x1D711}(t)$
satisfies
and determines a complex structure
![]() $X_{t}$
on the underlying differentiable manifold of
$X_{t}$
on the underlying differentiable manifold of
![]() $X_{0}$
. More importantly,
$X_{0}$
. More importantly,
![]() $\unicode[STIX]{x1D711}(t)$
represents the complete holomorphic family
$\unicode[STIX]{x1D711}(t)$
represents the complete holomorphic family
![]() $\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
of complex manifolds. Roughly speaking, the Kuranishi family
$\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
of complex manifolds. Roughly speaking, the Kuranishi family
![]() $\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
contains all sufficiently small differentiable deformations of
$\unicode[STIX]{x1D71B}:{\mathcal{K}}\rightarrow T$
contains all sufficiently small differentiable deformations of
![]() $X_{0}$
.
$X_{0}$
.
By means of these, one can reduce the local stability Theorem 4.1 to the Kuranishi family by shrinking
![]() $E$
if necessary, that is, it suffices to construct a
$E$
if necessary, that is, it suffices to construct a
![]() $p$
-Kähler metric on each
$p$
-Kähler metric on each
![]() $X_{t}$
. From now on, we use
$X_{t}$
. From now on, we use
![]() $\unicode[STIX]{x1D711}(t)$
and
$\unicode[STIX]{x1D711}(t)$
and
![]() $\unicode[STIX]{x1D711}$
interchangeably to denote this holomorphic family of integrable Beltrami differentials, and assume
$\unicode[STIX]{x1D711}$
interchangeably to denote this holomorphic family of integrable Beltrami differentials, and assume
![]() $m=1$
for simplicity.
$m=1$
for simplicity.
4.2 Obstruction equation and construction of power series
Now we begin to prove the
![]() $d$
-closed smooth extension of
$d$
-closed smooth extension of
![]() $(p,q)$
-forms as in Theorem 4.1 by using the power series method.
$(p,q)$
-forms as in Theorem 4.1 by using the power series method.
As both
![]() $e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}$
and
$e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}$
and
![]() $e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}$
are invertible operators when
$e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}$
are invertible operators when
![]() $t$
is sufficiently small, it follows that for any
$t$
is sufficiently small, it follows that for any
![]() $\unicode[STIX]{x1D6FA}\in A^{p,q}(X_{0})$
,
$\unicode[STIX]{x1D6FA}\in A^{p,q}(X_{0})$
,
Set
where
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\tilde{\unicode[STIX]{x1D6FA}}$
apparently have a one-to-one correspondence. Here we follow the notation:
$\tilde{\unicode[STIX]{x1D6FA}}$
apparently have a one-to-one correspondence. Here we follow the notation:
![]() $\overline{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}\lrcorner \overline{\unicode[STIX]{x1D711}}$
,
$\overline{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}\lrcorner \overline{\unicode[STIX]{x1D711}}$
,
![]() $\unicode[STIX]{x1D7D9}$
is the identity operator defined as
$\unicode[STIX]{x1D7D9}$
is the identity operator defined as
when it acts on
![]() $(p,q)$
-forms of a complex manifold, and similarly for others. And it is easy to check that the operator
$(p,q)$
-forms of a complex manifold, and similarly for others. And it is easy to check that the operator
preserves the form types and thus
![]() $\tilde{\unicode[STIX]{x1D6FA}}$
is still a
$\tilde{\unicode[STIX]{x1D6FA}}$
is still a
![]() $(p,q)$
-form. In fact, for any
$(p,q)$
-form. In fact, for any
![]() $(p,q)$
-form
$(p,q)$
-form
![]() $\unicode[STIX]{x1D6FC}$
on
$\unicode[STIX]{x1D6FC}$
on
![]() $X_{0}$
, we will find
$X_{0}$
, we will find
where
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i_{1}\cdots i_{p}\overline{j_{1}}\cdots \overline{j_{q}}}\,dz^{i_{1}}\wedge \cdots \wedge \,dz^{i_{p}}\wedge \,d\bar{z}^{j_{1}}\wedge \cdots \wedge \,d\bar{z}^{j_{q}}$
. Together with (8) and (9), Proposition 2.3 implies that
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i_{1}\cdots i_{p}\overline{j_{1}}\cdots \overline{j_{q}}}\,dz^{i_{1}}\wedge \cdots \wedge \,dz^{i_{p}}\wedge \,d\bar{z}^{j_{1}}\wedge \cdots \wedge \,d\bar{z}^{j_{q}}$
. Together with (8) and (9), Proposition 2.3 implies that
 $$\begin{eqnarray}\displaystyle d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})) & = & \displaystyle d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ (\bar{\unicode[STIX]{x2202}}+[\unicode[STIX]{x2202},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}]+\unicode[STIX]{x2202})\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}(\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}+\unicode[STIX]{x2202})\mathop{\sum }_{k=0}^{+\infty }A_{k}\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\biggl(\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}A_{0}+\mathop{\sum }_{k=0}^{+\infty }(\unicode[STIX]{x2202}A_{k}+\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}A_{k+1})\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})) & = & \displaystyle d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ (\bar{\unicode[STIX]{x2202}}+[\unicode[STIX]{x2202},\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}]+\unicode[STIX]{x2202})\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}(\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}+\unicode[STIX]{x2202})\mathop{\sum }_{k=0}^{+\infty }A_{k}\nonumber\\ \displaystyle & = & \displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\biggl(\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}A_{0}+\mathop{\sum }_{k=0}^{+\infty }(\unicode[STIX]{x2202}A_{k}+\bar{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D711}}A_{k+1})\biggr),\end{eqnarray}$$
where
is a
![]() $(p+k,q-k)$
-form and
$(p+k,q-k)$
-form and
Thus,
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
amounts to
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
amounts to
Proposition 4.2. For any given
![]() $(p,q)$
-form
$(p,q)$
-form
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
is equivalent to
where
![]() $\max \{1,n-p-q\}\leqslant l\leqslant \min \{2n-p-q,n+1\}$
,
$\max \{1,n-p-q\}\leqslant l\leqslant \min \{2n-p-q,n+1\}$
,
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}=0$
for
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}=0$
for
![]() $k<0$
and
$k<0$
and
![]() $0!=1$
.
$0!=1$
.
Proof. Recall that
![]() $\tilde{\unicode[STIX]{x1D6FA}}=e^{-\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}\circ e^{-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})$
and then
$\tilde{\unicode[STIX]{x1D6FA}}=e^{-\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}\circ e^{-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})$
and then
 $$\begin{eqnarray}\displaystyle d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})) & = & \displaystyle d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle (\bar{\unicode[STIX]{x2202}}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}+\unicode[STIX]{x2202}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}})(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k_{1},k_{2}=0}^{+\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k_{1}}}{k_{1}!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k_{1}}}{k_{1}!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k_{2}}}{k_{2}!}(\tilde{\unicode[STIX]{x1D6FA}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})) & = & \displaystyle d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle (\bar{\unicode[STIX]{x2202}}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}+\unicode[STIX]{x2202}\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}})(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k_{1},k_{2}=0}^{+\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k_{1}}}{k_{1}!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k_{1}}}{k_{1}!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k_{2}}}{k_{2}!}(\tilde{\unicode[STIX]{x1D6FA}}).\nonumber\end{eqnarray}$$
Note that the part of degree
![]() $(+(n-p-l+1),-(n-p-l))$
in the operator
$(+(n-p-l+1),-(n-p-l))$
in the operator
![]() $d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}$
is
$d\circ e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}}\circ e^{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}}$
is
since
This is exactly the left-hand side of (11). So
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
is equivalent to the vanishing of (12) for each
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
is equivalent to the vanishing of (12) for each
![]() $l$
such that
$l$
such that
i.e.,
![]() $\max \{1,n-p-q\}\leqslant l\leqslant \min \{2n-p-q,n+1\}$
.◻
$\max \{1,n-p-q\}\leqslant l\leqslant \min \{2n-p-q,n+1\}$
.◻
Remark 4.3. We consider two special cases of Proposition 4.2.
(i) For
 $p=q=n-1$
, (11) is reduced to which is exactly the system of obstruction equations given in [Reference Rao, Wan and ZhaoRWZ16, (3.8)].
$p=q=n-1$
, (11) is reduced to which is exactly the system of obstruction equations given in [Reference Rao, Wan and ZhaoRWZ16, (3.8)]. $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x2202}A_{0}+(\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})A_{1}=0,\quad \\ (\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})A_{0}+(\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2})A_{1}=0,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x2202}A_{0}+(\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})A_{1}=0,\quad \\ (\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})A_{0}+(\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2})A_{1}=0,\quad \end{array}\right.\end{eqnarray}$$
(ii) For
 $p=q=1$
, (11) is reduced to Since
$p=q=1$
, (11) is reduced to Since $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}-\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA})+(\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \\ (\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA}))+(\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2})\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \\ \unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}-\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA})+(\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \\ (\bar{\unicode[STIX]{x2202}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})(\unicode[STIX]{x1D6FA}-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA}))+(\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2})\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \\ \unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0.\quad \end{array}\right.\end{eqnarray}$$
 $-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}+\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}=-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}\bar{\unicode[STIX]{x1D711}}}+\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
and
$-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}+\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}=-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}\bar{\unicode[STIX]{x1D711}}}+\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
and
 $2\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FC})$
for
$2\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{2}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FC})$
for
 $(1,1)$
-form
$(1,1)$
-form
 $\unicode[STIX]{x1D6FC}$
as shown in [Reference Rao, Wan and ZhaoRWZ16, Proposition 2.6], we have which is exactly the system of obstruction equations given in [Reference Rao, Wan and ZhaoRWZ16, Proposition 2.7].
$\unicode[STIX]{x1D6FC}$
as shown in [Reference Rao, Wan and ZhaoRWZ16, Proposition 2.6], we have which is exactly the system of obstruction equations given in [Reference Rao, Wan and ZhaoRWZ16, Proposition 2.7]. $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D6FA}=\bar{\unicode[STIX]{x2202}}\circ (\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}})(\unicode[STIX]{x1D6FA})-\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA}),\quad \\ \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}=\unicode[STIX]{x2202}\circ (\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}\bar{\unicode[STIX]{x1D711}}}-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})(\unicode[STIX]{x1D6FA})-\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA}),\quad \\ \unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\bar{\unicode[STIX]{x2202}}\unicode[STIX]{x1D6FA}=\bar{\unicode[STIX]{x2202}}\circ (\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}})(\unicode[STIX]{x1D6FA})-\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FA}),\quad \\ \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}=\unicode[STIX]{x2202}\circ (\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}\bar{\unicode[STIX]{x1D711}}}-\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}})(\unicode[STIX]{x1D6FA})-\bar{\unicode[STIX]{x2202}}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA}),\quad \\ \unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D6FA})=0,\quad \end{array}\right.\end{eqnarray}$$
Unfortunately, the system (11) of obstruction equations consists of too many equations, and is difficult to solve. We try to reduce it to one with only two equations as in Proposition 4.5.
We will use the homogenous notation for a power series here and henceforth. Assuming that
![]() $\unicode[STIX]{x1D6FC}(t)$
is a power series of (bundle-valued)
$\unicode[STIX]{x1D6FC}(t)$
is a power series of (bundle-valued)
![]() $(p,q)$
-forms, expanded as
$(p,q)$
-forms, expanded as
we use the notation
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D6FC}(t)=\mathop{\sum }_{k=0}^{\infty }\unicode[STIX]{x1D6FC}_{k},\quad \\ \displaystyle \unicode[STIX]{x1D6FC}_{k}=\mathop{\sum }_{i+j=k}\unicode[STIX]{x1D6FC}_{i,j}t^{i}\overline{t}^{j},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D6FC}(t)=\mathop{\sum }_{k=0}^{\infty }\unicode[STIX]{x1D6FC}_{k},\quad \\ \displaystyle \unicode[STIX]{x1D6FC}_{k}=\mathop{\sum }_{i+j=k}\unicode[STIX]{x1D6FC}_{i,j}t^{i}\overline{t}^{j},\quad \end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{k}$
is the
$\unicode[STIX]{x1D6FC}_{k}$
is the
![]() $k$
-order homogeneous part in the expansion of
$k$
-order homogeneous part in the expansion of
![]() $\unicode[STIX]{x1D6FC}(t)$
and all
$\unicode[STIX]{x1D6FC}(t)$
and all
![]() $\unicode[STIX]{x1D6FC}_{i,j}$
are smooth (bundle-valued)
$\unicode[STIX]{x1D6FC}_{i,j}$
are smooth (bundle-valued)
![]() $(p,q)$
-forms on
$(p,q)$
-forms on
![]() $X_{0}$
with
$X_{0}$
with
![]() $\unicode[STIX]{x1D6FC}(0)=\unicode[STIX]{x1D6FC}_{0,0}$
.
$\unicode[STIX]{x1D6FC}(0)=\unicode[STIX]{x1D6FC}_{0,0}$
.
Lemma 4.4. If
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
for any
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
for any
![]() $N_{1}\leqslant N$
, then
$N_{1}\leqslant N$
, then
for any
![]() $N_{1}\leqslant N$
.
$N_{1}\leqslant N$
.
Proof. From (10), it follows that
For any
![]() $N_{1}\leqslant N$
,
$N_{1}\leqslant N$
,
By comparing degrees, we complete the proof. ◻
As for (10), one can also have
A long local calculation shows that
Here we use the notation ![]() , first introduced in[Reference Rao, Wan and ZhaoRWZ16, §2.1], to denote the simultaneous contraction on each component of a complex differential form. For example,
, first introduced in[Reference Rao, Wan and ZhaoRWZ16, §2.1], to denote the simultaneous contraction on each component of a complex differential form. For example, ![]() means that the operator
means that the operator
![]() $(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}+\bar{\unicode[STIX]{x1D711}})$
acts on
$(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711}+\bar{\unicode[STIX]{x1D711}})$
acts on
![]() $\unicode[STIX]{x1D6FC}$
simultaneously as
$\unicode[STIX]{x1D6FC}$
simultaneously as

if
![]() $\unicode[STIX]{x1D6FC}$
is locally expressed by
$\unicode[STIX]{x1D6FC}$
is locally expressed by
This new simultaneous contraction is well defined since
![]() $\unicode[STIX]{x1D711}(t)$
is a global
$\unicode[STIX]{x1D711}(t)$
is a global
![]() $(1,0)$
-vector valued
$(1,0)$
-vector valued
![]() $(0,1)$
-form on
$(0,1)$
-form on
![]() $X_{0}$
(see [Reference Morrow and KodairaMK71, pp. 150–151]) as reasoned in [Reference Rao and ZhaoRZ18, Proof of Lemma 2.8]. Moreover, we know that
$X_{0}$
(see [Reference Morrow and KodairaMK71, pp. 150–151]) as reasoned in [Reference Rao and ZhaoRZ18, Proof of Lemma 2.8]. Moreover, we know that
Thus, by carefully comparing the types of forms in both sides of (13), we have
See [Reference Rao and ZhaoRZ18, Proposition 2.13] and [Reference Rao, Wan and ZhaoRWZ16, (2.14)] for more details of (14).
Here and henceforth we denote by
![]() $(\unicode[STIX]{x1D6FC})^{p,q}$
the
$(\unicode[STIX]{x1D6FC})^{p,q}$
the
![]() $(p,q)$
-type part of a
$(p,q)$
-type part of a
![]() $(p+q)$
-degree complex differential form
$(p+q)$
-degree complex differential form
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Proposition 4.5. The obstruction equation
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
is also equivalent to
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
is also equivalent to
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{k=0}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \mathop{\sum }_{k=0}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k-1}}{(k-1)!}(\tilde{\unicode[STIX]{x1D6FA}})=0.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \mathop{\sum }_{k=0}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \mathop{\sum }_{k=0}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k-1}}{(k-1)!}(\tilde{\unicode[STIX]{x1D6FA}})=0.\quad \end{array}\right.\end{eqnarray}$$
Proof. From the proof of Proposition 4.2, it is easy to see that the left-hand side of the first equation in (15) is
![]() $(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p+1,q}$
, while the other one is
$(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p+1,q}$
, while the other one is
![]() $(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p,q+1}$
. Thus, (15) holds if
$(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p,q+1}$
. Thus, (15) holds if
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
.
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))=0$
.
Conversely, we assume that (15) holds. By (14) and (10), we compare types of forms to get

Similarly, we get
where
![]() $\overline{\bullet }$
in the last term means that
$\overline{\bullet }$
in the last term means that
![]() $\unicode[STIX]{x2202},\bar{\unicode[STIX]{x2202}},\unicode[STIX]{x1D711},\bar{\unicode[STIX]{x1D711}}$
are replaced by
$\unicode[STIX]{x2202},\bar{\unicode[STIX]{x2202}},\unicode[STIX]{x1D711},\bar{\unicode[STIX]{x1D711}}$
are replaced by
![]() $\bar{\unicode[STIX]{x2202}},\unicode[STIX]{x2202},\bar{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D711}$
, respectively, while
$\bar{\unicode[STIX]{x2202}},\unicode[STIX]{x2202},\bar{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D711}$
, respectively, while
![]() $\unicode[STIX]{x1D6FA}$
takes no conjugation.
$\unicode[STIX]{x1D6FA}$
takes no conjugation.
If (15) holds, i.e.,
![]() $(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p+1,q}=0$
and
$(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p+1,q}=0$
and
![]() $(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p,q+1}=0$
, we will prove
$(d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})))^{p,q+1}=0$
, we will prove
by induction on orders. Obviously,
Now we assume that for any
![]() $N_{1}\leqslant N$
,
$N_{1}\leqslant N$
,
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
. By Lemma 4.4, we have
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
. By Lemma 4.4, we have
for any
![]() $N_{1}\leqslant N$
. For the
$N_{1}\leqslant N$
. For the
![]() $(N+1)$
th order, (16) and the induction assumption for any
$(N+1)$
th order, (16) and the induction assumption for any
![]() $N_{1}\leqslant N$
imply
$N_{1}\leqslant N$
imply

Similarly, we have
![]() $(\unicode[STIX]{x2202}_{t}e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}=0$
. So
$(\unicode[STIX]{x2202}_{t}e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}=0$
. So
Thus, we complete the proof. ◻
Remark 4.6. For
![]() $p=q=1$
, if solving
$p=q=1$
, if solving
![]() $de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})=0$
for the orders
$de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA})=0$
for the orders
![]() ${\leqslant}N$
, we proceed to the
${\leqslant}N$
, we proceed to the
![]() $(N+1)$
th order. It is necessary to prove
$(N+1)$
th order. It is necessary to prove
From (10), we have
where the last equality follows from Lemma 4.4.
Now we begin to solve (15) with two more lemmas. For the resolution of
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equations, we need a lemma due to [Reference PopoviciPop15, Theorem 4.1] (or [Reference Rao, Wan and ZhaoRWZ16, Lemma 3.14]).
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equations, we need a lemma due to [Reference PopoviciPop15, Theorem 4.1] (or [Reference Rao, Wan and ZhaoRWZ16, Lemma 3.14]).
Lemma 4.7. Let
![]() $(X,\unicode[STIX]{x1D714})$
be a compact Hermitian complex manifold with the pure-type complex differential forms
$(X,\unicode[STIX]{x1D714})$
be a compact Hermitian complex manifold with the pure-type complex differential forms
![]() $x$
and
$x$
and
![]() $y$
. Assume that the
$y$
. Assume that the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation
admits a solution. Then an explicit solution of the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation (17) can be chosen as
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation (17) can be chosen as
which uniquely minimizes the
![]() $L^{2}$
-norms of all the solutions with respect to
$L^{2}$
-norms of all the solutions with respect to
![]() $\unicode[STIX]{x1D714}$
. Besides, the equalities
$\unicode[STIX]{x1D714}$
. Besides, the equalities
hold, where
![]() $\mathbb{G}_{\text{BC}}$
and
$\mathbb{G}_{\text{BC}}$
and
![]() $\mathbb{G}_{\text{A}}$
are the associated Green’s operators of
$\mathbb{G}_{\text{A}}$
are the associated Green’s operators of
![]() $\Box _{\text{BC}}$
and
$\Box _{\text{BC}}$
and
![]() $\Box _{\text{A}}$
, respectively. Here
$\Box _{\text{A}}$
, respectively. Here
![]() $\Box _{\text{BC}}$
is defined in (7) and
$\Box _{\text{BC}}$
is defined in (7) and
![]() $\Box _{\text{A}}$
is the second Kodaira–Spencer operator (often also called Aeppli Laplacian)
$\Box _{\text{A}}$
is the second Kodaira–Spencer operator (often also called Aeppli Laplacian)
Sketch of Proof for Lemma 4.7.
We shall use the Hodge decomposition of
![]() $\Box _{\text{BC}}$
on
$\Box _{\text{BC}}$
on
![]() $X$
,
$X$
,
whose three parts are orthogonal to each other with respect to the
![]() $L^{2}$
-scalar product defined by
$L^{2}$
-scalar product defined by
![]() $\unicode[STIX]{x1D714}$
, combined with the equality
$\unicode[STIX]{x1D714}$
, combined with the equality
where
![]() $\mathbb{H}_{\text{BC}}$
is the harmonic projection operator. Then two observations follow:
$\mathbb{H}_{\text{BC}}$
is the harmonic projection operator. Then two observations follow:
(1)
 $\Box _{\text{BC}}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\Box _{\text{BC}}$
;
$\Box _{\text{BC}}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\Box _{\text{BC}}$
;(2)
 $\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}$
.
$\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }=\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}$
.
It is clear that (1) implies (2), while the statement (1) is proved by a direct calculation,
Hence, we have
where
![]() $y\in \operatorname{Im}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
due to the solution-existence of the
$y\in \operatorname{Im}\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
due to the solution-existence of the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation.
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation.
To see that the solution
![]() $(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}y$
is the unique
$(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}y$
is the unique
![]() $L^{2}$
-norm minimum, we resort to the Hodge decomposition of the operator
$L^{2}$
-norm minimum, we resort to the Hodge decomposition of the operator
![]() $\Box _{\text{A}}$
,
$\Box _{\text{A}}$
,
where
![]() $\ker \Box _{\text{A}}=\ker (\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})\cap \ker \unicode[STIX]{x2202}^{\ast }\cap \ker \overline{\unicode[STIX]{x2202}}^{\ast }$
. Let
$\ker \Box _{\text{A}}=\ker (\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})\cap \ker \unicode[STIX]{x2202}^{\ast }\cap \ker \overline{\unicode[STIX]{x2202}}^{\ast }$
. Let
![]() $z$
be an arbitrary solution of the
$z$
be an arbitrary solution of the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation (17), which decomposes into three components
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-equation (17), which decomposes into three components
![]() $z_{1}+z_{2}+z_{3}$
with respect to the Hodge decomposition (18) of
$z_{1}+z_{2}+z_{3}$
with respect to the Hodge decomposition (18) of
![]() $\Box _{\text{A}}$
. And we are able to obtain that
$\Box _{\text{A}}$
. And we are able to obtain that
Therefore,
and the equality holds if and only if
![]() $z_{1}=z_{2}=0$
, i.e.,
$z_{1}=z_{2}=0$
, i.e.,
![]() $z=z_{3}=(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}y$
.◻
$z=z_{3}=(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}y$
.◻
Lemma 4.8. Let
![]() $X$
be a complex manifold satisfying the
$X$
be a complex manifold satisfying the
![]() $(p,q+1)$
th and
$(p,q+1)$
th and
![]() $(q,p+1)$
th mild
$(q,p+1)$
th mild
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata. Consider the system of equations
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemmata. Consider the system of equations
where
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D709}$
are
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D709}$
are
![]() $(p+1,q-1)$
- and
$(p+1,q-1)$
- and
![]() $(q+1,p-1)$
-forms on
$(q+1,p-1)$
-forms on
![]() $X$
, respectively. The system of equations (19) has a solution if and only if
$X$
, respectively. The system of equations (19) has a solution if and only if
Proof. This lemma is inspired by [Reference Rao, Wan and ZhaoRWZ16, Observation 2.11]. The lemmata assumption will produce
![]() $\unicode[STIX]{x1D707}\in A^{p,q-1}$
and
$\unicode[STIX]{x1D707}\in A^{p,q-1}$
and
![]() $\unicode[STIX]{x1D708}\in A^{p-1,q}$
, satisfying the system of equations
$\unicode[STIX]{x1D708}\in A^{p-1,q}$
, satisfying the system of equations
The combined expression
is our choice for the solution of the system (19). ◻
By Lemmata 4.7 and 4.8, we have the following proposition.
Proposition 4.9. With the same notation as in Lemmata 4.7 and 4.8, the system of equations (19) has a canonical solution
Now we assume that
![]() $X_{0}$
is a complex manifold that satisfies the
$X_{0}$
is a complex manifold that satisfies the
![]() $(q,p+1)$
th and
$(q,p+1)$
th and
![]() $(p,q+1)$
th mild
$(p,q+1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata. The obstruction (15) can be rewritten as
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata. The obstruction (15) can be rewritten as
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6FA}}+\mathop{\sum }_{k=1}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \bar{\unicode[STIX]{x2202}}\tilde{\unicode[STIX]{x1D6FA}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}(\tilde{\unicode[STIX]{x1D6FA}})+\mathop{\sum }_{k=2}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k-1}}{(k-1)!}(\tilde{\unicode[STIX]{x1D6FA}})=0.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6FA}}+\mathop{\sum }_{k=1}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \bar{\unicode[STIX]{x2202}}\tilde{\unicode[STIX]{x1D6FA}}+\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}(\tilde{\unicode[STIX]{x1D6FA}})+\mathop{\sum }_{k=2}^{\infty }\biggl(\bar{\unicode[STIX]{x2202}}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}+\unicode[STIX]{x2202}\circ \frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\biggr)\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k-1}}{(k-1)!}(\tilde{\unicode[STIX]{x1D6FA}})=0.\quad \end{array}\right.\end{eqnarray}$$
Set
Then (20) becomes
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6FA}}^{\prime }=-\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}}),\quad \\ \displaystyle \bar{\unicode[STIX]{x2202}}\tilde{\unicode[STIX]{x1D6FA}}^{\prime }=-\unicode[STIX]{x2202}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}}).\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6FA}}^{\prime }=-\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}}),\quad \\ \displaystyle \bar{\unicode[STIX]{x2202}}\tilde{\unicode[STIX]{x1D6FA}}^{\prime }=-\unicode[STIX]{x2202}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}}).\quad \end{array}\right.\end{eqnarray}$$
In order to use the
![]() $(q,p+1)$
th and
$(q,p+1)$
th and
![]() $(p,q+1)$
th mild
$(p,q+1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, we need to prove
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata, we need to prove
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \\ \displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})=0,\quad \end{array}\right.\end{eqnarray}$$
at the
![]() $(N+1)$
th order if it has been solved for the orders
$(N+1)$
th order if it has been solved for the orders
![]() ${\leqslant}N$
.
${\leqslant}N$
.
Now we prove (21). Firstly, note that
Thus,
 $$\begin{eqnarray}\displaystyle \mathop{\biggl(\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{N+1} & = & \displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}((e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))^{p-1,q+1})_{N+1}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p,q+2}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x2202}de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p,q+2}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p-1,q+2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\biggl(\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{N+1} & = & \displaystyle \unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}((e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))^{p-1,q+1})_{N+1}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p,q+2}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x2202}de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p,q+2}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}(de^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N+1}^{p-1,q+2}\nonumber\end{eqnarray}$$
since the obstruction equation is solved for the orders
![]() ${\leqslant}N$
, i.e.,
${\leqslant}N$
, i.e.,
![]() $d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
for any
$d(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\bar{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D6FA}))_{N_{1}}=0$
for any
![]() $N_{1}\leqslant N$
. By Lemma 4.4, we have
$N_{1}\leqslant N$
. By Lemma 4.4, we have
for any
![]() $N_{1}\leqslant N$
. It follows from (10) that
$N_{1}\leqslant N$
. It follows from (10) that
So
Hence, we have proved the second equation of (21). Similarly, by the same argument (i.e., replace all
![]() $\unicode[STIX]{x1D711}$
(respectively,
$\unicode[STIX]{x1D711}$
(respectively,
![]() $\bar{\unicode[STIX]{x1D711}}$
) by
$\bar{\unicode[STIX]{x1D711}}$
) by
![]() $\bar{\unicode[STIX]{x1D711}}$
(respectively,
$\bar{\unicode[STIX]{x1D711}}$
(respectively,
![]() $\unicode[STIX]{x1D711}$
)), the first equation of (21) also holds.
$\unicode[STIX]{x1D711}$
)), the first equation of (21) also holds.
By Proposition 4.9, one obtains a formal solution of (20) by induction
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D6FA}}_{l} & = & \displaystyle -\mathop{\biggl(\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\biggl(\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\biggl(\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\biggl(\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\biggl(\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\biggl(\mathop{\sum }_{k=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D6FA}}_{l} & = & \displaystyle -\mathop{\biggl(\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\biggl(\mathop{\sum }_{k=1}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\biggl(\mathop{\sum }_{k=0}^{\infty }\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\biggl(\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\biggl(\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\biggl(\mathop{\sum }_{k=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\biggr)}\nolimits_{l}.\end{eqnarray}$$
Remark 4.10. We are possibly able to obtain this (formal) solution (22) of (20) backwards by the invertibility of some operator in small
![]() $t$
as shown in [Reference Liu, Rao and WanLRW17, Remark 4.6], but it seems that to figure out this solution explicitly by the power series method is indispensable in this process.
$t$
as shown in [Reference Liu, Rao and WanLRW17, Remark 4.6], but it seems that to figure out this solution explicitly by the power series method is indispensable in this process.
4.3 Regularity argument
Here we adopt a strategy for a convergence argument [Reference Liu and ZhuLZ18] suggested by Liu, which simplifies our argument involved in [Reference Rao, Wan and ZhaoRWZ16, Reference Rao and ZhaoRZ18].
From the induction expression (22), one obtains the formal expression of
![]() $\tilde{\unicode[STIX]{x1D6FA}}$
$\tilde{\unicode[STIX]{x1D6FA}}$
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D6FA}} & = & \displaystyle -\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i}}{i!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i-1}}{(i-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{i=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i+1}}{(i+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})+\unicode[STIX]{x1D6FA}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D6FA}} & = & \displaystyle -\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i}}{i!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})-\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i-1}}{(i-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{i=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i+1}}{(i+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}(\tilde{\unicode[STIX]{x1D6FA}})+\unicode[STIX]{x1D6FA}_{0}.\end{eqnarray}$$
Set
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle \unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{i=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i+1}}{(i+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i}}{i!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\\ \displaystyle & & \displaystyle -\,\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i-1}}{(i-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle \unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{i=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i+1}}{(i+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i}}{i!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\\ \displaystyle & & \displaystyle -\,\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{i=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{i-1}}{(i-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{i}}{i!}\nonumber\end{eqnarray}$$
and write
We claim that
![]() $\tilde{\unicode[STIX]{x1D6FA}}(t)$
converges in Hölder norm as
$\tilde{\unicode[STIX]{x1D6FA}}(t)$
converges in Hölder norm as
![]() $t\rightarrow 0$
by use of the following two a priori elliptic estimates: for any complex differential form
$t\rightarrow 0$
by use of the following two a priori elliptic estimates: for any complex differential form
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
and
where
![]() $k>3$
and
$k>3$
and
![]() $C_{k,\unicode[STIX]{x1D6FC}}$
depends only on
$C_{k,\unicode[STIX]{x1D6FC}}$
depends only on
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
, not on
$\unicode[STIX]{x1D6FC}$
, not on
![]() $\unicode[STIX]{x1D719}$
(cf. [Reference KodairaKod86, Appendix.Theorem 7.4] for example). And we note that
$\unicode[STIX]{x1D719}$
(cf. [Reference KodairaKod86, Appendix.Theorem 7.4] for example). And we note that
![]() $\unicode[STIX]{x1D711}(t)$
converges smoothly to zero as
$\unicode[STIX]{x1D711}(t)$
converges smoothly to zero as
![]() $t\rightarrow 0$
. Thus, by (24), we estimate
$t\rightarrow 0$
. Thus, by (24), we estimate
where
![]() $0<\unicode[STIX]{x1D716}_{k,\unicode[STIX]{x1D6FC}}\ll 1$
is some constant depending on
$0<\unicode[STIX]{x1D716}_{k,\unicode[STIX]{x1D6FC}}\ll 1$
is some constant depending on
![]() $k,\unicode[STIX]{x1D6FC}$
.
$k,\unicode[STIX]{x1D6FC}$
.
Finally, we proceed to the regularity of
![]() $\tilde{\unicode[STIX]{x1D6FA}}(t)$
since there is possibly no uniform lower bound for the convergence radius obtained as above in the
$\tilde{\unicode[STIX]{x1D6FA}}(t)$
since there is possibly no uniform lower bound for the convergence radius obtained as above in the
![]() $C^{k,\unicode[STIX]{x1D6FC}}$
-norm when
$C^{k,\unicode[STIX]{x1D6FC}}$
-norm when
![]() $k$
converges to
$k$
converges to
![]() $+\infty$
. This argument lies heavily in the elliptic estimates [Reference KodairaKod86, Appendix 8], [Reference Douglis and NirenbergDN55] and also [Reference Rao, Wan and ZhaoRWZ16, §3.2].
$+\infty$
. This argument lies heavily in the elliptic estimates [Reference KodairaKod86, Appendix 8], [Reference Douglis and NirenbergDN55] and also [Reference Rao, Wan and ZhaoRWZ16, §3.2].
Without loss of generality, we just consider the equation
 $$\begin{eqnarray}\displaystyle \Box \tilde{\unicode[STIX]{x1D6FA}} & = & \displaystyle -\Box \mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})-\overline{\unicode[STIX]{x2202}}\overline{\unicode[STIX]{x2202}}^{\ast }\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\Box \unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{k=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Box \tilde{\unicode[STIX]{x1D6FA}} & = & \displaystyle -\Box \mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k}}{k!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})-\overline{\unicode[STIX]{x2202}}\overline{\unicode[STIX]{x2202}}^{\ast }\overline{\unicode[STIX]{x2202}}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\overline{\unicode[STIX]{x2202}}\mathop{\sum }_{k=1}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k-1}}{(k-1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\\ \displaystyle & & \displaystyle +\,\Box \unicode[STIX]{x2202}(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}})^{\ast }\mathbb{G}_{\text{BC}}\unicode[STIX]{x2202}\mathop{\sum }_{k=0}^{\min \{q,n-p\}}\frac{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}^{k+1}}{(k+1)!}\circ \frac{\unicode[STIX]{x1D704}_{(\unicode[STIX]{x1D7D9}-\bar{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D711})^{-1}\bar{\unicode[STIX]{x1D711}}}^{k}}{k!}(\tilde{\unicode[STIX]{x1D6FA}})\nonumber\end{eqnarray}$$
by applying the
![]() $\overline{\unicode[STIX]{x2202}}$
-Laplacian
$\overline{\unicode[STIX]{x2202}}$
-Laplacian
![]() $\Box =\overline{\unicode[STIX]{x2202}}^{\ast }\overline{\unicode[STIX]{x2202}}+\overline{\unicode[STIX]{x2202}}\overline{\unicode[STIX]{x2202}}^{\ast }$
to the expression formula (23) and omitting the lower-order term
$\Box =\overline{\unicode[STIX]{x2202}}^{\ast }\overline{\unicode[STIX]{x2202}}+\overline{\unicode[STIX]{x2202}}\overline{\unicode[STIX]{x2202}}^{\ast }$
to the expression formula (23) and omitting the lower-order term
![]() $\Box \unicode[STIX]{x1D6FA}_{0}$
in this expression. By replacing the roles of
$\Box \unicode[STIX]{x1D6FA}_{0}$
in this expression. By replacing the roles of
in the analogous strongly elliptic second-order pseudo-differential equation in the regularity argument of [Reference Rao, Wan and ZhaoRWZ16, §3.2]
by
respectively, we prove the following result. For each
![]() $l=1,2,\ldots \,$
, choose a smooth function
$l=1,2,\ldots \,$
, choose a smooth function
![]() $\unicode[STIX]{x1D702}^{l}(t)$
with values in
$\unicode[STIX]{x1D702}^{l}(t)$
with values in
![]() $[0,1]$
$[0,1]$
 $$\begin{eqnarray}\unicode[STIX]{x1D702}^{l}(t)\equiv \left\{\begin{array}{@{}l@{}}\displaystyle 1\quad \text{for }|t|\leqslant \biggl(\frac{1}{2}+\frac{1}{2^{l+1}}\biggr)r;\quad \\ \displaystyle 0\quad \text{for }|t|\geqslant \biggl(\frac{1}{2}+\frac{1}{2^{l}}\biggr)r,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}^{l}(t)\equiv \left\{\begin{array}{@{}l@{}}\displaystyle 1\quad \text{for }|t|\leqslant \biggl(\frac{1}{2}+\frac{1}{2^{l+1}}\biggr)r;\quad \\ \displaystyle 0\quad \text{for }|t|\geqslant \biggl(\frac{1}{2}+\frac{1}{2^{l}}\biggr)r,\quad \end{array}\right.\end{eqnarray}$$
where
![]() $r$
is a positive constant to be determined. Inductively, by Douglis–Nirenberg’s interior estimates [Reference KodairaKod86, Appendix.Theorem 2.3], [Reference Douglis and NirenbergDN55], for any
$r$
is a positive constant to be determined. Inductively, by Douglis–Nirenberg’s interior estimates [Reference KodairaKod86, Appendix.Theorem 2.3], [Reference Douglis and NirenbergDN55], for any
![]() $l=1,2,\ldots \,$
,
$l=1,2,\ldots \,$
,
![]() $\unicode[STIX]{x1D702}^{2l+1}\tilde{\unicode[STIX]{x1D6FA}}(t)$
is
$\unicode[STIX]{x1D702}^{2l+1}\tilde{\unicode[STIX]{x1D6FA}}(t)$
is
![]() $C^{k+l,\unicode[STIX]{x1D6FC}}$
, where
$C^{k+l,\unicode[STIX]{x1D6FC}}$
, where
![]() $r$
can be chosen independent of
$r$
can be chosen independent of
![]() $l$
. Since
$l$
. Since
![]() $\unicode[STIX]{x1D702}^{2l+1}(t)$
is identically equal to
$\unicode[STIX]{x1D702}^{2l+1}(t)$
is identically equal to
![]() $1$
on
$1$
on
![]() $|t|<r/2$
, which is independent of
$|t|<r/2$
, which is independent of
![]() $l$
,
$l$
,
![]() $\tilde{\unicode[STIX]{x1D6FA}}(t)$
is
$\tilde{\unicode[STIX]{x1D6FA}}(t)$
is
![]() $C^{\infty }$
on
$C^{\infty }$
on
![]() $X_{0}$
with
$X_{0}$
with
![]() $|t|<r/2$
. Then
$|t|<r/2$
. Then
![]() $\tilde{\unicode[STIX]{x1D6FA}}(t)$
can be considered as a real analytic family of
$\tilde{\unicode[STIX]{x1D6FA}}(t)$
can be considered as a real analytic family of
![]() $(p,q)$
-forms in
$(p,q)$
-forms in
![]() $t$
and thus is smooth on
$t$
and thus is smooth on
![]() $t$
.
$t$
.
5 Deformation invariance of Bott–Chern numbers
The main goal of this section is to study deformation invariance of Bott–Chern numbers on complex manifolds.
Theorem 5.1. If the reference fiber
![]() $X_{0}$
satisfies the
$X_{0}$
satisfies the
![]() $(p,q\,+\,1)$
th and
$(p,q\,+\,1)$
th and
![]() $(q,p\,+\,1)$
th mild
$(q,p\,+\,1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata and the deformation invariance of the
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemmata and the deformation invariance of the
![]() $(p-1,q-1)$
-Aeppli number
$(p-1,q-1)$
-Aeppli number
![]() $h_{\text{A}}^{p-1,q-1}(X_{t})$
holds, then
$h_{\text{A}}^{p-1,q-1}(X_{t})$
holds, then
![]() $h_{\text{BC}}^{p,q}(X_{t})$
are deformation invariant.
$h_{\text{BC}}^{p,q}(X_{t})$
are deformation invariant.
The following is a direct corollary.
Corollary 5.2. If the reference fiber
![]() $X_{0}$
satisfies the
$X_{0}$
satisfies the
![]() $(p,1)$
th mild
$(p,1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma, then
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma, then
![]() $h_{\text{BC}}^{p,0}(X_{t})$
and
$h_{\text{BC}}^{p,0}(X_{t})$
and
![]() $h_{\text{BC}}^{0,p}(X_{t})$
are deformation invariant.
$h_{\text{BC}}^{0,p}(X_{t})$
are deformation invariant.
Resorting to the calculations for the Hodge and Bott–Chern numbers of manifolds in the Kuranishi family of the Iwasawa manifold (cf. [Reference AngellaAng13, Appendix]), we find the following example where neither the deformation invariance of the
![]() $(p,0)$
- nor
$(p,0)$
- nor
![]() $(0,p)$
-Bott–Chern numbers is true when the condition of the
$(0,p)$
-Bott–Chern numbers is true when the condition of the
![]() $(p,1)$
th mild
$(p,1)$
th mild
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma does not hold on the reference fiber in Corollary 5.2. It indicates that the condition involved may not be omitted in order for the deformation invariance of
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma does not hold on the reference fiber in Corollary 5.2. It indicates that the condition involved may not be omitted in order for the deformation invariance of
![]() $(p,0)$
- and
$(p,0)$
- and
![]() $(0,p)$
-Bott–Chern numbers.
$(0,p)$
-Bott–Chern numbers.
Let
![]() $\mathbb{I}_{3}$
be the Iwasawa manifold of complex dimension
$\mathbb{I}_{3}$
be the Iwasawa manifold of complex dimension
![]() $3$
with
$3$
with
![]() $\unicode[STIX]{x1D702}^{1},\unicode[STIX]{x1D702}^{2},\unicode[STIX]{x1D702}^{3}$
denoted by the basis of the holomorphic one form
$\unicode[STIX]{x1D702}^{1},\unicode[STIX]{x1D702}^{2},\unicode[STIX]{x1D702}^{3}$
denoted by the basis of the holomorphic one form
![]() $H^{0}(\mathbb{I}_{3},\unicode[STIX]{x1D6FA}^{1})$
of
$H^{0}(\mathbb{I}_{3},\unicode[STIX]{x1D6FA}^{1})$
of
![]() $\mathbb{I}_{3}$
, satisfying the relation
$\mathbb{I}_{3}$
, satisfying the relation
And the convention
![]() $\unicode[STIX]{x1D702}^{12\bar{1}\bar{3}}:=\unicode[STIX]{x1D702}^{1}\wedge \unicode[STIX]{x1D702}^{2}\wedge \overline{\unicode[STIX]{x1D702}}^{1}\wedge \overline{\unicode[STIX]{x1D702}}^{3}$
will be used for simplicity.
$\unicode[STIX]{x1D702}^{12\bar{1}\bar{3}}:=\unicode[STIX]{x1D702}^{1}\wedge \unicode[STIX]{x1D702}^{2}\wedge \overline{\unicode[STIX]{x1D702}}^{1}\wedge \overline{\unicode[STIX]{x1D702}}^{3}$
will be used for simplicity.
Example 5.3 (The cases
 $(p,q)=(2,0)$
and
$(p,q)=(2,0)$
and
 $(0,2)$
).
$(0,2)$
).
The injectivity of
![]() $\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{2,1}$
does not hold on
$\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{2,1}$
does not hold on
![]() $\mathbb{I}_{3}$
and in these cases
$\mathbb{I}_{3}$
and in these cases
![]() $h_{\text{BC}}^{2,0}(X_{t})$
and
$h_{\text{BC}}^{2,0}(X_{t})$
and
![]() $h_{\text{BC}}^{0,2}(X_{t})$
are deformation variant.
$h_{\text{BC}}^{0,2}(X_{t})$
are deformation variant.
Proof. It is easy to check that the left-invariant
![]() $(2,1)$
-form
$(2,1)$
-form
stands for a non-trivial Bott–Chern class but a trivial class in
![]() $H_{\unicode[STIX]{x2202}}^{2,1}(\mathbb{I}_{3})$
, which indicates non-injectivity of
$H_{\unicode[STIX]{x2202}}^{2,1}(\mathbb{I}_{3})$
, which indicates non-injectivity of
![]() $\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{2,1}$
. The deformation variance of
$\unicode[STIX]{x1D704}_{\text{BC},\unicode[STIX]{x2202}}^{2,1}$
. The deformation variance of
![]() $h_{\text{BC}}^{2,0}(X_{t})$
and
$h_{\text{BC}}^{2,0}(X_{t})$
and
![]() $h_{\text{BC}}^{0,2}(X_{t})$
can be got from [Reference AngellaAng13, Appendix].◻
$h_{\text{BC}}^{0,2}(X_{t})$
can be got from [Reference AngellaAng13, Appendix].◻
Now let us describe our basic philosophy to consider the deformation invariance of Bott–Chern numbers briefly. The Kodaira–Spencer’s upper semi-continuity theorem [Reference Kodaira and SpencerKS60, Theorem 4] tells us that the function
is always upper semi-continuous for
![]() $t\in B$
and thus, to approach the deformational invariance of
$t\in B$
and thus, to approach the deformational invariance of
![]() $h_{\text{BC}}^{p,q}(X_{t})$
, we only need to obtain the lower semi-continuity. Here our main strategy is a modified iteration procedure, originally from [Reference Liu, Sun and YauLSY09] and developed in [Reference SunSun12, Reference Sun and YauSY11, Reference Zhao and RaoZR13, Reference Liu, Rao and YangLRY15], which is to look for an injective extension map from
$h_{\text{BC}}^{p,q}(X_{t})$
, we only need to obtain the lower semi-continuity. Here our main strategy is a modified iteration procedure, originally from [Reference Liu, Sun and YauLSY09] and developed in [Reference SunSun12, Reference Sun and YauSY11, Reference Zhao and RaoZR13, Reference Liu, Rao and YangLRY15], which is to look for an injective extension map from
![]() $H_{\text{BC}}^{p,q}(X_{0})$
to
$H_{\text{BC}}^{p,q}(X_{0})$
to
![]() $H_{\text{BC}}^{p,q}(X_{t})$
. More precisely, for the unique harmonic representative
$H_{\text{BC}}^{p,q}(X_{t})$
. More precisely, for the unique harmonic representative
![]() $\unicode[STIX]{x1D70E}_{0}$
of the initial Bott–Chern cohomology class in
$\unicode[STIX]{x1D70E}_{0}$
of the initial Bott–Chern cohomology class in
![]() $H_{\text{BC}}^{p,q}(X_{0})$
, we try to construct a convergent power series
$H_{\text{BC}}^{p,q}(X_{0})$
, we try to construct a convergent power series
with
![]() $\unicode[STIX]{x1D70E}_{t}$
varying smoothly on
$\unicode[STIX]{x1D70E}_{t}$
varying smoothly on
![]() $t$
such that for each small
$t$
such that for each small
![]() $t$
:
$t$
:
(i)
 $e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E}_{t})\in A^{p,q}(X_{t})$
is
$e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E}_{t})\in A^{p,q}(X_{t})$
is
 $d$
-closed with respect to the differential structure on
$d$
-closed with respect to the differential structure on
 $X_{t}$
with the induced family
$X_{t}$
with the induced family
 $\unicode[STIX]{x1D711}$
of Beltrami differentials;
$\unicode[STIX]{x1D711}$
of Beltrami differentials;(ii) the extension map
 $H_{\text{BC}}^{p,q}(X_{0})\rightarrow H_{\text{BC}}^{p,q}(X_{t}):[\unicode[STIX]{x1D70E}_{0}]_{d}\mapsto [e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E}_{t})]_{d}$
is injective.
$H_{\text{BC}}^{p,q}(X_{0})\rightarrow H_{\text{BC}}^{p,q}(X_{t}):[\unicode[STIX]{x1D70E}_{0}]_{d}\mapsto [e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E}_{t})]_{d}$
is injective.
Obviously, (i) amounts to Theorem 4.1. To guarantee (ii), it suffices to prove the following proposition.
Proposition 5.4. If the
![]() $d$
-extension of
$d$
-extension of
![]() $H_{\text{BC}}^{p,q}(X_{0})$
as in Theorem 4.1 holds for a complex manifold
$H_{\text{BC}}^{p,q}(X_{0})$
as in Theorem 4.1 holds for a complex manifold
![]() $X_{0}$
, then the deformation invariance of
$X_{0}$
, then the deformation invariance of
![]() $h_{\text{A}}^{p-1,q-1}(X_{t})$
assures that the extension map
$h_{\text{A}}^{p-1,q-1}(X_{t})$
assures that the extension map
is injective.
Proof. Here we follow an idea in [Reference Rao and ZhaoRZ18, Proposition 3.15]. Let us fix a family of smoothly varying Hermitian metrics
![]() ${\{\unicode[STIX]{x1D714}_{t}\}}_{t\in B}$
for the infinitesimal deformation
${\{\unicode[STIX]{x1D714}_{t}\}}_{t\in B}$
for the infinitesimal deformation
![]() $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow B$
of
![]() $X_{0}$
. Thus, if the Aeppli numbers
$X_{0}$
. Thus, if the Aeppli numbers
![]() $h_{\text{A}}^{p-1,q-1}(X_{t})$
are deformation invariant, the Green’s operator
$h_{\text{A}}^{p-1,q-1}(X_{t})$
are deformation invariant, the Green’s operator
![]() $\mathbb{G}_{\text{A},t}$
, acting on the
$\mathbb{G}_{\text{A},t}$
, acting on the
![]() $A^{p-1,q-1}(X_{t})$
, depends differentiably with respect to
$A^{p-1,q-1}(X_{t})$
, depends differentiably with respect to
![]() $t$
from [Reference Kodaira and SpencerKS60, Theorem 7] by Kodaira and Spencer. Using this, we ensure that this extension map cannot send a nonzero class in
$t$
from [Reference Kodaira and SpencerKS60, Theorem 7] by Kodaira and Spencer. Using this, we ensure that this extension map cannot send a nonzero class in
![]() $H_{\text{BC}}^{p,q}(X_{0})$
to a zero class in
$H_{\text{BC}}^{p,q}(X_{0})$
to a zero class in
![]() $H_{\text{BC}}^{p,q}(X_{t})$
.
$H_{\text{BC}}^{p,q}(X_{t})$
.
If we suppose that
for some
![]() $\unicode[STIX]{x1D702}_{t}\in A^{p-1,q-1}(X_{t})$
when
$\unicode[STIX]{x1D702}_{t}\in A^{p-1,q-1}(X_{t})$
when
![]() $t\in B\setminus \{0\}$
, the Hodge decomposition of Bott–Chern Laplacian and the commutativity
$t\in B\setminus \{0\}$
, the Hodge decomposition of Bott–Chern Laplacian and the commutativity
in Lemma 4.7 yield that
 $$\begin{eqnarray}\displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}(\unicode[STIX]{x1D70E}_{t}) & = & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\unicode[STIX]{x1D702}_{t}=(\mathbb{H}_{\text{BC},t}+\Box _{\text{BC},t}\mathbb{G}_{\text{BC},t})\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{G}_{\text{BC},t}\Box _{\text{BC},t}\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{G}_{\text{BC},t}\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\overline{\unicode[STIX]{x2202}}_{t}^{\ast }\unicode[STIX]{x2202}_{t}^{\ast }\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\mathbb{G}_{\text{A},t}\overline{\unicode[STIX]{x2202}}_{t}^{\ast }\unicode[STIX]{x2202}_{t}^{\ast }(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}(\unicode[STIX]{x1D70E}_{t})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}(\unicode[STIX]{x1D70E}_{t}) & = & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\unicode[STIX]{x1D702}_{t}=(\mathbb{H}_{\text{BC},t}+\Box _{\text{BC},t}\mathbb{G}_{\text{BC},t})\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{G}_{\text{BC},t}\Box _{\text{BC},t}\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{G}_{\text{BC},t}\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\overline{\unicode[STIX]{x2202}}_{t}^{\ast }\unicode[STIX]{x2202}_{t}^{\ast }\unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}(\unicode[STIX]{x1D702}_{t})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x2202}_{t}\overline{\unicode[STIX]{x2202}}_{t}\mathbb{G}_{\text{A},t}\overline{\unicode[STIX]{x2202}}_{t}^{\ast }\unicode[STIX]{x2202}_{t}^{\ast }(e^{\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}(t)}|\unicode[STIX]{x1D704}_{\overline{\unicode[STIX]{x1D711}(t)}}}(\unicode[STIX]{x1D70E}_{t})),\nonumber\end{eqnarray}$$
where
![]() $\mathbb{H}_{\text{BC},t}$
,
$\mathbb{H}_{\text{BC},t}$
,
![]() $\Box _{\text{BC},t}$
are the harmonic projectors and the Bott–Chern Laplacian with respect to
$\Box _{\text{BC},t}$
are the harmonic projectors and the Bott–Chern Laplacian with respect to
![]() $(X_{t},\unicode[STIX]{x1D714}_{t})$
, respectively. Let
$(X_{t},\unicode[STIX]{x1D714}_{t})$
, respectively. Let
![]() $t$
converge to
$t$
converge to
![]() $0$
on both sides of the equality
$0$
on both sides of the equality
which turns out that
![]() $\unicode[STIX]{x1D70E}_{0}$
is
$\unicode[STIX]{x1D70E}_{0}$
is
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact on the reference fiber
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-exact on the reference fiber
![]() $X_{0}$
. Here we use the fact that the Green’s operator
$X_{0}$
. Here we use the fact that the Green’s operator
![]() $\mathbb{G}_{\text{A},t}$
depends differentiably with respect to
$\mathbb{G}_{\text{A},t}$
depends differentiably with respect to
![]() $t$
.◻
$t$
.◻
Acknowledgements
The authors would like to express their gratitude to Professor Kefeng Liu for his constant help, especially in the formal convergence argument here, and to Professor L. Ugarte for pointing out an example to us. This work started from the first author’s visit to Institut Fourier, Université Grenoble Alpes from March to June 2017, and was mostly completed during his visit to Institute of Mathematics, Academia Sinica since September 2017. He would like to thank both institutes for their hospitality and excellent working space. The third author is grateful to Professors Fangyang Zheng and Bo Guan for their help and interests during his visit to the Ohio State University in November 2017.