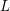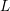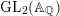Simple zeros of automorphic $L$-functions

Abstract

We prove that the complete $L$-function associated to any cuspidal automorphic representation of $\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$ has infinitely many simple zeros.

1 Introduction

In [Boo16], the first author showed that the complete $L$ -functions associated to classical holomorphic newforms have infinitely many simple zeros. The purpose of this paper is to extend that result to the remaining degree- $2$ automorphic $L$ -functions over $\mathbb{Q}$ , that is, those associated to cuspidal Maass newforms. This also extends work of the second author [Cho13] which established a quantitative estimate for the first few Maass forms of level $1$ . When combined with the holomorphic case from [Boo16], we obtain the following theorem.

Theorem 1.1. Let $\mathbb{A}_{\mathbb{Q}}$ denote the adèle ring of $\mathbb{Q}$ , and let $\unicode[STIX]{x1D70B}$ be a cuspidal automorphic representation of $\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$ . Then the associated complete $L$ -function $\unicode[STIX]{x1D6EC}(s,\unicode[STIX]{x1D70B})$ has infinitely many simple zeros.

The basic idea of the proof is the same as in [Boo16], which is in turn based on the method of Conrey and Ghosh [CG88]. Let $f$ be a primitive Maass cuspform of weight $k\in \{0,1\}$ for $\unicode[STIX]{x1D6E4}_{0}(N)$ with nebentypus character $\unicode[STIX]{x1D709}$ , and let $L_{f}(s)$ be the finite $L$ -function attached to $f$ :

$$\begin{eqnarray}L_{f}(s)=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}_{f}(n)n^{-s}.\end{eqnarray}$$

We define

$$\begin{eqnarray}D_{f}(s)=L_{f}(s)\frac{d^{2}}{ds^{2}}\log L_{f}(s)=\mathop{\sum }_{n=1}^{\infty }c_{f}(n)n^{-s}.\end{eqnarray}$$

Then it is easy to see that $D_{f}(s)$ has a pole at some point if and only if $L_{f}(s)$ has a simple zero there.

For $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ and $j\geqslant 0$ we define the additive twists

$$\begin{eqnarray}L_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(j)})=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}_{f}(n)\cos ^{(j)}(2\unicode[STIX]{x1D70B}n\unicode[STIX]{x1D6FC})n^{-s},\quad D_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(j)})=\mathop{\sum }_{n=1}^{\infty }c_{f}(n)\cos ^{(j)}(2\unicode[STIX]{x1D70B}n\unicode[STIX]{x1D6FC})n^{-s},\end{eqnarray}$$

where $\cos ^{(j)}$ denotes the $j$ th derivative of the cosine function. Let $q\nmid N$ be a prime and $\unicode[STIX]{x1D712}_{0}$ the principal character mod $q$ . Then we have the following expansions of the trigonometric functions in terms of Dirichlet characters:

$$\begin{eqnarray}\displaystyle \cos \biggl(\frac{2\unicode[STIX]{x1D70B}n}{q}\biggr) & = & \displaystyle 1-\frac{q}{q-1}\unicode[STIX]{x1D712}_{0}(n)+\frac{\sqrt{q}}{q-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}(modq) \\ \unicode[STIX]{x1D712}(-1)=1 \\ \unicode[STIX]{x1D712}\neq \unicode[STIX]{x1D712}_{0}}}\overline{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D712}}}\unicode[STIX]{x1D712}(n),\nonumber\\ \displaystyle \sin \biggl(\frac{2\unicode[STIX]{x1D70B}n}{q}\biggr) & = & \displaystyle \frac{\sqrt{q}}{q-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}(modq) \\ \unicode[STIX]{x1D712}(-1)=-1}}\overline{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D712}}}\unicode[STIX]{x1D712}(n),\nonumber\end{eqnarray}$$

where $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D712}}$ denotes the root number of the Dirichlet $L$ -function $L(s,\unicode[STIX]{x1D712})$ . In particular, we have

$$\begin{eqnarray}D_{f}\biggl(s,\frac{1}{q},\cos \biggr)=D_{f}(s)-\frac{q}{q-1}D_{f}(s,\unicode[STIX]{x1D712}_{0})+\frac{\sqrt{q}}{q-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}(modq) \\ \unicode[STIX]{x1D712}(-1)=1 \\ \unicode[STIX]{x1D712}\neq \unicode[STIX]{x1D712}_{0}}}\overline{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D712}}}D_{f}(s,\unicode[STIX]{x1D712}),\end{eqnarray}$$

where

$$\begin{eqnarray}D_{f}(s,\unicode[STIX]{x1D712})=\mathop{\sum }_{n=1}^{\infty }c_{f}(n)\unicode[STIX]{x1D712}(n)n^{-s}\end{eqnarray}$$

is the corresponding multiplicative twist.

By the non-vanishing results for automorphic $L$ -functions [JS77], all non-trivial poles of $D_{f}(s)$ and $D_{f}(s,\unicode[STIX]{x1D712})$ for $\unicode[STIX]{x1D712}\neq \unicode[STIX]{x1D712}_{0}$ are located in the critical strip $\{s\in \mathbb{C}:0<\Re (s)<1\}$ . However, for the case of the principal character, since

$$\begin{eqnarray}L_{f}(s,\unicode[STIX]{x1D712}_{0})=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}_{f}(n)\unicode[STIX]{x1D712}_{0}(n)n^{-s}=(1-\unicode[STIX]{x1D706}_{f}(q)q^{-s}+\unicode[STIX]{x1D709}(q)q^{-2s})L_{f}(s),\end{eqnarray}$$

$D_{f}(s,\unicode[STIX]{x1D712}_{0})$ has a pole at every simple zero of the local Euler factor polynomial, $1-\unicode[STIX]{x1D706}_{f}(q)q^{-s}+\unicode[STIX]{x1D709}(q)q^{-2s}$ , at which $L_{f}(s)$ does not vanish.

Since $f$ is cuspidal, the Rankin–Selberg method implies that the average of $|\unicode[STIX]{x1D706}_{f}(q)|^{2}$ over primes $q$ is $1$ , that is,

(1) $$\begin{eqnarray}\lim _{x\rightarrow \infty }\frac{\mathop{\sum }_{\substack{ q\text{ prime},\,q\leqslant x}}|\unicode[STIX]{x1D706}_{f}(q)|^{2}}{\#\{q\text{ prime}:q\leqslant x\}}=1.\end{eqnarray}$$

To see this, write

$$\begin{eqnarray}-\frac{L_{f}^{\prime }}{L_{f}}(s)=\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D6EC}(n)a_{n}n^{-s},\end{eqnarray}$$

where $\unicode[STIX]{x1D6EC}$ is the von Mangoldt function and $a_{n}=0$ unless $n$ is prime or a prime power. Then, by [LY07, Lemma 5.2], we have

(2) $$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)|a_{n}|^{2}\sim x\quad \text{as }x\rightarrow \infty .\end{eqnarray}$$

By the estimate of Kim and Sarnak [Kim03], we have $|a_{n}|\leqslant n^{7/64}+n^{-7/64}$ , so the contribution of composite $n$ to (2) is $O(x^{23/32})$ . Since $a_{q}=\unicode[STIX]{x1D706}_{f}(q)$ for primes $q$ , this implies that

$$\begin{eqnarray}\mathop{\sum }_{\substack{ q\text{ prime} \\ q\leqslant x}}(\log q)|\unicode[STIX]{x1D706}_{f}(q)|^{2}\sim x,\end{eqnarray}$$

and (1) follows by partial summation and the prime number theorem.

In particular, there are infinitely many $q\nmid N$ such that $|\unicode[STIX]{x1D706}_{f}(q)|<2$ . For any such $q$ , it follows that $D_{f}(s,\unicode[STIX]{x1D712}_{0})$ has infinitely many poles on the line $\Re (s)=0$ . In view of the above, $D_{f}(s,1/q,\cos )$ inherits these poles when they occur. On the other hand, under the assumption that $L_{f}(s)$ has at most finitely many non-trivial simple zeros, we will show that $D_{f}(s,1/q,\cos )$ is holomorphic apart from possible poles along two horizontal lines. The contradiction between these two implies the main theorem.

1.1 Overview

We begin with an overview of the proof. First, by [DFI02, (4.36)], $f$ has the Fourier–Whittaker expansion

$$\begin{eqnarray}f(x+iy)=\mathop{\sum }_{n=1}^{\infty }(\unicode[STIX]{x1D70C}(n)W_{k/2,\unicode[STIX]{x1D708}}(4\unicode[STIX]{x1D70B}ny)e(nx)+\unicode[STIX]{x1D70C}(-n)W_{-k/2,\unicode[STIX]{x1D708}}(4\unicode[STIX]{x1D70B}ny)e(-nx)),\end{eqnarray}$$

where $W_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$ is the Whittaker function defined in [DFI02, (4.20)] and $\unicode[STIX]{x1D708}=\sqrt{{\textstyle \frac{1}{4}}-\unicode[STIX]{x1D706}}$ , where $\unicode[STIX]{x1D706}$ is the eigenvalue of $f$ with respect to the weight- $k$ Laplace operator. When $k=1$ , the Selberg eigenvalue conjecture holds, so that $\unicode[STIX]{x1D708}\in i[0,\infty )$ . When $k=0$ the conjecture remains open, but we have the partial result of Kim and Sarnak [Kim03] that $\unicode[STIX]{x1D708}\in (0,{\textstyle \frac{7}{64}}]\cup i[0,\infty )$ .

Since $f$ is primitive, it is an eigenfunction of the operator $Q_{sk}$ defined in [DFI02, (4.65)], so that

$$\begin{eqnarray}\unicode[STIX]{x1D70C}(-n)=\unicode[STIX]{x1D716}\frac{\unicode[STIX]{x1D6E4}((1+k)/2+\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}((1-k)/2+\unicode[STIX]{x1D708})}\unicode[STIX]{x1D70C}(n)=\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}^{k}\unicode[STIX]{x1D70C}(n)\end{eqnarray}$$

for some $\unicode[STIX]{x1D716}\in \{\pm 1\}$ . Further, we have $\unicode[STIX]{x1D70C}(n)=\unicode[STIX]{x1D70C}(1)\unicode[STIX]{x1D706}_{f}(n)/\sqrt{n}$ . Choosing the normalization $\unicode[STIX]{x1D70C}(1)=\unicode[STIX]{x1D70B}^{-k/2}$ and writing $e(\pm nx)=\cos (2\unicode[STIX]{x1D70B}nx)\pm i\sin (2\unicode[STIX]{x1D70B}nx)$ , we obtain the expansion

(3) $$\begin{eqnarray}f(x+iy)=\mathop{\sum }_{n=1}^{\infty }\frac{\unicode[STIX]{x1D706}_{f}(n)}{\sqrt{n}}(V_{f}^{+}(ny)\cos (2\unicode[STIX]{x1D70B}nx)+iV_{f}^{-}(ny)\sin (2\unicode[STIX]{x1D70B}nx)),\end{eqnarray}$$

where

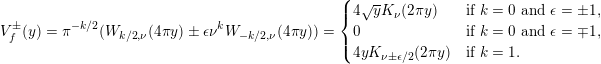(4) $$\begin{eqnarray}V_{f}^{\pm }(y)=\unicode[STIX]{x1D70B}^{-k/2}(W_{k/2,\unicode[STIX]{x1D708}}(4\unicode[STIX]{x1D70B}y)\pm \unicode[STIX]{x1D716}\unicode[STIX]{x1D708}^{k}W_{-k/2,\unicode[STIX]{x1D708}}(4\unicode[STIX]{x1D70B}y))=\left\{\begin{array}{@{}ll@{}}4\sqrt{y}K_{\unicode[STIX]{x1D708}}(2\unicode[STIX]{x1D70B}y)\quad & \text{if }k=0\text{ and }\unicode[STIX]{x1D716}=\pm 1,\\ 0\quad & \text{if }k=0\text{ and }\unicode[STIX]{x1D716}=\mp 1,\\ 4yK_{\unicode[STIX]{x1D708}\pm \unicode[STIX]{x1D716}/2}(2\unicode[STIX]{x1D70B}y)\quad & \text{if }k=1.\end{array}\right.\end{eqnarray}$$

Let $\bar{f}(z):=\overline{f(-\bar{z})}$ denote the dual of $f$ . Since $f$ is primitive, it is also an eigenfunction of the operator $\overline{W}_{k}$ defined in [DFI02, (6.10)], so we have

(5) $$\begin{eqnarray}f(z)=\unicode[STIX]{x1D702}\biggl(i\frac{|z|}{z}\biggr)^{k}\bar{f}\biggl(-\frac{1}{Nz}\biggr)\end{eqnarray}$$

for some $\unicode[STIX]{x1D702}\in \mathbb{C}$ with $|\unicode[STIX]{x1D702}|=1$ .

Next we define a formal Fourier series $F(z)$ associated to $D_{f}(s)$ by replacing $\unicode[STIX]{x1D706}_{f}(n)$ in the above by $c_{f}(n)$ :

$$\begin{eqnarray}\displaystyle F(x+iy)=\mathop{\sum }_{n=1}^{\infty }\frac{c_{f}(n)}{\sqrt{n}}(V_{f}^{+}(ny)\cos (2\unicode[STIX]{x1D70B}nx)+iV_{f}^{-}(ny)\sin (2\unicode[STIX]{x1D70B}nx)). & & \displaystyle \nonumber\end{eqnarray}$$

We expect $F(z)$ to satisfy a relation similar to the modularity relation (5). To make this precise, we first recall the functional equation for $L_{f}(s)$ . Define

(6) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{f}^{\pm }(s)=\unicode[STIX]{x1D6E4}_{\mathbb{ R}}\biggl(s+\frac{1\mp (-1)^{k}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708}\biggr)\unicode[STIX]{x1D6E4}_{\mathbb{R}}\biggl(s+\frac{1\mp \unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708}\biggr).\end{eqnarray}$$

Then the complete $L$ -function $\unicode[STIX]{x1D6EC}_{f}(s):=\unicode[STIX]{x1D6FE}_{f}^{+}(s)L_{f}(s)$ satisfies

(7) $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{f}(s)=\unicode[STIX]{x1D702}\unicode[STIX]{x1D716}^{1-k}N^{1/2-s}\unicode[STIX]{x1D6EC}_{\bar{f}}(1-s),\end{eqnarray}$$

with $\unicode[STIX]{x1D702}$ as above.

We define a completed version of $D_{f}(s)$ by multiplying by the same $\unicode[STIX]{x1D6E4}$ -factor: $\unicode[STIX]{x1D6E5}_{f}(s):=\unicode[STIX]{x1D6FE}_{f}^{+}(s)D_{f}(s)$ . Then, differentiating the functional equation (7), we obtain

(8) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{f}(s)+(\unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s))\unicode[STIX]{x1D6EC}_{f}(s)=\unicode[STIX]{x1D702}\unicode[STIX]{x1D716}^{1-k}N^{1/2-s}\unicode[STIX]{x1D6E5}_{\bar{f}}(1-s),\end{eqnarray}$$

where $\unicode[STIX]{x1D713}_{f}(s):=(d/ds)\log \unicode[STIX]{x1D6FE}_{f}^{+}(s)$ . In §2, we take a suitable inverse Mellin transform of (8). Under the assumption that $\unicode[STIX]{x1D6EC}_{f}(s)$ has at most finitely many simple zeros, this yields a pseudo-modularity relation for $F$ of the form

(9) $$\begin{eqnarray}F(z)+A(z)=\unicode[STIX]{x1D702}\biggl(i\frac{|z|}{z}\biggr)^{k}\overline{F}\biggl(-\frac{1}{Nz}\biggr)+B(z),\end{eqnarray}$$

for certain auxiliary functions $A$ and $B$ , where $\overline{F}(z):=\overline{F(-\bar{z})}$ . Roughly speaking, $A$ is the contribution from the correction term $(\unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s))\unicode[STIX]{x1D6EC}_{f}(s)$ in (8), and $B$ comes from the non-trivial poles of $\unicode[STIX]{x1D6E5}_{f}(s)$ .

The main technical ingredient needed to carry this out is the following pair of Mellin transforms involving the $K$ -Bessel function and trigonometric functions [GR15, 6.699(3) and 6.699(4)]:

(10) $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }x^{\unicode[STIX]{x1D706}+1}K_{\unicode[STIX]{x1D707}}(ax)\sin (bx)\frac{dx}{x} & = & \displaystyle 2^{\unicode[STIX]{x1D706}}b\unicode[STIX]{x1D6E4}\biggl(\frac{2+\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}{2}\biggr)\unicode[STIX]{x1D6E4}\biggl(\frac{2+\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}}{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\operatorname{2F1}\biggl(\frac{2+\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}{2},\frac{2+\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}}{2};\frac{3}{2};-\frac{b^{2}}{a^{2}}\biggr)\end{eqnarray}$$

and

(11) $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }x^{\unicode[STIX]{x1D706}+1}K_{\unicode[STIX]{x1D707}}(ax)\cos (bx)\frac{dx}{x} & = & \displaystyle \frac{2^{\unicode[STIX]{x1D706}-1}}{a^{\unicode[STIX]{x1D706}+1}}\unicode[STIX]{x1D6E4}\biggl(\frac{1+\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}{2}\biggr)\unicode[STIX]{x1D6E4}\biggl(\frac{1+\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}}{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\operatorname{2F1}\biggl(\frac{1+\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}{2},\frac{1+\unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}}{2};\frac{1}{2};-\frac{b^{2}}{a^{2}}\biggr),\end{eqnarray}$$

where

(12) $$\begin{eqnarray}\operatorname{2F1}(a,b;c;z)=\mathop{\sum }_{j=1}^{\infty }\frac{a(a+1)\cdots (a+j-1)\cdot b(b+1)\cdots (b+j-1)}{c(c+1)\cdots (c+j-1)}\frac{z^{j}}{j!}\end{eqnarray}$$

is the Gauss hypergeometric function. The origin of these hypergeometric factors is explained in the introduction to [BT18], and the need to analyze them is the main difference between this paper and the holomorphic case from [Boo16] (for which the corresponding factors are elementary functions).

Specializing (9) to $z=\unicode[STIX]{x1D6FC}+iy$ for $\unicode[STIX]{x1D6FC}\in \mathbb{Q}^{\times }$ , we have

(13) $$\begin{eqnarray}F(\unicode[STIX]{x1D6FC}+iy)+A(\unicode[STIX]{x1D6FC}+iy)=\unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D6FC}+iy|}{\unicode[STIX]{x1D6FC}+iy}\biggr)^{k}\overline{F}\biggl(-\frac{1}{N(\unicode[STIX]{x1D6FC}+iy)}\biggr)+B(\unicode[STIX]{x1D6FC}+iy).\end{eqnarray}$$

We will take the Mellin transform of (13). Without difficulty the reader can guess that the transform of $F(\unicode[STIX]{x1D6FC}+iy)$ will be a combination of $D_{f}(s,\unicode[STIX]{x1D6FC},\cos )$ and $D_{f}(s,\unicode[STIX]{x1D6FC},\sin )$ . The calculation of the other terms is non-trivial, but ultimately we obtain the following proposition, which will play the role of [Boo16, Proposition 2.1].

Proposition 1.2. Suppose that $\unicode[STIX]{x1D6EC}_{f}(s)$ has at most finitely many simple zeros. Then, for every $M\in \mathbb{Z}_{{\geqslant}0}$ and $a\in \{0,1\}$ ,

$$\begin{eqnarray}\displaystyle & & \displaystyle P_{f}(s;a,0)\unicode[STIX]{x1D6E5}_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(a+k)})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D702}(-\!\operatorname{sgn}\unicode[STIX]{x1D6FC})^{k}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}\mathop{\sum }_{m=0}^{M-1}\frac{(2\unicode[STIX]{x1D70B}N\unicode[STIX]{x1D6FC})^{m}}{m!}P_{f}(s;a,m)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+m,-\frac{1}{N\unicode[STIX]{x1D6FC}},\cos ^{(a+m)}\biggr)\nonumber\end{eqnarray}$$

is holomorphic for $\Re (s)>{\textstyle \frac{3}{2}}-M$ except for possible poles for $s\pm \unicode[STIX]{x1D708}\in \mathbb{Z}$ , where

$$\begin{eqnarray}P_{f}(s;a,m)=\frac{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a}}(1-s)}{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a}}(1-s-2\lfloor m/2\rfloor )}\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{s+2\lfloor m/2\rfloor -(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}}{2\unicode[STIX]{x1D70B}}}\quad & \text{if }k=1\text{ and }2\nmid m,\\ 0\quad & \text{if }k=0\text{ and }(-1)^{a}=-\unicode[STIX]{x1D716},\\ 1\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$

and

$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(a)})=\unicode[STIX]{x1D6FE}_{f}^{(-)^{a}}(s)D_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(a)}).\end{eqnarray}$$

1.2 Proof of Theorem 1.1

Assuming Proposition 1.2 for the moment, we can complete the proof of Theorem 1.1 for the case of $\unicode[STIX]{x1D70B}$ corresponding to a Maass cusp form, $f$ . First, as noted above, we may choose a prime $q\nmid N$ for which $D_{f}(s,1/q,\cos )$ has infinitely many poles on the line $\Re (s)=0$ . Then, by Dirichlet’s theorem on primes in an arithmetic progression, for any $M\in \mathbb{Z}_{{>}0}$ there are distinct primes $q_{0},q_{1},\ldots ,q_{M-1}$ such that $q_{j}\equiv q(modN)$ and $D_{\bar{f}}(s,-q_{j}/N,\cos ^{(a)})=D_{\bar{f}}(s,-q/N,\cos ^{(a)})$ for all $j$ , $a$ .

Let $m_{0}$ be an integer with $0\leqslant m_{0}\leqslant M-1$ . By the Vandermonde determinant, there exist rational numbers $c_{0},c_{1},\ldots ,c_{M-1}$ such that

$$\begin{eqnarray}\mathop{\sum }_{j=0}^{M-1}c_{j}q_{j}^{-m}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }m=m_{0}\\ 0\quad & \text{if }m\neq m_{0}\end{array}\right.\quad \text{for all }m\in \{0,1,\ldots ,M-1\}.\end{eqnarray}$$

We fix $\unicode[STIX]{x1D6FF}\in \{0,1\}$ and apply Proposition 1.2 with $a\equiv \unicode[STIX]{x1D6FF}+m_{0}(mod2)$ and $\unicode[STIX]{x1D6FC}=1/q_{j}$ for $j=0,1,\ldots ,M-1$ . Multiplying by $(-1)^{k}c_{j}(q_{j}^{2}/N)^{s-1/2}$ , summing over $j$ and replacing $s$ by $s-m_{0}$ , we find that

$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=0}^{M-1}(-1)^{k}c_{j}\biggl(\frac{q_{j}^{2}}{N}\biggr)^{s-m_{0}-1/2}P_{f}(s-m_{0};\unicode[STIX]{x1D6FF}+m_{0},0)\unicode[STIX]{x1D6E5}_{f}\biggl(s-m_{0},\frac{1}{q_{j}},\cos ^{(\unicode[STIX]{x1D6FF}+m_{0}+k)}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D702}\frac{(-2\unicode[STIX]{x1D70B}N)^{m_{0}}}{m_{0}!}P_{f}(s-m_{0};\unicode[STIX]{x1D6FF}+m_{0},m_{0})\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s,-\frac{q}{N},\cos ^{(\unicode[STIX]{x1D6FF})}\biggr)\nonumber\end{eqnarray}$$

is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)>\frac{3}{2}+m_{0}-M\}$ , where we set

$$\begin{eqnarray}\unicode[STIX]{x1D6FA}=\{s\in \mathbb{C}:s\pm \unicode[STIX]{x1D708}\notin \mathbb{Z}\}.\end{eqnarray}$$

Since $D_{f}(s-m_{0},1/q_{j},\cos ^{(\unicode[STIX]{x1D6FF}+m_{0}+k)})$ is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)<m_{0}-\frac{1}{2}\}$ , choosing $m_{0}=2+\unicode[STIX]{x1D6FF}+(1-\unicode[STIX]{x1D716})/2$ and $M$ arbitrarily large, we conclude that $D_{\bar{f}}(s,-q/N,\cos ^{(\unicode[STIX]{x1D6FF})})$ is holomorphic on $\unicode[STIX]{x1D6FA}$ .

Next we apply Proposition 1.2 again with $a=k$ , $\unicode[STIX]{x1D6FC}=1/q$ and $M=2$ . When $k=1$ or $k=0$ and $\unicode[STIX]{x1D716}=1$ , we see that $D_{f}(s,1/q,\cos )$ is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)=0\}$ . This is a contradiction, and Theorem 1.1 follows in these cases.

The remaining case is that of odd Maass forms of weight $0$ . The above argument with $\unicode[STIX]{x1D6FF}=1$ shows that $D_{f}(s,-q/N,\sin )$ is entire apart from possible poles for $s\pm \unicode[STIX]{x1D708}\in \mathbb{Z}$ . Applying Proposition 1.2 with $a=1$ , $\unicode[STIX]{x1D6FC}=-q/N$ and $M=3$ , we find that

$$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D6E5}_{f}\biggl(s,-\frac{q}{N},\sin \biggr)+\unicode[STIX]{x1D702}\biggl(\frac{q^{2}}{N}\biggr)^{s-1/2} [\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s,\frac{1}{q},\sin \biggr)-2\unicode[STIX]{x1D70B}q\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+1,\frac{1}{q},\cos \biggr)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{(2\unicode[STIX]{x1D70B}q)^{2}}{2!}P_{f}(s;1,2)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+2,\frac{1}{q},\sin \biggr)\!]\nonumber\end{eqnarray}$$

is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)>-\frac{5}{2}\}$ . Since $D_{\bar{f}}(s,1/q,\sin )$ is holomorphic on the lines $\Re (s)=-1$ and $\Re (s)=1$ , we see that $D_{\bar{f}}(s,1/q,\cos )$ is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)=0\}$ . This is again a contradiction, and concludes the proof.

2 Proof of Proposition 1.2

Using expansion (3), we take the Mellin transform of (5) along the line $z=(\unicode[STIX]{x1D714}+i)y$ . First, the left-hand side becomes, for $\Re (s)\gg 1$ ,

(14) $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }f(\unicode[STIX]{x1D714}y+iy)y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }\frac{\unicode[STIX]{x1D706}_{f}(n)}{\sqrt{n}}\int _{0}^{\infty }(V_{f}^{+}(ny)\cos (2\unicode[STIX]{x1D70B}n\unicode[STIX]{x1D714}y)+iV_{f}^{-}(ny)\sin (2\unicode[STIX]{x1D70B}n\unicode[STIX]{x1D714}y))y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =G_{f}(s,\unicode[STIX]{x1D714})L_{f}(s),\end{eqnarray}$$

where, by (4), (10) and (11),

(15) $$\begin{eqnarray}\displaystyle & & \displaystyle G_{f}(s,\unicode[STIX]{x1D714})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }(V_{f}^{+}(y)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}y)+iV_{f}^{-}(y)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}y))y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}(2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D714})^{(1-\unicode[STIX]{x1D716})/2}\unicode[STIX]{x1D6FE}_{f}^{+}(s)\operatorname{2F1}\biggl({\displaystyle \frac{s+(1-\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708}}{2}},{\displaystyle \frac{s+(1-\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708}}{2}};1-{\displaystyle \frac{\unicode[STIX]{x1D716}}{2}};-\unicode[STIX]{x1D714}^{2}\biggr)\quad & \text{if }k=0,\\ \unicode[STIX]{x1D6FE}_{f}^{+}(s)\operatorname{2F1}\biggl({\displaystyle \frac{s+(1+\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708}}{2}},{\displaystyle \frac{s+(1-\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708}}{2}};{\displaystyle \frac{1}{2}};-\unicode[STIX]{x1D714}^{2}\biggr)\quad \\ \quad +\,2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FE}_{f}^{-}(s+1)\operatorname{2F1}\biggl({\displaystyle \frac{s+(3-\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708}}{2}},{\displaystyle \frac{s+(3+\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708}}{2}};{\displaystyle \frac{3}{2}};-\unicode[STIX]{x1D714}^{2}\biggr)\quad & \text{if }k=1.\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Note that we have $G_{\bar{f}}(s,\unicode[STIX]{x1D714})=\overline{G_{f}(\bar{s},-\unicode[STIX]{x1D714})}$ .

On the other hand, the Mellin transform of the right-hand side of (5) is, for $-\Re (s)\gg 1$ ,

$$\begin{eqnarray}\unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}\int _{0}^{\infty }\bar{f}\biggl(-\frac{\unicode[STIX]{x1D714}}{N(\unicode[STIX]{x1D714}^{2}+1)y}+\frac{i}{N(\unicode[STIX]{x1D714}^{2}+1)y}\biggr)y^{s-1/2}\frac{dy}{y}.\end{eqnarray}$$

Making the substitution $y\mapsto (N(\unicode[STIX]{x1D714}^{2}+1)y)^{-1}$ , this becomes

(16) $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}(N(1+\unicode[STIX]{x1D714}^{2}))^{1/2-s}\int _{0}^{\infty }\bar{f}(-\unicode[STIX]{x1D714}y+iy)y^{1/2-s}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}(N(1+\unicode[STIX]{x1D714}^{2}))^{1/2-s}G_{\bar{f}}(1-s,-\unicode[STIX]{x1D714})L_{\bar{f}}(1-s).\end{eqnarray}$$

By (5), (14) and (16) must continue to entire functions and equal each other. In particular, taking $\unicode[STIX]{x1D714}\rightarrow 0$ , we recover the functional equation (7). Equating (14) with (16) and dividing by (7), we discover the functional equation for the hypergeometric factor $H_{f}(s,\unicode[STIX]{x1D714}):=G_{f}(s,\unicode[STIX]{x1D714})/\unicode[STIX]{x1D6FE}_{f}^{+}(s)$ :

(17) $$\begin{eqnarray}H_{f}(s,\unicode[STIX]{x1D714})=\unicode[STIX]{x1D716}^{1-k}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}(1+\unicode[STIX]{x1D714}^{2})^{1/2-s}H_{\bar{f}}(1-s,-\unicode[STIX]{x1D714}).\end{eqnarray}$$

Next, for $z=x+iy\in \mathbb{H}$ , define

$$\begin{eqnarray}A(z)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}(\unicode[STIX]{x1D713}^{\prime }(s+\unicode[STIX]{x1D708})+\unicode[STIX]{x1D713}^{\prime }(s-\unicode[STIX]{x1D708}))H_{f}(s,x/y)\unicode[STIX]{x1D6EC}_{f}(s)y^{1/2-s}\,ds\end{eqnarray}$$

and

(18) $$\begin{eqnarray}B(z)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}X_{f}(s)\unicode[STIX]{x1D6EC}_{f}(s)H_{f}(s,x/y)y^{1/2-s}\,ds-\mathop{\sum }_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6EC}_{f}^{\prime }(\unicode[STIX]{x1D70C})H_{f}(\unicode[STIX]{x1D70C},x/y)y^{1/2-\unicode[STIX]{x1D70C}},\end{eqnarray}$$

where the sum runs over all simple zeros of $\unicode[STIX]{x1D6EC}_{f}(s)$ , and

$$\begin{eqnarray}X_{f}(s)=\frac{\unicode[STIX]{x1D70B}^{2}}{4}\biggl[\csc ^{2}\biggl(\frac{\unicode[STIX]{x1D70B}}{2}\biggl[s+\frac{1+(-1)^{k}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708}\biggr]\biggr)+\csc ^{2}\biggl(\frac{\unicode[STIX]{x1D70B}}{2}\biggl[s+\frac{1+\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708}\biggr]\biggr)\biggr].\end{eqnarray}$$

Lemma 2.1.

$$\begin{eqnarray}F(z)+A(z)=\unicode[STIX]{x1D702}\biggl(i\frac{|z|}{z}\biggr)^{k}\overline{F}\biggl(-\frac{1}{Nz}\biggr)+B(z)\quad \text{for all }z\in \mathbb{H}.\end{eqnarray}$$

Proof. Fix $z=x+iy\in \mathbb{H}$ , and put $\unicode[STIX]{x1D714}=x/y$ . Applying Mellin inversion as in (14), we have

$$\begin{eqnarray}F(z)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}D_{f}(s)G_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s}\,ds\end{eqnarray}$$

and

$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D702}\biggl(i\frac{|z|}{z}\biggr)^{k}\overline{F}\biggl(-\frac{1}{Nz}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}\cdot \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}G_{\bar{f}}(s,-\unicode[STIX]{x1D714})D_{\bar{f}}(s)(N(1+\unicode[STIX]{x1D714}^{2})y)^{s-1/2}\,ds\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D702}\biggl(i\frac{|\unicode[STIX]{x1D714}+i|}{\unicode[STIX]{x1D714}+i}\biggr)^{k}\cdot \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=-1}H_{\bar{f}}(1-s,-\unicode[STIX]{x1D714})\unicode[STIX]{x1D6E5}_{\bar{f}}(1-s)(N(1+\unicode[STIX]{x1D714}^{2})y)^{1/2-s}\,ds.\nonumber\end{eqnarray}$$

Applying (17) and (8), and using the fact that $\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s)$ is holomorphic for $\Re (s)\leqslant \frac{1}{2}$ , the last line becomes

$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=-1}\unicode[STIX]{x1D702}\unicode[STIX]{x1D716}^{1-k}H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D6E5}_{\bar{f}}(1-s)(Ny)^{1/2-s}\,ds\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=-1}H_{f}(s,\unicode[STIX]{x1D714})[\unicode[STIX]{x1D6E5}_{f}(s)+(\unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s))\unicode[STIX]{x1D6EC}_{f}(s)]y^{1/2-s}\,ds\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=-1}H_{f}(s,\unicode[STIX]{x1D714})[\unicode[STIX]{x1D6E5}_{f}(s)+\unicode[STIX]{x1D713}_{f}^{\prime }(s)\unicode[STIX]{x1D6EC}_{f}(s)]y^{1/2-s}\,ds\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s)\unicode[STIX]{x1D6EC}_{f}(s)y^{1/2-s}\,ds.\nonumber\end{eqnarray}$$

Shifting the contour of the first integral to the right and using that $\unicode[STIX]{x1D713}_{f}^{\prime }(s)$ is holomorphic for $\Re (s)\geqslant \frac{1}{2}$ , we get

$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D6E5}_{f}(s)y^{1/2-s}\,ds-\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{{\mathcal{C}}}H_{f}(s,\unicode[STIX]{x1D714})(\unicode[STIX]{x1D6E5}_{f}(s)+\unicode[STIX]{x1D713}_{f}^{\prime }(s)\unicode[STIX]{x1D6EC}_{f}(s))y^{1/2-s}\,ds\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}(\unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s))H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D6EC}_{f}(s)y^{1/2-s}\,ds,\nonumber\end{eqnarray}$$

where ${\mathcal{C}}$ is the contour running from $2-i\infty$ to $2+i\infty$ and from $-1+i\infty$ to $-1-i\infty$ . Note that

$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{f}(s)+\unicode[STIX]{x1D713}_{f}^{\prime }(s)\unicode[STIX]{x1D6EC}_{f}(s)=\unicode[STIX]{x1D6EC}_{f}(s)\frac{d^{2}}{ds^{2}}\log \unicode[STIX]{x1D6EC}_{f}(s),\end{eqnarray}$$

which has a pole at every simple zero $\unicode[STIX]{x1D70C}$ of $\unicode[STIX]{x1D6EC}_{f}(s)$ , with residue $-\unicode[STIX]{x1D6EC}_{f}^{\prime }(\unicode[STIX]{x1D70C})$ . Hence,

$$\begin{eqnarray}-\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{{\mathcal{C}}}H_{f}(s,\unicode[STIX]{x1D714})(\unicode[STIX]{x1D6E5}_{f}(s)+\unicode[STIX]{x1D713}_{f}^{\prime }(s)\unicode[STIX]{x1D6EC}_{f}(s))y^{1/2-s}\,ds=\mathop{\sum }_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6EC}_{f}^{\prime }(\unicode[STIX]{x1D70C})H_{f}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D714})y^{1/2-\unicode[STIX]{x1D70C}}.\end{eqnarray}$$

Next, writing $\unicode[STIX]{x1D713}_{\mathbb{R}}(s)=(\unicode[STIX]{x1D6E4}_{\mathbb{R}}^{\prime }/\unicode[STIX]{x1D6E4}_{\mathbb{R}})(s)$ , we have

$$\begin{eqnarray}\unicode[STIX]{x1D713}_{f}(s)=\unicode[STIX]{x1D713}_{\mathbb{R}}\biggl(s+\frac{1-(-1)^{k}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708}\biggr)+\unicode[STIX]{x1D713}_{\mathbb{R}}\biggl(s+\frac{1-\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708}\biggr).\end{eqnarray}$$

Applying the reflection formula and Legendre duplication formula in the form

$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\mathbb{R}}^{\prime }(s)=\frac{\unicode[STIX]{x1D70B}^{2}}{4}\csc ^{2}\biggl(\frac{\unicode[STIX]{x1D70B}s}{2}\biggr)-\unicode[STIX]{x1D713}_{\mathbb{R}}^{\prime }(2-s)\quad \text{and}\quad \unicode[STIX]{x1D713}_{\mathbb{ R}}^{\prime }(s)+\unicode[STIX]{x1D713}_{\mathbb{ R}}^{\prime }(s+1)=\unicode[STIX]{x1D713}^{\prime }(s),\end{eqnarray}$$

we derive

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s)=\unicode[STIX]{x1D713}^{\prime }(s+\unicode[STIX]{x1D708})+\unicode[STIX]{x1D713}^{\prime }(s-\unicode[STIX]{x1D708})-X_{f}(s). & & \displaystyle \nonumber\end{eqnarray}$$

Thus,

$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}(\unicode[STIX]{x1D713}_{f}^{\prime }(s)-\unicode[STIX]{x1D713}_{\bar{f}}^{\prime }(1-s))H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D6EC}_{f}(s)y^{1/2-s}\,ds\nonumber\\ \displaystyle & & \displaystyle \quad =A(z)-\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=1/2}X_{f}(s)H_{f}(s,\unicode[STIX]{x1D714})\unicode[STIX]{x1D6EC}_{f}(s)y^{1/2-s}\,ds.\nonumber\end{eqnarray}$$

Rearranging terms completes the proof. ◻

Lemma 2.2. For any $\unicode[STIX]{x1D6FC}\in \mathbb{Q}^{\times }$ ,

$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D6E4}(s+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}(s-\unicode[STIX]{x1D708})}\int _{0}^{\infty }A(\unicode[STIX]{x1D6FC}+iy)y^{s-1/2}\frac{dy}{y}\end{eqnarray}$$

continues to an entire function of $s$ .

Proof. Define $\unicode[STIX]{x1D6F7}(s)=\unicode[STIX]{x1D713}^{\prime }(s+\unicode[STIX]{x1D708})+\unicode[STIX]{x1D713}^{\prime }(s-\unicode[STIX]{x1D708})$ . Then we have $\unicode[STIX]{x1D6F7}(s)=\int _{1}^{\infty }\unicode[STIX]{x1D719}(x)x^{1/2-s}\,dx$ , where $\unicode[STIX]{x1D719}(x)=\cosh (\unicode[STIX]{x1D708}\log x)\log x/\text{sinh}((1/2)\log x)$ . Applying (15) and the change of variables $y\mapsto xt$ , we have

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}(s)G_{f}(s,\unicode[STIX]{x1D714}) & = & \displaystyle \int _{1}^{\infty }\int _{0}^{\infty }\unicode[STIX]{x1D719}(x)(V_{f}^{+}(y)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}y)+iV_{f}^{-}(y)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}y))\biggl(\frac{y}{x}\biggr)^{s-1/2}\frac{dy}{y}\,dx\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }\biggl(\int _{1}^{\infty }\unicode[STIX]{x1D719}(x)(V_{f}^{+}(tx)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}tx)+iV_{f}^{-}(tx)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}tx))\,dx\biggr)t^{s-1/2}\frac{dt}{t}.\nonumber\end{eqnarray}$$

Hence, writing $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}/y$ , we have

$$\begin{eqnarray}\displaystyle A(\unicode[STIX]{x1D6FC}+iy) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}\unicode[STIX]{x1D6EC}_{f}(s)\unicode[STIX]{x1D6F7}(s)H_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s}\,ds\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\unicode[STIX]{x1D706}_{f}(n)}{\sqrt{n}}\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}\unicode[STIX]{x1D6F7}(s)G_{f}(s,\unicode[STIX]{x1D714})(ny)^{1/2-s}\,ds\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\frac{\unicode[STIX]{x1D706}_{f}(n)}{\sqrt{n}}\int _{1}^{\infty }\unicode[STIX]{x1D719}(x)(V_{f}^{+}(nxy)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)+iV_{f}^{-}(nxy)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx))\,dx,\nonumber\end{eqnarray}$$

so that

$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }A(\unicode[STIX]{x1D6FC}+iy)y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }\frac{\unicode[STIX]{x1D706}_{f}(n)}{\sqrt{n}}\int _{1}^{\infty }\unicode[STIX]{x1D719}(x)\int _{0}^{\infty }(V_{f}^{+}(nxy)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)+iV_{f}^{-}(nxy)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx))y^{s-1/2}\frac{dy}{y}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}_{f}(n)n^{-s}\int _{1}^{\infty }\unicode[STIX]{x1D719}(x)x^{1/2-s}(\widetilde{V}_{f}^{+}(s)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)+i\widetilde{V}_{f}^{-}(s)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx))\,dx,\nonumber\end{eqnarray}$$

where

(19) $$\begin{eqnarray}\widetilde{V}_{f}^{\pm }(s)=\int _{0}^{\infty }V_{f}^{\pm }(y)y^{s-1/2}\frac{dy}{y}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FE}_{f}^{\pm }(s)\quad & \text{if }k=1\text{ or }\unicode[STIX]{x1D716}=\pm 1,\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$

A case-by-case inspection of (6) shows that $\widetilde{V}_{f}^{\pm }(s)/(\unicode[STIX]{x1D6E4}(s+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}(s-\unicode[STIX]{x1D708}))$ is entire for both choices of sign.

Define $\unicode[STIX]{x1D719}_{j}=\unicode[STIX]{x1D719}_{j}(x,s)$ for $j\geqslant 0$ by

$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D719}\quad \text{and}\quad \unicode[STIX]{x1D719}_{j+1}=x\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{j}}{\unicode[STIX]{x2202}x}-\biggl(s+j-\frac{1}{2}\biggr)\unicode[STIX]{x1D719}_{j}.\end{eqnarray}$$

Then, applying integration by parts $m$ times, we see that

$$\begin{eqnarray}\displaystyle \int _{1}^{\infty }\unicode[STIX]{x1D719}(x)\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)x^{1/2-s}\,dx & = & \displaystyle \mathop{\sum }_{j=0}^{m-1}\frac{\cos ^{(j+1)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)^{j+1}}\unicode[STIX]{x1D719}_{j}(1,s)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{1}^{\infty }\frac{\cos ^{(m)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)^{m}}\unicode[STIX]{x1D719}_{k}(x,s)x^{1/2-m-s}\,dx\nonumber\end{eqnarray}$$

and

$$\begin{eqnarray}\displaystyle \int _{1}^{\infty }\unicode[STIX]{x1D719}(x)\sin (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)x^{1/2-s}\,dx & = & \displaystyle \mathop{\sum }_{j=0}^{m-1}\frac{\sin ^{(j+1)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)^{j+1}}\unicode[STIX]{x1D719}_{j}(1,s)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{1}^{\infty }\frac{\sin ^{(m)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}n)^{m}}\unicode[STIX]{x1D719}_{k}(x,s)x^{1/2-m-s}\,dx.\nonumber\end{eqnarray}$$

Thus,

$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }A(\unicode[STIX]{x1D6FC}+iy)y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\widetilde{V}_{f}^{+}(s)(\mathop{\sum }_{j=0}^{m-1}\frac{\unicode[STIX]{x1D719}_{j}(1,s)L(f,s+j+1,\unicode[STIX]{x1D6FC},\cos ^{(j+1)})}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC})^{j+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC})^{m}}\mathop{\sum }_{n=1}^{\infty }\frac{a_{f}(n)}{n^{s+m}}\int _{1}^{\infty }\cos ^{(m)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)\unicode[STIX]{x1D719}_{m}(x,s)x^{1/2-m-s}\,dx\!)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,i\widetilde{V}_{f}^{-}(s)(\mathop{\sum }_{j=0}^{m-1}\frac{\unicode[STIX]{x1D719}_{j}(1,s)L(f,s+j+1,\unicode[STIX]{x1D6FC},\sin ^{(j+1)})}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC})^{j+1}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC})^{m}}\mathop{\sum }_{n=1}^{\infty }\frac{a_{f}(n)}{n^{s+m}}\int _{1}^{\infty }\sin ^{(m)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}nx)\unicode[STIX]{x1D719}_{m}(x,s)x^{1/2-m-s}\,dx\!).\nonumber\end{eqnarray}$$

It follows from [BK11, Proposition 3.1] that $L_{f}(s,\unicode[STIX]{x1D6FC},\cos )$ and $L_{f}(s,\unicode[STIX]{x1D6FC},\sin )$ continue to entire functions. We see by induction that $\unicode[STIX]{x1D719}_{m}(x,s)\ll _{m}((1+|s|)(1+|\unicode[STIX]{x1D708}|))^{m}x^{-1}$ uniformly for $x\geqslant 1$ , and thus the integral terms above are holomorphic for $\Re (s)>\frac{1}{2}-m$ . Choosing $m$ arbitrarily large, the lemma follows.◻

Lemma 2.3. For any $\unicode[STIX]{x1D70E}\geqslant 0$ and any $l\in \mathbb{Z}_{{\geqslant}0}$ , we have

$$\begin{eqnarray}\frac{y^{l}}{l!}(V_{\bar{f}}^{\pm })^{(l)}(y)\ll _{\unicode[STIX]{x1D70E}}2^{l}y^{-\unicode[STIX]{x1D70E}}\quad \text{for }y>0.\end{eqnarray}$$

Proof. In view of (19), since $|\Re (\unicode[STIX]{x1D708})|<\frac{1}{2}$ , for any $\unicode[STIX]{x1D70E}\geqslant 0$ we have the integral representation

$$\begin{eqnarray}V_{\bar{f}}^{\pm }(y)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=\unicode[STIX]{x1D70E}+1/2}\widetilde{V}_{\bar{f}}^{\pm }(s)y^{1/2-s}\,ds.\end{eqnarray}$$

Differentiating $l$ times, we obtain

$$\begin{eqnarray}\frac{y^{l}}{l!}(V_{\bar{f}}^{\pm })^{(l)}(y)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=\unicode[STIX]{x1D70E}+1/2}\binom{\frac{1}{2}-s}{l}\widetilde{V}_{\bar{f}}^{\pm }(s)y^{1/2-s}\,ds.\end{eqnarray}$$

Using the estimate

$$\begin{eqnarray}\biggl|\binom{\frac{1}{2}-s}{l}\biggr|=\biggl|\binom{s-\frac{1}{2}+l}{l}\biggr|\leqslant 2^{|s-1/2|+l},\end{eqnarray}$$

we have

$$\begin{eqnarray}\frac{y^{l}}{l!}(V_{\bar{f}}^{\pm })^{(l)}(y)\leqslant 2^{l}y^{-\unicode[STIX]{x1D70E}}\cdot \frac{1}{2\unicode[STIX]{x1D70B}}\int _{\Re (s)=\unicode[STIX]{x1D70E}+1/2}2^{|s-1/2|}|\widetilde{V}_{\bar{f}}^{\pm }(s)\,ds|\ll _{\unicode[STIX]{x1D70E}}2^{l}y^{-\unicode[STIX]{x1D70E}},\end{eqnarray}$$

where the last inequality is justified by Stirling’s formula. ◻

Lemma 2.4. Let $\unicode[STIX]{x1D6FC}\in \mathbb{Q}^{\times }$ and $z=\unicode[STIX]{x1D6FC}+iy$ for some $y\in (0,|\unicode[STIX]{x1D6FC}|/2]$ . Then, for any integer $T\geqslant 0$ , we have

(20) $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(i\frac{|z|}{z}\biggr)^{k}\overline{F}\biggl(-\frac{1}{Nz}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =O_{\unicode[STIX]{x1D6FC},T}(y^{T-1})+(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{t=0}^{T-1}\frac{(2\unicode[STIX]{x1D70B}iN\unicode[STIX]{x1D6FC})^{t}}{t!}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{a\in \{0,1\}}\frac{i^{-a}}{2\unicode[STIX]{x1D70B}i}\int _{\Re (s)=2}P_{f}(s;a+t,t)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+t,-\frac{1}{N\unicode[STIX]{x1D6FC}},\cos ^{(a)}\biggr)\biggl(\frac{y}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)^{1/2-s}\,ds.\end{eqnarray}$$

Proof. Let $z=\unicode[STIX]{x1D6FC}+iy$ , $\unicode[STIX]{x1D6FD}=-1/N\unicode[STIX]{x1D6FC}$ and $u=y/\unicode[STIX]{x1D6FC}$ . Then

$$\begin{eqnarray}-\frac{1}{Nz}=\frac{\unicode[STIX]{x1D6FD}}{1+u^{2}}+i\frac{|\unicode[STIX]{x1D6FD}u|}{1+u^{2}},\end{eqnarray}$$

so that

$$\begin{eqnarray}\displaystyle \biggl(i\frac{|z|}{z}\biggr)^{k}\overline{F}\biggl(-\frac{1}{Nz}\biggr) & = & \displaystyle \biggl(i\operatorname{sgn}(\unicode[STIX]{x1D6FC})\frac{|1+iu|}{1+iu}\biggr)^{k}\overline{F}\biggl(\frac{\unicode[STIX]{x1D6FD}}{1+u^{2}}+i\frac{|\unicode[STIX]{x1D6FD}u|}{1+u^{2}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(i\operatorname{sgn}(\unicode[STIX]{x1D6FC})\frac{|1+iu|}{1+iu}\biggr)^{k}\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)}{\sqrt{n}}\biggl(V_{\bar{f}}^{+}\biggl(\frac{|\unicode[STIX]{x1D6FD}nu|}{1+u^{2}}\biggr)\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+u^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,iV_{\bar{f}}^{-}\biggl(\frac{|\unicode[STIX]{x1D6FD}nu|}{1+u^{2}}\biggr)\sin \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+u^{2}}\biggr)\!\biggr).\nonumber\end{eqnarray}$$

By Lemma 2.3, for any $\unicode[STIX]{x1D70E}\geqslant 0$ and any $l_{0}\in \mathbb{Z}_{{\geqslant}0}$ , we have

$$\begin{eqnarray}\displaystyle V_{\bar{f}}^{\pm }\biggl(\frac{|\unicode[STIX]{x1D6FD}nu|}{1+u^{2}}\biggr) & = & \displaystyle \mathop{\sum }_{l=0}^{\infty }\frac{1}{l!}(V_{\bar{f}}^{\pm })^{(l)}(|\unicode[STIX]{x1D6FD}nu|)\biggl(\frac{\unicode[STIX]{x1D6FD}nu^{3}}{1+u^{2}}\biggr)^{l}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{l=0}^{l_{0}-1}\frac{1}{l!}(V_{\bar{f}}^{\pm })^{(l)}(|\unicode[STIX]{x1D6FD}nu|)\biggl(\frac{\unicode[STIX]{x1D6FD}nu^{3}}{1+u^{2}}\biggr)^{l}+O_{\unicode[STIX]{x1D70E}}\biggl(|\unicode[STIX]{x1D6FD}nu|^{-\unicode[STIX]{x1D70E}}\mathop{\sum }_{l=l_{0}}^{\infty }\biggl(\frac{2u^{2}}{1+u^{2}}\biggr)^{l}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{l=0}^{l_{0}-1}\frac{1}{l!}(V_{\bar{f}}^{\pm })^{(l)}(|\unicode[STIX]{x1D6FD}nu|)\biggl(\frac{\unicode[STIX]{x1D6FD}nu^{3}}{1+u^{2}}\biggr)^{l}+O_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E},l_{0}}(|nu|^{-\unicode[STIX]{x1D70E}}u^{2l_{0}}).\nonumber\end{eqnarray}$$

Similarly, for any $a\in \{0,1\}$ , we have

$$\begin{eqnarray}\displaystyle \cos ^{(a)}\biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+u^{2}}\biggr) & = & \displaystyle \mathop{\sum }_{j=0}^{\infty }\frac{1}{j!}\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(-\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}nu^{2}}{1+u^{2}}\biggr)^{j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{j=0}^{j_{0}-1}\frac{1}{j!}\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(-\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}nu^{2}}{1+u^{2}}\biggr)^{j}+O\biggl(\frac{1}{j_{0}!}\biggl|\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}nu^{2}}{1+u^{2}}\biggr|^{j_{0}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{j=0}^{j_{0}-1}\frac{1}{j!}\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(-\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}nu^{2}}{1+u^{2}}\biggr)^{j}+O_{\unicode[STIX]{x1D6FC},j_{0}}((nu^{2})^{j_{0}}),\nonumber\end{eqnarray}$$

by the Lagrange form of the error in Taylor’s theorem. Taking $j_{0}=2(l_{0}-l)$ and applying Lemma 2.3 with $\unicode[STIX]{x1D70E}$ replaced by $\unicode[STIX]{x1D70E}+2(l_{0}-l)$ , we obtain

$$\begin{eqnarray}\displaystyle & & \displaystyle V_{\bar{f}}^{(-)^{a}}\biggl(\frac{|\unicode[STIX]{x1D6FD}nu|}{1+u^{2}}\biggr)\cos ^{(a)}\biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+u^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j+2l<2l_{0}}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!l!}(V_{\bar{f}}^{(-)^{a}})^{(l)}(|\unicode[STIX]{x1D6FD}nu|)\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)u^{l}\biggl(\frac{\unicode[STIX]{x1D6FD}nu^{2}}{1+u^{2}}\biggr)^{j+l}+O_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E},l_{0}}(|nu|^{-\unicode[STIX]{x1D70E}}u^{2l_{0}}).\nonumber\end{eqnarray}$$

Next, defining

$$\begin{eqnarray}b_{j,k,l,m}=\left\{\begin{array}{@{}ll@{}}\left(\begin{array}{@{}c@{}}j+l-1+\biggl\lfloor{\displaystyle \frac{m}{2}}\biggr\rfloor+{\displaystyle \frac{k}{2}}\\ \biggl\lfloor{\displaystyle \frac{m}{2}}\biggr\rfloor\end{array}\right)\quad & \text{if }k=1\text{ or }k=0\text{ and }2\mid m,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$

we have

$$\begin{eqnarray}\displaystyle \biggl(\frac{|1+iu|}{1+iu}\biggr)^{k}(1+u^{2})^{-j-l} & = & \displaystyle (1-iu)^{k}(1+u^{2})^{-j-l-k/2}=\mathop{\sum }_{m=0}^{\infty }b_{j,k,l,m}(-iu)^{m}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{m_{0}-1}b_{j,k,l,m}(-iu)^{m}+O\biggl(\mathop{\sum }_{m=m_{0}}^{\infty }2^{j+l+m/2}|u|^{m}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m=0}^{m_{0}-1}b_{j,k,l,m}(-iu)^{m}+O_{j,l,m_{0}}(|u|^{m_{0}}).\nonumber\end{eqnarray}$$

Taking $m_{0}=2l_{0}-j-2l$ and applying Lemma 2.3 with $\unicode[STIX]{x1D70E}$ replaced by $\unicode[STIX]{x1D70E}+j$ , we obtain

$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(i\operatorname{sgn}(\unicode[STIX]{x1D6FC})\frac{|1+iu|}{1+iu}\biggr)^{k}V_{\bar{f}}^{(-)^{a}}\biggl(\frac{|\unicode[STIX]{x1D6FD}nu|}{1+u^{2}}\biggr)\cos ^{(a)}\biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+u^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{j+2l+m<2l_{0}}\frac{(-2\unicode[STIX]{x1D70B})^{j}(-i)^{m}}{j!l!}b_{j,k,l,m}(\unicode[STIX]{x1D6FD}nu)^{j+l}(V_{\bar{f}}^{(-)^{a}})^{(l)}(|\unicode[STIX]{x1D6FD}nu|)\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)u^{j+2l+m}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E},l_{0}}(|nu|^{-\unicode[STIX]{x1D70E}}u^{2l_{0}}).\nonumber\end{eqnarray}$$

Recalling the definition of $u$ , multiplying by $c_{\bar{f}}(n)/\sqrt{n}$ and summing over $n$ and both choices of $a$ , the error term converges if $\unicode[STIX]{x1D70E}\geqslant 1$ , to give

$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{a\in \{0,1\}}i^{-a}\biggl(i\frac{|\unicode[STIX]{x1D6FC}+iy|}{\unicode[STIX]{x1D6FC}+iy}\biggr)^{k}\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)}{\sqrt{n}}V_{\bar{f}}^{(-)^{a}}\biggl(\frac{ny}{N(\unicode[STIX]{x1D6FC}^{2}+y^{2})}\biggr)\cos ^{(a)}\biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n}{1+(y/\unicode[STIX]{x1D6FC})^{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j+2l+m<2l_{0}}(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)}{\sqrt{n}}\frac{(2\unicode[STIX]{x1D70B}i)^{j}}{j!l!}b_{j,k,l,m}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)^{j+l}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(V_{\bar{f}}^{(-)^{a}})^{(l)}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)\cos ^{(j+a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(\frac{y}{i\unicode[STIX]{x1D6FC}}\biggr)^{j+2l+m}+O_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E},l_{0}}(y^{2l_{0}-\unicode[STIX]{x1D70E}})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j+2l+m<2l_{0}}(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)}{\sqrt{n}}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!l!}b_{j,k,l,m}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)^{j+l}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(V_{\bar{f}}^{(-)^{a+j}})^{(l)}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)\cos ^{(a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(\frac{y}{i\unicode[STIX]{x1D6FC}}\biggr)^{j+2l+m}+O_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E},l_{0}}(y^{2l_{0}-\unicode[STIX]{x1D70E}}).\nonumber\end{eqnarray}$$

Taking the Mellin transform of a single term of the sum over $j,l,m$ and making the change of variables $y\mapsto N\unicode[STIX]{x1D6FC}^{2}y/n$ , we get

$$\begin{eqnarray}\displaystyle & & \displaystyle (i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\int _{0}^{\infty }\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)}{\sqrt{n}}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!l!}b_{j,k,l,m}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)^{j+l}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(V_{\bar{f}}^{(-)^{a+j}})^{(l)}\biggl(\frac{ny}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)\cos ^{(a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)\biggl(\frac{y}{i\unicode[STIX]{x1D6FC}}\biggr)^{j+2l+m}y^{s-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{j+2l+m}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}b_{j,k,l,m}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{n=1}^{\infty }\frac{c_{\bar{f}}(n)\cos ^{(a)}(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}n)}{n^{s+j+2l+m}}\int _{0}^{\infty }\frac{y^{l}}{l!}(V_{\bar{f}}^{(-)^{a+j}})^{(l)}(y)y^{s+2j+2l+m-1/2}\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}b_{j,k,l,m}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\binom{\frac{1}{2}-s-t-j}{l}\widetilde{V}_{\bar{f}}^{(-)^{a+j}}(s+t+j),\nonumber\end{eqnarray}$$

where $t=j+2l+m$ .

Next we fix $t\in \mathbb{Z}_{{\geqslant}0}$ and sum over all $(j,l,m)$ satisfying $j+2l+m=t$ . When $k=0$ , $b_{j,k,l,m}$ vanishes unless $m$ is even. Hence, defining

$$\begin{eqnarray}I_{k}(m)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }k=1\text{ or }2\mid m,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$

we get

$$\begin{eqnarray}\displaystyle & & \displaystyle (i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{j+2l+m=t}I_{k}(t-j)\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}\binom{j+l-1+\lfloor \frac{m}{2}\rfloor +\frac{k}{2}}{\lfloor \frac{m}{2}\rfloor }\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\binom{\frac{1}{2}-s-t-j}{l}\widetilde{V}_{\bar{f}}^{(-)^{a+j}}(s+t+j)\nonumber\\ \displaystyle & & \displaystyle \quad =(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{j=0}^{t}I_{k}(t-j)\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\widetilde{V}_{\bar{f}}^{(-)^{a+j}}(s+t+j)\mathop{\sum }_{l=0}^{\lfloor (t-j)/2\rfloor }\binom{j+\lfloor \frac{t-j}{2}\rfloor +\frac{k}{2}-1}{\lfloor \frac{t-j}{2}\rfloor -l}\binom{\frac{1}{2}-s-t-j}{l}\nonumber\\ \displaystyle & & \displaystyle \quad =(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{a\in \{0,1\}}i^{-a}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{j=0}^{t}I_{k}(t-j)\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\widetilde{V}_{\bar{f}}^{(-)^{a+j}}(s+t+j)\binom{\lfloor \frac{t-j}{2}\rfloor +\frac{k-1}{2}-s-t}{\lfloor \frac{t-j}{2}\rfloor },\nonumber\end{eqnarray}$$

by the Chu–Vandermonde identity.

We now consider two cases according to the weight, $k$ . When $k=0$ , the inner sum vanishes identically when $(-1)^{a+t}=-\unicode[STIX]{x1D716}$ , so we may assume that $(-1)^{a+t}=\unicode[STIX]{x1D716}$ . Thus, in this case, we have

$$\begin{eqnarray}\displaystyle (N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(iN\unicode[STIX]{x1D6FC})^{t}i^{-a}D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\mathop{\sum }_{\substack{ j\leqslant t \\ j\equiv t(mod2)}}\frac{(2\unicode[STIX]{x1D70B})^{j}}{j!}\unicode[STIX]{x1D6FE}_{\bar{f}}^{(-)^{a+t}}(s+t+j)\binom{\frac{t-j}{2}-\frac{1}{2}-s-t}{\frac{t-j}{2}}. & & \displaystyle \nonumber\end{eqnarray}$$

Put $t=2n+b$ , with $b\in \{0,1\}$ . Then, writing $j=2r+b$ , the above becomes

$$\begin{eqnarray}\displaystyle & & \displaystyle (N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(iN\unicode[STIX]{x1D6FC})^{t}i^{-a}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{r=0}^{n}\frac{(2\unicode[STIX]{x1D70B})^{2r+b}}{(2r+b)!}\frac{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+2r+b+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+2r+b-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+b+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+b-\unicode[STIX]{x1D708})}\binom{n-r-\frac{1}{2}-s-t}{n-r}\nonumber\\ \displaystyle & & \displaystyle \quad =(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(iN\unicode[STIX]{x1D6FC})^{t}i^{-a}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})(-1)^{n}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{r=0}^{n}\biggl(\frac{2\unicode[STIX]{x1D70B}}{2r+1}\biggr)^{b}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t+b+\unicode[STIX]{x1D708})/2}{r}\binom{-(s+t+b-\unicode[STIX]{x1D708})/2}{r}\binom{s+t-\frac{1}{2}}{n-r}.\nonumber\end{eqnarray}$$

Applying [BK11, Lemma A.1(ii)–(iii)], we get

$$\begin{eqnarray}\displaystyle & & \displaystyle (N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(iN\unicode[STIX]{x1D6FC})^{t}i^{-a}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\frac{2\unicode[STIX]{x1D70B}}{2n+1}\biggr)^{b}\frac{4^{n}n!^{2}}{(2n)!}\binom{(s+t-1-b+\unicode[STIX]{x1D708})/2}{n}\binom{(s+t-1-b-\unicode[STIX]{x1D708})/2}{n}\nonumber\\ \displaystyle & & \displaystyle \quad =(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}\frac{(2\unicode[STIX]{x1D70B}iN\unicode[STIX]{x1D6FC})^{t}}{t!}i^{-a}\frac{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s)}{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s-2n)}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)}).\nonumber\end{eqnarray}$$

Turning to $k=1$ , we have

$$\begin{eqnarray}\displaystyle & & \displaystyle i\operatorname{sgn}(\unicode[STIX]{x1D6FC})(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\mathop{\sum }_{j=0}^{t}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\unicode[STIX]{x1D6FE}_{\bar{f}}^{(-)^{a+j}}(s+t+j)\binom{\lfloor \frac{t-j}{2}\rfloor -s-t}{\lfloor \frac{t-j}{2}\rfloor }\nonumber\\ \displaystyle & & \displaystyle \quad =i\operatorname{sgn}(\unicode[STIX]{x1D6FC})(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{a\in \{0,1\}}i^{-a}D_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{j=0}^{t}\frac{(-2\unicode[STIX]{x1D70B})^{j}}{j!}\unicode[STIX]{x1D6FE}_{\bar{f}}^{(-1)^{a+j}}(s+t+j)\binom{\lfloor \frac{t-j}{2}\rfloor -s-t}{\lfloor \frac{t-j}{2}\rfloor }.\nonumber\end{eqnarray}$$

Writing $j=2r-c$ with $c\in \{0,1\}$ , this is

$$\begin{eqnarray}\displaystyle & & \displaystyle i\operatorname{sgn}(\unicode[STIX]{x1D6FC})(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{c\in \{0,1\}}\mathop{\sum }_{2r-c\leqslant t}\frac{(-2\unicode[STIX]{x1D70B})^{2r-c}}{(2r-c)!}\binom{n-r+\lfloor \frac{b+c}{2}\rfloor -s-t}{n-r+\lfloor \frac{b+c}{2}\rfloor }\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\frac{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+2r-c+(1-(-1)^{a+c}\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}_{\mathbb{ R}}(s+t+2r-c+(1+(-1)^{a+c}\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+(1-(-1)^{a}\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708})\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+t+(1+(-1)^{a}\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708})}\nonumber\\ \displaystyle & & \displaystyle \quad =i\operatorname{sgn}(\unicode[STIX]{x1D6FC})(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}(-iN\unicode[STIX]{x1D6FC})^{t}\mathop{\sum }_{a\in \{0,1\}}i^{-a}\unicode[STIX]{x1D6E5}_{\bar{f}}(s+t,\unicode[STIX]{x1D6FD},\cos ^{(a)})\mathop{\sum }_{c\in \{0,1\}}(-1)^{n+bc}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{2r-c\leqslant t}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{r-c\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}}\binom{-(s+t+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{r-c\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}}\binom{s+t-1}{n+bc-r}.\nonumber\end{eqnarray}$$

For $b=0$ , applying [BK11, Lemma A.1(ii)], the sum over $c$ becomes

$$\begin{eqnarray}\displaystyle & & \displaystyle (-1)^{n}\mathop{\sum }_{r=0}^{n}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t-1+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{r}\!\binom{-(s+t-1+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{r}\!\binom{s+t-1}{n-r}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{4^{n}n!^{2}}{(2n)!}\binom{(s+2n-2+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{n}\binom{(s+2n-2+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{n}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-2\unicode[STIX]{x1D70B})^{2n}}{(2n)!}\frac{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(1-s+(1+(-1)^{a}\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(1-s-2n+(1+(-1)^{a}\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708})}\frac{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(1-s+(1-(-1)^{a}\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}_{\mathbb{R}}(1-s-2n+(1-(-1)^{a}\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708})}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-2\unicode[STIX]{x1D70B})^{t}}{t!}\frac{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a}}(1-s)}{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a}}(1-s-2n)}=\frac{(-2\unicode[STIX]{x1D70B})^{t}}{t!}\frac{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s)}{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s-2\lfloor t/2\rfloor )}.\nonumber\end{eqnarray}$$

For $b=1$ and $c=0$ , the inner sum is

$$\begin{eqnarray}(-1)^{n}\mathop{\sum }_{r=0}^{n}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{r}\binom{-(s+t+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{r}\binom{s+t-1}{n-r}.\end{eqnarray}$$

Writing $\binom{s+t-1}{n-r}=\binom{s+t}{n-r+1}-\binom{s+t-1}{n-r+1}$ and applying [BK11, Lemma A.1(ii)], we get

$$\begin{eqnarray}\displaystyle & & \displaystyle (-1)^{n} [\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{(s+t-\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{n+1}\binom{(s+t-\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{-(s+t+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{n+1}\binom{-(s+t+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{n+1}\! ]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{n+1} [\mathop{\sum }_{r=0}^{n+1}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{r}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\binom{-(s+t+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{r}\binom{s+t-1}{n-r+1}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{-(s+t+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{n+1}\binom{-(s+t+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{n+1}\! ]\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{n}\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{(s+t-1+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\binom{(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{n+1}\mathop{\sum }_{r=0}^{n+1}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}+1)/2}{r}\binom{-(s+t+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{r}\binom{s+t-1}{n-r+1}.\nonumber\end{eqnarray}$$

For $b=1$ and $c=1$ the inner sum is

$$\begin{eqnarray}\displaystyle (-1)^{n+1}\mathop{\sum }_{r=1}^{n+1}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{-(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}+1)/2}{r-1}\binom{-(s+t+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{r}\binom{s+t-1}{n+1-r}, & & \displaystyle \nonumber\end{eqnarray}$$

and, adding this to the contribution from $c=0$ , for $b=1$ we obtain

$$\begin{eqnarray}\displaystyle & & \displaystyle (-1)^{n}\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{(s+t-1+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\binom{(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}+(-1)^{n+1}\binom{s+t-1}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{n+1}\mathop{\sum }_{r=1}^{n+1}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{1-(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}+1)/2}{r}\binom{-(s+t+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{r}\binom{s+t-1}{n-r+1}\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{n}\frac{(-4)^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{(s+t-1+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\binom{(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{n+1}\mathop{\sum }_{r=0}^{n+1}\frac{(-4)^{r}r!^{2}}{(2r)!}\binom{1-(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}+1)/2}{r}\!\binom{-(s+t+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{r}\!\binom{s+t-1}{n-r+1}.\nonumber\end{eqnarray}$$

Applying [BK11, Lemma A.1(ii)], this is

$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{4^{n+1}(n+1)!^{2}}{(2n+2)!}\binom{(s+t-1+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl[\binom{(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2}{n+1}-\binom{(s+t-(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})/2-1}{n+1}\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{4^{n+1}(n+1)!^{2}}{(2n+2)!}\frac{(s+(-1)^{a}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}+2n)/2}{n+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\binom{(s+2n-2+\frac{1+(-1)^{a}\unicode[STIX]{x1D716}}{2}-\unicode[STIX]{x1D708})/2}{n}\binom{(s+2n-2+\frac{1-(-1)^{a}\unicode[STIX]{x1D716}}{2}+\unicode[STIX]{x1D708})/2}{n}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{s+2\lfloor t/2\rfloor -(-1)^{a+t}\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}}{2\unicode[STIX]{x1D70B}}\frac{(-2\unicode[STIX]{x1D70B})^{t}}{t!}\frac{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s)}{\unicode[STIX]{x1D6FE}_{f}^{(-)^{a+t}}(1-s-2\lfloor t/2\rfloor )}.\nonumber\end{eqnarray}$$

In all cases, the result matches the formula for $P_{f}(s;a+t,t)$ . Taking $l_{0}=\lceil T/2\rceil$ , $\unicode[STIX]{x1D70E}=1$ and applying Mellin inversion, we get (20), with $T+1$ in place of $T$ when $T$ is odd. In that case, we estimate the final term of the sum by shifting the contour to $\Re (s)=\frac{3}{2}-T$ , which yields $O(y^{T-1})$ .◻

Lemma 2.5. Assume that $\unicode[STIX]{x1D6EC}_{f}(s)$ has at most finitely many simple zeros, and let $\unicode[STIX]{x1D6FC}\in \mathbb{Q}^{\times }$ and $z=\unicode[STIX]{x1D6FC}+iy$ for some $y\in (0,|\unicode[STIX]{x1D6FC}|/4]$ . Then there are numbers $a_{j}(\unicode[STIX]{x1D6FC}),b_{j}(\unicode[STIX]{x1D6FC})\in \mathbb{C}$ such that, for any integer $M\geqslant 0$ , we have

(21) $$\begin{eqnarray}B(\unicode[STIX]{x1D6FC}+iy)=O_{\unicode[STIX]{x1D6FC},f,M}(y^{M})+\mathop{\sum }_{j=0}^{M-1}y^{j+1/2}\left\{\begin{array}{@{}ll@{}}a_{j}(\unicode[STIX]{x1D6FC})+b_{j}(\unicode[STIX]{x1D6FC})\log y\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC})y^{\unicode[STIX]{x1D708}}+b_{j}(\unicode[STIX]{x1D6FC})y^{-\unicode[STIX]{x1D708}}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$

Proof. Let $s\in \mathbb{C}$ with $\Re (s)\in (0,1)$ , and set $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}/y$ . We will show that there are numbers $a_{j}(\unicode[STIX]{x1D6FC},s),b_{j}(\unicode[STIX]{x1D6FC},s)\in \mathbb{C}$ satisfying

(22) $$\begin{eqnarray}H_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s}=\mathop{\sum }_{j=0}^{\infty }y^{j+1/2}\left\{\begin{array}{@{}ll@{}}a_{j}(\unicode[STIX]{x1D6FC},s)+b_{j}(\unicode[STIX]{x1D6FC},s)\log y\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC},s)y^{\unicode[STIX]{x1D708}}+b_{j}(\unicode[STIX]{x1D6FC},s)y^{-\unicode[STIX]{x1D708}}\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$

and

(23) $$\begin{eqnarray}a_{j}(\unicode[STIX]{x1D6FC},s),b_{j}(\unicode[STIX]{x1D6FC},s)\ll _{f,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}}(2e^{\unicode[STIX]{x1D70B}/2})^{(1+\unicode[STIX]{x1D700})|s|}|2/\unicode[STIX]{x1D6FC}|^{j+1/2}\sqrt{j+1}\quad \text{for all }\unicode[STIX]{x1D700}>0.\end{eqnarray}$$

Let us assume this for now. Then, since $y\leqslant |\unicode[STIX]{x1D6FC}|/4$ , we have

$$\begin{eqnarray}\mathop{\sum }_{j=M}^{\infty }\biggl(\frac{2y}{|\unicode[STIX]{x1D6FC}|}\biggr)^{j+1/2}\sqrt{j+1}\ll _{\unicode[STIX]{x1D6FC},M}y^{M+1/2},\end{eqnarray}$$

so that (by the trivial estimate $|\Re (\unicode[STIX]{x1D708})|<{\textstyle \frac{1}{2}}$ ),

(24) $$\begin{eqnarray}\displaystyle H_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s} & = & \displaystyle O_{f,\unicode[STIX]{x1D6FC},M,\unicode[STIX]{x1D700}}((2e^{\unicode[STIX]{x1D70B}/2})^{(1+\unicode[STIX]{x1D700})|s|}y^{M})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=0}^{M-1}y^{j+1/2}\left\{\begin{array}{@{}ll@{}}a_{j}(\unicode[STIX]{x1D6FC},s)+b_{j}(\unicode[STIX]{x1D6FC},s)\log y\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC},s)y^{\unicode[STIX]{x1D708}}+b_{j}(\unicode[STIX]{x1D6FC},s)y^{-\unicode[STIX]{x1D708}}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$

We substitute this expansion into (18). By hypothesis, $\unicode[STIX]{x1D6EC}_{f}(s)$ has at most finitely many simple zeros, so the sum over $\unicode[STIX]{x1D70C}$ in (18) is a finite linear combination of the series (24) with $s=\unicode[STIX]{x1D70C}$ , which yields an expansion of the shape (21). As for the integral term in (18), by the convexity bound and Stirling’s formula, we have

$$\begin{eqnarray}X_{f}(s)\unicode[STIX]{x1D6EC}_{f}(s)\ll _{f,\unicode[STIX]{x1D700}}e^{-(3\unicode[STIX]{x1D70B}/2-\unicode[STIX]{x1D700})|s|}\quad \text{for }\Re (s)={\textstyle \frac{1}{2}},~\unicode[STIX]{x1D700}>0.\end{eqnarray}$$

Since $2<e^{\unicode[STIX]{x1D70B}}$ , the integral converges absolutely and again yields something of the shape (21).

It remains to show (22) and (23). First suppose that $k=0$ . Then, by (15), we have

$$\begin{eqnarray}H_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s}=|\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D714}|^{1/2-s}(2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D714})^{(1-\unicode[STIX]{x1D716})/2}\operatorname{ 2F1}\biggl(\frac{s+(1-\unicode[STIX]{x1D716})/2+\unicode[STIX]{x1D708}}{2},\frac{s+(1-\unicode[STIX]{x1D716})/2-\unicode[STIX]{x1D708}}{2};1-\frac{\unicode[STIX]{x1D716}}{2};-\unicode[STIX]{x1D714}^{2}\biggr).\end{eqnarray}$$

Applying the hypergeometric transformation [GR15, 9.132(2)] and the defining series (12), this is

(25) $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D70B}i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{(1-\unicode[STIX]{x1D716})/2}|\unicode[STIX]{x1D6FC}|^{1/2-s}\unicode[STIX]{x1D70B}^{1/2}\mathop{\sum }_{\pm }\frac{|y/\unicode[STIX]{x1D6FC}|^{1/2\pm \unicode[STIX]{x1D708}}\unicode[STIX]{x1D6E4}(\mp \unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}(1-(s+(1+\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708})/2)\unicode[STIX]{x1D6E4}((s+(1-\unicode[STIX]{x1D716})/2\mp \unicode[STIX]{x1D708})/2)}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\operatorname{2F1}\biggl(\frac{s+(1-\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708}}{2},\frac{s+(1+\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708}}{2};1\pm \unicode[STIX]{x1D708};-\biggl(\frac{y}{\unicode[STIX]{x1D6FC}}\biggr)^{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =(\unicode[STIX]{x1D70B}i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{(1-\unicode[STIX]{x1D716})/2}|\unicode[STIX]{x1D6FC}|^{1/2-s}\unicode[STIX]{x1D70B}^{1/2}\mathop{\sum }_{j=0}^{\infty }\mathop{\sum }_{\pm }\frac{\unicode[STIX]{x1D6E4}(\mp \unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}(1-(s+(1+\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708})/2)\unicode[STIX]{x1D6E4}((s+(1-\unicode[STIX]{x1D716})/2\mp \unicode[STIX]{x1D708})/2)}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\frac{\binom{-\frac{s+(1-\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708}}{2}}{j}\binom{-\frac{s+(1+\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708}}{2}}{j}}{\binom{-1\mp \unicode[STIX]{x1D708}}{j}}\biggl|\frac{y}{\unicode[STIX]{x1D6FC}}\biggr|^{2j+1/2\pm \unicode[STIX]{x1D708}}.\end{eqnarray}$$

To pass from this to (22), we replace $2j$ by $j$ and set $a_{j}=b_{j}=0$ when $j$ is odd.

When $\unicode[STIX]{x1D708}\neq 0$ we use the estimates

$$\begin{eqnarray}\biggl|\binom{-\frac{s+a\pm \unicode[STIX]{x1D708}}{2}}{j}\biggr|=\biggl|\binom{\frac{s+a\pm \unicode[STIX]{x1D708}}{2}+j-1}{j}\biggr|\leqslant 2^{|s+a\pm \unicode[STIX]{x1D708}|/2+j}\ll _{f}2^{|s|/2+j}\quad \text{for }a\in \{0,1\},\end{eqnarray}$$

$$\begin{eqnarray}\biggl|\binom{-1\mp \unicode[STIX]{x1D708}}{j}\biggr|=\mathop{\prod }_{l=1}^{j}\biggl|1\pm \frac{\unicode[STIX]{x1D708}}{l}\biggr|\geqslant \mathop{\prod }_{l=1}^{j}\biggl|1-\frac{1}{2l}\biggr|=\biggl|\binom{-\frac{1}{2}}{j}\biggr|\gg \frac{1}{\sqrt{2j+1}}\end{eqnarray}$$

and

$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D70B}i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{(1-\unicode[STIX]{x1D716})/2}|\unicode[STIX]{x1D6FC}|^{1/2-s}\unicode[STIX]{x1D70B}^{1/2}\frac{\unicode[STIX]{x1D6E4}(\mp \unicode[STIX]{x1D708})}{\unicode[STIX]{x1D6E4}(1-(s+(1+\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708})/2)\unicode[STIX]{x1D6E4}((s+(1-\unicode[STIX]{x1D716})/2\mp \unicode[STIX]{x1D708})/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \ll _{f,\unicode[STIX]{x1D700}}e^{(\unicode[STIX]{x1D70B}/2+\unicode[STIX]{x1D700})|s|}\quad \text{for all }\unicode[STIX]{x1D700}>0\nonumber\end{eqnarray}$$

to obtain (23).

When $\unicode[STIX]{x1D708}=0$ , (25) has a singularity arising from the $\unicode[STIX]{x1D6E4}(\pm \unicode[STIX]{x1D708})$ factors, but we can still understand the formula by analytic continuation. To remove the singularity, we replace $y^{\pm \unicode[STIX]{x1D708}}$ by $(y^{\pm \unicode[STIX]{x1D708}}-1)+1$ . Since

$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D708}\rightarrow 0}\unicode[STIX]{x1D6E4}(\pm \unicode[STIX]{x1D708})(y^{\pm \unicode[STIX]{x1D708}}-1)=\log y,\end{eqnarray}$$

in the terms with $y^{\pm \unicode[STIX]{x1D708}}-1$ we can simply take the limit and estimate the remaining factors as before; this gives the $b_{j}$ terms in (22) and (23). The terms with $1$ can be written in the form $y^{2j+1/2}(h_{j}(\unicode[STIX]{x1D708})+h_{j}(-\unicode[STIX]{x1D708}))$ , where $h_{j}$ is meromorphic with a simple pole at $\unicode[STIX]{x1D708}=0$ , and independent of $y$ . Then $h_{j}(\unicode[STIX]{x1D708})+h_{j}(-\unicode[STIX]{x1D708})$ is even, so it has a removable singularity at $\unicode[STIX]{x1D708}=0$ . By the Cauchy integral formula, we have

$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D708}\rightarrow 0}(h_{j}(\unicode[STIX]{x1D708})+h_{j}(-\unicode[STIX]{x1D708}))=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{|\unicode[STIX]{x1D708}|=1/2}\frac{h_{j}(\unicode[STIX]{x1D708})+h_{j}(-\unicode[STIX]{x1D708})}{\unicode[STIX]{x1D708}}\,d\unicode[STIX]{x1D708}.\end{eqnarray}$$

Since the above estimates hold uniformly for $\unicode[STIX]{x1D708}\in \mathbb{C}$ with $|\unicode[STIX]{x1D708}|=\frac{1}{2}$ , they also hold for $\lim _{\unicode[STIX]{x1D708}\rightarrow 0}(h_{j}(\unicode[STIX]{x1D708})+h_{j}(-\unicode[STIX]{x1D708}))$ . This concludes the proof of (22) and (23) when $k=0$ .

Turning to $k=1$ , by (15) we have

$$\begin{eqnarray}\displaystyle & & \displaystyle H_{f}(s,\unicode[STIX]{x1D714})y^{1/2-s}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \{0,1\}}\biggl|\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D714}}\biggr|^{1/2-s}(i\unicode[STIX]{x1D714}(s-\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}))^{\unicode[STIX]{x1D6FF}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\operatorname{2F1}\biggl(\frac{s+(-1)^{\unicode[STIX]{x1D6FF}}((1+\unicode[STIX]{x1D716})/2)+\unicode[STIX]{x1D708}}{2}+\unicode[STIX]{x1D6FF},\frac{s+(-1)^{\unicode[STIX]{x1D6FF}}((1-\unicode[STIX]{x1D716})/2)-\unicode[STIX]{x1D708}}{2}+\unicode[STIX]{x1D6FF};\frac{1}{2}+\unicode[STIX]{x1D6FF};-\unicode[STIX]{x1D714}^{2}\biggr),\nonumber\end{eqnarray}$$

and applying [GR15, 9.132(2)], this becomes

$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70B}^{1/2}|\unicode[STIX]{x1D6FC}|^{1/2-s}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \{0,1\}}\biggl(\frac{i\operatorname{sgn}(\unicode[STIX]{x1D6FC})(s-\unicode[STIX]{x1D716}\unicode[STIX]{x1D708})}{2}\biggr)^{\unicode[STIX]{x1D6FF}}\mathop{\sum }_{\pm }\biggl|\frac{y}{\unicode[STIX]{x1D6FC}}\biggr|^{1/2+(1\pm (-1)^{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D716})/2\pm \unicode[STIX]{x1D708}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D6E4}(\mp (\unicode[STIX]{x1D708}+(-1)^{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D716}/2)))}{\unicode[STIX]{x1D6E4}((s+(-1)^{\unicode[STIX]{x1D6FF}}((1\mp \unicode[STIX]{x1D716})/2)\mp \unicode[STIX]{x1D708})/2+\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D6E4}(1/2-(s+(-1)^{\unicode[STIX]{x1D6FF}}((1\pm \unicode[STIX]{x1D716})/2)\pm \unicode[STIX]{x1D708})/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \cdot \,\operatorname{2F1} (\frac{s+(-1)^{\unicode[STIX]{x1D6FF}}((1\pm \unicode[STIX]{x1D716})/2)\pm \unicode[STIX]{x1D708}}{2}+\unicode[STIX]{x1D6FF},\frac{s+(-1)^{\unicode[STIX]{x1D6FF}}((1\pm \unicode[STIX]{x1D716})/2)\pm \unicode[STIX]{x1D708}}{2}+\frac{1}{2};\nonumber\\ \displaystyle & & \displaystyle \qquad 1\pm \biggl(\unicode[STIX]{x1D708}+(-1)^{\unicode[STIX]{x1D6FF}}\frac{\unicode[STIX]{x1D716}}{2}\biggr);-\biggl(\frac{y}{\unicode[STIX]{x1D6FC}}\biggr)^{2} ).\nonumber\end{eqnarray}$$

In this case no singularity arises from the $\unicode[STIX]{x1D6E4}$ -factor in the numerator, so expanding the final $\operatorname{2F1}$ as a series and applying a similar analysis to the above, we arrive at (22) and (23).◻

With the lemmas in place, we can now complete the proof of Proposition 1.2. Let

$$\begin{eqnarray}\unicode[STIX]{x1D712}_{(0,|\unicode[STIX]{x1D6FC}|/4]}(y)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }y\leqslant {\displaystyle \frac{|\unicode[STIX]{x1D6FC}|}{4}},\\ 0\quad & \text{if }y>{\displaystyle \frac{|\unicode[STIX]{x1D6FC}|}{4}},\end{array}\right.\end{eqnarray}$$

and define

$$\begin{eqnarray}\displaystyle g(y) & = & \displaystyle F(\unicode[STIX]{x1D6FC}+iy)+A(\unicode[STIX]{x1D6FC}+iy)-\unicode[STIX]{x1D712}_{(0,|\unicode[STIX]{x1D6FC}|/4]}(y)\mathop{\sum }_{j=0}^{M-1}y^{j+1/2}\left\{\begin{array}{@{}ll@{}}a_{j}(\unicode[STIX]{x1D6FC})+b_{j}(\unicode[STIX]{x1D6FC})\log y\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC})y^{\unicode[STIX]{x1D708}}+b_{j}(\unicode[STIX]{x1D6FC})y^{-\unicode[STIX]{x1D708}}\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D702}(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}\mathop{\sum }_{t=0}^{M-1}\frac{(2\unicode[STIX]{x1D70B}iN\unicode[STIX]{x1D6FC})^{t}}{t!}\mathop{\sum }_{a\in \{0,1\}}\frac{i^{-a}}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{\Re (s)=2}P_{f}(s;a+t,t)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+t,-\frac{1}{N\unicode[STIX]{x1D6FC}},\cos ^{(a)}\biggr)\biggl(\frac{y}{N\unicode[STIX]{x1D6FC}^{2}}\biggr)^{1/2-s}\,ds.\nonumber\end{eqnarray}$$

By Lemmas 2.1, 2.4 and 2.5, we have $g(y)=O_{\unicode[STIX]{x1D6FC},M}(y^{M-1})$ for $y\leqslant |\unicode[STIX]{x1D6FC}|/4$ . On the other hand, shifting the contour of the above to the right, we see that $g$ decays rapidly as $y\rightarrow \infty$ . Hence, $\int _{0}^{\infty }g(y)y^{s-1/2}(dy/y)$ converges absolutely and defines a holomorphic function for $\Re (s)>\frac{5}{2}-M$ .

We have

$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }F(\unicode[STIX]{x1D6FC}+iy)y^{s-1/2}\frac{dy}{y}=\mathop{\sum }_{a\in \{0,1\}}i^{-a}\unicode[STIX]{x1D6E5}_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(a)})\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }k=1\text{ or }(-1)^{a}=\unicode[STIX]{x1D716},\\ 0\quad & \text{otherwise.}\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$

By Lemma 2.2, $\int _{0}^{\infty }A(\unicode[STIX]{x1D6FC}+iy)y^{s-1/2}(dy/y)$ continues to a holomorphic function on $\unicode[STIX]{x1D6FA}$ . Similarly,

$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }y^{s-1/2}\frac{dy}{y}\cdot \unicode[STIX]{x1D712}_{(0,|\unicode[STIX]{x1D6FC}|/4]}(y)\mathop{\sum }_{j=0}^{M-1}y^{j+1/2}\left\{\begin{array}{@{}ll@{}}a_{j}(\unicode[STIX]{x1D6FC})+b_{j}(\unicode[STIX]{x1D6FC})\log y\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC})y^{\unicode[STIX]{x1D708}}+b_{j}(\unicode[STIX]{x1D6FC})y^{-\unicode[STIX]{x1D708}}\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j=0}^{M-1}\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{|\unicode[STIX]{x1D6FC}/4|^{s+j}}{s+j}}\biggl[a_{j}(\unicode[STIX]{x1D6FC})+b_{j}(\unicode[STIX]{x1D6FC})\biggl(\log |\unicode[STIX]{x1D6FC}/4|-{\displaystyle \frac{1}{s+j}}\biggr)\biggr]\quad & \text{if }\unicode[STIX]{x1D708}=k=0,\\ a_{j}(\unicode[STIX]{x1D6FC}){\displaystyle \frac{|\unicode[STIX]{x1D6FC}/4|^{s+j+\unicode[STIX]{x1D708}}}{s+j+\unicode[STIX]{x1D708}}}+b_{j}(\unicode[STIX]{x1D6FC}){\displaystyle \frac{|\unicode[STIX]{x1D6FC}/4|^{s+j-\unicode[STIX]{x1D708}}}{s+j-\unicode[STIX]{x1D708}}}\quad & \text{otherwise},\end{array}\right.\nonumber\end{eqnarray}$$

is holomorphic on $\unicode[STIX]{x1D6FA}$ . Hence, by Mellin inversion,

(26) $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{a\in \{0,1\}}i^{-a}\unicode[STIX]{x1D6E5}_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(a)})\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }k=1\text{ or }(-1)^{a}=\unicode[STIX]{x1D716},\\ 0\quad & \text{otherwise,}\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle \quad -\unicode[STIX]{x1D702}(i\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}\mathop{\sum }_{t=0}^{M-1}\frac{(2\unicode[STIX]{x1D70B}iN\unicode[STIX]{x1D6FC})^{t}}{t!}\mathop{\sum }_{a\in \{0,1\}}i^{-a}P_{f}(s;a+t,t)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+t,-\frac{1}{N\unicode[STIX]{x1D6FC}},\cos ^{(a)}\biggr)\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)>\frac{5}{2}-M\}$ .

Denoting (26) by $h(\unicode[STIX]{x1D6FC})$ , we consider the combination $\frac{1}{2}(i^{k+a_{0}}h(\unicode[STIX]{x1D6FC})+i^{-k-a_{0}}h(-\unicode[STIX]{x1D6FC}))$ for some $a_{0}\in \{0,1\}$ . This picks out the term with $a\equiv k+a_{0}(mod2)$ in the first sum over $a$ , and $a\equiv t+a_{0}(mod2)$ in the second. Therefore, since

$$\begin{eqnarray}P_{f}(s;a_{0},0)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }k=1\text{ or }(-1)^{a_{0}}=\unicode[STIX]{x1D716},\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$

we find that

(27) $$\begin{eqnarray}\displaystyle & & \displaystyle P_{f}(s;a_{0},0)\unicode[STIX]{x1D6E5}_{f}(s,\unicode[STIX]{x1D6FC},\cos ^{(k+a_{0})})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D702}(-\!\operatorname{sgn}(\unicode[STIX]{x1D6FC}))^{k}(N\unicode[STIX]{x1D6FC}^{2})^{s-1/2}\mathop{\sum }_{t=0}^{M-1}\frac{(2\unicode[STIX]{x1D70B}N\unicode[STIX]{x1D6FC})^{t}}{t!}P_{f}(s;a_{0},t)\unicode[STIX]{x1D6E5}_{\bar{f}}\biggl(s+t,-\frac{1}{N\unicode[STIX]{x1D6FC}},\cos ^{(t+a_{0})}\biggr)\end{eqnarray}$$

is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)>\frac{5}{2}-M\}$ . Finally, replacing $M$ by $M+1$ and discarding the final term of the sum, we see that (27) is holomorphic on $\{s\in \unicode[STIX]{x1D6FA}:\Re (s)>\frac{3}{2}-M\}$ , as required.