Bayesian Downscaling Methods for Aggregated Count Data

Abstract

Policy-critical, micro-level statistical data are often unavailable at the desired level of disaggregation. We present a Bayesian methodology for “downscaling” aggregated count data to the micro level, using an outside statistical sample. Our procedure combines numerical simulation with exact calculation of combinatorial probabilities. We motivate our approach with an application estimating the number of farms in a region, using count totals at higher levels of aggregation. In a simulation analysis over varying population sizes, we demonstrate both robustness to sampling variability and outperformance relative to maximum likelihood. Spatial considerations, implementation of “informative” priors, non-spatial classification problems, and best practices are discussed.

Local economic planning often relies on micro-level data that are not always available at the desired level of disaggregation. For example, Federal government-provided economic and employment data for key industry sectors are often reported at the county level, and obtaining city or ZIP-code level data may require time-consuming special requests or considerable expense, or the data may simply be unavailable. In this article, we address the need for micro-level count data by developing a Bayesian methodology to “downscale” aggregated count data to lower levels of aggregation using the information contained in an outside statistical sample.

Suppose a researcher knows the true size of a population (e.g., farmers, voters, customers) and would like to classify members of that population into distinct subgroups (e.g., by farm type, county/region, political party, or demographic attributes) using independent data sampled from the full population. In this setting, we demonstrate a method for estimating the population proportion in each subgroup, in a manner that provides more stable and robust estimates than maximum likelihood estimation (MLE) in the face of sampling variability. The method consists primarily of using simulated random sampling combined with exact calculation of combinatorial probabilities to estimate the posterior distribution over combinations of counts. We leverage two key restrictions: (i) the subgroup counts must add up to the population total, and (ii) the subgroup counts cannot be smaller than their observed counts in the outside sample, nor larger than the population minus the sum of observed samples in the other subgroups. This explicit handling of sampling variability, especially in small- to medium-sized samples, results in smaller normalized errors and, consequently, more reliably accurate estimates.

We are not the first to address the demand for more disaggregated data from aggregated sources. Gocht and Roder (2011), for example, employ a Bayesian procedure to downscale county-level German Agricultural Census estimates of land devoted to agricultural use. Their method incorporates land-use data from GIS to facilitate micro-level environmental impact studies, which would otherwise be hindered by data protection rules (i.e., censoring). Other relevant studies include Chakir (2009), Dendoncker, Bogaert, and Rounsevell (2006), Gärtner, Keller, and Schulin (2013), Howitt and Reynaud (2003), Polasek, Llano, and Sellner (2010), and Purcell and Kish (1980). These papers share a common thread of attempting to estimate land-use patterns using a variety and/or combination of methods, including regression, multinomial logit, maximum entropy, cross-entropy, and various iterative fitting procedures. However, while these procedures perform well in their intended domain, they are ill-suited to solving the downscaling problem for count data. Intuitively, multinomial logit might be mapped to a count model in which sampling probabilities are estimated but many observations and covariates are required. The methods we introduce here are designed to overcome this problem when the outside sample contains only limited categorical information.

Another popular application of downscaling involves disaggregation of global climate data (typically reported at grid levels of 100–200 km²) to a level of resolution more useful for decision makers and impact assessors. Such procedures are outlined, for example, in Coelho et al. (2006), Fasbender and Ouarda (2010), Hashmi, Shamseldin, and Melville (2009), Murphy (1999), and von Storch, Zorita, and Cubasch (1993). The goals of such estimation procedures, however, are to disaggregate weather/climate data not only spatially, but temporally as well, in order to model various potential weather outcomes for use in forecasting. The procedures outlined by these studies are both unnecessarily complex, given our particular problem of interest, and potentially ill-suited to the count data problem due to highly detailed data requirements in the outside sample.

In an attempt to balance precision with tractability, we develop a method that is adaptable to the data and computational resources of the applied researcher. Namely, we show that reasonable performance can be obtained using a uniform prior distribution over combinations of counts, but we also demonstrate a method for researchers to incorporate “informative” prior information generated by a simple linear regression or one of the more spatially explicit and computationally demanding methods described above. In our simulation analysis, we demonstrate a means for testing the best performance among MLE, the uniform prior, or an informative spatial prior, over a range of population counts and sample sizes. As might be expected, an informative prior performs best for the smallest sample sizes and smallest population counts. However, we find that the uninformative, uniform prior performs best over an unexpectedly wide range of sample size and population count combinations.

To provide context, we introduce and apply our methods in the setting of estimating spatially disaggregated farm counts by subregion from regional data, using a sample of Rhode Island farms combined with aggregated data from the 2012 United States Department of Agriculture (USDA) Census of Agriculture (herein, “Ag Census”). We explore both county-to-city downscaling and state-to-county downscaling, and show how spatial patterns at higher levels of aggregation might be used to construct an informative prior. We take special advantage of state-to-county downscaling as an example where the true underlying distribution is known and can be used to validate our methods. We also use published estimates of uncertainty in the Ag Census total counts to demonstrate the robustness of our methods to uncertainty in the top-level population count.

Despite the focus of much of the literature, and our own application, on spatial downscaling problems, it is important to note that there is nothing inherently spatial about the mathematics involved. Our method is equally well adapted to arbitrary classification problems in which it is desired to estimate the size of population subgroups according to a number of discrete categories. These applications might include political polling, estimation of workforce participation rates, demographic breakdowns by gender, age, race, or educational attainment, or market segmentation analysis. At the same time, though our method does not require spatial information per se, it is flexible enough to incorporate arbitrarily complex spatial information as an input to the estimation procedure, by way of the informative prior.

The remainder of this article is organized as follows. The next section outlines and derives our estimation methodology, and the following section discusses selection of a prior. The fourth and fifth sections outline our sample data and methods, and the sixth section covers the results. The next section discusses applications of our findings and areas for future research, and the final section concludes.

Bayesian Downscaling of Aggregated Count Data

Consider a source of aggregated count data for which estimated count data are required at the subpopulation (e.g., subregion, demographic classifications) level, for each subpopulation, s = 1, . . . , S. Let N denote counts at the aggregate level, i.e., population size. We denote the counts to be estimated at the subpopulation level as N _s, such that the sum of subpopulations counts is equal to the total population count, $\sum {N_{\rm s} = N} $. We supplement this population level data with an outside, independently sampled data set with subpopulation counts, n _s, where $\sum {n_{\rm s} = n \lt N} $. That is, the outside sample of subregion data is a subset of the population to be estimated. The immediate impact of the outside data set is to constrain the range of eligible values, which we will denote as ${N}^{\prime}_{\rm s}$ within each combination. Namely,

(1)$$n_{\rm s} \le {N}^{\prime}_{\rm s} \le N - \sum\nolimits_{{\rm s}{\rm ^{\prime}} \ne {\rm s}} {n_{{\rm s}{\rm ^{\prime}}}}. $$

Thus, we define C to be the set of all valid combinations of integer-valued counts satisfying equation 1. The cardinality of this set is denoted |C| and is given by:

(2)$${\rm \vert} {\bi C}{\rm \vert} = \left({\matrix{ {N - n + S - 1} \cr {S - 1} \cr}} \right)= \displaystyle{{\lpar N - n + S - 1\rpar !} \over {\lpar S - 1\rpar !\lpar N - n\rpar !}}.$$

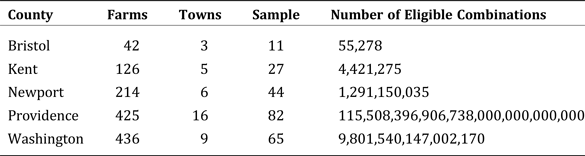
For example, consider Bristol County, Rhode Island. Bristol County comprises three municipalities and is reported by the Ag Census as containing 42 farms. Our sample counts for these three subregions are (6, 3, 2). A valid combination would therefore be any triple with each value equal to or exceeding the sample count and with the total count equal to 42. Thus, (2, 21, 19) is not a valid combination because there are not enough farms in the first town, and (25, 12, 7) is not valid because there are too many total farms (44), but both (6, 34, 2) and (15, 15, 12) are valid combinations.

We have now developed sufficient notation to outline our estimation procedure. First, recall Bayes’ Rule:

(3)$$\Pr\! \lpar A{\rm \vert} B\rpar = \displaystyle{{\Pr \lpar B{\rm \vert} A\rpar \Pr \lpar A\rpar } \over {\Pr \lpar B\rpar }}{\rm \propto} \Pr \lpar B{\rm \vert} A\rpar \Pr \lpar A\rpar .$$

For our purposes, Pr(A|B) in equation 3 represents the probability of a specific combination of subpopulation counts given the data, or Pr(C _i|N, n ₁, . . . , n _s), and the other terms translate similarly. That is:

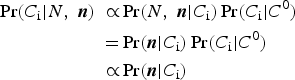(4)$$\eqalign{\Pr \lpar C_{\rm i} \vert N\comma \; {\bi n}\rpar \;\propto& \Pr \lpar N\comma \; {\bi n} \vert C_{\rm i}\rpar \Pr \lpar C_{\rm i} \vert C^0\rpar \cr =& \Pr \lpar {\bi n} \vert C_{\rm i}\rpar \Pr \lpar C_{\rm i} \vert C^0\rpar \cr \propto& \Pr \lpar {\bi n} \vert C_{\rm i}\rpar } $$

where (i) n = (n ₁, . . . , n _S) denotes the vector of subpopulation counts in the outside data, (ii) the equality follows from the constraint in equation 1 because only combinations that sum to N are considered, and (iii) the final proportionality comparison relies on the assumption that the unconditional probability of a combination is uniform across combinations, representing the prior in our Bayesian approach. This is the simplest case of a uniform (“uninformative”) prior over combinations, which we will later generalize. Equation 4 therefore tells us that the posterior probability of a given combination is proportional to the probability of our outside data sample conditional on that combination. For the case of a non-uniform prior this proportionality does not hold and the final reduction in equation 4 does not apply.

The analysis is further simplified because the conditional probability of our data given a combination, Pr(n|C _i), has a closed form according to the formula for sampling without replacement. Namely,

(5)$${\rm Pr}\lpar {\bi n} \vert C_{\rm i}\rpar = \prod\limits_{s = 1}^S {\left({\prod\limits_{k = 0}^{k_{\rm s} - 1} {\displaystyle{{C_{{\rm s\comma i}} - k} \over {N - \lpar s - 1\rpar n_{\rm s} - k}}}} \right)}. $$

Given equation 5, it is theoretically possible to iterate over all eligible combinations of counts at the subpopulation level and exactly calculate the posterior distribution over those counts given the outside sample data in n. Unfortunately, the number of combinations given in equation 2 grows astronomically large rather quickly in real-world applications. Table 1 provides examples for our application.

Table 1. Number of Eligible Combinations per County

Because it is not computationally feasible using contemporary hardware to calculate equation 5 for each possible combination, we propose a (pseudo) random sampling procedure in which valid combinations are sample uniformly from C. These samples are generated by recognizing that each subpopulation's count falls in a range containing N − n + 1 consecutive integers, whose lower bound is found in our sample for that subpopulation. Revisiting our previous Bristol County example, wherein N − n + 1 = 42 − 11 + 1 = 32, it is only possible for subregional values to fall in the set, {n _s (+0), n _s + 1, . . . , n _s + 31}. Since each subregion must have the same size range, the problem reduces to picking uniform integers in this range. If we offset the uniform integers by their minimum values, then all the random choices must add up to the same total (also N − n + 1 = 32) to be a valid combination as described above.

This is a well-known problem for which the solution is to randomly choose switching points, s _s ∈ {s ₂, . . . , s _S}, without replacement from the set of integers, {1, 2, . . . , N − n}. The sampled combination is then derived by differencing the switching points after setting s ₁ = 0 and s _S+1 = N − n + 1. In order to handle the minimum switching interval being size 1, the resulting differences are added to the sample value, minus 1, and the sampled switching points are taken from N − n + S − 1 candidate values. Downscaling Bristol County into three subregions provides N − n + S − 1 = 42 − 11 + 3 + 1 = 35. We would thus randomly sample S − 1 = 2 switching points from {1, . . . , 35}, setting s ₁ = 0 and s ₄ = 36.

Choosing a Prior

Researchers have two broad choices for estimating the Bayesian prior used in our estimation method: an uninformative (uniform) prior or an informative one. While in its most generalized form, our method has no requirement that subpopulations have additional characteristics from which to estimate a prior, researchers may be able to elicit a more informative prior based on additional characteristics of the sampling units. For example, in the case of classifying farms into subregions, these additional data may include population, land area, demographic data, etc., at the subregion level. We now outline a rigorous procedure for eliciting an informative prior. In cases where such additional characteristic information is unavailable for whatever reason, researchers have little choice but to assume a uniform prior across the subpopulations.

In many cases, the assumption that counted units have an equal probability of occurrence across subpopulations is unrealistic, particularly in our example application of estimating farm counts. If the data available to the researchers consist of aggregate count data for multiple populations, as well as additional covariates at the subregional level (and can thus be summed to the regional level, e.g., population, land area, demographics, spatial information), one can test and identify potential informative priors by regressing these covariates (summed to the population level) on the population-level count data. By identifying the covariates that are most predictive of (correlated with) counts at the population level, one can use these relationships to estimate subregional farm counts. In this fashion, a more informative prior is elicited than the simple uniform prior. See Figure 1 for an illustration of how the data analysis is structured.

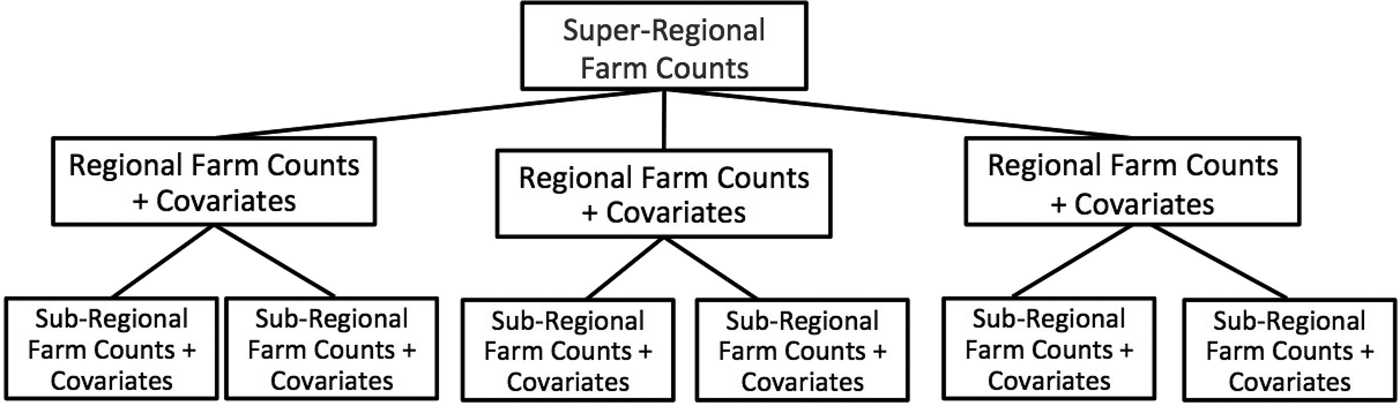
Figure 1. Structure of Sample Data Analysis

To compare the accuracy of estimates resulting from an informative versus an uninformative prior, we used the above procedure to elicit and compare various informative priors using supplemental subregional data obtained from the 2010 United States Census. Using county-level Census data, we performed a comprehensive regression analysis, regressing various combinations of potentially relevant covariates such as population, area, and population density on our five county-level farm counts. Land area was by far the most predictive covariate, being significantly positively correlated with farm counts (0.928). In calculating our prior, we ignore the constant term in the regression to reduce bias introduced by the fact that the constant term is only meaningful at the aggregated level because we scaled up the data. Removing the constant term also imposes the intuitive constraint that a subregion with zero land area must also contain zero farms. Because of the combinatorial nature of this problem, the regression-based priors are normalized to sum to the known aggregate counts. This makes the elicitation of the informative prior in our example equivalent to distributing N across subregions based on their proportional land area, such that $n_{\rm n}^{\rm 0} = \hbox{Land Area}_n/ \hbox{Land Area}_N$.

In what follows, we will explicitly compare predictions of the uniform prior against those of this simple informative prior and compare both against maximum likelihood.

Although geographic downscaling is traditionally a spatial problem, the general form of our method ignores issues of spatial dependency in favor of a more parsimonious method that requires much less data (and less technical expertise in the area of spatial modeling). However, the generalized method can be easily expanded and the use of an informative prior in our procedure makes the incorporation of features such as spatial dependence relatively straightforward. While we opt for a simple, one-parameter, area-based prior as an example here, myriad potential models for eliciting an informative prior exist, including those discussed in the introduction. Researchers with the prior belief that the posterior distribution follows a spatial dependency structure (such as spatial lag or autocorrelation) can easily incorporate such beliefs into this methodology by eliciting their priors using a spatial model such as geographically weighted regression (GWR), among many choices.

Sample Data

Rhode Island has 39 municipalities grouped into five counties: Bristol, Kent, Newport, Providence, and Washington County. Counties range in size from 3 towns in Bristol County to 16 in Providence County. Our aggregated data source comes from the 2012 Ag Census, which contains farm counts by county and consequently, at the state level. Our outside sample data comes from a survey administered by the University of Rhode Island in 2011–2012, in collaboration with local government agencies and agricultural organizations. It contains a list of addresses for 229 of the 1,243 farms reported in the Ag Census. We further supplement these data with additional subregional data provided by the 2010 Census. of these data, only land area was used in our final estimation procedure (indirectly, to elicit the informative prior). This information is presented in Table 2.

Table 2. Farms, Municipalities, and Land Area (mi²) per County

Note: Pearson's Rho = 0.928.

Methods

Clearly the unknowns in our data set are the city-level counts. We focus instead on the county totals, as if unknown, so that we can compare the results of our procedure against the true underlying distribution. By aggregating our regional counts to the state level and aggregating our sample data to the county level, we can compare the accuracy of our estimates using (i) a uniform prior, (ii) a simple spatial prior, and (iii) maximum likelihood. The maximum likelihood estimates (MLE) differ from those of the Bayesian estimates under the uniform prior since because N and n are known, MLE estimates for N _s simplify to $ \hat N_{\rm s}^{{\rm MLE}} = \lpar n_{\rm s}/n\rpar N$.

For each methodology, we evaluate the normalized root mean squared error (NRMSE) of our posterior point estimates relative to the values reported in the Ag Census. The NRMSE is simply the familiar root mean squared error (RMSE), scaled by the average region-size, $ \bar N_{\rm s} = N/S $. Using NRMSE supports our goals of estimating the effects of both population size, N, and sample size, n/N, on the relative performance of each method.

To obtain estimates for the Bayesian methods, we use the sampling procedure described in “Bayesian Downscaling of Aggregated Count Data” to calculate estimates from 100,000 sample combinations. We report as point estimates the means of the posterior count distributions, which is why decimal values are observed in the estimates despite only considering integer-valued combinations. We repeat the procedure 200 times for each estimate to obtain standard errors of our estimates and calculate the NRMSE of our posterior estimates relative to the values reported in the Ag Census.

To test the effect of population size, N, on estimation performance, we simulate five subregions with our county-size proportions and sample proportion (approx. 0.2), at varying population sizes from N = 50 up to N = 5,000. To test the effect of sample size on estimation performance, we again simulate five subregions with our county-size proportions, this time with a fixed population size of N = 1,250 and with varying sample sizes from n/N = 0.01 up to n/N = 0.50.

For each comparison, we conduct two simulations, one with observations bootstrapped from our observed Rhode Island sample, and another randomly sampled from a multinomial distribution taken only from the population parameters. The results are nearly identical across the paired simulations, indicating that the sample data we collected do not contain extreme deviations from the projected sampling distribution.

Results

The mean NRMSE and standard error for each method are presented in Table 3, as a function of varying sample size. For a population of 1,250, the Bayesian methods consistently outperform MLE for all sample sizes up to half of the population. Among the Bayesian methods, the simple, area-based, informative prior was best for small samples (due to greater sampling variability), but the uninformative (uniform) prior was best for samples comprising at least 5 percent of the population. These results suggest a somewhat counterintuitive finding: namely, that even in cases where detailed spatial information is available, many applied problems will get more accurate results using the uninformative prior, even when it might not seem realistic to the application at hand. The reasoning is that even relatively small samples will quickly become more representative of the underlying population than a good informative prior, but not so representative as to obviate the need for a Bayesian approach over MLE.

Table 3. Mean Normalized Root Mean Square Error by Estimate Type: Fixed Population Size (1,250) with Increasing Sample Size

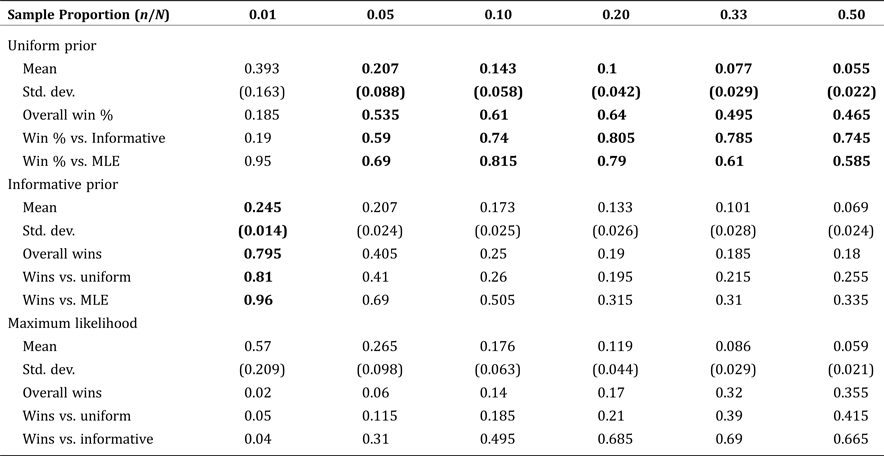
Note: Boldface indicates estimates with the smallest RMSE compared to the true, known values.

When examining Table 3, it is important to note that the conventional wisdom regarding standard errors and statistical significance does not hold because of correlated testing. That is, we are not testing whether one measure produces a lower NRMSE on average over independent tests, rather, we are testing whether one measure produced a statistically significantly lower NRMSE than the others across the same simulation tests. So, we do not present p-values or a fully developed hypothesis testing framework with our results. Rather, the “winning method” which is bold-faced in each column of Table 3, is determined according to a single transferable vote system as outlined in Tideman (1995) based on the percentage of “wins” (lower observed NRMSE) out of 200 trials. In essence, the winning model is chosen according to winning a simple majority of trials outright, or else winning a “runoff” between the top two candidates.

For the interested reader, pairwise tests of statistically significant better performance between two estimators can be determined as follows. The null hypothesis for pairwise comparison of two identical estimators is that the number of wins for each estimator follows the binomial distribution with n = 200 draws and p = 0.5. So, for individual, pairwise tests of performance, the threshold for statistical significance at the 95 percent and 99 percent levels are 113 wins (56.5 percent) and 117 wins (58.5 percent), respectively. Clearly, to evaluate every possible pairwise test in Table 3 involves many hypotheses, so p-values would need to be adjusted using either a Bonferroni correction or stepdown methods to control the family-wise error rate (e.g., Romano and Wolf 2005). Explicit testing of multiple hypotheses in this fashion is beyond the scope of this paper.

Table 4 is structured similarly but shows the effect of varying population size, given the sample size held fixed at $ n/N = 20\percnt $ of the population. The table also shows the Bayesian methods consistently outperforming MLE, but show subtly different patterns of performance of the informative prior against the uniform prior. With the sample size held at a fixed percentage, the informative prior outperforms for populations smaller than 500, while the uniform outperforms for larger populations. For populations of exactly 500, the performance of the two priors is not statistically different at conventional levels.

Table 4. Mean Normalized Root Mean Square Error by Estimate Type: Fixed Sample Proportion (0.20) and Increasing Population Size

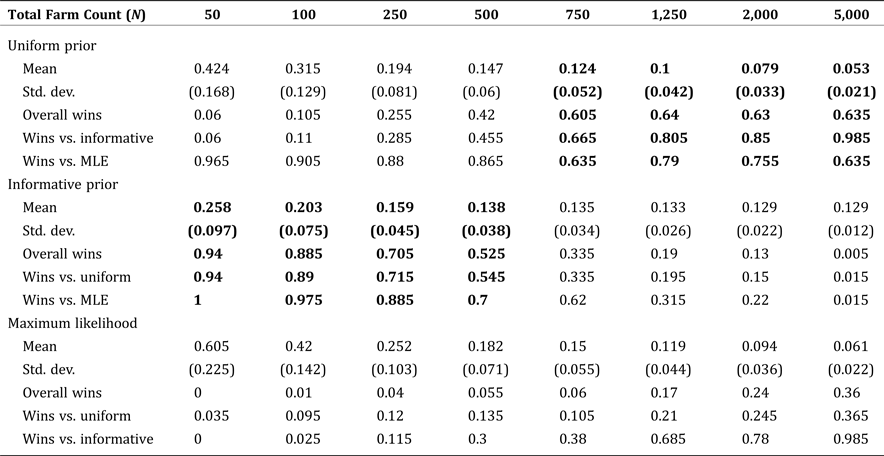
Note: Boldface indicates estimates with the smallest RMSE compared to the true, known values.

Discussion

The above results are primarily focused on evaluating the performance of our Bayesian methods for a case where the underlying distribution is known. However, our method is only designed to be useful in cases where this information is unavailable. Furthermore, applications of our procedure to new problems will likely involve variation in population size, sample size(s) and availability of an informative prior, distinct from the permutations described here. In this section, we consider the possibility that future researchers have access to data at higher levels of aggregation, similar to how we have both state-level and county-level farm counts for Rhode Island from the Ag Census, and county-level land area data from the U.S. Census.

If it can be assumed that spatial (or other group-wise dependence) patterns are likely to hold at higher levels of aggregation, then an informative prior can be calibrated from that data and applied in the downscaling problem. In our application, that would mean calibrating the land-area prior from county-level data and then applying it to the city-level downscaling problem. Depending on the application, however, this assumption may not be palatable. Spatial econometric models can be conceptualized as having a direct effect from the covariates and an indirect effect from the spatial dependence structure. If this indirect effect is relatively smaller at higher levels of aggregation, then calibrating the prior at higher levels will cause it to appear more informative than it actually will be in the downscaled analysis. Identifying when this problem materially affects the analysis is an area for future research. That said, there is no reason why spatial dependence observed in an econometric model would predict non-random sampling, so whenever the spatial prior is suspect, researchers can always default to the uninformative prior for reasonable performance.

Beyond spatial dependence defined econometrically, there is also the possibility that the outside data sample is non-random, in the sense that spatial factors influence response rates. At higher levels of aggregation, this can be tested simply be evaluating the degree to which the sample contains outliers relative to a typical sample from a multinomial distribution. A further verification step is possible using the simulation methods outlined above at higher levels of aggregation. Namely, the bootstrapped analysis can be replicated with counts drawn directly from a multinomial distribution instead of from the sample data. Below, we give an example of simulation results obtained in this fashion in Tables 5 and 6, which replicate our Tables 3 and 4 but do not use our sample data. For our specific application, it can be observed that the results are nearly identical, the desired outcome indicating that systematic sampling bias is unlikely to be a problem in our application.

Table 5. Mean Normalized Root Mean Square Error by Estimate Type using Simulated Sample: Fixed Population Size (1,250) with Increasing Sample Size

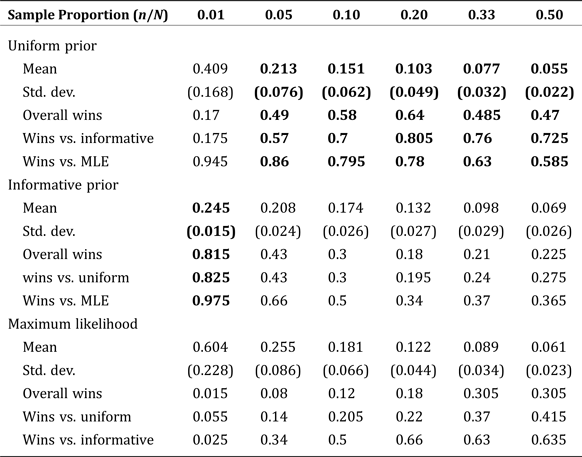
Note: Boldface indicates estimates with the smallest RMSE compared to the true, known values.

Table 6. Mean Normalized Root Mean Square Error by Estimate Type using Simulated Sample: Fixed Sample Proportion (0.20) and Increasing Population Size

Note: Boldface indicates estimates with the smallest RMSE compared to the true, known values.

If we consider the city-level downscaling problem in our application, the above procedures indicate that every county in Rhode Island should be estimated using the informative, area-based prior. Clearly, we do not have the underlying, true distribution of city-level farm counts for verification, so we include this observation only for completeness.

Two issues not previously addressed are (i) the effects of uncertainty in the top-level population estimates, and (ii) the scenarios in which MLE does outperform the Bayesian estimators, according to conventional wisdom based on asymptotic results. While our procedure is designed to mitigate potential estimation error resulting from the increased sampling variability inherent in relatively small samples, it does not account for potential error in the aggregate count data. In our application, for example, the Ag Census farm counts for Rhode Island are reported as 1,243 total farms with a standard error of 236 (USDA 2014). The analysis thus far suggests that incorporating an error term on the total count may have non-linear effects because of simultaneous changes both in the population size, N, and in the sample proportion, n/N.

To address this concern, we repeated the simulation analysis using the uniform prior, with each replication using a different total farm count drawn from a normal distribution with mean and standard deviation according to the reported Ag Census mean and standard error. The mean estimated farm counts arising from this procedure were within 1 percent of the values estimated with N = 1,243. This suggests that errors in top-level counts are less of a concern, as long as (i) it is recognized that the division of the population into groups will necessarily result in estimates that are proportional to the total used, and (ii) that the estimation error in the total count is not so large as to make the collected sample size unlikely or impossible.

Finally, it is important to give proper context to our finding that these Bayesian methods outperform MLE. Clearly, this is a finite sample result since, asymptotically, Bayesian updating with a uniform prior converges to MLE, whereas in small samples MLE is equivalent to Bayesian updating with zero sample weight on the prior. Also, it may not be immediately obvious, but our application data set includes considerable variation in the group sizes to be estimated: 42, 126, 214, 425, and 436 (from Table 2). Having extremes in the group sizes, especially on the small end, leads to inherently noisier sampling of the smaller groups. This problem can be conceptualized as arising from the probability that a given sample will be representative of the population conditional on population size and sample size.

To show how variation across group sizes affects the performance of MLE relative to the Bayesian methods described here, we ran some preliminary simulations. The simulated group sizes were all drawn IID from a normal distribution with sigma given by a fraction of the mean value, and samples were then drawn from the resulting multinomial distribution. Our sample data had a standard deviation of 71 percent of the mean count, and MLE did not outperform the Bayesian methods for any population of N = 5,000 or below. Reducing the standard deviation to 50 percent of the mean count, we found that MLE was statistically significantly best (lowest NRMSE) for populations above 2,000 (as might appear in Table 6). These preliminary results suggest that the efficacy of MLE relative to the Bayesian methods is not only a function of population size and sample size, but also of the degree of heterogeneity in the subpopulation counts to be estimated. We leave exact quantification of these tradeoffs as an area for future research.

Conclusion

Micro-level statistical data are often unavailable at the desired level of disaggregation, despite their critical importance for applied policy research. Herein, we present a Bayesian methodology for “downscaling” aggregated count data to the micro-level, using an outside statistical sample. Our procedure combines numerical simulation with exact calculation of combinatorial probabilities. We motivate our approach with an application estimating the number of farms in a region, using count totals at higher levels of aggregation, and data sourced from the 2012 USDA Ag Census. In a simulation analysis over varying population sizes, we demonstrate both robustness to sampling variability and outperformance relative to maximum likelihood. Our results show that Bayesian methods have better finite sample performance than MLE in many cases relevant to applied research, especially for relatively small populations (N < 5,000).

We develop a number of methods for applied researchers to calibrate informative prior probabilities, and to estimate whether the combination of sample size and population size in their application will perform best with their informative prior, or with an uninformative alternative. In many cases, the uninformative prior performs reasonably well and can be used as a default in cases where an informative prior is unavailable, or cannot be reasonably calibrated due to spatial considerations. We also show how the process of calibrating the priors can be simulated to verify that they are not being affected adversely by outside sample data that contains too many outliers. Our methods appear to be robust, both to sampling variability in the outside data sample and also to uncertainty in the top-level population counts. An area for future research is determining the effects of heterogeneity in subpopulation sizes on the relative performance of MLE in smaller populations.