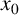1 Introduction and preliminaries
Many papers examine disruptions of functions and dynamical systems with respect to certain properties (see, for example, [Reference Loranty and Pawlak7, Reference Pawlak10, Reference Poprawa11]). The basis of our considerations is an observation articulated in Proposition 2.4, which states that distributional chaos for continuous functions at an arbitrary point may be disrupted by the family of all continuous functions. This prompts a natural question about the possibility of approximating a continuous function by a ‘big’ family of functions resistant to disruptions. Whereas approximating functions cannot be continuous, a natural requirement is to determine a property ‘close’ to continuity. Taking into account research conducted in [Reference Cao and McCluskey1, Reference Crannel and Martelli3, Reference Pawlak and Pawlak9], the chosen property is quasicontinuity (which is widely examined in real analysis).
Throughout the paper, we will use standard definitions and notation. Unless otherwise stated, we will consider functions mapping the unit interval
![]() $[0,1]$
into itself. Therefore, we will write
$[0,1]$
into itself. Therefore, we will write
![]() $(a,b), [a,b]$
and so on, instead of the intersections
$(a,b), [a,b]$
and so on, instead of the intersections
![]() $(a,b)\cap [0,1], [a,b]\cap [0,1]$
. By
$(a,b)\cap [0,1], [a,b]\cap [0,1]$
. By
![]() $\mathbb {N}$
, we denote the positive integers. The symbol
$\mathbb {N}$
, we denote the positive integers. The symbol
![]() $\operatorname {\mathrm {\#}} (A)$
means the cardinality of A. The symbol
$\operatorname {\mathrm {\#}} (A)$
means the cardinality of A. The symbol
![]() $f|_{A}$
denotes a restriction of the function f to A. We denote the set of all fixed points of f by
$f|_{A}$
denotes a restriction of the function f to A. We denote the set of all fixed points of f by
![]() $\textrm {Fix}(f)$
(that is,
$\textrm {Fix}(f)$
(that is,
![]() $x\in \textrm {Fix}(f)$
, if
$x\in \textrm {Fix}(f)$
, if
![]() $f(x)=x$
).
$f(x)=x$
).
We employ the concept of a (discrete) dynamical system, following [Reference Čiklová2, Reference Ruette12]. Let X be a compact space. A topological dynamical system
![]() $(X,f)$
(denoted by
$(X,f)$
(denoted by
![]() $(f)$
) is given by a map
$(f)$
) is given by a map
![]() $f:X\rightarrow X$
. The evolution of the system is given by the successive iterations of the map, that is,
$f:X\rightarrow X$
. The evolution of the system is given by the successive iterations of the map, that is,
![]() $f^{0}(x)=x$
and
$f^{0}(x)=x$
and
![]() $f^{n}(x)=(f\circ f^{n-1})(x)$
for
$f^{n}(x)=(f\circ f^{n-1})(x)$
for
![]() $x\in X$
and
$x\in X$
and
![]() $n\in \mathbb {N}$
. For
$n\in \mathbb {N}$
. For
![]() $x\in X$
, the set
$x\in X$
, the set
![]() $O_{f}(x)=\{f^{i}(x): i=0,1,2,\ldots \}$
is called an orbit.
$O_{f}(x)=\{f^{i}(x): i=0,1,2,\ldots \}$
is called an orbit.
Let
![]() $(f)$
be a dynamical system and let
$(f)$
be a dynamical system and let
![]() $Y\subset X$
. For
$Y\subset X$
. For
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\varepsilon> 0$
, we say that a set
$\varepsilon> 0$
, we say that a set
![]() $E\subset Y$
is an
$E\subset Y$
is an
![]() $(n,Y,\varepsilon )$
-separated set if for all distinct points
$(n,Y,\varepsilon )$
-separated set if for all distinct points
![]() $x,y\in E$
, there exists
$x,y\in E$
, there exists
![]() $k\in [0,n-1]\cap \mathbb {N}$
such that
$k\in [0,n-1]\cap \mathbb {N}$
such that
![]() $|f^{k}(x)-f^{k}(y)|> \varepsilon $
. Let
$|f^{k}(x)-f^{k}(y)|> \varepsilon $
. Let
![]() $s_{n}(f,Y,\varepsilon )$
denote the maximal cardinality of an
$s_{n}(f,Y,\varepsilon )$
denote the maximal cardinality of an
![]() $(n,\varepsilon )$
-separated set in Y. The entropy of a dynamical system
$(n,\varepsilon )$
-separated set in Y. The entropy of a dynamical system
![]() $(f)$
on
$(f)$
on
![]() $Y\subset X$
is the number
$Y\subset X$
is the number
If
![]() $Y=X$
, then we will omit the symbol X.
$Y=X$
, then we will omit the symbol X.
Let
![]() $f:I\rightarrow I$
, where I is a nondegenerate compact interval, be a continuous function and let
$f:I\rightarrow I$
, where I is a nondegenerate compact interval, be a continuous function and let
![]() $n\in \{2,3,\ldots \}$
. If
$n\in \{2,3,\ldots \}$
. If
![]() $J_{1},J_{2},\ldots ,J_{n}$
are nondegenerate, closed and pairwise disjoint intervals such that
$J_{1},J_{2},\ldots ,J_{n}$
are nondegenerate, closed and pairwise disjoint intervals such that
![]() $J_{1}\cup J_{2}\cup \cdots \cup J_{n}\subset f(J_{i})$
for all
$J_{1}\cup J_{2}\cup \cdots \cup J_{n}\subset f(J_{i})$
for all
![]() $i\in \{ 1,2,\ldots ,n\}$
, then
$i\in \{ 1,2,\ldots ,n\}$
, then
![]() $(J_{1}, J_{2},\ldots , J_{n})$
is called an n-horseshoe for f.
$(J_{1}, J_{2},\ldots , J_{n})$
is called an n-horseshoe for f.
Following [Reference Kempisty5], we say that a function f is quasicontinuous at a point
![]() $x_{0}\in [0,1]$
if for any neighbourhood V of
$x_{0}\in [0,1]$
if for any neighbourhood V of
![]() $x_{0}$
and for any neighbourhood W of
$x_{0}$
and for any neighbourhood W of
![]() $f(x_{0})$
, there exists a nonempty open set
$f(x_{0})$
, there exists a nonempty open set
![]() $U\subset V$
such that
$U\subset V$
such that
![]() $f(U)\subset W$
. The function f is called quasicontinuous if it is quasicontinuous at every point
$f(U)\subset W$
. The function f is called quasicontinuous if it is quasicontinuous at every point
![]() $x\in [0,1]$
. From now on, by DQc, we denote the family of all Darboux and quasicontinuous functions.
$x\in [0,1]$
. From now on, by DQc, we denote the family of all Darboux and quasicontinuous functions.
Quasicontinuous dynamical systems (that is, systems such that
![]() $f^{n}$
is quasicontinuous for
$f^{n}$
is quasicontinuous for
![]() $n\in \mathbb {N}$
) have been considered in [Reference Cao and McCluskey1, Reference Crannel and Martelli3]. To ensure that all iterations of a quasicontinuous dynamical system have this property, in [Reference Pawlak and Pawlak9], quasicontinuity was connected with the Darboux property for the first time. The following lemma refers to these considerations in a more general situation.
$n\in \mathbb {N}$
) have been considered in [Reference Cao and McCluskey1, Reference Crannel and Martelli3]. To ensure that all iterations of a quasicontinuous dynamical system have this property, in [Reference Pawlak and Pawlak9], quasicontinuity was connected with the Darboux property for the first time. The following lemma refers to these considerations in a more general situation.
Lemma 1.1. If
![]() $f,g\in \mathrm {DQc}$
, then
$f,g\in \mathrm {DQc}$
, then
![]() $g\circ f\in \mathrm {DQc}$
.
$g\circ f\in \mathrm {DQc}$
.
Proof. Assume that
![]() $f,g\in \mathrm {DQc}$
. Obviously,
$f,g\in \mathrm {DQc}$
. Obviously,
![]() $g\circ f$
is Darboux. For simplicity of notation, we will use symbols
$g\circ f$
is Darboux. For simplicity of notation, we will use symbols
![]() $(a,b), [a,b]$
and so on even in the case where
$(a,b), [a,b]$
and so on even in the case where
![]() $a>b$
.
$a>b$
.
Now, let
![]() $x_{0}\in [0,1]$
,
$x_{0}\in [0,1]$
,
![]() $V=(x_{0}-\delta ,x_{0}+\delta )$
and
$V=(x_{0}-\delta ,x_{0}+\delta )$
and
![]() $W=(g(f(x_{0}))-{\varepsilon },g(f(x_{0}))+{\varepsilon })$
. Of course, it is sufficient to consider only the case when there is
$W=(g(f(x_{0}))-{\varepsilon },g(f(x_{0}))+{\varepsilon })$
. Of course, it is sufficient to consider only the case when there is
![]() $\delta _{1}>0$
such that
$\delta _{1}>0$
such that
![]() $f([x_{0}-\delta _{1},x_{0}+\delta _{1}])\neq \{f(x_{0})\}$
.
$f([x_{0}-\delta _{1},x_{0}+\delta _{1}])\neq \{f(x_{0})\}$
.
Put
![]() $A_{0}=[x_{0}-\delta ,x_{0}+\delta ]$
. Then
$A_{0}=[x_{0}-\delta ,x_{0}+\delta ]$
. Then
![]() $f(A_{0})\ni f(x_{0})$
is a nondegenerate interval. Obviously, there exists
$f(A_{0})\ni f(x_{0})$
is a nondegenerate interval. Obviously, there exists
![]() $p_{1}\in (f(x_{0})-{\varepsilon },f(x_{0})+{\varepsilon })\cap (f(A_{0})\backslash \{f(x_{0})\})$
.
$p_{1}\in (f(x_{0})-{\varepsilon },f(x_{0})+{\varepsilon })\cap (f(A_{0})\backslash \{f(x_{0})\})$
.
Now, let
![]() $A_{1}=[f(x_{0}),p_{1}]$
. Then
$A_{1}=[f(x_{0}),p_{1}]$
. Then
![]() $A_{1}\subset f(A_{0})$
. In the case where
$A_{1}\subset f(A_{0})$
. In the case where
![]() $g(A_{1})=\{g(f(x_{0}))\}$
, the proof is straightforward. So let us consider the situation
$g(A_{1})=\{g(f(x_{0}))\}$
, the proof is straightforward. So let us consider the situation
![]() $g(A_{1})\neq \{g(f(x_{0}))\}$
. The Darboux property of g implies that there is
$g(A_{1})\neq \{g(f(x_{0}))\}$
. The Darboux property of g implies that there is
![]() $p_{2}\in (g(f(x_{0}))-{\varepsilon },g(f(x_{0}))+{\varepsilon })\cap (g(A_{1})\backslash \{g(f(x_{0}))\})$
. Put
$p_{2}\in (g(f(x_{0}))-{\varepsilon },g(f(x_{0}))+{\varepsilon })\cap (g(A_{1})\backslash \{g(f(x_{0}))\})$
. Put
![]() $A_{2}=[g(f(x_{0})),p_{2}]\subset g(A_{1})$
. It is immediate that there exists
$A_{2}=[g(f(x_{0})),p_{2}]\subset g(A_{1})$
. It is immediate that there exists
![]() $y_{2}\in A_{2}\backslash \{g(f(x_{0})), g(f(x_{0}-\delta )),g(f(x_{0}+\delta )),g(p_{1}),p_{2}\}\subset (g(f(x_{0})),p_{2})$
. Consequently, there is
$y_{2}\in A_{2}\backslash \{g(f(x_{0})), g(f(x_{0}-\delta )),g(f(x_{0}+\delta )),g(p_{1}),p_{2}\}\subset (g(f(x_{0})),p_{2})$
. Consequently, there is
![]() $y_{1}\in A_{1}$
such that
$y_{1}\in A_{1}$
such that
![]() $y_{2}=g(y_{1})$
. Obviously,
$y_{2}=g(y_{1})$
. Obviously,
![]() $y_{1}\in (f(x_{0}),p_{1})\backslash \{f(x_{0}-\delta ),f(x_{0}+\delta )\}$
. By quasicontinuity of g at
$y_{1}\in (f(x_{0}),p_{1})\backslash \{f(x_{0}-\delta ),f(x_{0}+\delta )\}$
. By quasicontinuity of g at
![]() $y_{1}$
, there is an open set
$y_{1}$
, there is an open set
![]() $U_{1}\subset (f(x_{0}),p_{1})\backslash \{f(x_{0}-\delta ),f(x_{0}+\delta )\}$
such that
$U_{1}\subset (f(x_{0}),p_{1})\backslash \{f(x_{0}-\delta ),f(x_{0}+\delta )\}$
such that
![]() $g(U_{1})\subset (g(f(x_{0})),p_{2})\subset A_{2}\subset W$
.
$g(U_{1})\subset (g(f(x_{0})),p_{2})\subset A_{2}\subset W$
.
Now, choose
![]() $z_{1}\in U_{1}$
. One can find
$z_{1}\in U_{1}$
. One can find
![]() $y_{0}\in A_{0}$
such that
$y_{0}\in A_{0}$
such that
![]() $z_{1}=f(y_{0})$
. Then
$z_{1}=f(y_{0})$
. Then
![]() $y_{0}\in V\backslash \{x_{0}\}$
. By quasicontinuity of f at
$y_{0}\in V\backslash \{x_{0}\}$
. By quasicontinuity of f at
![]() $y_{0}$
, we infer that there is an open set
$y_{0}$
, we infer that there is an open set
![]() $U_{0}\subset V\backslash \{x_{0}\}$
such that
$U_{0}\subset V\backslash \{x_{0}\}$
such that
![]() $f(U_{0})\subset U_{1}$
. It is easy to check that
$f(U_{0})\subset U_{1}$
. It is easy to check that
![]() $g(f(U_{0}))\subset W$
.
$g(f(U_{0}))\subset W$
.
In connection with distributional chaos, we will use the notation and concepts introduced in [Reference Schweizer and Smítal13]. Let
![]() $(f)$
be a dynamical system and
$(f)$
be a dynamical system and
![]() $x,y\in [0,1]$
. For
$x,y\in [0,1]$
. For
![]() $t>0$
, the functions,
$t>0$
, the functions,
 $$ \begin{align*} \Phi^{*(f)}_{x,y} (t) &=\limsup\limits_{n\longrightarrow \infty}\frac{1}{n}\operatorname{\mathrm{\#}}(\{\kern1.5pt j\in [0,n-1]\cap\mathbb{N}:|f^{\,j}(x)-f^{\,j}(y)|<t\}),\\ \Phi^{(f)}_{x,y} (t) &=\liminf\limits_{n\longrightarrow \infty}\frac{1}{n}\operatorname{\mathrm{\#}}(\{\kern1.5pt j\in[0,n-1]\cap\mathbb{N}:|f^{\,j}(x)-f^{\,j}(y)|<t\}), \end{align*} $$
$$ \begin{align*} \Phi^{*(f)}_{x,y} (t) &=\limsup\limits_{n\longrightarrow \infty}\frac{1}{n}\operatorname{\mathrm{\#}}(\{\kern1.5pt j\in [0,n-1]\cap\mathbb{N}:|f^{\,j}(x)-f^{\,j}(y)|<t\}),\\ \Phi^{(f)}_{x,y} (t) &=\liminf\limits_{n\longrightarrow \infty}\frac{1}{n}\operatorname{\mathrm{\#}}(\{\kern1.5pt j\in[0,n-1]\cap\mathbb{N}:|f^{\,j}(x)-f^{\,j}(y)|<t\}), \end{align*} $$
are respectively called upper and lower distribution function of x and y for the dynamical system
![]() $(f)$
.
$(f)$
.
Let
![]() $x,y\in [0,1]$
. We shall say that a pair
$x,y\in [0,1]$
. We shall say that a pair
![]() $(x,y)$
is a DC-pair for a dynamical system
$(x,y)$
is a DC-pair for a dynamical system
![]() $(f)$
if
$(f)$
if
![]() $\Phi ^{*(f)}_{x,y} (t)=1$
for any
$\Phi ^{*(f)}_{x,y} (t)=1$
for any
![]() $t>0$
and there exists
$t>0$
and there exists
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
![]() $\Phi ^{(f)}_{x,y} (t_{0})=0.$
A set
$\Phi ^{(f)}_{x,y} (t_{0})=0.$
A set
![]() $S\subset [0,1]$
is called a distributionally scrambled set (DS-set for brevity) for a dynamical system
$S\subset [0,1]$
is called a distributionally scrambled set (DS-set for brevity) for a dynamical system
![]() $(f)$
if
$(f)$
if
![]() $\operatorname {\mathrm {\#}} (S)>1$
and each pair of distinct points
$\operatorname {\mathrm {\#}} (S)>1$
and each pair of distinct points
![]() $x,y\in S$
forms a DC-pair. A dynamical system
$x,y\in S$
forms a DC-pair. A dynamical system
![]() $(f)$
is distributionally chaotic if there exists an uncountable DS-set for this system.
$(f)$
is distributionally chaotic if there exists an uncountable DS-set for this system.
The concept of the S-DC1 point is a slight modification of the DC1 point introduced in [Reference Loranty and Pawlak7]. We say that
![]() $x_{0}$
is an S-DC1 point (point focusing distributional chaos) for a dynamical system
$x_{0}$
is an S-DC1 point (point focusing distributional chaos) for a dynamical system
![]() $(f)$
(briefly,
$(f)$
(briefly,
![]() $x_{0}$
is an S-DC1 point for f) if for any
$x_{0}$
is an S-DC1 point for f) if for any
![]() ${\varepsilon }>0$
, there exist an uncountable DS-set S for the dynamical system
${\varepsilon }>0$
, there exist an uncountable DS-set S for the dynamical system
![]() $(f)$
and a strictly increasing sequence
$(f)$
and a strictly increasing sequence
![]() $\{n_{k}\}_{k\in \mathbb {N}}\subset \mathbb {N}$
such that
$\{n_{k}\}_{k\in \mathbb {N}}\subset \mathbb {N}$
such that
![]() $f^{ n_{k}}(S) \subset (x_{0}-{\varepsilon },x_{0}+{\varepsilon })$
.
$f^{ n_{k}}(S) \subset (x_{0}-{\varepsilon },x_{0}+{\varepsilon })$
.
In our considerations a special role is played by the ‘local approximation of functions’, which we obtain by means of equivalence classes considered in [Reference Korczak-Kubiak, Loranty and Pawlak6, Reference Poprawa11]. Let
![]() $f,g$
be some functions,
$f,g$
be some functions,
![]() $x_{0}\in [0,1]$
and
$x_{0}\in [0,1]$
and
![]() ${\varepsilon }>0$
. Then one can consider the equivalence relation
${\varepsilon }>0$
. Then one can consider the equivalence relation
![]() , where
, where
![]() . By the symbol
. By the symbol
![]() $[f]_{x_{0}}^{{\varepsilon }}$
, we denote the equivalence class of f under relation
$[f]_{x_{0}}^{{\varepsilon }}$
, we denote the equivalence class of f under relation
![]() ${{\varepsilon }}/{x_{0}}$
.
${{\varepsilon }}/{x_{0}}$
.
Many papers treat disruptions of dynamical systems (for example, [Reference Loranty and Pawlak7, Reference Pawlak10, Reference Poprawa11]). We will adapt this term to the situation which we consider.
Let f be a function,
![]() $\mathcal {F}$
a family of functions and let
$\mathcal {F}$
a family of functions and let
![]() ${\varepsilon }>0$
,
${\varepsilon }>0$
,
![]() $x_{0}\in [0,1]$
. We define the family
$x_{0}\in [0,1]$
. We define the family
![]() $D_{{\varepsilon }}(f,\mathcal {F},x_{0})=\{g\circ f\in [f]_{x_{0}}^{{\varepsilon }}:g\in \mathcal {F}\}$
. Each function belonging to
$D_{{\varepsilon }}(f,\mathcal {F},x_{0})=\{g\circ f\in [f]_{x_{0}}^{{\varepsilon }}:g\in \mathcal {F}\}$
. Each function belonging to
![]() $D_{{\varepsilon }}(f,\mathcal {F},x_{0})$
is called an
$D_{{\varepsilon }}(f,\mathcal {F},x_{0})$
is called an
![]() ${\varepsilon }$
-disruption of f at
${\varepsilon }$
-disruption of f at
![]() $x_{0}$
.
$x_{0}$
.
By C, we mean the family of all continuous functions
![]() $f:[0,1]\rightarrow [0,1]$
and we put
$f:[0,1]\rightarrow [0,1]$
and we put
![]() $\textrm {FIX} (C,x_{0})=\{f\in C:x_{0}\in \textrm {Fix}(f)\}$
.
$\textrm {FIX} (C,x_{0})=\{f\in C:x_{0}\in \textrm {Fix}(f)\}$
.
Let us observe that if we consider any function
![]() $f\in \textrm {FIX}(C,x_{0})$
, then for all
$f\in \textrm {FIX}(C,x_{0})$
, then for all
![]() ${\varepsilon }>0$
, it is easy to find a function
${\varepsilon }>0$
, it is easy to find a function
![]() $g\in D_{{\varepsilon }}(f,\textrm {FIX}(C,x_{0}),x_{0})$
such that
$g\in D_{{\varepsilon }}(f,\textrm {FIX}(C,x_{0}),x_{0})$
such that
![]() $x_{0}$
is not an S-DC1 point of g. Therefore, our attention will be focused on a situation when
$x_{0}$
is not an S-DC1 point of g. Therefore, our attention will be focused on a situation when
![]() $x_{0}\in \textrm {S-DC1}$
cannot be removed by disruptions. It is why we adopt the following definition.
$x_{0}\in \textrm {S-DC1}$
cannot be removed by disruptions. It is why we adopt the following definition.
Let
![]() $P(x_{0})$
be some property of functions at
$P(x_{0})$
be some property of functions at
![]() $x_{0}\in [0,1]$
. We will say that a family of functions
$x_{0}\in [0,1]$
. We will say that a family of functions
![]() $\mathcal {K}$
is resistant to disruptions by a family of functions
$\mathcal {K}$
is resistant to disruptions by a family of functions
![]() $\mathcal {F}$
with respect to the property
$\mathcal {F}$
with respect to the property
![]() $P(x_{0})$
if each function
$P(x_{0})$
if each function
![]() $f\in \mathcal {K}$
has the property
$f\in \mathcal {K}$
has the property
![]() $P(x_{0})$
and there exists
$P(x_{0})$
and there exists
![]() $\mu>0$
such that for any function
$\mu>0$
such that for any function
![]() $g\in \mathcal {K}$
, each function
$g\in \mathcal {K}$
, each function
![]() $\xi \in D_{\mu }(g,\mathcal {F},x_{0})$
has the property
$\xi \in D_{\mu }(g,\mathcal {F},x_{0})$
has the property
![]() $P(x_{0})$
. If
$P(x_{0})$
. If
![]() $\mathcal {K}=\{f\}$
, we will say that the function f is resistant to disruptions by a family
$\mathcal {K}=\{f\}$
, we will say that the function f is resistant to disruptions by a family
![]() $\mathcal {F}$
with respect to the property
$\mathcal {F}$
with respect to the property
![]() $P(x_{0})$
. Otherwise, we will say that f is not resistant to disruptions by
$P(x_{0})$
. Otherwise, we will say that f is not resistant to disruptions by
![]() $\mathcal {F}$
with respect to
$\mathcal {F}$
with respect to
![]() $P(x_{0})$
.
$P(x_{0})$
.
2 Various kinds of points and resistance to disruptions
In the theory of dynamical systems, a special role is played by attraction (for example, the well-known Lorenz attractor), including attracting points [Reference Devaney4]. Usually, this relates to fixed points, even for noncontinuous functions [Reference Pawlak and Pawlak8]. In our considerations, we examine points with the opposite property, although they will also be associated with fixed points.
We say that
![]() $x_{0}\in [0,1]$
is a nonattracting point of a function f if for any
$x_{0}\in [0,1]$
is a nonattracting point of a function f if for any
![]() $\alpha>0$
, there exists
$\alpha>0$
, there exists
![]() $\sigma \in (0,\alpha )$
such that
$\sigma \in (0,\alpha )$
such that
Proposition 2.1. If
![]() $x_{0}\in [0,1]$
is a nonattracting point of f, then
$x_{0}\in [0,1]$
is a nonattracting point of f, then
![]() $x_{0}\in \mathrm {Fix}(f)$
.
$x_{0}\in \mathrm {Fix}(f)$
.
Proof. Assume that f and
![]() $x_{0}$
satisfy the assumptions of the proposition. Fix
$x_{0}$
satisfy the assumptions of the proposition. Fix
![]() ${\varepsilon }>0$
and let
${\varepsilon }>0$
and let
![]() $\{\delta _{n}\}_{n\in \mathbb {N}}\subset (0,{\varepsilon })$
be a strictly decreasing sequence converging to
$\{\delta _{n}\}_{n\in \mathbb {N}}\subset (0,{\varepsilon })$
be a strictly decreasing sequence converging to
![]() $0$
such that
$0$
such that
![]() $f([x_{0}-\delta _{n},x_{0}+\delta _{n}])= [x_{0}-\delta _{n},x_{0}+\delta _{n}] \;\mathrm { for }\; n\in \mathbb {N}$
. Obviously, for any
$f([x_{0}-\delta _{n},x_{0}+\delta _{n}])= [x_{0}-\delta _{n},x_{0}+\delta _{n}] \;\mathrm { for }\; n\in \mathbb {N}$
. Obviously, for any
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
![]() $f(x_{0})\in f([x_{0}-\delta _{n},x_{0}+\delta _{n}])$
. Hence,
$f(x_{0})\in f([x_{0}-\delta _{n},x_{0}+\delta _{n}])$
. Hence,
![]() $f(x_{0})\in \bigcap _{n=1}^{\infty }f([x_{0}-\delta _{n},x_{0}+\delta _{n}])=\bigcap _{n=1}^{\infty }[x_{0}-\delta _{n},x_{0}+\delta _{n}]=\{x_{0}\}$
.
$f(x_{0})\in \bigcap _{n=1}^{\infty }f([x_{0}-\delta _{n},x_{0}+\delta _{n}])=\bigcap _{n=1}^{\infty }[x_{0}-\delta _{n},x_{0}+\delta _{n}]=\{x_{0}\}$
.
The following proposition explains the name ‘nonattracting point’.
Proposition 2.2. If
![]() $x_{0}\in [0,1]$
is a nonattracting point of f, then for any
$x_{0}\in [0,1]$
is a nonattracting point of f, then for any
![]() $x\neq x_{0}$
, there exists
$x\neq x_{0}$
, there exists
![]() $\delta _{x}>0$
such that
$\delta _{x}>0$
such that
![]() $O_{f}(x)\cap [x_{0}-\delta _{x},x_{0}+\delta _{x}]=\emptyset $
.
$O_{f}(x)\cap [x_{0}-\delta _{x},x_{0}+\delta _{x}]=\emptyset $
.
Proof. Let us adopt the notation used in the proposition. Without loss of generality, we can assume that
![]() $x_{0}\in (0,1)$
. Let
$x_{0}\in (0,1)$
. Let
![]() $x\in [0,1]\backslash \{x_{0}\}$
and let
$x\in [0,1]\backslash \{x_{0}\}$
and let
![]() $\alpha =|x-x_{0}|$
. It follows that there exists
$\alpha =|x-x_{0}|$
. It follows that there exists
![]() $\delta _{x}\in (0,\alpha )$
such that
$\delta _{x}\in (0,\alpha )$
such that
![]() $f([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]=f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])$
.
$f([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]=f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])$
.
Now we will proceed by induction to show that
![]() $f^{n}(x)\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
for
$f^{n}(x)\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
for
![]() $n=0,1,2,\ldots .$
Put
$n=0,1,2,\ldots .$
Put
![]() $n=0$
. Since
$n=0$
. Since
![]() $\delta _{x}\in (0,\alpha )$
, it it easy to see that
$\delta _{x}\in (0,\alpha )$
, it it easy to see that
![]() $f^{0}(x)=x\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
.
$f^{0}(x)=x\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
.
Now put
![]() $n=1$
. Suppose, contrary to our claim, that
$n=1$
. Suppose, contrary to our claim, that
![]() $f(x)\in [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. This clearly forces
$f(x)\in [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. This clearly forces
![]() $x\in f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. However,
$x\in f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. However,
![]() $x\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
, which is a contradiction.
$x\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
, which is a contradiction.
Finally, let us assume that
![]() $f^{i}(x)\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
for some
$f^{i}(x)\notin [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
for some
![]() $i\in \mathbb {N}$
and suppose that
$i\in \mathbb {N}$
and suppose that
![]() $f^{i+1}(x)\in [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. Then,
$f^{i+1}(x)\in [x_{0}-\delta _{x},x_{0}+\delta _{x}]$
. Then,
![]() $f^{i}(x)\in f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]$
, which leads us to a contradiction.
$f^{i}(x)\in f^{-1}([x_{0}-\delta _{x},x_{0}+\delta _{x}])=[x_{0}-\delta _{x},x_{0}+\delta _{x}]$
, which leads us to a contradiction.
Let us now note a useful lemma.
Lemma 2.3. Let f be a function. If there is
![]() $x_{0}\in [0,1]$
such that
$x_{0}\in [0,1]$
such that
![]() $f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
and
$f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
and
![]() $x_{0}-\delta \in (0,1)$
for some
$x_{0}-\delta \in (0,1)$
for some
![]() $\delta>0$
(respectively
$\delta>0$
(respectively
![]() $x_{0}+\delta \in (0,1)$
) is a continuity point of f, then
$x_{0}+\delta \in (0,1)$
) is a continuity point of f, then
![]() $f(x_{0}-\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
(respectively
$f(x_{0}-\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
(respectively
![]() $f(x_{0}+\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
).
$f(x_{0}+\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
).
Proof. Consider
![]() $f, \delta , x_{0}$
and
$f, \delta , x_{0}$
and
![]() $x_{0}-\delta $
satisfying the assumptions of the lemma. There is no loss of generality in assuming that
$x_{0}-\delta $
satisfying the assumptions of the lemma. There is no loss of generality in assuming that
![]() $x_{0}\in (0,1)$
. Thus,
$x_{0}\in (0,1)$
. Thus,
![]() $f(x_{0}-\delta )\in [x_{0}-\delta ,x_{0}+\delta ]$
. Suppose, contrary to our claim, that
$f(x_{0}-\delta )\in [x_{0}-\delta ,x_{0}+\delta ]$
. Suppose, contrary to our claim, that
![]() $f(x_{0}-\delta )\in (x_{0}-\delta ,x_{0}+\delta )$
.
$f(x_{0}-\delta )\in (x_{0}-\delta ,x_{0}+\delta )$
.
Fix
![]() ${\varepsilon }>0$
such that
${\varepsilon }>0$
such that
![]() $f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon }\in (x_{0}-\delta ,x_{0}+\delta )$
. Since f is continuous at
$f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon }\in (x_{0}-\delta ,x_{0}+\delta )$
. Since f is continuous at
![]() $x_{0}-\delta $
, it follows that there is
$x_{0}-\delta $
, it follows that there is
![]() $r\in (0,{\varepsilon })$
such that
$r\in (0,{\varepsilon })$
such that
![]() $f((x_{0}-\delta -r,x_{0}-\delta ))\subset (f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon })$
.
$f((x_{0}-\delta -r,x_{0}-\delta ))\subset (f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon })$
.
Now, choose
![]() $y\in (x_{0}-\delta -r,x_{0}-\delta )$
so that
$y\in (x_{0}-\delta -r,x_{0}-\delta )$
so that
![]() $f(y)\in (f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon })\subset [x_{0}-\delta ,x_{0}+\delta ]$
. According to our assumption
$f(y)\in (f(x_{0}-\delta )-{\varepsilon },f(x_{0}-\delta )+{\varepsilon })\subset [x_{0}-\delta ,x_{0}+\delta ]$
. According to our assumption
![]() $f^{-1}([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]$
and
$f^{-1}([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]$
and
![]() $f(y)\in [x_{0}-\delta ,x_{0}+\delta ]$
, we have
$f(y)\in [x_{0}-\delta ,x_{0}+\delta ]$
, we have
![]() $f^{-1}(f(y))\subset [x_{0}-\delta ,x_{0}+\delta ]$
. In particular,
$f^{-1}(f(y))\subset [x_{0}-\delta ,x_{0}+\delta ]$
. In particular,
![]() $y\in f^{-1}(f(y))$
, so that
$y\in f^{-1}(f(y))$
, so that
![]() $y\in [x_{0}-\delta ,x_{0}+\delta ]$
, which contradicts the fact that
$y\in [x_{0}-\delta ,x_{0}+\delta ]$
, which contradicts the fact that
![]() $y\in (x_{0}-\delta -r,x_{0}-\delta )$
.
$y\in (x_{0}-\delta -r,x_{0}-\delta )$
.
The proof of
![]() $f(x_{0}+\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
runs in a similar way.
$f(x_{0}+\delta )\in \{x_{0}-\delta ,x_{0}+\delta \}$
runs in a similar way.
The following statement shows the purposefulness of the considerations in Theorem 2.8.
Proposition 2.4. Let f be a continuous function such that
![]() $x_{0}\in (0,1)$
is a nonattracting point of f. Then f is not resistant to disruptions by
$x_{0}\in (0,1)$
is a nonattracting point of f. Then f is not resistant to disruptions by
![]() $\mathrm {FIX}(C,x_{0})$
with respect to the property ‘
$\mathrm {FIX}(C,x_{0})$
with respect to the property ‘
![]() $x_{0}$
is an S-DC1 point’.
$x_{0}$
is an S-DC1 point’.
Proof. Let us adopt the notation used in the proposition. Fix
![]() $\mu>0$
. Since
$\mu>0$
. Since
![]() $x_{0}$
is a nonattracting point of f, it follows that there is
$x_{0}$
is a nonattracting point of f, it follows that there is
![]() $\gamma \in (0,\mu )$
such that
$\gamma \in (0,\mu )$
such that
![]() $f([x_{0}-\gamma ,x_{0}+\gamma ])=[x_{0}-\gamma ,x_{0}+\gamma ]=f^{-1}([x_{0}-\gamma ,x_{0}+\gamma ])$
. Again, let us fix
$f([x_{0}-\gamma ,x_{0}+\gamma ])=[x_{0}-\gamma ,x_{0}+\gamma ]=f^{-1}([x_{0}-\gamma ,x_{0}+\gamma ])$
. Again, let us fix
![]() $\delta \in (0,\gamma )$
such that
$\delta \in (0,\gamma )$
such that
![]() $f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
. Now, consider the function g given by the formula
$f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
. Now, consider the function g given by the formula
 $$ \begin{align*} g(x)= \begin{cases} x & \mathrm{for}\ x\in [0,x_{0}-\gamma]\cup [x_{0}+\gamma,1],\\ x_{0}& \mathrm{for}\ x\in [x_{0}-\delta,x_{0}+\delta],\\ \mathrm{linear}& \mathrm{on\; the\; intervals}\ [x_{0}-\gamma,x_{0}-\delta],[x_{0}+\delta,x_{0}+\gamma]. \end{cases} \end{align*} $$
$$ \begin{align*} g(x)= \begin{cases} x & \mathrm{for}\ x\in [0,x_{0}-\gamma]\cup [x_{0}+\gamma,1],\\ x_{0}& \mathrm{for}\ x\in [x_{0}-\delta,x_{0}+\delta],\\ \mathrm{linear}& \mathrm{on\; the\; intervals}\ [x_{0}-\gamma,x_{0}-\delta],[x_{0}+\delta,x_{0}+\gamma]. \end{cases} \end{align*} $$
It is easy to see that g is continuous and
![]() $g\circ f\in [f]_{x_{0}}^{\mu }$
. Furthermore,
$g\circ f\in [f]_{x_{0}}^{\mu }$
. Furthermore,
![]() $x_{0}$
is not an S-DC1 point for
$x_{0}$
is not an S-DC1 point for
![]() $g\circ f$
, since this function is constant on
$g\circ f$
, since this function is constant on
![]() $[x_{0}-\delta ,x_{0}+\delta ]$
.
$[x_{0}-\delta ,x_{0}+\delta ]$
.
For later reference, we note a known fact.
Lemma 2.5 [Reference Ruette12]
If
![]() $f:I\rightarrow I$
is a continuous function, where I is a nondegenerate compact interval, then
$f:I\rightarrow I$
is a continuous function, where I is a nondegenerate compact interval, then
![]() $(f)$
is distributionally chaotic if and only if there exists an integer
$(f)$
is distributionally chaotic if and only if there exists an integer
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $f^{n}$
has a 2-horseshoe.
$f^{n}$
has a 2-horseshoe.
Note that the term ‘S-DC1 point’ has been introduced for self maps. In the next theorem, we do not have that situation, so we refer to the relevant properties without using this notion.
Theorem 2.6. Let
![]() $p'\leq p<q\leq q'$
and let
$p'\leq p<q\leq q'$
and let
![]() $f:[p,q]\rightarrow [p',q']$
be a continuous function, for which there exist points
$f:[p,q]\rightarrow [p',q']$
be a continuous function, for which there exist points
![]() $p<a<b<c<d<q$
such that
$p<a<b<c<d<q$
such that
![]() $f(a)=a=f(d)$
and
$f(a)=a=f(d)$
and
![]() $f(b)=d=f(c)$
. Then there exists an uncountable set S such that
$f(b)=d=f(c)$
. Then there exists an uncountable set S such that
and if
![]() $s,z\in S$
are distinct points, then
$s,z\in S$
are distinct points, then
![]() $\Phi _{s,z}^{*(f)}(t)=1$
for all
$\Phi _{s,z}^{*(f)}(t)=1$
for all
![]() $t>0$
, and there is some
$t>0$
, and there is some
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
![]() $\Phi _{s,z}^{(f)}(t_{0})=0$
.
$\Phi _{s,z}^{(f)}(t_{0})=0$
.
Proof. Let us adopt the notation in the lemma. Set
![]() $a_{1}\kern1.5pt{=}\kern1.5pt \sup \{x\kern1.5pt{\in}\kern1.5pt [a,b]:f(x)\kern1.5pt{=}\kern1.5pt a\}$
,
$a_{1}\kern1.5pt{=}\kern1.5pt \sup \{x\kern1.5pt{\in}\kern1.5pt [a,b]:f(x)\kern1.5pt{=}\kern1.5pt a\}$
,
![]() $b_{1}\kern1.5pt{=}\kern1.5pt \inf \{x\in [a,b]:f(x)\kern1.5pt{=}\kern1.5pt d,x>a_{1}\}$
,
$b_{1}\kern1.5pt{=}\kern1.5pt \inf \{x\in [a,b]:f(x)\kern1.5pt{=}\kern1.5pt d,x>a_{1}\}$
,
![]() $c_{1}\kern1.5pt{=}\kern1.5pt \sup \{x\kern1.5pt{\in}\kern1.5pt [c,d]:f(x)\kern1.5pt{=}\kern1.5pt d\}$
,
$c_{1}\kern1.5pt{=}\kern1.5pt \sup \{x\kern1.5pt{\in}\kern1.5pt [c,d]:f(x)\kern1.5pt{=}\kern1.5pt d\}$
,
![]() $d_{1}\kern1.5pt{=}\kern1.5pt \inf \{x\kern1.5pt{\in}\kern1.5pt [c,d]: f(x)=a,x>c_{1}\}$
. We see at once that
$d_{1}\kern1.5pt{=}\kern1.5pt \inf \{x\kern1.5pt{\in}\kern1.5pt [c,d]: f(x)=a,x>c_{1}\}$
. We see at once that
![]() $f(a_{1})=a=f(d_{1})$
,
$f(a_{1})=a=f(d_{1})$
,
![]() $f(b_{1})=d=f(c_{1})$
and
$f(b_{1})=d=f(c_{1})$
and
![]() $p<a_{1}<b_{1}<c_{1}<d_{1}<q$
.
$p<a_{1}<b_{1}<c_{1}<d_{1}<q$
.
Now, let us consider the function
![]() $f_{0}:[p,q]\rightarrow [p,q]$
defined by
$f_{0}:[p,q]\rightarrow [p,q]$
defined by
 $$ \begin{align*} f_{0}(x)= \begin{cases} a&\mathrm{ for }\ x\in [p,a_{1}]\cup [d_{1},q], \\ f(x)&\mathrm{ for }\ x\in [a_{1},b_{1}]\cup [c_{1},d_{1}], \\ d&\mathrm{ for }\ x\in [b_{1},c_{1}]. \end{cases} \end{align*} $$
$$ \begin{align*} f_{0}(x)= \begin{cases} a&\mathrm{ for }\ x\in [p,a_{1}]\cup [d_{1},q], \\ f(x)&\mathrm{ for }\ x\in [a_{1},b_{1}]\cup [c_{1},d_{1}], \\ d&\mathrm{ for }\ x\in [b_{1},c_{1}]. \end{cases} \end{align*} $$
One can easily see that
![]() $f_{0}$
is a continuous function with the property
$f_{0}$
is a continuous function with the property
![]() $f_{0}([a_{1},b_{1}])=[a,d]=f_{0}([c_{1},d_{1}])$
.
$f_{0}([a_{1},b_{1}])=[a,d]=f_{0}([c_{1},d_{1}])$
.
We will show that there exists a DS-set S for
![]() $(f_{0})$
. Clearly,
$(f_{0})$
. Clearly,
![]() $([a_{1},b_{1}],[c_{1},d_{1}])$
forms a horseshoe for
$([a_{1},b_{1}],[c_{1},d_{1}])$
forms a horseshoe for
![]() $f_{0}$
. By Lemma 2.5, there exists an uncountable DS-set
$f_{0}$
. By Lemma 2.5, there exists an uncountable DS-set
![]() $S_{0}$
for
$S_{0}$
for
![]() $(f_{0})$
.
$(f_{0})$
.
Now, we will prove that
Suppose, contrary to our claim, that there exist two distinct points
![]() $x_{1}$
,
$x_{1}$
,
![]() $x_{2}\in S_{0}$
and
$x_{2}\in S_{0}$
and
![]() $n_{1},n_{2}\in \mathbb {N}$
such that
$n_{1},n_{2}\in \mathbb {N}$
such that
![]() $(f_{0})^{n_{i}}(x_{i})\notin [a_{1},b_{1}]\cup [c_{1},d_{1}]$
for
$(f_{0})^{n_{i}}(x_{i})\notin [a_{1},b_{1}]\cup [c_{1},d_{1}]$
for
![]() $i\in \{1,2\}$
. Therefore,
$i\in \{1,2\}$
. Therefore,
![]() $(f_{0})^{n_{i}+1}(x_{i})\in \{a,d\}$
. Let us note that if
$(f_{0})^{n_{i}+1}(x_{i})\in \{a,d\}$
. Let us note that if
![]() $(f_{0})^{n_{i}+1}(x_{i})=a$
(for some
$(f_{0})^{n_{i}+1}(x_{i})=a$
(for some
![]() $i\in \{1,2\}$
), then
$i\in \{1,2\}$
), then
![]() $(f_{0})^{m}(x_{i})=a$
for
$(f_{0})^{m}(x_{i})=a$
for
![]() $m\geq n_{i}+1$
and likewise, if
$m\geq n_{i}+1$
and likewise, if
![]() $(f_{0})^{n_{i}+1}(x_{i})=d$
, then
$(f_{0})^{n_{i}+1}(x_{i})=d$
, then
![]() $(f_{0})^{n_{i}+2}(x_{i})=a$
. Put
$(f_{0})^{n_{i}+2}(x_{i})=a$
. Put
![]() $n_{0}=\max \{n_{1}+ 2, n_{2}+2\}$
. It follows that
$n_{0}=\max \{n_{1}+ 2, n_{2}+2\}$
. It follows that
![]() $(f_{0})^{n}(x_{i})=a\;\mathrm { for }\; n\geq n_{0}\;\mathrm { and }\; i\in \{1,2\}$
. Recall that
$(f_{0})^{n}(x_{i})=a\;\mathrm { for }\; n\geq n_{0}\;\mathrm { and }\; i\in \{1,2\}$
. Recall that
![]() $x_{1},x_{2}\in S_{0}$
, and hence for some
$x_{1},x_{2}\in S_{0}$
, and hence for some
![]() $t_{0}>0$
,
$t_{0}>0$
,
However, one can infer that
which obviously leads us to a contradiction with (2.2). This proves (2.1).
Put
![]() $S=S_{0}\backslash \{x\in S_{0}: O_{f_{0}}(x)\not \subset [a_{1},b_{1}]\cup [c_{1},d_{1}]\}$
. From (2.1), we conclude that S is an uncountable set. Of course, if
$S=S_{0}\backslash \{x\in S_{0}: O_{f_{0}}(x)\not \subset [a_{1},b_{1}]\cup [c_{1},d_{1}]\}$
. From (2.1), we conclude that S is an uncountable set. Of course, if
![]() $x\in S$
, then
$x\in S$
, then
![]() $O_{f_{0}}(x)\subset [a_{1},b_{1}]\cup [c_{1},d_{1}]$
, which leads to the conclusion that
$O_{f_{0}}(x)\subset [a_{1},b_{1}]\cup [c_{1},d_{1}]$
, which leads to the conclusion that
![]() $S\subset [a_{1},b_{1}]\cup [c_{1},d_{1}]$
.
$S\subset [a_{1},b_{1}]\cup [c_{1},d_{1}]$
.
What is left is to show that S is a DS-set for
![]() $(f)$
. It is easy to prove, by induction, that
$(f)$
. It is easy to prove, by induction, that
![]() $(f_{0})^{n}(x)=f^{n}(x)$
for all
$(f_{0})^{n}(x)=f^{n}(x)$
for all
![]() $x\in S$
and all
$x\in S$
and all
![]() $n\in \mathbb {N}\cup \{0\}$
. Hence, for any
$n\in \mathbb {N}\cup \{0\}$
. Hence, for any
![]() $z_{1},z_{2}\in S$
and any
$z_{1},z_{2}\in S$
and any
![]() $t>0$
, we have
$t>0$
, we have
![]() $1=\Phi _{z_{1},z_{2}}^{*(f_{0})}(t)=\Phi _{z_{1},z_{2}}^{*(f)}(t)$
. Now, fix
$1=\Phi _{z_{1},z_{2}}^{*(f_{0})}(t)=\Phi _{z_{1},z_{2}}^{*(f)}(t)$
. Now, fix
![]() $t_{1}>0$
such that
$t_{1}>0$
such that
![]() $\Phi _{z_{1},z_{2}}^{(f_{0})}(t_{1})=0$
. Thus, by (2.2),
$\Phi _{z_{1},z_{2}}^{(f_{0})}(t_{1})=0$
. Thus, by (2.2),
![]() $0=\Phi _{z_{1},z_{2}}^{(f_{0})}(t_{1})= \Phi _{z_{1},z_{2}}^{(f)}(t_{1})$
. This finishes the proof of the theorem.
$0=\Phi _{z_{1},z_{2}}^{(f_{0})}(t_{1})= \Phi _{z_{1},z_{2}}^{(f)}(t_{1})$
. This finishes the proof of the theorem.
Building the intuition related to the concept of a nonattracting point, let us note the following statement.
Proposition 2.7. Let f be a Darboux function and
![]() $x_{0}\in (0,1)$
be a nonattracting point of f. Then, for any
$x_{0}\in (0,1)$
be a nonattracting point of f. Then, for any
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
, there are two possibilities:
$f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
, there are two possibilities:
or
Proof. Let us adopt the notation used in the proposition. Clearly, Proposition 2.1 implies that
![]() $x_{0}\in \mathrm {Fix}(f)$
. First, let us prove that
$x_{0}\in \mathrm {Fix}(f)$
. First, let us prove that
Suppose, contrary to our claim, that
![]() $x_{0}\in f([x_{0}-\delta ,x_{0}+\delta ]\backslash \{x_{0}\})$
. Assume, for example, that
$x_{0}\in f([x_{0}-\delta ,x_{0}+\delta ]\backslash \{x_{0}\})$
. Assume, for example, that
![]() $x_{0}\in f([x_{0}-\delta ,x_{0}))$
. Then there is
$x_{0}\in f([x_{0}-\delta ,x_{0}))$
. Then there is
![]() $t\in [x_{0}-\delta ,x_{0})$
such that
$t\in [x_{0}-\delta ,x_{0})$
such that
![]() $f(t)=x_{0}$
. By the definition of a nonattracting point, we conclude that there exists
$f(t)=x_{0}$
. By the definition of a nonattracting point, we conclude that there exists
![]() $\sigma \in (0,x_{0}-t)$
such that
$\sigma \in (0,x_{0}-t)$
such that
Of course,
![]() $t\in f^{-1}([x_{0}-\sigma ,x_{0}+\sigma ])$
. Moreover, we have
$t\in f^{-1}([x_{0}-\sigma ,x_{0}+\sigma ])$
. Moreover, we have
![]() $t\notin [x_{0}-\sigma ,x_{0}+\sigma ]$
(because
$t\notin [x_{0}-\sigma ,x_{0}+\sigma ]$
(because
![]() $t<x_{0}-\sigma $
), and hence
$t<x_{0}-\sigma $
), and hence
![]() $f^{-1}([x_{0}-\sigma ,x_{0}+\sigma ])\backslash [x_{0}-\sigma ,x_{0}+\sigma ]\neq \emptyset $
, contrary to (2.4). This contradiction proves that
$f^{-1}([x_{0}-\sigma ,x_{0}+\sigma ])\backslash [x_{0}-\sigma ,x_{0}+\sigma ]\neq \emptyset $
, contrary to (2.4). This contradiction proves that
![]() $x_{0}\notin f([x_{0}-\delta ,x_{0}))$
.
$x_{0}\notin f([x_{0}-\delta ,x_{0}))$
.
In the case where
![]() $x_{0}\in f((x_{0},x_{0}+\delta ])$
, the proof runs in a similar way. This finishes the proof of (2.3).
$x_{0}\in f((x_{0},x_{0}+\delta ])$
, the proof runs in a similar way. This finishes the proof of (2.3).
Now, let
![]() $\alpha \in f([x_{0}-\delta ,x_{0}))$
. Then there exists
$\alpha \in f([x_{0}-\delta ,x_{0}))$
. Then there exists
![]() $a\in [x_{0}-\delta ,x_{0}) $
such that
$a\in [x_{0}-\delta ,x_{0}) $
such that
![]() $f(a)=\alpha $
. According to (2.3), we obtain
$f(a)=\alpha $
. According to (2.3), we obtain
![]() $\alpha \neq x_{0}$
. Consequently, we have two possibilities. First, let us suppose that
$\alpha \neq x_{0}$
. Consequently, we have two possibilities. First, let us suppose that
![]() $\alpha \in [x_{0}-\delta ,x_{0})$
. We start by showing that in this case,
$\alpha \in [x_{0}-\delta ,x_{0})$
. We start by showing that in this case,
Suppose, contrary to (2.5), that there is a point
![]() $b\in [x_{0}-\delta ,x_{0})$
such that
$b\in [x_{0}-\delta ,x_{0})$
such that
![]() $f(b)>x_{0}$
. Then,
$f(b)>x_{0}$
. Then,
![]() $a,b\in [x_{0}-\delta ,x_{0})$
and
$a,b\in [x_{0}-\delta ,x_{0})$
and
![]() $f(a)=\alpha <x_{0}<f(b)$
. Since f is Darboux, it follows that there exists
$f(a)=\alpha <x_{0}<f(b)$
. Since f is Darboux, it follows that there exists
![]() $c\in [x_{0}-\delta ,x_{0})$
satisfying
$c\in [x_{0}-\delta ,x_{0})$
satisfying
![]() $f(c)=x_{0}$
, and in consequence,
$f(c)=x_{0}$
, and in consequence,
![]() $x_{0}\in f([x_{0}-\delta ,x_{0}))$
, contrary to (2.3). Thus,
$x_{0}\in f([x_{0}-\delta ,x_{0}))$
, contrary to (2.3). Thus,
![]() $f([x_{0}-\delta ,x_{0}))\subset (-\infty ,x_{0})$
. According to our assumption
$f([x_{0}-\delta ,x_{0}))\subset (-\infty ,x_{0})$
. According to our assumption
![]() $f([x_{0}-\delta ,x_{0}))\subset [x_{0}-\delta ,x_{0}+\delta ]$
, it follows that
$f([x_{0}-\delta ,x_{0}))\subset [x_{0}-\delta ,x_{0}+\delta ]$
, it follows that
![]() $f([x_{0}-\delta ,x_{0}))\subset [x_{0}-\delta ,x_{0}]$
. This combined with (2.3) proves (2.5).
$f([x_{0}-\delta ,x_{0}))\subset [x_{0}-\delta ,x_{0}]$
. This combined with (2.3) proves (2.5).
Now, we will show that in this case,
From the considerations above and the equality
![]() $f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]$
, it follows that
$f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]$
, it follows that
Now we will show the opposite inclusion. Let
![]() $e\in (x_{0},x_{0}+\delta ]$
. From (2.7), there exists
$e\in (x_{0},x_{0}+\delta ]$
. From (2.7), there exists
![]() $o\in (x_{0},x_{0}+\delta ]$
such that
$o\in (x_{0},x_{0}+\delta ]$
such that
![]() $e=f(o)$
. Suppose, contrary to our claim, that there is
$e=f(o)$
. Suppose, contrary to our claim, that there is
![]() $h\in (x_{0},x_{0}+\delta ]$
such that
$h\in (x_{0},x_{0}+\delta ]$
such that
![]() $f(h)<x_{0}$
. We have
$f(h)<x_{0}$
. We have
![]() $o,h\in (x_{0},x_{0}+\delta ]$
and
$o,h\in (x_{0},x_{0}+\delta ]$
and
![]() $f(h)<x_{0}<e=f(o)$
. Since f is Darboux, there exists
$f(h)<x_{0}<e=f(o)$
. Since f is Darboux, there exists
![]() $z\in (x_{0},x_{0}+\delta ]$
satisfying
$z\in (x_{0},x_{0}+\delta ]$
satisfying
![]() $f(z)=x_{0}$
, that is,
$f(z)=x_{0}$
, that is,
![]() $x_{0}\in f((x_{0},x_{0}+\delta ])$
, contrary to (2.3). Thus,
$x_{0}\in f((x_{0},x_{0}+\delta ])$
, contrary to (2.3). Thus,
![]() $f((x_{0},x_{0}+\delta ])\subset (x_{0},\infty )$
. Moreover,
$f((x_{0},x_{0}+\delta ])\subset (x_{0},\infty )$
. Moreover,
![]() $f((x_{0},x_{0}+\delta ])\subset [x_{0}-\delta ,x_{0}+\delta ]\cap (x_{0},\infty )=(x_{0},x_{0}+\delta ]$
. Thus from (2.7), we obtain
$f((x_{0},x_{0}+\delta ])\subset [x_{0}-\delta ,x_{0}+\delta ]\cap (x_{0},\infty )=(x_{0},x_{0}+\delta ]$
. Thus from (2.7), we obtain
![]() $f((x_{0},x_{0}+\delta ])=(x_{0},x_{0}+\delta ]$
, which proves (2.6).
$f((x_{0},x_{0}+\delta ])=(x_{0},x_{0}+\delta ]$
, which proves (2.6).
From (2.3), (2.5), (2.6) and the assumed equality
![]() ${f([x_{0}\kern1.5pt{-}\kern1.5pt\delta ,x_{0}\kern1.5pt{+}\kern1.5pt\delta ])\kern1.5pt{=}\kern1.5pt[x_{0}\kern1.5pt{-}\kern1.5pt\delta ,x_{0}\kern1.5pt{+}\kern1.5pt\delta ]}$
, we have
${f([x_{0}\kern1.5pt{-}\kern1.5pt\delta ,x_{0}\kern1.5pt{+}\kern1.5pt\delta ])\kern1.5pt{=}\kern1.5pt[x_{0}\kern1.5pt{-}\kern1.5pt\delta ,x_{0}\kern1.5pt{+}\kern1.5pt\delta ]}$
, we have
![]() $f([x_{0}-\delta ,x_{0}))=[x_{0}-\delta ,x_{0})$
.
$f([x_{0}-\delta ,x_{0}))=[x_{0}-\delta ,x_{0})$
.
For other cases, the proof runs in a similar way.
As pointed out in the Section 1, Proposition 2.4 suggests a question about the possibility of approximating the continuous functions by a family resistant to disruptions with respect to the property connected with an S-DC1 point. The answer is given in the next theorem.
Let
![]() $\mathrm {Qc}(x_{0})$
(respectively S-DC1
$\mathrm {Qc}(x_{0})$
(respectively S-DC1
![]() $(x_{0})$
) denote the property of functions such that
$(x_{0})$
) denote the property of functions such that
![]() $x_{0}$
is a quasicontinuity point of a function (respectively
$x_{0}$
is a quasicontinuity point of a function (respectively
![]() $x_{0}$
is an S-DC1 point of a function). Now we will state and prove the main result of our paper.
$x_{0}$
is an S-DC1 point of a function). Now we will state and prove the main result of our paper.
Theorem 2.8. Let f be a continuous function such that
![]() $x_{0}\in [0,1]$
is a nonattracting point of f. Then for any
$x_{0}\in [0,1]$
is a nonattracting point of f. Then for any
![]() ${\varepsilon }>0$
, there exists an uncountable family
${\varepsilon }>0$
, there exists an uncountable family
![]() $\mathcal {K}\subset D_{{\varepsilon }}(f,\mathrm {DQc},x_{0})$
, which is resistant to disruptions by the family
$\mathcal {K}\subset D_{{\varepsilon }}(f,\mathrm {DQc},x_{0})$
, which is resistant to disruptions by the family
![]() $\mathrm {FIX} (C,x_{0})$
with respect to the following properties:
$\mathrm {FIX} (C,x_{0})$
with respect to the following properties:
-
(a) the property
 $\mathrm {Qc}(x_{0})$
;
$\mathrm {Qc}(x_{0})$
; -
(b) the property S-DC1
 $(x_{0})$
.
$(x_{0})$
.
Proof. Without loss of generality, we can assume that
![]() $x_{0}\in (0,1)$
(if
$x_{0}\in (0,1)$
(if
![]() $x_{0}\in \{0,1\}$
, the proof is analogous). By Proposition 2.1, it is obvious that
$x_{0}\in \{0,1\}$
, the proof is analogous). By Proposition 2.1, it is obvious that
![]() $x_{0}\in \mathrm {Fix}(f)$
. We shall examine this proof for fixed
$x_{0}\in \mathrm {Fix}(f)$
. We shall examine this proof for fixed
![]() ${\varepsilon }>0$
. Obviously, there exists
${\varepsilon }>0$
. Obviously, there exists
![]() $\delta \in (0,{\varepsilon })$
, which is a number such that
$\delta \in (0,{\varepsilon })$
, which is a number such that
![]() $f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
.
$f([x_{0}-\delta ,x_{0}+\delta ])=[x_{0}-\delta ,x_{0}+\delta ]=f^{-1}([x_{0}-\delta ,x_{0}+\delta ])$
.
By Proposition 2.7, we can find a strictly monotone sequence
![]() $\{x_{n}\}_{n\in \mathbb {N}}\subset (x_{0}-\delta ,x_{0})$
converging to
$\{x_{n}\}_{n\in \mathbb {N}}\subset (x_{0}-\delta ,x_{0})$
converging to
![]() $x_{0}$
such that
$x_{0}$
such that
![]() $\{f(x_{n})\}_{n\in \mathbb {N}}$
is strictly monotone and
$\{f(x_{n})\}_{n\in \mathbb {N}}$
is strictly monotone and
![]() $f(x_{n})\neq x_{0}$
for all
$f(x_{n})\neq x_{0}$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
We will consider the case when
![]() $\{f(x_{n})\}_{n\in \mathbb {N}}$
is strictly decreasing. This implies that
$\{f(x_{n})\}_{n\in \mathbb {N}}$
is strictly decreasing. This implies that
![]() $\{f(x_{n})\}_{n\in \mathbb {N}}\subset (x_{0},x_{0}+\delta ]$
. Let us put
$\{f(x_{n})\}_{n\in \mathbb {N}}\subset (x_{0},x_{0}+\delta ]$
. Let us put
![]() $s_{n}=\min \{x\in [x_{n},x_{n+1}]:f(x)=f(x_{n+1})\}$
for
$s_{n}=\min \{x\in [x_{n},x_{n+1}]:f(x)=f(x_{n+1})\}$
for
![]() $n\in \mathbb {N}$
. Continuity of f implies that
$n\in \mathbb {N}$
. Continuity of f implies that
For each
![]() $\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
, let
$\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
, let
![]() $\beta _{\alpha }=x_{0}+\alpha \in (x_{0},x_{0}+\delta )$
. Let us choose
$\beta _{\alpha }=x_{0}+\alpha \in (x_{0},x_{0}+\delta )$
. Let us choose
![]() $z_{n}\in [x_{n},s_{n}]$
such that
$z_{n}\in [x_{n},s_{n}]$
such that
![]() $f(z_{n})=f(s_{n})+\tfrac 12(f(x_{n})-f(s_{n}))$
for
$f(z_{n})=f(s_{n})+\tfrac 12(f(x_{n})-f(s_{n}))$
for
![]() $n\in \mathbb {N}$
. Then, we define the functions
$n\in \mathbb {N}$
. Then, we define the functions
![]() $g_{\alpha }:[0,1]\rightarrow [0,1]$
for
$g_{\alpha }:[0,1]\rightarrow [0,1]$
for
![]() $\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
by
$\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
by
 $$ \begin{align*} g_{\alpha}(x)= \begin{cases} x & \mathrm{for} \ x\in [0,x_{0}]\cup [x_{0}+\delta,1]\mathrm{,}\\ x_{1}& \mathrm{for} \ x\in \{f(x_{n}):n\in\mathbb{N}\}\textrm{,} \\ \beta_{\alpha}& \mathrm{for} \ x\in \{f(z_{n}):n\in\mathbb{N}\}\textrm{,}\\ \mathrm{linear} & \mathrm{on\; the\; intervals} \ [f(x_{n+1}),f(z_{n})], [f(z_{n}),f(x_{n})], \,[f(x_{1}),x_{0}+\delta] \\ & \quad \mathrm{ for }\; n\in\mathbb{N}\textrm{.} \end{cases} \end{align*} $$
$$ \begin{align*} g_{\alpha}(x)= \begin{cases} x & \mathrm{for} \ x\in [0,x_{0}]\cup [x_{0}+\delta,1]\mathrm{,}\\ x_{1}& \mathrm{for} \ x\in \{f(x_{n}):n\in\mathbb{N}\}\textrm{,} \\ \beta_{\alpha}& \mathrm{for} \ x\in \{f(z_{n}):n\in\mathbb{N}\}\textrm{,}\\ \mathrm{linear} & \mathrm{on\; the\; intervals} \ [f(x_{n+1}),f(z_{n})], [f(z_{n}),f(x_{n})], \,[f(x_{1}),x_{0}+\delta] \\ & \quad \mathrm{ for }\; n\in\mathbb{N}\textrm{.} \end{cases} \end{align*} $$
Put
![]() $f_{\alpha }=g_{\alpha }\circ f$
for
$f_{\alpha }=g_{\alpha }\circ f$
for
![]() $\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
and let
$\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
and let
![]() $\mathcal {K}=\{f_{\alpha }:\alpha \in (x_{0}-x_{2},x_{0}-x_{1})\}$
. An easy computation shows that
$\mathcal {K}=\{f_{\alpha }:\alpha \in (x_{0}-x_{2},x_{0}-x_{1})\}$
. An easy computation shows that
![]() $\mathcal {K}\subset [f]_{x_{0}}^{{\varepsilon }}$
.
$\mathcal {K}\subset [f]_{x_{0}}^{{\varepsilon }}$
.
We are now in a position to show that for each
![]() $\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
, the function
$\alpha \in (x_{0}-x_{2},x_{0}-x_{1})$
, the function
![]() $f_{\alpha }$
is resistant to disruptions by the family
$f_{\alpha }$
is resistant to disruptions by the family
![]() $\mathrm {FIX} (C,x_{0})$
with respect to each of the properties (a) and (b). Fix
$\mathrm {FIX} (C,x_{0})$
with respect to each of the properties (a) and (b). Fix
![]() $\alpha _{0}\in (x_{0}-x_{2},x_{0}-x_{1})$
and put
$\alpha _{0}\in (x_{0}-x_{2},x_{0}-x_{1})$
and put
![]() $\mu ={(x_{0}-x_{3})}/{2}$
. Obviously,
$\mu ={(x_{0}-x_{3})}/{2}$
. Obviously,
![]() $f_{\alpha _{0}}\in \mathrm {DQc}$
. Fix
$f_{\alpha _{0}}\in \mathrm {DQc}$
. Fix
![]() $\xi \in D_{\mu }(f_{\alpha _{0}},\mathrm {FIX} (C,x_{0}),x_{0})$
, that is,
$\xi \in D_{\mu }(f_{\alpha _{0}},\mathrm {FIX} (C,x_{0}),x_{0})$
, that is,
![]() $\xi =\tau \circ f_{\alpha _{0}}$
, where
$\xi =\tau \circ f_{\alpha _{0}}$
, where
![]() $\tau \in \mathrm {FIX} (C,x_{0})$
. By Lemma 1.1, the function
$\tau \in \mathrm {FIX} (C,x_{0})$
. By Lemma 1.1, the function
![]() $\xi \in \mathrm {DQc}$
.
$\xi \in \mathrm {DQc}$
.
Now we will prove that
![]() $x_{0}$
is an S-DC1 point for the dynamical system
$x_{0}$
is an S-DC1 point for the dynamical system
![]() $(\xi )$
. To do so, fix
$(\xi )$
. To do so, fix
![]() $\sigma \in (0,\mu )$
. Recall that
$\sigma \in (0,\mu )$
. Recall that
![]() $\xi =\tau \circ f_{\alpha _{0}}=\tau \circ g_{\alpha _{0}}\circ f$
, where
$\xi =\tau \circ f_{\alpha _{0}}=\tau \circ g_{\alpha _{0}}\circ f$
, where
![]() $\tau \in \mathrm {FIX} (C,x_{0})$
and, moreover,
$\tau \in \mathrm {FIX} (C,x_{0})$
and, moreover,
![]() $\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
. Obviously, there exists
$\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
. Obviously, there exists
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $x_{m}\in (x_{0}-\sigma ,x_{0})$
. Note that
$x_{m}\in (x_{0}-\sigma ,x_{0})$
. Note that
![]() $f_{\alpha _{0}}(x_{m})=x_{1}=f_{\alpha _{0}}(x_{m+1})$
and
$f_{\alpha _{0}}(x_{m})=x_{1}=f_{\alpha _{0}}(x_{m+1})$
and
![]() $f_{\alpha _{0}}(z_{m})=\beta _{\alpha _{0}}$
. Moreover,
$f_{\alpha _{0}}(z_{m})=\beta _{\alpha _{0}}$
. Moreover,
The first inequality of (2.8) is obtained by showing that
![]() $\xi (x_{m})<x_{1}+\mu $
. Indeed, we show that
$\xi (x_{m})<x_{1}+\mu $
. Indeed, we show that
![]() $\xi (x_{m})=x_{1}$
. Conversely, suppose that
$\xi (x_{m})=x_{1}$
. Conversely, suppose that
![]() $\xi (x_{m})\neq x_{1}$
. Since
$\xi (x_{m})\neq x_{1}$
. Since
![]() $\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
, we conclude by our supposition that
$\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
, we conclude by our supposition that
![]() $x_{m},f_{\alpha _{0}}(x_{m})\in (x_{0}-\mu ,x_{0}+\mu )$
. However,
$x_{m},f_{\alpha _{0}}(x_{m})\in (x_{0}-\mu ,x_{0}+\mu )$
. However,
![]() $f_{\alpha _{0}}(x_{m})=x_{1}\notin (x_{0}-\mu ,x_{0}+\mu )\subset (x_{1},x_{0}+\alpha _{0})$
, which is a contradiction. Thus,
$f_{\alpha _{0}}(x_{m})=x_{1}\notin (x_{0}-\mu ,x_{0}+\mu )\subset (x_{1},x_{0}+\alpha _{0})$
, which is a contradiction. Thus,
![]() $\xi (x_{m})=f_{\alpha _{0}}(x_{m})=x_{1}<x_{1}+\mu <x_{1}+\tfrac 12\alpha _{0}<x_{0}-\tfrac 12\alpha _{0}$
.
$\xi (x_{m})=f_{\alpha _{0}}(x_{m})=x_{1}<x_{1}+\mu <x_{1}+\tfrac 12\alpha _{0}<x_{0}-\tfrac 12\alpha _{0}$
.
To prove the last inequality of (2.8), it is sufficient to observe that
![]() $\xi (z_{m})=\beta _{\alpha _{0}}$
. Indeed, suppose contrary to our claim that
$\xi (z_{m})=\beta _{\alpha _{0}}$
. Indeed, suppose contrary to our claim that
![]() $\xi (z_{m})\neq \beta _{\alpha _{0}}$
. Since
$\xi (z_{m})\neq \beta _{\alpha _{0}}$
. Since
![]() $\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
, we have
$\xi \in [f_{\alpha _{0}}]_{x_{0}}^{\mu }$
, we have
![]() $z_{m},f_{\alpha _{0}}(z_{m})\kern1.5pt{\in}\kern1.5pt (x_{0}-\mu ,x_{0}+\mu )$
. However,
$z_{m},f_{\alpha _{0}}(z_{m})\kern1.5pt{\in}\kern1.5pt (x_{0}-\mu ,x_{0}+\mu )$
. However,
![]() $f_{\alpha _{0}}(z_{m})\kern1.5pt{=}\kern1.5pt\beta _{\alpha _{0}}\kern1.5pt{\notin}\kern1.5pt (x_{0}-\mu ,x_{0}+\mu )\kern1.5pt{\subset}\kern1.5pt (x_{1},x_{0}+\alpha _{0})$
, which is a contradiction. Therefore,
$f_{\alpha _{0}}(z_{m})\kern1.5pt{=}\kern1.5pt\beta _{\alpha _{0}}\kern1.5pt{\notin}\kern1.5pt (x_{0}-\mu ,x_{0}+\mu )\kern1.5pt{\subset}\kern1.5pt (x_{1},x_{0}+\alpha _{0})$
, which is a contradiction. Therefore,
![]() $\xi (z_{m})>\beta _{\alpha _{0}}-\mu >\beta _{\alpha _{0}}-\tfrac 12\alpha _{0}=x_{0}+\tfrac 12\alpha _{0}$
. Since
$\xi (z_{m})>\beta _{\alpha _{0}}-\mu >\beta _{\alpha _{0}}-\tfrac 12\alpha _{0}=x_{0}+\tfrac 12\alpha _{0}$
. Since
![]() $\xi |_{[x_{m},s_{m}]}$
is a continuous function, (2.8) shows that there is
$\xi |_{[x_{m},s_{m}]}$
is a continuous function, (2.8) shows that there is
![]() $a\in (x_{m},z_{m})$
such that
$a\in (x_{m},z_{m})$
such that
![]() $\xi (a)=a$
. Moreover, there exists
$\xi (a)=a$
. Moreover, there exists
![]() $d\in (z_{m},s_{m})$
such that
$d\in (z_{m},s_{m})$
such that
![]() $\xi (d)=a$
. We shall also conclude from (2.8) that
$\xi (d)=a$
. We shall also conclude from (2.8) that
![]() $\xi (z_{m})>x_{0}+\tfrac 12\alpha _{0}>d$
and
$\xi (z_{m})>x_{0}+\tfrac 12\alpha _{0}>d$
and
![]() $\xi (d)=a<d$
. By continuity of
$\xi (d)=a<d$
. By continuity of
![]() $\xi |_{[x_{m},s_{m}]}$
, it follows that there exists
$\xi |_{[x_{m},s_{m}]}$
, it follows that there exists
![]() $c\in (z_{m},d)$
such that
$c\in (z_{m},d)$
such that
![]() $\xi (c)=d$
. Furthermore,
$\xi (c)=d$
. Furthermore,
![]() $\xi (a)=a<d<\xi (z_{m})$
and
$\xi (a)=a<d<\xi (z_{m})$
and
![]() $\xi |_{[x_{m},s_{m}]}$
is Darboux, and hence there is a point
$\xi |_{[x_{m},s_{m}]}$
is Darboux, and hence there is a point
![]() $b\in (a,z_{m})$
such that
$b\in (a,z_{m})$
such that
![]() $\xi (b)=d$
.
$\xi (b)=d$
.
Finally,
![]() $x_{m}< a<b<c<d< s_{m}$
. The above considerations show that
$x_{m}< a<b<c<d< s_{m}$
. The above considerations show that
![]() $\xi |_{[x_{m},s_{m}]}:[x_{m},s_{m}]\rightarrow [0,1]$
satisfies the assumptions of Theorem 2.6 (with
$\xi |_{[x_{m},s_{m}]}:[x_{m},s_{m}]\rightarrow [0,1]$
satisfies the assumptions of Theorem 2.6 (with
![]() $p'=0,p=x_{m},q=s_{m},q'=1$
). Consequently, there exists an uncountable DS-set S for
$p'=0,p=x_{m},q=s_{m},q'=1$
). Consequently, there exists an uncountable DS-set S for
![]() $(\xi )$
such that
$(\xi )$
such that
![]() $O_{\xi }(s)\subset [a,b]\cup [c,d]$
for all
$O_{\xi }(s)\subset [a,b]\cup [c,d]$
for all
![]() $s\in S$
.
$s\in S$
.
What is left is to show that there is a sequence
![]() $\{n_{k}\}_{k\in \mathbb {N}}$
such that
$\{n_{k}\}_{k\in \mathbb {N}}$
such that
![]() $S\subset \xi ^{n_{k}}(S)\subset (x_{0}-\sigma ,x_{0}+\sigma )$
. For this purpose, let us put
$S\subset \xi ^{n_{k}}(S)\subset (x_{0}-\sigma ,x_{0}+\sigma )$
. For this purpose, let us put
![]() $\{n_{k}\}_{k\in \mathbb {N}}=\{1,2,\ldots \}$
. Fix
$\{n_{k}\}_{k\in \mathbb {N}}=\{1,2,\ldots \}$
. Fix
![]() $s\in S$
. Then, by Theorem 2.6, we have
$s\in S$
. Then, by Theorem 2.6, we have
![]() $\xi ^{n_{k}}(s)\in O_{\xi }(s)\subset [a,b]\cup [c,d] \subset (x_{0}-\sigma ,x_{0}+\sigma )$
for any
$\xi ^{n_{k}}(s)\in O_{\xi }(s)\subset [a,b]\cup [c,d] \subset (x_{0}-\sigma ,x_{0}+\sigma )$
for any
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.