Clay minerals, which are predominant components of expansive clays and clayey rocks, are ubiquitous in the Earth's crust. Their mechanical attributes considerably influence the overarching properties of both clay soil and rock, marking them pivotal subjects in the realm of geotechnical and geological engineering (Zheng et al., Reference Zheng, Zaoui and Shahrour2011; Liu et al., Reference Liu, Shao, Xie, Conil and Talandier2018; Yotsuji et al., Reference Yotsuji, Tachi, Sakuma and Kawamura2021). Previous literature underscores the pronounced sensitivity of these minerals’ mechanical properties to variations in water content and inherent structural anisotropy (Zhang et al., Reference Zhang, Xie, Hu, Shao and Gatmiri2012; Liu et al., Reference Liu, Xie, Shao and Conil2015; Zheng & Zaoui, Reference Zheng and Zaoui2018). A plethora of experimental and computational methodologies have been adopted to investigate the structural (Vanorio et al., Reference Vanorio, Prasad and Nur2003; Bobko & Ulm, Reference Bobko and Ulm2008; Mondol et al., Reference Mondol, Jahren, Bjorlykke and Brevik2008; Hedan et al., Reference Hedan, Hubert, Prêt, Ferrage, Valle and Cosenza2015; Húlan et al., Reference Húlan, Trník, Štubňa, Bačík, Kaljuvee and Vozár2015) and mechanical nuances (Hueckel, Reference Hueckel2002; Chen & Evans, Reference Chen and Evans2006; Ortega et al., Reference Ortega, Ulm and Abousleiman2007) of clay minerals and associated rock forms. Existing research evidence corroborates the decline in the mechanical resilience of clay minerals as water content increases, alongside a notable display of anisotropy in their mechanical robustness and rupture mechanisms.
Molecular dynamics (MD) simulations have emerged as an instrumental technique for modelling systems with atomic granularity, facilitating the observation of deformation and failure pathways at the nano-scale (Yang et al., Reference Yang, He, Lu and Gong2019b; Wei et al., Reference Wei, Zheng, Xiong, Zhou, Al-Zaoari and Zaoui2022). These simulations have been prolifically employed to discern the elastic and structural attributes of diverse clay minerals such as montmorillonite (Manevitch & Rutledge, Reference Manevitch and Rutledge2004; Wang, Reference Wang2005; Suter et al., Reference Suter, Coveney, Greenwell and Thyveetil2007; Ebrahimi et al., Reference Ebrahimi, Pellenq and Whittle2012), illite (Hantal et al., Reference Hantal, Brochard, Laubie, Ebrahimi, Pellenq, Ulm and Coasne2014; Wang et al., Reference Wang, Li and Sun2017) and kaolinite (Benazzouz & Zaoui, Reference Benazzouz and Zaoui2012; Ma, Reference Ma2022). Specifically, Xu (Reference Xu2012) probed into the hydration dynamics of sodium montmorillonite, while investigations by Kuang and colleagues investigated the interplay of the structure and mechanics of water molecules interspersed within sodium montmorillonite's crystal layers (Kuang, Reference Kuang2013; Kuang et al., Reference Kuang, Zhou, Shang and Zhao2013). Schmidt et al. (Reference Schmidt, Katti, Ghosh and Katti2005) studied how sodium montmorillonite's mechanical responses evolve with increasing hydration. In another study, Yang et al. (Reference Yang, Han, Hu and He2019a) employed MD simulations to capture the fracturing intricacies of kaolinite microstructures. The mechanical dynamics of kaolinite, in both dehydrated and hydrated states, under varied stresses have been meticulously examined, accounting for variables such as temperature and hydration level (Han et al., Reference Han, Yang and He2019; Zhang et al., Reference Zhang, Zheng, Wei, Diao and Yin2021). Seppälä et al. (Reference Seppälä, Puhakka and Olin2016), via MD simulations, illustrated the expansion behaviours of various montmorillonites, revealing a direct correlation between self-diffusion coefficients and hydration level. In addition, Katti et al. (Reference Katti, Schmidt, Ghosh and Katti2007) highlighted the nuanced mechanical responses of both dehydrated and hydrated montmorillonite, further enriching our comprehension of clay mineral mechanics.
Materials Studio represents a prominent simulation platform. This toolkit enables the construction of three-dimensional molecular architectures and offers insights into the interactions and properties of polymers and crystalline substances (Wang, Reference Wang2019). Its diverse simulation arsenal encompasses quantum mechanical density functional theory, semi-empirical methods, molecular mechanics and dynamics and meso-scale simulations (Zhuang et al., Reference Zhuang, Yue and Zhang2010).
While existing research offers valuable insights into the mechanics and hydration processes of clay minerals at both the macro- and micro-level, a comprehensive understanding of the disparate mechanical behaviours across different clay mineral types remains elusive. Addressing this gap, the present investigation focuses on three prevalent clay minerals: illite, montmorillonite and kaolinite. Utilizing MD simulations, this work seeks to shed light on the intricacies of atomic structural evolution and the associated mechanical responses of these clay mineral microstructures under tensile strain, especially considering varying hydration levels. The overarching objective is to elucidate how the inherent microstructure of these clay minerals modulates their hydration and consequent tensile strength degradation.
Research protocol
Model
The fundamental architecture of clay minerals is delineated by silicon–oxygen tetrahedra (T) juxtaposed with aluminium–oxygen octahedra (O). Illite and montmorillonite are classified as 2:1-type clay minerals (represented as TOT), whereas kaolinite falls under the 1:1 category, represented as TO (as illustrated in Fig. 1). Within the silicon–oxygen tetrahedra, aluminium atoms occasionally substitute for silicon atoms. Similarly, in the aluminium–oxygen octahedra, lower-valence cations such as magnesium or iron may take the place of aluminium atoms, imbuing the clay structure with a negative charge. To equilibrate this charge, interstitial cations intersperse between the layers of clay minerals. For this research, molecular models of three clay minerals were configured using Materials Studio software: illite, denoted as KAl2(SiAl)4O10(OH)2 (Drits et al., Reference Drits, Zviagina, McCarty and Salyn2010); montmorillonite, described as CaSi2(SiAl)2O12 (Viani & Artioli, 2002); and kaolinite, represented by (SiAl)2O5(OH)4 (Richard & Rendtorff, 2019). Their crystalline parameters are given in Table 1. Both illite and montmorillonite are 2:1-type clay minerals. Their primary differentiation lies in the intervening metal cations: illite incorporates K+ ions that uniformly intersperse between layers, maintaining a defined spacing from the crystalline layer. Conversely, montmorillonite's interlayer region houses Ca2+ ions, with its tetrahedral and octahedral framework exhibiting a more chaotic organization than illite's. These Ca2+ ions tend to cluster towards one side of the crystal layer. Distinctly, kaolinite, as a 1:1-type clay mineral, lacks an additional silicon–oxygen tetrahedral layer and also lacks the presence of supplementary metal cations between its layers. Furthermore, the aluminium–oxygen octahedron has hydrogen bonds on one side, whereas the tetrahedron on the other side does not have hydrogen bonds.

Figure 1. (a) Illite, (b) montmorillonite and (c) kaolinite models.
Table 1. Lattice parameters of illite, montmorillonite and kaolinite.

Research methods
To determine the interplay between clay mineral microstructures and the effects of hydration and tensile strength degradation, this study examined three prominent clay minerals: illite, montmorillonite and kaolinite. Uniaxial tensile strength tests were conducted across three orthogonal axes (x, y, z) on these minerals, aiming to illuminate the interaction dynamics between mineral microstructures and water across varying clay types. This investigation also probed the impacts of hydration states on both microstructural and mechanical attributes. Initially, a model was constructed with incremental moisture content, ranging from 0% to 10% in 1% gradations. This allowed for a meticulous examination of clay mineral microstructural alterations under multiaxial tensile strains. The interactivity between clay minerals and water molecules under low-hydration conditions was examined. Subsequently, a distinct model was developed, wherein the moisture content spanned from 0% to 50% in 10% increments. This aimed to elucidate the ramifications of interlayer cations and the interfacing of clay laminates with water molecules in terms of tensile strength degradation at increased hydration levels. A comprehensive analysis of the mechanical characteristics and structural transitions of the clay minerals offered insights into the correlation between distinct clay mineral microstructures and their susceptibility to tensile strength degradation in moist environments. Collectively, this research aims to improve our understanding of hydration-induced tensile strength degradation across different clay minerals, contextualized by their inherent microstructures.
Simulation methods
MD simulations for this research were performed utilizing the LAMMPS software suite. The system modelling relied on the Clayff force field, as delineated by Cygan et al. (Reference Cygan, Liang and Kalinichev2004). Within this framework, cations in the clay strata are depicted as ionic entities without covalent bonds. The total potential energy E total can be expressed using the Clayff force field according to Equation 1:
where the E VDM is van der Waals energy and E Coul is coulomb energy, representing non-bonded energy components. The last two components in Equation 1 represent bond energy components related to bond stretching, where E bond stretch is bond stretching and E angle bend is angular bend.
The van der Waals interactions of all atoms are described by the Lennard–Jones potential, and this is expressed as in Equation 2:
 $$E_{{\rm VDW}} = \mathop \sum \limits_{i\ne j} 4{\rm \varepsilon }_{ij}\left[{{\left({\displaystyle{{{\rm \sigma }_{ij}} \over {{ r}_{ ij}}}} \right)}^{12}-{\left({\displaystyle{{{\rm \sigma }_{ij}} \over {{ r}_{ij}}}} \right)}^6} \right]$$
$$E_{{\rm VDW}} = \mathop \sum \limits_{i\ne j} 4{\rm \varepsilon }_{ij}\left[{{\left({\displaystyle{{{\rm \sigma }_{ij}} \over {{ r}_{ ij}}}} \right)}^{12}-{\left({\displaystyle{{{\rm \sigma }_{ij}} \over {{ r}_{ij}}}} \right)}^6} \right]$$where r ij is the distance between atom i and atom j. The distance parameter σij can be formulated as in Equation 3:
where σi and σj are the distance parameters between atoms i and j. The energy parameter ![]() $\rm \varepsilon _{ij}$ represents the minimum value of E VDM in the interaction curve and is expressed as in Equation 4:
$\rm \varepsilon _{ij}$ represents the minimum value of E VDM in the interaction curve and is expressed as in Equation 4:
where ![]() ${\rm \varepsilon }_i$ and
${\rm \varepsilon }_i$ and ![]() ${\rm \varepsilon }_j$ are the energy parameters of atoms i and j. The charge of all atoms is defined as the point charge within the Clayff force field. In addition, oxygen and hydrogen charges depend on their local charge and bridged charge environment. E Coul is defined as in Equation 5:
${\rm \varepsilon }_j$ are the energy parameters of atoms i and j. The charge of all atoms is defined as the point charge within the Clayff force field. In addition, oxygen and hydrogen charges depend on their local charge and bridged charge environment. E Coul is defined as in Equation 5:
where q i and q j represent the partial charges of two interacting atoms i and j, e is the electron charge and ![]() ${\rm \varepsilon }_0$ is the permittivity of the vacuum. In addition, SPC/E parameterization utilizes water molecules, which is the only bonding interaction clearly defined in the Clayff force field. Thus, the energy component associated with hydrogen bond stretching E bond stretch is described by a simple harmonic oscillation based on Hooke's law, as in Equation 6:
${\rm \varepsilon }_0$ is the permittivity of the vacuum. In addition, SPC/E parameterization utilizes water molecules, which is the only bonding interaction clearly defined in the Clayff force field. Thus, the energy component associated with hydrogen bond stretching E bond stretch is described by a simple harmonic oscillation based on Hooke's law, as in Equation 6:
where k1 is a force constant and r 0 is the length of the balance bond. The energy component E angle bend concerning the bending angle is similar to hydrogen bond stretching as can be described as in Equation 7:
where k2 is a force constant, θij represents the metal/hydrogen–oxygen–hydrogen bond angle and θ0 represents the equilibrium bond angle.
Once the computational model was configured, energy minimization was conducted at 0 K in a vacuum environment. Subsequently, a 100 ps MD simulation was executed at 300 K and 1 atm (NPT), leveraging the Clayff force field. Atomic trajectories were integrated using the Verlet leapfrog approach with a time step of 0.25 fs. The Nose–Hoover thermostat and barostat were employed to maintain temperature and pressure, respectively. Throughout this simulation phase, atomic coordinates were recorded to monitor the microstructural shifts within the system. In the final step, the interactions between the clay mineral lamellae and water molecules were modelled to determine the ramifications of the hydration state on the system's architecture, as well as stress–strain responses, tensile strength and Young's modulus.
Inherently, the mechanical attributes of clay minerals manifest anisotropy, attributed to the varied atomic configurations in the mineral lattice both along and orthogonal to the mineral layers. To probe this mechanical anisotropy, uniaxial tensile strength assays were performed in the x-, y- and z-axes under the NVT ensemble, followed by analysis of the system's stress trajectories and strength dynamics across these orientations.
Results and discussion
Effects of clay mineral microstructure on hydration phenomena
To investigate the impacts of the clay mineral microstructure on hydration phenomena, initial observations were made on the clay minerals in an anhydrous state. Subsequently, moisture content was incrementally introduced to examine its effect on microstructural shifts during tensile deformation. Specifically, a model containing a moisture content gradient of 0–10% was developed. Uniaxial tensile strength tests were performed along three orthogonal axes (x, y and z), with a particular focus on identifying the interaction dynamics between clay minerals and water molecules under low water contents. Next, we developed a model with a 10% moisture content gradient ranging from 0% to 50%. The setup was designed to carefully study the role of interlaminar cations and the interactions between clay laminates and water molecules, particularly with regard to intensity degradation under high-humidity conditions. Mechanical and structural analyses were carried out to examine these relationships.
Through a comparative analysis of clay mineral microstructures at varying moisture levels and their subsequent adaptations during tensile strength modifications, this study aims to elucidate the nuanced shifts in both microstructure and mechanical attributes of clay minerals across different hydration states.
Initial structural differences between the three clay minerals
In the preliminary, water-free models, three distinct clay minerals were delineated, as illustrated in Fig. 1. Both illite and montmorillonite fall under the 2:1 clay mineral category (TOT). Within the foundational structure of the illite model, K+ ions are uniformly dispersed across the crystal layer's surface, ensuring a consistent separation from it. This results in a systematic arrangement of silicon–oxygen tetrahedrons and aluminium–oxygen octahedrons. Conversely, in the montmorillonite model, Ca2+ ions gravitate towards one side of the silicon–oxygen tetrahedron, inducing some disparities in the tetrahedron and octahedron structures. Distinct from these, kaolinite represents the 1:1 clay mineral variant (TO) and lacks interlayer metal cations.
Mechanism of interaction between water molecules and clay minerals
To elucidate the interaction dynamics between water molecules and clay minerals, we constructed a model with a progressive moisture increment of 1%, ranging from 0% to 10%. The objective was to investigate the engagement patterns of water molecules with clay minerals under sparse water content conditions. Upon the introduction of minimal water to the mineral substrate, montmorillonite and kaolinite exhibited a pronounced expansion in layer spacing. By contrast, illite's layering exhibited negligible alterations. Within illite, a modest congregation of water molecules is discernible around the interstitial K+ ions. For montmorillonite, water molecules are anchored by the intercalated Ca2+ ions, residing proximal to the crystal layer's surface. In kaolinite's context, the extant hydrogen bonds on the layer's side facilitate a degree of water molecule adsorption, causing these molecules to aggregate on the bond-rich side. Subsequently, we probed the radial distribution functions of the three clay minerals at various hydration states: 1%, 10% and 50%. Although the representative cations differ across the minerals (illite's K+ ion, montmorillonite's Ca2+ ion and kaolinite's H+ ion), the radial distribution function for the H+ ion and O2– ion is depicted in Fig. 2, which showcases multi-modal traits, approaching unity at extended ranges. A comparative assessment amongst the three clay minerals reveals that in both illite and montmorillonite the O2– ion's curve in the radial distribution function precedes the H+ ion's curve, suggesting the O2– ions’ closer proximity to the crystalline layer and, thus, the heightened likelihood of their presence.

Figure 2. Radial distribution functions of illite, montmorillonite and kaolinite at 1%, 10% and 50% moisture content.
Structural changes at high moisture contents
Upon introducing a modest quantity of water molecules to assess the changes in the microstructural properties of the clay minerals, a model was devised with a moisture gradient spanning from 0% to 50%. Observations under increased hydration scenarios revealed that an increase in moisture content was directly proportional to the widening of clay mineral layer spacings, as illustrated in Fig. 3. Montmorillonite's architectural constituents (i.e. the silicon–oxygen tetrahedron and the aluminium–oxygen octahedron) demonstrated discernible structural transformations. As the hydration level increased, the tetrahedron's structural integrity exhibited progressive deterioration. A closer examination revealed that water molecules in the montmorillonite strata were predominantly aligned proximal to the crystal layer's Ca2+ ion side. A void that was devoid of water molecules persisted centrally, with a sparse set of molecules tethered around the Ca2+ ions. By contrast, within illite, water molecules presented a uniform distribution interstitially amongst the crystal strata, maintaining a clear separation from the embedded K+ ions, as depicted in Fig. 4. Regarding kaolinite, given the presence of hydrogen bonds solely on one side of its crystal layer, water molecules preferentially clustered on this bond-rich side, staying away from the opposite side.

Figure 3. Layer spacing of the three clay minerals.

Figure 4. Interlaminar ionic densities of illite and montmorillonite. Z = layer spacing.
Within the density profiles of water molecules interspersed amongst the three distinct clay minerals, illite displays notable stratification, as shown in Fig. 5. In the model with a 10% hydration level, illite's water molecules present a four-layered distribution pattern, becoming more accentuated as moisture content increases. Given the presence of potassium ions at both extremities of the crystal strata, there is an intervening gap hindering direct interaction between water molecules and the crystal layer, leading to a near-zero density on either side of the distribution spectrum. Conversely, water molecules in montmorillonite display a more erratic dispersal. The binding influence of calcium ions on water molecules and the inherently unstable disposition of these calcium ions culminate in a distribution lacking consistent patterning. Kaolinite's hydration profile starkly contrasts with the aforementioned minerals. Due to the presence of hydrogen bonds solely on one side, water molecules predominantly congregate on this bond-rich side. Conversely, the opposing side, devoid of such bonds, remains without water molecules.

Figure 5. Water molecular density distributions of the three clay minerals. Z = layer spacing.
Hydration deterioration effect on clay mineral tensile strength
Hydration and deterioration law of clay mineral tensile strength
Uniaxial tensile strength tests, executed in the x-, y- and z-directions, were employed on illite, montmorillonite and kaolinite. Stress–strain curves at moisture contents of 0%, 10%, 30% and 50% are depicted in Fig. 6.

Figure 6. Stress–strain curves of (a) illite, (b) montmorillonite and (c) kaolinite at various moisture contents in three directions (x, y and z).
Analysis of Fig. 7 reveals a pronounced decline in tensile strength across all three minerals when the moisture content is incrementally increased from 0% to 1%. While the tensile strengths of montmorillonite and kaolinite exhibit minimal differences, illite demonstrated a notably superior tensile strength. However, at a 10% moisture threshold, illite's tensile strength dropped precipitously, aligning it closer to the tensile strengths of montmorillonite and kaolinite. As hydration continued to increase, the tensile strengths amongst the three clay minerals became increasingly congruent. A comparative analysis between the 0% and 10% moisture contents indicated that illite's tensile strength at 10% moisture was 34% of its initial tensile strength in a dry state. By contrast, both montmorillonite and kaolinite retained ~60% of their initial tensile strengths. These data underscore the profound influence of hydration on the tensile properties of clay minerals, with illite being particularly vulnerable.

Figure 7. Stress–strain peak change curves of the three clay minerals in three directions (x, y and z).
As illustrated in Fig. 8, for all three clay minerals, the Young's modulus in the y-direction outperforms the tensile strength in the x-direction and is markedly superior to the tensile strength in the z-direction. Furthermore, there is a discernible decline in the Young's modulus for each clay mineral with increasing moisture content. This observation underscores the inference that water presence diminishes the minerals’ resilience against deformation and fracture.

Figure 8. Young's modulus values of the three clay minerals in three directions (x, y and z).
Mechanism of hydration deterioration of clay mineral tensile strength
To investigate the movement trajectories of water molecules during the tensile deformation of clay minerals, samples of illite, montmorillonite and kaolinite with 0% and 50% moisture contents were analysed. Tensile deformation was executed in both the x- and z-directions, selecting model structures from three distinct instances within the stretching process for a comparative analysis.
Initially, a pronounced interlayer spacing is evident under varying moisture content levels (as illustrated in Fig. 9), with the interlayer distance increasing in conjunction with increasing moisture content. During the x-directional deformation, the illite model exhibits fracturing. Influenced by the force exerted by K+ ions, water molecules’ trajectories become adsorbed and attached to the illite structure. Conversely, during z-directional tensile deformation, the gap between crystal layers progressively enlarges. Under the impact of K+ ion forces, water molecules manifest in a columnar configuration. Notably, by contrast to the lateral direction, the intermolecular bonds within the crystal layer remain intact.
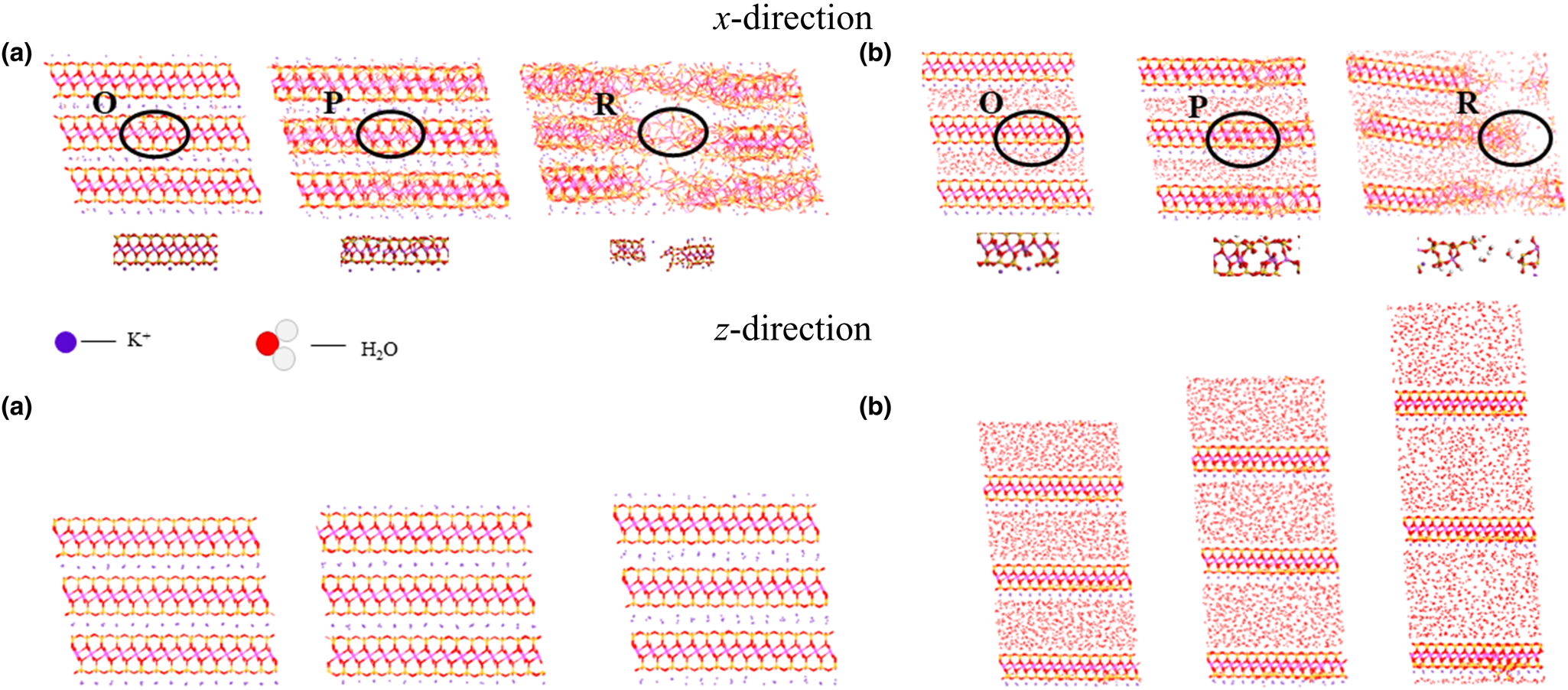
Figure 9. Illite tensile deformation at moisture contents of (a) 0% and (b) 50%. O, P and R in the image represent the three stages of the illite stress–strain curve in Fig. 6a.
Upon subjecting montmorillonite with incorporated water molecules to tensile deformation (see Fig. 10), it becomes evident that the presence of Ca2+ ions prompts the water molecules to preferentially adsorb to both sides of the montmorillonite crystal layer and in proximity to the Ca2+ ions. By juxtaposing the tensile deformation trajectories across both axes, it can be seen that water molecules exert a pronounced influence on montmorillonite, precipitating more extensive structural disruptions. As the z-directional tensile deformation ensues, disparities or discontinuities emerge in the distribution of water molecules within the montmorillonite interlayers. These molecules exhibit a tendency to accumulate adjacent to the Ca2+ ions on either side of the crystal layer, contrasting with the behaviour shown by illite, where water molecules uniformly populate the entire interlayer space.

Figure 10. Montmorillonite tensile deformation at moisture contents of (a) 0% and (b) 50%. O, P and R in the image represent the three stages of the montmorillonite stress–strain curve in Fig. 6b.
In the kaolinite model, the structural changes observed pre- and post-tensile deformation upon the introduction of water molecules are intrinsically linked to the hydrogen bonds inherent to kaolinite (as depicted in Fig. 11). These hydrogen bonds, in conjunction with the adsorptive interactions between water molecules and hydrogen–oxygen bonds, play a pivotal role in directing the movement trajectories of water molecules. Prior to any tensile deformation, water molecules adhere to the crystal surfaces enriched with hydrogen bonds. Conversely, those crystal planes devoid of such bonds exhibit no discernible clustering of water molecules. Upon undergoing tensile deformation, a similar affinity of water molecules for hydrogen bond-rich sides of the crystal layer persists. As the x-directional tensile deformation progresses, not only does the crystal plane exhibit fractures, but also its entire morphology undergoes substantial transformation. Initial planar configurations are replaced with marked curvatures post-deformation. Yet, throughout these structural transitions, water molecules predominantly remain concentrated on the hydrogen bond-rich sides of the crystal layer.

Figure 11. Kaolinite tensile deformation at moisture contents of (a) 0% and (b) 50%. O, P and R in the image represent the three stages of the kaolinite stress–strain curve in Fig. 6c.
Figures 9–11 demonstrate the tensile processes of three distinct clay minerals in both dry and hydrated states. A pronounced increase in layer spacing post-tensioning is evident in the presence of water. Furthermore, lateral tensile stresses induce a heightened predisposition towards structural fractures, culminating in a profound compromise of the minerals’ integrity and consequent diminishment in tensile strength. Notably, kaolinite exhibits a marked increase in its bending magnitude. It is clear that the presence of water modulates the microstructural behaviour of these clay minerals, leading to a deterioration of their mechanical robustness.
Conclusion
Utilizing MD simulations, we probed the mechanical attributes of illite, montmorillonite and kaolinite, specifically under varying moisture levels, elucidating concomitant microstructural evolutions. The study juxtaposed clay minerals in both hydrated and anhydrous states. Illite, characterized as a 2:1-type clay mineral, harbours potassium ions interlaced neatly between its layers, spanning both crystal surfaces. Introduction of water culminates in a quasi-uniform dispersion of these molecules, thereby engendering distinct stratified patterns. Conversely, montmorillonite, another 2:1-type clay mineral, exhibits calcium ions interspersed freely amidst its crystalline layers. These ions seemingly attract and tether the infused water molecules. Kaolinite, a 1:1-type clay mineral, lacks interlayer metallic cations. Notably, one side of kaolinite employs hydrogen bonds to attract water molecules, while the opposing side remains relatively inert in this respect.
Upon contrasting clay mineral structures under high- and low-moisture conditions, it becomes clear that increased moisture is directly proportional to increased interlayer spacing. This elevates the propensity for structural vulnerabilities. During uniaxial tensile strength evaluations across moisture gradients, vertical strains primarily increase the layer separations without perturbing the tetrahedral and octahedral structures. However, lateral strains led to discernible damage in both of these configurations. Illite, in particular, demonstrated a conspicuous crystal-layer curvature, inducing notable tensile strength fluctuations. Incremental water molecule infusion exacerbated this strength degradation. Amongst these three clay minerals, illite experienced the most pronounced tensile strength diminution, suggesting maximal structural deterioration, whereas montmorillonite's structural integrity, approximating that of kaolinite, underwent minimal degradation.
In summation, the infusion of water molecules into these clay minerals predominantly disrupts their inherent structural frameworks, culminating in diminished mechanical resilience. While this investigation demonstrated the ramifications of tensile strength testing, a comprehensive understanding of these minerals’ mechanical properties requires a broader spectrum of mechanical evaluations.
Acknowledgements
None.
Financial support
This work was supported by the National Natural Science Foundation of China (Grant No. 42002280) and the Science and Technology Foundation of Guizhou Province (No. ZK[2022]Key018).
Conflicts of interest
The authors declare none.
Data availability
Some or all data, models or code generated or used during the study are available from the corresponding author by request.














