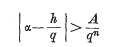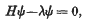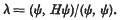In a recent paper [4], I introduced the notion of recursive formal Lie groups (of infinite dimension) over a field of characteristic p > 0, and studied a particular class of such groups, the groups of hyperexponential type; these can be characterized either as being (recursively) isomorphic to a special group of that class, the hyperexponential group, or by simple conditions on their Lie hyperalgebra. An interesting example of a group of that class is the additive Witt group W, whose “infinitesimal” structure can therefore be considered as known, at least “up to an isomorphism”. However, the intrinsic importance of the Witt group (which, as well known, is the “formalization”, so to speak, of the additive group of a p-adic field) leads one to think that it may be worth while to study in greater detail that group itself, instead of being content with the mere existence of an unspecified isomorphism with the hyperexponential group. This is what we intend to do here; it turns out that, although it seems hopeless to write down explicitly the group law of the Witt group, the multiplication table of its hyperalgebra is, on the contrary, as simple as one could hope, and is, in fact, identical to that of the hyperalgebra of the hyperexponential group (although the two groups are distinct). Moreover, this leads to a new and quite unexpected definition of the Witt group, which links it still closer to the hyperexponential group, and provides a well-determined isomorphism between the two groups.