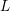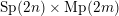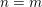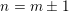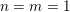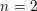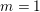1 Introduction
In this paper, we propose a conjectural identity between the Fourier–Jacobi periods on symplectic groups and the central value of certain Rankin–Selberg
![]() $L$
-functions. This identity can be viewed as a refinement to the (global) Gan–Gross–Prasad conjecture [Reference Gan, Gross and PrasadGGP12] for
$L$
-functions. This identity can be viewed as a refinement to the (global) Gan–Gross–Prasad conjecture [Reference Gan, Gross and PrasadGGP12] for
 $\operatorname{Sp}(2n)\times \operatorname{Mp}(2m)$
.
$\operatorname{Sp}(2n)\times \operatorname{Mp}(2m)$
.
The Gan–Gross–Prasad conjecture predicts that the nonvanishing of certain periods is equivalent to the nonvanishing of the central value of certain
![]() $L$
-functions. There are two types of periods: Bessel periods and Fourier–Jacobi periods. Bessel periods are periods of automorphic forms on orthogonal groups or hermitian unitary groups. A lot of work has been devoted to the study of Bessel periods, starting from the pioneering work of Waldspurger [Reference WaldspurgerWal81]. In their seminal work [Reference Ichino and IkedaII10], based on an extensive study of the known low-rank examples, Ichino and Ikeda proposed a precise formula relating the Bessel periods on
$L$
-functions. There are two types of periods: Bessel periods and Fourier–Jacobi periods. Bessel periods are periods of automorphic forms on orthogonal groups or hermitian unitary groups. A lot of work has been devoted to the study of Bessel periods, starting from the pioneering work of Waldspurger [Reference WaldspurgerWal81]. In their seminal work [Reference Ichino and IkedaII10], based on an extensive study of the known low-rank examples, Ichino and Ikeda proposed a precise formula relating the Bessel periods on
 $\operatorname{SO}(n+1)\times \operatorname{SO}(n)$
and the central value of some Rankin–Selberg
$\operatorname{SO}(n+1)\times \operatorname{SO}(n)$
and the central value of some Rankin–Selberg
![]() $L$
-functions. The analogous formula for Bessel periods on the hermitian unitary groups
$L$
-functions. The analogous formula for Bessel periods on the hermitian unitary groups
 $\operatorname{U}(n+1)\times \operatorname{U}(n)$
has been worked out by Harris in his thesis [Reference HarrisHar11]. Zhang [Reference ZhangZha14a, Reference ZhangZha14b] then proved a large part of the conjectural formula for
$\operatorname{U}(n+1)\times \operatorname{U}(n)$
has been worked out by Harris in his thesis [Reference HarrisHar11]. Zhang [Reference ZhangZha14a, Reference ZhangZha14b] then proved a large part of the conjectural formula for
 $\operatorname{U}(n+1)\times \operatorname{U}(n)$
, using the relative trace formulae proposed by Jacquet and Rallis [Reference Jacquet and RallisJR11]. This has been further improved by Beuzart-Plessis [Reference Beuzart-PlessisBeu16]. Recently, Liu [Reference LiuLiu16] proposed a conjectural formula for Bessel periods in general, i.e. the Bessel periods on
$\operatorname{U}(n+1)\times \operatorname{U}(n)$
, using the relative trace formulae proposed by Jacquet and Rallis [Reference Jacquet and RallisJR11]. This has been further improved by Beuzart-Plessis [Reference Beuzart-PlessisBeu16]. Recently, Liu [Reference LiuLiu16] proposed a conjectural formula for Bessel periods in general, i.e. the Bessel periods on
 $\operatorname{SO}(n+2r+1)\times \operatorname{SO}(n)$
or
$\operatorname{SO}(n+2r+1)\times \operatorname{SO}(n)$
or
 $\operatorname{U}(n+2r+1)\times \operatorname{U}(n)$
. Some low-rank cases have also been considered in [Reference LiuLiu16].
$\operatorname{U}(n+2r+1)\times \operatorname{U}(n)$
. Some low-rank cases have also been considered in [Reference LiuLiu16].
There is a parallel theory for the Fourier–Jacobi periods. They are the periods of automorphic forms on
 $\operatorname{Mp}(2n+2r)\times \operatorname{Sp}(2n)$
or
$\operatorname{Mp}(2n+2r)\times \operatorname{Sp}(2n)$
or
 $\operatorname{U}(n+2r)\times \operatorname{U}(n)$
. The case of Fourier–Jacobi periods on
$\operatorname{U}(n+2r)\times \operatorname{U}(n)$
. The case of Fourier–Jacobi periods on
 $\operatorname{U}(n)\times \operatorname{U}(n)$
has been considered in [Reference XueXue14, Reference XueXue16]. We proposed a conjectural formula relating the Fourier–Jacobi periods on
$\operatorname{U}(n)\times \operatorname{U}(n)$
has been considered in [Reference XueXue14, Reference XueXue16]. We proposed a conjectural formula relating the Fourier–Jacobi periods on
 $\operatorname{U}(n)\times \operatorname{U}(n)$
and the central value of some
$\operatorname{U}(n)\times \operatorname{U}(n)$
and the central value of some
![]() $L$
-functions. We proved this conjectural formula in some cases, using the relative trace formula proposed by Liu [Reference LiuLiu14]. In the other extreme case, where one of the groups is trivial, the Fourier–Jacobi periods are simply the Whittaker–Fourier coefficients. In this situation, Lapid and Mao [Reference Lapid and MaoLM15a] proposed a formula computing the norm of the Whittaker–Fourier coefficients. In a series of papers [Reference Lapid and MaoLM15c, Reference Lapid and MaoLM15b, Reference Lapid and MaoLM14], they proved the formula for Whittaker–Fourier coefficients on
$L$
-functions. We proved this conjectural formula in some cases, using the relative trace formula proposed by Liu [Reference LiuLiu14]. In the other extreme case, where one of the groups is trivial, the Fourier–Jacobi periods are simply the Whittaker–Fourier coefficients. In this situation, Lapid and Mao [Reference Lapid and MaoLM15a] proposed a formula computing the norm of the Whittaker–Fourier coefficients. In a series of papers [Reference Lapid and MaoLM15c, Reference Lapid and MaoLM15b, Reference Lapid and MaoLM14], they proved the formula for Whittaker–Fourier coefficients on
 $\operatorname{Mp}(2n)$
, under some simplifying conditions at the archimedean places.
$\operatorname{Mp}(2n)$
, under some simplifying conditions at the archimedean places.
The goal of this paper is to formulate a conjectural identity between the Fourier–Jacobi periods and the central value of some Rankin–Selberg
![]() $L$
-functions for symplectic groups. We also verify that this conjecture is compatible with the Ichino–Ikeda conjecture in some cases. As a corollary, the conjectural identity holds in some low-rank cases. We now describe our results in more detail.
$L$
-functions for symplectic groups. We also verify that this conjecture is compatible with the Ichino–Ikeda conjecture in some cases. As a corollary, the conjectural identity holds in some low-rank cases. We now describe our results in more detail.
For simplicity, in the introduction, we consider only the Fourier–Jacobi periods on
 $\operatorname{Sp}(2n+2r)\times \operatorname{Mp}(2n)$
(
$\operatorname{Sp}(2n+2r)\times \operatorname{Mp}(2n)$
(
![]() $r\geqslant 0$
). The case
$r\geqslant 0$
). The case
![]() $r<0$
will be explained in the main context of the paper. Let
$r<0$
will be explained in the main context of the paper. Let
![]() $F$
be a number field and
$F$
be a number field and
 $\unicode[STIX]{x1D713}:F\backslash \mathbb{A}_{F}\rightarrow \mathbb{C}^{\times }$
be a nontrivial additive character. Let
$\unicode[STIX]{x1D713}:F\backslash \mathbb{A}_{F}\rightarrow \mathbb{C}^{\times }$
be a nontrivial additive character. Let
 $(W_{2},q_{2})$
be the symplectic space over
$(W_{2},q_{2})$
be the symplectic space over
![]() $F$
with an orthogonal decomposition
$F$
with an orthogonal decomposition
 $W_{0}+R+R^{\ast }$
where
$W_{0}+R+R^{\ast }$
where
![]() $R$
and
$R$
and
![]() $R^{\ast }$
are isotropic subspaces and
$R^{\ast }$
are isotropic subspaces and
![]() $R+R^{\ast }$
is the direct sum of
$R+R^{\ast }$
is the direct sum of
![]() $r-1$
hyperbolic planes. We fix a complete filtration of
$r-1$
hyperbolic planes. We fix a complete filtration of
![]() $R$
and let
$R$
and let
![]() $N_{r-1}$
be the unipotent radical of the parabolic subgroup of
$N_{r-1}$
be the unipotent radical of the parabolic subgroup of
![]() $G_{2}$
fixing the complete filtration.
$G_{2}$
fixing the complete filtration.
Let
 $G_{2}=\operatorname{Sp}(W_{2})$
,
$G_{2}=\operatorname{Sp}(W_{2})$
,
 $G_{0}=\operatorname{Sp}(W_{0})$
and
$G_{0}=\operatorname{Sp}(W_{0})$
and
 $\widetilde{G_{0}}=\operatorname{Mp}(W_{0})$
(the metaplectic double cover). Let
$\widetilde{G_{0}}=\operatorname{Mp}(W_{0})$
(the metaplectic double cover). Let
![]() $\unicode[STIX]{x1D70B}_{2}$
(respectively
$\unicode[STIX]{x1D70B}_{2}$
(respectively
![]() $\unicode[STIX]{x1D70B}_{0}$
) be an irreducible cuspidal tempered (respectively genuine) automorphic representation of
$\unicode[STIX]{x1D70B}_{0}$
) be an irreducible cuspidal tempered (respectively genuine) automorphic representation of
 $G_{2}(\mathbb{A}_{F})$
(respectively
$G_{2}(\mathbb{A}_{F})$
(respectively
 $\widetilde{G_{0}}(\mathbb{A}_{F})$
). Let
$\widetilde{G_{0}}(\mathbb{A}_{F})$
). Let
 $\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
and
 $\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
. Let
$\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
. Let
 $H=W_{0}\ltimes F$
be the Heisenberg group attached to
$H=W_{0}\ltimes F$
be the Heisenberg group attached to
![]() $W_{0}$
and
$W_{0}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
 $H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
which is realized on the Schwartz space
$H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
which is realized on the Schwartz space
![]() ${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Let
${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Let
 $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
be a Schwartz function and
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
be a Schwartz function and
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(\cdot ,\unicode[STIX]{x1D719})$
be a theta series on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(\cdot ,\unicode[STIX]{x1D719})$
be a theta series on
 $H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
. Let
$H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
. Let
![]() $\unicode[STIX]{x1D713}_{r-1}$
be an automorphic generic character of
$\unicode[STIX]{x1D713}_{r-1}$
be an automorphic generic character of
 $N_{r-1}(\mathbb{A}_{F})$
which is stable under the conjugation action of
$N_{r-1}(\mathbb{A}_{F})$
which is stable under the conjugation action of
 $H(\mathbb{A}_{F})\rtimes G_{0}(\mathbb{A}_{F})$
. The Fourier–Jacobi period of
$H(\mathbb{A}_{F})\rtimes G_{0}(\mathbb{A}_{F})$
. The Fourier–Jacobi period of
 $(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})$
is the following integral
$(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})$
is the following integral
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\int _{N_{r-1}(F)\backslash N_{r-1}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}_{2}(uhg_{0})\unicode[STIX]{x1D711}_{0}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})}\,du\,dh\,dg_{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\int _{N_{r-1}(F)\backslash N_{r-1}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}_{2}(uhg_{0})\unicode[STIX]{x1D711}_{0}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})}\,du\,dh\,dg_{0}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
This integral is absolutely convergent since
![]() $\unicode[STIX]{x1D711}_{2}$
and
$\unicode[STIX]{x1D711}_{2}$
and
![]() $\unicode[STIX]{x1D711}_{0}$
are both cuspidal. It defines an element in
$\unicode[STIX]{x1D711}_{0}$
are both cuspidal. It defines an element in
 $$\begin{eqnarray}\operatorname{Hom}_{N_{r-1}(\mathbb{A}_{F})\rtimes (H(\mathbb{A}_{F})\rtimes G_{0}(\mathbb{A}_{F}))}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D713}_{r-1}},\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{N_{r-1}(\mathbb{A}_{F})\rtimes (H(\mathbb{A}_{F})\rtimes G_{0}(\mathbb{A}_{F}))}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D713}_{r-1}},\mathbb{C}).\end{eqnarray}$$
This space is at most one dimensional [Reference Liu and SunLS13, Reference SunSun12].
The Gan–Gross–Prasad conjecture predicts [Reference Gan, Gross and PrasadGGP12, Conjecture 26.1] that if the above
![]() $\operatorname{Hom}$
-space is not zero, then the integral (1.0.1) does not vanish identically if and only if
$\operatorname{Hom}$
-space is not zero, then the integral (1.0.1) does not vanish identically if and only if
 $L_{\unicode[STIX]{x1D713}}^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is nonvanishing, where
$L_{\unicode[STIX]{x1D713}}^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is nonvanishing, where
![]() $S$
is a sufficiently large finite set of places of
$S$
is a sufficiently large finite set of places of
![]() $F$
and
$F$
and
 $L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is the tensor product
$L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is the tensor product
![]() $L$
-function of
$L$
-function of
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
(note that this
$\unicode[STIX]{x1D70B}_{0}$
(note that this
![]() $L$
-function depends on
$L$
-function depends on
![]() $\unicode[STIX]{x1D713}$
).
$\unicode[STIX]{x1D713}$
).
The conjectural identity that we propose is
 $$\begin{eqnarray}|{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})|^{2}=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}^{S}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}\frac{L_{\unicode[STIX]{x1D713}}^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L^{S}(1,\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{0},\text{Ad})}\times \mathop{\prod }_{v\in S}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v}),\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})|^{2}=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}^{S}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}\frac{L_{\unicode[STIX]{x1D713}}^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L^{S}(1,\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{0},\text{Ad})}\times \mathop{\prod }_{v\in S}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v}),\end{eqnarray}$$
where:
-
–
 $\unicode[STIX]{x1D711}_{2}=\bigotimes \unicode[STIX]{x1D711}_{2,v}$
,
$\unicode[STIX]{x1D711}_{2}=\bigotimes \unicode[STIX]{x1D711}_{2,v}$
,
 $\unicode[STIX]{x1D711}_{0,v}=\bigotimes \unicode[STIX]{x1D711}_{0,v}$
,
$\unicode[STIX]{x1D711}_{0,v}=\bigotimes \unicode[STIX]{x1D711}_{0,v}$
,
 $\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}$
;
$\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}$
; -
–
 $\unicode[STIX]{x1D6E5}_{G_{2}}^{S}=\prod _{i=1}^{n+r}\unicode[STIX]{x1D701}_{F}^{S}(2i)$
;
$\unicode[STIX]{x1D6E5}_{G_{2}}^{S}=\prod _{i=1}^{n+r}\unicode[STIX]{x1D701}_{F}^{S}(2i)$
; -
–
 $L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is the tensor product
$L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
is the tensor product
 $L$
-function and
$L$
-function and
 $L^{S}(s,\unicode[STIX]{x1D70B}_{2},\text{Ad})$
,
$L^{S}(s,\unicode[STIX]{x1D70B}_{2},\text{Ad})$
,
 $L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{0},\text{Ad})$
are adjoint
$L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{0},\text{Ad})$
are adjoint
 $L$
-functions;
$L$
-functions; -
–
 $\unicode[STIX]{x1D6FC}_{v}$
is a local linear form defined by integration of matrix coefficients (see § 2.2 for the definition); it is expected that
$\unicode[STIX]{x1D6FC}_{v}$
is a local linear form defined by integration of matrix coefficients (see § 2.2 for the definition); it is expected that
 $\unicode[STIX]{x1D6FC}_{v}\not =0$
if and only if
$\unicode[STIX]{x1D6FC}_{v}\not =0$
if and only if
 $\operatorname{Hom}_{N_{r-1}(F_{v})\rtimes (H(F_{v})\rtimes G_{0}(F_{v}))}(\unicode[STIX]{x1D70B}_{2,v}\otimes \unicode[STIX]{x1D70B}_{0,v}\otimes \overline{\unicode[STIX]{x1D713}_{r-1,v}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}},\mathbb{C})\not =0$
;
$\operatorname{Hom}_{N_{r-1}(F_{v})\rtimes (H(F_{v})\rtimes G_{0}(F_{v}))}(\unicode[STIX]{x1D70B}_{2,v}\otimes \unicode[STIX]{x1D70B}_{0,v}\otimes \overline{\unicode[STIX]{x1D713}_{r-1,v}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}},\mathbb{C})\not =0$
; -
–
 $dg_{0}$
in the definition of
$dg_{0}$
in the definition of
 ${\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}$
is the Tamagawa measure on
${\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}$
is the Tamagawa measure on
 $G_{0}(\mathbb{A}_{F})$
,
$G_{0}(\mathbb{A}_{F})$
,
 $du$
and
$du$
and
 $dh$
are the self-dual measures on
$dh$
are the self-dual measures on
 $N_{r-1}(\mathbb{A}_{F})$
and
$N_{r-1}(\mathbb{A}_{F})$
and
 $H(\mathbb{A}_{F})$
respectively;
$H(\mathbb{A}_{F})$
respectively; -
–
 $S_{\unicode[STIX]{x1D70B}_{2}}$
and
$S_{\unicode[STIX]{x1D70B}_{2}}$
and
 $S_{\unicode[STIX]{x1D70B}_{0}}$
are centralizers of the
$S_{\unicode[STIX]{x1D70B}_{0}}$
are centralizers of the
 $L$
-parameters of
$L$
-parameters of
 $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
 $\unicode[STIX]{x1D70B}_{0}$
, respectively; they are abelian 2-groups (see § 2.3 for a discussion).
$\unicode[STIX]{x1D70B}_{0}$
, respectively; they are abelian 2-groups (see § 2.3 for a discussion).
This conjectural identity can be viewed as a refinement to the Gan–Gross–Prasad conjecture. It is motivated by the existing conjectural identities of this type [Reference Ichino and IkedaII10, Reference LiuLiu16, Reference HarrisHar11, Reference XueXue16]. The conjectural identity claims that we should expect the same for both of the Bessel periods and the Fourier–Jacobi periods. In the first part of this paper, we show that the conjectural identity (1.0.2) is well-defined, i.e. the local linear form
![]() $\unicode[STIX]{x1D6FC}_{v}$
is well-defined and the right-hand side of (1.0.2) is independent of the set
$\unicode[STIX]{x1D6FC}_{v}$
is well-defined and the right-hand side of (1.0.2) is independent of the set
![]() $S$
. In the definition of the local linear form
$S$
. In the definition of the local linear form
![]() $\unicode[STIX]{x1D6FC}_{v}$
, we introduce a new way to regularize a divergent oscillating integral over a unipotent group. This gives the same results as the existing regularizations [Reference Lapid and MaoLM15a, Reference LiuLiu16], but has the advantage of being elementary, purely function theoretic and uniform for both archimedean and non-archimedean places.
$\unicode[STIX]{x1D6FC}_{v}$
, we introduce a new way to regularize a divergent oscillating integral over a unipotent group. This gives the same results as the existing regularizations [Reference Lapid and MaoLM15a, Reference LiuLiu16], but has the advantage of being elementary, purely function theoretic and uniform for both archimedean and non-archimedean places.
One might be asking what happens for the Fourier–Jacobi periods on skew-hermitian unitary groups. An identity similar to (1.0.2) should also hold. We exclude that in the present paper for two reasons. First, sticking to the symplectic groups greatly simplifies the notation. More importantly, in showing that the right-hand side of (1.0.2) is independent of
![]() $S$
, we make use of some results in [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11]. The analogue results for unitary groups have not appeared in print yet. Jiang has informed the author that Shen and Zhang are working on a more general version of the results in [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11], which should cover Fourier–Jacobi periods for both symplectic groups and skew-hermitian unitary groups. Once such results are available, one can then formulate the refined Gan–Gross–Prasad conjecture in the context of skew-hermitian unitary groups.
$S$
, we make use of some results in [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11]. The analogue results for unitary groups have not appeared in print yet. Jiang has informed the author that Shen and Zhang are working on a more general version of the results in [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11], which should cover Fourier–Jacobi periods for both symplectic groups and skew-hermitian unitary groups. Once such results are available, one can then formulate the refined Gan–Gross–Prasad conjecture in the context of skew-hermitian unitary groups.
To support our conjecture, in the second part of this paper, we show, under some hypothesis on the local and global Langlands correspondences which we will state in § 5, that our conjecture is compatible with the Ichino–Ikeda conjecture in some cases. Thus (1.0.2) holds in some low-rank cases when the Ichino–Ikeda conjecture is known. We have the following cases.
(i) If
![]() $n=1$
and
$n=1$
and
![]() $r=0$
, then (1.0.2) has been proved in [Reference QiuQiu14, Theorem 4.5].
$r=0$
, then (1.0.2) has been proved in [Reference QiuQiu14, Theorem 4.5].
(ii) If
![]() $r=0$
and
$r=0$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
is a theta lift of some irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}_{2}$
is a theta lift of some irreducible cuspidal tempered automorphic representation of
![]() $\operatorname{O}(2n)$
, then (1.0.2) can be deduced from the Ichino–Ikeda conjecture for
$\operatorname{O}(2n)$
, then (1.0.2) can be deduced from the Ichino–Ikeda conjecture for
 $\operatorname{SO}(2n+1)\times \operatorname{SO}(2n)$
. In this case, if
$\operatorname{SO}(2n+1)\times \operatorname{SO}(2n)$
. In this case, if
![]() $\unicode[STIX]{x1D70B}_{0}$
is not a theta lift from any
$\unicode[STIX]{x1D70B}_{0}$
is not a theta lift from any
 $\operatorname{O}(2n+1)$
, then both sides of (1.0.2) vanish.
$\operatorname{O}(2n+1)$
, then both sides of (1.0.2) vanish.
(iii) If
![]() $r=1$
and
$r=1$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
is a theta lift of some irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}_{2}$
is a theta lift of some irreducible cuspidal tempered automorphic representation of
 $\operatorname{O}(2n+2)$
, then (1.0.2) can be deduced from the Ichino–Ikeda conjecture for
$\operatorname{O}(2n+2)$
, then (1.0.2) can be deduced from the Ichino–Ikeda conjecture for
 $\operatorname{SO}(2n+2)\times \operatorname{SO}(2n+1)$
. In this case, if
$\operatorname{SO}(2n+2)\times \operatorname{SO}(2n+1)$
. In this case, if
![]() $\unicode[STIX]{x1D70B}_{0}$
is not a theta lift from
$\unicode[STIX]{x1D70B}_{0}$
is not a theta lift from
 $\operatorname{O}(2n+1)$
, then both sides of (1.0.2) vanish. In particular, when
$\operatorname{O}(2n+1)$
, then both sides of (1.0.2) vanish. In particular, when
![]() $n=1$
, (1.0.2) holds for
$n=1$
, (1.0.2) holds for
 $\operatorname{Sp}(4)\times \operatorname{Mp}(2)$
, if the automorphic representation on
$\operatorname{Sp}(4)\times \operatorname{Mp}(2)$
, if the automorphic representation on
![]() $\operatorname{Sp}(4)$
is a theta lift from
$\operatorname{Sp}(4)$
is a theta lift from
![]() $\operatorname{O}(4)$
.
$\operatorname{O}(4)$
.
See Theorems 7.1.1 and 8.1.1 for the precise statements. See also Theorem 8.6.1 for an analogous statement in the case
![]() $r=-1$
. In the course of proving these results, we derive a variant for the Ichino–Ikeda conjecture for the full orthogonal group, cf. Conjecture 6.3.1 and Proposition 6.3.3. The author hopes that this variant is of some independent interest. See [Reference Gan and IchinoGI11] for the case of the triple product formula on
$r=-1$
. In the course of proving these results, we derive a variant for the Ichino–Ikeda conjecture for the full orthogonal group, cf. Conjecture 6.3.1 and Proposition 6.3.3. The author hopes that this variant is of some independent interest. See [Reference Gan and IchinoGI11] for the case of the triple product formula on
![]() $\operatorname{GO}(4)$
.
$\operatorname{GO}(4)$
.
Ichino informed the author that there are some minor inaccuracies in the original formulation of the Ichino–Ikeda conjecture [Reference Ichino and IkedaII10, Conjecture 2.1] when the automorphic representation on the even orthogonal group appears with multiplicity two in the discrete automorphic spectrum. In this case, one needs to specify an automorphic realization. Moreover, the size of the centralizer of the Arthur parameter needs to be modified accordingly. We will take care of this modification in § 6.
It is expected that our conjecture is compatible with the refined Gan–Gross–Prasad conjecture for
 $\operatorname{SO}(2n+2r+1)\times \operatorname{SO}(2n)$
proposed by Liu [Reference LiuLiu16]. To keep this paper within a reasonable length, we postpone to check this more general compatibility in a future paper.
$\operatorname{SO}(2n+2r+1)\times \operatorname{SO}(2n)$
proposed by Liu [Reference LiuLiu16]. To keep this paper within a reasonable length, we postpone to check this more general compatibility in a future paper.
This paper is organized as follows. The first part of the paper consists of §§ 2–4. In § 2, we first define the Fourier–Jacobi periods and the local linear form
![]() $\unicode[STIX]{x1D6FC}_{v}$
. Then we state the conjectural formula for the Fourier–Jacobi periods. In § 3, we show that the local linear form
$\unicode[STIX]{x1D6FC}_{v}$
. Then we state the conjectural formula for the Fourier–Jacobi periods. In § 3, we show that the local linear form
![]() $\unicode[STIX]{x1D6FC}_{v}$
is well-defined, i.e. its defining integral is either absolutely convergent or can be regularized. We also prove a positivity result for
$\unicode[STIX]{x1D6FC}_{v}$
is well-defined, i.e. its defining integral is either absolutely convergent or can be regularized. We also prove a positivity result for
![]() $\unicode[STIX]{x1D6FC}_{v}$
. In § 4, we compute
$\unicode[STIX]{x1D6FC}_{v}$
. In § 4, we compute
![]() $\unicode[STIX]{x1D6FC}_{v}$
when all of the data involved are unramified. The argument is mostly adapted from [Reference LiuLiu16]. The second part of this paper consists of §§ 5–8. In § 5, we state some working hypotheses on the local and global Langlands correspondences and make some remarks on the theta correspondences. For orthogonal groups and symplectic groups, these hypotheses should follow from the work of Arthur [Reference ArthurArt13]. For metaplectic groups, they should eventually follow from the on-going work of Li (e.g. [Reference LiLi15]). In § 6, we review the Ichino–Ikeda conjecture and derive a variant of it for the full orthogonal group. In § 7, we study the conjecture in the case
$\unicode[STIX]{x1D6FC}_{v}$
when all of the data involved are unramified. The argument is mostly adapted from [Reference LiuLiu16]. The second part of this paper consists of §§ 5–8. In § 5, we state some working hypotheses on the local and global Langlands correspondences and make some remarks on the theta correspondences. For orthogonal groups and symplectic groups, these hypotheses should follow from the work of Arthur [Reference ArthurArt13]. For metaplectic groups, they should eventually follow from the on-going work of Li (e.g. [Reference LiLi15]). In § 6, we review the Ichino–Ikeda conjecture and derive a variant of it for the full orthogonal group. In § 7, we study the conjecture in the case
 $\operatorname{Mp}(2n)\times \operatorname{Sp}(2n)$
via a seesaw argument. This type of argument has also been used in [Reference AtobeAto15, Reference Gan and IchinoGI16, Reference XueXue16]. In § 8, we study the conjecture in the case
$\operatorname{Mp}(2n)\times \operatorname{Sp}(2n)$
via a seesaw argument. This type of argument has also been used in [Reference AtobeAto15, Reference Gan and IchinoGI16, Reference XueXue16]. In § 8, we study the conjecture in the case
 $\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
. For the convenience of the readers, we remark that §§ 3 and 4 and the second part of the paper are logically independent. Sections 7 and 8 are also logically independent. They can be read in any order.
$\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
. For the convenience of the readers, we remark that §§ 3 and 4 and the second part of the paper are logically independent. Sections 7 and 8 are also logically independent. They can be read in any order.
Notation and convention
The following notation will be used throughout this paper. Let
![]() $F$
be a number field,
$F$
be a number field,
![]() $\mathfrak{o}_{F}$
the ring of integers and
$\mathfrak{o}_{F}$
the ring of integers and
![]() $\mathbb{A}_{F}$
the ring of adeles. For any finite place
$\mathbb{A}_{F}$
the ring of adeles. For any finite place
![]() $v$
, let
$v$
, let
![]() $\mathfrak{o}_{F,v}$
be the ring of integers of
$\mathfrak{o}_{F,v}$
be the ring of integers of
![]() $F_{v}$
and
$F_{v}$
and
![]() $\unicode[STIX]{x1D71B}_{v}$
a uniformizer. Let
$\unicode[STIX]{x1D71B}_{v}$
a uniformizer. Let
 $q_{v}=|\mathfrak{o}_{F,v}/\unicode[STIX]{x1D71B}_{v}|$
be the number of elements in the residue field of
$q_{v}=|\mathfrak{o}_{F,v}/\unicode[STIX]{x1D71B}_{v}|$
be the number of elements in the residue field of
![]() $v$
. We fix a nontrivial additive character
$v$
. We fix a nontrivial additive character
 $\unicode[STIX]{x1D713}=\bigotimes \unicode[STIX]{x1D713}_{v}:F\backslash \mathbb{A}_{F}\rightarrow \mathbb{C}^{\times }$
. We assume that
$\unicode[STIX]{x1D713}=\bigotimes \unicode[STIX]{x1D713}_{v}:F\backslash \mathbb{A}_{F}\rightarrow \mathbb{C}^{\times }$
. We assume that
![]() $\unicode[STIX]{x1D713}$
is unitary, thus
$\unicode[STIX]{x1D713}$
is unitary, thus
 $\unicode[STIX]{x1D713}^{-1}=\overline{\unicode[STIX]{x1D713}}$
. For any
$\unicode[STIX]{x1D713}^{-1}=\overline{\unicode[STIX]{x1D713}}$
. For any
![]() $a\in F^{\times }$
, we define an additive character
$a\in F^{\times }$
, we define an additive character
![]() $\unicode[STIX]{x1D713}_{a}$
of
$\unicode[STIX]{x1D713}_{a}$
of
![]() $F\backslash \mathbb{A}_{F}$
by
$F\backslash \mathbb{A}_{F}$
by
 $\unicode[STIX]{x1D713}_{a}(x)=\unicode[STIX]{x1D713}(ax)$
. For any place
$\unicode[STIX]{x1D713}_{a}(x)=\unicode[STIX]{x1D713}(ax)$
. For any place
![]() $v$
of
$v$
of
![]() $F$
, let
$F$
, let
![]() $(\cdot ,\cdot )_{F_{v}}$
be the Hilbert symbol of
$(\cdot ,\cdot )_{F_{v}}$
be the Hilbert symbol of
![]() $F_{v}$
and
$F_{v}$
and
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}$
the Weil index, which is an eighth root of unity. Note that
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}$
the Weil index, which is an eighth root of unity. Note that
 $\prod _{v}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}=1$
.
$\prod _{v}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}=1$
.
Suppose that
![]() $V$
is a vector space and
$V$
is a vector space and
 $v_{1},\ldots ,v_{r}\in V$
. Then we denote by
$v_{1},\ldots ,v_{r}\in V$
. Then we denote by
 $\langle v_{1},\ldots ,v_{r}\rangle$
the subspace of
$\langle v_{1},\ldots ,v_{r}\rangle$
the subspace of
![]() $V$
generated by
$V$
generated by
 $v_{1},\ldots ,v_{r}$
. We write
$v_{1},\ldots ,v_{r}$
. We write
![]() ${\mathcal{S}}(V)$
for the space of Schwartz functions on
${\mathcal{S}}(V)$
for the space of Schwartz functions on
![]() $V$
.
$V$
.
Let
![]() $(V,q_{V})$
be a quadratic space of dimension
$(V,q_{V})$
be a quadratic space of dimension
![]() $n$
over
$n$
over
![]() $F$
where
$F$
where
![]() $V$
is the underlying vector space and
$V$
is the underlying vector space and
![]() $q_{V}$
is the quadratic form. We can choose a basis of
$q_{V}$
is the quadratic form. We can choose a basis of
![]() $V$
so that its quadratic form is represented by a diagonal matrix with entries
$V$
so that its quadratic form is represented by a diagonal matrix with entries
 $a_{1},\ldots ,a_{n}$
. We define the discriminant
$a_{1},\ldots ,a_{n}$
. We define the discriminant
![]() $\operatorname{disc}V$
of
$\operatorname{disc}V$
of
![]() $V$
by
$V$
by
 $$\begin{eqnarray}\operatorname{disc}V=(-1)^{n(n-1)/2}a_{1}\cdots a_{n}\in F^{\times }/F^{\times ,2}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{disc}V=(-1)^{n(n-1)/2}a_{1}\cdots a_{n}\in F^{\times }/F^{\times ,2}.\end{eqnarray}$$
Define a quadratic character
 $\unicode[STIX]{x1D712}_{V}:F^{\times }\backslash \mathbb{A}_{F}^{\times }\rightarrow \{\pm 1\}$
by
$\unicode[STIX]{x1D712}_{V}:F^{\times }\backslash \mathbb{A}_{F}^{\times }\rightarrow \{\pm 1\}$
by
 $\unicode[STIX]{x1D712}_{V}(x)=(x,\operatorname{disc}V)_{F}$
.
$\unicode[STIX]{x1D712}_{V}(x)=(x,\operatorname{disc}V)_{F}$
.
Let
 $(W,q_{W})$
be a symplectic space of dimension
$(W,q_{W})$
be a symplectic space of dimension
![]() $2n$
over
$2n$
over
![]() $F$
where
$F$
where
![]() $W$
is the underlying vector space and
$W$
is the underlying vector space and
![]() $q_{W}$
is the symplectic form. Then we denote by
$q_{W}$
is the symplectic form. Then we denote by
![]() $\operatorname{Sp}(W)$
or
$\operatorname{Sp}(W)$
or
![]() $\operatorname{Sp}(2n)$
the symplectic group attached to
$\operatorname{Sp}(2n)$
the symplectic group attached to
![]() $W$
and
$W$
and
 $\operatorname{Mp}(W)$
or
$\operatorname{Mp}(W)$
or
 $\operatorname{Mp}(2n)$
the metaplectic double cover. By definition, if
$\operatorname{Mp}(2n)$
the metaplectic double cover. By definition, if
![]() $v$
is a place of
$v$
is a place of
![]() $F$
, then
$F$
, then
 $\operatorname{Mp}(W)(F_{v})=\operatorname{Sp}(W)(F_{v})\ltimes \{\pm 1\}$
and the multiplication is given by
$\operatorname{Mp}(W)(F_{v})=\operatorname{Sp}(W)(F_{v})\ltimes \{\pm 1\}$
and the multiplication is given by
 $$\begin{eqnarray}(g_{1},\unicode[STIX]{x1D716}_{1})(g_{2},\unicode[STIX]{x1D716}_{2})=(g_{1}g_{2},\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}c(g_{1},g_{2})),\end{eqnarray}$$
$$\begin{eqnarray}(g_{1},\unicode[STIX]{x1D716}_{1})(g_{2},\unicode[STIX]{x1D716}_{2})=(g_{1}g_{2},\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{2}c(g_{1},g_{2})),\end{eqnarray}$$
where
 $c(g_{1},g_{2})$
is some 2-cocycle on
$c(g_{1},g_{2})$
is some 2-cocycle on
![]() $\operatorname{Sp}(W)$
valued in
$\operatorname{Sp}(W)$
valued in
![]() $\{\pm 1\}$
(see [Reference Ranga RaoRan93]). Moreover,
$\{\pm 1\}$
(see [Reference Ranga RaoRan93]). Moreover,
 $$\begin{eqnarray}\operatorname{Mp}(W)(\mathbb{A}_{F})=\mathop{\prod }_{v}\hspace{0.0pt}^{\prime }\operatorname{Mp}(W)(F_{v})/\biggl\{(1,\unicode[STIX]{x1D716}_{v})_{v}\biggm\vert\mathop{\prod }_{v}\unicode[STIX]{x1D716}_{v}=1\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Mp}(W)(\mathbb{A}_{F})=\mathop{\prod }_{v}\hspace{0.0pt}^{\prime }\operatorname{Mp}(W)(F_{v})/\biggl\{(1,\unicode[STIX]{x1D716}_{v})_{v}\biggm\vert\mathop{\prod }_{v}\unicode[STIX]{x1D716}_{v}=1\biggr\}.\end{eqnarray}$$
If
 $g\in \operatorname{Sp}(W)(\mathbb{A}_{F})$
(respectively
$g\in \operatorname{Sp}(W)(\mathbb{A}_{F})$
(respectively
 $\operatorname{Sp}(W)(F_{v})$
), then we define
$\operatorname{Sp}(W)(F_{v})$
), then we define
 $\unicode[STIX]{x1D704}(g)=(g,1)\in \operatorname{Mp}(W)(\mathbb{A}_{F})$
(respectively
$\unicode[STIX]{x1D704}(g)=(g,1)\in \operatorname{Mp}(W)(\mathbb{A}_{F})$
(respectively
 $\operatorname{Mp}(F_{v})$
). Note that
$\operatorname{Mp}(F_{v})$
). Note that
 $g\mapsto \unicode[STIX]{x1D704}(g)$
is not a group homomorphism.
$g\mapsto \unicode[STIX]{x1D704}(g)$
is not a group homomorphism.
By a genuine function on
 $\operatorname{Mp}(W)(F_{v})$
, we mean a function on
$\operatorname{Mp}(W)(F_{v})$
, we mean a function on
 $\operatorname{Mp}(W)(F_{v})$
which is not the pullback of a function on
$\operatorname{Mp}(W)(F_{v})$
which is not the pullback of a function on
 $\operatorname{Sp}(W)(F_{v})$
. We always identify a function on
$\operatorname{Sp}(W)(F_{v})$
. We always identify a function on
 $\operatorname{Sp}(W)(F_{v})$
with a non-genuine function on
$\operatorname{Sp}(W)(F_{v})$
with a non-genuine function on
 $\operatorname{Mp}(W)(F_{v})$
. Suppose that
$\operatorname{Mp}(W)(F_{v})$
. Suppose that
 $f_{1},\ldots ,f_{r}$
are genuine functions on
$f_{1},\ldots ,f_{r}$
are genuine functions on
 $\operatorname{Mp}(W)(F_{v})$
and
$\operatorname{Mp}(W)(F_{v})$
and
 $h_{1},\ldots h_{s}$
are functions on
$h_{1},\ldots h_{s}$
are functions on
 $\operatorname{Sp}(W)(F_{v})$
such that the product
$\operatorname{Sp}(W)(F_{v})$
such that the product
 $f_{1}\cdots f_{r}$
is not genuine. Then we write
$f_{1}\cdots f_{r}$
is not genuine. Then we write
 $$\begin{eqnarray}\int _{\operatorname{Sp}(W)(F_{v})}f_{1}(g)\cdots f_{r}(g)h_{1}(g)\cdots h_{s}(g)\,dg=\int _{\operatorname{Sp}(W)(F_{v})}f_{1}(\unicode[STIX]{x1D704}(g))\cdots f_{r}(\unicode[STIX]{x1D704}(g))h_{1}(g)\cdots h_{s}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\operatorname{Sp}(W)(F_{v})}f_{1}(g)\cdots f_{r}(g)h_{1}(g)\cdots h_{s}(g)\,dg=\int _{\operatorname{Sp}(W)(F_{v})}f_{1}(\unicode[STIX]{x1D704}(g))\cdots f_{r}(\unicode[STIX]{x1D704}(g))h_{1}(g)\cdots h_{s}(g)\,dg.\end{eqnarray}$$
An irreducible representation of
 $\operatorname{Mp}(W)(F_{v})$
is said to be genuine if the element
$\operatorname{Mp}(W)(F_{v})$
is said to be genuine if the element
![]() $(1,\unicode[STIX]{x1D716})$
acts by
$(1,\unicode[STIX]{x1D716})$
acts by
![]() $\unicode[STIX]{x1D716}$
. We always identify an irreducible representation of
$\unicode[STIX]{x1D716}$
. We always identify an irreducible representation of
 $\operatorname{Sp}(W)(F_{v})$
with a non-genuine representation of
$\operatorname{Sp}(W)(F_{v})$
with a non-genuine representation of
 $\operatorname{Mp}(W)(F_{v})$
. We make similar definitions for genuine functions and representations of
$\operatorname{Mp}(W)(F_{v})$
. We make similar definitions for genuine functions and representations of
 $\operatorname{Mp}(W)(\mathbb{A}_{F})$
.
$\operatorname{Mp}(W)(\mathbb{A}_{F})$
.
Suppose
![]() $v$
is a non-archimedean place of
$v$
is a non-archimedean place of
![]() $F$
whose residue characteristic is not two. Let
$F$
whose residue characteristic is not two. Let
 $B=TU$
is a Borel subgroup of
$B=TU$
is a Borel subgroup of
![]() $\operatorname{Sp}(2n)$
and
$\operatorname{Sp}(2n)$
and
 $\widetilde{B}=\widetilde{T}U$
the inverse image of
$\widetilde{B}=\widetilde{T}U$
the inverse image of
![]() $B$
in
$B$
in
 $\operatorname{Mp}(2n)(F_{v})$
. Then
$\operatorname{Mp}(2n)(F_{v})$
. Then
 $\widetilde{T}\simeq (F_{v}^{\times })^{n}\ltimes \{\pm 1\}$
. We define a genuine character
$\widetilde{T}\simeq (F_{v}^{\times })^{n}\ltimes \{\pm 1\}$
. We define a genuine character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(t)$
of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(t)$
of
![]() $\widetilde{T}$
by
$\widetilde{T}$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}_{v}}((t_{1},\ldots ,t_{n}),\unicode[STIX]{x1D716})=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v,t_{1}\cdots t_{n}}}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}_{v}}((t_{1},\ldots ,t_{n}),\unicode[STIX]{x1D716})=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D713}_{v,t_{1}\cdots t_{n}}}^{-1}.\end{eqnarray}$$
Suppose that the conductor of
![]() $\unicode[STIX]{x1D713}_{v}$
is
$\unicode[STIX]{x1D713}_{v}$
is
![]() $\mathfrak{o}_{F,v}$
. By an unramified principal series representation of
$\mathfrak{o}_{F,v}$
. By an unramified principal series representation of
 $\operatorname{Mp}(2n)(F_{v})$
, we mean the induced representation
$\operatorname{Mp}(2n)(F_{v})$
, we mean the induced representation
 $I(\unicode[STIX]{x1D712})=\operatorname{Ind}_{\widetilde{B}}^{\operatorname{Mp}(2n)(F_{v})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D712}$
, where
$I(\unicode[STIX]{x1D712})=\operatorname{Ind}_{\widetilde{B}}^{\operatorname{Mp}(2n)(F_{v})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D712}$
, where
![]() $\unicode[STIX]{x1D712}$
be a character of
$\unicode[STIX]{x1D712}$
be a character of
 $T\simeq F_{v}^{n}$
defined by
$T\simeq F_{v}^{n}$
defined by
 $\unicode[STIX]{x1D712}(t_{1},\ldots ,t_{n})=|t_{1}|^{\unicode[STIX]{x1D6FC}_{1}}\cdots |t_{n}|^{\unicode[STIX]{x1D6FC}_{n}}$
,
$\unicode[STIX]{x1D712}(t_{1},\ldots ,t_{n})=|t_{1}|^{\unicode[STIX]{x1D6FC}_{1}}\cdots |t_{n}|^{\unicode[STIX]{x1D6FC}_{n}}$
,
 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}\in \mathbb{C}$
. This convention of parabolic inductions of the metaplectic group is the one in [Reference Gan and SavinGS12]. If
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}\in \mathbb{C}$
. This convention of parabolic inductions of the metaplectic group is the one in [Reference Gan and SavinGS12]. If
![]() $\unicode[STIX]{x1D70B}_{v}$
is an unramified representation of
$\unicode[STIX]{x1D70B}_{v}$
is an unramified representation of
 $\operatorname{Mp}(2n)(F_{v})$
, then we can find an unramified character
$\operatorname{Mp}(2n)(F_{v})$
, then we can find an unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $T$
as above and
$T$
as above and
 $\unicode[STIX]{x1D70B}_{v}\subset I(\unicode[STIX]{x1D712})$
. The complex numbers
$\unicode[STIX]{x1D70B}_{v}\subset I(\unicode[STIX]{x1D712})$
. The complex numbers
 $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
are called the Satake parameters of
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
are called the Satake parameters of
![]() $\unicode[STIX]{x1D70B}_{v}$
. Note that the Satake parameters of
$\unicode[STIX]{x1D70B}_{v}$
. Note that the Satake parameters of
![]() $\unicode[STIX]{x1D70B}_{v}$
depend also on
$\unicode[STIX]{x1D70B}_{v}$
depend also on
![]() $\unicode[STIX]{x1D713}_{v}$
.
$\unicode[STIX]{x1D713}_{v}$
.
We write
![]() $1_{r}$
for the
$1_{r}$
for the
![]() $r\times r$
identity matrix. We recursively define
$r\times r$
identity matrix. We recursively define
 $\mathsf{w}_{1}=\{1\}$
and
$\mathsf{w}_{1}=\{1\}$
and
 $\mathsf{w}_{r}=(\!\begin{smallmatrix} & \mathsf{w}_{r-1}\\ 1 & \end{smallmatrix}\!)$
. Suppose
$\mathsf{w}_{r}=(\!\begin{smallmatrix} & \mathsf{w}_{r-1}\\ 1 & \end{smallmatrix}\!)$
. Suppose
 $a=(a_{1},\ldots ,a_{r})\in (F^{\times })^{r}$
. We let
$a=(a_{1},\ldots ,a_{r})\in (F^{\times })^{r}$
. We let
 $\operatorname{diag}[a_{1},\ldots ,a_{r}]$
be the diagonal matrix with diagonal entries
$\operatorname{diag}[a_{1},\ldots ,a_{r}]$
be the diagonal matrix with diagonal entries
 $a_{1},\ldots ,a_{r}$
.
$a_{1},\ldots ,a_{r}$
.
Suppose that
![]() $G$
is a unimodular locally compact topological group and
$G$
is a unimodular locally compact topological group and
![]() $dg$
a Haar measure. Suppose that
$dg$
a Haar measure. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is a representation of
$\unicode[STIX]{x1D70B}$
is a representation of
![]() $G$
, realized on some space
$G$
, realized on some space
![]() $V$
. Let
$V$
. Let
![]() $f$
be a continuous function on
$f$
be a continuous function on
![]() $G$
. Then we put (whenever it makes sense, e.g.
$G$
. Then we put (whenever it makes sense, e.g.
![]() $f$
is compactly supported and locally constant)
$f$
is compactly supported and locally constant)
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(f)v=\int _{G}f(g)\unicode[STIX]{x1D70B}(g).v\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(f)v=\int _{G}f(g)\unicode[STIX]{x1D70B}(g).v\,dg.\end{eqnarray}$$
Let
![]() $S$
be a finite set of places of
$S$
be a finite set of places of
![]() $F$
. We define a constant
$F$
. We define a constant
![]() $\unicode[STIX]{x1D6E5}_{G}^{S}$
as follows. If
$\unicode[STIX]{x1D6E5}_{G}^{S}$
as follows. If
 $G=\operatorname{Mp}(2n)$
or
$G=\operatorname{Mp}(2n)$
or
![]() $\operatorname{Sp}(2n)$
, we define
$\operatorname{Sp}(2n)$
, we define
 $\unicode[STIX]{x1D6E5}_{G}^{S}=\prod _{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)$
. If
$\unicode[STIX]{x1D6E5}_{G}^{S}=\prod _{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)$
. If
 $G=\operatorname{O}(V)$
or
$G=\operatorname{O}(V)$
or
![]() $\operatorname{SO}(V)$
when
$\operatorname{SO}(V)$
when
 $n=\dim V\geqslant 3$
, then we define
$n=\dim V\geqslant 3$
, then we define
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{G}^{S}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D701}_{F}^{S}(2)\unicode[STIX]{x1D701}_{F}^{S}(4)\cdots \unicode[STIX]{x1D701}_{F}^{S}(n-1) & \text{if }n\text{ is odd},\\ \unicode[STIX]{x1D701}_{F}^{S}(2)\unicode[STIX]{x1D701}_{F}^{S}(4)\cdots \unicode[STIX]{x1D701}_{F}^{S}(n-2)L^{S}\biggl(\displaystyle \frac{n}{2},\unicode[STIX]{x1D712}_{V}\biggr) & \text{if }n\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{G}^{S}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D701}_{F}^{S}(2)\unicode[STIX]{x1D701}_{F}^{S}(4)\cdots \unicode[STIX]{x1D701}_{F}^{S}(n-1) & \text{if }n\text{ is odd},\\ \unicode[STIX]{x1D701}_{F}^{S}(2)\unicode[STIX]{x1D701}_{F}^{S}(4)\cdots \unicode[STIX]{x1D701}_{F}^{S}(n-2)L^{S}\biggl(\displaystyle \frac{n}{2},\unicode[STIX]{x1D712}_{V}\biggr) & \text{if }n\text{ is even}.\end{array}\right.\end{eqnarray}$$
Suppose that
![]() $v$
is a place
$v$
is a place
![]() $F$
, then we define
$F$
, then we define
![]() $\unicode[STIX]{x1D6E5}_{G,v}$
in an analogous way, replacing the partial
$\unicode[STIX]{x1D6E5}_{G,v}$
in an analogous way, replacing the partial
![]() $L$
-functions by the local Euler factors at
$L$
-functions by the local Euler factors at
![]() $v$
. In this case, if
$v$
. In this case, if
![]() $T$
is a split maximal torus in
$T$
is a split maximal torus in
![]() $\operatorname{Sp}(2n)$
and
$\operatorname{Sp}(2n)$
and
![]() $\widetilde{T}$
is the inverse image of
$\widetilde{T}$
is the inverse image of
![]() $T$
in
$T$
in
 $\operatorname{Mp}(2n)$
, then we define
$\operatorname{Mp}(2n)$
, then we define
 $\unicode[STIX]{x1D6E5}_{\widetilde{T},v}=\unicode[STIX]{x1D6E5}_{T,v}=(1-q_{v}^{-1})^{-n}$
.
$\unicode[STIX]{x1D6E5}_{\widetilde{T},v}=\unicode[STIX]{x1D6E5}_{T,v}=(1-q_{v}^{-1})^{-n}$
.
Part I. Conjectures
2 Conjectures for the Fourier–Jacobi periods
2.1 Global Fourier–Jacobi periods
Let
 $(W_{2},q_{2})$
be a
$(W_{2},q_{2})$
be a
![]() $2m$
-dimensional symplectic space over
$2m$
-dimensional symplectic space over
![]() $F$
. We choose a basis
$F$
. We choose a basis
 $\{e_{m}^{\ast },\ldots ,e_{1}^{\ast },e_{1},\ldots ,e_{m}\}$
of
$\{e_{m}^{\ast },\ldots ,e_{1}^{\ast },e_{1},\ldots ,e_{m}\}$
of
![]() $W_{2}$
so that
$W_{2}$
so that
 $q_{2}(e_{i}^{\ast },e_{j})=\unicode[STIX]{x1D6FF}_{ij}$
. For
$q_{2}(e_{i}^{\ast },e_{j})=\unicode[STIX]{x1D6FF}_{ij}$
. For
 $1\leqslant i\leqslant m$
, let
$1\leqslant i\leqslant m$
, let
 $R_{i}=\langle e_{m-i+1},\ldots ,e_{m}\rangle$
and
$R_{i}=\langle e_{m-i+1},\ldots ,e_{m}\rangle$
and
 $R_{i}^{\ast }=\langle e_{m}^{\ast },\ldots ,e_{m-i+1}^{\ast }\rangle$
be isotropic subspaces of
$R_{i}^{\ast }=\langle e_{m}^{\ast },\ldots ,e_{m-i+1}^{\ast }\rangle$
be isotropic subspaces of
![]() $W_{2}$
. Put
$W_{2}$
. Put
 $R_{0}=R_{0}^{\ast }=\{0\}$
. Let
$R_{0}=R_{0}^{\ast }=\{0\}$
. Let
 $0\leqslant r\leqslant m$
be an integer and put
$0\leqslant r\leqslant m$
be an integer and put
 $n=m-r$
and
$n=m-r$
and
 $(W_{0},q_{0})$
the orthogonal complement of
$(W_{0},q_{0})$
the orthogonal complement of
 $R_{r}+R_{r}^{\ast }$
. We define
$R_{r}+R_{r}^{\ast }$
. We define
 $(W_{1},q_{1})=W_{0}+\langle e_{n+1},e_{n+1}^{\ast }\rangle$
. Let
$(W_{1},q_{1})=W_{0}+\langle e_{n+1},e_{n+1}^{\ast }\rangle$
. Let
 $G_{i}=\operatorname{Sp}(W_{i})$
and
$G_{i}=\operatorname{Sp}(W_{i})$
and
 $\widetilde{G_{i}}=\operatorname{Mp}(W_{i})$
.
$\widetilde{G_{i}}=\operatorname{Mp}(W_{i})$
.
Let
 $0\leqslant i\leqslant n$
be an integer. Let
$0\leqslant i\leqslant n$
be an integer. Let
![]() $P_{i}$
be the parabolic subgroup of
$P_{i}$
be the parabolic subgroup of
![]() $G_{2}$
stabilizing the flag
$G_{2}$
stabilizing the flag
 $$\begin{eqnarray}0=R_{0}\subset R_{1}\subset \cdots \subset R_{i},\end{eqnarray}$$
$$\begin{eqnarray}0=R_{0}\subset R_{1}\subset \cdots \subset R_{i},\end{eqnarray}$$
with the Levi decomposition
 $P_{i}=M_{i}N_{i}$
. Here and below in this article, the notation
$P_{i}=M_{i}N_{i}$
. Here and below in this article, the notation
 $P=MN$
signifies that
$P=MN$
signifies that
![]() $M$
is the Levi subgroup and
$M$
is the Levi subgroup and
![]() $N$
is the unipotent radical of
$N$
is the unipotent radical of
![]() $P$
. We denote by
$P$
. We denote by
![]() $W^{i}$
the orthogonal complement of
$W^{i}$
the orthogonal complement of
 $R_{i}+R_{i}^{\ast }$
and
$R_{i}+R_{i}^{\ast }$
and
 $G^{i}=\operatorname{Sp}(W^{i})$
. Then
$G^{i}=\operatorname{Sp}(W^{i})$
. Then
 $M_{i}=G^{i}\times \operatorname{GL}_{1}^{i}$
. Let
$M_{i}=G^{i}\times \operatorname{GL}_{1}^{i}$
. Let
![]() $\unicode[STIX]{x1D713}_{m}$
be the character of
$\unicode[STIX]{x1D713}_{m}$
be the character of
![]() $N_{m}$
defined by
$N_{m}$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{m}(n)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{j=1}^{m-1}q_{2}(ne_{m-j+1}^{\ast },e_{m-j})+q_{2}(ne_{1}^{\ast },e_{1}^{\ast })\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{m}(n)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{j=1}^{m-1}q_{2}(ne_{m-j+1}^{\ast },e_{m-j})+q_{2}(ne_{1}^{\ast },e_{1}^{\ast })\biggr).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D713}_{i}$
be the restriction of
$\unicode[STIX]{x1D713}_{i}$
be the restriction of
![]() $\unicode[STIX]{x1D713}_{m}$
to
$\unicode[STIX]{x1D713}_{m}$
to
![]() $N_{i}$
.
$N_{i}$
.
Let
 $H=H(W_{0})$
be the Heisenberg group attached to the symplectic space
$H=H(W_{0})$
be the Heisenberg group attached to the symplectic space
![]() $W_{0}$
. By definition,
$W_{0}$
. By definition,
 $H=W_{0}\ltimes F$
and the group law is given by
$H=W_{0}\ltimes F$
and the group law is given by
 $$\begin{eqnarray}(w_{1},t_{1})(w_{2},t_{2})=(w_{1}+w_{2},t_{1}+t_{2}+q_{0}(w_{1},w_{2})).\end{eqnarray}$$
$$\begin{eqnarray}(w_{1},t_{1})(w_{2},t_{2})=(w_{1}+w_{2},t_{1}+t_{2}+q_{0}(w_{1},w_{2})).\end{eqnarray}$$
The group
![]() $H$
embeds in
$H$
embeds in
![]() $G_{2}$
as a subgroup of
$G_{2}$
as a subgroup of
![]() $G_{1}$
and
$G_{1}$
and
 $H=G_{1}\cap N_{r}$
,
$H=G_{1}\cap N_{r}$
,
 $N_{r}=N_{r-1}H$
. Let
$N_{r}=N_{r-1}H$
. Let
 $L=\langle e_{1},\ldots ,e_{n}\rangle$
and
$L=\langle e_{1},\ldots ,e_{n}\rangle$
and
 $L^{\ast }=\langle e_{n}^{\ast },\ldots ,e_{1}^{\ast }\rangle$
. Then
$L^{\ast }=\langle e_{n}^{\ast },\ldots ,e_{1}^{\ast }\rangle$
. Then
 $W_{0}=L+L^{\ast }$
is a complete polarization. We sometimes write an element
$W_{0}=L+L^{\ast }$
is a complete polarization. We sometimes write an element
![]() $h\in H$
as
$h\in H$
as
 $h(l+l^{\ast },t)$
where
$h(l+l^{\ast },t)$
where
![]() $l\in L$
,
$l\in L$
,
![]() $l^{\ast }\in L^{\ast }$
and
$l^{\ast }\in L^{\ast }$
and
![]() $t\in F$
. Let
$t\in F$
. Let
![]() $v$
be a place of
$v$
be a place of
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
be the Weil representation of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
be the Weil representation of
![]() $H(F_{v})$
which is realized on
$H(F_{v})$
which is realized on
 ${\mathcal{S}}(L^{\ast }(F_{v}))$
. It is defined by
${\mathcal{S}}(L^{\ast }(F_{v}))$
. It is defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}(h(y+x,t))f(l^{\ast }) & = & \displaystyle \unicode[STIX]{x1D713}(t+q_{2}(2x+l^{\ast },y))f(l^{\ast }+x),\nonumber\\ \displaystyle & & \displaystyle \quad f\in {\mathcal{S}}(L^{\ast }(F_{v})),\;l^{\ast },x\in L^{\ast }(F_{v}),\;y\in L(F_{v}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}(h(y+x,t))f(l^{\ast }) & = & \displaystyle \unicode[STIX]{x1D713}(t+q_{2}(2x+l^{\ast },y))f(l^{\ast }+x),\nonumber\\ \displaystyle & & \displaystyle \quad f\in {\mathcal{S}}(L^{\ast }(F_{v})),\;l^{\ast },x\in L^{\ast }(F_{v}),\;y\in L(F_{v}).\nonumber\end{eqnarray}$$
This is the unique irreducible infinite-dimensional representation of
![]() $H(F_{v})$
whose central character is
$H(F_{v})$
whose central character is
![]() $\unicode[STIX]{x1D713}_{v}$
. It induces an action of
$\unicode[STIX]{x1D713}_{v}$
. It induces an action of
![]() $\widetilde{G_{0}}(F_{v})$
on
$\widetilde{G_{0}}(F_{v})$
on
 ${\mathcal{S}}(L^{\ast }(F_{v}))$
. We denote the joint action of
${\mathcal{S}}(L^{\ast }(F_{v}))$
. We denote the joint action of
 $H(F_{v})\rtimes \widetilde{G_{0}}(F_{v})$
on
$H(F_{v})\rtimes \widetilde{G_{0}}(F_{v})$
on
 ${\mathcal{S}}(L^{\ast }(F_{v}))$
again by
${\mathcal{S}}(L^{\ast }(F_{v}))$
again by
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
. We take the convention that if
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
. We take the convention that if
 $W_{0}=\{0\}$
, then
$W_{0}=\{0\}$
, then
 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}=\unicode[STIX]{x1D713}_{v}$
.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}=\unicode[STIX]{x1D713}_{v}$
.
Taking restricted tensor product of the Weil representations
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
, we obtain a global Weil representation
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
, we obtain a global Weil representation
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
of
 $H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
which is realized on
$H(\mathbb{A}_{F})\rtimes \widetilde{G_{0}}(\mathbb{A}_{F})$
which is realized on
 ${\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
. We define the theta series
${\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
. We define the theta series
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})=\mathop{\sum }_{l^{\ast }\in L^{\ast }(F)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\unicode[STIX]{x1D719}(l^{\ast }),\quad \unicode[STIX]{x1D719}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F})),~h\in H(\mathbb{A}_{F}),~g_{0}\in \widetilde{G_{0}}(\mathbb{A}_{F}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})=\mathop{\sum }_{l^{\ast }\in L^{\ast }(F)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\unicode[STIX]{x1D719}(l^{\ast }),\quad \unicode[STIX]{x1D719}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F})),~h\in H(\mathbb{A}_{F}),~g_{0}\in \widetilde{G_{0}}(\mathbb{A}_{F}).\end{eqnarray}$$
We now talk about automorphic representations. There are two cases.
Case
![]() $\operatorname{Mp}$
. Let
$\operatorname{Mp}$
. Let
 $\unicode[STIX]{x1D70B}_{2}=\bigotimes \unicode[STIX]{x1D70B}_{2,v}$
be an irreducible cuspidal genuine automorphic representation of
$\unicode[STIX]{x1D70B}_{2}=\bigotimes \unicode[STIX]{x1D70B}_{2,v}$
be an irreducible cuspidal genuine automorphic representation of
 $\widetilde{G_{2}}(\mathbb{A}_{F})$
and
$\widetilde{G_{2}}(\mathbb{A}_{F})$
and
 $\unicode[STIX]{x1D70B}_{0}=\bigotimes \unicode[STIX]{x1D70B}_{0,v}$
be an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}_{0}=\bigotimes \unicode[STIX]{x1D70B}_{0,v}$
be an irreducible cuspidal automorphic representation of
 $G_{0}(\mathbb{A}_{F})$
.
$G_{0}(\mathbb{A}_{F})$
.
Case
![]() $\operatorname{Sp}$
. Let
$\operatorname{Sp}$
. Let
 $\unicode[STIX]{x1D70B}_{2}=\bigotimes \unicode[STIX]{x1D70B}_{2,v}$
be an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}_{2}=\bigotimes \unicode[STIX]{x1D70B}_{2,v}$
be an irreducible cuspidal automorphic representation of
 $G_{2}(\mathbb{A}_{F})$
and
$G_{2}(\mathbb{A}_{F})$
and
 $\unicode[STIX]{x1D70B}_{0}=\bigotimes \unicode[STIX]{x1D70B}_{0,v}$
be an irreducible cuspidal genuine automorphic representation of
$\unicode[STIX]{x1D70B}_{0}=\bigotimes \unicode[STIX]{x1D70B}_{0,v}$
be an irreducible cuspidal genuine automorphic representation of
 $\widetilde{G_{0}}(\mathbb{A}_{F})$
.
$\widetilde{G_{0}}(\mathbb{A}_{F})$
.
Let
![]() $S$
be a sufficiently large finite set of places of
$S$
be a sufficiently large finite set of places of
![]() $F$
containing all archimedean places and finite places whose residue characteristic is two, such that
$F$
containing all archimedean places and finite places whose residue characteristic is two, such that
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are both unramified and the conductor of
$\unicode[STIX]{x1D70B}_{0,v}$
are both unramified and the conductor of
![]() $\unicode[STIX]{x1D713}_{v}$
is
$\unicode[STIX]{x1D713}_{v}$
is
![]() $\mathfrak{o}_{F,v}$
if
$\mathfrak{o}_{F,v}$
if
![]() $v\not \in S$
. Let
$v\not \in S$
. Let
 $(\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v})$
and
$(\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v})$
and
 $(\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v})$
be the Satake parameters of
$(\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v})$
be the Satake parameters of
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
, respectively. Put
$\unicode[STIX]{x1D70B}_{0,v}$
, respectively. Put
 $$\begin{eqnarray}A_{2}=\left\{\begin{array}{@{}ll@{}}\operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v},\unicode[STIX]{x1D6FC}_{m,v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Mp},\\ \operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v},1,\unicode[STIX]{x1D6FC}_{m,v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Sp},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A_{2}=\left\{\begin{array}{@{}ll@{}}\operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v},\unicode[STIX]{x1D6FC}_{m,v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Mp},\\ \operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{m,v},1,\unicode[STIX]{x1D6FC}_{m,v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Sp},\end{array}\right.\end{eqnarray}$$
and
 $$\begin{eqnarray}A_{0}=\left\{\begin{array}{@{}ll@{}}\operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v},1,\unicode[STIX]{x1D6FD}_{n,v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Mp},\\ \operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v},\unicode[STIX]{x1D6FD}_{n,v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Sp}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A_{0}=\left\{\begin{array}{@{}ll@{}}\operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v},1,\unicode[STIX]{x1D6FD}_{n,v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Mp},\\ \operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{n,v},\unicode[STIX]{x1D6FD}_{n,v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}]\quad & \text{Case }\operatorname{Sp}.\end{array}\right.\end{eqnarray}$$
We then define the tensor product
![]() $L$
-function
$L$
-function
 $$\begin{eqnarray}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v})=\det (1-A_{2}\otimes A_{0}\cdot q_{v}^{-s})^{-1},\quad L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})=\mathop{\prod }_{v\not \in S}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v}).\end{eqnarray}$$
$$\begin{eqnarray}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v})=\det (1-A_{2}\otimes A_{0}\cdot q_{v}^{-s})^{-1},\quad L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})=\mathop{\prod }_{v\not \in S}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v}).\end{eqnarray}$$
The partial
![]() $L$
-function is convergent for
$L$
-function is convergent for
![]() $\Re s\gg 0$
. We denote by
$\Re s\gg 0$
. We denote by
 $L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{i,v},\operatorname{Ad})$
and
$L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{i,v},\operatorname{Ad})$
and
 $L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})=\prod _{v\not \in S}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{i,v},\operatorname{Ad})$
the (local and partial) adjoint
$L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})=\prod _{v\not \in S}L_{\unicode[STIX]{x1D713}_{v}}(s,\unicode[STIX]{x1D70B}_{i,v},\operatorname{Ad})$
the (local and partial) adjoint
![]() $L$
-functions of
$L$
-functions of
![]() $\unicode[STIX]{x1D70B}_{i}$
. If
$\unicode[STIX]{x1D70B}_{i}$
. If
![]() $\unicode[STIX]{x1D70B}_{i}$
is an automorphic representation of the metaplectic group (respectively symplectic group), then they depend (respectively do not depend) on
$\unicode[STIX]{x1D70B}_{i}$
is an automorphic representation of the metaplectic group (respectively symplectic group), then they depend (respectively do not depend) on
![]() $\unicode[STIX]{x1D713}$
. We include the subscript
$\unicode[STIX]{x1D713}$
. We include the subscript
![]() $\unicode[STIX]{x1D713}$
in both cases to unify notation. We assume that these
$\unicode[STIX]{x1D713}$
in both cases to unify notation. We assume that these
![]() $L$
-functions can be meromorphically continued to the whole complex plane.
$L$
-functions can be meromorphically continued to the whole complex plane.
Let
 $\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
,
$\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
,
 $\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
and
$\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
and
 $\unicode[STIX]{x1D719}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
. Define
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
. Define
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\int _{N_{r-1}(F)\backslash N_{r-1}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}_{2}(uhg_{0})\unicode[STIX]{x1D711}_{0}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})}\,du\,dh\,dg_{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\int _{N_{r-1}(F)\backslash N_{r-1}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}_{2}(uhg_{0})\unicode[STIX]{x1D711}_{0}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(hg_{0},\unicode[STIX]{x1D719})}\,du\,dh\,dg_{0}.\nonumber\end{eqnarray}$$
The measures
![]() $du$
and
$du$
and
![]() $dh$
are the self-dual measures on
$dh$
are the self-dual measures on
 $N_{r-1}(\mathbb{A}_{F})$
and
$N_{r-1}(\mathbb{A}_{F})$
and
![]() $H(\mathbb{A}_{F})$
, respectively. The measure
$H(\mathbb{A}_{F})$
, respectively. The measure
![]() $dg_{0}$
is the Tamagawa measures on
$dg_{0}$
is the Tamagawa measures on
 $G_{0}(\mathbb{A}_{F})$
.
$G_{0}(\mathbb{A}_{F})$
.
2.2 Local Fourier–Jacobi periods
We fix a Haar measure
![]() $dg_{0,v}$
on
$dg_{0,v}$
on
![]() $G_{0}(F_{v})$
for each
$G_{0}(F_{v})$
for each
![]() $v$
such that the volume of
$v$
such that the volume of
![]() $G_{0}(\mathfrak{o}_{v})$
equals one for almost all
$G_{0}(\mathfrak{o}_{v})$
equals one for almost all
![]() $v$
. Then there is a constant
$v$
. Then there is a constant
![]() $C_{0}$
such that
$C_{0}$
such that
 $dg_{0}=C_{0}\prod _{v}\,dg_{0,v}$
. Following [Reference Ichino and IkedaII10], we call
$dg_{0}=C_{0}\prod _{v}\,dg_{0,v}$
. Following [Reference Ichino and IkedaII10], we call
![]() $C_{0}$
the measure constant.
$C_{0}$
the measure constant.
Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i}}$
(
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i}}$
(
![]() $i=0,2$
) be the canonical bilinear pairing between
$i=0,2$
) be the canonical bilinear pairing between
![]() $\unicode[STIX]{x1D70B}_{i}$
and
$\unicode[STIX]{x1D70B}_{i}$
and
![]() $\unicode[STIX]{x1D70B}_{i}^{\vee }$
defined by
$\unicode[STIX]{x1D70B}_{i}^{\vee }$
defined by
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee })=\int _{G_{2}(F)\backslash G_{2}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\vee }(g)\,dg,\quad \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70B}_{i},~\unicode[STIX]{x1D711}^{\vee }\in \unicode[STIX]{x1D70B}_{i}^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee })=\int _{G_{2}(F)\backslash G_{2}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\vee }(g)\,dg,\quad \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70B}_{i},~\unicode[STIX]{x1D711}^{\vee }\in \unicode[STIX]{x1D70B}_{i}^{\vee }.\end{eqnarray}$$
We fix a bilinear pairing
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}$
between
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}$
between
![]() $\unicode[STIX]{x1D70B}_{i,v}$
and
$\unicode[STIX]{x1D70B}_{i,v}$
and
![]() $\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
for each place
$\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
for each place
![]() $v$
such that
$v$
such that
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}$
. Put
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}$
. Put
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }}(g)={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}(\unicode[STIX]{x1D70B}_{i,v}(g)\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee })$
if
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }}(g)={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}(\unicode[STIX]{x1D70B}_{i,v}(g)\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee })$
if
 $\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i,v}$
and
$\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i,v}$
and
 $\unicode[STIX]{x1D711}_{i,v}^{\vee }\in \unicode[STIX]{x1D70B}_{i,v}^{\vee }$
.
$\unicode[STIX]{x1D711}_{i,v}^{\vee }\in \unicode[STIX]{x1D70B}_{i,v}^{\vee }$
.
The contragredient representation of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
is
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
is
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}^{-1}}$
(again realized on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}^{-1}}$
(again realized on
 ${\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
) and there is a canonical pairing between
${\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
) and there is a canonical pairing between
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}^{-1}}$
given by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}^{-1}}$
given by
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })=\int _{L^{\ast }(\mathbb{A}_{F})}\unicode[STIX]{x1D719}(l^{\ast })\unicode[STIX]{x1D719}^{\vee }(l^{\ast })\,dl^{\ast },\quad \unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F})),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })=\int _{L^{\ast }(\mathbb{A}_{F})}\unicode[STIX]{x1D719}(l^{\ast })\unicode[STIX]{x1D719}^{\vee }(l^{\ast })\,dl^{\ast },\quad \unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F})),\end{eqnarray}$$
where the measure
![]() $dl^{\ast }$
is the self-dual measure on
$dl^{\ast }$
is the self-dual measure on
![]() $L^{\ast }(\mathbb{A}_{F})$
. Similarly, for any place
$L^{\ast }(\mathbb{A}_{F})$
. Similarly, for any place
![]() $v$
, there is a canonical pairing between
$v$
, there is a canonical pairing between
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}^{-1}}$
given by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}^{-1}}$
given by
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\int _{L^{\ast }(F_{v})}\unicode[STIX]{x1D719}_{v}(l^{\ast })\unicode[STIX]{x1D719}_{v}^{\vee }(l^{\ast })\,dl^{\ast },\quad \unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }\in {\mathcal{S}}(L^{\ast }(F_{v})),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\int _{L^{\ast }(F_{v})}\unicode[STIX]{x1D719}_{v}(l^{\ast })\unicode[STIX]{x1D719}_{v}^{\vee }(l^{\ast })\,dl^{\ast },\quad \unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }\in {\mathcal{S}}(L^{\ast }(F_{v})),\end{eqnarray}$$
where the measure
![]() $dl^{\ast }$
is the self-dual measure on
$dl^{\ast }$
is the self-dual measure on
![]() $L^{\ast }(F_{v})$
. Then
$L^{\ast }(F_{v})$
. Then
 ${\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}\!.$
Put
${\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}\!.$
Put
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }}(g)={\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })$
.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }}(g)={\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })$
.
We now fix a place
![]() $v$
of
$v$
of
![]() $F$
. Recall that the group
$F$
. Recall that the group
![]() $P_{m}$
of
$P_{m}$
of
![]() $G_{2}$
is a minimal parabolic subgroup which is contained in
$G_{2}$
is a minimal parabolic subgroup which is contained in
![]() $P_{r-1}$
. For any real number
$P_{r-1}$
. For any real number
![]() $\unicode[STIX]{x1D6FE}$
or
$\unicode[STIX]{x1D6FE}$
or
 $\unicode[STIX]{x1D6FE}=-\infty$
, define
$\unicode[STIX]{x1D6FE}=-\infty$
, define
 $$\begin{eqnarray}N_{m,\unicode[STIX]{x1D6FE}}=\{u\in N_{m}(F_{v})\mid |q_{2}(ue_{1}^{\ast },e_{1}^{\ast })|\leqslant e^{\unicode[STIX]{x1D6FE}},|q_{2}(ue_{i+1}^{\ast },e_{i})|\leqslant e^{\unicode[STIX]{x1D6FE}},~1\leqslant i\leqslant m-1\}.\end{eqnarray}$$
$$\begin{eqnarray}N_{m,\unicode[STIX]{x1D6FE}}=\{u\in N_{m}(F_{v})\mid |q_{2}(ue_{1}^{\ast },e_{1}^{\ast })|\leqslant e^{\unicode[STIX]{x1D6FE}},|q_{2}(ue_{i+1}^{\ast },e_{i})|\leqslant e^{\unicode[STIX]{x1D6FE}},~1\leqslant i\leqslant m-1\}.\end{eqnarray}$$
For any
 $\unicode[STIX]{x1D6FE}\geqslant -\infty$
, we define
$\unicode[STIX]{x1D6FE}\geqslant -\infty$
, we define
 $N_{i,\unicode[STIX]{x1D6FE}}=N_{i}(F_{v})\cap N_{m,\unicode[STIX]{x1D6FE}}$
. Define
$N_{i,\unicode[STIX]{x1D6FE}}=N_{i}(F_{v})\cap N_{m,\unicode[STIX]{x1D6FE}}$
. Define
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0})=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}(F_{v})}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0}u)\overline{\unicode[STIX]{x1D713}_{r-1,v}(u)}\,du,\quad \unicode[STIX]{x1D711}_{2,v}\in \unicode[STIX]{x1D70B}_{2,v},~\unicode[STIX]{x1D711}_{2,v}^{\vee }\in \unicode[STIX]{x1D70B}_{2,v}^{\vee },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0})=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}(F_{v})}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0}u)\overline{\unicode[STIX]{x1D713}_{r-1,v}(u)}\,du,\quad \unicode[STIX]{x1D711}_{2,v}\in \unicode[STIX]{x1D70B}_{2,v},~\unicode[STIX]{x1D711}_{2,v}^{\vee }\in \unicode[STIX]{x1D70B}_{2,v}^{\vee },\end{eqnarray}$$
where
 $h\in H(F_{v})$
and
$h\in H(F_{v})$
and
 $g_{0}\in G_{0}(F_{v})$
in the case
$g_{0}\in G_{0}(F_{v})$
in the case
![]() $\operatorname{Sp}$
(respectively
$\operatorname{Sp}$
(respectively
 $g_{0}\in \widetilde{G_{0}}(F_{v})$
in the case
$g_{0}\in \widetilde{G_{0}}(F_{v})$
in the case
![]() $\operatorname{Mp}$
). Define
$\operatorname{Mp}$
). Define
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\int _{G_{0}(F_{v})}\int _{H(F_{v})}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee }}(g_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }}(hg_{0})\,dh\,dg_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\int _{G_{0}(F_{v})}\int _{H(F_{v})}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}(hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee }}(g_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }}(hg_{0})\,dh\,dg_{0},\end{eqnarray}$$
for
 $\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }\in \unicode[STIX]{x1D70B}_{i,v}^{\vee }$
,
$\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }\in \unicode[STIX]{x1D70B}_{i,v}^{\vee }$
,
 $\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }\in {\mathcal{S}}(L^{\ast }(F_{v}))$
. If
$\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }\in {\mathcal{S}}(L^{\ast }(F_{v}))$
. If
![]() $r\leqslant 1$
, then it is to be understood that
$r\leqslant 1$
, then it is to be understood that
 ${\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}$
. Moreover, if
${\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}$
. Moreover, if
![]() $r=0$
, then it is to be understood that the integral over
$r=0$
, then it is to be understood that the integral over
![]() $H(F_{v})$
is void.
$H(F_{v})$
is void.
Proposition 2.2.1. Assume that
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are both tempered. Then the limit in the definition of
$\unicode[STIX]{x1D70B}_{0,v}$
are both tempered. Then the limit in the definition of
 ${\mathcal{F}}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}$
exists. Moreover, the defining integral of
${\mathcal{F}}_{\unicode[STIX]{x1D713}_{v}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee }}$
exists. Moreover, the defining integral of
![]() $\unicode[STIX]{x1D6FC}_{v}$
is absolutely convergent.
$\unicode[STIX]{x1D6FC}_{v}$
is absolutely convergent.
If
![]() $\unicode[STIX]{x1D70B}_{i,v}$
is unitary, then we may identify
$\unicode[STIX]{x1D70B}_{i,v}$
is unitary, then we may identify
![]() $\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
with
$\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
with
![]() $\overline{\unicode[STIX]{x1D70B}_{i,v}}$
. We then define
$\overline{\unicode[STIX]{x1D70B}_{i,v}}$
. We then define
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\overline{\unicode[STIX]{x1D711}_{2,v}},\unicode[STIX]{x1D711}_{0,v},\overline{\unicode[STIX]{x1D711}_{0,v}},\unicode[STIX]{x1D719}_{v},\overline{\unicode[STIX]{x1D719}_{v}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\overline{\unicode[STIX]{x1D711}_{2,v}},\unicode[STIX]{x1D711}_{0,v},\overline{\unicode[STIX]{x1D711}_{0,v}},\unicode[STIX]{x1D719}_{v},\overline{\unicode[STIX]{x1D719}_{v}}).\end{eqnarray}$$
Proposition 2.2.2. Assume that
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are unitary and tempered. Then
$\unicode[STIX]{x1D70B}_{0,v}$
are unitary and tempered. Then
 $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})\geqslant 0$
for all smooth vectors
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})\geqslant 0$
for all smooth vectors
 $\unicode[STIX]{x1D711}_{2,v}\in \unicode[STIX]{x1D70B}_{2,v}$
,
$\unicode[STIX]{x1D711}_{2,v}\in \unicode[STIX]{x1D70B}_{2,v}$
,
 $\unicode[STIX]{x1D711}_{0,v}\in \unicode[STIX]{x1D70B}_{0,v}$
and
$\unicode[STIX]{x1D711}_{0,v}\in \unicode[STIX]{x1D70B}_{0,v}$
and
 $\unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(L^{\ast }(F_{v}))$
.
$\unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(L^{\ast }(F_{v}))$
.
These two propositions will be proved in § 3.
We now consider the unramified situation. Note first that the symplectic spaces
![]() $W_{i}$
, the isotropic subspaces
$W_{i}$
, the isotropic subspaces
![]() $R_{i}$
and hence the groups
$R_{i}$
and hence the groups
![]() $G_{i}$
are naturally defined over
$G_{i}$
are naturally defined over
![]() $\mathfrak{o}_{F}$
. Let
$\mathfrak{o}_{F}$
. Let
![]() $S$
be a sufficiently large finite set of places of
$S$
be a sufficiently large finite set of places of
![]() $F$
containing all archimedean places and finite places whose residue characteristic is two, such that if
$F$
containing all archimedean places and finite places whose residue characteristic is two, such that if
![]() $v\not \in S$
, then the following conditions hold.
$v\not \in S$
, then the following conditions hold.
-
(i) The conductor of
 $\unicode[STIX]{x1D713}_{v}$
is
$\unicode[STIX]{x1D713}_{v}$
is
 $\mathfrak{o}_{F,v}$
.
$\mathfrak{o}_{F,v}$
. -
(ii) We have
 $\unicode[STIX]{x1D719}_{v}=\unicode[STIX]{x1D719}_{v}^{\vee }=\operatorname{1}_{L^{\ast }(\mathfrak{o}_{F,v})}$
.
$\unicode[STIX]{x1D719}_{v}=\unicode[STIX]{x1D719}_{v}^{\vee }=\operatorname{1}_{L^{\ast }(\mathfrak{o}_{F,v})}$
. -
(iii) For
 $i=0,2$
,
$i=0,2$
,
 $\unicode[STIX]{x1D711}_{i,v}$
and
$\unicode[STIX]{x1D711}_{i,v}$
and
 $\unicode[STIX]{x1D711}_{i,v}^{\vee }$
are fixed by
$\unicode[STIX]{x1D711}_{i,v}^{\vee }$
are fixed by
 $G_{i}(\mathfrak{o}_{F,v})$
and satisfy
$G_{i}(\mathfrak{o}_{F,v})$
and satisfy
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}(\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee })=1$
. In particular, the representations
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{i,v}}(\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee })=1$
. In particular, the representations
 $\unicode[STIX]{x1D70B}_{i,v}$
and
$\unicode[STIX]{x1D70B}_{i,v}$
and
 $\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
are unramified.
$\unicode[STIX]{x1D70B}_{i,v}^{\vee }$
are unramified. -
(iv) We have
 $\int _{G_{0}(\mathfrak{o}_{F,v})}\,dg_{0,v}=1$
.
$\int _{G_{0}(\mathfrak{o}_{F,v})}\,dg_{0,v}=1$
.
Proposition 2.2.3. If
![]() $v\not \in S$
and the defining integral of
$v\not \in S$
and the defining integral of
![]() $\unicode[STIX]{x1D6FC}_{v}$
is convergent, then
$\unicode[STIX]{x1D6FC}_{v}$
is convergent, then
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\unicode[STIX]{x1D6E5}_{G_{2},v}\frac{L_{\unicode[STIX]{x1D713}_{v}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v})}{L_{\unicode[STIX]{x1D713}_{v}}(1,\unicode[STIX]{x1D70B}_{0,v},\text{Ad})L_{\unicode[STIX]{x1D713}_{v}}(1,\unicode[STIX]{x1D70B}_{2,v},\text{Ad})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })=\unicode[STIX]{x1D6E5}_{G_{2},v}\frac{L_{\unicode[STIX]{x1D713}_{v}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2,v}\times \unicode[STIX]{x1D70B}_{0,v})}{L_{\unicode[STIX]{x1D713}_{v}}(1,\unicode[STIX]{x1D70B}_{0,v},\text{Ad})L_{\unicode[STIX]{x1D713}_{v}}(1,\unicode[STIX]{x1D70B}_{2,v},\text{Ad})}.\end{eqnarray}$$
We will prove this proposition in § 4. Note that in this proposition, we do not assume that the representations
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are tempered.
$\unicode[STIX]{x1D70B}_{0,v}$
are tempered.
2.3 Conjectures
Following [Reference Ichino and IkedaII10] and [Reference LiuLiu16], we say that the representations
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
are almost locally generic if for almost all places
$\unicode[STIX]{x1D70B}_{0}$
are almost locally generic if for almost all places
![]() $v$
of
$v$
of
![]() $F$
, the local components
$F$
, the local components
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are generic. Suppose that we are in the case of
$\unicode[STIX]{x1D70B}_{0,v}$
are generic. Suppose that we are in the case of
![]() $\operatorname{Mp}$
. As explained in [Reference Ichino and IkedaII10], the automorphic representations
$\operatorname{Mp}$
. As explained in [Reference Ichino and IkedaII10], the automorphic representations
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
should come from some elliptic Arthur parameters
$\unicode[STIX]{x1D70B}_{0}$
should come from some elliptic Arthur parameters
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{2}:L_{F}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow \widehat{\widetilde{G_{2}}}=\operatorname{Sp}(2m,\mathbb{C}),\quad \unicode[STIX]{x1D6F9}_{0}:L_{F}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow \widehat{G_{0}}=\operatorname{SO}(2n+1,\mathbb{C}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{2}:L_{F}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow \widehat{\widetilde{G_{2}}}=\operatorname{Sp}(2m,\mathbb{C}),\quad \unicode[STIX]{x1D6F9}_{0}:L_{F}\times \operatorname{SL}_{2}(\mathbb{C})\rightarrow \widehat{G_{0}}=\operatorname{SO}(2n+1,\mathbb{C}),\end{eqnarray}$$
where
![]() $L_{F}$
is the (hypothetical) Langlands group of
$L_{F}$
is the (hypothetical) Langlands group of
![]() $F$
. If
$F$
. If
![]() $\unicode[STIX]{x1D70B}_{i}$
is tempered, then
$\unicode[STIX]{x1D70B}_{i}$
is tempered, then
![]() $\unicode[STIX]{x1D6F9}_{i}$
is trivial on
$\unicode[STIX]{x1D6F9}_{i}$
is trivial on
![]() $\operatorname{SL}_{2}(\mathbb{C})$
. It is believed (Ramanujan conjecture) that almost locally generic representations are tempered. We define
$\operatorname{SL}_{2}(\mathbb{C})$
. It is believed (Ramanujan conjecture) that almost locally generic representations are tempered. We define
![]() $S_{\unicode[STIX]{x1D70B}_{2}}$
(respectively
$S_{\unicode[STIX]{x1D70B}_{2}}$
(respectively
![]() $S_{\unicode[STIX]{x1D70B}_{0}}$
) to be the centralizer of the image of
$S_{\unicode[STIX]{x1D70B}_{0}}$
) to be the centralizer of the image of
![]() $\unicode[STIX]{x1D6F9}_{2}$
in
$\unicode[STIX]{x1D6F9}_{2}$
in
![]() $\widehat{\widetilde{G_{2}}}$
(respectively
$\widehat{\widetilde{G_{2}}}$
(respectively
![]() $\widehat{G_{0}}$
). They are finite abelian 2-groups. In the case
$\widehat{G_{0}}$
). They are finite abelian 2-groups. In the case
![]() $\operatorname{Sp}$
, we have the same discussion, except that we replace
$\operatorname{Sp}$
, we have the same discussion, except that we replace
![]() $\widetilde{G_{2}}$
by
$\widetilde{G_{2}}$
by
![]() $G_{2}$
and replace
$G_{2}$
and replace
![]() $G_{0}$
by
$G_{0}$
by
![]() $\widetilde{G_{0}}$
.
$\widetilde{G_{0}}$
.
Conjecture 2.3.1. Assume that
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
are irreducible cuspidal automorphic representations that are almost locally generic. Then the following statements hold.
$\unicode[STIX]{x1D70B}_{0}$
are irreducible cuspidal automorphic representations that are almost locally generic. Then the following statements hold.
-
(i) The defining integral of
 $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })$
is convergent for any
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{2,v}^{\vee },\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D711}_{0,v}^{\vee },\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee })$
is convergent for any
 $K_{i}$
-finite vectors
$K_{i}$
-finite vectors
 $\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }$
and
$\unicode[STIX]{x1D711}_{i,v},\unicode[STIX]{x1D711}_{i,v}^{\vee }$
and
 $K_{0}$
-finite Schwartz functions
$K_{0}$
-finite Schwartz functions
 $\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }$
, where
$\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v}^{\vee }$
, where
 $K_{i}$
is a maximal compact subgroup of
$K_{i}$
is a maximal compact subgroup of
 $G_{i}(F_{v})$
,
$G_{i}(F_{v})$
,
 $i=0,2$
.
$i=0,2$
. -
(ii) We have
 $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})\geqslant 0$
for any
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})\geqslant 0$
for any
 $K_{i}$
-finite vectors
$K_{i}$
-finite vectors
 $\unicode[STIX]{x1D711}_{i,v}$
and
$\unicode[STIX]{x1D711}_{i,v}$
and
 $K_{0}$
-finite Schwartz function
$K_{0}$
-finite Schwartz function
 $\unicode[STIX]{x1D719}_{v}$
. Moreover,
$\unicode[STIX]{x1D719}_{v}$
. Moreover,
 $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})=0$
for all
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v})=0$
for all
 $K_{i}$
-finite
$K_{i}$
-finite
 $\unicode[STIX]{x1D711}_{i,v}$
and
$\unicode[STIX]{x1D711}_{i,v}$
and
 $K_{0}$
-finite
$K_{0}$
-finite
 $\unicode[STIX]{x1D719}_{v}$
precisely when
$\unicode[STIX]{x1D719}_{v}$
precisely when  $$\begin{eqnarray}\operatorname{Hom}_{N_{r-1}(F_{v})\rtimes (H(F_{v})\rtimes G_{0}(F_{v}))}(\unicode[STIX]{x1D70B}_{2,v}\otimes \unicode[STIX]{x1D70B}_{0,v}\otimes \overline{\unicode[STIX]{x1D713}_{r-1,v}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}},\mathbb{C})=0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{N_{r-1}(F_{v})\rtimes (H(F_{v})\rtimes G_{0}(F_{v}))}(\unicode[STIX]{x1D70B}_{2,v}\otimes \unicode[STIX]{x1D70B}_{0,v}\otimes \overline{\unicode[STIX]{x1D713}_{r-1,v}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{v}}},\mathbb{C})=0.\end{eqnarray}$$
-
(iii) Assume that
 $\unicode[STIX]{x1D711}_{i}=\bigotimes _{v}\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i}$
(
$\unicode[STIX]{x1D711}_{i}=\bigotimes _{v}\unicode[STIX]{x1D711}_{i,v}\in \unicode[STIX]{x1D70B}_{i}$
(
 $i=0,2$
) and
$i=0,2$
) and
 $\unicode[STIX]{x1D719}=\bigotimes _{v}\unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
are factorizable, then (2.3.1)
$\unicode[STIX]{x1D719}=\bigotimes _{v}\unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(L^{\ast }(\mathbb{A}_{F}))$
are factorizable, then (2.3.1) $$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{C_{0}\unicode[STIX]{x1D6E5}_{G_{2}}^{S}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}\frac{L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L_{\unicode[STIX]{x1D713}}^{S}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}^{S}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0},\text{Ad})}\biggr|_{s=1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{C_{0}\unicode[STIX]{x1D6E5}_{G_{2}}^{S}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}\frac{L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L_{\unicode[STIX]{x1D713}}^{S}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}^{S}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0},\text{Ad})}\biggr|_{s=1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D711}_{2,v},\unicode[STIX]{x1D711}_{0,v},\unicode[STIX]{x1D719}_{v}).\end{eqnarray}$$
Remark 2.3.2. It follows from the Proposition 2.2.3 that the right-hand side of (2.3.1) does not depend on the finite set
![]() $S$
.
$S$
.
Remark 2.3.3. Assume that
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
are both tempered. It is then believed that
$\unicode[STIX]{x1D70B}_{0}$
are both tempered. It is then believed that
 $L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
and
$L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})$
and
 $L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})$
should be holomorphic for
$L_{\unicode[STIX]{x1D713}}^{S}(s,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})$
should be holomorphic for
![]() $\Re s>0$
. Moreover,
$\Re s>0$
. Moreover,
 $L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})\not =0$
.
$L_{\unicode[STIX]{x1D713}}^{S}(1,\unicode[STIX]{x1D70B}_{i},\operatorname{Ad})\not =0$
.
Remark 2.3.4. Without the assumption of almost local genericity of
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
, we expect that local linear forms
$\unicode[STIX]{x1D70B}_{0}$
, we expect that local linear forms
![]() $\unicode[STIX]{x1D6FC}_{v}$
can be ‘analytically continued’ in some way so that it is defined for all representations
$\unicode[STIX]{x1D6FC}_{v}$
can be ‘analytically continued’ in some way so that it is defined for all representations
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
. This is indeed the case if
$\unicode[STIX]{x1D70B}_{0,v}$
. This is indeed the case if
![]() $v\not \in S$
. Thus
$v\not \in S$
. Thus
![]() $\unicode[STIX]{x1D6FC}_{v}$
is well-defined for all
$\unicode[STIX]{x1D6FC}_{v}$
is well-defined for all
![]() $v$
if
$v$
if
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
satisfy the property that
$\unicode[STIX]{x1D70B}_{0}$
satisfy the property that
![]() $\unicode[STIX]{x1D70B}_{2,v}$
and
$\unicode[STIX]{x1D70B}_{2,v}$
and
![]() $\unicode[STIX]{x1D70B}_{0,v}$
are both tempered if
$\unicode[STIX]{x1D70B}_{0,v}$
are both tempered if
![]() $v\in S$
. Moreover, we expect that the identity (2.3.1) holds with the quantity
$v\in S$
. Moreover, we expect that the identity (2.3.1) holds with the quantity
 $|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|$
replaced by some
$|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|$
replaced by some
![]() $2^{-\unicode[STIX]{x1D6FD}}$
where
$2^{-\unicode[STIX]{x1D6FD}}$
where
![]() $\unicode[STIX]{x1D6FD}$
is an integer. The nature of
$\unicode[STIX]{x1D6FD}$
is an integer. The nature of
![]() $\unicode[STIX]{x1D6FD}$
, however, remains mysterious at this moment.
$\unicode[STIX]{x1D6FD}$
, however, remains mysterious at this moment.
We end this section by writing Conjecture 2.3.1(3) in an equivalent form which does not involve the finite set
![]() $S$
. We may define the completed
$S$
. We may define the completed
![]() $L$
-functions
$L$
-functions
 $$\begin{eqnarray}L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0}),\quad L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{i},\text{Ad}),\quad i=0,2.\end{eqnarray}$$
$$\begin{eqnarray}L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0}),\quad L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{i},\text{Ad}),\quad i=0,2.\end{eqnarray}$$
The actual definition of the local Euler factor of these
![]() $L$
-functions is not essential to us since Conjecture 2.3.1 does not depend on the definition of these Euler factors. Put
$L$
-functions is not essential to us since Conjecture 2.3.1 does not depend on the definition of these Euler factors. Put
 $$\begin{eqnarray}{\mathcal{L}}=\unicode[STIX]{x1D6E5}_{G_{2}}\frac{L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L_{\unicode[STIX]{x1D713}}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0},\text{Ad})}\bigg|_{s=1/2}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}=\unicode[STIX]{x1D6E5}_{G_{2}}\frac{L_{\unicode[STIX]{x1D713}}(s,\unicode[STIX]{x1D70B}_{2}\times \unicode[STIX]{x1D70B}_{0})}{L_{\unicode[STIX]{x1D713}}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{2},\text{Ad})L_{\unicode[STIX]{x1D713}}(s+{\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0},\text{Ad})}\bigg|_{s=1/2}\end{eqnarray}$$
and let
![]() ${\mathcal{L}}_{v}$
be its local Euler factor evaluated at
${\mathcal{L}}_{v}$
be its local Euler factor evaluated at
![]() $s=\frac{1}{2}$
at the place
$s=\frac{1}{2}$
at the place
![]() $v$
. Define
$v$
. Define
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}^{\natural }={\mathcal{L}}_{v}^{-1}\unicode[STIX]{x1D6FC}_{v}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{v}^{\natural }={\mathcal{L}}_{v}^{-1}\unicode[STIX]{x1D6FC}_{v}.\end{eqnarray}$$
Then the identity (2.3.1) can be rewritten as
 $$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}\cdot \overline{{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}}=\frac{C_{0}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}{\mathcal{L}}\cdot \mathop{\prod }_{v}\unicode[STIX]{x1D6FC}_{v}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}\cdot \overline{{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}}=\frac{C_{0}}{|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|}{\mathcal{L}}\cdot \mathop{\prod }_{v}\unicode[STIX]{x1D6FC}_{v}^{\natural }.\end{eqnarray}$$
The product is convergent since there are only finitely many terms which do not equal to one. This is an equality of elements in
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D713}_{r-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}},\mathbb{C})\otimes \overline{\operatorname{Hom}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D713}_{r-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}},\mathbb{C})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D713}_{r-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}},\mathbb{C})\otimes \overline{\operatorname{Hom}(\unicode[STIX]{x1D70B}_{2}\otimes \unicode[STIX]{x1D70B}_{0}\otimes \overline{\unicode[STIX]{x1D713}_{r-1}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}},\mathbb{C})}.\end{eqnarray}$$
Note that by [Reference SunSun12, Reference Sun and ZhuSZ12, Reference Liu and SunLS13], this space is at most one dimensional. So we know a priori that there is a constant
![]() $C$
such that
$C$
such that
 $$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}\cdot \overline{{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}}=C\cdot \mathop{\prod }_{v}\unicode[STIX]{x1D6FC}_{v}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}\cdot \overline{{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}}}=C\cdot \mathop{\prod }_{v}\unicode[STIX]{x1D6FC}_{v}^{\natural }.\end{eqnarray}$$
The point of Conjecture 2.3.1 is thus to compute the constant
![]() $C$
.
$C$
.
3 Convergence and positivity
For the rest of Part I of this paper, we fix a place
![]() $v$
of
$v$
of
![]() $F$
and suppress it from all notation. Thus
$F$
and suppress it from all notation. Thus
![]() $F$
is a local field of characteristic zero. To shorten notation, for any algebraic group
$F$
is a local field of characteristic zero. To shorten notation, for any algebraic group
![]() $G$
or
$G$
or
 $G=\operatorname{Mp}(2n)$
over
$G=\operatorname{Mp}(2n)$
over
![]() $F$
, we denote by
$F$
, we denote by
![]() $G$
instead of
$G$
instead of
![]() $G(F)$
for its group of
$G(F)$
for its group of
![]() $F$
-points. We have fixed a basis
$F$
-points. We have fixed a basis
 $\{e_{m}^{\ast },\ldots ,e_{1}^{\ast },e_{1},\ldots ,e_{m}\}$
of
$\{e_{m}^{\ast },\ldots ,e_{1}^{\ast },e_{1},\ldots ,e_{m}\}$
of
![]() $W_{2}$
. We thus realize the group
$W_{2}$
. We thus realize the group
![]() $G_{2}$
and its various subgroups as groups of matrices. We also identify
$G_{2}$
and its various subgroups as groups of matrices. We also identify
![]() $W_{i}$
,
$W_{i}$
,
![]() $L,L^{\ast }$
as spaces of row vectors. We put
$L,L^{\ast }$
as spaces of row vectors. We put
 $K_{i}=G_{i}(\mathfrak{o}_{F})$
. This is a maximal compact subgroup of
$K_{i}=G_{i}(\mathfrak{o}_{F})$
. This is a maximal compact subgroup of
![]() $G_{i}$
. The group
$G_{i}$
. The group
![]() $P_{m}$
consists of upper triangular matrices. The group
$P_{m}$
consists of upper triangular matrices. The group
 $P_{m}\cap G_{i}$
is a minimal parabolic subgroup of
$P_{m}\cap G_{i}$
is a minimal parabolic subgroup of
![]() $G_{i}$
.
$G_{i}$
.
Suppose
 $a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
. Then we let
$a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
. Then we let
 $d(a)\in G_{0}$
so that
$d(a)\in G_{0}$
so that
 $d(a)e_{i}^{\ast }=a_{i}e_{i}^{\ast }$
for any
$d(a)e_{i}^{\ast }=a_{i}e_{i}^{\ast }$
for any
 $1\leqslant i\leqslant n$
. We also put
$1\leqslant i\leqslant n$
. We also put
 $\text{}\underline{a}=\operatorname{diag}[a_{n},\ldots ,a_{1}]\in \operatorname{GL}_{n}$
.
$\text{}\underline{a}=\operatorname{diag}[a_{n},\ldots ,a_{1}]\in \operatorname{GL}_{n}$
.
3.1 Preliminaries
We recall some basic estimates in this subsection. We follow [Reference Ichino and IkedaII10, § 4] rather closely.
Let
![]() $G$
be a reductive group over
$G$
be a reductive group over
![]() $F$
. Let
$F$
. Let
![]() $A_{G}$
be a maximal split subtorus of
$A_{G}$
be a maximal split subtorus of
![]() $G$
,
$G$
,
![]() $M_{0}$
the centralizer of
$M_{0}$
the centralizer of
![]() $A_{G}$
in
$A_{G}$
in
![]() $G$
. We fix a minimal parabolic subgroup
$G$
. We fix a minimal parabolic subgroup
![]() $P_{0}$
of
$P_{0}$
of
![]() $G$
with the Levi decomposition
$G$
with the Levi decomposition
 $P_{0}=M_{0}N_{0}$
. Let
$P_{0}=M_{0}N_{0}$
. Let
![]() $\unicode[STIX]{x1D6E5}$
be the set of simple roots of
$\unicode[STIX]{x1D6E5}$
be the set of simple roots of
 $(P_{0},A_{G})$
. Let
$(P_{0},A_{G})$
. Let
![]() $\unicode[STIX]{x1D6FF}_{P_{0}}$
be the modulus character of
$\unicode[STIX]{x1D6FF}_{P_{0}}$
be the modulus character of
![]() $P_{0}$
. Let
$P_{0}$
. Let
 $$\begin{eqnarray}A_{G}^{+}=\{a\in A_{0}\mid |\unicode[STIX]{x1D6FC}(a)|\leqslant 1~\text{for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}.\end{eqnarray}$$
$$\begin{eqnarray}A_{G}^{+}=\{a\in A_{0}\mid |\unicode[STIX]{x1D6FC}(a)|\leqslant 1~\text{for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}.\end{eqnarray}$$
We fix a special maximal compact subgroup
![]() $K$
of
$K$
of
![]() $G$
. Then we have a Cartan decomposition
$G$
. Then we have a Cartan decomposition
 $G=KA_{G}^{+}K$
. We also have the Iwasawa decomposition
$G=KA_{G}^{+}K$
. We also have the Iwasawa decomposition
 $$\begin{eqnarray}G=M_{0}N_{0}K,\quad g=m_{0}(g)n_{0}(g)k_{0}(g).\end{eqnarray}$$
$$\begin{eqnarray}G=M_{0}N_{0}K,\quad g=m_{0}(g)n_{0}(g)k_{0}(g).\end{eqnarray}$$
Let
![]() $f$
and
$f$
and
![]() $f^{\prime }$
be two nonnegative functions on
$f^{\prime }$
be two nonnegative functions on
![]() $G$
. We say that
$G$
. We say that
![]() $f\ll f^{\prime }$
if there is a constant
$f\ll f^{\prime }$
if there is a constant
![]() $C$
such that
$C$
such that
 $f(g)\leqslant Cf^{\prime }(g)$
for all
$f(g)\leqslant Cf^{\prime }(g)$
for all
![]() $g\in G$
. We say that
$g\in G$
. We say that
![]() $f\sim f^{\prime }$
if
$f\sim f^{\prime }$
if
![]() $f\ll f^{\prime }$
and
$f\ll f^{\prime }$
and
![]() $f^{\prime }\ll f$
. In this case we say that
$f^{\prime }\ll f$
. In this case we say that
![]() $f$
and
$f$
and
![]() $f^{\prime }$
are equivalent.
$f^{\prime }$
are equivalent.
For any function
 $f\in L^{1}(G)$
,
$f\in L^{1}(G)$
,
 $$\begin{eqnarray}\int _{G}f(g)\,dg=\int _{A_{G}^{+}}\unicode[STIX]{x1D708}(m)\iint _{K\times K}f(k_{1}mk_{2})\,dk_{1}\,dk_{2}\,dm,\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}f(g)\,dg=\int _{A_{G}^{+}}\unicode[STIX]{x1D708}(m)\iint _{K\times K}f(k_{1}mk_{2})\,dk_{1}\,dk_{2}\,dm,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D708}(m)$
is a positive function on
$\unicode[STIX]{x1D708}(m)$
is a positive function on
![]() $A_{G}^{+}$
such that
$A_{G}^{+}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D708}(m)\sim \unicode[STIX]{x1D6FF}_{P_{0}}(m)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(m)\sim \unicode[STIX]{x1D6FF}_{P_{0}}(m)^{-1}.\end{eqnarray}$$
Let
![]() $\operatorname{1}$
be the trivial representation of
$\operatorname{1}$
be the trivial representation of
![]() $M_{0}$
and let
$M_{0}$
and let
 $e(g)=\unicode[STIX]{x1D6FF}_{P_{0}}(m_{0}(g))^{1/2}$
be an element in
$e(g)=\unicode[STIX]{x1D6FF}_{P_{0}}(m_{0}(g))^{1/2}$
be an element in
![]() $\operatorname{Ind}_{P_{0}}^{G}\operatorname{1}$
. Let
$\operatorname{Ind}_{P_{0}}^{G}\operatorname{1}$
. Let
![]() $dk$
be the measure on
$dk$
be the measure on
![]() $K$
such that
$K$
such that
 $\operatorname{vol}K=1$
. We define the Harish-Chandra function
$\operatorname{vol}K=1$
. We define the Harish-Chandra function
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(g)=\int _{K}e(kg)\,dk=\int _{K}\unicode[STIX]{x1D6FF}_{P_{0}}(m_{0}(kg))^{1/2}\,dk.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(g)=\int _{K}e(kg)\,dk=\int _{K}\unicode[STIX]{x1D6FF}_{P_{0}}(m_{0}(kg))^{1/2}\,dk.\end{eqnarray}$$
This function is bi-
![]() $K$
-invariant. This function depends on the choice of
$K$
-invariant. This function depends on the choice of
![]() $K$
. However, different choices of
$K$
. However, different choices of
![]() $K$
give equivalent functions on
$K$
give equivalent functions on
![]() $G$
. So this choice will not affect our estimates.
$G$
. So this choice will not affect our estimates.
We define a height function on
![]() $G$
. We fix an embedding
$G$
. We fix an embedding
 $\unicode[STIX]{x1D70F}:G\rightarrow \operatorname{GL}_{n}$
. Write
$\unicode[STIX]{x1D70F}:G\rightarrow \operatorname{GL}_{n}$
. Write
 $\unicode[STIX]{x1D70F}(g)=(a_{ij})$
and
$\unicode[STIX]{x1D70F}(g)=(a_{ij})$
and
 $\unicode[STIX]{x1D70F}(g^{-1})=(b_{ij})$
. Define
$\unicode[STIX]{x1D70F}(g^{-1})=(b_{ij})$
. Define
 $$\begin{eqnarray}\unicode[STIX]{x1D70D}(g)=\sup \{1,\log |a_{ij}|,\log |b_{ij}|\mid 1\leqslant i,j\leqslant n\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70D}(g)=\sup \{1,\log |a_{ij}|,\log |b_{ij}|\mid 1\leqslant i,j\leqslant n\}.\end{eqnarray}$$
There is a positive real number
![]() $d$
such that
$d$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{0}(a)^{1/2}\ll \unicode[STIX]{x1D6EF}(a)\ll \unicode[STIX]{x1D6FF}_{0}(a)^{1/2}\unicode[STIX]{x1D70D}(a)^{d},\quad a\in A_{0}^{+}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{0}(a)^{1/2}\ll \unicode[STIX]{x1D6EF}(a)\ll \unicode[STIX]{x1D6FF}_{0}(a)^{1/2}\unicode[STIX]{x1D70D}(a)^{d},\quad a\in A_{0}^{+}.\end{eqnarray}$$
Now let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible admissible tempered representation of
$\unicode[STIX]{x1D70B}$
be an irreducible admissible tempered representation of
![]() $G$
. Let
$G$
. Let
![]() $\unicode[STIX]{x1D6F7}$
be a smooth matrix coefficient of
$\unicode[STIX]{x1D6F7}$
be a smooth matrix coefficient of
![]() $G$
. Then there is a constant
$G$
. Then there is a constant
![]() $B$
such that
$B$
such that
 $$\begin{eqnarray}|\unicode[STIX]{x1D6F7}(g)|\ll \unicode[STIX]{x1D6EF}(g)\unicode[STIX]{x1D70D}(g)^{B}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6F7}(g)|\ll \unicode[STIX]{x1D6EF}(g)\unicode[STIX]{x1D70D}(g)^{B}.\end{eqnarray}$$
This is classical and is called the weak inequality when
![]() $\unicode[STIX]{x1D6F7}$
is
$\unicode[STIX]{x1D6F7}$
is
![]() $K$
-finite and due to [Reference SunSun09] when
$K$
-finite and due to [Reference SunSun09] when
![]() $\unicode[STIX]{x1D6F7}$
is smooth.
$\unicode[STIX]{x1D6F7}$
is smooth.
We finally assume that
 $G=\operatorname{Mp}(2n)$
. This is not an algebraic group, but it behaves in many ways like an algebraic group. In particular, we have a Cartan decomposition for
$G=\operatorname{Mp}(2n)$
. This is not an algebraic group, but it behaves in many ways like an algebraic group. In particular, we have a Cartan decomposition for
![]() $G$
, i.e.
$G$
, i.e.
 $G=KA_{G}^{+}K$
where
$G=KA_{G}^{+}K$
where
![]() $K$
is the inverse image of a special maximal compact subgroup of
$K$
is the inverse image of a special maximal compact subgroup of
![]() $\operatorname{Sp}(2n)$
(e.g.
$\operatorname{Sp}(2n)$
(e.g.
 $\operatorname{Sp}(2n)(\mathfrak{o}_{F})$
if
$\operatorname{Sp}(2n)(\mathfrak{o}_{F})$
if
![]() $F$
is non-archimedean and
$F$
is non-archimedean and
![]() $\operatorname{U}(n)$
is
$\operatorname{U}(n)$
is
![]() $F$
is archimedean) and
$F$
is archimedean) and
![]() $A_{G}^{+}$
is the inverse image of
$A_{G}^{+}$
is the inverse image of
![]() $A_{\operatorname{Sp}(2n)}^{+}$
in
$A_{\operatorname{Sp}(2n)}^{+}$
in
![]() $G$
. We define
$G$
. We define
 $\unicode[STIX]{x1D6EF}_{G}=\unicode[STIX]{x1D6EF}_{\operatorname{Sp}(2n)}\circ p$
where
$\unicode[STIX]{x1D6EF}_{G}=\unicode[STIX]{x1D6EF}_{\operatorname{Sp}(2n)}\circ p$
where
 $p:G\rightarrow \operatorname{Sp}(2n)$
is the canonical projection. Then the weak inequality holds for tempered representations of
$p:G\rightarrow \operatorname{Sp}(2n)$
is the canonical projection. Then the weak inequality holds for tempered representations of
![]() $G$
.
$G$
.
3.2 Some estimates
Lemma 3.2.1. There is a
![]() $d>0$
, such that
$d>0$
, such that
 $$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{-d}\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{-d}\,du\end{eqnarray}$$
is absolutely convergent for all
 $m\in G_{0}$
. Moreover, in this case, there is an
$m\in G_{0}$
. Moreover, in this case, there is an
![]() $\unicode[STIX]{x1D6FD}>0$
so that
$\unicode[STIX]{x1D6FD}>0$
so that
 $$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{-d}\,du\ll \unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}},\quad m\in G_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{-d}\,du\ll \unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}},\quad m\in G_{0}.\end{eqnarray}$$
Proof. In the archimedean case, this is [Har75, § 10, Lemma 2]. In the non-archimedean case, this is [Reference SilbergerSil79, Theorem 4.3.20].◻
Lemma 3.2.2. There is some constant
![]() $c>0$
so that
$c>0$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{G^{i}}(gg^{\prime })\ll \unicode[STIX]{x1D6EF}_{G^{i}}(g)e^{c\unicode[STIX]{x1D70D}(g^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{G^{i}}(gg^{\prime })\ll \unicode[STIX]{x1D6EF}_{G^{i}}(g)e^{c\unicode[STIX]{x1D70D}(g^{\prime })}.\end{eqnarray}$$
In particular, if
![]() $g=1$
, then we have
$g=1$
, then we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(g^{\prime })\gg e^{-c\unicode[STIX]{x1D70D}(g^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(g^{\prime })\gg e^{-c\unicode[STIX]{x1D70D}(g^{\prime })}.\end{eqnarray}$$
Proof. This can be proved by mimicking the argument in [Reference WaldspurgerWal12, § 3.3] and [Reference LiuLiu16, Lemma 3.11]. ◻
Lemma 3.2.3. Fix a real number
![]() $D$
. Then there exists some
$D$
. Then there exists some
![]() $\unicode[STIX]{x1D6FD}>0$
, such that
$\unicode[STIX]{x1D6FD}>0$
, such that
 $$\begin{eqnarray}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\ll \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\quad m\in G^{i+1}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\ll \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\quad m\in G^{i+1}.\end{eqnarray}$$
Proof. We fix some real number
![]() $b$
to be determined later. We denote the left-hand side of the inequality by
$b$
to be determined later. We denote the left-hand side of the inequality by
![]() $I$
. Then,
$I$
. Then,
 $I=I_{{<}b}+I_{{\geqslant}b}$
with
$I=I_{{<}b}+I_{{\geqslant}b}$
with
 $$\begin{eqnarray}\displaystyle I_{{<}b} & = & \displaystyle \int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}<b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\nonumber\\ \displaystyle I_{{\geqslant}b} & = & \displaystyle \int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{{<}b} & = & \displaystyle \int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}<b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\nonumber\\ \displaystyle I_{{\geqslant}b} & = & \displaystyle \int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du,\nonumber\end{eqnarray}$$
where
![]() $\operatorname{1}_{\unicode[STIX]{x1D70D}<b}$
is the characteristic function of
$\operatorname{1}_{\unicode[STIX]{x1D70D}<b}$
is the characteristic function of
 $\{u\in N_{i+1}\cap G^{i}\mid \unicode[STIX]{x1D70D}(u)<b\}$
and
$\{u\in N_{i+1}\cap G^{i}\mid \unicode[STIX]{x1D70D}(u)<b\}$
and
![]() $\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}$
is the characteristic function of
$\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}$
is the characteristic function of
 $\{u\in N_{i+1}\cap G^{i}\mid \unicode[STIX]{x1D70D}(u)\geqslant b\}$
.
$\{u\in N_{i+1}\cap G^{i}\mid \unicode[STIX]{x1D70D}(u)\geqslant b\}$
.
By Lemma 3.2.1, we have
 $$\begin{eqnarray}\displaystyle I_{{<}b} & \ll & \displaystyle b^{d}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}<b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D-d}\,du\nonumber\\ \displaystyle & \ll & \displaystyle b^{d}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{{<}b} & \ll & \displaystyle b^{d}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}<b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D-d}\,du\nonumber\\ \displaystyle & \ll & \displaystyle b^{d}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FD}_{1}$
is a positive real number and
$\unicode[STIX]{x1D6FD}_{1}$
is a positive real number and
![]() $d$
is a positive real number so that the integral
$d$
is a positive real number so that the integral
 $$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D-d}\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D-d}\,du\end{eqnarray}$$
is convergent.
Let
 $\unicode[STIX]{x1D706}:N_{i+1}\cap G^{i}\rightarrow F$
be a character defined by
$\unicode[STIX]{x1D706}:N_{i+1}\cap G^{i}\rightarrow F$
be a character defined by
 $\unicode[STIX]{x1D706}(n)=q_{2}(ne_{m-i}^{\ast },e_{m-i-1})$
. Then by [Reference Beuzart-PlessisBeu15, Corollary B.3.1], there is an
$\unicode[STIX]{x1D706}(n)=q_{2}(ne_{m-i}^{\ast },e_{m-i-1})$
. Then by [Reference Beuzart-PlessisBeu15, Corollary B.3.1], there is an
![]() $\unicode[STIX]{x1D716}>0$
, such that the integral
$\unicode[STIX]{x1D716}>0$
, such that the integral
 $$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(u)e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}\unicode[STIX]{x1D70D}(u)^{D}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(u)e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}\unicode[STIX]{x1D70D}(u)^{D}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\end{eqnarray}$$
is convergent. We have
 $\unicode[STIX]{x1D6EF}_{G^{i}}(um)\ll e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)}\unicode[STIX]{x1D6EF}_{G^{i}}(u)$
for some
$\unicode[STIX]{x1D6EF}_{G^{i}}(um)\ll e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)}\unicode[STIX]{x1D6EF}_{G^{i}}(u)$
for some
![]() $\unicode[STIX]{x1D6FC}>0$
, cf. Lemma 3.2.2. It follows that
$\unicode[STIX]{x1D6FC}>0$
, cf. Lemma 3.2.2. It follows that
 $$\begin{eqnarray}\displaystyle I_{{\geqslant}b} & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}e^{-\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{{\geqslant}b} & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)}\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}e^{-\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\int _{N_{i+1,\unicode[STIX]{x1D6FE}}\cap G^{i}}\operatorname{1}_{\unicode[STIX]{x1D70D}\geqslant b}(u)\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\int _{N_{i+1}\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(u)\unicode[STIX]{x1D70D}(u)^{D}e^{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70D}(u)}(1+|\unicode[STIX]{x1D706}(u)|)^{-1}\,du\nonumber\\ \displaystyle & \ll & \displaystyle e^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}}).\nonumber\end{eqnarray}$$
There is a constant
![]() $c>0$
, such that
$c>0$
, such that
 $\unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\gg e^{-c\unicode[STIX]{x1D70D}(m)}$
, then we have
$\unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\gg e^{-c\unicode[STIX]{x1D70D}(m)}$
, then we have
 $$\begin{eqnarray}I\ll b^{d}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}+e^{(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
$$\begin{eqnarray}I\ll b^{d}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m)\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}+e^{(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m)-\unicode[STIX]{x1D716}b}(1+e^{\unicode[STIX]{x1D6FE}})\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
We may thus choose
 $b=\unicode[STIX]{x1D716}^{-1}(\log (1+e^{\unicode[STIX]{x1D6FE}})+(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m))$
and get
$b=\unicode[STIX]{x1D716}^{-1}(\log (1+e^{\unicode[STIX]{x1D6FE}})+(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m))$
and get
 $$\begin{eqnarray}I\ll (\unicode[STIX]{x1D716}^{-d}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}(\unicode[STIX]{x1D6FE}+(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m))^{d}+1)\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
$$\begin{eqnarray}I\ll (\unicode[STIX]{x1D716}^{-d}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}_{1}}(\unicode[STIX]{x1D6FE}+(\unicode[STIX]{x1D6FC}+c)\unicode[STIX]{x1D70D}(m))^{d}+1)\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
Note that
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}_{1}$
,
$\unicode[STIX]{x1D6FD}_{1}$
,
![]() $d$
and
$d$
and
![]() $c$
are constants which are independent of
$c$
are constants which are independent of
![]() $\unicode[STIX]{x1D6FE}$
or
$\unicode[STIX]{x1D6FE}$
or
![]() $m$
. We therefore conclude that there is some
$m$
. We therefore conclude that there is some
![]() $\unicode[STIX]{x1D6FD}>0$
, such that
$\unicode[STIX]{x1D6FD}>0$
, such that
 $$\begin{eqnarray}I\ll \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
$$\begin{eqnarray}I\ll \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m).\end{eqnarray}$$
This proves the lemma.◻
Lemma 3.2.4. Fix a real number
![]() $D$
. Then there is some
$D$
. Then there is some
![]() $\unicode[STIX]{x1D6FD}>0$
such that
$\unicode[STIX]{x1D6FD}>0$
such that
 $$\begin{eqnarray}\int _{N_{i+1,-\infty }\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\ll \unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\quad m\in G^{i+1}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{i+1,-\infty }\cap G^{i}}\unicode[STIX]{x1D6EF}_{G^{i}}(um)\unicode[STIX]{x1D70D}(u)^{D}\,du\ll \unicode[STIX]{x1D70D}(m)^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G^{i+1}}(m),\quad m\in G^{i+1}.\end{eqnarray}$$
Proof. Choose a subgroup
![]() $N^{\dagger }$
of
$N^{\dagger }$
of
 $N_{i+1}\cap G^{i}$
so that the multiplication map
$N_{i+1}\cap G^{i}$
so that the multiplication map
 $N^{\dagger }\times (N_{i+1,-\infty }\cap G^{i})\rightarrow N_{i+1}\cap G^{i}$
is an isomorphism. Recall that
$N^{\dagger }\times (N_{i+1,-\infty }\cap G^{i})\rightarrow N_{i+1}\cap G^{i}$
is an isomorphism. Recall that
![]() $\unicode[STIX]{x1D6EF}_{G^{i}}$
is itself a matrix coefficient of a (unitary) tempered representation which we temporarily denote by
$\unicode[STIX]{x1D6EF}_{G^{i}}$
is itself a matrix coefficient of a (unitary) tempered representation which we temporarily denote by
![]() $e$
. Thus
$e$
. Thus
 $\unicode[STIX]{x1D6EF}_{G^{i}}(g)=\langle e(g)v,v^{\vee }\rangle$
where
$\unicode[STIX]{x1D6EF}_{G^{i}}(g)=\langle e(g)v,v^{\vee }\rangle$
where
![]() $\langle -,-\rangle$
is the inner product on
$\langle -,-\rangle$
is the inner product on
![]() $e$
and
$e$
and
 $v,v^{\vee }\in e$
. It follows from the Dixmier–Milliavin theorem [Reference Dixmier and MalliavinDM78] that
$v,v^{\vee }\in e$
. It follows from the Dixmier–Milliavin theorem [Reference Dixmier and MalliavinDM78] that
![]() $v^{\vee }$
is a finite linear combination of the elements of the form
$v^{\vee }$
is a finite linear combination of the elements of the form
 $$\begin{eqnarray}\int _{N_{\dagger }}f(n)e(n^{-1})v^{\prime \vee }\,dn,\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{\dagger }}f(n)e(n^{-1})v^{\prime \vee }\,dn,\end{eqnarray}$$
where
 $f\in {\mathcal{C}}_{c}^{\infty }(N_{\dagger })$
. Thus
$f\in {\mathcal{C}}_{c}^{\infty }(N_{\dagger })$
. Thus
![]() $\unicode[STIX]{x1D6EF}_{G^{i}}$
is a finite linear combination of the functions of the form
$\unicode[STIX]{x1D6EF}_{G^{i}}$
is a finite linear combination of the functions of the form
 $$\begin{eqnarray}g\mapsto \int _{N^{\dagger }}f(n)\unicode[STIX]{x1D6F7}(ng)\,dn,\end{eqnarray}$$
$$\begin{eqnarray}g\mapsto \int _{N^{\dagger }}f(n)\unicode[STIX]{x1D6F7}(ng)\,dn,\end{eqnarray}$$
where
![]() $f(n)$
is a compactly supported function on
$f(n)$
is a compactly supported function on
![]() $N^{\dagger }$
and
$N^{\dagger }$
and
![]() $\unicode[STIX]{x1D6F7}$
is a smooth matrix coefficient of a tempered representation of
$\unicode[STIX]{x1D6F7}$
is a smooth matrix coefficient of a tempered representation of
![]() $G^{i}$
, namely
$G^{i}$
, namely
![]() $e$
. The lemma then follows from Lemma 3.2.3.◻
$e$
. The lemma then follows from Lemma 3.2.3.◻
Lemma 3.2.5. Let
![]() $f$
be a nonnegative function on
$f$
be a nonnegative function on
![]() $L^{\ast }$
such that
$L^{\ast }$
such that
 $P(x)f(x)$
is bounded for any polynomial function
$P(x)f(x)$
is bounded for any polynomial function
![]() $P(x)$
on
$P(x)$
on
![]() $L^{\ast }$
(e.g.
$L^{\ast }$
(e.g.
![]() $f$
is compactly supported). Let
$f$
is compactly supported). Let
 $p:H\rtimes G_{0}\rightarrow L^{\ast }$
be the projection given by
$p:H\rtimes G_{0}\rightarrow L^{\ast }$
be the projection given by
 $$\begin{eqnarray}hg_{0}\mapsto \mathop{\sum }_{i=1}^{n}q_{2}(hg_{0}e_{n+1}^{\ast },e_{i})e_{i}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}hg_{0}\mapsto \mathop{\sum }_{i=1}^{n}q_{2}(hg_{0}e_{n+1}^{\ast },e_{i})e_{i}^{\ast }.\end{eqnarray}$$
Then there is a real number
![]() $B$
such that
$B$
such that
 $$\begin{eqnarray}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})f(p(hg_{0}))\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\unicode[STIX]{x1D70D}(g_{0})^{B},\quad g_{0}\in G_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})f(p(hg_{0}))\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\unicode[STIX]{x1D70D}(g_{0})^{B},\quad g_{0}\in G_{0}.\end{eqnarray}$$
Proof. By the Cartan decomposition of
![]() $G_{0}$
, we may assume that
$G_{0}$
, we may assume that
 $g=d(a)$
where
$g=d(a)$
where
 $a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
,
$a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
,
 $|a_{n}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1$
. Then
$|a_{n}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1$
. Then
 $p(h(l+l^{\ast },t)d(a))=l^{\ast }\text{}\underline{a}$
where
$p(h(l+l^{\ast },t)d(a))=l^{\ast }\text{}\underline{a}$
where
 $\text{}\underline{a}=\operatorname{diag}[a_{n},\ldots ,a_{1}]$
.
$\text{}\underline{a}=\operatorname{diag}[a_{n},\ldots ,a_{1}]$
.
We fix some
![]() $\unicode[STIX]{x1D6FE}$
which will be determined later. Let
$\unicode[STIX]{x1D6FE}$
which will be determined later. Let
 $H_{\unicode[STIX]{x1D6FE}}=H\cap N_{m,\unicode[STIX]{x1D6FE}}$
and
$H_{\unicode[STIX]{x1D6FE}}=H\cap N_{m,\unicode[STIX]{x1D6FE}}$
and
![]() $H^{\unicode[STIX]{x1D6FE}}$
be the complement of
$H^{\unicode[STIX]{x1D6FE}}$
be the complement of
![]() $H_{\unicode[STIX]{x1D6FE}}$
in
$H_{\unicode[STIX]{x1D6FE}}$
in
![]() $H$
. Then
$H$
. Then
 $$\begin{eqnarray}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh=\int _{H_{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh+\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh=\int _{H_{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh+\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh.\end{eqnarray}$$
By Lemma 3.2.3, the first integral is bounded by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{B}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{B}.\end{eqnarray}$$
Write
 $l^{\ast }=(l_{1}^{\ast },\ldots ,l_{n}^{\ast })$
and
$l^{\ast }=(l_{1}^{\ast },\ldots ,l_{n}^{\ast })$
and
 $l^{\prime \ast }=(0,l_{2}^{\ast },\ldots ,l_{n}^{\ast })\in F^{n}$
. Then
$l^{\prime \ast }=(0,l_{2}^{\ast },\ldots ,l_{n}^{\ast })\in F^{n}$
. Then
 $$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})f(l^{\ast }\text{}\underline{a})\,dh=\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a)h(l_{1}^{\ast }a_{n},0,\ldots ,0))f(l^{\ast }\text{}\underline{a})\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})f(l^{\ast }\text{}\underline{a})\,dh=\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a)h(l_{1}^{\ast }a_{n},0,\ldots ,0))f(l^{\ast }\text{}\underline{a})\,dh.\end{eqnarray}$$
There is some positive constant
![]() $\unicode[STIX]{x1D6FC}$
such that
$\unicode[STIX]{x1D6FC}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a)h(l_{1}^{\ast }a_{n},0))\ll \unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a))e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a)h(l_{1}^{\ast }a_{n},0))\ll \unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\prime \ast },t)d(a))e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh\ll \int _{H_{-\infty }}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))\,dh\times \int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l^{\ast }\text{}\underline{a})\,dh\ll \int _{H_{-\infty }}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))\,dh\times \int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast },\end{eqnarray}$$
where
![]() $f_{1}$
is a function on
$f_{1}$
is a function on
![]() $F$
such that
$F$
such that
 $f_{1}(x)P(x)$
is bounded for any polynomial function
$f_{1}(x)P(x)$
is bounded for any polynomial function
![]() $P$
on
$P$
on
![]() $F$
. It follows from Lemma 3.2.4 that there is a positive real number
$F$
. It follows from Lemma 3.2.4 that there is a positive real number
![]() $D$
such that
$D$
such that
 $$\begin{eqnarray}\int _{H_{-\infty }}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{D}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{-\infty }}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{D}.\end{eqnarray}$$
Since
 $f_{1}(x)P(x)$
is bounded for any polynomial function
$f_{1}(x)P(x)$
is bounded for any polynomial function
![]() $P$
on
$P$
on
![]() $F$
, we have
$F$
, we have
 $$\begin{eqnarray}\int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast }\ll |a_{n}|^{-1}e^{-\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
$$\begin{eqnarray}\int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast }\ll |a_{n}|^{-1}e^{-\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
where the implicit constant in
![]() $\ll$
does not depend on
$\ll$
does not depend on
![]() $a_{n}$
or
$a_{n}$
or
![]() $\unicode[STIX]{x1D6FE}$
. We may choose
$\unicode[STIX]{x1D6FE}$
. We may choose
![]() $\unicode[STIX]{x1D6FE}$
with
$\unicode[STIX]{x1D6FE}$
with
 $\unicode[STIX]{x1D6FE}>-\!\log |a_{n}|$
. Then
$\unicode[STIX]{x1D6FE}>-\!\log |a_{n}|$
. Then
 $$\begin{eqnarray}\int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast }\ll 1.\end{eqnarray}$$
$$\begin{eqnarray}\int _{|l_{1}^{\ast }a_{n}|\geqslant e^{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FC}\log \max \{|l_{1}^{\ast }a_{n}|,1\}}f_{1}(l_{1}^{\ast }a_{n})\,dl_{1}^{\ast }\ll 1.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l\text{}\underline{a})\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{D}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H^{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6EF}_{G_{1}}(hd(a))f(l\text{}\underline{a})\,dh\ll \unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D70D}(d(a))^{D}.\end{eqnarray}$$
The desired estimate then follows.◻
Lemma 3.2.6. Let
![]() $\unicode[STIX]{x1D6F7}$
be a smooth matrix coefficient of a tempered representation
$\unicode[STIX]{x1D6F7}$
be a smooth matrix coefficient of a tempered representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G_{2}$
. Then the limit
$G_{2}$
. Then the limit
 $$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\quad g\in G_{2}\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\quad g\in G_{2}\end{eqnarray}$$
exists and defines a continuous function in
![]() $\unicode[STIX]{x1D713}_{r-1}$
(for a fixed
$\unicode[STIX]{x1D713}_{r-1}$
(for a fixed
![]() $g$
). If
$g$
). If
![]() $F$
is non-archimedean, then the integral is in fact a constant for sufficiently large
$F$
is non-archimedean, then the integral is in fact a constant for sufficiently large
![]() $\unicode[STIX]{x1D6FE}$
. Moreover if
$\unicode[STIX]{x1D6FE}$
. Moreover if
![]() $g\in G_{1}$
, then
$g\in G_{1}$
, then
 $$\begin{eqnarray}\biggl|\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\biggr|\ll \unicode[STIX]{x1D6EF}_{G_{1}}(g)\unicode[STIX]{x1D70D}(g)^{D}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\biggr|\ll \unicode[STIX]{x1D6EF}_{G_{1}}(g)\unicode[STIX]{x1D70D}(g)^{D}.\end{eqnarray}$$
Proof. First recall that
![]() $N_{r-1}$
is the unipotent subgroup of some parabolic subgroup
$N_{r-1}$
is the unipotent subgroup of some parabolic subgroup
![]() $P_{r-1}$
of
$P_{r-1}$
of
![]() $G_{2}$
, the Levi part being isomorphic to
$G_{2}$
, the Levi part being isomorphic to
 $G_{1}\times \operatorname{GL}_{1}^{r-1}$
. Put
$G_{1}\times \operatorname{GL}_{1}^{r-1}$
. Put
 $T=\operatorname{GL}_{1}^{r-1}$
and denote an element in
$T=\operatorname{GL}_{1}^{r-1}$
and denote an element in
![]() $T$
by
$T$
by
 $a=(a_{1},\ldots ,a_{r-1})$
where
$a=(a_{1},\ldots ,a_{r-1})$
where
 $a_{i}\in F^{\times }$
.
$a_{i}\in F^{\times }$
.
If
![]() $F$
is non-archimedean, the constancy of the integral when
$F$
is non-archimedean, the constancy of the integral when
![]() $\unicode[STIX]{x1D6FE}$
is large can be proved in the same way as [Reference WaldspurgerWal12, Lemma 3.5]. In fact, suppose that
$\unicode[STIX]{x1D6FE}$
is large can be proved in the same way as [Reference WaldspurgerWal12, Lemma 3.5]. In fact, suppose that
 $\unicode[STIX]{x1D6F7}(g)=\langle \unicode[STIX]{x1D70B}(g)v,v^{\vee }\rangle$
where
$\unicode[STIX]{x1D6F7}(g)=\langle \unicode[STIX]{x1D70B}(g)v,v^{\vee }\rangle$
where
![]() $v\in \unicode[STIX]{x1D70B}$
,
$v\in \unicode[STIX]{x1D70B}$
,
 $v^{\vee }\in \unicode[STIX]{x1D70B}^{\vee }$
and
$v^{\vee }\in \unicode[STIX]{x1D70B}^{\vee }$
and
![]() $\langle -,-\rangle$
stands for the pairing between
$\langle -,-\rangle$
stands for the pairing between
![]() $\unicode[STIX]{x1D70B}$
and its contragradient
$\unicode[STIX]{x1D70B}$
and its contragradient
![]() $\unicode[STIX]{x1D70B}^{\vee }$
. Suppose that
$\unicode[STIX]{x1D70B}^{\vee }$
. Suppose that
![]() $K^{\prime }$
is an open compact subgroup of
$K^{\prime }$
is an open compact subgroup of
![]() $G_{2}$
such that
$G_{2}$
such that
![]() $v$
and
$v$
and
![]() $v^{\vee }$
are fixed by
$v^{\vee }$
are fixed by
![]() $K^{\prime }$
. Let
$K^{\prime }$
. Let
 $K^{\prime \prime }=K^{\prime }\cap gK^{\prime }g^{-1}$
. This is an open compact subgroup of
$K^{\prime \prime }=K^{\prime }\cap gK^{\prime }g^{-1}$
. This is an open compact subgroup of
![]() $G_{2}$
. Let
$G_{2}$
. Let
![]() $c>0$
and
$c>0$
and
![]() $T_{c}$
be the subgroup of
$T_{c}$
be the subgroup of
![]() $T$
consisting of elements
$T$
consisting of elements
 $a=(a_{1},\ldots ,a_{r-1})$
so that
$a=(a_{1},\ldots ,a_{r-1})$
so that
 $|a_{i}-1|\leqslant e^{-c}$
for all
$|a_{i}-1|\leqslant e^{-c}$
for all
![]() $i$
. The intersection
$i$
. The intersection
![]() $T\cap K^{\prime \prime }$
is an open subgroup of
$T\cap K^{\prime \prime }$
is an open subgroup of
![]() $T$
. Moreover,
$T$
. Moreover,
![]() $\unicode[STIX]{x1D70B}(g)v$
and
$\unicode[STIX]{x1D70B}(g)v$
and
![]() $v^{\vee }$
are both fixed by
$v^{\vee }$
are both fixed by
![]() $T\cap K^{\prime \prime }$
. Thus there is some
$T\cap K^{\prime \prime }$
. Thus there is some
 $c(g)>0$
depending on
$c(g)>0$
depending on
![]() $g$
, and
$g$
, and
 $c(g)\simeq \unicode[STIX]{x1D70D}(g)$
, such that
$c(g)\simeq \unicode[STIX]{x1D70D}(g)$
, such that
![]() $\unicode[STIX]{x1D70B}(g)v$
and
$\unicode[STIX]{x1D70B}(g)v$
and
![]() $v^{\vee }$
are fixed by
$v^{\vee }$
are fixed by
![]() $T_{c(g)}$
. We have
$T_{c(g)}$
. We have
 $$\begin{eqnarray}\displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn & = & \displaystyle \int _{N_{r-1},\unicode[STIX]{x1D6FE}}\int _{T_{c(g)}}\langle \unicode[STIX]{x1D70B}(a^{-1}nag)v,v^{\vee }\rangle \overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,da\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1},\unicode[STIX]{x1D6FE}}\langle \unicode[STIX]{x1D70B}(ng)v,v^{\vee }\rangle \biggl(\int _{T_{c(g)}}\overline{\unicode[STIX]{x1D713}_{r-1}(ana^{-1})}\,da\biggr)\,dn.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn & = & \displaystyle \int _{N_{r-1},\unicode[STIX]{x1D6FE}}\int _{T_{c(g)}}\langle \unicode[STIX]{x1D70B}(a^{-1}nag)v,v^{\vee }\rangle \overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,da\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1},\unicode[STIX]{x1D6FE}}\langle \unicode[STIX]{x1D70B}(ng)v,v^{\vee }\rangle \biggl(\int _{T_{c(g)}}\overline{\unicode[STIX]{x1D713}_{r-1}(ana^{-1})}\,da\biggr)\,dn.\nonumber\end{eqnarray}$$
There is some
![]() $c^{\prime }(g)$
,
$c^{\prime }(g)$
,
 $c^{\prime }(g)\simeq \unicode[STIX]{x1D70D}(g)$
, so that if
$c^{\prime }(g)\simeq \unicode[STIX]{x1D70D}(g)$
, so that if
 $\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
and
$\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
and
 $n\in N_{r-1,\unicode[STIX]{x1D6FE}}\backslash N_{r-1,c^{\prime }(g)}$
, then the inner integral vanishes. It follows that if
$n\in N_{r-1,\unicode[STIX]{x1D6FE}}\backslash N_{r-1,c^{\prime }(g)}$
, then the inner integral vanishes. It follows that if
 $\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
, then
$\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
, then
 $$\begin{eqnarray}\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn=\int _{N_{r-1,c^{\prime }(g)}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn=\int _{N_{r-1,c^{\prime }(g)}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn.\end{eqnarray}$$
It also follows, by Lemma 3.2.3, that if
 $\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
, then there is some
$\unicode[STIX]{x1D6FE}>c^{\prime }(g)$
, then there is some
![]() $D>0$
so that
$D>0$
so that
 $$\begin{eqnarray}\biggl|\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\biggr|\ll c^{\prime }(g)^{D}\unicode[STIX]{x1D6EF}_{G_{1}}(g)\unicode[STIX]{x1D70D}(g)^{D},\quad g\in G_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(g)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\biggr|\ll c^{\prime }(g)^{D}\unicode[STIX]{x1D6EF}_{G_{1}}(g)\unicode[STIX]{x1D70D}(g)^{D},\quad g\in G_{1}.\end{eqnarray}$$
As
 $c^{\prime }(g)\simeq \unicode[STIX]{x1D70D}(g)$
, we get the desired estimate (possibly for some larger
$c^{\prime }(g)\simeq \unicode[STIX]{x1D70D}(g)$
, we get the desired estimate (possibly for some larger
![]() $D$
). This proves the lemma in the non-archimedean case.
$D$
). This proves the lemma in the non-archimedean case.
From now on we assume that
![]() $F$
is archimedean.
$F$
is archimedean.
To simplify notation, we put
 $$\begin{eqnarray}I(\unicode[STIX]{x1D6FE},g,\unicode[STIX]{x1D6F7})=\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\quad g\in G_{1}.\end{eqnarray}$$
$$\begin{eqnarray}I(\unicode[STIX]{x1D6FE},g,\unicode[STIX]{x1D6F7})=\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(ng)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\quad g\in G_{1}.\end{eqnarray}$$
Note that to prove the limit exists, we may even assume that
![]() $g=1$
. By the Dixmier–Malliavin theorem, it is enough to prove the lemma for
$g=1$
. By the Dixmier–Malliavin theorem, it is enough to prove the lemma for
 $\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }I(\unicode[STIX]{x1D6FE},g,f\ast \unicode[STIX]{x1D6F7})$
where
$\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }I(\unicode[STIX]{x1D6FE},g,f\ast \unicode[STIX]{x1D6F7})$
where
 $f\in {\mathcal{C}}_{c}^{\infty }(T)$
and
$f\in {\mathcal{C}}_{c}^{\infty }(T)$
and
 $$\begin{eqnarray}f\ast \unicode[STIX]{x1D6F7}(g)=\int _{T}f(t)\unicode[STIX]{x1D6F7}(t^{-1}gt)\,dt\end{eqnarray}$$
$$\begin{eqnarray}f\ast \unicode[STIX]{x1D6F7}(g)=\int _{T}f(t)\unicode[STIX]{x1D6F7}(t^{-1}gt)\,dt\end{eqnarray}$$
is a function on
![]() $G_{2}$
. When there is no confusion, we write
$G_{2}$
. When there is no confusion, we write
 $I(\unicode[STIX]{x1D6FE})=I(\unicode[STIX]{x1D6FE},g,f\ast \unicode[STIX]{x1D6F7})$
for short.
$I(\unicode[STIX]{x1D6FE})=I(\unicode[STIX]{x1D6FE},g,f\ast \unicode[STIX]{x1D6F7})$
for short.
Let
 $(x_{1},\ldots ,x_{r-1})\in F^{r-1}$
and
$(x_{1},\ldots ,x_{r-1})\in F^{r-1}$
and
 $n(x_{1},\ldots ,x_{r-1})\in N_{r-1}$
so that
$n(x_{1},\ldots ,x_{r-1})\in N_{r-1}$
so that
 $n(x_{1},\ldots ,n_{r-1})e_{n+i}^{\ast }=e_{n+i}^{\ast }+x_{i-1}e_{n+i-1}^{\ast }$
for
$n(x_{1},\ldots ,n_{r-1})e_{n+i}^{\ast }=e_{n+i}^{\ast }+x_{i-1}e_{n+i-1}^{\ast }$
for
 $i=2,\ldots ,r$
. Let
$i=2,\ldots ,r$
. Let
 $N_{\dagger }=\{n(x_{1},\ldots ,x_{r-1})\mid (x_{1},\ldots ,x_{r-1})\in F^{r-1}\}$
. It is a subgroup of
$N_{\dagger }=\{n(x_{1},\ldots ,x_{r-1})\mid (x_{1},\ldots ,x_{r-1})\in F^{r-1}\}$
. It is a subgroup of
![]() $N_{r-1}$
which is stable under the conjugation by
$N_{r-1}$
which is stable under the conjugation by
![]() $T$
and the multiplication map
$T$
and the multiplication map
 $N_{\dagger }\times N_{r-1,-\infty }\rightarrow N_{r-1}$
is an isomorphism. Let
$N_{\dagger }\times N_{r-1,-\infty }\rightarrow N_{r-1}$
is an isomorphism. Let
 $N_{\dagger ,\unicode[STIX]{x1D6FE}}=N_{\dagger }\cap N_{r-1,\unicode[STIX]{x1D6FE}}$
. We denote by
$N_{\dagger ,\unicode[STIX]{x1D6FE}}=N_{\dagger }\cap N_{r-1,\unicode[STIX]{x1D6FE}}$
. We denote by
![]() $\widehat{N_{\dagger }}$
the group of additive characters of
$\widehat{N_{\dagger }}$
the group of additive characters of
![]() $N_{\dagger }$
and by
$N_{\dagger }$
and by
![]() $\widehat{N_{\dagger }}^{\text{reg}}$
the open subset consisting of generic characters. Then
$\widehat{N_{\dagger }}^{\text{reg}}$
the open subset consisting of generic characters. Then
 $\unicode[STIX]{x1D713}_{r-1}\in \widehat{N_{\dagger }}^{\text{reg}}$
. Let
$\unicode[STIX]{x1D713}_{r-1}\in \widehat{N_{\dagger }}^{\text{reg}}$
. Let
![]() $\unicode[STIX]{x1D713}^{t}$
be the character of
$\unicode[STIX]{x1D713}^{t}$
be the character of
![]() $N_{\dagger }$
defined by
$N_{\dagger }$
defined by
 $\unicode[STIX]{x1D713}^{t}(n)=\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})$
. The map
$\unicode[STIX]{x1D713}^{t}(n)=\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})$
. The map
![]() $t\mapsto \unicode[STIX]{x1D713}^{t}$
defines a homeomorphism from
$t\mapsto \unicode[STIX]{x1D713}^{t}$
defines a homeomorphism from
![]() $T$
to
$T$
to
![]() $\widehat{N_{\dagger }}^{\text{reg}}$
. A compactly supported function on
$\widehat{N_{\dagger }}^{\text{reg}}$
. A compactly supported function on
![]() $T$
is then identified with a compactly supported function on
$T$
is then identified with a compactly supported function on
![]() $\widehat{N_{\dagger }}^{\text{reg}}$
. We may thus talk about the Fourier transform of
$\widehat{N_{\dagger }}^{\text{reg}}$
. We may thus talk about the Fourier transform of
![]() $f$
, which is a Schwartz function on
$f$
, which is a Schwartz function on
![]() $N_{\dagger }$
. Let
$N_{\dagger }$
. Let
 $t_{1},\ldots ,t_{r-1}\in F^{\times }$
and
$t_{1},\ldots ,t_{r-1}\in F^{\times }$
and
![]() $t\in T$
so that
$t\in T$
so that
 $tn(x_{1},\ldots ,x_{r-1})t^{-1}=n(t_{1}x_{1},\ldots ,t_{r-1}x_{r-1})$
. The measure
$tn(x_{1},\ldots ,x_{r-1})t^{-1}=n(t_{1}x_{1},\ldots ,t_{r-1}x_{r-1})$
. The measure
 $|t_{1}\ldots t_{r-1}|\,dt$
is, up to a positive constant, the restriction of the self-dual measure of
$|t_{1}\ldots t_{r-1}|\,dt$
is, up to a positive constant, the restriction of the self-dual measure of
![]() $\widehat{N}$
to
$\widehat{N}$
to
![]() $\widehat{N}^{\text{reg}}$
under this homeomorphism. We may assume that the constant is one.
$\widehat{N}^{\text{reg}}$
under this homeomorphism. We may assume that the constant is one.
We have
 $$\begin{eqnarray}\displaystyle I(\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\int _{T}f(t)\unicode[STIX]{x1D6F7}(t^{-1}ntg)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dt\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1}}\int _{T}f(t)\operatorname{1}_{N_{r-1,\unicode[STIX]{x1D6FE}}}(n)\unicode[STIX]{x1D6F7}(t^{-1}ntg)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dt\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\biggl(\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr)\biggl(\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\biggr)\,dn,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\int _{T}f(t)\unicode[STIX]{x1D6F7}(t^{-1}ntg)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dt\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1}}\int _{T}f(t)\operatorname{1}_{N_{r-1,\unicode[STIX]{x1D6FE}}}(n)\unicode[STIX]{x1D6F7}(t^{-1}ntg)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dt\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\biggl(\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr)\biggl(\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\biggr)\,dn,\end{eqnarray}$$
where in the last identity, we have made the change of variable
 $n\mapsto tnt^{-1}$
and split the integral over
$n\mapsto tnt^{-1}$
and split the integral over
![]() $N_{r-1}$
as a double integral over
$N_{r-1}$
as a double integral over
 $N_{\dagger }\times N_{r-1,-\infty }$
.
$N_{\dagger }\times N_{r-1,-\infty }$
.
We claim that there is a constant
![]() $C$
which does not depend on
$C$
which does not depend on
![]() $\unicode[STIX]{x1D6FE}$
so that
$\unicode[STIX]{x1D6FE}$
so that
 $$\begin{eqnarray}\biggl|\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr|\leqslant C\mathop{\prod }_{i=1}^{r-1}\max \{1,|x_{i}|\}^{-1},\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr|\leqslant C\mathop{\prod }_{i=1}^{r-1}\max \{1,|x_{i}|\}^{-1},\end{eqnarray}$$
where
 $n=n(x_{1},\ldots ,x_{r-1})\in N_{\dagger }$
. In fact, we integrate
$n=n(x_{1},\ldots ,x_{r-1})\in N_{\dagger }$
. In fact, we integrate
![]() $t_{i}\in F^{\times }$
with
$t_{i}\in F^{\times }$
with
![]() $|x_{i}|\leqslant 1$
via integration by parts. The anti-derivative of
$|x_{i}|\leqslant 1$
via integration by parts. The anti-derivative of
 $\operatorname{1}_{\{|\cdot |\leqslant e^{\unicode[STIX]{x1D6FE}}\}}(xt)\unicode[STIX]{x1D713}(xt)$
is a function of the form
$\operatorname{1}_{\{|\cdot |\leqslant e^{\unicode[STIX]{x1D6FE}}\}}(xt)\unicode[STIX]{x1D713}(xt)$
is a function of the form
 $|x|^{-1}X_{\unicode[STIX]{x1D6FE}}(xt)$
where
$|x|^{-1}X_{\unicode[STIX]{x1D6FE}}(xt)$
where
![]() $X_{\unicode[STIX]{x1D6FE}}$
is bounded by a constant independent of
$X_{\unicode[STIX]{x1D6FE}}$
is bounded by a constant independent of
![]() $\unicode[STIX]{x1D6FE}$
. It then follows that
$\unicode[STIX]{x1D6FE}$
. It then follows that
 $$\begin{eqnarray}\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt=\int _{F^{r-1}}\mathop{\prod }_{i:|x_{i}|\leqslant 1}|x_{i}|^{-1}X_{\unicode[STIX]{x1D6FE}}(x_{i}t_{i})\unicode[STIX]{x2202}f_{1}(t_{1},\ldots ,t_{r-1})\,dt,\end{eqnarray}$$
$$\begin{eqnarray}\int _{T}f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt=\int _{F^{r-1}}\mathop{\prod }_{i:|x_{i}|\leqslant 1}|x_{i}|^{-1}X_{\unicode[STIX]{x1D6FE}}(x_{i}t_{i})\unicode[STIX]{x2202}f_{1}(t_{1},\ldots ,t_{r-1})\,dt,\end{eqnarray}$$
where
 $f_{1}(t_{1},\ldots ,t_{r-1})=f(t_{1},\ldots ,t_{r-1})|t_{1}\cdots t_{r-1}|^{-1}$
and
$f_{1}(t_{1},\ldots ,t_{r-1})=f(t_{1},\ldots ,t_{r-1})|t_{1}\cdots t_{r-1}|^{-1}$
and
![]() $\unicode[STIX]{x2202}f_{1}$
is the partial derivative of
$\unicode[STIX]{x2202}f_{1}$
is the partial derivative of
![]() $f_{1}$
with respect to all
$f_{1}$
with respect to all
![]() $t_{i}$
such that
$t_{i}$
such that
![]() $|x_{i}|\leqslant 1$
. As
$|x_{i}|\leqslant 1$
. As
![]() $f$
, so
$f$
, so
![]() $f_{1}$
, are in
$f_{1}$
, are in
![]() ${\mathcal{C}}_{c}^{\infty }(T)$
, and
${\mathcal{C}}_{c}^{\infty }(T)$
, and
![]() $X_{\unicode[STIX]{x1D6FE}}$
is bounded by a constant independent of
$X_{\unicode[STIX]{x1D6FE}}$
is bounded by a constant independent of
![]() $\unicode[STIX]{x1D6FE}$
, the desired estimate (3.2.2) follows.
$\unicode[STIX]{x1D6FE}$
, the desired estimate (3.2.2) follows.
By [Reference Beuzart-PlessisBeu15, Corollary B.3.1], the integral
 $$\begin{eqnarray}\int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\mathop{\prod }_{i=1}^{r-1}\max \{1,|x_{i}|\}^{-1}\unicode[STIX]{x1D6F7}(n(x_{1},\ldots ,x_{r-1})n^{\prime }g)\,dn^{\prime }\,dn\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\mathop{\prod }_{i=1}^{r-1}\max \{1,|x_{i}|\}^{-1}\unicode[STIX]{x1D6F7}(n(x_{1},\ldots ,x_{r-1})n^{\prime }g)\,dn^{\prime }\,dn\end{eqnarray}$$
is convergent. By the Lebesgue dominated convergence theorem, we have
 $$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }I(\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{N_{\dagger }}\biggl(\int _{T}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr)\biggl(\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\biggr)\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\widehat{f_{1}}(n)\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\,dn.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }I(\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{N_{\dagger }}\biggl(\int _{T}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }f(t)\operatorname{1}_{N_{\dagger ,\unicode[STIX]{x1D6FE}}}(tnt^{-1})\overline{\unicode[STIX]{x1D713}^{t}(n)}\,dt\biggr)\biggl(\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\biggr)\,dn\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\widehat{f_{1}}(n)\unicode[STIX]{x1D6F7}(nn^{\prime }g)\,dn^{\prime }\,dn.\nonumber\end{eqnarray}$$
The rest of the assertions of the lemma follow easily from this expression.◻
3.3 Proof of Proposition 2.2.1
The case
![]() $r=0$
is rather straightforward. Indeed, in this case
$r=0$
is rather straightforward. Indeed, in this case
 $G_{0}=G_{1}=G_{2}$
. By the weak inequality, we only need to prove that
$G_{0}=G_{1}=G_{2}$
. By the weak inequality, we only need to prove that
 $$\begin{eqnarray}\int _{G_{0}}\unicode[STIX]{x1D6EF}_{G_{0}}(g)^{2}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(g)|\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\unicode[STIX]{x1D6EF}_{G_{0}}(g)^{2}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(g)|\,dg\end{eqnarray}$$
is absolutely convergent. By the Cartan decomposition and the estimates (3.1.2) and (3.1.4), the convergence is reduced to the convergence of
 $$\begin{eqnarray}\int _{|a_{n}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1}|a_{1}\cdots a_{n}|^{1/2}\biggl(-\mathop{\sum }_{i=1}^{n}\log |a_{i}|\biggr)^{D}\,da_{1}\cdots da_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{|a_{n}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1}|a_{1}\cdots a_{n}|^{1/2}\biggl(-\mathop{\sum }_{i=1}^{n}\log |a_{i}|\biggr)^{D}\,da_{1}\cdots da_{n}.\end{eqnarray}$$
This is clear. Proposition 2.2.1 is thus proved when
![]() $r=0$
.
$r=0$
.
The case
![]() $r\geqslant 2$
follows from the case
$r\geqslant 2$
follows from the case
![]() $r=1$
by Lemma 3.2.6.
$r=1$
by Lemma 3.2.6.
We now treat the case
![]() $r=1$
. In this case
$r=1$
. In this case
 $G_{2}=G_{1}$
. The defining integral of
$G_{2}=G_{1}$
. The defining integral of
![]() $\unicode[STIX]{x1D6FC}$
reduces to
$\unicode[STIX]{x1D6FC}$
reduces to
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{2}^{\vee },\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}^{\vee },\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })=\int _{G_{0}}\int _{H}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee }}(hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}^{\vee }}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hg_{0})}\,dh\,dg_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{2}^{\vee },\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}^{\vee },\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })=\int _{G_{0}}\int _{H}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee }}(hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}^{\vee }}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hg_{0})}\,dh\,dg_{0},\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{0}$
are both tempered, we need to prove that
$\unicode[STIX]{x1D70B}_{0}$
are both tempered, we need to prove that
 $$\begin{eqnarray}\int _{G_{0}}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hg_{0})|\,dh\,dg_{0}\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hg_{0})|\,dh\,dg_{0}\end{eqnarray}$$
is convergent.
Let
 $g_{0}=k_{1}d(a)k_{2}$
be the Cartan decomposition of
$g_{0}=k_{1}d(a)k_{2}$
be the Cartan decomposition of
![]() $g_{0}$
where
$g_{0}$
where
 $a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
with
$a=(a_{1},\ldots ,a_{n})\in (F^{\times })^{n}$
with
 $|a_{s}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1$
. We first estimate
$|a_{s}|\leqslant \cdots \leqslant |a_{1}|\leqslant 1$
. We first estimate
 $|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hd(a))|$
. We claim that there is a function
$|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(hd(a))|$
. We claim that there is a function
![]() $f$
on
$f$
on
![]() $L^{\ast }$
so that
$L^{\ast }$
so that
 $f(l^{\ast })P(l^{\ast })$
is bounded for any polynomial function
$f(l^{\ast })P(l^{\ast })$
is bounded for any polynomial function
![]() $P$
on
$P$
on
![]() $L^{\ast }$
, such that
$L^{\ast }$
, such that
 $$\begin{eqnarray}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(h(l+l^{\ast },t)d(a))|\ll |\text{det}\,\text{}\underline{a}|^{1/2}f(l^{\ast }\text{}\underline{a}).\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(h(l+l^{\ast },t)d(a))|\ll |\text{det}\,\text{}\underline{a}|^{1/2}f(l^{\ast }\text{}\underline{a}).\end{eqnarray}$$
Indeed
 $$\begin{eqnarray}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(h(l+l^{\ast },t)d(a))|\leqslant |\text{det}\,\text{}\underline{a}|^{1/2}\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+l^{\ast }\text{}\underline{a})\unicode[STIX]{x1D719}^{\vee }(x)|\,dx.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee }}(h(l+l^{\ast },t)d(a))|\leqslant |\text{det}\,\text{}\underline{a}|^{1/2}\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+l^{\ast }\text{}\underline{a})\unicode[STIX]{x1D719}^{\vee }(x)|\,dx.\end{eqnarray}$$
Thus, to prove (3.3.1), it is enough to prove that for any polynomial function
![]() $P$
on
$P$
on
![]() $L^{\ast }$
,
$L^{\ast }$
,
 $$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)|\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)\unicode[STIX]{x1D719}^{\vee }(x)|\,dx<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)|\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)\unicode[STIX]{x1D719}^{\vee }(x)|\,dx<\infty .\end{eqnarray}$$
We have
 $$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)|\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)\unicode[STIX]{x1D719}^{\vee }(x)|\,dx\leqslant \int _{L^{\ast }}\biggl(\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\biggr)|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)|\int _{L^{\ast }}|\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)\unicode[STIX]{x1D719}^{\vee }(x)|\,dx\leqslant \int _{L^{\ast }}\biggl(\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\biggr)|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx.\end{eqnarray}$$
Since
![]() $P$
is a polynomial function, we may choose a sufficiently large
$P$
is a polynomial function, we may choose a sufficiently large
![]() $N$
, such that
$N$
, such that
 $$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\ll (1+|x_{1}a_{n}|+\cdots |x_{n}a_{1}|)^{N}\leqslant (1+|x_{1}|+\cdots |x_{n}|)^{N},\end{eqnarray}$$
$$\begin{eqnarray}\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\ll (1+|x_{1}a_{n}|+\cdots |x_{n}a_{1}|)^{N}\leqslant (1+|x_{1}|+\cdots |x_{n}|)^{N},\end{eqnarray}$$
where
 $x=(x_{1},\ldots ,x_{n})\in L^{\ast }$
. We have the second inequality because
$x=(x_{1},\ldots ,x_{n})\in L^{\ast }$
. We have the second inequality because
![]() $|a_{i}|\leqslant 1$
for all
$|a_{i}|\leqslant 1$
for all
![]() $i$
. Then
$i$
. Then
 $$\begin{eqnarray}\int _{L^{\ast }}\Bigl(\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\Bigr)|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx\ll \int _{L^{\ast }}(1+|x_{1}|+\cdots |x_{n}|)^{N}|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\int _{L^{\ast }}\Bigl(\sup _{y\in L^{\ast }}|P(y)\unicode[STIX]{x1D719}(x\text{}\underline{a}+y)|\Bigr)|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx\ll \int _{L^{\ast }}(1+|x_{1}|+\cdots |x_{n}|)^{N}|\unicode[STIX]{x1D719}^{\vee }(x)|\,dx<\infty .\end{eqnarray}$$
We have thus proved (3.3.1).
By (3.1.1), to prove the convergence of the defining integral of
![]() $\unicode[STIX]{x1D6FC}$
, it is enough to show the convergence of
$\unicode[STIX]{x1D6FC}$
, it is enough to show the convergence of
 $$\begin{eqnarray}\int _{A_{G_{0}}^{+}}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\ast },t)d(a))\unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D6FF}_{P_{m}\cap G_{0}}^{-1}(d(a))|\text{det}\,\text{}\underline{a}|^{1/2}f(l^{\ast }\text{}\underline{a})\,dh\,da.\end{eqnarray}$$
$$\begin{eqnarray}\int _{A_{G_{0}}^{+}}\int _{H}\unicode[STIX]{x1D6EF}_{G_{1}}(h(l+l^{\ast },t)d(a))\unicode[STIX]{x1D6EF}_{G_{0}}(d(a))\unicode[STIX]{x1D6FF}_{P_{m}\cap G_{0}}^{-1}(d(a))|\text{det}\,\text{}\underline{a}|^{1/2}f(l^{\ast }\text{}\underline{a})\,dh\,da.\end{eqnarray}$$
Then Lemma 3.2.5 reduces the convergence of this integral to the case
![]() $r=0$
.
$r=0$
.
3.4 Proof of Proposition 2.2.2
We are going to use the notation in the proof of Lemma 3.2.6, one paragraph before (3.2.1). To simplify notation, we write
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i}}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i},\unicode[STIX]{x1D711}_{i}}$
,
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i}}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{i},\unicode[STIX]{x1D711}_{i}}$
,
![]() $i=0,2$
and
$i=0,2$
and
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}$
.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}$
.
To facilitate understanding, we divide the proof into several steps.
Step 1. The goal is to reduce the Proposition to the inequality (3.4.1).
In order to prove that
 $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\geqslant 0$
, it is enough to show that for any function
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D711}_{2},\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D719})\geqslant 0$
, it is enough to show that for any function
 $f\in {\mathcal{C}}_{c}^{\infty }(T)$
, we have
$f\in {\mathcal{C}}_{c}^{\infty }(T)$
, we have
 $$\begin{eqnarray}\int _{T}\int _{G_{0}}\int _{H}\biggl(\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}f(t)\overline{f(t)}\,dh\,dg_{0}\,dt\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{T}\int _{G_{0}}\int _{H}\biggl(\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}f(t)\overline{f(t)}\,dh\,dg_{0}\,dt\geqslant 0.\end{eqnarray}$$
We denote this expression by
![]() $I$
. Since
$I$
. Since
![]() $f(t)$
is compactly supported, by Fubini’s theorem, we have
$f(t)$
is compactly supported, by Fubini’s theorem, we have
 $$\begin{eqnarray}I=\int _{G_{0}}\int _{H}\biggl(\int _{T}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\,dt\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dh\,dg_{0}.\end{eqnarray}$$
$$\begin{eqnarray}I=\int _{G_{0}}\int _{H}\biggl(\int _{T}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\,dt\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dh\,dg_{0}.\end{eqnarray}$$
We denote the integral in the parentheses by
![]() $\mathit{II}$
. It follows from Lemma 3.2.6 that
$\mathit{II}$
. It follows from Lemma 3.2.6 that
 $$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\end{eqnarray}$$
is bounded by a constant which depends continuously on
![]() $\unicode[STIX]{x1D713}_{r-1}$
. Since
$\unicode[STIX]{x1D713}_{r-1}$
. Since
![]() $f$
is compactly supported on
$f$
is compactly supported on
![]() $T$
, we can choose this constant to be independent of
$T$
, we can choose this constant to be independent of
![]() $t$
(but depends on
$t$
(but depends on
![]() $hg_{0}$
). Then by the Lebesgue dominated convergence theorem, we have
$hg_{0}$
). Then by the Lebesgue dominated convergence theorem, we have
 $$\begin{eqnarray}\mathit{II}=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{T}\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\,dt.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{II}=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{T}\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dn\,dt.\end{eqnarray}$$
Moreover, the double integral on the right-hand side is absolutely convergent. We can thus interchange the order of integration. Finally, we conclude that
 $$\begin{eqnarray}\mathit{II}=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\int _{T}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dt\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{II}=\lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\int _{T}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(nhg_{0})f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dt\,dn.\end{eqnarray}$$
Let
 $f_{1}(t)=f(t)|t_{1}\cdots t_{r-1}|^{-1/2}\in {\mathcal{C}}_{c}^{\infty }(T)$
. Recall that the map
$f_{1}(t)=f(t)|t_{1}\cdots t_{r-1}|^{-1/2}\in {\mathcal{C}}_{c}^{\infty }(T)$
. Recall that the map
![]() $t\mapsto \unicode[STIX]{x1D713}^{t}$
identifies
$t\mapsto \unicode[STIX]{x1D713}^{t}$
identifies
![]() $T$
with
$T$
with
![]() $\widehat{N_{\dagger }}^{\text{reg}}$
which is an open subset of
$\widehat{N_{\dagger }}^{\text{reg}}$
which is an open subset of
![]() $\widehat{N_{\dagger }}$
consisting of generic characters. The measure
$\widehat{N_{\dagger }}$
consisting of generic characters. The measure
 $|t_{1}\cdots t_{r-1}|\,dt$
is identified with the self-dual measure on
$|t_{1}\cdots t_{r-1}|\,dt$
is identified with the self-dual measure on
![]() $\widehat{N_{\dagger }}$
under this map. In this way,
$\widehat{N_{\dagger }}$
under this map. In this way,
![]() $f$
, as well as
$f$
, as well as
![]() $f_{1}$
, are viewed as compactly supported functions on
$f_{1}$
, are viewed as compactly supported functions on
![]() $\widehat{N_{\dagger }}$
and we may talk about their Fourier transform
$\widehat{N_{\dagger }}$
and we may talk about their Fourier transform
![]() $\widehat{f}$
and
$\widehat{f}$
and
![]() $\widehat{f_{1}}$
which are functions on
$\widehat{f_{1}}$
which are functions on
![]() $N_{\dagger }$
. The Fourier transform of a product of two functions is the convolution of the Fourier transforms of these two functions. We conclude that
$N_{\dagger }$
. The Fourier transform of a product of two functions is the convolution of the Fourier transforms of these two functions. We conclude that
 $$\begin{eqnarray}\int _{T}f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dt=\int _{N_{\dagger }}\widehat{f_{1}}(n_{1}n_{2})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{T}f(t)\overline{f(t)}\overline{\unicode[STIX]{x1D713}_{r-1}(tnt^{-1})}\,dt=\int _{N_{\dagger }}\widehat{f_{1}}(n_{1}n_{2})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\displaystyle \mathit{II} & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{\dagger ,\unicode[STIX]{x1D6FE}}}\int _{N_{r-1,-\infty }}\int _{N_{\dagger }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n_{1}n^{\prime }hg_{0})\widehat{f_{1}}(n_{1}n_{2})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}\,dn^{\prime }\,dn_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n_{1}n_{2}^{-1}n^{\prime }hg_{0})\widehat{f_{1}}(n_{1})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}\,dn^{\prime }\,dn_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\,dn^{\prime },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{II} & = & \displaystyle \lim _{\unicode[STIX]{x1D6FE}\rightarrow \infty }\int _{N_{\dagger ,\unicode[STIX]{x1D6FE}}}\int _{N_{r-1,-\infty }}\int _{N_{\dagger }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n_{1}n^{\prime }hg_{0})\widehat{f_{1}}(n_{1}n_{2})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}\,dn^{\prime }\,dn_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{\dagger }}\int _{N_{\dagger }}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n_{1}n_{2}^{-1}n^{\prime }hg_{0})\widehat{f_{1}}(n_{1})\widehat{\overline{f_{1}}}(n_{2})\,dn_{2}\,dn^{\prime }\,dn_{1}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\,dn^{\prime },\nonumber\end{eqnarray}$$
where
 $\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}=\int _{N_{\dagger }}\widehat{f_{1}}(n)\unicode[STIX]{x1D70B}_{2}(n)\unicode[STIX]{x1D711}_{2}\,dn$
. This expression makes sense since
$\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}=\int _{N_{\dagger }}\widehat{f_{1}}(n)\unicode[STIX]{x1D70B}_{2}(n)\unicode[STIX]{x1D711}_{2}\,dn$
. This expression makes sense since
![]() $\widehat{f_{1}}$
is a Schwartz function on
$\widehat{f_{1}}$
is a Schwartz function on
![]() $N_{\dagger }$
. Thus to show that
$N_{\dagger }$
. Thus to show that
![]() $I\geqslant 0$
, it remains to show that
$I\geqslant 0$
, it remains to show that
 $$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}_{2}(\widehat{f_{1}})\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\geqslant 0.\end{eqnarray}$$
Actually, we will show that
 $$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\geqslant 0,\end{eqnarray}$$
for all smooth vectors
 $\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
and
 $\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
. Unlike the proof of [Reference Ichino and IkedaII10, Proposition 1.1] and [Reference LiuLiu16, Theorem 2.1(2)], we cannot apply [Reference HeHe03, Theorem 2.1] directly, as
$\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
. Unlike the proof of [Reference Ichino and IkedaII10, Proposition 1.1] and [Reference LiuLiu16, Theorem 2.1(2)], we cannot apply [Reference HeHe03, Theorem 2.1] directly, as
 $G_{2}\times HG_{0}$
is not reductive. However, we are going to mimic the proof of [Reference HeHe03, Theorem 2.1] to prove (3.4.1).
$G_{2}\times HG_{0}$
is not reductive. However, we are going to mimic the proof of [Reference HeHe03, Theorem 2.1] to prove (3.4.1).
Step 2. The goal is to reduce (3.4.1) to the case of
![]() $K$
-finite vectors.
$K$
-finite vectors.
We claim that it is enough to prove (3.4.1) for a
![]() $K_{2}$
-finite (respectively
$K_{2}$
-finite (respectively
![]() $K_{0}$
-finite) vector
$K_{0}$
-finite) vector
 $\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
(respectively
$\unicode[STIX]{x1D711}_{2}\in \unicode[STIX]{x1D70B}_{2}$
(respectively
 $\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
). This is only an issue when
$\unicode[STIX]{x1D711}_{0}\in \unicode[STIX]{x1D70B}_{0}$
). This is only an issue when
![]() $F$
is archimedean. So we assume temporarily that
$F$
is archimedean. So we assume temporarily that
![]() $F$
is archimedean. Since
$F$
is archimedean. Since
![]() $K_{2}$
-finite vectors are dense in the space of smooth vectors in
$K_{2}$
-finite vectors are dense in the space of smooth vectors in
![]() $\unicode[STIX]{x1D70B}_{2}$
, we may choose a sequence of
$\unicode[STIX]{x1D70B}_{2}$
, we may choose a sequence of
![]() $K_{2}$
-finite vectors
$K_{2}$
-finite vectors
![]() $\unicode[STIX]{x1D711}_{2}^{(i)}$
which is convergent to
$\unicode[STIX]{x1D711}_{2}^{(i)}$
which is convergent to
![]() $\unicode[STIX]{x1D711}_{2}$
. It follows that
$\unicode[STIX]{x1D711}_{2}$
. It follows that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}$
is approximated pointwisely by
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}$
is approximated pointwisely by
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}$
. Moreover, by [Reference SunSun09], there exists an element
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}$
. Moreover, by [Reference SunSun09], there exists an element
![]() $X$
in the Lie algebra of
$X$
in the Lie algebra of
![]() $G_{2}$
, which depends on
$G_{2}$
, which depends on
![]() $K_{2}$
only, such that
$K_{2}$
only, such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}(g_{2})\leqslant {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)},\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)})\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2})=|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)}|^{2}\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}(g_{2})\leqslant {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)},\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)})\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2})=|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)}|^{2}\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2}).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D711}_{2}^{(i)}$
is convergent to
$\unicode[STIX]{x1D711}_{2}^{(i)}$
is convergent to
![]() $\unicode[STIX]{x1D711}_{2}$
, we see that
$\unicode[STIX]{x1D711}_{2}$
, we see that
 $|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)}|^{2}$
is convergent to
$|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}^{(i)}|^{2}$
is convergent to
 $|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}|^{2}$
. In particular, it is bounded by some constant which is independent of
$|\unicode[STIX]{x1D70B}_{2}(X)\unicode[STIX]{x1D711}_{2}|^{2}$
. In particular, it is bounded by some constant which is independent of
![]() $\unicode[STIX]{x1D711}_{2}^{(i)}$
. Similarly we choose a sequence
$\unicode[STIX]{x1D711}_{2}^{(i)}$
. Similarly we choose a sequence
![]() $\unicode[STIX]{x1D711}_{0}^{(i)}$
of
$\unicode[STIX]{x1D711}_{0}^{(i)}$
of
![]() $K_{0}$
-finite vectors in
$K_{0}$
-finite vectors in
![]() $\unicode[STIX]{x1D70B}_{0}$
which approximate
$\unicode[STIX]{x1D70B}_{0}$
which approximate
![]() $\unicode[STIX]{x1D711}_{0}$
. Since
$\unicode[STIX]{x1D711}_{0}$
. Since
 $$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6EF}_{G_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6EF}_{G_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\end{eqnarray}$$
is absolutely convergent, by the Lebesgue dominated convergence theorem
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\nonumber\\ \displaystyle & & \displaystyle \qquad =\lim _{i\rightarrow \infty }\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}^{(i)}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}\nonumber\\ \displaystyle & & \displaystyle \qquad =\lim _{i\rightarrow \infty }\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}^{(i)}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}^{(i)}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dn^{\prime }\,dh\,dg_{0}.\nonumber\end{eqnarray}$$
So the positivity in (3.4.1) for smooth vectors follows from the positivity for
![]() $K$
-finite vectors.
$K$
-finite vectors.
From now on, we assume that
![]() $\unicode[STIX]{x1D711}_{2}$
and
$\unicode[STIX]{x1D711}_{2}$
and
![]() $\unicode[STIX]{x1D711}_{0}$
in (3.4.1) are
$\unicode[STIX]{x1D711}_{0}$
in (3.4.1) are
![]() $K_{2}$
-finite and
$K_{2}$
-finite and
![]() $K_{0}$
-finite, respectively. We come back to the situation
$K_{0}$
-finite, respectively. We come back to the situation
![]() $F$
being an arbitrary local field of characteristic zero.
$F$
being an arbitrary local field of characteristic zero.
Step 3. The goal is to reduce (3.4.1) to the inequality (3.4.2).
Since
![]() $\unicode[STIX]{x1D70B}_{2}$
is tempered, by (the proof of) [Reference HeHe03, Theorem 2.1] (which is also valid when
$\unicode[STIX]{x1D70B}_{2}$
is tempered, by (the proof of) [Reference HeHe03, Theorem 2.1] (which is also valid when
![]() $F$
is non-archimedean), one can find a sequence of compactly supported continuous functions
$F$
is non-archimedean), one can find a sequence of compactly supported continuous functions
![]() $f_{2,j}^{(i)}$
on
$f_{2,j}^{(i)}$
on
![]() $G_{2}$
and a sequence of positive real numbers
$G_{2}$
and a sequence of positive real numbers
![]() $a_{j}^{(i)}$
,
$a_{j}^{(i)}$
,
 $j=1,\ldots ,s_{i}$
, such that
$j=1,\ldots ,s_{i}$
, such that
 $\sum _{j=1}^{s_{i}}a_{j}^{(i)}=1$
and the functions
$\sum _{j=1}^{s_{i}}a_{j}^{(i)}=1$
and the functions
 $$\begin{eqnarray}g_{2}^{\prime }\mapsto A^{(i)}(g_{2}^{\prime })=\mathop{\sum }_{j=1}^{s_{i}}a_{j}^{(i)}\int _{G_{2}}f_{2,j}^{(i)}(g_{2}g_{2}^{\prime })\overline{f_{2,j}^{(i)}(g_{2})}\,dg_{2}\end{eqnarray}$$
$$\begin{eqnarray}g_{2}^{\prime }\mapsto A^{(i)}(g_{2}^{\prime })=\mathop{\sum }_{j=1}^{s_{i}}a_{j}^{(i)}\int _{G_{2}}f_{2,j}^{(i)}(g_{2}g_{2}^{\prime })\overline{f_{2,j}^{(i)}(g_{2})}\,dg_{2}\end{eqnarray}$$
approximate
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(g_{2}^{\prime })$
pointwisely. Moreover, there is a constant
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{2}}(g_{2}^{\prime })$
pointwisely. Moreover, there is a constant
![]() $C_{2}$
, such that
$C_{2}$
, such that
 $$\begin{eqnarray}|A^{(i)}(g_{2}^{\prime })|\leqslant C_{2}\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}|A^{(i)}(g_{2}^{\prime })|\leqslant C_{2}\unicode[STIX]{x1D6EF}_{G_{2}}(g_{2}^{\prime }).\end{eqnarray}$$
Similarly, we can find a sequence of compactly supported continuous functions
![]() $f_{0,j}^{(i)}$
on
$f_{0,j}^{(i)}$
on
![]() $G_{0}$
and a sequence of positive real numbers
$G_{0}$
and a sequence of positive real numbers
![]() $b_{j}^{(i)}$
,
$b_{j}^{(i)}$
,
 $j=1,\ldots ,k_{i}$
, such that
$j=1,\ldots ,k_{i}$
, such that
 $\sum _{j=1}^{k_{i}}b_{j}^{(i)}=1$
and the functions
$\sum _{j=1}^{k_{i}}b_{j}^{(i)}=1$
and the functions
 $$\begin{eqnarray}g_{0}^{\prime }\mapsto B^{(i)}(g_{0}^{\prime })=\mathop{\sum }_{j=1}^{k_{i}}b_{j}^{(i)}\int _{G_{0}}f_{0,j}^{(i)}(g_{0}g_{0}^{\prime })\overline{f_{0,j}^{(i)}(g_{0})}\,dg_{0}\end{eqnarray}$$
$$\begin{eqnarray}g_{0}^{\prime }\mapsto B^{(i)}(g_{0}^{\prime })=\mathop{\sum }_{j=1}^{k_{i}}b_{j}^{(i)}\int _{G_{0}}f_{0,j}^{(i)}(g_{0}g_{0}^{\prime })\overline{f_{0,j}^{(i)}(g_{0})}\,dg_{0}\end{eqnarray}$$
approximate
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0}^{\prime })$
pointwisely. Moreover, there is a constant
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D711}_{0}}(g_{0}^{\prime })$
pointwisely. Moreover, there is a constant
![]() $C_{0}$
, such that
$C_{0}$
, such that
 $$\begin{eqnarray}|B^{(i)}(g_{0}^{\prime })|\leqslant C_{0}\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}|B^{(i)}(g_{0}^{\prime })|\leqslant C_{0}\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0}^{\prime }).\end{eqnarray}$$
Since the integral
 $$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6EF}_{G_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})\,dn^{\prime }\,dh\,dg_{0}\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\unicode[STIX]{x1D6EF}_{G_{2}}(n^{\prime }hg_{0})\unicode[STIX]{x1D6EF}_{G_{0}}(g_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})\,dn^{\prime }\,dh\,dg_{0}\end{eqnarray}$$
is absolutely convergent, by the Lebesgue dominated convergence theorem, to prove (3.4.1), it is enough to prove that for any
![]() $i,j$
,
$i,j$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2,j}^{(i)}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2,j}^{(i)}(g_{2})}\,dg_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\int _{G_{0}}f_{0,j}^{(i)}(g_{0}g_{0}^{\prime })\overline{f_{0,j}^{(i)}(g_{0})}\,dg_{0}\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0}^{\prime })\,dn^{\prime }\,dh\,dg_{0}^{\prime }\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2,j}^{(i)}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2,j}^{(i)}(g_{2})}\,dg_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\int _{G_{0}}f_{0,j}^{(i)}(g_{0}g_{0}^{\prime })\overline{f_{0,j}^{(i)}(g_{0})}\,dg_{0}\biggr)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0}^{\prime })\,dn^{\prime }\,dh\,dg_{0}^{\prime }\geqslant 0.\end{eqnarray}$$
We denote the left-hand side by
![]() $Q$
. Note that this integral is absolutely convergent. To simplify notation, we write
$Q$
. Note that this integral is absolutely convergent. To simplify notation, we write
 $f_{2}=f_{2,j}^{(i)}$
and
$f_{2}=f_{2,j}^{(i)}$
and
 $f_{0}=f_{0,j}^{(i)}$
.
$f_{0}=f_{0,j}^{(i)}$
.
Step 4. Proof of (3.4.2).
We can write the inner product on
![]() ${\mathcal{S}}(L^{\ast })$
as
${\mathcal{S}}(L^{\ast })$
as
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime })=\int _{L+F\backslash H}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}(0)\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}^{\prime }(0)}\,dh^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\prime })=\int _{L+F\backslash H}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}(0)\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}^{\prime }(0)}\,dh^{\prime }.\end{eqnarray}$$
Using this expression of the inner product, we have
 $$\begin{eqnarray}\displaystyle Q & = & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2})}\,dg_{2}\biggr)\biggl(\int _{G_{0}}f_{0}(g_{0}g_{0}^{\prime })\overline{f_{0}(g_{0})}\,dg_{0}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{L+F\backslash H}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}(0)\,dh^{\prime }\biggr)\,dn^{\prime }\,dh\,dg_{0}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2})}\,dg_{2}\biggr)\biggl(\int _{G_{0}}f_{0}(g_{0}g_{0}^{\prime })\overline{f_{0}(g_{0})}\,dg_{0}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{L+F\backslash H}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0}hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0})\unicode[STIX]{x1D719}(0)\,dh^{\prime }\biggr)\,dn^{\prime }\,dh\,dg_{0}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q & = & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2})}\,dg_{2}\biggr)\biggl(\int _{G_{0}}f_{0}(g_{0}g_{0}^{\prime })\overline{f_{0}(g_{0})}\,dg_{0}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{L+F\backslash H}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime })\unicode[STIX]{x1D719}(0)\,dh^{\prime }\biggr)\,dn^{\prime }\,dh\,dg_{0}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{G_{0}}\int _{H}\int _{N_{r-1,-\infty }}\biggl(\int _{G_{2}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2})}\,dg_{2}\biggr)\biggl(\int _{G_{0}}f_{0}(g_{0}g_{0}^{\prime })\overline{f_{0}(g_{0})}\,dg_{0}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{L+F\backslash H}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0}hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0})\unicode[STIX]{x1D719}(0)\,dh^{\prime }\biggr)\,dn^{\prime }\,dh\,dg_{0}^{\prime }.\nonumber\end{eqnarray}$$
Note that we have used the fact the pairing
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}$
is
${\mathcal{B}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}}$
is
![]() $G_{0}$
-invariant.
$G_{0}$
-invariant.
We make the following change of variables
 $$\begin{eqnarray}g_{0}^{\prime }\mapsto g_{0}^{-1}g_{0}^{\prime },\quad h\mapsto g_{0}^{-1}h^{\prime -1}hg_{0},\quad n^{\prime }\mapsto g_{0}^{-1}h^{\prime -1}n^{\prime }h^{\prime }g_{0},\quad g_{2}\mapsto g_{2}h^{\prime }g_{0}.\end{eqnarray}$$
$$\begin{eqnarray}g_{0}^{\prime }\mapsto g_{0}^{-1}g_{0}^{\prime },\quad h\mapsto g_{0}^{-1}h^{\prime -1}hg_{0},\quad n^{\prime }\mapsto g_{0}^{-1}h^{\prime -1}n^{\prime }h^{\prime }g_{0},\quad g_{2}\mapsto g_{2}h^{\prime }g_{0}.\end{eqnarray}$$
Then
 $$\begin{eqnarray}\displaystyle Q & = & \displaystyle \int _{G_{2}}\int _{N_{r-1,-\infty }}\iint _{(L+F)\backslash H\times H}\iint _{G_{0}\times G_{0}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2}h^{\prime }g_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,f_{0}(g_{0}^{\prime })\overline{f_{0}(g_{0})}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0})\unicode[STIX]{x1D719}(0)\,dg_{0}\,dg_{0}^{\prime }\,dh\,dh^{\prime }\,dn^{\prime }\,dg_{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q & = & \displaystyle \int _{G_{2}}\int _{N_{r-1,-\infty }}\iint _{(L+F)\backslash H\times H}\iint _{G_{0}\times G_{0}}f_{2}(g_{2}n^{\prime }hg_{0}^{\prime })\overline{f_{2}(g_{2}h^{\prime }g_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,f_{0}(g_{0}^{\prime })\overline{f_{0}(g_{0})}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0}^{\prime })\unicode[STIX]{x1D719}(0)}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h^{\prime }g_{0})\unicode[STIX]{x1D719}(0)\,dg_{0}\,dg_{0}^{\prime }\,dh\,dh^{\prime }\,dn^{\prime }\,dg_{2},\nonumber\end{eqnarray}$$
where
![]() $L+F$
embeds in
$L+F$
embeds in
![]() $H\times H$
diagonally.
$H\times H$
diagonally.
Finally we decompose the integral over
![]() $G_{2}$
as
$G_{2}$
as
 $$\begin{eqnarray}\int _{G_{2}/(N_{r-1,-\infty }\rtimes (L+F))}\int _{N_{r-1,-\infty }}\int _{L+F}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{2}/(N_{r-1,-\infty }\rtimes (L+F))}\int _{N_{r-1,-\infty }}\int _{L+F}.\end{eqnarray}$$
We conclude that
 $$\begin{eqnarray}Q=\int _{G_{2}/(N_{r-1,-\infty }\rtimes (L+F))}\biggl|\int _{N_{r-1,-\infty }}\int _{H}\int _{G_{0}}f_{2}(g_{2}nhg_{0})f_{0}(g_{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D707}}(hg_{0})\unicode[STIX]{x1D719}(0)}\,dg_{0}\,dh\,dn\biggr|^{2}\,dg_{2}\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}Q=\int _{G_{2}/(N_{r-1,-\infty }\rtimes (L+F))}\biggl|\int _{N_{r-1,-\infty }}\int _{H}\int _{G_{0}}f_{2}(g_{2}nhg_{0})f_{0}(g_{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D707}}(hg_{0})\unicode[STIX]{x1D719}(0)}\,dg_{0}\,dh\,dn\biggr|^{2}\,dg_{2}\geqslant 0.\end{eqnarray}$$
3.5 Regularization via stable unipotent integral
In this subsection, we give an alternative but equivalent way to define the linear functional
![]() $\unicode[STIX]{x1D6FC}$
when
$\unicode[STIX]{x1D6FC}$
when
![]() $F$
is non-archimedean following [Reference Lapid and MaoLM15a, Reference LiuLiu16]. This definition is better for the unramified computation and is valid for nontempered representations. In this subsection,
$F$
is non-archimedean following [Reference Lapid and MaoLM15a, Reference LiuLiu16]. This definition is better for the unramified computation and is valid for nontempered representations. In this subsection,
![]() $F$
is always assumed to be non-archimedean.
$F$
is always assumed to be non-archimedean.
Let
![]() $N$
be a unipotent group over
$N$
be a unipotent group over
![]() $F$
and
$F$
and
![]() $f$
a smooth function on
$f$
a smooth function on
![]() $N$
. We say that
$N$
. We say that
![]() $f$
is compactly supported on average if there are compact subsets
$f$
is compactly supported on average if there are compact subsets
![]() $U$
and
$U$
and
![]() $U^{\prime }$
of
$U^{\prime }$
of
![]() $N$
, such that
$N$
, such that
 $\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f$
is compactly supported. Here
$\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f$
is compactly supported. Here
![]() $\unicode[STIX]{x1D6FF}_{U}$
stands for the Dirac measure on
$\unicode[STIX]{x1D6FF}_{U}$
stands for the Dirac measure on
![]() $U$
, i.e.
$U$
, i.e.
 $\unicode[STIX]{x1D6FF}_{U}=(\operatorname{vol}U)^{-1}\operatorname{1}_{U}$
, and
$\unicode[STIX]{x1D6FF}_{U}=(\operatorname{vol}U)^{-1}\operatorname{1}_{U}$
, and
 $$\begin{eqnarray}\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f(n)=\int _{N}\int _{N}\unicode[STIX]{x1D6FF}_{U^{\prime }}(u^{\prime })\unicode[STIX]{x1D6FF}_{U}(u)f(u^{\prime }nu)\,du^{\prime }\,du.\end{eqnarray}$$
$$\begin{eqnarray}\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f(n)=\int _{N}\int _{N}\unicode[STIX]{x1D6FF}_{U^{\prime }}(u^{\prime })\unicode[STIX]{x1D6FF}_{U}(u)f(u^{\prime }nu)\,du^{\prime }\,du.\end{eqnarray}$$
If
![]() $f$
is compactly supported on average, we then define
$f$
is compactly supported on average, we then define
 $$\begin{eqnarray}\int _{N}^{\text{st}}f(n)\,dn:=\int _{N}\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f(n)\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N}^{\text{st}}f(n)\,dn:=\int _{N}\text{L}(\unicode[STIX]{x1D6FF}_{U^{\prime }})\text{R}(\unicode[STIX]{x1D6FF}_{U})f(n)\,dn.\end{eqnarray}$$
This is called the stable integral of
![]() $f$
on
$f$
on
![]() $N$
. The definition is independent of the choice of
$N$
. The definition is independent of the choice of
![]() $U$
and
$U$
and
![]() $U^{\prime }$
.
$U^{\prime }$
.
We denote temporarily by
![]() $G$
a reductive group over
$G$
a reductive group over
![]() $F$
. Let
$F$
. Let
 $P_{\text{min}}=M_{\text{min}}N_{\text{min}}$
be a fixed minimal parabolic subgroup of
$P_{\text{min}}=M_{\text{min}}N_{\text{min}}$
be a fixed minimal parabolic subgroup of
![]() $G$
. Let
$G$
. Let
 $P=MN\supset P_{\text{min}}$
be a parabolic subgroup of
$P=MN\supset P_{\text{min}}$
be a parabolic subgroup of
![]() $G$
. Let
$G$
. Let
![]() $\unicode[STIX]{x1D6F9}$
be a generic character of
$\unicode[STIX]{x1D6F9}$
be a generic character of
![]() $N$
, i.e. the stabilizer of
$N$
, i.e. the stabilizer of
![]() $\unicode[STIX]{x1D6F9}$
in
$\unicode[STIX]{x1D6F9}$
in
![]() $M_{\text{min}}$
is the center of
$M_{\text{min}}$
is the center of
![]() $M_{\text{min}}$
. Let
$M_{\text{min}}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible admissible representation of
$\unicode[STIX]{x1D70B}$
be an irreducible admissible representation of
![]() $G$
and
$G$
and
![]() $\unicode[STIX]{x1D6F7}$
a matrix coefficient of
$\unicode[STIX]{x1D6F7}$
a matrix coefficient of
![]() $\unicode[STIX]{x1D70B}$
. Then we have the following result.
$\unicode[STIX]{x1D70B}$
. Then we have the following result.
Proposition 3.5.1 [Reference LiuLiu16, Proposition 3.3].
The function
 $\unicode[STIX]{x1D6F7}|_{N_{P}}\cdot \unicode[STIX]{x1D6F9}$
is compactly supported on average.
$\unicode[STIX]{x1D6F7}|_{N_{P}}\cdot \unicode[STIX]{x1D6F9}$
is compactly supported on average.
Now let
 $G=\operatorname{Mp}(2n)$
. Then Proposition 3.5.1 still holds. The same proof as in [Reference LiuLiu16, Proposition 3.3] goes through as it uses only the Bruhat decomposition and Jacquet’s subrepresentation theorem, which are valid for
$G=\operatorname{Mp}(2n)$
. Then Proposition 3.5.1 still holds. The same proof as in [Reference LiuLiu16, Proposition 3.3] goes through as it uses only the Bruhat decomposition and Jacquet’s subrepresentation theorem, which are valid for
![]() $G$
.
$G$
.
Now we retain the notation
![]() $G_{0}$
,
$G_{0}$
,
![]() $G_{1}$
,
$G_{1}$
,
![]() $G_{2}$
, etc. Let
$G_{2}$
, etc. Let
![]() $\unicode[STIX]{x1D6F7}$
be a matrix coefficient on
$\unicode[STIX]{x1D6F7}$
be a matrix coefficient on
![]() $G_{2}$
(respectively
$G_{2}$
(respectively
![]() $\widetilde{G_{2}}$
). Define
$\widetilde{G_{2}}$
). Define
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}(g)=\int _{N_{r-1}}^{\text{st}}\unicode[STIX]{x1D6F7}(gn)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}(g)=\int _{N_{r-1}}^{\text{st}}\unicode[STIX]{x1D6F7}(gn)\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn,\end{eqnarray}$$
which is a function on
![]() $G_{2}$
(respectively
$G_{2}$
(respectively
![]() $\widetilde{G_{2}}$
). This definition makes sense because of Proposition 3.5.1.
$\widetilde{G_{2}}$
). This definition makes sense because of Proposition 3.5.1.
Lemma 3.5.2. Assume that
![]() $\unicode[STIX]{x1D6F7}$
is a matrix coefficient of a tempered representation of
$\unicode[STIX]{x1D6F7}$
is a matrix coefficient of a tempered representation of
![]() $G_{2}$
(respectively
$G_{2}$
(respectively
![]() $\widetilde{G_{2}}$
). Then
$\widetilde{G_{2}}$
). Then
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}(hg_{0})={\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}(hg_{0}),\quad h\in H,~g_{0}\in G_{0},~(\text{respectively }g_{0}\in \widetilde{G_{0}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}(hg_{0})={\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}(hg_{0}),\quad h\in H,~g_{0}\in G_{0},~(\text{respectively }g_{0}\in \widetilde{G_{0}}).\end{eqnarray}$$
Proof. By definition,
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}_{2}(hg_{0})=\int _{N_{r-1}}\biggl((\operatorname{vol}U)^{-1}\int _{U}\unicode[STIX]{x1D6F7}(unhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(un)}\,du\biggr)\,dn,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}_{2}(hg_{0})=\int _{N_{r-1}}\biggl((\operatorname{vol}U)^{-1}\int _{U}\unicode[STIX]{x1D6F7}(unhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(un)}\,du\biggr)\,dn,\end{eqnarray}$$
where
![]() $U$
is an open compact set of
$U$
is an open compact set of
![]() $N_{r-1}$
. The inner integral, as a function of
$N_{r-1}$
. The inner integral, as a function of
![]() $n$
, is compactly supported. Therefore, we may take a sufficiently large
$n$
, is compactly supported. Therefore, we may take a sufficiently large
![]() $\unicode[STIX]{x1D6FE}$
, such that
$\unicode[STIX]{x1D6FE}$
, such that
![]() $N_{r-1,\unicode[STIX]{x1D6FE}}$
contains
$N_{r-1,\unicode[STIX]{x1D6FE}}$
contains
![]() $U$
and the support of the inner integral (as a function of
$U$
and the support of the inner integral (as a function of
![]() $n$
) and that
$n$
) and that
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{2}(hg_{0})=\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{2}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{2}(hg_{0})=\int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}_{2}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn.\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}_{2}(hg_{0}) & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}(\operatorname{vol}U)^{-1}\int _{U}\unicode[STIX]{x1D6F7}(unhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(un)}\,du\,dn,\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\times (\operatorname{vol}U)^{-1}\int _{U}\,du\nonumber\\ \displaystyle & = & \displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{2}(hg_{0}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}\unicode[STIX]{x1D6F7}_{2}(hg_{0}) & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}(\operatorname{vol}U)^{-1}\int _{U}\unicode[STIX]{x1D6F7}(unhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(un)}\,du\,dn,\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1,\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F7}(nhg_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(n)}\,dn\times (\operatorname{vol}U)^{-1}\int _{U}\,du\nonumber\\ \displaystyle & = & \displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{2}(hg_{0}),\nonumber\end{eqnarray}$$
where in the second equality, we have made a change of variable
 $n\mapsto u^{-1}n$
.◻
$n\mapsto u^{-1}n$
.◻
Thanks to Lemma 3.5.2, if
![]() $F$
is non-archimedean, then we may use
$F$
is non-archimedean, then we may use
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}$
instead of
${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}$
instead of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
in the definition of the local linear form
${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
in the definition of the local linear form
![]() $\unicode[STIX]{x1D6FC}$
. We will not distinguish
$\unicode[STIX]{x1D6FC}$
. We will not distinguish
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}$
and
${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\text{st}}$
and
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
from now on and write just
${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
from now on and write just
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
.
${\mathcal{F}}_{\unicode[STIX]{x1D713}}$
.
4 Unramified computations
In this section, we assume the conditions prior to Proposition 2.2.3. In particular,
![]() $F$
is a non-archimedean local field of residue characteristic different from two. The argument is mostly adapted from [Reference LiuLiu16], except that at the end we use a different trick, which avoids the use of the explicit formulae of the Whittkaer–Shintani functions as in [Reference LiuLiu16, Appendix]. Some of the arguments which are identical to [Reference LiuLiu16] are only sketched.
$F$
is a non-archimedean local field of residue characteristic different from two. The argument is mostly adapted from [Reference LiuLiu16], except that at the end we use a different trick, which avoids the use of the explicit formulae of the Whittkaer–Shintani functions as in [Reference LiuLiu16, Appendix]. Some of the arguments which are identical to [Reference LiuLiu16] are only sketched.
4.1 Setup
For
 $i=0,1,2$
, let
$i=0,1,2$
, let
 $B_{i}=P_{m}\cap G_{i}=T_{i}U_{i}$
be the upper triangular Borel subgroup of
$B_{i}=P_{m}\cap G_{i}=T_{i}U_{i}$
be the upper triangular Borel subgroup of
![]() $G_{i}$
where
$G_{i}$
where
![]() $T_{i}$
is the diagonal maximal torus of
$T_{i}$
is the diagonal maximal torus of
![]() $G_{i}$
. We have a hyperspecial subgroup
$G_{i}$
. We have a hyperspecial subgroup
 $K_{i}=\operatorname{Sp}(W_{i})(\mathfrak{o}_{F})$
of
$K_{i}=\operatorname{Sp}(W_{i})(\mathfrak{o}_{F})$
of
![]() $\operatorname{Sp}(W_{i})$
. Recall that the twofold cover
$\operatorname{Sp}(W_{i})$
. Recall that the twofold cover
 $\widetilde{G_{i}}\rightarrow G_{i}$
splits uniquely over
$\widetilde{G_{i}}\rightarrow G_{i}$
splits uniquely over
![]() $K_{i}$
. We can thus view
$K_{i}$
. We can thus view
![]() $K_{i}$
as a subgroup of
$K_{i}$
as a subgroup of
![]() $\widetilde{G_{i}}$
. Let
$\widetilde{G_{i}}$
. Let
![]() $\unicode[STIX]{x1D6EF}$
(respectively
$\unicode[STIX]{x1D6EF}$
(respectively
![]() $\unicode[STIX]{x1D709}$
) be an unramified character of
$\unicode[STIX]{x1D709}$
) be an unramified character of
![]() $T_{2}$
(respectively
$T_{2}$
(respectively
![]() $T_{0}$
). In the case
$T_{0}$
). In the case
![]() $\operatorname{Sp}$
, we consider the unramified principal series
$\operatorname{Sp}$
, we consider the unramified principal series
 $\unicode[STIX]{x1D70B}_{2}=I(\unicode[STIX]{x1D6EF})$
of
$\unicode[STIX]{x1D70B}_{2}=I(\unicode[STIX]{x1D6EF})$
of
![]() $G_{2}$
and
$G_{2}$
and
 $\unicode[STIX]{x1D70B}_{0}=I(\unicode[STIX]{x1D709})$
of
$\unicode[STIX]{x1D70B}_{0}=I(\unicode[STIX]{x1D709})$
of
![]() $\widetilde{G_{0}}$
. In the case
$\widetilde{G_{0}}$
. In the case
![]() $\operatorname{Mp}$
, we consider the unramified principal series
$\operatorname{Mp}$
, we consider the unramified principal series
 $\unicode[STIX]{x1D70B}_{2}=I(\unicode[STIX]{x1D6EF})$
of
$\unicode[STIX]{x1D70B}_{2}=I(\unicode[STIX]{x1D6EF})$
of
![]() $\widetilde{G_{2}}$
and
$\widetilde{G_{2}}$
and
 $\unicode[STIX]{x1D70B}_{0}=I(\unicode[STIX]{x1D709})$
of
$\unicode[STIX]{x1D70B}_{0}=I(\unicode[STIX]{x1D709})$
of
![]() $G_{0}$
. Note that the unramified principal series representation of the metaplectic group depends on the additive character
$G_{0}$
. Note that the unramified principal series representation of the metaplectic group depends on the additive character
![]() $\unicode[STIX]{x1D713}$
, even though this is not reflected in the notation. We frequently identify
$\unicode[STIX]{x1D713}$
, even though this is not reflected in the notation. We frequently identify
![]() $\unicode[STIX]{x1D6EF}$
with an element in
$\unicode[STIX]{x1D6EF}$
with an element in
![]() $\mathbb{C}^{m}$
which we also denote by
$\mathbb{C}^{m}$
which we also denote by
 $\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{m})$
, the correspondence being given by
$\unicode[STIX]{x1D6EF}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{m})$
, the correspondence being given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\operatorname{diag}[a_{m},\ldots ,a_{1},a_{1}^{-1},\ldots ,a_{m}^{-1}])=|a_{1}|^{\unicode[STIX]{x1D6EF}_{1}}\cdots |a_{m}|^{\unicode[STIX]{x1D6EF}_{m}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\operatorname{diag}[a_{m},\ldots ,a_{1},a_{1}^{-1},\ldots ,a_{m}^{-1}])=|a_{1}|^{\unicode[STIX]{x1D6EF}_{1}}\cdots |a_{m}|^{\unicode[STIX]{x1D6EF}_{m}}.\end{eqnarray}$$
Similarly we identify
![]() $\unicode[STIX]{x1D709}$
with an element in
$\unicode[STIX]{x1D709}$
with an element in
![]() $\mathbb{C}^{n}$
. The contragredient of
$\mathbb{C}^{n}$
. The contragredient of
![]() $\unicode[STIX]{x1D70B}_{2}$
(respectively
$\unicode[STIX]{x1D70B}_{2}$
(respectively
![]() $\unicode[STIX]{x1D70B}_{0}$
) is
$\unicode[STIX]{x1D70B}_{0}$
) is
![]() $I(\unicode[STIX]{x1D6EF}^{-1})$
(respectively
$I(\unicode[STIX]{x1D6EF}^{-1})$
(respectively
![]() $I(\unicode[STIX]{x1D709}^{-1})$
). Let
$I(\unicode[STIX]{x1D709}^{-1})$
). Let
 $f_{\unicode[STIX]{x1D6EF}}\in I(\unicode[STIX]{x1D6EF})$
,
$f_{\unicode[STIX]{x1D6EF}}\in I(\unicode[STIX]{x1D6EF})$
,
 $f_{\unicode[STIX]{x1D6EF}^{-1}}\in I(\unicode[STIX]{x1D6EF}^{-1})$
(respectively
$f_{\unicode[STIX]{x1D6EF}^{-1}}\in I(\unicode[STIX]{x1D6EF}^{-1})$
(respectively
 $f_{\unicode[STIX]{x1D709}}\in I(\unicode[STIX]{x1D709})$
,
$f_{\unicode[STIX]{x1D709}}\in I(\unicode[STIX]{x1D709})$
,
 $f_{\unicode[STIX]{x1D709}^{-1}}\in I(\unicode[STIX]{x1D709}^{-1})$
) be the
$f_{\unicode[STIX]{x1D709}^{-1}}\in I(\unicode[STIX]{x1D709}^{-1})$
) be the
![]() $K_{2}$
-fixed (respectively
$K_{2}$
-fixed (respectively
![]() $K_{0}$
-fixed) elements with
$K_{0}$
-fixed) elements with
 $f_{\unicode[STIX]{x1D6EF}}(1)=f_{\unicode[STIX]{x1D6EF}^{-1}}(1)=1$
(respectively
$f_{\unicode[STIX]{x1D6EF}}(1)=f_{\unicode[STIX]{x1D6EF}^{-1}}(1)=1$
(respectively
 $f_{\unicode[STIX]{x1D709}}(1)=f_{\unicode[STIX]{x1D709}^{-1}}(1)=1$
). Let
$f_{\unicode[STIX]{x1D709}}(1)=f_{\unicode[STIX]{x1D709}^{-1}}(1)=1$
). Let
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2})=\int _{K_{2}}f_{\unicode[STIX]{x1D6EF}}(k_{2}g_{2})\,dk_{2},\quad \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D709}}(g_{0})=\int _{K_{0}}f_{\unicode[STIX]{x1D709}}(k_{0}g_{0})\,dk_{0}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})=\int _{L(\mathfrak{o}_{F})}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\operatorname{1}_{L^{\ast }(\mathfrak{o}_{F})}(x)\,dx, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2})=\int _{K_{2}}f_{\unicode[STIX]{x1D6EF}}(k_{2}g_{2})\,dk_{2},\quad \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D709}}(g_{0})=\int _{K_{0}}f_{\unicode[STIX]{x1D709}}(k_{0}g_{0})\,dk_{0}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})=\int _{L(\mathfrak{o}_{F})}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\operatorname{1}_{L^{\ast }(\mathfrak{o}_{F})}(x)\,dx, & \displaystyle \nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{H}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dh\,dg_{0}.\end{eqnarray}$$
$$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{H}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}hg_{0})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D719}}(hg_{0})}\,dh\,dg_{0}.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D6FC}(f_{\unicode[STIX]{x1D6EF}},f_{\unicode[STIX]{x1D6EF}^{-1}},f_{\unicode[STIX]{x1D709}},f_{\unicode[STIX]{x1D709}^{-1}},\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})=I(1,\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.
$\unicode[STIX]{x1D6FC}(f_{\unicode[STIX]{x1D6EF}},f_{\unicode[STIX]{x1D6EF}^{-1}},f_{\unicode[STIX]{x1D709}},f_{\unicode[STIX]{x1D709}^{-1}},\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})=I(1,\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.
Let
 $J=H\rtimes G_{0}$
and
$J=H\rtimes G_{0}$
and
 $\widetilde{J}=H\rtimes \widetilde{G_{0}}$
. We define the Borel subgroup
$\widetilde{J}=H\rtimes \widetilde{G_{0}}$
. We define the Borel subgroup
![]() $B_{J}$
(respectively
$B_{J}$
(respectively
![]() $B_{\widetilde{J}}$
) of
$B_{\widetilde{J}}$
) of
![]() $J$
(respectively
$J$
(respectively
![]() $\widetilde{J}$
) as a subgroup of
$\widetilde{J}$
) as a subgroup of
![]() $J$
(respectively
$J$
(respectively
![]() $\widetilde{J}$
) consisting of elements of the form
$\widetilde{J}$
) consisting of elements of the form
![]() $hb_{0}$
where
$hb_{0}$
where
![]() $b_{0}\in B_{0}$
(respectively
$b_{0}\in B_{0}$
(respectively
![]() $\widetilde{B_{0}}$
, the inverse image of
$\widetilde{B_{0}}$
, the inverse image of
![]() $B_{0}$
in
$B_{0}$
in
![]() $\widetilde{G_{0}}$
) and
$\widetilde{G_{0}}$
) and
![]() $h\in H$
is of the form
$h\in H$
is of the form
![]() $h(l,t)$
,
$h(l,t)$
,
![]() $l\in L$
. We define the unramified principal series representation of
$l\in L$
. We define the unramified principal series representation of
![]() $J$
(respectively
$J$
(respectively
![]() $\widetilde{J}$
) as
$\widetilde{J}$
) as
 $$\begin{eqnarray}I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})=\{f\in {\mathcal{C}}^{\infty }(J)\mid f(h(l,t)b_{0}hg_{0})=\unicode[STIX]{x1D6FF}_{B_{J}}^{1/2}(b_{0})\unicode[STIX]{x1D709}(b_{0})\overline{\unicode[STIX]{x1D713}}(t)f(hg_{0})\},\end{eqnarray}$$
$$\begin{eqnarray}I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})=\{f\in {\mathcal{C}}^{\infty }(J)\mid f(h(l,t)b_{0}hg_{0})=\unicode[STIX]{x1D6FF}_{B_{J}}^{1/2}(b_{0})\unicode[STIX]{x1D709}(b_{0})\overline{\unicode[STIX]{x1D713}}(t)f(hg_{0})\},\end{eqnarray}$$
respectively
 $$\begin{eqnarray}I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})=\{f\in {\mathcal{C}}^{\infty }(\widetilde{J})\mid f(h(l,t)b_{0}hg_{0})=\unicode[STIX]{x1D6FF}_{B_{J}}^{1/2}(b_{0})\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(b_{0})\overline{\unicode[STIX]{x1D713}}(t)f(hg_{0})\},\end{eqnarray}$$
$$\begin{eqnarray}I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})=\{f\in {\mathcal{C}}^{\infty }(\widetilde{J})\mid f(h(l,t)b_{0}hg_{0})=\unicode[STIX]{x1D6FF}_{B_{J}}^{1/2}(b_{0})\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(b_{0})\overline{\unicode[STIX]{x1D713}}(t)f(hg_{0})\},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(b_{0})=\unicode[STIX]{x1D709}(\operatorname{diag}[t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}])\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(t_{1}\cdots t_{n})$
and
$\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(b_{0})=\unicode[STIX]{x1D709}(\operatorname{diag}[t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}])\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}(t_{1}\cdots t_{n})$
and
 $t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}$
are diagonal entries of
$t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}$
are diagonal entries of
![]() $b_{0}$
.
$b_{0}$
.
The group
![]() $J$
(respectively
$J$
(respectively
![]() $\widetilde{J}$
) acts on
$\widetilde{J}$
) acts on
 $I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
(respectively
$I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
(respectively
 $I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
) via the right translation. Let
$I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
) via the right translation. Let
 $K_{J}=J\cap K_{1}$
. There is a canonical
$K_{J}=J\cap K_{1}$
. There is a canonical
![]() $J$
(respectively
$J$
(respectively
![]() $\widetilde{J}$
)-invariant pairing given by
$\widetilde{J}$
)-invariant pairing given by
 $$\begin{eqnarray}{\mathcal{B}}_{J}(f,f^{\vee })=\int _{L^{\ast }}\int _{K_{0}}f(h(l^{\ast },0)k_{0})f^{\vee }(h(l^{\ast },0)k_{0})\,dk_{0}\,dl^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{J}(f,f^{\vee })=\int _{L^{\ast }}\int _{K_{0}}f(h(l^{\ast },0)k_{0})f^{\vee }(h(l^{\ast },0)k_{0})\,dk_{0}\,dl^{\ast },\end{eqnarray}$$
where
 $f\in I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),f^{\vee }\in I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})$
(respectively
$f\in I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),f^{\vee }\in I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})$
(respectively
 $f\in I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),f^{\vee }\in I^{\widetilde{J}}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})$
).
$f\in I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),f^{\vee }\in I^{\widetilde{J}}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})$
).
In the case
![]() $\operatorname{Mp}$
, there is a canonical inner product preserving isomorphism
$\operatorname{Mp}$
, there is a canonical inner product preserving isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}\otimes I(\unicode[STIX]{x1D709})\rightarrow I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),\quad \unicode[STIX]{x1D719}\otimes f_{\unicode[STIX]{x1D709}}\rightarrow f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}\otimes I(\unicode[STIX]{x1D709})\rightarrow I^{\widetilde{J}}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),\quad \unicode[STIX]{x1D719}\otimes f_{\unicode[STIX]{x1D709}}\rightarrow f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},\end{eqnarray}$$
where
 $f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(hg_{0})=\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}(hg_{0})\unicode[STIX]{x1D719}(0)f_{\unicode[STIX]{x1D709}}(g_{0})$
,
$f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(hg_{0})=\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}(hg_{0})\unicode[STIX]{x1D719}(0)f_{\unicode[STIX]{x1D709}}(g_{0})$
,
![]() $h\in H$
and
$h\in H$
and
 $g_{0}\in \widetilde{G_{0}}$
. In the case
$g_{0}\in \widetilde{G_{0}}$
. In the case
![]() $\operatorname{Sp}$
, there is a canonical inner product preserving isomorphism
$\operatorname{Sp}$
, there is a canonical inner product preserving isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}\otimes I(\unicode[STIX]{x1D709})\rightarrow I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),\quad \unicode[STIX]{x1D719}\otimes f_{\unicode[STIX]{x1D709}}\rightarrow f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}\otimes I(\unicode[STIX]{x1D709})\rightarrow I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}),\quad \unicode[STIX]{x1D719}\otimes f_{\unicode[STIX]{x1D709}}\rightarrow f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},\end{eqnarray}$$
where
 $f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(hg_{0})=\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}(h\unicode[STIX]{x1D704}(g_{0}))\unicode[STIX]{x1D719}(0)f_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D704}(g_{0}))$
. Analogous isomorphism also holds in the case
$f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(hg_{0})=\unicode[STIX]{x1D714}_{\overline{\unicode[STIX]{x1D713}}}(h\unicode[STIX]{x1D704}(g_{0}))\unicode[STIX]{x1D719}(0)f_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D704}(g_{0}))$
. Analogous isomorphism also holds in the case
![]() $\operatorname{Mp}$
.
$\operatorname{Mp}$
.
For the ease of the exposition, we slightly modify our notation in the case
![]() $\operatorname{Mp}$
for the rest of this section. For
$\operatorname{Mp}$
for the rest of this section. For
 $i=0,1,2$
, we put
$i=0,1,2$
, we put
 $G_{i}=\operatorname{Mp}(W_{i})$
and
$G_{i}=\operatorname{Mp}(W_{i})$
and
![]() $B_{i}$
the standard Borel subgroup of
$B_{i}$
the standard Borel subgroup of
![]() $G_{i}$
. Denote by
$G_{i}$
. Denote by
 $J=H\rtimes \operatorname{Mp}(W_{0})$
, which is a subgroup of
$J=H\rtimes \operatorname{Mp}(W_{0})$
, which is a subgroup of
![]() $G_{1}$
, and
$G_{1}$
, and
![]() $B_{J}$
its Borel subgroup. We denote by
$B_{J}$
its Borel subgroup. We denote by
 $K_{i}=\operatorname{Sp}(W_{i})(\mathfrak{o}_{F})$
a hyperspecial maximal subgroup of
$K_{i}=\operatorname{Sp}(W_{i})(\mathfrak{o}_{F})$
a hyperspecial maximal subgroup of
![]() $\operatorname{Sp}(W_{i})$
. The metaplectic cover
$\operatorname{Sp}(W_{i})$
. The metaplectic cover
 $\operatorname{Mp}(W_{i})\rightarrow \operatorname{Sp}(W_{i})$
splits canonically over
$\operatorname{Mp}(W_{i})\rightarrow \operatorname{Sp}(W_{i})$
splits canonically over
![]() $K_{i}$
, so we view
$K_{i}$
, so we view
![]() $K_{i}$
as a compact (but not maximal) subgroup of
$K_{i}$
as a compact (but not maximal) subgroup of
![]() $G_{i}$
and an element in
$G_{i}$
and an element in
![]() $K_{i}$
is naturally viewed as an element in
$K_{i}$
is naturally viewed as an element in
![]() $G_{i}$
. Let
$G_{i}$
. Let
 $K_{J}=K_{1}\cap J$
. The subgroup
$K_{J}=K_{1}\cap J$
. The subgroup
 $P_{i}=M_{i}N_{i}$
(
$P_{i}=M_{i}N_{i}$
(
 $i=1,\ldots ,r-1$
) is a parabolic subgroup of
$i=1,\ldots ,r-1$
) is a parabolic subgroup of
![]() $\operatorname{Sp}(W_{2})$
as before. The metaplectic double cover splits canonically over
$\operatorname{Sp}(W_{2})$
as before. The metaplectic double cover splits canonically over
![]() $N_{i}$
, so we consider
$N_{i}$
, so we consider
![]() $N_{i}$
as subgroups of
$N_{i}$
as subgroups of
![]() $G_{2}$
. By the Weyl group of
$G_{2}$
. By the Weyl group of
 $\operatorname{Mp}(W_{i})$
, we mean the Weyl group of
$\operatorname{Mp}(W_{i})$
, we mean the Weyl group of
![]() $\operatorname{Sp}(W_{i})$
. We let
$\operatorname{Sp}(W_{i})$
. We let
 $$\begin{eqnarray}w_{2,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{m}\\ -\mathsf{w}_{m}\end{array}\right),\quad w_{1,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{n+1}\\ -\mathsf{w}_{n+1}\end{array}\right),\quad w_{0,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{n}\\ -\mathsf{w}_{n}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}w_{2,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{m}\\ -\mathsf{w}_{m}\end{array}\right),\quad w_{1,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{n+1}\\ -\mathsf{w}_{n+1}\end{array}\right),\quad w_{0,\text{long}}=\left(\begin{array}{@{}cc@{}} & \mathsf{w}_{n}\\ -\mathsf{w}_{n}\end{array}\right)\end{eqnarray}$$
be representatives of the longest elements in the Weyl groups
![]() $W_{G_{2}}$
,
$W_{G_{2}}$
,
![]() $W_{G_{1}}$
and
$W_{G_{1}}$
and
![]() $W_{G_{0}}$
, respectively. They are viewed as elements in
$W_{G_{0}}$
, respectively. They are viewed as elements in
![]() $G_{2}$
,
$G_{2}$
,
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{0}$
, respectively.
$G_{0}$
, respectively.
For
 $(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{m})\in \mathbb{C}^{m}$
and
$(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{m})\in \mathbb{C}^{m}$
and
 $(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n})\in \mathbb{C}^{n}$
, we denote by
$(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n})\in \mathbb{C}^{n}$
, we denote by
![]() $\unicode[STIX]{x1D6EF}$
and
$\unicode[STIX]{x1D6EF}$
and
![]() $\unicode[STIX]{x1D709}$
the genuine character of
$\unicode[STIX]{x1D709}$
the genuine character of
![]() $B_{2}$
and
$B_{2}$
and
![]() $B_{0}$
, respectively, defined by
$B_{0}$
, respectively, defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}((\operatorname{diag}[t_{m},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{m}^{-1}],\unicode[STIX]{x1D716})) & = & \displaystyle \unicode[STIX]{x1D716}\cdot (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6EF}_{1})(t_{1})\cdots (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6EF}_{m})(t_{m}),\nonumber\\ \displaystyle \unicode[STIX]{x1D709}((\operatorname{diag}[t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}],\unicode[STIX]{x1D716})) & = & \displaystyle \unicode[STIX]{x1D716}\cdot (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{1})(t_{1})\cdots (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{n})(t_{n}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}((\operatorname{diag}[t_{m},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{m}^{-1}],\unicode[STIX]{x1D716})) & = & \displaystyle \unicode[STIX]{x1D716}\cdot (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6EF}_{1})(t_{1})\cdots (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6EF}_{m})(t_{m}),\nonumber\\ \displaystyle \unicode[STIX]{x1D709}((\operatorname{diag}[t_{n},\ldots ,t_{1},t_{1}^{-1},\ldots ,t_{n}^{-1}],\unicode[STIX]{x1D716})) & = & \displaystyle \unicode[STIX]{x1D716}\cdot (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{1})(t_{1})\cdots (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D709}_{n})(t_{n}).\nonumber\end{eqnarray}$$
We have the unramified principal series representation
![]() $I(\unicode[STIX]{x1D6EF})$
of
$I(\unicode[STIX]{x1D6EF})$
of
![]() $G_{2}$
and
$G_{2}$
and
![]() $I(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
of
$I(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
of
![]() $J$
. We let
$J$
. We let
![]() $f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}$
be the
$f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}$
be the
![]() $K_{J}$
fixed element in
$K_{J}$
fixed element in
![]() $I(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
such that
$I(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})$
such that
 $f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(1)=1$
. We will need to integrate over
$f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(1)=1$
. We will need to integrate over
 $\operatorname{Mp}(W_{0})$
. For this, we pick a measure
$\operatorname{Mp}(W_{0})$
. For this, we pick a measure
![]() $dx$
on
$dx$
on
 $\operatorname{Mp}(W_{0})$
, such that for any
$\operatorname{Mp}(W_{0})$
, such that for any
 $f\in {\mathcal{C}}_{c}^{\infty }(\operatorname{Sp}(W_{0}))$
, we have
$f\in {\mathcal{C}}_{c}^{\infty }(\operatorname{Sp}(W_{0}))$
, we have
 $\int _{\operatorname{Sp}(W_{0})}f(g)\,dg=\int _{\operatorname{Mp}(W_{0})}f(x)\,dx$
. When integrating over
$\int _{\operatorname{Sp}(W_{0})}f(g)\,dg=\int _{\operatorname{Mp}(W_{0})}f(x)\,dx$
. When integrating over
![]() $K_{i}$
’s or
$K_{i}$
’s or
![]() $K_{J}$
, we always use the measure so that the volume of the domain of the integration is one.
$K_{J}$
, we always use the measure so that the volume of the domain of the integration is one.
With this modification of notation, the integral
 $I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
in both cases
$I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
in both cases
![]() $\operatorname{Mp}$
and
$\operatorname{Mp}$
and
![]() $\operatorname{Sp}$
can be written as
$\operatorname{Sp}$
can be written as
 $$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{J}\int _{K_{J}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J})\,dk_{J}\,dg_{J}.\end{eqnarray}$$
$$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{J}\int _{K_{J}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J})\,dk_{J}\,dg_{J}.\end{eqnarray}$$
4.2 Reduction steps:
 $r\geqslant 1$
$r\geqslant 1$
We distinguish two cases:
![]() $r=0$
and
$r=0$
and
![]() $r\geqslant 1$
. We treat the case
$r\geqslant 1$
. We treat the case
![]() $r\geqslant 1$
first.
$r\geqslant 1$
first.
Let
 ${\dot{w}}=w_{1,\text{long}}^{-1}w_{2,\text{long}}$
be a representative of the longest element in
${\dot{w}}=w_{1,\text{long}}^{-1}w_{2,\text{long}}$
be a representative of the longest element in
 $W_{G_{1}}\backslash W_{G_{2}}$
.
$W_{G_{1}}\backslash W_{G_{2}}$
.
Lemma 4.2.1. If
 $g_{2}\in G_{2}$
and
$g_{2}\in G_{2}$
and
![]() $g_{J}\in J$
, then
$g_{J}\in J$
, then
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})(k_{1}{\dot{w}}n)\,dn\,dk_{1},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})(k_{1}{\dot{w}}n)\,dn\,dk_{1},\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathbf{w}=\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}({\dot{w}}n)f_{\unicode[STIX]{x1D6EF}^{-1}}({\dot{w}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}=\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}({\dot{w}}n)f_{\unicode[STIX]{x1D6EF}^{-1}}({\dot{w}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
Proof. By definition,
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J}) & = & \displaystyle \int _{N_{r-1}}^{\text{st}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(g_{2}^{-1}g_{J}u)f_{\unicode[STIX]{x1D6EF}},f_{\unicode[STIX]{x1D6EF}^{-1}})\unicode[STIX]{x1D713}(u)^{-1}\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1}}^{\text{st}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(g_{J}u)f_{\unicode[STIX]{x1D6EF}},\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})\unicode[STIX]{x1D713}(u)^{-1}\,du.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J}) & = & \displaystyle \int _{N_{r-1}}^{\text{st}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(g_{2}^{-1}g_{J}u)f_{\unicode[STIX]{x1D6EF}},f_{\unicode[STIX]{x1D6EF}^{-1}})\unicode[STIX]{x1D713}(u)^{-1}\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{r-1}}^{\text{st}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(g_{J}u)f_{\unicode[STIX]{x1D6EF}},\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})\unicode[STIX]{x1D713}(u)^{-1}\,du.\nonumber\end{eqnarray}$$
By [Reference LiuLiu16, Lemma 3.2] (it is valid also for metaplectic groups since the Bruhat decomposition is valid for metaplectic groups), there is an open compact subgroup
![]() $U$
of
$U$
of
![]() $N_{r-1}$
, such that
$N_{r-1}$
, such that
 $(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }=\operatorname{R}(\unicode[STIX]{x1D6FF}_{U}\unicode[STIX]{x1D713})(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})$
and
$(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }=\operatorname{R}(\unicode[STIX]{x1D6FF}_{U}\unicode[STIX]{x1D713})(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})$
and
 $(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})^{\circ }=\operatorname{R}(\unicode[STIX]{x1D6FF}_{U}\unicode[STIX]{x1D713})(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})$
are supported in
$(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})^{\circ }=\operatorname{R}(\unicode[STIX]{x1D6FF}_{U}\unicode[STIX]{x1D713})(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})$
are supported in
 $B_{2}{\dot{w}}P_{r-1}$
. Then
$B_{2}{\dot{w}}P_{r-1}$
. Then
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\int _{N_{r-1}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(u)(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})^{\circ },(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ })\unicode[STIX]{x1D713}(u)^{-1}\,du.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\int _{N_{r-1}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D70B}_{2}(u)(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})^{\circ },(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ })\unicode[STIX]{x1D713}(u)^{-1}\,du.\end{eqnarray}$$
We use the following realization of
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}$
:
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}$
:
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee })=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\unicode[STIX]{x1D711}(k_{1}{\dot{w}}n)\unicode[STIX]{x1D711}^{\vee }(k_{1}{\dot{w}}n)\,dn\,dk_{1},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\vee })=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\unicode[STIX]{x1D711}(k_{1}{\dot{w}}n)\unicode[STIX]{x1D711}^{\vee }(k_{1}{\dot{w}}n)\,dn\,dk_{1},\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathbf{w}=\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}({\dot{w}}n)f_{\unicode[STIX]{x1D6EF}^{-1}}({\dot{w}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}=\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}({\dot{w}}n)f_{\unicode[STIX]{x1D6EF}^{-1}}({\dot{w}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
In fact, the pairing is
![]() $G_{2}$
invariant since
$G_{2}$
invariant since
 $B_{2}K_{1}{\dot{w}}N_{r-1}$
is an open subset of
$B_{2}K_{1}{\dot{w}}N_{r-1}$
is an open subset of
![]() $G_{2}$
. The evaluation of
$G_{2}$
. The evaluation of
![]() $\mathbf{w}$
is as follows. Denote temporarily by
$\mathbf{w}$
is as follows. Denote temporarily by
![]() $f_{i}$
(
$f_{i}$
(
![]() $i=1,2$
) the function on
$i=1,2$
) the function on
![]() $\operatorname{Sp}(W_{i})$
which satisfies
$\operatorname{Sp}(W_{i})$
which satisfies
 $f_{i}|_{K_{i}}=1$
,
$f_{i}|_{K_{i}}=1$
,
 $f_{i}(bg)=\unicode[STIX]{x1D6FF}_{i}(b)f_{i}(g)$
for all
$f_{i}(bg)=\unicode[STIX]{x1D6FF}_{i}(b)f_{i}(g)$
for all
![]() $b\in B_{i}$
where
$b\in B_{i}$
where
![]() $B_{i}$
is the Borel subgroup of
$B_{i}$
is the Borel subgroup of
![]() $\operatorname{Sp}(W_{i})$
and
$\operatorname{Sp}(W_{i})$
and
![]() $\unicode[STIX]{x1D6FF}_{i}$
is the modulus character of
$\unicode[STIX]{x1D6FF}_{i}$
is the modulus character of
![]() $B_{i}$
. Define a function
$B_{i}$
. Define a function
![]() $f_{1}^{\prime }$
on
$f_{1}^{\prime }$
on
![]() $\operatorname{Sp}(W_{1})$
by
$\operatorname{Sp}(W_{1})$
by
 $$\begin{eqnarray}f_{1}^{\prime }(g)=\int _{N_{r-1}}f_{2}({\dot{w}}ng)\,dn.\end{eqnarray}$$
$$\begin{eqnarray}f_{1}^{\prime }(g)=\int _{N_{r-1}}f_{2}({\dot{w}}ng)\,dn.\end{eqnarray}$$
Then
 $\mathbf{w}=f_{1}^{\prime }(1)$
. Since
$\mathbf{w}=f_{1}^{\prime }(1)$
. Since
 $f_{1}^{\prime }(bg)=\unicode[STIX]{x1D6FF}_{1}(b)f_{1}^{\prime }(g)$
and
$f_{1}^{\prime }(bg)=\unicode[STIX]{x1D6FF}_{1}(b)f_{1}^{\prime }(g)$
and
![]() $f_{1}^{\prime }|_{K_{1}}$
is a constant, it follows that
$f_{1}^{\prime }|_{K_{1}}$
is a constant, it follows that
 $f_{1}^{\prime }=\mathbf{w}f_{1}$
. Therefore,
$f_{1}^{\prime }=\mathbf{w}f_{1}$
. Therefore,
 $$\begin{eqnarray}\int _{N_{m}\cap \operatorname{Sp}(W_{1})}f_{1}^{\prime }(w_{1,\text{long}}n)\,dn=\mathbf{w}\int _{N_{m}\cap \operatorname{Sp}(W_{1})}f_{1}(w_{1,\text{long}}n)\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{m}\cap \operatorname{Sp}(W_{1})}f_{1}^{\prime }(w_{1,\text{long}}n)\,dn=\mathbf{w}\int _{N_{m}\cap \operatorname{Sp}(W_{1})}f_{1}(w_{1,\text{long}}n)\,dn.\end{eqnarray}$$
The left-hand side equals
 $$\begin{eqnarray}\int _{N_{m}}f_{2}(w_{2,\text{long}}n)\,dn\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{m}}f_{2}(w_{2,\text{long}}n)\,dn\end{eqnarray}$$
by the definition of
![]() $f_{1}^{\prime }$
. It follows from [Reference GrossGro97, Proposition 4.7] that
$f_{1}^{\prime }$
. It follows from [Reference GrossGro97, Proposition 4.7] that
 $$\begin{eqnarray}\int _{N_{m}\cap \operatorname{Sp}(W_{i})}f_{i}(w_{i,\text{long}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{i}}}{\unicode[STIX]{x1D6E5}_{G_{i}}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{m}\cap \operatorname{Sp}(W_{i})}f_{i}(w_{i,\text{long}}n)\,dn=\frac{\unicode[STIX]{x1D6E5}_{T_{i}}}{\unicode[STIX]{x1D6E5}_{G_{i}}}.\end{eqnarray}$$
We then conclude that
 $$\begin{eqnarray}\mathbf{w}=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}=\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{1}}}{\unicode[STIX]{x1D6E5}_{G_{1}}}\biggr)^{-1}.\end{eqnarray}$$
We continue the computation of
 ${\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})$
. We have
${\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})$
. We have
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\mathbf{w}^{-1}\int _{N_{r-1}}\int _{K_{1}}\int _{N_{r-1}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})^{\circ }(k_{1}{\dot{w}}nu)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }(k_{1}{\dot{w}}n)\unicode[STIX]{x1D713}(u)^{-1}\,dn\,dk_{1}\,du,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EF}}(g_{2}^{-1}g_{J})=\mathbf{w}^{-1}\int _{N_{r-1}}\int _{K_{1}}\int _{N_{r-1}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})^{\circ }(k_{1}{\dot{w}}nu)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }(k_{1}{\dot{w}}n)\unicode[STIX]{x1D713}(u)^{-1}\,dn\,dk_{1}\,du,\end{eqnarray}$$
where the integrand is compactly supported. It equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }(k_{1}{\dot{w}}n)\,dn\,dk_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})(k_{1}{\dot{w}}n)\,dn\,dk_{1}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})^{\circ }(k_{1}{\dot{w}}n)\,dn\,dk_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{J})f_{\unicode[STIX]{x1D6EF}})(k_{1}{\dot{w}}n)(\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}})(k_{1}{\dot{w}}n)\,dn\,dk_{1}.\Box \nonumber\end{eqnarray}$$
By Lemma 4.2.1, we have
 $$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\mathbf{w}^{-1}\int _{J}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(k_{1}{\dot{w}}ng_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J})\,dk_{J}\,dn\,dk_{1}\,dg_{J}.\end{eqnarray}$$
$$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\mathbf{w}^{-1}\int _{J}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(k_{1}{\dot{w}}ng_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J})\,dk_{J}\,dn\,dk_{1}\,dg_{J}.\end{eqnarray}$$
Let
 $$\begin{eqnarray}l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast },\quad \unicode[STIX]{x1D702}_{1}=w_{1,\text{long}}h(l_{0}^{\ast },0)\in G_{1},\quad \unicode[STIX]{x1D702}={\dot{w}}\unicode[STIX]{x1D702}_{1}\in G_{2}.\end{eqnarray}$$
$$\begin{eqnarray}l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast },\quad \unicode[STIX]{x1D702}_{1}=w_{1,\text{long}}h(l_{0}^{\ast },0)\in G_{1},\quad \unicode[STIX]{x1D702}={\dot{w}}\unicode[STIX]{x1D702}_{1}\in G_{2}.\end{eqnarray}$$
Lemma 4.2.2. The double coset
 $B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J})$
is open dense in
$B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J})$
is open dense in
![]() $G_{2}$
.
$G_{2}$
.
Proof. This is straightforward to check.◻
Thanks to this lemma, we can define a function
![]() $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
![]() $G_{2}$
with the following properties:
$G_{2}$
with the following properties:
-
(i)
 $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{2}g_{2}h(l,t)b_{0}u)=(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{B_{2}}^{1/2})(b_{2})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{B_{J}}^{-1/2})(b_{0})\overline{\unicode[STIX]{x1D713}(t)\unicode[STIX]{x1D713}_{r-1}(u)}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})$
for any
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{2}g_{2}h(l,t)b_{0}u)=(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{B_{2}}^{1/2})(b_{2})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{B_{J}}^{-1/2})(b_{0})\overline{\unicode[STIX]{x1D713}(t)\unicode[STIX]{x1D713}_{r-1}(u)}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})$
for any
 $b_{2}\in B_{2}$
,
$b_{2}\in B_{2}$
,
 $b_{0}\in B_{0}$
,
$b_{0}\in B_{0}$
,
 $l\in L$
and
$l\in L$
and
 $u\in N_{r-1}$
;
$u\in N_{r-1}$
; -
(ii) the support of
 $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is
 $B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J})$
;
$B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J})$
; -
(iii)
 $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})=1$
.
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})=1$
.
The space of functions that satisfy the first two conditions is one dimensional by Lemma 4.2.2. We have
 $$\begin{eqnarray}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{2}\unicode[STIX]{x1D702}h(l,t)b_{0}u)=(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{B_{J}}^{-1/2})(b_{0})\overline{\unicode[STIX]{x1D713}(t)\unicode[STIX]{x1D713}_{r-1}(u)},\end{eqnarray}$$
$$\begin{eqnarray}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{2}\unicode[STIX]{x1D702}h(l,t)b_{0}u)=(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{B_{J}}^{-1/2})(b_{0})\overline{\unicode[STIX]{x1D713}(t)\unicode[STIX]{x1D713}_{r-1}(u)},\end{eqnarray}$$
for
![]() $b_{2}\in B_{2}$
,
$b_{2}\in B_{2}$
,
![]() $b_{0}\in B_{0}$
,
$b_{0}\in B_{0}$
,
![]() $l\in L$
and
$l\in L$
and
 $u\in N_{r-1}$
. We define a function
$u\in N_{r-1}$
. We define a function
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
![]() $G_{2}$
as
$G_{2}$
as
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{J}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(g_{2}g_{J})f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J})\,dg_{J}\quad & g_{2}\in B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{J}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(g_{2}g_{J})f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J})\,dg_{J}\quad & g_{2}\in B_{2}\unicode[STIX]{x1D702}(N_{r-1}\rtimes B_{J}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
If the defining integral of
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent, then we have
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent, then we have
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(g_{2}),\quad g_{2}\in G_{2}.\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(g_{2}),\quad g_{2}\in G_{2}.\end{eqnarray}$$
We assume that the defining integral of
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent for the moment. This will be proved later. It follows that
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent for the moment. This will be proved later. It follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathbf{w}^{-1}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}.\nonumber\end{eqnarray}$$
Define
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(g_{2})=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}.\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(g_{2})=\mathbf{w}^{-1}\int _{K_{1}}\int _{N_{r-1}}^{\text{st}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(k_{1}{\dot{w}}nk_{J})\unicode[STIX]{x1D70B}_{2}^{\vee }(g_{2})f_{\unicode[STIX]{x1D6EF}^{-1}}(k_{1}{\dot{w}}n)\,dk_{J}\,dn\,dk_{1}.\end{eqnarray}$$
Then we have
 $$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(g_{2}).\end{eqnarray}$$
$$\begin{eqnarray}I(g_{2},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(g_{2}).\end{eqnarray}$$
4.3 Reduction steps:
 $r=0$
$r=0$
We now treat the case
![]() $r=0$
.
$r=0$
.
The integral we need to compute is
 $$\begin{eqnarray}I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{K_{J}}\int _{K_{0}}f_{\unicode[STIX]{x1D6EF}}(k_{0}g)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J}^{-1}g)\,dk_{0}\,dk_{J}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{K_{J}}\int _{K_{0}}f_{\unicode[STIX]{x1D6EF}}(k_{0}g)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(k_{J}g_{J}^{-1}g)\,dk_{0}\,dk_{J}\,dg.\end{eqnarray}$$
We define
 $$\begin{eqnarray}l_{0}=(1,\ldots ,1)\in L,\quad \unicode[STIX]{x1D702}=w_{0,\text{long}}h(l_{0},0)\in J.\end{eqnarray}$$
$$\begin{eqnarray}l_{0}=(1,\ldots ,1)\in L,\quad \unicode[STIX]{x1D702}=w_{0,\text{long}}h(l_{0},0)\in J.\end{eqnarray}$$
Similar to Lemma 4.2.2, it is straightforward to prove the following lemma.
Lemma 4.3.1. The double coset
![]() $B_{J}\unicode[STIX]{x1D702}B_{0}$
is open dense in
$B_{J}\unicode[STIX]{x1D702}B_{0}$
is open dense in
![]() $J$
.
$J$
.
We define a function
![]() $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
![]() $J$
which is supported on
$J$
which is supported on
![]() $B_{J}\unicode[STIX]{x1D702}B_{0}$
by
$B_{J}\unicode[STIX]{x1D702}B_{0}$
by
 $$\begin{eqnarray}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(h(l,t)b_{0}^{\prime }\unicode[STIX]{x1D702}b_{0})=(\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}_{J}^{1/2})(b_{0}^{\prime })(\unicode[STIX]{x1D6EF}\unicode[STIX]{x1D6FF}_{0}^{1/2})(b_{0})\unicode[STIX]{x1D713}(t),\quad b_{0},b_{0}^{\prime }\in B_{0},~l\in L.\end{eqnarray}$$
$$\begin{eqnarray}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(h(l,t)b_{0}^{\prime }\unicode[STIX]{x1D702}b_{0})=(\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}_{J}^{1/2})(b_{0}^{\prime })(\unicode[STIX]{x1D6EF}\unicode[STIX]{x1D6FF}_{0}^{1/2})(b_{0})\unicode[STIX]{x1D713}(t),\quad b_{0},b_{0}^{\prime }\in B_{0},~l\in L.\end{eqnarray}$$
We define the function
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
on
![]() $J$
by
$J$
by
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J})=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{G_{0}}f_{\unicode[STIX]{x1D6EF}}(g)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J}g)\,dg\quad & g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0},\\ 0\quad & \text{otherwise}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J})=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{G_{0}}f_{\unicode[STIX]{x1D6EF}}(g)f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J}g)\,dg\quad & g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0},\\ 0\quad & \text{otherwise}\end{array}\right.\end{eqnarray}$$
and the function
![]() $S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
by
$S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
by
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J})=\int _{K_{J}}\int _{K_{0}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{J}g_{J}^{-1}k_{0})\,dk_{0}\,dk_{J}.\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J})=\int _{K_{J}}\int _{K_{0}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{J}g_{J}^{-1}k_{0})\,dk_{0}\,dk_{J}.\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(g_{J}).\end{eqnarray}$$
$$\begin{eqnarray}I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}(g_{J}).\end{eqnarray}$$
We now prove the convergence of the defining integral of
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
 $S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
. Assume that
$S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
. Assume that
![]() $r\geqslant 0$
.
$r\geqslant 0$
.
Lemma 4.3.2. The defining integrals for
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
 $S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
are absolutely convergent if
$S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
are absolutely convergent if
![]() $\unicode[STIX]{x1D6EF}^{\prime }$
and
$\unicode[STIX]{x1D6EF}^{\prime }$
and
![]() $\unicode[STIX]{x1D709}$
are sufficiently close to the unitary axis, where
$\unicode[STIX]{x1D709}$
are sufficiently close to the unitary axis, where
![]() $\unicode[STIX]{x1D6EF}^{\prime }$
is the restriction of
$\unicode[STIX]{x1D6EF}^{\prime }$
is the restriction of
![]() $\unicode[STIX]{x1D6EF}$
to
$\unicode[STIX]{x1D6EF}$
to
![]() $T_{1}$
.
$T_{1}$
.
Proof. If
![]() $r=0$
, then it follows from Proposition 2.2.1 (or its proof, applied to
$r=0$
, then it follows from Proposition 2.2.1 (or its proof, applied to
![]() $|\unicode[STIX]{x1D6EF}|$
and
$|\unicode[STIX]{x1D6EF}|$
and
![]() $|\unicode[STIX]{x1D709}|$
) that
$|\unicode[STIX]{x1D709}|$
) that
 $I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
is convergent if
$I(g_{J},\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
is convergent if
![]() $\unicode[STIX]{x1D6EF}$
and
$\unicode[STIX]{x1D6EF}$
and
![]() $\unicode[STIX]{x1D709}$
are sufficiently close to the unitary axis. It then follows that for a fixed
$\unicode[STIX]{x1D709}$
are sufficiently close to the unitary axis. It then follows that for a fixed
![]() $g_{J}\in J$
, the defining integral of
$g_{J}\in J$
, the defining integral of
 $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{J}g_{J}k_{0})$
is convergent for almost all
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{J}g_{J}k_{0})$
is convergent for almost all
 $k_{J}\in K_{J}$
and
$k_{J}\in K_{J}$
and
 $k_{0}\in K_{0}$
such that
$k_{0}\in K_{0}$
such that
 $k_{J}g_{J}^{-1}k_{0}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
. By the definition of
$k_{J}g_{J}^{-1}k_{0}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
. By the definition of
![]() $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
, its defining integral is convergent for some
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
, its defining integral is convergent for some
 $g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
is and only if it is convergent for all
$g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
is and only if it is convergent for all
 $g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
. Therefore, the defining integral of
$g_{J}\in B_{J}\unicode[STIX]{x1D702}B_{0}$
. Therefore, the defining integral of
 $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})$
is convergent. This then implies that the defining integral of
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})$
is convergent. This then implies that the defining integral of
 $S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
is convergent.
$S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}$
is convergent.
The convergence in the case of
![]() $r=1$
can be proved similarly. We only need to change the notation at several places.
$r=1$
can be proved similarly. We only need to change the notation at several places.
Now assume that
![]() $r\geqslant 2$
. By [Reference LiuLiu16, Lemma 3.3], there is an open compact subgroup
$r\geqslant 2$
. By [Reference LiuLiu16, Lemma 3.3], there is an open compact subgroup
![]() $U$
of
$U$
of
![]() $N_{r-1}$
, such that for all
$N_{r-1}$
, such that for all
![]() $g_{J}\in J$
,
$g_{J}\in J$
,
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J})=\int _{U}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J}u)\overline{\unicode[STIX]{x1D713}_{r-1}(u)}\,du.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J})=\int _{U}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J}u)\overline{\unicode[STIX]{x1D713}_{r-1}(u)}\,du.\end{eqnarray}$$
Therefore there is a constant
![]() $C$
, such that
$C$
, such that
 $$\begin{eqnarray}|{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J})|\leqslant C\times f_{|\unicode[STIX]{x1D6EF}^{\prime }|}(\unicode[STIX]{x1D702}_{1}g_{J}).\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{F}}_{\unicode[STIX]{x1D713}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}g_{J})|\leqslant C\times f_{|\unicode[STIX]{x1D6EF}^{\prime }|}(\unicode[STIX]{x1D702}_{1}g_{J}).\end{eqnarray}$$
The lemma in the case
![]() $r\geqslant 2$
then follows from the case
$r\geqslant 2$
then follows from the case
![]() $r=1$
.◻
$r=1$
.◻
4.4 Proof of Proposition 2.2.3
Assume that
![]() $r\geqslant 1$
. Let
$r\geqslant 1$
. Let
 $\unicode[STIX]{x1D6EF}^{0}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{n})\in \mathbb{C}^{n}$
. Let
$\unicode[STIX]{x1D6EF}^{0}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{n})\in \mathbb{C}^{n}$
. Let
![]() $\unicode[STIX]{x1D70E}$
be the unramified principal series representation of
$\unicode[STIX]{x1D70E}$
be the unramified principal series representation of
![]() $G_{0}$
defined by
$G_{0}$
defined by
![]() $\unicode[STIX]{x1D6EF}^{0}$
. We let
$\unicode[STIX]{x1D6EF}^{0}$
. We let
![]() $\unicode[STIX]{x1D70F}$
be the unramified principal series representation of
$\unicode[STIX]{x1D70F}$
be the unramified principal series representation of
![]() $\operatorname{GL}_{r}$
defined by the unramified characters
$\operatorname{GL}_{r}$
defined by the unramified characters
 $(\unicode[STIX]{x1D6EF}_{n+1},\ldots ,\unicode[STIX]{x1D6EF}_{m})$
.
$(\unicode[STIX]{x1D6EF}_{n+1},\ldots ,\unicode[STIX]{x1D6EF}_{m})$
.
Following the notation of [Reference Ichino and IkedaII10] and [Reference LiuLiu16], we shall denote
 $T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})$
by
$T_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})$
by
 $\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.
$\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.
Lemma 4.4.1. We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\quad & \text{Case}~\operatorname{Sp},\\ \displaystyle \frac{L({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L_{\unicode[STIX]{x1D713}}(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\operatorname{Sym}^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\quad & \text{Case}~\operatorname{Mp}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\quad & \text{Case}~\operatorname{Sp},\\ \displaystyle \frac{L({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L_{\unicode[STIX]{x1D713}}(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\operatorname{Sym}^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\quad & \text{Case}~\operatorname{Mp}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Recall that
 $l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast }$
. By definition,
$l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast }$
. By definition,
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{H}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)uhg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\unicode[STIX]{x1D719}(0)}\,du\,dh\,dg_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{H}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)uhg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(u)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(hg_{0})\unicode[STIX]{x1D719}(0)}\,du\,dh\,dg_{0}.\end{eqnarray}$$
We combine the integral over
![]() $H$
and
$H$
and
![]() $N_{r-1}$
to get an integral over
$N_{r-1}$
to get an integral over
![]() $N_{r}$
and get
$N_{r}$
and get
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)vg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(\ell (v)g_{0})\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)vg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(\ell (v)g_{0})\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\end{eqnarray}$$
where
 $\ell :N_{r}\rightarrow H$
is the natural projection whose kernel is
$\ell :N_{r}\rightarrow H$
is the natural projection whose kernel is
![]() $N_{r-1}$
. We make a change of variable
$N_{r-1}$
. We make a change of variable
 $v\mapsto h(l_{0}^{\ast },0)^{-1}v$
and get
$v\mapsto h(l_{0}^{\ast },0)^{-1}v$
and get
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}vg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h(l_{0}^{\ast },0)^{-1}\ell (v)g_{0})\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}g_{0}v)f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h(l_{0}^{\ast },0)^{-1}g_{0}\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}vg_{0})f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h(l_{0}^{\ast },0)^{-1}\ell (v)g_{0})\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \int _{G_{0}}\int _{N_{r}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}g_{0}v)f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D713}_{r-1}(v)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(h(l_{0}^{\ast },0)^{-1}g_{0}\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\nonumber\end{eqnarray}$$
where in the second equality we made a chance of variable
 $v\mapsto g_{0}vg_{0}^{-1}$
and used the fact that
$v\mapsto g_{0}vg_{0}^{-1}$
and used the fact that
 $\unicode[STIX]{x1D713}_{r-1}(g_{0}vg_{0}^{-1})=\unicode[STIX]{x1D713}_{r-1}(v)$
.
$\unicode[STIX]{x1D713}_{r-1}(g_{0}vg_{0}^{-1})=\unicode[STIX]{x1D713}_{r-1}(v)$
.
Let
![]() $N_{R}$
be the unipotent radical of the upper triangular Borel subgroup of
$N_{R}$
be the unipotent radical of the upper triangular Borel subgroup of
![]() $\operatorname{GL}_{r}$
and
$\operatorname{GL}_{r}$
and
 $$\begin{eqnarray}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(g)=\int _{N_{R}}f_{\unicode[STIX]{x1D6EF}}(\mathsf{w}_{r}ng)\overline{\unicode[STIX]{x1D713}_{r}(n)}\,dn,\quad g\in G_{2}.\end{eqnarray}$$
$$\begin{eqnarray}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(g)=\int _{N_{R}}f_{\unicode[STIX]{x1D6EF}}(\mathsf{w}_{r}ng)\overline{\unicode[STIX]{x1D713}_{r}(n)}\,dn,\quad g\in G_{2}.\end{eqnarray}$$
Then by the Casselman–Shalika formula, we have
 $$\begin{eqnarray}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(1)=\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}.\end{eqnarray}$$
$$\begin{eqnarray}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(1)=\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}.\end{eqnarray}$$
We can then write the integral (4.4.1) as
 $$\begin{eqnarray}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\times \int _{N_{R}\backslash N_{r}}\int _{G_{0}}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(w_{0,\text{long}}g_{0}\ddot{w}v)f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D714}(h(l_{0}^{\ast },0)^{-1}g_{0}\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\times \int _{N_{R}\backslash N_{r}}\int _{G_{0}}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(w_{0,\text{long}}g_{0}\ddot{w}v)f_{\unicode[STIX]{x1D709}}(g_{0})\overline{\unicode[STIX]{x1D714}(h(l_{0}^{\ast },0)^{-1}g_{0}\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg_{0},\end{eqnarray}$$
where
 $\ddot{w}=(\begin{smallmatrix} & & 1_{r}\\ & 1_{2n}\\ -1_{r}\end{smallmatrix})$
. We make a change of variable
$\ddot{w}=(\begin{smallmatrix} & & 1_{r}\\ & 1_{2n}\\ -1_{r}\end{smallmatrix})$
. We make a change of variable
 $g\mapsto w_{0,\text{long}}^{-1}gw_{0,\text{long}}$
and
$g\mapsto w_{0,\text{long}}^{-1}gw_{0,\text{long}}$
and
 $v\mapsto w_{0,\text{long}}^{-1}vw_{0,\text{long}}$
. Then since
$v\mapsto w_{0,\text{long}}^{-1}vw_{0,\text{long}}$
. Then since
 $w_{0,\text{long}}\in K_{0}$
and
$w_{0,\text{long}}\in K_{0}$
and
![]() $f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}$
,
$f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}$
,
![]() $f_{\unicode[STIX]{x1D709}}$
,
$f_{\unicode[STIX]{x1D709}}$
,
![]() $\unicode[STIX]{x1D719}$
are all
$\unicode[STIX]{x1D719}$
are all
![]() $K_{0}$
-fixed, we conclude that
$K_{0}$
-fixed, we conclude that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{N_{R}\backslash N_{r}}\int _{G_{0}}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(g\ddot{w}v)f_{\unicode[STIX]{x1D709}}(w_{0,\text{long}}g)\overline{\unicode[STIX]{x1D714}(w_{0,\text{long}}h(l_{0}^{\ast },0)g\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{N_{R}\backslash N_{r}}\int _{G_{0}}f_{W_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D6EF}^{0}}(g\ddot{w}v)f_{\unicode[STIX]{x1D709}}(w_{0,\text{long}}g)\overline{\unicode[STIX]{x1D714}(w_{0,\text{long}}h(l_{0}^{\ast },0)g\ell (v))\unicode[STIX]{x1D719}(0)}\,dv\,dg.\nonumber\end{eqnarray}$$
By definition,
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}f_{\unicode[STIX]{x1D6EF}^{0}}(g)f_{\unicode[STIX]{x1D709}}(w_{0,\text{long}}g)\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(w_{0,\text{long}}h(l_{0}^{\ast },0)g)\unicode[STIX]{x1D719}(0)}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})=\int _{G_{0}}f_{\unicode[STIX]{x1D6EF}^{0}}(g)f_{\unicode[STIX]{x1D709}}(w_{0,\text{long}}g)\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}(w_{0,\text{long}}h(l_{0}^{\ast },0)g)\unicode[STIX]{x1D719}(0)}\,dg.\end{eqnarray}$$
We then apply [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11, Theorem 4.3] and [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11, End of § 4, (4.7)] to get the lemma. (In the notation of [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11], we apply this to the case
![]() $r=0$
and
$r=0$
and
 $b_{\unicode[STIX]{x1D708}}(f_{\unicode[STIX]{x1D6EF}^{0}},f_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D719})=\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.)◻
$b_{\unicode[STIX]{x1D708}}(f_{\unicode[STIX]{x1D6EF}^{0}},f_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D719})=\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})$
.)◻
We now compute
 $S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(1)$
. Define the projection
$S_{\unicode[STIX]{x1D6EF}^{-1},\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713}^{-1}}^{\prime }(1)$
. Define the projection
 $\operatorname{pr}_{2}:{\mathcal{C}}_{c}^{\infty }(G_{2})\rightarrow I(\unicode[STIX]{x1D6EF})$
by
$\operatorname{pr}_{2}:{\mathcal{C}}_{c}^{\infty }(G_{2})\rightarrow I(\unicode[STIX]{x1D6EF})$
by
 $$\begin{eqnarray}\operatorname{pr}_{2}(F_{2})(g_{2})=\int _{B_{2}}F_{2}(b_{2}g_{2})(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\,db_{2},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{2}(F_{2})(g_{2})=\int _{B_{2}}F_{2}(b_{2}g_{2})(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\,db_{2},\end{eqnarray}$$
where the measure
![]() $db_{2}$
is the left invariant measure on
$db_{2}$
is the left invariant measure on
![]() $B_{2}$
so that
$B_{2}$
so that
 $\operatorname{pr}_{2}(\operatorname{1}_{K_{2}})=f_{\unicode[STIX]{x1D6EF}}$
. Then we define
$\operatorname{pr}_{2}(\operatorname{1}_{K_{2}})=f_{\unicode[STIX]{x1D6EF}}$
. Then we define
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}\in \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}\in \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})\end{eqnarray}$$
by
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(f_{2})(g_{J})=\int _{G_{2}}f_{2}^{\prime }(g_{2}g_{J})Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})\,dg_{2},\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(f_{2})(g_{J})=\int _{G_{2}}f_{2}^{\prime }(g_{2}g_{J})Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})\,dg_{2},\end{eqnarray}$$
where
![]() $f_{2}^{\prime }$
is any element in
$f_{2}^{\prime }$
is any element in
 ${\mathcal{C}}_{c}^{\infty }(G_{2})$
with
${\mathcal{C}}_{c}^{\infty }(G_{2})$
with
 $\operatorname{pr}_{2}(f_{2}^{\prime })=f_{2}$
. It is not hard to check that
$\operatorname{pr}_{2}(f_{2}^{\prime })=f_{2}$
. It is not hard to check that
![]() $l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is independent of the choice of
$l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is independent of the choice of
![]() $f_{2}^{\prime }$
. We define
$f_{2}^{\prime }$
. We define
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})={\mathcal{B}}_{I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})}(f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})).\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{2})={\mathcal{B}}_{I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})}(f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})).\end{eqnarray}$$
The defining integral of
![]() $l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent if
$l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is convergent if
![]() $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous. By [Reference ShenShe14, § 3], whose method is valid for both cases
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous. By [Reference ShenShe14, § 3], whose method is valid for both cases
![]() $\operatorname{Mp}$
and
$\operatorname{Mp}$
and
![]() $\operatorname{Sp}$
,
$\operatorname{Sp}$
,
![]() $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous if
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous if
![]() $(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709})$
lie in some (nonempty) open subset of
$(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709})$
lie in some (nonempty) open subset of
 $\mathbb{C}^{r+s}\times \mathbb{C}^{s}$
. We refer the readers to [Reference ShenShe14, § 3] for a precise description of this open subset.
$\mathbb{C}^{r+s}\times \mathbb{C}^{s}$
. We refer the readers to [Reference ShenShe14, § 3] for a precise description of this open subset.
Lemma 4.4.2. We have
 $S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }=S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
.
$S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }=S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
.
Proof. We check that
![]() $S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
$S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
and
![]() $S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }$
agree when
$S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }$
agree when
![]() $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous. We divide the proof into two steps.
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}$
is continuous. We divide the proof into two steps.
Step 1. The goal is to reduce the lemma to the identity (4.4.2).
Let
 $\unicode[STIX]{x1D6EF}^{1}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{n+1})$
and
$\unicode[STIX]{x1D6EF}^{1}=(\unicode[STIX]{x1D6EF}_{1},\ldots ,\unicode[STIX]{x1D6EF}_{n+1})$
and
![]() $I(\unicode[STIX]{x1D6EF}^{1})$
be the unramified principal series representation of
$I(\unicode[STIX]{x1D6EF}^{1})$
be the unramified principal series representation of
![]() $G_{1}$
defined by the character
$G_{1}$
defined by the character
![]() $\unicode[STIX]{x1D6EF}^{1}$
. Let
$\unicode[STIX]{x1D6EF}^{1}$
. Let
 ${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})(g_{2}):={\mathcal{F}}_{\unicode[STIX]{x1D713}}(f_{2})(g_{2}{\dot{w}})$
. Then
${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})(g_{2}):={\mathcal{F}}_{\unicode[STIX]{x1D713}}(f_{2})(g_{2}{\dot{w}})$
. Then
 ${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})|_{G_{1}}\in I(\unicode[STIX]{x1D6EF}^{1})$
. Define the projection
${\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})|_{G_{1}}\in I(\unicode[STIX]{x1D6EF}^{1})$
. Define the projection
 $\operatorname{pr}_{1}:{\mathcal{C}}_{c}^{\infty }(G_{1})\rightarrow I(\unicode[STIX]{x1D6EF}^{1})$
by
$\operatorname{pr}_{1}:{\mathcal{C}}_{c}^{\infty }(G_{1})\rightarrow I(\unicode[STIX]{x1D6EF}^{1})$
by
 $$\begin{eqnarray}\operatorname{pr}_{1}(F)(g_{1})=\int _{B_{1}}F(b_{1}g_{1})((\unicode[STIX]{x1D6EF}^{1})^{-1}\unicode[STIX]{x1D6FF}_{1}^{1/2})(b_{1})\,db_{1},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{1}(F)(g_{1})=\int _{B_{1}}F(b_{1}g_{1})((\unicode[STIX]{x1D6EF}^{1})^{-1}\unicode[STIX]{x1D6FF}_{1}^{1/2})(b_{1})\,db_{1},\end{eqnarray}$$
where the left invariant measure
![]() $db_{1}$
is the one so that
$db_{1}$
is the one so that
 $\operatorname{pr}_{1}(\operatorname{1}_{K_{1}})=f_{\unicode[STIX]{x1D6EF}^{1}}$
. Note that
$\operatorname{pr}_{1}(\operatorname{1}_{K_{1}})=f_{\unicode[STIX]{x1D6EF}^{1}}$
. Note that
![]() $\operatorname{pr}_{1}$
is surjective and for any element
$\operatorname{pr}_{1}$
is surjective and for any element
 $f\in I(\unicode[STIX]{x1D6EF}^{1})$
, one can choose
$f\in I(\unicode[STIX]{x1D6EF}^{1})$
, one can choose
![]() $F$
whose support lies in
$F$
whose support lies in
![]() $K_{1}$
such that
$K_{1}$
such that
 $\operatorname{pr}_{1}(F)=f$
.
$\operatorname{pr}_{1}(F)=f$
.
Define the intertwining operator
 $l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }\in \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})$
by
$l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }\in \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})$
by
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(f_{2})(g_{J})=\int _{G_{1}}f_{2}^{\prime \prime }(g_{1}g_{J})Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{1}{\dot{w}})\,dg_{1},\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(f_{2})(g_{J})=\int _{G_{1}}f_{2}^{\prime \prime }(g_{1}g_{J})Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{1}{\dot{w}})\,dg_{1},\end{eqnarray}$$
where
![]() $f_{2}^{\prime \prime }$
is any element in
$f_{2}^{\prime \prime }$
is any element in
 ${\mathcal{C}}_{c}^{\infty }(G_{1})$
with
${\mathcal{C}}_{c}^{\infty }(G_{1})$
with
 $\operatorname{pr}_{1}(f_{2}^{\prime \prime })={\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})|_{G_{1}}\!$
.
$\operatorname{pr}_{1}(f_{2}^{\prime \prime })={\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(f_{2})|_{G_{1}}\!$
.
Fix
 $g_{2}\in G_{2}$
and let
$g_{2}\in G_{2}$
and let
 $f_{2}^{\prime \prime }\in {\mathcal{C}}_{c}^{\infty }(G_{1})$
be a smooth function whose support is contained in
$f_{2}^{\prime \prime }\in {\mathcal{C}}_{c}^{\infty }(G_{1})$
be a smooth function whose support is contained in
![]() $K_{1}$
and
$K_{1}$
and
 $\operatorname{pr}_{1}(f_{2}^{\prime \prime })={\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})|_{G_{1}}\!$
. Then
$\operatorname{pr}_{1}(f_{2}^{\prime \prime })={\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})|_{G_{1}}\!$
. Then
 $$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(g_{2}) & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}k_{J}){\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})(k_{1})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}k_{J})f_{2}^{\prime \prime }(k_{1})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}})f_{2}^{\prime \prime }(k_{1}k_{J})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}{\mathcal{B}}_{I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})}(f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(g_{2}) & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}k_{J}){\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})(k_{1})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}}k_{J})f_{2}^{\prime \prime }(k_{1})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}\int _{K_{1}}\int _{K_{J}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{1}{\dot{w}})f_{2}^{\prime \prime }(k_{1}k_{J})\,dk_{J}\,dk_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathbf{w}^{-1}{\mathcal{B}}_{I^{J}(\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}})}(f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}},l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D70B}_{2}(g_{2})f_{\unicode[STIX]{x1D6EF}})).\nonumber\end{eqnarray}$$
Therefore, in order to prove the lemma, we only need to show
 $\mathbf{w}\cdot l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}=l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }$
. We have
$\mathbf{w}\cdot l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}=l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }$
. We have
 $$\begin{eqnarray}\dim \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})=1.\end{eqnarray}$$
$$\begin{eqnarray}\dim \operatorname{Hom}_{N_{r-1}\rtimes J}(I(\unicode[STIX]{x1D6EF}),I^{J}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D713})\otimes \unicode[STIX]{x1D713}_{r-1})=1.\end{eqnarray}$$
This is proved in [Reference ShenShe14] in the case
![]() $\operatorname{Sp}$
, but the proof works equally well in the case
$\operatorname{Sp}$
, but the proof works equally well in the case
![]() $\operatorname{Mp}$
as it uses only the decomposition
$\operatorname{Mp}$
as it uses only the decomposition
 $G_{i}=B_{i}K_{i}$
. Therefore, we only have to find a function
$G_{i}=B_{i}K_{i}$
. Therefore, we only have to find a function
 $\unicode[STIX]{x1D711}\in I(\unicode[STIX]{x1D6EF})$
such that
$\unicode[STIX]{x1D711}\in I(\unicode[STIX]{x1D6EF})$
such that
 $l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711})(1)\not =0$
and show that
$l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711})(1)\not =0$
and show that
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D711})(1)/l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711})(1)=\mathbf{w}.\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\unicode[STIX]{x1D711})(1)/l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711})(1)=\mathbf{w}.\end{eqnarray}$$
Step 2. Proof of (4.4.2).
Let
![]() $K_{i}^{(1)}$
be the Iwahori subgroup of
$K_{i}^{(1)}$
be the Iwahori subgroup of
![]() $K_{i}$
. Let
$K_{i}$
. Let
 $T_{i}^{(0)}=T_{i}(\mathfrak{o}_{F})$
and
$T_{i}^{(0)}=T_{i}(\mathfrak{o}_{F})$
and
![]() $T_{i}^{(1)}$
be the kernel of the reduction map
$T_{i}^{(1)}$
be the kernel of the reduction map
 $T_{i}^{(0)}\rightarrow T_{i}(\mathfrak{o}_{F}/\unicode[STIX]{x1D71B})$
. Note here that by
$T_{i}^{(0)}\rightarrow T_{i}(\mathfrak{o}_{F}/\unicode[STIX]{x1D71B})$
. Note here that by
![]() $T_{i}$
, we mean the diagonal torus of
$T_{i}$
, we mean the diagonal torus of
![]() $\operatorname{Sp}(W_{i})$
in both cases
$\operatorname{Sp}(W_{i})$
in both cases
![]() $\operatorname{Sp}$
and
$\operatorname{Sp}$
and
![]() $\operatorname{Mp}$
. Let
$\operatorname{Mp}$
. Let
![]() $\overline{B}_{i}$
be the opposite Borel subgroup of
$\overline{B}_{i}$
be the opposite Borel subgroup of
![]() $G_{i}$
and
$G_{i}$
and
![]() $\overline{N}_{i}$
be its unipotent radical. Let
$\overline{N}_{i}$
be its unipotent radical. Let
 $N_{i}^{(0)}=N_{i}\cap K_{i}$
,
$N_{i}^{(0)}=N_{i}\cap K_{i}$
,
 $\overline{N}_{i}^{(1)}=\overline{N}_{i}\cap K_{i}^{(1)}$
and
$\overline{N}_{i}^{(1)}=\overline{N}_{i}\cap K_{i}^{(1)}$
and
 $N_{i}^{(1)}=w_{i,\text{long}}^{-1}\overline{N}_{i}^{(1)}w_{i,\text{long}}$
. Let
$N_{i}^{(1)}=w_{i,\text{long}}^{-1}\overline{N}_{i}^{(1)}w_{i,\text{long}}$
. Let
 $N_{r-1}^{(1)}=N_{r-1}\cap N_{2}^{(1)}$
. Note that in the case
$N_{r-1}^{(1)}=N_{r-1}\cap N_{2}^{(1)}$
. Note that in the case
![]() $\operatorname{Mp}$
, these subgroups of
$\operatorname{Mp}$
, these subgroups of
![]() $K_{i}$
are considered as subgroups of
$K_{i}$
are considered as subgroups of
![]() $G_{i}$
via the splitting
$G_{i}$
via the splitting
 $K_{i}\rightarrow G_{i}$
.
$K_{i}\rightarrow G_{i}$
.
Let
 $\unicode[STIX]{x1D711}=\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})\in {\mathcal{C}}_{c}^{\infty }(G_{2})$
. Then
$\unicode[STIX]{x1D711}=\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})\in {\mathcal{C}}_{c}^{\infty }(G_{2})$
. Then
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})(1)=\int _{K_{2}^{(1)}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{2}\unicode[STIX]{x1D702})\,dk_{2}.\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})(1)=\int _{K_{2}^{(1)}}Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{2}\unicode[STIX]{x1D702})\,dk_{2}.\end{eqnarray}$$
Recall that
 $l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast }$
and
$l_{0}^{\ast }=(1,\ldots ,1)\in L^{\ast }$
and
 $\unicode[STIX]{x1D702}=w_{2,\text{long}}h(l_{0}^{\ast },0)$
. By the Iwahori decomposition of
$\unicode[STIX]{x1D702}=w_{2,\text{long}}h(l_{0}^{\ast },0)$
. By the Iwahori decomposition of
![]() $K_{2}^{(1)}$
, it is not hard to check that
$K_{2}^{(1)}$
, it is not hard to check that
 $$\begin{eqnarray}K_{2}^{(1)}\unicode[STIX]{x1D702}=T_{2}^{(0)}N_{2}^{(0)}w_{2,\text{long}}h(l_{0}^{\ast },0)T_{0}^{(1)}N_{J}^{(1)}N_{r-1}^{(1)}.\end{eqnarray}$$
$$\begin{eqnarray}K_{2}^{(1)}\unicode[STIX]{x1D702}=T_{2}^{(0)}N_{2}^{(0)}w_{2,\text{long}}h(l_{0}^{\ast },0)T_{0}^{(1)}N_{J}^{(1)}N_{r-1}^{(1)}.\end{eqnarray}$$
Therefore,
 $Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{2}\unicode[STIX]{x1D702})=Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})=1$
for any
$Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(k_{2}\unicode[STIX]{x1D702})=Y_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D702})=1$
for any
 $k_{2}\in K_{2}^{(1)}$
. Thus,
$k_{2}\in K_{2}^{(1)}$
. Thus,
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})(1)=\operatorname{vol}K_{2}^{(1)}.\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}})(1)=\operatorname{vol}K_{2}^{(1)}.\end{eqnarray}$$
We now compute
 $l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(1)$
. First
$l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(1)$
. First
 $$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(g_{1})=\int _{N_{r-1}}\int _{B_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}g_{1}{\dot{w}}u)(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\overline{\unicode[STIX]{x1D713}_{r-1}(u)}\,db_{2}\,du,\quad g_{1}\in G_{1}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(g_{1})=\int _{N_{r-1}}\int _{B_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}g_{1}{\dot{w}}u)(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\overline{\unicode[STIX]{x1D713}_{r-1}(u)}\,db_{2}\,du,\quad g_{1}\in G_{1}.\end{eqnarray}$$
By the decomposition (4.4.3) again, for any
 $u\in N_{r-1}$
, if
$u\in N_{r-1}$
, if
 $b_{2}g_{1}{\dot{w}}u\in K_{2}^{(1)}\unicode[STIX]{x1D702}$
, then
$b_{2}g_{1}{\dot{w}}u\in K_{2}^{(1)}\unicode[STIX]{x1D702}$
, then
 $u\in N_{r-1}^{(1)}$
and
$u\in N_{r-1}^{(1)}$
and
 $b_{2}g_{1}{\dot{w}}\in K_{2}^{(1)}\unicode[STIX]{x1D702}$
. Therefore,
$b_{2}g_{1}{\dot{w}}\in K_{2}^{(1)}\unicode[STIX]{x1D702}$
. Therefore,
 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(g_{1}) & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{B_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}g_{1}{\dot{w}})(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\,db_{2}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{B_{1}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{1}g_{1}{\dot{w}})((\unicode[STIX]{x1D6EF}^{1})^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{1})\,db_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(g_{1}) & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{B_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}g_{1}{\dot{w}})(\unicode[STIX]{x1D6EF}^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{2})\,db_{2}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{B_{1}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{1}g_{1}{\dot{w}})((\unicode[STIX]{x1D6EF}^{1})^{-1}\unicode[STIX]{x1D6FF}_{2}^{1/2})(b_{1})\,db_{1}.\nonumber\end{eqnarray}$$
Thus,
 $$\begin{eqnarray}\displaystyle l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(1) & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{G_{1}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(g_{1}{\dot{w}})Y_{\unicode[STIX]{x1D6EF}^{1},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{1}{\dot{w}})\,dg_{1}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \operatorname{vol}K_{1}^{(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}^{\prime }(\operatorname{pr}_{2}(\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}))(1) & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \int _{G_{1}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(g_{1}{\dot{w}})Y_{\unicode[STIX]{x1D6EF}^{1},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{1}{\dot{w}})\,dg_{1}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{vol}N_{r-1}^{(1)}\cdot \operatorname{vol}K_{1}^{(1)}.\nonumber\end{eqnarray}$$
The lemma then follows since
 $\operatorname{vol}N_{r-1}^{(1)}\cdot \operatorname{vol}K_{1}^{(1)}=\mathbf{w}\operatorname{vol}K_{2}^{(1)}$
.◻
$\operatorname{vol}N_{r-1}^{(1)}\cdot \operatorname{vol}K_{1}^{(1)}=\mathbf{w}\operatorname{vol}K_{2}^{(1)}$
.◻
Lemma 4.4.3. We have
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}),\quad S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}),\quad S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\end{eqnarray}$$
Proof. We claim that the restriction of the measure
![]() $dg$
to the open subset
$dg$
to the open subset
 $B_{2}\unicode[STIX]{x1D702}B_{J}N_{r-1}$
decomposes as
$B_{2}\unicode[STIX]{x1D702}B_{J}N_{r-1}$
decomposes as
 $$\begin{eqnarray}dg|_{B_{2}\unicode[STIX]{x1D702}B_{J}N_{r-1}}=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\,db_{2}\,dn_{r-1}\,db_{J},\end{eqnarray}$$
$$\begin{eqnarray}dg|_{B_{2}\unicode[STIX]{x1D702}B_{J}N_{r-1}}=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\,db_{2}\,dn_{r-1}\,db_{J},\end{eqnarray}$$
where
 $db_{J}=db_{0}\,dl\,dt$
if
$db_{J}=db_{0}\,dl\,dt$
if
 $b_{J}=b_{0}h(l,t)$
. In fact, on the one hand,
$b_{J}=b_{0}h(l,t)$
. In fact, on the one hand,
 $$\begin{eqnarray}\int _{G_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(g)\,dg=[K_{2}:K_{2}^{(1)}]^{-1}=q^{-\!\dim G_{2}+\dim N_{2}+\dim T_{2}}\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{2}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(g)\,dg=[K_{2}:K_{2}^{(1)}]^{-1}=q^{-\!\dim G_{2}+\dim N_{2}+\dim T_{2}}\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}}.\end{eqnarray}$$
On the other hand, it follows from (4.4.3) that
 $$\begin{eqnarray}\int _{B_{2}}\int _{N_{r-1}}\int _{B_{J}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}\unicode[STIX]{x1D702}b_{J}n_{r-1})\,db_{2}\,dn_{r-1}\,db_{J}=q^{-\!\dim T_{0}-\dim N_{J}-\dim N_{r-1}}\unicode[STIX]{x1D6E5}_{T_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{B_{2}}\int _{N_{r-1}}\int _{B_{J}}\operatorname{1}_{K_{2}^{(1)}\unicode[STIX]{x1D702}}(b_{2}\unicode[STIX]{x1D702}b_{J}n_{r-1})\,db_{2}\,dn_{r-1}\,db_{J}=q^{-\!\dim T_{0}-\dim N_{J}-\dim N_{r-1}}\unicode[STIX]{x1D6E5}_{T_{0}}.\end{eqnarray}$$
The claim then follows. Therefore,
 $$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(f_{\unicode[STIX]{x1D6EF}})(g_{J})=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{B_{J}}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}b_{J}n_{r-1}g_{J})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{J}^{-1/2})(b_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}\,db_{J}\,dn_{r-1}.\end{eqnarray}$$
$$\begin{eqnarray}l_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(f_{\unicode[STIX]{x1D6EF}})(g_{J})=\frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{B_{J}}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(\unicode[STIX]{x1D702}b_{J}n_{r-1}g_{J})(\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FF}_{J}^{-1/2})(b_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}\,db_{J}\,dn_{r-1}.\end{eqnarray}$$
We have
 $$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{L^{\ast }}\int _{K_{0}}\int _{B_{J}}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)b_{J}n_{r-1}h(l^{\ast },0)k)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}_{J}^{1/2})(b_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(h(l^{\ast },0)k)\,dn_{r-1}\,db_{J}\,dk\,dl^{\ast }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{L^{\ast }}\int _{K_{0}}\int _{B_{J}}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)b_{J}n_{r-1}h(l^{\ast },0)k)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D6FF}_{J}^{1/2})(b_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(h(l^{\ast },0)k)\,dn_{r-1}\,db_{J}\,dk\,dl^{\ast }.\nonumber\end{eqnarray}$$
We combine the integration over
![]() $L$
,
$L$
,
![]() $K_{0}$
and
$K_{0}$
and
![]() $B_{J}$
as an integral over
$B_{J}$
as an integral over
![]() $J$
and then conclude that
$J$
and then conclude that
 $$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{J}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)n_{r-1}g_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J})\,dn_{r-1}\,dg_{J}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\int _{J}\int _{N_{r-1}}f_{\unicode[STIX]{x1D6EF}}(w_{2,\text{long}}h(l_{0}^{\ast },0)n_{r-1}g_{J})\overline{\unicode[STIX]{x1D713}_{r-1}(n_{r-1})}f_{\unicode[STIX]{x1D709},\overline{\unicode[STIX]{x1D713}}}(g_{J})\,dn_{r-1}\,dg_{J}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{2}}}{\unicode[STIX]{x1D6E5}_{T_{2}}\unicode[STIX]{x1D6E5}_{T_{0}}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\nonumber\end{eqnarray}$$
The equality
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1)=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713})\end{eqnarray}$$
can be proved similarly. In fact,
 $$\begin{eqnarray}dg_{J}|_{B_{J}\unicode[STIX]{x1D702}B_{0}}=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\,db_{J}\,db_{0}.\end{eqnarray}$$
$$\begin{eqnarray}dg_{J}|_{B_{J}\unicode[STIX]{x1D702}B_{0}}=\frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\,db_{J}\,db_{0}.\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \int _{J}\int _{G_{0}}\operatorname{1}_{K_{J}}(g_{J})\operatorname{1}_{K_{0}}(g_{0})Y_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J}g_{0}^{-1})\,dg_{J}\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\int _{G_{0}}\int _{B_{J}}\int _{B_{0}}\operatorname{1}_{K_{J}}(b_{J}\unicode[STIX]{x1D702}b_{0}g_{0})\operatorname{1}_{K_{0}}(g_{0})Y_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{J}\unicode[STIX]{x1D702}b_{0})\,db_{J}\,db_{0}\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(1) & = & \displaystyle \int _{J}\int _{G_{0}}\operatorname{1}_{K_{J}}(g_{J})\operatorname{1}_{K_{0}}(g_{0})Y_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(g_{J}g_{0}^{-1})\,dg_{J}\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\int _{G_{0}}\int _{B_{J}}\int _{B_{0}}\operatorname{1}_{K_{J}}(b_{J}\unicode[STIX]{x1D702}b_{0}g_{0})\operatorname{1}_{K_{0}}(g_{0})Y_{\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}}(b_{J}\unicode[STIX]{x1D702}b_{0})\,db_{J}\,db_{0}\,dg_{0}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6E5}_{G_{0}}}{\unicode[STIX]{x1D6E5}_{T_{0}}^{2}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}).\Box \nonumber\end{eqnarray}$$
Proof of Proposition 2.2.3.
If
![]() $r=0$
, then Proposition 2.2.3 can be proved in exactly the same way as [Reference XueXue16, Appendix D.3]. We omit the details. See also Lemma 7.2.2.
$r=0$
, then Proposition 2.2.3 can be proved in exactly the same way as [Reference XueXue16, Appendix D.3]. We omit the details. See also Lemma 7.2.2.
Assume that
![]() $r\geqslant 1$
. Suppose that we are in the case
$r\geqslant 1$
. Suppose that we are in the case
![]() $\operatorname{Sp}$
. It follows from Lemmas 4.4.1 and 4.4.3 that
$\operatorname{Sp}$
. It follows from Lemmas 4.4.1 and 4.4.3 that
 $$\begin{eqnarray}\displaystyle I(1,\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggr)^{-1}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{0}}}{\unicode[STIX]{x1D6E5}_{G_{0}}}\biggr)\biggl(\frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}^{\vee }\times \unicode[STIX]{x1D70F}^{\vee })}{L(1,\unicode[STIX]{x1D70E}^{\vee }\times \unicode[STIX]{x1D70F}^{\vee })L(1,\unicode[STIX]{x1D70F}^{\vee },\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}^{-1}\unicode[STIX]{x1D6EF}_{n+j})}\biggr)I(1,\unicode[STIX]{x1D709},\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D713}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(1,\unicode[STIX]{x1D6EF},\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}) & = & \displaystyle \biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{2}}}{\unicode[STIX]{x1D6E5}_{G_{2}}}\biggr)^{-1}\biggl(\frac{\unicode[STIX]{x1D6E5}_{T_{0}}}{\unicode[STIX]{x1D6E5}_{G_{0}}}\biggr)\biggl(\frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}\times \unicode[STIX]{x1D70F})}{L(1,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70F})L(1,\unicode[STIX]{x1D70F},\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}\unicode[STIX]{x1D6EF}_{n+j}^{-1})}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\frac{L_{\unicode[STIX]{x1D713}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{0}^{\vee }\times \unicode[STIX]{x1D70F}^{\vee })}{L(1,\unicode[STIX]{x1D70E}^{\vee }\times \unicode[STIX]{x1D70F}^{\vee })L(1,\unicode[STIX]{x1D70F}^{\vee },\wedge ^{2})}\mathop{\prod }_{1\leqslant i<j\leqslant r}\frac{1}{L(1,\unicode[STIX]{x1D6EF}_{n+i}^{-1}\unicode[STIX]{x1D6EF}_{n+j})}\biggr)I(1,\unicode[STIX]{x1D709},\unicode[STIX]{x1D6EF}^{0},\unicode[STIX]{x1D713}).\nonumber\end{eqnarray}$$
Proposition 2.2.3 in the case
![]() $r\geqslant 1$
is then reduced to the case
$r\geqslant 1$
is then reduced to the case
![]() $r=0$
. The case
$r=0$
. The case
![]() $\operatorname{Mp}$
can be proved in the same way. We only need to change notation at all necessary places.◻
$\operatorname{Mp}$
can be proved in the same way. We only need to change notation at all necessary places.◻
Part II. Compatibility with the Ichino–Ikeda conjecture
The notation in this part of the paper is independent from Part I. We keep the notation and convention from the Introduction. Additional notation will be fixed in each section.
5 Some assumptions and remarks
5.1 Parameters
We will prove that Conjecture 2.3.1(3) is compatible with the Ichino–Ikeda conjecture [Reference Ichino and IkedaII10, Conjecture 2.1]. The most subtle part is the appearance of the size of the centralizer of the global
![]() $L$
-parameters in the formula. To address this issue, of course, one has to assume that the Langlands correspondence exists and satisfies some expected properties. We begin by setting down the precise hypotheses that we require. We remark that for orthogonal groups and symplectic groups, they follow from the work of Arthur [Reference ArthurArt13] and the recent work of Atobe and Gan [Reference Atobe and GanAG16]. For metaplectic groups, they should eventually follow from the on-going work of Wen-Wei Li (e.g. [Reference LiLi15]).
$L$
-parameters in the formula. To address this issue, of course, one has to assume that the Langlands correspondence exists and satisfies some expected properties. We begin by setting down the precise hypotheses that we require. We remark that for orthogonal groups and symplectic groups, they follow from the work of Arthur [Reference ArthurArt13] and the recent work of Atobe and Gan [Reference Atobe and GanAG16]. For metaplectic groups, they should eventually follow from the on-going work of Wen-Wei Li (e.g. [Reference LiLi15]).
We first state the hypothesis on the local Langlands correspondences.
Hypothesis (LLC). We assume the Hypotheses (LLC), (Local factors), (Plancherel measures) from [Reference Gan and IchinoGI14, Appendix C] at all non-archimedean places
![]() $v$
of
$v$
of
![]() $F$
. Thus [Reference Gan and IchinoGI14, Theorem C.5] holds if
$F$
. Thus [Reference Gan and IchinoGI14, Theorem C.5] holds if
![]() $v$
is non-archimedean. It also holds if
$v$
is non-archimedean. It also holds if
![]() $v$
is archimedean by [Reference PaulPau05].
$v$
is archimedean by [Reference PaulPau05].
We note that if
![]() $v$
is an archimedean place, then the Hypothesis (LLC) is established by Langlands [Reference LanglandsLan89]. Hypothesis (Local factors) is proved in [Reference Lapid and RallisLR05]. Hypothesis (Plancherel measures) is proved by [Reference ArthurArt89]. If
$v$
is an archimedean place, then the Hypothesis (LLC) is established by Langlands [Reference LanglandsLan89]. Hypothesis (Local factors) is proved in [Reference Lapid and RallisLR05]. Hypothesis (Plancherel measures) is proved by [Reference ArthurArt89]. If
![]() $v$
is non-archimedean, then they should follow from [Reference ArthurArt13, Theorems 1.5.1, 9.4.1, Conjecture 9.4.2].
$v$
is non-archimedean, then they should follow from [Reference ArthurArt13, Theorems 1.5.1, 9.4.1, Conjecture 9.4.2].
Thus, if
![]() $v$
is a place of
$v$
is a place of
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D70B}_{v}$
is an irreducible admissible representation of
$\unicode[STIX]{x1D70B}_{v}$
is an irreducible admissible representation of
![]() $G(F_{v})$
, where
$G(F_{v})$
, where
 $G=\operatorname{SO}(2n+1)$
(respectively
$G=\operatorname{SO}(2n+1)$
(respectively
![]() $\operatorname{SO}(2n)$
, respectively
$\operatorname{SO}(2n)$
, respectively
![]() $\operatorname{Sp}(2n)$
) gives rise to a
$\operatorname{Sp}(2n)$
) gives rise to a
![]() $2n$
(respectively
$2n$
(respectively
![]() $2n$
, respectively
$2n$
, respectively
 $(2n+1)$
)-dimensional selfdual representation
$(2n+1)$
)-dimensional selfdual representation
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}$
of the Weil–Deligne group
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}$
of the Weil–Deligne group
 $\operatorname{WD}(F_{v})$
of sign
$\operatorname{WD}(F_{v})$
of sign
![]() $-1$
(respectively
$-1$
(respectively
![]() $+1$
, respectively
$+1$
, respectively
![]() $+1$
). We call it the local
$+1$
). We call it the local
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}_{v}$
.
$\unicode[STIX]{x1D70B}_{v}$
.
Let
![]() $\unicode[STIX]{x1D70B}_{v}$
be an irreducible admissible genuine representation of
$\unicode[STIX]{x1D70B}_{v}$
be an irreducible admissible genuine representation of
 $\operatorname{Mp}(2n)(F_{v})$
and
$\operatorname{Mp}(2n)(F_{v})$
and
 $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})$
be the restriction to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})$
be the restriction to
 $\operatorname{SO}(V)(F_{v})$
of its theta lift to
$\operatorname{SO}(V)(F_{v})$
of its theta lift to
 $\operatorname{O}(V)(F_{v})$
where
$\operatorname{O}(V)(F_{v})$
where
![]() $V$
is a
$V$
is a
 $(2n+1)$
-dimensional orthogonal space over
$(2n+1)$
-dimensional orthogonal space over
![]() $F_{v}$
of discriminant
$F_{v}$
of discriminant
![]() $1$
. By [Reference Gan and IchinoGI14, Theorem 1.1], the map
$1$
. By [Reference Gan and IchinoGI14, Theorem 1.1], the map
 $\unicode[STIX]{x1D70B}_{v}\mapsto \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})$
gives a bijection between the set of irreducible admissible genuine representations of
$\unicode[STIX]{x1D70B}_{v}\mapsto \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})$
gives a bijection between the set of irreducible admissible genuine representations of
 $\operatorname{Mp}(2n)(F_{v})$
and the union of the sets of irreducible admissible representations of
$\operatorname{Mp}(2n)(F_{v})$
and the union of the sets of irreducible admissible representations of
 $\operatorname{SO}(V)(F_{v})$
where
$\operatorname{SO}(V)(F_{v})$
where
![]() $V$
ranges over all
$V$
ranges over all
 $(2n+1)$
-dimensional orthogonal spaces over
$(2n+1)$
-dimensional orthogonal spaces over
![]() $F_{v}$
of discriminant
$F_{v}$
of discriminant
![]() $1$
. This bijection satisfies several expected properties (cf. [Reference Gan and IchinoGI14, Theorem 1.3] for a list). The local
$1$
. This bijection satisfies several expected properties (cf. [Reference Gan and IchinoGI14, Theorem 1.3] for a list). The local
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}_{v}$
is defined to be
$\unicode[STIX]{x1D70B}_{v}$
is defined to be
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}$
. Note that the local
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}$
. Note that the local
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}_{v}$
depends on
$\unicode[STIX]{x1D70B}_{v}$
depends on
![]() $\unicode[STIX]{x1D713}_{v}$
.
$\unicode[STIX]{x1D713}_{v}$
.
We now turn to the global Langlands correspondences. We shall be concerned only with tempered cuspidal automorphic representations. To avoid mentioning the hypothetical Langlands group
![]() $L_{F}$
, we use the following substitute of the global
$L_{F}$
, we use the following substitute of the global
![]() $L$
-parameters following [Reference ArthurArt13, § 1.4] and [Reference Gan, Gross and PrasadGGP12, § 25, pp. 103–105].
$L$
-parameters following [Reference ArthurArt13, § 1.4] and [Reference Gan, Gross and PrasadGGP12, § 25, pp. 103–105].
Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
![]() $G(\mathbb{A}_{F})$
, where
$G(\mathbb{A}_{F})$
, where
 $G=\operatorname{SO}(2n+1)$
(respectively
$G=\operatorname{SO}(2n+1)$
(respectively
![]() $\operatorname{SO}(2n)$
,
$\operatorname{SO}(2n)$
,
![]() $\operatorname{Sp}(2n)$
,
$\operatorname{Sp}(2n)$
,
 $\operatorname{Mp}(2n)$
). By the global
$\operatorname{Mp}(2n)$
). By the global
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}$
, we mean the following data:
$\unicode[STIX]{x1D70B}$
, we mean the following data:
-
– a partition
 $N=N_{1}+\cdots +N_{r}$
, where
$N=N_{1}+\cdots +N_{r}$
, where
 $N=2n$
(respectively
$N=2n$
(respectively
 $2n$
,
$2n$
,
 $2n+1$
,
$2n+1$
,
 $2n$
);
$2n$
); -
– a collection of pairwisely inequivalent selfdual irreducible cuspidal automorphic representations
 $\unicode[STIX]{x1D6F1}_{i}$
of
$\unicode[STIX]{x1D6F1}_{i}$
of
 $\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
of sign
$\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
of sign
 $-1$
(respectively
$-1$
(respectively
 $+1$
,
$+1$
,
 $+1$
,
$+1$
,
 $-1$
),
$-1$
),
 $i=1,\ldots ,r$
;
$i=1,\ldots ,r$
;
which satisfy the condition that for all places
![]() $v$
of
$v$
of
![]() $F$
,
$F$
,
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\simeq \bigoplus _{i=1}^{r}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6F1}_{i,v}}$
as representations of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\simeq \bigoplus _{i=1}^{r}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6F1}_{i,v}}$
as representations of
 $\operatorname{WD}(F_{v})$
, where
$\operatorname{WD}(F_{v})$
, where
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6F1}_{i,v}}$
is an
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6F1}_{i,v}}$
is an
![]() $N_{i}$
-dimensional representation of
$N_{i}$
-dimensional representation of
 $\operatorname{WD}(F_{v})$
associated to
$\operatorname{WD}(F_{v})$
associated to
![]() $\unicode[STIX]{x1D6F1}_{i,v}$
by the local Langlands correspondences for
$\unicode[STIX]{x1D6F1}_{i,v}$
by the local Langlands correspondences for
![]() $\operatorname{GL}_{N_{i}}$
(which is known due to [Reference Harris and TaylorHT01] and [Reference HenniartHen00]). By [Reference Jacquet and ShalikaJS81, Theorem 4.4], the global
$\operatorname{GL}_{N_{i}}$
(which is known due to [Reference Harris and TaylorHT01] and [Reference HenniartHen00]). By [Reference Jacquet and ShalikaJS81, Theorem 4.4], the global
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}$
is unique if it exists. We write formally
$\unicode[STIX]{x1D70B}$
is unique if it exists. We write formally
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
.
We now state the hypothesis on the global Langlands correspondences.
Hypothesis GLC. The global
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}$
exists.
$\unicode[STIX]{x1D70B}$
exists.
For orthogonal and symplectic groups, a weaker version of this (namely, replacing the requirement ‘for all places
![]() $v$
’ by ‘for almost all places
$v$
’ by ‘for almost all places
![]() $v$
’) follows from [Reference ArthurArt13, Theorems 1.5.2, 9.5.3]. For metaplectic groups, this should follow from the work of Wen-Wei Li.
$v$
’) follows from [Reference ArthurArt13, Theorems 1.5.2, 9.5.3]. For metaplectic groups, this should follow from the work of Wen-Wei Li.
With this reformulation of the
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}$
, we (re-)define the centralizer
$\unicode[STIX]{x1D70B}$
, we (re-)define the centralizer
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D70B}}=S_{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=1\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D70B}}=S_{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=1\}.\end{eqnarray}$$
From now on, when we speak of the global
![]() $L$
-parameters and their centralizers, we always mean the one defined here.
$L$
-parameters and their centralizers, we always mean the one defined here.
We end this subsection by some discussions on the automorphic representations on the even orthogonal groups. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
is an irreducible cuspidal tempered automorphic representation of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
. We are interested in the restriction
$\operatorname{O}(2n)(\mathbb{A}_{F})$
. We are interested in the restriction
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. Here by
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. Here by
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
, we mean the following. Suppose that
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
, we mean the following. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is realized on
$\unicode[STIX]{x1D70B}$
is realized on
![]() $V$
, which is a subspace of the cuspidal automorphic spectrum of
$V$
, which is a subspace of the cuspidal automorphic spectrum of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
. Let
$\operatorname{O}(2n)(\mathbb{A}_{F})$
. Let
 $V^{0}=\{f|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}\mid f\in V\}$
. Then
$V^{0}=\{f|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}\mid f\in V\}$
. Then
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
stands for the natural action of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
stands for the natural action of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
on
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
on
![]() $V^{0}$
. We summarize some recent results of Atobe and Gan [Reference Atobe and GanAG16] as the following Hypothesis O.
$V^{0}$
. We summarize some recent results of Atobe and Gan [Reference Atobe and GanAG16] as the following Hypothesis O.
Hypothesis O. Each tempered automorphic representation
![]() $\unicode[STIX]{x1D70B}$
appears with multiplicity one in the discrete spectrum of
$\unicode[STIX]{x1D70B}$
appears with multiplicity one in the discrete spectrum of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
. The following three cases exhaust all possibilities of
$\operatorname{O}(2n)(\mathbb{A}_{F})$
. The following three cases exhaust all possibilities of
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
.
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
.
-
(i) We have that
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity one in the discrete spectrum of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity one in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
.
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. -
(ii) We have that
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity two in the discrete spectrum of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity two in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
. In this case, there is an automorphic representation
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. In this case, there is an automorphic representation
 $\unicode[STIX]{x1D70B}^{\prime }$
of
$\unicode[STIX]{x1D70B}^{\prime }$
of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
such that
$\operatorname{O}(2n)(\mathbb{A}_{F})$
such that
 $\unicode[STIX]{x1D70B}\not =\unicode[STIX]{x1D70B}^{\prime }$
and
$\unicode[STIX]{x1D70B}\not =\unicode[STIX]{x1D70B}^{\prime }$
and
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}\oplus \unicode[STIX]{x1D70B}^{\prime }|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is the
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}\oplus \unicode[STIX]{x1D70B}^{\prime }|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is the
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
-isotypic component of the discrete spectrum of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
-isotypic component of the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Note that
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Note that
 $\unicode[STIX]{x1D70B}^{\prime }$
is not uniquely determined.
$\unicode[STIX]{x1D70B}^{\prime }$
is not uniquely determined. -
(iii) We have
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}=\unicode[STIX]{x1D70B}^{+}\oplus \unicode[STIX]{x1D70B}^{-}$
where
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}=\unicode[STIX]{x1D70B}^{+}\oplus \unicode[STIX]{x1D70B}^{-}$
where
 $\unicode[STIX]{x1D70B}^{+}$
and
$\unicode[STIX]{x1D70B}^{+}$
and
 $\unicode[STIX]{x1D70B}^{-}$
are inequivalent automorphic representations of
$\unicode[STIX]{x1D70B}^{-}$
are inequivalent automorphic representations of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Both
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Both
 $\unicode[STIX]{x1D70B}^{+}$
and
$\unicode[STIX]{x1D70B}^{+}$
and
 $\unicode[STIX]{x1D70B}^{-}$
appear with multiplicity one in the discrete spectrum of
$\unicode[STIX]{x1D70B}^{-}$
appear with multiplicity one in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Moreover,
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. Moreover,
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{+}}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{-}}$
.
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{+}}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{-}}$
.
In each case, let
![]() $\unicode[STIX]{x1D70B}^{0}$
be an irreducible component of
$\unicode[STIX]{x1D70B}^{0}$
be an irreducible component of
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. Then we define the
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. Then we define the
![]() $L$
-parameter
$L$
-parameter
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
of
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{0}}$
. Suppose that
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{0}}$
. Suppose that
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
where
![]() $\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
 $\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
. Then in the first (respectively second and third) case (respectively cases), at least one of
$\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
. Then in the first (respectively second and third) case (respectively cases), at least one of
![]() $N_{i}$
is odd (respectively all
$N_{i}$
is odd (respectively all
![]() $N_{i}$
are even).
$N_{i}$
are even).
Let
 $\unicode[STIX]{x1D716}\in \operatorname{O}(2n)(F)\backslash \operatorname{SO}(2n)(F)$
. Conjugation by
$\unicode[STIX]{x1D716}\in \operatorname{O}(2n)(F)\backslash \operatorname{SO}(2n)(F)$
. Conjugation by
![]() $\unicode[STIX]{x1D716}$
induces an outer automorphism of order two of
$\unicode[STIX]{x1D716}$
induces an outer automorphism of order two of
![]() $\operatorname{SO}(2n)$
which does not depend on the choice of the element
$\operatorname{SO}(2n)$
which does not depend on the choice of the element
![]() $\unicode[STIX]{x1D716}$
. We denote this outer automorphism also by
$\unicode[STIX]{x1D716}$
. We denote this outer automorphism also by
![]() $\unicode[STIX]{x1D716}$
. If
$\unicode[STIX]{x1D716}$
. If
![]() $n\not =2$
, then this is the unique nontrivial outer automorphism of
$n\not =2$
, then this is the unique nontrivial outer automorphism of
![]() $\operatorname{SO}(2n)$
. For any automorphic representation
$\operatorname{SO}(2n)$
. For any automorphic representation
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
, we let
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
, we let
![]() $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}$
be its twist by
$\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}$
be its twist by
![]() $\unicode[STIX]{x1D716}$
. In the first two cases,
$\unicode[STIX]{x1D716}$
. In the first two cases,
 $(\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})})^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. In the third case,
$(\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})})^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
. In the third case,
 $(\unicode[STIX]{x1D70B}^{\pm })^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D70B}^{\mp }$
. Here we use ‘
$(\unicode[STIX]{x1D70B}^{\pm })^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D70B}^{\mp }$
. Here we use ‘
![]() $=$
’ to indicate that not only the automorphic representations are isomorphic, but the spaces on which they realize are the same.
$=$
’ to indicate that not only the automorphic representations are isomorphic, but the spaces on which they realize are the same.
The automorphic representation
![]() $\unicode[STIX]{x1D70B}$
appears with multiplicity one in the discrete spectrum of
$\unicode[STIX]{x1D70B}$
appears with multiplicity one in the discrete spectrum of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
, so the space on which it realizes is canonical. Suppose that
$\operatorname{O}(2n)(\mathbb{A}_{F})$
, so the space on which it realizes is canonical. Suppose that
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity two in the discrete spectrum of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
is irreducible and appears with multiplicity two in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
. The restrictions of
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
. The restrictions of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}^{\prime }$
to
$\unicode[STIX]{x1D70B}^{\prime }$
to
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
are canonical subspaces of the discrete spectrum of
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
are canonical subspaces of the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
and give a canonical decomposition of the
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
and give a canonical decomposition of the
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
-isotypic component of the discrete spectrum of
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(2n)(\mathbb{A}_{F})}$
-isotypic component of the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
(we are not able to distinguish the restrictions of
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
(we are not able to distinguish the restrictions of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}^{\prime }$
). Moreover, these subspaces are characterized by the fact that they are invariant under the outer twist
$\unicode[STIX]{x1D70B}^{\prime }$
). Moreover, these subspaces are characterized by the fact that they are invariant under the outer twist
![]() $\unicode[STIX]{x1D716}$
. In other words, if
$\unicode[STIX]{x1D716}$
. In other words, if
![]() $\unicode[STIX]{x1D70B}^{0}$
(as an abstract representation) is an automorphic representation of
$\unicode[STIX]{x1D70B}^{0}$
(as an abstract representation) is an automorphic representation of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
and appears with multiplicity two in the discrete spectrum of
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
and appears with multiplicity two in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
, then there are precisely two automorphic realizations
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
, then there are precisely two automorphic realizations
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
of
$V_{2}$
of
![]() $\unicode[STIX]{x1D70B}^{0}$
that are invariant under the outer twist by
$\unicode[STIX]{x1D70B}^{0}$
that are invariant under the outer twist by
![]() $\unicode[STIX]{x1D716}$
. Both
$\unicode[STIX]{x1D716}$
. Both
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
can be extended to automorphic representations of
$V_{2}$
can be extended to automorphic representations of
 $\operatorname{O}(2n)(\mathbb{A}_{F})$
. Moreover,
$\operatorname{O}(2n)(\mathbb{A}_{F})$
. Moreover,
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are orthogonal in the discrete spectrum of
$V_{2}$
are orthogonal in the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
and
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
and
![]() $V_{1}\oplus V_{2}$
is the
$V_{1}\oplus V_{2}$
is the
![]() $\unicode[STIX]{x1D70B}^{0}$
-isotypic component of the discrete spectrum of
$\unicode[STIX]{x1D70B}^{0}$
-isotypic component of the discrete spectrum of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
.
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
.
Finally, assume that
![]() $\operatorname{SO}(2n)$
is quasi-split and
$\operatorname{SO}(2n)$
is quasi-split and
![]() $\unicode[STIX]{x1D70B}^{0}$
is an irreducible cuspidal tempered generic automorphic representation of
$\unicode[STIX]{x1D70B}^{0}$
is an irreducible cuspidal tempered generic automorphic representation of
 $\operatorname{SO}(2n)(\mathbb{A}_{F})$
which appears with multiplicity two in the discrete spectrum. Suppose that
$\operatorname{SO}(2n)(\mathbb{A}_{F})$
which appears with multiplicity two in the discrete spectrum. Suppose that
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{0}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
. Then (at least conjecturally) the descent construction [Reference Ginzburg, Rallis and SoudryGRS11] provides us with an automorphic realization of
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{0}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
. Then (at least conjecturally) the descent construction [Reference Ginzburg, Rallis and SoudryGRS11] provides us with an automorphic realization of
![]() $\unicode[STIX]{x1D70B}^{0}$
which is invariant under the outer twist
$\unicode[STIX]{x1D70B}^{0}$
which is invariant under the outer twist
![]() $\unicode[STIX]{x1D716}$
. We refer the reader to [Reference Lapid and MaoLM15c, § 5] for some further discussions on the descent construction.
$\unicode[STIX]{x1D716}$
. We refer the reader to [Reference Lapid and MaoLM15c, § 5] for some further discussions on the descent construction.
Convention. We assume the Hypotheses LLC, GLC and O from now on, unless otherwise specified.
5.2 Theta correspondences
We are going to use the Rallis inner product formula in the later sections of this paper. We will not recall the precise form of this formula in various cases, but refer the readers to [Reference YamanaYam11, Reference YamanaYam14] for the formula in the first term range and to [Reference Gan, Qiu and TakedaGQT14] for the formula in the second term range.
We now consider the behavior of the
![]() $L$
-parameters under theta correspondences.
$L$
-parameters under theta correspondences.
Lemma 5.2.1. Let
![]() $V$
be a
$V$
be a
![]() $2n$
-dimensional orthogonal space over
$2n$
-dimensional orthogonal space over
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D70B}$
an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
an irreducible cuspidal tempered automorphic representation of
 $\operatorname{O}(V)(\mathbb{A}_{F})$
. Let
$\operatorname{O}(V)(\mathbb{A}_{F})$
. Let
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be its theta lift to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be its theta lift to
 $\operatorname{Sp}(2n)(\mathbb{A}_{F})$
with additive character
$\operatorname{Sp}(2n)(\mathbb{A}_{F})$
with additive character
![]() $\unicode[STIX]{x1D713}$
. Suppose that
$\unicode[STIX]{x1D713}$
. Suppose that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
is nonzero and cuspidal. Let
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
is nonzero and cuspidal. Let
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
be the
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
be the
![]() $L$
-parameter of
$L$
-parameter of
![]() $\unicode[STIX]{x1D70B}$
. Then
$\unicode[STIX]{x1D70B}$
. Then
![]() $\unicode[STIX]{x1D6F1}_{i}\not =\operatorname{1}$
(the trivial character of
$\unicode[STIX]{x1D6F1}_{i}\not =\operatorname{1}$
(the trivial character of
![]() $\mathbb{A}_{F}^{\times }$
) for all
$\mathbb{A}_{F}^{\times }$
) for all
![]() $i$
.
$i$
.
Proof. Suppose that
![]() $\unicode[STIX]{x1D6F1}_{i}=\operatorname{1}$
for some
$\unicode[STIX]{x1D6F1}_{i}=\operatorname{1}$
for some
![]() $i$
. We may assume that
$i$
. We may assume that
![]() $i=1$
. Then by Hypothesis O,
$i=1$
. Then by Hypothesis O,
 $\unicode[STIX]{x1D70B}|_{\operatorname{SO}(V)(\mathbb{A}_{F})}$
is irreducible. We prove that
$\unicode[STIX]{x1D70B}|_{\operatorname{SO}(V)(\mathbb{A}_{F})}$
is irreducible. We prove that
![]() $\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
$\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
 $\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. The lemma then follows from the tower property of the theta lift [Reference RallisRal84].
$\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. The lemma then follows from the tower property of the theta lift [Reference RallisRal84].
If
![]() $\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
$\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
 $\operatorname{Sp}(2n-2r)(\mathbb{A}_{F})$
for some
$\operatorname{Sp}(2n-2r)(\mathbb{A}_{F})$
for some
![]() $r>1$
, then by the tower property of the theta lift,
$r>1$
, then by the tower property of the theta lift,
![]() $\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
$\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
 $\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. Thus, we may assume that
$\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. Thus, we may assume that
![]() $\unicode[STIX]{x1D70B}$
does not have a nonzero theta lift to any
$\unicode[STIX]{x1D70B}$
does not have a nonzero theta lift to any
 $\operatorname{Sp}(2n-2r)(\mathbb{A}_{F})$
for any
$\operatorname{Sp}(2n-2r)(\mathbb{A}_{F})$
for any
![]() $r>1$
.
$r>1$
.
We fix a sufficiently large finite set
![]() $S$
of places of
$S$
of places of
![]() $F$
which contains all the archimedean places, so that if
$F$
which contains all the archimedean places, so that if
![]() $v\not \in S$
, then
$v\not \in S$
, then
![]() $\unicode[STIX]{x1D70B}$
(hence,
$\unicode[STIX]{x1D70B}$
(hence,
![]() $\unicode[STIX]{x1D6F1}_{i}$
) is unramified. By the Hypotheses LLC and GLC,
$\unicode[STIX]{x1D6F1}_{i}$
) is unramified. By the Hypotheses LLC and GLC,
 $$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B})=\mathop{\prod }_{i=1}^{r}L^{S}(s,\unicode[STIX]{x1D6F1}_{i}),\end{eqnarray}$$
$$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B})=\mathop{\prod }_{i=1}^{r}L^{S}(s,\unicode[STIX]{x1D6F1}_{i}),\end{eqnarray}$$
where the left-hand side is the standard
![]() $L$
-function of
$L$
-function of
![]() $\unicode[STIX]{x1D70B}$
defined by the doubling method and the right-hand side is the standard
$\unicode[STIX]{x1D70B}$
defined by the doubling method and the right-hand side is the standard
![]() $L$
-function of
$L$
-function of
![]() $\unicode[STIX]{x1D6F1}_{i}$
. If
$\unicode[STIX]{x1D6F1}_{i}$
. If
![]() $i\not =1$
, then
$i\not =1$
, then
 $L^{S}(s,\unicode[STIX]{x1D6F1}_{i})$
is holomorphic and does not vanish at
$L^{S}(s,\unicode[STIX]{x1D6F1}_{i})$
is holomorphic and does not vanish at
![]() $s=1$
(see [Reference Jacquet and ShalikaJS76/77]) and
$s=1$
(see [Reference Jacquet and ShalikaJS76/77]) and
 $L^{S}(s,\operatorname{1})$
have a simple pole at
$L^{S}(s,\operatorname{1})$
have a simple pole at
![]() $s=1$
. Therefore,
$s=1$
. Therefore,
 $L^{S}(s,\unicode[STIX]{x1D70B})$
has a simple pole at
$L^{S}(s,\unicode[STIX]{x1D70B})$
has a simple pole at
![]() $s=1$
.
$s=1$
.
Let
![]() $v$
be a place of
$v$
be a place of
![]() $F$
. By assumption,
$F$
. By assumption,
 $\unicode[STIX]{x1D70B}_{v}|_{\operatorname{SO}(V)(F_{v})}$
is irreducible. By [Reference Gan and IchinoGI14, Theorem C.5], there is an irreducible admissible representation
$\unicode[STIX]{x1D70B}_{v}|_{\operatorname{SO}(V)(F_{v})}$
is irreducible. By [Reference Gan and IchinoGI14, Theorem C.5], there is an irreducible admissible representation
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
 $\operatorname{Sp}(2n-2)(F_{v})$
such that
$\operatorname{Sp}(2n-2)(F_{v})$
such that
 $\unicode[STIX]{x1D70B}_{v}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E})$
. This means that
$\unicode[STIX]{x1D70B}_{v}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E})$
. This means that
![]() $\unicode[STIX]{x1D70B}_{v}$
has a nonzero theta lift to
$\unicode[STIX]{x1D70B}_{v}$
has a nonzero theta lift to
 $\operatorname{Sp}(2n-2)(F_{v})$
.
$\operatorname{Sp}(2n-2)(F_{v})$
.
It then follows from [Reference YamanaYam14, Theorem 10.1] that
![]() $\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
$\unicode[STIX]{x1D70B}$
has a nonzero theta lift to
 $\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. This proves the lemma.◻
$\operatorname{Sp}(2n-2)(\mathbb{A}_{F})$
. This proves the lemma.◻
Lemma 5.2.2. Let
![]() $V$
be a
$V$
be a
![]() $2n+1$
(respectively
$2n+1$
(respectively
![]() $2n$
)-dimensional orthogonal space over
$2n$
)-dimensional orthogonal space over
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
 $\operatorname{O}(V)(\mathbb{A}_{F})$
. Let
$\operatorname{O}(V)(\mathbb{A}_{F})$
. Let
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be its theta lift to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be its theta lift to
 $\operatorname{Mp}(2n)(\mathbb{A}_{F})$
(respectively
$\operatorname{Mp}(2n)(\mathbb{A}_{F})$
(respectively
 $\operatorname{Sp}(2n)(\mathbb{A}_{F})$
) with additive character
$\operatorname{Sp}(2n)(\mathbb{A}_{F})$
) with additive character
![]() $\unicode[STIX]{x1D713}$
. Assume that
$\unicode[STIX]{x1D713}$
. Assume that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
is cuspidal and nonzero. Then
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
is cuspidal and nonzero. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\otimes \unicode[STIX]{x1D712}_{V},\quad \text{respectively }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\boxplus \operatorname{1})\otimes \unicode[STIX]{x1D712}_{V},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\otimes \unicode[STIX]{x1D712}_{V},\quad \text{respectively }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\boxplus \operatorname{1})\otimes \unicode[STIX]{x1D712}_{V},\end{eqnarray}$$
where
![]() $\operatorname{1}$
stands for the trivial character of
$\operatorname{1}$
stands for the trivial character of
![]() $\mathbb{A}_{F}^{\times }$
.
$\mathbb{A}_{F}^{\times }$
.
Proof. Let
![]() $v$
be a place of
$v$
be a place of
![]() $F$
. By [Reference Gan and IchinoGI14, Theorem C.5] and [Reference Gan and SavinGS12], we see that
$F$
. By [Reference Gan and IchinoGI14, Theorem C.5] and [Reference Gan and SavinGS12], we see that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\otimes \unicode[STIX]{x1D712}_{V,v},\quad \text{respectively }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}=(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\oplus \operatorname{1}_{v})\otimes \unicode[STIX]{x1D712}_{V,v},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\otimes \unicode[STIX]{x1D712}_{V,v},\quad \text{respectively }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})}=(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{v}}\oplus \operatorname{1}_{v})\otimes \unicode[STIX]{x1D712}_{V,v},\end{eqnarray}$$
By the previous lemma, in the case
 $\dim V=2n$
,
$\dim V=2n$
,
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
does not contain
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$
does not contain
![]() $\operatorname{1}$
. The lemma then follows from [Reference Jacquet and ShalikaJS81, Theorem 4.4].◻
$\operatorname{1}$
. The lemma then follows from [Reference Jacquet and ShalikaJS81, Theorem 4.4].◻
Lemma 5.2.3. Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
 $\operatorname{O}(V)(\mathbb{A}_{F})$
where
$\operatorname{O}(V)(\mathbb{A}_{F})$
where
![]() $V$
is a
$V$
is a
![]() $2n$
-dimensional orthogonal space over
$2n$
-dimensional orthogonal space over
![]() $F$
. There is a canonical injective map
$F$
. There is a canonical injective map
 $S_{\unicode[STIX]{x1D70B}}\rightarrow S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}$
. It is not bijective if and only if
$S_{\unicode[STIX]{x1D70B}}\rightarrow S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}$
. It is not bijective if and only if
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D6F1}_{1}\boxplus \cdots \boxplus \unicode[STIX]{x1D6F1}_{r}$
where
![]() $\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
 $\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
with
$\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
with
![]() $N_{i}$
being even. In this case,
$N_{i}$
being even. In this case,
![]() $S_{\unicode[STIX]{x1D70B}}$
is an index two subgroup of
$S_{\unicode[STIX]{x1D70B}}$
is an index two subgroup of
![]() $S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}$
.
$S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}$
.
Proof. Suppose that
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
, where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x229E}_{i=1}^{r}\unicode[STIX]{x1D6F1}_{i}$
, where
![]() $\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
 $\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
and
$\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
and
 $\sum _{i=1}^{r}=2n$
. By Lemma 5.2.2,
$\sum _{i=1}^{r}=2n$
. By Lemma 5.2.2,
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D70B}}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=1\},\quad S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r+1}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}a_{r+1}=1\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D70B}}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=1\},\quad S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}=\{(a_{i})\in (\mathbb{Z}/2\mathbb{Z})^{r+1}\mid a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}a_{r+1}=1\}.\end{eqnarray}$$
The map
 $(a_{1},\ldots ,a_{r})\mapsto (a_{1},\ldots ,a_{r},1)$
is clearly injective. It is not bijective if and only if there are elements
$(a_{1},\ldots ,a_{r})\mapsto (a_{1},\ldots ,a_{r},1)$
is clearly injective. It is not bijective if and only if there are elements
 $(a_{1},\ldots ,a_{r})\in (\mathbb{Z}/2\mathbb{Z})^{r}$
so that
$(a_{1},\ldots ,a_{r})\in (\mathbb{Z}/2\mathbb{Z})^{r}$
so that
 $a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=-1$
. This is equivalent to that at least one of the
$a_{1}^{N_{1}}\cdots a_{r}^{N_{r}}=-1$
. This is equivalent to that at least one of the
![]() $N_{i}$
is odd.◻
$N_{i}$
is odd.◻
6 The Ichino–Ikeda conjecture for the full orthogonal group
We review in this section the conjecture of Ichino and Ikeda [Reference Ichino and IkedaII10] and extend it to the full orthogonal group. There are minor inaccuracies in the formulation of the conjecture in [Reference Ichino and IkedaII10] when the automorphic representation on the even orthogonal group appears with multiplicity two in the discrete automorphic spectrum. We will take care of this issue in § 6.2. The Ichino–Ikeda conjecture for the full orthogonal groups is stated in § 6.3. We will show that it follows from the Ichino–Ikeda conjecture for the special orthogonal groups. The argument is close to [Reference Gan and IchinoGI11, §§ 2, 3] at various points. We give details on the new difficulties that arise in our situation (mainly due to the failure of multiplicity one in the discrete automorphic spectrum) and only state the result when its proof is identical to that in [Reference Gan and IchinoGI11].
6.1 Inner products
Let
![]() $F$
be a number field and
$F$
be a number field and
![]() $(U,q_{U})$
be an
$(U,q_{U})$
be an
![]() $n$
-dimensional orthogonal group over
$n$
-dimensional orthogonal group over
![]() $F$
. Let
$F$
. Let
 $H=\operatorname{O}(U)$
and
$H=\operatorname{O}(U)$
and
 $H^{0}=\operatorname{SO}(U)$
. Recall that there is an exact sequence
$H^{0}=\operatorname{SO}(U)$
. Recall that there is an exact sequence
 $$\begin{eqnarray}1\rightarrow H^{0}\rightarrow H\rightarrow \unicode[STIX]{x1D707}_{2}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow H^{0}\rightarrow H\rightarrow \unicode[STIX]{x1D707}_{2}\rightarrow 1.\end{eqnarray}$$
We view
![]() $\unicode[STIX]{x1D707}_{2}$
as an algebraic group over
$\unicode[STIX]{x1D707}_{2}$
as an algebraic group over
![]() $F$
. We write
$F$
. We write
![]() $t$
for the nonidentity element in
$t$
for the nonidentity element in
![]() $\unicode[STIX]{x1D707}_{2}(F)$
and
$\unicode[STIX]{x1D707}_{2}(F)$
and
![]() $t_{v}$
its image in
$t_{v}$
its image in
![]() $\unicode[STIX]{x1D707}_{2}(F_{v})$
for each place
$\unicode[STIX]{x1D707}_{2}(F_{v})$
for each place
![]() $v$
of
$v$
of
![]() $F$
. Note that if
$F$
. Note that if
![]() $n$
is odd, then we may take
$n$
is odd, then we may take
![]() $t=-1$
. The sequence splits canonically and gives an isomorphism
$t=-1$
. The sequence splits canonically and gives an isomorphism
 $H\simeq H^{0}\times \unicode[STIX]{x1D707}_{2}$
.
$H\simeq H^{0}\times \unicode[STIX]{x1D707}_{2}$
.
Let
![]() $d\unicode[STIX]{x1D716}_{v}$
be the measure on
$d\unicode[STIX]{x1D716}_{v}$
be the measure on
![]() $\unicode[STIX]{x1D707}_{2}(F_{v})$
so that
$\unicode[STIX]{x1D707}_{2}(F_{v})$
so that
 $\operatorname{vol}\unicode[STIX]{x1D707}_{2}(F_{v})=1$
. Then
$\operatorname{vol}\unicode[STIX]{x1D707}_{2}(F_{v})=1$
. Then
 $d\unicode[STIX]{x1D716}=\prod _{v}\,d\unicode[STIX]{x1D716}_{v}$
is the Tamagawa measure of
$d\unicode[STIX]{x1D716}=\prod _{v}\,d\unicode[STIX]{x1D716}_{v}$
is the Tamagawa measure of
![]() $\unicode[STIX]{x1D707}_{2}(\mathbb{A}_{F})$
. Let
$\unicode[STIX]{x1D707}_{2}(\mathbb{A}_{F})$
. Let
![]() $Z$
be the center of
$Z$
be the center of
![]() $H^{0}$
. Note that the group
$H^{0}$
. Note that the group
![]() $Z$
is trivial unless
$Z$
is trivial unless
![]() $n=2$
. Let
$n=2$
. Let
![]() $dh$
and
$dh$
and
![]() $dh^{0}$
be the Tamagawa measure of
$dh^{0}$
be the Tamagawa measure of
 $Z(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
and
$Z(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
and
 $Z(\mathbb{A}_{F})\backslash H^{0}(\mathbb{A}_{F})$
, respectively. Then we have
$Z(\mathbb{A}_{F})\backslash H^{0}(\mathbb{A}_{F})$
, respectively. Then we have
 $$\begin{eqnarray}\int _{Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F})}f(h)\,dh=\int _{\unicode[STIX]{x1D707}_{2}(F)\backslash \unicode[STIX]{x1D707}_{2}(\mathbb{A}_{F})}\int _{Z(\mathbb{A}_{F})H^{0}(F)\backslash H^{0}(\mathbb{A}_{F})}f(h^{0}\unicode[STIX]{x1D716})\,dh^{0}\,d\unicode[STIX]{x1D716},\end{eqnarray}$$
$$\begin{eqnarray}\int _{Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F})}f(h)\,dh=\int _{\unicode[STIX]{x1D707}_{2}(F)\backslash \unicode[STIX]{x1D707}_{2}(\mathbb{A}_{F})}\int _{Z(\mathbb{A}_{F})H^{0}(F)\backslash H^{0}(\mathbb{A}_{F})}f(h^{0}\unicode[STIX]{x1D716})\,dh^{0}\,d\unicode[STIX]{x1D716},\end{eqnarray}$$
for all
 $f\in L^{1}(Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F}))$
.
$f\in L^{1}(Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F}))$
.
We fix a decomposition
 $dh=\prod _{v}\,dh_{v}$
where
$dh=\prod _{v}\,dh_{v}$
where
![]() $dh_{v}$
is a measure on
$dh_{v}$
is a measure on
![]() $H(F_{v})$
. Let
$H(F_{v})$
. Let
 $dh_{v}^{0}=2\,dh_{v}|_{H^{0}(F_{v})}$
be a measure on
$dh_{v}^{0}=2\,dh_{v}|_{H^{0}(F_{v})}$
be a measure on
![]() $H^{0}(F_{v})$
. Then
$H^{0}(F_{v})$
. Then
 $dh^{0}=\prod _{v}\,dh_{v}^{0}$
.
$dh^{0}=\prod _{v}\,dh_{v}^{0}$
.
Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal automorphic representation of
![]() $H(\mathbb{A}_{F})$
. We denote by
$H(\mathbb{A}_{F})$
. We denote by
![]() $V$
the space of automorphic functions on which
$V$
the space of automorphic functions on which
![]() $\unicode[STIX]{x1D70B}$
is realized. Let
$\unicode[STIX]{x1D70B}$
is realized. Let
 $\unicode[STIX]{x1D70B}^{0}=\unicode[STIX]{x1D70B}|_{H^{0}(\mathbb{A}_{F})}$
and
$\unicode[STIX]{x1D70B}^{0}=\unicode[STIX]{x1D70B}|_{H^{0}(\mathbb{A}_{F})}$
and
 $V^{0}=\{f|_{H^{0}(\mathbb{A}_{F})}\mid f\in V\}$
. Let
$V^{0}=\{f|_{H^{0}(\mathbb{A}_{F})}\mid f\in V\}$
. Let
![]() $\mathfrak{S}$
be the set of places
$\mathfrak{S}$
be the set of places
![]() $v$
of
$v$
of
![]() $F$
such that
$F$
such that
 $\unicode[STIX]{x1D70B}_{v}|_{H^{0}(F_{v})}$
is reducible. This is also the set of places
$\unicode[STIX]{x1D70B}_{v}|_{H^{0}(F_{v})}$
is reducible. This is also the set of places
![]() $v$
of
$v$
of
![]() $F$
so that
$F$
so that
 $\unicode[STIX]{x1D70B}_{v}\otimes \det _{v}\simeq \unicode[STIX]{x1D70B}_{v}$
. Let
$\unicode[STIX]{x1D70B}_{v}\otimes \det _{v}\simeq \unicode[STIX]{x1D70B}_{v}$
. Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}}$
be the Petersson inner product on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}}$
be the Petersson inner product on
![]() $V$
given by
$V$
given by
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}}(f,f^{\prime })=\int _{Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F})}f(h)\overline{f^{\prime }(h)}\,dh,\quad f,f^{\prime }\in V,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}}(f,f^{\prime })=\int _{Z(\mathbb{A}_{F})H(F)\backslash H(\mathbb{A}_{F})}f(h)\overline{f^{\prime }(h)}\,dh,\quad f,f^{\prime }\in V,\end{eqnarray}$$
We fix a decomposition
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
where
${\mathcal{B}}_{\unicode[STIX]{x1D70B}}=\prod _{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
where
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
is an inner product on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
is an inner product on
![]() $\unicode[STIX]{x1D70B}_{v}$
.
$\unicode[STIX]{x1D70B}_{v}$
.
We distinguish two cases.
Case I:
![]() $\mathfrak{S}=\varnothing$
. In this case,
$\mathfrak{S}=\varnothing$
. In this case,
![]() $\unicode[STIX]{x1D70B}^{0}$
is irreducible and the restriction to
$\unicode[STIX]{x1D70B}^{0}$
is irreducible and the restriction to
 $H^{0}(\mathbb{A}_{F})$
as functions induces an isomorphism
$H^{0}(\mathbb{A}_{F})$
as functions induces an isomorphism
 $V\simeq V^{0}$
as representations of
$V\simeq V^{0}$
as representations of
 $H^{0}(\mathbb{A}_{F})$
. Let
$H^{0}(\mathbb{A}_{F})$
. Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}^{0}}$
be the Petersson inner product on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}^{0}}$
be the Petersson inner product on
![]() $V^{0}$
(defined using the Tamagawa measure on
$V^{0}$
(defined using the Tamagawa measure on
 $H^{0}(\mathbb{A}_{F})$
).
$H^{0}(\mathbb{A}_{F})$
).
Lemma 6.1.1. For any
 $f,f^{\prime }\in V$
, we have
$f,f^{\prime }\in V$
, we have
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}^{0}}(f|_{H^{0}(\mathbb{A}_{F})},f^{\prime }|_{H^{0}(\mathbb{A}_{F})})=2{\mathcal{B}}_{\unicode[STIX]{x1D70B}}(f,f^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}^{0}}(f|_{H^{0}(\mathbb{A}_{F})},f^{\prime }|_{H^{0}(\mathbb{A}_{F})})=2{\mathcal{B}}_{\unicode[STIX]{x1D70B}}(f,f^{\prime }).\end{eqnarray}$$
Proof. This can be proved in the same way as [Reference Gan and IchinoGI11, Lemma 2.1].◻
Case II:
![]() $\mathfrak{S}\not =\varnothing$
. We fix an isomorphism
$\mathfrak{S}\not =\varnothing$
. We fix an isomorphism
 $$\begin{eqnarray}V\simeq \lim _{\substack{ \longrightarrow \\ S}}\biggl(\bigotimes _{v\in S}V_{v}\biggr)\otimes \biggl(\bigotimes _{v\not \in S}\unicode[STIX]{x1D719}_{v}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}V\simeq \lim _{\substack{ \longrightarrow \\ S}}\biggl(\bigotimes _{v\in S}V_{v}\biggr)\otimes \biggl(\bigotimes _{v\not \in S}\unicode[STIX]{x1D719}_{v}\biggr),\end{eqnarray}$$
where
![]() $V_{v}$
is the space on which
$V_{v}$
is the space on which
![]() $\unicode[STIX]{x1D70B}_{v}$
is realized and
$\unicode[STIX]{x1D70B}_{v}$
is realized and
![]() $\unicode[STIX]{x1D719}_{v}$
is an
$\unicode[STIX]{x1D719}_{v}$
is an
 $H(\mathfrak{o}_{F,v})$
-invariant vector in
$H(\mathfrak{o}_{F,v})$
-invariant vector in
![]() $V_{v}$
for
$V_{v}$
for
![]() $v\not \in S$
.
$v\not \in S$
.
If
![]() $v\in \mathfrak{S}$
, then
$v\in \mathfrak{S}$
, then
 $\unicode[STIX]{x1D70B}_{v}\otimes \det _{v}\not \simeq \unicode[STIX]{x1D70B}_{v}$
and
$\unicode[STIX]{x1D70B}_{v}\otimes \det _{v}\not \simeq \unicode[STIX]{x1D70B}_{v}$
and
 $\unicode[STIX]{x1D70B}_{v}^{0}\simeq \unicode[STIX]{x1D70B}_{v}^{+}\oplus \unicode[STIX]{x1D70B}_{v}^{-}$
where
$\unicode[STIX]{x1D70B}_{v}^{0}\simeq \unicode[STIX]{x1D70B}_{v}^{+}\oplus \unicode[STIX]{x1D70B}_{v}^{-}$
where
![]() $\unicode[STIX]{x1D70B}_{v}^{\pm }$
are irreducible admissible representations of
$\unicode[STIX]{x1D70B}_{v}^{\pm }$
are irreducible admissible representations of
![]() $H^{0}(F_{v})$
. We have
$H^{0}(F_{v})$
. We have
 $V_{v}^{0}\simeq V_{v}^{+}\oplus V_{v}^{-}$
where
$V_{v}^{0}\simeq V_{v}^{+}\oplus V_{v}^{-}$
where
![]() $V_{v}^{\ast }$
is the space on which
$V_{v}^{\ast }$
is the space on which
![]() $\unicode[STIX]{x1D70B}_{v}^{\ast }$
are realized and
$\unicode[STIX]{x1D70B}_{v}^{\ast }$
are realized and
![]() $\ast =\pm$
or
$\ast =\pm$
or
![]() $0$
. Note that
$0$
. Note that
 $V_{v}^{-}\simeq \unicode[STIX]{x1D70B}_{v}(t)V_{v}^{+}$
. For almost all places
$V_{v}^{-}\simeq \unicode[STIX]{x1D70B}_{v}(t)V_{v}^{+}$
. For almost all places
![]() $v\in \mathfrak{S}$
, we have
$v\in \mathfrak{S}$
, we have
 $\unicode[STIX]{x1D719}_{v}=\unicode[STIX]{x1D719}_{v}^{+}+\unicode[STIX]{x1D719}_{v}^{-}$
where
$\unicode[STIX]{x1D719}_{v}=\unicode[STIX]{x1D719}_{v}^{+}+\unicode[STIX]{x1D719}_{v}^{-}$
where
![]() $\unicode[STIX]{x1D719}_{v}^{\pm }$
is an
$\unicode[STIX]{x1D719}_{v}^{\pm }$
is an
 $H^{0}(\mathfrak{o}_{F,v})$
-invariant element in
$H^{0}(\mathfrak{o}_{F,v})$
-invariant element in
![]() $V_{v}^{\pm }$
and
$V_{v}^{\pm }$
and
 $\unicode[STIX]{x1D719}_{v}^{-}=\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v}^{+}$
. If
$\unicode[STIX]{x1D719}_{v}^{-}=\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v}^{+}$
. If
![]() $v\not \in \mathfrak{S}$
, then
$v\not \in \mathfrak{S}$
, then
![]() $\unicode[STIX]{x1D70B}_{v}^{0}$
is an irreducible admissible representation on the space
$\unicode[STIX]{x1D70B}_{v}^{0}$
is an irreducible admissible representation on the space
![]() $V_{v}$
.
$V_{v}$
.
In this case, by the Hypothesis O, there are two irreducible cuspidal automorphic representations
![]() $\unicode[STIX]{x1D70B}^{+}$
and
$\unicode[STIX]{x1D70B}^{+}$
and
![]() $\unicode[STIX]{x1D70B}^{-}$
so that
$\unicode[STIX]{x1D70B}^{-}$
so that
 $\unicode[STIX]{x1D70B}^{0}\simeq \unicode[STIX]{x1D70B}^{+}\oplus \unicode[STIX]{x1D70B}^{-}$
,
$\unicode[STIX]{x1D70B}^{0}\simeq \unicode[STIX]{x1D70B}^{+}\oplus \unicode[STIX]{x1D70B}^{-}$
,
 $\unicode[STIX]{x1D70B}^{-}\simeq \unicode[STIX]{x1D70B}^{+}\circ \operatorname{Ad}t$
,
$\unicode[STIX]{x1D70B}^{-}\simeq \unicode[STIX]{x1D70B}^{+}\circ \operatorname{Ad}t$
,
 $V^{0}=V^{+}\oplus V^{-}$
where
$V^{0}=V^{+}\oplus V^{-}$
where
![]() $V^{\pm }$
are the spaces on which
$V^{\pm }$
are the spaces on which
![]() $\unicode[STIX]{x1D70B}^{\pm }$
are realized. We may label the two irreducible components of
$\unicode[STIX]{x1D70B}^{\pm }$
are realized. We may label the two irreducible components of
![]() $\unicode[STIX]{x1D70B}_{v}^{0}$
for
$\unicode[STIX]{x1D70B}_{v}^{0}$
for
![]() $v\in \mathfrak{S}$
so that
$v\in \mathfrak{S}$
so that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}^{\pm } & \simeq & \displaystyle \biggl(\bigotimes _{v\in \mathfrak{S}}\unicode[STIX]{x1D70B}_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{v\not \in \mathfrak{S}}\unicode[STIX]{x1D70B}_{v}^{0}\biggr),\nonumber\\ \displaystyle V^{\pm } & = & \displaystyle \lim _{\substack{ \longrightarrow \\ S}}\biggl(\bigotimes _{\substack{ v\in S \\ v\in \mathfrak{S}}}V_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{\substack{ v\in S \\ v\not \in \mathfrak{S}}}V_{v}\biggr)\otimes \biggl(\bigotimes _{\substack{ v\not \in S \\ v\in \mathfrak{S}}}\unicode[STIX]{x1D719}_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{\substack{ v\not \in S \\ v\not \in \mathfrak{S}}}\unicode[STIX]{x1D719}_{v}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}^{\pm } & \simeq & \displaystyle \biggl(\bigotimes _{v\in \mathfrak{S}}\unicode[STIX]{x1D70B}_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{v\not \in \mathfrak{S}}\unicode[STIX]{x1D70B}_{v}^{0}\biggr),\nonumber\\ \displaystyle V^{\pm } & = & \displaystyle \lim _{\substack{ \longrightarrow \\ S}}\biggl(\bigotimes _{\substack{ v\in S \\ v\in \mathfrak{S}}}V_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{\substack{ v\in S \\ v\not \in \mathfrak{S}}}V_{v}\biggr)\otimes \biggl(\bigotimes _{\substack{ v\not \in S \\ v\in \mathfrak{S}}}\unicode[STIX]{x1D719}_{v}^{\pm }\biggr)\otimes \biggl(\bigotimes _{\substack{ v\not \in S \\ v\not \in \mathfrak{S}}}\unicode[STIX]{x1D719}_{v}\biggr).\nonumber\end{eqnarray}$$
Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}^{+}}$
be the Petersson inner product on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}^{+}}$
be the Petersson inner product on
![]() $V^{+}$
with a fixed decomposition
$V^{+}$
with a fixed decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}^{+}}=\mathop{\prod }_{v\in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}\mathop{\prod }_{v\not \in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}^{+}}=\mathop{\prod }_{v\in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}\mathop{\prod }_{v\not \in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}},\end{eqnarray}$$
where:
-
–
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}$
is an
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}$
is an
 $H^{0}(F_{v})$
invariant pairing on
$H^{0}(F_{v})$
invariant pairing on
 $V_{v}^{+}$
if
$V_{v}^{+}$
if
 $v\in \mathfrak{S}$
and
$v\in \mathfrak{S}$
and
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
is an
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}}$
is an
 $H(F_{v})$
invariant pairing on
$H(F_{v})$
invariant pairing on
 $V_{v}$
if
$V_{v}$
if
 $v\not \in \mathfrak{S}$
;
$v\not \in \mathfrak{S}$
; -
–
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}(\unicode[STIX]{x1D719}_{v}^{+},\unicode[STIX]{x1D719}_{v}^{+})={\mathcal{B}}_{v}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})=1$
for almost all
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{v}^{+}}(\unicode[STIX]{x1D719}_{v}^{+},\unicode[STIX]{x1D719}_{v}^{+})={\mathcal{B}}_{v}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})=1$
for almost all
 $v$
.
$v$
.
If
![]() $v\in \mathfrak{S}$
, we define an
$v\in \mathfrak{S}$
, we define an
![]() $H^{0}(F_{v})$
invariant pairing on
$H^{0}(F_{v})$
invariant pairing on
![]() $V_{v}^{-}$
by
$V_{v}^{-}$
by
 ${\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})={\mathcal{B}}_{v}^{+}(\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v})$
. Then for almost all
${\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})={\mathcal{B}}_{v}^{+}(\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D70B}_{v}(t_{v})\unicode[STIX]{x1D719}_{v})$
. Then for almost all
![]() $v$
, we have
$v$
, we have
 ${\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v}^{-},\unicode[STIX]{x1D719}_{v}^{-})=1$
. We then define an
${\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v}^{-},\unicode[STIX]{x1D719}_{v}^{-})=1$
. We then define an
![]() $H(F_{v})$
invariant pairing on
$H(F_{v})$
invariant pairing on
![]() $V_{v}$
by
$V_{v}$
by
 $$\begin{eqnarray}{\mathcal{B}}_{v}^{\natural }(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})=\left\{\begin{array}{@{}ll@{}}\frac{1}{2}({\mathcal{B}}_{v}^{+}(\unicode[STIX]{x1D719}_{v}^{+},\unicode[STIX]{x1D719}_{v}^{+})+{\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v}^{-},\unicode[STIX]{x1D719}_{v}^{-}))\quad & \text{if }v\in \mathfrak{S},\\ {\mathcal{B}}_{v}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})\quad & \text{if }v\not \in \mathfrak{S}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{v}^{\natural }(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})=\left\{\begin{array}{@{}ll@{}}\frac{1}{2}({\mathcal{B}}_{v}^{+}(\unicode[STIX]{x1D719}_{v}^{+},\unicode[STIX]{x1D719}_{v}^{+})+{\mathcal{B}}_{v}^{-}(\unicode[STIX]{x1D719}_{v}^{-},\unicode[STIX]{x1D719}_{v}^{-}))\quad & \text{if }v\in \mathfrak{S},\\ {\mathcal{B}}_{v}(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})\quad & \text{if }v\not \in \mathfrak{S}.\end{array}\right.\end{eqnarray}$$
Then for almost all
![]() $v$
,
$v$
,
 ${\mathcal{B}}_{v}^{\natural }(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})=1$
.
${\mathcal{B}}_{v}^{\natural }(\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})=1$
.
Lemma 6.1.2. We have
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}}=\mathop{\prod }_{v}{\mathcal{B}}_{v}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}}=\mathop{\prod }_{v}{\mathcal{B}}_{v}^{\natural }.\end{eqnarray}$$
Proof. This can be proved in the same way as [Reference Gan and IchinoGI11, Lemma 2.3].◻
6.2 The Ichino–Ikeda conjecture for special orthogonal groups
We review the Ichino–Ikeda conjecture [Reference Ichino and IkedaII10, Conjecture 2.1] in this subsection. There is a slight inaccuracy in its original formulation in [Reference Ichino and IkedaII10] when the multiplicity of the automorphic representation on the even orthogonal group in the discrete automorphic spectrum is two. We will make some modifications to the conjecture in this case.
Let
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $U_{n+1}$
and
$U_{n+1}$
and
![]() $U_{n}$
be orthogonal spaces of dimension
$U_{n}$
be orthogonal spaces of dimension
![]() $n+1$
and
$n+1$
and
![]() $n$
with an embedding
$n$
with an embedding
 $U_{n}\subset U_{n+1}$
. Let
$U_{n}\subset U_{n+1}$
. Let
 $H_{i}^{0}=\operatorname{SO}(U_{i})$
(
$H_{i}^{0}=\operatorname{SO}(U_{i})$
(
 $i=n,n+1$
). Let
$i=n,n+1$
). Let
![]() $dh$
be the Tamagawa measure on
$dh$
be the Tamagawa measure on
 $H_{n}^{0}(\mathbb{A}_{F})$
and we fix a decomposition
$H_{n}^{0}(\mathbb{A}_{F})$
and we fix a decomposition
 $dh=\prod _{v}\,dh_{v}$
where
$dh=\prod _{v}\,dh_{v}$
where
![]() $dh_{v}$
is a Haar measure on
$dh_{v}$
is a Haar measure on
![]() $H_{n}^{0}(F_{v})$
and
$H_{n}^{0}(F_{v})$
and
 $\operatorname{vol}H_{n}^{0}(\mathfrak{o}_{F,v})=1$
for almost all
$\operatorname{vol}H_{n}^{0}(\mathfrak{o}_{F,v})=1$
for almost all
![]() $v$
.
$v$
.
Let
 $\unicode[STIX]{x1D70B}_{n+1}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n+1,v}$
and
$\unicode[STIX]{x1D70B}_{n+1}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n+1,v}$
and
 $\unicode[STIX]{x1D70B}_{n}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n,v}$
be irreducible cuspidal tempered automorphic representations of
$\unicode[STIX]{x1D70B}_{n}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n,v}$
be irreducible cuspidal tempered automorphic representations of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
and
$H_{n+1}^{0}(\mathbb{A}_{F})$
and
 $H_{n}^{0}(\mathbb{A}_{F})$
, respectively. Let
$H_{n}^{0}(\mathbb{A}_{F})$
, respectively. Let
 $V_{n+1}=\bigotimes _{v}V_{n+1,v}$
and
$V_{n+1}=\bigotimes _{v}V_{n+1,v}$
and
 $V_{n}=\bigotimes _{v}V_{n,v}$
be the space on which
$V_{n}=\bigotimes _{v}V_{n,v}$
be the space on which
![]() $\unicode[STIX]{x1D70B}_{n+1}$
and
$\unicode[STIX]{x1D70B}_{n+1}$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
are realized, respectively. Let
$\unicode[STIX]{x1D70B}_{n}$
are realized, respectively. Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}$
and
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}$
and
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}$
be the Petersson inner products on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}$
be the Petersson inner products on
![]() $V_{n+1}$
and
$V_{n+1}$
and
![]() $V_{n}$
, respectively. We fix a decomposition
$V_{n}$
, respectively. We fix a decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}},\quad {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}},\quad {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}\end{eqnarray}$$
where
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}$
and
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}$
and
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}$
are inner products on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}$
are inner products on
![]() $V_{n+1,v}$
and
$V_{n+1,v}$
and
![]() $V_{n,v}$
respectively.
$V_{n,v}$
respectively.
Let
 $f_{n+1}=\bigotimes f_{n+1,v},f_{n+1}^{\prime }=\bigotimes f_{n+1,v}^{\prime }\in V_{n+1}$
and
$f_{n+1}=\bigotimes f_{n+1,v},f_{n+1}^{\prime }=\bigotimes f_{n+1,v}^{\prime }\in V_{n+1}$
and
 $f_{n}=\bigotimes f_{n,v},f_{n}^{\prime }=\bigotimes f_{n,v}^{\prime }\in V_{n}$
. Define
$f_{n}=\bigotimes f_{n,v},f_{n}^{\prime }=\bigotimes f_{n,v}^{\prime }\in V_{n}$
. Define
 $$\begin{eqnarray}{\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime })=\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\cdot \overline{\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}^{\prime }(h)f_{n}^{\prime }(h)\,dh}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime })=\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\cdot \overline{\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}^{\prime }(h)f_{n}^{\prime }(h)\,dh}.\end{eqnarray}$$
For each place
![]() $v$
, we define
$v$
, we define
 $$\begin{eqnarray}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime })=\int _{H_{n}^{0}(F_{v})}{\mathcal{B}}_{n+1,v}(\unicode[STIX]{x1D70B}_{n+1,v}(h_{v})f_{n+1,v},f_{n+1,v}^{\prime }){\mathcal{B}}_{n,v}(\unicode[STIX]{x1D70B}_{n,v}(h_{v})f_{n,v},f_{n,v}^{\prime })\,dh_{v}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime })=\int _{H_{n}^{0}(F_{v})}{\mathcal{B}}_{n+1,v}(\unicode[STIX]{x1D70B}_{n+1,v}(h_{v})f_{n+1,v},f_{n+1,v}^{\prime }){\mathcal{B}}_{n,v}(\unicode[STIX]{x1D70B}_{n,v}(h_{v})f_{n,v},f_{n,v}^{\prime })\,dh_{v}.\end{eqnarray}$$
Let
![]() $S$
be a sufficiently large finite set of places of
$S$
be a sufficiently large finite set of places of
![]() $F$
containing all archimedean places so that if
$F$
containing all archimedean places so that if
![]() $v\not \in S$
, then
$v\not \in S$
, then
 $f_{n+1,v},f_{n+1,v}^{\prime }$
(respectively
$f_{n+1,v},f_{n+1,v}^{\prime }$
(respectively
![]() $f_{n,v}$
,
$f_{n,v}$
,
![]() $f_{n,v}^{\prime }$
) are
$f_{n,v}^{\prime }$
) are
 $H_{n+1}^{0}(\mathfrak{o}_{F,v})$
(respectively
$H_{n+1}^{0}(\mathfrak{o}_{F,v})$
(respectively
 $H_{n}^{0}(\mathfrak{o}_{F,v})$
) fixed and
$H_{n}^{0}(\mathfrak{o}_{F,v})$
) fixed and
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}(f_{n+1,v},f_{n+1,v}^{\prime })={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}(f_{n,v},f_{n,v}^{\prime })=1$
. In particular,
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}(f_{n+1,v},f_{n+1,v}^{\prime })={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}(f_{n,v},f_{n,v}^{\prime })=1$
. In particular,
![]() $\unicode[STIX]{x1D70B}_{n+1,v}$
and
$\unicode[STIX]{x1D70B}_{n+1,v}$
and
![]() $\unicode[STIX]{x1D70B}_{n,v}$
are both unramified if
$\unicode[STIX]{x1D70B}_{n,v}$
are both unramified if
![]() $v\not \in S$
. Let
$v\not \in S$
. Let
 $\{\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{[(n+1)/2],v}\}$
and
$\{\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{[(n+1)/2],v}\}$
and
 $\{\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{[n/2],v}\}$
be the Satake parameters of
$\{\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{[n/2],v}\}$
be the Satake parameters of
![]() $\unicode[STIX]{x1D70B}_{n+1,v}$
and
$\unicode[STIX]{x1D70B}_{n+1,v}$
and
![]() $\unicode[STIX]{x1D70B}_{n,v}$
, respectively. Let
$\unicode[STIX]{x1D70B}_{n,v}$
, respectively. Let
 $$\begin{eqnarray}\displaystyle A_{n+1,v} & = & \displaystyle \operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{[(n+1)/2],v},\unicode[STIX]{x1D6FC}_{[(n+1)/2],v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\nonumber\\ \displaystyle A_{n,v} & = & \displaystyle \operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{[n/2],v},\unicode[STIX]{x1D6FD}_{[n/2],v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{n+1,v} & = & \displaystyle \operatorname{diag}[\unicode[STIX]{x1D6FC}_{1,v},\ldots ,\unicode[STIX]{x1D6FC}_{[(n+1)/2],v},\unicode[STIX]{x1D6FC}_{[(n+1)/2],v}^{-1},\ldots ,\unicode[STIX]{x1D6FC}_{1,v}^{-1}]\nonumber\\ \displaystyle A_{n,v} & = & \displaystyle \operatorname{diag}[\unicode[STIX]{x1D6FD}_{1,v},\ldots ,\unicode[STIX]{x1D6FD}_{[n/2],v},\unicode[STIX]{x1D6FD}_{[n/2],v}^{-1},\ldots ,\unicode[STIX]{x1D6FD}_{1,v}^{-1}].\nonumber\end{eqnarray}$$
Let
 $$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=\mathop{\prod }_{v\not \in S}\det (1-A_{n+1,v}\otimes A_{n,v}\cdot q_{v}^{-s})^{-1}\end{eqnarray}$$
$$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=\mathop{\prod }_{v\not \in S}\det (1-A_{n+1,v}\otimes A_{n,v}\cdot q_{v}^{-s})^{-1}\end{eqnarray}$$
be the tensor product
![]() $L$
-function and
$L$
-function and
 $L^{S}(s,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})$
and
$L^{S}(s,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})$
and
 $L^{S}(s,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})$
be the adjoint
$L^{S}(s,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})$
be the adjoint
![]() $L$
-functions.
$L$
-functions.
Conjecture 6.2.1 (Ichino–Ikeda [Reference Ichino and IkedaII10, Conjecture 2.1]).
(i) Suppose that
![]() $\unicode[STIX]{x1D70B}_{n+1}$
and
$\unicode[STIX]{x1D70B}_{n+1}$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
appear with multiplicity one in the discrete spectrum. Then the automorphic realization
$\unicode[STIX]{x1D70B}_{n}$
appear with multiplicity one in the discrete spectrum. Then the automorphic realization
![]() $V_{n+1}$
(respectively
$V_{n+1}$
(respectively
![]() $V_{n}$
) of
$V_{n}$
) of
![]() $\unicode[STIX]{x1D70B}_{n+1}$
(respectively
$\unicode[STIX]{x1D70B}_{n+1}$
(respectively
![]() $\unicode[STIX]{x1D70B}_{n}$
) is canonical. We have
$\unicode[STIX]{x1D70B}_{n}$
) is canonical. We have
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime }) & = & \displaystyle \frac{1}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}^{0}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime }) & = & \displaystyle \frac{1}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}^{0}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime }).\nonumber\end{eqnarray}$$
(ii) Suppose that
![]() $n$
is odd and
$n$
is odd and
![]() $\unicode[STIX]{x1D70B}_{n+1}$
appears with multiplicity two in the discrete spectrum of
$\unicode[STIX]{x1D70B}_{n+1}$
appears with multiplicity two in the discrete spectrum of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
. Then the automorphic realization
$H_{n+1}^{0}(\mathbb{A}_{F})$
. Then the automorphic realization
![]() $V_{n}$
of
$V_{n}$
of
![]() $\unicode[STIX]{x1D70B}_{n}$
is canonical. Let
$\unicode[STIX]{x1D70B}_{n}$
is canonical. Let
![]() $L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
be the isotypic component of
$L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
be the isotypic component of
![]() $\unicode[STIX]{x1D70B}_{n+1}$
in the discrete automorphic spectrum of
$\unicode[STIX]{x1D70B}_{n+1}$
in the discrete automorphic spectrum of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
. Then there are two possibilities.
$H_{n+1}^{0}(\mathbb{A}_{F})$
. Then there are two possibilities.
-
(a) The linear form
 ${\mathcal{J}}$
is identically zero on
${\mathcal{J}}$
is identically zero on
 $L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}\times \unicode[STIX]{x0141}_{\unicode[STIX]{x1D70B}_{n+1}}^{2}\times V_{n}\times V_{n}$
. This is equivalent to that either
$L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}\times \unicode[STIX]{x0141}_{\unicode[STIX]{x1D70B}_{n+1}}^{2}\times V_{n}\times V_{n}$
. This is equivalent to that either
 $\operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})=0$
or
$\operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})=0$
or
 $L^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=0$
.
$L^{S}(\frac{1}{2},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=0$
. -
(b) There is a unique irreducible subrepresentation
 $V_{n+1}$
of
$V_{n+1}$
of
 $L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
such that it is invariant under the outer automorphism of
$L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
such that it is invariant under the outer automorphism of
 $H_{n+1}^{0}$
and
$H_{n+1}^{0}$
and
 ${\mathcal{J}}$
is not identically zero on
${\mathcal{J}}$
is not identically zero on
 $V_{n+1}\times V_{n+1}\times V_{n}\times V_{n}$
. We have if
$V_{n+1}\times V_{n+1}\times V_{n}\times V_{n}$
. We have if $$\begin{eqnarray}\displaystyle {\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime }) & = & \displaystyle \frac{2}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}^{0}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}{\mathcal{I}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}(f_{n+1},f_{n+1}^{\prime },f_{n},f_{n}^{\prime }) & = & \displaystyle \frac{2}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}^{0}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}{\mathcal{I}}_{v}(f_{n+1,v},f_{n+1,v}^{\prime },f_{n,v},f_{n,v}^{\prime }),\nonumber\end{eqnarray}$$
 $f_{n+1},f_{n+1}^{\prime }\in V_{n+1}$
,
$f_{n+1},f_{n+1}^{\prime }\in V_{n+1}$
,
 $f_{n},f_{n}^{\prime }\in V_{n}$
. Let
$f_{n},f_{n}^{\prime }\in V_{n}$
. Let
 $V_{n+1}^{\prime }$
(
$V_{n+1}^{\prime }$
(
 $\not =V_{n+1}$
) be the other irreducible subrepresentation of
$\not =V_{n+1}$
) be the other irreducible subrepresentation of
 $L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
that is invariant under the outer automorphism of
$L_{\unicode[STIX]{x1D70B}_{n+1}}^{2}$
that is invariant under the outer automorphism of
 $H_{n+1}^{0}$
. Then
$H_{n+1}^{0}$
. Then
 ${\mathcal{J}}$
is identically zero on
${\mathcal{J}}$
is identically zero on
 $V_{n+1}^{\prime }\times V_{n+1}^{\prime }\times V_{n}\times V_{n}$
.
$V_{n+1}^{\prime }\times V_{n+1}^{\prime }\times V_{n}\times V_{n}$
.
If
![]() $n$
is even, then we have a similar statement, with the role of
$n$
is even, then we have a similar statement, with the role of
![]() $\unicode[STIX]{x1D70B}_{n+1}$
and
$\unicode[STIX]{x1D70B}_{n+1}$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
being switched.
$\unicode[STIX]{x1D70B}_{n}$
being switched.
Remark 6.2.2. The same inaccuracy also occurs in [Reference LiuLiu16]. One also needs to modify [Reference LiuLiu16, Conjecture 2.5] in a similar way when the automorphic representation on the even orthogonal group has multiplicity two. In this case, the automorphic realization is required to be invariant under the outer twist and (in the notation of [Reference LiuLiu16])
 $1/|S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{2})}||S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{0})}|$
needs to be replaced by
$1/|S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{2})}||S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{0})}|$
needs to be replaced by
 $2/|S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{2})}||S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{0})}|$
.
$2/|S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{2})}||S_{\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D70B}_{0})}|$
.
6.3 The Ichino–Ikeda conjecture for full orthogonal groups
Let
![]() $U_{n+1}$
and
$U_{n+1}$
and
![]() $U_{n}$
be orthogonal spaces of dimension
$U_{n}$
be orthogonal spaces of dimension
![]() $n+1$
and
$n+1$
and
![]() $n$
with an embedding
$n$
with an embedding
 $U_{n}\subset U_{n+1}$
. Let
$U_{n}\subset U_{n+1}$
. Let
 $H_{i}=\operatorname{O}(U_{i})$
and
$H_{i}=\operatorname{O}(U_{i})$
and
 $H_{i}^{0}=\operatorname{SO}(U_{i})$
(
$H_{i}^{0}=\operatorname{SO}(U_{i})$
(
 $i=n,n+1$
). Let
$i=n,n+1$
). Let
![]() $dh$
be the Tamagawa measure on
$dh$
be the Tamagawa measure on
 $H_{n}(\mathbb{A}_{F})$
and we fix a decomposition
$H_{n}(\mathbb{A}_{F})$
and we fix a decomposition
 $dh=\prod _{v}\,dh_{v}$
where
$dh=\prod _{v}\,dh_{v}$
where
![]() $dh_{v}$
is a Haar measure on
$dh_{v}$
is a Haar measure on
![]() $H_{n}(F_{v})$
and
$H_{n}(F_{v})$
and
 $\operatorname{vol}H_{n}(\mathfrak{o}_{F,v})=1$
for almost all
$\operatorname{vol}H_{n}(\mathfrak{o}_{F,v})=1$
for almost all
![]() $v$
.
$v$
.
Let
 $\unicode[STIX]{x1D70B}_{n+1}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n+1,v}$
and
$\unicode[STIX]{x1D70B}_{n+1}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n+1,v}$
and
 $\unicode[STIX]{x1D70B}_{n}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n,v}$
be irreducible cuspidal tempered automorphic representations of
$\unicode[STIX]{x1D70B}_{n}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{n,v}$
be irreducible cuspidal tempered automorphic representations of
 $H_{n+1}(\mathbb{A}_{F})$
and
$H_{n+1}(\mathbb{A}_{F})$
and
 $H_{n}(\mathbb{A}_{F})$
, respectively. Let
$H_{n}(\mathbb{A}_{F})$
, respectively. Let
 $V_{n+1}=\bigotimes _{v}V_{n+1,v}$
and
$V_{n+1}=\bigotimes _{v}V_{n+1,v}$
and
 $V_{n}=\bigotimes _{v}V_{n,v}$
be the space on which
$V_{n}=\bigotimes _{v}V_{n,v}$
be the space on which
![]() $\unicode[STIX]{x1D70B}_{n+1}$
and
$\unicode[STIX]{x1D70B}_{n+1}$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
are realized, respectively. Let
$\unicode[STIX]{x1D70B}_{n}$
are realized, respectively. Let
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}$
and
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}$
and
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}$
be the Petersson inner products on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}$
be the Petersson inner products on
![]() $V_{n+1}$
and
$V_{n+1}$
and
![]() $V_{n}$
, respectively. We fix a decomposition
$V_{n}$
, respectively. We fix a decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}},\quad {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}},\quad {\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}}=\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}\end{eqnarray}$$
where
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}$
and
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}$
and
![]() ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}$
are inner products on
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}$
are inner products on
![]() $V_{n+1,v}$
and
$V_{n+1,v}$
and
![]() $V_{n,v}$
, respectively.
$V_{n,v}$
, respectively.
Let
 $f_{n+1}=\bigotimes f_{n+1,v}\in V_{n+1}$
and
$f_{n+1}=\bigotimes f_{n+1,v}\in V_{n+1}$
and
 $f_{n}=\bigotimes f_{n,v}\in V_{n}$
. Define
$f_{n}=\bigotimes f_{n,v}\in V_{n}$
. Define
 $$\begin{eqnarray}{\mathcal{I}}(f_{n+1},f_{n})=\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\cdot \overline{\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}(f_{n+1},f_{n})=\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\cdot \overline{\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh}.\end{eqnarray}$$
For each place
![]() $v$
, we define
$v$
, we define
 $$\begin{eqnarray}{\mathcal{I}}_{v}(f_{n+1,v},f_{n,v})=\int _{H_{n}(F_{v})}{\mathcal{B}}_{n+1,v}(\unicode[STIX]{x1D70B}_{n+1,v}(h_{v})f_{n+1,v},f_{n+1,v}){\mathcal{B}}_{n,v}(\unicode[STIX]{x1D70B}_{n,v}(h_{v})f_{n,v},f_{n,v})\,dh_{v}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{v}(f_{n+1,v},f_{n,v})=\int _{H_{n}(F_{v})}{\mathcal{B}}_{n+1,v}(\unicode[STIX]{x1D70B}_{n+1,v}(h_{v})f_{n+1,v},f_{n+1,v}){\mathcal{B}}_{n,v}(\unicode[STIX]{x1D70B}_{n,v}(h_{v})f_{n,v},f_{n,v})\,dh_{v}.\end{eqnarray}$$
Let
![]() $S$
be a sufficiently large finite set of places of
$S$
be a sufficiently large finite set of places of
![]() $F$
containing all archimedean places so that if
$F$
containing all archimedean places so that if
![]() $v\not \in S$
, then
$v\not \in S$
, then
![]() $f_{n+1,v}$
(respectively
$f_{n+1,v}$
(respectively
![]() $f_{n,v}$
) is
$f_{n,v}$
) is
 $H_{n+1}(\mathfrak{o}_{F,v})$
(respectively
$H_{n+1}(\mathfrak{o}_{F,v})$
(respectively
 $H_{n}(\mathfrak{o}_{F,v})$
) fixed and
$H_{n}(\mathfrak{o}_{F,v})$
) fixed and
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}(f_{n+1,v},f_{n+1,v})={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}(f_{n,v},f_{n,v})=1$
. In particular,
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}(f_{n+1,v},f_{n+1,v})={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}(f_{n,v},f_{n,v})=1$
. In particular,
![]() $\unicode[STIX]{x1D70B}_{n+1,v}$
and
$\unicode[STIX]{x1D70B}_{n+1,v}$
and
![]() $\unicode[STIX]{x1D70B}_{n,v}$
are both unramified if
$\unicode[STIX]{x1D70B}_{n,v}$
are both unramified if
![]() $v\not \in S$
. We define the partial
$v\not \in S$
. We define the partial
![]() $L$
-functions
$L$
-functions
 $$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=L^{S}(s,\dot{\unicode[STIX]{x1D70B}}_{n+1}\times \dot{\unicode[STIX]{x1D70B}}_{n}),\quad L^{S}(s,\unicode[STIX]{x1D70B}_{i},\text{Ad})=L^{S}(s,\dot{\unicode[STIX]{x1D70B}}_{i},\text{Ad}),\quad i=n,n+1,\end{eqnarray}$$
$$\begin{eqnarray}L^{S}(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=L^{S}(s,\dot{\unicode[STIX]{x1D70B}}_{n+1}\times \dot{\unicode[STIX]{x1D70B}}_{n}),\quad L^{S}(s,\unicode[STIX]{x1D70B}_{i},\text{Ad})=L^{S}(s,\dot{\unicode[STIX]{x1D70B}}_{i},\text{Ad}),\quad i=n,n+1,\end{eqnarray}$$
where
![]() $\dot{\unicode[STIX]{x1D70B}}_{i}$
is an irreducible constituent of
$\dot{\unicode[STIX]{x1D70B}}_{i}$
is an irreducible constituent of
![]() $\unicode[STIX]{x1D70B}_{i}^{0}$
which is invariant by the nontrivial outer automorphism
$\unicode[STIX]{x1D70B}_{i}^{0}$
which is invariant by the nontrivial outer automorphism
![]() $\unicode[STIX]{x1D716}$
. The
$\unicode[STIX]{x1D716}$
. The
![]() $L$
-functions on the right-hand side of each equality is independent of the choice of this irreducible constituent.
$L$
-functions on the right-hand side of each equality is independent of the choice of this irreducible constituent.
The Ichino–Ikeda conjecture for the full orthogonal group is the following.
Conjecture 6.3.1. We have
 $$\begin{eqnarray}{\mathcal{I}}(f_{n+1},f_{n})=\frac{2^{\unicode[STIX]{x1D6FE}}}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\mathop{\prod }_{v\in S}{\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}(f_{n+1},f_{n})=\frac{2^{\unicode[STIX]{x1D6FE}}}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\mathop{\prod }_{v\in S}{\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}$
is given as follows. Suppose that
$\unicode[STIX]{x1D6FE}$
is given as follows. Suppose that
![]() $n$
is even (respectively odd). Let
$n$
is even (respectively odd). Let
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{n}}=\unicode[STIX]{x229E}\unicode[STIX]{x1D6F1}_{i}$
(respectively
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{n}}=\unicode[STIX]{x229E}\unicode[STIX]{x1D6F1}_{i}$
(respectively
 $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{n+1}}=\unicode[STIX]{x229E}\unicode[STIX]{x1D6F1}_{i}$
) where
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}_{n+1}}=\unicode[STIX]{x229E}\unicode[STIX]{x1D6F1}_{i}$
) where
![]() $\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}_{i}$
is an irreducible cuspidal automorphic representation of
 $\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
. Then
$\operatorname{GL}_{N_{i}}(\mathbb{A}_{F})$
. Then
![]() $\unicode[STIX]{x1D6FE}=0$
(respectively
$\unicode[STIX]{x1D6FE}=0$
(respectively
![]() $1$
) if at least one of
$1$
) if at least one of
![]() $N_{i}$
is odd (respectively all
$N_{i}$
is odd (respectively all
![]() $N_{i}$
are even).
$N_{i}$
are even).
Remark 6.3.2. We may have a neater formulation of the conjecture if we replace our definition of the centralizers
![]() $S_{\unicode[STIX]{x1D70B}_{i}}$
by the one given in [Reference Atobe and GanAG16] for parameters of full orthogonal groups. We stick to our current formulation as it is more convenient for the applications in this paper.
$S_{\unicode[STIX]{x1D70B}_{i}}$
by the one given in [Reference Atobe and GanAG16] for parameters of full orthogonal groups. We stick to our current formulation as it is more convenient for the applications in this paper.
Similar to Conjecture 2.3.1, we may rewrite the identity (6.3.3) in an equivalent form, which does not involve the finite set
![]() $S$
. We may define the completed
$S$
. We may define the completed
![]() $L$
-function
$L$
-function
 $$\begin{eqnarray}L(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=\mathop{\prod }_{v}L(s,\unicode[STIX]{x1D70B}_{n+1,v}\times \unicode[STIX]{x1D70B}_{n,v}),\quad L(s,\unicode[STIX]{x1D70B}_{i},\text{Ad})=\mathop{\prod }_{v}L(s,\unicode[STIX]{x1D70B}_{i,v},\text{Ad}),\quad i=n,n+1.\end{eqnarray}$$
$$\begin{eqnarray}L(s,\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})=\mathop{\prod }_{v}L(s,\unicode[STIX]{x1D70B}_{n+1,v}\times \unicode[STIX]{x1D70B}_{n,v}),\quad L(s,\unicode[STIX]{x1D70B}_{i},\text{Ad})=\mathop{\prod }_{v}L(s,\unicode[STIX]{x1D70B}_{i,v},\text{Ad}),\quad i=n,n+1.\end{eqnarray}$$
The actually definition of the local Euler factors outside the set
![]() $S$
is irrelevant to our discussion since the conjecture does not reply on how these Euler factors are defined. Let
$S$
is irrelevant to our discussion since the conjecture does not reply on how these Euler factors are defined. Let
 $$\begin{eqnarray}{\mathcal{L}}=\unicode[STIX]{x1D6E5}_{H_{n+1}}\frac{L({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L(1,\unicode[STIX]{x1D70B}_{n+1},\text{Ad})L(1,\unicode[STIX]{x1D70B}_{n},\text{Ad})},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}=\unicode[STIX]{x1D6E5}_{H_{n+1}}\frac{L({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L(1,\unicode[STIX]{x1D70B}_{n+1},\text{Ad})L(1,\unicode[STIX]{x1D70B}_{n},\text{Ad})},\end{eqnarray}$$
and by
![]() ${\mathcal{L}}_{v}$
the Euler factor of
${\mathcal{L}}_{v}$
the Euler factor of
![]() ${\mathcal{L}}$
at the place
${\mathcal{L}}$
at the place
![]() $v$
. We define
$v$
. We define
 $$\begin{eqnarray}{\mathcal{I}}_{v}^{\natural }={\mathcal{L}}_{v}^{-1}\cdot {\mathcal{I}}_{v}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{v}^{\natural }={\mathcal{L}}_{v}^{-1}\cdot {\mathcal{I}}_{v}.\end{eqnarray}$$
Then Conjecture 6.3.1 can be written as a decomposition of linear forms
 $$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}}}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}{\mathcal{L}}\cdot \mathop{\prod }_{v}{\mathcal{I}}_{v}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}}}{|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}{\mathcal{L}}\cdot \mathop{\prod }_{v}{\mathcal{I}}_{v}^{\natural }.\end{eqnarray}$$
The product on the right-hand side ranges over all places
![]() $v$
of
$v$
of
![]() $F$
. It is convergent since for almost all
$F$
. It is convergent since for almost all
![]() $v$
, i.e.
$v$
, i.e.
![]() $v\not \in S$
,
$v\not \in S$
,
![]() ${\mathcal{I}}_{v}^{\natural }=1$
. We may write Conjecture 6.2.1 in a similar forms.
${\mathcal{I}}_{v}^{\natural }=1$
. We may write Conjecture 6.2.1 in a similar forms.
Proof. We assume that
![]() $n$
is odd. The case
$n$
is odd. The case
![]() $n$
being even can be handled similarly, with modifications of notation at various places. Then
$n$
being even can be handled similarly, with modifications of notation at various places. Then
 $H_{n}\simeq H_{n}^{0}\times \unicode[STIX]{x1D707}_{2}$
. So
$H_{n}\simeq H_{n}^{0}\times \unicode[STIX]{x1D707}_{2}$
. So
![]() $\unicode[STIX]{x1D70B}_{n,v}^{0}$
is irreducible for all places
$\unicode[STIX]{x1D70B}_{n,v}^{0}$
is irreducible for all places
![]() $v$
of
$v$
of
![]() $F$
. Let
$F$
. Let
![]() $\mathfrak{S}$
be the set of places of
$\mathfrak{S}$
be the set of places of
![]() $F$
such that
$F$
such that
![]() $\unicode[STIX]{x1D70B}_{n+1,v}^{0}$
is reducible.
$\unicode[STIX]{x1D70B}_{n+1,v}^{0}$
is reducible.
If
![]() $v\not \in S$
, then
$v\not \in S$
, then
 $f_{n+1,v}=\unicode[STIX]{x1D719}_{n+1,v}$
is fixed by
$f_{n+1,v}=\unicode[STIX]{x1D719}_{n+1,v}$
is fixed by
 $H_{n+1}(\mathfrak{o}_{F,v})$
and
$H_{n+1}(\mathfrak{o}_{F,v})$
and
![]() $f_{n,v}$
is fixed by
$f_{n,v}$
is fixed by
 $H_{n}(\mathfrak{o}_{F,v})$
. We may further assume that
$H_{n}(\mathfrak{o}_{F,v})$
. We may further assume that
 $f_{n+1,v}=f_{n+1,v}^{+}\in V_{n+1,v}^{+}$
if
$f_{n+1,v}=f_{n+1,v}^{+}\in V_{n+1,v}^{+}$
if
 $v\in S\cap \mathfrak{S}$
. Thus,
$v\in S\cap \mathfrak{S}$
. Thus,
 $$\begin{eqnarray}f_{n+1,v}=\mathop{\prod }_{v\in S\cap \mathfrak{S}}f_{n+1,v}^{+}\mathop{\prod }_{v\in S,v\not \in \mathfrak{S}}f_{n+1,v}\mathop{\prod }_{v\not \in S}\unicode[STIX]{x1D719}_{n+1,v}.\end{eqnarray}$$
$$\begin{eqnarray}f_{n+1,v}=\mathop{\prod }_{v\in S\cap \mathfrak{S}}f_{n+1,v}^{+}\mathop{\prod }_{v\in S,v\not \in \mathfrak{S}}f_{n+1,v}\mathop{\prod }_{v\not \in S}\unicode[STIX]{x1D719}_{n+1,v}.\end{eqnarray}$$
Put
 $$\begin{eqnarray}S^{\prime }=S\backslash (S\cap \mathfrak{S}),\quad s=|S\cap \mathfrak{S}|,\quad s^{\prime }=|S^{\prime }|.\end{eqnarray}$$
$$\begin{eqnarray}S^{\prime }=S\backslash (S\cap \mathfrak{S}),\quad s=|S\cap \mathfrak{S}|,\quad s^{\prime }=|S^{\prime }|.\end{eqnarray}$$
For any finite set of places
![]() $T$
of
$T$
of
![]() $F$
, we define
$F$
, we define
 $F_{T}=\prod _{v\in T}F_{v}$
.
$F_{T}=\prod _{v\in T}F_{v}$
.
If
![]() $\mathfrak{S}\not =\varnothing$
, then
$\mathfrak{S}\not =\varnothing$
, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}(f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})+f_{n+1}(h\unicode[STIX]{x1D716}t)f_{n}(h\unicode[STIX]{x1D716}t))\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}(f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})+f_{n+1}(h\unicode[STIX]{x1D716}t)f_{n}(h\unicode[STIX]{x1D716}t))\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{1}{2^{s+s^{\prime }}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh.\nonumber\end{eqnarray}$$
If
![]() $\mathfrak{S}=\varnothing$
, then
$\mathfrak{S}=\varnothing$
, then
 $$\begin{eqnarray}\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh=\frac{1}{2^{s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{n}(F)\backslash H_{n}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh=\frac{1}{2^{s^{\prime }+1}}\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D707}_{2}(F_{S})}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h\unicode[STIX]{x1D716})f_{n}(h\unicode[STIX]{x1D716})\,dh.\end{eqnarray}$$
We fix a decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}^{+}}=\mathop{\prod }_{v\in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{+}}\mathop{\prod }_{v\not \in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}},\quad \text{respectively }{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}^{0}}=2\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}^{+}}=\mathop{\prod }_{v\in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{+}}\mathop{\prod }_{v\not \in \mathfrak{S}}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}},\quad \text{respectively }{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1}^{0}}=2\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}}\end{eqnarray}$$
if
![]() $\mathfrak{S}\not =\varnothing$
(respectively
$\mathfrak{S}\not =\varnothing$
(respectively
![]() $\mathfrak{S}=\varnothing$
), so that
$\mathfrak{S}=\varnothing$
), so that
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}^{\natural }$
if
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}^{\natural }$
if
![]() $v\in \mathfrak{S}$
(respectively
$v\in \mathfrak{S}$
(respectively
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}}$
if
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n+1,v}^{0}}$
if
![]() $v\not \in \mathfrak{S}$
). We fix a decomposition
$v\not \in \mathfrak{S}$
). We fix a decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}^{0}}=2\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}^{0}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n}^{0}}=2\mathop{\prod }_{v}{\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}^{0}},\end{eqnarray}$$
so that
 ${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}^{0}}$
.
${\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}}={\mathcal{B}}_{\unicode[STIX]{x1D70B}_{n,v}^{0}}$
.
We say that we are in the exceptional case if the following conditions are satisfied.
-
– We have that
 $\unicode[STIX]{x1D70B}_{n+1}^{0}$
is irreducible and appears with multiplicity two in the discrete spectrum of
$\unicode[STIX]{x1D70B}_{n+1}^{0}$
is irreducible and appears with multiplicity two in the discrete spectrum of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
.
$H_{n+1}^{0}(\mathbb{A}_{F})$
. -
– The period integral
is identically zero on $$\begin{eqnarray}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\end{eqnarray}$$
 $V_{n+1}^{0}\times V_{n}^{0}$
, where we denote as before
$V_{n+1}^{0}\times V_{n}^{0}$
, where we denote as before
 $V_{i}^{0}=\{f|_{H_{i}^{0}(\mathbb{A}_{F})}\mid f\in V_{i}\}$
,
$V_{i}^{0}=\{f|_{H_{i}^{0}(\mathbb{A}_{F})}\mid f\in V_{i}\}$
,
 $i=n,n+1$
.
$i=n,n+1$
.
-
– The period integral is not identically zero on the isotypic component of
 $\unicode[STIX]{x1D70B}_{n+1}^{0}$
.
$\unicode[STIX]{x1D70B}_{n+1}^{0}$
.
Suppose that we are not in the exceptional case. Then Conjecture 6.2.1 implies that
 $$\begin{eqnarray}\displaystyle {\mathcal{I}}(f_{n+1},f_{n}) & = & \displaystyle \frac{2^{m+\unicode[STIX]{x1D6FE}^{\prime }}}{2^{2s+2s^{\prime }}|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}^{\prime }\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\mathop{\prod }_{v\in S}{\mathcal{J}}_{v}(\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716})f_{n+1,v},\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716}^{\prime })f_{n+1,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716})f_{n,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716}^{\prime })f_{n,v}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}}(f_{n+1},f_{n}) & = & \displaystyle \frac{2^{m+\unicode[STIX]{x1D6FE}^{\prime }}}{2^{2s+2s^{\prime }}|S_{\unicode[STIX]{x1D70B}_{n+1}}||S_{\unicode[STIX]{x1D70B}_{n}}|}\unicode[STIX]{x1D6E5}_{H_{n+1}}^{S}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{n+1}\times \unicode[STIX]{x1D70B}_{n})}{L^{S}(1,\unicode[STIX]{x1D70B}_{n+1},\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70B}_{n},\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}^{\prime }\in \unicode[STIX]{x1D707}_{2}(F_{S^{\prime }})}\mathop{\prod }_{v\in S}{\mathcal{J}}_{v}(\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716})f_{n+1,v},\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716}^{\prime })f_{n+1,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716})f_{n,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716}^{\prime })f_{n,v}),\nonumber\end{eqnarray}$$
where:
-
–
 $\unicode[STIX]{x1D6FE}^{\prime }=1$
(respectively
$\unicode[STIX]{x1D6FE}^{\prime }=1$
(respectively
 $0$
) if
$0$
) if
 $\unicode[STIX]{x1D70B}_{n+1}^{0}$
is reducible (respectively irreducible);
$\unicode[STIX]{x1D70B}_{n+1}^{0}$
is reducible (respectively irreducible); -
–
 $m=1$
(respectively
$m=1$
(respectively
 $0$
) if
$0$
) if
 $\unicode[STIX]{x1D70B}_{n+1}^{0}$
is irreducible and appears with multiplicity two (respectively any irreducible constituent appears with multiplicity one) in the discrete spectrum of
$\unicode[STIX]{x1D70B}_{n+1}^{0}$
is irreducible and appears with multiplicity two (respectively any irreducible constituent appears with multiplicity one) in the discrete spectrum of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
.
$H_{n+1}^{0}(\mathbb{A}_{F})$
.
We note that
 $\unicode[STIX]{x1D6FE}=m+\unicode[STIX]{x1D6FE}^{\prime }$
. In fact, in the first (respectively second, respectively third) case in Hypothesis O, we have
$\unicode[STIX]{x1D6FE}=m+\unicode[STIX]{x1D6FE}^{\prime }$
. In fact, in the first (respectively second, respectively third) case in Hypothesis O, we have
 $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }=m=0$
(respectively
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}^{\prime }=m=0$
(respectively
 $\unicode[STIX]{x1D6FE}=1,m=1,\unicode[STIX]{x1D6FE}^{\prime }=0$
, respectively
$\unicode[STIX]{x1D6FE}=1,m=1,\unicode[STIX]{x1D6FE}^{\prime }=0$
, respectively
 $\unicode[STIX]{x1D6FE}=1,m=0,\unicode[STIX]{x1D6FE}^{\prime }=1$
). Therefore, to deduce Conjecture 6.3.1 from Conjecture 6.2.1, we only need to prove the following two identities. If
$\unicode[STIX]{x1D6FE}=1,m=0,\unicode[STIX]{x1D6FE}^{\prime }=1$
). Therefore, to deduce Conjecture 6.3.1 from Conjecture 6.2.1, we only need to prove the following two identities. If
![]() $v\in \mathfrak{S}$
, then
$v\in \mathfrak{S}$
, then
 $$\begin{eqnarray}{\textstyle \frac{1}{4}}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v},f_{n,v},f_{n,v})={\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{4}}{\mathcal{J}}_{v}(f_{n+1,v},f_{n+1,v},f_{n,v},f_{n,v})={\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
If
![]() $v\not \in \mathfrak{S}$
, then
$v\not \in \mathfrak{S}$
, then
 $$\begin{eqnarray}\frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}^{\prime }\in \unicode[STIX]{x1D707}_{2}(F_{v})}{\mathcal{J}}_{v}(\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716})f_{n+1,v},\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716}^{\prime })f_{n+1,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716})f_{n,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716}^{\prime })f_{n,v})={\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{4}\mathop{\sum }_{\unicode[STIX]{x1D716},\unicode[STIX]{x1D716}^{\prime }\in \unicode[STIX]{x1D707}_{2}(F_{v})}{\mathcal{J}}_{v}(\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716})f_{n+1,v},\unicode[STIX]{x1D70B}_{n+1}(\unicode[STIX]{x1D716}^{\prime })f_{n+1,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716})f_{n,v},\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D716}^{\prime })f_{n,v})={\mathcal{I}}_{v}(f_{n+1,v},f_{n,v}).\end{eqnarray}$$
These two identities can be proved in the same way as [Reference Ichino and IkedaII10, Lemma 3.4]. Therefore Conjecture 6.3.1 follows from Conjecture 6.2.1 if we are not in the exceptional case.
Now assume that we are in the exceptional case. Let
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}$
be an irreducible cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}$
be an irreducible cuspidal automorphic representation of
 $H_{n+1}^{0}(\mathbb{A}_{F})$
which realizes on
$H_{n+1}^{0}(\mathbb{A}_{F})$
which realizes on
![]() $V_{n+1}^{\prime 0}$
such that
$V_{n+1}^{\prime 0}$
such that
![]() $V_{n+1}^{\prime 0}$
is invariant under the outer automorphism of
$V_{n+1}^{\prime 0}$
is invariant under the outer automorphism of
![]() $H_{n+1}^{0}$
,
$H_{n+1}^{0}$
,
 $V_{n+1}^{\prime 0}\not =V_{n+1}^{0}$
and
$V_{n+1}^{\prime 0}\not =V_{n+1}^{0}$
and
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}$
is isomorphic to
$\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}$
is isomorphic to
![]() $\unicode[STIX]{x1D70B}_{n+1}^{0}$
(as abstract representations). Then the period integral
$\unicode[STIX]{x1D70B}_{n+1}^{0}$
(as abstract representations). Then the period integral
 $$\begin{eqnarray}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{n}^{0}(F)\backslash H_{n}^{0}(\mathbb{A}_{F})}f_{n+1}(h)f_{n}(h)\,dh\end{eqnarray}$$
is not identically zero on
 $V_{n+1}^{\prime 0}\times V_{n}^{0}$
. Therefore,
$V_{n+1}^{\prime 0}\times V_{n}^{0}$
. Therefore,
 $$\begin{eqnarray}\operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}\otimes \unicode[STIX]{x1D70B}_{n}^{0},\mathbb{C})\not =0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime 0}\otimes \unicode[STIX]{x1D70B}_{n}^{0},\mathbb{C})\not =0.\end{eqnarray}$$
Since
![]() $V_{n+1}^{\prime 0}$
is invariant under the outer automorphism of
$V_{n+1}^{\prime 0}$
is invariant under the outer automorphism of
![]() $H_{n+1}^{0}$
, there is an automorphic representation
$H_{n+1}^{0}$
, there is an automorphic representation
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime }$
of
$\unicode[STIX]{x1D70B}_{n+1}^{\prime }$
of
 $H_{n+1}(\mathbb{A}_{F})$
which is realized on
$H_{n+1}(\mathbb{A}_{F})$
which is realized on
![]() $V_{n+1}^{\prime }$
whose restriction to
$V_{n+1}^{\prime }$
whose restriction to
 $H_{n+1}^{0}(\mathbb{A}_{F})$
is
$H_{n+1}^{0}(\mathbb{A}_{F})$
is
![]() $V_{n+1}^{\prime 0}$
.
$V_{n+1}^{\prime 0}$
.
Let
![]() $T$
be a finite subset of places of
$T$
be a finite subset of places of
![]() $F$
and we let
$F$
and we let
![]() $\det _{T}$
be the character of
$\det _{T}$
be the character of
 $H_{n+1}(\mathbb{A}_{F})$
defined by
$H_{n+1}(\mathbb{A}_{F})$
defined by
 $$\begin{eqnarray}(g_{v})\mapsto \mathop{\prod }_{v\in T}\det g_{v}\in \{\pm 1\},\quad (g_{v})\in H_{n+1}(\mathbb{A}_{F}).\end{eqnarray}$$
$$\begin{eqnarray}(g_{v})\mapsto \mathop{\prod }_{v\in T}\det g_{v}\in \{\pm 1\},\quad (g_{v})\in H_{n+1}(\mathbb{A}_{F}).\end{eqnarray}$$
Then
![]() $\det _{T}$
is automorphic if and only if
$\det _{T}$
is automorphic if and only if
![]() $|T|$
is even.
$|T|$
is even.
Note that
![]() $n\geqslant 3$
in this case. Let
$n\geqslant 3$
in this case. Let
 $Z_{n}\simeq \unicode[STIX]{x1D707}_{2}$
be the center of
$Z_{n}\simeq \unicode[STIX]{x1D707}_{2}$
be the center of
![]() $H_{n}$
and it is identified with a subgroup of
$H_{n}$
and it is identified with a subgroup of
![]() $H_{n+1}$
via the embedding
$H_{n+1}$
via the embedding
 $H_{n}\rightarrow H_{n+1}$
. Let
$H_{n}\rightarrow H_{n+1}$
. Let
 $l=\bigotimes l_{v}\in \operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})$
and
$l=\bigotimes l_{v}\in \operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})$
and
 $\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{v})\in Z_{n}(\mathbb{A}_{F})$
. Let
$\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{v})\in Z_{n}(\mathbb{A}_{F})$
. Let
 $l^{\unicode[STIX]{x1D703}}=\bigotimes l_{v}^{\unicode[STIX]{x1D703}_{v}}\in \operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})$
be defined by
$l^{\unicode[STIX]{x1D703}}=\bigotimes l_{v}^{\unicode[STIX]{x1D703}_{v}}\in \operatorname{Hom}_{H_{n}^{0}(\mathbb{A}_{F})}(\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n},\mathbb{C})$
be defined by
 $$\begin{eqnarray}l_{v}^{\unicode[STIX]{x1D703}_{v}}(\unicode[STIX]{x1D709}_{n+1,v}\otimes \unicode[STIX]{x1D709}_{n,v})=l_{v}(\unicode[STIX]{x1D70B}_{n+1,v}(\unicode[STIX]{x1D703}_{v})\unicode[STIX]{x1D709}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v}(\unicode[STIX]{x1D703}_{v})\unicode[STIX]{x1D709}_{n,v}),\end{eqnarray}$$
$$\begin{eqnarray}l_{v}^{\unicode[STIX]{x1D703}_{v}}(\unicode[STIX]{x1D709}_{n+1,v}\otimes \unicode[STIX]{x1D709}_{n,v})=l_{v}(\unicode[STIX]{x1D70B}_{n+1,v}(\unicode[STIX]{x1D703}_{v})\unicode[STIX]{x1D709}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v}(\unicode[STIX]{x1D703}_{v})\unicode[STIX]{x1D709}_{n,v}),\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D703}_{v}^{2}=1$
and
$\unicode[STIX]{x1D703}_{v}^{2}=1$
and
 $\dim \operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=1$
, we have
$\dim \operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=1$
, we have
 $l_{v}^{\unicode[STIX]{x1D703}_{v}}=\pm l_{v}$
. It follows that there is finite set
$l_{v}^{\unicode[STIX]{x1D703}_{v}}=\pm l_{v}$
. It follows that there is finite set
![]() $T$
of places of
$T$
of places of
![]() $F$
so that
$F$
so that
 $l^{\unicode[STIX]{x1D703}}=\det _{T}(\unicode[STIX]{x1D703})\cdot l$
. Since
$l^{\unicode[STIX]{x1D703}}=\det _{T}(\unicode[STIX]{x1D703})\cdot l$
. Since
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime }$
and
$\unicode[STIX]{x1D70B}_{n+1}^{\prime }$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
are automorphic,
$\unicode[STIX]{x1D70B}_{n}$
are automorphic,
![]() $\det _{T}$
is also automorphic. It follows that
$\det _{T}$
is also automorphic. It follows that
![]() $|T|$
is even.
$|T|$
is even.
Let
 $\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }=\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \det _{T}$
. Then
$\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }=\unicode[STIX]{x1D70B}_{n+1}^{\prime }\otimes \det _{T}$
. Then
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }$
is an automorphic representation of
$\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }$
is an automorphic representation of
 $H_{n+1}(\mathbb{A}_{F})$
and is realized on
$H_{n+1}(\mathbb{A}_{F})$
and is realized on
![]() $V_{n+1}^{\prime \prime }$
. Its restriction to
$V_{n+1}^{\prime \prime }$
. Its restriction to
 $H_{n+1}^{0}(\mathbb{A}_{F})$
is
$H_{n+1}^{0}(\mathbb{A}_{F})$
is
![]() $V_{n+1}^{\prime 0}$
. Moreover, for any place
$V_{n+1}^{\prime 0}$
. Moreover, for any place
![]() $v$
of
$v$
of
![]() $F$
,
$F$
,
 $$\begin{eqnarray}\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})\not =0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})\not =0.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70B}_{n+1}$
and
$\unicode[STIX]{x1D70B}_{n+1}$
and
![]() $\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }$
are not isomorphic but their restrictions to
$\unicode[STIX]{x1D70B}_{n+1}^{\prime \prime }$
are not isomorphic but their restrictions to
 $H_{n+1}^{0}(\mathbb{A}_{F})$
are isomorphic, there is at least one place
$H_{n+1}^{0}(\mathbb{A}_{F})$
are isomorphic, there is at least one place
![]() $v$
, such that
$v$
, such that
 $\unicode[STIX]{x1D70B}_{n+1,v}\simeq \unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \det _{v}$
. We claim that
$\unicode[STIX]{x1D70B}_{n+1,v}\simeq \unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \det _{v}$
. We claim that
 $$\begin{eqnarray}\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=0.\end{eqnarray}$$
In fact,
 $\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})\not =0$
is the
$\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})\not =0$
is the
![]() $+1$
eigenspace of
$+1$
eigenspace of
 $\unicode[STIX]{x1D703}_{v}=-1\in Z_{n}(F_{v})$
on
$\unicode[STIX]{x1D703}_{v}=-1\in Z_{n}(F_{v})$
on
 $\operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{0}\otimes \unicode[STIX]{x1D70B}_{n,v}^{0},\mathbb{C})$
while
$\operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{0}\otimes \unicode[STIX]{x1D70B}_{n,v}^{0},\mathbb{C})$
while
 $\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})$
is the
$\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})$
is the
![]() $-1$
eigenspace. Since
$-1$
eigenspace. Since
 $\dim \operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{0}\otimes \unicode[STIX]{x1D70B}_{n,v}^{0},\mathbb{C})=\dim \operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=1$
, we conclude that
$\dim \operatorname{Hom}_{H_{n}^{0}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{0}\otimes \unicode[STIX]{x1D70B}_{n,v}^{0},\mathbb{C})=\dim \operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}^{\prime \prime }\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=1$
, we conclude that
 $\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=0$
.
$\operatorname{Hom}_{H_{n}(F_{v})}(\unicode[STIX]{x1D70B}_{n+1,v}\otimes \unicode[STIX]{x1D70B}_{n,v},\mathbb{C})=0$
.
It follows that the linear form
![]() ${\mathcal{I}}_{v}$
is identically zero in the exceptional case. Therefore, both sides of (6.3.3) are zero.◻
${\mathcal{I}}_{v}$
is identically zero in the exceptional case. Therefore, both sides of (6.3.3) are zero.◻
7 Compactibility with the Ichino–Ikeda conjecture:
 $\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
$\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
7.1 The theorem
The goal of this section is to study Conjecture 2.3.1 for
 $\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
. We are going to show that Conjecture 2.3.1 is compatible with the Ichino–Ikeda conjecture for
$\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
. We are going to show that Conjecture 2.3.1 is compatible with the Ichino–Ikeda conjecture for
 $\operatorname{SO}(2n+1)\times \operatorname{SO}(2n)$
in some cases. A result of this sort for unitary groups appeared in [Reference XueXue16, Proposition 1.4.1]. The local counterpart of this argument has been used to establish the local Gan–Gross–Prasad conjecture for the Fourier–Jacobi models [Reference AtobeAto15, Reference Gan and IchinoGI16].
$\operatorname{SO}(2n+1)\times \operatorname{SO}(2n)$
in some cases. A result of this sort for unitary groups appeared in [Reference XueXue16, Proposition 1.4.1]. The local counterpart of this argument has been used to establish the local Gan–Gross–Prasad conjecture for the Fourier–Jacobi models [Reference AtobeAto15, Reference Gan and IchinoGI16].
Let
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
. Let
$\unicode[STIX]{x1D706}\in F^{\times }$
. Let
![]() $(V,q_{V})$
be a
$(V,q_{V})$
be a
 $(2n+1)$
-dimensional orthogonal space and
$(2n+1)$
-dimensional orthogonal space and
![]() $V_{\unicode[STIX]{x1D706}}$
is a
$V_{\unicode[STIX]{x1D706}}$
is a
![]() $2n$
-dimensional subspace such that
$2n$
-dimensional subspace such that
![]() $V_{\unicode[STIX]{x1D706}}^{\bot }$
is a one-dimensional orthogonal space of discriminant
$V_{\unicode[STIX]{x1D706}}^{\bot }$
is a one-dimensional orthogonal space of discriminant
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
 $H=\operatorname{O}(V)$
and
$H=\operatorname{O}(V)$
and
 $H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
and
$H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
and
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}:H_{\unicode[STIX]{x1D706}}\rightarrow H$
be the natural embedding.
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}:H_{\unicode[STIX]{x1D706}}\rightarrow H$
be the natural embedding.
Let
![]() $W$
be a
$W$
be a
![]() $2n$
-dimensional symplectic space and
$2n$
-dimensional symplectic space and
 $G=\operatorname{Sp}(W)$
,
$G=\operatorname{Sp}(W)$
,
 $\widetilde{G}=\operatorname{Mp}(W)$
. Let
$\widetilde{G}=\operatorname{Mp}(W)$
. Let
![]() $\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}$
(respectively
$\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}$
(respectively
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
) be the Weil representation of
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
) be the Weil representation of
 $\widetilde{G}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
(respectively
$\widetilde{G}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
(respectively
 $G(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
) which is realized on
$G(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
) which is realized on
 ${\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
(respectively
${\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
(respectively
 ${\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
). Let
${\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
). Let
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}$
be the Weil representation of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}$
be the Weil representation of
![]() $\widetilde{G}(\mathbb{A}_{F})$
realized on
$\widetilde{G}(\mathbb{A}_{F})$
realized on
![]() ${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Then we have the theta series
${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Then we have the theta series
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h,\unicode[STIX]{x1D6F7}),\quad \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\quad \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g},\unicode[STIX]{x1D719})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h,\unicode[STIX]{x1D6F7}),\quad \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\quad \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g},\unicode[STIX]{x1D719})\end{eqnarray}$$
on
 $\widetilde{G}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
,
$\widetilde{G}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
,
 $G(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
and
$G(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
and
![]() $\widetilde{G}(\mathbb{A}_{F})$
respectively, where
$\widetilde{G}(\mathbb{A}_{F})$
respectively, where
 $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
,
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
,
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
and
 $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
.
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
.
Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered genuine automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered genuine automorphic representation of
![]() $\widetilde{G}(\mathbb{A}_{F})$
. Let
$\widetilde{G}(\mathbb{A}_{F})$
. Let
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be the theta lift of
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
be the theta lift of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $H(\mathbb{A}_{F})$
, i.e. the automorphic representation generated by the functions of the form
$H(\mathbb{A}_{F})$
, i.e. the automorphic representation generated by the functions of the form
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})(\cdot )=\int _{G(F)\backslash G(\mathbb{A}_{F})}\overline{\unicode[STIX]{x1D711}(g)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\cdot ,\unicode[STIX]{x1D6F7})\,dg,\quad \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70B},~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})(\cdot )=\int _{G(F)\backslash G(\mathbb{A}_{F})}\overline{\unicode[STIX]{x1D711}(g)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\cdot ,\unicode[STIX]{x1D6F7})\,dg,\quad \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70B},~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n}).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered automorphic representation of
 $H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
. Let
$H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
. Let
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
be the theta lift of
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
be the theta lift of
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
![]() $G(\mathbb{A}_{F})$
, i.e. the automorphic representation generated by the functions of the form
$G(\mathbb{A}_{F})$
, i.e. the automorphic representation generated by the functions of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})(\cdot )=\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}})}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\cdot ,h_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}},\quad f\in \unicode[STIX]{x1D70E},~\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})(\cdot )=\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}})}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\cdot ,h_{\unicode[STIX]{x1D706}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}},\quad f\in \unicode[STIX]{x1D70E},~\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n}).\end{eqnarray}$$
Theorem 7.1.1. Suppose that
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
and
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal (possibly zero). If Conjecture 6.3.1 holds for
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal (possibly zero). If Conjecture 6.3.1 holds for
 $(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
, then Conjecture 2.3.1(3) holds for
$(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
, then Conjecture 2.3.1(3) holds for
 $(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
with the additive character
$(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
with the additive character
![]() $\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}$
.
$\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}$
.
Remark 7.1.2. We have shown in Proposition 6.3.3 that Conjecture 6.3.1 can be deduced from the original conjecture of Ichino–Ikeda (Conjecture 6.2.1). The theorem thus says that Conjecture 2.3.1(3) and Ichino–Ikeda’s conjecture are compatible in this situation. The same remark also applies to Theorem 8.1.1 in the next section.
7.2 A seesaw diagram
The proof of Theorem 7.1.1 is very similar to [Reference XueXue16, Proposition 1.4.1]. It makes use of the following seesaw diagram.

Suppose that
 $f=\bigotimes f_{v}\in \unicode[STIX]{x1D70E}$
,
$f=\bigotimes f_{v}\in \unicode[STIX]{x1D70E}$
,
 $\unicode[STIX]{x1D711}=\bigotimes \unicode[STIX]{x1D711}_{v}\in \unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D711}=\bigotimes \unicode[STIX]{x1D711}_{v}\in \unicode[STIX]{x1D70B}$
,
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}=\bigotimes \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}=\bigotimes \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
and
 $\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
are all factorizable.
$\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
are all factorizable.
Lemma 7.2.1. We have
 $$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})=\overline{\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}f(h)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h))\,dh}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})=\overline{\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}f(h)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h))\,dh}.\end{eqnarray}$$
Proof. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{G(F)\backslash G(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(g,\unicode[STIX]{x1D719})}\,dh\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\int _{G(F)\backslash G(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h),\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\otimes \overline{\unicode[STIX]{x1D719}})\overline{f(h)}\,dg\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\overline{\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}f(h)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h))\,dh}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{G(F)\backslash G(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(g,\unicode[STIX]{x1D719})}\,dh\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\int _{G(F)\backslash G(\mathbb{A}_{F})}\unicode[STIX]{x1D711}(g)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h),\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}\otimes \overline{\unicode[STIX]{x1D719}})\overline{f(h)}\,dg\,dh\nonumber\\ \displaystyle & & \displaystyle \qquad =\overline{\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}f(h)\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D706}}(h))\,dh}.\Box \nonumber\end{eqnarray}$$
Let
![]() $v$
be a place of
$v$
be a place of
![]() $F$
. We use
$F$
. We use
![]() ${\mathcal{B}}$
to denote the inner products on various unitary representations.
${\mathcal{B}}$
to denote the inner products on various unitary representations.
Lemma 7.2.2. The integral
 $$\begin{eqnarray}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}\int _{G(F_{v})}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70E}_{v}(h)f_{v},f_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(g,h)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706},v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg\,dh\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}\int _{G(F_{v})}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70E}_{v}(h)f_{v},f_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(g,h)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706},v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg\,dh\end{eqnarray}$$
is absolutely convergent.
Proof. To simplify notation, we suppress the subscript
![]() $v$
from the notation in the proof. Put
$v$
from the notation in the proof. Put
 $$\begin{eqnarray}\unicode[STIX]{x1D6F6}(x)=\left\{\begin{array}{@{}ll@{}}1\quad & |x|\leqslant 1;\\ |x|^{-1}\quad & |x|>1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F6}(x)=\left\{\begin{array}{@{}ll@{}}1\quad & |x|\leqslant 1;\\ |x|^{-1}\quad & |x|>1.\end{array}\right.\end{eqnarray}$$
By the weak inequality (3.1.5) and the estimates (3.1.2), (3.1.4), it is enough to prove that the double integral
 $$\begin{eqnarray}\int _{A_{H_{\unicode[STIX]{x1D706}}}^{+}}\int _{A_{G}^{+}}\unicode[STIX]{x1D6FF}_{H_{\unicode[STIX]{x1D706}}}^{-1/2}(b)\unicode[STIX]{x1D6FF}_{G}^{-1/2}(a)|a_{1}\cdots a_{n}|^{(2n+1)/2}\mathop{\prod }_{i=1}^{n}\mathop{\prod }_{j=1}^{r}\unicode[STIX]{x1D6F6}(a_{i}b_{j}^{-1})\unicode[STIX]{x1D70D}(a)^{M}\unicode[STIX]{x1D70D}(b)^{M}\,da\,db\end{eqnarray}$$
$$\begin{eqnarray}\int _{A_{H_{\unicode[STIX]{x1D706}}}^{+}}\int _{A_{G}^{+}}\unicode[STIX]{x1D6FF}_{H_{\unicode[STIX]{x1D706}}}^{-1/2}(b)\unicode[STIX]{x1D6FF}_{G}^{-1/2}(a)|a_{1}\cdots a_{n}|^{(2n+1)/2}\mathop{\prod }_{i=1}^{n}\mathop{\prod }_{j=1}^{r}\unicode[STIX]{x1D6F6}(a_{i}b_{j}^{-1})\unicode[STIX]{x1D70D}(a)^{M}\unicode[STIX]{x1D70D}(b)^{M}\,da\,db\end{eqnarray}$$
is convergent, where
![]() $M$
is some positive real number,
$M$
is some positive real number,
![]() $r$
is the Witt index of
$r$
is the Witt index of
![]() $V_{\unicode[STIX]{x1D706}}$
and
$V_{\unicode[STIX]{x1D706}}$
and
 $$\begin{eqnarray}a=\operatorname{diag}[a_{1},\ldots ,a_{n},a_{n}^{-1},\ldots ,a_{1}^{-1}]\in A_{G}^{+},\quad b=\operatorname{diag}[b_{1},\ldots ,b_{r},1,\ldots ,1,b_{r}^{-1},\ldots ,b_{1}^{-1}]\in A_{H_{\unicode[STIX]{x1D706}}}^{+}.\end{eqnarray}$$
$$\begin{eqnarray}a=\operatorname{diag}[a_{1},\ldots ,a_{n},a_{n}^{-1},\ldots ,a_{1}^{-1}]\in A_{G}^{+},\quad b=\operatorname{diag}[b_{1},\ldots ,b_{r},1,\ldots ,1,b_{r}^{-1},\ldots ,b_{1}^{-1}]\in A_{H_{\unicode[STIX]{x1D706}}}^{+}.\end{eqnarray}$$
We assume that
![]() $r<n$
. The case
$r<n$
. The case
![]() $r=n$
is very similar and needs only a slight modification. We left it to the interested readers.
$r=n$
is very similar and needs only a slight modification. We left it to the interested readers.
We have
 $|b_{1}|\leqslant \cdots \leqslant |b_{r}|\leqslant 1$
. Let
$|b_{1}|\leqslant \cdots \leqslant |b_{r}|\leqslant 1$
. Let
 $\text{}\underline{j}=(j_{1},\ldots ,j_{r})$
be
$\text{}\underline{j}=(j_{1},\ldots ,j_{r})$
be
![]() $r$
nonnegative integers such that
$r$
nonnegative integers such that
 $j_{1}+\cdots +j_{r}\leqslant n$
and let
$j_{1}+\cdots +j_{r}\leqslant n$
and let
![]() $I_{\text{}\underline{j}}$
be the subset of
$I_{\text{}\underline{j}}$
be the subset of
 $A_{G}^{+}\times A_{H_{\unicode[STIX]{x1D706}}}^{+}$
consisting of elements
$A_{G}^{+}\times A_{H_{\unicode[STIX]{x1D706}}}^{+}$
consisting of elements
 $$\begin{eqnarray}a_{1}\leqslant \cdots \leqslant a_{j_{1}}\leqslant b_{1}\leqslant a_{j_{1}+1}\leqslant \cdots \leqslant a_{j_{1}+j_{2}}\leqslant b_{2}\leqslant \cdots \leqslant b_{r}\leqslant a_{j_{1}+\cdots +j_{r}+1}\leqslant \cdots \leqslant a_{n}\leqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}a_{1}\leqslant \cdots \leqslant a_{j_{1}}\leqslant b_{1}\leqslant a_{j_{1}+1}\leqslant \cdots \leqslant a_{j_{1}+j_{2}}\leqslant b_{2}\leqslant \cdots \leqslant b_{r}\leqslant a_{j_{1}+\cdots +j_{r}+1}\leqslant \cdots \leqslant a_{n}\leqslant 1.\end{eqnarray}$$
Then
 $A_{G}^{+}\times A_{H_{\unicode[STIX]{x1D706}}}^{+}=\bigcup _{\text{}\underline{j}}I_{\text{}\underline{j}}$
. Thus, it is enough to prove the convergence of (7.2.1) when the domain is replaced by
$A_{G}^{+}\times A_{H_{\unicode[STIX]{x1D706}}}^{+}=\bigcup _{\text{}\underline{j}}I_{\text{}\underline{j}}$
. Thus, it is enough to prove the convergence of (7.2.1) when the domain is replaced by
![]() $I_{\text{}\underline{j}}$
.
$I_{\text{}\underline{j}}$
.
Over the region
![]() $I_{\text{}\underline{j}}$
, the integrand of (7.2.1) equals
$I_{\text{}\underline{j}}$
, the integrand of (7.2.1) equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle |a_{1}|^{1/2}\cdots |a_{j_{1}}|^{(2j_{1}+1)/2}|b_{1}|^{-j_{1}+1}|a_{j_{1}+1}|^{(2j_{1}+1)/2}\cdots |a_{j_{1}+j_{2}}|^{(2j_{1}+2j_{2}-3)/2}|b_{2}|^{-j_{1}-j_{2}+2}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots |b_{r}|^{-j_{1}-\cdots -j_{r}+r}|a_{j_{1}+\cdots +j_{r}+1}|^{(2(j_{1}+\cdots +j_{r})+1-2r)/2}\cdots |a_{n}|^{(2n-1-2r)/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |a_{1}|^{1/2}\cdots |a_{j_{1}}|^{(2j_{1}+1)/2}|b_{1}|^{-j_{1}+1}|a_{j_{1}+1}|^{(2j_{1}+1)/2}\cdots |a_{j_{1}+j_{2}}|^{(2j_{1}+2j_{2}-3)/2}|b_{2}|^{-j_{1}-j_{2}+2}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdots |b_{r}|^{-j_{1}-\cdots -j_{r}+r}|a_{j_{1}+\cdots +j_{r}+1}|^{(2(j_{1}+\cdots +j_{r})+1-2r)/2}\cdots |a_{n}|^{(2n-1-2r)/2}.\nonumber\end{eqnarray}$$
Then lemma then follows from the following elementary fact.
Fact. Fix
![]() $D$
a positive real number. The integral
$D$
a positive real number. The integral
 $$\begin{eqnarray}\int _{|x_{1}|\leqslant \cdots \leqslant |x_{s}|\leqslant 1}|x_{1}|^{n_{1}-1}\cdots |x_{s}|^{n_{s}-1}\biggl(-\!\mathop{\sum }_{i=1}^{s}\log |x_{i}|\biggr)^{D}\,dx_{1}\cdots \,dx_{s}\end{eqnarray}$$
$$\begin{eqnarray}\int _{|x_{1}|\leqslant \cdots \leqslant |x_{s}|\leqslant 1}|x_{1}|^{n_{1}-1}\cdots |x_{s}|^{n_{s}-1}\biggl(-\!\mathop{\sum }_{i=1}^{s}\log |x_{i}|\biggr)^{D}\,dx_{1}\cdots \,dx_{s}\end{eqnarray}$$
is convergent if
 $n_{1}+\cdots +n_{t}>0$
for all
$n_{1}+\cdots +n_{t}>0$
for all
 $1\leqslant t\leqslant s$
.◻
$1\leqslant t\leqslant s$
.◻
7.3 Proof of Theorem 7.1.1
Let
![]() $S$
be a sufficiently large finite set of places of
$S$
be a sufficiently large finite set of places of
![]() $F$
, such that if
$F$
, such that if
![]() $v\not \in S$
, then the following conditions hold:
$v\not \in S$
, then the following conditions hold:
-
(i)
 $v$
is non-archimedean,
$v$
is non-archimedean,
 $2$
and
$2$
and
 $\unicode[STIX]{x1D706}$
are in
$\unicode[STIX]{x1D706}$
are in
 $\mathfrak{o}_{F,v}^{\times }$
, the conductor of
$\mathfrak{o}_{F,v}^{\times }$
, the conductor of
 $\unicode[STIX]{x1D713}_{v}$
is
$\unicode[STIX]{x1D713}_{v}$
is
 $\mathfrak{o}_{F,v}$
;
$\mathfrak{o}_{F,v}$
; -
(ii) the group
 $A$
is unramified with a hyperspecial subgroup
$A$
is unramified with a hyperspecial subgroup
 $A(\mathfrak{o}_{F,v})$
, where
$A(\mathfrak{o}_{F,v})$
, where
 $A=H,H_{\unicode[STIX]{x1D706}},G$
;
$A=H,H_{\unicode[STIX]{x1D706}},G$
; -
(iii)
 $f_{v}$
is
$f_{v}$
is
 $H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
fixed and
$H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
fixed and
 $\unicode[STIX]{x1D711}_{v}$
is
$\unicode[STIX]{x1D711}_{v}$
is
 $G(\mathfrak{o}_{F,v})$
fixed; moreover
$G(\mathfrak{o}_{F,v})$
fixed; moreover
 ${\mathcal{B}}(f_{v},f_{v})={\mathcal{B}}(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})=1$
;
${\mathcal{B}}(f_{v},f_{v})={\mathcal{B}}(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})=1$
; -
(iv)
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
is the characteristic function of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}$
is the characteristic function of
 $V_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})^{n}$
and
$V_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})^{n}$
and
 $\unicode[STIX]{x1D719}_{v}$
is the characteristic function of
$\unicode[STIX]{x1D719}_{v}$
is the characteristic function of
 $\mathfrak{o}_{F,v}^{n}$
;
$\mathfrak{o}_{F,v}^{n}$
; -
(v) the volume of the hyperspecial subgroup
 $K_{A_{v}}$
is
$K_{A_{v}}$
is
 $1$
under the chosen measure on
$1$
under the chosen measure on
 $A(F_{v})$
, where
$A(F_{v})$
, where
 $A=H,H_{\unicode[STIX]{x1D706}},G$
.
$A=H,H_{\unicode[STIX]{x1D706}},G$
.
We may assume that
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}^{-1}}(\unicode[STIX]{x1D70B})\not =0$
. If this is not the case, it follows from the computation below that both sides of Conjecture 2.3.1(3) vanish. Applying Lemma 7.2.1, Conjecture 6.3.1 and the Rallis inner product formula (for theta lifting from
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}^{-1}}(\unicode[STIX]{x1D70B})\not =0$
. If this is not the case, it follows from the computation below that both sides of Conjecture 2.3.1(3) vanish. Applying Lemma 7.2.1, Conjecture 6.3.1 and the Rallis inner product formula (for theta lifting from
![]() $\widetilde{G}$
to
$\widetilde{G}$
to
![]() $H$
), we get
$H$
), we get
 $$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}^{S}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{L^{S}({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{-1}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}\int _{G(F_{v})}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70E}_{v}(h)f_{v},f_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(g,h)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706},v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg\,dh,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}^{S}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{L^{S}({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{-1}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v\in S}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}\int _{G(F_{v})}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70E}_{v}(h)f_{v},f_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(g,h)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706},v}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg\,dh,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}$
is described as in Conjecture 6.3.1. We explain the use the Rallis inner product formula here in detail. In the remaining part of this paper, we are going to apply the same sort of argument several times. We will simply say that we apply the Rallis inner product for the rest of the paper.
$\unicode[STIX]{x1D6FE}$
is described as in Conjecture 6.3.1. We explain the use the Rallis inner product formula here in detail. In the remaining part of this paper, we are going to apply the same sort of argument several times. We will simply say that we apply the Rallis inner product for the rest of the paper.
First by Lemma 7.2.1, we have
 $$\begin{eqnarray}|{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})|^{2}={\mathcal{I}}(f,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})),\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}),\unicode[STIX]{x1D719})|^{2}={\mathcal{I}}(f,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719})),\end{eqnarray}$$
where
![]() ${\mathcal{I}}$
is defined in § 6.3. Apply Conjecture 6.3.1 (in the form (6.3.4)), we have
${\mathcal{I}}$
is defined in § 6.3. Apply Conjecture 6.3.1 (in the form (6.3.4)), we have
 $$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6E5}_{H}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\mathop{\prod }_{v}{\mathcal{I}}_{v}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6E5}_{H}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\mathop{\prod }_{v}{\mathcal{I}}_{v}^{\natural }.\end{eqnarray}$$
Note that here the local linear form
![]() ${\mathcal{I}}_{v}^{\natural }$
is defined using an inner product
${\mathcal{I}}_{v}^{\natural }$
is defined using an inner product
![]() ${\mathcal{B}}_{v}$
on
${\mathcal{B}}_{v}$
on
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})_{v}$
so that
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})_{v}$
so that
![]() $\prod _{v}{\mathcal{B}}_{v}$
equals the Petersson inner product on
$\prod _{v}{\mathcal{B}}_{v}$
equals the Petersson inner product on
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
(defined using the Tamagawa measure on
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
(defined using the Tamagawa measure on
![]() $H(\mathbb{A}_{F})$
). We view the Rallis inner product as another decomposition of the Petersson inner product on
$H(\mathbb{A}_{F})$
). We view the Rallis inner product as another decomposition of the Petersson inner product on
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
. The integral
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
. The integral
 $$\begin{eqnarray}\int _{G(F_{v})}{\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}(g,1)\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D6F7}_{v}^{\prime }){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v}^{\prime })\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{G(F_{v})}{\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}(g,1)\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D6F7}_{v}^{\prime }){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v}^{\prime })\,dg,\end{eqnarray}$$
where we have used
![]() ${\mathcal{B}}$
to denote inner products on
${\mathcal{B}}$
to denote inner products on
![]() $\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}$
and on
$\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}$
and on
![]() $\unicode[STIX]{x1D70B}_{v}$
by abuse of notation, defines a linear form on
$\unicode[STIX]{x1D70B}_{v}$
by abuse of notation, defines a linear form on
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}\otimes \unicode[STIX]{x1D70B}_{v}\otimes \overline{\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}\otimes \unicode[STIX]{x1D70B}_{v}}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}\otimes \unicode[STIX]{x1D70B}_{v}\otimes \overline{\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}_{v}}\otimes \unicode[STIX]{x1D70B}_{v}}\end{eqnarray}$$
which descends to an inner product on
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1,v}}(\unicode[STIX]{x1D70B}_{v})$
which we denote by
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1,v}}(\unicode[STIX]{x1D70B}_{v})$
which we denote by
![]() ${\mathcal{B}}_{v}^{\prime }$
. Put
${\mathcal{B}}_{v}^{\prime }$
. Put
 $$\begin{eqnarray}{\mathcal{B}}_{v}^{\prime \natural }={\mathcal{B}}_{v}^{\prime }\biggl(\frac{L_{\unicode[STIX]{x1D713}_{v,-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{v}\times \unicode[STIX]{x1D712}_{V,v})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F_{v}}(2i)}\biggr)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{v}^{\prime \natural }={\mathcal{B}}_{v}^{\prime }\biggl(\frac{L_{\unicode[STIX]{x1D713}_{v,-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{v}\times \unicode[STIX]{x1D712}_{V,v})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F_{v}}(2i)}\biggr)^{-1}.\end{eqnarray}$$
Then in this case, the Rallis inner product formula claims that
 $$\begin{eqnarray}\frac{1}{2}\frac{L_{\unicode[STIX]{x1D713}_{-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}(2i)}\mathop{\prod }_{v}{\mathcal{B}}_{v}^{\prime \natural }\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2}\frac{L_{\unicode[STIX]{x1D713}_{-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}(2i)}\mathop{\prod }_{v}{\mathcal{B}}_{v}^{\prime \natural }\end{eqnarray}$$
equals the Petersson inner product on
 $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
. Let
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})$
. Let
![]() ${\mathcal{I}}_{v}^{\prime }$
be the linear form defined in the same way as
${\mathcal{I}}_{v}^{\prime }$
be the linear form defined in the same way as
![]() ${\mathcal{I}}_{v}$
but using the inner product
${\mathcal{I}}_{v}$
but using the inner product
![]() ${\mathcal{B}}_{v}^{\prime }$
. Define
${\mathcal{B}}_{v}^{\prime }$
. Define
 $$\begin{eqnarray}{\mathcal{I}}_{v}^{\prime \natural }={\mathcal{I}}_{v}^{\prime }\cdot \biggl(\unicode[STIX]{x1D6E5}_{H_{v}}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1},v}(\unicode[STIX]{x1D70B}_{v})\times \unicode[STIX]{x1D70E}_{v})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1},v}(\unicode[STIX]{x1D70B}_{v}),\text{Ad})L(1,\unicode[STIX]{x1D70E}_{v},\text{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{v,-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{v}\times \unicode[STIX]{x1D712}_{V,v})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F_{v}}(2i)}\biggr)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{v}^{\prime \natural }={\mathcal{I}}_{v}^{\prime }\cdot \biggl(\unicode[STIX]{x1D6E5}_{H_{v}}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1},v}(\unicode[STIX]{x1D70B}_{v})\times \unicode[STIX]{x1D70E}_{v})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1},v}(\unicode[STIX]{x1D70B}_{v}),\text{Ad})L(1,\unicode[STIX]{x1D70E}_{v},\text{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{v,-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}_{v}\times \unicode[STIX]{x1D712}_{V,v})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F_{v}}(2i)}\biggr)^{-1}.\end{eqnarray}$$
It follows that we have a decomposition
 $$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}(2i)}\mathop{\prod }_{v}{\mathcal{I}}_{v}^{\prime \natural }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}=\frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\frac{L({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\frac{L_{\unicode[STIX]{x1D713}_{-1}}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}(2i)}\mathop{\prod }_{v}{\mathcal{I}}_{v}^{\prime \natural }.\end{eqnarray}$$
This is an identity of elements in
 $$\begin{eqnarray}\operatorname{Hom}_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70B}\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})\otimes \overline{\operatorname{Hom}_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70B}\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70B}\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})\otimes \overline{\operatorname{Hom}_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70B}\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})},\end{eqnarray}$$
which descends to an identity of elements in
 $$\begin{eqnarray}\operatorname{Hom}_{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})\otimes \overline{\operatorname{Hom}_{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})\otimes \overline{\operatorname{Hom}_{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}(\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\otimes \overline{\unicode[STIX]{x1D70E}},\mathbb{C})}.\end{eqnarray}$$
We now compute
 ${\mathcal{I}}(f,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719}))$
using decomposition (7.3.2). Note that
${\mathcal{I}}(f,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D711},\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}}}\otimes \unicode[STIX]{x1D719}))$
using decomposition (7.3.2). Note that
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}|_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\simeq \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}|_{\widetilde{G}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\simeq \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$
where
![]() $\widetilde{G}(\mathbb{A}_{F})$
acts on both factors on the right-hand side and
$\widetilde{G}(\mathbb{A}_{F})$
acts on both factors on the right-hand side and
 $H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
acts only on
$H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
acts only on
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
. We also note that if
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
. We also note that if
![]() $v\not \in S$
, then
$v\not \in S$
, then
 $$\begin{eqnarray}{\mathcal{I}}_{v}^{\prime \natural }(\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}}\otimes \unicode[STIX]{x1D719}_{v},\overline{\unicode[STIX]{x1D711}_{v}},f_{v})=1.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{v}^{\prime \natural }(\overline{\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v}}\otimes \unicode[STIX]{x1D719}_{v},\overline{\unicode[STIX]{x1D711}_{v}},f_{v})=1.\end{eqnarray}$$
Then the identity (7.3.1) follows.
We continue the proof of Theorem 7.1.1. The double integral on the right-hand side of (7.3.1) is absolutely convergent by Lemma 7.2.2. Thus, we can change the order of integration by integrating over
 $g\in G(F_{v})$
first. Then we apply Rallis inner product formula (for theta lifting from
$g\in G(F_{v})$
first. Then we apply Rallis inner product formula (for theta lifting from
![]() $H_{\unicode[STIX]{x1D706}}$
to
$H_{\unicode[STIX]{x1D706}}$
to
![]() $G$
), and get
$G$
), and get
 $$\begin{eqnarray}\displaystyle & & \displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D709},\unicode[STIX]{x1D719})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}^{S}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\cdot \frac{L^{S}({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\biggl(\frac{L^{S}(1,\unicode[STIX]{x1D70E})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\biggr)^{-1}\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\frac{L_{\unicode[STIX]{x1D713}_{-1}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\mathop{\prod }_{v\in S}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E}_{v})(g)\unicode[STIX]{x1D709}_{v},\unicode[STIX]{x1D709}_{v}){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D709},\unicode[STIX]{x1D719})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2^{\unicode[STIX]{x1D6FE}-1}\unicode[STIX]{x1D6E5}_{H}^{S}}{|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|}\cdot \frac{L^{S}({\textstyle \frac{1}{2}},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})\times \unicode[STIX]{x1D70E})}{L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B}),\operatorname{Ad})L^{S}(1,\unicode[STIX]{x1D70E},\operatorname{Ad})}\biggl(\frac{L^{S}(1,\unicode[STIX]{x1D70E})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\biggr)^{-1}\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\frac{L_{\unicode[STIX]{x1D713}_{-1}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D712}_{V})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)}\mathop{\prod }_{v\in S}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})}{\mathcal{B}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E}_{v})(g)\unicode[STIX]{x1D709}_{v},\unicode[STIX]{x1D709}_{v}){\mathcal{B}}(\unicode[STIX]{x1D70B}_{v}(g)\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{-\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}\,dg,\nonumber\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})=\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}\in \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
. Here we fixed a surjective map
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706}})=\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}\in \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
. Here we fixed a surjective map
 $\unicode[STIX]{x1D717}_{v}:\overline{\unicode[STIX]{x1D70E}}_{v}\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}\rightarrow \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E}_{v})$
for each
$\unicode[STIX]{x1D717}_{v}:\overline{\unicode[STIX]{x1D70E}}_{v}\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}\rightarrow \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70E}_{v})$
for each
![]() $v$
and put
$v$
and put
 $\unicode[STIX]{x1D717}_{v}(f_{v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v})=\unicode[STIX]{x1D709}_{v}$
, so that
$\unicode[STIX]{x1D717}_{v}(f_{v},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D706},v})=\unicode[STIX]{x1D709}_{v}$
, so that
 $\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}$
holds. By Lemma 5.2.3,
$\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}$
holds. By Lemma 5.2.3,
 $|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|=2^{\unicode[STIX]{x1D6FE}-1}|S_{\unicode[STIX]{x1D70B}}||S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|$
. Theorem 7.1.1 then follows from Lemma 5.2.2.
$|S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}_{-1}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|=2^{\unicode[STIX]{x1D6FE}-1}|S_{\unicode[STIX]{x1D70B}}||S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|$
. Theorem 7.1.1 then follows from Lemma 5.2.2.
7.4 Some remarks
We end this section by some remarks on Theorem 7.1.1.
Remark 7.4.1. We have proved in the theorem that we can deduce Conjecture 2.3.1(3) from Conjecture 6.3.1 under the assumptions of the theorem. Similarly, we may also deduce Conjecture 6.3.1 from Conjecture 2.3.1(3). We only need to run the above argument backwards.
Remark 7.4.2. Instead of the seesaw diagram that has been used in the proof of Theorem 7.1.1, we may consider the following seesaw diagram.

Then we can go back and forth between Conjecture 2.3.1(3) for
 $\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
and the Ichino–Ikeda conjecture for
$\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
and the Ichino–Ikeda conjecture for
 $\operatorname{SO}(2n+2)\times \operatorname{SO}(2n+1)$
.
$\operatorname{SO}(2n+2)\times \operatorname{SO}(2n+1)$
.
In particular, if
![]() $n=1$
, then the Ichino–Ikeda conjecture, hence Conjecture 6.3.1 is known. In this case, without assuming Hypotheses LLC, GLC and O, [Reference QiuQiu14, Theorem 4.5] proved Conjecture 2.3.1(3) with
$n=1$
, then the Ichino–Ikeda conjecture, hence Conjecture 6.3.1 is known. In this case, without assuming Hypotheses LLC, GLC and O, [Reference QiuQiu14, Theorem 4.5] proved Conjecture 2.3.1(3) with
 $|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|$
replaced by
$|S_{\unicode[STIX]{x1D70B}_{2}}||S_{\unicode[STIX]{x1D70B}_{0}}|$
replaced by
![]() $\frac{1}{4}$
. This result is compatible with our conjecture if we assume Hypotheses LLC, GLC and O.
$\frac{1}{4}$
. This result is compatible with our conjecture if we assume Hypotheses LLC, GLC and O.
Remark 7.4.3. Instead of the seesaw diagrams above, we may consider the following.

In this way, the Conjecture 2.3.1(3) for tempered representations on
 $\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
will be related to the Ichino–Ikeda conjecture for nontempered representations. Ichino [Reference IchinoIch05] and Ichino and Ikeda [Reference Ichino and IkedaII02] made use of the following seesaw diagrams respectively.
$\operatorname{Sp}(2n)\times \operatorname{Mp}(2n)$
will be related to the Ichino–Ikeda conjecture for nontempered representations. Ichino [Reference IchinoIch05] and Ichino and Ikeda [Reference Ichino and IkedaII02] made use of the following seesaw diagrams respectively.

At this moment, there is no precise form of the refined Gan–Gross–Prasad conjecture for nontempered representations. We hope that Conjecture 2.3.1(3) together with the seesaw diagrams as above could shed some light on the formulation of this conjecture.
8 Compactibility with the Ichino–Ikeda conjecture:
 $\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
$\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
8.1 The theorem
The goal of this section is to study Conjecture 2.3.1(3) for
 $\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
.
$\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
.
Let
![]() $W$
be a
$W$
be a
 $(2n+2)$
-dimensional symplectic space and
$(2n+2)$
-dimensional symplectic space and
 $G=\operatorname{Sp}(W)$
. We choose a basis
$G=\operatorname{Sp}(W)$
. We choose a basis
 $\{e_{1},\ldots ,e_{n+1},e_{1}^{\ast },\ldots ,e_{n+1}^{\ast }\}$
of
$\{e_{1},\ldots ,e_{n+1},e_{1}^{\ast },\ldots ,e_{n+1}^{\ast }\}$
of
![]() $W$
so that symplectic form on
$W$
so that symplectic form on
![]() $W$
is given by the matrix
$W$
is given by the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}} & 1_{n}\\ -1_{n}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}} & 1_{n}\\ -1_{n}\end{array}\right).\end{eqnarray}$$
Let
 $X=\langle e_{n+1}\rangle$
,
$X=\langle e_{n+1}\rangle$
,
 $X^{\ast }=\langle e_{n+1}^{\ast }\rangle$
and
$X^{\ast }=\langle e_{n+1}^{\ast }\rangle$
and
 $W_{0}=\langle e_{1},\ldots ,e_{n},e_{1}^{\ast },\ldots ,e_{n}^{\ast }\rangle$
. With this choice of basis, we identify
$W_{0}=\langle e_{1},\ldots ,e_{n},e_{1}^{\ast },\ldots ,e_{n}^{\ast }\rangle$
. With this choice of basis, we identify
![]() $W$
with
$W$
with
![]() $F^{2n+2}$
and
$F^{2n+2}$
and
![]() $W_{0}$
with
$W_{0}$
with
![]() $F^{2n}$
. Let
$F^{2n}$
. Let
 $L=\langle e_{1},\ldots ,e_{n}\rangle \simeq F^{n}$
and
$L=\langle e_{1},\ldots ,e_{n}\rangle \simeq F^{n}$
and
 $L^{\ast }=\langle e_{1}^{\ast },\ldots ,e_{n}^{\ast }\rangle \simeq F^{n}$
. Then
$L^{\ast }=\langle e_{1}^{\ast },\ldots ,e_{n}^{\ast }\rangle \simeq F^{n}$
. Then
 $W_{0}=L+L^{\ast }$
is a complete polarization of
$W_{0}=L+L^{\ast }$
is a complete polarization of
![]() $W_{0}$
. We represent elements in
$W_{0}$
. We represent elements in
![]() $G$
as matrices.
$G$
as matrices.
Let
 $R=R(W_{0})=NG_{0}$
be the Jacobi group associated to
$R=R(W_{0})=NG_{0}$
be the Jacobi group associated to
![]() $W_{0}$
, where
$W_{0}$
, where
![]() $N$
is the unipotent radical and
$N$
is the unipotent radical and
 $G_{0}\simeq \operatorname{Sp}(W_{0})$
. The group
$G_{0}\simeq \operatorname{Sp}(W_{0})$
. The group
![]() $R$
takes the form
$R$
takes the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}1_{n} & & & \text{}^{t}y\\ x & 1 & y & \unicode[STIX]{x1D705}\\ & & 1_{n} & \text{}^{t}x\\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}a & & b\\ & 1\\ c & & d\\ & & & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}1_{n} & & & \text{}^{t}y\\ x & 1 & y & \unicode[STIX]{x1D705}\\ & & 1_{n} & \text{}^{t}x\\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}a & & b\\ & 1\\ c & & d\\ & & & 1\end{array}\right)\end{eqnarray}$$
where
 $x,y\in F^{n}$
,
$x,y\in F^{n}$
,
![]() $\unicode[STIX]{x1D705}\in F$
and
$\unicode[STIX]{x1D705}\in F$
and
 $(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in G_{0}$
. We write the first matrix as
$(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in G_{0}$
. We write the first matrix as
 $n=n(x,y,\unicode[STIX]{x1D705})$
. Let
$n=n(x,y,\unicode[STIX]{x1D705})$
. Let
 $\widetilde{G_{0}}=\operatorname{Mp}(W_{0})$
and
$\widetilde{G_{0}}=\operatorname{Mp}(W_{0})$
and
 $\widetilde{R}=R\widetilde{G_{0}}$
.
$\widetilde{R}=R\widetilde{G_{0}}$
.
Let
![]() $(V,q_{V})$
be a
$(V,q_{V})$
be a
 $(2n+2)$
-dimensional orthogonal space and
$(2n+2)$
-dimensional orthogonal space and
 $H=\operatorname{O}(V)$
. Let
$H=\operatorname{O}(V)$
. Let
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
and
$\unicode[STIX]{x1D706}\in F^{\times }$
and
![]() $v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
$v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
 $q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. Let
$q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. Let
![]() $V_{\unicode[STIX]{x1D706}}$
be the orthogonal complement of
$V_{\unicode[STIX]{x1D706}}$
be the orthogonal complement of
![]() $\langle v_{\unicode[STIX]{x1D706}}^{0}\rangle$
and
$\langle v_{\unicode[STIX]{x1D706}}^{0}\rangle$
and
 $H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
.
$H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
.
Let
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}$
be the Weil representation of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}$
be the Weil representation of
![]() $\widetilde{R}(\mathbb{A}_{F})$
which is realized on
$\widetilde{R}(\mathbb{A}_{F})$
which is realized on
![]() ${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Let
${\mathcal{S}}(\mathbb{A}_{F}^{n})$
. Let
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
 $G(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
which is realized on
$G(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
which is realized on
 ${\mathcal{S}}(V(\mathbb{A}_{F})^{n+1})$
. Let
${\mathcal{S}}(V(\mathbb{A}_{F})^{n+1})$
. Let
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}$
be the Weil representation of
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}$
be the Weil representation of
 $G_{0}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
which is realized on
$G_{0}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
which is realized on
 ${\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
. Let
${\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
. Let
![]() $\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
$\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}$
be the Weil representation of
 $\widetilde{G_{0}}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
which is realized on
$\widetilde{G_{0}}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
which is realized on
 ${\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
. Suppose that
${\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
. Suppose that
 $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
(respectively
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\mathbb{A}_{F}^{n})$
(respectively
 $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V^{n+1}(\mathbb{A}_{F}))$
, respectively
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V^{n+1}(\mathbb{A}_{F}))$
, respectively
 $\widetilde{\unicode[STIX]{x1D6F7}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
). Then we have the theta series on
$\widetilde{\unicode[STIX]{x1D6F7}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
). Then we have the theta series on
![]() $\widetilde{R}(\mathbb{A}_{F})$
(respectively
$\widetilde{R}(\mathbb{A}_{F})$
(respectively
 $G(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
, respectively
$G(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
, respectively
 $\widetilde{G_{0}}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
)
$\widetilde{G_{0}}(\mathbb{A}_{F})\times H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
)
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(r,\unicode[STIX]{x1D719}),\quad \text{respectively }\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h,\unicode[STIX]{x1D6F7}),\quad \text{respectively }\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}},\widetilde{\unicode[STIX]{x1D6F7}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(r,\unicode[STIX]{x1D719}),\quad \text{respectively }\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(g,h,\unicode[STIX]{x1D6F7}),\quad \text{respectively }\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}},\widetilde{\unicode[STIX]{x1D6F7}}).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
![]() $H(\mathbb{A}_{F})$
. We denote by
$H(\mathbb{A}_{F})$
. We denote by
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
the global theta lifting of
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
the global theta lifting of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $G(\mathbb{A}_{F})$
, i.e. the automorphic representation of
$G(\mathbb{A}_{F})$
, i.e. the automorphic representation of
![]() $G(\mathbb{A}_{F})$
generated by the functions of the form
$G(\mathbb{A}_{F})$
generated by the functions of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7})(\cdot )=\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\cdot ,h,\unicode[STIX]{x1D6F7})\,dh,\quad f\in \unicode[STIX]{x1D70B},~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n+1}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7})(\cdot )=\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\cdot ,h,\unicode[STIX]{x1D6F7})\,dh,\quad f\in \unicode[STIX]{x1D70B},~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n+1}).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered genuine automorphic representation of
$\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered genuine automorphic representation of
 $\widetilde{G_{0}}(\mathbb{A}_{F})$
and
$\widetilde{G_{0}}(\mathbb{A}_{F})$
and
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
be the theta lifting of
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
be the theta lifting of
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
 $H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
, i.e. the automorphic representation of
$H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
, i.e. the automorphic representation of
 $H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
generated by the functions of the form
$H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
generated by the functions of the form
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\widetilde{\unicode[STIX]{x1D6F7}})(\cdot )=\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\overline{\unicode[STIX]{x1D711}(g)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\cdot ,\widetilde{\unicode[STIX]{x1D6F7}})\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\widetilde{\unicode[STIX]{x1D6F7}})(\cdot )=\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\overline{\unicode[STIX]{x1D711}(g)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(g,\cdot ,\widetilde{\unicode[STIX]{x1D6F7}})\,dg.\end{eqnarray}$$
Theorem 8.1.1. Assume that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
and
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
and
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal. If Conjecture 6.3.1 holds for
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal. If Conjecture 6.3.1 holds for
 $(\unicode[STIX]{x1D70B},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
, then Conjecture 2.3.1(3) holds for
$(\unicode[STIX]{x1D70B},\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
, then Conjecture 2.3.1(3) holds for
 $(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
$(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
). In particular, if
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
). In particular, if
![]() $n=1$
, then Conjecture 2.3.1(3) holds for
$n=1$
, then Conjecture 2.3.1(3) holds for
 $(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
$(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
).
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
).
The proof of this theorem will occupy the following four subsections. The last assertion follows from the fact that the Ichino–Ikeda conjecture is known for
 $\operatorname{SO}(4)\times \operatorname{SO}(3)$
. Thus, Conjecture 6.3.1 holds for
$\operatorname{SO}(4)\times \operatorname{SO}(3)$
. Thus, Conjecture 6.3.1 holds for
 $\operatorname{O}(4)\times \operatorname{O}(3)$
.
$\operatorname{O}(4)\times \operatorname{O}(3)$
.
Remark 8.1.2. We do not assume that
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
is not zero. In fact, if
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
is not zero. In fact, if
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
is zero, then it follows from the computation below that both sides of the identity in Conjecture 2.3.1(3) are zero.
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
is zero, then it follows from the computation below that both sides of the identity in Conjecture 2.3.1(3) are zero.
Remark 8.1.3. By assumption, there is a
![]() $v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
$v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
 $q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. If follows from the computation below that if such a
$q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. If follows from the computation below that if such a
![]() $v_{\unicode[STIX]{x1D706}}^{0}$
does not exist, then both sides of the identity in Conjecture 2.3.1(3) are zero.
$v_{\unicode[STIX]{x1D706}}^{0}$
does not exist, then both sides of the identity in Conjecture 2.3.1(3) are zero.
8.2 Measures
Without saying to the contrary, we always take the Tamagawa measure on the group of adelic points of an algebraic group. Note that
 $\operatorname{vol}A(F)\backslash A(\mathbb{A}_{F})=1$
where
$\operatorname{vol}A(F)\backslash A(\mathbb{A}_{F})=1$
where
 $A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
. Note also that
$A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
. Note also that
 $\operatorname{vol}G_{0}(F)\backslash \widetilde{G_{0}}(\mathbb{A}_{F})=1$
. Suppose that
$\operatorname{vol}G_{0}(F)\backslash \widetilde{G_{0}}(\mathbb{A}_{F})=1$
. Suppose that
 $A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
or
$A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
or
![]() $\widetilde{G_{0}}$
. We fix a decomposition
$\widetilde{G_{0}}$
. We fix a decomposition
 $dg=\prod _{v}\,dg_{v}$
where
$dg=\prod _{v}\,dg_{v}$
where
![]() $dg_{v}$
is a measure on
$dg_{v}$
is a measure on
![]() $A(F_{v})$
so that for almost all places
$A(F_{v})$
so that for almost all places
![]() $v$
,
$v$
,
 $\operatorname{vol}K_{v}=1$
where
$\operatorname{vol}K_{v}=1$
where
 $K_{v}=A(\mathfrak{o}_{F,v})$
is a hyperspecial maximal compact subgroup of
$K_{v}=A(\mathfrak{o}_{F,v})$
is a hyperspecial maximal compact subgroup of
![]() $A(F_{v})$
.
$A(F_{v})$
.
Lemma 8.2.1. Let
 $f\in {\mathcal{S}}(V(\mathbb{A}_{F}))$
. Then
$f\in {\mathcal{S}}(V(\mathbb{A}_{F}))$
. Then
 $$\begin{eqnarray}\int _{\mathbb{A}_{F}}\biggl(\int _{V(\mathbb{A}_{F})}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}=\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{A}_{F}}\biggl(\int _{V(\mathbb{A}_{F})}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}=\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\end{eqnarray}$$
Proof. Suppose that
![]() $V$
is not a four-dimensional split quadratic space. Then the lemma follows from the Siegel–Weil formula for
$V$
is not a four-dimensional split quadratic space. Then the lemma follows from the Siegel–Weil formula for
 $\operatorname{SL}_{2}\times H$
. Let
$\operatorname{SL}_{2}\times H$
. Let
 $E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})$
be the Eisenstein series on
$E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})$
be the Eisenstein series on
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
where
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
where
 $\unicode[STIX]{x1D6F7}_{f}^{(s)}\in \operatorname{Ind}_{B}^{\operatorname{SL}_{2}(\mathbb{A}_{F})}\unicode[STIX]{x1D712}_{V}|\cdot |^{s}$
is the Siegel–Weil section where
$\unicode[STIX]{x1D6F7}_{f}^{(s)}\in \operatorname{Ind}_{B}^{\operatorname{SL}_{2}(\mathbb{A}_{F})}\unicode[STIX]{x1D712}_{V}|\cdot |^{s}$
is the Siegel–Weil section where
![]() $B$
is the standard upper triangular Borel subgroup of
$B$
is the standard upper triangular Borel subgroup of
![]() $\operatorname{SL}_{2}$
. Then the left-hand side of (8.2.1) is the
$\operatorname{SL}_{2}$
. Then the left-hand side of (8.2.1) is the
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
-Fourier coefficient of
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
-Fourier coefficient of
 $E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})$
at
$E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})$
at
 $s=s_{0}=n$
. The right-hand side of (8.2.1) is the
$s=s_{0}=n$
. The right-hand side of (8.2.1) is the
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
-Fourier coefficient of the theta integral
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
-Fourier coefficient of the theta integral
 $$\begin{eqnarray}\int _{H(F)\backslash H(\mathbb{A}_{F})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)\,dh,\end{eqnarray}$$
$$\begin{eqnarray}\int _{H(F)\backslash H(\mathbb{A}_{F})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)\,dh,\end{eqnarray}$$
where
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)$
is the theta series on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)$
is the theta series on
 $\operatorname{SL}_{2}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
. The lemma then follows from the (convergent) Siegel–Weil formula
$\operatorname{SL}_{2}(\mathbb{A}_{F})\times H(\mathbb{A}_{F})$
. The lemma then follows from the (convergent) Siegel–Weil formula
 $$\begin{eqnarray}E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})|_{s=s_{0}}=\int _{H(F)\backslash H(\mathbb{A}_{F})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)\,dh.\end{eqnarray}$$
$$\begin{eqnarray}E(g,\unicode[STIX]{x1D6F7}_{f}^{(s)})|_{s=s_{0}}=\int _{H(F)\backslash H(\mathbb{A}_{F})}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(g,h,f)\,dh.\end{eqnarray}$$
Suppose that
![]() $V$
is split and
$V$
is split and
 $\dim V=4$
. Without loss of generality, we may assume that
$\dim V=4$
. Without loss of generality, we may assume that
![]() $\unicode[STIX]{x1D706}=1$
. Then
$\unicode[STIX]{x1D706}=1$
. Then
![]() $V$
is identified with the space of
$V$
is identified with the space of
![]() $2\times 2$
matrices over
$2\times 2$
matrices over
![]() $F$
and the quadratic form is given by the determinant. We may assume
$F$
and the quadratic form is given by the determinant. We may assume
 $v_{1}^{0}=1_{2}\in V$
. Under this identification,
$v_{1}^{0}=1_{2}\in V$
. Under this identification,
 $H_{1}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
is identified with
$H_{1}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
is identified with
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
and the quotient measure is identified with the Tamagawa measure on
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
and the quotient measure is identified with the Tamagawa measure on
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
. This is because the volume of
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
. This is because the volume of
 $H(F)H_{1}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
equals one.
$H(F)H_{1}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})$
equals one.
We write an element in
![]() $V$
as
$V$
as
![]() $(\begin{smallmatrix}x_{1} & x_{2}\\ x_{3} & x_{4}\end{smallmatrix}\!)$
. The left-hand side of the desired identity equals
$(\begin{smallmatrix}x_{1} & x_{2}\\ x_{3} & x_{4}\end{smallmatrix}\!)$
. The left-hand side of the desired identity equals
 $$\begin{eqnarray}\int _{\mathbb{A}_{F}}\int _{\mathbb{A}_{F}^{4}}f(x_{1},x_{2},x_{3},x_{4})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}(x_{1}x_{4}-x_{2}x_{3})-\unicode[STIX]{x1D705})\,dx_{1}\,dx_{2}\,dx_{3}\,dx_{4}\,d\unicode[STIX]{x1D705}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{A}_{F}}\int _{\mathbb{A}_{F}^{4}}f(x_{1},x_{2},x_{3},x_{4})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}(x_{1}x_{4}-x_{2}x_{3})-\unicode[STIX]{x1D705})\,dx_{1}\,dx_{2}\,dx_{3}\,dx_{4}\,d\unicode[STIX]{x1D705}.\end{eqnarray}$$
By the Fourier inversion formula, it equals
 $$\begin{eqnarray}\int _{\mathbb{A}_{F}^{2}}\int _{\mathbb{A}_{F}}f(x_{1}^{0}+ax_{3},x_{2}^{0}+ax_{4},x_{3},x_{4})\,da\,dx_{3}\,dx_{4},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{A}_{F}^{2}}\int _{\mathbb{A}_{F}}f(x_{1}^{0}+ax_{3},x_{2}^{0}+ax_{4},x_{3},x_{4})\,da\,dx_{3}\,dx_{4},\end{eqnarray}$$
where
 $(x_{1}^{0},x_{2}^{0})\in \mathbb{A}_{F}^{2}$
is a fixed vector of norm one and perpendicular to
$(x_{1}^{0},x_{2}^{0})\in \mathbb{A}_{F}^{2}$
is a fixed vector of norm one and perpendicular to
![]() $(x_{3},x_{4})$
under the usual Euclidean inner product on
$(x_{3},x_{4})$
under the usual Euclidean inner product on
![]() $\mathbb{A}_{F}^{2}$
. The choice of
$\mathbb{A}_{F}^{2}$
. The choice of
![]() $(x_{1}^{0},x_{2}^{0})$
is not unique, but the above formula does not depend on the choice. The measure
$(x_{1}^{0},x_{2}^{0})$
is not unique, but the above formula does not depend on the choice. The measure
 $da\,dx_{3}\,dx_{4}$
gives a measure on
$da\,dx_{3}\,dx_{4}$
gives a measure on
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
which is invariant under the right multiplication of
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
which is invariant under the right multiplication of
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
. It is clear that it gives
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
. It is clear that it gives
 $\operatorname{SL}_{2}(F)\backslash \operatorname{SL}_{2}(\mathbb{A}_{F})$
volume one, hence it is the Tamagawa measure on
$\operatorname{SL}_{2}(F)\backslash \operatorname{SL}_{2}(\mathbb{A}_{F})$
volume one, hence it is the Tamagawa measure on
 $\operatorname{SL}_{2}(\mathbb{A}_{F})$
. The lemma then follows.◻
$\operatorname{SL}_{2}(\mathbb{A}_{F})$
. The lemma then follows.◻
8.3 Global Fourier–Jacobi periods of theta liftings
The goal of this subsection is to compute
 $$\begin{eqnarray}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{N(F)\backslash N(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})}\unicode[STIX]{x1D711}(g)\,dh\,dn\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{N(F)\backslash N(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})}\unicode[STIX]{x1D711}(g)\,dh\,dn\,dg.\end{eqnarray}$$
The idea of the computation is putting in the definition of the theta series and unfolding the integrals. The essential step is the identity (8.3.2). In this identity, the summation over rational points in
![]() $V$
of norm
$V$
of norm
![]() $\unicode[STIX]{x1D706}$
is replaced by the summation over
$\unicode[STIX]{x1D706}$
is replaced by the summation over
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
. This is the key step which enable us to unfold the integrals. We divide the computation in several steps.
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
. This is the key step which enable us to unfold the integrals. We divide the computation in several steps.
Step 1. The goal is to unwind the definition of the theta functions.
Suppose that
 $n=n(x,y,\unicode[STIX]{x1D705})$
,
$n=n(x,y,\unicode[STIX]{x1D705})$
,
 $\unicode[STIX]{x1D705}\in F\backslash \mathbb{A}_{F}$
,
$\unicode[STIX]{x1D705}\in F\backslash \mathbb{A}_{F}$
,
 $x=(x_{1},\ldots ,x_{n})\in (F\backslash \mathbb{A}_{F})^{n}$
and
$x=(x_{1},\ldots ,x_{n})\in (F\backslash \mathbb{A}_{F})^{n}$
and
 $y=(y_{1},\ldots ,y_{n})\in (F\backslash \mathbb{A}_{F})^{n}$
. By definition, we have
$y=(y_{1},\ldots ,y_{n})\in (F\backslash \mathbb{A}_{F})^{n}$
. By definition, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})=\mathop{\sum }_{l_{1},\ldots ,l_{n}\in F}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})+\cdots +\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n})+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})=\mathop{\sum }_{l_{1},\ldots ,l_{n}\in F}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})+\cdots +\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n})+\unicode[STIX]{x1D706}\unicode[STIX]{x1D705}).\end{eqnarray}$$
Suppose that
 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
where
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
where
 $\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
and
$\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V(\mathbb{A}_{F})^{n})$
and
 $\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V(\mathbb{A}_{F}))$
. We have an
$\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V(\mathbb{A}_{F}))$
. We have an
 $H(\mathbb{A}_{F})\times G_{0}(\mathbb{A}_{F})$
equivariant isomorphism
$H(\mathbb{A}_{F})\times G_{0}(\mathbb{A}_{F})$
equivariant isomorphism
 $$\begin{eqnarray}{\mathcal{S}}(V(\mathbb{A}_{F})^{n+1})\simeq {\mathcal{S}}(V(\mathbb{A}_{F})^{n})\otimes {\mathcal{S}}(V(\mathbb{A}_{F})),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}(V(\mathbb{A}_{F})^{n+1})\simeq {\mathcal{S}}(V(\mathbb{A}_{F})^{n})\otimes {\mathcal{S}}(V(\mathbb{A}_{F})),\end{eqnarray}$$
where the left-hand side is the Weil representation
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
restricted to
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}$
restricted to
 $H(\mathbb{A}_{F})\times G_{0}(\mathbb{A}_{F})$
and this group acts on the first factor via the Weil representation
$H(\mathbb{A}_{F})\times G_{0}(\mathbb{A}_{F})$
and this group acts on the first factor via the Weil representation
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}$
and on the second factor via projection to
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}$
and on the second factor via projection to
![]() $H(\mathbb{A}_{F})$
and multiplication from the left.
$H(\mathbb{A}_{F})$
and multiplication from the left.
Then we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7}) & = & \displaystyle \mathop{\sum }_{v_{1},\ldots ,v_{n},v_{n+1}\in V}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots +2y_{n}q_{V}(v_{n},v_{n+1})+(\unicode[STIX]{x1D705}+y\text{}^{t}x)q_{V}(v_{n+1},v_{n+1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7}) & = & \displaystyle \mathop{\sum }_{v_{1},\ldots ,v_{n},v_{n+1}\in V}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots +2y_{n}q_{V}(v_{n},v_{n+1})+(\unicode[STIX]{x1D705}+y\text{}^{t}x)q_{V}(v_{n+1},v_{n+1})).\nonumber\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F\backslash \mathbb{A}_{F}}\unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D705})}\,d\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ q_{V}(v_{n+1},v_{n+1})=\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \quad \qquad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots +2y_{n}q_{V}(v_{n},v_{n+1})+y\text{}^{t}x\unicode[STIX]{x1D706}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F\backslash \mathbb{A}_{F}}\unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D705})}\,d\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ q_{V}(v_{n+1},v_{n+1})=\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \quad \qquad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots +2y_{n}q_{V}(v_{n},v_{n+1})+y\text{}^{t}x\unicode[STIX]{x1D706}).\nonumber\end{eqnarray}$$
From this we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{N(F)\backslash N(\mathbb{A}_{F})}\unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g),\unicode[STIX]{x1D719})}\,dn\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ q_{V}(v_{n+1},v_{n+1})=\unicode[STIX]{x1D706} \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{n+1})-l_{1}\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\cdots +2y_{n}(q_{V}(v_{n},v_{n+1})-l_{n}\unicode[STIX]{x1D706}))\,dx\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{N(F)\backslash N(\mathbb{A}_{F})}\unicode[STIX]{x1D6E9}(ng,h,\unicode[STIX]{x1D6F7})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g),\unicode[STIX]{x1D719})}\,dn\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ q_{V}(v_{n+1},v_{n+1})=\unicode[STIX]{x1D706} \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{n+1})-l_{1}\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,\cdots +2y_{n}(q_{V}(v_{n},v_{n+1})-l_{n}\unicode[STIX]{x1D706}))\,dx\,dy.\nonumber\end{eqnarray}$$
Recall that if
![]() $g\in G_{0}$
, then we define
$g\in G_{0}$
, then we define
 $\unicode[STIX]{x1D704}(g)=(g,1)\in \widetilde{G_{0}}$
.
$\unicode[STIX]{x1D704}(g)=(g,1)\in \widetilde{G_{0}}$
.
Step 2. This is the key step. We replace the summation over rational points in
![]() $V$
of norm
$V$
of norm
![]() $\unicode[STIX]{x1D706}$
by the summation over
$\unicode[STIX]{x1D706}$
by the summation over
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
.
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
.
Let
 $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}=\{v\in V\mid q_{V}(v,v)=\unicode[STIX]{x1D706}\}$
. Then the group
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}=\{v\in V\mid q_{V}(v,v)=\unicode[STIX]{x1D706}\}$
. Then the group
![]() $H(F)$
acts transitively on
$H(F)$
acts transitively on
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(F)$
and identifies
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(F)$
and identifies
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
with
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
with
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(F)$
by
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(F)$
by
 $h\mapsto h^{-1}v_{\unicode[STIX]{x1D706}}^{0}$
. It follows that
$h\mapsto h^{-1}v_{\unicode[STIX]{x1D706}}^{0}$
. It follows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle (8.3.1)=\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{\unicode[STIX]{x1D706}}^{0})-l_{1}\unicode[STIX]{x1D706})+\cdots +2y_{n}(q_{V}(v_{n},v_{\unicode[STIX]{x1D706}}^{0})-l_{n}\unicode[STIX]{x1D706}))\unicode[STIX]{x1D711}(g)\,dh\,dg\,dx\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (8.3.1)=\mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{\unicode[STIX]{x1D706}}^{0})-l_{1}\unicode[STIX]{x1D706})+\cdots +2y_{n}(q_{V}(v_{n},v_{\unicode[STIX]{x1D706}}^{0})-l_{n}\unicode[STIX]{x1D706}))\unicode[STIX]{x1D711}(g)\,dh\,dg\,dx\,dy.\end{eqnarray}$$
Then
 $$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{\unicode[STIX]{x1D706}}^{0})-l_{1}\unicode[STIX]{x1D706})+\cdots +2y_{n}(q_{V}(v_{n},v_{\unicode[STIX]{x1D706}}^{0})-l_{n}\unicode[STIX]{x1D706}))\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{2n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}(q_{V}(v_{1},v_{\unicode[STIX]{x1D706}}^{0})-l_{1}\unicode[STIX]{x1D706})+\cdots +2y_{n}(q_{V}(v_{n},v_{\unicode[STIX]{x1D706}}^{0})-l_{n}\unicode[STIX]{x1D706}))\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx\,dy.\nonumber\end{eqnarray}$$
Step 3. Simplifying the expression. This step is mostly formal.
Integrations over
![]() $y_{i}$
yield
$y_{i}$
yield
 $$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F \\ q_{V}(v_{i},v_{\unicode[STIX]{x1D706}}^{0})=l_{i}\unicode[STIX]{x1D706},\forall i}}\int _{(F\backslash \mathbb{A}_{F})^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{f(h_{\unicode[STIX]{x1D706}}h)}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ v_{1},\ldots ,v_{n}\in V \\ l_{1},\ldots ,l_{n}\in F \\ q_{V}(v_{i},v_{\unicode[STIX]{x1D706}}^{0})=l_{i}\unicode[STIX]{x1D706},\forall i}}\int _{(F\backslash \mathbb{A}_{F})^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{f(h_{\unicode[STIX]{x1D706}}h)}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}v_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
The variables
![]() $v_{i}$
have to be of the form
$v_{i}$
have to be of the form
 $l_{i}v_{\unicode[STIX]{x1D706}}^{0}+w_{i}$
where
$l_{i}v_{\unicode[STIX]{x1D706}}^{0}+w_{i}$
where
 $w_{i}\in V_{\unicode[STIX]{x1D706}}$
. Therefore,
$w_{i}\in V_{\unicode[STIX]{x1D706}}$
. Therefore,
 $$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ w_{1},\ldots ,w_{n}\in V_{\unicode[STIX]{x1D706}} \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{f(h_{\unicode[STIX]{x1D706}}h)}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{1}+(l_{1}+x_{1})h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{n}+(l_{n}+x_{n})h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{\substack{ w_{1},\ldots ,w_{n}\in V_{\unicode[STIX]{x1D706}} \\ l_{1},\ldots ,l_{n}\in F}}\int _{(F\backslash \mathbb{A}_{F})^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{f(h_{\unicode[STIX]{x1D706}}h)}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{1}+(l_{1}+x_{1})h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{n}+(l_{n}+x_{n})h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
Thus
 $$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{w_{1},\ldots ,w_{n}\in V_{\unicode[STIX]{x1D706}}}\int _{\mathbb{A}_{F}^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.3.1) & = & \displaystyle \mathop{\sum }_{w_{1},\ldots ,w_{n}\in V_{\unicode[STIX]{x1D706}}}\int _{\mathbb{A}_{F}^{n}}\int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{1}+x_{1}h^{-1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,h^{-1}h_{\unicode[STIX]{x1D706}}^{-1}w_{n}+x_{n}h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\unicode[STIX]{x1D711}(g)\,dh_{\unicode[STIX]{x1D706}}\,dh\,dg\,dx.\nonumber\end{eqnarray}$$
We define
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}(w_{1},\ldots ,w_{n})=\int _{\mathbb{A}_{F}^{n}}\unicode[STIX]{x1D6F7}^{0}(w_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,w_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\,dx_{1}\cdots dx_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}(w_{1},\ldots ,w_{n})=\int _{\mathbb{A}_{F}^{n}}\unicode[STIX]{x1D6F7}^{0}(w_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,w_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\,dx_{1}\cdots dx_{n}.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
.
$\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})^{n})$
.
It is straightforward to check that
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}})=(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h_{\unicode[STIX]{x1D706}})\unicode[STIX]{x1D6F7}^{0})\ast \overline{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719})},\quad \widetilde{g}\in \widetilde{G_{0}}(\mathbb{A}_{F}),h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}})=(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h_{\unicode[STIX]{x1D706}})\unicode[STIX]{x1D6F7}^{0})\ast \overline{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719})},\quad \widetilde{g}\in \widetilde{G_{0}}(\mathbb{A}_{F}),h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F}),\end{eqnarray}$$
where
![]() $g$
is the image of
$g$
is the image of
![]() $\widetilde{g}$
in
$\widetilde{g}$
in
 $G_{0}(\mathbb{A}_{F})$
. With this definition, we have
$G_{0}(\mathbb{A}_{F})$
. With this definition, we have
 $$\begin{eqnarray}(8.3.1)=\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\end{eqnarray}$$
$$\begin{eqnarray}(8.3.1)=\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\end{eqnarray}$$
We summarize the above computation in the following lemma.
Lemma 8.3.1. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{N(F)\backslash N(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(ng,h,\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})}\unicode[STIX]{x1D711}(g)\,dh\,dn\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}(F)\backslash G_{0}(\mathbb{A}_{F})}\int _{N(F)\backslash N(\mathbb{A}_{F})}\int _{H(F)\backslash H(\mathbb{A}_{F})}\overline{f(h)}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(ng,h,\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1})\overline{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng,\unicode[STIX]{x1D719})}\unicode[STIX]{x1D711}(g)\,dh\,dn\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F})}\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,dh.\nonumber\end{eqnarray}$$
8.4 Local Fourier–Jacobi periods of theta liftings
We now switch to the local situation. We fix a place
![]() $v$
of
$v$
of
![]() $F$
and suppress it from all notation. So
$F$
and suppress it from all notation. So
![]() $F$
stands for a local field of characteristic zero. We have the local version of all of the previous objects, e.g. Weil representations, the representations
$F$
stands for a local field of characteristic zero. We have the local version of all of the previous objects, e.g. Weil representations, the representations
![]() $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
![]() $\unicode[STIX]{x1D70E}$
, and the theta liftings
$\unicode[STIX]{x1D70E}$
, and the theta liftings
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
,
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
,
![]() $\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
, the orbit
$\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
, the orbit
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}$
of
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}$
of
![]() $v_{\unicode[STIX]{x1D706}}^{0}$
under the action of
$v_{\unicode[STIX]{x1D706}}^{0}$
under the action of
![]() $H(F)$
, which is identified with
$H(F)$
, which is identified with
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, etc. We denote by
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, etc. We denote by
![]() ${\mathcal{B}}$
the inner products on various unitary representations.
${\mathcal{B}}$
the inner products on various unitary representations.
The goal is to compute
 $$\begin{eqnarray}\int _{G_{0}(F)}\int _{N(F)}\int _{H(F)}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng)\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\,dh\,dn\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{0}(F)}\int _{N(F)}\int _{H(F)}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng)\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\,dh\,dn\,dg,\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
with
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
with
 $\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V^{n})$
and
$\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V^{n})$
and
 $\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V)$
.
$\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V)$
.
The computation is parallel to the global computation as given in the previous subsection. The idea is again to unwind the definition of the Weil representations. The unfolding argument in the global situation is replaced by several integration formulas in the local case. The computation, however, is messy and technical. We list the main steps.
-
(i) Showing that the integral (8.4.1) is absolutely convergent. Thus, we may change the order of integration.
-
(ii) Computation of the integral over
 $N(F)$
, namely, for
$N(F)$
, namely, for $$\begin{eqnarray}\int _{N(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}\,dn\end{eqnarray}$$
$$\begin{eqnarray}\int _{N(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}\,dn\end{eqnarray}$$
 $g\in G_{0}(F)$
and
$g\in G_{0}(F)$
and
 $h\in H(F)$
. The goal is to unwind the definition of the Weil representations and show that this integral equals (8.4.6). The key point in this step is the integral formula Lemma 8.4.3.
$h\in H(F)$
. The goal is to unwind the definition of the Weil representations and show that this integral equals (8.4.6). The key point in this step is the integral formula Lemma 8.4.3.
-
(iii) Simplifying the results from the previous step. Here we make use of the integration formula Lemma 8.4.4 which is a variant of the fact that Fourier transform preserves
 $L^{2}$
norm of Schwartz functions. The final outcome is a clean expression (8.4.7) of the integral over
$L^{2}$
norm of Schwartz functions. The final outcome is a clean expression (8.4.7) of the integral over
 $N(F)$
.
$N(F)$
. -
(iv) Computing (8.4.1) using (8.4.7). The final result is summarized in Lemma 8.4.5. This steps requires no more than making change of variables.
We organize the following computation in the above described steps.
Step 1. Absolute convergence.
Lemma 8.4.1. The integral (8.4.1) is absolutely convergent.
Proof. In view of Proposition 2.2.1 (the case
![]() $r=1$
), we only need to prove that for some
$r=1$
), we only need to prove that for some
![]() $A>0$
, we have
$A>0$
, we have
 $$\begin{eqnarray}\int _{H(F)}\unicode[STIX]{x1D6EF}(h)|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|\,dh\ll \unicode[STIX]{x1D6EF}(g)(1+\unicode[STIX]{x1D70D}(g))^{A},\quad g\in G(F).\end{eqnarray}$$
$$\begin{eqnarray}\int _{H(F)}\unicode[STIX]{x1D6EF}(h)|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|\,dh\ll \unicode[STIX]{x1D6EF}(g)(1+\unicode[STIX]{x1D70D}(g))^{A},\quad g\in G(F).\end{eqnarray}$$
Note that
 $$\begin{eqnarray}\biggl|\int _{H(F)}\unicode[STIX]{x1D6EF}(h){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\,dh\biggr|\ll \unicode[STIX]{x1D6EF}(g)(1+\unicode[STIX]{x1D70D}(g))^{A},\quad g\in G(F),\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\int _{H(F)}\unicode[STIX]{x1D6EF}(h){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\,dh\biggr|\ll \unicode[STIX]{x1D6EF}(g)(1+\unicode[STIX]{x1D70D}(g))^{A},\quad g\in G(F),\end{eqnarray}$$
since the left-hand side is a matrix coefficient of a tempered representation.
Even though in general
 $|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|$
is not a matrix coefficient of the Weil representation, we claim that it is dominated by a matrix coefficient of the Weil representation. In fact, by the Cartan decomposition, we only need to prove this when
$|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|$
is not a matrix coefficient of the Weil representation, we claim that it is dominated by a matrix coefficient of the Weil representation. In fact, by the Cartan decomposition, we only need to prove this when
 $g=a\in A_{G}^{+}$
and
$g=a\in A_{G}^{+}$
and
 $h=b\in A_{H}^{+}$
. Then
$h=b\in A_{H}^{+}$
. Then
 $$\begin{eqnarray}|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|\leqslant \int _{V(F)^{n+1}}|\unicode[STIX]{x1D6F7}(b^{-1}va)\unicode[STIX]{x1D6F7}(v)|\,dv.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})|\leqslant \int _{V(F)^{n+1}}|\unicode[STIX]{x1D6F7}(b^{-1}va)\unicode[STIX]{x1D6F7}(v)|\,dv.\end{eqnarray}$$
We may find a Schwartz function
![]() $\unicode[STIX]{x1D6F7}^{+}$
so that
$\unicode[STIX]{x1D6F7}^{+}$
so that
 $|\unicode[STIX]{x1D6F7}|\leqslant \unicode[STIX]{x1D6F7}^{+}$
(pointwise). We have proved the claim and hence the lemma.◻
$|\unicode[STIX]{x1D6F7}|\leqslant \unicode[STIX]{x1D6F7}^{+}$
(pointwise). We have proved the claim and hence the lemma.◻
Step 2. Computing the integral over
![]() $N(F)$
.
$N(F)$
.
We recall the following well-known lemma.
Lemma 8.4.2 [Reference LiuLiu16, Lemma 3.18].
There is a unique measure
![]() $\text{}\underline{d}h$
on
$\text{}\underline{d}h$
on
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, such that for any
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, such that for any
 $f\in {\mathcal{S}}(V)$
, we have
$f\in {\mathcal{S}}(V)$
, we have
 $$\begin{eqnarray}\int _{V}f(v)\,dv=\int _{F^{\times }}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h\,d\unicode[STIX]{x1D706},\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}f(v)\,dv=\int _{F^{\times }}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h\,d\unicode[STIX]{x1D706},\end{eqnarray}$$
where
![]() $dv$
is the self-dual measure on
$dv$
is the self-dual measure on
![]() $V$
and
$V$
and
![]() $d\unicode[STIX]{x1D706}$
is the self-dual measure on
$d\unicode[STIX]{x1D706}$
is the self-dual measure on
![]() $F$
.
$F$
.
For the rest of this section, when we use the notation
![]() $\text{}\underline{d}$
to denote a measure on
$\text{}\underline{d}$
to denote a measure on
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, we always mean the measure defined in this lemma.
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
, we always mean the measure defined in this lemma.
We need the following integration formula.
Lemma 8.4.3. Let
 $f\in {\mathcal{S}}(V)$
. Then
$f\in {\mathcal{S}}(V)$
. Then
 $\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
is absolutely integrable as a function of
$\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
is absolutely integrable as a function of
![]() $\unicode[STIX]{x1D705}$
. Moreover,
$\unicode[STIX]{x1D705}$
. Moreover,
 $$\begin{eqnarray}\int _{F}\biggl(\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}=\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h.\end{eqnarray}$$
$$\begin{eqnarray}\int _{F}\biggl(\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}=\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h.\end{eqnarray}$$
Proof. The integral
 $\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
equals
$\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
equals
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{f}^{n}\left(\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{f}^{n}\left(\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}_{f}^{n}$
is the Siegel–Weil section of
$\unicode[STIX]{x1D6F7}_{f}^{n}$
is the Siegel–Weil section of
 $\operatorname{Ind}^{\operatorname{SL}_{2}(F)}\unicode[STIX]{x1D712}_{V}|\cdot |^{s}$
at
$\operatorname{Ind}^{\operatorname{SL}_{2}(F)}\unicode[STIX]{x1D712}_{V}|\cdot |^{s}$
at
 $s=s_{0}=n$
. Then by the decomposition
$s=s_{0}=n$
. Then by the decomposition
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}-\unicode[STIX]{x1D705}^{-1} & 1\\ & -\unicode[STIX]{x1D705}\end{array}\right)\left(\begin{array}{@{}cc@{}}1\\ \unicode[STIX]{x1D705}^{-1} & 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}-\unicode[STIX]{x1D705}^{-1} & 1\\ & -\unicode[STIX]{x1D705}\end{array}\right)\left(\begin{array}{@{}cc@{}}1\\ \unicode[STIX]{x1D705}^{-1} & 1\end{array}\right),\end{eqnarray}$$
the order of magnitude of
 $\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
is
$\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv$
is
![]() $|\unicode[STIX]{x1D705}|^{-n-1}$
when
$|\unicode[STIX]{x1D705}|^{-n-1}$
when
![]() $|\unicode[STIX]{x1D705}|$
is large. The integrability then follows.
$|\unicode[STIX]{x1D705}|$
is large. The integrability then follows.
By Lemma 8.4.2,
 $$\begin{eqnarray}\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv=\int _{F^{\times }}\biggl(\int _{H_{\unicode[STIX]{x1D706}^{\prime }}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}^{\prime }}^{0})\,\text{}\underline{d}h\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D706}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\int _{V}f(v)\unicode[STIX]{x1D713}(\unicode[STIX]{x1D705}q_{V}(v,v))\,dv=\int _{F^{\times }}\biggl(\int _{H_{\unicode[STIX]{x1D706}^{\prime }}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}^{\prime }}^{0})\,\text{}\underline{d}h\biggr)\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}^{\prime }\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D706}^{\prime }.\end{eqnarray}$$
Since
![]() $f$
is Schwartz,
$f$
is Schwartz,
 $\int _{H_{\unicode[STIX]{x1D706}^{\prime }}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}^{\prime }}^{0})\,\text{}\underline{d}h$
is integrable as a function of
$\int _{H_{\unicode[STIX]{x1D706}^{\prime }}(F)\backslash H(F)}f(h^{-1}v_{\unicode[STIX]{x1D706}^{\prime }}^{0})\,\text{}\underline{d}h$
is integrable as a function of
![]() $\unicode[STIX]{x1D706}^{\prime }$
and is continuous on
$\unicode[STIX]{x1D706}^{\prime }$
and is continuous on
![]() $F^{\times }$
. The lemma then follows from the Fourier inversion formula.◻
$F^{\times }$
. The lemma then follows from the Fourier inversion formula.◻
Thanks to Lemma 8.4.1, we may change the order of integrations in (8.4.1). We integrate over
![]() $N(F)$
first. By definition,
$N(F)$
first. By definition,
 $$\begin{eqnarray}\displaystyle {\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7}) & = & \displaystyle \int _{V^{n+1}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots 2y_{n}q_{V}(v_{n},v_{n+1})+(\unicode[STIX]{x1D705}+y\text{}^{t}x)q_{V}(v_{n+1},v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\overline{\unicode[STIX]{x1D6F7}_{n+1}(v_{n+1})}\,dv_{1}\cdots dv_{n+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7}) & = & \displaystyle \int _{V^{n+1}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}v_{n+1}),\ldots ,h^{-1}(v_{n}+x_{n}v_{n+1}))\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v_{n+1})+\cdots 2y_{n}q_{V}(v_{n},v_{n+1})+(\unicode[STIX]{x1D705}+y\text{}^{t}x)q_{V}(v_{n+1},v_{n+1}))\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{n+1})\overline{\unicode[STIX]{x1D6F7}_{n+1}(v_{n+1})}\,dv_{1}\cdots dv_{n+1}.\nonumber\end{eqnarray}$$
Here
 $n=n(x,y,\unicode[STIX]{x1D705})$
and
$n=n(x,y,\unicode[STIX]{x1D705})$
and
 $x=(x_{1},\ldots ,x_{n})\in F^{n}$
,
$x=(x_{1},\ldots ,x_{n})\in F^{n}$
,
 $y=(y_{1},\ldots ,y_{n})\in F^{n}$
,
$y=(y_{1},\ldots ,y_{n})\in F^{n}$
,
![]() $\unicode[STIX]{x1D705}\in F$
. It follows from Lemma 8.4.3 that
$\unicode[STIX]{x1D705}\in F$
. It follows from Lemma 8.4.3 that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F}\int _{V^{n+1}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})\overline{\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})}\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,dv_{1}\cdots dv_{n}\,dv_{n+1}\,d\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}))\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+\cdots 2y_{n}q_{V}(v_{n},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+(x_{1}y_{1}+\cdots x_{n}y_{n})\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F}\int _{V^{n+1}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})\overline{\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})}\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,dv_{1}\cdots dv_{n}\,dv_{n+1}\,d\unicode[STIX]{x1D705}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}))\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+\cdots 2y_{n}q_{V}(v_{n},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+(x_{1}y_{1}+\cdots x_{n}y_{n})\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
The integral on the right-hand side is absolutely convergent. In fact, the integrand is bounded by
 $$\begin{eqnarray}C|\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})|,\end{eqnarray}$$
$$\begin{eqnarray}C|\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})|,\end{eqnarray}$$
where
![]() $C$
is a constant which is independent of
$C$
is a constant which is independent of
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
By definition,
 $$\begin{eqnarray}\displaystyle {\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}) & = & \displaystyle \int _{F^{n}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})+\cdots +\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n}))\,dl_{1}\cdots dl_{n},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}) & = & \displaystyle \int _{F^{n}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}(\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})+\cdots +\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n}))\,dl_{1}\cdots dl_{n},\nonumber\end{eqnarray}$$
where
![]() $\widetilde{g}\in \widetilde{G_{0}}$
.
$\widetilde{g}\in \widetilde{G_{0}}$
.
We claim that
 $$\begin{eqnarray}\int _{F^{2n}}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}|\ast ||{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})|\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }\,dx\,dy\end{eqnarray}$$
$$\begin{eqnarray}\int _{F^{2n}}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}|\ast ||{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})|\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }\,dx\,dy\end{eqnarray}$$
is convergent, where
![]() $\ast$
stands for the integrand of the right-hand side of (8.4.4). Indeed, this integral is bounded by the convergent integral
$\ast$
stands for the integrand of the right-hand side of (8.4.4). Indeed, this integral is bounded by the convergent integral
 $$\begin{eqnarray}\displaystyle & & \displaystyle C\times \int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}|\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})|\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }\nonumber\\ \displaystyle & & \displaystyle \qquad \times \int _{F^{2n}}|{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D706}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})|\,dx\,dy,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C\times \int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{V^{n}}|\unicode[STIX]{x1D6F7}(v_{1},\ldots ,v_{n},v_{n+1})\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})|\,dv_{1}\cdots dv_{n}\,\text{}\underline{d}h^{\prime }\nonumber\\ \displaystyle & & \displaystyle \qquad \times \int _{F^{2n}}|{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D706}}(n(x,y,0)\widetilde{g})\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})|\,dx\,dy,\nonumber\end{eqnarray}$$
where
![]() $C$
is some constant.
$C$
is some constant.
Thanks to the convergence of (8.4.5), we can change the order of the integration of
 $x,y\in F^{n}$
and
$x,y\in F^{n}$
and
 $h^{\prime }\in H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
. We end up with
$h^{\prime }\in H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
. We end up with
 $$\begin{eqnarray}\int _{N(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}\,dn\end{eqnarray}$$
$$\begin{eqnarray}\int _{N(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(n\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}\,dn\end{eqnarray}$$
equals the following integral:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{F^{2n}}\int _{V^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+\cdots +2y_{n}q_{V}(v_{n},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+(x_{1}y_{1}+\cdots x_{n}y_{n})\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})-\cdots -\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dl_{1}\cdots dl_{n}\,dv_{1}\cdots dv_{n}\,dy_{1}\cdots dy_{n}\,dx_{1}\cdots dx_{n}\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}\int _{F^{2n}}\int _{V^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}(v_{1}+x_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}(v_{n}+x_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(v_{1},\ldots ,v_{n})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+\cdots +2y_{n}q_{V}(v_{n},h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})+(x_{1}y_{1}+\cdots x_{n}y_{n})\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\unicode[STIX]{x1D713}(-\unicode[STIX]{x1D706}y_{1}(x_{1}+2l_{1})-\cdots -\unicode[STIX]{x1D706}y_{n}(x_{n}+2l_{n}))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dl_{1}\cdots dl_{n}\,dv_{1}\cdots dv_{n}\,dy_{1}\cdots dy_{n}\,dx_{1}\cdots dx_{n}\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
Step 3. Simplifying the three inner integrals of (8.4.6).
We need the following integration formula.
Lemma 8.4.4. Let
![]() $f$
be a Schwartz function on
$f$
be a Schwartz function on
![]() $V^{n}$
and
$V^{n}$
and
![]() $\unicode[STIX]{x1D719}$
a Schwartz function on
$\unicode[STIX]{x1D719}$
a Schwartz function on
![]() $F^{n}$
. Let
$F^{n}$
. Let
![]() $v^{0}\in V$
with
$v^{0}\in V$
with
 $q_{V}(v^{0},v^{0})=\unicode[STIX]{x1D706}$
and
$q_{V}(v^{0},v^{0})=\unicode[STIX]{x1D706}$
and
![]() $\{v^{0}\}^{\bot }$
be its orthogonal complement. Then
$\{v^{0}\}^{\bot }$
be its orthogonal complement. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F^{n}}\int _{V^{n}}\int _{F^{n}}\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v^{0})+\cdots 2y_{n}q_{V}(v_{n},v^{0})-2y_{1}l_{1}\unicode[STIX]{x1D706}-\cdots -2y_{n}l_{n}\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,f(v_{1},\ldots ,v_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\,dl_{1}\cdots dl_{n}\,dv_{1}\cdots dv_{n}\,dy_{1}\cdots dy_{n}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{F^{n}}\int _{V^{n}}\int _{F^{n}}\unicode[STIX]{x1D713}(2y_{1}q_{V}(v_{1},v^{0})+\cdots 2y_{n}q_{V}(v_{n},v^{0})-2y_{1}l_{1}\unicode[STIX]{x1D706}-\cdots -2y_{n}l_{n}\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,f(v_{1},\ldots ,v_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\,dl_{1}\cdots dl_{n}\,dv_{1}\cdots dv_{n}\,dy_{1}\cdots dy_{n}\nonumber\end{eqnarray}$$
equals
 $$\begin{eqnarray}|2\unicode[STIX]{x1D706}|^{-n}\int _{(\{v^{0}\}^{\bot })^{n}}\int _{F^{n}}f(l_{1}v^{0}+w_{1},\ldots l_{n}v^{0}+w_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\,dl_{1}\cdots dl_{n}\,dw_{1}\cdots dw_{n}.\end{eqnarray}$$
$$\begin{eqnarray}|2\unicode[STIX]{x1D706}|^{-n}\int _{(\{v^{0}\}^{\bot })^{n}}\int _{F^{n}}f(l_{1}v^{0}+w_{1},\ldots l_{n}v^{0}+w_{n})\overline{\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})}\,dl_{1}\cdots dl_{n}\,dw_{1}\cdots dw_{n}.\end{eqnarray}$$
Proof. Let
![]() $\widehat{f}$
and
$\widehat{f}$
and
![]() $\widehat{\unicode[STIX]{x1D719}}$
be the Fourier transform of
$\widehat{\unicode[STIX]{x1D719}}$
be the Fourier transform of
![]() $f$
and
$f$
and
![]() $\unicode[STIX]{x1D719}$
respectively (with respect to
$\unicode[STIX]{x1D719}$
respectively (with respect to
![]() $\unicode[STIX]{x1D713}$
). Then the first integral in the lemma equals
$\unicode[STIX]{x1D713}$
). Then the first integral in the lemma equals
 $$\begin{eqnarray}\int _{F^{n}}\widehat{f}(2y_{1}v^{0},\ldots ,2y_{n}v^{0})\overline{\widehat{\unicode[STIX]{x1D719}}(2y_{1}\unicode[STIX]{x1D706},\ldots ,2y_{n}\unicode[STIX]{x1D706})}\,dy_{1}\cdots dy_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{F^{n}}\widehat{f}(2y_{1}v^{0},\ldots ,2y_{n}v^{0})\overline{\widehat{\unicode[STIX]{x1D719}}(2y_{1}\unicode[STIX]{x1D706},\ldots ,2y_{n}\unicode[STIX]{x1D706})}\,dy_{1}\cdots dy_{n}.\end{eqnarray}$$
The lemma then follows from the fact that the Fourier transform preserves the inner product of Schwartz functions.◻
Applying this lemma, we see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inner three integrals of }(8.4.6)\nonumber\\ \displaystyle & & \displaystyle =|2\unicode[STIX]{x1D706}|^{-n}\int _{V_{\unicode[STIX]{x1D706}}^{n}}\int _{F^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h^{\prime -1}(w_{1}+l_{1}v_{\unicode[STIX]{x1D706}}^{0}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}h^{\prime -1}(w_{n}+l_{n}v_{\unicode[STIX]{x1D706}}^{0}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(w_{1}+l_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,w_{n}+l_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,dw_{1}\cdots dw_{n}\,dl_{1}\cdots dl_{n}\,dx_{1}\cdots dx_{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inner three integrals of }(8.4.6)\nonumber\\ \displaystyle & & \displaystyle =|2\unicode[STIX]{x1D706}|^{-n}\int _{V_{\unicode[STIX]{x1D706}}^{n}}\int _{F^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h^{\prime -1}(w_{1}+l_{1}v_{\unicode[STIX]{x1D706}}^{0}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}h^{\prime -1}(w_{n}+l_{n}v_{\unicode[STIX]{x1D706}}^{0}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(w_{1}+l_{1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,w_{n}+l_{n}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(l_{1}+x_{1},\ldots ,l_{n}+x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,dw_{1}\cdots dw_{n}\,dl_{1}\cdots dl_{n}\,dx_{1}\cdots dx_{n}.\nonumber\end{eqnarray}$$
This integral is absolutely convergent. We then make change of variables
 $x_{i}\mapsto x_{i}-l_{i}$
. Then
$x_{i}\mapsto x_{i}-l_{i}$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inner three integrals of }(8.4.6)\nonumber\\ \displaystyle & & \displaystyle =|2\unicode[STIX]{x1D706}|^{-n}\int _{V_{\unicode[STIX]{x1D706}}^{n}}\int _{F^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h^{\prime -1}(w_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}h^{\prime -1}(w_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(h^{\prime -1}(w_{1}+l_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{\prime -1}(w_{n}+l_{n}v_{\unicode[STIX]{x1D706}}^{0}))}\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\,dl_{1}\cdots \,dl_{n}\,dw_{1}\cdots dw_{n}\,dx_{1}\cdots dx_{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inner three integrals of }(8.4.6)\nonumber\\ \displaystyle & & \displaystyle =|2\unicode[STIX]{x1D706}|^{-n}\int _{V_{\unicode[STIX]{x1D706}}^{n}}\int _{F^{n}}\int _{F^{n}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g)\unicode[STIX]{x1D6F7}^{0}(h^{-1}h^{\prime -1}(w_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{-1}h^{\prime -1}(w_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0}))\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\overline{\unicode[STIX]{x1D6F7}^{0}(h^{\prime -1}(w_{1}+l_{1}v_{\unicode[STIX]{x1D706}}^{0}),\ldots ,h^{\prime -1}(w_{n}+l_{n}v_{\unicode[STIX]{x1D706}}^{0}))}\nonumber\\ \displaystyle & & \displaystyle \quad \quad \times \,\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D704}(g))\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\unicode[STIX]{x1D719}(l_{1},\ldots ,l_{n})\,dl_{1}\cdots \,dl_{n}\,dw_{1}\cdots dw_{n}\,dx_{1}\cdots dx_{n}.\nonumber\end{eqnarray}$$
We define a local analogue of (8.3.3), i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}(v_{1},\ldots ,v_{n})=\int _{F^{n}}\unicode[STIX]{x1D6F7}^{0}(v_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,v_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\,dx_{1}\cdots dx_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}(v_{1},\ldots ,v_{n})=\int _{F^{n}}\unicode[STIX]{x1D6F7}^{0}(v_{1}+x_{1}v_{\unicode[STIX]{x1D706}}^{0},\ldots ,v_{n}+x_{n}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D719}(x_{1},\ldots ,x_{n})}\,dx_{1}\cdots dx_{n}.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}^{n})$
and
$\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}}\in {\mathcal{S}}(V_{\unicode[STIX]{x1D706}}^{n})$
and
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}})=(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h_{\unicode[STIX]{x1D706}})\unicode[STIX]{x1D6F7}^{0})\ast \overline{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719})},\quad \widetilde{g}\in \widetilde{G_{0}}(F),h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}(F),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(\widetilde{g},h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6F7}^{0}\ast \overline{\unicode[STIX]{x1D719}})=(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h_{\unicode[STIX]{x1D706}})\unicode[STIX]{x1D6F7}^{0})\ast \overline{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\widetilde{g})\unicode[STIX]{x1D719})},\quad \widetilde{g}\in \widetilde{G_{0}}(F),h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}(F),\end{eqnarray}$$
where
![]() $g$
is the image of
$g$
is the image of
![]() $\widetilde{g}$
in
$\widetilde{g}$
in
![]() $G_{0}(F)$
.
$G_{0}(F)$
.
We conclude that
 $$\begin{eqnarray}\displaystyle (8.4.6) & = & \displaystyle |2\unicode[STIX]{x1D706}|^{-n}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h^{\prime }h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.4.6) & = & \displaystyle |2\unicode[STIX]{x1D706}|^{-n}\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h^{\prime }h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,\text{}\underline{d}h^{\prime }.\end{eqnarray}$$
Step 4. Computing (8.4.1) using (8.4.7).
Recall that we have fixed a measure on
![]() $H(F)$
and
$H(F)$
and
![]() $H_{\unicode[STIX]{x1D706}}(F)$
, respectively. Let
$H_{\unicode[STIX]{x1D706}}(F)$
, respectively. Let
![]() $dh^{\prime }$
be the quotient measure on
$dh^{\prime }$
be the quotient measure on
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
and
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
and
![]() $c$
a constant so that
$c$
a constant so that
 $c\cdot dh^{\prime }=\text{}\underline{d}h^{\prime }$
where
$c\cdot dh^{\prime }=\text{}\underline{d}h^{\prime }$
where
![]() $\text{}\underline{d}h^{\prime }$
is the measure on
$\text{}\underline{d}h^{\prime }$
is the measure on
 $H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
defined in Lemma 8.4.2. Then we get
$H_{\unicode[STIX]{x1D706}}(F)\backslash H(F)$
defined in Lemma 8.4.2. Then we get
 $$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{H_{\unicode[STIX]{x1D706}}\backslash H}\int _{H}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h^{\prime }h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{H_{\unicode[STIX]{x1D706}}\backslash H}\int _{H}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h^{\prime }h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
We make a change of variable
 $h\mapsto h^{\prime -1}h$
and get
$h\mapsto h^{\prime -1}h$
and get
 $$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\iint _{H_{\unicode[STIX]{x1D706}}\backslash H\times H}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\iint _{H_{\unicode[STIX]{x1D706}}\backslash H\times H}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(g,h)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(g)\unicode[STIX]{x1D719}},\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}})\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
The group
![]() $H_{\unicode[STIX]{x1D706}}$
embeds in
$H_{\unicode[STIX]{x1D706}}$
embeds in
![]() $H\times H$
diagonally. This integral is absolutely convergent.
$H\times H$
diagonally. This integral is absolutely convergent.
We further split the integration over
![]() $h$
as
$h$
as
![]() $h_{\unicode[STIX]{x1D706}}h$
where
$h_{\unicode[STIX]{x1D706}}h$
where
 $h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}$
and
$h_{\unicode[STIX]{x1D706}}\in H_{\unicode[STIX]{x1D706}}$
and
 $h\in H_{\unicode[STIX]{x1D706}}\backslash H$
. Then
$h\in H_{\unicode[STIX]{x1D706}}\backslash H$
. Then
 $$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{(H_{\unicode[STIX]{x1D706}}\backslash H)^{2}}\int _{H_{\unicode[STIX]{x1D706}}}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h_{\unicode[STIX]{x1D706}}h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}),(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh_{\unicode[STIX]{x1D706}}\,dh^{\prime }\,dh.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (8.4.1) & = & \displaystyle c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{(H_{\unicode[STIX]{x1D706}}\backslash H)^{2}}\int _{H_{\unicode[STIX]{x1D706}}}\int _{G_{0}}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h_{\unicode[STIX]{x1D706}}h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}),(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}))\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dg\,dh_{\unicode[STIX]{x1D706}}\,dh^{\prime }\,dh.\nonumber\end{eqnarray}$$
We summarize the above computation into the following lemma.
Lemma 8.4.5. Suppose
 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
where
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{0}\otimes \unicode[STIX]{x1D6F7}_{n+1}$
where
 $\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V^{n})$
and
$\unicode[STIX]{x1D6F7}^{0}\in {\mathcal{S}}(V^{n})$
and
 $\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V)$
. Then
$\unicode[STIX]{x1D6F7}_{n+1}\in {\mathcal{S}}(V)$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}(F)}\int _{N(F)}\int _{H(F)}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng)\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\,dh\,dn\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{(H_{\unicode[STIX]{x1D706}}\backslash H)^{2}}\int _{H_{\unicode[STIX]{x1D706}}}\biggl(\int _{G_{0}}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}),(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}))\,dg\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h_{\unicode[STIX]{x1D706}}h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dh_{\unicode[STIX]{x1D706}}\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{G_{0}(F)}\int _{N(F)}\int _{H(F)}\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h)f,f)}{\mathcal{B}}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}(ng,h)\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6F7})\overline{{\mathcal{B}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(ng)\unicode[STIX]{x1D719},\unicode[STIX]{x1D719})}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711})\,dh\,dn\,dg\nonumber\\ \displaystyle & & \displaystyle \qquad =c\cdot |2\unicode[STIX]{x1D706}|^{-n}\int _{(H_{\unicode[STIX]{x1D706}}\backslash H)^{2}}\int _{H_{\unicode[STIX]{x1D706}}}\biggl(\int _{G_{0}}{\mathcal{B}}(\unicode[STIX]{x1D70E}(g)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}){\mathcal{B}}(\widetilde{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D713}}(g,h_{\unicode[STIX]{x1D706}})(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}),(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}\ast \overline{\unicode[STIX]{x1D719}}))\,dg\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\overline{{\mathcal{B}}(\unicode[STIX]{x1D70B}(h_{\unicode[STIX]{x1D706}}h)f,\unicode[STIX]{x1D70B}(h^{\prime })f)}\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\,dh_{\unicode[STIX]{x1D706}}\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
8.5 Proof of Theorem 8.1.1
By Lemma 8.3.1, we have
 $$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}),\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \iint _{(H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F}))^{2}}\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}^{\prime }h^{\prime })}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}}^{\prime })\,dh_{\unicode[STIX]{x1D706}}^{\prime }\biggr)}\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}),\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \iint _{(H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})\backslash H(\mathbb{A}_{F}))^{2}}\unicode[STIX]{x1D6F7}_{n+1}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\overline{\unicode[STIX]{x1D6F7}_{n+1}(h^{\prime -1}v_{\unicode[STIX]{x1D706}}^{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}h)}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h)\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}})\,dh_{\unicode[STIX]{x1D706}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{\biggl(\int _{H_{\unicode[STIX]{x1D706}}(F)\backslash H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})}\overline{f(h_{\unicode[STIX]{x1D706}}^{\prime }h^{\prime })}\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\overline{\unicode[STIX]{x1D711}},(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}}^{0}(h^{\prime })\unicode[STIX]{x1D6F7}^{0})\ast \overline{\unicode[STIX]{x1D719}})(h_{\unicode[STIX]{x1D706}}^{\prime })\,dh_{\unicode[STIX]{x1D706}}^{\prime }\biggr)}\,dh\,dh^{\prime }.\nonumber\end{eqnarray}$$
We fix a sufficiently large finite set of places
![]() $S$
of
$S$
of
![]() $F$
so that if
$F$
so that if
![]() $v\not \in S$
, then the following conditions hold:
$v\not \in S$
, then the following conditions hold:
-
(i)
 $v$
is non-archimedean,
$v$
is non-archimedean,
 $2$
and
$2$
and
 $\unicode[STIX]{x1D706}$
are in
$\unicode[STIX]{x1D706}$
are in
 $\mathfrak{o}_{F,v}^{\times }$
, the conductor of
$\mathfrak{o}_{F,v}^{\times }$
, the conductor of
 $\unicode[STIX]{x1D713}$
is
$\unicode[STIX]{x1D713}$
is
 $\mathfrak{o}_{F,v}$
;
$\mathfrak{o}_{F,v}$
; -
(ii) the group
 $A$
is unramified with a hyperspecial maximal compact subgroup
$A$
is unramified with a hyperspecial maximal compact subgroup
 $K_{A_{v}}=A(\mathfrak{o}_{F,v})$
where
$K_{A_{v}}=A(\mathfrak{o}_{F,v})$
where
 $A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
;
$A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
; -
(iii)
 $f_{v}$
and
$f_{v}$
and
 $\unicode[STIX]{x1D711}_{v}$
are
$\unicode[STIX]{x1D711}_{v}$
are
 $K_{H_{v}}$
and
$K_{H_{v}}$
and
 $K_{G_{0,v}}$
fixed respectively; moreover, they are normalized so that
$K_{G_{0,v}}$
fixed respectively; moreover, they are normalized so that
 ${\mathcal{B}}(f_{v},f_{v})={\mathcal{B}}(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})=1$
; in particular,
${\mathcal{B}}(f_{v},f_{v})={\mathcal{B}}(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})=1$
; in particular,
 $\unicode[STIX]{x1D70B}_{v}$
and
$\unicode[STIX]{x1D70B}_{v}$
and
 $\unicode[STIX]{x1D70E}_{v}$
are both unramified;
$\unicode[STIX]{x1D70E}_{v}$
are both unramified; -
(iv)
 $\unicode[STIX]{x1D6F7}_{v}$
is the characteristic function of
$\unicode[STIX]{x1D6F7}_{v}$
is the characteristic function of
 $V(\mathfrak{o}_{F,v})^{n+1}$
,
$V(\mathfrak{o}_{F,v})^{n+1}$
,
 $\unicode[STIX]{x1D719}_{v}$
is the characteristic function of
$\unicode[STIX]{x1D719}_{v}$
is the characteristic function of
 $\mathfrak{o}_{F,v}^{n}$
;
$\mathfrak{o}_{F,v}^{n}$
; -
(v) the volume of the hyperspecial maximal compact subgroup
 $K_{A_{v}}$
is
$K_{A_{v}}$
is
 $1$
under the chosen measure on
$1$
under the chosen measure on
 $A(F_{v})$
, where
$A(F_{v})$
, where
 $A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
.
$A=G,G_{0},H,H_{\unicode[STIX]{x1D706}}$
.
Lemma 8.5.1. If
![]() $v\not \in S$
, then
$v\not \in S$
, then
 $c_{v}=L_{v}(n+1,\unicode[STIX]{x1D712}_{V_{v}})^{-1}$
. Recall that
$c_{v}=L_{v}(n+1,\unicode[STIX]{x1D712}_{V_{v}})^{-1}$
. Recall that
 $\text{}\underline{d}h_{v}=c_{v}\cdot dh_{\unicode[STIX]{x1D706},v}\backslash \,dh_{v}$
where
$\text{}\underline{d}h_{v}=c_{v}\cdot dh_{\unicode[STIX]{x1D706},v}\backslash \,dh_{v}$
where
![]() $\text{}\underline{d}h_{v}$
is the measure defined in Lemma 8.4.2.
$\text{}\underline{d}h_{v}$
is the measure defined in Lemma 8.4.2.
Proof. We denote temporarily by
![]() $f_{v}$
the characteristic function of
$f_{v}$
the characteristic function of
![]() $V(\mathfrak{o}_{F,v})$
. Recall from the proof of Lemma 8.4.3 that
$V(\mathfrak{o}_{F,v})$
. Recall from the proof of Lemma 8.4.3 that
 $$\begin{eqnarray}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})\backslash H(F_{v})}f_{v}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h=\int _{F_{v}}\unicode[STIX]{x1D6F7}_{f_{v}}^{n}\left(\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)\right)\unicode[STIX]{x1D713}_{v}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705},\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{\unicode[STIX]{x1D706}}(F_{v})\backslash H(F_{v})}f_{v}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})\,\text{}\underline{d}h=\int _{F_{v}}\unicode[STIX]{x1D6F7}_{f_{v}}^{n}\left(\left(\begin{array}{@{}cc@{}} & 1\\ -1\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & \unicode[STIX]{x1D705}\\ & 1\end{array}\right)\right)\unicode[STIX]{x1D713}_{v}(-\unicode[STIX]{x1D706}\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}_{f_{v}}^{n}$
is the Siegel–Weil section of
$\unicode[STIX]{x1D6F7}_{f_{v}}^{n}$
is the Siegel–Weil section of
 $\operatorname{Ind}^{\operatorname{SL}_{2}(F_{v})}\unicode[STIX]{x1D712}_{V_{v}}|\cdot |^{s}$
at
$\operatorname{Ind}^{\operatorname{SL}_{2}(F_{v})}\unicode[STIX]{x1D712}_{V_{v}}|\cdot |^{s}$
at
 $s=s_{0}=n$
. It is well-known that the right-hand side equals
$s=s_{0}=n$
. It is well-known that the right-hand side equals
 $L_{v}(n+1,\unicode[STIX]{x1D712}_{V_{v}})^{-1}$
.
$L_{v}(n+1,\unicode[STIX]{x1D712}_{V_{v}})^{-1}$
.
We note that since
 $\unicode[STIX]{x1D706}\in \mathfrak{o}_{F,v}^{\times }$
, the orbit
$\unicode[STIX]{x1D706}\in \mathfrak{o}_{F,v}^{\times }$
, the orbit
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}$
of
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}$
of
![]() $v_{\unicode[STIX]{x1D706}}^{0}$
is defined over
$v_{\unicode[STIX]{x1D706}}^{0}$
is defined over
![]() $\mathfrak{o}_{F,v}$
. The group
$\mathfrak{o}_{F,v}$
. The group
 $H(\mathfrak{o}_{F,v})$
acts transitively on
$H(\mathfrak{o}_{F,v})$
acts transitively on
 $V_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
. Therefore,
$V_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
. Therefore,
 $H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})\backslash H(\mathfrak{o}_{F,v})\rightarrow \unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
is a bijection. Thus,
$H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})\backslash H(\mathfrak{o}_{F,v})\rightarrow \unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})$
is a bijection. Thus,
 $f_{v}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})=\operatorname{1}_{H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})\backslash H(\mathfrak{o}_{F,v})}(h)$
. Therefore, under the quotient measure
$f_{v}(h^{-1}v_{\unicode[STIX]{x1D706}}^{0})=\operatorname{1}_{H_{\unicode[STIX]{x1D706}}(\mathfrak{o}_{F,v})\backslash H(\mathfrak{o}_{F,v})}(h)$
. Therefore, under the quotient measure
 $dh_{\unicode[STIX]{x1D706},v}\backslash \,dh_{v}$
, the left-hand side equals one. The lemma then follows.◻
$dh_{\unicode[STIX]{x1D706},v}\backslash \,dh_{v}$
, the left-hand side equals one. The lemma then follows.◻
Lemma 8.5.2. We have
 $$\begin{eqnarray}\mathop{\prod }_{v\in S}c_{v}=L^{S}(n+1,\unicode[STIX]{x1D712}_{V}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S}c_{v}=L^{S}(n+1,\unicode[STIX]{x1D712}_{V}).\end{eqnarray}$$
Proof. It follows from Lemma 8.2.1 that
 $\prod _{v}c_{v}=1$
. Then
$\prod _{v}c_{v}=1$
. Then
 $$\begin{eqnarray}\mathop{\prod }_{v\in S}c_{v}=\mathop{\prod }_{v\not \in S}c_{v}^{-1}=L^{S}(n+1,\unicode[STIX]{x1D712}_{V}).\Box\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\in S}c_{v}=\mathop{\prod }_{v\not \in S}c_{v}^{-1}=L^{S}(n+1,\unicode[STIX]{x1D712}_{V}).\Box\end{eqnarray}$$
Conjecture 6.3.1, the Rallis’ inner product formula (for theta lifting from
![]() $\widetilde{G_{0}}$
to
$\widetilde{G_{0}}$
to
![]() $H_{\unicode[STIX]{x1D706}}$
) and Lemma 8.4.5 lead to
$H_{\unicode[STIX]{x1D706}}$
) and Lemma 8.4.5 lead to
 $$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}),\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{2^{\unicode[STIX]{x1D6FE}-1}}{|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))}{L^{S}(1,\unicode[STIX]{x1D70B},\operatorname{Ad})L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}),\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{H(V)}^{S}\cdot \frac{L_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D712}_{V_{\unicode[STIX]{x1D706}}})}{\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2j)}\mathop{\prod }_{v\in S}c_{v}^{-1}\int _{G_{0}(F_{v})}\int _{N(F_{v})}\int _{H(F_{v})}\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}_{v}(\overline{\unicode[STIX]{x1D70B}(h_{v})f_{v},f_{v}}){\mathcal{B}}_{v}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(h_{v},n_{v}g_{v})\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D6F7}_{v})\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{{\mathcal{B}}_{v}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706},v}}(n_{v}g_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D70E}_{v}(g_{v})\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\,dh_{v}\,dn_{v}\,dg_{v},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(f,\unicode[STIX]{x1D6F7}),\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2} & = & \displaystyle \frac{2^{\unicode[STIX]{x1D6FE}-1}}{|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))}{L^{S}(1,\unicode[STIX]{x1D70B},\operatorname{Ad})L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}),\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E5}_{H(V)}^{S}\cdot \frac{L_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D712}_{V_{\unicode[STIX]{x1D706}}})}{\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2j)}\mathop{\prod }_{v\in S}c_{v}^{-1}\int _{G_{0}(F_{v})}\int _{N(F_{v})}\int _{H(F_{v})}\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{B}}_{v}(\overline{\unicode[STIX]{x1D70B}(h_{v})f_{v},f_{v}}){\mathcal{B}}_{v}(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{v}}(h_{v},n_{v}g_{v})\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D6F7}_{v})\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{{\mathcal{B}}_{v}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706},v}}(n_{v}g_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D70E}_{v}(g_{v})\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\,dh_{v}\,dn_{v}\,dg_{v},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}$
is described as in Conjecture 6.3.1.
$\unicode[STIX]{x1D6FE}$
is described as in Conjecture 6.3.1.
We then apply the Rallis inner product formula for the theta lifting from
![]() $H$
to
$H$
to
![]() $G$
. We conclude that
$G$
. We conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2^{\unicode[STIX]{x1D6FE}-1}}{|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))}{L^{S}(1,\unicode[STIX]{x1D70B},\operatorname{Ad})L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}),\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E5}_{H}^{S}\cdot \frac{L_{\unicode[STIX]{x1D713}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D712}_{V_{\unicode[STIX]{x1D706}}})}{\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2j)}\biggl(\frac{L^{S}(1,\unicode[STIX]{x1D70B})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)L^{S}(n+1,\unicode[STIX]{x1D712}_{V})}\biggr)^{-1}L^{S}(n+1,\unicode[STIX]{x1D712}_{V})^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{v\in S}\int _{G_{0}(F_{v})}\int _{N(F_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})(n_{v}g_{v})\unicode[STIX]{x1D709}_{v},\unicode[STIX]{x1D709}_{v})\overline{{\mathcal{B}}_{v}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706},v}}(n_{v}g_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D70E}_{v}(g_{v})\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\,dn_{v}\,dg_{v},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |{\mathcal{F}}{\mathcal{J}}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2^{\unicode[STIX]{x1D6FE}-1}}{|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|}\frac{L^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70B}\times \widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))}{L^{S}(1,\unicode[STIX]{x1D70B},\operatorname{Ad})L^{S}(1,\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}),\operatorname{Ad})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D6E5}_{H}^{S}\cdot \frac{L_{\unicode[STIX]{x1D713}}^{S}({\textstyle \frac{1}{2}},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D712}_{V_{\unicode[STIX]{x1D706}}})}{\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2j)}\biggl(\frac{L^{S}(1,\unicode[STIX]{x1D70B})}{\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D701}_{F}^{S}(2i)L^{S}(n+1,\unicode[STIX]{x1D712}_{V})}\biggr)^{-1}L^{S}(n+1,\unicode[STIX]{x1D712}_{V})^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{v\in S}\int _{G_{0}(F_{v})}\int _{N(F_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}_{v}}(\unicode[STIX]{x1D70B}_{v})(n_{v}g_{v})\unicode[STIX]{x1D709}_{v},\unicode[STIX]{x1D709}_{v})\overline{{\mathcal{B}}_{v}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706},v}}(n_{v}g_{v})\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D719}_{v})}{\mathcal{B}}_{v}(\unicode[STIX]{x1D70E}_{v}(g_{v})\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D711}_{v})\,dn_{v}\,dg_{v},\nonumber\end{eqnarray}$$
where
 $\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}\in \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
. Note that
$\unicode[STIX]{x1D709}=\bigotimes \unicode[STIX]{x1D709}_{v}\in \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
. Note that
 $|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|=2^{\unicode[STIX]{x1D6FE}-1}|S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|$
by Lemma 5.2.3. Conjecture 2.3.1(3) then follows from Lemma 5.2.2.
$|S_{\unicode[STIX]{x1D70B}}||S_{\widetilde{\unicode[STIX]{x1D6E9}}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})}|=2^{\unicode[STIX]{x1D6FE}-1}|S_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})}||S_{\unicode[STIX]{x1D70E}}|$
by Lemma 5.2.3. Conjecture 2.3.1(3) then follows from Lemma 5.2.2.
8.6 A variant
So far we considered the case
 $\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
. The case
$\operatorname{Sp}(2n+2)\times \operatorname{Mp}(2n)$
. The case
 $\operatorname{Mp}(2n+2)\times \operatorname{Sp}(2n)$
is similar. We only mention the following theorem.
$\operatorname{Mp}(2n+2)\times \operatorname{Sp}(2n)$
is similar. We only mention the following theorem.
Let
![]() $(V,q_{V})$
be a
$(V,q_{V})$
be a
 $(2n+3)$
-dimensional orthogonal space and
$(2n+3)$
-dimensional orthogonal space and
 $H=\operatorname{O}(V)$
. Suppose that
$H=\operatorname{O}(V)$
. Suppose that
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
and there is an element
$\unicode[STIX]{x1D706}\in F^{\times }$
and there is an element
![]() $v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
$v_{\unicode[STIX]{x1D706}}^{0}\in V$
such that
 $q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. Let
$q_{V}(v_{\unicode[STIX]{x1D706}}^{0},v_{\unicode[STIX]{x1D706}}^{0})=\unicode[STIX]{x1D706}$
. Let
![]() $V_{\unicode[STIX]{x1D706}}$
be the orthogonal complement of
$V_{\unicode[STIX]{x1D706}}$
be the orthogonal complement of
![]() $v_{\unicode[STIX]{x1D706}}^{0}$
and
$v_{\unicode[STIX]{x1D706}}^{0}$
and
 $H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
. Let
$H_{\unicode[STIX]{x1D706}}=\operatorname{O}(V_{\unicode[STIX]{x1D706}})$
. Let
![]() $\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70B}$
be an irreducible cuspidal tempered automorphic representation of
![]() $H(\mathbb{A}_{F})$
and
$H(\mathbb{A}_{F})$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
its theta lift to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
its theta lift to
 $\operatorname{Mp}(2n+2)(\mathbb{A}_{F})$
(with additive character
$\operatorname{Mp}(2n+2)(\mathbb{A}_{F})$
(with additive character
![]() $\unicode[STIX]{x1D713}$
). Let
$\unicode[STIX]{x1D713}$
). Let
![]() $\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered automorphic representation of
$\unicode[STIX]{x1D70E}$
be an irreducible cuspidal tempered automorphic representation of
 $\operatorname{Sp}(2n)(\mathbb{A}_{F})$
and
$\operatorname{Sp}(2n)(\mathbb{A}_{F})$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
its theta lift to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
its theta lift to
 $H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
.
$H_{\unicode[STIX]{x1D706}}(\mathbb{A}_{F})$
.
Theorem 8.6.1. Suppose that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
and
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B})$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal. If Conjecture 6.3.1 holds for
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$
are both cuspidal. If Conjecture 6.3.1 holds for
 $(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
, then Conjecture 2.3.1(3) holds for
$(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E}))$
, then Conjecture 2.3.1(3) holds for
 $(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
$(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70B}),\unicode[STIX]{x1D70E})$
(with the additive character
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
).
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}}$
).
The proof of Theorem 8.6.1 is analogues to Theorem 8.1.1 and we leave the details to the interested reader.
Acknowledgements
I thank Atsushi Ichino for pointing out to me the inaccuracy in [Reference Ichino and IkedaII10] and some inaccuracies in an early draft of this paper. I thank Raphael Beuzart-Plessis, Wee Teck Gan, Yifeng Liu, Bin Xu, Wei Zhang and Shou-Wu Zhang for many helpful discussions. I am also grateful for the anonymous referee for the careful reading of the manuscript and the numerous suggestions which greatly improve the exposition of this paper.