Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-01T19:48:35.975Z Has data issue: false hasContentIssue false
  • English
  • Français

On function spaces equipped with Isbell topology and Scott topology

Published online by Cambridge University Press:  05 February 2023

Xiaoquan Xu Open the ORCID record for Xiaoquan Xu [Opens in a new window] ,
Meng Bao  and
Xiaoyuan Zhang Open the ORCID record for Xiaoyuan Zhang [Opens in a new window]
Xiaoquan Xu*
Affiliation:
Fujian Key Laboratory of Granular Computing and Applications, Minnan Normal University, Zhangzhou 363000, China
Meng Bao
Affiliation:
College of Mathematics, Sichuan University, Chengdu 610064, China
Xiaoyuan Zhang
Affiliation:
School of Big Data Science, Hebei Finance University, Baoding 071051, China
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

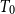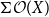In this paper, we mainly study the function spaces related to H-sober spaces. For an irreducible subset system H and $T_{0}$ spaces X and Y, it is proved that the following three conditions are equivalent: (1) the Scott space $\Sigma \mathcal O(X)$ of the lattice of all open sets of X is H-sober; (2) for every H-sober space Y, the function space 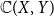$\mathbb{C}(X, Y)$ of all continuous mappings from X to Y equipped with the Isbell topology is H-sober; (3) for every H-sober space Y, the Isbell topology on $\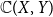mathbb{C}(X, Y)$ has property S with respect to H. 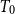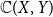One immediate corollary is that for a $T_{0}$ space X, Y is a d-space (resp., well-filtered space) iff the function space $\mathbb{C}(X, Y)$ equipped with the Isbell topology is a d-space (resp., well-filtered space). 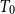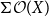It is shown that for any $T_0$ space X for which the Scott space $\Sigma \mathcal O(X)$ is non-sober, the function space 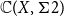$\mathbb{C}(X, \Sigma 2)$ equipped with the Isbell topology is not sober. The function spaces 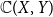$\mathbb{C}(X, Y)$ equipped with the Scott topology, the compact-open topology and the pointwise convergence topology are also discussed. Our study also leads to a number of questions, whose answers will deepen our understanding of the function spaces related to H-sober spaces.

Keywords

Function spaceIsbell topologyScott topologycompact-open topologypointwise convergence topologyH-sober space
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 32 , Issue 8 , September 2022 , pp. 1099 - 1116
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This research was supported by the National Natural Science Foundation of China (Nos. 12071199, 11661057), and the Science and Technology Project of Education Bureau of Hebei Province, China (No. QN2023023).

References

Engelking, R. (1989). General Topology , Warzawa, Polish Scientific Publishers.Google Scholar
Ershov, Y. and Schwidefsky, M. (2020). On function spaces. Siberian Electronic Mathematical Reports 17 999–1008.Google Scholar
Gierz, G., Hofmann, K., Keimel, K., Lawson, J., Mislove, M. and Scott, D. (2003). Continuous Lattices and Domains, Cambridge, Cambridge University Press.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2003). Non-Hausdorff Topology and Domain Theory , New Mathematical Monographs, vol. 22, Cambridge, Cambridge University Press.Google Scholar
Isbell, J. (1982). Completion of a construction of Johnstone. Proceedings of the American Mathematical Society 85 333–334.CrossRefGoogle Scholar
Johnstone, P. (1981). Scott is not always sober. In Continuous Lattices, Lecture Notes in Mathematics, Berlin, Springer-Verlag, 282–283.CrossRefGoogle Scholar
Jung, A. (1989). Cartesian Closed Categories of Domains , CWI Tract, vol. 66, Amsterdam.Google Scholar
Jung, A. (1990). The classification of continuous domains. In: Proceedings, Fifth Annual IEEE Symposium on Logic in Computer Science, IEEE Computer Society Press, 35–40.CrossRefGoogle Scholar
Keimel, K. and Lawson, J. (2009). D-completion and d-topology. Annals of Pure and Applied Logic 159 292–306.CrossRefGoogle Scholar
Liu, B., Li, Q. and Ho, W. (2021). On function spaces related to d-spaces. Topology and Its Applications 300 107757.CrossRefGoogle Scholar
Lu, C. and Li, Q. (2017). Weak well-filtered spaces and coherence. Topology and Its Applications 230 373–380.CrossRefGoogle Scholar
Plotkin, G. (1976). A powerdomain construction. SIAM Journal on Computing 5 452–487.CrossRefGoogle Scholar
Scott, D. (1970). Outline of a mathematical theory of computation. In: Proceedings of the 4th Annual Princeton Conference on Information Sciences and Systems, Princeton University Press, 169–176.Google Scholar
Shen, C., Xi, X., Xu, X. and Zhao, D. (2019). On well-filtered reflections of inline926 spaces. Topology and Its Applications 267 106869.CrossRefGoogle Scholar
Smyth, M. (1983). The largest cartesian closed category of domains. Theoretical Computer Science 27 109–119.CrossRefGoogle Scholar
Xi, X. and Lawson, J. (2017). On well-filtered spaces and ordered sets. Topology and Its Applications 228 139–144.CrossRefGoogle Scholar
Xu, X. (2021). On H-sober spaces and H-sobrifications of inline927 spaces. Topology and Its Applications 289 107548.CrossRefGoogle Scholar
Xu, X., Shen, C., Xi, X. and Zhao, D. (2020). On inline928 spaces determined by well-filtered spaces. Topology and Its Applications 282 107323.CrossRefGoogle Scholar
Xu, X., Xi, X. and Zhao, D. (2021). A complete Heyting algebra whose Scott topology is not sober. Fundamenta Mathematicae 252 315–323.CrossRefGoogle Scholar
Zhao, D. and Ho, W. (2015). On topologies defined by irreducible sets. Journal of Logical and Algebraic Methods in Programming 84(1) 185–195.CrossRefGoogle Scholar