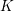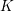1 Introduction
Knutson–Vakil [Reference Coşkun and VakilCV09, §5] conjectured a combinatorial rule for the structure coefficients of the torus-equivariant
![]() $K$
-theory ring of a Grassmannian. The structure coefficients are with respect to the basis of Schubert structure sheaves. Their rule extends puzzles, combinatorial objects founded in work of Knutson and Tao [Reference Knutson and TaoKT03] and in their collaboration with Woodward [Reference Knutson, Tao and WoodwardKTW04]. The various puzzle rules play a prominent role in modern Schubert calculus; see, e.g., [Reference Buch, Kresch and TamvakisBKT03, Reference VakilVak06, Reference Coşkun and VakilCV09], recent developments [Reference KnutsonKnu10, Reference Knutson and PurbhooKP11, Reference Buch, Kresch, Purbhoo and TamvakisBKPT16, Reference BuchBuc15] and the references therein.
$K$
-theory ring of a Grassmannian. The structure coefficients are with respect to the basis of Schubert structure sheaves. Their rule extends puzzles, combinatorial objects founded in work of Knutson and Tao [Reference Knutson and TaoKT03] and in their collaboration with Woodward [Reference Knutson, Tao and WoodwardKTW04]. The various puzzle rules play a prominent role in modern Schubert calculus; see, e.g., [Reference Buch, Kresch and TamvakisBKT03, Reference VakilVak06, Reference Coşkun and VakilCV09], recent developments [Reference KnutsonKnu10, Reference Knutson and PurbhooKP11, Reference Buch, Kresch, Purbhoo and TamvakisBKPT16, Reference BuchBuc15] and the references therein.
This paper is a sequel to [Reference Pechenik and YongPY15], where we gave the first proved tableau rules for these structure coefficients, including a conjecture of Thomas and the second author [Reference Thomas and YongTY12]. Here we use these results to prove a mild correction of the puzzle conjecture.
1.1 The puzzle conjecture
Let
![]() $X=\text{Gr}_{k}(\mathbb{C}^{n})$
denote the Grassmannian of
$X=\text{Gr}_{k}(\mathbb{C}^{n})$
denote the Grassmannian of
![]() $k$
-dimensional subspaces of
$k$
-dimensional subspaces of
![]() $\mathbb{C}^{n}$
. The general linear group
$\mathbb{C}^{n}$
. The general linear group
![]() $\mathsf{GL}_{n}$
acts transitively on
$\mathsf{GL}_{n}$
acts transitively on
![]() $X$
by change of basis. The Borel subgroup
$X$
by change of basis. The Borel subgroup
![]() $\mathsf{B}\subset \mathsf{GL}_{\mathsf{n}}$
of invertible lower triangular matrices acts on
$\mathsf{B}\subset \mathsf{GL}_{\mathsf{n}}$
of invertible lower triangular matrices acts on
![]() $X$
with finitely many orbits, i.e., the Schubert cells
$X$
with finitely many orbits, i.e., the Schubert cells
![]() $X_{\unicode[STIX]{x1D706}}^{\circ }$
. These orbits are indexed by
$X_{\unicode[STIX]{x1D706}}^{\circ }$
. These orbits are indexed by
![]() $\{0,1\}$
-sequences
$\{0,1\}$
-sequences
![]() $\unicode[STIX]{x1D706}$
of length
$\unicode[STIX]{x1D706}$
of length
![]() $n$
with
$n$
with
![]() $k$
-many
$k$
-many
![]() $1$
’s. The Schubert varieties are the Zariski closures
$1$
’s. The Schubert varieties are the Zariski closures
![]() $X_{\unicode[STIX]{x1D706}}:=\overline{X_{\unicode[STIX]{x1D706}}^{\circ }}$
. The
$X_{\unicode[STIX]{x1D706}}:=\overline{X_{\unicode[STIX]{x1D706}}^{\circ }}$
. The
![]() $X_{\unicode[STIX]{x1D706}}$
are stable under the action of the maximal torus
$X_{\unicode[STIX]{x1D706}}$
are stable under the action of the maximal torus
![]() $\mathsf{T}\subset \mathsf{B}$
of invertible diagonal matrices. Therefore, their structure sheaves
$\mathsf{T}\subset \mathsf{B}$
of invertible diagonal matrices. Therefore, their structure sheaves
![]() ${\mathcal{O}}_{X_{\unicode[STIX]{x1D706}}}$
admit classes in
${\mathcal{O}}_{X_{\unicode[STIX]{x1D706}}}$
admit classes in
![]() $K_{\mathsf{T}}(X)$
, the Grothendieck ring of T-equivariant vector bundles over
$K_{\mathsf{T}}(X)$
, the Grothendieck ring of T-equivariant vector bundles over
![]() $X$
. Now
$X$
. Now
![]() $K_{\mathsf{T}}(X)$
is a
$K_{\mathsf{T}}(X)$
is a
![]() $K_{\mathsf{T}}(\text{pt})$
-module and the
$K_{\mathsf{T}}(\text{pt})$
-module and the
![]() $\binom{n}{k}$
Schubert classes form a module basis. One may make a standard identification
$\binom{n}{k}$
Schubert classes form a module basis. One may make a standard identification
![]() $K_{\mathsf{T}}(\text{pt})\cong \mathbb{Z}[t_{i}^{\pm 1}:1\leqslant i\leqslant n]$
. The structure coefficients
$K_{\mathsf{T}}(\text{pt})\cong \mathbb{Z}[t_{i}^{\pm 1}:1\leqslant i\leqslant n]$
. The structure coefficients
![]() $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}\in K_{\mathsf{T}}(\text{pt})$
are defined by
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}\in K_{\mathsf{T}}(\text{pt})$
are defined by
Consider the
![]() $n$
-length equilateral triangle oriented as
$n$
-length equilateral triangle oriented as
![]() $\unicode[STIX]{x1D6E5}$
. A puzzle is a filling of
$\unicode[STIX]{x1D6E5}$
. A puzzle is a filling of
![]() $\unicode[STIX]{x1D6E5}$
with the following puzzle pieces:
$\unicode[STIX]{x1D6E5}$
with the following puzzle pieces:

The double-labeled edges are gashed. A filling requires that the common (non-gashed) edges of adjacent puzzle pieces share the same label. Two gashed edges may not be overlayed. The pieces on either side of a gash must have the indicated labels. The first three may be rotated but the fourth (equivariant piece) may not [Reference Knutson and TaoKT03]. We call the remainder KV-pieces; these may not be rotated. The fifth piece may only be placed if the equivariant piece is attached to its left. There is a ‘non-local’ requirement [Reference Coşkun and VakilCV09, §5] for using the sixth piece: it ‘may only be placed (when completing the puzzle from top to bottom and left to right as usual) if the edges to its right are a (possibly empty) series of horizontal 0’s followed by a 1’. A KV-puzzle is a puzzle filling of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
For simplicity, we will illustrate these six puzzle pieces by the following respective shaded versions (colour online):

Let
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
be
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
be
![]() $\unicode[STIX]{x1D6E5}$
with the boundary given by:
$\unicode[STIX]{x1D6E5}$
with the boundary given by:
-
∙
 $\unicode[STIX]{x1D706}$
as read
$\unicode[STIX]{x1D706}$
as read
 ${\nearrow}$
along the left-hand side;
${\nearrow}$
along the left-hand side; -
∙
 $\unicode[STIX]{x1D707}$
as read
$\unicode[STIX]{x1D707}$
as read
 ${\searrow}$
along the right-hand side; and
${\searrow}$
along the right-hand side; and -
∙
 $\unicode[STIX]{x1D708}$
as read
$\unicode[STIX]{x1D708}$
as read
 $\rightarrow$
along the bottom side.
$\rightarrow$
along the bottom side.
The weight
![]() $\text{wt}(P)$
of a KV-puzzle
$\text{wt}(P)$
of a KV-puzzle
![]() $P$
is a product of the following factors. Each KV-piece contributes a factor of
$P$
is a product of the following factors. Each KV-piece contributes a factor of
![]() $-1$
. For each equivariant piece one draws a
$-1$
. For each equivariant piece one draws a
![]() ${\searrow}$
diagonal arrow from the center of the piece to the
${\searrow}$
diagonal arrow from the center of the piece to the
![]() $\unicode[STIX]{x1D708}$
-side of
$\unicode[STIX]{x1D708}$
-side of
![]() $\unicode[STIX]{x1D6E5}$
; let
$\unicode[STIX]{x1D6E5}$
; let
![]() $a$
be the unit segment of the
$a$
be the unit segment of the
![]() $\unicode[STIX]{x1D708}$
-boundary, as counted from the right. Similarly, one determines
$\unicode[STIX]{x1D708}$
-boundary, as counted from the right. Similarly, one determines
![]() $b$
by drawing a
$b$
by drawing a
![]() $\swarrow$
antidiagonal arrow. The equivariant piece contributes a factor of
$\swarrow$
antidiagonal arrow. The equivariant piece contributes a factor of
![]() $1-t_{a}/t_{b}$
.
$1-t_{a}/t_{b}$
.
Conjecture 1.1 (The Knutson–Vakil puzzle conjecture).
![]() $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all KV-puzzles of
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all KV-puzzles of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
.
We consider the structure coefficient
![]() $K_{01001,00101}^{10010}$
for
$K_{01001,00101}^{10010}$
for
![]() $\text{Gr}_{2}(\mathbb{C}^{5})$
. The reader can check that there are six KV-puzzles
$\text{Gr}_{2}(\mathbb{C}^{5})$
. The reader can check that there are six KV-puzzles
![]() $P_{1},P_{2},\ldots ,P_{6}$
with the indicated weights.
$P_{1},P_{2},\ldots ,P_{6}$
with the indicated weights.


Using double Grothendieck polynomials [Reference Lascoux and SchützenbergerLS82] (see also [Reference Fulton and LascouxFL94] and references therein), one computes
![]() $K_{01001,00101}^{10010}=-(t_{2}/t_{4})=\text{wt}(P_{2})+\text{wt}(P_{3})+\text{wt}(P_{5})+\text{wt}(P_{6})$
. This gives a counterexample to Conjecture 1.1. Actually, this subset of four puzzles is explained by the rule of Theorem 1.2 below.
$K_{01001,00101}^{10010}=-(t_{2}/t_{4})=\text{wt}(P_{2})+\text{wt}(P_{3})+\text{wt}(P_{5})+\text{wt}(P_{6})$
. This gives a counterexample to Conjecture 1.1. Actually, this subset of four puzzles is explained by the rule of Theorem 1.2 below.
1.2 A modified puzzle rule
We define a modified KV-puzzle to be a KV-puzzle with the non-local condition on the second KV-piece replaced by the requirement that the second KV-piece only appears in the combination pieces
Theorem 1.2.
![]() $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all modified KV-puzzles of
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all modified KV-puzzles of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
.
We have a few remarks. First, the rule of Theorem 1.2 is ‘positive’ in the sense of Anderson et al. [Reference Anderson, Griffeth and MillerAGM11]; cf. the discussion in [Reference Pechenik and YongPY15, §1.4]. Second, it is a natural objective to interpret Theorem 1.2 via geometric degeneration; see [Reference Coşkun and VakilCV09, Reference KnutsonKnu10]. Third, the first author has found a tableau formulation similar to that of [Reference Pechenik and YongPY15] to complement the puzzle rule of [Reference KnutsonKnu10] for the different Schubert calculus problem in
![]() $K_{\mathsf{T}}(\mathsf{X})$
of multiplying a class of a Schubert variety by that of an opposite Schubert variety; further discussion may appear elsewhere. Fourth, we observe that the rule of Theorem 1.2 may be easily reformulated to avoid gashed edges and restricted placement rules, as in the following result.
$K_{\mathsf{T}}(\mathsf{X})$
of multiplying a class of a Schubert variety by that of an opposite Schubert variety; further discussion may appear elsewhere. Fourth, we observe that the rule of Theorem 1.2 may be easily reformulated to avoid gashed edges and restricted placement rules, as in the following result.
Corollary 1.3.
![]() $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all tilings of
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\sum _{P}\text{wt}(P)$
, where the sum is over all tilings of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
by

(where only the first three may be rotated and the pieces are given the appropriate weights).
While this latter formulation is arguably simpler and involves fewer puzzles, we focus here on the modified KV-puzzles of Theorem 1.2 to emphasize the close connection to Conjecture 1.1.
To prove Theorem 1.2, we first give a variant of the main theorem of [Reference Pechenik and YongPY15]; see §2. In §3, we then give a weight-preserving bijection between modified KV-puzzles and the objects of the rule of §2.
2 A tableau rule for
 $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}$
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}$
We need to briefly recall the definitions of [Reference Pechenik and YongPY15, §§1.2–1.3]; there the Schubert varieties
![]() $X_{\unicode[STIX]{x1D706}}$
are indexed by Young diagrams
$X_{\unicode[STIX]{x1D706}}$
are indexed by Young diagrams
![]() $\unicode[STIX]{x1D706}$
contained in a
$\unicode[STIX]{x1D706}$
contained in a
![]() $k\times (n-k)$
rectangle. (Throughout, we orient Young diagrams and tableaux according to the English convention.)
$k\times (n-k)$
rectangle. (Throughout, we orient Young diagrams and tableaux according to the English convention.)
An edge-labeled genomic tableau is a filling of the boxes and horizontal edges of a skew diagram
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
with subscripted labels
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
with subscripted labels
![]() $i_{j}$
, where
$i_{j}$
, where
![]() $i$
is a positive integer and the
$i$
is a positive integer and the
![]() $j$
that appear for each
$j$
that appear for each
![]() $i$
form an initial interval of positive integers. Each box of
$i$
form an initial interval of positive integers. Each box of
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
contains one label, whereas the horizontal edges weakly between the southern border of
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
contains one label, whereas the horizontal edges weakly between the southern border of
![]() $\unicode[STIX]{x1D706}$
and the northern border of
$\unicode[STIX]{x1D706}$
and the northern border of
![]() $\unicode[STIX]{x1D708}$
are filled by (possibly empty) sets of labels. A genomic edge-labeled tableau
$\unicode[STIX]{x1D708}$
are filled by (possibly empty) sets of labels. A genomic edge-labeled tableau
![]() $T$
is semistandard if:
$T$
is semistandard if:
(S.1) the box labels of each row strictly increase lexicographically from left to right;
(S.2) ignoring subscripts, each label is strictly less than any label strictly south in its column;
(S.3) ignoring subscripts, the labels appearing on a given edge are distinct;
(S.4) if
![]() $i_{j}$
appears strictly west of
$i_{j}$
appears strictly west of
![]() $i_{k}$
, then
$i_{k}$
, then
![]() $j\leqslant k$
.
$j\leqslant k$
.
Index the rows of
![]() $\unicode[STIX]{x1D708}$
from the top starting at
$\unicode[STIX]{x1D708}$
from the top starting at
![]() $1$
. We say that a label
$1$
. We say that a label
![]() $i_{j}$
is too high if it appears weakly above the north edge of row
$i_{j}$
is too high if it appears weakly above the north edge of row
![]() $i$
. We refer to the collection of all
$i$
. We refer to the collection of all
![]() $i_{j}$
(for fixed
$i_{j}$
(for fixed
![]() $i,j$
) as a gene of family
$i,j$
) as a gene of family
![]() $i$
. The content of
$i$
. The content of
![]() $T$
is the composition
$T$
is the composition
![]() $(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots \,)$
, where
$(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots \,)$
, where
![]() $\unicode[STIX]{x1D6FC}_{i}$
is greatest so that
$\unicode[STIX]{x1D6FC}_{i}$
is greatest so that
![]() $i_{\unicode[STIX]{x1D6FC}_{i}}$
is a gene of
$i_{\unicode[STIX]{x1D6FC}_{i}}$
is a gene of
![]() $T$
.
$T$
.
Recall that in the classical tableau theory, a semistandard tableau
![]() $S$
is ballot if, reading the labels down columns from right to left, we obtain a word
$S$
is ballot if, reading the labels down columns from right to left, we obtain a word
![]() $W$
with the following property: for each
$W$
with the following property: for each
![]() $i$
, every initial segment of
$i$
, every initial segment of
![]() $W$
contains at least as many
$W$
contains at least as many
![]() $i$
’s as
$i$
’s as
![]() $(i+1)$
’s. Given an edge-labeled genomic tableau
$(i+1)$
’s. Given an edge-labeled genomic tableau
![]() $T$
, choose one label from each gene and delete all others; now delete all subscripts. We say that
$T$
, choose one label from each gene and delete all others; now delete all subscripts. We say that
![]() $T$
is ballot if, regardless of our choices from genes, the resulting tableau (possibly containing holes) is necessarily ballot in the above classical sense. (In the case of multiple labels on a edge, read them from least to greatest.)
$T$
is ballot if, regardless of our choices from genes, the resulting tableau (possibly containing holes) is necessarily ballot in the above classical sense. (In the case of multiple labels on a edge, read them from least to greatest.)
We now diverge slightly from the treatment of [Reference Pechenik and YongPY15], borrowing notation from [Reference Thomas and YongTY12]. Given a box
![]() $\mathsf{x}$
in an edge-labeled genomic tableau
$\mathsf{x}$
in an edge-labeled genomic tableau
![]() $T$
, we say that
$T$
, we say that
![]() $\mathsf{x}$
is starrable if it contains
$\mathsf{x}$
is starrable if it contains
![]() $i_{j}$
, is in row
$i_{j}$
, is in row
![]() ${>}i$
and
${>}i$
and
![]() $i_{j+1}$
is not a box label to its immediate right. Let
$i_{j+1}$
is not a box label to its immediate right. Let
![]() $\mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
be the set of all ballot semistandard edge-labeled genomic tableaux of shape
$\mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
be the set of all ballot semistandard edge-labeled genomic tableaux of shape
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
and content
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
and content
![]() $\unicode[STIX]{x1D707}$
with no label too high, where the label of each starrable box may freely be marked by
$\unicode[STIX]{x1D707}$
with no label too high, where the label of each starrable box may freely be marked by
![]() $\star$
or not. The tableau
$\star$
or not. The tableau
![]() $T$
illustrated in Figure 2 is an element of
$T$
illustrated in Figure 2 is an element of
![]() $\mathtt{StarBallotGen}_{(10,5,3)}((15,8,5)/(12,2,1))$
. There are three starrable boxes in
$\mathtt{StarBallotGen}_{(10,5,3)}((15,8,5)/(12,2,1))$
. There are three starrable boxes in
![]() $T$
, in only one of which the label has been starred.
$T$
, in only one of which the label has been starred.
Let
![]() $\mathsf{Man}(\mathsf{x})$
denote the length of any
$\mathsf{Man}(\mathsf{x})$
denote the length of any
![]() $\{\uparrow ,\rightarrow \}$
-lattice path from the southwest corner of
$\{\uparrow ,\rightarrow \}$
-lattice path from the southwest corner of
![]() $k\times (n-k)$
to the northwest corner of
$k\times (n-k)$
to the northwest corner of
![]() $\mathsf{x}$
. For
$\mathsf{x}$
. For
![]() $\mathsf{x}$
in row
$\mathsf{x}$
in row
![]() $r$
containing
$r$
containing
![]() $i_{j}^{\star }$
, set
$i_{j}^{\star }$
, set
![]() $\mathtt{starfactor}(\mathsf{x}):=1-(t_{\mathsf{Man}(\mathsf{x})+1})/(t_{r-i+\unicode[STIX]{x1D707}_{i}-j+1+\mathsf{Man}(\mathsf{x})})$
. For an edge label
$\mathtt{starfactor}(\mathsf{x}):=1-(t_{\mathsf{Man}(\mathsf{x})+1})/(t_{r-i+\unicode[STIX]{x1D707}_{i}-j+1+\mathsf{Man}(\mathsf{x})})$
. For an edge label
![]() $\ell =i_{j}$
in the southern edge of
$\ell =i_{j}$
in the southern edge of
![]() $\mathsf{x}$
in row
$\mathsf{x}$
in row
![]() $r$
, set
$r$
, set
![]() $\mathtt{edgefactor}:=1-(t_{\mathsf{Man}(\mathsf{x})})/(t_{r-i+\unicode[STIX]{x1D707}_{i}-j+1+\mathsf{Man}(\mathsf{x})})$
. Finally for
$\mathtt{edgefactor}:=1-(t_{\mathsf{Man}(\mathsf{x})})/(t_{r-i+\unicode[STIX]{x1D707}_{i}-j+1+\mathsf{Man}(\mathsf{x})})$
. Finally for
![]() $T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
, define
$T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
, define
here the products are respectively over edge labels
![]() $\ell$
and boxes
$\ell$
and boxes
![]() $\mathsf{x}$
containing starred labels, while
$\mathsf{x}$
containing starred labels, while
![]() $\hat{d}(T):=\#(\text{labels in }T)+\#(\star \text{'s in }T)-|\unicode[STIX]{x1D707}|$
. Let
$\hat{d}(T):=\#(\text{labels in }T)+\#(\star \text{'s in }T)-|\unicode[STIX]{x1D707}|$
. Let
where the sum is over all
![]() $T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
.
$T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
.
We need a reformulation of [Reference Pechenik and YongPY15, Theorem 1.3]; the proof is a simple application of the ‘inclusion–exclusion’ identity
![]() $\prod _{i\in [m]}a_{i}=\sum _{S\subseteq [m]}(-1)^{|S|}\prod _{i\in S}(1-a_{i})$
.
$\prod _{i\in [m]}a_{i}=\sum _{S\subseteq [m]}(-1)^{|S|}\prod _{i\in S}(1-a_{i})$
.
Theorem 2.1.
![]() $K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\hat{L}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}.$
$K_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}=\hat{L}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}.$
Example 2.2. Let
![]() $k=2,n=5$
and
$k=2,n=5$
and
![]() $\unicode[STIX]{x1D706}=(2,0)$
,
$\unicode[STIX]{x1D706}=(2,0)$
,
![]() $\unicode[STIX]{x1D707}=(1,0)$
and
$\unicode[STIX]{x1D707}=(1,0)$
and
![]() $\unicode[STIX]{x1D708}=(3,1)$
. The four tableaux contributing to
$\unicode[STIX]{x1D708}=(3,1)$
. The four tableaux contributing to
![]() $\hat{L}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}$
are
$\hat{L}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D708}}$
are

Our indexing of these tableaux alludes to the precise connection to the four puzzles
![]() $P_{2},P_{3},P_{5}$
and
$P_{2},P_{3},P_{5}$
and
![]() $P_{6}$
of §1.1, as explained in the next section.◻
$P_{6}$
of §1.1, as explained in the next section.◻
3 Proof of Theorem 1.2: bijecting the tableau and puzzle rules
3.1 Description of the bijection
To relate the modified KV-puzzle rule of Theorem 1.2 with the tableau rule of Theorem 2.1, we give a variant of Tao’s ‘proof without words’ [Reference VakilVak06] (and its modification by Purbhoo [Reference PurbhooPur08]) that bijects cohomological puzzles (using the first three pieces) and a tableau Littlewood–Richardson rule. An extension of this proof for equivariant puzzles (i.e., fillings that additionally use the equivariant piece) was given by Kreiman [Reference KreimanKre10]; we also incorporate elements of his bijection in our analysis.
Figure 1 gives a ‘generic’ example of a (modified) KV-puzzle
![]() $P$
. We will define a track
$P$
. We will define a track
![]() $\unicode[STIX]{x1D70B}_{i}$
from the
$\unicode[STIX]{x1D70B}_{i}$
from the
![]() $i$
th
$i$
th
![]() $1$
(from the left) on the
$1$
(from the left) on the
![]() $\unicode[STIX]{x1D708}$
-boundary of
$\unicode[STIX]{x1D708}$
-boundary of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
to the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
to the
![]() $i$
th
$i$
th
![]() $1$
(from the top) on the
$1$
(from the top) on the
![]() $\unicode[STIX]{x1D707}$
-boundary. To do this, we describe the flow through the (oriented, non-KV) puzzle pieces that use a
$\unicode[STIX]{x1D707}$
-boundary. To do this, we describe the flow through the (oriented, non-KV) puzzle pieces that use a
![]() $1$
and four combination pieces (possible ways one can use the KV-pieces under the rules for a modified KV-puzzle):
$1$
and four combination pieces (possible ways one can use the KV-pieces under the rules for a modified KV-puzzle):

Thinking of the (combination) pieces in (A.1)–(A.9) as letters of an alphabet, we can encode the northernmost track in
![]() $P$
(from Figure 1) as the word
$P$
(from Figure 1) as the word
Recall, if
![]() $\unicode[STIX]{x1D705}$
is a letter/word in some alphabet, then the Kleene star is
$\unicode[STIX]{x1D705}$
is a letter/word in some alphabet, then the Kleene star is
![]() $\unicode[STIX]{x1D705}^{\ast }:=\{\emptyset ,\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}\unicode[STIX]{x1D705},\ldots \}$
.
$\unicode[STIX]{x1D705}^{\ast }:=\{\emptyset ,\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}\unicode[STIX]{x1D705},\ldots \}$
.
Proposition 3.1 (Decomposition of
 $\unicode[STIX]{x1D70B}_{i}$
).
$\unicode[STIX]{x1D70B}_{i}$
).
The list of (combination) pieces that appear in
![]() $\unicode[STIX]{x1D70B}_{i}$
, as read from southwest to northeast, is a word from the following formal grammar:
$\unicode[STIX]{x1D70B}_{i}$
, as read from southwest to northeast, is a word from the following formal grammar:
where

Proof. This is by inspection of the rules for modified KV-puzzles.◻

Figure 1. A ‘generic’ modified KV-puzzle
![]() $P$
(
$P$
(
![]() $k=3,n=20$
).
$k=3,n=20$
).
The remaining filling of the puzzle is forced, which we explain in two steps. First there is the NWray of each
![]() $\blacktriangle$
, i.e., the (possibly empty) path of upward-pointing rhombi
$\blacktriangle$
, i.e., the (possibly empty) path of upward-pointing rhombi
Lemma 3.2. The NWray of
![]() $\blacktriangle$
ends either at the
$\blacktriangle$
ends either at the
![]() $\unicode[STIX]{x1D706}$
-boundary of
$\unicode[STIX]{x1D706}$
-boundary of
![]() $\unicode[STIX]{x1D6E5}$
or with a piece from startrow. In the latter case, the shared edge is the south-then-easternmost edge of the (combination) piece.
$\unicode[STIX]{x1D6E5}$
or with a piece from startrow. In the latter case, the shared edge is the south-then-easternmost edge of the (combination) piece.
Proof. The north
![]() $/$
of
$/$
of
Second, pieces of the puzzle not in a track or NWray are
![]() $0$
-triangles (depicted white).
$0$
-triangles (depicted white).
We correspond Young diagrams to
![]() $\{0,1\}$
-sequences. Trace the
$\{0,1\}$
-sequences. Trace the
![]() $\{\leftarrow ,\downarrow \}$
-lattice path defined by the southern boundary of
$\{\leftarrow ,\downarrow \}$
-lattice path defined by the southern boundary of
![]() $\unicode[STIX]{x1D706}$
(as placed in the northwest corner of
$\unicode[STIX]{x1D706}$
(as placed in the northwest corner of
![]() $k\times (n-k)$
) starting from the northeast corner of
$k\times (n-k)$
) starting from the northeast corner of
![]() $k\times (n-k)$
towards the southeast corner of
$k\times (n-k)$
towards the southeast corner of
![]() $k\times (n-k)$
. Record each
$k\times (n-k)$
. Record each
![]() $\leftarrow$
step with ‘
$\leftarrow$
step with ‘
![]() $0$
’ and each
$0$
’ and each
![]() $\downarrow$
step with ‘
$\downarrow$
step with ‘
![]() $1$
’.
$1$
’.
We now convert
![]() $P$
into (we claim) an edge-labeled starred genomic tableau
$P$
into (we claim) an edge-labeled starred genomic tableau
![]() $T:=\unicode[STIX]{x1D719}(P)$
of shape
$T:=\unicode[STIX]{x1D719}(P)$
of shape
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
with content
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
with content
![]() $\unicode[STIX]{x1D707}$
. The placement of the labels of family
$\unicode[STIX]{x1D707}$
. The placement of the labels of family
![]() $i$
is governed by the decomposition (3.1) of
$i$
is governed by the decomposition (3.1) of
![]() $\unicode[STIX]{x1D70B}_{i}$
. The initial sequence of
$\unicode[STIX]{x1D70B}_{i}$
. The initial sequence of
![]() $k$
$k$

Applying
![]() $\unicode[STIX]{x1D719}$
to the puzzle
$\unicode[STIX]{x1D719}$
to the puzzle
![]() $P$
of Figure 1 gives the tableau
$P$
of Figure 1 gives the tableau
![]() $T$
of Figure 2. Here
$T$
of Figure 2. Here
![]() $\unicode[STIX]{x1D706}=0^{5}10^{10}1010$
, corresponding to the inner shape
$\unicode[STIX]{x1D706}=0^{5}10^{10}1010$
, corresponding to the inner shape
![]() $(12,2,1)$
(which is shaded in grey). Since
$(12,2,1)$
(which is shaded in grey). Since
![]() $\unicode[STIX]{x1D707}=0^{7}10^{5}10^{2}10^{3}$
, the content of
$\unicode[STIX]{x1D707}=0^{7}10^{5}10^{2}10^{3}$
, the content of
![]() $T$
is
$T$
is
![]() $(10,5,3)$
. Finally, since
$(10,5,3)$
. Finally, since
![]() $\unicode[STIX]{x1D708}=0^{2}10^{7}10^{3}10^{5}$
, the outer shape of
$\unicode[STIX]{x1D708}=0^{2}10^{7}10^{3}10^{5}$
, the outer shape of
![]() $T$
is
$T$
is
![]() $(15,8,5)$
. As another example,
$(15,8,5)$
. As another example,
![]() $\unicode[STIX]{x1D719}$
connects the puzzles
$\unicode[STIX]{x1D719}$
connects the puzzles
![]() $P_{2},P_{3},P_{5}$
and
$P_{2},P_{3},P_{5}$
and
![]() $P_{6}$
of §1 respectively with the tableaux
$P_{6}$
of §1 respectively with the tableaux
![]() $T_{2},T_{3},T_{5}$
and
$T_{2},T_{3},T_{5}$
and
![]() $T_{6}$
of Example 2.2.
$T_{6}$
of Example 2.2.

Figure 2. The tableau
![]() $T:=\unicode[STIX]{x1D719}(P)$
corresponding to the modified KV-puzzle
$T:=\unicode[STIX]{x1D719}(P)$
corresponding to the modified KV-puzzle
![]() $P$
of Figure 1.
$P$
of Figure 1.
Conversely, given
![]() $T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
, construct a word
$T\in \mathtt{StarBallotGen}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706})$
, construct a word
![]() $\unicode[STIX]{x1D70E}_{i}$
using the correspondences (B.1)–(B.9), for
$\unicode[STIX]{x1D70E}_{i}$
using the correspondences (B.1)–(B.9), for
![]() $1\leqslant i\leqslant k$
. That is, read the occurrences (possibly zero) of family
$1\leqslant i\leqslant k$
. That is, read the occurrences (possibly zero) of family
![]() $i$
in
$i$
in
![]() $T$
from right to left and from the
$T$
from right to left and from the
![]() $i$
th row down. We note about (B.6) in the degenerate case that there are no labels of family
$i$
th row down. We note about (B.6) in the degenerate case that there are no labels of family
![]() $i$
in the next row: use
$i$
in the next row: use
![]() $\blacktriangle$
after reading the leftmost box in that row of
$\blacktriangle$
after reading the leftmost box in that row of
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
(i.e., the one without any family-
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
(i.e., the one without any family-
![]() $i$
box entries) without a label of family
$i$
box entries) without a label of family
![]() ${<}i$
.
${<}i$
.
Lemma 3.3. Each
![]() $\unicode[STIX]{x1D70E}_{i}$
is of the form (3.1).
$\unicode[STIX]{x1D70E}_{i}$
is of the form (3.1).
Proof. Since
![]() $T$
is semistandard, in any row, all box labels of family
$T$
is semistandard, in any row, all box labels of family
![]() $i$
are contiguous and strictly right of any (lower) edge labels of that family on that row. The lemma follows.◻
$i$
are contiguous and strictly right of any (lower) edge labels of that family on that row. The lemma follows.◻
We describe a claimed filling
![]() $P:=\unicode[STIX]{x1D713}(T)$
of
$P:=\unicode[STIX]{x1D713}(T)$
of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
. There are
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
. There are
![]() $k$
$k$
![]() $1$
’s on each side of
$1$
’s on each side of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
; to the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
; to the
![]() $i$
th
$i$
th
![]() $1$
from the left on the
$1$
from the left on the
![]() $\unicode[STIX]{x1D708}$
-boundary of
$\unicode[STIX]{x1D708}$
-boundary of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
, place puzzle pieces in the order indicated by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
, place puzzle pieces in the order indicated by
![]() $\unicode[STIX]{x1D70E}_{i}$
. That is, attach the next (combination) piece using the northernmost
$\unicode[STIX]{x1D70E}_{i}$
. That is, attach the next (combination) piece using the northernmost
![]() $\backslash$
edge on its west side, if it exists. Otherwise attach at the piece’s unique southern edge. We attach at the unique — or
$\backslash$
edge on its west side, if it exists. Otherwise attach at the piece’s unique southern edge. We attach at the unique — or
![]() $\backslash$
edge of the thus far constructed track. Fill in the order
$\backslash$
edge of the thus far constructed track. Fill in the order
![]() $i=1,2,3,\ldots ,k$
. Now stack
$i=1,2,3,\ldots ,k$
. Now stack
Sections 3.2–3.4 prove that
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
are well-defined and weight-preserving maps between
$\unicode[STIX]{x1D713}$
are well-defined and weight-preserving maps between
Semistandardness (specifically (S.4)) implies that knowing the locations of labels of family
![]() $i$
, and which labels are repeated or
$i$
, and which labels are repeated or
![]() $\star$
-ed, uniquely determines the gene(s) in each location. The injectivity of
$\star$
-ed, uniquely determines the gene(s) in each location. The injectivity of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
is easy from this. Moreover, by construction (cf. Lemma 3.3), the two maps are mutually reversing. Thus, Theorem 1.2 follows from Theorem 2.1.◻
$\unicode[STIX]{x1D713}$
is easy from this. Moreover, by construction (cf. Lemma 3.3), the two maps are mutually reversing. Thus, Theorem 1.2 follows from Theorem 2.1.◻
3.2 Well definedness of
 $\unicode[STIX]{x1D719}:{\mathcal{P}}\rightarrow {\mathcal{T}}$
$\unicode[STIX]{x1D719}:{\mathcal{P}}\rightarrow {\mathcal{T}}$
Let
![]() $P\in {\mathcal{P}}$
be a modified KV-puzzle for
$P\in {\mathcal{P}}$
be a modified KV-puzzle for
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
. For the track
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
. For the track
![]() $\unicode[STIX]{x1D70B}_{i}$
, let
$\unicode[STIX]{x1D70B}_{i}$
, let
![]() $\blacktriangle _{i,j}$
refer to the
$\blacktriangle _{i,j}$
refer to the
![]() $j$
th
$j$
th
![]() $\blacktriangle$
seen along
$\blacktriangle$
seen along
![]() $\unicode[STIX]{x1D70B}_{i}$
(as read from southwest to northeast). Let
$\unicode[STIX]{x1D70B}_{i}$
(as read from southwest to northeast). Let
![]() $\mathbb{S}$
denote any of the (combination) pieces that appear in startrow. Similarly, we let
$\mathbb{S}$
denote any of the (combination) pieces that appear in startrow. Similarly, we let
![]() $\mathbb{S}_{i,j}$
be the
$\mathbb{S}_{i,j}$
be the
![]() $j$
th such piece on
$j$
th such piece on
![]() $\unicode[STIX]{x1D70B}_{i}$
.
$\unicode[STIX]{x1D70B}_{i}$
.
Figure 1 illustrates the ‘ragged honeycomb’ structure of modified KV-puzzles. To formalize this, first note by inspection that the
![]() $\unicode[STIX]{x1D70B}_{i}$
do not intersect. Second, we have the following claim.
$\unicode[STIX]{x1D70B}_{i}$
do not intersect. Second, we have the following claim.
Claim 3.4. There is a bijective correspondence between the
![]() $1$
’s on the
$1$
’s on the
![]() $\unicode[STIX]{x1D706}$
-boundary and the
$\unicode[STIX]{x1D706}$
-boundary and the
![]() $\blacktriangle$
’s in
$\blacktriangle$
’s in
![]() $\unicode[STIX]{x1D70B}_{1}$
. Specifically, the
$\unicode[STIX]{x1D70B}_{1}$
. Specifically, the
![]() $j$
th
$j$
th
![]() $1$
on the
$1$
on the
![]() $\unicode[STIX]{x1D706}$
-boundary is the terminus of the NWray of
$\unicode[STIX]{x1D706}$
-boundary is the terminus of the NWray of
![]() $\blacktriangle _{1,j}$
. Similarly, there is a bijective correspondence between
$\blacktriangle _{1,j}$
. Similarly, there is a bijective correspondence between
![]() $\blacktriangle _{i+1,j}$
and
$\blacktriangle _{i+1,j}$
and
![]() $\mathbb{S}_{i,j}$
in that the former’s NWray terminates at the southernmost
$\mathbb{S}_{i,j}$
in that the former’s NWray terminates at the southernmost
![]() $/$
edge of the latter.
$/$
edge of the latter.
Define
![]() ${\mathcal{L}}_{i}$
to be the left sequence of
${\mathcal{L}}_{i}$
to be the left sequence of
![]() $\unicode[STIX]{x1D70B}_{i}$
: start at the southwest corner of
$\unicode[STIX]{x1D70B}_{i}$
: start at the southwest corner of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
and read the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$
and read the
![]() $\{\rightarrow ,{\nearrow}\}$
-lattice path that starts along the
$\{\rightarrow ,{\nearrow}\}$
-lattice path that starts along the
![]() $\unicode[STIX]{x1D708}$
-boundary and travels up the left-hand boundary of
$\unicode[STIX]{x1D708}$
-boundary and travels up the left-hand boundary of
![]() $\unicode[STIX]{x1D70B}_{i}$
. The
$\unicode[STIX]{x1D70B}_{i}$
. The
![]() $\{0,1\}$
-sequence records the labels of the edges seen. Similarly, define
$\{0,1\}$
-sequence records the labels of the edges seen. Similarly, define
![]() ${\mathcal{R}}_{i}$
to be the right sequence of
${\mathcal{R}}_{i}$
to be the right sequence of
![]() $\unicode[STIX]{x1D70B}_{i}$
by traveling up the right-hand side of
$\unicode[STIX]{x1D70B}_{i}$
by traveling up the right-hand side of
![]() $\unicode[STIX]{x1D70B}_{i}$
but only reading the
$\unicode[STIX]{x1D70B}_{i}$
but only reading the
![]() $\rightarrow$
and
$\rightarrow$
and
![]() ${\nearrow}$
edges. (In Figure 1,
${\nearrow}$
edges. (In Figure 1,
![]() ${\mathcal{L}}_{1}=0^{5}10^{10}1010(=\unicode[STIX]{x1D706})$
while
${\mathcal{L}}_{1}=0^{5}10^{10}1010(=\unicode[STIX]{x1D706})$
while
![]() ${\mathcal{R}}_{1}=0^{2}10^{11}10^{2}10^{2}$
.)
${\mathcal{R}}_{1}=0^{2}10^{11}10^{2}10^{2}$
.)
In view of Claim 3.4, the following is ‘graphically’ clear by considering the
![]() $n$
diagonal strips through
$n$
diagonal strips through
![]() $P$
.
$P$
.
Claim 3.5.
![]() ${\mathcal{L}}_{1}=\unicode[STIX]{x1D706}$
,
${\mathcal{L}}_{1}=\unicode[STIX]{x1D706}$
,
![]() ${\mathcal{L}}_{i+1}={\mathcal{R}}_{i}$
for
${\mathcal{L}}_{i+1}={\mathcal{R}}_{i}$
for
![]() $1\leqslant i\leqslant k-1$
and
$1\leqslant i\leqslant k-1$
and
![]() $R_{k}=\unicode[STIX]{x1D708}$
.
$R_{k}=\unicode[STIX]{x1D708}$
.
Let
![]() $T^{(i)}$
be the tableau after adding labels of family
$T^{(i)}$
be the tableau after adding labels of family
![]() $1,2,\ldots ,i$
. We declare
$1,2,\ldots ,i$
. We declare
![]() $T^{(0)}$
to be the empty tableau of shape
$T^{(0)}$
to be the empty tableau of shape
![]() $\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
. Let
![]() $\unicode[STIX]{x1D708}^{(i)}$
be the outer shape of
$\unicode[STIX]{x1D708}^{(i)}$
be the outer shape of
![]() $T^{(i)}$
(interpreted as the
$T^{(i)}$
(interpreted as the
![]() $\{0,1\}$
-sequence for its lattice path).
$\{0,1\}$
-sequence for its lattice path).
Claim 3.6.
![]() ${\mathcal{L}}_{i}=\unicode[STIX]{x1D708}^{(i-1)}$
and
${\mathcal{L}}_{i}=\unicode[STIX]{x1D708}^{(i-1)}$
and
![]() ${\mathcal{R}}_{i}=\unicode[STIX]{x1D708}^{(i)}$
.
${\mathcal{R}}_{i}=\unicode[STIX]{x1D708}^{(i)}$
.
Proof. Both assertions follow by inspection of the correspondences (B.1)–(B.9). (Also, the second follows from the first, by Claim 3.5.)◻
It is straightforward from Claims 3.5 and 3.6 that
![]() $T=\unicode[STIX]{x1D719}(P)$
is semistandard in the sense of (S.1)–(S.4) of [Reference Pechenik and YongPY15]. By Proposition 3.1, no label of
$T=\unicode[STIX]{x1D719}(P)$
is semistandard in the sense of (S.1)–(S.4) of [Reference Pechenik and YongPY15]. By Proposition 3.1, no label of
![]() $T$
is
$T$
is
![]() $\star$
-ed unless it is the rightmost box label of its family in a row (
$\star$
-ed unless it is the rightmost box label of its family in a row (
![]() ${>}i$
). Since labels of family
${>}i$
). Since labels of family
![]() $i$
are placed in the boxes of row
$i$
are placed in the boxes of row
![]() $i$
or below, no label of
$i$
or below, no label of
![]() $T$
can be too high. Since
$T$
can be too high. Since
![]() ${\mathcal{R}}_{k}=\unicode[STIX]{x1D708}$
, the shape of
${\mathcal{R}}_{k}=\unicode[STIX]{x1D708}$
, the shape of
![]() $T$
is
$T$
is
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
.
Claim 3.7.
![]() $T$
has content
$T$
has content
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FD}$
be the content of
$\unicode[STIX]{x1D6FD}$
be the content of
![]() $T$
. Then
$T$
. Then
![]() $\unicode[STIX]{x1D6FD}_{i}$
is the number of (distinct) genes of family
$\unicode[STIX]{x1D6FD}_{i}$
is the number of (distinct) genes of family
![]() $i$
that appear in
$i$
that appear in
![]() $T$
, which, in terms of
$T$
, which, in terms of
![]() $P$
, is the number of
$P$
, is the number of
Finally, we have the following claim.
Claim 3.8.
![]() $T$
is ballot.
$T$
is ballot.
Proof. The height of a (combination) piece is the distance of any northernmost point to the
![]() $\unicode[STIX]{x1D708}$
-boundary as measured along any (anti)diagonal. The height
$\unicode[STIX]{x1D708}$
-boundary as measured along any (anti)diagonal. The height
![]() $h$
of
$h$
of
![]() $\blacktriangle _{i+1,j}$
equals the number of
$\blacktriangle _{i+1,j}$
equals the number of
3.3 Well definedness of
 $\unicode[STIX]{x1D713}:{\mathcal{T}}\rightarrow {\mathcal{P}}$
$\unicode[STIX]{x1D713}:{\mathcal{T}}\rightarrow {\mathcal{P}}$
Let
![]() $T\in {\mathcal{T}}$
be a starred ballot genomic tableau of shape
$T\in {\mathcal{T}}$
be a starred ballot genomic tableau of shape
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
and content
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}$
and content
![]() $\unicode[STIX]{x1D707}$
. Let
$\unicode[STIX]{x1D707}$
. Let
![]() $P=\unicode[STIX]{x1D713}(T)$
. Let
$P=\unicode[STIX]{x1D713}(T)$
. Let
![]() $\unicode[STIX]{x1D70B}_{i}$
be the track associated to
$\unicode[STIX]{x1D70B}_{i}$
be the track associated to
![]() $\unicode[STIX]{x1D70E}_{i}$
. As in §3.2, we define the
$\unicode[STIX]{x1D70E}_{i}$
. As in §3.2, we define the
![]() $\{0,1\}$
-sequences
$\{0,1\}$
-sequences
![]() ${\mathcal{L}}_{i}$
and
${\mathcal{L}}_{i}$
and
![]() ${\mathcal{R}}_{i}$
associated to
${\mathcal{R}}_{i}$
associated to
![]() $\unicode[STIX]{x1D70B}_{i}$
. Here
$\unicode[STIX]{x1D70B}_{i}$
. Here
![]() $T^{(i)}$
is defined as the subtableau of
$T^{(i)}$
is defined as the subtableau of
![]() $T$
using the labels of family
$T$
using the labels of family
![]() $1,2,\ldots ,i$
. Hence,
$1,2,\ldots ,i$
. Hence,
![]() $T^{(0)}$
is the empty tableau of shape
$T^{(0)}$
is the empty tableau of shape
![]() $\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
. Let
![]() $\unicode[STIX]{x1D708}^{(i)}$
be the outer shape of
$\unicode[STIX]{x1D708}^{(i)}$
be the outer shape of
![]() $T^{(i)}$
.
$T^{(i)}$
.
Claim 3.9 (Cf. Claim 3.6).
![]() ${\mathcal{L}}_{i}=\unicode[STIX]{x1D708}^{(i-1)}$
and
${\mathcal{L}}_{i}=\unicode[STIX]{x1D708}^{(i-1)}$
and
![]() ${\mathcal{R}}_{i}=\unicode[STIX]{x1D708}^{(i)}$
.
${\mathcal{R}}_{i}=\unicode[STIX]{x1D708}^{(i)}$
.
Proof. By inspection of the correspondences (B.1)–(B.9). ◻
By the lattice path definition, each
![]() $\unicode[STIX]{x1D708}^{(j)}$
is a length-
$\unicode[STIX]{x1D708}^{(j)}$
is a length-
![]() $n$
sequence. So,
$n$
sequence. So,
![]() $\unicode[STIX]{x1D70B}_{i}$
is a track that (by definition) starts at the south border of
$\unicode[STIX]{x1D70B}_{i}$
is a track that (by definition) starts at the south border of
![]() $\unicode[STIX]{x1D6E5}$
and terminates at the east border of
$\unicode[STIX]{x1D6E5}$
and terminates at the east border of
![]() $\unicode[STIX]{x1D6E5}$
. Also, define
$\unicode[STIX]{x1D6E5}$
. Also, define
![]() $\blacktriangledown _{i,j}$
and
$\blacktriangledown _{i,j}$
and
![]() $\mathbb{S}_{i,j}$
as before.
$\mathbb{S}_{i,j}$
as before.
Claim 3.10.
![]() $\mathbb{S}_{i,j}$
and
$\mathbb{S}_{i,j}$
and
![]() $\blacktriangle _{i+1,j}$
share a diagonal with the former strictly northwest of the latter.
$\blacktriangle _{i+1,j}$
share a diagonal with the former strictly northwest of the latter.
Proof. The
![]() $1$
’s in
$1$
’s in
![]() ${\mathcal{L}}_{i+1}$
result solely from the
${\mathcal{L}}_{i+1}$
result solely from the
![]() $\blacktriangle$
’s appearing in
$\blacktriangle$
’s appearing in
![]() $\unicode[STIX]{x1D70B}_{i+1}$
while the
$\unicode[STIX]{x1D70B}_{i+1}$
while the
![]() $1$
’s appearing in
$1$
’s appearing in
![]() ${\mathcal{R}}_{i}$
result solely from the
${\mathcal{R}}_{i}$
result solely from the
![]() $\mathbb{S}$
(combination) pieces. Thus, that the pieces share a diagonal follows from Claim 3.9. For the ‘northwest’ assertion, repeat Claim 3.8’s argument but reverse the logic of the final sentence: since by assumption
$\mathbb{S}$
(combination) pieces. Thus, that the pieces share a diagonal follows from Claim 3.9. For the ‘northwest’ assertion, repeat Claim 3.8’s argument but reverse the logic of the final sentence: since by assumption
![]() $T$
is ballot, it follows that
$T$
is ballot, it follows that
![]() $h^{\prime }\geqslant h$
.◻
$h^{\prime }\geqslant h$
.◻
Since Claims 3.9 and 3.10 combine to imply that the
![]() $\unicode[STIX]{x1D70B}_{i}$
are non-intersecting, attaching NWrays to each
$\unicode[STIX]{x1D70B}_{i}$
are non-intersecting, attaching NWrays to each
![]() $\blacktriangle$
and filling with white
$\blacktriangle$
and filling with white
![]() $0$
-triangles as prescribed, we have a filling
$0$
-triangles as prescribed, we have a filling
![]() $P$
of
$P$
of
![]() $\unicode[STIX]{x1D6E5}_{\widetilde{\unicode[STIX]{x1D706}},\widetilde{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D708}}$
satisfying the modified KV-puzzle rule. It remains to check the
$\unicode[STIX]{x1D6E5}_{\widetilde{\unicode[STIX]{x1D706}},\widetilde{\unicode[STIX]{x1D707}},\unicode[STIX]{x1D708}}$
satisfying the modified KV-puzzle rule. It remains to check the
![]() $\unicode[STIX]{x1D706}$
- and
$\unicode[STIX]{x1D706}$
- and
![]() $\unicode[STIX]{x1D707}$
-boundaries.
$\unicode[STIX]{x1D707}$
-boundaries.
Claim 3.11.
![]() $\widetilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}$
.
$\widetilde{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}$
.
Proof. Graphically,
![]() $\widetilde{\unicode[STIX]{x1D706}}={\mathcal{L}}_{1}$
. On the other hand, by Claim 3.9, we know that
$\widetilde{\unicode[STIX]{x1D706}}={\mathcal{L}}_{1}$
. On the other hand, by Claim 3.9, we know that
![]() ${\mathcal{L}}_{1}=\unicode[STIX]{x1D706}$
.◻
${\mathcal{L}}_{1}=\unicode[STIX]{x1D706}$
.◻
Claim 3.12.
![]() $\widetilde{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}$
.
$\widetilde{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}$
.
Proof. This is given by reversing the logic of the proof of Claim 3.7; here we are given the content of
![]() $T$
and are determining the heights of the tracks
$T$
and are determining the heights of the tracks
![]() $\unicode[STIX]{x1D70B}_{i}$
.◻
$\unicode[STIX]{x1D70B}_{i}$
.◻
3.4 Weight preservation
We wish to show the following result.
Claim 3.13.
![]() $\unicode[STIX]{x1D719}$
is weight preserving, i.e.,
$\unicode[STIX]{x1D719}$
is weight preserving, i.e.,
![]() $\text{wt}(P)=\widehat{\text{wt}}(T)$
.
$\text{wt}(P)=\widehat{\text{wt}}(T)$
.
Proof. The
![]() $\pm 1$
sign associated to
$\pm 1$
sign associated to
![]() $P$
and
$P$
and
![]() $T$
is the same since each usage of a KV-piece in
$T$
is the same since each usage of a KV-piece in
![]() $P$
corresponds to a
$P$
corresponds to a
![]() $\star$
-ed label or a repetition of a gene in
$\star$
-ed label or a repetition of a gene in
![]() $T$
.
$T$
.
Now consider the weight
![]() $1-t_{a}/t_{b}$
assigned to an equivariant piece
$1-t_{a}/t_{b}$
assigned to an equivariant piece
![]() $p$
in
$p$
in
![]() $P$
. Here
$P$
. Here
![]() $a$
is the ordinal (counted from the right) of the line segment
$a$
is the ordinal (counted from the right) of the line segment
![]() $s$
on the
$s$
on the
![]() $\unicode[STIX]{x1D708}$
-boundary hit by the diagonal ‘right leg’ emanating from
$\unicode[STIX]{x1D708}$
-boundary hit by the diagonal ‘right leg’ emanating from
![]() $p$
. Then
$p$
. Then
![]() $b$
equals
$b$
equals
![]() $a+h-1$
, where
$a+h-1$
, where
![]() $h$
is the height of the piece
$h$
is the height of the piece
![]() $p$
. Suppose that
$p$
. Suppose that
![]() $p$
lies in track
$p$
lies in track
![]() $\unicode[STIX]{x1D70B}_{i}$
, and corresponds either to
$\unicode[STIX]{x1D70B}_{i}$
, and corresponds either to
![]() $i_{j}$
on the lower edge of box
$i_{j}$
on the lower edge of box
![]() $\mathsf{x}$
in row
$\mathsf{x}$
in row
![]() $r$
or to
$r$
or to
![]() $i_{j}^{\star }\in \mathsf{x}$
in row
$i_{j}^{\star }\in \mathsf{x}$
in row
![]() $r$
. Consider the edge
$r$
. Consider the edge
![]() $e$
on the left boundary of
$e$
on the left boundary of
![]() $\unicode[STIX]{x1D70B}_{i}$
that is on the same diagonal as
$\unicode[STIX]{x1D70B}_{i}$
that is on the same diagonal as
![]() $s$
. If
$s$
. If
![]() $p$
is not attached to the first KV-piece, so it corresponds to an edge label, then
$p$
is not attached to the first KV-piece, so it corresponds to an edge label, then
![]() $e$
’s index from the right in the string
$e$
’s index from the right in the string
![]() ${\mathcal{L}}_{i}$
equals
${\mathcal{L}}_{i}$
equals
![]() $\mathsf{Man}(\mathsf{x})$
. Otherwise
$\mathsf{Man}(\mathsf{x})$
. Otherwise
![]() $e$
’s index from the right in the string
$e$
’s index from the right in the string
![]() ${\mathcal{L}}_{i}$
equals
${\mathcal{L}}_{i}$
equals
![]() $\mathsf{Man}(\mathsf{x})+1$
.
$\mathsf{Man}(\mathsf{x})+1$
.
Note that
![]() $h$
equals the number of
$h$
equals the number of
Acknowledgements
We thank Hugh Thomas for enlightening conversations during our work on [Reference Pechenik and YongPY15] and also thank Allen Knutson and Ravi Vakil for helpful correspondence. We thank two anonymous reviewers for helpful comments. O. P. was supported by an Illinois Distinguished Fellowship, an NSF Graduate Research Fellowship and NSF MCTP grant DMS 0838434. A. Y. was supported by NSF grants.