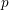1 Introduction
Simply connected minimal complex surfaces of general type of geometric genus zero, i.e. without global holomorphic
![]() $2$
-forms, occupy a special place in the geography of surfaces; see the excellent survey [Reference Bauer, Catanese and PignatelliBCP11]. These surfaces are homeomorphic (but not diffeomorphic) to del Pezzo surfaces, i.e. blowups of
$2$
-forms, occupy a special place in the geography of surfaces; see the excellent survey [Reference Bauer, Catanese and PignatelliBCP11]. These surfaces are homeomorphic (but not diffeomorphic) to del Pezzo surfaces, i.e. blowups of
![]() $\mathbb{P}^{2}$
in
$\mathbb{P}^{2}$
in
![]() $9-K^{2}$
points where
$9-K^{2}$
points where
 $1\leqslant K^{2}\leqslant 8$
. Describing their Gieseker moduli space of canonically polarized surfaces, or even finding explicit examples, is difficult. The first example was found by Barlow [Reference BarlowBar85]. Her surface has
$1\leqslant K^{2}\leqslant 8$
. Describing their Gieseker moduli space of canonically polarized surfaces, or even finding explicit examples, is difficult. The first example was found by Barlow [Reference BarlowBar85]. Her surface has
![]() $K^{2}=1$
and contains four
$K^{2}=1$
and contains four
![]() $(-2)$
-curves. Contracting them gives a canonically polarized surface with four
$(-2)$
-curves. Contracting them gives a canonically polarized surface with four
![]() $A_{1}$
singularities. One can show by deformation theory that the local Gieseker moduli space of the Barlow surface is smooth and eight-dimensional, and there exist nearby surfaces which are smooth (see [Reference LeBrun and CataneseLC97, Theorem 7] and [Reference LeeLee02]).
$A_{1}$
singularities. One can show by deformation theory that the local Gieseker moduli space of the Barlow surface is smooth and eight-dimensional, and there exist nearby surfaces which are smooth (see [Reference LeBrun and CataneseLC97, Theorem 7] and [Reference LeeLee02]).
More examples, including examples for every
 $1\leqslant K^{2}\leqslant 4$
, were found using
$1\leqslant K^{2}\leqslant 4$
, were found using
![]() $\mathbb{Q}$
-Gorenstein deformation theory, starting with the pioneering work of Lee and Park [Reference Lee and ParkLP07]; see also [Reference Park, Park and ShinPPS09a, Reference Park, Park and ShinPPS09b, Reference Stern and UrzúaSU16]. From the moduli space perspective, the Gieseker moduli space of canonically polarized surfaces with ADE singularities is compactified by the Kollár–Shepherd-Barron–Alexeev (KSBA) moduli space of canonically polarized surfaces with semi log canonical singularities [Reference Kollár and Shepherd-BarronKS88]. We call the complement of the Gieseker space the KSBA boundary. Lee, Park, and others explicitly constructed special points on the KSBA boundary, and proved (using deformation theory) that the local KSBA moduli space is smooth at these points, and that one can find nearby surfaces which are smooth. To compute the fundamental group of the smoothing, one has to look into what happens when the singularity is replaced with the Milnor fiber. In the presence of special curves on the singular surface, one can use Van Kampen’s theorem to compute the fundamental group of the smoothing; see the proof of Theorem 6.2.
$\mathbb{Q}$
-Gorenstein deformation theory, starting with the pioneering work of Lee and Park [Reference Lee and ParkLP07]; see also [Reference Park, Park and ShinPPS09a, Reference Park, Park and ShinPPS09b, Reference Stern and UrzúaSU16]. From the moduli space perspective, the Gieseker moduli space of canonically polarized surfaces with ADE singularities is compactified by the Kollár–Shepherd-Barron–Alexeev (KSBA) moduli space of canonically polarized surfaces with semi log canonical singularities [Reference Kollár and Shepherd-BarronKS88]. We call the complement of the Gieseker space the KSBA boundary. Lee, Park, and others explicitly constructed special points on the KSBA boundary, and proved (using deformation theory) that the local KSBA moduli space is smooth at these points, and that one can find nearby surfaces which are smooth. To compute the fundamental group of the smoothing, one has to look into what happens when the singularity is replaced with the Milnor fiber. In the presence of special curves on the singular surface, one can use Van Kampen’s theorem to compute the fundamental group of the smoothing; see the proof of Theorem 6.2.
Another remarkable surface was found by Craighero and Gattazzo [Reference Craighero and GattazzoCG94]. Their surface
![]() $S$
is the minimal resolution of singularities of an explicit quintic surface (2.1) with four elliptic singularities. This surface has
$S$
is the minimal resolution of singularities of an explicit quintic surface (2.1) with four elliptic singularities. This surface has
![]() $K_{S}^{2}=1$
. It was proved by Dolgachev and Werner [Reference Dolgachev and WernerDW99] that
$K_{S}^{2}=1$
. It was proved by Dolgachev and Werner [Reference Dolgachev and WernerDW99] that
![]() $S$
is canonically polarized and that its algebraic fundamental group (i.e. the profinite completion of the fundamental group) is trivial. In addition, it was proved by Catanese and Pignatelli [Reference Catanese and PignatelliCP00, Theorem 0.31] that the local moduli space of
$S$
is canonically polarized and that its algebraic fundamental group (i.e. the profinite completion of the fundamental group) is trivial. In addition, it was proved by Catanese and Pignatelli [Reference Catanese and PignatelliCP00, Theorem 0.31] that the local moduli space of
![]() $S$
is smooth of dimension eight. It was originally claimed in [Reference Dolgachev and WernerDW99] that
$S$
is smooth of dimension eight. It was originally claimed in [Reference Dolgachev and WernerDW99] that
![]() $S$
is simply connected, but a serious flaw was discovered in the proof; see [Reference Dolgachev and WernerDW99, Erratum].
$S$
is simply connected, but a serious flaw was discovered in the proof; see [Reference Dolgachev and WernerDW99, Erratum].
The goal of this paper is to prove that
![]() $S$
is simply connected using an algebraic reduction mod
$S$
is simply connected using an algebraic reduction mod
![]() $p$
technique and deformation theory. We would like to use the Lee–Park argument involving the Milnor fiber of a
$p$
technique and deformation theory. We would like to use the Lee–Park argument involving the Milnor fiber of a
![]() $\mathbb{Q}$
-Gorenstein deformation and Van Kampen’s theorem. In order to do that, we need a
$\mathbb{Q}$
-Gorenstein deformation and Van Kampen’s theorem. In order to do that, we need a
![]() $\mathbb{Q}$
-Gorenstein family of complex surfaces
$\mathbb{Q}$
-Gorenstein family of complex surfaces
![]() ${\mathcal{S}}\rightarrow U$
over a smooth irreducible complex curve
${\mathcal{S}}\rightarrow U$
over a smooth irreducible complex curve
![]() $U$
, such that one of the fibers is the Craighero–Gattazzo surface
$U$
, such that one of the fibers is the Craighero–Gattazzo surface
![]() $S$
and another fiber is a simply connected surface with a cyclic quotient singularity and containing a special curve configuration needed to prove simply connectedness. However, it is not clear how to explicitly construct a family containing the Craighero–Gattazzo as a fiber because no explicit model of the moduli space is known.
$S$
and another fiber is a simply connected surface with a cyclic quotient singularity and containing a special curve configuration needed to prove simply connectedness. However, it is not clear how to explicitly construct a family containing the Craighero–Gattazzo as a fiber because no explicit model of the moduli space is known.
Our trick is to work out an integral model of the Craighero–Gattazzo surface over a ring of algebraic integers. One obvious model is given by the quintic equation. In an REU (research experience for undergraduates) directed by the first two authors, Charles Boyd discovered that this arithmetic threefold has a non-reduced fiber in characteristic seven, and its local equation has a very special form. Over the complex disc, analogous families of quintic surfaces were studied by the first author in [Reference RanaRan14], where it was proved that the KSBA replacement acquires a
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity in the special fiber. In fact, it is proved in [Reference RanaRan14] that numerical quintic surfaces with a
${\textstyle \frac{1}{4}}(1,1)$
singularity in the special fiber. In fact, it is proved in [Reference RanaRan14] that numerical quintic surfaces with a
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity form a divisor in the KSBA moduli space (and this divisor is explicitly described). The upshot is that, to some degree, it can be hoped that this singularity appears in one-parameter families of surfaces, including families over a ring of algebraic integers. We show that the KSBA limit of
${\textstyle \frac{1}{4}}(1,1)$
singularity form a divisor in the KSBA moduli space (and this divisor is explicitly described). The upshot is that, to some degree, it can be hoped that this singularity appears in one-parameter families of surfaces, including families over a ring of algebraic integers. We show that the KSBA limit of
![]() $S$
over the
$S$
over the
![]() $7$
-adic disc is a surface
$7$
-adic disc is a surface
![]() $S_{0}$
with a
$S_{0}$
with a
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity. We use the word ‘KSBA limit’ somewhat loosely here because existence of the mixed characteristic KSBA moduli space (or even canonical KSBA integral models) is still only conjectural.
${\textstyle \frac{1}{4}}(1,1)$
singularity. We use the word ‘KSBA limit’ somewhat loosely here because existence of the mixed characteristic KSBA moduli space (or even canonical KSBA integral models) is still only conjectural.
The minimal resolution of
![]() $S_{0}$
turns out to be a very special and beautiful Dolgachev surface, i.e. an elliptic fibration over
$S_{0}$
turns out to be a very special and beautiful Dolgachev surface, i.e. an elliptic fibration over
![]() $\mathbb{P}^{1}$
with two multiple fibers, one of multiplicity two and one of multiplicity three. We call it the Boyd surface. By pure luck, it carries a special curve, which, if it were a complex surface, would have allowed us to conclude that the Craighero–Gattazzo surface
$\mathbb{P}^{1}$
with two multiple fibers, one of multiplicity two and one of multiplicity three. We call it the Boyd surface. By pure luck, it carries a special curve, which, if it were a complex surface, would have allowed us to conclude that the Craighero–Gattazzo surface
![]() $S$
is simply connected. Of course our degeneration is over the
$S$
is simply connected. Of course our degeneration is over the
![]() $7$
-adic unit disc, so we can not use Van Kampen’s theorem directly. Our main idea is to use deformation theory to conclude that
$7$
-adic unit disc, so we can not use Van Kampen’s theorem directly. Our main idea is to use deformation theory to conclude that
![]() $S$
admits an analogous (but no longer explicit) degeneration over the complex unit disc to a complex surface
$S$
admits an analogous (but no longer explicit) degeneration over the complex unit disc to a complex surface
![]() $D_{0}$
with a
$D_{0}$
with a
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity such that its minimal resolution is a complex Dolgachev surface analogous to the Boyd surface.
${\textstyle \frac{1}{4}}(1,1)$
singularity such that its minimal resolution is a complex Dolgachev surface analogous to the Boyd surface.
As an application of our construction, we show in Theorem 7.2 that there exist simply connected Dolgachev surfaces (with multiple fibers of multiplicity
![]() $2,3$
) which carry algebraic genus two Lefschetz fibrations, specifically genus two fibrations without multiple components in fibers and such that the only singularities of fibers are nodes. Dolgachev and Werner showed existence of a genus two fibration on the Craighero–Gattazzo surface [Reference Dolgachev and WernerDW99, Proposition 3.2]. If this fibration had only nodal singular fibers, then by combining our theorem that the Craighero–Gattazzo surface is simply connected, we would have the existence of a simply connected numerical Godeaux surface with a genus two Lefschetz fibration. By [Reference FreedmanFre82], these surfaces are homeomorphic to
$2,3$
) which carry algebraic genus two Lefschetz fibrations, specifically genus two fibrations without multiple components in fibers and such that the only singularities of fibers are nodes. Dolgachev and Werner showed existence of a genus two fibration on the Craighero–Gattazzo surface [Reference Dolgachev and WernerDW99, Proposition 3.2]. If this fibration had only nodal singular fibers, then by combining our theorem that the Craighero–Gattazzo surface is simply connected, we would have the existence of a simply connected numerical Godeaux surface with a genus two Lefschetz fibration. By [Reference FreedmanFre82], these surfaces are homeomorphic to
![]() $\mathbb{P}^{2}$
blown-up in nine or eight points, respectively. In the symplectic category, Lefschetz fibrations on knot surgered elliptic surfaces in the homotopy class of
$\mathbb{P}^{2}$
blown-up in nine or eight points, respectively. In the symplectic category, Lefschetz fibrations on knot surgered elliptic surfaces in the homotopy class of
![]() $\mathbb{P}^{2}$
blown-up at nine points were constructed in [Reference Fintushel and SternFS04] and in the homotopy classes of
$\mathbb{P}^{2}$
blown-up at nine points were constructed in [Reference Fintushel and SternFS04] and in the homotopy classes of
![]() $\mathbb{P}^{2}$
blown-up at eight or seven points in [Reference Baykur and KorkmazBK15].
$\mathbb{P}^{2}$
blown-up at eight or seven points in [Reference Baykur and KorkmazBK15].
2 Stable limit of the Craighero–Gattazzo surface in characteristic seven
Let
 $X\subset \mathbb{P}_{\mathbb{C}}^{3}$
be the quintic surface (see Figure 1)
$X\subset \mathbb{P}_{\mathbb{C}}^{3}$
be the quintic surface (see Figure 1)
 $$\begin{eqnarray}\displaystyle & & \displaystyle a^{2}(x^{2}y^{3}+x^{3}t^{2}+y^{2}z^{3}+z^{2}t^{3})+m^{2}(x^{3}z^{2}+x^{2}z^{3}+y^{3}t^{2}+y^{2}t^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,2am(xyz^{3}+xy^{3}t+x^{3}zt+yzt^{3})+14m(x^{3}yz+y^{3}zt+xz^{3}t+xyt^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,7b(x^{2}y^{2}z+y^{2}z^{2}t+x^{2}yt^{2}+xz^{2}t^{2})+14a(xy^{3}z+x^{3}yt+yz^{3}t+xzt^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,c(x^{2}yz^{2}+x^{2}z^{2}t+xy^{2}t^{2}+y^{2}zt^{2})+7e(xy^{2}z^{2}+x^{2}y^{2}t+x^{2}zt^{2}+yz^{2}t^{2})\nonumber\\ \displaystyle & & \displaystyle \quad +\,f(x^{2}yzt+xy^{2}zt+xyz^{2}t+xyzt^{2})+49(x^{3}y^{2}+y^{3}z^{2}+z^{3}t^{2}+x^{2}t^{3})=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a^{2}(x^{2}y^{3}+x^{3}t^{2}+y^{2}z^{3}+z^{2}t^{3})+m^{2}(x^{3}z^{2}+x^{2}z^{3}+y^{3}t^{2}+y^{2}t^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,2am(xyz^{3}+xy^{3}t+x^{3}zt+yzt^{3})+14m(x^{3}yz+y^{3}zt+xz^{3}t+xyt^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,7b(x^{2}y^{2}z+y^{2}z^{2}t+x^{2}yt^{2}+xz^{2}t^{2})+14a(xy^{3}z+x^{3}yt+yz^{3}t+xzt^{3})\nonumber\\ \displaystyle & & \displaystyle \quad +\,c(x^{2}yz^{2}+x^{2}z^{2}t+xy^{2}t^{2}+y^{2}zt^{2})+7e(xy^{2}z^{2}+x^{2}y^{2}t+x^{2}zt^{2}+yz^{2}t^{2})\nonumber\\ \displaystyle & & \displaystyle \quad +\,f(x^{2}yzt+xy^{2}zt+xyz^{2}t+xyzt^{2})+49(x^{3}y^{2}+y^{3}z^{2}+z^{3}t^{2}+x^{2}t^{3})=0.\end{eqnarray}$$

Figure 1. The Craighero–Gattazzo quintic.
The coefficients are (from [Reference Catanese and PignatelliCP00, p. 25], multiplied by
![]() $49$
)
$49$
)
 $$\begin{eqnarray}\displaystyle & \displaystyle a=7r^{2},\quad b=-2r^{2}+13r+18,\quad c=73r^{2}+75r+92, & \displaystyle \nonumber\\ \displaystyle & \displaystyle e=-r^{2}+24r+9,\quad f=181r^{2}+241r+163,\quad m=3r^{2}+5r+1, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a=7r^{2},\quad b=-2r^{2}+13r+18,\quad c=73r^{2}+75r+92, & \displaystyle \nonumber\\ \displaystyle & \displaystyle e=-r^{2}+24r+9,\quad f=181r^{2}+241r+163,\quad m=3r^{2}+5r+1, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $r$
is a complex root of the equation
$r$
is a complex root of the equation
 $$\begin{eqnarray}r^{3}+r^{2}-1=0.\end{eqnarray}$$
$$\begin{eqnarray}r^{3}+r^{2}-1=0.\end{eqnarray}$$
The surface is invariant under the
![]() $\unicode[STIX]{x1D707}_{4}$
action which cyclically permutes the variables as follows:
$\unicode[STIX]{x1D707}_{4}$
action which cyclically permutes the variables as follows:
 $x\rightarrow y\rightarrow z\rightarrow t\rightarrow x$
. It is singular at the points
$x\rightarrow y\rightarrow z\rightarrow t\rightarrow x$
. It is singular at the points
 $$\begin{eqnarray}P_{1}=[1:0:0:0],\quad P_{2}=[0:1:0:0],\quad P_{3}=[0:0:1:0],\quad P_{4}=[0:0:0:1].\end{eqnarray}$$
$$\begin{eqnarray}P_{1}=[1:0:0:0],\quad P_{2}=[0:1:0:0],\quad P_{3}=[0:0:1:0],\quad P_{4}=[0:0:0:1].\end{eqnarray}$$
Its minimal resolution is the Craighero–Gattazzo surface
![]() $S$
. Exceptional divisors over
$S$
. Exceptional divisors over
 $P_{1},\ldots ,P_{4}$
are elliptic curves
$P_{1},\ldots ,P_{4}$
are elliptic curves
 ${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{4}$
such that
${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{4}$
such that
 ${\mathcal{E}}_{i}^{2}=-1$
for each
${\mathcal{E}}_{i}^{2}=-1$
for each
![]() $i$
. These singularities are sometimes called singularities of type
$i$
. These singularities are sometimes called singularities of type
![]() $\tilde{E}_{8}$
.
$\tilde{E}_{8}$
.
Equation (2.1) gives an integral model of
![]() $X$
over
$X$
over
 $\operatorname{Spec}\mathbb{Z}[r]$
. Since
$\operatorname{Spec}\mathbb{Z}[r]$
. Since
![]() $3$
is a simple root of (2.2) in
$3$
is a simple root of (2.2) in
![]() $\mathbb{Z}/(7)$
, by Hensel’s lemma we have a section
$\mathbb{Z}/(7)$
, by Hensel’s lemma we have a section
 $\operatorname{Spec}\mathbb{Z}_{7}\rightarrow \operatorname{Spec}\mathbb{Z}_{7}[r]$
, where
$\operatorname{Spec}\mathbb{Z}_{7}\rightarrow \operatorname{Spec}\mathbb{Z}_{7}[r]$
, where
![]() $\mathbb{Z}_{7}$
is the ring of
$\mathbb{Z}_{7}$
is the ring of
![]() $7$
-adic integers. Pulling back the integral model with respect to the base change
$7$
-adic integers. Pulling back the integral model with respect to the base change
 $\operatorname{Spec}\mathbb{Z}_{7}\rightarrow \operatorname{Spec}\mathbb{Z}_{7}[r]\rightarrow \operatorname{Spec}\mathbb{Z}[r]$
gives the family
$\operatorname{Spec}\mathbb{Z}_{7}\rightarrow \operatorname{Spec}\mathbb{Z}_{7}[r]\rightarrow \operatorname{Spec}\mathbb{Z}[r]$
gives the family
![]() ${\mathcal{X}}$
over
${\mathcal{X}}$
over
 $\operatorname{Spec}\mathbb{Z}_{7}$
. The corresponding root of (2.2) modulo
$\operatorname{Spec}\mathbb{Z}_{7}$
. The corresponding root of (2.2) modulo
![]() $7^{3}$
is equal to
$7^{3}$
is equal to
![]() $143$
and after some manipulations the equation of
$143$
and after some manipulations the equation of
![]() ${\mathcal{X}}$
to the order of
${\mathcal{X}}$
to the order of
![]() $7^{3}$
takes the form
$7^{3}$
takes the form
 $$\begin{eqnarray}f_{1}f_{2}^{2}+7f_{2}f_{3}+7^{2}f_{5}+\text{(higher order terms)},\end{eqnarray}$$
$$\begin{eqnarray}f_{1}f_{2}^{2}+7f_{2}f_{3}+7^{2}f_{5}+\text{(higher order terms)},\end{eqnarray}$$
where
 $f_{1},f_{2},f_{3},f_{5}\in \mathbb{Z}/(7)[x,y,z,t]$
are the following forms (the subscript indicates the degree):
$f_{1},f_{2},f_{3},f_{5}\in \mathbb{Z}/(7)[x,y,z,t]$
are the following forms (the subscript indicates the degree):
 $$\begin{eqnarray}\displaystyle & \displaystyle f_{1}=x+y+z+t, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{2}=xz+yt, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{3}=2(x^{2}y+y^{2}z+z^{2}t+xt^{2})+x^{2}z+xz^{2}+y^{2}t+yt^{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad \qquad -3(xy^{2}+yz^{2}+x^{2}t+zt^{2}+xyz+xyt+xzt+yzt), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}=x+y+z+t, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{2}=xz+yt, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{3}=2(x^{2}y+y^{2}z+z^{2}t+xt^{2})+x^{2}z+xz^{2}+y^{2}t+yt^{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad \qquad -3(xy^{2}+yz^{2}+x^{2}t+zt^{2}+xyz+xyt+xzt+yzt), & \displaystyle \nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle f_{5} & = & \displaystyle x^{3}y^{2}+x^{3}z^{2}+y^{3}z^{2}+x^{2}z^{3}+y^{3}t^{2}+z^{3}t^{2}+x^{2}t^{3}+y^{2}t^{3}\nonumber\\ \displaystyle & & \displaystyle +\,x^{3}yz+y^{3}zt+xz^{3}t+xyt^{3}-xy^{2}z^{2}-x^{2}y^{2}t-x^{2}zt^{2}-yz^{2}t^{2}\nonumber\\ \displaystyle & & \displaystyle -\,x^{2}yzt-xy^{2}zt-xyz^{2}t-xyzt^{2}--3x^{2}y^{3}-3y^{2}z^{3}-3x^{3}t^{2}-3z^{2}t^{3}\nonumber\\ \displaystyle & & \displaystyle -\,2x^{2}y^{2}z-2x^{2}yz^{2}-2x^{2}z^{2}t-2y^{2}z^{2}t-2x^{2}yt^{2}-2xy^{2}t^{2}-2y^{2}zt^{2}-2xz^{2}t^{2}\nonumber\\ \displaystyle & & \displaystyle -\,3xy^{3}z-3x^{3}yt-3yz^{3}t-3xzt^{3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{5} & = & \displaystyle x^{3}y^{2}+x^{3}z^{2}+y^{3}z^{2}+x^{2}z^{3}+y^{3}t^{2}+z^{3}t^{2}+x^{2}t^{3}+y^{2}t^{3}\nonumber\\ \displaystyle & & \displaystyle +\,x^{3}yz+y^{3}zt+xz^{3}t+xyt^{3}-xy^{2}z^{2}-x^{2}y^{2}t-x^{2}zt^{2}-yz^{2}t^{2}\nonumber\\ \displaystyle & & \displaystyle -\,x^{2}yzt-xy^{2}zt-xyz^{2}t-xyzt^{2}--3x^{2}y^{3}-3y^{2}z^{3}-3x^{3}t^{2}-3z^{2}t^{3}\nonumber\\ \displaystyle & & \displaystyle -\,2x^{2}y^{2}z-2x^{2}yz^{2}-2x^{2}z^{2}t-2y^{2}z^{2}t-2x^{2}yt^{2}-2xy^{2}t^{2}-2y^{2}zt^{2}-2xz^{2}t^{2}\nonumber\\ \displaystyle & & \displaystyle -\,3xy^{3}z-3x^{3}yt-3yz^{3}t-3xzt^{3}.\nonumber\end{eqnarray}$$
This expansion shows that the special fiber of
![]() ${\mathcal{X}}$
is the union of the plane
${\mathcal{X}}$
is the union of the plane
 $L=(f_{1}=0)$
and the quadric surface
$L=(f_{1}=0)$
and the quadric surface
 $Q=(f_{2}=0)$
with multiplicity two. In particular, it is not reduced.
$Q=(f_{2}=0)$
with multiplicity two. In particular, it is not reduced.
Let
![]() $k$
be an algebraically closed field of characteristic
$k$
be an algebraically closed field of characteristic
![]() $7$
and let
$7$
and let
![]() ${\mathcal{R}}$
be its ring of Witt vectors. We denote the pull-back of
${\mathcal{R}}$
be its ring of Witt vectors. We denote the pull-back of
![]() ${\mathcal{X}}$
to
${\mathcal{X}}$
to
![]() $\operatorname{Spec}{\mathcal{R}}$
(with respect to the canonical inclusion
$\operatorname{Spec}{\mathcal{R}}$
(with respect to the canonical inclusion
 $\mathbb{Z}_{7}{\hookrightarrow}{\mathcal{R}}$
) by the same letter
$\mathbb{Z}_{7}{\hookrightarrow}{\mathcal{R}}$
) by the same letter
![]() ${\mathcal{X}}$
. We also pullback
${\mathcal{X}}$
. We also pullback
![]() $L$
and
$L$
and
![]() $Q$
to
$Q$
to
![]() $k$
.
$k$
.
We would like to compute the stable limit of the generic fiber of
![]() ${\mathcal{X}}$
. Over the complex disc, stable
${\mathcal{X}}$
. Over the complex disc, stable
![]() $\mathbb{Q}$
-Gorenstein limits of families of the form (2.3) were computed by the first author [Reference RanaRan14], and semi-stable Gorenstein limits of sufficiently general families by Ashikaga and Konno [Reference Ashikaga and KonnoAK91]. In our case the disc is
$\mathbb{Q}$
-Gorenstein limits of families of the form (2.3) were computed by the first author [Reference RanaRan14], and semi-stable Gorenstein limits of sufficiently general families by Ashikaga and Konno [Reference Ashikaga and KonnoAK91]. In our case the disc is
![]() $7$
-adic but the computation is the same. We now describe what the stable limit is, postponing the proof to Lemma 2.4.
$7$
-adic but the computation is the same. We now describe what the stable limit is, postponing the proof to Lemma 2.4.
Let
 $\unicode[STIX]{x1D6E5}=L\cap Q\subset Q\simeq \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
. It is a curve in the linear system
$\unicode[STIX]{x1D6E5}=L\cap Q\subset Q\simeq \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
. It is a curve in the linear system
 $|{\mathcal{O}}(1,1)|$
. The curve
$|{\mathcal{O}}(1,1)|$
. The curve
 $$\begin{eqnarray}Q\cap (f_{3}^{2}-4f_{1}f_{5}=0)\subset \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}\end{eqnarray}$$
$$\begin{eqnarray}Q\cap (f_{3}^{2}-4f_{1}f_{5}=0)\subset \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}\end{eqnarray}$$
is the union of two curves in the linear system
 $|{\mathcal{O}}(3,3)|$
:
$|{\mathcal{O}}(3,3)|$
:
 $$\begin{eqnarray}B_{1}=Q\cap (xy^{2}+3x^{2}z-3y^{2}z+3xz^{2}-3xt^{2}+zt^{2}=0)\end{eqnarray}$$
$$\begin{eqnarray}B_{1}=Q\cap (xy^{2}+3x^{2}z-3y^{2}z+3xz^{2}-3xt^{2}+zt^{2}=0)\end{eqnarray}$$
and
 $$\begin{eqnarray}B_{2}=Q\cap (yz^{2}+3y^{2}t-3z^{2}t+3yt^{2}-3yx^{2}+tx^{2}=0).\end{eqnarray}$$
$$\begin{eqnarray}B_{2}=Q\cap (yz^{2}+3y^{2}t-3z^{2}t+3yt^{2}-3yx^{2}+tx^{2}=0).\end{eqnarray}$$
Figure 2 shows how these curves intersect, where
 $A_{1},\ldots ,A_{4}$
are rulings of
$A_{1},\ldots ,A_{4}$
are rulings of
 $\mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
and
$\mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
and
 $\{Q_{1},Q_{2}\}=\unicode[STIX]{x1D6E5}\cap B_{1}\cap B_{2}$
.
$\{Q_{1},Q_{2}\}=\unicode[STIX]{x1D6E5}\cap B_{1}\cap B_{2}$
.

Figure 2. Data in
 $Q\simeq \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
.
$Q\simeq \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}$
.
Lemma 2.1. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}:Z\rightarrow \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:Z\rightarrow \mathbb{P}_{k}^{1}\times \mathbb{P}_{k}^{1}\end{eqnarray}$$
be the double cover branched along
 $B_{1}\cup B_{2}$
. The surface
$B_{1}\cup B_{2}$
. The surface
![]() $Z$
has four simple elliptic singularities of type
$Z$
has four simple elliptic singularities of type
![]() $\tilde{E}_{8}$
over
$\tilde{E}_{8}$
over
 $P_{1},\ldots ,P_{4}$
, and two
$P_{1},\ldots ,P_{4}$
, and two
![]() $A_{1}$
singularities over
$A_{1}$
singularities over
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
. It is smooth elsewhere.
$Q_{2}$
. It is smooth elsewhere.
Proof. Direct calculation. ◻
We denote the ramification curves in
![]() $Z$
by
$Z$
by
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
, and we denote the singular points of
$B_{2}$
, and we denote the singular points of
![]() $Z$
by the same letters as their images in
$Z$
by the same letters as their images in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Finally,
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Finally,
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6E5})$
is the union of two smooth rational curves:
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6E5})$
is the union of two smooth rational curves:
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
.
$\unicode[STIX]{x1D6E5}_{2}$
.
Unless it causes confusion, we adopt the following convention throughout this paper: we use the same letter to denote an irreducible curve and its proper transform after some birational transformation.
Definition 2.2. We call the minimal resolution
![]() $Y$
of
$Y$
of
![]() $Z$
the Boyd surface.
$Z$
the Boyd surface.
The Boyd surface contains elliptic curves
 $E_{1},\ldots ,E_{4}$
of self-intersection
$E_{1},\ldots ,E_{4}$
of self-intersection
![]() $-1$
(preimages of elliptic singularities of
$-1$
(preimages of elliptic singularities of
![]() $Z$
),
$Z$
),
![]() $(-2)$
-curves
$(-2)$
-curves
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
(preimages of
$N_{2}$
(preimages of
![]() $A_{1}$
singularities of
$A_{1}$
singularities of
![]() $Z$
), and
$Z$
), and
![]() $(-4)$
-curves
$(-4)$
-curves
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
.
$\unicode[STIX]{x1D6E5}_{2}$
.
Definition 2.3. Let
![]() $S_{0}$
be the surface obtained by contracting the
$S_{0}$
be the surface obtained by contracting the
![]() $(-4)$
-curve
$(-4)$
-curve
![]() $\unicode[STIX]{x1D6E5}_{1}$
.
$\unicode[STIX]{x1D6E5}_{1}$
.
Lemma 2.4 (Cf. [Reference RanaRan14]).
There exists a flat family
 $S\rightarrow \operatorname{Spec}{\mathcal{R}}$
with special fiber
$S\rightarrow \operatorname{Spec}{\mathcal{R}}$
with special fiber
![]() $S_{0}$
and generic fiber the Craighero–Gattazzo surface
$S_{0}$
and generic fiber the Craighero–Gattazzo surface
![]() $S$
(after pull-back to
$S$
(after pull-back to
![]() $\mathbb{C}$
). Near the singular point of the special fiber, the family is formally isomorphic to
$\mathbb{C}$
). Near the singular point of the special fiber, the family is formally isomorphic to
 $$\begin{eqnarray}(xy=z^{2}+7)\subset {\textstyle \frac{1}{2}}(1,1,1)_{{\mathcal{R}}}:=\operatorname{Spec}{\mathcal{R}}[x,y,z]^{\unicode[STIX]{x1D707}_{2}},\end{eqnarray}$$
$$\begin{eqnarray}(xy=z^{2}+7)\subset {\textstyle \frac{1}{2}}(1,1,1)_{{\mathcal{R}}}:=\operatorname{Spec}{\mathcal{R}}[x,y,z]^{\unicode[STIX]{x1D707}_{2}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{2}$
acts by
$\unicode[STIX]{x1D707}_{2}$
acts by
 $x\mapsto -x$
,
$x\mapsto -x$
,
 $y\mapsto -y$
,
$y\mapsto -y$
,
 $z\mapsto -z$
.
$z\mapsto -z$
.
Proof. We first produce the stable limit of the Craighero–Gattazzo quintic
![]() $X$
in characteristic seven. Let
$X$
in characteristic seven. Let
![]() ${\mathcal{X}}^{0}$
be the generic fiber of
${\mathcal{X}}^{0}$
be the generic fiber of
![]() ${\mathcal{X}}$
given by (2.3). Consider the family
${\mathcal{X}}$
given by (2.3). Consider the family
 $\hat{{\mathcal{X}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
given by equations
$\hat{{\mathcal{X}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
given by equations
 $$\begin{eqnarray}(f_{1}w^{2}+f_{3}w+f_{5}+\text{h.o.t.}=0,\;f_{2}=7w)\subset \mathbb{P}_{[x:y:z:t:w]}^{4}(1,1,1,1,2)_{{\mathcal{R}}}\end{eqnarray}$$
$$\begin{eqnarray}(f_{1}w^{2}+f_{3}w+f_{5}+\text{h.o.t.}=0,\;f_{2}=7w)\subset \mathbb{P}_{[x:y:z:t:w]}^{4}(1,1,1,1,2)_{{\mathcal{R}}}\end{eqnarray}$$
obtained by substituting
![]() $f_{2}$
for
$f_{2}$
for
![]() $7w$
in the first three terms of (2.3) and dividing by
$7w$
in the first three terms of (2.3) and dividing by
![]() $343$
. Here, and throughout, ‘h.o.t.’ refers to higher-order terms with respect to the
$343$
. Here, and throughout, ‘h.o.t.’ refers to higher-order terms with respect to the
![]() $7$
-adic valuation. The generic fiber of
$7$
-adic valuation. The generic fiber of
![]() $\hat{{\mathcal{X}}}$
is clearly isomorphic to
$\hat{{\mathcal{X}}}$
is clearly isomorphic to
![]() ${\mathcal{X}}^{0}$
.
${\mathcal{X}}^{0}$
.
The special fiber
![]() $\hat{{\mathcal{X}}}_{0}$
is given by
$\hat{{\mathcal{X}}}_{0}$
is given by
 $$\begin{eqnarray}(f_{1}w^{2}+f_{3}w+f_{5}=0,\;f_{2}=0)\subset \mathbb{P}_{[x:y:z:t:w]}^{4}(1,1,1,1,2)_{k}.\end{eqnarray}$$
$$\begin{eqnarray}(f_{1}w^{2}+f_{3}w+f_{5}=0,\;f_{2}=0)\subset \mathbb{P}_{[x:y:z:t:w]}^{4}(1,1,1,1,2)_{k}.\end{eqnarray}$$
We claim that it is isomorphic to the surface
![]() $Z^{\prime }$
obtained by blowing down four elliptic
$Z^{\prime }$
obtained by blowing down four elliptic
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $S_{0}$
to
$S_{0}$
to
![]() $\tilde{E}_{8}$
-singularities.
$\tilde{E}_{8}$
-singularities.
The point
 $(0:0:0:0:1)$
is an isolated singularity with equation, in a local chart,
$(0:0:0:0:1)$
is an isolated singularity with equation, in a local chart,
 $$\begin{eqnarray}(f_{1}+f_{3}+f_{5}=0,\;f_{2}=0)\subset {\textstyle \frac{1}{2}}(1,1,1,1).\end{eqnarray}$$
$$\begin{eqnarray}(f_{1}+f_{3}+f_{5}=0,\;f_{2}=0)\subset {\textstyle \frac{1}{2}}(1,1,1,1).\end{eqnarray}$$
The singularity is formally isomorphic to
 $$\begin{eqnarray}(xy=z^{2})\subset {\textstyle \frac{1}{2}}(1,1,1)_{k},\end{eqnarray}$$
$$\begin{eqnarray}(xy=z^{2})\subset {\textstyle \frac{1}{2}}(1,1,1)_{k},\end{eqnarray}$$
which has a
![]() $(-4)$
-curve as the resolution graph. Moreover, the equation of the whole family
$(-4)$
-curve as the resolution graph. Moreover, the equation of the whole family
![]() $\hat{{\mathcal{X}}}$
near this point is formally isomorphic to
$\hat{{\mathcal{X}}}$
near this point is formally isomorphic to
 $$\begin{eqnarray}(xy=z^{2}+7)\subset {\textstyle \frac{1}{2}}(1,1,1)_{{\mathcal{R}}}.\end{eqnarray}$$
$$\begin{eqnarray}(xy=z^{2}+7)\subset {\textstyle \frac{1}{2}}(1,1,1)_{{\mathcal{R}}}.\end{eqnarray}$$
Next we analyze
![]() $\hat{{\mathcal{X}}}_{0}$
away from
$\hat{{\mathcal{X}}}_{0}$
away from
 $t_{0}=(0:0:0:0:1)$
. We use the generically two-to-one map
$t_{0}=(0:0:0:0:1)$
. We use the generically two-to-one map
 $\unicode[STIX]{x1D70B}:S_{0}\setminus \{t_{0}\}\rightarrow Q$
given by
$\unicode[STIX]{x1D70B}:S_{0}\setminus \{t_{0}\}\rightarrow Q$
given by
 $[x:y:z:t:w]\rightarrow [x:y:z:t]$
. Away from
$[x:y:z:t:w]\rightarrow [x:y:z:t]$
. Away from
 $\unicode[STIX]{x1D6E5}=L\cap Q$
,
$\unicode[STIX]{x1D6E5}=L\cap Q$
,
![]() $\unicode[STIX]{x1D70B}$
is a double cover branched along
$\unicode[STIX]{x1D70B}$
is a double cover branched along
 $(f_{3}^{2}-4f_{1}f_{5}=0)=B_{1}\cup B_{2}$
. Thus, it can be identified with
$(f_{3}^{2}-4f_{1}f_{5}=0)=B_{1}\cup B_{2}$
. Thus, it can be identified with
 $Z^{\prime }\setminus (\unicode[STIX]{x1D6E5}_{2}\cup N_{1}\cup N_{2})$
. Over
$Z^{\prime }\setminus (\unicode[STIX]{x1D6E5}_{2}\cup N_{1}\cup N_{2})$
. Over
![]() $\unicode[STIX]{x1D6E5}$
, but away from
$\unicode[STIX]{x1D6E5}$
, but away from
![]() $t_{0}$
(which includes
$t_{0}$
(which includes
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
) the map
$Q_{2}$
) the map
![]() $\unicode[STIX]{x1D70B}$
is one-to-one. The preimages of
$\unicode[STIX]{x1D70B}$
is one-to-one. The preimages of
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
are lines (with coordinate
$Q_{2}$
are lines (with coordinate
![]() $w$
). The preimages of the other four points where
$w$
). The preimages of the other four points where
![]() $f_{3}=0$
are empty; in Figure 2 these are the points where
$f_{3}=0$
are empty; in Figure 2 these are the points where
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are tangent to
$B_{2}$
are tangent to
![]() $\unicode[STIX]{x1D6E5}$
. It follows that
$\unicode[STIX]{x1D6E5}$
. It follows that
![]() $\hat{{\mathcal{X}}}_{0}$
and
$\hat{{\mathcal{X}}}_{0}$
and
![]() $Z^{\prime }$
are normal surfaces isomorphic in codimension one, and therefore isomorphic.
$Z^{\prime }$
are normal surfaces isomorphic in codimension one, and therefore isomorphic.
It remains to note that the family
![]() $\hat{{\mathcal{X}}}$
has
$\hat{{\mathcal{X}}}$
has
![]() $\tilde{E}_{8}$
singularities along the sections
$\tilde{E}_{8}$
singularities along the sections
 $(1:0:0:0:0)$
,
$(1:0:0:0:0)$
,
 $(0:1:0:0:0)$
,
$(0:1:0:0:0)$
,
 $(0:0:1:0:0)$
, and
$(0:0:1:0:0)$
, and
 $(0:0:0:1:0)$
. Resolving them gives a family
$(0:0:0:1:0)$
. Resolving them gives a family
 ${\mathcal{S}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with special fiber
${\mathcal{S}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with special fiber
![]() $S_{0}$
and generic fiber (after pulling back to
$S_{0}$
and generic fiber (after pulling back to
![]() $\operatorname{Spec}\mathbb{C}$
) the Craighero–Gattazzo surface
$\operatorname{Spec}\mathbb{C}$
) the Craighero–Gattazzo surface
![]() $S$
.◻
$S$
.◻
3 Study of the Boyd surface: vanishing of obstructions
We have a commutative diagram,

where the vertical maps are double covers and the horizontal maps are birational. Here
![]() $\mathbb{P}$
is obtained by blowing up
$\mathbb{P}$
is obtained by blowing up
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
(let
$Q_{2}$
(let
![]() $\bar{N}_{1}$
and
$\bar{N}_{1}$
and
![]() $\bar{N}_{2}$
be the exceptional divisors), blowing up
$\bar{N}_{2}$
be the exceptional divisors), blowing up
 $P_{1},\ldots ,P_{4}$
(let
$P_{1},\ldots ,P_{4}$
(let
 $\bar{G}_{1},\ldots ,\bar{G}_{4}$
be the exceptional divisors), and then blowing up these four points again in the direction of the tangent cone to
$\bar{G}_{1},\ldots ,\bar{G}_{4}$
be the exceptional divisors), and then blowing up these four points again in the direction of the tangent cone to
 $B_{1}\cup B_{2}$
(let
$B_{1}\cup B_{2}$
(let
 $\bar{E}_{1},\ldots ,\bar{E}_{4}$
be the exceptional divisors).
$\bar{E}_{1},\ldots ,\bar{E}_{4}$
be the exceptional divisors).
Since
 $$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 6\unicode[STIX]{x1D70E}^{\ast }({\mathcal{O}}_{Q}(1,1))-3\mathop{\sum }_{i=1}^{4}\bar{G}_{i}-6\mathop{\sum }_{i=1}^{4}\bar{E}_{i},\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 6\unicode[STIX]{x1D70E}^{\ast }({\mathcal{O}}_{Q}(1,1))-3\mathop{\sum }_{i=1}^{4}\bar{G}_{i}-6\mathop{\sum }_{i=1}^{4}\bar{E}_{i},\end{eqnarray}$$
we have
 $$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 3\biggl(\mathop{\sum }_{i=1}^{4}A_{i}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 3\biggl(\mathop{\sum }_{i=1}^{4}A_{i}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr)\end{eqnarray}$$
as well as
 $$\begin{eqnarray}B_{1}+B_{2}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\sim 2\biggl(3\unicode[STIX]{x1D70E}^{\ast }({\mathcal{O}}_{Q}(1,1))-\bar{N}_{1}-\bar{N}_{2}-3\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\sim 2\biggl(3\unicode[STIX]{x1D70E}^{\ast }({\mathcal{O}}_{Q}(1,1))-\bar{N}_{1}-\bar{N}_{2}-3\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr).\end{eqnarray}$$
We define
![]() $W$
to be the double cover of
$W$
to be the double cover of
![]() $\mathbb{P}$
branched along the smooth curve
$\mathbb{P}$
branched along the smooth curve
 $$\begin{eqnarray}B=B_{1}+B_{2}+\bar{G}_{1}+\cdots +\bar{G}_{4}.\end{eqnarray}$$
$$\begin{eqnarray}B=B_{1}+B_{2}+\bar{G}_{1}+\cdots +\bar{G}_{4}.\end{eqnarray}$$
Let
 $N_{i},E_{i},G_{i}\subset W$
be the preimages of
$N_{i},E_{i},G_{i}\subset W$
be the preimages of
 $\bar{N}_{i},\bar{E}_{i},\bar{G}_{i}$
, respectively. The curves
$\bar{N}_{i},\bar{E}_{i},\bar{G}_{i}$
, respectively. The curves
 $G_{1},\ldots ,G_{4}$
are
$G_{1},\ldots ,G_{4}$
are
![]() $(-1)$
-curves, and contracting them gives the Boyd surface
$(-1)$
-curves, and contracting them gives the Boyd surface
![]() $Y$
. The curves
$Y$
. The curves
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
are
$N_{2}$
are
![]() $(-2)$
-curves on
$(-2)$
-curves on
![]() $Y$
, while
$Y$
, while
 $E_{1},\ldots ,E_{4}$
are elliptic
$E_{1},\ldots ,E_{4}$
are elliptic
![]() $(-1)$
-curves (i.e. elliptic curves with self-intersection
$(-1)$
-curves (i.e. elliptic curves with self-intersection
![]() $-1$
).
$-1$
).
Theorem 3.1. We have
 $H^{2}(Y,T_{Y}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))=0$
.
$H^{2}(Y,T_{Y}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))=0$
.
Proof. We follow [Reference RanaRan14, 4.8, 4.10] closely. It suffices to show that
 $$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))=0.\end{eqnarray}$$
Indeed, if this is the case, then Serre duality implies
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle H^{0}(W,\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K_{W}))\nonumber\\ \displaystyle & = & \displaystyle H^{0}(Y,\unicode[STIX]{x1D70F}_{\ast }[\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(G_{1}+\cdots +G_{4})](K_{Y}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle H^{0}(W,\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K_{W}))\nonumber\\ \displaystyle & = & \displaystyle H^{0}(Y,\unicode[STIX]{x1D70F}_{\ast }[\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(G_{1}+\cdots +G_{4})](K_{Y}))\nonumber\end{eqnarray}$$
(by Lemma 3.3)
 $$\begin{eqnarray}=H^{0}(Y,\unicode[STIX]{x1D6FA}_{Y}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K_{Y}))=H^{2}(Y,T_{Y}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}=H^{0}(Y,\unicode[STIX]{x1D6FA}_{Y}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K_{Y}))=H^{2}(Y,T_{Y}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+N_{1})))^{\vee }.\end{eqnarray}$$
Arguing as in [Reference RanaRan14, 4.8], (3.3) will follow if we can show that
 $$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{-}=0,\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{-}=0,\end{eqnarray}$$
and
 $$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(N_{1})))_{+}=0,\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(N_{1})))_{+}=0,\end{eqnarray}$$
where
![]() $+/-$
denotes the symmetric/skew-symmetric part with respect to the
$+/-$
denotes the symmetric/skew-symmetric part with respect to the
![]() $\unicode[STIX]{x1D707}_{2}$
-action on the double cover. Explicitly, and using Serre duality multiple times, if
$\unicode[STIX]{x1D707}_{2}$
-action on the double cover. Explicitly, and using Serre duality multiple times, if
 $\unicode[STIX]{x1D6FC}\in H^{0}(W,\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K))$
, then since
$\unicode[STIX]{x1D6FC}\in H^{0}(W,\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K))$
, then since
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K)\subset \unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))(K)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+N_{1}))(K)\subset \unicode[STIX]{x1D6FA}_{W}^{1}(\log (\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))(K)\end{eqnarray}$$
the one-form
![]() $\unicode[STIX]{x1D6FC}$
must be invariant. But
$\unicode[STIX]{x1D6FC}$
must be invariant. But
![]() $\unicode[STIX]{x1D707}_{2}$
interchanges
$\unicode[STIX]{x1D707}_{2}$
interchanges
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
, so that
$\unicode[STIX]{x1D6E5}_{2}$
, so that
![]() $\unicode[STIX]{x1D6FC}$
does not have a pole along
$\unicode[STIX]{x1D6FC}$
does not have a pole along
![]() $\unicode[STIX]{x1D6E5}_{1}$
. Thus,
$\unicode[STIX]{x1D6E5}_{1}$
. Thus,
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}_{W}^{1}(\log N_{1})(K)$
is an invariant one-form. Equation (3.5) implies that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}_{W}^{1}(\log N_{1})(K)$
is an invariant one-form. Equation (3.5) implies that
![]() $\unicode[STIX]{x1D6FC}=0$
.
$\unicode[STIX]{x1D6FC}=0$
.
Proof of (3.4).
At each of the points
 $Q_{3},\ldots ,Q_{6}$
(the remaining points of
$Q_{3},\ldots ,Q_{6}$
(the remaining points of
![]() $B_{i}\cap \unicode[STIX]{x1D6E5}$
) we blowup twice to obtain a surface
$B_{i}\cap \unicode[STIX]{x1D6E5}$
) we blowup twice to obtain a surface
![]() $\mathbb{P}_{1}$
where
$\mathbb{P}_{1}$
where
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $B_{i}$
have normal crossings. Let
$B_{i}$
have normal crossings. Let
![]() $\bar{C}_{i}$
,
$\bar{C}_{i}$
,
![]() $\bar{F}_{i}$
,
$\bar{F}_{i}$
,
 $i=3,\ldots ,6$
be the exceptional divisors of these blowups, so that on
$i=3,\ldots ,6$
be the exceptional divisors of these blowups, so that on
![]() $\mathbb{P}_{1}$
we have
$\mathbb{P}_{1}$
we have
 $\bar{C}_{i}^{2}=-2$
and
$\bar{C}_{i}^{2}=-2$
and
 $\bar{F}_{i}^{2}=-1$
. Let
$\bar{F}_{i}^{2}=-1$
. Let
 $\unicode[STIX]{x1D70E}^{\prime }:\mathbb{P}_{1}\rightarrow Q$
be the composition of these blowups, and let
$\unicode[STIX]{x1D70E}^{\prime }:\mathbb{P}_{1}\rightarrow Q$
be the composition of these blowups, and let
 $f:W_{1}\rightarrow \mathbb{P}_{1}$
be the double cover branched over
$f:W_{1}\rightarrow \mathbb{P}_{1}$
be the double cover branched over
 $B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}$
.
$B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}$
.
The surface
![]() $W_{1}$
contains
$W_{1}$
contains
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $C_{i}$
and
$C_{i}$
and
![]() $(-2)$
-curves
$(-2)$
-curves
![]() $F_{i}$
which contract to give the surface
$F_{i}$
which contract to give the surface
![]() $W$
. By the
$W$
. By the
![]() $(-1)$
- and
$(-1)$
- and
![]() $(-2)$
-curve principles [Reference Park, Shin and UrzúaPSU13, Proposition 4.3, Theorem 4.4] (here we only need the
$(-2)$
-curve principles [Reference Park, Shin and UrzúaPSU13, Proposition 4.3, Theorem 4.4] (here we only need the
![]() $(-1)$
-curve principle), we have
$(-1)$
-curve principle), we have
 $$\begin{eqnarray}H^{2}(W_{1},T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))\simeq H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))).\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(W_{1},T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))\simeq H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))).\end{eqnarray}$$
Note that the double cover
![]() $f$
is defined by (see (3.2))
$f$
is defined by (see (3.2))
 $$\begin{eqnarray}B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}\sim 2L,\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}\sim 2L,\end{eqnarray}$$
where
 $$\begin{eqnarray}L\sim 3{\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{G}_{i}-3\sum \bar{E}_{i}-\sum \bar{N}_{i}-\sum \bar{F}_{i}.\end{eqnarray}$$
$$\begin{eqnarray}L\sim 3{\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{G}_{i}-3\sum \bar{E}_{i}-\sum \bar{N}_{i}-\sum \bar{F}_{i}.\end{eqnarray}$$
Also we have
 $$\begin{eqnarray}K_{\mathbb{P}_{1}}=-2{\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i}+\sum \bar{C}_{i}+2\sum \bar{F}_{i},\end{eqnarray}$$
$$\begin{eqnarray}K_{\mathbb{P}_{1}}=-2{\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i}+\sum \bar{C}_{i}+2\sum \bar{F}_{i},\end{eqnarray}$$
and so
 $$\begin{eqnarray}K_{\mathbb{P}_{1}}+L\sim {\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}.\end{eqnarray}$$
$$\begin{eqnarray}K_{\mathbb{P}_{1}}+L\sim {\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}.\end{eqnarray}$$
By Lemma 3.2, we have
 $$\begin{eqnarray}f_{\ast }(T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{-}=T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+\bar{N}_{1}))(-L).\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }(T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{-}=T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+\bar{N}_{1}))(-L).\end{eqnarray}$$
By Serre duality, it suffices to prove vanishing of
 $$\begin{eqnarray}H^{0}(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))(K_{\mathbb{P}_{1}}+L)),\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))(K_{\mathbb{P}_{1}}+L)),\end{eqnarray}$$
or
 $$\begin{eqnarray}H^{0}\biggl(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))\biggl({\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}\biggl(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))\biggl({\unicode[STIX]{x1D70E}^{\prime }}^{\ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr).\end{eqnarray}$$
By Lemma 3.3, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))\biggl(\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \subset \unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\biggl(\unicode[STIX]{x1D6E5}+\bar{N}_{1}+\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\biggl(\unicode[STIX]{x1D70E}^{\prime \ast }(\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\bar{N}_{2}-\sum \bar{E}_{i}-\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \subset \unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)\otimes {\mathcal{I}}_{Q_{2}}\bigotimes _{i=1}^{4}{\mathcal{I}}_{P_{i}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}(\log (\unicode[STIX]{x1D6E5}+\bar{N}_{1}))\biggl(\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \subset \unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\biggl(\unicode[STIX]{x1D6E5}+\bar{N}_{1}+\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}_{\ast }^{\prime }\biggl(\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\biggl(\unicode[STIX]{x1D70E}^{\prime \ast }(\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D70E}^{\prime \ast }({\mathcal{O}}_{Q}(1,1))-\bar{N}_{2}-\sum \bar{E}_{i}-\sum \bar{F}_{i}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \subset \unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)\otimes {\mathcal{I}}_{Q_{2}}\bigotimes _{i=1}^{4}{\mathcal{I}}_{P_{i}}.\nonumber\end{eqnarray}$$
Since
 $\unicode[STIX]{x1D6FA}_{Q}^{1}={\mathcal{O}}_{Q}(-2,0)\oplus {\mathcal{O}}_{Q}(0,-2)$
, we have
$\unicode[STIX]{x1D6FA}_{Q}^{1}={\mathcal{O}}_{Q}(-2,0)\oplus {\mathcal{O}}_{Q}(0,-2)$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)={\mathcal{O}}_{Q}(0,2)\oplus {\mathcal{O}}_{Q}(2,0).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)={\mathcal{O}}_{Q}(0,2)\oplus {\mathcal{O}}_{Q}(2,0).\end{eqnarray}$$
Thus, any global section of
 $\unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)\otimes {\mathcal{I}}_{Q_{2}}\bigotimes _{i=1}^{4}{\mathcal{I}}_{P_{i}}$
is a global section of
$\unicode[STIX]{x1D6FA}_{Q}^{1}\otimes {\mathcal{O}}_{Q}(2,2)\otimes {\mathcal{I}}_{Q_{2}}\bigotimes _{i=1}^{4}{\mathcal{I}}_{P_{i}}$
is a global section of
 ${\mathcal{O}}_{Q}(0,2)\oplus {\mathcal{O}}_{Q}(2,0)$
vanishing at the points
${\mathcal{O}}_{Q}(0,2)\oplus {\mathcal{O}}_{Q}(2,0)$
vanishing at the points
 $Q_{2},P_{1},\ldots ,P_{4}$
. Since these points are in three distinct horizontal and vertical fibers of
$Q_{2},P_{1},\ldots ,P_{4}$
. Since these points are in three distinct horizontal and vertical fibers of
![]() $Q$
, any such global section must be zero. This completes the proof of (3.4).
$Q$
, any such global section must be zero. This completes the proof of (3.4).
Lemma 3.2. Let
![]() $Y$
be a smooth projective surface defined over an algebraically closed field of characteristic
$Y$
be a smooth projective surface defined over an algebraically closed field of characteristic
![]() $\neq 2$
. Let
$\neq 2$
. Let
 $f:X\rightarrow Y$
be a double cover with a smooth branch divisor
$f:X\rightarrow Y$
be a double cover with a smooth branch divisor
![]() $B\subset Y$
. Let
$B\subset Y$
. Let
 $C=f^{-1}(D)$
be the preimage of a smooth curve
$C=f^{-1}(D)$
be the preimage of a smooth curve
![]() $D$
on
$D$
on
![]() $Y$
, and suppose that
$Y$
, and suppose that
![]() $D$
intersects
$D$
intersects
![]() $B$
transversally. Then
$B$
transversally. Then
 $$\begin{eqnarray}f_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(\log C))=\unicode[STIX]{x1D6FA}_{Y}^{1}(\log (D))\oplus \unicode[STIX]{x1D6FA}_{Y}^{1}(\log (D+B))(-L)\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(\log C))=\unicode[STIX]{x1D6FA}_{Y}^{1}(\log (D))\oplus \unicode[STIX]{x1D6FA}_{Y}^{1}(\log (D+B))(-L)\end{eqnarray}$$
and
 $$\begin{eqnarray}f_{\ast }(T_{X}(-\text{log}\,C))=T_{Y}(-\text{log}(D+B))\oplus T_{Y}(-\text{log}(D))(-L),\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }(T_{X}(-\text{log}\,C))=T_{Y}(-\text{log}(D+B))\oplus T_{Y}(-\text{log}(D))(-L),\end{eqnarray}$$
where
 $B\sim 2L$
. Moreover, these decompositions break the sheaves into their invariant and anti-invariant subspaces under the action of
$B\sim 2L$
. Moreover, these decompositions break the sheaves into their invariant and anti-invariant subspaces under the action of
![]() $\unicode[STIX]{x1D707}_{2}$
by deck transformations.
$\unicode[STIX]{x1D707}_{2}$
by deck transformations.
Proof. The surface
![]() $X$
is defined in the total space of the line bundle
$X$
is defined in the total space of the line bundle
![]() $L$
by the equation
$L$
by the equation
![]() $z^{2}=x$
where
$z^{2}=x$
where
![]() $x$
is a global section of
$x$
is a global section of
 ${\mathcal{O}}_{Y}(2L)$
. This allows us to work étale-locally, using the argument of [Reference RanaRan14, 4.6].◻
${\mathcal{O}}_{Y}(2L)$
. This allows us to work étale-locally, using the argument of [Reference RanaRan14, 4.6].◻
Lemma 3.3. Let
![]() $Y$
be a smooth projective surface defined over an algebraically closed field. Let
$Y$
be a smooth projective surface defined over an algebraically closed field. Let
 $\unicode[STIX]{x1D70E}:X\rightarrow Y$
be the blowup of
$\unicode[STIX]{x1D70E}:X\rightarrow Y$
be the blowup of
![]() $p\in Y$
with exceptional divisor
$p\in Y$
with exceptional divisor
![]() $E$
. Then for every integer
$E$
. Then for every integer
![]() $m\geqslant 0$
, we have
$m\geqslant 0$
, we have
 $\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))=\unicode[STIX]{x1D6FA}_{Y}^{1}$
. Moreover,
$\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))=\unicode[STIX]{x1D6FA}_{Y}^{1}$
. Moreover,
 $\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(-E))=\unicode[STIX]{x1D6FA}_{Y}^{1}\otimes {\mathcal{I}}_{p}$
, where
$\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(-E))=\unicode[STIX]{x1D6FA}_{Y}^{1}\otimes {\mathcal{I}}_{p}$
, where
![]() ${\mathcal{I}}_{p}$
is the ideal sheaf of the point
${\mathcal{I}}_{p}$
is the ideal sheaf of the point
![]() $p$
.
$p$
.
Proof. Let
![]() $\unicode[STIX]{x1D702}$
be the generic point of
$\unicode[STIX]{x1D702}$
be the generic point of
![]() $Y$
. The sheaves
$Y$
. The sheaves
 $\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))$
and
$\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))$
and
![]() $\unicode[STIX]{x1D6FA}_{Y}^{1}$
are subsheaves of the constant sheaf with stalk
$\unicode[STIX]{x1D6FA}_{Y}^{1}$
are subsheaves of the constant sheaf with stalk
![]() $\unicode[STIX]{x1D6FA}_{Y,\unicode[STIX]{x1D702}}^{1}$
(the sheaf of rational differentials). A local section of
$\unicode[STIX]{x1D6FA}_{Y,\unicode[STIX]{x1D702}}^{1}$
(the sheaf of rational differentials). A local section of
 $\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))$
is regular outside of
$\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))$
is regular outside of
![]() $p$
and therefore regular at
$p$
and therefore regular at
![]() $p$
since
$p$
since
![]() $\unicode[STIX]{x1D6FA}_{Y}^{1}$
is locally free. Thus, we have an injective map
$\unicode[STIX]{x1D6FA}_{Y}^{1}$
is locally free. Thus, we have an injective map
 $i:\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))\rightarrow \unicode[STIX]{x1D6FA}_{Y}^{1}$
. It is surjective because given a local
$i:\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(mE))\rightarrow \unicode[STIX]{x1D6FA}_{Y}^{1}$
. It is surjective because given a local
![]() $1$
-form
$1$
-form
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}_{Y}^{1}(U)$
, the
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FA}_{Y}^{1}(U)$
, the
![]() $1$
-form
$1$
-form
 $\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FC})\in \unicode[STIX]{x1D6FA}_{X}^{1}(\unicode[STIX]{x1D70E}^{-1}(U))\subset \unicode[STIX]{x1D6FA}_{X}^{1}(mE)(\unicode[STIX]{x1D70E}^{-1}(U))$
maps to
$\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6FC})\in \unicode[STIX]{x1D6FA}_{X}^{1}(\unicode[STIX]{x1D70E}^{-1}(U))\subset \unicode[STIX]{x1D6FA}_{X}^{1}(mE)(\unicode[STIX]{x1D70E}^{-1}(U))$
maps to
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
For the second part, we have an injective map
 $i:\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(-E))\rightarrow \unicode[STIX]{x1D6FA}_{Y}^{1}$
, as above. Moreover, any one-form
$i:\unicode[STIX]{x1D70E}_{\ast }(\unicode[STIX]{x1D6FA}_{X}^{1}(-E))\rightarrow \unicode[STIX]{x1D6FA}_{Y}^{1}$
, as above. Moreover, any one-form
![]() $i(\unicode[STIX]{x1D6FC})$
in the image of
$i(\unicode[STIX]{x1D6FC})$
in the image of
![]() $i$
vanishes at
$i$
vanishes at
![]() $p$
, since
$p$
, since
![]() $\unicode[STIX]{x1D6FC}$
vanishes along
$\unicode[STIX]{x1D6FC}$
vanishes along
![]() $E$
. Thus, the image of
$E$
. Thus, the image of
![]() $i$
is the sheaf
$i$
is the sheaf
 $\unicode[STIX]{x1D6FA}_{Y}^{1}\otimes {\mathcal{I}}_{p}$
.◻
$\unicode[STIX]{x1D6FA}_{Y}^{1}\otimes {\mathcal{I}}_{p}$
.◻
Proof of (3.5). Note that we have the short exact sequence
 $$\begin{eqnarray}0\rightarrow T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))\rightarrow T_{W}(-\text{log},N_{1})\rightarrow {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{1}/W}\oplus {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{2}/W}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1}))\rightarrow T_{W}(-\text{log},N_{1})\rightarrow {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{1}/W}\oplus {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{2}/W}\rightarrow 0.\end{eqnarray}$$
Since
 $H^{2}(W,{\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{1}/W}\oplus {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{2}/W})=0$
, it suffices to prove that
$H^{2}(W,{\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{1}/W}\oplus {\mathcal{N}}_{\unicode[STIX]{x1D6E5}_{2}/W})=0$
, it suffices to prove that
 $$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{+}=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(W,T_{W}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{+}=0.\end{eqnarray}$$
This part is more delicate and the proof occupies the rest of the section.
By Lemma 3.2, we have
 $$\begin{eqnarray}f_{\ast }(T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{+}=T_{\mathbb{P}_{1}}\biggl(-\text{log}\biggl(\unicode[STIX]{x1D6E5}+\bar{N}_{1}+B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }(T_{W_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+N_{1})))_{+}=T_{\mathbb{P}_{1}}\biggl(-\text{log}\biggl(\unicode[STIX]{x1D6E5}+\bar{N}_{1}+B_{1}+B_{2}+\sum \bar{G}_{i}+\sum \bar{C}_{i}\biggr)\biggr).\end{eqnarray}$$
Again applying the
![]() $(-1)$
and
$(-1)$
and
![]() $(-2)$
-curve principles, it suffices to show that
$(-2)$
-curve principles, it suffices to show that
 $$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))=0.\end{eqnarray}$$
To begin with, we claim that
 $$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))=0.\end{eqnarray}$$
Because
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
have simple normal crossings after contracting the curves
$B_{2}$
have simple normal crossings after contracting the curves
![]() $\bar{C}_{i}$
and
$\bar{C}_{i}$
and
![]() $\bar{F}_{i}$
, it suffices to show that
$\bar{F}_{i}$
, it suffices to show that
 $$\begin{eqnarray}H^{2}(\mathbb{P},T_{\mathbb{ P}}(-\text{log}(B_{1}+B_{2})))=0\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{P},T_{\mathbb{ P}}(-\text{log}(B_{1}+B_{2})))=0\end{eqnarray}$$
or equivalently (by Serre duality)
 $$\begin{eqnarray}H^{0}\biggl(\mathbb{P},\unicode[STIX]{x1D6FA}_{\mathbb{ P}}^{1}(\log (B_{1}+B_{2}))\biggl(-2D+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i}\biggr)\biggr)=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{0}\biggl(\mathbb{P},\unicode[STIX]{x1D6FA}_{\mathbb{ P}}^{1}(\log (B_{1}+B_{2}))\biggl(-2D+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i}\biggr)\biggr)=0.\end{eqnarray}$$
Letting
 ${\mathcal{F}}={\mathcal{O}}_{\mathbb{P}}(-2D+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i})$
, we have the short exact sequence
${\mathcal{F}}={\mathcal{O}}_{\mathbb{P}}(-2D+\sum \bar{N}_{i}+\sum \bar{G}_{i}+2\sum \bar{E}_{i})$
, we have the short exact sequence
 $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\otimes {\mathcal{F}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{ P}}^{1}(\log (B_{1}+B_{2}))\otimes {\mathcal{F}}\rightarrow ({\mathcal{O}}_{B_{1}}\oplus {\mathcal{O}}_{B_{2}})\otimes {\mathcal{F}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\otimes {\mathcal{F}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{ P}}^{1}(\log (B_{1}+B_{2}))\otimes {\mathcal{F}}\rightarrow ({\mathcal{O}}_{B_{1}}\oplus {\mathcal{O}}_{B_{2}})\otimes {\mathcal{F}}\rightarrow 0.\end{eqnarray}$$
The products
 $B_{j}\cdot {\mathcal{F}}=-4<0$
for
$B_{j}\cdot {\mathcal{F}}=-4<0$
for
 $j=1,2$
and thus
$j=1,2$
and thus
 $$\begin{eqnarray}H^{0}(({\mathcal{O}}_{B_{1}}\oplus {\mathcal{O}}_{B_{2}})\otimes {\mathcal{F}})=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(({\mathcal{O}}_{B_{1}}\oplus {\mathcal{O}}_{B_{2}})\otimes {\mathcal{F}})=0.\end{eqnarray}$$
The projection formula and Lemma 3.3 give
 $$\begin{eqnarray}H^{0}(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\otimes {\mathcal{F}})\simeq H^{0}(Q,\unicode[STIX]{x1D6FA}_{Q}^{1}(-2D)).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(\mathbb{P}_{1},\unicode[STIX]{x1D6FA}_{\mathbb{P}_{1}}^{1}\otimes {\mathcal{F}})\simeq H^{0}(Q,\unicode[STIX]{x1D6FA}_{Q}^{1}(-2D)).\end{eqnarray}$$
The sheaf
 $\unicode[STIX]{x1D6FA}_{Q}^{1}(-2D)={\mathcal{O}}_{Q}(-4,-2)\oplus {\mathcal{O}}_{Q}(-2,-4)$
has no global sections, completing the proof of claim (3.6).
$\unicode[STIX]{x1D6FA}_{Q}^{1}(-2D)={\mathcal{O}}_{Q}(-4,-2)\oplus {\mathcal{O}}_{Q}(-2,-4)$
has no global sections, completing the proof of claim (3.6).
Now consider the short exact sequence
 $$\begin{eqnarray}0\rightarrow T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2}))\rightarrow T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2}))\rightarrow {\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2}))\rightarrow T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2}))\rightarrow {\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}}\rightarrow 0.\end{eqnarray}$$
By claim (3.6), vanishing of
 $H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))$
will be complete once we show that the map
$H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))$
will be complete once we show that the map
 $$\begin{eqnarray}H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})\end{eqnarray}$$
is surjective. We identify
 $H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))$
with the space of first-order infinitesimal deformations of
$H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(B_{1}+B_{2})))$
with the space of first-order infinitesimal deformations of
![]() $\mathbb{P}_{1}$
which contain an embedded first-order deformation of
$\mathbb{P}_{1}$
which contain an embedded first-order deformation of
 $B_{1}\cup B_{2}$
. We identify
$B_{1}\cup B_{2}$
. We identify
 $H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
with the space of obstructions to deforming
$H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
with the space of obstructions to deforming
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() $\mathbb{P}_{1}$
. Thus, the map (3.7) factors through the natural map
$\mathbb{P}_{1}$
. Thus, the map (3.7) factors through the natural map
 $$\begin{eqnarray}H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}})\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}})\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})\end{eqnarray}$$
which sends an infinitesimal first-order deformation of
![]() $\mathbb{P}_{1}$
to the obstruction to deforming
$\mathbb{P}_{1}$
to the obstruction to deforming
![]() $\unicode[STIX]{x1D6E5}$
in this first-order deformation of
$\unicode[STIX]{x1D6E5}$
in this first-order deformation of
![]() $\mathbb{P}_{1}$
. We have to show that given any such obstruction, there is a deformation of the pair
$\mathbb{P}_{1}$
. We have to show that given any such obstruction, there is a deformation of the pair
 $(\mathbb{P}_{1},B_{1}+B_{2})$
that maps to the given obstruction.
$(\mathbb{P}_{1},B_{1}+B_{2})$
that maps to the given obstruction.
Recall that
![]() $\mathbb{P}_{1}$
is obtained from
$\mathbb{P}_{1}$
is obtained from
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
by blowing up once at each of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
by blowing up once at each of
 $Q_{1},\ldots ,Q_{6};P_{1},\ldots ,P_{4}$
, and again at each of
$Q_{1},\ldots ,Q_{6};P_{1},\ldots ,P_{4}$
, and again at each of
 $Q_{3},\ldots ,Q_{6}$
in the direction of the proper transform of
$Q_{3},\ldots ,Q_{6}$
in the direction of the proper transform of
![]() $\unicode[STIX]{x1D6E5}$
and at each of
$\unicode[STIX]{x1D6E5}$
and at each of
 $P_{1},\ldots ,P_{4}$
in the direction of tangent cone of
$P_{1},\ldots ,P_{4}$
in the direction of tangent cone of
 $B_{1}\cup B_{2}$
. We denote by
$B_{1}\cup B_{2}$
. We denote by
 $\unicode[STIX]{x1D70E}_{2}:\mathbb{P}_{1}\rightarrow \tilde{Q}$
the ‘intermediate’ blowup, i.e. the map which contracts the last eight
$\unicode[STIX]{x1D70E}_{2}:\mathbb{P}_{1}\rightarrow \tilde{Q}$
the ‘intermediate’ blowup, i.e. the map which contracts the last eight
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $\mathbb{P}_{1}$
.
$\mathbb{P}_{1}$
.
We have the following exact sequence of sheaves on
![]() $\tilde{Q}$
$\tilde{Q}$
 $$\begin{eqnarray}0\rightarrow (\unicode[STIX]{x1D70E}_{2})_{\ast }T_{\mathbb{P}_{1}}\rightarrow T_{\tilde{Q}}\rightarrow \bigoplus _{i=3}^{6}k_{Q_{i}}^{2}\oplus \bigoplus _{i=1}^{4}k_{P_{i}}^{2}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow (\unicode[STIX]{x1D70E}_{2})_{\ast }T_{\mathbb{P}_{1}}\rightarrow T_{\tilde{Q}}\rightarrow \bigoplus _{i=3}^{6}k_{Q_{i}}^{2}\oplus \bigoplus _{i=1}^{4}k_{P_{i}}^{2}\rightarrow 0.\end{eqnarray}$$
Looking at the corresponding exact sequence in cohomology, we see that every infinitesimal first-order deformation of
![]() $\mathbb{P}_{1}$
arises from either an infinitesimal first-order deformation of
$\mathbb{P}_{1}$
arises from either an infinitesimal first-order deformation of
![]() $\tilde{Q}$
(corresponding to an element of
$\tilde{Q}$
(corresponding to an element of
 $H^{1}(\tilde{Q},T_{\tilde{Q}})$
) or from an infinitesimal first-order deformation of the points
$H^{1}(\tilde{Q},T_{\tilde{Q}})$
) or from an infinitesimal first-order deformation of the points
 $Q_{3},\ldots ,Q_{6},P_{1},\ldots ,P_{4}$
on
$Q_{3},\ldots ,Q_{6},P_{1},\ldots ,P_{4}$
on
![]() $\tilde{Q}$
, or both. This latter space is isomorphic to a vector space
$\tilde{Q}$
, or both. This latter space is isomorphic to a vector space
 $V=(k^{2})^{8}$
. We note that
$V=(k^{2})^{8}$
. We note that
![]() $V$
has a linear subspace
$V$
has a linear subspace
 $V_{1}\simeq k^{8}$
corresponding to infinitesimal first-order deformations of the points
$V_{1}\simeq k^{8}$
corresponding to infinitesimal first-order deformations of the points
 $Q_{3},\ldots ,Q_{6}$
,
$Q_{3},\ldots ,Q_{6}$
,
 $P_{1},\ldots ,P_{4}$
to points along the exceptional divisors of
$P_{1},\ldots ,P_{4}$
to points along the exceptional divisors of
![]() $\unicode[STIX]{x1D70E}_{2}$
, i.e. changing the tangent direction of the infinitely-near blowup.
$\unicode[STIX]{x1D70E}_{2}$
, i.e. changing the tangent direction of the infinitely-near blowup.
Similarly, because
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
is rigid, every first-order infinitesimal deformation of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
is rigid, every first-order infinitesimal deformation of
![]() $\tilde{Q}$
arises from a first-order infinitesimal deformation of the points
$\tilde{Q}$
arises from a first-order infinitesimal deformation of the points
 $Q_{1},\ldots ,Q_{6};P_{1},\ldots ,P_{4}$
in
$Q_{1},\ldots ,Q_{6};P_{1},\ldots ,P_{4}$
in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. This latter deformation space is isomorphic to the vector space
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. This latter deformation space is isomorphic to the vector space
 $W=(k^{2})^{10}$
. Thus, we have short exact sequences
$W=(k^{2})^{10}$
. Thus, we have short exact sequences
 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow V\rightarrow H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}})\rightarrow H^{1}(\tilde{Q},T_{\tilde{Q}})\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow H^{0}(\mathbb{P}^{1}\times \mathbb{P}^{1},T_{\mathbb{P}^{1}\times \mathbb{P}^{1}})\rightarrow W\rightarrow H^{1}(\tilde{Q},T_{\tilde{Q}})\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow V\rightarrow H^{1}(\mathbb{P}_{1},T_{\mathbb{P}_{1}})\rightarrow H^{1}(\tilde{Q},T_{\tilde{Q}})\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow H^{0}(\mathbb{P}^{1}\times \mathbb{P}^{1},T_{\mathbb{P}^{1}\times \mathbb{P}^{1}})\rightarrow W\rightarrow H^{1}(\tilde{Q},T_{\tilde{Q}})\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
signifying that every first-order infinitesimal deformation of
![]() $\mathbb{P}_{1}$
, and therefore of
$\mathbb{P}_{1}$
, and therefore of
 $(\mathbb{P}_{1},B_{1}\cup B_{2})$
, arises from a first-order infinitesimal deformation of the points
$(\mathbb{P}_{1},B_{1}\cup B_{2})$
, arises from a first-order infinitesimal deformation of the points
 $Q_{1},\ldots ,Q_{6}$
;
$Q_{1},\ldots ,Q_{6}$
;
 $P_{1},\ldots ,P_{4}$
in
$P_{1},\ldots ,P_{4}$
in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
(i.e. an element of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
(i.e. an element of
![]() $W$
) or a first-order deformation of
$W$
) or a first-order deformation of
 $Q_{3},\ldots ,Q_{6},P_{1},\ldots ,P_{4}$
in
$Q_{3},\ldots ,Q_{6},P_{1},\ldots ,P_{4}$
in
![]() $\tilde{Q}$
, or both.
$\tilde{Q}$
, or both.
We note that (3.8), and even
 $V_{1}\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
, is surjective, i.e. each obstruction in
$V_{1}\rightarrow H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
, is surjective, i.e. each obstruction in
 $H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
arises from a first-order infinitesimal deformation of
$H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
arises from a first-order infinitesimal deformation of
 $Q_{1},\ldots ,Q_{6}$
and the tangent directions of
$Q_{1},\ldots ,Q_{6}$
and the tangent directions of
 $Q_{3},\ldots ,Q_{6}$
in
$Q_{3},\ldots ,Q_{6}$
in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
that fails to induce a first-order embedded deformation of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
that fails to induce a first-order embedded deformation of
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Lemma 3.4. The space
 $H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
has dimension seven and has the following distinguished basis. Each basis element comes from a first-order deformation of
$H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
has dimension seven and has the following distinguished basis. Each basis element comes from a first-order deformation of
![]() $\mathbb{P}_{1}$
which fixes
$\mathbb{P}_{1}$
which fixes
![]() $Q_{1}$
,
$Q_{1}$
,
![]() $Q_{2}$
,
$Q_{2}$
,
![]() $Q_{3}$
(this takes care of infinitesimal automorphisms of
$Q_{3}$
(this takes care of infinitesimal automorphisms of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
) and either:
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
) and either:
-
∙
 $I_{k}$
for
$I_{k}$
for
 $k=1,2,3$
leaves the tangent direction at
$k=1,2,3$
leaves the tangent direction at
 $Q_{3}$
fixed, i.e. parallel to
$Q_{3}$
fixed, i.e. parallel to
 $\unicode[STIX]{x1D6E5}$
, and moves
$\unicode[STIX]{x1D6E5}$
, and moves
 $Q_{k+3}\in \{Q_{4},Q_{5},Q_{6}\}$
off
$Q_{k+3}\in \{Q_{4},Q_{5},Q_{6}\}$
off
 $\unicode[STIX]{x1D6E5}$
while keeping the remaining points and their tangent directions fixed, i.e. parallel to
$\unicode[STIX]{x1D6E5}$
while keeping the remaining points and their tangent directions fixed, i.e. parallel to
 $\unicode[STIX]{x1D6E5}$
; or
$\unicode[STIX]{x1D6E5}$
; or -
∙
 $I_{k}$
for
$I_{k}$
for
 $k=4,5,6,7$
fixes
$k=4,5,6,7$
fixes
 $Q_{k-1}\in \{Q_{3},Q_{4},Q_{5},Q_{6}\}$
and changes the tangent direction at
$Q_{k-1}\in \{Q_{3},Q_{4},Q_{5},Q_{6}\}$
and changes the tangent direction at
 $Q_{k-1}$
, moving the remaining points of
$Q_{k-1}$
, moving the remaining points of
 $Q_{4},Q_{5},Q_{6}$
along
$Q_{4},Q_{5},Q_{6}$
along
 $\unicode[STIX]{x1D6E5}$
and keeping the tangent directions at these remaining points fixed, i.e. parallel to
$\unicode[STIX]{x1D6E5}$
and keeping the tangent directions at these remaining points fixed, i.e. parallel to
 $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
Proof. Simple calculation. ◻
To show that the map (3.7) is surjective, it suffices to show that for each deformation type listed, there exists an equisingular deformation of
 $B_{1}\cup B_{2}$
in
$B_{1}\cup B_{2}$
in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
which passes through the points to which
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
which passes through the points to which
 $Q_{1},\ldots ,Q_{6}$
deform and which has the desired tangent direction at each point.
$Q_{1},\ldots ,Q_{6}$
deform and which has the desired tangent direction at each point.
To begin, let us choose bi-homogeneous coordinates
 $((\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FC}^{\prime }),(\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6FD}^{\prime }))$
on
$((\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FC}^{\prime }),(\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6FD}^{\prime }))$
on
 $Q=\mathbb{P}^{1}\times \mathbb{P}^{1}$
so that
$Q=\mathbb{P}^{1}\times \mathbb{P}^{1}$
so that
 $\unicode[STIX]{x1D6FC}=x/y=-t/z$
and
$\unicode[STIX]{x1D6FC}=x/y=-t/z$
and
 $\unicode[STIX]{x1D6FD}=x/t=-y/z$
. Let
$\unicode[STIX]{x1D6FD}=x/t=-y/z$
. Let
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
be the equations (bihomogeneous of degree
$g_{2}$
be the equations (bihomogeneous of degree
![]() $(3,3)$
) of
$(3,3)$
) of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
, respectively. Referring to (2.4) and (2.5), we have
$B_{2}$
, respectively. Referring to (2.4) and (2.5), we have
 $$\begin{eqnarray}\displaystyle g_{1} & = & \displaystyle -\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}^{3}+3\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }-3\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }{\unicode[STIX]{x1D6FC}^{\prime }}^{3}-3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}+3\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}+\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }{\unicode[STIX]{x1D6FD}^{\prime }}^{3}\nonumber\\ \displaystyle g_{2} & = & \displaystyle -\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}{\unicode[STIX]{x1D6FC}^{\prime }}^{3}-3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }+3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}{\unicode[STIX]{x1D6FD}^{\prime }}^{3}-3\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }+3\unicode[STIX]{x1D6FD}^{3}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }-\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }\unicode[STIX]{x1D6FC}^{3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{1} & = & \displaystyle -\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}^{3}+3\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }-3\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }{\unicode[STIX]{x1D6FC}^{\prime }}^{3}-3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}+3\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}+\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }{\unicode[STIX]{x1D6FD}^{\prime }}^{3}\nonumber\\ \displaystyle g_{2} & = & \displaystyle -\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}{\unicode[STIX]{x1D6FC}^{\prime }}^{3}-3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }+3\unicode[STIX]{x1D6FC}{\unicode[STIX]{x1D6FC}^{\prime }}^{2}{\unicode[STIX]{x1D6FD}^{\prime }}^{3}-3\unicode[STIX]{x1D6FD}{\unicode[STIX]{x1D6FD}^{\prime }}^{2}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }+3\unicode[STIX]{x1D6FD}^{3}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FC}^{\prime }-\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D6FD}^{\prime }\unicode[STIX]{x1D6FC}^{3}.\nonumber\end{eqnarray}$$
Global first-order deformations
![]() $\tilde{B}_{1}$
and
$\tilde{B}_{1}$
and
![]() $\tilde{B}_{2}$
of
$\tilde{B}_{2}$
of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are given by equations
$B_{2}$
are given by equations
 $$\begin{eqnarray}g_{1}+\unicode[STIX]{x1D700}\bar{g_{1}}=g_{1}+\unicode[STIX]{x1D700}\mathop{\sum }_{0\leqslant i,j\leqslant 3}a_{ij}\unicode[STIX]{x1D6FC}^{i}{\unicode[STIX]{x1D6FC}^{\prime }}^{3-i}\unicode[STIX]{x1D6FD}^{j}{\unicode[STIX]{x1D6FD}^{\prime }}^{3-j}\end{eqnarray}$$
$$\begin{eqnarray}g_{1}+\unicode[STIX]{x1D700}\bar{g_{1}}=g_{1}+\unicode[STIX]{x1D700}\mathop{\sum }_{0\leqslant i,j\leqslant 3}a_{ij}\unicode[STIX]{x1D6FC}^{i}{\unicode[STIX]{x1D6FC}^{\prime }}^{3-i}\unicode[STIX]{x1D6FD}^{j}{\unicode[STIX]{x1D6FD}^{\prime }}^{3-j}\end{eqnarray}$$
and
 $$\begin{eqnarray}g_{2}+\unicode[STIX]{x1D700}\bar{g_{2}}=g_{2}+\unicode[STIX]{x1D700}\mathop{\sum }_{0\leqslant i,j\leqslant 3}b_{ij}\unicode[STIX]{x1D6FC}^{i}{\unicode[STIX]{x1D6FC}^{\prime }}^{3-i}\unicode[STIX]{x1D6FD}^{j}{\unicode[STIX]{x1D6FD}^{\prime }}^{3-j},\end{eqnarray}$$
$$\begin{eqnarray}g_{2}+\unicode[STIX]{x1D700}\bar{g_{2}}=g_{2}+\unicode[STIX]{x1D700}\mathop{\sum }_{0\leqslant i,j\leqslant 3}b_{ij}\unicode[STIX]{x1D6FC}^{i}{\unicode[STIX]{x1D6FC}^{\prime }}^{3-i}\unicode[STIX]{x1D6FD}^{j}{\unicode[STIX]{x1D6FD}^{\prime }}^{3-j},\end{eqnarray}$$
respectively. In order to describe equisingular first-order deformations of
 $B_{1}\cup B_{2}$
, we move the singularities of
$B_{1}\cup B_{2}$
, we move the singularities of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
at
$B_{2}$
at
 $P_{1},\ldots ,P_{4}$
to the points
$P_{1},\ldots ,P_{4}$
to the points
 $(\unicode[STIX]{x1D700}c_{1},\unicode[STIX]{x1D700}d_{1}),\ldots ,(\unicode[STIX]{x1D700}c_{4},\unicode[STIX]{x1D700}d_{4})$
, given in local coordinates on
$(\unicode[STIX]{x1D700}c_{1},\unicode[STIX]{x1D700}d_{1}),\ldots ,(\unicode[STIX]{x1D700}c_{4},\unicode[STIX]{x1D700}d_{4})$
, given in local coordinates on
 $U_{1},\ldots ,U_{4}\subset Q$
, respectively, where
$U_{1},\ldots ,U_{4}\subset Q$
, respectively, where
 $$\begin{eqnarray}\displaystyle & \displaystyle U_{1}=\{\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=1\},\quad U_{2}=\{\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FD}=1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle U_{3}=\{\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}^{\prime }=1\},\quad U_{4}=\{\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }=1\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{1}=\{\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=1\},\quad U_{2}=\{\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FD}=1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle U_{3}=\{\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}^{\prime }=1\},\quad U_{4}=\{\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }=1\}. & \displaystyle \nonumber\end{eqnarray}$$
To simplify calculations, we change coordinates on
 $U_{1},\ldots ,U_{4}$
, so that the points
$U_{1},\ldots ,U_{4}$
, so that the points
 $(\unicode[STIX]{x1D700}c_{1},\unicode[STIX]{x1D700}d_{1}),\ldots ,(\unicode[STIX]{x1D700}c_{4},\unicode[STIX]{x1D700}d_{4})$
are at the origin.
$(\unicode[STIX]{x1D700}c_{1},\unicode[STIX]{x1D700}d_{1}),\ldots ,(\unicode[STIX]{x1D700}c_{4},\unicode[STIX]{x1D700}d_{4})$
are at the origin.
Letting
 $g_{ij}+\unicode[STIX]{x1D700}\bar{g}_{ij}$
be the degree
$g_{ij}+\unicode[STIX]{x1D700}\bar{g}_{ij}$
be the degree
![]() $j$
part of the equation
$j$
part of the equation
![]() $g_{i}+\unicode[STIX]{x1D700}\bar{g}_{i}$
with respect to the new coordinates, we have the following conditions. These ensure that
$g_{i}+\unicode[STIX]{x1D700}\bar{g}_{i}$
with respect to the new coordinates, we have the following conditions. These ensure that
 $B_{1}\cup B_{2}$
maintains the singularities, with possibly different tangent cones, at the points to which
$B_{1}\cup B_{2}$
maintains the singularities, with possibly different tangent cones, at the points to which
 $P_{1},\ldots ,P_{4}$
deform. For simplicity we use the same notation for
$P_{1},\ldots ,P_{4}$
deform. For simplicity we use the same notation for
 $P_{1},\ldots ,P_{4}$
and the points to which they deform:
$P_{1},\ldots ,P_{4}$
and the points to which they deform:
-
(1)
 $g_{10}+\unicode[STIX]{x1D700}\bar{g}_{10}=0$
on each
$g_{10}+\unicode[STIX]{x1D700}\bar{g}_{10}=0$
on each
 $U_{i}$
; this forces
$U_{i}$
; this forces
 $\tilde{B}_{1}$
to pass through
$\tilde{B}_{1}$
to pass through
 $P_{1},\ldots ,P_{4}$
;
$P_{1},\ldots ,P_{4}$
; -
(2)
 $g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11}=0$
on
$g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11}=0$
on
 $U_{1}$
,
$U_{1}$
,
 $U_{4}$
; this forces
$U_{4}$
; this forces
 $\tilde{B}_{1}$
to be singular at
$\tilde{B}_{1}$
to be singular at
 $P_{1}$
and
$P_{1}$
and
 $P_{4}$
;
$P_{4}$
; -
(3)
 $g_{12}+\unicode[STIX]{x1D700}\bar{g}_{12}=(m+m_{1}\unicode[STIX]{x1D700})(g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21})^{2}$
, for some constants
$g_{12}+\unicode[STIX]{x1D700}\bar{g}_{12}=(m+m_{1}\unicode[STIX]{x1D700})(g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21})^{2}$
, for some constants
 $m,m_{1}$
, on
$m,m_{1}$
, on
 $U_{1}$
,
$U_{1}$
,
 $U_{4}$
(where
$U_{4}$
(where
 $m,m_{1}$
may differ on
$m,m_{1}$
may differ on
 $U_{1}$
,
$U_{1}$
,
 $U_{4}$
); this forces the tangent cones of
$U_{4}$
); this forces the tangent cones of
 $\tilde{B}_{1}$
at
$\tilde{B}_{1}$
at
 $P_{1}$
and
$P_{1}$
and
 $P_{4}$
to be the same as those of
$P_{4}$
to be the same as those of
 $\tilde{B}_{2}$
at
$\tilde{B}_{2}$
at
 $P_{1}$
and
$P_{1}$
and
 $P_{4}$
;
$P_{4}$
; -
(4)
 $g_{13}+\unicode[STIX]{x1D700}\bar{g}_{13}=(g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21})(h+\unicode[STIX]{x1D700}h_{1})$
, where
$g_{13}+\unicode[STIX]{x1D700}\bar{g}_{13}=(g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21})(h+\unicode[STIX]{x1D700}h_{1})$
, where
 $h$
and
$h$
and
 $h_{1}$
are quadratic forms; by Lemma 3.6, this forces
$h_{1}$
are quadratic forms; by Lemma 3.6, this forces
 $\tilde{B}_{1}$
to have tacnodes at the points
$\tilde{B}_{1}$
to have tacnodes at the points
 $P_{1}$
and
$P_{1}$
and
 $P_{4}$
;
$P_{4}$
; -
(5)
 $g_{20}+\unicode[STIX]{x1D700}\bar{g}_{20}=0$
on each
$g_{20}+\unicode[STIX]{x1D700}\bar{g}_{20}=0$
on each
 $U_{i}$
; this forces and
$U_{i}$
; this forces and
 $\tilde{B}_{2}$
to pass through
$\tilde{B}_{2}$
to pass through
 $P_{1},\ldots ,P_{4}$
;
$P_{1},\ldots ,P_{4}$
; -
(6)
 $g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21}=0$
on
$g_{21}+\unicode[STIX]{x1D700}\bar{g}_{21}=0$
on
 $U_{2}$
,
$U_{2}$
,
 $U_{3}$
; this forces
$U_{3}$
; this forces
 $\tilde{B}_{2}$
to be singular at
$\tilde{B}_{2}$
to be singular at
 $P_{2}$
and
$P_{2}$
and
 $P_{3}$
;
$P_{3}$
; -
(7)
 $g_{22}+\unicode[STIX]{x1D700}\bar{g}_{22}=(n+n_{1}\unicode[STIX]{x1D700})(g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11})^{2}$
, for some constants
$g_{22}+\unicode[STIX]{x1D700}\bar{g}_{22}=(n+n_{1}\unicode[STIX]{x1D700})(g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11})^{2}$
, for some constants
 $n,n_{1}$
, on
$n,n_{1}$
, on
 $U_{2}$
,
$U_{2}$
,
 $U_{3}$
(where
$U_{3}$
(where
 $n,n_{1}$
may differ on
$n,n_{1}$
may differ on
 $U_{2}$
,
$U_{2}$
,
 $U_{3}$
); this forces the tangent cones of
$U_{3}$
); this forces the tangent cones of
 $\tilde{B}_{2}$
at
$\tilde{B}_{2}$
at
 $P_{2}$
and
$P_{2}$
and
 $P_{3}$
to be the same as those of
$P_{3}$
to be the same as those of
 $\tilde{B}_{1}$
at
$\tilde{B}_{1}$
at
 $P_{2}$
and
$P_{2}$
and
 $P_{3}$
;
$P_{3}$
; -
(8)
 $g_{23}+\unicode[STIX]{x1D700}\bar{g}_{23}=(g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11})(h+\unicode[STIX]{x1D700}h_{1})$
, where
$g_{23}+\unicode[STIX]{x1D700}\bar{g}_{23}=(g_{11}+\unicode[STIX]{x1D700}\bar{g}_{11})(h+\unicode[STIX]{x1D700}h_{1})$
, where
 $h$
and
$h$
and
 $h_{1}$
are quadratic forms; by Lemma 3.6, this forces
$h_{1}$
are quadratic forms; by Lemma 3.6, this forces
 $\tilde{B}_{2}$
to have tacnodes at the points
$\tilde{B}_{2}$
to have tacnodes at the points
 $P_{2}$
and
$P_{2}$
and
 $P_{3}$
.
$P_{3}$
.
Returning to original coordinates, and after simple algebraic manipulations, this gives the following system of
![]() $28$
linear equations in
$28$
linear equations in
 $c_{i},d_{i},a_{ij},b_{ij}$
(four blocks for four charts).
$c_{i},d_{i},a_{ij},b_{ij}$
(four blocks for four charts).
Equations 3.5.
 $$\begin{eqnarray}\displaystyle & \displaystyle a_{33}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{33}=d_{1}-3c_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{32}=-3c_{1}-6d_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{23}=2c_{1}-3d_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{22}=a_{31}+b_{23}+3b_{32} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{13}=2a_{31}-2b_{32}+4b_{23} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 2c_{1}-d_{1}+3a_{12}+a_{03}+2a_{21}-a_{30}=0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{33}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{33}=d_{1}-3c_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{32}=-3c_{1}-6d_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{23}=2c_{1}-3d_{1} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{22}=a_{31}+b_{23}+3b_{32} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{13}=2a_{31}-2b_{32}+4b_{23} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 2c_{1}-d_{1}+3a_{12}+a_{03}+2a_{21}-a_{30}=0 & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle a_{30}=-c_{2}-3d_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{30}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{31}=3c_{2}+2d_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{20}=3d_{2}+c_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{32}=2b_{10}+4a_{31}+2a_{20} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{21}=6b_{10}+6a_{31}+3a_{20} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 5c_{2}+3d_{2}+5b_{00}+3b_{11}+6b_{22}+5b_{33}=0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{30}=-c_{2}-3d_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{30}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{31}=3c_{2}+2d_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{20}=3d_{2}+c_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{32}=2b_{10}+4a_{31}+2a_{20} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{21}=6b_{10}+6a_{31}+3a_{20} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 5c_{2}+3d_{2}+5b_{00}+3b_{11}+6b_{22}+5b_{33}=0 & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle a_{03}=c_{3}+3d_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{03}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{02}=2d_{3}+3c_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{13}=3d_{3}+c_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{01}=5a_{13}+2b_{23}+3a_{02} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{12}=4a_{13}+6b_{23}+a_{02} & \displaystyle \nonumber\\ \displaystyle & \displaystyle c_{3}+2d_{3}-3b_{11}+b_{33}+2b_{22}+b_{00}=0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{03}=c_{3}+3d_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{03}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{02}=2d_{3}+3c_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{13}=3d_{3}+c_{3} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{01}=5a_{13}+2b_{23}+3a_{02} & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{12}=4a_{13}+6b_{23}+a_{02} & \displaystyle \nonumber\\ \displaystyle & \displaystyle c_{3}+2d_{3}-3b_{11}+b_{33}+2b_{22}+b_{00}=0 & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle a_{00}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{00}=d_{4}-3c_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{01}=3c_{4}+6d_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{10}=3d_{4}-2c_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{20}=2a_{02}+2b_{01}+3b_{10} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{11}=a_{02}+4b_{01}+6b_{10} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 4c_{4}+5d_{4}+2a_{03}+3a_{12}+a_{21}+5a_{30}=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{00}=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{00}=d_{4}-3c_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{01}=3c_{4}+6d_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{10}=3d_{4}-2c_{4} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{20}=2a_{02}+2b_{01}+3b_{10} & \displaystyle \nonumber\\ \displaystyle & \displaystyle a_{11}=a_{02}+4b_{01}+6b_{10} & \displaystyle \nonumber\\ \displaystyle & \displaystyle 4c_{4}+5d_{4}+2a_{03}+3a_{12}+a_{21}+5a_{30}=0. & \displaystyle \nonumber\end{eqnarray}$$
Next, we determine all additional conditions on
![]() $a_{ij}$
,
$a_{ij}$
,
![]() $b_{ij}$
,
$b_{ij}$
,
![]() $c_{i}$
,
$c_{i}$
,
![]() $d_{i}$
which ensure that
$d_{i}$
which ensure that
![]() $\tilde{B}_{1}$
and
$\tilde{B}_{1}$
and
![]() $\tilde{B}_{2}$
pass through the points to which
$\tilde{B}_{2}$
pass through the points to which
 $Q_{1},\ldots ,Q_{6}$
deform, with the desired multiplicities at each point. To do so, we look in the chart
$Q_{1},\ldots ,Q_{6}$
deform, with the desired multiplicities at each point. To do so, we look in the chart
![]() $U_{4}$
. Here, the equation of
$U_{4}$
. Here, the equation of
![]() $\unicode[STIX]{x1D6E5}$
is
$\unicode[STIX]{x1D6E5}$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(1+\unicode[STIX]{x1D6FD})+\unicode[STIX]{x1D6FD}-1=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(1+\unicode[STIX]{x1D6FD})+\unicode[STIX]{x1D6FD}-1=0.\end{eqnarray}$$
Solving for
![]() $\unicode[STIX]{x1D6FC}$
gives
$\unicode[STIX]{x1D6FC}$
gives
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{1-\unicode[STIX]{x1D6FD}}{1+\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{1-\unicode[STIX]{x1D6FD}}{1+\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
Thus, the points at which
![]() $\unicode[STIX]{x1D6E5}$
intersects
$\unicode[STIX]{x1D6E5}$
intersects
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are the roots of the following polynomials:
$B_{2}$
are the roots of the following polynomials:
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{2}+1)(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D6FD}+6)^{2}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{2}+1)(\unicode[STIX]{x1D6FD}^{2}+4\unicode[STIX]{x1D6FD}+6)^{2}\end{eqnarray}$$
and
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{2}+1)(\unicode[STIX]{x1D6FD}^{2}+6\unicode[STIX]{x1D6FD}+6)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{2}+1)(\unicode[STIX]{x1D6FD}^{2}+6\unicode[STIX]{x1D6FD}+6)^{2}.\end{eqnarray}$$
This gives the six points at which
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
intersect
$B_{2}$
intersect
![]() $\unicode[STIX]{x1D6E5}$
:
$\unicode[STIX]{x1D6E5}$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle Q_{1}=(-i,i),\quad Q_{2}=(i,-i), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{3}=(3-5i,-2+4i),\quad Q_{4}=(3+5i,-2-4i), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{5}=(-5+4i,-3+5i),\quad Q_{6}=(-5-4i,-3-5i), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Q_{1}=(-i,i),\quad Q_{2}=(i,-i), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{3}=(3-5i,-2+4i),\quad Q_{4}=(3+5i,-2-4i), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{5}=(-5+4i,-3+5i),\quad Q_{6}=(-5-4i,-3-5i), & \displaystyle \nonumber\end{eqnarray}$$
where
 $i^{2}+1=0~\text{mod}~7$
.
$i^{2}+1=0~\text{mod}~7$
.
The intersections of
![]() $\bar{g}_{1}=0$
and
$\bar{g}_{1}=0$
and
![]() $\bar{g}_{2}=0$
with
$\bar{g}_{2}=0$
with
![]() $\unicode[STIX]{x1D6E5}$
are given by the zeros of the following polynomials:
$\unicode[STIX]{x1D6E5}$
are given by the zeros of the following polynomials:
 $$\begin{eqnarray}\displaystyle {\hat{g}}_{1} & = & \displaystyle (1+\unicode[STIX]{x1D6FD})^{3}(a_{00}+a_{01}\unicode[STIX]{x1D6FD}+a_{02}\unicode[STIX]{x1D6FD}^{2}+a_{03}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})^{2}(1-\unicode[STIX]{x1D6FD})(a_{10}+a_{11}\unicode[STIX]{x1D6FD}+a_{12}\unicode[STIX]{x1D6FD}^{2}+a_{13}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})(1-\unicode[STIX]{x1D6FD})^{2}(a_{20}+a_{21}\unicode[STIX]{x1D6FD}+a_{22}\unicode[STIX]{x1D6FD}^{2}+a_{23}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D6FD})^{3}(a_{30}+a_{31}\unicode[STIX]{x1D6FD}+a_{32}\unicode[STIX]{x1D6FD}^{2}+a_{33}\unicode[STIX]{x1D6FD}^{3})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\hat{g}}_{1} & = & \displaystyle (1+\unicode[STIX]{x1D6FD})^{3}(a_{00}+a_{01}\unicode[STIX]{x1D6FD}+a_{02}\unicode[STIX]{x1D6FD}^{2}+a_{03}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})^{2}(1-\unicode[STIX]{x1D6FD})(a_{10}+a_{11}\unicode[STIX]{x1D6FD}+a_{12}\unicode[STIX]{x1D6FD}^{2}+a_{13}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})(1-\unicode[STIX]{x1D6FD})^{2}(a_{20}+a_{21}\unicode[STIX]{x1D6FD}+a_{22}\unicode[STIX]{x1D6FD}^{2}+a_{23}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D6FD})^{3}(a_{30}+a_{31}\unicode[STIX]{x1D6FD}+a_{32}\unicode[STIX]{x1D6FD}^{2}+a_{33}\unicode[STIX]{x1D6FD}^{3})\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\hat{g}}_{2} & = & \displaystyle (1+\unicode[STIX]{x1D6FD})^{3}(b_{00}+b_{01}\unicode[STIX]{x1D6FD}+b_{02}\unicode[STIX]{x1D6FD}^{2}+b_{03}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})^{2}(1-\unicode[STIX]{x1D6FD})(b_{10}+b_{11}\unicode[STIX]{x1D6FD}+b_{12}\unicode[STIX]{x1D6FD}^{2}+b_{13}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+b)(1-\unicode[STIX]{x1D6FD})^{2}(b_{20}+b_{21}\unicode[STIX]{x1D6FD}+b_{22}\unicode[STIX]{x1D6FD}^{2}+b_{23}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D6FD})^{3}(b_{30}+b_{31}\unicode[STIX]{x1D6FD}+b_{32}\unicode[STIX]{x1D6FD}^{2}+b_{33}\unicode[STIX]{x1D6FD}^{3}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\hat{g}}_{2} & = & \displaystyle (1+\unicode[STIX]{x1D6FD})^{3}(b_{00}+b_{01}\unicode[STIX]{x1D6FD}+b_{02}\unicode[STIX]{x1D6FD}^{2}+b_{03}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+\unicode[STIX]{x1D6FD})^{2}(1-\unicode[STIX]{x1D6FD})(b_{10}+b_{11}\unicode[STIX]{x1D6FD}+b_{12}\unicode[STIX]{x1D6FD}^{2}+b_{13}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1+b)(1-\unicode[STIX]{x1D6FD})^{2}(b_{20}+b_{21}\unicode[STIX]{x1D6FD}+b_{22}\unicode[STIX]{x1D6FD}^{2}+b_{23}\unicode[STIX]{x1D6FD}^{3})\nonumber\\ \displaystyle & & \displaystyle +\,(1-\unicode[STIX]{x1D6FD})^{3}(b_{30}+b_{31}\unicode[STIX]{x1D6FD}+b_{32}\unicode[STIX]{x1D6FD}^{2}+b_{33}\unicode[STIX]{x1D6FD}^{3}).\nonumber\end{eqnarray}$$
Using these equations, we obtain eight additional linear equations in
![]() $a_{ij}$
,
$a_{ij}$
,
![]() $b_{ij}$
,
$b_{ij}$
,
![]() $c_{i}$
,
$c_{i}$
,
![]() $d_{i}$
. These ensure that
$d_{i}$
. These ensure that
![]() $\tilde{B}_{1}$
and
$\tilde{B}_{1}$
and
![]() $\tilde{B}_{2}$
pass through
$\tilde{B}_{2}$
pass through
![]() $Q_{1},Q_{2}$
, that
$Q_{1},Q_{2}$
, that
![]() $\tilde{B}_{1}$
passes through
$\tilde{B}_{1}$
passes through
![]() $Q_{3},Q_{4}$
, and that
$Q_{3},Q_{4}$
, and that
![]() $\tilde{B}_{2}$
passes through
$\tilde{B}_{2}$
passes through
![]() $Q_{5},Q_{6}$
. Note that each restriction arises from setting
$Q_{5},Q_{6}$
. Note that each restriction arises from setting
![]() $\unicode[STIX]{x1D6FD}$
equal to
$\unicode[STIX]{x1D6FD}$
equal to
![]() $i$
,
$i$
,
![]() $-i$
,
$-i$
,
 $-2+4i$
,
$-2+4i$
,
 $-2-4i$
,
$-2-4i$
,
 $-3+5i$
, or
$-3+5i$
, or
 $-3-5i$
in the appropriate equation.
$-3-5i$
in the appropriate equation.
(B1Q1)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{1}-3c_{4}+3d_{1}+d_{4}-2a_{20}-2a_{21}-a_{31}+3a_{02}-a_{12}+3a_{03}-2b_{10}+3b_{32}+2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-3c_{4}+3d_{1}+d_{4}+2a_{20}-2a_{21}+a_{31}-3a_{02}-a_{12}+3a_{03}+2b_{10}-3b_{32}-2b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{1}-3c_{4}+3d_{1}+d_{4}-2a_{20}-2a_{21}-a_{31}+3a_{02}-a_{12}+3a_{03}-2b_{10}+3b_{32}+2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-3c_{4}+3d_{1}+d_{4}+2a_{20}-2a_{21}+a_{31}-3a_{02}-a_{12}+3a_{03}+2b_{10}-3b_{32}-2b_{23}=0\nonumber\end{eqnarray}$$
(B1Q2)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{1}+3c_{4}-3d_{1}-d_{4}+2a_{20}+2a_{21}+a_{31}-3a_{02}+a_{12}-3a_{03}+2b_{10}-3b_{32}-2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-3c_{4}+3d_{1}+d_{4}+2a_{20}-2a_{21}+a_{31}-3a_{02}-a_{12}+3a_{03}+2b_{10}-3b_{32}-2b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{1}+3c_{4}-3d_{1}-d_{4}+2a_{20}+2a_{21}+a_{31}-3a_{02}+a_{12}-3a_{03}+2b_{10}-3b_{32}-2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-3c_{4}+3d_{1}+d_{4}+2a_{20}-2a_{21}+a_{31}-3a_{02}-a_{12}+3a_{03}+2b_{10}-3b_{32}-2b_{23}=0\nonumber\end{eqnarray}$$
(B2Q1)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{2}-c_{3}-3d_{3}-a_{20}-3a_{31}-a_{02}-2b_{11}+b_{22}+3b_{32}+b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{2}+c_{3}+3d_{3}-a_{20}-3a_{31}-a_{02}+2b_{11}-b_{22}+3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{2}-c_{3}-3d_{3}-a_{20}-3a_{31}-a_{02}-2b_{11}+b_{22}+3b_{32}+b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{2}+c_{3}+3d_{3}-a_{20}-3a_{31}-a_{02}+2b_{11}-b_{22}+3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
(B2Q2)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{2}+c_{3}+3d_{3}+a_{20}+3a_{31}+a_{02}+2b_{11}-b_{22}-3b_{32}-b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{2}+c_{3}+3d_{3}-a_{20}-3a_{31}-a_{02}+2b_{11}-b_{22}+3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{2}+c_{3}+3d_{3}+a_{20}+3a_{31}+a_{02}+2b_{11}-b_{22}-3b_{32}-b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{2}+c_{3}+3d_{3}-a_{20}-3a_{31}-a_{02}+2b_{11}-b_{22}+3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
(B1Q3)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{4}+2d_{1}-2d_{4}+3a_{20}+3a_{21}-a_{31}+3a_{12}+2b_{10}-2b_{32}-3b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-c_{4}-3d_{1}-2d_{4}-2a_{20}+3a_{21}-3a_{31}+a_{02}+a_{12}-a_{03}-3b_{10}-3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{4}+2d_{1}-2d_{4}+3a_{20}+3a_{21}-a_{31}+3a_{12}+2b_{10}-2b_{32}-3b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-c_{4}-3d_{1}-2d_{4}-2a_{20}+3a_{21}-3a_{31}+a_{02}+a_{12}-a_{03}-3b_{10}-3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
(B1Q4)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (c_{4}-2d_{1}+2d_{4}-3a_{20}-3a_{21}+a_{31}-3a_{12}-2b_{10}+2b_{32}+3b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-c_{4}-3d_{1}-2d_{4}-2a_{20}+3a_{21}-3a_{31}+a_{02}+a_{12}-a_{03}-3b_{10}-3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (c_{4}-2d_{1}+2d_{4}-3a_{20}-3a_{21}+a_{31}-3a_{12}-2b_{10}+2b_{32}+3b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,3c_{1}-c_{4}-3d_{1}-2d_{4}-2a_{20}+3a_{21}-3a_{31}+a_{02}+a_{12}-a_{03}-3b_{10}-3b_{32}+b_{23}=0\nonumber\end{eqnarray}$$
(B2Q5)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (c_{1}+3c_{2}+2c_{3}+2d_{1}-d_{3}+a_{20}-3a_{31}+2a_{02}-b_{10}+3b_{11}-b_{22}+b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,2c_{1}-2c_{2}+2c_{3}-3d_{1}+3d_{2}-d_{3}-2a_{20}-a_{31}+3a_{02}+b_{10}+3b_{11}-3b_{22}+b_{32}-3b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (c_{1}+3c_{2}+2c_{3}+2d_{1}-d_{3}+a_{20}-3a_{31}+2a_{02}-b_{10}+3b_{11}-b_{22}+b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,2c_{1}-2c_{2}+2c_{3}-3d_{1}+3d_{2}-d_{3}-2a_{20}-a_{31}+3a_{02}+b_{10}+3b_{11}-3b_{22}+b_{32}-3b_{23}=0\nonumber\end{eqnarray}$$
(B2Q6)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{1}-3c_{2}-2c_{3}-2d_{1}+d_{3}-a_{20}+3a_{31}-2a_{02}+b_{10}-3b_{11}+b_{22}-b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,2c_{1}-2c_{2}+2c_{3}-3d_{1}+3d_{2}-d_{3}-2a_{20}-a_{31}+3a_{02}+b_{10}+3b_{11}-3b_{22}+b_{32}-3b_{23}=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{1}-3c_{2}-2c_{3}-2d_{1}+d_{3}-a_{20}+3a_{31}-2a_{02}+b_{10}-3b_{11}+b_{22}-b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad +\,2c_{1}-2c_{2}+2c_{3}-3d_{1}+3d_{2}-d_{3}-2a_{20}-a_{31}+3a_{02}+b_{10}+3b_{11}-3b_{22}+b_{32}-3b_{23}=0.\nonumber\end{eqnarray}$$
Taking the derivatives of
![]() ${\hat{g}}_{1}$
and
${\hat{g}}_{1}$
and
![]() ${\hat{g}}_{2}$
with respect to
${\hat{g}}_{2}$
with respect to
![]() $\unicode[STIX]{x1D6FD}$
and setting
$\unicode[STIX]{x1D6FD}$
and setting
![]() $\unicode[STIX]{x1D6FD}$
equal to
$\unicode[STIX]{x1D6FD}$
equal to
 $-2+4i$
,
$-2+4i$
,
 $-2-4i$
,
$-2-4i$
,
 $-3+5i$
, or
$-3+5i$
, or
 $-3-5i$
as appropriate gives the final four linear equations in
$-3-5i$
as appropriate gives the final four linear equations in
 $a_{ij},b_{ij},c_{i},d_{i}$
. These ensure that
$a_{ij},b_{ij},c_{i},d_{i}$
. These ensure that
![]() $\tilde{B}_{1}$
and
$\tilde{B}_{1}$
and
![]() $\tilde{B}_{2}$
are tangent to
$\tilde{B}_{2}$
are tangent to
![]() $\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D6E5}$
at
![]() $Q_{3},Q_{4}$
and
$Q_{3},Q_{4}$
and
![]() $Q_{5},Q_{6}$
, respectively.
$Q_{5},Q_{6}$
, respectively.
(dB1Q3)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{1}-2c_{4}-3d_{1}+3d_{4}+a_{21}+2a_{31}+2a_{02}+a_{03}-b_{10}-2b_{32})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{1}+c_{4}-2d_{1}+2d_{4}+2a_{20}+a_{21}+3a_{02}+a_{03}-3b_{10}-2b_{32}-b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (3c_{1}-2c_{4}-3d_{1}+3d_{4}+a_{21}+2a_{31}+2a_{02}+a_{03}-b_{10}-2b_{32})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{1}+c_{4}-2d_{1}+2d_{4}+2a_{20}+a_{21}+3a_{02}+a_{03}-3b_{10}-2b_{32}-b_{23}=0\nonumber\end{eqnarray}$$
(dB1Q4)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{1}+2c_{4}+3d_{1}-3d_{4}-a_{21}-2a_{31}-2a_{02}-a_{03}+b_{10}+2b_{32})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{1}+c_{4}-2d_{1}+2d_{4}+2a_{20}+a_{21}+3a_{02}+a_{03}-3b_{10}-2b_{32}-b_{23}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-3c_{1}+2c_{4}+3d_{1}-3d_{4}-a_{21}-2a_{31}-2a_{02}-a_{03}+b_{10}+2b_{32})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{1}+c_{4}-2d_{1}+2d_{4}+2a_{20}+a_{21}+3a_{02}+a_{03}-3b_{10}-2b_{32}-b_{23}=0\nonumber\end{eqnarray}$$
(dB2Q5)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (c_{1}-3c_{2}-c_{3}+2d_{1}+d_{2}-3d_{3}+3a_{20}+2a_{31}+3a_{02}+2b_{10}-2b_{11}-3b_{22}-2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{2}-3c_{3}-3d_{2}-2d_{3}-3a_{31}-3a_{02}-b_{10}-b_{22}-3b_{32}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (c_{1}-3c_{2}-c_{3}+2d_{1}+d_{2}-3d_{3}+3a_{20}+2a_{31}+3a_{02}+2b_{10}-2b_{11}-3b_{22}-2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{2}-3c_{3}-3d_{2}-2d_{3}-3a_{31}-3a_{02}-b_{10}-b_{22}-3b_{32}=0\nonumber\end{eqnarray}$$
(dB2Q6)
 $$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{1}+3c_{2}+c_{3}-2d_{1}-d_{2}+3d_{3}-3a_{20}-2a_{31}-3a_{02}-2b_{10}+2b_{11}+3b_{22}+2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{2}-3c_{3}-3d_{2}-2d_{3}-3a_{31}-3a_{02}-b_{10}-b_{22}-3b_{32}=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (-c_{1}+3c_{2}+c_{3}-2d_{1}-d_{2}+3d_{3}-3a_{20}-2a_{31}-3a_{02}-2b_{10}+2b_{11}+3b_{22}+2b_{23})i\nonumber\\ \displaystyle & & \displaystyle \quad -\,c_{2}-3c_{3}-3d_{2}-2d_{3}-3a_{31}-3a_{02}-b_{10}-b_{22}-3b_{32}=0.\nonumber\end{eqnarray}$$
Consider a basis element in
 $H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
corresponding via Lemma 3.4 to some deformation of the points
$H^{1}(\mathbb{P}_{1},{\mathcal{N}}_{\unicode[STIX]{x1D6E5}/\mathbb{P}_{1}})$
corresponding via Lemma 3.4 to some deformation of the points
 $P_{1},\ldots ,P_{4},Q_{1},\ldots ,Q_{6}$
together with the tangent directions of
$P_{1},\ldots ,P_{4},Q_{1},\ldots ,Q_{6}$
together with the tangent directions of
 $P_{1},\ldots ,P_{4},Q_{4},\ldots ,Q_{6}$
in
$P_{1},\ldots ,P_{4},Q_{4},\ldots ,Q_{6}$
in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. There are two cases, as in Lemma 3.4.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. There are two cases, as in Lemma 3.4.
Consider for example the basis element
![]() $I_{1}$
. The existence of an equisingular deformation of
$I_{1}$
. The existence of an equisingular deformation of
 $(\mathbb{P}_{1},B_{1}\cup B_{2})$
mapping to
$(\mathbb{P}_{1},B_{1}\cup B_{2})$
mapping to
![]() $I_{1}$
is equivalent to the existence of
$I_{1}$
is equivalent to the existence of
 $a_{ij},b_{ij},c_{i},d_{i}$
which satisfy (3.5), as well as B1Q1, B1Q2, B2Q1, B2Q2, B1Q3, dB1Q3, B1Q4-1, B2Q5, B2Q6. Here, we use Lemma 3.7.
$a_{ij},b_{ij},c_{i},d_{i}$
which satisfy (3.5), as well as B1Q1, B1Q2, B2Q1, B2Q2, B1Q3, dB1Q3, B1Q4-1, B2Q5, B2Q6. Here, we use Lemma 3.7.
Next we consider the basis element
![]() $I_{4}$
. The existence of an equisingular deformation of
$I_{4}$
. The existence of an equisingular deformation of
 $(\mathbb{P}_{1},B_{1}\cup B_{2})$
mapping to
$(\mathbb{P}_{1},B_{1}\cup B_{2})$
mapping to
![]() $I_{4}$
is equivalent to the existence of
$I_{4}$
is equivalent to the existence of
 $a_{ij},b_{ij},c_{i},d_{i}$
which satisfy (3.5), as well as B1Q1, B1Q2, B2Q1, B2Q2, B1Q3, dB1Q3, dB1Q3-1, B2Q4, B2Q5, B2Q6. Here, we use Lemma 3.7.
$a_{ij},b_{ij},c_{i},d_{i}$
which satisfy (3.5), as well as B1Q1, B1Q2, B2Q1, B2Q2, B1Q3, dB1Q3, dB1Q3-1, B2Q4, B2Q5, B2Q6. Here, we use Lemma 3.7.
Thus, each of the seven basis elements corresponds to finding a non-trivial solution of a large system of linear equations. As working with such large matrices is unwieldy, we use Macaulay2 to check this (see the code included in the Appendix). In each case, we find that solutions indeed form either a three- or four-dimensional vector space, depending on the basis element, completing the proof. ◻
Lemma 3.6. The singularity
 $(h_{1}^{2}+h_{1}h_{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
, where
$(h_{1}^{2}+h_{1}h_{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
, where
![]() $h_{i}$
is a form of degree
$h_{i}$
is a form of degree
![]() $i$
, is a tacnode (or a degeneration of a tacnode).
$i$
, is a tacnode (or a degeneration of a tacnode).
Proof. Completing the square, the equation becomes
 $((h_{1}+{\textstyle \frac{1}{2}}h_{2})^{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
. Letting
$((h_{1}+{\textstyle \frac{1}{2}}h_{2})^{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
. Letting
 $h=h_{1}+{\textstyle \frac{1}{2}}h_{2}$
, the singularity becomes
$h=h_{1}+{\textstyle \frac{1}{2}}h_{2}$
, the singularity becomes
 $(h^{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
. As there are no terms of degree
$(h^{2}+\text{h.o.t.}=0)\subset \mathbb{A}^{2}$
. As there are no terms of degree
![]() $3$
, this is a tacnode.◻
$3$
, this is a tacnode.◻
Lemma 3.7. Let
 $B=(g=0)$
be the germ of a smooth curve in
$B=(g=0)$
be the germ of a smooth curve in
![]() $\mathbb{A}^{2}$
which is simply tangent to the
$\mathbb{A}^{2}$
which is simply tangent to the
![]() $x$
-axis at the origin, and let
$x$
-axis at the origin, and let
 $\tilde{B}=(g+\unicode[STIX]{x1D700}\bar{g}=0)$
be its first-order infinitesimal embedded deformation. Then
$\tilde{B}=(g+\unicode[STIX]{x1D700}\bar{g}=0)$
be its first-order infinitesimal embedded deformation. Then
![]() $\tilde{B}$
is tangent to the
$\tilde{B}$
is tangent to the
![]() $x$
-axis if and only if
$x$
-axis if and only if
 $\bar{g}(0,0)=0$
.
$\bar{g}(0,0)=0$
.
Proof. Suppose
 $\bar{g}(0,0)=0$
. We have to show that there exists
$\bar{g}(0,0)=0$
. We have to show that there exists
![]() $x_{0}$
with
$x_{0}$
with
 $$\begin{eqnarray}g(\unicode[STIX]{x1D700}x_{0},0)+\unicode[STIX]{x1D700}\bar{g}(\unicode[STIX]{x1D700}x_{0},0)=0\end{eqnarray}$$
$$\begin{eqnarray}g(\unicode[STIX]{x1D700}x_{0},0)+\unicode[STIX]{x1D700}\bar{g}(\unicode[STIX]{x1D700}x_{0},0)=0\end{eqnarray}$$
and that
 $$\begin{eqnarray}\frac{d}{dx}(g(\unicode[STIX]{x1D700}x_{0},0)+\unicode[STIX]{x1D700}\bar{g}(\unicode[STIX]{x1D700}x_{0},0))=0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dx}(g(\unicode[STIX]{x1D700}x_{0},0)+\unicode[STIX]{x1D700}\bar{g}(\unicode[STIX]{x1D700}x_{0},0))=0.\end{eqnarray}$$
Taking the Taylor expansion of these with respect to
![]() $\unicode[STIX]{x1D700}$
, the first of these obviously holds. The second holds for
$\unicode[STIX]{x1D700}$
, the first of these obviously holds. The second holds for
 $$\begin{eqnarray}x_{0}=\frac{-\bar{g}_{1}^{\prime }(0,0)}{g_{1}^{\prime \prime }(0,0)}.\end{eqnarray}$$
$$\begin{eqnarray}x_{0}=\frac{-\bar{g}_{1}^{\prime }(0,0)}{g_{1}^{\prime \prime }(0,0)}.\end{eqnarray}$$
◻
4 The Boyd surface is a Dolgachev surface
Lemma 4.1. Blowing-down
![]() $\bar{N}_{1}$
and
$\bar{N}_{1}$
and
![]() $\bar{N}_{2}$
on
$\bar{N}_{2}$
on
![]() $\mathbb{P}$
gives a Halphen surface of index three [Reference Cossec and DolgachevCD89, ch. V, § 6] with a multiple fiber
$\mathbb{P}$
gives a Halphen surface of index three [Reference Cossec and DolgachevCD89, ch. V, § 6] with a multiple fiber
 $A_{1}+\cdots +A_{4}+\bar{G}_{1}+\cdots \bar{G}_{4}$
of type
$A_{1}+\cdots +A_{4}+\bar{G}_{1}+\cdots \bar{G}_{4}$
of type
![]() $I_{8}$
.
$I_{8}$
.
Proof. By 3.1,
![]() $\mathbb{P}$
has a fibration
$\mathbb{P}$
has a fibration
 $\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
with connected fibers such that the general fiber is smooth of genus one; see [Reference BǎdescuBǎd01, § 7]. Moreover, the
$\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
with connected fibers such that the general fiber is smooth of genus one; see [Reference BǎdescuBǎd01, § 7]. Moreover, the
![]() $I_{8}$
fiber
$I_{8}$
fiber
 $\sum _{i=1}^{4}A_{i}+\sum _{i=1}^{4}\bar{G}_{i}$
has multiplicity three. Thus, this elliptic fibration is a Halphen surface of index three (after one blows down
$\sum _{i=1}^{4}A_{i}+\sum _{i=1}^{4}\bar{G}_{i}$
has multiplicity three. Thus, this elliptic fibration is a Halphen surface of index three (after one blows down
![]() $\bar{N}_{1}$
and
$\bar{N}_{1}$
and
![]() $\bar{N}_{2}$
); see [Reference Cossec and DolgachevCD89, ch. V, Theorem 5.6.1].◻
$\bar{N}_{2}$
); see [Reference Cossec and DolgachevCD89, ch. V, Theorem 5.6.1].◻
Lemma 4.2. The Boyd surface
![]() $Y$
is a Dolgachev surface in characteristic seven. The elliptic fibration
$Y$
is a Dolgachev surface in characteristic seven. The elliptic fibration
 $Y\rightarrow \mathbb{P}_{k}^{1}$
has four singular fibers: one
$Y\rightarrow \mathbb{P}_{k}^{1}$
has four singular fibers: one
![]() $I_{4}$
with multiplicity three, one
$I_{4}$
with multiplicity three, one
![]() $I_{4}$
with multiplicity two, and two reduced
$I_{4}$
with multiplicity two, and two reduced
![]() $I_{2}$
.
$I_{2}$
.
Proof. We denote by
![]() $\unicode[STIX]{x1D6FC}$
the composition
$\unicode[STIX]{x1D6FC}$
the composition
 $W\rightarrow \mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
. Since this is a projective morphism, we have a Stein factorization for
$W\rightarrow \mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
. Since this is a projective morphism, we have a Stein factorization for
![]() $\unicode[STIX]{x1D6FC}$
, i.e. maps
$\unicode[STIX]{x1D6FC}$
, i.e. maps
 $\unicode[STIX]{x1D6FD}:W\rightarrow C$
with connected fibers and
$\unicode[STIX]{x1D6FD}:W\rightarrow C$
with connected fibers and
 $\unicode[STIX]{x1D6FE}:C\rightarrow \mathbb{P}_{k}^{1}$
a finite morphism such that
$\unicode[STIX]{x1D6FE}:C\rightarrow \mathbb{P}_{k}^{1}$
a finite morphism such that
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D6FD}$
. Note that the multiplicity of the fiber
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D6FD}$
. Note that the multiplicity of the fiber
 $B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
of
$B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
of
![]() $\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
is
$\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
is
![]() $1$
, and so
$1$
, and so
 $\unicode[STIX]{x1D6FE}:C\rightarrow \mathbb{P}_{k}^{1}$
is a finite separable morphism. Note also that the fibers
$\unicode[STIX]{x1D6FE}:C\rightarrow \mathbb{P}_{k}^{1}$
is a finite separable morphism. Note also that the fibers
 $B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
and
$B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
and
![]() $I_{8}$
in
$I_{8}$
in
 $\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
pull back to connected fibers of
$\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
pull back to connected fibers of
![]() $\unicode[STIX]{x1D6FC}$
with multiplicities two and three, respectively. Since these multiplicities are coprime, we must have that the degree of
$\unicode[STIX]{x1D6FC}$
with multiplicities two and three, respectively. Since these multiplicities are coprime, we must have that the degree of
![]() $\unicode[STIX]{x1D6FE}$
is one, and so
$\unicode[STIX]{x1D6FE}$
is one, and so
![]() $\unicode[STIX]{x1D6FE}$
is an isomorphism. In this way
$\unicode[STIX]{x1D6FE}$
is an isomorphism. In this way
![]() $\unicode[STIX]{x1D6FC}$
has connected fibers. In addition, since it has two multiple fibers, the Kodaira dimension of
$\unicode[STIX]{x1D6FC}$
has connected fibers. In addition, since it has two multiple fibers, the Kodaira dimension of
![]() $Y$
is non-negative [Reference Cossec and DolgachevCD89].
$Y$
is non-negative [Reference Cossec and DolgachevCD89].
The double cover
 $W\rightarrow \mathbb{P}$
induces a connected étale cover between the non-multiple fibers of
$W\rightarrow \mathbb{P}$
induces a connected étale cover between the non-multiple fibers of
![]() $\unicode[STIX]{x1D6FC}$
. Note that
$\unicode[STIX]{x1D6FC}$
. Note that
 $\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
can only have irreducible singular fibers apart from
$\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
can only have irreducible singular fibers apart from
 $B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
and
$B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
and
![]() $I_{8}$
, because the Picard number of
$I_{8}$
, because the Picard number of
![]() $\mathbb{P}$
is
$\mathbb{P}$
is
![]() $12$
. Therefore, we can have either two
$12$
. Therefore, we can have either two
![]() $I_{1}$
or one II as extra singular fibers. But a fiber of type II is étale simply connected, and so it does not have a connected étale cover of degree two. Thus,
$I_{1}$
or one II as extra singular fibers. But a fiber of type II is étale simply connected, and so it does not have a connected étale cover of degree two. Thus,
 $\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
has precisely two extra
$\mathbb{P}\rightarrow \mathbb{P}_{k}^{1}$
has precisely two extra
![]() $I_{1}$
singular fibers, and their pre-images under
$I_{1}$
singular fibers, and their pre-images under
 $W\rightarrow \mathbb{P}$
give two
$W\rightarrow \mathbb{P}$
give two
![]() $I_{2}$
reduced fibers for
$I_{2}$
reduced fibers for
![]() $\unicode[STIX]{x1D6FC}$
. This elliptic fibration induces a relatively minimal elliptic fibration
$\unicode[STIX]{x1D6FC}$
. This elliptic fibration induces a relatively minimal elliptic fibration
 $Y\rightarrow \mathbb{P}_{k}^{1}$
, after we blow-down the curves
$Y\rightarrow \mathbb{P}_{k}^{1}$
, after we blow-down the curves
 $G_{1},\ldots ,G_{4}$
.
$G_{1},\ldots ,G_{4}$
.
Using well-known facts on double covers, one can easily verify that
 $K_{Y}^{2}=0$
,
$K_{Y}^{2}=0$
,
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{Y})=1$
, and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{Y})=1$
, and
 $$\begin{eqnarray}p_{g}(Y)=h^{2}(-L)=h^{0}(K_{\mathbb{ P}}+L)=0,\end{eqnarray}$$
$$\begin{eqnarray}p_{g}(Y)=h^{2}(-L)=h^{0}(K_{\mathbb{ P}}+L)=0,\end{eqnarray}$$
where
 $$\begin{eqnarray}L=3\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6E5})-\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-2\mathop{\sum }_{i=1}^{4}\bar{G}_{i}-\bar{N}_{1}-\bar{N}_{2}\end{eqnarray}$$
$$\begin{eqnarray}L=3\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6E5})-\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-2\mathop{\sum }_{i=1}^{4}\bar{G}_{i}-\bar{N}_{1}-\bar{N}_{2}\end{eqnarray}$$
is the line bundle defining the double cover
![]() $\unicode[STIX]{x1D70B}^{\prime }$
. Thus,
$\unicode[STIX]{x1D70B}^{\prime }$
. Thus,
 $q(Y)=0$
.◻
$q(Y)=0$
.◻
The previous lemma shows the canonical class of
![]() $Y$
has the form
$Y$
has the form
 $$\begin{eqnarray}K_{Y}\sim -F+\unicode[STIX]{x1D6E4}_{2}+2\unicode[STIX]{x1D6E4}_{3}\equiv 1/6F,\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}\sim -F+\unicode[STIX]{x1D6E4}_{2}+2\unicode[STIX]{x1D6E4}_{3}\equiv 1/6F,\end{eqnarray}$$
where
![]() $F$
is a general fiber,
$F$
is a general fiber,
![]() $\unicode[STIX]{x1D6E4}_{2}$
is the
$\unicode[STIX]{x1D6E4}_{2}$
is the
![]() $I_{4}$
with multiplicity two, and
$I_{4}$
with multiplicity two, and
![]() $\unicode[STIX]{x1D6E4}_{3}$
is the
$\unicode[STIX]{x1D6E4}_{3}$
is the
![]() $I_{4}$
with multiplicity three.
$I_{4}$
with multiplicity three.
Lemma 4.3. We have that
![]() $K_{S_{0}}$
is nef.
$K_{S_{0}}$
is nef.
Proof. The Boyd surface
![]() $Y$
is the minimal resolution of the surface
$Y$
is the minimal resolution of the surface
![]() $S_{0}$
, which has log terminal singularities. Therefore, it suffices to show that
$S_{0}$
, which has log terminal singularities. Therefore, it suffices to show that
![]() $K_{Y}$
is nef, which follows from (4.2).◻
$K_{Y}$
is nef, which follows from (4.2).◻
5 Some mixed characteristic deformation theory
In this section we show that the Craighero–Gattazzo surface can be degenerated to a special complex surface with a
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity. Our argument is based on the following simple fact.
${\textstyle \frac{1}{4}}(1,1)$
singularity. Our argument is based on the following simple fact.
Lemma 5.1. Let
![]() ${\mathcal{R}}$
be a DVR with residue field
${\mathcal{R}}$
be a DVR with residue field
![]() $k$
and quotient field
$k$
and quotient field
![]() $K$
. Let
$K$
. Let
![]() $\bar{K}$
be the algebraic closure of
$\bar{K}$
be the algebraic closure of
![]() $K$
. Let
$K$
. Let
![]() $T$
be a smooth
$T$
be a smooth
![]() ${\mathcal{R}}$
-scheme. Let
${\mathcal{R}}$
-scheme. Let
![]() $o\in T$
be a
$o\in T$
be a
![]() $k$
-point. Let
$k$
-point. Let
 $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}:\operatorname{Spec}{\mathcal{R}}\rightarrow T$
be two sections passing through
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}:\operatorname{Spec}{\mathcal{R}}\rightarrow T$
be two sections passing through
![]() $o$
. Then there exists an irreducible smooth
$o$
. Then there exists an irreducible smooth
![]() $\bar{K}$
-curve
$\bar{K}$
-curve
![]() $C$
and a morphism
$C$
and a morphism
 $C\rightarrow T_{\bar{K}}$
such that its image contains
$C\rightarrow T_{\bar{K}}$
such that its image contains
![]() $\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D702})$
and
$\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D702})$
and
![]() $\unicode[STIX]{x1D70E}_{2}(\unicode[STIX]{x1D702})$
, where
$\unicode[STIX]{x1D70E}_{2}(\unicode[STIX]{x1D702})$
, where
 $\unicode[STIX]{x1D702}\in \operatorname{Spec}{\mathcal{R}}$
is the generic point.
$\unicode[STIX]{x1D702}\in \operatorname{Spec}{\mathcal{R}}$
is the generic point.
Remark 5.2. For the proof we only need
![]() $\unicode[STIX]{x1D70E}_{1}$
to be a section;
$\unicode[STIX]{x1D70E}_{1}$
to be a section;
![]() $\unicode[STIX]{x1D70E}_{2}$
can be a section
$\unicode[STIX]{x1D70E}_{2}$
can be a section
 $\operatorname{Spec}{\mathcal{R}}^{\prime }\rightarrow T_{{\mathcal{R}}^{\prime }}$
after a finite surjective base change
$\operatorname{Spec}{\mathcal{R}}^{\prime }\rightarrow T_{{\mathcal{R}}^{\prime }}$
after a finite surjective base change
 $\operatorname{Spec}{\mathcal{R}}^{\prime }\rightarrow \operatorname{Spec}{\mathcal{R}}$
.
$\operatorname{Spec}{\mathcal{R}}^{\prime }\rightarrow \operatorname{Spec}{\mathcal{R}}$
.
Proof. We can substitute
![]() $T$
with an affine connected component
$T$
with an affine connected component
![]() $\operatorname{Spec}A$
of
$\operatorname{Spec}A$
of
![]() $o$
. By [Reference MumfordMum70, p. 56], it suffices to prove that
$o$
. By [Reference MumfordMum70, p. 56], it suffices to prove that
![]() $T_{K}$
is geometrically connected. Since it is smooth over
$T_{K}$
is geometrically connected. Since it is smooth over
![]() $\operatorname{Spec}K$
and has a
$\operatorname{Spec}K$
and has a
![]() $K$
-point
$K$
-point
![]() $\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D702})$
, it suffices to prove that it is connected. Arguing by contradiction, suppose it is disconnected. Then
$\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D702})$
, it suffices to prove that it is connected. Arguing by contradiction, suppose it is disconnected. Then
 $H^{0}(T_{K},{\mathcal{O}}_{T_{K}})$
contains a non-trivial idempotent
$H^{0}(T_{K},{\mathcal{O}}_{T_{K}})$
contains a non-trivial idempotent
![]() $e$
. Let
$e$
. Let
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{R}}$
be a uniformizer. Since
$\unicode[STIX]{x1D70B}\in {\mathcal{R}}$
be a uniformizer. Since
![]() $T$
is flat over
$T$
is flat over
![]() $\operatorname{Spec}{\mathcal{R}}$
,
$\operatorname{Spec}{\mathcal{R}}$
,
![]() $\unicode[STIX]{x1D70B}$
is not a zero-divisor in
$\unicode[STIX]{x1D70B}$
is not a zero-divisor in
![]() $A$
, and so
$A$
, and so
 $e\in A[1/\unicode[STIX]{x1D70B}]$
. Let
$e\in A[1/\unicode[STIX]{x1D70B}]$
. Let
![]() $n$
be the minimal non-negative integer such that
$n$
be the minimal non-negative integer such that
![]() $e$
can be written as
$e$
can be written as
![]() $a/\unicode[STIX]{x1D70B}^{n}$
with
$a/\unicode[STIX]{x1D70B}^{n}$
with
![]() $a\in A$
. Then
$a\in A$
. Then
 $a^{2}=\unicode[STIX]{x1D70B}^{n}a$
. Since
$a^{2}=\unicode[STIX]{x1D70B}^{n}a$
. Since
![]() $T$
is smooth over
$T$
is smooth over
![]() $\operatorname{Spec}{\mathcal{R}}$
, its special fiber is reduced. It follows that
$\operatorname{Spec}{\mathcal{R}}$
, its special fiber is reduced. It follows that
![]() $n=0$
because otherwise
$n=0$
because otherwise
 $a^{2}=0\operatorname{mod}(\unicode[STIX]{x1D70B})$
and therefore
$a^{2}=0\operatorname{mod}(\unicode[STIX]{x1D70B})$
and therefore
 $a=0\operatorname{mod}(\unicode[STIX]{x1D70B})$
, which implies that
$a=0\operatorname{mod}(\unicode[STIX]{x1D70B})$
, which implies that
![]() $n$
is not minimal. So
$n$
is not minimal. So
![]() $e\in A$
, which contradicts the connectedness of
$e\in A$
, which contradicts the connectedness of
![]() $T$
.◻
$T$
.◻
Lemma 5.3. Let
![]() ${\mathcal{R}}$
be a complete DVR with residue field
${\mathcal{R}}$
be a complete DVR with residue field
![]() $k$
and quotient field
$k$
and quotient field
![]() $K$
. Let
$K$
. Let
![]() $\bar{K}$
be the algebraic closure of
$\bar{K}$
be the algebraic closure of
![]() $K$
. Let
$K$
. Let
![]() $F$
be a limit-preserving contravariant functor from the category of
$F$
be a limit-preserving contravariant functor from the category of
![]() ${\mathcal{R}}$
-schemes to the category of sets.
${\mathcal{R}}$
-schemes to the category of sets.
Fix
 $\unicode[STIX]{x1D701}_{0}\in F(\operatorname{Spec}k)$
. Let
$\unicode[STIX]{x1D701}_{0}\in F(\operatorname{Spec}k)$
. Let
![]() $F_{\unicode[STIX]{x1D701}_{0}}$
be its ‘deformation functor’, i.e. a functor from the category of pointed
$F_{\unicode[STIX]{x1D701}_{0}}$
be its ‘deformation functor’, i.e. a functor from the category of pointed
![]() ${\mathcal{R}}$
-schemes
${\mathcal{R}}$
-schemes
![]() $(X,x_{0})$
, where
$(X,x_{0})$
, where
![]() $x_{0}$
is a closed point with residue field
$x_{0}$
is a closed point with residue field
![]() $k$
, to sets. Specifically,
$k$
, to sets. Specifically,
 $F_{\unicode[STIX]{x1D701}_{0}}(X,x_{0})=\{\unicode[STIX]{x1D709}\in F(X)\,|\,F(i)\unicode[STIX]{x1D709}=\unicode[STIX]{x1D701}_{0}\}$
, where
$F_{\unicode[STIX]{x1D701}_{0}}(X,x_{0})=\{\unicode[STIX]{x1D709}\in F(X)\,|\,F(i)\unicode[STIX]{x1D709}=\unicode[STIX]{x1D701}_{0}\}$
, where
 $i:\operatorname{Spec}k=\operatorname{Spec}k(x_{0}){\hookrightarrow}X$
is the inclusion.
$i:\operatorname{Spec}k=\operatorname{Spec}k(x_{0}){\hookrightarrow}X$
is the inclusion.
Suppose the restriction of
![]() $F_{\unicode[STIX]{x1D701}_{0}}$
to the category of spectra of local artinian
$F_{\unicode[STIX]{x1D701}_{0}}$
to the category of spectra of local artinian
![]() ${\mathcal{R}}$
-algebras with residue field
${\mathcal{R}}$
-algebras with residue field
![]() $k$
is smooth and satisfies Schlessinger’s conditions [Reference SchlessingerSch68]. Suppose also that the natural map
$k$
is smooth and satisfies Schlessinger’s conditions [Reference SchlessingerSch68]. Suppose also that the natural map
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}A)\rightarrow \lim _{\longleftarrow }F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}A/\mathfrak{m}^{n})\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}A)\rightarrow \lim _{\longleftarrow }F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}A/\mathfrak{m}^{n})\end{eqnarray}$$
is bijective for every complete local Noetherian
![]() ${\mathcal{R}}$
-algebra
${\mathcal{R}}$
-algebra
![]() $(A,\mathfrak{m})$
with residue field
$(A,\mathfrak{m})$
with residue field
![]() $k$
.
$k$
.
Let
 $\unicode[STIX]{x1D6F4}_{1},\unicode[STIX]{x1D6F4}_{2}\in F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}{\mathcal{R}})$
and let
$\unicode[STIX]{x1D6F4}_{1},\unicode[STIX]{x1D6F4}_{2}\in F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}{\mathcal{R}})$
and let
 $\bar{\unicode[STIX]{x1D6F4}}_{1},\bar{\unicode[STIX]{x1D6F4}}_{2}\in F(\operatorname{Spec}\bar{K})$
be their pull-backs to
$\bar{\unicode[STIX]{x1D6F4}}_{1},\bar{\unicode[STIX]{x1D6F4}}_{2}\in F(\operatorname{Spec}\bar{K})$
be their pull-backs to
![]() $\operatorname{Spec}\bar{K}$
. Then there exists an irreducible smooth
$\operatorname{Spec}\bar{K}$
. Then there exists an irreducible smooth
![]() $\bar{K}$
-curve
$\bar{K}$
-curve
![]() $C$
,
$C$
,
![]() $\bar{K}$
-points
$\bar{K}$
-points
 $y_{1},y_{2}\in C$
, and an element
$y_{1},y_{2}\in C$
, and an element
 $\unicode[STIX]{x1D6F4}\in F(C)$
which restricts to
$\unicode[STIX]{x1D6F4}\in F(C)$
which restricts to
![]() $\bar{\unicode[STIX]{x1D6F4}}_{1}$
and
$\bar{\unicode[STIX]{x1D6F4}}_{1}$
and
![]() $\bar{\unicode[STIX]{x1D6F4}}_{2}$
at
$\bar{\unicode[STIX]{x1D6F4}}_{2}$
at
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
, respectively.
$y_{2}$
, respectively.
Proof. By [Reference SchlessingerSch68],
![]() $F_{\unicode[STIX]{x1D701}_{0}}$
admits a hull, and by (5.1) we can assume that the hull is induced by an element
$F_{\unicode[STIX]{x1D701}_{0}}$
admits a hull, and by (5.1) we can assume that the hull is induced by an element
 $\bar{\unicode[STIX]{x1D701}}\in F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}{\mathcal{H}})$
, where
$\bar{\unicode[STIX]{x1D701}}\in F_{\unicode[STIX]{x1D701}_{0}}(\operatorname{Spec}{\mathcal{H}})$
, where
![]() $({\mathcal{H}},\mathfrak{m})$
is a complete local Noetherian
$({\mathcal{H}},\mathfrak{m})$
is a complete local Noetherian
![]() ${\mathcal{R}}$
-algebra with residue field
${\mathcal{R}}$
-algebra with residue field
![]() $k$
. By Artin’s algebraization theorem [Reference ArtinArt69, Theorem 1.6], there exists an
$k$
. By Artin’s algebraization theorem [Reference ArtinArt69, Theorem 1.6], there exists an
![]() ${\mathcal{R}}$
-scheme of finite type
${\mathcal{R}}$
-scheme of finite type
![]() $T$
, a closed
$T$
, a closed
![]() $k$
-point
$k$
-point
![]() $o\in T$
, an element
$o\in T$
, an element
 $\unicode[STIX]{x1D701}\in F_{\unicode[STIX]{x1D701}_{0}}(T,o)$
, and an isomorphism
$\unicode[STIX]{x1D701}\in F_{\unicode[STIX]{x1D701}_{0}}(T,o)$
, and an isomorphism
 $\unicode[STIX]{x1D70E}:\hat{{\mathcal{O}}}_{T,o}\rightarrow {\mathcal{H}}$
such that
$\unicode[STIX]{x1D70E}:\hat{{\mathcal{O}}}_{T,o}\rightarrow {\mathcal{H}}$
such that
![]() $F(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D701}$
and
$F(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D701}$
and
![]() $\bar{\unicode[STIX]{x1D701}}$
agree on
$\bar{\unicode[STIX]{x1D701}}$
agree on
![]() ${\mathcal{H}}/\mathfrak{m}^{n}$
for all
${\mathcal{H}}/\mathfrak{m}^{n}$
for all
![]() $n\geqslant 1$
. By (5.1), in fact
$n\geqslant 1$
. By (5.1), in fact
 $F(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D701}=\bar{\unicode[STIX]{x1D701}}$
.
$F(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D701}=\bar{\unicode[STIX]{x1D701}}$
.
Since
![]() $F_{\unicode[STIX]{x1D701}_{0}}$
is smooth,
$F_{\unicode[STIX]{x1D701}_{0}}$
is smooth,
 $T\rightarrow \operatorname{Spec}{\mathcal{R}}$
is formally smooth at
$T\rightarrow \operatorname{Spec}{\mathcal{R}}$
is formally smooth at
![]() $o$
, and therefore we can assume that
$o$
, and therefore we can assume that
![]() $T$
is a smooth
$T$
is a smooth
![]() ${\mathcal{R}}$
-scheme after shrinking it if necessary.
${\mathcal{R}}$
-scheme after shrinking it if necessary.
Since
![]() ${\mathcal{R}}$
is complete, we can find sections
${\mathcal{R}}$
is complete, we can find sections
 $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}:\operatorname{Spec}{\mathcal{R}}\rightarrow T$
such that
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}:\operatorname{Spec}{\mathcal{R}}\rightarrow T$
such that
 $F(\unicode[STIX]{x1D70E}_{i})(\unicode[STIX]{x1D701})$
and
$F(\unicode[STIX]{x1D70E}_{i})(\unicode[STIX]{x1D701})$
and
![]() $\unicode[STIX]{x1D6F4}_{i}$
agree on
$\unicode[STIX]{x1D6F4}_{i}$
agree on
![]() ${\mathcal{R}}/\mathfrak{n}^{n}$
for any
${\mathcal{R}}/\mathfrak{n}^{n}$
for any
![]() $n\geqslant 1$
, where
$n\geqslant 1$
, where
![]() $\mathfrak{n}\subset {\mathcal{R}}$
is the maximal ideal. By (5.1),
$\mathfrak{n}\subset {\mathcal{R}}$
is the maximal ideal. By (5.1),
 $F(\unicode[STIX]{x1D70E}_{i})(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6F4}_{i}$
. It remains to apply Lemma 5.1.◻
$F(\unicode[STIX]{x1D70E}_{i})(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6F4}_{i}$
. It remains to apply Lemma 5.1.◻
In our application
![]() $F$
will be a functor of
$F$
will be a functor of
![]() $\mathbb{Q}$
-Gorenstein deformations, as worked out in [Reference HackingHac04] in characteristic zero and [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11] in general. For simplicity, we allow only Cohen–Macaulay surfaces. Following [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11], let
$\mathbb{Q}$
-Gorenstein deformations, as worked out in [Reference HackingHac04] in characteristic zero and [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11] in general. For simplicity, we allow only Cohen–Macaulay surfaces. Following [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11], let
![]() ${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
be the category of Kollár families fibered in groupoids over the category of schemes. An object of
${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
be the category of Kollár families fibered in groupoids over the category of schemes. An object of
![]() ${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
over a scheme
${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
over a scheme
![]() $B$
is a triple
$B$
is a triple
 $(f:X\rightarrow B,F,\unicode[STIX]{x1D719})$
, where
$(f:X\rightarrow B,F,\unicode[STIX]{x1D719})$
, where
![]() $f$
is a proper flat family of connected reduced Cohen–Macaulay surfaces,
$f$
is a proper flat family of connected reduced Cohen–Macaulay surfaces,
![]() $F$
is a coherent sheaf, and
$F$
is a coherent sheaf, and
 $\unicode[STIX]{x1D719}:F\rightarrow \unicode[STIX]{x1D714}_{X/B}$
is an isomorphism. Moreover, we assume that the formation of every reflexive power
$\unicode[STIX]{x1D719}:F\rightarrow \unicode[STIX]{x1D714}_{X/B}$
is an isomorphism. Moreover, we assume that the formation of every reflexive power
![]() $F^{[n]}$
commutes with arbitrary base change (we call this the Kollár condition) and that for every geometric point
$F^{[n]}$
commutes with arbitrary base change (we call this the Kollár condition) and that for every geometric point
![]() $s$
of
$s$
of
![]() $B$
there exists a positive integer
$B$
there exists a positive integer
![]() $N_{s}$
such that
$N_{s}$
such that
 $F^{[N_{s}]}|_{X_{s}}$
is invertible and ample. See [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11] for the description of morphisms in
$F^{[N_{s}]}|_{X_{s}}$
is invertible and ample. See [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11] for the description of morphisms in
![]() ${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
and for the proof that it is an algebraic stack. The functor
${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
and for the proof that it is an algebraic stack. The functor
![]() $\operatorname{Def}^{\mathbb{Q}G}$
of
$\operatorname{Def}^{\mathbb{Q}G}$
of
![]() $\mathbb{Q}$
-Gorenstein deformations is the associated set-valued functor of isomorphism classes of Kollár families.
$\mathbb{Q}$
-Gorenstein deformations is the associated set-valued functor of isomorphism classes of Kollár families.
Theorem 5.4. Let
![]() ${\mathcal{R}}$
be a complete DVR with algebraically closed residue field
${\mathcal{R}}$
be a complete DVR with algebraically closed residue field
![]() $k$
and quotient field
$k$
and quotient field
![]() $K$
. Let
$K$
. Let
![]() $\bar{K}$
be the algebraic closure of
$\bar{K}$
be the algebraic closure of
![]() $K$
. Let
$K$
. Let
![]() ${\mathcal{X}}_{1}$
and
${\mathcal{X}}_{1}$
and
![]() ${\mathcal{X}}_{2}$
be two
${\mathcal{X}}_{2}$
be two
![]() $\mathbb{Q}$
-Gorenstein families over
$\mathbb{Q}$
-Gorenstein families over
![]() $\operatorname{Spec}{\mathcal{R}}$
. Suppose their special fibers are both isomorphic to a
$\operatorname{Spec}{\mathcal{R}}$
. Suppose their special fibers are both isomorphic to a
![]() $k$
-surface
$k$
-surface
![]() $X$
. Let
$X$
. Let
![]() ${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
be the restriction of
${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
be the restriction of
![]() ${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
to the category of
${\mathcal{K}}^{\unicode[STIX]{x1D714}}$
to the category of
![]() ${\mathcal{R}}$
-schemes. Suppose it is
${\mathcal{R}}$
-schemes. Suppose it is
![]() ${\mathcal{R}}$
-smooth at
${\mathcal{R}}$
-smooth at
 $X\rightarrow \operatorname{Spec}k$
. Then there exists an irreducible smooth
$X\rightarrow \operatorname{Spec}k$
. Then there exists an irreducible smooth
![]() $\bar{K}$
-curve
$\bar{K}$
-curve
![]() $C$
,
$C$
,
![]() $\bar{K}$
-points
$\bar{K}$
-points
 $y_{1},y_{2}\in C$
, and a
$y_{1},y_{2}\in C$
, and a
![]() $\mathbb{Q}$
-Gorenstein family over
$\mathbb{Q}$
-Gorenstein family over
![]() $C$
with fibers at
$C$
with fibers at
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
isomorphic to
$y_{2}$
isomorphic to
![]() $({\mathcal{X}}_{1})_{\bar{K}}$
and
$({\mathcal{X}}_{1})_{\bar{K}}$
and
![]() $({\mathcal{X}}_{2})_{\bar{K}}$
, respectively.
$({\mathcal{X}}_{2})_{\bar{K}}$
, respectively.
Proof. Since
![]() ${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is an algebraic
${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is an algebraic
![]() ${\mathcal{R}}$
-stack, its associated set-valued functor
${\mathcal{R}}$
-stack, its associated set-valued functor
![]() $\operatorname{Def}_{{\mathcal{R}}}^{\mathbb{Q}G}$
satisfies the conditions of Lemma 5.3 by Artin’s criterion [Reference ArtinArt74].◻
$\operatorname{Def}_{{\mathcal{R}}}^{\mathbb{Q}G}$
satisfies the conditions of Lemma 5.3 by Artin’s criterion [Reference ArtinArt74].◻
In our situation,
![]() ${\mathcal{X}}_{1}$
will be a degeneration of the Craighero–Gattazzo surface to the contraction
${\mathcal{X}}_{1}$
will be a degeneration of the Craighero–Gattazzo surface to the contraction
![]() $S_{0}$
of the Boyd surface
$S_{0}$
of the Boyd surface
![]() $Y$
. To construct the second family, we will need the following well-known fact.
$Y$
. To construct the second family, we will need the following well-known fact.
Lemma 5.5. Let
![]() $k$
be an algebraically closed field, let
$k$
be an algebraically closed field, let
![]() ${\mathcal{R}}$
be a complete DVR with residue field
${\mathcal{R}}$
be a complete DVR with residue field
![]() $k$
, let
$k$
, let
![]() $Y$
be a smooth projective surface over
$Y$
be a smooth projective surface over
![]() $k$
and let
$k$
and let
 $C_{1},\ldots ,C_{r}\subset Y$
be smooth curves intersecting transversally. Suppose
$C_{1},\ldots ,C_{r}\subset Y$
be smooth curves intersecting transversally. Suppose
 $$\begin{eqnarray}H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=H^{2}(Y,{\mathcal{O}}_{Y})=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=H^{2}(Y,{\mathcal{O}}_{Y})=0.\end{eqnarray}$$
Then there exists a smooth projective family of surfaces
 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with closed subschemes
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with closed subschemes
 ${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{r}\subset {\mathcal{Y}}$
smooth and proper over
${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{r}\subset {\mathcal{Y}}$
smooth and proper over
![]() $\operatorname{Spec}{\mathcal{R}}$
such that the special fiber is
$\operatorname{Spec}{\mathcal{R}}$
such that the special fiber is
 $(Y;C_{1},\ldots ,C_{r})$
.
$(Y;C_{1},\ldots ,C_{r})$
.
Proof. This is well-known but we sketch a proof for completeness. Let
![]() $\mathfrak{m}\subset {\mathcal{R}}$
be the maximal ideal and let
$\mathfrak{m}\subset {\mathcal{R}}$
be the maximal ideal and let
 ${\mathcal{R}}_{n}={\mathcal{R}}/\mathfrak{m}^{n+1}$
for each
${\mathcal{R}}_{n}={\mathcal{R}}/\mathfrak{m}^{n+1}$
for each
 $n=0,1,\ldots .$
We first lift
$n=0,1,\ldots .$
We first lift
 $(Y;C_{1},\ldots ,C_{r})$
to a scheme and a collection of subschemes flat over
$(Y;C_{1},\ldots ,C_{r})$
to a scheme and a collection of subschemes flat over
 $\operatorname{Spec}{\mathcal{R}}_{n}$
for each
$\operatorname{Spec}{\mathcal{R}}_{n}$
for each
![]() $n$
by induction on
$n$
by induction on
![]() $n$
. So assume we already have a lift
$n$
. So assume we already have a lift
 $(Y^{n};C_{1}^{n},\ldots ,C_{r}^{n})$
to
$(Y^{n};C_{1}^{n},\ldots ,C_{r}^{n})$
to
 $\operatorname{Spec}{\mathcal{R}}_{n}$
. We have an exact sequence
$\operatorname{Spec}{\mathcal{R}}_{n}$
. We have an exact sequence
 $$\begin{eqnarray}0\rightarrow T_{Y}(-\text{log}(C_{1}+\cdots +C_{r}))\rightarrow T_{Y}\rightarrow i_{1\ast }N_{C_{1}/Y}\oplus \cdots \oplus i_{r\ast }N_{C_{r}/Y}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T_{Y}(-\text{log}(C_{1}+\cdots +C_{r}))\rightarrow T_{Y}\rightarrow i_{1\ast }N_{C_{1}/Y}\oplus \cdots \oplus i_{r\ast }N_{C_{r}/Y}\rightarrow 0\end{eqnarray}$$
of sheaves on
![]() $Y$
, where
$Y$
, where
 $i_{j}:C_{j}\rightarrow Y$
denotes the embedding for each
$i_{j}:C_{j}\rightarrow Y$
denotes the embedding for each
![]() $j$
. Since
$j$
. Since
 $H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=0$
, we have
$H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=0$
, we have
 $H^{2}(Y,T_{Y})=0$
as well. Therefore, we can lift
$H^{2}(Y,T_{Y})=0$
as well. Therefore, we can lift
![]() $Y^{n}$
to a scheme
$Y^{n}$
to a scheme
![]() $Y^{n+1}$
flat (and then automatically smooth and proper) over
$Y^{n+1}$
flat (and then automatically smooth and proper) over
 $\operatorname{Spec}{\mathcal{R}}_{n+1}$
. Moreover, all possible lifts form an affine space with underlying vector space
$\operatorname{Spec}{\mathcal{R}}_{n+1}$
. Moreover, all possible lifts form an affine space with underlying vector space
 $H^{1}(Y,T_{Y})$
. Since
$H^{1}(Y,T_{Y})$
. Since
 $$\begin{eqnarray}H^{1}(Y,T_{Y})\rightarrow H^{1}(C_{1},N_{C_{1}/Y})\oplus \cdots \oplus H^{1}(C_{r},N_{C_{r}/Y})\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(Y,T_{Y})\rightarrow H^{1}(C_{1},N_{C_{1}/Y})\oplus \cdots \oplus H^{1}(C_{r},N_{C_{r}/Y})\end{eqnarray}$$
is surjective by
 $H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=0$
, we can choose a lift such that the corresponding class in
$H^{2}(Y,T_{Y}(-\text{log}(C_{1}+\cdots +C_{r})))=0$
, we can choose a lift such that the corresponding class in
 $H^{1}(C_{i},N_{C_{i}/Y})$
vanishes for each
$H^{1}(C_{i},N_{C_{i}/Y})$
vanishes for each
![]() $i$
. This class can be interpreted as an obstruction to lifting
$i$
. This class can be interpreted as an obstruction to lifting
 $C_{i}^{n}\subset Y^{n}$
to a subscheme
$C_{i}^{n}\subset Y^{n}$
to a subscheme
 $C_{i}^{n+1}\subset Y^{n+1}$
flat over
$C_{i}^{n+1}\subset Y^{n+1}$
flat over
 $\operatorname{Spec}{\mathcal{R}}_{n+1}$
. So we can lift all
$\operatorname{Spec}{\mathcal{R}}_{n+1}$
. So we can lift all
![]() $C_{i}$
to subschemes
$C_{i}$
to subschemes
 $C_{i}^{n+1}\subset Y^{n+1}$
flat (and automatically smooth and proper) over
$C_{i}^{n+1}\subset Y^{n+1}$
flat (and automatically smooth and proper) over
 $\operatorname{Spec}{\mathcal{R}}_{n+1}$
. The projective limit
$\operatorname{Spec}{\mathcal{R}}_{n+1}$
. The projective limit
 $\hat{{\mathcal{Y}}}=\mathop{\lim }_{\leftarrow }Y^{n}$
is a formal scheme smooth and proper over
$\hat{{\mathcal{Y}}}=\mathop{\lim }_{\leftarrow }Y^{n}$
is a formal scheme smooth and proper over
![]() $\operatorname{Spf}{\mathcal{R}}$
. The projective limits
$\operatorname{Spf}{\mathcal{R}}$
. The projective limits
 $\hat{{\mathcal{C}}}_{i}=\mathop{\lim }_{\leftarrow }C_{i}^{n}$
for
$\hat{{\mathcal{C}}}_{i}=\mathop{\lim }_{\leftarrow }C_{i}^{n}$
for
 $i=1,\ldots ,n$
are closed formal subschemes smooth and proper over
$i=1,\ldots ,n$
are closed formal subschemes smooth and proper over
![]() $\operatorname{Spf}{\mathcal{R}}$
.
$\operatorname{Spf}{\mathcal{R}}$
.
Since
 $H^{2}(Y,{\mathcal{O}}_{Y})=0$
, we can lift any ample invertible sheaf on
$H^{2}(Y,{\mathcal{O}}_{Y})=0$
, we can lift any ample invertible sheaf on
![]() $Y$
to an (automatically ample) invertible sheaf on
$Y$
to an (automatically ample) invertible sheaf on
![]() $\hat{{\mathcal{Y}}}$
. By Grothendieck’s existence theorem [Reference Grothendieck and DieudonnéEGAIII, 5.4.5], there exists a scheme
$\hat{{\mathcal{Y}}}$
. By Grothendieck’s existence theorem [Reference Grothendieck and DieudonnéEGAIII, 5.4.5], there exists a scheme
![]() ${\mathcal{Y}}$
projective and flat (and then automatically smooth) over
${\mathcal{Y}}$
projective and flat (and then automatically smooth) over
![]() $\operatorname{Spec}{\mathcal{R}}$
such that
$\operatorname{Spec}{\mathcal{R}}$
such that
![]() $\hat{{\mathcal{Y}}}$
is a completion of its special fiber. By [Reference Grothendieck and DieudonnéEGAIII, 5.1.8], there exist closed subschemes
$\hat{{\mathcal{Y}}}$
is a completion of its special fiber. By [Reference Grothendieck and DieudonnéEGAIII, 5.1.8], there exist closed subschemes
 ${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{r}\subset {\mathcal{Y}}$
such that
${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{r}\subset {\mathcal{Y}}$
such that
 $\hat{{\mathcal{C}}}_{1},\ldots ,\hat{{\mathcal{C}}}_{r}$
are completions of their special fibers. They are flat (and automatically smooth and proper) over
$\hat{{\mathcal{C}}}_{1},\ldots ,\hat{{\mathcal{C}}}_{r}$
are completions of their special fibers. They are flat (and automatically smooth and proper) over
![]() $\operatorname{Spec}{\mathcal{R}}$
.◻
$\operatorname{Spec}{\mathcal{R}}$
.◻
Notation 5.6. We revert to the notation of the previous sections; in particular,
![]() ${\mathcal{R}}$
will denote the ring of Witt vectors of an algebraically closed field
${\mathcal{R}}$
will denote the ring of Witt vectors of an algebraically closed field
![]() $k$
of characteristic seven. We denote by
$k$
of characteristic seven. We denote by
![]() $Y$
the Boyd surface over
$Y$
the Boyd surface over
![]() $k$
. The
$k$
. The
![]() $(-4)$
-curve
$(-4)$
-curve
![]() $\unicode[STIX]{x1D6E5}_{1}$
and the
$\unicode[STIX]{x1D6E5}_{1}$
and the
![]() $(-2)$
-curve
$(-2)$
-curve
![]() $N_{1}$
of
$N_{1}$
of
![]() $Y$
intersect transversally and in one point.
$Y$
intersect transversally and in one point.
Lemma 5.7. There exists a smooth projective family of surfaces
 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with closed subschemes
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
with closed subschemes
 ${\mathcal{C}},{\mathcal{N}}\subset {\mathcal{Y}}$
smooth and proper over
${\mathcal{C}},{\mathcal{N}}\subset {\mathcal{Y}}$
smooth and proper over
![]() $\operatorname{Spec}{\mathcal{R}}$
such that their geometric fibers are transversal rational curves of self-intersection
$\operatorname{Spec}{\mathcal{R}}$
such that their geometric fibers are transversal rational curves of self-intersection
![]() $-4$
and
$-4$
and
![]() $-2$
, respectively. The special fiber is the Boyd surface
$-2$
, respectively. The special fiber is the Boyd surface
 $(Y,\unicode[STIX]{x1D6E5}_{1},N_{1})$
.
$(Y,\unicode[STIX]{x1D6E5}_{1},N_{1})$
.
We need a few facts about the
![]() ${\textstyle \frac{1}{4}}(1,1)$
singularity. Let
${\textstyle \frac{1}{4}}(1,1)$
singularity. Let
![]() $\unicode[STIX]{x1D707}_{4}$
be the
$\unicode[STIX]{x1D707}_{4}$
be the
![]() $\mathbb{Z}$
-group scheme
$\mathbb{Z}$
-group scheme
 $\operatorname{Spec}\mathbb{Z}[\unicode[STIX]{x1D704}]/(\unicode[STIX]{x1D704}^{4}-1)$
with comultiplication
$\operatorname{Spec}\mathbb{Z}[\unicode[STIX]{x1D704}]/(\unicode[STIX]{x1D704}^{4}-1)$
with comultiplication
 $\unicode[STIX]{x1D704}\rightarrow \unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D704}$
. Let
$\unicode[STIX]{x1D704}\rightarrow \unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D704}$
. Let
 $$\begin{eqnarray}\mathbb{X}=\operatorname{Spec}\mathbb{Z}[u,v]^{\unicode[STIX]{x1D707}_{4}}=\operatorname{Spec}\mathbb{Z}[u^{4},u^{3}v,u^{2}v^{2},uv^{3},v^{4}],\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{X}=\operatorname{Spec}\mathbb{Z}[u,v]^{\unicode[STIX]{x1D707}_{4}}=\operatorname{Spec}\mathbb{Z}[u^{4},u^{3}v,u^{2}v^{2},uv^{3},v^{4}],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{4}$
acts on
$\unicode[STIX]{x1D707}_{4}$
acts on
![]() $\mathbb{A}^{2}$
with weights
$\mathbb{A}^{2}$
with weights
![]() $(\unicode[STIX]{x1D704},\unicode[STIX]{x1D704})$
. For any scheme
$(\unicode[STIX]{x1D704},\unicode[STIX]{x1D704})$
. For any scheme
![]() $S$
, we say that
$S$
, we say that
 $\mathbb{X}_{S}\rightarrow S$
is the standard family of surfaces with
$\mathbb{X}_{S}\rightarrow S$
is the standard family of surfaces with
![]() $\frac{1}{4}(1,1)$
singularity. If
$\frac{1}{4}(1,1)$
singularity. If
![]() $k$
is a field, then
$k$
is a field, then
![]() $\mathbb{X}_{k}$
is isomorphic to the cone over the rational normal curve in
$\mathbb{X}_{k}$
is isomorphic to the cone over the rational normal curve in
![]() $\mathbb{P}_{k}^{4}$
.
$\mathbb{P}_{k}^{4}$
.
Definition 5.8. Let
![]() $S$
be a locally Noetherian scheme and let
$S$
be a locally Noetherian scheme and let
![]() ${\mathcal{X}}\rightarrow S$
be a flat family of geometrically connected reduced surfaces smooth outside of a section
${\mathcal{X}}\rightarrow S$
be a flat family of geometrically connected reduced surfaces smooth outside of a section
 $\unicode[STIX]{x1D6F4}:S\rightarrow {\mathcal{X}}$
. We say that
$\unicode[STIX]{x1D6F4}:S\rightarrow {\mathcal{X}}$
. We say that
![]() ${\mathcal{X}}\rightarrow S$
has a
${\mathcal{X}}\rightarrow S$
has a
![]() $\frac{1}{4}(1,1)$
singularity along
$\frac{1}{4}(1,1)$
singularity along
![]() $\unicode[STIX]{x1D6F4}$
if there exists a (not necessarily cartesian) commutative diagram
$\unicode[STIX]{x1D6F4}$
if there exists a (not necessarily cartesian) commutative diagram

of morphisms with commuting sections
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
 $\unicode[STIX]{x1D6F4}^{\prime }:S^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
such that
$\unicode[STIX]{x1D6F4}^{\prime }:S^{\prime }\rightarrow {\mathcal{X}}^{\prime }$
such that
![]() $f$
is surjective étale,
$f$
is surjective étale,
![]() $g$
is étale, and
$g$
is étale, and
![]() ${\mathcal{X}}^{\prime }$
is isomorphic to an étale neighborhood of the section in the standard family
${\mathcal{X}}^{\prime }$
is isomorphic to an étale neighborhood of the section in the standard family
![]() $\mathbb{X}_{S^{\prime }}$
.
$\mathbb{X}_{S^{\prime }}$
.
Lemma 5.9. Let
![]() ${\mathcal{X}}\rightarrow S$
be a flat family of geometrically connected reduced surfaces with a section
${\mathcal{X}}\rightarrow S$
be a flat family of geometrically connected reduced surfaces with a section
 $\unicode[STIX]{x1D6F4}:S\rightarrow {\mathcal{X}}$
over a locally Noetherian base scheme
$\unicode[STIX]{x1D6F4}:S\rightarrow {\mathcal{X}}$
over a locally Noetherian base scheme
![]() $S$
and smooth outside of
$S$
and smooth outside of
![]() $\unicode[STIX]{x1D6F4}$
. Then
$\unicode[STIX]{x1D6F4}$
. Then
![]() ${\mathcal{X}}$
has
${\mathcal{X}}$
has
![]() $\frac{1}{4}(1,1)$
singularity along
$\frac{1}{4}(1,1)$
singularity along
![]() $\unicode[STIX]{x1D6F4}$
if and only if there exists a morphism
$\unicode[STIX]{x1D6F4}$
if and only if there exists a morphism
 $\unicode[STIX]{x1D70B}:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
over
$\unicode[STIX]{x1D70B}:{\mathcal{Y}}\rightarrow {\mathcal{X}}$
over
![]() $S$
such that
$S$
such that
![]() ${\mathcal{Y}}\rightarrow S$
is smooth,
${\mathcal{Y}}\rightarrow S$
is smooth,
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism outside of
$\unicode[STIX]{x1D70B}$
is an isomorphism outside of
![]() $\unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6F4}$
, and
 $\mathbb{P}=\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6F4})$
is a
$\mathbb{P}=\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6F4})$
is a
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $S$
such that all geometric fibers have self-intersection
$S$
such that all geometric fibers have self-intersection
![]() $-4$
. In this case
$-4$
. In this case
![]() ${\mathcal{X}}\rightarrow S$
satisfies the Kollár condition.
${\mathcal{X}}\rightarrow S$
satisfies the Kollár condition.
Proof. In one direction, we obtain
![]() ${\mathcal{Y}}$
by blowing up
${\mathcal{Y}}$
by blowing up
![]() $\unicode[STIX]{x1D6F4}$
. In the opposite direction, since the question is étale-local on
$\unicode[STIX]{x1D6F4}$
. In the opposite direction, since the question is étale-local on
![]() $S$
and
$S$
and
![]() ${\mathcal{X}}$
, we can assume that
${\mathcal{X}}$
, we can assume that
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() $S$
are spectra of Henselian local rings. By [Reference Lee and NakayamaLN13, Theorem 2.13], it suffices to find relative Cartier divisors
$S$
are spectra of Henselian local rings. By [Reference Lee and NakayamaLN13, Theorem 2.13], it suffices to find relative Cartier divisors
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
of
$D_{2}$
of
![]() ${\mathcal{X}}\rightarrow S$
such that their scheme-theoretic intersections with
${\mathcal{X}}\rightarrow S$
such that their scheme-theoretic intersections with
![]() $\mathbb{P}$
are disjoint sections of the
$\mathbb{P}$
are disjoint sections of the
![]() $\mathbb{P}^{1}$
-bundle. As in the proof of [Reference Lee and NakayamaLN13, Theorem 2.11], their existence follows from surjectivity of
$\mathbb{P}^{1}$
-bundle. As in the proof of [Reference Lee and NakayamaLN13, Theorem 2.11], their existence follows from surjectivity of
 $\operatorname{Pic}{\mathcal{X}}\rightarrow \operatorname{Pic}\mathbb{P}_{s}^{1}$
(see [Reference Grothendieck and DieudonnéEGAIV, Corollary 21.9.12]), where
$\operatorname{Pic}{\mathcal{X}}\rightarrow \operatorname{Pic}\mathbb{P}_{s}^{1}$
(see [Reference Grothendieck and DieudonnéEGAIV, Corollary 21.9.12]), where
![]() $s\in S$
is the closed point. Finally,
$s\in S$
is the closed point. Finally,
![]() $\mathbb{X}_{S^{\prime }}$
(being toric) and hence
$\mathbb{X}_{S^{\prime }}$
(being toric) and hence
![]() ${\mathcal{X}}$
satisfy the Kollár condition.◻
${\mathcal{X}}$
satisfy the Kollár condition.◻
Recall that we have a contraction
 $Y\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}S_{0}$
of
$Y\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}S_{0}$
of
![]() $\unicode[STIX]{x1D6E5}_{1}$
to a
$\unicode[STIX]{x1D6E5}_{1}$
to a
![]() $\frac{1}{4}(1,1)$
singularity.
$\frac{1}{4}(1,1)$
singularity.
Lemma 5.10. We can ‘blow down’ the deformation
 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
of
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
of
![]() $Y$
to the deformation
$Y$
to the deformation
 $\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
of
$\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
of
![]() $S_{0}$
, i.e. there exists a morphism
$S_{0}$
, i.e. there exists a morphism
![]() ${\mathcal{Y}}\rightarrow \bar{{\mathcal{Y}}}$
of deformations over
${\mathcal{Y}}\rightarrow \bar{{\mathcal{Y}}}$
of deformations over
![]() $\operatorname{Spec}{\mathcal{R}}$
which on the special fiber gives
$\operatorname{Spec}{\mathcal{R}}$
which on the special fiber gives
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
This morphism contracts
![]() ${\mathcal{C}}$
to a section
${\mathcal{C}}$
to a section
![]() $\unicode[STIX]{x1D6F4}$
of
$\unicode[STIX]{x1D6F4}$
of
 $\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
and it is an isomorphism outside
$\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
and it is an isomorphism outside
![]() $\unicode[STIX]{x1D6F4}$
. The family
$\unicode[STIX]{x1D6F4}$
. The family
 $\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
has a
$\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
has a
![]() $\frac{1}{4}(1,1)$
singularity along
$\frac{1}{4}(1,1)$
singularity along
![]() $\unicode[STIX]{x1D6F4}$
and is smooth elsewhere. It is
$\unicode[STIX]{x1D6F4}$
and is smooth elsewhere. It is
![]() $\mathbb{Q}$
-Gorenstein.
$\mathbb{Q}$
-Gorenstein.
Proof. This follows from the fact that
 $R^{1}\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}_{Y})=0$
as in [Reference WahlWah76] (where the equi-characteristic local case is worked out). Specifically, let
$R^{1}\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}_{Y})=0$
as in [Reference WahlWah76] (where the equi-characteristic local case is worked out). Specifically, let
![]() $\hat{{\mathcal{Y}}}$
be the formal completion of the special fiber in
$\hat{{\mathcal{Y}}}$
be the formal completion of the special fiber in
![]() ${\mathcal{Y}}$
. Let
${\mathcal{Y}}$
. Let
![]() $\hat{\bar{{\mathcal{Y}}}}$
be a formal scheme with underlying topological space
$\hat{\bar{{\mathcal{Y}}}}$
be a formal scheme with underlying topological space
![]() $S_{0}$
and sheaf of rings
$S_{0}$
and sheaf of rings
![]() $\unicode[STIX]{x1D6FC}_{\ast }{\mathcal{O}}_{\hat{{\mathcal{Y}}}}$
. The vanishing of
$\unicode[STIX]{x1D6FC}_{\ast }{\mathcal{O}}_{\hat{{\mathcal{Y}}}}$
. The vanishing of
 $R^{1}\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}_{Y})$
implies that
$R^{1}\unicode[STIX]{x1D6FC}_{\ast }({\mathcal{O}}_{Y})$
implies that
![]() $\hat{\bar{{\mathcal{Y}}}}$
is flat over
$\hat{\bar{{\mathcal{Y}}}}$
is flat over
![]() $\operatorname{Spf}{\mathcal{R}}$
by [Reference WahlWah76, 0.4.4]. Since
$\operatorname{Spf}{\mathcal{R}}$
by [Reference WahlWah76, 0.4.4]. Since
 $H^{2}(S_{0},{\mathcal{O}}_{S_{0}})=0$
and
$H^{2}(S_{0},{\mathcal{O}}_{S_{0}})=0$
and
![]() $S_{0}$
is projective,
$S_{0}$
is projective,
![]() $\hat{\bar{{\mathcal{Y}}}}$
carries an ample line bundle, and therefore is a formal fiber of a scheme
$\hat{\bar{{\mathcal{Y}}}}$
carries an ample line bundle, and therefore is a formal fiber of a scheme
![]() $\bar{{\mathcal{Y}}}$
projective and flat over
$\bar{{\mathcal{Y}}}$
projective and flat over
![]() $\operatorname{Spec}{\mathcal{R}}$
, by Grothendieck’s existence theorem [Reference Grothendieck and DieudonnéEGAIII, 5.4.5]. Since the formal fiber functor is fully faithful [Reference Grothendieck and DieudonnéEGAIII, 5.4.1], the morphism
$\operatorname{Spec}{\mathcal{R}}$
, by Grothendieck’s existence theorem [Reference Grothendieck and DieudonnéEGAIII, 5.4.5]. Since the formal fiber functor is fully faithful [Reference Grothendieck and DieudonnéEGAIII, 5.4.1], the morphism
![]() $\hat{{\mathcal{Y}}}\rightarrow \hat{\bar{{\mathcal{Y}}}}$
is induced by the morphism
$\hat{{\mathcal{Y}}}\rightarrow \hat{\bar{{\mathcal{Y}}}}$
is induced by the morphism
 $\unicode[STIX]{x1D6FC}:{\mathcal{Y}}\rightarrow \bar{{\mathcal{Y}}}$
. The rest follows from Lemma 5.9.◻
$\unicode[STIX]{x1D6FC}:{\mathcal{Y}}\rightarrow \bar{{\mathcal{Y}}}$
. The rest follows from Lemma 5.9.◻
Lemma 5.11. The
![]() ${\mathcal{R}}$
-stack
${\mathcal{R}}$
-stack
![]() ${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is smooth at
${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is smooth at
 $S_{0}\rightarrow \operatorname{Spec}k$
.
$S_{0}\rightarrow \operatorname{Spec}k$
.
Proof. It suffices to prove that the special fiber of
![]() ${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
, i.e. the algebraic stack of Kollár families over
${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
, i.e. the algebraic stack of Kollár families over
![]() $k$
, is smooth at
$k$
, is smooth at
 $S_{0}\rightarrow \operatorname{Spec}k$
. There are several ways to deduce this from Theorem 3.1. One is to use the theory of index one covers as in [Reference HackingHac04, § 3] (which assumes characteristic zero but in our case this is not important because the index of the singularity two is not divisible by the characteristic seven). One can also mimic calculations in [Reference HackingHac04] in the setting of [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11]. Finally, one can apply [Reference WahlWah81, Proposition 6.4] (or [Reference Lee and NakayamaLN13, Theorem 4.6]), which shows that the morphism of deformation functors of artinian rings
$S_{0}\rightarrow \operatorname{Spec}k$
. There are several ways to deduce this from Theorem 3.1. One is to use the theory of index one covers as in [Reference HackingHac04, § 3] (which assumes characteristic zero but in our case this is not important because the index of the singularity two is not divisible by the characteristic seven). One can also mimic calculations in [Reference HackingHac04] in the setting of [Reference Abramovich, Hassett, Faber, van der Geer and LooijengaAH11]. Finally, one can apply [Reference WahlWah81, Proposition 6.4] (or [Reference Lee and NakayamaLN13, Theorem 4.6]), which shows that the morphism of deformation functors of artinian rings
 $\operatorname{Def}X\rightarrow \operatorname{Def}^{\text{loc}}X$
is smooth and that local
$\operatorname{Def}X\rightarrow \operatorname{Def}^{\text{loc}}X$
is smooth and that local
![]() $\mathbb{Q}$
-Gorenstein deformations of a
$\mathbb{Q}$
-Gorenstein deformations of a
![]() $\frac{1}{4}(1,1)$
-singularity are unobstructed.◻
$\frac{1}{4}(1,1)$
-singularity are unobstructed.◻
Let
 $(D;\unicode[STIX]{x1D6E4},N)$
be the general fiber of the family
$(D;\unicode[STIX]{x1D6E4},N)$
be the general fiber of the family
 $({\mathcal{Y}};{\mathcal{C}},{\mathcal{N}})\rightarrow \operatorname{Spec}{\mathcal{R}}$
after pull-back to
$({\mathcal{Y}};{\mathcal{C}},{\mathcal{N}})\rightarrow \operatorname{Spec}{\mathcal{R}}$
after pull-back to
![]() $\operatorname{Spec}\mathbb{C}$
. Let
$\operatorname{Spec}\mathbb{C}$
. Let
 $D\rightarrow D_{0}$
be the contraction of
$D\rightarrow D_{0}$
be the contraction of
![]() $\unicode[STIX]{x1D6E4}$
. Here
$\unicode[STIX]{x1D6E4}$
. Here
![]() $D_{0}$
is the general fiber of
$D_{0}$
is the general fiber of
 $\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
(after pull-back to
$\bar{{\mathcal{Y}}}\rightarrow \operatorname{Spec}{\mathcal{R}}$
(after pull-back to
![]() $\operatorname{Spec}\mathbb{C}$
). Figure 3 shows the big picture.
$\operatorname{Spec}\mathbb{C}$
). Figure 3 shows the big picture.
Theorem 5.12. There exists a
![]() $\mathbb{Q}$
-Gorenstein family of complex surfaces
$\mathbb{Q}$
-Gorenstein family of complex surfaces
![]() $\mathbb{S}\rightarrow U$
over a smooth irreducible complex curve such that one of the fibers is
$\mathbb{S}\rightarrow U$
over a smooth irreducible complex curve such that one of the fibers is
![]() $D_{0}$
and another fiber is the Craighero–Gattazzo surface
$D_{0}$
and another fiber is the Craighero–Gattazzo surface
![]() $S$
.
$S$
.

Figure 3. The big picture.
The following corollary (of the proof) was first proved in [Reference Catanese and PignatelliCP00, Theorem 0.31].
Porism 5.13. The Craighero–Gattazzo surface is unobstructed and its local moduli space is smooth of dimension eight.
Proof. Since the stack of Kollár families
![]() ${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is
${\mathcal{K}}_{{\mathcal{R}}}^{\unicode[STIX]{x1D714}}$
is
![]() ${\mathcal{R}}$
-smooth at
${\mathcal{R}}$
-smooth at
 $S_{0}\rightarrow \operatorname{Spec}k$
, the stack
$S_{0}\rightarrow \operatorname{Spec}k$
, the stack
![]() ${\mathcal{K}}_{\mathbb{C}}^{\unicode[STIX]{x1D714}}$
is
${\mathcal{K}}_{\mathbb{C}}^{\unicode[STIX]{x1D714}}$
is
![]() $\mathbb{C}$
-smooth at
$\mathbb{C}$
-smooth at
 $S\rightarrow \operatorname{Spec}\mathbb{C}$
. But in the neighborhood of a smooth surface such as
$S\rightarrow \operatorname{Spec}\mathbb{C}$
. But in the neighborhood of a smooth surface such as
![]() $S$
,
$S$
,
![]() ${\mathcal{K}}_{\mathbb{C}}^{\unicode[STIX]{x1D714}}$
can be identified with the Deligne–Mumford stack of Gieseker families of canonically polarized surfaces with canonical singularities.◻
${\mathcal{K}}_{\mathbb{C}}^{\unicode[STIX]{x1D714}}$
can be identified with the Deligne–Mumford stack of Gieseker families of canonically polarized surfaces with canonical singularities.◻
6 Calculation of the fundamental group
Proposition 6.1. The surface
![]() $D$
is a complex Dolgachev surface with multiple fibers of multiplicity two and three. In particular,
$D$
is a complex Dolgachev surface with multiple fibers of multiplicity two and three. In particular,
 $\unicode[STIX]{x1D70B}_{1}(D)=1$
.
$\unicode[STIX]{x1D70B}_{1}(D)=1$
.
Proof. We first claim that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})=1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})=1.\end{eqnarray}$$
We are going to use that
 $\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)=1$
(see [Reference Dolgachev and WernerDW99]). Since this is the only fact about
$\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)=1$
(see [Reference Dolgachev and WernerDW99]). Since this is the only fact about
![]() $S$
that we need, we can shrink the curve
$S$
that we need, we can shrink the curve
![]() $U$
from Theorem 5.12 and without loss of generality assume that
$U$
from Theorem 5.12 and without loss of generality assume that
![]() $U$
is a complex disc. Since
$U$
is a complex disc. Since
![]() ${\mathcal{S}}$
contracts onto
${\mathcal{S}}$
contracts onto
![]() $D_{0}$
, we have
$D_{0}$
, we have
 $\unicode[STIX]{x1D70B}_{1}({\mathcal{S}})=\unicode[STIX]{x1D70B}_{1}(D_{0})$
. Now using the same argument as in [Reference XiaoXia91, p. 601], we have an exact sequence
$\unicode[STIX]{x1D70B}_{1}({\mathcal{S}})=\unicode[STIX]{x1D70B}_{1}(D_{0})$
. Now using the same argument as in [Reference XiaoXia91, p. 601], we have an exact sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(S)\rightarrow \unicode[STIX]{x1D70B}_{1}({\mathcal{S}})\rightarrow \unicode[STIX]{x1D70B}_{1}(U)\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(S)\rightarrow \unicode[STIX]{x1D70B}_{1}({\mathcal{S}})\rightarrow \unicode[STIX]{x1D70B}_{1}(U)\rightarrow 1,\end{eqnarray}$$
and so
![]() $\unicode[STIX]{x1D70B}_{1}(S)$
surjects onto
$\unicode[STIX]{x1D70B}_{1}(S)$
surjects onto
![]() $\unicode[STIX]{x1D70B}_{1}(D_{0})$
. The right exactness of profinite completions [Reference Ribes and ZalesskiiRZ10, Proposition 3.2.5] implies that
$\unicode[STIX]{x1D70B}_{1}(D_{0})$
. The right exactness of profinite completions [Reference Ribes and ZalesskiiRZ10, Proposition 3.2.5] implies that
![]() $\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)$
surjects onto
$\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)$
surjects onto
 $\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
, which implies (6.1). Alternatively, surjectivity of
$\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
, which implies (6.1). Alternatively, surjectivity of
 $\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)\rightarrow \unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
follows from the Grothendieck’s specialization theorem [Reference Grothendieck and RaynaudSGA1, Corollary 2.3].
$\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(S)\rightarrow \unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
follows from the Grothendieck’s specialization theorem [Reference Grothendieck and RaynaudSGA1, Corollary 2.3].
We have
 $K_{D}^{2}=0$
. By Lemma 4.3 and Corollary 5.12,
$K_{D}^{2}=0$
. By Lemma 4.3 and Corollary 5.12,
![]() $K_{D_{0}}$
is nef. Therefore,
$K_{D_{0}}$
is nef. Therefore,
![]() $D$
is not rational. Indeed, if
$D$
is not rational. Indeed, if
![]() $D$
is rational, then by Riemann–Roch
$D$
is rational, then by Riemann–Roch
 $h^{0}(D,-K_{D})\geqslant 1$
and so
$h^{0}(D,-K_{D})\geqslant 1$
and so
 $-K_{D}\sim E\geqslant 0$
. Since
$-K_{D}\sim E\geqslant 0$
. Since
 $K_{D}\cdot \unicode[STIX]{x1D6E4}=2$
, we have
$K_{D}\cdot \unicode[STIX]{x1D6E4}=2$
, we have
![]() $\unicode[STIX]{x1D6E4}\subset E$
. We know that
$\unicode[STIX]{x1D6E4}\subset E$
. We know that
 $f^{\ast }(2K_{D_{0}})\sim -2E+\unicode[STIX]{x1D6E4}$
where
$f^{\ast }(2K_{D_{0}})\sim -2E+\unicode[STIX]{x1D6E4}$
where
 $f:D\rightarrow D_{0}$
is the minimal resolution. But
$f:D\rightarrow D_{0}$
is the minimal resolution. But
![]() $E\neq \unicode[STIX]{x1D6E4}$
, and so
$E\neq \unicode[STIX]{x1D6E4}$
, and so
 $f^{\ast }(2K_{D_{0}})$
cannot be nef. Also, the Kodaira dimension of
$f^{\ast }(2K_{D_{0}})$
cannot be nef. Also, the Kodaira dimension of
![]() $D$
cannot be zero because of the Enriques classification and
$D$
cannot be zero because of the Enriques classification and
 $K_{D}\cdot \unicode[STIX]{x1D6E4}=2$
, and cannot be two because of Kawamata’s argument [Reference KawamataKaw92] (see [Reference RanaRan14, Lemma 2.4]). Therefore, the Kodaira dimension is one, and so
$K_{D}\cdot \unicode[STIX]{x1D6E4}=2$
, and cannot be two because of Kawamata’s argument [Reference KawamataKaw92] (see [Reference RanaRan14, Lemma 2.4]). Therefore, the Kodaira dimension is one, and so
![]() $D$
is an elliptic fibration over
$D$
is an elliptic fibration over
![]() $\mathbb{P}^{1}$
(since
$\mathbb{P}^{1}$
(since
 $q(D)=0$
).
$q(D)=0$
).
Say we have
![]() $r$
multiple fibers of multiplicities
$r$
multiple fibers of multiplicities
 $m_{1},\ldots ,m_{r}$
. By [Reference XiaoXia91, p. 601],
$m_{1},\ldots ,m_{r}$
. By [Reference XiaoXia91, p. 601],
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(D)\simeq \langle a_{1},\ldots ,a_{r}:a_{1}\cdots a_{r}=a_{1}^{m_{1}}=\cdots =a_{r}^{m_{r}}=1\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1}(D)\simeq \langle a_{1},\ldots ,a_{r}:a_{1}\cdots a_{r}=a_{1}^{m_{1}}=\cdots =a_{r}^{m_{r}}=1\rangle .\end{eqnarray}$$
But this group is residually finite (see [Reference Lyndon and SchuppLS77, p. 126] and [Reference Lyndon and SchuppLS77, p. 141 last paragraph]). We also have
 $\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D)=\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
(see [Reference KollárKol93]), and so by the above we get
$\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D)=\unicode[STIX]{x1D70B}_{1}^{\text{alg}}(D_{0})$
(see [Reference KollárKol93]), and so by the above we get
 $\unicode[STIX]{x1D70B}_{1}(D)=1$
. This implies that there are only two multiple fibers
$\unicode[STIX]{x1D70B}_{1}(D)=1$
. This implies that there are only two multiple fibers
 $m_{1}F_{1},m_{2}F_{2}$
with coprime multiplicities
$m_{1}F_{1},m_{2}F_{2}$
with coprime multiplicities
![]() $m_{1},m_{2}$
. Let
$m_{1},m_{2}$
. Let
![]() $F$
be a general fiber of
$F$
be a general fiber of
 $D\rightarrow \mathbb{P}^{1}$
, and let
$D\rightarrow \mathbb{P}^{1}$
, and let
 $\unicode[STIX]{x1D6E4}\cdot F=d$
. Then, since
$\unicode[STIX]{x1D6E4}\cdot F=d$
. Then, since
 $K_{D}\sim -F+(m_{1}-1)F_{1}+(m_{2}-1)F_{2}$
, we have
$K_{D}\sim -F+(m_{1}-1)F_{1}+(m_{2}-1)F_{2}$
, we have
 $\unicode[STIX]{x1D6E4}\cdot K_{D}=d-d/m_{1}-d/m_{2}=2$
. In addition, since
$\unicode[STIX]{x1D6E4}\cdot K_{D}=d-d/m_{1}-d/m_{2}=2$
. In addition, since
 $\unicode[STIX]{x1D6E4}\cdot F_{1}=d/m_{1}$
and
$\unicode[STIX]{x1D6E4}\cdot F_{1}=d/m_{1}$
and
 $\unicode[STIX]{x1D6E4}\cdot F_{2}=d/m_{2}$
, we have
$\unicode[STIX]{x1D6E4}\cdot F_{2}=d/m_{2}$
, we have
 $d=\unicode[STIX]{x1D706}m_{1}m_{2}$
, and so
$d=\unicode[STIX]{x1D706}m_{1}m_{2}$
, and so
 $\unicode[STIX]{x1D706}(m_{1}m_{2}-m_{1}-m_{2})=2$
. The only possible solutions, up to permuting one and two, are
$\unicode[STIX]{x1D706}(m_{1}m_{2}-m_{1}-m_{2})=2$
. The only possible solutions, up to permuting one and two, are
![]() $\unicode[STIX]{x1D706}=2$
,
$\unicode[STIX]{x1D706}=2$
,
![]() $m_{1}=2$
,
$m_{1}=2$
,
![]() $m_{2}=3$
.◻
$m_{2}=3$
.◻
Theorem 6.2. We have
 $\unicode[STIX]{x1D70B}_{1}(S)=1$
.
$\unicode[STIX]{x1D70B}_{1}(S)=1$
.
Proof. Here we use the method of [Reference Lee and ParkLP07], which applies Van Kampen’s theorem and the Milnor fiber of the
![]() $\mathbb{Q}$
-Gorenstein smoothing of
$\mathbb{Q}$
-Gorenstein smoothing of
![]() $\frac{1}{4}(1,1)$
. We only need
$\frac{1}{4}(1,1)$
. We only need
 $\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})=1$
. By Van Kampen’s theorem, we have
$\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})=1$
. By Van Kampen’s theorem, we have
 $\unicode[STIX]{x1D70B}_{1}(D)\simeq \unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})/\overline{\langle \unicode[STIX]{x1D6FC}\rangle }$
where
$\unicode[STIX]{x1D70B}_{1}(D)\simeq \unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})/\overline{\langle \unicode[STIX]{x1D6FC}\rangle }$
where
![]() $\unicode[STIX]{x1D6FC}$
is a loop around
$\unicode[STIX]{x1D6FC}$
is a loop around
![]() $\unicode[STIX]{x1D6E4}$
, and
$\unicode[STIX]{x1D6E4}$
, and
![]() $\overline{\langle \unicode[STIX]{x1D6FC}\rangle }$
is the smallest normal subgroup of
$\overline{\langle \unicode[STIX]{x1D6FC}\rangle }$
is the smallest normal subgroup of
 $\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})$
containing
$\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})$
containing
![]() $\langle \unicode[STIX]{x1D6FC}\rangle$
. We can and do consider
$\langle \unicode[STIX]{x1D6FC}\rangle$
. We can and do consider
![]() $\unicode[STIX]{x1D6FC}$
as given by a loop around
$\unicode[STIX]{x1D6FC}$
as given by a loop around
![]() $N$
, since
$N$
, since
![]() $N$
and
$N$
and
![]() $\unicode[STIX]{x1D6E4}$
intersect transversally. As
$\unicode[STIX]{x1D6E4}$
intersect transversally. As
 $N\cdot \unicode[STIX]{x1D6E4}=1$
, the set
$N\cdot \unicode[STIX]{x1D6E4}=1$
, the set
 $N^{\prime }:=N\cap (D\setminus \unicode[STIX]{x1D6E4})$
is simply connected, and so
$N^{\prime }:=N\cap (D\setminus \unicode[STIX]{x1D6E4})$
is simply connected, and so
 $\unicode[STIX]{x1D6FC}\subset N^{\prime }\subset D\setminus \unicode[STIX]{x1D6E4}$
is homotopically trivial. Therefore,
$\unicode[STIX]{x1D6FC}\subset N^{\prime }\subset D\setminus \unicode[STIX]{x1D6E4}$
is homotopically trivial. Therefore,
![]() $\overline{\langle \unicode[STIX]{x1D6FC}\rangle }=1$
, and so
$\overline{\langle \unicode[STIX]{x1D6FC}\rangle }=1$
, and so
 $\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})=1$
since by Proposition 6.1 we have
$\unicode[STIX]{x1D70B}_{1}(D\setminus \unicode[STIX]{x1D6E4})=1$
since by Proposition 6.1 we have
 $\unicode[STIX]{x1D70B}_{1}(D)=1$
. After this, one directly applies [Reference Lee and ParkLP07, pp. 493 and 499].◻
$\unicode[STIX]{x1D70B}_{1}(D)=1$
. After this, one directly applies [Reference Lee and ParkLP07, pp. 493 and 499].◻
7 Genus two Lefschetz fibration on a Dolgachev surface
In § 5 we constructed a lifting of the Boyd surface
![]() $Y$
(a Dolgachev surface in characteristic seven) to some Dolgachev surface
$Y$
(a Dolgachev surface in characteristic seven) to some Dolgachev surface
![]() $D$
in characteristic zero. Using results of § 3 we can be much more explicit.
$D$
in characteristic zero. Using results of § 3 we can be much more explicit.
Theorem 7.1. The Boyd surface
![]() $Y$
can be lifted to a complex Dolgachev surface
$Y$
can be lifted to a complex Dolgachev surface
![]() $D$
of type
$D$
of type
![]() $2,3$
, which possesses an
$2,3$
, which possesses an
![]() $I_{4}$
fiber of multiplicity two, two
$I_{4}$
fiber of multiplicity two, two
![]() $(-4)$
curves, and four elliptic
$(-4)$
curves, and four elliptic
![]() $(-1)$
curves
$(-1)$
curves
 $E_{1},\ldots ,E_{4}$
. This surface has a Campedelli-type description as the minimal resolution of singularities of the double cover of
$E_{1},\ldots ,E_{4}$
. This surface has a Campedelli-type description as the minimal resolution of singularities of the double cover of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
with four elliptic singularities and two
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
with four elliptic singularities and two
![]() $A_{1}$
singularities.
$A_{1}$
singularities.
Proof. In § 3, the main point was to prove that
 $$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{P}_{1},T_{\mathbb{P}_{1}}(-\text{log}(\unicode[STIX]{x1D6E5}+B_{1}+B_{2})))=0.\end{eqnarray}$$
By applying the
![]() $(-1)$
and
$(-1)$
and
![]() $(-2)$
principles as before, we have
$(-2)$
principles as before, we have
 $$\begin{eqnarray}H^{2}\biggl(\mathbb{P}_{1},T_{\mathbb{P}_{1}}\biggl(-\text{log}\biggl(\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\biggr)=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}\biggl(\mathbb{P}_{1},T_{\mathbb{P}_{1}}\biggl(-\text{log}\biggl(\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}\biggr)\biggr)\biggr)=0.\end{eqnarray}$$
By Lemma 5.5, preservation of intersection numbers, and
 $H^{2}(\mathbb{P}_{1},{\mathcal{O}}_{\mathbb{P}_{1}})=0$
, we have that the configuration of curves
$H^{2}(\mathbb{P}_{1},{\mathcal{O}}_{\mathbb{P}_{1}})=0$
, we have that the configuration of curves
 $\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
exists in
$\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
exists in
![]() $\mathbb{P}_{1}$
over
$\mathbb{P}_{1}$
over
![]() $\mathbb{C}$
. We will use the same notation as in characteristic seven. Then, by contracting
$\mathbb{C}$
. We will use the same notation as in characteristic seven. Then, by contracting
 $\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
, we obtain curves
$\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
, we obtain curves
 $\unicode[STIX]{x1D6E5}+B_{1}+B_{2}$
in
$\unicode[STIX]{x1D6E5}+B_{1}+B_{2}$
in
 $\mathbb{P}_{\mathbb{C}}^{1}\times \mathbb{P}_{\mathbb{C}}^{1}$
with the corresponding singularities. In this way, we can check that
$\mathbb{P}_{\mathbb{C}}^{1}\times \mathbb{P}_{\mathbb{C}}^{1}$
with the corresponding singularities. In this way, we can check that
 $\unicode[STIX]{x1D6E5}\sim (1,1)$
and
$\unicode[STIX]{x1D6E5}\sim (1,1)$
and
 $B_{i}\sim (3,3)$
in Pic
$B_{i}\sim (3,3)$
in Pic
 $(\mathbb{P}^{1}\times \mathbb{P}^{1})$
. Note that the two singularities of
$(\mathbb{P}^{1}\times \mathbb{P}^{1})$
. Note that the two singularities of
![]() $B_{1}$
and the two singularities of
$B_{1}$
and the two singularities of
![]() $B_{2}$
may not be located at the special position we had in characteristic seven. Let us call these points
$B_{2}$
may not be located at the special position we had in characteristic seven. Let us call these points
 $P_{1},\ldots ,P_{4}$
as before.
$P_{1},\ldots ,P_{4}$
as before.
The linear system
 $|{\mathcal{O}}(2,2)|$
contains a member, which we call
$|{\mathcal{O}}(2,2)|$
contains a member, which we call
![]() $\unicode[STIX]{x1D6E4}$
, that passes through
$\unicode[STIX]{x1D6E4}$
, that passes through
 $P_{1},\ldots ,P_{4}$
with the direction of the tangent cone to
$P_{1},\ldots ,P_{4}$
with the direction of the tangent cone to
 $B_{1}\cup B_{2}$
. Indeed,
$B_{1}\cup B_{2}$
. Indeed,
![]() $\unicode[STIX]{x1D6E4}$
exists because
$\unicode[STIX]{x1D6E4}$
exists because
 $h^{0}(\mathbb{P}^{1}\times \mathbb{P}^{1},{\mathcal{O}}(2,2))=9$
and passing through four points with four given directions imposes eight conditions.
$h^{0}(\mathbb{P}^{1}\times \mathbb{P}^{1},{\mathcal{O}}(2,2))=9$
and passing through four points with four given directions imposes eight conditions.
Then one easily checks in
![]() $\mathbb{P}_{1}$
that
$\mathbb{P}_{1}$
that
 $$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 3\unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+2\bar{N}_{1}+2\bar{N}_{2}\sim 3\unicode[STIX]{x1D6E4}\end{eqnarray}$$
as well as
 $$\begin{eqnarray}B_{1}+B_{2}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\sim 2\biggl(3\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6E5})-\bar{N}_{1}-\bar{N}_{2}-3\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}B_{1}+B_{2}+\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\sim 2\biggl(3\unicode[STIX]{x1D70E}^{\ast }(\unicode[STIX]{x1D6E5})-\bar{N}_{1}-\bar{N}_{2}-3\mathop{\sum }_{i=1}^{4}\bar{E}_{i}-\mathop{\sum }_{i=1}^{4}\bar{G}_{i}\biggr).\end{eqnarray}$$
In this way, (7.1) gives an elliptic fibration
 $\mathbb{P}_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
with one multiple fiber
$\mathbb{P}_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
with one multiple fiber
![]() $\unicode[STIX]{x1D6E4}$
of multiplicity three, and (7.2) gives a double cover
$\unicode[STIX]{x1D6E4}$
of multiplicity three, and (7.2) gives a double cover
 $W\rightarrow \mathbb{P}_{1}$
of
$W\rightarrow \mathbb{P}_{1}$
of
![]() $\mathbb{P}_{1}$
branched along
$\mathbb{P}_{1}$
branched along
 $B_{1}+B_{2}+\sum _{i=1}^{4}\bar{G}_{i}$
, just as before. Again the pre-images of
$B_{1}+B_{2}+\sum _{i=1}^{4}\bar{G}_{i}$
, just as before. Again the pre-images of
 $\bar{G}_{1},\ldots ,\bar{G}_{4}$
give
$\bar{G}_{1},\ldots ,\bar{G}_{4}$
give
![]() $(-1)$
-curves in
$(-1)$
-curves in
![]() $W$
, which we contract to obtain a surface
$W$
, which we contract to obtain a surface
![]() $D$
. Using the standard formulas for double covers, as before, we get
$D$
. Using the standard formulas for double covers, as before, we get
 $K_{D}^{2}=0$
and
$K_{D}^{2}=0$
and
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{D})=1$
. Also, we can directly compute
$\unicode[STIX]{x1D712}({\mathcal{O}}_{D})=1$
. Also, we can directly compute
 $p_{g}(D)=0$
using the defining line bundle of the double cover, and so
$p_{g}(D)=0$
using the defining line bundle of the double cover, and so
 $q(D)=0$
. The pull-back of the elliptic fibration
$q(D)=0$
. The pull-back of the elliptic fibration
 $\mathbb{P}_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
gives an elliptic fibration
$\mathbb{P}_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
gives an elliptic fibration
 $D\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
with two multiple fibers: the pre-images of
$D\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
with two multiple fibers: the pre-images of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
 $B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
, with multiplicities three and two, respectively. The two
$B_{1}+B_{2}+\bar{N}_{1}+\bar{N}_{2}$
, with multiplicities three and two, respectively. The two
![]() $(-4)$
curves are pre-images of
$(-4)$
curves are pre-images of
![]() $\unicode[STIX]{x1D6E5}$
.◻
$\unicode[STIX]{x1D6E5}$
.◻
Moreover, we note that the pull-backs of the two rulings of
 $\mathbb{P}_{\mathbb{C}}^{1}\times \mathbb{P}_{\mathbb{C}}^{1}$
give two distinct genus two fibrations
$\mathbb{P}_{\mathbb{C}}^{1}\times \mathbb{P}_{\mathbb{C}}^{1}$
give two distinct genus two fibrations
 $D\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
.
$D\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
.
Theorem 7.2. There exist Dolgachev surfaces (with multiple fibers of multiplicity
![]() $2,3$
) which carry genus two Lefschetz fibrations, specifically genus two fibrations without multiple components in fibers and such that the only singularities of fibers are nodes.
$2,3$
) which carry genus two Lefschetz fibrations, specifically genus two fibrations without multiple components in fibers and such that the only singularities of fibers are nodes.
Proof. In characteristic seven, we have two genus two fibrations on the Boyd surface induced by the two rulings in
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We first want to find out the singular fibers of these fibrations. For that, we need to look at the induced morphisms
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We first want to find out the singular fibers of these fibrations. For that, we need to look at the induced morphisms
 $B_{i}\subset \mathbb{P}\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
for each
$B_{i}\subset \mathbb{P}\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
for each
![]() $i$
and for each ruling.
$i$
and for each ruling.
Using (2.4) and (2.5) of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
, respectively, we obtain that, for the ruling
$B_{2}$
, respectively, we obtain that, for the ruling
 $\unicode[STIX]{x1D6FD}=x/t$
, the morphism
$\unicode[STIX]{x1D6FD}=x/t$
, the morphism
 $B_{1}\rightarrow \mathbb{P}^{1}$
has branch points at
$B_{1}\rightarrow \mathbb{P}^{1}$
has branch points at
![]() $\unicode[STIX]{x1D6FD}$
satisfying
$\unicode[STIX]{x1D6FD}$
satisfying
 $(\unicode[STIX]{x1D6FD}^{2}+1)^{2}=0$
, and the morphism
$(\unicode[STIX]{x1D6FD}^{2}+1)^{2}=0$
, and the morphism
 $B_{2}\rightarrow \mathbb{P}^{1}$
is branched at
$B_{2}\rightarrow \mathbb{P}^{1}$
is branched at
![]() $\unicode[STIX]{x1D6FD}$
satisfying
$\unicode[STIX]{x1D6FD}$
satisfying
 $\unicode[STIX]{x1D6FD}^{4}+4\unicode[STIX]{x1D6FD}^{2}+1=0$
. One verifies that in the first case, the points of ramification are
$\unicode[STIX]{x1D6FD}^{4}+4\unicode[STIX]{x1D6FD}^{2}+1=0$
. One verifies that in the first case, the points of ramification are
 $Q_{1}=(-i,i)$
and
$Q_{1}=(-i,i)$
and
 $Q_{2}=(i,-i)$
, and
$Q_{2}=(i,-i)$
, and
![]() $B_{1}$
is tangent to the ruling with flex points at
$B_{1}$
is tangent to the ruling with flex points at
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
. For the second ruling, the roles of
$Q_{2}$
. For the second ruling, the roles of
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are interchanged in relation to ramification, and
$B_{2}$
are interchanged in relation to ramification, and
![]() $B_{2}$
is tangent to the ruling with flex points at
$B_{2}$
is tangent to the ruling with flex points at
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
for
$Q_{2}$
for
![]() $B_{2}$
.
$B_{2}$
.
Using the previous observations on the ramification points of
 $B_{1}\rightarrow \mathbb{P}^{1}$
and
$B_{1}\rightarrow \mathbb{P}^{1}$
and
 $B_{2}\rightarrow \mathbb{P}^{1}$
, we obtain the following singular fibers for the genus two fibrations
$B_{2}\rightarrow \mathbb{P}^{1}$
, we obtain the following singular fibers for the genus two fibrations
 $Y\rightarrow \mathbb{P}^{1}$
(we take it from one ruling, the other is analogous).
$Y\rightarrow \mathbb{P}^{1}$
(we take it from one ruling, the other is analogous).
-
(1) Two reduced singular fibers consisting of
 $E_{1}\cup A_{1}\cup E_{4}$
and
$E_{1}\cup A_{1}\cup E_{4}$
and
 $E_{2}\cup A_{2}\cup E_{3}$
where
$E_{2}\cup A_{2}\cup E_{3}$
where
 $E_{i}$
are disjoint elliptic
$E_{i}$
are disjoint elliptic
 $(-1)$
curves, and
$(-1)$
curves, and
 $A_{i}$
are
$A_{i}$
are
 $(-2)$
rational curves, each intersecting two
$(-2)$
rational curves, each intersecting two
 $E_{j}$
at one nodal point.
$E_{j}$
at one nodal point. -
(2) Two reduced singular fibers over
 $\unicode[STIX]{x1D6FD}=i,-i$
consisting of one nodal rational curve together with
$\unicode[STIX]{x1D6FD}=i,-i$
consisting of one nodal rational curve together with
 $N_{1}$
, and another rational nodal curve with
$N_{1}$
, and another rational nodal curve with
 $N_{2}$
. Each of the
$N_{2}$
. Each of the
 $N_{i}$
passes through the corresponding node, forming a simple triple point for the fiber.
$N_{i}$
passes through the corresponding node, forming a simple triple point for the fiber. -
(3) Four reduced singular curves, each consisting of a nodal curve whose resolution is an elliptic curve.
We claim that there exists a lifting of this Dolgachev surface to characteristic zero as in Theorem 7.1 such that case (2) is eliminated. In other words, we have to construct a lifting of
![]() $\mathbb{P}_{1}$
together with the curves
$\mathbb{P}_{1}$
together with the curves
 $\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
such that the flex ramification points for
$\unicode[STIX]{x1D6E5}+B_{1}+B_{2}+\sum \bar{N}_{i}+\sum \bar{G}_{i}+\sum \bar{E}_{i}+\sum \bar{C}_{i}+\sum \bar{F}_{i}$
such that the flex ramification points for
 $B_{1}\rightarrow \mathbb{P}^{1}$
disappear, becoming simple ramification for a degree three morphism
$B_{1}\rightarrow \mathbb{P}^{1}$
disappear, becoming simple ramification for a degree three morphism
 $B_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
. Using the Macaulay2 code in the Appendix, we show the existence of a first other deformation of that type. This together with unobstructed deformations, as in the remark above, gives a lifting to
$B_{1}\rightarrow \mathbb{P}_{\mathbb{C}}^{1}$
. Using the Macaulay2 code in the Appendix, we show the existence of a first other deformation of that type. This together with unobstructed deformations, as in the remark above, gives a lifting to
![]() $\operatorname{Spec}{\mathcal{R}}$
such that, over the generic point, the curve
$\operatorname{Spec}{\mathcal{R}}$
such that, over the generic point, the curve
![]() $B_{1}$
is not flex with respect to any ruling. In this way, at least for one ruling, the corresponding genus two fibration on the complex
$B_{1}$
is not flex with respect to any ruling. In this way, at least for one ruling, the corresponding genus two fibration on the complex
![]() $2,3$
Dolgachev surface has only singular fibers which are reduced and with nodes as singularities, i.e. it is a Lefschetz fibration.◻
$2,3$
Dolgachev surface has only singular fibers which are reduced and with nodes as singularities, i.e. it is a Lefschetz fibration.◻
Acknowledgements
We are grateful to Paul Hacking for numerous discussions about moduli of stable surfaces, to Inanc Baykur for his suggestion to construct Lefschetz fibrations mentioned above and to Charles Boyd for writing and testing Macaulay2 scripts which were used to find the KSBA limit of the Craighero–Gattazzo surface in characteristic seven. The first author was partially supported by the NSF grant DMS-1502154. The second author was supported by the NSF grant DMS-1303415. The third author was supported by the FONDECYT regular grant 1150068.