Langfjordjøkelen, a rapidly shrinking glacier in northern Norway

Abstract

In this paper we document changes of Langfjordjøkelen, a small ice cap in northern Norway. Surface mass-balance measurements have been carried out on an east-facing part (3.2 km²) of the ice cap since 1989. Measurements reveal a strong thinning; the balance year 2008/09 was the 13th successive year with significant negative annual balance (≤-0.30 m w.e.). The average annual deficit was 0.9m w.e. over 1989-2009. The recent thinning of Langfjordjøkelen is stronger than observed for any other glacier in mainland Norway. Maps from 1966, 1994 and 2008 show that the whole ice cap is shrinking. The total volume loss over 1966-2008 was 0.264 km³. The east-facing part has been greatly reduced in volume (46%), area (38%) and length (20%). For this part over 1994-2008, the cumulative direct mass balance (-14.5 m w.e.) is less negative than the geodetic mass balance (-17.7 m w.e.). A surface mass-balance model using upper-air meteorological data was used to reconstruct annual balances back to 1948 and to reconstruct unmeasured years 1994 and 1995. Sensitivity of annual balance to 1°C warming is -0.76 m w.e. and to 10% increase in precipitation is +0.20 m w.e.

Introduction

Norwegian glaciers span large distances and cover different climatic regimes from wet to dry conditions and from south to north. While several maritime glaciers experienced mass surplus from 1962-2000, resulting in re-advances in the 1990s, continental glaciers with small summer and winter balances had a mass deficit and a steady frontal retreat (Andreassen and others, 2005; Nesje and others, 2008). Since 2000 most glaciers have experienced mass deficit, although years with positive balances still occur as in 2005 and 2007 for many of the maritime glaciers (e.g. Kjøllmoen and others, 2008).

The Norwegian mass-balance record is extensive; how- ever, most glaciers are unmeasured, and measurements are biased towards southern Norway (Andreassen and others, 2005; Kjøllmoen and others, 2010). Systematic measurements of mass balance started in the 1960s and reveal both temporal and spatial variability. To gain knowledge of glaciers in the northernmost parts of mainland Norway, the Norwegian Water Resources and Energy Directorate (NVE) began investigations in 1989 on an east-facing outlet of the maritime ice cap Langfjordjøkelen; measurements have been carried out each year except for 1994 and 1995. Within the International Polar Year (IPY) project Glaciodyn, Langfjordjøkelen was selected as a target glacier together with other glaciers for field campaigns for the period 200710. Additional data such as ice thickness measurements and laser scanning of the glacier surface were collected in 2008.

Glacier surface mass balance may be assessed by the direct (also called glaciological, traditional or conventional) method, indirectly assessed by the geodetic (or cartographic) method or modelled using a mass-balance model. Direct and geodetic measurements are independent of each other, but differences between the methods can be substantial (Krim-mel, 1999; Cogley, 2009; Haug and others, 2009). Mass- balance models are often calibrated with direct mass-balance data (Kuhn and others, 1999; Schuler and others, 2005) and are then dependent on measurements. The direct mass- balance method measures mass balance at point locations, and data are extrapolated over the entire glacier surface to obtain glacier-wide averages. Many mass-balance programmes include measurements of the seasonal components of the mass balance (Østrem and Brugman, 1991). The cumulative mass balance is the sum of the annual balances. Systematic errors may cause large cumulative errors in longterm mass-balance series. For outlets from ice caps, the choice of glacier boundary can also have a significant effect on annual and cumulative values (Elvehøy and others, 2009).

In the geodetic method, cumulative balance is calculated from glacier surface elevations measured in different years by differencing digital terrain models (DTMs) and by converting the volume change to mass using density estimates. This method is used to control the traditional method (Andreassen, 1999; Thibert and others, 2008; Fischer, 2010) or to assess changes in unmeasured areas or periods (Kjøllmoen and Østrem, 1997; Bauder and others, 2007; Nuth and others, 2010). The accuracy of the geodetic method is limited by the quality of the maps and DTMs; unknown accuracy of topographical maps derived from aerial photographs may lessen the reliability of these comparisons. Errors in datum surface or inaccuracies in maps may call for reprocessing of maps to achieve a homogeneous dataset (Koblet and others, 2010). In recent years new technologies such as airborne laser scanning (altimetry) have produced good results for mapping glacier areas at high resolution and accuracy (Geist and others, 2005; Rees and Arnold, 2007; Abermann and others, 2010). To reconstruct annual mass balance and study the climate sensitivity of glaciers, mass-balance models are needed. Numerous models exist, from simple regression models to complex energy-balance models. To model glacier mass balance for a longer time, simpler models with less detailed data requirements are usually applied.

In this paper we aim to give an overall report on changes of Langfjordjøkelen, and we compare direct and geodetic mass balance. A simple model using upper-air values is used to reconstruct the mass balance back to 1948 and to estimate the glacier’s climate sensitivity. To obtain a series reflecting the influence of climate during that period we also created a 1948-2009 reference-surface mass-balance series (Elsberg and others, 2001; Cogley and others, 2011) based on 1994 topography. This was done to isolate the effects of climate from the effects of changing glacier topography.

Setting

Langfjordjøkelen (70°10’ N, 21°45’ E) is a small ice cap in northern Norway (Fig. 1a). It is one of five small ice caps in this region, and this is the northernmost area in mainland Norway with glaciers (Fig. 1b). Langfjordj0kelen has an area of ˜-7.7km² (2008), of which 3.2 km² drains eastward. The mass-balance investigations are performed on this east-facing part, hereafter called Langfjord East, ranging from 302 to 1050ma.s.l. (Figs 1c and 2).

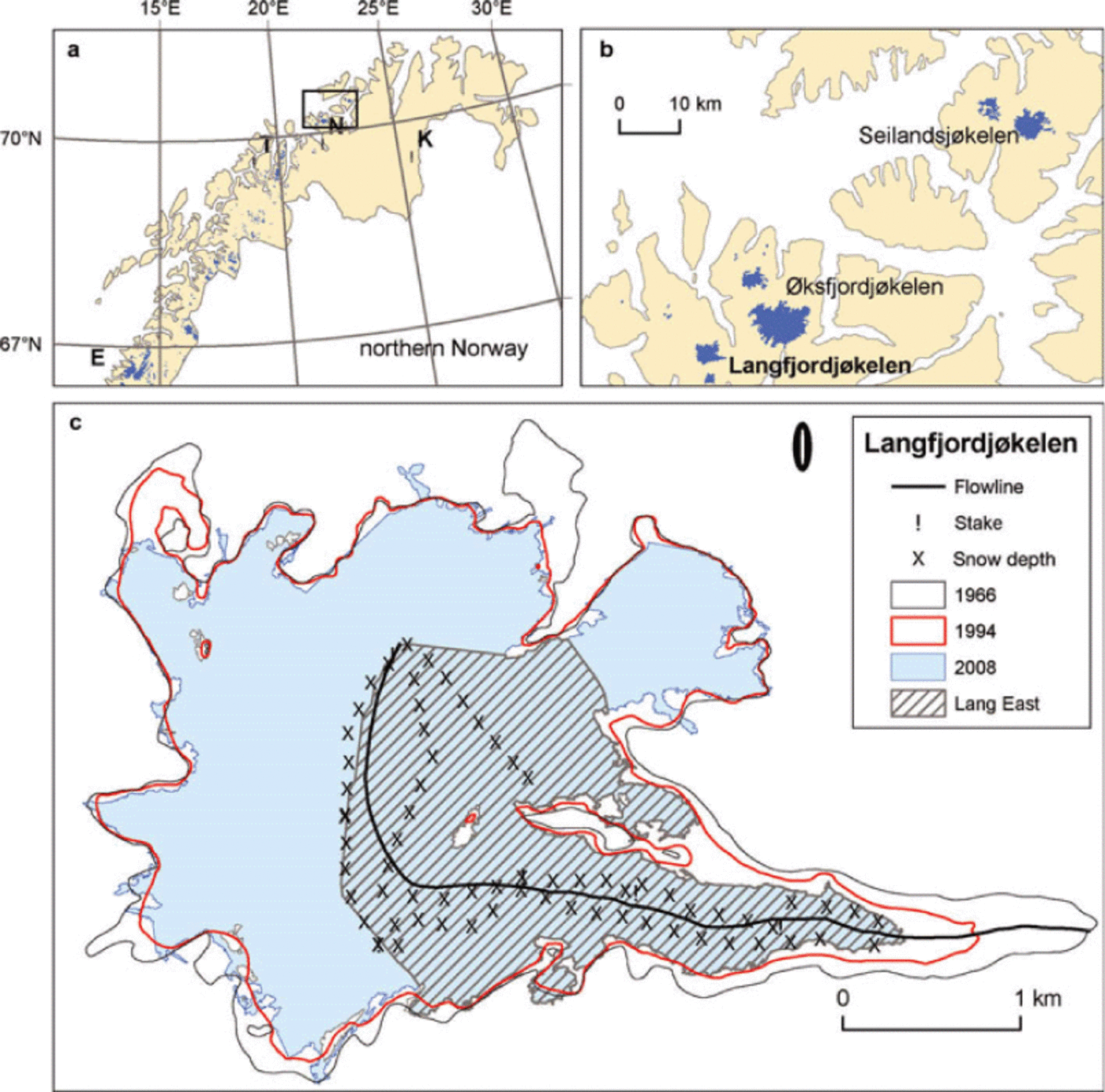
Fig. 1. Maps showing (a) location in northern Norway with positions of Engabreen (E) and meteorological stations Nordstraum in Kv?nangen (N), Tromsø (T) and Karasjok (K); (b) the northernmost glaciers in mainland Norway including Langfjordjøkelen; and (c) locations of stakes and snow depth soundings of Langfjordjøkelen. Mass-balance investigations are carried out on the east-facing part of Langfjordjøkelen (Langfjord East).

Fig. 2. Elevation–area distribution of Langfjordjøkelen (entire ice cap and east) in 1966, 1994 and 2008. Elevation interval is 100 m.

The climate in the area of Langfjordjøkelen is to a large extent determined by the ice-free Norwegian Sea, its northern latitude, and the coastal mountains that generate orographic precipitation. The area has a typical maritime climate, with relatively high precipitation during winter, with a maximum in the autumn and a minimum in the spring. Its maritime climate is also confirmed by the small difference between the warmest and coldest months in the year. The mean July and January temperatures over 1971-2000 at Nordstraum were 12.3°C and -4.0°C respectively, compared with the continental climate at Finnmarksvidda where temperatures at Karasjok were 13.4°C and -16.1 °C respectively (for location of stations see Fig. 1a; data from http:\\www.met.no).

Data and Methods

Surface mass-balance observations

Langfjordjøkelen has been the subject of annual mass- balance measurements since 1989, with the exception of 1994 and 1995. The accumulated snow (winter balance, b _w) is measured in May or early June by several point measurements of snow depth (stakes and soundings) and one snow density measurement. The snow density is usually measured at ˜900ma.s.l. (Fig. 1) and is assumed to be representative of the rest of the glacier. Ablation of snow and ice is the main component of summer balance, b _s, which is measured at the end of summer in September or early October at stakes in five locations (Fig. 1). The annual balance, b _a, is the sum of these two components:

(1)

where b _s is negative. Glacier-wide surface winter balance B _w is obtained by integrating average values of point values b_w within each 50 m altitude interval:

(2)

in which a_i is the area within the interval and A is the total glacier area; a similar equation holds for B_s.

The annual mass-balance calculations have been based on three different maps. First measurements were calculated based on a map from 1966. When the new map from the 1994 photos became available in 1997 the entire mass- balance series from 1989 was recalculated using the 1994 map for the stake and sounding elevations and the area- altitude distribution. This map was used for annual calculations up to and including 2007. The 2008 map has been used since 2008. Details on observation programme, methods and results are reported annually or biannually in NVE reports (Giadoiogicai investigations in Norway; see, e.g., Kjøllmoen and others, 2010). As shown later, the changes in elevation distribution are large for Langfjordjøkelen from 1994 to 2008. We therefore obtain significantly different values from Eqn (2) depending on which elevation distribution is used. To minimize the effects of changing elevation distribution on the results, we obtained glacierwide balance values from Eqn (2) for 1995-2007 using both area-altitude distributions. The values of B _w and B _s presented here are obtained by linearly time-weighting the values derived using the two elevation distributions, by applying the equation:

(3)

Climate data

Temporal development in temperature in the melting season, and precipitation in the accumulation season was studied using data from two meteorological stations: Nordstraum and Tromsø (N and Tin Fig. 1a). Nordstraum in Kv?nangen is the nearest long-term meteorological station to Langfjordjøkelen at 6 m a.s.l., 34 km to the south. The station has been in operation since 1965. To obtain a longer time series of the climatic variations in the area, data from Tromsø (in operation since 1867), 120 km west-southwest of Langfjordjøkelen at 100ma.s.l., were used.

Mass-balance model

To model the sensitivity of the glacier to climate change and to reconstruct the mass balance prior to 1989, we used a simple model using upper-air values at 70.0° N, 22.5° E in the NCEP-NCAR Reanalysis database (US National Centers for Environmental Prediction and US National Center for Atmospheric Research). The model was previously applied to ten glaciers in Norway and two in Sweden (Rasmussen and Conway, 2005). It separately estimates glacier average values of winter balance, B_w ^* and summer balance B_s ^* , then forms annual balance as B_a ^* = B_w ^* + B_s ^* .

The model estimates the snow flux unless in which case f = 0. Here RH is the dimensionless 850 hPa relative humidity, is the speed of the 850 hPa wind (m s^-1) and φ is its direction. Temperature 7 at 750 m, near the middle of the altitude range of the glacier, is interpolated between the 1000 and 850 hPa levels. The critical direction φ’ = 280° was determined empirically for best fit to the observed glacier-wide winter balance, B _w, obtained by integrating the observed b _w over the 1994 topography. This is not to say snow never occurs when the wind has no component in that direction, just that the component in that direction gives the best empirical fit to observed B _w. Model results are only moderately sensitive to the value of φ’ used.

Winter balance is estimated from the linear regression between measured B _w and the October-May mean of f:

(4)

Summer balance is estimated from the linear regression with the measured summer balance B _s, using T ⁺, the mean of June-September daily temperatures interpolated to 850m, near the mean equilibrium-line altitude (ELA), considering only days when T>0:

(5)

Here the glacier-wide surface mass balances B _w and B _s used in the regressions are those obtained by integrating the observed b(z) profile over the 1994 topography (Eqn (2)). The model is calibrated over 1989-2009 except for 1994 and 1995, when B _w and B _s were not observed. Accuracy is expressed by the root-mean-square error (rmse) (0.19 m w.e. for B_w ^* and 0.29 m w.e. for B_s ^* ) between observed and measured values, and coefficient of determination r ² (0.82 for B_w ^* and 0.70 for B_s ^* ). For annual balance B_a ^* they are 0.30 m w.e. and 0.85. The reason B_a ^* has a higher r ², even with a higher rms model error, is that the standard deviation, α, of the observed B _a is also larger than for either B _w or B _s. The three quantities are related through

(6)

The three values are σ _w = 0.45, σ _s = 0.52, σ _a = 0.78. Model error is comparable to uncertainty in mass-balance measurements. The model was run with these model coefficients over 1948-2009. It does not create b(z) profiles and then integrate them over the glacier surface to obtain a glacier-wide value B. Instead, it relies on the strong correlation between B and b at a point in the middle of the altitude range of the glacier (Rasmussen and Andreassen, 2005) and calculates it there as detailed in Eqns (4) and (5). Further description of the model can be found in Rasmussen and Conway (2005).

Digital terrain models

DTMs from 1966, 1994 and 2008 were used to calculate changes in geometry and the geodetic mass balance (Fig. 3). The DTMs cover the entire ice cap, and calculations were made both for the entire ice cap and Langfjord East. The 1966 and 1994 data were based on aerial photography. The 2008 DTM was derived from airborne laser scanning.

Fig. 3. Source of DTMs of Langfjordjøkelen : contour maps made from aerial photos in 1966 and 1994 and airborne laser scanning in 2008.

The 1966 aerial photos were taken on 11 July; the 1994 photos were taken on 1 August. Both maps were constructed by Fjellanger Wideoe AS in 1997 using digital stereo- photogrammetry. Numerous pass points were used in the map construction, 19 for 1966 and 14 for 1994; four of these points were used for both map constructions. A contour interval of 10 m was used for the glacier surface and 20 m for outside the glacier (Fig. 3). Both the 1966 and 1994 photos show seasonal snow outside the glacier. The 1966 photos show more glacier ice exposed than the 1994 photos.

Laser scanning of Langfjordjøkelen was performed on 9 September 2008 by Blom Geomatics AS, which also carried out the laser raw data processing. The flying height above ground was ˜2500m and the point density 0.6 points m^-2 in areas with no overlapping zones. Analysis of the homogeneity of the dataset was done by analysing height differences in overlapping zones and showed an rms value of <0.10 m in the vertical over the glacier. From the quality-checked point dataset delivered by Blom Geomatics a DTM with 5 m cell size was derived and used in the further processing. The glacier outline was partly generated from the laser data by interpretation of the intensity image and the relief image of the DTM. Due to fresh snow at the time of laser scanning, a complete outline was not detectable from these data and the outline was completed by manual digitizing based on the 1994 outline and a Landsat satellite image from 28 August 2006.

The GIS-data processing of maps, DTMs and ice thickness data was done using ArcGIS 9.3 software (© 1999-2008 ESRI). Contour maps from 1966 and 1994 were converted to regular grids of 5 m cell size using the function ‘Topo to Raster’ (ArcGIS) (Hutchinson, 1989; Hutchinson and Dowling, 1991). Surface elevation changes were calculated by subtracting the DTMs on a cell-by-cell basis for 1966-94 and 1994-2008. Volume change was computed for both the whole ice cap and for Langfjord East. The average of the 1966 and 1994 areas was used for the 1966-94 calculation and similarly for the 1994-2008 calculation. Glacier-wide mass balance over each period was calculated by dividing the volume change by the area. The calculated altitude difference represents glacier ice, firn and snow. We converted to water equivalents by multiplying the altitude difference by the density of ice, 900 kg m^-3 (Paterson, 1994) assuming Sorge’s law, that the density profile from the surface to the firn-ice transition remained unchanged between the DTMs (Bader, 1954).

Finally, the geodetic results were modified to account for any difference in additional melting that might have occurred between the date of photography and the end of the melting season. The melting was estimated using the described mass- balance model, and values were extrapolated to obtain a value for the entire ice cap. For the first period, corrections were -0.3 m w.e. (ice cap) and -0.4 m w.e. (Langfjord East), and for the second period they were -1.0 m w.e. (ice cap) and -1.2 mw.e. (Langfjord East). The uncertainty in this estimate is ±0.3 mw.e. for Langfjord East and ±0.5 mw.e. for the entire ice cap.

Accuracy of the final result depends on several factors such as the quality of mapping and interpolation, and density assumption (Krimmel, 1999; Thibert and others, 2008; Zemp and others, 2010). Estimation of ablation between time of measurement and the end of melting will also introduce errors. Obviously, results depend on the quality of the input datasets. The differences between repeated DTMs should reveal the change in elevation between the corresponding times of data acquisition, and not changes due to systematic errors in the DTMs. Such systematic errors can be vertical or horizontal shifts between DTMs, or scale or rotation terms. Horizontal and vertical shifts between multitemporal datasets that are not related to actual terrain changes can be corrected (Kääb, 2005). To test whether shifts had to be adjusted for, we plotted vertical difference of the terrain, Δh, outside the glacier border against aspect and Δh/tan θ against aspect, where θ is the angle of the slope. We detected no dependency of height differences on terrain aspect or slope, for either the period 1966-94 or the period 1994-2008, and therefore did not apply any correction.

The quality of the DTMs can also be assessed by comparing the DTMs outside the glacier, a common way of estimating uncertainty (Nuth and others, 2007; Haug and others, 2009), but also debatable as the quality of the DTM outside the glacier is only an indication of the quality of the DTM on the glacier surface (Rolstad, 2009; Nuth and others, 2010). On the one hand, DTM interpolation of glacier surfaces with limited roughness introduces fewer errors than mountainous terrain outside the glacier with higher topographic roughness. On the other hand, poor optical contrast of snow-covered parts of the glacier surfaces may cause larger uncertainties in derived contours. Data derived from laser-scanned data are, however, very accurate on snow-covered surfaces with low roughness; thus increased uncertainty applies only to the 1966 and 1994 maps derived from aerial photographs. Hence, the 1966 and 1994 DTMs have a larger uncertainty than the high-quality 2008 DTM derived from laser scanning, in general, but in particular in the snow-covered parts of the glacier.

On Langfjordjøkelen the contours constructed outside the 1966 and 1994 glacier are in very steep topography with mean slope of nearly 40°, whereas the mean slope of Langfjordjøkelen (Langfjord East) is only 12° (13°). Although laser-scanned data have high precision in general, the error increases with slope (Baltsavias, 1999; Hodgson and Bresnahan, 2004). Furthermore, as the 1966 and 1994 DTM is based on 20m contour intervals outside the glacier and 10 m on the glacier, the 1966 and 1994 data are poorer outside the glacier than on the glacier. Nonetheless, to indicate the quality of the 1994 data on bedrock we compared 60 points with slope less than 30° (using breakpoints (vertices) of the digitally constructed contours) on the nunatak in the middle of the glacier. The points were outside the glacier extent both in 1994 and 2008 and had a mean slope of 18.3° (range 7.5-29.4°). The mean difference for 2008-1994 was -0.18 m, with values ranging from -5.0 to +3.2 and standard deviation of 1.6 m. Assuming the 2008 DTM is ground truth, the rmse is 1.6 m. This nunatak was smaller and partly snow-covered in 1966, so no comparison was made for 2008-1966. This agreement is very good, but not necessarily representative for the glacier or for other bedrock outside the glacier. Comparison of contours from 1994 and 1966 outside the glacier reveals that they overlap very well in some areas and deviate more in others. In particular, differences grow large at the end of the contours outside the glacier. Owing to the high terrain steepness we chose not to use these areas for quantitative assessment of the quality of the map construction as it was the contours on the glacier that were used for deriving volume change and geodetic balance.

The uncertainty of the difference between two DTMs, where σ_DTM is the accuracy of a model, can be calculated as

(7)

assuming errors in the two are uncorrelated. Using an elevation accuracy of the glacier surface of 0.15 m for the 2008 DTM and 2.0 m for both the 1994 and 1966 DTMs gives an estimated uncertainty of the difference between the 2008 and 1994 DTMs of 2.0 m, and between the 1994 and 1966 DTMs of 2.8 m. If the accuracy of the surface of the 1966 and 1994 DTM was 1.5 m (2.5 m), the uncertainty is reduced (increased) to 2.1 (3.5 m).

Ice thickness and bed topography

To determine ice thickness and bed topography, radio-echo sounding (RES) data were collected in two 1 day campaigns (13 March and 21 May 2008) providing wide spatial coverage, mainly on the east-facing part (Fig. 1c). We used non-commercial ground-penetrating radar (GPR) with 8 MHz transmitter and receiver antenna and bandwidth of ˜10MHz. The equipment is similar to that described by Sverrisson and others (1980), but with technological improvements. Antennas were 10 m long and towed by a snowmobile or skier. The total dataset collected for Langfjordjøkelen consisted of 15 000 points.

The RES data were interpreted in two steps: first, bedrock echoes were digitized, and then data were positioned. We used a computer-assisted digitizing routine available in the Reflexw^® software (Sandmeier Scientific Software) to pick the bed reflector. The local ice thickness was determined assuming a homogeneous propagation velocity of the electromagnetic wave in ice (168m μs^-1) and that all reflectors were located vertically beneath the trace location (radar results were not migrated). The traces were positioned by post-processed kinematic differential global navigation satellite systems (GNSS) (in March 2008) and hand-held GPS (in May 2008) respectively. GPS data were acquired simultaneously with the RES survey, but using a different time interval.

To derive an ice thickness map from the point measurements, an interpolation procedure developed by Liu and others (1999) using a combination of inverse distance weighting (IDW) and triangulated irregular network (TIN) methods was applied to interpolate and extrapolate data. The glacier outline was used as the boundary condition with zero ice thickness. Smoothed contour maps were drawn from a first interpolated ice thickness map. The smoothed contour map was checked and contours were redrawn manually, where necessary, before a final ice thickness grid was compiled. Bedrock topography was obtained by subtracting the ice thickness grid from the surface DTM of September 2008. A comparison between the differential GPS data of March 2008 and the DTM of September 2008 shows that elevation differences range from 1.1 to 6.4 m, with a mean of about 3.2 m.

Uncertainties in the calculation of ice thickness arise from uncertainties in propagation velocity of the electromagnetic wave in ice, inaccuracies when picking reflectors (inaccurate travel-time determination) and the resolution of the radar system. Uncertainties in the electromagnetic wave velocity in the snow and ice are about ±1%. This corresponds to an error of up to ±5 m. The picking of the ice-base reflections has similar accuracy, and an error of ±0.05 ms in travel time corresponds to an error of ±8m travelled by the received pulse in ice. Hence, this uncertainty introduces errors in the final ice thickness estimation of ±4m. The maximum resolutions that can be achieved correspond to one-quarter of the used wavelength, and thus about 5.3 m. In areas with steeper slope, the effect of not carrying out migration could significantly increase error in the estimated ice thickness (Moran and others, 2000). Uncertainty in determining bedrock elevation is also affected by inaccurate positioning of the radar traces. To obtain a large dataset for comparison and to account for errors associated with assumptions concerning the position of the GPR and ice thickness, we selected thickness data at crossover points that were within a horizontal distance of 20 m and obtained a set of 45 validation data points. At each point, only the two nearest points from two different radar profiles were compared. The maximum difference between the two datasets was 43 m (ice thickness was about 150 m) and the mean difference was 9 m. In areas where differences were larger than 20 m, often areas with steep slopes or with problems determining horizontal coordinates, the less reliable dataset was moved to fit more reliable data or completely removed. After this procedure, all datasets were considered to be comparable and were combined to produce a thickness DTM as described above. The overall error in ice thickness is estimated to be ±20 m in the central study area.

Result

Direct surface mass balance

Surface mass-balance measurements on Langfjord East, the eastern part of Langfjordjøkelen, reveal a large annual mass turnover (Figs 4 and 5). The mass turnover is comparable to that at the maritime glaciers located much farther south in Norway. Mean surface summer balance, B_s (-3.04 mw.e.), exceeds surface winter balance, B _w (2.17mw.e.), resulting in an annual balance of -0.87 m w.e. a^-1 for the period 1989-2009 (excluding 1994 and 1995). Including modelled values of 1994 and 1995 the cumulative and mean annual balances are -17.0 and -0.81 m w.e. respectively. The similar official values reported annually in the NVE publications are more negative, -18.2 and -0.87mw.e. respectively, as they include 1994 topography up to 2008. This is because B _w decreases and B _s becomes more negative when using the 1994 map instead of the 2008 map in the calculations. For example, in 2008 B _w is reduced from 1.67m w.e. to 1.59m w.e., and B _s changes from -2.02 to -2.14m w.e. using 1994 instead of 2008 topography.

Fig. 4. Reconstructed (1948–88, 1994–95) and measured (1989–93, 1996–2009) glacier-average annual balance (B _a) and cumulative mass balance (cum B _a) referred to 1994 topography.

Fig. 5. Reconstructed (1948–88, 1994–95) and measured (1989–93, 1996–2009) annual values of the components of surface mass balance B _w, B _a, B _s. Each series is fitted with a piecewise-constant function, stages of which are determined empirically so that the probability P{t} is small according to Student’s t-test that the values in two successive stages are from the same population. For all pairs of successive stages, P{t} < 0.01. All values are referred to 1994 topography.

Most of the mass loss has occurred over balance years 1997-2009 (Fig. 4). All years in this period had significantly negative surface annual balance (≤-0.30 m w.e.) resulting in a cumulative mass balance of -16.1 m w.e. or -1.24 m w.e. a^-1.

In the period 1989-95 the glacier had a slightly negative mass balance (-1.0 m w.e. or -0.14 m w.e. a^-1), while all the other observed glaciers in mainland Norway, including the continental glaciers, had a transient mass surplus (Andreassen and others, 2005). The accumulation-area ratio (AAR) record derived from the ELA (which is determined by the z value where the b(z) profile crosses zero) in measured years shows that in 7 of 19 years with measurements the AAR was 0%, so no accumulation area was left at the end of the balance year (Fig. 6). For the modelled years 1994 and 1995 we estimate that the AAR was 46% and 69% respectively, based on the relationship between ELA and AAR over the years with measurements. The mean AAR over 1989-2009 (modelled years 1994-95 included) was thus 35%. Over 1989-2009, except for 1994 and 1995, the mean vertical profile of annual balance was found to be b _a(z) = 7.0z- 6.40m w.e. (z in kma.s.l.), by Rasmussen and Andreassen (2005), who show that the b _a(z) profiles from individual years were well approximated by linear functions that differed little from year to year in slope. At the top of the eastern part this gives b _a(1030) = +0.76 m w.e. Over the most recent 10 years 2000-09 only, b _a(1030) =+0.31 m w.e.

Fig. 6. Accumulation–area ratio (AAR) of Langfjordjøkelen 1989–2009.

Vertical profiles of mass balance, b(z), are remarkably linear (Fig. 7), with gradient b’ = db/dz changing little from year to year. Their means and standard deviations are 2.3 ± 0.6, 7.0 ± 1.0 and 4.5 ± 1.1m w.e.per km of altitude, for b’_{w ’} b’_a and b’_{s ’} respectively. The correlation r between b’ and glacier-wide balance B is positive for all three components, but is not statistically significant. A consequence of the regularity of the profiles is that b measured at 750 m a.s.l. is strongly and significantly correlated with B, with rmse ≈0.15 m w.e. for each of the three components. The correlation between B and b measured at other altitudes near the middle of the altitude range is also high but tails off at both the top and bottom of the range.

Fig. 7. Langfjordjøkelen balance profiles for 1989–93 and 1996–2009 (19 individual years).

Modelled and reconstructed surface mass balance

The reconstructed series from 1948/49 until 1988/89 (40 years) reveals a cumulative annual balance of 24.4 m w.e. or -0.61 m w.e. a^-1. (Fig. 4). Annual values of the three reconstructed measured components B _w, B _a, B _s indicate that 65% of the decrease in B _a from 1996/97 is due to B _s becoming more negative and 35% is due to B _w becoming less positive (Fig. 5). The reconstructed values prior to 1989 suggest that, of the 40 years, only 5 years had positive balance of >0.30mw.e., the majority of the years (25) had negative balances of <-0.30mw.e. and 10 years had balances between 0.30 and -0.30mw.e. Although the reconstruction suggested strong deficits in many years, the most negative year on record, 2006, is unprecedented in the reconstructed series. Because the 1989-2005 glacier- average balances were all integrated over the same topography (1994) model, results here are reference-topography balances (Elsberg and others, 2001), both over that period and for the reconstructed values back to 1948.

Climate sensitivity was calculated by applying perturbations of temperature and precipitation to the entire period 1948-2009. Sensitivity of annual balance B _a to a 1°C warming was calculated to be -0.76m w.e. and to a 10% increase in precipitation was +0.19 m w.e. The -0.76 m w.e. results from -0.65 m w.e. due to increase in ablation and -0.11 m w.e. due to decrease in the fraction of precipitation falling as snow. Thus, under even a 1 °C additional warming beyond 2000-09, the entire b _a(z) profile would, on average, be negative. It should be noted that the derived climate sensitivities pertain to the glacier topography of 1994 for Langfjord East.

Length, area, ice thickness, elevation and volume change

The difference maps derived by DTM subtraction show a marked thinning of Langfjordjøkelen over both periods 1966-94 and 1994-2008 (Fig. 8). For the first period, thinning (>2 m) occurred over 96% of the entire glacier surface. The greatest mass loss was, as expected, on the glacier tongue, where the thinning was more than 100 m. Some areas in the middle and north of the glacier experienced little or no elevation change (±2 m). There were even some minor areas (2%) indicating increase in surface elevation. The glacier thinning continued over 1994-2008, and 97% of the glacier surface sank more than 2 m in this period. Half of the glacier area experienced thinning of 10-20 m. A small patch in the northeast revealed surface rising according to the maps, but this might be erroneous owing to inaccuracy of the 1994 DTM or interpolation errors. The greatest thinning over the period 1994-2008 occurred in the lower part of the eastern outlet (up to 73 m).

Fig. 8. Elevation change of Langfjordjøkelen 1994–2008 and 1966–94.

The area-altitude distribution for 1966, 1994 and 2008 also illustrates the thinning (Fig. 2). The greatest area changes during the periods 1966-94 and 1994-2008 occurred in the topmost interval (1000-1050 m a.s.l.). The area for the whole ice cap reduced from 9.8 km² in 1966 to 7.7 km² in 2008, a decrease in area of 22% (Table 1). The area for Langfjord East reduced from 5.17 km² in 1966 to 3.21 km² in 2008, a decrease of 38%. Almost all this area shrinkage was caused by retreat of the tongue.

The length along Langfjord East was determined by digitizing the central flowline perpendicular to the elevation contours (Fig. 1c). The calculated length of the glacier in 1966 was 5.3 km, which reduced to 4.7 km in 1994 and 4.2 km in 2008 (Table 1). The total reduction in length along this flowline is ˜1.1 km or 20%, which represents a mean annual retreat of 26 m over 1966-2008. The determined total length and the percentage length change will of course be sensitive to the choice of flowline. Annual length-change measurements on this outlet began in 1998 and show a total retreat of 319 m during 1998-2008, a mean annual retreat of more than 30 m (Kjøllmoen and others, 2009, NVE data).

The derived ice thickness from the ˜15 000 individual point measurements gave ice depths ranging from 11 m to 211 m below the 2008 surface, with a mean of 92 m. The ice thickness map of Langfjordjøkelen, which was interpolated and extrapolated from the point measurements, suggests a mean depth of 47 m for the whole ice cap and 67 m for Langfjord East (Fig. 9). Measurements were few outside Langfjord East, and the thickness in these parts is highly uncertain.

Fig. 9. Ice thickness map of Langfjordjøkelen derived from measurements in March and May 2008. Radar profiles shown with black line. The glacier extent and 50m contour lines are from 2008. The ice divide for Langfjord East is also marked.

The ice thickness and bedrock along the central flowline (Fig. 1) of Langfjordjøkelen show that the greatest ice thicknesses are in the middle parts of Langfjord East (Fig. 9). The 2008 mean ice thickness along the flowline was 93 m (Fig. 10), and the mean loss along the profile over 19662008 was 36 m. The mean thinning over 1994-2008 was 17.5m or 1.25 m a^-1, whereas the thinning over 1966-94 was 18.4m or 0.66 m a^-1. Hence, the thinning rate nearly doubled from 1966-94 to 1994-2008. The volume loss over Langfjord East is 0.180 km³ over 1966-2008, and with a present ice thickness of 67m we estimate a volume loss of 46% over 1966-2008. The total volume loss of the ice cap over 1966-2008 is 0.264 km³. The overall volume loss of the ice cap from 1966 to 2008 may be estimated to be about 40% assuming a mean ice thickness of 47 m; however, as stated above, the ice thickness is very uncertain outside Langfjord East owing to the small number of measurements so this is only a crude estimate.

Fig. 10. Profile along the central flowline (see Fig. 1c for location) of the east-facing part (Langfjord East) of Langfjordjøkelen, showing the bed profile and the surfaces of 1966, 1994 and 2008.

Geodetic mass balance

The geodetic mass balance for the period 1966-94 was -13.2 m w.e. over the entire ice cap and -21.8 m w.e. for Langfjord East (Table 2). For 1994-2008 the geodetic mass balance was -13.5 m w.e. for the entire ice cap and -17.7m w.e. for Langfjord East. The cumulative value for the direct method calculated for Langfjord East is -14.5 m w.e. The annual mass loss over 1994-2008 (14 years) is thus 1.26 m w.e. for the geodetic method and 1.04 m w.e. for the direct method for Langfjord East. For the first period 1966-94 (28 years) the mean annual mass loss is 0.78 m w.e. The geodetic mass balance is more negative for Langfjord East than for the entire ice cap, which is natural as only Langfjord East has areas at lower altitudes (<600 m a.s.l.) where losses are greatest (Figs 2 and 8).

Discussion

Comparison of direct and geodetic mass balance

The 3.2m w.e. difference between direct and geodetic mass balance over 1994–2008 for Langfjord East represents a deviation of 0.22m w.e. a^–1; this is within the accuracy of the measurements which is estimated to be 0.3m w.e. a^–1. Differences between the geodetic and direct method are found at many others glaciers (Krimmel, 1999; Østrem and Haakensen, 1999; Haug and others, 2009). Smaller or larger parts of the difference may be caused by small but systematic errors in the direct observations or calculations. The difference may call for revision of the mass-balance values or programme.

Table 1. Area (A), length (L) and volume (V) for Langfjordjøkelen 1966, 1994 and 2008, and change over 1966–2008. Values are for the entire ice cap and Langfjord East

A typical source of errors in the direct method is the spatial sampling of observations and the related interpolation to cover the whole drainage basin. This might also be a source of error at Langfjord East, but as it is a relatively small and narrow glacier and almost all parts of it can be reached by foot, this glacier might be easier to measure correctly than a glacier with inaccessible parts due to crevassing, or with very wide areas for example. Another problem that may cause errors in mass-balance programmes is identifying the previous summer surface to estimate winter accumulation correctly. Probing to the right summer surface can be difficult in the firn areas in years with much snow remaining from the previous year, particularly on maritime glaciers with high mass turnover. At Langfjordjøkelen, however, there have been few years with mass surpluses, and the summer surface has been relatively easy to identify in most years. In other words, a shrinking glacier like Langfjord East with clear summer surfaces due to high melting may be easier to measure than a growing glacier with much snow remaining.

Although the DTM differencing also clearly reveals a high mass deficit and marked shrinking over Langfjordjøkelen, the absolute values of the shrinkage will depend not only on errors in map sources, but also on the choices of density and area made for the calculations. The geodetic mass balance was calculated assuming Sorge’s law and thus unchanged density profiles. This is a common approach (Andreassen, 1999;Arendt and others, 2009), but requires a steady-state glacier to be completely valid. No density profiles were available to test this assumption on Langfjordjøkelen, but it is most likely that the amounts of firn and snow were not identical in the three mapping years 1966, 1994 and 2008. Reconstructed, modelled and measured values show that prior to 1966 and 1994 there were two years with a small surplus, whereas mass balance prior to 2008 had been highly negative every year and in several years there had been no winter snow left (AAR 0%). We therefore must assume that there was less firn and snow on the glacier in 2008 than in 1994 and such a loss of firn and snow will lead to overestimation of the geodetic mass balance in the 1994-2008 period since densities of firn and snow are lower. Negative mass balances occurred in most years prior to all three mapping years, so the firn reservoirs were probably not very thick or extensive, but we do not account for possible changes in them. Another uncertainty is the value used for the density of ice. We used 900 kg m^-3, but values may be in the range 830-917 kgm^-3 (Paterson, 1994). As the absolute value of geodetic mass balance is high for both periods, the density used will influence the result considerably. Using a value of 830 (917)kgm^-3 instead will result in a change of + 1.5 (-0.4)m w.e. of the geodetic mass balance for Langfjord East for the 1994-2008 period.

On the strong thinning and retreat

Although absolute values of the geodetic and cumulative direct mass balance may vary due to uncertainties in data sources and methods, there is no doubt that Langfjordjøkelen has shrunk remarkably over the past few decades. The 18.2 mw.e. officially reported (or 17.0 mw.e. if using interpolated values for the 1994 and 2008 area) mass deficit of Langfjordjokelen over 1989-2009 is stronger than observed for any other glacier in mainland Norway. Official data published annually or biannually in the report series Gladological investigations in Norway (see, e.g., Kjøllmoen and others, 2010, NVE data) reveal that over the same period Storbreen had a cumulative net loss of 5.6 m w.e., Hellstugubreen 8.8 m w.e., Grasubreen 8.4mw.e. and Austdalsbreen 5.1 m w.e. Records from northern Sweden show that Storglaci?ren and Marmaglaci?ren had a cumulative balance of -0.4 m w.e. (period 1989-2008) and -7.4 m w.e. (period 1990-2008) respectively (WGMS, 2009; with updates WGMS).

In contrast, NVE records show that Engabreen, located ˜500km south of Langfjordjøkelen, had a strong mass surplus in the same period (+13.1 m w.e.). The absolute value for Engabreen is dependent on the choice of drainage divide, however, and could be halved by using a different divide (Elvehøy and others, 2009). Moreover, Engabreen’s cumulative record is assumed to be overestimated as geodetic calculations indicate a glacier in balance over 1985-2002 (Haug and others, 2009). The mass- balance record of Engabreen is now being homogenized and re-evaluated.

Table 2. Elevation change and geodetic mass balance for Langfjordjøkelen 1966–94 and 1994–2008. Values are for the entire ice cap and Langfjord East including adjustment for melt. Direct mass balance only for Langfjord East in the 1994–2008 period

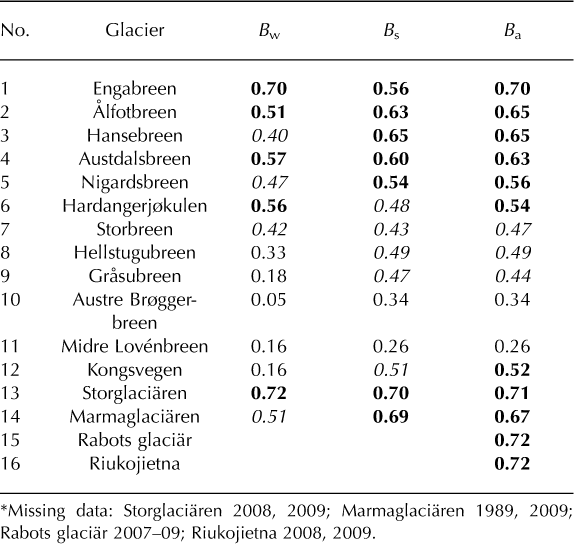
Table 3. Correlation (r) of Langfjordjøkelen Bs, Bw and Ba over 1989–2009 (21 years*) with other glaciers in mainland Norway (Nos. 1–9), Svalbard (Nos. 10–12) and Sweden (Nos. 13–16) with long-term mass-balance programmes. Bold values are significant at 99%, italic at 95%

Nevertheless, the difference between the huge deficit of Langfjordjøkelen and the positive or balanced mass balance of Engabreen in the same period is striking. While Langfjordjøkelen seems to have been in constant retreat since mass-balance measurements began in 1989, Engabreen had a frontal advance in the 1990s.

Why has Langfjordjøkelen had such a strong retreat and thinning, and why is the thinning stronger than that of other glaciers in Norway? At all ten glaciers in Norway with longterm mass-balance measurements, heavy accumulation occurred during 1989-95, the period of strongly positive North Atlantic Oscillation (NAO) (Hurrell, 1995). Neither B _w nor B _a at Langfjordjøkelen correlates well with NAO (+0.30 for B _a and +0.09 for B _w), whereas glaciers in maritime southern Norway had NAO correlations r> +0.6 for both components (Rasmussen, 2007). Nevertheless, the ratio of B _w during 1989-95 to B _w during1996-2009 was ˜1.3 at all ten glaciers. Thus, lack of strong accumulation during 198995 was not a cause of Langfjordjøkelen’s exceptional mass deficit over 1989-2009. By contrast, correlation with the Arctic Oscillation (AO) (Thompson and Wallace, 2000), is better, r = +0.6 for B _w and r = +0.4 for B _a, but negligible for B_s. For the other nine glaciers in Norway with mass-balance measurements, both B _a and B _w correlated as well or better with NAO than Langfjordjøkelen (Rasmussen, 2007).

Glaciers with gentle slope tend to adjust to the end of the Little Ice Age (LIA) more slowly than those with steep slope (Rasmussen and Conway, 2001; Fountain and others, 2009). The slope of Langfjordjøkelen’s lower part (˜0.20) is representative of those of the other glaciers (˜0.10-0.25) in the NVE programme, so atypical bed topography is not the reason why Langfjordjkelen had a greater mass deficit than the other glaciers.

Although Langfjordjøkelen has had an exceptional mass deficit since 1989, it did correlate well on a year-to-year basis with other glaciers in Scandinavia for all three components B _w, B _s, B _a (Table 3). The best correlation was found for glaciers in northern Sweden (Nos. 13-16 in Table 3): r for B_a is 0.67-0.72. Langfjordjøkelen correlated well with Storglaci?ren for B _w and B _s. It also correlated well with Engabreen in northern Norway (No. 1 in Table 3) and the maritime glaciers in southern Norway (Nos. 2-6 in Table 3), but correlation weakens with distance from the coast towards the continental glaciers in Jotunheimen (Nos. 7-9 in Table 3). Mass balance correlated poorly between Langfjordjøkelen and two of the Svalbard glaciers (Nos. 10 and 11 in Table 3) and only slightly better at the other (No. 12 in Table 3). A similar situation exists with South Cascade Glacier, Washington, USA, which had a much greater longterm mass loss than other glaciers in the region but correlated well with them on a year-to-year basis (Rasmussen and Conway, 2001; Fountain and others, 2009).

Another possible explanation for Langfjordjøkelen’s excessive mass deficit is the timing of the LIA extent. Whereas glaciers in southern Norway and Engabreen reached their maximum LIA extent about 1750 (Hoel and Werenskiold, 1962; Matthews, 2005), glaciers in northernmost Scandinavia had a later maximum according to several studies. In Lyngen, east of Tromsø, the LIA glacier maximum is suggested to have occurred about 1900-10 (Ballantyne, 1990; Bakke and others, 2005) and in northern Sweden about 1900 (Holmlund and Jansson, 1999). Thus, the excessive mass deficit at Langfjordjøkelen might be the result of still having an extensive area at low altitude, where the mass-balance profile is strongly negative, because it is still adjusting to the end of the LIA in northern Scandinavia.

Langfjordjøkelen is far from an equilibrium state. That Langfjord East had no accumulation area left (AAR 0%) in 7 of the last 12 years (1998-2009) reveals that the glacier simply does not have enough area at high altitude for the present climate. Ice caps with flat accumulation areas are sensitive to climate change owing to their hypsometry, because modest warming may turn large parts of the accumulation area into a melting zone as shown in model simulations for other Norwegian ice caps (e.g. Nigardsbreen (Oerlemans, 1997);Hardangerjøkulen (Giesen and Oerle-mans, 2010)).

In the region where Langfjordjøkelen is situated, the well- known Early Twentieth-Century Warming event was very pronounced, and mean summer temperature increased by about 1^oC during a few years in the 1910s (Hanssen-Bauer and Nordli, 1998) and peaked in the 1930s. This might well be seen as the end of the LIA on the high latitudes of the Atlantic region. The temperature decreased from the 1930s to about 1980 and after that increased to an even higher level than in the 1930s.

Meteorological records from Nordstraum in Kvænangen reveal that mean summer temperature (June-September) passed the 1971-2000 normal value in 1988 and has been above the mean in all years except three since then (Fig. 11a), whereas winter precipitation (October-May) at Nordstraum peaked in the early 1990s and has decreased since then (Fig. 11b). Precipitation data from Tromsø, which has a longer time series, indicate that winter precipitation in the period 1920-80 was lower than during the monitoring

period of the glacier, except for some wet years in the mid- 1940s. For summer temperatures, the Early Twentieth- Century Warming is very characteristic in Tromsø as in other coastal districts of northern Norway (Fig. 11).

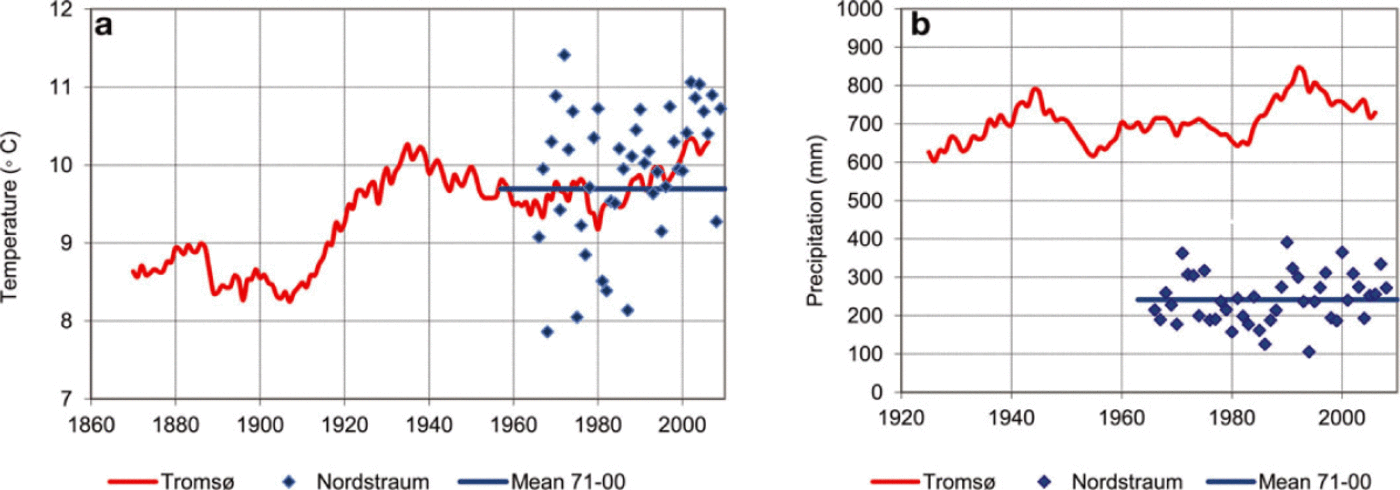
Fig. 11. Summer temperature (a) and winter precipitation (b) for Tromsø and Nordstraum in Kvænangen. Values are shown as a running 10 year filter for Tromsø and yearly values for Nordstraum. The mean of 1971–2000 for Nordstraum is also shown. Summer temperature is defined as June–September, and winter precipitation comprises the precipitation sums for October–May. The data are downloaded from the website of the Norwegian Meteorological Institute by the portal eklima (www.eklima.no).

Climate projections show increase in regional winter (December-February) precipitation and regional summer (June-August) temperature, but the projections show a large spread, particularly for precipitation (Hanssen-Bauer and others, 2009). Summer temperature will increase by approximately 2°C and winter precipitation by 10% from 1961-90 to 2021-50 (Hanssen-Bauer and others, 2009) according to the middle projection. Temperature and precipitation projections obtained with regional climate models for Nordstraum station have been bias-corrected (Engen-Skaugen, 2007) and analysed for this study;7_s is expected to increase by ˜1.8°C [1.6-2.2°C] and P_w will increase by 12% [4-18%] from 1961-90 to 2021-50 (the values in square brackets show the range of the projections). Thus the projections for the Nordstraum station do not differ much from the regional ones in spite of the somewhat different definitions of the seasons.

Although the increase in precipitation, which will make B _w more positive, will partly counteract the increase in temperature, which will make B_s more negative and will also decrease the fraction of precipitation falling as snow, the temperature increase will also extend the melt season and raise the ELA of the glacier. It is likely that in most years the ELA will be above the glacier. Hence, Langfjordjøkelen will continue to shrink and retreat and might disappear completely during the next 50-100 years.

Conclusion

We have documented a strong decrease in mass, area and volume of a small ice cap in northern Norway. Maps reveal a change (for Langfjord East) in mass (-35 ± 2 m w.e.), volume (-46%), area (-38%) and length (-20%) over the period 1966-2008. Ice thickness measurements of Langfjord East reveal a 2008 average thickness of ˜70 m. The total 1966-94 and 1994-2008 changes are comparable, but on an annual basis the 1994-2008 changes are about twice as large. Geodetic and direct mass balance differed over 1994-2008: -17.7 m w.e. vs -14.5 m w.e. Although there are uncertainties in both methods, the difference may call for a revision of the published direct values. Nevertheless, results from both methods show a strong mass deficit. The recent thinning and retreat of Langfjordjøkelen is stronger than observed for any other glacier in mainland Norway. Langfjordjøkelen is far from an equilibrium state; in most recent years the glacier had no accumulation area left at the end of the season. It simply does not have enough area at high altitude for the present climate and will continue to shrink.

The new accurate surface map of the glacier provides an excellent reference surface for a future new geodetic comparison. The derived bed topography of the glacier together with projected climate scenarios can be used to model the response of Langfjordjøkelen to future climate changes. Owing to the strong changes of Langfjordjøkelen it is recommended that a new map survey by laser scanning be conducted in 10-15 years’ time.