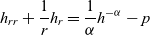Steady states of thin-film equations with van der Waals force with mass constraint

Abstract

We consider steady states with mass constraint of the fourth-order thin-film equation with van der Waals force in a bounded domain which leads to a singular elliptic equation for the thickness with an unknown pressure term. By studying second-order nonlinear ordinary differential equation,

\begin{equation*}h_{rr}+\frac{1}{r}h_{r}=\frac{1}{\alpha}h^{-\alpha}-p\end{equation*}

we prove the existence of infinitely many radially symmetric solutions. Also, we perform rigorous asymptotic analysis to identify the blow-up limit when the steady state is close to a constant solution and the blow-down limit when the maximum of the steady state goes to the infinity.

1. Introduction

The equation

(1.1) \begin{equation}h_{t}=\nabla\cdot\left( M(h) \nabla p\right) \end{equation}

has been used to model the dynamics of long-wave unstable thin films of viscous fluids. Here h is the thickness of the thin film and the nonlinear mobility is given by

\begin{equation*}M(h) =h^{n}+\lambda h^{b}\end{equation*}

with $\lambda\geq0,$ $n>0$ , and $b\in\left( 0,3\right) $ where $\lambda=0$ corresponds to the no-slip boundary condition. And we assume the pressure

(1.2) \begin{equation}p=-\Delta h+\frac{1}{\alpha}h^{-\alpha}, \end{equation}

where $\alpha>1$ is a sum of contributions from disjointing pressure due to an attractive van der Waals force and a linearised curvature term corresponding to surface tension effects.

With different formulations of coefficient M(h) and pressure p, equation (1.1) could model thin film under various practical physical forces and boundary conditions between fluid and the solid surface. For $M(h) = h$ and $\alpha= -1$ , it models the thin film in a gravity-driven Hele-Shaw cell [1, 9, 10, 12]. For $M(h) = h^{3}$ and $\alpha= -3$ , it models the fluid droplet hanging from a ceiling [11]. The existence and evolution of solutions to thin-film equations have been studied by a lot of authors [2, 3, 4, 5, 6, 7, 8, 14, 15, 24, 25, 26]. Also, extensive mathematical analysis has been made for the steady states on the above thin-film equation in one-dimensional space [18, 19, 20, 21].

Back to thin-film equation driven by van der Waals force, we consider viscous fluids in a cylindrical container whose bottom is represented by $\Omega$ , a bounded smooth domain in $\mathbb{R}^{2}$ . Since there is no flux across the boundary, we have the Neumann boundary condition

(1.3) \begin{equation}\frac{\partial p}{\partial\nu}=0\text{ on }\partial\Omega.\end{equation}

We also ignore the wetting or non-wetting effect and assume that the fluid surface is orthogonal to the boundary of the container, i.e.

(1.4) \begin{equation}\frac{\partial h}{\partial\nu}=0\text{ on }\partial\Omega.\end{equation}

Let

(1.5) \begin{equation}E(h) =\int_{\Omega}\left( \frac{1}{2}\left\vert \nabla h\right\vert^{2}-\frac{1}{\alpha\left( \alpha-1\right) }h^{1-\alpha}\right)\end{equation}

be the associated energy functional to (1.1). Formally, using (1.1) and the boundary conditions (1.3) (1.4), we have

\begin{align*}\frac{d}{dt}E(h) & =\int_{\Omega}\nabla h\nabla h_{t}+\frac{1}{\alpha}h^{-\alpha}h_{t}\\[3pt] & =\int_{\Omega}\left( -\Delta h+\frac{1}{\alpha}h^{-\alpha}\right) h_{t}\\[3pt] & =\int_{\Omega}p \nabla\cdot\left( M(h) \nabla p\right) \\[3pt] & =-\int_{\Omega}M(h) \left\vert \nabla p\right\vert ^{2}\leq0.\end{align*}

Hence, for a thin-film fluid at rest, the pressure p has to be a constant, and h satisfies the elliptic equation (1.2) with the Neumann boundary condition (1.4).

In physical experiments, usually the total volume of the fluid is a known parameter, i.e.

\begin{equation*}\bar{h}=\frac{1}{\left\vert \Omega\right\vert }\int_{\Omega}h(x)dx\end{equation*}

is given. Therefore for any given $\bar{h}>0$ , we need to find a function h and an unknown constant p satisfying

(1.6) \begin{equation}\left\{\begin{array}{c}\Delta h=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ \Omega,\\ \\[-7pt] \dfrac{1}{\left\vert \Omega\right\vert }\int_{\Omega}h(x)dx=\bar{h},\\ \\[-7pt] \dfrac{\partial h}{\partial\nu}=0\ \ \ \ \ \ \ \ \ \text{on}\ \ \partial\Omega.\end{array}\right. \end{equation}

Obviously, $h\equiv\bar{h}$ with $p=\frac{1}{\alpha}\bar{h}^{-\alpha}$ is always a solution. However, the solutions are not unique even if we restrict to radially symmetric thin-film distributions.

For equation (1.6) without the volume constraint, Jiang and Ni [17] have provided a complete description to the radial solution with $h(0)=\eta$ . The existence of radial rupture solution in our physical dimension space $\mathbb{R}^{2}$ has been extended to a larger class of equations in [16]. Guo et al. [13] have obtained a singular solution in $\mathbb{R}^{N}$ with $N\geq3$ .

Let $\left\{ r_{k}^{\ast}\right\} $ be the increasing divergent sequence of all positive critical points of

(1.7) \begin{equation}J_{0}(x)=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(n!)^{2}}\left( \frac{x}{2}\right) ^{2n} \end{equation}

which is known as the Bessel’s function of the first kind with order 0.

Theorem 1. Let $\Omega=B_{1}(0)$ be the unit disk in $\mathbb{R}^{2}$ . Given $\bar{h}>0$ . Let

\begin{equation*}K=\min\left\{ k\in\mathbb{N}:\bar{h}>(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}\right\} .\end{equation*}

Then for any $k\geq K$ , (1.6) admits a radially symmetric solution $\left( h_{k},p_{k}\right) $ such that $h_{k}$ has exactly k critical points for $r\in\left( 0,1\right] $ . In particular, there are infinitely many radially symmetric solutions to (1.6) for any given $\bar{h}>0$ .

We remark here that K is finite since $\lim_{k\rightarrow\infty}(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}=0$ .

An early version of the result is also presented in the third author’s thesis [22].

This result provides an answer to the question raised in [17] by the second author and W. Ni on the number of solutions with given mass constraint. Our result is interesting since it seems rare to have a mass constraint elliptic problem to have infinitely many symmetric solutions.

We also want to compare our result with an interesting uniqueness result by M. del Pino and G. Hernandez which implies

Proposition 1. [23] There exists a constant $p_{0}$ , such that for any $0< p\leq p_{0}$ , constant solution $h\equiv( \alpha p )^{-\frac{1}{\alpha}}$ is the only radial solution of the Neumann boundary value problem

\begin{align*}\Delta h & =\frac{1}{\alpha}h^{-\alpha}-p\ \text{in}\ B_{1}(0) ,\\[3pt] \frac{\partial h}{\partial\nu} & =0\text{ on }\partial B_{1}(0) .\end{align*}

Hence, any nontrivial radial solutions to (1.6) must satisfy $p>p_{0}$ . Since

\begin{equation*}p=\frac{1}{\left\vert B_{1}(0) \right\vert }\int_{B_{1}(0) }\frac{1}{\alpha}h^{-\alpha}(x) dx,\end{equation*}

naively, large p implies small h. We may ask about the existence of a critical average film thickness $\bar{h}_{0}$ so that there is no nontrivial solutions to (1.6) whenever $h>\bar{h}_{0}$ . Our result shows such $\bar{h}_{0}$ does not exist. Physically, when the film is thick enough, we do expect that it will be evenly distributed. Our result suggests that either the equation we are using could not accurately describe the thin film which is not too thin or the nontrivial solutions we constructed are highly unstable. We will investigate the linear and nonlinear stability of the steady states in future researches.

The paper is organised in the following manner: we will first discuss the scaling property of global radial solutions following the framework of [17]. It was shown that all non-constant radial solutions to (1.6) with assumption $p=\frac{1}{\alpha}$ and without volume constraint form a two parameter family $h^{\eta,k}$ where $\eta:=h(0)\in\left[ 0,1\right) \cup\left( 1,\infty\right) $ and $k\in\mathbb{N}$ is the number of critical points. We remark here that the case $\eta=1$ is special since it corresponds to the constant solution. We will prove Theorem 1 while postponing the analysis of asymptotic behaviour of $h^{\eta,k}$ to later sections: We consider the limit behaviours of $h^{\eta,k}$ as $\eta\rightarrow1$ in Section 3 and as $\eta\rightarrow\infty$ in Sections 4 and 5 to obtain the dependency of average thickness $\bar{h}=\bar{h}^{\eta,k}$ on initial value $\eta$ . In Section 6, we discuss some properties of blowing down limit profile of $h^{\eta,k}$ as $\eta\rightarrow\infty$ by performing the inductive calculations of the local minimum to the limiting problem.

2. Scaling property of global radial solutions

Given $\bar{h}>0$ and let $h=h\left( \left\vert x\right\vert \right) $ be a radial solution to (1.6) in $\Omega=B_{1}(0) $ , we have

(2.1) \begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-p\ \ \text{in}\ \ B_{1}(0),\\ \\[-7pt] 2\int_{0}^{1}rh(r)dr=\bar{h},\\ \\[-7pt] h^{\prime}(1) =0.\end{array}\right. \end{equation}

From the elliptic theory, h is smooth whenever it is positive; hence, we also require that $h^{\prime}(0) =0$ if $h(0) >0$ .

We follow the construction of radial solutions in [17]. Fixing $p=\frac{1}{\alpha}$ , we consider the ordinary differential equation

(2.2) \begin{equation}h_{rr}+\frac{1}{r}h_{r}=\frac{1}{\alpha}h^{-\alpha}-\frac{1}{\alpha}\end{equation}

defined on $\left[ 0,\infty\right) $ . It has been shown in [17] that for any $\eta>0$ ,

(2.3) \begin{equation}\left\{\begin{array}{l}h_{rr}+\dfrac{1}{r}h_{r}=\dfrac{1}{\alpha}h^{-\alpha}-\dfrac{1}{\alpha},\\ \\[-9pt] h(0) = \eta,\\ \\[-9pt] h^{\prime}(0) = 0\end{array}\right. \end{equation}

has a unique positive solution $h^{\eta}$ defined on $\left[ 0,\infty\right)$ . And when $\eta=0$ , there exists a unique rupture solution $h^{0}$ which is continuous on $\left[ 0,\infty\right) $ such that $h\left( 0\right) =0$ and h is positive and satisfies (2.2) on $\left( 0,\infty\right) $ . We remark here that $h^{0}$ is a weak solution to (2.2) in the sense of distribution even though $\left( h^{0}\right)_{r}(0) =\infty$ . Please see Remark 4.3 in [17] for the definition of weak solutions which have higher integrability.

Obviously $h\equiv1$ if $\eta=1$ . When $\eta\geq0$ , $\eta\not =1$ , $h^{\eta}$ oscillates around 1 and there exists an increasing sequence of positive critical radii $\left\{ r_{k}^{\eta}\right\} _{k=1}^{\infty}$ satisfying

\begin{equation*}\lim_{k\rightarrow\infty}r_{k}^{\eta}=\infty,\end{equation*}

such that $\left( h^{\eta} \right) ^{\prime}( r_{k}^{\eta} )=0$ .

Remark 1. The local maximum and minimum values of $h^{\eta}$ at $r_{k}^{\eta}$ form two monotone sequences converging to 1. [17]

Given $\eta\geq0$ , $\eta\not =1$ and a positive integer k, $h^{\eta}(r)$ satisfies the Neumann boundary condition at $r=r_{k}^{\eta}$ . We now define a scaled function

\begin{equation*}h^{\eta,k}(r) =(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}h^{\eta}(r_{k}^{\eta}r)\end{equation*}

and a constant

\begin{equation*}p^{\eta,k}=\frac{1}{\alpha}\left( r_{k}^{\eta}\right) ^{\frac{2\alpha}{1+\alpha}}.\end{equation*}

One can easily verify that $h^{\eta,k}\left( x\right) =h^{\eta,k}(\left\vert x\right\vert ) $ satisfies the elliptic equation

\begin{equation*}\Delta h=\frac{1}{\alpha} h^{-\alpha}-p^{\eta,k}\ \ in\ \ B_{1}(0)\end{equation*}

with Neumann boundary condition

\begin{equation*}\frac{\partial h}{\partial\nu}=0\ on\ \ \partial B_{1}(0).\end{equation*}

We can also calculate the average thickness for $h^{\eta,k}$ ,

\begin{align*}\bar{h}^{\eta,k} & = \frac{1}{|B_{1}(0)|}\int_{B_{1}(0)}h^{\eta,k}(x)dx=\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr\\[3pt] & =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr.\end{align*}

So far we constructed a solution $h^{\eta,k}$ to (2.1) with

\begin{equation*}\bar{h}=\bar{h}^{\eta,k}.\end{equation*}

Actually, all non-constant radial solutions to (2.1) could be obtained in this fashion. Hence, solving (2.1) for given $\bar{h}$ is reduced to find $\eta,k$ so that $\bar{h}=\bar{h}^{\eta,k}$ . So we will analyse the dependence of $\bar{h}^{\eta,k}$ on $\eta$ and k.

Denote $\bar{h}( \eta,k ) =\bar{h}^{\eta,k}$ as a function of $\eta$ and k for averaging thickness. Fixing a positive integer k, from the continuous dependence of ordinary differential equations on the initial data, $\bar{h}(\eta,k ) $ is continuous for $\eta$ in $\left( 0,1 \right) \cup\left(1,\infty\right) $ . As $\eta\rightarrow0^{+}$ , $h^{\eta}$ converges uniformly to the rupture solution $h^{0}$ on $\left[ 0,\infty\right) $ as proved in [16]. Hence, $\bar{h}( \eta,k ) $ is continuous at $\eta=0$ . Moreover, we have

\begin{equation*}\lim_{k\rightarrow\infty}\sqrt{k\pi}\bar{h}( 0,k ) =1.\end{equation*}

Please refer to Theorem 1.6 of [17].

Function $\bar{h}( \eta,k ) $ is not well defined when $\eta=1$ . We will discuss the behaviour of $\bar{h}( \eta,k ) $ when $\eta\rightarrow1$ and $\eta\rightarrow\infty$ , respectively, in the next sections. We will first show that

\begin{equation*}\lim_{\eta\rightarrow1}\bar{h}^{\eta,k}=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}},\end{equation*}

where $\left\{ r_{k}^{\ast} \right\} $ is the increasing divergent sequence of the positive critical points of $J_{0}$ , the Bessel’s function of the first kind with order 0 given by (1.7). Hence, $\bar{h}( \eta,k ) $ is a continuous positive function for $\eta\in\left[ 0,\infty\right) $ if we define $\bar{h}( 1,k )=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}$ . When $\eta\rightarrow\infty$ , we will show in Section 4 that

\begin{equation*}\lim_{\eta\rightarrow\infty}\frac{\bar{h}( \eta,k ) }{\eta^{\frac{\alpha}{1+\alpha}}}=A_{k}\end{equation*}

for some $A_{k}\in\left( 0,\infty\right) $ . That is,

\begin{equation*}\lim_{\eta\rightarrow\infty}\bar{h}( \eta,k ) = \infty.\end{equation*}

Now we are ready to prove our main theorem.

Proof of Theorem 1. Given any $\bar{h}\in\left(0,\infty\right) $ . Define

\begin{equation*}K=\min\left\{ k\in\mathbb{N}:\bar{h}>(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}\right\} .\end{equation*}

Then we have

\begin{equation*}\bar{h}>(r_{K}^{\ast})^{-\frac{2}{1+\alpha}}\geq(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}\end{equation*}

for any $k\geq K$ . Now $\bar{h}( \eta,k ) $ is a continuous positive function of $\eta$ on $\left( 1,\infty\right) $ with

\begin{equation*}\lim_{\eta\rightarrow1^{+}}\bar{h}^{\eta,k}=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}\end{equation*}

and

\begin{equation*}\lim_{\eta\rightarrow\infty}\bar{h}( \eta,k ) =\infty.\end{equation*}

Intermediate value theorem implies the existence of $\eta^{k}>1$ , such that

\begin{equation*}\bar{h}=\bar{h}( \eta^{k},k ) .\end{equation*}

Hence, (1.6) admits a radially symmetric solution $\left( h_{k},p_{k}\right) $ where

\begin{equation*}h_{k}(x) =h^{\eta^{k},k}( \left\vert x\right\vert ) =( r_{k}^{\eta^{k})^{-\frac{2}{1+\alpha}}} h^{\eta^{k}}(r_{k}^{\eta^{k}}\left\vert x\right\vert)\end{equation*}

and the pressure

\begin{equation*}p_{k}=p^{\eta_{k},k}=\frac{1}{\alpha}\left( r_{k}^{\eta_{k}}\right)^{\frac{2\alpha}{1+\alpha}}.\end{equation*}

Moreover, $h_{k}$ has exactly k critical points for $r = |x| \in\left( 0,1\right]$ .

3. Behaviour of $\bar{h}( \eta,k ) $ when $\eta\rightarrow1$

To understand the behaviour of $\bar{h}( \eta,k )$ as $\eta\rightarrow1$ , we need to understand the behaviour of $h^{\eta}(r)$ as $\eta\rightarrow1$ . Recall that $h^{\eta}$ is a solution to (2.2) with $h^{\eta}(0) =\eta$ and $\left( h^{\eta}\right) _{r}(0) =0$ . Let $\varepsilon=\eta-1$ and

\begin{equation*}w^{\eta}(r) =\frac{h^{\eta}(r) - 1 }{\varepsilon}.\end{equation*}

Then $w^{\eta}$ is a solution to the differential equation

(3.1) \begin{equation}w_{rr}+\frac{1}{r}w_{r}=\frac{1}{\varepsilon}\left[ \frac{1}{\alpha}\left(1+\varepsilon w\right) ^{-\alpha}-\frac{1}{\alpha}\right]\end{equation}

with initial condition

(3.2) \begin{equation}w(0) = 1,\,w_{r}(0) = 0. \end{equation}

As $\eta\rightarrow1$ , $\varepsilon\rightarrow0$ , formally, (3.1) converges to the Bessel’s differential equation with order 0,

\begin{equation*}w_{rr}^{\ast}+\frac{1}{r}w_{r}^{\ast}+w^{\ast}=0\end{equation*}

with the initial condition $w^{\ast}( 0 ) =1,\,w^{\ast\prime}( 0 ) = 0$ . Such limiting initial value problem has a unique solution $J_{0}$ given by (1.7).

We remark here that $J_{0}$ is oscillating around 0. Denote $r_{k}$ to be the increasing sequence of the critical points of w and $r_{k}^{\ast}$ to be the increasing sequence of the critical points of $J_{0}$ , we have

Proposition 2. As $\eta\rightarrow1$ , the solution $w^{\eta}$ to (3.1) with initial data (3.2) converges uniformly to $J_{0}$ in $\left[ 0,\infty\right) $ . Furthermore, for any positive integer k,

\begin{equation*}\lim_{\eta\rightarrow1}r_{k}=r_{k}^{\ast}.\end{equation*}

Proof. We first show that $w^{\eta}$ is uniformly bounded as $\eta\rightarrow1$ . For simplicity, we will suppress $\eta$ here. Since h is the solution to (2.3), we define energy function

\begin{equation*}e(r)=\frac{1}{2}(h^{\prime}(r))^{2}+F(h(r))\text{ with }F(h)=\frac{1}{\alpha(\alpha-1)}h^{1-\alpha}+\frac{1}{\alpha}h.\end{equation*}

F(h) attains its minimum $\frac{1}{\alpha-1}$ in $\left( 0,\infty\right) $ at $h=1.$ We have

\begin{equation*}\frac{d}{dr}[e(r)]=-\frac{1}{r}(h^{\prime}(r))^{2}\leq0.\end{equation*}

It yields that $F(h(r))\leq e(r)\leq e(0)=F(\eta)$ . Note that as $\eta\rightarrow1$ ,

\begin{align*}& F(1+2(1-\eta))-F(\eta)\\& =[F(1)+\frac{1}{2}F^{\prime\prime}(1)\left[ 2(1-\eta)\right]^{2}]-[F(1)+\frac{1}{2}F^{\prime\prime}(1)(\eta-1)^{2}]+O((\eta-1)^{3})\\& =\frac{3}{2}(1-\eta)^{2}+O((\eta-1)^{3}),\end{align*}

hence for some constant $\delta>0$ , $F(1+2(1-\eta))\geq F(\eta)$ holds whenever $\left\vert \eta-1\right\vert <\delta$ . If $1<\eta<1+\delta$ , then $F(h(r))\leq F( \eta) $ implies $1+2(1-\eta)\leq h(r)\leq\eta$ and if $1-\delta<\eta<1$ , then $\eta\leq h(r)\leq1+2(1-\eta)$ , in both cases

\begin{equation*}-2=\frac{2(1-\eta)}{\varepsilon}\leq w=\frac{h-1}{\varepsilon}\leq\frac{\eta-1}{\varepsilon}=1.\end{equation*}

Thus, $|w\left( r\right) |\leq2$ for any $r>0$ whenever $\left\vert\eta-1\right\vert <\delta$ .

The uniform boundedness of w, as $\eta\rightarrow1$ , implies

\begin{equation*}w_{rr}+\frac{1}{r}w_{r}+w=\frac{1}{\varepsilon}\left[ \frac{1}{\alpha}\left(1+\varepsilon w\right) ^{-\alpha}-\frac{1}{\alpha}\right] +w=O(\varepsilon),\end{equation*}

hence w(x) and $w^{\prime}(x)$ converge uniformly to $J_{0}(x)$ and $J_{0}^{\prime}(x)$ on any bounded interval which implies the convergence of critical points as $\eta\rightarrow1$ since both w and $J_{0}$ are oscillating around 0. From Remark 1, the local maximum and minimum values of $\omega$ at $r_{k}^{\eta}$ form two monotone sequences converging to zero; hence, the local convergence of w(x) to $J_{0}( x ) $ implies the uniform convergence on $\left[ 0,\infty\right) $ .

Since $h^{\eta}=1+\varepsilon w^{\eta}\rightarrow1$ uniformly as $\eta\rightarrow1$ , we have

\begin{equation*}\lim_{\eta\rightarrow1}\bar{h}^{\eta,k}=\lim_{\eta\rightarrow1}\frac{(r_{k}^{\eta})^{-\frac{2}{1+\alpha}}}{|B_{r_{k}^{\eta}}(0)|}\int_{B_{r_{k}^{\eta}}(0)}h^{\eta}(r)dr=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}.\end{equation*}

Hence, $\bar{h}^{\eta,k}$ is a continuous function in $\eta$ on $\left[0,\infty\right) $ if we define

\begin{equation*}\bar{h}(1,k)=\bar{h}^{1,k}=(r_{k}^{\ast})^{-\frac{2}{1+\alpha}}.\end{equation*}

4. Limiting profile when $\eta\rightarrow\infty$

In this section, we will analyse the behaviour of $\bar{h}(\eta,k)=\bar{h}^{\eta,k}$ as $\eta\rightarrow\infty$ .

Let $\eta>1$ and $h^{\eta}$ be the solution to (2.3). We define the blow-down solution z by $z\left( x\right) =\frac{1}{\eta}h^{\eta}(r)$ with $r=\sqrt{\alpha\eta}x$ . Then we have

\begin{align*}z_{xx}+\frac{1}{x}z_{x} & =\alpha\left( h_{rr}+\frac{1}{r}h_{r}\right)=h^{-\alpha}-1 =\frac{\eta^{-\alpha}}{z^{\alpha}}-1.\end{align*}

Denoting $\varepsilon=\frac{1}{\eta}$ , we have $\varepsilon\rightarrow0^{+}$ as $\eta\rightarrow\infty$ . The blow-down function z is a solution to the initial value problem

(4.1) \begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=\dfrac{\varepsilon^{\alpha}}{z^{\alpha}}-1\text{ for }x\in\left( 0,\infty\right) ,\\ \\[-9pt] z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right. \end{equation}

Formally, as $\varepsilon\rightarrow0^{+}$ , (4.1) converges to the limiting equation

(4.2) \begin{equation}\left\{\begin{array}{l}z^{\prime\prime}+\dfrac{1}{x}z^{\prime}=-1,\\ \\[-9pt] z(0) =1,\ \ \text{and}\ \ z^{\prime}(0) =0.\end{array}\right.\end{equation}

which has a unique global solution

\begin{equation*}z(x) =1-\frac{1}{4}x^{2}.\end{equation*}

However, we cannot expect

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}z^{\varepsilon}(x) =1-\frac{1}{4}x^{2}\end{equation*}

since the function $1-\frac{1}{4}x^{2}$ becomes negative when $x>2$ .

Nonetheless, we can establish the following theorem:

Theorem 2. For every $\varepsilon>0$ , let $z^{\varepsilon}(x) $ be the unique solution of the initial value problem (4.1). Then as $\varepsilon\rightarrow0^{+}$ , $z^{\varepsilon}(x) $ converges uniformly to $z_{\ast}(x)$ , the solution of the limiting initial value problem

(4.3) \begin{equation}\left\{\begin{array}{c}z_{\ast}^{\prime\prime}+\frac{1}{x}z_{\ast}^{\prime}=-1,\ \ z_{\ast}>0\ \text{in }\bigcup_{j=0}^{\infty}(a_{j},a_{j+1}).\\ \\[-9pt] z_{\ast}(0) =1,\ \ \text{and}\ \ z_{\ast}^{\prime}(0) =0,\\ \\[-9pt] z_{\ast}( a_{j} ) =0,\ \ z_{\ast}^{\prime}( a_{j}^{+} ) =-z_{\ast}^{\prime}(a_{j}^{-} ),\end{array}\right. \end{equation}

where $a_{0}=0$ , $2=a_{1}<a_{2}<\cdots$ could be inductively computed by solving the initial value problem (4.3).

We will prove Theorem 2 in Section 5 and perform the inductive calculations in Section 6 to obtain the asymptotic behaviour of $a_{k}$ .

The above theorem implies that $z^{\varepsilon}( x ) \ $ converges uniformly to $1-\frac{1}{4}x^{2}$ on $\left[ 0,2\right] $ as $\varepsilon\rightarrow0$ and $\frac{r_{1}^{\eta}}{\sqrt{\alpha\eta}}$ converges to $a_{1}=2$ as $\eta\rightarrow\infty$ . More generally, we have for $k=1,2,3,\cdots$ ,

\begin{equation*}\lim_{\eta\rightarrow\infty}\frac{r_{2k-1}^{\eta}}{\sqrt{\alpha\eta}}=a_{k}\text{ and }\lim_{\eta\rightarrow\infty}\frac{r_{2k}^{\eta}}{\sqrt{\alpha\eta}}=b_{k},\end{equation*}

where $b_{k}$ is the maximum point of $z_{\ast}$ in $\left( a_{k},a_{k+1}\right) $ .

Given a positive integer k and given $\eta>1$ , we have

\begin{align*}\bar{h}^{\eta,k} & =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\int_{0}^{r_{k}^{\eta}}rh^{\eta}(r)dr\\& =2(r_{k}^{\eta})^{-\frac{2}{1+\alpha}-2}\alpha\eta^{2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds\\& =2\alpha^{-\frac{1}{1+\alpha}}\eta^{\frac{\alpha}{1+\alpha}}\left(\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}\right) ^{-\frac{2}{1+\alpha}-2}\int_{0}^{\frac{r_{k}^{\eta}}{\sqrt{\alpha\eta}}}sz(s)ds.\end{align*}

Hence, we have for $k=1,2,3,\cdots$ ,

\begin{equation*}\lim_{\eta\rightarrow\infty}\frac{\bar{h}^{\eta,2k-1}}{\eta^{\frac{\alpha}{1+\alpha}}}=2\alpha^{-\frac{1}{1+\alpha}}a_{k}^{-\frac{2}{1+\alpha}-2}\int_{0}^{a_{k}}sz_{\ast}(s)ds\end{equation*}

and

\begin{equation*}\lim_{\eta\rightarrow\infty}\frac{\bar{h}^{\eta,2k}}{\eta^{\frac{\alpha}{1+\alpha}}}=2\alpha^{-\frac{1}{1+\alpha}}b_{k}^{-\frac{2}{1+\alpha}-2}\int_{0}^{b_{k}}sz_{\ast}(s)ds.\end{equation*}

We remark here that for each positive integer k, $\bar{h}^{\eta,k}\rightarrow\infty$ as $\eta\rightarrow\infty$ .

5. Convergence to the limiting profile

In this section, our goal here is to prove Theorem 2.

Let $\varepsilon\in(0,1) $ , and recall z(x), $x\geq0$ , be the unique solution to (4.1). We need to show that z converges uniformly to $z_{\ast}$ in $\left[0,\infty\right) $ as $\varepsilon\rightarrow0^{+}$ where $z_{\ast}$ is defined by (4.3).

We define an energy function

(5.1) \begin{equation}e(x) =\frac{1}{2}\left( z^{\prime}(x) \right) ^{2}+G(z(x)),\end{equation}

where

\begin{equation*}G(z) =\frac{\varepsilon^{\alpha}}{\alpha-1}z^{1-\alpha}+z.\end{equation*}

It is easy to check that G, defined for $z\in\left( 0,\infty\right) $ , has the following properties:

\begin{equation*}\left\{\begin{array}[c]{l}G( \varepsilon) =\min_{z\in\left( 0,\infty\right) } G(z) =\frac{\alpha}{\alpha-1}\varepsilon,\\ \\[-9pt] G^{\prime}(z) >0\text{ for }z>\varepsilon\text{ and }G^{\prime}(z) <0\text{for }0<z<\varepsilon,\\ \\[-9pt] G^{\prime\prime}(z) >0\text{ for any }z\in\left( 0,\infty\right) ,\\ \\[-9pt] \lim_{z\rightarrow0}G\left( z\right) =\lim_{z\rightarrow\infty}G(z) =\infty.\end{array}\right.\end{equation*}

Since

\begin{equation*}\frac{d}{dx}e(x) =-\frac{1}{x}\left( z^{\prime}(x) \right) ^{2},\end{equation*}

e(x) is monotone decreasing. Hence, for any $x\in\left[ 0,\infty\right)$ ,

\begin{equation*}e(x) \leq e(0) = G(1) =\frac{\varepsilon^{\alpha}}{\alpha-1}+1\end{equation*}

which implies the bounds

\begin{equation*}0<z(x) \leq1\text{, }\left\vert z^{\prime}(x) \right\vert \leq\sqrt{2\left(\frac{\varepsilon^{\alpha}}{\alpha-1}+1\right) }\text{ for any }x\in\left[0,\infty\right) .\end{equation*}

A direct calculation also yields the following simple but useful formulas:

Lemma 1.

(5.2) \begin{equation}\frac{d}{dx}\left( x^{2}\left( z^{\prime}\right) ^{2}\right) = -2x^{2} ( G\circ z ) ^{\prime} (x), \end{equation}

(5.3) \begin{equation}\frac{d}{dx}\left( xz^{\prime}\right) =x\frac{\varepsilon^{\alpha}}{z^{\alpha}}-x. \end{equation}

Applying the convexity property of G, we have

Lemma 2. Suppose $m<\varepsilon$ , for any $z\in\left( m,\varepsilon\right] $ , we have

(5.4) \begin{equation}\frac{G(m) -G( \varepsilon) }{\varepsilon-m} \leq\frac{G(m) - G(z) }{z-m}\leq-G^{\prime}(m) =\left( \frac{\varepsilon}{m}\right) ^{\alpha}-1.\end{equation}

Suppose $M>\varepsilon$ , for any $z\in\left[ \varepsilon,M\right) $ , we have

(5.5) \begin{equation}\frac{G(M) -G( \varepsilon) }{M-\varepsilon}\leq\frac{G(M) -G(z) }{M-z}\leq G^{\prime}(M) =1-\left( \frac{\varepsilon}{M}\right) ^{\alpha}.\end{equation}

Proof. G(z) is a convex function with minimum at $z=\varepsilon$ . The estimates follow from the geometry of convex functions.

For any $\varepsilon\in\left( 0,1\right) $ , z(x) is oscillating around $\varepsilon$ and the roots to $z(x)=\varepsilon$ could be listed in order as

\begin{equation*}0<x_{1}<y_{1}<x_{2}<y_{2}<\cdots<x_{k}<y_{k}<\cdots\end{equation*}

such that

\begin{align*}z & >\varepsilon\text{ for any }x\in\left( 0,x_{1}\right) \cup\left(\cup_{k=1}^{\infty}\left( y_{k},x_{k+1}\right) \right) ,\\[3pt] z & <\varepsilon\text{ for any }x\in\cup_{k=1}^{\infty}\left( x_{k},y_{k}\right) .\end{align*}

We refer the readers to [17] for more details.

Our first step is to show the convergence of z to $z_{\ast}$ on $\left[0,x_{1} \right) $ as $\varepsilon\rightarrow0^{+}$ :

Proposition 3.

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}x_{1} & =a_{1}=2,\\[3pt] \lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{1} ) & = z_{\ast}^{\prime}(a_{1}^{-} ) =-1.\end{align*}

Moreover,

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\sup_{x\in\left[ 0,x_{1}\right]}\left\vert z(x) -z_{\ast}(x) \right\vert =0.\end{equation*}

Proof. Integrating (5.3) from 0 to x, we have

(5.6) \begin{equation}xz^{\prime}(x) =\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy-\frac{x^{2}}{2}\geq-\frac{x^{2}}{2} \end{equation}

hence $z^{\prime}(x)\geq-\frac{x}{2}$ . Integrating again, we obtain

\begin{equation*}z(x)\geq1-\frac{x^{2}}{4}\text{ for any }x\in\left[ 0,\infty\right) .\text{}\end{equation*}

Plugging the lower bound for z back into (5.6), we have for any $x\in\left( 0,2\right) $ ,

\begin{equation*}xz^{\prime}(x) =\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx-\frac{x^{2}}{2}\leq\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left(1-\frac{y^{2}}{4}\right) ^{\alpha}}dy-\frac{x^{2}}{2}\end{equation*}

hence

\begin{equation*}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{\left( 1-\frac{y^{2}}{4}\right) ^{\alpha}}dy\leq\frac{x\varepsilon^{\alpha}}{2\left( 1-\frac{x^{2}}{4}\right) ^{\alpha}}.\end{equation*}

Fix any $a\in\left( 0,2\right) $ , we have

(5.7) \begin{equation}0\leq z^{\prime}(x) +\frac{x}{2}\leq\frac{a\varepsilon^{\alpha}}{2\left(1-\frac{a^{2}}{4}\right) ^{\alpha}} \end{equation}

holds for any $x\in\left[ 0,a\right] $ . Hence, for any $x\in\left[0,a\right] $

\begin{equation*}1-\frac{x^{2}}{4}\leq z(x) \leq1-\frac{x^{2}}{4}+\frac{a^{2}\varepsilon^{\alpha}}{2\left( 1-\frac{a^{2}}{4}\right) ^{\alpha}}.\end{equation*}

In particular, z converges to $1-\frac{x^{2}}{4}$ uniformly on $\left[ 0,a\right] $ as $\varepsilon\rightarrow0^{+}$ , such fact actually follows directly from the continuously dependence of ordinary differential equations since singularity can be avoided on $\left[ 0,a\right] $ with fixed $a<2$ .

Such convergence implies $x_{1}>1$ for sufficiently small $\varepsilon$ . (5.3) implies $xz^{\prime}(x) $ is decreasing on $\left( 0,x_{1}\right) $ , hence for any $x\in\left[1,x_{1}\right] $ , $xz^{\prime}(x) \leq z^{\prime}(1) <0$ and

\begin{equation*}\ln x_{1}=\int_{1}^{x_{1}}\frac{1}{x}dx\leq\int_{\varepsilon}^{z(1) }\frac{1}{\left\vert z^{\prime}(1) \right\vert }dz=\frac{z(1) -\varepsilon}{\left\vert z^{\prime}(1) \right\vert }.\end{equation*}

Since

\begin{equation*}\,\lim_{\varepsilon\rightarrow0^{+}}z(1) =\frac{3}{4},\,\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}(1) =-\frac{1}{2}\end{equation*}

the above estimate implies that $x_{1}\leq C$ for some constant C independent of $\varepsilon\in\left( 0,1\right) $ .

For any $x\in\left[ 1,x_{1}\right] $ , we have

\begin{align*}0 & \leq z^{\prime}(x)+\frac{x}{2}=\frac{1}{x}\int_{0}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\leq\int_{0}^{1}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy+\int_{1}^{x_{1}}y\frac{\varepsilon^{\alpha}}{z^{\alpha}}dy\\[3pt] & \leq\frac{1}{2}\left( z\left( 1\right) \right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z(1)}\frac{y\varepsilon^{\alpha}}{z^{\alpha}\left\vert \frac{dz}{dy}\right\vert }dz\\[3pt] & \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\int_{\varepsilon}^{z\left( 1\right) }\frac{y^{2}\varepsilon^{\alpha}}{z^{\alpha}\left\vert z^{\prime}(1)\right\vert }dz\\[3pt] & \leq\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}}{\left\vert z^{\prime}(1)\right\vert }\int_{\varepsilon}^{\infty}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dz\\[3pt] & =\frac{1}{2}\left( z(1)\right) ^{-\alpha}\varepsilon^{\alpha}+\frac{x_{1}^{2}\varepsilon}{\left\vert z^{\prime}(1)\right\vert \left(\alpha-1\right) }\leq C\varepsilon\end{align*}

for some constant C independent of $\varepsilon\in\left( 0,1\right) $ . Combining the estimate (5.7) with $a=1$ , we conclude for any $x\in\left( 0,x_{1}\right] $

(5.8) \begin{equation}0\leq z^{\prime}(x)+\frac{x}{2}\leq C\varepsilon,\end{equation}

where C is some constant independent of $\varepsilon\in\left( 0,1\right)$ . Integrating from 0 to x, we have for any $x\in\left[ 0,x_{1}\right]$ ,

\begin{equation*}0\leq z(x)-\left( 1-\frac{x^{2}}{4}\right) \leq C\varepsilon x_{1}\leq C\varepsilon.\end{equation*}

In particular, evaluating at $x=x_{1}$ ,

\begin{equation*}0\leq\varepsilon-\left( 1-\frac{x_{1}^{2}}{4}\right) \leq C\varepsilon,\end{equation*}

we deduce

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}x_{1}=2=a_{1}.\end{equation*}

And (5.8) implies

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}(x_{1})=-1=z_{\ast}^{\prime}(a_{1}^{-}).\end{equation*}

Next, we work on intervals $\left( x_{k},y_{k}\right) $ , $k=1,2,3,\cdots$ .

Proposition 4. Let $1<a<b$ and z(x), $x\in\left[ a,b\right] $ be the solution to

(5.9) \begin{equation}\left\{\begin{array}{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt] z(a)=z(b)=\varepsilon.\end{array}\right.\end{equation}

Assume that:

1. (1) $z<\varepsilon\ in\ (a,b).$

2. (2) $\textit{z}\ attains\ its\ unique\ minimum\ \textit{m}\ at\ x_{\min}\in(a,b).$

3. (3) $z^{\prime}<0\ in\ \left[ a,x_{\min}\right)\ and\ z^{\prime}>0\ in\ \left( x_{\min},b\right] .$

Then there exists $\varepsilon_{0}>0$ such that for any $\varepsilon\in\left(0,\varepsilon_{0}\right] $ , $b-a\leq C_{1}\varepsilon$ and

(5.10) \begin{equation}\int_{a}^{b}\frac{(z^{\prime}(x))^{2}}{x}dx\leq C_{2}\varepsilon,\end{equation}

where $\varepsilon_{0}$ , $C_{1}$ , $C_{2}$ are positive constants only depending on $A,B,\alpha$ if $a<A$ , $e(a)<A$ and $\left\vert z^{\prime}(a)\right\vert >B>0$ .

Proof. Integrating (5.2) from $x_{\min}$ to x yields

\begin{equation*}x^{2}\left( z^{\prime}\right) ^{2}=-2\int_{x_{\min}}^{x}y^{2} \left( G \circ z \right) ^{\prime} (y) dy \text{ for any }x\in\left[ a,b\right] .\end{equation*}

Suppose $x\in\left[ a, x_{\min} \right] $ , we deduce

\begin{equation*}2\left( G(m) - G(z) \right) \leq\left\vert \frac{dz}{dx}\right\vert ^{2}\leq\frac{2x_{\min}^{2}}{x^{2}}\left( G(m)-G(z) \right) .\end{equation*}

Evaluating at $x=a$ , we have

\begin{equation*}a^{2}\left( z^{\prime}(a) \right) ^{2}\leq2x_{\min}^{2}\left[ G(m)-G(\varepsilon) \right] .\end{equation*}

Next, applying (5.4),

\begin{align*}x_{\min}-a & =\int_{a}^{x_{\min}}dx\leq\int_{m}^{\varepsilon}\frac{dz}{\sqrt{2\left( G(m)-G(z) \right) }} \leq\frac{\sqrt{2} \varepsilon}{\sqrt{G(m)-G( \varepsilon) }}.\end{align*}

Hence,

\begin{align*}a^{2}\left( z^{\prime}(a) \right) ^{2} & \leq2x_{\min}^{2}\left[G(m)-G(\varepsilon) \right] \\[3pt] & \leq2\left( a+\frac{\sqrt{2} \varepsilon}{\sqrt{G(m) -G(\varepsilon) }}\right) ^{2}\left[ G(m) -G(\varepsilon) \right] \\[3pt] & \leq2\left( a\sqrt{G(m) }+\sqrt{2}\varepsilon\right) ^{2}.\end{align*}

So if

\begin{equation*}\varepsilon_{0}\leq\frac{B}{4}\leq\frac{a\left\vert z^{\prime}(a) \right\vert}{4},\end{equation*}

we have for any $\varepsilon\leq\varepsilon_{0}$ ,

\begin{equation*}G(m) \geq\left( \frac{\left\vert z^{\prime}(a) \right\vert }{\sqrt{2}}-\frac{\sqrt{2}\varepsilon}{a}\right) ^{2}\geq\frac{\left\vert z^{\prime}(a)\right\vert ^{2}}{8}\geq\frac{B^{2}}{8}.\end{equation*}

Hence from the structure of function G, we have $m\leq C\varepsilon^{\frac{\alpha}{\alpha-1}}$ . Now with $\varepsilon_{0}$ sufficiently small, we have for any $\varepsilon\leq\varepsilon_{0}$ , $m\leq\frac{\varepsilon}{2}$ . Hence,

\begin{equation*}x_{\min}-a\leq\frac{\sqrt{2} \varepsilon }{\sqrt{G(m)-G(\varepsilon) }} \leq C_{1} \varepsilon\end{equation*}

since

\begin{equation*}G(m) \geq\frac{B^{2}}{8}\text{ and }G(\varepsilon) =\frac{\alpha}{\alpha-1}\varepsilon.\end{equation*}

And

\begin{align*}\int_{a}^{x_{\min}}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & =\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{x_{\min}\left( \sqrt{2\left[ G(m)-G(z) \right]}\right) }{x^{2}}dz\\[3pt] & \leq\frac{x_{\min}\sqrt{2G(m)}}{a^{2}}\varepsilon\leq\frac{\left(a+C_{1}\varepsilon\right) \sqrt{2e(a) }}{a^{2}}\varepsilon.\end{align*}

Suppose $x\in\left[ x_{\min},b\right] $ , we have

\begin{equation*}2\frac{x_{\min}^{2}}{x^{2}}\left( G(m)-G(z) \right) \leq\left\vert \frac{dz}{dx}\right\vert ^{2}\leq2\left( G(m)-G(z) \right) .\end{equation*}

Applying (5.4) again,

\begin{equation*}\left\vert \frac{dz}{dx}\right\vert \geq\frac{x_{\min}}{x}\sqrt{2\left(G(m)-G(z) \right) }\geq\frac{x_{\min}}{x}\sqrt{\frac{G(m) -G(\varepsilon)}{\varepsilon-m}2\left( z-m\right) }\end{equation*}

so we have

\begin{align*}\frac{x_{\min}}{b}\left( b-x_{\min}\right) & \leq\int_{x_{\min}}^{b}\frac{x_{\min}}{x}dx\leq\int_{m}^{\varepsilon}\frac{dz}{\sqrt{\frac{2 ( G(m)-G(\varepsilon) ) }{\varepsilon-m}}\sqrt{z-m}}\\& =\frac{\sqrt{2}\left( \varepsilon-m\right) }{\sqrt{G(m)-G(\varepsilon) }}\leq C_{1}\varepsilon.\end{align*}

Hence for sufficient small $\varepsilon$ ,

\begin{equation*}b-x_{\min}\leq\frac{C_{1}\varepsilon}{1-\frac{C_{1}\varepsilon}{x_{\min}}}\leq2C_{1}\varepsilon.\end{equation*}

And

\begin{align*}\int_{x_{\min}}^{b}\frac{\left( z^{\prime}\right) ^{2}}{x}dx & \leq\int_{m}^{\varepsilon}\frac{\left\vert z^{\prime}\right\vert }{x}dz\leq\int_{m}^{\varepsilon}\frac{\sqrt{2\left[ G(m)-G(z) \right] }}{x}dz\\[3pt] & \leq\frac{\sqrt{ 2G(m) }}{ x_{\min} }\varepsilon\leq\frac{\sqrt{2e(a)}}{a}\varepsilon.\\[-30pt] \end{align*}

Corollary 1. Suppose

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}x_{k} & =a_{k} \text{ and } \lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{k} ) =z_{\ast}^{\prime}(a_{k}^{-} ) .\end{align*}

Then

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}y_{k} & =a_{k} \text{ and } \lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( y_{k} ) = z_{\ast}^{\prime}(a_{k}^{+} ) .\end{align*}

Moreover

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\sup_{x\in\left[ x_{k},y_{k} \right]}\left\vert z(x)-z_{\ast}(x) \right\vert =0.\end{equation*}

Proof. Since

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\left( y_{k}-x_{k}\right) =0\text{, }\end{equation*}

we have $\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$ . Now

\begin{equation*}0\leq e( x_{k} ) -e( y_{k} ) =\int_{x_{k}}^{y_{k}}\frac{\left( z^{\prime}\right) ^{2}}{x}dx\rightarrow0\text{ as } \varepsilon\rightarrow0^{+},\end{equation*}

hence

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\frac{1}{2}\left( \left\vert z^{\prime}(x_{k} ) \right\vert ^{2}-\left\vert z^{\prime}( y_{k} ) \right\vert^{2}\right) =\lim_{\varepsilon\rightarrow0^{+}}\left( e( x_{k} ) -e( y_{k} )\right) =0.\end{equation*}

Since $z^{\prime}( y_{k} ) >0$ , we conclude

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( y_{k} ) =-\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{k} ) =-z^{\prime}_{\ast}( a_{k}^{-} ) =z^{\prime}_{\ast}( a_{k}^{+} ) .\end{equation*}

The convergence

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\sup_{x\in\left[ x_{k},y_{k}\right]}\left\vert z(x) -z_{\ast}(x) \right\vert =0.\end{equation*}

follows from the fact that both z and $z_{\ast}$ converge to 0 in the shrinking to a point interval $\left[ x_{k},y_{k}\right] $ .

Finally, we deal with intervals $\left( y_{k},x_{k+1}\right) $ , $k=1,2,3,\cdots$ .

Proposition 5. Let $1<a<b$ and z(x), $x\in\left[ a,b\right] $ be the solution to

(5.11) \begin{equation}\left\{\begin{array}[c]{c}z^{\prime\prime}+\frac{1}{x}z^{\prime}=\frac{\varepsilon^{\alpha}}{z^{\alpha}}-1,\\ \\[-9pt] z(a) = z(b) = \varepsilon.\end{array}\right.\end{equation}

Assume that:

1. (1) $z>\varepsilon\ in\ (a,b).$

2. (2) $\textit{z}\ attains\ its\ unique\ maximum\ M<1\ at\ x_{\max}\ \in(a,b).$

3. (3) $z^{\prime}>0\ in\ \left[a,x_{\max}\right)\ and\ z^{\prime}<0\ in\ \left( x_{\max},b\right] .$

Then for any $0<\varepsilon\leq\varepsilon_{0}$ , $C_{1}\leq b-a\leq C_{2}$ and

\begin{equation*}\int_{a}^{b}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx\leq C_{3}\varepsilon,\end{equation*}

where $\varepsilon_{0}$ , $C_{i}$ are constants depending only on $\alpha$ , the upper bound of a and the positive lower bound of $z^{\prime}\left(a\right) $ .

Proof. Integrating (5.3) from a to x, we have

\begin{equation*}xz^{\prime}-az^{\prime}(a) \geq-\frac{1}{2}\left( x^{2}-a^{2}\right) .\end{equation*}

So

\begin{equation*}z^{\prime}\geq\frac{1}{x}\left[ az^{\prime}(a) -\frac{1}{2}\left(x^{2}-a^{2}\right) \right] \geq0\end{equation*}

whenever

\begin{equation*}x\leq\sqrt{a^{2}+2az^{\prime}(a) }.\end{equation*}

Hence,

\begin{equation*}x_{\max}\geq\sqrt{a^{2}+2az^{\prime}(a) },\end{equation*}

and

\begin{align*}M & \geq z\left( \sqrt{a^{2}+2az^{\prime}(a) }\right) \\ \\[-9pt] & \geq\int_{a}^{\sqrt{a^{2}+2az^{\prime}(a) }}\frac{1} {x}\left[ az^{\prime}(a) -\frac{1}{2}\left( x^{2} - a^{2}\right) \right] dx =\frac{a^{2}}{4}u(\frac{2z^{\prime}(a)}{a}) \geq C,\end{align*}

where $u(x)=\left( 1+x\right) \ln(1+x) -x$ is positive and increasing for $x>0$ and C is some constant independent of $\varepsilon$ . We could see that M is uniformly bounded in $\left[ C,1 \right] $ and then we could assume for any $\varepsilon\leq\varepsilon_{0}$ by taking $\varepsilon_{0}$ sufficiently small and any $z\in\left[ \varepsilon,M\right] $

\begin{equation*}\frac{G(M)-G(z)}{M-z}\geq\frac{G(M)-G(\varepsilon)}{M-\varepsilon}\geq\frac{1}{2}.\end{equation*}

Next, integrating (5.2) from $x_{\max}$ to x yields

\begin{equation*}x^{2}\left( z^{\prime}\right) ^{2}=-2\int_{x_{\max}}^{x}y^{2}( G \circ z)^{\prime} (y) dy.\end{equation*}

Suppose $x \in\left[ a,x_{\max} \right] $ , we have

\begin{equation*}2\left( G(M)-G(z) \right) \leq\left\vert \frac{dz}{dx}\right\vert ^{2}\leq\frac{2x_{\max}^{2}}{x^{2}}\left( G(M)-G(z) \right) ,\end{equation*}

hence

\begin{align*}x_{\max}-a & = \int_{a}^{x_{\max}}dx\leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\[3pt] & \leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{M-z}} \leq2\sqrt{M}.\end{align*}

Now we estimate

\begin{align*}\int_{a}^{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\\ \\[-9pt] & \leq\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} = \int_{\varepsilon}^{M/2}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}+\int_{M/2}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}}\\ \\[-9pt] & \leq\frac{\varepsilon}{\left( \alpha-1\right) \sqrt{M/2}}+\frac{2^{\alpha}\varepsilon^{\alpha}}{M^{\alpha}}2\sqrt{M} \leq C_{2}\varepsilon.\end{align*}

On the other hand, suppose $x\in\left[ x_{\max},b\right] $ , we have

\begin{equation*}\frac{2x_{\max}^{2}}{x^{2}}\left( G(M)-G(z) \right) \leq\left\vert \frac{dz}{dx}\right\vert ^{2}\leq2\left( G(M)-G(z) \right) ,\end{equation*}

hence

\begin{equation*}x_{\max}\ln\frac{b}{x_{\max}} = \int_{x_{\max}}^{b}\frac{x_{\max}}{x}dx \leq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right) }}\leq2\sqrt{M}\end{equation*}

which yields

\begin{equation*}b \leq x_{\max}e^{\frac{2\sqrt{M}}{x_{\max}}} \leq\left( a+2\sqrt{M} \right)e^{\frac{2\sqrt{M}}{a}}.\end{equation*}

We also have

\begin{equation*}b-x_{\max}\geq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( G(M)-G(z) \right)}} \geq\int_{\varepsilon}^{M}\frac{dz}{\sqrt{2\left( M - z \right) }} =\sqrt{2\left( M - \varepsilon\right) }\end{equation*}

and

\begin{align*}\int_{x_{\max}}^{b}\frac{\varepsilon^{\alpha}}{z^{\alpha}}dx & \leq\int_{\varepsilon}^{M}\frac{x}{x_{\max}}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{2\left( G(M) -G(z) \right) }}\\& \leq\frac{b}{x_{\max}}\int_{\varepsilon}^{M}\frac{\varepsilon^{\alpha}}{z^{\alpha}}\frac{dz}{\sqrt{M-z}} \leq\frac{b}{x_{\max}}C_{2}\varepsilon\leq C_{3}\varepsilon.\\[-40pt]\end{align*}

Corollary 2. Suppose that

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}y_{k} & =a_{k} \text{ and } \lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( y_{k} ) = z_{\ast}^{\prime}(a_{k}^{+} ) .\end{align*}

Then

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}x_{k+1} & =a_{k+1} \text{ and }\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{k+1} ) = z_{\ast}^{\prime}(a_{k+1}^{-} ) .\end{align*}

Moreover,

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\sup_{x\in\left[ y_{k},x_{k+1}\right]}\left\vert z(x) -z_{\ast}(x) \right\vert =0.\end{equation*}

Proof. We define $\tilde{z}$ on $\left[ y_{k},x_{k+1}\right] $ as a solution to

\begin{equation*}\tilde{z}^{\prime\prime}+\frac{1}{x}\tilde{z}^{\prime}=-1\end{equation*}

satisfying $\tilde{z}(y_{k}) = z(y_{k}) $ and $\tilde{z}^{\prime}( y_{k} ) =z^{\prime}( y_{k} )$ . Integrating

\begin{equation*}\left( xz^{\prime}-x\tilde{z}^{\prime} \right) ^{\prime}=x\frac{\varepsilon^{\alpha}}{z^{\alpha}}\end{equation*}

from $y_{k}$ , we have

\begin{equation*}0\leq z^{\prime}-\tilde{z}^{\prime}=\frac{1}{x}\int_{y_{k}}^{x}y\frac{\varepsilon^{\alpha}}{z^{\alpha}(y) }dy\leq\frac{x_{k+1}}{y_{k}}\int_{y_{k}}^{x_{k+1}}\frac{\varepsilon^{\alpha}}{z^{\alpha}(y) }dy\leq C_{1}\varepsilon.\end{equation*}

Integrating again, we obtain

\begin{equation*}0\leq z(x) -\tilde{z}(x) \leq C_{1}\left( x_{k+1}-y_{k}\right)\varepsilon=C_{2}\varepsilon.\end{equation*}

In particular, at $x_{k+1}$ , we have

\begin{equation*}\left( 1-C_{2}\right) \varepsilon\leq\tilde{z}( x_{k+1} ) \leq\varepsilon.\end{equation*}

Let $\tilde{z}^{\ast}$ , defined for $x\geq\min\left( y_{k},a_{k}\right) $ be the solution to

\begin{equation*}z^{\prime\prime}+\frac{1}{x}z^{\prime}=-1\end{equation*}

satisfying

\begin{equation*}z( a_{k} ) =0\text{ and }z^{\prime}( a_{k} ) =z_{\ast}^{\prime}( a_{k}^{+} ).\end{equation*}

Since $x_{k+1}-y_{k}\geq C$ and $\lim_{\varepsilon\rightarrow0^{+}}y_{k}=a_{k}$ , we have $x_{k+1}-a_{k}\geq C$ . The continuously dependence of differential equations with initial data implies

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}\tilde{z}^{\ast}( x_{k+1} ) =0.\end{equation*}

Since

\begin{equation*}\tilde{z}^{\ast}=\left( a_{k}z_{\ast}^{\prime}( a_{k}^{+} ) +\frac{a_{k}^{2}}{2} \right) \ln\frac{x}{a_{k}}-\frac{x^{2}-a_{k}^{2}}{4}\end{equation*}

has a unique root $a_{k+1}$ in $\left( a_{k},\infty\right) $ , we conclude

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}x_{k+1}=a_{k+1}.\end{equation*}

And

\begin{equation*}\lim_{\varepsilon\rightarrow0^{+}}z^{\prime}( x_{k+1} ) =\lim_{\varepsilon\rightarrow0^{+}}\tilde{z}^{\prime}( x_{k+1} ) =\lim_{\varepsilon\rightarrow0^{+}}\tilde{z}^{\ast\prime}( x_{k+1} ) =\tilde{z}^{\ast\prime}(a_{k+1} ) = z_{\ast}^{\prime}( a_{k+1} ) .\end{equation*}

Since

\begin{equation*}\left\vert z(x)-z_{\ast}(x) \right\vert \leq\left\vert z(x)-\tilde{z}(x)\right\vert + \left\vert \tilde{z}(x)-\tilde{z}^{\ast}(x) \right\vert+\left\vert \tilde{z}^{\ast}(x)-z_{\ast}(x) \right\vert\end{equation*}

and all the functions are uniformly small near $a_{k}$ and $a_{k+1}$ , it is easy to check

\begin{align*}\lim_{\varepsilon\rightarrow0^{+}}\sup_{x\in\left[ y_{k},x_{k+1}\right]}\left\vert z(x)-z_{\ast}(x) \right\vert =0.\\[-30pt] \end{align*}

Now we are ready to prove Theorem 2 using the asymptotic behaviour of limit solution $z_{\ast}$ which we will prove in the next section.

Proof of Theorem 2. Note that energy function e(x) defined by (5.1) is bounded by e(0). Combining Proposition 3, Corollary 1 and 2 hold, we conclude z(x) converges to $z_{\ast}(x)$ locally uniformly on $\left[ 0,\infty\right) $ as $\varepsilon\rightarrow0^{+}$ . From Remark 1, the local maximum and the local minimum of z(x) form two monotone sequences converging to $\varepsilon$ . Since $\lim_{x\rightarrow\infty}z_{\ast}(x)=0$ , the local uniform convergence of z to $z_{\ast}$ implies the global uniform convergence on $\left[0,\infty\right) $ as $\varepsilon\rightarrow0^{+}$ .

6. Asymptotic behaviour of limit solution

From Theorem 2, we have as $\varepsilon\rightarrow0^{+}$ , z(x) converges uniformly on $\left[0,\infty\right) $ to the limit $z_{\ast}(x)$ satisfying (4.3). Now we are going to apply inductive calculations to compute $a_{j}$ and analyse the asymptotic behaviours in the following manner. Similarly as previous, we define the energy function

\begin{equation*}e(x) = \frac{1}{2} \left( z_{\ast}^{\prime}(x) \right) ^{2} + z_{\ast}(x)\end{equation*}

and $e_{j} = e(a_{j})$ . It is easy to check that e(x) is decreasing in x and $e_{j}$ is decreasing in j.

(i) In $\left[0,a_{1}\right] $ , we have

\begin{equation*}z_{\ast}(x) =1-\frac{x^{2}}{4}.\end{equation*}

Hence,

\begin{equation*}a_{1}=2 \text{ and } e_{1}=|z_{\ast}^{\prime}(a_{1})|^{2}=1.\end{equation*}

(ii) In $[a_{1},a_{2}],$

\begin{equation*}(xz_{\ast}^{\prime})^{\prime}=-x\text{ and }z_{\ast}^{\prime}(2^{+})=1.\end{equation*}

Then

\begin{equation*}z_{\ast}(x)=4\ln\frac{x}{2}+\frac{4-x^{2}}{4}.\end{equation*}

Note that $z_{\ast}^{\prime\prime}(x)=-\frac{4}{x^{2}}-\frac{1}{2}<0,$ $z_{\ast}(x)$ is concave down. Therefore, there exists a unique solution $a_{2}\in(2,\infty)$ to

\begin{equation*}4\ln\frac{a_{2}}{2}+\frac{4-a_{2}^{2}}{4}=0.\end{equation*}

That is,

\begin{equation*}a_{2}\approx3.74853 \text{ and } e_{2}=\left\vert z_{\ast}^{\prime}(a_{2})\right\vert ^{2}=\left( \frac{a_{2}}{2}-\frac{4}{a_{2}}\right) ^{2}\approx0.6515.\end{equation*}

(iii) In $[a_{j},a_{j+1}]$ , $j\geq2$ , $z_{\ast}$ is defined by the initial value problem

\begin{equation*}(xz_{\ast}^{\prime})^{\prime}=-x \text{, } z_{\ast}( a_{j} ) =0 \text{ and }z_{\ast}^{\prime}(a_{j}^{+})=\sqrt{e_{j}}.\end{equation*}

For any $x\geq a_{j}$ , integrating twice from $a_{j}$ to x, we obtain

\begin{equation*}z_{\ast}(x) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right) \ln\frac{x}{a_{j}}-\frac{x^{2}-a_{j}^{2}}{4}.\end{equation*}

Since

\begin{equation*}z_{\ast}^{\prime\prime}(x) = -\frac{a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}}{x^{2}}-\frac{1}{2}<0\end{equation*}

on $\left( a_{j},\infty\right) $ , there is a unique root $a_{j+1}\in(a_{j},\infty)$ such that

(6.1) \begin{equation}z_{\ast} ( a_{j+1} ) =\left( a_{j}\sqrt{e_{j}}+\frac{a_{j}^{2}}{2}\right)\ln\frac{a_{j+1}}{a_{j}}-\frac{a_{j+1}^{2}-a_{j}^{2}}{4}=0.\end{equation}

And $\sqrt{e_{j+1}}$ is given by

(6.2) \begin{equation}\sqrt{e_{j+1}}=-z_{\ast}^{\prime}( a_{j+1} ) =-\frac{a_{j}}{a_{j+1}}\sqrt{e_{j}} + \frac{ a_{j+1}^{2} -a_{j}^{2} }{ 2 a_{j+1} }.\end{equation}

Next, we consider the asymptotic behaviour of $a_{j}$ and $e_{j}$ as $j\rightarrow\infty$ .

Theorem 3. There exists positive constant A such that as $j\rightarrow\infty$ ,

\begin{equation*}a_{j}\sim Aj^{\frac{3}{4}}\text{ and }\sqrt{e_{j}}\sim\frac{3}{8}Aj^{-\frac{1}{4}}.\end{equation*}

Proof. Let $b_{j}=\frac{\sqrt{e_{j}}}{a_{j}}$ , (6.2) implies

(6.3) \begin{equation}b_{j+1}=\frac{1}{2}-\frac{1}{2}\left( \frac{a_{j}}{a_{j+1}}\right)^{2}\left( 1+2b_{j}\right) . \end{equation}

Since $\sqrt{e_{j}}$ is decreasing and $a_{j}$ is increasing in j, $b_{j}$ is decreasing. If $\lim_{j\rightarrow\infty}b_{j}\not =0$ , then $a_{j}=\frac{\sqrt{e_{j}}}{b_{j}}$ is bounded and hence $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$ . If $\lim_{j\rightarrow\infty}b_{j}=0$ , then (6.3) implies $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$ . Hence, in any case, $\lim_{j\rightarrow\infty}\frac{a_{j}}{a_{j+1}}=1$ which also implies $\lim_{j\rightarrow\infty}b_{j}=0$ . Denote $t_j=(\frac{a_{j+1}}{a_{j}})^{2}-1$ , we have $\lim_{j\rightarrow\infty}t_j=0$ . Now (6.1) could be rewritten into

\begin{equation*}\frac{t_j}{\ln(t_j+1)}=2b_{j}+1.\end{equation*}

By Taylor expansion, we have

\begin{equation*}2b_{j}=\frac{t_j}{2}-\frac{t_j^{2}}{12}+O\left(t_j^{3}\right)\end{equation*}

which yields

\begin{equation*}t_j=4b_{j}+\frac{t_j^{2}}{6}+O\left(t_j^{3}\right) = 4b_{j}+\frac{8}{3}b_{j}^{2}+O\left(b_{j}^{3}\right).\end{equation*}

Therefore,

\begin{align*}\frac{a_{j}}{a_{j+1}} & =\left( 1+t_j\right)^{-\frac{1}{2}}=1-\frac{1}{2}t_j+\frac{3t_j^{2}}{8}+O\left(t_j^{3}\right) \\& =1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3}).\end{align*}

Plug the above expansion into (6.3), we have

\begin{align*}b_{j+1} & =\frac{1}{2}-\frac{1}{2}\left( 1-2b_{j}+\frac{14}{3}b_{j}^{2}+O(b_{j}^{3})\right) ^{2}\left( 1+2b_{j}\right) \\& =b_{j}-\frac{8}{3}b_{j}^{2}+O(b_{j}^{3})\end{align*}

which implies

\begin{equation*}\frac{1}{b_{j+1}}=\frac{1}{b_{j}}+\frac{8}{3}+O(b_{j}).\end{equation*}

As $b_{j}$ is decreasing and converges to 0, we conclude

\begin{equation*}\lim_{j\rightarrow\infty}jb_{j}=\frac{3}{8}.\end{equation*}

Next, since

\begin{align*}\frac{b_{j+1}a_{j+1}^{\frac{4}{3}}}{b_{j}a_{j}^{\frac{4}{3}}} &=\frac{b_{j+1}}{b_{j}}\left( \frac{a_{j+1}}{a_{j}}\right) ^{\frac{4}{3}}=\frac{\left( 1-\frac{8}{3}b_{j}+O(b_{j}^{2})\right) }{\left[1-2b_{j}+O(b_{j}^{2})\right] ^{4/3}}\\& =1+O(b_{j}^{2}),\end{align*}

the order of $b_{j}$ implies the limit $\gamma=\lim_{j\rightarrow\infty}b_{j}a_{j}^{\frac{4}{3}}>0$ exists. Hence,

\begin{equation*}\lim_{j\rightarrow\infty}\frac{a_{j}}{j^{\frac{3}{4}}}=\lim_{j\rightarrow\infty}\left( \frac{b_{j}a_{j}^{\frac{4}{3}}}{jb_{j}}\right) ^{\frac{3}{4}}=\left( \frac{8\gamma}{3}\right) ^{\frac{3}{4}}=A\end{equation*}

and finally

\begin{align*}\lim_{j\rightarrow\infty}\frac{\sqrt{e_{j}}}{j^{-\frac{1}{4}}}=\lim_{j\rightarrow\infty}jb_{j}\frac{a_{j}}{j^{\frac{3}{4}}}=\frac{3}{8}A.\\[-40pt] \end{align*}