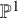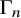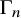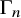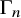1 Introduction
1.1 Euler continuants
Fix a string
![]() $\mathtt {S}=`x_1\dots x_k$
’ of
$\mathtt {S}=`x_1\dots x_k$
’ of
![]() $k\geq 1$
indeterminates, which are not necessarily invertible or commuting. We define the k-th Euler continuant (polynomial), denoted
$k\geq 1$
indeterminates, which are not necessarily invertible or commuting. We define the k-th Euler continuant (polynomial), denoted
![]() $(x_1,\dots ,x_k)$
, by starting with the product
$(x_1,\dots ,x_k)$
, by starting with the product
![]() $x_1\cdots x_k$
and then taking the sum of all the distinct substrings of
$x_1\cdots x_k$
and then taking the sum of all the distinct substrings of
![]() $\mathtt {S}$
obtained by removing adjacent pairs
$\mathtt {S}$
obtained by removing adjacent pairs
![]() $x_{\ell } x_{\ell +1}$
in all possible ways, with
$x_{\ell } x_{\ell +1}$
in all possible ways, with
![]() $+1$
assigned to the empty substring. The first instances of this family were already written in 1764 by Euler [Reference Euler28, p. 55] as
$+1$
assigned to the empty substring. The first instances of this family were already written in 1764 by Euler [Reference Euler28, p. 55] as
 $$ \begin{align*} (x_1)&=x_1\,, \\ (x_1,x_2)&=x_1x_2+1\,, \\ (x_1,x_2,x_3)&=x_1x_2x_3+x_3+x_1\,, \\ (x_1,x_2,x_3,x_4)&=x_1x_2x_3x_4+x_1x_2+x_1x_4+x_3x_4+1\,, \\ (x_1,x_2,x_3,x_4,x_5)&=x_1x_2x_3x_4x_5+x_1x_2x_3+x_1x_2x_5+x_1x_4x_5+x_3x_4x_5+x_1+x_3+x_5\,.\\[-15pt] \end{align*} $$
$$ \begin{align*} (x_1)&=x_1\,, \\ (x_1,x_2)&=x_1x_2+1\,, \\ (x_1,x_2,x_3)&=x_1x_2x_3+x_3+x_1\,, \\ (x_1,x_2,x_3,x_4)&=x_1x_2x_3x_4+x_1x_2+x_1x_4+x_3x_4+1\,, \\ (x_1,x_2,x_3,x_4,x_5)&=x_1x_2x_3x_4x_5+x_1x_2x_3+x_1x_2x_5+x_1x_4x_5+x_3x_4x_5+x_1+x_3+x_5\,.\\[-15pt] \end{align*} $$
More succinctly, Euler continuants can be defined by the following recurrence:
Originally, Euler introduced this class of polynomials to grasp the numerators and denominators of continued fractions (hence the name ‘continuants’). For example,
 $$\begin{align*}x_1+\frac{1}{x_2}=\frac{(x_1,x_2)}{(x_2)}\,, \quad x_1+\frac{1}{x_2+\frac{1}{x_3}}=\frac{(x_1,x_2,x_3)}{(x_2,x_3)}\,, \quad x_1+\frac{1}{x_2+\frac{1}{x_3+\frac{1}{x_4}}}=\frac{(x_1,x_2,x_3,x_4)}{(x_2,x_3,x_4)}\,.\\[-15pt] \end{align*}$$
$$\begin{align*}x_1+\frac{1}{x_2}=\frac{(x_1,x_2)}{(x_2)}\,, \quad x_1+\frac{1}{x_2+\frac{1}{x_3}}=\frac{(x_1,x_2,x_3)}{(x_2,x_3)}\,, \quad x_1+\frac{1}{x_2+\frac{1}{x_3+\frac{1}{x_4}}}=\frac{(x_1,x_2,x_3,x_4)}{(x_2,x_3,x_4)}\,.\\[-15pt] \end{align*}$$
Since then, Euler continuants have appeared in many unexpected areas of research, and they have become essential in mathematics. In the context of number theory, Euler continuants are closely related to Euclid’s algorithm; see, for example, [Reference Graham, Knuth and Patashnik34] for a more detailed account. The number of terms of the k-th Euler continuant is the
![]() $(k+1)$
-th Fibonacci number, while the Catalan numbers count the factorisations of the continuant via triangulations of polygons—see [Reference Paluba38], where a connection to Loday’s free duplicial algebras is also stated. In knot theory, the Conway polynomial of an oriented two-bridge link is related to Euler continuants [Reference Koseleff and Pecker36]; in contact and symplectic geometry, the braid varieties associated with two-stranded braids are smooth varieties whose defining equations are closely linked to Euler continuants [Reference Casals, Gorsky, Gorsky and Simental21]. Another appearance of Euler continuants occurs when we consider a matrix version of the Stern–Brocot tree [Reference Graham, Knuth and Patashnik34], which is a classical construction of all nonnegative fractions whose numerators and denominators are coprime. If we let
$(k+1)$
-th Fibonacci number, while the Catalan numbers count the factorisations of the continuant via triangulations of polygons—see [Reference Paluba38], where a connection to Loday’s free duplicial algebras is also stated. In knot theory, the Conway polynomial of an oriented two-bridge link is related to Euler continuants [Reference Koseleff and Pecker36]; in contact and symplectic geometry, the braid varieties associated with two-stranded braids are smooth varieties whose defining equations are closely linked to Euler continuants [Reference Casals, Gorsky, Gorsky and Simental21]. Another appearance of Euler continuants occurs when we consider a matrix version of the Stern–Brocot tree [Reference Graham, Knuth and Patashnik34], which is a classical construction of all nonnegative fractions whose numerators and denominators are coprime. If we let
 $$\begin{align*}L= \left(\begin{array}{cc} 1&1\\0&1 \end{array} \right) ,\quad R= \left(\begin{array}{cc} 1&0\\1&1 \end{array} \right),\\[-15pt] \end{align*}$$
$$\begin{align*}L= \left(\begin{array}{cc} 1&1\\0&1 \end{array} \right) ,\quad R= \left(\begin{array}{cc} 1&0\\1&1 \end{array} \right),\\[-15pt] \end{align*}$$
each node in the matrix Stern–Brocot tree can be represented as a sequence
and n is even. Then it is not difficult to prove that the four entries of the obtained matrix can be rewritten in terms of Euler continuants. To show this, it suffices to note that
 $$ \begin{align} \left(\begin{array}{cc} 1&\alpha \\0&1 \end{array} \right) = \left(\begin{array}{cc} 0&1\\1&0 \end{array} \right) \left(\begin{array}{cc} 0&1\\1&\alpha \end{array} \right) \,, \quad \left(\begin{array}{cc} 1&0\\\alpha&1 \end{array} \right) = \left(\begin{array}{cc} 0&1\\1&\alpha \end{array} \right) \left(\begin{array}{cc} 0&1\\1&0 \end{array} \right) \,,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \left(\begin{array}{cc} 1&\alpha \\0&1 \end{array} \right) = \left(\begin{array}{cc} 0&1\\1&0 \end{array} \right) \left(\begin{array}{cc} 0&1\\1&\alpha \end{array} \right) \,, \quad \left(\begin{array}{cc} 1&0\\\alpha&1 \end{array} \right) = \left(\begin{array}{cc} 0&1\\1&\alpha \end{array} \right) \left(\begin{array}{cc} 0&1\\1&0 \end{array} \right) \,,\\[-15pt]\nonumber \end{align} $$
for any constant
![]() $\alpha $
and then use that, given
$\alpha $
and then use that, given
![]() $k\geq 2$
and constants
$k\geq 2$
and constants
![]() $x_i$
for
$x_i$
for
![]() $1\leq i \leq k$
, we have
$1\leq i \leq k$
, we have
 $$ \begin{align} \left(\begin{array}{cc} 0&1\\ 1&x_k \end{array} \right) \left(\begin{array}{cc} 0&1\\1&x_{k-1} \end{array} \right) \cdots \left(\begin{array}{cc} 0&1\\ 1&x_1 \end{array} \right) = \left(\begin{array}{cc} (x_{k-1},\ldots,x_2)&(x_{k-1},\ldots,x_1)\\ (x_{k},\ldots,x_2)&(x_{k},\ldots,x_1) \end{array} \right)\,.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \left(\begin{array}{cc} 0&1\\ 1&x_k \end{array} \right) \left(\begin{array}{cc} 0&1\\1&x_{k-1} \end{array} \right) \cdots \left(\begin{array}{cc} 0&1\\ 1&x_1 \end{array} \right) = \left(\begin{array}{cc} (x_{k-1},\ldots,x_2)&(x_{k-1},\ldots,x_1)\\ (x_{k},\ldots,x_2)&(x_{k},\ldots,x_1) \end{array} \right)\,.\\[-15pt]\nonumber \end{align} $$
This remarkable matrix identity can be proven by induction and it will be crucial in §1.2.
Finally, beyond the recurrence (1.1), an effective way to define Euler continuants uses the determinant of a tridiagonal matrix. For such a matrix, the only nonzero entries are given by the indeterminates
![]() $x_i$
along the main diagonal,
$x_i$
along the main diagonal,
![]() $-1$
on the first diagonal below it and
$-1$
on the first diagonal below it and
![]() $+1$
on the first diagonal above it. This approach suggests how to introduce new families of continuants; for instance, by taking determinants of other tridiagonal matrices. They have appeared in interesting contexts such as Coxeter’s frieze patterns, Ptolemy–Plücker relations and cluster algebras, or the discrete Sturm–Liouville, Hill or Schrödinger equations (see [Reference Morier-Genoud and Ovsienko37] and references therein).
$+1$
on the first diagonal above it. This approach suggests how to introduce new families of continuants; for instance, by taking determinants of other tridiagonal matrices. They have appeared in interesting contexts such as Coxeter’s frieze patterns, Ptolemy–Plücker relations and cluster algebras, or the discrete Sturm–Liouville, Hill or Schrödinger equations (see [Reference Morier-Genoud and Ovsienko37] and references therein).
Quite strikingly, Boalch [Reference Boalch15] realised that Euler continuants naturally appear in the setting of certain wild character varieties linked to the work of Sibuya [Reference Sibuya40]. In that case, the continuants can be understood as Lie group valued moment maps [Reference Alekseev, Malkin and Meinrenken1, Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2]; we will explain these links in §1.2. In this article, we are able to further prove that Euler continuants are noncommutative moment maps in the sense of Van den Bergh’s noncommutative quasi-Poisson geometry—see §1.3. This is another step towards the programme that we have initiated in [Reference Fairon and Fernández31] which aims at understanding the Poisson geometry of wild character varieties in terms of Hamiltonian double quasi-Poisson algebras attached to quivers. Our programme is based on two main tools. First, the interpretation of such varieties using graphs/quivers undertaken by Boalch [Reference Boalch11]–[Reference Boalch and Yamakawa16]. Second, the application of the Kontsevich–Rosenberg principle [Reference Kontsevich and Rosenberg35], whereby one studies a noncommutative structure on an associative algebra whenever it induces the corresponding standard algebro-geometric structures on representation spaces. Whereas in [Reference Fairon and Fernández31] we pursued this idea by varying the number of vertices of the quivers under consideration (typically, complete graphs with some additional data), in this article we fix the quivers to have two vertices and we vary the number of arrows between them.
1.2 Euler continuants as moment maps
Character varieties of Riemann surfaces have become central objects in modern mathematics. This is essentially due to their dual nature: They can be defined as moduli spaces of monodromy data of regular singular connections or as spaces of representations of the fundamental group. Partially motivated by works on two-dimensional gauge theory concerning the Atiyah–Bott symplectic form, Boalch started in [Reference Boalch7, Reference Boalch8] a groundbreaking programme to investigate the geometry of wild character varieties (note this terminology appeared in [Reference Boalch13]). These spaces generalise character varieties by considering moduli spaces of monodromy data classifying irregular meromorphic connections on bundles over Riemann surfaces; alternatively, wild character varieties parametrise fundamental group representations enriched by adding Stokes data at each singularity. This led to the construction of many new holomorphic symplectic manifolds [Reference Boalch6, Reference Boalch7], which turn out to admit hyperkähler metrics, as shown in [Reference Biquard and Boalch5]. These developments prompted Boalch in [Reference Boalch9] to begin an extensive study of wild character varieties from an alternative algebraic perspective. Indeed, he realised that such varieties can be constructed as finite-dimensional multiplicative symplectic quotients of smooth affine varieties, involving a distinguished holomorphic 2-form. This point of view required the introduction of a complex-analytic version of quasi-Hamiltonian geometry [Reference Alekseev, Malkin and Meinrenken1], which builds on the key operations of fission and fusion. Whereas the former consists in breaking the structure group into some relevant subgroups—see [Reference Boalch10, Reference Boalch13]—the latter provides a way to glue pieces of surfaces together out of building blocks given by conjugacy classes, pairs of pants and the important fission spaces [Reference Boalch13]. In the rest of this subsection, we will come across one of these building blocks: The (reduced) fission space
![]() $\mathcal {B}^{n+1}$
; see equation (1.5).
$\mathcal {B}^{n+1}$
; see equation (1.5).
In [Reference Boalch15], Boalch examined an interesting class of wild character varieties arising as specific moduli spaces of points on
![]() $\mathbb {P}^1$
; they were originally studied by Sibuya [Reference Sibuya40], and for certain values they give rise to the prominent gravitational instantons. These wild character varieties are multiplicative analogues of a family of Hyperkähler varieties introduced by Calabi [Reference Calabi20] in 1979 as higher-dimensional examples of the Eguchi–Hanson spaces. If we denote by
$\mathbb {P}^1$
; they were originally studied by Sibuya [Reference Sibuya40], and for certain values they give rise to the prominent gravitational instantons. These wild character varieties are multiplicative analogues of a family of Hyperkähler varieties introduced by Calabi [Reference Calabi20] in 1979 as higher-dimensional examples of the Eguchi–Hanson spaces. If we denote by
![]() $\Gamma _n$
the quiver with two vertices
$\Gamma _n$
the quiver with two vertices
![]() $\{1,2\}$
and n arrows
$\{1,2\}$
and n arrows
![]() $a_i:1\to 2$
(whose double
$a_i:1\to 2$
(whose double
![]() $\overline {\Gamma }_n$
has n extra arrows
$\overline {\Gamma }_n$
has n extra arrows
![]() $b_i:2\to 1$
; see Figure 1), Calabi’s varieties can be described as (Nakajima/additive) quiver varieties attached to
$b_i:2\to 1$
; see Figure 1), Calabi’s varieties can be described as (Nakajima/additive) quiver varieties attached to
![]() $\Gamma _n$
. They are obtained by Hamiltonian reduction from the moduli space of representations of
$\Gamma _n$
. They are obtained by Hamiltonian reduction from the moduli space of representations of
![]() $\overline {\Gamma }_n$
with dimension vector
$\overline {\Gamma }_n$
with dimension vector
![]() $d=(1,1)$
. This prompted Boalch [Reference Boalch15] to make the crucial observation that Sibuya’s varieties, as multiplicative analogues of Calabi’s varieties, could also be defined using the quiver
$d=(1,1)$
. This prompted Boalch [Reference Boalch15] to make the crucial observation that Sibuya’s varieties, as multiplicative analogues of Calabi’s varieties, could also be defined using the quiver
![]() $\Gamma _n$
. This point of view naturally leads to Euler continuants as we explain now.
$\Gamma _n$
. This point of view naturally leads to Euler continuants as we explain now.

Figure 1 The quiver
![]() $\overline {\Gamma }_n$
with
$\overline {\Gamma }_n$
with
![]() $2n$
arrows is the double of
$2n$
arrows is the double of
![]() $\Gamma _n$
, which is only formed of the n arrows
$\Gamma _n$
, which is only formed of the n arrows
![]() $a_i:1\to 2$
.
$a_i:1\to 2$
.
If
![]() $G:=\operatorname {GL}_2(\mathbb {C})$
, let
$G:=\operatorname {GL}_2(\mathbb {C})$
, let
![]() $U_{+}$
(resp.
$U_{+}$
(resp.
![]() $U_-$
) be the subgroup of unipotent upper (resp. lower) triangular matrices, T be the maximal diagonal torus of G and we let
$U_-$
) be the subgroup of unipotent upper (resp. lower) triangular matrices, T be the maximal diagonal torus of G and we let
![]() $G_{\circ } =U_+TU_-$
denote the subspace of matrices in G admitting a Gauss decomposition. Recall that, for a matrix
$G_{\circ } =U_+TU_-$
denote the subspace of matrices in G admitting a Gauss decomposition. Recall that, for a matrix
![]() $M=(M_{ij})\in G$
, we have that
$M=(M_{ij})\in G$
, we have that
![]() $M\in G_{\circ }$
is equivalent to the condition
$M\in G_{\circ }$
is equivalent to the condition
![]() $M_{22}\neq 0$
, in which case we can write that
$M_{22}\neq 0$
, in which case we can write that
 $$ \begin{align} M= \left(\begin{array}{cc} 1&M_{12}M_{22}^{-1}\\0&1 \end{array} \right) \left(\begin{array}{cc} M_{11}-M_{12}M_{22}^{-1}M_{21}&0\\0&M_{22} \end{array} \right) \left(\begin{array}{cc} 1&0\\M_{22}^{-1}M_{21}&1 \end{array} \right) \,.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} M= \left(\begin{array}{cc} 1&M_{12}M_{22}^{-1}\\0&1 \end{array} \right) \left(\begin{array}{cc} M_{11}-M_{12}M_{22}^{-1}M_{21}&0\\0&M_{22} \end{array} \right) \left(\begin{array}{cc} 1&0\\M_{22}^{-1}M_{21}&1 \end{array} \right) \,.\\[-15pt]\nonumber \end{align} $$
Following Boalch [Reference Boalch15] from now on (see also Paluba’s thesis [Reference Paluba38] and even more generally [Reference Boalch9, Reference Boalch13]), we introduce for any
![]() $n\geq 1$
the reduced fission space
$n\geq 1$
the reduced fission space
![]() $\mathcal {B}^{n+1}\subset (U_-\times U_+)^{n}$
, which is the smooth complex variety defined by
$\mathcal {B}^{n+1}\subset (U_-\times U_+)^{n}$
, which is the smooth complex variety defined by
The condition of admitting a Gauss decomposition has a deep geometric meaning. Indeed, there is a natural action of T on
![]() $\mathcal {B}^{n+1}$
by simultaneous conjugation, which preserves a
$\mathcal {B}^{n+1}$
by simultaneous conjugation, which preserves a
![]() $2$
-form, and the inverse
$2$
-form, and the inverse
![]() $\mu _T$
of the diagonal part of the Gauss decomposition can be interpreted as a Lie group valued moment map, in the sense of [Reference Alekseev, Malkin and Meinrenken1]. Furthermore, since we consider the Gauss decomposition of a product of unipotent matrices,
$\mu _T$
of the diagonal part of the Gauss decomposition can be interpreted as a Lie group valued moment map, in the sense of [Reference Alekseev, Malkin and Meinrenken1]. Furthermore, since we consider the Gauss decomposition of a product of unipotent matrices,
![]() $\mu _T$
takes value in
$\mu _T$
takes value in
![]() $T\cap \operatorname {SL}_2(\mathbb {C})$
. This implies that, if we fix the T-valued moment map
$T\cap \operatorname {SL}_2(\mathbb {C})$
. This implies that, if we fix the T-valued moment map
![]() $\mu _T$
to
$\mu _T$
to
![]() $t_{\gamma }:=\operatorname {diag}(\gamma ,\gamma ^{-1})\in T \cap \operatorname {SL}_2(\mathbb {C})$
for generic
$t_{\gamma }:=\operatorname {diag}(\gamma ,\gamma ^{-1})\in T \cap \operatorname {SL}_2(\mathbb {C})$
for generic
![]() $\gamma \in \mathbb {C}^{\times }$
, the corresponding geometric invariant theory (GIT) quotient
$\gamma \in \mathbb {C}^{\times }$
, the corresponding geometric invariant theory (GIT) quotient
![]() $\mathcal {M}_n(t_{\gamma })=\mu _T^{-1}(t_{\gamma })/\!/T$
admits a symplectic form. The space
$\mathcal {M}_n(t_{\gamma })=\mu _T^{-1}(t_{\gamma })/\!/T$
admits a symplectic form. The space
![]() $\mathcal {M}_n(t_{\gamma })$
hence obtained is an example of the Sibuya spaces mentioned earlier.
$\mathcal {M}_n(t_{\gamma })$
hence obtained is an example of the Sibuya spaces mentioned earlier.
To relate the construction of
![]() $\mathcal {M}_n(t_{\gamma })$
to quivers and Euler continuants, we let
$\mathcal {M}_n(t_{\gamma })$
to quivers and Euler continuants, we let
 $$ \begin{align} S_{b,i}=\left(\begin{array}{cc} 1&0\\B_i&1 \end{array} \right)\,, \quad S_{a,i}= \left(\begin{array}{cc} 1&A_i\\0&1 \end{array} \right) \,, \quad 1\leq i \leq n\,, \end{align} $$
$$ \begin{align} S_{b,i}=\left(\begin{array}{cc} 1&0\\B_i&1 \end{array} \right)\,, \quad S_{a,i}= \left(\begin{array}{cc} 1&A_i\\0&1 \end{array} \right) \,, \quad 1\leq i \leq n\,, \end{align} $$
for constants
![]() $A_i,B_i\in \mathbb {C}$
at a point of
$A_i,B_i\in \mathbb {C}$
at a point of
![]() $\mathcal {B}^{n+1}$
. Then, by equations (1.2) and (1.3), we can see that
$\mathcal {B}^{n+1}$
. Then, by equations (1.2) and (1.3), we can see that
 $$ \begin{align} \begin{aligned} S_{b,n}S_{a,n}\cdots S_{b,1}S_{a,1} =& \left(\begin{array}{cc} 0&1\\1&B_n \end{array} \right) \left(\begin{array}{cc} 0&1\\1&A_n \end{array} \right) \ldots \left(\begin{array}{cc} 0&1\\1&B_1 \end{array} \right) \left(\begin{array}{cc} 0&1\\1&A_1 \end{array} \right) \\ =& \left(\begin{array}{cc} (A_{n},\ldots,B_1)&(A_{n},\ldots,A_1)\\ (B_{n},\ldots,B_1)&(B_{n},\ldots,A_1) \end{array} \right)\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S_{b,n}S_{a,n}\cdots S_{b,1}S_{a,1} =& \left(\begin{array}{cc} 0&1\\1&B_n \end{array} \right) \left(\begin{array}{cc} 0&1\\1&A_n \end{array} \right) \ldots \left(\begin{array}{cc} 0&1\\1&B_1 \end{array} \right) \left(\begin{array}{cc} 0&1\\1&A_1 \end{array} \right) \\ =& \left(\begin{array}{cc} (A_{n},\ldots,B_1)&(A_{n},\ldots,A_1)\\ (B_{n},\ldots,B_1)&(B_{n},\ldots,A_1) \end{array} \right)\,. \end{aligned} \end{align} $$
Thus, the condition that this product belongs to
![]() $G_{\circ }$
is equivalent to requiring the invertibility of the Euler continuant
$G_{\circ }$
is equivalent to requiring the invertibility of the Euler continuant
![]() $(B_{n},\ldots ,A_1)$
placed in the (2,2)-entry. In view of equation (1.4), we get that the diagonal part of the Gauss decomposition is
$(B_{n},\ldots ,A_1)$
placed in the (2,2)-entry. In view of equation (1.4), we get that the diagonal part of the Gauss decomposition is
![]() $\operatorname {diag}(\tilde {s}_n,(B_{n},\ldots ,A_1))$
, where
$\operatorname {diag}(\tilde {s}_n,(B_{n},\ldots ,A_1))$
, where
By taking the determinant in equation (1.7), we can find thatFootnote
1
![]() $\tilde {s}_n=(A_1,B_1,\ldots ,A_n,B_n)^{-1}$
. The upshot is that we can reexpress
$\tilde {s}_n=(A_1,B_1,\ldots ,A_n,B_n)^{-1}$
. The upshot is that we can reexpress
![]() $\mathcal {B}^{n+1}$
and its Lie group valued moment map
$\mathcal {B}^{n+1}$
and its Lie group valued moment map
![]() $\mu _T:\mathcal {B}^{n+1}\to T$
in terms of the space
$\mu _T:\mathcal {B}^{n+1}\to T$
in terms of the space
and the map
From this point of view, we can realise
![]() $\widehat {\mathcal {B}}^{n+1}$
as an affine subspaceFootnote
2
inside
$\widehat {\mathcal {B}}^{n+1}$
as an affine subspaceFootnote
2
inside
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(1,1))$
, where we assign
$\operatorname {Rep}(\overline {\Gamma }_n,(1,1))$
, where we assign
![]() $A_i,B_i$
to the arrows
$A_i,B_i$
to the arrows
![]() $a_i,b_i$
, respectively. Moreover, the subspace
$a_i,b_i$
, respectively. Moreover, the subspace
![]() $\mu _T^{-1}(t_{\gamma })$
needed to define the wild character variety
$\mu _T^{-1}(t_{\gamma })$
needed to define the wild character variety
![]() $\mathcal {M}_n(t_{\gamma })$
can be identified with
$\mathcal {M}_n(t_{\gamma })$
can be identified with
![]() $\widehat {\mu }^{-1}(\gamma ,\gamma ^{-1})$
, which can be further seen as a moduli space of representations of a noncommutative algebra, the fission algebra
$\widehat {\mu }^{-1}(\gamma ,\gamma ^{-1})$
, which can be further seen as a moduli space of representations of a noncommutative algebra, the fission algebra
![]() $\mathcal {F}^{q_{\gamma }}(\overline {\Gamma }_n)$
; see equation (3.8) with parameter
$\mathcal {F}^{q_{\gamma }}(\overline {\Gamma }_n)$
; see equation (3.8) with parameter
![]() $q_{\gamma }=(\gamma ,\gamma ^{-1})$
. Introduced in [Reference Boalch14], fission algebras generalise the (deformed) multiplicative preprojective algebras of [Reference Crawley-Boevey and Shaw25], and they are linked to the generalised double affine Hecke algebras of Etingof, Oblomkov and Rains, as explained in [Reference Etingof, Oblomkov and Rains27].
$q_{\gamma }=(\gamma ,\gamma ^{-1})$
. Introduced in [Reference Boalch14], fission algebras generalise the (deformed) multiplicative preprojective algebras of [Reference Crawley-Boevey and Shaw25], and they are linked to the generalised double affine Hecke algebras of Etingof, Oblomkov and Rains, as explained in [Reference Etingof, Oblomkov and Rains27].
The importance of the discussion made so far is that we do not really need to consider the elements
![]() $\{A_i,B_i\}$
parametrising
$\{A_i,B_i\}$
parametrising
![]() $\widehat {\mathcal {B}}^{n+1}$
as numbers, but, more generally, we can use matrices
$\widehat {\mathcal {B}}^{n+1}$
as numbers, but, more generally, we can use matrices
![]() $A_i\in \operatorname {Mat}_{d_2\times d_1}(\mathbb {C})$
,
$A_i\in \operatorname {Mat}_{d_2\times d_1}(\mathbb {C})$
,
![]() $B_i\in \operatorname {Mat}_{d_1\times d_2}(\mathbb {C})$
for any
$B_i\in \operatorname {Mat}_{d_1\times d_2}(\mathbb {C})$
for any
![]() $d_1,d_2\geq 1$
. Indeed, we get in that way other examples of reduced fission spaces [Reference Boalch13]; see [Reference Paluba38]. Hence, we can work with a space of invertible representations inside
$d_1,d_2\geq 1$
. Indeed, we get in that way other examples of reduced fission spaces [Reference Boalch13]; see [Reference Paluba38]. Hence, we can work with a space of invertible representations inside
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
, rather than
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
, rather than
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(1,1))$
. Therefore, it seems natural to try to understand the structures unveiled by Boalch directly at the level of the quiver
$\operatorname {Rep}(\overline {\Gamma }_n,(1,1))$
. Therefore, it seems natural to try to understand the structures unveiled by Boalch directly at the level of the quiver
![]() $\overline {\Gamma }_n$
by using noncommutative quasi-Poisson geometry [Reference Van den Bergh41]. In that case, we define from
$\overline {\Gamma }_n$
by using noncommutative quasi-Poisson geometry [Reference Van den Bergh41]. In that case, we define from
![]() $\overline {\Gamma }_n$
the noncommutative
$\overline {\Gamma }_n$
the noncommutative
![]() $(2n)$
-th Euler continuants
$(2n)$
-th Euler continuants
which shall play the role of noncommutative moment maps. This will be the aim of this article, whose main achievements will be presented in §1.3.
To gain insight into this noncommutative framework, it may be illuminating to illustrate the case
![]() $n=1$
. Given two complex vector spaces
$n=1$
. Given two complex vector spaces
![]() $V_1,V_2$
of finite dimensions
$V_1,V_2$
of finite dimensions
![]() $d_1,d_2$
, respectively, we can introduce the Van den Bergh space (see [Reference Bezrukavnikov and Kapranov4, Reference Boalch13, Reference Braverman, Etingof and Finkelberg17, Reference Yamakawa43])
$d_1,d_2$
, respectively, we can introduce the Van den Bergh space (see [Reference Bezrukavnikov and Kapranov4, Reference Boalch13, Reference Braverman, Etingof and Finkelberg17, Reference Yamakawa43])
Van den Bergh proved in [Reference Van den Bergh41, Reference Van den Bergh42] that this space is a complex quasi-Hamiltonian manifold in the sense of [Reference Alekseev, Malkin and Meinrenken1] for the natural action of
![]() $H=\operatorname {GL}(V_1)\times \operatorname {GL}(V_2)$
. Furthermore, its Lie group valued moment map is given by
$H=\operatorname {GL}(V_1)\times \operatorname {GL}(V_2)$
. Furthermore, its Lie group valued moment map is given by
Note that we easily recover
![]() $(\widehat {\mathcal {B}}^{2},\widehat {\mu })$
from
$(\widehat {\mathcal {B}}^{2},\widehat {\mu })$
from
![]() $(\mathcal {B}^{\operatorname {VdB}},\mu ^{\operatorname {VdB}})$
when
$(\mathcal {B}^{\operatorname {VdB}},\mu ^{\operatorname {VdB}})$
when
![]() $V_1=V_2=\mathbb {C}$
. In the setting of multiplicative quiver varieties, Van den Bergh crucially observed that the pair
$V_1=V_2=\mathbb {C}$
. In the setting of multiplicative quiver varieties, Van den Bergh crucially observed that the pair
![]() $\big (\mathcal {B}^{\operatorname {VdB}},\mu ^{\operatorname {VdB}}\big )$
and its corresponding
$\big (\mathcal {B}^{\operatorname {VdB}},\mu ^{\operatorname {VdB}}\big )$
and its corresponding
![]() $2$
-form can be understood at the level of the quiver
$2$
-form can be understood at the level of the quiver
![]() $\Gamma _1$
. Indeed, he introduced the notion of a quasi-bisymplectic algebra [Reference Van den Bergh42] as a noncommutative analogue of a quasi-Hamiltonian manifold, and he showed that an appropriate localisation, denoted
$\Gamma _1$
. Indeed, he introduced the notion of a quasi-bisymplectic algebra [Reference Van den Bergh42] as a noncommutative analogue of a quasi-Hamiltonian manifold, and he showed that an appropriate localisation, denoted
![]() $\mathcal {A}(\Gamma _1)$
, of the path algebra of the double quiver
$\mathcal {A}(\Gamma _1)$
, of the path algebra of the double quiver
![]() $\overline {\Gamma }_1$
is endowed with such a structure. In fact, Van den Bergh first introduced a ‘quasi-Poisson version’ of this result, when he derived in [Reference Van den Bergh41] that
$\overline {\Gamma }_1$
is endowed with such a structure. In fact, Van den Bergh first introduced a ‘quasi-Poisson version’ of this result, when he derived in [Reference Van den Bergh41] that
![]() $\mathcal {A}(\Gamma _1)$
is a Hamiltonian double quasi-Poisson algebra; this is the noncommutative version of a Hamiltonian quasi-Poisson manifold in the sense of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2]; see Definition 2.5. The key point is that this structure is such that the second Euler continuants
$\mathcal {A}(\Gamma _1)$
is a Hamiltonian double quasi-Poisson algebra; this is the noncommutative version of a Hamiltonian quasi-Poisson manifold in the sense of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2]; see Definition 2.5. The key point is that this structure is such that the second Euler continuants
![]() $(b,a)^{-1}$
and
$(b,a)^{-1}$
and
![]() $(a,b)$
become noncommutative moment maps. Our aim is to generalise this result of Van den Bergh: We want to prove that we can attach to each quiver
$(a,b)$
become noncommutative moment maps. Our aim is to generalise this result of Van den Bergh: We want to prove that we can attach to each quiver
![]() $\Gamma _n$
an explicit Hamiltonian double quasi-Poisson algebra structure, whose moment map is given in terms of the
$\Gamma _n$
an explicit Hamiltonian double quasi-Poisson algebra structure, whose moment map is given in terms of the
![]() $(2n)$
-th Euler continuants
$(2n)$
-th Euler continuants
![]() $(a_1,\dots ,b_n)$
and
$(a_1,\dots ,b_n)$
and
![]() $(b_n,\dots ,a_1)^{-1}$
.
$(b_n,\dots ,a_1)^{-1}$
.
1.3 Main results
We fix a field
![]() $\Bbbk $
of characteristic zero. Recall that
$\Bbbk $
of characteristic zero. Recall that
![]() $\overline {\Gamma }_n$
denotes the quiver on
$\overline {\Gamma }_n$
denotes the quiver on
![]() $2$
vertices and
$2$
vertices and
![]() $2n$
arrows labelled
$2n$
arrows labelled
![]() $\{a_i,b_i\mid 1\leq i\leq n\}$
as in Figure 1. We introduce the Boalch algebra
$\{a_i,b_i\mid 1\leq i\leq n\}$
as in Figure 1. We introduce the Boalch algebra
![]() $\mathcal {B}(\Gamma _n)$
which is obtained from the path algebra
$\mathcal {B}(\Gamma _n)$
which is obtained from the path algebra
![]() $\Bbbk \overline {\Gamma }_n$
by requiring that the
$\Bbbk \overline {\Gamma }_n$
by requiring that the
![]() $(2n)$
-th Euler continuants
$(2n)$
-th Euler continuants
![]() $(a_1,\dots ,b_n)$
and
$(a_1,\dots ,b_n)$
and
![]() $ (b_n,\dots ,a_1)$
are inverted (see § 3.1 for the definition of Euler continuants in
$ (b_n,\dots ,a_1)$
are inverted (see § 3.1 for the definition of Euler continuants in
![]() $\Bbbk \overline {\Gamma }_n$
). The main result of this article is Theorem 3.4: We prove that
$\Bbbk \overline {\Gamma }_n$
). The main result of this article is Theorem 3.4: We prove that
![]() $\mathcal {B}(\Gamma _n)$
is endowed with a double quasi-Poisson bracket
$\mathcal {B}(\Gamma _n)$
is endowed with a double quasi-Poisson bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
, explicitly defined in equation (3.10), which is such that
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
, explicitly defined in equation (3.10), which is such that
![]() $\Phi := (a_1,\dots ,b_n) + (b_n,\dots ,a_1)^{-1}$
is a multiplicative moment map. In other words, the triple
$\Phi := (a_1,\dots ,b_n) + (b_n,\dots ,a_1)^{-1}$
is a multiplicative moment map. In other words, the triple
![]() $\big (\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi \big )$
is a Hamiltonian double quasi-Poisson algebra. As a consequence of this result, we obtain in Corollary 3.5 that the corresponding fission algebra
$\big (\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi \big )$
is a Hamiltonian double quasi-Poisson algebra. As a consequence of this result, we obtain in Corollary 3.5 that the corresponding fission algebra
![]() $\mathcal {F}^q(\Gamma _n)$
defined by Boalch [Reference Boalch15] carries a noncommutative Poisson structure, called an
$\mathcal {F}^q(\Gamma _n)$
defined by Boalch [Reference Boalch15] carries a noncommutative Poisson structure, called an
![]() $H_0$
-Poisson structure, as introduced in [Reference Crawley-Boevey23]. Such an
$H_0$
-Poisson structure, as introduced in [Reference Crawley-Boevey23]. Such an
![]() $H_0$
-Poisson structure induces a Poisson bracket on the corresponding varieties
$H_0$
-Poisson structure induces a Poisson bracket on the corresponding varieties
when
![]() $\Bbbk $
is algebraically closed. If
$\Bbbk $
is algebraically closed. If
![]() $\Bbbk =\mathbb {C}$
,
$\Bbbk =\mathbb {C}$
,
![]() $(d_1,d_2)=(1,1)$
and
$(d_1,d_2)=(1,1)$
and
![]() $q=(\gamma ,\gamma ^{-1})$
, we recover the wild character variety
$q=(\gamma ,\gamma ^{-1})$
, we recover the wild character variety
![]() $\mathcal {M}_n(t_{\gamma })$
from § 1.2. In particular, the Poisson bracket hence obtained is nondegenerate and corresponds to Boalch’s symplectic form [Reference Boalch15]; see § 5.6. We will investigate this nondegeneracy property for a general field
$\mathcal {M}_n(t_{\gamma })$
from § 1.2. In particular, the Poisson bracket hence obtained is nondegenerate and corresponds to Boalch’s symplectic form [Reference Boalch15]; see § 5.6. We will investigate this nondegeneracy property for a general field
![]() $\Bbbk $
in a future work.
$\Bbbk $
in a future work.
It is important to observe that, if
![]() $n=1$
, the Boalch algebra
$n=1$
, the Boalch algebra
![]() $\mathcal {B}(\Gamma _1)$
coincides with Van den Bergh’s algebra
$\mathcal {B}(\Gamma _1)$
coincides with Van den Bergh’s algebra
![]() $\mathcal {A}(\Gamma _1)$
described above, and the Hamiltonian double quasi-Poisson structures are the same. Thus, Theorem 3.4 can be regarded as a generalisation of [Reference Van den Bergh41, Theorem 6.5.1]. We also note that, in the inductive proof of Theorem 3.4 carried out in Section 4, formulae (3.5) and (3.6) play a key role since they enable us to rewrite Euler continuants in terms of lower ones. To the best of our knowledge, these formulae are new and may be of independent interest. After that, using the correspondence between double (quasi-Poisson) brackets and noncommutative bivectors explained in [Reference Van den Bergh41, §4.2], we exhibit in Proposition 3.6 the bivector
$\mathcal {A}(\Gamma _1)$
described above, and the Hamiltonian double quasi-Poisson structures are the same. Thus, Theorem 3.4 can be regarded as a generalisation of [Reference Van den Bergh41, Theorem 6.5.1]. We also note that, in the inductive proof of Theorem 3.4 carried out in Section 4, formulae (3.5) and (3.6) play a key role since they enable us to rewrite Euler continuants in terms of lower ones. To the best of our knowledge, these formulae are new and may be of independent interest. After that, using the correspondence between double (quasi-Poisson) brackets and noncommutative bivectors explained in [Reference Van den Bergh41, §4.2], we exhibit in Proposition 3.6 the bivector
![]() ${\mathrm {P}}_n$
that gives rise to the double quasi-Poisson bracket from Theorem 3.4. As in [Reference Van den Bergh42, Proposition 8.3.1], we expect that this result will be important in the future to prove that the double quasi-Poisson bracket (3.10) is nondegenerate.
${\mathrm {P}}_n$
that gives rise to the double quasi-Poisson bracket from Theorem 3.4. As in [Reference Van den Bergh42, Proposition 8.3.1], we expect that this result will be important in the future to prove that the double quasi-Poisson bracket (3.10) is nondegenerate.
Furthermore, Boalch observed [Reference Boalch15, Remark 5] that, at certain values (
![]() $n=2$
),
$n=2$
),
![]() $\mathcal {M}_n^{\Bbbk }(q)$
is isomorphic to the Flaschka–Newell surface [Reference Flaschka and Newell32]. This is an affine cubic surface endowed with a Poisson structure; in the setting of integrable systems, it is closely related to solutions to Painlevé II equation (see also [Reference Chekhov, Mazzocco and Rubtsov22]). Recently, based on [Reference Flaschka and Newell33] (see also [Reference Boalch15, §5]), Bertola and Tarricone [Reference Bertola and Tarricone3] explicitly wrote the Poisson bracket on the wild character variety
$\mathcal {M}_n^{\Bbbk }(q)$
is isomorphic to the Flaschka–Newell surface [Reference Flaschka and Newell32]. This is an affine cubic surface endowed with a Poisson structure; in the setting of integrable systems, it is closely related to solutions to Painlevé II equation (see also [Reference Chekhov, Mazzocco and Rubtsov22]). Recently, based on [Reference Flaschka and Newell33] (see also [Reference Boalch15, §5]), Bertola and Tarricone [Reference Bertola and Tarricone3] explicitly wrote the Poisson bracket on the wild character variety
![]() $\mathcal {M}_n(t_{\gamma })$
(with no restriction on n); note that an explicit expression for the corresponding symplectic 2-form is well-known by experts. Whereas we originally obtained the Hamiltonian double quasi-Poisson structure of Theorem 3.4 employing entirely noncommutative arguments, in §3.4 we are able to show that it induces the Poisson bracket due to Flaschka and Newell on
$\mathcal {M}_n(t_{\gamma })$
(with no restriction on n); note that an explicit expression for the corresponding symplectic 2-form is well-known by experts. Whereas we originally obtained the Hamiltonian double quasi-Poisson structure of Theorem 3.4 employing entirely noncommutative arguments, in §3.4 we are able to show that it induces the Poisson bracket due to Flaschka and Newell on
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
(i.e., before performing quasi-Hamiltonian reduction to end up with
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
(i.e., before performing quasi-Hamiltonian reduction to end up with
![]() $\mathcal {M}_n(t_{\gamma })$
). In particular, this shows that our Theorem 3.4 should be regarded as the natural noncommutative counterpart of the well-known commutative theory.
$\mathcal {M}_n(t_{\gamma })$
). In particular, this shows that our Theorem 3.4 should be regarded as the natural noncommutative counterpart of the well-known commutative theory.
Finally, one of the driving ideas in quasi-Hamiltonian geometry consists of constructing interesting moduli spaces from simple pieces by using the operation of fusion [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2, §5]; algebraically, it endows the category of quasi-Hamiltonian manifolds with a symmetric monoidal category structure. As we explain in §2.2, Van den Bergh [Reference Van den Bergh41, §5.3] unveiled a noncommutative analogue of this method to obtain a double quasi-Poisson bracket and a multiplicative moment map from a Hamiltonian double quasi-Poisson algebra by identifying several idempotents. The last important result of this article is Theorem 5.1 which states that, after further localisation at
![]() $2n-2$
Euler continuants, the structure of Hamiltonian double quasi-Poisson algebra of
$2n-2$
Euler continuants, the structure of Hamiltonian double quasi-Poisson algebra of
![]() $\mathcal {B}(\Gamma _n)$
unveiled in Theorem 3.4 can be obtained by fusing the idempotents in n copies of
$\mathcal {B}(\Gamma _n)$
unveiled in Theorem 3.4 can be obtained by fusing the idempotents in n copies of
![]() $\mathcal {B}(\Gamma _1)$
. In the simplest case
$\mathcal {B}(\Gamma _1)$
. In the simplest case
![]() $n=2$
, this can be interpreted as a way to get the factorisation
$n=2$
, this can be interpreted as a way to get the factorisation
of the fourth Euler continuant in terms of a product of second ones through the substitution
The proof of Theorem 5.1 is based on an explicit description of the Hamiltonian double quasi-Poisson algebra structure obtained after the change of coordinates (5.16) that generalises equation (1.11) for any
![]() $n\geq 2$
. We also note that this result relies on the curious identity of Lemma 3.3, which commutes the adjacent arrows in a product of Euler continuants.
$n\geq 2$
. We also note that this result relies on the curious identity of Lemma 3.3, which commutes the adjacent arrows in a product of Euler continuants.
Layout of the article
In Section 2, we recall the basics of Van den Bergh’s noncommutative quasi-Poisson geometry [Reference Van den Bergh41]. We introduce the important notions of double quasi-Poisson brackets and Hamiltonian double quasi-Poisson algebras, as well as the method of fusion. In this context, we also present an example associated with the quiver
![]() $\Gamma _1$
by Van den Bergh [Reference Van den Bergh41, Reference Van den Bergh42], which is generalised in the rest of this work. In Section 3, we state as part of Theorem 3.4 that we can obtain a Hamiltonian double quasi-Poisson algebra
$\Gamma _1$
by Van den Bergh [Reference Van den Bergh41, Reference Van den Bergh42], which is generalised in the rest of this work. In Section 3, we state as part of Theorem 3.4 that we can obtain a Hamiltonian double quasi-Poisson algebra
![]() $\mathcal {B}(\Gamma _n)$
by localisation of the path algebra
$\mathcal {B}(\Gamma _n)$
by localisation of the path algebra
![]() $\Bbbk \overline {\Gamma }_n$
of the double of the quiver
$\Bbbk \overline {\Gamma }_n$
of the double of the quiver
![]() $\Gamma _n$
. This structure is such that its noncommutative moment map is given in terms of Euler continuants. We then write down the corresponding noncommutative bivector
$\Gamma _n$
. This structure is such that its noncommutative moment map is given in terms of Euler continuants. We then write down the corresponding noncommutative bivector
![]() ${\mathrm {P}}_n$
in Proposition 3.6, and we link our result to the Flaschka–Newell Poisson bracket [Reference Flaschka and Newell33] in § 3.4. The proof of Theorem 3.4 is the subject of Section 4. Finally, in Section 5 we exhibit a factorisation of (a localisation of) the algebra
${\mathrm {P}}_n$
in Proposition 3.6, and we link our result to the Flaschka–Newell Poisson bracket [Reference Flaschka and Newell33] in § 3.4. The proof of Theorem 3.4 is the subject of Section 4. Finally, in Section 5 we exhibit a factorisation of (a localisation of) the algebra
![]() $\mathcal {B}(\Gamma _n)$
in terms of n copies of
$\mathcal {B}(\Gamma _n)$
in terms of n copies of
![]() $\mathcal {B}(\Gamma _1)$
through the method of fusion.
$\mathcal {B}(\Gamma _1)$
through the method of fusion.
2 Noncommutative quasi-Poisson geometry
2.1 Hamiltonian double quasi-Poisson algebras
Hereafter, we follow [Reference Van den Bergh41, Reference Crawley-Boevey, Etingof and Ginzburg24, Reference Fairon29].
2.1.1 Double derivations
We fix a finitely generated associative unital algebra A over a field
![]() $\Bbbk $
of characteristic zero, and we use the unadorned notations
$\Bbbk $
of characteristic zero, and we use the unadorned notations
![]() $\otimes =\otimes _{\Bbbk }$
,
$\otimes =\otimes _{\Bbbk }$
,
![]() $\operatorname {Hom}=\operatorname {Hom}_{\Bbbk }$
for brevity. The opposite algebra and the enveloping algebra of A will be denoted
$\operatorname {Hom}=\operatorname {Hom}_{\Bbbk }$
for brevity. The opposite algebra and the enveloping algebra of A will be denoted
![]() $A^{\operatorname {op}}$
and
$A^{\operatorname {op}}$
and
![]() $A^{\operatorname {e}}:=A\otimes A^{\operatorname {op}}$
, respectively. We shall identify the category of A-bimodules and the category of (left)
$A^{\operatorname {e}}:=A\otimes A^{\operatorname {op}}$
, respectively. We shall identify the category of A-bimodules and the category of (left)
![]() $A^{\operatorname {e}}$
-modules. Note that the underlying A-bimodule of A carries two A-bimodule structures with the same underlying vector space
$A^{\operatorname {e}}$
-modules. Note that the underlying A-bimodule of A carries two A-bimodule structures with the same underlying vector space
![]() $A\otimes A$
, namely the outer and the inner A-bimodule structures, respectively denoted by
$A\otimes A$
, namely the outer and the inner A-bimodule structures, respectively denoted by
![]() $(A\otimes A)_{\operatorname {out}}$
and
$(A\otimes A)_{\operatorname {out}}$
and
![]() $(A\otimes A)_{\operatorname {inn}}$
; they are given by
$(A\otimes A)_{\operatorname {inn}}$
; they are given by
 $$ \begin{align*} a_1(a'\otimes a'')a_2&:=(a_1a')\otimes (a''a_2)\quad \text{on }(A\otimes A)_{\operatorname{out}}\,; \\ a_1*(a'\otimes a'')*a_2&:=(a'a_2)\otimes (a_1a'')\quad \text{on }(A\otimes A)_{\operatorname{inn}}\,, \end{align*} $$
$$ \begin{align*} a_1(a'\otimes a'')a_2&:=(a_1a')\otimes (a''a_2)\quad \text{on }(A\otimes A)_{\operatorname{out}}\,; \\ a_1*(a'\otimes a'')*a_2&:=(a'a_2)\otimes (a_1a'')\quad \text{on }(A\otimes A)_{\operatorname{inn}}\,, \end{align*} $$
for all
![]() $a',a'',a_1,a_2\in A$
.
$a',a'',a_1,a_2\in A$
.
Given another unital associative
![]() $\Bbbk $
-algebra B, A is called a B-algebra if there exists a unit preserving
$\Bbbk $
-algebra B, A is called a B-algebra if there exists a unit preserving
![]() $\Bbbk $
-algebra morphism
$\Bbbk $
-algebra morphism
![]() $B\to A$
. Let M be an arbitrary A-bimodule and
$B\to A$
. Let M be an arbitrary A-bimodule and
![]() $\operatorname {Der}_B(A,M)$
be the vector space of B-derivations of A into M, that is, additive maps
$\operatorname {Der}_B(A,M)$
be the vector space of B-derivations of A into M, that is, additive maps
![]() $\theta \colon A\to M$
satisfying the Leibniz rule and
$\theta \colon A\to M$
satisfying the Leibniz rule and
![]() $\theta (b)=0$
, for all
$\theta (b)=0$
, for all
![]() $b\in B$
. Following [Reference Cuntz and Quillen26], we define the A-bimodule of noncommutative differential 1-forms as
$b\in B$
. Following [Reference Cuntz and Quillen26], we define the A-bimodule of noncommutative differential 1-forms as
![]() $\Omega ^1_B A:=\operatorname {ker}(m\colon A\otimes _B A\to A)$
, where m is the product of A. As in the commutative case, it carries a canonical B-derivation
$\Omega ^1_B A:=\operatorname {ker}(m\colon A\otimes _B A\to A)$
, where m is the product of A. As in the commutative case, it carries a canonical B-derivation
![]() $\operatorname {d}\colon A\to \Omega ^1_B A$
,
$\operatorname {d}\colon A\to \Omega ^1_B A$
,
![]() $a\mapsto \operatorname {d}{a}:=a\otimes _B 1-1\otimes _B a$
, and the pair
$a\mapsto \operatorname {d}{a}:=a\otimes _B 1-1\otimes _B a$
, and the pair
![]() $(\Omega ^1_B A,\operatorname {d})$
has a universal property ([Reference Quillen39, §2]), which can be rephrased as
$(\Omega ^1_B A,\operatorname {d})$
has a universal property ([Reference Quillen39, §2]), which can be rephrased as
By taking
![]() $M=(A\otimes A)_{\operatorname {out}}$
in equation (2.1), we define the A-bimodule of double derivations
$M=(A\otimes A)_{\operatorname {out}}$
in equation (2.1), we define the A-bimodule of double derivations
If
![]() $\delta \in \operatorname {\mathbb {D}er}_B A$
, we systematically use Sweedler’s notation:
$\delta \in \operatorname {\mathbb {D}er}_B A$
, we systematically use Sweedler’s notation:
![]() $\delta \colon A\to A\otimes A$
,
$\delta \colon A\to A\otimes A$
,
![]() $a\mapsto \delta (a)^{\prime }\otimes \delta (a)''$
. Note that the A-bimodule structure on
$a\mapsto \delta (a)^{\prime }\otimes \delta (a)''$
. Note that the A-bimodule structure on
![]() $\operatorname {\mathbb {D}er}_B A$
is induced from the inner bimodule structure:
$\operatorname {\mathbb {D}er}_B A$
is induced from the inner bimodule structure:
![]() $(a_1\delta a_2)(a):=\delta (a)'a_2\otimes a_1\delta (a)^{\prime \prime }$
, for all
$(a_1\delta a_2)(a):=\delta (a)'a_2\otimes a_1\delta (a)^{\prime \prime }$
, for all
![]() $a,a_1,a_2\in A$
.
$a,a_1,a_2\in A$
.
The A-bimodule
![]() $\operatorname {\mathbb {D}er}_BA$
carries a distinguished element, called the gauge element E, defined by
$\operatorname {\mathbb {D}er}_BA$
carries a distinguished element, called the gauge element E, defined by
Note that this element was also introduced in [Reference Crawley-Boevey, Etingof and Ginzburg24, §3] and denoted by
![]() $\Delta $
.
$\Delta $
.
Following [Reference Van den Bergh41, §3.1], we define the algebra of poly-vector fields as
![]() $D_BA=T_A(\operatorname {\mathbb {D}er}_B A)$
, which is the tensor algebra of the A-bimodule
$D_BA=T_A(\operatorname {\mathbb {D}er}_B A)$
, which is the tensor algebra of the A-bimodule
![]() $\operatorname {\mathbb {D}er}_B A$
(over A). The n-th component is the n-fold
$\operatorname {\mathbb {D}er}_B A$
(over A). The n-th component is the n-fold
![]() $(D_BA)_n=(\operatorname {\mathbb {D}er}_B A)^{\otimes _ An}$
for
$(D_BA)_n=(\operatorname {\mathbb {D}er}_B A)^{\otimes _ An}$
for
![]() $n\geq 1$
.
$n\geq 1$
.
2.1.2 Double derivations for quivers
A quiver Q is an oriented graph. We denote its set of vertices by I and its set of arrows (oriented edges) by Q. We can define on Q the tail (resp. head) map
![]() $t\colon Q\to I$
(resp.
$t\colon Q\to I$
(resp.
![]() $h\colon Q\to I$
) assigning to any arrow
$h\colon Q\to I$
) assigning to any arrow
![]() $a\in Q$
its tail/starting vertex
$a\in Q$
its tail/starting vertex
![]() $t(a)\in Q$
(resp. its head/ending vertex
$t(a)\in Q$
(resp. its head/ending vertex
![]() $h(a)\in Q$
). We can then form the double
$h(a)\in Q$
). We can then form the double
![]() $\overline {Q}$
of Q with the same vertex set I by adding an opposite arrow
$\overline {Q}$
of Q with the same vertex set I by adding an opposite arrow
![]() $a^{\ast } : h(a)\to t(a)$
for each
$a^{\ast } : h(a)\to t(a)$
for each
![]() $a\in Q$
. We naturally extend
$a\in Q$
. We naturally extend
![]() $h,t$
to
$h,t$
to
![]() $\overline {Q}$
.
$\overline {Q}$
.
Now, given a quiver Q (not necessarily a double quiver), we form the path algebra
![]() $\Bbbk Q$
which is the
$\Bbbk Q$
which is the
![]() $\Bbbk $
-algebra generated by the arrows
$\Bbbk $
-algebra generated by the arrows
![]() $a\in Q$
and idempotents
$a\in Q$
and idempotents
![]() $(e_s)_{s\in I}$
labelled by the vertices such that
$(e_s)_{s\in I}$
labelled by the vertices such that
and the product is given by concatenation of paths (if possible; otherwise, the idempotent decomposition makes the product vanish). In this article, we will regard
![]() $\Bbbk Q$
as a B-algebra with
$\Bbbk Q$
as a B-algebra with
![]() $B=\oplus _{s\in I}\Bbbk e_s$
. Then, if
$B=\oplus _{s\in I}\Bbbk e_s$
. Then, if
![]() $A=\Bbbk Q$
, the A-bimodule of double derivations
$A=\Bbbk Q$
, the A-bimodule of double derivations
![]() $\operatorname {\mathbb {D}er}_B A$
is generated as an A-bimodule by
$\operatorname {\mathbb {D}er}_B A$
is generated as an A-bimodule by
![]() $\big \{\frac {\partial }{\partial a}\mid a\in Q\big \}$
, where if
$\big \{\frac {\partial }{\partial a}\mid a\in Q\big \}$
, where if
![]() $b\in Q$
,
$b\in Q$
,
Remark 2.1. Note that equation (2.3) implies that we read paths from right to left. This is the convention followed by Boalch in [Reference Boalch14, Reference Boalch15] and Crawley-Boevey and Shaw [Reference Crawley-Boevey and Shaw25], but it contrasts with [Reference Van den Bergh41], where Van den Bergh uses the opposite convention (i.e.,
![]() $a=e_{t(a)}a e_{h(a)}$
).
$a=e_{t(a)}a e_{h(a)}$
).
2.1.3 Double quasi-Poisson brackets
Let A be a finitely generated associative unital B-algebra. A B-linear n-bracket [Reference Van den Bergh41] is a map
![]() $\{\mkern -6mu\{-,\cdots ,-\}\mkern -6mu\}\colon A^{\times n}\to A^{\otimes n}$
which
$\{\mkern -6mu\{-,\cdots ,-\}\mkern -6mu\}\colon A^{\times n}\to A^{\otimes n}$
which
-
(a) is linear in all its arguments;
-
(b) is cyclically antisymmetric, that is,
for the cyclic permutation $$ \begin{align*} \tau_{(1\cdots n)}\circ\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}\circ \tau^{-1}_{(1\cdots n)}=(-1)^{n+1}\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\} \end{align*} $$
$$ \begin{align*} \tau_{(1\cdots n)}\circ\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}\circ \tau^{-1}_{(1\cdots n)}=(-1)^{n+1}\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\} \end{align*} $$
 $\tau _{(1\cdots n)}(a_1\otimes \cdots \otimes a_{n-1}\otimes a_n)=a_n\otimes a_1\otimes \cdots \otimes a_{n-1}$
;
$\tau _{(1\cdots n)}(a_1\otimes \cdots \otimes a_{n-1}\otimes a_n)=a_n\otimes a_1\otimes \cdots \otimes a_{n-1}$
;
-
(c) vanishes when its last argument (hence any argument) is in the image of B;
-
(d) is a derivation
 $A\to A^{\otimes n}$
in its last argument for the outer bimodule structure on
$A\to A^{\otimes n}$
in its last argument for the outer bimodule structure on
 $A^{\otimes n}$
given by
$A^{\otimes n}$
given by
 $b(a_1\otimes a_2 \otimes \cdots \otimes a_{n-1}\otimes a_n)c= (ba_1)\otimes a_2 \otimes \cdots \otimes a_{n-1}\otimes (a_nc)$
.
$b(a_1\otimes a_2 \otimes \cdots \otimes a_{n-1}\otimes a_n)c= (ba_1)\otimes a_2 \otimes \cdots \otimes a_{n-1}\otimes (a_nc)$
.
We call a 2- and 3-bracket a double and triple bracket, respectively. For the reader’s convenience, we explicitly write the definition of the former.
Definition 2.2 [Reference Van den Bergh41]
A B-linear double bracket on the B-algebra A is a
![]() $\Bbbk $
-bilinear map
$\Bbbk $
-bilinear map
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}:A\times A \to A \otimes A$
, which satisfies for any
$\{\mkern -6mu\{-,-\}\mkern -6mu\}:A\times A \to A \otimes A$
, which satisfies for any
![]() $a,b,c \in A$
,
$a,b,c \in A$
,
and which is such that
![]() $\{\mkern -6mu\{-,e\}\mkern -6mu\}=0$
for all
$\{\mkern -6mu\{-,e\}\mkern -6mu\}=0$
for all
![]() $e\in B$
.
$e\in B$
.
Assuming that equation (2.4) holds, it is easy to check that equation (2.5) is equivalent to
From the derivation rules (2.5) and (2.6), observe that it suffices to define double brackets on generators of A. From now on, if the context is clear, by a double bracket we will mean a B-linear double bracket. The following result will be used in §3.3.
Proposition 2.3 ([Reference Van den Bergh41], Proposition 4.1.1)
There exists a well-defined linear map
 $$ \begin{align*} \mu\colon (D_B A)_n\longrightarrow&\, \{B\text{-linear }n\text{-brackets on }A\} \\ Q\,\,\longmapsto&\, \{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}_Q=\sum^{n-1}_{i=0}(-1)^{(n-1)i}\,\tau^{i}_{(1\cdots n)}\circ\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}^{\sim}_Q\circ\tau^{-i}_{(1\cdots n)}\, , \end{align*} $$
$$ \begin{align*} \mu\colon (D_B A)_n\longrightarrow&\, \{B\text{-linear }n\text{-brackets on }A\} \\ Q\,\,\longmapsto&\, \{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}_Q=\sum^{n-1}_{i=0}(-1)^{(n-1)i}\,\tau^{i}_{(1\cdots n)}\circ\{\mkern-6mu\{-,\cdots,-\}\mkern-6mu\}^{\sim}_Q\circ\tau^{-i}_{(1\cdots n)}\, , \end{align*} $$
where we set for
![]() $Q=\delta _1\cdots \delta _n$
and
$Q=\delta _1\cdots \delta _n$
and
![]() $a_1,\dots ,a_n\in A$
,
$a_1,\dots ,a_n\in A$
,
Note that, if
![]() $\Omega ^1_B A$
is a projective
$\Omega ^1_B A$
is a projective
![]() $A^{\operatorname {e}}$
-module—for instance, if A is the path algebra of a quiver—
$A^{\operatorname {e}}$
-module—for instance, if A is the path algebra of a quiver—
![]() $\mu $
is an isomorphism (see [Reference Van den Bergh41, Proposition 4.1.2]). Also, since it will be used in § 3.3, we specialise the previous formula to noncommutative bivectors
$\mu $
is an isomorphism (see [Reference Van den Bergh41, Proposition 4.1.2]). Also, since it will be used in § 3.3, we specialise the previous formula to noncommutative bivectors
![]() $Q=\delta _1\delta _2\in (D_B A)_2=(\operatorname {\mathbb {D}er}_B A) \otimes _A (\operatorname {\mathbb {D}er}_B A)$
:
$Q=\delta _1\delta _2\in (D_B A)_2=(\operatorname {\mathbb {D}er}_B A) \otimes _A (\operatorname {\mathbb {D}er}_B A)$
:
for any
![]() $a_1,a_2\in A$
.
$a_1,a_2\in A$
.
To develop a noncommutative version of quasi-Poisson geometry, as introduced in [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2], we need a nonvanishing noncommutative Jacobi identity. Firstly, given a double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
on A and
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
on A and
![]() $a,b,c\in A$
, Van den Bergh [Reference Van den Bergh41] introduced a suitable extension of the double bracket, given by
$a,b,c\in A$
, Van den Bergh [Reference Van den Bergh41] introduced a suitable extension of the double bracket, given by
![]() $\{\mkern -6mu\{a,b\otimes c\}\mkern -6mu\}_L:=\{\mkern -6mu\{a,b\}\mkern -6mu\}\otimes c\in A^{\otimes 3}$
. Next, he defined a natural triple bracket associated with
$\{\mkern -6mu\{a,b\otimes c\}\mkern -6mu\}_L:=\{\mkern -6mu\{a,b\}\mkern -6mu\}\otimes c\in A^{\otimes 3}$
. Next, he defined a natural triple bracket associated with
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
by setting
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
by setting
Note that
![]() $\tau _{(123)}(a_1\otimes a_2\otimes a_3)=a_{3}\otimes a_1 \otimes a_{2}$
and
$\tau _{(123)}(a_1\otimes a_2\otimes a_3)=a_{3}\otimes a_1 \otimes a_{2}$
and
![]() $\tau _{(132)}(a_1\otimes a_2\otimes a_3)=a_2\otimes a_3\otimes a_1$
, for all
$\tau _{(132)}(a_1\otimes a_2\otimes a_3)=a_2\otimes a_3\otimes a_1$
, for all
![]() $a_1,a_2,a_3\in A$
. Secondly, we assume that the unit in A admits a decomposition
$a_1,a_2,a_3\in A$
. Secondly, we assume that the unit in A admits a decomposition
![]() $1=\sum _{s\in I} e_s$
in terms of a finite set of orthogonal idempotents, that is,
$1=\sum _{s\in I} e_s$
in terms of a finite set of orthogonal idempotents, that is,
![]() $|I|\in \mathbb {N}^{\times }$
and
$|I|\in \mathbb {N}^{\times }$
and
![]() $e_s e_t = \delta _{st} e_s$
. In that case, we view A as a B-algebra for
$e_s e_t = \delta _{st} e_s$
. In that case, we view A as a B-algebra for
![]() $B=\oplus _{s\in I} \Bbbk e_s$
. Now, using the distinguished double derivation E defined in equation (2.2), we have
$B=\oplus _{s\in I} \Bbbk e_s$
. Now, using the distinguished double derivation E defined in equation (2.2), we have
![]() $E_s=e_s E e_s\in D_B A$
and we can apply Proposition 2.3 to
$E_s=e_s E e_s\in D_B A$
and we can apply Proposition 2.3 to
![]() $\sum _{s\in I}E_s^3\in (D_B A)_3$
and define the following triple bracket:
$\sum _{s\in I}E_s^3\in (D_B A)_3$
and define the following triple bracket:
 $$ \begin{align} \begin{aligned} &\quad \{\mkern-6mu\{a,b,c\}\mkern-6mu\}_{\mathrm{qP}}:=\frac{1}{12}\sum_{s\in I} \{\mkern-6mu\{a,b,c\}\mkern-6mu\}_{E^3_s} \\ &=\frac14 \sum_{s\in I} \Big( c e_s a \otimes e_s b \otimes e_s - c e_s a \otimes e_s \otimes b e_s - c e_s \otimes a e_s b \otimes e_s + c e_s \otimes a e_s \otimes b e_s \\ &\qquad \quad - e_s a \otimes e_s b \otimes e_s c + e_s a \otimes e_s \otimes b e_s c + e_s \otimes a e_s b \otimes e_s c - e_s \otimes a e_s \otimes b e_s c \Big)\,, \end{aligned}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} &\quad \{\mkern-6mu\{a,b,c\}\mkern-6mu\}_{\mathrm{qP}}:=\frac{1}{12}\sum_{s\in I} \{\mkern-6mu\{a,b,c\}\mkern-6mu\}_{E^3_s} \\ &=\frac14 \sum_{s\in I} \Big( c e_s a \otimes e_s b \otimes e_s - c e_s a \otimes e_s \otimes b e_s - c e_s \otimes a e_s b \otimes e_s + c e_s \otimes a e_s \otimes b e_s \\ &\qquad \quad - e_s a \otimes e_s b \otimes e_s c + e_s a \otimes e_s \otimes b e_s c + e_s \otimes a e_s b \otimes e_s c - e_s \otimes a e_s \otimes b e_s c \Big)\,, \end{aligned}\\[-15pt]\nonumber \end{align} $$
for any
![]() $a,b,c\in A$
.
$a,b,c\in A$
.
Definition 2.4 [Reference Van den Bergh41]
Let A be an associative B-algebra endowed with a double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. We say that the double bracket is quasi-Poisson if the triple brackets (2.8) and (2.9) coincide:
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. We say that the double bracket is quasi-Poisson if the triple brackets (2.8) and (2.9) coincide:
for all
![]() $a,b,c\in A$
. The pair
$a,b,c\in A$
. The pair
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
is called a double quasi-Poisson algebra.
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
is called a double quasi-Poisson algebra.
Note that
![]() $\{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
and
$\{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
and
![]() $\{\mkern -6mu\{-,-,-\}\mkern -6mu\}_{\mathrm {qP}}$
are triple brackets according to the terminology given at the beginning of this subsection. Thus, since triple brackets are cyclic and enjoy a derivation property, it suffices to check equation (2.10) on generators of A.
$\{\mkern -6mu\{-,-,-\}\mkern -6mu\}_{\mathrm {qP}}$
are triple brackets according to the terminology given at the beginning of this subsection. Thus, since triple brackets are cyclic and enjoy a derivation property, it suffices to check equation (2.10) on generators of A.
2.1.4 Multiplicative moment maps
In addition to the introduction of a noncommutative version of quasi-Poisson brackets, Van den Bergh adapted the notion of Lie group valued moment maps from [Reference Alekseev, Malkin and Meinrenken1, Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2] as follows.
Definition 2.5 [Reference Van den Bergh41]
Let
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
be a double quasi-Poisson algebra over
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
be a double quasi-Poisson algebra over
![]() $B=\oplus _{s\in I} \Bbbk e_s$
. An invertible element
$B=\oplus _{s\in I} \Bbbk e_s$
. An invertible element
![]() $\Phi \in A$
is a multiplicative moment map if it can be decomposed as
$\Phi \in A$
is a multiplicative moment map if it can be decomposed as
![]() $\Phi =\sum _{s\in I}\Phi _s$
with
$\Phi =\sum _{s\in I}\Phi _s$
with
![]() $\Phi _s\in e_sAe_s$
, and it satisfies that for all
$\Phi _s\in e_sAe_s$
, and it satisfies that for all
![]() $a\in A$
and
$a\in A$
and
![]() $s\in I$
$s\in I$
Then we call the triple
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
a Hamiltonian double quasi-Poisson algebra.Footnote
3
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
a Hamiltonian double quasi-Poisson algebra.Footnote
3
The invertibility of
![]() $\Phi $
implies that
$\Phi $
implies that
![]() $\Phi _s^{-1}:=e_s\Phi ^{-1}e_s$
is an inverse for
$\Phi _s^{-1}:=e_s\Phi ^{-1}e_s$
is an inverse for
![]() $\Phi _s$
in
$\Phi _s$
in
![]() $e_s A e_s$
. Then the identity (2.11) yields for all
$e_s A e_s$
. Then the identity (2.11) yields for all
![]() $a\in A$
that
$a\in A$
that
Finally, we can define morphisms between such algebras, which we use in Section 5.
Definition 2.6 [Reference Fairon30]
Let
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
and
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
and
![]() $(A',\{\mkern -6mu\{-,-\}\mkern -6mu\}',\Phi ')$
be two Hamiltonian double quasi-Poisson algebras over B. An isomorphism
$(A',\{\mkern -6mu\{-,-\}\mkern -6mu\}',\Phi ')$
be two Hamiltonian double quasi-Poisson algebras over B. An isomorphism
![]() $\psi :A\to A'$
of B-algebras is said to be an isomorphism of Hamiltonian double quasi-Poisson algebras if it preserves the double quasi-Poisson brackets and the multiplicative moment maps, that is,
$\psi :A\to A'$
of B-algebras is said to be an isomorphism of Hamiltonian double quasi-Poisson algebras if it preserves the double quasi-Poisson brackets and the multiplicative moment maps, that is,
for all
![]() $a_1,a_2\in A$
.
$a_1,a_2\in A$
.
2.2 Fusion of Hamiltonian double quasi-Poisson algebras
Given an algebra A, the method of fusion allows to construct a new algebra
![]() $A^f$
by identifying two orthogonal idempotents in A. More importantly, if A is a Hamiltonian double quasi-Poisson algebra, it is possible to obtain such a structure on
$A^f$
by identifying two orthogonal idempotents in A. More importantly, if A is a Hamiltonian double quasi-Poisson algebra, it is possible to obtain such a structure on
![]() $A^f$
after performing fusion. Below, we recall the main results associated with this method, which are due to Van den Bergh [Reference Van den Bergh41, §2.5, 5.3] (see also [Reference Brüstle18, §2.1] without the perspective of double brackets); alternative presentations can be found in [Reference Fairon29, 30]. These results are noncommutative analogues of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2, §5].
$A^f$
after performing fusion. Below, we recall the main results associated with this method, which are due to Van den Bergh [Reference Van den Bergh41, §2.5, 5.3] (see also [Reference Brüstle18, §2.1] without the perspective of double brackets); alternative presentations can be found in [Reference Fairon29, 30]. These results are noncommutative analogues of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2, §5].
As in §2.1, we assumeFootnote
4
that there exist orthogonal idempotents
![]() $e_i,e_j\in B$
. First, we extend the algebra A along the (ordered) idempotents
$e_i,e_j\in B$
. First, we extend the algebra A along the (ordered) idempotents
![]() $(e_i,e_j)$
as
$(e_i,e_j)$
as
Here, we have set
![]() $\hat {e}=1-e_i-e_j$
, and
$\hat {e}=1-e_i-e_j$
, and
![]() $\operatorname {Mat}_2(\Bbbk )$
is the
$\operatorname {Mat}_2(\Bbbk )$
is the
![]() $\Bbbk $
-algebra generated by the elements
$\Bbbk $
-algebra generated by the elements
![]() $e_i=e_{ii},e_{ij},e_{ji},e_j=e_{jj}$
subject to the matrix relations
$e_i=e_{ii},e_{ij},e_{ji},e_j=e_{jj}$
subject to the matrix relations
![]() $e_{st}e_{uv}=\delta _{tu}e_{sv}$
. Second, we can introduce the fusion algebra
$e_{st}e_{uv}=\delta _{tu}e_{sv}$
. Second, we can introduce the fusion algebra
![]() $A^f_{e_j \to e_i}$
obtained by fusing
$A^f_{e_j \to e_i}$
obtained by fusing
![]() $e_j$
onto
$e_j$
onto
![]() $e_i$
, which we abbreviate as
$e_i$
, which we abbreviate as
![]() $A^f$
. It is simply defined as
$A^f$
. It is simply defined as
The fusion algebra
![]() $A^f$
can be seen as dismissing the elements of
$A^f$
can be seen as dismissing the elements of
![]() $e_j \bar {A} + \bar {A} e_j$
inside
$e_j \bar {A} + \bar {A} e_j$
inside
![]() $\bar {A}$
. Note that
$\bar {A}$
. Note that
![]() $A^f$
is a
$A^f$
is a
![]() $B^f$
-algebra, where
$B^f$
-algebra, where
![]() $B^f:=\epsilon \bar {B} \epsilon $
. Furthermore, there exists a projection onto the fusion algebra
$B^f:=\epsilon \bar {B} \epsilon $
. Furthermore, there exists a projection onto the fusion algebra
from which we can get a set of generators in
![]() $A^f$
, which we split into four types. Namely,
$A^f$
, which we split into four types. Namely,
We assume that
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
is a Hamiltonian double quasi-Poisson algebra over
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
is a Hamiltonian double quasi-Poisson algebra over
![]() $B=\oplus _{s\in I} \Bbbk e_s$
from now on. Then, the double bracket uniquely extends from A to
$B=\oplus _{s\in I} \Bbbk e_s$
from now on. Then, the double bracket uniquely extends from A to
![]() $\bar A$
by requiring it to be
$\bar A$
by requiring it to be
![]() $\bar {B}$
-linear, and it can then be restricted to
$\bar {B}$
-linear, and it can then be restricted to
![]() $A^f$
. We also denote the double bracket hence induced on
$A^f$
. We also denote the double bracket hence induced on
![]() $A^f$
by
$A^f$
by
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. The image in
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. The image in
![]() $A^f$
of the component
$A^f$
of the component
![]() $\Phi _s$
of the multiplicative moment map is either
$\Phi _s$
of the multiplicative moment map is either
![]() $\Phi _s^f=\epsilon \Phi _s\epsilon =\Phi _s$
if
$\Phi _s^f=\epsilon \Phi _s\epsilon =\Phi _s$
if
![]() $s\neq j$
, or
$s\neq j$
, or
![]() $\Phi _s^f=e_{ij}\Phi _j e_{ji}$
if
$\Phi _s^f=e_{ij}\Phi _j e_{ji}$
if
![]() $s=j$
. However, the data
$s=j$
. However, the data
![]() $(\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi ^f)$
do not turn
$(\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi ^f)$
do not turn
![]() $A^f$
into a Hamiltonian double quasi-Poisson algebra.
$A^f$
into a Hamiltonian double quasi-Poisson algebra.
Lemma 2.7. There exists a unique double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
on
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
on
![]() $A^f$
such that for any
$A^f$
such that for any
we have that
Proof. Defining a double bracket on
![]() $A^f$
is equivalent to specifying the double bracket on a set of generators. But we know that the image in
$A^f$
is equivalent to specifying the double bracket on a set of generators. But we know that the image in
![]() $A^f$
of all the elements of the form (2.21) provides a set of generators, thus specifying equations (2.22a)–(2.22j) and using the cyclic antisymmetry (2.4) is enough to determine uniquely the double bracket
$A^f$
of all the elements of the form (2.21) provides a set of generators, thus specifying equations (2.22a)–(2.22j) and using the cyclic antisymmetry (2.4) is enough to determine uniquely the double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
. Since any relation in A can be decomposed in components of
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
. Since any relation in A can be decomposed in components of
![]() $\epsilon A \epsilon $
,
$\epsilon A \epsilon $
,
![]() $e_j A \epsilon $
,
$e_j A \epsilon $
,
![]() $\epsilon A e_j$
and
$\epsilon A e_j$
and
![]() $e_j A e_j$
which, in turn, induce relations in
$e_j A e_j$
which, in turn, induce relations in
![]() $A^f$
, this yields a well-defined double bracket
$A^f$
, this yields a well-defined double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
.
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
.
The double bracket from Lemma 2.7 is due to Van den Bergh [Reference Van den Bergh41, Theorem 5.3.1]; it was introduced to get a Hamiltonian double quasi-Poisson structure on
![]() $A^f$
.
$A^f$
.
Theorem 2.8 [Reference Van den Bergh41, 29]
Let
![]() $A^f=A^f_{e_j \to e_i}$
be the fusion algebra. Then
$A^f=A^f_{e_j \to e_i}$
be the fusion algebra. Then
![]() $A^f$
is a Hamiltonian double quasi-Poisson algebra, whose double quasi-Poisson bracket is given by
$A^f$
is a Hamiltonian double quasi-Poisson algebra, whose double quasi-Poisson bracket is given by
where
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
is induced in
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
is induced in
![]() $A^f$
by the double quasi-Poisson bracket of A, while
$A^f$
by the double quasi-Poisson bracket of A, while
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
is defined in Lemma 2.7. Its multiplicative moment map is given by
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {fus}}$
is defined in Lemma 2.7. Its multiplicative moment map is given by
This result was derived in [Reference Van den Bergh41, Theorems 5.3.1 and 5.3.2] under mild assumptions, which were removed in [Reference Fairon29, Theorems 2.14 and 2.15].
Let us note that fusing the two idempotents
![]() $e_i,e_j$
in the opposite order yields an isomorphic algebra. Indeed, each
$e_i,e_j$
in the opposite order yields an isomorphic algebra. Indeed, each
![]() $a\in A$
has a unique image in both
$a\in A$
has a unique image in both
![]() $A^f_{e_j \to e_i}$
and
$A^f_{e_j \to e_i}$
and
![]() $A^f_{e_i \to e_j}$
through the projection map (2.16). By mapping one projection onto the other, we get an algebra isomorphism
$A^f_{e_i \to e_j}$
through the projection map (2.16). By mapping one projection onto the other, we get an algebra isomorphism
![]() $A^f_{e_j \to e_i}\longrightarrow A^f_{e_i \to e_j}$
which is induced by the identity map on A. However, this is not an isomorphism of Hamiltonian double quasi-Poisson algebras as in Definition 2.6. To preserve the double quasi-Poisson structure, one needs a different isomorphism
$A^f_{e_j \to e_i}\longrightarrow A^f_{e_i \to e_j}$
which is induced by the identity map on A. However, this is not an isomorphism of Hamiltonian double quasi-Poisson algebras as in Definition 2.6. To preserve the double quasi-Poisson structure, one needs a different isomorphism
![]() $A^f_{e_j \to e_i}\longrightarrow A^f_{e_i \to e_j}$
that involves (images of)
$A^f_{e_j \to e_i}\longrightarrow A^f_{e_i \to e_j}$
that involves (images of)
![]() $\Phi _j\in A$
; see [Reference Fairon30, §4.1.1].
$\Phi _j\in A$
; see [Reference Fairon30, §4.1.1].
2.3
 $H_0$
-Poisson algebras
$H_0$
-Poisson algebras
The zeroth Hochschild homology of A, denoted
![]() $H_0(A)$
, is the vector space obtained by identifying all the commutators to zero. This means that
$H_0(A)$
, is the vector space obtained by identifying all the commutators to zero. This means that
![]() $H_0(A)=A/[A,A]$
, where
$H_0(A)=A/[A,A]$
, where
![]() $[A,A]\subset A$
is spanned by commutators. We write
$[A,A]\subset A$
is spanned by commutators. We write
![]() $\overline {a}$
for the image of
$\overline {a}$
for the image of
![]() $a\in A$
under the natural projection map
$a\in A$
under the natural projection map
![]() $A\to A/[A,A]$
.
$A\to A/[A,A]$
.
Definition 2.9 [Reference Crawley-Boevey23]
Let
![]() $\{-,-\}$
be a Lie bracket on
$\{-,-\}$
be a Lie bracket on
![]() $H_0 (A)$
. We say that A is endowed with an
$H_0 (A)$
. We say that A is endowed with an
![]() $H_0$
-Poisson structure if, for all
$H_0$
-Poisson structure if, for all
![]() $\overline {a}\in H_0(A)$
, the map
$\overline {a}\in H_0(A)$
, the map
![]() $\{\overline {a},-\}\colon H_0(A)\to H_0(A)$
, which is obtained from the Lie bracket, is induced by a derivation
$\{\overline {a},-\}\colon H_0(A)\to H_0(A)$
, which is obtained from the Lie bracket, is induced by a derivation
![]() $A\to A$
.
$A\to A$
.
Interestingly, double quasi-Poisson brackets induce
![]() $H_0$
-Poisson structures as follows. By [Reference Van den Bergh41, §2.4 and §5.1], the associated bracket
$H_0$
-Poisson structures as follows. By [Reference Van den Bergh41, §2.4 and §5.1], the associated bracket
![]() $\{-,-\}:=m\circ \{\mkern -6mu\{-,-\}\mkern -6mu\}:A\to A$
obtained by multiplication descends to a Lie bracket on
$\{-,-\}:=m\circ \{\mkern -6mu\{-,-\}\mkern -6mu\}:A\to A$
obtained by multiplication descends to a Lie bracket on
![]() $H_0(A)$
. Moreover, since the associated bracket on A is a derivation in its second argument, we get an
$H_0(A)$
. Moreover, since the associated bracket on A is a derivation in its second argument, we get an
![]() $H_0$
-Poisson structure on A. Furthermore,
$H_0$
-Poisson structure on A. Furthermore,
![]() $H_0$
-Poisson structures naturally arise after performing quotients of Hamiltonian double quasi-Poisson algebras using the corresponding multiplicative moment map as in Definition 2.5.
$H_0$
-Poisson structures naturally arise after performing quotients of Hamiltonian double quasi-Poisson algebras using the corresponding multiplicative moment map as in Definition 2.5.
Proposition 2.10 [Reference Van den Bergh41]
Let
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
be a Hamiltonian double quasi-Poisson algebra. Fix
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
be a Hamiltonian double quasi-Poisson algebra. Fix
![]() $q\in B^{\times }$
, and set
$q\in B^{\times }$
, and set
![]() $\overline {A}^q=A/(\Phi -q)$
. Then the associated bracket
$\overline {A}^q=A/(\Phi -q)$
. Then the associated bracket
![]() $\{-,-\}$
descends to an
$\{-,-\}$
descends to an
![]() $H_0$
-Poisson structure on
$H_0$
-Poisson structure on
![]() $\overline {A}^q$
.
$\overline {A}^q$
.
Remark 2.11. Proposition 2.10 is an analogue in the noncommutative setting of quasi-Hamiltonian reduction [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2]. To see this, note that a Hamiltonian double quasi-Poisson algebra
![]() $(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
induces a structure of Hamiltonian quasi-Poisson variety on its representation spaces—see [Reference Van den Bergh41, §7.12 and §7.13]. This structure further induces a Poisson structure on the GIT quotient obtained from the representation space of
$(A,\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi )$
induces a structure of Hamiltonian quasi-Poisson variety on its representation spaces—see [Reference Van den Bergh41, §7.12 and §7.13]. This structure further induces a Poisson structure on the GIT quotient obtained from the representation space of
![]() $\overline {A}^q=A/(\Phi -q)$
. This (commutative) Poisson structure is determined by the (noncommutative)
$\overline {A}^q=A/(\Phi -q)$
. This (commutative) Poisson structure is determined by the (noncommutative)
![]() $H_0$
-Poisson structure on
$H_0$
-Poisson structure on
![]() $\overline {A}^q$
obtained in Proposition 2.10; see [Reference Crawley-Boevey23, Theorem 4.5].
$\overline {A}^q$
obtained in Proposition 2.10; see [Reference Crawley-Boevey23, Theorem 4.5].
2.4 Example from a one-arrow quiver
Let
![]() $\Gamma _1:=A_2$
be the quiver with one arrow
$\Gamma _1:=A_2$
be the quiver with one arrow
![]() $a:1\to 2$
and
$a:1\to 2$
and
![]() $\overline {\Gamma }_1$
be its double with the additional arrow
$\overline {\Gamma }_1$
be its double with the additional arrow
![]() $b=a^{\ast }:2\to 1$
. We form the path algebra
$b=a^{\ast }:2\to 1$
. We form the path algebra
![]() $\Bbbk \overline {\Gamma }_1$
as explained in § 2.1.2. Now, let
$\Bbbk \overline {\Gamma }_1$
as explained in § 2.1.2. Now, let
![]() $\mathcal {A}(\Gamma _1)$
be the algebra obtained by universal localisation from the set
$\mathcal {A}(\Gamma _1)$
be the algebra obtained by universal localisation from the set
![]() $S=\{1+ab,1+ba \}$
. This is equivalent to adding the local inverse
$S=\{1+ab,1+ba \}$
. This is equivalent to adding the local inverse
![]() $(e_2+ab)^{-1}$
to
$(e_2+ab)^{-1}$
to
![]() $e_2+ab$
in
$e_2+ab$
in
![]() $e_{2}\mathcal {A}(\Gamma _1) e_{2}$
, as well as to adding
$e_{2}\mathcal {A}(\Gamma _1) e_{2}$
, as well as to adding
![]() $(e_1+ba)^{-1}$
to
$(e_1+ba)^{-1}$
to
![]() $e_1+ba$
in
$e_1+ba$
in
![]() $e_{1}\mathcal {A}(\Gamma _1) e_{1}$
. Finally, note that
$e_{1}\mathcal {A}(\Gamma _1) e_{1}$
. Finally, note that
![]() $\mathcal {A}(\Gamma _1)$
is a B-algebra for
$\mathcal {A}(\Gamma _1)$
is a B-algebra for
![]() $B=\Bbbk e_1\oplus \Bbbk e_2$
.
$B=\Bbbk e_1\oplus \Bbbk e_2$
.
Following [Reference Crawley-Boevey and Shaw25], we define the multiplicative preprojective algebra
Footnote
5
of
![]() $\Gamma _1$
with parameter
$\Gamma _1$
with parameter
![]() $q=(q_1,q_2)\in (\Bbbk ^{\times })^2$
as the algebra
$q=(q_1,q_2)\in (\Bbbk ^{\times })^2$
as the algebra
where
![]() $R^q$
is the ideal generated by
$R^q$
is the ideal generated by
Theorem 2.12 ([Reference Van den Bergh41], Theorem 6.5.1 and Proposition 6.8.1)
-
(i) The algebra
 $\mathcal {A}(\Gamma _1)$
possesses a Hamiltonian double quasi-Poisson structure given by the double quasi-Poisson bracket and by the multiplicative moment map
$\mathcal {A}(\Gamma _1)$
possesses a Hamiltonian double quasi-Poisson structure given by the double quasi-Poisson bracket and by the multiplicative moment map $$ \begin{align*} \{\mkern-6mu\{a,a\}\mkern-6mu\}&=\;\;\,0\,,\qquad \{\mkern-6mu\{b,b\}\mkern-6mu\}=0\,; \\ \{\mkern-6mu\{a,b\}\mkern-6mu\}&=\;\;\,\frac{1}{2}\Big(ba\otimes e_{2}+e_{1}\otimes ab\Big)+e_{1}\otimes e_{2}\,; \\ \{\mkern-6mu\{b,a\}\mkern-6mu\}&=-\frac{1}{2}\Big(e_{2}\otimes ba+ab\otimes e_{1}\Big)-e_{2}\otimes e_{1}\,; \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a,a\}\mkern-6mu\}&=\;\;\,0\,,\qquad \{\mkern-6mu\{b,b\}\mkern-6mu\}=0\,; \\ \{\mkern-6mu\{a,b\}\mkern-6mu\}&=\;\;\,\frac{1}{2}\Big(ba\otimes e_{2}+e_{1}\otimes ab\Big)+e_{1}\otimes e_{2}\,; \\ \{\mkern-6mu\{b,a\}\mkern-6mu\}&=-\frac{1}{2}\Big(e_{2}\otimes ba+ab\otimes e_{1}\Big)-e_{2}\otimes e_{1}\,; \end{align*} $$
 $$\begin{align*}\Phi=(e_2+ab)+(e_1+ba)^{-1}\,. \end{align*}$$
$$\begin{align*}\Phi=(e_2+ab)+(e_1+ba)^{-1}\,. \end{align*}$$
-
(ii) The multiplicative preprojective algebra (with parameter q)
 $\Lambda ^q(\Gamma _1)$
is endowed with an
$\Lambda ^q(\Gamma _1)$
is endowed with an
 $H_0$
-Poisson structure, as defined in [Reference Crawley-Boevey23].
$H_0$
-Poisson structure, as defined in [Reference Crawley-Boevey23].
Remark 2.13. Note that Theorem 2.12 can be adapted to an arbitrary quiver Q. Indeed, it suffices to use fusion and Theorem 2.8. We will not need this general result which the reader can find in [Reference Van den Bergh41, Theorem 6.7.1] (keeping in mind Remark 2.1). A particular case of this generalisation is derived in § 5.2 for the quiver
![]() $Q=\Gamma _n$
.
$Q=\Gamma _n$
.
3 Euler continuants and Hamiltonian double quasi-Poisson algebras
3.1 Euler continuants with idempotents
Given an integer
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\Gamma _n$
be the quiver whose set of vertices is
$\Gamma _n$
be the quiver whose set of vertices is
![]() $\{1,2\}$
and whose set of arrows is
$\{1,2\}$
and whose set of arrows is
![]() $\{a_i\mid 1\leq i \leq n\}$
, where
$\{a_i\mid 1\leq i \leq n\}$
, where
![]() $a_i$
is an arrow from the vertex
$a_i$
is an arrow from the vertex
![]() $1$
to
$1$
to
![]() $2$
. We form the double
$2$
. We form the double
![]() $\overline {\Gamma }_n$
of
$\overline {\Gamma }_n$
of
![]() $\Gamma _n$
by adding the arrows
$\Gamma _n$
by adding the arrows
![]() $\{b_i \mid 1\leq i \leq n\}$
, where
$\{b_i \mid 1\leq i \leq n\}$
, where
![]() $b_i$
is an arrow from the vertex
$b_i$
is an arrow from the vertex
![]() $2$
to
$2$
to
![]() $1$
; see Figure 1.
$1$
; see Figure 1.
We form the path algebra
![]() $\Bbbk \overline {\Gamma }_n$
of
$\Bbbk \overline {\Gamma }_n$
of
![]() $\overline {\Gamma }_n$
as in §2.1.2. This allows us to see this algebra as being generated by the orthogonal idempotents
$\overline {\Gamma }_n$
as in §2.1.2. This allows us to see this algebra as being generated by the orthogonal idempotents
![]() $e_1,e_2$
and the symbols
$e_1,e_2$
and the symbols
![]() $\{a_i,b_i\mid 1\!\leq \! i\!\leq \! n\}$
subject to the relations
$\{a_i,b_i\mid 1\!\leq \! i\!\leq \! n\}$
subject to the relations
Since
![]() $a_ib_j$
and
$a_ib_j$
and
![]() $b_ja_i$
are not trivially vanishing in
$b_ja_i$
are not trivially vanishing in
![]() $\Bbbk \overline {\Gamma }_n$
, we can slightly adapt the definition of Euler continuants from Section 1 as follows. We introduce the first and second Euler continuants by setting
$\Bbbk \overline {\Gamma }_n$
, we can slightly adapt the definition of Euler continuants from Section 1 as follows. We introduce the first and second Euler continuants by setting
 $$ \begin{align} \begin{aligned} (a_i)&:=a_i\in e_2(\Bbbk \overline{\Gamma}_n)e_1\,,&\quad (b_i)&:=b_i \in e_1(\Bbbk \overline{\Gamma}_n)e_2\,, \\ (a_i,b_j)&:= e_2+a_ib_j\in e_2(\Bbbk \overline{\Gamma}_n)e_2\,,&\quad (b_i,a_j)&:= e_1+b_ia_j\in e_1(\Bbbk \overline{\Gamma}_n)e_1\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (a_i)&:=a_i\in e_2(\Bbbk \overline{\Gamma}_n)e_1\,,&\quad (b_i)&:=b_i \in e_1(\Bbbk \overline{\Gamma}_n)e_2\,, \\ (a_i,b_j)&:= e_2+a_ib_j\in e_2(\Bbbk \overline{\Gamma}_n)e_2\,,&\quad (b_i,a_j)&:= e_1+b_ia_j\in e_1(\Bbbk \overline{\Gamma}_n)e_1\,, \end{aligned} \end{align} $$
for
![]() $i,j=1,\ldots ,n$
. We also put
$i,j=1,\ldots ,n$
. We also put
![]() $(a_i,a_j)=0=(b_i,b_j)$
as
$(a_i,a_j)=0=(b_i,b_j)$
as
![]() $a_ia_j=0=b_ib_j$
in
$a_ia_j=0=b_ib_j$
in
![]() $\Bbbk \overline {\Gamma }_n$
. This ensures that the first and second Euler continuants respect the idempotent decomposition, that is, if
$\Bbbk \overline {\Gamma }_n$
. This ensures that the first and second Euler continuants respect the idempotent decomposition, that is, if
![]() $y_1,y_2\in \{a_i,b_i\mid 1\leq i\leq n\}$
, we have
$y_1,y_2\in \{a_i,b_i\mid 1\leq i\leq n\}$
, we have
![]() $(y_1,y_2)=e_{h(y_1)}(y_1,y_2)e_{t(y_2)}$
. Then, given elements
$(y_1,y_2)=e_{h(y_1)}(y_1,y_2)e_{t(y_2)}$
. Then, given elements
![]() $y_1,\ldots ,y_k\in \{a_i,b_i\mid 1\leq i\leq n\}$
for
$y_1,\ldots ,y_k\in \{a_i,b_i\mid 1\leq i\leq n\}$
for
![]() $k\geq 3$
, we have that the k-th Euler continuant is obtained recursively using the rule
$k\geq 3$
, we have that the k-th Euler continuant is obtained recursively using the rule
We will only consider the Euler continuant
![]() $(y_1,\dots ,y_k)$
when the elements
$(y_1,\dots ,y_k)$
when the elements
![]() $\{y_{\ell }\}$
are alternating with respect to the generators
$\{y_{\ell }\}$
are alternating with respect to the generators
![]() $\{a_i,b_i\mid 1\leq i\leq n\}$
; that is, if
$\{a_i,b_i\mid 1\leq i\leq n\}$
; that is, if
![]() $y_{\ell }=a_i$
(resp.
$y_{\ell }=a_i$
(resp.
![]() $y_{\ell }=b_i$
), then
$y_{\ell }=b_i$
), then
![]() $y_{\ell +1}=b_{j}$
(resp.
$y_{\ell +1}=b_{j}$
(resp.
![]() $y_{\ell +1}=a_{j}$
) for some
$y_{\ell +1}=a_{j}$
) for some
![]() $1\leq i,j\leq n$
.
$1\leq i,j\leq n$
.
Remark 3.1. Alternatively to equation (1.1), observe that the recursive rule used to define Euler continuants can be expressed as
Then, when dealing with idempotents, we can also use equation (3.4) instead of equation (3.3) to define the k-th Euler continuants for
![]() $k\geq 3$
.
$k\geq 3$
.
We close this subsection by proving several identities involving Euler continuants that will be important for later purposes.
Lemma 3.2. For
![]() $n\geq 1$
, we have that
$n\geq 1$
, we have that
 $$ \begin{align} (a_1,b_1,\dots, b_{n-1},a_n)=\sum^{n+1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1\, , \end{align} $$
$$ \begin{align} (a_1,b_1,\dots, b_{n-1},a_n)=\sum^{n+1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1\, , \end{align} $$
and for
![]() $n\geq 2$
, we have that
$n\geq 2$
, we have that
 $$ \begin{align} (a_1,b_1,\dots,a_n ,b_n)=(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\,. \end{align} $$
$$ \begin{align} (a_1,b_1,\dots,a_n ,b_n)=(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\,. \end{align} $$
Proof. We prove equation (3.5) by induction. The base case occurs when
![]() $n=1$
, which follows by definition:
$n=1$
, which follows by definition:
![]() $(a_1)=a_1$
. Now, by equation (3.3) and the inductive hypothesis, we have that
$(a_1)=a_1$
. Now, by equation (3.3) and the inductive hypothesis, we have that
 $$ \begin{align*} (a_1,b_1,&\dots ,a_{n-1},b_{n-1},a_n)=(a_1,b_1,\dots ,a_{n-1},b_{n-1})a_n+(a_1,b_1,\dots,a_{n-1}) \\ &=(a_1,b_1,\dots ,a_{n-1},b_{n-1})a_n+\sum^{n}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1 \\ &=\sum^{n+1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1\,. \end{align*} $$
$$ \begin{align*} (a_1,b_1,&\dots ,a_{n-1},b_{n-1},a_n)=(a_1,b_1,\dots ,a_{n-1},b_{n-1})a_n+(a_1,b_1,\dots,a_{n-1}) \\ &=(a_1,b_1,\dots ,a_{n-1},b_{n-1})a_n+\sum^{n}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1 \\ &=\sum^{n+1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+a_1\,. \end{align*} $$
To prove (3.6), it suffices to use the recursive relation (3.3) and (3.5):
 $$ \begin{align*} (a_1,b_1,&\dots,a_n ,b_n)=(a_1,\dots ,a_n)b_n+(a_1,\dots ,b_{n-1}) \\ &=\Big[(a_1,\dots ,b_{n-1})a_n+ (a_1,\dots ,a_{n-1})\Big]b_n+(a_1,\dots ,b_{n-1}) \\ &=(a_1,\dots ,b_{n-1})(a_n,b_n)+ (a_1,\dots ,a_{n-1})b_n \\ &=(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\, .\\[-48pt] \end{align*} $$
$$ \begin{align*} (a_1,b_1,&\dots,a_n ,b_n)=(a_1,\dots ,a_n)b_n+(a_1,\dots ,b_{n-1}) \\ &=\Big[(a_1,\dots ,b_{n-1})a_n+ (a_1,\dots ,a_{n-1})\Big]b_n+(a_1,\dots ,b_{n-1}) \\ &=(a_1,\dots ,b_{n-1})(a_n,b_n)+ (a_1,\dots ,a_{n-1})b_n \\ &=(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\, .\\[-48pt] \end{align*} $$
Lemma 3.3. For
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
Proof. For
![]() $n=1$
, we can write that
$n=1$
, we can write that
Now, using the induction hypothesis and the recursive relations (3.3) and (3.4) of the Euler continuants, we have
 $$ \begin{align*} (a_1,\ldots,&a_{n})(b_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})a_{n}(b_{n},\ldots,a_1)+(a_1,\ldots,a_{n-1})(b_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})a_{n}(b_{n},\ldots,a_1)+(a_1,\ldots,a_{n-1})\Big[b_{n}(a_{n},\ldots,a_1)+(b_{n-1},\ldots,a_1)\Big] \\ &=(a_1,\ldots,b_{n-1})\Big[a_{n}(b_{n},\ldots,a_1)+(a_{n-1},\ldots,a_1) \Big]+(a_1,\ldots,a_{n-1})b_{n}(a_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})(a_{n},b_{n},\ldots,a_1) + (a_1,\ldots,a_{n-1})b_{n}(a_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n})(a_{n},\ldots,a_1)\,. \\[-38pt] \end{align*} $$
$$ \begin{align*} (a_1,\ldots,&a_{n})(b_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})a_{n}(b_{n},\ldots,a_1)+(a_1,\ldots,a_{n-1})(b_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})a_{n}(b_{n},\ldots,a_1)+(a_1,\ldots,a_{n-1})\Big[b_{n}(a_{n},\ldots,a_1)+(b_{n-1},\ldots,a_1)\Big] \\ &=(a_1,\ldots,b_{n-1})\Big[a_{n}(b_{n},\ldots,a_1)+(a_{n-1},\ldots,a_1) \Big]+(a_1,\ldots,a_{n-1})b_{n}(a_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n-1})(a_{n},b_{n},\ldots,a_1) + (a_1,\ldots,a_{n-1})b_{n}(a_{n},\ldots,a_1) \\ &=(a_1,\ldots,b_{n})(a_{n},\ldots,a_1)\,. \\[-38pt] \end{align*} $$
3.2 The result
We consider the
![]() $(2n)$
-th Euler continuants
$(2n)$
-th Euler continuants
 $$ \begin{align} \begin{aligned} (a_1,b_1,a_2,b_2,\dots,a_n,b_n)&\in e_2(\Bbbk\overline{\Gamma}_n)e_2\, , \\ (b_n,a_n,b_{n-1},a_{n-1},\dots,b_1,a_1)&\in e_1(\Bbbk\overline{\Gamma}_n)e_1\, , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (a_1,b_1,a_2,b_2,\dots,a_n,b_n)&\in e_2(\Bbbk\overline{\Gamma}_n)e_2\, , \\ (b_n,a_n,b_{n-1},a_{n-1},\dots,b_1,a_1)&\in e_1(\Bbbk\overline{\Gamma}_n)e_1\, , \end{aligned} \end{align} $$
and we form the Boalch algebra
![]() $\mathcal {B}(\Gamma _n)$
as the path algebra
$\mathcal {B}(\Gamma _n)$
as the path algebra
![]() $\Bbbk \overline {\Gamma }_n$
with
$\Bbbk \overline {\Gamma }_n$
with
![]() $(a_1,\dots ,b_n)$
and
$(a_1,\dots ,b_n)$
and
![]() $ (b_n,\dots ,a_1)$
inverted. As in [Reference Van den Bergh41, §6.5], this means that we introduce elements
$ (b_n,\dots ,a_1)$
inverted. As in [Reference Van den Bergh41, §6.5], this means that we introduce elements
![]() $A,B$
such that
$A,B$
such that
![]() $A=Ae_2=e_2A$
,
$A=Ae_2=e_2A$
,
![]() $B=Be_1=e_1B$
and
$B=Be_1=e_1B$
and
![]() $A(a_1,\dots ,b_n)=(a_1,\dots ,b_n)A=e_2$
and
$A(a_1,\dots ,b_n)=(a_1,\dots ,b_n)A=e_2$
and
![]() $B(b_n,\dots ,a_1)=(b_n,\dots ,a_1)B=e_1$
. From now on, we use the notation
$B(b_n,\dots ,a_1)=(b_n,\dots ,a_1)B=e_1$
. From now on, we use the notation
![]() $(a_1,\dots ,b_n)^{-1}$
and
$(a_1,\dots ,b_n)^{-1}$
and
![]() $(b_n,\dots ,a_1)^{-1}$
for A and B, respectively. This entails that
$(b_n,\dots ,a_1)^{-1}$
for A and B, respectively. This entails that
![]() $e_1+(a_1,\dots ,b_n)$
and
$e_1+(a_1,\dots ,b_n)$
and
![]() $e_2+(b_n,\dots ,a_1)$
are invertible in
$e_2+(b_n,\dots ,a_1)$
are invertible in
![]() $\mathcal {B}(\Gamma _n)$
in the usual sense.
$\mathcal {B}(\Gamma _n)$
in the usual sense.
Next, we follow Boalch [Reference Boalch15, Remark 17] and define the fission algebra
where
![]() $R^q$
is the ideal generated by the two relations
$R^q$
is the ideal generated by the two relations
Note that
![]() $\mathcal {B}(\Gamma _n)$
is a generalisation of
$\mathcal {B}(\Gamma _n)$
is a generalisation of
![]() $\mathcal {B}(\Gamma _1)=\mathcal {A}(\Gamma _1)$
introduced in § 2.4, while
$\mathcal {B}(\Gamma _1)=\mathcal {A}(\Gamma _1)$
introduced in § 2.4, while
![]() $\mathcal {F}^q(\Gamma _n)$
is a generalisation of the multiplicative preprojective algebra
$\mathcal {F}^q(\Gamma _n)$
is a generalisation of the multiplicative preprojective algebra
![]() $\mathcal {F}^q(\Gamma _1)=\Lambda ^q(\Gamma _1)$
of [Reference Crawley-Boevey and Shaw25].
$\mathcal {F}^q(\Gamma _1)=\Lambda ^q(\Gamma _1)$
of [Reference Crawley-Boevey and Shaw25].
Finally, let
![]() $B=\Bbbk e_1\oplus \Bbbk e_2$
, and we introduce a B-linear double bracket
$B=\Bbbk e_1\oplus \Bbbk e_2$
, and we introduce a B-linear double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
on the arrows of
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
on the arrows of
![]() $\overline {\Gamma }_n$
(seen as generators of
$\overline {\Gamma }_n$
(seen as generators of
![]() $\mathcal {B}(\Gamma _n)$
) as
$\mathcal {B}(\Gamma _n)$
) as
 $$ \begin{align} \{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(a_i\otimes a_j+a_j\otimes a_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\, , &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(a_i\otimes a_j+a_j\otimes a_i\big), & \mbox{if } i>j \end{cases}\,; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(a_i\otimes a_j+a_j\otimes a_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\, , &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(a_i\otimes a_j+a_j\otimes a_i\big), & \mbox{if } i>j \end{cases}\,; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(b_i\otimes b_j+b_j\otimes b_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(b_i\otimes b_j+b_j\otimes b_i\big)\,, & \mbox{if } i>j \end{cases}\,; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(b_i\otimes b_j+b_j\otimes b_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(b_i\otimes b_j+b_j\otimes b_i\big)\,, & \mbox{if } i>j \end{cases}\,; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{a_i,b_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes a_ib_j+b_ja_i\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(b_ia_i\otimes e_2+e_1\otimes a_ib_i\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(b_ja_{i}\otimes e_2+e_1\otimes a_{i}b_j\big)-\delta_{i-j,1}(e_1\otimes e_2)\,, &\mbox{if } i>j \end{cases}\,; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{a_i,b_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes a_ib_j+b_ja_i\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(b_ia_i\otimes e_2+e_1\otimes a_ib_i\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(b_ja_{i}\otimes e_2+e_1\otimes a_{i}b_j\big)-\delta_{i-j,1}(e_1\otimes e_2)\,, &\mbox{if } i>j \end{cases}\,; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{b_i,a_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_2\otimes b_ia_j+ a_jb_i\otimes e_1\big)+\delta_{j-i,1}(e_2\otimes e_1)\, , &\mbox{if } i<j \\ - \frac{1}{2}\big(e_2\otimes b_ia_i+ a_ib_i\otimes e_1\big)-e_2\otimes e_1\,, &\mbox{if } i=j \\ -\frac{1}{2}\big(a_jb_i\otimes e_1+ e_2\otimes b_ia_j)\,, &\mbox{if } i>j \end{cases}\,; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{b_i,a_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_2\otimes b_ia_j+ a_jb_i\otimes e_1\big)+\delta_{j-i,1}(e_2\otimes e_1)\, , &\mbox{if } i<j \\ - \frac{1}{2}\big(e_2\otimes b_ia_i+ a_ib_i\otimes e_1\big)-e_2\otimes e_1\,, &\mbox{if } i=j \\ -\frac{1}{2}\big(a_jb_i\otimes e_1+ e_2\otimes b_ia_j)\,, &\mbox{if } i>j \end{cases}\,; \end{align} $$
where
![]() $i,j\in \{1,\dots ,n\}$
, and we extend
$i,j\in \{1,\dots ,n\}$
, and we extend
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
to
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
to
![]() $\mathcal {B}(\Gamma _n)$
by the Leibniz rules (2.5) and (2.6).
$\mathcal {B}(\Gamma _n)$
by the Leibniz rules (2.5) and (2.6).
It is worth noting how the double bracket can be determined on the inverses of the elements (3.7) so that it is is uniquely defined on
![]() $\mathcal {B}(\Gamma _n)$
and not only on
$\mathcal {B}(\Gamma _n)$
and not only on
![]() $\Bbbk \overline {\Gamma }_n$
. By B-linearity
$\Bbbk \overline {\Gamma }_n$
. By B-linearity
![]() $\{\mkern -6mu\{c,(b_n,\ldots ,a_1)(b_n,\ldots ,a_1)^{-1}\}\mkern -6mu\}=\{\mkern -6mu\{c,e_1\}\mkern -6mu\}=0$
for any
$\{\mkern -6mu\{c,(b_n,\ldots ,a_1)(b_n,\ldots ,a_1)^{-1}\}\mkern -6mu\}=\{\mkern -6mu\{c,e_1\}\mkern -6mu\}=0$
for any
![]() $c\in \mathcal {B}(\Gamma _n)$
, hence by equation (2.5)
$c\in \mathcal {B}(\Gamma _n)$
, hence by equation (2.5)
A similar relation holds for
![]() $\{\mkern -6mu\{c,(a_1,\ldots ,b_n)^{-1}\}\mkern -6mu\}$
.
$\{\mkern -6mu\{c,(a_1,\ldots ,b_n)^{-1}\}\mkern -6mu\}$
.
Theorem 3.4. Given an integer
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\overline {\Gamma }_n$
be the quiver with vertices
$\overline {\Gamma }_n$
be the quiver with vertices
![]() $\{1,2\}$
and arrows
$\{1,2\}$
and arrows
![]() $\{a_i,b_i\mid 1\leq i\leq n\}$
such that
$\{a_i,b_i\mid 1\leq i\leq n\}$
such that
![]() $a_i=e_2a_ie_1$
and
$a_i=e_2a_ie_1$
and
![]() $b_i=e_1b_ie_2$
. Let
$b_i=e_1b_ie_2$
. Let
![]() $B:=\Bbbk e_1\oplus \Bbbk e_2$
and
$B:=\Bbbk e_1\oplus \Bbbk e_2$
and
![]() $\Bbbk \overline {\Gamma }_n$
be the path algebra of
$\Bbbk \overline {\Gamma }_n$
be the path algebra of
![]() $\overline {\Gamma }_n$
over B. Finally, if
$\overline {\Gamma }_n$
over B. Finally, if
![]() $(a_1,\dots ,b_n)$
and
$(a_1,\dots ,b_n)$
and
![]() $ (b_n,\dots ,a_1)$
are
$ (b_n,\dots ,a_1)$
are
![]() $(2n)$
-th Euler continuants, let
$(2n)$
-th Euler continuants, let
![]() $\mathcal {B}(\Gamma _n)$
denote
$\mathcal {B}(\Gamma _n)$
denote
![]() $\Bbbk \overline {\Gamma }_n$
with
$\Bbbk \overline {\Gamma }_n$
with
![]() $(a_1,\dots ,b_n)$
and
$(a_1,\dots ,b_n)$
and
![]() $ (b_n,\dots ,a_1)$
inverted.
$ (b_n,\dots ,a_1)$
inverted.
Let
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
be the B-linear double bracket defined on
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
be the B-linear double bracket defined on
![]() $\mathcal {B}(\Gamma _n)$
by equation (3.10). In addition, we introduce the following element of
$\mathcal {B}(\Gamma _n)$
by equation (3.10). In addition, we introduce the following element of
![]() $\mathcal {B}(\Gamma _n)$
$\mathcal {B}(\Gamma _n)$
Then the triple
![]() $\big (\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi \big )$
is a Hamiltonian double quasi-Poisson algebra.
$\big (\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\},\Phi \big )$
is a Hamiltonian double quasi-Poisson algebra.
We postpone the proof of Theorem 3.4 to Section 4. We remark that, in the case
![]() $n=1$
where
$n=1$
where
![]() $\mathcal {B}(\Gamma _1)=\mathcal {A}(\Gamma _1)$
, Theorem 3.4 recovers Van den Bergh’s double quasi-Poisson bracket described in Theorem 2.12(i). Furthermore, using Proposition 2.10, we can obtain the following generalisation of Theorem 2.12(ii).
$\mathcal {B}(\Gamma _1)=\mathcal {A}(\Gamma _1)$
, Theorem 3.4 recovers Van den Bergh’s double quasi-Poisson bracket described in Theorem 2.12(i). Furthermore, using Proposition 2.10, we can obtain the following generalisation of Theorem 2.12(ii).
Corollary 3.5. The fission algebra
![]() $\mathcal {F}^q(\Gamma _n)$
attached to
$\mathcal {F}^q(\Gamma _n)$
attached to
![]() $\Gamma _n$
carries an
$\Gamma _n$
carries an
![]() $H_0$
-Poisson structure.
$H_0$
-Poisson structure.
Using the Kontsevich–Rosenberg principle, Theorem 3.4 turns the representation space
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(d_1,d_2)\big )$
into a Hamiltonian quasi-Poisson space for the canonical action of
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(d_1,d_2)\big )$
into a Hamiltonian quasi-Poisson space for the canonical action of
![]() $H:=\operatorname {GL}(d_1)\times \operatorname {GL}(d_2)$
. Similarly, Corollary 3.5 induces a Poisson structure on the reduced spaces
$H:=\operatorname {GL}(d_1)\times \operatorname {GL}(d_2)$
. Similarly, Corollary 3.5 induces a Poisson structure on the reduced spaces
![]() $\operatorname {Rep}\big (\mathcal {F}^q(\Gamma _n),(d_1,d_2)\big )/\!/H$
, which coincides with the structure obtained by quasi-Hamiltonian reduction; we refer to [Reference Fairon and Fernández31, §2.3] for a review of this general construction based on [Reference Crawley-Boevey23, Reference Van den Bergh41].
$\operatorname {Rep}\big (\mathcal {F}^q(\Gamma _n),(d_1,d_2)\big )/\!/H$
, which coincides with the structure obtained by quasi-Hamiltonian reduction; we refer to [Reference Fairon and Fernández31, §2.3] for a review of this general construction based on [Reference Crawley-Boevey23, Reference Van den Bergh41].
As pointed out in the introduction, if
![]() $\Bbbk =\mathbb {C}$
and
$\Bbbk =\mathbb {C}$
and
![]() $(d_1,d_2)=(1,1)$
, we are in the situation of the Sibuya spaces [Reference Sibuya40] whose symplectic geometry was studied by Boalch in [Reference Boalch15]. In § 3.4, we give the precise form of the bracket obtained from equation (3.10) in this specific case, and we explain its connection to the Flaschka–Newell Poisson bracket [Reference Flaschka and Newell33]. More generally, if
$(d_1,d_2)=(1,1)$
, we are in the situation of the Sibuya spaces [Reference Sibuya40] whose symplectic geometry was studied by Boalch in [Reference Boalch15]. In § 3.4, we give the precise form of the bracket obtained from equation (3.10) in this specific case, and we explain its connection to the Flaschka–Newell Poisson bracket [Reference Flaschka and Newell33]. More generally, if
![]() $\Bbbk =\mathbb {C}$
and the dimension vector
$\Bbbk =\mathbb {C}$
and the dimension vector
![]() $(d_1,d_2)$
is arbitrary, we get that the Poisson structure induced on any reduced space
$(d_1,d_2)$
is arbitrary, we get that the Poisson structure induced on any reduced space
![]() $\operatorname {Rep}\big (\mathcal {F}^q(\Gamma _n),(d_1,d_2)\big )/\!/H$
corresponds (on its smooth locus) to the symplectic structure defined by Boalch. This follows from Proposition 5.16 presented in §5.6, where we prove that the Hamiltonian quasi-Poisson structure that we obtain on the representation space
$\operatorname {Rep}\big (\mathcal {F}^q(\Gamma _n),(d_1,d_2)\big )/\!/H$
corresponds (on its smooth locus) to the symplectic structure defined by Boalch. This follows from Proposition 5.16 presented in §5.6, where we prove that the Hamiltonian quasi-Poisson structure that we obtain on the representation space
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(d_1,d_2)\big )$
corresponds to the quasi-Hamiltonian structure introduced by Boalch [Reference Boalch9, 13] and conveniently studied by Paluba [Reference Paluba38, Ch. 5].
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(d_1,d_2)\big )$
corresponds to the quasi-Hamiltonian structure introduced by Boalch [Reference Boalch9, 13] and conveniently studied by Paluba [Reference Paluba38, Ch. 5].
3.3 The noncommutative bivector
In the case of Theorem 3.4, it is possible to write explicitly the bivector defining the double bracket on the Boalch algebra
![]() $\mathcal {B}(\Gamma _n)$
through Proposition 2.3. As in §2.1.2, we consider the double derivations
$\mathcal {B}(\Gamma _n)$
through Proposition 2.3. As in §2.1.2, we consider the double derivations
which are defined for
![]() $i,k=1,\ldots ,n$
by
$i,k=1,\ldots ,n$
by
Then the following result is a direct application of the equivalence given by Proposition 2.3 since path algebras of quivers are smooth.
Proposition 3.6. The double quasi-Poisson bracket from Theorem 3.4 is associated with the following bivector:
 $$ \begin{align} \begin{aligned} {\mathrm{P}_n}&=\frac12 \sum_{i>j} \left[ \frac{\partial}{\partial a_i}a_i \frac{\partial}{\partial a_j} a_j + \frac{\partial}{\partial a_i} a_j \frac{\partial}{\partial a_j} a_i \right] +\frac12 \sum_{i>j} \left[ \frac{\partial}{\partial b_i}b_i \frac{\partial}{\partial b_j} b_j + \frac{\partial}{\partial b_i} b_j \frac{\partial}{\partial b_j} b_i \right] \\ &\quad+\frac12 \sum_{i\neq j} \operatorname{sgn}(j-i) \left[ \frac{\partial}{\partial a_i}a_i b_j \frac{\partial}{\partial b_j} + a_i \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_j} b_j \right] -\sum_{i=2}^n \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_{i-1}} \\ &\quad +\frac12 \sum_{i=1}^n\left[ \frac{\partial}{\partial a_i}a_i b_i \frac{\partial}{\partial b_i} + a_i\frac{\partial}{\partial a_i} \frac{\partial}{\partial b_i} b_i \right] +\sum_{i=1}^n \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_{i}}\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathrm{P}_n}&=\frac12 \sum_{i>j} \left[ \frac{\partial}{\partial a_i}a_i \frac{\partial}{\partial a_j} a_j + \frac{\partial}{\partial a_i} a_j \frac{\partial}{\partial a_j} a_i \right] +\frac12 \sum_{i>j} \left[ \frac{\partial}{\partial b_i}b_i \frac{\partial}{\partial b_j} b_j + \frac{\partial}{\partial b_i} b_j \frac{\partial}{\partial b_j} b_i \right] \\ &\quad+\frac12 \sum_{i\neq j} \operatorname{sgn}(j-i) \left[ \frac{\partial}{\partial a_i}a_i b_j \frac{\partial}{\partial b_j} + a_i \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_j} b_j \right] -\sum_{i=2}^n \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_{i-1}} \\ &\quad +\frac12 \sum_{i=1}^n\left[ \frac{\partial}{\partial a_i}a_i b_i \frac{\partial}{\partial b_i} + a_i\frac{\partial}{\partial a_i} \frac{\partial}{\partial b_i} b_i \right] +\sum_{i=1}^n \frac{\partial}{\partial a_i} \frac{\partial}{\partial b_{i}}\,. \end{aligned} \end{align} $$
Proof. It suffices to show that the double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {P}_n}$
defined through equation (2.7) using
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\mathrm {P}_n}$
defined through equation (2.7) using
![]() ${\mathrm {P}_n}$
gives equations (3.10a)–(3.10c) when evaluated on generators. If
${\mathrm {P}_n}$
gives equations (3.10a)–(3.10c) when evaluated on generators. If
![]() $i>j$
, we note that the only terms contributing to
$i>j$
, we note that the only terms contributing to
![]() $\{\mkern -6mu\{a_i,a_j\}\mkern -6mu\}_{\mathrm {P}_n}$
come from the first term of equation (3.14) as
$\{\mkern -6mu\{a_i,a_j\}\mkern -6mu\}_{\mathrm {P}_n}$
come from the first term of equation (3.14) as
 $$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left( \frac{\partial}{\partial a_j} a_j\right) + \frac12 \left(\frac{\partial}{\partial a_i} a_j\right) \left(\frac{\partial}{\partial a_j} a_i \right)\,, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left( \frac{\partial}{\partial a_j} a_j\right) + \frac12 \left(\frac{\partial}{\partial a_i} a_j\right) \left(\frac{\partial}{\partial a_j} a_i \right)\,, \end{aligned} \end{align*} $$
so that equation (2.7) yields
Clearly,
![]() $\{\mkern -6mu\{a_i,a_i\}\mkern -6mu\}_{\mathrm {P}_n}=0$
, so by cyclic antisymmetry (2.4) we get that
$\{\mkern -6mu\{a_i,a_i\}\mkern -6mu\}_{\mathrm {P}_n}=0$
, so by cyclic antisymmetry (2.4) we get that
![]() $\{\mkern -6mu\{a_i,a_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10a) for all
$\{\mkern -6mu\{a_i,a_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10a) for all
![]() $1\leq i,j \leq n$
. We can show in the same way that
$1\leq i,j \leq n$
. We can show in the same way that
![]() $\{\mkern -6mu\{b_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10b) for all indices.
$\{\mkern -6mu\{b_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10b) for all indices.
We now compute
![]() $\{\mkern -6mu\{a_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
. If
$\{\mkern -6mu\{a_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
. If
![]() $i<j$
, the only terms that contribute come from the third term of equation (3.14) as
$i<j$
, the only terms that contribute come from the third term of equation (3.14) as
 $$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_j \frac{\partial}{\partial b_j}\right) + \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} b_j \right)\,, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_j \frac{\partial}{\partial b_j}\right) + \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} b_j \right)\,, \end{aligned} \end{align*} $$
and we get from equation (2.7) that
If
![]() $i=j$
, we only need the following terms from the last line in equation (3.14)
$i=j$
, we only need the following terms from the last line in equation (3.14)
 $$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_i \frac{\partial}{\partial b_i}\right) + \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_i} b_i \right) + \left( \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_i} \right)\,, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_i \frac{\partial}{\partial b_i}\right) + \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_i} b_i \right) + \left( \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_i} \right)\,, \end{aligned} \end{align*} $$
and equation (2.7) yields
In the case
![]() $i>j$
, the contributing terms come from the third and fourth sums in equation (3.14) as
$i>j$
, the contributing terms come from the third and fourth sums in equation (3.14) as
 $$ \begin{align*} \begin{aligned} -\frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_j \frac{\partial}{\partial b_j}\right) - \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} b_j \right) -\delta_{i-j,1} \left( \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} \right)\,, \end{aligned}\\[-15pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} -\frac12 \left(\frac{\partial}{\partial a_i}a_i\right) \left(b_j \frac{\partial}{\partial b_j}\right) - \frac12 \left(a_i \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} b_j \right) -\delta_{i-j,1} \left( \frac{\partial}{\partial a_i} \right) \left( \frac{\partial}{\partial b_j} \right)\,, \end{aligned}\\[-15pt] \end{align*} $$
and equation (2.7) yields
Gathering the three cases, we get that
![]() $\{\mkern -6mu\{a_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10c) for all indices.
$\{\mkern -6mu\{a_i,b_j\}\mkern -6mu\}_{\mathrm {P}_n}$
coincides with equation (3.10c) for all indices.
Remark 3.7. In the case
![]() $n=1$
, the noncommutative bivector
$n=1$
, the noncommutative bivector
![]() ${\mathrm {P}}_1$
can directly be compared with the one of Van den Bergh [Reference Van den Bergh41, Theorem 6.5.1]. Setting
${\mathrm {P}}_1$
can directly be compared with the one of Van den Bergh [Reference Van den Bergh41, Theorem 6.5.1]. Setting
![]() $a:=a_1$
,
$a:=a_1$
,
![]() $b:=b_1$
, we have that modulo graded-commutator
$b:=b_1$
, we have that modulo graded-commutator
![]() ${\mathrm {P}}_1$
equals
${\mathrm {P}}_1$
equals
which was constructed by Van den Bergh. It is an easy exercise (see [Reference Van den Bergh41, §4.1] in full generalities) to check that the double bracket induced by an element
![]() $Q\in (D_BA)_2$
by Proposition 2.3 only depends on Q modulo graded commutators. Thus,
$Q\in (D_BA)_2$
by Proposition 2.3 only depends on Q modulo graded commutators. Thus,
![]() ${\mathrm {P}}_1$
and
${\mathrm {P}}_1$
and
![]() ${\mathrm {P}}_{\operatorname {VdB}}$
induce the same double quasi-Poisson bracket on
${\mathrm {P}}_{\operatorname {VdB}}$
induce the same double quasi-Poisson bracket on
![]() $\mathcal {B}(\Gamma _1)= \mathcal {A}(\Gamma _1)$
.
$\mathcal {B}(\Gamma _1)= \mathcal {A}(\Gamma _1)$
.
3.4 The Flaschka–Newell Poisson bracket
The representation space of dimension
![]() $(1,1)$
, denoted
$(1,1)$
, denoted
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
, is parametrised by assigning
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
, is parametrised by assigning
![]() $A_i,B_i\in \mathbb {C}$
to the generators
$A_i,B_i\in \mathbb {C}$
to the generators
![]() $a_i,b_i$
for each
$a_i,b_i$
for each
![]() $ 1\leq i\leq n$
, where we require the invertibility of the (scalar) matrices representing the two elements (3.7). Denoting by
$ 1\leq i\leq n$
, where we require the invertibility of the (scalar) matrices representing the two elements (3.7). Denoting by
![]() $A_i,B_i$
the corresponding evaluation functions on
$A_i,B_i$
the corresponding evaluation functions on
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
, this gives precisely the parametrisation (1.9) of the space
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
, this gives precisely the parametrisation (1.9) of the space
![]() $\widehat {\mathcal {B}}^{n+1}$
from the introduction. It is endowed with the action of
$\widehat {\mathcal {B}}^{n+1}$
from the introduction. It is endowed with the action of
![]() $\mathbb {C}^{\times } \times \mathbb {C}^{\times }$
through
$\mathbb {C}^{\times } \times \mathbb {C}^{\times }$
through
This is a Hamiltonian quasi-Poisson space using Theorem 3.4 and [Reference Van den Bergh41, Proposition 7.13.2], in application of the Kontsevich–Rosenberg principle. Using [Reference Van den Bergh41, Proposition 7.5.1], the quasi-Poisson bracket is given byFootnote 6
 $$ \begin{align} \{ A_i,B_j \}=&\left\{ \begin{array}{cc} A_iB_j \,, &\mbox{if }i<j\\ A_iB_i+1\,, &\mbox{if }i=j\\ -A_iB_j-\delta_{i-j,1}\,, &\mbox{if }i>j \end{array} \right.\,.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \{ A_i,B_j \}=&\left\{ \begin{array}{cc} A_iB_j \,, &\mbox{if }i<j\\ A_iB_i+1\,, &\mbox{if }i=j\\ -A_iB_j-\delta_{i-j,1}\,, &\mbox{if }i>j \end{array} \right.\,.\\[-15pt]\nonumber \end{align} $$
The corresponding moment map
![]() $\widehat {\mu }$
is given by equation (1.10) and, noting that the variables
$\widehat {\mu }$
is given by equation (1.10) and, noting that the variables
![]() $A_i,B_i$
commute, it can be simply written as
$A_i,B_i$
commute, it can be simply written as
Since
![]() $\lambda $
represents the component
$\lambda $
represents the component
![]() $\Phi _2$
of the (noncommutative) moment map from Theorem 3.4, we have from [Reference Van den Bergh41, Proposition 7.5.1] and equations (4.12) and (4.13) that
$\Phi _2$
of the (noncommutative) moment map from Theorem 3.4, we have from [Reference Van den Bergh41, Proposition 7.5.1] and equations (4.12) and (4.13) that
Let us note that, since the group
![]() $\mathbb {C}^{\times } \times \mathbb {C}^{\times }$
acting on
$\mathbb {C}^{\times } \times \mathbb {C}^{\times }$
acting on
![]() $\widehat {\mathcal {B}}^{n+1}$
is abelian, the quasi-Poisson bracket is in fact a Poisson bracket. This will be important in view of the following change of variables, motivated by a standard parametrisation connected to Stokes matrices [Reference Bertola and Tarricone3, Reference Boalch15]. We set
$\widehat {\mathcal {B}}^{n+1}$
is abelian, the quasi-Poisson bracket is in fact a Poisson bracket. This will be important in view of the following change of variables, motivated by a standard parametrisation connected to Stokes matrices [Reference Bertola and Tarricone3, Reference Boalch15]. We set
for
![]() $s_j\in \mathbb {C}$
with
$s_j\in \mathbb {C}$
with
![]() $2\leq j\leq 2n+1$
. (The parameters
$2\leq j\leq 2n+1$
. (The parameters
![]() $s_k$
with odd/even indices are the
$s_k$
with odd/even indices are the
![]() $A_i$
/
$A_i$
/
![]() $B_i$
respectively, and they appear with decreasing indices.) We also denote by
$B_i$
respectively, and they appear with decreasing indices.) We also denote by
![]() $s_j$
the corresponding evaluation function on
$s_j$
the corresponding evaluation function on
![]() $\widehat {\mathcal {B}}^{n+1}$
. Then, using this change of coordinates, the moment map
$\widehat {\mathcal {B}}^{n+1}$
. Then, using this change of coordinates, the moment map
![]() $\lambda $
in equation (3.21) becomes
$\lambda $
in equation (3.21) becomes
![]() $\lambda =(s_2,\ldots ,s_{2n+1})$
. It is an easy exercise using equation (3.20a) to see that we can write
$\lambda =(s_2,\ldots ,s_{2n+1})$
. It is an easy exercise using equation (3.20a) to see that we can write
We can also note that equation (3.20b) yields
 $$ \begin{align*} \{ s_k,s_l \}=\left\{ \begin{array}{ll} s_ks_l \,, &\mbox{if } k>l\\ s_ks_l+1\,, &\mbox{if }k=l+1\\ -s_ks_l-1\,, &\mbox{if } k=l-1\\ -s_ks_l\,, &\mbox{if }k<l-1 \end{array} \right. \quad \text{ for } k \text{ odd and } l \text{ even}\,. \end{align*} $$
$$ \begin{align*} \{ s_k,s_l \}=\left\{ \begin{array}{ll} s_ks_l \,, &\mbox{if } k>l\\ s_ks_l+1\,, &\mbox{if }k=l+1\\ -s_ks_l-1\,, &\mbox{if } k=l-1\\ -s_ks_l\,, &\mbox{if }k<l-1 \end{array} \right. \quad \text{ for } k \text{ odd and } l \text{ even}\,. \end{align*} $$
This is equivalent to
 $$ \begin{align*} \{ s_k,s_l \}=\left\{ \begin{array}{ll} -s_ks_l\,, &\mbox{if }k<l\\ -s_ks_l-1\,, &\mbox{if }k=l-1\\ s_ks_l+1\,, &\mbox{if }k=l+1\\ s_ks_l\,, &\mbox{if }k>l+1 \end{array} \right. \quad \text{ for } k \text{ even and } l \text{ odd}\,. \end{align*} $$
$$ \begin{align*} \{ s_k,s_l \}=\left\{ \begin{array}{ll} -s_ks_l\,, &\mbox{if }k<l\\ -s_ks_l-1\,, &\mbox{if }k=l-1\\ s_ks_l+1\,, &\mbox{if }k=l+1\\ s_ks_l\,, &\mbox{if }k>l+1 \end{array} \right. \quad \text{ for } k \text{ even and } l \text{ odd}\,. \end{align*} $$
Gathering these identities with the moment map identity (3.22), we get that the Poisson bracket is completely determined by
Using equation (1.7) and the subsequent Gauss decomposition, we note that we can equivalently parametrise
![]() $\widehat {\mathcal {B}}^{n+1}$
in terms of the elements
$\widehat {\mathcal {B}}^{n+1}$
in terms of the elements
![]() $\{s_j \mid 2\leq j\leq 2n+1\}$
such that
$\{s_j \mid 2\leq j\leq 2n+1\}$
such that
 $$ \begin{align} \begin{aligned} &\left(\begin{array}{cc} 1&0\\s_2&1 \end{array} \right) \left(\begin{array}{cc} 1&s_3\\0&1 \end{array} \right) \ldots \left(\begin{array}{cc} 1&0\\s_{2n}&1 \end{array} \right) \left(\begin{array}{cc} 1&s_{2n+1}\\0&1 \end{array} \right) \\ =& \left(\begin{array}{cc} 1&(s_3,\ldots,s_{2n+1})\lambda^{-1}\\0&1 \end{array} \right) \left(\begin{array}{cc} \lambda^{-1}&0\\0&\lambda \end{array} \right) \left(\begin{array}{cc} 1&0\\ \lambda^{-1} (s_2,\ldots,s_{2n})&1 \end{array} \right)\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left(\begin{array}{cc} 1&0\\s_2&1 \end{array} \right) \left(\begin{array}{cc} 1&s_3\\0&1 \end{array} \right) \ldots \left(\begin{array}{cc} 1&0\\s_{2n}&1 \end{array} \right) \left(\begin{array}{cc} 1&s_{2n+1}\\0&1 \end{array} \right) \\ =& \left(\begin{array}{cc} 1&(s_3,\ldots,s_{2n+1})\lambda^{-1}\\0&1 \end{array} \right) \left(\begin{array}{cc} \lambda^{-1}&0\\0&\lambda \end{array} \right) \left(\begin{array}{cc} 1&0\\ \lambda^{-1} (s_2,\ldots,s_{2n})&1 \end{array} \right)\,. \end{aligned} \end{align} $$
Consequently,
![]() $\widehat {\mathcal {B}}^{n+1}$
can be written as the following subspace of
$\widehat {\mathcal {B}}^{n+1}$
can be written as the following subspace of
![]() $\mathbb {C}^{2n+2}\times \mathbb {C}^{\times }$
:
$\mathbb {C}^{2n+2}\times \mathbb {C}^{\times }$
:
 $$ \begin{align} \left\{ \left(\begin{array}{cc} 1&s_1\\0&1 \end{array} \right)\left(\begin{array}{cc} 1&0\\s_2&1 \end{array} \right) \ldots \left(\begin{array}{cc} 1&s_{2n+1}\\0&1 \end{array} \right) \left(\begin{array}{cc} 1&0\\s_{2n+2}&1 \end{array} \right) \left(\begin{array}{cc} \lambda&0\\0&\lambda^{-1} \end{array} \right) = \operatorname{Id}_2 \right\}\,. \end{align} $$
$$ \begin{align} \left\{ \left(\begin{array}{cc} 1&s_1\\0&1 \end{array} \right)\left(\begin{array}{cc} 1&0\\s_2&1 \end{array} \right) \ldots \left(\begin{array}{cc} 1&s_{2n+1}\\0&1 \end{array} \right) \left(\begin{array}{cc} 1&0\\s_{2n+2}&1 \end{array} \right) \left(\begin{array}{cc} \lambda&0\\0&\lambda^{-1} \end{array} \right) = \operatorname{Id}_2 \right\}\,. \end{align} $$
Indeed, we recover equation (3.25) from equation (3.26) because the Gauss decomposition yields
Using the description of
![]() $\widehat {\mathcal {B}}^{n+1}$
given in equation (3.26), Bertola and Tarricone [Reference Bertola and Tarricone3] recently wrote the following Poisson bracket
$\widehat {\mathcal {B}}^{n+1}$
given in equation (3.26), Bertola and Tarricone [Reference Bertola and Tarricone3] recently wrote the following Poisson bracket
which was originally introduced by Flaschka and Newell [Reference Flaschka and Newell33]. By comparing the expressions (3.24a) and (3.28a) on the generators
![]() $\{s_j \mid 2\leq j\leq 2n+1\}$
, we directly see that the double quasi-Poisson bracket from Theorem 3.4 induces the Flaschka–Newell Poisson bracket on the representation space
$\{s_j \mid 2\leq j\leq 2n+1\}$
, we directly see that the double quasi-Poisson bracket from Theorem 3.4 induces the Flaschka–Newell Poisson bracket on the representation space
![]() $\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
(up to an irrelevant factor). In particular, equation (3.28b) is nothing else than the moment map condition.
$\operatorname {Rep}\big (\mathcal {B}(\Gamma _n),(1,1)\big )$
(up to an irrelevant factor). In particular, equation (3.28b) is nothing else than the moment map condition.
4 Proof of Theorem 3.4
In order to prove Theorem 3.4, we will show in § 4.2 that the double bracket defined by equation (3.10) is quasi-Poisson, that is, it satisfies equation (2.10). We then prove in § 4.3 that the components of the moment map
![]() $\Phi $
given in equation (3.11) satisfy equation (2.11), which finishes the proof. Before tackling these two steps, we will derive some preliminary identities in §4.1.
$\Phi $
given in equation (3.11) satisfy equation (2.11), which finishes the proof. Before tackling these two steps, we will derive some preliminary identities in §4.1.
4.1 Preparation for the proof
In this subsection we shall prove two results that we will extensively use in the proof of Theorem 3.4 below. We recall
![]() $(a_n,b_n)=e_2+a_nb_n$
, and
$(a_n,b_n)=e_2+a_nb_n$
, and
![]() $\ast $
denotes the inner bimodule multiplication from §2.1.1.
$\ast $
denotes the inner bimodule multiplication from §2.1.1.
Lemma 4.1. Consider the double bracket defined in equation (3.10). Then the following identities hold:
-
(i)
 $\{\mkern -6mu\{(a_n,b_n),a_i\}\mkern -6mu\}\!= \begin {cases} \;\;\,\frac {1}{2}\Big ((a_n,b_n)\otimes a_i-e_2\otimes (a_n,b_n)a_i\Big ), &\mbox {if } 1\leq i\leq n-1 \\ -\frac {1}{2}\Big ((a_n,b_n)\otimes a_n+e_2\otimes (a_n,b_n)a_n\Big ), &\mbox {if } i=n \end {cases}; $
$\{\mkern -6mu\{(a_n,b_n),a_i\}\mkern -6mu\}\!= \begin {cases} \;\;\,\frac {1}{2}\Big ((a_n,b_n)\otimes a_i-e_2\otimes (a_n,b_n)a_i\Big ), &\mbox {if } 1\leq i\leq n-1 \\ -\frac {1}{2}\Big ((a_n,b_n)\otimes a_n+e_2\otimes (a_n,b_n)a_n\Big ), &\mbox {if } i=n \end {cases}; $
-
(ii)
 $ \{\mkern -6mu\{(a_n,b_n),b_i\}\mkern -6mu\}\!= \begin {cases} \frac {1}{2}\Big (b_i\otimes (a_n,b_n)-b_i(a_n,b_n)\otimes e_2 \Big ), &\!\!\!\mbox {if } 1\leq i\leq n-2 \\ \frac {1}{2}\Big (b_{n-1}\otimes (a_n,b_n)-b_{n-1} (a_n,b_n)\otimes e_2\Big )\!-\!b_n\!\otimes \!e_2, &\!\!\!\mbox {if } i=n-1 \\ \frac {1}{2}\Big (b_n\otimes (a_n,b_n)+b_n(a_n,b_n)\otimes e_2\Big ), &\!\!\!\mbox {if } i=n \end {cases}. $
$ \{\mkern -6mu\{(a_n,b_n),b_i\}\mkern -6mu\}\!= \begin {cases} \frac {1}{2}\Big (b_i\otimes (a_n,b_n)-b_i(a_n,b_n)\otimes e_2 \Big ), &\!\!\!\mbox {if } 1\leq i\leq n-2 \\ \frac {1}{2}\Big (b_{n-1}\otimes (a_n,b_n)-b_{n-1} (a_n,b_n)\otimes e_2\Big )\!-\!b_n\!\otimes \!e_2, &\!\!\!\mbox {if } i=n-1 \\ \frac {1}{2}\Big (b_n\otimes (a_n,b_n)+b_n(a_n,b_n)\otimes e_2\Big ), &\!\!\!\mbox {if } i=n \end {cases}. $
Proof. To prove (i), if
![]() $1\leq i\leq n-1$
, by equations (2.6), (3.10a) and (3.10d), we obtain
$1\leq i\leq n-1$
, by equations (2.6), (3.10a) and (3.10d), we obtain
 $$ \begin{align*} \{\mkern-6mu\{(a_n,b_n),a_i\}\mkern-6mu\}&=a_n*\{\mkern-6mu\{b_n,a_i\}\mkern-6mu\}+\{\mkern-6mu\{a_n,a_i\}\mkern-6mu\}*b_n \\ &=-a_n*\Big(\frac{1}{2}\big(a_ib_n\otimes e_1+e_2\otimes b_na_i\big)\Big)+\Big(\frac{1}{2}\big(a_n\otimes a_i+a_i\otimes a_n\big)\Big)*b_n \\ &=\frac{1}{2}a_nb_n\otimes a_i-\frac{1}{2}e_2\otimes a_nb_na_i =\frac{1}{2}\Big((a_n,b_n)\otimes a_i-e_2\otimes (a_n,b_n)a_i\Big)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_n,b_n),a_i\}\mkern-6mu\}&=a_n*\{\mkern-6mu\{b_n,a_i\}\mkern-6mu\}+\{\mkern-6mu\{a_n,a_i\}\mkern-6mu\}*b_n \\ &=-a_n*\Big(\frac{1}{2}\big(a_ib_n\otimes e_1+e_2\otimes b_na_i\big)\Big)+\Big(\frac{1}{2}\big(a_n\otimes a_i+a_i\otimes a_n\big)\Big)*b_n \\ &=\frac{1}{2}a_nb_n\otimes a_i-\frac{1}{2}e_2\otimes a_nb_na_i =\frac{1}{2}\Big((a_n,b_n)\otimes a_i-e_2\otimes (a_n,b_n)a_i\Big)\,, \end{align*} $$
where we used
![]() $(a_n,b_n)=a_nb_n+e_2$
. Similarly, in (ii), the reader can prove the identity
$(a_n,b_n)=a_nb_n+e_2$
. Similarly, in (ii), the reader can prove the identity
![]() $2\{\mkern -6mu\{(a_n,b_n),b_i\}\mkern -6mu\}=b_i\otimes (a_n,b_n)-b_i(a_n,b_n)\otimes e_2 $
, for
$2\{\mkern -6mu\{(a_n,b_n),b_i\}\mkern -6mu\}=b_i\otimes (a_n,b_n)-b_i(a_n,b_n)\otimes e_2 $
, for
![]() $1\leq i\leq n-2$
.
$1\leq i\leq n-2$
.
Now, to prove the second formula in (i), since
![]() $\{\mkern -6mu\{a_n,a_n\}\mkern -6mu\}=0$
, by equation (3.10d) we have
$\{\mkern -6mu\{a_n,a_n\}\mkern -6mu\}=0$
, by equation (3.10d) we have
 $$ \begin{align*} \{\mkern-6mu\{(a_n,b_n),a_n\}\mkern-6mu\}&=a_n*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\} \\ &=-a_n*\Big(\frac{1}{2}\big(e_2\otimes b_na_n+a_nb_n\otimes e_2\big)+e_2\otimes e_1\Big) \\ &=-\frac{1}{2}\Big( (a_n,b_n)\otimes a_n+e_2\otimes (a_n,b_n)a_n\Big)\, , \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_n,b_n),a_n\}\mkern-6mu\}&=a_n*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\} \\ &=-a_n*\Big(\frac{1}{2}\big(e_2\otimes b_na_n+a_nb_n\otimes e_2\big)+e_2\otimes e_1\Big) \\ &=-\frac{1}{2}\Big( (a_n,b_n)\otimes a_n+e_2\otimes (a_n,b_n)a_n\Big)\, , \end{align*} $$
where we used again that
![]() $(a_n,b_n)=a_nb_n+e_2$
. Similarly, the reader can check that
$(a_n,b_n)=a_nb_n+e_2$
. Similarly, the reader can check that
![]() $2\{\mkern -6mu\{(a_n,b_n),b_n\}\mkern -6mu\}=b_n\otimes (a_n,b_n)+b_n(a_n,b_n)\otimes e_2$
holds in (ii).
$2\{\mkern -6mu\{(a_n,b_n),b_n\}\mkern -6mu\}=b_n\otimes (a_n,b_n)+b_n(a_n,b_n)\otimes e_2$
holds in (ii).
Finally, we prove the remaining identity in (ii). By equations (3.10b) and (3.10c),
 $$ \begin{align*} \{\mkern-6mu\{(&a_n,b_n),b_{n-1}\}\mkern-6mu\}=a_n*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_n,b_{n-1}\}\mkern-6mu\}*b_n \\ &=a_n*\Big(\frac{1}{2}\big(b_n\otimes b_{n-1}+b_{n-1}\otimes b_n\big)\Big) -\Big(\frac{1}{2}\big(b_{n-1}a_n\otimes e_2+e_1\otimes a_nb_{n-1}\big)+e_1\otimes e_2\Big)*b_n \\ &=\frac{1}{2}b_{n-1}\otimes a_nb_n-\frac{1}{2}b_{n-1}a_nb_n\otimes e_2-b_n\otimes e_2 \\ &=\frac{1}{2}\Big(b_{n-1}\otimes (a_n,b_n)-b_{n-1}(a_n,b_n)\otimes e_2\Big)-b_n\otimes e_2\,.\\[-45pt] \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(&a_n,b_n),b_{n-1}\}\mkern-6mu\}=a_n*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_n,b_{n-1}\}\mkern-6mu\}*b_n \\ &=a_n*\Big(\frac{1}{2}\big(b_n\otimes b_{n-1}+b_{n-1}\otimes b_n\big)\Big) -\Big(\frac{1}{2}\big(b_{n-1}a_n\otimes e_2+e_1\otimes a_nb_{n-1}\big)+e_1\otimes e_2\Big)*b_n \\ &=\frac{1}{2}b_{n-1}\otimes a_nb_n-\frac{1}{2}b_{n-1}a_nb_n\otimes e_2-b_n\otimes e_2 \\ &=\frac{1}{2}\Big(b_{n-1}\otimes (a_n,b_n)-b_{n-1}(a_n,b_n)\otimes e_2\Big)-b_n\otimes e_2\,.\\[-45pt] \end{align*} $$
Lemma 4.2. Consider the double bracket defined in equation (3.10). Then the following identities hold:
-
(i)
 $2\{\mkern -6mu\{(a_1,\dots , b_i),b_j\}\mkern -6mu\}=b_j(a_1,\dots , b_i)\otimes e_2-b_j\otimes (a_1,\dots , b_i)$
, with
$2\{\mkern -6mu\{(a_1,\dots , b_i),b_j\}\mkern -6mu\}=b_j(a_1,\dots , b_i)\otimes e_2-b_j\otimes (a_1,\dots , b_i)$
, with
 $1\leq i<j\leq n$
;
$1\leq i<j\leq n$
; -
(ii)
 $2\{\mkern -6mu\{(a_1,\dots , b_i),a_j\}\mkern -6mu\}=e_2\otimes (a_1,\dots , b_i)a_j- (a_1,\dots , b_i)\otimes a_j$
, with
$2\{\mkern -6mu\{(a_1,\dots , b_i),a_j\}\mkern -6mu\}=e_2\otimes (a_1,\dots , b_i)a_j- (a_1,\dots , b_i)\otimes a_j$
, with
 $j\geq i+2$
;
$j\geq i+2$
; -
(iii)
 $\{\mkern -6mu\{(a_1,\dots , b_i),a_{i+1}\}\mkern -6mu\}=\frac {1}{2}\Big (e_2\otimes (a_1,\dots , b_i)a_{i+1}- (a_1,\dots , b_i)\otimes a_{i+1}\Big )+e_2\otimes (a_1,\dots , a_i)$
, with
$\{\mkern -6mu\{(a_1,\dots , b_i),a_{i+1}\}\mkern -6mu\}=\frac {1}{2}\Big (e_2\otimes (a_1,\dots , b_i)a_{i+1}- (a_1,\dots , b_i)\otimes a_{i+1}\Big )+e_2\otimes (a_1,\dots , a_i)$
, with
 $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
Proof. We will prove these formulas by strong induction. To prove (i), we start noting that, by equations (3.10b) and (3.10c),
 $$ \begin{align} \begin{aligned} \{\mkern-6mu\{(a_i,b_i),b_j\}\mkern-6mu\}&=a_i*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_j\}\mkern-6mu\}*b_i \\ &=\frac{1}{2}b_ja_ib_i\otimes e_2-\frac{1}{2}b_j\otimes a_ib_i =\frac{1}{2}\Big(b_j(a_i,b_i)\otimes e_2-b_j\otimes (a_i,b_i)\Big)\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \{\mkern-6mu\{(a_i,b_i),b_j\}\mkern-6mu\}&=a_i*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_j\}\mkern-6mu\}*b_i \\ &=\frac{1}{2}b_ja_ib_i\otimes e_2-\frac{1}{2}b_j\otimes a_ib_i =\frac{1}{2}\Big(b_j(a_i,b_i)\otimes e_2-b_j\otimes (a_i,b_i)\Big)\,. \end{aligned} \end{align} $$
Then the base case arises when
![]() $i=1$
. Now, if
$i=1$
. Now, if
![]() $i\geq 2$
, by equation (3.6), we have
$i\geq 2$
, by equation (3.6), we have
 $$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, b_i),\,b_j\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\Big]+a_1b_i\Big),b_j\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{i-1})*\{\mkern-6mu\{(a_i,b_i),b_j\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{i-1}),b_j\}\mkern-6mu\}*(a_i,b_i) \\ &\quad +\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_j\}\mkern-6mu\}*b_i\Big] \\ &\quad +\sum^i_{\ell=3}\Big[ \{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_j\}\mkern-6mu\}*a_{\ell-1}b_i\Big]+a_1*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\}*b_i\,. \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, b_i),\,b_j\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\Big]+a_1b_i\Big),b_j\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{i-1})*\{\mkern-6mu\{(a_i,b_i),b_j\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{i-1}),b_j\}\mkern-6mu\}*(a_i,b_i) \\ &\quad +\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_j\}\mkern-6mu\}*b_i\Big] \\ &\quad +\sum^i_{\ell=3}\Big[ \{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_j\}\mkern-6mu\}*a_{\ell-1}b_i\Big]+a_1*\{\mkern-6mu\{b_i,b_j\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\}*b_i\,. \end{align*} $$
If we apply equation (4.1) in the first term and the inductive hypothesis in the second and fifth terms, we obtain
 $$ \begin{align*} &=\frac{1}{2}b_j(a_i,b_i)\otimes (a_1,\dots,b_{i-1})-\frac{1}{2}b_j\otimes (a_1,\dots,b_{i-1})(a_i,b_i) \\ &\quad +\frac{1}{2}\Big(b_j(a_1,\dots,b_{i-1})(a_i,b_i)\otimes e_2-b_j(a_i,b_i)\otimes (a_1,\dots,b_{i-1})\Big) \\ &\quad -\frac{1}{2}\sum^i_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_j+b_j\otimes (a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\Big] \\ &\quad+ \frac{1}{2}\sum^i_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_j+b_ja_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad+ \frac{1}{2}\sum^i_{\ell=3}\Big[b_j (a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes e_2-b_ja_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad -\frac{1}{2}\Big(b_i\otimes a_1b_j+b_j\otimes a_1b_i\Big)+\frac{1}{2}\Big(b_i\otimes a_1b_j+b_ja_1b_i\otimes e_2\Big) \\ &=\frac{1}{2}\Big(b_j (a_1,\dots,b_{i-1})(a_i,b_i)\otimes e_2+\sum^i_{\ell=3}\Big[b_j(a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\otimes e_2\Big]+b_ja_1b_i\otimes e_2\Big) \\ &\quad -\frac{1}{2}\Big(b_j\otimes (a_1,\dots,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[b_j\otimes(a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\Big]+b_j\otimes a_1b_i\Big) \\ &=\frac{1}{2}\Big(b_j(a_1,\dots,b_i)\otimes e_2-b_j\otimes (a_1,\dots, b_i)\Big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}b_j(a_i,b_i)\otimes (a_1,\dots,b_{i-1})-\frac{1}{2}b_j\otimes (a_1,\dots,b_{i-1})(a_i,b_i) \\ &\quad +\frac{1}{2}\Big(b_j(a_1,\dots,b_{i-1})(a_i,b_i)\otimes e_2-b_j(a_i,b_i)\otimes (a_1,\dots,b_{i-1})\Big) \\ &\quad -\frac{1}{2}\sum^i_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_j+b_j\otimes (a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\Big] \\ &\quad+ \frac{1}{2}\sum^i_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_j+b_ja_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad+ \frac{1}{2}\sum^i_{\ell=3}\Big[b_j (a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes e_2-b_ja_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad -\frac{1}{2}\Big(b_i\otimes a_1b_j+b_j\otimes a_1b_i\Big)+\frac{1}{2}\Big(b_i\otimes a_1b_j+b_ja_1b_i\otimes e_2\Big) \\ &=\frac{1}{2}\Big(b_j (a_1,\dots,b_{i-1})(a_i,b_i)\otimes e_2+\sum^i_{\ell=3}\Big[b_j(a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\otimes e_2\Big]+b_ja_1b_i\otimes e_2\Big) \\ &\quad -\frac{1}{2}\Big(b_j\otimes (a_1,\dots,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[b_j\otimes(a_1,\dots ,b_{\ell-2})a_{\ell-1}b_i\Big]+b_j\otimes a_1b_i\Big) \\ &=\frac{1}{2}\Big(b_j(a_1,\dots,b_i)\otimes e_2-b_j\otimes (a_1,\dots, b_i)\Big)\,, \end{align*} $$
where we used equation (3.6).
The proof of the formula in (ii) is pretty similar to (i), so it is left to the reader. Nevertheless, the formula in (iii) is slightly more delicate, so we prove it now. If
![]() $1\leq i\leq n-1$
, note that by equations (3.10a) and (3.10d), we get
$1\leq i\leq n-1$
, note that by equations (3.10a) and (3.10d), we get
 $$ \begin{align} \{\mkern-6mu\{(a_i,b_i),a_{i+1}\}\mkern-6mu\}&=a_i*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{a_i,a_{i+1}\}\mkern-6mu\}*b_{i} \nonumber\\ &=a_i*\Big(\frac{1}{2}\big(e_2\otimes b_ia_{i+1}+a_{i+1}b_i\otimes e_1\big)+e_2\otimes e_1\Big)-\frac{1}{2}\Big(a_i\otimes a_{i+1}+a_{i+1}\otimes a_i\Big)*b_i \nonumber\\ &=\frac{1}{2}e_2\otimes a_ib_ia_{i+1}+e_2\otimes a_{i}-\frac{1}{2}a_ib_i\otimes a_{i+1} \\ &=\frac{1}{2}\Big(e_2\otimes (a_i,b_i)a_{i+1}-(a_i,b_i)\otimes a_{i+1}\Big)+e_2\otimes (a_i)\,.\nonumber \end{align} $$
$$ \begin{align} \{\mkern-6mu\{(a_i,b_i),a_{i+1}\}\mkern-6mu\}&=a_i*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{a_i,a_{i+1}\}\mkern-6mu\}*b_{i} \nonumber\\ &=a_i*\Big(\frac{1}{2}\big(e_2\otimes b_ia_{i+1}+a_{i+1}b_i\otimes e_1\big)+e_2\otimes e_1\Big)-\frac{1}{2}\Big(a_i\otimes a_{i+1}+a_{i+1}\otimes a_i\Big)*b_i \nonumber\\ &=\frac{1}{2}e_2\otimes a_ib_ia_{i+1}+e_2\otimes a_{i}-\frac{1}{2}a_ib_i\otimes a_{i+1} \\ &=\frac{1}{2}\Big(e_2\otimes (a_i,b_i)a_{i+1}-(a_i,b_i)\otimes a_{i+1}\Big)+e_2\otimes (a_i)\,.\nonumber \end{align} $$
In particular, if
![]() $i=1$
, we have the base case of (iii).
$i=1$
, we have the base case of (iii).
Next, we address the general case by assuming that
![]() $i\geq 2$
. By equation (3.6),
$i\geq 2$
. By equation (3.6),
 $$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, b_i),a_{i+1}\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\Big]+a_1b_i\Big),a_{i+1}\right\}\!\!\!\right\} \\ &=(a_1,\dots, b_{i-1})*\{\mkern-6mu\{(a_i,b_i),a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{i-1}),a_{i+1}\}\mkern-6mu\}*(a_i,b_i) \\ &\quad +\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_{i+1}\}\mkern-6mu\}*b_i\Big] \\ &\quad +\sum^i_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_{i+1}\}\mkern-6mu\}*a_{\ell-1}b_i\Big] +a_1*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_{i+1}\}\mkern-6mu\}*b_i\,. \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, b_i),a_{i+1}\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{i-1})(a_i,b_i)+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\Big]+a_1b_i\Big),a_{i+1}\right\}\!\!\!\right\} \\ &=(a_1,\dots, b_{i-1})*\{\mkern-6mu\{(a_i,b_i),a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{i-1}),a_{i+1}\}\mkern-6mu\}*(a_i,b_i) \\ &\quad +\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_{i+1}\}\mkern-6mu\}*b_i\Big] \\ &\quad +\sum^i_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_{i+1}\}\mkern-6mu\}*a_{\ell-1}b_i\Big] +a_1*\{\mkern-6mu\{b_i,a_{i+1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_{i+1}\}\mkern-6mu\}*b_i\,. \end{align*} $$
Now, we apply equation (4.2) in the first summand and Lemma 4.2(ii) in the second and fifth summands to obtain
 $$ \begin{align*} &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{i-1})(a_i,b_i)a_{i+1}-(a_i,b_i)\otimes (a_1,\dots,b_{i-1})a_{i+1}\Big)+e_2\otimes (a_1,\dots,b_{i-1})a_i \\ &\; +\frac{1}{2}\Big((a_i,b_i)\otimes (a_1,\dots,b_{i-1})a_{i+1}-(a_1,\dots,b_{i-1})(a_i,b_i)\otimes a_{i+1}\Big) \\ &\; +\sum^i_{\ell=3}\Big[\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_ia_{i+1}+a_{i+1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big)+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\; -\frac{1}{2}\sum^i_{\ell=3}\Big[a_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{i+1}+a_{i+1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\; +\frac{1}{2}\sum^i_{\ell=3}\Big[a_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{i+1}-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes a_{i+1}\Big] \\ &\; +\frac{1}{2}\Big(e_2\otimes a_1b_ia_{i+1}+a_{i+1}b_i\otimes a_1\Big)+e_2\otimes a_1 -\frac{1}{2}\Big(a_1b_i\otimes a_{i+1}+a_{i+1}b_i\otimes a_1\Big) \\ &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{i-1})(a_i,b_i)a_{i+1}+\sum^i_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_ia_{i+1}\Big]+e_2\otimes a_1b_ia_{i+1}\Big) \\ &\;-\frac{1}{2}\Big((a_1,\dots,b_{i-1})(a_i,b_i)\otimes a_{i+1}+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes a_{i+1}+a_1b_i\otimes a_{i+1}\Big) \\ &\;+e_2\otimes (a_1,\dots,b_{i-1})a_i+\sum^i_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+e_2\otimes a_1 \\ &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_i)a_{i+1}-(a_1,\dots,b_i)\otimes a_{i+1}\Big)+e_2\otimes (a_1,\dots,a_i)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{i-1})(a_i,b_i)a_{i+1}-(a_i,b_i)\otimes (a_1,\dots,b_{i-1})a_{i+1}\Big)+e_2\otimes (a_1,\dots,b_{i-1})a_i \\ &\; +\frac{1}{2}\Big((a_i,b_i)\otimes (a_1,\dots,b_{i-1})a_{i+1}-(a_1,\dots,b_{i-1})(a_i,b_i)\otimes a_{i+1}\Big) \\ &\; +\sum^i_{\ell=3}\Big[\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_ia_{i+1}+a_{i+1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big)+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\; -\frac{1}{2}\sum^i_{\ell=3}\Big[a_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{i+1}+a_{i+1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\; +\frac{1}{2}\sum^i_{\ell=3}\Big[a_{\ell-1}b_i\otimes (a_1,\dots,b_{\ell-2})a_{i+1}-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes a_{i+1}\Big] \\ &\; +\frac{1}{2}\Big(e_2\otimes a_1b_ia_{i+1}+a_{i+1}b_i\otimes a_1\Big)+e_2\otimes a_1 -\frac{1}{2}\Big(a_1b_i\otimes a_{i+1}+a_{i+1}b_i\otimes a_1\Big) \\ &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{i-1})(a_i,b_i)a_{i+1}+\sum^i_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_ia_{i+1}\Big]+e_2\otimes a_1b_ia_{i+1}\Big) \\ &\;-\frac{1}{2}\Big((a_1,\dots,b_{i-1})(a_i,b_i)\otimes a_{i+1}+\sum^i_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_i\otimes a_{i+1}+a_1b_i\otimes a_{i+1}\Big) \\ &\;+e_2\otimes (a_1,\dots,b_{i-1})a_i+\sum^i_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]+e_2\otimes a_1 \\ &=\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_i)a_{i+1}-(a_1,\dots,b_i)\otimes a_{i+1}\Big)+e_2\otimes (a_1,\dots,a_i)\,, \end{align*} $$
where in the last identity we used equations (3.6) and (3.5).
4.2 The double bracket (3.10) is quasi-Poisson
By its definition, it is clear that
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
, as given in equation (3.10), is a B-linear double bracket on
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
, as given in equation (3.10), is a B-linear double bracket on
![]() $\mathcal {B}(\Gamma _n)$
. In order to prove that the pair
$\mathcal {B}(\Gamma _n)$
. In order to prove that the pair
![]() $(\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\})$
is a double quasi-Poisson algebra, we need to show that
$(\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\})$
is a double quasi-Poisson algebra, we need to show that
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
satisfies equation (2.10) for every triple of generators
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
satisfies equation (2.10) for every triple of generators
![]() $\{x_i,y_j,z_k\}$
, with
$\{x_i,y_j,z_k\}$
, with
![]() $x_i,y_j,z_k\in \{a_{\ell },b_{\ell }\mid 1\leq \ell \leq n\}$
, by distinguishing every possible case. To do that, we need to attend to the number of a’s and b’s occurring in such a triple. We essentially have four cases:Footnote
7
$x_i,y_j,z_k\in \{a_{\ell },b_{\ell }\mid 1\leq \ell \leq n\}$
, by distinguishing every possible case. To do that, we need to attend to the number of a’s and b’s occurring in such a triple. We essentially have four cases:Footnote
7
![]() $(a_i,a_j,a_k)$
,
$(a_i,a_j,a_k)$
,
![]() $(a_i,a_j,b_k)$
,
$(a_i,a_j,b_k)$
,
![]() $(b_i,b_j,a_k)$
and
$(b_i,b_j,a_k)$
and
![]() $(b_i,b_j,b_k)$
. Then, we shall keep track of the relations of the indices
$(b_i,b_j,b_k)$
. Then, we shall keep track of the relations of the indices
![]() $i,j,k$
with respect to the natural total order
$i,j,k$
with respect to the natural total order
![]() $\leq $
on
$\leq $
on
![]() $\mathbb {N}$
. By cyclicity of the triple bracket without loss of generality, we will assume that the distinct element, if any, is in the third position.
$\mathbb {N}$
. By cyclicity of the triple bracket without loss of generality, we will assume that the distinct element, if any, is in the third position.
Firstly, we note the following general result.
Lemma 4.3. Let
![]() $A_0$
be an algebra over
$A_0$
be an algebra over
![]() $B_0$
, where
$B_0$
, where
![]() $B_0$
contains orthogonal idempotents
$B_0$
contains orthogonal idempotents
![]() $e_1,e_2$
. Assume that
$e_1,e_2$
. Assume that
![]() $A_0$
is endowed with a
$A_0$
is endowed with a
![]() $B_0$
-linear double bracket
$B_0$
-linear double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
and that there exist elements
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
and that there exist elements
![]() $c_i\in e_2 A_0 e_1$
,
$c_i\in e_2 A_0 e_1$
,
![]() $i\in \{1,\ldots ,n\}$
, such that
$i\in \{1,\ldots ,n\}$
, such that
with
![]() $\epsilon _{ij}\in \Bbbk $
. Then
$\epsilon _{ij}\in \Bbbk $
. Then
![]() $\epsilon _{ij}=-\epsilon _{ji}$
, and we have that the quasi-Poisson property (2.10) is satisfied when evaluated on any triples from
$\epsilon _{ij}=-\epsilon _{ji}$
, and we have that the quasi-Poisson property (2.10) is satisfied when evaluated on any triples from
![]() $\{c_i\}$
if and only if
$\{c_i\}$
if and only if
for all
![]() $i,j,k\in \{1,\ldots ,n\}$
with
$i,j,k\in \{1,\ldots ,n\}$
with
![]() $(i,j,k)\neq (i,i,i)$
, that is, the three indices are not all equal.
$(i,j,k)\neq (i,i,i)$
, that is, the three indices are not all equal.
Proof. Clearly, the cyclic antisymmetry implies that
![]() $\epsilon _{ij}=-\epsilon _{ji}$
. The quasi-Poisson property (2.10) on
$\epsilon _{ij}=-\epsilon _{ji}$
. The quasi-Poisson property (2.10) on
![]() $c_i,c_j,c_k$
reads:
$c_i,c_j,c_k$
reads:
Now, we can compute that
 $$ \begin{align*} \{\mkern-6mu\{c_i,\{\mkern-6mu\{c_j,c_k\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{jk} [\epsilon_{ij} (c_i \otimes c_j \otimes c_k + c_j \otimes c_i \otimes c_k) + \epsilon_{ik} (c_i \otimes c_k \otimes c_j + c_k \otimes c_i \otimes c_j) ] \\ \tau_{(123)}\{\mkern-6mu\{c_j,\{\mkern-6mu\{c_k,c_i\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{ki} [\epsilon_{jk} (c_i \otimes c_j \otimes c_k + c_i \otimes c_k \otimes c_j) + \epsilon_{ji} (c_k \otimes c_j \otimes c_i + c_k \otimes c_i \otimes c_j) ] \\ \tau_{(132)}\{\mkern-6mu\{c_k,\{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{ij} [\epsilon_{ki} (c_i \otimes c_j \otimes c_k + c_k \otimes c_j \otimes c_i) + \epsilon_{kj} (c_j \otimes c_i \otimes c_k + c_k \otimes c_i \otimes c_j) ]. \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{c_i,\{\mkern-6mu\{c_j,c_k\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{jk} [\epsilon_{ij} (c_i \otimes c_j \otimes c_k + c_j \otimes c_i \otimes c_k) + \epsilon_{ik} (c_i \otimes c_k \otimes c_j + c_k \otimes c_i \otimes c_j) ] \\ \tau_{(123)}\{\mkern-6mu\{c_j,\{\mkern-6mu\{c_k,c_i\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{ki} [\epsilon_{jk} (c_i \otimes c_j \otimes c_k + c_i \otimes c_k \otimes c_j) + \epsilon_{ji} (c_k \otimes c_j \otimes c_i + c_k \otimes c_i \otimes c_j) ] \\ \tau_{(132)}\{\mkern-6mu\{c_k,\{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}\}\mkern-6mu\}_L &= \epsilon_{ij} [\epsilon_{ki} (c_i \otimes c_j \otimes c_k + c_k \otimes c_j \otimes c_i) + \epsilon_{kj} (c_j \otimes c_i \otimes c_k + c_k \otimes c_i \otimes c_j) ]. \end{align*} $$
Using the identity
![]() $\epsilon _{ij}=-\epsilon _{ji}$
, we obtain
$\epsilon _{ij}=-\epsilon _{ji}$
, we obtain
which satisfies equation (4.5) if and only if
![]() $C_{ijk}=-\frac 14$
when
$C_{ijk}=-\frac 14$
when
![]() $i,j,k$
are not all equal.
$i,j,k$
are not all equal.
In our case, we note that, if we consider
![]() $A_0=\Bbbk \overline {\Gamma }_n$
(or
$A_0=\Bbbk \overline {\Gamma }_n$
(or
![]() $\mathcal {B}(\Gamma _n)$
directly),
$\mathcal {B}(\Gamma _n)$
directly),
![]() $B_0=B$
and the elements
$B_0=B$
and the elements
![]() $c_i=a_i$
, then equation (3.10a) takes the form (4.3) for
$c_i=a_i$
, then equation (3.10a) takes the form (4.3) for
We can then directly verify that the condition (4.4) holds in the cases
Due to the cyclic antisymmetry (2.4), these are the only cases to check, and we obtain from Lemma 4.3 that equation (2.10) holds on any triple
![]() $(a_i,a_j, a_k)$
with
$(a_i,a_j, a_k)$
with
![]() $i,j,k\in \{1,\dots , n\}$
.
$i,j,k\in \{1,\dots , n\}$
.
Secondly, we shall show that equation (2.10) holds for every triple
![]() $(b_i,b_j,b_k)$
, where
$(b_i,b_j,b_k)$
, where
![]() $1\leq i,j,k\leq n$
. In fact, this can be obtained by an application of Lemma 4.3, but we shall use a different method that we will employ below. As in the proof of [Reference Van den Bergh41, Theorem 6.5.1], we note the existence of an automorphism of order two on
$1\leq i,j,k\leq n$
. In fact, this can be obtained by an application of Lemma 4.3, but we shall use a different method that we will employ below. As in the proof of [Reference Van den Bergh41, Theorem 6.5.1], we note the existence of an automorphism of order two on
![]() $\Bbbk \overline {\Gamma }_n$
, namely S, given by
$\Bbbk \overline {\Gamma }_n$
, namely S, given by
for all
![]() $1\leq \ell \leq n$
. By inspection on equation (3.10), we can see that this automorphism has the effect
$1\leq \ell \leq n$
. By inspection on equation (3.10), we can see that this automorphism has the effect
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}\mapsto -\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. Moreover, this automorphism has no effect on the triple bracket
$\{\mkern -6mu\{-,-\}\mkern -6mu\}\mapsto -\{\mkern -6mu\{-,-\}\mkern -6mu\}$
. Moreover, this automorphism has no effect on the triple bracket
![]() $\{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
defined by equation (2.8); in other words,
$\{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
defined by equation (2.8); in other words,
![]() $\{\mkern -6mu\{-,-,-\}\mkern -6mu\}\mapsto \{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
. Once we have just proved that the identity
$\{\mkern -6mu\{-,-,-\}\mkern -6mu\}\mapsto \{\mkern -6mu\{-,-,-\}\mkern -6mu\}$
. Once we have just proved that the identity
![]() $4\{\mkern -6mu\{a_i,a_j,a_k\}\mkern -6mu\}=a_k\otimes a_i\otimes a_j-a_i\otimes a_j\otimes a_k$
is satisfied for all
$4\{\mkern -6mu\{a_i,a_j,a_k\}\mkern -6mu\}=a_k\otimes a_i\otimes a_j-a_i\otimes a_j\otimes a_k$
is satisfied for all
![]() $1\leq i,j,k\leq n$
, we can apply the automorphism S to this identity to obtain
$1\leq i,j,k\leq n$
, we can apply the automorphism S to this identity to obtain
for all
![]() $1\leq i,j,k\leq n$
. In this way, we can conclude that equation (2.10) also holds for every triple
$1\leq i,j,k\leq n$
. In this way, we can conclude that equation (2.10) also holds for every triple
![]() $(b_i,b_j,b_k)$
, where
$(b_i,b_j,b_k)$
, where
![]() $1\leq i,j,k\leq n$
.
$1\leq i,j,k\leq n$
.
Thirdly, we will prove that the bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
defined in equation (3.10) satisfies equation (2.10) for triples
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
defined in equation (3.10) satisfies equation (2.10) for triples
![]() $(a_i,a_j,b_k)$
, where
$(a_i,a_j,b_k)$
, where
![]() $1\leq i,j,k\leq n$
. To achieve this purpose, we shall distinguish the different cases attending to the different values of the indices
$1\leq i,j,k\leq n$
. To achieve this purpose, we shall distinguish the different cases attending to the different values of the indices
![]() $i,j,k$
. To begin with, note that in this case the right-hand side of equation (2.10) reduces to
$i,j,k$
. To begin with, note that in this case the right-hand side of equation (2.10) reduces to
Now, the simplest case occurs when the three indices are equal, namely
![]() $i=j=k$
. Then, since
$i=j=k$
. Then, since
![]() $\{\mkern -6mu\{a_i,a_i\}\mkern -6mu\}=0$
, and by equations (3.10a), (3.10c) and (3.10d), at the left-hand side of equation (2.10) we obtain
$\{\mkern -6mu\{a_i,a_i\}\mkern -6mu\}=0$
, and by equations (3.10a), (3.10c) and (3.10d), at the left-hand side of equation (2.10) we obtain
 $$ \begin{align*} \{\mkern-6mu\{a_i,a_i,b_i\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_i,\{\mkern-6mu\{b_i,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(a_i\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ia_i\otimes a_i\otimes e_2+e_1\otimes a_ib_ia_i\otimes e_2+2e_1\otimes a_i\otimes e_2\Big) \\ &\quad-\frac{\tau_{(123)}}{4}\Big(a_ib_ia_i\otimes e_2\otimes e_1+a_i\otimes a_ib_i\otimes e_1+2a_i\otimes e_2\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ia_i\otimes a_i\otimes e_2-e_1\otimes a_i\otimes a_ib_i\Big)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i,a_i,b_i\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_i,\{\mkern-6mu\{b_i,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(a_i\{\mkern-6mu\{a_i,b_i\}\mkern-6mu\}\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ia_i\otimes a_i\otimes e_2+e_1\otimes a_ib_ia_i\otimes e_2+2e_1\otimes a_i\otimes e_2\Big) \\ &\quad-\frac{\tau_{(123)}}{4}\Big(a_ib_ia_i\otimes e_2\otimes e_1+a_i\otimes a_ib_i\otimes e_1+2a_i\otimes e_2\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ia_i\otimes a_i\otimes e_2-e_1\otimes a_i\otimes a_ib_i\Big)\,, \end{align*} $$
which coincides with equation (4.10).
Now, we address the cases when two indices coincide. If
![]() $i=j$
and
$i=j$
and
![]() $i<k$
, by equations (3.10c) and (3.10d),
$i<k$
, by equations (3.10c) and (3.10d),
 $$ \begin{align*} \{\mkern-6mu\{a_i,a_i,b_k\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_i,\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(a_i\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}\otimes e_1\Big) \\ &=\frac{1}{4}\Big(e_1\otimes a_ib_ka_i\otimes e_2+b_ka_i\otimes a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_ib_k\otimes e_1+a_ib_ka_i\otimes e_2\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_i\otimes e_2-e_1\otimes a_i\otimes a_ib_k\Big)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i,a_i,b_k\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_i,\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(a_i\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}\otimes e_1\Big) \\ &=\frac{1}{4}\Big(e_1\otimes a_ib_ka_i\otimes e_2+b_ka_i\otimes a_i\otimes e_2\Big)-\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_ib_k\otimes e_1+a_ib_ka_i\otimes e_2\otimes e_1\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_i\otimes e_2-e_1\otimes a_i\otimes a_ib_k\Big)\,, \end{align*} $$
as we wished. Similarly, the reader can check that the four cases occurring when
![]() $i=k$
and
$i=k$
and
![]() $j\neq k$
, and
$j\neq k$
, and
![]() $j=k$
and
$j=k$
and
![]() $i\neq k$
are completely analogous to the previous ones.
$i\neq k$
are completely analogous to the previous ones.
Finally, we address the six possible cases of triples
![]() $(a_i,a_j,b_k)$
when
$(a_i,a_j,b_k)$
when
![]() $i,j,k$
are all distinct. Let
$i,j,k$
are all distinct. Let
![]() $(a_i,a_j,b_k)$
with
$(a_i,a_j,b_k)$
with
![]() $i<j<k$
. Then, by equations (3.10a), (3.10c) and (3.10d), we obtain
$i<j<k$
. Then, by equations (3.10a), (3.10c) and (3.10d), we obtain
 $$ \begin{align*} \{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_j,\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(132)}\{\mkern-6mu\{b_k,\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) -\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=-\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2-b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1+a_j\otimes a_ib_k\otimes e_1+a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j+a_jb_k\otimes e_1\otimes a_i+e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,; \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\}&=\{\mkern-6mu\{a_i,\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(123)}\{\mkern-6mu\{a_j,\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\}\mkern-6mu\}_L+\tau_{(132)}\{\mkern-6mu\{b_k,\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}\}\mkern-6mu\}_L \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) -\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=-\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2-b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1+a_j\otimes a_ib_k\otimes e_1+a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j+a_jb_k\otimes e_1\otimes a_i+e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,; \end{align*} $$
consequently, equation (2.10) holds. The following case occurs when
![]() $i<j$
,
$i<j$
,
![]() $i<k$
and
$i<k$
and
![]() $j>k$
:
$j>k$
:
 $$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k \big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2-b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad +\frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1+2\delta_{j-k,1}(a_i\otimes e_2\otimes e_1)-a_j\otimes a_ib_k\otimes e_1 \\ &\qquad \qquad -a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j-e_2\otimes b_ka_j\otimes a_i-a_jb_k\otimes e_1\otimes a_i \\ &\qquad \qquad -2\delta_{j-k,1}(e_2\otimes e_1\otimes a_i)\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big)-\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k \big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2-b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad +\frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1+2\delta_{j-k,1}(a_i\otimes e_2\otimes e_1)-a_j\otimes a_ib_k\otimes e_1 \\ &\qquad \qquad -a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j-e_2\otimes b_ka_j\otimes a_i-a_jb_k\otimes e_1\otimes a_i \\ &\qquad \qquad -2\delta_{j-k,1}(e_2\otimes e_1\otimes a_i)\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
which is tantamount to equation (4.10). The next case occurs when
![]() $i<j$
,
$i<j$
,
![]() $i>k$
and
$i>k$
and
![]() $j>k$
. It is important to note that with these constraints
$j>k$
. It is important to note that with these constraints
![]() $j-k\neq 1$
because the condition
$j-k\neq 1$
because the condition
![]() $j-k=1$
would imply that
$j-k=1$
would imply that
![]() $0<i-k<1$
, which is a contradiction since
$0<i-k<1$
, which is a contradiction since
![]() $i,k\in \mathbb {N}$
. Then, by equations (3.10a), (3.10c) and (3.10d), we have
$i,k\in \mathbb {N}$
. Then, by equations (3.10a), (3.10c) and (3.10d), we have
 $$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) +\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2+b_ka_i\otimes a_j\otimes e_2+e_1\otimes a_ib_ka_j\otimes e_2+2\delta_{i-k,1}(e_1\otimes a_j\otimes e_2)\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+2\delta_{i-k,1}(e_2\otimes e_1\otimes a_j)+e_2\otimes b_ka_j\otimes a_i \\ &\qquad \qquad +a_jb_k\otimes e_1\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) +\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2+b_ka_i\otimes a_j\otimes e_2+e_1\otimes a_ib_ka_j\otimes e_2+2\delta_{i-k,1}(e_1\otimes a_j\otimes e_2)\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+2\delta_{i-k,1}(e_2\otimes e_1\otimes a_j)+e_2\otimes b_ka_j\otimes a_i \\ &\qquad \qquad +a_jb_k\otimes e_1\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
which is equation (4.10). Next, to prove that the bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
as defined in equation (3.10) is a double quasi-Poisson bracket, we need to check that equation (2.10) holds for the triple
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
as defined in equation (3.10) is a double quasi-Poisson bracket, we need to check that equation (2.10) holds for the triple
![]() $(a_i,a_j,b_k)$
, whose indices are subject to the constraints
$(a_i,a_j,b_k)$
, whose indices are subject to the constraints
![]() $i>j$
,
$i>j$
,
![]() $j>k$
and
$j>k$
and
![]() $i>k$
. Note that
$i>k$
. Note that
![]() $i-k\neq 1$
. If not,
$i-k\neq 1$
. If not,
![]() $0<j-k<1$
that contradicts the fact that
$0<j-k<1$
that contradicts the fact that
![]() $j,k\in \mathbb {N}$
. Then,
$j,k\in \mathbb {N}$
. Then,
 $$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big)+\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=-\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2\Big) \\ &\quad - \frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1+2\delta_{j-k,1}(a_i\otimes e_2\otimes e_1)+a_j\otimes a_ib_k\otimes e_1 \\ &\qquad \qquad +a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_j\otimes a_i+a_jb_k\otimes e_1\otimes a_i \\ &\qquad \qquad +2\delta_{j-k,1}(e_2\otimes e_1\otimes a_i)\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big) \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=-\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big)+\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=-\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2\Big) \\ &\quad - \frac{\tau_{(123)}}{4}\Big(a_ib_ka_j\otimes e_2\otimes e_1+a_i\otimes a_jb_k\otimes e_1+2\delta_{j-k,1}(a_i\otimes e_2\otimes e_1)+a_j\otimes a_ib_k\otimes e_1 \\ &\qquad \qquad +a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_j\otimes a_i+a_jb_k\otimes e_1\otimes a_i \\ &\qquad \qquad +2\delta_{j-k,1}(e_2\otimes e_1\otimes a_i)\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big) \end{align*} $$
that is just the right-hand side of equation (2.10). Next, the fifth case that we need to study comes from the triple
![]() $(a_i,a_j,b_k)$
such that
$(a_i,a_j,b_k)$
such that
![]() $i>j$
,
$i>j$
,
![]() $j<k$
and
$j<k$
and
![]() $i>k$
. Then
$i>k$
. Then
 $$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) +\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2 \\ &\qquad \qquad -2\delta_{i-k,1}(e_1\otimes a_j\otimes e_2)\Big) \\ &\quad +\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+2\delta_{i-k,1}(e_2\otimes e_1\otimes a_j)-a_jb_k\otimes e_1\otimes a_i \\ &\qquad\qquad -e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) +\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2-b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_ib_ka_j\otimes e_2 \\ &\qquad \qquad -2\delta_{i-k,1}(e_1\otimes a_j\otimes e_2)\Big) \\ &\quad +\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{4}\Big(e_2\otimes b_ka_i\otimes a_j+a_ib_k\otimes e_1\otimes a_j+2\delta_{i-k,1}(e_2\otimes e_1\otimes a_j)-a_jb_k\otimes e_1\otimes a_i \\ &\qquad\qquad -e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
which proves equation (2.10). The final case for a triple
![]() $(a_i,a_j,b_k)$
, with
$(a_i,a_j,b_k)$
, with
![]() $i,j,k$
distinct occurs when
$i,j,k$
distinct occurs when
![]() $i>j$
,
$i>j$
,
![]() $j<k$
and
$j<k$
and
![]() $i<k$
. So, by equations (3.10a), (3.10c) and (3.10d), we can write
$i<k$
. So, by equations (3.10a), (3.10c) and (3.10d), we can write
 $$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) -\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2+e_1\otimes a_ib_ka_j\otimes e_2+b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j+a_jb_k\otimes e_1\otimes a_i+e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{a_i,a_j,b_k\}\mkern-6mu\} \\ &=\frac{1}{2}\Big(\big(b_k\{\mkern-6mu\{a_i,a_j\}\mkern-6mu\}+\{\mkern-6mu\{a_i,b_k\}\mkern-6mu\}a_j\big)\otimes e_2\Big) -\frac{\tau_{(123)}}{2}\Big(\big(a_i\{\mkern-6mu\{a_j,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_j,a_i\}\mkern-6mu\}b_k\big)\otimes e_1\Big) \\ &\quad +\frac{\tau_{(132)}}{2}\Big(\{\mkern-6mu\{b_k,a_i\}\mkern-6mu\}\otimes a_j+\{\mkern-6mu\{b_k,a_j\}\mkern-6mu\}\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2+b_ka_j\otimes a_i\otimes e_2+e_1\otimes a_ib_ka_j\otimes e_2+b_ka_i\otimes a_j\otimes e_2\Big) \\ &\quad -\frac{\tau_{(123)}}{4}\Big(a_i\otimes a_jb_k\otimes e_1+a_ib_ka_j\otimes e_2\otimes e_1-a_j\otimes a_ib_k\otimes e_1-a_i\otimes a_jb_k\otimes e_1\Big) \\ &\quad -\frac{\tau_{(132)}}{4}\Big(a_ib_k\otimes e_1\otimes a_j+e_2\otimes b_ka_i\otimes a_j+a_jb_k\otimes e_1\otimes a_i+e_2\otimes b_ka_j\otimes a_i\Big) \\ &=\frac{1}{4}\Big(b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k\Big)\,, \end{align*} $$
as we wanted. So we can conclude that equation (2.10) holds for every triple
![]() $(a_i,a_j,b_k)$
, where
$(a_i,a_j,b_k)$
, where
![]() $1\leq i,j,k\leq n$
.
$1\leq i,j,k\leq n$
.
Finally, we deal with the case
![]() $(b_i,b_j,a_k)$
, with
$(b_i,b_j,a_k)$
, with
![]() $1\leq i,j,k\leq n$
. Since we proved that equation (2.10) is fulfilled for every triple
$1\leq i,j,k\leq n$
. Since we proved that equation (2.10) is fulfilled for every triple
![]() $(a_i,a_j,b_k)$
, that is,
$(a_i,a_j,b_k)$
, that is,
![]() $4\{\mkern -6mu\{a_i,a_j,b_k\}\mkern -6mu\}=b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k$
, we can apply the automorphism S on
$4\{\mkern -6mu\{a_i,a_j,b_k\}\mkern -6mu\}=b_ka_i\otimes a_j\otimes e_2-e_1\otimes a_i\otimes a_jb_k$
, we can apply the automorphism S on
![]() $\Bbbk \overline {\Gamma }_n$
defined in equation (4.9) to obtain the identity
$\Bbbk \overline {\Gamma }_n$
defined in equation (4.9) to obtain the identity
which holds for all indices
![]() $i,j,k\in \{1,\dots ,n\}$
. Hence, equation (2.10) is also satisfied for a given triple
$i,j,k\in \{1,\dots ,n\}$
. Hence, equation (2.10) is also satisfied for a given triple
![]() $(b_i,b_j,a_k)$
with
$(b_i,b_j,a_k)$
with
![]() $1\leq i,j,k\leq n$
.
$1\leq i,j,k\leq n$
.
To sum up, we proved that the pair
![]() $(\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\})$
(in fact, the pair
$(\mathcal {B}(\Gamma _n),\{\mkern -6mu\{-,-\}\mkern -6mu\})$
(in fact, the pair
![]() $(\Bbbk \overline {\Gamma }_n,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
), where
$(\Bbbk \overline {\Gamma }_n,\{\mkern -6mu\{-,-\}\mkern -6mu\})$
), where
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
was defined in equation (3.10), is a double quasi-Poisson algebra (over B).
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
was defined in equation (3.10), is a double quasi-Poisson algebra (over B).
4.3 The element (3.11) is a multiplicative moment map
In this subsection, we proceed to prove that equation (3.11) is a multiplicative moment map; in other words, we show that equation (3.11) satisfies equation (2.11) for
![]() $s\in \{1,2\}$
and
$s\in \{1,2\}$
and
![]() $a_1,\dots ,a_n,b_1,\dots , b_n$
, which are the generators of
$a_1,\dots ,a_n,b_1,\dots , b_n$
, which are the generators of
![]() $\mathcal {B}(\Gamma _n)$
. We write
$\mathcal {B}(\Gamma _n)$
. We write
![]() $\Phi =\Phi _1+\Phi _2$
, where
$\Phi =\Phi _1+\Phi _2$
, where
Since Euler continuants are defined by the recursive relation (3.3), we shall use strong induction. Note that the base case is given by Theorem 2.12(i). Next, to fix ideas, the inductive hypothesis states that lower Euler continuants satisfy equation (2.11). In particular, using the orthogonality of the idempotents, the inductive hypothesis gives rise to the formulas
where
![]() $\ell \in \{1,\dots ,n-1\}$
and
$\ell \in \{1,\dots ,n-1\}$
and
![]() $1\leq i\leq \ell $
.
$1\leq i\leq \ell $
.
By the very definition of the double quasi-Poisson bracket (3.10), we need to distinguish different cases, depending on the use of the inductive hypothesis and Lemma 4.2.
Let
![]() $b_i\in \{b_1,\dots ,b_n\}$
. Then, since
$b_i\in \{b_1,\dots ,b_n\}$
. Then, since
![]() $e_ie_j=\delta _{i,j}e_i$
for
$e_ie_j=\delta _{i,j}e_i$
for
![]() $i,j\in \{1,2\}$
, the identity (2.11) reduces to
$i,j\in \{1,2\}$
, the identity (2.11) reduces to
 $$ \begin{align} \begin{aligned} \{\mkern-6mu\{\Phi_2,b_i\}\mkern-6mu\}&=\frac{1}{2}\Big(b_i\otimes \Phi_2+b_i\Phi_2\otimes e_2\Big) \\ &=\frac{1}{2}\Big(b_i\otimes(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_i\otimes a_1b_n \\ &\quad + b_i(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_i(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_ia_1b_n\otimes e_2\Big)\,, \end{aligned}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} \{\mkern-6mu\{\Phi_2,b_i\}\mkern-6mu\}&=\frac{1}{2}\Big(b_i\otimes \Phi_2+b_i\Phi_2\otimes e_2\Big) \\ &=\frac{1}{2}\Big(b_i\otimes(a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_i\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_i\otimes a_1b_n \\ &\quad + b_i(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_i(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_ia_1b_n\otimes e_2\Big)\,, \end{aligned}\\[-15pt]\nonumber \end{align} $$
where in the last identity we applied equation (3.6).
To begin with, we shall check equation (2.11) for
![]() $b_1$
. Using the left Leibniz rule (2.6) in the first argument (that makes the inner action appear) and separating the case
$b_1$
. Using the left Leibniz rule (2.6) in the first argument (that makes the inner action appear) and separating the case
![]() $\ell =3$
in the sum to keep track of
$\ell =3$
in the sum to keep track of
![]() $\{\mkern -6mu\{a_2,b_1\}\mkern -6mu\}$
, we can write
$\{\mkern -6mu\{a_2,b_1\}\mkern -6mu\}$
, we can write
 $$ \begin{align*} \{\mkern-6mu\{&\Phi_2,b_1\}\mkern-6mu\}=\{\mkern-6mu\{(a_1,\dots,b_n),b_1\}\mkern-6mu\} \\ &= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_1\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_1\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots ,b_{n-1}),b_1\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots, b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_1\}\mkern-6mu\}\Big] +(a_1,b_1)*\{\mkern-6mu\{a_2,b_1\}\mkern-6mu\}*b_n \\ &\quad +\sum^{n}_{\ell=4}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_1\}\mkern-6mu\}*b_n \Big] +\sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_1\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad + a_1*\{\mkern-6mu\{b_n,b_1\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_1\}\mkern-6mu\}*b_n\,. \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{&\Phi_2,b_1\}\mkern-6mu\}=\{\mkern-6mu\{(a_1,\dots,b_n),b_1\}\mkern-6mu\} \\ &= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_1\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_1\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots ,b_{n-1}),b_1\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots, b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_1\}\mkern-6mu\}\Big] +(a_1,b_1)*\{\mkern-6mu\{a_2,b_1\}\mkern-6mu\}*b_n \\ &\quad +\sum^{n}_{\ell=4}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_1\}\mkern-6mu\}*b_n \Big] +\sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_1\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad + a_1*\{\mkern-6mu\{b_n,b_1\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_1\}\mkern-6mu\}*b_n\,. \end{align*} $$
By Lemma 4.1(ii), the inductive hypothesis (4.11b) and equation (3.10), we have
 $$ \begin{align*} &=\frac{1}{2}\Big(b_1\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_1(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_1(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_1(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_1+b_1\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad -\frac{1}{2}\Big(b_1a_2b_n\otimes (a_1,b_1)+b_n\otimes (a_1,b_1)a_2b_1\Big)-b_n\otimes (a_1,b_1) \\ &\quad -\frac{1}{2}\sum^n_{\ell=4}\Big[b_1a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_1\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_1a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_1(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_1+b_1\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_1a_1b_n\otimes e_2+b_n\otimes a_1b_1\Big)+b_n\otimes e_2 \\ &=\frac{1}{2}\Big(b_1\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_1\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_1\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_1(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_1(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_1a_1b_n\otimes e_2\Big] \\ &\quad -b_n\otimes (a_1,b_1)+b_n\otimes a_1b_1+b_n\otimes e_2 \\ &=\frac{1}{2}\big(b_1\otimes \Phi_2+b_1\Phi_2\otimes e_2\big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_1\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_1(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_1(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_1(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_1+b_1\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad -\frac{1}{2}\Big(b_1a_2b_n\otimes (a_1,b_1)+b_n\otimes (a_1,b_1)a_2b_1\Big)-b_n\otimes (a_1,b_1) \\ &\quad -\frac{1}{2}\sum^n_{\ell=4}\Big[b_1a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_1\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_1a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_1(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_1+b_1\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_1a_1b_n\otimes e_2+b_n\otimes a_1b_1\Big)+b_n\otimes e_2 \\ &=\frac{1}{2}\Big(b_1\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_1\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_1\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_1(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_1(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_1a_1b_n\otimes e_2\Big] \\ &\quad -b_n\otimes (a_1,b_1)+b_n\otimes a_1b_1+b_n\otimes e_2 \\ &=\frac{1}{2}\big(b_1\otimes \Phi_2+b_1\Phi_2\otimes e_2\big)\,, \end{align*} $$
where the last identity is due to equation (3.6).
Now, we need to check equation (2.11) for an arrow
![]() $b_k$
, where
$b_k$
, where
![]() $k\in \{2,\dots ,n-2\}$
is fixed. Then,
$k\in \{2,\dots ,n-2\}$
is fixed. Then,
 $$ \begin{align*} \{\mkern-6mu\{&\Phi_2,b_k\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_k\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_k\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_k\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_k\}\mkern-6mu\}\Big]+\sum^k_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_k\}\mkern-6mu\}*b_n\Big] \\ &\quad +(a_1,\dots,b_{k-1})*\{\mkern-6mu\{a_k,b_k\}\mkern-6mu\}*b_n+(a_1,\dots,b_k)*\{\mkern-6mu\{a_{k+1},b_k\}\mkern-6mu\}*b_n \\ &\quad + \sum^n_{\ell=k+3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_k\}\mkern-6mu\}*b_n\Big] +\sum^{k+1}_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +\sum^n_{\ell=k+2}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] +a_1*\{\mkern-6mu\{b_n,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_k\}\mkern-6mu\}*b_n\,. \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{&\Phi_2,b_k\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots ,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_k\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_k\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_k\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_k\}\mkern-6mu\}\Big]+\sum^k_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_k\}\mkern-6mu\}*b_n\Big] \\ &\quad +(a_1,\dots,b_{k-1})*\{\mkern-6mu\{a_k,b_k\}\mkern-6mu\}*b_n+(a_1,\dots,b_k)*\{\mkern-6mu\{a_{k+1},b_k\}\mkern-6mu\}*b_n \\ &\quad + \sum^n_{\ell=k+3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_k\}\mkern-6mu\}*b_n\Big] +\sum^{k+1}_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +\sum^n_{\ell=k+2}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] +a_1*\{\mkern-6mu\{b_n,b_k\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_k\}\mkern-6mu\}*b_n\,. \end{align*} $$
Applying Lemma 4.1(ii) in the first summand, the inductive hypothesis (4.11b) in the second and ninth summands and Lemma 4.2(i) in the eighth one, we obtain:
 $$ \begin{align*} &=\frac{1}{2}\Big(b_k\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_k(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_k(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_k(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k+b_k\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad +\frac{1}{2}\sum^k_{\ell=3}\Big[b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big] \\ &\quad +\frac{1}{2}\Big(b_ka_kb_n\otimes (a_1,\dots ,b_{k-1}) +b_n\otimes (a_1,\dots,b_{k-1})a_kb_k\Big)+b_n\otimes (a_1,\dots,b_{k-1}) \\ &\quad-\frac{1}{2}\Big(b_ka_{k+1}b_n\otimes (a_1,\dots ,b_k)+b_n\otimes (a_1,\dots,b_k)a_{k+1}b_k\Big)-b_n\otimes (a_1,\dots ,b_k) \\ &\quad -\frac{1}{2}\sum^n_{\ell=k+3}\Big[b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big] \\ &\quad +\frac{1}{2}\sum^{k+1}_{\ell=3}\Big[b_k(a_1,\dots, b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\sum^{n}_{\ell=k+2}\Big[b_k(a_1,\dots, b_{\ell-2})a_{\ell-1}b_n\otimes e_2+b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_k+b_k\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_ka_1b_n\otimes e_2+b_n\otimes a_1b_k\Big). \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_k\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_k(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_k(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_k(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k+b_k\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad +\frac{1}{2}\sum^k_{\ell=3}\Big[b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big] \\ &\quad +\frac{1}{2}\Big(b_ka_kb_n\otimes (a_1,\dots ,b_{k-1}) +b_n\otimes (a_1,\dots,b_{k-1})a_kb_k\Big)+b_n\otimes (a_1,\dots,b_{k-1}) \\ &\quad-\frac{1}{2}\Big(b_ka_{k+1}b_n\otimes (a_1,\dots ,b_k)+b_n\otimes (a_1,\dots,b_k)a_{k+1}b_k\Big)-b_n\otimes (a_1,\dots ,b_k) \\ &\quad -\frac{1}{2}\sum^n_{\ell=k+3}\Big[b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})+b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big] \\ &\quad +\frac{1}{2}\sum^{k+1}_{\ell=3}\Big[b_k(a_1,\dots, b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\sum^{n}_{\ell=k+2}\Big[b_k(a_1,\dots, b_{\ell-2})a_{\ell-1}b_n\otimes e_2+b_ka_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_k+b_k\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_ka_1b_n\otimes e_2+b_n\otimes a_1b_k\Big). \end{align*} $$
At this point, if in the third line we rewrite
 $$ \begin{align*} \begin{split} \sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]=\sum^k_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]+b_n\otimes (a_1,\dots,b_{k-1})a_kb_k \\ +\ b_n\otimes (a_1,\dots,b_{k})a_{k+1}b_k+\sum^n_{\ell=k+3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]\,, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]=\sum^k_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]+b_n\otimes (a_1,\dots,b_{k-1})a_kb_k \\ +\ b_n\otimes (a_1,\dots,b_{k})a_{k+1}b_k+\sum^n_{\ell=k+3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]\,, \end{split} \end{align*} $$
we can cancel some terms, obtaining
 $$ \begin{align*} &=\frac{1}{2}\Big(b_k\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_k\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_k\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_k(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_k(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_ka_1b_n\otimes e_2\Big) \\ &\quad -b_n\otimes (a_1,,\dots,b_k)+b_n\otimes (a_1,\dots,b_{k-1})(a_k,b_k)\\&\quad +\sum^k_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]+b_n\otimes a_1b_k \\ &=\frac{1}{2}\big(b_k\otimes \Phi_2+b_k\Phi_2\otimes e_2\big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_k\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_k\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_k\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_k(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2+\sum^n_{\ell=3}\Big[b_k(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2\Big]+b_ka_1b_n\otimes e_2\Big) \\ &\quad -b_n\otimes (a_1,,\dots,b_k)+b_n\otimes (a_1,\dots,b_{k-1})(a_k,b_k)\\&\quad +\sum^k_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_k\Big]+b_n\otimes a_1b_k \\ &=\frac{1}{2}\big(b_k\otimes \Phi_2+b_k\Phi_2\otimes e_2\big)\,, \end{align*} $$
where in the last identity we used equation (3.6).
Now, we shall show the validity of equation (2.11) for
![]() $b_{n-1}$
. By equation (3.5) and the left Leibniz rule (2.6) of the double bracket, we can write
$b_{n-1}$
. By equation (3.5) and the left Leibniz rule (2.6) of the double bracket, we can write
 $$ \begin{align*} &\{\mkern-6mu\{\Phi_2,b_{n-1}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_{n-1}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_{n-1}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}\Big] \\ &\quad +\sum^{n-1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_{n-1}\}\mkern-6mu\}*b_n\Big]+(a_1,\dots,b_{n-2})*\{\mkern-6mu\{a_{n-1},b_{n-1}\}\mkern-6mu\}*b_n \\ &\quad +\sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_{n-1}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+a_1*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_{n-1}\}\mkern-6mu\}*b_n\,. \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{\Phi_2,b_{n-1}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_{n-1}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_{n-1}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}\Big] \\ &\quad +\sum^{n-1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_{n-1}\}\mkern-6mu\}*b_n\Big]+(a_1,\dots,b_{n-2})*\{\mkern-6mu\{a_{n-1},b_{n-1}\}\mkern-6mu\}*b_n \\ &\quad +\sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_{n-1}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+a_1*\{\mkern-6mu\{b_n,b_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,b_{n-1}\}\mkern-6mu\}*b_n\,. \end{align*} $$
Applying Lemma 4.1(ii) in the first term, the inductive hypothesis in the second one and Lemma 4.2(i), we obtain
 $$ \begin{align*} &=\frac{1}{2}\Big(b_{n-1}\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_{n-1}(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big)-b_n\otimes (a_1,\dots,b_{n-1}) \\ &\quad +\frac{1}{2}\Big(b_{n-1}(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_{n-1}(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}+b_{n-1}\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad +\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}+b_{n-1}a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad + \frac{1}{2}\Big(b_{n-1}a_{n-1}b_n\otimes (a_1,\dots,b_{n-2})+b_n\otimes (a_1,\dots,b_{n-2})a_{n-1}b_{n-1}\Big)+b_n\otimes (a_1,\dots,b_{n-2}) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_{n-1}(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_{n-1}a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_{n-1}+b_{n-1}\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_n\otimes a_1b_{n-1}+b_{n-1}a_1b_n\otimes e_2\Big)\,. \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_{n-1}\otimes (a_1,\dots,b_{n-1})(a_n,b_n)-b_{n-1}(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big)-b_n\otimes (a_1,\dots,b_{n-1}) \\ &\quad +\frac{1}{2}\Big(b_{n-1}(a_n,b_n)\otimes (a_1,\dots,b_{n-1})+b_{n-1}(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}+b_{n-1}\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big] \\ &\quad +\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}+b_{n-1}a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad + \frac{1}{2}\Big(b_{n-1}a_{n-1}b_n\otimes (a_1,\dots,b_{n-2})+b_n\otimes (a_1,\dots,b_{n-2})a_{n-1}b_{n-1}\Big)+b_n\otimes (a_1,\dots,b_{n-2}) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_{n-1}(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_{n-1}a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_{n-1}+b_{n-1}\otimes a_1b_n\Big)+\frac{1}{2}\Big(b_n\otimes a_1b_{n-1}+b_{n-1}a_1b_n\otimes e_2\Big)\,. \end{align*} $$
We can cancel some terms to obtain
 $$ \begin{align*} &=\frac{1}{2}\Big(b_{n-1}\otimes(a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_{n-1}\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_{n-1}\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_{n-1}(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2 +\sum^n_{\ell=3}\Big[b_{n-1}(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2 +b_{n-1}a_1b_n\otimes e_2\Big) \\ &\quad -b_n\otimes (a_1,\dots,b_{n-1})+b_n\otimes (a_1,\dots,b_{n-2})(a_{n-1},b_{n-1})+\sum^{n-1}_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}\Big] \\ &\quad +b_n\otimes a_1b_{n-1} \\ &=\frac{1}{2}\big(b_{n-1}\otimes \Phi_2+b_{n-1}\Phi_2\otimes e_2\big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_{n-1}\otimes(a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[b_{n-1}\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+b_{n-1}\otimes a_1b_n\Big) \\ &\quad +\frac{1}{2}\Big(b_{n-1}(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2 +\sum^n_{\ell=3}\Big[b_{n-1}(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2 +b_{n-1}a_1b_n\otimes e_2\Big) \\ &\quad -b_n\otimes (a_1,\dots,b_{n-1})+b_n\otimes (a_1,\dots,b_{n-2})(a_{n-1},b_{n-1})+\sum^{n-1}_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_{n-1}\Big] \\ &\quad +b_n\otimes a_1b_{n-1} \\ &=\frac{1}{2}\big(b_{n-1}\otimes \Phi_2+b_{n-1}\Phi_2\otimes e_2\big)\,, \end{align*} $$
which is tantamount to equation (4.12).
Finally, we shall prove that equation (2.11) holds for
![]() $b_n$
via equation (4.12). Then,
$b_n$
via equation (4.12). Then,
 $$ \begin{align*} &\{\mkern-6mu\{\Phi_2,b_{n}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_{n}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_{n}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_{n}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^{n}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_{n}\}\mkern-6mu\}*b_n+\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_{n}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+\{\mkern-6mu\{a_1,b_{n}\}\mkern-6mu\}*b_n\,, \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{\Phi_2,b_{n}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),b_{n}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),b_{n}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),b_{n}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^{n}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},b_{n}\}\mkern-6mu\}*b_n+\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),b_{n}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+\{\mkern-6mu\{a_1,b_{n}\}\mkern-6mu\}*b_n\,, \end{align*} $$
where we used that
![]() $\{\mkern -6mu\{b_n,b_n\}\mkern -6mu\}=0$
. Now, by Lemma 4.1(ii) and Lemma 4.2(i), we have
$\{\mkern -6mu\{b_n,b_n\}\mkern -6mu\}=0$
. Now, by Lemma 4.1(ii) and Lemma 4.2(i), we have
 $$ \begin{align*} &=\frac{1}{2}\Big(b_n\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+b_n(a_n,b_n)\otimes (a_1,\dots, b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_n(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2-b_n(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1} b_n+b_na_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_na_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_n+b_na_1b_n\otimes e_2\Big) \\ &=\frac{1}{2}\big(b_{n}\otimes \Phi_2+b_{n}\Phi_2\otimes e_2\big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big(b_n\otimes (a_1,\dots,b_{n-1})(a_n,b_n)+b_n(a_n,b_n)\otimes (a_1,\dots, b_{n-1})\Big) \\ &\quad +\frac{1}{2}\Big(b_n(a_1,\dots,b_{n-1})(a_n,b_n)\otimes e_2-b_n(a_n,b_n)\otimes (a_1,\dots,b_{n-1})\Big) \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1} b_n+b_na_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[b_n(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes e_2-b_na_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})\Big] \\ &\quad +\frac{1}{2}\Big(b_n\otimes a_1b_n+b_na_1b_n\otimes e_2\Big) \\ &=\frac{1}{2}\big(b_{n}\otimes \Phi_2+b_{n}\Phi_2\otimes e_2\big)\,, \end{align*} $$
where, once again, in the last identity we applied equation (3.6). To sum up, so far, we proved that equation (2.11) holds for
![]() $\Phi _2$
and
$\Phi _2$
and
![]() $b_i\in \{b_1,\dots ,b_n\}$
.
$b_i\in \{b_1,\dots ,b_n\}$
.
Next, let
![]() $a_i\in \{a_1,\dots ,a_n\}$
. Then, since
$a_i\in \{a_1,\dots ,a_n\}$
. Then, since
![]() $e_ie_j=\delta _{i,j}e_i$
for
$e_ie_j=\delta _{i,j}e_i$
for
![]() $i,j\in \{1,2\}$
, equation (2.11) reduces to
$i,j\in \{1,2\}$
, equation (2.11) reduces to
 $$ \begin{align} \begin{aligned} \{\mkern-6mu\{&\Phi_2,a_i\}\mkern-6mu\}=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_i+\Phi_2\otimes a_i\Big) \\ &=-\frac{1}{2}\Big(e_2\otimes(a_1,\dots ,b_{n-1})(a_n,b_n)a_i+ \sum^n_{\ell=3} \Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_i\Big]+e_2\otimes a_1b_na_i \\ &\quad + (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_i+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_i\Big]+a_1b_n\otimes a_i\Big)\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \{\mkern-6mu\{&\Phi_2,a_i\}\mkern-6mu\}=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_i+\Phi_2\otimes a_i\Big) \\ &=-\frac{1}{2}\Big(e_2\otimes(a_1,\dots ,b_{n-1})(a_n,b_n)a_i+ \sum^n_{\ell=3} \Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_i\Big]+e_2\otimes a_1b_na_i \\ &\quad + (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_i+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_i\Big]+a_1b_n\otimes a_i\Big)\,, \end{aligned} \end{align} $$
where we used equation (3.6).
Now, applying the left Leibniz rule (2.6) and using that
![]() $\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
, we can write
$\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
, we can write
 $$ \begin{align*} &\{\mkern-6mu\{\Phi_2,a_1\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_1\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_1\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots, b_{n-1}),a_1\}\mkern-6mu\}*(a_n,b_n) \\ &\quad+ \sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_1\}\mkern-6mu\} +(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_1\}\mkern-6mu\}*b_n\Big] \\ &\quad + \sum^n_{\ell=3}\Big[ \{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_1\}\mkern-6mu\}*a_{\ell-1}b_n\Big] +a_1*\{\mkern-6mu\{b_n,a_1\}\mkern-6mu\}\,. \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{\Phi_2,a_1\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_1\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_1\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots, b_{n-1}),a_1\}\mkern-6mu\}*(a_n,b_n) \\ &\quad+ \sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_1\}\mkern-6mu\} +(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_1\}\mkern-6mu\}*b_n\Big] \\ &\quad + \sum^n_{\ell=3}\Big[ \{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_1\}\mkern-6mu\}*a_{\ell-1}b_n\Big] +a_1*\{\mkern-6mu\{b_n,a_1\}\mkern-6mu\}\,. \end{align*} $$
Using Lemma 4.1(i) in the first term and the inductive hypothesis (4.11a) in the second and fifth terms,
 $$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_1-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_1\Big) \\ &\quad -\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_1+(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_1\Big) \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_1b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_1\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_1+a_1b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_1+(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_1 \Big] \\ &\quad -\frac{1}{2}\Big(a_1b_n\otimes a_1+e_2\otimes a_1b_na_1\Big) \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_1+\Phi_2\otimes a_1\Big)\,, \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_1-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_1\Big) \\ &\quad -\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_1+(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_1\Big) \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_1b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_1\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_1+a_1b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_1+(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_1 \Big] \\ &\quad -\frac{1}{2}\Big(a_1b_n\otimes a_1+e_2\otimes a_1b_na_1\Big) \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_1+\Phi_2\otimes a_1\Big)\,, \end{align*} $$
where we used equation (3.6) in the last identity. Thus, equation (2.11) holds for
![]() $a_1$
.
$a_1$
.
Next, we need to prove first that equation (2.11) holds for
![]() $a_2,\dots , a_{n-2}$
. Since the proof is similar, we are going to fix
$a_2,\dots , a_{n-2}$
. Since the proof is similar, we are going to fix
![]() $k\in \{2,\dots , n-2\}$
, and we shall show that equation (2.11) is satisfied for the arrow
$k\in \{2,\dots , n-2\}$
, and we shall show that equation (2.11) is satisfied for the arrow
![]() $a_k$
. By equation (3.6),
$a_k$
. By equation (3.6),
 $$ \begin{align*} \{\mkern-6mu\{\Phi_2,a_k\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots, b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_k\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_k\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_k\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_k\}\mkern-6mu\}\Big] +\sum^k_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_k\}\mkern-6mu\}*b_n\Big] \\ &\quad +\sum^n_{\ell=k+2}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_k\}\mkern-6mu\}*b_n\Big] +\sum^k_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +\{\mkern-6mu\{(a_1,\dots,b_{k-1}),a_k\}\mkern-6mu\}*a_kb_n +\sum^n_{\ell=k+2}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +a_1*\{\mkern-6mu\{b_n,a_k\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_k\}\mkern-6mu\}*b_n\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{\Phi_2,a_k\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots, b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_k\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_k\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_k\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_k\}\mkern-6mu\}\Big] +\sum^k_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_k\}\mkern-6mu\}*b_n\Big] \\ &\quad +\sum^n_{\ell=k+2}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_k\}\mkern-6mu\}*b_n\Big] +\sum^k_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +\{\mkern-6mu\{(a_1,\dots,b_{k-1}),a_k\}\mkern-6mu\}*a_kb_n +\sum^n_{\ell=k+2}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_k\}\mkern-6mu\}*a_{\ell-1}b_n\Big] \\ &\quad +a_1*\{\mkern-6mu\{b_n,a_k\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_k\}\mkern-6mu\}*b_n\,, \end{align*} $$
where we used that
![]() $\{\mkern -6mu\{a_k,a_k\}\mkern -6mu\}=0$
. Now, we use Lemma 4.1(i) in the first summand, the inductive hypothesis in the second and eighth terms, Lemma 4.2(ii) in the sixth term and Lemma 4.2(iii) in the seventh summand.
$\{\mkern -6mu\{a_k,a_k\}\mkern -6mu\}=0$
. Now, we use Lemma 4.1(i) in the first summand, the inductive hypothesis in the second and eighth terms, Lemma 4.2(ii) in the sixth term and Lemma 4.2(iii) in the seventh summand.
 $$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_k-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_k\Big) \\ &\quad -\frac{1}{2}\Big((a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_k+(a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_k\Big) \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_k\Big] \\ &\quad -\frac{1}{2}\sum^k_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=k+2}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^k_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big] \\ &\quad +\frac{1}{2}\Big(a_kb_n\otimes (a_1,\dots,b_{k-1})a_k-(a_1,\dots,b_{k-1})a_kb_n\otimes a_k\Big)+a_kb_n\otimes (a_1,\dots,a_{k-1}) \\ &\quad-\frac{1}{2}\sum^n_{\ell=k+2}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big] \\ &\quad -\frac{1}{2}\Big(a_kb_n\otimes a_1+e_2\otimes a_1b_na_k\Big)-\frac{1}{2}\Big(a_1b_n\otimes a_k+a_kb_n\otimes a_1\Big)\,. \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_k-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_k\Big) \\ &\quad -\frac{1}{2}\Big((a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_k+(a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_k\Big) \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_k\Big] \\ &\quad -\frac{1}{2}\sum^k_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=k+2}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^k_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big] \\ &\quad +\frac{1}{2}\Big(a_kb_n\otimes (a_1,\dots,b_{k-1})a_k-(a_1,\dots,b_{k-1})a_kb_n\otimes a_k\Big)+a_kb_n\otimes (a_1,\dots,a_{k-1}) \\ &\quad-\frac{1}{2}\sum^n_{\ell=k+2}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_k+(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big] \\ &\quad -\frac{1}{2}\Big(a_kb_n\otimes a_1+e_2\otimes a_1b_na_k\Big)-\frac{1}{2}\Big(a_1b_n\otimes a_k+a_kb_n\otimes a_1\Big)\,. \end{align*} $$
Some terms cancel each other, giving
 $$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_k+\sum^n_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_k\Big]+e_2\otimes a_1b_na_k\Big) \\ &\quad -\frac{1}{2}\Big((a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_k+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big]+a_1b_n\otimes a_k\Big) \\ &\quad +a_kb_n\otimes (a_1,\dots,a_{k-1})-\sum^k_{\ell=3}\Big[a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]-a_kb_n\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_k+\Phi_2\otimes a_k\Big)\,. \end{align*} $$
$$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_k+\sum^n_{\ell=3}\Big[e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_k\Big]+e_2\otimes a_1b_na_k\Big) \\ &\quad -\frac{1}{2}\Big((a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_k+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_k\Big]+a_1b_n\otimes a_k\Big) \\ &\quad +a_kb_n\otimes (a_1,\dots,a_{k-1})-\sum^k_{\ell=3}\Big[a_kb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]-a_kb_n\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_k+\Phi_2\otimes a_k\Big)\,. \end{align*} $$
Consequently, we can conclude that equation (2.11) holds for
![]() $a_2,\dots ,a_{n-2}$
.
$a_2,\dots ,a_{n-2}$
.
Now, we proceed to prove that
![]() $a_{n-1}$
satisfies equation (2.11), that is, we need to show that
$a_{n-1}$
satisfies equation (2.11), that is, we need to show that
![]() $2\{\mkern -6mu\{\Phi _2,a_{n-1}\}\mkern -6mu\}=-\big (e_2\otimes \Phi _2a_{n-1}+\Phi _2\otimes a_{n-1}\big )$
. By equation (3.6),
$2\{\mkern -6mu\{\Phi _2,a_{n-1}\}\mkern -6mu\}=-\big (e_2\otimes \Phi _2a_{n-1}+\Phi _2\otimes a_{n-1}\big )$
. By equation (3.6),
 $$ \begin{align*} \{\mkern-6mu\{\Phi_2,a_{n-1}\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_{n-1}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_{n-1}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_{n-1}\}\mkern-6mu\}\Big]+\sum^{n-1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_{n-1}\}\mkern-6mu\}*b_n\Big] \\ &\quad+ \sum^{n-1}_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_{n-1}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+\{\mkern-6mu\{(a_1,\dots,b_{n-2}),a_{n-1}\}\mkern-6mu\}*a_{n-1}b_n \\ &\quad + a_1*\{\mkern-6mu\{b_n,a_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_{n-1}\}\mkern-6mu\}*b_n\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{\Phi_2,a_{n-1}\}\mkern-6mu\}&= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_{n-1}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_{n-1}\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_{n-1}\}\mkern-6mu\}\Big]+\sum^{n-1}_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_{n-1}\}\mkern-6mu\}*b_n\Big] \\ &\quad+ \sum^{n-1}_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_{n-1}\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+\{\mkern-6mu\{(a_1,\dots,b_{n-2}),a_{n-1}\}\mkern-6mu\}*a_{n-1}b_n \\ &\quad + a_1*\{\mkern-6mu\{b_n,a_{n-1}\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_{n-1}\}\mkern-6mu\}*b_n\,, \end{align*} $$
where we used that
![]() $\{\mkern -6mu\{a_{n-1},a_{n-1}\}\mkern -6mu\}=0$
. Next, we apply Lemma 4.1(i) to the first summand, the inductive hypothesis to the second summand, Lemma 4.2(ii) to the fifth term and Lemma 4.2(iii) in the sixth one.
$\{\mkern -6mu\{a_{n-1},a_{n-1}\}\mkern -6mu\}=0$
. Next, we apply Lemma 4.1(i) to the first summand, the inductive hypothesis to the second summand, Lemma 4.2(ii) to the fifth term and Lemma 4.2(iii) in the sixth one.
 $$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_{n-1}-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_{n-1}\Big) \\ &\quad -\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_{n-1}+(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_{n-1}\Big) \\ &\quad -\frac{1}{2}\sum^{n}_{\ell=3}\Big[a_{n-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_{n-1}\Big] \\ &\quad -\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{n-1}+a_{n-1}b_n\otimes (a_1,\dots, b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{n-1}-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_{n-1}\Big] \\ &\quad +\frac{1}{2}\Big(a_{n-1}b_n\otimes (a_1,\dots,b_{n-2})a_{n-1}-(a_1,\dots,b_{n-2})a_{n-1}b_n\otimes a_{n-1}\Big)+a_{n-1}b_n\otimes (a_1,\dots, a_{n-2}) \\ &\quad -\frac{1}{2}\Big(a_{n-1}b_n\otimes a_1+e_2\otimes a_1b_na_{n-1}\Big)-\frac{1}{2}\Big(a_1b_n\otimes a_{n-1}+a_{n-1}b_n\otimes a_1\Big)\,. \end{align*} $$
$$ \begin{align*} &=\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_{n-1}-e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_{n-1}\Big) \\ &\quad -\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_{n-1}+(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_{n-1}\Big) \\ &\quad -\frac{1}{2}\sum^{n}_{\ell=3}\Big[a_{n-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_{n-1}\Big] \\ &\quad -\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{n-1}+a_{n-1}b_n\otimes (a_1,\dots, b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^{n-1}_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{n-1}-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_{n-1}\Big] \\ &\quad +\frac{1}{2}\Big(a_{n-1}b_n\otimes (a_1,\dots,b_{n-2})a_{n-1}-(a_1,\dots,b_{n-2})a_{n-1}b_n\otimes a_{n-1}\Big)+a_{n-1}b_n\otimes (a_1,\dots, a_{n-2}) \\ &\quad -\frac{1}{2}\Big(a_{n-1}b_n\otimes a_1+e_2\otimes a_1b_na_{n-1}\Big)-\frac{1}{2}\Big(a_1b_n\otimes a_{n-1}+a_{n-1}b_n\otimes a_1\Big)\,. \end{align*} $$
If we cancel some terms and use both equations (3.6) and (3.5), we obtain
 $$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_{n-1} +\sum^n_{\ell=3}\Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_{n-1}\Big] +e_2\otimes a_1b_na_{n-1} \Big) \\ &\quad -\frac{1}{2} \Big( (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_{n-1} +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_{n-1}\Big] + a_1b_n\otimes a_{n-1} \Big) \\ &\quad +a_{n-1}b_n\otimes (a_1,\dots,a_{n-2})-\sum^{n-1}_{\ell=3}\Big[a_{n-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]- a_{n-1}b_n\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_{n-1}+\Phi_2\otimes a_{n-1}\Big)\,. \end{align*} $$
$$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_{n-1} +\sum^n_{\ell=3}\Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_{n-1}\Big] +e_2\otimes a_1b_na_{n-1} \Big) \\ &\quad -\frac{1}{2} \Big( (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_{n-1} +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_{n-1}\Big] + a_1b_n\otimes a_{n-1} \Big) \\ &\quad +a_{n-1}b_n\otimes (a_1,\dots,a_{n-2})-\sum^{n-1}_{\ell=3}\Big[a_{n-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]- a_{n-1}b_n\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_{n-1}+\Phi_2\otimes a_{n-1}\Big)\,. \end{align*} $$
Finally, we check equation (2.11) for
![]() $a_{n}$
via equation (4.13). Once again, by equation (3.6),
$a_{n}$
via equation (4.13). Once again, by equation (3.6),
 $$ \begin{align*} &\{\mkern-6mu\{\Phi_2,a_{n}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_{n}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_n\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_n\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_n\}\mkern-6mu\}*b_n\Big] \\ &\quad + \sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_n\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+ a_1*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_n\}\mkern-6mu\}*b_n\,. \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{\Phi_2,a_{n}\}\mkern-6mu\}= \left\{\!\!\!\left\{\Big((a_1,\dots,b_{n-1})(a_n,b_n)+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\Big]+a_1b_n\Big),a_{n}\right\}\!\!\!\right\} \\ &=(a_1,\dots,b_{n-1})*\{\mkern-6mu\{(a_n,b_n),a_n\}\mkern-6mu\}+\{\mkern-6mu\{(a_1,\dots,b_{n-1}),a_n\}\mkern-6mu\}*(a_n,b_n) \\ &\quad +\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\}+(a_1,\dots,b_{\ell-2})*\{\mkern-6mu\{a_{\ell-1},a_n\}\mkern-6mu\}*b_n\Big] \\ &\quad + \sum^n_{\ell=3}\Big[\{\mkern-6mu\{(a_1,\dots,b_{\ell-2}),a_n\}\mkern-6mu\}*a_{\ell-1}b_n\Big]+ a_1*\{\mkern-6mu\{b_n,a_n\}\mkern-6mu\}+\{\mkern-6mu\{a_1,a_n\}\mkern-6mu\}*b_n\,. \end{align*} $$
Now, applying Lemma 4.1(i) to the first summand, Lemma 4.2(iii) in the second term, and Lemma 4.2(ii) in the fifth term, we get
 $$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots ,b_{n-1})(a_n,b_n)a_n+(a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_n\Big) \\ &\quad +\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_n-(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_n\Big)+(a_n,b_n)\otimes (a_1,\dots,a_{n-1}) \\ &\quad -\sum^n_{\ell=3}\Big[\frac{1}{2}\big(e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_n+a_nb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\big)+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_n+a_nb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_n-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_n\Big] \\ &\quad -\frac{1}{2}\Big(e_2\otimes a_1b_na_n+a_nb_n\otimes a_1\Big)-e_2\otimes a_1 -\frac{1}{2}\Big(a_1b_n\otimes a_n+a_nb_n\otimes a_1\Big)\,. \end{align*} $$
$$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots ,b_{n-1})(a_n,b_n)a_n+(a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_n\Big) \\ &\quad +\frac{1}{2}\Big((a_n,b_n)\otimes (a_1,\dots,b_{n-1})a_n-(a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_n\Big)+(a_n,b_n)\otimes (a_1,\dots,a_{n-1}) \\ &\quad -\sum^n_{\ell=3}\Big[\frac{1}{2}\big(e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_n+a_nb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\big)+e_2\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad -\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_n+a_nb_n\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big] \\ &\quad +\frac{1}{2}\sum^n_{\ell=3}\Big[a_{\ell-1}b_n\otimes (a_1,\dots,b_{\ell-2})a_n-(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_n\Big] \\ &\quad -\frac{1}{2}\Big(e_2\otimes a_1b_na_n+a_nb_n\otimes a_1\Big)-e_2\otimes a_1 -\frac{1}{2}\Big(a_1b_n\otimes a_n+a_nb_n\otimes a_1\Big)\,. \end{align*} $$
Using that
![]() $(a_n,b_n)=a_nb_n+e_2$
and equations (3.6) and (3.5), we finally obtain
$(a_n,b_n)=a_nb_n+e_2$
and equations (3.6) and (3.5), we finally obtain
 $$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_n+\sum^n_{\ell=3}\Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_n\Big]+e_2\otimes a_1b_na_n\Big) \\ &\quad -\frac{1}{2} \Big( (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_n+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_n\Big]+a_1b_n\otimes a_n\Big) \\ &\quad+ (a_n,b_n)\otimes (a_1,\dots,a_{n-1})-\sum^n_{\ell=3}\Big[(a_n,b_n)\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]-(a_n,b_n)\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_{n}+\Phi_2\otimes a_{n}\Big)\,. \end{align*} $$
$$ \begin{align*} &=-\frac{1}{2}\Big(e_2\otimes (a_1,\dots,b_{n-1})(a_n,b_n)a_n+\sum^n_{\ell=3}\Big[e_2\otimes(a_1,\dots,b_{\ell-2})a_{\ell-1}b_na_n\Big]+e_2\otimes a_1b_na_n\Big) \\ &\quad -\frac{1}{2} \Big( (a_1,\dots,b_{n-1})(a_n,b_n)\otimes a_n+\sum^n_{\ell=3}\Big[(a_1,\dots,b_{\ell-2})a_{\ell-1}b_n\otimes a_n\Big]+a_1b_n\otimes a_n\Big) \\ &\quad+ (a_n,b_n)\otimes (a_1,\dots,a_{n-1})-\sum^n_{\ell=3}\Big[(a_n,b_n)\otimes (a_1,\dots,b_{\ell-2})a_{\ell-1}\Big]-(a_n,b_n)\otimes a_1 \\ &=-\frac{1}{2}\Big(e_2\otimes \Phi_2a_{n}+\Phi_2\otimes a_{n}\Big)\,. \end{align*} $$
To sum up, we proved that
![]() $\Phi _2=(a_1,\dots , b_n)$
satisfies equation (2.11) in
$\Phi _2=(a_1,\dots , b_n)$
satisfies equation (2.11) in
![]() $\mathcal {B}(\Gamma _n)$
. Now, we need to prove that
$\mathcal {B}(\Gamma _n)$
. Now, we need to prove that
![]() $\Phi _1=(b_n,\dots , a_1)^{-1}\in e_1 \mathcal {B}(\Gamma _n) e_1$
satisfies equation (2.11) as well. The automorphism S of order two (see equation (4.9)) has the effect
$\Phi _1=(b_n,\dots , a_1)^{-1}\in e_1 \mathcal {B}(\Gamma _n) e_1$
satisfies equation (2.11) as well. The automorphism S of order two (see equation (4.9)) has the effect
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}\mapsto -\{\mkern -6mu\{-,-\}\mkern -6mu\}$
and
$\{\mkern -6mu\{-,-\}\mkern -6mu\}\mapsto -\{\mkern -6mu\{-,-\}\mkern -6mu\}$
and
![]() $(a_1,\dots ,b_n)\mapsto (b_n,\dots , a_1)$
. By applying S to the just proved identity
$(a_1,\dots ,b_n)\mapsto (b_n,\dots , a_1)$
. By applying S to the just proved identity
![]() $2\{\mkern -6mu\{(a_1,\dots , b_n),a_i\}\mkern -6mu\}=-\big (e_2\otimes \Phi _2a_{i}+\Phi _2\otimes a_{i}\big )$
—see equation (4.13)—for
$2\{\mkern -6mu\{(a_1,\dots , b_n),a_i\}\mkern -6mu\}=-\big (e_2\otimes \Phi _2a_{i}+\Phi _2\otimes a_{i}\big )$
—see equation (4.13)—for
![]() $1\leq i\leq n$
, we obtain
$1\leq i\leq n$
, we obtain
for
![]() $1\leq i\leq n$
. Then, by equation (2.6) and noting that
$1\leq i\leq n$
. Then, by equation (2.6) and noting that
![]() $\Phi _1(b_n,\dots ,a_1)=(b_n,\dots ,a_1)\Phi _1=e_1$
, we finally obtain
$\Phi _1(b_n,\dots ,a_1)=(b_n,\dots ,a_1)\Phi _1=e_1$
, we finally obtain
 $$ \begin{align*} \{\mkern-6mu\{\Phi_1,b_{n+1-i}\}\mkern-6mu\}&=-\Phi_1*\{\mkern-6mu\{(b_n,\dots, a_1),b_{n+1-i}\}\mkern-6mu\}*\Phi_1 \\ &=-\Phi_1*\Big(\frac{1}{2}\big(e_1\otimes (b_n,\dots,a_1)b_{n+1-i}+(b_n,\dots, a_1)\otimes b_{n+1-i}\big)\Big)*\Phi_1 \\ &=-\frac{1}{2}\Big(\Phi_1\otimes b_{n+1-i}+e_1\otimes \Phi_1b_{n+1-i}\Big)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{\Phi_1,b_{n+1-i}\}\mkern-6mu\}&=-\Phi_1*\{\mkern-6mu\{(b_n,\dots, a_1),b_{n+1-i}\}\mkern-6mu\}*\Phi_1 \\ &=-\Phi_1*\Big(\frac{1}{2}\big(e_1\otimes (b_n,\dots,a_1)b_{n+1-i}+(b_n,\dots, a_1)\otimes b_{n+1-i}\big)\Big)*\Phi_1 \\ &=-\frac{1}{2}\Big(\Phi_1\otimes b_{n+1-i}+e_1\otimes \Phi_1b_{n+1-i}\Big)\,, \end{align*} $$
for all
![]() $1\leq i\leq n$
, which is tantamount to equation (2.11) since
$1\leq i\leq n$
, which is tantamount to equation (2.11) since
![]() $b_{n+1-i}e_1=0$
. Similarly, applying the automorphism S to equation (4.12), we get the identity
$b_{n+1-i}e_1=0$
. Similarly, applying the automorphism S to equation (4.12), we get the identity
By equation (2.6) and the fact
![]() $e_1a_{n+1-i}=0$
, we have
$e_1a_{n+1-i}=0$
, we have
 $$ \begin{align*} \{\mkern-6mu\{\Phi_1,a_{n+1-i}\}\mkern-6mu\}&=-\Phi_1*\{\mkern-6mu\{(b_n,\dots, a_1),a_{n+1-i}\}\mkern-6mu\}*\Phi_1 \\ &=\Phi_1*\Big(\frac{1}{2}\big(a_{n+1-i}\otimes (b_n,\dots, a_1)+a_{n+1-i}(b_n,\dots, a_1)\otimes e_1\big)\Big)*\Phi_1 \\ &=\frac{1}{2}\Big(a_{n+1-i}\Phi_1\otimes e_1+a_{n+1-i}\otimes \Phi_1\Big)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{\Phi_1,a_{n+1-i}\}\mkern-6mu\}&=-\Phi_1*\{\mkern-6mu\{(b_n,\dots, a_1),a_{n+1-i}\}\mkern-6mu\}*\Phi_1 \\ &=\Phi_1*\Big(\frac{1}{2}\big(a_{n+1-i}\otimes (b_n,\dots, a_1)+a_{n+1-i}(b_n,\dots, a_1)\otimes e_1\big)\Big)*\Phi_1 \\ &=\frac{1}{2}\Big(a_{n+1-i}\Phi_1\otimes e_1+a_{n+1-i}\otimes \Phi_1\Big)\,, \end{align*} $$
as we wished. So, we conclude that equation (2.11) holds for
![]() $\Phi _1$
; therefore,
$\Phi _1$
; therefore,
![]() $\Phi $
, as defined in equation (3.11), is a multiplicative moment map for the double quasi-Poisson bracket (3.10). This finishes the proof of Theorem 3.4.
$\Phi $
, as defined in equation (3.11), is a multiplicative moment map for the double quasi-Poisson bracket (3.10). This finishes the proof of Theorem 3.4.
5 Factorisation after localisation at several Euler continuants
5.1 The result
Recall from § 3.2 that
![]() $\mathcal {B}(\Gamma _n)$
denotes the algebra obtained from
$\mathcal {B}(\Gamma _n)$
denotes the algebra obtained from
![]() $\Bbbk \overline {\Gamma }_n$
after localisation at the Euler continuants (3.7). We now consider the algebra
$\Bbbk \overline {\Gamma }_n$
after localisation at the Euler continuants (3.7). We now consider the algebra
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
obtained by further localising
$\mathcal {B}_{n}^{\operatorname {loc}}$
obtained by further localising
![]() $\mathcal {B}(\Gamma _n)$
at the elements
$\mathcal {B}(\Gamma _n)$
at the elements
 $$ \begin{align} \begin{aligned} &(a_1,b_1)\,,\ldots\,,(a_1,b_1,\dots,a_{n-1},b_{n-1})\in e_2(\Bbbk\overline{\Gamma}_n)e_2\,, \\ &(b_1,a_1)\,,\ldots,(b_{n-1},a_{n-1}\,,\dots,b_1,a_1)\in e_1(\Bbbk\overline{\Gamma}_n)e_1\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &(a_1,b_1)\,,\ldots\,,(a_1,b_1,\dots,a_{n-1},b_{n-1})\in e_2(\Bbbk\overline{\Gamma}_n)e_2\,, \\ &(b_1,a_1)\,,\ldots,(b_{n-1},a_{n-1}\,,\dots,b_1,a_1)\in e_1(\Bbbk\overline{\Gamma}_n)e_1\,. \end{aligned} \end{align} $$
In other words,
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is obtained from
$\mathcal {B}_{n}^{\operatorname {loc}}$
is obtained from
![]() $\Bbbk \overline {\Gamma }_n$
by requiring that the following elements are inverted (in the sense of §3.2):
$\Bbbk \overline {\Gamma }_n$
by requiring that the following elements are inverted (in the sense of §3.2):
The structure on
![]() $\mathcal {B}(\Gamma _n)$
given in Theorem 3.4 descends to
$\mathcal {B}(\Gamma _n)$
given in Theorem 3.4 descends to
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
by localisation.
$\mathcal {B}_{n}^{\operatorname {loc}}$
by localisation.
Theorem 5.1. There exists an isomorphism of Hamiltonian double quasi-Poisson algebras between
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
endowed with the structure induced by localisation of
$\mathcal {B}_{n}^{\operatorname {loc}}$
endowed with the structure induced by localisation of
![]() $\mathcal {B}(\Gamma _n)$
and the fusion algebra
$\mathcal {B}(\Gamma _n)$
and the fusion algebra
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
obtained by identifying the idempotents in n copies of
$\mathcal {A}_{n}^{\operatorname {fus}}$
obtained by identifying the idempotents in n copies of
![]() $\mathcal {B}(\Gamma _1)$
endowed with the structure from Theorem 3.4.
$\mathcal {B}(\Gamma _1)$
endowed with the structure from Theorem 3.4.
The algebra
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
is obtained by fusion which, as we recalled in § 2.2, is a method to get a double quasi-Poisson bracket and a multiplicative moment map from a Hamiltonian double quasi-Poisson algebra by identifying several idempotents. We describe the structure of
$\mathcal {A}_{n}^{\operatorname {fus}}$
is obtained by fusion which, as we recalled in § 2.2, is a method to get a double quasi-Poisson bracket and a multiplicative moment map from a Hamiltonian double quasi-Poisson algebra by identifying several idempotents. We describe the structure of
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
in § 5.2. In particular, we will notice in Remark 5.5 that the algebra
$\mathcal {A}_{n}^{\operatorname {fus}}$
in § 5.2. In particular, we will notice in Remark 5.5 that the algebra
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
is, by construction, an example of Hamiltonian double quasi-Poisson algebra associated with the quiver
$\mathcal {A}_{n}^{\operatorname {fus}}$
is, by construction, an example of Hamiltonian double quasi-Poisson algebra associated with the quiver
![]() $\Gamma _n$
(where we see
$\Gamma _n$
(where we see
![]() $\overline {\Gamma }_n$
as its double quiver for
$\overline {\Gamma }_n$
as its double quiver for
![]() $b_k=a_k^{\ast }$
) by Van den Bergh; see Remark 2.13. Thus, the next result is a direct consequence of Theorem 5.1.
$b_k=a_k^{\ast }$
) by Van den Bergh; see Remark 2.13. Thus, the next result is a direct consequence of Theorem 5.1.
Corollary 5.2. After localisation at the Euler continuants (5.2), the Boalch algebra
![]() $\mathcal {B}(\Gamma _n)$
associated with the quiver
$\mathcal {B}(\Gamma _n)$
associated with the quiver
![]() $\Gamma _n$
is isomorphic as a Hamiltonian double quasi-Poisson algebra to the algebra
$\Gamma _n$
is isomorphic as a Hamiltonian double quasi-Poisson algebra to the algebra
![]() $\mathcal {A}(\Gamma _n)$
associated with the quiver
$\mathcal {A}(\Gamma _n)$
associated with the quiver
![]() $\Gamma _n$
by Van den Bergh.
$\Gamma _n$
by Van den Bergh.
Remark 5.3. Theorem 5.1 and Corollary 5.2 are motivated by the fact that, at the level of representation spaces,
![]() $\operatorname {Rep}(\mathcal {B}(\Gamma _n),(d_1,d_2))$
can be seen as a ‘partial compactification’ of
$\operatorname {Rep}(\mathcal {B}(\Gamma _n),(d_1,d_2))$
can be seen as a ‘partial compactification’ of
![]() $\operatorname {Rep}(\mathcal {A}(\Gamma _n),(d_1,d_2))$
. We are grateful to Philip Boalch for mentioning this geometric property which can be found in [Reference Paluba38, §5.3–5.5].
$\operatorname {Rep}(\mathcal {A}(\Gamma _n),(d_1,d_2))$
. We are grateful to Philip Boalch for mentioning this geometric property which can be found in [Reference Paluba38, §5.3–5.5].
5.2 The algebra
 $\mathcal {A}_{n}^{\operatorname {fus}}$
$\mathcal {A}_{n}^{\operatorname {fus}}$
We consider n copies of the algebra
![]() $\mathcal {B}(\Gamma _1)$
, that we denote by
$\mathcal {B}(\Gamma _1)$
, that we denote by
![]() $\mathcal {A}(\Gamma _1)$
for the rest of this subsection, since the Hamiltonian double quasi-Poisson structures of Theorems 2.12 and 3.4 (with
$\mathcal {A}(\Gamma _1)$
for the rest of this subsection, since the Hamiltonian double quasi-Poisson structures of Theorems 2.12 and 3.4 (with
![]() $n=1$
) coincide. We respectively denote the two generators
$n=1$
) coincide. We respectively denote the two generators
![]() $a_1,b_1$
in the
$a_1,b_1$
in the
![]() $\ell $
-th copy as
$\ell $
-th copy as
![]() $c_{\ell },d_{\ell }$
and the two idempotents
$c_{\ell },d_{\ell }$
and the two idempotents
![]() $e_1,e_2$
in the
$e_1,e_2$
in the
![]() $\ell $
-th copy as
$\ell $
-th copy as
![]() $e_{1,\ell },e_{2,\ell }$
. In particular, the continuants
$e_{1,\ell },e_{2,\ell }$
. In particular, the continuants
![]() $(c_{\ell },d_{\ell })$
and
$(c_{\ell },d_{\ell })$
and
![]() $(d_{\ell },c_{\ell })$
are inverted in each copy. We can naturally see
$(d_{\ell },c_{\ell })$
are inverted in each copy. We can naturally see
![]() $\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
as a Hamiltonian double quasi-Poisson algebra over
$\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
as a Hamiltonian double quasi-Poisson algebra over
![]() $\tilde {B}$
, where
$\tilde {B}$
, where
![]() $\tilde B = (\oplus _{\ell =1}^n \Bbbk e_{1,\ell }) \bigoplus (\oplus _{\ell =1}^n \Bbbk e_{2,\ell })$
; see [Reference Fairon29, Remark 2.13].
$\tilde B = (\oplus _{\ell =1}^n \Bbbk e_{1,\ell }) \bigoplus (\oplus _{\ell =1}^n \Bbbk e_{2,\ell })$
; see [Reference Fairon29, Remark 2.13].
Next, we identify idempotents in
![]() $\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
. We let
$\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
. We let
![]() $e_1:=e_{1,1}$
and
$e_1:=e_{1,1}$
and
![]() $e_2:=e_{2,1}$
, and we inductively perform fusion (2.2) of the idempotents
$e_2:=e_{2,1}$
, and we inductively perform fusion (2.2) of the idempotents
![]() $e_{1,\ell }$
onto
$e_{1,\ell }$
onto
![]() $e_1$
and
$e_1$
and
![]() $e_{2,\ell }$
onto
$e_{2,\ell }$
onto
![]() $e_2$
for
$e_2$
for
![]() $\ell =2,\ldots ,n$
. The algebra
$\ell =2,\ldots ,n$
. The algebra
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
obtained in this way can be described as being generated by the orthogonal idempotents
$\mathcal {A}_{n}^{\operatorname {fus}}$
obtained in this way can be described as being generated by the orthogonal idempotents
![]() $e_1,e_2$
satisfying
$e_1,e_2$
satisfying
![]() $e_1+e_2=1$
, together with the elements
$e_1+e_2=1$
, together with the elements
and the following elements are inverted:
The choice of order in which we perform fusion gives a Hamiltonian double quasi-Poisson algebra structure on
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
by [Reference Van den Bergh41, §5.3].
$\mathcal {A}_{n}^{\operatorname {fus}}$
by [Reference Van den Bergh41, §5.3].
Proposition 5.4. The Hamiltonian double quasi-Poisson structure on
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
is given by the B-linear double bracket
$\mathcal {A}_{n}^{\operatorname {fus}}$
is given by the B-linear double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(n)}$
which is defined on generators by
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(n)}$
which is defined on generators by
 $$ \begin{align} \{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}^{(n)}&= \begin{cases} -\frac{1}{2}\big(c_i\otimes c_j+c_j\otimes c_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(c_i\otimes c_j+c_j\otimes c_i\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}^{(n)}&= \begin{cases} -\frac{1}{2}\big(c_i\otimes c_j+c_j\otimes c_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(c_i\otimes c_j+c_j\otimes c_i\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{d_i,d_j\}\mkern-6mu\}^{(n)}&= \begin{cases} -\frac{1}{2}\big(d_i\otimes d_j+d_j\otimes d_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(d_i\otimes d_j+d_j\otimes d_i\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{d_i,d_j\}\mkern-6mu\}^{(n)}&= \begin{cases} -\frac{1}{2}\big(d_i\otimes d_j+d_j\otimes d_i\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(d_i\otimes d_j+d_j\otimes d_i\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{c_i,d_j\}\mkern-6mu\}^{(n)}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes c_id_j+d_jc_i\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(e_1\otimes c_id_i+ d_ic_i\otimes e_2\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(e_1\otimes c_id_j+d_jc_i\otimes e_2\big)\,, &\mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{c_i,d_j\}\mkern-6mu\}^{(n)}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes c_id_j+d_jc_i\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(e_1\otimes c_id_i+ d_ic_i\otimes e_2\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(e_1\otimes c_id_j+d_jc_i\otimes e_2\big)\,, &\mbox{if } i>j \end{cases}; \end{align} $$
and which we extend to
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
by the Leibniz rule and cyclic antisymmetry. The multiplicative moment map
$\mathcal {A}_{n}^{\operatorname {fus}}$
by the Leibniz rule and cyclic antisymmetry. The multiplicative moment map
![]() $\Phi ^{(n)}=\Phi _1^{(n)}+\Phi _2^{(n)}$
is given by
$\Phi ^{(n)}=\Phi _1^{(n)}+\Phi _2^{(n)}$
is given by
Proof. The Hamiltonian double quasi-Poisson structure on
![]() $\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
is given by the double quasi-Poisson bracket
$\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
is given by the double quasi-Poisson bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{\operatorname {sep}}$
satisfying for
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{\operatorname {sep}}$
satisfying for
![]() $1\leq i,j\leq n$
$1\leq i,j\leq n$
 $$ \begin{align} \begin{aligned} &\{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}^{\operatorname{sep}}=0\,, \quad\{\mkern-6mu\{d_i,d_j\}\mkern-6mu\}^{\operatorname{sep}}=0\,, \\ &\{\mkern-6mu\{c_i,d_j\}\mkern-6mu\}^{\operatorname{sep}}=\delta_{ij} \,e_{1,i}\otimes e_{2,i}+\frac12 \delta_{ij} (e_{1,i}\otimes c_i d_i + d_i c_i \otimes e_{2,i})\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\{\mkern-6mu\{c_i,c_j\}\mkern-6mu\}^{\operatorname{sep}}=0\,, \quad\{\mkern-6mu\{d_i,d_j\}\mkern-6mu\}^{\operatorname{sep}}=0\,, \\ &\{\mkern-6mu\{c_i,d_j\}\mkern-6mu\}^{\operatorname{sep}}=\delta_{ij} \,e_{1,i}\otimes e_{2,i}+\frac12 \delta_{ij} (e_{1,i}\otimes c_i d_i + d_i c_i \otimes e_{2,i})\,, \end{aligned} \end{align} $$
and the multiplicative moment map
![]() $\Phi ^{\operatorname {sep}}$
for
$\Phi ^{\operatorname {sep}}$
for
 $$ \begin{align} \Phi^{\operatorname{sep}}=\sum_{\ell=1}^n (\Phi_{1,\ell}+\Phi_{2,\ell})\,, \quad \Phi_{1,\ell}:=(e_{1,\ell}+d_{\ell} c_{\ell})^{-1},\quad \Phi_{2,\ell}:=e_{2,\ell}+c_{\ell} d_{\ell}\,. \end{align} $$
$$ \begin{align} \Phi^{\operatorname{sep}}=\sum_{\ell=1}^n (\Phi_{1,\ell}+\Phi_{2,\ell})\,, \quad \Phi_{1,\ell}:=(e_{1,\ell}+d_{\ell} c_{\ell})^{-1},\quad \Phi_{2,\ell}:=e_{2,\ell}+c_{\ell} d_{\ell}\,. \end{align} $$
We inductively perform fusion of
![]() $e_{1,\ell }$
onto
$e_{1,\ell }$
onto
![]() $e_1=e_{1,1}$
and of
$e_1=e_{1,1}$
and of
![]() $e_{2,\ell }$
onto
$e_{2,\ell }$
onto
![]() $e_2=e_{2,1}$
for
$e_2=e_{2,1}$
for
![]() $\ell =2,\ldots ,n$
. When such fusions have been performed for all
$\ell =2,\ldots ,n$
. When such fusions have been performed for all
![]() $\ell =1,\ldots ,k$
,
$\ell =1,\ldots ,k$
,
![]() $2\leq k\leq n$
, we have by Theorem 2.8 that the multiplicative moment map
$2\leq k\leq n$
, we have by Theorem 2.8 that the multiplicative moment map
![]() $\Phi ^{(k)}$
becomes
$\Phi ^{(k)}$
becomes
 $$ \begin{align} \begin{aligned} & \Phi^{(k)}=\Phi_1^{(k)}+ \Phi_2^{(k)} +\sum_{\ell=k+1}^n (\Phi_{1,\ell}+\Phi_{2,\ell})\,, \\ &\Phi_{1}^{(k)}=(e_{1}+d_1 c_1)^{-1}\cdots (e_{1}+d_k c_k)^{-1},\quad \Phi_{2}^{(k)}=(e_{2}+c_1 d_1)\cdots (e_{2}+c_k d_k)\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \Phi^{(k)}=\Phi_1^{(k)}+ \Phi_2^{(k)} +\sum_{\ell=k+1}^n (\Phi_{1,\ell}+\Phi_{2,\ell})\,, \\ &\Phi_{1}^{(k)}=(e_{1}+d_1 c_1)^{-1}\cdots (e_{1}+d_k c_k)^{-1},\quad \Phi_{2}^{(k)}=(e_{2}+c_1 d_1)\cdots (e_{2}+c_k d_k)\,. \end{aligned} \end{align} $$
In particular,
![]() $\Phi ^{(n)}_1=e_1 \Phi ^{(n)}e_1$
and
$\Phi ^{(n)}_1=e_1 \Phi ^{(n)}e_1$
and
![]() $\Phi ^{(n)}_2=e_2\Phi ^{(n)}e_2$
are the components of the multiplicative moment map on
$\Phi ^{(n)}_2=e_2\Phi ^{(n)}e_2$
are the components of the multiplicative moment map on
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
by construction, and this is just equation (5.6).
$\mathcal {A}_{n}^{\operatorname {fus}}$
by construction, and this is just equation (5.6).
Using again Theorem 2.8, we get that the double quasi-Poisson bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}$
obtained after fusing together the first k copies of
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}$
obtained after fusing together the first k copies of
![]() $\mathcal {A}(\Gamma _1)$
in
$\mathcal {A}(\Gamma _1)$
in
![]() $\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
is defined by adding an extra ‘fusion’ double bracket
$\oplus _{\ell =1}^n \mathcal {A}(\Gamma _1)$
is defined by adding an extra ‘fusion’ double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
to the previously obtained one
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
to the previously obtained one
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k-1)}$
(where
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k-1)}$
(where
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(0)}=\{\mkern -6mu\{-,-\}\mkern -6mu\}^{\operatorname {sep}}$
). It can be read from Lemma 2.7 that the fusions of
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(0)}=\{\mkern -6mu\{-,-\}\mkern -6mu\}^{\operatorname {sep}}$
). It can be read from Lemma 2.7 that the fusions of
![]() $e_{1,k}$
onto
$e_{1,k}$
onto
![]() $e_1$
and of
$e_1$
and of
![]() $e_{2,k}$
onto
$e_{2,k}$
onto
![]() $e_2$
result in the additional fusion double bracket
$e_2$
result in the additional fusion double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
which satisfies the following relations
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
which satisfies the following relations
Let us derive equation (5.10a). When we fuse
![]() $e_{1,k}$
onto
$e_{1,k}$
onto
![]() $e_1$
, according to the terminology of § 2.2 the element
$e_1$
, according to the terminology of § 2.2 the element
![]() $c_i$
(for
$c_i$
(for
![]() $i<k$
) is a generator of first type, and
$i<k$
) is a generator of first type, and
![]() $c_k$
is a generator of third type. Hence, this fusion results in the following added term in
$c_k$
is a generator of third type. Hence, this fusion results in the following added term in
![]() $\{\mkern -6mu\{c_i,c_k\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
by equation (2.22c):
$\{\mkern -6mu\{c_i,c_k\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
by equation (2.22c):
When we fuse
![]() $e_{2,k}$
onto
$e_{2,k}$
onto
![]() $e_2$
, the element
$e_2$
, the element
![]() $c_i$
(for
$c_i$
(for
![]() $i<k$
) is again of first type, but
$i<k$
) is again of first type, but
![]() $c_k$
is of second type, so we add the following term in
$c_k$
is of second type, so we add the following term in
![]() $\{\mkern -6mu\{c_i,c_k\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
by equation (2.22b):
$\{\mkern -6mu\{c_i,c_k\}\mkern -6mu\}^{(k)}_{\operatorname {fus}}$
by equation (2.22b):
Putting together equations (5.11) and (5.12), we get the two terms in equation (5.10a).
To conclude, note that the double bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(n)}$
on
$\{\mkern -6mu\{-,-\}\mkern -6mu\}^{(n)}$
on
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
is obtained by adding all the double brackets
$\mathcal {A}_{n}^{\operatorname {fus}}$
is obtained by adding all the double brackets
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\operatorname {fus}}^{(\ell )}$
for
$\{\mkern -6mu\{-,-\}\mkern -6mu\}_{\operatorname {fus}}^{(\ell )}$
for
![]() $2\leq \ell \leq n$
to equation (5.7). It is easy to see that it coincides with equation (5.5).
$2\leq \ell \leq n$
to equation (5.7). It is easy to see that it coincides with equation (5.5).
Remark 5.5. We can relate Proposition 5.4 to Remark 2.13 as follows. Recall that the Hamiltonian double quasi-Poisson structure on
![]() $\mathcal {A}(\Gamma _1)$
is the structureFootnote
8
constructed by Van den Bergh on
$\mathcal {A}(\Gamma _1)$
is the structureFootnote
8
constructed by Van den Bergh on
![]() $\Bbbk \overline {\Gamma }_1$
localised at
$\Bbbk \overline {\Gamma }_1$
localised at
![]() $e_2+ab$
and
$e_2+ab$
and
![]() $e_1+ba$
.
$e_1+ba$
.
Denote by
![]() $\Gamma _n$
the quiver consisting of n arrows
$\Gamma _n$
the quiver consisting of n arrows
![]() $c_{\ell }:1\to 2$
, and denote by
$c_{\ell }:1\to 2$
, and denote by
![]() $d_{\ell }=c_{\ell }^{\ast }:2\to 1$
the corresponding arrows in the double
$d_{\ell }=c_{\ell }^{\ast }:2\to 1$
the corresponding arrows in the double
![]() $\overline {\Gamma }_n$
. For a fixed ordering of the arrows starting at each vertex, Van den Bergh obtained a Hamiltonian double quasi-Poisson structure on
$\overline {\Gamma }_n$
. For a fixed ordering of the arrows starting at each vertex, Van den Bergh obtained a Hamiltonian double quasi-Poisson structure on
![]() $\mathcal {A}(\Gamma _n)$
, which is defined as the algebra
$\mathcal {A}(\Gamma _n)$
, which is defined as the algebra
![]() $\Bbbk \overline {\Gamma }_n$
localised at all the
$\Bbbk \overline {\Gamma }_n$
localised at all the
![]() $e_2+c_{\ell } d_{\ell }$
and
$e_2+c_{\ell } d_{\ell }$
and
![]() $e_1+d_{\ell } c_{\ell }$
. This structure is obtained by fusion, starting with n copies of
$e_1+d_{\ell } c_{\ell }$
. This structure is obtained by fusion, starting with n copies of
![]() $\Bbbk \overline {\Gamma }_1$
. By construction, it was noticed by Van den Bergh that the order in which we perform fusion can be encoded in an ordering taken at each vertex on the arrows which start at that vertex. In our case the Hamiltonian double quasi-Poisson structure for the orderings
$\Bbbk \overline {\Gamma }_1$
. By construction, it was noticed by Van den Bergh that the order in which we perform fusion can be encoded in an ordering taken at each vertex on the arrows which start at that vertex. In our case the Hamiltonian double quasi-Poisson structure for the orderings
is precisely the result obtained in Proposition 5.4. The comparison is easily made using the explicit form of Van den Bergh’s double bracket written in [Reference Fairon29, Theorem 3.3] (keeping in mind footnote 8). Note that, up to isomorphism, Van den Bergh’s Hamiltonian double quasi-Poisson algebra structure associated with
![]() $\Gamma _n$
only depends on the quiver seen as an undirected graph [Reference Fairon30, Theorem 4.12].
$\Gamma _n$
only depends on the quiver seen as an undirected graph [Reference Fairon30, Theorem 4.12].
Remark 5.6. Fix
![]() $q=(q_1,q_2)\in (\Bbbk ^{\times })^2$
. Building on the previous remark, the quotient algebra
$q=(q_1,q_2)\in (\Bbbk ^{\times })^2$
. Building on the previous remark, the quotient algebra
![]() $\mathcal {A}_{n}^{\operatorname {fus}}/(\Phi ^{(n)}-q_1e_1-q_2 e_2)$
(for
$\mathcal {A}_{n}^{\operatorname {fus}}/(\Phi ^{(n)}-q_1e_1-q_2 e_2)$
(for
![]() $\Phi ^{(n)}=\Phi ^{(n)}_1+\Phi ^{(n)}_2$
defined in equation (5.6)) is the multiplicative preprojective algebra
$\Phi ^{(n)}=\Phi ^{(n)}_1+\Phi ^{(n)}_2$
defined in equation (5.6)) is the multiplicative preprojective algebra
![]() $\Lambda ^q(\Gamma _n)$
of the quiver
$\Lambda ^q(\Gamma _n)$
of the quiver
![]() $\Gamma _n$
as introduced by Crawley-Boevey and Shaw [Reference Crawley-Boevey and Shaw25]. Furthermore, by Theorem 5.1, we obtain that the fission algebra
$\Gamma _n$
as introduced by Crawley-Boevey and Shaw [Reference Crawley-Boevey and Shaw25]. Furthermore, by Theorem 5.1, we obtain that the fission algebra
![]() $\mathcal {F}^q(\Gamma _n)$
attached to
$\mathcal {F}^q(\Gamma _n)$
attached to
![]() $\Gamma _n$
is, after localisation at the elements (5.1), isomorphic to
$\Gamma _n$
is, after localisation at the elements (5.1), isomorphic to
![]() $\Lambda ^q(\Gamma _n)$
.
$\Lambda ^q(\Gamma _n)$
.
5.3 Alternative description of the algebra
 $\mathcal {B}_{n}^{\operatorname {loc}}$
$\mathcal {B}_{n}^{\operatorname {loc}}$
By construction,
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is generated by the orthogonal idempotents
$\mathcal {B}_{n}^{\operatorname {loc}}$
is generated by the orthogonal idempotents
![]() $e_1,e_2$
satisfying
$e_1,e_2$
satisfying
![]() $e_1+e_2=1$
, together with the elements
$e_1+e_2=1$
, together with the elements
while the elements in equation (5.2) are inverted. By localisation, the double quasi-Poisson bracket and the multiplicative moment map can be written as in Theorem 3.4 in terms of the generators (5.14).
Let us introduce the following elements of
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
:
$\mathcal {B}_{n}^{\operatorname {loc}}$
:
 $$ \begin{align} \begin{aligned} b_{\ell}'&=b_{\ell}\,, & &\text{for }1\leq \ell\leq n\,, \\ a_1'&=a_1\,, & &a_{\ell}'=a_{\ell}+(a_1,\ldots,b_{\ell-1})^{-1}(a_1,\ldots,a_{\ell-1})\,,\quad \text{for }2\leq \ell\leq n\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} b_{\ell}'&=b_{\ell}\,, & &\text{for }1\leq \ell\leq n\,, \\ a_1'&=a_1\,, & &a_{\ell}'=a_{\ell}+(a_1,\ldots,b_{\ell-1})^{-1}(a_1,\ldots,a_{\ell-1})\,,\quad \text{for }2\leq \ell\leq n\,. \end{aligned} \end{align} $$
Though the formulae are cumbersome, we can see by induction that the elements (5.14) can be expressed in terms of the elements
![]() $\{a_{\ell }',b_{\ell }'\}$
in equation (5.15). Hence, the elements
$\{a_{\ell }',b_{\ell }'\}$
in equation (5.15). Hence, the elements
![]() $\{a_{\ell }',b_{\ell }'\}$
can be used as a set of generators for
$\{a_{\ell }',b_{\ell }'\}$
can be used as a set of generators for
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
(where the elements in equation (5.2) written in terms of
$\mathcal {B}_{n}^{\operatorname {loc}}$
(where the elements in equation (5.2) written in terms of
![]() $\{a_{\ell }',b_{\ell }'\}$
are inverted). We can also write
$\{a_{\ell }',b_{\ell }'\}$
are inverted). We can also write
due to Lemma 3.3.
Proposition 5.7. In terms of the generators
![]() $\{a_k',b_k'\mid 1\leq k \leq n\}$
, the Hamiltonian double quasi-Poisson algebra structure on
$\{a_k',b_k'\mid 1\leq k \leq n\}$
, the Hamiltonian double quasi-Poisson algebra structure on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is given by the B-linear double bracket
$\mathcal {B}_{n}^{\operatorname {loc}}$
is given by the B-linear double bracket
 $$ \begin{align} \{\mkern-6mu\{a_i',a_j'\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(a_i'\otimes a_j'+a_j'\otimes a_i'\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(a_i'\otimes a_j'+a_j'\otimes a_i'\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{a_i',a_j'\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(a_i'\otimes a_j'+a_j'\otimes a_i'\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(a_i'\otimes a_j'+a_j'\otimes a_i'\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{b_i',b_j'\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(b_i'\otimes b_j'+b_j'\otimes b_i'\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(b_i'\otimes b_j'+b_j'\otimes b_i'\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{b_i',b_j'\}\mkern-6mu\}&= \begin{cases} -\frac{1}{2}\big(b_i'\otimes b_j'+b_j'\otimes b_i'\big)\,, &\mbox{if } i<j \\ \;\;\; 0\,, &\mbox{if } i=j \\ \;\;\; \frac{1}{2}\big(b_i'\otimes b_j'+b_j'\otimes b_i'\big)\,, & \mbox{if } i>j \end{cases}; \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes a_i'b_j'+b_j'a_i'\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(e_1\otimes a_i'b_i'+ b_i'a_i'\otimes e_2\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(e_1\otimes a_i'b_j'+b_j'a_i'\otimes e_2\big)\,, &\mbox{if } i>j \end{cases}; \end{align} $$
$$ \begin{align} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac{1}{2}\big(e_1\otimes a_i'b_j'+b_j'a_i'\otimes e_2\big)\,, &\mbox{if } i<j \\ \;\;\; \frac{1}{2}\big(e_1\otimes a_i'b_i'+ b_i'a_i'\otimes e_2\big)+e_1\otimes e_2\,, &\mbox{if } i=j \\ - \frac{1}{2}\big(e_1\otimes a_i'b_j'+b_j'a_i'\otimes e_2\big)\,, &\mbox{if } i>j \end{cases}; \end{align} $$
and the multiplicative moment map
![]() $\Phi =\Phi _1+\Phi _2$
for
$\Phi =\Phi _1+\Phi _2$
for
5.4 Proof of Theorem 5.1
We consider the generators introduced in §5.2 for
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
and §5.3 for
$\mathcal {A}_{n}^{\operatorname {fus}}$
and §5.3 for
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
. We first note that we have a B-linear isomorphism given by
$\mathcal {B}_{n}^{\operatorname {loc}}$
. We first note that we have a B-linear isomorphism given by
for
![]() $\ell =1,\ldots ,n$
. To see that this map is well-defined, note that the invertibility of the elements (5.2) in
$\ell =1,\ldots ,n$
. To see that this map is well-defined, note that the invertibility of the elements (5.2) in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is equivalent to the invertibility of the elements
$\mathcal {B}_{n}^{\operatorname {loc}}$
is equivalent to the invertibility of the elements
![]() $(a_{\ell }',b_{\ell }')=e_2+a_{\ell }'b_{\ell }'$
and
$(a_{\ell }',b_{\ell }')=e_2+a_{\ell }'b_{\ell }'$
and
![]() $(b_{\ell }',a_{\ell }')=e_1+b_{\ell }' a_{\ell }'$
in
$(b_{\ell }',a_{\ell }')=e_1+b_{\ell }' a_{\ell }'$
in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
for
$\mathcal {B}_{n}^{\operatorname {loc}}$
for
![]() $1\leq \ell \leq n$
due to equation (5.24), which we obtain as part of the proof of Proposition 5.7. But these elements are precisely mapped onto the invertible elements
$1\leq \ell \leq n$
due to equation (5.24), which we obtain as part of the proof of Proposition 5.7. But these elements are precisely mapped onto the invertible elements
![]() $(c_{\ell },d_{\ell })$
and
$(c_{\ell },d_{\ell })$
and
![]() $(d_{\ell },c_{\ell })$
in
$(d_{\ell },c_{\ell })$
in
![]() $\mathcal {A}_{n}^{\operatorname {fus}}$
.
$\mathcal {A}_{n}^{\operatorname {fus}}$
.
Next, by comparing Propositions 5.4 and 5.7, we can see that
 $$ \begin{align} \begin{aligned} & \{\mkern-6mu\{\psi(a_i'),\psi(a_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{a_i',a_j'\}\mkern-6mu\})\,, \\ &\{\mkern-6mu\{\psi(b_i'),\psi(b_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{b_i',b_j'\}\mkern-6mu\})\,, \\ & \{\mkern-6mu\{\psi(a_i'),\psi(b_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\})\,, \quad \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \{\mkern-6mu\{\psi(a_i'),\psi(a_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{a_i',a_j'\}\mkern-6mu\})\,, \\ &\{\mkern-6mu\{\psi(b_i'),\psi(b_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{b_i',b_j'\}\mkern-6mu\})\,, \\ & \{\mkern-6mu\{\psi(a_i'),\psi(b_j')\}\mkern-6mu\}^{(n)}=\psi^{\otimes 2}(\{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\})\,, \quad \end{aligned} \end{align} $$
for any
![]() $i,j=1,\ldots ,n$
. We thus get that, for all
$i,j=1,\ldots ,n$
. We thus get that, for all
![]() $a,b\in \mathcal {B}_{n}^{\operatorname {loc}}$
,
$a,b\in \mathcal {B}_{n}^{\operatorname {loc}}$
,
It is also clear that
![]() $\psi (\Phi _1)=\Phi _1^{(n)}$
and
$\psi (\Phi _1)=\Phi _1^{(n)}$
and
![]() $\psi (\Phi _2)=\Phi _2^{(n)}$
, so
$\psi (\Phi _2)=\Phi _2^{(n)}$
, so
![]() $\psi $
is an isomorphism of Hamiltonian double quasi-Poisson algebras.
$\psi $
is an isomorphism of Hamiltonian double quasi-Poisson algebras.
5.5 Proof of Proposition 5.7
5.5.1 Preparation
Recall that the double quasi-Poisson bracket on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
takes the form (3.10) on the elements
$\mathcal {B}_{n}^{\operatorname {loc}}$
takes the form (3.10) on the elements
![]() $\{a_i,b_i\}$
since it is obtained by localisation of
$\{a_i,b_i\}$
since it is obtained by localisation of
![]() $\mathcal {B}(\Gamma _n)$
.
$\mathcal {B}(\Gamma _n)$
.
Lemma 5.8. The double bracket on
![]() $\mathcal {B}(\Gamma _n)$
is such that
$\mathcal {B}(\Gamma _n)$
is such that
 $$ \begin{align} \{\mkern-6mu\{(a_1,\dots, b_i),b_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac12\Big(b_j(a_1,\dots, b_i)\otimes e_2-b_j\otimes (a_1,\dots, b_i)\Big) \,, &\mbox{if } i<j, \\ \;\;\;\frac12\Big(b_j(a_1,\dots, b_i)\otimes e_2+b_j\otimes (a_1,\dots, b_i)\Big) \,, &\mbox{if } i\geq j , \end{cases} \end{align} $$
$$ \begin{align} \{\mkern-6mu\{(a_1,\dots, b_i),b_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac12\Big(b_j(a_1,\dots, b_i)\otimes e_2-b_j\otimes (a_1,\dots, b_i)\Big) \,, &\mbox{if } i<j, \\ \;\;\;\frac12\Big(b_j(a_1,\dots, b_i)\otimes e_2+b_j\otimes (a_1,\dots, b_i)\Big) \,, &\mbox{if } i\geq j , \end{cases} \end{align} $$
 $$ \begin{align} \{\mkern-6mu\{(a_1,\dots, b_i),a_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac12 \Big(e_2\otimes (a_1,\dots, b_i)a_j- (a_1,\dots, b_i)\otimes a_j\Big)\,, &\mbox{if } i<j\!-\!1 , \\ \;\;\; \frac{1}{2}\Big(e_2\otimes (a_1,\dots, b_i)a_{j}- (a_1,\dots, b_i)\otimes a_{j}\Big)& \\ \qquad\; +\,e_2\otimes (a_1,\dots, a_i)\,, &\mbox{if } i=j\!-\!1 ,\\ -\frac12 \Big(e_2\otimes (a_1,\dots, b_i)a_j+ (a_1,\dots, b_i)\otimes a_j\Big)\,, & \mbox{if } i\geq j. \end{cases}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \{\mkern-6mu\{(a_1,\dots, b_i),a_j\}\mkern-6mu\}&= \begin{cases} \;\;\; \frac12 \Big(e_2\otimes (a_1,\dots, b_i)a_j- (a_1,\dots, b_i)\otimes a_j\Big)\,, &\mbox{if } i<j\!-\!1 , \\ \;\;\; \frac{1}{2}\Big(e_2\otimes (a_1,\dots, b_i)a_{j}- (a_1,\dots, b_i)\otimes a_{j}\Big)& \\ \qquad\; +\,e_2\otimes (a_1,\dots, a_i)\,, &\mbox{if } i=j\!-\!1 ,\\ -\frac12 \Big(e_2\otimes (a_1,\dots, b_i)a_j+ (a_1,\dots, b_i)\otimes a_j\Big)\,, & \mbox{if } i\geq j. \end{cases}\\[-15pt]\nonumber \end{align} $$
In particular, these identities hold in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
.
$\mathcal {B}_{n}^{\operatorname {loc}}$
.
Proof. If
![]() $i<j$
, these relations have been derived in Lemma 4.2.
$i<j$
, these relations have been derived in Lemma 4.2.
If
![]() $i\geq j$
, note by inspecting Theorem 3.4 that the double brackets involving the elements
$i\geq j$
, note by inspecting Theorem 3.4 that the double brackets involving the elements
![]() $\{a_{\ell },b_{\ell }\mid 1\leq \ell \leq i\}$
of
$\{a_{\ell },b_{\ell }\mid 1\leq \ell \leq i\}$
of
![]() $\mathcal {B}(\Gamma _n)$
are exactly the same as the double brackets in
$\mathcal {B}(\Gamma _n)$
are exactly the same as the double brackets in
![]() $\mathcal {B}(\Gamma _i)$
. But since
$\mathcal {B}(\Gamma _i)$
. But since
![]() $(a_1,\dots , b_i)$
is the component in
$(a_1,\dots , b_i)$
is the component in
![]() $e_2 \mathcal {B}(\Gamma _i) e_2$
of the multiplicative moment map of
$e_2 \mathcal {B}(\Gamma _i) e_2$
of the multiplicative moment map of
![]() $\mathcal {B}(\Gamma _i)$
, the claim followsFootnote
9
from equation (2.11).
$\mathcal {B}(\Gamma _i)$
, the claim followsFootnote
9
from equation (2.11).
We compute double brackets with the
![]() $(2i-1)$
-th Euler continuant
$(2i-1)$
-th Euler continuant
![]() $(a_1,b_1,\ldots ,a_{i-1},b_{i-1},a_i)$
. By equation (3.5), we can use the decomposition
$(a_1,b_1,\ldots ,a_{i-1},b_{i-1},a_i)$
. By equation (3.5), we can use the decomposition
 $$ \begin{align} (a_1,\ldots,a_i)=\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\,.\\[-20pt]\nonumber \end{align} $$
$$ \begin{align} (a_1,\ldots,a_i)=\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\,.\\[-20pt]\nonumber \end{align} $$
(The formula holds for
![]() $i=1$
since the sum is over an empty set, hence we omit it).
$i=1$
since the sum is over an empty set, hence we omit it).
Lemma 5.9. The double bracket on
![]() $\mathcal {B}(\Gamma _n)$
is such that
$\mathcal {B}(\Gamma _n)$
is such that
 $$ \begin{align*} \begin{aligned} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}&= \begin{cases} \frac12\Big(b_j(a_1,\dots, a_i)\otimes e_2+ e_1 \otimes (a_1,\dots, a_i)b_j\Big)\, , &\mbox{if } i<j, \\ \frac12\Big(b_i(a_1,\dots, a_i)\otimes e_2+ e_1 \otimes (a_1,\dots, a_i)b_i\Big) & \\ \qquad +\, e_1 \otimes (a_1,\ldots,b_{i-1}) \,, &\mbox{if } i=j, \\ \frac12\Big(b_j(a_1,\dots, a_i)\otimes e_2 - e_1 \otimes (a_1,\dots, a_i)b_j\Big) \,, &\mbox{if } i>j. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}&= \begin{cases} \frac12\Big(b_j(a_1,\dots, a_i)\otimes e_2+ e_1 \otimes (a_1,\dots, a_i)b_j\Big)\, , &\mbox{if } i<j, \\ \frac12\Big(b_i(a_1,\dots, a_i)\otimes e_2+ e_1 \otimes (a_1,\dots, a_i)b_i\Big) & \\ \qquad +\, e_1 \otimes (a_1,\ldots,b_{i-1}) \,, &\mbox{if } i=j, \\ \frac12\Big(b_j(a_1,\dots, a_i)\otimes e_2 - e_1 \otimes (a_1,\dots, a_i)b_j\Big) \,, &\mbox{if } i>j. \end{cases} \end{aligned} \end{align*} $$
In particular, these identities hold in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
.
$\mathcal {B}_{n}^{\operatorname {loc}}$
.
Proof. If
![]() $i< j$
, by equation (5.22a), we have
$i< j$
, by equation (5.22a), we have
 $$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}=& \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^i \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2-b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell}\\ &+\frac12\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_j\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 +\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_j\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}=& \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^i \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2-b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell}\\ &+\frac12\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_j\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 +\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_j\,, \end{align*} $$
which is the desired result by equation (5.23).
If
![]() $i=j=1$
, this is just
$i=j=1$
, this is just
![]() $\{\mkern -6mu\{a_1,b_1\}\mkern -6mu\}$
equation (3.10c). If
$\{\mkern -6mu\{a_1,b_1\}\mkern -6mu\}$
equation (3.10c). If
![]() $i=j$
is distinct from
$i=j$
is distinct from
![]() $1$
, we use again equation (5.22a) to get
$1$
, we use again equation (5.22a) to get
 $$ \begin{align*} &\{\mkern-6mu\{(a_1,\dots, a_i),b_i\}\mkern-6mu\} \\ =& \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_i\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_i\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_i\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^i \Big(b_i(a_1,\dots, b_{\ell-1})\otimes e_2-b_i\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=2}^{i-1} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_i + b_i a_{\ell} \otimes e_2\Big) \\ &+\frac12 (a_1,\ldots,b_{i-1})\ast \Big(e_1 \otimes a_i b_i + b_i a_i \otimes e_2 + 2 e_1 \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_i\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 +\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_i + e_1 \otimes (a_1,\ldots,b_{i-1}), \end{align*} $$
$$ \begin{align*} &\{\mkern-6mu\{(a_1,\dots, a_i),b_i\}\mkern-6mu\} \\ =& \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_i\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_i\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_i\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^i \Big(b_i(a_1,\dots, b_{\ell-1})\otimes e_2-b_i\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=2}^{i-1} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_i + b_i a_{\ell} \otimes e_2\Big) \\ &+\frac12 (a_1,\ldots,b_{i-1})\ast \Big(e_1 \otimes a_i b_i + b_i a_i \otimes e_2 + 2 e_1 \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_i\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 +\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_i + e_1 \otimes (a_1,\ldots,b_{i-1}), \end{align*} $$
which is the claimed result by equation (5.23).
If
![]() $i>j$
, we only prove the result for
$i>j$
, we only prove the result for
![]() $j\neq 1$
and leave the easier case
$j\neq 1$
and leave the easier case
![]() $j=1$
to the reader. We can use equation (5.22a) one last time to obtain
$j=1$
to the reader. We can use equation (5.22a) one last time to obtain
 $$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}= & \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^j \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2-b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=j+1}^i \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2 + b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) \\ &+\frac12 (a_1,\ldots,b_{j-1})\ast \Big(e_1 \otimes a_j b_j + b_j a_j \otimes e_2 + 2 e_1 \otimes e_2\Big) \\ &-\frac12 (a_1,\ldots,b_{j})\ast \Big(e_1 \otimes a_{j+1} b_j + b_j a_{j+1} \otimes e_2 + 2 e_1 \otimes e_2\Big) \\ &-\frac12\sum_{\ell=j+2}^{i} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_j\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 -\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_j \\ &+ e_1 \otimes \Big[ (a_1,\ldots,b_{j-1}) + (a_1,\ldots,a_{j})b_j - (a_1,\ldots, b_j) \Big], \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{(a_1,\dots, a_i),b_j\}\mkern-6mu\}= & \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,\ldots,b_{\ell-1}),b_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},b_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,b_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^j \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2-b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=j+1}^i \Big(b_j(a_1,\dots, b_{\ell-1})\otimes e_2 + b_j\otimes (a_1,\dots, b_{\ell-1})\Big) \ast a_{\ell} \\ &+\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) \\ &+\frac12 (a_1,\ldots,b_{j-1})\ast \Big(e_1 \otimes a_j b_j + b_j a_j \otimes e_2 + 2 e_1 \otimes e_2\Big) \\ &-\frac12 (a_1,\ldots,b_{j})\ast \Big(e_1 \otimes a_{j+1} b_j + b_j a_{j+1} \otimes e_2 + 2 e_1 \otimes e_2\Big) \\ &-\frac12\sum_{\ell=j+2}^{i} (a_1,\ldots,b_{\ell-1})\ast \Big(e_1 \otimes a_{\ell} b_j + b_j a_{\ell} \otimes e_2\Big) +\frac12 (e_1 \otimes a_1 b_j + b_j a_1 \otimes e_2) \\ =&\frac12b_j\left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right]\otimes e_2 -\frac12 e_1 \otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] b_j \\ &+ e_1 \otimes \Big[ (a_1,\ldots,b_{j-1}) + (a_1,\ldots,a_{j})b_j - (a_1,\ldots, b_j) \Big], \end{align*} $$
which is the claimed result if we use equation (5.23) as well as the recursive relation for
![]() $(a_1,\ldots , b_j)$
, so that the last term disappears.
$(a_1,\ldots , b_j)$
, so that the last term disappears.
Lemma 5.10. The double bracket on
![]() $\mathcal {B}(\Gamma _n)$
is such that
$\mathcal {B}(\Gamma _n)$
is such that
 $$ \begin{align*} \begin{aligned} \{\mkern-6mu\{(a_1,\dots, a_i),a_j\}\mkern-6mu\}&= \begin{cases} \;\;\, \frac12\Big(a_j \otimes (a_1,\dots, a_i) - (a_1,\dots, a_i) \otimes a_j\Big)\, , &\mbox{if } i\geq j, \\ -\frac12\Big(a_j \otimes (a_1,\dots, a_i) + (a_1,\dots, a_i) \otimes a_j\Big)\, , &\mbox{if } i=j-1,\, j\neq 1. \\ \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{\mkern-6mu\{(a_1,\dots, a_i),a_j\}\mkern-6mu\}&= \begin{cases} \;\;\, \frac12\Big(a_j \otimes (a_1,\dots, a_i) - (a_1,\dots, a_i) \otimes a_j\Big)\, , &\mbox{if } i\geq j, \\ -\frac12\Big(a_j \otimes (a_1,\dots, a_i) + (a_1,\dots, a_i) \otimes a_j\Big)\, , &\mbox{if } i=j-1,\, j\neq 1. \\ \end{cases} \end{aligned} \end{align*} $$
In particular, these identities hold in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
.
$\mathcal {B}_{n}^{\operatorname {loc}}$
.
Proof. We first assume that
![]() $i>j>1$
, and we leave the case
$i>j>1$
, and we leave the case
![]() $i>j$
with
$i>j$
with
![]() $j=1$
to the reader. Using equations (5.23) and (5.22b), we can write
$j=1$
to the reader. Using equations (5.23) and (5.22b), we can write
![]() $\{\mkern -6mu\{(a_1,\dots , a_i),a_j\}\mkern -6mu\}$
as
$\{\mkern -6mu\{(a_1,\dots , a_i),a_j\}\mkern -6mu\}$
as
 $$ \begin{align*} \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &+\frac12 \Big(e_2 \otimes (a_1,\dots, b_{j-1}) a_j - (a_1,\dots, b_{j-1})\otimes a_j + 2 e_2 \otimes (a_1,\ldots,a_{j-1}) \Big) \ast a_j \\ &-\frac12\sum_{\ell=j+1}^i \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j + (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) \\ &+\frac12\sum_{\ell=j+1}^{i} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&\frac12a_j\otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] -\frac12 \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ &+ a_j \otimes \left[ (a_1,\ldots,a_{j-1}) -\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} -a_1 \right] \\ =& \frac12\Big(a_j \otimes (a_1,\dots, a_i) - (a_1,\dots, a_i) \otimes a_j\Big)\,. \end{align*} $$
$$ \begin{align*} \sum_{\ell=2}^i \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &+\frac12 \Big(e_2 \otimes (a_1,\dots, b_{j-1}) a_j - (a_1,\dots, b_{j-1})\otimes a_j + 2 e_2 \otimes (a_1,\ldots,a_{j-1}) \Big) \ast a_j \\ &-\frac12\sum_{\ell=j+1}^i \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j + (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) \\ &+\frac12\sum_{\ell=j+1}^{i} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&\frac12a_j\otimes \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] -\frac12 \left[\sum_{\ell=2}^i (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ &+ a_j \otimes \left[ (a_1,\ldots,a_{j-1}) -\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} -a_1 \right] \\ =& \frac12\Big(a_j \otimes (a_1,\dots, a_i) - (a_1,\dots, a_i) \otimes a_j\Big)\,. \end{align*} $$
Next, let
![]() $i=j$
. If
$i=j$
. If
![]() $j=1$
,
$j=1$
,
![]() $\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
, and we are done. If
$\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
, and we are done. If
![]() $j\neq 1$
, we compute
$j\neq 1$
, we compute
![]() $\{\mkern -6mu\{(a_1,\dots , a_j),a_j\}\mkern -6mu\}$
as in the previous case and find
$\{\mkern -6mu\{(a_1,\dots , a_j),a_j\}\mkern -6mu\}$
as in the previous case and find
 $$ \begin{align*} \sum_{\ell=2}^j \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &+\frac12 \Big(e_2 \otimes (a_1,\dots, b_{j-1}) a_j - (a_1,\dots, b_{j-1})\otimes a_j + 2 e_2 \otimes (a_1,\ldots,a_{j-1}) \Big) \ast a_j \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&\frac12a_j\otimes \left[(a_1,\dots, b_{j-1}) a_j + 2 (a_1,\ldots,a_{j-1})-\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,-a_1\right] \\ & -\frac12 \left[\sum_{\ell=2}^j (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ =&\frac12a_j\otimes \Big[(a_1,\dots, b_{j-1}) a_j + (a_1,\ldots,a_{j-1}) \Big] -\frac12 (a_1,\dots, a_j) \otimes a_j \\ =& \frac12\Big(a_j \otimes (a_1,\dots, a_j) - (a_1,\dots, a_j) \otimes a_j\Big)\,, \end{align*} $$
$$ \begin{align*} \sum_{\ell=2}^j \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &+\frac12 \Big(e_2 \otimes (a_1,\dots, b_{j-1}) a_j - (a_1,\dots, b_{j-1})\otimes a_j + 2 e_2 \otimes (a_1,\ldots,a_{j-1}) \Big) \ast a_j \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&\frac12a_j\otimes \left[(a_1,\dots, b_{j-1}) a_j + 2 (a_1,\ldots,a_{j-1})-\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,-a_1\right] \\ & -\frac12 \left[\sum_{\ell=2}^j (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ =&\frac12a_j\otimes \Big[(a_1,\dots, b_{j-1}) a_j + (a_1,\ldots,a_{j-1}) \Big] -\frac12 (a_1,\dots, a_j) \otimes a_j \\ =& \frac12\Big(a_j \otimes (a_1,\dots, a_j) - (a_1,\dots, a_j) \otimes a_j\Big)\,, \end{align*} $$
where we needed to use the recursive relation for
![]() $(a_1,\ldots ,a_{j})$
in the last line.
$(a_1,\ldots ,a_{j})$
in the last line.
Finally, for
![]() $i=j-1$
with
$i=j-1$
with
![]() $j\neq 1$
, we get for
$j\neq 1$
, we get for
![]() $\{\mkern -6mu\{(a_1,\dots , a_{j-1}),a_j\}\mkern -6mu\}$
that
$\{\mkern -6mu\{(a_1,\dots , a_{j-1}),a_j\}\mkern -6mu\}$
that
 $$ \begin{align*} \sum_{\ell=2}^{j-1} \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&-\frac12a_j\otimes \Big[ \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,+ a_1\Big] -\frac12 \left[\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ =& - \frac12\Big(a_j \otimes (a_1,\dots, a_{j-1}) + (a_1,\dots, a_{j-1}) \otimes a_j\Big)\,. \\[-38pt] \end{align*} $$
$$ \begin{align*} \sum_{\ell=2}^{j-1} \Big[\{\mkern-6mu\{(a_1,&\ldots,b_{\ell-1}),a_j\}\mkern-6mu\}\ast a_{\ell} + (a_1,\ldots,b_{\ell-1})\ast \{\mkern-6mu\{a_{\ell},a_j\}\mkern-6mu\}\Big]\,+\{\mkern-6mu\{a_1,a_j\}\mkern-6mu\} \\ =& \frac12\sum_{\ell=2}^{j-1} \Big(e_2 \otimes (a_1,\dots, b_{\ell-1}) a_j - (a_1,\dots, b_{\ell-1})\otimes a_j \Big) \ast a_{\ell} \\ &-\frac12\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})\ast \Big( a_{\ell} \otimes a_j + a_j \otimes a_{\ell}\Big) -\frac12 (a_1 \otimes a_j + a_j \otimes a_1) \\ =&-\frac12a_j\otimes \Big[ \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,+ a_1\Big] -\frac12 \left[\sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell}\,+a_1\right] \otimes a_j \\ =& - \frac12\Big(a_j \otimes (a_1,\dots, a_{j-1}) + (a_1,\dots, a_{j-1}) \otimes a_j\Big)\,. \\[-38pt] \end{align*} $$
We now perform computations in
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
involving the elements
$\mathcal {B}_{n}^{\operatorname {loc}}$
involving the elements
![]() $\{a_j'\mid 1\leq j\leq n\}$
for which we use the definition in equation (5.15).
$\{a_j'\mid 1\leq j\leq n\}$
for which we use the definition in equation (5.15).
Lemma 5.11. The double bracket on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
$\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
 $$ \begin{align*} \begin{aligned} \{\mkern-6mu\{a_i',a_j\}\mkern-6mu\}&= \begin{cases} \frac12\Big(a_i' \otimes a_j + a_j \otimes a_i' \Big)\, , &\mbox{if } i> j, \\ \frac12\Big(a_j' \otimes a_j + a_j \otimes a_j' \Big) - a_j' \otimes a_j' \,, &\mbox{if } i=j. \\ \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{\mkern-6mu\{a_i',a_j\}\mkern-6mu\}&= \begin{cases} \frac12\Big(a_i' \otimes a_j + a_j \otimes a_i' \Big)\, , &\mbox{if } i> j, \\ \frac12\Big(a_j' \otimes a_j + a_j \otimes a_j' \Big) - a_j' \otimes a_j' \,, &\mbox{if } i=j. \\ \end{cases} \end{aligned} \end{align*} $$
Proof. We will repeatedly use equations (3.10a), (5.22b) and Lemma 5.10. If
![]() $i>j>1$
, we have that
$i>j>1$
, we have that
![]() $\{\mkern -6mu\{a_i',a_j\}\mkern -6mu\}$
equals
$\{\mkern -6mu\{a_i',a_j\}\mkern -6mu\}$
equals
 $$ \begin{align*} & \left\{\!\!\left\{\Big(a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big),a_j\right\}\!\!\right\} \\ =& \frac12 (a_i \otimes a_j + a_j \otimes a_i) +\frac12 (a_1,\ldots,b_{i-1})^{-1}\ast \Big(a_j \otimes (a_1,\ldots,a_{i-1}) - (a_1,\ldots,a_{i-1}) \otimes a_j \Big) \\ &-\!\frac12 (a_1,\ldots,b_{i-1})^{-1}\!\!\ast \!\big(\!- e_2\! \otimes \!(a_1,\ldots,b_{i-1})a_j \!- (a_1,\ldots,b_{i-1}) \!\otimes\! a_j \big) \!\ast\! (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \\ =&\frac12 \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big]\otimes a_j + \frac12 a_j \otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big]\\ =& \frac12\Big(a_i' \otimes a_j + a_j \otimes a_i' \Big) \,. \end{align*} $$
$$ \begin{align*} & \left\{\!\!\left\{\Big(a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big),a_j\right\}\!\!\right\} \\ =& \frac12 (a_i \otimes a_j + a_j \otimes a_i) +\frac12 (a_1,\ldots,b_{i-1})^{-1}\ast \Big(a_j \otimes (a_1,\ldots,a_{i-1}) - (a_1,\ldots,a_{i-1}) \otimes a_j \Big) \\ &-\!\frac12 (a_1,\ldots,b_{i-1})^{-1}\!\!\ast \!\big(\!- e_2\! \otimes \!(a_1,\ldots,b_{i-1})a_j \!- (a_1,\ldots,b_{i-1}) \!\otimes\! a_j \big) \!\ast\! (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \\ =&\frac12 \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big]\otimes a_j + \frac12 a_j \otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big]\\ =& \frac12\Big(a_i' \otimes a_j + a_j \otimes a_i' \Big) \,. \end{align*} $$
If
![]() $i=j=1$
, we have
$i=j=1$
, we have
![]() $\{\mkern -6mu\{a_1',a_1\}\mkern -6mu\}=\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
. If
$\{\mkern -6mu\{a_1',a_1\}\mkern -6mu\}=\{\mkern -6mu\{a_1,a_1\}\mkern -6mu\}=0$
. If
![]() $i=j$
is distinct from
$i=j$
is distinct from
![]() $1$
, we have that
$1$
, we have that
![]() $\{\mkern -6mu\{a_j',a_j\}\mkern -6mu\}$
can be computed as follows:
$\{\mkern -6mu\{a_j',a_j\}\mkern -6mu\}$
can be computed as follows:
 $$ \begin{align*} & \left\{\!\!\left\{\Big(a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\Big),a_j\right\}\!\!\right\} \\ =& -\frac12 (a_1,\ldots,b_{j-1})^{-1}\ast \Big(a_j \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_j \Big) \\ &-\frac12 (a_1,\ldots,b_{j-1})^{-1}\ast \Big( e_2 \otimes (a_1,\ldots,b_{j-1})a_j - (a_1,\ldots,b_{j-1}) \otimes a_j \\ &\qquad \qquad \qquad \qquad \qquad \quad + 2 e_2 \otimes (a_1,\ldots,a_{j-1})\Big) \ast (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&-\frac12 (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\otimes a_j - \frac12 a_j \otimes (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\\ &-(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \otimes (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =& -\frac12\Big((a_j' - a_j) \otimes a_j + a_j \otimes (a_j'-a_j) \Big) - (a_j'-a_j)\otimes (a_j'-a_j) \\ =&\frac12\Big(a_j' \otimes a_j + a_j \otimes a_j' \Big) - a_j' \otimes a_j' \,.\\[-38pt] \end{align*} $$
$$ \begin{align*} & \left\{\!\!\left\{\Big(a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\Big),a_j\right\}\!\!\right\} \\ =& -\frac12 (a_1,\ldots,b_{j-1})^{-1}\ast \Big(a_j \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_j \Big) \\ &-\frac12 (a_1,\ldots,b_{j-1})^{-1}\ast \Big( e_2 \otimes (a_1,\ldots,b_{j-1})a_j - (a_1,\ldots,b_{j-1}) \otimes a_j \\ &\qquad \qquad \qquad \qquad \qquad \quad + 2 e_2 \otimes (a_1,\ldots,a_{j-1})\Big) \ast (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&-\frac12 (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\otimes a_j - \frac12 a_j \otimes (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1})\\ &-(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \otimes (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =& -\frac12\Big((a_j' - a_j) \otimes a_j + a_j \otimes (a_j'-a_j) \Big) - (a_j'-a_j)\otimes (a_j'-a_j) \\ =&\frac12\Big(a_j' \otimes a_j + a_j \otimes a_j' \Big) - a_j' \otimes a_j' \,.\\[-38pt] \end{align*} $$
5.5.2 Proof of Proposition 5.7
We show that we can write
![]() $\Phi $
as in equation (5.18), then we show that the double bracket takes the form (5.17) on the generators
$\Phi $
as in equation (5.18), then we show that the double bracket takes the form (5.17) on the generators
![]() $\{ a_{\ell }',b_{\ell }'\}$
.
$\{ a_{\ell }',b_{\ell }'\}$
.
Step 1: Rewriting
![]() $\Phi $
. For
$\Phi $
. For
![]() $1\leq \ell \leq n$
, we prove that,
$1\leq \ell \leq n$
, we prove that,
 $$ \begin{align} \begin{aligned} (a_1,\ldots,b_{\ell})&=(e_2+a_1'b_1')\cdots(e_2+a_{\ell}' b_{\ell}')\,, \\ (b_{\ell},\ldots,a_1)&= (e_1+b_{\ell}'a_{\ell}')\cdots (e_1+b_1' a_1')\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (a_1,\ldots,b_{\ell})&=(e_2+a_1'b_1')\cdots(e_2+a_{\ell}' b_{\ell}')\,, \\ (b_{\ell},\ldots,a_1)&= (e_1+b_{\ell}'a_{\ell}')\cdots (e_1+b_1' a_1')\,. \end{aligned} \end{align} $$
This gives in particular that
![]() $\Phi $
takes the form (5.18) when
$\Phi $
takes the form (5.18) when
![]() $\ell =n$
. We prove equation (5.24) by induction. The case
$\ell =n$
. We prove equation (5.24) by induction. The case
![]() $\ell =1$
is obvious. If we assume that equation (5.24) holds for
$\ell =1$
is obvious. If we assume that equation (5.24) holds for
![]() $\ell -1$
, we have
$\ell -1$
, we have
 $$ \begin{align*} \begin{aligned} (a_1,\ldots,b_{\ell})&=(a_1,\ldots,b_{\ell-1})(e_2+a_{\ell} b_{\ell}) + (a_1,\ldots,a_{\ell-1})b_{\ell}\\ &=(a_1,\ldots,b_{\ell-1}) (e_2+\underbrace{[a_{\ell}+(a_1,\ldots,b_{\ell-1})^{-1}(a_1,\ldots,a_{\ell-1})]}_{=\,a_{\ell}'\text{ by equation } (5.15) }b_{\ell})\\ &=(e_2+a_1'b_1')\cdots(e_2+a_{\ell-1}' b_{\ell-1}')(e_2+a_{\ell}' b_{\ell}')\,, \\ (b_{\ell},\ldots,a_1)&=(e_1+b_{\ell} a_{\ell}) (b_{\ell-1},\ldots,a_1) + (b_{\ell-1},\ldots,a_1)\\ &=(e_1+b_{\ell} \underbrace{[a_{\ell}+(a_{\ell-1},\ldots,a_1)(b_{\ell-1},\ldots,a_1)^{-1}]}_{=\,a_{\ell}'\text{ by equation } (5.16)} (b_{\ell-1},\ldots,a_1) \\ &=(e_1+b_{\ell}'a_{\ell}')(e_1+b_{\ell-1}'a_{\ell-1}')\cdots (e_1+b_1'a_1')\,. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (a_1,\ldots,b_{\ell})&=(a_1,\ldots,b_{\ell-1})(e_2+a_{\ell} b_{\ell}) + (a_1,\ldots,a_{\ell-1})b_{\ell}\\ &=(a_1,\ldots,b_{\ell-1}) (e_2+\underbrace{[a_{\ell}+(a_1,\ldots,b_{\ell-1})^{-1}(a_1,\ldots,a_{\ell-1})]}_{=\,a_{\ell}'\text{ by equation } (5.15) }b_{\ell})\\ &=(e_2+a_1'b_1')\cdots(e_2+a_{\ell-1}' b_{\ell-1}')(e_2+a_{\ell}' b_{\ell}')\,, \\ (b_{\ell},\ldots,a_1)&=(e_1+b_{\ell} a_{\ell}) (b_{\ell-1},\ldots,a_1) + (b_{\ell-1},\ldots,a_1)\\ &=(e_1+b_{\ell} \underbrace{[a_{\ell}+(a_{\ell-1},\ldots,a_1)(b_{\ell-1},\ldots,a_1)^{-1}]}_{=\,a_{\ell}'\text{ by equation } (5.16)} (b_{\ell-1},\ldots,a_1) \\ &=(e_1+b_{\ell}'a_{\ell}')(e_1+b_{\ell-1}'a_{\ell-1}')\cdots (e_1+b_1'a_1')\,. \end{aligned} \end{align*} $$
Step 2: The double bracket
![]() $\{\mkern -6mu\{b_i',b_j'\}\mkern -6mu\}$
. It is clear that equation (5.17b) holds since it is just equation (3.10b) because by definition
$\{\mkern -6mu\{b_i',b_j'\}\mkern -6mu\}$
. It is clear that equation (5.17b) holds since it is just equation (3.10b) because by definition
![]() $b^{\prime }_{\ell }=b_{\ell }$
.
$b^{\prime }_{\ell }=b_{\ell }$
.
Step 3: The double bracket
![]() $\{\mkern -6mu\{a_i',b_j'\}\mkern -6mu\}$
. We have to check equation (5.17c). It directly holds for
$\{\mkern -6mu\{a_i',b_j'\}\mkern -6mu\}$
. We have to check equation (5.17c). It directly holds for
![]() $i=1$
by equation (3.10c) since
$i=1$
by equation (3.10c) since
![]() $\{\mkern -6mu\{a_1',b_j'\}\mkern -6mu\}=\{\mkern -6mu\{a_1,b_j\}\mkern -6mu\}$
. So, hereafter, we assume
$\{\mkern -6mu\{a_1',b_j'\}\mkern -6mu\}=\{\mkern -6mu\{a_1,b_j\}\mkern -6mu\}$
. So, hereafter, we assume
![]() $i\neq 1$
. Then, we need to compute
$i\neq 1$
. Then, we need to compute
 $$ \begin{align*} \begin{aligned} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}=& \left\{\!\!\left\{\Big(a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big), b_j\right\}\!\!\right\} \\ =& \{\mkern-6mu\{a_i,b_j\}\mkern-6mu\} + (a_1,\ldots,b_{i-1})^{-1}\ast \{\mkern-6mu\{(a_1,\ldots,a_{i-1}) ,b_j\}\mkern-6mu\} \\ &- (a_1,\ldots,b_{i-1})^{-1}\ast \{\mkern-6mu\{(a_1,\ldots,b_{i-1}),b_j\}\mkern-6mu\} \ast (a_1,\ldots,b_{i-1})^{-1} (a_1,\ldots,a_{i-1}) \,, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}=& \left\{\!\!\left\{\Big(a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big), b_j\right\}\!\!\right\} \\ =& \{\mkern-6mu\{a_i,b_j\}\mkern-6mu\} + (a_1,\ldots,b_{i-1})^{-1}\ast \{\mkern-6mu\{(a_1,\ldots,a_{i-1}) ,b_j\}\mkern-6mu\} \\ &- (a_1,\ldots,b_{i-1})^{-1}\ast \{\mkern-6mu\{(a_1,\ldots,b_{i-1}),b_j\}\mkern-6mu\} \ast (a_1,\ldots,b_{i-1})^{-1} (a_1,\ldots,a_{i-1}) \,, \end{aligned} \end{align*} $$
and this can be obtained from equation (3.10c) and Lemmas 5.8 and 5.9. If
![]() $i<j$
, we find
$i<j$
, we find
 $$ \begin{align*} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}=&\frac12 (e_1 \otimes a_ib_j+b_j a_i \otimes e_2) \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} + e_1 \otimes (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) b_j \Big) \\ &-\frac12 \Big(b_j(a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} - b_j (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \otimes e_2 \Big) \\ =&\frac12 e_1 \otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big] b_j \\ &+\frac12\, b_j \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \Big] \otimes e_2\\ =& \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\}=&\frac12 (e_1 \otimes a_ib_j+b_j a_i \otimes e_2) \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} + e_1 \otimes (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) b_j \Big) \\ &-\frac12 \Big(b_j(a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} - b_j (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \otimes e_2 \Big) \\ =&\frac12 e_1 \otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big] b_j \\ &+\frac12\, b_j \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \Big] \otimes e_2\\ =& \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
as expected. The proof is basically the same for
![]() $i=j$
as we add a term
$i=j$
as we add a term
![]() $+e_1 \otimes e_2$
coming from
$+e_1 \otimes e_2$
coming from
![]() $\{\mkern -6mu\{a_i,b_i\}\mkern -6mu\}$
.
$\{\mkern -6mu\{a_i,b_i\}\mkern -6mu\}$
.
If
![]() $i=j+1$
, we get
$i=j+1$
, we get
 $$ \begin{align*} \{\mkern-6mu\{a_{j+1}',b_j'\}\mkern-6mu\} =&-\frac12 (e_1 \otimes a_{j+1}b_j+b_j a_{j+1} \otimes e_2) - e_1 \otimes e_2 \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{j}) \otimes (a_1,\ldots,b_{j})^{-1} + e_1 \otimes (a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) b_j\Big) \\ &+ e_1 \otimes (a_1,\ldots,b_j)^{-1} (a_1,\ldots,b_{j-1})\\ &-\frac12 \Big(b_j(a_1,\ldots,a_{j}) \otimes (a_1,\ldots,b_{j})^{-1} + b_j (a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) \otimes e_2 \Big) \\ =&-\frac12 e_1 \!\otimes \!\Big[a_{j+1}+(a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j})\Big] b_j \\ &-\frac12\, b_j \Big[a_{j+1}+(a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) \Big]\! \otimes e_2\\ &+ e_1 \otimes (a_1,\ldots,b_{j})^{-1}\Big[ (a_1,\ldots,a_{j}) b_j + (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j})\Big] \\ =&- \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_{j+1}',b_j'\}\mkern-6mu\} =&-\frac12 (e_1 \otimes a_{j+1}b_j+b_j a_{j+1} \otimes e_2) - e_1 \otimes e_2 \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{j}) \otimes (a_1,\ldots,b_{j})^{-1} + e_1 \otimes (a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) b_j\Big) \\ &+ e_1 \otimes (a_1,\ldots,b_j)^{-1} (a_1,\ldots,b_{j-1})\\ &-\frac12 \Big(b_j(a_1,\ldots,a_{j}) \otimes (a_1,\ldots,b_{j})^{-1} + b_j (a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) \otimes e_2 \Big) \\ =&-\frac12 e_1 \!\otimes \!\Big[a_{j+1}+(a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j})\Big] b_j \\ &-\frac12\, b_j \Big[a_{j+1}+(a_1,\ldots,b_{j})^{-1}(a_1,\ldots,a_{j}) \Big]\! \otimes e_2\\ &+ e_1 \otimes (a_1,\ldots,b_{j})^{-1}\Big[ (a_1,\ldots,a_{j}) b_j + (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j})\Big] \\ =&- \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
where we used the recursive relation for
![]() $(a_1,\ldots , b_j)$
.
$(a_1,\ldots , b_j)$
.
If
![]() $i>j+1$
, we finally obtain
$i>j+1$
, we finally obtain
 $$ \begin{align*} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\} =&-\frac12 (e_1 \otimes a_ib_j+b_j a_i \otimes e_2) \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} - e_1 \otimes (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) b_j \Big) \\ &-\frac12 \Big(b_j(a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} + b_j (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \otimes e_2 \Big) \\ =&-\frac12 e_1 \!\otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big] b_j\\ &-\frac12\, b_j \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \Big]\! \otimes e_2\\ =&- \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i',b_j'\}\mkern-6mu\} =&-\frac12 (e_1 \otimes a_ib_j+b_j a_i \otimes e_2) \\ &+ \frac12 \Big(b_j (a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} - e_1 \otimes (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) b_j \Big) \\ &-\frac12 \Big(b_j(a_1,\ldots,a_{i-1}) \otimes (a_1,\ldots,b_{i-1})^{-1} + b_j (a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \otimes e_2 \Big) \\ =&-\frac12 e_1 \!\otimes \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1})\Big] b_j\\ &-\frac12\, b_j \Big[a_i+(a_1,\ldots,b_{i-1})^{-1}(a_1,\ldots,a_{i-1}) \Big]\! \otimes e_2\\ =&- \frac12 (e_1 \otimes a_i' b_j' + b_j' a_i'\otimes e_2)\,, \end{align*} $$
as we wanted.
Step 4: Interlude (some double brackets involving
![]() $a_i'$
). For the sake of clarity, let us rewrite the following two identities which were obtained in Lemma 5.11 and in equation (5.17b) with
$a_i'$
). For the sake of clarity, let us rewrite the following two identities which were obtained in Lemma 5.11 and in equation (5.17b) with
![]() $b_j=b_j'$
(the latter has just been checked):
$b_j=b_j'$
(the latter has just been checked):
Lemma 5.12. The double bracket on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
$\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
Proof. Using equation (5.25), we get for
![]() $i>j$
that
$i>j$
that
 $$ \begin{align*} \{\mkern-6mu\{a_i',(a_j,b_j)\}\mkern-6mu\}=& \{\mkern-6mu\{a_i',a_jb_j\}\mkern-6mu\} \\ =& \frac12 (a_i' \otimes a_j + a_j \otimes a_i')b_j -\frac12 a_j(e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2) \\ =& \frac12 a_i' \otimes (e_2+a_j b_j) -\frac12 (e_2+a_j b_j) a_i' \otimes e_2\,.\\[-38pt] \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i',(a_j,b_j)\}\mkern-6mu\}=& \{\mkern-6mu\{a_i',a_jb_j\}\mkern-6mu\} \\ =& \frac12 (a_i' \otimes a_j + a_j \otimes a_i')b_j -\frac12 a_j(e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2) \\ =& \frac12 a_i' \otimes (e_2+a_j b_j) -\frac12 (e_2+a_j b_j) a_i' \otimes e_2\,.\\[-38pt] \end{align*} $$
Lemma 5.13. The double bracket on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
$\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
Proof. We prove the result by induction on j. Note that the case
![]() $j=1$
is directly obtained from Lemma 5.12. If
$j=1$
is directly obtained from Lemma 5.12. If
![]() $i>j>1$
, by equation (3.6),
$i>j>1$
, by equation (3.6),
 $$ \begin{align*} \{\mkern-6mu\{a_i',(a_1,\ldots,b_j)\}\mkern-6mu\}=\{\mkern-6mu\{a_i',(a_1,\ldots,b_{j-1})(a_j,b_j)\}\mkern-6mu\} + \sum_{\ell=2}^{j-1}\{\mkern-6mu\{a_i',(a_1,\ldots,b_{\ell-1})a_{\ell} b_j \}\mkern-6mu\} + \{\mkern-6mu\{a_i',a_1 b_j\}\mkern-6mu\}\\[-20pt] \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i',(a_1,\ldots,b_j)\}\mkern-6mu\}=\{\mkern-6mu\{a_i',(a_1,\ldots,b_{j-1})(a_j,b_j)\}\mkern-6mu\} + \sum_{\ell=2}^{j-1}\{\mkern-6mu\{a_i',(a_1,\ldots,b_{\ell-1})a_{\ell} b_j \}\mkern-6mu\} + \{\mkern-6mu\{a_i',a_1 b_j\}\mkern-6mu\}\\[-20pt] \end{align*} $$
which can be computed using the induction hypothesis together with Lemma 5.12 and equation (5.25) as
 $$ \begin{align*} =&\frac12 \Big( a_i' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_i' \otimes e_2 \Big) (a_j,b_j) \\ &+\frac12 (a_1,\ldots,b_{j-1})\Big( a_i' \otimes (a_j,b_j) - (a_j,b_j) a_i' \otimes e_2 \Big) \\ &+\frac12 \sum_{\ell=2}^{j-1} \Big( a_i' \otimes (a_1,\ldots,b_{\ell-1}) - (a_1,\ldots,b_{\ell-1}) a_i' \otimes e_2 \Big) a_{\ell} b_j \\ &+\frac12 \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1}) \Big(a_i' \otimes a_{\ell} + a_{\ell} \otimes a_i'\Big) b_j - \frac12 \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1}) a_{\ell} \Big(e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2\Big) \\ &+ \frac12 (a_i' \otimes a_1 + a_1 \otimes a_i') b_j - \frac12 a_1 (e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2) \\ =&\frac12 a_i' \otimes \Big[(a_1,\ldots,b_{j-1})(a_j,b_j) + \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} b_j + a_1 b_j \Big] \\ &-\frac12 \Big[ (a_1,\ldots,b_{j-1})(a_j,b_j) + \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} b_j + a_1 b_j \Big] a_i' \otimes e_2\,, \end{align*} $$
$$ \begin{align*} =&\frac12 \Big( a_i' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_i' \otimes e_2 \Big) (a_j,b_j) \\ &+\frac12 (a_1,\ldots,b_{j-1})\Big( a_i' \otimes (a_j,b_j) - (a_j,b_j) a_i' \otimes e_2 \Big) \\ &+\frac12 \sum_{\ell=2}^{j-1} \Big( a_i' \otimes (a_1,\ldots,b_{\ell-1}) - (a_1,\ldots,b_{\ell-1}) a_i' \otimes e_2 \Big) a_{\ell} b_j \\ &+\frac12 \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1}) \Big(a_i' \otimes a_{\ell} + a_{\ell} \otimes a_i'\Big) b_j - \frac12 \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1}) a_{\ell} \Big(e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2\Big) \\ &+ \frac12 (a_i' \otimes a_1 + a_1 \otimes a_i') b_j - \frac12 a_1 (e_1 \otimes a_i' b_j + b_j a_i' \otimes e_2) \\ =&\frac12 a_i' \otimes \Big[(a_1,\ldots,b_{j-1})(a_j,b_j) + \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} b_j + a_1 b_j \Big] \\ &-\frac12 \Big[ (a_1,\ldots,b_{j-1})(a_j,b_j) + \sum_{\ell=2}^{j-1} (a_1,\ldots,b_{\ell-1})a_{\ell} b_j + a_1 b_j \Big] a_i' \otimes e_2\,, \end{align*} $$
and this is the claimed result due to equation (3.6).
Lemma 5.14. The double bracket on
![]() $\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
$\mathcal {B}_{n}^{\operatorname {loc}}$
is such that
Proof. We prove the result by induction on j, and the case
![]() $j=1$
is a special case of equation (5.25b). We can use equation (5.23) to write
$j=1$
is a special case of equation (5.25b). We can use equation (5.23) to write
 $$ \begin{align*} \{\mkern-6mu\{a_i',(a_1,\ldots,a_j)\}\mkern-6mu\}=\sum_{\ell=2}^{j}\{\mkern-6mu\{a_i',(a_1,\ldots,b_{\ell-1})a_{\ell}\}\mkern-6mu\} + \{\mkern-6mu\{a_i',a_1\}\mkern-6mu\}\,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a_i',(a_1,\ldots,a_j)\}\mkern-6mu\}=\sum_{\ell=2}^{j}\{\mkern-6mu\{a_i',(a_1,\ldots,b_{\ell-1})a_{\ell}\}\mkern-6mu\} + \{\mkern-6mu\{a_i',a_1\}\mkern-6mu\}\,, \end{align*} $$
and due to equation (5.25b) and Lemma 5.13 we find
 $$ \begin{align*} =&\frac12 \sum_{\ell=2}^{j} \Big( a_i' \otimes (a_1,\ldots,b_{\ell-1}) - (a_1,\ldots,b_{\ell-1}) a_i' \otimes e_2 \Big) a_{\ell} \\ &+\frac12\sum_{\ell=2}^{j} (a_1,\ldots,b_{\ell-1}) \Big( a_i' \otimes a_{\ell} + a_{\ell} \otimes a_i' \Big) + \Big( a_i' \otimes a_1 + a_1 \otimes a_i' \Big) \\ =&\frac12 a_i' \otimes \Big[\sum_{\ell=2}^{j}(a_1,\ldots,b_{\ell-1}) a_{\ell} + a_1 \Big] + \frac12 \Big[\sum_{\ell=2}^{j}(a_1,\ldots,b_{\ell-1}) a_{\ell} + a_1 \Big] \otimes a_i'\,, \end{align*} $$
$$ \begin{align*} =&\frac12 \sum_{\ell=2}^{j} \Big( a_i' \otimes (a_1,\ldots,b_{\ell-1}) - (a_1,\ldots,b_{\ell-1}) a_i' \otimes e_2 \Big) a_{\ell} \\ &+\frac12\sum_{\ell=2}^{j} (a_1,\ldots,b_{\ell-1}) \Big( a_i' \otimes a_{\ell} + a_{\ell} \otimes a_i' \Big) + \Big( a_i' \otimes a_1 + a_1 \otimes a_i' \Big) \\ =&\frac12 a_i' \otimes \Big[\sum_{\ell=2}^{j}(a_1,\ldots,b_{\ell-1}) a_{\ell} + a_1 \Big] + \frac12 \Big[\sum_{\ell=2}^{j}(a_1,\ldots,b_{\ell-1}) a_{\ell} + a_1 \Big] \otimes a_i'\,, \end{align*} $$
which is the desired result by equation (5.23).
Step 5: The double bracket
![]() $\{\mkern -6mu\{a_i',a_j'\}\mkern -6mu\}$
. It remains to prove that
$\{\mkern -6mu\{a_i',a_j'\}\mkern -6mu\}$
. It remains to prove that
![]() $\{\mkern -6mu\{a_i',a_j'\}\mkern -6mu\}$
takes the form (5.17a), and it suffices to do so for
$\{\mkern -6mu\{a_i',a_j'\}\mkern -6mu\}$
takes the form (5.17a), and it suffices to do so for
![]() $i\geq j$
due to the cyclic antisymmetry.
$i\geq j$
due to the cyclic antisymmetry.
Firstly, we consider the case when
![]() $i>j$
. We write
$i>j$
. We write
![]() $a_j'$
using equation (5.15). The case
$a_j'$
using equation (5.15). The case
![]() $j=1$
is just equation (5.25b), while for
$j=1$
is just equation (5.25b), while for
![]() $i>j>1$
we have that
$i>j>1$
we have that
This can be computed using equation (5.25b) and Lemmas 5.13 and 5.14, as
 $$ \begin{align*} =&\frac12 (a_i'\otimes a_j + a_j \otimes a_i') +\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_i' \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_i' \Big) \\ &-\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_i' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_i' \otimes e_2 \Big) (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&\frac12 a_i' \otimes \Big[ a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] +\frac12 \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big]\otimes a_i' \\ =&\frac12( a_i' \otimes a_j' + a_j' \otimes a_i')\,. \end{align*} $$
$$ \begin{align*} =&\frac12 (a_i'\otimes a_j + a_j \otimes a_i') +\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_i' \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_i' \Big) \\ &-\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_i' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_i' \otimes e_2 \Big) (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&\frac12 a_i' \otimes \Big[ a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] +\frac12 \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big]\otimes a_i' \\ =&\frac12( a_i' \otimes a_j' + a_j' \otimes a_i')\,. \end{align*} $$
When
![]() $i=j$
, this is obviously zero if
$i=j$
, this is obviously zero if
![]() $j=1$
by equation (3.10a). If
$j=1$
by equation (3.10a). If
![]() $j> 1$
we use Lemma 5.11 to get
$j> 1$
we use Lemma 5.11 to get
![]() $\{\mkern -6mu\{a_j',a_j\}\mkern -6mu\}$
so that as in the previous case we can compute
$\{\mkern -6mu\{a_j',a_j\}\mkern -6mu\}$
so that as in the previous case we can compute
 $$ \begin{align*} \{\mkern-6mu\{a&_j',a_j'\}\mkern-6mu\} \\ =&\frac12 (a_j'\otimes a_j + a_j \otimes a_j') - a_j' \otimes a_j'\\ &+\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_j' \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_j' \Big) \\ &-\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_j' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_j' \otimes e_2 \Big) (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&\frac12 a_j' \otimes \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] \\ &+\frac12 \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] \otimes a_j' - a_j' \otimes a_j' \,, \end{align*} $$
$$ \begin{align*} \{\mkern-6mu\{a&_j',a_j'\}\mkern-6mu\} \\ =&\frac12 (a_j'\otimes a_j + a_j \otimes a_j') - a_j' \otimes a_j'\\ &+\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_j' \otimes (a_1,\ldots,a_{j-1}) + (a_1,\ldots,a_{j-1}) \otimes a_j' \Big) \\ &-\frac12(a_1,\ldots,b_{j-1})^{-1} \Big( a_j' \otimes (a_1,\ldots,b_{j-1}) - (a_1,\ldots,b_{j-1}) a_j' \otimes e_2 \Big) (a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \\ =&\frac12 a_j' \otimes \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] \\ &+\frac12 \Big[a_j+(a_1,\ldots,b_{j-1})^{-1}(a_1,\ldots,a_{j-1}) \Big] \otimes a_j' - a_j' \otimes a_j' \,, \end{align*} $$
which is zero, as expected. So
![]() $\{\mkern -6mu\{a^{\prime }_j,a^{\prime }_j\}\mkern -6mu\}$
takes the form (5.17a), and Proposition 5.17 follows.
$\{\mkern -6mu\{a^{\prime }_j,a^{\prime }_j\}\mkern -6mu\}$
takes the form (5.17a), and Proposition 5.17 follows.
5.6 Towards the quasi-bisymplectic form
Working in full generalities as in §2.1, we consider a finitely generated unital algebra A over
![]() $B=\oplus _{s\in I} \Bbbk e_s$
and the A-bimodule
$B=\oplus _{s\in I} \Bbbk e_s$
and the A-bimodule
![]() $\Omega ^1_B A$
of (B-relative) noncommutative differential
$\Omega ^1_B A$
of (B-relative) noncommutative differential
![]() $1$
-forms. Following [Reference Cuntz and Quillen26], we put
$1$
-forms. Following [Reference Cuntz and Quillen26], we put
![]() $\Omega _B A:=T_A \Omega ^1_B A$
and note that
$\Omega _B A:=T_A \Omega ^1_B A$
and note that
![]() $\operatorname {d}\colon A\to \Omega ^1_B A$
can be extended to a differential on
$\operatorname {d}\colon A\to \Omega ^1_B A$
can be extended to a differential on
![]() $\Omega _B A$
. If A is freely generated by elements
$\Omega _B A$
. If A is freely generated by elements
![]() $\{a_j\mid j\in J\}$
, with
$\{a_j\mid j\in J\}$
, with
![]() $|J|<\infty $
and
$|J|<\infty $
and
![]() $a_j=e_{h_j} a_j e_{t_j}$
, we can introduce the map
$a_j=e_{h_j} a_j e_{t_j}$
, we can introduce the map
 $$ \begin{align} \tilde{\operatorname{d}}:=\sum_{j\in J}\operatorname{d}\! a_j\frac{\partial}{\partial a_j}:A\longrightarrow A\otimes \Omega_B^1A\,, \quad \tilde{\operatorname{d}}(b)= \sum_{j\in J}\left(\frac{\partial b}{\partial a_j}\right)'\otimes \operatorname{d}\! a_j\left(\frac{\partial b}{\partial a_j}\right)''\, \end{align} $$
$$ \begin{align} \tilde{\operatorname{d}}:=\sum_{j\in J}\operatorname{d}\! a_j\frac{\partial}{\partial a_j}:A\longrightarrow A\otimes \Omega_B^1A\,, \quad \tilde{\operatorname{d}}(b)= \sum_{j\in J}\left(\frac{\partial b}{\partial a_j}\right)'\otimes \operatorname{d}\! a_j\left(\frac{\partial b}{\partial a_j}\right)''\, \end{align} $$
for the double derivations
![]() $\partial /\partial a_j\in \operatorname {\mathbb {D}er}_BA$
given by
$\partial /\partial a_j\in \operatorname {\mathbb {D}er}_BA$
given by
![]() $\partial a_i/\partial a_j=\delta _{ij} \, e_{h_j}\otimes e_{t_j}$
. Since we have that
$\partial a_i/\partial a_j=\delta _{ij} \, e_{h_j}\otimes e_{t_j}$
. Since we have that
![]() $A\otimes \Omega _B^1A\subset \Omega _BA\otimes \Omega _BA$
, we can decompose the differential as
$A\otimes \Omega _B^1A\subset \Omega _BA\otimes \Omega _BA$
, we can decompose the differential as
through the multiplication map
![]() $\tilde {\operatorname {m}}$
on
$\tilde {\operatorname {m}}$
on
![]() $\Omega _BA$
. By iterating
$\Omega _BA$
. By iterating
![]() $\tilde {\operatorname {d}}$
, we can introduce
$\tilde {\operatorname {d}}$
, we can introduce
 $$ \begin{align} \begin{aligned} \operatorname{D}^2:=&\tilde{\operatorname{m}}\circ (\operatorname{d}\otimes 1)\circ \tilde{\operatorname{d}}:A\longrightarrow \Omega^2_BA \subset \Omega_BA\,,\\ \operatorname{D}^2(b)=&\sum_{i,j\in J} \left(\frac{\partial}{\partial a_i}\left(\frac{\partial b}{\partial a_j}\right)'\right)' \operatorname{d}\! a_i \left(\frac{\partial}{\partial a_i}\left(\frac{\partial b}{\partial a_j}\right)'\right)'' \operatorname{d}\! a_j\left(\frac{\partial b}{\partial a_j}\right)''\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{D}^2:=&\tilde{\operatorname{m}}\circ (\operatorname{d}\otimes 1)\circ \tilde{\operatorname{d}}:A\longrightarrow \Omega^2_BA \subset \Omega_BA\,,\\ \operatorname{D}^2(b)=&\sum_{i,j\in J} \left(\frac{\partial}{\partial a_i}\left(\frac{\partial b}{\partial a_j}\right)'\right)' \operatorname{d}\! a_i \left(\frac{\partial}{\partial a_i}\left(\frac{\partial b}{\partial a_j}\right)'\right)'' \operatorname{d}\! a_j\left(\frac{\partial b}{\partial a_j}\right)''\,. \end{aligned} \end{align} $$
The above construction can be applied to the algebra
![]() $\Bbbk \overline {\Gamma }_n$
and after localisation to
$\Bbbk \overline {\Gamma }_n$
and after localisation to
![]() $\mathcal {B}(\Gamma _n)$
. Using the double derivations given in equation (3.12), we have
$\mathcal {B}(\Gamma _n)$
. Using the double derivations given in equation (3.12), we have
 $$ \begin{align*} \tilde{\operatorname{d}}=\sum_{j=1}^n \left( \operatorname{d}\! a_j\frac{\partial}{\partial a_j}+ \operatorname{d}\! b_j\frac{\partial}{\partial b_j}\right)\,. \end{align*} $$
$$ \begin{align*} \tilde{\operatorname{d}}=\sum_{j=1}^n \left( \operatorname{d}\! a_j\frac{\partial}{\partial a_j}+ \operatorname{d}\! b_j\frac{\partial}{\partial b_j}\right)\,. \end{align*} $$
In particular, we can define the map
![]() $\operatorname {D}^2:\mathcal {B}(\Gamma _n)\to \Omega _B^2(\mathcal {B}(\Gamma _n))$
by equation (5.30). Motivated by the construction of Paluba [Reference Paluba38, §5.6] (see below), we introduce the element
$\operatorname {D}^2:\mathcal {B}(\Gamma _n)\to \Omega _B^2(\mathcal {B}(\Gamma _n))$
by equation (5.30). Motivated by the construction of Paluba [Reference Paluba38, §5.6] (see below), we introduce the element
Note that we use the two Euler continuants that are inverted in
![]() $\mathcal {B}(\Gamma _n)$
and which occur in the moment map
$\mathcal {B}(\Gamma _n)$
and which occur in the moment map
![]() $\Phi $
, as defined in equation (3.11).
$\Phi $
, as defined in equation (3.11).
Conjecture 5.15. The triple
![]() $(\mathcal {B}(\Gamma _n),\Phi ,\omega _n)$
is a quasi-bisymplectic algebra. Furthermore, the double quasi-Poisson bracket
$(\mathcal {B}(\Gamma _n),\Phi ,\omega _n)$
is a quasi-bisymplectic algebra. Furthermore, the double quasi-Poisson bracket
![]() $\{\mkern -6mu\{-,-\}\mkern -6mu\}$
given by equation (3.10) is nondegenerate, and it is compatible with
$\{\mkern -6mu\{-,-\}\mkern -6mu\}$
given by equation (3.10) is nondegenerate, and it is compatible with
![]() $\omega _n$
.
$\omega _n$
.
Since we are not going to prove this result here,Footnote
10
the precise definitions (of quasi-bisymplectic algebra, nondegeneracy or compatibility) are omitted, and the reader can find them in [Reference Van den Bergh42]. Let us nevertheless remark that by [Reference Van den Bergh42, Proposition 6.1], if the conjecture holds, we will have that
![]() $\omega _n$
turns any representation space
$\omega _n$
turns any representation space
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
(with its natural
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
(with its natural
![]() $\operatorname {GL}_{d_1}(\Bbbk )\times \operatorname {GL}_{d_2}(\Bbbk )$
-action) into a quasi-Hamiltonian space in the sense of [Reference Alekseev, Malkin and Meinrenken1]. Moreover, the induced
$\operatorname {GL}_{d_1}(\Bbbk )\times \operatorname {GL}_{d_2}(\Bbbk )$
-action) into a quasi-Hamiltonian space in the sense of [Reference Alekseev, Malkin and Meinrenken1]. Moreover, the induced
![]() $2$
-form will be compatible with the quasi-Poisson bracket on
$2$
-form will be compatible with the quasi-Poisson bracket on
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
induced by the double quasi-Poisson bracket from Theorem 3.4, which will be nondegenerate by [Reference Van den Bergh42, §6–7]. We should emphasise that, in the previous sentence, compatibility and nondegeneracy are meant in the geometric sense of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2], not at the noncommutative/associative algebra level stated in the conjecture. To strengthen Conjecture 5.15, we explain how the induced results on
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
induced by the double quasi-Poisson bracket from Theorem 3.4, which will be nondegenerate by [Reference Van den Bergh42, §6–7]. We should emphasise that, in the previous sentence, compatibility and nondegeneracy are meant in the geometric sense of [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2], not at the noncommutative/associative algebra level stated in the conjecture. To strengthen Conjecture 5.15, we explain how the induced results on
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
hold in the particular case of
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
hold in the particular case of
![]() $\Bbbk =\mathbb {C}$
thanks to the factorisation presented in this section.
$\Bbbk =\mathbb {C}$
thanks to the factorisation presented in this section.
Fix
![]() $\Bbbk =\mathbb {C}$
and
$\Bbbk =\mathbb {C}$
and
![]() $d_1,d_2\geq 1$
. Let
$d_1,d_2\geq 1$
. Let
![]() ${\mathrm {P}}_{\operatorname {Rep}}$
and
${\mathrm {P}}_{\operatorname {Rep}}$
and
![]() $\omega _{\operatorname {Rep}}$
be the (matrix) bivectors and
$\omega _{\operatorname {Rep}}$
be the (matrix) bivectors and
![]() $2$
-forms induced on
$2$
-forms induced on
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
by
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
by
![]() ${\mathrm {P}_n}$
and
${\mathrm {P}_n}$
and
![]() $\omega _n$
, respectively. Their explicit expressions can be obtained using the formalism of [Reference Van den Bergh41, §7].
$\omega _n$
, respectively. Their explicit expressions can be obtained using the formalism of [Reference Van den Bergh41, §7].
Proposition 5.16. The
![]() $2$
-form
$2$
-form
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
is the
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
is the
![]() $2$
-form from the quasi-Hamiltonian structure on
$2$
-form from the quasi-Hamiltonian structure on
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
constructed by Boalch in [Reference Boalch13] (through the identification with the fission variety
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
constructed by Boalch in [Reference Boalch13] (through the identification with the fission variety
![]() $\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
). Furthermore,
$\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
). Furthermore,
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
corresponds to the quasi-Poisson bivector
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
corresponds to the quasi-Poisson bivector
![]() $\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
.
$\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
.
Proof. Let
![]() $A_i\in \operatorname {Mat}_{d_2\times d_1}(\mathbb {C})$
,
$A_i\in \operatorname {Mat}_{d_2\times d_1}(\mathbb {C})$
,
![]() $B_i\in \operatorname {Mat}_{d_1\times d_2}(\mathbb {C})$
be the matrix-valued functions on
$B_i\in \operatorname {Mat}_{d_1\times d_2}(\mathbb {C})$
be the matrix-valued functions on
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
returning the elements representing
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
returning the elements representing
![]() $a_i,b_i$
for any
$a_i,b_i$
for any
![]() $1\leq i \leq n$
. Then, we can write from equation (5.31) that
$1\leq i \leq n$
. Then, we can write from equation (5.31) that
 $$ \begin{align} \begin{aligned} \operatorname{tr}(\omega_{\operatorname{Rep}})=&\frac12 \operatorname{tr}\Big( (B_n,\ldots,A_1)^{-1} \operatorname{D}^2(B_n,\ldots,A_1) \Big) \\ &- \frac12 \operatorname{tr}\Big( (A_1,\ldots,B_n)^{-1} \operatorname{D}^2 (A_1,\ldots,B_n) \Big)\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{tr}(\omega_{\operatorname{Rep}})=&\frac12 \operatorname{tr}\Big( (B_n,\ldots,A_1)^{-1} \operatorname{D}^2(B_n,\ldots,A_1) \Big) \\ &- \frac12 \operatorname{tr}\Big( (A_1,\ldots,B_n)^{-1} \operatorname{D}^2 (A_1,\ldots,B_n) \Big)\,, \end{aligned} \end{align} $$
where the matrix
![]() $2$
-forms occurring on the right-hand side are given by
$2$
-forms occurring on the right-hand side are given by
with matrix
![]() $1$
-forms
$1$
-forms
![]() $(dC_j)$
defined in the obvious way. Upon relabelling the matrices as
$(dC_j)$
defined in the obvious way. Upon relabelling the matrices as
 $$ \begin{align} \mathrm{b}_{\ell}=\left\{ \begin{array}{cc} A_{(2n-\ell+2)/2} & \text{ for }\ell \text{ even}, \\ B_{(2n-\ell+1)/2}& \text{ for } \ell \text{ odd}, \end{array} \right. \qquad \ell=1,\ldots,2n\,, \end{align} $$
$$ \begin{align} \mathrm{b}_{\ell}=\left\{ \begin{array}{cc} A_{(2n-\ell+2)/2} & \text{ for }\ell \text{ even}, \\ B_{(2n-\ell+1)/2}& \text{ for } \ell \text{ odd}, \end{array} \right. \qquad \ell=1,\ldots,2n\,, \end{align} $$
(these are not the elements
![]() $b_j\in \mathcal {B}(\Gamma _n)$
), we have that
$b_j\in \mathcal {B}(\Gamma _n)$
), we have that
 $$ \begin{align} \begin{aligned} \operatorname{tr}(\omega_{\operatorname{Rep}})=&\frac12 \operatorname{tr}\Big( (\mathrm{b}_1,\ldots,\mathrm{b}_{2n})^{-1} \operatorname{D}^2(\mathrm{b}_1,\ldots,\mathrm{b}_{2n}) \Big) \\ &- \frac12 \operatorname{tr}\Big( (\mathrm{b}_{2n},\ldots,\mathrm{b}_1)^{-1} \operatorname{D}^2 (\mathrm{b}_{2n},\ldots,\mathrm{b}_1) \Big)\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{tr}(\omega_{\operatorname{Rep}})=&\frac12 \operatorname{tr}\Big( (\mathrm{b}_1,\ldots,\mathrm{b}_{2n})^{-1} \operatorname{D}^2(\mathrm{b}_1,\ldots,\mathrm{b}_{2n}) \Big) \\ &- \frac12 \operatorname{tr}\Big( (\mathrm{b}_{2n},\ldots,\mathrm{b}_1)^{-1} \operatorname{D}^2 (\mathrm{b}_{2n},\ldots,\mathrm{b}_1) \Big)\,. \end{aligned} \end{align} $$
Using the
![]() $2n$
matrices
$2n$
matrices
![]() $(\mathrm {b}_{\ell })$
, the space
$(\mathrm {b}_{\ell })$
, the space
![]() $\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
can be directly identified with the higher fission space
$\operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
can be directly identified with the higher fission space
![]() $\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
using the parametrisation given by Paluba in [Reference Paluba38, Chapter 5]. Furthermore, the formula (5.34) for
$\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
using the parametrisation given by Paluba in [Reference Paluba38, Chapter 5]. Furthermore, the formula (5.34) for
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
exactly matchesFootnote
11
the quasi-Hamiltonian
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
exactly matchesFootnote
11
the quasi-Hamiltonian
![]() $2$
-form on
$2$
-form on
![]() $\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
from [Reference Boalch13] in the form written by Paluba in [Reference Paluba38, Theorem 5.6.1]. (In the case
$\mathcal {B}^{n+1}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
from [Reference Boalch13] in the form written by Paluba in [Reference Paluba38, Theorem 5.6.1]. (In the case
![]() $n=1$
, the
$n=1$
, the
![]() $2$
-form on
$2$
-form on
![]() $\mathcal {B}^{2}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
is already written in that way in [Reference Boalch13, Theorem 2.9]).
$\mathcal {B}^{2}(\mathbb {C}^{d_1},\mathbb {C}^{d_2})$
is already written in that way in [Reference Boalch13, Theorem 2.9]).
For
![]() $n=1$
,
$n=1$
,
![]() $\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
is Van den Bergh’s quasi-Poisson bivector [Reference Van den Bergh41], which corresponds to
$\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
is Van den Bergh’s quasi-Poisson bivector [Reference Van den Bergh41], which corresponds to
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
[Reference Van den Bergh42, Reference Yamakawa43], establishing the second part of the statement in that case. If
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
[Reference Van den Bergh42, Reference Yamakawa43], establishing the second part of the statement in that case. If
![]() $n\geq 2$
, note that the factorisation from Theorem 5.1 yields a dense embedding of Hamiltonian quasi-Poisson manifolds
$n\geq 2$
, note that the factorisation from Theorem 5.1 yields a dense embedding of Hamiltonian quasi-Poisson manifolds
where the Hamiltonian quasi-Poisson structure on the left is obtained by fusion. Denote by
![]() $M^{\textrm {inv}} \subset \operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
this dense subspace. Thus, when restricted to
$M^{\textrm {inv}} \subset \operatorname {Rep}(\overline {\Gamma }_n,(d_1,d_2))$
this dense subspace. Thus, when restricted to
![]() $M^{\textrm {inv}}$
,
$M^{\textrm {inv}}$
,
![]() $\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
is obtained by fusion from n copies of the
$\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
is obtained by fusion from n copies of the
![]() $n=1$
case. We get from [Reference Paluba38, Theorem 5.6.1] that
$n=1$
case. We get from [Reference Paluba38, Theorem 5.6.1] that
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
admits the same factorisationFootnote
12
on
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
admits the same factorisationFootnote
12
on
![]() $M^{\textrm {inv}}$
in terms of n copies of the
$M^{\textrm {inv}}$
in terms of n copies of the
![]() $n=1$
case. As we recalled, the correspondence of the bivector and the
$n=1$
case. As we recalled, the correspondence of the bivector and the
![]() $2$
-form is already known on
$2$
-form is already known on
![]() $\operatorname {Rep}(\overline {\Gamma }_1,(d_1,d_2))$
so that
$\operatorname {Rep}(\overline {\Gamma }_1,(d_1,d_2))$
so that
![]() $\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
and
$\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
and
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
correspond to one another on
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
correspond to one another on
![]() $M^{\textrm {inv}}$
. Being in correspondence (see [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2, Lemma 10.2]) means that the composite
$M^{\textrm {inv}}$
. Being in correspondence (see [Reference Alekseev, Kosmann-Schwarzbach and Meinrenken2, Lemma 10.2]) means that the composite
coincides with a specific holomorphic function when restricted to
![]() $TM^{\textrm {inv}}$
. By holomorphicity, these functions must then coincide globally, so
$TM^{\textrm {inv}}$
. By holomorphicity, these functions must then coincide globally, so
![]() $\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
and
$\operatorname {tr}({\mathrm {P}}_{\operatorname {Rep}})$
and
![]() $\operatorname {tr}(\omega _{\operatorname {Rep}})$
correspond to one another globally.
$\operatorname {tr}(\omega _{\operatorname {Rep}})$
correspond to one another globally.
Acknowledgements
We are deeply grateful to Luis Álvarez-Cónsul, Philip Boalch, Oleg Chalykh, William Crawley-Boevey and Vladimir Rubtsov for useful discussions and their encouragement and to Thomas Brüstle for bringing [Reference Brüstle18] to our attention. Special thanks are due to Philip Boalch for suggesting that Proposition 5.16 should hold and to the referees for useful comments. M. F. (corresponding author) was supported by a Rankin-Sneddon Research Fellowship of the University of Glasgow. D. F. was supported by the Alexander von Humboldt Stiftung in the framework of an Alexander von Humboldt professorship endowed by the German Federal Ministry of Education and Research.
Conflict of Interests
None.