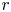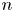1. Introduction
Modern industries use different kinds of systems which are not only costly but also very complex in nature. The failure of such a system may cause catastrophic damage to the concerned industry. If there are more than one systems of similar types available (which is often the case), then the key question is: how to choose the best one among them, keeping in mind that the lifetime of a system is a random quantity? Stochastic orders are often used as an effective solution to this problem. Another important problem related to the system reliability is: how to analyze the lifetime behavior of a system which has already been operated over a period of time? The notion of stochastic agings can be used to address this problem.
Most of the real-life systems are structurally the same as the coherent systems defined in reliability theory (see [Reference Barlow and Proschan5] for the definition). An ![]() $r$-out-of-
$r$-out-of-![]() $n$ system is a special type of coherent system. A system of
$n$ system is a special type of coherent system. A system of ![]() $n$ components is said to be the
$n$ components is said to be the ![]() $r$-out-of-
$r$-out-of-![]() $n$ system if it functions as long as at least
$n$ system if it functions as long as at least ![]() $r$ of its
$r$ of its ![]() $n$ components function. Again, two special cases of
$n$ components function. Again, two special cases of ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems are
$n$ systems are ![]() $1$-out-of-
$1$-out-of-![]() $n$ system (parallel system) and
$n$ system (parallel system) and ![]() $n$-out-of-
$n$-out-of-![]() $n$ system (series system). It is worthwhile to mention here that the lifetime of an
$n$ system (series system). It is worthwhile to mention here that the lifetime of an ![]() $r$-out-of-
$r$-out-of-![]() $n$ system can be represented by the
$n$ system can be represented by the ![]() $(n-r+1)$th order statistic (of lifetimes of
$(n-r+1)$th order statistic (of lifetimes of ![]() $n$ components). This means that the study of an
$n$ components). This means that the study of an ![]() $r$-out-of-
$r$-out-of-![]() $n$ system is the same as the study of the
$n$ system is the same as the study of the ![]() $(n-r+1)$th order statistic of nonnegative random variables.
$(n-r+1)$th order statistic of nonnegative random variables.
The study of stochastic comparisons of coherent systems is considered as one of the important problems in reliability theory. Among all, Pledger and Proschan [Reference Pledger and Proschan43], to the best of our knowledge, are the first who studied stochastic comparisons of two ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems with heterogeneous components. Different variations of this problem were further studied by numerous researchers (see [Reference Balakrishnan and Zhao2,Reference Barmalzan, Haidari and Balakrishnan6,Reference Bon and Păltănea10,Reference Dykstra, Kochar and Rojo12,Reference Hazra, Kuiti, Finkelstein and Nanda22,Reference Hazra, Kuiti, Finkelstein and Nanda23,Reference Khaledi and Kochar25,Reference Samaniego45,Reference Samaniego and Navarro46,Reference Zhao, Li and Balakrishnan50,Reference Zhao, Li and Da51], to name a few). Stochastic comparisons of coherent systems with independent and nonidentically distributed components were considered in [Reference Belzunce, Franco, Ruiz and Ruiz8,Reference Boland, El-Neweihi and Proschan9,Reference Nanda, Jain and Singh34]. Furthermore, the same problem for coherent systems with dependent components was studied by Navarro [Reference Navarro35], Navarro et al. [Reference Navarro, Águila, Sordo and Suárez-Liorens38,Reference Navarro, Pellerey and Di Crescenzo40,Reference Navarro, Águila, Sordo and Suárez-Liorens41], Navarro and Rubio [Reference Navarro and Rubio37], Amini-Seresht et al. [Reference Amini-Seresht, Zhang and Balakrishnan1], Hazra and Finkelstein [Reference Hazra and Finkelstein18], Navarro and Mulero [Reference Navarro and Mulero36], Kelkinnama and Asadi [Reference Kelkinnama and Asadi24], and Hazra and Misra [Reference Hazra and Misra19,Reference Hazra and Misra20]. Recently, Li and Fang [Reference Li and Fang30] studied ordering properties of order statistics where the dependency structure between random variables was described by an Archimedean copula. They have considered the order statistics from a single sample. Later, this problem for two samples under a specific semi-parametric model was considered by numerous researchers (see [Reference Barmalzan, Ayat, Balakrishnan and Roozegar7,Reference Fang, Li and Li14,Reference Li and Lu32], and the references therein). In all these studies, it is assumed that the lifetimes of the components of a system either have a specific distribution (namely, exponential, Weibull, Gamma, etc.) or follow a semi-parametric model (namely, proportional hazard rate model, scale model, proportional odds model, etc.). To the best of our knowledge, no study has been carried out for general systems (namely,
$n$ systems with heterogeneous components. Different variations of this problem were further studied by numerous researchers (see [Reference Balakrishnan and Zhao2,Reference Barmalzan, Haidari and Balakrishnan6,Reference Bon and Păltănea10,Reference Dykstra, Kochar and Rojo12,Reference Hazra, Kuiti, Finkelstein and Nanda22,Reference Hazra, Kuiti, Finkelstein and Nanda23,Reference Khaledi and Kochar25,Reference Samaniego45,Reference Samaniego and Navarro46,Reference Zhao, Li and Balakrishnan50,Reference Zhao, Li and Da51], to name a few). Stochastic comparisons of coherent systems with independent and nonidentically distributed components were considered in [Reference Belzunce, Franco, Ruiz and Ruiz8,Reference Boland, El-Neweihi and Proschan9,Reference Nanda, Jain and Singh34]. Furthermore, the same problem for coherent systems with dependent components was studied by Navarro [Reference Navarro35], Navarro et al. [Reference Navarro, Águila, Sordo and Suárez-Liorens38,Reference Navarro, Pellerey and Di Crescenzo40,Reference Navarro, Águila, Sordo and Suárez-Liorens41], Navarro and Rubio [Reference Navarro and Rubio37], Amini-Seresht et al. [Reference Amini-Seresht, Zhang and Balakrishnan1], Hazra and Finkelstein [Reference Hazra and Finkelstein18], Navarro and Mulero [Reference Navarro and Mulero36], Kelkinnama and Asadi [Reference Kelkinnama and Asadi24], and Hazra and Misra [Reference Hazra and Misra19,Reference Hazra and Misra20]. Recently, Li and Fang [Reference Li and Fang30] studied ordering properties of order statistics where the dependency structure between random variables was described by an Archimedean copula. They have considered the order statistics from a single sample. Later, this problem for two samples under a specific semi-parametric model was considered by numerous researchers (see [Reference Barmalzan, Ayat, Balakrishnan and Roozegar7,Reference Fang, Li and Li14,Reference Li and Lu32], and the references therein). In all these studies, it is assumed that the lifetimes of the components of a system either have a specific distribution (namely, exponential, Weibull, Gamma, etc.) or follow a semi-parametric model (namely, proportional hazard rate model, scale model, proportional odds model, etc.). To the best of our knowledge, no study has been carried out for general systems (namely, ![]() $r$-out-of-
$r$-out-of-![]() $n$ system, etc.) with components’ lifetimes having arbitrary distributions (i.e., without any specific distribution/semi-parametric model). Thus, in this paper, we study some stochastic comparisons results for series, parallel, and general
$n$ system, etc.) with components’ lifetimes having arbitrary distributions (i.e., without any specific distribution/semi-parametric model). Thus, in this paper, we study some stochastic comparisons results for series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems with arbitrary components’ lifetimes.
$n$ systems with arbitrary components’ lifetimes.
The systems that are used in real life are mostly composed either by new components or by used components. Consider two systems, namely, a used system and a system of used components (see the definitions in Subsection 3.2). An important research problem in this context is whether a system of used components has larger lifetime than a used system in some stochastic sense. This problem was first considered in [Reference Li and Lu32]. Later, many other researchers (namely, [Reference Gupta16,Reference Gupta, Misra and Kumar17,Reference Hazra and Nanda21], and the references therein) have shown their interest to study this problem. Although there is a vast literature on this topic, no research has been carried out for the systems with dependent components governed by the Archimedean copula. Thus, another goal of this paper is to study the aforementioned problem for the systems with d.i.d. components governed by the Archimedean copula.
The study of stochastic agings is another important problem in reliability theory. Closure properties of various aging classes (namely, IFR, DFR, IFRA, DRFR, etc.) under the formation of coherent systems with independent components were studied by Esary and Proschan [Reference Esary and Proschan13], Barlow and Proschan [Reference Barlow and Proschan5], Sengupta and Nanda [Reference Sengupta and Nanda48], Franco et al. [Reference Franco, Ruiz and Ruiz15], Lai and Xie [Reference Lai and Xie29], and others. The same problem for coherent systems with dependent components was considered in [Reference Navarro and Mulero36,Reference Navarro, Águila, Sordo and Suárez-Liorens39]. However, the study of aging properties of coherent systems (especially, ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems) with dependent components governed by the Archimedean copula has not yet been considered in the literature. In this paper, we focus to study the closure properties of different aging classes under the formation of
$n$ systems) with dependent components governed by the Archimedean copula has not yet been considered in the literature. In this paper, we focus to study the closure properties of different aging classes under the formation of ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems with dependent and identically distributed components, where the dependency structures are described by Archimedean copulas.
$n$ systems with dependent and identically distributed components, where the dependency structures are described by Archimedean copulas.
The rest of the paper is organized as follows. In Section 2, we discuss some useful concepts and introduce some notations and definitions. In Section 3, we discuss the main results of this paper. To be more specific, in Subsection 3.1, we give some stochastic comparisons results for series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems. In Subsection 3.2, we investigate whether a system of used components performs better than a used system with respect to different stochastic orders. Different aging properties of series, parallel, and general
$n$ systems. In Subsection 3.2, we investigate whether a system of used components performs better than a used system with respect to different stochastic orders. Different aging properties of series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems are discussed in Subsection 3.3. Furthermore, in Section 4, we give some numerical examples. Finally, the concluding remarks are given in Section 5.
$n$ systems are discussed in Subsection 3.3. Furthermore, in Section 4, we give some numerical examples. Finally, the concluding remarks are given in Section 5.
All proofs of theorems, wherever given, are deferred to the Appendix.
2. Preliminaries
For an absolutely continuous random variable ![]() $Z$, we denote the probability density function (pdf) by
$Z$, we denote the probability density function (pdf) by ![]() $f_Z(\cdot )$, the cumulative distribution function (cdf) by
$f_Z(\cdot )$, the cumulative distribution function (cdf) by ![]() $F_Z(\cdot )$, the reliability/survival function (sf) by
$F_Z(\cdot )$, the reliability/survival function (sf) by ![]() $\bar F_Z(\cdot )$, the hazard/failure rate function by
$\bar F_Z(\cdot )$, the hazard/failure rate function by ![]() $r_Z(\cdot )$, and the reverse hazard/failure rate function by
$r_Z(\cdot )$, and the reverse hazard/failure rate function by ![]() $\tilde {r}_Z(\cdot )$; here
$\tilde {r}_Z(\cdot )$; here ![]() $\bar F_Z(\cdot )\equiv 1-F_Z(\cdot )$,
$\bar F_Z(\cdot )\equiv 1-F_Z(\cdot )$, ![]() $r_Z(\cdot )=f_Z(\cdot )/\bar F_Z(\cdot )$, and
$r_Z(\cdot )=f_Z(\cdot )/\bar F_Z(\cdot )$, and ![]() $\tilde r_Z(\cdot )=f_Z(\cdot )/F_Z(\cdot )$.
$\tilde r_Z(\cdot )=f_Z(\cdot )/F_Z(\cdot )$.
Copula is a very useful notion in describing the dependency structure between components of a random vector. It builds a bridge between a multivariate distribution function and its corresponding one-dimensional marginal distribution functions. The joint cdf of a random vector ![]() $\boldsymbol {X}=(X_1,X_2, \ldots,X_n)$ can be written, in terms of a copula, as
$\boldsymbol {X}=(X_1,X_2, \ldots,X_n)$ can be written, in terms of a copula, as
where ![]() $C(\cdot )$ is a copula. Similarly, the joint reliability function of
$C(\cdot )$ is a copula. Similarly, the joint reliability function of ![]() $\boldsymbol {X}$ can be represented as
$\boldsymbol {X}$ can be represented as
where ![]() $\bar C(\cdot )$ is a survival copula. In the literature, different types of survival copulas have been introduced to describe different dependency structures between components of a random vector. The commonly used copulas are the Farlie–Gumbel–Morgenstern (FGM) copula, the extreme-value copulas, the family of Archimedean copulas, the Clayton–Oakes (CO) copula, etc. Among all these copulas, the family of Archimedean copulas is the one that has paid more attention from the researchers due to its wide range of capturing the dependency structures. Moreover, these are mathematically tractable, and there is a large number of results available in the literature which can be used on a ready-made basis in different problems. More information on this topic could be found in the monograph written by Nelsen [Reference Nelsen42]. In what follows, we give the definition of the Archimedean copula (see [Reference McNeil and Nĕslehová33]).
$\bar C(\cdot )$ is a survival copula. In the literature, different types of survival copulas have been introduced to describe different dependency structures between components of a random vector. The commonly used copulas are the Farlie–Gumbel–Morgenstern (FGM) copula, the extreme-value copulas, the family of Archimedean copulas, the Clayton–Oakes (CO) copula, etc. Among all these copulas, the family of Archimedean copulas is the one that has paid more attention from the researchers due to its wide range of capturing the dependency structures. Moreover, these are mathematically tractable, and there is a large number of results available in the literature which can be used on a ready-made basis in different problems. More information on this topic could be found in the monograph written by Nelsen [Reference Nelsen42]. In what follows, we give the definition of the Archimedean copula (see [Reference McNeil and Nĕslehová33]).
Definition 2.1 Let ![]() $\phi : [0, +\infty ]\longrightarrow [0,1]$ be a decreasing continuous function such that
$\phi : [0, +\infty ]\longrightarrow [0,1]$ be a decreasing continuous function such that ![]() $\phi (0)=1$ and
$\phi (0)=1$ and ![]() $\phi (+\infty )=0$, and let
$\phi (+\infty )=0$, and let ![]() $\psi \equiv \phi ^{-1}$ be the pseudo-inverse of
$\psi \equiv \phi ^{-1}$ be the pseudo-inverse of ![]() $\phi$. Then,
$\phi$. Then,
is called the Archimedean copula with generator ![]() $\phi$ if
$\phi$ if ![]() $(-1)^{k}\phi ^{(k)}(x)\geq 0$, for
$(-1)^{k}\phi ^{(k)}(x)\geq 0$, for ![]() $k=0,1,\ldots,n-2$, and
$k=0,1,\ldots,n-2$, and ![]() $(-1)^{n-2}\phi ^{(n-2)}(x)$ is decreasing and convex in
$(-1)^{n-2}\phi ^{(n-2)}(x)$ is decreasing and convex in ![]() $x\geq 0$.
$x\geq 0$.
Stochastic orders are frequently used to compare two random variables/vectors. In the last seven decades, it has widely been used in various disciplines of science and engineering including actuarial science, econometrics, finance, risk management, and reliability theory. In the literature, different types of stochastic orders (namely, usual stochastic order, hazard rate order, dispersive order, Lorenz order, etc.) have been developed to study different kinds of problems. This topic is explicitly covered in the book written by Shaked and Shanthikumar [Reference Shaked and Shanthikumar49]. Below we give the definitions of stochastic orders that are used in this paper (see [Reference Razaei, Gholizadeh and Izadkhah44,Reference Sengupta and Deshpande47,Reference Shaked and Shanthikumar49]).
Definition 2.2 Let ![]() $X$ and
$X$ and ![]() $Y$ be two absolutely continuous random variables with nonnegative supports. Then,
$Y$ be two absolutely continuous random variables with nonnegative supports. Then, ![]() $X$ is said to be smaller than
$X$ is said to be smaller than ![]() $Y$ in the
$Y$ in the
(a) usual stochastic order, denoted by
 $X\leq _{\textrm {st}}Y$, if
$X\leq _{\textrm {st}}Y$, if  $\bar F_X(x)\leq \bar F_Y(x) \text { for all }x\in [0,\infty );$
$\bar F_X(x)\leq \bar F_Y(x) \text { for all }x\in [0,\infty );$(b) hazard rate order, denoted by
 $X\leq _{\textrm {hr}}Y$, if
$X\leq _{\textrm {hr}}Y$, if  ${\bar F_Y(x)}/{\bar F_X(x)}\text { is increasing in } x \in [0,\infty );$
${\bar F_Y(x)}/{\bar F_X(x)}\text { is increasing in } x \in [0,\infty );$(c) reversed hazard rate order, denoted by
 $X\leq _{\textrm {rhr}}Y$, if
$X\leq _{\textrm {rhr}}Y$, if  ${F_Y(x)}/{ F_X(x)}\text { is increasing in }$
${F_Y(x)}/{ F_X(x)}\text { is increasing in }$  $x\in [0,\infty );$
$x\in [0,\infty );$(d) likelihood ratio order, denoted by
 $X\leq _{\textrm {lr}}Y$, if
$X\leq _{\textrm {lr}}Y$, if  ${f_Y(x)}/{f_X(x)}\;\text { is increasing in } x\in (0,\infty );$
${f_Y(x)}/{f_X(x)}\;\text { is increasing in } x\in (0,\infty );$(e) aging faster order in terms of the failure rate, denoted by
 $X\leq _{c} Y$, if
$X\leq _{c} Y$, if  $r_X(x)/r_Y(x)$ is increasing in
$r_X(x)/r_Y(x)$ is increasing in  $x\in [0,\infty );$
$x\in [0,\infty );$(f) aging faster order in terms of the reversed failure rate, denoted by
 $X\leq _{b}Y$, if
$X\leq _{b}Y$, if  $\tilde r_X(x)/\tilde r_Y(x)$ is decreasing in
$\tilde r_X(x)/\tilde r_Y(x)$ is decreasing in  $x\in [0,\infty )$.
$x\in [0,\infty )$.
Like stochastic orders, the notion of stochastic agings is another important concept in reliability theory. Stochastic agings largely describe how a system behaves as time progresses. There are three types of agings, namely, positive aging, negative aging, and no aging. A system has the positive aging property if its residual lifetime decreases in some stochastic sense as time progresses. On the other hand, negative aging describes the scenario where the residual lifetime of a system increases in some stochastic sense as the system ages. No aging means that the system does not age over time. A variety of positive and negative aging classes (namely, IFR, IFRA, DFR, DLR, etc.) have been introduced in the literature to describe different aging characteristics of a system (see [Reference Barlow and Proschan5,Reference Lai and Xie29], and the references therein). For the sake of completeness, we give the following definitions of aging classes that are used in this paper.
Definition 2.3 Let ![]() $X$ be an absolutely continuous random variable with nonnegative support. Then,
$X$ be an absolutely continuous random variable with nonnegative support. Then, ![]() $X$ is said to have the
$X$ is said to have the
(a) increasing likelihood ratio (ILR) (resp. decreasing likelihood ratio (DLR)) property if
 $f'_X(x)/f_X(x)$ is decreasing (resp. increasing) in
$f'_X(x)/f_X(x)$ is decreasing (resp. increasing) in  $x\geq 0;$
$x\geq 0;$(b) increasing failure rate (IFR) (resp. decreasing failure rate (DFR)) property if
 $r_X(x)$ is increasing (resp. decreasing) in
$r_X(x)$ is increasing (resp. decreasing) in  $x\geq 0;$
$x\geq 0;$(c) decreasing reversed failure rate (DRFR) property if
 $\tilde r_X(x)\ \text {is decreasing in}\ x\geq 0;$
$\tilde r_X(x)\ \text {is decreasing in}\ x\geq 0;$(d) increasing failure rate in average (IFRA) (resp. decreasing failure rate in average (DFRA)) property if
 ${-\ln \bar F_X(x)}/{x}\text { is increasing (resp. decreasing) in }x\geq 0$.
${-\ln \bar F_X(x)}/{x}\text { is increasing (resp. decreasing) in }x\geq 0$.
Throughout the paper, we use the words “increasing” and “decreasing” to mean “nondecreasing” and “nonincreasing”, respectively. Furthermore, the words “positive” and “negative” mean “nonnegative” and “nonpositive”, respectively. By ![]() $a\stackrel {\text {def.}}=b$, we mean that
$a\stackrel {\text {def.}}=b$, we mean that ![]() $a$ is defined as
$a$ is defined as ![]() $b$. For a twice differentiable function
$b$. For a twice differentiable function ![]() $u(\cdot )$, we write
$u(\cdot )$, we write ![]() $u'(t)$ and
$u'(t)$ and ![]() $u''(t)$ to mean the first and the second derivatives of
$u''(t)$ to mean the first and the second derivatives of ![]() $u(t)$ with respect to
$u(t)$ with respect to ![]() $t$. We use the acronyms “i.i.d.” and “d.i.d.” to mean “independent and identically distributed” and “dependent and identically distributed”, respectively. All random variables considered in this paper are assumed to be absolutely continuous with nonnegative supports.
$t$. We use the acronyms “i.i.d.” and “d.i.d.” to mean “independent and identically distributed” and “dependent and identically distributed”, respectively. All random variables considered in this paper are assumed to be absolutely continuous with nonnegative supports.
3. Main results
In this section, we first discuss some stochastic comparisons results for series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems. Then, we study whether a system of used components performs better than a used system with respect to different stochastic orders. Lastly, the closure properties of different aging classes under formations of different systems have been studied.
$n$ systems. Then, we study whether a system of used components performs better than a used system with respect to different stochastic orders. Lastly, the closure properties of different aging classes under formations of different systems have been studied.
Let ![]() $\tau ^{\phi _1}_{r|n}(\boldsymbol {X})$ and
$\tau ^{\phi _1}_{r|n}(\boldsymbol {X})$ and ![]() $\tau ^{\phi _2}_{r|n}(\boldsymbol {Y})$ be the lifetimes of two
$\tau ^{\phi _2}_{r|n}(\boldsymbol {Y})$ be the lifetimes of two ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems formed by two different sets of
$n$ systems formed by two different sets of ![]() $n$ d.i.d. components with the lifetime vectors
$n$ d.i.d. components with the lifetime vectors ![]() $\boldsymbol {X}=(X_1,X_2,\ldots,X_n)$ and
$\boldsymbol {X}=(X_1,X_2,\ldots,X_n)$ and ![]() $\boldsymbol {Y}=(Y_1,Y_2,\ldots,Y_n)$, respectively, where the distributions of
$\boldsymbol {Y}=(Y_1,Y_2,\ldots,Y_n)$, respectively, where the distributions of ![]() $\boldsymbol {X}$ and
$\boldsymbol {X}$ and ![]() $\boldsymbol {Y}$ are described by the Archimedean copulas with generators
$\boldsymbol {Y}$ are described by the Archimedean copulas with generators ![]() $\phi _1(\cdot )$ and
$\phi _1(\cdot )$ and ![]() $\phi _2(\cdot )$, respectively. Furthermore, let
$\phi _2(\cdot )$, respectively. Furthermore, let ![]() $X_i\stackrel {d}=X$ and
$X_i\stackrel {d}=X$ and ![]() $Y_i\stackrel {d}=Y$,
$Y_i\stackrel {d}=Y$, ![]() $i=1,2,\ldots,n$, for some nonnegative random variables
$i=1,2,\ldots,n$, for some nonnegative random variables ![]() $X$ and
$X$ and ![]() $Y$; here
$Y$; here ![]() $\stackrel {d}=$ stands for equality in distribution. In what follows, we introduce some notation:
$\stackrel {d}=$ stands for equality in distribution. In what follows, we introduce some notation:
Since ![]() $\phi _i(\cdot )$,
$\phi _i(\cdot )$, ![]() $i=1,2$, are decreasing convex functions, it follows that
$i=1,2$, are decreasing convex functions, it follows that ![]() $H_i(\cdot )$,
$H_i(\cdot )$, ![]() $R_i(\cdot )$, and
$R_i(\cdot )$, and ![]() $G_i(\cdot )$ are all negative-valued functions. Furthermore, we write
$G_i(\cdot )$ are all negative-valued functions. Furthermore, we write ![]() $\tau ^{\phi _1}_{r|n}=\tau ^{\phi _2}_{r|n}=\tau ^{\phi }_{r|n}$ (say),
$\tau ^{\phi _1}_{r|n}=\tau ^{\phi _2}_{r|n}=\tau ^{\phi }_{r|n}$ (say), ![]() $H_1(\cdot )=H_2(\cdot )=H(\cdot )$ (say),
$H_1(\cdot )=H_2(\cdot )=H(\cdot )$ (say), ![]() $R_1(\cdot )=R_2(\cdot )=R(\cdot )$ (say), and
$R_1(\cdot )=R_2(\cdot )=R(\cdot )$ (say), and ![]() $G_1(\cdot )=G_2(\cdot )=G(\cdot )$ (say) whenever the distributions of both
$G_1(\cdot )=G_2(\cdot )=G(\cdot )$ (say) whenever the distributions of both ![]() $\boldsymbol {X}$ and
$\boldsymbol {X}$ and ![]() $\boldsymbol {Y}$ are described by the same Archimedean copula with generator
$\boldsymbol {Y}$ are described by the same Archimedean copula with generator ![]() $\phi _1(\cdot )=\phi _2(\cdot )=\phi (\cdot )$ (say). Furthermore, we introduce a few more notations as follows:
$\phi _1(\cdot )=\phi _2(\cdot )=\phi (\cdot )$ (say). Furthermore, we introduce a few more notations as follows:
 \begin{align*} & C(u)=\left(\frac{u\phi''(u)}{\phi'(u)}+\frac{u\phi'(u)}{1-\phi(u)}+1\right)=\frac{uH'(u)}{H(u)},\quad u>0,\\ & C_{r,n}^{j}=\left({-}1\right)^{j-r}\binom{j-1}{r-1}\binom{n}{j},\quad 1\leq r\leq j\leq n,\\ & P_{r,n}^{j}(u)=\frac{C_{r,n}^{j}\phi\left(ju\right)}{\sum_{j=r}^{n} C_{r,n}^{j}\phi\left(ju\right)},\quad Q_{r,n}^{j}(u)=\frac{C_{r,n}^{j}\left(1-\phi\left(ju\right)\right)}{1-\sum_{j=r}^{n} C_{r,n}^{j}\phi\left(ju\right)},\quad u>0,\;1\leq r\leq j\leq n,\\ & K_j(u)=\frac{R\left(ju\right)}{R(u)},\quad L_j(u)=\frac{H\left(ju\right)}{H(u)},\quad u>0,\ 1\leq j\leq n. \end{align*}
\begin{align*} & C(u)=\left(\frac{u\phi''(u)}{\phi'(u)}+\frac{u\phi'(u)}{1-\phi(u)}+1\right)=\frac{uH'(u)}{H(u)},\quad u>0,\\ & C_{r,n}^{j}=\left({-}1\right)^{j-r}\binom{j-1}{r-1}\binom{n}{j},\quad 1\leq r\leq j\leq n,\\ & P_{r,n}^{j}(u)=\frac{C_{r,n}^{j}\phi\left(ju\right)}{\sum_{j=r}^{n} C_{r,n}^{j}\phi\left(ju\right)},\quad Q_{r,n}^{j}(u)=\frac{C_{r,n}^{j}\left(1-\phi\left(ju\right)\right)}{1-\sum_{j=r}^{n} C_{r,n}^{j}\phi\left(ju\right)},\quad u>0,\;1\leq r\leq j\leq n,\\ & K_j(u)=\frac{R\left(ju\right)}{R(u)},\quad L_j(u)=\frac{H\left(ju\right)}{H(u)},\quad u>0,\ 1\leq j\leq n. \end{align*}3.1. Stochastic comparisons of two systems
In this subsection, we study some comparisons results for series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems using different stochastic orders.
$n$ systems using different stochastic orders.
In the following theorem, we compare two ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems with respect to the usual stochastic order, the hazard rate order, and the reversed hazard rate order. Here, we assume that both systems have the same dependency structure described by the Archimedean copula with generator
$n$ systems with respect to the usual stochastic order, the hazard rate order, and the reversed hazard rate order. Here, we assume that both systems have the same dependency structure described by the Archimedean copula with generator ![]() $\phi .$ The proof of the first part of this theorem is straightforward, whereas the proof of the third part is similar to that of the second part and hence omitted.
$\phi .$ The proof of the first part of this theorem is straightforward, whereas the proof of the third part is similar to that of the second part and hence omitted.
Theorem 3.1 The following results hold true.
(a) Assume that
 $\sum _{j=r}^{n} C_{r,n}^{j}\phi \left (ju\right )$ (or
$\sum _{j=r}^{n} C_{r,n}^{j}\phi \left (ju\right )$ (or  $\sum _{j=n-r+1}^{n} C_{n-r+1,n}^{j}\phi \left (ju\right )$) is decreasing in
$\sum _{j=n-r+1}^{n} C_{n-r+1,n}^{j}\phi \left (ju\right )$) is decreasing in  $u>0$. If
$u>0$. If  $X \leq _{\textrm {st}} Y$, then
$X \leq _{\textrm {st}} Y$, then  $\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {st}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$;
$\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {st}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$;(b) Assume that
 $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in  $u>0$, or
$u>0$, or  $\sum _{j=n-r+1}^{n} Q_{n-r+1,n}^{j}(u)L_j(u)$ is decreasing in
$\sum _{j=n-r+1}^{n} Q_{n-r+1,n}^{j}(u)L_j(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X \leq _{\textrm {hr}} Y$, then
$X \leq _{\textrm {hr}} Y$, then  $\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {hr}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$;
$\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {hr}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$;(c) Assume that
 $\sum _{j=n-r+1}^{n} P_{n-r+1,n}^{j}(u)K_j(u)$ is increasing in
$\sum _{j=n-r+1}^{n} P_{n-r+1,n}^{j}(u)K_j(u)$ is increasing in  $u>0$, or
$u>0$, or  $\sum _{j=r}^{n} Q_{r,n}^{j}(u)L_j(u)$ is decreasing in
$\sum _{j=r}^{n} Q_{r,n}^{j}(u)L_j(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X \leq _{\textrm {rh}} Y$, then
$X \leq _{\textrm {rh}} Y$, then  $\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {rh}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$.
$\tau ^{\phi }_{r|n}(\boldsymbol {X}) \leq _{\textrm {rh}} \tau ^{\phi }_{r|n}\left (\boldsymbol {Y}\right )$.
Stochastic comparisons of two series/parallel systems (in the sense of the usual stochastic order, the hazard rate order, and the reversed hazard rate order) are given in the following corollary which is obtained from Theorem 3.1.
Corollary 3.1 The following results hold true.
(a) If
 $X\leq _{\textrm {st}} Y$, then
$X\leq _{\textrm {st}} Y$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {st}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$ and
$\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {st}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$ and  $\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {st}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {st}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;(b) Assume that
 $uH'(u)/H(u)$ is decreasing in
$uH'(u)/H(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {hr}} Y$, then
$X\leq _{\textrm {hr}} Y$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {hr}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {hr}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$;(c) Assume that
 $uR'(u)/R(u)$ is increasing in
$uR'(u)/R(u)$ is increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {hr}} Y$, then
$X\leq _{\textrm {hr}} Y$, then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {hr}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {hr}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;(d) Assume that
 $uR'(u)/R(u)$ is increasing in
$uR'(u)/R(u)$ is increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {rh}} Y$, then
$X\leq _{\textrm {rh}} Y$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {rh}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {rh}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$;(e) Assume that
 $uH'(u)/H(u)$ is decreasing in
$uH'(u)/H(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {rh}} Y$, then
$X\leq _{\textrm {rh}} Y$, then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
$\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
In the next theorem, we compare two series/parallel systems with respect to the likelihood ratio order and the aging faster orders. The proof of the third part of this theorem can be done in the same line as in the second part and hence omitted.
Theorem 3.2 The following results hold true.
(a) Assume that
 $({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing in
$({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {lr}} Y$, then
$X\leq _{\textrm {lr}} Y$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {lr}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$ and
$\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{\textrm {lr}}\tau ^{\phi }_{1|n}(\boldsymbol {Y})$ and  $\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {lr}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{\textrm {lr}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$;(b) Assume that
 $({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in
$({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in  $u>0$. If
$u>0$. If  $Y\leq _{\textrm {rh}} X$ and
$Y\leq _{\textrm {rh}} X$ and  $X\leq _{c} Y$, then
$X\leq _{c} Y$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{c} \tau ^{\phi }_{1|n}(\boldsymbol {Y})$;
$\tau ^{\phi }_{1|n}(\boldsymbol {X})\leq _{c} \tau ^{\phi }_{1|n}(\boldsymbol {Y})$;(c) Assume that
 $({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in
$({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {hr}} Y$ and
$X\leq _{\textrm {hr}} Y$ and  $X\leq _{b} Y$, then
$X\leq _{b} Y$, then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{b} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
$\tau ^{\phi }_{n|n}(\boldsymbol {X})\leq _{b} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
The following remark provides sufficient conditions for the assumptions given in Theorem 3.2.
Remark 3.1 The following observations can be made.
(a) If
 $uG'(u)/G(u)$ is positive and increasing (resp. decreasing) in
$uG'(u)/G(u)$ is positive and increasing (resp. decreasing) in  $u>0$, and
$u>0$, and  $G(u)/R(u)$ is increasing (resp. decreasing) in
$G(u)/R(u)$ is increasing (resp. decreasing) in  $u>0$, then
$u>0$, then  $({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing (resp. decreasing) in
$({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing (resp. decreasing) in  $u>0$.
$u>0$.(b) If both
 $uC'(u)/C(u)$ and
$uC'(u)/C(u)$ and  $C(u)/R(u)$ are positive and increasing in
$C(u)/R(u)$ are positive and increasing in  $u>0$, then
$u>0$, then  $({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in
$({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in  $u>0$.
$u>0$.
In the following theorem, we compare two parallel systems with respect to the usual stochastic order, the hazard rate order, and the reversed hazard rate order. Here, we assume that the dependency structure of one system differs from that of the other system. The proof of the third part of this theorem can be done in the same line, as in the second part, and hence omitted.
Theorem 3.3 The following results hold true.
(a) Assume that
 $\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in
$\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {st}} Y$, then
$X\leq _{\textrm {st}} Y$, then  $\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {st}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$;
$\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {st}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$;(b) Assume that
 $\psi _1(w)\leq \psi _2(v)$, for all
$\psi _1(w)\leq \psi _2(v)$, for all  $0\leq v\leq w\leq 1$, and
$0\leq v\leq w\leq 1$, and  $H_1(u)/H_2(u)$ is increasing in
$H_1(u)/H_2(u)$ is increasing in  $u>0$. Furthermore, assume that either
$u>0$. Furthermore, assume that either  $uH_1'(u)/H_1(u)$ or
$uH_1'(u)/H_1(u)$ or  $uH_2'(u)/H_2(u)$ is decreasing in
$uH_2'(u)/H_2(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {hr}} Y$, then
$X\leq _{\textrm {hr}} Y$, then  $\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {hr}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$;
$\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {hr}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$;(c) Assume that
 $\psi _1(w)\leq \psi _2(v)$, for all
$\psi _1(w)\leq \psi _2(v)$, for all  $0\leq v\leq w\leq 1$, and
$0\leq v\leq w\leq 1$, and  $R_1(u)/R_2(u)$ is decreasing in
$R_1(u)/R_2(u)$ is decreasing in  $u>0$. Furthermore, assume that either
$u>0$. Furthermore, assume that either  $uR_1'(u)/R_1(u)$ or
$uR_1'(u)/R_1(u)$ or  $uR_2'(u)/R_2(u)$ is increasing in
$uR_2'(u)/R_2(u)$ is increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {rh}} Y$, then
$X\leq _{\textrm {rh}} Y$, then  $\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {rh}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$.
$\tau ^{\phi _1}_{1|n}(\boldsymbol {X})\leq _{\textrm {rh}}\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$.
In the next theorem, we study the same set of results, as in Theorem 3.3, for the series system. The proofs are similar to those of Theorem 3.3 and hence omitted.
Theorem 3.4 The following results hold true.
(a) Assume that
 $\phi _1^{-1}\left (\phi _2(u)\right )$ is sub-additive in
$\phi _1^{-1}\left (\phi _2(u)\right )$ is sub-additive in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {st}} Y$, then
$X\leq _{\textrm {st}} Y$, then  $\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {st}} \tau ^{\phi _2}_{n|n}(\boldsymbol {Y})$;
$\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {st}} \tau ^{\phi _2}_{n|n}(\boldsymbol {Y})$;(b) Assume that
 $\psi _1(w)\geq \psi _2(v)$, for all
$\psi _1(w)\geq \psi _2(v)$, for all  $0\leq w\leq v\leq 1$, and
$0\leq w\leq v\leq 1$, and  $R_1(u)/R_2(u)$ is increasing in
$R_1(u)/R_2(u)$ is increasing in  $u>0$. Furthermore, assume that either
$u>0$. Furthermore, assume that either  $uR_1'(u)/R_1(u)$ or
$uR_1'(u)/R_1(u)$ or  $uR_2'(u)/R_2(u)$ is increasing in
$uR_2'(u)/R_2(u)$ is increasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {hr}} Y$, then
$X\leq _{\textrm {hr}} Y$, then  $\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {hr}} \tau ^{\phi _2}_{n|n}(\boldsymbol {Y})$;
$\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {hr}} \tau ^{\phi _2}_{n|n}(\boldsymbol {Y})$;(c) Assume that
 $\psi _1(w)\geq \psi _2(v)$, for all
$\psi _1(w)\geq \psi _2(v)$, for all  $0\leq w\leq v\leq 1$, and
$0\leq w\leq v\leq 1$, and  $H_1(u)/H_2(u)$ is decreasing in
$H_1(u)/H_2(u)$ is decreasing in  $u>0$. Furthermore, assume that
$u>0$. Furthermore, assume that  $uH_1'(u)/H_1(u)$ or
$uH_1'(u)/H_1(u)$ or  $uH_2'(u)/H_2(u)$ is decreasing in
$uH_2'(u)/H_2(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X\leq _{\textrm {rh}} Y$, then
$X\leq _{\textrm {rh}} Y$, then  $\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
$\tau ^{\phi _1}_{n|n}(\boldsymbol {X})\leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {Y})$.
Remark 3.2 The following observations can be made.
(a) If
 ${\phi _2^{-1}(w)}/{\phi _1^{-1}(w)}$ is increasing in
${\phi _2^{-1}(w)}/{\phi _1^{-1}(w)}$ is increasing in  $w \in (0,1]$, then
$w \in (0,1]$, then  $\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in
$\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in  $u>0$;
$u>0$;(b) If
 $\phi _1(u) \leq \phi _2(u)$, for all
$\phi _1(u) \leq \phi _2(u)$, for all  $u>0$, then
$u>0$, then  $\psi _1(w) \leq \psi _2(v)$, for all
$\psi _1(w) \leq \psi _2(v)$, for all  $0\leq v\leq w\leq 1$.
$0\leq v\leq w\leq 1$.
3.2. Stochastic comparisons between a used system and a system of used components
Let ![]() $X$ be a random variable representing the lifetime of a component/system. Then, its residual lifetime at a time instant
$X$ be a random variable representing the lifetime of a component/system. Then, its residual lifetime at a time instant ![]() $t \;(\geq 0)$ is given by
$t \;(\geq 0)$ is given by ![]() $X_t = \left (X-t|X>t\right )$. We call
$X_t = \left (X-t|X>t\right )$. We call ![]() $X_t$ as a used component/system. Further, let
$X_t$ as a used component/system. Further, let ![]() $\boldsymbol {X} = \left (X_1, X_2,\ldots, X_n\right )$ be a random vector representing the lifetimes of
$\boldsymbol {X} = \left (X_1, X_2,\ldots, X_n\right )$ be a random vector representing the lifetimes of ![]() $n$ d.i.d. components governed by the Archimedean copula with generator
$n$ d.i.d. components governed by the Archimedean copula with generator ![]() $\phi$, where
$\phi$, where ![]() $X_i\stackrel {d}=X$,
$X_i\stackrel {d}=X$, ![]() $i=1,2,\ldots,n$, for some nonnegative random variable
$i=1,2,\ldots,n$, for some nonnegative random variable ![]() $X$. We denote the vector of
$X$. We denote the vector of ![]() $n$ used components by
$n$ used components by ![]() $\boldsymbol {X}_t =\left (X_1)_t, (X_2)_t,\ldots, (X_n)_t\right )$, for some fixed
$\boldsymbol {X}_t =\left (X_1)_t, (X_2)_t,\ldots, (X_n)_t\right )$, for some fixed ![]() $t>0$. Consequently, we denote the lifetimes of the parallel and the series systems made by a set of used components with the lifetime vector
$t>0$. Consequently, we denote the lifetimes of the parallel and the series systems made by a set of used components with the lifetime vector ![]() $\boldsymbol {X}_t$ by
$\boldsymbol {X}_t$ by ![]() $\tau _{1|n}^{\phi }(\boldsymbol {X}_t)$ and
$\tau _{1|n}^{\phi }(\boldsymbol {X}_t)$ and ![]() $\tau _{n|n}^{\phi }(\boldsymbol {X}_t)$, respectively. Further, we denote the lifetimes of the used parallel system and the used series system formed by a set of components with the lifetime vector
$\tau _{n|n}^{\phi }(\boldsymbol {X}_t)$, respectively. Further, we denote the lifetimes of the used parallel system and the used series system formed by a set of components with the lifetime vector ![]() $\boldsymbol {X}$ by
$\boldsymbol {X}$ by ![]() $(\tau _{1|n}^{\phi }(\boldsymbol {X}))_t$ and
$(\tau _{1|n}^{\phi }(\boldsymbol {X}))_t$ and ![]() $(\tau _{n|n}^{\phi }(\boldsymbol {X}))_t$, respectively, where
$(\tau _{n|n}^{\phi }(\boldsymbol {X}))_t$, respectively, where ![]() $(\tau _{i|n}^{\phi }(\boldsymbol {X}))_t = \tau _{i|n}^{\phi }(\boldsymbol {X})-t|\tau _{i|n}^{\phi }(\boldsymbol {X})>t$, for
$(\tau _{i|n}^{\phi }(\boldsymbol {X}))_t = \tau _{i|n}^{\phi }(\boldsymbol {X})-t|\tau _{i|n}^{\phi }(\boldsymbol {X})>t$, for ![]() $t\geq 0$ and
$t\geq 0$ and ![]() $i=1,n$.
$i=1,n$.
In the following theorem, we compare a used system and a system made by used components with respect to different stochastic orders. Here, we particularly consider the series and the parallel systems formed by d.i.d. components governed by the Archimedean copula with generator ![]() $\phi$. The proofs of the fourth, the sixth, and the seventh parts of this theorem are given in the Appendix. Furthermore, the proof of the first part is straightforward, whereas the proofs of the second, the third, and the fifth parts are similar to that of the fourth part and hence omitted.
$\phi$. The proofs of the fourth, the sixth, and the seventh parts of this theorem are given in the Appendix. Furthermore, the proof of the first part is straightforward, whereas the proofs of the second, the third, and the fifth parts are similar to that of the fourth part and hence omitted.
Theorem 3.5 The following results hold true.
(a)
 $(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {st}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$ and
$(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {st}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$ and  $(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {st}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {st}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(b) If
 $uH'(u)/H(u)$ is decreasing in
$uH'(u)/H(u)$ is decreasing in  $u>0$, then
$u>0$, then  $(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {hr}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {hr}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(c) If
 $uR'(u)/R(u)$ is increasing in
$uR'(u)/R(u)$ is increasing in  $u>0$, then
$u>0$, then  $(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {hr}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {hr}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(d) If
 $uR'(u)/R(u)$ is positive and increasing in
$uR'(u)/R(u)$ is positive and increasing in  $u>0$, then
$u>0$, then  $(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {rh}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {rh}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(e) If
 $uH'(u)/H(u)$ is negative and decreasing in
$uH'(u)/H(u)$ is negative and decreasing in  $u>0$, then
$u>0$, then  $(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {rh}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(f) If
 $({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing in
$({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing in  $u>0$, then
$u>0$, then  $(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {lr}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$ and
$(\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t \leq _{\textrm {lr}} \tau ^{\phi }_{1|n}(\boldsymbol {X}_t)$ and  $(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {lr}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed
$(\tau ^{\phi }_{n|n}(\boldsymbol {X}))_t \leq _{\textrm {lr}} \tau ^{\phi }_{n|n}(\boldsymbol {X}_t)$, for any fixed  $t\geq 0$;
$t\geq 0$;(g) If
 $({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in
$({C(nu)}-{C(u)})/{R(u)}$ is positive and increasing in  $u>0$, then
$u>0$, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X}_t) \leq _{c} (\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t$, for any fixed
$\tau ^{\phi }_{1|n}(\boldsymbol {X}_t) \leq _{c} (\tau ^{\phi }_{1|n}(\boldsymbol {X}))_t$, for any fixed  $t\geq 0$.
$t\geq 0$.
3.3. Preservation of aging classes under the formation of a system
In this subsection, we discuss the closure properties of different aging classes under the formation of ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems.
$n$ systems.
In the following theorem, we provide some sufficient conditions to show that the IFR, the DFR, and the DRFR classes are preserved under the formation of an ![]() $r$-out-of-
$r$-out-of-![]() $n$ system. The proof of the second part of this theorem is similar to that of the first part and hence omitted.
$n$ system. The proof of the second part of this theorem is similar to that of the first part and hence omitted.
Theorem 3.6 The following results hold true.
(a) Assume that
 $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in  $u>0$, or
$u>0$, or  $\sum _{j=n-r+1}^{n} Q_{n-r+1,n}^{j}(u)L_j(u)$ is decreasing (resp. increasing) in
$\sum _{j=n-r+1}^{n} Q_{n-r+1,n}^{j}(u)L_j(u)$ is decreasing (resp. increasing) in  $u>0$. If
$u>0$. If  $X$ is IFR (resp. DFR), then
$X$ is IFR (resp. DFR), then  $\tau ^{\phi }_{r|n}(\boldsymbol {X})$ is IFR (resp. DFR);
$\tau ^{\phi }_{r|n}(\boldsymbol {X})$ is IFR (resp. DFR);(b) Assume that
 $\sum _{j=n-r+1}^{n} P_{n-r+1,n}^{j}(u)K_j(u)$ is increasing in
$\sum _{j=n-r+1}^{n} P_{n-r+1,n}^{j}(u)K_j(u)$ is increasing in  $u>0$, or
$u>0$, or  $\sum _{j=r}^{n} Q_{r,n}^{j}(u)L_j(u)$ is decreasing in
$\sum _{j=r}^{n} Q_{r,n}^{j}(u)L_j(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X$ is DRFR, then
$X$ is DRFR, then  $\tau ^{\phi }_{r|n}(\boldsymbol {X})$ is DRFR.
$\tau ^{\phi }_{r|n}(\boldsymbol {X})$ is DRFR.
The following corollary immediately follows from Theorem 3.6.
Corollary 3.2 The following results hold true.
(a) Assume that
 $uR'(u)/R(u)$ is increasing (resp. decreasing) in
$uR'(u)/R(u)$ is increasing (resp. decreasing) in  $u>0$. If
$u>0$. If  $X$ is IFR (resp. DFR), then
$X$ is IFR (resp. DFR), then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is IFR (resp. DFR);
$\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is IFR (resp. DFR);(b) Assume that
 $uH'(u)/H(u)$ is decreasing (resp. increasing) in
$uH'(u)/H(u)$ is decreasing (resp. increasing) in  $u>0$. If
$u>0$. If  $X$ is IFR (resp. DFR), then
$X$ is IFR (resp. DFR), then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is IFR (resp. DFR);
$\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is IFR (resp. DFR);(c) Assume that
 $uH'(u)/H(u)$ is decreasing in
$uH'(u)/H(u)$ is decreasing in  $u>0$. If
$u>0$. If  $X$ is DRFR, then
$X$ is DRFR, then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is DRFR;
$\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is DRFR;(d) Assume that
 $uR'(u)/R(u)$ is increasing in
$uR'(u)/R(u)$ is increasing in  $u>0$. If
$u>0$. If  $X$ is DRFR, then
$X$ is DRFR, then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is DRFR.
$\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is DRFR.
In the following theorem, we show that the ILR, the DLR, the IFRA, and the DFRA classes are preserved under the formation of the parallel and the series systems.
Theorem 3.7 The following results hold true.
(a) Assume that
 $({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing (resp. decreasing) in
$({G(nu)}-{G(u)})/{R(u)}$ is positive and increasing (resp. decreasing) in  $u>0$. If
$u>0$. If  $X$ is ILR (resp. DLR), then both
$X$ is ILR (resp. DLR), then both  $\tau ^{\phi }_{n|n}(\boldsymbol {X})$ and
$\tau ^{\phi }_{n|n}(\boldsymbol {X})$ and  $\tau ^{\phi }_{1|n}(\boldsymbol {X})$ are ILR (resp. DLR);
$\tau ^{\phi }_{1|n}(\boldsymbol {X})$ are ILR (resp. DLR);(b) Assume that
 $uR'(u)/R(u)$ is increasing (resp. decreasing) in
$uR'(u)/R(u)$ is increasing (resp. decreasing) in  $u>0$. If
$u>0$. If  $X$ is IFRA (resp. DFRA), then
$X$ is IFRA (resp. DFRA), then  $\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is IFRA (resp. DFRA);
$\tau ^{\phi }_{n|n}(\boldsymbol {X})$ is IFRA (resp. DFRA);(c) Assume that
 $H(u)/\ln (1-\phi (u))$ is increasing (resp. decreasing) in
$H(u)/\ln (1-\phi (u))$ is increasing (resp. decreasing) in  $u>0$. If
$u>0$. If  $X$ is IFRA (resp. DFRA), then
$X$ is IFRA (resp. DFRA), then  $\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is IFRA (resp. DFRA).
$\tau ^{\phi }_{1|n}(\boldsymbol {X})$ is IFRA (resp. DFRA).
4. Examples
In this section, we give some examples to illustrate the sufficient conditions used in the previous section. Here, we specifically consider the copulas that are frequently used in practice, namely, the Clayton copula ![]() $C(\boldsymbol {u}) =(\prod _{i=1}^{n} u_i^{-\theta } - n + 1)^{-1/\theta }$ with the generator
$C(\boldsymbol {u}) =(\prod _{i=1}^{n} u_i^{-\theta } - n + 1)^{-1/\theta }$ with the generator ![]() $\phi (t) = (\theta t + 1)^{-1/\theta }$, for
$\phi (t) = (\theta t + 1)^{-1/\theta }$, for ![]() $\theta \geq 0$, the Ali-Mikhail-Haq (AMH) copula
$\theta \geq 0$, the Ali-Mikhail-Haq (AMH) copula ![]() $C(\boldsymbol {u}) =((1 - \theta )\prod _{i=1}^{n} u_i)/(\prod _{i=1}^{n}(1- \theta +\theta u_i) -\theta \prod _{i=1}^{n} u_i)$ with the generator
$C(\boldsymbol {u}) =((1 - \theta )\prod _{i=1}^{n} u_i)/(\prod _{i=1}^{n}(1- \theta +\theta u_i) -\theta \prod _{i=1}^{n} u_i)$ with the generator ![]() $\phi (t) = (1 - \theta )/(e^{t}-\theta )$, for
$\phi (t) = (1 - \theta )/(e^{t}-\theta )$, for ![]() $\theta \in [0, 1)$, etc.
$\theta \in [0, 1)$, etc.
We begin with the following example that demonstrates the conditions given in Theorem 3.1(b) and (c), and Theorem 3.6.
Example 4.1 Consider the Archimedean copula with generator
Then,
 $$k_1(u)\stackrel{\text{def.}}=\sum_{j=2}^{3}P_{2,3}^{j}(u)K_j(u)= \frac{(e^{u}-\alpha_{1})\left(\frac{6e^{u}}{(e^{2u}-\alpha_{1})^{2}}-\frac{6e^{2u}}{\left(e^{3u}-\alpha_{1}\right)^{2}}\right)}{\left(\frac{3}{e^{2u}-\alpha_{1}}-\frac{2}{e^{3u}-\alpha_{1}}\right)},\quad u>0,$$
$$k_1(u)\stackrel{\text{def.}}=\sum_{j=2}^{3}P_{2,3}^{j}(u)K_j(u)= \frac{(e^{u}-\alpha_{1})\left(\frac{6e^{u}}{(e^{2u}-\alpha_{1})^{2}}-\frac{6e^{2u}}{\left(e^{3u}-\alpha_{1}\right)^{2}}\right)}{\left(\frac{3}{e^{2u}-\alpha_{1}}-\frac{2}{e^{3u}-\alpha_{1}}\right)},\quad u>0,$$and
 $$k_2(u)\stackrel{\text{def.}}=\sum_{j=2}^{3}Q_{2,3}^{j}(u)L_j(u) =\frac{(e^{u}-\alpha_{1})(e^{u}-1)\left(\frac{6e^{u}}{(e^{2u}-\alpha_{1})^{2}}- \frac{6e^{2u}}{(e^{3u}-\alpha_{1})^{2}}\right)}{1-(1-\alpha_1) \left(\frac{3}{e^{2u}-\alpha_{1}}-\frac{2}{e^{3u}-\alpha_{1}}\right)},\quad u>0.$$
$$k_2(u)\stackrel{\text{def.}}=\sum_{j=2}^{3}Q_{2,3}^{j}(u)L_j(u) =\frac{(e^{u}-\alpha_{1})(e^{u}-1)\left(\frac{6e^{u}}{(e^{2u}-\alpha_{1})^{2}}- \frac{6e^{2u}}{(e^{3u}-\alpha_{1})^{2}}\right)}{1-(1-\alpha_1) \left(\frac{3}{e^{2u}-\alpha_{1}}-\frac{2}{e^{3u}-\alpha_{1}}\right)},\quad u>0.$$In Figure 1, we plot ![]() $k_{1}(-\ln (v))$ against
$k_{1}(-\ln (v))$ against ![]() $v\in (0,1]$, for fixed
$v\in (0,1]$, for fixed ![]() $\alpha _{1}=0.3$,
$\alpha _{1}=0.3$, ![]() $0.4$,
$0.4$, ![]() $0.5$, and
$0.5$, and ![]() $0.6$. This shows that
$0.6$. This shows that ![]() $k_{1}(-\ln (v))$ is decreasing in
$k_{1}(-\ln (v))$ is decreasing in ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $k_{1}(u)$ is increasing in
$k_{1}(u)$ is increasing in ![]() $u>0$. Furthermore, we plot
$u>0$. Furthermore, we plot ![]() $k_{2}(-\ln (v))$ against
$k_{2}(-\ln (v))$ against ![]() $v\in (0,1]$, for fixed
$v\in (0,1]$, for fixed ![]() $\alpha _{1}=0.8$,
$\alpha _{1}=0.8$, ![]() $0.85$, and
$0.85$, and ![]() $0.9$. From Figure 2, we see that
$0.9$. From Figure 2, we see that ![]() $k_{2}(-\ln (v))$ is increasing in
$k_{2}(-\ln (v))$ is increasing in ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $k_{2}(u)$ is decreasing in
$k_{2}(u)$ is decreasing in ![]() $u>0$. Thus, the required conditions are satisfied.
$u>0$. Thus, the required conditions are satisfied.

Figure 1. Plot of ![]() $k_{1}(-\ln (v))$ against
$k_{1}(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.

Figure 2. Plot of ![]() $k_{2}(-\ln (v))$ against
$k_{2}(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.
The following example demonstrates the condition given in Corollary 3.1(c) and (d), Theorem 3.5(c) and (d), Corollary 3.2(a) and (d), and Theorem 3.7(b).
Example 4.2 Consider the Archimedean copula with generator
From this, we have
and
It can be easily shown that ![]() $l_{1}(u)$ is positive and increasing in
$l_{1}(u)$ is positive and increasing in ![]() $u>0$, for all
$u>0$, for all ![]() $\beta _1 \in (0, 1)$. Thus, the required condition holds.
$\beta _1 \in (0, 1)$. Thus, the required condition holds.
The next example illustrates the condition given in Theorems 3.2(a), 3.5(f), and 3.7(a).
Example 4.3 Consider the Archimedean copula with generator
Then
Let us fix ![]() $\gamma _1=0.4$,
$\gamma _1=0.4$, ![]() $0.6$, and
$0.6$, and ![]() $0.8.$ In Figure 3, we plot
$0.8.$ In Figure 3, we plot ![]() $l_2(-\ln (v))$ against
$l_2(-\ln (v))$ against ![]() $v\in (0,1]$. This shows that
$v\in (0,1]$. This shows that ![]() $l_2(-\ln (v))$ is positive and decreasing in
$l_2(-\ln (v))$ is positive and decreasing in ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $l_2(u)$ is positive and increasing in
$l_2(u)$ is positive and increasing in ![]() $u>0$. Furthermore, it can easily be checked that
$u>0$. Furthermore, it can easily be checked that ![]() $l_3(u)$ is increasing in
$l_3(u)$ is increasing in ![]() $u>0$. Thus, the required condition holds from Remark 3.1.
$u>0$. Thus, the required condition holds from Remark 3.1.

Figure 3. Plot of ![]() $l_2(-\ln (v))$ against
$l_2(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.
Below we cite an example that illustrates the condition given in Theorem 3.2(b) and (c), and Theorem 3.5(g).
Example 4.4 Consider the Archimedean copula with generator
which gives
 $$R(u)={-}\frac{1}{\alpha_2}u^{{1}/{\alpha_2}}\quad \text{and}\quad C(u)=\frac{1}{\alpha_2}-\frac{u^{{1}/{\alpha_2}}e^{{-}u^{{1}/{\alpha_2}}}}{\alpha_2\left(1-e^{{-}u^{{1}/{\alpha_2}}}\right)}-\frac{1}{\alpha_2}u^{{1}/{\alpha_2}},\quad u>0.$$
$$R(u)={-}\frac{1}{\alpha_2}u^{{1}/{\alpha_2}}\quad \text{and}\quad C(u)=\frac{1}{\alpha_2}-\frac{u^{{1}/{\alpha_2}}e^{{-}u^{{1}/{\alpha_2}}}}{\alpha_2\left(1-e^{{-}u^{{1}/{\alpha_2}}}\right)}-\frac{1}{\alpha_2}u^{{1}/{\alpha_2}},\quad u>0.$$Let us fix ![]() $\alpha _2=7$ and
$\alpha _2=7$ and ![]() $8$. Furthermore, let
$8$. Furthermore, let ![]() $k_{3}(u)=uC'(u)/C(u)$ and
$k_{3}(u)=uC'(u)/C(u)$ and ![]() $k_{4}(u)=C(u)/R(u),$ for
$k_{4}(u)=C(u)/R(u),$ for ![]() $u>0$. From Figures 4 and 5, we see that both
$u>0$. From Figures 4 and 5, we see that both ![]() $k_{3}(-\ln (v))$ and
$k_{3}(-\ln (v))$ and ![]() $k_{4}(-\ln (v))$ are decreasing and positive for all
$k_{4}(-\ln (v))$ are decreasing and positive for all ![]() $v\in (0,1]$. Hence, both
$v\in (0,1]$. Hence, both ![]() $k_{3}(u)$ and
$k_{3}(u)$ and ![]() $k_{4}(u)$ are increasing and positive for all
$k_{4}(u)$ are increasing and positive for all ![]() $u>0$. Thus, the required conditions hold from Remark 3.1.
$u>0$. Thus, the required conditions hold from Remark 3.1.

Figure 4. Plot of ![]() $k_{3}(-\ln (v))$ against
$k_{3}(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.

Figure 5. Plot of ![]() $k_{4}(-\ln (v))$ against
$k_{4}(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.
The next example demonstrates the condition given in Theorem 3.3(b). Furthermore, this may also be used to illustrate the condition given in Corollary 3.1(b) and (e), Theorem 3.5(b) and (e), and Corollary 3.2(b) and (c).
Example 4.5 Consider two parallel systems ![]() $\tau ^{\phi _1}_{1|n}(\boldsymbol {X})$ and
$\tau ^{\phi _1}_{1|n}(\boldsymbol {X})$ and ![]() $\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$, where
$\tau ^{\phi _2}_{1|n}(\boldsymbol {Y})$, where ![]() $X\le _{\textrm {hr}}Y$. Consider the Archimedean copulas with generators
$X\le _{\textrm {hr}}Y$. Consider the Archimedean copulas with generators
and
respectively. Consequently,
Let us fix ![]() $(\beta _2,\gamma _2)=(14, 0.3),(14,0.4),(15,0.3)$, and
$(\beta _2,\gamma _2)=(14, 0.3),(14,0.4),(15,0.3)$, and ![]() $(15,0.4)$. Figure 6 shows that
$(15,0.4)$. Figure 6 shows that ![]() $k_5\left (-\ln \left (v\right )\right )$ is negative for all
$k_5\left (-\ln \left (v\right )\right )$ is negative for all ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $k_5(u)$ is negative for all
$k_5(u)$ is negative for all ![]() $u>0$. Thus,
$u>0$. Thus, ![]() $\phi _1(u)\leq \phi _2(u)$, for all
$\phi _1(u)\leq \phi _2(u)$, for all ![]() $u>0$, which, by Remark 3.2, gives
$u>0$, which, by Remark 3.2, gives ![]() $\psi _1(w) \leq \psi _2(v)$, for all
$\psi _1(w) \leq \psi _2(v)$, for all ![]() $0\leq v\leq w\leq 1$. Again,
$0\leq v\leq w\leq 1$. Again,
 \begin{align*} & k_6(u)\stackrel{\text{def.}}=\frac{H_1(u)}{H_2(u)}=\frac{e^{u}-\gamma_2}{\beta_2\left(1-\gamma_2\right)e^{u}}\\ \text{and}\quad & k_7(u)\stackrel{\text{def.}}=\frac{uH_2'(u)}{H_2(u)}={-}\frac{ue^{u}}{e^{u}-\gamma_2}-\frac{ue^{u}}{e^{u}-1}+1+u,\quad u>0. \end{align*}
\begin{align*} & k_6(u)\stackrel{\text{def.}}=\frac{H_1(u)}{H_2(u)}=\frac{e^{u}-\gamma_2}{\beta_2\left(1-\gamma_2\right)e^{u}}\\ \text{and}\quad & k_7(u)\stackrel{\text{def.}}=\frac{uH_2'(u)}{H_2(u)}={-}\frac{ue^{u}}{e^{u}-\gamma_2}-\frac{ue^{u}}{e^{u}-1}+1+u,\quad u>0. \end{align*}From Figure 7, we see that ![]() $k_6(-\ln (v))$ is decreasing in
$k_6(-\ln (v))$ is decreasing in ![]() $v\in (0,1]$, whereas Figure 8 shows that
$v\in (0,1]$, whereas Figure 8 shows that ![]() $k_7(-\ln (v))$ is increasing and negative for all
$k_7(-\ln (v))$ is increasing and negative for all ![]() $v\in (0,1]$. Hence,
$v\in (0,1]$. Hence, ![]() $k_6(u)$ is increasing in
$k_6(u)$ is increasing in ![]() $u>0$, and
$u>0$, and ![]() $k_7(u)$ is decreasing and negative for all
$k_7(u)$ is decreasing and negative for all ![]() $u>0$. Thus, the condition of Theorem 3.3(b) holds.
$u>0$. Thus, the condition of Theorem 3.3(b) holds.

Figure 6. Plot of ![]() $k_5\left (-\ln \left (v\right )\right )$ against
$k_5\left (-\ln \left (v\right )\right )$ against ![]() $v \in \left (0,1\right ].$
$v \in \left (0,1\right ].$

Figure 7. Plot of ![]() $k_6(-\ln (v))$ against
$k_6(-\ln (v))$ against ![]() $v \in \left (0,1\right ]$.
$v \in \left (0,1\right ]$.

Figure 8. Plot of ![]() $k_7(-\ln (v))$ against
$k_7(-\ln (v))$ against ![]() $v \in \left (0,1\right ]$.
$v \in \left (0,1\right ]$.
Below we give an example that illustrates the condition given in Theorem 3.4(a).
Example 4.6 Consider the Archimedean copulas with generators
and
respectively. By writing ![]() $l_{5}(w)=\phi _1^{-1}(w)/\phi _2^{-1}(w)$, we have
$l_{5}(w)=\phi _1^{-1}(w)/\phi _2^{-1}(w)$, we have
In Figure 9, we plot ![]() $l_5(w)$ against
$l_5(w)$ against ![]() $w\in (0,1]$, for fixed
$w\in (0,1]$, for fixed ![]() $(\alpha _3,\beta _3)=(0.3, 1.1),(0.3, 1.2),(0.4, 1.1)$, and
$(\alpha _3,\beta _3)=(0.3, 1.1),(0.3, 1.2),(0.4, 1.1)$, and ![]() $(0.4, 1.2)$. This shows that
$(0.4, 1.2)$. This shows that ![]() $l_5(w)$ is increasing in
$l_5(w)$ is increasing in ![]() $w\in (0,1]$, and hence, the condition of Theorem 3.4(a) is satisfied.
$w\in (0,1]$, and hence, the condition of Theorem 3.4(a) is satisfied.

Figure 9. Plot of ![]() $l_{5}(w)$ against
$l_{5}(w)$ against ![]() $w\in (0,1]$.
$w\in (0,1]$.
The following example demonstrates the conditions given in Theorem 3.4(b).
Example 4.7 Consider the Archimedean copulas with generators
and
respectively. Consequently,
Let us fix ![]() $(\alpha _4,\beta _4)=(3.8, 13),(3.8,16),(4.9,13)$, and
$(\alpha _4,\beta _4)=(3.8, 13),(3.8,16),(4.9,13)$, and ![]() $(4.9,16)$. In Figure 10, we plot
$(4.9,16)$. In Figure 10, we plot ![]() $l_{6}\left (-\ln \left (v\right )\right )$ against
$l_{6}\left (-\ln \left (v\right )\right )$ against ![]() $v\in (0,1]$. This shows that
$v\in (0,1]$. This shows that ![]() $l_{6}\left (-\ln \left (v\right )\right )$ is positive for all
$l_{6}\left (-\ln \left (v\right )\right )$ is positive for all ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $l_{6}(t)$ is positive for all
$l_{6}(t)$ is positive for all ![]() $u>0$. Thus,
$u>0$. Thus, ![]() $\phi _1(u)\geq \phi _2(u)$, for all
$\phi _1(u)\geq \phi _2(u)$, for all ![]() $u>0$, which, by Remark 3.2, gives
$u>0$, which, by Remark 3.2, gives ![]() $\psi _1(w)\geq \psi _2(v)$, for all
$\psi _1(w)\geq \psi _2(v)$, for all ![]() $0\leq w\leq v\leq 1$. Again,
$0\leq w\leq v\leq 1$. Again,
In Figure 11, we plot ![]() $l_{7}(-\ln (v))$ against
$l_{7}(-\ln (v))$ against ![]() $v\in (0,1]$. This shows that
$v\in (0,1]$. This shows that ![]() $l_{7}(-\ln (v))$ is decreasing in
$l_{7}(-\ln (v))$ is decreasing in ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $l_{7}(u)$ is increasing in
$l_{7}(u)$ is increasing in ![]() $u>0$. Furthermore, it is trivially true that
$u>0$. Furthermore, it is trivially true that ![]() ${uR_2'(u)}/{R_2(u)}$ is increasing in
${uR_2'(u)}/{R_2(u)}$ is increasing in ![]() $u>0$. Thus, the required conditions are satisfied.
$u>0$. Thus, the required conditions are satisfied.

Figure 10. Plot of ![]() $l_{6}\left (-\ln \left (v\right )\right )$ against
$l_{6}\left (-\ln \left (v\right )\right )$ against ![]() $v\in \left (0,1\right ]$.
$v\in \left (0,1\right ]$.

Figure 11. Plot of ![]() $l_{7}(-\ln (v))$ against
$l_{7}(-\ln (v))$ against ![]() $v\in \left (0,1\right ]$.
$v\in \left (0,1\right ]$.
The following example demonstrates the condition given in Theorem 3.7(c).
Example 4.8 Consider the Archimedean copula with generator
which gives
Let us fix ![]() $\gamma _{3}=3$,
$\gamma _{3}=3$, ![]() $4$, and
$4$, and ![]() $5$. By writing
$5$. By writing ![]() $l_{8}(u)=H(u)/(\ln \left (1-\phi (u)\right )),$
$l_{8}(u)=H(u)/(\ln \left (1-\phi (u)\right )),$ ![]() $u>0$, we plot
$u>0$, we plot ![]() $l_{8}(-\ln (v))$ against
$l_{8}(-\ln (v))$ against ![]() $v\in (0,1]$. From Figure 12, we see that
$v\in (0,1]$. From Figure 12, we see that ![]() $l_{8}(-\ln (v))$ is decreasing in
$l_{8}(-\ln (v))$ is decreasing in ![]() $v\in (0,1]$ and hence,
$v\in (0,1]$ and hence, ![]() $l_{8}(u)$ is increasing in
$l_{8}(u)$ is increasing in ![]() $u>0$. Thus, the required condition is satisfied.
$u>0$. Thus, the required condition is satisfied.

Figure 12. Plot of ![]() $l_{8}(-\ln (v))$ against
$l_{8}(-\ln (v))$ against ![]() $v\in (0,1]$.
$v\in (0,1]$.
5. Concluding remarks
In this paper, we consider different coherent systems (especially, series, parallel, and general ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems) formed by d.i.d. components, where the dependency structures are described by Archimedean copulas. We provide some sufficient conditions (in terms of the generators of Archimedean copulas) to show that one system performs better than another one with respect to the usual stochastic order, the hazard rate order, the reversed hazard rate order, the likelihood ratio order, and the aging faster orders in terms of the failure rate and the reversed failure rate. In the same spirit, we compare a used system and a system made by used components with respect to different stochastic orders. Furthermore, we study the closure properties of different aeing classes (namely, IFR, DFR, DRFR, ILR, DLR, IFRA and DFRA) under the formation of
$n$ systems) formed by d.i.d. components, where the dependency structures are described by Archimedean copulas. We provide some sufficient conditions (in terms of the generators of Archimedean copulas) to show that one system performs better than another one with respect to the usual stochastic order, the hazard rate order, the reversed hazard rate order, the likelihood ratio order, and the aging faster orders in terms of the failure rate and the reversed failure rate. In the same spirit, we compare a used system and a system made by used components with respect to different stochastic orders. Furthermore, we study the closure properties of different aeing classes (namely, IFR, DFR, DRFR, ILR, DLR, IFRA and DFRA) under the formation of ![]() $r$-out-of-
$r$-out-of-![]() $n$ systems. Moreover, we illustrate the proposed results through various examples.
$n$ systems. Moreover, we illustrate the proposed results through various examples.
As we discussed, the main idea of this paper is to consider the dependency structure between components of a system by an Archimedean copula. Most of the systems used in real life have inter-dependency structures between their components, and hence, the assumption of “independent components” sometimes oversimplifies the actual scenario. Thus, we consider the coherent systems that are formed by dependent components governed by the Archimedean copula. As mentioned in the Introduction section, Archimedean copulas are extensively used in the literature due to their wide spectrum of capturing the dependency structures. Furthermore, Archimedean copulas enjoy nice mathematical properties which make them popular. Thus, our study based on the Archimedean copulas may be useful in different practical scenarios where systems with dependent components are considered.
Even though we derived a large number of results in this paper, there remains ample scope to develop further results for systems with dependent components under the Archimedean copula. Here, we only consider the systems with dependent and identically distributed components. The same study for the systems with dependent and nonidentically distributed components may be considered in future.
Acknowledgments
The authors are thankful to the Editor-in-Chief, the Associate Editor, and the anonymous Reviewers for their valuable constructive comments/suggestions which lead to an improved version of the manuscript. The first author sincerely acknowledges the financial support received from UGC, Govt. of India. The work of the second author was supported by IIT Jodhpur, India.
Competing interest
The authors declare no conflict of interest.
Appendix
Proof of Theorem 3.1(b). We only prove the result under the assumption that ![]() $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in ![]() $u>0$. The proof for the other case follows in the same line. From
$u>0$. The proof for the other case follows in the same line. From ![]() $(3.4.3)$ of David and Nagaraja [Reference David and Nagaraja11], we have
$(3.4.3)$ of David and Nagaraja [Reference David and Nagaraja11], we have
 $$\bar{F}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)=\sum_{j=r}^{n} C_{r,n}^{j}\phi(j\psi(\bar{F}_X(x))), \quad x>0,$$
$$\bar{F}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)=\sum_{j=r}^{n} C_{r,n}^{j}\phi(j\psi(\bar{F}_X(x))), \quad x>0,$$which gives
 \begin{align} {r}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)& ={r}_X(x)\frac{\sum_{j=r}^{n} C_{r,n}^{j}\phi(j\psi(\bar{F}_X(x)))\frac{R(j\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))}}{\sum_{i=r}^{n} C_{r,n}^{i}\phi(i\psi(\bar{F}_X(x)))} \nonumber\\ & ={r}_X(t)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))), \quad x>0, \end{align}
\begin{align} {r}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)& ={r}_X(x)\frac{\sum_{j=r}^{n} C_{r,n}^{j}\phi(j\psi(\bar{F}_X(x)))\frac{R(j\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))}}{\sum_{i=r}^{n} C_{r,n}^{i}\phi(i\psi(\bar{F}_X(x)))} \nonumber\\ & ={r}_X(t)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))), \quad x>0, \end{align}Similarly, we get
 $${r}_{\tau^{\phi}_{r|n}(\boldsymbol{Y})}(x) ={r}_Y(x)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_Y(x)))K_{j}(\psi(\bar{F}_Y(x))), \quad x>0.$$
$${r}_{\tau^{\phi}_{r|n}(\boldsymbol{Y})}(x) ={r}_Y(x)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_Y(x)))K_{j}(\psi(\bar{F}_Y(x))), \quad x>0.$$Since ![]() $X\leq _{\textrm {hr}} Y$ and
$X\leq _{\textrm {hr}} Y$ and ![]() $\psi$ is a decreasing function, we have
$\psi$ is a decreasing function, we have ![]() ${r}_X(x)\geq {r}_Y(x)$ and
${r}_X(x)\geq {r}_Y(x)$ and ![]() $\psi (\bar {F}_X(x))\geq \psi (\bar {F}_Y(x))$, for all
$\psi (\bar {F}_X(x))\geq \psi (\bar {F}_Y(x))$, for all ![]() $x>0$. Then, by using the assumption “
$x>0$. Then, by using the assumption “![]() $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing in ![]() $u>0$”, we get
$u>0$”, we get
 $$\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))) \geq \sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_Y(x)))K_{j}(\psi(\bar{F}_Y(x))),\quad \text{for all } x>0,$$
$$\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))) \geq \sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_Y(x)))K_{j}(\psi(\bar{F}_Y(x))),\quad \text{for all } x>0,$$which is equivalent to mean that ![]() ${r}_{\tau ^{\phi }_{r|n}(\boldsymbol {X})}(x)\geq {r}_{\tau ^{\phi }_{r|n}(\boldsymbol {Y})}(x)$, for all
${r}_{\tau ^{\phi }_{r|n}(\boldsymbol {X})}(x)\geq {r}_{\tau ^{\phi }_{r|n}(\boldsymbol {Y})}(x)$, for all ![]() $x>0$. Hence, the result is proved.
$x>0$. Hence, the result is proved.
Proof of Theorem 3.2(a). We only prove the result for the parallel system. The proof for the series system follows in the same line. We have
which gives
 \begin{align} \frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)} & =\frac{f'_X(x)}{f_X(x)}+\frac{f_X(x)}{F_X(x)} \left[\frac{F_X(t)\psi''({F}_X(x))}{\psi'{F}_X(x)}+\frac{F_X(x)\psi'({F}_X(x))}{\psi({F}_X(x))} \frac{n\psi(F_X(x))\phi''(n{F}_X(x))}{\phi'(n{F}_X(x))}\right] \nonumber\\ & =\frac{f'_X(x)}{f_X(x)}+\tilde{r}_X(x)\left[\frac{G(n\psi(F_X(x)))}{R(\psi(F_X(x)))}- \frac{G(\psi(F_X(x)))}{R(\psi(F_X(x)))}\right],\quad x>0, \end{align}
\begin{align} \frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)} & =\frac{f'_X(x)}{f_X(x)}+\frac{f_X(x)}{F_X(x)} \left[\frac{F_X(t)\psi''({F}_X(x))}{\psi'{F}_X(x)}+\frac{F_X(x)\psi'({F}_X(x))}{\psi({F}_X(x))} \frac{n\psi(F_X(x))\phi''(n{F}_X(x))}{\phi'(n{F}_X(x))}\right] \nonumber\\ & =\frac{f'_X(x)}{f_X(x)}+\tilde{r}_X(x)\left[\frac{G(n\psi(F_X(x)))}{R(\psi(F_X(x)))}- \frac{G(\psi(F_X(x)))}{R(\psi(F_X(x)))}\right],\quad x>0, \end{align}where the last equality follows from the fact that
Similarly, we have
 $$\frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)} =\frac{f'_Y(x)}{f_Y(x)}+\tilde{r}_Y(x)\left[\frac{G(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{G(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right],\quad x>0.$$
$$\frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)} =\frac{f'_Y(x)}{f_Y(x)}+\tilde{r}_Y(x)\left[\frac{G(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{G(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right],\quad x>0.$$Then, the result holds if, and only if,
 \begin{align} & \frac{f'_X(x)}{f_X(x)}+\tilde{r}_X(x)\left[\frac{G(n\psi(F_X(x)))}{R(\psi(F_X(x)))}- \frac{G(\psi(F_X(x)))}{R(\psi(F_X(x)))}\right]\nonumber\\ & \quad \leq \frac{f'_Y(x)}{f_Y(x)}+\tilde{r}_Y(x)\left[\frac{G(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{G(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right],\quad x>0. \end{align}
\begin{align} & \frac{f'_X(x)}{f_X(x)}+\tilde{r}_X(x)\left[\frac{G(n\psi(F_X(x)))}{R(\psi(F_X(x)))}- \frac{G(\psi(F_X(x)))}{R(\psi(F_X(x)))}\right]\nonumber\\ & \quad \leq \frac{f'_Y(x)}{f_Y(x)}+\tilde{r}_Y(x)\left[\frac{G(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{G(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right],\quad x>0. \end{align}Since ![]() $X\leq _{\textrm {lr}} Y$, we have
$X\leq _{\textrm {lr}} Y$, we have
and
Since ![]() $\psi$ is a decreasing function, we have, from (A.5),
$\psi$ is a decreasing function, we have, from (A.5),
Again, from the assumption, we have that
which, by (A.7), gives
for all ![]() $x>0$. On combining (A.5), (A.6), and (A.8), we get (A.4) and hence, the result follows.
$x>0$. On combining (A.5), (A.6), and (A.8), we get (A.4) and hence, the result follows.
Proof of Theorem 3.2(b). From (A.2), we have
 \begin{align*} r_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)& =r_X(x)\left[\frac{\left(1-F_X(x)\right)\psi'(F_X(x))}{\psi(F_X(x))}\right] \left[\frac{n\psi(F_X(x))\phi'(n\psi(F_X(x)))}{1-\phi(n\psi(F_X(x)))}\right]\nonumber\\ & =r_X(x)\frac{H(n\psi(F_X(x)))}{H(\psi(F_X(x)))}, \quad t>0. \end{align*}
\begin{align*} r_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)& =r_X(x)\left[\frac{\left(1-F_X(x)\right)\psi'(F_X(x))}{\psi(F_X(x))}\right] \left[\frac{n\psi(F_X(x))\phi'(n\psi(F_X(x)))}{1-\phi(n\psi(F_X(x)))}\right]\nonumber\\ & =r_X(x)\frac{H(n\psi(F_X(x)))}{H(\psi(F_X(x)))}, \quad t>0. \end{align*}Similarly,
Then,
 $$\frac{r_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)}{r_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)} =\frac{r_{X}(x)}{r_{Y}(x)}\frac{\frac{H(n\psi(F_X(x)))}{H(\psi(F_X(x)))}}{\frac{H(n\psi(F_Y(x)))}{H(\psi(F_Y(x)))}},\quad x>0.$$
$$\frac{r_{\tau^{\phi}_{1|n}(\boldsymbol{X})}(x)}{r_{\tau^{\phi}_{1|n}(\boldsymbol{Y})}(x)} =\frac{r_{X}(x)}{r_{Y}(x)}\frac{\frac{H(n\psi(F_X(x)))}{H(\psi(F_X(x)))}}{\frac{H(n\psi(F_Y(x)))}{H(\psi(F_Y(x)))}},\quad x>0.$$Since ![]() $X\leq _{c} Y$, we have that
$X\leq _{c} Y$, we have that ![]() ${r_X(x)}/{r_Y(x)}$ is increasing in
${r_X(x)}/{r_Y(x)}$ is increasing in ![]() $x>0$. Thus, to prove the result, it suffices to show that
$x>0$. Thus, to prove the result, it suffices to show that
or equivalently,
 \begin{align} & \tilde{r}_X(x)\left[\frac{C(n\psi(F_X(x)))}{R(\psi(F_X(x)))} -\frac{C(\psi_1(F_X(x)))}{R(\psi_1(F_X(x)))}\right]\nonumber\\ & \quad \geq \tilde{r}_Y(x)\left[\frac{C(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{C(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right], \end{align}
\begin{align} & \tilde{r}_X(x)\left[\frac{C(n\psi(F_X(x)))}{R(\psi(F_X(x)))} -\frac{C(\psi_1(F_X(x)))}{R(\psi_1(F_X(x)))}\right]\nonumber\\ & \quad \geq \tilde{r}_Y(x)\left[\frac{C(n\psi(F_Y(x)))}{R(\psi(F_Y(x)))}- \frac{C(\psi(F_Y(x)))}{R(\psi(F_Y(x)))}\right], \end{align}for all ![]() $x>0$. Since
$x>0$. Since ![]() $Y\leq _{\textrm {rh}} X$, we have
$Y\leq _{\textrm {rh}} X$, we have
Since ![]() $\psi$ is a decreasing function, we have, from the above inequality,
$\psi$ is a decreasing function, we have, from the above inequality,
Again, from the assumption, we have that
which, by (A.11), gives
for all ![]() $x>0$. On combining (A.10) and (A.12), we get (A.9) and hence, the result follows.
$x>0$. On combining (A.10) and (A.12), we get (A.9) and hence, the result follows.
Proof of Theorem 3.3(a). We have
Since ![]() $X\leq _{\textrm {st}}Y$ and
$X\leq _{\textrm {st}}Y$ and ![]() $\psi _1$ is a decreasing function, we have
$\psi _1$ is a decreasing function, we have ![]() $\phi _1(n\psi _1(F_X(x)))\geq \phi _1(n\psi _1(F_Y(x)))$ for all
$\phi _1(n\psi _1(F_X(x)))\geq \phi _1(n\psi _1(F_Y(x)))$ for all ![]() $x>0$. Furthermore, from the assumption “
$x>0$. Furthermore, from the assumption “![]() $\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in
$\phi _2^{-1}\left (\phi _1(u)\right )$ is sub-additive in ![]() $u>0$”, we have
$u>0$”, we have ![]() $\phi _1(n\psi _1(F_Y(x)))\geq \phi _2(n\psi _2(F_Y(x)))$ for all
$\phi _1(n\psi _1(F_Y(x)))\geq \phi _2(n\psi _2(F_Y(x)))$ for all ![]() $x>0.$ On combining these two inequalities, we get
$x>0.$ On combining these two inequalities, we get ![]() $\phi _1(n\psi _1(F_X(x)))\geq \phi _2(n\psi _2(F_Y(x)))$ for all
$\phi _1(n\psi _1(F_X(x)))\geq \phi _2(n\psi _2(F_Y(x)))$ for all ![]() $x>0$ and hence, the result follows
$x>0$ and hence, the result follows
Proof of Theorem 3.3(b). We only prove the result under the condition that ![]() $uH_2'(u)/H_2(u)$ is decreasing in
$uH_2'(u)/H_2(u)$ is decreasing in ![]() $u>0$. The proof follows in the same line for the other case. Note that, for all
$u>0$. The proof follows in the same line for the other case. Note that, for all ![]() $p\in (0,1)$,
$p\in (0,1)$,
Now, from (A.13), we get
 \begin{align*} r_{\tau^{\phi_1}_{1|n}(\boldsymbol{X})}(x)& =\frac{f_X(x)\phi_1'(n\psi_1(F_X(x)))n\psi_1'(F_X(x))}{1-\phi_1(n\psi_1(F_X(x)))}\nonumber\\ & =r_X(x)\left[\frac{\left(1-F_X(x)\right)\psi_1'(F_X(x))}{\psi_1(F_X(x))}\right] \left[\frac{n\psi_1(F_X(x))\phi_1'(n\psi_1(F_X(x)))}{1-\phi_1(n\psi_1(F_X(x)))}\right]\nonumber\\ & =r_X(x)\frac{H_1(n\psi_1(F_X(x)))}{H_1(\psi_1(F_X(x)))}, \quad x>0, \end{align*}
\begin{align*} r_{\tau^{\phi_1}_{1|n}(\boldsymbol{X})}(x)& =\frac{f_X(x)\phi_1'(n\psi_1(F_X(x)))n\psi_1'(F_X(x))}{1-\phi_1(n\psi_1(F_X(x)))}\nonumber\\ & =r_X(x)\left[\frac{\left(1-F_X(x)\right)\psi_1'(F_X(x))}{\psi_1(F_X(x))}\right] \left[\frac{n\psi_1(F_X(x))\phi_1'(n\psi_1(F_X(x)))}{1-\phi_1(n\psi_1(F_X(x)))}\right]\nonumber\\ & =r_X(x)\frac{H_1(n\psi_1(F_X(x)))}{H_1(\psi_1(F_X(x)))}, \quad x>0, \end{align*}where the last equality follows from (A.14). Similarly, from (A.13) and (A.14), we get
Thus, the result holds if, only if,
Since ![]() $X\leq _{\textrm {hr}} Y$, we have
$X\leq _{\textrm {hr}} Y$, we have ![]() $r_X(x)\geq r_Y(x)$. Thus, the above inequality holds if
$r_X(x)\geq r_Y(x)$. Thus, the above inequality holds if
Now, from the assumptions “![]() $\psi _1(w)\leq \psi _2(v)$ for all
$\psi _1(w)\leq \psi _2(v)$ for all ![]() $0\leq v\leq w\leq 1$” and “
$0\leq v\leq w\leq 1$” and “![]() $X\leq _{\textrm {hr}} Y$”, we have
$X\leq _{\textrm {hr}} Y$”, we have
Again, we have that ![]() $u{H_2'(u)}/{H_2(u)}$ is decreasing in
$u{H_2'(u)}/{H_2(u)}$ is decreasing in ![]() $u>0$. This implies that
$u>0$. This implies that
which further, by (A.16), gives
Again, on using the condition “![]() $H_1(u)/H_2(u)$ is increasing in
$H_1(u)/H_2(u)$ is increasing in ![]() $u>0$”, we get
$u>0$”, we get
On combining (A.17) and (A.18), we get (A.15). Thus, the result is proved.
Proof of Theorem 3.5(d). We only prove the result for the parallel system. The proof for the series system can be done in the same line. Now, for any fixed ![]() $t\geq 0$, we have
$t\geq 0$, we have
and
which give
 \begin{align*} \tilde{r}_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)& = \frac{f_X(x+t)\phi'(n\psi({F}_X(x+t))n\psi'({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))} \\ & \quad \times\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}\\ & =\tilde{r}_X(x+t)\left[\frac{({F}_X(x+t))\psi'({F}_X(x+t))}{\psi({F}_X(x+t))}\right] \\ & \quad \times\left[\frac{n\psi({F}_X(x+t))\phi'(n\psi({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))}\right] \nonumber \\ & \quad \times\left[\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}\right]\nonumber \\ & =\tilde{r}_X(x+t)\frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))} \nonumber \\ & \quad \times\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}, \quad x>0, \end{align*}
\begin{align*} \tilde{r}_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)& = \frac{f_X(x+t)\phi'(n\psi({F}_X(x+t))n\psi'({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))} \\ & \quad \times\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}\\ & =\tilde{r}_X(x+t)\left[\frac{({F}_X(x+t))\psi'({F}_X(x+t))}{\psi({F}_X(x+t))}\right] \\ & \quad \times\left[\frac{n\psi({F}_X(x+t))\phi'(n\psi({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))}\right] \nonumber \\ & \quad \times\left[\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}\right]\nonumber \\ & =\tilde{r}_X(x+t)\frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))} \nonumber \\ & \quad \times\frac{\phi(n\psi(F_X(x+t)))}{\phi(n\psi(F_X(x+t)))-\phi(n\psi({F_X}(t)))}, \quad x>0, \end{align*}and
 \begin{align*} \tilde{r}_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x) & =\frac{f_X(x+t)\phi'\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)n\psi' \left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}{\bar{F}_X(t)\phi\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)} \\ & =\tilde{r}_X(x+t)\left[\frac{\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\psi' \left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}{\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}\right] \\ & \quad \times\left[\frac{n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\phi' \left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}{\phi\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}\right]\nonumber \\ & \quad \times\left[\frac{\phi(\psi(F_X(x+t)))}{\phi(\psi(F_X(x+t)))-\phi(\psi({F_X}(t)))}\right]\nonumber \\ & =\tilde{r}_X(x+t)\frac{R\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}{R\left(\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}\nonumber \\ & \quad \times\frac{\phi(\psi(F_X(x+t)))}{\phi(\psi(F_X(x+t)))-\phi(\psi({F_X}(t)))}, \quad x>0. \end{align*}
\begin{align*} \tilde{r}_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x) & =\frac{f_X(x+t)\phi'\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)n\psi' \left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}{\bar{F}_X(t)\phi\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)} \\ & =\tilde{r}_X(x+t)\left[\frac{\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\psi' \left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}{\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)}\right] \\ & \quad \times\left[\frac{n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\phi' \left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}{\phi\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}\right]\nonumber \\ & \quad \times\left[\frac{\phi(\psi(F_X(x+t)))}{\phi(\psi(F_X(x+t)))-\phi(\psi({F_X}(t)))}\right]\nonumber \\ & =\tilde{r}_X(x+t)\frac{R\left(n\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}{R\left(\psi\left(\frac{{F_X}(x+t)-F_X(t)}{1-{F_X}(t)}\right)\right)}\nonumber \\ & \quad \times\frac{\phi(\psi(F_X(x+t)))}{\phi(\psi(F_X(x+t)))-\phi(\psi({F_X}(t)))}, \quad x>0. \end{align*}Thus, to prove the result, it suffices to show that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
 \begin{align} & \frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))} \frac{\phi(n\psi({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))-\phi\left(n\psi({F}_X(t))\right)} \nonumber\\ & \quad \leq \frac{R\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}{R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} \frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}, \quad x>0. \end{align}
\begin{align} & \frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))} \frac{\phi(n\psi({F}_X(x+t))}{\phi(n\psi({F}_X(x+t))-\phi\left(n\psi({F}_X(t))\right)} \nonumber\\ & \quad \leq \frac{R\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}{R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} \frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}, \quad x>0. \end{align}Since ![]() $uR'(u)/R(u)\geq 0$ for all
$uR'(u)/R(u)\geq 0$ for all ![]() $u\geq 0$, we get that
$u\geq 0$, we get that ![]() $R(u)$ is decreasing in
$R(u)$ is decreasing in ![]() $u>0$. This implies that, for any fixed
$u>0$. This implies that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
for all ![]() $x>0$. Note that, for any fixed
$x>0$. Note that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
which, by decreasing property of ![]() $\psi$, gives
$\psi$, gives
Again, we have that ![]() $uR'(u)/R(u)$ is increasing in
$uR'(u)/R(u)$ is increasing in ![]() $u>0$. This implies that
$u>0$. This implies that
which further, by (A.23), gives
 \begin{equation} \frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}\leq \frac{R\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}, \end{equation}
\begin{equation} \frac{R(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}\leq \frac{R\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}, \end{equation}for all ![]() $x>0$ and for fixed
$x>0$ and for fixed ![]() $t\geq 0$. On combining (A.22) and (A.24), we get (A.21) and hence, the result is proved.
$t\geq 0$. On combining (A.22) and (A.24), we get (A.21) and hence, the result is proved.
Proof of Theorem 3.5(f). From (A.19) and (A.20), we have that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
 \begin{align*} \frac{f'_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)}{f_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)} & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)n\psi'({F}_X(x+t))\phi''(n\psi({F}_X(x+t))}{\phi'(n\psi({F}_X(x+t))} \\ & \quad +\frac{f_X(x+t)\psi''({F}_X(x+t))}{\psi'({F}_X(x+t))} \\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)}{{F}_X(x+t)} \left[\frac{{F}_X(x+t)\psi''({F}_X(x+t))}{\psi'({F}_X(x+t))} \right.\\ & \quad \left. +\frac{{F}_X(x+t)\psi'({F}_X(x+t))}{\psi({F}_X(x+t))} \frac{n\psi({F}_X(x+t))\phi''(n\psi({F}_X(x+t))}{\phi'(n\psi({F}_X(x+t))}\right] \\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\tilde{r}_X(x+t)\left[\frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\right],\quad x>0, \end{align*}
\begin{align*} \frac{f'_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)}{f_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)} & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)n\psi'({F}_X(x+t))\phi''(n\psi({F}_X(x+t))}{\phi'(n\psi({F}_X(x+t))} \\ & \quad +\frac{f_X(x+t)\psi''({F}_X(x+t))}{\psi'({F}_X(x+t))} \\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)}{{F}_X(x+t)} \left[\frac{{F}_X(x+t)\psi''({F}_X(x+t))}{\psi'({F}_X(x+t))} \right.\\ & \quad \left. +\frac{{F}_X(x+t)\psi'({F}_X(x+t))}{\psi({F}_X(x+t))} \frac{n\psi({F}_X(x+t))\phi''(n\psi({F}_X(x+t))}{\phi'(n\psi({F}_X(x+t))}\right] \\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\tilde{r}_X(x+t)\left[\frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\right],\quad x>0, \end{align*}and
 \begin{align} \frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)} & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)n\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right) \phi''\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}{\bar{F}_X(t) \phi'\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} \nonumber\\ & \quad +\frac{f_X(x+t)\psi''\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\bar{F}_X(t)\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} \nonumber\\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)}{{F}_X(x+t)} \left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right] \nonumber\\ & \quad \times\left[\frac{\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\psi'' \left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} +\frac{\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} {\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} \right.\nonumber\\ & \quad \left.\times\frac{n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\phi'' \left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {\phi'\left(n\psi(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)})\right)}\right] \nonumber\\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\tilde{r}_X(x+t) \nonumber\\ & \quad \times\left[\frac{G\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right] \nonumber\\ & \quad \times\left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right], \quad x>0. \end{align}
\begin{align} \frac{f'_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)}{f_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)} & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)n\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right) \phi''\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}{\bar{F}_X(t) \phi'\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} \nonumber\\ & \quad +\frac{f_X(x+t)\psi''\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\bar{F}_X(t)\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} \nonumber\\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\frac{f_X(x+t)}{{F}_X(x+t)} \left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right] \nonumber\\ & \quad \times\left[\frac{\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\psi'' \left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} +\frac{\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\psi'\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} {\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)} \right.\nonumber\\ & \quad \left.\times\frac{n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\phi'' \left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {\phi'\left(n\psi(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)})\right)}\right] \nonumber\\ & =\frac{f'_X(x+t)}{f_X(x+t)}+\tilde{r}_X(x+t) \nonumber\\ & \quad \times\left[\frac{G\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right] \nonumber\\ & \quad \times\left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right], \quad x>0. \end{align}Thus, to prove the result, it suffices to show that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
 \begin{align} & \frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}-\frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\nonumber\\ & \quad \leq\left[\frac{G\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right]\nonumber\\ & \qquad \times\left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right], \quad x>0. \end{align}
\begin{align} & \frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}-\frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\nonumber\\ & \quad \leq\left[\frac{G\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right]\nonumber\\ & \qquad \times\left[\frac{\phi(\psi({F}_X(x+t)))}{\phi(\psi({F}_X(x+t)))-\phi(\psi({F}_X(t)))}\right], \quad x>0. \end{align}Since ![]() $\phi$ is a decreasing function, we have that, for any fixed
$\phi$ is a decreasing function, we have that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
Again, from the assumption, we have that
which, by (A.23), gives
 \begin{align} 0& \leq \frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))} \nonumber\\ & \leq \frac{G\left(n\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)}, \end{align}
\begin{align} 0& \leq \frac{G(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{G(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))} \nonumber\\ & \leq \frac{G\left(n\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)}- \frac{G\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-{F}_X(t)}{{F}_X(t)}\right)\right)}, \end{align}for any fixed ![]() $t\geq 0$ and for all
$t\geq 0$ and for all ![]() $x>0$. Finally, by combining (A.27) and (A.28), we get (A.26) and hence, the result follows.
$x>0$. Finally, by combining (A.27) and (A.28), we get (A.26) and hence, the result follows.
Proof of Theorem 3.5(g). From (A.19) and (A.20), we have that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
 \begin{align*} r_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x) & =\frac{f_X(x+t)\phi'(n\psi({F}_X(x+t))n\psi'({F}_X(x+t))}{1-\phi(n\psi(\bar{F}_X(x+t)))} \\ & =r_X(x+t)\left[\frac{(1-{F}_X(x+t))\psi'({F}_X(x+t))}{\psi({F}_X(x+t))}\right] \left[\frac{n\psi({F}_X(x+t))\phi'(n\psi({F}_X(x+t))}{1-\phi(n\psi({F}_X(x+t))}\right]\\ & =r_X(x+t)\frac{H(n\psi({F}_X(x+t))}{H(\psi({F}_X(x+t)))},\quad x>0, \end{align*}
\begin{align*} r_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x) & =\frac{f_X(x+t)\phi'(n\psi({F}_X(x+t))n\psi'({F}_X(x+t))}{1-\phi(n\psi(\bar{F}_X(x+t)))} \\ & =r_X(x+t)\left[\frac{(1-{F}_X(x+t))\psi'({F}_X(x+t))}{\psi({F}_X(x+t))}\right] \left[\frac{n\psi({F}_X(x+t))\phi'(n\psi({F}_X(x+t))}{1-\phi(n\psi({F}_X(x+t))}\right]\\ & =r_X(x+t)\frac{H(n\psi({F}_X(x+t))}{H(\psi({F}_X(x+t)))},\quad x>0, \end{align*}and
 \begin{align*} r_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x) & =\frac{f_X(x+t)\phi'\left(n\psi\left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)\right)n\psi' \left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)}{\bar{F}(t)\left(1-\phi\left(n\psi\left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)\right)\right)} \\ & =r_X(x+t)\left[\frac{\left(1-\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\psi' \left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}\right]\\ & \quad \times\left[\frac{n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\phi' \left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {1-\phi\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right]\nonumber \\ & =r_X(x+t)\frac{H\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {H\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)},\quad x>0. \end{align*}
\begin{align*} r_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x) & =\frac{f_X(x+t)\phi'\left(n\psi\left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)\right)n\psi' \left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)}{\bar{F}(t)\left(1-\phi\left(n\psi\left(\frac{{F}(x+t)-F(t)}{1-{F}(t)}\right)\right)\right)} \\ & =r_X(x+t)\left[\frac{\left(1-\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\psi' \left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}{\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)}\right]\\ & \quad \times\left[\frac{n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\phi' \left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {1-\phi\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right]\nonumber \\ & =r_X(x+t)\frac{H\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {H\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)},\quad x>0. \end{align*}Thus, to prove the result, it suffices to show that, for any fixed ![]() $t\geq 0$,
$t\geq 0$,
 $$\frac{r_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)}{r_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)} =\frac{H\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)H(\psi({F}_X(x+t)))} {H\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)H(n\psi({F}_X(x+t))} \quad \text{is increasing in }x>0,$$
$$\frac{r_{\tau^{\phi}_{1|n}(\boldsymbol{X}_t)}(x)}{r_{(\tau^{\phi}_{1|n}(\boldsymbol{X}))_t}(x)} =\frac{H\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)H(\psi({F}_X(x+t)))} {H\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)H(n\psi({F}_X(x+t))} \quad \text{is increasing in }x>0,$$or equivalently,
 \begin{align} & \left[\frac{C\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{C\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right] \left[\frac{F_X(x+t)}{F_X(x+t)-F_X(t)}\right] \nonumber\\ & \quad \geq \left[\frac{C(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{C(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\right], \quad \text{for all }x>0. \end{align}
\begin{align} & \left[\frac{C\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{C\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}\right] \left[\frac{F_X(x+t)}{F_X(x+t)-F_X(t)}\right] \nonumber\\ & \quad \geq \left[\frac{C(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}- \frac{C(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))}\right], \quad \text{for all }x>0. \end{align}Since ![]() $F\left (\cdot \right )$ is a increasing function, we have
$F\left (\cdot \right )$ is a increasing function, we have
Again, from the assumption, we have that
which, by (A.23), gives
 \begin{align} 0& \leq \frac{C(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}-\frac{C(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))} \nonumber\\ & \leq\frac{C\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{C\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}, \end{align}
\begin{align} 0& \leq \frac{C(n\psi({F}_X(x+t))}{R(\psi({F}_X(x+t)))}-\frac{C(\psi({F}_X(x+t)))}{R(\psi({F}_X(x+t)))} \nonumber\\ & \leq\frac{C\left(n\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}- \frac{C\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)} {R\left(\psi\left(\frac{{F}_X(x+t)-F_X(t)}{1-{F}_X(t)}\right)\right)}, \end{align}for any fixed ![]() $t\geq 0$ and for all
$t\geq 0$ and for all ![]() $x>0$. On combining (A.30) and (A.31), we get (A.29) and hence, the result follows.
$x>0$. On combining (A.30) and (A.31), we get (A.29) and hence, the result follows.
Proof of Theorem 3.6(a). We only prove the result under the condition that ![]() $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in ![]() $u>0$. The proof follows in the same line for the other case. From (A.1), we have
$u>0$. The proof follows in the same line for the other case. From (A.1), we have
 $${r}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)={r}_X(x)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))), \quad x>0.$$
$${r}_{\tau^{\phi}_{r|n}(\boldsymbol{X})}(x)={r}_X(x)\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x))), \quad x>0.$$Since ![]() $X$ is IFR (resp. DFR), we have that
$X$ is IFR (resp. DFR), we have that ![]() ${r}_X(x)$ is increasing (resp. decreasing) in
${r}_X(x)$ is increasing (resp. decreasing) in ![]() $x>0$. Thus, to prove the result, it suffices to show that
$x>0$. Thus, to prove the result, it suffices to show that
 \begin{equation} \sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\quad \text{is increasing (resp. decreasing) in } x>0. \end{equation}
\begin{equation} \sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\quad \text{is increasing (resp. decreasing) in } x>0. \end{equation}Now,
 $$\frac{d}{dx}\left(\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\right) = \frac{d}{du}\left(\sum_{j=r}^{n} P_{r,n}^{j}(u)K_{j}(u)\right)\frac{du}{dt},$$
$$\frac{d}{dx}\left(\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\right) = \frac{d}{du}\left(\sum_{j=r}^{n} P_{r,n}^{j}(u)K_{j}(u)\right)\frac{du}{dt},$$where ![]() $u=\psi \left (\bar {F}_X(t)\right )$. Since
$u=\psi \left (\bar {F}_X(t)\right )$. Since ![]() $\psi$ is a decreasing function, we have
$\psi$ is a decreasing function, we have ![]() ${du}/{dt}\geq 0$. On using this together with the condition “
${du}/{dt}\geq 0$. On using this together with the condition “![]() $\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in
$\sum _{j=r}^{n} P_{r,n}^{j}(u)K_j(u)$ is increasing (resp. decreasing) in ![]() $u>0$”, we get
$u>0$”, we get
 $$\frac{d}{dx}\left(\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\right)\geq(\text{resp. }\leq)\;0,$$
$$\frac{d}{dx}\left(\sum_{j=r}^{n} P_{r,n}^{j}(\psi(\bar{F}_X(x)))K_{j}(\psi(\bar{F}_X(x)))\right)\geq(\text{resp. }\leq)\;0,$$which implies that (A.32) is true. Hence, the result is proved.
Proof of Theorem 3.7(a). We only prove the result for the series system. The result for the parallel system can be shown in the same line. We have
which gives
 $$\frac{f'_{\tau^{\phi}_{n|n}(\boldsymbol{X})}(x)}{f_{\tau^{\phi}_{n|n}(\boldsymbol{X})}(x)} =\frac{f'_X(x)}{f_X(x)}-r_X(x)\left[\frac{G(n\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))} -\frac{G(\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))}\right],\quad x>0.$$
$$\frac{f'_{\tau^{\phi}_{n|n}(\boldsymbol{X})}(x)}{f_{\tau^{\phi}_{n|n}(\boldsymbol{X})}(x)} =\frac{f'_X(x)}{f_X(x)}-r_X(x)\left[\frac{G(n\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))} -\frac{G(\psi(\bar{F}_X(x)))}{R(\psi(\bar{F}_X(x)))}\right],\quad x>0.$$Since X is ILR (resp. DLR), we have that ![]() ${f'_X(x)}/{f_X(x)}$ is decreasing (resp. increasing) in
${f'_X(x)}/{f_X(x)}$ is decreasing (resp. increasing) in ![]() $x>0$, and
$x>0$, and ![]() $r_X(x)$ is increasing (resp. decreasing) in
$r_X(x)$ is increasing (resp. decreasing) in ![]() $x>0$. Thus, to prove the result, it suffices to show that
$x>0$. Thus, to prove the result, it suffices to show that
is positive and increasing (resp. decreasing) in ![]() $x>0$. Since
$x>0$. Since ![]() $\psi$ is a decreasing function, we have that
$\psi$ is a decreasing function, we have that
Again, from the assumption, we have that
On combining (A.34) and (A.35), we get (A.33) and hence, the result is proved.
Proof of Theorem 3.7(b). To prove the result, we have to show that
or equivalently,
Since ![]() $X$ is IFRA (resp. DFRA), we have
$X$ is IFRA (resp. DFRA), we have
On using the decreasing property of ![]() $\phi$ in the above inequality, we get
$\phi$ in the above inequality, we get
for all ![]() $x>0 \text { and }0<\alpha <1$. Again, the assumption “
$x>0 \text { and }0<\alpha <1$. Again, the assumption “![]() $uR'(u)/R(u)$ is increasing (resp. decreasing) in
$uR'(u)/R(u)$ is increasing (resp. decreasing) in ![]() $u>0$” implies that
$u>0$” implies that
which further implies that
or equivalently,
Furthermore, this implies that
and hence,
for all ![]() $x>0$ and
$x>0$ and ![]() $0<\alpha <1$. On combining (A.37) and (A.38), we get (A.36). Hence, the result is proved.
$0<\alpha <1$. On combining (A.37) and (A.38), we get (A.36). Hence, the result is proved.
Proof of Theorem 3.7(c). Note that, for all ![]() $x>0$,
$x>0$,
Since ![]() $X$ is IFRA (resp. DFRA), we have that
$X$ is IFRA (resp. DFRA), we have that
Again, from the assumption “![]() $H(u)/\log (1-\phi (u))$ is increasing (resp. decreasing) in
$H(u)/\log (1-\phi (u))$ is increasing (resp. decreasing) in ![]() $u>0$”, we get that
$u>0$”, we get that
On combing (A.39) and (A.40), we get that
or equivalently,
and hence, the result follows.