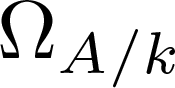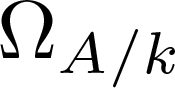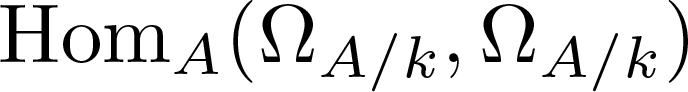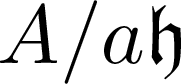1. Introduction
A long-standing conjecture posed by R. W. Berger [Reference Berger3] states the following:
Berger’s Conjecture. Let k be a field of characteristic zero and let A be a one-dimensional reduced local ring which is either
 \begin{equation*}k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}/\mathfrak{A} \quad \mbox{or} \quad k[[X_1, \ldots, X_n]]/\mathfrak{A},\end{equation*}
\begin{equation*}k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}/\mathfrak{A} \quad \mbox{or} \quad k[[X_1, \ldots, X_n]]/\mathfrak{A},\end{equation*}where the X i’s are  $n\geq 2$ indeterminates over k and
$n\geq 2$ indeterminates over k and  $\mathfrak{A}$ stands for an ideal. If the (universally finite) module
$\mathfrak{A}$ stands for an ideal. If the (universally finite) module  $\Omega_{A/k}$ of k-differentials of A is torsion-free, then A is regular.
$\Omega_{A/k}$ of k-differentials of A is torsion-free, then A is regular.
Example 1. The standard and easiest illustration is the cuspidal plane cubic, that is, the local domain  $A= {\mathbb C}[[X, Y]]/(Y^2-X^3) =
{\mathbb C}[[x, y]]$. We have
$A= {\mathbb C}[[X, Y]]/(Y^2-X^3) =
{\mathbb C}[[x, y]]$. We have  $\Omega_{A/{\mathbb C}} \cong A^2/A (-3x^2, 2y)$, which, as expected, has non-trivial torsion. For instance, if
$\Omega_{A/{\mathbb C}} \cong A^2/A (-3x^2, 2y)$, which, as expected, has non-trivial torsion. For instance, if  $\omega \in \Omega_{A/{\mathbb C}}\setminus \{0\}$ is the differential corresponding to the image of the vector
$\omega \in \Omega_{A/{\mathbb C}}\setminus \{0\}$ is the differential corresponding to the image of the vector  $(-3xy, 2x^2)\in A^2$, then
$(-3xy, 2x^2)\in A^2$, then  $x\omega =0$.
$x\omega =0$.
Remark 2. In Berger’s problem, the local k-algebra A is not required to be an integral domain (even though this constitutes a fundamental case), and moreover, in the algebroid case, its defining ideal is not required to be generated by polynomials. Also, the original statement assumes the field k to be perfect only, but as in Berger’s survey [Reference Berger5] we restrict ourselves to the characteristic zero case. The conjecture has been confirmed in a number of special situations; see, for instance, Bassein [Reference Bassein2], Berger [Reference Berger3, Reference Berger4], Buchweitz and Greuel [Reference Buchweitz and Greuel7], Cortiñas et al. [Reference Cortiñas, Geller and Weibel11], Cortiñas and Krongold [Reference Cortiñas and Krongold10], Güttes [Reference Güttes15], Herzog [Reference Herzog17], Herzog and Waldi [Reference Herzog and Waldi21, Reference Herzog and Waldi22], Isogawa [Reference Isogawa26], Pohl [Reference Pohl28], Scheja [Reference Scheja29] and Ulrich [Reference Ulrich31]. We also refer to Herzog’s survey [Reference Herzog19] about this and other differential conjectures, for instance, the so-called rigidity conjecture (cf. also Herzog [Reference Herzog17, Reference Herzog18] and Ulrich [Reference Ulrich31]), which is closely related to the problem considered here (see Remark 13).
In this note, we start from the fact that the key hypothesis of the conjecture allows us to realize the endomorphism module  ${\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k})$ as an ideal
${\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k})$ as an ideal  $\mathfrak{h}_{A/k}$ of A (Lemma 2). Then, our main result (Theorem 4) characterizes when A is regular and shows that, in order to solve Berger’s Conjecture, it suffices to prove that
$\mathfrak{h}_{A/k}$ of A (Lemma 2). Then, our main result (Theorem 4) characterizes when A is regular and shows that, in order to solve Berger’s Conjecture, it suffices to prove that  $A/a\mathfrak{h}_{A/k}$ can be taken as Gorenstein for some parameter a of A.
$A/a\mathfrak{h}_{A/k}$ can be taken as Gorenstein for some parameter a of A.
Several other characterizations for the regularity of  $(A, \mathfrak{m})$ in the context of Berger’s Conjecture (hence, assuming
$(A, \mathfrak{m})$ in the context of Berger’s Conjecture (hence, assuming  $\Omega_{A/k}$ to be torsion-free) are given. Later, we mention some of them.
$\Omega_{A/k}$ to be torsion-free) are given. Later, we mention some of them.
Proposition 6 makes use, in particular, of the vanishing of (co)homology modules and shows, among other equivalences, that A is regular if and only if
 \begin{equation*}{\rm Ext}_A^i(\Omega_{A/k}, \mathfrak{m}^{\nu}) = 0 \quad \mbox{for some} \, i, \nu \geq 1.\end{equation*}
\begin{equation*}{\rm Ext}_A^i(\Omega_{A/k}, \mathfrak{m}^{\nu}) = 0 \quad \mbox{for some} \, i, \nu \geq 1.\end{equation*} In Proposition 8 and Corollary 9, we apply a similar approach but eventually exploring the finiteness of the injective dimension of certain modules; for instance, in the latter, it is observed that A is regular if and only if  ${\rm injdim}\,{\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k}) \lt \infty$.
${\rm injdim}\,{\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k}) \lt \infty$.
In Lemma 12, we use a suitable Artinian derivation module to provide a numerical characterization of the vanishing of  ${\rm Ext}_A^1(\Omega_{A/k}, A)$, and this turns out to be one of the key ingredients to Corollary 14, which also characterizes when A is regular.
${\rm Ext}_A^1(\Omega_{A/k}, A)$, and this turns out to be one of the key ingredients to Corollary 14, which also characterizes when A is regular.
Another result, Corollary 16, has as a consequence the fact that if in addition A is a Gorenstein domain, then A is regular, provided that the tensor product module  $\mathfrak{h}_{A/k}\otimes_A{\rm Hom}_A(\mathfrak{h}_{A/k}, A)$ is torsion-free and
$\mathfrak{h}_{A/k}\otimes_A{\rm Hom}_A(\mathfrak{h}_{A/k}, A)$ is torsion-free and
 \begin{equation*}\bigcup_{j\geq 1}\mathfrak{h}_{A/k}^j :_{A^\prime} \mathfrak{h}_{A/k}^j = \mathfrak{h}_{A/k} :_{A^\prime} \mathfrak{h}_{A/k},\end{equation*}
\begin{equation*}\bigcup_{j\geq 1}\mathfrak{h}_{A/k}^j :_{A^\prime} \mathfrak{h}_{A/k}^j = \mathfrak{h}_{A/k} :_{A^\prime} \mathfrak{h}_{A/k},\end{equation*}where A ʹ is the integral closure of A in its fraction field.
Finally, Corollary 19 shows that A is regular if and only if the quotient ring
 \begin{equation*}{\mathfrak R}_A(\mathfrak{h}_{A/k})/(t^2+at+b)A[t]\cap {\mathfrak R}_A(\mathfrak{h}_{A/k})\end{equation*}
\begin{equation*}{\mathfrak R}_A(\mathfrak{h}_{A/k})/(t^2+at+b)A[t]\cap {\mathfrak R}_A(\mathfrak{h}_{A/k})\end{equation*}is Gorenstein for some – equivalently, all –  $a, b\in A$, where
$a, b\in A$, where  ${\mathfrak R}_A(\mathfrak{h}_{A/k})=\bigoplus_{i\geq 0}\mathfrak{h}_{A/k}^it^i$ (hence, an A-subalgebra of
${\mathfrak R}_A(\mathfrak{h}_{A/k})=\bigoplus_{i\geq 0}\mathfrak{h}_{A/k}^it^i$ (hence, an A-subalgebra of  $A[t]$) is the Rees algebra of the ideal
$A[t]$) is the Rees algebra of the ideal  $\mathfrak{h}_{A/k}$.
$\mathfrak{h}_{A/k}$.
2. Preliminaries
2.1. Conventions and basics
Throughout the paper, by ring, we tacitly mean Noetherian, commutative, unital ring. The set of zero divisors of a ring S is equal to  $\bigcup_{\mathfrak{p}\in {\rm Ass}\,S}\mathfrak{p}$, where as usual
$\bigcup_{\mathfrak{p}\in {\rm Ass}\,S}\mathfrak{p}$, where as usual  ${\rm Ass}\,S$ denotes the (finite) set of associated primes of S. We say that an S-module M is finite, simply, if it is finitely generated over S. The S-torsion submodule of M is formed by the elements that are killed by some non-zero-divisor of S. If such submodule is trivial, then M is said to be torsion-free (over S). We say that a finite S-module M has a (generic, constant) rank, say
${\rm Ass}\,S$ denotes the (finite) set of associated primes of S. We say that an S-module M is finite, simply, if it is finitely generated over S. The S-torsion submodule of M is formed by the elements that are killed by some non-zero-divisor of S. If such submodule is trivial, then M is said to be torsion-free (over S). We say that a finite S-module M has a (generic, constant) rank, say  $r\geq 0$, if the
$r\geq 0$, if the  $S_{\mathfrak{p}}$-module
$S_{\mathfrak{p}}$-module  $M_{\mathfrak{p}}=M\otimes_SS_{\mathfrak{p}}$ is free of rank r for every
$M_{\mathfrak{p}}=M\otimes_SS_{\mathfrak{p}}$ is free of rank r for every  $\mathfrak{p}\in {\rm Ass}\,S$. For instance, an ideal containing a non-zero-divisor has rank 1, and any finite module over a domain has a rank.
$\mathfrak{p}\in {\rm Ass}\,S$. For instance, an ideal containing a non-zero-divisor has rank 1, and any finite module over a domain has a rank.
Now let  $(S, \mathfrak{n})$ be a local ring. We denote the
$(S, \mathfrak{n})$ be a local ring. We denote the ![]() $\mathfrak{n}$-depth of a finite S-module M by
$\mathfrak{n}$-depth of a finite S-module M by  ${\rm depth}\,M$. Thus, M is maximal Cohen-Macaulay over S if
${\rm depth}\,M$. Thus, M is maximal Cohen-Macaulay over S if  ${\rm depth}\,M={\rm dim}\,S$. If S is a Cohen–Macaulay local ring with a canonical module, say ω S (which is unique up to isomorphism), then it is well-known that M is maximal Cohen–Macaulay if and only if
${\rm depth}\,M={\rm dim}\,S$. If S is a Cohen–Macaulay local ring with a canonical module, say ω S (which is unique up to isomorphism), then it is well-known that M is maximal Cohen–Macaulay if and only if  ${\rm Ext}^i_S(M, \omega_S) = 0$ for all
${\rm Ext}^i_S(M, \omega_S) = 0$ for all  $i\geq 1$. For further information, see [Reference Bruns and Herzog6].
$i\geq 1$. For further information, see [Reference Bruns and Herzog6].
2.2. Differentials
Let k be a ring and S be a k-algebra. Consider the tensor product algebra  $S\otimes_kS$ and the ‘diagonal’ ideal
$S\otimes_kS$ and the ‘diagonal’ ideal  $\mathfrak{D}\subset S\otimes_kS$ generated by all elements of the form
$\mathfrak{D}\subset S\otimes_kS$ generated by all elements of the form  $x\otimes 1 - 1\otimes x$, with
$x\otimes 1 - 1\otimes x$, with  $x \in S$. It is easy to see that
$x \in S$. It is easy to see that  $\mathfrak{D}$ is the kernel of the natural multiplication map
$\mathfrak{D}$ is the kernel of the natural multiplication map  $S\otimes_kS\rightarrow S$, so that
$S\otimes_kS\rightarrow S$, so that  $(S\otimes_kS)/\mathfrak{D} \cong S$. This endows
$(S\otimes_kS)/\mathfrak{D} \cong S$. This endows  $\mathfrak{D}/\mathfrak{D}^2$ with a natural structure of an S-module, which is denoted
$\mathfrak{D}/\mathfrak{D}^2$ with a natural structure of an S-module, which is denoted
 \begin{equation*}{\rm D}_{S/k} := \mathfrak{D}/\mathfrak{D}^2,\end{equation*}
\begin{equation*}{\rm D}_{S/k} := \mathfrak{D}/\mathfrak{D}^2,\end{equation*}the so-called module of Kähler differentials of S over k. This S-module is finite if, for example, the k-algebra S is essentially of finite type, but it is important to recall that  ${\rm D}_{S/k}$ may not be finite in general and such a pathology can occur even if S is a regular local ring; for instance, if
${\rm D}_{S/k}$ may not be finite in general and such a pathology can occur even if S is a regular local ring; for instance, if  $S=k[[X_1, \ldots, X_n]]$ is a formal power series ring over a field k of characteristic zero, then
$S=k[[X_1, \ldots, X_n]]$ is a formal power series ring over a field k of characteristic zero, then  ${\rm D}_{S/k}$ is not finite (see [Reference Kunz27, Example 5.5(a)]).
${\rm D}_{S/k}$ is not finite (see [Reference Kunz27, Example 5.5(a)]).
For some classes of k-algebras S, there exists, however, a suitable modification of  ${\rm D}_{S/k}$, typically written
${\rm D}_{S/k}$, typically written  ${\Omega_{S/k}}$ and called universally finite differential module of S over k, which turns out to be a finite S-module. For instance, if S is either essentially of finite type over k or a complete local ring
${\Omega_{S/k}}$ and called universally finite differential module of S over k, which turns out to be a finite S-module. For instance, if S is either essentially of finite type over k or a complete local ring  $(S, \mathfrak{n})$ such that
$(S, \mathfrak{n})$ such that  $S/\mathfrak{n}$ is a finite extension of a field k, then
$S/\mathfrak{n}$ is a finite extension of a field k, then  ${\Omega_{S/k}}$ does exist; in the former case, we simply put
${\Omega_{S/k}}$ does exist; in the former case, we simply put  ${\Omega_{S/k}}:={\rm D}_{S/k}$, and, in the latter,
${\Omega_{S/k}}:={\rm D}_{S/k}$, and, in the latter,
 \begin{equation*}\Omega_{S/k} := {\rm D}_{S/k}/\bigcap_{i\geq 0}\mathfrak{n}^i{\rm D}_{S/k}.\end{equation*}
\begin{equation*}\Omega_{S/k} := {\rm D}_{S/k}/\bigcap_{i\geq 0}\mathfrak{n}^i{\rm D}_{S/k}.\end{equation*} If, for example, k is a field and  $S=k[[X_1, \ldots, X_n]]$, then
$S=k[[X_1, \ldots, X_n]]$, then  ${\Omega_{S/k}}$ is free of rank n. Finally, it should be mentioned that the formation of the universally finite differential module does not commute with localization in general. For the theory, see [Reference Kunz27], also [Reference Herzog19].
${\Omega_{S/k}}$ is free of rank n. Finally, it should be mentioned that the formation of the universally finite differential module does not commute with localization in general. For the theory, see [Reference Kunz27], also [Reference Herzog19].
3. One-dimensional regular local rings
3.1. Main result
Before stating our main result, we introduce some notation as well as a basic lemma.
Notation 1.
Let k be a field of characteristic zero and let A be a local ring which is a quotient of either  $k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or
$k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or  $k[[X_1, \ldots, X_n]]$; in particular,
$k[[X_1, \ldots, X_n]]$; in particular,  $\Omega_{A/k}$ exists. Throughout the paper, we set
$\Omega_{A/k}$ exists. Throughout the paper, we set
 \begin{equation*}{\rm H}_{A/k} := {\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k}).\end{equation*}
\begin{equation*}{\rm H}_{A/k} := {\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k}).\end{equation*}Lemma 2. Let k be a field of characteristic zero and let A be a one-dimensional reduced local ring which is a quotient of either  $k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or
$k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or  $k[[X_1, \ldots, X_n]]$. The following assertions hold:
$k[[X_1, \ldots, X_n]]$. The following assertions hold:
(i)
 $\Omega_{A/k}$ has rank 1 as an A-module.
$\Omega_{A/k}$ has rank 1 as an A-module.(ii) If
 $\Omega_{A/k}$ is torsion-free, then
$\Omega_{A/k}$ is torsion-free, then  ${\rm H}_{A/k}$ can be identified with an ideal of A.
${\rm H}_{A/k}$ can be identified with an ideal of A.
Proof. First, note that, being a reduced one-dimensional local ring, A must be Cohen–Macaulay. The assertion (i) is well known and standard notably in the algebraic case. In the algebroid case, it was mentioned, for example, in [Reference Pohl28, proof of Lemma 1], and moreover proofs can be found in the literature under the hypothesis that A is an integral domain. Below we give a proof without assuming this condition.
Write  $A=B/\mathfrak{A}$, where
$A=B/\mathfrak{A}$, where  $B=k[[X_1, \ldots, X_n]]$ is a formal power series ring over k and
$B=k[[X_1, \ldots, X_n]]$ is a formal power series ring over k and  $\mathfrak{A}\subset B$ is a radical proper ideal. By [Reference Kunz27, Corollary 11.10], the A-module
$\mathfrak{A}\subset B$ is a radical proper ideal. By [Reference Kunz27, Corollary 11.10], the A-module  $\Omega_{A/k}$ fits into the conormal sequence
$\Omega_{A/k}$ fits into the conormal sequence
 \begin{equation*}\mathfrak{A}/\mathfrak{A}^2\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0.\end{equation*}
\begin{equation*}\mathfrak{A}/\mathfrak{A}^2\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0.\end{equation*} Explicitly, the map  $\mathfrak{A}/\mathfrak{A}^2\rightarrow A^n$ sends the class (modulo
$\mathfrak{A}/\mathfrak{A}^2\rightarrow A^n$ sends the class (modulo  $\mathfrak{A}^2$) of any given
$\mathfrak{A}^2$) of any given  $f\in \mathfrak{A}$ to
$f\in \mathfrak{A}$ to  $(\partial f/\partial x_1, \ldots, \partial f/\partial x_n)\in A^n$, where
$(\partial f/\partial x_1, \ldots, \partial f/\partial x_n)\in A^n$, where  $\partial f/\partial x_j$ stands for the image in A of the formal partial derivative
$\partial f/\partial x_j$ stands for the image in A of the formal partial derivative  $\partial f/\partial X_j$, for every
$\partial f/\partial X_j$, for every  $j=1, \ldots, n$. Hence, this map has kernel
$j=1, \ldots, n$. Hence, this map has kernel  $\mathfrak{A}^{\langle 2\rangle}/\mathfrak{A}^2$, where
$\mathfrak{A}^{\langle 2\rangle}/\mathfrak{A}^2$, where  $\mathfrak{A}^{\langle 2\rangle}$ is the so-called second differential power of
$\mathfrak{A}^{\langle 2\rangle}$ is the so-called second differential power of  $\mathfrak{A}$, that is, the subideal formed by the
$\mathfrak{A}$, that is, the subideal formed by the  $g\in \mathfrak{A}$ such that
$g\in \mathfrak{A}$ such that  $\partial g/\partial X_j\in \mathfrak{A}$ for every
$\partial g/\partial X_j\in \mathfrak{A}$ for every  $j=1, \ldots, n$. Now, consider the second symbolic power
$j=1, \ldots, n$. Now, consider the second symbolic power  $\mathfrak{A}^{(2)} = \bigcap_{\mathfrak{P}}(\mathfrak{A}^2B_{\mathfrak{P}}\cap B)$, where
$\mathfrak{A}^{(2)} = \bigcap_{\mathfrak{P}}(\mathfrak{A}^2B_{\mathfrak{P}}\cap B)$, where  ${\mathfrak{P}}\subset B$ ranges over the associated primes of the B-module
${\mathfrak{P}}\subset B$ ranges over the associated primes of the B-module  $B/{\mathfrak{A}}$. Since
$B/{\mathfrak{A}}$. Since  $\mathfrak{A}$ is radical and
$\mathfrak{A}$ is radical and  ${\rm char}\,k=0$, we have
${\rm char}\,k=0$, we have  $\mathfrak{A}^{(2)}=\mathfrak{A}^{\langle 2\rangle}$ by the general versions of the Zariski–Nagata theorem obtained in [Reference Dao, De Stefani, Grifo, Huneke and Núñez-Betancourt12,
$\mathfrak{A}^{(2)}=\mathfrak{A}^{\langle 2\rangle}$ by the general versions of the Zariski–Nagata theorem obtained in [Reference Dao, De Stefani, Grifo, Huneke and Núñez-Betancourt12, ![]() $\S$ 2.1] (which, as pointed out therein, hold as well in the present case of power series rings). It follows a short exact sequence
$\S$ 2.1] (which, as pointed out therein, hold as well in the present case of power series rings). It follows a short exact sequence
 \begin{equation*}0\longrightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0.\end{equation*}
\begin{equation*}0\longrightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0.\end{equation*} Therefore, in order to prove that  $\Omega_{A/k}$ has rank 1, it suffices to show that
$\Omega_{A/k}$ has rank 1, it suffices to show that  $\mathfrak{A}/\mathfrak{A}^{(2)}$ has rank n − 1. As is well-known, the torsion of the conormal module
$\mathfrak{A}/\mathfrak{A}^{(2)}$ has rank n − 1. As is well-known, the torsion of the conormal module  $\mathfrak{A}/\mathfrak{A}^{2}$ is precisely
$\mathfrak{A}/\mathfrak{A}^{2}$ is precisely  $\mathfrak{A}^{(2)}/\mathfrak{A}^{2}$, which then has rank zero. Thus, by the short exact sequence of A-modules
$\mathfrak{A}^{(2)}/\mathfrak{A}^{2}$, which then has rank zero. Thus, by the short exact sequence of A-modules  $0\rightarrow \mathfrak{A}^{(2)}/\mathfrak{A}^{2}\rightarrow \mathfrak{A}/\mathfrak{A}^{2}\rightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\rightarrow 0$, it suffices to check that
$0\rightarrow \mathfrak{A}^{(2)}/\mathfrak{A}^{2}\rightarrow \mathfrak{A}/\mathfrak{A}^{2}\rightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\rightarrow 0$, it suffices to check that  $\mathfrak{A}/\mathfrak{A}^{2}$ has rank n − 1. But this is true (see, e.g., [Reference Bruns and Herzog6, Exercise 4.7.17]) since A is reduced – hence, generically a complete intersection – and Cohen–Macaulay, and since
$\mathfrak{A}/\mathfrak{A}^{2}$ has rank n − 1. But this is true (see, e.g., [Reference Bruns and Herzog6, Exercise 4.7.17]) since A is reduced – hence, generically a complete intersection – and Cohen–Macaulay, and since  $n-1= {\rm height}\,\mathfrak{A}$.
$n-1= {\rm height}\,\mathfrak{A}$.
Finally, to prove (ii), set  ${\rm H}:={\rm H}_{A/k}$ for simplicity. Having shown that
${\rm H}:={\rm H}_{A/k}$ for simplicity. Having shown that  $\Omega_{A/k}$ has rank 1 as an A-module, we get that
$\Omega_{A/k}$ has rank 1 as an A-module, we get that  ${\rm H}$ has rank 1 as well; indeed, we can write
${\rm H}$ has rank 1 as well; indeed, we can write
 \begin{equation*}{\rm H}_{\mathfrak{p}} \cong {\rm Hom}_{A_{\mathfrak{p}}}(({\Omega_{A/k})}_{\mathfrak{p}}, ({\Omega_{A/k})}_{\mathfrak{p}}) \cong {\rm Hom}_{A_{\mathfrak{p}}}(A_{\mathfrak{p}},A_{\mathfrak{p}}) \cong A_{\mathfrak{p}}\end{equation*}
\begin{equation*}{\rm H}_{\mathfrak{p}} \cong {\rm Hom}_{A_{\mathfrak{p}}}(({\Omega_{A/k})}_{\mathfrak{p}}, ({\Omega_{A/k})}_{\mathfrak{p}}) \cong {\rm Hom}_{A_{\mathfrak{p}}}(A_{\mathfrak{p}},A_{\mathfrak{p}}) \cong A_{\mathfrak{p}}\end{equation*}for any minimal prime ![]() $\mathfrak{p}$ of A. It is also clear that
$\mathfrak{p}$ of A. It is also clear that  ${\rm H}$ is torsion-free since so is
${\rm H}$ is torsion-free since so is  $\Omega_{A/k}$ by assumption. It follows that
$\Omega_{A/k}$ by assumption. It follows that  ${\rm H}$ affords an embedding into A and hence is isomorphic to the image, which is a non-zero ideal of A.
${\rm H}$ affords an embedding into A and hence is isomorphic to the image, which is a non-zero ideal of A.
Notation 3.
Consider the setting and hypotheses of Lemma 2(ii). As we have seen, we can fix an A-module isomorphism between  ${\rm H}_{A/k}$ and an ideal of A; throughout the paper, such an ideal will be denoted
${\rm H}_{A/k}$ and an ideal of A; throughout the paper, such an ideal will be denoted  $\mathfrak{h}_{A/k}$, or simply
$\mathfrak{h}_{A/k}$, or simply ![]() $\mathfrak{h}$. Theoretically, its generators can be seen in the usual way. Consider generators
$\mathfrak{h}$. Theoretically, its generators can be seen in the usual way. Consider generators  ${\rm H}_{A/k} = \sum_{j=1}^{\mu}A\xi_j$ of
${\rm H}_{A/k} = \sum_{j=1}^{\mu}A\xi_j$ of  ${\rm H}_{A/k}$ as an A-module. According to the fixed embedding
${\rm H}_{A/k}$ as an A-module. According to the fixed embedding  ${\rm H}_{A/k}\subset A$, each ξ j corresponds to a uniquely determined
${\rm H}_{A/k}\subset A$, each ξ j corresponds to a uniquely determined  ${\alpha}_j\in A$, so that
${\alpha}_j\in A$, so that  $\mathfrak{h}_{A/k}=({\alpha}_1, \ldots, {\alpha}_{\mu})$.
$\mathfrak{h}_{A/k}=({\alpha}_1, \ldots, {\alpha}_{\mu})$.
Our result is as follows.
Theorem 4. Assume the setting and hypotheses of Berger’s Conjecture. The following assertions are equivalent:
(i) A is regular.
(ii)
 $A/a\mathfrak{h}_{A/k}$ is a hypersurface ring for some
$A/a\mathfrak{h}_{A/k}$ is a hypersurface ring for some  $($any
$($any $)$ parameter
$)$ parameter  $a\in \mathfrak{m}$.
$a\in \mathfrak{m}$.(iii)
 $A/a\mathfrak{h}_{A/k}$ is Gorenstein for some
$A/a\mathfrak{h}_{A/k}$ is Gorenstein for some  $($any
$($any $)$ parameter
$)$ parameter  $a\in \mathfrak{m}$.
$a\in \mathfrak{m}$.
Proof. It is a well-known fact that  $\Omega_{A/k}$ is free if and only if A is regular (see [Reference Kunz27, Theorem 14.1], where the hypothesis
$\Omega_{A/k}$ is free if and only if A is regular (see [Reference Kunz27, Theorem 14.1], where the hypothesis  ${\rm char}\,k=0$ is required). Consequently, if the one-dimensional local ring A is regular, then
${\rm char}\,k=0$ is required). Consequently, if the one-dimensional local ring A is regular, then  ${\rm H}_{A/k}$ is free, that is, the ideal
${\rm H}_{A/k}$ is free, that is, the ideal ![]() $\mathfrak{h}$ is principally generated by a non-zero-divisor, say b. Hence, if
$\mathfrak{h}$ is principally generated by a non-zero-divisor, say b. Hence, if ![]() $a\in \mathfrak{m}$ is a parameter, the ring
$a\in \mathfrak{m}$ is a parameter, the ring  $A/a\mathfrak{h} = A/(ab)$ is a hypersurface ring. Also recall that hypersurface rings are Gorenstein. This proves (i)
$A/a\mathfrak{h} = A/(ab)$ is a hypersurface ring. Also recall that hypersurface rings are Gorenstein. This proves (i)![]() $\Rightarrow$(ii)
$\Rightarrow$(ii)![]() $\Rightarrow$(iii).
$\Rightarrow$(iii).
It remains to show that (iii)![]() $\Rightarrow$(i), which is the core of the proof. Since
$\Rightarrow$(i), which is the core of the proof. Since  $\Omega_{A/k}$ is torsion-free of rank 1, we can fix a proper ideal
$\Omega_{A/k}$ is torsion-free of rank 1, we can fix a proper ideal ![]() $\mathfrak{o}$ of A such that
$\mathfrak{o}$ of A such that
 \begin{equation*}\Omega_{A/k} \cong \mathfrak{o}.\end{equation*}
\begin{equation*}\Omega_{A/k} \cong \mathfrak{o}.\end{equation*} Since A is one-dimensional and  $\Omega_{A/k}$ is torsion-free,
$\Omega_{A/k}$ is torsion-free, ![]() $\mathfrak{o}$ is a maximal Cohen–Macaulay A-module and then, as an ideal, it must be
$\mathfrak{o}$ is a maximal Cohen–Macaulay A-module and then, as an ideal, it must be ![]() $\mathfrak{m}$-primary. Hence, as, in addition, the residue field of A is infinite, there exists a non-zero-divisor
$\mathfrak{m}$-primary. Hence, as, in addition, the residue field of A is infinite, there exists a non-zero-divisor ![]() $x\in \mathfrak{m}$ such that the principal ideal (x) is a (minimal) reduction of
$x\in \mathfrak{m}$ such that the principal ideal (x) is a (minimal) reduction of ![]() $\mathfrak{o}$ (this follows, e.g., from [Reference Huneke and Swanson24, Theorem 8.6.3]). Let T denote the total quotient ring of A, that is,
$\mathfrak{o}$ (this follows, e.g., from [Reference Huneke and Swanson24, Theorem 8.6.3]). Let T denote the total quotient ring of A, that is,  $T=W^{-1}A,$ where W is the multiplicative set formed by the non-zero-divisors of A. Consider the A-submodule
$T=W^{-1}A,$ where W is the multiplicative set formed by the non-zero-divisors of A. Consider the A-submodule  $\mathfrak{F}\subset T$ formed by the fractions
$\mathfrak{F}\subset T$ formed by the fractions  $y/x$ with
$y/x$ with  $y\in \mathfrak{o}$. Clearly,
$y\in \mathfrak{o}$. Clearly,  $\mathfrak{F}\cong \mathfrak{o}$ as A-modules. Let
$\mathfrak{F}\cong \mathfrak{o}$ as A-modules. Let  $\mathfrak{F}\colon \mathfrak{F}=\{\sigma \in T \,|\, \sigma \mathfrak{F}\subset \mathfrak{F}\}$. Each
$\mathfrak{F}\colon \mathfrak{F}=\{\sigma \in T \,|\, \sigma \mathfrak{F}\subset \mathfrak{F}\}$. Each  $a\in A$ satisfies
$a\in A$ satisfies  $ay/x\in \mathfrak{F}$ for all
$ay/x\in \mathfrak{F}$ for all  $y\in \mathfrak{o}$, and moreover,
$y\in \mathfrak{o}$, and moreover,  $1=x/x\in \mathfrak{F}$. Hence,
$1=x/x\in \mathfrak{F}$. Hence,  $A \subset \mathfrak{F}\colon \mathfrak{F} \subset \mathfrak{F}$. Observe that the co-kernel
$A \subset \mathfrak{F}\colon \mathfrak{F} \subset \mathfrak{F}$. Observe that the co-kernel  $\overline{\mathfrak{F}}$ of the latter inclusion is of finite length; the argument is standard, but for completeness, we provide it here. First, we may identify
$\overline{\mathfrak{F}}$ of the latter inclusion is of finite length; the argument is standard, but for completeness, we provide it here. First, we may identify  $A\cong \{a/x \,|\, a\in (x)\}\subset \mathfrak{F}$, which is the kernel of the natural epimorphism
$A\cong \{a/x \,|\, a\in (x)\}\subset \mathfrak{F}$, which is the kernel of the natural epimorphism  $\mathfrak{F}\rightarrow \mathfrak{o}/(x)$ given by
$\mathfrak{F}\rightarrow \mathfrak{o}/(x)$ given by  $y/x\mapsto y\,{\rm mod} (x)$ for
$y/x\mapsto y\,{\rm mod} (x)$ for  $y\in \mathfrak{o}$. In the present setting, the A-module
$y\in \mathfrak{o}$. In the present setting, the A-module  $\mathfrak{o}/(x)$ is of finite length, and so is
$\mathfrak{o}/(x)$ is of finite length, and so is  $\mathfrak{F}/A$, and the induced epimorphism
$\mathfrak{F}/A$, and the induced epimorphism
 \begin{equation*}\mathfrak{F}/A\longrightarrow \mathfrak{F}/(\mathfrak{F}\colon \mathfrak{F}) = \overline{\mathfrak{F}}\end{equation*}
\begin{equation*}\mathfrak{F}/A\longrightarrow \mathfrak{F}/(\mathfrak{F}\colon \mathfrak{F}) = \overline{\mathfrak{F}}\end{equation*}forces  $\overline{\mathfrak{F}}$ to be of finite length as well. It will be also useful to notice that
$\overline{\mathfrak{F}}$ to be of finite length as well. It will be also useful to notice that  $1\notin \mathfrak{m}\mathfrak{F}$. Indeed, assuming otherwise and using the fact that the integral closure A ʹ of A in T contains
$1\notin \mathfrak{m}\mathfrak{F}$. Indeed, assuming otherwise and using the fact that the integral closure A ʹ of A in T contains  $\mathfrak{F}$ (to see this, recall (x) is a reduction of
$\mathfrak{F}$ (to see this, recall (x) is a reduction of ![]() $\mathfrak{o}$ and apply [Reference Huneke and Swanson24, Corollary 1.2.5]), we would get
$\mathfrak{o}$ and apply [Reference Huneke and Swanson24, Corollary 1.2.5]), we would get  $1\in \mathfrak{m}A^\prime$, hence
$1\in \mathfrak{m}A^\prime$, hence  $1\in \mathfrak{m}A^\prime \cap A=\mathfrak{m}$, a contradiction.
$1\in \mathfrak{m}A^\prime \cap A=\mathfrak{m}$, a contradiction.
Now we claim that, even more, the hypothesis (iii) forces the equality  $\mathfrak{F}\colon \mathfrak{F}=\mathfrak{F}$ to hold. To prove this, suppose by way of contradiction that the finite length A-module
$\mathfrak{F}\colon \mathfrak{F}=\mathfrak{F}$ to hold. To prove this, suppose by way of contradiction that the finite length A-module  $\overline{\mathfrak{F}}$ is non-zero. Then its socle contains a non-zero element, say u. Note there exists
$\overline{\mathfrak{F}}$ is non-zero. Then its socle contains a non-zero element, say u. Note there exists  $F_u \in {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$, which sends 1 to u. To obtain this map, first notice that the natural A-module isomorphism
$F_u \in {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$, which sends 1 to u. To obtain this map, first notice that the natural A-module isomorphism
 \begin{equation*}{\rm Soc}_A(\overline{\mathfrak{F}}) \cong {\rm Hom}_A(k, \overline{\mathfrak{F}})\end{equation*}
\begin{equation*}{\rm Soc}_A(\overline{\mathfrak{F}}) \cong {\rm Hom}_A(k, \overline{\mathfrak{F}})\end{equation*}gives the well-defined non-zero A-linear map  $k\rightarrow \overline{\mathfrak{F}}$ given by
$k\rightarrow \overline{\mathfrak{F}}$ given by  $1+\mathfrak{m}\mapsto u$. Moreover, as shown earlier, 1 is part of a minimal generating set of
$1+\mathfrak{m}\mapsto u$. Moreover, as shown earlier, 1 is part of a minimal generating set of  $\mathfrak{F}$, so that
$\mathfrak{F}$, so that  $1+\mathfrak{m}\mathfrak{F}$ is part of a basis for the k-vector space
$1+\mathfrak{m}\mathfrak{F}$ is part of a basis for the k-vector space  $\mathfrak{F}/\mathfrak{m}\mathfrak{F}$. Hence, there is a k-linear map (which is also an A-module homomorphism)
$\mathfrak{F}/\mathfrak{m}\mathfrak{F}$. Hence, there is a k-linear map (which is also an A-module homomorphism)  $\mathfrak{F}/\mathfrak{m}\mathfrak{F}\rightarrow k$ such that
$\mathfrak{F}/\mathfrak{m}\mathfrak{F}\rightarrow k$ such that  $1+\mathfrak{m}\mathfrak{F}\mapsto 1+\mathfrak{m}$. Finally, we define F u simply by the composite
$1+\mathfrak{m}\mathfrak{F}\mapsto 1+\mathfrak{m}$. Finally, we define F u simply by the composite  $\mathfrak{F} \rightarrow \mathfrak{F}/\mathfrak{m}\mathfrak{F}\rightarrow k \rightarrow \overline{\mathfrak{F}}$. Now, let
$\mathfrak{F} \rightarrow \mathfrak{F}/\mathfrak{m}\mathfrak{F}\rightarrow k \rightarrow \overline{\mathfrak{F}}$. Now, let  $\pi \in {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$ denote the natural projection. We have an exact sequence
$\pi \in {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$ denote the natural projection. We have an exact sequence
 \begin{equation*}{\rm Hom}_A(\mathfrak{F}, \mathfrak{F})\longrightarrow {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})\longrightarrow {\rm Ext}_A^1(\mathfrak{F}, \mathfrak{F}\colon \mathfrak{F}).\end{equation*}
\begin{equation*}{\rm Hom}_A(\mathfrak{F}, \mathfrak{F})\longrightarrow {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})\longrightarrow {\rm Ext}_A^1(\mathfrak{F}, \mathfrak{F}\colon \mathfrak{F}).\end{equation*} Because A is reduced and T is a direct product of finitely many fields (namely, the residue class fields corresponding to the minimal primes of A), the natural A-module homomorphism  $\mathfrak{F}\colon \mathfrak{F}\rightarrow {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$ is surjective and has kernel
$\mathfrak{F}\colon \mathfrak{F}\rightarrow {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$ is surjective and has kernel  $0\colon \mathfrak{F}\subset T$ (see [Reference Huneke and Swanson24, Lemma 2.4.2]). But
$0\colon \mathfrak{F}\subset T$ (see [Reference Huneke and Swanson24, Lemma 2.4.2]). But  $0\colon \mathfrak{F}=0$ since
$0\colon \mathfrak{F}=0$ since  $1\in \mathfrak{F}$. Therefore,
$1\in \mathfrak{F}$. Therefore,  $\mathfrak{F}\colon \mathfrak{F} \cong {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$. Furthermore, as
$\mathfrak{F}\colon \mathfrak{F} \cong {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$. Furthermore, as  $\mathfrak{F}\cong \mathfrak{o}$, we obtain
$\mathfrak{F}\cong \mathfrak{o}$, we obtain
 \begin{equation*}{\rm Ext}_A^1(\mathfrak{F}, \mathfrak{F}\colon \mathfrak{F}) \cong {\rm Ext}_A^1(\mathfrak{o}, {\rm Hom}_A(\mathfrak{o}, \mathfrak{o})) \cong {\rm Ext}_A^1(\mathfrak{o}, \mathfrak{h}).\end{equation*}
\begin{equation*}{\rm Ext}_A^1(\mathfrak{F}, \mathfrak{F}\colon \mathfrak{F}) \cong {\rm Ext}_A^1(\mathfrak{o}, {\rm Hom}_A(\mathfrak{o}, \mathfrak{o})) \cong {\rm Ext}_A^1(\mathfrak{o}, \mathfrak{h}).\end{equation*} Now, by [Reference Elias13, Proposition 2.2], the hypothesis (iii) gives that ![]() $\mathfrak{h}$ is isomorphic to a canonical module of A, so that
$\mathfrak{h}$ is isomorphic to a canonical module of A, so that  ${\rm Ext}_A^1(\mathfrak{o}, \mathfrak{h}) = 0$ as
${\rm Ext}_A^1(\mathfrak{o}, \mathfrak{h}) = 0$ as ![]() $\mathfrak{o}$ is maximal Cohen–Macaulay (see 2.1). It follows that the map
$\mathfrak{o}$ is maximal Cohen–Macaulay (see 2.1). It follows that the map  ${\rm Hom}_A(\mathfrak{F}, \mathfrak{F})\rightarrow {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$ induced by π is surjective. In particular, we can pick
${\rm Hom}_A(\mathfrak{F}, \mathfrak{F})\rightarrow {\rm Hom}_A(\mathfrak{F}, \overline{\mathfrak{F}})$ induced by π is surjective. In particular, we can pick  $G\in {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$ satisfying
$G\in {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$ satisfying  $F_u = \pi \circ G$. According to the isomorphism
$F_u = \pi \circ G$. According to the isomorphism  $\mathfrak{F}\colon \mathfrak{F}\cong {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$, there exists
$\mathfrak{F}\colon \mathfrak{F}\cong {\rm Hom}_A(\mathfrak{F}, \mathfrak{F})$, there exists  $\alpha \in \mathfrak{F}\colon \mathfrak{F}$ such that G is given by multiplication by α. Hence,
$\alpha \in \mathfrak{F}\colon \mathfrak{F}$ such that G is given by multiplication by α. Hence,  $G(1)=\alpha$, and thus
$G(1)=\alpha$, and thus  $F_u(1) = \pi(\alpha) = 0$, which is a contradiction because
$F_u(1) = \pi(\alpha) = 0$, which is a contradiction because  $F_u(1)=u\neq 0$. This proves the claim.
$F_u(1)=u\neq 0$. This proves the claim.
To finish the proof, the equality  $\mathfrak{F}\colon \mathfrak{F}=\mathfrak{F}$ can be expressed as an isomorphism
$\mathfrak{F}\colon \mathfrak{F}=\mathfrak{F}$ can be expressed as an isomorphism  ${\rm Hom}_A(\mathfrak{o}, \mathfrak{o}) \cong \mathfrak{o}$, that is,
${\rm Hom}_A(\mathfrak{o}, \mathfrak{o}) \cong \mathfrak{o}$, that is,  $\mathfrak{h}\cong \mathfrak{o}$. It follows that
$\mathfrak{h}\cong \mathfrak{o}$. It follows that ![]() $\mathfrak{o}$ is a canonical module of A because so is
$\mathfrak{o}$ is a canonical module of A because so is ![]() $\mathfrak{h}$. But then
$\mathfrak{h}$. But then  ${\rm Hom}_A(\mathfrak{o}, \mathfrak{o})\cong A$, so that
${\rm Hom}_A(\mathfrak{o}, \mathfrak{o})\cong A$, so that  $\mathfrak{o}\cong A$. Therefore,
$\mathfrak{o}\cong A$. Therefore,  $\Omega_{A/k}$ is free, as needed.
$\Omega_{A/k}$ is free, as needed.
Remark 5. (a) The final part of the above proof (from the use of [Reference Elias13, Proposition 2.2] on) admits a more general statement, to wit, if ![]() $\mathfrak{b}$ is an ideal of height 1 in A such that
$\mathfrak{b}$ is an ideal of height 1 in A such that  ${\rm Hom}_A(\mathfrak{b}, \mathfrak{b})\cong \omega_A$, then
${\rm Hom}_A(\mathfrak{b}, \mathfrak{b})\cong \omega_A$, then  $\mathfrak{b}\cong A$. To see this, let
$\mathfrak{b}\cong A$. To see this, let  $B={\rm Hom}_A(\mathfrak{b}, \mathfrak{b})=\mathfrak{b}:_T\mathfrak{b}$, which we can choose to be ω A. Consequently,
$B={\rm Hom}_A(\mathfrak{b}, \mathfrak{b})=\mathfrak{b}:_T\mathfrak{b}$, which we can choose to be ω A. Consequently,
 \begin{equation*}B:_TB=\omega_A:_T\omega_A=A.\end{equation*}
\begin{equation*}B:_TB=\omega_A:_T\omega_A=A.\end{equation*} But  $B\subset B:_TB=A\subset B$, that is, B = A, which shows that A is Gorenstein. Now, because
$B\subset B:_TB=A\subset B$, that is, B = A, which shows that A is Gorenstein. Now, because  ${\rm Hom}_A(\mathfrak{b}, \mathfrak{b})\cong A$, we can apply [Reference Vasconcelos33, Theorem 3.1] to conclude that
${\rm Hom}_A(\mathfrak{b}, \mathfrak{b})\cong A$, we can apply [Reference Vasconcelos33, Theorem 3.1] to conclude that  $\mathfrak{b}\cong A$, as claimed. In the same spirit, by replacing
$\mathfrak{b}\cong A$, as claimed. In the same spirit, by replacing  $\Omega_{A/k}$ with any torsion-free A-module M of rank 1, our theorem (as well as related results given in this note, such as Proposition 6, Proposition 8 and Corollary 9) admits an easy adaptation, which in fact yields
$\Omega_{A/k}$ with any torsion-free A-module M of rank 1, our theorem (as well as related results given in this note, such as Proposition 6, Proposition 8 and Corollary 9) admits an easy adaptation, which in fact yields  $M\cong A$ instead of A being regular.
$M\cong A$ instead of A being regular.
(b) A comment on the condition of  $A/a\mathfrak{h}_{A/k}$ being Gorenstein. It was proved in [Reference Huneke23] that if B is an unramified regular local ring and
$A/a\mathfrak{h}_{A/k}$ being Gorenstein. It was proved in [Reference Huneke23] that if B is an unramified regular local ring and ![]() $\mathfrak{b}$ is an ideal such that
$\mathfrak{b}$ is an ideal such that  $B/\mathfrak{b}$ is Gorenstein, then
$B/\mathfrak{b}$ is Gorenstein, then ![]() $\mathfrak{b}$ cannot be a product if
$\mathfrak{b}$ cannot be a product if  ${\rm height}\,\mathfrak{b}\geq 2$ (in particular,
${\rm height}\,\mathfrak{b}\geq 2$ (in particular,  ${\rm dim}\,B\geq 2$). Also note B is already assumed to be regular. So, there is no conflict with our setting here.
${\rm dim}\,B\geq 2$). Also note B is already assumed to be regular. So, there is no conflict with our setting here.
3.2. Other characterizations
Proposition 6 describes (co)homological characterizations of the regularity of  $(A, \mathfrak{m})$ in the presence of the torsion-freeness of
$(A, \mathfrak{m})$ in the presence of the torsion-freeness of  $\Omega_{A/k}$ – see also Proposition 8 and, in the next subsection, Corollary 9 and Corollary 14. Wherever they appear throughout the paper,
$\Omega_{A/k}$ – see also Proposition 8 and, in the next subsection, Corollary 9 and Corollary 14. Wherever they appear throughout the paper, ![]() $\mathfrak{E}$ and projdimA denote, respectively, the injective hull of
$\mathfrak{E}$ and projdimA denote, respectively, the injective hull of  $A/\mathfrak{m}$ and projective dimension over A.
$A/\mathfrak{m}$ and projective dimension over A.
Proposition 6. Assume the setting and hypotheses of Berger’s Conjecture. The following assertions are equivalent:
(i) A is regular.
(ii)
 ${\rm Tor}^A_i({\Omega}_{A/k}, A/\mathfrak{m}^{\nu})=0$ for some
${\rm Tor}^A_i({\Omega}_{A/k}, A/\mathfrak{m}^{\nu})=0$ for some  $i, \nu \geq 1$.
$i, \nu \geq 1$.(iii)
 ${\rm Ext}^i_A(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))=0$ for some
${\rm Ext}^i_A(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))=0$ for some  $i, \nu \geq 1$.
$i, \nu \geq 1$.(iv)
 ${\rm Ext}_A^i(\Omega_{A/k}, \mathfrak{m}^{\nu})=0$ for some
${\rm Ext}_A^i(\Omega_{A/k}, \mathfrak{m}^{\nu})=0$ for some  $i, \nu \geq 1$.
$i, \nu \geq 1$.(v)
 $\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ is torsion-free for some
$\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ is torsion-free for some  $\nu \geq 1$.
$\nu \geq 1$.(vi)
 $\mathfrak{m}^{\nu}\otimes_A{\rm Hom}_A(\mathfrak{m}^{\nu}, A)$ is torsion-free for some
$\mathfrak{m}^{\nu}\otimes_A{\rm Hom}_A(\mathfrak{m}^{\nu}, A)$ is torsion-free for some  $\nu \geq 1$.
$\nu \geq 1$.
Proof. If we assume that A is regular, then  $\Omega_{A/k}$ is a free A-module and hence (ii), (iii) and (iv) hold. In addition,
$\Omega_{A/k}$ is a free A-module and hence (ii), (iii) and (iv) hold. In addition, ![]() $\mathfrak{m}$ is a principal generated by a non-zero-divisor; hence,
$\mathfrak{m}$ is a principal generated by a non-zero-divisor; hence,  $\mathfrak{m}^{\nu}\cong A$ as A-modules for any
$\mathfrak{m}^{\nu}\cong A$ as A-modules for any  $\nu \geq 1$, so that (v) and (vi) hold as well.
$\nu \geq 1$, so that (v) and (vi) hold as well.
The equivalence between (ii) and (iii) follows by Ext-Tor duality (see [Reference Schenzel and Simon30, 1.4.1]), which gives for each  $i\geq 0$ an isomorphism
$i\geq 0$ an isomorphism
 \begin{equation*}\mathrm{Ext}^i_A(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})) \cong {\rm Hom}_A(\mathrm{Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu}),\mathfrak{E}),\end{equation*}
\begin{equation*}\mathrm{Ext}^i_A(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})) \cong {\rm Hom}_A(\mathrm{Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu}),\mathfrak{E}),\end{equation*}the latter being the Matlis dual of  ${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu})$.
${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu})$.
Now we show that (ii)![]() $\Rightarrow$(i). So, assume
$\Rightarrow$(i). So, assume  ${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu})=0$ for some
${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m}^{\nu})=0$ for some  $i, \nu \geq 1$, and consider first the case i = 1. Then there is a short exact sequence
$i, \nu \geq 1$, and consider first the case i = 1. Then there is a short exact sequence
 \begin{equation*}0\longrightarrow \mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}\longrightarrow \Omega_{A/k}\longrightarrow (A/\mathfrak{m}^{\nu})\otimes_A\Omega_{A/k}\longrightarrow 0,\end{equation*}
\begin{equation*}0\longrightarrow \mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}\longrightarrow \Omega_{A/k}\longrightarrow (A/\mathfrak{m}^{\nu})\otimes_A\Omega_{A/k}\longrightarrow 0,\end{equation*}which yields  $\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}\cong \mathfrak{m}^{\nu}\Omega_{A/k}$. This gives an embedding
$\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}\cong \mathfrak{m}^{\nu}\Omega_{A/k}$. This gives an embedding
 \begin{equation*}\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k} \subset \Omega_{A/k}.\end{equation*}
\begin{equation*}\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k} \subset \Omega_{A/k}.\end{equation*} On the other hand, we know that  $\Omega_{A/k}$ possesses a rank as an A-module (see Lemma 2(i)), and being by hypothesis torsion-free, it embeds into a free A-module of finite rank. It follows that
$\Omega_{A/k}$ possesses a rank as an A-module (see Lemma 2(i)), and being by hypothesis torsion-free, it embeds into a free A-module of finite rank. It follows that  $\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ is torsion-free. Thus, since A is a reduced local ring of positive depth, we are in a position to apply [Reference Celikbas and Takahashi8, Corollary 2.7] in order to conclude that
$\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ is torsion-free. Thus, since A is a reduced local ring of positive depth, we are in a position to apply [Reference Celikbas and Takahashi8, Corollary 2.7] in order to conclude that  $\Omega_{A/k}$ is free as an A-module, that is, A is regular.
$\Omega_{A/k}$ is free as an A-module, that is, A is regular.
Next, we consider the case  $i\geq 2$. Then (ii) gives
$i\geq 2$. Then (ii) gives
 \begin{equation*}{\rm Tor}^A_{i-1}(\Omega_{A/k}, \mathfrak{m}^{\nu}) = 0,\end{equation*}
\begin{equation*}{\rm Tor}^A_{i-1}(\Omega_{A/k}, \mathfrak{m}^{\nu}) = 0,\end{equation*} and this in turn implies, by [Reference Celikbas and Takahashi8, Corollary 1.3], that  ${\rm projdim}_A\Omega_{A/k} \lt \infty$. Since
${\rm projdim}_A\Omega_{A/k} \lt \infty$. Since  $\Omega_{A/k}$ is torsion-free and
$\Omega_{A/k}$ is torsion-free and  ${\rm dim}\,A=1$, we have
${\rm dim}\,A=1$, we have  ${\rm depth }\,\Omega_{A/k} = 1$ and then the well-known Auslander–Buchsbaum formula forces
${\rm depth }\,\Omega_{A/k} = 1$ and then the well-known Auslander–Buchsbaum formula forces  $\Omega_{A/k}$ to be free, as needed.
$\Omega_{A/k}$ to be free, as needed.
Now let us prove that (iv)![]() $\Rightarrow$(i). By [Reference Celikbas and Takahashi8, Corollary 1.3], the module
$\Rightarrow$(i). By [Reference Celikbas and Takahashi8, Corollary 1.3], the module  $\mathfrak{m}^{\nu}$ has for any
$\mathfrak{m}^{\nu}$ has for any  $\nu \geq 1$ the so-called strongly rigid property (i.e.,
$\nu \geq 1$ the so-called strongly rigid property (i.e.,  ${\rm projdim}_AN \lt \infty$ whenever N is a finite A-module satisfying
${\rm projdim}_AN \lt \infty$ whenever N is a finite A-module satisfying  ${\rm Tor}^A_{s}(N, \mathfrak{m}^{\nu})=0$ for some
${\rm Tor}^A_{s}(N, \mathfrak{m}^{\nu})=0$ for some  $s\geq 1$). Therefore, since
$s\geq 1$). Therefore, since  ${\rm depth}\,A=1$ and assuming (iv), we are in a position to apply [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Theorem 5.8(2)] (with r = 0) to get
${\rm depth}\,A=1$ and assuming (iv), we are in a position to apply [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Theorem 5.8(2)] (with r = 0) to get
 \begin{equation*}{\rm projdim}_A\Omega_{A/k} \leq i-1 \lt \infty.\end{equation*}
\begin{equation*}{\rm projdim}_A\Omega_{A/k} \leq i-1 \lt \infty.\end{equation*} By the Auslander–Buchsbaum formula once again, we obtain that  $\Omega_{A/k}$ is free.
$\Omega_{A/k}$ is free.
Finally, the implication (v)![]() $\Rightarrow$(i) (respectively, (vi)
$\Rightarrow$(i) (respectively, (vi)![]() $\Rightarrow$(i)) follows by [Reference Celikbas and Takahashi8, Corollary 2.7] (respectively, [Reference Celikbas and Takahashi8, Corollary 1.5]).
$\Rightarrow$(i)) follows by [Reference Celikbas and Takahashi8, Corollary 2.7] (respectively, [Reference Celikbas and Takahashi8, Corollary 1.5]).
We provide some remarks about Proposition 6.
Remark 7. (a) Regarding the assertion (ii) (also (iii)), it is clear that the case of interest is  $\nu \geq 2$, since for ν = 1, the condition
$\nu \geq 2$, since for ν = 1, the condition  ${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m})=0$ forces
${\rm Tor}^A_i(\Omega_{A/k}, A/\mathfrak{m})=0$ forces  ${\rm projdim}_A\Omega_{A/k} \lt \infty$ (and hence
${\rm projdim}_A\Omega_{A/k} \lt \infty$ (and hence  $\Omega_{A/k}$ must be free). Indeed, the
$\Omega_{A/k}$ must be free). Indeed, the  $A/\mathfrak{m}$-vector space dimension of
$A/\mathfrak{m}$-vector space dimension of  $\mathrm{Tor}_i^A(\Omega_{A/k}, A/\mathfrak{m})$ is equal to the ith Betti number of
$\mathrm{Tor}_i^A(\Omega_{A/k}, A/\mathfrak{m})$ is equal to the ith Betti number of  $\Omega_{A/k}$ (see [Reference Bruns and Herzog6, Proposition 1.3.1]).
$\Omega_{A/k}$ (see [Reference Bruns and Herzog6, Proposition 1.3.1]).
(b) The implications (v)![]() $\Rightarrow$(i) and (vi)
$\Rightarrow$(i) and (vi)![]() $\Rightarrow$(i) do not use the torsion-freeness of
$\Rightarrow$(i) do not use the torsion-freeness of  $\Omega_{A/k}$. So it seems natural to ask whether, for some
$\Omega_{A/k}$. So it seems natural to ask whether, for some  $\nu \geq 1$, at least one of the A-modules
$\nu \geq 1$, at least one of the A-modules  $\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ and
$\mathfrak{m}^{\nu}\otimes_A\Omega_{A/k}$ and  $\mathfrak{m}^{\nu}\otimes_A{\rm Hom}_A(\mathfrak{m}^{\nu}, A)$ must be torsion-free if so is
$\mathfrak{m}^{\nu}\otimes_A{\rm Hom}_A(\mathfrak{m}^{\nu}, A)$ must be torsion-free if so is  $\Omega_{A/k}$. According to Proposition 6, an affirmative answer would imply the validity of Berger’s Conjecture.
$\Omega_{A/k}$. According to Proposition 6, an affirmative answer would imply the validity of Berger’s Conjecture.
(c) It is also worth noticing that the A-module  ${\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})$ (which appears as an ingredient of (iii)) is finite in the complete case, that is, the situation where A is a quotient of
${\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})$ (which appears as an ingredient of (iii)) is finite in the complete case, that is, the situation where A is a quotient of  $k[[X_1, \ldots, X_n]]$. This follows from [Reference Bruns and Herzog6, Theorem 3.2.13(b)]. Such a Matlis dual module will also play a role in Proposition 8.
$k[[X_1, \ldots, X_n]]$. This follows from [Reference Bruns and Herzog6, Theorem 3.2.13(b)]. Such a Matlis dual module will also play a role in Proposition 8.
We close the subsection with further characterizations for the regularity of A, involving in particular the finiteness of the injective dimension over A – which we denote injdimA – of suitable modules (see also Corollary 9 in the next subsection). For item (v) below, we recall for completeness the notion of integral closure of ideals. Given an ideal ![]() $\mathfrak{a}$ of A, an element
$\mathfrak{a}$ of A, an element  $a\in A$ is said to be integral over
$a\in A$ is said to be integral over ![]() $\mathfrak{a}$ if there exists an equation
$\mathfrak{a}$ if there exists an equation  $a^n +b_1a^{n-1}+\cdots +b_n = 0$, with
$a^n +b_1a^{n-1}+\cdots +b_n = 0$, with  $ b_i\in \mathfrak{a}^i$,
$ b_i\in \mathfrak{a}^i$,  $i=1, \ldots, n$. The elements of A that are integral over
$i=1, \ldots, n$. The elements of A that are integral over ![]() $\mathfrak{a}$ form an ideal, denoted
$\mathfrak{a}$ form an ideal, denoted ![]() $\overline{\mathfrak{a}}$. Clearly,
$\overline{\mathfrak{a}}$. Clearly,  $\mathfrak{a}\subset \overline{\mathfrak{a}}$, and
$\mathfrak{a}\subset \overline{\mathfrak{a}}$, and ![]() $\mathfrak{a}$ is integrally closed if
$\mathfrak{a}$ is integrally closed if  $\mathfrak{a}=\overline{\mathfrak{a}}$. In part (vii), A ʹ stands for the integral closure of A in its total quotient ring.
$\mathfrak{a}=\overline{\mathfrak{a}}$. In part (vii), A ʹ stands for the integral closure of A in its total quotient ring.
Proposition 8. Assume the setting and hypotheses of Berger’s Conjecture. Let ω A denote the canonical module of A. The following assertions are equivalent:
(i) A is regular.
(ii)
 ${\rm injdim}_A{\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}) \lt \infty$ for some
${\rm injdim}_A{\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}) \lt \infty$ for some  $\nu \geq 1$.
$\nu \geq 1$.(iii)
 ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \mathfrak{m}^{\nu}\otimes_A\omega_A)=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \mathfrak{m}^{\nu}\otimes_A\omega_A)=0$ for some  $i\geq 2$ and
$i\geq 2$ and  $\nu \geq 1$.
$\nu \geq 1$.(iv)
 ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some  $i\geq 2$ and
$i\geq 2$ and  $\nu \geq 1$, and
$\nu \geq 1$, and  ${\rm Ext}^j_A(\mathfrak{m}^{\mu}, A)=0$ for all
${\rm Ext}^j_A(\mathfrak{m}^{\mu}, A)=0$ for all  $j\gg 0$ and some
$j\gg 0$ and some  $\mu \geq 1$.
$\mu \geq 1$.(v)
 ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some  $i\geq 2$ and
$i\geq 2$ and  $\nu \geq 1$, and
$\nu \geq 1$, and  ${\rm Ext}^j_A(\mathfrak{a}, A)=0$ for some
${\rm Ext}^j_A(\mathfrak{a}, A)=0$ for some  $j\geq 1$ and some integrally closed
$j\geq 1$ and some integrally closed  $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal  $\mathfrak{a}$ of A.
$\mathfrak{a}$ of A.(vi)
 ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some  $i\geq 2$ and
$i\geq 2$ and  $\nu \geq 1$, and
$\nu \geq 1$, and  ${\rm Ext}^1_A(\omega_A, A)=0$.
${\rm Ext}^1_A(\omega_A, A)=0$.(vii)
 ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some  $i\geq 2$ and
$i\geq 2$ and  $\nu \geq 1$, and
$\nu \geq 1$, and  ${\rm Ext}^1_A(A^\prime, A)=0$.
${\rm Ext}^1_A(A^\prime, A)=0$.
Proof. If (i) takes place, then all A-modules have finite injective dimension and the A-modules  $\mathfrak{m}^{\nu}$ and ω A are free, so that all items hold. Notice that the second part of (v) holds by taking
$\mathfrak{m}^{\nu}$ and ω A are free, so that all items hold. Notice that the second part of (v) holds by taking  $\mathfrak{a}=\mathfrak{m}\cong A$, and the second part of (vii) follows because a regular ring is normal, that is,
$\mathfrak{a}=\mathfrak{m}\cong A$, and the second part of (vii) follows because a regular ring is normal, that is,  $A^\prime=A$.
$A^\prime=A$.
Now suppose (ii) and set  $\rho:={\rm injdim}_A{\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})$. It follows that the module
$\rho:={\rm injdim}_A{\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E})$. It follows that the module  ${\rm Ext}_A^{\rho + 1}(M, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))$ vanishes for every A-module M. In particular,
${\rm Ext}_A^{\rho + 1}(M, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))$ vanishes for every A-module M. In particular,
 \begin{equation*}{\rm Ext}_A^{\rho + 1}(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))= 0\end{equation*}
\begin{equation*}{\rm Ext}_A^{\rho + 1}(\Omega_{A/k}, {\rm Hom}_A(A/\mathfrak{m}^{\nu}, \mathfrak{E}))= 0\end{equation*}and thus A must be regular by Proposition 6.
Let us show that (iii)![]() $\Rightarrow$(i). As we have recalled in the proof of Proposition 6, the module
$\Rightarrow$(i). As we have recalled in the proof of Proposition 6, the module  $\mathfrak{m}^{\nu}$ is strongly rigid for any
$\mathfrak{m}^{\nu}$ is strongly rigid for any  $\nu \geq 1$. By (iii) and [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Proposition 3.6], we get
$\nu \geq 1$. By (iii) and [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Proposition 3.6], we get
 \begin{equation*}{\rm injdim}_A\mathfrak{m}^{\nu}\otimes_A\omega_A \lt \infty,\end{equation*}
\begin{equation*}{\rm injdim}_A\mathfrak{m}^{\nu}\otimes_A\omega_A \lt \infty,\end{equation*}and then the regularity of A follows by applying [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Corollary 6.11] (with  $C=\omega_A$).
$C=\omega_A$).
Next, we verify that (iv)![]() $\Rightarrow$(i). Because
$\Rightarrow$(i). Because  ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, \Omega_{A/k})=0$ for some  $i\geq 2={\rm dim}\,A+1$, and since
$i\geq 2={\rm dim}\,A+1$, and since  $\mathfrak{m}^{\nu}$ is strongly rigid, we have
$\mathfrak{m}^{\nu}$ is strongly rigid, we have  ${\rm injdim}_A\Omega_{A/k} \lt \infty$ by [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Proposition 3.6]. Now, since A is not Artinian, the asymptotic vanishing of
${\rm injdim}_A\Omega_{A/k} \lt \infty$ by [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Proposition 3.6]. Now, since A is not Artinian, the asymptotic vanishing of  ${\rm Ext}^j_A(\mathfrak{m}^{\mu}, A)$ is equivalent to A being Gorenstein, according to [Reference Celikbas and Takahashi8, Proposition 1.6]. By a well-known fact (see [Reference Bruns and Herzog6, Exercise 3.1.25]), we get
${\rm Ext}^j_A(\mathfrak{m}^{\mu}, A)$ is equivalent to A being Gorenstein, according to [Reference Celikbas and Takahashi8, Proposition 1.6]. By a well-known fact (see [Reference Bruns and Herzog6, Exercise 3.1.25]), we get  ${\rm projdim}_A\Omega_{A/k} \lt \infty$, which in the present setting, as we have seen, implies (i).
${\rm projdim}_A\Omega_{A/k} \lt \infty$, which in the present setting, as we have seen, implies (i).
In order to prove (v)![]() $\Rightarrow$(i), note we must have, as above,
$\Rightarrow$(i), note we must have, as above,  ${\rm injdim}_A\Omega_{A/k} \lt \infty$. By virtue of [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Corollary 3.9], the vanishing of
${\rm injdim}_A\Omega_{A/k} \lt \infty$. By virtue of [Reference Zargar, Celikbas, Gheibi and Sadeghi34, Corollary 3.9], the vanishing of  ${\rm Ext}^j_A(\mathfrak{a}, A)$ for some
${\rm Ext}^j_A(\mathfrak{a}, A)$ for some  $j\geq 1={\rm dim}\,A$ forces
$j\geq 1={\rm dim}\,A$ forces  ${\rm injdim}_AA \lt \infty$, that is, A is Gorenstein. It follows, as above, that A is regular.
${\rm injdim}_AA \lt \infty$, that is, A is Gorenstein. It follows, as above, that A is regular.
Finally, assume that (vi) or (vii) takes place. In either case, we once again have  ${\rm injdim}_A\Omega_{A/k} \lt \infty$. If (vi) holds, then since A is reduced (hence generically Gorenstein) and
${\rm injdim}_A\Omega_{A/k} \lt \infty$. If (vi) holds, then since A is reduced (hence generically Gorenstein) and  ${\rm dim}\,A=1$, the condition
${\rm dim}\,A=1$, the condition  ${\rm Ext}^1_A(\omega_A, A)=0$ is equivalent to A being Gorenstein (see [Reference Hanes and Huneke16, Corollary 2.2]). Now if (vii) holds, then as A is a reduced excellent local ring (hence analytically unramified) and
${\rm Ext}^1_A(\omega_A, A)=0$ is equivalent to A being Gorenstein (see [Reference Hanes and Huneke16, Corollary 2.2]). Now if (vii) holds, then as A is a reduced excellent local ring (hence analytically unramified) and  ${\rm dim}\,A=1$, the vanishing of
${\rm dim}\,A=1$, the vanishing of  ${\rm Ext}^1_A(A^\prime, A)$ is equivalent to A having the Gorenstein property, by [Reference Ulrich32, Corollary 2.3]. Thus, (i) follows.
${\rm Ext}^1_A(A^\prime, A)$ is equivalent to A having the Gorenstein property, by [Reference Ulrich32, Corollary 2.3]. Thus, (i) follows.
3.3. On the Gorenstein case and more characterizations
In order to tackle Berger’s Conjecture in the case where A is Gorenstein, one option is to show that the torsion-freeness of  $\Omega_{A/k}$ yields an A-module isomorphism
$\Omega_{A/k}$ yields an A-module isomorphism  ${\rm H}_{A/k} \cong A$. This follows from a more general fact: if S is a one-dimensional Gorenstein local ring and M is a finite S-module such that
${\rm H}_{A/k} \cong A$. This follows from a more general fact: if S is a one-dimensional Gorenstein local ring and M is a finite S-module such that  ${\rm Hom}_S(M, M)$ is free, then M is free (see [Reference Vasconcelos33, Theorem 3.1]). A different proof, in the context of Berger’s Conjecture, is contained in the following byproduct of Theorem 4.
${\rm Hom}_S(M, M)$ is free, then M is free (see [Reference Vasconcelos33, Theorem 3.1]). A different proof, in the context of Berger’s Conjecture, is contained in the following byproduct of Theorem 4.
Corollary 9. Assume the setting and hypotheses of Berger’s Conjecture. The following assertions are equivalent:
(i) A is regular.
(ii) A is Gorenstein and
 ${\rm H}_{A/k}$ is free.
${\rm H}_{A/k}$ is free.(iii)
 ${\rm injdim}_A{\rm H}_{A/k} \lt \infty$.
${\rm injdim}_A{\rm H}_{A/k} \lt \infty$.
Proof. The implications (i)![]() $\Rightarrow$(ii) and (i)
$\Rightarrow$(ii) and (i)![]() $\Rightarrow$(iii) are clear. Now set
$\Rightarrow$(iii) are clear. Now set  ${\rm H}:={\rm H}_{A/k}$ and note this A-module has rank 1, which follows by Lemma 2. Assume first that A is Gorenstein and
${\rm H}:={\rm H}_{A/k}$ and note this A-module has rank 1, which follows by Lemma 2. Assume first that A is Gorenstein and  ${\rm H}$ is free. In particular, because of the identification
${\rm H}$ is free. In particular, because of the identification  ${\rm H}=\mathfrak{h}$ as an ideal (see Notation 3), we have
${\rm H}=\mathfrak{h}$ as an ideal (see Notation 3), we have  $\mathfrak{h}=(b)$ for some parameter
$\mathfrak{h}=(b)$ for some parameter  $b\in \mathfrak{m}$. Now, for any parameter
$b\in \mathfrak{m}$. Now, for any parameter ![]() $a\in \mathfrak{m}$, the local ring
$a\in \mathfrak{m}$, the local ring  $A/a\mathfrak{h}=A/(ab)$ is Gorenstein since so is A. By Theorem 4, A must be regular.
$A/a\mathfrak{h}=A/(ab)$ is Gorenstein since so is A. By Theorem 4, A must be regular.
Finally, suppose (iii) holds, and recall that  ${\rm H}$ is torsion-free because so is
${\rm H}$ is torsion-free because so is  $\Omega_{A/k}$ by assumption. Hence, in the present setting, we must have
$\Omega_{A/k}$ by assumption. Hence, in the present setting, we must have  ${\rm depth}\,{\rm H} = 1 = {\rm depth}\,A$. Thus, by [Reference Ghosh and Takahashi14, Proposition 3.2], the condition
${\rm depth}\,{\rm H} = 1 = {\rm depth}\,A$. Thus, by [Reference Ghosh and Takahashi14, Proposition 3.2], the condition  ${\rm injdim}_A{\rm H} \lt \infty$ forces A to be Gorenstein. Using [Reference Bruns and Herzog6, Exercise 3.1.25], we get
${\rm injdim}_A{\rm H} \lt \infty$ forces A to be Gorenstein. Using [Reference Bruns and Herzog6, Exercise 3.1.25], we get  ${\rm projdim}_A{\rm H} \lt \infty$ and hence
${\rm projdim}_A{\rm H} \lt \infty$ and hence  ${\rm H}$ is necessarily free. It follows that (ii) holds, and so (i) holds by the preceding part.
${\rm H}$ is necessarily free. It follows that (ii) holds, and so (i) holds by the preceding part.
Remark 10. Recall that, for an A-module N, a k-derivation of A with values in N is a k-linear map  $\delta \colon A\rightarrow N$ satisfying
$\delta \colon A\rightarrow N$ satisfying  $\delta(ab)=a\delta(b)+b\delta(a)$ for all
$\delta(ab)=a\delta(b)+b\delta(a)$ for all  $a, b\in A$. Such derivations are collected in an A-module denoted
$a, b\in A$. Such derivations are collected in an A-module denoted  ${\rm Der}_k(A, N)$. Now we recall that
${\rm Der}_k(A, N)$. Now we recall that  $\Omega_{A/k}$ comes equipped with a universal derivation
$\Omega_{A/k}$ comes equipped with a universal derivation  ${\delta}_{A/k}\colon A\rightarrow \Omega_{A/k}$, that is, a k-derivation with the property that the A-linear map
${\delta}_{A/k}\colon A\rightarrow \Omega_{A/k}$, that is, a k-derivation with the property that the A-linear map  ${\rm Hom}_A(\Omega_{A/k}, N)\rightarrow {\rm Der}_k(A, N)$ given by composition with
${\rm Hom}_A(\Omega_{A/k}, N)\rightarrow {\rm Der}_k(A, N)$ given by composition with  ${\delta}_{A/k}$ is an isomorphism. In particular, taking
${\delta}_{A/k}$ is an isomorphism. In particular, taking  $N=\Omega_{A/k}$,
$N=\Omega_{A/k}$,
 \begin{equation*}{\rm H}_{A/k} \cong {\rm Der}_k(A, \Omega_{A/k}).\end{equation*}
\begin{equation*}{\rm H}_{A/k} \cong {\rm Der}_k(A, \Omega_{A/k}).\end{equation*}It follows that the assertions of Corollary 9 are also equivalent to the following one:
(iv) A is Gorenstein and
 ${\rm Der}_k(A, \Omega_{A/k})= A {\delta}_{A/k}$.
${\rm Der}_k(A, \Omega_{A/k})= A {\delta}_{A/k}$.
The proof of Corollary 14 – where A is not required to be Gorenstein a priori – will crucially rely on Corollary 9 together with suitable Gorensteiness criteria from the literature. First, we provide a lemma which characterizes (e.g., by means of the length of a certain Artinian module) the vanishing
 \begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, A) = 0\end{equation*}
\begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, A) = 0\end{equation*}in the context of Berger’s Conjecture; see also Remark 13. The characterizations will automatically provide some of the equivalences to be presented in Corollary 14.
Before stating the lemma, we introduce for convenience a piece of notation.
Notation 11.
For a non-zero-divisor ![]() $a\in \mathfrak{m}$, we consider the relative derivation module
$a\in \mathfrak{m}$, we consider the relative derivation module  ${\rm Der}_k(A, A/(a))$, which has finite length since
${\rm Der}_k(A, A/(a))$, which has finite length since  $A/(a)$ is Artinian. We put
$A/(a)$ is Artinian. We put
 \begin{equation*}\mathfrak{d}(A, a) := {\rm length}\,{\rm Der}_k(A, A/(a)).\end{equation*}
\begin{equation*}\mathfrak{d}(A, a) := {\rm length}\,{\rm Der}_k(A, A/(a)).\end{equation*} Notice for completeness that, since  ${\rm dim}\,A=1$, the Hilbert–Samuel multiplicity
${\rm dim}\,A=1$, the Hilbert–Samuel multiplicity  $\mathfrak{e}(A)$ of A is simply the leading coefficient of the Hilbert–Samuel polynomial of A. Also we recall that the property of a parameter
$\mathfrak{e}(A)$ of A is simply the leading coefficient of the Hilbert–Samuel polynomial of A. Also we recall that the property of a parameter  $a\in \mathfrak{m}\setminus \mathfrak{m}^2$ being superficial in the one-dimensional local ring A – note such an element does exist as A has infinite residue field – forces (and is in fact equivalent to) the principal ideal (a) being a minimal reduction of
$a\in \mathfrak{m}\setminus \mathfrak{m}^2$ being superficial in the one-dimensional local ring A – note such an element does exist as A has infinite residue field – forces (and is in fact equivalent to) the principal ideal (a) being a minimal reduction of ![]() $\mathfrak{m}$. For more information, see [Reference Herzog and Waldi20, Remark 1.5], also [Reference Huneke and Swanson24, 8.6].
$\mathfrak{m}$. For more information, see [Reference Herzog and Waldi20, Remark 1.5], also [Reference Huneke and Swanson24, 8.6].
Lemma 12. Assume the setting and hypotheses of Berger’s Conjecture. The following assertions are equivalent:
(i)
 ${\rm Ext}^1_A(\Omega_{A/k}, A)=0$.
${\rm Ext}^1_A(\Omega_{A/k}, A)=0$.(ii)
 $\Omega_{A/k}\otimes_A\omega_A$ is torsion-free.
$\Omega_{A/k}\otimes_A\omega_A$ is torsion-free.(iii)
 $\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for some
$\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for some  $($any
$($any $)$ superficial element a.
$)$ superficial element a.
Proof. Under the present hypotheses,  $\Omega_{A/k}$ is a maximal Cohen–Macaulay A-module possessing a rank, and the one-dimensional local ring A, being reduced, is Gorenstein locally at the prime ideals of height zero (hence, Gorenstein locally on its punctured spectrum). Now, the equivalence (i)
$\Omega_{A/k}$ is a maximal Cohen–Macaulay A-module possessing a rank, and the one-dimensional local ring A, being reduced, is Gorenstein locally at the prime ideals of height zero (hence, Gorenstein locally on its punctured spectrum). Now, the equivalence (i)![]() $\Leftrightarrow$(ii) follows directly by [Reference Hanes and Huneke16, Lemma 2.1].
$\Leftrightarrow$(ii) follows directly by [Reference Hanes and Huneke16, Lemma 2.1].
In order to prove that (i) and (iii) are equivalent, we apply once again [Reference Hanes and Huneke16, Lemma 2.1], which gives that (i) holds if and only if there is a length equality
 \begin{equation*}{\rm length}\,{\rm Hom}_{A/(a)}(\Omega_{A/k}/a\Omega_{A/k}, A/(a)) = {\rm length}\,\Omega_{A/k}/a\Omega_{A/k},\end{equation*}
\begin{equation*}{\rm length}\,{\rm Hom}_{A/(a)}(\Omega_{A/k}/a\Omega_{A/k}, A/(a)) = {\rm length}\,\Omega_{A/k}/a\Omega_{A/k},\end{equation*}where a is any given parameter of A. Now, by standard homological algebra, there are  $A/(a)$-module isomorphisms
$A/(a)$-module isomorphisms
 \begin{equation*}{\rm Hom}_{A/(a)}(\Omega_{A/k}/a\Omega_{A/k}, A/(a)) \cong {\rm Hom}_{A}(\Omega_{A/k}, {\rm Hom}_{A/(a)}(A/(a), A/(a))),\end{equation*}
\begin{equation*}{\rm Hom}_{A/(a)}(\Omega_{A/k}/a\Omega_{A/k}, A/(a)) \cong {\rm Hom}_{A}(\Omega_{A/k}, {\rm Hom}_{A/(a)}(A/(a), A/(a))),\end{equation*} \begin{equation*}\cong {\rm Hom}_{A}(\Omega_{A/k}, A/(a)) \cong {\rm Der}_k(A, A/(a)),\end{equation*}
\begin{equation*}\cong {\rm Hom}_{A}(\Omega_{A/k}, A/(a)) \cong {\rm Der}_k(A, A/(a)),\end{equation*} $N=A/(a)$. Thus, we have shown that (i) holds if and only if
$N=A/(a)$. Thus, we have shown that (i) holds if and only if  $\mathfrak{d}(A, a)={\rm length}\,\Omega_{A/k}/a\Omega_{A/k}$. On the other hand, because
$\mathfrak{d}(A, a)={\rm length}\,\Omega_{A/k}/a\Omega_{A/k}$. On the other hand, because  $\Omega_{A/k}$ is Cohen–Macaulay and, by Lemma 2(i), has a well-defined rank equal to 1, we can write (see [Reference Herzog17])
$\Omega_{A/k}$ is Cohen–Macaulay and, by Lemma 2(i), has a well-defined rank equal to 1, we can write (see [Reference Herzog17])
 \begin{equation*}{\rm length}\,\Omega_{A/k}/a\Omega_{A/k} = {\rm length}\,A/(a).\end{equation*}
\begin{equation*}{\rm length}\,\Omega_{A/k}/a\Omega_{A/k} = {\rm length}\,A/(a).\end{equation*} But  ${\rm length}\,A/(a)=\mathfrak{e}(A)$ whenever (a) is a minimal reduction of
${\rm length}\,A/(a)=\mathfrak{e}(A)$ whenever (a) is a minimal reduction of ![]() $\mathfrak{m}$ (see [Reference Huneke and Swanson24, Proposition 11.2.2]), that is, if a is superficial. It follows that (i) is equivalent to
$\mathfrak{m}$ (see [Reference Huneke and Swanson24, Proposition 11.2.2]), that is, if a is superficial. It follows that (i) is equivalent to  $\mathfrak{d}(A, a)=\mathfrak{e}(A)$.
$\mathfrak{d}(A, a)=\mathfrak{e}(A)$.
Remark 13. Consider the setting and hypotheses of Berger’s Conjecture, and in addition, suppose A is complete and k is algebraically closed. The local ring A is said to be rigid if it admits no infinitesimal deformations, which is known to be equivalent to the condition  ${\rm Ext}^1_A(\Omega_{A/k}, A)=0$ characterized in Lemma 12. The rigidity conjecture predicts that A is rigid if and only if A is regular. Now, by Lemma 12, the algebra A is rigid if and only if
${\rm Ext}^1_A(\Omega_{A/k}, A)=0$ characterized in Lemma 12. The rigidity conjecture predicts that A is rigid if and only if A is regular. Now, by Lemma 12, the algebra A is rigid if and only if  $\Omega_{A/k}\otimes_A\omega_A$ is torsion-free, which can alternatively be seen by means of an isomorphism
$\Omega_{A/k}\otimes_A\omega_A$ is torsion-free, which can alternatively be seen by means of an isomorphism
 \begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, A)\cong {\rm Hom}_A(\tau_A(\Omega_{A/k}\otimes_A\omega_A), \mathfrak{E}),\end{equation*}
\begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, A)\cong {\rm Hom}_A(\tau_A(\Omega_{A/k}\otimes_A\omega_A), \mathfrak{E}),\end{equation*}where the latter is the Matlis dual of the A-torsion of  $\Omega_{A/k}\otimes_A\omega_A$. It follows that, in the Gorenstein case, Berger’s Conjecture is equivalent to the rigidity conjecture. We refer to [Reference Herzog19, p. 11, first paragraph].
$\Omega_{A/k}\otimes_A\omega_A$. It follows that, in the Gorenstein case, Berger’s Conjecture is equivalent to the rigidity conjecture. We refer to [Reference Herzog19, p. 11, first paragraph].
Recall that the embedding dimension  ${\rm edim}\,A$ of a local ring
${\rm edim}\,A$ of a local ring  $(A, \mathfrak{m})$ is the minimal number of generators of
$(A, \mathfrak{m})$ is the minimal number of generators of ![]() $\mathfrak{m}$. The corollary is as follows.
$\mathfrak{m}$. The corollary is as follows.
Corollary 14. Assume the setting and hypotheses of Berger’s Conjecture. Let ω A denote the canonical module of A. The following assertions are equivalent:
(i) A is regular.
(ii)
 ${\rm H}_{A/k}$ is free,
${\rm H}_{A/k}$ is free,  $\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for a superficial element a and
$\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for a superficial element a and  $\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.
$\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.(iii)
 ${\rm H}_{A/k}$ is free,
${\rm H}_{A/k}$ is free,  $\Omega_{A/k}\otimes_A\omega_A$ is torsion-free and
$\Omega_{A/k}\otimes_A\omega_A$ is torsion-free and  $\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.
$\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.(iv)
 ${\rm H}_{A/k}$ is free,
${\rm H}_{A/k}$ is free,  ${\rm Ext}^1_A(\Omega_{A/k}, A)=0$ and
${\rm Ext}^1_A(\Omega_{A/k}, A)=0$ and  $\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.
$\mathfrak{e}(A)\leq 2\,{\rm edim}\,A -1$.(v)
 ${\rm H}_{A/k}$ is free, and
${\rm H}_{A/k}$ is free, and  ${\rm Ext}^i_A(\mathfrak{m}^{\nu}, A)=0$ for some
${\rm Ext}^i_A(\mathfrak{m}^{\nu}, A)=0$ for some  $\nu \geq 1$ and all
$\nu \geq 1$ and all  $i\gg 0$.
$i\gg 0$.(vi)
 ${\rm H}_{A/k}$ is free, and
${\rm H}_{A/k}$ is free, and  ${\rm Ext}^i_A(\mathfrak{a}, A)=0$ for some
${\rm Ext}^i_A(\mathfrak{a}, A)=0$ for some  $i\geq 1$ and some integrally closed
$i\geq 1$ and some integrally closed  $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal  $\mathfrak{a}$ of A.
$\mathfrak{a}$ of A.(vii)
 ${\rm H}_{A/k}$ is free, and
${\rm H}_{A/k}$ is free, and  ${\rm Ext}^1_A(\omega_A, A)=0$.
${\rm Ext}^1_A(\omega_A, A)=0$.(viii)
 ${\rm H}_{A/k}$ is free, and
${\rm H}_{A/k}$ is free, and  ${\rm Ext}^1_A(A', A)=0$.
${\rm Ext}^1_A(A', A)=0$.
Proof. First, suppose (i). Then  $\mathfrak{e}(A)=1$ and
$\mathfrak{e}(A)=1$ and  ${\rm edim}\,A={\rm dim}\,A=1$, so that
${\rm edim}\,A={\rm dim}\,A=1$, so that  $\mathfrak{e}(A)= 2\,{\rm edim}\,A -1$. Moreover,
$\mathfrak{e}(A)= 2\,{\rm edim}\,A -1$. Moreover,  $\Omega_{A/k}\cong A$; hence,
$\Omega_{A/k}\cong A$; hence,  ${\rm H}_{A/k}\cong A$ and, for any
${\rm H}_{A/k}\cong A$ and, for any ![]() $a\in \mathfrak{m}$, we have
$a\in \mathfrak{m}$, we have  ${\rm Der}_k(A, A/(a))\cong {\rm Hom}_A(\Omega_{A/k}, A/(a)) \cong A/(a)$, so that
${\rm Der}_k(A, A/(a))\cong {\rm Hom}_A(\Omega_{A/k}, A/(a)) \cong A/(a)$, so that  $\mathfrak{d}(A, a)={\rm length}\,A/(a)$, which by [Reference Huneke and Swanson24, Proposition 11.2.2] is equal to
$\mathfrak{d}(A, a)={\rm length}\,A/(a)$, which by [Reference Huneke and Swanson24, Proposition 11.2.2] is equal to  $\mathfrak{e}(A)$ if for instance
$\mathfrak{e}(A)$ if for instance  $a\in \mathfrak{m}\setminus \mathfrak{m}^2$ is any uniformizing parameter of A. In addition, the A-modules ω A and
$a\in \mathfrak{m}\setminus \mathfrak{m}^2$ is any uniformizing parameter of A. In addition, the A-modules ω A and  $\mathfrak{m}^{\nu}$ (for any
$\mathfrak{m}^{\nu}$ (for any  $\nu \geq 1$) are free as well, and in particular, we can take
$\nu \geq 1$) are free as well, and in particular, we can take  $\mathfrak{a}=\mathfrak{m}\cong A$ in (vi). Finally,
$\mathfrak{a}=\mathfrak{m}\cong A$ in (vi). Finally,  $A^\prime=A$ if A is regular. Therefore, all items follow.
$A^\prime=A$ if A is regular. Therefore, all items follow.
Lemma 12 immediately gives (ii)![]() $\Leftrightarrow$(iii)
$\Leftrightarrow$(iii)![]() $\Leftrightarrow$(iv).
$\Leftrightarrow$(iv).
Now we prove (iv)![]() $\Rightarrow$(i). Recall that
$\Rightarrow$(i). Recall that  $\Omega_{A/k}$ is a rank 1 A-module (see Lemma 2(i)), which is, in addition, minimally generated by
$\Omega_{A/k}$ is a rank 1 A-module (see Lemma 2(i)), which is, in addition, minimally generated by  ${\rm edim}\,A$ elements; for the latter fact in the algebraic (respectively, algebroid) case, see [Reference Kunz27, Corollary 6.5(b)] (respectively, [Reference Kunz27, Corollary 13.15]). Thus, condition
${\rm edim}\,A$ elements; for the latter fact in the algebraic (respectively, algebroid) case, see [Reference Kunz27, Corollary 6.5(b)] (respectively, [Reference Kunz27, Corollary 13.15]). Thus, condition  $2\, {\rm edim}\,A \gt \mathfrak{e}(A)$ along with the vanishing of
$2\, {\rm edim}\,A \gt \mathfrak{e}(A)$ along with the vanishing of  ${\rm Ext}^1_A(\Omega_{A/k}, A)$ put us in a position to apply [Reference Ulrich32, Theorem 3.1], which gives that A is Gorenstein. Now the regularity of A follows by Corollary 9.
${\rm Ext}^1_A(\Omega_{A/k}, A)$ put us in a position to apply [Reference Ulrich32, Theorem 3.1], which gives that A is Gorenstein. Now the regularity of A follows by Corollary 9.
Finally, in each of the assertions (v), (vi), (vii) and (viii), we observe that, apart from the condition of  ${\rm H}_{A/k}$ being free, the remaining hypotheses guarantee that A is Gorenstein, as explained in the proof of Proposition 8. Once again, we apply Corollary 9 to conclude that (i) holds.
${\rm H}_{A/k}$ being free, the remaining hypotheses guarantee that A is Gorenstein, as explained in the proof of Proposition 8. Once again, we apply Corollary 9 to conclude that (i) holds.
Remark 15. If in addition A is a domain, we can add some equivalent statements to the list of Corollary 14 without supposing the freeness of  ${\rm H}_{A/k}$. Indeed, from the proof above and [Reference Güttes15, Satz 6] (see also [Reference Berger5, Theorem 10]), we have for instance the following assertions:
${\rm H}_{A/k}$. Indeed, from the proof above and [Reference Güttes15, Satz 6] (see also [Reference Berger5, Theorem 10]), we have for instance the following assertions:
(ix)
 $\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for a superficial element a, and
$\mathfrak{d}(A, a)=\mathfrak{e}(A)$ for a superficial element a, and  $\mathfrak{e}(A)\leq {\rm min}\{13,\,2\,{\rm edim}\,A -1\}$.
$\mathfrak{e}(A)\leq {\rm min}\{13,\,2\,{\rm edim}\,A -1\}$.(x)
 $\mathfrak{e}(A)\leq 13$ and
$\mathfrak{e}(A)\leq 13$ and  ${\rm Ext}^i_A(\mathfrak{a}, A)=0$ for some
${\rm Ext}^i_A(\mathfrak{a}, A)=0$ for some  $i\geq 1$ and some integrally closed
$i\geq 1$ and some integrally closed  $\mathfrak{m}$-primary ideal
$\mathfrak{m}$-primary ideal  $\mathfrak{a}$ of A.
$\mathfrak{a}$ of A.
A natural question is whether, in item (vi) of Proposition 6, the ideal  $\mathfrak{m}^{\nu}$ can be replaced with
$\mathfrak{m}^{\nu}$ can be replaced with  $\mathfrak{h}_{A/k}$. The answer is affirmative if we require suitable extra conditions. To see this, let
$\mathfrak{h}_{A/k}$. The answer is affirmative if we require suitable extra conditions. To see this, let  $(A, \mathfrak{m})$ be as above and assume in addition that it is a domain. Recall that, for a non-zero ideal
$(A, \mathfrak{m})$ be as above and assume in addition that it is a domain. Recall that, for a non-zero ideal ![]() $\mathfrak{a}$ of A, we can consider
$\mathfrak{a}$ of A, we can consider
 \begin{equation*}A^{\mathfrak{a}} := \bigcup_{s\geq 1}\mathfrak{a}^s\colon \mathfrak{a}^s\end{equation*}
\begin{equation*}A^{\mathfrak{a}} := \bigcup_{s\geq 1}\mathfrak{a}^s\colon \mathfrak{a}^s\end{equation*}as a subring of the integral closure of A in its fraction field (note that taking ![]() $\mathfrak{a}=\mathfrak{m}$, we get the quadratic transform
$\mathfrak{a}=\mathfrak{m}$, we get the quadratic transform  $A^{\mathfrak{m}}$ of A). The ideal
$A^{\mathfrak{m}}$ of A). The ideal ![]() $\mathfrak{a}$ is said to be stable if
$\mathfrak{a}$ is said to be stable if  $A^{\mathfrak{a}}=\mathfrak{a}\colon \mathfrak{a}$.
$A^{\mathfrak{a}}=\mathfrak{a}\colon \mathfrak{a}$.
Corollary 16. Assume the setting and hypotheses of Berger’s Conjecture, and in addition that A is a domain. Suppose the following conditions hold:
(i)
 ${\rm Ext}^1_A(\mathfrak{F}, A)=0$ for some non-zero fractional ideal
${\rm Ext}^1_A(\mathfrak{F}, A)=0$ for some non-zero fractional ideal  $\mathfrak{F}$ in
$\mathfrak{F}$ in  $A^{\mathfrak{m}}$.
$A^{\mathfrak{m}}$.(ii)
 $\mathfrak{h}_{A/k}$ is stable.
$\mathfrak{h}_{A/k}$ is stable.(iii)
 $\mathfrak{h}_{A/k}\otimes_A{\rm Hom}_A(\mathfrak{h}_{A/k}, A)$ is torsion-free.
$\mathfrak{h}_{A/k}\otimes_A{\rm Hom}_A(\mathfrak{h}_{A/k}, A)$ is torsion-free.
Then, A is regular.
Proof. By [Reference Ulrich32, Corollary 3.2], condition (i) is equivalent to A being Gorenstein. Now, under the hypotheses (ii) and (iii), the ideal ![]() $\mathfrak{h}$ must be principal by [Reference Constapel9, Proposition 3.1]. This means precisely that
$\mathfrak{h}$ must be principal by [Reference Constapel9, Proposition 3.1]. This means precisely that  ${\rm H}_{A/k}$ is free as an A-module. Thus, Corollary 9 applies.
${\rm H}_{A/k}$ is free as an A-module. Thus, Corollary 9 applies.
Remark 17. The above corollaries deal – directly or indirectly – with the module  ${\rm H}_{A/k}={\rm Ext}^0_A(\Omega_{A/k}, \Omega_{A/k})$. Thus, it is natural to ask whether
${\rm H}_{A/k}={\rm Ext}^0_A(\Omega_{A/k}, \Omega_{A/k})$. Thus, it is natural to ask whether  ${\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})$ also plays a role in the problem. First, it has been predicted in [Reference Huneke, Iyengar and Wiegand25, Conjecture 1.2] that if S is a one-dimensional Gorenstein local domain and M is a torsion-free finite S-module such that
${\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})$ also plays a role in the problem. First, it has been predicted in [Reference Huneke, Iyengar and Wiegand25, Conjecture 1.2] that if S is a one-dimensional Gorenstein local domain and M is a torsion-free finite S-module such that  ${\rm Ext}^1_S(M, M)=0$, then M must be a free S-module. Now, assuming the validity of this conjecture, then in order to settle Berger’s Conjecture in case A is a Gorenstein domain, it suffices to prove that the torsion-freeness of
${\rm Ext}^1_S(M, M)=0$, then M must be a free S-module. Now, assuming the validity of this conjecture, then in order to settle Berger’s Conjecture in case A is a Gorenstein domain, it suffices to prove that the torsion-freeness of  $\Omega_{A/k}$ forces
$\Omega_{A/k}$ forces
 \begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k}) = 0.\end{equation*}
\begin{equation*}{\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k}) = 0.\end{equation*} This vanishing condition is, in turn, equivalent to the surjectivity of a certain map involving the torsion-free module  $\Omega_{A/k}$ and the conormal module of the ideal
$\Omega_{A/k}$ and the conormal module of the ideal  $\mathfrak{A}$ defining A as a quotient of either
$\mathfrak{A}$ defining A as a quotient of either  $k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or
$k[X_1, \ldots, X_n]_{(X_1, \ldots, X_n)}$ or  $k[[X_1, \ldots, X_n]]$. More precisely, as recalled in the proof of Lemma 2(i), we have first a short exact sequence
$k[[X_1, \ldots, X_n]]$. More precisely, as recalled in the proof of Lemma 2(i), we have first a short exact sequence
 \begin{equation*}0\longrightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0,\end{equation*}
\begin{equation*}0\longrightarrow \mathfrak{A}/\mathfrak{A}^{(2)}\longrightarrow A^n\longrightarrow \Omega_{A/k}\longrightarrow 0,\end{equation*}to which we can apply the functor  ${\rm Hom}_A(-, \Omega_{A/k})$. Identifying
${\rm Hom}_A(-, \Omega_{A/k})$. Identifying  ${\rm Hom}_A(A^n, \Omega_{A/k})\cong \Omega_{A/k}^{\oplus n}$ and noticing that
${\rm Hom}_A(A^n, \Omega_{A/k})\cong \Omega_{A/k}^{\oplus n}$ and noticing that  $ {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{(2)}, \Omega_{A/k}) \cong {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{2}, \Omega_{A/k})$ (since
$ {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{(2)}, \Omega_{A/k}) \cong {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{2}, \Omega_{A/k})$ (since  $\Omega_{A/k}$ is torsion-free and
$\Omega_{A/k}$ is torsion-free and  $\mathfrak{A}^{(2)}/\mathfrak{A}^{2}$ is the torsion of
$\mathfrak{A}^{(2)}/\mathfrak{A}^{2}$ is the torsion of  $\mathfrak{A}/\mathfrak{A}^{2}$), we get an exact sequence
$\mathfrak{A}/\mathfrak{A}^{2}$), we get an exact sequence
 \begin{equation*}\Omega_{A/k}^{\oplus n}\stackrel{\Phi}{\longrightarrow} {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{2}, \Omega_{A/k})\longrightarrow {\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})\longrightarrow 0.\end{equation*}
\begin{equation*}\Omega_{A/k}^{\oplus n}\stackrel{\Phi}{\longrightarrow} {\rm Hom}_A(\mathfrak{A}/\mathfrak{A}^{2}, \Omega_{A/k})\longrightarrow {\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})\longrightarrow 0.\end{equation*} It follows that the module  ${\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})$ vanishes if and only if Φ is an epimorphism. Also notice that
${\rm Ext}^1_A(\Omega_{A/k}, \Omega_{A/k})$ vanishes if and only if Φ is an epimorphism. Also notice that  ${\rm kernel}\,\Phi \cong {\rm H}_{A/k}$.
${\rm kernel}\,\Phi \cong {\rm H}_{A/k}$.
3.4. A connection to Rees algebras
We close the paper by pointing out a quite surprising link to the theory of blowup rings. First, as a preparation for Corollary 19 below, recall that the Rees algebra of an ideal ![]() $\mathfrak{a}$ in a ring A is the graded algebra
$\mathfrak{a}$ in a ring A is the graded algebra
 \begin{equation*}{\mathfrak R}_A(\mathfrak{a}) = \bigoplus_{i\geq 0}\mathfrak{a}^it^i \subset A[t],\end{equation*}
\begin{equation*}{\mathfrak R}_A(\mathfrak{a}) = \bigoplus_{i\geq 0}\mathfrak{a}^it^i \subset A[t],\end{equation*}where t is an indeterminate over A. In terms of generators, if  $\mathfrak{a}=(a_1, \ldots, a_r)$ then
$\mathfrak{a}=(a_1, \ldots, a_r)$ then  ${\mathfrak R}_A(\mathfrak{a})=A[a_1t, \ldots, a_rt]$.
${\mathfrak R}_A(\mathfrak{a})=A[a_1t, \ldots, a_rt]$.
Notation 18.
Given  $a, b\in A$, we consider the monic polynomial
$a, b\in A$, we consider the monic polynomial  $t^2+at+b\in A[t]$. Now, following [Reference Barucci, D’Anna and Strazzanti1], we set
$t^2+at+b\in A[t]$. Now, following [Reference Barucci, D’Anna and Strazzanti1], we set
 \begin{equation*}{\rm R}(\mathfrak{a})_{a, b} := {\mathfrak R}_A(\mathfrak{a})/(t^2+at+b)A[t] \cap {\mathfrak R}_A(\mathfrak{a}).\end{equation*}
\begin{equation*}{\rm R}(\mathfrak{a})_{a, b} := {\mathfrak R}_A(\mathfrak{a})/(t^2+at+b)A[t] \cap {\mathfrak R}_A(\mathfrak{a}).\end{equation*} It follows from [Reference Barucci, D’Anna and Strazzanti1, p. 138] that if A is a one-dimensional reduced local ring and the ideal ![]() $\mathfrak{a}$ contains a non-zero-divisor, then
$\mathfrak{a}$ contains a non-zero-divisor, then  ${\rm R}(\mathfrak{a})_{a, b}$ is Cohen–Macaulay. The next result reveals that the Gorensteiness of this algebra plays a role in regard to Berger’s Conjecture.
${\rm R}(\mathfrak{a})_{a, b}$ is Cohen–Macaulay. The next result reveals that the Gorensteiness of this algebra plays a role in regard to Berger’s Conjecture.
Corollary 19. Assume the setting and hypotheses of Berger’s Conjecture. The following assertions are equivalent:
(i) A is regular.
(ii)
 ${\rm R}(\mathfrak{h}_{A/k})_{a, b}$ is Gorenstein for all
${\rm R}(\mathfrak{h}_{A/k})_{a, b}$ is Gorenstein for all  $a, b\in A$.
$a, b\in A$.(iii)
 ${\rm R}(\mathfrak{h}_{A/k})_{a, b}$ is Gorenstein for some
${\rm R}(\mathfrak{h}_{A/k})_{a, b}$ is Gorenstein for some  $a, b\in A$.
$a, b\in A$.
Proof. If A is regular, then  $\Omega_{A/k}$ is free and consequently
$\Omega_{A/k}$ is free and consequently  $\mathfrak{h}\cong A$ as A-modules. In this case, the ring
$\mathfrak{h}\cong A$ as A-modules. In this case, the ring  ${\mathfrak R}_A(\mathfrak{h})$ can be identified with the regular domain
${\mathfrak R}_A(\mathfrak{h})$ can be identified with the regular domain  $A[t]$. Thus, for any pair
$A[t]$. Thus, for any pair  $a, b\in A$, we have
$a, b\in A$, we have  ${\rm R}(\mathfrak{h})_{a, b}= A[t]/(t^2 + at + b)$, which clearly is Gorenstein. This shows (i)
${\rm R}(\mathfrak{h})_{a, b}= A[t]/(t^2 + at + b)$, which clearly is Gorenstein. This shows (i)![]() $\Rightarrow$(ii)
$\Rightarrow$(ii)![]() $\Rightarrow$(iii).
$\Rightarrow$(iii).
Finally, by [Reference Barucci, D’Anna and Strazzanti1, Corollary 3.3], the ring  ${\rm R}(\mathfrak{h})_{a, b}$ is Gorenstein for some
${\rm R}(\mathfrak{h})_{a, b}$ is Gorenstein for some  $a, b\in A$ if and only if
$a, b\in A$ if and only if ![]() $\mathfrak{h}$ is isomorphic to a canonical module of A. In this case, the proof of Theorem 4 applies and we thus conclude that A is regular if (iii) holds.
$\mathfrak{h}$ is isomorphic to a canonical module of A. In this case, the proof of Theorem 4 applies and we thus conclude that A is regular if (iii) holds.
Acknowledgements
The author thanks J. Elias and S. Zarzuela for some conversations on an earlier version of the manuscript. He is especially grateful to the anonymous referee for helpful comments and for suggesting several additions (e.g., Remark 5(a) and some interesting references on Berger’s Conjecture), which improved the quality of the paper.
Funding Statement
The author was partially supported by the CNPq-Brazil grants 301029/2019-9 and 406377/2021-9.
Competing interests
The author declares no competing interests.