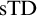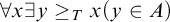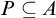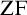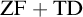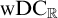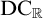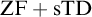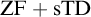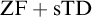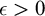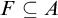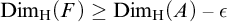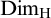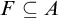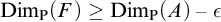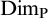1 Introduction
1.1 Turing Determinacy and strong Turing Determinacy
Turing reduction
![]() $\leq _T$
is a quasi-order over reals.
$\leq _T$
is a quasi-order over reals.
![]() $x\leq _T y$
, or x is Turing reducible to y, means x can be computed by a Turing machine with oracle y. The reduction naturally induces an equivalence relation
$x\leq _T y$
, or x is Turing reducible to y, means x can be computed by a Turing machine with oracle y. The reduction naturally induces an equivalence relation
![]() $\equiv _T$
. Given a real x, its corresponded Turing degree
$\equiv _T$
. Given a real x, its corresponded Turing degree
![]() ${\mathbf {x}}$
is a set of reals defined as
${\mathbf {x}}$
is a set of reals defined as
![]() $\{y\mid y\equiv _T x\}$
. We say
$\{y\mid y\equiv _T x\}$
. We say
![]() ${\mathbf {x}}\leq \mathbf {y}$
if
${\mathbf {x}}\leq \mathbf {y}$
if
![]() $x\leq _T y$
. We use
$x\leq _T y$
. We use
![]() $\mathcal {D}$
to denote the set of Turing degrees. An upper cone of Turing degrees is a set of form
$\mathcal {D}$
to denote the set of Turing degrees. An upper cone of Turing degrees is a set of form
![]() $\{\mathbf {y}\mid \mathbf {y}\geq \mathbf {x} \}$
for some
$\{\mathbf {y}\mid \mathbf {y}\geq \mathbf {x} \}$
for some
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
We say that a perfect set P is pointed if there is a perfect tree
![]() $T\subseteq 2^{<\omega }$
such that
$T\subseteq 2^{<\omega }$
such that
![]() $[T]=P$
and for any
$[T]=P$
and for any
![]() $x\in P$
,
$x\in P$
,
![]() $T\leq _T x$
, where
$T\leq _T x$
, where
![]() $[T]=\{x\in 2^{\omega }\mid \forall n (x{\upharpoonright} n \in T)\}$
.
$[T]=\{x\in 2^{\omega }\mid \forall n (x{\upharpoonright} n \in T)\}$
.
Definition 1.1.
-
• Turing Determinacy, or
 ${\mathrm {TD}}$
, is the statement that for every set A of Turing degrees, either A or
${\mathrm {TD}}$
, is the statement that for every set A of Turing degrees, either A or
 $\mathcal {D}\setminus A$
contains an upper cone of Turing degrees.
$\mathcal {D}\setminus A$
contains an upper cone of Turing degrees. -
• Strong Turing Determinacy, or
 ${\mathrm {sTD}}$
, is the statement that for every set A of reals, if
${\mathrm {sTD}}$
, is the statement that for every set A of reals, if
 $\forall x\exists y\geq _T x (y\in A)$
, then there is a pointed set P such that
$\forall x\exists y\geq _T x (y\in A)$
, then there is a pointed set P such that
 $P\subseteq A$
.
$P\subseteq A$
.
Clearly
![]() ${\mathrm {sTD}}$
implies
${\mathrm {sTD}}$
implies
![]() ${\mathrm {TD}}$
. Martin proves the following famous theorem, which partly justifies why Turing degrees are important to set theory.
${\mathrm {TD}}$
. Martin proves the following famous theorem, which partly justifies why Turing degrees are important to set theory.
Theorem 1.2 (Martin [Reference Martin16])
Over
![]() ${\mathrm {ZF}}$
, Axiom of Determinacy, or
${\mathrm {ZF}}$
, Axiom of Determinacy, or
![]() ${\mathrm {AD}}$
, implies
${\mathrm {AD}}$
, implies
![]() ${\mathrm {sTD}}$
and so
${\mathrm {sTD}}$
and so
![]() ${\mathrm {TD}}$
.
${\mathrm {TD}}$
.
Definition 1.3.
-
• Countable choice axiom for sets of reals, or
 ${\mathrm {CC}_{\mathbb {R}}}$
, is the statement that for every countable sequence
${\mathrm {CC}_{\mathbb {R}}}$
, is the statement that for every countable sequence
 $\{A_n\}_{n\in \omega }$
of nonempty sets of reals, there is a function
$\{A_n\}_{n\in \omega }$
of nonempty sets of reals, there is a function
 $f:\omega \to \mathbb {R}$
such that for every n,
$f:\omega \to \mathbb {R}$
such that for every n,
 $f(n)\in A_n$
.
$f(n)\in A_n$
. -
• Dependent choice axiom for sets of reals, or
 ${\mathrm {DC}_{\mathbb {R}}}$
, is the statement that for every binary relation R over reals such that
${\mathrm {DC}_{\mathbb {R}}}$
, is the statement that for every binary relation R over reals such that
 $\forall x \exists y R(x,y)$
, there is a function
$\forall x \exists y R(x,y)$
, there is a function
 $f:\omega \to \mathbb {R}$
such that for every n,
$f:\omega \to \mathbb {R}$
such that for every n,
 $R(f(n), f(n+1))$
.
$R(f(n), f(n+1))$
.
Turing Determinacy is an important and very useful consequence of
![]() ${\mathrm {AD}}$
. In many situations,
${\mathrm {AD}}$
. In many situations,
![]() ${\mathrm {TD}}$
seems sufficient to be used to prove set theory theorems. The following theorem partly justifies this phenomenon. Actually Woodin shows that under
${\mathrm {TD}}$
seems sufficient to be used to prove set theory theorems. The following theorem partly justifies this phenomenon. Actually Woodin shows that under
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
, every Suslin set is determined (see [Reference Woodin28, Theorem 1.2]).
${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
, every Suslin set is determined (see [Reference Woodin28, Theorem 1.2]).
Theorem 1.4 (Woodin [Reference Woodin28, Theorem 1.1])
Assume
![]() ${\mathrm {ZF}}+V=L(\mathbb {R})+{\mathrm {DC}_{\mathbb {R}}}$
.
${\mathrm {ZF}}+V=L(\mathbb {R})+{\mathrm {DC}_{\mathbb {R}}}$
.
![]() ${\mathrm {AD}}$
is equivalent to
${\mathrm {AD}}$
is equivalent to
![]() ${\mathrm {TD}}$
.
${\mathrm {TD}}$
.
Moreover, as we shall see in this paper, the consequences of
![]() ${\mathrm {TD}}$
(and
${\mathrm {TD}}$
(and
![]() ${\mathrm {sTD}}$
) may be proved in a uniform way, unlike the proofs that assume
${\mathrm {sTD}}$
) may be proved in a uniform way, unlike the proofs that assume
![]() ${\mathrm {AD}}$
, which often require a very genius, tricky, and case-by-case design of games.
${\mathrm {AD}}$
, which often require a very genius, tricky, and case-by-case design of games.
The first result in this paper concerns the relationship between
![]() ${\mathrm {AD}}$
and Axiom of Choice, or
${\mathrm {AD}}$
and Axiom of Choice, or
![]() $\mathrm {AC}$
. Although
$\mathrm {AC}$
. Although
![]() ${\mathrm {AD}}$
contradicts
${\mathrm {AD}}$
contradicts
![]() $\mathrm {AC}$
, Mycielski proves the following theorem.
$\mathrm {AC}$
, Mycielski proves the following theorem.
Theorem 1.5 (Mycielski [Reference Mycielski18])
Over
![]() ${\mathrm {ZF}}$
,
${\mathrm {ZF}}$
,
![]() ${\mathrm {AD}}$
implies
${\mathrm {AD}}$
implies
![]() ${\mathrm {CC}_{\mathbb {R}}}$
.
${\mathrm {CC}_{\mathbb {R}}}$
.
The question if
![]() ${\mathrm {AD}}$
implies
${\mathrm {AD}}$
implies
![]() ${\mathrm {DC}_{\mathbb {R}}}$
remains open for a long time.
${\mathrm {DC}_{\mathbb {R}}}$
remains open for a long time.
Question 1.6 (Solovay [Reference Solovay, Kechris and Moschovakis26])
Over
![]() ${\mathrm {ZF}}$
, does
${\mathrm {ZF}}$
, does
![]() ${\mathrm {AD}}$
imply
${\mathrm {AD}}$
imply
![]() ${\mathrm {DC}_{\mathbb {R}}}$
?
${\mathrm {DC}_{\mathbb {R}}}$
?
Kechris proves the following result.
Theorem 1.7 (Kechris [Reference Kechris12])
Assume
![]() ${\mathrm {ZF}}+V=L(\mathbb {R})$
.
${\mathrm {ZF}}+V=L(\mathbb {R})$
.
![]() ${\mathrm {AD}}$
implies
${\mathrm {AD}}$
implies
![]() ${\mathrm {DC}_{\mathbb {R}}}$
.
${\mathrm {DC}_{\mathbb {R}}}$
.
It is unknown whether the assumption
![]() $V=L(\mathbb {R})$
can be removed. Recently, the following “unconditional” result is proved.
$V=L(\mathbb {R})$
can be removed. Recently, the following “unconditional” result is proved.
Theorem 1.8 (Peng and Yu [Reference Peng and Yu20])
Over
![]() ${\mathrm {ZF}}$
,
${\mathrm {ZF}}$
,
![]() ${\mathrm {TD}}$
implies
${\mathrm {TD}}$
implies
![]() ${\mathrm {CC}_{\mathbb {R}}}$
.
${\mathrm {CC}_{\mathbb {R}}}$
.
We will use
![]() ${\mathrm {CC}_{\mathbb {R}}}$
throughout the paper even without mentioning it.
${\mathrm {CC}_{\mathbb {R}}}$
throughout the paper even without mentioning it.
The first result in this paper is a partial solution to Question 1.6. We prove in Theorem 4.3 that
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
implies
${\mathrm {ZF}}+{\mathrm {TD}}$
implies
![]() $\mathrm {wDC}_{\mathbb {R}}$
, a weaker version of
$\mathrm {wDC}_{\mathbb {R}}$
, a weaker version of
![]() ${\mathrm {DC}_{\mathbb {R}}}$
(for the definition of
${\mathrm {DC}_{\mathbb {R}}}$
(for the definition of
![]() $\mathrm {wDC}_{\mathbb {R}}$
, see Definition 4.1).
$\mathrm {wDC}_{\mathbb {R}}$
, see Definition 4.1).
The second result in this paper is about the regularity properties of sets of reals. Although
![]() ${\mathrm {TD}}$
seems unlikely as strong as
${\mathrm {TD}}$
seems unlikely as strong as
![]() ${\mathrm {AD}}$
, a natural question is whether
${\mathrm {AD}}$
, a natural question is whether
![]() ${\mathrm {TD}}$
is as “useful” as
${\mathrm {TD}}$
is as “useful” as
![]() ${\mathrm {AD}}$
. Sami initiated this project by proving (in [Reference Sami23]) that
${\mathrm {AD}}$
. Sami initiated this project by proving (in [Reference Sami23]) that
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
implies
${\mathrm {ZF}}+{\mathrm {TD}}$
implies
![]() $\mathrm {CH}$
, the continuum hypothesis. But it seems a rather difficult (and long-standing) question whether
$\mathrm {CH}$
, the continuum hypothesis. But it seems a rather difficult (and long-standing) question whether
![]() ${\mathrm {ZF}}+{\mathrm {TD}}(+\mathrm {DC})$
implies regularity properties for sets of reals. A progress is made in [Reference Hamel, Horowitz and Shelah8] by showing that the perfect set property for all Turing invariant sets of reals implies the perfect set property for all sets of reals. A partial answer (Theorem 5.1) to this question is due to Woodin and remains unpublished (email communication between Woodin and Yu in April 2021). In this paper, we give another proof of Theorem 5.1 that strong Turing Determinacy,
${\mathrm {ZF}}+{\mathrm {TD}}(+\mathrm {DC})$
implies regularity properties for sets of reals. A progress is made in [Reference Hamel, Horowitz and Shelah8] by showing that the perfect set property for all Turing invariant sets of reals implies the perfect set property for all sets of reals. A partial answer (Theorem 5.1) to this question is due to Woodin and remains unpublished (email communication between Woodin and Yu in April 2021). In this paper, we give another proof of Theorem 5.1 that strong Turing Determinacy,
![]() ${\mathrm {sTD}}$
–a stronger version of
${\mathrm {sTD}}$
–a stronger version of
![]() ${\mathrm {TD}}$
—implies the regularity properties for sets of reals via a recursion theoretical method that is different from Woodin’s.
${\mathrm {TD}}$
—implies the regularity properties for sets of reals via a recursion theoretical method that is different from Woodin’s.
A basis for a class
![]() $\mathscr {C}$
of linearly ordered sets is a collection
$\mathscr {C}$
of linearly ordered sets is a collection
![]() $\mathscr {B}\subseteq \mathscr {C}$
such that for each
$\mathscr {B}\subseteq \mathscr {C}$
such that for each
![]() $L_1\in \mathscr {C}$
, there is an
$L_1\in \mathscr {C}$
, there is an
![]() $L_2\in \mathscr {B}$
such that
$L_2\in \mathscr {B}$
such that
![]() $L_2$
is isomorphic to a subset of
$L_2$
is isomorphic to a subset of
![]() $L_1$
. Investigating basis for linear ordering is a very active area in set theory today. For example, Moore [Reference Moore17] proves that under proper forcing axioms,
$L_1$
. Investigating basis for linear ordering is a very active area in set theory today. For example, Moore [Reference Moore17] proves that under proper forcing axioms,
![]() $\mathrm {PFA}$
, a five-element basis for uncountable linear orders exists. But it seems that basis theorems for linear orderings under
$\mathrm {PFA}$
, a five-element basis for uncountable linear orders exists. But it seems that basis theorems for linear orderings under
![]() ${\mathrm {AD}}$
remain untouched. In this paper, we prove a basis theorem for linear orderings over
${\mathrm {AD}}$
remain untouched. In this paper, we prove a basis theorem for linear orderings over
![]() $\mathbb {R}$
under the assumption
$\mathbb {R}$
under the assumption
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every uncountable set of reals has a perfect subset"}$
by showing that for every linear order
${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every uncountable set of reals has a perfect subset"}$
by showing that for every linear order
![]() $\leq _L$
over
$\leq _L$
over
![]() $\mathbb {R}$
, there is an order-preserving embedding from
$\mathbb {R}$
, there is an order-preserving embedding from
![]() $(2^{\omega },\leq )$
to
$(2^{\omega },\leq )$
to
![]() $(\mathbb {R},\leq _L)$
. In other words,
$(\mathbb {R},\leq _L)$
. In other words,
![]() $\{(2^{\omega },\leq )\}$
is a basis for
$\{(2^{\omega },\leq )\}$
is a basis for
![]() $\{(\mathbb {R},\leq _L)\mid \leq _L \mbox { is a linear ordering over } \mathbb {R}\}.$
$\{(\mathbb {R},\leq _L)\mid \leq _L \mbox { is a linear ordering over } \mathbb {R}\}.$
The last result in this paper is an application of recursion theory to fractal geometry theory. Besicovitch and Davis [Reference Besicovitch1, Reference Davies5] prove that for every analytic set, its Hausdorff dimension can be approximated arbitrarily close by the Hausdorff dimension of its closed subsets. Joyce and Preiss [Reference Joyce and Preiss11] prove a similar result for packing dimension. Recently Slaman [Reference Slaman25] proves that both Besicovitch–Davis and Joyce–Preiss theorems fail for some
![]() $\Pi ^1_1$
-set under the assumption
$\Pi ^1_1$
-set under the assumption
![]() $V=L$
. However, we prove in Theorem 6.5 that both theorems hold for arbitrary sets of reals over
$V=L$
. However, we prove in Theorem 6.5 that both theorems hold for arbitrary sets of reals over
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. So the phenomenon can be viewed as a new regularity property for the sets of reals. This weakens the assumption of the following result in [Reference Crone, Fishman and Jackson3].
${\mathrm {ZF}}+{\mathrm {sTD}}$
. So the phenomenon can be viewed as a new regularity property for the sets of reals. This weakens the assumption of the following result in [Reference Crone, Fishman and Jackson3].
Theorem 1.9 (Crone, Fishman, and Jackson [Reference Crone, Fishman and Jackson3])
Assume
![]() ${\mathrm {ZF}}+{\mathrm {AD}}+{\mathrm {DC}_{\mathbb {R}}}$
. For every set A and
${\mathrm {ZF}}+{\mathrm {AD}}+{\mathrm {DC}_{\mathbb {R}}}$
. For every set A and
![]() $\epsilon>0$
, there is a closed set
$\epsilon>0$
, there is a closed set
![]() $F\subseteq A$
such that
$F\subseteq A$
such that
![]() $\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)- \epsilon $
.
$\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)- \epsilon $
.
The proof of this theorem is direct and uses some rather deep results from set theory. However, we believe that our proof is simpler and, most importantly, it does not depend on
![]() ${\mathrm {DC}_{\mathbb {R}}}$
.
${\mathrm {DC}_{\mathbb {R}}}$
.
1.2 Point to set principle
Relativization opens a door between recursion theory and other mathematical branches. In recursion theory, for a real x, a relativization to x, roughly speaking, is a way to add prefix x- to every appearance of any notion in the statement. Then if a notion is defined in recursion theory, its relativization is defined naturally. And if a theorem in recursion theory is proved, then its relativization also follows naturally. For example, every continuous function is a recursive function relative to a real, and a Borel set is a hyperarithmeitc set relative to a real. From this point of view, one may apply recursion theory results to analysis.
The “point to set” principle is a more concrete way, by using relativization, to apply recursion theory to other areas of mathematics. Generally speaking, the principle says that a set A having certain property is equivalent to that it contains some special points. Such argument can be dated back to Sacks, who (in [Reference Sacks21]) gave a recursion theoretical proof of the classical result that every analytic set is measurable. For one more example, given a relativizable algorithmic randomness notion
![]() $\Gamma $
(such as Martin-Löf and Schnorr), we have the following fact.
$\Gamma $
(such as Martin-Löf and Schnorr), we have the following fact.
Fact 1.10. Assume
![]() ${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
. A set
${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
. A set
![]() $A\subseteq \mathbb {R}$
is null if and only if there is some real x such that no
$A\subseteq \mathbb {R}$
is null if and only if there is some real x such that no
![]() $\Gamma (x)$
-random real is in A.
$\Gamma (x)$
-random real is in A.
So a set A is not null is equivalent to say that for every real x, there is a
![]() $\Gamma (x)$
-random real in A. One may also replace randomness with genericity and obtain the corresponding results. In this paper, we apply some recent results in recursion theory and algorithmic randomness theory to descriptive set theory and fractal geometry theory. Especially some deep results concerning the lowness properties for various recursion theory notations turned to be crucial to our proof. The so-called “lowness properties” is a kind of property preserving some algorithmic property that was considered as very unique in algorithmic randomness theory. For example, a real x is low for Turing jump (or just low) if
$\Gamma (x)$
-random real in A. One may also replace randomness with genericity and obtain the corresponding results. In this paper, we apply some recent results in recursion theory and algorithmic randomness theory to descriptive set theory and fractal geometry theory. Especially some deep results concerning the lowness properties for various recursion theory notations turned to be crucial to our proof. The so-called “lowness properties” is a kind of property preserving some algorithmic property that was considered as very unique in algorithmic randomness theory. For example, a real x is low for Turing jump (or just low) if
![]() $x'\equiv _T \emptyset '$
, and a real x is called low for Schnorr random (for the definition of Schnorr randomness, see the paragraphs below Theorem 4.3) if every Schnorr random real is Schnorr random relative to x, etc. Ironically, different from the “slowdown” properties of themselves, these notions will be used to prove some “speedup” results. We expect to see more such applications in the near future.
$x'\equiv _T \emptyset '$
, and a real x is called low for Schnorr random (for the definition of Schnorr randomness, see the paragraphs below Theorem 4.3) if every Schnorr random real is Schnorr random relative to x, etc. Ironically, different from the “slowdown” properties of themselves, these notions will be used to prove some “speedup” results. We expect to see more such applications in the near future.
In [Reference Lutz and Lutz15], a specific theorem (i.e., Theorem 6.6) is called the “point to set” principle. It can be viewed as a dual principle to the randomness in geometric measure theory.
We organize the paper as follows. In Section 2, we give some terminologies and notions. In Section 3, we sketch a recursion theoretical reformulation of Sami’s proof that
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
implies
${\mathrm {ZF}}+{\mathrm {TD}}$
implies
![]() $\mathrm {CH}$
. The result will be used in Section 5. In Section 4, we prove
$\mathrm {CH}$
. The result will be used in Section 5. In Section 4, we prove
![]() $\mathrm {wDC}_{\mathbb {R}}$
within
$\mathrm {wDC}_{\mathbb {R}}$
within
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
. In Section 5, we prove that
${\mathrm {ZF}}+{\mathrm {TD}}$
. In Section 5, we prove that
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
implies regularity properties for sets of reals. In the same section, we also prove a basis theorem for linear orderings over sets of reals within
${\mathrm {ZF}}+{\mathrm {sTD}}$
implies regularity properties for sets of reals. In the same section, we also prove a basis theorem for linear orderings over sets of reals within
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every uncountable set of reals has a perfect subset."}$
In Section 6, we prove that the Besicovitch–Davis theorem holds for every set of reals within
${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every uncountable set of reals has a perfect subset."}$
In Section 6, we prove that the Besicovitch–Davis theorem holds for every set of reals within
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
.
${\mathrm {ZF}}+{\mathrm {sTD}}$
.
2 Terminologies and notions
We assume that readers have some knowledge of descriptive set theory and recursion theory. The major references are [Reference Chong and Yu2, Reference Downey and Hirschfeldt6, Reference Jech10, Reference Lerman14, Reference Nies19, Reference Sacks22].
2.1 Set theory
We assume that readers have some knowledge of axiomatic set theory.
![]() ${\mathrm {ZF}}$
is the Zermelo–Fraenkel axiom system.
${\mathrm {ZF}}$
is the Zermelo–Fraenkel axiom system.
![]() ${\mathrm {AD}}$
is the axiom of Determinacy.
${\mathrm {AD}}$
is the axiom of Determinacy.
When we say that
![]() $T\subseteq 2^{<\omega }$
is a tree, we mean that T is a tree without dead nodes.
$T\subseteq 2^{<\omega }$
is a tree, we mean that T is a tree without dead nodes.
![]() $[T]$
is the collection of infinite paths through T. Given any
$[T]$
is the collection of infinite paths through T. Given any
![]() $x\in \omega ^{\omega }$
and natural number n, we use
$x\in \omega ^{\omega }$
and natural number n, we use
![]() $x{\upharpoonright} n$
to denote an initial segment of x with length n. In other words,
$x{\upharpoonright} n$
to denote an initial segment of x with length n. In other words,
![]() $x{\upharpoonright} n$
is a finite string
$x{\upharpoonright} n$
is a finite string
![]() $\sigma \in \omega ^{<\omega }$
of length n such that for any
$\sigma \in \omega ^{<\omega }$
of length n such that for any
![]() $i<n$
,
$i<n$
,
![]() $\sigma (i)=x(i)$
.
$\sigma (i)=x(i)$
.
2.2 Recursion theory
We use
![]() $\leq _T$
to denote Turing reduction and
$\leq _T$
to denote Turing reduction and
![]() $\leq _h$
to denote hyperarithmetic reduction. We use
$\leq _h$
to denote hyperarithmetic reduction. We use
![]() $\Phi ^x$
to denote a Turing machine with oracle x. Sometimes we also say that
$\Phi ^x$
to denote a Turing machine with oracle x. Sometimes we also say that
![]() $\Phi ^x$
is a recursive functional. We fix an effective enumeration
$\Phi ^x$
is a recursive functional. We fix an effective enumeration
![]() $\{\Phi _e^x\}_{e\in \omega }$
of recursive functionals.
$\{\Phi _e^x\}_{e\in \omega }$
of recursive functionals.
We use Kleene’s
![]() $\mathcal {O}$
and we write
$\mathcal {O}$
and we write
![]() $\omega _1^{\mathrm {CK}}$
for the least non-recursive ordinal,
$\omega _1^{\mathrm {CK}}$
for the least non-recursive ordinal,
![]() $\omega _1^x$
for the least ordinal not recursive in x.
$\omega _1^x$
for the least ordinal not recursive in x.
We say a set A ranges Turing degrees cofinally if for every real x, there is some
![]() $y\geq _T x$
in A. We use
$y\geq _T x$
in A. We use
![]() $x'$
to denote the Turing jump relative to x. More generally, if
$x'$
to denote the Turing jump relative to x. More generally, if
![]() $\alpha <\omega _1^x$
, then
$\alpha <\omega _1^x$
, then
![]() $x^{(\alpha )}$
is that
$x^{(\alpha )}$
is that
![]() $\alpha $
-th Turing jump of x. Then,
$\alpha $
-th Turing jump of x. Then,
![]() $x\leq _h y$
if
$x\leq _h y$
if
![]() $x\leq _T y^{(\alpha )}$
for some
$x\leq _T y^{(\alpha )}$
for some
![]() $\alpha <\omega _1^y$
.
$\alpha <\omega _1^y$
.
The following fact is folklore and a sketched proof can be found in [Reference Peng and Yu20].
Lemma 2.1. Assume
![]() ${\mathrm {ZF}}$
. For any Turing degree
${\mathrm {ZF}}$
. For any Turing degree
![]() ${\mathbf {x}}$
, there is a family of Turing degrees
${\mathbf {x}}$
, there is a family of Turing degrees
![]() $\{{\mathbf {y}}_r\mid r\in \mathbb {R}\}$
satisfying the following properties
$\{{\mathbf {y}}_r\mid r\in \mathbb {R}\}$
satisfying the following properties
![]() $:$
$:$
-
(1) For any
 $r\in \mathbb {R}$
,
$r\in \mathbb {R}$
,
 ${\mathbf {x}}<{\mathbf {y}}_r$
.
${\mathbf {x}}<{\mathbf {y}}_r$
. -
(2) For any
 $r_0\neq r_1\in \mathbb {R}$
and
$r_0\neq r_1\in \mathbb {R}$
and
 ${\mathbf {z}}<{\mathbf {y}}_{r_0},{\mathbf {y}}_{r_1}$
, we have that
${\mathbf {z}}<{\mathbf {y}}_{r_0},{\mathbf {y}}_{r_1}$
, we have that
 ${\mathbf {z}}\leq {\mathbf {x}}$
.
${\mathbf {z}}\leq {\mathbf {x}}$
. -
(3) For any
 ${\mathbf {z}}\geq {\mathbf {x}}"$
, the Turing double jump of
${\mathbf {z}}\geq {\mathbf {x}}"$
, the Turing double jump of
 ${\mathbf {x}}$
, there is an infinite set
${\mathbf {x}}$
, there is an infinite set
 $C_{{\mathbf {z}}}\subset \mathbb {R}$
such that
$C_{{\mathbf {z}}}\subset \mathbb {R}$
such that
 ${\mathbf {y}}_r"={\mathbf {z}}$
for any
${\mathbf {y}}_r"={\mathbf {z}}$
for any
 $r\in C_{{\mathbf {z}}}$
.
$r\in C_{{\mathbf {z}}}$
.
3 On Sami’s theorem
Theorem 3.1 (Sami [Reference Sami23])
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+\mathrm {DC}$
proves
${\mathrm {ZF}}+{\mathrm {TD}}+\mathrm {DC}$
proves
![]() $\mathrm {CH}$
.
$\mathrm {CH}$
.
In this section, we sketch a recursion theoretical proof of Theorem 3.1 to show that
![]() $\mathrm {DC}$
can be removed from the assumption, which was also observed by Sami. So we can give another proof of the following result.
$\mathrm {DC}$
can be removed from the assumption, which was also observed by Sami. So we can give another proof of the following result.
Proposition 3.2 (Sami, email communication between Sami and Yu in June 2021)
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
proves
${\mathrm {ZF}}+{\mathrm {TD}}$
proves
![]() $\mathrm {CH}$
.
$\mathrm {CH}$
.
Proof Given an uncountable set
![]() $A\subseteq \mathbb {R}$
, by Lemma 2.1, for any real x, there is a real
$A\subseteq \mathbb {R}$
, by Lemma 2.1, for any real x, there is a real
![]() $y>_T x$
such that there is some real
$y>_T x$
such that there is some real
![]() $r\in A$
Turing below
$r\in A$
Turing below
![]() $y"$
but not below y. So, by
$y"$
but not below y. So, by
![]() ${\mathrm {TD}}$
, there is some real
${\mathrm {TD}}$
, there is some real
![]() $z_0$
such that for any
$z_0$
such that for any
![]() $y\geq _T z_0$
, there is some real
$y\geq _T z_0$
, there is some real
![]() $r\in A$
Turing below
$r\in A$
Turing below
![]() $y"$
but not below y.
$y"$
but not below y.
Now it is simple to construct a
![]() $\Sigma ^1_1(z_0)$
set B so that:
$\Sigma ^1_1(z_0)$
set B so that:
-
(i) For any
 $y\leq _h z_0$
and
$y\leq _h z_0$
and
 $x\in B$
, we have that
$x\in B$
, we have that
 $y\leq _T x$
.
$y\leq _T x$
. -
(ii) For any
 $x_0\neq x_1\in B$
, if
$x_0\neq x_1\in B$
, if
 $y\leq _h x_0, x_1$
, then
$y\leq _h x_0, x_1$
, then
 $y\leq _h z_0$
.
$y\leq _h z_0$
.
To see the existence of such B, first note that the set
![]() $\{y\mid \forall r\leq _h z_0(r\leq _T y)\}$
is an uncountable
$\{y\mid \forall r\leq _h z_0(r\leq _T y)\}$
is an uncountable
![]() $\Sigma ^1_1(z_0)$
-set. Then one may construct a perfect set
$\Sigma ^1_1(z_0)$
-set. Then one may construct a perfect set
![]() $P\subseteq B$
so that any two different members from P form a minimal pair over
$P\subseteq B$
so that any two different members from P form a minimal pair over
![]() $z_0$
in the hyperarithmetic degree sense.
$z_0$
in the hyperarithmetic degree sense.
Now for every real
![]() $x\in B$
, let
$x\in B$
, let
![]() $y_x=\Phi ^{x"}_e$
where e is the least n such that
$y_x=\Phi ^{x"}_e$
where e is the least n such that
![]() $\Phi ^{x"}_n$
is in A and not Turing below x. For any
$\Phi ^{x"}_n$
is in A and not Turing below x. For any
![]() $x_0\neq x_1\in B$
, if
$x_0\neq x_1\in B$
, if
![]() $y_{x_0}=y_{x_1}$
, then by (ii),
$y_{x_0}=y_{x_1}$
, then by (ii),
![]() $y_{x_0}=y_{x_1}\leq _h z_0$
. By (i), we have that
$y_{x_0}=y_{x_1}\leq _h z_0$
. By (i), we have that
![]() $y_{x_0}=y_{x_1}\leq _T x_0$
, which is a contradiction.
$y_{x_0}=y_{x_1}\leq _T x_0$
, which is a contradiction.
So
![]() $x\mapsto y_x$
is a
$x\mapsto y_x$
is a
![]() $1$
–
$1$
–
![]() $1$
map from B to A. It is known that every uncountable analytic set has a perfect subset and so A has the same power as
$1$
map from B to A. It is known that every uncountable analytic set has a perfect subset and so A has the same power as
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
From the proof of Proposition 3.2, we can see the following fact that will be used later. Actually by the remark after the proof of [Reference Sami23, Theorem 1.3], Sami proves that
![]() $f_n$
below can be chosen to be continuous. But we only need this weaker version here.
$f_n$
below can be chosen to be continuous. But we only need this weaker version here.
Lemma 3.3 (Sami [Reference Sami23])
Assume
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
. For every uncountable set A of reals, there is a perfect set B of reals and a sequence of arithmetical functions
${\mathrm {ZF}}+{\mathrm {TD}}$
. For every uncountable set A of reals, there is a perfect set B of reals and a sequence of arithmetical functions
![]() $\{f_n\}_{n\in \omega }$
from B to
$\{f_n\}_{n\in \omega }$
from B to
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $B\subseteq \bigcup _{n\in \omega }f_n^{-1}(A)$
. Moreover, restricted to B,
$B\subseteq \bigcup _{n\in \omega }f_n^{-1}(A)$
. Moreover, restricted to B,
![]() $f_n$
is 1–1 for every n.
$f_n$
is 1–1 for every n.
Proof Fix an effective enumeration of Turing functional
![]() $\{\Phi _n\}_{n\in \omega }$
. Going to a subset, assume that in the proof of Proposition 3.2, B is perfect. Define
$\{\Phi _n\}_{n\in \omega }$
. Going to a subset, assume that in the proof of Proposition 3.2, B is perfect. Define
![]() $f_n: B\to \mathbb {R}$
by
$f_n: B\to \mathbb {R}$
by
 $$ \begin{align} f_n(x)=\left\{ \begin{array}{rcl} \uparrow, & &(\exists m \Phi_n^{x"}(m)\mbox{ is not defined}) \vee( \Phi_n^{x"}\leq_T x),\\[2pt] \Phi_n^{x"}, & & \mathrm{otherwise}.\\ \end{array} \right. \end{align} $$
$$ \begin{align} f_n(x)=\left\{ \begin{array}{rcl} \uparrow, & &(\exists m \Phi_n^{x"}(m)\mbox{ is not defined}) \vee( \Phi_n^{x"}\leq_T x),\\[2pt] \Phi_n^{x"}, & & \mathrm{otherwise}.\\ \end{array} \right. \end{align} $$
Clearly
![]() $f_n$
is arithmetical for every n. We have that
$f_n$
is arithmetical for every n. We have that
![]() $B\subseteq \bigcup _{n\in \omega }f_n^{-1}(A)$
. Moreover, if
$B\subseteq \bigcup _{n\in \omega }f_n^{-1}(A)$
. Moreover, if
![]() $x\in B$
and
$x\in B$
and
![]() $f_n(x)$
is defined, then
$f_n(x)$
is defined, then
![]() $f_n(x)\leq _T x"\wedge f_n(x)\not \leq _T x$
. Then by the same reason as in the proof of Proposition 3.2,
$f_n(x)\leq _T x"\wedge f_n(x)\not \leq _T x$
. Then by the same reason as in the proof of Proposition 3.2,
![]() $f_n$
must be 1–1 on B. So
$f_n$
must be 1–1 on B. So
![]() $\{f_n\}_{n\in \omega }$
is as required.
$\{f_n\}_{n\in \omega }$
is as required.
4 Weakly dependent choice
Throughout the section, we work within
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
.
${\mathrm {ZF}}+{\mathrm {TD}}$
.
Definition 4.1. Weakly dependent choice for sets of reals, or
![]() $\mathrm {wDC}_{\mathbb {R}}$
, is the statement that for every binary relation R over
$\mathrm {wDC}_{\mathbb {R}}$
, is the statement that for every binary relation R over
![]() $\mathbb {R}$
with the property that the set
$\mathbb {R}$
with the property that the set
![]() $\{y\mid R(x,y)\}$
has positive inner measure for any real x, there is a sequence
$\{y\mid R(x,y)\}$
has positive inner measure for any real x, there is a sequence
![]() $\{x_n\}_{n\in \omega }$
of reals such that
$\{x_n\}_{n\in \omega }$
of reals such that
![]() $\forall n R(x_n,x_{n+1})$
.
$\forall n R(x_n,x_{n+1})$
.
Remark.
![]() $\mathrm {wDC}_{\mathbb {R}}$
is not a consequence of
$\mathrm {wDC}_{\mathbb {R}}$
is not a consequence of
![]() ${\mathrm {ZF}}$
. To see this, let V be a model of ZFC+GCH and
${\mathrm {ZF}}$
. To see this, let V be a model of ZFC+GCH and
![]() $\kappa =\aleph _\omega ^V$
. Let G be
$\kappa =\aleph _\omega ^V$
. Let G be
![]() $Col(\omega , <\kappa )$
-generic over V. Let
$Col(\omega , <\kappa )$
-generic over V. Let
![]() $A_n=\kappa ^\omega \cap V[G\cap Col(\omega , <\aleph _n^V)]$
. Let
$A_n=\kappa ^\omega \cap V[G\cap Col(\omega , <\aleph _n^V)]$
. Let
Then in M:
-
•
 $2^\omega \cap M=2^\omega \cap (\bigcup A_n)$
. [See, e.g., the proof of [Reference Schindler24, Theorem 6.69].]
$2^\omega \cap M=2^\omega \cap (\bigcup A_n)$
. [See, e.g., the proof of [Reference Schindler24, Theorem 6.69].] -
•
 $A_n$
is countable.
$A_n$
is countable. -
• Every countable subset of reals intersects at most finitely many
 $A_{n+1}\setminus A_n$
’s.
$A_{n+1}\setminus A_n$
’s.
For every
![]() $x\in 2^\omega \cap M$
, let
$x\in 2^\omega \cap M$
, let
![]() $n(x)$
be the least n such that
$n(x)$
be the least n such that
![]() $x\in A_n$
. Then in M,
$x\in A_n$
. Then in M,
witnesses the failure of
![]() $\mathrm {wDC}_{\mathbb {R}}$
.
$\mathrm {wDC}_{\mathbb {R}}$
.
Proposition 4.2.
![]() $\mathrm {wDC}_{\mathbb {R}}$
does not imply
$\mathrm {wDC}_{\mathbb {R}}$
does not imply
![]() ${\mathrm {CC}_{\mathbb {R}}}$
.
${\mathrm {CC}_{\mathbb {R}}}$
.
Proof To see this, let
![]() $V=L[A]$
for some set
$V=L[A]$
for some set
![]() $A $
of ordinals,
$A $
of ordinals,
![]() $\mathbb {P}$
be the random forcing over
$\mathbb {P}$
be the random forcing over
![]() $2^{\omega \times \omega }$
, G be
$2^{\omega \times \omega }$
, G be
![]() $\mathbb {P}$
-generic over V, and
$\mathbb {P}$
-generic over V, and
![]() $r_G: \omega \times \omega \rightarrow 2$
be the induced random real. Let
$r_G: \omega \times \omega \rightarrow 2$
be the induced random real. Let
![]() $x_n=r_G(n,\cdot ): \omega \rightarrow 2$
for each
$x_n=r_G(n,\cdot ): \omega \rightarrow 2$
for each
![]() $n<\omega $
and
$n<\omega $
and
![]() $X=\{x_n: n<\omega \}$
. Let
$X=\{x_n: n<\omega \}$
. Let
First note that any bijection
![]() $\pi : \omega \rightarrow \omega $
will induce a homeomorphism
$\pi : \omega \rightarrow \omega $
will induce a homeomorphism
![]() $\tilde {\pi }$
of
$\tilde {\pi }$
of
![]() $2^{\omega \times \omega }$
to itself by:
$2^{\omega \times \omega }$
to itself by:
![]() $\tilde {\pi }(x)(n,m)=x(\pi (n),m)$
. Moreover,
$\tilde {\pi }(x)(n,m)=x(\pi (n),m)$
. Moreover,
![]() $\tilde {\pi }$
preserves measure and X. Then the following hold in M.
$\tilde {\pi }$
preserves measure and X. Then the following hold in M.
-
(1) M satisfies
 $\mathrm {wDC}_{\mathbb {R}}$
. [Let R be a binary relation in M satisfying the assumption of
$\mathrm {wDC}_{\mathbb {R}}$
. [Let R be a binary relation in M satisfying the assumption of
 $\mathrm {wDC}_{\mathbb {R}}$
. Find
$\mathrm {wDC}_{\mathbb {R}}$
. Find
 $a\in V$
,
$a\in V$
,
 $x_0,\ldots ,x_{m-1}\in X$
and formula
$x_0,\ldots ,x_{m-1}\in X$
and formula
 $\varphi $
such that
$\varphi $
such that
 $x R y$
iff
$x R y$
iff
 $V[G]\vDash \varphi (x,y, a,x_0,\ldots ,x_{m-1}, X).$
We may assume that there is no occurrence of
$V[G]\vDash \varphi (x,y, a,x_0,\ldots ,x_{m-1}, X).$
We may assume that there is no occurrence of
 $x_i$
in
$x_i$
in
 $\varphi $
since, e.g., we may view
$\varphi $
since, e.g., we may view
 $L[A, x_0,\ldots ,x_{m-1}]$
as the ground model and
$L[A, x_0,\ldots ,x_{m-1}]$
as the ground model and
 $r_G\upharpoonright _{[m,\omega )\times \omega }$
as the random real over
$r_G\upharpoonright _{[m,\omega )\times \omega }$
as the random real over
 $L[A, x_0,\ldots ,x_{m-1}]$
. So Recall that
$L[A, x_0,\ldots ,x_{m-1}]$
. So Recall that $$ \begin{align*}x R y\text{ iff }V[G]\vDash \varphi(x,y, a, X).\end{align*} $$
$$ \begin{align*}x R y\text{ iff }V[G]\vDash \varphi(x,y, a, X).\end{align*} $$
 $\mathbb {R}\cap V$
has full outer measure in
$\mathbb {R}\cap V$
has full outer measure in
 $V[G]$
. Consequently, for any
$V[G]$
. Consequently, for any
 $x\in \mathbb {R}\cap V$
, there is some
$x\in \mathbb {R}\cap V$
, there is some
 $y\in V$
such that
$y\in V$
such that
 $x R y$
. We will be done if
$x R y$
. We will be done if
 $R\cap (\mathbb {R}\cap V)^2\in V$
. Now it suffices to prove that for any
$R\cap (\mathbb {R}\cap V)^2\in V$
. Now it suffices to prove that for any
 $x, y\in \mathbb {R}\cap V$
, for any
$x, y\in \mathbb {R}\cap V$
, for any
 $p, q\in \mathbb {P}$
, Suppose towards a contradiction that
$p, q\in \mathbb {P}$
, Suppose towards a contradiction that $$ \begin{align*}p\Vdash \varphi(x,y,a, \dot{X}) \text{ iff } q\Vdash \varphi(x,y,a, \dot{X}).\end{align*} $$
$$ \begin{align*}p\Vdash \varphi(x,y,a, \dot{X}) \text{ iff } q\Vdash \varphi(x,y,a, \dot{X}).\end{align*} $$
 $p\Vdash \varphi (x,y,a, \dot {X}) \text { and } q\Vdash \neg \varphi (x,y,a, \dot {X}).$
Find finite unions of basis open sets
$p\Vdash \varphi (x,y,a, \dot {X}) \text { and } q\Vdash \neg \varphi (x,y,a, \dot {X}).$
Find finite unions of basis open sets
 $O_p$
and
$O_p$
and
 $O_q$
such that for some n:
$O_q$
such that for some n:
-
•
 $\mu (O_p)=\mu (O_q)=\epsilon $
for some
$\mu (O_p)=\mu (O_q)=\epsilon $
for some
 $\epsilon>0$
;
$\epsilon>0$
; -
•
 $\mu (O_p\setminus p)+\mu (O_q\setminus q)<\epsilon ^2$
;
$\mu (O_p\setminus p)+\mu (O_q\setminus q)<\epsilon ^2$
; -
•
 $O_p=\bigcup _{i<k} O_{\sigma _i}$
and each
$O_p=\bigcup _{i<k} O_{\sigma _i}$
and each
 $\sigma _i: n\times \omega \rightarrow 2$
is a finite partial map;
$\sigma _i: n\times \omega \rightarrow 2$
is a finite partial map; -
•
 $O_q=\bigcup _{i<k^*} O_{\tau _i}$
and each
$O_q=\bigcup _{i<k^*} O_{\tau _i}$
and each
 $\tau _i: n\times \omega \rightarrow 2$
is a finite partial map.
$\tau _i: n\times \omega \rightarrow 2$
is a finite partial map.
Fix a bijection
 $\pi : \omega \rightarrow \omega $
such that
$\pi : \omega \rightarrow \omega $
such that
 $\pi [[0,n)]\subset [n, \omega )$
. Then But recall that
$\pi [[0,n)]\subset [n, \omega )$
. Then But recall that $$ \begin{align*}\mu(p\cap \tilde{\pi}(q))\geq \mu(O_p\cap \tilde{\pi}[O_q])-\mu(O_p\setminus p)-\mu(\tilde{\pi}[O_q\setminus q])>0.\end{align*} $$
$$ \begin{align*}\mu(p\cap \tilde{\pi}(q))\geq \mu(O_p\cap \tilde{\pi}[O_q])-\mu(O_p\setminus p)-\mu(\tilde{\pi}[O_q\setminus q])>0.\end{align*} $$
 $\tilde {\pi }[\dot {X}]=\dot {X}$
. So A contradiction.]
$\tilde {\pi }[\dot {X}]=\dot {X}$
. So A contradiction.] $$ \begin{align*}p\cap \tilde{\pi}(q)\Vdash \varphi(x,y,a, \dot{X})\wedge \neg \varphi(x,y,a, \dot{X}).\end{align*} $$
$$ \begin{align*}p\cap \tilde{\pi}(q)\Vdash \varphi(x,y,a, \dot{X})\wedge \neg \varphi(x,y,a, \dot{X}).\end{align*} $$
-
-
(2) There is no injection from
 $\omega $
to X. [Suppose otherwise, f is an injection. Then for some
$\omega $
to X. [Suppose otherwise, f is an injection. Then for some
 $a\in V$
,
$a\in V$
,
 $x_0,\ldots ,x_{m-1}\in X$
and formula
$x_0,\ldots ,x_{m-1}\in X$
and formula
 $\varphi $
, for any
$\varphi $
, for any
 $(n, x)\in \omega \times X$
,
$(n, x)\in \omega \times X$
,
 $f(n)=x$
iff
$f(n)=x$
iff
 $V[G]\vDash \varphi (n,x,a,x_0,\ldots ,x_{m-1}, X).$
Choose n such that
$V[G]\vDash \varphi (n,x,a,x_0,\ldots ,x_{m-1}, X).$
Choose n such that
 $f(n)=x_k\notin \{x_0,\ldots ,x_{m-1}\}$
and
$f(n)=x_k\notin \{x_0,\ldots ,x_{m-1}\}$
and
 $p\in G$
such that
$p\in G$
such that
 $p\Vdash \varphi (n,\dot {x}_k,a,\dot {x}_0,\ldots ,\dot {x}_{m-1}, \dot {X}).$
It is straightforward to find a bijection
$p\Vdash \varphi (n,\dot {x}_k,a,\dot {x}_0,\ldots ,\dot {x}_{m-1}, \dot {X}).$
It is straightforward to find a bijection
 $\pi : \omega \rightarrow \omega $
such that
$\pi : \omega \rightarrow \omega $
such that
 $\pi $
is identity on
$\pi $
is identity on
 $\{0,\ldots , m-1\}$
,
$\{0,\ldots , m-1\}$
,
 $\pi (k)\neq k$
and
$\pi (k)\neq k$
and
 $\mu (p\cap \tilde {\pi }[p])>0$
. But then
$\mu (p\cap \tilde {\pi }[p])>0$
. But then
 $p\cap \tilde {\pi }[p]\Vdash \dot {x}_k=\dot {f}(n)=\dot {x}_{\pi (k)}$
. A contradiction.]
$p\cap \tilde {\pi }[p]\Vdash \dot {x}_k=\dot {f}(n)=\dot {x}_{\pi (k)}$
. A contradiction.]
So M does not satisfy
![]() ${\mathrm {CC}_{\mathbb {R}}}$
. To see this, find a sequence of disjoint rational intervals
${\mathrm {CC}_{\mathbb {R}}}$
. To see this, find a sequence of disjoint rational intervals
![]() $\langle I_n: n<\omega \rangle $
such that
$\langle I_n: n<\omega \rangle $
such that
![]() $I_n\cap X\neq \emptyset $
for each n. Then by (2),
$I_n\cap X\neq \emptyset $
for each n. Then by (2),
![]() $\langle I_n\cap X: n<\omega \rangle $
admits no choice function.
$\langle I_n\cap X: n<\omega \rangle $
admits no choice function.
If we use Cohen forcing instead of random forcing in the above argument, then we conclude that the category version of
![]() $\mathrm {wDC}_{\mathbb {R}}$
does not imply
$\mathrm {wDC}_{\mathbb {R}}$
does not imply
![]() ${\mathrm {CC}_{\mathbb {R}}}$
. But we do not know if
${\mathrm {CC}_{\mathbb {R}}}$
. But we do not know if
![]() ${\mathrm {CC}_{\mathbb {R}}}$
implies
${\mathrm {CC}_{\mathbb {R}}}$
implies
![]() $\mathrm {wDC}_{\mathbb {R}}$
.
$\mathrm {wDC}_{\mathbb {R}}$
.
Theorem 4.3.
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
implies
${\mathrm {ZF}}+{\mathrm {TD}}$
implies
![]() $\mathrm {wDC}_{\mathbb {R}}$
.
$\mathrm {wDC}_{\mathbb {R}}$
.
We remark that if “having positive inner measure” is replaced by having Baire property and non-meager in the definition of
![]() $\mathrm {wDC}_{\mathbb {R}}$
, then the theorem still holds.
$\mathrm {wDC}_{\mathbb {R}}$
, then the theorem still holds.
A Schnorr test relative to x is an x-recursive sequence of x-recursive open sets
![]() $\{V_{n}\}_{n\in \omega }$
such that
$\{V_{n}\}_{n\in \omega }$
such that
![]() $\forall n \mu (V_n)=2^{-n}$
. A real r is called x-Schnorr random if
$\forall n \mu (V_n)=2^{-n}$
. A real r is called x-Schnorr random if
![]() $r\not \in \bigcap _{n\in \omega } V_n$
for any Schnorr test
$r\not \in \bigcap _{n\in \omega } V_n$
for any Schnorr test
![]() $\{V_{n}\}_{n\in \omega }$
relative to x. If x is recursive, then we simply use Schnorr randomness instead of x-Schnorr randomness. It is not difficult to see that there is a Schnorr random
$\{V_{n}\}_{n\in \omega }$
relative to x. If x is recursive, then we simply use Schnorr randomness instead of x-Schnorr randomness. It is not difficult to see that there is a Schnorr random
![]() $r\leq _T \emptyset '$
. And it is clear from the definition that if r is x-Schnorr random and
$r\leq _T \emptyset '$
. And it is clear from the definition that if r is x-Schnorr random and
![]() $z\leq _T x$
, then r is also z-Schnorr random. Also note that if
$z\leq _T x$
, then r is also z-Schnorr random. Also note that if
![]() $x\geq _T \emptyset '$
and r is x-Schnorr random, then x is Turing incomparable with r.
$x\geq _T \emptyset '$
and r is x-Schnorr random, then x is Turing incomparable with r.
A real x is called low for Schnorr random if every Schnorr random real is Schnorr random relative to x. The following theorem, which was proved by Sacks forcing, is due to Terwijn and Zambella.
Theorem 4.4 (Terwijn and Zambella [Reference Terwijn and Zambella27])
For every real
![]() $y\geq _T \emptyset "$
, there is a real x low for Schnorr random such that
$y\geq _T \emptyset "$
, there is a real x low for Schnorr random such that
![]() $x"\equiv _T y$
.
$x"\equiv _T y$
.

Figure 1
![]() $R(r_n,r_{n+1})$
.
$R(r_n,r_{n+1})$
.
Proof of Theorem 4.3
Fix a binary relation R as stated in
![]() $\mathrm {wDC}_{\mathbb {R}}$
. To prove
$\mathrm {wDC}_{\mathbb {R}}$
. To prove
![]() $\mathrm {wDC}_{\mathbb {R}}$
, we may assume that for any real x, the set
$\mathrm {wDC}_{\mathbb {R}}$
, we may assume that for any real x, the set
![]() $R_x=\{y\mid R(x,y)\}$
is upward closed under Turing reduction (and so
$R_x=\{y\mid R(x,y)\}$
is upward closed under Turing reduction (and so
![]() $R_x$
is co-null for any x). I.e., for any y and z, if
$R_x$
is co-null for any x). I.e., for any y and z, if
![]() $y\leq _T z$
and
$y\leq _T z$
and
![]() $y\in R_x$
, then
$y\in R_x$
, then
![]() $z\in R_x$
. To see this, we may define a new relation
$z\in R_x$
. To see this, we may define a new relation
![]() $\tilde {R}$
so that
$\tilde {R}$
so that
![]() $\tilde {R}(x,y)$
if and only if
$\tilde {R}(x,y)$
if and only if
![]() $\forall z_0\leq _T x \exists z_1\leq _T y \ R(z_0,z_1)$
. Then for every real x, the set
$\forall z_0\leq _T x \exists z_1\leq _T y \ R(z_0,z_1)$
. Then for every real x, the set
![]() $\tilde {R}_x=\{y\mid \tilde {R}(x,y)\}$
is upward closed under Turing reduction and has positive measure, and so co-null. Moreover, if there is a sequence
$\tilde {R}_x=\{y\mid \tilde {R}(x,y)\}$
is upward closed under Turing reduction and has positive measure, and so co-null. Moreover, if there is a sequence
![]() $\{y_n\}_{n\in \omega }$
such that
$\{y_n\}_{n\in \omega }$
such that
![]() $\forall n\tilde {R}(y_n,y_{n+1})$
. Then we build a sequence
$\forall n\tilde {R}(y_n,y_{n+1})$
. Then we build a sequence
![]() $\{x_n\}_{n\in \omega }$
so that
$\{x_n\}_{n\in \omega }$
so that
![]() $\forall nR(x_n,x_{n+1})$
as follows.
$\forall nR(x_n,x_{n+1})$
as follows.
First let
![]() $x_0= y_0$
. By the definition of
$x_0= y_0$
. By the definition of
![]() $\tilde {R}$
, we may choose the least
$\tilde {R}$
, we may choose the least
![]() $m_1$
such that
$m_1$
such that
![]() $\Phi _{m_1}^{y_1}$
is defined and
$\Phi _{m_1}^{y_1}$
is defined and
![]() $R(x_0, \Phi _{m_1}^{y_1})$
. Let
$R(x_0, \Phi _{m_1}^{y_1})$
. Let
![]() $x_1=\Phi _{m_1}^{y_1}$
. Generally, if
$x_1=\Phi _{m_1}^{y_1}$
. Generally, if
![]() $x_n$
is defined, then
$x_n$
is defined, then
![]() $x_n\leq _T y_n$
. So by the definition of
$x_n\leq _T y_n$
. So by the definition of
![]() $\tilde {R}$
, we may choose the least index
$\tilde {R}$
, we may choose the least index
![]() $m_{n+1}$
such that
$m_{n+1}$
such that
![]() $\Phi _{m_{n+1}}^{y_{n+1}}$
is defined and
$\Phi _{m_{n+1}}^{y_{n+1}}$
is defined and
![]() $R(x_n, \Phi _{m_{n+1}}^{y_{n+1}})$
. Set
$R(x_n, \Phi _{m_{n+1}}^{y_{n+1}})$
. Set
![]() $x_{n+1}=\Phi _{m_{n+1}}^{y_{n+1}}$
. Then we have that
$x_{n+1}=\Phi _{m_{n+1}}^{y_{n+1}}$
. Then we have that
![]() $\forall n R(x_n,x_{n+1})$
.
$\forall n R(x_n,x_{n+1})$
.
Now fix a real z. Note that by the assumption on R,
![]() $\bigcap _{y\leq _T z'} R_y$
is co-null. Then by Fact 1.10, there is a real
$\bigcap _{y\leq _T z'} R_y$
is co-null. Then by Fact 1.10, there is a real
![]() $z_0\geq _T z'$
such that for every
$z_0\geq _T z'$
such that for every
![]() $y\leq _T z'$
and every
$y\leq _T z'$
and every
![]() $z_0$
-Schnorr random r,
$z_0$
-Schnorr random r,
![]() $R(y,r)$
. Also by relativizing Theorem 4.4 to z, there is a real
$R(y,r)$
. Also by relativizing Theorem 4.4 to z, there is a real
![]() $x>_T z$
low for z-Schnorr random such that
$x>_T z$
low for z-Schnorr random such that
![]() $x"\geq _T z_0$
. So for every
$x"\geq _T z_0$
. So for every
![]() $y\leq _T z'$
and every
$y\leq _T z'$
and every
![]() $x"$
-Schnorr random r,
$x"$
-Schnorr random r,
![]() $R(y,r)$
. Also note that there is a z-Schnorr random, and so x-Schnorr random, real
$R(y,r)$
. Also note that there is a z-Schnorr random, and so x-Schnorr random, real
![]() $r\leq _T z'$
. Since
$r\leq _T z'$
. Since
![]() $x"\geq _T z'$
, there is some index of Turing functional e such that
$x"\geq _T z'$
, there is some index of Turing functional e such that
![]() $\Phi _e^{x"}=z'$
. For every number
$\Phi _e^{x"}=z'$
. For every number
![]() $e\in \omega $
, define the set
$e\in \omega $
, define the set
 $$ \begin{align*} A_e=\{x\mid \exists r(r\mbox{ is }x\mbox{-Schnorr random }\wedge r\leq_T \Phi_e^{x"})\\ \wedge \forall r_0\leq_T \Phi_e^{x"}\forall r_1(r_1\mbox{ is }x"\mbox{-Schnorr random}\rightarrow R(r_0,r_1))\}. \end{align*} $$
$$ \begin{align*} A_e=\{x\mid \exists r(r\mbox{ is }x\mbox{-Schnorr random }\wedge r\leq_T \Phi_e^{x"})\\ \wedge \forall r_0\leq_T \Phi_e^{x"}\forall r_1(r_1\mbox{ is }x"\mbox{-Schnorr random}\rightarrow R(r_0,r_1))\}. \end{align*} $$
Then by the discussion above,
![]() $\bigcup _{e\in \omega }A_e$
ranges Turing degrees cofinally. So there must be some
$\bigcup _{e\in \omega }A_e$
ranges Turing degrees cofinally. So there must be some
![]() $e_0$
such that
$e_0$
such that
![]() $A_{e_0}$
ranges Turing degrees cofinally. By
$A_{e_0}$
ranges Turing degrees cofinally. By
![]() ${\mathrm {TD}}$
, there is some
${\mathrm {TD}}$
, there is some
![]() $x_0$
such that every
$x_0$
such that every
![]() $y\geq _T x_0$
is
$y\geq _T x_0$
is
![]() $\equiv _T$
equivalent to some
$\equiv _T$
equivalent to some
![]() $y_0$
in
$y_0$
in
![]() $A_{e_0}$
. We may assume that
$A_{e_0}$
. We may assume that
![]() $x_0\in A_{e_0}$
. Recursively in
$x_0\in A_{e_0}$
. Recursively in
![]() $x_0^{(\omega )}$
, we first find a sequence of reals
$x_0^{(\omega )}$
, we first find a sequence of reals
Then find a sequence of reals
![]() $\{r_n\}_{n\in \omega }$
so that for every n,
$\{r_n\}_{n\in \omega }$
so that for every n,
![]() $r_n\leq _T \Phi _{e_0}^{y_n"}$
is
$r_n\leq _T \Phi _{e_0}^{y_n"}$
is
![]() $y_n\equiv _T x^{(2n)}_0$
-Schnorr random. Note that for every n,
$y_n\equiv _T x^{(2n)}_0$
-Schnorr random. Note that for every n,
![]() $r_n\leq _T \Phi _{e_0}^{y_n"}$
and
$r_n\leq _T \Phi _{e_0}^{y_n"}$
and
![]() $r_{n+1}$
is
$r_{n+1}$
is
![]() $x^{(2n+2)}_0\equiv _T y_n"$
-Schnorr random (see Figure 1). So by the definition of
$x^{(2n+2)}_0\equiv _T y_n"$
-Schnorr random (see Figure 1). So by the definition of
![]() $A_{e_0}$
,
$A_{e_0}$
,
![]() $R(r_n,r_{n+1})$
.
$R(r_n,r_{n+1})$
.
The reason we choose Schnorr randomness, instead of Martin-Löf randomness that is the standard randomness notion, is that every low for Martin-Löf random real is Turing below
![]() $\emptyset '$
. So for any real x low for Martin-Löf random, there is no way to make the Turing jumps of x be very high.
$\emptyset '$
. So for any real x low for Martin-Löf random, there is no way to make the Turing jumps of x be very high.
5 Regularity properties of sets of reals
In this section, we prove some regularity properties for sets of reals under
![]() ${\mathrm {ZF}}+{\mathrm {sTD}} (+{\mathrm {DC}_{\mathbb {R}}})$
. Woodin already considered
${\mathrm {ZF}}+{\mathrm {sTD}} (+{\mathrm {DC}_{\mathbb {R}}})$
. Woodin already considered
![]() ${\mathrm {sTD}}$
long time ago. All the results in Sections 5.1 and 5.2 have been known to him (email communication between Woodin and Yu in April 2021).
${\mathrm {sTD}}$
long time ago. All the results in Sections 5.1 and 5.2 have been known to him (email communication between Woodin and Yu in April 2021).
Theorem 5.1 (Woodin, unpublished)
-
(1)
 ${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that every set is measurable and has Baire property.
${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that every set is measurable and has Baire property. -
(2)
 ${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that every uncountable set of reals has a perfect subset.
${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that every uncountable set of reals has a perfect subset.
5.1 The proof of part (1)
We only prove that every set is measurable and leave the second part to readers.
It suffices to prove that for any set A, if every measurable subset of A is null, then A must be null. Now suppose, for a contradiction, that every measurable subset of A is null but A is not null. Then, by Fact 1.10 with Schnorr randomness, for every real z, there is a z-Schnorr random real
![]() $z_0$
in A. By Theorem 4.4 relative to z, there is a real
$z_0$
in A. By Theorem 4.4 relative to z, there is a real
![]() $x\geq _T z$
low for z-Schnorr random and
$x\geq _T z$
low for z-Schnorr random and
![]() $x"\geq _T z_0$
.
$x"\geq _T z_0$
.
Now for every
![]() $e\in \omega $
, let
$e\in \omega $
, let
The argument in the previous paragraph shows that
![]() $\bigcup _{e\in \omega } B_e$
ranges Turing degrees cofinally. Then there is some
$\bigcup _{e\in \omega } B_e$
ranges Turing degrees cofinally. Then there is some
![]() $e_0$
such that
$e_0$
such that
![]() $B_{e_0}$
ranges Turing degrees cofinally. By
$B_{e_0}$
ranges Turing degrees cofinally. By
![]() ${\mathrm {sTD}}$
, there is a pointed subset
${\mathrm {sTD}}$
, there is a pointed subset
![]() $P\subseteq B_{e_0}$
.
$P\subseteq B_{e_0}$
.
Let
C is an analytic set and so measurable. Since P is a pointed set, by the definition of
![]() $B_{e_0}$
and Fact 1.10 with Schnorr randomness, C is not null. This is absurd.
$B_{e_0}$
and Fact 1.10 with Schnorr randomness, C is not null. This is absurd.
Remark. Clearly the proof can be localized if we assume
![]() ${\mathrm {CC}_{\mathbb {R}}}$
, as pointed out by one of the referees. For example, assuming
${\mathrm {CC}_{\mathbb {R}}}$
, as pointed out by one of the referees. For example, assuming
![]() ${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
, if
${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
, if
![]() ${\mathrm {sTD}}$
holds for
${\mathrm {sTD}}$
holds for
![]() $\mathbf {\Sigma }^1_n$
-sets, then every
$\mathbf {\Sigma }^1_n$
-sets, then every
![]() $\mathbf {\Sigma }^1_n$
-set is measurable.
$\mathbf {\Sigma }^1_n$
-set is measurable.
5.2 The proof of part (2)
We first prove the following lemma.
Lemma 5.2. Assume
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. For every perfect set P of reals and every partition
${\mathrm {ZF}}+{\mathrm {sTD}}$
. For every perfect set P of reals and every partition
![]() $P=\bigcup _{n<\omega } B_n$
, there exists n such that
$P=\bigcup _{n<\omega } B_n$
, there exists n such that
![]() $B_n$
has a perfect subset.
$B_n$
has a perfect subset.
Proof Clearly we may assume that
![]() $P=2^\omega $
via a homeomorphism. Then for some n,
$P=2^\omega $
via a homeomorphism. Then for some n,
![]() $B_n$
ranges Turing degrees cofinally. By sTD,
$B_n$
ranges Turing degrees cofinally. By sTD,
![]() $B_n$
contains a perfect subset.
$B_n$
contains a perfect subset.
Proof of part (2) of Theorem 5.1
Suppose that A is uncountable. By Lemma 3.3, we may fix a perfect set B and a sequence of functions
![]() $\{f_n\}_{n\in \omega }$
as in the lemma. Then by Lemma 5.2, we can choose a perfect
$\{f_n\}_{n\in \omega }$
as in the lemma. Then by Lemma 5.2, we can choose a perfect
![]() $Q\subset f^{-1}_n[A]$
for some n. Now
$Q\subset f^{-1}_n[A]$
for some n. Now
![]() $f_n[Q]$
is an uncountable analytic subset of A. So
$f_n[Q]$
is an uncountable analytic subset of A. So
![]() $f_n[Q]$
and hence A contains a perfect subset.
$f_n[Q]$
and hence A contains a perfect subset.
Remark. We would like to thank the referee who pointed out to us that the proof derived the result that
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+\mbox {"every set of reals has Baire property"}$
implies every uncountable set of reals has a perfect subset.
${\mathrm {ZF}}+{\mathrm {TD}}+\mbox {"every set of reals has Baire property"}$
implies every uncountable set of reals has a perfect subset.
Here we mention another approach, within
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}+{\mathrm {DC}_{\mathbb {R}}}$
, to get a perfect subset due to Sami. A set A of reals is called Bernstein if neither A nor
${\mathrm {ZF}}+{\mathrm {sTD}}+{\mathrm {DC}_{\mathbb {R}}}$
, to get a perfect subset due to Sami. A set A of reals is called Bernstein if neither A nor
![]() $\mathbb {R}\setminus A$
has a perfect subset. Notice that the nonexistence of a Bernstein set implies that for every perfect set P and its subset
$\mathbb {R}\setminus A$
has a perfect subset. Notice that the nonexistence of a Bernstein set implies that for every perfect set P and its subset
![]() $A\subseteq P$
, either A or
$A\subseteq P$
, either A or
![]() $P\setminus A$
has a perfect subset. Sami observed the following relationship between the existence of a Bernstein set and perfect subset property.
$P\setminus A$
has a perfect subset. Sami observed the following relationship between the existence of a Bernstein set and perfect subset property.
Lemma 5.3 (Sami [Reference Sami23])
Assume
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
. If there is no Bernstein set, then every uncountable set of reals has a perfect subset.
${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
. If there is no Bernstein set, then every uncountable set of reals has a perfect subset.
Proof Suppose that A is uncountable. By Lemma 3.3, we may fix a perfect set B and a sequence of functions
![]() $\{f_n\}_{n\in \omega }$
as in the lemma.
$\{f_n\}_{n\in \omega }$
as in the lemma.
Let
![]() $T^0\subseteq 2^{<\omega }$
be a perfect tree such that
$T^0\subseteq 2^{<\omega }$
be a perfect tree such that
![]() $[T^0]=B$
. We will inductively choose a decreasing sequence of perfect trees
$[T^0]=B$
. We will inductively choose a decreasing sequence of perfect trees
![]() $T^0\supset T^1\supset \cdots \supset T^n\supset \cdots $
until the procedure terminates. Suppose that
$T^0\supset T^1\supset \cdots \supset T^n\supset \cdots $
until the procedure terminates. Suppose that
![]() $T^n$
has been chosen and we choose
$T^n$
has been chosen and we choose
![]() $T^{n+1}$
.
$T^{n+1}$
.
Case
![]() $(1)$
. There is some perfect tree
$(1)$
. There is some perfect tree
![]() $T^{*}\subseteq T^n$
such that
$T^{*}\subseteq T^n$
such that
![]() $f_n$
is defined on every member in
$f_n$
is defined on every member in
![]() $[T^*]$
and
$[T^*]$
and
![]() $f_n([T^*])\subseteq A$
. Fix such
$f_n([T^*])\subseteq A$
. Fix such
![]() $T^*$
. Then
$T^*$
. Then
![]() $f_n([T^*])\subseteq A$
is an uncountable analytic set. Thus A must have a perfect subset. The procedure terminates and we are done.
$f_n([T^*])\subseteq A$
is an uncountable analytic set. Thus A must have a perfect subset. The procedure terminates and we are done.
Case
![]() $(2)$
. Otherwise. Then by the assumption of no Bernstein set, choose
$(2)$
. Otherwise. Then by the assumption of no Bernstein set, choose
![]() $T^{n+1}$
to be a perfect subtree of
$T^{n+1}$
to be a perfect subtree of
![]() $ T^n$
such that for every
$ T^n$
such that for every
![]() $x\in [T^{n+1}]$
, either
$x\in [T^{n+1}]$
, either
![]() $f_n(x)$
is not defined or
$f_n(x)$
is not defined or
![]() $f_n(x)\not \in A$
.
$f_n(x)\not \in A$
.
Either we stop at Case (1) of some n, then we find a perfect subset of A. Or else, the construction goes through all of n’s. Then
![]() $\bigcap _{n<\omega } [T^n]$
is non-empty. Moreover, for every
$\bigcap _{n<\omega } [T^n]$
is non-empty. Moreover, for every
![]() $x\in \bigcap _{n<\omega } [T^n]$
and every n, either
$x\in \bigcap _{n<\omega } [T^n]$
and every n, either
![]() $f_n(x)$
is not defined or
$f_n(x)$
is not defined or
![]() $f_n(x)\not \in A$
. This contradicts the fact that
$f_n(x)\not \in A$
. This contradicts the fact that
![]() $B\subseteq \bigcup _{n\in \omega } f^{-1}_n(A)$
.
$B\subseteq \bigcup _{n\in \omega } f^{-1}_n(A)$
.
Thus we must stop at Case (1) of some n and so A must have a perfect subset.
![]() ${\mathrm {sTD}}$
implies that every set is measurable and so there is no Bernstein set. Thus
${\mathrm {sTD}}$
implies that every set is measurable and so there is no Bernstein set. Thus
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}+{\mathrm {DC}_{\mathbb {R}}}$
implies every uncountable set of reals has a perfect subset.
${\mathrm {ZF}}+{\mathrm {sTD}}+{\mathrm {DC}_{\mathbb {R}}}$
implies every uncountable set of reals has a perfect subset.
5.3 An application of regularity properties to linear orderings over
 $\mathbb {R}$
$\mathbb {R}$
Lemma 5.4. Assume
![]() ${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}+\mbox {"every set of reals is measurable."}$
Given any linear order
${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}+\mbox {"every set of reals is measurable."}$
Given any linear order
![]() $\leq _L$
of
$\leq _L$
of
![]() $\mathbb {R}$
and any non-null set
$\mathbb {R}$
and any non-null set
![]() $A\subseteq \mathbb {R}$
, the collection of all
$A\subseteq \mathbb {R}$
, the collection of all
![]() $x\in A$
such that either
$x\in A$
such that either
![]() $\{y\in A\mid y\leq _L x\}$
is null or
$\{y\in A\mid y\leq _L x\}$
is null or
![]() $\{y\in A\mid x\leq _L y\}$
is null is a null set.
$\{y\in A\mid x\leq _L y\}$
is null is a null set.
Proof Given a linear order
![]() $\leq _L$
over
$\leq _L$
over
![]() $\mathbb {R}$
, let
$\mathbb {R}$
, let
![]() $A\subseteq \mathbb {R}$
be any non-null set. Fix a non-null set
$A\subseteq \mathbb {R}$
be any non-null set. Fix a non-null set
![]() $B\subseteq A$
. By Fubini’s theorem, the set
$B\subseteq A$
. By Fubini’s theorem, the set
![]() $\{(x,y)\mid x\leq _L y\wedge x\in B\wedge y\in B\}$
is measurable and has positive measure. Let
$\{(x,y)\mid x\leq _L y\wedge x\in B\wedge y\in B\}$
is measurable and has positive measure. Let
be a subset of B. Then by Fubini’s theorem again, the set
![]() $B\setminus L^B$
is not null. So the set
$B\setminus L^B$
is not null. So the set
is a null subset of A.
By the same method, the set
is also a null subset of A.
Finally, we have the following basis theorem for linear orderings over
![]() $\mathbb {R}$
under
$\mathbb {R}$
under
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. In what follows, we use
${\mathrm {ZF}}+{\mathrm {sTD}}$
. In what follows, we use
![]() $\leq $
to denote the usual order on reals. Since the lexicographic order on
$\leq $
to denote the usual order on reals. Since the lexicographic order on
![]() $2^\omega $
is order isomorphic to the real order on the Cantor set through the standard bijection, we also use
$2^\omega $
is order isomorphic to the real order on the Cantor set through the standard bijection, we also use
![]() $\leq $
to denote this order on
$\leq $
to denote this order on
![]() $2^\omega $
.
$2^\omega $
.
Theorem 5.5. Assume
![]() ${\mathrm {ZF}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every set of reals is measurable."}$
For every linear order
${\mathrm {ZF}}+{\mathrm {DC}_{\mathbb {R}}}+\mbox {"every set of reals is measurable."}$
For every linear order
![]() $\leq _L$
over
$\leq _L$
over
![]() $\mathbb {R}$
, there is an order-preserving embedding from
$\mathbb {R}$
, there is an order-preserving embedding from
![]() $(2^{\omega },\leq )$
to
$(2^{\omega },\leq )$
to
![]() $(\mathbb {R},\leq _L)$
.
$(\mathbb {R},\leq _L)$
.
Proof First we set
![]() $P_{\emptyset }=[0, 1]$
.
$P_{\emptyset }=[0, 1]$
.
By Lemma 5.4, there is a real
![]() $x\in P_{\emptyset }$
such that both the sets
$x\in P_{\emptyset }$
such that both the sets
![]() $\{y\in A\mid y\leq _L x\}$
and
$\{y\in A\mid y\leq _L x\}$
and
![]() $\{y\in A\mid x\leq _L y\}$
have positive measure. So both of them have disjoint perfect subsets
$\{y\in A\mid x\leq _L y\}$
have positive measure. So both of them have disjoint perfect subsets
![]() $P_0$
and
$P_0$
and
![]() $P_1$
with positive measure, respectively. Moreover, we may require that for any
$P_1$
with positive measure, respectively. Moreover, we may require that for any
![]() $i\in \{0,1\}$
and
$i\in \{0,1\}$
and
![]() $y,z\in P_{i}$
,
$y,z\in P_{i}$
,
![]() $|y-z|\leq 2^{-1}$
.
$|y-z|\leq 2^{-1}$
.
Now, by an induction, it is not difficult to construct a sequence
![]() $\{P_{\sigma }\}_{\sigma \in 2^{<\omega }}$
of perfect sets so that:
$\{P_{\sigma }\}_{\sigma \in 2^{<\omega }}$
of perfect sets so that:
-
• If
 $\sigma $
extends
$\sigma $
extends
 $\tau $
, written as
$\tau $
, written as
 $\sigma \succ \tau $
, then
$\sigma \succ \tau $
, then
 $P_{\sigma }\subset P_{\tau }$
has positive measure.
$P_{\sigma }\subset P_{\tau }$
has positive measure. -
• If
 $\sigma $
and
$\sigma $
and
 $\tau $
are incompatible, then
$\tau $
are incompatible, then
 $P_{\sigma }\cap P_{\tau }=\emptyset $
.
$P_{\sigma }\cap P_{\tau }=\emptyset $
. -
• If for some n,
 $\sigma \upharpoonright _n=\tau \upharpoonright _n$
and
$\sigma \upharpoonright _n=\tau \upharpoonright _n$
and
 $\sigma (n)<\tau (n)$
, then
$\sigma (n)<\tau (n)$
, then
 $\forall x\in P_{\sigma }\forall y\in P_{\tau }(x\leq _L y)$
.
$\forall x\in P_{\sigma }\forall y\in P_{\tau }(x\leq _L y)$
. -
• For any
 $\sigma $
and
$\sigma $
and
 $x,y\in P_{\sigma }$
,
$x,y\in P_{\sigma }$
,
 $|x-y|\leq 2^{-|\sigma |}$
.
$|x-y|\leq 2^{-|\sigma |}$
.
Define
![]() $f:2^{\omega }\to \mathbb {R}$
so that
$f:2^{\omega }\to \mathbb {R}$
so that
![]() $f(x)$
is the unique real in
$f(x)$
is the unique real in
![]() $\bigcap _n P_{x{\upharpoonright} n}$
. Then f is an order-preserving embedding from
$\bigcap _n P_{x{\upharpoonright} n}$
. Then f is an order-preserving embedding from
![]() $(2^{\omega },\leq )$
to
$(2^{\omega },\leq )$
to
![]() $(\mathbb {R},\leq _L)$
.
$(\mathbb {R},\leq _L)$
.
One may wonder what happens to Lemma 5.4 under
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
. Since it is unknown whether
${\mathrm {ZF}}+{\mathrm {TD}}$
. Since it is unknown whether
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
implies that every set of reals is measurable, we have to use a more involved argument.
${\mathrm {ZF}}+{\mathrm {TD}}$
implies that every set of reals is measurable, we have to use a more involved argument.
Definition 5.6. A linear order
![]() $(L,\leq _L)$
is locally countable if for any
$(L,\leq _L)$
is locally countable if for any
![]() $l\in L$
, the set
$l\in L$
, the set
![]() $\{x\leq _L l\mid x\in L\}$
is countable.
$\{x\leq _L l\mid x\in L\}$
is countable.
A typical locally countable order is
![]() $(\omega _1,\leq )$
.
$(\omega _1,\leq )$
.
For a set A of reals that is closed under Turing equivalence relation, a real x is a minimal upper bound of A if:
-
• every member of A is recursive in x; and
-
• there is no real
 $y<_T x$
such that every member of A is recursive in y.
$y<_T x$
such that every member of A is recursive in y.
By a classical theorem in recursion theory (see Theorem 4.11 in [Reference Lerman14]), every countable set of reals has a minimal upper bound.
Lemma 5.7. Assume
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
. There is no uncountable set
${\mathrm {ZF}}+{\mathrm {TD}}$
. There is no uncountable set
![]() $A\subseteq \mathbb {R}$
with a locally countable linear order over A.
$A\subseteq \mathbb {R}$
with a locally countable linear order over A.
Proof By Proposition 3.2, it suffices to prove that there is no locally countable linear order on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Suppose not. Let
![]() $(\mathbb {R},\leq _L)$
be a locally countable order. For every real x, let
$(\mathbb {R},\leq _L)$
be a locally countable order. For every real x, let
![]() $I_x$
be the Turing downward closure of the set
$I_x$
be the Turing downward closure of the set
![]() $\{z\mid z\leq _L x\}$
. I.e.,
$\{z\mid z\leq _L x\}$
. I.e.,
Obviously
![]() $x\leq _L y$
implies
$x\leq _L y$
implies
![]() $I_x\subseteq I_y$
.
$I_x\subseteq I_y$
.
Note that for any real z, there is a real x such that
![]() $z\in I_x$
. So there is a real
$z\in I_x$
. So there is a real
![]() $z_0\geq _T z$
such that
$z_0\geq _T z$
such that
![]() $z_0$
is a minimal upper bound of
$z_0$
is a minimal upper bound of
![]() $I_x$
. By
$I_x$
. By
![]() ${\mathrm {TD}}$
, there is a real
${\mathrm {TD}}$
, there is a real
![]() $z_1$
such that every real
$z_1$
such that every real
![]() $z_2\geq _T z_1$
is a minimal upper bound over
$z_2\geq _T z_1$
is a minimal upper bound over
![]() $I_x$
for some x.
$I_x$
for some x.
For every real z, let
and
Note that
![]() $M_{z_2}$
is nonempty for every
$M_{z_2}$
is nonempty for every
![]() $z_2\geq _T z_1$
. We have the following fact:
$z_2\geq _T z_1$
. We have the following fact:
-
• For any
 $z_2, z_3\geq _T z_1$
, either
$z_2, z_3\geq _T z_1$
, either
 $N_{z_3}\subseteq N_{z_2}$
or
$N_{z_3}\subseteq N_{z_2}$
or
 $N_{z_2}\subseteq N_{z_3}$
. [To see this, suppose that
$N_{z_2}\subseteq N_{z_3}$
. [To see this, suppose that
 $N_{z_3}\not \subseteq N_{z_2}$
. Then there must be some
$N_{z_3}\not \subseteq N_{z_2}$
. Then there must be some
 $x_3\in M_{z_3}$
such that for any
$x_3\in M_{z_3}$
such that for any
 $x_2\in M_{z_2}$
,
$x_2\in M_{z_2}$
,
 $x_3\not \leq _L x_2$
. In other words,
$x_3\not \leq _L x_2$
. In other words,
 $x_2\leq _L x_3$
for any
$x_2\leq _L x_3$
for any
 $x_2\in M_{z_2}$
. So
$x_2\in M_{z_2}$
. So
 $N_{z_2}\subseteq N_{z_3}$
.]
$N_{z_2}\subseteq N_{z_3}$
.]
Now fix a pair of minimal covers
![]() $z_2\not \equiv _T z_3$
of
$z_2\not \equiv _T z_3$
of
![]() $z_1$
(i.e., for
$z_1$
(i.e., for
![]() $i\in \{2,3\}$
,
$i\in \{2,3\}$
,
![]() $z_i>_T z_1$
but there is no real y strictly between
$z_i>_T z_1$
but there is no real y strictly between
![]() $z_1$
and
$z_1$
and
![]() $z_i$
in the Turing reduction order sense. For the existence of such a pair, see Lemma 2.1). By the fact above, WLOG, we may assume
$z_i$
in the Turing reduction order sense. For the existence of such a pair, see Lemma 2.1). By the fact above, WLOG, we may assume
![]() $N_{z_2}\subseteq N_{z_3}$
and fix some
$N_{z_2}\subseteq N_{z_3}$
and fix some
![]() $x\in M_{z_2}$
. Then every real in
$x\in M_{z_2}$
. Then every real in
![]() $I_x\subseteq N_{z_2}\subseteq N_{z_3}$
is recursive in both
$I_x\subseteq N_{z_2}\subseteq N_{z_3}$
is recursive in both
![]() $z_2$
and
$z_2$
and
![]() $z_3$
. So every real in
$z_3$
. So every real in
![]() $I_x$
is recursive in
$I_x$
is recursive in
![]() $z_1$
. This contradicts the fact that
$z_1$
. This contradicts the fact that
![]() $z_2$
is a minimal upper bound of
$z_2$
is a minimal upper bound of
![]() $I_x$
and
$I_x$
and
![]() $z_1<_T z_2$
.
$z_1<_T z_2$
.
Corollary 5.8. Assume
![]() ${\mathrm {ZF}}+{\mathrm {TD}}$
. For every uncountable set
${\mathrm {ZF}}+{\mathrm {TD}}$
. For every uncountable set
![]() $A\subseteq \mathbb {R}$
and linear order
$A\subseteq \mathbb {R}$
and linear order
![]() $\leq _L$
over A, there are uncountably many reals
$\leq _L$
over A, there are uncountably many reals
![]() $x\in A$
such that both
$x\in A$
such that both
![]() $\{y\in A\mid y\leq _L x\}$
and
$\{y\in A\mid y\leq _L x\}$
and
![]() $\{y\in A\mid x\leq _L y\}$
are uncountable.
$\{y\in A\mid x\leq _L y\}$
are uncountable.
Proof Given a linear order
![]() $\leq _L$
over
$\leq _L$
over
![]() $\mathbb {R}$
, let
$\mathbb {R}$
, let
and
By Lemma 5.7, both L and R are countable. So there are uncountably many reals
![]() $x\in A$
such that both
$x\in A$
such that both
![]() $\{y\mid y\leq _L x\}$
and
$\{y\mid y\leq _L x\}$
and
![]() $\{y\mid x\leq _L y\}$
are uncountable.
$\{y\mid x\leq _L y\}$
are uncountable.
Now we may obtain the following result.
Theorem 5.9. Assume
![]() ${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
. The following are equivalent.
${\mathrm {ZF}}+{\mathrm {TD}}+{\mathrm {DC}_{\mathbb {R}}}$
. The following are equivalent.
-
1. Every uncountable set of reals has a perfect subset.
-
2. For every linear order
 $\leq _L$
over
$\leq _L$
over
 $\mathbb {R}$
, there is an order-preserving embedding from
$\mathbb {R}$
, there is an order-preserving embedding from
 $(2^{\omega },\leq )$
to
$(2^{\omega },\leq )$
to
 $(\mathbb {R},\leq _L)$
.
$(\mathbb {R},\leq _L)$
.
Proof (1)
![]() $\Rightarrow $
(2). The argument of Theorem 5.5 works here. Just replace “set with positive measure” by “uncountable set.”
$\Rightarrow $
(2). The argument of Theorem 5.5 works here. Just replace “set with positive measure” by “uncountable set.”
(2)
![]() $\Rightarrow $
(1). Fix an uncountable set of reals A. By Proposition 3.2,
$\Rightarrow $
(1). Fix an uncountable set of reals A. By Proposition 3.2,
![]() $|A|=|\mathbb {R}|$
. So
$|A|=|\mathbb {R}|$
. So
![]() $(A, \leq )$
is order isomorphic to
$(A, \leq )$
is order isomorphic to
![]() $(\mathbb {R}, \leq _L)$
for some
$(\mathbb {R}, \leq _L)$
for some
![]() $\leq _L$
. By (2), there is an order-preserving map from
$\leq _L$
. By (2), there is an order-preserving map from
![]() $(2^\omega , \leq )$
to
$(2^\omega , \leq )$
to
![]() $(\mathbb {R}, \leq _L)$
and hence
$(\mathbb {R}, \leq _L)$
and hence
![]() $(A, \leq )$
.
$(A, \leq )$
.
Fix
![]() $\pi : 2^\omega \to A$
that preserves order and so is monotonic. Then
$\pi : 2^\omega \to A$
that preserves order and so is monotonic. Then
![]() $\pi $
is continuous on all but countably many points. In particular,
$\pi $
is continuous on all but countably many points. In particular,
![]() $\pi $
is continuous (and injective) on a perfect subset P. So
$\pi $
is continuous (and injective) on a perfect subset P. So
![]() $\pi [P]$
is a perfect subset of A.
$\pi [P]$
is a perfect subset of A.
6 Regularity properties for dimension theory
For the notions and terminologies in fractal geometry, we follow the book [Reference Falconer7].
Given a non-empty
![]() $U\subseteq \mathbb {R}$
, the diameter of U is
$U\subseteq \mathbb {R}$
, the diameter of U is
Given any set
![]() $E\subseteq \mathbb {R}$
and
$E\subseteq \mathbb {R}$
and
![]() $d\geq 0$
, let
$d\geq 0$
, let
 $$ \begin{align*} \mathcal{P}_0^d(E)=\lim_{\delta\to 0}\sup\{\sum_{i<\omega} |B_i|^d: \{B_i\}\mbox{ is a collection of disjoint balls of radii at}\\ \mbox{ most }\delta \mbox{ with centres in }E\}, \end{align*} $$
$$ \begin{align*} \mathcal{P}_0^d(E)=\lim_{\delta\to 0}\sup\{\sum_{i<\omega} |B_i|^d: \{B_i\}\mbox{ is a collection of disjoint balls of radii at}\\ \mbox{ most }\delta \mbox{ with centres in }E\}, \end{align*} $$
and
Definition 6.1. Given any set
![]() $E$
:
$E$
:
-
(1) The Hausdorff dimension of E, or
 $\mathrm {Dim_H}(E)$
, is
$\mathrm {Dim_H}(E)$
, is  $$ \begin{align*}\inf\{d\mid \mathcal{H}^d(E)=0\}.\end{align*} $$
$$ \begin{align*}\inf\{d\mid \mathcal{H}^d(E)=0\}.\end{align*} $$
-
(2) The Packing dimension of E, or
 $\mathrm {Dim_P}(E)$
, is
$\mathrm {Dim_P}(E)$
, is  $$ \begin{align*}\inf\{d\mid \mathcal{P}^d(E)=0\}.\end{align*} $$
$$ \begin{align*}\inf\{d\mid \mathcal{P}^d(E)=0\}.\end{align*} $$
By the same reason as in the Lebesgue measure, it can be proved with
![]() ${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
that for every Borel set B and
${\mathrm {ZF}}+{\mathrm {CC}_{\mathbb {R}}}$
that for every Borel set B and
![]() $\epsilon>0$
, there is a closed set
$\epsilon>0$
, there is a closed set
![]() $F\subseteq B$
such that
$F\subseteq B$
such that
![]() $\mathrm {Dim_H}(F)>\mathrm {Dim_H}(B)-\epsilon $
.
$\mathrm {Dim_H}(F)>\mathrm {Dim_H}(B)-\epsilon $
.
Theorem 6.2 (Besicovitch [Reference Besicovitch1] and Davis [Reference Davies5])
For every analytic set A and every
![]() $\epsilon>0$
, there is a closed set
$\epsilon>0$
, there is a closed set
![]() $F\subseteq A$
such that
$F\subseteq A$
such that
![]() $\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)- \epsilon $
.
$\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)- \epsilon $
.
Theorem 6.3 (Joyce and Preiss [Reference Joyce and Preiss11])
For every analytic set A and every
![]() $\epsilon>0$
, there is a closed set
$\epsilon>0$
, there is a closed set
![]() $F\subseteq A$
such that
$F\subseteq A$
such that
![]() $\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)- \epsilon $
.
$\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)- \epsilon $
.
However Slaman proves that both Theorems 6.2 and 6.3 may fail even for some
![]() $\Pi ^1_1$
set under certain assumptions.
$\Pi ^1_1$
set under certain assumptions.
Theorem 6.4 (Slaman [Reference Slaman25])
Suppose that the set of constructible reals is not null, then there is a
![]() $\Pi ^1_1$
set C with
$\Pi ^1_1$
set C with
![]() $\mathrm {Dim_H}(C)=1$
but for any Borel
$\mathrm {Dim_H}(C)=1$
but for any Borel
![]() $F\subset C$
,
$F\subset C$
,
![]() $\mathrm {Dim_P}(F)=0$
.
$\mathrm {Dim_P}(F)=0$
.
We prove that Theorems 6.2 and 6.3 both remain true for all sets of reals under
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. As pointed out by one of the referees, the following result can be localized similarly as the localization of Theorem 5.1.
${\mathrm {ZF}}+{\mathrm {sTD}}$
. As pointed out by one of the referees, the following result can be localized similarly as the localization of Theorem 5.1.
Theorem 6.5.
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that for every set of reals A and every
${\mathrm {ZF}}+{\mathrm {sTD}}$
implies that for every set of reals A and every
![]() $\epsilon>0:$
$\epsilon>0:$
-
(1) There is a closed set
 $F\subseteq A$
such that
$F\subseteq A$
such that
 $\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)-\epsilon $
.
$\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)-\epsilon $
. -
(2) There is a closed set
 $F\subseteq A$
such that
$F\subseteq A$
such that
 $\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)-\epsilon $
.
$\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)-\epsilon $
.
To show the theorem, we use the “point-to-set” method.
Some more facts from algorithmic randomness theory are needed. Let K denote the prefix-free Kolmogorov complexity. We use
![]() $K^x$
to denote the prefix-free Kolmogorov complexity with oracle, which is a real, x. The following “point to set” style theorem is due to Lutz and Lutz. A similar form was also discovered by Cutler. See [Reference Cutler4, Theorem 1.4].
$K^x$
to denote the prefix-free Kolmogorov complexity with oracle, which is a real, x. The following “point to set” style theorem is due to Lutz and Lutz. A similar form was also discovered by Cutler. See [Reference Cutler4, Theorem 1.4].
Theorem 6.6 (Lutz and Lutz [Reference Lutz and Lutz15])
For every set
![]() $A\subseteq \mathbb {R}$
,
$A\subseteq \mathbb {R}$
,
 $$ \begin{align*}\mathrm{Dim_H}(A)=\inf_{x\in\mathbb{R}} \sup_{y\in A} \underline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\end{align*} $$
$$ \begin{align*}\mathrm{Dim_H}(A)=\inf_{x\in\mathbb{R}} \sup_{y\in A} \underline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\end{align*} $$
and
 $$ \begin{align*}\mathrm{Dim_P}(A)=\inf_{x\in\mathbb{R}} \sup_{y\in A} \overline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}.\end{align*} $$
$$ \begin{align*}\mathrm{Dim_P}(A)=\inf_{x\in\mathbb{R}} \sup_{y\in A} \overline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}.\end{align*} $$
The following lowness property is crucial to our proof.
Theorem 6.7 (Herbert [Reference Herbert9]; Lempp, Miller, Ng, Turetsky, Weber [Reference Lempp, Miller, Ng, Turetsky and Weber13])
-
• There is a perfect tree
 $T\subseteq 2^{<\omega }$
recursive in
$T\subseteq 2^{<\omega }$
recursive in
 $\emptyset '$
such that for any real
$\emptyset '$
such that for any real
 $x\in [T]$
,
$x\in [T]$
,  $$ \begin{align*}\forall y\in \mathbb{R}\Bigg(\underline{\lim}_{n\to \infty}\frac{K(y{\upharpoonright} n)}{n}=\underline{\lim}_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\Bigg).\end{align*} $$
$$ \begin{align*}\forall y\in \mathbb{R}\Bigg(\underline{\lim}_{n\to \infty}\frac{K(y{\upharpoonright} n)}{n}=\underline{\lim}_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\Bigg).\end{align*} $$
-
• There is a perfect tree
 $T\subseteq 2^{<\omega }$
recursive in
$T\subseteq 2^{<\omega }$
recursive in
 $\emptyset '$
such that for any real
$\emptyset '$
such that for any real
 $x\in [T]$
,
$x\in [T]$
,  $$ \begin{align*}\forall y\in \mathbb{R}\Bigg(\overline{\lim}_{n\to \infty}\frac{K(y{\upharpoonright} n)}{n}=\overline{\lim}_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\Bigg).\end{align*} $$
$$ \begin{align*}\forall y\in \mathbb{R}\Bigg(\overline{\lim}_{n\to \infty}\frac{K(y{\upharpoonright} n)}{n}=\overline{\lim}_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\Bigg).\end{align*} $$
Now we are ready to prove our major theorem of this section.
Proof of Theorem 6.5
(1). Suppose that
![]() $A\subseteq \mathbb {R}$
with
$A\subseteq \mathbb {R}$
with
![]() $\mathrm {Dim_H}(A)>0$
. Fix any
$\mathrm {Dim_H}(A)>0$
. Fix any
![]() $\epsilon>0$
. By Theorem 6.6, for every real z, there is some real
$\epsilon>0$
. By Theorem 6.6, for every real z, there is some real
![]() $x\in A$
such that
$x\in A$
such that
By Theorem 6.7 relative to z, there is a real
![]() $y>_T z$
such that
$y>_T z$
such that
So there must be some
![]() $e_0$
such that the set
$e_0$
such that the set
 $$ \begin{align*}B_{e_0}=\Bigg\{y\mid \Phi_{e_0}^{y'}\in A\wedge \underline{\lim}_{n\to \infty}\frac{K^y(\Phi_{e_0}^{y'}{\upharpoonright} n)}{n}>\mathrm{Dim_H}(A)-\frac{\epsilon}{2}\Bigg\}\end{align*} $$
$$ \begin{align*}B_{e_0}=\Bigg\{y\mid \Phi_{e_0}^{y'}\in A\wedge \underline{\lim}_{n\to \infty}\frac{K^y(\Phi_{e_0}^{y'}{\upharpoonright} n)}{n}>\mathrm{Dim_H}(A)-\frac{\epsilon}{2}\Bigg\}\end{align*} $$
ranges Turing degrees cofinally. By
![]() ${\mathrm {sTD}}$
, there is a pointed set
${\mathrm {sTD}}$
, there is a pointed set
![]() $P\subseteq B_{e_0}$
.
$P\subseteq B_{e_0}$
.
Then the set
is an analytic subset of A. By Theorem 6.6,
By Theorem 6.2, C has a closed subset F such that
Thus
(2). The same proof as (1) except replacing Hausdorff dimension with packing dimension. We leave the details to readers.
To continue our study, we need the following folklore technique lemma of which we sketch a proof for the completeness.
Lemma 6.8 (Folklore)
Assume
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. If
${\mathrm {ZF}}+{\mathrm {sTD}}$
. If
![]() $f:\mathbb {R}\to Ord$
is a degree invariant
$f:\mathbb {R}\to Ord$
is a degree invariant
![]() $($
i.e.,
$($
i.e.,
![]() $x\equiv _T y\implies f(x)=f(y))$
map such that
$x\equiv _T y\implies f(x)=f(y))$
map such that
![]() $f(x)<\omega _1^x$
, then there is an ordinal
$f(x)<\omega _1^x$
, then there is an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $f(x)=\alpha $
over an upper cone of Turing degrees.
$f(x)=\alpha $
over an upper cone of Turing degrees.
Proof Fix such a map f. Since there are countably many recursive functionals, by
![]() ${\mathrm {sTD}}$
, there is some recursive functional
${\mathrm {sTD}}$
, there is some recursive functional
![]() $\Phi $
such that
$\Phi $
such that
![]() $\Phi ^x$
codes a linear order for every real x, and a pointed set P such that
$\Phi ^x$
codes a linear order for every real x, and a pointed set P such that
![]() $f(x)\cong \Phi ^x$
for any
$f(x)\cong \Phi ^x$
for any
![]() $x\in P$
. Let T be a tree representing P such that
$x\in P$
. Let T be a tree representing P such that
![]() $\forall x\in P(T\leq _T x)$
. Then the set
$\forall x\in P(T\leq _T x)$
. Then the set
is a
![]() $\Sigma ^1_1(T)$
set and so
$\Sigma ^1_1(T)$
set and so
![]() $\Phi ^x$
represents an ordinal smaller than
$\Phi ^x$
represents an ordinal smaller than
![]() $\omega _1^T$
for any
$\omega _1^T$
for any
![]() $x\in P$
by
$x\in P$
by
![]() $\Sigma ^1_1$
-boundedness relative to T (see [Reference Chong and Yu2]). By
$\Sigma ^1_1$
-boundedness relative to T (see [Reference Chong and Yu2]). By
![]() ${\mathrm {sTD}}$
again, there must be some
${\mathrm {sTD}}$
again, there must be some
![]() $\alpha <\omega _1^T$
and a pointed set
$\alpha <\omega _1^T$
and a pointed set
![]() $Q\subseteq P$
such that
$Q\subseteq P$
such that
![]() $f(x)=\alpha $
for any
$f(x)=\alpha $
for any
![]() $x\in Q$
. This finishes the proof.
$x\in Q$
. This finishes the proof.
Crone, Fishman, and Jackson also proved the following result.
Theorem 6.9 (Crone, Fishman, and Jackson [Reference Crone, Fishman and Jackson3])
Assume
![]() ${\mathrm {ZF}}+{\mathrm {AD}}+\mathrm {DC}$
. If
${\mathrm {ZF}}+{\mathrm {AD}}+\mathrm {DC}$
. If
![]() $A=\bigcup _{\alpha <\kappa }A_{\alpha }$
for some ordinal
$A=\bigcup _{\alpha <\kappa }A_{\alpha }$
for some ordinal
![]() $\kappa $
, then
$\kappa $
, then
![]() $\mathrm {Dim_H}(A)=\sup \{\mathrm {Dim_H}( A_{\alpha })\mid \alpha <\kappa \}$
.
$\mathrm {Dim_H}(A)=\sup \{\mathrm {Dim_H}( A_{\alpha })\mid \alpha <\kappa \}$
.
We may provide an “elementary” proof of the following weaker result under
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
.
${\mathrm {ZF}}+{\mathrm {sTD}}$
.
Theorem 6.10. Assume
![]() ${\mathrm {ZF}}+{\mathrm {sTD}}$
. If
${\mathrm {ZF}}+{\mathrm {sTD}}$
. If
![]() $A=\bigcup _{\alpha <\omega _1}A_{\alpha }$
, then
$A=\bigcup _{\alpha <\omega _1}A_{\alpha }$
, then
Proof Let
![]() $r=\mathrm {Dim_H}(A)$
and for every real x,
$r=\mathrm {Dim_H}(A)$
and for every real x,
 $$ \begin{align*}\gamma_x=\min\Bigg\{\gamma|\sup_{y\in \bigcup_{\alpha< \gamma}A_{\alpha}} \underline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\geq r\Bigg\}.\end{align*} $$
$$ \begin{align*}\gamma_x=\min\Bigg\{\gamma|\sup_{y\in \bigcup_{\alpha< \gamma}A_{\alpha}} \underline\lim_{n\to \infty}\frac{K^x(y{\upharpoonright} n)}{n}\geq r\Bigg\}.\end{align*} $$
By Theorem 6.6,
![]() $\gamma _x$
is defined for every real x.
$\gamma _x$
is defined for every real x.
For any real z, by Theorem 6.7 and the assumption, there is a real
![]() $x>_T z$
such that
$x>_T z$
such that
![]() $\gamma _x=\gamma _z$
but
$\gamma _x=\gamma _z$
but
![]() $\omega _1^{x'}>\gamma _z$
. So
$\omega _1^{x'}>\gamma _z$
. So
In other words,
![]() $x\mapsto \gamma _x$
is a degree invariant function such that
$x\mapsto \gamma _x$
is a degree invariant function such that
![]() $\gamma _x<\omega _1^x$
over an upper cone of Turing degrees. Then by Lemma 6.8,
$\gamma _x<\omega _1^x$
over an upper cone of Turing degrees. Then by Lemma 6.8,
![]() $x\mapsto \gamma _x$
is a constant, say
$x\mapsto \gamma _x$
is a constant, say
![]() $\eta $
, over an upper cone. Then, by the countability of
$\eta $
, over an upper cone. Then, by the countability of
![]() $\eta $
, for every
$\eta $
, for every
![]() $m\in \omega $
, there must be some
$m\in \omega $
, there must be some
![]() $\alpha _m<\eta $
such that the set
$\alpha _m<\eta $
such that the set
![]() $\{x\mid \sup _{y\in A_{\alpha _m}} \underline \lim _{n\to \infty }\frac {K^x(y{\upharpoonright} n)}{n}\geq r-\frac {1}{m}\}$
ranges Turing degrees cofinally. Then by Theorem 6.6,
$\{x\mid \sup _{y\in A_{\alpha _m}} \underline \lim _{n\to \infty }\frac {K^x(y{\upharpoonright} n)}{n}\geq r-\frac {1}{m}\}$
ranges Turing degrees cofinally. Then by Theorem 6.6,
![]() $\mathrm {Dim_H}(A_{\alpha _m})\geq r-\frac {1}{m}$
. So
$\mathrm {Dim_H}(A_{\alpha _m})\geq r-\frac {1}{m}$
. So
We leave the proof of the second part to readers.
Some remarks:
Acknowledgement
We thank Denis Hirschfeldt, Ramez Sami, Theodore Slaman, and Hugh Woodin for their helpful discussions, especially for Slaman’s introducing Hausdorff dimension regularity to us.
Funding
Peng was partially supported by the NSF of China (Grant No. 11901562) and a program of the Chinese Academy of Sciences. Wu was partially supported by the NSFC (Grant No. 11871464). Yu was partially supported by the NSF of China (Grant Nos. 11671196 and 12025103).