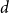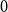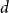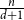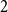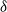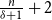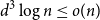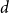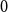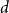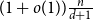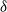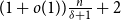Irregular subgraphs

Abstract

We suggest two related conjectures dealing with the existence of spanning irregular subgraphs of graphs. The first asserts that any $d$ -regular graph on $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between $0$ and $d$ deviates from $\frac{n}{d+1}$ by at most $2$ . The second is that every graph on $n$ vertices with minimum degree $\delta$ contains a spanning subgraph in which the number of vertices of each degree does not exceed $\frac{n}{\delta +1}+2$ . Both conjectures remain open, but we prove several asymptotic relaxations for graphs with a large number of vertices $n$ . In particular we show that if $d^3 \log n \leq o(n)$ then every $d$ -regular graph with $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between $0$ and $d$ is $(1+o(1))\frac{n}{d+1}$ . We also prove that any graph with $n$ vertices and minimum degree $\delta$ contains a spanning subgraph in which no degree is repeated more than $(1+o(1))\frac{n}{\delta +1}+2$ times.

1. Introduction

All graphs considered here are simple, that is, contain no loops and no parallel edges. For a graph $G$ and a non-negative integer $k$ , let $m(G,k)$ denote the number of vertices of degree $k$ in $G$ , and let $m(G)=\max _k m(G,k)$ denote the maximum number of vertices of the same degree in $G$ . One of the basic facts in Graph Theory is the statement that for every graph $G$ with at least $2$ vertices, $m(G) \geq 2$ . In this paper, we suggest the following two related conjectures.

Conjecture 1.1. Every $d$ -regular graph $G$ on $n$ vertices contains a spanning subgraph $H$ so that for every $k$ , $0 \leq k \leq d$ , $ \left \lceil \left | m(H,k)-\frac{n}{d+1}\right |\right \rceil \leq 2.$

Conjecture 1.2. Every graph $G$ with $n$ vertices and minimum degree $\delta$ contains a spanning subgraph $H$ satisfying $\lceil m(H) - \frac{n}{\delta +1} \rceil \leq 2$ .

If true, both conjectures are tight. One example showing it is the vertex disjoint union of two cycles of length $4$ . There are also many examples showing that an extra additive $1$ is needed even when $\frac{n}{d+1}$ is an integer. Indeed, if $G$ is any $d$ -regular graph with $n$ vertices, then by the pigeonhole principle, for any spanning subgraph $H$ of $G$ , $m(H) \geq \frac{n}{d+1}$ , as the degree of each vertex of $H$ is an integer between $0$ and $d$ . If, in addition, $n$ is divisible by $d+1$ , then the equality $m(H)=\frac{n}{d+1}$ is possible only if $m(H,k)=\frac{n}{d+1}$ for any $0 \leq k \leq d$ . However, this is impossible if $\left (\lfloor \frac{d+1}{2} \rfloor \right ) \frac{n}{d+1}$ is odd, as the number of vertices of odd degree in $H$ must be even. Note that a small value of $m(H)$ can be viewed as a measure of the irregularity of the graph $H$ . Thus both conjectures address the question of the existence of highly irregular subgraphs of graphs, stating that with this interpretation every graph $G$ contains a spanning subgraph $H$ which is nearly as irregular as the degrees of $G$ permit.

We have not been able to prove any of the two conjectures above, but can establish the following results, showing that some natural asymptotic versions of both do hold. In the following two results the $o(1)$ terms tend to $0$ as $n$ tends to infinity.

Theorem 1.3. If $d^3 \log n =o(n)$ then any $d$ -regular graph with $n$ vertices contains a spanning subgraph $H$ so that for every $0 \leq k \leq d$ , $m(H,k)=(1+o(1))\frac{n}{d+1}.$

Theorem 1.4. Any graph with $n$ vertices and minimum degree $\delta$ contains a spanning subgraph $H$ satisfying $m(H) \leq (1+o(1)) \left \lceil \frac{n}{\delta +1 } \right \rceil +2.$

In addition, if $\delta ^{1.24} \geq n$ and $n$ is sufficiently large, there is such an $H$ so that $m(H) \leq \left \lceil \frac{n}{\delta +1} \right \rceil + 2$ .

For any values of $d$ or $\delta$ and $n$ , without the assumption that $n$ is sufficiently large, we can prove a weaker universal bound showing that there is always a spanning subgraph $H$ with $m(H)$ bounded by $O(n/\delta )$ .

Theorem 1.5. Any $d$ -regular graph $G$ with $n$ vertices contains a spanning subgraph $H$ satisfying $m(H) \leq 8\frac{n}{d} +2$ .

Theorem 1.6. Any graph $G$ with $n$ vertices and minimum degree $\delta$ contains a spanning subgraph $H$ satisfying $m(H) \leq 16\frac{n}{\delta } +4$ .

We can improve the constants $8$ and $16$ above by a more complicated argument, but since it is clear that these improved constants are not tight we prefer to present the shorter proofs of the results above.

Our proofs combine some of the ideas used in the earlier work on the so called irregularity strength of graphs with techniques from discrepancy theory. The irregularity strength $s(G)$ of a graph $G$ with at most one isolated vertex and no isolated edges is the smallest integer $s$ so that one can assign a positive integer weight between $1$ and $s$ to each edge of $G$ so that for any two distinct vertices $u$ and $v$ , the sum of weights of all edges incident with $u$ differs from the sum of weights of all edges incident with $v$ . This notion was introduced in the 80s in [5]. Faudree and Lehel conjectured in [7] that there exists an absolute constant $C$ so that for every $d$ -regular graph $G$ with $n$ vertices, where $d \geq 2$ , $s(G)\leq \frac{n}{d}+C$ . The notion of irregularity strength and in particular the Faudree-Lehel conjecture received a considerable amount of attention, see for example [6, 8, 10–15]. The theorems above improve some of the results in these papers. In particular, Theorems 1.3 and 1.4 improve a result of [8] which implies that any $d$ -regular graph with $n$ vertices contains a spanning subgraph $H$ satisfying $m(H) \leq 2n/d$ provided $d^4 \log n \leq n$ . (The result there is stated in terms of assigning weights $1$ and $2$ to edges, for regular graphs this is equivalent.)

Theorems 1.4, 1.5 and 1.6 improve another result of [8] which implies that any $d$ -regular graph with $n \geq 10$ vertices, where $d \geq 10 \log n$ , contains a spanning subgraph $H$ with $m(H) \leq 48 \log n \frac{n}{d}$ , as well as a result that for all sufficiently large $n$ any $d$ -regular $G$ contains a spanning $H$ with $m(H) \leq 2\frac{n}{\sqrt d}$ . They also strengthen a result in [6] that shows that any $d$ -regular graph on $n$ vertices contains a spanning $H$ in which the number of vertices with degrees in any interval of length $c_1 \log n$ does not exceed $c_2 n \log n/d$ where $c_2\gt c_1$ are some absolute constants.

Our final results demonstrate a direct connection between the irregularity strength of graphs and our problem here.

Theorem 1.7. Let $G$ be a bipartite graph and let $s=s(G)$ be its irregularity strength. Then $G$ contains a spanning subgraph $H$ satisfying $m(H) \leq 2s-1$ . If $G$ is regular this can be improved to $m(H) \leq 2s-3$ .

A similar result, with a somewhat more complicated proof, holds without the assumption that $G$ is bipartite.

Theorem 1.8. Let $G$ be a graph and let $s=s(G)$ be its irregularity strength. Then $G$ contains a spanning subgraph $H$ satisfying $m(H) \leq 2s$ . If $G$ is regular this can be improved to $m(H) \leq 2s-2$ .

The rest of the paper contains the proofs as well as a brief final section suggesting natural versions of the two conjectures that may be simpler.

2. Proof of Theorem 1.3 and a special case of Theorem 1.4

In this section we prove Theorem 1.3 and describe also a short proof of Theorem 1.4 for the special case that the minimum degree $\delta$ satisfies $\delta ^4 =o (n/ \log n)$ . The proof of the theorem for larger $\delta$ requires more work, and is presented in Section 5.

We need several combinatorial and probabilistic lemmas. The first is the standard estimate of Chernoff for Binomial distributions.

Lemma 2.1 (Chernoff’s Inequality, c.f., for example, [3], Appendix A). Let $B(m,p)$ denote the Binomial random variable with parameters $m$ and $p$ , that is, the sum of $m$ independent, identically distributed Bernoulli random variables, each being $1$ with probability $p$ and $0$ with probability $1-p$ . Then for every $0\lt a \leq mp$ , $\mathbb{P}(X-mp \geq a) \leq e^{-a^2/3mp}$ and $\mathbb{P}(|X-mp| \geq a) \leq 2e^{-a^2/3mp}$ . If $a \geq mp$ then $\mathbb{P}(|X-mp| \geq a) \leq 2e^{-a/3}$ .

Another result we need is the following, proved (in a slightly different form) in [8].

Lemma 2.2 ([8]). Let $G=(V,E)$ be a graph and let $H$ be the spanning random subgraph of $G$ obtained as follows. For each vertex $v \in V$ let $x(v)$ be a uniform random weight in $[0,1]$ , where all choices are independent. An edge $uv \in E$ is an edge of $H$ iff $x(u)+x(v) \gt 1$ . Let $v$ be a vertex of $G$ and suppose its degree in $G$ is $d$ . Then for every $k$ , $0 \leq k \leq d$ , the probability that the degree of $v$ in $H$ is $k$ is exactly $\frac{1}{d+1}$ .

The (simple) proof given in [8] proceeds by computing the corresponding integral. Here is a combinatorial proof, avoiding this computation. Let $Y=x(v)$ and let $X_1,X_2, \ldots,X_d$ be the random weights of the neighbours of $v$ . Then the random variables $1-Y, X_1, X_2, \ldots,X_d$ are i.i.d uniform random variables in $[0,1]$ . By symmetry, $1-Y$ is equally likely to be the $k+1$ -st largest among the variables $1-Y, X_1, \ldots,X_d$ for all $1 \leq k+1 \leq d+1$ , that is, the probability that $1-Y$ is smaller than exactly $k$ of the variables $X_i$ is exactly $1/(d+1)$ . The desired results follows as $1-Y \lt X_i$ iff $X_i+Y \gt 1$ .

We will also use the following well known result of Hajnal and Szemerédi.

Lemma 2.3 ([9]). Any graph with $n$ vertices and maximum degree at most $D$ admits a proper vertex colouring by $D+1$ colours in which every colour class is of size either $\lfloor n/(D+1) \rfloor$ or $\lceil n/(D+1) \rceil$ .

We are now ready to prove Theorem 1.3 in the following explicit form.

Proposition 2.4. Let $G=(V,E)$ be a $d$ -regular graph on $n$ vertices. Suppose $0\lt{\varepsilon }\lt 1/3$ and assume that the following inequality holds.

(1) \begin{equation} (d+1)(d^2+1) 2e^{-\frac{1}{3}{\varepsilon }^2 \lfloor n/(d^2+1) \rfloor \cdot 1/(d+1)} \lt 1. \end{equation}

Then there is a spanning subgraph $H$ of $G$ so that for every integer $k$ , $0 \leq k \leq d$ ,

\begin{equation*} \left |m(H,k)-\frac {n}{d+1}\right | \leq {\varepsilon }\frac {n}{d+1}. \end{equation*}

Proof. For each vertex $v \in V$ , let $x(v)$ be a random weight chosen uniformly in $[0,1]$ , where all choices are independent. Let $H$ be the random spanning subgraph of $G$ consisting of all edges $uv \in E$ that satisfy $x(u)+x(v) \gt 1$ . Let $G^{(2)}$ denote the auxiliary graph on the set of vertices $V$ in which two distinct vertices are adjacent if and only if their distance in $G$ is either $1$ or $2$ . The maximum degree of $G^{(2)}$ is at most $d+d(d-1)=d^2$ and hence by Lemma 2.3 the set of vertices $V$ has a partition into $t=d^2+1$ pairwise disjoint subsets $V_1,V_2, \ldots,V_t$ , where

\begin{equation*}|V_i|=n_i \in \{ \lfloor n/(d^2+1) \rfloor, \lceil n/(d^2+1) \rceil \}\end{equation*}

for all $i$ and each $V_i$ is an independent set in $G^{(2)}$ . Note that this means that the distance in $G$ between any two distinct vertices $u,v \in V_i$ is larger than $2$ . As the degree of each vertex $v$ of $G$ in $H$ is determined by the random weights assigned to it and to its neighbours, it follows that for every fixed $0 \leq k \leq d$ , the $n_i$ indicator random variables $\{Z_{v,k}\;:\;v \in V_i\}$ where $Z_{v,k}=1$ iff the degree of $v$ in $H$ is $k$ , are mutually independent. By Lemma 2.2 each $Z_{v,k}$ is a Bernoulli random variable with expectation $1/(d+1)$ . For any fixed $k$ as above it thus follows, by Lemma 2.1 and the assumption inequality (1), that the probability that the number of vertices in $V_i$ whose degree in $H$ is $k$ deviates from $n_i/(d+1)$ by at least ${\varepsilon } n_i/(d+1)$ is smaller than $\frac{1}{(d^2+1)(d+1)}$ . By the union bound over all pairs $V_i,k$ , with positive probability this does not happen for any $k$ and any $V_i$ . But in this case for every $0 \leq k \leq d$ the total number of vertices with degree $k$ in $H$ deviates from $n/(d+1)$ by less than ${\varepsilon } \sum _i n_i/(d+1)={\varepsilon } n/(d+1).$ This completes the proof.

Remark: The proof above is similar to the proof of Lemma 7 in [8]. The improved estimate here is obtained by replacing the application of Azuma’s Inequality in [8] by the argument using the Hajnal-Szemerédi Theorem (Lemma 2.3), and by an appropriate different choice of parameters.

By a simple modification of the proof of Proposition 2.4 we next prove the following.

Proposition 2.5. Let $G=(V,E)$ be a graph on $n$ vertices with minimum degree $\delta$ and maximum degree $\Delta$ . Suppose $0\lt{\varepsilon }\lt 1/3$ and assume that the following inequality holds.

(2) \begin{equation} (\Delta +1)(\delta \Delta +1) e^{-\frac{1}{3}{\varepsilon }^2 \lfloor n/(\delta \Delta +1) \rfloor \cdot 1/(\delta +1)} \lt 1. \end{equation}

Then there is a spanning subgraph $H$ of $G$ so that

\begin{equation*} m(H) \leq (1+{\varepsilon })\frac {n}{\delta +1}. \end{equation*}

Proof. Start by modifying $G$ to a graph $G'$ obtained by repeatedly deleting any edge connecting two vertices, both of degrees larger than $\delta$ , as long as there are such edges. Thus $G'$ is a spanning subgraph of $G$ . It has minimum degree $\delta$ and every edge in it has at least one end-point of degree exactly $\delta$ . Let $G'^{(2)}$ denote the auxiliary graph on the set of vertices $V$ in which two distinct vertices are adjacent iff they are either adjacent or have a common neighbour in $G'$ . The maximum degree in $G'^{(2)}$ is at most

\begin{equation*}\max \{ \delta +\delta (\Delta -1), \Delta +\Delta (\delta -1)\}= \delta \Delta .\end{equation*}

We can now follow the argument in the proof of the previous proposition, splitting $V$ into $\delta \Delta +1$ nearly equal pairwise disjoint sets $V_i$ , and defining a spanning random subgraph $H$ of $G'$ (and hence of $G$ ) using independent random uniform weights in $[0,1]$ as before. Here for every vertex $v$ and every integer $k$ , the probability that the degree of $v$ in $H$ is $k$ , is at most $1/(\delta +1)$ . This, the obvious monotonicity, and the fact that the events corresponding to distinct members of $V_i$ are independent, imply, by Lemma 2.1 and by the assumption inequality (2), that the probability that $V_i$ contains at least $(1+{\varepsilon })|V_i|/(\delta +1)$ vertices of degree $k$ is smaller than $\frac{1}{(\delta \Delta +1)(\Delta +1)}$ . The desired result follows from the union bound, as before.

Similarly, we can prove the following strengthening of the last proposition.

Proposition 2.6. Let $G=(V,E)$ be a graph with at least $n$ vertices, minimum degree $\delta$ and maximum degree $\Delta$ . Suppose $0\lt{\varepsilon }\lt 1/3$ . Let $X \subset V$ be a set of $n$ vertices of $G$ and assume that the inequality ( 2 ) holds. Then there is a spanning subgraph $H$ of $G$ so that for every $k$ the number of vertices in $X$ of degree $k$ in $H$ is at most $(1+{\varepsilon })\frac{n}{\delta +1}$ .

Proof. The proof is a slight modification of the previous one. Let $G'$ be the graph obtained from $G$ as before. Let $F$ denote the auxiliary graph on the set of vertices $X$ in which two distinct vertices are adjacent iff they are either adjacent or have a common neighbour in $G'$ . The maximum degree in this graph is at most $\delta \Delta .$ We can thus follow the argument in the proof of the previous proposition, splitting $X$ into $\delta \Delta +1$ nearly equal pairwise disjoint sets $X_i$ , and defining a spanning random subgraph $H$ of $G'$ (and hence of $G$ ) using the independent random uniform weights in $[0,1]$ as before.

We can now prove the assertion of Theorem 1.4 provided $\delta ^4 =o(n/ \log n)$ in the following explicit form.

Proposition 2.7. Let $G=(V,E)$ be a graph on $n$ vertices with minimum degree $\delta$ . Suppose $0\lt{\varepsilon }\lt 1/3$ . Define $D=\frac{\delta (\delta +1)}{{\varepsilon }}$ and assume that the following inequality holds.

(3) \begin{equation} (D+1)(\delta D+1) e^{-\frac{1}{3}{\varepsilon }^2 \lfloor n/(\delta D+1) \rfloor \cdot 1/(\delta +1)} \lt 1. \end{equation}

Then there is a spanning subgraph $H$ of $G$ so that

\begin{equation*} m(H) \leq (1+2{\varepsilon })\frac {n}{\delta +1}. \end{equation*}

Proof. Let $G=(V,E)$ , $\delta$ , $\varepsilon$ and $D$ be as above. As in the previous proofs we start by modifying $G$ to a graph $G'$ obtained by repeatedly deleting any edge connecting two vertices, both of degrees larger than $\delta$ , as long as there are such edges. Thus $G'$ is a spanning subgraph of $G$ ; it has minimum degree $\delta$ and the set of all its vertices of degree exceeding $\delta$ is an independent set. Let $A$ denote the set of all vertices of degree $\delta$ in $G'$ , $B$ the set of all vertices of degrees larger than $\delta$ and at most $D$ in $G'$ (if there are any), and $C$ the set of all vertices of degree exceeding $D$ . Since all edges from the vertices of $C$ lead to vertices of $A$ (as $B \cup C$ is an independent set) it follows, by double-counting, that $|C| D \lt |A| \delta \leq n \delta$ and thus $|C| \leq n \delta/D ={\varepsilon }\frac{n}{\delta +1}.$

If $C=\emptyset$ define $G''=G'$ ; otherwise let $G''$ be the graph obtained from $G'$ as follows. For every vertex $v \in C$ of degree $d (\gt D)$ replace $v$ by a set $S_v$ of $k_v=\lfloor d/\delta \rfloor$ new vertices $v_1,v_2, \ldots,v_{k_v}$ . Split the set of neighbours of $v$ in $G'$ (that are all in $A$ ) into $k_v$ pairwise disjoint sets $N_1, N_2, \ldots, N_{k_v}$ , each of size at least $\delta$ and at most $2 \delta$ , and join the vertex $v_i$ to all vertices in $N_i$ $(1 \leq i \leq k_v)$ . Thus $G''$ is obtained by splitting all vertices of $C$ , and there is a clear bijection between the edges of $G''$ and those of $G'$ . Let $X$ be an arbitrary subset of $n$ vertices of $G''$ containing all vertices in $A \cup B$ . The graph $G''$ has minimum degree $\delta$ and maximum degree at most $D$ ; hence by Proposition 2.6 [which can be applied by the assumption inequality (3)] it has a spanning subgraph $H''$ so that no degree is repeated more than $(1+{\varepsilon })\frac{n}{\delta +1}$ times among the vertices of $X$ . Let $H$ be the spanning subgraph of $G'$ (and hence of $G$ ) consisting of exactly the set of edges of $H''$ . The degree of each vertex in $A \cup B$ in $H''$ is the same as its degree in $H$ , hence $H$ contains at most $(1+{\varepsilon })\frac{n}{\delta +1}$ vertices of each fixed degree in $A \cup B$ (which is a subset of $X$ ). We have no control on the degrees of the vertices of $C$ in $H$ , but their total number is at most ${\varepsilon } \frac{n}{\delta +1}$ . Therefore $m(H) \leq (1+2{\varepsilon })\frac{n}{\delta +1}$ , completing the proof.

3. Proof of Theorems 1.5 and 1.6

The main tool in the proofs of Theorems 1.5 and 1.6 is the following result of [1]. A similar application of this result appears in [13].

Lemma 3.1 ([1]). Let $G=(V,E)$ be a graph. For each vertex $v \in V$ let $\deg\!(v)$ denote the degree of $v$ in $G$ . For each vertex $v$ , let $a(v)$ and $b(v)$ be two non-negative integers satisfying

(4) \begin{equation} a(v) \leq \left \lfloor \frac{\deg\!(v)}{2} \right \rfloor \leq b(v) \lt \deg\!(v) \end{equation}

and

(5) \begin{equation} b(v) \leq \frac{\deg\!(v)+a(v)}{2}+1 \ \text{and} \ b(v) \leq 2a(v)+3. \end{equation}

Then there is a spanning subgraph $H$ of $G$ so that for every vertex $v$ the degree of $v$ in $H$ lies in the set $\{a(v), a(v)+1,b(v),b(v)+1\}$ .

Theorem 1.5 is an easy consequence of this lemma, as we show next.

Proof of Theorem 1.5 : Let $G=(V,E)$ be a $d$ -regular graph on $n$ vertices. Since the assertion is trivial for $d \leq 8$ assume $d\gt 8$ . Put $k=\lceil d/4 \rceil$ and split $V$ arbitrarily into $k$ pairwise disjoint sets of vertices $V_1, \ldots,V_k$ , each of size at most $\lceil n/k \rceil$ . For each vertex $v \in V_i$ define $a(v)=\lceil d/2 \rceil -i$ and $b(v)=\lceil d/2 \rceil +k -i$ . It is easy to check that $\deg\!(v)=d$ and each such $a(v),b(v)$ satisfy (4) and (5). By Lemma 3.1 there is a spanning subgraph $H$ of $G$ in which the degree of every $v \in V_i$ is in the set

\begin{equation*}S_i=\{\lceil d/2 \rceil -i, \lceil d/2 \rceil -i+1, \lceil d/2 \rceil +k -i, \lceil d/2 \rceil +k -i+1\}.\end{equation*}

It is easy to check that no integer belongs to more than $2$ of the sets $S_i$ , implying that $m(H) \leq 2\lceil n/k \rceil \lt 8n/d+2,$ and completing the proof.

The proof of Theorem 1.6 is similar, combining the reasoning above with one additional argument.

Proof of Theorem 1.6 : Let $G=(V,E)$ be a graph with $n$ vertices and minimum degree $\delta$ . As the result is trivial for $\delta \leq 16$ , assume $\delta \gt 16$ . Order the vertices of $G$ by degrees, that is, put $V=\{v_1, v_2, \ldots,v_n\}$ , where the degree of $v_i$ is $d_i$ and $d_1 \geq d_2 \geq \ldots \geq d_n$ . Put $k=\lceil \delta/4 \rceil$ and split the set of vertices into $m=\lceil n/k \rceil$ blocks $B_1, B_2, \ldots,B_m$ of consecutive vertices in the order above, each (besides possibly the last) containing $k$ vertices. Thus $B_i=\{v_{(i-1)k+1}, v_{(i-1)k+2}, \ldots,v_{ik}\}$ for all $i\lt m$ and $B_m=V-\cup _{i\lt m} B_i$ . Fix a block $B=B_i$ ; let $w_1, w_2, \ldots, w_k$ denote its vertices and let $f_1 \geq f_2 \geq \ldots \geq f_k$ be their degrees (assume now that $B$ is not the last block). For each vertex $w_i$ define $a_i=\lceil f_i/2 \rceil -i$ , $b_i=\lceil f_i/2 \rceil +k-i$ . For the last block $B_m$ define the numbers $a_i,b_i$ similarly, taking only the first $|B_m| (\leq k)$ terms defined as above. Note that the sequence $(a_1,a_2, \ldots,a_k)$ (as well as the possibly shorter one for the last block) is strictly decreasing, and so are the sequences $(a_1+1,a_2+1, \ldots,a_k+1)$ , $(b_1,b_2, \ldots,b_k)$ and $(b_1+1, b_2+1, \ldots,b_k+1)$ . Therefore, no integer belongs to more than $4$ of the sets $S(w_i)=\{a_i,a_i+1,b_i,b_i+1\}$ , $1 \leq i \leq k$ . Note also that the numbers $\deg\!(v)=f_i, a(v)=a_i, b(v)=b_i$ satisfy (4) and (5). By Lemma 3.1 there is a spanning subgraph $H$ of $G$ in which the degree of every vertex $v$ lies in the corresponding set $S(v)$ . Therefore $m(H) \leq 4m \lt 16\frac{n}{\delta }+4$ , completing the proof.

4. Proof of Theorems 1.7 and 1.8

Proof of Theorem 1.7 : The proof is based on the simple known fact that the incidence matrix of any bipartite graph is totally unimodular (see, e.g., [17], page 318). Let $G=(V,E)$ be a bipartite graph and let $s=s(G)$ be its irregularity strength. By the definition of $s(G)$ there is a weight function assigning to each edge $e \in E$ a weight $w(e)$ which is a positive integer between $1$ and $s$ , so that all the sums $\sum _{e \ni v} w(e)$ , $v \in V$ are pairwise distinct. Consider the following system of linear inequalities in the variables $x(e), e \in E$ .

\begin{equation*} 0 \leq x(e) \leq 1 \ \text {for all} \ e \in E \end{equation*}

and

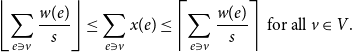\begin{equation*} \left \lfloor \sum _{e \ni v} \frac {w(e)}{s} \right \rfloor \leq \sum _{e \ni v} x(e) \leq \left \lceil \sum _{e \ni v} \frac {w(e)}{s} \right \rceil \ \text {for all} \ v \in V. \end{equation*}

This system has a real solution given by $x(e)=\frac{w(e)}{s}$ for all $e \in E$ . Since the $V \times E$ incidence matrix of $G$ is totally unimodular there is an integer solution as well, namely, a solution in which $x(e) \in \{0,1\}$ for all $e \in E$ . Let $H$ be the spanning subgraph of $G$ consisting of all edges $e$ with $x(e)=1$ . For each integer $k$ the vertex $v$ can have degree $k$ in $H$ only if $k-1 \lt \sum _{e \ni v} \frac{w(e)}{s} \lt k+1$ , that is, only if the integer $\sum _{e \ni v} w(e)$ is strictly between $s(k-1)$ and $s(k+1)$ . As there are only $2s-1$ such integers, and the integers $\sum _{e \ni v} w(e)$ are pairwise distinct, it follows that $m(H,k) \leq 2s-1$ .

If $G$ is regular one can repeat the above proof replacing $w(e)$ by $w(e)-1$ for every $e$ and replacing $s$ by $s-1$ . This completes the proof of Theorem 1.7.

The proof of Theorem 1.8 is similar to the last proof, but requires an additional argument, as the incidence matrix of a non-bipartite graph is not totally unimodular. We thus prove the following lemma. Its proof is based on some of the techniques of Discrepancy Theory, following the approach of Beck and Fiala in [4]. This lemma will also be useful in the proof of Theorem 1.4 described in the next section.

Lemma 4.1. Let $G=(V,E)$ be a graph, and let $z\;:\;E \mapsto [0,1]$ be a weight function assigning to each edge $e \in E$ a real weight $z(e)$ in $[0,1]$ . Then there is a function $x\;:\;E \mapsto \{0,1\}$ assigning to each edge an integer value in $\{0,1\}$ so that for every $v \in V$

(6) \begin{equation} \sum _{e \ni v} z(e)-1 \lt \sum _{e \ni v} x(e) \leq \sum _{e \ni v} z(e)+ 1. \end{equation}

Note that the deviation of $1$ in this inequality is tight, as shown by any odd cycle and the function $z$ assigning weight $1/2$ to each of its edges.

Proof. We describe an algorithm for generating the required numbers $x(e)$ . Think of these values as variables. During the algorithm, the variables $x(e)$ will always lie in the continuous interval $[0,1]$ . Call a variable $x(e)$ fixed if $x(e) \in \{0,1\}$ , otherwise call it floating. At the beginning of the algorithm, some (or all) variables $x(e)$ will possibly be floating, and as the algorithm proceeds, floating variables will become fixed. Once fixed, a variable does not change anymore during the algorithm, and at the end all variables will be fixed. For convenience, call an edge $e$ floating iff $x(e)$ is floating.

For each edge $e \in E$ , let $y_e$ denote the corresponding column of the $V \times E$ incidence matrix of $G$ , that is, the vector of length $|V|$ defined by $y_e(v)=1$ if $v \in e$ and $y_e(v)=0$ otherwise.

Start the algorithm with $x(e)=z(e)$ for all $e \in E$ . As long as the vectors $y_e$ corresponding to the floating edges $e$ (assuming there are such edges) are not linearly independent over the reals, let $\sum _{e \in E'} c_e y_e=0$ be a linear dependence, where $E'$ is a set of floating edges and $c_e \neq 0$ for all $e \in E'$ . Note that for any real $\nu$ , if we replace $x(e)$ by $x(e)+\nu c_e$ then the values of the sums

(7) \begin{equation} \sum _{e \ni v} x(e) \ \text{for all} \ v \in V \end{equation}

stay unchanged. As $\nu$ varies this determines a line of values of the variables $x(e)$ (in which the only ones that change are the variables $x(e)$ for $e \in E'$ ) so that the sums in (7) stay fixed along the line. By choosing $\nu$ appropriately we can find a point along this line in which all variables stay in $[0,1]$ and at least one of the floating variables in $E'$ reaches $0$ or $1$ . We now update the variables $x(e)$ as determined by this point, thus fixing at least one of the floating variables. Continuing in this manner the algorithm finds an assignment of the variables $x(e)$ so that for each $v \in V$ , $\sum _{e \ni v} x(e)=\sum _{e \ni v} z(e)$ and the set of vectors $y_e, e \in E'$ , where $E'$ is the set of floating edges, is linearly independent. Note that this implies that the set of edges in each connected component of the graph $(V,E')$ is either a tree, or contains exactly one cycle, which is odd.

As long as there is a connected component consisting of floating edges, which is not an odd cycle or a single edge, let $V''$ be the set of all vertices of such a component whose degree in the component exceeds $1$ . Let $E''$ be the set of edges of this component (recall that all of these edges are floating). Consider the following system of linear equations.

(8) \begin{equation} \sum _{e \ni v} x(e)=\sum _{e \ni v} z(e) \ \text{for all} \ v \in V''. \end{equation}

This system is viewed as one in which the only variables are $x(e)$ for $e \in E''$ . The other $x(e)$ appearing in the system are already fixed, and are thus considered as constants, and the values $z(e)$ are also constants. It is easy to check that the number of variables in this system, which is $|E''|$ , exceeds the number of equations, which is the number of vertices of degree at least $2$ in the component. Therefore there is a line of solutions, and as before we move to a point on this line which keeps all variables $x(e)$ in $[0,1]$ and fixes at least one variable $x(e)$ for some $e \in E''$ , shifting it to either $0$ or $1$ . Note, crucially, that each of the sums $\sum _{e \ni v} x(e)$ for $v \in V''$ stays unchanged, but the value of this sum for vertices of degree $1$ in the component may change.

Continuing this process we keep reducing the number of floating edges. When the graph of floating edges contains only connected components which are odd cycles or isolated edges we finish by rounding each floating variable $x(e)$ to either $0$ or $1$ , whichever is closer to its current value, where $x(e)=1/2$ is always rounded to $1$ . Once this is done, all variables $x(e)$ are fixed, that is $x(e) \in \{0,1\}$ for all $e$ . It remains to show that (6) holds for each $v \in V$ . To this end note that as long as the degree of $v$ in the graph consisting of all floating edges is at least $2$ , and the component in which it lies is not an odd cycle, the value of the sum $\sum _{e \ni v} x(e)$ stays unchanged (and is thus equal exactly to $\sum _{e \ni v} z(e)$ ) even after modifying the variables $x(e)$ in the corresponding step of the algorithm. Therefore, at the first time the degree of $v$ in this floating graph (the graph of floating edges) becomes $1$ , if this ever happens, the sum $\sum _{e \ni v} x(e)$ is still exactly $\sum _{e \ni v} z(e)$ . Afterwards this sum can change only by the change in the value of the unique floating edge incident with it, which is less than $1$ (as this value has been in the open interval $(0,1)$ and will end being either $0$ or $1$ ). The only case in which the final sum $\sum _{e \ni v} x(e)$ can differ by $1$ from $\sum _{e \ni v} z(e)$ is if the final step in which all floating edges incident with $v$ become fixed is a step in which the connected component of $v$ in the floating graph is an odd cycle, $x(e)=1/2$ for both edges of this component incident with $v$ , and both are rounded to the same value $1$ . In this case (6) holds with equality, and in all other cases it holds with a strict inequality. This completes the proof of the lemma.

Proof of Theorem 1.8 : The proof is similar to that of Theorem 1.7, replacing the argument using the total unimodularity of the incidence matrix of the graph by Lemma 4.1. Let $G=(V,E)$ be a graph let $s=s(G)$ be its irregularity strength. Thus there is a weight function assigning to each edge $e \in E$ a weight $w(e)$ which is a positive integer between $1$ and $s$ , so that all the sums $\sum _{e \ni v} w(e)$ , $v \in V$ are pairwise distinct. Define $z: E \mapsto [0,1]$ by $z(e)=w(e)/s$ for each $e \in E$ . By Lemma 4.1 there is a function $x: E \mapsto \{0,1\}$ so that for every $v \in V$ (6) holds. Let $H$ be the spanning subgraph of $G$ consisting of all edges $e$ with $x(e)=1$ . For each integer $k$ the vertex $v$ can have degree $k$ in $H$ only if

\begin{equation*} k-1 \leq \sum _{e \ni v} z(e) =\sum _{e \ni v} \frac {w(e)}{s} \lt k+1, \end{equation*}

that is, only if the integer $\sum _{e \ni v} w(e)$ is at least $s(k-1)$ and strictly smaller than $s(k+1)$ . As there are only $2s$ such integers, and the integers $\sum _{e \ni v} w(e)$ are pairwise distinct, it follows that $m(H,k) \leq 2s$ .

If $G$ is regular one can repeat the above proof replacing $w(e)$ by $w(e)-1$ for every $e$ and replacing $s$ by $s-1$ . This completes the proof.

5. Proof of Theorem 1.4

In this section we describe the proof of Theorem 1.4 for all $\delta$ and $n$ where $n$ is sufficiently large. If $\delta =o((n/\log n)^{1/4})$ the assertion of the theorem holds, as proved in Section 2. We thus can and will assume that $\delta$ is larger. In particular it will be convenient to fix a small $\epsilon \gt 0$ and assume that $\delta \geq \ln ^{2/\epsilon } n (\ln \ln n)^{1/\epsilon }$ . The argument here is more complicated than the one for smaller $\delta$ . To simplify the presentation we omit, throughout the proof, all floor and ceiling signs whenever these are not crucial (but leave these signs when this is important). We further assume whenever this is needed that $n$ is sufficiently large as a function of $\epsilon$ . The explicit version of the theorem we prove here is the following.

Theorem 5.1. Fix $\epsilon \in (0,1/4)$ . Every graph $G$ with $n$ vertices and minimum degree $\delta$ with $\delta \geq \ln ^{2/\epsilon } n (\ln \ln n)^{1/\epsilon }$ and $n$ sufficiently large in terms of $\epsilon$ contains a spanning subgraph $H$ satisfying

\begin{equation*} m(H) \lt \left \lceil \frac {n}{\delta } + \frac {5\sqrt {(n/\delta )(\ln n)}} {\delta ^{1/4}} \right \rceil + \left \lfloor \frac {2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \right \rfloor + 1. \end{equation*}

In particular, when $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ , and $n$ is sufficiently large, then

\begin{equation*} m(H) \leq \lceil n/(\delta +1) \rceil + 2. \end{equation*}

The constants $5, 2016$ and the assumption $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ can be improved, but as this will not lead to any significant change in the asymptotic statement given in Theorem 1.4 it is convenient to prove the result as stated above.

In the proof we assign binary weights to the edges of the graph $G$ , where weight one corresponds to edges in $H$ and zero to non-edges. The weight of a vertex will always be the sum of weights of the edges incident to it. We use $\deg\!(v)$ to denote the degree of the vertex $v$ in $G$ . By assumption $\deg\!(v) \geq \delta$ for every $v$ .

Put ${s^*} = \delta ^{1/2+\epsilon }, k = \delta ^{1/2-\epsilon }/\ln \ln n$ . By our assumption on $\delta$ we have $k \geq \ln ^2 n$ . We will assume that both $s^*$ and $k$ are integers, and $\delta -{s^*}$ is divisible by $\lfloor \sqrt{\delta }\rfloor$ . ¹ We start by partitioning the vertices randomly into a big set $B$ and a small set $S$ , where each is further partitioned into $B = B_1 \ldots \cup B_{\delta -{s^*}}$ and $S = S_1 \cup \ldots \cup S_{k}$ . This random partition is achieved in the following way. Let $X_v$ , $v \in V(G)$ be i.i.d. uniform random variables $X_v\sim U[0,1]$ . For each integer $1 \leq i \leq \delta -{s^*}$ , if $X_v \in [\frac{i-1}{\delta }, \frac{i}{\delta })$ , then place $v$ in $B_i$ . For each integer $1 \leq j \leq k-1$ , if $X_v \in \left [\frac{\delta -{s^*}}{\delta } + \frac{(j-1){s^*}}{\delta k},\frac{\delta -{s^*}}{\delta } + \frac{j{s^*}}{\delta k}\right )$ , place $v$ in $S_j$ ; if $X_v \in \left [\frac{\delta -{s^*}}{\delta } + \frac{(k-1){s^*}}{\delta k},1\right ]$ , place $v$ in $S_k$ .

The weight assignment will be done in three steps. The first two steps only concern edges in $B$ and between $B$ and $S$ . The last step only concerns edges within $S$ . We will randomly label some edges between $S$ and $B$ to be active and removable. Active edges denote the edges between $S$ and $B$ that will be assigned weight one in Step 1, and active and removable edges denote ones whose weights can be modified back to zero in Step 2. For each $1 \leq i \leq k$ , vertex $v \in S_i$ and its neighbour $u\in B$ , the edge $uv$ is active randomly and independently with probability $\frac{\delta - 4{s^*} i }{\delta -{s^*}}$ . It is removable randomly and independently with probability $\frac{32 \delta \ln n}{{s^*} \sqrt{\deg\!(u)}}$ .

The next lemma shows that the quantities we care about in $G$ are not far from their expected values with high probability.

Lemma 5.2. Let $\epsilon \in (0,1/4)$ . Suppose $n$ is sufficiently large in terms of $\epsilon$ and assume that $\delta ^{\epsilon } \geq \ln n \ln \ln n$ . Let $h\;:\;[n]\times [\delta -{s^*}] \to \mathbb{R}$ be a function $h(d, i) = c_1(d) i +c_2 d + c_3 \sqrt{d} + c_4$ where $c_1(d) \geq 1$ for all $d \geq \delta$ and $c_2, c_3, c_4 \in \mathbb{R}$ . Then, with probability at least $1 - 7/n^2$ , the following statements hold simultaneously with the random choices described above.

1. (i) For any integer $0 \leq j \leq n-1$ , the number of vertices $v \in B$ satisfying $h(\!\deg\!(v), Z(v)) \in [j, j+\lfloor \sqrt{\delta } \rfloor )$ is at most $ \lfloor \sqrt{\delta } \rfloor \frac{n}{\delta } +4 \sqrt{\frac{n }{\delta } \cdot \sqrt{\delta } \ln n}$ , where $Z(v) \in [\delta -{s^*}]$ is the random variable satisfying $v \in B_{Z(v)}$ .

2. (ii) For any vertex $v$ , its degree to $S$ is in the interval $[0.5{s^*} \deg\!(v)/ \delta, 1.5{s^*} \deg\!(v)/ \delta ]$ .

3. (iii) For each $1 \leq i \leq \delta -{s^*}$ and for each vertex $v \in B_i$ , its degree to $\{\bigcup B_j, \delta -{s^*} - i + 1 \leq j \leq \delta -{s^*}\}$ is in $\left [\frac{i\deg\!(v)}{\delta } -12\sqrt{\frac{i\deg\!(v)}{\delta }} \ln n, \ \frac{i\deg\!(v)}{\delta } + 12\sqrt{\frac{i\deg\!(v)}{\delta }} \ln n\right ]$ .

4. (iv) For each $1 \leq i \leq k$ and each vertex $v \in S_i$ , the number of edges between $v$ and $B$ that are active is in the interval

   \begin{equation*}\left [\frac {(\delta - 4{s^*} i)\deg\!(v)}{\delta } - \sqrt {\deg\!(v) }\ln n, \frac {(\delta - 4{s^*} i)\deg\!(v)}{\delta } +\sqrt {\deg\!(v)} \ln n\right ].\end{equation*}
   The number of edges between $v \in S$ and $B$ that are both active and removable is at most $ \frac{33(\delta - 4{s^*} i)\deg\!(v) \ln n}{\sqrt{\delta }{s^*}}$ .

5. (v) For each $1 \leq i \leq k$ and each $u \in B$ , the number of edges between $u$ and $S_i$ that are active is in the interval

   \begin{equation*}\left [\frac {{s^*} \deg\!(u)}{\delta k} \cdot \frac {\delta - 4{s^*} i}{\delta - {s^*}} - \sqrt {\frac {\deg\!(u) {s^*}}{\delta k}} \ln n, \frac {{s^*} \deg\!(u)}{\delta k} \cdot \frac {\delta - 4{s^*} i}{\delta - {s^*}} + \sqrt {\frac {\deg\!(u) {s^*}}{\delta k}} \ln n\right ].\end{equation*}
   The number of edges between $u \in B$ and $S$ that are both active and removable is at least $27\sqrt{\deg\!(u)} \ln n$ .

Proof. We first prove (i). Given $j$ and $v$ , since $c_1(\!\deg\!(v)) \geq 1$ as $\deg\!(v) \geq \delta$ , there is at most one integer $1 \leq i \leq \delta -{s^*}$ such that $h(\!\deg\!(v), i) = c_1(\!\deg\!(v)) i + c_2 \cdot \deg\!(v) + c_3{\sqrt{\deg\!(v)}} + c_4 \in [j, j+1)$ . Thus each vertex independently has probability at most $\lfloor \sqrt{\delta } \rfloor/ \delta$ to satisfy $h(\!\deg\!(v), Z(v)) \in [j, j+\lfloor \sqrt{\delta } \rfloor )$ . By Chernoff’s Inequality (Lemma 2.1) and a union bound over $0 \leq j \leq n-1$ and $v$ , the probability that (i) is violated is at most $ n^2 e^{-(16(n/\delta ) (\sqrt{\delta }) \ln n)/(3 (n/\delta )(\sqrt{\delta }))} \lt n^2 e^{-4 \ln n} = 1/n^2$ .

To prove (ii), note that for each vertex $v$ , each of its neighbours independently has probability $\frac{{s^*}}{\delta }$ to be in $S$ . Therefore its expected degree in $S$ is $\frac{\deg\!(v){s^*}}{\delta }$ . By Chernoff’s Inequality and a union bound over $v$ , (ii) is violated with probability at most $2ne^{- 0.25 \deg\!(v){s^*}/(3\delta )} \lt 1/n^2$ .

To prove (iii), note that for each $1 \leq i \leq \delta -{s^*}$ , each neighbour of $v$ independently has probability $i/\delta$ to be in $B_{\delta -{s^*}-i+1} \cup \ldots \cup B_{\delta -{s^*}}$ , and thus the expected number of its neighbours in $B_{\delta -{s^*}-i+1} \cup \ldots \cup B_{\delta -{s^*}}$ is $\frac{i\deg\!(v)}{\delta }$ . By Chernoff’s Inequality, for any positive value $\mu$ , given $v \in B_i$ , the probability that (iii) is violated is at most $2e^{-\mu ^{2}/(3\max (i\deg\!(v)/\delta, \mu ))}$ . Plugging in $\mu = 12\sqrt{i \deg\!(v)/\delta } \ln n$ and noting that $\max (i\deg\!(v)/\delta, \mu )) \leq 12 \frac{i \deg\!(v)}{\delta } \ln n$ , the probability that (iii) is violated for $v \in B_i$ is at most $2 e^{- 12 \ln n/ 3}= 2/n^4$ . By a union bound over all vertices the probability that (iii) is violated is much smaller than $1/n^2$ .

Similarly we can prove (iv). Given $v \in S_i$ , each edge incident to $v$ independently has probability $\frac{\delta -{s^*}}{\delta } \cdot \frac{\delta - 4{s^*} i}{\delta -{s^*}} = \frac{\delta - 4{s^*} i}{\delta }$ to be active. Thus the expected number of active edges incident to $v \in S_i$ is $\frac{\deg\!(v)(\delta - 4{s^*} i)}{\delta }$ . Again by Chernoff’s Inequality and a union bound over $v$ , the first statement in (iv) is violated with probability at most $n 2e^{- \deg\!(v) \ln ^2 n/ (3(\delta - 4{s^*} i)\deg\!(v)/\delta )} \lt n2e^{-\ln ^2n/3}\lt 1/n^2$ . Similarly, for a neighbour $u$ of $v \in S_i$ , the edge $(v, u)$ randomly and independently has probability $\frac{\delta - 4{s^*} i}{\delta } \frac{32\delta \ln n}{{s^*} \sqrt{\deg\!(u)}} \leq \frac{32 (\delta - 4{s^*} i) \ln n}{{s^*} \sqrt{\delta }}$ to be both active and removable. By Chernoff’s Inequality and a union bound over $v$ the probability that the second statement is violated is much smaller than $1/n^2$ .

(v) is proved in almost the same way. Fix $1 \leq i \leq k$ and $u \in B$ . Each edge $uv$ independently has probability $\frac{{s^*}}{k\delta } \cdot \frac{\delta - 4{s^*} i}{\delta -{s^*}}$ to be active and satisfy $v \in S_i$ ; and it has probability $\frac{{s^*}}{k\delta } \cdot \frac{\delta - 4{s^*} i}{\delta -{s^*}} \cdot \frac{32\delta \ln n}{{s^*} \sqrt{\deg\!(u)}} = \frac{32 \ln n}{k} \cdot \frac{\delta - 4{s^*} i}{(\delta -{s^*})\sqrt{\deg\!(u)}} \gt \frac{30 \ln n}{k \sqrt{\deg\!(u)}}$ to be both active and removable and incident to $S_i$ . Thus for any $u \in B$ the expected number of edges $uv$ with $v \in S$ which are both active and removable is at least ${30\ln n}{\sqrt{\deg\!(u)}}$ . Applying Chernoff’s Inequality and a union bound it follows that the probability that the statement fails is much smaller than $2/n^2$ .

Therefore, with probability at least $1- 7/n^2$ all assertions of Lemma 5.2 hold, where the function $h(\!\deg\!(v), i)$ in (i) is

\begin{equation*}h_B(\!\deg\!(v),i) = \frac {i\deg\!(v)}{\delta }+ \frac {{s^*} \deg\!(v)}{\delta }\frac {\delta - 2{s^*} (k+1)}{\delta - {s^*}} - 13\sqrt {\deg\!(v)} \ln n.\end{equation*}

Since $\deg\!(v) \geq \delta$ , $k{s^*} = \delta/\ln \ln n$ and by the lower bounds on $\delta$ in the assumption, it is easy to see that $h_B(d,i) \gt{s^*}/ 2 \gt \sqrt{\delta }$ . Note that $h_B$ satisfies the requirement of $h(d,i)$ in Lemma 5.2. We can now proceed assigning weights in $\{0,1\}$ to the edges in $G$ in three steps.

In Step 1, we assign the following edges weight one: (1) for all $1 \leq i \leq \delta -{s^*}$ , all the edges between $B_i$ and $\{ \bigcup _j B_j, \delta -{s^*} - i + 1 \leq j \leq \delta -{s^*}\}$ ; (2) all the active edges between $B$ and $S$ .

In Step 2, the goal is to ensure that each vertex weight appears in at most

(9) \begin{equation} \lceil n/\delta + 5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4}\rceil \end{equation}

vertices in $B$ . This is achieved by making two modifications. First ensure that each vertex $v$ in $B_i$ has weight exactly $\lfloor h_B(\!\deg\!(v),i) \rfloor$ . By Lemma 5.2 applied with $h_B(d,i)$ , with probability at least $1-7/n^2$ after Step 1, for each $1 \leq i \leq \delta -{s^*}$ , the weight of $v \in B_i$ deviates from

\begin{equation*} \frac {i\deg\!(v)}{\delta }+ \sum _{j=1}^k \frac {{s^*} \deg\!(v)}{\delta k} \cdot \frac {\delta - 4{s^*} j}{\delta - {s^*}} = h_B(\!\deg\!(v),i) + 13\sqrt {\deg\!(v)} \ln n \end{equation*}

by at most $k\sqrt{\frac{\deg\!(v){s^*} }{\delta k}} \ln n + 12\sqrt{\deg\!(v)} \ln n \lt 13\sqrt{\deg\!(v)} \ln n$ by Lemma 5.2 (iii) and the first statement in (v). Thus it is possible to transform the weight of $v$ to exactly $\lfloor h_B(\!\deg\!(v),i) \rfloor$ by reducing the weights of at most $26\sqrt{\deg\!(v)} \ln n +1 \lt 26.5\sqrt{\deg\!(v)} \ln n$ (active and removable) edges from $v$ to $S$ from one to zero.

Suppose this first modification is possible, in the second modification, by Lemma 5.2 (i) and the fact that $h_B(\!\deg\!(v),i) \gt \sqrt{\delta }$ for each vertex $v$ and $1\leq i \leq \delta -{s^*}$ and that $\delta -{s^*}$ is divisible by $\lfloor \sqrt{\delta } \rfloor$ , we can further reduce the weights of at most $2(\sqrt{\delta })$ edges between each $v \in B$ and $S$ ensuring that each integer vertex weight appears in at most $ \lceil ( \lfloor \sqrt{\delta } \rfloor n/\delta + 4 \sqrt{(n/\delta )(\sqrt{\delta }) \ln n} )/ \lfloor \sqrt{\delta } \rfloor \rceil \leq \lceil n/\delta + 5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4}\rceil$ vertices in $B$ , as desired. Indeed, this can be done by considering, for any fixed admissible $j\gt 1$ , all vertices whose weight after the first modification lies in $[(j-1)( \lfloor \sqrt{\delta } \rfloor ), j( \lfloor \sqrt{\delta } \rfloor ))$ . Their weights can be reduced and distributed uniformly among the possible weights in the interval $[(j-2)( \lfloor \sqrt{\delta } \rfloor ), (j-1)( \lfloor \sqrt{\delta } \rfloor ))$ .

It is not difficult to check that these two modifications can be accomplished by reducing only the weights of some edges which are both active and removable. Indeed, for every vertex $v \in B$ it is only needed to reduce its weight by at most $26.5\sqrt{\deg\!(v)} \ln n+ 2 \sqrt{\delta } \lt 27\sqrt{\deg\!(v)} \ln n$ . By Lemma 5.2 (v), the number of edges between $v$ and $S$ which are both active and removable is at least $27 \sqrt{\deg\!(v)}\ln n$ , and as all active edges between $B$ and $S$ have weight one prior to Step 2 there are enough edges whose weights can be reduced from one to zero to allow the two modifications.

In Step 3, we will only adjust the weights of edges within $S$ to ensure that each weight appears in at most $ \lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor + 1$ vertices in $S$ . We first use a method developed in a paper in preparation by the second author and J. Przybyło [16] to identify which vertices in $S$ might have the same weight. For each vertex $v \in S$ , we will define a set $L(v)$ such that $v,u \in S$ cannot have the same weight at the end of Step 3 if $u \notin L(v)$ . We will then show that with high probability all sets $L(v)$ will not be large.

To start, we relax the problem where the weight of each edge in $S$ can be any real number in $[0,1]$ . We first analyse the range of weight for each $v \in S$ after adjusting weights in $S$ .

By Lemma 5.2 (iv), after Step 2, since $\sqrt{\deg\!(v)} \ln n \leq \deg\!(v)\ln n/\sqrt{\delta }$ , the weight of $v \in S_i$ is at least the number of edges incident to $v$ which are active but not removable, which is bounded below by

\begin{align*} & \frac{(\delta - 4{s^*} i)\deg\!(v)}{\delta } - \frac{\deg\!(v)\ln n}{\sqrt{\delta }} - \frac{33(\delta - 4{s^*} i)\deg\!(v) \ln n}{\sqrt{\delta }{s^*}} \\ & \quad = \deg\!(v)\!\left (\left (1-\frac{4{s^*} i}{\delta }\right )\!\left (1 - \frac{33\ln n}{\delta ^{\epsilon }}\right )- \frac{\ln n}{\sqrt{\delta }} \right ) \geq \deg\!(v)\!\left (1-\frac{4{s^*} i}{\delta } - \frac{34\ln n}{\delta ^{\epsilon }} \right ). \end{align*}

This is also a lower bound on the weight of $v \in S_i$ after Step 3. By Lemma 5.2 (ii), the additional weight each vertex $v \in S$ can gain in Step 3 is at most $\deg _S\!(v) \cdot 1 \leq 1.5 \deg\!(v){s^*}/\delta$ . Again together with Lemma 5.2 (iv), the weight of $v \in S_i$ after Step 3 is at most $\left (\frac{(\delta - 4{s^*} i)\deg\!(v)}{\delta }+\frac{\deg\!(v)\ln n}{\sqrt{\delta }} \right ) +1.5 \deg\!(v){s^*}/\delta = \deg\!(v)\!\left ( 1 - \frac{4{s^*} i}{\delta } + \frac{\ln n}{\sqrt{\delta }} + \frac{1.5{s^*}}{\delta } \right ) \lt \deg\!(v)\!\left ( 1 - \frac{4{s^*} i}{\delta } + \frac{3{s^*}}{{\delta }} \right )$ . In summary, the weight of $v \in S_i$ after assigning arbitrary weights in $[0,1]$ to edges in $S$ is always in the interval

(10) \begin{equation} I_{v, i}= \left [ \deg\!(v)\!\left (1-\frac{4{s^*} i}{\delta } - \frac{34\ln n}{\delta ^{\epsilon }} \right ), \deg\!(v)\!\left ( 1 - \frac{4{s^*} i}{\delta } + \frac{3{s^*}}{\delta } \right ) \right ]. \end{equation}

Therefore, vertex $v \in S_i$ and $u\in S_j$ can have the same weight after Step 3 only if $I_{v,i} \cap I_{u,j} \neq \emptyset$ , which is equivalent to

(11) \begin{align} \deg\!(v)\!\left (1-\frac{4{s^*} i}{\delta } - \frac{34\ln n}{\delta ^{\epsilon }} \right ) \leq & \deg\!(u)\!\left ( 1 - \frac{4{s^*} j}{\delta } + \frac{3{s^*}}{\delta } \right ); \text{ and } \end{align}

(12) \begin{align} \deg\!(u)\!\left (1-\frac{4{s^*} j}{\delta } - \frac{34\ln n}{\delta ^{\epsilon }} \right ) \leq & \deg\!(v)\!\left ( 1 - \frac{4{s^*} i}{\delta } + \frac{3{s^*}}{\delta } \right ).\end{align}

Let $u \in L(v)$ if and only if $u \neq v$ , $u \in S$ , and both (11) and (12) hold if $u \in S_j$ . Clearly $u \notin L(v)$ implies the distinct vertices $u,v \in S$ have distinct weights.

Claim 5.3. With probability at least $1-1/n^2$ , $|L(v)| \leq \frac{42n\deg\!(v) \ln n}{k \delta ^{1+\epsilon } }$ for all $v \in S$ .

Proof. Given $v \in S_i$ we bound the number of vertices $u$ in $L(v)$ by bounding the number of vertices $u$ in all sets $S_j$ where $j$ satisfies both inequalities (11) and (12). These two inequalities together imply

\begin{equation*} \frac {\deg\!(v)}{\deg\!(u)} \left (1-\frac {4{s^*} i}{\delta } - \frac {34\ln n}{\delta ^{\epsilon }} \right ) - \frac {3{s^*}}{\delta } \leq 1-\frac {4{s^*} j}{\delta } \leq \frac {\deg\!(v)}{\deg\!(u)} \left ( 1 - \frac {4{s^*} i}{\delta } + \frac {3{s^*}}{\delta } \right ) + \frac {34\ln n}{\delta ^{\epsilon }}. \end{equation*}

This means the value of $\frac{4{s^*} j}{ \delta }$ can only lie in an interval of length $\frac{\deg\!(v)}{\deg\!(u)}\left (\frac{3{s^*}}{\delta } + \frac{34\ln n}{\delta ^{\epsilon }} \right ) + \frac{34\ln n}{\delta ^{\epsilon }} +\frac{3{s^*}}{\delta } \leq \frac{2\deg\!(v)}{\delta }\left (\frac{3{s^*}}{\delta } + \frac{34\ln n}{\delta ^{\epsilon }} \right ) \leq \frac{2\deg\!(v)}{\delta } \frac{37\ln n}{\delta ^{\epsilon }}$ where the last inequality uses $\epsilon \lt 1/4$ . This implies $j$ can only lie in an interval of length at most $\frac{\delta }{4{s^*}} \frac{2\deg\!(v)}{\delta } \frac{37\ln n}{\delta ^{\epsilon }} = \frac{\deg\!(v)}{2{s^*}} \frac{37\ln n}{\delta ^{\epsilon }}$ .

Since with probability $\frac{{s^*}}{k \delta }$ , the vertex $u$ lies in $S_j$ for any given $j$ , the probability that $u$ satisfies $u \in S_j$ for some $j$ with $I_{v,i} \cap I_{u,j} \neq \emptyset$ is at most

\begin{equation*}\frac {{s^*}}{k \delta } \left (\frac {\deg\!(v)}{2{s^*} } \frac {37\ln n}{\delta ^{\epsilon }}+1\right ) \leq \frac {{s^*}}{k \delta }\frac {\deg\!(v)}{{s^*} } \frac {37\ln n}{\delta ^{\epsilon }} = \frac {37\deg\!(v) \ln n}{k \delta ^{1+\epsilon } }. \end{equation*}

The first inequality uses the fact that $\epsilon \lt 1/4$ . Thus $\mathbb{E}[|L(v)|] \leq n\frac{37\deg\!(v) \ln n}{k \delta ^{1+\epsilon } }$ . Since the events for different vertices $u$ are independent, by Chernoff’s Inequality the probability that $|L(v)| \geq n\frac{42\deg\!(v) \ln n}{k \delta ^{1+\epsilon } }$ is at most $n^{-4}$ . By a union bound over $v$ , the desired result follows.

We are now ready to adjust the weights of edges in $S$ . First we show there is a desired weighting with edges in $S$ having fractional weights in $\{0, 1/4, 1/2, 3/4, 1\}$ .

Claim 5.4. With probability at least $1-8/n^2$ one can assign each edge in $S$ a weight in $\{0, 1/4, 1/2, 3/4, 1\}$ such that for each vertex $v \in S$ , the number of vertices in $L(v)$ whose weight (including the weight to $B$ ) differs from that of $v$ by strictly less than $11/4$ is at most $\lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor$ .

In particular, if $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ , for any two vertices $v, u \in S$ where $u \in L(v)$ , the difference between the weights of $v$ and $u$ is at least $11/4$ .

Proof. We use a modified version of the algorithm by Kalkowski, Karoński, and Pfender [10]. All edge weights in $S$ are initialized to be $1/2$ .

Order the vertices of $S$ arbitrarily as $v_1, v_2, \ldots$ and process them sequentially starting from $v_1$ . When processing $v_i$ , we will find a set $\Lambda _{v_i}$ of the form $\{\frac{12a}{4}, \frac{12a+1}{4}\}$ for some $a \in \mathbb{Z}$ , such that throughout the later stages of the algorithm, $\Lambda _{v_i}$ will stay unchanged and the weight of $v_i$ will always stay in $\Lambda _{v_i}$ . Suppose we are processing $v_i$ for $i \geq 1$ . For each forward edge, that is, edge $v_i v_j$ where $j \gt i$ if exists, we allow to change the edge weight by increasing it by $0$ or $1/4$ ; for each backward edge $v_i v_j$ where $j \lt i$ if exists, we allow to change the weight by adding an element of $\{-1/4, 0, 1/4\}$ , where if the current weight of $v_j$ is the maximum value in $\Lambda _{v_j}$ , we can only change this backward edge by adding a member of $\{-1/4, 0\}$ , whereas if the current weight of $v_j$ is the minimum value in $\Lambda _{v_j}$ , we can only change this backward edge by adding a member of $\{0, 1/4\}$ . This rule guarantees the weight of $v_j$ which has been processed always stays in $\Lambda _{v_j}$ . Furthermore, by all combinations of the allowable changes, the weight of $v_i$ can achieve any value in an arithmetic progression $P_i$ with common difference $1/4$ and of length $\deg _S(v_i)$ . In addition, by our constraints on the structure of the sets $\Lambda _{v_i}$ , a vertex $v_i$ has weight in $\Lambda _{v_i} = \{\frac{12a}{4}, \frac{12a+1}{4}\}$ if and only if $v_i$ has weight in $J_{v_i} = \{\frac{12a}{4}, \frac{12a+1}{4}, \frac{12a+2}{4}, \ldots, \frac{12a+11}{4}\}$ . Thus there must be a set $ \{\frac{12b}{4}, \frac{12b+1}{4}, \frac{12b+2}{4}, \ldots, \frac{12b+11}{4}\} \subset P_i$ for some $b \in \mathbb{Z}$ which is shared by at most $\lfloor |L(v)|/ (( |P_i| -22)/12) \rfloor$ sets $J_{v_j}$ for $v_j \in L(v)$ and $j \lt i$ . Fix such a set $\{\frac{12b}{4}, \frac{12b+1}{4}, \frac{12b+2}{4}, \ldots, \frac{12b+11}{4}\} \subset P_i$ as $J_{v_i}$ and then ensure that the weight of $v_i$ lies in $\{ \frac{12b}{4}, \frac{12b+1}{4}\} = \Lambda _{v_i}$ by adjusting the weights of forward and backward edges appropriately, and then continue to $v_{i+1}$ . By Claim 5.3 and Lemma 5.2 (ii) which implies that $|P_i| \geq 0.5{s^*} \deg\!(v)/\delta$ ,

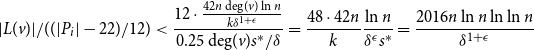\begin{equation*} |L(v)|/ (( |P_i| -22)/12) \lt \frac {12 \cdot \frac {42n\deg\!(v) \ln n}{k \delta ^{1+\epsilon } } }{ 0.25 \deg\!(v) {s^*}/ \delta } = \frac {48\cdot 42 n}{k } \frac {\ln n}{\delta ^{\epsilon } {s^*} } = \frac {2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \end{equation*}

where the equality is by plugging in $k{s^*} = \delta/ \ln \ln n$ . Therefore we have shown that each set $J_{v_i}$ can be shared by at most $\lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor$ other $J_{v_j}$ for $v_j \in L(v_i)$ . Furthermore, if $J_v$ is different from $J_u$ which implies $J_v$ is disjoint from $J_u$ , then since the weight of $v$ is in $\Lambda _v \subset J_v$ and the weight of $u$ is in $\Lambda _u \subset J_u$ , the difference between the weights of $u$ and $v$ is at least $11/4$ . Lastly, notice that each edge changes its weight at most twice (once as a forward edge and once as a backward edge), so all edge weights in $S$ stay in $\{0, 1/4, 1/2, 3/4, 1\}$ . Therefore the first statement holds. The second statement holds by noticing that when $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ , then $\lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor = 0$ .

Suppose $\delta ^{\epsilon } \geq \ln ^2 n \ln \ln n$ . We are now ready to finish the construction and the proof. Suppose $z(e)$ are the current weights of edges $e$ in $E(G)$ where when $e \in E(S)$ , $z(e) \in \{0, 1/4, 1/2, 3/4, 1\}$ and when $e \notin E(S)$ , $z(e) \in \{0,1\}$ . We now show that we can change the edge weights in $S$ to be in $\{0,1\}$ so that each weight is shared by at most $ \lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor + 1$ vertices in $S$ . To achieve this, we apply Lemma 4.1 to the induced subgraph on $S$ to conclude that there is a binary weighting $x\;:\;E(G) \to \{0,1\}$ such that $x(e) = z(e)$ for $e \notin E(S)$ , and for each $v\in S$ ,

(13) \begin{equation} \sum _{e \ni v} z(e) - 1 \lt \sum _{e \ni v} x(e) \leq \sum _{e \ni v} z(e) + 1. \end{equation}

We now bound the number of vertices in $S$ sharing the same weight. Given $v \in S$ , if a different vertex $u\in S$ satisfies $\sum _{e \ni v} x(e)= \sum _{e \ni u} x(e)$ , then $u \in L(v)$ . Furthermore, by the triangle inequality and (13),

\begin{equation*} 0 = \left |\sum _{e \ni v} x(e) - \sum _{e \ni u} x(e)\right | \geq \left |\sum _{e \ni v} z(e) - \sum _{e \ni u} z(e)\right | - 2, \end{equation*}

which implies $ |\sum _{e \ni v} z(e) - \sum _{e \ni u} z(e) | \leq 2 \lt 11/4$ . By Claim 5.4, there are at most $\lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor$ different $u \in L(v)$ with $ | \sum _{e \ni v} z(e) - \sum _{e \ni u} z(e) | \lt 11/4$ . Thus each weight with respect to $x$ is shared by at most $\lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \rfloor + 1$ vertices in $S$ , as desired.

We have shown in (9) in Step 2 that the number of vertices in $B$ with the same weight is at most $\lceil n/\delta + 5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4}\rceil$ , and note that weights of vertices in $B$ do not change after Step 2. Therefore we have shown that there is a spanning subgraph $H$ of $G$ (corresponding to the edges with $x(e)=1$ ) satisfying $m(H) \leq \left \lceil n/\delta + 5 \sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4} \right \rceil + \left \lfloor \frac{2016 n \ln n \ln \ln n}{\delta ^{1+\epsilon }} \right \rfloor + 1$ . This completes the proof of the first statement in Theorem 5.1. In case $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ , $m(H) \leq \lceil n/\delta + 5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4}\rceil + 1 = \lceil n/(\delta +1) + n/(\delta (\delta +1)) +5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4} \rceil + 1$ . Since $\delta ^{1+\epsilon } \gt 2016 n \ln n \ln \ln n$ , the value of $n/(\delta (\delta +1)) + 5\sqrt{n/\delta } \sqrt{\ln n}/\delta ^{1/4}$ is arbitrarily small when $n$ is sufficiently large. Thus in this case, $m(H) \leq \lceil n/(\delta +1) \rceil +2$ , as needed.

To see the first statement in Theorem 1.4 holds, notice that when $\delta ^{1+\epsilon } \geq 2016 n \ln n \ln \ln n$ then it is implied by the second statement in Theorem 5.1. Otherwise it follows from the first statement of this theorem and the fact that we may assume that $\delta \geq \Omega ((n/\log n)^{1/4})$ by the results in Section 2, that $m(H) \leq (n/\delta ) (1+o(1)) = (n/(\delta +1))(1+o(1))$ . The second statement in Theorem 1.4 holds since the condition $\delta ^{1.24} \geq n$ implies that for sufficiently large $n$ , $\delta ^{1.245} \gt 2016 n \ln n \ln \ln n$ and the desired result follows from the second statement in Theorem 5.1.

6. Open problems

The two Conjectures 1.1 and 1.2 remain open, although we have established some weaker asymptotic versions. It is possible that the constant $2$ in both conjectures can even be replaced by $1$ provided the number of vertices in the graphs considered is large. As proved by Axenovich and Füredi in [2] this is indeed the case for Conjecture 1.2 provided $ \delta \geq 7n/8 + cn^{3/4}$ for an appropriate absolute constant $c$ . It may be interesting to prove that the assertions of the two conjectures hold if we replace the constant $2$ in each of them by some absolute constant $C$ . It will also be nice to prove that every $d$ -regular graph on $n$ vertices, where $d=o(n)$ , contains a spanning subgraph $H$ in which every degree between $0$ and $d$ appears $(1+o(1))\frac{n}{d+1}$ times, even when $d$ is nearly linear in $n$ . As is the case throughout the paper, the $o(1)$ -term here tends to $0$ as $n$ tends to infinity. Finally, Theorems 1.7 and 1.8 suggest the question of deciding whether or not there is an absolute constant $C$ so that every graph $G$ (with a finite irregularity strength $s(G)$ ) contains a spanning subgraph $H$ satisfying $m(H) \leq s(G)+C$ .