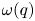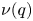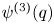Partitions with parts separated by parity: conjugation, congruences and the mock theta functions

Abstract

Noting a curious link between Andrews’ even-odd crank and the Stanley rank, we adopt a combinatorial approach building on the map of conjugation and continue the study of integer partitions with parts separated by parity. Our motivation is twofold. Firstly, we derive results for certain restricted partitions with even parts below odd parts. These include a Franklin-type involution proving a parametrized identity that generalizes Andrews’ bivariate generating function, and two families of Andrews–Beck type congruences. Secondly, we introduce several new subsets of partitions that are stable (i.e. invariant under conjugation) and explore their connections with three third-order mock theta functions $\omega (q)$, $\nu (q)$, and $\psi ^{(3)}(q)$, introduced by Ramanujan and Watson.

1. Introduction

A partition $\lambda =(\lambda _1,\lambda _2,\ldots,\lambda _r)$ of a positive integer $n$ is a finite weakly decreasing sequence of positive integers $\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{r}\ge 1$ such that $\sum _{i=1}^{r}\lambda _{i}=n$, denoted as $\lambda \vdash n$. The $\lambda _{i}$ are called the parts of the partition $\lambda$. As usual, we denote the number being partitioned $n$, and the number of parts $r$, as $|\lambda |$ and $\#(\lambda )$, respectively. The partition function $p(n)$ is the number of partitions of $n$. For the sake of convenience, we denote the empty partition of $0$ as $\epsilon$ and agree that it is contained in the set of ordinary partitions and various subclasses of restricted partitions. Hence, for example, $p(0)=1$. Unless otherwise noted, we will follow the notations used in [1].

In 1944, Dyson [20] defined the rank of a partition as the largest part minus the number of parts, and then observed that the rank appears to give combinatorial interpretations for the first two (i.e. (1.1) and (1.2)) of Ramanujan's celebrated partition congruences, namely,

(1.1)\begin{align} p(5n+4) & \equiv0\pmod{5}, \end{align}

(1.2)\begin{align} p(7n+5) & \equiv0\pmod{7}, \end{align}

(1.3)\begin{align} p(11n+6) & \equiv0\pmod{11}. \end{align}

Since the map of conjugation (see § 2 for definition) swaps the largest part and the number of parts between a partition $\lambda$ and its conjugate $\lambda '$, Dyson's rank can be rephrased as

\[ \textrm{rank}(\lambda)=\#(\lambda')-\#(\lambda). \]

A similar looking partition statistic, the so-called Stanley rank, was introduced by Stanley [39] in his study of sign-balanced, labelled posets (see also [2, 9, 10]), and can be defined as

(1.4)\begin{equation} \textrm{srank}(\lambda)=\mathcal{O}(\lambda)-\mathcal{O}(\lambda'),\end{equation}

where $\mathcal {O}(\lambda )$ is the number of odd parts in $\lambda$. This statistic also refines Ramanujan's first congruence (1.1); see [2, Corollary 1.2].

Our starting point is an observation that connects the Stanley rank with Andrews’ recent work [4] on partitions with even parts below odd parts. We need some further definitions before we can state this observation.

Let $\mathfrak {EO}_n$ denote the set of partitions of $n$ in which every even part is less than each odd part, and let $\mathcal {EO}(n):=|\mathfrak {EO}_n|$, $\mathfrak {EO}:=\bigcup _{n\geq 0}\mathfrak {EO}_n$. Let $\overline {\mathfrak {EO}}_n$ denote the set of partitions in $\mathfrak {EO}_n$ in which ONLY the largest even part, if any, appears an odd number of times, then $\overline {\mathcal {EO}}(n)$ and $\overline {\mathfrak {EO}}$ can be defined analogously. More generally, if $\mathfrak {P}$ denote a set of partitions with certain restrictions, then $\mathfrak {P}_n:=\{\lambda \in \mathfrak {P}\colon |\lambda |=n\}$, and $\mathcal {P}(n):=|\mathfrak {P}_n|$.

The third-order mock theta functions $\nu (q)$ and $\omega (q)$ due to Ramanujan and Watson (see, e.g. [7]) are given by

(1.5)\begin{align} \nu(q) & =\sum_{n=0}^{\infty}\frac{q^{n^2+n}}{({-}q;q^2)_{n+1}}, \end{align}

(1.6)\begin{align} \omega(q) & =\sum_{n=0}^{\infty}\frac{q^{2n^2+2n}}{(q;q^2)_{n+1}^2}, \end{align}

where, here and throughout the rest of this paper, we always assume that $q$ is a complex number such that $|q|<1$ and adopt the following customary abbreviations in partitions and $q$-series:

\[ (a;q)_n:=\prod_{j=0}^{n-1}(1-aq^j)\quad\textrm{and}\quad (a;q)_\infty:=\prod_{j=0}^\infty(1-aq^j). \]

Noting the connection with the third-order mock theta function $\nu (q)$, Andrews deduced in [4] that for any $n\geq 0$,

(1.7)\begin{equation} \overline{\mathcal{EO}}(10n+8)\equiv0\pmod{5}. \end{equation}

In order to explain (1.7) combinatorially as the rank does for (1.1) and (1.2), he went on to introduce the even-odd crank for any partition $\lambda \in \mathfrak {EO}$, to be

(1.8)\begin{equation} \textrm{eoc}(\lambda)=\textrm{the~largest~even~part~of~}\lambda-\mathcal{O}(\lambda). \end{equation}

Of course, $\textrm {eoc}(\lambda )$ is always an even number when $\lambda \in \overline {\mathfrak {EO}}$. Let $N_{\textrm {eo}}(k,m,n)$ denote the number of partitions in $\overline {\mathfrak {EO}}_n$ whose even-odd cranks are congruent to $k$ modulo $m$. Andrews [4, Theorem 3.3] proved that for any $n\geq 0$ and $0\leq i\leq 4$,

(1.9)\begin{equation} N_{\textrm{eo}}(i,5,10n+8)=\dfrac{1}{5}\overline{\mathcal{EO}}(10n+8).\end{equation}

The key observation mentioned earlier is as follows.

Observation 1.1 For any partition $\lambda$, $\lambda \in \overline {\mathfrak {EO}}$ if and only if $\lambda '\in \overline {\mathfrak {EO}}$. In this case, we have

(1.10)\begin{equation} {\rm eoc}(\lambda)=\mathcal{O}(\lambda')-\mathcal{O}(\lambda)={-}{\rm srank}(\lambda). \end{equation}

This link sheds new light on the study of $\overline {\mathcal {EO}}(n)$, since now we can utilize the symmetry of $\overline {\mathfrak {EO}}$, imposed by the map of conjugation.

Motivated by (1.1), (1.2) and the statistic rank, Beck conjectured some surprising congruences. Let $NT(k,m,n)$ denote the total number of parts in the partitions of $n$ with rank congruent to $k$ modulo $m$, Andrews [6] proved these conjectural congruences due to Beck. More precisely, he [6, Theorems 1 and 2] proved that for any $n\geq 0$,

(1.11)\begin{align} & \big(NT(1,5,5n+i)-NT(4,5,5n+i)\big)\nonumber\\ & \quad+2\big(NT(2,5,5n+i)-NT(3,5,5n+i)\big) \equiv0\pmod{5},\text{ if } i\in\{1,4\}, \end{align}

(1.12)\begin{align} & \big(NT(1,7,7n+j)-NT(6,7,7n+j)\big)\nonumber\\ & \quad+ \big(NT(2,7,7n+j)-NT(5,7,7n+j)\big)\quad\nonumber\\& \quad- \big(NT(3,7,7n+j)-NT(4,7,7n+j)\big) \equiv0\pmod{7},\text{ if }j\in\{1,5\}. \end{align}

Congruences (1.11) and (1.12) are in general called Andrews–Beck type congruences. Motivated by these two congruences, many authors have recently established many Andrews–Beck type congruences for various types of partitions with their associated statistics; see, for example, [12, 14–16, 18, 19, 27, 30, 31, 33–35, 42]. Let $NT_{\textrm {eo}}(k,m,n)$ denote the total number of odd parts among partitions in $\overline {\mathfrak {EO}}_n$, whose even-odd cranks are congruent to $k$ modulo $m$. Our first result is the following Andrews–Beck type congruences for $NT_{\textrm {eo}}(k,m,n)$. Unlike the methods used in the aforementioned literature, the proofs of (1.13) and (1.14) need to take advantage of the map of conjugation and (1.10).

Theorem 1.2 For any $n\geq 0$,

(1.13)\begin{align} & \big(NT_{{\rm eo}}(1,5,10n)-NT_{{\rm eo}}(4,5,10n)\big)\nonumber\\ & \quad+ 2\big(NT_{{\rm eo}}(2,5,10n)-NT_{{\rm eo}}(3,5,10n)\big) \equiv 0 \pmod{10}, \end{align}

(1.14)\begin{align} & \big(NT_{{\rm eo}}(1,5,10n+8)-NT_{{\rm eo}}(4,5,10n+8)\big)\nonumber\\& \quad+ 2\big(NT_{{\rm eo}}(2,5,10n+8)-NT_{{\rm eo}}(3,5,10n+8)\big) \equiv 0 \pmod{20}. \end{align}

In a follow-up paper, Andrews [5] further considered various types of partitions with parts separated by parity. Motivated by this work, we also consider some subclasses of partitions with parts separated by parity. Let $\mathcal {OE}(n)$ denote the number of partitions of $n$ in which each odd part is less than each even part. Denote by $\overline {\mathcal {OE}}(n)$ the number of partitions counted by $\mathcal {OE}(n)$ in which both even and odd parts appear, and ONLY the largest odd part and the largest even part appear an odd number of times, so in particular, $\overline {\mathcal {OE}}(n)>0$ only for any odd $n\ge 3$. For example $\overline {\mathcal {OE}}(9)=8$, with the eligible partitions being $(8,1)$, $(6,3)$, $(6,1,1,1)$, $(4,3,1,1)$, $(4,2,2,1)$, $(4,1,1,1,1,1)$, $(2,2,2,1,1,1)$, and $(2,1,1,1,1,1,1,1)$.

Relating to the Stanley rank, we define $\overline {\mathcal {OE}}(m,n)$ to be the number of partitions enumerated by $\overline {\mathcal {OE}}(n)$ whose Stanley rank equals $m$ and let

\[ \overline{\textrm{OE}}(z,q):=\sum_{\pi\in\overline{\mathfrak{OE}}} z^{\textrm{srank}(\pi)}q^{|\pi|}=\sum_{n=0}^\infty\sum_{m={-}\infty}^{\infty} \overline{\mathcal{OE}}(m,n)z^mq^n \]

be the bivariate generating function of $\overline {\mathcal {OE}}(m,n)$. The following theorem gives an explicit formula for $\overline {\textrm {OE}}(z,q)$.

Theorem 1.3 We have

(1.15)\begin{equation} \overline{{\rm OE}}(z,q)=\sum_{m=1}^{\infty}\sum_{n=1}^{\infty} \dfrac{q^{4mn-1}}{(z^2q^2;q^4)_{m}(q^2/z^2;q^4)_{n}}. \end{equation}

The rest of this paper is organized as follows. We introduce the pivotal concept of ‘stable’ sets of partitions in § 2 (see definition 2.1), after which observation 1.1 is explained, and a complete characterization of the parity of $\overline {\mathcal {OE}}(n)$ is rederived with ease. Theorem 1.2 is proved in § 3, where three further stable subsets contained in $\mathfrak {EO}$ and their connections with mock theta functions are considered as well. In § 4, we prove theorem 1.3 and explore further subsets of $\overline {\mathfrak {OE}}$. We raise three conjectures to conclude the paper.

2. Preliminaries

We set further notations and lay the groundwork in this section.

To each partition $\lambda$, we associate a graphical representation called Ferrers graph, which is a left-justified array of unit squares such that the $i$-th row contains $\lambda _i$ squares. Ferrers graph facilitates the illustration of the following three notions that will appear frequently in this paper (see figure 1). Suppose we are given a partition $\lambda =(\lambda _1,\lambda _2,\ldots,\lambda _r)$.

• • Conjugation: The conjugate of $\lambda$ is obtained by transposing its Ferrers graph. Equivalently, the conjugate partition of $\lambda$ is $\lambda '=(\lambda _1',\lambda '_2,\ldots,\lambda _{\lambda _1}')$, where $\lambda _i'=|\{1\le j\le r:\lambda _j\ge i\}|$.

• • Durfee square: The Durfee square of $\lambda$ is the largest square that can fit into the top-left corner of its Ferrers graph. If we denote the side of the Durfee square of $\lambda$ as $d(\lambda )$, then $d(\lambda )=|\{1\le j\le r:\lambda _j\ge j\}|$. Note that $\lambda$ has a unique decomposition $\lambda =(d(\lambda );\mu,\nu )$, with $\mu$ and $\nu$ being the subpartition below the Durfee square of $\lambda$ and the conjugate of the subpartition to the right of the Durfee square, respectively. Clearly, $|\lambda |=d^2+|\mu |+|\nu |$.

• • Profile: The profile of a nonempty partition $\lambda$ is the sequence of southmost and eastmost border edges in its Ferrers graph, that starts with an east edge and ends with a north edge. We use the profile word to record the profile of $\lambda \colon w_{\lambda }=(e_1,n_1,\ldots,e_k,n_k)$, where for each $1\le i\le k\le \min \{r,\lambda _1\}$, $e_i$ and $n_i$ are the numbers of consecutive east and north edges appearing alternately in the profile, respectively. It is worth noting that Dyson's rank can be rephrased as $\textrm {rank}(\lambda )=\sum _i e_i-\sum _i n_i$.

Figure 1. Ferrers graph, conjugation, Durfee square and profile.

Note that both the conjugation and the Durfee square are standard notions that have been widely applied in the study of partition theory [1]. While the partition profile, whose definition follows [28], was involved in our previous work [22]; see also [21, 32] for recent works demonstrating the usefulness of this alternative way of recording a partition. A closely related notion, the rim hook, makes an appearance in the famed Murnaghan–Nakayama rule (see, e.g. [38, Theorem 4.10.2]) and is crucial in the study of symmetric functions in general.

As a standard tool in the realm of enumerative combinatorics, the theory of enumeration under group action, or Pólya theory, seems to lack application in the study of integer partitions. Nonetheless, one notable and enlightening exception was the paper by Garvan et al. [24], in which they utilized three dihedral groups’ actions on the partitions of $5n+4$, $7n+5$, and $11n+6$, to give a uniform proof of all three Ramanujan congruences (1.1)–(1.3); see also Hirschhorn's paper [25] and book [26, Chapter 4] for a more direct version of their proof. We would also like to mention the recent work of Kim [29], in which a $\mathbb {Z}_2$-action similar to conjugation was discussed and interesting congruences were derived.

Motivated by these previous works and our observation 1.1, we view the map of conjugation as a $\mathbb {Z}_2$-action on the set of partitions. From this perspective, it is natural to consider those subsets that are invariant under this group action. We give a name to such subsets now.

Definition 2.1 A collection of partitions, say $\mathfrak {C}$, is said to be (conjugationally) stable, if the following is true:

\[ \lambda\in\mathfrak{C}\text{ if and only if }\lambda'\in\mathfrak{C}. \]

For instance, we state without proof in observation 1.1 that $\overline {\mathfrak {EO}}$ is stable. To see this, simply note that for any $\lambda \in \overline {\mathfrak {EO}}$, its profile word $w_{\lambda }=(e_1,n_1,\ldots,e_k,n_k)$ must contain a consecutive pair of odd numbers $(n_i,e_{i+1})$ for some $0\le i\le k$ (set $n_0=e_{k+1}=1$ by convention), and all remaining letters in $w_{\lambda }$ are even. This property is clearly seen to be preserved by the reversal, thus $\lambda '\in \overline {\mathfrak {EO}}$ as well (see proposition 2.2). Furthermore, we see that the largest even part of $\lambda$ is given by $e_1+e_2+\cdots +e_i$, which, upon reversal, outputs exactly $\mathcal {O}(\lambda ')$, the number of odd parts in $\lambda '$, hence (1.10) follows and observation 1.1 is true.

From now on, we will use stability as a guideline for discovering new subclasses of partitions with parts separated by parity. For any class of partitions $\mathfrak {C}$, we use $\mathfrak {C}_{c}$ to denote the subset of partitions $\lambda \in \mathfrak {C}$ that are self-conjugate, i.e. $\lambda =\lambda '$. The following two facts are simple but useful.

Proposition 2.2 For a partition $\lambda$ with its profile word $w_{\lambda }=(e_1,n_1,\ldots,e_k,n_k)$, the profile word for its conjugate is obtained from reversing $w_{\lambda }$, i.e.:

\[ w_{\lambda'}=(n_k,e_k,\ldots,n_1,e_1). \]

In particular, $\lambda$ is self-conjugate if and only if $w_{\lambda }$ is palindromic, i.e. $e_1=n_k$, $n_1=e_k,\ldots$.

Proposition 2.3 Let $\mathcal {C}(n):=|\{\lambda \in \mathfrak {C}:|\lambda |=n\}|$ and $\mathcal {C}_c(n):=|\{\lambda \in \mathfrak {C}_c:|\lambda |=n\}|$. Then

(2.1)\begin{equation} \mathcal{C}(n)\equiv\mathcal{C}_c(n)\pmod 2. \end{equation}

Based on proposition 2.3, we provide another proof of the following complete characterization for the parity of $\overline {\mathcal {EO}}(n)$, first derived by Passary [36, Equation (2.1.24)].

Corollary 2.4 For any $n\ge 0$,

(2.2)\begin{equation} \overline{\mathcal{EO}}(n) \equiv \begin{cases} 1 \pmod 2 & \text{if }n=4k(3k-1) \text{ for some }k,\\ 0 \pmod 2 & \text{otherwise.} \end{cases} \end{equation}

Proof. Let $\overline {\mathcal {EO}}_c(n)$ denote the number of self-conjugate partitions in $\overline {\mathfrak {EO}}_n$. Then, by (2.1), one easily gets $\overline {\mathcal {EO}}(n)\equiv \overline {\mathcal {EO}}_c(n)\pmod 2$. Now, each self-conjugate partition $\lambda \in \overline {\mathfrak {EO}}_n$ can be decomposed as $\lambda =(2m;\mu,\mu )$, where $2\,m$ is the side of $\lambda$'s Durfee square, and $\mu$ is the subpartition below the Durfee square, which has an odd number of largest part $2\,m$, with the remaining parts all being even and all occurring an even number of times. Together with another copy of $\mu$ to the right of the Durfee square, they are generated by $(q^{2m}\cdot q^{2m})/(q^8;q^8)_{m}$. This amounts to give the generating function:

(2.3)\begin{align} \sum_{n=0}^{\infty}\overline{\mathcal{EO}}_c(n)q^n & =\sum_{m=0}^{\infty}\frac{q^{(2m)^2+4m}}{(q^8;q^8)_m}\nonumber\\ & =({-}q^8;q^8)_{\infty} \end{align}

(2.4)\begin{align} & \equiv (q^8;q^8)_{\infty}\pmod 2\nonumber\\& =\sum_{m={-}\infty}^{\infty}({-}1)^m q^{4m(3m-1)}, \end{align}

where (2.3) and (2.4) follow from Euler's identity [1, p. 19, Equation (2.2.6)] and Euler's pentagonal number theorem [1, p. 11, Corollary 1.7], respectively. Now, (2.2) follows by comparing the coefficients.

Remark 2.5 Two remarks on corollary 2.4 are in order. For one thing, in a recent paper of Ray and Barman [37], utilizing the theory of modular forms, they derived, among some other things, an infinite family of congruences modulo $2$ for $\overline {\mathcal {EO}}(n)$ (see [37, Theorem 1.1]), and a result concerning the parity of $\overline {\mathcal {EO}}(n)$ in any arithmetic progression [37, Theorem 1.4]. For another, the identities (2.3) and (2.4) both possess classical combinatorial proofs. From this perspective, our proof is a combinatorial proof.

3. Stable sets in $\mathfrak {EO}$

Equipped with the combinatorial insights from § 2, we investigate in this section various stable subsets contained in $\mathfrak {EO}$.

3.1. Further results for $\overline {\mathfrak {EO}}$

We begin by answering a problem raised by Andrews in [4]:

‘Problem 2. Prove proposition 3.1 combinatorially. (Hopefully more directly than invoking [1].)’

Proposition 3.1 referred to above is the following generating function of $\overline {\mathcal {EO}}(m,n)$, the number of partitions in $\overline {\mathfrak {EO}}_n$ whose even-odd crank equals $m$:

(3.1)\begin{equation} \sum_{n=0}^{\infty}\sum_{m={-}\infty}^{\infty}\overline{\mathcal{EO}}(m,n)z^m q^n =\dfrac{(q^4;q^4)_\infty}{(z^2q^2;q^4)_\infty(q^2/z^2;q^4)_\infty}.\end{equation}

We construct an involution on a certain set of $2$-coloured partition pairs to establish theorem 3.3, which is a bivariate generalization of (3.1). This approach is reminiscent of Franklin's proof of Euler's pentagonal number theorem. For this purpose, we need to make some further definitions.

We consider $2$-coloured partitions, wherein each part of size $k$ can be coloured as either $b$ or $ab$ (when $k\ge 2$), such that $ab$-coloured parts are all distinct. We remark that this notion of $2$-coloured partition is essentially Corteel and Lovejoy's overpartition [17], probably appended with parts of zero (nonoverlined), but we introduce it this way for our convenience.

Using its Ferrers graph, we realize every $2$-coloured partition by assigning the neutral weight $q$, and colour weights $b$ or $ab$, such that the leftmost cell of each part is always filled with $b$, while the rightmost cell of each $ab$-coloured part is filled with $a$, with the remaining cells all filled with $q$. We call such cell-labelled Ferrers graph a Ferrers diagram. The weight for each Ferrers diagram $\mu$ is the product over all the weights of its cells, and is denoted as $w(\mu )$; see figure 2 for an example. Note that when there are two parts with the same size but different colour, we always put the $ab$-coloured one below the $b$-coloured one. Consequently, each cell filled with $a$ must be an outer corner cell. Denote the set of all Ferrers diagrams as $\mathfrak {F}(a,b;q)$. From now on, we will speak of Ferrers diagram and $2$-coloured partition interchangeably. It is now routine to find its generating function.

Proposition 3.1 The weight generating function of Ferrers diagrams is given by

\[ \sum_{\mu\in\mathfrak{F}(a,b;q)}w(\mu)=\dfrac{({-}ab;q)_{\infty}}{(b;q)_{\infty}}. \]

Figure 2. Ferrers diagram for $\mu$ with $w(\mu )=a^2b^7q^{20}$.

Clearly, $\mathfrak {F}(0,q;q)$ is in bijection with the set of ordinary partitions. Now, define a peculiar set of $2$-coloured partition pairs

\begin{align*} \mathfrak{F}(a,b,c,d;q)& :=\big\{(\lambda,\mu)\in\mathfrak{F}(a,b;q)\times\mathfrak{F}(c,d;q)\colon \lambda=\epsilon~\text{or}\\ & \qquad\text{the smallest part of }\lambda>\#(\mu)\big\}. \end{align*}

Lemma 3.2 There exists a bijection

\[ \varphi\colon\mathfrak{F}\big(0,q^2/z^2,0,z^2q^2;q^4\big)\to\overline{\mathfrak{EO}}, \]

such that a pair of Ferrers diagrams $(\lambda,\mu )\in \mathfrak {F}(0,q^2/z^2,0,z^2q^2;q^4)$ weighted by $w(\lambda )w(\mu )=z^mq^n$ corresponds to a partition counted by $\overline {\mathcal {EO}}(m,n)$.

Proof. Let $(\lambda,\mu )\in \mathfrak {F}(0,q^2/z^2,0,z^2q^2;q^4)$ with $\#(\lambda )=s$ and $\#(\mu )=t$, then $\lambda _s>t$ from the definition. Moreover, $\lambda \in \mathfrak {F}(0,q^2/z^2;q^4)$ implies that $\lambda$ corresponds to a partition $\hat {\lambda }\vdash (4|\lambda |-2\,s)$ into $2\,s$ odd parts, wherein each part appears an even number of times and each occurrence is weighted by $z^{-1}$. Thus $\hat {\lambda }$ is weighted by $z^{-2s}$. On the contrary, the conjugate partition of $\mu \in \mathfrak {F}(0,z^2q^2;q^4)$ is seen to be corresponding to a partition $\hat {\mu }\vdash (4|\mu |-2t)$ into even parts, with the largest part $2t$ occurring an odd number of times while all remaining parts occurring an even number of times. $\hat {\mu }$ is weighted by $z^{2t}$.

Now, let $\pi$ be the unique partition obtained from appending $\hat {\mu }$ to $\hat {\lambda }$. We see that the condition $\lambda _s>t$ ensures that $\pi \in \overline {\mathfrak {EO}}$. In addition, we have indeed $\textrm {eoc}(\pi )=2t-2\,s$. Conversely, it should be clear how to start with a partition in $\overline {\mathfrak {EO}}$ and recover a unique pair in $\mathfrak {F}(0,q^2/z^2,0,z^2q^2;q^4)$. See figure 3 for a concrete example.

Figure 3. Correspondence $\varphi \colon (\lambda,\mu )\to \pi$ with $\textrm {eoc}(\pi )=4-6=-2$.

In view of lemma 3.2, the following theorem indeed covers Andrews's formula (3.1) as the special case of setting $a\to q^2/z^2$, $b\to z^2q^2$, $q\to q^4$.

Theorem 3.3 We have

(3.2)\begin{align} \sum_{(\lambda,\mu)\in\mathfrak{F}(0,a;q) \times\mathfrak{F}({-}a,b;q)}w(\lambda)w(\mu) & =\dfrac{(ab;q)_{\infty}}{(a;q)_{\infty}(b;q)_{\infty}}, \end{align}

(3.3)\begin{align} \sum_{(\lambda,\mu)\in\mathfrak{F}(0,a;q) \times\mathfrak{F}({-}a,b;q)}w(\lambda)w(\mu) & =\sum_{(\lambda,\mu)\in\mathfrak{F}(0,a,0,b;q)}w(\lambda)w(\mu). \end{align}

Proof. Identity (3.2) follows immediately from applying proposition 3.1 for the pair $(\lambda,\mu )$. To show the weight equivalence between $\mathfrak {F}(0,a;q)\times \mathfrak {F}(-a,b;q)$ and $\mathfrak {F}(0,a,0,b;q)$, it suffices to construct a weight-preserving, sign-reversing involution,¹ say $\ast \colon (\lambda,\mu )\mapsto (\lambda ^\ast,\mu ^\ast )$, over $\mathfrak {F}(0,a;q)\times \mathfrak {F}(-a,b;q)$, with $\mathfrak {F}(0,a,0,b;q)$ being precisely the set of fixed pairs; see figure 4 for an example of the map $\ast$, where we use $\bar {a}$ in place of the weight $-a$ to save space.

Figure 4. Example of the involution $\ast$ (case (ii) with $\lambda _i=3>j=2$).

Given a pair $(\lambda,\mu )$ with $\#(\mu )=t$, let $\lambda _i$ be the largest part of $\lambda$ that is no greater than $t$, note that the leftmost cell of $\lambda _i$ is filled with $a$ since $\lambda \in \mathfrak {F}(0,a;q)$. Also let $j$ be the largest index of an $ab$-coloured part of $\mu$, note that the rightmost cell of $\mu _j$ is filled with $-a$ since $\mu \in \mathfrak {F}(-a,b;q)$. If such a $\lambda _i$ (resp. $j$) does not exist, we simply set $\lambda _i=0$ (resp. $j=0$). Now, we compare $\lambda _i$ with $j$, and consider the following three cases.

1. (i) $\lambda _i\le j\neq 0$. Insert $j$ as a new part into $\lambda$ to get $\lambda ^\ast$, and convert $\mu$ to $\mu ^\ast$ whose parts are given by

   \[ \mu^\ast_k=\begin{cases} \mu_k-1, & \textrm{if}~1\le k\le j,\\ \mu_k, & \textrm{otherwise.}\\ \end{cases} \]
   Note that $\mu _j$ is $ab$-coloured hence $\mu _j>\mu _{j+1}$, which ensures $\mu ^\ast _j\ge \mu ^\ast _{j+1}$, and thus $\mu ^\ast$ is well-defined.

2. (ii) $\lambda _i>j$. Remove part $\lambda _i$ from $\lambda$ to get $\lambda ^\ast$. Convert $\mu$ to $\mu ^\ast$ whose parts are given by

   \[ \mu^\ast_k=\begin{cases} \mu_k+1, & \textrm{if}~1\le k\le \lambda_i,\\ \mu_k, & \textrm{otherwise.}\\ \end{cases} \]
   We fill the rightmost cell of $\mu ^\ast _{\lambda _i}$ with $-a$, while other inserted cells are filled with $q$. Note that originally $\mu _{\lambda _i}$ cannot be $ab$-coloured, or we are not in case (ii). Therefore, colour part $\mu ^\ast _{\lambda _i}$ as $ab$ is legitimate.

3. (iii) $\lambda _i=j=0$. We say put and take $(\lambda ^\ast,\mu ^\ast )=(\lambda,\mu )$. Note that we are in this case if and only if all parts of $\lambda$ are greater than $t$ (or $\lambda =\epsilon$), and none part of $\mu$ is $ab$-coloured. In other words, $(\lambda,\mu )\in \mathfrak {F}(0,a,0,b;q)$, as desired.

It should be clear that the operations conducted in cases (i) and (ii) are inverses of each other, and $\ast \colon (\lambda,\mu )\mapsto (\lambda ^\ast,\mu ^\ast )$ as described above is an involution over $\mathfrak {F}(0,a;q)\times \mathfrak {F}(-a,b;q)$, such that $w(\lambda ^\ast )w(\mu ^\ast )=-w(\lambda )w(\mu )$ whenever $(\lambda ^\ast,\mu ^\ast )\neq (\lambda,\mu )$. And the set of pairs fixed by $\ast$ is exactly $\mathfrak {F}(0,a,0,b;q)$. We have now proven (3.3).

Next, we proceed to establish theorem 1.2. The first step is to note the vanishing property of certain $N_{\textrm {eo}}(k,m,n)$, which can be readily deduced from lemma 3.2.

Corollary 3.4 For any $n\geq 0$,

(3.4)\begin{equation} N_{{\rm eo}}(0,4,4n+2)=N_{{\rm eo}}(2,4,4n+4)=0.\end{equation}

Proof. As explained in the proof of lemma 3.2, for each $\pi =\varphi (\lambda,\mu )$ with $\#(\lambda )=s$ and $\#(\mu )=t$, we have

\[ \textrm{eoc}(\pi)=2t-2s\equiv 2t+2s\equiv|\pi|\pmod 4, \]

which is clearly equivalent to (3.4).

Proof of theorem 1.2 We first show the divisibility of $5$. Note that when $r\not \equiv 0 \pmod k$, $N_{\textrm {eo}}(r,k,n)=N_{\textrm {eo}}(k-r,k,n)$ via the map of conjugation, hence for $0< r< k/2$, we have

\begin{align*} r\big(N_{\textrm{eo}}(r,k,n)-N_{\textrm{eo}}(k-r,k,n)\big) & =r\sum_{\substack{\lambda\in\overline{\mathfrak{EO}}_n \\ \textrm{eoc}(\lambda)\equiv r\pmod{k}}} \big(\mathcal{O}(\lambda)-\mathcal{O}(\lambda')\big) \\ & \equiv{-}r^2N_{\textrm{eo}}(r,k,n)\pmod k~(\text{by~(1.10)}) \end{align*}

In particular, if $\gcd (r,k)=1$,

\[ N_{\textrm{eo}}(r,k,n)-N_{\textrm{eo}}(k-r,k,n)\equiv{-}rN_{\textrm{eo}}(r,k,n)\pmod{k}. \]

Therefore,

\begin{align*} & \big(N_{\textrm{eo}}(1,5,n)-N_{\textrm{eo}}(4,5,n)\big) +2\big(N_{\textrm{eo}}(2,5,n)-N_{\textrm{eo}}(3,5,n)\big)\\ & \quad\equiv{-}N_{\textrm{eo}}(1,5,n)-4N_{\textrm{eo}}(2,5,n)\pmod{5}. \end{align*}

Finally, according to [36, Theorem 2.1.5], we have

\[ N_{\textrm{eo}}(1,5,10n)=N_{\textrm{eo}}(2,5,10n), \]

and (1.9) already gives us

\[ N_{\textrm{eo}}(1,5,10n+8)=N_{\textrm{eo}}(2,5,10n+8). \]

So, both congruences (1.13) and (1.14) hold modulo $5$. Since each partition $\lambda \in \overline {\mathfrak {EO}}$ has an even number of odd parts, we get the modulo $2$ results immediately. All that remains is to show that

(3.5)\begin{align} & NT_{\textrm{eo}}(1,5,10n+8)-NT_{\textrm{eo}}(4,5,10n+8)\nonumber\\ & \quad=\sum_{\substack{\lambda\in\overline{\mathfrak{EO}}_{10n+8}\\ \textrm{eoc}(\lambda)\equiv 1\pmod{5}}} \big(\mathcal{O}(\lambda)-\mathcal{O}(\lambda')\big)\nonumber\\ & \quad={-}\sum_{\substack{\lambda\in\overline{\mathfrak{EO}}_{10n+8}\\ \textrm{eoc}(\lambda)\equiv1\pmod{5}}} \textrm{eoc}(\lambda)\equiv0\pmod 4. \end{align}

To this end, we write $n=4m+i$ with $i=0,1,2,3$, and discuss the following two cases:

1. (i) Case $i\equiv 0\pmod {2}$. In this case $10n+8\equiv 0\pmod 4$ so each $\lambda \in \overline {\mathfrak {EO}}_{10n+8}$ satisfies $\textrm {eoc}(\lambda )\equiv 0\pmod 4$ by (3.4), thus (3.5) holds.

2. (ii) Case $i\equiv 1\pmod {2}$. In this case $10n+8\equiv 2\pmod 4$ so each $\lambda \in \overline {\mathfrak {EO}}_{10n+8}$ satisfies $\textrm {eoc}(\lambda )\equiv 2\pmod 4$ by (3.4), and the total number of summands is

   \[ N_{\textrm{eo}}(1,5,40m+10i+8)=\frac{1}{5}\overline{\mathcal{EO}}(40m+10i+8)\equiv0\pmod{2}~ \text{(by~(2.2))} \]
   i.e. it is an even number. So, (3.5) still holds.

This completes the proof.

3.2. Three more stable subsets of $\mathfrak {EO}$

With the discussion of $\overline {\mathfrak {EO}}$ after definition 2.1 in mind, other stable subsets of $\mathfrak {EO}$ besides $\overline {\mathfrak {EO}}$ naturally present themselves. We study three of them in this subsection. First note that $\mathfrak {EO}$ itself is not stable, as can be seen from figure 1, wherein $\lambda '\in \mathfrak {EO}$ but $\lambda \not \in \mathfrak {EO}$. The three stable subsets of $\mathfrak {EO}$ are defined as follows: the first of which is the largest one, in the sense that there exists no stable subset $\mathfrak {C}$, such that $\mathfrak {EO}^{(1)}\subsetneq \mathfrak {C}\subsetneq \mathfrak {EO}$:

\begin{align*} \mathfrak{EO}^{(1)} & :=\{\lambda\in\mathfrak{EO}\colon\text{at most one part of }\lambda\text{ aont}\},\\ \mathfrak{EO}^{(2)} & :=\{\lambda\in\mathfrak{EO}\colon \text{ only the smallest odd part of }\lambda\text{ aont}\},\\ \mathfrak{EO}^{(3)} & :=\{\lambda\in\mathfrak{EO}\colon \text{all parts of }\lambda\text{ odd and only the largest odd part of }\lambda\text{ aont}\}. \end{align*}

Here, ‘aont’ stands for ‘appears an odd number of times’. Note that $\epsilon \not \in \mathfrak {EO}^{(2)}\cup \mathfrak {EO}^{(3)}$. Interpreting the defining conditions for $\mathfrak {EO}^{(1)}$, $\mathfrak {EO}^{(2)}$, and $\mathfrak {EO}^{(3)}$ in terms of the profile words for the respective partitions, we obtain the following connection with mock theta functions $\nu (q)$ and $\omega (q)$.

Theorem 3.5 The three subsets $\mathfrak {EO}^{(1)}$, $\mathfrak {EO}^{(2)}$, and $\mathfrak {EO}^{(3)}$ are all stable. Furthermore, we have

(3.6)\begin{align} \sum_{n=1}^\infty\mathcal{EO}^{(2)}(n)q^n & =\dfrac{1}{2}q\big(\nu(q)+\nu({-}q)\big), \end{align}

(3.7)\begin{align} \sum_{n=1}^\infty\mathcal{EO}^{(3)}(n)q^n & =q\!\:\omega(q^2), \end{align}

where $\nu (q)$ and $\omega (q)$ are defined as in (1.5) and (1.6).

Proof. Given a profile word $w_{\lambda }=(e_1,n_1,\ldots,e_k,n_k)$ associated with partition $\lambda$. It can be characterized respectively as having at most one odd number among all $n_i$'s when $\lambda \in \mathfrak {EO}^{(1)}$, having a consecutive odd pair $(e_i,n_i)$ when $\lambda \in \mathfrak {EO}^{(2)}$, and having only $e_1$ and $n_k$ as odd components when $\lambda \in \mathfrak {EO}^{(3)}$. Each of the above characterizations is clearly invariant under the reversal $w_{\lambda }\to w_{\lambda '}$, hence all three subsets $\mathfrak {EO}^{(1)}$, $\mathfrak {EO}^{(2)}$, and $\mathfrak {EO}^{(3)}$ are stable.

To obtain (3.6), we observe that there is a natural bijection between the set $\mathfrak {EO}^{(2)}_n$ and $\overline {\mathfrak {EO}}_{n-1}$. For a given partition $\lambda \in \mathfrak {EO}^{(2)}_n$ with $n\ge 1$, subtract one from the last smallest odd part of $\lambda$ and denote this new partition by $\mu$. Obviously, $\mu \in \overline {\mathfrak {EO}}_{n-1}$. Conversely, for a given partition $\mu \in \overline {\mathfrak {EO}}_{n-1}$, adding one to its first largest even part² recovers for us a partition $\lambda \in \mathfrak {EO}^{(2)}_n$. Therefore,

\[ \sum_{n=1}^\infty\mathcal{EO}^{(2)}(n)q^n=\sum_{n=1}^\infty\overline{\mathcal{EO}}(n-1)q^{n} =q\dfrac{(q^4;q^4)_\infty^3}{(q^2;q^2)_\infty^2}=\dfrac{1}{2}q\big(\nu(q)+\nu({-}q)\big), \]

where the second and last equalities follow from Corollary 3.2 and Theorem 1.1 in [4].

To handle the connection with $\omega (q)$ and prove (3.7), we recall a variation of the standard Ferrers graph introduced by Andrews in [3], called the ‘odd Ferrers graph’. It consists of a Ferrers graph using $2$'s with a surrounding border of $1$'s; see figure 5 for an illustration along with its ‘$2$-dilation’. As noted in [3, p. 60], the generating function for odd Ferrers graphs is $q\!\:\omega (q)$. Now, we immediately have (3.7) by noticing that each partition in $\mathfrak {EO}^{(3)}$ can be uniquely represented by a $2$-dilated odd Ferrers graph with its top-left corner cell subtracted by $1$.

Figure 5. Odd Ferrers graph and its $2$-dilation.

Remark 3.6 Several remarks on theorem 3.5 are necessary. First, the coefficients of $\nu (-q)$ and $\omega (q)$ also possess their own partition-theoretic interpretations, so it is interesting to give a bijective proof of (3.6) and (3.7). Second, there are various investigations on arithmetic properties of coefficients of $\nu (q)$ and $\omega (q)$ (see, e.g. [8, 11, 23]). This suggests that there should be various congruences for functions $\mathcal {EO}^{(2)}(n)$ and $\mathcal {EO}^{(3)}(n)$, inherited from those of $\nu (q)$ and $\omega (q)$. Finally, it is not easy to find the generating function for $\mathcal {EO}^{(1)}(n)$ following a similar line of proving (3.6) and (3.7).

Let

\[ \nu({-}q):=\sum_{n=0}^\infty p_{\nu}(n)q^n. \]

Then, Andrews et al. [7, Theorem 4.1] proved that $p_{\nu }(n)$ counts the number of distinct partitions of $n$ in which all odd parts are less than twice the smallest part.³ Thanks to the new connections made in theorem 3.5, we are rewarded with an alternative interpretation of $p_{\nu }(n)$. Note that the even $n$ case of the following result is essentially rephrasing Theorem 1.1 of [4]. From this perspective, the next corollary is a companion to Theorem 1.1 of [4].

Corollary 3.7 For any $n\ge 0$, $p_\nu (n)$ also counts the number of partitions of $n$ in $\mathfrak {EO}$, such that when $n$ is even, then only the largest even part appears an odd number of times; when $n$ is odd, then all parts are odd and only the largest odd part appears an odd number of times.

Proof. According to [41, p. 72], we find that

(3.8)\begin{equation} \nu(q)+q\!\:\omega(q^2)=\dfrac{(q^4;q^4)_\infty^3}{(q^2;q^2)_\infty^2}. \end{equation}

Replacing $q$ by $-q$ yields

(3.9)\begin{equation} \nu({-}q)-q\!\:\omega(q^2)=\dfrac{(q^4;q^4)_\infty^3}{(q^2;q^2)_\infty^2}. \end{equation}

In view of (3.6)–(3.9), we find that

\[ \sum_{n=1}^\infty\mathcal{EO}^{(2)}(n)q^n+\sum_{n=1}^\infty\mathcal{EO}^{(3)}(n)q^{n+1} =q\nu({-}q)=\sum_{n=0}^\infty p_\nu(n)q^{n+1}: \]

from which we obtain that for any $n\geq 0$,

\[ \mathcal{EO}^{(2)}(n+1)+\mathcal{EO}^{(3)}(n)=p_\nu(n). \]

Finally, we observe that the powers of $q$ in both $q(\nu (q)+\nu (-q))/2$ and $q\!\:\omega (q^2)$ are odd, which results in $\mathcal {EO}^{(2)}(2m)=\mathcal {EO}^{(3)}(2m)=0$ for every integer $m\ge 0$. Now, we apply the identity $\mathcal {EO}^{(2)}(n+1)=\overline {\mathcal {EO}}(n)$ to finish the proof.

4. Stable sets in $\mathfrak {OE}$

In the first subsection, we give a proof of theorem 1.3 and characterize completely the parity of $\overline {\mathcal {OE}}(n)$. We consider further subsets of $\overline {\mathfrak {OE}}$ in subsection 4.2.

4.1. Results for $\overline {\mathfrak {OE}}$

For a partition $\lambda \in \overline {\mathfrak {OE}}$, its profile word $w_{\lambda }$ begins and ends with an odd number $e_1$ and $n_k$ respectively, and contains precisely one consecutive odd pair $(n_i,e_{i+1})$, with remaining letters all being even. This characterization is seen to be invariant under conjugation thus $\overline {\mathfrak {OE}}$ is stable. Then, with observation 1.1 in mind, we see (1.15), which we prove next, parallels Andrews’ generating function (3.1) of $\overline {\mathfrak {OE}}(m,n)$ nicely.

Proof of theorem 1.3 Recall that for each $\lambda \in \overline {\mathfrak {OE}}$, it contains both even and odd parts, each odd part is smaller than each even part, and ONLY the largest odd part and the largest even part appear an odd number of times. Suppose $\lambda$ (resp. $\lambda '$) has $2n-1$ (resp. $2m-1$) even parts, for certain $n$, $m\ge 1$. From these constraints we can uniquely dissect $\lambda$ into five pieces; see figure 6 for an illustration. The top-left rectangle contains $(2n-1)\times (2m-1)$ cells which contribute $q^{(2m-1)(2n-1)}$ to the generating function; a horizontal strip representing the largest odd part of $\lambda$ with contribution $zq^{2m-1}$; a vertical strip representing the largest odd part of $\lambda '$ with contribution $z^{-1}q^{2n-1}$; a subpartition $\alpha$ below the horizontal strip; and a subpartition $\beta$ to the right of the vertical strip. Note that $\alpha$ is a partition into odd parts each occurring an even number of times, with the largest part no greater than $2m-1$, and its contribution is $z^{\#(\alpha )}q^{|\alpha |}$. Similarly, $\beta$'s conjugation $\beta '$ is also a partition into odd parts each occurring an even number of times, with the largest part no greater than $2n-1$, and its contribution is $z^{-\#(\beta ')}q^{|\beta '|}$. Finally, it suffices to note that all such $\alpha$'s (resp. $\beta$'s) are generated by $1/(z^2q^2;q^4)_m$ (resp. $1/(q^2/z^2;q^4)_n$). Putting together all five pieces we arrive at (1.15).

Figure 6. Dissection of a partition $\lambda \in \overline {\mathfrak {OE}}$.

Next, we investigate the parity of $\overline {\mathcal {OE}}(n)$, in the hope of getting a complete characterization analogous to corollary 2.4.

Another third-order mock theta function due to Watson [41, p. 62] is given by

(4.1)\begin{equation} \psi^{(3)}(q)=\sum_{n=1}^\infty\dfrac{q^{n^2}}{(q;q^2)_n}:=\sum_{n=1}^\infty p_\psi(n)q^n. \end{equation}

Utilizing some techniques from analytic and algebraic number theory, Wang [40, Theorem 4.2] established the following complete characterization modulo $2$ for $p_\psi (n)$:

(4.2)\begin{align} p_\psi(m)& \equiv1\pmod{2}~\Longleftrightarrow24m-1=p^{4\alpha+1}k^2\nonumber\\ & \text{for some prime }p\text{ coprime to }k. \end{align}

Relying on Wang's result, we are able to fully characterize $\overline {\mathcal {OE}}(n)$ modulo $2$.

Theorem 4.1 For any $n\geq 1$,

(4.3)\begin{equation} \overline{\mathcal{OE}}(n)\equiv \begin{cases} 1 \pmod 2 & \text{if }n\equiv3\pmod4 \text{ and }6n+5=p^{4\alpha+1}k^2\\ & \text{for some prime }p\text{ coprime to }k,\\ 0 \pmod 2 & \textrm{otherwise}. \end{cases} \end{equation}

Proof. By proposition 2.3, it suffices to consider only self-conjugate partitions in $\overline {\mathfrak {OE}}$. Their generating function is given by

\[ \sum_{n=0}^\infty\overline{\mathcal{OE}}_c(n)q^n = q^{{-}1}\sum_{n=1}^{\infty} \dfrac{q^{4n^2}}{(q^4;q^8)_n}=q^{{-}1}\sum_{m=1}^{\infty}p_{\psi}(m)q^{4m}~ \textrm{(by~(4.1))} \]

It follows that

(4.4)\begin{equation} \overline{\mathcal{OE}}(n)\equiv \begin{cases} p_\psi(m)\pmod2 & \text{if }n=4m-1,\\ \quad0\quad\;\pmod 2 & \textrm{otherwise.} \end{cases}\end{equation}

Now, (4.3) follows from (4.4) and (4.2) immediately.

With the aid of theorem 4.1, it is possible to deduce Ramanujan-type congruences for a certain arithmetic progression. We record one example below.

Corollary 4.2 For any $n\geq 0$,

\begin{align*} \overline{\mathcal{OE}}(100n+15)\equiv\overline{\mathcal{OE}}(100n+35) & \equiv0\pmod 2,\\ \overline{\mathcal{OE}}(100n+55)\equiv\overline{\mathcal{OE}}(100n+75) & \equiv0\pmod 2. \end{align*}

Proof. In view of relation (4.4), we only need to show that:

(4.5)\begin{align} p_\psi(25n+4)\equiv p_\psi(25n+19) & \equiv0\pmod{2},\nonumber\\ p_\psi(25n+9)\equiv p_{\psi}(25n+14) & \equiv0\pmod 2. \end{align}

Here, we only prove the congruence $p_{\psi }(25n+4)\equiv 0\pmod {2}$, because the proofs of the remaining cases are quite similar.

For any $n\geq 0$, note that $24(25n+4)-1=5(120n+19)$, $5\nmid (120n+19)$ and $120n+19$ cannot be a square (a square is congruent to $0$ or $1$ modulo $4$). According to (4.2), we obtain the desired congruence.

Remark 4.3 Quite recently, Chen and Garvan [13, Equation (4.31)] derived an infinite family of congruences modulo $4$ satisfied by $p_\psi (n)$. One easily derives from their results the following strengthening of (4.5), namely, for any $n\geq 0$,

\[ p_\psi(25n+9)\equiv p_\psi(25n+14)\equiv0\pmod{4}. \]

From this perspective, it might be interesting to pursue modulo $4$ results for $\overline {\mathcal {OE}}(n)$.

4.2. Subsets of $\overline {\mathfrak {OE}}$

Given a partition $\lambda$, let $\mathcal {E}(\lambda )$ be the number of even parts in $\lambda$. We further refine $\overline {\mathfrak {OE}}$ as follows. Let $k\geq 0$ and

\[ \overline{\mathfrak{OE}}_{k}:=\big\{\lambda\in\overline{\mathfrak{OE}} \colon\mathcal{E}(\lambda)-\mathcal{E}(\lambda')=2k\big\}. \]

Noting that each partition $\lambda \in \overline {\mathfrak {OE}}$ must be a partition of an odd number, we define $p_k(0)=p_k(1)=0$, and for all $n\ge 2$, let

\[ p_k(n):=\big|\big\{\lambda\in\overline{\mathfrak{OE}}_k:|\lambda|=2n-1\big\}\big|. \]

The following explicit generating functions for $p_0(n)$ and $p_1(n)$ presage their connection with the mock theta function $\omega (q)$ (see corollary 4.6).

Corollary 4.4 There holds

(4.6)\begin{align} \sum_{n=0}^\infty p_0(n)q^n & =\sum_{n=1}^{\infty}\frac{q^{2n^2}}{(q;q^2)_{n}^2}, \end{align}

(4.7)\begin{align} \sum_{n=0}^\infty p_1(n)q^n & =\sum_{n=1}^{\infty}\frac{q^{2n^2+2n}}{(q;q^2)_{n}(q;q^2)_{n+1}}. \end{align}

Proof. The length of the vertical (resp. horizontal) strip that arises in the proof of theorem 1.3 is precisely $\mathcal {E}(\lambda )$ (resp. $\mathcal {E}(\lambda ')$). Therefore, by setting $n=m$ and putting $z\to 1$, $q\to q^{1/2}$ in (1.15), we immediately arrive at (4.6). Similarly, with $n=m+1$ we can deduce (4.7).

Remark 4.5 Combining (4.1) and (4.6), one obtains $p_0(2n)\equiv p_\psi (n)\pmod {2}$ immediately. Alternatively, this congruence could be combinatorially justified as we derive (4.4).

Let $p_\omega (n)$ denote the number of partitions of $n$ in which each odd part is less than twice the smallest part. Just like the partition-theoretical interpretation for $p_{\nu }(n)$, it was first noticed in the same paper by Andrews et al. [7, Theorem 3.1] that

\[ q\!\:\omega(q)=\sum_{n=1}^{\infty}p_{\omega}(n)q^n. \]

Corollary 4.6 For any $n\geq 1$,

(4.8)\begin{equation} p_0(n)+p_1(n-1)+1=p_\omega(n).\end{equation}

Proof. It follows from (4.6) and (4.7) that

\begin{align*} & \sum_{n=0}^\infty p_0(n)q^n+\sum_{n=0}^\infty p_1(n)q^{n+1}+\sum_{n=1}^\infty q^n\\ & \quad=\sum_{n=0}^\infty\frac{q^{2n^2+4n+2}}{(q;q^2)_{n+1}^2} +\sum_{n=1}^{\infty}\frac{q^{2n^2+2n+1}}{(q;q^2)_n(q;q^2)_{n+1}}+\dfrac{q}{1-q}\\ & \quad=\sum_{n=0}^\infty\frac{q^{2n^2+4n+2}}{(q;q^2)_{n+1}^2}+ \sum_{n=1}^{\infty}\frac{q^{2n^2+2n+1}(1-q^{2n+1})}{(q;q^2)_{n+1}^2}+\dfrac{q}{1-q}\\ & \quad=\sum_{n=1}^\infty\dfrac{q^{2n^2+2n+1}}{(q;q^2)_{n+1}^2} +\dfrac{q^2}{(1-q)^2}+\dfrac{q}{1-q}\\ & \quad=\sum_{n=0}^\infty\dfrac{q^{2n^2+2n+1}}{(q;q^2)_{n+1}^2} =q\!\:\omega(q)=\sum_{n=1}^\infty p_\omega(n)q^n. \end{align*}

Then, (4.8) follows by comparing the coefficients of $q^n$ on both sides of the identity above.

Problem 4.7 Prove (4.8) combinatorially via their partition-theoretical interpretations.

5. Final remarks

We conclude this paper with several conjectures to motivate further investigation.

Conjecture 5.1 Let $\ell >3$ be a prime number such that $\ell \not \equiv 23\pmod {24}$. Then, for any $n\geq 0$,

\[ p_0\big(2\ell^2n+2\ell j+2\delta_\ell\big)\equiv0\pmod{4}, \]

where $0\leq j\leq \ell -2$ and $\delta _\ell$ is the least positive integer such that $24\delta _\ell \equiv 1\pmod {\ell }$.

Conjecture 5.2 We have

\[ \lim_{X\rightarrow\infty} \dfrac{\#\{0\leq n< X\colon p_0(n)\equiv0\pmod{4}\}}{X}=\dfrac{1}{2}. \]

Conjecture 5.3

1. (i) For any $n\geq 3$,

   \[ \overline{\mathcal{OE}}(2n+1)>\overline{\mathcal{EO}}(2n). \]

2. (ii) For any $n\geq 1$,

   \[ p_0(n)\ge p_1(n), \]
   where the strict inequality holds if $n\neq 1$, $10$ or $13$.