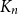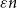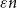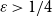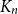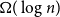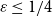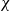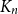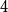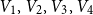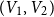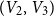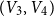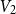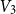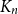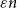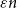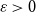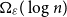1. Introduction
Ramsey’s theorem guarantees that any
![]() $r$
-edge-colouring of a large complete graph yields a large monochromatic complete subgraph. In general, we cannot guarantee the existence of anything but monochromatic subgraphs. Indeed, nothing prevents the host graph from being monochromatic itself. However, in recent years, there have been many results stating that in colourings where each colour is well-represented, a richer family of patterns can be guaranteed. The following, initially suggested by Bollobás [Reference Cutler and Montágh4], is a prototypical result of this form. Here,
$r$
-edge-colouring of a large complete graph yields a large monochromatic complete subgraph. In general, we cannot guarantee the existence of anything but monochromatic subgraphs. Indeed, nothing prevents the host graph from being monochromatic itself. However, in recent years, there have been many results stating that in colourings where each colour is well-represented, a richer family of patterns can be guaranteed. The following, initially suggested by Bollobás [Reference Cutler and Montágh4], is a prototypical result of this form. Here,
![]() $\mathcal{F}_t$
denotes the family of
$\mathcal{F}_t$
denotes the family of
![]() $2$
-edge-coloured complete graphs on
$2$
-edge-coloured complete graphs on
![]() $2t$
vertices in which one colour forms either a complete bipartite graph with
$2t$
vertices in which one colour forms either a complete bipartite graph with
![]() $t$
vertices on each side
$t$
vertices on each side
![]() $(K_{t,t})$
or a clique of order
$(K_{t,t})$
or a clique of order
![]() $t$
$t$
![]() $(K_t)$
. See Figure 1 for a depiction of the four colourings in
$(K_t)$
. See Figure 1 for a depiction of the four colourings in
![]() $\mathcal{F}_t$
(up to isomorphism).
$\mathcal{F}_t$
(up to isomorphism).
Theorem 1.1 (Fox-Sudakov, Cutler-Montágh [Reference Cutler and Montágh4, Reference Fox and Sudakov9]). Let
![]() $G$
be a
$G$
be a
![]() $2$
-edge-coloured
$2$
-edge-coloured
![]() $K_n$
where each colour class has at least
$K_n$
where each colour class has at least
![]() $\varepsilon n^2$
edges, and suppose
$\varepsilon n^2$
edges, and suppose
![]() $n\geq (1/\varepsilon )^{16 t}$
. Then,
$n\geq (1/\varepsilon )^{16 t}$
. Then,
![]() $G$
contains a member of
$G$
contains a member of
![]() $\mathcal{F}_t$
.
$\mathcal{F}_t$
.
A probabilistic construction shows that the above is asymptotically tight up to the constant factor in the exponent. The theorem is also optimal from a structural standpoint. Namely,
![]() $2$
-edge-colourings of
$2$
-edge-colourings of
![]() $K_n$
where one colour class forms two disjoint cliques of size
$K_n$
where one colour class forms two disjoint cliques of size
![]() $\lfloor n/2 \rfloor$
and
$\lfloor n/2 \rfloor$
and
![]() $\lceil n/2 \rceil$
or one colour class forms a
$\lceil n/2 \rceil$
or one colour class forms a
![]() $K_{cn}$
(with
$K_{cn}$
(with
![]() $c \sim \sqrt{2}/2$
) satisfy the hypothesis of Theorem 1.1 with
$c \sim \sqrt{2}/2$
) satisfy the hypothesis of Theorem 1.1 with
![]() $\varepsilon \sim 1/2$
, and thus certify that one cannot hope to find patterns which are more complex than those in Figure 1. Similarly, Theorem 1.1 becomes false if we delete any of the four patterns contained in
$\varepsilon \sim 1/2$
, and thus certify that one cannot hope to find patterns which are more complex than those in Figure 1. Similarly, Theorem 1.1 becomes false if we delete any of the four patterns contained in
![]() $\mathcal{F}_t$
.
$\mathcal{F}_t$
.
There are numerous extensions of Theorem 1.1, including multicolour and infinite variants [Reference Bowen, Lamaison and Müyesser1], variants where
![]() $K_n$
is replaced by another dense host subgraph [Reference Müyesser and Tait15], and variants where
$K_n$
is replaced by another dense host subgraph [Reference Müyesser and Tait15], and variants where
![]() $\varepsilon$
is allowed to depend on
$\varepsilon$
is allowed to depend on
![]() $n$
[Reference Caro, Hansberg and Montejano2, Reference Girão and Hancock11, Reference Girão and Narayanan13]. In this paper, we are concerned with the following question, initially raised by Wesley Pegden (personal communication).
$n$
[Reference Caro, Hansberg and Montejano2, Reference Girão and Hancock11, Reference Girão and Narayanan13]. In this paper, we are concerned with the following question, initially raised by Wesley Pegden (personal communication).

Figure 1. The four types of colourings in
![]() $\mathcal{F}_t$
. The circles denote cliques of size
$\mathcal{F}_t$
. The circles denote cliques of size
![]() $t$
, whereas the lines connecting the circles denote complete bipartite graphs. In the first row, one colour class forms a
$t$
, whereas the lines connecting the circles denote complete bipartite graphs. In the first row, one colour class forms a
![]() $K_{t,t}$
, whereas on the second row, one colour class forms a
$K_{t,t}$
, whereas on the second row, one colour class forms a
![]() $K_t$
.
$K_t$
.
Question 1.2.
Let
![]() $\varepsilon \gt 0$
. Suppose that
$\varepsilon \gt 0$
. Suppose that
![]() $K_n$
is
$K_n$
is
![]() $2$
-edge-coloured so that each vertex is incident to at least
$2$
-edge-coloured so that each vertex is incident to at least
![]() $\varepsilon n$
edges in each colour. Which subgraphs must
$\varepsilon n$
edges in each colour. Which subgraphs must
![]() $K_n$
necessarily contain?
$K_n$
necessarily contain?
We call
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
as in Question 1.2 locally
$K_n$
as in Question 1.2 locally
![]() $\varepsilon$
-balanced. Of course, this is a stronger hypothesis on the colouring compared to Theorem 1.1. Hence, any locally
$\varepsilon$
-balanced. Of course, this is a stronger hypothesis on the colouring compared to Theorem 1.1. Hence, any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $K_n$
must contain a complete subgraph on
$K_n$
must contain a complete subgraph on
![]() $2t$
vertices where one colour forms a
$2t$
vertices where one colour forms a
![]() $K_{t,t}$
or a
$K_{t,t}$
or a
![]() $K_t$
, where
$K_t$
, where
![]() $t = \Omega _{\varepsilon }(\log n)$
. However, this is not necessarily a complete answer to Question 1.2 as it cannot be the case that in a locally
$t = \Omega _{\varepsilon }(\log n)$
. However, this is not necessarily a complete answer to Question 1.2 as it cannot be the case that in a locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $K_n$
one colour class consists entirely of a clique. This motivates the following question: does any locally
$K_n$
one colour class consists entirely of a clique. This motivates the following question: does any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $K_n$
contain a complete
$K_n$
contain a complete
![]() $2t$
-vertex subgraph in which one colour class forms a
$2t$
-vertex subgraph in which one colour class forms a
![]() $K_{t,t}$
?
$K_{t,t}$
?
The answer turns out to be negative for any value of
![]() $\varepsilon \leq 1/4$
and
$\varepsilon \leq 1/4$
and
![]() $t\geq 2$
. To see this, consider the following
$t\geq 2$
. To see this, consider the following
![]() $2$
-colouring of
$2$
-colouring of
![]() $K_{4k}$
, where each vertex is adjacent to at least
$K_{4k}$
, where each vertex is adjacent to at least
![]() $k$
red and blue edges, illustrated in Figure 2 (labelled
$k$
red and blue edges, illustrated in Figure 2 (labelled
![]() $P_3$
). Partition
$P_3$
). Partition
![]() $V(K_{4k})$
into four equal-sized sets as
$V(K_{4k})$
into four equal-sized sets as
![]() $V_1,V_2,V_3$
and
$V_1,V_2,V_3$
and
![]() $V_4$
. Colour all edges with both endpoints in
$V_4$
. Colour all edges with both endpoints in
![]() $V_1\cup V_4$
red, colour all edges with both endpoints in
$V_1\cup V_4$
red, colour all edges with both endpoints in
![]() $V_2\cup V_3$
blue, and colour edges between
$V_2\cup V_3$
blue, and colour edges between
![]() $V_1$
,
$V_1$
,
![]() $V_3$
, and between
$V_3$
, and between
![]() $V_2$
,
$V_2$
,
![]() $V_4$
red, and colour the remaining edges (between
$V_4$
red, and colour the remaining edges (between
![]() $V_1$
,
$V_1$
,
![]() $V_2$
and between
$V_2$
and between
![]() $V_3$
,
$V_3$
,
![]() $V_4$
) blue. Denote by
$V_4$
) blue. Denote by
![]() $\mathcal{P}_k$
the resulting
$\mathcal{P}_k$
the resulting
![]() $2$
-coloured
$2$
-coloured
![]() $K_{4k}$
(so the number of vertices is
$K_{4k}$
(so the number of vertices is
![]() $n=4k$
). It is easy to see that
$n=4k$
). It is easy to see that
![]() $\mathcal{P}_k$
contains no complete subgraph with
$\mathcal{P}_k$
contains no complete subgraph with
![]() $4$
vertices in which one colour class forms two disjoint cliques of size
$4$
vertices in which one colour class forms two disjoint cliques of size
![]() $2$
each. One can also check that
$2$
each. One can also check that
![]() $\mathcal{P}_k$
is locally
$\mathcal{P}_k$
is locally
![]() $1/4$
-balanced.
$1/4$
-balanced.

Figure 2. An illustration of the relevant two-coloured and totally two-coloured graphs.
Perhaps surprisingly,
![]() $\mathcal{P}_k$
is an optimal construction in the following sense. For any
$\mathcal{P}_k$
is an optimal construction in the following sense. For any
![]() $\gamma \gt 0$
, a locally
$\gamma \gt 0$
, a locally
![]() $(1/4+\gamma )$
-balanced
$(1/4+\gamma )$
-balanced
![]() $K_n$
must contain large complete subgraphs where one colour class forms a complete bipartite graph. Our first result makes this precise, thereby answering Question 1.2 when
$K_n$
must contain large complete subgraphs where one colour class forms a complete bipartite graph. Our first result makes this precise, thereby answering Question 1.2 when
![]() $\varepsilon \gt 1/4$
.
$\varepsilon \gt 1/4$
.
Theorem 1.3.
Let
![]() $G$
be a
$G$
be a
![]() $2$
-coloured locally
$2$
-coloured locally
![]() $(1/4+\varepsilon )$
-balanced
$(1/4+\varepsilon )$
-balanced
![]() $K_n$
for
$K_n$
for
![]() $\varepsilon \gt 0$
, and suppose
$\varepsilon \gt 0$
, and suppose
![]() $n\geq 2^{t \cdot 2^{-C\log (1/\varepsilon )^8}}$
for some absolute constant
$n\geq 2^{t \cdot 2^{-C\log (1/\varepsilon )^8}}$
for some absolute constant
![]() $C$
. Then,
$C$
. Then,
![]() $G$
contains a complete subgraph on
$G$
contains a complete subgraph on
![]() $2t$
vertices where one colour class forms a
$2t$
vertices where one colour class forms a
![]() $K_{t,t}$
.
$K_{t,t}$
.
The earlier construction (
![]() $\mathcal{P}_k$
) shows that Theorem 1.3 does not hold when
$\mathcal{P}_k$
) shows that Theorem 1.3 does not hold when
![]() $1/4+\varepsilon$
is replaced by
$1/4+\varepsilon$
is replaced by
![]() $1/4$
. Moreover,
$1/4$
. Moreover,
![]() $n$
has to be exponentially large in
$n$
has to be exponentially large in
![]() $t$
for the conclusion to hold (e.g. by considering a random colouring), but we believe that the dependence of
$t$
for the conclusion to hold (e.g. by considering a random colouring), but we believe that the dependence of
![]() $n$
on
$n$
on
![]() $\varepsilon$
should be far from optimal. We discuss this further in Section 5.
$\varepsilon$
should be far from optimal. We discuss this further in Section 5.
We now turn our attention to answering Question 1.2 when
![]() $\varepsilon \leq 1/4$
. In light of the earlier construction (
$\varepsilon \leq 1/4$
. In light of the earlier construction (
![]() $\mathcal{P}_k$
), it is not clear at all if anything interesting can be said about this case. One might guess there exists a
$\mathcal{P}_k$
), it is not clear at all if anything interesting can be said about this case. One might guess there exists a
![]() $2$
-colouring of
$2$
-colouring of
![]() $K_n$
, say
$K_n$
, say
![]() $\mathcal{P}'_k$
, that is locally
$\mathcal{P}'_k$
, that is locally
![]() $1/8$
-balanced, but
$1/8$
-balanced, but
![]() $\mathcal{P}'_k$
does not contain a complete subgraph isomorphic to
$\mathcal{P}'_k$
does not contain a complete subgraph isomorphic to
![]() $\mathcal{P}_2$
, or a complete graph on
$\mathcal{P}_2$
, or a complete graph on
![]() $4$
vertices where one colour class forms two disjoint cliques of size
$4$
vertices where one colour class forms two disjoint cliques of size
![]() $2$
. And perhaps, there exists another colouring which is locally
$2$
. And perhaps, there exists another colouring which is locally
![]() $1/16$
-balanced, which does not contain
$1/16$
-balanced, which does not contain
![]() $\mathcal{P}_2'$
or any of the former patterns. Hence, maybe, the answer to Question 1.2 is a family of patterns
$\mathcal{P}_2'$
or any of the former patterns. Hence, maybe, the answer to Question 1.2 is a family of patterns
![]() $\mathcal{F}_\varepsilon$
which increases with
$\mathcal{F}_\varepsilon$
which increases with
![]() $\varepsilon ^{-1}$
. Indeed, Theorem 1.3 could feasibly be interpreted as evidence towards such a phenomenon. Our next result rules out any such possibility in a strong sense, demonstrating that the answer to Question 1.2 depends only on whether
$\varepsilon ^{-1}$
. Indeed, Theorem 1.3 could feasibly be interpreted as evidence towards such a phenomenon. Our next result rules out any such possibility in a strong sense, demonstrating that the answer to Question 1.2 depends only on whether
![]() $\varepsilon \leq 1/4$
or not.
$\varepsilon \leq 1/4$
or not.
Theorem 1.4.
Let
![]() $G$
be a
$G$
be a
![]() $2$
-coloured locally
$2$
-coloured locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $K_n$
for some
$K_n$
for some
![]() $\varepsilon \gt 0$
, and suppose
$\varepsilon \gt 0$
, and suppose
![]() $n \geq 2^{C t/\varepsilon ^{16}}$
for some absolute constant
$n \geq 2^{C t/\varepsilon ^{16}}$
for some absolute constant
![]() $C$
. Then,
$C$
. Then,
![]() $G$
contains a complete subgraph on
$G$
contains a complete subgraph on
![]() $2t$
vertices where one colour class forms a
$2t$
vertices where one colour class forms a
![]() $K_{t,t}$
, or a complete subgraph isomorphic to
$K_{t,t}$
, or a complete subgraph isomorphic to
![]() $\mathcal{P}_{t}$
.
$\mathcal{P}_{t}$
.
In [Reference Bowen, Lamaison and Müyesser1], Theorem 1.1 was generalised to
![]() $r$
-edge-colourings of
$r$
-edge-colourings of
![]() $K_n$
, and we refer the reader to that paper to see what kind of patterns can be guaranteed in the multicolour version of the problem. It is also natural to investigate a locally balanced version of the multicolour problem. The situation here is unexpectedly more difficult, as already for locally
$K_n$
, and we refer the reader to that paper to see what kind of patterns can be guaranteed in the multicolour version of the problem. It is also natural to investigate a locally balanced version of the multicolour problem. The situation here is unexpectedly more difficult, as already for locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $3$
-colourings there is no straightforward analogue of Theorem 1.4. We formalise this negative statement in Section 4, and obtain some complementary positive results.
$3$
-colourings there is no straightforward analogue of Theorem 1.4. We formalise this negative statement in Section 4, and obtain some complementary positive results.
Organisation of the paper. In Section 3.2, we introduce a general tool to find patterns (such as those depicted in Figure 3) efficiently in edge-coloured complete graphs. Our main tool is a technique of Nikiforov which uses subgraph count estimates to find large blow-ups of small subgraphs. This is in contrast to many of the related results in this area for which the main tool is the dependent random choice method. In Section 2.2, we compare these two approaches and give an overview of the proofs of Theorem 1.3 and Theorem 1.4. Section 3 contains formal proofs of both of these results. In Section 4, we treat the multicolour version of the problem.

Figure 3. A three-colouring of
![]() $K_n$
in which any locally balanced subgraph has at least
$K_n$
in which any locally balanced subgraph has at least
![]() $6$
vertices, where
$6$
vertices, where
![]() $6$
is the number of parts. This colouring is locally
$6$
is the number of parts. This colouring is locally
![]() $(1/6)$
-balanced. Colourings of this type (where two colour classes form a blow-up of an alternating cycle) show that there is no analogue of Theorem 1.4 for more than two colours.
$(1/6)$
-balanced. Colourings of this type (where two colour classes form a blow-up of an alternating cycle) show that there is no analogue of Theorem 1.4 for more than two colours.
Remark. After the submission of this paper, Theorem 1.3 and Theorem 1.4 have been strengthened by Gir ao and Munhá Correia [Reference Girão and Correia12] to give a dependence between
![]() $n$
and
$n$
and
![]() $\varepsilon$
which is optimal up to constant factors in the exponent.
$\varepsilon$
which is optimal up to constant factors in the exponent.
2. Preliminaries and proof outline
2.1 Notation
In this subsection, in preparation to give an overview of the proofs, we introduce and recall some notation. An
![]() $r$
-edge-coloured (or just an
$r$
-edge-coloured (or just an
![]() $r$
-coloured) graph is a graph together with a labelled partition of its edge-set into
$r$
-coloured) graph is a graph together with a labelled partition of its edge-set into
![]() $r$
parts. We view the parts of this partition as being labelled by different colours. We say that one coloured graph
$r$
parts. We view the parts of this partition as being labelled by different colours. We say that one coloured graph
![]() $G$
contains another coloured graph
$G$
contains another coloured graph
![]() $H$
if there exists an injection
$H$
if there exists an injection
![]() $\phi \colon V(H)\to V(G)$
such that
$\phi \colon V(H)\to V(G)$
such that
![]() $(a,b)\in E(H)$
implies that
$(a,b)\in E(H)$
implies that
![]() $(\phi (a),\phi (b))\in E(G)$
and
$(\phi (a),\phi (b))\in E(G)$
and
![]() $(\phi (a),\phi (b))$
has the same colour as
$(\phi (a),\phi (b))$
has the same colour as
![]() $(a,b)$
.
$(a,b)$
.
We say that a coloured graph
![]() $G$
is a homogeneous
$G$
is a homogeneous
![]() $t$
-blow-up of another coloured graph
$t$
-blow-up of another coloured graph
![]() $H$
if
$H$
if
![]() $V(G)$
can be partitioned into
$V(G)$
can be partitioned into
![]() $t$
-sized sets
$t$
-sized sets
![]() $V_1,\cdots, V_{|V(H)|}$
, each
$V_1,\cdots, V_{|V(H)|}$
, each
![]() $G[V_i]$
is a monochromatic clique (in some colour), and for each
$G[V_i]$
is a monochromatic clique (in some colour), and for each
![]() $(i,j)\in E(H)$
of colour
$(i,j)\in E(H)$
of colour
![]() $c$
,
$c$
,
![]() $G[V_i,V_j]$
is a complete bipartite graph where each edge gets colour
$G[V_i,V_j]$
is a complete bipartite graph where each edge gets colour
![]() $c$
.
$c$
.
An
![]() $r$
-totally coloured graph is a graph whose vertices as well as its edges are given an
$r$
-totally coloured graph is a graph whose vertices as well as its edges are given an
![]() $r$
-colouring. A coloured graph
$r$
-colouring. A coloured graph
![]() $G$
is a
$G$
is a
![]() $t$
-blow-up of a totally coloured graph
$t$
-blow-up of a totally coloured graph
![]() $H$
if
$H$
if
![]() $G$
is a
$G$
is a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $H$
with respect to the edge-colouring of
$H$
with respect to the edge-colouring of
![]() $H$
, and
$H$
, and
![]() $G[V_i]$
is a monochromatic clique in the same colour as the vertex
$G[V_i]$
is a monochromatic clique in the same colour as the vertex
![]() $i\in H$
.
$i\in H$
.
If
![]() $G$
is
$G$
is
![]() $2$
-coloured,
$2$
-coloured,
![]() $\overline{G}$
is used to denote the coloured graph with the two colours interchanged.
$\overline{G}$
is used to denote the coloured graph with the two colours interchanged.
We say that an
![]() $r$
-coloured
$r$
-coloured
![]() $G$
is locally
$G$
is locally
![]() $\varepsilon$
-balanced if each vertex of
$\varepsilon$
-balanced if each vertex of
![]() $G$
is incident to at least
$G$
is incident to at least
![]() $\varepsilon |V(G)|$
edges in each of the
$\varepsilon |V(G)|$
edges in each of the
![]() $r$
colours. We say that an
$r$
colours. We say that an
![]() $r$
-coloured graph
$r$
-coloured graph
![]() $G$
is globally
$G$
is globally
![]() $\varepsilon$
-balanced if each colour class has size at least
$\varepsilon$
-balanced if each colour class has size at least
![]() $\varepsilon \binom{n}{2}$
. Throughout the paper,
$\varepsilon \binom{n}{2}$
. Throughout the paper,
![]() $\epsilon$
is assumed to be a positive real number.
$\epsilon$
is assumed to be a positive real number.
For the convenience of the reader, in the following paragraph we collect every coloured and totally coloured graph we make reference to throughout the paper. For further clarity, in Figure 2, we provide an illustration of each of these graphs.
Let
![]() $P_1$
be the totally coloured
$P_1$
be the totally coloured
![]() $K_2$
with vertices receiving colour red, and the unique edge receiving colour blue. Note that the
$K_2$
with vertices receiving colour red, and the unique edge receiving colour blue. Note that the
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
is a blue induced
$P_1$
is a blue induced
![]() $K_{t,t}$
. Let
$K_{t,t}$
. Let
![]() $P_2$
be the totally coloured
$P_2$
be the totally coloured
![]() $K_2$
with one vertex receiving colour red, the other receiving colour blue, and the edge receiving colour red. Let
$K_2$
with one vertex receiving colour red, the other receiving colour blue, and the edge receiving colour red. Let
![]() $P_3$
be the totally coloured
$P_3$
be the totally coloured
![]() $K_4$
with edges
$K_4$
with edges
![]() $(1,2),(2,3), (3,4)$
and vertices
$(1,2),(2,3), (3,4)$
and vertices
![]() $2$
and
$2$
and
![]() $3$
coloured blue, and all other edges and vertices coloured red. Note that a
$3$
coloured blue, and all other edges and vertices coloured red. Note that a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_3$
is locally
$P_3$
is locally
![]() $1/4$
-balanced. Moreover, let
$1/4$
-balanced. Moreover, let
![]() $P_{3}^{\circ }$
be the (not totally) coloured graph obtained from
$P_{3}^{\circ }$
be the (not totally) coloured graph obtained from
![]() $P_3$
by discarding the vertex colours. Let
$P_3$
by discarding the vertex colours. Let
![]() $C_4$
be a
$C_4$
be a
![]() $2$
-edge-coloured
$2$
-edge-coloured
![]() $K_4$
with the red edges forming a
$K_4$
with the red edges forming a
![]() $4$
-cycle. Let
$4$
-cycle. Let
![]() $M_1$
be the properly
$M_1$
be the properly
![]() $2$
-edge-coloured
$2$
-edge-coloured
![]() $K_{2,2}$
.
$K_{2,2}$
.
With our notation, the aforementioned theorems can be stated as follows.
Theorem 1.1. (Fox-Sudakov, Cutler-Montágh) Suppose
![]() $n\geq (1/\varepsilon )^{16t}$
. Then, any globally
$n\geq (1/\varepsilon )^{16t}$
. Then, any globally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
contains a
$K_n$
contains a
![]() $t$
-blow-up of one of
$t$
-blow-up of one of
![]() $P_1$
,
$P_1$
,
![]() $P_2$
,
$P_2$
,
![]() $\overline{P_1}$
,
$\overline{P_1}$
,
![]() $\overline{P_2}$
.
$\overline{P_2}$
.
Theorem 1.2.
Suppose
![]() $n\geq 2^{t\cdot 2^{-C\log (1/\varepsilon )^8}}$
for a sufficiently large absolute constant
$n\geq 2^{t\cdot 2^{-C\log (1/\varepsilon )^8}}$
for a sufficiently large absolute constant
![]() $C$
. Then, any locally
$C$
. Then, any locally
![]() $(1/4+\varepsilon )$
-balanced
$(1/4+\varepsilon )$
-balanced
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
contains a
$K_n$
contains a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
or
$P_1$
or
![]() $\overline{P_1}$
.
$\overline{P_1}$
.
Theorem 1.3.
Suppose
![]() $n\geq 2^{C t/\varepsilon ^{16}}$
for a sufficiently large absolute constant
$n\geq 2^{C t/\varepsilon ^{16}}$
for a sufficiently large absolute constant
![]() $C$
. Then, any locally
$C$
. Then, any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
contains a
$K_n$
contains a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
,
$P_1$
,
![]() $\overline{P_1}$
or
$\overline{P_1}$
or
![]() $P_3$
.
$P_3$
.
Note that
![]() $\overline{P_3}$
is not included in the above list as
$\overline{P_3}$
is not included in the above list as
![]() $\overline{P_3}=P_3$
.
$\overline{P_3}=P_3$
.
2.2 Proof overview
Although our proofs are short, the method is quite different from the other papers in the area. In this section, we aim to motivate our approach and give heuristic explanations for why Theorems 3 and 4 are true, at least qualitatively (i.e. with some finite
![]() $n=n(t,\varepsilon )$
). We begin with a brief discussion of Theorem 1.1 in order to compare the different approaches. It is rather straightforward to obtain a proof of Theorem 1.1 if one is only concerned with obtaining
$n=n(t,\varepsilon )$
). We begin with a brief discussion of Theorem 1.1 in order to compare the different approaches. It is rather straightforward to obtain a proof of Theorem 1.1 if one is only concerned with obtaining
![]() $t$
-blow-ups where
$t$
-blow-ups where
![]() $t$
tends to infinity with
$t$
tends to infinity with
![]() $n$
. Indeed, applying the well-known Kővari-Sós-Turán Theorem to both red and blue colour classes, we can obtain one red and one blue
$n$
. Indeed, applying the well-known Kővari-Sós-Turán Theorem to both red and blue colour classes, we can obtain one red and one blue
![]() $K_{s,s}$
, say
$K_{s,s}$
, say
![]() $T_1$
and
$T_1$
and
![]() $T_2$
, respectively, where
$T_2$
, respectively, where
![]() $s\sim \log n$
(we can ensure that
$s\sim \log n$
(we can ensure that
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are vertex-disjoint). Apply Ramsey’s theorem to the four parts coming from
$T_2$
are vertex-disjoint). Apply Ramsey’s theorem to the four parts coming from
![]() $T_1$
and
$T_1$
and
![]() $T_2$
, and delete all vertices outside of the monochromatic cliques guaranteed by this application. Similarly, for each pair of the
$T_2$
, and delete all vertices outside of the monochromatic cliques guaranteed by this application. Similarly, for each pair of the
![]() $4$
parts, in turn, apply the Kővari-Sós-Turán theorem to the majority colour class in the bipartite graph between the pair of parts to guarantee a monochromatic complete bipartite subgraph, at each iteration reducing the size of the parts logarithmically. This produces a
$4$
parts, in turn, apply the Kővari-Sós-Turán theorem to the majority colour class in the bipartite graph between the pair of parts to guarantee a monochromatic complete bipartite subgraph, at each iteration reducing the size of the parts logarithmically. This produces a
![]() $t$
-blow-up of a totally coloured
$t$
-blow-up of a totally coloured
![]() $K_4$
(where
$K_4$
(where
![]() $t\to \infty$
as
$t\to \infty$
as
![]() $n\to \infty$
) where we do not have precise control over the colouring; however, we know that the colouring is not monochromatic (there exists at least one blue and one red edge). It is easy to see that this implies that the totally coloured
$n\to \infty$
) where we do not have precise control over the colouring; however, we know that the colouring is not monochromatic (there exists at least one blue and one red edge). It is easy to see that this implies that the totally coloured
![]() $K_4$
must contain one of
$K_4$
must contain one of
![]() $P_1$
,
$P_1$
,
![]() $P_2$
,
$P_2$
,
![]() $\overline{P_1}$
,
$\overline{P_1}$
,
![]() $\overline{P_2}$
, as desired.
$\overline{P_2}$
, as desired.
In [Reference Fox and Sudakov9], the dependent random choice method (see, e.g. [Reference Fox and Sudakov10]) is employed to obtain optimal bounds for Theorem 1.1, eliminating the need for nested applications of the Theorems of Ramsey and Kővari-Sós-Turán. However, the argument still boils down to finding a blow-up of a totally coloured graph which is not monochromatic, thereby producing a structure which necessarily contains one of the desired patterns. To prove Theorems 1.3 and 1.4, we find blow-ups of totally coloured graphs where each vertex is adjacent to edges of both colours. The argument given in the previous paragraph is too weak to achieve this, since it does not make use of the assumption that our colouring is locally balanced. The dependent random choice is quantitatively much stronger, but does not give any additional structural information.
Hence, we need an argument which will make use of the global structure of the colouring. Specifically, our main tool (Lemma 2.4), a strengthening of a theorem due to Nikiforov [Reference Nikiforov17], reduces the problem to finding certain small subgraphs appearing in
![]() $G$
with a positive density. Using Lemma 2.4, the statements of Theorem 1.3 and 1.4 reduce to the following two statements, respectively.
$G$
with a positive density. Using Lemma 2.4, the statements of Theorem 1.3 and 1.4 reduce to the following two statements, respectively.
Proposition 2.1.
There exists a constant
![]() $C_1$
such that the following holds. Any locally
$C_1$
such that the following holds. Any locally
![]() $(1/4 + \varepsilon )$
-balanced 2-coloured
$(1/4 + \varepsilon )$
-balanced 2-coloured
![]() $K_n$
contains
$K_n$
contains
![]() $2^{-C_1\log (1/\varepsilon )^8} n^4$
copies of
$2^{-C_1\log (1/\varepsilon )^8} n^4$
copies of
![]() $C_4$
or
$C_4$
or
![]() $\overline{C_4}$
.
$\overline{C_4}$
.
Proposition 2.2.
Let
![]() $n\geq \varepsilon ^{-100}$
. Any locally
$n\geq \varepsilon ^{-100}$
. Any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
contains
$K_n$
contains
![]() $\varepsilon ^4n^4/10^5$
copies of
$\varepsilon ^4n^4/10^5$
copies of
![]() $P_{3}^{\circ }, C_4$
or
$P_{3}^{\circ }, C_4$
or
![]() $\overline{C_4}$
.
$\overline{C_4}$
.
A natural tool for proving statements such as Proposition 2.1 and 2.2 is the Szemerédi Regularity Lemma and closely related removal lemmas (see, e.g. [Reference Conlon and Fox3]). For the sake of obtaining better bounds and more cogent proofs, we do not use the regularity method. However, the regularity method does provide a shorter proof of a quantitatively weaker version of Proposition 2.1, and thus Theorem 1.3. Indeed, using the Regularity Lemma, it is not hard to show that the vertex set of a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
with a vanishing density of both
$K_n$
with a vanishing density of both
![]() $C_4$
and
$C_4$
and
![]() $\overline{C}_4$
can essentially (i.e. after recolouring
$\overline{C}_4$
can essentially (i.e. after recolouring
![]() $o(n^2)$
edges), be partitioned into a red and a blue clique. Such a
$o(n^2)$
edges), be partitioned into a red and a blue clique. Such a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
can at best be locally
$K_n$
can at best be locally
![]() $(1/4+o(1))$
-balanced, by an easy optimisation argument (see Proposition 3.5), implying Proposition 2.1.
$(1/4+o(1))$
-balanced, by an easy optimisation argument (see Proposition 3.5), implying Proposition 2.1.
Proposition 2.2 is, however, more subtle, since even finding a single copy of the desired small subgraphs is a non-obvious extremal problem. To give some intuition on why the statement holds, let us prove an idealised version of it.
Proposition 2.3.
Let
![]() $(A,B)$
be a
$(A,B)$
be a
![]() $2$
-coloured complete bipartite graph with
$2$
-coloured complete bipartite graph with
![]() $|A|,|B|\gt 2$
so that each vertex of
$|A|,|B|\gt 2$
so that each vertex of
![]() $A$
has at least one blue neighbour, and each vertex of
$A$
has at least one blue neighbour, and each vertex of
![]() $B$
has at least one red neighbour. Then,
$B$
has at least one red neighbour. Then,
![]() $(A,B)$
contains a cycle of length
$(A,B)$
contains a cycle of length
![]() $4$
whose edges are alternating red and blue.
$4$
whose edges are alternating red and blue.
Proof. Suppose without loss of generality that
![]() $|A|\gt |B|$
. Let
$|A|\gt |B|$
. Let
![]() $v,w\in A$
. Suppose there exists no alternating red and blue
$v,w\in A$
. Suppose there exists no alternating red and blue
![]() $4$
-cycle. Observe that the blue neighbourhood of
$4$
-cycle. Observe that the blue neighbourhood of
![]() $v$
must be contained in that of
$v$
must be contained in that of
![]() $w$
, or vice versa, otherwise we immediately obtain an alternating
$w$
, or vice versa, otherwise we immediately obtain an alternating
![]() $4$
-cycle. Hence, the collection of blue neighbourhoods of vertices in
$4$
-cycle. Hence, the collection of blue neighbourhoods of vertices in
![]() $A$
forms a chain where the smallest subset has at least one element, say
$A$
forms a chain where the smallest subset has at least one element, say
![]() $q\in B$
, by assumption. Hence,
$q\in B$
, by assumption. Hence,
![]() $q$
is in the blue neighbourhood of every vertex of
$q$
is in the blue neighbourhood of every vertex of
![]() $A$
, meaning
$A$
, meaning
![]() $q$
has no red neighbours, a contradiction.
$q$
has no red neighbours, a contradiction.
To clarify the connection between Proposition 2.3 and Proposition 2.2, notice that completing a colouring of an alternating red-blue 4-cycle to an edge-colouring of
![]() $K_4$
yields a
$K_4$
yields a
![]() $C_4, \overline{C_4}$
or a
$C_4, \overline{C_4}$
or a
![]() $P_{3}^{\circ }$
.
$P_{3}^{\circ }$
.
Finally, we state our main technical tool, which allows us to deduce Theorems 1.3 and 1.4 from the aforementioned Propositions. Nikiforov [Reference Nikiforov17] showed that any graph with a positive density of
![]() $K_\ell$
-copies contains a large complete
$K_\ell$
-copies contains a large complete
![]() $\ell$
-partite subgraph. We strengthen this statement to find homogeneous blow-ups in
$\ell$
-partite subgraph. We strengthen this statement to find homogeneous blow-ups in
![]() $r$
-coloured graphs. Recall that our definition of a homogeneous blow-up in a coloured graph requires that the parts of the blow-up induce monochromatic cliques, but the colours of the cliques are not specified.
$r$
-coloured graphs. Recall that our definition of a homogeneous blow-up in a coloured graph requires that the parts of the blow-up induce monochromatic cliques, but the colours of the cliques are not specified.
Lemma 2.4.
Let
![]() $H$
be an
$H$
be an
![]() $\ell$
-vertex
$\ell$
-vertex
![]() $r$
-coloured graph. Let
$r$
-coloured graph. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $r$
-coloured graph containing at least
$r$
-coloured graph containing at least
![]() $c n^\ell$
copies of
$c n^\ell$
copies of
![]() $H$
. Then
$H$
. Then
![]() $G$
contains a homogeneous
$G$
contains a homogeneous
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $H$
with
$H$
with
![]() $ t \geq \min \left \{ \frac{c}{2\ell }, \frac{1}{2 r \log r} \right \} ^\ell \log n$
.
$ t \geq \min \left \{ \frac{c}{2\ell }, \frac{1}{2 r \log r} \right \} ^\ell \log n$
.
Lemma 2.4 is proved in Section 3.2. We remark that the Lemma also gives a short proof of Theorem 1.1 with the stronger hypothesis that
![]() $n\geq 2^{100t/\varepsilon }$
. Indeed, an easy counting argument implies that any globally
$n\geq 2^{100t/\varepsilon }$
. Indeed, an easy counting argument implies that any globally
![]() $\varepsilon$
-balanced 2-colouring of
$\varepsilon$
-balanced 2-colouring of
![]() $K_n$
contains
$K_n$
contains
![]() $\Omega (\varepsilon n^3)$
properly coloured two-edge paths (i.e.
$\Omega (\varepsilon n^3)$
properly coloured two-edge paths (i.e.
![]() $K_{1, 2}$
-copies), so Lemma 2.4 yields a homogeneous
$K_{1, 2}$
-copies), so Lemma 2.4 yields a homogeneous
![]() $t$
-blow-up of the non-monochromatic edge-colouring of
$t$
-blow-up of the non-monochromatic edge-colouring of
![]() $K_{1,2}$
. A simple case distinction then gives a blow-up of
$K_{1,2}$
. A simple case distinction then gives a blow-up of
![]() $P_1$
,
$P_1$
,
![]() $P_2$
or one of their complements. A similar argument gives a concise proof (with a weaker dependence between
$P_2$
or one of their complements. A similar argument gives a concise proof (with a weaker dependence between
![]() $n$
and
$n$
and
![]() $\varepsilon$
) of Theorem 1.4 from [Reference Bowen, Lamaison and Müyesser1], which is a generalisation of Theorem 1.1 to an arbitrary number of colours, originally proved via nested applications of the dependent random choice method.
$\varepsilon$
) of Theorem 1.4 from [Reference Bowen, Lamaison and Müyesser1], which is a generalisation of Theorem 1.1 to an arbitrary number of colours, originally proved via nested applications of the dependent random choice method.
3. Proofs for patterns in two-colourings
3.1 Proofs of the main theorems
We now show how the main theorems follow easily from the two propositions on subgraph counts and Lemma 2.4.
Proof of Theorem
1.3. By Proposition 2.1, we may assume (without loss of generality) that
![]() $G$
contains at least
$G$
contains at least
![]() $2^{-C_1\log (1/\varepsilon )^8} n^4$
copies of
$2^{-C_1\log (1/\varepsilon )^8} n^4$
copies of
![]() $C_4$
. By Lemma 2.4 applied with
$C_4$
. By Lemma 2.4 applied with
![]() $c = 2^{-C_1\log (1/\varepsilon )^8}$
,
$c = 2^{-C_1\log (1/\varepsilon )^8}$
,
![]() $G$
contains a homogeneous
$G$
contains a homogeneous
![]() $(2^{-C\log (1/\varepsilon )^8} \log n)$
-blow-up of
$(2^{-C\log (1/\varepsilon )^8} \log n)$
-blow-up of
![]() $C_4$
for some absolute constant
$C_4$
for some absolute constant
![]() $C$
. Note that by assumption on
$C$
. Note that by assumption on
![]() $n$
,
$n$
,
![]() $2^{-C\log (1/\varepsilon )^8} \log n \geq t$
. Let
$2^{-C\log (1/\varepsilon )^8} \log n \geq t$
. Let
![]() $V_1, \ldots, V_4$
be the parts of this blow-up, and recall that
$V_1, \ldots, V_4$
be the parts of this blow-up, and recall that
![]() $G[V_i]$
are monochromatic cliques.
$G[V_i]$
are monochromatic cliques.
We claim that
![]() $G[V_1 \cup V_2 \cup V_3 \cup V_4]$
contains a
$G[V_1 \cup V_2 \cup V_3 \cup V_4]$
contains a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
or
$P_1$
or
![]() $\overline{P_1}$
. Assume the opposite. At least one vertex part has to be blue, so assume that
$\overline{P_1}$
. Assume the opposite. At least one vertex part has to be blue, so assume that
![]() $G[V_1]$
is blue. Then
$G[V_1]$
is blue. Then
![]() $G[V_2]$
and
$G[V_2]$
and
![]() $G[V_4]$
are red, so they form a blow-up of
$G[V_4]$
are red, so they form a blow-up of
![]() $P_1$
, which is a contradiction.
$P_1$
, which is a contradiction.
Proof of Theorem
1.4. Proposition 2.2 implies that
![]() $G$
contains
$G$
contains
![]() $\varepsilon ^4 n^4/10^5$
copies of
$\varepsilon ^4 n^4/10^5$
copies of
![]() $C_4$
,
$C_4$
,
![]() $\overline{C_4}$
or
$\overline{C_4}$
or
![]() $P_{3}^{\circ }$
in
$P_{3}^{\circ }$
in
![]() $G$
. Let
$G$
. Let
![]() $t = \left (\varepsilon ^4 \cdot 10^{-6} \right )^4 \log n$
, noting that this satisfies the claimed bound on
$t = \left (\varepsilon ^4 \cdot 10^{-6} \right )^4 \log n$
, noting that this satisfies the claimed bound on
![]() $n(t, \varepsilon )$
. In the cases with many copies of
$n(t, \varepsilon )$
. In the cases with many copies of
![]() $C_4$
or
$C_4$
or
![]() $\overline{C_4}$
, the above argument from the proof of Theorem 1.3 yields a
$\overline{C_4}$
, the above argument from the proof of Theorem 1.3 yields a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
or
$P_1$
or
![]() $\overline{P_1}$
. In the latter case, applying Lemma 2.4, we obtain that
$\overline{P_1}$
. In the latter case, applying Lemma 2.4, we obtain that
![]() $G$
contains a homogeneous
$G$
contains a homogeneous
![]() $(\varepsilon ^{16}10^{-7}\log n)$
-blow-up of
$(\varepsilon ^{16}10^{-7}\log n)$
-blow-up of
![]() $P_{3}^{\circ }$
on the vertex parts
$P_{3}^{\circ }$
on the vertex parts
![]() $V_1, V_2, V_3$
and
$V_1, V_2, V_3$
and
![]() $V_4$
. Suppose that this structure does not contain the
$V_4$
. Suppose that this structure does not contain the
![]() $t$
-blow-up of a
$t$
-blow-up of a
![]() $P_1$
or
$P_1$
or
![]() $\overline{P}_1$
, otherwise we are done. Suppose that
$\overline{P}_1$
, otherwise we are done. Suppose that
![]() $G[V_1]$
is blue. Then
$G[V_1]$
is blue. Then
![]() $G[V_3]$
and
$G[V_3]$
and
![]() $G[V_4]$
are red, and hence they form a blow-up of
$G[V_4]$
are red, and hence they form a blow-up of
![]() $P_1$
, contradiction. Hence
$P_1$
, contradiction. Hence
![]() $G[V_1]$
is red, and consequently,
$G[V_1]$
is red, and consequently,
![]() $G[V_2]$
is blue, so
$G[V_2]$
is blue, so
![]() $G[V_4]$
is red, and finally,
$G[V_4]$
is red, and finally,
![]() $G[V_3]$
is blue. This yields a
$G[V_3]$
is blue. This yields a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_3$
, as required.
$P_3$
, as required.
3.2 Finding homogeneous blow-ups of small patterns
In this subsection, we prove Lemma 2.4, a variant of a result due to Nikiforov [Reference Nikiforov17]. The main ingredient is Lemma 3.1, which is about dense
![]() $\ell$
-uniform hypergraphs. Before stating and proving Lemma 3.1, we give the following definitions which are central due to the inductive nature of the proof.
$\ell$
-uniform hypergraphs. Before stating and proving Lemma 3.1, we give the following definitions which are central due to the inductive nature of the proof.
Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $\ell$
-partite
$\ell$
-partite
![]() $\ell$
-uniform hypergraph
$\ell$
-uniform hypergraph
![]() $\mathcal{H}$
on parts
$\mathcal{H}$
on parts
![]() $V_1, \ldots, V_\ell$
. We usually specify the members of
$V_1, \ldots, V_\ell$
. We usually specify the members of
![]() $E({\mathcal{H}})$
as
$E({\mathcal{H}})$
as
![]() $\ell$
-tuples
$\ell$
-tuples
![]() $(v_1, \ldots v_\ell )$
(where
$(v_1, \ldots v_\ell )$
(where
![]() $v_i\in V_i$
), but we also abuse notation by saying that
$v_i\in V_i$
), but we also abuse notation by saying that
![]() $(v_1, \ldots, v_\ell )$
contains
$(v_1, \ldots, v_\ell )$
contains
![]() $v_1$
, or by writing
$v_1$
, or by writing
![]() $(v_1, \ldots v_\ell ) = (v_1, \ldots, v_{\ell -1})+v_\ell$
. Let
$(v_1, \ldots v_\ell ) = (v_1, \ldots, v_{\ell -1})+v_\ell$
. Let
![]() $K_2({\mathcal{H}})$
be the vertex pairs contained in edges of
$K_2({\mathcal{H}})$
be the vertex pairs contained in edges of
![]() $\mathcal{H}$
. Moreover, we write
$\mathcal{H}$
. Moreover, we write
![]() $\partial{\mathcal{H}}$
for the collection of
$\partial{\mathcal{H}}$
for the collection of
![]() $(\ell -1)$
-tuples
$(\ell -1)$
-tuples
![]() $(v_1, \ldots, v_{\ell -1})$
which are contained in some edge
$(v_1, \ldots, v_{\ell -1})$
which are contained in some edge
![]() $(v_1, \ldots, v_\ell )$
of
$(v_1, \ldots, v_\ell )$
of
![]() $\mathcal{H}$
, with
$\mathcal{H}$
, with
![]() $v_i \in V_i$
for
$v_i \in V_i$
for
![]() $i \in [\ell ]$
. We emphasise that this notation is not standard since
$i \in [\ell ]$
. We emphasise that this notation is not standard since
![]() $\partial{\mathcal{H}}$
only contains
$\partial{\mathcal{H}}$
only contains
![]() $(\ell -1)$
-tuples from
$(\ell -1)$
-tuples from
![]() $V_1 \times \dots \times V_{\ell -1}$
. Given a graph
$V_1 \times \dots \times V_{\ell -1}$
. Given a graph
![]() $G$
isomorphic to a
$G$
isomorphic to a
![]() $K_{\ell }(m)$
(the complete
$K_{\ell }(m)$
(the complete
![]() $\ell$
-partite graph with vertex parts of size
$\ell$
-partite graph with vertex parts of size
![]() $m$
), we say that
$m$
), we say that
![]() $\mathcal{H}$
covers
$\mathcal{H}$
covers
![]() $G$
if
$G$
if
![]() $E(G) \subset K_2({\mathcal{H}})$
and there are
$E(G) \subset K_2({\mathcal{H}})$
and there are
![]() $m$
disjoint
$m$
disjoint
![]() $S \in E({\mathcal{H}})$
with
$S \in E({\mathcal{H}})$
with
![]() $S \subset V(G)$
(in other words,
$S \subset V(G)$
(in other words,
![]() $\mathcal{H}$
contains a matching of size
$\mathcal{H}$
contains a matching of size
![]() $m$
on
$m$
on
![]() $V(G)$
).
$V(G)$
).
Lemma 3.1.
Let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $\ell$
-partite
$\ell$
-partite
![]() $\ell$
-uniform hypergraph on parts
$\ell$
-uniform hypergraph on parts
![]() $V_1, \ldots, V_\ell$
of size
$V_1, \ldots, V_\ell$
of size
![]() $n$
with least
$n$
with least
![]() $\ell c n^\ell$
edges. Let
$\ell c n^\ell$
edges. Let
![]() $\varphi$
be an
$\varphi$
be an
![]() $r$
-colouring of the complete (
$r$
-colouring of the complete (
![]() $2$
-uniform) graphs on
$2$
-uniform) graphs on
![]() $V_1, \ldots, V_\ell$
. Then, there are vertex sets
$V_1, \ldots, V_\ell$
. Then, there are vertex sets
![]() $S_1, \ldots, S_\ell$
with
$S_1, \ldots, S_\ell$
with
![]() $|S_i| \geq \left ( \min \{\frac c2, \frac{1}{2r \log r}\} \right )^\ell \log n$
such that
$|S_i| \geq \left ( \min \{\frac c2, \frac{1}{2r \log r}\} \right )^\ell \log n$
such that
![]() $\varphi$
is constant on each
$\varphi$
is constant on each
![]() $S_i$
, and
$S_i$
, and
![]() $\mathcal{H}$
covers the complete
$\mathcal{H}$
covers the complete
![]() $\ell$
-partite graph on
$\ell$
-partite graph on
![]() $S_1, \ldots, S_\ell$
.
$S_1, \ldots, S_\ell$
.
To prove Lemma 3.1, we need the following lemma for finding unbalanced complete bipartite graphs, which can be proved using the classical double counting argument of Kővari, Sós and Turán [Reference Kővari, Sós and Turán14].
Lemma 3.2. (Lemma 2 from [Reference Nikiforov17]). Let
![]() $F$
be a bipartite graph with parts
$F$
be a bipartite graph with parts
![]() $A$
and
$A$
and
![]() $B$
. Let
$B$
. Let
![]() $|A| = m$
,
$|A| = m$
,
![]() $|B| = n$
and
$|B| = n$
and
![]() $c, \alpha \in (0, 1/2)$
. If
$c, \alpha \in (0, 1/2)$
. If
![]() $\alpha \log n \leq \frac{cm}{2} + 1$
and
$\alpha \log n \leq \frac{cm}{2} + 1$
and
![]() $e(F) \geq cmn$
, then
$e(F) \geq cmn$
, then
![]() $F$
contains a complete bipartite graph with parts
$F$
contains a complete bipartite graph with parts
![]() $S \subset A$
and
$S \subset A$
and
![]() $T \subset B$
of size
$T \subset B$
of size
![]() $|S| = \alpha \log n$
and
$|S| = \alpha \log n$
and
![]() $|T| \gt n^{1-\alpha/c}$
.
$|T| \gt n^{1-\alpha/c}$
.
We also need a standard upper bound on the
![]() $r$
-colour Ramsey number due to Erdős and Szekeres [Reference Erdős and Szekeres6]. Namely, any
$r$
-colour Ramsey number due to Erdős and Szekeres [Reference Erdős and Szekeres6]. Namely, any
![]() $r$
-colouring of
$r$
-colouring of
![]() $K_n$
contains a monochromatic clique on
$K_n$
contains a monochromatic clique on
![]() $\frac{\log n}{r \log r}$
vertices. We emphasise that we are mostly concerned with the case
$\frac{\log n}{r \log r}$
vertices. We emphasise that we are mostly concerned with the case
![]() $r =2$
. We can now proceed with the proof.
$r =2$
. We can now proceed with the proof.
Proof of Lemma
3.1. Assume that
![]() $c \leq (r \log r)^{-1}$
, since the statement for larger values of
$c \leq (r \log r)^{-1}$
, since the statement for larger values of
![]() $c$
then follows. We prove the statement by induction on
$c$
then follows. We prove the statement by induction on
![]() $\ell$
. The case
$\ell$
. The case
![]() $\ell =1$
follows from Ramsey’s Theorem – a colouring of
$\ell =1$
follows from Ramsey’s Theorem – a colouring of
![]() $K_{cn}$
contains a monochromatic clique of size
$K_{cn}$
contains a monochromatic clique of size
![]() $ (r \log r)^{-1} \log (cn) \geq (2 r \log r)^{-1} \log (n) \geq \frac c2 \log n$
. Assume that the statement holds for
$ (r \log r)^{-1} \log (cn) \geq (2 r \log r)^{-1} \log (n) \geq \frac c2 \log n$
. Assume that the statement holds for
![]() $\ell -1$
, and let
$\ell -1$
, and let
![]() $\mathcal{H}$
be as in the statement.
$\mathcal{H}$
be as in the statement.
For a hypergraph
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $R= (v_1, \ldots, v_{\ell -1})$
, we write
$R= (v_1, \ldots, v_{\ell -1})$
, we write
![]() $d_{\mathcal{L}}(R)$
for the number of edges of
$d_{\mathcal{L}}(R)$
for the number of edges of
![]() $\mathcal{L}$
containing
$\mathcal{L}$
containing
![]() $R$
. A standard deletion argument shows that there is
$R$
. A standard deletion argument shows that there is
![]() $\mathcal{L} \subset{\mathcal{H}}$
with
$\mathcal{L} \subset{\mathcal{H}}$
with
![]() $|\mathcal{L}| \geq (\ell -1)cn^\ell$
such that
$|\mathcal{L}| \geq (\ell -1)cn^\ell$
such that
indeed, one can iteratively remove all edges containing
![]() $R$
for any
$R$
for any
![]() $R$
violating (1), removing at most
$R$
violating (1), removing at most
![]() $cn \cdot n^{\ell -1}$
edges in total.
$cn \cdot n^{\ell -1}$
edges in total.
We have
![]() $|\partial \mathcal{L}| \geq |\mathcal{L}|/ n \geq (\ell -1) cn^{\ell -1}$
, since each
$|\partial \mathcal{L}| \geq |\mathcal{L}|/ n \geq (\ell -1) cn^{\ell -1}$
, since each
![]() $R \in \partial \mathcal{L}$
is contained in at most
$R \in \partial \mathcal{L}$
is contained in at most
![]() $n$
edges of
$n$
edges of
![]() $\mathcal{L}$
. Applying the induction hypothesis to
$\mathcal{L}$
. Applying the induction hypothesis to
![]() $\partial \mathcal{L}$
, we obtain sets
$\partial \mathcal{L}$
, we obtain sets
![]() $U_1, \ldots U_{\ell -1}\subseteq V_1,\ldots, V_{\ell -1}$
with
$U_1, \ldots U_{\ell -1}\subseteq V_1,\ldots, V_{\ell -1}$
with
![]() $|U_i| = m = \left (\frac c2 \right )^{\ell -1} \log n$
such that
$|U_i| = m = \left (\frac c2 \right )^{\ell -1} \log n$
such that
![]() $\partial \mathcal{L}$
covers the complete
$\partial \mathcal{L}$
covers the complete
![]() $(\ell -1)$
-partite graph on
$(\ell -1)$
-partite graph on
![]() $U_1 \cup \ldots \cup U_{\ell -1}$
, and
$U_1 \cup \ldots \cup U_{\ell -1}$
, and
![]() $\varphi [U_i]$
is constant for each
$\varphi [U_i]$
is constant for each
![]() $i\in [\ell -1]$
.
$i\in [\ell -1]$
.
Let
![]() $\mathcal{A}$
be a set of
$\mathcal{A}$
be a set of
![]() $m$
disjoint
$m$
disjoint
![]() $(\ell -1)$
-tuples in
$(\ell -1)$
-tuples in
![]() $\partial \mathcal{L}$
, which exists by the definition of a covering. The graph structure of
$\partial \mathcal{L}$
, which exists by the definition of a covering. The graph structure of
![]() $K_2(\mathcal{L})$
will now be used by noticing that it suffices to find a large subset of vertices
$K_2(\mathcal{L})$
will now be used by noticing that it suffices to find a large subset of vertices
![]() $T \subset V_\ell$
such that
$T \subset V_\ell$
such that
![]() $R+v_\ell \in \mathcal{L}$
for all
$R+v_\ell \in \mathcal{L}$
for all
![]() $R \in \mathcal{A}$
and
$R \in \mathcal{A}$
and
![]() $v_\ell \in T$
. To this end, consider the bipartite graph
$v_\ell \in T$
. To this end, consider the bipartite graph
![]() $F$
with parts
$F$
with parts
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $V_\ell$
such that
$V_\ell$
such that
![]() $(R, v_\ell ) \in F$
whenever
$(R, v_\ell ) \in F$
whenever
![]() $R+ v_\ell$
lies in
$R+ v_\ell$
lies in
![]() $\mathcal{L}$
. Since
$\mathcal{L}$
. Since
![]() $d_{\mathcal{L}}(R) \gt cn$
for all
$d_{\mathcal{L}}(R) \gt cn$
for all
![]() $R \in \mathcal{A} \subset \partial \mathcal{L}$
, we have that
$R \in \mathcal{A} \subset \partial \mathcal{L}$
, we have that
![]() $e(F) \geq cmn$
.
$e(F) \geq cmn$
.
We can apply Lemma 3.2 to
![]() $F$
with
$F$
with
![]() $\alpha =(c/2)^\ell$
. We also set
$\alpha =(c/2)^\ell$
. We also set
![]() $s\;:\!=\; \left (\frac c2 \right )^\ell \log n =\alpha \log n \leq \frac c2 m + 1$
and
$s\;:\!=\; \left (\frac c2 \right )^\ell \log n =\alpha \log n \leq \frac c2 m + 1$
and
![]() $t\;:\!=\; n^{1-2^{-\ell }c^{\ell -1}} = n^{1-\alpha/ c}$
. It follows that
$t\;:\!=\; n^{1-2^{-\ell }c^{\ell -1}} = n^{1-\alpha/ c}$
. It follows that
![]() $F$
contains a complete bipartite graph with parts
$F$
contains a complete bipartite graph with parts
![]() $\mathcal{A}'$
and
$\mathcal{A}'$
and
![]() $T$
such that
$T$
such that
![]() $|\mathcal{A}'| = s$
and
$|\mathcal{A}'| = s$
and
![]() $|T| = t$
. Let
$|T| = t$
. Let
![]() $G = K_2(\mathcal{L})$
. Let
$G = K_2(\mathcal{L})$
. Let
![]() $S_1, \ldots, S_{\ell -1}$
be the vertex sets of the edges of
$S_1, \ldots, S_{\ell -1}$
be the vertex sets of the edges of
![]() $\mathcal{A}'$
, and recall that they induce a
$\mathcal{A}'$
, and recall that they induce a
![]() $K_{\ell -1}(s)$
in
$K_{\ell -1}(s)$
in
![]() $ G$
since
$ G$
since
![]() $S_i \subset U_i$
. Moreover, we claim that
$S_i \subset U_i$
. Moreover, we claim that
![]() $w v_\ell$
is in
$w v_\ell$
is in
![]() $G$
for any
$G$
for any
![]() $v_\ell \in T$
and
$v_\ell \in T$
and
![]() $w \in S_i$
with
$w \in S_i$
with
![]() $i \in [\ell -1]$
. This follows from the fact that there is an
$i \in [\ell -1]$
. This follows from the fact that there is an
![]() $R \in \mathcal{A}'$
containing
$R \in \mathcal{A}'$
containing
![]() $w$
, and
$w$
, and
![]() $R+v_\ell \in \mathcal{L}$
.
$R+v_\ell \in \mathcal{L}$
.
Finally, by Ramsey’s theorem, there is a subset
![]() $S_\ell \subset T$
with
$S_\ell \subset T$
with
![]() $|S_\ell | = s = \left (\frac c2 \right )^\ell \log n \leq \frac{1}{r\log r} \log |T|$
on which
$|S_\ell | = s = \left (\frac c2 \right )^\ell \log n \leq \frac{1}{r\log r} \log |T|$
on which
![]() $\varphi$
is constant. Recalling that
$\varphi$
is constant. Recalling that
![]() $\varphi [S_i]$
is constant for
$\varphi [S_i]$
is constant for
![]() $i \in [\ell -1]$
by induction hypothesis, we obtain our desired sets
$i \in [\ell -1]$
by induction hypothesis, we obtain our desired sets
![]() $S_1, \ldots, S_\ell$
. To verify that
$S_1, \ldots, S_\ell$
. To verify that
![]() $\mathcal{L}$
covers
$\mathcal{L}$
covers
![]() $S_1, \ldots, S_\ell$
, note that the edges of
$S_1, \ldots, S_\ell$
, note that the edges of
![]() $\mathcal{A}'$
with the vertices of
$\mathcal{A}'$
with the vertices of
![]() $S_\ell$
(in an arbitrary order) form a matching of size
$S_\ell$
(in an arbitrary order) form a matching of size
![]() $s$
in
$s$
in
![]() $\mathcal{L}$
.
$\mathcal{L}$
.
We now give the proof of Lemma 2.4.
Proof that Lemma
2.4 follows from Lemma 3.1. Let
![]() $V_1, \ldots, V_\ell$
be a uniformly random partition of the vertex set of
$V_1, \ldots, V_\ell$
be a uniformly random partition of the vertex set of
![]() $G$
with parts of size at least
$G$
with parts of size at least
![]() $n' = \lfloor \frac{n}{\ell } \rfloor$
, and associate
$n' = \lfloor \frac{n}{\ell } \rfloor$
, and associate
![]() $V_1, \ldots, V_{\ell }$
to the vertices of
$V_1, \ldots, V_{\ell }$
to the vertices of
![]() $v_1,v_2,\ldots, v_\ell$
of
$v_1,v_2,\ldots, v_\ell$
of
![]() $H$
. We say that a copy of
$H$
. We say that a copy of
![]() $H$
in
$H$
in
![]() $G$
is canonical with respect to this partition if
$G$
is canonical with respect to this partition if
![]() $v_i$
is embedded to
$v_i$
is embedded to
![]() $V_i$
for each
$V_i$
for each
![]() $i\in [\ell ]$
. We claim that a copy of
$i\in [\ell ]$
. We claim that a copy of
![]() $H$
in
$H$
in
![]() $G$
is canonical with probability at least
$G$
is canonical with probability at least
![]() $(n'/ n)^{\ell }$
. Indeed, each vertex
$(n'/ n)^{\ell }$
. Indeed, each vertex
![]() $v_i$
of this
$v_i$
of this
![]() $H$
-copy is placed into
$H$
-copy is placed into
![]() $V_i$
with probability at least
$V_i$
with probability at least
![]() $\frac{n'}{n}$
. Moreover, the events that the vertices of this
$\frac{n'}{n}$
. Moreover, the events that the vertices of this
![]() $H$
-copy are placed into the corresponding parts are positively correlated, which implies the lower bound
$H$
-copy are placed into the corresponding parts are positively correlated, which implies the lower bound
![]() $(n'/ n)^{\ell }$
.
$(n'/ n)^{\ell }$
.
Hence, using linearity of expectation, we may assume that the number of
![]() $H$
-copies respecting our partition is at least
$H$
-copies respecting our partition is at least
![]() $\left (\frac{n'}{n} \right )^\ell cn^{\ell }= cn'^\ell$
. Let
$\left (\frac{n'}{n} \right )^\ell cn^{\ell }= cn'^\ell$
. Let
![]() $\mathcal{H}$
be the hypergraph corresponding to those copies. We may apply Lemma 3.1 with
$\mathcal{H}$
be the hypergraph corresponding to those copies. We may apply Lemma 3.1 with
![]() $c' = \frac c\ell$
, to obtain the desired sets
$c' = \frac c\ell$
, to obtain the desired sets
![]() $S_1, \ldots S_\ell$
with
$S_1, \ldots S_\ell$
with
![]() $|S_i| =\min \left \{ \frac{c}{2\ell }, \frac{1}{2 r \log r} \right \} ^\ell \log n$
.
$|S_i| =\min \left \{ \frac{c}{2\ell }, \frac{1}{2 r \log r} \right \} ^\ell \log n$
.
3.3 Small subgraphs in locally balanced colourings
We now prove Proposition 2.1, which follows immediately from Lemma 3.4 and Proposition 3.5. As discussed above, in Lemma 3.4 we actually describe the structure of colourings with a vanishing density of
![]() $C_4$
and
$C_4$
and
![]() $\overline{C_4}$
. We call a
$\overline{C_4}$
. We call a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
split if its vertex set can be partitioned into a red clique and a blue clique. We call two
$K_n$
split if its vertex set can be partitioned into a red clique and a blue clique. We call two
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
$K_n$
![]() $\delta$
-close if the first can be made isomorphic to the second after flipping the colours of at most
$\delta$
-close if the first can be made isomorphic to the second after flipping the colours of at most
![]() $\delta n^2$
many edges. The following result can be thought of as a substitute for the regularity method which is sufficient for our purposes.
$\delta n^2$
many edges. The following result can be thought of as a substitute for the regularity method which is sufficient for our purposes.
Lemma 3.3. (Fox-Sudakov [Reference Fox and Sudakov8] (Theorem 4.4)). There exists an absolute constant
![]() $c$
such that for each
$c$
such that for each
![]() $\varepsilon \in (0,1)$
and graph
$\varepsilon \in (0,1)$
and graph
![]() $H$
on
$H$
on
![]() $k$
vertices, there are constants
$k$
vertices, there are constants
![]() $\kappa \;:\!=\;(\varepsilon/4)^k2^{-c(k\log (1/\varepsilon ))^2}$
and
$\kappa \;:\!=\;(\varepsilon/4)^k2^{-c(k\log (1/\varepsilon ))^2}$
and
![]() $C=4/(\varepsilon 2^{-ck(\log (1/\varepsilon ))^2})$
such the following holds. For any
$C=4/(\varepsilon 2^{-ck(\log (1/\varepsilon ))^2})$
such the following holds. For any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with fewer than
$G$
with fewer than
![]() $\kappa n^k$
induced copies of
$\kappa n^k$
induced copies of
![]() $H$
, there is an equitable partition of
$H$
, there is an equitable partition of
![]() $V(G)$
into at most
$V(G)$
into at most
![]() $C$
parts such that each part induces a subgraph of density at most
$C$
parts such that each part induces a subgraph of density at most
![]() $\varepsilon$
or at least
$\varepsilon$
or at least
![]() $1-\varepsilon$
.
$1-\varepsilon$
.
We now use the above lemma to show that a
![]() $2$
-coloured graph with a vanishing density of
$2$
-coloured graph with a vanishing density of
![]() $C_4$
and
$C_4$
and
![]() $\overline{C_4}$
is
$\overline{C_4}$
is
![]() $o(1)$
-close to being split.
$o(1)$
-close to being split.
Lemma 3.4.
There exists an absolute constant
![]() $C_2$
so that the following holds for any
$C_2$
so that the following holds for any
![]() $n$
and
$n$
and
![]() $\delta$
. Let
$\delta$
. Let
![]() $G$
be a
$G$
be a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
. Then, at least one of the following is true.
$K_n$
. Then, at least one of the following is true.
-
1.
 $G$
contains at least
$G$
contains at least
 $2^{-C_2\log (1/\delta )^8} n^4$
many distinct copies of
$2^{-C_2\log (1/\delta )^8} n^4$
many distinct copies of
 $C_4$
or
$C_4$
or
 $\overline{C_4}$
$\overline{C_4}$
-
2.
 $G$
is
$G$
is
 $\delta$
-close to being split.
$\delta$
-close to being split.
Proof. Suppose that
![]() $(1)$
does not hold. Then, by Lemma 3.3 applied with
$(1)$
does not hold. Then, by Lemma 3.3 applied with
![]() $\delta ^{5}$
in place of
$\delta ^{5}$
in place of
![]() $\varepsilon$
, we have that there is an equitable partition of
$\varepsilon$
, we have that there is an equitable partition of
![]() $G$
into at most
$G$
into at most
parts, each of which has either red or blue density above
![]() $1-\delta ^5$
. Let us refer to the parts with high red density as red parts, and label them by
$1-\delta ^5$
. Let us refer to the parts with high red density as red parts, and label them by
![]() $V_1,\ldots, V_\ell$
.
$V_1,\ldots, V_\ell$
.
Proof. We claim that
![]() $G[V_1 \cup \dots \cup V_\ell ]$
contains at most
$G[V_1 \cup \dots \cup V_\ell ]$
contains at most
![]() $\delta n^2/2$
blue edges. If
$\delta n^2/2$
blue edges. If
![]() $\ell = 1$
, this is trivial, and otherwise it follows from the following claim.
$\ell = 1$
, this is trivial, and otherwise it follows from the following claim.
Claim 1.
Let
![]() $V_i$
and
$V_i$
and
![]() $V_j$
be two parts with density
$V_j$
be two parts with density
![]() $\geq 1-\delta ^5$
in red. Then the bipartite graph
$\geq 1-\delta ^5$
in red. Then the bipartite graph
![]() $G[V_i, V_j]$
has red density at least
$G[V_i, V_j]$
has red density at least
![]() $1-\delta$
.
$1-\delta$
.
Suppose that the blue density between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
is at least
$V_j$
is at least
![]() $\delta$
. It follows that the blue subgraph of
$\delta$
. It follows that the blue subgraph of
![]() $G[V_i\cup V_j]$
must contain at least
$G[V_i\cup V_j]$
must contain at least
![]() $2^{-10} \delta ^4 (n/C)^4$
copies of a cycle on
$2^{-10} \delta ^4 (n/C)^4$
copies of a cycle on
![]() $4$
vertices (see, for example, Theorem 1.9(iv) from [Reference Nagy16]). At most
$4$
vertices (see, for example, Theorem 1.9(iv) from [Reference Nagy16]). At most
![]() $2\delta ^5 (n/C)^4$
such
$2\delta ^5 (n/C)^4$
such
![]() $4$
-cycles can contain a blue edge from
$4$
-cycles can contain a blue edge from
![]() $G[V_i]$
or
$G[V_i]$
or
![]() $G[V_j]$
, by the density assumption. The remaining
$G[V_j]$
, by the density assumption. The remaining
![]() $4$
-cycles must correspond to a copy of
$4$
-cycles must correspond to a copy of
![]() $\overline{C_4}$
in
$\overline{C_4}$
in
![]() $G[V_i\cup V_j]$
. Note that for some absolute constant
$G[V_i\cup V_j]$
. Note that for some absolute constant
![]() $C_2$
, we have that
$C_2$
, we have that
![]() $\delta ^4 (n/C)^4\geq 2^{-C_2\log (1/\delta )^8} n^4$
, so as we assumed that
$\delta ^4 (n/C)^4\geq 2^{-C_2\log (1/\delta )^8} n^4$
, so as we assumed that
![]() $(1)$
does not hold, we conclude that
$(1)$
does not hold, we conclude that
![]() $G[V_i, V_j]$
has red density at least
$G[V_i, V_j]$
has red density at least
![]() $1-\delta$
.
$1-\delta$
.
The same argument implies that the union of blue parts contains at most
![]() $\delta n^2/ 2$
blue edges. Hence, combining the red parts as well as the blue parts gives a partition certifying that
$\delta n^2/ 2$
blue edges. Hence, combining the red parts as well as the blue parts gives a partition certifying that
![]() $G$
is
$G$
is
![]() $\delta$
-close to a split graph, as required.
$\delta$
-close to a split graph, as required.
We now show that graphs which are
![]() $\delta$
-close to being split cannot be
$\delta$
-close to being split cannot be
![]() $(1/4+2\delta )$
-balanced. When combined with Lemma 3.4, this immediately implies Proposition 2.1.
$(1/4+2\delta )$
-balanced. When combined with Lemma 3.4, this immediately implies Proposition 2.1.
Proposition 3.5.
If a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
is
$K_n$
is
![]() $\delta$
-close to being split, then it has a vertex with at most
$\delta$
-close to being split, then it has a vertex with at most
![]() $(1/4+3\delta )n$
red or at most
$(1/4+3\delta )n$
red or at most
![]() $(1/4+3\delta )n$
blue neighbours.
$(1/4+3\delta )n$
blue neighbours.
Proof. Assume for the sake of a contradiction that
![]() $G$
is a
$G$
is a
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
in which all vertices have more than
$K_n$
in which all vertices have more than
![]() $(1/4+3\delta )n$
red and more than
$(1/4+3\delta )n$
red and more than
![]() $(1/4+3\delta )n$
blue neighbours. Consider a split graph
$(1/4+3\delta )n$
blue neighbours. Consider a split graph
![]() $G'$
which is
$G'$
which is
![]() $\delta$
-close to
$\delta$
-close to
![]() $G$
. The vertex set of
$G$
. The vertex set of
![]() $G'$
is the union of a red clique
$G'$
is the union of a red clique
![]() $X$
and a blue clique
$X$
and a blue clique
![]() $Y$
. In
$Y$
. In
![]() $G$
, the sum of the blue degrees of the vertices in
$G$
, the sum of the blue degrees of the vertices in
![]() $X$
is
$X$
is
![]() $\gt (1/4+3\delta )n|X|$
. Since
$\gt (1/4+3\delta )n|X|$
. Since
![]() $X$
contains at most
$X$
contains at most
![]() $\delta n^2$
blue edges by the
$\delta n^2$
blue edges by the
![]() $\delta$
-closeness assumption between
$\delta$
-closeness assumption between
![]() $G$
and
$G$
and
![]() $G'$
, the edges inside
$G'$
, the edges inside
![]() $X$
contribute at most
$X$
contribute at most
![]() $2\delta n^2$
to the previous sum. This implies that in
$2\delta n^2$
to the previous sum. This implies that in
![]() $G$
, between
$G$
, between
![]() $X$
and
$X$
and
![]() $Y$
, there are at least
$Y$
, there are at least
![]() $(1/4+\delta )n|X|$
blue edges. Similarly, we can derive that between
$(1/4+\delta )n|X|$
blue edges. Similarly, we can derive that between
![]() $X$
and
$X$
and
![]() $Y$
, there are at least
$Y$
, there are at least
![]() $(1/4+\delta )n|Y|$
red edges, giving in total
$(1/4+\delta )n|Y|$
red edges, giving in total
![]() $(1/4+\delta )n^2\gt n^2/4$
edges between two disjoint subsets of
$(1/4+\delta )n^2\gt n^2/4$
edges between two disjoint subsets of
![]() $G$
. This is a contradiction.
$G$
. This is a contradiction.
Now we move on to Proposition 2.2. Recall that
![]() $M_1$
denotes a properly
$M_1$
denotes a properly
![]() $2$
-edge-coloured
$2$
-edge-coloured
![]() $K_{2,2}$
. The following lemma is a robust version of Proposition 2.3. For a graph
$K_{2,2}$
. The following lemma is a robust version of Proposition 2.3. For a graph
![]() $G$
, let
$G$
, let
![]() $\delta _G(S)$
denote the minimum degree (in
$\delta _G(S)$
denote the minimum degree (in
![]() $G$
) of a vertex in
$G$
) of a vertex in
![]() $S \subset V(G)$
.
$S \subset V(G)$
.
Lemma 3.6.
Let
![]() $\varepsilon \gt 0$
, and consider a two-colouring
$\varepsilon \gt 0$
, and consider a two-colouring
![]() $R \cup B$
of
$R \cup B$
of
![]() $K_{n,n}$
with vertex parts
$K_{n,n}$
with vertex parts
![]() $X, Y$
of order
$X, Y$
of order
![]() $n$
such that
$n$
such that
![]() $\delta _R(X), \delta _B(Y)\geq \varepsilon n$
. Then, this two-colouring of
$\delta _R(X), \delta _B(Y)\geq \varepsilon n$
. Then, this two-colouring of
![]() $K_{n,n}$
contains at least
$K_{n,n}$
contains at least
![]() $\varepsilon ^4 n^4/2000$
many distinct copies of
$\varepsilon ^4 n^4/2000$
many distinct copies of
![]() $M_1$
.
$M_1$
.
Proof. Let
![]() $A$
be the set of vertices in
$A$
be the set of vertices in
![]() $X$
contained in at least
$X$
contained in at least
![]() $\varepsilon ^3 n^3/500$
copies of
$\varepsilon ^3 n^3/500$
copies of
![]() $M_1$
. We will show that
$M_1$
. We will show that
![]() $| A | \geq \frac{\varepsilon n }{2}$
. This implies the lemma, since the number of copies of
$| A | \geq \frac{\varepsilon n }{2}$
. This implies the lemma, since the number of copies of
![]() $M_1$
is at least
$M_1$
is at least
![]() $|A|\varepsilon ^3 n^3/ 1000$
.
$|A|\varepsilon ^3 n^3/ 1000$
.
Assume that
![]() $|A | \lt \frac{\varepsilon n }{2}$
, and let
$|A | \lt \frac{\varepsilon n }{2}$
, and let
![]() $A' = X \setminus A$
. Note that
$A' = X \setminus A$
. Note that
![]() $\delta _R(A'), \delta _B(Y)\geq \varepsilon n/2$
by the assumption on the size of
$\delta _R(A'), \delta _B(Y)\geq \varepsilon n/2$
by the assumption on the size of
![]() $A'$
. Let
$A'$
. Let
![]() $v$
be a vertex of
$v$
be a vertex of
![]() $A'$
with minimum red degree, and let
$A'$
with minimum red degree, and let
![]() $S\subseteq Y$
be the red neighbourhood of
$S\subseteq Y$
be the red neighbourhood of
![]() $v$
. In
$v$
. In
![]() $A'\setminus \{v\}\times S$
, there are at least
$A'\setminus \{v\}\times S$
, there are at least
![]() $\varepsilon n^2/3$
blue edges. It is well-known that every graph with average degree
$\varepsilon n^2/3$
blue edges. It is well-known that every graph with average degree
![]() $\mu$
contains a subgraph with minimum degree
$\mu$
contains a subgraph with minimum degree
![]() $\mu/2$
(see [Reference Diestel5], Proposition 1.2.2). So,
$\mu/2$
(see [Reference Diestel5], Proposition 1.2.2). So,
![]() $A'\setminus \{v\}\times S$
has a subgraph
$A'\setminus \{v\}\times S$
has a subgraph
![]() $(C,D)$
with minimum blue degree at least
$(C,D)$
with minimum blue degree at least
![]() $\varepsilon n/6$
(in particular,
$\varepsilon n/6$
(in particular,
![]() $|C|, |D|\geq \varepsilon n/6$
). Observe now that for each element
$|C|, |D|\geq \varepsilon n/6$
). Observe now that for each element
![]() $d$
of
$d$
of
![]() $D$
, each blue neighbour of
$D$
, each blue neighbour of
![]() $d$
in
$d$
in
![]() $C$
, say
$C$
, say
![]() $c$
, and each red neighbour of
$c$
, and each red neighbour of
![]() $c$
in
$c$
in
![]() $Y\setminus S$
, say
$Y\setminus S$
, say
![]() $b$
,
$b$
,
![]() $\{v,d,c,b\}$
induce a copy of
$\{v,d,c,b\}$
induce a copy of
![]() $M_1$
. This is because
$M_1$
. This is because
![]() $(v,b)$
must be blue by the assumption that
$(v,b)$
must be blue by the assumption that
![]() $b\notin S$
. There are at least
$b\notin S$
. There are at least
![]() $|D|\varepsilon n/ 6$
choices for such
$|D|\varepsilon n/ 6$
choices for such
![]() $d$
and
$d$
and
![]() $c$
, and we claim that any
$c$
, and we claim that any
![]() $c \in C$
has at least
$c \in C$
has at least
![]() $\varepsilon n/ 6$
red neighbours in
$\varepsilon n/ 6$
red neighbours in
![]() $Y \setminus S$
, all of which can play the role of
$Y \setminus S$
, all of which can play the role of
![]() $b$
. To see this, note that by minimality of
$b$
. To see this, note that by minimality of
![]() $v$
,
$v$
,
![]() $c$
must have at least
$c$
must have at least
![]() $|S|$
red neighbours in
$|S|$
red neighbours in
![]() $Y$
, and that at most
$Y$
, and that at most
![]() $|S|-\varepsilon n/6$
of these neighbours are contained in
$|S|-\varepsilon n/6$
of these neighbours are contained in
![]() $S$
(since
$S$
(since
![]() $c$
has at least
$c$
has at least
![]() $\varepsilon n/6$
blue neighbours in
$\varepsilon n/6$
blue neighbours in
![]() $D \subset S$
). Hence, we can find at least
$D \subset S$
). Hence, we can find at least
![]() $(\varepsilon/6)^3n^3 \gt \varepsilon ^3 n^3/500$
distinct triples
$(\varepsilon/6)^3n^3 \gt \varepsilon ^3 n^3/500$
distinct triples
![]() $(d,c,b)$
giving rise to distinct
$(d,c,b)$
giving rise to distinct
![]() $M_1$
containing
$M_1$
containing
![]() $v$
. This contradicts the definition of
$v$
. This contradicts the definition of
![]() $A$
, so we conclude that
$A$
, so we conclude that
![]() $|A| \geq \varepsilon n/2$
.
$|A| \geq \varepsilon n/2$
.
Proposition 2.2 follows easily from the previous result.
Proof of Proposition
2.2. Let
![]() $G$
be locally
$G$
be locally
![]() $\varepsilon$
-balanced 2-coloured
$\varepsilon$
-balanced 2-coloured
![]() $K_n$
. By assigning each vertex to a set
$K_n$
. By assigning each vertex to a set
![]() $X$
or
$X$
or
![]() $Y$
uniformly at random, we can find a bipartite subgraph
$Y$
uniformly at random, we can find a bipartite subgraph
![]() $G' = (X, Y)$
of
$G' = (X, Y)$
of
![]() $G$
which satisfies the hypotheses of Lemma 3.6 with
$G$
which satisfies the hypotheses of Lemma 3.6 with
![]() $n_{(3.6)}\;:\!=\;0.49n$
and
$n_{(3.6)}\;:\!=\;0.49n$
and
![]() $\varepsilon _{(3.6)}\;:\!=\;0.99 \varepsilon$
(Chernoff’s bound is sufficient here, using the assumption
$\varepsilon _{(3.6)}\;:\!=\;0.99 \varepsilon$
(Chernoff’s bound is sufficient here, using the assumption
![]() $n\geq (1/\varepsilon )^{100}$
). It follows by Lemma 3.6 that
$n\geq (1/\varepsilon )^{100}$
). It follows by Lemma 3.6 that
![]() $G$
contains
$G$
contains
![]() $\varepsilon ^4 n^4/10^5$
many distinct copies of
$\varepsilon ^4 n^4/10^5$
many distinct copies of
![]() $M_1$
. Note that each copy of
$M_1$
. Note that each copy of
![]() $M_1$
yields a copy of
$M_1$
yields a copy of
![]() $P_{3}^{\circ }$
,
$P_{3}^{\circ }$
,
![]() $C_4$
or
$C_4$
or
![]() $\overline{C_4}$
, depending on the colour of the remaining two edges spanned by
$\overline{C_4}$
, depending on the colour of the remaining two edges spanned by
![]() $V(M_1)$
. This implies the proposition.
$V(M_1)$
. This implies the proposition.
4. Multiple colours
In this section, we investigate the
![]() $r$
-colour variant of Question 1.2. To allow for a more precise discussion, we give the following two definitions. Given a totally coloured graph
$r$
-colour variant of Question 1.2. To allow for a more precise discussion, we give the following two definitions. Given a totally coloured graph
![]() $H$
, the
$H$
, the
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $H$
is denoted by
$H$
is denoted by
![]() $H[t]$
. A totally
$H[t]$
. A totally
![]() $r$
-coloured graph
$r$
-coloured graph
![]() $H$
is called unibalanced if each vertex of
$H$
is called unibalanced if each vertex of
![]() $H[2]$
is incident to an edge in each of the
$H[2]$
is incident to an edge in each of the
![]() $r$
colours.Footnote 1 For instance, the patterns
$r$
colours.Footnote 1 For instance, the patterns
![]() $P_1$
and
$P_1$
and
![]() $P_3$
are unibalanced, but
$P_3$
are unibalanced, but
![]() $P_2$
is not. Observe that for a totally coloured graph
$P_2$
is not. Observe that for a totally coloured graph
![]() $H$
,
$H$
,
![]() $H[t]$
is locally
$H[t]$
is locally
![]() $\varepsilon$
-balanced for some value of
$\varepsilon$
-balanced for some value of
![]() $\varepsilon \gt 0$
if and only if
$\varepsilon \gt 0$
if and only if
![]() $H$
is unibalanced. We call a family
$H$
is unibalanced. We call a family
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $r$
-colourings of
$r$
-colourings of
![]() $K_n$
locally
$K_n$
locally
![]() $(r,\varepsilon )$
-unavoidable if every locally
$(r,\varepsilon )$
-unavoidable if every locally
![]() $\varepsilon$
-balanced colouring of
$\varepsilon$
-balanced colouring of
![]() $K_n$
where
$K_n$
where
![]() $n$
is sufficiently large contains a copy of some
$n$
is sufficiently large contains a copy of some
![]() $F\in \mathcal{F}$
.
$F\in \mathcal{F}$
.
Question 4.1.
Suppose
![]() $K_n$
is given a locally
$K_n$
is given a locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $r$
-edge-colouring. Which subgraphs must
$r$
-edge-colouring. Which subgraphs must
![]() $K_n$
necessarily contain?
$K_n$
necessarily contain?
Obviously, colourings as in Question 4.1 are globally
![]() $\varepsilon$
-balanced as well. In [Reference Bowen, Lamaison and Müyesser1], a multicolour version of Theorem 1.1 is provided (see Theorem 4). This result guarantees, just using a global balancedness assumption, the existence of a rich family of patterns, say
$\varepsilon$
-balanced as well. In [Reference Bowen, Lamaison and Müyesser1], a multicolour version of Theorem 1.1 is provided (see Theorem 4). This result guarantees, just using a global balancedness assumption, the existence of a rich family of patterns, say
![]() $\mathcal{F}^{(r)}$
, where each pattern in the family uses all
$\mathcal{F}^{(r)}$
, where each pattern in the family uses all
![]() $r$
colours (see Figure 1 in [Reference Bowen, Lamaison and Müyesser1] for a depiction of patterns guaranteed when
$r$
colours (see Figure 1 in [Reference Bowen, Lamaison and Müyesser1] for a depiction of patterns guaranteed when
![]() $r=3$
). In particular,
$r=3$
). In particular,
![]() $\mathcal{F}^{(r)}$
is locally
$\mathcal{F}^{(r)}$
is locally
![]() $(r,\varepsilon )$
-unavoidable for every
$(r,\varepsilon )$
-unavoidable for every
![]() $\varepsilon \gt 0$
. Yet,
$\varepsilon \gt 0$
. Yet,
![]() $\mathcal{F}^{(r)}$
does not give a satisfying answer to Question 1.2, for the same reason the family
$\mathcal{F}^{(r)}$
does not give a satisfying answer to Question 1.2, for the same reason the family
![]() $\mathcal{F}_t$
(see Figure 1) does not give a satisfying answer to Question 1.2. That is, elements of
$\mathcal{F}_t$
(see Figure 1) does not give a satisfying answer to Question 1.2. That is, elements of
![]() $\mathcal{F}^{(r)}$
are not locally balanced, leaving open the possibility that there exists either a smaller (as in Theorem 1.3) or more complex (as in Theorem 1.4) family of unavoidable patterns. On the other hand, as in the two-colour case, any
$\mathcal{F}^{(r)}$
are not locally balanced, leaving open the possibility that there exists either a smaller (as in Theorem 1.3) or more complex (as in Theorem 1.4) family of unavoidable patterns. On the other hand, as in the two-colour case, any
![]() $(r,\varepsilon )$
-unavoidable family
$(r,\varepsilon )$
-unavoidable family
![]() $\mathcal{F}$
consisting of blow-ups of a finite family of unibalanced totally coloured graphs
$\mathcal{F}$
consisting of blow-ups of a finite family of unibalanced totally coloured graphs
![]() $\mathcal{F}'$
(assuming that no member of
$\mathcal{F}'$
(assuming that no member of
![]() $\mathcal{F}'$
contains another member) would give a structurally optimal answer to Question 1.2. Indeed, members of such
$\mathcal{F}'$
contains another member) would give a structurally optimal answer to Question 1.2. Indeed, members of such
![]() $\mathcal{F}$
would be themselves locally
$\mathcal{F}$
would be themselves locally
![]() $\varepsilon$
-balanced for some
$\varepsilon$
-balanced for some
![]() $\varepsilon \gt 0$
, making it impossible for a smaller, or more complex family of
$\varepsilon \gt 0$
, making it impossible for a smaller, or more complex family of
![]() $(r,\varepsilon )$
-unavoidable graphs to exist (for
$(r,\varepsilon )$
-unavoidable graphs to exist (for
![]() $\varepsilon$
sufficiently small).
$\varepsilon$
sufficiently small).
We can now explain why already for
![]() $r\geq 3$
, the problem is rather different. A consequence of Theorem 1.4 is that for any
$r\geq 3$
, the problem is rather different. A consequence of Theorem 1.4 is that for any
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $t\geq 1$
, the family
$t\geq 1$
, the family
![]() $\{P_1[t],\bar{P_1}[t], P_3[t]\}$
is
$\{P_1[t],\bar{P_1}[t], P_3[t]\}$
is
![]() $(2,\varepsilon )$
-unavoidable. For
$(2,\varepsilon )$
-unavoidable. For
![]() $r= 3$
, if
$r= 3$
, if
![]() $\mathcal{F}$
is a finite family consisting of unibalanced totally coloured graphs whose blow-ups are
$\mathcal{F}$
is a finite family consisting of unibalanced totally coloured graphs whose blow-ups are
![]() $(3,\varepsilon )$
-unavoidable, then the following proposition shows that
$(3,\varepsilon )$
-unavoidable, then the following proposition shows that
![]() $|\mathcal{F}|$
has to have size at least
$|\mathcal{F}|$
has to have size at least
![]() $1/\varepsilon$
.
$1/\varepsilon$
.
Proposition 4.2.
There exists a locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $3$
-colouring of
$3$
-colouring of
![]() $K_n$
in which any unibalanced subgraph has at least
$K_n$
in which any unibalanced subgraph has at least
![]() $\lfloor \varepsilon ^{-1} \rfloor -1$
vertices.
$\lfloor \varepsilon ^{-1} \rfloor -1$
vertices.
Proof. Partition the vertex set into parts
![]() $V_1, \ldots, V_\ell$
of order at least
$V_1, \ldots, V_\ell$
of order at least
![]() $\varepsilon n$
, where
$\varepsilon n$
, where
![]() $\ell \geq \lfloor \varepsilon ^{-1} \rfloor -1$
is an even number. Colour the bipartite graphs between
$\ell \geq \lfloor \varepsilon ^{-1} \rfloor -1$
is an even number. Colour the bipartite graphs between
![]() $V_i$
and
$V_i$
and
![]() $V_{i+1}$
red and blue alternatingly (with indices modulo
$V_{i+1}$
red and blue alternatingly (with indices modulo
![]() $\ell$
). Colour the remaining edges green. For an illustration of the case when
$\ell$
). Colour the remaining edges green. For an illustration of the case when
![]() $\ell =6$
, see Figure 3. This colouring is locally
$\ell =6$
, see Figure 3. This colouring is locally
![]() $\varepsilon$
-balanced and any non-empty unibalanced subgraph of this colouring must contain a vertex from each of
$\varepsilon$
-balanced and any non-empty unibalanced subgraph of this colouring must contain a vertex from each of
![]() $V_1, \ldots, V_\ell$
, as required.
$V_1, \ldots, V_\ell$
, as required.
Proposition 4.2 implies that there can be no straightforward generalisation of Theorem 1.4 for more than two colours. That is, there is no single finite family of unibalanced totally coloured (with
![]() $r$
colours) graphs whose blow-ups are
$r$
colours) graphs whose blow-ups are
![]() $(r,\varepsilon )$
-unavoidable for every
$(r,\varepsilon )$
-unavoidable for every
![]() $\varepsilon \gt 0$
. However, we can still prove a version of Theorem 1.4, with the caveat that the size of the family of unavoidable patterns depends on
$\varepsilon \gt 0$
. However, we can still prove a version of Theorem 1.4, with the caveat that the size of the family of unavoidable patterns depends on
![]() $\varepsilon$
.
$\varepsilon$
.
Theorem 4.3.
Given
![]() $\varepsilon \gt 0$
, an integer
$\varepsilon \gt 0$
, an integer
![]() $r\geq 2$
, and
$r\geq 2$
, and
![]() $C = \frac{80}{\varepsilon } \log \frac 1 \varepsilon$
, there is a constant
$C = \frac{80}{\varepsilon } \log \frac 1 \varepsilon$
, there is a constant
![]() $\alpha$
such that the following holds for sufficiently large
$\alpha$
such that the following holds for sufficiently large
![]() $n$
. Any locally
$n$
. Any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $r$
-colouring of an
$r$
-colouring of an
![]() $n$
-vertex complete graph contains a homogeneous
$n$
-vertex complete graph contains a homogeneous
![]() $\alpha \log n$
-blow-up of some unibalanced graph on at most
$\alpha \log n$
-blow-up of some unibalanced graph on at most
![]() $C$
vertices.
$C$
vertices.
Proof. Let
![]() $\varepsilon \gg \eta \gg \alpha \gg 1/n$
. We have the following claim.
$\varepsilon \gg \eta \gg \alpha \gg 1/n$
. We have the following claim.
Claim 2.
There exists
![]() $k \leq C$
such that there are at least
$k \leq C$
such that there are at least
![]() $\frac 14 \binom nk$
vertex subsets
$\frac 14 \binom nk$
vertex subsets
![]() $S$
of order
$S$
of order
![]() $k$
inducing a unibalanced
$k$
inducing a unibalanced
![]() $r$
-coloured subgraph.
$r$
-coloured subgraph.
Proof. Denote the family of subsets
![]() $S \subset [n]$
which induce a unibalanced subgraph by
$S \subset [n]$
which induce a unibalanced subgraph by
![]() $\mathcal{U}$
. Let
$\mathcal{U}$
. Let
![]() $S$
be a random set of vertices where each vertex is sampled independently with probability
$S$
be a random set of vertices where each vertex is sampled independently with probability
![]() $\frac{\zeta }{n}$
, with
$\frac{\zeta }{n}$
, with
![]() $\zeta = \frac{20}{\varepsilon } \left (\log r+ \log \frac{1}{\varepsilon } \right ) \leq \frac C2$
. We will show that the probability that
$\zeta = \frac{20}{\varepsilon } \left (\log r+ \log \frac{1}{\varepsilon } \right ) \leq \frac C2$
. We will show that the probability that
![]() $S \notin \mathcal{U}$
is at most
$S \notin \mathcal{U}$
is at most
![]() $\frac 12$
.
$\frac 12$
.
For
![]() $v \in V(G)$
, let
$v \in V(G)$
, let
![]() $A_i(v)$
be the event that there is a vertex
$A_i(v)$
be the event that there is a vertex
![]() $u \in S$
such that
$u \in S$
such that
![]() $uv$
has colour
$uv$
has colour
![]() $i$
(note that this event does not depend on whether
$i$
(note that this event does not depend on whether
![]() $v$
is in
$v$
is in
![]() $S$
), and let
$S$
), and let
![]() $A(v) = \bigcap _{i \in [r]} A_i(v)$
.
$A(v) = \bigcap _{i \in [r]} A_i(v)$
.
Since
![]() $A_i(v)$
are mutually independent for
$A_i(v)$
are mutually independent for
![]() $i \in [r]$
, we have
$i \in [r]$
, we have
Moreover, by the locally
![]() $\varepsilon$
-balancedness assumption, we have that
$\varepsilon$
-balancedness assumption, we have that
![]() $\mathbb{P} \left [ A_i(v) \right ] \geq 1- \left ( 1- \frac{\zeta }{n}\right )^{\varepsilon n} \geq 1- e^{-\zeta \varepsilon/2}$
for
$\mathbb{P} \left [ A_i(v) \right ] \geq 1- \left ( 1- \frac{\zeta }{n}\right )^{\varepsilon n} \geq 1- e^{-\zeta \varepsilon/2}$
for
![]() $n$
sufficiently large, so
$n$
sufficiently large, so
Since
![]() $A(v)$
and
$A(v)$
and
![]() $v \in S$
are independent events, we have, for any
$v \in S$
are independent events, we have, for any
![]() $v \in [n]$
,
$v \in [n]$
,
Denoting the random variable counting the vertices
![]() $v \in S$
for which
$v \in S$
for which
![]() $A(v)$
does not occur by
$A(v)$
does not occur by
![]() $X$
and substituting for
$X$
and substituting for
![]() $\zeta$
, we have
$\zeta$
, we have
 \begin{align*}{\mathbb{E} \left [{X} \right ]} &\leq \zeta r e^{-\zeta \varepsilon/2} \leq \frac{20}{\varepsilon }\left ( \log r + \log \frac{1}{\varepsilon } \right ) r e^{-10 \log r - 10\log \frac{1}{\varepsilon }} \\[5pt] &\leq 40r^2 \varepsilon ^{-2}\cdot r^{-10}\varepsilon ^{10} \lt 40\left (\varepsilon r^{-1} \right )^{8} \lt 40\cdot 4^{-8} \lt \frac 12. \end{align*}
\begin{align*}{\mathbb{E} \left [{X} \right ]} &\leq \zeta r e^{-\zeta \varepsilon/2} \leq \frac{20}{\varepsilon }\left ( \log r + \log \frac{1}{\varepsilon } \right ) r e^{-10 \log r - 10\log \frac{1}{\varepsilon }} \\[5pt] &\leq 40r^2 \varepsilon ^{-2}\cdot r^{-10}\varepsilon ^{10} \lt 40\left (\varepsilon r^{-1} \right )^{8} \lt 40\cdot 4^{-8} \lt \frac 12. \end{align*}
Note that in the fifth inequality, we used that
![]() $\varepsilon \leq 1/2$
and
$\varepsilon \leq 1/2$
and
![]() $r\geq 2$
. Clearly,
$r\geq 2$
. Clearly,
![]() $S\notin \mathcal{U}$
only if
$S\notin \mathcal{U}$
only if
![]() $X\geq 1$
. By Markov’s inequality, the probability that
$X\geq 1$
. By Markov’s inequality, the probability that
![]() $X \geq 1$
is at most
$X \geq 1$
is at most
![]() $1/2$
, so
$1/2$
, so
![]() $\mathbb{P} \left [ S \notin \mathcal{U} \right ] \leq \frac 12$
, as claimed.
$\mathbb{P} \left [ S \notin \mathcal{U} \right ] \leq \frac 12$
, as claimed.
To complete the proof of the claim, assume that
It follows that
 \begin{equation*} \mathbb {P} \left [ S \in \mathcal {U} \right ] \leq \sum _{k=0}^{C} \mathbb {P} \left [ S \in \mathcal U \;\middle |\; |S| = k \right ] + \mathbb {P} \left [ |S| \gt C \right ] \leq \sum _{k=0}^{C} \frac 14 \cdot \mathbb {P} \left [ |S| = k \right ] + \frac 18 \leq \frac 38, \end{equation*}
\begin{equation*} \mathbb {P} \left [ S \in \mathcal {U} \right ] \leq \sum _{k=0}^{C} \mathbb {P} \left [ S \in \mathcal U \;\middle |\; |S| = k \right ] + \mathbb {P} \left [ |S| \gt C \right ] \leq \sum _{k=0}^{C} \frac 14 \cdot \mathbb {P} \left [ |S| = k \right ] + \frac 18 \leq \frac 38, \end{equation*}
where the second inequality follows from (2) and the Chernoff bound. We reached a contradiction, completing the proof of the Claim.
Hence, for some
![]() $k$
-vertex unibalanced graph
$k$
-vertex unibalanced graph
![]() $H$
,
$H$
,
![]() $G$
contains at least
$G$
contains at least
![]() $\frac 14 r^{-C^2} \binom nk$
copies of
$\frac 14 r^{-C^2} \binom nk$
copies of
![]() $H$
; to see this, note that there are at most
$H$
; to see this, note that there are at most
![]() $r^{C^2}$
options for
$r^{C^2}$
options for
![]() $H$
. Applying Lemma 2.4, we obtain a homogeneous
$H$
. Applying Lemma 2.4, we obtain a homogeneous
![]() $\alpha \log n$
-blow-up of
$\alpha \log n$
-blow-up of
![]() $H$
, as required.
$H$
, as required.
5. Concluding remarks
Asymptotics. It remains an interesting open problem to improve the quantitative estimates from Theorems 1.3 and 1.4. There is more room for improvement in Theorem 1.3 compared to Theorem 1.4, but we believe both estimates should be quite far away from the truth. In particular, we don’t see an inherent reason why the asymptotics of the locally balanced Ramsey problem should be different from the globally balanced Ramsey problem. That is, we believe that there should be an absolute constant
![]() $C$
so that when
$C$
so that when
![]() $n\geq (1/\varepsilon )^{Ct}$
, the conclusions of Theorems 1.3 and 1.4 hold. Such a bound would be of the same order of magnitude as the bound from Theorem 1.1. This bound would also be tight up to the value of
$n\geq (1/\varepsilon )^{Ct}$
, the conclusions of Theorems 1.3 and 1.4 hold. Such a bound would be of the same order of magnitude as the bound from Theorem 1.1. This bound would also be tight up to the value of
![]() $C$
, as can be justified with a simple probabilistic construction.
$C$
, as can be justified with a simple probabilistic construction.
The main obstacle to proving a bound of this form comes from our reliance on Lemma 2.4. Fox, Luo, and Wigderson [Reference Fox, Luo and Wigderson7] have recently combined the method of Nikiforov with ideas from graph regularity to obtain better estimates for a version of Lemma 2.4 where the blow-up guaranteed is not necessarily homogeneous. Their ideas could quite possibly be modified to guarantee homogeneous blow-ups, but the resulting bound would still be rather far from being able to prove optimal bounds for Theorems 1.3 and 1.4.
Remark. While this paper was under revision, Girão and Munhá Correia [Reference Girão and Correia12] have addressed the above problem.
The extremal aspect. A fruitful direction of research in the globally balanced version of the problem has been finding patterns in globally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $K_n$
where
$K_n$
where
![]() $\varepsilon$
is a function of
$\varepsilon$
is a function of
![]() $n$
. This seems to be an intriguing direction in the locally balanced setting as well, especially in the setting of Theorem 1.4. Namely, we raise the following problem. Let
$n$
. This seems to be an intriguing direction in the locally balanced setting as well, especially in the setting of Theorem 1.4. Namely, we raise the following problem. Let
![]() $t\geq 1$
be some integer. What is the smallest function
$t\geq 1$
be some integer. What is the smallest function
![]() $\varepsilon \;:\!=\;\varepsilon (n,t)$
as
$\varepsilon \;:\!=\;\varepsilon (n,t)$
as
![]() $n\to \infty$
such that any locally
$n\to \infty$
such that any locally
![]() $\varepsilon$
-balanced
$\varepsilon$
-balanced
![]() $2$
-coloured
$2$
-coloured
![]() $K_n$
contains a
$K_n$
contains a
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $P_1$
,
$P_1$
,
![]() $\overline{P_1}$
or
$\overline{P_1}$
or
![]() $P_3$
? It already seems like an interesting challenge to prove
$P_3$
? It already seems like an interesting challenge to prove
![]() $\varepsilon \leq n^{C/t^2}$
for some absolute constant
$\varepsilon \leq n^{C/t^2}$
for some absolute constant
![]() $C$
.
$C$
.
Acknowledgements
We are grateful to Kyriakos Katsamaktsis for stimulating discussions at the early stages of this project, especially for the formulation of Lemma 3.6, and to Shoham Letzter for helpful comments on the manuscript. We would also like to thank the anonymous referee for their careful reading and helpful comments.