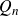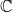Coniveau filtrations and Milnor operation $Q_n$

Abstract

Let BG be the classifying space of an algebraic group G over the field ${\mathbb C}$ of complex numbers. There are smooth projective approximations X of $BG\times {\mathbb P}^{\infty}$, by Ekedahl. We compute a new stable birational invariant of X defined by the difference of two coniveau filtrations of X, by Benoist and Ottem. Hence we give many examples such that two coniveau filtrations are different.

1. Introduction

Let p be a prime number and $A={\mathbb Q},{\mathbb Z}$ or ${\mathbb Z}/p^i$ for $i\ge 1$ . Let X be a smooth algebraic variety over $k={\mathbb C}$ . Let us recall the coniveau filtration of the cohomology with coefficients in A,

\begin{equation*} N^cH^i(X;\,A)=\sum_{Z\subset X} ker\!\left(j^*:H^i(X;\,A)\longrightarrow H^i(X-Z,A)\right),\end{equation*}

where $Z\subset X$ runs through the closed subvarieties of codimension at least c of X, and $j\,:\,X-Z\subset X$ is the complementary open immersion.

Similarly, we can define the strong coniveau filtration by

\begin{equation*} \tilde N^cH^i(X;\,A)=\sum_{f\,:\,Y\to X} im\!\left(f_*\,:\,H^{i-2r}(Y;\,A)\longrightarrow H^i(X,A)\right),\end{equation*}

where the sum is over all proper morphism $f\,:\, Y\to X$ from a smooth complex variety Y of $dim(Y)=dim(X)-r$ with $r\ge c$ , and $f_*$ its transfer (Gysin map). It is immediate that $\tilde N^cH^*(X;\,A)\subset N^cH^*(X;\,A)$ .

It was hoped that when X is proper, the strong coniveau filtration was just the coniveau filtration, i.e., $ \tilde N^cH^i(X;\,A)=N^cH^i(X;\,A)$ . In fact Deligne shows that they are the same for $A={\mathbb Q}$ . However, Benoist and Ottem ([ 1 ]) recently show that they are not equal for $A={\mathbb Z}$ .

Let G be an algebraic group such that $H^*(BG;\,{\mathbb Z})$ has p-torsion for the (geometric) classifying space BG defined by Totaro [ 17 ] as a colimit of smooth quasi-projective varieties. Moreover, Ekedahl [ 4 ] shows that $BG\times {\mathbb P}^{\infty} $ can be approximated by smooth projective varieties X in the following sense.

Here a (degree N) approximation is the projective smooth variety $X=X(N)$ such that there is a map $g\,:\,X\to BG\times {\mathbb P}^{\infty}$ with

\begin{equation*}g^*\,:\,H^*(BG\times {\mathbb P}^{\infty};\,A)\cong H^*(X;\,A) \quad for \ all\ degree \ *<N. \end{equation*}

The aim of this paper is to compute the mod(p) stable birational invariant of X [ 1 , proposition 2·4]

\begin{equation*} DH^*(X;\,A)=N^1H^*(X;\,A)/\left(p,\tilde N^1H^*(X;\,A)\right) \end{equation*}

for projective approximations X of $BG\times {\mathbb P}^{\infty}$ ([ 4 , 10 ]). In fact, we see that $DH^*(X;\,{\mathbb Z})\not =0$ happen very frequently in the above cases. In this paper, we say that X is an approximation for BG when it is that of $BG\times {\mathbb P}^{\infty} $ strictly speaking. Let us write $DH^*(X;\,{\mathbb Z})$ by $DH^*(X)$ simply as usual.

Here we give an example that we can compute a nonzero $DH^*(X)$ . For $G=({\mathbb Z}/p)^3$ the elementary abelian p-group of $rank=3$ , we know (for p odd)

\begin{equation*} H^*(BG;\,{\mathbb Z}/p)\cong {\mathbb Z}/p\!\left[y_1,y_2,y_3 \right]\otimes \Lambda\!\left(x_1,x_2,x_3\right),\ \ degree\ |x_i|=1,\ Q_0(x_i)=y_i,\end{equation*}

\begin{equation*}H^*(BG)/p\cong {\mathbb Z}/p\!\left[y_1,y_2,y_3\right]\left(1,Q_0\left(x_ix_j\right),Q_0\left(x_1x_2x_3\right)|1\le i<j\le 3\right), \end{equation*}

where $Q_0=\beta$ is the Bockstein operation, $\Lambda(a,...,b)$ is the ${\mathbb Z}/p$ -exterior algebra generated by $a,...,b$ . and the notation $R(a,...,b)$ (resp. $R\{a,..., b\}$ ) means the R-submodule (resp. the free R-module) generated by $a,...,b$ .

Theorem 1·1. Let $G=({\mathbb Z}/p)^3$ . For all $N>2p+3$ and all (degree N) approximations $X=X(N)$ for BG, we have

\begin{equation*} DH^*(X)\cong DH^3(X)\oplus DH^4(X)\end{equation*}

\begin{equation*}\cong {\mathbb Z}/p\!\left\{Q_0\left(x_ix_j\right),Q_0\left(x_1x_2x_3\right)|1\le i<j\le 3\right\}\quad for \ all \ degree\ *<N.\end{equation*}

But we have $DH^*(X;\,{\mathbb Z}/p)=0$ for all degree $*<N$ .

Remark. In general, $DH^*(X)$ seems not to be an invariant of BG, but the above case is determined by BG. Many cases of examples in this paper have this property.

Benoist and Ottem also study approximations of $BG\times {\mathbb P}^{\infty}$ . They compute for example $G=({\mathbb Z}/2)^3$ and show that the invariant is nonzero for $A={\mathbb Z}_{(2)}$ by using compositions of the Steenrod squares and Wu theorems. On the other hand, we show that arguments can be extended for $A={\mathbb Z}_{(p)}$ for all prims p by using the Milnor operation $Q_n$ , which commutes with all Gysin maps.

However it seems not so easy to give a nontrivial example for $A={\mathbb Z}/p$ in the case X is an approximation for BG as the above examples show.

For connected groups we have

Theorem 1·2. Let G be a simply connected group such that $H^*(BG)$ has p-torsion. Let $N>2p+3$ . Then all degree N approximation X for BG, we have $ DH^4(X)\not =0.$

Theorem 1·3. Let p be an odd prime number, and $G=PGL_p$ . Let $N>2p+2$ . Then for all degree N approximation X for BG, we have $DH^3(X)\not =0$ .

Theorem 1·4. Let $p=2$ and $X_{2m+1}=X_{2m+1}(N)$ be an approximation for $BSO_{2m+1}$ of degree $N\ge 3$ . Then there exists $0<L=L(m)$ such that for all approximations $X_{2m+1}$ of degree $N>L$ , we have

\begin{equation*} DH^*\left(X_{2m+1}\right)\supset {\mathbb Z}/2\!\left\{w_3,w_5,...,w_{2m+1}\right\}\quad for \ all\ 2m+1\le *<N,\end{equation*}

where $w_i$ is the ith Stiefel–Whiteny class for $SO_{2m+1}\subset O_{2m+1}$ .

2. Transfer and $Q_n$

The Milnor operation (in $H^*({-};\,{\mathbb Z}/p)$ ) is defined by $Q_0=\beta$ and for $n\ge 1$

\begin{equation*} Q_n=P^{\Delta_n} \beta-\beta P^{\Delta_n}, \quad \Delta_n=\left(0,..,0,\stackrel{n}{1},0,...\right) \end{equation*}

(for details see [ 8 ], [ 18 , section 3·1]), where $\beta$ is the Bockstein operation and $P^{\alpha}$ for $\alpha=(\alpha_1,\alpha_2,...)$ is the fundamental base of the module of finite sums of products of reduced powers.

Lemma 2·1. Let $f_*$ be the transfer (Gysin) map (for proper smooth) $f\,:\,X\to Y$ . Then $Q_nf_*(x)=f_*Q_n(x)$ for $x\in H^*(X;\,{\mathbb Z}/p)$ .

The above lemma is known (see the proof of [ 23 , lemma 7·1]). The transfer $f_*$ is expressed as $g^*f^{\prime}_*$ such that

\begin{equation*} f^{\prime}_*(x)=i^*(Th(1)\cdot x), \quad x\in H^*(X;\,{\mathbb Z}/p)\end{equation*}

for some maps g, f ^′, i and the Thom class Th(1). Since $Q_n(Th(1))=0$ and $Q_n$ is a derivation, we get the lemma. However, we give here the another computational proof.

Proof of Lemma 2·1. Recall the following Grothendieck formula (e.g., [Q1])

(1) \begin{equation} P_t(f_*(x))=f_*(c_t\cdot P_t(x)).\end{equation}

Here the total reduced powers $P_t(x)$ are defined

\begin{equation*}P_t(x)=\sum_{\alpha}P^{\alpha}(x)t^{\alpha}\in H^*\left(X;\,{\mathbb Z}/p\right)\left[t_1,t_2,...\right]\quad with\ t^{\alpha}=t_1^{\alpha_1}t_2^{\alpha_2}...,\end{equation*}

where $\alpha=(\alpha_1,\alpha_2,...)$ and $degree(t^{\alpha})=\sum_i 2\alpha_i\left(p^i-1\right)$ (each element in the cohomology $H^*(X;\,{\mathbb Z}/p)$ is represented as a homogeneous part respective to the above degree). The total Chern class $c_t$ is defined similarly, for the Chern classes of the normal bundle of the map f.

We consider the above equation with the assumption such that $t_n^2=0$ and $t_j=0$ for $j\not =n$ , i.e., $P_t(x)\in H^*(X;\,{\mathbb Z}/p)\otimes \Lambda(t_n)$ . That means

(2) \begin{equation} P_t(f_*(x))=\left(1+P^{\Delta_n}t_n\right)(f_*(x))\end{equation}

(3) \begin{align} f_*\left(c_t\cdot P_t(x)\right) & =f_*\left(\left(1+c_{p^n-1}t_n\right)\left(x+P^{\Delta_n}(x)t_n\right)\right)\nonumber\\& =f_*\left(x+\left(c_{p^n-1}x+P^{\Delta_n}(x)\right)t_n\right).\end{align}

From (1), we see $(2)=(3)$ and we have

(4) \begin{equation} P^{\Delta_n}\left(f_*(x)\right)=f_*\left(c_{p^n-1}x+P^{\Delta_n}(x)\right).\end{equation}

By the definition, $\beta$ commutes with $f_*$ , and we have

(5) \begin{equation}P^{\Delta_n}\beta(f_*(x))=P^{\Delta_n}f_*(\beta x)=f_*\left(c_{p^n-1}\beta x+P^{\Delta_n}(\beta x)\right).\end{equation}

On the other hand

(6) \begin{equation}\beta P^{\Delta_n}f_*(x)\stackrel{(4)}{=}\beta f_*\left(c_{p^n-1}x+P^{\Delta_n}(x)\right)=f_*\left(c_{p^n-1}\beta x+\beta P^{\Delta_n}(x)\right).\end{equation}

Then (5)–(6) gives that $\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)f_*(x)=f_*\left(P^{\Delta_n} \beta-\beta P^{\Delta_n}\right)(x).$ Thus we can prove Lemma 2·1.

By the definition, each cohomology operation h (i.e., an element in the Steenrod algebra) is written $\big($ with $Q^B=Q_0^{b_0}Q_1^{b_1}...\big)$ by

\begin{equation*}h=\sum_{A,B}P^AQ^B\quad {with}\ A=(a_1,...),\ B=(b_0,...)\ b_i=0\ {or}\ 1.\end{equation*}

Corollary 2·2. We have $ P_tQ^B\left(f_*(x)\right)=f_*\left(c_t\cdot P_tQ^B(x)\right).$

Hence cohomology operations h (for $H^*({-};\,{\mathbb Z}/p))$ which commute with all transfer $f_*$ are cases $c_t=1$ , i.e. $A=0$ which are only products $Q^B$ of Milnor operations $Q_i$ .

3. Coniveau filtrations

Bloch–Ogus [ 2 ] give a spectral sequence such that its $E_2$ -term is given by

\begin{equation*}E(c)_2^{c,*-c}\cong H_{Zar}^c\!\left(X,\mathcal{H}_{A}^{*-c}\right)\Longrightarrow H_{et}^*(X;\,A),\end{equation*}

where $\mathcal{H}_{A}^*$ is the Zariski sheaf induced from the presheaf given by $U\mapsto H_{et}^*(U;\,A)$ for an open $U\subset X$ .

The filtration for this spectral sequence is defined as the coniveau filtration

\begin{equation*}N^cH_{et}^*(X;\,A)= F(c)^{c,*-c},\end{equation*}

where the infinite term $ E(c)^{c,*-c}_{\infty}\cong F(c)^{c,*-c}/F(c)^{c+1,*-c-1}$ and

\begin{equation*} N^cH^*_{et}(X;\,A)=\sum_{Z\subset X;codim_X(Z)\le c} ker\!\left(j^*\,:\,H^*_{et}(X;\,A)\to H^*_{et}(X-Z,A)\right).\end{equation*}

Here we recall the motivic cohomology $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$ defined by Voevodsky and Suslin ([ 18 , 20 , 21 ]) so that

\begin{equation*} H^{i,i}(X;\,{\mathbb Z}/p)\cong H^i_{et}(X;\,{\mathbb Z}/p)\cong H^i(X;\,{\mathbb Z}/p).\end{equation*}

Let us write $H^*_{et}(X;\,{\mathbb Z} )$ simply by $H^*_{et}(X)$ as usual. Note that $H^*_{et}(X)\not \cong H^*(X)$ in general, while we have the natural map $H_{et}^*(X)\to H^*(X)$ .

Let $0\not =\tau \in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$ . Then by the multiplying $\tau$ , we can define a map $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)\to H^{*,*^{\prime}+1}(X;\,{\mathbb Z}/p)$ . By Deligne ([ 2 , foot note (1) in Remark 6·4]) and Paranjape ([ 9 , corollary 4·4]), it is proven that there is an isomorphism of the coniveau spectral sequence with the $\tau$ -Bockstein spectral sequence $E(\tau)_r^{*,*^{\prime}}$ (see also [ 16 , 22 ]).

Lemma 3·1. (Deligne) Let $A={\mathbb Z}/p$ . Then we have the isomorphism of spectral sequence

\begin{equation*}E(c)_r^{c,*-c}\cong E(\tau)_{r-1}^{*,*-c} \quad for \ r\ge 2.\end{equation*}

Hence the filtrations are the same, i.e. $N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$ where

\begin{equation*}F_{\tau}^{*,*-c}=Im({\times}\tau^c\,:\,H^{*,*-c}(X;\,{\mathbb Z}/p)\longrightarrow H^{*,*}(X;\,{\mathbb Z}/p)).\end{equation*}

Lemma 3·2. Suppose that $x\in H^{*,*}(X)$ and for $c>0$ its mod(p) reduction $r(x)\in N^cH^*(X;\,{\mathbb Z}/p)$ . Then if the map $f\,:\,H^{*+1,*-c}(X)\to H^{*+1,*}(X)$ is injective, then $x\in N^cH^*(X)$ mod(p).

Proof. Consider the exact sequences

.

By the assumption of this lemma, we can take $x^{\prime}\in H^{*,*-c}(X;\,{\mathbb Z}/p)$ such that $r_2(x)=f_2(x^{\prime})$ . So $\delta_2f_2(x^{\prime})=0$ . Since $f_3$ is injective, we see $\delta_1(x^{\prime})=0$ , Hence there is $x^{\prime\prime}\in H^{*.*-c^{\prime}}(X)$ such that $r_1(x^{\prime\prime})=x^{\prime}$ . Thus we have the lemma.

Let $cl\,:\, CH^*(X)\otimes A\to H^{2*}(X;\,A)$ be the cycle map, and $Im(cl)^+$ be the positive degree parts of its image.

Lemma 3·3. We see that $Im(cl)^+\subset N^*H^{2*}(X;\,A)$ .

Proof. Recall that $H^{*.*^{\prime}}(X;\,A)\to N^{*-*^{\prime}}H^*(X;\,A)$ . We have $H^{2*,*}(X;\,A)\cong CH^*(X)\otimes A.$ Since $2*>*$ for $*\ge 1$ , we see $cl(y)\in N^{1}H^{2*}(X;\,A)$ .

Each element $y\in CH^*(X)\otimes A$ is represented by closed algebraic set supported Y, while Y may be singular. On the other hand, by Totaro [ 17 ], we have the modified cycle map $\bar cl$

\begin{equation*} cl\,:\,CH^*(X)\otimes A\stackrel{\bar cl}{\longrightarrow} MU^{2*}(X)\otimes_{MU^*}A\stackrel{\rho}{\longrightarrow} H^{2*}(X;\,A)\end{equation*}

for the complex cobordism theory $MU^*(X)$ . It is known [ 11 ] that elements in $MU^{2*}(X)$ can be represented by proper maps to X from stable almost complex manifolds Y. (The manifold Y is not necessarily a complex manifold.)

The following lemma is well known.

Lemma 3·4. If $x\in Im(\rho)$ for $\rho\,:\, MU^*(X)/p\to H^*(X;\,{\mathbb Z}/p)$ , then we have $Q_i(x)=0$ for all $i\ge 0$ .

Proof. Recall the connective Morava K-theory $k(i)^*(X)$ with $k(i)^*={\mathbb Z}/p[v_i]$ , $|v_i|=-2p^i+2$ , which has natural maps

\begin{equation*} \rho\,:\,MU^*(X)/p \stackrel{\rho_1}{\longrightarrow} k(i)^*(X)\stackrel{\rho_2}{\longrightarrow} H^*(X\,:\,{\mathbb Z}/p).\end{equation*}

It is known that $d_{2p^i-1}=Q_i$ for the first nonzero differential $d_{2p^i-1}$ of the Atiyah-Hirzebruch spectral sequence converging to $k(i)^*(X)$ ,

\begin{equation*} E_2^{*,*^{\prime}}\cong H^*(X;\,{\mathbb Z}/p)\otimes k(i)^*\Longrightarrow k(i)^*(X).\end{equation*}

Hence $Q_i\rho_2(x)=0$ which implies $Q_i\rho(x)=0$ .

Lemma 3·5. (reciprocity law) If $a\in \tilde N^1H^{*}(X;\,A)$ , then for each $g\in H^{*^{\prime}}(X;\,A)$ we have $ag\in \tilde N^1H^{*+*^{\prime}}(X;\,A)$ .

Proof. Suppose we have $f\,:\,Y\to X$ with $f_*(a^{\prime})=a$ . Then

\begin{equation*} f_*\left(a^{\prime}f^*(g)\right)=f_*\left(a^{\prime}\right)g=ag\end{equation*}

by Frobenius reciprocity law.

Let G be an algebraic group (over ${\mathbb C}$ ) and r be a complex representation $r\,:\,G\to U_n$ for the unitary group $U_n$ . Then we can define the Chern class $c_i=r^*c_i^U$ . Here the Chern classes $c_i^U$ in $H^*(BU_n)\cong {\mathbb Z}\!\left[c_1^U,...,c_n^U\right]$ are defined by the Gysin map $c_n^U=i_{n*}(1)$ for the inclusion $i_n\,:\,\{0\}\subset {\mathbb C}^{\times n}$ , that is,

\begin{equation*} i_{n*} \,:\, H^*(BU_n)\cong H_{U_n}^*(\{0\})\stackrel{i_{n*}}{\longrightarrow} H_{U_n}^{*+2n}({\mathbb C}^{\times n})\cong H^{*+2i}(BU_n),\end{equation*}

where $H_{U_n}({-})=H^*(EU_n\times_{U_n}-)$ is the $U_n$ -equivariant cohomology. Hence for the approximation $XU_n$ for $U_n$ , we see $c_i^{U}\in \tilde N^1H^*(XU_n)$ . So $c_i=r^*c_i^U\in\tilde N ^{1}H^*(X)$ for the approximation X for BG.

By the reciprocity law (Lemma 3·5) we have

Lemma 3·6. Let $c_i=r^*c_i^U\in H^*(BG)$ be a Chern class for some representation $r\,:\, G\to U_n$ . For an approximation X for BG and for each $g\in H^{*^{\prime}}(BG)$ , we have $gc_i\in \tilde N^1H^*(X)$ .

The following lemma is proved by Colliot Thérène and Voisin [ 3 ] by using the affirmative answer of the Bloch–Kato conjecture by Voevodsky ([ 20 , 21 ]).

Lemma 3·7. ([ 3 ]) Let X be a smooth complex variety. Then any torsion element in $H^*(X)$ is in $N^1H^*(X)$ .

4. The main lemmas

The following lemma is the $Q_i$ -version of one of results by Benoist and Ottem.

Lemma 4·1. Let $\alpha\in N^1H^s(X)$ for $s=3$ or 4. If $Q_i(\alpha)\not =0\in H^*(X;\,{\mathbb Z}/p)$ for some $i\ge 1$ , then

\begin{equation*} DH^s(X)\supset {\mathbb Z}/p\{\alpha\},\quad DH^s\left(X;\,{\mathbb Z}/p^t\right)\supset {\mathbb Z}/p\{\alpha\}\ \ for\ t\ge 2.\end{equation*}

Proof. Suppose $\alpha\in \tilde N^1H^s(X)$ for $s=3$ or 4, i.e. there is a smooth Y with $f\,:\,Y\to X$ such that the transfer $f_*\left(\alpha^{\prime}\right)=\alpha$ for $\alpha^{\prime}\in H^*(Y)$ . Then for $s=4$

\begin{align*} Q_i\left(\alpha^{\prime}\right) & =\left(P^{\Delta_i}\beta-\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right)=\left({-}\beta P^{\Delta_i}\right)\left(\alpha^{\prime}\right) = -\beta \!\left(\alpha^{\prime}\right)^{p^i}\\[4pt]& =-p^i\left(\beta \alpha^{\prime}\right)\left(\alpha^{\prime}\right)^{p^i-1}=0 \quad (by\ Cartan\ formula)\end{align*}

since $\beta\!\left(\alpha^{\prime}\right)=0$ and $P^{\Delta_i}(y)=y^{p^i}$ for $deg(y)=2$ . (For $s=3$ , we get also $Q_i\left(\alpha^{\prime}\right)=0$ since $ P^{\Delta_i}(x)=0$ for $deg(x)=1$ .) This contradicts the commutativity of $Q_i$ and $f_*$ .

The case $A={\mathbb Z}/p^t$ , $t\ge 2$ is proved similarly, since for $\alpha^{\prime}\in H^*(X;\,A)$ we see $\beta \alpha^{\prime}=0\in H^*(X;\,{\mathbb Z}/p)$ . Thus we have this lemma.

We will extend Lemma 4·1 to $s>4$ , by using MU-theory of Eilenberg–MacLane spaces. Recall that $K=K({\mathbb Z},n)$ is the Eilenberg–MacLane space such that the homotopy group $[X,K]\cong H^n(X\,:\,{\mathbb Z})$ , i.e., each element $x\in H^n(X;\,{\mathbb Z})$ is represented by a homotopy map $x\,:\, X\to K$ . Let $\eta_n\in H^n(K;\,{\mathbb Z})$ corresponding the identity map. (For $K^{\prime}=K({\mathbb Z}/p,n)$ define $\eta^{\prime}_n\in H^n(K^{\prime};\,{\mathbb Z}/p)$ by the identity element of K ^′.) We know the image $\rho(MU^*(K))\subset H^*(K;\,{\mathbb Z})/p$ .

Lemma 4·2. ([ 13 , 15 ]) We have the isomorphism

\begin{equation*} \rho \,:\, MU^*(K)\otimes _{MU^*}{\mathbb Z}/{p}\cong{\mathbb Z}/{p}\left[Q_{i_1}...Q_{i_{n-2}}\eta_n|0<i_1<...<i_{n-2}\right],\end{equation*}

\begin{equation*} \rho \,:\, MU^*(K^{\prime})\otimes _{MU^*}{\mathbb Z}/{p}\cong{\mathbb Z}/{p}\left[Q_{i_1}...Q_{i_{n-1}}Q_0\eta^{\prime}_{n}|0<i_1<...<i_{n-1}\right] , \end{equation*}

where the notation ${\mathbb Z}/p[a,...]$ exactly means ${\mathbb Z}/p[a,...]/\left(a^2|\ |a|=odd\right)$ .

The following lemma is an extension of Lemma 4·1 to $s> 4$ .

Lemma 4·3. Let $\alpha\in N^cH^{n+2c}(X)$ , $n\ge 2$ , $c\ge 1$ . Suppose that there is a sequence $0<i_1< \cdots <i_{n-1}$ with

\begin{equation*} Q_{i_1}...Q_{i_{n-1}}\alpha \not =0 \quad in\ H^*(X;\,{\mathbb Z}/p).\end{equation*}

Then $D^cH^{*}(X)=N^cH^{*}(X)/(p,\tilde N^cH^{*}(X)) \supset {\mathbb Z}/p\{\alpha\}$ .

Proof. Suppose $\alpha\in \tilde N^cH^{n+2c}(X)$ , i.e. there is a smooth Y of $dim(Y)=dim(X)-c$ with $f\,:\,Y\to X$ such that the transfer $f_*\left(\alpha^{\prime}\right)=\alpha$ for $\alpha^{\prime}\in H^n(Y)$ .

Identify the map $\alpha^{\prime}\,:\, Y\to K$ with $\alpha^{\prime}=\left(\alpha^{\prime}\right)^*\eta_n.$ We still see from Lemma 4·2,

\begin{equation*}Q\!\left(\alpha^{\prime}\right)= Q_{i_1}...Q_{i_{n-2}}(\left(\alpha^{\prime}\right)^*\eta_n)\in Im(MU^*(Y)\longrightarrow H^*(Y;\,{\mathbb Z}/p)).\end{equation*}

From Lemma 3·4, we see

\begin{equation*}Q_{i_{n-1}}Q\!\left(\alpha^{\prime}\right)=Q_{i_{n-1}}Q_{i_1}...Q_{i_{n-2}}\left(\alpha^{\prime}\right)=0 \in H^*(Y;\,{\mathbb Z}/p).\end{equation*}

Therefore $Q_{i_{n-1}}Q(\alpha)$ must be zero by the commutativity of $f_*$ and $Q_i$ .

Remark. For $\alpha\in N^cH^{n+2c}(X;\,{\mathbb Z}/p)$ , one can prove an $A={\mathbb Z}/p$ version of the above lemma using the second isomorphism in Lemma 4·2. But we can see $Q_{i_1}...Q_{i_n}Q_0\alpha=0$ always (even when $Q_{i_1}...Q_{i_{n-1}}\alpha\not=0$ ), hence ${\mathbb Z}/p$ version would be vacuous.

5. Classifying spaces for finite groups

Let G be a finite group or an algebraic group, and BG its (geometric) classifying space. For example, when $G=G_m$ is the multiplicative group, we see

\begin{equation*} BG_m=BS^1\cong {\mathbb P}^{\infty}, \quad H^*({\mathbb P}^{\infty})\cong {\mathbb Z}[y]\ \ with\ degree\ |y=c_1|=2,\end{equation*}

for the infinite (complex) projective space ${\mathbb P}^{\infty}$ . Note that $BG_m$ is a colimit of complex projective spaces.

Though BG itself is not a colimit of complex projective varieties, we can take a complex projective variety X(N) ([ 4 ]) for a given $N\ge 3$ such that there is a map $ j\,:\,X(N)\to BG\times {\mathbb P}^{\infty} $ with

\begin{equation*} H^*(BG\times {\mathbb P}^{\infty};\,A)\stackrel{j^*}{\cong} H^*(X(N);\,A)\quad {for \ all} < N.\end{equation*}

In this paper, we call the above X(N) a (degree $\ N$ ) complex projective approximation for BG (which is an approximation of $BG\times {\mathbb P}^{\infty}$ strictly speaking).

Note that the quotient

\begin{equation*} N^nH^*(X;\,A)/(\tilde N^nH^*(X;\,A)) \end{equation*}

is an invariant under replacing X with $X\times {\mathbb P}^m$ for all n and all abelian groups A. In fact, from K $\ddot{{u}}$ nneth formula,

\begin{equation*} H^*\left(X\times {\mathbb P}^m;\, A\right)\cong H^*(X;\,A)\otimes {\mathbb Z}[y]/\left(y^{m+1}\right),\end{equation*}

where $y\in CH^1({\mathbb P}^m)$ is the first Chern class. Let Ideal(y) be the ideal of $H^*(X\times {\mathbb P}^m;\,A)$ generated by y. Then $Ideal(y)\subset \tilde N^*H^*(X\times {\mathbb P}^{m};\,A)$ by the Frobenius reciprocity law (Lemma 3·5). Moreover Benoist and Ottem show that the above quotient when $n=1$ is a stable birational invariant of X ([ 1 , proposition 2·4]).

In this paper, we will study the following (mod(p)) stable rational invariant

\begin{equation*}DH^*(X;\,A)=N^1H^*(X;\,A)/\left(p,\tilde N^1H^*(X;\,A)\right).\end{equation*}

Hereafter, we consider $DH^*(X;\,A)$ when $A={\mathbb Z}$ . Let p be an odd prime. (The case $p=2$ is different but a similar argument works.) Let $G=({\mathbb Z}/p)^3$ the $rank=3$ elementary abelian p-group. Then the mod(p) cohomology is

\begin{equation*}H^*(BG;\,{\mathbb Z}/p)\cong H^*(B{\mathbb Z}/p;\,{\mathbb Z}/p)^{3\otimes }\cong {\mathbb Z}/p[y_1,y_2,y_3]\otimes \Lambda(x_1,x_2,x_3).\end{equation*}

Here degree $|y_i|=2, |x_i|=1, \beta(x_i)=y_i$ , and $\Lambda(a,...,b)$ is the ${\mathbb Z}/p$ -exterior algebra generated by $a,...,b$ .

The integral cohomology (modulo p) is isomorphic to

\begin{equation*} H^*(BG)/p\cong Ker(Q_0)\cong H(H^*(BG;\,{\mathbb Z}/p);\,Q_0)\oplus Im(Q_0),\end{equation*}

where $H({-};\,Q_0)=Ker(Q_0)/Im(Q_0)$ is the homology with the differential $Q_0$ . It is immediate that $H(H^*(B{\mathbb Z}/p;\,{\mathbb Z}/p);\, Q_0)\cong {\mathbb Z}/p$ . By the K $\ddot{u}$ nneth formula, we have $H(H^*((BG;\,{\mathbb Z}/p);\,Q_0)\cong ( {\mathbb Z}/p)^{3\otimes}\cong {\mathbb Z}/p$ . Hence we have

\begin{equation*} H^*(BG)/p\cong {\mathbb Z}/p\{1\}\oplus Im(Q_0)\end{equation*}

\begin{equation*} \cong {\mathbb Z}/p[y_1,y_2,y_3]\left(1,Q_0(x_ix_j),Q_0\left(x_1x_2x_3\right)|i<j\right),\end{equation*}

where the notation $R(a,...,b)$ (resp. $R\{a,..., b\}$ ) means the R-submodule (resp. the free R-module) generated by $a,...,b$ . Here we note $H^+(BG)$ is just p-torsion.

Also note that $y_1,y_2,y_3$ are represented by the Chern classes $c_1$ . From Lemma 3·6, we see

\begin{equation*} Ideal(y_1,y_2,y_3)=0\in DH^*(X).\end{equation*}

We know $Q_i(y_j)=y_j^{p^i}$ and $Q_j$ is a derivation. Let us write

\begin{equation*} \alpha=Q_0(x_1x_2x_3)=y_1x_2x_3-y_2x_1x_3+y_3x_1x_2.\end{equation*}

Note $\alpha\in H^4(X)$ , $p\alpha=0$ , and $\alpha\in N^1H^*(X)$ from Lemma 3·7. Moreover

\begin{equation*}Q_1(\alpha)=Q_1(y_1x_2x_3)-...=y_1y_2^px_3-y_1y_3^px_2-...\not =0 \in H^*(X;\,{\mathbb Z}/p).\end{equation*}

Similarly, for $\alpha_{ij}=Q_0(x_ix_{j})$ , we see $Q_1(\alpha_{ij})\not =0$ . Hence from Lemma 4·1 and Lemma 3·6, we have

Theorem 5·1. Let $X=X(N)$ with $N> 2p+3$ be a (degree N) approximation for $B({\mathbb Z}/p)^3$ . Then we have

\begin{equation*}DH^*(X)\cong{\mathbb Z}/p\{\alpha_{ij}, \alpha|1\le i<j\le 3\}\quad for\ all \ *<N.\end{equation*}

Proof. We see $H^*(BG)/(p,y_1,y_2,y_3)\cong {\mathbb Z}/p\{1,\alpha_{ij},\alpha\}$ . Of course $1\not \in N^1H^*(X)$ , we have the theorem from Lemma 4·1.

Theorem 5·2. Let $X=X(N)_n$ be an approximation for $(B{\mathbb Z}/p)^n$ with $N>|Q_0Q_1...Q_{n-1}(x_1...x_n)|$ . Then we have for $\alpha_{i_1,...,i_s}=Q_0(x_{i_1}...x_{i_s})$ ,

\begin{equation*}DH^*(X)\supset{\mathbb Z}/p\!\left\{\alpha_{i_1,...,i_s }|2\le s,\ 0<i_1<i_2...<i_s\le n\right\}\quad for\ *<N.\end{equation*}

Here the notation $DH^*(X)\supset B^*$ means $DH^t(X)\supset B^t$ for the degree t-homogeneous parts of B for all $t<N$ strictly speaking.

Proof. We have the theorem from Lemma 4·3 and $ Q_{i_1}...Q_{i_{s-2}}(\alpha_{i_1,...,i_s})$ is

\begin{equation*} Q_{i_1}...Q_{i_{s-2}}Q_0(x_{i_1}...x_{i_s})=y_{i_1}^{p^{i_1}}...y_{i_{s-2}}^ {p^{i_{s-2}}}y_{i_{s-1}}x_{i_s}+...\not =0.\end{equation*}

(Note the $n=|\alpha^{\prime}|$ in Lemma 4·3 is written by $s-1$ here.)

Corollary 5·3. If $n\not =m\ge 3$ , then $X(N)_n$ and $X(N)_m$ are not stable birational equivalent.

Next we study small non-abelian p-groups. Let G be a non-abelian group of order $p^3$ (see Section 8, for details). Then $H^{even}(BG)$ is generated by Chern classes, and $H^{odd}(BG)$ is a (just) p-torsion. We can identify $H^{odd}(BG)\subset H^{odd}(BG;\,{\mathbb Z}/p)$ .The operation $Q_1$ acts on $H^{odd}(X)$ , and induces the injection

\begin{equation*} Q_1\,:\, H^{odd}(BG)\hookrightarrow H^{even}(BG).\end{equation*}

Such groups are four types (see Section 8 below), and they are called extraspecial p-groups $G=p_{\pm}^{1+2}$ of order $p^3$ . When $G=Q_8=2_-^{1+2}$ the quaternion group of order 8, we know $H^{odd}(X)=0$ . However when $G=D_8=2_+^{1+2}$ the dihedral group of order 8, the cohomology $H^{odd}(BG)$ is generated as an $H^{even}(BG)$ module by an element e of $deg(e)=3$ . When $G=E=p_+^{1+2}$ for $p\ge 3$ , $H^{odd}(BG)$ is generated by $e_1,e_2$ with $deg(e_i)=3$ . When $G=M=p_-^{1+2}$ for $p\ge 3$ , $H^{odd}(BG)$ is generated by e ^′ but $deg(e^{\prime})=2p+1$ .

From Lemma 3·5 (Frobenius reciprocity) and the main lemma (Lemma 4·1), we have the following theorem.

Theorem 5·4. Let $X=X(N)$ with $N>2p+3$ be an approximation for an extraspecial p-group G of order $p^3$ . Then we have for all $*<N$ :

\begin{equation*} DH^*(X)\cong\begin{cases} 0\quad for \ G=Q_8\\[3pt] {\mathbb Z}/2\{e\}\quad for \ G=D_8\\[3pt] 0\ or \ {\mathbb Z}/p\{e^{\prime}\} \quad for\ G=M \\[3pt] {\mathbb Z}/p\{e_1,e_2\} \quad for \ G=E.\end{cases} \end{equation*}

In particular, the above theorem implies that when $G=p_+^{1+2}$ , all $X=X(N)$ satisfy $DH^3(X)\not =0$ but $ DH^*(X)=0$ for all $4\le *<N.$

In this paper, we can not decide $DH^*(X)$ when $G=M$ .

6. Connected groups

At first, we consider when $G=U_n$ , $SU_n$ or $Sp_{2n}$ for all p, where the cohomology $H^*(BG)$ has no torsion. Then $H^*(BG)$ is generated by Chern classes, e.g.,

\begin{equation*}H^*(BU_n)\cong CH^*(BU_n)\cong {\mathbb Z}_{(p)}[c_1,...,c_n],\end{equation*}

\begin{equation*} H^*(BSp_{2n})\cong CH^*(BSp_{2n})\cong{\mathbb Z}_{(p)}[c_2,c_4,...,c_{2n}].\end{equation*}

Hence $DH^*(X)=0$ for the approximations X for these groups.

Next we consider the case $G=SO_3$ and $p=2$ . Then

\begin{equation*} H^*(BG;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[w_1,w_2,w_3]/(w_1)\cong {\mathbb Z}/2[w_2,w_3],\end{equation*}

where $w_i$ is the ith Stiefel–Whitney class for $SO_3\subset O_3$ and $w_i^2=c_i$ is the ith Chern class for $SO_3\subset U_3$ . (Also it is the elementary symmetric polynomial in ${\mathbb Z}/2[y_1,...,y_i]$ .)

Here we know $Q_0(w_2)=w_3,$ and $Q_1(w_3)=w_3^2=c_3$ . Therefore we have [ 22 ]

\begin{equation*} H^*(BG;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[c_2,c_3]\{1,w_2,w_3=Q_0(w_2),w_2w_3=Q_1w_2\}\end{equation*}

\begin{equation*} \cong {\mathbb Z}/2[c_2,c_3]\{w_2,Q_0(w_2),Q_1(w_2),Q_0Q_1(w_2)=c_3\}\oplus {\mathbb Z}/2[c_2] \end{equation*}

\begin{equation*}\cong {\mathbb Z}/2[c_2,c_3]\otimes \Lambda(Q_0,Q_1)\{w_2\}\oplus {\mathbb Z}/2[c_2].\end{equation*}

In particular $H^*(BG)/2\cong Ker(Q_0)\cong {\mathbb Z}/2[c_2,c_3]\{1,w_3\}. $ Then from Lemma 4·1, we have

Theorem 6·1. Let $G=SO_3$ and X be an approximation of BG for $6<N$ . Then $DH^*(X)\cong{\mathbb Z}/2\{w_3\}$ for $*<N.$

Using Lemma 4·3, we have

Theorem 6·2. Let $X_n=X_n(N)$ be approximations for $BSO_n$ for $n\ge 3$ . Moreover, let $|Q_1...Q_{2m-1}(w_{2m+1})|<N$ . Then we have

\begin{equation*} DH^*(X_{2m+1})\supset {\mathbb Z}/2\{w_3,w_5,...,w_{2m+1}\}\quad for \ all \ 2m+1\le *<N.\end{equation*}

Proof. Since $Q_0w_{2i}=w_{2i+1}$ , we see $w_{2i+1}\in N^1H^{2i+1}(X)$ from Lemma 3·7. We have the theorem, from Lemma 4·3 and the restriction to $H^*(B({\mathbb Z}/2)^{2i};\,{\mathbb Z}/2),$

\begin{equation*} Q_1...Q_{2i-2}(w_{2i+1})=Q_1...Q_{2i-2}Q_0(w_{2i})=y_1y_2^2...y_{2i-1}^{2^{2i-2}}x_{2i}+\cdots\not =0.\end{equation*}

Remark. The same inclusion

\begin{equation*} DH^*(X)\supset {\mathbb Z}/2\{w_3,w_5, ...,w_{2m+1}\}.\end{equation*}

holds for $G=SO_{2m+2}$ . Since $O_{2m+1}\cong SO_{2m+1}\times {\mathbb Z}/2$ , the orthogonal group $O_{2m+1}$ (hence $O_{2m+2}$ ) also has the same property.

We next consider simply connected groups. Let us write by X an approximation for $BG_2$ for the exceptional simple group $G_2$ of $rank=2$ . The mod (2) cohomology is generated by the Stiefel–Whitney classes $w_i$ of the real representation $G_2\to SO_7$

\begin{equation*} H^*(BG_2;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[w_4,w_6,w_7],\quad P^1(w_4)=w_6,\ Q_0(w_6)=w_7, \end{equation*}

\begin{equation*}H^*(BG_2)\cong \left(D^{\prime}\oplus D^{\prime}/2[w_7]^+\right)\quad where \ \ D^{\prime}={\mathbb Z}[w_4,c_6].\end{equation*}

Then we have $Q_1w_4=w_7, Q_2(w_7)=w_7^2=c_7$ (the Chern class).

The Chow ring of $BG_2$ is also known

\begin{equation*} CH^*(BG_2)\cong \left(D\{1,2w_4\} \oplus D/2[c_7]^+\right)\quad where \ \ D={\mathbb Z}[c_4,c_6]\ \ c_i=w_i^2.\end{equation*}

In particular the cycle map $cl\,:\, CH^*(BG)\to H^*(BG)$ is injective.

It is known $w_4\in N^1H^*(X;\,{\mathbb Z}/2)$ ([ 22 ]) and from Lemma 3·2, we see $w_4\in N^1H^*(X)$ . Since $Q_1(w_4)=w_7\not =0$ , from Lemma 4·1, we have $DH^4(X)\not =0$ . This fact is known in [ 1 ]. Moreover $H^*(BG)/(c_4,c_6,c_7)\cong\Lambda(w_4,w_7)$ implies:

Proposition 6·3. For X an approximation for $BG_2$ , we have the surjection

\begin{equation*} \Lambda(w_4,w_7)^+\twoheadrightarrow DH^*(X)\quad for\ all \ *<N.\end{equation*}

By Voevodsky [ 18 , 19 ], we have the $Q_i$ operation also in the motivic cohomology $H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$ with $deg(Q_i)=(2p^i-1,p-1)$ . Then we can take

\begin{equation*} deg(w_4)=(4,3),\ deg(w_6)=(6,4),\ deg(w_7)=(7,4),\ deg(c_7)=(14,7).\end{equation*}

By Theorem 3·1, the above means

\begin{equation*} w_7=Q_1w_4\in N^{7-4}H^*(X;\,{\mathbb Z}/2)=N^{3}H^*(X;\,{\mathbb Z}/2).\end{equation*}

We cannot see here that $0\not =w_7\in DH^*(X)$ , but see the following proposition.

Proposition 6·4. Let $N>|Q_2w_7|=14$ . For an approximation $X=X(N)$ for $BG_2$ , we have

\begin{equation*}{\mathbb Z}/2\{w_7\}\subset D^3H^*(X)=N^3H^*(X)/(2,\tilde N^3H^*(X)).\end{equation*}

Proof. Suppose $w_7\in \tilde N^3H^*(X)$ . That is, there is $x\in H^1(Y)$ with $f_*(x)=w_7$ for $f\,:\,Y\to X$ . Act $Q_2$ on $H^*(Y;\,{\mathbb Z}/2)$ , and

\begin{equation*} Q_2(x)=\left(P^{\Delta_2}\beta +\beta P^{\Delta_2}\right)(x)=0\end{equation*}

since $\beta(x)=0$ and $P^{i}(x)=Sq^{2i}(x)=0$ for $i>0$ . But $Q_2w_7=c_7\not =0$ . This contradicts to the commutativity of $f_*$ and $Q_2$ .

Theorem 6·5. Let G be a simply connected group such that $H^*(BG)$ has p-torsion. Let $X=X(N)$ be an approximation for BG for $N\ge 2p+3$ . Then $ DH^4(X)\not =0$ .

Proof. We only need to prove the theorem when G is a simple group having p torsion in $H^*(BG)$ . Let $p=2$ . It is well known that there is an embedding $j\,:\,G_2\subset G$ such that (see [ 10 , 25 ] for details)

\begin{equation*} H^4(BG)\stackrel{j^*}{\cong} H^4(BG_2)\cong {\mathbb Z}\{w_4\}.\end{equation*}

Let $x=(j^{*})^{-1}w_4\in H^4(BG)$ . From [ 25 , lemma 3·1], we see that 2x is represented by Chern classes. Hence 2x is the image from $CH^*(X)$ , and so $2x\in N^1H^4(X)$ . This means there is an open set $U\subset X$ such that $ 2x=0\in H^*(U)$ that is. x is 2-torsion in $H^*(U)$ . Hence from Lemma 3·5, we have $x\in N^1H^4(U)$ , and so there is $U^{\prime}\subset U$ such that $x=0\in H^4(U^{\prime})$ . This implies $x\in N^1H^4(X)$ .

Since $j^*(Q_1x)=Q_1w_4=w_7$ , we see $Q_1x\not =0$ . From the main lemma (Lemma 4·1), we see $DH^4(X)\not =0$ for G.

For the cases $p=3,5$ , we consider the exceptional groups $F_4,E_8$ respectively. Each simply connected simple group G contains $F_4$ for $p=3$ , $E_8$ for $p=5$ . There is $x\in H^4(BG)$ such that px is a Chern class [ 25 ], and $Q_1(x)\not =0\in H^*(BG;\,{\mathbb Z}/p).$ In fact, there is embedding $j\,:\,({\mathbb Z}/p)^3\subset G$ with $j^*(x)=Q_0(x_1x_2x_3)$ . Hence we have the theorem.

Corollary 6·6. Let X be an approximation for $BSpin_n$ with $n\ge 7$ or BG for an exceptional group G. Then X is not stable rational.

Remark. Kordonskii [ 6 ], Merkurjev ([ 7 , corollary 5·8]), and Reichstein–Scavia show [ 14 ] that the classifying space $BSpin_n$ itself is stably rational when $n\le 14$ . Hence the (Ekedahl) approximation X is not stable rationally equivalent to BG. In fact, these X is constructed from a quasi projective variety BG as taking intersections of subspaces of ${\mathbb P}^{M}$ for a large M. (The author thanks Federico Scavia who pointed out this remark.)

At last of this section, we consider the case $G=PGL_p$ . We have (for example [ 5 , theorems 1·5, 1·7]) additively

\begin{equation*}H^*(BG;\,{\mathbb Z}/p)\cong M\oplus N \quad with \ \ M\stackrel{add.}{\cong}{\mathbb Z}/p\!\left[x_4,x_6,...,x_{2p}\right],\quad \end{equation*}

\begin{equation*} N= SD\otimes \Lambda(Q_0,Q_1)\{u_2\}\quad with\ \ SD={\mathbb Z}/p\!\left[x_{2p+2},x_{2p^2-2p}\right],\end{equation*}

where $x_{2p+2}=Q_1Q_0u_2$ and suffix means its degree. The Chow ring is given as

\begin{equation*} CH^*(BG)/p\cong M\oplus SD\{Q_0Q_1(u_2)\}.\end{equation*}

From Lemma 4·1, we have:

Theorem 6·7. Let p be odd. For an approximation X for $BPGL_p$ , we see $ {\mathbb Z}/p\{Q_0u_2\}\subset DH^*(X)$ , and moreover there is a surjection

\begin{equation*} {\mathbb Z}/p\!\left[x_{2p^2-2p}\right]\{Q_0u_2\}\twoheadrightarrow DH^*(X)/(Im(cl))\quad for\ all \ * <N\end{equation*}

for the cycle map $cl\,:\,CH^*(X)\to H^{2*}(X)$ .

In the above case, we do not see here that $DH^*(X)$ for $*<N$ is invariant of BG. (See the remark in the introduction.)

7. ${\mathbb Z}/p$ -coefficient cohomology for abelian groups

In the preceding sections, we have seen that cases $DH^*(X;\,A)\not =0$ are not so rare for $A={\mathbb Z}_{(p)}$ , ${\mathbb Z}/p^i$ , $i\ge 2$ . However currently it seems difficult to make such example for $A={\mathbb Z}/p$ . (Recall the final remark in Section 4.)

Question 7·1. Is $DH^*(X;\,{\mathbb Z}/p)=0$ for each smooth projective variety X?

At first, we consider the case $G=({\mathbb Z}/p)^3$ .

Lemma 7·2. Let $X=X(N), N>3$ be an approximation for $(B{\mathbb Z}/p)^3$ . Then we have $DH^*(X;\,{\mathbb Z}/p)=0$ for all $*<N.$

Proof. Recall the mod p cohomology

\begin{equation*}H^*(BG;\,{\mathbb Z}/p)\cong {\mathbb Z}/p[y_1,y_2,y_3]\otimes \Lambda(x_1,x_2,x_3).\end{equation*}

Here $y_i$ is a Chern class. Hence $x_jy_i=0 \in DH^*(X;\,{\mathbb Z}/p)$ by reciprocity law. Hence we only need to check it for $z\in \Lambda(x_1,x_2,x_3)$ . But these $z\not \in N^1H^*(X;\,{\mathbb Z}/p)$ (see Lemma 7·4 below). Hence $DH^*(X;\,{\mathbb Z}/p)=0$ .

Example of Gysin maps. We can take a quasi projective approximation $\bar X(N)$ of $B{\mathbb Z}/p$ explicitly by the quotient (the N-dimensional lens space)

\begin{equation*}\bar X(N)={\mathbb C}^{N*}/({\mathbb Z}/p)\quad where \ {\mathbb C}^{N*}=\left({\mathbb C}^N-\{0\}\right).\end{equation*}

Next we consider the projective approximation

\begin{equation*}X(N)\longrightarrow \bar X(N)\times {\mathbb P}^{N}\longrightarrow B{\mathbb Z}/p\times {\mathbb P}^{\infty}.\end{equation*}

Let us write $X_i$ (resp. $X^{\prime}_i$ ) for $i=1,2,3$ the above $\bar X(N)$ (resp. $\bar X(N-1))$ for a sufficient large number N. Let

\begin{equation*} i_1\,:\,Y_1=X^{\prime}_1\times X_2\times X_3\longrightarrow X=X_1\times X_2\times X_3.\end{equation*}

Similarly we define $Y_2,Y_3$ , and the disjoin union $Y=Y_1\sqcup Y_2\sqcup Y_3$ .

Recall that for $p\,:\,odd$

\begin{equation*}H^*(X;\,{\mathbb Z}/p)\cong {\mathbb Z}/p[y_1,y_2,y_3]/\left(y_1^{N+1},y_1^{N+1},y_3^{N+1}\right)\otimes\Lambda(x_1,x_2,x_3),\end{equation*}

and $H^*(Y_i;\,{\mathbb Z}/p)\cong H^*(X;\,{\mathbb Z}/p)/\left(y_i^N\right)$ for $i=1,2,3$ . For $p=2$ , some graded ring $grH^*(X;\,{\mathbb Z}/2)$ is isomorphic to the above ring (in fact $x^2_i=y_i$ ).

For the embedding $f_i\,:\,X^{\prime}_i\to X_i$ , it is known $f_{i*}(1)=c_1(N_i)$ where $N_i$ is the normal bundle for $X^{\prime}_i\subset X_i$ . Hence the Gysin map is given by

\begin{equation*} f_{1*}(1)=y_1,\quad f_{2*}(1)=y_2,\quad f_{3*}(1)=y_3.\end{equation*}

Therefore we have for $x=(x_2x_3+ x_3x_1+x_1x_2)\in H^*(Y_1\sqcup Y_2\sqcup Y_3;\,{\mathbb Z}/p)$ ,

\begin{equation*} f_*(x)=y_1x_2x_3+y_2x_3x_1+y_3x_1x_2=Q_0(x_1x_2x_3)=\alpha.\end{equation*}

(Note that the element $x=(x_1x_2+x_2x_3+x_3x_1)$ is not in the integral cohomology $H^*(Y)$ .) Thus we see $\alpha\in \tilde N^cH^*(X;\,{\mathbb Z}/p).$ More generally, we see

Theorem 7·3. Let $X=X(N)$ be an approximation for $(B{\mathbb Z}/p)^n$ with ${\mathbb Z}/p$ -coefficients. Then we have

\begin{equation*}DH^*(X;\,{\mathbb Z}/p)=0 \quad for\ all\ *<N.\end{equation*}

We recall here the motivic cohomology. By Voevodsky [ 18 ], $H^{*,*^{\prime}}(B{\mathbb Z}/p;\,{\mathbb Z}/p)$ satisfies the K $\ddot{{u}}$ nneth formula so that (for p odd)

\begin{equation*}H^{*,*^{\prime}}(B({\mathbb Z}/p)^n;\,{\mathbb Z}/p)\cong {\mathbb Z}/p[\tau, y_1,...,,y_n]/\left(y_1^{N+1},...,y_n^{N+1}\right)\otimes\Lambda(x_1,...,x_n).\end{equation*}

Here $0\not =\tau\in H^{0,1}(Spec({\mathbb C});\,{\mathbb Z}/p)$ , and $deg(y_i)=(2,1)$ , $deg(x_i)=(1,1)$ .

From Lemma 3·1, we can identify $N^cH_{et}^*(X;\,{\mathbb Z}/p)= F_{\tau}^{*,*-c}$ where

$F_{\tau}^{*,*-c}=Im(\times \tau^c\,:\,H^{*,*-c}(X;\,{\mathbb Z}/p)\to H^{*,*}(X;\,{\mathbb Z}/p)).$

Lemma 7·4. ([ 16 , theorem 5·1]) Let $X=X(N)$ be an approximation for $(B{\mathbb Z}/p)^n$ for a sufficient large N. Then we have

\begin{equation*} H^*(X;\,{\mathbb Z}/p)/N^1H^*(X;\,{\mathbb Z}/p)\cong \Lambda(x_1,....,x_n).\end{equation*}

Proof. Let $x\in Ideal(y_1,...,y_n)\subset H^{*,*^{\prime}}(X;\,{\mathbb Z}/p)$ . Then $deg(x)=(*,*^{\prime})$ with $*>*^{\prime}$ , and x is a multiplying of $\tau$ . Hence $x\in N^1H^*(X;\,{\mathbb Z}/p)$ .

Proof of Theorem 7·3. Let $x\in N^1H^*(X;\,{\mathbb Z}/p)$ . From the above lemma, $x\in Ideal(y_1,...,y_n)$ which is in the image of the Gysin map. That is $x\in \tilde N^1H^*(X;\,{\mathbb Z}/p)$ .

We can extend Theorem 7·3, by using the following lemma. Let us write by XG an approximation for BG. Let $j\,:\, BS\to BG$ and $i;\, Y\to XS$ . We consider maps:

Lemma 7·5. Let G have a Sylow p-subgroup S. If $ DH^*(XS;\,{\mathbb Z}/p)=0$ , then $DH^*(XG\,:\,{\mathbb Z}/p)=0$ also for BG.

Proof. Let $j\,:\, BS\to BG$ so that $j_*=cor_S^G$ is the transfer (with the codimension $c=0$ ) for finite groups. Note that $j^*N^1H^*(XG;\,{\mathbb Z}/p)\subset N^1H^*(XS;\,{\mathbb Z}/p)$ by the naturality of $j^*$ . Hence given $x\in N^1H^*(XG;\,{\mathbb Z}/p)$ , the element $y=j^*(x)$ is in $N^1H^*(XS;\,{\mathbb Z}/p)$ .

By the assumption in this lemma, there are $i\,:\,Y\to XS$ and y ^′ such that $y^{\prime}\in H^*(Y;\,{\mathbb Z}/p)$ with $i_*(y^{\prime})=y$ . We consider maps:

\begin{equation*} H^*(Y;\,{\mathbb Z}/p)\stackrel{i_*}{\to} H^*(XS;\,{\mathbb Z}/p)\stackrel{j_*}{\to}H^*(XG;\,{\mathbb Z}/p).\end{equation*}

Then we have $\ j_*i_*(y^{\prime})=j_*y=j_*j^*(x)=[G;\,S]x.$

Similarly, we can prove:

Corollary 7·6. Let G have an abelian Sylow p-subgroup. Let $X=X(N)$ be an approximation for BG. Then we have $ DH^*(X;\,{\mathbb Z}/p)=0$ for all $ *<N$ .

8. The groups $Q_8$ and $D_8$

When $|G|=p^3$ , we have the short exact sequence

\begin{equation*} 0\longrightarrow C\longrightarrow G\longrightarrow V \longrightarrow 0,\end{equation*}

where $C\cong {\mathbb Z}/p$ is in the center and $ V\cong {\mathbb Z}/p\times {\mathbb Z}/p$ . Let us take generators such that $C={\langle} c{\rangle}, V={\langle} a,b {\rangle}.$ Moreover we can take $[a,b]=c$ when G is non-abelian.

There are two cases, when $p=2$ , the quaternion group $Q_8$ and the dihedral group $D_8$ . We will show here

Theorem 8·1. Let $X=X(N)$ be an approximation for $Q_8$ or $D_8$ . Then $DH^*(X;\,{\mathbb Z}/2)=0$ for all $*<N$ .

8·1. The case $G=Q_8$ . Then $a^2=b^2=c$ . Its cohomologies are well known (see [ 12 ]):

\begin{equation*}H^*(BG)/2\cong {\mathbb Z}/2[y_1,y_2,c_2]/\left(y_i^2,y_1y_2\right)\ \|y_i|=2,\end{equation*}

\begin{equation*}H^*(BG;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[x_1,x_2,c_2]/(x_1x_2+y_1+y_2,x_1y_2+x_2y_1)\end{equation*}

\begin{equation*}\cong {\mathbb Z}/2\{1,x_1,y_1,x_2,y_2,w\}\otimes {\mathbb Z}/2[c_2],\end{equation*}

where $ x_i^2=y_i$ $|x_i|=1$ , and $w=y_1x_2=y_2x_1$ , $|w|=3$ .

Therefore, we see

\begin{equation*}H^*(BG;\,{\mathbb Z}/2)/(y_1,y_2,c_2)\cong {\mathbb Z}/2\{1,x_1,x_2\}.\end{equation*}

Of course $deg(x_i)=(1,1)$ in $H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$ and they are not in $N^1H^*(BG;\,{\mathbb Z}/2)$ . Thus we have Theorem 8·1 for $G=Q_8$ .

8·2. The case $G=D_8$ . Then $a^2=c, b^2=1$ . It is well known

\begin{equation*} H^*(BG)/2\cong {\mathbb Z}/2[y_1,y_2,c_2]/(y_1y_2)\{1,e\}\quad with \ |e|=3.\end{equation*}

The mod 2 cohomlogy is written [ 12 ]

\begin{equation*} H^*(BG;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[x_1,x_2,u]/(x_1x_2)\quad (with\ |u|=2)\end{equation*}

\begin{equation*} \cong \left(\!\oplus_{j=1}^2 {\mathbb Z}/2[y_j]\{y_j, x_j,y_ju,x_ju\}\oplus{\mathbb Z}/2\{1,u\}\right)\otimes {\mathbb Z}/2[c_2].\end{equation*}

Here $y_j=x_j^2, u^2=c_2$ and $Q_0(u)=(x_1+x_2)u=e,Q_1Q_0(u)=(y_1+y_2)c_2$ .

We note $y_1,y_2,c_2\in CH^*(BG)/2$ and

\begin{equation*} H^*(BG;\,{\mathbb Z}/2)/(y_1,y_2,c_2)\cong\left(\oplus _{j=1}^2{\mathbb Z}/2\{x_j,x_ju\}\right)\oplus {\mathbb Z}/2\{1,u\}.\end{equation*}

Moreover, $deg(x_j)=(1,1)$ , $deg(u)=(2,2)$ in the motivic cohomology

$H^{*,*^{\prime}}(BG;\,{\mathbb Z}/2)$ and they are not in $N^1H^*(BG;\,{\mathbb Z}/2)$ . Here we note $deg(x_ju)=(3,3)$ , but there is $u^{\prime}_j\in H^{3,2}(BG;\,{\mathbb Z}/2)$ with $x_ju=\tau u^{\prime}_j$ from [ 24 , lemma 6·2] (i.e., $x_ju\in N^1H^*(X;\,{\mathbb Z}/2)$ ).

Hence for the proof of Lemma 8·1 (for $G=D_8$ ), it is only needed to show

Lemma 8·2. Let $N>4$ and X be an approximation for BG. Then we have $x_iu\in \tilde N^1H^*(X;\,{\mathbb Z}/2)$ .

To prove the above lemma, for a G-variety H, we consider the equivariant cohomology (recall the arguments just before Lemma 3·6)

\begin{equation*} H_G^*(H;\,{\mathbb Z}/p)=H^*(E(N)\times _{G}H;\,{\mathbb Z}/p),\end{equation*}

where E(N) is an (approximation of) contractible free G-variety. Let us write

\begin{equation*} X_GH=approx. \ of\ E(N)\times_GH \ so\ that\ H_G^*(H;\,{\mathbb Z}/p)\cong H^*(X_GH;\,{\mathbb Z}/p).\end{equation*}

For a closed embedding $i\,:\,H\subset K$ of G-varieties, we can define the Gysin map

\begin{equation*} i_*\,:\, H_G^*(H;\,{\mathbb Z}/p)\longrightarrow H^*_G(K;\,{\mathbb Z}/p)\quad by \ i\,:\,X_GH\stackrel{id\times_Gi}{\longrightarrow} X_GK. \end{equation*}

Hereafter in this section, let $G=D_8$ . We recall arguments in [ 24 ]. We define the 2-dimensional representation $\tilde c\,:\, G\to U_2$ such that $\tilde c(a)=diag(i,-i)$ and $\bar c(b)$ is the permutation matrix (1,2). By this representation, we identify that $W={\mathbb C}^{2*}={\mathbb C}^2-\{0\}$ is an G-variety. Note G acts freely on $W\times {\mathbb C}^*$ but it does not act freely on $W={\mathbb C}^{2*}.$

The fixed points set on W under b is

\begin{equation*} W^{{\langle} b{\rangle}}=\{(x,x)|x\in {\mathbb C}^*\}={\mathbb C}^*\{e^{\prime}\} ,\quad e^{\prime}=diag(1,1)\in GL_2({\mathbb C}).\end{equation*}

Similarly $W^{{\langle} bc{\rangle}}={\mathbb C}^*\{a^{-1}e^{\prime}\}.$ Take

\begin{equation*} H_0={\mathbb C}^{*}\{e^{\prime},ae^{\prime}\},\quad H_1={\mathbb C}^{*}\left\{g^{-1}e^{\prime},q^{-1}ae^{\prime}\right\},\end{equation*}

where $g\in GL_2({\mathbb C})$ with $g^{-1}bg=ab$ (note $(ab)^2=1$ ).

Let us write $ H=H_0\sqcup H_1.$ Then G acts on $H_i$ and acts freely on ${\mathbb C}^{2*}-H$ . In fact it does not contain fixed points of non-trivial stabiliser groups. We consider the transfer for some G-variety H in ${\mathbb C}^{2*}$ , and induced equivariant cohomology

\begin{equation*} i_*\,:\, H^*_G(H;\,{\mathbb Z}/2)\longrightarrow H^*_G\!\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right).\end{equation*}

Lemma 8·3. We have

\begin{equation*}H^*_G(H_0;\,{\mathbb Z}/2)\cong {\mathbb Z}/2[y] \otimes \Lambda(x,z)\quad with \ y=x^2,\ |x|= |z|=1.\end{equation*}

Proof. We consider the group extension $0\to {\langle} a{\rangle} \to G\to {\langle} b {\rangle} \to 0$ and the induced spectral sequence

\begin{equation*}E_2^{*,*^{\prime}}=H^*(B{\langle} b{\rangle};\, H^{*^{\prime}}_{{\langle} a{\rangle} }(H_0;\,{\mathbb Z}/2))\Longrightarrow H_G^*(H_0;\,{\mathbb Z}/2).\end{equation*}

Since ${\langle} a{\rangle}\cong {\mathbb Z}/4$ acts freely on $H_0$ , we see $H_0/{\langle} a{\rangle} \cong {\mathbb C}^{*}\{e^{\prime},ae^{\prime}\}/{\langle} a{\rangle}\cong {\mathbb C}^{*}.$ Therefore we have

\begin{equation*}H^*_{{\langle} a{\rangle}}(H_0;\,{\mathbb Z}/2)\cong H^*({\mathbb C}^*/{\langle} a{\rangle};\,{\mathbb Z}/2)\cong H^*({\mathbb C}^*;\,{\mathbb Z}/2)\cong \Lambda (z),\quad |z|=1.\end{equation*}

Since ${\langle} b{\rangle}$ acts trivially on $\Lambda(z)$ we have this lemma

\begin{equation*} H^*_G(H_0;\,{\mathbb Z}/2)\cong H^*(B{\langle} b{\rangle};\,{\mathbb Z}/2)\otimes \Lambda(z)\cong {\mathbb Z}/2[y]\otimes \Lambda(x,z).\end{equation*}

Note $H_G^*(H_0;\,{\mathbb Z}/2)\cong H_G^*(H_1;\,{\mathbb Z}/2)$ and hence we see

\begin{equation*}H^*_G(H;\,{\mathbb Z}/2)\cong \oplus_{j=1}^2 {\mathbb Z}/2[y_j]\left\{1_j,y_j, x_j,x_jz_j,z_j\right\}.\end{equation*}

We consider the long exact sequence

\begin{equation*} \quad\quad\cdots\longrightarrow H^{*}_G(\{0\};\,{\mathbb Z}/2)\stackrel{i_*=c_2}{\longrightarrow}H^{*+4}_G\left({\mathbb C}^2;\,{\mathbb Z}/2\right) \longrightarrow H^{*+4}_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\longrightarrow \cdots \qquad({\ast})\end{equation*}

and we have $H^*_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\cong H^*(BG;\,{\mathbb Z}/2)/(c_2)$ . Hence, we get

\begin{equation*}H^*_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\cong \left( \oplus_{j=1}^2 {\mathbb Z}/2[y_j]\left\{y_j,x_j,x_ju^{\prime}_j,u^{\prime}_j\right\}\right)\oplus{\mathbb Z}/2\{1,u\}.\end{equation*}

Now we consider the transfer $H^*_G(H;\,{\mathbb Z}/2) \stackrel{i_*}{\to} H^{*+2}_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)$ . We have explicitly ([ 24 , p. 527])

\begin{equation*} i_*(1_j)=y_j,\ i_*(x_j)=y_jx_j,\ i_*(x_jz_j)=x_ju^{\prime}_j,\ i_*(z_j)=u^{\prime}_j.\end{equation*}

Therefore we have Lemma 8·2 and hence Theorem 8·1 for $G=D_8$ .

To see the above $i_*$ , we recall the long exact sequence for $i\,:\,H \subset {\mathbb C}^{2*}$

\begin{equation*} \quad\qquad\cdots\longrightarrow H^{*+1}_G\left({\mathbb C}^{2*}-H;\,{\mathbb Z}/2\right)\stackrel{\delta}{\longrightarrow}H^*_G(H;\,{\mathbb Z}/2) \stackrel{i_*}{\longrightarrow} H^{*+2}_G\left({\mathbb C}^{2*};\,{\mathbb Z}/2\right)\quad\quad({\ast\ast})\end{equation*}

\begin{equation*}\stackrel{j^*}{\longrightarrow} H^{*+2}_G\left({\mathbb C}^{2*}-H;\,{\mathbb Z}/2\right)\longrightarrow\cdots\end{equation*}

The transfer $i_*$ is determined by the following lemma.

Lemma 8·4. In the above $({**})$ , we see $\delta=0$ , and hence $i_*$ is injective.

Proof. Since G acts freely on ${\mathbb C}^{2*}-H$ , we have

\begin{equation*} H^*_G\left({\mathbb C}^{2*}-H\,:\,{\mathbb Z}/2\right)\cong H^*\left(\left({\mathbb C}^{2*}-H\right)/G;\,{\mathbb Z}/2\right),\end{equation*}

which is zero when $*>4=2dim(({\mathbb C}^{2*}-H)/G)$ . Hence $\delta$ must be zero for $*>4$ , and $i_*$ is injective for $*>4$ . In particular, $i_*\left(y^2_jz_j\right)=y_j^2u^{\prime}_j$ . Since $H^*_G(H;\,{\mathbb Z}/2)$ is ${\mathbb Z}/2[y_1]$ -free (or $Z/2[y_2]$ -free,) we see $i_*(z_j)=u^{\prime}_j$ .