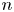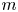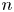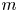1. Introduction
This paper studies an apparently novel insurance product: a policy that pays off if at least ![]() $m$-out-of-
$m$-out-of-![]() $n$ sites have a catastrophic event in a given time interval. Although the literature on catastrophe insurance scarcely mentions this product, there are hints that insurers have offered it to clients who are exposed to multiple perils.Footnote 1
$n$ sites have a catastrophic event in a given time interval. Although the literature on catastrophe insurance scarcely mentions this product, there are hints that insurers have offered it to clients who are exposed to multiple perils.Footnote 1
As motivation, consider a multi-national company (MNC) with ![]() $n$ sites, widely dispersed geographically. (Geographic dispersion allows us to regard events at different sites as independent. See Section 1.3 for discussion of dependent risks.) The company wants to buy insurance to compensate for potential losses arising from a variety of catastrophic events such as earthquakes, hurricanes, wildfires, volcanic eruptions, or other natural hazards. Although a catastrophic event at any one site is rare, the company is likely to experience an increasing number of these events per year on average as
$n$ sites, widely dispersed geographically. (Geographic dispersion allows us to regard events at different sites as independent. See Section 1.3 for discussion of dependent risks.) The company wants to buy insurance to compensate for potential losses arising from a variety of catastrophic events such as earthquakes, hurricanes, wildfires, volcanic eruptions, or other natural hazards. Although a catastrophic event at any one site is rare, the company is likely to experience an increasing number of these events per year on average as ![]() $n$ increases, ergo the potential for financial loss increases. Hereafter, we refer to catastrophic events generically as quakes and to a global company seeking insurance as a customer.
$n$ increases, ergo the potential for financial loss increases. Hereafter, we refer to catastrophic events generically as quakes and to a global company seeking insurance as a customer.
One coverage option, Strategy A, has an insurance company offering the MNC individual policies with a fixed amount of coverage on each site. Because the total premium increases linearly with the number of sites, a customer with many sites would find this approach overly expensive, especially when quakes are rare events. The approach also holds limited appeal for a customer who has contingency cash reserves that allow it to absorb some of the financial loss associated with multiple quakes occurring within the coverage period. As a consequence, a customer, able to absorb the loss from quakes at ![]() $m-1$ sites, may need a cash infusion, presumably from insurance, only if
$m-1$ sites, may need a cash infusion, presumably from insurance, only if ![]() $m$ or more sites have quakes during the coverage period.
$m$ or more sites have quakes during the coverage period.
Insurance policies that provide less than full coverage of customers' losses are common. They usually contain a deductible clause requiring a customer to self-insure the first ![]() $x$ dollars, where
$x$ dollars, where ![]() $x$ is the deductible. But in the context of multi-peril catastrophes spread out over time and space, there is the alternative coverage option in which the deductible takes the form of a minimal number of sites suffering losses rather than a minimal dollar amount before a customer receives a payout.
$x$ is the deductible. But in the context of multi-peril catastrophes spread out over time and space, there is the alternative coverage option in which the deductible takes the form of a minimal number of sites suffering losses rather than a minimal dollar amount before a customer receives a payout.
1.1. Potential applications
Many multi-national companies (MNCs) now develop a captive: an insurance company that operates within the set of companies comprising the MNC and its subsidiaries. Using capital provided by the MNC, the captive insures the risks of the MNC, leveraging the geographic and product diversification of the MNC, and then organizes external (re)insurance for losses exceeding the retention limit of the captive. Thus, an MNC with a captive might choose an ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy. Quoting from Westover [Reference Westover17]: “Many captives are established because insurance in the commercial market is prohibitively expensive, poorly matched to the insured's needs, or not available at all. A captive insurer can successfully provide coverage for difficult risks that is tailored to fit the exact needs of the insured.” Indeed, when it comes to obtaining
$n$ policy. Quoting from Westover [Reference Westover17]: “Many captives are established because insurance in the commercial market is prohibitively expensive, poorly matched to the insured's needs, or not available at all. A captive insurer can successfully provide coverage for difficult risks that is tailored to fit the exact needs of the insured.” Indeed, when it comes to obtaining ![]() $m$-out-of-
$m$-out-of-![]() $n$ coverage, there may be no alternative to a captive, since providers in the commercial market seem to have little interest in offering such a “boutique” insurance product.
$n$ coverage, there may be no alternative to a captive, since providers in the commercial market seem to have little interest in offering such a “boutique” insurance product.
Another potential application with increasing relevance as global temperatures increase is insurance against damages from wildfires. For example, an electric power company with power lines in ![]() $n$ geographically dispersed locations may want insurance which pays if
$n$ geographically dispersed locations may want insurance which pays if ![]() $m$ or more of these locations have wildfires caused by power-line malfunctions resulting in liability claims against the company. The power company may be able to go to reinsurers to provide policies on individual locations.
$m$ or more of these locations have wildfires caused by power-line malfunctions resulting in liability claims against the company. The power company may be able to go to reinsurers to provide policies on individual locations.
1.2. Preview of results
To offer a policy with ![]() $m$-out-of-
$m$-out-of-![]() $n$ coverage, an insurance company needs a strategy for determining the premium to charge to a customer. This study describes Strategies B and C, both of which provide this coverage. Each determines a minimal premium for which the insurance company is indifferent between offering and not offering the policy. Whereas Strategy B is relatively static, Strategy C is adaptive. As the covered properties’ quake history evolves, it periodically adjusts its reinsurance level based on a review of the number of sites that have had quakes so far. In particular, it exploits the rarity of more than one quake occurring between successive reviews. The study principally focuses on Strategy C, comparing the risk of loss to which it exposes an insurance company with Strategy B's corresponding risk of loss for the minimal premiums at which the company is willing to offer the policy under each strategy. The study also describes decision rules for choosing between strategies, based in large part on utility theory.
$n$ coverage, an insurance company needs a strategy for determining the premium to charge to a customer. This study describes Strategies B and C, both of which provide this coverage. Each determines a minimal premium for which the insurance company is indifferent between offering and not offering the policy. Whereas Strategy B is relatively static, Strategy C is adaptive. As the covered properties’ quake history evolves, it periodically adjusts its reinsurance level based on a review of the number of sites that have had quakes so far. In particular, it exploits the rarity of more than one quake occurring between successive reviews. The study principally focuses on Strategy C, comparing the risk of loss to which it exposes an insurance company with Strategy B's corresponding risk of loss for the minimal premiums at which the company is willing to offer the policy under each strategy. The study also describes decision rules for choosing between strategies, based in large part on utility theory.
Strategy C exploits the property that the event, ![]() $m$-out-of-
$m$-out-of-![]() $n$ sites have quakes, is a contingent claim: it is completely determined by whether or not the individual sites have quakes, events for which the insurer can purchase reinsurance policies. The situation is analogous to the pricing of derivatives in financial markets, but unlike the latter, the market for reinsurance is typically neither complete nor necessarily free from arbitrage. For this and other reasons, the powerful theory for pricing financial derivatives using dynamic hedging (buying and selling a portfolio of cash and stock) is not fully applicable to the
$n$ sites have quakes, is a contingent claim: it is completely determined by whether or not the individual sites have quakes, events for which the insurer can purchase reinsurance policies. The situation is analogous to the pricing of derivatives in financial markets, but unlike the latter, the market for reinsurance is typically neither complete nor necessarily free from arbitrage. For this and other reasons, the powerful theory for pricing financial derivatives using dynamic hedging (buying and selling a portfolio of cash and stock) is not fully applicable to the ![]() $m$-out-of-
$m$-out-of-![]() $n$ problem. For a more detailed discussion of these issues, see Section 3.
$n$ problem. For a more detailed discussion of these issues, see Section 3.
1.3. Related research
The present paper employs utility functions (primarily exponential) to set premiums and compare strategies. The use of utility theory in insurance models goes back at least to the 1960s (see, e.g., [Reference Arrow1,Reference Arrow2,Reference Borch6]). As an alternative to traditional actuarial methods for setting premiums, Bühlmann [Reference Bühlmann7] develops an economic model based on an equilibrium solution for prices in a market with utility-maximizing insurers and reinsurers, each with a concave utility function. For the special case of an exponential utility function, this solution is closely related to the traditional actuarial premium principle introduced by Esscher [Reference Esscher12].
Embrechts and Meister [Reference Embrechts and Meister11] combine utility theory with dynamic hedging to study the pricing of insurance derivatives, using more abstract mathematical models than the present paper. A common thread in both papers is acknowledgement that markets for insurance are typically incomplete and therefore do not admit a unique price even in a no-arbitrage context.
Cummins and Trainar [Reference Cummins and Trainar9] provide a comprehensive survey of the literature on the relative merits of reinsurance and securitization for managing insurable risks. Their setting is that of an insurer deciding how much of a specific risk to cede to one or more reinsurers versus shedding some or all of that risk by means of an insurance-linked security (ILS). There is an analogy between this situation and the comparison of Strategy B and Strategy C for insuring an ![]() $m$-out-of-
$m$-out-of-![]() $n$ risk. The analysis of Strategy B in this paper yields an upper bound on how much the insurer would be willing to pay a reinsurer to assume the risk in its entirety. By the same token, Strategy C is analogous to an ILS, in that the insurer is transferring some (indeed, most) of the risk to an external market, in this case not a financial market but rather a market (typically not complete) for policies on the individual sites. By contrast, the kind of ILS considered by Cummins and Trainor [Reference Cummins and Trainar9] is a conventional financial instrument, such as a catastrophe bond based on a risk index, which trades on a conventional financial market. For the insurer in their setting, there is typically a basis risk associated with the ILS, inasmuch as it is not 100% correlated with the insurer's risk. By contrast, the basis risk associated with Strategy C comes from the small but positive probability that more than one site will have a quake during the review period. (There is also a risk that the seller of the single-site insurance will default, which this paper does not consider.)
$n$ risk. The analysis of Strategy B in this paper yields an upper bound on how much the insurer would be willing to pay a reinsurer to assume the risk in its entirety. By the same token, Strategy C is analogous to an ILS, in that the insurer is transferring some (indeed, most) of the risk to an external market, in this case not a financial market but rather a market (typically not complete) for policies on the individual sites. By contrast, the kind of ILS considered by Cummins and Trainor [Reference Cummins and Trainar9] is a conventional financial instrument, such as a catastrophe bond based on a risk index, which trades on a conventional financial market. For the insurer in their setting, there is typically a basis risk associated with the ILS, inasmuch as it is not 100% correlated with the insurer's risk. By contrast, the basis risk associated with Strategy C comes from the small but positive probability that more than one site will have a quake during the review period. (There is also a risk that the seller of the single-site insurance will default, which this paper does not consider.)
The present paper assumes that insurers and reinsurers are risk averse. An alternative model assumes that they are risk neutral with convex capital costs (e.g., [Reference Froot13]). Higher capital costs in adverse states cause firms to avoid these states, which leads to behavior that looks like risk aversion. Risk aversion in firms can be a type of short-hand for cases like this.
Risk-shedding instruments based on the ![]() $m$-out-of-
$m$-out-of-![]() $n$ concept have arisen in finance, in particular, as a basket of credit default swaps. Originally developed to allow lending institutions to shed the risk of default associated with a commercial loan, a credit default swap (CDS) is a transaction between two parties in which the seller of the CDS agrees to compensate the buyer (e.g., a bank making a loan) in the event of a default on a credit obligation. In return, the buyer periodically pays the seller a premium. Therefore, a CDS is a form of insurance that lacks the regulatory features associated with conventional insurance products.
$n$ concept have arisen in finance, in particular, as a basket of credit default swaps. Originally developed to allow lending institutions to shed the risk of default associated with a commercial loan, a credit default swap (CDS) is a transaction between two parties in which the seller of the CDS agrees to compensate the buyer (e.g., a bank making a loan) in the event of a default on a credit obligation. In return, the buyer periodically pays the seller a premium. Therefore, a CDS is a form of insurance that lacks the regulatory features associated with conventional insurance products.
A basket of credit default swaps is a contract involving more than one credit obligation. One variation, called an ![]() $m$-out-of-
$m$-out-of-![]() $n$ basket of CDSs, is a contract that pays the buyer an agreed-upon sum if and when
$n$ basket of CDSs, is a contract that pays the buyer an agreed-upon sum if and when ![]() $m$-out-of-
$m$-out-of-![]() $n$ credit obligations have defaulted. As previously mentioned, our
$n$ credit obligations have defaulted. As previously mentioned, our ![]() $m$-out-of-
$m$-out-of-![]() $n$ catastrophic insurance model on globally distributed sites assumes that quakes occur independently. However, defaults among the credit obligations in a basket rarely are probabilistically independent. (An extreme example of the danger of ignoring dependence among default risks is the failure of AIG to hedge its portfolio of default swaps tied to subprime mortgages in 2008.) This dependence has prompted substantial research on baskets of CDSs that focusses on models that explicitly take dependence into account.
$n$ catastrophic insurance model on globally distributed sites assumes that quakes occur independently. However, defaults among the credit obligations in a basket rarely are probabilistically independent. (An extreme example of the danger of ignoring dependence among default risks is the failure of AIG to hedge its portfolio of default swaps tied to subprime mortgages in 2008.) This dependence has prompted substantial research on baskets of CDSs that focusses on models that explicitly take dependence into account.
Assuming a complete trading market for individual CDSs with no arbitrage, Bielecki et al. [Reference Bielecki, Jeanblanc and Rutkowski4] develop a general theory for pricing a basket of correlated credit default swaps based on dynamic replication by trading individual CDSs (see also [Reference Hull and White14]). By contrast, the present paper presents a model that assumes that the risks at individual sites are independent (a realistic assumption for widely dispersed sites), but does not assume that the underlying entities (reinsurance contracts on individual sites) trade in a complete market with no arbitrage. (To assume so would not be realistic.)
In principle, the ideas behind the present paper's dynamic reinsurance model could be extended to dependent risks, but at the cost of confronting the well-known curse of dimensionality associated with multi-dimensional dynamic models, a task better left to future research.
1.4. Organization of paper
To set the stage, Section 2 describes Strategy B, including a mechanism, based on expected utility, for determining the minimal premium that the insurance company requires before offering the ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy. Section 3 introduces Strategy C. In particular, it specifies Condition (7) for the coverage period's quake history which, if satisfied, guarantees that Strategy C is self-financing when purchasing reinsurance coverage periodically as dictated by the minimal working capital scheme derived in Section 3.1. It also determines the minimal premium to charge that, together with the schedule, accounts for the reduction in the insurance company's risk exposure. It also derives the indifference premium for Strategy C, again based on expected utility. To fix ideas, the study principally focuses on one-year coverage with daily review. Of course, daily reinsurance on individual sites may not exist. Later sections illustrate the analysis for 7 and 30-day review intervals. A review interval denotes the number of days between successive reviews.
$n$ policy. Section 3 introduces Strategy C. In particular, it specifies Condition (7) for the coverage period's quake history which, if satisfied, guarantees that Strategy C is self-financing when purchasing reinsurance coverage periodically as dictated by the minimal working capital scheme derived in Section 3.1. It also determines the minimal premium to charge that, together with the schedule, accounts for the reduction in the insurance company's risk exposure. It also derives the indifference premium for Strategy C, again based on expected utility. To fix ideas, the study principally focuses on one-year coverage with daily review. Of course, daily reinsurance on individual sites may not exist. Later sections illustrate the analysis for 7 and 30-day review intervals. A review interval denotes the number of days between successive reviews.
How well Strategy C sheds risk depends on how often quake histories satisfy Condition (7). Section 3.2 derives a bound on C's loss probability that, for ![]() $m$ small relative to
$m$ small relative to ![]() $n$, often is considerably less than the corresponding loss probability for Strategy B. Section 3.3 next describes how Strategy C induces a sometimes substantial profit when at least
$n$, often is considerably less than the corresponding loss probability for Strategy B. Section 3.3 next describes how Strategy C induces a sometimes substantial profit when at least ![]() $m$ quakes occur but Condition (7) is not satisfied, offering an additional advantage over Strategy B, which realizes a profit only if fewer than
$m$ quakes occur but Condition (7) is not satisfied, offering an additional advantage over Strategy B, which realizes a profit only if fewer than ![]() $m$ quakes occur.
$m$ quakes occur.
Section 4 provides guidance for choosing between the two strategies based on expected utility, loss probabilities, and the premium dictated by the market for this form of ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy. Section 5 carries the analysis further by examining the scenario,
$n$ policy. Section 5 carries the analysis further by examining the scenario, ![]() $(m, n) = (2, 5)$, in considerably more detail. In particular, it shows how premium and loss probability vary for insurance companies with different levels of risk aversion. Section 5.1 then describes how Strategy C may induce a profit when
$(m, n) = (2, 5)$, in considerably more detail. In particular, it shows how premium and loss probability vary for insurance companies with different levels of risk aversion. Section 5.1 then describes how Strategy C may induce a profit when ![]() $m$ or more quakes occur during the first review interval that experiences quakes. Most notably, it shows how the probability of a profit increases as the review interval increases.
$m$ or more quakes occur during the first review interval that experiences quakes. Most notably, it shows how the probability of a profit increases as the review interval increases.
To fix ideas, Sections 3 through 4 assume daily reviews. Later, Sections 5 through 6 examine how increasing the length of the review interval affects the premium and loss probability. Sections 3 through 5 also assume that the reinsurer's markup remains constant over the entire coverage period. Section 6 relaxes that assumption and examines how the reinsurer's markup varies in response to changing risk exposure over the coverage period and how those changes affect the insurance company's minimal working capital scheme. Most notably, the varying reinsurer's markup lowers the insurance company's indifference premium at the expense of modestly increasing Strategy C's working-capital loss probability. Both premium and loss probability are substantially less than those for Strategy B. For this variable–reinsurer–markup environment, Section 6.1 describes how Strategy C can induce a profit when ![]() $m$ or more quakes occur during the first review interval that experiences quakes. Section 6.2 then shows how dividing reinsurance coverage on each active site into multiple policies affects premiums and loss probabilities. An active site denotes a site where no quake has occurred during the elapsed coverage period.
$m$ or more quakes occur during the first review interval that experiences quakes. Section 6.2 then shows how dividing reinsurance coverage on each active site into multiple policies affects premiums and loss probabilities. An active site denotes a site where no quake has occurred during the elapsed coverage period.
1.5. Basic model and notation
Suppose a quake occurs at a given site during a fixed coverage period of ![]() $T$ days with probability
$T$ days with probability ![]() $q$. For example,
$q$. For example, ![]() $T = 365$ implies one-year coverage with annual quake rate
$T = 365$ implies one-year coverage with annual quake rate ![]() $q$. The probability that
$q$. The probability that ![]() $j$ quakes occur among the
$j$ quakes occur among the ![]() $n$ sites during a year is
$n$ sites during a year is
![]() $j \in \{0,1,\ldots,n\}$, and the probability of
$j \in \{0,1,\ldots,n\}$, and the probability of ![]() $m$ or more quakes during a year is
$m$ or more quakes during a year is ![]() $1 - F(m-1; n, q)$, where
$1 - F(m-1; n, q)$, where
 $$F(m; n, q) = \sum_{j=0}^{m} f(j; n, q).$$
$$F(m; n, q) = \sum_{j=0}^{m} f(j; n, q).$$The following definitions are used throughout the paper:
 \begin{equation} \begin{aligned} \pi & := \text{premium per dollar of coverage for}\, T\, \text {days} \\ w_{{{\rm I}}} & := \text{insurance company's wealth at the beginning of the coverage period} \\ \theta & :=\text{total coverage in dollars} \\ \kappa(\pi) & :=\text{insurance company's final working capital at the} \\ & \qquad \text{end of the coverage period, given premium}\, \pi \\ & = w_{{{\rm I}}}+\theta\pi-\theta\times (\text{payout per coverage dollar}). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \pi & := \text{premium per dollar of coverage for}\, T\, \text {days} \\ w_{{{\rm I}}} & := \text{insurance company's wealth at the beginning of the coverage period} \\ \theta & :=\text{total coverage in dollars} \\ \kappa(\pi) & :=\text{insurance company's final working capital at the} \\ & \qquad \text{end of the coverage period, given premium}\, \pi \\ & = w_{{{\rm I}}}+\theta\pi-\theta\times (\text{payout per coverage dollar}). \end{aligned} \end{equation}2. Strategy B
Suppose a customer wants a one-year ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy for
$n$ policy for ![]() $\theta$ dollars of coverage, and an insurance company, embracing Strategy B, offers the policy for a premium of
$\theta$ dollars of coverage, and an insurance company, embracing Strategy B, offers the policy for a premium of ![]() $\pi$ per dollar of coverage. If fewer than
$\pi$ per dollar of coverage. If fewer than ![]() $m$ quakes occur during the coverage period, the insurance company pays out nothing with probability
$m$ quakes occur during the coverage period, the insurance company pays out nothing with probability ![]() $1-F(m-1;n,q)$. If
$1-F(m-1;n,q)$. If ![]() $m$ or more quakes occur, it pays out
$m$ or more quakes occur, it pays out ![]() $\theta$ dollars with probability
$\theta$ dollars with probability ![]() $F(m-1;n,q)$. As a consequence, the insurance company has final working capital
$F(m-1;n,q)$. As a consequence, the insurance company has final working capital
That is, it increases its wealth by ![]() $\theta \pi$ if fewer than
$\theta \pi$ if fewer than ![]() $m$ quakes occur, but incurs a
$m$ quakes occur, but incurs a ![]() $-\theta (1-\pi )$ loss in wealth if more than
$-\theta (1-\pi )$ loss in wealth if more than ![]() $m-1$ occur.
$m-1$ occur.
As one basis for comparing strategies, the study relies on ![]() $expected ~utility$ for determining the premiums per dollar of coverage under each strategy. For a given strategy, the insurance company wants to determine the minimal
$expected ~utility$ for determining the premiums per dollar of coverage under each strategy. For a given strategy, the insurance company wants to determine the minimal ![]() $\pi$ at which it is indifferent between offering and not offering the policy. Let
$\pi$ at which it is indifferent between offering and not offering the policy. Let ![]() $\{u(w),\ -\infty < w<\infty \}$ denote a concave increasing utility function in wealth
$\{u(w),\ -\infty < w<\infty \}$ denote a concave increasing utility function in wealth ![]() $w$. Then,
$w$. Then, ![]() $\pi ^{\ast }$ is the minimal
$\pi ^{\ast }$ is the minimal ![]() $\pi$ that solves
$\pi$ that solves
where the expectation is taken with respect to the (real-world) distribution of the random payout per unit coverage. For Strategy B, (2) becomes
 \begin{align} {{{\rm E}}}u(\kappa^{({{{\rm B}}})}(\pi))& = F(m-1;n,q)\times u(w_{{{\rm I}}} +\theta\pi)\nonumber\\ & \quad +[1-F(m-1;n,q)]\times u(w_{{{\rm I}}}+\theta(\pi-1))\nonumber\\ & = u(w_{{{\rm I}}}). \end{align}
\begin{align} {{{\rm E}}}u(\kappa^{({{{\rm B}}})}(\pi))& = F(m-1;n,q)\times u(w_{{{\rm I}}} +\theta\pi)\nonumber\\ & \quad +[1-F(m-1;n,q)]\times u(w_{{{\rm I}}}+\theta(\pi-1))\nonumber\\ & = u(w_{{{\rm I}}}). \end{align}As illustration, the utility function
leads (from (2)) to
Here, increasing ![]() $\alpha$ denotes increasing aversion to risk. Moreover, as
$\alpha$ denotes increasing aversion to risk. Moreover, as ![]() $\alpha \to 0$,
$\alpha \to 0$, ![]() $\pi \to {\rm E}\,(\text {payout per coverage dollar})$, that is, the standard net premium.
$\pi \to {\rm E}\,(\text {payout per coverage dollar})$, that is, the standard net premium.
It follows that the premium for Strategy B is
Strategy B responds to increased aversion to risk by increasing the premium, while the loss probability, ![]() $1 - F(m-1;n,q)$, remains constant. To facilitate comparison of the properties of Strategies B and C, all indifference premiums in this study are based on the exponential utility function (4). Use of the exponential utility function dramatically simplifies the analysis since the indifference premiums for both strategies do not depend on the initial wealth,
$1 - F(m-1;n,q)$, remains constant. To facilitate comparison of the properties of Strategies B and C, all indifference premiums in this study are based on the exponential utility function (4). Use of the exponential utility function dramatically simplifies the analysis since the indifference premiums for both strategies do not depend on the initial wealth, ![]() $w_{{{\rm I}}}$. Additional motivation comes from the property that with an exponential utility function the premium is closely related to the one determined by the Esscher premium principle, which may be thought of as an exponential tilting of the original distribution, in this case the binomial distribution. See Bühlmann [Reference Bühlmann7,Reference Bühlmann8]. Note that Strategy B has the property that its (random) payout is proportional to
$w_{{{\rm I}}}$. Additional motivation comes from the property that with an exponential utility function the premium is closely related to the one determined by the Esscher premium principle, which may be thought of as an exponential tilting of the original distribution, in this case the binomial distribution. See Bühlmann [Reference Bühlmann7,Reference Bühlmann8]. Note that Strategy B has the property that its (random) payout is proportional to ![]() $\theta$ and, as a result, the indifference premium
$\theta$ and, as a result, the indifference premium ![]() $\pi ^{\ast }_{{{\rm B}}}$ depends on
$\pi ^{\ast }_{{{\rm B}}}$ depends on ![]() $\alpha$ and
$\alpha$ and ![]() $\theta$ only through their product,
$\theta$ only through their product, ![]() $\alpha \theta$.
$\alpha \theta$.
3. Strategy C
Although an insurer's exposure to risk for an ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy varies as the policy's coverage period elapses, Strategy B commits the company to offer the policy based on perceived risk at the beginning of the coverage period. Strategy C overcomes that limitation by providing a means for the insurer to shed some or all this risk in a costless way as the coverage period elapses.
$n$ policy varies as the policy's coverage period elapses, Strategy B commits the company to offer the policy based on perceived risk at the beginning of the coverage period. Strategy C overcomes that limitation by providing a means for the insurer to shed some or all this risk in a costless way as the coverage period elapses.
During that period, any one of a multiplicity of quake histories may evolve. For expository convenience, assume that reviews occur daily. The following definitions are used throughout the rest of the paper:
 \begin{equation} \begin{aligned} T & := \text{coverage per period in days} \\ p & := \text{one-day quake probability at a given site}, \\ & \qquad \text{given annual probability} \,q \\ & = 1-(1-q)^{1/T} \\ t & := \text{remaining number of coverage days} \\ L & :=\text{the random first coverage day on which the number} \\ & \qquad \text{of active sites becomes less than}\, n-m \\ K_t & :=\text{the random number of active sites at} \\ & \qquad \text{the beginning of remaining day} \, t \\ J_t & :=\text{the random number of sites that} \\ & \qquad \text{have quakes on remaining day} \, t \\ & = K_t-K_{t-1}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} T & := \text{coverage per period in days} \\ p & := \text{one-day quake probability at a given site}, \\ & \qquad \text{given annual probability} \,q \\ & = 1-(1-q)^{1/T} \\ t & := \text{remaining number of coverage days} \\ L & :=\text{the random first coverage day on which the number} \\ & \qquad \text{of active sites becomes less than}\, n-m \\ K_t & :=\text{the random number of active sites at} \\ & \qquad \text{the beginning of remaining day} \, t \\ J_t & :=\text{the random number of sites that} \\ & \qquad \text{have quakes on remaining day} \, t \\ & = K_t-K_{t-1}. \end{aligned} \end{equation}Strategy C gains its advantage by focussing most attention on a particular subset of quake histories, namely those for which:
 \begin{equation} \begin{array}{c} {\rm either}\\ {\rm a.}\ \text{Fewer than} \,m \, \text{quakes occur during the coverage period} \\ \text{and no more than one quake occurs on each quake day;} \\ {\rm or}\\ {\rm b.}\ \text{More than} \, m-1 \, \text{quakes occur during the coverage period} \\ \text{but no more than one quake occurs on each of the first } \\ \quad m-1 \, \text{quake days.} \end{array} \end{equation}
\begin{equation} \begin{array}{c} {\rm either}\\ {\rm a.}\ \text{Fewer than} \,m \, \text{quakes occur during the coverage period} \\ \text{and no more than one quake occurs on each quake day;} \\ {\rm or}\\ {\rm b.}\ \text{More than} \, m-1 \, \text{quakes occur during the coverage period} \\ \text{but no more than one quake occurs on each of the first } \\ \quad m-1 \, \text{quake days.} \end{array} \end{equation}Hereafter, we refer to this property as Condition (7).
Strategy C first divides the coverage period into smaller intervals of equal size. For illustration, we take the interval as one day. Later, Section 5 describes how longer and shorter intervals affect final working capital. Then,
• For each remaining day of coverage,
 $t$, with
$t$, with  $k$ sites remaining active (i.e., having had no quake so far), Schedule C provides a schedule for purchasing one-day coverage in a daily reinsurance market with given daily markup per dollar of coverage,
$k$ sites remaining active (i.e., having had no quake so far), Schedule C provides a schedule for purchasing one-day coverage in a daily reinsurance market with given daily markup per dollar of coverage,  $g$, that remains constant for the entire coverage period. Later, Section 6 extends the study to a reinsurer's markup that varies on successive review intervals.
$g$, that remains constant for the entire coverage period. Later, Section 6 extends the study to a reinsurer's markup that varies on successive review intervals.• If the quake history satisfies Condition (7) during the coverage period, the schedule provides the minimal premium per dollar of coverage to charge a customer at the beginning of the coverage period that for a premium,
 $\pi$, no less than this minimal premium, guarantees w.p.1 that final working capital,
$\pi$, no less than this minimal premium, guarantees w.p.1 that final working capital,  $\kappa ^{({{{\rm C}}})}(\pi )$, is no less than initial wealth
$\kappa ^{({{{\rm C}}})}(\pi )$, is no less than initial wealth  $w_{{{\rm I}}}$.
$w_{{{\rm I}}}$.
That is, whenever either a or b in Condition (7) holds, this ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy is self-financing, regardless of how many quakes actually occurred during the coverage period.
$n$ policy is self-financing, regardless of how many quakes actually occurred during the coverage period.
The ability to shed risk in this way clearly depends on how probable is a quake history satisfying Condition (7) during a coverage period. As illustration, suppose at least one quake occurs at a given site during a year with probability ![]() $q=0.1$ with corresponding daily quake probability
$q=0.1$ with corresponding daily quake probability ![]() $p=2.886\times 10 ^{-4}$ (see (6)). Consider an
$p=2.886\times 10 ^{-4}$ (see (6)). Consider an ![]() $(m,n)=(2,5)$ one-year policy. Because the probability of daily satisfying Condition (7) for one year is
$(m,n)=(2,5)$ one-year policy. Because the probability of daily satisfying Condition (7) for one year is ![]() $1- 2.364\times 10^{-4}$ (see Table 1), Strategy C incurs a loss with probability no greater than
$1- 2.364\times 10^{-4}$ (see Table 1), Strategy C incurs a loss with probability no greater than ![]() $2.364\times 10^{-4}$. In contrast, Strategy B would incur a loss with probability 0.0815. Therefore, an insurance company using Strategy C incurs a loss with considerably less probability than with Strategy B, thus establishing the efficacy of Strategy C.
$2.364\times 10^{-4}$. In contrast, Strategy B would incur a loss with probability 0.0815. Therefore, an insurance company using Strategy C incurs a loss with considerably less probability than with Strategy B, thus establishing the efficacy of Strategy C.
Table 1. Loss probability for ![]() $m=2$ (
$m=2$ (![]() $\theta =1$,
$\theta =1$, ![]() $T=365$,
$T=365$, ![]() $\pi '\in (0,1)$,
$\pi '\in (0,1)$, ![]() $\pi \geq v_{Tn}$).
$\pi \geq v_{Tn}$).

3.1. Schedule
Shedding risk in this way depends crucially on the amount of coverage scheduled for purchase on each of the active sites on each coverage day. To make these purchases, the insurer needs to have working capital. In particular, the schedule derives the minimal working capital needed on each day to guarantee no loss w.p.1. if Condition (7) is satisfied. This section derives the schedule that satisfies that requirement and determines the minimal annual premium per dollar charged at the beginning of the coverage that makes that minimal working capital sequence feasible.
Let ![]() $t$ denote the number of remaining days of coverage and
$t$ denote the number of remaining days of coverage and ![]() $k$, the number of sites that remain active. Suppose Condition (7) is satisfied. Let
$k$, the number of sites that remain active. Suppose Condition (7) is satisfied. Let ![]() $w_{{{\rm I}}}+v_{tk}$ denote the minimal working capital in state
$w_{{{\rm I}}}+v_{tk}$ denote the minimal working capital in state ![]() $(t,k)$ that guarantees that working capital on the final coverage day,
$(t,k)$ that guarantees that working capital on the final coverage day, ![]() $\min (L,T)$, is no less than
$\min (L,T)$, is no less than ![]() $w_{{{\rm I}}}$. For coverage
$w_{{{\rm I}}}$. For coverage ![]() $\theta$, this ending condition determines the boundary values for the bivariate function
$\theta$, this ending condition determines the boundary values for the bivariate function ![]() $\{v_{tk}\}$ as:
$\{v_{tk}\}$ as:
Consider a particular state ![]() $(t,k)$,
$(t,k)$, ![]() $t \in \{1,\ldots,T\}$,
$t \in \{1,\ldots,T\}$, ![]() $k \in \{n-m+1,\ldots,n\}$, and suppose we already know the values
$k \in \{n-m+1,\ldots,n\}$, and suppose we already know the values ![]() $v_{t-1,i}$ for all
$v_{t-1,i}$ for all ![]() $i \in \{0,1,\ldots,k\}$.
$i \in \{0,1,\ldots,k\}$.
Let ![]() $x$ denote the amount of reinsurance to purchase on each active site and
$x$ denote the amount of reinsurance to purchase on each active site and ![]() $y$ denote the amount of cash held in reserve in state
$y$ denote the amount of cash held in reserve in state ![]() $(t,k)$. If
$(t,k)$. If ![]() $j$ sites have quakes, then working capital available at the end of the day is
$j$ sites have quakes, then working capital available at the end of the day is ![]() $w_{{{\rm I}}}+j x + y$ for
$w_{{{\rm I}}}+j x + y$ for ![]() $j \in \{0,1,\ldots,k\}$. To satisfy the criterion that
$j \in \{0,1,\ldots,k\}$. To satisfy the criterion that ![]() $v_{tk}$ is the minimal working capital at remaining time
$v_{tk}$ is the minimal working capital at remaining time ![]() $t$ that guarantees that the working capital at remaining time 0 is no less than
$t$ that guarantees that the working capital at remaining time 0 is no less than ![]() $w_{{{\rm I}}}$, no matter what the value of
$w_{{{\rm I}}}$, no matter what the value of ![]() $j$, we must have
$j$, we must have
 \begin{equation} \begin{aligned} v_{tk} & = \min_{x,y} \{ k g p x + y \} \\ \text{s.t. } j x + y & \geq v_{t-1,n-m+1-j} \quad j \geq 0. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} v_{tk} & = \min_{x,y} \{ k g p x + y \} \\ \text{s.t. } j x + y & \geq v_{t-1,n-m+1-j} \quad j \geq 0. \end{aligned} \end{equation} Suppose either Condition (7a) or (7b) holds. First, consider the case ![]() $k \geq n-m+2$. Condition (7a) implies that at most one of the
$k \geq n-m+2$. Condition (7a) implies that at most one of the ![]() $k$ active sites has a quake at remaining time
$k$ active sites has a quake at remaining time ![]() $t$. Thus, the constrained minimization (9) defining
$t$. Thus, the constrained minimization (9) defining ![]() $v_{tk}$ reduces to
$v_{tk}$ reduces to
 \begin{equation} \begin{aligned} v_{tk} & = \min_{x,y} \{ k g p x + y \} \\ \text{s.t. } x + y & \geq v_{t-1,k-1} \\ y & \geq v_{t-1,k}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} v_{tk} & = \min_{x,y} \{ k g p x + y \} \\ \text{s.t. } x + y & \geq v_{t-1,k-1} \\ y & \geq v_{t-1,k}. \end{aligned} \end{equation}The solutions are
To fund the policies with face value ![]() $x$ on each of the
$x$ on each of the ![]() $k$ active sites, we must pay a total premium of
$k$ active sites, we must pay a total premium of ![]() $k \times g \times p\times x$. It follows that the minimal working capital needed in state
$k \times g \times p\times x$. It follows that the minimal working capital needed in state ![]() $(t,k)$ is given by
$(t,k)$ is given by
for all ![]() $k \in \{n-m+2,\ldots,n\}$.
$k \in \{n-m+2,\ldots,n\}$.
Now consider the case ![]() $k = n-m+1$. Condition (7b) allows the number of quakes at remaining time
$k = n-m+1$. Condition (7b) allows the number of quakes at remaining time ![]() $t$ to be any value
$t$ to be any value ![]() $j \in \{0,1,\ldots,n-m+1\}$. But because
$j \in \{0,1,\ldots,n-m+1\}$. But because ![]() $v_{t-1,n-m+1-j} = 1$ for
$v_{t-1,n-m+1-j} = 1$ for ![]() $j \geq 1$, the constrained minimization problem is again equivalent to (10), the solution to which is again given by (12), now with
$j \geq 1$, the constrained minimization problem is again equivalent to (10), the solution to which is again given by (12), now with ![]() $k=n-m+1$. It follows that the total working capital needed in state
$k=n-m+1$. It follows that the total working capital needed in state ![]() $(t,k)$ equals
$(t,k)$ equals ![]() $w_{{{\rm I}}} + v_{tk}$, where
$w_{{{\rm I}}} + v_{tk}$, where ![]() $v_{tk}$ is given by (12) for all
$v_{tk}$ is given by (12) for all ![]() $k \in \{n-m+1,\ldots,n\}$.
$k \in \{n-m+1,\ldots,n\}$.
Starting from the boundary equations (8) and using the backward recursion (12) for ![]() $k \in \{n-m+1,n\}$, for
$k \in \{n-m+1,n\}$, for ![]() $t \in \{1,\ldots,T\}$, we can calculate all values of the function,
$t \in \{1,\ldots,T\}$, we can calculate all values of the function, ![]() $\{v_{tk}\}$, and in particular,
$\{v_{tk}\}$, and in particular, ![]() $v_{Tn}$, the minimal premium that guarantees that final working capital is not less than
$v_{Tn}$, the minimal premium that guarantees that final working capital is not less than ![]() $w_{{{\rm I}}}$ when following Strategy C, provided that Condition (7) holds.
$w_{{{\rm I}}}$ when following Strategy C, provided that Condition (7) holds.
The minimal capital array ![]() $\{v_{tk}\}$, together with the rule for purchasing daily reinsurance, makes it possible to characterize working capital for any quake history, regardless of whether or not Condition (7) is satisfied. Let
$\{v_{tk}\}$, together with the rule for purchasing daily reinsurance, makes it possible to characterize working capital for any quake history, regardless of whether or not Condition (7) is satisfied. Let ![]() $K_t$ denote the random number of active sites at the beginning of
$K_t$ denote the random number of active sites at the beginning of ![]() $t$ during the coverage period. Then, for an initial premium per coverage dollar,
$t$ during the coverage period. Then, for an initial premium per coverage dollar, ![]() $\pi$, Strategy C induces final working capital
$\pi$, Strategy C induces final working capital
 \begin{equation} \kappa^{({{{\rm C}}})}(\pi)= w_{{{\rm I}}}+\pi+\sum_{s=T}^{\max(0,T-L)}[(K_s-K_{s-1}-gpK_s)(v_{s-1,K_s-1}-v_{s-1,K_s})- \theta I_{K_{s-1}\leq n-m}], \end{equation}
\begin{equation} \kappa^{({{{\rm C}}})}(\pi)= w_{{{\rm I}}}+\pi+\sum_{s=T}^{\max(0,T-L)}[(K_s-K_{s-1}-gpK_s)(v_{s-1,K_s-1}-v_{s-1,K_s})- \theta I_{K_{s-1}\leq n-m}], \end{equation}where
and
Most notably, ![]() $\kappa ^{({{{\rm C}}})}(\pi )>w_{{{\rm I}}}$ implies that the insurance company makes a profit on the
$\kappa ^{({{{\rm C}}})}(\pi )>w_{{{\rm I}}}$ implies that the insurance company makes a profit on the ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy whereas
$n$ policy whereas ![]() $\kappa ^{({{{\rm C}}})}(\pi )< w_{{{\rm I}}}$ implies a loss. Proposition 3.1 formally shows that Condition (7) is sufficient for Strategy C to be self-financing.
$\kappa ^{({{{\rm C}}})}(\pi )< w_{{{\rm I}}}$ implies a loss. Proposition 3.1 formally shows that Condition (7) is sufficient for Strategy C to be self-financing.
Proposition 3.1 Suppose an insurance company adopts Strategy C and offers a customer an ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy for a premium per dollar of coverage,
$n$ policy for a premium per dollar of coverage, ![]() $\pi$, no less than
$\pi$, no less than ![]() $v_{Tn}$. Then,
$v_{Tn}$. Then,
i. If no quakes occur, then
 $\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1.
$\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1.ii. If no more than one quake occurs on any coverage day, then
 $\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1.
$\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1.iii. If a single quake occurs on each of the first
 $m-1$ quake days, then
$m-1$ quake days, then  $\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1 regardless of how many quakes occur on a subsequent, remaining coverage day.
$\kappa ^{({{{\rm C}}})}(\pi )\geq w_{{{\rm I}}}$ w.p.1 regardless of how many quakes occur on a subsequent, remaining coverage day.
The derivation of ![]() $\{v_{tk}\}$ by backward recursion implicitly proves the proposition by induction. Appendix A provides an alternative algebraic proof. That proof reveals that for a quake history
$\{v_{tk}\}$ by backward recursion implicitly proves the proposition by induction. Appendix A provides an alternative algebraic proof. That proof reveals that for a quake history ![]() $(\underbrace {1,\ldots,1}_{m-1{\text { ones}}},r)$ (Condition (7b)) with
$(\underbrace {1,\ldots,1}_{m-1{\text { ones}}},r)$ (Condition (7b)) with ![]() $r>1$ and ending on coverage day
$r>1$ and ending on coverage day ![]() $s$ (part iii), final working capital is
$s$ (part iii), final working capital is
implying a net profit that increases with ![]() $r$.
$r$.
One particular property of ![]() $\{v_{tk}\}$ facilitates later analysis. Appendix A contains the proof.
$\{v_{tk}\}$ facilitates later analysis. Appendix A contains the proof.
Proposition 3.2 For the schedule ![]() $\{v_{tk}\}$ determined by (12) with boundary conditions (8),
$\{v_{tk}\}$ determined by (12) with boundary conditions (8), ![]() $v_{tk}$ is non-increasing in
$v_{tk}$ is non-increasing in ![]() $k$ for all
$k$ for all ![]() $k\in \{n-m+1,\ldots,n\}$ for each
$k\in \{n-m+1,\ldots,n\}$ for each ![]() $t\in \{1,\ldots,T\}$.
$t\in \{1,\ldots,T\}$.
Remark As noted in the Introduction, the event, ![]() $m$-out-of-
$m$-out-of-![]() $n$ sites have quakes, is a contingent claim. This property suggests using dynamic pricing techniques such as those used to price derivatives in financial markets.
$n$ sites have quakes, is a contingent claim. This property suggests using dynamic pricing techniques such as those used to price derivatives in financial markets.
Derivative pricing theory following Black and Scholes [Reference Black and Scholes5] assumes a complete market in which arbitrage is not possible and uses dynamic hedging, while modeling fluctuations in the stock's price as geometric Brownian motion in continuous time or as a Bernoulli process in discrete time. However, pricing an ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy does not allow an analogous protocol unless one imposes similar restrictions. In a model with discrete review points such as the model in this paper, these restrictions would include no arbitrage and at most one quake in each review period, in effect requiring that Condition (7) hold for all quake histories.
$n$ policy does not allow an analogous protocol unless one imposes similar restrictions. In a model with discrete review points such as the model in this paper, these restrictions would include no arbitrage and at most one quake in each review period, in effect requiring that Condition (7) hold for all quake histories.
Although making these assumptions would be tempting from a theoretical vantage point, the present paper offers a more realistic, nuanced model which allows multiple quakes during a review period. As the quake history evolves during the coverage period, Strategy C exploits the rarity of multiple-quake review periods in the procedures for pricing the ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy and for setting reinsurance coverage levels at each review point. The resulting coverage schedule and policy price reduce the insurance company's loss probability to a level substantially lower than under Strategy B, a beneficial property that follows from the fact that the
$n$ policy and for setting reinsurance coverage levels at each review point. The resulting coverage schedule and policy price reduce the insurance company's loss probability to a level substantially lower than under Strategy B, a beneficial property that follows from the fact that the ![]() $m$-out-of-
$m$-out-of-![]() $n$ event almost satisfies the conditions for eliminating risk by dynamic hedging. As a result, Strategy C removes most, but not all, the risk for the insurance company, as the analyses in the next and following sections show.
$n$ event almost satisfies the conditions for eliminating risk by dynamic hedging. As a result, Strategy C removes most, but not all, the risk for the insurance company, as the analyses in the next and following sections show.
3.2. Bounding loss probability
Because Strategy C applies schedule ![]() $\{v_{tk}\}$ to purchase daily reinsurance coverage regardless of whether or not Condition (7) is satisfied, the insurer may have to ante up cash from his initial wealth to pay for this reinsurance and possibly for a customer payout during the coverage period. This possibility implies that for
$\{v_{tk}\}$ to purchase daily reinsurance coverage regardless of whether or not Condition (7) is satisfied, the insurer may have to ante up cash from his initial wealth to pay for this reinsurance and possibly for a customer payout during the coverage period. This possibility implies that for ![]() $\pi \geq v_{Tn}$
$\pi \geq v_{Tn}$
This section determines this upper bound as a function of ![]() $m,~n$, and
$m,~n$, and ![]() $p$, with equality when
$p$, with equality when ![]() $\pi =v_{Tn}$.
$\pi =v_{Tn}$.
For ![]() $j_i\in \{1,\ldots,n\}\text { for }i=1,\ldots,n \text { s.t. } j_1+\cdots +j_{l-1}< m\text { and } j_1+\cdots +j_{l}\geq m$, let
$j_i\in \{1,\ldots,n\}\text { for }i=1,\ldots,n \text { s.t. } j_1+\cdots +j_{l-1}< m\text { and } j_1+\cdots +j_{l}\geq m$, let
 \begin{equation} \begin{aligned} P_n(j_1,\ldots,j_l) & = \left(\begin{array}{c} \text{probability that} \, j_1 \, \text{quakes occur on} \\ \text{the first quake day},\ j_2 \,\text{on the second} \\ \text{quake day,} \ldots, \, j_l \, \text{on the}\, l \text{th quake day} \end{array}\right)\\ P_n(j_1\geq m) & = \sum_{j_1=m}^{n} P_n(j_1) \\ P_n(j_1,j_2\geq r) & = \sum_{j_2=r}^{n-j_1}P_n(j_1,j_2),\quad r\in \{1,\ldots, n-j_1\},\ j_1\in\{1,\ldots, m-1\}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} P_n(j_1,\ldots,j_l) & = \left(\begin{array}{c} \text{probability that} \, j_1 \, \text{quakes occur on} \\ \text{the first quake day},\ j_2 \,\text{on the second} \\ \text{quake day,} \ldots, \, j_l \, \text{on the}\, l \text{th quake day} \end{array}\right)\\ P_n(j_1\geq m) & = \sum_{j_1=m}^{n} P_n(j_1) \\ P_n(j_1,j_2\geq r) & = \sum_{j_2=r}^{n-j_1}P_n(j_1,j_2),\quad r\in \{1,\ldots, n-j_1\},\ j_1\in\{1,\ldots, m-1\}. \end{aligned} \end{equation} We first consider scenarios with ![]() $m=2\leq n$. During a
$m=2\leq n$. During a ![]() $T$-day coverage period, one of several different events occurs: No quakes (0), one quake (1), two or more quakes on the same day
$T$-day coverage period, one of several different events occurs: No quakes (0), one quake (1), two or more quakes on the same day ![]() $(j_1\geq 2)$, two quakes on different days (1,1), and one quake on the first quake day and two or more on a second day
$(j_1\geq 2)$, two quakes on different days (1,1), and one quake on the first quake day and two or more on a second day ![]() $(1,j_2\geq 2)$ exhaust the list. These events occur with probabilities
$(1,j_2\geq 2)$ exhaust the list. These events occur with probabilities
 \begin{equation} \begin{aligned} P_n(0) & = (1-q)^{n} \\ P_n(1) & = nq(1-q)^{n-1} \\ P_n(j_1\geq 2) & = \frac{1-(1-p)^{nT}}{1-(1-p)^{n}}[1- (1-p)^{n}-np(1-p)^{n-1}] \\ P_n(1,1) & = \frac{f(1;n,p)f(1;n-1,p)}{p}(1-p)^{(n-2)(T-1)} \\ & \quad \times\left\{\frac{1-(1-p)^{2T}}{1-(1-p)^{2}} -\frac{(1-p)^{T-1}[1-(1-p)^{T}]}{p}\right\}\\ P_n(1,j_2\geq 2) & = f(1;n,p)[1-f(0;n-1,p)-f(1;n-1,p)] \\ & \quad \times \sum_{s=1}^{T-1}(1-p)^{n(s-1)}\left[\frac{1-(1-p)^{(n-1)(T-s)}}{1-(1-p)^{n-1}}\right], \end{aligned}\end{equation}
\begin{equation} \begin{aligned} P_n(0) & = (1-q)^{n} \\ P_n(1) & = nq(1-q)^{n-1} \\ P_n(j_1\geq 2) & = \frac{1-(1-p)^{nT}}{1-(1-p)^{n}}[1- (1-p)^{n}-np(1-p)^{n-1}] \\ P_n(1,1) & = \frac{f(1;n,p)f(1;n-1,p)}{p}(1-p)^{(n-2)(T-1)} \\ & \quad \times\left\{\frac{1-(1-p)^{2T}}{1-(1-p)^{2}} -\frac{(1-p)^{T-1}[1-(1-p)^{T}]}{p}\right\}\\ P_n(1,j_2\geq 2) & = f(1;n,p)[1-f(0;n-1,p)-f(1;n-1,p)] \\ & \quad \times \sum_{s=1}^{T-1}(1-p)^{n(s-1)}\left[\frac{1-(1-p)^{(n-1)(T-s)}}{1-(1-p)^{n-1}}\right], \end{aligned}\end{equation}so that
Moreover,
Then, for any premiums ![]() $\pi \geq v_{Tn}$ and
$\pi \geq v_{Tn}$ and ![]() $\pi '\in (0,1)$,
$\pi '\in (0,1)$,
 \begin{equation} \begin{aligned} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi)< w_{{{\rm I}}}] & \leq 1-{{{\rm pr}}}[\text{Condition (7)}] \\ & = P_n(j_1\geq 2) \\ & \leq{{{\rm pr}}}[\kappa^{({{{\rm B}}})}(\pi')< w_{{{\rm I}}}]=1-(1-q)^{n}-nq(1-q)^{n-1}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi)< w_{{{\rm I}}}] & \leq 1-{{{\rm pr}}}[\text{Condition (7)}] \\ & = P_n(j_1\geq 2) \\ & \leq{{{\rm pr}}}[\kappa^{({{{\rm B}}})}(\pi')< w_{{{\rm I}}}]=1-(1-q)^{n}-nq(1-q)^{n-1}. \end{aligned} \end{equation} Table 1 (at the beginning of this section) shows the substantial reduction in loss probability that Strategy C induces for ![]() $m=2$ and
$m=2$ and ![]() $\theta =1$.
$\theta =1$.
More generally, for ![]() $2\leq m\leq n$, Strategy C with premium
$2\leq m\leq n$, Strategy C with premium ![]() $\pi \geq v_{Tn}$ has loss probability
$\pi \geq v_{Tn}$ has loss probability ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(v_{Tn})< w_{{{\rm I}}}]\leq \beta _{mn}$, where
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(v_{Tn})< w_{{{\rm I}}}]\leq \beta _{mn}$, where
 \begin{align} \beta_{mn}& := 1-{{{\rm pr}}}[\text{Condition (7) }] \nonumber\\ & = 1-P_n(0)-\sum_{l=1}^{m-1}P_n(\underbrace{1,\ldots,1}_{l\text{ ones}}) -\sum_{r=1}^{n-m+1}P_n(\underbrace{1,\ldots,1}_{m-1\text{ ones}},r), \end{align}
\begin{align} \beta_{mn}& := 1-{{{\rm pr}}}[\text{Condition (7) }] \nonumber\\ & = 1-P_n(0)-\sum_{l=1}^{m-1}P_n(\underbrace{1,\ldots,1}_{l\text{ ones}}) -\sum_{r=1}^{n-m+1}P_n(\underbrace{1,\ldots,1}_{m-1\text{ ones}},r), \end{align}where for ![]() $1\leq l\leq m$,
$1\leq l\leq m$, ![]() $i\in \{1,\ldots,l\}$,
$i\in \{1,\ldots,l\}$, ![]() $j_i\geq 1$,
$j_i\geq 1$, ![]() $j_1+\cdots +j_{l-1}< m$,
$j_1+\cdots +j_{l-1}< m$, ![]() $k_0=n$, and
$k_0=n$, and ![]() $k_i=k_{i-1}-j_i$,
$k_i=k_{i-1}-j_i$,
 \begin{align} & P_n(j_1,\ldots,j_l)= \prod_{i=1}^{l}f(j_i;k_{i-1},p) \nonumber\\ & \qquad \times \sum_{1\leq s_1< s_2<\cdots< s_l\leq T} \left[(1-p)^{\sum_{i=1}^{l}{k_{i-1}(s_i-s_{i-1}-1)} }\right] \times \left\{\begin{array}{ll} (1-p)^{k_l(T-s_l)}, & \text{if } k_l>n-m \\ 1, & \text{otherwise} \end{array}\right. \nonumber\\ & \quad= \left[\prod_{i=1}^{l}f(j_i;k_{i-1},p)\right]\times (1-p)^{-\sum_{i=1}^{l}k_{i-1}} \times\sum_{s_l=l}^{T} \underbrace{\left[\sum_{1\leq s_1<\cdots< s_{l-1}\leq s_l}(1-p)^{\sum_{i=1}^{l-1}j_is_i} \rho(s_l)\right],}_{\omega_{1}(s_l)} \end{align}
\begin{align} & P_n(j_1,\ldots,j_l)= \prod_{i=1}^{l}f(j_i;k_{i-1},p) \nonumber\\ & \qquad \times \sum_{1\leq s_1< s_2<\cdots< s_l\leq T} \left[(1-p)^{\sum_{i=1}^{l}{k_{i-1}(s_i-s_{i-1}-1)} }\right] \times \left\{\begin{array}{ll} (1-p)^{k_l(T-s_l)}, & \text{if } k_l>n-m \\ 1, & \text{otherwise} \end{array}\right. \nonumber\\ & \quad= \left[\prod_{i=1}^{l}f(j_i;k_{i-1},p)\right]\times (1-p)^{-\sum_{i=1}^{l}k_{i-1}} \times\sum_{s_l=l}^{T} \underbrace{\left[\sum_{1\leq s_1<\cdots< s_{l-1}\leq s_l}(1-p)^{\sum_{i=1}^{l-1}j_is_i} \rho(s_l)\right],}_{\omega_{1}(s_l)} \end{align}where
and
 \begin{equation} \omega_{i}(x)= \left\{\begin{array}{lll} \rho(x), & i=l, \\ \displaystyle (1-p)^{j_ix}\sum_{y=x}^{T} \omega_{i+1}(y), & i\in\{l-1,\ldots,1\}, \end{array}\right.\quad x\in\{i,\ldots,T-l+i\}. \end{equation}
\begin{equation} \omega_{i}(x)= \left\{\begin{array}{lll} \rho(x), & i=l, \\ \displaystyle (1-p)^{j_ix}\sum_{y=x}^{T} \omega_{i+1}(y), & i\in\{l-1,\ldots,1\}, \end{array}\right.\quad x\in\{i,\ldots,T-l+i\}. \end{equation} The ![]() $(m,n,q)$ scenarios in Table 2 reveal that Condition (7) induces
$(m,n,q)$ scenarios in Table 2 reveal that Condition (7) induces ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi )< w_{{{\rm I}}}]>\beta _{mn}\geq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ')< w_{{{\rm I}}}]$ for
${{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi )< w_{{{\rm I}}}]>\beta _{mn}\geq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ')< w_{{{\rm I}}}]$ for ![]() $m$ small relative to
$m$ small relative to ![]() $n$. However, Strategy C offers an additional benefit. The next section and later Section 6.1 reveal that it can further reduce loss probability for quake histories
$n$. However, Strategy C offers an additional benefit. The next section and later Section 6.1 reveal that it can further reduce loss probability for quake histories ![]() $(j_1,\ldots,j_{l+1})=(\underbrace {1,\ldots,1}_{{l< m-1\text { ones}}},r)$ for some
$(j_1,\ldots,j_{l+1})=(\underbrace {1,\ldots,1}_{{l< m-1\text { ones}}},r)$ for some ![]() $r +l\geq n-m$.
$r +l\geq n-m$.
Table 2. Loss probability for ![]() $n=5$ and
$n=5$ and ![]() $10\ (\theta =1$,
$10\ (\theta =1$, ![]() $T=365$,
$T=365$, ![]() $\pi '\in (0,1)$,
$\pi '\in (0,1)$, ![]() $\pi \geq v_{T,n}$).
$\pi \geq v_{T,n}$).

3.3. An additional benefit
Whereas Strategy B incurs a loss of ![]() $-(1-\pi ^{\ast }_{{{\rm B}}}$) for any quake history with
$-(1-\pi ^{\ast }_{{{\rm B}}}$) for any quake history with ![]() $m$ or more quakes during the coverage period, for some of these quake histories Strategy C may have positive probability of producing a profit. Recall that Proposition 3.1(iii) exemplifies this for a history in which a single quake occurs on each of the first
$m$ or more quakes during the coverage period, for some of these quake histories Strategy C may have positive probability of producing a profit. Recall that Proposition 3.1(iii) exemplifies this for a history in which a single quake occurs on each of the first ![]() $m-1$ quakes regardless of how many quakes occur on a subsequent quake day. A similar result holds if one quake occurs on each of the first
$m-1$ quakes regardless of how many quakes occur on a subsequent quake day. A similar result holds if one quake occurs on each of the first ![]() $l\ (< m-1)$ quake days followed by
$l\ (< m-1)$ quake days followed by ![]() $j\ (\geq m-l)$ quakes on the
$j\ (\geq m-l)$ quakes on the ![]() $(l+1)$st quake day. Assume
$(l+1)$st quake day. Assume ![]() $\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ and recall that
$\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ and recall that ![]() $\pi ^{\ast }_{{{\rm C}}}- v_{Tn}+v_{t,k}$ denotes working capital on remaining day
$\pi ^{\ast }_{{{\rm C}}}- v_{Tn}+v_{t,k}$ denotes working capital on remaining day ![]() $t$ with
$t$ with ![]() $k$ active sites. If
$k$ active sites. If ![]() $j\ (\geq m-l)$ quakes occur on the
$j\ (\geq m-l)$ quakes occur on the ![]() $(l+1)$st quake day, then coverage ends on remaining day
$(l+1)$st quake day, then coverage ends on remaining day ![]() $t$ and, after pay out, final working capital is
$t$ and, after pay out, final working capital is
 \begin{align} \kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})& =w_{{{\rm I}}} +\pi^{{\ast}}_{{{\rm C}}} -v_{Tn}+v_{t,n-l}+j(v_{t-1,n-l-1}-v_{t-1,n-l}) \nonumber\\ & \quad -(n-l)gp(v_{t-1,n-l-1}-v_{t-1,n-l})-1. \end{align}
\begin{align} \kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})& =w_{{{\rm I}}} +\pi^{{\ast}}_{{{\rm C}}} -v_{Tn}+v_{t,n-l}+j(v_{t-1,n-l-1}-v_{t-1,n-l}) \nonumber\\ & \quad -(n-l)gp(v_{t-1,n-l-1}-v_{t-1,n-l})-1. \end{align} Because ![]() $v_{t,n-l}=(n-l)gp(v_{t-1,n-l-1}-v_{t-1,n-l})+v_{t-1,n-l}$ (see Section 3.1), the insurance company realizes a profit (i.e.,
$v_{t,n-l}=(n-l)gp(v_{t-1,n-l-1}-v_{t-1,n-l})+v_{t-1,n-l}$ (see Section 3.1), the insurance company realizes a profit (i.e., ![]() $\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}$) if
$\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}$) if
Consider the events
 \begin{align} {{{\mathcal{E}}}}_{jl} & = \left(\begin{array}{c} \text{one quake occurs on each of the} \\ \text{first}\, l \, \text{quake days followed by}\, j \\ \text{quakes on the}\, (l+1) \text{st quake day} \end{array}\right) \nonumber\\ & = (\underbrace{1,\ldots,1}_{l\text{ ones}},j) \end{align}
\begin{align} {{{\mathcal{E}}}}_{jl} & = \left(\begin{array}{c} \text{one quake occurs on each of the} \\ \text{first}\, l \, \text{quake days followed by}\, j \\ \text{quakes on the}\, (l+1) \text{st quake day} \end{array}\right) \nonumber\\ & = (\underbrace{1,\ldots,1}_{l\text{ ones}},j) \end{align}and
for ![]() $j\in \{m-l,\ldots,n-l\}$,
$j\in \{m-l,\ldots,n-l\}$, ![]() $s\in \{l+1,\ldots,T\}$, and
$s\in \{l+1,\ldots,T\}$, and ![]() $l\in \{0,1,\ldots, m-1\}$. If
$l\in \{0,1,\ldots, m-1\}$. If ![]() $l=m-1$ on remaining day
$l=m-1$ on remaining day ![]() $t$, then
$t$, then ![]() $B_{T-t+1}={(1-\pi ^{\ast }_{{{\rm C}}}+v_{Tn}-v_{t-1,n-m+1})}/{(1-v_{t-1,n-m+1})}\leq 1$ so that (22) is satisfied w.p.1 (as per Proposition 3.1(iii)). However, for
$B_{T-t+1}={(1-\pi ^{\ast }_{{{\rm C}}}+v_{Tn}-v_{t-1,n-m+1})}/{(1-v_{t-1,n-m+1})}\leq 1$ so that (22) is satisfied w.p.1 (as per Proposition 3.1(iii)). However, for ![]() $l\leq m-2$,
$l\leq m-2$, ![]() $v_{t-1,n-l-1}<1$, so that
$v_{t-1,n-l-1}<1$, so that ![]() $B_{T-t+1}$ may exceed 1. Therefore, for
$B_{T-t+1}$ may exceed 1. Therefore, for ![]() $l\leq m-2$
$l\leq m-2$
where
This result implies the tighter bound on loss probability
 $${{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta_{mn}-\sum_{l=0}^{m-2}\sum_{j=m-l}^{n-l}\sum_{s\in{{{\mathcal{T}}}}_{jl}}{{{\rm pr}}}({{{\mathcal{E}}}}_{jls}),$$
$${{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta_{mn}-\sum_{l=0}^{m-2}\sum_{j=m-l}^{n-l}\sum_{s\in{{{\mathcal{T}}}}_{jl}}{{{\rm pr}}}({{{\mathcal{E}}}}_{jls}),$$where (see (19))
Moreover, it implies a profit with probability
 $${{{\rm pr}}}\left[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})> w_{{{\rm I}}},\bigcup_{j=m-l}^{n-l}{{{\mathcal{E}}}}_{jl}\right] =\sum_{l=0}^{m-2}\sum_{j=m-l}^{n-l}\sum_{s\in{{{\mathcal{T}}}}_{jl}}{{{\rm pr}}}({{{\mathcal{E}}}}_{jls}),$$
$${{{\rm pr}}}\left[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})> w_{{{\rm I}}},\bigcup_{j=m-l}^{n-l}{{{\mathcal{E}}}}_{jl}\right] =\sum_{l=0}^{m-2}\sum_{j=m-l}^{n-l}\sum_{s\in{{{\mathcal{T}}}}_{jl}}{{{\rm pr}}}({{{\mathcal{E}}}}_{jls}),$$where
 \begin{align*} {{{\rm pr}}}({{{\mathcal{E}}}}_{jls})& = \sum_{s_0< s_1<\cdots< s_l< s<\infty}\left\{\left[\prod_{i=1}^{l} f(1;n-i+1,p)(1-p)^{(n-i+1)(s_i-s_{i-1}-1)}\right]\right. \\ & \quad \left. \times f(j;n-l,p)(1-p)^{(n-l)(s-s_l-1)}\right\} \quad j=1,\ldots, n-l,\ l=1,\ldots,m-1. \end{align*}
\begin{align*} {{{\rm pr}}}({{{\mathcal{E}}}}_{jls})& = \sum_{s_0< s_1<\cdots< s_l< s<\infty}\left\{\left[\prod_{i=1}^{l} f(1;n-i+1,p)(1-p)^{(n-i+1)(s_i-s_{i-1}-1)}\right]\right. \\ & \quad \left. \times f(j;n-l,p)(1-p)^{(n-l)(s-s_l-1)}\right\} \quad j=1,\ldots, n-l,\ l=1,\ldots,m-1. \end{align*} Sections 5.1 and 6.1 offer examples that show positive probability of profit when the most catastrophic event, ![]() $(j\geq 2)$, occurs for the
$(j\geq 2)$, occurs for the ![]() $(m,n)=(2,5)$ scenario.
$(m,n)=(2,5)$ scenario.
4. Choosing a strategy
Recall that ![]() $\pi ^{\ast }_{{{\rm B}}}$ denotes the premium at which the insurance company, using Strategy B, is indifferent between offering and not offering the
$\pi ^{\ast }_{{{\rm B}}}$ denotes the premium at which the insurance company, using Strategy B, is indifferent between offering and not offering the ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy, where (5) determines
$n$ policy, where (5) determines ![]() $\pi ^{\ast }_{{{\rm B}}}$ for the exponential utility function (4). For Strategy C,
$\pi ^{\ast }_{{{\rm B}}}$ for the exponential utility function (4). For Strategy C,
gives the corresponding indifference premium. (In the case of ![]() $\theta \ne 1$, (25) determines the indifference premium with
$\theta \ne 1$, (25) determines the indifference premium with ![]() $\alpha \theta$ replacing
$\alpha \theta$ replacing ![]() $\alpha$.) Appendix B describes a procedure for computing
$\alpha$.) Appendix B describes a procedure for computing ![]() $\pi ^{\ast }_{{{\rm C}}}$. Note that
$\pi ^{\ast }_{{{\rm C}}}$. Note that ![]() $\kappa ^{(C)}(0) - w_{{{\rm I}}}$ is the random total payout when following Strategy C, which does not depend on
$\kappa ^{(C)}(0) - w_{{{\rm I}}}$ is the random total payout when following Strategy C, which does not depend on ![]() $w_{{{\rm I}}}$. Whereas (5) implies that
$w_{{{\rm I}}}$. Whereas (5) implies that ![]() $\pi ^{\ast }_{{{\rm B}}}<1$ for utility function (4),
$\pi ^{\ast }_{{{\rm B}}}<1$ for utility function (4), ![]() $\pi ^{\ast }_{{{\rm C}}}>1$ for sufficiently large
$\pi ^{\ast }_{{{\rm C}}}>1$ for sufficiently large ![]() $\alpha$ or
$\alpha$ or ![]() $g$. When this occurs, Strategy C with premium
$g$. When this occurs, Strategy C with premium ![]() $\pi ^{\ast }_{{{\rm C}}}$ has no appeal.
$\pi ^{\ast }_{{{\rm C}}}$ has no appeal.
For an adaptive approach such as Strategy C to be implementable, a market must exist for daily reinsurance purchases. Motivation for reinsurers to make this market comes from considerations of the markup per coverage dollar, ![]() $g$, on daily policies. A reinsurer presumably would charge a higher markup per dollar of reinsurance coverage for shorter than for longer term policies. Section 6 contains a fuller treatment of this issue. See Proposition 6.1 for example. In particular, one can expect
$g$, on daily policies. A reinsurer presumably would charge a higher markup per dollar of reinsurance coverage for shorter than for longer term policies. Section 6 contains a fuller treatment of this issue. See Proposition 6.1 for example. In particular, one can expect ![]() $g$ to exceed any yearly markup for Strategy B. Moreover,
$g$ to exceed any yearly markup for Strategy B. Moreover, ![]() $g$ may contribute to a larger indifference premium for Strategy C than for Strategy B. However, Section 5 shows that Strategy C can have a considerably smaller loss probability than Strategy B. This lower probability counters a strict preference for Strategy B based on a smaller indifference premium.
$g$ may contribute to a larger indifference premium for Strategy C than for Strategy B. However, Section 5 shows that Strategy C can have a considerably smaller loss probability than Strategy B. This lower probability counters a strict preference for Strategy B based on a smaller indifference premium.
The premiums, ![]() $\pi ^{\ast }_{{{\rm B}}}$ and
$\pi ^{\ast }_{{{\rm B}}}$ and ![]() $\pi ^{\ast }_{{{\rm C}}}$, together with the minimal
$\pi ^{\ast }_{{{\rm C}}}$, together with the minimal ![]() $v_{Tn}$, provide a basis for deciding the appeal of each strategy in practice. For the moment, assume
$v_{Tn}$, provide a basis for deciding the appeal of each strategy in practice. For the moment, assume ![]() $\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ and suppose the insurance market for
$\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ and suppose the insurance market for ![]() $m$-out-of-
$m$-out-of-![]() $n$ policies dictates an annual premium,
$n$ policies dictates an annual premium, ![]() $\pi _{{{\rm M}}}$. (As noted below,
$\pi _{{{\rm M}}}$. (As noted below, ![]() $\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ in all but one of the scenarios in Table 3. Although the assumption that a market exists for
$\pi ^{\ast }_{{{\rm C}}}\geq v_{Tn}$ in all but one of the scenarios in Table 3. Although the assumption that a market exists for ![]() $m$-out-of-
$m$-out-of-![]() $n$ policies may be unrealistic in some situations, the insurer may still have competitors willing to offer coverage in one or more particular scenarios.) Then:
$n$ policies may be unrealistic in some situations, the insurer may still have competitors willing to offer coverage in one or more particular scenarios.) Then:
A1. If
 $\min (\pi ^{\ast }_{{{\rm B}}},\pi ^{\ast }_{{{\rm C}}})> \pi _{{{\rm M}}}$, the insurance company is averse to offering the policy, regardless of strategy.
$\min (\pi ^{\ast }_{{{\rm B}}},\pi ^{\ast }_{{{\rm C}}})> \pi _{{{\rm M}}}$, the insurance company is averse to offering the policy, regardless of strategy.A2. If
 $\pi ^{\ast }_{{{\rm C}}}>\pi _{{{\rm M}}}>\pi ^{\ast }_{{{\rm B}}}$, the insurance company can offer the policy at premium
$\pi ^{\ast }_{{{\rm C}}}>\pi _{{{\rm M}}}>\pi ^{\ast }_{{{\rm B}}}$, the insurance company can offer the policy at premium  $\pi _{{{\rm M}}}$, follow Strategy B, and realize final working capital
$\pi _{{{\rm M}}}$, follow Strategy B, and realize final working capital  $\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}})=w_{{{\rm I}}}+\pi _{{{\rm M}}}~(>w_{{{\rm I}}}+\pi ^{\ast }_{{{\rm B}}})$ if fewer than
$\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}})=w_{{{\rm I}}}+\pi _{{{\rm M}}}~(>w_{{{\rm I}}}+\pi ^{\ast }_{{{\rm B}}})$ if fewer than  $m$ quakes occur, or
$m$ quakes occur, or  $\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}})=w_{{{\rm I}}}+\pi _{{{\rm M}}}-1~(>w_{{{\rm I}}}+\pi ^{\ast }_{{{\rm B}}}-1)$ otherwise. Moreover,
$\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}})=w_{{{\rm I}}}+\pi _{{{\rm M}}}-1~(>w_{{{\rm I}}}+\pi ^{\ast }_{{{\rm B}}}-1)$ otherwise. Moreover,  ${{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}}))>{{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}}))= {{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}}))$. But the corresponding loss probability remains
${{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi _{{{\rm M}}}))>{{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}}))= {{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}}))$. But the corresponding loss probability remains  $1-F(m-1;n,q)$ which for
$1-F(m-1;n,q)$ which for  $m$ small relative to
$m$ small relative to  $n$, tends to exceed
$n$, tends to exceed  $\beta _{mn}$.
$\beta _{mn}$.A3. If
 $\pi ^{\ast }_{{{\rm B}}}>\>\pi _{{{\rm M}}}>\pi ^{\ast }_{{{\rm C}}}$, then adopting Strategy C with premium
$\pi ^{\ast }_{{{\rm B}}}>\>\pi _{{{\rm M}}}>\pi ^{\ast }_{{{\rm C}}}$, then adopting Strategy C with premium  $\pi _{{{\rm M}}}$ implies
$\pi _{{{\rm M}}}$ implies  ${{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi _{{{\rm M}}}))> {{{\rm E}}}u(\kappa ^{({{{\rm B}}})} (\pi ^{\ast }_{{{\rm B}}}))= {{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}}))$ and
${{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi _{{{\rm M}}}))> {{{\rm E}}}u(\kappa ^{({{{\rm B}}})} (\pi ^{\ast }_{{{\rm B}}}))= {{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}}))$ and  ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi _{{{\rm M}}})< w_{{{\rm I}}}]\leq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta _{mn}$.
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi _{{{\rm M}}})< w_{{{\rm I}}}]\leq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta _{mn}$.A4. If
 $\pi _{{{\rm M}}}>\max (\pi ^{\ast }_{{{\rm B}}},\pi ^{\ast }_{{{\rm C}}})$, then adopting either strategy with premium
$\pi _{{{\rm M}}}>\max (\pi ^{\ast }_{{{\rm B}}},\pi ^{\ast }_{{{\rm C}}})$, then adopting either strategy with premium  $\pi _{{{\rm M}}}$ increases potential profit and increases expected utility. If
$\pi _{{{\rm M}}}$ increases potential profit and increases expected utility. If  $\beta _{mn}<1-F(m-1;n,q)$, choosing Strategy C implies
$\beta _{mn}<1-F(m-1;n,q)$, choosing Strategy C implies  ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})} (\pi _{{{\rm M}}})< w_{{{\rm I}}}]\leq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta _{mn}$.
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})} (\pi _{{{\rm M}}})< w_{{{\rm I}}}]\leq {{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]\leq \beta _{mn}$.A5. If
 $v_{Tn}>\pi ^{\ast }_{{{\rm C}}}$, then A1 through A4 continue to apply with
$v_{Tn}>\pi ^{\ast }_{{{\rm C}}}$, then A1 through A4 continue to apply with  $v_{Tn}$ replacing
$v_{Tn}$ replacing  $\pi ^{\ast }_{{{\rm C}}}$. In this case
$\pi ^{\ast }_{{{\rm C}}}$. In this case  ${{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(v_{Tn}))>{{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}}))$.
${{{\rm E}}}u(\kappa ^{({{{\rm C}}})}(v_{Tn}))>{{{\rm E}}}u(\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}}))$.
Table 3. Premiums for ![]() $n=5$ and
$n=5$ and ![]() $10\ (g=4$,
$10\ (g=4$, ![]() $\theta =1$, and
$\theta =1$, and ![]() $T=365$).
$T=365$).

Note that for all ![]() $\pi _{{{\rm M}}}\in (\pi ^{*}_{{{\rm C}}},1)$
$\pi _{{{\rm M}}}\in (\pi ^{*}_{{{\rm C}}},1)$
By way of comparison, Table 3 displays ![]() $\pi ^{\ast }_{{{\rm B}}}$,
$\pi ^{\ast }_{{{\rm B}}}$, ![]() $\pi ^{\ast }_{{{\rm C}}}$, and
$\pi ^{\ast }_{{{\rm C}}}$, and ![]() $v_{Tn}$ for selected
$v_{Tn}$ for selected ![]() $\alpha,~g,~m,~n$, and
$\alpha,~g,~m,~n$, and ![]() $q$. Most notably,
$q$. Most notably, ![]() $\pi ^{\ast }_{{{\rm C}}}>v_{Tn}$ for all but scenario
$\pi ^{\ast }_{{{\rm C}}}>v_{Tn}$ for all but scenario ![]() $(\alpha,m,n,q)=(4,5,5,0.01)$. For
$(\alpha,m,n,q)=(4,5,5,0.01)$. For ![]() $\alpha =4$,
$\alpha =4$, ![]() $\pi ^{\ast }_{{{\rm B}}}$ is less than the corresponding
$\pi ^{\ast }_{{{\rm B}}}$ is less than the corresponding ![]() $\pi ^{\ast }_{{{\rm C}}}$ for both
$\pi ^{\ast }_{{{\rm C}}}$ for both ![]() $q=0.01$ and 0.1. For
$q=0.01$ and 0.1. For ![]() $\alpha =8$, a mixed picture obtains.
$\alpha =8$, a mixed picture obtains.
5. Example:  $(m,n,\theta )=(2,5,1)$
$(m,n,\theta )=(2,5,1)$
This section focuses on the scenario ![]() $(m,n,\theta )=(2,5,1)$, examining in detail how Strategy C's indifference premium,
$(m,n,\theta )=(2,5,1)$, examining in detail how Strategy C's indifference premium, ![]() $\pi ^{\ast }_{{{\rm C}}}$, loss probability,
$\pi ^{\ast }_{{{\rm C}}}$, loss probability, ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$, and its corresponding upper bound,
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$, and its corresponding upper bound, ![]() $\beta _{mn}$, behave as functions of annual quake probability,
$\beta _{mn}$, behave as functions of annual quake probability, ![]() $q$, level of risk aversion,
$q$, level of risk aversion, ![]() $\alpha$, markup,
$\alpha$, markup, ![]() $g$, and review interval,
$g$, and review interval, ![]() $\Delta$, (in days). Although previous sections assume
$\Delta$, (in days). Although previous sections assume ![]() $\Delta =1$, Strategy C applies more generally. For example, a policy with one year coverage may have intervals
$\Delta =1$, Strategy C applies more generally. For example, a policy with one year coverage may have intervals ![]() $\Delta =$1, 7, 30, 90, or 180 days, with 365, 52, 12, 4, and 2 reviews, respectively. (The corresponding total coverage periods are 365, 364, 360, 360, and 360 days, respectively. Presumably, these slight differences in coverage period should have negligible effect when comparing results for different
$\Delta =$1, 7, 30, 90, or 180 days, with 365, 52, 12, 4, and 2 reviews, respectively. (The corresponding total coverage periods are 365, 364, 360, 360, and 360 days, respectively. Presumably, these slight differences in coverage period should have negligible effect when comparing results for different ![]() $\Delta$.) The present analysis focuses on
$\Delta$.) The present analysis focuses on ![]() $\Delta =1$, 7, and 30 with
$\Delta =1$, 7, and 30 with
 \begin{align} p_\Delta& :=\text{probability of a quake at a site during a period of} \, \Delta \text{days} \nonumber\\ & = 1-(1-q)^{1/\lfloor T/\Delta\rfloor}. \end{align}
\begin{align} p_\Delta& :=\text{probability of a quake at a site during a period of} \, \Delta \text{days} \nonumber\\ & = 1-(1-q)^{1/\lfloor T/\Delta\rfloor}. \end{align}The corresponding upper bound on loss probability takes the form
 \begin{align*} \beta_{25}& = 1-P_5(0) -P_5(1)-P_5(1,j_2\geq 1) \\ & = P_5(j_1\geq 2) \\ & =[1-(1-p_\Delta)^{4}(1+4p_\Delta)]\times\frac{1-(1-p_\Delta)^{5\lfloor T/\Delta\rfloor}}{1-(1-p_\Delta)^{5}}, \end{align*}
\begin{align*} \beta_{25}& = 1-P_5(0) -P_5(1)-P_5(1,j_2\geq 1) \\ & = P_5(j_1\geq 2) \\ & =[1-(1-p_\Delta)^{4}(1+4p_\Delta)]\times\frac{1-(1-p_\Delta)^{5\lfloor T/\Delta\rfloor}}{1-(1-p_\Delta)^{5}}, \end{align*}Table 4(a) characterizes Strategy B with regard to premium, loss, and loss probability. Tables 4(b) and 4(c) do likewise for Strategy C. They reveal that:
• For final working capital, Strategy B concentrates probability
 $1-F(1;5,q)$ on loss,
$1-F(1;5,q)$ on loss,  $-(1- \pi ^{\ast }_{{{\rm B}}})$, and
$-(1- \pi ^{\ast }_{{{\rm B}}})$, and  $F(1;5,q)$ on profit,
$F(1;5,q)$ on profit,  $\pi ^{\ast }_{{{\rm B}}}$. By contrast, Strategy C concentrates virtually all its probability mass in a small profit interval
$\pi ^{\ast }_{{{\rm B}}}$. By contrast, Strategy C concentrates virtually all its probability mass in a small profit interval  $[0,d)$, where
$[0,d)$, where  $d$ increases as
$d$ increases as  $\pi ^{\ast }_{{{\rm C}}}-v_{Tn}$ increases. Its modal value is in
$\pi ^{\ast }_{{{\rm C}}}-v_{Tn}$ increases. Its modal value is in  $(0,d)$.
$(0,d)$.• For each 4-tuple
 $(\alpha,g,q,\Delta )$,
$(\alpha,g,q,\Delta )$,  ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]<{{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}})< w_{{{\rm I}}}]$.
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]<{{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}})< w_{{{\rm I}}}]$.• For given
 $\alpha$,
$\alpha$,  $g$, and
$g$, and  $q$,
$q$,  $\pi ^{\ast }_{{{\rm C}}}$ increases relatively little as
$\pi ^{\ast }_{{{\rm C}}}$ increases relatively little as  $\Delta$ increases.
$\Delta$ increases.• For given interval,
 $g$, and
$g$, and  $q$,
$q$,  $\pi ^{\ast }_{{{\rm B}}}$ increases substantially as
$\pi ^{\ast }_{{{\rm B}}}$ increases substantially as  $\alpha$ increases from 4 to 8, whereas
$\alpha$ increases from 4 to 8, whereas  $\pi ^{\ast }_{{{\rm C}}}$ increases relatively little.
$\pi ^{\ast }_{{{\rm C}}}$ increases relatively little.• For
 $q=0.01$,
$q=0.01$,  $\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$ for
$\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$ for  $\alpha =4$ but
$\alpha =4$ but  $\pi ^{\ast }_{{{\rm B}}}>\pi ^{\ast }_{{{\rm C}}}$ for
$\pi ^{\ast }_{{{\rm B}}}>\pi ^{\ast }_{{{\rm C}}}$ for  $\alpha =8$.
$\alpha =8$.• For
 $q=0.1$ both strategies have relatively large indifference premiums, with
$q=0.1$ both strategies have relatively large indifference premiums, with  $\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$ for
$\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$ for  $g=8$ and
$g=8$ and  $(\alpha,g,\Delta )=(8,4,30)$. For one dollar coverage, Strategy C clearly is not a serious alternative if
$(\alpha,g,\Delta )=(8,4,30)$. For one dollar coverage, Strategy C clearly is not a serious alternative if  $\pi ^{\ast }_{{{\rm C}}}>1.$
$\pi ^{\ast }_{{{\rm C}}}>1.$• For each given
 $(\alpha,g,q)$ in Table 4(c),
$(\alpha,g,q)$ in Table 4(c),  $\max -\min$ decreases as
$\max -\min$ decreases as  $\Delta$ increases. The reduction is most noticeable for
$\Delta$ increases. The reduction is most noticeable for  $q=0.1$ and
$q=0.1$ and  $\Delta =90$ and 180 days.
$\Delta =90$ and 180 days.• The maximal profit
 $(>3)$ occurs for the quake history (1,4) which has positive, but negligible, probability of occurring.
$(>3)$ occurs for the quake history (1,4) which has positive, but negligible, probability of occurring.
Table 4. Premiums, probabilities and ![]() $\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})$ range, for
$\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})$ range, for ![]() $(m,n,\theta )=(2,5,1)$.
$(m,n,\theta )=(2,5,1)$.

Additional computation reveals that for 90 and 180 day intervals, Strategy C has loss probabilities ![]() $2.460\times 10^{-4}$ and
$2.460\times 10^{-4}$ and ![]() $4.913\times 10^{-4}$, respectively, for
$4.913\times 10^{-4}$, respectively, for ![]() $q=0.01$ and all
$q=0.01$ and all ![]() $\alpha$ and
$\alpha$ and ![]() $g$. These are again less than the corresponding loss probabilities for Strategy B. A similar property holds for
$g$. These are again less than the corresponding loss probabilities for Strategy B. A similar property holds for ![]() $q=0.1$. For both intervals and both
$q=0.1$. For both intervals and both ![]() $q$,
$q$, ![]() $\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$.
$\pi ^{\ast }_{{{\rm B}}}<\pi ^{\ast }_{{{\rm C}}}$.
The entries in Table 4 for ![]() $q = 0.1$ offer an example in which both
$q = 0.1$ offer an example in which both ![]() $v_{Tn}$ and
$v_{Tn}$ and ![]() $\pi _{{{\rm C}}}^{\ast }$ decrease as
$\pi _{{{\rm C}}}^{\ast }$ decrease as ![]() $\Delta$ decreases, thus showing that Strategy C's use of dynamic reinsurance sometimes provides the largest benefit to the insurer when the review interval is shortest (
$\Delta$ decreases, thus showing that Strategy C's use of dynamic reinsurance sometimes provides the largest benefit to the insurer when the review interval is shortest (![]() $\Delta = 1$). Additional computations for other parameter values also exhibit such behavior. (Note, however, that the entries in Table 4 for
$\Delta = 1$). Additional computations for other parameter values also exhibit such behavior. (Note, however, that the entries in Table 4 for ![]() $q = 0.01$ do not.)
$q = 0.01$ do not.)
One might argue, nevertheless, that the assumption that ![]() $g$ is constant gives an unfair advantage to shorter review intervals. As noted in Section 4, the conventional wisdom is that over a shorter interval an insurer or reinsurer will demand a larger markup for coverage of the same risk (i.e., the same value of
$g$ is constant gives an unfair advantage to shorter review intervals. As noted in Section 4, the conventional wisdom is that over a shorter interval an insurer or reinsurer will demand a larger markup for coverage of the same risk (i.e., the same value of ![]() $q$ in the present setting). In the context of utility theory, this conventional wisdom can be explained as a consequence of risk aversion (see Proposition 6.1).
$q$ in the present setting). In the context of utility theory, this conventional wisdom can be explained as a consequence of risk aversion (see Proposition 6.1).
Section 6 below generalizes the model with different review intervals to accommodate a reinsurer's markup that depends on both the quake probability and the coverage amount in the review interval, under the assumption that the reinsurer, like the insurer, has an exponential utility function with a positive risk-aversion coefficient.
5.1. Profit from multiple quakes
Table 5 shows how ![]() $\beta _{25}$, the upper bound in (18) on loss probability when applying Strategy C to the scenario
$\beta _{25}$, the upper bound in (18) on loss probability when applying Strategy C to the scenario ![]() $(m,n)=(2,5)$, varies with
$(m,n)=(2,5)$, varies with ![]() $\Delta$. Comparing them to their corresponding loss probabilities in Table 4(b) reveals that:
$\Delta$. Comparing them to their corresponding loss probabilities in Table 4(b) reveals that:
• For
 $q=0.01$ and all
$q=0.01$ and all  $\alpha$,
$\alpha$, $g$, and
$g$, and  $\Delta$,
$\Delta$,  ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ and
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ and  $\beta _{25}$ agree to four digits.
$\beta _{25}$ agree to four digits.• For
 $q=0.1$ and all
$q=0.1$ and all  $\alpha$,
$\alpha$,  $g$, and
$g$, and  $\Delta$,
$\Delta$,  ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ is considerably less than
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ is considerably less than  $\beta _{25}$.
$\beta _{25}$.
Table 5. ![]() $\beta _{25}$ for varying review intervals for
$\beta _{25}$ for varying review intervals for ![]() $(m,n)=(2,5)$.
$(m,n)=(2,5)$.

To reconcile these similarities and differences, we first focus on ![]() $\alpha =4$,
$\alpha =4$, ![]() $g=4$, and
$g=4$, and ![]() $q=0.01$ and examine the event
$q=0.01$ and examine the event ![]() $(j\geq 2)$, using the nomenclature of Section 3.3. In order for a profit to materialize, the bound
$(j\geq 2)$, using the nomenclature of Section 3.3. In order for a profit to materialize, the bound ![]() $B_{T-t+1}$ in (22) must be less than 5 for the
$B_{T-t+1}$ in (22) must be less than 5 for the ![]() $(m,n)=(2,5)$ scenario. However,
$(m,n)=(2,5)$ scenario. However, ![]() $\min _{1\leq t\leq T}B_{T-t+1}\geq 7.359$, 7.405, and 7.911 for
$\min _{1\leq t\leq T}B_{T-t+1}\geq 7.359$, 7.405, and 7.911 for ![]() $\Delta =1$, 7, and 30, respectively. Therefore,
$\Delta =1$, 7, and 30, respectively. Therefore, ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}\,|\,{{{\mathcal {E}}}}]=0$, where
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}\,|\,{{{\mathcal {E}}}}]=0$, where
 \begin{align} {{{\mathcal{E}}}}& = \bigcup_{j=2}^{5}{{{\mathcal{E}}}}_{j0} \nonumber\\ & = \left(\begin{array}{c} \text{at least two events occur} \\ \text{on the first quake day} \end{array}\right). \end{align}
\begin{align} {{{\mathcal{E}}}}& = \bigcup_{j=2}^{5}{{{\mathcal{E}}}}_{j0} \nonumber\\ & = \left(\begin{array}{c} \text{at least two events occur} \\ \text{on the first quake day} \end{array}\right). \end{align} The case of ![]() $q=0.1$ presents a considerably different picture. It has
$q=0.1$ presents a considerably different picture. It has ![]() $\min _{1\leq t\leq T}B_{T-t+1}\geq 1.725$, 1.711, and 1.649 for
$\min _{1\leq t\leq T}B_{T-t+1}\geq 1.725$, 1.711, and 1.649 for ![]() $\Delta =1$, 7, and 30, respectively, implying a profit if as few as two quakes occur during the first review period in which a quake occurs. For example,
$\Delta =1$, 7, and 30, respectively, implying a profit if as few as two quakes occur during the first review period in which a quake occurs. For example, ![]() $\Delta =1$ has
$\Delta =1$ has
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}]& = \sum_{s=1}^{117}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{249}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{290}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{309}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 8.901\times 10^{{-}5}, \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}]& = \sum_{s=1}^{117}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{249}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{290}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{309}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 8.901\times 10^{{-}5}, \end{align*}leading to the tighter upper bound on loss probability
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}] & = \beta_{25}-\sum_{s=1}^{117}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{249}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s})-\sum_{s=1}^{290}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})-\sum_{s=1}^{309}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})\\ & = 2.175\times 10^{{-}4}. \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}] & = \beta_{25}-\sum_{s=1}^{117}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{249}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s})-\sum_{s=1}^{290}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})-\sum_{s=1}^{309}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})\\ & = 2.175\times 10^{{-}4}. \end{align*} That is, the insurance company realizes a profit if two quakes occur during any of the first 117 coverage days, three quakes on any of the first 249 coverage days, four quakes on any of the first 290 coverage days, or five quakes on any of the first 309 coverage days. For monthly review intervals (![]() $\Delta =30$),
$\Delta =30$),
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}]& = \sum_{s=1}^{5}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{8}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{9}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{10}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 3.461\times 10^{{-}3}. \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}]& = \sum_{s=1}^{5}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{8}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{9}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{10}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 3.461\times 10^{{-}3}. \end{align*}implying a noticeably larger probability than for ![]() $q=0.01$. Moreover, it reduces the bound on loss probability by about one half to
$q=0.01$. Moreover, it reduces the bound on loss probability by about one half to
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}]& = \beta_{25}-\sum_{s=1}^{5}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{8}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) -\sum_{s=1}^{9}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})-\sum_{s=1}^{10}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 3.698\times 10^{{-}3}. \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}]& = \beta_{25}-\sum_{s=1}^{5}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{8}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) -\sum_{s=1}^{9}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})-\sum_{s=1}^{10}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 3.698\times 10^{{-}3}. \end{align*}Interestingly, among all possible quake histories that can occur during a coverage period, the most catastrophic event, two or more quakes occurring within the same 30-day review interval, has positive, although small, probability of generating a profit for the insurance company.
6. Reinsurer's markup
Section 3.1 assumes that for ![]() $k$ active sites at the beginning of remaining day
$k$ active sites at the beginning of remaining day ![]() $t$, the insurance company pays the premium,
$t$, the insurance company pays the premium, ![]() $kgp\phi _{tk}$, to buy reinsurance coverage,
$kgp\phi _{tk}$, to buy reinsurance coverage, ![]() $\phi _{tk}=v_{t-1,k-1}-v_{t-1,k}$, on each of the
$\phi _{tk}=v_{t-1,k-1}-v_{t-1,k}$, on each of the ![]() $k$ sites for
$k$ sites for ![]() $\Delta$ days. (This form of reinsurance is merely Strategy A applied to a coverage interval shorter than one year.) Moreover, it treats the reinsurer's markup,
$\Delta$ days. (This form of reinsurance is merely Strategy A applied to a coverage interval shorter than one year.) Moreover, it treats the reinsurer's markup, ![]() $g$, as constant over the entire coverage period, presumably a function of the interval quake probability,
$g$, as constant over the entire coverage period, presumably a function of the interval quake probability, ![]() $p_\Delta$. In reality, the markup may vary on successive reviews as the risk facing the reinsurer varies with changing coverage,
$p_\Delta$. In reality, the markup may vary on successive reviews as the risk facing the reinsurer varies with changing coverage, ![]() $\phi _{tk}$. This section extends the analysis of Section 3.1 by allowing the markup to be a function of both coverage and the quake probability. It again illustrates the development for the
$\phi _{tk}$. This section extends the analysis of Section 3.1 by allowing the markup to be a function of both coverage and the quake probability. It again illustrates the development for the ![]() $(m,n,\theta )=(2,5,1)$ scenario.
$(m,n,\theta )=(2,5,1)$ scenario.
On each of ![]() $k$ sites at the beginning of remaining day
$k$ sites at the beginning of remaining day ![]() $t$, the insurance company wants to purchase reinsurance that pays it
$t$, the insurance company wants to purchase reinsurance that pays it ![]() $\phi _{tk}$ dollars if a quake occurs at the site during the subsequent
$\phi _{tk}$ dollars if a quake occurs at the site during the subsequent ![]() $\Delta$ coverage days. Each potential reinsurer presumably determines the premium that would make him indifferent between offering and not offering the coverage. In a competitive insurance market, the insurance company purchases the policy at the current market price from a reinsurer who is willing to sell; that is, one whose indifference premium is no greater than the market price. In the case of
$\Delta$ coverage days. Each potential reinsurer presumably determines the premium that would make him indifferent between offering and not offering the coverage. In a competitive insurance market, the insurance company purchases the policy at the current market price from a reinsurer who is willing to sell; that is, one whose indifference premium is no greater than the market price. In the case of ![]() $k$ active sites, we assume that the market is large enough that all
$k$ active sites, we assume that the market is large enough that all ![]() $k$ policies are available (from one or more reinsurers) at the current market price.
$k$ policies are available (from one or more reinsurers) at the current market price.
Once again we rely on expected utility theory; this time to characterize the markup, and therefore the premium, required to make the reinsurer indifferent between offering and not offering the policy for given ![]() $p_\Delta$ and
$p_\Delta$ and ![]() $\phi _{tk}$. Suppose the reinsurer's utility function,
$\phi _{tk}$. Suppose the reinsurer's utility function, ![]() $\{u(w)\}$, is concave increasing in initial wealth,
$\{u(w)\}$, is concave increasing in initial wealth, ![]() $w$. Then
$w$. Then ![]() $g(p_\Delta,\phi _{tk})\times p_\Delta$ is the premium per dollar of coverage that makes him indifferent between offering and not offering the coverage for
$g(p_\Delta,\phi _{tk})\times p_\Delta$ is the premium per dollar of coverage that makes him indifferent between offering and not offering the coverage for ![]() $\Delta$ days, where
$\Delta$ days, where ![]() $g(p_\Delta,\phi _{tk})$ solves the expected utility indifference equation
$g(p_\Delta,\phi _{tk})$ solves the expected utility indifference equation
Except to avoid ambiguity, we hereafter write ![]() $g(p,\phi )$ for
$g(p,\phi )$ for ![]() $g(p_\Delta,\phi _{tk})$.
$g(p_\Delta,\phi _{tk})$.
Propositions 6.1 and 6.2 characterize how ![]() $g(p,\phi )$ varies with
$g(p,\phi )$ varies with ![]() $p$ and
$p$ and ![]() $\phi$.
$\phi$.
Proposition 6.1 If the Arrow-Pratt measure of absolute risk aversion, ![]() $-{u''(w)}/{u'(w)}$, decreases in
$-{u''(w)}/{u'(w)}$, decreases in ![]() $w$, then for all
$w$, then for all ![]() $t$ and
$t$ and ![]() $k$,
$k$, ![]() $g(p,\phi )$ is decreasing in
$g(p,\phi )$ is decreasing in ![]() $p$ for given
$p$ for given ![]() $\phi$.
$\phi$.
Proposition 6.2 For given ![]() $p$,
$p$, ![]() $g(p,\phi )$ is strictly increasing in
$g(p,\phi )$ is strictly increasing in ![]() $\phi$.
$\phi$.
See Appendix A for the proofs. The property for the Arrow-Pratt measure is a common requirement of utility theory because it is consistent with the property that an individual's aversion to risk does not increase as his wealth increases. Because ![]() $v_{t,n-m}=1$ and
$v_{t,n-m}=1$ and ![]() $v_{tk}$ is monotone non-increasing in
$v_{tk}$ is monotone non-increasing in ![]() $k\in \{n-m,\ldots,n\}$ for given
$k\in \{n-m,\ldots,n\}$ for given ![]() $t$ (Proposition 3.2),
$t$ (Proposition 3.2), ![]() $\phi$ is bounded above by 1.
$\phi$ is bounded above by 1.
Suppose the reinsurer has the exponential utility function, ![]() $u(w)=-{{{\rm e}}}^{-\gamma w}$, for
$u(w)=-{{{\rm e}}}^{-\gamma w}$, for ![]() $-\infty < w<\infty$ and level of risk aversion,
$-\infty < w<\infty$ and level of risk aversion, ![]() $\gamma >0$. Solving for
$\gamma >0$. Solving for ![]() $g(p,\phi )$ yields
$g(p,\phi )$ yields
Because Proposition 6.1 implies that ![]() $g(p,\phi )$ decreases as
$g(p,\phi )$ decreases as ![]() $q$,
$q$, ![]() $\Delta$, or both increase,
$\Delta$, or both increase, ![]() $g(p,\phi )$ in (29) has upper bounds
$g(p,\phi )$ in (29) has upper bounds
Table 6 reveals that ![]() $g(p,1)$ differs little from its limiting upper bound for quake probabilities
$g(p,1)$ differs little from its limiting upper bound for quake probabilities ![]() $q\leq 0.1$ and
$q\leq 0.1$ and ![]() $\Delta =1$, 7, and 30. Although one might be tempted to choose
$\Delta =1$, 7, and 30. Although one might be tempted to choose ![]() $g(p,1)$ as the constant markup in Section 3.1, doing can lead to a needlessly larger markup than necessary, as we now show.
$g(p,1)$ as the constant markup in Section 3.1, doing can lead to a needlessly larger markup than necessary, as we now show.
Table 6. Strategy C: Upper bound on reinsurer's indifference markup (![]() $p=1-(1-q)^{1/\lfloor {T/\Delta \rfloor }}$).
$p=1-(1-q)^{1/\lfloor {T/\Delta \rfloor }}$).

Using the indifference markup ![]() $g_{tk}(p_\Delta,\phi _{tk})$ in (29) in place of a constant
$g_{tk}(p_\Delta,\phi _{tk})$ in (29) in place of a constant ![]() $g$, we extend the development in Section 3.1 by computing the schedule,
$g$, we extend the development in Section 3.1 by computing the schedule, ![]() $\{v_{tk}\}$, as
$\{v_{tk}\}$, as
subject to the boundary conditions (8). Again, ![]() $v_{Tn}$ is the minimal premium that guarantees no loss for the insurance company when the quake history satisfies Condition (7), whereas
$v_{Tn}$ is the minimal premium that guarantees no loss for the insurance company when the quake history satisfies Condition (7), whereas ![]() $k\times p\times g_{tk}(p,\phi _{tk})$ is the reinsurer's indifference premium at review
$k\times p\times g_{tk}(p,\phi _{tk})$ is the reinsurer's indifference premium at review ![]() $t$ with
$t$ with ![]() $k$ active sites. Figure 1 displays coverage, reinsurer's indifference markup, and
$k$ active sites. Figure 1 displays coverage, reinsurer's indifference markup, and ![]() ${{{\rm pr}}}(\text {one quake on the first quake day})$ for
${{{\rm pr}}}(\text {one quake on the first quake day})$ for ![]() $\Delta =1$ and reinsurer risk aversion level,
$\Delta =1$ and reinsurer risk aversion level, ![]() $\gamma =4$. Most notably, Figure 1(b) shows that over the coverage year, markups considerably smaller than the corresponding upper bounds
$\gamma =4$. Most notably, Figure 1(b) shows that over the coverage year, markups considerably smaller than the corresponding upper bounds ![]() $g(p,1)$ in Table 6 suffice to make the reinsurer indifferent between offering or not offering the coverage. As illustration, let
$g(p,1)$ in Table 6 suffice to make the reinsurer indifferent between offering or not offering the coverage. As illustration, let ![]() $\phi _{\max }$ denote the maximal coverage during the entire coverage period. Then for
$\phi _{\max }$ denote the maximal coverage during the entire coverage period. Then for ![]() $(\alpha,\gamma,\Delta )=(4,4,1)$, we have
$(\alpha,\gamma,\Delta )=(4,4,1)$, we have
 \begin{align*} & \left. \begin{array}{rcl} {{{\rm pr}}}(\phi_{\max}=0.1805) & = & 1-(1-p)^{5(T-1)}\\ & = & 0.9511 \\ {{{\rm pr}}}(0.1805<\phi_{\max}\leq 1) & = & 0.0489 \end{array}\right\} \quad \text{for }q=0.01 \\ & \left.\begin{array}{rcl} {{{\rm pr}}}(\phi_{\max}=0.3909) & = & 0.5916 \\ {{{\rm pr}}}(0.3909<\phi_{\max}\leq 1) & = & 0.4087 \end{array}\right\}\quad \text{for }q=0.1, \end{align*}
\begin{align*} & \left. \begin{array}{rcl} {{{\rm pr}}}(\phi_{\max}=0.1805) & = & 1-(1-p)^{5(T-1)}\\ & = & 0.9511 \\ {{{\rm pr}}}(0.1805<\phi_{\max}\leq 1) & = & 0.0489 \end{array}\right\} \quad \text{for }q=0.01 \\ & \left.\begin{array}{rcl} {{{\rm pr}}}(\phi_{\max}=0.3909) & = & 0.5916 \\ {{{\rm pr}}}(0.3909<\phi_{\max}\leq 1) & = & 0.4087 \end{array}\right\}\quad \text{for }q=0.1, \end{align*}where

Figure 1. Coverage and reinsurer's indifference markup for ![]() $(m,n,\theta )=(2,5,1)$,
$(m,n,\theta )=(2,5,1)$, ![]() $\alpha =4$,
$\alpha =4$, ![]() $\gamma =4$, and
$\gamma =4$, and ![]() $\Delta =1$ (solid:
$\Delta =1$ (solid: ![]() $k=4$, dash:
$k=4$, dash: ![]() $k=5$).
$k=5$).
For premium, ![]() $\pi$,
$\pi$, ![]() $\{v_{tk}\}$ as in (31), and
$\{v_{tk}\}$ as in (31), and ![]() $g(p_\Delta,\phi _{tk})$ as in (29), final working capital now becomes
$g(p_\Delta,\phi _{tk})$ as in (29), final working capital now becomes
 \begin{equation} \kappa^{({{{\rm C}}})}(\pi)= w_{{{\rm I}}}+\pi+\sum_{s=T}^{\max(0,T-L)}\{[K_s-K_{s-1}-K_sg(p,\phi_{s,K_s})p]\phi_{s,K_s}- \theta I_{K_{s-1}\leq n-m}\}, \end{equation}
\begin{equation} \kappa^{({{{\rm C}}})}(\pi)= w_{{{\rm I}}}+\pi+\sum_{s=T}^{\max(0,T-L)}\{[K_s-K_{s-1}-K_sg(p,\phi_{s,K_s})p]\phi_{s,K_s}- \theta I_{K_{s-1}\leq n-m}\}, \end{equation}and the insurance company's corresponding indifference premium follows from (25). Table 7 displays ![]() $\pi ^{\ast }_{{{\rm C}}}$,
$\pi ^{\ast }_{{{\rm C}}}$, ![]() $v_{Tn}$, and
$v_{Tn}$, and ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$ based on the reinsurer's indifference markup,
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$ based on the reinsurer's indifference markup, ![]() $g(p_\Delta,\phi _{tk})$, in (29). Comparing its entries with those in Table 4 for Strategy B reveals that
$g(p_\Delta,\phi _{tk})$, in (29). Comparing its entries with those in Table 4 for Strategy B reveals that ![]() $\pi ^{\ast }_{{{\rm C}}}\leq \pi ^{\ast }_{{{\rm B}}}$ and
$\pi ^{\ast }_{{{\rm C}}}\leq \pi ^{\ast }_{{{\rm B}}}$ and ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}] \leq {{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}})\leq w_{{{\rm I}}}]$ for the same
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}] \leq {{{\rm pr}}}[\kappa ^{({{{\rm B}}})}(\pi ^{\ast }_{{{\rm B}}})\leq w_{{{\rm I}}}]$ for the same ![]() $\alpha$,
$\alpha$, ![]() $\Delta$, and
$\Delta$, and ![]() $q$. This occurs for both
$q$. This occurs for both ![]() $\gamma =3$ and 4. But
$\gamma =3$ and 4. But ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$ tends to be greater than the corresponding entries in Table 4 for fixed reinsurer's markups,
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})\leq w_{{{\rm I}}}]$ tends to be greater than the corresponding entries in Table 4 for fixed reinsurer's markups, ![]() $g=4$ and 8.
$g=4$ and 8.
Table 7. Strategy C: ![]() $\pi ^{\ast }_{{{\rm C}}},~v_{Tn}$, and
$\pi ^{\ast }_{{{\rm C}}},~v_{Tn}$, and ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}} ]$ for variable markup (
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}} ]$ for variable markup (![]() $(m,n,\theta )=(2,5,1$) and
$(m,n,\theta )=(2,5,1$) and ![]() $\gamma =4$).
$\gamma =4$).

Whereas Section 3.1 takes the reinsurer's markup, ![]() $g$, as a known constant for the total
$g$, as a known constant for the total ![]() $T$ day coverage period, the present development takes the reinsurer's level of risk aversion,
$T$ day coverage period, the present development takes the reinsurer's level of risk aversion, ![]() $\gamma$, as known. Although the insurance company knows neither of these with certainty, it is not unreasonable to assume
$\gamma$, as known. Although the insurance company knows neither of these with certainty, it is not unreasonable to assume ![]() $\gamma \leq \alpha$. That is, the insurance company is at least as risk averse as reinsurers are.Footnote 2 Then the resulting
$\gamma \leq \alpha$. That is, the insurance company is at least as risk averse as reinsurers are.Footnote 2 Then the resulting ![]() $\{g(p_\Delta,\phi _{tk})\}$ provides an upper bound on the unknown markups, but for which the gap between them decreases as
$\{g(p_\Delta,\phi _{tk})\}$ provides an upper bound on the unknown markups, but for which the gap between them decreases as ![]() $\gamma$ approaches
$\gamma$ approaches ![]() $\alpha$. This assumption is more plausible than assuming a constant markup.
$\alpha$. This assumption is more plausible than assuming a constant markup.
In Table 7, note that ![]() $v_{Tn}$ increases as
$v_{Tn}$ increases as ![]() $\Delta$ increases for
$\Delta$ increases for ![]() $q = 0.1$ and decreases as
$q = 0.1$ and decreases as ![]() $\Delta$ increases for
$\Delta$ increases for ![]() $q = 0.01$, with
$q = 0.01$, with ![]() $\gamma = 4$ and
$\gamma = 4$ and ![]() $\Delta = 1$, 7, and
$\Delta = 1$, 7, and ![]() $30$. Additional computations suggest that in general for given
$30$. Additional computations suggest that in general for given ![]() $q$ and sufficiently small (large) values of
$q$ and sufficiently small (large) values of ![]() $\gamma$,
$\gamma$, ![]() $v_{Tn}$ decreases (increases) as the length of the review interval increases, whereas for an intermediate range of values of
$v_{Tn}$ decreases (increases) as the length of the review interval increases, whereas for an intermediate range of values of ![]() $\gamma$,
$\gamma$, ![]() $v_{Tn}$ first decreases then increases as the length of the review interval increases.
$v_{Tn}$ first decreases then increases as the length of the review interval increases.
An important and perhaps unexpected implication of these results is that smaller values of ![]() $v_{Tn}$ and
$v_{Tn}$ and ![]() $\pi _{{{\rm C}}}^{\ast }$ can still be associated with shorter review intervals even though the markups demanded by a risk-averse reinsurer now vary with the length of the review interval. As was the case in Table 4 (where the reinsurer's markup
$\pi _{{{\rm C}}}^{\ast }$ can still be associated with shorter review intervals even though the markups demanded by a risk-averse reinsurer now vary with the length of the review interval. As was the case in Table 4 (where the reinsurer's markup ![]() $g$ was constant), the entries in Table 7 for
$g$ was constant), the entries in Table 7 for ![]() $q = 0.1$ show both
$q = 0.1$ show both ![]() $v_{Tn}$ and
$v_{Tn}$ and ![]() $\pi _{{{\rm C}}}^{\ast }$ decreasing as
$\pi _{{{\rm C}}}^{\ast }$ decreasing as ![]() $\Delta$ decreases. The reason for this behavior, which at first may seem to contradict the conventional wisdom, is that Strategy C's schedule assigns smaller coverage amounts
$\Delta$ decreases. The reason for this behavior, which at first may seem to contradict the conventional wisdom, is that Strategy C's schedule assigns smaller coverage amounts ![]() $\phi$ as well as smaller probabilities
$\phi$ as well as smaller probabilities ![]() $p$ to shorter review intervals. Whereas the reinsurer's markup
$p$ to shorter review intervals. Whereas the reinsurer's markup ![]() $g(p, \phi )$ increases as
$g(p, \phi )$ increases as ![]() $p$ decreases, it decreases as
$p$ decreases, it decreases as ![]() $\phi$ decreases (see Proposition 6.2). The net effect, as shown by the entries in Table 7 for
$\phi$ decreases (see Proposition 6.2). The net effect, as shown by the entries in Table 7 for ![]() $q = 0.1$, can once again be that the shortest review interval provides the largest benefit to the insurer, just as in the case of constant markup
$q = 0.1$, can once again be that the shortest review interval provides the largest benefit to the insurer, just as in the case of constant markup ![]() $g$.
$g$.
6.1. Profit from multiple quakes
Recall from Section 3.3 for constant reinsurer's markup that a profit may occur if on remaining day ![]() $t$ the event
$t$ the event ![]() ${{{\mathcal {E}}}}_{j,l,T-t+1}$ occurs for some
${{{\mathcal {E}}}}_{j,l,T-t+1}$ occurs for some ![]() $l< m-1$ and
$l< m-1$ and ![]() $j\geq m-l$. A similar property holds for the variable markup case, with
$j\geq m-l$. A similar property holds for the variable markup case, with ![]() $g(p_\Delta,\phi _{T-s+1,n})$ replacing
$g(p_\Delta,\phi _{T-s+1,n})$ replacing ![]() $g$ in expressions (21) and (22). As illustration for
$g$ in expressions (21) and (22). As illustration for ![]() $(m,n)=(2,5)$,
$(m,n)=(2,5)$, ![]() $\gamma =4$,
$\gamma =4$, ![]() $\alpha =4$,
$\alpha =4$, ![]() $\Delta =1$, and
$\Delta =1$, and ![]() $q=0.01$, the bound in (22) satisfies
$q=0.01$, the bound in (22) satisfies
so that a profit accrues for ![]() $j\geq 4$ with probability
$j\geq 4$ with probability
 $${{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}] =\sum_{s=1}^{56}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{149}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})={{{\rm O}}}(10^{{-}12}).$$
$${{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}] =\sum_{s=1}^{56}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{149}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})={{{\rm O}}}(10^{{-}12}).$$ This is consistent with the observation that ![]() $\beta _{25}$ in Table 5 and
$\beta _{25}$ in Table 5 and ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ in Table 7 are identical to at least four digits.
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ in Table 7 are identical to at least four digits.
Realizing a profit when more than one quake occurs on the first quake day is more probable for ![]() $q=0.1$. Specifically,
$q=0.1$. Specifically,
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}] & = \sum_{s=1}^{186}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{314}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{335}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{344}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})\\ & = 1.359\times 10^{{-}4}, \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})>w_{{{\rm I}}},{{{\mathcal{E}}}}] & = \sum_{s=1}^{186}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})+\sum_{s=1}^{314}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s}) +\sum_{s=1}^{335}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s})+\sum_{s=1}^{344}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s})\\ & = 1.359\times 10^{{-}4}, \end{align*}substantially reducing the upper bound, ![]() $\beta _{25}=2.364\times 10^{-4}$, on loss probability to
$\beta _{25}=2.364\times 10^{-4}$, on loss probability to
 \begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}] & = \beta_{25}-\sum_{s=1}^{185}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{314}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s})-\sum_{s=1}^{335}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s}) -\sum_{s=1}^{344}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 1.005\times 10^{{-}4}. \end{align*}
\begin{align*} {{{\rm pr}}}[\kappa^{({{{\rm C}}})}(\pi^{{\ast}}_{{{\rm C}}})< w_{{{\rm I}}}] & = \beta_{25}-\sum_{s=1}^{185}{{{\rm pr}}}({{{\mathcal{E}}}}_{20s})-\sum_{s=1}^{314}{{{\rm pr}}}({{{\mathcal{E}}}}_{30s})-\sum_{s=1}^{335}{{{\rm pr}}}({{{\mathcal{E}}}}_{40s}) -\sum_{s=1}^{344}{{{\rm pr}}}({{{\mathcal{E}}}}_{50s}) \\ & = 1.005\times 10^{{-}4}. \end{align*} For event ![]() ${{{\mathcal {E}}}}$, as defined in (27), Table 8 shows that profit becomes more probable as the review interval,
${{{\mathcal {E}}}}$, as defined in (27), Table 8 shows that profit becomes more probable as the review interval, ![]() $\Delta$, increases. In particular, given that two or more quakes occur in the same interval, the insurance company has a substantial conditional probability,
$\Delta$, increases. In particular, given that two or more quakes occur in the same interval, the insurance company has a substantial conditional probability, ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}\,|\,{{{\mathcal {E}}}}]$, of realizing a profit.
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})>w_{{{\rm I}}}\,|\,{{{\mathcal {E}}}}]$, of realizing a profit.
Table 8. Strategy C: Profit probability on first quake interval with variable reinsurer's markup (![]() $(m,n,\theta )=(2,5,1$),
$(m,n,\theta )=(2,5,1$), ![]() $\alpha =4$,
$\alpha =4$, ![]() $\gamma =4$, and
$\gamma =4$, and ![]() $q=0.1$).
$q=0.1$).

6.2. More than  $k$ reinsurance policies for
$k$ reinsurance policies for  $k$ active sites
$k$ active sites
Because ![]() $g(p,\phi )$ increases with
$g(p,\phi )$ increases with ![]() $\phi$, the insurance company has an incentive to purchase reinsurance in the form of
$\phi$, the insurance company has an incentive to purchase reinsurance in the form of ![]() $\lambda >1$ policies on each active site, each with coverage
$\lambda >1$ policies on each active site, each with coverage ![]() $\phi /\lambda$. Doing so lowers the risk of individual reinsurers, with the result that the insurer's total cost of reinsurance on a site, based on the indifference markup in (29), is
$\phi /\lambda$. Doing so lowers the risk of individual reinsurers, with the result that the insurer's total cost of reinsurance on a site, based on the indifference markup in (29), is
where the inequality follows from Proposition 6.2.
As illustration, Table 9 shows the effect of halving coverage per policy on each site but having ![]() $\lambda =2$ policies on each. Comparing these entries with corresponding results in Table 7 reveals substantial reductions in
$\lambda =2$ policies on each. Comparing these entries with corresponding results in Table 7 reveals substantial reductions in ![]() $\pi ^{\ast }_{{{\rm C}}}$ and
$\pi ^{\ast }_{{{\rm C}}}$ and ![]() $v_{Tn}$ with no change in
$v_{Tn}$ with no change in ![]() ${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ for
${{{\rm pr}}}[\kappa ^{({{{\rm C}}})}(\pi ^{\ast }_{{{\rm C}}})< w_{{{\rm I}}}]$ for ![]() $q=0.01$ and small changes for
$q=0.01$ and small changes for ![]() $q=0.1$. Nevertheless, these loss probabilities remain considerably smaller than those for Strategy B.
$q=0.1$. Nevertheless, these loss probabilities remain considerably smaller than those for Strategy B.
Table 9. Strategy C: Two reinsurers and variable reinsurer markup (![]() $(m,n,\theta )=(2,5,1$),
$(m,n,\theta )=(2,5,1$), ![]() $\gamma =4$, and
$\gamma =4$, and ![]() $\lambda =2$).
$\lambda =2$).

7. Concluding remarks
In contrast to other more conventional forms of insurance such as those mentioned in Embrechts [Reference Embrechts10], an ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy is ideally suited to pricing via the techniques of dynamic hedging developed for pricing financial derivatives. Indeed, if the hedging could be done (nearly) instantaneously (i.e., if, when a quake occurs, new reinsurance could be purchased before another quake occurs) dynamic hedging would remove all risk for the insurer: the policy would become self-financing. Rather than make this strong and probably unrealistic assumption, the present paper uses a combination of probabilistic analysis and utility theory to study the risk of loss on the part of the insurer making dynamic purchases of reinsurance and to compare it to actuarial pricing without reinsurance.
$n$ policy is ideally suited to pricing via the techniques of dynamic hedging developed for pricing financial derivatives. Indeed, if the hedging could be done (nearly) instantaneously (i.e., if, when a quake occurs, new reinsurance could be purchased before another quake occurs) dynamic hedging would remove all risk for the insurer: the policy would become self-financing. Rather than make this strong and probably unrealistic assumption, the present paper uses a combination of probabilistic analysis and utility theory to study the risk of loss on the part of the insurer making dynamic purchases of reinsurance and to compare it to actuarial pricing without reinsurance.
In principle, the techniques used in this paper extend to other insurance products that are contingent claims on events for which there is a reinsurance market. Indeed, the desirable properties of such compound products could serve as an incentive for reinsurers to create and offer products which could be used as components in more complicated products, just as insurance policies on individual sites constitute the components used to price the ![]() $m$-out-of-
$m$-out-of-![]() $n$ policy.
$n$ policy.
Appendix A. Proofs of propositions
Assume ![]() $\Delta =1$ and
$\Delta =1$ and ![]() $\theta =1$. For
$\theta =1$. For ![]() $\Delta >1$,
$\Delta >1$, ![]() $p_\Delta$ replaces
$p_\Delta$ replaces ![]() $p$ and
$p$ and ![]() $\lfloor {{T}/{\Delta }}\rfloor$ replaces
$\lfloor {{T}/{\Delta }}\rfloor$ replaces ![]() $T$.
$T$.
Alternative Proof of Proposition 3.1. This is an alternative proof to the proof by induction in Section 3.1.
Part i. If no quakes occur on coverage days one through ![]() $T$, then the insurance company has anted up
$T$, then the insurance company has anted up
 \begin{align*} ngp\sum_{t=1}^{T}(v_{t-1,n-1}-v_{t-1,n})& = \sum_{t=T}^{1}(v_{tn}-v_{t-1,n}) \\ & = v_{Tn}-v_{0n} \\ & =v_{Tn}. \end{align*}
\begin{align*} ngp\sum_{t=1}^{T}(v_{t-1,n-1}-v_{t-1,n})& = \sum_{t=T}^{1}(v_{tn}-v_{t-1,n}) \\ & = v_{Tn}-v_{0n} \\ & =v_{Tn}. \end{align*} Therefore, any premium, ![]() $\pi$, no less than
$\pi$, no less than ![]() $=v_{Tn}$ would cover that expense, proving part i.
$=v_{Tn}$ would cover that expense, proving part i.
Part ii. Suppose a single quake occurs on each of ![]() $l\in \{1,\ldots,m-1\}$ coverage days,
$l\in \{1,\ldots,m-1\}$ coverage days, ![]() $1\leq s_1<\ldots < s_l\leq T$. Then, on days
$1\leq s_1<\ldots < s_l\leq T$. Then, on days ![]() $s_{i-1}+1$ through
$s_{i-1}+1$ through ![]() $s_{i}$, the insurance company pays a total of
$s_{i}$, the insurance company pays a total of
 \begin{align*} \zeta_i& = (n-i+1)gp\sum_{s=s_{i-1}}^{s_{i}-1}(v_{T-s-1,n-i}-v_{T-s-1,n-i+1}) \\ & =v_{T-s_{i-1},n-i+1}-v_{T-s_{i},n-i+1} \end{align*}
\begin{align*} \zeta_i& = (n-i+1)gp\sum_{s=s_{i-1}}^{s_{i}-1}(v_{T-s-1,n-i}-v_{T-s-1,n-i+1}) \\ & =v_{T-s_{i-1},n-i+1}-v_{T-s_{i},n-i+1} \end{align*}for daily reinsurance coverage and receives
from the reinsurer for the quake on day ![]() $s_i$. For the remaining coverage days, the insurance company pays
$s_i$. For the remaining coverage days, the insurance company pays
 \begin{align*} \zeta_{l+1}& = (n-l)gp\sum_{s=s_l}^{T-1}(v_{T-s-1,n-l}-v_{T-s-1,n-l+1}) \\ & = v_{T-s_l,n-l+1}-v_{0,n-l+1}. \end{align*}
\begin{align*} \zeta_{l+1}& = (n-l)gp\sum_{s=s_l}^{T-1}(v_{T-s-1,n-l}-v_{T-s-1,n-l+1}) \\ & = v_{T-s_l,n-l+1}-v_{0,n-l+1}. \end{align*} Then, the change in working capital during the ![]() $T$ days is
$T$ days is
 \begin{align*} -\zeta_{l+1}+\sum_{i=1}^{l}(-\zeta_i+\lambda_i) & ={-}v_{T-s_l,n-l+1}-v_{0,n-l+1} +\sum_{i=1}^{l}(v_{T-s_i,n-i}-v_{T-s_{i-1},n-i+1})\\ & =v_{T-s_l,n-l}-v_{T-s_l,n-l+1}-v_{0,n-l+1}-v_{Tn} \end{align*}
\begin{align*} -\zeta_{l+1}+\sum_{i=1}^{l}(-\zeta_i+\lambda_i) & ={-}v_{T-s_l,n-l+1}-v_{0,n-l+1} +\sum_{i=1}^{l}(v_{T-s_i,n-i}-v_{T-s_{i-1},n-i+1})\\ & =v_{T-s_l,n-l}-v_{T-s_l,n-l+1}-v_{0,n-l+1}-v_{Tn} \end{align*} Expression (8) implies ![]() $v_{0,n-l+1}=0$ for
$v_{0,n-l+1}=0$ for ![]() $l< m$. Because
$l< m$. Because ![]() $\{v_{tk}\}$ is non-increasing in
$\{v_{tk}\}$ is non-increasing in ![]() $k$ (see Proposition 3.2),
$k$ (see Proposition 3.2), ![]() $v_{T-s_l,n-l}-v_{T-s_l,n-l+1}\geq 0$. Therefore,
$v_{T-s_l,n-l}-v_{T-s_l,n-l+1}\geq 0$. Therefore,
 \begin{align*} \kappa^{({{{\rm C}}})}(\pi)-w_{{{\rm I}}}& = \pi+v_{T-s_l,n-l}-v_{T-s_l,n-l+1}-v_{0,n-l+1}-v_{Tn}\\ & =\pi-v_{Tn}\geq 0, \end{align*}
\begin{align*} \kappa^{({{{\rm C}}})}(\pi)-w_{{{\rm I}}}& = \pi+v_{T-s_l,n-l}-v_{T-s_l,n-l+1}-v_{0,n-l+1}-v_{Tn}\\ & =\pi-v_{Tn}\geq 0, \end{align*}proving part ii.
Part iii. Suppose ![]() $r\in \{1,\ldots, n-m+1\}$ quakes occur on the
$r\in \{1,\ldots, n-m+1\}$ quakes occur on the ![]() $m$th quake day. On days
$m$th quake day. On days ![]() $s_{m-1}+1$ through
$s_{m-1}+1$ through ![]() $s_m$, the insurance company had paid out
$s_m$, the insurance company had paid out ![]() $\zeta _m$ for daily reinsurance and on day
$\zeta _m$ for daily reinsurance and on day ![]() $s_m$ receives
$s_m$ receives ![]() $\lambda _m$ as a payout from the reinsurer for the
$\lambda _m$ as a payout from the reinsurer for the ![]() $r$ quakes, where
$r$ quakes, where
The insurance company also pays out one dollar to the customer. The resulting change in capital during the total coverage interval is
 \begin{align*} \kappa^{({{{\rm C}}})}(\pi)-w_{{{\rm I}}} & = \pi+\sum_{i=1}^{m}(v_{T-s_i,n-i}-v_{T-s_{i-1},n-i+1})+(k-1)(v_{T-s_m,n-m}-v_{T-s_m,n-m+1})-\theta \\ & = \pi+v_{T-s_m,n-m}-v_{Tn}+(r-1)(v_{T-s_m,n-m}-v_{T-s_m,n-m+1})-\theta. \end{align*}
\begin{align*} \kappa^{({{{\rm C}}})}(\pi)-w_{{{\rm I}}} & = \pi+\sum_{i=1}^{m}(v_{T-s_i,n-i}-v_{T-s_{i-1},n-i+1})+(k-1)(v_{T-s_m,n-m}-v_{T-s_m,n-m+1})-\theta \\ & = \pi+v_{T-s_m,n-m}-v_{Tn}+(r-1)(v_{T-s_m,n-m}-v_{T-s_m,n-m+1})-\theta. \end{align*} From (8), ![]() $v_{T-s_m,n-m}=\theta$,
$v_{T-s_m,n-m}=\theta$, ![]() $\kappa ^{({{{\rm C}}})}(\pi )-w_{{{\rm I}}}\geq 0$ for
$\kappa ^{({{{\rm C}}})}(\pi )-w_{{{\rm I}}}\geq 0$ for ![]() $\pi \geq v_{Tn}$, proving part iii.
$\pi \geq v_{Tn}$, proving part iii.
Proof of Proposition 3.2. For ![]() $t=0$, we have
$t=0$, we have
so that ![]() $v_{0k}$ is non-increasing in
$v_{0k}$ is non-increasing in ![]() $n-m \leq k \leq n$.
$n-m \leq k \leq n$.
Let ![]() $0 \leq t \leq T-1$ and suppose
$0 \leq t \leq T-1$ and suppose ![]() $v_{tk}$ is non-increasing (the induction hypothesis). From (12), we have, for
$v_{tk}$ is non-increasing (the induction hypothesis). From (12), we have, for ![]() $n-m+1 \leq k \leq n-1$,
$n-m+1 \leq k \leq n-1$,
 \begin{align} v_{t+1,k+1} - v_{t+1,k} & = (k+1)gp v_{tk} + [1 - (k+1)gp] v_{t,k+1}- k gp v_{t,k-1} - (1 - k gp)v_{tk} \nonumber\\ & = k gp (v_{tk} - v_{t,k-1}) + gp v_{tk} + [1 - (k+1)gp] (v_{t,k+1} - v_{tk}) - gp v_{tk} \nonumber\\ & = k gp (v_{tk} - v_{t,k-1}) + [1 - (k+1)gp] (v_{t,k+1} - v_{tk})\nonumber\\ & \leq 0, \end{align}
\begin{align} v_{t+1,k+1} - v_{t+1,k} & = (k+1)gp v_{tk} + [1 - (k+1)gp] v_{t,k+1}- k gp v_{t,k-1} - (1 - k gp)v_{tk} \nonumber\\ & = k gp (v_{tk} - v_{t,k-1}) + gp v_{tk} + [1 - (k+1)gp] (v_{t,k+1} - v_{tk}) - gp v_{tk} \nonumber\\ & = k gp (v_{tk} - v_{t,k-1}) + [1 - (k+1)gp] (v_{t,k+1} - v_{tk})\nonumber\\ & \leq 0, \end{align}and for ![]() $k = n-m$,
$k = n-m$,
 \begin{align} v_{t+1,k+1} - v_{t+1,k} & = v_{t+1,n-m+1} - v_{t+1,n-m} \nonumber\\ & = (n-m+1)gp v_{t,n-m} + [1 -(n-m+1)gp] v_{t,n-m+1} - v_{t+1,n-m}\nonumber\\ & \leq (n-m+1)gp + \theta - (n+m-1)gp - \theta \nonumber\\ & = \theta - \theta \nonumber\\ & \leq 0, \end{align}
\begin{align} v_{t+1,k+1} - v_{t+1,k} & = v_{t+1,n-m+1} - v_{t+1,n-m} \nonumber\\ & = (n-m+1)gp v_{t,n-m} + [1 -(n-m+1)gp] v_{t,n-m+1} - v_{t+1,n-m}\nonumber\\ & \leq (n-m+1)gp + \theta - (n+m-1)gp - \theta \nonumber\\ & = \theta - \theta \nonumber\\ & \leq 0, \end{align}so that
It follows by induction on ![]() $t$ that
$t$ that ![]() $\{v_{tk}\}$ is non-increasing in
$\{v_{tk}\}$ is non-increasing in ![]() $k$,
$k$, ![]() $n-m \leq k \leq n$, for all
$n-m \leq k \leq n$, for all ![]() $0 \leq t \leq T$.
$0 \leq t \leq T$.
Proof of Proposition 6.1. Assume ![]() $\phi =1$. We determine conditions under which
$\phi =1$. We determine conditions under which ![]() $g'(p) < 0$, that is, the indifference markup decreases as the probability of loss increases (or, equivalently, the indifference markup increases as the probability of loss decreases). Differentiating both sides of (28) with respect to
$g'(p) < 0$, that is, the indifference markup decreases as the probability of loss increases (or, equivalently, the indifference markup increases as the probability of loss decreases). Differentiating both sides of (28) with respect to ![]() $p$ yields (upon setting
$p$ yields (upon setting ![]() $\pi = g(p)p$)
$\pi = g(p)p$)
or equivalently,
Solving for ![]() $g'(p)$ we obtain
$g'(p)$ we obtain
Since the denominator is positive (because ![]() $u(\cdot )$ is increasing), to show
$u(\cdot )$ is increasing), to show ![]() $g'(p) < 0$ it is (necessary and) sufficient to show that
$g'(p) < 0$ it is (necessary and) sufficient to show that
or equivalently,
Because ![]() $p [u(w+\pi ) - u(w+\pi -1)] = u(w+\pi ) - u(w)$ (from (28)) this inequality is, in turn, equivalent to
$p [u(w+\pi ) - u(w+\pi -1)] = u(w+\pi ) - u(w)$ (from (28)) this inequality is, in turn, equivalent to
Note that both sides of (A.5) approach ![]() $u'(w)$ as
$u'(w)$ as ![]() $p$ approaches zero. Therefore, to show (A.5) it suffices to show that for all
$p$ approaches zero. Therefore, to show (A.5) it suffices to show that for all ![]() $p > 0$ and
$p > 0$ and ![]() $\pi = g(p) p$,
$\pi = g(p) p$,
The first of these inequalities follows from the (strict) concavity of ![]() $u(\cdot )$. For the second inequality, we shall need another condition on
$u(\cdot )$. For the second inequality, we shall need another condition on ![]() $u(\cdot )$ (in addition to strictly increasing and strictly concave), namely,
$u(\cdot )$ (in addition to strictly increasing and strictly concave), namely,
Under this condition (strict convexity of ![]() $u'(\cdot )$) we have
$u'(\cdot )$) we have ![]() $(1-p) u'(w+\pi ) + p u'(w+\pi -1) > u'(w)$, since
$(1-p) u'(w+\pi ) + p u'(w+\pi -1) > u'(w)$, since ![]() $w+\pi -1 < w < w+\pi$.
$w+\pi -1 < w < w+\pi$.
Note that condition (A.6) is satisfied if the utility function ![]() $u(\cdot )$ has the property that the Arrow-Pratt measure of absolute risk aversion [Reference Arrow2,Reference Pratt16],
$u(\cdot )$ has the property that the Arrow-Pratt measure of absolute risk aversion [Reference Arrow2,Reference Pratt16],
is decreasing in ![]() $w$. This is a common requirement in utility theory because it is consistent with the property that an individual's aversion to risk does not increase as his wealth increases.
$w$. This is a common requirement in utility theory because it is consistent with the property that an individual's aversion to risk does not increase as his wealth increases.
Proof of Proposition 6.2. For conciseness of notation, let ![]() $g=g(p,\phi )$. Recall that
$g=g(p,\phi )$. Recall that ![]() $\{u(w),\ -\infty < w<\infty \}$ denotes the reinsurer's concave increasing utlity function. For given initial reinsurer's wealth,
$\{u(w),\ -\infty < w<\infty \}$ denotes the reinsurer's concave increasing utlity function. For given initial reinsurer's wealth, ![]() $w_{{{\rm R}}}$, and
$w_{{{\rm R}}}$, and ![]() $p \in [0,1]$, let
$p \in [0,1]$, let
 \begin{align} \psi(g,\phi)& := (1-p) u(w_{{{\rm R}}}+g p \phi) + p u(w_{{{\rm R}}}+g p \phi - \phi) - u(w_{{{\rm R}}}) \quad g \geq 1\text{ and }\phi > 0 \nonumber\\ & = \left(\begin{array}{c} \text{difference between the expected utilities of the} \\ \text{reinsurer's ending wealth and his initial wealth} \end{array}\right). \end{align}
\begin{align} \psi(g,\phi)& := (1-p) u(w_{{{\rm R}}}+g p \phi) + p u(w_{{{\rm R}}}+g p \phi - \phi) - u(w_{{{\rm R}}}) \quad g \geq 1\text{ and }\phi > 0 \nonumber\\ & = \left(\begin{array}{c} \text{difference between the expected utilities of the} \\ \text{reinsurer's ending wealth and his initial wealth} \end{array}\right). \end{align} Then, the reinsurer is indifferent between offering and not offering the reinsurance at all points ![]() $(g,\phi )$ satisfying
$(g,\phi )$ satisfying
For given ![]() $g > 1$, let
$g > 1$, let ![]() $\phi (g)$ denote the maximal value of
$\phi (g)$ denote the maximal value of ![]() $\phi$ satisfying (A.8), and for given
$\phi$ satisfying (A.8), and for given ![]() $\phi$, let
$\phi$, let ![]() $g(\phi )$ denote the minimal value of
$g(\phi )$ denote the minimal value of ![]() $g$ satisfying (A.8), where the dependence on the fixed values of
$g$ satisfying (A.8), where the dependence on the fixed values of ![]() $w_{{{\rm R}}}$ and
$w_{{{\rm R}}}$ and ![]() $p$ have been suppressed. We determine conditions under which
$p$ have been suppressed. We determine conditions under which ![]() $g^{\prime }(\phi ) > 0$, for all
$g^{\prime }(\phi ) > 0$, for all ![]() $\phi > 0$.
$\phi > 0$.
Setting ![]() $g = g(\phi )$ in (A.7) and differentiating both sides of (A.8) with respect to
$g = g(\phi )$ in (A.7) and differentiating both sides of (A.8) with respect to ![]() $\phi$ yield
$\phi$ yield
Rearranging terms and setting ![]() $\zeta = g(\phi ) p \phi$ yield
$\zeta = g(\phi ) p \phi$ yield
Because the r.h.s denominator is positive, the condition
suffices for ![]() $g'(\phi )>0$ for all
$g'(\phi )>0$ for all ![]() $\phi >0$. To show this, consider a different problem:
$\phi >0$. To show this, consider a different problem:
• Find the value of
 $\phi$ that maximizes
$\phi$ that maximizes  $\psi (g,\phi )$ for a given value of
$\psi (g,\phi )$ for a given value of  $g > 1$.
$g > 1$.
Because ![]() $\{u(w)\}$ is concave in
$\{u(w)\}$ is concave in ![]() $w$,
$w$, ![]() $\{\psi (g,\phi )\}$ is concave in
$\{\psi (g,\phi )\}$ is concave in ![]() $\phi$ and, therefore, maximized at
$\phi$ and, therefore, maximized at ![]() $\phi ^{*}(g)$, where
$\phi ^{*}(g)$, where
 $$\left.\frac{\partial \psi(g,\phi)}{\partial \phi}\right|_{\phi=\phi^{{\ast}}(g)} = p [ (g (1-p) u^{\prime} (w_{{{\rm R}}}+g p \phi) - (1 - g p) u^{\prime} (w_{{{\rm R}}}+g p \phi - \phi)] = 0.$$
$$\left.\frac{\partial \psi(g,\phi)}{\partial \phi}\right|_{\phi=\phi^{{\ast}}(g)} = p [ (g (1-p) u^{\prime} (w_{{{\rm R}}}+g p \phi) - (1 - g p) u^{\prime} (w_{{{\rm R}}}+g p \phi - \phi)] = 0.$$ Equivalently, at ![]() $\phi =\phi ^{\ast }(g)$
$\phi =\phi ^{\ast }(g)$
But
for ![]() $\phi > \phi ^{\ast }(g)$, in particular, for
$\phi > \phi ^{\ast }(g)$, in particular, for ![]() $\phi = \phi (g)$ or, equivalently, for
$\phi = \phi (g)$ or, equivalently, for ![]() $g = g(\phi )$. Therefore, (A.10) is satisfied, implying that
$g = g(\phi )$. Therefore, (A.10) is satisfied, implying that ![]() $g^{\prime }(\phi ) > 0$.
$g^{\prime }(\phi ) > 0$.
Appendix B. Computing  $\pi ^{\ast }_{{{\rm C}}}$
$\pi ^{\ast }_{{{\rm C}}}$
Assume the availability of the ![]() $\{v_{tk}\}$ schedule computed in (12) for constant reinusrer's markup,
$\{v_{tk}\}$ schedule computed in (12) for constant reinusrer's markup, ![]() $g$, and review interval,
$g$, and review interval, ![]() $\Delta =1$. For a variable markup, (31) replaces (12). For
$\Delta =1$. For a variable markup, (31) replaces (12). For ![]() $\Delta >1$,
$\Delta >1$, ![]() $p_\Delta$ replaces
$p_\Delta$ replaces ![]() $p$ and
$p$ and ![]() $\lfloor {{T}/{\Delta }}\rfloor$ replaces
$\lfloor {{T}/{\Delta }}\rfloor$ replaces ![]() $T$. From expression (32) for (random) final working capital,
$T$. From expression (32) for (random) final working capital, ![]() $\kappa ^{({{{\rm C}}})}( \pi )$, it follows that the insurance company's random total payout (the difference between initial and final working capital) is given by
$\kappa ^{({{{\rm C}}})}( \pi )$, it follows that the insurance company's random total payout (the difference between initial and final working capital) is given by
 \begin{equation} w_{{{\rm I}}} + \pi - \kappa^{({{{\rm C}}})}(\pi) = \sum_{s=T}^{\max(0,T-L)} [(g p K_s - (K_s - K_{s-1}) )(v_{s-1,K_{s-1}} - v_{s-1,K_s}) + \theta I_{K_{s-1} \leq n-m} ]. \end{equation}
\begin{equation} w_{{{\rm I}}} + \pi - \kappa^{({{{\rm C}}})}(\pi) = \sum_{s=T}^{\max(0,T-L)} [(g p K_s - (K_s - K_{s-1}) )(v_{s-1,K_{s-1}} - v_{s-1,K_s}) + \theta I_{K_{s-1} \leq n-m} ]. \end{equation} Note that the expression on the r.h.s. of the equality is independent of both ![]() $w_{{{\rm I}}}$ and
$w_{{{\rm I}}}$ and ![]() $\pi$. Because the total payout equals
$\pi$. Because the total payout equals ![]() $v_{Tn}$ if no more than one site has a quake on any day, (B.1) is equivalent to
$v_{Tn}$ if no more than one site has a quake on any day, (B.1) is equivalent to
where
 $$H_T:=\left(\begin{array}{c} \text{the insurance company's total additional expenditure} \\ \text{over the coverage interval as a result of quake days} \\ \text{on which more than one site has a quake} \end{array}\right).$$
$$H_T:=\left(\begin{array}{c} \text{the insurance company's total additional expenditure} \\ \text{over the coverage interval as a result of quake days} \\ \text{on which more than one site has a quake} \end{array}\right).$$Therefore,
where ![]() $\pi ^{\ast }_{{{\rm C}}}$ satisfies the indifference equation
$\pi ^{\ast }_{{{\rm C}}}$ satisfies the indifference equation
which in the case of the exponential utility function, ![]() $u(x) = - {{{\rm e}}}^{- \alpha x}$, reduces to
$u(x) = - {{{\rm e}}}^{- \alpha x}$, reduces to
where
Therefore, it remains to calculate ![]() ${{{{\rm E}}}}({{{\rm e}}}^{\alpha H_T})$.
${{{{\rm E}}}}({{{\rm e}}}^{\alpha H_T})$.
Define
By way of interpretation, suppose the working capital at the beginning of remaining day ![]() $t$ is
$t$ is ![]() $v_{tk}$; that is, the amount dictated by the entry in the
$v_{tk}$; that is, the amount dictated by the entry in the ![]() $\{v_{tk}\}$ schedule for
$\{v_{tk}\}$ schedule for ![]() $k$ active sites. If
$k$ active sites. If ![]() $j$ quakes occur on remaining day
$j$ quakes occur on remaining day ![]() $t$, then
$t$, then ![]() $\eta _{tkj}$ is the amount that the insurance company must ante up at the end of the day in order to restore the working capital at the beginning of the next day to the level,
$\eta _{tkj}$ is the amount that the insurance company must ante up at the end of the day in order to restore the working capital at the beginning of the next day to the level, ![]() $v_{t-1,k-j}$, dictated by the schedule. Note that
$v_{t-1,k-j}$, dictated by the schedule. Note that ![]() $\eta _{tkj} \geq 0$ for all
$\eta _{tkj} \geq 0$ for all ![]() $j\in \{0,1,\ldots,k\}$ and
$j\in \{0,1,\ldots,k\}$ and ![]() $\eta _{tkj}= 0$ for
$\eta _{tkj}= 0$ for ![]() $j=0,1$. Moreover, for
$j=0,1$. Moreover, for ![]() $k\in \{0,1,\ldots, n-m\}$,
$k\in \{0,1,\ldots, n-m\}$, ![]() $\eta _{tkj}=0$ for all
$\eta _{tkj}=0$ for all ![]() $j\in \{0,1,\ldots,k\}$, whereas for
$j\in \{0,1,\ldots,k\}$, whereas for ![]() $k=n-m+1$,
$k=n-m+1$,
Recall that ![]() $K_t$ denotes the random number of active sites at the beginning of remaining day
$K_t$ denotes the random number of active sites at the beginning of remaining day ![]() $t$ and
$t$ and ![]() $J_t: = K_t - K_{t-1}$, the random number of sites that have quakes on remaining day
$J_t: = K_t - K_{t-1}$, the random number of sites that have quakes on remaining day ![]() $t$, so that the random ante required at the end of remaining day
$t$, so that the random ante required at the end of remaining day ![]() $t$ is
$t$ is ![]() $\eta _{t,K_t,J_t}$. Also, recall that coverage starts on remaining day
$\eta _{t,K_t,J_t}$. Also, recall that coverage starts on remaining day ![]() $T$ with
$T$ with ![]() $n$ active sites, so that
$n$ active sites, so that ![]() $K_T = n$. Define
$K_T = n$. Define
 \begin{align*} H_t& := \sum_{\tau=t}^{1} \eta_{\tau,K_\tau,J_\tau} \\ & = \left(\begin{array}{c} \text{the (random) total amount that the insurance } \\ \text{company antes up on remaining days} \\ \tau=t \,\text{through} \, \tau=1 \end{array}\right),\quad t \in \{1,\ldots,T\}. \end{align*}
\begin{align*} H_t& := \sum_{\tau=t}^{1} \eta_{\tau,K_\tau,J_\tau} \\ & = \left(\begin{array}{c} \text{the (random) total amount that the insurance } \\ \text{company antes up on remaining days} \\ \tau=t \,\text{through} \, \tau=1 \end{array}\right),\quad t \in \{1,\ldots,T\}. \end{align*}The quantity ![]() $H_T$ is the insurance company's total additional expenditure over the coverage interval as a result of quake days on which more than one site has a quake.
$H_T$ is the insurance company's total additional expenditure over the coverage interval as a result of quake days on which more than one site has a quake.
Define
The following backward recursive algorithm calculates ![]() $z_{tk}$ recursively for
$z_{tk}$ recursively for ![]() $k \in \{ 0,\ldots,n\}$ and
$k \in \{ 0,\ldots,n\}$ and ![]() $t \in \{1,\ldots,T\}$:
$t \in \{1,\ldots,T\}$:
 \begin{align} z_{tk} & = \sum_{j=0}^{k} f(j;k,p) {\rm E}({{{\rm e}}}^{\alpha H_t} \,|\, K_t = k,J_t=j) \nonumber\\ & =\sum_{j=0}^{k} f(j;k,p) {\rm E}({{{\rm e}}}^{\alpha (\eta_{tkj} + H_{t-1})} \,|\, K_t = k,J_t=j) \nonumber\\ & = \sum_{j=0}^{k} f(j;k,p) {{{\rm e}}}^{\alpha \eta_{tkj}} {\rm E}({{{\rm e}}}^{\alpha H_{t-1}} \,|\, K_{t-1} = k-j) \nonumber\\ & = \sum_{j=0}^{k} f(j;k,p) {{{\rm e}}}^{\alpha \eta_{tkj}} z_{t-1,k-j}, \end{align}
\begin{align} z_{tk} & = \sum_{j=0}^{k} f(j;k,p) {\rm E}({{{\rm e}}}^{\alpha H_t} \,|\, K_t = k,J_t=j) \nonumber\\ & =\sum_{j=0}^{k} f(j;k,p) {\rm E}({{{\rm e}}}^{\alpha (\eta_{tkj} + H_{t-1})} \,|\, K_t = k,J_t=j) \nonumber\\ & = \sum_{j=0}^{k} f(j;k,p) {{{\rm e}}}^{\alpha \eta_{tkj}} {\rm E}({{{\rm e}}}^{\alpha H_{t-1}} \,|\, K_{t-1} = k-j) \nonumber\\ & = \sum_{j=0}^{k} f(j;k,p) {{{\rm e}}}^{\alpha \eta_{tkj}} z_{t-1,k-j}, \end{align}where, most notably,
 \begin{align*} z_{Tn} & = {{{\rm E}}} ({{{\rm e}}}^{\alpha H_T} \,|\, K_T = n) \\ & = {{{\rm E}}}({{{\rm e}}}^{\alpha H_T}). \end{align*}
\begin{align*} z_{Tn} & = {{{\rm E}}} ({{{\rm e}}}^{\alpha H_T} \,|\, K_T = n) \\ & = {{{\rm E}}}({{{\rm e}}}^{\alpha H_T}). \end{align*}