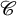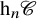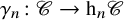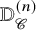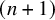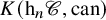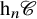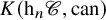1 Introduction
It has long been understood in homotopy theory that the homotopy category is only a crude invariant of a much richer homotopy-theoretic structure. The problem of finding a suitable formalism for this additional structure, one that encodes homotopy-theoretic extensions of ordinary categorical notions, led to several foundational approaches, each with its own distinctive advantages and special characteristics. The theory of ![]() $\infty $-categories (or quasi–categories) [Reference Joyal20, Reference Lurie21, Reference Lurie22, Reference Cisinski4] is one of several successful approaches to develop useful foundations for the study of homotopy theories and has led to groundbreaking new perspectives and results in the field.
$\infty $-categories (or quasi–categories) [Reference Joyal20, Reference Lurie21, Reference Lurie22, Reference Cisinski4] is one of several successful approaches to develop useful foundations for the study of homotopy theories and has led to groundbreaking new perspectives and results in the field.
Even though passing to the homotopy category certainly neglects homotopy-theoretic information, the general problem of understanding how much information this process retains still poses interesting questions in specific contexts. This has inspired many important developments, for example, in the context of rigidity theorems for homotopy theories [Reference Franke12, Reference Schwede35, Reference Roitzheim33, Reference Patchkoria31], derived/homotopical Morita and tilting theory (see [Reference Schwede36] for a nice survey) or in connection with K-theory regarded as an invariant of homotopy theories [Reference Dugger and Shipley9, Reference Neeman28, Reference Schlichting34, Reference Maltsiniotis24].
The theory of derivators, first introduced and developed by Grothendieck [Reference Grothendieck16], Heller [Reference Heller19] and Franke [Reference Franke12], is a different foundational approach based on the idea of considering the homotopy categories of all diagram categories as a remedy to the defects of the homotopy category (see also [Reference Groth18]). By supplementing the homotopy category with the network of all these (homotopy) categories, it is possible to encode the collection of homotopy (co)limit functors and general homotopy Kan extensions as an enhancement of the homotopy category. This approach provides a different, lower (= 2–) categorical formalism for expressing homotopy-theoretic universal properties (see [Reference Cisinski5] and [Reference Tabuada37, Reference Cisinski and Tabuada7] for some interesting applications). Moreover, Maltsiniotis [Reference Maltsiniotis24] defined K-theory in the context of derivators with a view towards partially recovering Waldhausen K-theory from the derivator. The K-theory of derivators and its comparison with Waldhausen K-theory has been studied extensively in [Reference Cisinski and Neeman6, Reference Garkusha14, Reference Garkusha15, Reference Maltsiniotis24, Reference Muro25, Reference Muro and Raptis26, Reference Muro and Raptis27]. In the context of the theory of derivators, the question about the information retained by the homotopy category is then upgraded to the analogous question for the derivator. The theory of derivators still does not provide in general faithful representations of homotopy theories; however, it is possible in certain cases to recover in a non-canonical way the homotopy theory from the derivator (see [Reference Renaudin32]).
The purpose of this paper is to extend these ideas on the comparison between homotopy theories and homotopy categories or derivators to n-categories (= ![]() $(n,1)$-categories), where the ordinary homotopy category is now replaced by the homotopy n-category of an
$(n,1)$-categories), where the ordinary homotopy category is now replaced by the homotopy n-category of an ![]() $\infty $-category. More specifically:
$\infty $-category. More specifically:
(a) Higher homotopy categories. Using the definition of the higher homotopy categories by Lurie [Reference Lurie22], we consider the tower of homotopy n-categories
 $\{\mathrm {h}_n \mathscr {C}\}_{n \geq 1}$ associated to an
$\{\mathrm {h}_n \mathscr {C}\}_{n \geq 1}$ associated to an  $\infty $-category
$\infty $-category  $\mathscr {C}$, together with the canonical (localization) functors
$\mathscr {C}$, together with the canonical (localization) functors  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n\mathscr {C}$, and we analyse the properties of
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n\mathscr {C}$, and we analyse the properties of  $\mathrm {h}_n\mathscr {C}$ inherited from
$\mathrm {h}_n\mathscr {C}$ inherited from  $\mathscr {C}$. (Sections 2–3, 6.1–6.2)
$\mathscr {C}$. (Sections 2–3, 6.1–6.2)(b) Higher derivators. We introduce a higher categorical notion of a derivator that takes values in n-categories. Then we develop the basic theory of higher derivators with a special emphasis on the examples that arise from
 $\infty $-categories. (Section 4)
$\infty $-categories. (Section 4)(c) K-theory of higher derivators. We extend the definition of derivator K-theory by Maltsiniotis [Reference Maltsiniotis24] and Garkusha [Reference Garkusha14, Reference Garkusha15] to n-derivators and study the comparison map from Waldhausen K-theory. Our main result shows that the comparison map is
 $(n+1)$-connected (Theorem 5.5). Moreover, following [Reference Muro and Raptis26], we prove that this comparison map has a universal property (Theorem 5.13).
$(n+1)$-connected (Theorem 5.5). Moreover, following [Reference Muro and Raptis26], we prove that this comparison map has a universal property (Theorem 5.13).(d) K-theory of homotopy n-categories. In analogy with the K-theory of triangulated categories [Reference Neeman28], we introduce K-theory for n-categories equipped with distinguished squares. In the case of a homotopy n-category, we study the comparison map from Waldhausen K-theory and prove that it is n-connected (Theorem 6.5).
(a) Higher homotopy categories. Every ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ has an associated homotopy n-category
$\mathscr {C}$ has an associated homotopy n-category ![]() $\mathrm {h}_n \mathscr {C}$ and a canonical functor
$\mathrm {h}_n \mathscr {C}$ and a canonical functor ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. The construction of the homotopy n-category and its properties are studied in [Reference Lurie22]. We will review this construction and its properties in Section 2. Intuitively, for
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. The construction of the homotopy n-category and its properties are studied in [Reference Lurie22]. We will review this construction and its properties in Section 2. Intuitively, for ![]() $n \geq 1$,
$n \geq 1$, ![]() $\mathrm {h}_n \mathscr {C}$ is an
$\mathrm {h}_n \mathscr {C}$ is an ![]() $\infty $-category with the same objects as
$\infty $-category with the same objects as ![]() $\mathscr {C}$ and whose mapping spaces are the appropriate Postnikov truncations of the mapping spaces in
$\mathscr {C}$ and whose mapping spaces are the appropriate Postnikov truncations of the mapping spaces in ![]() $\mathscr {C}$. For
$\mathscr {C}$. For ![]() $n=1$, the homotopy category
$n=1$, the homotopy category ![]() $\mathrm {h}_1 \mathscr {C}$ is the ordinary homotopy category of
$\mathrm {h}_1 \mathscr {C}$ is the ordinary homotopy category of ![]() $\mathscr {C}$. The collection of homotopy n-categories defines a tower of
$\mathscr {C}$. The collection of homotopy n-categories defines a tower of ![]() $\infty $-categories
$\infty $-categories
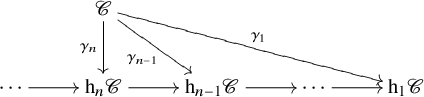
that approximates ![]() $\mathscr {C}$. One of the defects of the homotopy category
$\mathscr {C}$. One of the defects of the homotopy category ![]() $\mathrm {h}_1 \mathscr {C}$, which is essentially what the theory of derivators tries to rectify, is that it does not in general inherit (co)limits from
$\mathrm {h}_1 \mathscr {C}$, which is essentially what the theory of derivators tries to rectify, is that it does not in general inherit (co)limits from ![]() $\mathscr {C}$. As a general rule, if
$\mathscr {C}$. As a general rule, if ![]() $\mathscr {C}$ admits (co)limits, then
$\mathscr {C}$ admits (co)limits, then ![]() $\mathrm {h}_1 \mathscr {C}$ admits only weak (co)limits – which may or may not be induced from
$\mathrm {h}_1 \mathscr {C}$ admits only weak (co)limits – which may or may not be induced from ![]() $\mathscr {C}$. (We recall that a weak colimit of a diagram is a cocone on the diagram that admits a morphism to every other such cocone, but this morphism may not be unique in general.) Do the higher homotopy categories have better inheritance properties for (co)limits, and in what sense? This question is closely related to the problem of understanding how much information
$\mathscr {C}$. (We recall that a weak colimit of a diagram is a cocone on the diagram that admits a morphism to every other such cocone, but this morphism may not be unique in general.) Do the higher homotopy categories have better inheritance properties for (co)limits, and in what sense? This question is closely related to the problem of understanding how much information ![]() $\mathrm {h}_n \mathscr {C}$ retains from
$\mathrm {h}_n \mathscr {C}$ retains from ![]() $\mathscr {C}$. We introduce a higher categorical version of weak (co)limit in order to address this question. In analogy with ordinary weak (co)limits, a higher weak colimit is a cocone for which the mapping spaces to other cocones are highly connected but not necessarily contractible. The relative strength of the weak colimit is measured by how highly connected these mapping spaces are; the connectivity of these mapping spaces determines the order of the weak colimit. The properties of higher weak (co)limits will be discussed in Section 3. For any simplicial set K, there is a canonical functor
$\mathscr {C}$. We introduce a higher categorical version of weak (co)limit in order to address this question. In analogy with ordinary weak (co)limits, a higher weak colimit is a cocone for which the mapping spaces to other cocones are highly connected but not necessarily contractible. The relative strength of the weak colimit is measured by how highly connected these mapping spaces are; the connectivity of these mapping spaces determines the order of the weak colimit. The properties of higher weak (co)limits will be discussed in Section 3. For any simplicial set K, there is a canonical functor
which is usually not an equivalence. The properties of this functor are relevant for understanding the interaction of K-colimits in ![]() $\mathscr {C}$ and in
$\mathscr {C}$ and in ![]() $\mathrm {h}_n \mathscr {C}$. One of our conclusions (Corollary 3.17) is the following:
$\mathrm {h}_n \mathscr {C}$. One of our conclusions (Corollary 3.17) is the following:
Moreover, in connection with higher weak colimits in ![]() $\mathrm {h}_n \mathscr {C}$, we also conclude (Corollary 3.22):
$\mathrm {h}_n \mathscr {C}$, we also conclude (Corollary 3.22):
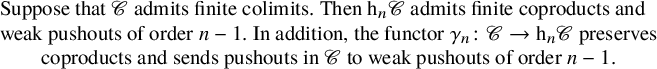 $$ \begin{align*} &\text{Suppose that}\ \mathscr{C}\ \text{admits finite colimits. Then}\ \mathrm{h}_n \mathscr{C}\ \text{admits finite coproducts and}\\[-3pt]& \text{weak pushouts of order}\ n-1.\ \text{In addition, the functor}\ \gamma_n \colon \mathscr{C} \to \mathrm{h}_n \mathscr{C}\ \text{preserves}\\[-3pt] &\qquad\text{coproducts and sends pushouts in}\ \mathscr{C}\ \text{to weak pushouts of order}\ n-1. \end{align*} $$
$$ \begin{align*} &\text{Suppose that}\ \mathscr{C}\ \text{admits finite colimits. Then}\ \mathrm{h}_n \mathscr{C}\ \text{admits finite coproducts and}\\[-3pt]& \text{weak pushouts of order}\ n-1.\ \text{In addition, the functor}\ \gamma_n \colon \mathscr{C} \to \mathrm{h}_n \mathscr{C}\ \text{preserves}\\[-3pt] &\qquad\text{coproducts and sends pushouts in}\ \mathscr{C}\ \text{to weak pushouts of order}\ n-1. \end{align*} $$These properties of homotopy n-categories ![]() $\mathrm {h}_n\mathscr {C}$ single out a class of n-categories for each
$\mathrm {h}_n\mathscr {C}$ single out a class of n-categories for each ![]() $n \geq 1$, called (finitely) weakly cocomplete n-categories (Definition 3.23). These classes of
$n \geq 1$, called (finitely) weakly cocomplete n-categories (Definition 3.23). These classes of ![]() $\infty $-categories form a sequence of refinements between ordinary categories with (finite) coproducts and weak pushouts and (finitely) cocomplete
$\infty $-categories form a sequence of refinements between ordinary categories with (finite) coproducts and weak pushouts and (finitely) cocomplete ![]() $\infty $-categories. We explore further the properties of these n-categories in connection with adjoint functor theorems and (higher) Brown representability in joint work with H. K. Nguyen and C. Schrade [Reference Nguyen, Raptis and Schrade30] (building on and extending our previous joint work in [Reference Nguyen, Raptis and Schrade29]).
$\infty $-categories. We explore further the properties of these n-categories in connection with adjoint functor theorems and (higher) Brown representability in joint work with H. K. Nguyen and C. Schrade [Reference Nguyen, Raptis and Schrade30] (building on and extending our previous joint work in [Reference Nguyen, Raptis and Schrade29]).
(b) Higher derivators. The main example of a (pre)derivator is given by the 2-functor that sends a small category I to the homotopy category ![]() $\mathrm {h}_1(\mathscr {C}^{N(I)})$, for suitable choices of an
$\mathrm {h}_1(\mathscr {C}^{N(I)})$, for suitable choices of an ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$. Using homotopy n-categories instead, we may consider more generally the example of the enriched functor that sends a simplicial set K to the homotopy n-category
$\mathscr {C}$. Using homotopy n-categories instead, we may consider more generally the example of the enriched functor that sends a simplicial set K to the homotopy n-category ![]() $\mathrm {h}_n(\mathscr {C}^K)$. Following the axiomatic definition of ordinary derivators, we introduce a definition of an n-derivator, which is meant to encapsulate the main abstract properties of this example. The basic definitions and properties of (left, right, pointed, stable) n-(pre)derivators,
$\mathrm {h}_n(\mathscr {C}^K)$. Following the axiomatic definition of ordinary derivators, we introduce a definition of an n-derivator, which is meant to encapsulate the main abstract properties of this example. The basic definitions and properties of (left, right, pointed, stable) n-(pre)derivators, ![]() $1 \leq n \leq \infty $, will be discussed in Section 4. For any
$1 \leq n \leq \infty $, will be discussed in Section 4. For any ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$, there is an associated n-prederivator
$\mathscr {C}$, there is an associated n-prederivator
where ![]() $\mathsf {Dia}$ denotes a category of diagram shapes and
$\mathsf {Dia}$ denotes a category of diagram shapes and ![]() $\mathsf {Cat_{n}}$ is the
$\mathsf {Cat_{n}}$ is the ![]() $\infty $-category of n-categories. These assemble to define a tower of
$\infty $-category of n-categories. These assemble to define a tower of ![]() $\infty $-prederivators
$\infty $-prederivators
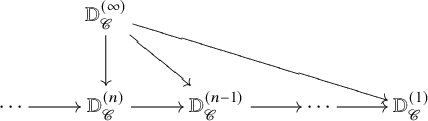
that approximates ![]() $\mathbb {D}^{(\infty )}_{\mathscr {C}} \colon K \mapsto \mathscr {C}^K$. The n-prederivator
$\mathbb {D}^{(\infty )}_{\mathscr {C}} \colon K \mapsto \mathscr {C}^K$. The n-prederivator ![]() $\mathbb {D}_{\mathscr {C}}^{(n)}$ is an n-derivator if certain homotopy Kan extensions exist in
$\mathbb {D}_{\mathscr {C}}^{(n)}$ is an n-derivator if certain homotopy Kan extensions exist in ![]() $\mathscr {C}$ and the corresponding base change transformations satisfy the Beck–Chevalley condition. For any fixed
$\mathscr {C}$ and the corresponding base change transformations satisfy the Beck–Chevalley condition. For any fixed ![]() $n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$, we prove the following fact, which can be used to obtain many examples of n-derivators (Proposition 4.17 and Theorem 4.18):
$n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$, we prove the following fact, which can be used to obtain many examples of n-derivators (Proposition 4.17 and Theorem 4.18):
 $$ \begin{align*} &\mathscr{C}\ \text{admits limits and colimits indexed by diagrams in}\ \mathsf{Dia}\\[-3pt] &\qquad\qquad\text{if and only if}\ \mathbb{D}_{\mathscr{C}}^{(n)}\ \text{is an}\ n\text{-derivator}. \end{align*} $$
$$ \begin{align*} &\mathscr{C}\ \text{admits limits and colimits indexed by diagrams in}\ \mathsf{Dia}\\[-3pt] &\qquad\qquad\text{if and only if}\ \mathbb{D}_{\mathscr{C}}^{(n)}\ \text{is an}\ n\text{-derivator}. \end{align*} $$The motivation for higher derivators is to bridge the gap between ![]() $\infty $-categories and derivators by introducing a hierarchy of intermediate notions, a different one for each categorical level, starting with ordinary derivators. For any fixed
$\infty $-categories and derivators by introducing a hierarchy of intermediate notions, a different one for each categorical level, starting with ordinary derivators. For any fixed ![]() $1 \leq n < \infty $, the theory of n-derivators is still not a faithful representation of homotopy theories; it dwells in an
$1 \leq n < \infty $, the theory of n-derivators is still not a faithful representation of homotopy theories; it dwells in an ![]() $(n+1)$-categorical context in the same way the classical theory of derivators is restricted to a 2-categorical context. In this respect, our approach using n-derivators remains close to the original idea of a derivator and differs from other recent perspectives on (pre)derivators in which (pre)derivators are reconsidered and revised into a model for the theory of
$(n+1)$-categorical context in the same way the classical theory of derivators is restricted to a 2-categorical context. In this respect, our approach using n-derivators remains close to the original idea of a derivator and differs from other recent perspectives on (pre)derivators in which (pre)derivators are reconsidered and revised into a model for the theory of ![]() $\infty $-categories [Reference Fuentes-Keuthan, Kedziorek and Rovelli13, Reference Arlin2, Reference Muro and Raptis26]. We will address the problem of comparing suitable nice classes of
$\infty $-categories [Reference Fuentes-Keuthan, Kedziorek and Rovelli13, Reference Arlin2, Reference Muro and Raptis26]. We will address the problem of comparing suitable nice classes of ![]() $\infty $-categories with n-derivators in future joint work with D.–C. Cisinski.
$\infty $-categories with n-derivators in future joint work with D.–C. Cisinski.
(c) K-theory of higher derivators. K-theory for (pointed, right) derivators was introduced by Maltsiniotis [Reference Maltsiniotis24] and Garkusha [Reference Garkusha14, Reference Garkusha15]. The basic feature of a derivator that allows this definition of K-theory is that there is a natural notion of cocartesian square for a derivator. The motivation for introducing this K-theory is connected with the problem of recovering Waldhausen K-theory from the derivator. Maltsiniotis [Reference Maltsiniotis24] conjectured that derivator K-theory of stable derivators satisfies additivity and localization and that it agrees with Quillen K-theory for exact categories. Cisinski and Neeman [Reference Cisinski and Neeman6] proved additivity for the derivator K-theory of stable derivators, and Coley [Reference Coley8] has recently extended this result to the unstable context. In joint work with Muro [Reference Muro and Raptis27], we proved that localization and agreement with Quillen K-theory cannot both hold. On the other hand, Muro [Reference Muro25] proved that agreement with Waldhausen K-theory holds for ![]() $K_0$ and
$K_0$ and ![]() $K_1$ (see also [Reference Maltsiniotis24, Section 6]). Moreover, Garkusha [Reference Garkusha15] obtained further positive results in the case of abelian categories. In Section 5, after a short review of the K-theory of
$K_1$ (see also [Reference Maltsiniotis24, Section 6]). Moreover, Garkusha [Reference Garkusha15] obtained further positive results in the case of abelian categories. In Section 5, after a short review of the K-theory of ![]() $\infty $-categories, we will define derivator K-theory for general (pointed, right)
$\infty $-categories, we will define derivator K-theory for general (pointed, right) ![]() $\infty $-derivators. For any pointed
$\infty $-derivators. For any pointed ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ with finite colimits, there is a comparison map to derivator K-theory,
$\mathscr {C}$ with finite colimits, there is a comparison map to derivator K-theory,
and these comparison maps assemble to give a tower of derivator K-theories and comparison maps
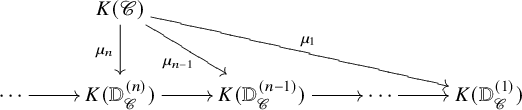
that approximates ![]() $K(\mathscr {C})$. Our main result on the comparison map
$K(\mathscr {C})$. Our main result on the comparison map ![]() $\mu _n$ is the following connectivity estimate (Theorem 5.5):
$\mu _n$ is the following connectivity estimate (Theorem 5.5):
We believe that this connectivity estimate is best possible in general (Remarks 5.7 and 5.8). Following the ideas of [Reference Muro and Raptis26], we also consider the Waldhausen K-theory ![]() $K^{W, \operatorname {Ob}}(\mathbb {D})$ (and
$K^{W, \operatorname {Ob}}(\mathbb {D})$ (and ![]() $K^W(\mathbb {D})$) of a general (pointed, right)
$K^W(\mathbb {D})$) of a general (pointed, right) ![]() $\infty $-derivator
$\infty $-derivator ![]() $\mathbb {D}$. This K-theory always agrees with the usual K-theory (Proposition 5.10); the proof is based on a version of the
$\mathbb {D}$. This K-theory always agrees with the usual K-theory (Proposition 5.10); the proof is based on a version of the ![]() $\textsf {s}_{\bullet }$-construction in the
$\textsf {s}_{\bullet }$-construction in the ![]() $\infty $-categorical context (Proposition 5.1). However, Waldhausen K-theory of derivators is not invariant under equivalences of derivators in general. Similarly to the case of ordinary derivators treated in [Reference Muro and Raptis26], we prove that the comparison map to derivator K-theory,
$\infty $-categorical context (Proposition 5.1). However, Waldhausen K-theory of derivators is not invariant under equivalences of derivators in general. Similarly to the case of ordinary derivators treated in [Reference Muro and Raptis26], we prove that the comparison map to derivator K-theory,
identifies derivator K-theory in terms of a universal property (Theorem 5.13):
(d) K-theory of homotopy n -categories. The motivation for introducing K-theory for homotopy n-categories is to identify the part of Waldhausen K-theory that may be reconstructed from the homotopy n-category. As a basic instance of this phenomenon, we recall that ![]() $K_0(\mathscr {C})$ can be recovered from the triangulated category
$K_0(\mathscr {C})$ can be recovered from the triangulated category ![]() $\mathrm {h}_1 \mathscr {C}$ for any stable
$\mathrm {h}_1 \mathscr {C}$ for any stable ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$. The main feature of the homotopy n-category that is needed for our definition of K-theory is the collection of higher weak pushouts that come from pushouts in
$\mathscr {C}$. The main feature of the homotopy n-category that is needed for our definition of K-theory is the collection of higher weak pushouts that come from pushouts in ![]() $\mathscr {C}$. We will revisit the properties of homotopy n-categories in Subsections 6.1–6.2 and discuss possible axiomatisations of these properties. We will then define K-theory for pointed n-categories with distinguished squares – this is a higher categorical, but much more elementary, version of Neeman’s K-theory of categories with squares [Reference Neeman28]. For a pointed
$\mathscr {C}$. We will revisit the properties of homotopy n-categories in Subsections 6.1–6.2 and discuss possible axiomatisations of these properties. We will then define K-theory for pointed n-categories with distinguished squares – this is a higher categorical, but much more elementary, version of Neeman’s K-theory of categories with squares [Reference Neeman28]. For a pointed ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ with finite colimits, we consider the K-theory
$\mathscr {C}$ with finite colimits, we consider the K-theory ![]() $K(\mathrm {h}_n\mathscr {C}, \mathrm {can})$ associated to
$K(\mathrm {h}_n\mathscr {C}, \mathrm {can})$ associated to ![]() $\mathrm {h}_n\mathscr {C}$ with the canonical structure of higher weak pushouts as distinguished squares. For every
$\mathrm {h}_n\mathscr {C}$ with the canonical structure of higher weak pushouts as distinguished squares. For every ![]() $n \geq 1$, there is a comparison map
$n \geq 1$, there is a comparison map
and these assemble to define a tower of K-theories and comparison maps

that approximates ![]() $K(\mathscr {C})$. Our main result in Section 6 on the comparison map
$K(\mathscr {C})$. Our main result in Section 6 on the comparison map ![]() $\rho _n$ is the following connectivity estimate (Theorem 6.5):
$\rho _n$ is the following connectivity estimate (Theorem 6.5):
This connectivity estimate is best possible in general (Remark 6.10). Let ![]() $P_n X$ denote the Postnikov n-truncation of a topological space X: that is, the homotopy groups of
$P_n X$ denote the Postnikov n-truncation of a topological space X: that is, the homotopy groups of ![]() $P_n X$ vanish in degrees
$P_n X$ vanish in degrees ![]() $> n$, and the canonical map
$> n$, and the canonical map ![]() $X \to P_n X$ is
$X \to P_n X$ is ![]() $(n+1)$-connected. Based on the connectivity estimate above, we conclude (Corollary 6.11):
$(n+1)$-connected. Based on the connectivity estimate above, we conclude (Corollary 6.11):
This confirms a recent conjecture of Antieau [Reference Antieau1, Conjecture 8.35] in the case of connective K-theory.
2 Higher homotopy categories
2.1 n-categories
We recall the definition and basic properties of n-categories following [Reference Lurie22, 2.3.4]. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $n \geq -1$ be an integer.
$n \geq -1$ be an integer. ![]() $\mathscr {C}$ is an n-category if it satisfies the following conditions:
$\mathscr {C}$ is an n-category if it satisfies the following conditions:
(1) Given a pair of maps
 $f,f': \Delta ^n \to \mathscr {C}$, if f and
$f,f': \Delta ^n \to \mathscr {C}$, if f and  $f'$ are homotopic relative to
$f'$ are homotopic relative to  $\partial \Delta ^n$, then
$\partial \Delta ^n$, then  $f = f'$. (We recall that the notion of homotopy employed here means that the two maps are homotopic via equivalences in
$f = f'$. (We recall that the notion of homotopy employed here means that the two maps are homotopic via equivalences in  $\mathscr {C}$.)
$\mathscr {C}$.)(2) Given a pair of maps
 $f, f': \Delta ^m \to \mathscr {C}$, where
$f, f': \Delta ^m \to \mathscr {C}$, where  $m> n$, if
$m> n$, if  $f_{|\partial \Delta ^m} = f^{\prime }_{|\partial \Delta ^m}$, then
$f_{|\partial \Delta ^m} = f^{\prime }_{|\partial \Delta ^m}$, then  $f = f'$.
$f = f'$.
These conditions say that ![]() $\mathscr {C}$ has no morphisms in degrees
$\mathscr {C}$ has no morphisms in degrees ![]() $> n$ and any two morphisms in degree n agree if they are equivalent. The conditions can be equivalently expressed as follows:
$> n$ and any two morphisms in degree n agree if they are equivalent. The conditions can be equivalently expressed as follows: ![]() $\mathscr {C}$ is an n-category,
$\mathscr {C}$ is an n-category, ![]() $n \geq 1$, if for every diagram
$n \geq 1$, if for every diagram
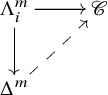
where ![]() $m> n$ and
$m> n$ and ![]() $0 < i < m$, there exists a unique dotted arrow that makes the diagram commutative [Reference Lurie22, Proposition 2.3.4.9]. Using an inductive argument (see [Reference Lurie22, Proposition 2.3.4.7]), it can also be shown that the conditions (1) and (2) together are equivalent to:
$0 < i < m$, there exists a unique dotted arrow that makes the diagram commutative [Reference Lurie22, Proposition 2.3.4.9]. Using an inductive argument (see [Reference Lurie22, Proposition 2.3.4.7]), it can also be shown that the conditions (1) and (2) together are equivalent to:
(3) Given a simplicial set K and maps
 $f,f': K \to \mathscr {C}$ such that
$f,f': K \to \mathscr {C}$ such that  $f_{| \mathrm {sk}_n(K)}$ and
$f_{| \mathrm {sk}_n(K)}$ and  $f^{\prime }_{|\mathrm {sk}_n(K)}$ are homotopic relative to
$f^{\prime }_{|\mathrm {sk}_n(K)}$ are homotopic relative to  $\mathrm {sk}_{n-1}(K)$, then
$\mathrm {sk}_{n-1}(K)$, then  $f = f'$.
$f = f'$.
An important immediate consequence of (3) is that for every n-category ![]() $\mathscr {C}$, the
$\mathscr {C}$, the ![]() $\infty $-category
$\infty $-category ![]() $\mathrm {Fun}(K, \mathscr {C})$ is again an n-category for any simplicial set K [Reference Lurie22, Corollary 2.3.4.8].
$\mathrm {Fun}(K, \mathscr {C})$ is again an n-category for any simplicial set K [Reference Lurie22, Corollary 2.3.4.8].
Example 2.1. The only ![]() $(-1)$-categories up to isomorphism are
$(-1)$-categories up to isomorphism are ![]() $\varnothing $ and
$\varnothing $ and ![]() $\Delta ^0$. An
$\Delta ^0$. An ![]() $\infty $-category is a
$\infty $-category is a ![]() $0$-category if and only if it is isomorphic to (the nerve of) a poset.
$0$-category if and only if it is isomorphic to (the nerve of) a poset. ![]() $1$-categories are up to isomorphism (nerves of) ordinary categories. See [Reference Lurie22, Examples 2.3.4.2–2.3.4.3, Proposition 2.3.4.5].
$1$-categories are up to isomorphism (nerves of) ordinary categories. See [Reference Lurie22, Examples 2.3.4.2–2.3.4.3, Proposition 2.3.4.5].
The property of being an n-category is not invariant under equivalences of ![]() $\infty $-categories. The following proposition gives a characterization of the invariant property that an
$\infty $-categories. The following proposition gives a characterization of the invariant property that an ![]() $\infty $-category is equivalent to an n-category. We recall that an
$\infty $-category is equivalent to an n-category. We recall that an ![]() $\infty $-groupoid (= Kan complex) X is n-truncated, where
$\infty $-groupoid (= Kan complex) X is n-truncated, where ![]() $n \geq -1$, if X has vanishing homotopy groups in degrees
$n \geq -1$, if X has vanishing homotopy groups in degrees ![]() $> n$. We say that X is (-2)-truncated if X is contractible.
$> n$. We say that X is (-2)-truncated if X is contractible.
Proposition 2.2. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $n \geq -1$ be an integer. Then
$n \geq -1$ be an integer. Then ![]() $\mathscr {C}$ is equivalent to an n-category if and only if
$\mathscr {C}$ is equivalent to an n-category if and only if ![]() $\mathrm {Map}_{\mathscr {C}}(x,y)$ is
$\mathrm {Map}_{\mathscr {C}}(x,y)$ is ![]() $(n-1)$-truncated for every pair of objects
$(n-1)$-truncated for every pair of objects ![]() $x,y \in \mathscr {C}$.
$x,y \in \mathscr {C}$.
Proof. See [Reference Lurie22, Proposition 2.3.4.18].
2.2 Homotopy n-categories
Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $n \geq 1$ be an integer. We recall from [Reference Lurie22] the construction of the homotopy n-category
$n \geq 1$ be an integer. We recall from [Reference Lurie22] the construction of the homotopy n-category ![]() $\mathrm {h}_n \mathscr {C}$ of
$\mathrm {h}_n \mathscr {C}$ of ![]() $\mathscr {C}$. Given a simplicial set K, we denote by
$\mathscr {C}$. Given a simplicial set K, we denote by ![]() $[K, \mathscr {C}]_n$ the set of maps
$[K, \mathscr {C}]_n$ the set of maps
which extend to ![]() $\mathrm {sk}_{n+1}(K)$. Two elements
$\mathrm {sk}_{n+1}(K)$. Two elements ![]() $f,g \in [K, \mathscr {C}]_n$ are called equivalent, denoted
$f,g \in [K, \mathscr {C}]_n$ are called equivalent, denoted ![]() $f \sim g$, if the maps
$f \sim g$, if the maps ![]() $f,g: \mathrm {sk}_n(K) \to \mathscr {C}$ are homotopic relative to
$f,g: \mathrm {sk}_n(K) \to \mathscr {C}$ are homotopic relative to ![]() $\mathrm {sk}_{n-1}(K)$. The equivalence classes of such maps for
$\mathrm {sk}_{n-1}(K)$. The equivalence classes of such maps for ![]() $K = \Delta ^m$ define the m-simplices of a simplicial set
$K = \Delta ^m$ define the m-simplices of a simplicial set ![]() $\mathrm {h}_n \mathscr {C}$: that is,
$\mathrm {h}_n \mathscr {C}$: that is,
Clearly an m-simplex of ![]() $\mathscr {C}$ defines an m-simplex in
$\mathscr {C}$ defines an m-simplex in ![]() $\mathrm {h}_n \mathscr {C}$, so we have a canonical map
$\mathrm {h}_n \mathscr {C}$, so we have a canonical map ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. Note that this map is a bijection in simplicial degrees
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. Note that this map is a bijection in simplicial degrees ![]() $< n$ and surjective in degrees n and
$< n$ and surjective in degrees n and ![]() $n+1$.
$n+1$.
The following proposition summarises some of the basic properties of this construction.
Proposition 2.3. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and
$\infty $-category and ![]() $n \geq 1$.
$n \geq 1$.
(a) The set of maps
 $K \to \mathrm {h}_n \mathscr {C}$ is in natural bijection with the set
$K \to \mathrm {h}_n \mathscr {C}$ is in natural bijection with the set  $[K, \mathscr {C} ]_n / \sim $.
$[K, \mathscr {C} ]_n / \sim $.(b)
 $\mathrm {h}_n \mathscr {C}$ is an n-category. In particular, it is an
$\mathrm {h}_n \mathscr {C}$ is an n-category. In particular, it is an  $\infty $-category.
$\infty $-category.(c)
 $\mathscr {C}$ is an n-category if and only if the map
$\mathscr {C}$ is an n-category if and only if the map  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ is an isomorphism.
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ is an isomorphism.(d) Let
 $\mathscr {D}$ be an n-category. Then the restriction functor along
$\mathscr {D}$ be an n-category. Then the restriction functor along  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$, is an isomorphism.
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$, is an isomorphism. $$ \begin{align*}\gamma_n^* \colon \mathrm{Fun}(\mathrm{h}_n \mathscr{C}, \mathscr{D}) \to \mathrm{Fun}(\mathscr{C}, \mathscr{D}),\end{align*} $$
$$ \begin{align*}\gamma_n^* \colon \mathrm{Fun}(\mathrm{h}_n \mathscr{C}, \mathscr{D}) \to \mathrm{Fun}(\mathscr{C}, \mathscr{D}),\end{align*} $$
Proof. See [Reference Lurie22, Proposition 2.3.4.12].
Example 2.4. For ![]() $n = 1$, the
$n = 1$, the ![]() $1$-category
$1$-category ![]() $\mathrm {h}_{1} \mathscr {C}$ is isomorphic to the (nerve of the) usual homotopy category of
$\mathrm {h}_{1} \mathscr {C}$ is isomorphic to the (nerve of the) usual homotopy category of ![]() $\mathscr {C}$.
$\mathscr {C}$.
Remark 2.5. For an ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$, the homotopy
$\mathscr {C}$, the homotopy ![]() $0$-category
$0$-category ![]() $\mathrm {h}_0 \mathscr {C}$ can be described in the following way. For
$\mathrm {h}_0 \mathscr {C}$ can be described in the following way. For ![]() $x, y \in \mathscr {C}$, we write
$x, y \in \mathscr {C}$, we write ![]() $x \leq y$ if
$x \leq y$ if ![]() $\mathrm {Map}_{\mathscr {C}}(x, y)$ is non-empty. This defines a reflexive and transitive relation. We say that two objects x and y are equivalent if
$\mathrm {Map}_{\mathscr {C}}(x, y)$ is non-empty. This defines a reflexive and transitive relation. We say that two objects x and y are equivalent if ![]() $x \leq y$ and
$x \leq y$ and ![]() $y \leq x$. Then the relation
$y \leq x$. Then the relation ![]() $\leq $ descends to a partial order on the set of equivalence classes of objects in
$\leq $ descends to a partial order on the set of equivalence classes of objects in ![]() $\mathscr {C}$. The homotopy
$\mathscr {C}$. The homotopy ![]() $0$-category
$0$-category ![]() $\mathrm {h}_0 \mathscr {C}$ is isomorphic to the nerve of this poset. We will often ignore the case
$\mathrm {h}_0 \mathscr {C}$ is isomorphic to the nerve of this poset. We will often ignore the case ![]() $n = 0$ and focus on the homotopy n-categories for
$n = 0$ and focus on the homotopy n-categories for ![]() $n \geq 1$.
$n \geq 1$.
Proposition 2.6. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and
$\infty $-category and ![]() $n \geq 1$. The functor
$n \geq 1$. The functor ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ is a categorical fibration between
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ is a categorical fibration between ![]() $\infty $-categories. In addition, for every lifting problem
$\infty $-categories. In addition, for every lifting problem
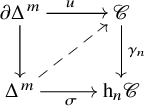
where ![]() $m \leq n + 1$ (respectively,
$m \leq n + 1$ (respectively, ![]() $m < n$), there is a (unique) filler
$m < n$), there is a (unique) filler ![]() $\Delta ^m \to \mathscr {C}$ that makes the diagram commutative.
$\Delta ^m \to \mathscr {C}$ that makes the diagram commutative.
Proof. Clearly, for any object c in ![]() $\mathscr {C}$ and any equivalence
$\mathscr {C}$ and any equivalence ![]() $f \colon c \to c'$ in
$f \colon c \to c'$ in ![]() $\mathrm {h}_n \mathscr {C}$, we may find a lift
$\mathrm {h}_n \mathscr {C}$, we may find a lift ![]() $\tilde {f} \colon c \to c'$ of f in
$\tilde {f} \colon c \to c'$ of f in ![]() $\mathscr {C}$ (uniquely if
$\mathscr {C}$ (uniquely if ![]() $n>1$), which is again an equivalence. Then we need to show that
$n>1$), which is again an equivalence. Then we need to show that ![]() $\gamma _n$ is an inner fibration. Consider a lifting problem
$\gamma _n$ is an inner fibration. Consider a lifting problem
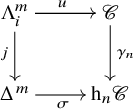
where ![]() $0 < i < m$. For
$0 < i < m$. For ![]() $m \leq n$, there is a diagonal filler
$m \leq n$, there is a diagonal filler ![]() $\Delta ^m \to \mathscr {C}$ because
$\Delta ^m \to \mathscr {C}$ because ![]() $\gamma _n$ is a bijection in simplicial degrees
$\gamma _n$ is a bijection in simplicial degrees ![]() $< n$ and surjective on n-simplices. For
$< n$ and surjective on n-simplices. For ![]() $m> n$, there is a map
$m> n$, there is a map ![]() $v \colon \Delta ^m \to \mathscr {C}$ that extends u because
$v \colon \Delta ^m \to \mathscr {C}$ that extends u because ![]() $\mathscr {C}$ is an
$\mathscr {C}$ is an ![]() $\infty $-category. We claim that v defines a diagonal filler for the diagram. To see this, note that an extension of
$\infty $-category. We claim that v defines a diagonal filler for the diagram. To see this, note that an extension of ![]() $\gamma _n u$ along j is unique up to homotopy relative to
$\gamma _n u$ along j is unique up to homotopy relative to ![]() $\Lambda ^m_i$ (
$\Lambda ^m_i$ (![]() $\supseteq \mathrm {sk}_{n-1} \Delta ^m$), since
$\supseteq \mathrm {sk}_{n-1} \Delta ^m$), since ![]() $\mathrm {h}_n \mathscr {C}$ is an
$\mathrm {h}_n \mathscr {C}$ is an ![]() $\infty $-category. In particular, the maps
$\infty $-category. In particular, the maps ![]() $\sigma $ and
$\sigma $ and ![]() $\gamma _n v$ are homotopic relative to
$\gamma _n v$ are homotopic relative to ![]() $\mathrm {sk}_{n-1} \Delta ^m$. Then the result follows because the n-category
$\mathrm {sk}_{n-1} \Delta ^m$. Then the result follows because the n-category ![]() $\mathrm {h}_n \mathscr {C}$ satisfies condition (3) (see Subsection 2.1). Therefore,
$\mathrm {h}_n \mathscr {C}$ satisfies condition (3) (see Subsection 2.1). Therefore, ![]() $\gamma _n$ is an inner fibration, and this completes the proof of the first claim.
$\gamma _n$ is an inner fibration, and this completes the proof of the first claim.
The second claim for ![]() $m \leq n$ follows again from the fact that
$m \leq n$ follows again from the fact that ![]() $\gamma _n$ is bijective in simplicial degrees
$\gamma _n$ is bijective in simplicial degrees ![]() $< n$ and surjective in degree n. For
$< n$ and surjective in degree n. For ![]() $m = n+1$, we may find a map
$m = n+1$, we may find a map ![]() $\sigma ' \colon \Delta ^{n+1} \to \mathscr {C}$ such that
$\sigma ' \colon \Delta ^{n+1} \to \mathscr {C}$ such that ![]() $\gamma _n \sigma ' = \sigma $, since
$\gamma _n \sigma ' = \sigma $, since ![]() $\gamma _n$ is surjective on
$\gamma _n$ is surjective on ![]() $(n+1)$-simplices. The maps
$(n+1)$-simplices. The maps
become equal after postcomposition with ![]() $\gamma _n$. By Proposition 2.3(a), this means they are homotopic (in the sense of the Joyal model category) relative to
$\gamma _n$. By Proposition 2.3(a), this means they are homotopic (in the sense of the Joyal model category) relative to ![]() $\mathrm {sk}_{n-1}(\partial \Delta ^{n+1})$. Using that the inclusion
$\mathrm {sk}_{n-1}(\partial \Delta ^{n+1})$. Using that the inclusion ![]() $\partial \Delta ^{n+1} \subset \Delta ^{n+1}$ is a cofibration, this homotopy can be extended to a homotopy on
$\partial \Delta ^{n+1} \subset \Delta ^{n+1}$ is a cofibration, this homotopy can be extended to a homotopy on ![]() $\Delta ^{n+1}$ between
$\Delta ^{n+1}$ between ![]() $\sigma '$ and a map
$\sigma '$ and a map ![]() $v \colon \Delta ^{n+1} \to \mathscr {C}$ such that
$v \colon \Delta ^{n+1} \to \mathscr {C}$ such that ![]() $v_{| \partial \Delta ^{n+1}} = u$. This new homotopy is still constant on
$v_{| \partial \Delta ^{n+1}} = u$. This new homotopy is still constant on ![]() $\mathrm {sk}_{n-1}(\partial \Delta ^{n+1}) = \mathrm {sk}_{n-1}(\Delta ^{n+1})$. Therefore, given that
$\mathrm {sk}_{n-1}(\partial \Delta ^{n+1}) = \mathrm {sk}_{n-1}(\Delta ^{n+1})$. Therefore, given that ![]() $\sigma '$ and v are homotopic relative to
$\sigma '$ and v are homotopic relative to ![]() $\mathrm {sk}_{n-1}(\Delta ^{n+1})$, it follows that
$\mathrm {sk}_{n-1}(\Delta ^{n+1})$, it follows that ![]() $\gamma _n v = \gamma _n \sigma ' = \sigma $; this shows that v defines a diagonal filler for the diagram.
$\gamma _n v = \gamma _n \sigma ' = \sigma $; this shows that v defines a diagonal filler for the diagram.
Corollary 2.7. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $n \geq 1$ be an integer. There is a (non-canonical) map
$n \geq 1$ be an integer. There is a (non-canonical) map
such that the following diagram commutes
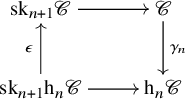
where the horizontal maps are the canonical inclusions.
Proof. We have a diagram as follows:
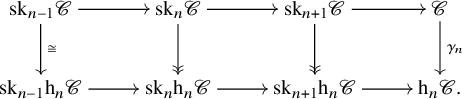
We may choose a section ![]() $\epsilon ' \colon \mathrm {sk}_n \mathrm {h}_n \mathscr {C} \to \mathrm {sk}_n \mathscr {C}$ – uniquely up to equivalence. We claim that this section can be extended further to a section
$\epsilon ' \colon \mathrm {sk}_n \mathrm {h}_n \mathscr {C} \to \mathrm {sk}_n \mathscr {C}$ – uniquely up to equivalence. We claim that this section can be extended further to a section ![]() $\epsilon $ as required. Let
$\epsilon $ as required. Let ![]() $\sigma \colon \Delta ^{n+1} \to \mathrm {h}_n\mathscr {C}$ denote a nondegenerate
$\sigma \colon \Delta ^{n+1} \to \mathrm {h}_n\mathscr {C}$ denote a nondegenerate ![]() $(n+1)$-simplex in
$(n+1)$-simplex in ![]() $\mathrm {h}_n \mathscr {C}$. Then we consider the composite map
$\mathrm {h}_n \mathscr {C}$. Then we consider the composite map
and this commutative diagram:
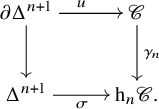
By Proposition 2.6, there is a diagonal filler ![]() $\tau \colon \Delta ^{n+1} \to \mathscr {C}$ – that is, an
$\tau \colon \Delta ^{n+1} \to \mathscr {C}$ – that is, an ![]() $(n+1)$-simplex of
$(n+1)$-simplex of ![]() $\mathscr {C}$ – that makes the diagram commutative. We set
$\mathscr {C}$ – that makes the diagram commutative. We set ![]() $\epsilon (\sigma ) := \tau $. Repeating this process for each
$\epsilon (\sigma ) := \tau $. Repeating this process for each ![]() $\sigma $, we obtain the required extension
$\sigma $, we obtain the required extension ![]() $\epsilon \colon \mathrm {sk}_{n+1} \mathrm {h}_n \mathscr {C} \to \mathrm {sk}_{n+1} \mathscr {C}$.
$\epsilon \colon \mathrm {sk}_{n+1} \mathrm {h}_n \mathscr {C} \to \mathrm {sk}_{n+1} \mathscr {C}$.
Example 2.8. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category. The functor
$\infty $-category. The functor ![]() $\gamma _1 \colon \mathscr {C} \to \mathrm {h}_1 \mathscr {C}$ is bijective on objects, so there is a unique section
$\gamma _1 \colon \mathscr {C} \to \mathrm {h}_1 \mathscr {C}$ is bijective on objects, so there is a unique section ![]() $\mathrm {sk}_0 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_0 \mathscr {C}$. By making choices of morphisms, one from each homotopy class, this map extends to a section
$\mathrm {sk}_0 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_0 \mathscr {C}$. By making choices of morphisms, one from each homotopy class, this map extends to a section ![]() $\mathrm {sk}_1 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_1 \mathscr {C}$. The last map extends further to a section
$\mathrm {sk}_1 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_1 \mathscr {C}$. The last map extends further to a section ![]() $\mathrm {sk}_2 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_2 \mathscr {C}$ by making (non-canonical) choices of homotopies for compositions.
$\mathrm {sk}_2 \mathrm {h}_1 \mathscr {C} \to \mathrm {sk}_2 \mathscr {C}$ by making (non-canonical) choices of homotopies for compositions.
The functor ![]() $\mathrm {h}_n(-)$ preserves categorical equivalences of
$\mathrm {h}_n(-)$ preserves categorical equivalences of ![]() $\infty $-categories. Using Proposition 2.3, it follows that there is a tower of
$\infty $-categories. Using Proposition 2.3, it follows that there is a tower of ![]() $\infty $-categories:
$\infty $-categories:
By construction, the canonical map
is an isomorphism, and by Proposition 2.6, this inverse limit defines also a homotopy limit in the Joyal model structure.
Example 2.9. As a consequence of Proposition 2.2, an ![]() $\infty $-groupoid X is categorically equivalent to an n-category if and only if it is n-truncated. For example, a Kan complex is equivalent to a
$\infty $-groupoid X is categorically equivalent to an n-category if and only if it is n-truncated. For example, a Kan complex is equivalent to a ![]() $0$-category if and only if it is homotopically discrete and to an
$0$-category if and only if it is homotopically discrete and to an ![]() $1$-category if and only if it is equivalent to the nerve of a groupoid. Given an
$1$-category if and only if it is equivalent to the nerve of a groupoid. Given an ![]() $\infty $-groupoid X, the canonical tower of
$\infty $-groupoid X, the canonical tower of ![]() $\infty $-groupoids
$\infty $-groupoids
models the Postnikov tower of X and the map ![]() $X \to \mathrm {h}_n X$ is
$X \to \mathrm {h}_n X$ is ![]() $(n+1)$-connected (i.e., for every
$(n+1)$-connected (i.e., for every ![]() $x \in X$, the map
$x \in X$, the map ![]() $\pi _k(X, x) \to \pi _k(\mathrm {h}_n X, x)$ is a bijection for
$\pi _k(X, x) \to \pi _k(\mathrm {h}_n X, x)$ is a bijection for ![]() $k \leq n$ and surjective for
$k \leq n$ and surjective for ![]() $k = n+1$.)
$k = n+1$.)
Remark 2.10. An n-category ![]() $\mathscr {C}$ is n-truncated in the
$\mathscr {C}$ is n-truncated in the ![]() $\infty $-category of
$\infty $-category of ![]() $\infty $-categories: that is, the
$\infty $-categories: that is, the ![]() $\infty $-groupoid
$\infty $-groupoid ![]() $\mathrm {Map}(K, \mathscr {C})$ is n-truncated for any
$\mathrm {Map}(K, \mathscr {C})$ is n-truncated for any ![]() $\infty $-category K (see [Reference Lurie22, 5.5.6] for the definition and properties of truncated objects in an
$\infty $-category K (see [Reference Lurie22, 5.5.6] for the definition and properties of truncated objects in an ![]() $\infty $-category). To see this, recall that
$\infty $-category). To see this, recall that ![]() $\mathrm {Fun}(K, \mathscr {C})$ is again an n-category, and then apply Proposition 2.2. But an n-truncated
$\mathrm {Fun}(K, \mathscr {C})$ is again an n-category, and then apply Proposition 2.2. But an n-truncated ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ is not equivalent to an n-category in general, so the analogue of Example 2.9 fails for general
$\mathscr {C}$ is not equivalent to an n-category in general, so the analogue of Example 2.9 fails for general ![]() $\infty $-categories. An
$\infty $-categories. An ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ is n-truncated if and only if
$\mathscr {C}$ is n-truncated if and only if ![]() $\mathscr {C}$ is equivalent to an
$\mathscr {C}$ is equivalent to an ![]() $(n+1)$-category and the maximal
$(n+1)$-category and the maximal ![]() $\infty $-subgroupoid
$\infty $-subgroupoid ![]() $\mathscr {C}^{\simeq } \subseteq \mathscr {C}$ is n-truncated. Indeed, given an n-truncated
$\mathscr {C}^{\simeq } \subseteq \mathscr {C}$ is n-truncated. Indeed, given an n-truncated ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$,
$\mathscr {C}$, ![]() $\mathscr {C}^{\simeq } \simeq \mathrm {Map}(\Delta ^0, \mathscr {C})$ is n-truncated. Moreover, since n-truncated objects are closed under limits, it follows that
$\mathscr {C}^{\simeq } \simeq \mathrm {Map}(\Delta ^0, \mathscr {C})$ is n-truncated. Moreover, since n-truncated objects are closed under limits, it follows that ![]() $\mathrm {Map}_{\mathscr {C}}(x, y)$ is n-truncated for every
$\mathrm {Map}_{\mathscr {C}}(x, y)$ is n-truncated for every ![]() $x, y \in \mathscr {C}$, using the fact that there is a pullback in the
$x, y \in \mathscr {C}$, using the fact that there is a pullback in the ![]() $\infty $-category of
$\infty $-category of ![]() $\infty $-categories:
$\infty $-categories:
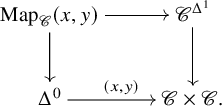
(Using the definition of n-truncated objects, we see that ![]() $\mathscr {C}^{\Delta ^1}$ is again n-truncated.) Conversely, if
$\mathscr {C}^{\Delta ^1}$ is again n-truncated.) Conversely, if ![]() $\mathscr {C}$ is an
$\mathscr {C}$ is an ![]() $(n+1)$-category and
$(n+1)$-category and ![]() $\mathscr {C}^{\simeq }$ is n-truncated, then it is possible to show that
$\mathscr {C}^{\simeq }$ is n-truncated, then it is possible to show that ![]() $\mathrm {Map}(\Delta ^k, \mathscr {C})$ is n-truncated by induction on
$\mathrm {Map}(\Delta ^k, \mathscr {C})$ is n-truncated by induction on ![]() $k \geq 0$, from which it follows that
$k \geq 0$, from which it follows that ![]() $\mathscr {C}$ is n-truncated. (I am grateful to Hoang Kim Nguyen for interesting discussions related to this remark.)
$\mathscr {C}$ is n-truncated. (I am grateful to Hoang Kim Nguyen for interesting discussions related to this remark.)
Let ![]() $\mathsf {Cat_{\infty }}$ denote the category of
$\mathsf {Cat_{\infty }}$ denote the category of ![]() $\infty $-categories, regarded as enriched in
$\infty $-categories, regarded as enriched in ![]() $\infty $-categories, and let
$\infty $-categories, and let ![]() $\mathsf {Cat_{n}}$ denote the full subcategory of
$\mathsf {Cat_{n}}$ denote the full subcategory of ![]() $\mathsf {Cat_{\infty }}$ that is spanned by n-categories.
$\mathsf {Cat_{\infty }}$ that is spanned by n-categories.
Proposition 2.11. Let ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {D}$ be
$\mathscr {D}$ be ![]() $\infty $-categories, and let
$\infty $-categories, and let ![]() $n \geq 1$ be an integer.
$n \geq 1$ be an integer.
(a) The natural map
 $\mathrm {h}_n (\mathscr {C} \times \mathscr {D}) \xrightarrow {\cong } \mathrm {h}_n \mathscr {C} \times \mathrm {h}_n \mathscr {D}$ is an isomorphism.
$\mathrm {h}_n (\mathscr {C} \times \mathscr {D}) \xrightarrow {\cong } \mathrm {h}_n \mathscr {C} \times \mathrm {h}_n \mathscr {D}$ is an isomorphism.(b) There is a functor
that is natural in $$ \begin{align*}\mathrm{h}_{n}^{\mathscr{C}, \mathscr{D}} \colon \mathrm{Fun}(\mathscr{C}, \mathscr{D}) \to \mathrm{Fun}(\mathrm{h}_n \mathscr{C}, \mathrm{h}_n \mathscr{D})\end{align*} $$
$$ \begin{align*}\mathrm{h}_{n}^{\mathscr{C}, \mathscr{D}} \colon \mathrm{Fun}(\mathscr{C}, \mathscr{D}) \to \mathrm{Fun}(\mathrm{h}_n \mathscr{C}, \mathrm{h}_n \mathscr{D})\end{align*} $$ $\mathscr {C}$ and
$\mathscr {C}$ and  $\mathscr {D}$. In particular,
$\mathscr {D}$. In particular,  $\mathrm {h}_n \colon \mathsf {Cat_{\infty }} \to \mathsf {Cat_{n}}$ is an enriched functor.
$\mathrm {h}_n \colon \mathsf {Cat_{\infty }} \to \mathsf {Cat_{n}}$ is an enriched functor.
Proof. (a) follows directly from the definition of ![]() $\mathrm {h}_n$. For (b), we define the functor
$\mathrm {h}_n$. For (b), we define the functor ![]() $\mathrm {h}_n^{\mathscr {C}, \mathscr {D}}$ as follows: a k-simplex
$\mathrm {h}_n^{\mathscr {C}, \mathscr {D}}$ as follows: a k-simplex ![]() $F \colon \mathscr {C} \times \Delta ^k \to \mathscr {D}$ is sent to the composite
$F \colon \mathscr {C} \times \Delta ^k \to \mathscr {D}$ is sent to the composite
The functor ![]() $\mathrm {h}_n^{\mathscr {C}, \mathscr {D}}$ is natural in
$\mathrm {h}_n^{\mathscr {C}, \mathscr {D}}$ is natural in ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {D}$ and turns
$\mathscr {D}$ and turns ![]() $\mathrm {h}_n$ into an enriched functor.
$\mathrm {h}_n$ into an enriched functor.
3 Higher weak colimits
3.1 Basic definitions and properties
It is well known that homotopy categories do not admit small (co)limits in general, even when the underlying ![]() $\infty $-category has small (co)limits. On the other hand, if the
$\infty $-category has small (co)limits. On the other hand, if the ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ admits pushouts (respectively, coproducts), for example, then the homotopy category
$\mathscr {C}$ admits pushouts (respectively, coproducts), for example, then the homotopy category ![]() $\mathrm {h}_1 \mathscr {C}$ admits weak pushouts (respectively, coproducts), which are induced from pushouts (respectively, coproducts) in
$\mathrm {h}_1 \mathscr {C}$ admits weak pushouts (respectively, coproducts), which are induced from pushouts (respectively, coproducts) in ![]() $\mathscr {C}$. Moreover, if
$\mathscr {C}$. Moreover, if ![]() $\mathscr {C}$ admits small colimits, then
$\mathscr {C}$ admits small colimits, then ![]() $\mathrm {h}_1 \mathscr {C}$ admits small weak colimits – which may or may not be induced from
$\mathrm {h}_1 \mathscr {C}$ admits small weak colimits – which may or may not be induced from ![]() $\mathscr {C}$. These observations suggest the following questions: does
$\mathscr {C}$. These observations suggest the following questions: does ![]() $\mathrm {h}_n \mathscr {C}$,
$\mathrm {h}_n \mathscr {C}$, ![]() $n> 1$, have in some sense more or better (co)limits than the homotopy category, and how do these compare with (co)limits in
$n> 1$, have in some sense more or better (co)limits than the homotopy category, and how do these compare with (co)limits in ![]() $\mathscr {C}$?
$\mathscr {C}$?
In this section, we introduce and study a notion of higher weak (co)limits in the context of ![]() $\infty $-categories. This is both a higher categorical version of the classical notion of weak (co)limits and a weak version of the higher categorical notion of (co)limits. We will mainly focus on the properties of higher weak (co)limits in the context of higher homotopy categories. We also refer to [Reference Nguyen, Raptis and Schrade30] for further properties and applications of higher weak (co)limits.
$\infty $-categories. This is both a higher categorical version of the classical notion of weak (co)limits and a weak version of the higher categorical notion of (co)limits. We will mainly focus on the properties of higher weak (co)limits in the context of higher homotopy categories. We also refer to [Reference Nguyen, Raptis and Schrade30] for further properties and applications of higher weak (co)limits.
We will restrict to higher weak colimits since the corresponding definitions and results about higher weak limits are obtained dually. First we recall that an ![]() $\infty $-groupoid (= Kan complex) X is k-connected, for some
$\infty $-groupoid (= Kan complex) X is k-connected, for some ![]() $k \geq -1$, if it is non-empty and
$k \geq -1$, if it is non-empty and ![]() $\pi _i(X, x) \cong 0$ for every
$\pi _i(X, x) \cong 0$ for every ![]() $x \in X$ and
$x \in X$ and ![]() $i \leq k$. For example, X is
$i \leq k$. For example, X is ![]() $(-1)$-connected (respectively,
$(-1)$-connected (respectively, ![]() $0$-connected,
$0$-connected, ![]() $\infty $-connected) if it is non-empty (respectively, connected, contractible).
$\infty $-connected) if it is non-empty (respectively, connected, contractible).
We begin with the definition of a weakly initial object. Fix ![]() $t \in \mathbb {Z}_{\geq 0} \cup \{\infty \}$.
$t \in \mathbb {Z}_{\geq 0} \cup \{\infty \}$.
Definition 3.1. An object x of an ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ is weakly initial of order t if the mapping space
$\mathscr {C}$ is weakly initial of order t if the mapping space ![]() $\mathrm {Map}_{\mathscr {C}}(x, y)$ is
$\mathrm {Map}_{\mathscr {C}}(x, y)$ is ![]() $(t-1)$-connected for every object
$(t-1)$-connected for every object ![]() $y \in \mathscr {C}$.
$y \in \mathscr {C}$.
Example 3.2. If ![]() $\mathscr {C}$ is an ordinary category, a weakly initial object
$\mathscr {C}$ is an ordinary category, a weakly initial object ![]() $x \in \mathscr {C}$ of order
$x \in \mathscr {C}$ of order ![]() $0$ is a weakly initial object in the classical sense. For a general n-category
$0$ is a weakly initial object in the classical sense. For a general n-category ![]() $\mathscr {C}$, a weakly initial object of order n is an initial object.
$\mathscr {C}$, a weakly initial object of order n is an initial object.
Proposition 3.3. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and
$\infty $-category and ![]() $x \in \mathscr {C}$. The following are equivalent:
$x \in \mathscr {C}$. The following are equivalent:
(1) x is weakly initial in
 $\mathscr {C}$ of order t.
$\mathscr {C}$ of order t.(2) x is weakly initial in
 $\mathrm {h}_n \mathscr {C}$ of order t for any
$\mathrm {h}_n \mathscr {C}$ of order t for any  $n> t$.
$n> t$.(3) x is initial in
 $\mathrm {h}_{t} \mathscr {C}$.
$\mathrm {h}_{t} \mathscr {C}$.
These imply:
(4) x is initial in
 $\mathrm {h}_n \mathscr {C}$ for any
$\mathrm {h}_n \mathscr {C}$ for any  $n < t$.
$n < t$.
Proof. This follows from the fact that the functor ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ restricts to an n-connected map
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ restricts to an n-connected map ![]() $\mathrm {Map}_{\mathscr {C}}(x, y) \to \mathrm {Map}_{\mathrm {h}_n \mathscr {C}}(x, y)$ for every
$\mathrm {Map}_{\mathscr {C}}(x, y) \to \mathrm {Map}_{\mathrm {h}_n \mathscr {C}}(x, y)$ for every ![]() $x, y \in \mathscr {C}$.
$x, y \in \mathscr {C}$.
Proposition 3.4. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $t> 0$. The full subcategory
$t> 0$. The full subcategory ![]() $\mathscr {C}'$ of
$\mathscr {C}'$ of ![]() $\mathscr {C}$, which is spanned by the weakly initial objects of order t is either empty or a t-connected
$\mathscr {C}$, which is spanned by the weakly initial objects of order t is either empty or a t-connected ![]() $\infty $-groupoid.
$\infty $-groupoid.
Proof. Suppose that the full subcategory ![]() $\mathscr {C}'$ is non-empty. Then the mapping spaces of
$\mathscr {C}'$ is non-empty. Then the mapping spaces of ![]() $\mathscr {C}'$ are
$\mathscr {C}'$ are ![]() $(t-1)$-connected, where
$(t-1)$-connected, where ![]() $t-1 \geq 0$. It follows that every morphism in
$t-1 \geq 0$. It follows that every morphism in ![]() $\mathscr {C}'$ is an equivalence, and therefore
$\mathscr {C}'$ is an equivalence, and therefore ![]() $\mathscr {C}'$ is an
$\mathscr {C}'$ is an ![]() $\infty $-groupoid.
$\infty $-groupoid.
Remark 3.5. The full subcategory ![]() $\mathscr {C}'$ of weakly initial objects in
$\mathscr {C}'$ of weakly initial objects in ![]() $\mathscr {C}$ of order 0 is not an
$\mathscr {C}$ of order 0 is not an ![]() $\infty $-groupoid in general. In this case, we only have that
$\infty $-groupoid in general. In this case, we only have that ![]() $\mathrm {Map}_{\mathscr {C}}(x, y)$ is non-empty for every
$\mathrm {Map}_{\mathscr {C}}(x, y)$ is non-empty for every ![]() $x, y \in \mathscr {C}'$.
$x, y \in \mathscr {C}'$.
Definition 3.6. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a simplicial set, and let
$\infty $-category and K a simplicial set, and let ![]() $F \colon K \to \mathscr {C}$ be a K-diagram in
$F \colon K \to \mathscr {C}$ be a K-diagram in ![]() $\mathscr {C}$. A weakly initial object
$\mathscr {C}$. A weakly initial object ![]() $G \in \mathscr {C}_{F/}$ of order t is called a weak colimit of F of order t.
$G \in \mathscr {C}_{F/}$ of order t is called a weak colimit of F of order t.
Example 3.7. If ![]() $\mathscr {C}$ is an n-category and
$\mathscr {C}$ is an n-category and ![]() $G \colon K^{\triangleright } \to \mathscr {C}$ is a weak colimit of
$G \colon K^{\triangleright } \to \mathscr {C}$ is a weak colimit of ![]() $F = G_{|K} \colon K \to \mathscr {C}$ order
$F = G_{|K} \colon K \to \mathscr {C}$ order ![]() $t \geq n$, then G is a colimit diagram. This follows from Example 3.2 using the fact that
$t \geq n$, then G is a colimit diagram. This follows from Example 3.2 using the fact that ![]() $\mathscr {C}_{F/}$ is again an n-category (see [Reference Lurie22, Corollary 2.3.4.10]). In particular, a weak colimit of order
$\mathscr {C}_{F/}$ is again an n-category (see [Reference Lurie22, Corollary 2.3.4.10]). In particular, a weak colimit of order ![]() $\infty $ is a colimit diagram. If
$\infty $ is a colimit diagram. If ![]() $\mathscr {C}$ is an ordinary category, then a weak colimit of order
$\mathscr {C}$ is an ordinary category, then a weak colimit of order ![]() $0$ is a weak colimit diagram in the classical sense.
$0$ is a weak colimit diagram in the classical sense.
Remark 3.8. There is an important difference between weak colimits of order ![]() $0$ and weak colimits of order
$0$ and weak colimits of order ![]() $> 0$: as a consequence of Proposition 3.4, any two weak colimits of F of order
$> 0$: as a consequence of Proposition 3.4, any two weak colimits of F of order ![]() $> 0$ are equivalent. In particular, if
$> 0$ are equivalent. In particular, if ![]() $G \in \mathscr {C}_{F/}$ is a weak colimit of order
$G \in \mathscr {C}_{F/}$ is a weak colimit of order ![]() $t> 0$ and
$t> 0$ and ![]() $G' \in \mathscr {C}_{F/}$ is a weak colimit of order
$G' \in \mathscr {C}_{F/}$ is a weak colimit of order ![]() $>0$, then
$>0$, then ![]() $G'$ is also a weak colimit of order t.
$G'$ is also a weak colimit of order t.
The following proposition gives an alternative characterization of higher weak colimits following the analogous characterization for colimits in [Reference Lurie22, Lemma 4.2.4.3].
Proposition 3.9. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a simplicial set, and let
$\infty $-category and K a simplicial set, and let ![]() $G \colon K^{\triangleright } \to \mathscr {C}$ be a diagram with cone object
$G \colon K^{\triangleright } \to \mathscr {C}$ be a diagram with cone object ![]() $x \in \mathscr {C}$. Then G is a weak colimit of
$x \in \mathscr {C}$. Then G is a weak colimit of ![]() $F = G_{| K}$ of order t if and only if the canonical restriction map
$F = G_{| K}$ of order t if and only if the canonical restriction map
is t-connected for every ![]() $y \in \mathscr {C}$, where
$y \in \mathscr {C}$, where ![]() $c_y$ denotes, respectively, the constant diagram at
$c_y$ denotes, respectively, the constant diagram at ![]() $y \in \mathscr {C}$.
$y \in \mathscr {C}$.
Proof. The fibre of the restriction map over ![]() $F' \colon K^{\triangleright } \to \mathscr {C}$ with cone object y is identified with
$F' \colon K^{\triangleright } \to \mathscr {C}$ with cone object y is identified with ![]() $\mathrm {Map}_{\mathscr {C}_{F/}}(G, F')$ (see the proof of [Reference Lurie22, Lemma 4.2.4.3]).
$\mathrm {Map}_{\mathscr {C}_{F/}}(G, F')$ (see the proof of [Reference Lurie22, Lemma 4.2.4.3]).
The basic rules for the manipulation of higher weak colimits can be established similarly as for colimits. The following procedure shows that higher weak colimits can be computed iteratively, exactly like colimits, but with the difference that the order of the weak colimit may decrease with each iteration.
Proposition 3.10. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $K = K_1 \cup _{K_0} K_2$ be a simplicial set, where
$K = K_1 \cup _{K_0} K_2$ be a simplicial set, where ![]() $K_0 \subseteq K_1$ is a simplicial subset. Let
$K_0 \subseteq K_1$ is a simplicial subset. Let ![]() $F \colon K \to \mathscr {C}$ be a diagram, and denote its restrictions by
$F \colon K \to \mathscr {C}$ be a diagram, and denote its restrictions by ![]() $F_i := F_{|K_i }$, for
$F_i := F_{|K_i }$, for ![]() $i = 0,1,2$. Suppose that
$i = 0,1,2$. Suppose that ![]() $G_i \colon K_i^{\triangleright } \to \mathscr {C}$ is a weak colimit of
$G_i \colon K_i^{\triangleright } \to \mathscr {C}$ is a weak colimit of ![]() $F_i$ of order
$F_i$ of order ![]() $t_i \geq 0$, for
$t_i \geq 0$, for ![]() $i = 0,1,2$.
$i = 0,1,2$.
(a) There are morphisms
 $G_0 \to G_1{}_{|K_0^{\triangleright }}$ and
$G_0 \to G_1{}_{|K_0^{\triangleright }}$ and  $G_0 \to G_2{}_{|K_0^{\triangleright }}$ in
$G_0 \to G_2{}_{|K_0^{\triangleright }}$ in  $\mathscr {C}_{F_0/}$. These together with
$\mathscr {C}_{F_0/}$. These together with  $G_1$ and
$G_1$ and  $G_2$ determine a diagram in
$G_2$ determine a diagram in  $\mathscr {C}$ as follows:
$\mathscr {C}$ as follows:  $$ \begin{align*}H \colon K_1^{\triangleright} \cup_{K_0 \ast \Delta^{\{1\}}} (K_0 \ast \Delta^1) \cup_{K_0 \ast \Delta^{\{0\}}} (K_0 \ast \Delta^1) \cup_{K_0 \ast \Delta^{\{1\}}} K_2^{\triangleright} \to \mathscr{C}.\end{align*} $$
$$ \begin{align*}H \colon K_1^{\triangleright} \cup_{K_0 \ast \Delta^{\{1\}}} (K_0 \ast \Delta^1) \cup_{K_0 \ast \Delta^{\{0\}}} (K_0 \ast \Delta^1) \cup_{K_0 \ast \Delta^{\{1\}}} K_2^{\triangleright} \to \mathscr{C}.\end{align*} $$(b) Let
 $H_{\ulcorner } \colon \Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \mathscr {C}$ be the restriction of H to the cone objects. Suppose that
$H_{\ulcorner } \colon \Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \mathscr {C}$ be the restriction of H to the cone objects. Suppose that  $H' \colon \Delta ^1 \times \Delta ^1 \to \mathscr {C}$ is a weak pushout of
$H' \colon \Delta ^1 \times \Delta ^1 \to \mathscr {C}$ is a weak pushout of  $H_{\ulcorner }$ of order k. Then
$H_{\ulcorner }$ of order k. Then  $H'$ determines a cocone
$H'$ determines a cocone  $G \colon K^{\triangleright } \to \mathscr {C}$ over F, with the same cone object as
$G \colon K^{\triangleright } \to \mathscr {C}$ over F, with the same cone object as  $H'$, which is a weak colimit of F of order
$H'$, which is a weak colimit of F of order  $\ell : = \mathrm {min}(k, t_1, t_0 -1, t_2)$.
$\ell : = \mathrm {min}(k, t_1, t_0 -1, t_2)$.
Proof. (a) follows directly from the properties of higher weak colimits. For (b), we first explain the construction of the cocone ![]() $G \colon K^{\triangleright } \to \mathscr {C}$. The functor
$G \colon K^{\triangleright } \to \mathscr {C}$. The functor ![]() $H'$ is represented by a diagram
$H'$ is represented by a diagram
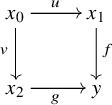
where ![]() $x_i$ is the cone object of
$x_i$ is the cone object of ![]() $G_i$ and the morphisms u and v are given, respectively, by the morphisms
$G_i$ and the morphisms u and v are given, respectively, by the morphisms ![]() $G_0 \to G_1{}_{|K_0^{\triangleright }}$ and
$G_0 \to G_1{}_{|K_0^{\triangleright }}$ and ![]() $G_0 \to G_2{}_{|K_0^{\triangleright }}$ in
$G_0 \to G_2{}_{|K_0^{\triangleright }}$ in ![]() $\mathscr {C}_{F_0/}$. The morphisms f and g produce two new cocones (essentially uniquely)
$\mathscr {C}_{F_0/}$. The morphisms f and g produce two new cocones (essentially uniquely) ![]() $G^{\prime }_1 \colon K_1^{\triangleright } \to \mathscr {C}$ over
$G^{\prime }_1 \colon K_1^{\triangleright } \to \mathscr {C}$ over ![]() $F_1$ and
$F_1$ and ![]() $G^{\prime }_2 \colon K_2^{\triangleright } \to \mathscr {C}$ over
$G^{\prime }_2 \colon K_2^{\triangleright } \to \mathscr {C}$ over ![]() $F_2$, with common cone object y. The restrictions
$F_2$, with common cone object y. The restrictions ![]() $G^{\prime }_1{}_{|K_0^{\triangleright }}$ and
$G^{\prime }_1{}_{|K_0^{\triangleright }}$ and ![]() $G^{\prime }_2{}_{|K_0^{\triangleright }}$ are equivalent as cocones over
$G^{\prime }_2{}_{|K_0^{\triangleright }}$ are equivalent as cocones over ![]() $F_0$. We may then extend
$F_0$. We may then extend ![]() $G^{\prime }_2{}_{|K_0^{\triangleright }}$ in an essentially unique way to a new cocone
$G^{\prime }_2{}_{|K_0^{\triangleright }}$ in an essentially unique way to a new cocone ![]() $G^{\prime \prime }_1 \colon K_1^{\triangleright } \to \mathscr {C}$ over
$G^{\prime \prime }_1 \colon K_1^{\triangleright } \to \mathscr {C}$ over ![]() $F_1$, which is equivalent to
$F_1$, which is equivalent to ![]() $G^{\prime }_1$. The resulting cocones
$G^{\prime }_1$. The resulting cocones
assemble to define the required cocone ![]() $G \colon K^{\triangleright } \to \mathscr {C}$. Then the claim in (b) is shown by applying Proposition 3.9, first for weak pushouts and then for
$G \colon K^{\triangleright } \to \mathscr {C}$. Then the claim in (b) is shown by applying Proposition 3.9, first for weak pushouts and then for ![]() $K_i$-diagrams, and using the fact that
$K_i$-diagrams, and using the fact that ![]() $\mathscr {C}^K$ is the homotopy pullback (in the Joyal model category) of the diagram of
$\mathscr {C}^K$ is the homotopy pullback (in the Joyal model category) of the diagram of ![]() $\infty $-categories (
$\infty $-categories (![]() $\mathscr {C}^{K_1} \to \mathscr {C}^{K_0} \leftarrow \mathscr {C}^{K_2}$), so its mapping spaces can also be identified with the corresponding (homotopy) pullbacks of mapping spaces.
$\mathscr {C}^{K_1} \to \mathscr {C}^{K_0} \leftarrow \mathscr {C}^{K_2}$), so its mapping spaces can also be identified with the corresponding (homotopy) pullbacks of mapping spaces.
Example 3.11. Let ![]() $\mathscr {C}$ be (the nerve of) an ordinary category that admits small coproducts and weak pushouts. By Proposition 3.10, every diagram
$\mathscr {C}$ be (the nerve of) an ordinary category that admits small coproducts and weak pushouts. By Proposition 3.10, every diagram ![]() $F \colon K \to \mathscr {C}$, where K is 1-dimensional, admits a weak colimit (of order 0). Now suppose that
$F \colon K \to \mathscr {C}$, where K is 1-dimensional, admits a weak colimit (of order 0). Now suppose that ![]() $F \colon I \to \mathscr {C}$ is a diagram where I is (the nerve of) an arbitrary ordinary small category. Since
$F \colon I \to \mathscr {C}$ is a diagram where I is (the nerve of) an arbitrary ordinary small category. Since ![]() $\mathscr {C}$ is an
$\mathscr {C}$ is an ![]() $1$-category, a cocone
$1$-category, a cocone ![]() $G \colon I^{\triangleright } \to \mathscr {C}$ over F is determined uniquely by its restriction to a cocone
$G \colon I^{\triangleright } \to \mathscr {C}$ over F is determined uniquely by its restriction to a cocone ![]() $G' \colon (\mathrm {sk}_1 I)^{\triangleright } \to \mathscr {C}$ over
$G' \colon (\mathrm {sk}_1 I)^{\triangleright } \to \mathscr {C}$ over ![]() $F_{|\mathrm {sk}_1 I}$, and similarly for morphisms between cocones. As a consequence, we may deduce the well-known fact that
$F_{|\mathrm {sk}_1 I}$, and similarly for morphisms between cocones. As a consequence, we may deduce the well-known fact that ![]() $\mathscr {C}$ has weak I-colimits.
$\mathscr {C}$ has weak I-colimits.
Example 3.12. Let ![]() $T \subset \Delta ^1 \times \Delta ^2$ be the full subcategory spanned by the objects
$T \subset \Delta ^1 \times \Delta ^2$ be the full subcategory spanned by the objects ![]() $(0, i)$, for
$(0, i)$, for ![]() $i = 0,1,2$, and
$i = 0,1,2$, and ![]() $(1,0)$. Let
$(1,0)$. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category with weak pushouts of order t, and let
$\infty $-category with weak pushouts of order t, and let ![]() $F \colon T \to \mathscr {C}$ be a T-diagram in
$F \colon T \to \mathscr {C}$ be a T-diagram in ![]() $\mathscr {C}$. Write
$\mathscr {C}$. Write ![]() $T = T_1 \cup _{T_0} T_2$, where
$T = T_1 \cup _{T_0} T_2$, where ![]() $T_1$ is spanned by
$T_1$ is spanned by ![]() $(0,i)$,
$(0,i)$, ![]() $i = 0,1$ and
$i = 0,1$ and ![]() $(1,0)$,
$(1,0)$, ![]() $T_2$ is spanned by
$T_2$ is spanned by ![]() $(0, i)$,
$(0, i)$, ![]() $i = 1,2$ and
$i = 1,2$ and ![]() $T_0 = \{(0,1)\}$. Using Proposition 3.10, we may compute a weak colimit of F of order t in terms of iterated weak pushouts of order t.
$T_0 = \{(0,1)\}$. Using Proposition 3.10, we may compute a weak colimit of F of order t in terms of iterated weak pushouts of order t.
3.2 Homotopy categories and (co)limits
Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let K be a simplicial set. By the universal property of
$\infty $-category, and let K be a simplicial set. By the universal property of ![]() $\mathrm {h}_n(-)$, the functor
$\mathrm {h}_n(-)$, the functor
which is given by composition with ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$, factors canonically through the homotopy n-category:
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$, factors canonically through the homotopy n-category:
The comparison between K-colimits in ![]() $\mathscr {C}$ and in
$\mathscr {C}$ and in ![]() $\mathrm {h}_n \mathscr {C}$ is essentially a question about the properties of the functor
$\mathrm {h}_n \mathscr {C}$ is essentially a question about the properties of the functor ![]() $\Phi ^K_n$. Note that for
$\Phi ^K_n$. Note that for ![]() $n=1$,
$n=1$, ![]() $\Phi ^K_1$ is simply the canonical functor of ordinary categories:
$\Phi ^K_1$ is simply the canonical functor of ordinary categories: ![]() $\mathrm {h}_1(\mathscr {C}^K) \to \mathrm {h}_1(\mathscr {C})^K$.
$\mathrm {h}_1(\mathscr {C}^K) \to \mathrm {h}_1(\mathscr {C})^K$.
Lemma 3.14. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a finite dimensional simplicial set of dimension
$\infty $-category and K a finite dimensional simplicial set of dimension ![]() $d> 0$, and let
$d> 0$, and let ![]() $n \geq 1$ be an integer. The functor
$n \geq 1$ be an integer. The functor
satisfies the following:
(a)
 $\Phi ^K_n$ is a bijection in simplicial degrees
$\Phi ^K_n$ is a bijection in simplicial degrees  $< n - d$.
$< n - d$.(b)
 $\Phi ^K_n$ is surjective in simplicial degree
$\Phi ^K_n$ is surjective in simplicial degree  $n-d$; it identifies
$n-d$; it identifies  $(n-d)$-simplices, which are homotopic relative to the
$(n-d)$-simplices, which are homotopic relative to the  $(n-1)$-skeleton of
$(n-1)$-skeleton of  $\Delta ^{n-d} \times K$.
$\Delta ^{n-d} \times K$.(c)
 $\Phi ^K_n$ is surjective in simplicial degree
$\Phi ^K_n$ is surjective in simplicial degree  $n-d+1$.
$n-d+1$.
Proof. The m-simplices of ![]() $\mathrm {Fun}(K, \mathrm {h}_n \mathscr {C})$ are equivalence classes of maps
$\mathrm {Fun}(K, \mathrm {h}_n \mathscr {C})$ are equivalence classes of maps
that extend to ![]() $\mathrm {sk}_{n+1}(\Delta ^m \times K)$. On the other hand, the m-simplices of
$\mathrm {sk}_{n+1}(\Delta ^m \times K)$. On the other hand, the m-simplices of ![]() $\mathrm {h}_n \mathrm {Fun}(K, \mathscr {C})$ are equivalence classes of maps
$\mathrm {h}_n \mathrm {Fun}(K, \mathscr {C})$ are equivalence classes of maps
that extend to ![]() $\mathrm {sk}_{n+1}(\Delta ^m) \times K$. The functor
$\mathrm {sk}_{n+1}(\Delta ^m) \times K$. The functor ![]() $\Phi ^K_n$ is induced by the canonical map
$\Phi ^K_n$ is induced by the canonical map
which is an isomorphism if ![]() $d \leq \mathrm {max}(n - m, 0)$. This shows that the map
$d \leq \mathrm {max}(n - m, 0)$. This shows that the map ![]() $\Phi ^K_n$ is surjective in simplicial degrees
$\Phi ^K_n$ is surjective in simplicial degrees ![]() $\leq n-d + 1$. Similarly, the map
$\leq n-d + 1$. Similarly, the map
is an isomorphism if ![]() $d \leq \mathrm {max}(n - m -1, 0)$, so the two equivalence relations agree for
$d \leq \mathrm {max}(n - m -1, 0)$, so the two equivalence relations agree for ![]() $m < n -d$.
$m < n -d$.
Remark 3.15. The case ![]() $d = 0$ is both special and essentially trivial, since the functor
$d = 0$ is both special and essentially trivial, since the functor ![]() $\Phi ^K_n$ is an isomorphism in this case.
$\Phi ^K_n$ is an isomorphism in this case.
Proposition 3.16. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a finite dimensional simplicial set of dimension
$\infty $-category and K a finite dimensional simplicial set of dimension ![]() $d> 0$, and let
$d> 0$, and let ![]() $n \geq 1$ be an integer. Then for every lifting problem
$n \geq 1$ be an integer. Then for every lifting problem
where ![]() $m \leq n-d+1$ (respectively,
$m \leq n-d+1$ (respectively, ![]() $m < n - d$), there is a (unique) filler
$m < n - d$), there is a (unique) filler ![]() $\Delta ^m \to \mathrm {h}_n (\mathscr {C}^K)$, which makes the diagram commutative.
$\Delta ^m \to \mathrm {h}_n (\mathscr {C}^K)$, which makes the diagram commutative.
Proof. The case ![]() $m < n-d + 1$ is a direct consequence of Lemma 3.14. For
$m < n-d + 1$ is a direct consequence of Lemma 3.14. For ![]() $m = n -d +1 \leq n$, Lemma 3.14 shows that there is a lift
$m = n -d +1 \leq n$, Lemma 3.14 shows that there is a lift ![]() $\tau \colon \Delta ^m \to \mathrm {h}_n(\mathscr {C}^K)$ of
$\tau \colon \Delta ^m \to \mathrm {h}_n(\mathscr {C}^K)$ of ![]() $\sigma $, represented by a map
$\sigma $, represented by a map ![]() $\tau ' \colon \Delta ^m \to \mathscr {C}^K$. The maps
$\tau ' \colon \Delta ^m \to \mathscr {C}^K$. The maps
become equal after composition with ![]() $\Phi ^K_n$. Moreover, note that u corresponds uniquely to a map
$\Phi ^K_n$. Moreover, note that u corresponds uniquely to a map ![]() $u \colon \partial \Delta ^m \to \mathscr {C}^K$. The maps
$u \colon \partial \Delta ^m \to \mathscr {C}^K$. The maps ![]() $\Phi ^K_n \circ u$ and
$\Phi ^K_n \circ u$ and ![]() $\Phi ^K_n \circ (\gamma _n \tau ^{\prime }_{|\partial \Delta ^m})$ correspond to the equivalence classes of maps (using here the same notation for the adjoint maps)
$\Phi ^K_n \circ (\gamma _n \tau ^{\prime }_{|\partial \Delta ^m})$ correspond to the equivalence classes of maps (using here the same notation for the adjoint maps)
so these last two maps are homotopic relative to ![]() $\mathrm {sk}_{n-1}(\partial \Delta ^m \times K)$ (see Proposition 2.3). Let
$\mathrm {sk}_{n-1}(\partial \Delta ^m \times K)$ (see Proposition 2.3). Let
be a homotopy from ![]() $\tau ^{\prime }_{| \partial \Delta ^m \times K}$ to u relative to the subspace
$\tau ^{\prime }_{| \partial \Delta ^m \times K}$ to u relative to the subspace ![]() $\mathrm {sk}_{n-1}(\partial \Delta ^m \times K)$, where
$\mathrm {sk}_{n-1}(\partial \Delta ^m \times K)$, where ![]() $J = N(0 \rightleftarrows 1)$ denotes the Joyal interval object. Using the fact that
$J = N(0 \rightleftarrows 1)$ denotes the Joyal interval object. Using the fact that
is a cofibration, this homotopy can be extended to a homotopy
where ![]() $\tau ' = H^{\prime }_{|\Delta ^m\times K \times \{0\}}$ and
$\tau ' = H^{\prime }_{|\Delta ^m\times K \times \{0\}}$ and ![]() $H'$ is constant on
$H'$ is constant on ![]() $\mathrm {sk}_{n-1}(\Delta ^m \times K)$. Then the map
$\mathrm {sk}_{n-1}(\Delta ^m \times K)$. Then the map
extends u. Moreover, the (adjoint) map ![]() $\widetilde {\tau } \colon \Delta ^m \to \mathscr {C}^K$ defines an element in
$\widetilde {\tau } \colon \Delta ^m \to \mathscr {C}^K$ defines an element in ![]() $\mathrm {h}_n(\mathscr {C})^K_m$, after composition with
$\mathrm {h}_n(\mathscr {C})^K_m$, after composition with ![]() $\gamma _n$, which agrees with
$\gamma _n$, which agrees with ![]() $\Phi ^K_n \circ \tau = \sigma $, so
$\Phi ^K_n \circ \tau = \sigma $, so ![]() $\widetilde {\tau }$ represents a diagonal filler, as required.
$\widetilde {\tau }$ represents a diagonal filler, as required.
As a consequence of Proposition 3.16, we obtain the following result about the comparison between the n-categories ![]() $\mathrm {h}_n(\mathscr {C}^K)$ and
$\mathrm {h}_n(\mathscr {C}^K)$ and ![]() $\mathrm {h}_n(\mathscr {C})^K$.
$\mathrm {h}_n(\mathscr {C})^K$.
Corollary 3.17. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a finite dimensional simplicial set of dimension
$\infty $-category and K a finite dimensional simplicial set of dimension ![]() $d> 0$, and let
$d> 0$, and let ![]() $n \geq d$ be an integer. The functor
$n \geq d$ be an integer. The functor ![]() $\Phi ^K_n \colon \mathrm {h}_n(\mathscr {C}^K) \to (\mathrm {h}_n \mathscr {C})^K$ is essentially surjective, and for every pair of objects
$\Phi ^K_n \colon \mathrm {h}_n(\mathscr {C}^K) \to (\mathrm {h}_n \mathscr {C})^K$ is essentially surjective, and for every pair of objects ![]() $F, G$ in
$F, G$ in ![]() $\mathrm {h}_n(\mathscr {C}^K)$, the induced map between mapping spaces
$\mathrm {h}_n(\mathscr {C}^K)$, the induced map between mapping spaces
is ![]() $(n-d)$-connected. As a consequence,
$(n-d)$-connected. As a consequence, ![]() $\Phi ^K_n$ induces an equivalence:
$\Phi ^K_n$ induces an equivalence:
Now assume that ![]() $\mathscr {C}$ is an
$\mathscr {C}$ is an ![]() $\infty $-category that admits K-colimits, where K is a simplicial set. We have colimit-functors:
$\infty $-category that admits K-colimits, where K is a simplicial set. We have colimit-functors:

Assuming also that ![]() $\mathscr {C}$ and K are as in Corollary 3.17, and passing to the homotopy
$\mathscr {C}$ and K are as in Corollary 3.17, and passing to the homotopy ![]() $(n-d)$-categories as in (3.18), we obtain the following corollary.
$(n-d)$-categories as in (3.18), we obtain the following corollary.
Corollary 3.19. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category and K a finite dimensional simplicial set of dimension
$\infty $-category and K a finite dimensional simplicial set of dimension ![]() $d> 0$, and let
$d> 0$, and let ![]() $n \geq d$ be an integer. Suppose that
$n \geq d$ be an integer. Suppose that ![]() $\mathscr {C}$ admits K-colimits. Then there is an adjoint pair
$\mathscr {C}$ admits K-colimits. Then there is an adjoint pair
where c denotes the constant K-diagram functor.
Proposition 3.20. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category with weak K-colimits of order k, where K is a simplicial set of dimension
$\infty $-category with weak K-colimits of order k, where K is a simplicial set of dimension ![]() $d> 0$, and let
$d> 0$, and let ![]() $n \geq 1$ be an integer. Then
$n \geq 1$ be an integer. Then ![]() $\mathrm {h}_n \mathscr {C}$ has weak K-colimits of order
$\mathrm {h}_n \mathscr {C}$ has weak K-colimits of order ![]() $\ell = \mathrm {min}(n-d, k)$. Moreover, the functor
$\ell = \mathrm {min}(n-d, k)$. Moreover, the functor ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ sends weak K-colimits of order k to weak K-colimits of order
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ sends weak K-colimits of order k to weak K-colimits of order ![]() $\ell $.
$\ell $.
Proof. We may assume that ![]() $n \geq d$, and therefore the functor
$n \geq d$, and therefore the functor ![]() $\mathscr {C}^K \to (\mathrm {h}_n \mathscr {C})^K$ is surjective on objects. Then it suffices to prove the second claim. Let
$\mathscr {C}^K \to (\mathrm {h}_n \mathscr {C})^K$ is surjective on objects. Then it suffices to prove the second claim. Let ![]() $G \colon K^{\triangleright } \to \mathscr {C}$ be a weak colimit of
$G \colon K^{\triangleright } \to \mathscr {C}$ be a weak colimit of ![]() $F = G_{|K}$ of order k with cone object
$F = G_{|K}$ of order k with cone object ![]() $x \in \mathscr {C}$. By Proposition 3.9, it suffices to prove that the canonical map
$x \in \mathscr {C}$. By Proposition 3.9, it suffices to prove that the canonical map
is ![]() $\ell $-connected for every
$\ell $-connected for every ![]() $y \in \mathscr {C}$. Note that there is a k-connected map:
$y \in \mathscr {C}$. Note that there is a k-connected map:
Hence it suffices to show that the canonical map
is ![]() $(n-d)$-connected. This follows from Corollary 3.17. (Alternatively, note that the last map is identified with the canonical map from the
$(n-d)$-connected. This follows from Corollary 3.17. (Alternatively, note that the last map is identified with the canonical map from the ![]() $(n-1)$-truncation of a
$(n-1)$-truncation of a ![]() $K^{\operatorname {op}}$-limit of
$K^{\operatorname {op}}$-limit of ![]() $\infty $-groupoids to the
$\infty $-groupoids to the ![]() $K^{\operatorname {op}}$-limit of the
$K^{\operatorname {op}}$-limit of the ![]() $(n-1)$-truncations of the
$(n-1)$-truncations of the ![]() $\infty $-groupoids:
$\infty $-groupoids:
An inductive argument on d shows that the map is ![]() $(n-d)$-connected.)
$(n-d)$-connected.)
Remark 3.21. A different proof of Proposition 3.20 is also possible using elementary lifting arguments based on Proposition 3.16.
Corollary 3.22. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category that admits finite (respectively, small) colimits.
$\infty $-category that admits finite (respectively, small) colimits.
(a) The homotopy n-category
 $\mathrm {h}_n \mathscr {C}$ admits finite (respectively, small) coproducts and weak pushouts of order
$\mathrm {h}_n \mathscr {C}$ admits finite (respectively, small) coproducts and weak pushouts of order  $n-1$. Moreover, the functor
$n-1$. Moreover, the functor  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ preserves finite (respectively, small) coproducts and sends pushouts in
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ preserves finite (respectively, small) coproducts and sends pushouts in  $\mathscr {C}$ to weak pushouts of order
$\mathscr {C}$ to weak pushouts of order  $n-1$.
$n-1$.(b) Suppose that
 $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ preserves finite colimits. Then
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ preserves finite colimits. Then  $\mathscr {C}$ is equivalent to an n-category.
$\mathscr {C}$ is equivalent to an n-category.
Proof. (a) ![]() $\mathrm {h}_n \mathscr {C}$ admits finite coproducts by Remark 3.15. The existence and preservation of higher weak pushouts is a consequence of Proposition 3.20. (b) is a consequence of [Reference Nguyen, Raptis and Schrade29, Corollary 3.3.5].
$\mathrm {h}_n \mathscr {C}$ admits finite coproducts by Remark 3.15. The existence and preservation of higher weak pushouts is a consequence of Proposition 3.20. (b) is a consequence of [Reference Nguyen, Raptis and Schrade29, Corollary 3.3.5].
These properties of homotopy n-categories of (finitely) cocomplete ![]() $\infty $-categories suggest considering the following class of n-categories as a convenient general context for the study of these n-categories.
$\infty $-categories suggest considering the following class of n-categories as a convenient general context for the study of these n-categories.
Definition 3.23. Let ![]() $n \geq 1$ be an integer or
$n \geq 1$ be an integer or ![]() $n=\infty $. A (finitely) weakly cocomplete n-category is an n-category
$n=\infty $. A (finitely) weakly cocomplete n-category is an n-category ![]() $\mathscr {C}$ that admits small (finite) coproducts and weak pushouts of order
$\mathscr {C}$ that admits small (finite) coproducts and weak pushouts of order ![]() $n-1$.
$n-1$.
These n-categories are studied further in [Reference Nguyen, Raptis and Schrade30] in connection with adjoint functor theorems and Brown representability theorems for n-categories (extending the results of [Reference Nguyen, Raptis and Schrade29]). Also, in Section 6 (which can be read independently of Sections 4 and 5), we will return to the properties of weak (co)limits in higher homotopy categories, especially, for pointed and stable ![]() $\infty $-categories, and use higher weak colimits in order to define K-theory for higher homotopy categories.
$\infty $-categories, and use higher weak colimits in order to define K-theory for higher homotopy categories.
Remark 3.24. Corollary 3.19 produces a truncated K-colimit functor for ![]() $\mathrm {h}_n \mathscr {C}$:
$\mathrm {h}_n \mathscr {C}$:
According to Proposition 3.16 (compare to Proposition 2.6 and Corollary 2.7), there is a (non-canonical) section
(Note that the target is closely related to ![]() $\mathrm {sk}_{n-d+1}(\mathscr {C}^K).$) Then we may define the partial K-colimit functor for
$\mathrm {sk}_{n-d+1}(\mathscr {C}^K).$) Then we may define the partial K-colimit functor for ![]() $\mathrm {h}_n (\mathscr {C})$ (which depends on
$\mathrm {h}_n (\mathscr {C})$ (which depends on ![]() $\mathscr {C}$ and the section
$\mathscr {C}$ and the section ![]() $\epsilon $)
$\epsilon $)
as the composition
Example 3.25. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category that has pushouts, and let K denote the (nerve of the) ‘corner’ category
$\infty $-category that has pushouts, and let K denote the (nerve of the) ‘corner’ category ![]() $\ulcorner : = \Delta ^1 \cup _{\Delta ^0} \Delta ^1$. The functor
$\ulcorner : = \Delta ^1 \cup _{\Delta ^0} \Delta ^1$. The functor
is surjective on objects and full. By Corollary 3.17, the pushout-functor on ![]() $\mathscr {C}$ induces a truncated pushout-functor
$\mathscr {C}$ induces a truncated pushout-functor
which is left adjoint to the constant diagram functor. Furthermore, we have a map as follows
which sends ![]() $F \colon K \to \mathrm {h}_1 \mathscr {C}$ to the pushout of a choice of a lift
$F \colon K \to \mathrm {h}_1 \mathscr {C}$ to the pushout of a choice of a lift ![]() $\widetilde {F} \colon K \to \mathscr {C}$. This is simply regarded as a map from the set of
$\widetilde {F} \colon K \to \mathscr {C}$. This is simply regarded as a map from the set of ![]() $0$-simplices. Moreover, (3.26) extends further to the
$0$-simplices. Moreover, (3.26) extends further to the ![]() $1$-skeleton, but this involves non-canonical choices that are not unique even up to homotopy. As explained in Remark 3.24, an extension of this type can be obtained from a section
$1$-skeleton, but this involves non-canonical choices that are not unique even up to homotopy. As explained in Remark 3.24, an extension of this type can be obtained from a section ![]() $\epsilon \colon \mathrm {sk}_1 \big (\mathrm {Fun}(K, \mathrm {h}_1\mathscr {C})\big ) \to \mathrm {sk}_1\big (\mathrm {h}_1(\mathscr {C}^K)\big ).$ The fact that this process cannot be continued to higher-dimensional skeleta is related to the non-functoriality of weak pushouts in the homotopy category.
$\epsilon \colon \mathrm {sk}_1 \big (\mathrm {Fun}(K, \mathrm {h}_1\mathscr {C})\big ) \to \mathrm {sk}_1\big (\mathrm {h}_1(\mathscr {C}^K)\big ).$ The fact that this process cannot be continued to higher-dimensional skeleta is related to the non-functoriality of weak pushouts in the homotopy category.
More generally, for ![]() $n \geq 1$, there is a left adjoint truncated pushout-functor
$n \geq 1$, there is a left adjoint truncated pushout-functor
and partial pushout-functors
that define weak pushouts in ![]() $\mathrm {h}_n(\mathscr {C})$ of order
$\mathrm {h}_n(\mathscr {C})$ of order ![]() $n-1$.
$n-1$.
4 Higher derivators
4.1 Basic definitions and properties
We recall that ![]() $\mathsf {Cat_{\infty }}$ denotes the category of
$\mathsf {Cat_{\infty }}$ denotes the category of ![]() $\infty $-categories, regarded as enriched in
$\infty $-categories, regarded as enriched in ![]() $\infty $-categories. Let
$\infty $-categories. Let ![]() $\mathsf {Dia}$ denote a full subcategory of
$\mathsf {Dia}$ denote a full subcategory of ![]() $\mathsf {Cat_{\infty }}$ that has the following properties:
$\mathsf {Cat_{\infty }}$ that has the following properties:
(Dia 0)
 $\mathsf {Dia}$ contains the (nerves of) finite posets.
$\mathsf {Dia}$ contains the (nerves of) finite posets.(Dia 1)
 $\mathsf {Dia}$ is closed under finite coproducts and under pullbacks along an inner fibration.
$\mathsf {Dia}$ is closed under finite coproducts and under pullbacks along an inner fibration.(Dia 2) For every
 $\mathsf {X} \in \mathsf {Dia}$ and
$\mathsf {X} \in \mathsf {Dia}$ and  $x \in \mathsf {X}$, the
$x \in \mathsf {X}$, the  $\infty $-category
$\infty $-category  $\mathsf {X}_{/x}$ is in
$\mathsf {X}_{/x}$ is in  $\mathsf {Dia}$.
$\mathsf {Dia}$.(Dia 3)
 $\mathsf {Dia}$ is closed under passing to the opposite
$\mathsf {Dia}$ is closed under passing to the opposite  $\infty $-category.
$\infty $-category.
The main examples of such subcategories of ![]() $\mathsf {Cat_{\infty }}$ are the following:
$\mathsf {Cat_{\infty }}$ are the following:
(i) The full subcategory of (nerves of) finite posets.
(ii) The full subcategory of (ordinary) finite direct categories
 $\mathcal {D}ir_{f}\kern-1pt$. (We recall that an ordinary category
$\mathcal {D}ir_{f}\kern-1pt$. (We recall that an ordinary category  $\mathsf {C}$ is called finite direct if its nerve is a finite simplicial set.)
$\mathsf {C}$ is called finite direct if its nerve is a finite simplicial set.)(iii) The full subcategory
 $\mathsf {Cat_{n}} \subset \mathsf {Cat_{\infty }}$ of n-categories for any
$\mathsf {Cat_{n}} \subset \mathsf {Cat_{\infty }}$ of n-categories for any  $n \geq 1$.
$n \geq 1$.(iv)
 $\mathsf {Cat_{\infty }}$.
$\mathsf {Cat_{\infty }}$.
We denote by ![]() $\mathsf {Dia}^{\operatorname {op}}$ the opposite category taken 1-categorically: that is, the enrichment of
$\mathsf {Dia}^{\operatorname {op}}$ the opposite category taken 1-categorically: that is, the enrichment of ![]() $\mathsf {Dia}^{\operatorname {op}}$ is given by
$\mathsf {Dia}^{\operatorname {op}}$ is given by
Definition 4.1. An ![]() $\infty $-prederivator with domain
$\infty $-prederivator with domain ![]() $\mathsf {Dia}$ is an enriched functor
$\mathsf {Dia}$ is an enriched functor
An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D}$ with domain
$\mathbb {D}$ with domain ![]() $\mathsf {Dia}$ is an n-prederivator if it factors through the inclusion
$\mathsf {Dia}$ is an n-prederivator if it factors through the inclusion ![]() $\mathsf {Cat_{n}} \subset \mathsf {Cat_{\infty }}$: that is,
$\mathsf {Cat_{n}} \subset \mathsf {Cat_{\infty }}$: that is, ![]() $\mathbb {D}$ is an enriched functor
$\mathbb {D}$ is an enriched functor
A strict morphism of ![]() $\infty $-prederivators is a natural transformation
$\infty $-prederivators is a natural transformation ![]() $F \colon \mathbb {D} \to \mathbb {D}'$ between enriched functors. Thus we obtain a category of
$F \colon \mathbb {D} \to \mathbb {D}'$ between enriched functors. Thus we obtain a category of ![]() $\infty $-prederivators, denoted by
$\infty $-prederivators, denoted by ![]() $\mathsf {PreDer}_{\infty }$, which is enriched in
$\mathsf {PreDer}_{\infty }$, which is enriched in ![]() $\infty $-categories. For any
$\infty $-categories. For any ![]() $n \geq 1$, there is a full subcategory
$n \geq 1$, there is a full subcategory ![]() $\mathsf {PreDer}_n \subset \mathsf {PreDer}_{\infty }$ spanned by the n-prederivators. In the same way that the classical theory of (pre)derivators is founded on a ((2,2)=)2-categorical context, the general theory of
$\mathsf {PreDer}_n \subset \mathsf {PreDer}_{\infty }$ spanned by the n-prederivators. In the same way that the classical theory of (pre)derivators is founded on a ((2,2)=)2-categorical context, the general theory of ![]() $\infty $-prederivators involves an
$\infty $-prederivators involves an ![]() $(\infty , 2)$-categorical context. We point out that it would be natural to also consider non-strict morphisms (aka pseudonatural transformations) between
$(\infty , 2)$-categorical context. We point out that it would be natural to also consider non-strict morphisms (aka pseudonatural transformations) between ![]() $\infty $-prederivators, but these will not be needed in this paper.
$\infty $-prederivators, but these will not be needed in this paper.
Notation. Let ![]() $\mathbb {D}$ be an
$\mathbb {D}$ be an ![]() $\infty $-prederivator with domain
$\infty $-prederivator with domain ![]() $\mathsf {Dia}$, and let
$\mathsf {Dia}$, and let ![]() $u \colon \mathsf {X} \to \mathsf {Y}$ be a functor in
$u \colon \mathsf {X} \to \mathsf {Y}$ be a functor in ![]() $\mathsf {Dia}$. We will often denote the induced functor
$\mathsf {Dia}$. We will often denote the induced functor ![]() $\mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y}) \to \mathbb {D}(\mathsf {X})$ by
$\mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y}) \to \mathbb {D}(\mathsf {X})$ by ![]() $u^*$. Moreover, if
$u^*$. Moreover, if ![]() $i_{\mathsf {Y}, y} \colon \Delta ^0 \to \mathsf {Y}$ is the inclusion of the object
$i_{\mathsf {Y}, y} \colon \Delta ^0 \to \mathsf {Y}$ is the inclusion of the object ![]() $y \in \mathsf {Y}$ and
$y \in \mathsf {Y}$ and ![]() $F \in \mathbb {D}(\mathsf {Y})$, we will often denote the object
$F \in \mathbb {D}(\mathsf {Y})$, we will often denote the object ![]() $\mathbb {D}(i_{\mathsf {Y}, y})(F)$ in
$\mathbb {D}(i_{\mathsf {Y}, y})(F)$ in ![]() $\mathbb {D}(\Delta ^0)$ by
$\mathbb {D}(\Delta ^0)$ by ![]() $F_{y}$.
$F_{y}$.
Example 4.2. A 1-prederivator with domain ![]() $\mathsf {Cat_1}$ is a prederivator in the usual sense [Reference Maltsiniotis24, Reference Groth18].
$\mathsf {Cat_1}$ is a prederivator in the usual sense [Reference Maltsiniotis24, Reference Groth18].
Example 4.3. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category. There is an associated
$\infty $-category. There is an associated ![]() $\infty $-prederivator (with domain
$\infty $-prederivator (with domain ![]() $\mathsf {Dia}$) defined by
$\mathsf {Dia}$) defined by ![]() $\mathbb {D}^{(\infty )}_{\mathscr {C}} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}, \ \mathsf {X} \mapsto \mathrm {Fun}(\mathsf {X}, \mathscr {C})$. Moreover, for any
$\mathbb {D}^{(\infty )}_{\mathscr {C}} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}, \ \mathsf {X} \mapsto \mathrm {Fun}(\mathsf {X}, \mathscr {C})$. Moreover, for any ![]() $n \geq 1$,
$n \geq 1$,
defines an n-prederivator.
Definition 4.4. An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a right
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a right ![]() $\infty $-derivator if it satisfies the following properties:
$\infty $-derivator if it satisfies the following properties:
(Der 1) For every pair of
 $\infty $-categories
$\infty $-categories  $\mathsf {X}$ and
$\mathsf {X}$ and  $\mathsf {Y}$ in
$\mathsf {Y}$ in  $\mathsf {Dia}$, the functor induced by the inclusions of the factors to the coproduct
$\mathsf {Dia}$, the functor induced by the inclusions of the factors to the coproduct  $\mathsf {X} \sqcup \mathsf {Y}$, is an equivalence. Moreover,
$\mathsf {X} \sqcup \mathsf {Y}$, is an equivalence. Moreover, $$ \begin{align*}\mathbb{D}(\mathsf{X} \sqcup \mathsf{Y})\rightarrow \mathbb{D}(\mathsf{X}) \times \mathbb{D}(\mathsf{Y})\end{align*} $$
$$ \begin{align*}\mathbb{D}(\mathsf{X} \sqcup \mathsf{Y})\rightarrow \mathbb{D}(\mathsf{X}) \times \mathbb{D}(\mathsf{Y})\end{align*} $$ $\mathbb {D}(\varnothing )$ is equivalent to the final
$\mathbb {D}(\varnothing )$ is equivalent to the final  $\infty $-category
$\infty $-category  $\Delta ^0$.
$\Delta ^0$.(Der 2) For every
 $\infty $-category
$\infty $-category  $\mathsf {X}$ in
$\mathsf {X}$ in  $\mathsf {Dia}$, the functor is conservative: that is, it detects equivalences. We recall that
$\mathsf {Dia}$, the functor is conservative: that is, it detects equivalences. We recall that $$ \begin{align*}(i_{\mathsf{X}, x}^{*} = \mathbb{D}(i_{\mathsf{X}, x}))_{x \in \mathsf{X}} \colon \mathbb{D}(\mathsf{X}) \rightarrow \prod_{x \in \mathsf{X}} \mathbb{D}(\Delta^0)\end{align*} $$
$$ \begin{align*}(i_{\mathsf{X}, x}^{*} = \mathbb{D}(i_{\mathsf{X}, x}))_{x \in \mathsf{X}} \colon \mathbb{D}(\mathsf{X}) \rightarrow \prod_{x \in \mathsf{X}} \mathbb{D}(\Delta^0)\end{align*} $$ $i_{\mathsf {X}, x} \colon \Delta ^0 \to \mathsf {X}$ is the functor that corresponds to the object
$i_{\mathsf {X}, x} \colon \Delta ^0 \to \mathsf {X}$ is the functor that corresponds to the object  $x \in \mathsf {X}$.
$x \in \mathsf {X}$.(Der 3) For every morphism
 $u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in
$u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in  $\mathsf {Dia}$, the functor
$\mathsf {Dia}$, the functor  $u^{*} = \mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y})\rightarrow \mathbb {D}(\mathsf {X})$ is a right adjoint. We denote a left adjoint of
$u^{*} = \mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y})\rightarrow \mathbb {D}(\mathsf {X})$ is a right adjoint. We denote a left adjoint of  $u^*$ by
$u^*$ by  $$ \begin{align*}u_{!}\colon \mathbb{D}(\mathsf{X})\rightarrow\mathbb{D}(\mathsf{Y}).\end{align*} $$
$$ \begin{align*}u_{!}\colon \mathbb{D}(\mathsf{X})\rightarrow\mathbb{D}(\mathsf{Y}).\end{align*} $$(Der 4) Given
 $u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in
$u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in  $\mathsf {Dia}$ and
$\mathsf {Dia}$ and  $y \in \mathsf {Y}$, consider the following pullback diagram in
$y \in \mathsf {Y}$, consider the following pullback diagram in  $\mathsf {Dia}$: Then the canonical base change natural transformation
$\mathsf {Dia}$: Then the canonical base change natural transformation is a natural equivalence of functors.
is a natural equivalence of functors. $$ \begin{align*}c_{u,y}\colon (p_{u/y})_{!} j^{*}_{u/y} \longrightarrow q^{*}_{\mathsf{Y} /y }u_{!}\end{align*} $$
$$ \begin{align*}c_{u,y}\colon (p_{u/y})_{!} j^{*}_{u/y} \longrightarrow q^{*}_{\mathsf{Y} /y }u_{!}\end{align*} $$
We define left ![]() $\infty $-derivators dually.
$\infty $-derivators dually.
Definition 4.5. An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a left
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a left ![]() $\infty $-derivator if it satisfies (Der1)–(Der2) as stated above together with the following dual versions of (Der3)–(Der4):
$\infty $-derivator if it satisfies (Der1)–(Der2) as stated above together with the following dual versions of (Der3)–(Der4):
(Der 3)* For every morphism
 $u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in
$u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in  $\mathsf {Dia}$, the functor
$\mathsf {Dia}$, the functor  $u^{*} = \mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y})\rightarrow \mathbb {D}(\mathsf {X})$ is a left adjoint. We denote a right adjoint of
$u^{*} = \mathbb {D}(u) \colon \mathbb {D}(\mathsf {Y})\rightarrow \mathbb {D}(\mathsf {X})$ is a left adjoint. We denote a right adjoint of  $u^*$ by
$u^*$ by  $$ \begin{align*}u_*\colon \mathbb{D}(\mathsf{X}) \to \mathbb{D}(\mathsf{Y}).\end{align*} $$
$$ \begin{align*}u_*\colon \mathbb{D}(\mathsf{X}) \to \mathbb{D}(\mathsf{Y}).\end{align*} $$(Der 4)* Given
 $u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in
$u \colon \mathsf {X} \rightarrow \mathsf {Y}$ in  $\mathsf {Dia}$ and
$\mathsf {Dia}$ and  $y \in \mathsf {Y}$, consider the following pullback diagram in
$y \in \mathsf {Y}$, consider the following pullback diagram in  $\mathsf {Dia}$: Then the canonical base change natural transformation
$\mathsf {Dia}$: Then the canonical base change natural transformation is a natural equivalence of functors.
is a natural equivalence of functors. $$ \begin{align*}c^{\prime}_{u,y} \colon q^{*}_{y / \mathsf{Y} }u_{*} \longrightarrow (p_{y/u})_{*} j^{*}_{y/u}\end{align*} $$
$$ \begin{align*}c^{\prime}_{u,y} \colon q^{*}_{y / \mathsf{Y} }u_{*} \longrightarrow (p_{y/u})_{*} j^{*}_{y/u}\end{align*} $$
Example 4.6. Let ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a left
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a left ![]() $\infty $-derivator. Then the
$\infty $-derivator. Then the ![]() $\infty $-prederivator
$\infty $-prederivator
is a right ![]() $\infty $-derivator.
$\infty $-derivator.
Definition 4.7. An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is an
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is an ![]() $\infty $-derivator if it is both a left and a right
$\infty $-derivator if it is both a left and a right ![]() $\infty $-derivator.
$\infty $-derivator.
We also specialise these definitions to n-prederivators as follows.
Definition 4.8. An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a (left, right) n-derivator if it is an n-prederivator and a (left, right)
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is a (left, right) n-derivator if it is an n-prederivator and a (left, right) ![]() $\infty $-derivator.
$\infty $-derivator.
Example 4.9. A (left, right) 1-derivator with domain ![]() $\mathsf {Cat_1}$ is a (left, right) derivator in the usual sense [Reference Maltsiniotis24, Reference Groth18]. Indeed, (Der 1)–(Der 3) are completely analogous to the usual axioms. (Der 4) is a convenient variation of the usual axiom for ordinary derivators; the equivalence of the definitions is based on known properties of homotopy exact squares in the context of ordinary derivators (see [Reference Groth18, Reference Maltsiniotis23]).
$\mathsf {Cat_1}$ is a (left, right) derivator in the usual sense [Reference Maltsiniotis24, Reference Groth18]. Indeed, (Der 1)–(Der 3) are completely analogous to the usual axioms. (Der 4) is a convenient variation of the usual axiom for ordinary derivators; the equivalence of the definitions is based on known properties of homotopy exact squares in the context of ordinary derivators (see [Reference Groth18, Reference Maltsiniotis23]).
Example 4.10. Let ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{n}}$ be an n-prederivator, where
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{n}}$ be an n-prederivator, where ![]() $n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. For any
$n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. For any ![]() $k < n$, there is an associated k-prederivator:
$k < n$, there is an associated k-prederivator:
If ![]() $\mathbb {D}$ is a left (right) n-derivator, then
$\mathbb {D}$ is a left (right) n-derivator, then ![]() $\mathrm {h}_k \mathbb {D}$ is a left (right) k-derivator.
$\mathrm {h}_k \mathbb {D}$ is a left (right) k-derivator.
As a consequence of the axioms of Definition 4.4, we have the following useful strong version of (Der 4) and (Der 4)*, which identifies a larger class of squares for which the base change transformations are equivalences. Similar results are known for ![]() $\infty $-categories and ordinary (
$\infty $-categories and ordinary (![]() $1$-)derivators (see, for example, [Reference Cisinski4] and [Reference Maltsiniotis23, Reference Groth18]).
$1$-)derivators (see, for example, [Reference Cisinski4] and [Reference Maltsiniotis23, Reference Groth18]).
Proposition 4.11. Let ![]() $\mathbb {D}$ be an
$\mathbb {D}$ be an ![]() $\infty $-derivator with domain
$\infty $-derivator with domain ![]() $\mathsf {Dia}$. Consider a pullback square in
$\mathsf {Dia}$. Consider a pullback square in ![]() $\mathsf {Dia}$:
$\mathsf {Dia}$:
(1) The canonical base change transformation
is a natural equivalence if u is a cocartesian fibration or if q is a cartesian fibration. $$ \begin{align*}p_! j^* \longrightarrow q^* u_!\end{align*} $$
$$ \begin{align*}p_! j^* \longrightarrow q^* u_!\end{align*} $$(2) The canonical base change transformation
is a natural equivalence if u is a cartesian fibration or if q is a cocartesian fibration. $$ \begin{align*}q^* u_* \longrightarrow p_* j^*\end{align*} $$
$$ \begin{align*}q^* u_* \longrightarrow p_* j^*\end{align*} $$
Proof. Using the duality ![]() $\mathbb {D} \mapsto \mathbb {D}(-^{\operatorname {op}})^{\operatorname {op}}$, it suffices to prove only (1). Indeed, we obtain (2) by applying (1) to the derivator
$\mathbb {D} \mapsto \mathbb {D}(-^{\operatorname {op}})^{\operatorname {op}}$, it suffices to prove only (1). Indeed, we obtain (2) by applying (1) to the derivator ![]() $\mathbb {D}(-^{\operatorname {op}})^{\operatorname {op}}$ in the case of the opposite pullback square in
$\mathbb {D}(-^{\operatorname {op}})^{\operatorname {op}}$ in the case of the opposite pullback square in ![]() $\mathsf {Dia}$.
$\mathsf {Dia}$.
Suppose that u is a cocartesian fibration. Applying (Der 2) and using the naturality properties of base change transformations, it suffices to prove the claim only in the case where ![]() $W = \Delta ^0$:
$W = \Delta ^0$:
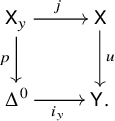
Using the following factorization of this square and applying (Der 4), it suffices to prove the claim for the left square in the following diagram:
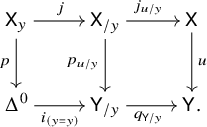
Note that the horizontal functors in the left square admit left adjoints
because u is a cocartesian fibration and ![]() $\mathsf {Y}_{/y}$ has a terminal object
$\mathsf {Y}_{/y}$ has a terminal object ![]() $(y = y)$. Thus, after applying
$(y = y)$. Thus, after applying ![]() $\mathbb {D}$, we obtain pairs of adjoint functors
$\mathbb {D}$, we obtain pairs of adjoint functors ![]() $(j^*, \ell _1^*)$ and
$(j^*, \ell _1^*)$ and ![]() $(i_{(y=y)}^*, \ell _2^*)$. Therefore, the base change transformation between compositions of left adjoints
$(i_{(y=y)}^*, \ell _2^*)$. Therefore, the base change transformation between compositions of left adjoints
is conjugate to the natural equivalence
which then implies that (4.12) is an equivalence, as required.
Suppose now that q is a cartesian fibration. Then it suffices to show that the conjugate base change transformation
is a natural equivalence. Again, by (Der 2), it suffices to restrict to the case where ![]() $X = \Delta ^0$
$X = \Delta ^0$

The proof of the equivalence (4.13) in this case is obtained similarly by dualizing the arguments in the previous proof.
In the context of ordinary derivators, there is a well-known additional axiom (Der 5), which is very useful in practice. Before we state the generalization of this axiom to higher derivators, we define (similarly to the classical case) for every ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D}$ and
$\mathbb {D}$ and ![]() $\mathsf {X}, \mathsf {Y} \in \mathsf {Dia}$, the underlying
$\mathsf {X}, \mathsf {Y} \in \mathsf {Dia}$, the underlying ![]() $(\mathsf {X}-)$diagram functor
$(\mathsf {X}-)$diagram functor
to be the adjoint of the following composition:
We say that a functor ![]() $F\colon \mathscr {C}\to \mathscr {D}$ between
$F\colon \mathscr {C}\to \mathscr {D}$ between ![]() $\infty $-categories is n–full if it restricts to
$\infty $-categories is n–full if it restricts to ![]() $(n-1)$-connected maps between the mapping spaces. For example, a full functor between ordinary categories is
$(n-1)$-connected maps between the mapping spaces. For example, a full functor between ordinary categories is ![]() $1$-full in this sense.
$1$-full in this sense.
Definition 4.14. Let ![]() $\mathbb {D}$ be an
$\mathbb {D}$ be an ![]() $\infty $-prederivator, and let
$\infty $-prederivator, and let ![]() $n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. We say that
$n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. We say that ![]() $\mathbb {D}$ is n-strong if the following axiom is satisfied:
$\mathbb {D}$ is n-strong if the following axiom is satisfied:
(Der 5n) For every
 $\mathsf {X} \in \mathsf {Dia}$, the underlying diagram functor is n-full and essentially surjective.
$\mathsf {X} \in \mathsf {Dia}$, the underlying diagram functor is n-full and essentially surjective. $$ \begin{align*}\mathrm{dia}_{\Delta^1, \mathsf{X}} \colon \mathbb{D}(\Delta^1 \times \mathsf{X}) \rightarrow \mathrm{Fun}(\Delta^1, \mathbb{D}(\mathsf{X}))\end{align*} $$
$$ \begin{align*}\mathrm{dia}_{\Delta^1, \mathsf{X}} \colon \mathbb{D}(\Delta^1 \times \mathsf{X}) \rightarrow \mathrm{Fun}(\Delta^1, \mathbb{D}(\mathsf{X}))\end{align*} $$
Remark 4.15. Similarly to the case of ordinary (pre)derivators, we may also consider a stronger form of the last axiom (compare to [Reference Heller19]), which states that the underlying diagram functor
is n-full and essentially surjective for every ![]() $\mathcal {I}$ in
$\mathcal {I}$ in ![]() $\mathsf {Dia}$, which is equivalent in the Joyal model category to a finite 1-dimensional simplicial set. Moreover, the following even stronger form of this axiom fits naturally in the higher categorical context:
$\mathsf {Dia}$, which is equivalent in the Joyal model category to a finite 1-dimensional simplicial set. Moreover, the following even stronger form of this axiom fits naturally in the higher categorical context:
(
 $\widetilde {\text {Der 5}_n}$) For every
$\widetilde {\text {Der 5}_n}$) For every  $\mathsf {X} \in \mathsf {Dia}$ and for every
$\mathsf {X} \in \mathsf {Dia}$ and for every  $\mathcal {I} \in \mathsf {Dia}$, which is equivalent (in the Joyal model category) to a d-dimensional simplicial set for some
$\mathcal {I} \in \mathsf {Dia}$, which is equivalent (in the Joyal model category) to a d-dimensional simplicial set for some  $d \leq n + 1$, the underlying diagram functor is
$d \leq n + 1$, the underlying diagram functor is $$ \begin{align*}\mathrm{dia}_{\mathcal{I}, \mathsf{X}} \colon \mathbb{D}(\mathcal{I} \times \mathsf{X}) \rightarrow \mathrm{Fun}(\mathcal{I}, \mathbb{D}(\mathsf{X}))\end{align*} $$
$$ \begin{align*}\mathrm{dia}_{\mathcal{I}, \mathsf{X}} \colon \mathbb{D}(\mathcal{I} \times \mathsf{X}) \rightarrow \mathrm{Fun}(\mathcal{I}, \mathbb{D}(\mathsf{X}))\end{align*} $$ $(n+1-d)$-full and essentially surjective.
$(n+1-d)$-full and essentially surjective.
Note that this axiom for ![]() $d = 0$ is also closely related to (Der 1).
$d = 0$ is also closely related to (Der 1).
Following the definitions of pointed and stable (1-)derivators [Reference Maltsiniotis24, Reference Groth18], we also define pointed and stable ![]() $\infty $-(pre)derivators as follows.
$\infty $-(pre)derivators as follows.
Definition 4.16. An ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is called pointed if it lifts to the
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is called pointed if it lifts to the ![]() $\infty $-category
$\infty $-category ![]() $\mathsf {Cat_{\infty }}_{,*}$ of pointed
$\mathsf {Cat_{\infty }}_{,*}$ of pointed ![]() $\infty $-categories and functors that preserve zero objects. An
$\infty $-categories and functors that preserve zero objects. An ![]() $\infty $-derivator
$\infty $-derivator ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is called stable if it is pointed and the associated 1-derivator
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ is called stable if it is pointed and the associated 1-derivator ![]() $\mathrm {h}_1 \mathbb {D}$ is stable.
$\mathrm {h}_1 \mathbb {D}$ is stable.
4.2 Examples of n-derivators
The examples of n-derivators we are mainly interested in are those where the underlying prederivator arises from an ![]() $\infty $-category as in Example 4.3. Let
$\infty $-category as in Example 4.3. Let ![]() $\mathsf {Dia} \subset \mathsf {Cat_{\infty }}$ be a fixed full subcategory satisfying the conditions (Dia 0)–(Dia 3).
$\mathsf {Dia} \subset \mathsf {Cat_{\infty }}$ be a fixed full subcategory satisfying the conditions (Dia 0)–(Dia 3).
Proposition 4.17. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category, and let
$\infty $-category, and let ![]() $n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$.
$n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$.
(a) The n-prederivator
 $\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies (Der 1), (Der 2) and (Der 5
$\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies (Der 1), (Der 2) and (Der 5 $_n$). Moreover, the underlying diagram functor is
$_n$). Moreover, the underlying diagram functor is $$ \begin{align*}\mathrm{dia}_{\mathcal{I}, \mathsf{X}} \colon \mathbb{D}^{(n)}_{\mathscr{C}}(\mathcal{I} \times \mathsf{X}) \rightarrow \mathrm{Fun}(\mathcal{I}, \mathbb{D}^{(n)}_{\mathscr{C}}(\mathsf{X}))\end{align*} $$
$$ \begin{align*}\mathrm{dia}_{\mathcal{I}, \mathsf{X}} \colon \mathbb{D}^{(n)}_{\mathscr{C}}(\mathcal{I} \times \mathsf{X}) \rightarrow \mathrm{Fun}(\mathcal{I}, \mathbb{D}^{(n)}_{\mathscr{C}}(\mathsf{X}))\end{align*} $$ $(n + 1 -d)$-full and essentially surjective for every
$(n + 1 -d)$-full and essentially surjective for every  $\mathcal {I}$ in
$\mathcal {I}$ in  $\mathsf {Dia}$, which is equivalent (in the Joyal model category) to a d-dimensional simplicial set for some
$\mathsf {Dia}$, which is equivalent (in the Joyal model category) to a d-dimensional simplicial set for some  $d \leq n + 1$ (i.e.,
$d \leq n + 1$ (i.e.,  $\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies
$\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies  $(\widetilde {\text {Der 5}_n})$, too).
$(\widetilde {\text {Der 5}_n})$, too).(b) Suppose that
 $\mathscr {C}$ admits
$\mathscr {C}$ admits  $\mathsf {X}$-colimits (respectively,
$\mathsf {X}$-colimits (respectively,  $\mathsf {X}$-limits) for any
$\mathsf {X}$-limits) for any  $\mathsf {X} \in \mathsf {Dia}$. Then
$\mathsf {X} \in \mathsf {Dia}$. Then  $\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies (Der 3) and (Der 4) (respectively, (Der 3)* and (Der 4)*). As a consequence,
$\mathbb {D}^{(n)}_{\mathscr {C}}$ satisfies (Der 3) and (Der 4) (respectively, (Der 3)* and (Der 4)*). As a consequence,  $\mathbb {D}^{(n)}_{\mathscr {C}}$ is a right (respectively, left) n-derivator, which is n-strong.
$\mathbb {D}^{(n)}_{\mathscr {C}}$ is a right (respectively, left) n-derivator, which is n-strong.
Proof. (a) (Der 1) is obvious. (Der 2) says that the equivalences in ![]() $\mathrm {h}_n(\mathscr {C}^{\mathsf {X}})$,
$\mathrm {h}_n(\mathscr {C}^{\mathsf {X}})$, ![]() $\mathsf {X} \in \mathsf {Dia}$, are given pointwise, which holds by a theorem of Joyal [Reference Joyal20, Chapter 5]. (Der 5
$\mathsf {X} \in \mathsf {Dia}$, are given pointwise, which holds by a theorem of Joyal [Reference Joyal20, Chapter 5]. (Der 5![]() $_n$) follows from Corollary 3.17. The second claim also follows from Corollary 3.17 (and Lemma 3.14) because we may replace
$_n$) follows from Corollary 3.17. The second claim also follows from Corollary 3.17 (and Lemma 3.14) because we may replace ![]() $\mathcal {I}$ by a d-dimensional simplicial set.
$\mathcal {I}$ by a d-dimensional simplicial set.
(b) It suffices to show that (Der 3) and (Der 4) hold for the ![]() $\infty $-prederivator
$\infty $-prederivator ![]() $\mathbb {D}^{(\infty )}_{\mathscr {C}}$: that is, it suffices to show that
$\mathbb {D}^{(\infty )}_{\mathscr {C}}$: that is, it suffices to show that ![]() $\mathscr {C}$ admits Kan extensions along functors in
$\mathscr {C}$ admits Kan extensions along functors in ![]() $\mathsf {Dia}$ and that Kan extensions are given pointwise by the usual formulas as axiomatised in (Der 4). These claims are established in [Reference Cisinski4, 6.4] (see also [Reference Lurie22, 4.3.2–4.3.3]).
$\mathsf {Dia}$ and that Kan extensions are given pointwise by the usual formulas as axiomatised in (Der 4). These claims are established in [Reference Cisinski4, 6.4] (see also [Reference Lurie22, 4.3.2–4.3.3]).
It is often possible to reduce statements about ![]() $\infty $-derivators to the corresponding (known) statements about
$\infty $-derivators to the corresponding (known) statements about ![]() $1$-derivators. This happens, for example, in the case of statements that involve the detection of equivalences. The following proposition shows another instance of this phenomenon and produces many examples of n-derivators from known examples of
$1$-derivators. This happens, for example, in the case of statements that involve the detection of equivalences. The following proposition shows another instance of this phenomenon and produces many examples of n-derivators from known examples of ![]() $1$-derivators.
$1$-derivators.
Theorem 4.18. Let ![]() $\mathscr {C}$ be an
$\mathscr {C}$ be an ![]() $\infty $-category. The following are equivalent:
$\infty $-category. The following are equivalent:
(1)
 $\mathscr {C}$ admits
$\mathscr {C}$ admits  $\mathsf {X}$-colimits and
$\mathsf {X}$-colimits and  $\mathsf {X}$-limits for every
$\mathsf {X}$-limits for every  $\mathsf {X} \in \mathsf {Dia}$.
$\mathsf {X} \in \mathsf {Dia}$.(2)
 $\mathbb {D}^{(\infty )}_{\mathscr {C}}$ is an
$\mathbb {D}^{(\infty )}_{\mathscr {C}}$ is an  $\infty $-derivator.
$\infty $-derivator.(3)
 $\mathbb {D}^{(n)}_{\mathscr {C}}$ is an n-derivator for every
$\mathbb {D}^{(n)}_{\mathscr {C}}$ is an n-derivator for every  $n \in \mathbb {Z}_{\geq 1}$.
$n \in \mathbb {Z}_{\geq 1}$.(4)
 $\mathbb {D}^{(n)}_{\mathscr {C}}$ is an n-derivator for some
$\mathbb {D}^{(n)}_{\mathscr {C}}$ is an n-derivator for some  $n \in \mathbb {Z}_{\geq 1}$.
$n \in \mathbb {Z}_{\geq 1}$.(5)
 $\mathbb {D}_{\mathscr {C}} = \mathbb {D}^{(1)}_{\mathscr {C}}$ is an
$\mathbb {D}_{\mathscr {C}} = \mathbb {D}^{(1)}_{\mathscr {C}}$ is an  $1$-derivator.
$1$-derivator.
Proof. (1) ![]() $\Rightarrow $ (2) was shown in Proposition 4.17, and the implications (2)
$\Rightarrow $ (2) was shown in Proposition 4.17, and the implications (2) ![]() $\Rightarrow $ (3)
$\Rightarrow $ (3) ![]() $\Rightarrow $ (4)
$\Rightarrow $ (4) ![]() $\Rightarrow $ (5) are obvious. We prove the implication (5)
$\Rightarrow $ (5) are obvious. We prove the implication (5) ![]() $\Rightarrow $ (1). We restrict to showing that
$\Rightarrow $ (1). We restrict to showing that ![]() $\mathscr {C}$ admits
$\mathscr {C}$ admits ![]() $\mathsf {X}$-colimits as the case of
$\mathsf {X}$-colimits as the case of ![]() $\mathsf {X}$-limits can be treated similarly by duality. Let
$\mathsf {X}$-limits can be treated similarly by duality. Let ![]() $F\colon \mathsf {X} \to \mathscr {C}$ be an
$F\colon \mathsf {X} \to \mathscr {C}$ be an ![]() $\mathsf {X}$-diagram, and let
$\mathsf {X}$-diagram, and let ![]() $G \colon \mathsf {X}^{\triangleright } \to \mathscr {C}$ be the diagram that is the image of
$G \colon \mathsf {X}^{\triangleright } \to \mathscr {C}$ be the diagram that is the image of ![]() $F \in \mathbb {D}_{\mathscr {C}}(\mathsf {X})$ under
$F \in \mathbb {D}_{\mathscr {C}}(\mathsf {X})$ under
where ![]() $u \colon \mathsf {X} \to \mathsf {X}^{\triangleright }$ is the canonical inclusion. As a consequence of (Der 4), the functor
$u \colon \mathsf {X} \to \mathsf {X}^{\triangleright }$ is the canonical inclusion. As a consequence of (Der 4), the functor ![]() $u_!$ is fully faithful because u is so. In particular, there is a canonical isomorphism
$u_!$ is fully faithful because u is so. In particular, there is a canonical isomorphism ![]() $F \cong u^* u_!(F),$ and therefore we may assume that G is an extension of the diagram F. We claim that G is a colimit diagram in
$F \cong u^* u_!(F),$ and therefore we may assume that G is an extension of the diagram F. We claim that G is a colimit diagram in ![]() $\mathscr {C}$ for the functor F. For this, it suffices to prove that for each sieve between (nerves of) finite posets
$\mathscr {C}$ for the functor F. For this, it suffices to prove that for each sieve between (nerves of) finite posets ![]() $v \colon \mathsf {Y}' \to \mathsf {Y}$ in
$v \colon \mathsf {Y}' \to \mathsf {Y}$ in ![]() $\mathsf {Dia}$, the canonical map
$\mathsf {Dia}$, the canonical map

is a ![]() $\pi _0$-isomorphism, where
$\pi _0$-isomorphism, where ![]() $c_y$ denotes the constant functor at
$c_y$ denotes the constant functor at ![]() $y \in \mathscr {C}$ in the respective functor
$y \in \mathscr {C}$ in the respective functor ![]() $\infty $-category. We will do this by first expressing
$\infty $-category. We will do this by first expressing ![]() $\pi _0$ of the domain and the target of this map (4.19) in terms of morphism sets in the (1-)category
$\pi _0$ of the domain and the target of this map (4.19) in terms of morphism sets in the (1-)category ![]() $\mathbb {D}_{\mathscr {C}}(\mathsf {X}^{\triangleright } \times \mathsf {Y})$ and then use the derivator properties of
$\mathbb {D}_{\mathscr {C}}(\mathsf {X}^{\triangleright } \times \mathsf {Y})$ and then use the derivator properties of ![]() $\mathbb {D}_{\mathscr {C}}$.
$\mathbb {D}_{\mathscr {C}}$.
First, note that we have a canonical isomorphism of morphism sets
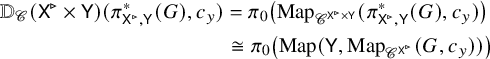 $$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{X}^{\triangleright} \times \mathsf{Y})(\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G), c_y) &= \pi_0 \big(\mathrm{Map}_{\mathscr{C}^{\mathsf{X}^{\triangleright} \times \mathsf{Y}}}(\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G), c_y)\big) \\ &\cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}^{\triangleright}}}(G, c_y)) \big) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{X}^{\triangleright} \times \mathsf{Y})(\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G), c_y) &= \pi_0 \big(\mathrm{Map}_{\mathscr{C}^{\mathsf{X}^{\triangleright} \times \mathsf{Y}}}(\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G), c_y)\big) \\ &\cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}^{\triangleright}}}(G, c_y)) \big) \end{aligned} \end{align} $$where ![]() $\pi _{\mathsf {X}^{\triangleright }, \mathsf {Y}} \colon \mathsf {X}^{\triangleright } \times \mathsf {Y} \to \mathsf {X}$ denotes the projection functor. Similarly, we have canonical isomorphisms
$\pi _{\mathsf {X}^{\triangleright }, \mathsf {Y}} \colon \mathsf {X}^{\triangleright } \times \mathsf {Y} \to \mathsf {X}$ denotes the projection functor. Similarly, we have canonical isomorphisms
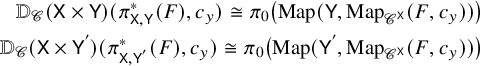 $$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{X} \times \mathsf{Y})(\pi_{\mathsf{X}, \mathsf{Y}}^*(F), c_y) \cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}}}(F, c_y)) \big) \\ \mathbb{D}_{\mathscr{C}}(\mathsf{X} \times \mathsf{Y}^{'})(\pi_{\mathsf{X}, \mathsf{Y}^{'}}^*(F), c_y) \cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}^{'}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}}}(F, c_y)) \big) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{X} \times \mathsf{Y})(\pi_{\mathsf{X}, \mathsf{Y}}^*(F), c_y) \cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}}}(F, c_y)) \big) \\ \mathbb{D}_{\mathscr{C}}(\mathsf{X} \times \mathsf{Y}^{'})(\pi_{\mathsf{X}, \mathsf{Y}^{'}}^*(F), c_y) \cong \pi_0 \big(\mathrm{Map}(\mathsf{Y}^{'}, \mathrm{Map}_{\mathscr{C}^{\mathsf{X}}}(F, c_y)) \big) \end{aligned} \end{align} $$where ![]() $\pi _{\mathsf {X}, \mathsf {Y}}$ and
$\pi _{\mathsf {X}, \mathsf {Y}}$ and ![]() $\pi _{\mathsf {X}, \mathsf {Y}'}$ denote again the projection functors.
$\pi _{\mathsf {X}, \mathsf {Y}'}$ denote again the projection functors.
Then consider the following pullback diagram in ![]() $\mathsf {Dia}$:
$\mathsf {Dia}$:

Since the horizontal functors are cartesian fibrations, it follows from (Der 4) and Proposition 4.11(1) that the canonical base change morphism in ![]() $\mathbb {D}_{\mathscr {C}}(\mathsf {X}^{\triangleright } \times \mathsf {Y})$
$\mathbb {D}_{\mathscr {C}}(\mathsf {X}^{\triangleright } \times \mathsf {Y})$
is an isomorphism.
Let ![]() $i \colon \mathsf {A} = \mathsf {X}^{\triangleright } \times \mathsf {Y}' \cup _{\mathsf {X} \times \mathsf {Y}'} \mathsf {X} \times \mathsf {Y} \subset \mathsf {X}^{\triangleright } \times \mathsf {Y}$ denote the full subcategory. This is again in
$i \colon \mathsf {A} = \mathsf {X}^{\triangleright } \times \mathsf {Y}' \cup _{\mathsf {X} \times \mathsf {Y}'} \mathsf {X} \times \mathsf {Y} \subset \mathsf {X}^{\triangleright } \times \mathsf {Y}$ denote the full subcategory. This is again in ![]() $\mathsf {Dia}$ by (Dia 1) and (Dia 3) because it can be described as the pullback of a functor
$\mathsf {Dia}$ by (Dia 1) and (Dia 3) because it can be described as the pullback of a functor ![]() $\mathsf {X}^{\triangleright } \times \mathsf {Y} \to \Delta ^1 \times \Delta ^1$ along the ‘upper corner’ inclusion
$\mathsf {X}^{\triangleright } \times \mathsf {Y} \to \Delta ^1 \times \Delta ^1$ along the ‘upper corner’ inclusion ![]() $\Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \Delta ^1 \times \Delta ^1$. Note that using (4.21), we can identify the set of components of the target of (4.19) canonically with the morphism set
$\Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \Delta ^1 \times \Delta ^1$. Note that using (4.21), we can identify the set of components of the target of (4.19) canonically with the morphism set
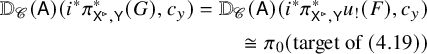 $$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{A})(i^* \pi^*_{\mathsf{X}^{\triangleright}, \mathsf{Y}}(G), c_y) = \mathbb{D}_{\mathscr{C}}(\mathsf{A})(i^*\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*u_!(F), c_y) \\ \cong \pi_0(\textrm{target of } (4.19)) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{D}_{\mathscr{C}}(\mathsf{A})(i^* \pi^*_{\mathsf{X}^{\triangleright}, \mathsf{Y}}(G), c_y) = \mathbb{D}_{\mathscr{C}}(\mathsf{A})(i^*\pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*u_!(F), c_y) \\ \cong \pi_0(\textrm{target of } (4.19)) \end{aligned} \end{align} $$and the map (4.19) on ![]() $\pi _0$ agrees using the identifications (4.20) and (4.23) with the map defined by the restriction functor
$\pi _0$ agrees using the identifications (4.20) and (4.23) with the map defined by the restriction functor
Since i is full, it follows from (Der 4) that the unit transformation ![]() $1 \to i^* i_!$ of the adjunction
$1 \to i^* i_!$ of the adjunction ![]() $(i_!, i^*)$ is a natural isomorphism. Therefore it suffices to show that the counit morphism
$(i_!, i^*)$ is a natural isomorphism. Therefore it suffices to show that the counit morphism
is an isomorphism.
Consider the following pullback diagram in ![]() $\mathsf {Dia}$:
$\mathsf {Dia}$:
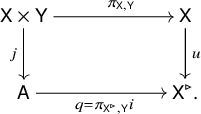
The bottom functor q is a cartesian fibration because it is the composition of cartesian fibrations. Therefore, it follows from (Der 4) and Proposition 4.11(1) that the canonical base change morphism in ![]() $\mathbb {D}_{\mathscr {C}}(\mathsf {A})$:
$\mathbb {D}_{\mathscr {C}}(\mathsf {A})$:
is an isomorphism. As a consequence of (4.22) and (4.25), we obtain canonical isomorphisms as follows:
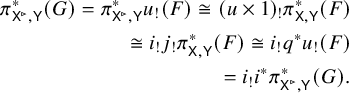 $$ \begin{align*} \begin{aligned} \pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G) = \pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^* u_!(F) \cong (u \times 1)_! \pi_{\mathsf{X}, \mathsf{Y}}^*(F) \\ \cong i_! j_! \pi_{\mathsf{X}, \mathsf{Y}}^*(F) \cong i_! q^* u_!(F) \\ = i_! i^* \pi^*_{\mathsf{X}^{\triangleright}, \mathsf{Y}}(G). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^*(G) = \pi_{\mathsf{X}^{\triangleright}, \mathsf{Y}}^* u_!(F) \cong (u \times 1)_! \pi_{\mathsf{X}, \mathsf{Y}}^*(F) \\ \cong i_! j_! \pi_{\mathsf{X}, \mathsf{Y}}^*(F) \cong i_! q^* u_!(F) \\ = i_! i^* \pi^*_{\mathsf{X}^{\triangleright}, \mathsf{Y}}(G). \end{aligned} \end{align*} $$This implies that (4.24) is an isomorphism; therefore, using the adjunction ![]() $(i_!, i^*)$ as explained above, it follows that the map in (4.19) is a
$(i_!, i^*)$ as explained above, it follows that the map in (4.19) is a ![]() $\pi _0$-isomorphism.
$\pi _0$-isomorphism.
Remark 4.26. We point out a significant simplification of the proof of Theorem 4.18 in the case where ![]() $\mathsf {Dia}$ is large enough that it can detect equivalences of
$\mathsf {Dia}$ is large enough that it can detect equivalences of ![]() $\infty $-groupoids – that is, in the case where the following holds: a map of
$\infty $-groupoids – that is, in the case where the following holds: a map of ![]() $\infty $-groupoids
$\infty $-groupoids ![]() $X \to X'$ is an equivalence if and only if
$X \to X'$ is an equivalence if and only if
is an isomorphism for every ![]() $\mathsf {Y} \in \mathsf {Dia}$. This happens, for example, when
$\mathsf {Y} \in \mathsf {Dia}$. This happens, for example, when ![]() $\mathsf {Dia}$ contains all posets – not just the finite ones. Assuming that
$\mathsf {Dia}$ contains all posets – not just the finite ones. Assuming that ![]() $\mathsf {Dia}$ is large enough in this sense, then we may restrict to the case
$\mathsf {Dia}$ is large enough in this sense, then we may restrict to the case ![]() $\mathsf {Y}' = \varnothing $ in the proof above, in which case the proof becomes more immediate.
$\mathsf {Y}' = \varnothing $ in the proof above, in which case the proof becomes more immediate.
5 K-theory of higher derivators
5.1 Preliminaries
We first recall the ![]() $\infty $-categorical version of Waldhausen’s
$\infty $-categorical version of Waldhausen’s ![]() $\mathrm {S}_{\bullet }$-construction [Reference Waldhausen39, Reference Blumberg, Gepner and Tabuada3]. Let
$\mathrm {S}_{\bullet }$-construction [Reference Waldhausen39, Reference Blumberg, Gepner and Tabuada3]. Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category that admits finite colimits. For every
$\infty $-category that admits finite colimits. For every ![]() $n \geq 0$, let
$n \geq 0$, let ![]() $\mathrm {Ar}[n]$ denote the (nerve of the) category of morphisms of the poset
$\mathrm {Ar}[n]$ denote the (nerve of the) category of morphisms of the poset ![]() $[n]$. The
$[n]$. The ![]() $\infty $-category
$\infty $-category ![]() $\mathrm {S}_n \mathscr {C}$ is the full subcategory of
$\mathrm {S}_n \mathscr {C}$ is the full subcategory of ![]() $\mathrm {Fun}(\mathrm {Ar}[n], \mathscr {C})$ spanned by the objects
$\mathrm {Fun}(\mathrm {Ar}[n], \mathscr {C})$ spanned by the objects ![]() $F \colon \mathrm {Ar}[n] \to \mathscr {C}$ such that:
$F \colon \mathrm {Ar}[n] \to \mathscr {C}$ such that:
(i)
 $F(i \to i)$ is a zero object for all
$F(i \to i)$ is a zero object for all  $i \in [n]$.
$i \in [n]$.(ii) For every
 $i \leq j \leq k$, the following diagram in
$i \leq j \leq k$, the following diagram in  $\mathscr {C}$ is a pushout.
$\mathscr {C}$ is a pushout.
The construction is clearly functorial in ![]() $[n]$,
$[n]$, ![]() $n \geq 0$, and
$n \geq 0$, and ![]() $\mathrm {S}_{\bullet } \mathscr {C}$ defines a simplicial object of pointed
$\mathrm {S}_{\bullet } \mathscr {C}$ defines a simplicial object of pointed ![]() $\infty $-categories, which is functorial in
$\infty $-categories, which is functorial in ![]() $\mathscr {C}$ with respect to functors that preserve zero objects and pushouts.
$\mathscr {C}$ with respect to functors that preserve zero objects and pushouts.
We denote by ![]() $\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}$ the associated simplicial object of pointed
$\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}$ the associated simplicial object of pointed ![]() $\infty $-groupoids, which is obtained by passing pointwise to the maximal
$\infty $-groupoids, which is obtained by passing pointwise to the maximal ![]() $\infty $-subgroupoids of
$\infty $-subgroupoids of ![]() $\mathrm {S}_{\bullet } \mathscr {C}$. For
$\mathrm {S}_{\bullet } \mathscr {C}$. For ![]() $n \geq 1$, the
$n \geq 1$, the ![]() $\infty $-groupoid
$\infty $-groupoid ![]() $\mathrm {S}_{n}^{\simeq } \mathscr {C}$ is equivalent to
$\mathrm {S}_{n}^{\simeq } \mathscr {C}$ is equivalent to ![]() $\mathrm {Map}(\Delta ^{n-1}, \mathscr {C})$. Moreover, we have
$\mathrm {Map}(\Delta ^{n-1}, \mathscr {C})$. Moreover, we have ![]() $\mathrm {S}^{\simeq }_{0} \mathscr {C} \simeq \Delta ^0$, so we may regard the geometric realization
$\mathrm {S}^{\simeq }_{0} \mathscr {C} \simeq \Delta ^0$, so we may regard the geometric realization ![]() $|\mathrm {S}^{\simeq }_{\bullet } \mathscr {C}|$ as canonically pointed by a zero object in
$|\mathrm {S}^{\simeq }_{\bullet } \mathscr {C}|$ as canonically pointed by a zero object in ![]() $\mathscr {C}$. The Waldhausen K-theory of
$\mathscr {C}$. The Waldhausen K-theory of ![]() $\mathscr {C}$ is defined to be the space
$\mathscr {C}$ is defined to be the space
If ![]() $\mathscr {C}$ arises from a nice Waldhausen category, this definition of K-theory agrees up to homotopy equivalence with the Waldhausen K-theory of the corresponding Waldhausen category (see [Reference Blumberg, Gepner and Tabuada3]). The definition of K-theory is functorial with respect to functors
$\mathscr {C}$ arises from a nice Waldhausen category, this definition of K-theory agrees up to homotopy equivalence with the Waldhausen K-theory of the corresponding Waldhausen category (see [Reference Blumberg, Gepner and Tabuada3]). The definition of K-theory is functorial with respect to functors ![]() $F \colon \mathscr {C} \to \mathscr {C}'$, which preserve the zero object and finite colimits.
$F \colon \mathscr {C} \to \mathscr {C}'$, which preserve the zero object and finite colimits.
Following [Reference Waldhausen39, Lemma 1.4.1] and [Reference Muro and Raptis26, Proposition 4.2.1], we consider also the following simpler model for Waldhausen K-theory. Restricting pointwise to the objects of ![]() $\mathrm {S}_{\bullet } \mathscr {C}$, we obtain a simplicial set
$\mathrm {S}_{\bullet } \mathscr {C}$, we obtain a simplicial set
There is a canonical comparison map, given by the inclusion of objects,
Proposition 5.1. The comparison map ![]() $\iota $ is a weak equivalence.
$\iota $ is a weak equivalence.
Proof. The proof is essentially the same as the proof of [Reference Waldhausen39, Lemma 1.4.1 and Corollary] (see also [Reference Muro and Raptis26, Proposition 4.2.1]).
5.2 Derivator K-theory
We extend the definition of derivator K-theory of Maltsiniotis [Reference Maltsiniotis24] and Garkusha [Reference Garkusha14, Reference Garkusha15] to general pointed right ![]() $\infty $-derivators. As in the case of ordinary derivators, this definition is based on the following intrinsic notion of cocartesian square.
$\infty $-derivators. As in the case of ordinary derivators, this definition is based on the following intrinsic notion of cocartesian square.
Let ![]() $i \colon \ulcorner = \Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \square = \Delta ^1 \times \Delta ^1$ denote the ‘upper corner’ inclusion. For any right
$i \colon \ulcorner = \Delta ^1 \cup _{\Delta ^0} \Delta ^1 \to \square = \Delta ^1 \times \Delta ^1$ denote the ‘upper corner’ inclusion. For any right ![]() $\infty $-derivator
$\infty $-derivator ![]() $\mathbb {D}$ (with domain
$\mathbb {D}$ (with domain ![]() $\mathsf {Dia}$), we have an adjunction
$\mathsf {Dia}$), we have an adjunction
Definition 5.2. Let ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a right
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a right ![]() $\infty $-derivator with domain
$\infty $-derivator with domain ![]() $\mathsf {Dia}$. An object
$\mathsf {Dia}$. An object ![]() $F \in \mathbb {D}(\square )$ is called cocartesian if the canonical morphism
$F \in \mathbb {D}(\square )$ is called cocartesian if the canonical morphism
is an equivalence in ![]() $\mathbb {D}(\square )$.
$\mathbb {D}(\square )$.
Let ![]() $\mathbb {D}$ be a pointed right
$\mathbb {D}$ be a pointed right ![]() $\infty $-derivator (with domain
$\infty $-derivator (with domain ![]() $\mathsf {Dia}$). Before we define the K-theory of
$\mathsf {Dia}$). Before we define the K-theory of ![]() $\mathbb {D}$, we first need to introduce some more notation. For every
$\mathbb {D}$, we first need to introduce some more notation. For every ![]() $0 \leq i \leq j \leq k \leq n$, we denote by
$0 \leq i \leq j \leq k \leq n$, we denote by ![]() $i_{i,j,k} \colon \square \to \mathrm {Ar}[n]$ the inclusion of the following square in
$i_{i,j,k} \colon \square \to \mathrm {Ar}[n]$ the inclusion of the following square in ![]() $\mathrm {Ar}[n]$:
$\mathrm {Ar}[n]$:
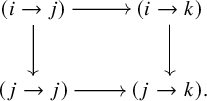
We define ![]() $\mathrm {S}_n \mathbb {D}$ to be the full subcategory of
$\mathrm {S}_n \mathbb {D}$ to be the full subcategory of ![]() $\mathbb {D}(\mathrm {Ar}[n])$, which is spanned by the objects
$\mathbb {D}(\mathrm {Ar}[n])$, which is spanned by the objects ![]() $F \in \mathbb {D}(\mathrm {Ar}[n])$ such that
$F \in \mathbb {D}(\mathrm {Ar}[n])$ such that
(i)
 $F_{(i \to i)}$ is a zero object for all
$F_{(i \to i)}$ is a zero object for all  $i \in [n]$.
$i \in [n]$.(ii) For every
 $i \leq j \leq k$, the object
$i \leq j \leq k$, the object  $i_{i,j,k}^*(F) \in \mathbb {D}(\square )$, which may be depicted as follows is cocartesian in
$i_{i,j,k}^*(F) \in \mathbb {D}(\square )$, which may be depicted as follows is cocartesian in
 $\mathbb {D}(\square )$.
$\mathbb {D}(\square )$.
The assignment ![]() $[n] \mapsto \mathrm {S}_n \mathbb {D}$ defines a simplicial object of pointed
$[n] \mapsto \mathrm {S}_n \mathbb {D}$ defines a simplicial object of pointed ![]() $\infty $-categories. Moreover, it is natural with respect to strict morphisms between pointed right
$\infty $-categories. Moreover, it is natural with respect to strict morphisms between pointed right ![]() $\infty $-derivators that preserve zero objects and cocartesian squares.
$\infty $-derivators that preserve zero objects and cocartesian squares.
Let ![]() $\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}$ denote the simplicial object of pointed
$\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}$ denote the simplicial object of pointed ![]() $\infty $-groupoids, which is obtained by passing pointwise to the maximal
$\infty $-groupoids, which is obtained by passing pointwise to the maximal ![]() $\infty $-subgroupoids of
$\infty $-subgroupoids of ![]() $\mathrm {S}_{\bullet } \mathbb {D}$. We have
$\mathrm {S}_{\bullet } \mathbb {D}$. We have ![]() $\mathrm {S}_0^{\simeq } \mathbb {D} \simeq \Delta ^0$, and we regard the geometric realization
$\mathrm {S}_0^{\simeq } \mathbb {D} \simeq \Delta ^0$, and we regard the geometric realization ![]() $|\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}|$ as based at a zero object of
$|\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}|$ as based at a zero object of ![]() $\mathbb {D}(\Delta ^0)$.
$\mathbb {D}(\Delta ^0)$.
Definition 5.3. Let ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a pointed right
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a pointed right ![]() $\infty $-derivator with domain
$\infty $-derivator with domain ![]() $\mathsf {Dia}$. The derivator K-theory of
$\mathsf {Dia}$. The derivator K-theory of ![]() $\mathbb {D}$ is defined to be the space
$\mathbb {D}$ is defined to be the space
We note that the definition of derivator K-theory is functorial with respect to strict morphisms ![]() $F \colon \mathbb {D} \to \mathbb {D}'$, which preserve the zero object and cocartesian squares. Moreover, derivator K-theory is invariant under those strict morphisms that are pointwise equivalences of
$F \colon \mathbb {D} \to \mathbb {D}'$, which preserve the zero object and cocartesian squares. Moreover, derivator K-theory is invariant under those strict morphisms that are pointwise equivalences of ![]() $\infty $-categories.
$\infty $-categories.
This definition of derivator K-theory clearly agrees with the usual derivator K-theory for ordinary derivators [Reference Garkusha14, Reference Muro and Raptis26]. Moreover, this definition of derivator K-theory is also an extension of the K-theory of pointed ![]() $\infty $-categories with finite colimits to pointed right
$\infty $-categories with finite colimits to pointed right ![]() $\infty $-derivators; by definition, for any pointed
$\infty $-derivators; by definition, for any pointed ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$ with finite colimits, the K-theory of
$\mathscr {C}$ with finite colimits, the K-theory of ![]() $\mathscr {C}$ agrees with the derivator K-theory of
$\mathscr {C}$ agrees with the derivator K-theory of ![]() $\mathbb {D}^{(\infty )}_{\mathscr {C}}$.
$\mathbb {D}^{(\infty )}_{\mathscr {C}}$.
Remark 5.4. Waldhausen’s Additivity Theorem [Reference Waldhausen39] establishes one of the fundamental properties of Waldhausen K-theory. The analogue of this theorem has been established for the derivator K-theory of stable ![]() $1$-derivators by Cisinski–Neeman [Reference Cisinski and Neeman6], confirming one of Maltsiniotis’ conjectures in [Reference Maltsiniotis24]. This theorem has recently been extended to general pointed right 1-derivators by Coley [Reference Coley8]. It would be interesting to know if the additivity theorem holds more generally for the derivator K-theory of pointed right
$1$-derivators by Cisinski–Neeman [Reference Cisinski and Neeman6], confirming one of Maltsiniotis’ conjectures in [Reference Maltsiniotis24]. This theorem has recently been extended to general pointed right 1-derivators by Coley [Reference Coley8]. It would be interesting to know if the additivity theorem holds more generally for the derivator K-theory of pointed right ![]() $\infty $-derivators.
$\infty $-derivators.
5.3 Comparison with Waldhausen K-theory
Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category with finite colimits. Applying pointwise the homotopy n-category functor to the simplicial object
$\infty $-category with finite colimits. Applying pointwise the homotopy n-category functor to the simplicial object ![]() $[k] \mapsto \mathrm {S}^{\simeq }_k \mathscr {C}$, we obtain a new simplicial object of (pointed)
$[k] \mapsto \mathrm {S}^{\simeq }_k \mathscr {C}$, we obtain a new simplicial object of (pointed) ![]() $\infty $-groupoids,
$\infty $-groupoids,
and there is a canonical comparison map:
(We note that the n-groupoid ![]() $\mathrm {h}_n(\mathscr {D}^{\simeq })$ is the maximal
$\mathrm {h}_n(\mathscr {D}^{\simeq })$ is the maximal ![]() $\infty $-subgroupoid of
$\infty $-subgroupoid of ![]() $\mathrm {h}_n(\mathscr {D})$ for every
$\mathrm {h}_n(\mathscr {D})$ for every ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {D}$; this can be seen directly from the definitions of
$\mathscr {D}$; this can be seen directly from the definitions of ![]() $\mathrm {h}_n(-)$ and
$\mathrm {h}_n(-)$ and ![]() $(-)^{\simeq }$. As a result, the order of the operations
$(-)^{\simeq }$. As a result, the order of the operations ![]() $\mathrm {h}_n(-)$ and
$\mathrm {h}_n(-)$ and ![]() $(-)^{\simeq }$ does not play an essential role in the definition of
$(-)^{\simeq }$ does not play an essential role in the definition of ![]() $\mathrm {h}_n \mathrm {S}_{\bullet }^{\simeq } \mathscr {C}$.)
$\mathrm {h}_n \mathrm {S}_{\bullet }^{\simeq } \mathscr {C}$.)
Let ![]() $\mathbb {D}^{(n)}_{\mathscr {C}}$ be the pointed right n-derivator associated to
$\mathbb {D}^{(n)}_{\mathscr {C}}$ be the pointed right n-derivator associated to ![]() $\mathscr {C}$ with domain
$\mathscr {C}$ with domain ![]() $\mathcal {D}ir_{f}$ (see Proposition 4.17). As a consequence of the natural identification between
$\mathcal {D}ir_{f}$ (see Proposition 4.17). As a consequence of the natural identification between ![]() $\mathrm {h}_n \big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C} \big )$ and
$\mathrm {h}_n \big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C} \big )$ and ![]() $\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}^{(n)}_{\mathscr {C}},$ we obtain a canonical comparison map from the Waldhausen K-theory of
$\mathrm {S}_{\bullet }^{\simeq } \mathbb {D}^{(n)}_{\mathscr {C}},$ we obtain a canonical comparison map from the Waldhausen K-theory of ![]() $\mathscr {C}$ to derivator K-theory:
$\mathscr {C}$ to derivator K-theory:
In addition, the natural morphisms of simplicial objects ![]() $\mathrm {h}_n\big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}\big ) \to \mathrm {h}_{n-1}\big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}\big )$, for
$\mathrm {h}_n\big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}\big ) \to \mathrm {h}_{n-1}\big (\mathrm {S}_{\bullet }^{\simeq } \mathscr {C}\big )$, for ![]() $n> 1$, define a tower of derivator K-theories for
$n> 1$, define a tower of derivator K-theories for ![]() $\mathscr {C}$ that is compatible with the comparison maps
$\mathscr {C}$ that is compatible with the comparison maps ![]() $\mu _n$:
$\mu _n$:

In the case of ordinary derivators, Maltsiniotis conjectured in [Reference Maltsiniotis24] that the comparison map ![]() $\mu _1$ is a weak equivalence for exact categories. The comparison map
$\mu _1$ is a weak equivalence for exact categories. The comparison map ![]() $\mu _1$ was subsequently studied in [Reference Garkusha15, Reference Muro25, Reference Muro and Raptis26, Reference Muro and Raptis27]. It is known (see [Reference Muro and Raptis27]) that
$\mu _1$ was subsequently studied in [Reference Garkusha15, Reference Muro25, Reference Muro and Raptis26, Reference Muro and Raptis27]. It is known (see [Reference Muro and Raptis27]) that ![]() $\mu _1$ is not a weak equivalence for general
$\mu _1$ is not a weak equivalence for general ![]() $\mathscr {C}$, and moreover that
$\mathscr {C}$, and moreover that ![]() $\mu _1$ will fail to be a weak equivalence even for exact categories if derivator K-theory satisfies localization – a property that was also conjectured by Maltsiniotis [Reference Maltsiniotis24].
$\mu _1$ will fail to be a weak equivalence even for exact categories if derivator K-theory satisfies localization – a property that was also conjectured by Maltsiniotis [Reference Maltsiniotis24].
We prove a general result about the connectivity of the comparison map ![]() $\mu _n$ for general
$\mu _n$ for general ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $n \geq 1$. This connectivity estimate is also a small improvement of the known estimate for
$n \geq 1$. This connectivity estimate is also a small improvement of the known estimate for ![]() $n=1$ that was shown by Muro [Reference Muro25].
$n=1$ that was shown by Muro [Reference Muro25].
Theorem 5.5. Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category that admits finite colimits. Then the comparison map
$\infty $-category that admits finite colimits. Then the comparison map ![]() $\mu _n: K(\mathscr {C}) \to K(\mathbb {D}^{(n)}_{\mathscr {C}})$ is
$\mu _n: K(\mathscr {C}) \to K(\mathbb {D}^{(n)}_{\mathscr {C}})$ is ![]() $(n+1)$-connected.
$(n+1)$-connected.
We will need the following useful elementary fact about simplicial spaces.
Lemma 5.6. Let ![]() $f_{\bullet } \colon X_{\bullet } \to Y_{\bullet }$ be a map of simplicial spaces. Suppose that
$f_{\bullet } \colon X_{\bullet } \to Y_{\bullet }$ be a map of simplicial spaces. Suppose that ![]() $f_k$ is
$f_k$ is ![]() $(m-k)$-connected for every
$(m-k)$-connected for every ![]() $k \geq 0$. Then the map
$k \geq 0$. Then the map ![]() $||f_{\bullet }|| \colon ||X_{\bullet }|| \to ||Y_{\bullet }||$ is m-connected. (Here
$||f_{\bullet }|| \colon ||X_{\bullet }|| \to ||Y_{\bullet }||$ is m-connected. (Here ![]() $||-||$ denotes the fat geometric realization of a simplicial space.)
$||-||$ denotes the fat geometric realization of a simplicial space.)
Proof. See [Reference Ebert and Randal-Williams11, Lemma 2.4].
Proof. (of Theorem 5.5) By Lemma 5.6, it suffices to show that the map of ![]() $\infty $-groupoids
$\infty $-groupoids
is ![]() $(n+2-k)$-connected for all
$(n+2-k)$-connected for all ![]() $k \geq 0$. This holds since the map is an equivalence for
$k \geq 0$. This holds since the map is an equivalence for ![]() $k = 0$ and
$k = 0$ and ![]() $(n+1)$-connected for
$(n+1)$-connected for ![]() $k> 0$ (Example 2.9).
$k> 0$ (Example 2.9).
Remark 5.7. The main result of [Reference Muro and Raptis27, Theorem 1.2] shows that the comparison map ![]() $\mu _1$ is not a
$\mu _1$ is not a ![]() $\pi _3$-isomorphism in general. (In addition, a closer inspection of the proofs in [Reference Muro and Raptis27] also shows that the map
$\pi _3$-isomorphism in general. (In addition, a closer inspection of the proofs in [Reference Muro and Raptis27] also shows that the map ![]() $\mu _1$ will not be 3-connected if derivator K-theory satisfies localization.) It seems likely that the connectivity estimate of Theorem 5.5 is best possible in general.
$\mu _1$ will not be 3-connected if derivator K-theory satisfies localization.) It seems likely that the connectivity estimate of Theorem 5.5 is best possible in general.
Remark 5.8. By [Reference Garkusha15, Theorem 7.1], the comparison map ![]() $\mu _1$ is
$\mu _1$ is ![]() $\pi _*$-split injective in the case where
$\pi _*$-split injective in the case where ![]() $\mathscr {C}$ is the bounded derived category of an abelian category. In fact, it is shown [Reference Garkusha15] that there is a retraction map to
$\mathscr {C}$ is the bounded derived category of an abelian category. In fact, it is shown [Reference Garkusha15] that there is a retraction map to ![]() $\mu _1$. As a consequence, the comparison map
$\mu _1$. As a consequence, the comparison map ![]() $\mu _n$ also admits a retraction in this case for all
$\mu _n$ also admits a retraction in this case for all ![]() $n \geq 1$. Related to this, an interesting problem suggested by B. Antieau is whether
$n \geq 1$. Related to this, an interesting problem suggested by B. Antieau is whether ![]() $\mu _n$ is a weak equivalence when
$\mu _n$ is a weak equivalence when ![]() $\mathscr {C}$ is a stable
$\mathscr {C}$ is a stable ![]() $\infty $-category that admits a bounded t-structure.
$\infty $-category that admits a bounded t-structure.
5.4 Waldhausen K-theory of derivators
Waldhausen K-theory for pointed right 1-derivators was defined in [Reference Muro and Raptis26]. It was shown in [Reference Muro and Raptis26] that this K-theory of derivators agrees with the usual Waldhausen K-theory for all well-behaved Waldhausen categories [Reference Muro and Raptis26, Theorem 4.3.1]. We consider an analogous definition of K-theory for general pointed right ![]() $\infty $-derivators.
$\infty $-derivators.
Let ![]() $\mathbb {D}$ be a pointed right
$\mathbb {D}$ be a pointed right ![]() $\infty $-derivator with domain
$\infty $-derivator with domain ![]() $\mathsf {Dia}$. Let
$\mathsf {Dia}$. Let ![]() $\mathrm {S}_{\bullet \bullet } \mathbb {D}$ be the bisimplicial set whose set of
$\mathrm {S}_{\bullet \bullet } \mathbb {D}$ be the bisimplicial set whose set of ![]() $(n,m)$-simplices
$(n,m)$-simplices ![]() $\mathrm {S}_{n,m} \mathbb {D}$ is the set of objects
$\mathrm {S}_{n,m} \mathbb {D}$ is the set of objects
such that
(1) For every
 $j\colon [0] \to [m]$, the object
$j\colon [0] \to [m]$, the object  $(j \times \mathrm {id})^*(F) \in \operatorname {Ob} \big (\mathbb {D}(\mathrm {Ar}[n])\big )$ is in
$(j \times \mathrm {id})^*(F) \in \operatorname {Ob} \big (\mathbb {D}(\mathrm {Ar}[n])\big )$ is in  $\mathrm {S}_n \mathbb {D}$.
$\mathrm {S}_n \mathbb {D}$.(2) The underlying diagram functor associated to F,
takes values in equivalences. $$ \begin{align*}\mathrm{dia}_{\Delta^m, \mathrm{Ar}[n]}(F) \colon \Delta^m \to \mathbb{D}(\mathrm{Ar}[n]),\end{align*} $$
$$ \begin{align*}\mathrm{dia}_{\Delta^m, \mathrm{Ar}[n]}(F) \colon \Delta^m \to \mathbb{D}(\mathrm{Ar}[n]),\end{align*} $$
The bisimplicial operators of ![]() $\mathrm {S}_{\bullet \bullet } \mathbb {D}$ are again defined using the structure of the underlying
$\mathrm {S}_{\bullet \bullet } \mathbb {D}$ are again defined using the structure of the underlying ![]() $\infty $-prederivator. Moreover, it is easy to see that the construction is functorial in
$\infty $-prederivator. Moreover, it is easy to see that the construction is functorial in ![]() $\mathbb {D}$ with respect to strict morphisms that preserve the zero objects and cocartesian squares. We regard the geometric realization
$\mathbb {D}$ with respect to strict morphisms that preserve the zero objects and cocartesian squares. We regard the geometric realization ![]() $| \mathrm {S}_{\bullet \bullet } \mathbb {D}|$ as based at a zero object of
$| \mathrm {S}_{\bullet \bullet } \mathbb {D}|$ as based at a zero object of ![]() $\mathbb {D}(\Delta ^0)$.
$\mathbb {D}(\Delta ^0)$.
Definition 5.9. Let ![]() $\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a pointed right
$\mathbb {D} \colon \mathsf {Dia}^{\operatorname {op}} \to \mathsf {Cat_{\infty }}$ be a pointed right ![]() $\infty $-derivator with domain
$\infty $-derivator with domain ![]() $\mathsf {Dia}$. The Waldhausen K-theory of
$\mathsf {Dia}$. The Waldhausen K-theory of ![]() $\mathbb {D}$ is defined to be the space
$\mathbb {D}$ is defined to be the space
Following [Reference Muro and Raptis26], we also consider the analogue of the ![]() $\textsf {s}_{\bullet }$-construction in this context. Restricting pointwise to the objects of
$\textsf {s}_{\bullet }$-construction in this context. Restricting pointwise to the objects of ![]() $\mathrm {S}_{\bullet } \mathbb {D}$, we obtain a simplicial set
$\mathrm {S}_{\bullet } \mathbb {D}$, we obtain a simplicial set
There is a canonical comparison map, given by the inclusion of ![]() $0$-simplices,
$0$-simplices,
This is the analogue of the comparison map in Proposition 5.1 for pointed right ![]() $\infty $-derivators.
$\infty $-derivators.
Proposition 5.10. (a) The comparison map ![]() $\iota $ is a weak equivalence. (b) Let
$\iota $ is a weak equivalence. (b) Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category with finite colimits, and let
$\infty $-category with finite colimits, and let ![]() $n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. There is a commutative diagram of weak equivalences:
$n \in \mathbb {Z}_{\geq 1} \cup \{\infty \}$. There is a commutative diagram of weak equivalences:

Proof. (a) The proof is essentially the same as the proof of [Reference Muro and Raptis26, Proposition 4.2.1] (see also [Reference Waldhausen39, Lemma 1.4.1 and Corollary]). (b) The bottom map is a weak equivalence (independently of n!) because we have ![]() $(\mathrm {S}_k^{\simeq } \mathscr {C})_m = \mathrm {S}_{k,m} \mathbb {D}^{(n)}_{\mathscr {C}}$. The left vertical map is a weak equivalence by Proposition 5.1. Then the result follows.
$(\mathrm {S}_k^{\simeq } \mathscr {C})_m = \mathrm {S}_{k,m} \mathbb {D}^{(n)}_{\mathscr {C}}$. The left vertical map is a weak equivalence by Proposition 5.1. Then the result follows.
5.5 Universal property of derivator K-theory
The comparison maps ![]() $\{\mu _n\}$ from Waldhausen K-theory to derivator K-theory can be defined more generally for pointed right
$\{\mu _n\}$ from Waldhausen K-theory to derivator K-theory can be defined more generally for pointed right ![]() $\infty $-derivators. Given a pointed right
$\infty $-derivators. Given a pointed right ![]() $\infty $-derivator
$\infty $-derivator ![]() $\mathbb {D}$ (with domain
$\mathbb {D}$ (with domain ![]() $\mathsf {Dia}$), the underlying diagram functors define a bisimplicial map as follows,
$\mathsf {Dia}$), the underlying diagram functors define a bisimplicial map as follows,
which after passing to the geometric realization and taking loop spaces defines a comparison map:
A universal property of this comparison map in the case of ![]() $1$-derivators was shown in [Reference Muro and Raptis26, Theorem 5.2.2]. More specifically, it was shown that
$1$-derivators was shown in [Reference Muro and Raptis26, Theorem 5.2.2]. More specifically, it was shown that ![]() $\mu $ is homotopically initial among all natural transformations from Waldhausen K-theory to a functor that is invariant under (pointwise) equivalences of pointed right derivators. The proof of this universal property extends similarly to our present
$\mu $ is homotopically initial among all natural transformations from Waldhausen K-theory to a functor that is invariant under (pointwise) equivalences of pointed right derivators. The proof of this universal property extends similarly to our present ![]() $\infty $-categorical context.
$\infty $-categorical context.
Let ![]() $\mathsf {Der}$ denote the (ordinary) category of pointed right
$\mathsf {Der}$ denote the (ordinary) category of pointed right ![]() $\infty $-derivators and strict morphisms that preserve the zero object and cocartesian squares. It will be convenient to work with the simpler model for the Waldhausen K-theory of derivators given by the
$\infty $-derivators and strict morphisms that preserve the zero object and cocartesian squares. It will be convenient to work with the simpler model for the Waldhausen K-theory of derivators given by the ![]() $\textsf {s}_{\bullet }$-construction. This will be denoted by
$\textsf {s}_{\bullet }$-construction. This will be denoted by
where ![]() $\mathrm {Top}$ denotes the ordinary category of topological spaces. Then we may regard the comparison map
$\mathrm {Top}$ denotes the ordinary category of topological spaces. Then we may regard the comparison map ![]() $\mu $ as a natural transformation
$\mu $ as a natural transformation ![]() $K^{W, \operatorname {Ob}} \to K$ between functors defined on
$K^{W, \operatorname {Ob}} \to K$ between functors defined on ![]() $\mathsf {Der}$.
$\mathsf {Der}$.
Definition 5.11. The category ![]() $\mathscr {E}$ of invariant approximations to Waldhausen K-theory is the full subcategory of the comma category
$\mathscr {E}$ of invariant approximations to Waldhausen K-theory is the full subcategory of the comma category ![]() $K^{W, \operatorname {Ob}} \downarrow \mathrm {Top}^{\mathsf {Der}}$ spanned by the objects
$K^{W, \operatorname {Ob}} \downarrow \mathrm {Top}^{\mathsf {Der}}$ spanned by the objects ![]() $(\eta \colon K^{W, \operatorname {Ob}} \to F)$ such that
$(\eta \colon K^{W, \operatorname {Ob}} \to F)$ such that ![]() $F \colon \mathsf {Der} \to \mathrm {Top}$ sends pointwise equivalences in
$F \colon \mathsf {Der} \to \mathrm {Top}$ sends pointwise equivalences in ![]() $\mathsf {Der}$ to weak equivalences. A morphism in
$\mathsf {Der}$ to weak equivalences. A morphism in ![]() $\mathscr {E}$
$\mathscr {E}$
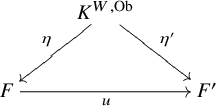
is a weak equivalence if the components of u are weak equivalences.
Remark 5.12. As defined in Definition 5.11, the category ![]() $\mathscr {E}$ (denoted by
$\mathscr {E}$ (denoted by ![]() $\mathtt {App}$ in [Reference Muro and Raptis26]) may not be locally small. This set–theoretical issue can be addressed by restricting to suitable small subcategories of
$\mathtt {App}$ in [Reference Muro and Raptis26]) may not be locally small. This set–theoretical issue can be addressed by restricting to suitable small subcategories of ![]() $\mathsf {Der}$, as was done in [Reference Muro and Raptis26].
$\mathsf {Der}$, as was done in [Reference Muro and Raptis26].
We recall from [Reference Dwyer, Hirschhorn, Kan and Smith10] that an object ![]() $x \in \mathcal {C}$ in an (ordinary) category with weak equivalences
$x \in \mathcal {C}$ in an (ordinary) category with weak equivalences ![]() $(\mathcal {C}, \mathcal {W})$ (satisfying in addition the ‘2-out-of-6’ property) is homotopically initial if there are functors
$(\mathcal {C}, \mathcal {W})$ (satisfying in addition the ‘2-out-of-6’ property) is homotopically initial if there are functors ![]() $F_0, F_1 \colon \mathcal {C} \to \mathcal {C}$ that preserve the weak equivalences and a natural transformation
$F_0, F_1 \colon \mathcal {C} \to \mathcal {C}$ that preserve the weak equivalences and a natural transformation ![]() $\phi \colon F_0 \Rightarrow F_1$ such that
$\phi \colon F_0 \Rightarrow F_1$ such that
(i)
 $F_0$ is naturally weakly equivalent to the constant functor at
$F_0$ is naturally weakly equivalent to the constant functor at  $x \in \mathcal {C}$.
$x \in \mathcal {C}$.(ii)
 $F_1$ is naturally weakly equivalent to the identity functor on
$F_1$ is naturally weakly equivalent to the identity functor on  $\mathcal {C}$.
$\mathcal {C}$.(iii)
 $\phi _x \colon F_0(x) \to F_1(x)$ is a weak equivalence.
$\phi _x \colon F_0(x) \to F_1(x)$ is a weak equivalence.
A homotopically initial object in ![]() $(\mathcal {C}, \mathcal {W})$ defines an initial object in the associated
$(\mathcal {C}, \mathcal {W})$ defines an initial object in the associated ![]() $\infty $-category.
$\infty $-category.
Theorem 5.13. The object ![]() $(\mu \colon K^{W, \operatorname {Ob}} \to K) \in \mathscr {E}$ is homotopically initial.
$(\mu \colon K^{W, \operatorname {Ob}} \to K) \in \mathscr {E}$ is homotopically initial.
Proof. (Sketch) The proof is similar to [Reference Muro and Raptis26, Theorem 5.2.2], so we only give a sketch of the proof. Given ![]() $\mathbb {D} \in \mathsf {Der}$ and
$\mathbb {D} \in \mathsf {Der}$ and ![]() $m \geq 0$, let
$m \geq 0$, let ![]() $\mathbb {D}^{\simeq }_{m}$ denote the
$\mathbb {D}^{\simeq }_{m}$ denote the ![]() $\infty $-prederivator whose value at
$\infty $-prederivator whose value at ![]() $\mathsf {X} \in \mathsf {Dia}$ is the full subcategory
$\mathsf {X} \in \mathsf {Dia}$ is the full subcategory ![]() $\mathrm {Fun}_{\simeq }(\Delta ^m, \mathbb {D}(\mathsf {X})) \subset \mathrm {Fun}(\Delta ^m, \mathbb {D}(\mathsf {X}))$ spanned by the functors
$\mathrm {Fun}_{\simeq }(\Delta ^m, \mathbb {D}(\mathsf {X})) \subset \mathrm {Fun}(\Delta ^m, \mathbb {D}(\mathsf {X}))$ spanned by the functors ![]() $\Delta ^m \to \mathbb {D}(\mathsf {X})$, which take values in equivalences. This
$\Delta ^m \to \mathbb {D}(\mathsf {X})$, which take values in equivalences. This ![]() $\infty $-prederivator is pointwise equivalent to
$\infty $-prederivator is pointwise equivalent to ![]() $\mathbb {D}$ and therefore also a pointed right
$\mathbb {D}$ and therefore also a pointed right ![]() $\infty $-derivator. Varying
$\infty $-derivator. Varying ![]() $m \geq 0$, we obtain a simplicial object
$m \geq 0$, we obtain a simplicial object ![]() $(\mathbb {D}^{\simeq }_{m})_{m \geq 0}$ in
$(\mathbb {D}^{\simeq }_{m})_{m \geq 0}$ in ![]() $\mathsf {Der}$ with
$\mathsf {Der}$ with ![]() $\mathbb {D}^{\simeq }_0 = \mathbb {D}$.
$\mathbb {D}^{\simeq }_0 = \mathbb {D}$.
For the proof of the theorem, it suffices to note that every object in ![]() $\mathscr {E}$,
$\mathscr {E}$,
is naturally weakly equivalent (as object in ![]() $\mathscr {E}$) to the composite functor
$\mathscr {E}$) to the composite functor
This uses the fact that F respects pointwise equivalences in ![]() $\mathsf {Der}$. Moreover, the first map above defines a natural transformation that is canonically identified with
$\mathsf {Der}$. Moreover, the first map above defines a natural transformation that is canonically identified with ![]() $\mu $. As a result, we have constructed a zigzag of natural transformations from the constant endofunctor at
$\mu $. As a result, we have constructed a zigzag of natural transformations from the constant endofunctor at ![]() $\mu $ to
$\mu $ to ![]() $\mathrm {id}_{\mathscr {E}}$ satisfying (i)–(iii).
$\mathrm {id}_{\mathscr {E}}$ satisfying (i)–(iii).
6 K-theory of homotopy n-categories
6.1 Revisiting the properties of homotopy n-categories
Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category with finite colimits. Then the associated homotopy n-category
$\infty $-category with finite colimits. Then the associated homotopy n-category ![]() $\mathrm {h}_n \mathscr {C}$ satisfies the following:
$\mathrm {h}_n \mathscr {C}$ satisfies the following:
(a)
 $\mathrm {h}_n \mathscr {C}$ is a pointed n-category.
$\mathrm {h}_n \mathscr {C}$ is a pointed n-category.(b) The suspension functor
 $\Sigma _{\mathscr {C}} \colon \mathscr {C} \to \mathscr {C}$ induces a functor
$\Sigma _{\mathscr {C}} \colon \mathscr {C} \to \mathscr {C}$ induces a functor  $\Sigma \colon \mathrm {h}_n \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. This is an equivalence if and only if
$\Sigma \colon \mathrm {h}_n \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. This is an equivalence if and only if  $\mathscr {C}$ is stable (see [Reference Lurie21, Corollary 1.4.2.27]).
$\mathscr {C}$ is stable (see [Reference Lurie21, Corollary 1.4.2.27]).(c)
 $\mathrm {h}_n \mathscr {C}$ admits finite coproducts and weak pushouts of order
$\mathrm {h}_n \mathscr {C}$ admits finite coproducts and weak pushouts of order  $n-1$. Moreover, these are preserved by the functor
$n-1$. Moreover, these are preserved by the functor  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ (Proposition 3.20).
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$ (Proposition 3.20).(d) For every
 $x \in \mathrm {h}_n \mathscr {C}$, there is a natural weak pushout of order
$x \in \mathrm {h}_n \mathscr {C}$, there is a natural weak pushout of order  $n-1$,
$n-1$, 
Assuming that ![]() $\mathscr {C}$ is a stable
$\mathscr {C}$ is a stable ![]() $\infty $-category, then the adjoint equivalence
$\infty $-category, then the adjoint equivalence ![]() $(\Sigma _{\mathscr {C}}, \Omega _{\mathscr {C}})$ induces an adjoint equivalence
$(\Sigma _{\mathscr {C}}, \Omega _{\mathscr {C}})$ induces an adjoint equivalence ![]() $\Sigma \colon \mathrm {h}_n \mathscr {C} \rightleftarrows \mathrm {h}_n \mathscr {C} \colon \Omega $. Moreover, by duality,
$\Sigma \colon \mathrm {h}_n \mathscr {C} \rightleftarrows \mathrm {h}_n \mathscr {C} \colon \Omega $. Moreover, by duality, ![]() $\mathrm {h}_n \mathscr {C}$ also satisfies in this case the following dual versions of (c)–(d):
$\mathrm {h}_n \mathscr {C}$ also satisfies in this case the following dual versions of (c)–(d):
(c)′
 $\mathrm {h}_n \mathscr {C}$ admits finite products and weak pullbacks of order
$\mathrm {h}_n \mathscr {C}$ admits finite products and weak pullbacks of order  $n-1$. Moreover, these are preserved by the functor
$n-1$. Moreover, these are preserved by the functor  $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$.
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$.(d)′ For every
 $x \in \mathrm {h}_n \mathscr {C}$, there is a natural weak pullback of order
$x \in \mathrm {h}_n \mathscr {C}$, there is a natural weak pullback of order  $n-1$
$n-1$ 
In addition, if ![]() $\mathscr {C}$ is a stable
$\mathscr {C}$ is a stable ![]() $\infty $-category,
$\infty $-category, ![]() $\mathrm {h}_n \mathscr {C}$ satisfies the following property:
$\mathrm {h}_n \mathscr {C}$ satisfies the following property:
(e) A square in
 $\mathrm {h}_n \mathscr {C}$ is a weak pushout of order
$\mathrm {h}_n \mathscr {C}$ is a weak pushout of order  $n-1$ if and only if it is a weak pullback of order
$n-1$ if and only if it is a weak pullback of order  $n-1$.
$n-1$.
Note that if ![]() $n> 1$, weak pushouts (respectively, weak pullbacks) of order
$n> 1$, weak pushouts (respectively, weak pullbacks) of order ![]() $n-1$ are unique up to (non-canonical) equivalence. This observation can be used to deduce (e) for
$n-1$ are unique up to (non-canonical) equivalence. This observation can be used to deduce (e) for ![]() $n> 1$. The validity of (e) for
$n> 1$. The validity of (e) for ![]() $n=1$ can be verified by a direct argument.
$n=1$ can be verified by a direct argument.
6.2 Towards stable n-categories
An attempt towards an axiomatization of the properties (a)–(d) would naturally lead to considering triples
where
(1)
 $\mathscr {D}$ is a pointed n-category.
$\mathscr {D}$ is a pointed n-category.(2)
 $\Sigma \colon \mathscr {D} \to \mathscr {D}$ is an endofunctor.
$\Sigma \colon \mathscr {D} \to \mathscr {D}$ is an endofunctor.(3)
 $\mathscr {D}$ admits finite coproducts and weak pushouts of order
$\mathscr {D}$ admits finite coproducts and weak pushouts of order  $n-1$.
$n-1$.(4) The functor
 $\sigma $ sends an object
$\sigma $ sends an object  $x \in \mathscr {D}$ to a weak pushout of order
$x \in \mathscr {D}$ to a weak pushout of order  $n-1$, which has the following form:
$n-1$, which has the following form: 
Then, specializing to the stable context and using (c)![]() $'$–(d)
$'$–(d)![]() $'$ and (e), it would be natural to require in addition:
$'$ and (e), it would be natural to require in addition:
(2)′
 $\Sigma \colon \mathscr {D} \to \mathscr {D}$ is an equivalence.
$\Sigma \colon \mathscr {D} \to \mathscr {D}$ is an equivalence.(3)′
 $\mathscr {D}$ admits finite products and weak pullbacks of order
$\mathscr {D}$ admits finite products and weak pullbacks of order  $n-1$.
$n-1$.(5) A square in
 $\mathscr {D}$ is a weak pushout of order
$\mathscr {D}$ is a weak pushout of order  $n-1$ if and only if it is a weak pullback of order
$n-1$ if and only if it is a weak pullback of order  $n-1$.
$n-1$.
Antieau [Reference Antieau1, Conjecture 8.28] conjectured that there is a good theory of stable n-categories, ![]() $1 \leq n \leq \infty $, satisfying the following properties:
$1 \leq n \leq \infty $, satisfying the following properties:
(i) Stable n-categories, exact functors and natural transformations form an
 $(n,2)$-category with a forgetful functor to
$(n,2)$-category with a forgetful functor to  $\mathsf {Cat_{n}}$.
$\mathsf {Cat_{n}}$.(ii) For each
 $n \geq k$, the homotopy k-category functor defines a functor from stable n-categories to stable k-categories.
$n \geq k$, the homotopy k-category functor defines a functor from stable n-categories to stable k-categories.(iii) For
 $n = \infty $, the theory recovers the theory of stable
$n = \infty $, the theory recovers the theory of stable  $\infty $-categories, exact functors and natural transformations.
$\infty $-categories, exact functors and natural transformations.(iv) For
 $n = 1$, the theory recovers the theory of triangulated categories, exact functors and natural transformations.
$n = 1$, the theory recovers the theory of triangulated categories, exact functors and natural transformations.
It seems reasonable to take properties (1)–(5) (including (2)![]() $'$–(3)
$'$–(3)![]() $'$) as a minimal basis for such a notion of stable n-category. Firstly, these properties are preserved after passing to lower homotopy categories (Proposition 3.20). Also, for any
$'$) as a minimal basis for such a notion of stable n-category. Firstly, these properties are preserved after passing to lower homotopy categories (Proposition 3.20). Also, for any ![]() $n> 2$ and any pointed n-category
$n> 2$ and any pointed n-category ![]() $\mathscr {D}$ that satisfies these properties, the associated homotopy category
$\mathscr {D}$ that satisfies these properties, the associated homotopy category ![]() $\mathrm {h}_1 \mathscr {D}$ can be equipped with a canonical triangulated structure. The proof is essentially exactly the same as that for stable
$\mathrm {h}_1 \mathscr {D}$ can be equipped with a canonical triangulated structure. The proof is essentially exactly the same as that for stable ![]() $\infty $-categories in [Reference Lurie21, 1.1.2], using the properties of weak pushouts of order
$\infty $-categories in [Reference Lurie21, 1.1.2], using the properties of weak pushouts of order ![]() $n-1> 1$ instead of actual pushouts; we believe this claim also holds for
$n-1> 1$ instead of actual pushouts; we believe this claim also holds for ![]() $n=2$. Also, it would be interesting to explore possible connections between properties of type (1)–(5) and n-angulated structures (on the ordinary homotopy category) in the sense of [Reference Geiss, Keller and Oppermann17]. Finally, for
$n=2$. Also, it would be interesting to explore possible connections between properties of type (1)–(5) and n-angulated structures (on the ordinary homotopy category) in the sense of [Reference Geiss, Keller and Oppermann17]. Finally, for ![]() $n=\infty $, these properties characterise stable
$n=\infty $, these properties characterise stable ![]() $\infty $-categories.
$\infty $-categories.
On the other hand, concerning the case ![]() $n = 1$, the notion of a triangulated structure includes more structure than what is required in (1)–(5). This could be regarded as a singularity that arises at the lowest level of coherence: since weak pushouts (of order 0) are not unique up to equivalence, they do not yield canonical connecting ‘boundary’ maps, not even up to homotopy, and therefore they do not suffice for defining distinguished triangles. Alternatively, it may be desirable to consider additional structure to (1)–(5), in the form of fixed choices of higher weak colimits, and stipulate their properties in analogy with triangulated structures. We will not attempt to give an axiomatic definition of a stable n-category in this paper, but we will propose to consider a triple satisfying (1)–(5) as a basic invariant of any good notion of a stable n-category.
$n = 1$, the notion of a triangulated structure includes more structure than what is required in (1)–(5). This could be regarded as a singularity that arises at the lowest level of coherence: since weak pushouts (of order 0) are not unique up to equivalence, they do not yield canonical connecting ‘boundary’ maps, not even up to homotopy, and therefore they do not suffice for defining distinguished triangles. Alternatively, it may be desirable to consider additional structure to (1)–(5), in the form of fixed choices of higher weak colimits, and stipulate their properties in analogy with triangulated structures. We will not attempt to give an axiomatic definition of a stable n-category in this paper, but we will propose to consider a triple satisfying (1)–(5) as a basic invariant of any good notion of a stable n-category.
6.3 K-theory of pointed n-categories with distinguished squares
We will define K-theory for certain n-categories equipped with distinguished squares. These distinguished squares are meant to play the role of the pushout squares in the definition of Waldhausen K-theory. In the case of ordinary categories, this notion of a category with distinguished squares and its K-theory can be viewed as a simpler and more basic version of Neeman’s K-theory of a category with squares as defined in [Reference Neeman28, Sections 5–7].
The main example we are interested in is the homotopy n-category ![]() $\mathrm {h}_n \mathscr {C}$ of a pointed
$\mathrm {h}_n \mathscr {C}$ of a pointed ![]() $\infty $-category
$\infty $-category ![]() $\mathscr {C}$, which admits finite colimits, equipped with the squares that come from pushout squares in
$\mathscr {C}$, which admits finite colimits, equipped with the squares that come from pushout squares in ![]() $\mathscr {C}$ as the distinguished squares. The main motivation for introducing K-theory for
$\mathscr {C}$ as the distinguished squares. The main motivation for introducing K-theory for ![]() $\mathrm {h}_n \mathscr {C}$ is to identify a part of Waldhausen K-theory
$\mathrm {h}_n \mathscr {C}$ is to identify a part of Waldhausen K-theory ![]() $K(\mathscr {C})$ that may canonically be recovered from
$K(\mathscr {C})$ that may canonically be recovered from ![]() $\mathrm {h}_n \mathscr {C}$, regarded as an n-category with distinguished squares. In particular, our main result (Theorem 6.5) generalises the well-known fact that
$\mathrm {h}_n \mathscr {C}$, regarded as an n-category with distinguished squares. In particular, our main result (Theorem 6.5) generalises the well-known fact that ![]() $K_0(\mathscr {C})$ can be recovered from
$K_0(\mathscr {C})$ can be recovered from ![]() $\mathrm {h}_1 \mathscr {C}$, regarded as a category equipped with those squares that arise from pushouts in
$\mathrm {h}_1 \mathscr {C}$, regarded as a category equipped with those squares that arise from pushouts in ![]() $\mathscr {C}$.
$\mathscr {C}$.
Definition 6.1. A pointed n-category with distinguished squares, ![]() $n \geq 1$, is a pair
$n \geq 1$, is a pair ![]() $(\mathscr {C}, \mathcal {T}\kern1.7pt)$, where
$(\mathscr {C}, \mathcal {T}\kern1.7pt)$, where ![]() $\mathscr {C}$ is a pointed n-category and
$\mathscr {C}$ is a pointed n-category and ![]() $\mathcal {T}$ is a collection of weak pushout squares in
$\mathcal {T}$ is a collection of weak pushout squares in ![]() $\mathscr {C}$ of order
$\mathscr {C}$ of order ![]() $n-1$ that contains the constant squares at a zero object. We call the diagrams in
$n-1$ that contains the constant squares at a zero object. We call the diagrams in ![]() $\mathcal {T}$ distinguished squares.
$\mathcal {T}$ distinguished squares.
An exact functor ![]() $F \colon (\mathscr {C}, \mathcal {T}\kern1.7pt) \to (\mathscr {C}', \mathcal {T}'\kern1pt)$ between pointed n-categories with distinguished squares is a functor
$F \colon (\mathscr {C}, \mathcal {T}\kern1.7pt) \to (\mathscr {C}', \mathcal {T}'\kern1pt)$ between pointed n-categories with distinguished squares is a functor ![]() $F \colon \mathscr {C} \to \mathscr {C}'$ that preserves zero objects and distinguished squares.
$F \colon \mathscr {C} \to \mathscr {C}'$ that preserves zero objects and distinguished squares.
Definition 6.2. Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category with finite colimits, and let
$\infty $-category with finite colimits, and let ![]() $n \geq 1$. We define the canonical structure of distinguished squares in
$n \geq 1$. We define the canonical structure of distinguished squares in ![]() $\mathrm {h}_n \mathscr {C}$ to be the collection of squares in
$\mathrm {h}_n \mathscr {C}$ to be the collection of squares in ![]() $\mathrm {h}_n \mathscr {C}$ that are equivalent in
$\mathrm {h}_n \mathscr {C}$ that are equivalent in ![]() $\mathrm {h}_n \mathscr {C}$ to the image of a pushout square in
$\mathrm {h}_n \mathscr {C}$ to the image of a pushout square in ![]() $\mathscr {C}$ under the functor
$\mathscr {C}$ under the functor ![]() $\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. By Proposition 3.20, these are weak pushout squares of order
$\gamma _n \colon \mathscr {C} \to \mathrm {h}_n \mathscr {C}$. By Proposition 3.20, these are weak pushout squares of order ![]() $n-1$. For
$n-1$. For ![]() $n>1$, they are precisely the weak pushouts of order
$n>1$, they are precisely the weak pushouts of order ![]() $n-1$. We will denote this pointed n-category with distinguished squares by
$n-1$. We will denote this pointed n-category with distinguished squares by ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can})$.
$(\mathrm {h}_n \mathscr {C}, \mathrm {can})$.
Remark 6.3. The canonical structure on ![]() $\mathrm {h}_n \mathscr {C}$ for
$\mathrm {h}_n \mathscr {C}$ for ![]() $n> 1$ is described in terms of an intrinsic property of
$n> 1$ is described in terms of an intrinsic property of ![]() $\mathrm {h}_n \mathscr {C}$ and therefore depends only on
$\mathrm {h}_n \mathscr {C}$ and therefore depends only on ![]() $\mathrm {h}_n \mathscr {C}$. This canonical structure can be defined more generally for any finitely weakly cocomplete n-category for
$\mathrm {h}_n \mathscr {C}$. This canonical structure can be defined more generally for any finitely weakly cocomplete n-category for ![]() $n> 1$ (see Definition 3.23). For
$n> 1$ (see Definition 3.23). For ![]() $n = 1$, the canonical structure is an additional structure on
$n = 1$, the canonical structure is an additional structure on ![]() $\mathrm {h}_1 \mathscr {C}$ that is canonically induced from
$\mathrm {h}_1 \mathscr {C}$ that is canonically induced from ![]() $\mathscr {C}$.
$\mathscr {C}$.
Let ![]() $(\mathscr {C}, \mathcal {T}\kern1.7pt)$ be a pointed n-category with distinguished squares. Let
$(\mathscr {C}, \mathcal {T}\kern1.7pt)$ be a pointed n-category with distinguished squares. Let ![]() $\mathrm {S}_q (\mathscr {C}, \mathcal {T}\kern1.7pt)$ denote the full subcategory of
$\mathrm {S}_q (\mathscr {C}, \mathcal {T}\kern1.7pt)$ denote the full subcategory of ![]() $\mathrm {Fun}(\mathrm {Ar}[q], \mathscr {C})$ that is spanned by the functors
$\mathrm {Fun}(\mathrm {Ar}[q], \mathscr {C})$ that is spanned by the functors ![]() $F \colon \mathrm {Ar}[q] \to \mathscr {C}$ such that
$F \colon \mathrm {Ar}[q] \to \mathscr {C}$ such that
(i)
 $F(i \to i)$ is a zero object for all
$F(i \to i)$ is a zero object for all  $i \in [q]$.
$i \in [q]$.(ii) For every
 $0 \leq i \leq j \leq k \leq m \leq q$, the following diagram in
$0 \leq i \leq j \leq k \leq m \leq q$, the following diagram in  $\mathscr {C}$ is a distinguished square in
$\mathscr {C}$ is a distinguished square in
 $(\mathscr {C}, \mathcal {T}\kern1.7pt)$.
$(\mathscr {C}, \mathcal {T}\kern1.7pt)$.
Note that the construction is functorial in ![]() $q \geq 0$, and therefore
$q \geq 0$, and therefore ![]() $\mathrm {S}_{\bullet } (\mathscr {C}, \mathcal {T}\kern1.7pt)$ defines a simplicial object of pointed n-categories. (Of course, the construction applies similarly to more general choices
$\mathrm {S}_{\bullet } (\mathscr {C}, \mathcal {T}\kern1.7pt)$ defines a simplicial object of pointed n-categories. (Of course, the construction applies similarly to more general choices ![]() $\mathcal {T}$ of distinguished squares, but we will be interested in collections
$\mathcal {T}$ of distinguished squares, but we will be interested in collections ![]() $\mathcal {T}$ that consist of higher weak pushouts.) Moreover, the construction is functorial with respect to exact functors between pointed n-categories with distinguished squares.
$\mathcal {T}$ that consist of higher weak pushouts.) Moreover, the construction is functorial with respect to exact functors between pointed n-categories with distinguished squares.
We denote by ![]() $\mathrm {S}_{\bullet }^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt)$ the associated simplicial object of
$\mathrm {S}_{\bullet }^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt)$ the associated simplicial object of ![]() $\infty $-groupoids that is obtained by passing to the maximal
$\infty $-groupoids that is obtained by passing to the maximal ![]() $\infty $-subgroupoids pointwise. We have
$\infty $-subgroupoids pointwise. We have ![]() $\mathrm {S}_0^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt) \simeq \Delta ^0$, and therefore we may regard the geometric realization
$\mathrm {S}_0^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt) \simeq \Delta ^0$, and therefore we may regard the geometric realization ![]() $|\mathrm {S}_{\bullet }^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt)|$ as based at a zero object of
$|\mathrm {S}_{\bullet }^{\simeq } (\mathscr {C}, \mathcal {T}\kern1.7pt)|$ as based at a zero object of ![]() $\mathscr {C}$.
$\mathscr {C}$.
Definition 6.4. Let ![]() $(\mathscr {C}, \mathcal {T}\kern1.7pt)$ be a pointed n-category with distinguished squares. The K-theory of
$(\mathscr {C}, \mathcal {T}\kern1.7pt)$ be a pointed n-category with distinguished squares. The K-theory of ![]() $(\mathscr {C}, \mathcal {T}\kern1.7pt)$ is defined to be the space
$(\mathscr {C}, \mathcal {T}\kern1.7pt)$ is defined to be the space
6.4 Comparison with Waldhausen K-theory
Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category that admits finite colimits. By Proposition 3.20, it follows that passing pointwise from
$\infty $-category that admits finite colimits. By Proposition 3.20, it follows that passing pointwise from ![]() $\mathrm {S}_{\bullet } \mathscr {C}$ to the respective homotopy n-categories defines a map of simplicial objects
$\mathrm {S}_{\bullet } \mathscr {C}$ to the respective homotopy n-categories defines a map of simplicial objects
and therefore also a comparison map between K-theory spaces
Note that this comparison map factors canonically through the comparison map ![]() $\mu _n \colon K(\mathscr {C}) \to K(\mathbb {D}^{(n)}_{\mathscr {C}})$ (Subsection 5.3).
$\mu _n \colon K(\mathscr {C}) \to K(\mathbb {D}^{(n)}_{\mathscr {C}})$ (Subsection 5.3).
By Proposition 3.20, the canonical functors ![]() $\gamma _{n-1} \colon \mathrm {h}_n \mathscr {C} \to \mathrm {h}_{n-1} \mathscr {C}$,
$\gamma _{n-1} \colon \mathrm {h}_n \mathscr {C} \to \mathrm {h}_{n-1} \mathscr {C}$, ![]() $n> 1$, define exact functors
$n> 1$, define exact functors ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can}) \to (\mathrm {h}_{n-1} \mathscr {C}, \mathrm {can})$. Therefore, we obtain a tower of K-theories associated to
$(\mathrm {h}_n \mathscr {C}, \mathrm {can}) \to (\mathrm {h}_{n-1} \mathscr {C}, \mathrm {can})$. Therefore, we obtain a tower of K-theories associated to ![]() $\mathscr {C}$ that is compatible with the comparison maps
$\mathscr {C}$ that is compatible with the comparison maps ![]() $\rho _n$,
$\rho _n$,
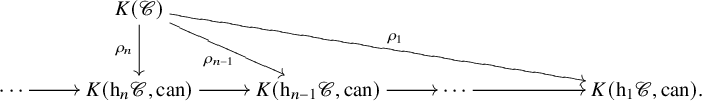
The next result gives a general connectivity estimate for the comparison map ![]() $\rho _n$.
$\rho _n$.
Theorem 6.5. Let ![]() $\mathscr {C}$ be a pointed
$\mathscr {C}$ be a pointed ![]() $\infty $-category that admits finite colimits. For
$\infty $-category that admits finite colimits. For ![]() $n \geq 1$, the comparison map
$n \geq 1$, the comparison map ![]() $\rho _n \colon K(\mathscr {C}) \to K(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ is n-connected.
$\rho _n \colon K(\mathscr {C}) \to K(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ is n-connected.
Proof. We write ![]() $\mathrm {h}_n \mathscr {C}$ for
$\mathrm {h}_n \mathscr {C}$ for ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ and
$(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ and ![]() $\mathrm {S}_{\bullet } \mathrm {h}_n\mathscr {C}$ for
$\mathrm {S}_{\bullet } \mathrm {h}_n\mathscr {C}$ for ![]() $\mathrm {S}_{\bullet }(\mathrm {h}_n \mathscr {C}, \mathrm {can})$, when the canonical structure is understood from the context, to simplify the notation in the proof. By Lemma 5.6, it suffices to show that the map of
$\mathrm {S}_{\bullet }(\mathrm {h}_n \mathscr {C}, \mathrm {can})$, when the canonical structure is understood from the context, to simplify the notation in the proof. By Lemma 5.6, it suffices to show that the map of ![]() $\infty $-groupoids
$\infty $-groupoids
is ![]() $(n+1-q)$-connected for every
$(n+1-q)$-connected for every ![]() $q \geq 0$. The claim is obvious for
$q \geq 0$. The claim is obvious for ![]() $q = 0$. For
$q = 0$. For ![]() $q = 1$, the map is
$q = 1$, the map is ![]() $(n+1)$-connected (Example 2.9). For
$(n+1)$-connected (Example 2.9). For ![]() $q = 2$ and
$q = 2$ and ![]() $n=1$, the map is
$n=1$, the map is ![]() $0$-connected by definition. This completes the proof for
$0$-connected by definition. This completes the proof for ![]() $n = 1$.
$n = 1$.
We may now restrict to the case ![]() $n> 1$. We claim that for every
$n> 1$. We claim that for every ![]() $q> 1$, the map (6.6) is
$q> 1$, the map (6.6) is ![]() $(n-1)$-connected. We consider the diagram
$(n-1)$-connected. We consider the diagram
where the vertical maps are given by restriction along the inclusion map of posets ![]() $[q-1] \subseteq \mathrm {Ar}[q], \ j \mapsto (0 \to j +1).$ The left vertical map in (6.7) is an equivalence. The lower left map is
$[q-1] \subseteq \mathrm {Ar}[q], \ j \mapsto (0 \to j +1).$ The left vertical map in (6.7) is an equivalence. The lower left map is ![]() $(n+1)$-connected (Example 2.9). The lower-right map in (6.7) is n-connected by Corollary 3.17, since we may replace
$(n+1)$-connected (Example 2.9). The lower-right map in (6.7) is n-connected by Corollary 3.17, since we may replace ![]() $\Delta ^{q-1}$ by its spine, which is
$\Delta ^{q-1}$ by its spine, which is ![]() $1$-dimensional.
$1$-dimensional.
Thus, it suffices to show that the right vertical map in (6.7) is n-connected for any ![]() $q> 0$. This claim is obvious for
$q> 0$. This claim is obvious for ![]() $q = 1$. For
$q = 1$. For ![]() $q> 1$, we proceed by induction on q and consider the following diagram:
$q> 1$, we proceed by induction on q and consider the following diagram:
For ![]() $0 \leq k \leq q$, let
$0 \leq k \leq q$, let ![]() $T^q_k \subseteq \mathrm {Ar}[q]$ be the full subcategory that contains the subposet
$T^q_k \subseteq \mathrm {Ar}[q]$ be the full subcategory that contains the subposet ![]() $\mathrm {Ar}[q-1] \subseteq \mathrm {Ar}[q]$ and the elements
$\mathrm {Ar}[q-1] \subseteq \mathrm {Ar}[q]$ and the elements ![]() $\{(j \to q) | \ 0 \leq j \leq k \}$. Moreover, let
$\{(j \to q) | \ 0 \leq j \leq k \}$. Moreover, let ![]() $\mathscr {T}^q_k$ denote the full subcategory of
$\mathscr {T}^q_k$ denote the full subcategory of ![]() $\mathrm {Map}(T^q_k, \mathrm {h}_n \mathscr {C})$ whose objects satisfy properties (i)–(ii) (Subsection 6.3) restricted to
$\mathrm {Map}(T^q_k, \mathrm {h}_n \mathscr {C})$ whose objects satisfy properties (i)–(ii) (Subsection 6.3) restricted to ![]() $T^q_k$. In other words, this is the full subcategory (indeed an
$T^q_k$. In other words, this is the full subcategory (indeed an ![]() $\infty $-groupoid), which is spanned by the image of
$\infty $-groupoid), which is spanned by the image of ![]() $\mathrm {S}_q^{\simeq } \mathrm {h}_n \mathscr {C}$ under the restriction map
$\mathrm {S}_q^{\simeq } \mathrm {h}_n \mathscr {C}$ under the restriction map ![]() $\mathrm {Map}(\mathrm {Ar}[q], \mathrm {h}_n \mathscr {C}) \to \mathrm {Map}(T^q_k, \mathrm {h}_n \mathscr {C})$. Then we may factorise the square above as the composition of the following squares
$\mathrm {Map}(\mathrm {Ar}[q], \mathrm {h}_n \mathscr {C}) \to \mathrm {Map}(T^q_k, \mathrm {h}_n \mathscr {C})$. Then we may factorise the square above as the composition of the following squares

followed by the pullback square
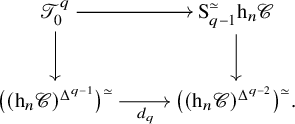
We note that all the horizontal and vertical maps in these diagrams are given by the respective restriction functors. We claim that each map ![]() $\mathscr {T}^q_k \to \mathscr {T}^q_{k-1}$ is n-connected, for any
$\mathscr {T}^q_k \to \mathscr {T}^q_{k-1}$ is n-connected, for any ![]() $1 \leq k < q$, from which the required result follows. To see this, we consider the pullback of
$1 \leq k < q$, from which the required result follows. To see this, we consider the pullback of ![]() $\infty $-groupoids
$\infty $-groupoids
where the bottom map is given by the restriction to the subposet of ![]() $\mathscr {T}^q_{k-1}$
$\mathscr {T}^q_{k-1}$

and ![]() $\big (\mathrm {h}_n(\mathscr {C})^{\square , \mathrm {can}}\big )^{\simeq } \subset \big (\mathrm {h}_n(\mathscr {C})^{\square }\big )^{\simeq }$ is the full subgroupoid that is spanned by the weak pushouts of order
$\big (\mathrm {h}_n(\mathscr {C})^{\square , \mathrm {can}}\big )^{\simeq } \subset \big (\mathrm {h}_n(\mathscr {C})^{\square }\big )^{\simeq }$ is the full subgroupoid that is spanned by the weak pushouts of order ![]() $n-1$. The right vertical map in (6.8) is given by restriction along the upper corner inclusion in
$n-1$. The right vertical map in (6.8) is given by restriction along the upper corner inclusion in ![]() $\square = \Delta ^1 \times \Delta ^1$. The fibre of this map at
$\square = \Delta ^1 \times \Delta ^1$. The fibre of this map at ![]() $F \in \big (\mathrm {h}_n(\mathscr {C})^{\ulcorner }\big )^{\simeq }$ is exactly the
$F \in \big (\mathrm {h}_n(\mathscr {C})^{\ulcorner }\big )^{\simeq }$ is exactly the ![]() $\infty $-groupoid of weak colimits of F of order
$\infty $-groupoid of weak colimits of F of order ![]() $n-1$. Since
$n-1$. Since ![]() $\mathrm {h}_n \mathscr {C}$ admits weak pushouts of order
$\mathrm {h}_n \mathscr {C}$ admits weak pushouts of order ![]() $n-1> 0$, it follows that the fibres of the right vertical map in (6.8) are
$n-1> 0$, it follows that the fibres of the right vertical map in (6.8) are ![]() $(n-1)$-connected. This means the vertical maps in (6.8) are n-connected, and the required result follows.
$(n-1)$-connected. This means the vertical maps in (6.8) are n-connected, and the required result follows.
Example 6.9. Theorem 6.5 for ![]() $n=1$ shows that the map
$n=1$ shows that the map ![]() $\rho _1 \colon K(\mathscr {C}) \to K(\mathrm {h}_1 \mathscr {C}, \mathrm {can})$ is
$\rho _1 \colon K(\mathscr {C}) \to K(\mathrm {h}_1 \mathscr {C}, \mathrm {can})$ is ![]() $1$-connected. In particular, this recovers the well-known fact that
$1$-connected. In particular, this recovers the well-known fact that ![]() $K_0(\mathscr {C})$ can be obtained from
$K_0(\mathscr {C})$ can be obtained from ![]() $\mathrm {h}_1 \mathscr {C}$ equipped with the canonical structure of distinguished squares.
$\mathrm {h}_1 \mathscr {C}$ equipped with the canonical structure of distinguished squares.
Remark 6.10. The connectivity estimate in Theorem 6.5 is best possible in general. Indeed, for ![]() $n=1$ and
$n=1$ and ![]() $\mathscr {E}$ an exact category, the comparison map
$\mathscr {E}$ an exact category, the comparison map ![]() $\rho _1$ for the
$\rho _1$ for the ![]() $\infty $-category associated to the Waldhausen category of bounded chain complexes in
$\infty $-category associated to the Waldhausen category of bounded chain complexes in ![]() $\mathscr {E}$ factors through the comparison map to Neeman’s K-theory of the triangulated category
$\mathscr {E}$ factors through the comparison map to Neeman’s K-theory of the triangulated category ![]() $D^b(\mathscr {E})$: that is, we have maps
$D^b(\mathscr {E})$: that is, we have maps
where the last map is induced by the forgetful map of simplicial objects ![]() ${}^d \mathrm {S}_{\bullet } D^b(\mathscr {E}) \to \mathrm {S}_{\bullet } (D^b(\mathscr {E}), \mathrm {can})$. (We refer to [Reference Neeman28] for a nice overview of the K-theory of triangulated categories and details about the comparison maps
${}^d \mathrm {S}_{\bullet } D^b(\mathscr {E}) \to \mathrm {S}_{\bullet } (D^b(\mathscr {E}), \mathrm {can})$. (We refer to [Reference Neeman28] for a nice overview of the K-theory of triangulated categories and details about the comparison maps ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $.) The map induced on
$\beta $.) The map induced on ![]() $K_1$ by
$K_1$ by ![]() $\beta \alpha $ is not injective in general by [Reference Neeman28, Section 11, Proposition 1]; see [Reference Vaknin38, Sections 2 and 5].
$\beta \alpha $ is not injective in general by [Reference Neeman28, Section 11, Proposition 1]; see [Reference Vaknin38, Sections 2 and 5].
Let us write ![]() $P_n X$ for the Postnikov n-section of a topological space X, which means the canonical map
$P_n X$ for the Postnikov n-section of a topological space X, which means the canonical map ![]() $X \to P_n X$ is
$X \to P_n X$ is ![]() $(n+1)$-connected – this agrees with the homotopy n-category of an
$(n+1)$-connected – this agrees with the homotopy n-category of an ![]() $\infty $-groupoid. Then Theorem 6.5 implies that the functor
$\infty $-groupoid. Then Theorem 6.5 implies that the functor ![]() $\mathscr {C} \mapsto P_{n-1}K(\mathscr {C})$ descends to a functor defined for
$\mathscr {C} \mapsto P_{n-1}K(\mathscr {C})$ descends to a functor defined for ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can})$. The following immediate corollary confirms a conjecture of Antieau in the case of connective K-theory [Reference Antieau1, Conjecture 8.35].
$(\mathrm {h}_n \mathscr {C}, \mathrm {can})$. The following immediate corollary confirms a conjecture of Antieau in the case of connective K-theory [Reference Antieau1, Conjecture 8.35].
Corollary 6.11. Let ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $\mathscr {C}'$ be stable
$\mathscr {C}'$ be stable ![]() $\infty $-categories such that there is an equivalence
$\infty $-categories such that there is an equivalence ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can}) \simeq (\mathrm {h}_n \mathscr {C}', \mathrm {can})$, as pointed n-categories with distinguished squares. Then there is a weak equivalence
$(\mathrm {h}_n \mathscr {C}, \mathrm {can}) \simeq (\mathrm {h}_n \mathscr {C}', \mathrm {can})$, as pointed n-categories with distinguished squares. Then there is a weak equivalence
Remark 6.12. As explained in Remark 6.3, the canonical structure on ![]() $(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ is preserved under equivalences for
$(\mathrm {h}_n \mathscr {C}, \mathrm {can})$ is preserved under equivalences for ![]() $n>1$: that is, an equivalence
$n>1$: that is, an equivalence ![]() $\mathrm {h}_n \mathscr {C} \simeq \mathrm {h}_n \mathscr {C}'$ for
$\mathrm {h}_n \mathscr {C} \simeq \mathrm {h}_n \mathscr {C}'$ for ![]() $n>1$ is automatically an equivalence of pointed n-categories with distinguished squares. For
$n>1$ is automatically an equivalence of pointed n-categories with distinguished squares. For ![]() $n=1$, note that an equivalence
$n=1$, note that an equivalence ![]() $\mathrm {h}_1 \mathscr {C} \stackrel {\Delta }{\simeq } \mathrm {h}_1 \mathscr {C}'$, as triangulated categories, clearly also respects the canonical structures of distinguished squares.
$\mathrm {h}_1 \mathscr {C} \stackrel {\Delta }{\simeq } \mathrm {h}_1 \mathscr {C}'$, as triangulated categories, clearly also respects the canonical structures of distinguished squares.
Acknowledgements
I would like to thank Benjamin Antieau, Denis–Charles Cisinski, Fernando Muro and Hoang Kim Nguyen for interesting discussions and their interest in this work. I also thank Martin Gallauer and Christoph Schrade for their interest and helpful comments. In addition, I thank the anonymous referee for their careful reading and useful comments.
Conflicts of Interest
none.
Financial Support
This work was partially supported by the SFB 1085 – Higher Invariants (University of Regensburg) funded by the DFG.