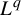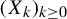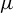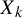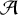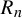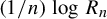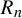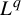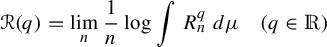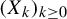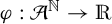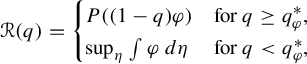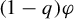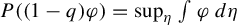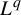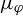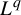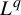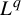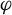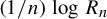Return-time $L^q$-spectrum for equilibrium states with potentials of summable variation

Abstract

Let $(X_k)_{k\geq 0}$ be a stationary and ergodic process with joint distribution $\mu $ , where the random variables $X_k$ take values in a finite set $\mathcal {A}$ . Let $R_n$ be the first time this process repeats its first n symbols of output. It is well known that $({1}/{n})\log R_n$ converges almost surely to the entropy of the process. Refined properties of $R_n$ (large deviations, multifractality, etc) are encoded in the return-time $L^q$ -spectrum defined as

provided the limit exists. We consider the case where $(X_k)_{k\geq 0}$ is distributed according to the equilibrium state of a potential with summable variation, and we prove that

where $P((1-q)\varphi )$ is the topological pressure of $(1-q)\varphi $ , the supremum is taken over all shift-invariant measures, and $q_\varphi ^*$ is the unique solution of $P((1-q)\varphi ) =\sup _\eta \int \varphi \,d\eta $ . Unexpectedly, this spectrum does not coincide with the $L^q$ -spectrum of $\mu _\varphi $ , which is $P((1-q)\varphi )$ , and it does not coincide with the waiting-time $L^q$ -spectrum in general. In fact, the return-time $L^q$ -spectrum coincides with the waiting-time $L^q$ -spectrum if and only if the equilibrium state of $\varphi $ is the measure of maximal entropy. As a by-product, we also improve the large deviation asymptotics of $({1}/{n})\log R_n$ .

1 Introduction

Consider the symbolic dynamical system $(\mathcal {A}^{\mathbb {N}},\mathscr {F},\mu ,\theta )$ in which $\mathcal A$ is a finite alphabet, $\theta $ is the left-shift map and $\mu $ is a shift-invariant probability measure, that is, $\mu \circ \theta ^{-1}=\mu $ . We are interested in the statistical properties of the return time $R_n(x)$ , the first time the orbit of x comes back in the nth cylinder $[x_0^{n-1}]=[x_0,\ldots ,x_{n-1}]$ (that is, the set of all $y\in \mathcal {A}^{\mathbb {N}}$ coinciding with x on the first n symbols ¹ ).

The main contribution of this paper is the calculation of the return-time $L^q$ -spectrum (or cumulant generating function) in the class of equilibrium states (a subclass of shift-invariant ergodic measures; see §2.1). More specifically, consider a potential $\varphi $ having summable variation (this includes Hölder continuous potentials for which the variation decreases exponentially fast). Our main result, Theorem 3.1, states that if its unique equilibrium state, denoted by $\mu _\varphi $ , is not of maximal entropy, then

where $P(\cdot )$ is the topological pressure, the supremum is taken over shift-invariant probability measures, and $q_\varphi ^*\in ]-1,0[$ is the unique solution of the equation

$$ \begin{align*} P((1-q)\varphi) =\sup_\eta \int \varphi \,d\eta. \end{align*} $$

We also prove that when $\varphi $ is a potential corresponding to the measure of maximal entropy, then $q^*_\varphi =-1$ and

is piecewise linear (Theorem 3.2). In this case, and only in this case, the return-time spectrum coincides with the waiting-time $L^q$ -spectrum

that was previously studied in [7] (see §2.2 for definitions). It is fair to say that the expressions of

and

are unexpected, and that it is surprising that they only coincide if $\mu _\varphi $ is the measure of maximal entropy.

Below we will list some implications of this result, and how it relates to the literature.

1.1 The ansatz $R_n(x)\longleftrightarrow 1/\mu _\varphi ([x_0^{n-1}])$

A remarkable result [15, 18] is that, for any ergodic measure $\mu $ ,

$$ \begin{align*} \lim_n\frac{1}{n} \log R_n(x)= h(\mu)\quad \mathrm{for\ }\mu\text{-}\mathrm{almost\ every}\, x, \end{align*} $$

where $h(\mu )=-\lim _n ({1}/{n}) \sum _{a_0^{n-1}\in \mathcal {A}^n} \mu ([a_0^{n-1}]) \log \mu ([a_0^{n-1}])$ is the entropy of $\mu $ . Compare this result with the Shannon–McMillan–Breiman theorem which says that

$$ \begin{align*} \lim_n -\frac{1}{n}\log\mu([x_0^{n-1}])= h(\mu) \quad \mathrm{for\ }\mu\text{-}\mathrm{almost\ every}\, x. \end{align*} $$

Hence, using return times, we do not need to know $\mu $ to estimate the entropy, but only to assume that we observe a typical output $x=x_0,x_1,\ldots $ of the process. In particular, combining the two previous pointwise convergences, we can write $R_n(x) \asymp 1/\mu ([x_0^{n-1}])$ for $\mu $ -almost every x ² . This yields the natural ansatz

(1) $$ \begin{align} R_n(x)\longleftrightarrow1/\mu_\varphi([x_0^{n-1}]) \end{align} $$

when integrating with respect to $\mu _\varphi $ . However, it is a consequence of our main result that this ansatz is not correct for the $L^q$ -spectra. Indeed, for the class of equilibrium states we consider (see §2.2),

which means that the $L^q$ -spectrum of the measure and

are different when $q<q^*_\varphi $ .

1.2 Fluctuations of return times

When $\mu _\varphi $ is the equilibrium state of a potential $\varphi $ of summable variation, there is a uniform control of the measure of cylinders, in the sense that $\log \mu _\varphi ([x_0^{n-1}])=\sum _{i=0}^{n-1} \varphi (x_i^{\infty })\pm \text {Const}$ , where the constant is independent of x and n. Moreover, $h(\mu _\varphi )=-\int \varphi \,d\mu _\varphi $ , so it is tempting to think that the fluctuations of $({1}/{n})\log R_n(x)$ should be the same as that of $-({1}/{n})\sum _{i=0}^{n-1} \varphi (x_i^{\infty })$ , in the sense of the central limit and large deviation asymptotics. Indeed, when $\varphi $ is Hölder continuous, it was proved in [8] that $\sqrt {n}(\log R_n/n-h(\mu ))$ converges in law to a Gaussian random variable $\mathcal {N}(0,\sigma ^2)$ , where $\sigma ^2$ is the asymptotic variance of $(({1}/{n})\sum _{i=0}^{n-1} \varphi (X_i^{\infty }))$ ³ . This was extended to potentials with summable variation in [7]. In plain words, $(({1}/{n})\log R_n(x))$ has the same central limit asymptotics as $(({1}/{n})\sum _{i=0}^{n-1} \varphi (x_i^{\infty }))$ ⁴ .

In [8], large deviation asymptotics of $(({1}/{n})\log R_n(x))$ , when $\varphi $ is Hölder continuous, were also considered. It is proved therein that, on a sufficiently small (non-explicit) interval around $h(\mu _\varphi )$ , the so-called rate function coincides with the rate function of $(-({1}/{n})\sum _{i=0}^{n-1} \varphi (x_i^{\infty }))$ . The latter is known to be the Legendre transform of $P((1-q)\varphi )$ . Using the Legendre transform of the return-time $L^q$ -spectrum, a direct consequence of our main result (see Theorem 3.3) is that, when $\varphi $ has summable variation, the coincidence of the rate functions holds on a much larger (and explicit, depending on $q^*_\varphi $ ) interval around $h(\mu _\varphi )$ . In other words, we extend the large deviation result of [8] in two ways: we deal with more general potentials and we get a much larger interval for the values of large deviations.

Notice that a similar result was deduced in [7] for the waiting time, based on the Legendre transform of the waiting-time $L^q$ -spectrum. In any case, this strategy cannot work to compute the rate functions of $(({1}/{n})\log R_n)$ and $(({1}/{n})\log W_n)$ , because the corresponding $L^q$ -spectra fail to be differentiable. Obtaining the complete description of large deviation asymptotics for $(({1}/{n})\log R_n)$ and $(({1}/{n})\log W_n)$ is an open question to date.

1.3 Relation to the return-time dimensions

Consider a general ergodic dynamical system $(M,T,\mu )$ and replace cylinders by (Euclidean) balls in the above return-time $L^q$ -spectrum, that is, consider the function $q\mapsto \int \tau _{B(x,\varepsilon )}^q(x) \,d\mu (x)$ , where $\tau _{B(x,\varepsilon )}(x)$ is the first time the orbit of x under T comes back to the ball $B(x,\varepsilon )$ of center x and radius $\varepsilon $ . The idea is to introduce return-time dimensions $D_\tau (q)$ by postulating that $\int \tau _{B(x,\varepsilon )}^q(x) \,d\mu (x)\approx \varepsilon ^{D_\tau (q)}$ , as $\varepsilon \downarrow 0$ . This was done in [11] (with a different ‘normalization’ in q) and compared numerically with the classical spectrum of generalized dimensions $D_\mu (q)$ defined in a similar way, with $\mu (B(x,\varepsilon ))^{-1}$ instead of $\tau _{B(x,\varepsilon )}(x)$ (geometric counterpart of the ansatz (1)). They studied a system of iterated functions in dimension one and numerically observed that return-time dimensions and generalized dimensions do not coincide. This can be understood with analytical arguments. For recent progress, more references and new perspectives, see [6]. Working with (Euclidean) balls in dynamical systems with a phase space M of dimension higher than one is more natural than working with cylinders, but it is much more difficult. It is an interesting open problem to obtain an analog of our main result even for uniform hyperbolic systems. We refer to [6] for recent developments.

1.4 Further recent literature

We now come back to large deviations for return times and comment on other results related to ours, besides [8]. In [12], the authors obtain the following result. For a $\phi $ -mixing process with an exponentially decaying rate, and satisfying a property called ‘exponential rates for entropy’, there exists an implicit positive function I such that $I(0)=0$ and

where h is the entropy of the process. In the same vein, [9] considered the case of (geometric) balls in smooth dynamical systems.

1.5 A few words about the proof of the main theorem

For $q>0$ , an important ingredient of the proof is an approximation of the distribution of $R_n(x)\mu _\varphi ([x_0^{n-1}])$ by an exponential law, with a precise error term, recently proved in [1]. Using this result, the computation of is straightforward. The range $q<0$ is much more delicate. To get upper and lower bounds for $\log \int R_n^q \,d\mu _{\varphi }$ , we have to partition $\mathcal {A}^{\mathbb {N}}$ over all cylinders; in particular, we cannot only take into account cylinders which are ‘typical’ for $\mu _\varphi $ . A crucial role is played by orbits which come back after less than n iterations under the shift in cylinders of length n. Such orbits are closely related to periodic orbits. What happens is roughly the following. There are two terms in competition in the ‘ $(1/2)\log $ limit’. The first one is

(2) $$ \begin{align} \sum_{a_0^{n-1}} \mu_\varphi([a_0^{n-1}]\cap \{T_{[a_0^{n-1}]}=\tau([a_0^{n-1}])\}), \end{align} $$

where $T_{[a_0^{n-1}]}(x)$ is the first time that the orbit of x enters $[a_0^{n-1}]$ , and $\tau ([a_0^{n-1}])$ is the smallest first return time among all $y\in [a_0^{n-1}]$ . The second term is

(3) $$ \begin{align} \sum_{a_0^{n-1}} \mu_\varphi([a_0^{n-1}])^{q}. \end{align} $$

Depending on the value of $q<0$ , when we take the logarithm and then divide by n, the first term (2) will beat the second one in the limit $n\to \infty $ , or vice-versa. Since the second term (3) behaves like ${e}^{nP((1-q)\varphi )}$ , and since we prove that the first one behaves like ${e}^{n \sup _\eta \int \varphi \,d\eta }$ , this indicates why the critical value $q^*_\varphi $ shows up. The asymptotic behavior of the first term (2) is rather delicate to analyze (see Proposition 4.2), and is an important ingredient of the present paper.

1.6 Organisation of the paper

The framework and the basic definitions are given in §2. In §2.1, we collect basic facts about equilibrium states and topological pressure. In §2.2, we define $L^q$ -spectra for measures, return times and waiting times. In §3, we give our main results and two simple examples in which all the involved quantities can be explicitly computed. The proofs are given in §4.

2 Setting and basic definitions

2.1 Shift space and equilibrium states

2.1.1 Notation and framework

For any sequence $(a_k)_{k\geq 0}$ where $a_k\in \mathcal {A}$ , we denote the partial sequence (‘string’) $(a_i,a_{i+1},\ldots ,a_j)$ by $a_i^j$ , for $i<j$ . (By convention, $a_i^i:=a_i$ .) In particular, $a_i^\infty $ denotes the sequence $(a_k)_{k \geq i}$ .

We consider the space $\mathcal {A}^{\mathbb {N}}$ of infinite sequences $x=(x_0,x_1,\ldots )$ , where $x_i\in \mathcal {A}$ , $i\in \mathbb {N}:=\{0,1,\ldots \}$ . Endowed with the product topology, $\mathcal {A}^{\mathbb {N}}$ is a compact space. The cylinder sets $[a_i^j]=\{x \in \mathcal {A}^{\mathbb {N}}: x_i^j=a_i^j\}$ , $i,j\in \mathbb {N}$ , generate the Borel $\sigma $ -algebra $\mathscr {F}$ . Now define the shift $\theta :\mathcal {A}^{\mathbb {N}}\to \mathcal {A}^{\mathbb {N}}$ by $(\theta x)_i=x_{i+1}$ , $i\in \mathbb {N}$ . Let $\mu $ be a shift-invariant probability measure on $\mathscr {F}$ , that is, $\mu (B)=\mu (\theta ^{-1}B)$ for each cylinder B. We then consider the stationary process $(X_k)_{k\geq 1}$ on the probability space $(\mathcal {A}^{\mathbb {N}},\mathscr {F},\mu )$ , where $X_n(x)=x_n$ , $n\in \mathbb {N}$ . We will use the shorthand notation $X_i^j$ for $(X_i,X_{i+1},\ldots ,X_j)$ , where $i<j$ . As usual, $\mathscr {F}_i^j$ is the $\sigma $ -algebra generated by $X_i^j$ , where $0\leq i\leq j\leq \infty $ . We denote by $\mathscr {M}_\theta (\mathcal {A}^{\mathbb {N}})$ the set of shift-invariant probability measures. This is a compact set in the weak topology.

2.1.2 Equilibrium states and topological pressure

We refer to [4, 22] for details on the material of this section. We consider potentials of the form $\beta \varphi $ , where and is of summable variation, that is,

$$ \begin{align*} \sum_n \operatorname{var}_n(\varphi)<\infty, \end{align*} $$

where

$$ \begin{align*} \operatorname{var}_n(\varphi)=\sup\{|\varphi(x)-\varphi(y)| : x_0^{n-1}=y_0^{n-1}\}. \end{align*} $$

Obviously, $\beta \varphi $ is of summable variation for each $\beta $ , and it has a unique equilibrium state denoted by $\mu _{\beta \varphi }$ . This means that it is the unique shift-invariant measure such that

(4) $$ \begin{align} \sup_{\eta\in \mathscr{M}_\theta(\mathcal{A}^{\mathbb{N}})}\bigg\{h(\eta)+\int \beta\varphi \,d\eta\bigg\}=h(\mu_{\beta\varphi})+ \int \beta\varphi \,d\mu_{\beta\varphi} =P(\beta\varphi), \end{align} $$

where $P(\beta \varphi )$ is the topological pressure of $\beta \varphi $ .

For convenience, we ‘normalize’ $\varphi $ as explained in [22, Corollary 3.3], which implies, in particular, that

$$ \begin{align*} P(\varphi)=0\quad\text{and}\quad\varphi<0. \end{align*} $$

This gives the same equilibrium state $\mu _\varphi $ . (Since $\sum _{a\in \mathcal {A}}{e}^{\varphi (ax)}=1$ for all $x\in \mathcal {A}^{\mathbb {N}}$ , we have $\varphi <0$ .)

The maximal entropy is $\log |\mathcal {A}|$ and, because $P(\varphi )=0$ , it is the equilibrium state of the potentials of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function .

We will use the following property, often referred to as the ‘Gibbs property’. There exists a constant $C=C_\varphi \geq 1$ such that, for any $n\geq 1$ , any cylinder $[a_0^{n-1}]$ and any $x\in [a_0^{n-1}]$ ,

(5) $$ \begin{align} C^{-1}\leq \frac{\mu_\varphi([a_0^{n-1}])}{\exp(\sum_{k=0}^{n-1} \varphi(x_k^\infty))}\leq C. \end{align} $$

See [16], where one can easily adapt the proof of their Proposition 3.2 to generalize their Corollary 3.2.1 to get (5) with $C=\exp (\sum _{k\geq 1}\operatorname {var}_k(\varphi ))$ . We will also often use the following direct consequence of (5). For $g\ge 0$ , $m,n\ge 1$ and $a_0^{m-1}\in \mathcal {A}^{m},b_0^{n-1}\in \mathcal {A}^n$ , we have

(6) $$ \begin{align} C^{-3} \leq \frac{\mu_\varphi([a_0^{m-1}]\cap \theta^{-m-g}[b_0^{n-1}])}{\mu_\varphi([a_0^{m-1}])\, \mu_\varphi([b_0^{n-1}])}\leq C^3=:D. \end{align} $$

For completeness, the proof is given in an appendix.

For the topological pressure of $\beta \varphi $ , we have the formula

(7) $$ \begin{align} P(\beta\varphi)=\lim_{n} \frac{1}{n}\log \sum_{a_0^{n-1}} {e}^{\beta \sup\{\sum_{k=0}^{n-1} \varphi(a_k^{n-1}x_n^\infty): x_n^\infty\in \mathcal{A}^{\mathbb{N}}\}}\!. \end{align} $$

One can easily check that $P(\psi +u-u\circ \theta +c)=P(\psi )+c$ for any continuous potential $\psi $ , any continuous and any . The map $\beta \mapsto P(\beta \varphi )$ is convex and continuously differentiable with

$$ \begin{align*} P'(\beta\varphi)=\int \varphi \,d\mu_{\beta\varphi}. \end{align*} $$

It is strictly decreasing since $\varphi <0$ . Moreover, it is strictly convex if and only if $\mu _\varphi $ is not the measure of maximal entropy, that is, the equilibrium state for a potential of the form $u-u\circ \theta -\log |\mathcal {A}|$ , where is continuous. We refer to [21] for a proof of these facts.

2.2 Hitting times, recurrence times and related $L^q$ -spectra

2.2.1 Hitting and recurrence times

Given $x\in \mathcal {A}^{\mathbb {N}}$ and $a_0^{n-1}\in \mathcal A^n$ , the (first) hitting time of x to $[a_0^{n-1}]$ is

$$ \begin{align*} T_{a_0^{n-1}}(x)=\inf\{k\ge1:x_k^{k+n-1}=a_0^{n-1}\}, \end{align*} $$

that is, the first time that the pattern $a_0^{n-1}$ appears in x. The (first) return time is defined by

$$ \begin{align*} R_n(x)=\inf\{k\ge1:x_k^{k+n-1}=x_0^{n-1}\},\, \end{align*} $$

that is, the first time that the first n symbols reappear in x. Finally, given $x,y\in \mathcal {A}^{\mathbb {N}}$ , we define the waiting time

$$ \begin{align*} W_n(x,y):=T_{x_0^{n-1}}(y), \end{align*} $$

which is the first time that the n first symbols of x appear in y.

2.2.2 $L^q$ -spectra

Consider a sequence $(U_n)_{n\ge 1}$ of positive measurable functions on some probability space $(\mathcal {A}^{\mathbb {N}},\mathscr {F},\mu )$ , where $\mu $ is shift-invariant, and define, for each

and $n\in \mathbb {N}^*$ , the quantities

(8)

and

Definition 2.1. ( $L^q$ -spectrum of $(U_n)_{n\ge 1}$ )

When for all , this defines the $L^q$ -spectrum of $(U_n)_{n\ge 1}$ , denoted by .

We will be mainly interested in three sequences of functions, which are, for $n\ge 1$ ,

$$ \begin{align*} \mu([x_0^{n-1}])^{-1}, \,\,R_n(x)\quad\text{and}\quad W_n(x,y). \end{align*} $$

Corresponding to (8), we naturally associate the functions

where for the third one, we mean that we integrate, in (8), with $\mu \otimes \mu $ : in other words, x and y are drawn independently and according to the same law $\mu $ . Finally, according to Definition 2.1, when the limits exist, we let

be the $L^q$ -spectrum of the measure, the return-time $L^q$ -spectrum and the waiting-time $L^q$ -spectrum, respectively.

The existence of these spectra is not known in general. Trivially, , and . It is easy to see that for ergodic measures (this follows from Kač’s lemma).

In this paper, we are interested in the particular case where $\mu =\mu _\varphi $ is an equilibrium state of a potential $\varphi $ of summable variation. In this setting, it is easy to see (this follows from (5) and (7)) that exists and that, for all ,

(9)

On the other hand, as mentioned in the introduction, [7] proved, in the same setting, that

(10)

It is one of the main objective of the present paper to compute (and, in particular, to show that it exists).

3 Main results

3.1 Two preparatory results

We start with two propositions about the critical value of q below which we will prove that the return-time $L^q$ -spectrum is different from the $L^q$ -spectrum of $\mu _\varphi $ .

Proposition 3.1. Let $\varphi $ be a potential of summable variation. Then, the equation

(11)

has a unique solution $q^*_\varphi \in [-1,0[$ . Moreover, $q_\varphi ^*=-1$ if and only if $\varphi =u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function .

See §4.1 for the proof.

The following (non-positive) quantity naturally shows up in the proof of the main theorem. Given a probability measure $\nu $ , let

$$ \begin{align*} \gamma_\nu^+:=\lim_n\frac{1}{n}\log\max_{a_0^{n-1}}\nu([a_0^{n-1}]) \end{align*} $$

whenever the limit exists. In fact, we have the following variational formula for $\gamma _{\mu _\varphi }^+$ .

Proposition 3.2. Let $\varphi $ be a potential of summable variation. Then $\gamma _\varphi ^+:=\gamma ^+(\mu _\varphi )$ exists and

(12) $$ \begin{align} \gamma_\varphi^+=\sup_{\eta\,\in\mathscr{M}_\theta(\mathcal{A}^{\mathbb{N}})} \int \varphi \,d\eta. \end{align} $$

The proof is given in §4.2.

3.2 Main results

We can now state our main results.

Theorem 3.1. (Return-time $L^q$ -spectrum)

Let $\varphi $ be a potential of summable variation. Assume that $\varphi $ is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function

(i.e., $\mu _\varphi $ is not the measure of maximal entropy). Then the return-time $L^q$ -spectrum

exists, and we have

where $q_\varphi ^*$ is given in Proposition 3.1.

In view of (9) and (12), the previous formula can be rewritten as

In other words, the return-time $L^q$ -spectrum coincides with the $L^q$ -spectrum of the equilibrium state only for $q\geq q_\varphi ^*$ .

We subsequently deal with the measure of maximal entropy because, for that measure, the return-time and the waiting-time spectra coincide.

In view of the waiting-time $L^q$ -spectrum , given in (10), which was computed by [7], we see that, if $\varphi $ is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ , then in the interval $]$ $-\infty ,q_\varphi ^*[\supsetneq ]-\infty , -1[$ . The fact that $P(2\varphi )<\sup _{\eta \in \mathscr {M}_\theta (\mathcal {A}^{\mathbb {N}})} \int \varphi \,d\eta $ follows from the proof of Proposition 3.1, in which we prove that $q_\varphi ^*>-1$ in that case.

Figure 1 illustrates Theorem 3.1.

Figure 1 Illustration of Theorem 3.1. Plot of when $\mu =m^{\mathbb {N}}$ (product measure) with m being the Bernoulli distribution (that is, $\mathcal A=\{0,1\}$ ) with parameter $p= 1/3$ . This corresponds to a potential $\varphi $ which is locally constant on the cylinders $[0]$ and $[1]$ , and therefore it obviously fulfils the conditions of the theorem. See Subsection 3.4). For a general potential of summable variation which is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ , the above graphs have the same shapes.

We now consider the case where $\mu _\varphi $ is the measure of maximal entropy.

Theorem 3.2. (Coincidence of and )

The return-time $L^q$ -spectrum coincides with the waiting-time $L^q$ -spectrum if and only if $\varphi =u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function

. In that case,

3.3 Consequences on large deviation asymptotics

Let $\varphi $ be a potential of summable variation and assume that it is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function u. Let

$$ \begin{align*} v^*_\varphi:=-\int \varphi \,d \mu_{(1-q_\varphi^*)\varphi} \quad\text{and}\quad v^+_\varphi:=-\inf_\eta \int\varphi \,d\eta. \end{align*} $$

We define the function

by

where $q(v)$ is the unique real number $q\in ]q^*_\varphi ,+\infty [$ such that

. It is easy to check that

. (This is because

is strictly convex, by the assumption we made on $\varphi $ , and is strictly increasing.) Notice that since

, we have $h(\mu _\varphi )\in ]v^*_\varphi ,v^+_\varphi [$ , and, in that interval,

is strictly convex and only vanishes at $v=h(\mu _\varphi )$ .

We have the following result.

Theorem 3.3. Let $\varphi $ be a potential of summable variation and assume that it is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function u. Then, for all $v\in [h(\mu _\varphi ),v^+_\varphi [$ ,

For all $v\in [v^*_\varphi ,h(\mu _\varphi )[$ ,

Proof. We apply a theorem from [17], a variant of the classical Gärtner–Ellis theorem [10], which roughly says that the rate function is the Legendre transform of the cumulant generating function in the interval where it is continuously differentiable. We have that is not differentiable at $q=q_\varphi ^*$ since and . Hence, we apply the large deviation theorem from [17] for $q\in ]q^*_\varphi ,+\infty [$ to prove the theorem.

Remark 3.1. Theorem 3.3 tells nothing about the asymptotic behaviour of ${\mu _\varphi ((1/2)\log R_n < v)}$ when $v\leq v^*_\varphi $ . Notice that the situation is similar for the large deviation rate function of waiting times; the only difference is that we take $-1$ in place of $q^*_\varphi $ and, therefore, $-\int \varphi \,d \mu _{2\varphi }$ in place of $v^*_\varphi $ . We believe that there exists a non-trivial rate function describing the large deviation asymptotic for these values of v for both return and waiting times, but this has to be proved using another method.

3.4 Some explicit examples

3.4.1 Independent random variables

The return-time and hitting-time spectra are non-trivial even when $\mu $ is a product measure, that is, even for a sequence of independent random variables taking values in $\mathcal {A}$ . Take, for instance, $\mathcal {A}=\{0,1\}$ and let $\mu =m^{\mathbb {N}}$ , where m is a Bernoulli measure on $\mathcal {A}$ with parameter $p_1\neq \tfrac 12$ . This corresponds to a potential $\varphi $ which is locally constant on the cylinders $[0]$ and $[1]$ . We can identify it with a function from $\mathcal {A}$ to

such that $\varphi (1)=\log p_1$ . For concreteness, let us take $p_1=\tfrac 13$ . Then, it is easy to verify that

and

and hence $P(2\varphi )<\gamma ^+_\varphi $ , as expected. Solving equation (11) numerically gives

$$ \begin{align*} q^*_\varphi\approx-0.672814. \end{align*} $$

So, in this case, Theorem 3.1 reads

We refer to Figure 1 where this spectrum is plotted, together with

and

.

Remark 3.2. One can check that, as $p_1\to \tfrac 12$ , and $\lim \nolimits _{p_1\to {1/2}} q^*_\varphi =-1$ , as expected.

3.4.2 Markov chains

If a potential $\varphi $ depends only on the first two symbols, that is, $\varphi (x)=\varphi (x_1,x_2)$ , then the corresponding process is a Markov chain. For Markov chains on $\mathcal {A}=\{1,\ldots ,K\}$ with matrix $(Q(a,b))_{a,b\in \mathcal {A}}$ , a well-known result [19, for instance] states that

(13) $$ \begin{align} \gamma^+_\varphi=\max_{1\le \ell\le K}\max_{a_1^{\ell}\in \mathcal{C}_{\ell}}\frac{1}{\ell}\log\prod_{i=1}^{\ell}Q(a_{i},a_{i+1}), \end{align} $$

where $\mathcal {C}_{\ell }$ is the set of cycles of distinct symbols of $\mathcal {A}$ , with the convention that $a_{i+1}=a_i$ (circuits). On the other hand, it is well known [19] that

where $\unicode{x3bb} _{\ell }$ is the largest eigenvalue of the matrix $((Q(a,b))^\ell )_{a,b\in \mathcal {A}}$ . This means that, in principle, everything is explicit for the Markov case. In practice, calculations are intractable even with some innocent-looking examples. Let us restrict to binary Markov chains ( $\mathcal {A}=\{0,1\}$ ) which enjoy reversibility. In this case, (13) simplifies to

(14) $$ \begin{align} \gamma_\varphi^+=\max_{i,j\in\mathcal{A}}\tfrac{1}{2}\log Q(i,j)Q(j,i). \end{align} $$

(See, for instance [14].) If we further assume symmetry, that is, $Q(1,1)=Q(0,0)$ , then we obtain

and $\gamma ^+_\varphi =\max \{\log Q(0,0),\log Q(0,1)\}$ . If we want to go beyond the symmetric case, the explicit expression of

gets cumbersome. As an illustration, consider the case $Q(0,0)=0.2$ and $Q(1,1)=0.6$ . Then

From (14) we easily obtain $\gamma _\varphi ^+=\log (0.6)$ . The solution of equation (11) can be found numerically: $q^*_\varphi \approx -0.870750$ .

4 Proofs

4.1 Proof of Proposition 3.1

Recall that

$$ \begin{align*} \mathcal M_\varphi(q)=P((1-q)\varphi)\quad\text{and}\quad \gamma_\varphi^+=\sup_{\eta\in\mathscr{M}_\theta(\mathcal{A}^{\mathbb{N}})} \int \varphi \,d\eta. \end{align*} $$

It follows easily from the basic properties of $\beta \to P(\beta \varphi )$ listed above that the map $q\mapsto \mathcal M_\varphi (q)$ is a bijection from to since it is a strictly increasing $C^1$ function. This implies that the equation $\mathcal M_\varphi (q)=\gamma _\varphi ^+$ has a unique solution $q_\varphi ^*$ that is necessarily strictly negative, since $\gamma _\varphi ^+<0$ (because $\varphi <0$ ) and $\mathcal M_\varphi (q)< 0$ if and only if $q< 0$ (since $P(\varphi )=0$ ).

We now prove that $q_\varphi ^*\geq -1$ . We use the variational principle (4) twice, first for $2\varphi $ and then for $\varphi $ , to get

$$ \begin{align*} \mathcal M_\varphi(-1) &=P(2\varphi)=h(\mu_{2\varphi})+2\int \varphi \,d\mu_{2\varphi}\\ & = h(\mu_{2\varphi})+\int \varphi \,d\mu_{2\varphi}+\int \varphi \,d\mu_{2\varphi}\\ & \leq P(\varphi) +\int \varphi \,d\mu_{2\varphi}=\int \varphi \,d\mu_{2\varphi}\quad\text{(since } P(\varphi)=0\text{)}\\ & \leq\gamma_\varphi^+. \end{align*} $$

Hence, $q_\varphi ^*\geq -1$ since $q\mapsto \mathcal M_\varphi (q)$ is increasing. Notice that $\mathcal M_\varphi $ is a bijection between $[-1,0]$ and $[P(2\varphi ),0]$ , and $\gamma _\varphi ^+\in [P(2\varphi ),0]$ .

It remains to analyze the ‘critical case’, that is, $q_\varphi ^*=-1$ .

If $\varphi =u-u\circ \theta -\log |\mathcal {A}|$ , where is continuous, then the equation $\mathcal M_\varphi (q)=\gamma _\varphi ^+$ boils down to the equation $q\log |\mathcal {A}|=-\log |\mathcal {A}|$ , and hence $q_\varphi ^*=-1$ .

We now prove the converse. It is convenient to introduce the auxiliary function

We collect its basic properties in the following lemma, the proof of which is given at the end of this section.

Lemma 4.1. The map has a continuous extension in $0$ , where it takes the value $h(\mu _\varphi )$ . It is $C^1$ and decreasing on $(0,+\infty )$ , and . Moreover, .

The condition $q_\varphi ^*=-1$ is equivalent to $\mathcal M_\varphi (-1)=\gamma _\varphi ^+$ , which, in turn, is equivalent to . But, since decreases to $-\gamma _\varphi ^+$ , we must have for all $q\geq 1$ , and hence the right derivative of at $1$ is equal to $0$ , but, since is differentiable, this implies that the left derivative of at $1$ is also equal to $0$ . Hence, . But, by the last statement of the lemma, this means that $h(\mu _{2\varphi })+\int \varphi \,d\mu _{2\varphi }=0$ , which is possible if and only if $\mu _{2\varphi }=\mu _\varphi $ , by the variational principle (since $h(\eta )+\int \varphi \,d\eta =0$ if and only if $\eta =\mu _\varphi $ ). In turn, this equality holds if and only if there exists a continuous function and such that $2\varphi =\varphi + u-u\circ \theta +c$ , which is equivalent to

$$ \begin{align*} \varphi=u-u\circ \theta+c. \end{align*} $$

Since $P(\varphi )=0$ , one must have $c=-\log |\mathcal {A}|$ .

The proof of the proposition is complete.

Proof of Lemma 4.1

Since

$$ \begin{align*} \frac{\,d}{\,d q} P(\varphi+q\varphi)\bigg|_{q=0}=\int \varphi \,d\mu_\varphi, \end{align*} $$

we can use l’Hospital’s rule to conclude that

$$ \begin{align*} -\frac{\mathcal M_\varphi(-q)}{q}\xrightarrow[]{q\to 0} -\int \varphi \,d\mu_\varphi=h(\mu_\varphi), \end{align*} $$

where we used the variational principle for $\varphi $ . Hence, we can extend

at $0$ (and denote the continuous extension by the same symbol). Then, since the pressure function is $C^1$ , we have for $q>0$ , and using the variational principle twice, that

Hence,

is $C^1$ and decreases on $(0,+\infty )$ . Taking $q=1$ gives the last statement of the lemma. Finally, we prove that

. By an obvious change of variable and a change of sign, it is equivalent to prove that

(15) $$ \begin{align} \lim_{q\to+\infty} \frac{P(q\varphi)}{q} =\gamma_\varphi^+. \end{align} $$

By the variational principle applied to $q\varphi $ ,

$$ \begin{align*} P(q\varphi) \geq h(\eta) + q \int \varphi \,d\eta \end{align*} $$

for any shift-invariant probability measure $\eta $ . Therefore, for any $q>0$ , we get

$$ \begin{align*} \frac{P(q\varphi)}{q} \geq \int \varphi \,d\eta +\frac{h(\eta)}{q} \end{align*} $$

and hence

$$ \begin{align*} \liminf_{q\to+\infty} \frac{P(q\varphi)}{q} \geq \int \varphi \,d\eta. \end{align*} $$

Taking $\eta $ to be a maximizing measure for $\varphi $ , we obtain

(16) $$ \begin{align} \liminf_{q\to+\infty} \frac{P(q\varphi)}{q} \geq \gamma_\varphi^+. \end{align} $$

(By compactness of $\mathscr {M}_\theta (\mathcal {A}^{\mathbb {N}})$ , there exists at least one shift-invariant measure maximizing $\int \varphi \,d\eta $ .) We now use (7). For any $q>0$ , we have the trivial bound

$$ \begin{align*} \frac{1}{n}\log \sum_{a_0^{n-1}} {e}^{q\sup\{\sum_{k=0}^{n-1} \varphi(a_k^{n-1}x_n^\infty): x_n^\infty\in \mathcal{A}^{\mathbb{N}}\}} \leq q\, \frac{1}{n} {\sup_y \sum_{k=0}^{n-1}\varphi(y_k^\infty)} + \log|\mathcal{A}|. \end{align*} $$

Hence, by taking the limit $n\to \infty $ on both sides, and using (19) (see the next subsection), we have, for any $q>0$ ,

$$ \begin{align*} \frac{P(q\varphi)}{q} \leq \gamma_\varphi^++ \frac{\log|\mathcal{A}|}{q} \end{align*} $$

and hence

$$ \begin{align*} \limsup_{q\to+\infty}\frac{P(q\varphi)}{q} \leq \gamma_\varphi^+. \end{align*} $$

Combining this inequality with (16) gives (15). The proof of the lemma is complete.

4.2 Proof of Proposition 3.2

For each $n\geq 1$ , let

$$ \begin{align*} \gamma_{\varphi,n}^+=\frac{1}{n} \max_{a_0^{n-1}} \log \mu_\varphi([a_0^{n-1}])\quad\text{and}\quad s_n(\varphi)=\max_y \sum_{k=0}^{n-1}\varphi(y_k^\infty). \end{align*} $$

(We can put a maximum instead of a supremum in the definition of $s_n(\varphi )$ since, by compactness of $\mathcal {A}^{\mathbb {N}}$ , the supremum of the continuous function $x\mapsto \sum _{k=0}^{n-1}\varphi (x_k^\infty )$ is attained for some y.) Fix $n\geq 1$ . We have

$$ \begin{align*} s_n(\varphi) =\max_{a_0^{n-1}}\max_{y:y_0^{n-1}=a_0^{n-1}} \sum_{k=0}^{n-1}\varphi(y_k^\infty) =\max_{a_0^{n-1}}\max_{y_{n}^\infty} \sum_{k=0}^{n-1}\varphi(a_k^{n-1} y_{n}^\infty). \end{align*} $$

Since $\mathcal {A}^{\mathbb {N}}$ is compact and $\varphi $ is continuous, for each n there exists a point $z^{(n)}\in \mathcal {A}^{\mathbb {N}}$ such that

(17) $$ \begin{align} s_n(\varphi)=\max_{a_0^{n-1}}\sum_{k=0}^{n-1}\varphi(a_k^{n-1} (z^{(n)})_{n}^\infty). \end{align} $$

Now, using (5), we get

(18) $$ \begin{align} \bigg| \gamma_{\varphi,n}^+- \frac{1}{n}\max_{a_0^{n-1}}\sum_{k=0}^{n-1} \varphi(a_{k}^{n-1} x_{n}^\infty)\bigg| \leq \frac{C}{n} \end{align} $$

for any choice of $x_{n}^\infty \in \mathcal {A}^{\mathbb {N}}$ , so we can take $x_{n}^\infty =(z^{(n)})_{n}^\infty $ . By using (18) and (17), we thus obtain

$$ \begin{align*} \bigg| \gamma_{\varphi,n}^+- \frac{s_n(\varphi)}{n}\bigg| \leq \frac{C}{n},\; n\geq 1. \end{align*} $$

Now, one can check that $(s_n(\varphi ))_n$ is a subadditive sequence such that $\inf _m m^{-1} s_m(\varphi ) \geq -\|\varphi \|_\infty $ . Hence, by Fekete’s lemma (see for example, [20]) $\lim _n n^{-1}s_n(\varphi )$ exists, so the limit of $(\gamma _{\varphi ,n}^+)_{n\ge 1}$ also exists and coincides with $\lim _n n^{-1}s_n(\varphi )$ . We now use the fact that

(19) $$ \begin{align} \lim_n \frac{s_n(\varphi)}{n}=\sup_{\eta\in\mathscr{M}_\theta(\mathcal{A}^{\mathbb{N}})} \int \varphi \,d \eta. \end{align} $$

The proof is found in [13, Proposition 2.1]. This finishes the proof of Proposition 3.2.

4.3 Auxiliary results concerning recurrence times

In this section, we state some auxiliary results which will be used in the proofs of the main theorems and are concerned with recurrence times.

4.3.1 Exponential approximation of return-time distribution

The following result of [1] will be important in the proof of Theorem 3.1 for $q>0$ .

We recall that a measure $\mu $ enjoys the $\psi $ -mixing property if there exists a sequence $(\psi (\ell ))_{\ell \geq 1}$ of positive numbers decreasing to zero where

$$ \begin{align*} \psi(\ell):=\sup_{j\geq 1}\sup_{B\in \mathscr{F}_0^j,\, B'\in \mathscr{F}_{j+\ell}^\infty} \bigg| \frac{\mu(B\cap B')}{\mu(B)\mu(B')}-1\bigg|. \end{align*} $$

Theorem 4.1. (Exponential approximation under $\psi $ -mixing)

Let $(X_k)_{k\geq 0}$ be a process distributed according to a $\psi $ -mixing measure $\mu $ . There exist constants $C,C'>0$ such that, for any $x\in \mathcal {A}^{\mathbb {N}}$ , $n\geq 1$ and $t\ge \tau (x_0^{n-1})$ ,

(20) $$ \begin{align} &|\,\mu_{x_0^{n-1}}(T_{x_0^{n-1}}> t)-\zeta_\mu(x_0^{n-1}){e}^{-\zeta_\mu(x_0^{n-1})\mu([x_0^{n-1}])(t-\tau(x_0^{n-1}))}|\nonumber\\ &\quad\le \begin{cases} C\epsilon_n & \text{if } t\le \dfrac{1}{2\mu([x_0^{n-1}])},\\[3pt] C\epsilon_n\mu([x_0^{n-1}])\,t{e}^{-(\zeta_\mu(x_0^{n-1})-C'\!\epsilon_n)\mu([x_0^{n-1}])t} & \text{if } t> \dfrac{1}{2\mu([x_0^{n-1}])}, \end{cases} \end{align} $$

where $(\epsilon _n)_n$ is a sequence of positive real numbers converging to $0$ , and where $\tau (x_0^{n-1})$ and $\zeta _\mu (x_0^{n-1})$ are defined in (22) and (23), respectively.

In [1], this is Theorem 1, statement 2, combined with Remark 2. A consequence of $\psi $ -mixing is that there exist $c_1,c_2>0$ such that $\mu ([x_0^{n-1}])\leq c_1 {e}^{-c_2 n}$ for all x and n. This also follows from (5) since $\varphi <0$ .

Remark 4.1. Notice that a previous version of the present paper relied on an exponential approximation of the return-time distribution given in [3], but their error term turned out to be wrong for $t\le {1}/{2\mu ([x_0^{n-1}])}$ . This mistake was fixed in [1].

Equilibrium states with potentials of summable variation are $\psi $ -mixing.

Proposition 4.1. Let $\varphi $ be a potential of summable variation. Then its equilibrium state $\mu _\varphi $ is $\psi $ -mixing.

Proof. The proof follows easily from (6), for $i=0$ . First, notice that this double inequality obviously holds for any $F\in \mathscr F_0^{m-1}$ in place of $a_0^{m-1}\in \mathcal {A}^{m}$ . Moreover, by the monotone class theorem, it also holds for any $G\in \mathscr F$ in place of $b_0^{n-1}\in \mathcal {A}^n$ , and we obtain that, for any $n\ge 1,F\in \mathscr F_0^{n-1}, G\in \mathscr F$ ,

(21) $$ \begin{align} C^{-3} \leq \frac{\mu_\varphi(F\cap \theta^{-m}G)}{\mu_\varphi(F)\,\mu_\varphi(G)}\leq C^3. \end{align} $$

We now apply Theorem 4.1(2) in [5] to conclude the proof.

Remark 4.2. Let us mention that, although the $\psi $ -mixing property, per se, is not studied in [22], it is a consequence of what is actually proved in the proof of Theorem 3.2 therein.

4.3.2 First possible return time and potential well

For the proof of the main theorem in the case $q<0$ , we will need to consider the short recurrence properties of the measures. The smallest possible return time in a cylinder $[a_0^{n-1}]$ , also called its period, will have a particularly important role. It is defined by

(22) $$ \begin{align} \tau(a_0^{n-1})=\inf_{x\in [a_0^{n-1}]} T_{a_0^{n-1}}(x). \end{align} $$

One can check that $\tau (a_0^{n-1})=\inf \{k\geq 1: [a_0^{n-1}]\cap \theta ^{-k}[a_0^{n-1}]\neq \emptyset \}$ . Observe that $\tau (a_0^{n-1})\leq n$ , for all $n\geq 1$ .

Let $\mu $ be a probability measure and assume that it has complete grammar, that is, it gives a positive measure to all cylinders. We denote by $\mu _{a_0^{n-1}}(\cdot ):=\mu ([a_0^{n-1}]\cap \cdot )/\mu ([a_0^{n-1}])$ the measure conditioned on $[a_0^{n-1}]$ . For any $a_0^{n-1}\in \mathcal {A}^n$ , define

(23) $$ \begin{align} \zeta_\mu(a_0^{n-1}) & := \mu_{a_0^{n-1}}( T_{a_0^{n-1}}\neq \tau(a_0^{n-1}))\\ \nonumber & =\mu_{a_0^{n-1}}( T_{a_0^{n-1}}> \tau(a_0^{n-1})). \end{align} $$

This quantity was called potential well in [1, 2], and shows up as an additional scaling factor in exponential approximations of the distributions of hitting and return times (see, for instance, the next subsection).

Remark 4.3. For $t<\mu ([a_0^{n-1}])\,\tau (a_0^{n-1})$ ,

$$ \begin{align*} \mu_{a_0^{n-1}}\bigg(T_{a_0^{n-1}}\le \frac{t}{\mu([a_0^{n-1}])}\bigg)=0 \end{align*} $$

since, by definition, $\mu _{a_0^{n-1}}(T_{a_0^{n-1}}< \tau (a_0^{n-1}) )=0$ (and hence the rightmost equality in (23)).

As already mentioned, equilibrium states with potential of summable variation are $\psi $ -mixing (see Proposition 4.1). Since, moreover, they have complete grammar, they, therefore, satisfy the conditions of Theorem 2 of [1]. This result states that the potential well is bounded away from $0$ , that is,

(24) $$ \begin{align} \zeta_\varphi^-:=\inf_{n\geq 1}\inf_{a_0^{n-1}} \zeta_{\varphi}(a_0^{n-1})>0 \end{align} $$

in which $\zeta _{\varphi }:=\zeta _{\mu _\varphi }$ .

We conclude this subsection with the following proposition which plays an important role in the proof of our main result. Its proof is quite long and, for this reason, it is postponed until §4.6.

Proposition 4.2. Let $\mu _\varphi $ be the equilibrium state of a potential $\varphi $ of summable variation. Then,

$$ \begin{align*} \Lambda_\varphi:=\lim_n\frac{1}{n}\log\sum_{a_0^{n-1}} (1-\zeta_{\varphi}(a_0^{n-1}))\, \mu_\varphi([a_0^{n-1}])=\gamma_\varphi^+. \end{align*} $$

4.4 Proof of Theorems 3.1 and 3.2 for $q\ge 0$

Notation 4.1. We will write $\sum _{A\in \mathcal {A}^n}$ for $\sum _{a_0^{n-1}\in \mathcal {A}^n}$ and $\mu _\varphi (A)$ for $\mu _\varphi ([a_0^{n-1}])$ . We will also use the notation $\mu _{\varphi ,A}(\cdot )=\mu _\varphi (A\cap \cdot )/\mu _\varphi (A)$ .

For the case of $q\ge 0$ , we proceed as in [7], but we give the proof for completeness. The case $q=0$ is trivial. For any $q>0$ , by a classical formula and a trivial change of variable,

$$ \begin{align*} \int R_n^{q}\,d\mu_\varphi & \!=\!\sum_{A\in\mathcal{A}^n}\!\mu_\varphi(A)\!\! \int T_{A}^{q} \,d\mu_{\varphi,A}\!=\! \sum_{A\in\mathcal{A}^n}\!\mu_\varphi(A)\int_{1}^\infty\! \mu_{\varphi,A}(T_{A}^{q}> s) \,d s\\ & \!=q\sum_{A\in\mathcal{A}^n} \mu_\varphi(A)\int^\infty_{\tau(A)} t^{q-1} \mu_{\varphi,A}(T_{A}> t) \,d t. \end{align*} $$

We take into account that $\mu _{\varphi ,A}(T_A\leq t)=0$ for $t<\tau (A)$ . Theorem 3.1 will be proved for $q>0$ if we prove that the above integral is of the order $C\mu _\varphi (A)^{-q}$ for any A. We use the exponential approximation (20) of Theorem 4.1, and the following facts.

• • By (24), we have $\inf _A \zeta _\varphi (A)\ge \zeta _\varphi ^->0$ , and, by definition, $\zeta _\varphi (A)\le 1$ for all A.

• • Consequently, there exists a constant $\varrho>0$ such that, for all n large enough, $\varrho \leq \inf _A \zeta _\varphi (A)-C'\epsilon _n\leq 1/2$ .

• • For all n large enough, we have $\sup _A(\zeta _\varphi (A)\mu _\varphi (A)\tau (A))\le 1$ since $\zeta _\varphi (A)\leq 1$ , $\tau (A)\leq n$ and $\mu _\varphi (A)$ decays exponentially fast to $0$ with a rate independent of A.

By (20), we thus have the following upper bound: there exists $n_0$ such that, for all $n\geq n_0$ and for all A,

$$ \begin{align*} \mu_{\varphi,A}(T_A> t)\leq 3 {e}^{-\zeta_\varphi^-\mu_\varphi(A)t} + \begin{cases} C\epsilon_n & \text{if } t\le \dfrac{1}{2\mu_\varphi(A)},\\[4pt] C\epsilon_n\,\mu_\varphi(A)\,t{e}^{-\varrho\mu_\varphi(A)t} & \text{if } t> \dfrac{1}{2\mu_\varphi(A)}. \end{cases} \end{align*} $$

Hence, we obtain (after an obvious change of variable)

$$ \begin{align*} & \int^\infty_{\tau(A)} t^{q-1} \mu_{\varphi,A}(T_{A}> t) \,d t \leq 3\mu_\varphi(A)^{-q} \int_{\tau(A)\mu_\varphi(A)}^\infty s^{q-1} {e}^{-\zeta^- s} \,d s \\ & \quad+ C\epsilon_n \mu_\varphi(A)^{-q}\bigg[ \int_{\tau(A)\mu_\varphi(A)}^{{1}/{2}} s^{q-1} \,d s + \int_{{1}/{2}}^\infty s^q {e}^{-\varrho s} \,d s\bigg]. \end{align*} $$

The right-hand side increases if we replace $\tau (A)\mu _\varphi (A)$ by $0$ in the first two integrals. It follows at once that there is a constant $\tilde {C}(q)>0$ such that, for all n larger than some $\tilde {n}_0$ and for all A,

$$ \begin{align*} \int^\infty_{\tau(A)} t^{q-1} \mu_{\varphi,A}(T_{A}> t) \,d t \leq \tilde{C}(q) \mu_\varphi(A)^{-q}. \end{align*} $$

Hence,

$$ \begin{align*} \int R_n^q \,d\mu_\varphi\leq q\,\tilde{C}(q) \sum_A \mu_\varphi(A)^{1-q} \end{align*} $$

and, therefore, using Proposition 9, we get

Now, by (20), we have the following lower bound: for all $n\geq n_0$ and for all A,

$$ \begin{align*} \mu_{\varphi,A}(T_A> t)\geq \zeta_- {e}^{-\mu_\varphi(A)t} - \begin{cases} C\epsilon_n & \text{if } t\le \dfrac{1}{2\mu_\varphi(A)},\\[4pt] C\epsilon_n\,\mu_\varphi(A)\,t\, {e}^{-\mu_\varphi(A)t/2} & \text{if } t> \dfrac{1}{2\mu_\varphi(A)}. \end{cases} \end{align*} $$

It is left to the reader to check that there exists a constant $\widehat {C}(q)>0$ such that, for n larger than some $\hat {n}_0$ ,

$$ \begin{align*} \int R_n^q \,d\mu_\varphi\geq q\,\widehat{C}(q) \sum_A \mu_\varphi(A)^{1-q} \end{align*} $$

and, therefore, using Proposition 9,

We have thus proved that

exists for all $q\geq 0$ , and

This proves both Theorems 3.1 and 3.2 in this regime. When $\varphi =u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function

, we have $P((1-q)\varphi )=q\log |\mathcal {A}|$ , and this is the only case when this function is not strictly convex.

4.5 Proofs of Theorems 3.1 and 3.2 for $q<0$

We continue using Notation 4.1.

Proceeding as above, for any $q<0$ ,

(25) $$ \begin{align} \int R_n^{-|q|}\,d\mu_\varphi = |q|\!\sum_{A\in\mathcal{A}^n}\mu_\varphi(A)^{|q|+1}\int^\infty_{\mu_\varphi(A){\tau(A)}}t^{-|q|-1} \mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg) \,d t, \end{align} $$

where we integrate from $\mu _\varphi (A){\tau (A)}$ since (see Remark 4.3)

$$ \begin{align*} \mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg)=0\quad\text{for } t<{\tau(A)}{\mu_\varphi(A)}. \end{align*} $$

Therefore, we want to estimate the integral

(26) $$ \begin{align} I(q,\![\mu_\varphi(A)\tau(A),\infty])\!:=\!\int^\infty_{\mu_\varphi(A)\tau(A)}\! t^{-|q|-1} \mu_{\varphi,A} \bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg) \,d t. \end{align} $$

Since $t^{-|q|-1}$ diverges close to $0$ , we see that we need a sufficiently precise control of $\mu _{\varphi ,A}(T_{A}\le {t}/{\mu _\varphi (A)})$ for ‘small’ t. This will be done ‘by hand’, using the results of §4.3.2 instead of Theorem 4.1.

4.5.1 Bounding $\mu _{\varphi ,A}(T_{A}\le {t}/{\mu _\varphi (A)})$

We first consider the case $t\in [\mu _\varphi (A)\tau (A),2[$ and then the case $t\geq 2$ to control the integral (26). (Since we will take the limit $n\to \infty $ , we implicitly assume that n is large enough so that $\mu _\varphi (A)\tau (A)$ is smaller that $2$ .)

For $t\in [\mu _\varphi (A)\tau (A),2[$ , we first observe that

$$ \begin{align*} \mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg)\ge \mu_{\varphi,A}( T_{A}= \tau(A)). \end{align*} $$

On the other hand, for any such t, we have

(27) $$ \begin{align} \nonumber & \mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg)\\[4pt] &\quad =\mu_{\varphi,A}(T_{A}\le n-1)+\mu_{\varphi,A}\bigg(n\le T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg). \end{align} $$

We want to get the upper bound (29) (see below) for the first term on the right-hand side of (27). To get this upper bound, first suppose that $\tau (A)=n$ . Then, in this case, $\mu _{\varphi ,A}(T_{A}\le n-1)=0$ and the inequality is obvious. Thus, we now suppose that $\tau (A)\le n-1$ . Since $\mu _{\varphi ,A}(T_{A}<\tau (A))=0$ and since for any $\tau (A)\le i\le n-1$ (remember that $A=a_0^{n-1}$ ), there is a constant $D\geq 1$ such that

(28) $$ \begin{align} \nonumber \mu_{\varphi,A}(T_{A}= i) & \le D\,\mu_\varphi([a_{n-i}^{n-1}])\le\! D\,\mu_\varphi([a_{n-\tau(a_0^{n-1})}^{n-1}])\\[4pt] &\le D^2\!\mu_{\varphi,A}(T_{A}= \tau(A)). \end{align} $$

The second inequality is trivial since $a_{n-\tau (a_0^{n-1})}^{n-1}$ is a substring of $a_{n-i}^{n-1}$ . The other two inequalities use (6) for $g=0$ . We deduce from (28) that

(29) $$ \begin{align} \mu_{\varphi,A}(T_{A}\le n-1)\le n D^2\mu_{\varphi,A}( T_{A}=\tau(A)). \end{align} $$

We now want an upper bound for the second term on the right-hand side of (27). Using (6) for $g=0$ , we get

$$ \begin{align*} & \mu_{\varphi,A}\bigg(n\le T_A\le \frac{t}{\mu_\varphi(A)}\bigg) =\mu_{\varphi,A}\bigg(\bigcup_{i=n}^{\lfloor{t}/{\mu_\varphi(A)}\rfloor}\{T_A=i\}\bigg)\\[4pt] &\quad\le \mu_{\varphi,A}\bigg(\bigcup_{i=n}^{\lfloor{t}/{\mu_\varphi(A)}\rfloor}\{X_i^{i+n-1}=A\}\bigg) \le D\mu_\varphi\bigg(\bigcup_{i=n}^{\lfloor{t}/{\mu_\varphi(A)}\rfloor}\{X_i^{i+n-1}=A\}\bigg)\\[4pt] &\quad\le D\sum_{i=n}^{\lfloor{t}/{\mu_\varphi(A)}\rfloor}\mu_\varphi(\{X_i^{i+n-1}=A\}) \le Dt. \end{align*} $$

Therefore, for any $t\in [\mu _\varphi (A)\tau (A),2[$ ,

(30) $$ \begin{align} \mu_{\varphi,A} ( T_{A}= \tau(A)) \leq \mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg) \leq nD^2\mu_{\varphi,A} ( T_{A}= \tau(A))+Dt. \end{align} $$

For $t\geq 2$ ,

(31) $$ \begin{align} \hspace{-14pt}1\ge\mu_{\varphi,A}\bigg(T_{A}\le \frac{t}{\mu_\varphi(A)}\bigg)&=1-\mu_{\varphi,A}\bigg(T_{A}> \frac{t}{\mu_\varphi(A)}\bigg) \end{align} $$

(32) $$ \begin{align} &\qquad\qquad\ge 1-\frac{\mathbb E_A(T_A)}{t/\mu_\varphi(A)}\nonumber\\[3pt] &\qquad\qquad=1-\frac{1}{t}\ge\frac{1}2, \end{align} $$

where we used Markov’s inequality and then Kač’s lemma (which holds since $\mu $ is ergodic).

4.5.2 Integral estimates

Using the bounds for $\mu _{\varphi ,A}(T_{A}\le {t}/{\mu _\varphi (A)})$ that we obtained in the preceding subsection, we can now bound the integral $I(q,[\tau (A)\mu _\varphi (A),\infty ])$ from above and from below.

Lower bound for any $q<0$ . Using (30) and (32), we get

$$ \begin{align*} I(q,[\mu_\varphi(A)\tau(A),\infty])\ge \frac{1}{|q|}(\mu_{\varphi,A}( T_{A}= \tau(A))[(\mu_\varphi(A)\tau(A))^{-|q|}-2^{-|q|}]+2^{-|q|-1}). \end{align*} $$

We can choose a suitable constant $c(q)>0$ , ensuring that, for any sufficiently large n, we have $(\mu _\varphi (A)\tau (A))^{-|q|}-2^{-|q|}\ge c(q)(\mu _\varphi (A)\tau (A))^{-|q|}$ , which is itself bounded below by $c(q)(\mu _\varphi (A)n)^{-|q|}$ since $\tau (A)\leq n$ . This gives, for all $q<0$ ,

(33) $$ \begin{align} I(q,[\mu_\varphi(A)\tau(A),\infty])\ge \frac{1}{|q|}(c(q)\mu_{\varphi,A}( T_{A}= \tau(A))(\mu_\varphi(A)n)^{-|q|}+2^{-|q|-1}). \end{align} $$

Upper bounds. Using the upper bounds of (30) and (31),

$$ \begin{align*} & I(q,[\mu_\varphi(A)\tau(A),\infty]) \le\\ &\quad \int_{\mu_\varphi(A)\tau(A)}^2 t^{-|q|-1} (nD^2\mu_{\varphi,A}( T_{A}= \tau(A))+Dt) \,d t+\int^\infty_{2} t^{-|q|-1}\,d t. \end{align*} $$

We have to consider three cases according to the values of q.

• • First, assume that $q<-1$ . Then,

  $$ \begin{align*} I(q,[\mu_\varphi(A)\tau(A),\infty])&\le \frac{1}{|q|}\bigg(nD^2\mu_{\varphi,A}( T_{A}= \tau(A))[\mu_\varphi(A)\tau(A)]^{-|q|} \\ &\quad+ \frac{D|q|}{|q|-1}(\mu_\varphi(A)\tau(A))^{-|q|+1}+2^{-|q|}\bigg). \end{align*} $$
  We can take a suitable constant $C(q)>0$ , ensuring that, for any sufficiently large n,
  $$ \begin{align*} \frac{D|q|}{|q|-1}(\mu_\varphi(A)\tau(A))^{-|q|+1}+2^{-|q|}\le C(q)(\mu_\varphi(A)\tau(A))^{-|q|+1}. \end{align*} $$
  Now using that $1\le \tau (A)$ , we get
  (34) $$ \begin{align} I(q,[\mu_\varphi(A)\tau(A),\infty]) \le\frac{1}{|q|} (nD^2\mu_{\varphi,A}( T_{A}\!=\! \tau(A))\mu_\varphi(A)^{-|q|}+C(q)\mu_\varphi(A)^{-|q|+1}). \end{align} $$

• • For $q\in (-1,0)$ , putting $C'(q):=({D|q|}/{|q|-1})2^{-|q|+1}+2^{-|q|}$ , we have

  (35) $$ \begin{align} I(q,[\mu_\varphi(A)\tau(A),\infty]) \le \frac{1}{|q|}(nD^2\mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)^{-|q|}+C'(q)). \end{align} $$

• • We conclude with the case $q=-1$ . Integrating, we get

  $$ \begin{align*} & I(-1,[\mu_\varphi(A)\tau(A),\infty])\\ &\quad \le nD^2\mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)^{-1}+D\log\frac{2}{\mu_\varphi(A)\tau(A)}+\frac{1}{2}\\ &\quad \le nD^2\mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)^{-1}+D\log\frac{2}{\mu_\varphi(A)}+\frac{1}{2}. \end{align*} $$
  Now, since $\mu _\varphi (A)\ge C^{-1}{e}^{-\|\varphi \|_\infty n}$ by (5) (where $C\geq 1$ is independent of A and n), we get, for all n large enough,
  (36) $$ \begin{align} I(-1,[\mu_\varphi(A)\tau(A),\infty]) \le nD^2\mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)^{-1}+2Dn\|\varphi\|_\infty. \end{align} $$

4.5.3 Conclusion of the proofs

Let $(a_n), (b_n)$ be two sequences of positive real numbers. The following notion of asymptotic equivalence is convenient in what follows.

$$ \begin{align*} a_n\asymp b_n\quad\text{means}\quad\lim_n\frac{1}{n}\log a_n=\lim_n \frac{1}{n}\log b_n. \end{align*} $$

We now list the properties that we are going to use to conclude the proofs. By (9), for all ,

(37)

By Proposition 4.2,

(38) $$ \begin{align} \sum_{A\in \mathcal{A}^n}\mu_{\varphi,A}(T_A=\tau(A))\mu_\varphi(A) \asymp {e}^{n\Lambda_\varphi}\quad\text{and}\quad \Lambda_\varphi=\gamma_\varphi^+ \end{align} $$

since $1-\zeta _\varphi (A)=\mu _{\varphi ,A}(T_A=\tau (A))$ (see (23)). By Proposition 3.1, the unique solution of the equation is $q_\varphi ^*\in [-1,0[$ . Finally, we also have to remember that is strictly increasing.

Up to prefactors that are negligible in the sense of $\asymp $ , the proofs will boil down to comparing with $\Lambda _\varphi $ , when q runs through , to see which one of the two ‘wins’ on the logarithmic scale.

We first prove that for $q\leq q_\varphi ^*$ , and for $q>q_\varphi ^*$ . By (25), (26) and (33), for all $q<0$ and for all n large enough,

$$ \begin{align*} \int R_n^{-|q|}\,d\mu_\varphi \geq \frac{c(q)}{n^{|q|}}\bigg(\sum_{A\in\mathcal{A}^n}\mu_{\varphi,A}(T_A=\tau(A))\mu_\varphi(A)+\sum_{A\in\mathcal{A}^n}\mu_\varphi(A)^{1+|q|}\bigg). \end{align*} $$

If $q>q_\varphi ^*$ , , and hence, by (37) and (38), we get . If $q\leq q_\varphi ^*$ , , and hence, by (37) and (38), we get .

We now prove that for $q\leq q_\varphi ^*$ , and for $q>q_\varphi ^*$ .

We first consider the case where $\varphi $ is not of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function , which is equivalent to $-1<q_\varphi ^*<0$ , by Proposition 3.1.

Suppose that $q<-1$ . By (34), for all n large enough, we get

$$ \begin{align*} \int R_n^{-|q|}\,d\mu_\varphi\leq nD^2\bigg(\sum_{A\in\mathcal{A}^n} \mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)+\sum_{A\in\mathcal{A}^n}\mu_\varphi(A)^{2}\bigg). \end{align*} $$

Since

, we obtain

For $-1<q<0$ , for all n large enough, by (35),

$$ \begin{align*} \int R_n^{-|q|}\,d\mu_\varphi\leq nD^2\bigg(\sum_{A\in\mathcal{A}^n} \mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)+\!\sum_{A\in\mathcal{A}^n}\!\mu_\varphi(A)^{|q|+1}\bigg). \end{align*} $$

Since

when $q\leq q_\varphi ^*$ , we conclude that

. When $q>q_\varphi ^*$ ,

, and hence

. When $q=-1$ , by (36),

$$ \begin{align*} \int\! R_n^{-|q|}\,d\mu_\varphi\leq n\max(D^2,2D\|\varphi\|_\infty)\bigg(\!\sum_{A\in\mathcal{A}^n} \mu_{\varphi,A}( T_{A}= \tau(A))\mu_\varphi(A)+\sum_{A\in\mathcal{A}^n}\mu_\varphi(A)^{2}\bigg), \end{align*} $$

so we conclude that

since $-1<q_\varphi ^*$ . Therefore,Theorem 3.1 is proved.

To conclude the proof of Theorem 3.2, we now suppose that $\varphi $ is of the form $u-u\circ \theta -\log |\mathcal {A}|$ for some continuous function

, which is equivalent to $q_\varphi ^*=-1$ , by Proposition 3.1. When $\varphi $ is of that form,

By (10),

coincides with

since $P(2\varphi )=P(0-2\log |\mathcal {A}|)=-\log |\mathcal {A}|$ (since, for any continuous potential $\psi $ , any continuous function v and any

, one has $P(\psi +v-v\circ \theta +c)=P(\psi )+c$ ).

4.6 Proof of Proposition 4.2

Proof of Proposition 4.2

Recall that

$$ \begin{align*} \zeta_{\varphi}(a_0^{n-1})= \mu_{\varphi,a_0^{n-1}}( T_{a_0^{n-1}}\neq \tau(a_0^{n-1})) =\mu_{\varphi,a_0^{n-1}}( T_{a_0^{n-1}}> \tau(a_0^{n-1})). \end{align*} $$

Since $a_0^{n-1}a_{n-\tau (a_0^{n-1})}^{n-1}=a_0^{\tau (a_0^{n-1})-1}a_0^{n-1}$ ,

$$ \begin{align*} (1-\zeta_{\varphi}(a_0^{n-1}))\, \mu_\varphi([a_0^{n-1}])=\mu_\varphi([a_0^{\tau(a_0^{n-1})-1}a_0^{n-1}]). \end{align*} $$

Let

$$ \begin{align*} \underline{\overline{\Lambda}}_\varphi:=\underline{\overline{\lim}}_n \frac{1}{n} \log \sum_{a_0^{n-1}} \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}a_0^{n-1}]). \end{align*} $$

We now prove that $\overline {\Lambda }_\varphi \le \gamma _\varphi ^+$ . By (6) (with $g=0$ ),

(39) $$ \begin{align} \nonumber & \sum_{a_0^{n-1}} \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}a_0^{n-1}]) \le D\sum_{a_0^{n-1}} \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}])\mu_\varphi([a_0^{n-1}])\\ & \quad \le D\max_{b_0^{n-1}}\mu_\varphi([b_0^{n-1}])\sum_{a_0^{n-1}}\mu_\varphi([a_0^{\tau(a_0^{n-1})-1}]). \end{align} $$

Partitioning according to the values of $\tau (a_0^{n-1})$ gives

$$ \begin{align*} & \sum_{a_0^{n-1}}\mu_\varphi([a_0^{\tau(a_0^{n-1})-1}])=\sum_{i=1}^n\sum_{\tau(a_0^{n-1})=i}\mu_\varphi([a_0^{i-1}]). \end{align*} $$

Now, observe that

$$ \begin{align*} \sum_{\tau(a_0^{n-1})=i}\mu_\varphi([a_0^{i-1}])= \mu_\varphi(\{x_0^{n-1}: \tau(x_0^{i-1})=i\}). \end{align*} $$

This implies, in particular, that $\sum _{a_0^{n-1}}\mu _\varphi ([a_0^{\tau (a_0^{n-1})-1}])\le n$ . Coming back to (39), we conclude by Proposition 3.2 that

$$ \begin{align*} \overline{\Lambda}_\varphi\le\limsup_n\frac{1}{n}\log (D\, n\max_{b_0^{n-1}}\mu_\varphi([b_0^{n-1}]))= \gamma_\varphi^+. \end{align*} $$

We now prove that $\underline {\Lambda }_\varphi \ge \gamma _\varphi ^+$ . We need the following lemma, the proof of which is given below.

Lemma 4.2. Let $\varphi $ be a potential of summable variation. Then there exists a sequence of strings $(A_n)_{n\geq 1}$ with $A_n\in \mathcal {A}^n$ such that

$$ \begin{align*} \lim_n\frac{1}{n}\log \mu_\varphi([A_n])=\gamma_\varphi^+\quad\text{and}\quad\lim_n \frac{\tau(A_n)}{n}=0. \end{align*} $$

For any $n\ge 1$ and any string $a_0^{n-1}$ , we introduce the notation $p_\tau (a_0^{n-1})=a_0^{\tau (a_0^{n-1})-1}$ , which is the prefix of $a_0^{n-1}$ of size $\tau (a_0^{n-1})$ . Now, using (6) (with $g=0$ ) gives

$$ \begin{align*} \sum_{a_0^{n-1}}\! \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}a_0^{n-1}]) \ge D^{-1}\sum_{a_0^{n-1}}\! \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}])\mu_\varphi([a_0^{n-1}]). \end{align*} $$

Therefore,

$$ \begin{align*} \frac{1}{n} \log \sum_{a_0^{n-1}} \mu_\varphi([a_0^{\tau(a_0^{n-1})-1}a_0^{n-1}]) \geq \frac{1}{n} \log(D^{-1}\mu_\varphi([\,p_\tau(A_n)])\mu_\varphi(A_n)). \end{align*} $$

We now use (5) and (6). For any point $x\in A_n$ , and using the fact that $\varphi (x)\geq -\inf \varphi>-\infty $ (since $\varphi $ is continuous and $\mathcal {A}^{\mathbb {N}}$ is compact), we obtain

$$ \begin{align*} & \frac{1}{n}\log(D^{-1}\mu_\varphi([\,p_\tau(A_n)])\,\mu_\varphi([A_n]))\\ &\quad\ge \frac{\log(D^{-1}C^{-1})}{n}+\frac{1}{n}\sum_{k=0}^{\tau(A_n)-1}\varphi(x_k^\infty)+\frac{1}{n}\log\mu_\varphi([A_n]) \\ &\quad\ge \frac{\log(D^{-1}C^{-1})}{n}+(\inf \varphi)\frac{\tau(A_n)}{n}+\frac{1}{n}\log\mu_\varphi([A_n]). \end{align*} $$

Therefore, by Lemma 4.2, we get

$$ \begin{align*} \underline{\Lambda}_\varphi\ge\liminf_n\frac{1}{n}\log\mu_\varphi([A_n])= \gamma_\varphi^+, \end{align*} $$

which concludes the proof of the proposition.

Proof of Lemma 4.2

We know that $\gamma _\varphi ^+$ exists by Proposition 3.2. This means that there exists a sequence of strings $(B_i)_{i\geq 1}$ with $B_i\in \mathcal {A}^i$ , such that

$$ \begin{align*} \lim_i\frac{1}{i}\log \mu_\varphi([B_i])=\gamma_\varphi^+. \end{align*} $$

Now, let $(k_i)_{i\geq 1}$ be a diverging sequence of positive integers. Then, for each $i\ge 1$ , consider the string $B_{i}^{k_i}$ obtained by concatenating $k_i$ times the string $B_{i}$ , that is,

$$ \begin{align*} B_{i}^{k_i}=\underbrace{B_i\cdots B_i}_{k_i\ \text{times}}. \end{align*} $$

Using (6) (with $g=0$ ) gives

(40) $$ \begin{align} \mu_\varphi([B_{i}])^{k_i} D^{-k_i}\le \mu_\varphi([B_{i}^{k_i}])\le\mu_\varphi([B_{i}])^{k_i} D^{k_i}. \end{align} $$

For any $n\ge 1$ , take the unique integer $i_n$ such that $n\in [ik_i,(i+1)k_{i}-1]$ (we omit the subscript n of $i_n$ to simplify the notation). We write $r=r(i,n):=n-ik_i$ and let $A_n=B_{i}^{k_i} B_{r(i)}$ , where $B_{r(i)}$ is the beginning (or prefix) of size $r(i)$ of $B_i$ , that is,

$$ \begin{align*} A_n=\underbrace{B_i\cdots B_i}_{k_i \text{ times}}B_{r(i)}. \end{align*} $$

Therefore,

$$ \begin{align*} \frac{\tau(A_n)}{n}\le \frac{i}{ik_i+r(i)}\xrightarrow[]{n\to\infty}0 \end{align*} $$

since i (and, therefore, $k_i$ ) diverges as $n\rightarrow \infty $ . Now, observe that

$$ \begin{align*} \frac{\log \mu_\varphi([B_{i}^{k_i+1}])}{n}\le\frac{1}{n}\log\mu_\varphi([A_n])\le\frac{\log \mu_\varphi([B_{i}^{k_i}])}{n}, \end{align*} $$

which gives, using (40),

$$ \begin{align*} \frac{\log (\mu_\varphi([B_{i}])^{k_i+1}D^{-(k_i+1)})}{ik_i+r}\le \frac{\log\mu_\varphi([A_n])}{n}\le\frac{\log (\mu_\varphi([B_{i}])^{k_i}D^{k_i})}{ik_i+r}. \end{align*} $$

The right-hand side is equal to

$$ \begin{align*} \frac{k_i}{k_i+\frac{r}{i}}\bigg(\frac{1}{i}\log \mu_\varphi([B_{i}])+\frac{\log D}{i}\bigg) \end{align*} $$

and $({1}/{i})\log \mu ([B_{i}])\rightarrow \gamma _\varphi ^+$ , whereas $k_i (k_i+{r}/{i})^{-1}\rightarrow 1$ . The limit of the left-hand side is also $\gamma _\varphi ^+$ . This concludes the proof of the lemma.