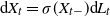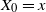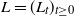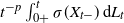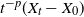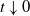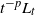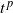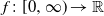Short-time behavior of solutions to Lévy-driven stochastic differential equations

Abstract

We consider solutions of Lévy-driven stochastic differential equations of the form $\textrm{d} X_t=\sigma(X_{t-})\textrm{d} L_t$, $X_0=x$, where the function $\sigma$ is twice continuously differentiable and the driving Lévy process $L=(L_t)_{t\geq0}$ is either vector or matrix valued. While the almost sure short-time behavior of Lévy processes is well known and can be characterized in terms of the characteristic triplet, there is no complete characterization of the behavior of the solution X. Using methods from stochastic calculus, we derive limiting results for stochastic integrals of the form $t^{-p}\int_{0+}^t\sigma(X_{t-})\,\textrm{d} L_t$ to show that the behavior of the quantity $t^{-p}(X_t-X_0)$ for $t\downarrow0$ almost surely reflects the behavior of $t^{-p}L_t$. Generalizing $t^{{\kern1pt}p}$ to a suitable function $f\colon[0,\infty)\rightarrow\mathbb{R}$ then yields a tool to derive explicit law of the iterated logarithm type results for the solution from the behavior of the driving Lévy process.

1. Introduction

This paper aims to study the almost sure short-time behavior of the solution $(X_t)_{t\geq0}$ to a Lévy-driven stochastic differential equation (SDE) of the form

(1) \begin{equation} \textrm{d} X_t=\sigma(X_{t-})\textrm{d} L_t, \qquad X_0=x\in\mathbb{R}^n \end{equation}

by relating it to the behavior of the driving process. Here, L is an $\mathbb{R}^d$ -valued Lévy process and the function $\sigma\colon\mathbb{R}^{n}\rightarrow\mathbb{R}^{n\times d}$ is chosen to be twice continuously differentiable and at most of linear growth. The latter conditions ensure that (1) has a unique strong solution (see, e.g., [12, Theorem 7, p. 259]) and that Itō’s formula is applicable for $\sigma(X)$ . Since the short-time behavior of a stochastic process is determined by its sample paths in an arbitrarily small neighborhood of zero, the linear growth condition may be omitted whenever the solution of the SDE is well defined on some interval $[0,\varepsilon]$ with $\varepsilon>0$ .

We characterize the short-time behavior of X by comparing the sample paths of the process to suitable functions. For real-valued Lévy processes, early results [14, 20] linked the almost sure convergence of the quotient $L_t/t$ for $t\downarrow0$ to the total variation of the sample paths of the process. This was generalized to determining the behavior of $L_t/t^{{\kern1pt}p}$ for arbitrary $p>0$ from the characteristic triplet of L in [2, 3, 13]. The exact scaling function f for law of the iterated logarithm type (LIL-type) results of the form $\limsup_{t\downarrow0}L_t/f(t)=c$ almost surely (a.s.) with a deterministic constant c was determined by Khinchine for Lévy processes with a Gaussian component (see, e.g., [15, Proposition 47.11]) and in, e.g., [16, 17] for more general types of Lévy processes. The multivariate counterpart to these LIL-type results was derived in [6], showing that the short-time behavior of the driving process in (1) is well understood overall.

For the solution X, the situation becomes less transparent. It was shown in [9, 18] that, under suitable conditions on the Lévy measure of L, the solution X is a Lévy-type Feller process, i.e. the symbol of X can be expressed through a triplet $(A(x),\nu(x),\gamma(x))$ that depends on the characteristics of the driving process, the initial condition, and the function $\sigma$ . The short- and long-time behavior of these particular Feller processes can be characterized in terms of power-law functions using a generalization of Blumenthal–Getoor indices (see [19]), where the symbol now plays the role of the characteristic exponent. Using similar methods, an explicit short-time LIL in one dimension was derived in [8], and the techniques have been explored further in [10]. The definition of a Lévy-type Feller process suggests that we can think of X as ‘locally Lévy’ and, since the short-time behavior of the process is determined by the sample paths in an arbitrarily small neighborhood of zero, the process X should directly reflect the short-time behavior of the driving Lévy process. We confirm this hypothesis in terms of power-law functions in Proposition 1 and Theorem 1 by showing that the almost sure finiteness of $\lim_{t\downarrow0}t^{-p}L_t$ implies the almost sure convergence of the quantity $t^{-p}(X_t-X_0)$ , and that similar results hold for $\limsup_{t\downarrow0} t^{-p}(X_t-X_0)$ and $\liminf_{t\downarrow0}t^{-p}(X_t-X_0)$ with probability 1 whenever $\lim_{t\downarrow0}t^{-p/2}L_t$ exists almost surely. The conditions on the driving process are readily checked from its characteristic triplet, e.g. from [2]. Using knowledge of the form of the scaling function for the driving Lévy process from [6], the limit theorems can be generalized to suitable functions $f\colon[0,\infty)\rightarrow\mathbb{R}$ to derive explicit LIL-type results for the solution of (1) that cover many frequently used models. As an application, we also briefly study convergence in distribution and in probability, showing that results on the short-time behavior of the driving process translate here as well. The results given partially overlap with characterizations obtained from other approaches such as the generalization of Blumenthal–Getoor indices for Lévy-type Feller processes discussed, e.g., in [19], while also covering new cases such as almost sure limits for $t\downarrow0$ . Compared to methods that rely on the symbol, the approach presented in this paper is less technical and more direct, as it only uses the behavior of the driving process as input. Whenever possible, we work with general semimartingales and include converse results to recover the limiting behavior of the driving process from the solution.

2. Preliminaries

A Lévy process $L=(L_t)_{t\geq0}$ is a stochastic process with stationary and independent increments, the paths of which are almost surely càdlàg, i.e. right-continuous with finite left limits, and start at zero with probability 1. In the following analysis, we consider both vector- and matrix-valued Lévy processes, identifying an $\mathbb{R}^{n\times d}$ -valued Lévy process with an $\mathbb{R}^{nd}$ -valued one by vectorization if needed. We follow the convention that a matrix m is vectorized by writing its entries columnwise into a vector $m^\mathrm{vec}$ . The symbols $\langle\cdot,\cdot\rangle$ and $\|\cdot\|$ denote the Euclidean scalar product and norm on $\mathbb{R}^d$ , respectively, and we write $x^\top$ for the transpose of a vector or matrix x.

By the Lévy–Khintchine formula (see, e.g., [15, Theorem 8.1]), the characteristic function of an $\mathbb{R}^d$ -valued Lévy process L is given by $\varphi_{L}(z)=\mathbb{E} \mathrm{e}^{\mathrm{i} z L_t} = \exp (t \psi_L(z))$ , $z\in \mathbb{R}^d$ , where $\psi_L$ denotes the characteristic exponent satisfying

\begin{align*} \psi_L(z)=-\frac{1}{2}\langle z,A_Lz\rangle+\mathrm{i}\langle \gamma_L,z\rangle+\int_{\mathbb{R}^d}\big(\exp(\mathrm{i}\langle z,s\rangle)-1-\mathrm{i}\langle z,s\rangle\textbf{1}_{\{\|s\|\leq1\}}\big)\nu_L(\textrm{d} s), \quad z\in \mathbb{R}^d.\end{align*}

Here, $A_L\in\mathbb{R}^{d\times d}$ is the Gaussian covariance matrix, $\nu_L$ is the Lévy measure, and $\gamma_L\in\mathbb{R}^d$ is the location parameter of L. The characteristic triplet of L is denoted by $(A_L,\nu_L,\gamma_L)$ . If $A_L=0$ , i.e. if the Lévy process has no Gaussian component, we refer to it as purely non-Gaussian. Whenever the Lévy measure satisfies the condition $\int_{\{\|x\|\leq 1\}} \|x\| \nu_L(\textrm{d} x)<\infty$ , we may also use the Lévy–Khintchine formula in the form

\begin{equation*} \psi_L(z)=-\frac{1}{2}\langle z,A_Lz\rangle+\mathrm{i}\langle \gamma_0,z\rangle+\int_{\mathbb{R}^d}\big(\exp(\mathrm{i}\langle z,s\rangle)-1\big)\nu_L(\textrm{d} s), \quad z\in \mathbb{R}^d ,\end{equation*}

and call $\gamma_0$ the drift of L.

For any càdlàg process X, we denote by $X_{s-}$ the left-hand limit of X at time ${s\in(0,\infty)}$ , and by $\Delta X_s=X_s-X_{s-}$ its jumps. The process $X_{s-}$ is càglàd, i.e. left-continuous with finite right limits. Any integrals are interpreted as integrals with respect to semimartingales as, e.g., in [12], and we generally consider a filtered probability space $\bigl(\Omega,\mathcal{F},(\mathcal{F}_t)_{t\geq0},\mathbb{P})$ satisfying the usual hypotheses (see, e.g., [12, p. 3]). The integral bounds are assumed to be included when the notation $\int_a^b$ is used, and the exclusion of the left or right bound is denoted by $\int_{a+}^b$ or $\int_a^{b-}$ . For semimartingales X, Y, and Z taking values in $\mathbb{R}^{n\times d}$ , $\mathbb{R}^{d\times m}$ , and $\mathbb{R}^{m\times d}$ , respectively, matrix-valued integrals are interpreted as

\begin{align*}\bigg(\int_{a+}^bX_{s-}\,\textrm{d} Y_s\bigg)_{i,j} & = \sum_{k=1}^d\int_{a+}^b(X_{i,k})_{s-}\,\textrm{d} (Y_{k,j})_s,\\[5pt] \bigg(\int_{a+}^b\textrm{d} Z_sX_{s-}\bigg)_{i,j} & = \sum_{k=1}^d\int_{a+}^b(X_{k,j})_{s-}\,\textrm{d} (Z_{i,k})_s ,\end{align*}

and the integration by parts formula takes the form

\begin{equation*} \int_{0+}^tX_{s-}\,\textrm{d} Y_s=X_tY_t-X_0Y_0-\int_{0+}^t\textrm{d} X_sY_{s-}-[X,Y]_{0+}^t.\end{equation*}

3. Main results and applications

The aim of this paper is a characterization of the almost sure short-time behavior of the solution to a Lévy-driven SDE by relating it to the behavior of the driving process. In Section 3.1, we first consider the setting of general semimartingales to show that the solution of (1) a.s. reflects the short-time behavior of the driving process. Specializing to Lévy processes in Section 3.2 then allows us to strengthen the results and, by referring to the explicit scaling functions obtained in [6], derive explicit LIL-type results for the solution process.

3.1. General SDEs

A key tool in the analysis is the following lemma, which gives the desired statement for a stochastic integral when the behavior of the integrand is known. We state the result in terms of power-law functions to match Proposition 1; however, the denominator $t^{{\kern1pt}p}$ may be replaced by an arbitrary continuous function $f\colon[0,\infty)\rightarrow\mathbb{R}$ that is increasing and satisfies $f(0)=0$ and $f(t)>0$ for all $t>0$ . The proofs of this lemma and all following results are given in Section 4.

Lemma 1. Let $X=(X_t)_{t\geq 0}$ be a real-valued semimartingale, $p>0$ , and $\varphi=(\varphi_t)_{t\geq0}$ an adapted càglàd process such that $\lim_{t\downarrow0}t^{-p}\varphi_t$ exists and is finite with probability 1. Then

(2) \begin{equation} \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\varphi_s\,\textrm{d} X_s= 0\quad \mathrm{a.s.} \end{equation}

Lemma 1 naturally extends to multivariate stochastic integrals, with $\psi$ and X being $\mathbb{R}^{n\times d}$ -valued and $\mathbb{R}^{d\times m}$ -valued semimartingales, respectively. We thus obtain a tool to derive the almost sure short-time behavior of the solution to (1) from the behavior of the driving process. Whenever we can ensure that $\sigma(X_{s-})$ is invertible, this implication is an equivalence which allows us to recover the behavior of the driving process from the solution. We hence get a counterpart to [19, Theorem 4.4] for almost sure limits at zero.

Proposition 1. Let L be an $\mathbb{R}^{d}$ -valued semimartingale with $L_0=0$ and ${\lim_{t\downarrow 0}t^{-p}L_t=v}$ a.s. for some $v\in\mathbb{R}^{d}$ , ${p>0}$ . Further, let $\sigma\colon\mathbb{R}^{d}\rightarrow\mathbb{R}^{n\times d}$ be twice continuously differentiable and at most of linear growth, and denote the solution of (1) by ${X=(X_t)_{t\geq0}}$ .

1. (i) The process X satisfies $\lim_{t\downarrow 0}({X_t-x})/{t^{{\kern1pt}p}}=\sigma(x)v$ a.s., and whenever $\sigma(X_{t-})$ with $X_{0-}=x$ has a.s. full rank for all t in a neighborhood of zero, we have the equivalence

   \begin{equation*} \lim_{t\downarrow0}\frac{L_t}{t^{{\kern1pt}p}}=v\quad \mathrm{a.s.} \quad \Longleftrightarrow \quad \lim_{t\downarrow0}\frac{X_t-x}{t^{{\kern1pt}p}}=\sigma(x)v\quad \mathrm{a.s.} \end{equation*}

2. (ii) If, additionally, $[L_k,L_k]_t=o(t^{2p})$ a.s. for $k=1,\dots,d$ , then

   \begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}\int_{0+}^tY_{s-}\,\textrm{d} L_s= Y_0v\quad \mathrm{a.s.} \end{equation*}
   for any $\mathbb{R}^{n\times d}$ -valued semimartingale Y, and whenever $\lim_{t\downarrow0}t^{-p}Y_t=w$ a.s. with ${w\in\mathbb{R}^{n\times d}}$ satisfying ${wv=0}$ , we have the stronger statement
   \begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{2p}}\int_{0+}^tY_{s-}\,\textrm{d} L_s= 0\quad \mathrm{a.s.} \end{equation*}

The above results naturally extend to matrix-valued L. Note that Proposition 1(ii) holds in particular when $Y_t=\sigma(L_t)$ , but the dependence on the driving process is not needed to conclude the convergence. As an example, we apply Proposition 1 to matrix-valued stochastic exponentials.

Example 1. Recall that for an $\mathbb{R}^{d\times d}$ -valued semimartingale ${L=(L_t)_{t\geq0}}$ , the (strong) solution to the stochastic differential equation $\textrm{d} X_t=X_{t-}\textrm{d} L_t$ or $\textrm{d} Y_t=\textrm{d} L_tY_{t-}$ with the initial condition given by the identity matrix Id is referred to as left or right stochastic exponential, respectively. Since the relevant properties of the process X carry over to Y by transposition, we restrict the following discussion to $X=\mathcal{E}(L)$ . Assuming that ${\det(\mathrm{Id}+\Delta L_s)\neq0}$ for all $s\geq0$ , the inverse $\mathcal{E}(L)^{-1}$ is well defined [7] and Proposition 1 yields the equivalence

(3) \begin{equation} \lim_{t\downarrow0}\frac{L_t}{t^{{\kern1pt}p}}=v\quad \mathrm{a.s.} \quad \Longleftrightarrow \quad \lim_{t\downarrow0}\frac{\mathcal{E}(L)-\mathrm{Id}}{t^{{\kern1pt}p}}=v\quad \mathrm{a.s.} \end{equation}

whenever one of the limits exists for some $v\in\mathbb{R}^{d\times d}$ and $p>0$ . If L is a Lévy process, the almost sure limit v appearing for $p=1$ is the drift of L. A result in [14, 20] directly links the existence of this limit to the total variation of the sample paths of L. Denoting the set of stochastic processes having sample paths of bounded variation by BV, (3) allows us to extend this connection to

\begin{equation*} \lim_{t\downarrow0}\frac{\mathcal{E}(L)-\mathrm{Id}}{t}\ \text{exists}\ \mathrm{a.s.} \quad \Longleftrightarrow \quad \lim_{t\downarrow0}\frac{L_t}{t}\ \text{exists}\ \mathrm{a.s.} \quad \Longleftrightarrow \quad L\in BV \quad \Longleftrightarrow \quad \mathcal{E}(L)\in BV, \end{equation*}

since $\mathcal{E}(L)$ has paths of bounded variation if and only if this holds for the paths of L.

Whenever L is a semimartingale satisfying both $\lim_{t\downarrow0}t^{-p}L_t=0$ and ${[L_k,L_k]_t=o(t^{2p})}$ a.s. for $k=1,\dots,d$ , an inspection of the proof of Proposition 1 shows that

$[\sigma_{i,k}(X),L_k]_t=O([L_1,L_1]_t+\dots+[L_d,L_d]_t) \; \text{a.s.}$

for $t\downarrow0$ , which implies that $[\sigma(X),L]_t=o(t^{2p})$ a.s. in the limit $t\downarrow0$ . We further use the stronger assumption on the quadratic variation to consider the $\limsup$ and $\liminf$ behavior of the quotient $t^{-p}(X_t-x)$ , including the divergent case.

Theorem 1. Let L be an $\mathbb{R}^{d}$ -valued semimartingale such that $\lim_{t\downarrow0}t^{-p/2}L_t=0$ a.s. for some $p>0$ , and $[L_k,L_k]_t=o(t^{{\kern1pt}p})$ a.s. for $k=1,\dots,d$ . Further, let $\sigma\colon\mathbb{R}^{n}\rightarrow\mathbb{R}^{n\times d}$ be twice continuously differentiable and at most of linear growth, and denote by X the solution of the SDE (1). Then, almost surely,

(4) \begin{equation} \lim_{t\downarrow0} \bigg(\frac{X_t-x}{t^{{\kern1pt}p}}-\frac{\sigma(X_t)L_t}{t^{{\kern1pt}p}}\bigg) = \lim_{t\downarrow0} \bigg(\frac{X_t-x}{t^{{\kern1pt}p}}-\frac{\sigma(x)L_t}{t^{{\kern1pt}p}}\bigg) = 0. \end{equation}

In particular, if $\sigma(x)$ has rank d, we have

(5) \begin{equation} \lim_{t\downarrow0}\frac{\|L_t\|}{t^{{\kern1pt}p}}=\infty\quad \mathrm{a.s.} \quad \Longrightarrow \quad \lim_{t\downarrow0}\frac{\|X_t-x\|}{t^{{\kern1pt}p}}=\infty\quad \mathrm{a.s.} \end{equation}

3.2. Lévy-driven SDEs

For the remainder of the section, we will assume that L is a Lévy process. In this case, the assumptions of Proposition 1 and Theorem 1 can be checked directly from the characteristic triplet of L. We give a brief overview of the behavior of $t^{-p}L_t$ for real-valued Lévy processes. Noting that the almost sure short-time behavior of L is dominated by Khintchine’s LIL (see, e.g., [15, Proposition 47.11]) whenever L contains a Gaussian component, and that the drift of L only occurs explicitly if $p=1$ and the process is of finite variation [20], we can further restrict the discussion to L being a pure-jump process and set its drift to zero whenever $\int_{\{\|x\|\leq 1\}}\|x\|\nu_L(\textrm{d} x)<\infty$ . A first indicator of the behavior of $t^{-p}L_t$ as $t\downarrow0$ is the (upper) Blumenthal–Getoor index

\begin{equation*} \beta\;:\!=\;\inf\bigg\{\kappa>0\colon\int_{\{|x|\leq1\}}|x|^\kappa\nu_L(\textrm{d} x)<\infty\bigg\}\in[0,2]\end{equation*}

introduced in [3], which yields

\begin{align*} \limsup_{t\downarrow0}\frac{|L_t|}{t^{{\kern1pt}p}}= \begin{cases} 0\quad &\text{if }p<1/\beta,\\[5pt] \infty\quad&\text{if }p>1/\beta \end{cases}\end{align*}

with probability 1 (see, e.g., [13]). A more direct criterion is given in [2, Section 2], showing that the condition $\lim_{t\downarrow0}t^{-p}L_t=0$ is a.s. satisfied for $p>\frac12$ whenever

(6) \begin{equation} \int_{[-1,1]}|x|^{1/p}\nu_L(\textrm{d} x)<\infty ,\end{equation}

and for $p=\frac12$ whenever

(7) \begin{equation} \lambda^*\;:\!=\;\inf\Bigg\{\lambda>0\colon \int_0^1x^{-1}\exp\Bigg(\frac{\lambda^2}{2\int_{\{|y|\leq x\}}y^2\nu_L(\textrm{d} y)}\Bigg)\textrm{d} x<\infty\Bigg\}=0.\end{equation}

If (6) or (7) fails, we have $\limsup_{t\downarrow0}t^{-p}|L_t|=\infty$ a.s. or ${\limsup_{t\downarrow0}t^{-1/2}|L_t|=\lambda^*\in(0,\infty]}$ a.s., respectively, instead.

Observe that the quadratic variation process of L is again a Lévy process, i.e. the integral test (6) in particular applies to [L, L]. For $d=1$ we have

(8) \begin{equation} [L,L]_t=a^2t+\sum_{0<s\leq t}(\Delta L_s)^2,\end{equation}

where a is the variance of the Gaussian part of L (if present). The additional assumption on the quadratic variation in Proposition 1(ii) and in Theorem 1 is always satisfied if L is a Lévy process.

Lemma 2. Let L be a real-valued Lévy process satisfying $\lim_{t\downarrow0}t^{-p}L_t=v$ a.s. for some $v\in\mathbb{R}$ and $p>0$ . Then, a.s., $[L,L]_t=o(t^{2p})$ as $t\downarrow0$ .

Note that Lemma 2 readily extends to the multivariate case by the Kunita–Watanabe inequality (see, e.g., [12, Theorem II.25]). So far, we have only characterized the almost sure short-time behavior of the solution to (1) in terms of power-law functions. To derive precise LIL-type results, we now consider more general scaling functions ${f\colon[0,\infty)\rightarrow\mathbb{R}}$ . Whenever the driving Lévy process has a Gaussian component, its almost sure short-time behavior is dominated by Khintchine’s LIL. In this setting, Lemma 2 directly generalizes to continuous increasing functions f with $f(0)=0$ and $f(t)>0$ for all $t>0$ . This is because any function f for which $\lim_{t\downarrow0}L_t/f(t)$ exists in $\mathbb{R}$ satisfies $\sqrt{2t\ln(\ln(1/t))}/f(t)\rightarrow0$ , implying

(9) \begin{equation}\lim_{t\downarrow0}\frac{[L,L]_t}{(f(t))^2}=\lim_{t\downarrow0}\bigg(\frac{[L,L]_t}{t}\frac{t}{2t\ln(\ln (1/t))}\frac{2t\ln(\ln (1/t))}{(f(t))^2}\bigg)=0\quad \mathrm{a.s.}\end{equation}

by [20, Theorem 1]. Hence, $[L,L]_t=o(f(t)^2)$ and we can replace the function $t^{p/2}$ in Theorem 1 by f, obtaining a precise short-time behavior for the solution whenever (1) includes a diffusion part. In the case that L does not include a Gaussian component, [L, L] is a finite variation process without drift satisfying ${\lim_{t\downarrow0}t^{-1}[L,L]_t=0}$ a.s. by [20, Theorem 1], but an argument similar to (9) is only applicable if f decays sufficiently fast as $t\downarrow0$ . For the general case, we combine Theorem 1 with the precise information on possible scaling functions derived in [6]. Note that the conditions of Corollary 1 immediately follow from Khintchine’s LIL whenever $h\equiv1$ , as the process does not include a Gaussian component by assumption.

Corollary 1. Let L be a purely non-Gaussian $\mathbb{R}^{d}$ -valued Lévy process and ${f\colon[0,\infty)\rightarrow\mathbb{R}}$ be of the form $f(t)=\sqrt{t\ln(\ln(1/t))}h(1/t)^{-1}$ , where $h\colon[0,\infty)\rightarrow[0,\infty)$ is a continuous and non-decreasing slowly varying function such that the set of cluster points of $L_t/f(t)$ as $t\downarrow0$ is bounded with probability 1. Further, let $\sigma\colon\mathbb{R}^{d}\rightarrow\mathbb{R}^{n\times d}$ be twice continuously differentiable and at most of linear growth, and denote by $X=(X_t)_{t\geq0}$ the solution of (1). Then, a.s.,

(10) \begin{equation} \lim_{t\downarrow0} \bigg(\frac{X_t-x}{f(t)}-\frac{\sigma(X_t)L_t}{f(t)}\bigg)=\lim_{t\downarrow0} \bigg(\frac{X_t-x}{f(t)}-\frac{\sigma(x)L_t}{f(t)}\bigg)=0. \end{equation}

In particular, if $\sigma(x)$ has rank d, we have

\begin{equation*} \lim_{t\downarrow0}\frac{\|L_t\|}{f(t)}=\infty\quad \mathrm{a.s.}\quad \Longrightarrow\quad \lim_{t\downarrow0}\frac{\|X_t-x\|}{f(t)}=\infty\quad \mathrm{a.s.} \end{equation*}

The above results show that the almost sure short-time LIL-type behavior of the driving Lévy process directly translates to the solution of the SDE (1). We also note the following statement for the corresponding cluster set.

Corollary 2. Under the assumptions of Corollary 1, let $\limsup_{t\downarrow0}\|L_t\|/f(t)$ be bounded with probability 1. Then there exists an almost sure cluster set ${C_X=C(\{X_t/f(t)\colon t\downarrow0\})}$ for the solution X of (1) which is obtained from the cluster set of ${C_L=C(\{L_t/f(t)\colon t\downarrow0\})}$ of the driving Lévy process L via $C_X=\sigma(x)C_L$ .

Corollary 2 implies in particular that $C_X$ shares the properties of $C_L$ derived in [6, Theorem 2.4], and that there is a one-to-one correspondence between the cluster sets whenever $\sigma(x)$ has rank d, e.g. $C_X=C_L$ for the stochastic exponential in Example 1. Another important special case is stable Lévy processes.

Example 2. Recall that a Lévy process L is called (strictly) stable with index ${\alpha\in(0,2]}$ if and only if the random variables $L_t$ and $t^{1/\alpha} L_1$ have the same law for each $t>0$ . For the following discussion, let $\alpha\neq2$ , i.e. L is a non-Gaussian Lévy process, and pick $d=1$ . In this case, the short-time behavior of $L_t/f(t)$ with ${f\colon(0,\infty)\rightarrow(0,\infty)}$ is determined by the behavior of the integral $\int_0^1f(t)^{-\alpha}\,\textrm{d} t$ in the sense that $\lim_{t\downarrow0} L_t/f(t)=0$ a.s. if the integral converges, and $\limsup_{t\downarrow0}|L_t|/f(t)=\infty$ a.s. if it does not (see [1, Chapter VIII, Theorem 5]). Hence, Lemma 2 yields $[L,L]_t=o(t^{2p})$ a.s., $0<p<1/\alpha$ , and Corollary 1 implies that the almost sure short-time behavior of the solution to (1) can be determined by the same integral criterion as the behavior of the driving Lévy process whenever $f\colon(0,\infty)\rightarrow(0,\infty)$ is of the specified form. For power functions, we get a strong resemblance to the Blumenthal–Getoor index, as

\begin{align*} \lim_{t\downarrow0}\frac{|X_t-x|}{t^{{\kern1pt}p}}=0\quad \mathrm{a.s.},\qquad p<1/\alpha , \end{align*}

by Proposition 1, while Theorem 1 implies that the alnmost sure lim sup behavior for $p>1/\alpha$ translates as well. See also [10] for generalizations of the above integral criterion which allow us to apply similar reasoning to a larger class of processes.

As an application of Theorem 1, we consider two similar statements concerning convergence in distribution and convergence in probability, which are denoted by $\overset{\mathrm{D}}{\rightarrow}$ and $\overset{\mathrm{P}}{\rightarrow}$ , respectively. Since the short-time behavior of Brownian motion is well known, we can assume that L does not have a Gaussian component. We further set the drift of L, whenever it exists, to zero. Sufficient conditions for the attraction of a Lévy process to a stable law are given, e.g., in [11, Theorem 2.3], and the conditions for the driving process in Corollary 3 are thus readily checked from the characteristic triplet. The special case of attraction to normality is, e.g., considered in [5, Theorem 2.5], with the condition being satisfied in particular for a Lévy process with a symmetric Lévy measure such as $\nu_L(\textrm{d} x)=\exp(-|x|)\textbf{1}_{[-1,1]}(x)\,\textrm{d} x$ . Attraction of Lévy processes to a stable law with index $\alpha<2$ is studied in [4].

Corollary 3. Let L be a real-valued non-Gaussian Lévy process such that the drift of L is equal to zero whenever it exists. Further, assume that there is a continuous increasing function $f\colon[0,\infty)\rightarrow[0,\infty)$ such that $f(t)^{-1}L_t\overset{\mathrm{D}}{\rightarrow}Y$ as $t\downarrow0$ , where the random variable Y follows a non-degenerate stable law with index $\alpha\in(0,2]$ . Also let $\sigma\colon\mathbb{R}\rightarrow\mathbb{R}$ be twice continuously differentiable and at most of linear growth, and choose $x\in\mathbb{R}^{n}$ such that $\sigma(x)\neq0$ . If X is the solution of (1) with initial condition x, then $({X_t-x})/{f(t)}\overset{\mathrm{D}}{\rightarrow}\sigma(x)Y$ . Whenever f is regularly varying with index $r\in\big(0,\frac12\big]$ at zero, this result also holds if the random variable Y is a.s. constant.

We give a further result for convergence in probability. The assumptions are again readily checked from the characteristic triplet of the driving Lévy process using [5, Theorem 2.2] and are, e.g., satisfied for finite variation Lévy processes. As the limiting random variable obtained is a.s. constant, the proof is immediate from Corollary 3.

Corollary 4. Let $d=1$ , L be as in Corollary 3, and assume that there is a continuous increasing function $f\colon[0,\infty)\rightarrow[0,\infty)$ that is regularly varying with index $r\in\big(0,\frac12\big]$ at zero and satisfies $f(t)^{-1}L_t\overset{\mathrm{P}}{\rightarrow}v$ for some finite value $v\in\mathbb{R}$ as $t\downarrow0$ . Also, let $\sigma\colon\mathbb{R}\rightarrow\mathbb{R}$ be twice continuously differentiable and at most of linear growth, and denote by X the solution of (1). Then $({X_t-x})/{f(t)}\overset{\mathrm{P}}{\rightarrow}\sigma(x)v$ .

4. Proof of Section 3

Proof of Lemma 1. Define the process $\psi$ ( $\omega$ -wise) by

\begin{equation*} \psi_t\;:\!=\; \begin{cases} t^{-p}\varphi_t, & t>0, \\[5pt] \lim_{s\downarrow0} s^{-p}\varphi_s,\quad & t=0, \end{cases} \end{equation*}

possibly setting $\psi_0(\omega)=0$ on the null set where the limit does not exist. By definition, $\psi$ is càglàd, and, as $\lim_{t\downarrow}t^{-p}\varphi_t$ exists a.s. in $\mathbb{R}$ , $\mathcal{F}_0$ contains all null sets by assumption, and the filtration is right-continuous, $\psi_0$ is $\mathcal{F}_0$ -measurable. Therefore, $\psi$ is also adapted. This implies that the semimartingale $Y_t\;:\!=\;\int_{0+}^t\psi_s\,\textrm{d} X_s$ is well defined, allowing us to rewrite the process considered in (2) as

$\int_{0+}^t\varphi_s\,\textrm{d} X_s=\int_{0+}^ts^{{\kern1pt}p}\psi_s\,\textrm{d} X_s=\int_{0+}^ts^{{\kern1pt}p}\,\textrm{d} Y_s$

, using the associativity of the stochastic integral. Applying integration by parts, we get

\begin{equation*} \frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\varphi_s\,\textrm{d} X_s = \frac{1}{t^{{\kern1pt}p}}\bigg(t^{{\kern1pt}p}Y_t-\int_{0+}^tY_s\,\textrm{d} (s^{{\kern1pt}p})\bigg) = Y_t-\frac{1}{t^{{\kern1pt}p}}\int_{0+}^tY_s\,\textrm{d} (s^{{\kern1pt}p}). \end{equation*}

As Y has almost sure càdlàg paths and satisfies $Y_0=0$ by definition, it follows that ${\lim_{t\downarrow0}Y_t=0}$ with probability 1. The term remaining on the right-hand side is a path-by-path Lebesgue–Stieltjes integral. Note that, as $p>0$ , the integrator is increasing, which implies the monotonicity of the corresponding integral. Hence,

\begin{equation*} \inf_{0<s\leq t}Y_s\leq\frac{1}{t^{{\kern1pt}p}}\int_{0+}^tY_s\,\textrm{d} (s^{{\kern1pt}p})\leq\sup_{0<s\leq t}Y_s. \end{equation*}

Recalling that $\lim_{t\downarrow0}Y_t=0$ a.s., the claim follows.

Proof of Proposition 1. (i) Let $\lim_{t\downarrow0}t^{-p}L_t=v$ with probability 1. Rearranging the integral equation for X and applying integration by parts to the components yields

(11) \begin{equation} \bigg(\frac{X_t-x}{t^{{\kern1pt}p}}\bigg)_i = \frac{1}{t^{{\kern1pt}p}}\sum_{k=1}^d\bigg(\sigma_{i,k}(X_t)(L_k)_t - \sigma_{i,k}(x)(L_k)_0 - \int_{0+}^t(L_k)_{s-}\,\textrm{d}\sigma_{i,k}(X_s) - \big[\sigma_{i,k}(X),L_k\big]_t\bigg). \end{equation}

As $\lim_{t\downarrow0}t^{-p}L_t=v$ a.s. by assumption, and $\lim_{t\downarrow0}X_t= x=X_0$ a.s. since X solves (1), the first term on the right-hand side of (11) converges a.s. to the desired limit. It thus remains to show that the other terms a.s. vanish as $t\downarrow0$ . For the second and third terms of (11), this follows from the assumption and Lemma 1, respectively. Finally, applying Itō’s formula for X in the quadratic covariation appearing in the last term yields

\begin{align*} \big[\sigma_{i,k}(X),L_k\big]_t & = \Bigg[\sigma_{i,k}(x) + \sum_{j=1}^n\int_{0+}^{\cdot}\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\,\textrm{d} (X_j)_s \\[5pt] & \qquad + \frac{1}{2}\sum_{j_1,j_2=1}^n\int_{0+}^{\cdot} \frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}}(X_{s-})\,\textrm{d} \big[X_{j_1},X_{j_2}\big]^c_s \\[5pt] & \qquad + \sum_{0<s\leq \cdot} \Bigg(\sigma_{i,k}(X_s) - \sigma_{i,k}(X_{s-}) - \sum_{j=1}^n\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\Delta(X_j)_s\Bigg),L_k\Bigg]_t. \end{align*}

By linearity, we can treat the terms on the right-hand side here separately. Using the associativity of the stochastic integral and noting that the continuous finite variation terms do not contribute to the quadratic covariation, we are left with

(12) \begin{align} \big[\sigma_{i,k}(X),L\big]_t & = \sum_{j=1}^n\int_{0+}^t\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\,\textrm{d} [X_j,L_k]_s \nonumber \\[5pt] & \quad + \Bigg[\sum_{0<s\leq \cdot} \Bigg(\sigma_{i,k}(X_s) - \sigma_{i,k}(X_{s-}) - \sum_{j=1}^n\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\Delta(X_j)_s\Bigg),L_k\Bigg]_t. \end{align}

As the integrators in the first term on the right-hand side of (12) are of finite variation, the corresponding integrals are path-by-path Lebesgue–Stieltjes integrals. Writing out

$[X_j,L_k]_t=\sum_{l=1}^d\int_{0+}^t\sigma_{j,l}(X_{s-})\,\textrm{d} [L_l,L_k]_s$

, and denoting integration with respect to the total variation measure of a process Y as $\textrm{d} TV_Y$ , the individual integrals can be estimated by

\begin{align*} \bigg|\int_{0+}^t\sigma_{j,l}(X_{s-})\,\textrm{d} [L_{l},L_{k}]_s\bigg| & \leq \int_{0+}^t\big|\sigma_{j,l}(X_{s-})|\,\textrm{d} TV_{[L_l,L_k]}(s) \\[5pt] & \leq \bigg(\int_{0+}^t\big|\sigma_{j,l}(X_{s-})\big|^2\,\textrm{d} [L_l,L_l]_s\bigg)^{\frac{1}{2}} \bigg(\int_{0+}^t\big|\sigma_{j,l}(X_{s-})\big|^2\,\textrm{d} [L_k,L_k]_s\bigg)^{\frac{1}{2}} \\[5pt] & \leq \sup_{0<s\leq t}\big|\sigma_{j,l}(X_{s-})\big|^2\sqrt{[L_l,L_l]_t}\sqrt{[L_k,L_k]_t}, \end{align*}

using the Kunita–Watanabe inequality and noting that the resulting integrals have increasing integrators. The above estimates show that the total variation of $\int_{0+}^t\sigma_{j,l}(X_{s-})\,\textrm{d}[L_l,L_k]_s$ also satisfies this estimate. For the quadratic variation terms, note that since ${(L_0)_{k,l}=0}$ a.s., it follows from the assumption and the one-dimensional version of Lemma 1 that

\begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}\bigg((L_k)_t^2-2\int_{0+}^t(L_k)_{s-}\,\textrm{d} (L_k)_s\bigg) = \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}\sqrt{[L_k,L_k]_t}\sqrt{[L_k,L_k]_t} = 0 \quad \text{a.s.} \end{equation*}

Therefore,

\begin{align*} 0 \leq \lim_{t\downarrow0}\sup\bigg|\frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\sigma_{j,l}(X_{s-})\,\textrm{d} [L_l,L_k]_s\bigg| = 0 \quad \mathrm{a.s.}, \end{align*}

and a similar estimate holds true for the total variation of $\int_{0+}^t\sigma_{j,l}(X_{s-})\,\textrm{d} [L_l,L_k]_s$ . Denoting the total variation process of a process Y at t by $TV(Y)_t$ , we obtain the bound

\begin{equation*} \frac{1}{t^{{\kern1pt}p}} \Bigg|\sum_{j=1}^n\int_{0+}^t\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\,\textrm{d} [X_j,L_k]_s\Bigg| \leq \sum_{j=1}^n\sup_{0<s\leq t}\bigg|\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\bigg|\frac{1}{t^{{\kern1pt}p}}TV\big([X_j,L_k]\big)_t \end{equation*}

for the first term on the right-hand side of (12), showing that it a.s. vanishes in the limit $t\downarrow0$ . Lastly, denote by

\begin{equation*} \Bigg[\sum_{0<s\leq t} \Bigg(\sigma_{i,k}(X_s)-\sigma_{i,k}(X_{s-})-\sum_{j=1}^n\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\Delta(X_j)_s\Bigg),L_k\Bigg]_t \;=\!:\; [J,L_k]_t \end{equation*}

the jump term remaining in (12). Using the Kunita–Watanabe inequality and recalling that $[L_k,L_k]=o(t^{{\kern1pt}p})$ by the previous estimate, it remains to consider the quadratic variation of J. Evaluating

\begin{align*} [J,J]_t = \sum_{0<s\leq t}(\Delta J_s)^2 = \sum_{0<s\leq t} \Bigg(\sigma_{i,k}(X_s)-\sigma_{i,k}(X_{s-}) - \sum_{j=1}^n\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\Delta(X_j)_s\Bigg)^2, \end{align*}

and noting that

\begin{equation*} \sup_{0<s\leq t}\bigg|\frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}}(X_{s-})\bigg| < \infty \end{equation*}

for all $j_1,j_2=1,\dots,n$ and a fixed $t\geq0$ due to the càdlàg paths of X, it follows that

\begin{align*} [J,J]_t \leq C \sum_{0<s\leq t}\|\Delta X_s\|^4\leq C\Bigg( \sum_{0<s\leq t}\|\Delta X_s\|^2\Bigg)^2 \end{align*}

by Taylor’s formula. Noting further that

\begin{equation*} \sum_{0<s\leq t}\|\Delta X_s\|^2 = C' \sum_{0<s\leq t}\|\sigma(X_{s-})\Delta L_s\|^2 \leq C''\sum_{0<s\leq t}\|\Delta L_s\|^2\leq C''\sum_{k=1}^d[L_k,L_k]_t \end{equation*}

for some finite (random) constants C ′,C′′, we can estimate $[J,J]_t$ in terms of the quadratic variation of L. In particular, both terms in (12) are a.s. of order $o(t^{{\kern1pt}p})$ and vanish when the limit $t\downarrow0$ is considered in (11).

Next, let $\lim_{t\downarrow0}t^{-p}(X_t-x)=\sigma(x)v$ with probability 1. As $\sigma(X_{s-})$ has a.s. full rank for all s in a neighborhood of zero, we can recover $L_t$ for small values of t through $L_t=\int_{0+}^t\bigl(\sigma(X_{s-})\bigr)^{-1}\,\textrm{d} X_s$ . Since $\|\sigma(X_t)-\sigma(x)\|<1$ a.s. for sufficiently small $t>0$ , it follows that

\begin{align*} \sigma(x)\sigma(X_t)^{-1} & = \bigl(\mathrm{Id}-(\mathrm{Id}-\sigma(X_t)\sigma(x)^{-1})\bigr)^{-1} \\[5pt] & =\sum_{k=0}^{\infty}\bigl(\mathrm{Id}-\sigma(X_t)\sigma(x)^{-1}\bigr)^k = \mathrm{Id}+\bigl(\mathrm{Id}-\sigma(X_t)\sigma(x)^{-1}\bigr)+R_t, \end{align*}

where the Neumann series converges a.s. in norm. By Taylor’s formula we have

\begin{equation*} \frac{1}{t^{{\kern1pt}p}}(\sigma(X_t)-\sigma(x))_{i,j} = \frac{1}{t^{{\kern1pt}p}}\sum_{k=1}^{n}\frac{\partial \sigma_{i,j}}{\partial x_k}(x)(X_t-x)_{i,j} + \frac{1}{t^{{\kern1pt}p}}r_{i,j}(t) , \end{equation*}

with a remainder that satisfies $r_{i,j}(t)=O((X_t-x)^2)=o(t^{{\kern1pt}p})$ . Thus,

\begin{align*} \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}(\mathrm{Id}-\sigma(X_t)\sigma(x)^{-1}\bigr) = \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}(\sigma(x)-\sigma(X_t)\bigr)\sigma(x)^{-1} \end{align*}

exists a.s., and it follows that also $R_t=o(t^{{\kern1pt}p})$ as $t\downarrow0$ with probability 1. Rewriting

\begin{align*} \sigma(x)\frac{1}{t^{{\kern1pt}p}}L_t & = \frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\bigl(\sigma(x)(\sigma(X_{s-}))^{-1}-\mathrm{Id}\bigr)\,\textrm{d} X_s + \frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\mathrm{Id}\, \textrm{d} X_s \\[5pt] & = \frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\bigl(\sigma(x)(\sigma(X_{s-}))^{-1}-\mathrm{Id}\bigr)\,\textrm{d} X_s + t^{-p}\bigl(X_t-x\bigr), \end{align*}

we conclude from Lemma 1 and the almost sure short-time behavior of X that the limit $t\downarrow0$ exists a.s. and is equal to $\sigma(x)v$ . In particular, the continuity of $\sigma$ and the assumption on the rank of $\sigma(X_{s-})$ ensure that the integrand $\sigma(x)(\sigma(X_{s-}))^{-1}-\mathrm{Id}$ converges a.s. as $t\downarrow0$ . Since $\sigma(x)$ is invertible, we recover the short-time behavior of L from the above convergence result for $\sigma(x)L$ , completing the proof of (i).

(ii) As $\lim_{t\downarrow0}t^{-p}Y_tL_t=Y_0v$ a.s. by assumption, consider $Y_t-Y_0$ and let $Y_0=0$ a.s. without loss of generality. Applying integration by parts to $t^{-p}\int_{0+}^tY_{s-}\,\textrm{d} L_s$ , we can estimate the covariation using the Kunita–Watanabe inequality. This yields

\begin{equation*} \bigg|\bigg(\frac{1}{t^{{\kern1pt}p}}[Y,L]_t\bigg)_i\bigg| \leq \sum_{k=1}^d\bigg|\frac{1}{t^{{\kern1pt}p}}[Y_k,L_k]_t\bigg| \leq \sum_{k=1}^d\frac{1}{t^{{\kern1pt}p}}\sqrt{[Y_k,Y_k]_t}\sqrt{[L_k,L_k]_t}. \end{equation*}

By assumption, we have $[L_k,L_k]_t=o(t^{2p})$ . This implies that $t^{-p}[Y,L]_t\rightarrow0$ a.s. for $t\downarrow0$ , yielding the first part of the proposition. Assume next that, additionally, ${\lim_{t\downarrow0}t^{-p}Y_t=w}$ for some $w\in\mathbb{R}^{n\times d}$ with $wv=0$ . Similar to the proof of Lemma 1, define an adapted stochastic process $\psi$ ( $\omega$ -wise) by

\begin{equation*} \psi_t \;:\!=\; \begin{cases} t^{-p}Y_t, & t>0, \\[5pt] \lim_{s\downarrow0} s^{-p}Y_s, \quad & t=0, \end{cases} \end{equation*}

possibly setting $\psi_0(\omega)=0$ on the null set where the limit does not exist. Rewriting the integral using $Z_t=\int_{0+}^t\psi_{s-}\,\textrm{d} L_s$ and applying integration by parts yields

(13) \begin{equation} \frac{1}{t^{2p}}\int_{0+}^tY_{s-}\,\textrm{d} L_s = \frac{1}{t^{2p}}\bigg(t^{{\kern1pt}p}Z_t-\int_{0+}^tZ_s\,\textrm{d} (s^{{\kern1pt}p})\bigg) = \frac{1}{t^{{\kern1pt}p}}Z_t-\frac{1}{t^{2p}}\int_{0+}^tZ_s\,\textrm{d} (s^{{\kern1pt}p}). \end{equation}

By the first part of the proposition we have

\begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}Z_t = \lim_{t\downarrow0}\frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\psi_{s-}\,\textrm{d} L_s = \psi_0v = wv=0 \quad \text{a.s.}, \end{equation*}

while the pathwise Lebesgue–Stieltjes integral can be estimated by

\begin{equation*} \frac{1}{t^{{\kern1pt}p}}\inf_{0<s\leq t}(Z_s)_i \leq \frac{1}{t^{2p}}\int_{0+}^t(Z_s)_i\,\textrm{d} (s^{{\kern1pt}p}) \leq \frac{1}{t^{{\kern1pt}p}}\sup_{0<s\leq t}(Z_s)_i,\qquad i=1,\dots,d. \end{equation*}

As $wv=0$ , both bounds converge to zero with probability 1, and hence

\begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{2p}}\int_{0+}^tZ_s\,\textrm{d} (s^{{\kern1pt}p})=0\quad \text{a.s.} \end{equation*}

Thus, the limit for $t\downarrow0$ of (13) exists a.s. and is equal to zero.

Proof of Theorem 1. Similar to the proof of Proposition 1, we use integration by parts and rewrite

\begin{equation*} \frac{X_t-x}{t^{{\kern1pt}p}} - \frac{\sigma(X_t)L_t}{t^{{\kern1pt}p}} = -\frac{1}{t^{{\kern1pt}p}}\int_{0+}^t\textrm{d}\sigma(X_s)L_{s-}-\frac{1}{t^{{\kern1pt}p}}[\sigma(X),L]_t. \end{equation*}

The claim follows by showing the desired limiting behavior for the right-hand side. For the covariation, this is immediate from the assumption and the previous calculations. Hence, it remains to study the behavior of the integral. Using Itō’s formula yields

\begin{align*} & \bigg(\int_{0+}^t\textrm{d} \sigma(X_s)L_{s-}\bigg)_i = \sum_{k=1}^d\int_{0+}^t(L_k)_{s-}\textrm{d}\Bigg(\sigma_{i,k}(x) + \sum_{j=1}^n\int_{0+}^s\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{r-})\,\textrm{d} (X_j)_r \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ + \frac{1}{2}\sum_{j_1,j_2=1}^n\int_{0+}^s\frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}} (X_{r-})\,\textrm{d} \big[X_{j_1},X_{j_2}\big]^c_r+(J_{i,k})_s\Bigg), \end{align*}

where the jump term is again denoted by J and the component of $\sigma$ included in it is carried as a subscript. Observe that, by associativity, it follows that

\begin{align*} \int_{0+}^t(L_k)_{s-} & \,\textrm{d}\bigg(\int_{0+}^s\frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}} (X_{r-})\,\textrm{d} \big[X_{j_1},X_{j_2}\big]_r^c\bigg) \\[5pt] & = \sum_{l_1=1}^n\sum_{l_2=1}^n\int_{0+}^t(L_k)_{s-} \frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}}(X_{s-}) \sigma_{j_1,l_1}(X_{s-})\sigma_{j_2,l_2}(X_{s-})\,\textrm{d}[L_{l_1},L_{l_2}]_s^c \\[5pt] & \;=\!:\; \sum_{l_1=1}^n\sum_{l_2=1}^n\int_{0+}^t(L_k)_{s-}M_{s-}\,\textrm{d}[L_{l_1},L_{l_2}]_s^c, \end{align*}

which is a sum of pathwise Lebesgue–Stieltjes integrals. Thus,

\begin{align*} &\frac{1}{t^{{\kern1pt}p}}\bigg|\int_{0+}^t(L_k)_{s-}\,\textrm{d}\bigg(\int_{0+}^s \frac{\partial^2\sigma_{i,k}}{\partial x_{j_1}\partial x_{j_2}}(X_{r-})\,\textrm{d} \big[X_{j_1},X_{j_2}\big]_r^c\bigg)\bigg| \\[5pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \leq \frac{1}{t^{{\kern1pt}p}}\sum_{l_1=1}^d\sum_{l_2=1}^d\sup_{0\lt s\leq t}\big|(L_k)_{s-}M_{s-}\big| \sqrt{[L_{l_1},L_{l_1}]_t}\sqrt{[L_{l_2},L_{l_2}]_t}. \end{align*}

As $\sigma$ is twice continuously differentiable, $\sup_{0<s\leq t}\big|(L_k)_{s-}M_{s-}\big|$ is bounded and the right-hand side of this inequality converges a.s. to zero. For the jump term we have

\begin{equation*} \frac{1}{t^{{\kern1pt}p}}\bigg|\int_{0+}^t(L_k)_{s-}\,\textrm{d} (J_{i,k})_s\bigg| \leq \frac{1}{t^{{\kern1pt}p}}\sum_{0<s\leq t}|(L_k)_{s-}|\cdot|\Delta (J_{i,k})_s| \end{equation*}

by definition. Using the assumption on $\sigma$ , it follows from Taylor’s formula that

\begin{equation*} |\Delta (J_{i,k})_s| = \Bigg|\sigma_{i,k}(X_s)-\sigma_{i,k}(X_{s-}) - \sum_{j=1}^n\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\Delta(X_j)_s\Bigg| \leq C\|\Delta X_s\|^2\leq C' \|\Delta L_s\|^2 \end{equation*}

for some finite (random) constants $C,C'\geq0$ . Thus,

\begin{equation*} \frac{1}{t^{{\kern1pt}p}}\bigg|\int_{0+}^t(L_k)_{s-}\,\textrm{d} (J_{i,k})_s\bigg| \leq \frac{1}{t^{{\kern1pt}p}}C'\sup_{0<s\leq t}|(L_k)_s|\sum_{j=1}^d[L_j,L_j]_t, \end{equation*}

which also converges a.s. to zero as $t\downarrow0$ . For the last term, observe first that

\begin{equation*} \int_{0+}^t(L_k)_{s-}\,\textrm{d}\bigg(\int_{0+}^s\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{r-})\textrm{d} (X_j)_r\bigg) = \sum_{l=1}^d\int_{0+}^t(L_k)_{s-}\frac{\partial\sigma_{i,k}}{\partial x_j}(X_{s-})\sigma_{j,l}(X_{s-})\,\textrm{d}(L_l)_s \end{equation*}

by associativity. This allows us to rewrite

\begin{align*} \sum_{k=1}^d\sum_{l=1}^d\int_{0+}^t(L_k)_{s-}\Bigg(\sum_{j=1}^d\frac{\partial\sigma_{i,k}}{\partial x_j} (X_{s-})\sigma_{j,l}(X_{s-})\Bigg)\,\textrm{d} (L_l)_s = \sum_{k=1}^d\sum_{l=1}^d\int_{0+}^t(L_k)_{s-}(M_{i,k,l})_{s-}\,\textrm{d} (L_l)_s. \end{align*}

Note that $\sup_{0<s\leq t}|(M_{i,k,l})_s|$ is bounded for any fixed small $t\geq0$ and continuous at zero due to the continuity of $\sigma$ and its derivatives. Since $\lim_{t\downarrow0}t^{-p/2}L_t=0$ a.s., it follows that $\lim_{t\downarrow0}t^{-p/2}(L_k)_t(M_{i,k,l})_t$ exists with probability 1. Thus, Proposition 1(ii) is applicable, implying that the integral a.s. vanishes in the limit. Since $\lim_{t\downarrow0}t^{-p/2}L_t=0$ a.s., we have

(14) \begin{align} 0 \leq \bigg\|\frac{\sigma(X_t)L_t}{t^{{\kern1pt}p}}-\frac{\sigma(x)L_t}{t^{{\kern1pt}p}}\bigg\| & \leq \bigg\|\frac{\sigma(X_t)-\sigma(x)}{t^{p/2}}\bigg\|\cdot\bigg\|\frac{L_t}{t^{p/2}}\bigg\| \nonumber \\[5pt] & \leq \sum_{j=1}^n\sup_{0<s\leq t}\bigg\|\frac{\partial\sigma}{\partial x_j}(X_s)\bigg\| \cdot \bigg\|\frac{X_t-x}{t^{p/2}}\bigg\|\cdot\bigg\|\frac{L_t}{t^{p/2}}\bigg\|. \end{align}

The assumptions on $\sigma$ ensure that the supremum on the right-hand side of (14) stays bounded as $t\downarrow0$ , while Proposition 1(i) applies for $t^{-p/2}(X_t-x)$ . Since ${\lim_{t\downarrow0}t^{-p/2}L_t=0}$ a.s., the right-hand side of (14) converges to zero a.s. as $t\downarrow0$ . In particular, the limits in (4) are indeed a.s. equal. If $\sigma(x)$ has rank d, (5) follows immediately from the convergence result in (4).

Proof of Lemma 2. Note that $([L,L]_t)_{t\geq0}$ always has sample paths of bounded variation. We distinguish three cases for $p>0$ . Recall that a denotes the diffusion coefficient of L.

Case 1 ( $p<\frac12$ ): Applying Khintchine’s LIL implies that ${\lim_{t\downarrow0}t^{-p}L_t=0}$ a.s. holds for any Lévy process. Since we also have $2p<1$ , [20, Theorem 1] yields, regardless of the value of a,

\begin{equation*} \lim_{t\downarrow0}\frac{1}{t^{2p}}[L,L]_t = \lim_{t\downarrow0}\bigg(\frac{1}{t}[L,L]_t\cdot t^{1-2p}\bigg) = 0 \quad \mathrm{a.s.} \end{equation*}

Case 2 ( $p=\frac12$ ): Here, Khinchine’s LIL yields $\limsup_{t\downarrow0} L_t/\sqrt{t}=\infty$ a.s. if the Gaussian part of L is non-zero. As the limit is assumed to be finite, the process L must satisfy $a=0$ . This implies that the quadratic variation process in (8) has no drift, so ${[L,L]_t=o(t)}$ a.s. by [20, Theorem 1].

Case 3 ( $p>\frac12$ ): Consider L with its drift (if present) subtracted from the process. This neither changes the structure of the quadratic variation nor the assumption on the almost sure convergence, but ensures that [2, Theorem 2.1] is applicable. Note that, whenever $p>1$ and L is of finite variation with non-zero drift, we have $\lim_{t\downarrow0}t^{-p}|L_t|=\infty$ by [14], showing that this case is excluded by the assumption. The almost sure existence of $\lim_{t\downarrow0}t^{-p}L_t$ further implies that the Lévy measure $\nu_L$ of L satisfies (cf. [2]) $\int_{[-1,1]}|x|^{1/p}\nu_L(\textrm{d} x)<\infty$ . Noting that $\Delta[L,L]_t=f(\Delta L_t)$ for $f(x)=x^2$ , it follows that $\nu_{[L,L]}(B)=\nu_L(f^{-1}(B))$ for all sets $B\subseteq[-1,1]$ . As we can now treat $\nu_{[L,L]}$ as an image measure, it is

\begin{equation*} \int_{[-1,1]}|x|^{1/2p}\nu_{[L,L]}(\textrm{d} x) = \int_{[0,1]}|x|^{1/2p}\nu_{[L,L]}(\textrm{d} x) = \int_{[-1,1]}|x|^{1/p}\nu_L(\textrm{d} x) < \infty. \end{equation*}

Thus, the quadratic variation satisfies the same integral condition with 2p instead of p. As $[L,L]_t$ is a bounded variation Lévy process without drift, part (i) of [2, Theorem 2.1] yields the claim in the last case.

Proof of Corollary 1. As the scaling function is of the form $f(t)=t^{1/2}\ell(1/t)$ with a slowly varying function $\ell$ by assumption, the almost sure boundedness of the cluster points of $L_t/f(t)$ in $\mathbb{R}^d$ implies that, for all $\varepsilon\in\big(0,\frac12\big)$ ,

\begin{equation*} \lim_{t\downarrow0}\frac{L_t}{t^{(1/2-\varepsilon)}} = \lim_{t\downarrow0}\frac{L_t}{f(t)} \cdot \ell(1/t)t^{\varepsilon}=0 \quad \text{a.s.} \end{equation*}

Thus, Theorem 1 is applicable with $p/2=\frac12-\varepsilon$ , yielding

\begin{equation*} \lim_{t\downarrow0} \bigg(\frac{X_t-x}{t^{1-2\varepsilon}}-\frac{\sigma(x)L_t}{t^{1-2\varepsilon}}\bigg) = 0 \quad \text{a.s.} \end{equation*}

Using the explicit form of f and choosing $\varepsilon\in(0,1/4)$ , it follows that

\begin{equation*} \lim_{t\downarrow0}\bigg(\frac{X_t-x-\sigma(x)L_t}{f(t)}\bigg) = \lim_{t\downarrow0}\bigg(\frac{X_t-x-\sigma(x)L_t}{t^{1-2\varepsilon}} \cdot \frac{t^{1-2\varepsilon}}{f(t)}\bigg)=0 \quad \text{a.s.}, \end{equation*}

which is (10), and the remaining claims follow by analogy with the proof of Theorem 1.

Now let L be a real-valued Lévy process with Lévy measure $\nu_L$ . For $x>0$ , we write $\overline{\Pi}^{(+)}_L(x) = \nu_L((x,\infty))$ , $\overline{\Pi}^{(-)}_L(x) = \nu_L((-\infty,-x))$ , and $\overline{\Pi}_L(x) = \overline{\Pi}^{(+)}_L(x) + \overline{\Pi}^{(-)}_L(x)$ for the tail function of $\nu_L$ .

Proof of Corollary 3. If $\alpha=2$ , i.e. Y is normally disributed, the convergence of $L_t/f(t)$ implies that

(15) \begin{equation} \lim_{t\downarrow0}t\overline{\Pi}^{(\#)}_L(xf(t))=0 \end{equation}

for all $x>0$ and $\#\in\{+,-\}$ by [11, Proposition 4.1]. Choosing $x=1$ , note that the condition (15) is not sufficient to imply the integrability of $\overline{\Pi}^{(\#)}_L(f(t))$ over [0,1]. However, since the distribution of Y is non-degenerate, the scaling function f is regularly varying with index $\frac12$ at zero (see [5, Theorem 2.5]). Thus, we also have $\lim_{t\downarrow0}t\overline{\Pi}^{\#}L(t^{1/2-\varepsilon})=0$ . This yields the estimate

(16) \begin{equation} \overline{\Pi}^{\#}_L\big(t^{(1/2-\varepsilon)k}\big)\leq\frac{C_t}{t^k} , \end{equation}

where $C_t$ is bounded as $t\downarrow0$ and the function is thus integrable over [0,1] for $0\leq k<1$ . By assumption, L does not have a Gaussian component and the drift of the process is equal to zero whenever it is defined. Hence, $\int_{0+}^t\overline{\Pi}^{\#}\big(t^{(1/2-\varepsilon)k}\big)\,\textrm{d} t<\infty$ for both $\#=+$ and $\#=-$ , and thus $\lim_{t\downarrow0}t^{-(1/2-\varepsilon)k}L_t=0$ a.s. by [2, Theorem 2.1]. Applying Theorem 1, we obtain

\begin{equation*} \lim_{t\downarrow0} \bigg(\frac{X_t-x}{t^{k-2\varepsilon k}}-\frac{\sigma(x)L_t}{t^{k-2\varepsilon k}}\bigg) = 0 \quad \text{a.s.} \end{equation*}

It now follows for $k-2\varepsilon k>\frac12$ that

\begin{equation*} \lim_{t\downarrow0}\bigg(\frac{X_t-x-\sigma(x)L_t}{f(t)}\bigg) = \lim_{t\downarrow0}\bigg(\frac{X_t-x-\sigma(x)L_t}{t^{k-2\varepsilon k}} \cdot \frac{t^{k-2\varepsilon k}}{f(t)}\bigg)=0 \quad \text{a.s.}, \end{equation*}

which yields the desired convergence of $f(t)^{-1}(X_t-x)$ . If Y follows a non-degenerate stable law with index $\alpha\in(0,2)$ , the right-hand side of (15) is replaced by the tail function $\overline{\Pi}^{\#}_Y(x)$ (see [11, Proposition 4.1]), and it follows from the proof of [11, Theorem 2.3] that the scaling function f is regularly varying with index $1/\alpha$ at zero in this case. Thus, we can derive a bound similar to (16) and argue as before. Noting that [11, Proposition 4.1] does not require the law of the limiting random variable to be non-degenerate, the argument is also applicable if Y is a.s. constant and f is regularly varying with index $r\in\big(0,\frac12\big]$ at zero.