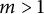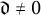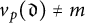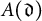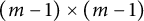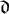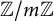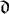The shape of cyclic number fields

Abstract

Let $m>1$ and $\mathfrak {d} \neq 0$ be integers such that $v_{p}(\mathfrak {d}) \neq m$ for any prime p. We construct a matrix $A(\mathfrak {d})$ of size $(m-1) \times (m-1)$ depending on only of $\mathfrak {d}$ with the following property: For any tame $ \mathbb {Z}/m \mathbb {Z}$ -number field K of discriminant $\mathfrak {d}$ , the matrix $A(\mathfrak {d})$ represents the Gram matrix of the integral trace-zero form of K. In particular, we have that the integral trace-zero form of tame cyclic number fields is determined by the degree and discriminant of the field. Furthermore, if in addition to the above hypotheses, we consider real number fields, then the shape is also determined by the degree and the discriminant.

1 Introduction

Let K be a number field of degree $n:=[K:\mathbb {Q}]$ , and let ${\mathfrak {o}}_{K}$ be its maximal order. The trace-zero module of ${\mathfrak {o}}_{K}$ is the $ \mathbb {Z}$ -submodule of ${\mathfrak {o}}_{K}$ given by the Kernel of the trace map, i.e., ${\mathfrak {o}}_{K}^{0}=K^{0} \cap {\mathfrak {o}}_{K}$ , where $K^{0}:= \{ x \in K : \mathrm {Tr}_{K/\mathbb {Q}}(x)=0 \}.$ The integral trace-zero form of K is the isometry class of the rank ( $n-1$ ) quadratic $ \mathbb {Z}$ -module $\langle {\mathfrak {o}}_{K}^{0}, \mathrm {Tr}_{K/ \mathbb {Q}}()_{{\mathfrak {o}}_K} \rangle $ given by restricting the trace pairing from ${\mathfrak {o}}_{K} \times {\mathfrak {o}}_{K}$ to ${\mathfrak {o}}_{K}^{0} \times {\mathfrak {o}}_{K}^{0}.$ For K of degree $n=1,2$ , it is clear, by checking the discriminant, that the isometry class of the quadratic module $\langle {\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\rangle $ determines the field K. For general degrees, this is not the case (see, for instance, [7, Section 3]). However, recently, the second-named author and one of his coauthors have shown that for square-free discriminants, with some extra conditions on the signature and the degree, the integral trace-zero form determines the conjugacy class of the field.

Theorem 1.1 [11, Theorem 2.13]

Suppose that K is a degree n totally real number field, of fundamental discriminant d, such that $\gcd (n,d)=1$ . If $( \mathbb {Z}/n \mathbb {Z})^{*}$ is cyclic, then $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right>$ is a complete invariant for K. In other words, for any number field L, we have that

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{ Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right> \simeq \left<{\mathfrak{o}}_L^{0} , \mathrm{Tr}_{L / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_L} \right> \ \mbox{if and only if} \ K \simeq L. \end{align*}$$

In contrast to the above result in the case of Galois number fields of prime degree $\ell =n$ , the integral trace-zero form does not discriminate beyond the discriminant. Moreover, in such a case, the integral trace-zero form is isometric to the root lattice $\mathbb {A}_{\ell -1}$ times a constant defined solely in terms of the discriminant. Recall that for a given positive integer m, the root lattice $\mathbb {A}_{m}$ is the m-dimensional lattice associated with the quadratic form

$$\begin{align*}\sum_{1 \leq i \leq m} 2x_{i}^{2} - \sum_{\substack{1\leq i,j \leq m \\ |i-j| = 1}} x_{i} x_{j} \end{align*}$$

or equivalently with a Gram matrix in some basis given by

$$\begin{align*}\mathcal{A}_{m}:=\begin{pmatrix} 2 & - 1 & 0 & 0 & \dots & 0 \\ - 1 & 2 & -1 & 0 & \cdots & 0 \\ 0 & -1 & 2 & -1 & \dots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & -1 & 2 & -1 \\ 0 & 0 & 0 & 0 & -1 & 2 \end{pmatrix}.\end{align*}$$

Given an integer d, let $\mathrm {rad}(d)$ be the square-free integer that has the same signature and the same prime factors as d.

Theorem 1.2 [6, Theorem 2.9]

Let $\ell $ be a prime, and let K be a $ \mathbb {Z}/\ell \mathbb {Z}$ -number field of discriminant $\mathfrak {d}(K)$ . Suppose that $\gcd (\ell , \mathfrak {d}(K))=1$ . Then, the Gram matrix of $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right>$ with respect to some basis is equal to

$$\begin{align*}\mathrm{rad}(\mathfrak{d}(K)) \mathcal{A}_{\ell -1}.\end{align*}$$

In particular, if L is a $ \mathbb {Z}/\ell \mathbb {Z}$ -number field with $\gcd (\ell , \mathfrak {d}(L))=1$ , then

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right> \simeq \left<{\mathfrak{o}}_L^{0} , \mathrm{Tr}_{L / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_L}\right> \ \mbox{if and only if} \ \mathfrak{d}(K)= \mathfrak{d}(L). \end{align*}$$

Remark 1.3 Note that the condition $\gcd (\ell , \mathfrak {d}(K))=1$ is equivalent to say that the field K is tame, i.e., that there is no rational prime that is wildly ramified in K.

The purpose of this paper is to generalize the result above to general cyclic number fields of arbitrary degree. Our main theorem is the following.

Theorem (cf. Theorem 2.10)

Let $m \neq 1$ be a positive integer, and let K be a $ \mathbb {Z}/m \mathbb {Z}$ -number field of discriminant $\mathfrak {d}(K)$ . Suppose that K is tame. There exists a matrix $A(\mathfrak {d}(K)) \in \mathrm {M}_{(m-1) \times (m-1)}( \mathbb {Z})$ depending only on $\mathfrak {d}(K)$ such that the Gram matrix of

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right>\end{align*}$$

with respect to some basis is equal to

$$\begin{align*}A(\mathfrak{d}(K)).\end{align*}$$

In particular, if L is a tame $ \mathbb {Z}/m \mathbb {Z}$ -number field, then

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right> \simeq \left<{\mathfrak{o}}_L^{0} , \mathrm{Tr}_{L / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_L}\right> \ \mbox{if and only if} \ \mathfrak{d}(K)= \mathfrak{d}(L). \end{align*}$$

Remark 1.4 In the case that $m=\ell $ is a prime number, $A(\mathfrak {d}(K))=\mathrm {rad}(\mathfrak {d}(K))\mathcal {A}_{\ell -1}$ . Hence, the construction here directly generalizes the results in [6].

1.1 The shape

Another quadratic invariant, with a more geometric interpretation and closely related to the trace zero form, that has been studied by several authors is the shape of K. Endow K with the real-valued $\mathbb {Q}$ -bilinear form $b_K$ whose associated quadratic form is given by

$$\begin{align*}b_K(x,x):= \sum_{\sigma : K \hookrightarrow \mathbb{C}} |\sigma(x)|^2.\end{align*}$$

The shape of K, denoted by $\textrm {Sh}(K)$ , is the isometry equivalence class of $ ({\mathfrak {o}}_ K^{\bot },b_K)$ up to scalar multiplication, where ${\mathfrak {o}}_ K^{\bot }$ is the image of ${\mathfrak {o}}_K$ under the projection map, $\alpha \mapsto \alpha _{\bot }:=n\alpha - \mathrm {Tr}_{K/\mathbb {Q}}(\alpha )$ , i.e.,

$$\begin{align*}{\mathfrak{o}}_ K^{\bot}:= \{\alpha_\bot : \alpha \in {\mathfrak{o}}_K \}=(\mathbb{Z}+n {\mathfrak{o}}_K) \cap {\mathfrak{o}}_{K}^{0}.\end{align*}$$

Thus, $\textrm {Sh}(K)=\textrm {Sh}(L)$ if and only if $({\mathfrak {o}}_K^{\bot },b_K) \simeq ({\mathfrak {o}}_L^{\bot }, \lambda b_L) $ for some $\lambda \in \mathbb {R}^{*}$ . Equivalently, $\mathrm {Sh}(K)$ can be thought as the $(n-1)$ -dimensional lattice inside $ \mathbb {R}^{n}$ , via the Minkowski embedding, that is the orthogonal complement of $1$ and that is defined up to reflection, rotations, and scaling by $ \mathbb {R}^{*}$ . Hence, Sh(K) corresponds to an element to the space of shapes

$$\begin{align*}\mathcal{S}_{n-1}:= \mathrm{GL}_{n-1}( \mathbb{Z}) \setminus \mathrm{GL}_{n-1}( \mathbb{R})/\mathrm{GO}_{n-1}( \mathbb{R}).\end{align*}$$

The distribution of shapes of number fields in $\mathcal {S}_{n}$ has been the subject of interesting current research (see [1, 3, 4, 6]). It turns out that, for cyclic real number fields, the Shape is determined by the discriminant, moreover:

Theorem (cf. Theorem 2.14)

Let m be a positive integer, and let K and L be two totally real tame $ \mathbb {Z}/m \mathbb {Z}$ -number fields. Then, the following are equivalent:

1. (a) $\left <{\mathfrak {o}}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> \simeq \left <{\mathfrak {o}}_L , \mathrm {Tr}_{L / {\mathbb {Q}}} () \right>.$

2. (b) $({\mathfrak {o}}_K^{\bot },b_K) \simeq ({\mathfrak {o}}_L^{\bot }, b_L).$

3. (c) $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right> \simeq \left <{\mathfrak {o}}_L^{0} , \mathrm {Tr}_{L / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_L}\right>.$

4. (d) $\mathfrak {d}(K)= \mathfrak {d}(L)$ .

2 The trace-zero module

In this section, we study the behavior of the trace-zero module of tamely ramified cyclic number fields and the connection with their discriminant. The main goal is to extend some results about trace-zero modules developed in [6, 7].

Definition 2.1 Let K be a number field, and let ${\mathfrak {o}}_K$ be its maximal order. The trace-zero module ${\mathfrak {o}}_K^{0}$ is defined as

$$ \begin{align*}{\mathfrak{o}}_K^{0}:= \{x \in {\mathfrak{o}}_K : \mathrm{Tr}_{K / {\mathbb{Q}}}(x) = 0 \}. \end{align*} $$

Lemma 2.1 Let K be a tamely ramified cyclic number field of degree m. Let $\sigma \in \text {Gal}(K / {\mathbb {Q}})$ be a generator of the Galois group. Suppose $B:=\{ {e}_{1},\ldots , {e}_{m}\}$ is a normal integral basis for ${\mathfrak {o}}_K$ , i.e., an integral basis such that $\sigma ({e}_{m}) ={e}_{1}$ and $\sigma ({e}_{j}) ={e}_{j+1}$ for $1 \leq j \leq m-1$ . Then, $B_{0}:=\{ {e}_1 - {e}_2, {e}_2 - {e}_3, \dots , {e}_{m-1} - {e}_{m}\}$ is an integral basis for ${\mathfrak {o}}_K^{0}$ .

Proof Since B is a normal basis, each element ${e}_j - {e}_{j+1}$ of $B_{0}$ belongs to ${\mathfrak {o}}_K^{0}$ . On the other hand, thanks to Hilbert’s 90, if $u \in K$ is such that $ \mathrm {Tr}_{K / {\mathbb {Q}}}(u) = 0$ , then there exist $b \in K$ such that $u = b - \sigma (b)$ . Therefore, if $u \in {\mathfrak {o}}_K^{0}$ , then

$$ \begin{align*} u & = b - \sigma(b) \\ & = (c_1 e_1 + c_2 e_2 + \dots + c_{m} e_{m}) - \sigma(c_1 e_1 + c_2 e_2 + \dots + c_{m}e_{m}) \\ &= (c_1 - c_{m})e_1 + (c_2 - c_1)e_2 + \dots + (c_m - c_{m-1})e_{m}, \end{align*} $$

for some $c_i \in {\mathbb {Q}}$ . Since $u \in {\mathfrak {o}}_K$ , we must have $c_{j+1} - c_j \in {\mathbb {Z}}$ for $j = 0, 1, \dots , (m-1)$ , where we define $c_0 := c_{m}$ . Moreover, since

$$\begin{align*}c_i - c_{m} = \sum_{j = 1}^{i} (c_j - c_{j-1}) \in {\mathbb{Z}},\end{align*}$$

by rearranging, we obtain

$$ \begin{align*} u & = (c_1 - c_{m})e_1 + (c_2 - c_1)e_2 + \dots + (c_m - c_{m-1})e_{m} \\ & = (c_1 - c_{m})(e_1 - e_2) + (c_2 - c_{m})(e_2 - e_3) + \dots + (c_{m-1} - c_{m})(e_{m-1} - e_{m}). \end{align*} $$

By ranks, we conclude that $\{ {e}_1 - {e}_2, {e}_2 - {e}_3, \dots , {e}_{m-1} - {e}_{m} \}$ is an integral basis for ${\mathfrak {o}}_{K}^0.$

2.1 A Gram matrix representation of the trace-zero form

In this section, we use a trace-zero basis, coming from a normal integral basis as in the previous section, to find a canonical Gram matrix for the integral trace zero form.

Lemma 2.2 Let K be a number field of degree m, and let $G_K := {\mathbb {Z}} + {\mathfrak {o}}_K^{0}$ . We have

$$\begin{align*}\left|{\mathfrak{o}}_K / G_K \right| = \left| \mathrm{Tr}_{K / {\mathbb{Q}}} ({\mathfrak{o}}_K) / m{\mathbb{Z}} \right|.\end{align*}$$

Proof By the isomorphism theorem on groups, the result follows from:

• • The group $G_K$ is a subgroup of ${\mathfrak {o}}_K$ that contains the Kernel of the trace map.

• • The image of $G_K$ under the trace is equal to $m{\mathbb {Z}}$ .

Corollary If K is a tamely ramified number field of degree m, then

$$ \begin{align*}\left|{\mathfrak{o}}_K / G_K \right| = m.\end{align*} $$

Proof Since K is tamely ramified, by [12, Corollary 5 to Theorem 4.24],

$$\begin{align*}\mathrm{Tr}_{K/ {\mathbb{Q}}}({\mathfrak{o}}_K) = {\mathbb{Z}}.\end{align*}$$

Using this, the result follows from Lemma 2.2.

Theorem 2.4 Let K and L be tamely ramified cyclic number fields of degree m. Then,

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right> \simeq \left<{\mathfrak{o}}_L^{0} , \mathrm{Tr}_{L / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_L} \right> \ \mbox{ if and only if} \ \ \mathfrak{d}(L) = \mathfrak{d}(K). \end{align*}$$

Proof Suppose that $ \left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right> \simeq \left <{\mathfrak {o}}_L^{0} , \mathrm {Tr}_{L / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_L} \right> $ . Since the decomposition of $G_{K}={\mathbb {Z}} + {\mathfrak {o}}_K^{0}$ (resp. $G_{L}={\mathbb {Z}} + {\mathfrak {o}}_L^{0}$ ) is an orthogonal decomposition with respect to the trace pairing, we have the following equalities between determinants of the trace in the respective modules:

$$\begin{align*}\mathfrak{d}(G_K) = \mathfrak{d}({\mathfrak{o}}_K^{0}) m = \mathfrak{d}({\mathfrak{o}}_L^{0}) m = \mathfrak{d}(G_L).\end{align*}$$

Since

$$\begin{align*}\mathfrak{d}(G_K) =\left| {\mathfrak{o}}_K / G_K \right|{}^2 \mathfrak{d}({\mathfrak{o}}_K) \ \mbox{and} \ \mathfrak{d}(G_L) =\left| {\mathfrak{o}}_L / G_L \right|{}^2 \mathfrak{d}({\mathfrak{o}}_L), \end{align*}$$

the result follows thanks to Corollary 2.3.

On the other hand, if $\mathfrak {d}(K) = \mathfrak {d}(L)$ , then, by [9, Theorems 4.2 and 4.5], there exist normal integral bases $B:=\{ {e}_{1},\ldots , {e}_{m}\}$ and $B':=\{ {e}^{\prime }_{1},\ldots , {e}^{\prime }_{m}\}$ of ${\mathfrak {o}}_K$ and ${\mathfrak {o}}_L$ , respectively, such that $\left <{\mathfrak {o}}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> $ and $ \left <{\mathfrak {o}}_L , \mathrm { Tr}_{L / {\mathbb {Q}}} () \right>$ are isometric via an isometry

$$\begin{align*}\gamma: {\mathfrak{o}}_K \to {\mathfrak{o}}_L\end{align*}$$

such that $\gamma ({e}_{i})={e}^{\prime }_{i}$ for all $1 \leq i \leq m$ . It follows from Lemma 2.1 that such an isometry $\gamma $ restricts to an isometry between the quadratic modules $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right>$ and $ \left <{\mathfrak {o}}_L^{0} , \mathrm {Tr}_{L / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_L} \right>$ .

Definition 2.2 Let m be a positive integer. For every d a positive divisor of m, we let $A_d$ be an $m \times m $ matrix defined as

$$\begin{align*}(A_d)_{i,j} := \left\{ \begin{array}{ll} 1, & \mbox{ if } \frac{m}{d} \big| (i-j), \\ & \\ 0, & \mathrm{otherwise}. \end{array} \right.\end{align*}$$

Suppose that K is a tame cyclic number field of degree m. Theorems 4.2 and 4.5 of [9] state that there exists a normal integral basis B of ${\mathfrak {o}}_K$ such that the Gram matrix of $\left <{\mathfrak {o}}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> $ in such basis is equal to

$$\begin{align*}\sum_{d|m} a_d A_d,\end{align*}$$

where $a_d$ are integers given in Lemma 4.3 of [9] that only depend on the discriminant of K. For the reader’s convenience, see also Definition 2.5.

We devote the rest of this section to describe a similar canonical decomposition, i.e., a Gram matrix depending only on the discriminant of the field, for the trace-zero module $\left <{\mathfrak {o}}^{0}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> $ .

Let $n \ge 2$ be an integer. Then, we define $\mathbb {B}_n$ as the $n \times n$ matrix

$$\begin{align*}\begin{pmatrix} 1 & 0 & 0& \dots & -1 \\ -1 & 1 & 0 & \dots & 0 \\ 0 & -1 & 1 & \dots & 0 \\ \vdots & 0 & \ddots & \ddots & \vdots \\ 0& 0 & \cdots & -1 & 1 \\ \end{pmatrix}.\end{align*}$$

In other words,

$$\begin{align*}(\mathbb{B}_n)_{i,j}:= \left\{ \begin{array}{rl} 1, & \mbox{ if } i=j, \\ -1, & \mbox{ if } i=j+1 \ \mathrm{or} \ (i,j) =(1,n),\\ 0, & \mbox{ otherwise. } \end{array} \right. \end{align*}$$

Proposition Let m be an integer bigger than $1$ , and let K be a degree m number field. Let M be the Gram Matrix of $ \left <{\mathfrak {o}}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> $ with respect to $\{ {e}_{1},\ldots , {e}_{m}\}$ , an integral basis of ${\mathfrak {o}}_K$ . Let $M_0$ be the Gram matrix of $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K^{0}} \right> $ with respect to $\{{e}_1 - {e}_2, {e}_2 - {e}_3, \dots , {e}_{m-1}- {e}_{m} \}$ . Then, $M_0$ is equal to $(\mathbb {B}_m^T M \mathbb {B}_m)_{(m,m)}$ , the $(m,m)$ minor of $\mathbb {B}_m^T M \mathbb {B}_m$ (the matrix obtained by deleting the last row and column).

Proof Let $i,j$ be integers such that $1\leq i,j < m$ . Then,

$$ \begin{align*} (\mathbb{B}_m^T M \mathbb{B}_m)_{i,j} &= \sum_{k=1}^{m}\sum_{l=1}^{m}\mathbb{B}_{k,i}M_{k,l}\mathbb{B}_{l,j} \\ &=M_{i,j}-M_{i,j+1}-M_{i+1,j}+ M_{i+1, j+1} \\ &= \mathrm{Tr}_{K / {\mathbb{Q}}} (e_{i}e_{j}) - \mathrm{Tr}_{K / {\mathbb{Q}}} (e_{i}e_{j+1})- \mathrm{Tr}_{K / {\mathbb{Q}}} (e_{i+1}e_{j})+ \mathrm{Tr}_{K / {\mathbb{Q}}} (e_{i+1}e_{j+1}) \\ &= \mathrm{Tr}_{K / {\mathbb{Q}}}\left( (e_{i}-e_{i+1})(e_{j}-e_{j+1})\right) \\ &= (M_{0})_{i,j}.\\[-35pt] \end{align*} $$

Corollary Let K be a tame cyclic number field of degree $m \neq 1$ . There exists a basis of ${\mathfrak {o}}_K^{0}$ such that the Gram matrix of $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K^{0}} \right> $ with respect to such basis is equal to the $(m,m)$ minor of

$$\begin{align*}\sum _{d | m} a_d \mathbb{B}_m^T A_d \mathbb{B}_m,\end{align*}$$

where the coefficients $a_d$ are given in Lemmas 3.7, 3.10, and 4.3 of [9] and depend solely on the discriminant of K. See also Definition 2.5.

Proof Since

$$\begin{align*}M = \sum _{d | m} a_d A_d, \end{align*}$$

the corollary is an immediate consequence of Proposition 2.5 and [9, Theorems 4.2 and 4.5].

2.1.1 The matrix $A(\mathfrak {d})$

Given a prime p, we denote by $v_{p}$ the usual p-adic valuation on the rationals.

Definition 2.3 Suppose that $m>0$ and $\mathfrak {d}$ are integers, and let p be a prime. Suppose that $m \neq v_{p}(\mathfrak {d})$ . The p-ramification index of $\mathfrak {d}$ is the rational number defined as

$$\begin{align*}e_{p}(\mathfrak{d}):=\frac{m}{m-v_{p}(\mathfrak{d})}.\end{align*}$$

Remark 2.7 The above definition is motivated by the following fact: If K is a Galois number field of degree m and discriminant $\mathfrak {d}$ , then $e_{p}(\mathfrak {d})$ is the ramification index of p in K for any prime p that is not wildly ramified in K.

Definition 2.4 Let $m>1$ and $\mathfrak {d} \neq 0$ be integers. Let $\mathrm {div}(\mathfrak {d})$ be the set of prime divisors of $\mathfrak {d}$ . Let $1 = d_1 < d_2 < \dots < d_{\tau (m)} = m$ be the set of positive divisors of m. Let

$$\begin{align*}P(m) := \left\{ \left(d_2^{\varepsilon_2}, d_3^{\varepsilon_3}, \dots , d_{\tau(m)}^{\varepsilon_{\tau(m)}} \right) \in {\mathbb{Z}}^{\tau(m)-1} : \varepsilon_i \in \{0,1\} \ \mbox{for all} \ i \right\},\end{align*}$$

and for every $\vec {v} \in P(m)$ , let

$$\begin{align*}\operatorname{\mathrm{lcm}}(\vec{v}) := \operatorname{\mathrm{lcm}}\left[ d_2^{\varepsilon_2}, d_3^{\varepsilon_3}, \dots , d_{\tau(m)}^{\varepsilon_{\tau(m)}}\right],\end{align*}$$

$$\begin{align*}\gcd(\vec{v}) := \gcd\left(d_2^{\varepsilon_2}, d_3^{\varepsilon_3}, \dots , d_{\tau(m)}^{\varepsilon_{\tau(m)}}\right),\end{align*}$$

and for every divisor d of m, let

$$\begin{align*}P_d := \{ \vec{v} \in P(m) : \operatorname{\mathrm{lcm}}(\vec{v}) = d \}. \end{align*}$$

If $d>1$ is a divisor of m, let

$$\begin{align*}\mathbb{P}_d:= \{ p \in \mathrm{div}(\mathfrak{d}) : e_{p}(\mathfrak{d}) = d \}\end{align*}$$

and

$$\begin{align*}w_{d}:=\prod_{p \in \mathbb{P}_d}p \ \mbox{and} \ f_d := \frac{w_d - 1}{d}. \end{align*}$$

Definition 2.5 Let $m>0$ and $\mathfrak {d}$ be integers. For d, a divisor of m not equal to $1$ , we let

$$\begin{align*}a_d := \sum\limits_{\vec{v} \in P_d} \left(\gcd(\vec{v}) \prod\limits_{\varepsilon_i = 0} w_{d_i} \prod\limits_{\varepsilon_j = 1}(- f_{d_j}) \right) \end{align*}$$

and let $a_1 := \prod \limits _{p \in \mathrm {div}(\mathfrak {d})} p $ . Let $A(\mathfrak {d})$ be the $(m-1)\times (m-1)$ matrix defined as

$$\begin{align*}A(\mathfrak{d}):=\sum_{ \substack{d \mid m \\ d \neq m}}a_{d}\widehat{A}_{d},\end{align*}$$

where $\displaystyle \widehat {A}_{d}:= \left (\mathbb {B}_m^T A_d \mathbb {B}_m \right )_{(m,m)}.$

Example 2.8 Let $m=9$ and $\mathfrak {d}= 9,644,443,241,083,841,416,681= 7^{6}\cdot 13^{6}\cdot 19^{8}.$ Here, the set of positive divisors of m is $1<3<9$ and $\mathrm {div}(\mathfrak {d})= \{7,13, 19\}$ . Hence, $P(9)$ is the subset of ${\mathbb {Z}}^{2}$ given by

$$\begin{align*}P(9)=\{ (1,1), (1,9), (3,1) ,(3, 9)\},\end{align*}$$

and thus

$$\begin{align*}P_{3}= \{ (3,1)\} \ \mbox{and} \ P_{9}= \{ (1,9), (3,9)\}.\end{align*}$$

On the other hand, $e_{7}(\mathfrak {d})=3, e_{13}(\mathfrak {d})=3$ , and $e_{19}(\mathfrak {d})=9$ . Thus, $\mathbb {P}_3=\{7,13\}$ and $\mathbb {P}_9=\{19\}.$ Therefore, $w_{3}=91, f_{3}=30$ , and $w_{9}=19, f_{9}=2$ . From this, we calculate that

$$\begin{align*}a_{3}= 1\cdot 19 \cdot (-30) =-570\ \mbox{and} \ a_{9}=1\cdot 91 \cdot (-2) + 3\cdot 1 \cdot (60)=-2; \end{align*}$$

moreover, $a_{1}=7\cdot 13\cdot 19=1,729.$ Since $A_{1}$ is the identity matrix of dimension $9$ , we have that

$$\begin{align*}A(\mathfrak{d})= 1,729 (\mathbb{B}_{9}^{t}\mathbb{B}_{9})_{(9,9)}-570(\mathbb{B}_{9}^{t}A_{3}\mathbb{B}_{9})_{(9,9)}.\end{align*}$$

In other words,

$$\begin{align*}A(\mathfrak{d})= \begin{pmatrix} \ 2,318 & -1,159 & \ 570 & -1,140 & \ 570 & \ 570 & -1,140 & \ 570 \\ -1,159 & \ 2,318 &-1,159 & \ 570 &-1,140 & \ 570 & \ 570 &-1,140 \\ \ 570 & -1,159 & \ 2,318 &-1,159 & \ 570 &-1,140 & \ 570 & 570\\ -1,140 & \ 570 &-1,159 & \ 2,318 &-1,159 & \ 570 &-1,140 & \ 570 \\ \ 570 &-1,140 & \ 570 &-1,159 & \ 2,318 &-1,159 & \ 570 &-1,140 \\ \ 570 & \ 570 &-1,140 & \ 570 &-1,159 & \ 2,318 &-1,159 & \ 570 \\ -1,140 & \ 570 & \ 570 &-1,140 & \ 570 &-1,159 & \ 2,318 &-1,159 \\ \ 570 &-1,140 & \ 570 & \ 570 &-1,140 & \ 570 &-1,159 & \ 2,318 \end{pmatrix}. \end{align*}$$

Example 2.9 Suppose that $m=\ell $ is a prime number. In such case,

$$\begin{align*}A(\mathfrak{d})=a_{1}\widehat{A}_{1}=\mathrm{rad}(\mathfrak{d})\left(\mathbb{B}_{\ell}^T A_1 \mathbb{B}_{\ell} \right)_{(\ell,\ell)}=\mathrm{ rad}(\mathfrak{d})\left(\mathbb{B}_{\ell}^T \mathbb{B}_{\ell} \right)_{(\ell,\ell)}=\mathrm{rad}(\mathfrak{d})\mathcal{A}_{\ell -1}.\end{align*}$$

Now, we are in position to state and prove one of the main theorems in the paper.

Theorem 2.10 Let m be an integer not equal to $1$ , and let K be a tame $ \mathbb {Z}/m \mathbb {Z}$ -number field of discriminant $\mathfrak {d}(K)$ . There exists a ${\mathbb {Z}}$ -basis of ${\mathfrak {o}}_K^{0}$ such that the Gram matrix of

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right>\end{align*}$$

with respect to such basis is equal to

$$\begin{align*}A(\mathfrak{d}(K)).\end{align*}$$

In particular, if L is a tame $ \mathbb {Z}/m \mathbb {Z}$ -number field, then

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_K}\right> \simeq \left<{\mathfrak{o}}_L^{0} , \mathrm{Tr}_{L / {\mathbb{Q}}} ()|_{{\mathfrak{o}}_L}\right> \ \mbox{if and only if} \ \mathfrak{d}(K)= \mathfrak{d}(L). \end{align*}$$

Proof For each d divisor of m, let

$$\begin{align*}\widehat{A}_{d}:= \left(\mathbb{B}_m^T A_d \mathbb{B}_m \right)_{(m,m)} \end{align*}$$

be the $(m-1) \times (m-1)$ matrix obtained by erasing the last row and column of $\mathbb {B}_m^T A_d \mathbb {B}_m$ . By definition, all the entries in $A_m$ are equal to $1$ , and hence the columns of $\mathbb {B}_m$ belong to $ \text {Ker}(A_m)$ . In particular, $\mathbb {B}_m^T A_m \mathbb {B}_m =0$ , and thus the result follows from Corollary 2.6 and [9, Theorems 4.2 and 4.5].

Example 2.11 There are four ${\mathbb {Z}}/9{\mathbb {Z}}$ -number fields with discriminant $\mathfrak {d}=7^{6}\cdot 13^{6}\cdot 19^{8}$ (see John Jones’ database [5]). Since 3 is unramified in any of those fields, neither of the fields have wild ramification. Such fields are defined, respectively, by the following polynomials:

• • $x^9 - x^8 - 578x^7 - 1,855x^6 + 87,155x^5 + 310,749x^4 - 4,599,958x^3 - 6,198,626x^2 + 102,071,235x - 169,800,379$ .

• • $x^9 - x^8 - 578x^7 - 1,855x^6 + 87,155x^5 + 518,229x^4 - 2,594,318x^3 - 22,409,730x^2 - 36,985,319x - 7,889,903.$

• • $x^9 - x^8 - 578x^7 + 1,603x^6 + 88,884x^5 - 430,992x^4 - 3,668,027x^3 + 27,283,459x^2 - 40,339,579x - 7,447,279.$

• • $x^9 - x^8 - 578x^7 + 1,603x^6 + 88,884x^5 - 119,772x^4 - 5,379,737x^3 - 3,169,418x^2 + 113,584,646x + 256,187,183.$

Let $A(\mathfrak {d})$ be the matrix calculated in Example 2.8. It follows from Theorem 2.10 that for each of those fields, there is a basis of the trace-zero integral module such that all the Gram matrices of the trace form in that basis are equal to the matrix $A(\mathfrak {d})$ . This can be verified computationally, for instance, in MAGMA [2], using the code found in [8, Section 3.1].

2.2 Another explicit description

In this subsection, we show that if we apply the results obtained here to the case $m=\ell $ , a prime, we recover the formulas obtained in [6]. We also see how some of the polynomial descriptions of the trace-zero form of [6] are extended to the general case of this paper.

Let n be a positive integer bigger than $1$ . The extended n-dimensional $\mathcal {A'}_n$ lattice is the lattice associated with the matrix

$$\begin{align*}\mathcal{A'}_n := \mathbb{B}_n^T \mathbb{B}_n = \begin{pmatrix} \ 2 & - 1 & \ 0 & \ 0 & \dots & -1 \\ - 1 & \ 2 & -1 & \ 0 & \cdots & \ 0 \\ \ 0 & -1 & \ 2 & -1 & \dots & \ 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ \ 0 & \ 0 & \ 0 & -1 & \ 2 & -1 \\ -1 & \ 0 & \ 0 & \ 0 & -1 & \ 2 \end{pmatrix}.\end{align*}$$

For any positive integer n, we denote by $1_{n}$ the $n\times n$ matrix with all its entries equal to $1$ and by $\mathrm {I}_{n}$ the identity matrix of dimension n

Lemma 2.12 Let m be an integer bigger than $1$ , and let $d\neq m$ be a positive divisor of m. Then,

$$\begin{align*}\mathbb{B}_m^T A_d \mathbb{B}_m = 1_{d}\otimes \mathcal{A'}_{\frac{m}{d}}.\end{align*}$$

Proof First notice that, for every $d|m$ , we have $\displaystyle A_d = 1_{d} \otimes \mathrm {I}_{\frac {m}{d}}.$ After doing block multiplication, the result follows from the definition of $\mathcal {A'}_n$ .

Applying Lemma 2.12 to the situation of Theorem 2.10, we deduce that the Gram matrix $M_0$ of $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K} \right> $ in the given basis has the form

(2.1) $$ \begin{align} M_0 = \left( \sum_{\substack{ d|m \\ d<m}} a_d 1_{d} \otimes \mathcal{A'}_{\frac{m}{d}}. \right)_{(m,m)}. \end{align} $$

If m is equal to a prime $\ell $ , then the above equation is simply

$$\begin{align*}M_0 = (a_1 \mathcal{A'}_{\ell} )_{(\ell, \ell)}.\end{align*}$$

Since $a_1 = \mathrm {rad}(\mathfrak {d}(K))$ and $(\mathcal {A'}_{\ell })_{(\ell ,\ell )}$ is the usual $(\ell -1)$ -dimensional root lattice $\mathcal {A}_{\ell -1}$ , the equation $\displaystyle M_0 = (a_1 \mathcal {A'}_{\ell } )_{(\ell ,\ell )}$ is precisely [6, Theorem 2.9].

An explicit polynomial description of the integral trace-zero form is the following.

Corollary Let K be a tame totally real cyclic number field of degree $m>1$ . Then,

$$\begin{align*}\left<{\mathfrak{o}}_K^{0} , \mathrm{Tr}_{K / {\mathbb{Q}}} ()\Big|_{{\mathfrak{o}}_K} \right> \end{align*}$$

is the lattice associated with the form

$$\begin{align*}\sum_{1 \leq i\leq j \leq m-1} c_{i,j} x_ix_j,\end{align*}$$

where

$$\begin{align*}c_{i,j}:= \sum_{\substack{ d \mid m, d \neq m \\ m \big| (i-j)d }} 2a_d - \sum_ {\substack{ d \mid m, d \neq m \\ m \big| (|i-j| -1)d }} a_d. \end{align*}$$

Proof Note that, for every $d|m$ and $d \neq m$ , we have

$$\begin{align*}1_d \otimes \mathcal{A'}_{\frac{m}{d}} := \left\{ \begin{array}{rl} 2, & \mbox{ if } (i-j) \equiv 0\quad \mod (\frac{m}{d}), \\ -1, & \mbox{ if } |i -j| \equiv 1\quad \mod (\frac{m}{d}), \\ 0, & \mbox{ otherwise. } \end{array} \right. \end{align*}$$

Then, the result follows from formula 2.1.

2.3 Equivalences on the shape of cyclic number fields

Finally, we show that for real cyclic fields, that have no wild ramification, the shape of the field is characterized by the discriminant. More specifically, we show the following theorem.

Theorem 2.14 Let m be a positive integer, and let K and L be two totally real tame $ \mathbb {Z}/m \mathbb {Z}$ -number fields. Then, the following are equivalent:

1. (a) $\left <{\mathfrak {o}}_K , \mathrm {Tr}_{K / {\mathbb {Q}}} ()\right> \simeq \left <{\mathfrak {o}}_L , \mathrm {Tr}_{L / {\mathbb {Q}}} () \right>.$

2. (b) $({\mathfrak {o}}_K^{\bot },b_K) \simeq ({\mathfrak {o}}_L^{\bot }, b_L).$

3. (c) $\left <{\mathfrak {o}}_K^{0} , \mathrm {Tr}_{K / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_K}\right> \simeq \left <{\mathfrak {o}}_L^{0} , \mathrm {Tr}_{L / {\mathbb {Q}}} ()|_{{\mathfrak {o}}_L}\right>.$

4. (d) $\mathfrak {d}(K)= \mathfrak {d}(L)$ .

Proof The equivalence between (c) and (d) is Theorem 2.4; however, this equivalence also follows from Theorem 2.10. The equivalence between (a) and (d) follows from [9, Theorems 4.2 and 4.5]. Since K and L are totally real, the bilinear forms $b_{K}$ and $b_{L}$ are just the corresponding trace forms. Hence, $(b) \Rightarrow (d)$ follows from [11, Lemma 2.1]. To check the missing implication, we see that $(a) \Rightarrow (b)$ follows from [10, Lemma 5.1]