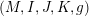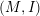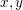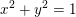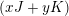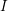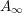1 Introduction
1.1 Background
Before stating our results, we recall some basic facts about hyperkähler manifolds. For more details and references, see [Reference BesseBes87].
Definition 1.1. A hypercomplex manifold is a manifold
![]() $M$
with three complex structures
$M$
with three complex structures
![]() $I,J,K$
, satisfying quaternionic relations
$I,J,K$
, satisfying quaternionic relations
A hyperkähler manifold is a hypercomplex manifold equipped with a metric
![]() $g$
which is Kähler with respect to
$g$
which is Kähler with respect to
![]() $I,J,K$
.
$I,J,K$
.
Definition 1.2. A holomorphic symplectic manifold is a manifold
![]() $M$
with a complex structure
$M$
with a complex structure
![]() $I$
and a closed non-degenerate holomorphic
$I$
and a closed non-degenerate holomorphic
![]() $(2,0)$
-form
$(2,0)$
-form
![]() $\unicode[STIX]{x1D6FA}$
. A complex submanifold
$\unicode[STIX]{x1D6FA}$
. A complex submanifold
![]() $L\subset M$
is holomorphic Lagrangian if
$L\subset M$
is holomorphic Lagrangian if
![]() $\unicode[STIX]{x1D6FA}|_{L}=0$
.
$\unicode[STIX]{x1D6FA}|_{L}=0$
.
Remark 1.3. A hyperkähler manifold
![]() $M$
is equipped with three symplectic forms
$M$
is equipped with three symplectic forms
![]() $\unicode[STIX]{x1D714}_{I}$
,
$\unicode[STIX]{x1D714}_{I}$
,
![]() $\unicode[STIX]{x1D714}_{J}$
,
$\unicode[STIX]{x1D714}_{J}$
,
![]() $\unicode[STIX]{x1D714}_{K}$
. The form
$\unicode[STIX]{x1D714}_{K}$
. The form
![]() $\unicode[STIX]{x1D6FA}_{I}:=\unicode[STIX]{x1D714}_{J}+\sqrt{-1}\unicode[STIX]{x1D714}_{K}$
is a holomorphic symplectic 2-form on
$\unicode[STIX]{x1D6FA}_{I}:=\unicode[STIX]{x1D714}_{J}+\sqrt{-1}\unicode[STIX]{x1D714}_{K}$
is a holomorphic symplectic 2-form on
![]() $(M,I)$
.
$(M,I)$
.
The following result is a consequence of the Calabi–Yau theorem [Reference YauYau78] and the Bochner technique.
Theorem 1.4. A compact, Kähler, holomorphically symplectic manifold admits a unique hyperkähler metric in any Kähler class.
In other words, ‘hyperkähler’ in the context of compact manifolds is essentially synonymous with ‘holomorphic symplectic’. Examples of non-compact hyperkähler manifolds include the moduli space of Higgs bundles [Reference HitchinHit87] and Nakajima quiver varieties [Reference NakajimaNak94]. The Fukaya categories of such manifolds have drawn considerable attention [Reference Kapustin and WittenKW07, Reference Seidel and SmithSS06].
Let
![]() $\unicode[STIX]{x1D6E9}$
be an almost complex structure on a manifold
$\unicode[STIX]{x1D6E9}$
be an almost complex structure on a manifold
![]() $M$
, that is, an automorphism of
$M$
, that is, an automorphism of
![]() $TM$
satisfying
$TM$
satisfying
![]() $\unicode[STIX]{x1D6E9}^{2}=-\text{Id}$
. Let
$\unicode[STIX]{x1D6E9}^{2}=-\text{Id}$
. Let
![]() $\unicode[STIX]{x1D6F4}$
be a Riemann surface with complex structure
$\unicode[STIX]{x1D6F4}$
be a Riemann surface with complex structure
![]() $j$
, possibly with boundary, and not necessarily compact.
$j$
, possibly with boundary, and not necessarily compact.
Definition 1.5. A map
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
is called
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
is called
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic if
$\unicode[STIX]{x1D6E9}$
-holomorphic if
The energy of
![]() $u$
with respect to a Riemannian metric
$u$
with respect to a Riemannian metric
![]() $g$
on
$g$
on
![]() $M$
is given by
$M$
is given by
1.2 Main results
We call a Riemann surface
![]() $\unicode[STIX]{x1D6F4}$
nice if it can be obtained by removing a finite number of boundary points from a compact connected Riemann surface with boundary
$\unicode[STIX]{x1D6F4}$
nice if it can be obtained by removing a finite number of boundary points from a compact connected Riemann surface with boundary
![]() $\overline{\unicode[STIX]{x1D6F4}}$
. We do not exclude the case
$\overline{\unicode[STIX]{x1D6F4}}$
. We do not exclude the case
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}=\emptyset$
. Let
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}=\emptyset$
. Let
denote the connected components of
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}$
. Let
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}$
. Let
denote the compactly supported Euler characteristic of
![]() $\unicode[STIX]{x1D6F4}$
. Let
$\unicode[STIX]{x1D6F4}$
. Let
![]() $(M,\unicode[STIX]{x1D714})$
be a symplectic manifold, and let
$(M,\unicode[STIX]{x1D714})$
be a symplectic manifold, and let
![]() ${\mathcal{L}}$
be a collection of Lagrangian submanifolds
${\mathcal{L}}$
be a collection of Lagrangian submanifolds
![]() $L_{i}\subset M,i\in A$
, where
$L_{i}\subset M,i\in A$
, where
![]() $A$
is a countable index set. An
$A$
is a countable index set. An
![]() $A$
-labeling of a nice Riemann surface
$A$
-labeling of a nice Riemann surface
![]() $\unicode[STIX]{x1D6F4}$
is a function
$\unicode[STIX]{x1D6F4}$
is a function
![]() $l:\{1,\ldots ,b(\unicode[STIX]{x1D6F4})\}\rightarrow A$
. An almost complex structure
$l:\{1,\ldots ,b(\unicode[STIX]{x1D6F4})\}\rightarrow A$
. An almost complex structure
![]() $\unicode[STIX]{x1D6E9}$
on
$\unicode[STIX]{x1D6E9}$
on
![]() $M$
is called
$M$
is called
![]() $\unicode[STIX]{x1D714}$
-tame if for all tangent vectors
$\unicode[STIX]{x1D714}$
-tame if for all tangent vectors
![]() $0\neq \unicode[STIX]{x1D709}\in T_{p}M$
, we have
$0\neq \unicode[STIX]{x1D709}\in T_{p}M$
, we have
![]() $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D709})>0$
. Let
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D709})>0$
. Let
![]() ${\mathcal{J}}_{\unicode[STIX]{x1D714}}$
denote the collection of all
${\mathcal{J}}_{\unicode[STIX]{x1D714}}$
denote the collection of all
![]() $\unicode[STIX]{x1D714}$
-tame almost complex structures. Assume there exists a compact set
$\unicode[STIX]{x1D714}$
-tame almost complex structures. Assume there exists a compact set
![]() $N\subset M$
such that
$N\subset M$
such that
for all
![]() $i,j$
. In particular, it suffices for
$i,j$
. In particular, it suffices for
![]() $M$
to be compact. Given a hypercomplex structure
$M$
to be compact. Given a hypercomplex structure
![]() $(I,J,K)$
on
$(I,J,K)$
on
![]() $M$
, let
$M$
, let
![]() $R_{I}\simeq S^{1}$
denote the space of complex structures on
$R_{I}\simeq S^{1}$
denote the space of complex structures on
![]() $M$
of the form
$M$
of the form
![]() $xJ+yK$
for
$xJ+yK$
for
![]() $x^{2}+y^{2}=1$
. The main result of this paper is the following theorem.
$x^{2}+y^{2}=1$
. The main result of this paper is the following theorem.
Theorem 1.6. Suppose there exists a complete hyperkähler structure
![]() $(I,J,K,g)$
on
$(I,J,K,g)$
on
![]() $M$
such that
$M$
such that
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and the Lagrangian submanifolds
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and the Lagrangian submanifolds
![]() $L_{i}$
for
$L_{i}$
for
![]() $i\in A$
are
$i\in A$
are
![]() $I$
-holomorphic. There exists a countable set
$I$
-holomorphic. There exists a countable set
![]() $P\subset R_{I}$
with the following significance. Let
$P\subset R_{I}$
with the following significance. Let
![]() $\unicode[STIX]{x1D6F4}$
be a nice Riemann surface and let
$\unicode[STIX]{x1D6F4}$
be a nice Riemann surface and let
![]() $l$
be an
$l$
be an
![]() $A$
-labeling. If
$A$
-labeling. If
![]() $\unicode[STIX]{x1D6E9}\in R_{I}\setminus P$
, then a
$\unicode[STIX]{x1D6E9}\in R_{I}\setminus P$
, then a
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map
$\unicode[STIX]{x1D6E9}$
-holomorphic map
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
with
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
with
![]() $u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
$u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
![]() $E_{g}(u)<\infty$
is necessarily constant.
$E_{g}(u)<\infty$
is necessarily constant.
It is crucially important in Theorem 1.6 that there is no restriction on how the Lagrangians
![]() $L_{i}$
intersect. Indeed, in the compact setting, moving the
$L_{i}$
intersect. Indeed, in the compact setting, moving the
![]() $L_{i}$
by any non-trivial Hamiltonian flow will destroy their holomorphicity. However, for the purposes of Lagrangian Floer cohomology and the Fukaya category, only Hamiltonian flows can be used to move the Lagrangians so they intersect transversely. See the end of § 2.1 and the end of § 2.3.
$L_{i}$
by any non-trivial Hamiltonian flow will destroy their holomorphicity. However, for the purposes of Lagrangian Floer cohomology and the Fukaya category, only Hamiltonian flows can be used to move the Lagrangians so they intersect transversely. See the end of § 2.1 and the end of § 2.3.
On the other hand, the standard construction of Lagrangian Floer cohomology and the Fukaya category uses Hamiltonian flows to move all Lagrangians so they intersect transversely, or at least cleanly. As
![]() $I$
-holomorphic Lagrangians
$I$
-holomorphic Lagrangians
![]() $L_{i}$
move under a Hamiltonian flow and loose their holomorphicity,
$L_{i}$
move under a Hamiltonian flow and loose their holomorphicity,
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic maps with boundary in the
$\unicode[STIX]{x1D6E9}$
-holomorphic maps with boundary in the
![]() $L_{i}$
can appear for all
$L_{i}$
can appear for all
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
. Nonetheless, as a consequence of Theorem 1.6 and Gromov compactness, we show that the
$\unicode[STIX]{x1D6E9}\in R_{I}$
. Nonetheless, as a consequence of Theorem 1.6 and Gromov compactness, we show that the
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic maps that appear can be forced to remain in an arbitrarily small neighborhood of the
$\unicode[STIX]{x1D6E9}$
-holomorphic maps that appear can be forced to remain in an arbitrarily small neighborhood of the
![]() $L_{i}$
for all but countably many
$L_{i}$
for all but countably many
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
. This is the content of the following Theorem 1.7. In § 2.4, Theorem 1.7 is used to show that in a certain sense the Fukaya category generated by
$\unicode[STIX]{x1D6E9}\in R_{I}$
. This is the content of the following Theorem 1.7. In § 2.4, Theorem 1.7 is used to show that in a certain sense the Fukaya category generated by
![]() $I$
-holomorphic Lagrangians in a hyperkähler manifold is local. In Remark 2.7, we discuss how this locality result provides evidence for a connection between the Fukaya category and the sheaf theoretic alternatives proposed by Kapustin [Reference KapustinKap04, Reference KapustinKap05], Behrend and Fantechi [Reference Behrend and FantechiBF09], and Brav et al. [Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15].
$I$
-holomorphic Lagrangians in a hyperkähler manifold is local. In Remark 2.7, we discuss how this locality result provides evidence for a connection between the Fukaya category and the sheaf theoretic alternatives proposed by Kapustin [Reference KapustinKap04, Reference KapustinKap05], Behrend and Fantechi [Reference Behrend and FantechiBF09], and Brav et al. [Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15].
Theorem 1.7. Suppose
![]() $(M,\unicode[STIX]{x1D714}),L_{i}$
and
$(M,\unicode[STIX]{x1D714}),L_{i}$
and
![]() $P$
, are as in Theorem 1.6. Then, for all
$P$
, are as in Theorem 1.6. Then, for all
![]() $\unicode[STIX]{x1D6E9}\in (R_{I}\setminus P)\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
, we have the following. Choose Hamiltonian flows
$\unicode[STIX]{x1D6E9}\in (R_{I}\setminus P)\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
, we have the following. Choose Hamiltonian flows
![]() $\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M$
, constants
$\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M$
, constants
![]() $E_{0}\geqslant 0,\unicode[STIX]{x1D712}_{0}\in \mathbb{Z}$
, a finite subset
$E_{0}\geqslant 0,\unicode[STIX]{x1D712}_{0}\in \mathbb{Z}$
, a finite subset
![]() $A_{0}\subset A$
, and an open
$A_{0}\subset A$
, and an open
![]() $V\subset M$
such that
$V\subset M$
such that
There exists
![]() $\unicode[STIX]{x1D700}>0$
such that if
$\unicode[STIX]{x1D700}>0$
such that if
![]() $t<\unicode[STIX]{x1D700}$
, then for all nice
$t<\unicode[STIX]{x1D700}$
, then for all nice
![]() $\unicode[STIX]{x1D6F4}$
, all
$\unicode[STIX]{x1D6F4}$
, all
![]() $A_{0}$
-labelings
$A_{0}$
-labelings
![]() $l$
and all
$l$
and all
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic maps
$\unicode[STIX]{x1D6E9}$
-holomorphic maps
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
with
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
with
we have
Remark 1.8. If we choose the Hamiltonian flows
![]() $\unicode[STIX]{x1D711}_{i,t}$
to be real analytic and fix the topological type of
$\unicode[STIX]{x1D711}_{i,t}$
to be real analytic and fix the topological type of
![]() $\unicode[STIX]{x1D6F4}$
as well as
$\unicode[STIX]{x1D6F4}$
as well as
![]() $l$
, it should be possible to replace hypothesis (1) with the weaker hypothesis
$l$
, it should be possible to replace hypothesis (1) with the weaker hypothesis
See Remark 8.1 for a more in depth discussion.
Our proof of Theorem 1.6 relies on the following result, which is valid in a more general setting. For
![]() $\unicode[STIX]{x1D6E9}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
, let
$\unicode[STIX]{x1D6E9}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
, let
![]() $g_{\unicode[STIX]{x1D6E9}}$
denote the Riemannian metric defined by
$g_{\unicode[STIX]{x1D6E9}}$
denote the Riemannian metric defined by
For
![]() $h$
a Riemannian metric, let
$h$
a Riemannian metric, let
![]() $d_{h}$
denote the associated distance function.
$d_{h}$
denote the associated distance function.
Theorem 1.9. Suppose
![]() $M,\unicode[STIX]{x1D714}$
, and the Lagrangian submanifolds
$M,\unicode[STIX]{x1D714}$
, and the Lagrangian submanifolds
![]() $L_{i}$
for
$L_{i}$
for
![]() $i\in A$
are real analytic. Let
$i\in A$
are real analytic. Let
![]() $\unicode[STIX]{x1D6E9}$
be an
$\unicode[STIX]{x1D6E9}$
be an
![]() $\unicode[STIX]{x1D714}$
-tame almost complex structure such that the metric
$\unicode[STIX]{x1D714}$
-tame almost complex structure such that the metric
![]() $g_{\unicode[STIX]{x1D6E9}}$
is complete. Choose a nice Riemann surface
$g_{\unicode[STIX]{x1D6E9}}$
is complete. Choose a nice Riemann surface
![]() $\unicode[STIX]{x1D6F4}$
, a Hermitian metric
$\unicode[STIX]{x1D6F4}$
, a Hermitian metric
![]() $h$
on
$h$
on
![]() $\overline{\unicode[STIX]{x1D6F4}}$
and an
$\overline{\unicode[STIX]{x1D6F4}}$
and an
![]() $A$
-labeling
$A$
-labeling
![]() $l$
. Let
$l$
. Let
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
be a
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
be a
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map with
$\unicode[STIX]{x1D6E9}$
-holomorphic map with
![]() $u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
$u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
![]() $E_{g_{\unicode[STIX]{x1D6E9}}}(u)<\infty$
. Then
$E_{g_{\unicode[STIX]{x1D6E9}}}(u)<\infty$
. Then
![]() $u$
extends to a continuous map
$u$
extends to a continuous map
![]() $\overline{u}:\overline{\unicode[STIX]{x1D6F4}}\rightarrow M$
. Moreover, there exist
$\overline{u}:\overline{\unicode[STIX]{x1D6F4}}\rightarrow M$
. Moreover, there exist
![]() $c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that for each
$c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that for each
![]() $p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
we have
$p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
we have
If the Lagrangian submanifolds
![]() $L_{i}$
intersect each other cleanly, then Theorem 1.9 is well known and holds without any real analyticity hypothesis [Reference WoodwardWoo11, Lemma 2.5]. In the general case, the proof uses Łojasiewicz’s inequalities [Reference ŁojasiewiczŁoj65] and through them the real analyticity hypothesis in an essential way. Of course, the holomorphic Lagrangians considered in Theorems 1.6 and 1.7 are a fortiori real analytic. The use of Łojasiewicz’s gradient inequality to obtain results in geometric analysis dates back to the work of Simon on harmonic map heat flow and minimal surfaces [Reference SimonSim83]. Related works include [Reference Colding and MinicozziCM15, Reference Morgan, Mrowka and RubermanMMR94, Reference TaubesTau93].
$L_{i}$
intersect each other cleanly, then Theorem 1.9 is well known and holds without any real analyticity hypothesis [Reference WoodwardWoo11, Lemma 2.5]. In the general case, the proof uses Łojasiewicz’s inequalities [Reference ŁojasiewiczŁoj65] and through them the real analyticity hypothesis in an essential way. Of course, the holomorphic Lagrangians considered in Theorems 1.6 and 1.7 are a fortiori real analytic. The use of Łojasiewicz’s gradient inequality to obtain results in geometric analysis dates back to the work of Simon on harmonic map heat flow and minimal surfaces [Reference SimonSim83]. Related works include [Reference Colding and MinicozziCM15, Reference Morgan, Mrowka and RubermanMMR94, Reference TaubesTau93].
1.3 Outline of paper
In § 2, after giving necessary background, we explain the implications of Theorems 1.6 and 1.7 for the Fukaya category. In § 3, we outline how Theorem 1.6 explains the unusual abundance of special Lagrangian submanifolds in hyperkähler manifolds.
The proof of Theorem 1.9 is contained in §§ 4–6. Section 4 uses the Whitney regularity of analytic sets [Reference BierstoneBie80, Reference HardtHar83] to prove that the symplectic action of a sufficiently short path between two analytic Lagrangians is well defined. Section 5 proves an isoperimetric inequality for the symplectic action based on Łojasiewicz’s gradient inequality [Reference ŁojasiewiczŁoj65]. Finally, § 6 combines the results of the preceding two sections with properties of holomorphic curves and a control-function argument of Łojasiewicz [Reference ŁojasiewiczŁoj84] to deduce Theorem 1.9.
The proof of Theorem 1.6 is given in §§ 7–8. The main idea is that each homotopy class
![]() $h$
of maps
$h$
of maps
![]() $u$
as in Theorem 1.6 gives rise to a functional
$u$
as in Theorem 1.6 gives rise to a functional
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
on
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
on
![]() $R_{I}$
. The functional
$R_{I}$
. The functional
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
either vanishes identically or attains its maximum at unique
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
either vanishes identically or attains its maximum at unique
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
. Moreover, if
$\unicode[STIX]{x1D6E9}\in R_{I}$
. Moreover, if
![]() $h$
is represented by a non-constant
$h$
is represented by a non-constant
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map, then
$\unicode[STIX]{x1D6E9}$
-holomorphic map, then
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
must attain its unique maximum at
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
must attain its unique maximum at
![]() $\unicode[STIX]{x1D6E9}$
. So, if we remove the set of
$\unicode[STIX]{x1D6E9}$
. So, if we remove the set of
![]() $\unicode[STIX]{x1D6E9}$
at which
$\unicode[STIX]{x1D6E9}$
at which
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
attains its maximum for some
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
attains its maximum for some
![]() $h,\unicode[STIX]{x1D6F4}$
, there are no non-constant
$h,\unicode[STIX]{x1D6F4}$
, there are no non-constant
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic maps for all the remaining
$\unicode[STIX]{x1D6E9}$
-holomorphic maps for all the remaining
![]() $\unicode[STIX]{x1D6E9}$
. Section 7 uses Łojasiewicz’s triangulation theorem for real analytic sets [Reference ŁojasiewiczŁoj64] to show the set of homotopy classes
$\unicode[STIX]{x1D6E9}$
. Section 7 uses Łojasiewicz’s triangulation theorem for real analytic sets [Reference ŁojasiewiczŁoj64] to show the set of homotopy classes
![]() $h$
is countable. Furthermore, it establishes a framework within which the functional
$h$
is countable. Furthermore, it establishes a framework within which the functional
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
can be defined. More specifically, the functional
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
can be defined. More specifically, the functional
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
is given by integrating a Kähler form pulled-back by a representative of
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
is given by integrating a Kähler form pulled-back by a representative of
![]() $h$
. However, since the Lagrangians
$h$
. However, since the Lagrangians
![]() $L_{i}$
may intersect each other in quite bad sets, there need not exist smooth homotopies between different representatives. Thus, the integral defining
$L_{i}$
may intersect each other in quite bad sets, there need not exist smooth homotopies between different representatives. Thus, the integral defining
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
could a priori depend on the choice of representative of
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
could a priori depend on the choice of representative of
![]() $h$
. The proof that
$h$
. The proof that
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
in fact depends only on
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
in fact depends only on
![]() $h$
is given in § 7 using the properties of the symplectic action proved in §§ 4–5. Section 8 combines the results of § 7 and Theorem 1.9 to complete the proof of Theorem 1.6. It concludes with the proof of Theorem 1.7.
$h$
is given in § 7 using the properties of the symplectic action proved in §§ 4–5. Section 8 combines the results of § 7 and Theorem 1.9 to complete the proof of Theorem 1.6. It concludes with the proof of Theorem 1.7.
A result analogous to Theorem 1.6 for maps from closed Riemann surfaces to compact hyperkähler manifolds was proved in [Reference VerbitskyVer95] using Hodge theory. This result was generalized to the non-compact case in [Reference VerbitskyVer04]. The present work builds on the approach of [Reference VerbitskyVer04].
2 Floer cohomology and the Fukaya category
In this section, we describe how Theorem 1.6 implies Floer cohomology and the Fukaya category are particularly well behaved for holomorphic Lagrangian submanifolds of a hyperkähler manifold.
2.1 Geometric framework
We start with a brief overview of Floer cohomology and Fukaya
![]() $A_{\infty }$
operations for Lagrangian submanifolds with vanishing Maslov class. We refer the reader to [Reference Fukaya, Oh, Ohta and OnoFOOO09, Reference SeidelSei08] for a detailed treatment. Let
$A_{\infty }$
operations for Lagrangian submanifolds with vanishing Maslov class. We refer the reader to [Reference Fukaya, Oh, Ohta and OnoFOOO09, Reference SeidelSei08] for a detailed treatment. Let
denote the Novikov field. Let
![]() $\Vert \cdot \Vert :\unicode[STIX]{x1D6EC}\rightarrow \mathbb{R}_{{>}0}$
be the non-Archimedean norm given by
$\Vert \cdot \Vert :\unicode[STIX]{x1D6EC}\rightarrow \mathbb{R}_{{>}0}$
be the non-Archimedean norm given by
![]() $\Vert 0\Vert =0$
and
$\Vert 0\Vert =0$
and
Let
![]() $(M,\unicode[STIX]{x1D714})$
be a symplectic manifold of dimension
$(M,\unicode[STIX]{x1D714})$
be a symplectic manifold of dimension
![]() $2n$
, either compact or with appropriately bounded geometry. Let
$2n$
, either compact or with appropriately bounded geometry. Let
![]() $\unicode[STIX]{x1D6E9}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. Assume there exists a non-vanishing complex
$\unicode[STIX]{x1D6E9}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. Assume there exists a non-vanishing complex
![]() $n$
-form
$n$
-form
![]() $\unicode[STIX]{x1D6F7}$
that is of type
$\unicode[STIX]{x1D6F7}$
that is of type
![]() $(n,0)$
with respect to
$(n,0)$
with respect to
![]() $\unicode[STIX]{x1D6E9}$
. A grading for an oriented Lagrangian submanifold
$\unicode[STIX]{x1D6E9}$
. A grading for an oriented Lagrangian submanifold
![]() $L\subset M$
is the choice of a function
$L\subset M$
is the choice of a function
![]() $\unicode[STIX]{x1D703}_{L}:L\rightarrow \mathbb{R}$
such that
$\unicode[STIX]{x1D703}_{L}:L\rightarrow \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D6F7}|_{L}=e^{\sqrt{-1}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{L}}\unicode[STIX]{x1D70C}$
where
$\unicode[STIX]{x1D6F7}|_{L}=e^{\sqrt{-1}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{L}}\unicode[STIX]{x1D70C}$
where
![]() $\unicode[STIX]{x1D70C}$
is a positive real
$\unicode[STIX]{x1D70C}$
is a positive real
![]() $n$
-form on
$n$
-form on
![]() $L$
. Consider a collection
$L$
. Consider a collection
![]() ${\mathcal{L}}$
of graded spin compact Lagrangian submanifolds
${\mathcal{L}}$
of graded spin compact Lagrangian submanifolds
![]() $L_{i}\subset M$
for
$L_{i}\subset M$
for
![]() $i$
belonging to an index set
$i$
belonging to an index set
![]() $A$
. Assume that the
$A$
. Assume that the
![]() $L_{i}$
intersect each other cleanly. That is, for
$L_{i}$
intersect each other cleanly. That is, for
![]() $B\subset A$
, the intersection
$B\subset A$
, the intersection
![]() $L_{B}=\bigcap _{i\in B}L_{i}$
is a smooth manifold, and
$L_{B}=\bigcap _{i\in B}L_{i}$
is a smooth manifold, and
For each connected component
![]() $C\subset L_{i}\,\cap \,L_{j}$
, the gradings on
$C\subset L_{i}\,\cap \,L_{j}$
, the gradings on
![]() $L_{i},L_{j}$
, give rise to an integer
$L_{i},L_{j}$
, give rise to an integer
![]() $m_{C}$
, called the Maslov index, in the following way. Let
$m_{C}$
, called the Maslov index, in the following way. Let
![]() $p\in C$
. Choose a direct sum decomposition
$p\in C$
. Choose a direct sum decomposition
![]() $T_{p}L_{i}=\bigoplus _{k}V_{k}$
and
$T_{p}L_{i}=\bigoplus _{k}V_{k}$
and
![]() $\unicode[STIX]{x1D6FC}_{k}\in [0,1)$
such that
$\unicode[STIX]{x1D6FC}_{k}\in [0,1)$
such that
![]() $T_{p}L_{j}=\bigoplus _{k}e^{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6E9}}V_{k}$
. Then,
$T_{p}L_{j}=\bigoplus _{k}e^{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6E9}}V_{k}$
. Then,
One verifies that
![]() $m_{C}$
does not depend on
$m_{C}$
does not depend on
![]() $p$
or the direct sum decomposition.
$p$
or the direct sum decomposition.
We define the Floer complex
![]() $\mathit{CF}^{\ast }(L_{i},L_{j})$
as follows. For
$\mathit{CF}^{\ast }(L_{i},L_{j})$
as follows. For
![]() $N$
a smooth manifold, let
$N$
a smooth manifold, let
![]() $A^{k}(N)$
denote the differential
$A^{k}(N)$
denote the differential
![]() $k$
-forms on
$k$
-forms on
![]() $N$
. Define
$N$
. Define
The norm
![]() $\Vert \cdot \Vert$
on
$\Vert \cdot \Vert$
on
![]() $\unicode[STIX]{x1D6EC}$
induces a norm, also denoted
$\unicode[STIX]{x1D6EC}$
induces a norm, also denoted
![]() $\Vert \cdot \Vert$
, on
$\Vert \cdot \Vert$
, on
![]() $\mathit{CF}^{\ast }(L_{i},L_{j})$
, which makes
$\mathit{CF}^{\ast }(L_{i},L_{j})$
, which makes
![]() $\mathit{CF}^{\ast }(L_{i},L_{j})$
a normed
$\mathit{CF}^{\ast }(L_{i},L_{j})$
a normed
![]() $\unicode[STIX]{x1D6EC}$
vector space. Here and below, all normed vector spaces are understood to be completed with respect to the norm. If
$\unicode[STIX]{x1D6EC}$
vector space. Here and below, all normed vector spaces are understood to be completed with respect to the norm. If
![]() $\unicode[STIX]{x1D6FC}\in \mathit{CF}^{m}(L_{i},L_{j})$
for some
$\unicode[STIX]{x1D6FC}\in \mathit{CF}^{m}(L_{i},L_{j})$
for some
![]() $m$
, write
$m$
, write
![]() $|\unicode[STIX]{x1D6FC}|=m$
.
$|\unicode[STIX]{x1D6FC}|=m$
.
The vector spaces
![]() $\mathit{CF}^{\ast }(L_{i},L_{j})$
come with a family of multilinear operations constructed using
$\mathit{CF}^{\ast }(L_{i},L_{j})$
come with a family of multilinear operations constructed using
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic curves. Let
$\unicode[STIX]{x1D6E9}$
-holomorphic curves. Let
![]() $D\subset \mathbb{C}$
denote the closed unit disk equipped with the complex orientation, and let
$D\subset \mathbb{C}$
denote the closed unit disk equipped with the complex orientation, and let
![]() $\unicode[STIX]{x1D6E5}\subset (\unicode[STIX]{x2202}D)^{k+1}$
denote the pairwise diagonal. For
$\unicode[STIX]{x1D6E5}\subset (\unicode[STIX]{x2202}D)^{k+1}$
denote the pairwise diagonal. For
let
![]() $\mathbf{z}$
denote the corresponding subset of
$\mathbf{z}$
denote the corresponding subset of
![]() $\unicode[STIX]{x2202}D$
. Say that
$\unicode[STIX]{x2202}D$
. Say that
![]() $\vec{z}$
is cyclically ordered if its order agrees with the cyclic order given by the induced orientation of
$\vec{z}$
is cyclically ordered if its order agrees with the cyclic order given by the induced orientation of
![]() $\unicode[STIX]{x2202}D$
. Let
$\unicode[STIX]{x2202}D$
. Let
![]() $(z_{i},z_{i+1})\subset \unicode[STIX]{x2202}D$
denote the open interval starting at
$(z_{i},z_{i+1})\subset \unicode[STIX]{x2202}D$
denote the open interval starting at
![]() $z_{i}$
and ending at
$z_{i}$
and ending at
![]() $z_{i+1}$
with respect to the induced orientation of
$z_{i+1}$
with respect to the induced orientation of
![]() $\unicode[STIX]{x2202}D$
. For
$\unicode[STIX]{x2202}D$
. For
![]() ${\mathcal{I}}=(i_{0},\ldots ,i_{k})\in A^{k+1}$
and
${\mathcal{I}}=(i_{0},\ldots ,i_{k})\in A^{k+1}$
and
![]() $E\in \mathbb{R}$
, define
$E\in \mathbb{R}$
, define
 $$\begin{eqnarray}\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})=\left\{(u,\vec{z})\left|\begin{array}{@{}l@{}}\displaystyle \vec{z}\in (\unicode[STIX]{x2202}D)^{k+1}\setminus \unicode[STIX]{x1D6E5},\text{ cyclically ordered,}\\ \displaystyle u:D\setminus \mathbf{z}\rightarrow M\text{ smooth},\\ \displaystyle \overline{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D6E9}}u=0,\\ \displaystyle u((z_{j},z_{j+1}))\subset L_{i_{j}},\\ \displaystyle \int u^{\ast }\unicode[STIX]{x1D714}=E\end{array}\right.\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})=\left\{(u,\vec{z})\left|\begin{array}{@{}l@{}}\displaystyle \vec{z}\in (\unicode[STIX]{x2202}D)^{k+1}\setminus \unicode[STIX]{x1D6E5},\text{ cyclically ordered,}\\ \displaystyle u:D\setminus \mathbf{z}\rightarrow M\text{ smooth},\\ \displaystyle \overline{\unicode[STIX]{x2202}}_{\unicode[STIX]{x1D6E9}}u=0,\\ \displaystyle u((z_{j},z_{j+1}))\subset L_{i_{j}},\\ \displaystyle \int u^{\ast }\unicode[STIX]{x1D714}=E\end{array}\right.\right\}.\end{eqnarray}$$
For
![]() $(u,\vec{z})\in \widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
, we have [Reference McDuff and SalamonMS12, Lemma 2.2.1]
$(u,\vec{z})\in \widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
, we have [Reference McDuff and SalamonMS12, Lemma 2.2.1]
So, if
![]() $E<0$
, then
$E<0$
, then
![]() $\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})=\emptyset$
. Furthermore, if
$\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})=\emptyset$
. Furthermore, if
![]() $E=0$
, then
$E=0$
, then
![]() $\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
consists of constant maps.
$\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
consists of constant maps.
An automorphism of the disk
![]() $\unicode[STIX]{x1D711}\in \operatorname{PSL}(2,\mathbb{R})$
acts on
$\unicode[STIX]{x1D711}\in \operatorname{PSL}(2,\mathbb{R})$
acts on
by
![]() $u\mapsto u\circ \unicode[STIX]{x1D711}$
and
$u\mapsto u\circ \unicode[STIX]{x1D711}$
and
![]() $z_{j}\mapsto \unicode[STIX]{x1D711}^{-1}(z_{j})$
. A pair
$z_{j}\mapsto \unicode[STIX]{x1D711}^{-1}(z_{j})$
. A pair
![]() $(I,E)$
is called stable if either
$(I,E)$
is called stable if either
![]() $E>0$
or
$E>0$
or
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $E=0$
. If
$E=0$
. If
![]() $(I,E)$
is stable, then the action of
$(I,E)$
is stable, then the action of
![]() $\operatorname{PSL}(2,\mathbb{R})$
on
$\operatorname{PSL}(2,\mathbb{R})$
on
![]() ${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
has finite order stabilizers. For stable
${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
has finite order stabilizers. For stable
![]() $(I,E)$
, set
$(I,E)$
, set
![]() ${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})=\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})/\operatorname{PSL}(2,\mathbb{R})$
. Otherwise, set
${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})=\widetilde{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})/\operatorname{PSL}(2,\mathbb{R})$
. Otherwise, set
![]() ${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})=\emptyset$
. For
${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})=\emptyset$
. For
![]() $[u,\vec{z}]\in {\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
, the condition
$[u,\vec{z}]\in {\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
, the condition
and the assumption that the Lagrangians
![]() $L_{i}$
intersect cleanly imply that
$L_{i}$
intersect cleanly imply that
![]() $u$
extends to a continuous map
$u$
extends to a continuous map
![]() $\overline{u}:D\rightarrow M$
. See [Reference WoodwardWoo11, Lemma 2.5]. So, we define evaluation maps
$\overline{u}:D\rightarrow M$
. See [Reference WoodwardWoo11, Lemma 2.5]. So, we define evaluation maps
by
![]() $ev_{j}^{E}((u,\vec{z}))=\overline{u}(z_{j})$
. The spaces
$ev_{j}^{E}((u,\vec{z}))=\overline{u}(z_{j})$
. The spaces
![]() ${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
admit stable map compactifications
${\mathcal{M}}({\mathcal{I}},E,{\mathcal{L}})$
admit stable map compactifications
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
to which the evaluation maps extend naturally, and we denote these extensions by
$\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
to which the evaluation maps extend naturally, and we denote these extensions by
![]() $ev_{j}^{E}$
as well.
$ev_{j}^{E}$
as well.
Although moduli spaces of stable maps are usually singular, it can been shown in many cases that they admit a virtual fundamental chain, which behaves like the fundamental chain of a smooth manifold. For the purpose of this discussion, we assume that operations of virtual pull-back (respectively push-forward) of differential forms along the maps
![]() $ev_{i}^{E}$
(respectively the map
$ev_{i}^{E}$
(respectively the map
![]() $ev_{0}^{E}$
) have been defined. These operations should satisfy the same properties as push-forward and pull-back along smooth maps of manifolds, with
$ev_{0}^{E}$
) have been defined. These operations should satisfy the same properties as push-forward and pull-back along smooth maps of manifolds, with
![]() $ev_{0}^{E}$
behaving like a proper submersion. When the moduli spaces are smooth of expected dimension, virtual pull-back and push-forward reduce to the usual pull-back and push-forward. Such operations were introduced in a similar context by Fukaya [Reference FukayaFuk10]. It is expected that polyfolds [Reference Hofer, Wysocki and ZehnderHWZ10] will give an alternate approach. We implicitly extend all operations on differential forms
$ev_{0}^{E}$
behaving like a proper submersion. When the moduli spaces are smooth of expected dimension, virtual pull-back and push-forward reduce to the usual pull-back and push-forward. Such operations were introduced in a similar context by Fukaya [Reference FukayaFuk10]. It is expected that polyfolds [Reference Hofer, Wysocki and ZehnderHWZ10] will give an alternate approach. We implicitly extend all operations on differential forms
![]() $\unicode[STIX]{x1D6EC}$
-linearly to the Floer complex
$\unicode[STIX]{x1D6EC}$
-linearly to the Floer complex
![]() $\mathit{CF}^{\ast }(L_{i},L_{j})$
.
$\mathit{CF}^{\ast }(L_{i},L_{j})$
.
Define maps
by
where
The sum is well defined by Gromov’s compactness theorem [Reference GromovGro85]. The maps
![]() $\unicode[STIX]{x1D707}_{k}$
preserve grading by a virtual dimension calculation along the lines of [Reference Fukaya, Oh, Ohta and OnoFOOO09, § 3.7.5]. It follows from the structure of the compactification
$\unicode[STIX]{x1D707}_{k}$
preserve grading by a virtual dimension calculation along the lines of [Reference Fukaya, Oh, Ohta and OnoFOOO09, § 3.7.5]. It follows from the structure of the compactification
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
and the properties of pull-back and push-forward that the operations
$\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
and the properties of pull-back and push-forward that the operations
![]() $\unicode[STIX]{x1D707}_{k}$
satisfy the
$\unicode[STIX]{x1D707}_{k}$
satisfy the
![]() $A_{\infty }$
relations,
$A_{\infty }$
relations,
where
![]() $\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. See [Reference Solomon and TukachinskyST16] for a detailed derivation including signs in the case of a single Lagrangian. The generalization to our setting is not hard.
$\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. See [Reference Solomon and TukachinskyST16] for a detailed derivation including signs in the case of a single Lagrangian. The generalization to our setting is not hard.
Considering (3) for
![]() $k=1$
, we have
$k=1$
, we have
So, if
![]() $\unicode[STIX]{x1D707}_{0}=0\in \mathit{CF}(L_{i},L_{i})$
for
$\unicode[STIX]{x1D707}_{0}=0\in \mathit{CF}(L_{i},L_{i})$
for
![]() $i\in A$
, then
$i\in A$
, then
![]() $\unicode[STIX]{x1D707}_{1}^{2}=0$
, and we can define the Floer cohomology of
$\unicode[STIX]{x1D707}_{1}^{2}=0$
, and we can define the Floer cohomology of
![]() $L_{i},L_{j}$
, by
$L_{i},L_{j}$
, by
In this case, we say the Lagrangians
![]() $L_{i},i\in A$
, are tautologically unobstructed with respect to
$L_{i},i\in A$
, are tautologically unobstructed with respect to
![]() $\unicode[STIX]{x1D6E9}$
. Floer [Reference FloerFlo88] introduced
$\unicode[STIX]{x1D6E9}$
. Floer [Reference FloerFlo88] introduced
![]() $\mathit{HF}^{\ast }(L_{i},L_{j})$
under the assumption
$\mathit{HF}^{\ast }(L_{i},L_{j})$
under the assumption
![]() $\unicode[STIX]{x1D70B}_{2}(M,L_{i})=0$
for
$\unicode[STIX]{x1D70B}_{2}(M,L_{i})=0$
for
![]() $i\in A$
. Then, a holomorphic disk with boundary in
$i\in A$
. Then, a holomorphic disk with boundary in
![]() $L_{i}$
must have energy zero, so the stability condition implies
$L_{i}$
must have energy zero, so the stability condition implies
![]() $\overline{{\mathcal{M}}}(i,E,{\mathcal{L}})=\emptyset$
for
$\overline{{\mathcal{M}}}(i,E,{\mathcal{L}})=\emptyset$
for
![]() $i\in A$
. It follows that the Lagrangians
$i\in A$
. It follows that the Lagrangians
![]() $L_{i}$
are tautologically unobstructed for all tame
$L_{i}$
are tautologically unobstructed for all tame
![]() $\unicode[STIX]{x1D6E9}$
. A similar case is when the ambient manifold
$\unicode[STIX]{x1D6E9}$
. A similar case is when the ambient manifold
![]() $M$
and the Lagrangians
$M$
and the Lagrangians
![]() $L_{i}$
are exact. That is, there exist
$L_{i}$
are exact. That is, there exist
![]() $\unicode[STIX]{x1D706}\in A^{1}(M)$
with
$\unicode[STIX]{x1D706}\in A^{1}(M)$
with
![]() $d\unicode[STIX]{x1D706}=\unicode[STIX]{x1D714}$
and
$d\unicode[STIX]{x1D706}=\unicode[STIX]{x1D714}$
and
![]() $f_{i}:L_{i}\rightarrow \mathbb{R}$
with
$f_{i}:L_{i}\rightarrow \mathbb{R}$
with
![]() $\unicode[STIX]{x1D706}|_{L_{i}}=df_{i}$
. Then, Stokes’ theorem implies that a holomorphic disk with boundary in
$\unicode[STIX]{x1D706}|_{L_{i}}=df_{i}$
. Then, Stokes’ theorem implies that a holomorphic disk with boundary in
![]() $L_{i}$
must have energy zero, so the stability condition implies
$L_{i}$
must have energy zero, so the stability condition implies
![]() $\overline{{\mathcal{M}}}(i,E,{\mathcal{L}})=\emptyset$
for
$\overline{{\mathcal{M}}}(i,E,{\mathcal{L}})=\emptyset$
for
![]() $i\in A$
. Again, it follows that the Lagrangians
$i\in A$
. Again, it follows that the Lagrangians
![]() $L_{i}$
are tautologically unobstructed for all tame
$L_{i}$
are tautologically unobstructed for all tame
![]() $\unicode[STIX]{x1D6E9}$
. This is the setting of [Reference SeidelSei08].
$\unicode[STIX]{x1D6E9}$
. This is the setting of [Reference SeidelSei08].
To deal with general Lagrangian submanifolds, which may not be tautologically unobstructed, Fukaya et al. [Reference Fukaya, Oh, Ohta and OnoFOOO09] introduce the notion of bounding cochains. A bounding cochain for
![]() $L_{i}$
is a cochain
$L_{i}$
is a cochain
![]() $b\in \mathit{CF}^{1}(L_{i},L_{i})$
with
$b\in \mathit{CF}^{1}(L_{i},L_{i})$
with
![]() $\Vert b\Vert <1$
that satisfies the Maurer–Cartan equation
$\Vert b\Vert <1$
that satisfies the Maurer–Cartan equation
Let
![]() $b_{i}$
be a bounding cochain for
$b_{i}$
be a bounding cochain for
![]() $L_{i}$
. We define
$L_{i}$
. We define
and we define
by
One verifies algebraically that (3) holds with
![]() $\unicode[STIX]{x1D707}_{k}$
replaced by
$\unicode[STIX]{x1D707}_{k}$
replaced by
![]() $\hat{\unicode[STIX]{x1D707}}_{k}$
. Moreover, (4) is the same as
$\hat{\unicode[STIX]{x1D707}}_{k}$
. Moreover, (4) is the same as
![]() $\hat{\unicode[STIX]{x1D707}}_{0}=0$
. Consequently,
$\hat{\unicode[STIX]{x1D707}}_{0}=0$
. Consequently,
![]() $\hat{\unicode[STIX]{x1D707}}_{1}^{2}=0$
. Thus, we define
$\hat{\unicode[STIX]{x1D707}}_{1}^{2}=0$
. Thus, we define
Equation (3) for
![]() $k=2$
implies that the composition map
$k=2$
implies that the composition map
given by
![]() $[\unicode[STIX]{x1D6FC}_{2}]\circ [\unicode[STIX]{x1D6FC}_{1}]=(-1)^{|a_{1}|}[\hat{\unicode[STIX]{x1D707}}_{2}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})]$
is well defined. This composition is associative by (3) for
$[\unicode[STIX]{x1D6FC}_{2}]\circ [\unicode[STIX]{x1D6FC}_{1}]=(-1)^{|a_{1}|}[\hat{\unicode[STIX]{x1D707}}_{2}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})]$
is well defined. This composition is associative by (3) for
![]() $k=3$
. In particular, the Floer cohomology
$k=3$
. In particular, the Floer cohomology
![]() $\mathit{HF}^{\ast }((L_{i_{0}},b_{i_{0}}),(L_{i_{0}},b_{i_{0}}))$
of a Lagrangian with itself is an associative algebra.
$\mathit{HF}^{\ast }((L_{i_{0}},b_{i_{0}}),(L_{i_{0}},b_{i_{0}}))$
of a Lagrangian with itself is an associative algebra.
A Hamiltonian flow
![]() $\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
gives rise to a series of maps
$\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
gives rise to a series of maps
defined using moduli spaces of holomorphic disks. The geometric construction is similar to [Reference Fukaya, Oh, Ohta and OnoFOOO09, § 4.6.1] and [Reference SeidelSei08, § 10e]. The maps
![]() $f_{k}^{\unicode[STIX]{x1D711}}$
satisfy
$f_{k}^{\unicode[STIX]{x1D711}}$
satisfy
![]() $\Vert f_{k}\Vert \leqslant 1$
with strict inequality for
$\Vert f_{k}\Vert \leqslant 1$
with strict inequality for
![]() $k=0$
, and
$k=0$
, and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ l \\ m_{1}+\cdots +m_{l}=k}}\unicode[STIX]{x1D707}_{l}(f_{m_{1}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{m_{1}}),\ldots ,f_{m_{l}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{k-m_{l}+1},\ldots ,\unicode[STIX]{x1D6FC}_{k}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ k_{1}+k_{2}=k+1 \\ 1\leqslant i\leqslant k_{1}}}(-1)^{\star }f_{k_{1}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D707}_{k_{2}}(\unicode[STIX]{x1D6FC}_{i},\ldots ,\unicode[STIX]{x1D6FC}_{i+k_{2}-1}),\ldots ,\unicode[STIX]{x1D6FC}_{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ l \\ m_{1}+\cdots +m_{l}=k}}\unicode[STIX]{x1D707}_{l}(f_{m_{1}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{m_{1}}),\ldots ,f_{m_{l}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{k-m_{l}+1},\ldots ,\unicode[STIX]{x1D6FC}_{k}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ k_{1}+k_{2}=k+1 \\ 1\leqslant i\leqslant k_{1}}}(-1)^{\star }f_{k_{1}}^{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D707}_{k_{2}}(\unicode[STIX]{x1D6FC}_{i},\ldots ,\unicode[STIX]{x1D6FC}_{i+k_{2}-1}),\ldots ,\unicode[STIX]{x1D6FC}_{k}),\end{eqnarray}$$
where
![]() $\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. One verifies algebraically that if
$\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. One verifies algebraically that if
![]() $b$
solves the Maurer–Cartan equation (4), then so does
$b$
solves the Maurer–Cartan equation (4), then so does
A fundamental property of Floer cohomology is that any Hamiltonian flow
![]() $\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
gives rise [Reference SeidelSei08, § 8c,8k] to a canonical element
$\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
gives rise [Reference SeidelSei08, § 8c,8k] to a canonical element
If
![]() $\unicode[STIX]{x1D711}_{t}=\mathsf{id}_{M}$
, then
$\unicode[STIX]{x1D711}_{t}=\mathsf{id}_{M}$
, then
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
is the unit of the algebra
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
is the unit of the algebra
![]() $\mathit{HF}^{\ast }((L_{i_{0}},b_{i_{0}}),(L_{i_{0}},b_{i_{0}}))$
. Moreover, if
$\mathit{HF}^{\ast }((L_{i_{0}},b_{i_{0}}),(L_{i_{0}},b_{i_{0}}))$
. Moreover, if
![]() $\unicode[STIX]{x1D713}_{t}:M\rightarrow M$
is another Hamiltonian flow, then
$\unicode[STIX]{x1D713}_{t}:M\rightarrow M$
is another Hamiltonian flow, then
It follows that
In particular, composition with
![]() $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
induces a canonical isomorphism
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D711}}$
induces a canonical isomorphism
If
![]() $L,L^{\prime }$
, are tautologically unobstructed but do not intersect cleanly, we define
$L,L^{\prime }$
, are tautologically unobstructed but do not intersect cleanly, we define
where
![]() $\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
is a Hamiltonian flow such that
$\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
is a Hamiltonian flow such that
![]() $\unicode[STIX]{x1D711}_{1}(L^{\prime })$
is transverse to
$\unicode[STIX]{x1D711}_{1}(L^{\prime })$
is transverse to
![]() $L$
. Since the choice of bounding chain is canonical, we omit it from the notation. By the preceding discussion, this definition does not depend on the choice of
$L$
. Since the choice of bounding chain is canonical, we omit it from the notation. By the preceding discussion, this definition does not depend on the choice of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
2.2 First applications
Let
![]() $(M,I,J,K,g)$
be a hyperkähler manifold, and let
$(M,I,J,K,g)$
be a hyperkähler manifold, and let
![]() $L_{i}\subset M$
be
$L_{i}\subset M$
be
![]() $I$
-holomorphic Lagrangians for
$I$
-holomorphic Lagrangians for
![]() $i$
belonging to a countable index set
$i$
belonging to a countable index set
![]() $A$
. In particular, the submanifolds
$A$
. In particular, the submanifolds
![]() $L_{i}$
are Lagrangian with respect to the symplectic form
$L_{i}$
are Lagrangian with respect to the symplectic form
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
. In the following, all Floer-theoretic constructions will be carried out with respect to this symplectic form.
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
. In the following, all Floer-theoretic constructions will be carried out with respect to this symplectic form.
Corollary 2.1. For all
![]() $\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, the
$\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, the
![]() $A_{\infty }$
operations
$A_{\infty }$
operations
are given by
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})=\left\{\begin{array}{@{}ll@{}}d\unicode[STIX]{x1D6FC}_{1}\quad & k=1,\\ (-1)^{|\unicode[STIX]{x1D6FC}_{1}|}\unicode[STIX]{x1D6FC}_{1}\wedge \unicode[STIX]{x1D6FC}_{2}\quad & k=2,\\ 0\quad & k\neq 1,2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})=\left\{\begin{array}{@{}ll@{}}d\unicode[STIX]{x1D6FC}_{1}\quad & k=1,\\ (-1)^{|\unicode[STIX]{x1D6FC}_{1}|}\unicode[STIX]{x1D6FC}_{1}\wedge \unicode[STIX]{x1D6FC}_{2}\quad & k=2,\\ 0\quad & k\neq 1,2.\end{array}\right.\end{eqnarray}$$
In particular, the Lagrangians
![]() $L_{i}$
are tautologically unobstructed.
$L_{i}$
are tautologically unobstructed.
Corollary 2.2. For all
![]() $\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, the Floer coboundary operator
$\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, the Floer coboundary operator
![]() $\unicode[STIX]{x1D707}_{1}:\mathit{CF}^{\ast }(L_{i},L_{j})\rightarrow \mathit{CF}^{\ast }(L_{i},L_{j})$
coincides with the exterior derivative
$\unicode[STIX]{x1D707}_{1}:\mathit{CF}^{\ast }(L_{i},L_{j})\rightarrow \mathit{CF}^{\ast }(L_{i},L_{j})$
coincides with the exterior derivative
![]() $d$
. Thus,
$d$
. Thus,
Proof of Corollaries 2.1 and 2.2.
Constant maps have energy zero, so Theorem 1.6 implies that the moduli spaces
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
are empty unless
$\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
are empty unless
![]() $E=0$
. On the other hand, for
$E=0$
. On the other hand, for
![]() ${\mathcal{I}}\in A^{k+1}$
with
${\mathcal{I}}\in A^{k+1}$
with
![]() $k\leqslant 1$
, the stability condition implies that
$k\leqslant 1$
, the stability condition implies that
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
is empty unless
$\overline{{\mathcal{M}}}({\mathcal{I}},E,{\mathcal{L}})$
is empty unless
![]() $E>0$
. Consequently, we obtain (6) when
$E>0$
. Consequently, we obtain (6) when
![]() $k=0,1$
as well as Corollary 2.2.
$k=0,1$
as well as Corollary 2.2.
When
![]() $k\geqslant 2$
, constant maps can be stable. Let
$k\geqslant 2$
, constant maps can be stable. Let
![]() $\overline{{\mathcal{M}}}_{k+1}$
denote the moduli space of stable disks with
$\overline{{\mathcal{M}}}_{k+1}$
denote the moduli space of stable disks with
![]() $k+1$
cyclically ordered boundary marked points, up to biholomorphism. For
$k+1$
cyclically ordered boundary marked points, up to biholomorphism. For
![]() ${\mathcal{I}}=(i,i,\ldots ,i)$
we have
${\mathcal{I}}=(i,i,\ldots ,i)$
we have
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})\simeq L_{i}\times \overline{{\mathcal{M}}}_{k+1}$
, and
$\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})\simeq L_{i}\times \overline{{\mathcal{M}}}_{k+1}$
, and
![]() $ev_{j}^{0}:\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})\rightarrow L_{i}$
is the projection to the first factor for
$ev_{j}^{0}:\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})\rightarrow L_{i}$
is the projection to the first factor for
![]() $j=0,\ldots ,k$
. Since
$j=0,\ldots ,k$
. Since
![]() $\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})$
is a smooth manifold of expected dimension, the virtual fundamental class coincides with the usual fundamental class. We have
$\overline{{\mathcal{M}}}({\mathcal{I}},0,{\mathcal{L}})$
is a smooth manifold of expected dimension, the virtual fundamental class coincides with the usual fundamental class. We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}) & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}ev_{0\ast }^{0}\biggl(\bigwedge _{j=1}^{k}ev_{j}^{0\ast }\unicode[STIX]{x1D6FC}_{j}\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}ev_{0\ast }^{0}ev_{0}^{0\ast }\biggl(\bigwedge _{j=1}^{k}\unicode[STIX]{x1D6FC}_{j}\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}\bigwedge _{j=1}^{k}\unicode[STIX]{x1D6FC}_{j}\wedge ev_{0\ast }^{0}(1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}) & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}ev_{0\ast }^{0}\biggl(\bigwedge _{j=1}^{k}ev_{j}^{0\ast }\unicode[STIX]{x1D6FC}_{j}\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}ev_{0\ast }^{0}ev_{0}^{0\ast }\biggl(\bigwedge _{j=1}^{k}\unicode[STIX]{x1D6FC}_{j}\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})}\bigwedge _{j=1}^{k}\unicode[STIX]{x1D6FC}_{j}\wedge ev_{0\ast }^{0}(1).\nonumber\end{eqnarray}$$
The fiber of
![]() $ev_{0}^{0}$
is zero-dimensional only when
$ev_{0}^{0}$
is zero-dimensional only when
![]() $k=2$
, and in this case
$k=2$
, and in this case
![]() $ev_{0}^{0}$
is the identity map. Equation (6) for
$ev_{0}^{0}$
is the identity map. Equation (6) for
![]() $k\geqslant 2$
follows.◻
$k\geqslant 2$
follows.◻
Remark 2.3. Even without the assumption that
![]() $M$
is hyperkähler and the
$M$
is hyperkähler and the
![]() $L_{i}$
are
$L_{i}$
are
![]() $I$
-holomorphic, the
$I$
-holomorphic, the
![]() $A_{\infty }$
algebra
$A_{\infty }$
algebra
![]() $(\mathit{CF}(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is a deformation of the differential graded algebra of differential forms on
$(\mathit{CF}(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is a deformation of the differential graded algebra of differential forms on
![]() $L_{i}$
. See [Reference Fukaya, Oh, Ohta and OnoFOOO09, Theorem X] and [Reference Solomon and TukachinskyST16, Theorem 3]. Corollary 2.1 says the deformation is trivial if
$L_{i}$
. See [Reference Fukaya, Oh, Ohta and OnoFOOO09, Theorem X] and [Reference Solomon and TukachinskyST16, Theorem 3]. Corollary 2.1 says the deformation is trivial if
![]() $L_{i}$
is
$L_{i}$
is
![]() $I$
-holomorphic and
$I$
-holomorphic and
![]() $M$
is hyperkähler.
$M$
is hyperkähler.
2.3 Algebraic framework
Before presenting further applications, we recall some definitions pertaining to abstract
![]() $A_{\infty }$
categories. In general, a curved
$A_{\infty }$
categories. In general, a curved
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() ${\mathcal{A}}$
consists of the following data:
${\mathcal{A}}$
consists of the following data:
– a collection of objects
 $\operatorname{Ob}{\mathcal{A}}$
;
$\operatorname{Ob}{\mathcal{A}}$
;– for each pair of objects
 $A,B\in \operatorname{Ob}{\mathcal{A}}$
, a graded normed
$A,B\in \operatorname{Ob}{\mathcal{A}}$
, a graded normed
 $\unicode[STIX]{x1D6EC}$
vector space
$\unicode[STIX]{x1D6EC}$
vector space
 $\mathit{Hom}_{{\mathcal{A}}}(A,B)$
;
$\mathit{Hom}_{{\mathcal{A}}}(A,B)$
;– for each
 $(k+1)$
-tuple of objects
$(k+1)$
-tuple of objects
 $A_{0},\ldots ,A_{k},k\geqslant 0$
, a multilinear map
$A_{0},\ldots ,A_{k},k\geqslant 0$
, a multilinear map  $$\begin{eqnarray}\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}:\bigotimes _{i=1}^{k}\mathit{Hom}_{{\mathcal{A}}}(A_{i-1},A_{i})\rightarrow \mathit{Hom}_{{\mathcal{A}}}(A_{0},A_{k})[2-k].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}:\bigotimes _{i=1}^{k}\mathit{Hom}_{{\mathcal{A}}}(A_{i-1},A_{i})\rightarrow \mathit{Hom}_{{\mathcal{A}}}(A_{0},A_{k})[2-k].\end{eqnarray}$$
The maps
![]() $\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}$
must satisfy
$\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}$
must satisfy
![]() $\Vert \unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}\Vert \leqslant 1$
with strict inequality for
$\Vert \unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}\Vert \leqslant 1$
with strict inequality for
![]() $k=0$
, as well as the
$k=0$
, as well as the
![]() $A_{\infty }$
relations (3). For example, we can take the objects to be Lagrangian submanifolds, define
$A_{\infty }$
relations (3). For example, we can take the objects to be Lagrangian submanifolds, define
![]() $\mathit{Hom}(L_{0},L_{1})=\mathit{CF}^{\ast }(L_{0},L_{1})$
, and define the maps
$\mathit{Hom}(L_{0},L_{1})=\mathit{CF}^{\ast }(L_{0},L_{1})$
, and define the maps
![]() $\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}$
as in § 2.1. An
$\unicode[STIX]{x1D707}_{k}^{{\mathcal{A}}}$
as in § 2.1. An
![]() $A_{\infty }$
category is a curved
$A_{\infty }$
category is a curved
![]() $A_{\infty }$
category with
$A_{\infty }$
category with
![]() $\unicode[STIX]{x1D707}_{0}=0$
.
$\unicode[STIX]{x1D707}_{0}=0$
.
A curved
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
consists of a map
$f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
consists of a map
![]() $f:\operatorname{Ob}{\mathcal{A}}\rightarrow \operatorname{Ob}{\mathcal{B}}$
along with multilinear maps
$f:\operatorname{Ob}{\mathcal{A}}\rightarrow \operatorname{Ob}{\mathcal{B}}$
along with multilinear maps
for each
![]() $k+1$
tuple of objects
$k+1$
tuple of objects
![]() $A_{0},\ldots ,A_{k}\in \operatorname{Ob}{\mathcal{A}}$
, for
$A_{0},\ldots ,A_{k}\in \operatorname{Ob}{\mathcal{A}}$
, for
![]() $k\geqslant 0$
. The maps
$k\geqslant 0$
. The maps
![]() $f_{k}$
must satisfy
$f_{k}$
must satisfy
![]() $\Vert f_{k}\Vert \leqslant 1$
with strict inequality for
$\Vert f_{k}\Vert \leqslant 1$
with strict inequality for
![]() $k=0$
, as well as the relation
$k=0$
, as well as the relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ l \\ m_{1}+\cdots +m_{l}=k}}\unicode[STIX]{x1D707}_{l}^{{\mathcal{B}}}(f_{m_{1}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{m_{1}}),\ldots ,f_{m_{l}}(\unicode[STIX]{x1D6FC}_{k-m_{l}+1},\ldots ,\unicode[STIX]{x1D6FC}_{k}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ k_{1}+k_{2}=k+1 \\ 1\leqslant i\leqslant k_{1}}}(-1)^{\star }f_{k_{1}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D707}_{k_{2}}^{{\mathcal{A}}}(\unicode[STIX]{x1D6FC}_{i},\ldots ,\unicode[STIX]{x1D6FC}_{i+k_{2}-1}),\ldots ,\unicode[STIX]{x1D6FC}_{k}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ l \\ m_{1}+\cdots +m_{l}=k}}\unicode[STIX]{x1D707}_{l}^{{\mathcal{B}}}(f_{m_{1}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{m_{1}}),\ldots ,f_{m_{l}}(\unicode[STIX]{x1D6FC}_{k-m_{l}+1},\ldots ,\unicode[STIX]{x1D6FC}_{k}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ k_{1}+k_{2}=k+1 \\ 1\leqslant i\leqslant k_{1}}}(-1)^{\star }f_{k_{1}}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D707}_{k_{2}}^{{\mathcal{A}}}(\unicode[STIX]{x1D6FC}_{i},\ldots ,\unicode[STIX]{x1D6FC}_{i+k_{2}-1}),\ldots ,\unicode[STIX]{x1D6FC}_{k}),\nonumber\end{eqnarray}$$
where
![]() $\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. The sum on the left-hand side converges because
$\star =q-1+\sum _{j=1}^{q-1}|\unicode[STIX]{x1D6FC}_{j}|$
. The sum on the left-hand side converges because
![]() $\Vert f_{0}\Vert <1$
. An
$\Vert f_{0}\Vert <1$
. An
![]() $A_{\infty }$
functor is a curved
$A_{\infty }$
functor is a curved
![]() $A_{\infty }$
functor with
$A_{\infty }$
functor with
![]() $f_{0}=0$
.
$f_{0}=0$
.
Let
![]() ${\mathcal{A}}$
be a curved
${\mathcal{A}}$
be a curved
![]() $A_{\infty }$
category and
$A_{\infty }$
category and
![]() $A\in \operatorname{Ob}{\mathcal{A}}$
. A Maurer–Cartan element or bounding cochain [Reference Fukaya, Oh, Ohta and OnoFOOO09] for
$A\in \operatorname{Ob}{\mathcal{A}}$
. A Maurer–Cartan element or bounding cochain [Reference Fukaya, Oh, Ohta and OnoFOOO09] for
![]() $A$
is an element
$A$
is an element
![]() $b\in \mathit{Hom}_{{\mathcal{A}}}(A,A)$
with
$b\in \mathit{Hom}_{{\mathcal{A}}}(A,A)$
with
![]() $\Vert b\Vert <1$
such that
$\Vert b\Vert <1$
such that
Let
![]() $f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
be a curved
$f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
be a curved
![]() $A_{\infty }$
functor. If
$A_{\infty }$
functor. If
![]() $b$
is a bounding cochain for
$b$
is a bounding cochain for
![]() $A\in \operatorname{Ob}{\mathcal{A}}$
, then
$A\in \operatorname{Ob}{\mathcal{A}}$
, then
is a bounding cochain for
![]() $f(A)\in \operatorname{Ob}{\mathcal{B}}$
.
$f(A)\in \operatorname{Ob}{\mathcal{B}}$
.
To a curved
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() ${\mathcal{A}}$
, we associate the
${\mathcal{A}}$
, we associate the
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() $\widehat{{\mathcal{A}}}$
defined as follows. An object of
$\widehat{{\mathcal{A}}}$
defined as follows. An object of
![]() $\widehat{{\mathcal{A}}}$
is a pair of an object
$\widehat{{\mathcal{A}}}$
is a pair of an object
![]() $A\in \operatorname{Ob}{\mathcal{A}}$
and a bounding cochain
$A\in \operatorname{Ob}{\mathcal{A}}$
and a bounding cochain
![]() $b$
for
$b$
for
![]() $A$
. For
$A$
. For
![]() $(A_{i},b_{i})\in \operatorname{Ob}\widehat{{\mathcal{A}}}$
we define
$(A_{i},b_{i})\in \operatorname{Ob}\widehat{{\mathcal{A}}}$
we define
For
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathit{Hom}_{\widehat{{\mathcal{A}}}}((A_{i-1},b_{i-1}),(A_{i},b_{i}))$
, we define
$\unicode[STIX]{x1D6FC}_{i}\in \mathit{Hom}_{\widehat{{\mathcal{A}}}}((A_{i-1},b_{i-1}),(A_{i},b_{i}))$
, we define
To a curved
![]() ${\mathcal{A}}_{\infty }$
functor
${\mathcal{A}}_{\infty }$
functor
![]() $f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
, we associate the
$f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
, we associate the
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $\hat{f}:\widehat{{\mathcal{A}}}\rightarrow \widehat{{\mathcal{B}}}$
defined as follows. The map
$\hat{f}:\widehat{{\mathcal{A}}}\rightarrow \widehat{{\mathcal{B}}}$
defined as follows. The map
![]() $\hat{f}:\operatorname{Ob}\widehat{{\mathcal{A}}}\rightarrow \operatorname{Ob}\widehat{{\mathcal{B}}}$
is given by
$\hat{f}:\operatorname{Ob}\widehat{{\mathcal{A}}}\rightarrow \operatorname{Ob}\widehat{{\mathcal{B}}}$
is given by
For
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathit{Hom}_{\widehat{{\mathcal{A}}}}((A_{i-1},b_{i-1}),(A_{i},b_{i}))$
, we define
$\unicode[STIX]{x1D6FC}_{i}\in \mathit{Hom}_{\widehat{{\mathcal{A}}}}((A_{i-1},b_{i-1}),(A_{i},b_{i}))$
, we define
Let
![]() ${\mathcal{A}}$
be an
${\mathcal{A}}$
be an
![]() $A_{\infty }$
category. The associated cohomological category
$A_{\infty }$
category. The associated cohomological category
![]() $H({\mathcal{A}})$
has the same objects, its morphism spaces are given by
$H({\mathcal{A}})$
has the same objects, its morphism spaces are given by
and the composition of morphisms is given by
Composition of morphisms is associative because of (3) for
![]() $k=3$
. If we drop the sign in (7), composition is no longer associative. Rather, we obtain an
$k=3$
. If we drop the sign in (7), composition is no longer associative. Rather, we obtain an
![]() $A_{\infty }$
category, called the cohomological
$A_{\infty }$
category, called the cohomological
![]() $A_{\infty }$
category, which has all operations zero except for
$A_{\infty }$
category, which has all operations zero except for
![]() $k=2$
. An
$k=2$
. An
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
induces a functor
$f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
induces a functor
![]() $H(f):H({\mathcal{A}})\rightarrow H(B)$
. Suppose
$H(f):H({\mathcal{A}})\rightarrow H(B)$
. Suppose
![]() $H({\mathcal{A}}),H({\mathcal{B}})$
, have identity morphisms. Then the functor
$H({\mathcal{A}}),H({\mathcal{B}})$
, have identity morphisms. Then the functor
![]() $f$
is called a quasi-equivalence if
$f$
is called a quasi-equivalence if
![]() $H(f)$
is an equivalence. An
$H(f)$
is an equivalence. An
![]() $A_{\infty }$
category is called formal if it is
$A_{\infty }$
category is called formal if it is
![]() $A_{\infty }$
equivalent to its cohomological
$A_{\infty }$
equivalent to its cohomological
![]() $A_{\infty }$
category.
$A_{\infty }$
category.
A paradigmatic example of quasi-equivalent
![]() $A_{\infty }$
categories is the following. Let
$A_{\infty }$
categories is the following. Let
![]() $(M,\unicode[STIX]{x1D714})$
be as in § 2.1 and let
$(M,\unicode[STIX]{x1D714})$
be as in § 2.1 and let
![]() ${\mathcal{L}}$
be a collection of graded spin compact Lagrangian submanifolds
${\mathcal{L}}$
be a collection of graded spin compact Lagrangian submanifolds
![]() $L_{i}\subset M,\,i\in A$
, that intersect cleanly. For
$L_{i}\subset M,\,i\in A$
, that intersect cleanly. For
![]() $j=0,1$
, let
$j=0,1$
, let
![]() ${\mathcal{A}}_{j}$
denote the curved
${\mathcal{A}}_{j}$
denote the curved
![]() $A_{\infty }$
category associated to
$A_{\infty }$
category associated to
![]() ${\mathcal{L}}$
using the almost complex structure
${\mathcal{L}}$
using the almost complex structure
![]() $\unicode[STIX]{x1D6E9}_{j}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. Since
$\unicode[STIX]{x1D6E9}_{j}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. Since
![]() ${\mathcal{J}}_{\unicode[STIX]{x1D714}}$
is contractible, one can always find a path
${\mathcal{J}}_{\unicode[STIX]{x1D714}}$
is contractible, one can always find a path
![]() $\unicode[STIX]{x1D6E9}_{t}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}},t\in [0,1]$
, from
$\unicode[STIX]{x1D6E9}_{t}\in {\mathcal{J}}_{\unicode[STIX]{x1D714}},t\in [0,1]$
, from
![]() $\unicode[STIX]{x1D6E9}_{0}$
to
$\unicode[STIX]{x1D6E9}_{0}$
to
![]() $\unicode[STIX]{x1D6E9}_{1}$
. To such a path one can associate a curved
$\unicode[STIX]{x1D6E9}_{1}$
. To such a path one can associate a curved
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $f^{\unicode[STIX]{x1D6E9}}:{\mathcal{A}}_{0}\rightarrow {\mathcal{A}}_{1}$
such that the
$f^{\unicode[STIX]{x1D6E9}}:{\mathcal{A}}_{0}\rightarrow {\mathcal{A}}_{1}$
such that the
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $\hat{f}^{\unicode[STIX]{x1D6E9}}:\widehat{{\mathcal{A}}}_{0}\rightarrow \widehat{{\mathcal{A}}}_{1}$
is a quasi-equivalence. Thus, one can associate an
$\hat{f}^{\unicode[STIX]{x1D6E9}}:\widehat{{\mathcal{A}}}_{0}\rightarrow \widehat{{\mathcal{A}}}_{1}$
is a quasi-equivalence. Thus, one can associate an
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
to
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
to
![]() ${\mathcal{L}}$
that, up to quasi-equivalence, depends only on the symplectic form
${\mathcal{L}}$
that, up to quasi-equivalence, depends only on the symplectic form
![]() $\unicode[STIX]{x1D714}$
. We call
$\unicode[STIX]{x1D714}$
. We call
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
the Fukaya category of
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
the Fukaya category of
![]() ${\mathcal{L}}$
.
${\mathcal{L}}$
.
Similarly, let
![]() $\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M,i\in A,t\in [0,1]$
, be a collection of Hamiltonian flows such that the Lagrangian submanifolds
$\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M,i\in A,t\in [0,1]$
, be a collection of Hamiltonian flows such that the Lagrangian submanifolds
![]() $\unicode[STIX]{x1D711}_{i,1}(L_{i})$
intersect cleanly. Let
$\unicode[STIX]{x1D711}_{i,1}(L_{i})$
intersect cleanly. Let
![]() ${\mathcal{L}}^{\unicode[STIX]{x1D711}}$
denote the collection of Lagrangians
${\mathcal{L}}^{\unicode[STIX]{x1D711}}$
denote the collection of Lagrangians
![]() $\unicode[STIX]{x1D711}_{i,1}(L_{i}),i\in A$
. Then we have a curved
$\unicode[STIX]{x1D711}_{i,1}(L_{i}),i\in A$
. Then we have a curved
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $f^{\unicode[STIX]{x1D711}}:{\mathcal{A}}_{{\mathcal{L}}}\rightarrow {\mathcal{A}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
such that the
$f^{\unicode[STIX]{x1D711}}:{\mathcal{A}}_{{\mathcal{L}}}\rightarrow {\mathcal{A}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
such that the
![]() $A_{\infty }$
functor
$A_{\infty }$
functor
![]() $\hat{f}^{\unicode[STIX]{x1D711}}:\widehat{{\mathcal{A}}}_{{\mathcal{L}}}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
is a quasi-equivalence. Thus, one sees that up to quasi-equivalence, the Fukaya category
$\hat{f}^{\unicode[STIX]{x1D711}}:\widehat{{\mathcal{A}}}_{{\mathcal{L}}}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
is a quasi-equivalence. Thus, one sees that up to quasi-equivalence, the Fukaya category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
depends only on the Hamiltonian isotopy classes of the Lagrangian submanifolds
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
depends only on the Hamiltonian isotopy classes of the Lagrangian submanifolds
![]() $L_{i},i\in A$
.
$L_{i},i\in A$
.
It follows that the Fukaya category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is well defined even when the Lagrangians
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is well defined even when the Lagrangians
![]() $L_{i}$
do not intersect cleanly. Indeed, it is always possible to choose
$L_{i}$
do not intersect cleanly. Indeed, it is always possible to choose
![]() $\unicode[STIX]{x1D711}_{i,t}$
such that the Lagrangians
$\unicode[STIX]{x1D711}_{i,t}$
such that the Lagrangians
![]() $\unicode[STIX]{x1D711}_{i,1}(L_{i})$
intersect cleanly, so we may define
$\unicode[STIX]{x1D711}_{i,1}(L_{i})$
intersect cleanly, so we may define
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}:=\widehat{{\mathcal{A}}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
. Any two choices of Hamiltonian flows
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}:=\widehat{{\mathcal{A}}}_{{\mathcal{L}}^{\unicode[STIX]{x1D711}}}$
. Any two choices of Hamiltonian flows
![]() $\unicode[STIX]{x1D711}_{i,t}$
differ by a Hamiltonian flow, so the preceding discussion shows that, up to quasi-equivalence, the definition does not depend on the choice of
$\unicode[STIX]{x1D711}_{i,t}$
differ by a Hamiltonian flow, so the preceding discussion shows that, up to quasi-equivalence, the definition does not depend on the choice of
![]() $\unicode[STIX]{x1D711}_{i,t}$
.
$\unicode[STIX]{x1D711}_{i,t}$
.
2.4 Locality
We return to the setting where
![]() $(M,I,J,K,g)$
is a hyperkähler manifold,
$(M,I,J,K,g)$
is a hyperkähler manifold,
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and
![]() ${\mathcal{L}}$
is a collection of graded spin compact
${\mathcal{L}}$
is a collection of graded spin compact
![]() $I$
-holomorphic Lagrangians
$I$
-holomorphic Lagrangians
![]() $L_{i}\subset M,i\in A$
, with
$L_{i}\subset M,i\in A$
, with
![]() $A$
finite now. We do not assume the Lagrangians
$A$
finite now. We do not assume the Lagrangians
![]() $L_{i}$
intersect cleanly. Let
$L_{i}$
intersect cleanly. Let
![]() $\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M,\,i\in A,t\in [0,1]$
, be a collection of real analytic Hamiltonian flows such that the Lagrangian submanifolds
$\unicode[STIX]{x1D711}_{i,t}:M\rightarrow M,\,i\in A,t\in [0,1]$
, be a collection of real analytic Hamiltonian flows such that the Lagrangian submanifolds
![]() $\unicode[STIX]{x1D711}_{i,t}(L_{i})$
intersect cleanly for
$\unicode[STIX]{x1D711}_{i,t}(L_{i})$
intersect cleanly for
![]() $t\in (0,1]$
. Let
$t\in (0,1]$
. Let
![]() ${\mathcal{L}}_{t}$
denote the collection of Lagrangian submanifolds
${\mathcal{L}}_{t}$
denote the collection of Lagrangian submanifolds
![]() $\unicode[STIX]{x1D711}_{i,t}(L_{i}),i\in A$
. The following is a special case of Theorem 1.7.
$\unicode[STIX]{x1D711}_{i,t}(L_{i}),i\in A$
. The following is a special case of Theorem 1.7.
Corollary 2.4. For all
![]() $\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, we have the following. Choose
$\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
except a countable set, we have the following. Choose
![]() $E_{0}\geqslant 0,K\in \mathbb{Z}_{{\geqslant}0}$
, and an open
$E_{0}\geqslant 0,K\in \mathbb{Z}_{{\geqslant}0}$
, and an open
![]() $V\subset M$
such that
$V\subset M$
such that
Then, there exists
![]() $\unicode[STIX]{x1D700}>0$
such that for all
$\unicode[STIX]{x1D700}>0$
such that for all
we have
As a consequence of Corollary 2.4 and the discussion in § 2.3, we obtain the following locality statement for
![]() $\widetilde{{\mathcal{A}}}_{{\mathcal{L}}}$
.
$\widetilde{{\mathcal{A}}}_{{\mathcal{L}}}$
.
Corollary 2.5. Choose
![]() $E_{0},K$
and
$E_{0},K$
and
![]() $V$
, as in Corollary 2.4. Then
$V$
, as in Corollary 2.4. Then
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is quasi-equivalent to an
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is quasi-equivalent to an
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() $\widehat{{\mathcal{B}}}$
with the same objects, such that there exist operations
$\widehat{{\mathcal{B}}}$
with the same objects, such that there exist operations
with
and
![]() $\unicode[STIX]{x1D707}_{k}^{V}$
only depends on the geometry of
$\unicode[STIX]{x1D707}_{k}^{V}$
only depends on the geometry of
![]() $V$
. In fact, we may take
$V$
. In fact, we may take
![]() $\widehat{{\mathcal{B}}}=\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}$
with
$\widehat{{\mathcal{B}}}=\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}$
with
![]() $t<\unicode[STIX]{x1D700}$
and
$t<\unicode[STIX]{x1D700}$
and
![]() $\unicode[STIX]{x1D700}$
as in Corollary 2.4.
$\unicode[STIX]{x1D700}$
as in Corollary 2.4.
Remark 2.6. Starting from Corollary 2.5, it should be possible to show that in fact, up to quasi-equivalence, the
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() $\widehat{A}_{{\mathcal{L}}}$
depends only on
$\widehat{A}_{{\mathcal{L}}}$
depends only on
![]() $V$
. The proof would use a categorical generalization of the obstruction theory of
$V$
. The proof would use a categorical generalization of the obstruction theory of
![]() $A_{n,K}$
algebras developed in [Reference Fukaya, Oh, Ohta and OnoFOOO09, § 7.2.6]. Indeed, by Corollary 2.5, for arbitrarily large
$A_{n,K}$
algebras developed in [Reference Fukaya, Oh, Ohta and OnoFOOO09, § 7.2.6]. Indeed, by Corollary 2.5, for arbitrarily large
![]() $E_{0}$
and
$E_{0}$
and
![]() $K$
, we can define an
$K$
, we can define an
![]() $A_{E_{0},K}$
category
$A_{E_{0},K}$
category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}^{V}$
depending only on
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}^{V}$
depending only on
![]() $V$
by replacing the usual structure maps of
$V$
by replacing the usual structure maps of
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}$
with the maps
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}$
with the maps
![]() $\unicode[STIX]{x1D707}_{k}^{V}$
. A generalization of Theorem 1.7 should imply that for arbitrarily large
$\unicode[STIX]{x1D707}_{k}^{V}$
. A generalization of Theorem 1.7 should imply that for arbitrarily large
![]() $E_{0},K$
there exists
$E_{0},K$
there exists
![]() $\unicode[STIX]{x1D700}>0$
such that for
$\unicode[STIX]{x1D700}>0$
such that for
![]() $t,t^{\prime }<\unicode[STIX]{x1D700}$
a truncated version of the usual quasi-equivalence
$t,t^{\prime }<\unicode[STIX]{x1D700}$
a truncated version of the usual quasi-equivalence
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t^{\prime }}}$
gives an
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t^{\prime }}}$
gives an
![]() $A_{E_{0},K}$
quasi-equivalence
$A_{E_{0},K}$
quasi-equivalence
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}^{V}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t^{\prime }}}^{V}$
. Then one can apply the categorical version of [Reference Fukaya, Oh, Ohta and OnoFOOO09, Theorem 7.2.72] to construct by a limiting procedure an
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t}}^{V}\rightarrow \widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t^{\prime }}}^{V}$
. Then one can apply the categorical version of [Reference Fukaya, Oh, Ohta and OnoFOOO09, Theorem 7.2.72] to construct by a limiting procedure an
![]() $A_{\infty }$
category
$A_{\infty }$
category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}^{V}$
depending only on
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}^{V}$
depending only on
![]() $V$
by extending the
$V$
by extending the
![]() $A_{n,K}$
structure on
$A_{n,K}$
structure on
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t_{0}}}^{V}$
for a fixed
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}_{t_{0}}}^{V}$
for a fixed
![]() $t_{0}$
. Examining the construction, one finds that
$t_{0}$
. Examining the construction, one finds that
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}^{V}$
is quasi-equivalent to
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}^{V}$
is quasi-equivalent to
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
.
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
.
Remark 2.7. Kapustin gives physical arguments [Reference KapustinKap04, Reference KapustinKap05] for the Fukaya category of a hyperkähler manifold
![]() $(M,I,J,K,g)$
equipped with the symplectic form
$(M,I,J,K,g)$
equipped with the symplectic form
![]() $\unicode[STIX]{x1D714}_{J}$
to coincide with the category of deformation quantization modules [Reference Kashiwara and SchapiraKS12] on the holomorphic symplectic manifold
$\unicode[STIX]{x1D714}_{J}$
to coincide with the category of deformation quantization modules [Reference Kashiwara and SchapiraKS12] on the holomorphic symplectic manifold
![]() $(M,I,\unicode[STIX]{x1D6FA}_{I})$
. Given a spin holomorphic Lagrangian submanifold
$(M,I,\unicode[STIX]{x1D6FA}_{I})$
. Given a spin holomorphic Lagrangian submanifold
![]() $L\subset M$
, D’Agnolo and Schapira [Reference D’Agnolo and SchapiraDS07] construct a deformation quantization module
$L\subset M$
, D’Agnolo and Schapira [Reference D’Agnolo and SchapiraDS07] construct a deformation quantization module
![]() $D_{L}^{\bullet }$
supported on
$D_{L}^{\bullet }$
supported on
![]() $L$
. Thus, one would expect that
$L$
. Thus, one would expect that
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is equivalent in some sense to the full subcategory
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
is equivalent in some sense to the full subcategory
![]() ${\mathcal{D}}_{{\mathcal{L}}}$
of deformation quantization modules on
${\mathcal{D}}_{{\mathcal{L}}}$
of deformation quantization modules on
![]() $M$
with objects
$M$
with objects
![]() $D_{L_{i}}^{\bullet }$
for
$D_{L_{i}}^{\bullet }$
for
![]() $i\in A$
. By definition, the category
$i\in A$
. By definition, the category
![]() ${\mathcal{D}}_{{\mathcal{L}}}$
depends only on an arbitrarily small open neighborhood
${\mathcal{D}}_{{\mathcal{L}}}$
depends only on an arbitrarily small open neighborhood
![]() $V$
of
$V$
of
![]() $\bigcup _{i\in A}L_{i}$
. Corollary 2.5 and Remark 2.6 show that although a priori the Fukaya category
$\bigcup _{i\in A}L_{i}$
. Corollary 2.5 and Remark 2.6 show that although a priori the Fukaya category
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
depends on the symplectic geometry of the whole manifold
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
depends on the symplectic geometry of the whole manifold
![]() $M$
, in fact,
$M$
, in fact,
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
also only depends on
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
also only depends on
![]() $V$
. This can be seen as a first step toward proving the expected equivalence of
$V$
. This can be seen as a first step toward proving the expected equivalence of
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
and
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
and
![]() ${\mathcal{D}}_{{\mathcal{L}}}$
.
${\mathcal{D}}_{{\mathcal{L}}}$
.
In a similar vein, Behrend and Fantechi [Reference Behrend and FantechiBF09] outline the construction of a differential graded category
![]() ${\mathcal{B}}$
associated to a collection of holomorphic Lagrangians in holomorphic symplectic manifold
${\mathcal{B}}$
associated to a collection of holomorphic Lagrangians in holomorphic symplectic manifold
![]() $(M,I,\unicode[STIX]{x1D6FA}_{I})$
and speculate on its relation to the corresponding Fukaya category. Again,
$(M,I,\unicode[STIX]{x1D6FA}_{I})$
and speculate on its relation to the corresponding Fukaya category. Again,
![]() ${\mathcal{B}}$
depends only on an arbitrarily small neighborhood of the Lagrangians. The cohomology of the morphism complex
${\mathcal{B}}$
depends only on an arbitrarily small neighborhood of the Lagrangians. The cohomology of the morphism complex
![]() $\mathit{Hom}_{{\mathcal{B}}}(L_{0},L_{1})$
is called the virtual de Rham cohomology of the intersection
$\mathit{Hom}_{{\mathcal{B}}}(L_{0},L_{1})$
is called the virtual de Rham cohomology of the intersection
![]() $L_{0}\,\cap \,L_{1}$
. If
$L_{0}\,\cap \,L_{1}$
. If
![]() $L_{0}$
and
$L_{0}$
and
![]() $L_{1}$
intersect cleanly, the virtual de Rham cohomology of
$L_{1}$
intersect cleanly, the virtual de Rham cohomology of
![]() $L_{0}\,\cap \,L_{1}$
coincides with the usual de Rham cohomology. When
$L_{0}\,\cap \,L_{1}$
coincides with the usual de Rham cohomology. When
![]() $M$
is hyperkähler, Corollary 2.2 asserts the same for the Floer cohomology
$M$
is hyperkähler, Corollary 2.2 asserts the same for the Floer cohomology
![]() $\mathit{HF}^{\ast }(L_{0},L_{1})$
up to tensoring with
$\mathit{HF}^{\ast }(L_{0},L_{1})$
up to tensoring with
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Brav et al. [Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15] and Bussi [Reference BussiBus14] give a construction of the virtual de Rham cohomology of a pair of Lagrangians
![]() $L_{0},L_{1}\subset M$
in terms of the hypercohomology of a perverse sheaf
$L_{0},L_{1}\subset M$
in terms of the hypercohomology of a perverse sheaf
![]() $P_{L_{0},L_{1}}^{\bullet }$
supported on
$P_{L_{0},L_{1}}^{\bullet }$
supported on
![]() $L_{0}\,\cap \,L_{1}$
. As explained in [Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15, Remark 6.15], it follows from the work of Kashiwara and Schapira [Reference Kashiwara and SchapiraKS08] that the perverse sheaf
$L_{0}\,\cap \,L_{1}$
. As explained in [Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15, Remark 6.15], it follows from the work of Kashiwara and Schapira [Reference Kashiwara and SchapiraKS08] that the perverse sheaf
![]() $P_{L_{0},L_{1}}$
can be recovered as
$P_{L_{0},L_{1}}$
can be recovered as
![]() $R{\mathcal{H}}om(D_{L_{0}}^{\bullet },D_{L_{1}}^{\bullet })$
. The same remark speculates on a connection between
$R{\mathcal{H}}om(D_{L_{0}}^{\bullet },D_{L_{1}}^{\bullet })$
. The same remark speculates on a connection between
![]() $\mathbb{H}^{\ast }(P_{L_{0},L_{1}}^{\bullet })$
and
$\mathbb{H}^{\ast }(P_{L_{0},L_{1}}^{\bullet })$
and
![]() $\mathit{HF}^{\ast }(L_{0},L_{1})$
.
$\mathit{HF}^{\ast }(L_{0},L_{1})$
.
2.5 Formality
Let
![]() $(M,I,J,K,g)$
be a hyperkähler manifold, take
$(M,I,J,K,g)$
be a hyperkähler manifold, take
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and let
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{J}$
and let
![]() ${\mathcal{L}}$
be a collection of graded spin compact
${\mathcal{L}}$
be a collection of graded spin compact
![]() $I$
-holomorphic Lagrangians
$I$
-holomorphic Lagrangians
![]() $L_{i}\subset M,i\in A$
, with
$L_{i}\subset M,i\in A$
, with
![]() $A$
countable. By Corollary 2.1, we may choose
$A$
countable. By Corollary 2.1, we may choose
![]() $\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
with respect to which
$\unicode[STIX]{x1D6E9}\in R_{I}\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
with respect to which
![]() $L_{i}$
is tautologically unobstructed for
$L_{i}$
is tautologically unobstructed for
![]() $i\in A$
.
$i\in A$
.
Corollary 2.8 (I. Smith).
The
![]() $A_{\infty }$
algebra
$A_{\infty }$
algebra
![]() $(\mathit{CF}^{\ast }(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is formal.
$(\mathit{CF}^{\ast }(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is formal.
Proof. Corollary 2.1 shows that
![]() $(\mathit{CF}^{\ast }(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is the usual dg algebra of differential forms on
$(\mathit{CF}^{\ast }(L_{i},L_{i}),\unicode[STIX]{x1D707}_{k})$
is the usual dg algebra of differential forms on
![]() $L_{i}$
with the product modified by a sign as in (7). Moreover,
$L_{i}$
with the product modified by a sign as in (7). Moreover,
![]() $\unicode[STIX]{x1D714}_{I}$
is a Kähler form for
$\unicode[STIX]{x1D714}_{I}$
is a Kähler form for
![]() $L_{i}$
. So, we apply the formality theorem of Deligne et al. [Reference Deligne, Griffiths, Morgan and SullivanDGMS75].◻
$L_{i}$
. So, we apply the formality theorem of Deligne et al. [Reference Deligne, Griffiths, Morgan and SullivanDGMS75].◻
The following question, suggested by I. Smith, is natural in light of Corollary 2.8. Let
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
denote the Fukaya category of
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
denote the Fukaya category of
![]() ${\mathcal{L}}$
as in § 2.3.
${\mathcal{L}}$
as in § 2.3.
Question 2.9. Is
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
formal?
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
formal?
Behrend and Fantechi [Reference Behrend and FantechiBF09, Conjecture 5.8] formulate a similar question concerning the degeneration of the spectral sequence computing the virtual de Rham cohomology of the intersection of two holomorphic Lagrangians.
Abouzaid and Smith [Reference Abouzaid and SmithAS16] prove a formality theorem for
![]() $\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
when
$\widehat{{\mathcal{A}}}_{{\mathcal{L}}}$
when
![]() $M$
belongs to a certain family of Nakajima quiver varieties and
$M$
belongs to a certain family of Nakajima quiver varieties and
![]() ${\mathcal{L}}$
is the collection of Lagrangians introduced in [Reference Seidel and SmithSS06]. Their proof does not make use of the hyperkähler structure on
${\mathcal{L}}$
is the collection of Lagrangians introduced in [Reference Seidel and SmithSS06]. Their proof does not make use of the hyperkähler structure on
![]() $M$
. It would be interesting to find an alternative proof that does.
$M$
. It would be interesting to find an alternative proof that does.
3 Special Lagrangian submanifolds
For the benefit of the reader, we recall some basic facts about special Lagrangian submanifolds. We follow [Reference Harvey and LawsonHL82].
Definition 3.1. A Calabi–Yau manifold is a Kähler manifold
![]() $(M,J,\unicode[STIX]{x1D714})$
of complex dimension
$(M,J,\unicode[STIX]{x1D714})$
of complex dimension
![]() $n$
along with a holomorphic
$n$
along with a holomorphic
![]() $(n,0)$
form
$(n,0)$
form
![]() $\unicode[STIX]{x1D6F7}$
such that
$\unicode[STIX]{x1D6F7}$
such that
An
![]() $n$
-dimensional submanifold
$n$
-dimensional submanifold
![]() $L\subset M$
is special Lagrangian if
$L\subset M$
is special Lagrangian if
The following lemmas concern a hyperkähler manifold
![]() $(M,I,J,K,g)$
of complex dimension
$(M,I,J,K,g)$
of complex dimension
![]() $2n$
. For complex structure
$2n$
. For complex structure
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
, write
$\unicode[STIX]{x1D6E9}\in R_{I}$
, write
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}$
for the corresponding Kähler form. Observe that if
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}$
for the corresponding Kähler form. Observe that if
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
, then also
$\unicode[STIX]{x1D6E9}\in R_{I}$
, then also
![]() $I\unicode[STIX]{x1D6E9}\in R_{I}$
.
$I\unicode[STIX]{x1D6E9}\in R_{I}$
.
Lemma 3.2. Let
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
. Then the
$\unicode[STIX]{x1D6E9}\in R_{I}$
. Then the
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic
$\unicode[STIX]{x1D6E9}$
-holomorphic
![]() $(2n,0)$
form
$(2n,0)$
form
makes the Kähler manifold
![]() $(M,\unicode[STIX]{x1D6E9},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}})$
into a Calabi–Yau manifold.
$(M,\unicode[STIX]{x1D6E9},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}})$
into a Calabi–Yau manifold.
Proof. We consider first a special case. Let
![]() $M=\mathbb{C}^{2n}$
with coordinates
$M=\mathbb{C}^{2n}$
with coordinates
![]() $z_{i},w_{i},i=1,\ldots ,n$
. Let
$z_{i},w_{i},i=1,\ldots ,n$
. Let
![]() $g$
be the standard Euclidean metric. Take
$g$
be the standard Euclidean metric. Take
![]() $\unicode[STIX]{x1D6E9}$
to be the standard complex structure, so
$\unicode[STIX]{x1D6E9}$
to be the standard complex structure, so
A
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic symplectic form is given by
$\unicode[STIX]{x1D6E9}$
-holomorphic symplectic form is given by
Let
![]() $I$
be the complex structure such that
$I$
be the complex structure such that
![]() $\unicode[STIX]{x1D714}_{I}=\operatorname{Re}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}$
. It follows that
$\unicode[STIX]{x1D714}_{I}=\operatorname{Re}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}$
. It follows that
![]() $\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}=-\text{Im}\,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}$
. Thus,
$\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}=-\text{Im}\,\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}$
. Thus,
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}=\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}^{n}/n!$
, and (8) with
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}=\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6E9}}^{n}/n!$
, and (8) with
![]() $2n$
in place of
$2n$
in place of
![]() $n$
follows by a straightforward calculation.
$n$
follows by a straightforward calculation.
To deal with a general hyperkähler manifold, it suffices to verify (8) at each point. At a given point, one can choose coordinates
![]() $z_{i},w_{i}$
, such that
$z_{i},w_{i}$
, such that
![]() $\unicode[STIX]{x1D714}_{I},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}},\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}$
, are given by the same expressions as in the preceding special case. Indeed, the triple
$\unicode[STIX]{x1D714}_{I},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}},\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}$
, are given by the same expressions as in the preceding special case. Indeed, the triple
![]() $I,J:=\unicode[STIX]{x1D6E9},K:=I\unicode[STIX]{x1D6E9}$
satisfies the standard quaternionic relations
$I,J:=\unicode[STIX]{x1D6E9},K:=I\unicode[STIX]{x1D6E9}$
satisfies the standard quaternionic relations
![]() $\mathit{IJ}=-\mathit{JI}=K$
, and
$\mathit{IJ}=-\mathit{JI}=K$
, and
![]() $I^{2}=J^{2}=K^{2}=-1$
.◻
$I^{2}=J^{2}=K^{2}=-1$
.◻
Lemma 3.3 [Reference Harvey and LawsonHL82, p. 154].
Let
![]() $\unicode[STIX]{x1D6FA}_{I}$
be as in Remark 1.3, let
$\unicode[STIX]{x1D6FA}_{I}$
be as in Remark 1.3, let
![]() $\unicode[STIX]{x1D6E9}\in R_{I}$
and let
$\unicode[STIX]{x1D6E9}\in R_{I}$
and let
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}$
be as in Lemma 3.2. Suppose
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}$
be as in Lemma 3.2. Suppose
![]() $L$
is a holomorphic Lagrangian submanifold of the holomorphic symplectic manifold
$L$
is a holomorphic Lagrangian submanifold of the holomorphic symplectic manifold
![]() $(M,I,\unicode[STIX]{x1D6FA}_{I})$
. Then
$(M,I,\unicode[STIX]{x1D6FA}_{I})$
. Then
![]() $L$
is a special Lagrangian submanifold of the Calabi–Yau
$L$
is a special Lagrangian submanifold of the Calabi–Yau
![]() $(M,\unicode[STIX]{x1D6E9},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}})$
.
$(M,\unicode[STIX]{x1D6E9},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}})$
.
Proof. Since
![]() $\unicode[STIX]{x1D6FA}_{I}|_{L}=0$
, we have
$\unicode[STIX]{x1D6FA}_{I}|_{L}=0$
, we have
![]() $\unicode[STIX]{x1D714}_{J}|_{L}=0$
and
$\unicode[STIX]{x1D714}_{J}|_{L}=0$
and
![]() $\unicode[STIX]{x1D714}_{K}|_{L}=0$
. It follows that
$\unicode[STIX]{x1D714}_{K}|_{L}=0$
. It follows that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}|_{L}=0$
for any
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}|_{L}=0$
for any
![]() $\unicode[STIX]{x1D6EC}\in R_{I}$
. In particular,
$\unicode[STIX]{x1D6EC}\in R_{I}$
. In particular,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}|_{L}=0$
. Moreover, since
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}|_{L}=0$
. Moreover, since
![]() $\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}|_{L}=0$
, we have
$\unicode[STIX]{x1D714}_{I\unicode[STIX]{x1D6E9}}|_{L}=0$
, we have
![]() $\operatorname{Im}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}|_{L}=\operatorname{Im}\unicode[STIX]{x1D714}_{I}^{n}|_{L}/n!=0$
since
$\operatorname{Im}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E9}}|_{L}=\operatorname{Im}\unicode[STIX]{x1D714}_{I}^{n}|_{L}/n!=0$
since
![]() $\unicode[STIX]{x1D714}_{I}$
is real.◻
$\unicode[STIX]{x1D714}_{I}$
is real.◻
Lemma 3.3 is one of the few known approaches to constructing special Lagrangian submanifolds. Another approach produces special Lagrangian submanifolds as the fixed points of anti-holomorphic isometric involutions [Reference BryantBry87]. In the non-compact setting, Lie group actions can be used to produce special Lagrangians [Reference Harvey and LawsonHL82]. Once a single special Lagrangian
![]() $L$
has been constructed, deformation theory can be used [Reference McLeanMcL98] to constructed a family of nearby special Lagrangians modeled on
$L$
has been constructed, deformation theory can be used [Reference McLeanMcL98] to constructed a family of nearby special Lagrangians modeled on
![]() $H^{1}(L)$
. In total, these techniques are only able to produce special Lagrangians in a handful of special situations.
$H^{1}(L)$
. In total, these techniques are only able to produce special Lagrangians in a handful of special situations.
On the other hand, ignoring instanton corrections, special Lagrangians are expected to be quite plentiful. Indeed, the existence of a special Lagrangian representative of an isomorphism class of objects in the Fukaya category ought to be roughly equivalent to stability in the sense of Douglas and Bridgeland [Reference BridgelandBri07, Reference DouglasDou02, Reference Thomas and YauTY02]. Thus there should be enough special Lagrangians for every object of the Fukaya category to admit a Harder–Narasimhan filtration.
To explain the apparent dearth of special Lagrangians, the first author and Tian [Reference Solomon and TianST] posit that instanton corrections cannot be ignored. For a Lagrangian
![]() $L$
together with a bounding chain
$L$
together with a bounding chain
![]() $b$
, they propose an explicit instanton corrected special Lagrangian equation. If
$b$
, they propose an explicit instanton corrected special Lagrangian equation. If
![]() $L$
is tautologically unobstructed and
$L$
is tautologically unobstructed and
![]() $b=0$
, the instanton-corrected special Lagrangian equation reduces to the usual special Lagrangian equation.
$b=0$
, the instanton-corrected special Lagrangian equation reduces to the usual special Lagrangian equation.
From the point of view of [Reference Solomon and TianST], Corollary 2.1 explains why Lemma 3.3 can be true. Namely, the hyperkähler structure suppresses the instanton corrections which would in general prevent the existence of ordinary special Lagrangians. Similarly, fixed points of anti-holomorphic isometric involutions are known to be tautologically unobstructed [Reference Fukaya, Oh, Ohta and OnoFOOO17].
4 Local symplectic action
Let
![]() $(M,\unicode[STIX]{x1D714})$
be a real analytic symplectic manifold, and let
$(M,\unicode[STIX]{x1D714})$
be a real analytic symplectic manifold, and let
be real analytic Lagrangian submanifolds. Let
![]() $\unicode[STIX]{x1D6E9}$
be an
$\unicode[STIX]{x1D6E9}$
be an
![]() $\unicode[STIX]{x1D714}$
-tame almost complex structure, not necessarily real analytic, and let
$\unicode[STIX]{x1D714}$
-tame almost complex structure, not necessarily real analytic, and let
![]() $g=g_{\unicode[STIX]{x1D6E9}}$
denote the associated Riemannian metric. Assume that
$g=g_{\unicode[STIX]{x1D6E9}}$
denote the associated Riemannian metric. Assume that
![]() $(M,g)$
is complete and there exists a compact set
$(M,g)$
is complete and there exists a compact set
![]() $N\subset M$
such that
$N\subset M$
such that
Write
for the intersection of the closed upper half-plane and the closed unit disk. We think of the intervals
![]() $[-1,0]$
and
$[-1,0]$
and
![]() $[0,1]$
as subsets of
$[0,1]$
as subsets of
![]() $\mathbb{R}$
and thus as subsets of
$\mathbb{R}$
and thus as subsets of
![]() $H\subset \mathbb{C}$
. Let
$H\subset \mathbb{C}$
. Let
![]() $B_{r}(p)\subset M$
denote the open ball of radius
$B_{r}(p)\subset M$
denote the open ball of radius
![]() $r$
centered at
$r$
centered at
![]() $p$
with respect to the metric
$p$
with respect to the metric
![]() $g$
. For a path
$g$
. For a path
![]() $\unicode[STIX]{x1D6FE}:[a,b]\rightarrow M$
, let
$\unicode[STIX]{x1D6FE}:[a,b]\rightarrow M$
, let
denote the length of
![]() $\unicode[STIX]{x1D6FE}$
with respect to
$\unicode[STIX]{x1D6FE}$
with respect to
![]() $g$
. For
$g$
. For
![]() $W,V$
, manifolds with corners, a continuous map
$W,V$
, manifolds with corners, a continuous map
![]() $f:W\rightarrow V$
is called piecewise smooth if we can find a smooth triangulation of
$f:W\rightarrow V$
is called piecewise smooth if we can find a smooth triangulation of
![]() $W$
such that
$W$
such that
![]() $f$
restricted to any simplex is smooth. The main result of this section is the following theorem.
$f$
restricted to any simplex is smooth. The main result of this section is the following theorem.
Theorem 4.1. There exists
![]() $\unicode[STIX]{x1D700}_{0}>0$
such that for each
$\unicode[STIX]{x1D700}_{0}>0$
such that for each
![]() $\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0}]$
there exists a
$\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0}]$
there exists a
![]() $\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700})>0$
with the following significance. Suppose
$\unicode[STIX]{x1D6FF}_{0}=\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700})>0$
with the following significance. Suppose
with
![]() $\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
$\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
![]() $i=0,1$
, and either
$i=0,1$
, and either
![]() $\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{0}$
or there exists a point
$\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{0}$
or there exists a point
![]() $p\in L_{0}\,\cap \,L_{1}$
with
$p\in L_{0}\,\cap \,L_{1}$
with
![]() $\unicode[STIX]{x1D6FE}([0,1])\subset B_{\unicode[STIX]{x1D700}/9}(p)$
.
$\unicode[STIX]{x1D6FE}([0,1])\subset B_{\unicode[STIX]{x1D700}/9}(p)$
.
(a) There exists a piecewise smooth
 $v_{\unicode[STIX]{x1D6FE}}:H\rightarrow B_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FE}(0))$
with
$v_{\unicode[STIX]{x1D6FE}}:H\rightarrow B_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FE}(0))$
with  $$\begin{eqnarray}\displaystyle & \displaystyle v_{\unicode[STIX]{x1D6FE}}([-1,0])\subset L_{1},\quad v_{\unicode[STIX]{x1D6FE}}([0,1])\subset L_{0}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle v_{\unicode[STIX]{x1D6FE}}(e^{\sqrt{-1}\unicode[STIX]{x1D70B}t})=\unicode[STIX]{x1D6FE}(t). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{\unicode[STIX]{x1D6FE}}([-1,0])\subset L_{1},\quad v_{\unicode[STIX]{x1D6FE}}([0,1])\subset L_{0}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle v_{\unicode[STIX]{x1D6FE}}(e^{\sqrt{-1}\unicode[STIX]{x1D70B}t})=\unicode[STIX]{x1D6FE}(t). & \displaystyle \nonumber\end{eqnarray}$$
(b) The integral
 $\int _{H}v_{\unicode[STIX]{x1D6FE}}^{\ast }\unicode[STIX]{x1D714}$
depends only on
$\int _{H}v_{\unicode[STIX]{x1D6FE}}^{\ast }\unicode[STIX]{x1D714}$
depends only on
 $\unicode[STIX]{x1D6FE}$
and not on the choice of
$\unicode[STIX]{x1D6FE}$
and not on the choice of
 $v_{\unicode[STIX]{x1D6FE}}$
.
$v_{\unicode[STIX]{x1D6FE}}$
.
Thus, we define the local symplectic action of
![]() $\unicode[STIX]{x1D6FE}$
to be
$\unicode[STIX]{x1D6FE}$
to be
where
![]() $v_{\unicode[STIX]{x1D6FE}}$
is as in (a).
$v_{\unicode[STIX]{x1D6FE}}$
is as in (a).
For the proof of Theorem 4.1, we use the following theorem on the Whitney regularity of real analytic sets [Reference BierstoneBie80, Reference HardtHar83].
Theorem 4.2. Let
![]() $X$
be a compact connected analytic subset of
$X$
be a compact connected analytic subset of
![]() $\mathbb{R}^{n}$
. Then there is a positive integer
$\mathbb{R}^{n}$
. Then there is a positive integer
![]() $\unicode[STIX]{x1D708}_{X}$
and a constant
$\unicode[STIX]{x1D708}_{X}$
and a constant
![]() $C_{X}$
such that any two points
$C_{X}$
such that any two points
![]() $x,y\in X$
can be joined by a semi-analytic curve
$x,y\in X$
can be joined by a semi-analytic curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $X$
of length
$X$
of length
The proof of Theorem 4.2 uses the Łojasiewicz inequality and local resolution of singularities. A concise exposition can be found in [Reference Bierstone and MilmanBM98, Theorem 6.1]. Using a covering argument, we obtain the following corollary.
Corollary 4.3. There is a positive integer
![]() $\unicode[STIX]{x1D708}$
and a constant
$\unicode[STIX]{x1D708}$
and a constant
![]() $C$
such that any two points
$C$
such that any two points
![]() $p,q$
, in the same connected component of
$p,q$
, in the same connected component of
![]() $L_{0}\,\cap \,L_{1}$
can be joined by a piecewise smooth curve
$L_{0}\,\cap \,L_{1}$
can be joined by a piecewise smooth curve
![]() $\unicode[STIX]{x1D6FC}:[0,1]\rightarrow L_{0}\,\cap \,L_{1}\subset M$
with
$\unicode[STIX]{x1D6FC}:[0,1]\rightarrow L_{0}\,\cap \,L_{1}\subset M$
with
We begin by proving the following lemma.
Lemma 4.4. Let
![]() $(X,h)$
be a complete Riemannian manifold, and let
$(X,h)$
be a complete Riemannian manifold, and let
![]() $Y\subset X$
be a subset such that injectivity radius of
$Y\subset X$
be a subset such that injectivity radius of
![]() $X$
at all points of
$X$
at all points of
![]() $Y$
is bounded below by
$Y$
is bounded below by
![]() $\unicode[STIX]{x1D6FF}$
. Suppose three paths
$\unicode[STIX]{x1D6FF}$
. Suppose three paths
![]() $\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1}:[0,1]\rightarrow Y$
form a triangle,
$\unicode[STIX]{x1D712},\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1}:[0,1]\rightarrow Y$
form a triangle,
with
![]() $\unicode[STIX]{x1D712}$
piecewise smooth and
$\unicode[STIX]{x1D712}$
piecewise smooth and
![]() $\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1}$
, smooth. Moreover, suppose
$\unicode[STIX]{x1D6FD}_{0},\unicode[STIX]{x1D6FD}_{1}$
, smooth. Moreover, suppose
Then there exists a piecewise smooth map
![]() $\unicode[STIX]{x1D701}:H\rightarrow B_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D712}(0))\subset X$
such that for
$\unicode[STIX]{x1D701}:H\rightarrow B_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D712}(0))\subset X$
such that for
![]() $x\in [0,1]$
we have
$x\in [0,1]$
we have
Proof. For
![]() $z=x+\sqrt{-1}y\in H$
, write
$z=x+\sqrt{-1}y\in H$
, write
 $$\begin{eqnarray}\displaystyle & \displaystyle u(z)=\frac{2x(y+1)}{x^{2}+(y+1)^{2}},\quad v(z)=\frac{(y+1)^{2}-x^{2}}{x^{2}+(y+1)^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle w(z)=u(z)+\sqrt{-1}v(z). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u(z)=\frac{2x(y+1)}{x^{2}+(y+1)^{2}},\quad v(z)=\frac{(y+1)^{2}-x^{2}}{x^{2}+(y+1)^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle w(z)=u(z)+\sqrt{-1}v(z). & \displaystyle \nonumber\end{eqnarray}$$
So,
![]() $w(z)$
is the stereographic projection of
$w(z)$
is the stereographic projection of
![]() $z$
from
$z$
from
![]() $-\sqrt{-1}$
to the unit circle. Write
$-\sqrt{-1}$
to the unit circle. Write
For
![]() $i=0,1$
, and
$i=0,1$
, and
![]() $x\in [0,1]$
, define
$x\in [0,1]$
, define
![]() $\unicode[STIX]{x1D709}_{i}(x)\in T_{\unicode[STIX]{x1D6FD}_{i}(x)}M$
by
$\unicode[STIX]{x1D709}_{i}(x)\in T_{\unicode[STIX]{x1D6FD}_{i}(x)}M$
by
Such
![]() $\unicode[STIX]{x1D709}_{i}$
exist because by the triangle inequality,
$\unicode[STIX]{x1D709}_{i}$
exist because by the triangle inequality,
![]() $\operatorname{dist}_{g}(\unicode[STIX]{x1D6FD}_{i}(s),\unicode[STIX]{x1D712}(t))<(2\unicode[STIX]{x1D6FF})/3$
for all
$\operatorname{dist}_{g}(\unicode[STIX]{x1D6FD}_{i}(s),\unicode[STIX]{x1D712}(t))<(2\unicode[STIX]{x1D6FF})/3$
for all
![]() $s,t$
. Write
$s,t$
. Write
for the stereographic projection of
![]() $z$
from
$z$
from
![]() $-\sqrt{-1}$
to
$-\sqrt{-1}$
to
![]() $\mathbb{R}$
. Take
$\mathbb{R}$
. Take
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(z)=\left\{\begin{array}{@{}ll@{}}\displaystyle \exp _{\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D71B}(z))}\biggl(\frac{y}{v(z)}\unicode[STIX]{x1D709}_{0}(\unicode[STIX]{x1D71B}(z))\biggr)\quad & x\geqslant 0,\\ \displaystyle \exp _{\unicode[STIX]{x1D6FD}_{1}(-\unicode[STIX]{x1D71B}(z))}\biggl(\frac{y}{v(z)}\unicode[STIX]{x1D709}_{1}(-\unicode[STIX]{x1D71B}(z))\biggr)\quad & x<0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(z)=\left\{\begin{array}{@{}ll@{}}\displaystyle \exp _{\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D71B}(z))}\biggl(\frac{y}{v(z)}\unicode[STIX]{x1D709}_{0}(\unicode[STIX]{x1D71B}(z))\biggr)\quad & x\geqslant 0,\\ \displaystyle \exp _{\unicode[STIX]{x1D6FD}_{1}(-\unicode[STIX]{x1D71B}(z))}\biggl(\frac{y}{v(z)}\unicode[STIX]{x1D709}_{1}(-\unicode[STIX]{x1D71B}(z))\biggr)\quad & x<0.\end{array}\right.\end{eqnarray}$$
Finally, for
![]() $i=0$
or
$i=0$
or
![]() $1$
depending on whether
$1$
depending on whether
![]() $x\geqslant 0$
or
$x\geqslant 0$
or
![]() $x<0$
, we have
$x<0$
, we have
 $$\begin{eqnarray}\displaystyle \operatorname{dist}_{g}(\unicode[STIX]{x1D701}(z),\unicode[STIX]{x1D712}(0)) & {\leqslant} & \displaystyle \operatorname{dist}_{g}(\unicode[STIX]{x1D701}(z),\unicode[STIX]{x1D701}(w(z)))+\operatorname{dist}_{g}(\unicode[STIX]{x1D701}(w(z)),\unicode[STIX]{x1D712}(0))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D709}_{i}((-1)^{i}\unicode[STIX]{x1D71B}(z))|+\operatorname{dist}_{g}(\unicode[STIX]{x1D712}(t(z)),\unicode[STIX]{x1D712}(0))\nonumber\\ \displaystyle & {<} & \displaystyle \frac{2\unicode[STIX]{x1D6FF}}{3}+\frac{\unicode[STIX]{x1D6FF}}{3}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{dist}_{g}(\unicode[STIX]{x1D701}(z),\unicode[STIX]{x1D712}(0)) & {\leqslant} & \displaystyle \operatorname{dist}_{g}(\unicode[STIX]{x1D701}(z),\unicode[STIX]{x1D701}(w(z)))+\operatorname{dist}_{g}(\unicode[STIX]{x1D701}(w(z)),\unicode[STIX]{x1D712}(0))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D709}_{i}((-1)^{i}\unicode[STIX]{x1D71B}(z))|+\operatorname{dist}_{g}(\unicode[STIX]{x1D712}(t(z)),\unicode[STIX]{x1D712}(0))\nonumber\\ \displaystyle & {<} & \displaystyle \frac{2\unicode[STIX]{x1D6FF}}{3}+\frac{\unicode[STIX]{x1D6FF}}{3}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}.\Box \nonumber\end{eqnarray}$$
For
![]() $r>0$
, let
$r>0$
, let
![]() $U_{r}$
denote the open
$U_{r}$
denote the open
![]() $r$
neighborhood of
$r$
neighborhood of
![]() $L_{0}\,\cap \,L_{1}$
with respect to
$L_{0}\,\cap \,L_{1}$
with respect to
![]() $g$
. If necessary replacing
$g$
. If necessary replacing
![]() $N$
with
$N$
with
![]() $N\cup \overline{U_{1}}$
, we may assume that
$N\cup \overline{U_{1}}$
, we may assume that
![]() $U_{1}\subset N$
. Let
$U_{1}\subset N$
. Let
![]() $g_{L_{i}}$
denote the induced metric on
$g_{L_{i}}$
denote the induced metric on
![]() $L_{i}$
for
$L_{i}$
for
![]() $i=0,1$
. Let
$i=0,1$
. Let
![]() $\unicode[STIX]{x1D700}_{N}$
denote the minimum injectivity radius of
$\unicode[STIX]{x1D700}_{N}$
denote the minimum injectivity radius of
![]() $(M,g)$
that occurs at a point
$(M,g)$
that occurs at a point
![]() $q\in N$
and let
$q\in N$
and let
![]() $\unicode[STIX]{x1D700}_{L_{i}}$
denote the minimum injectivity radius of
$\unicode[STIX]{x1D700}_{L_{i}}$
denote the minimum injectivity radius of
![]() $(L_{i},g_{L_{i}})$
that occurs at a point
$(L_{i},g_{L_{i}})$
that occurs at a point
![]() $q\in N\,\cap \,L_{i}$
. Choose
$q\in N\,\cap \,L_{i}$
. Choose
Let
![]() $B_{r}(q,L_{i})\subset L_{i}$
denote the ball of radius
$B_{r}(q,L_{i})\subset L_{i}$
denote the ball of radius
![]() $r$
centered at
$r$
centered at
![]() $q$
with respect to the metric
$q$
with respect to the metric
![]() $g_{L_{i}}$
. After possibly making
$g_{L_{i}}$
. After possibly making
![]() $\unicode[STIX]{x1D700}_{1}$
smaller, we may assume that for every
$\unicode[STIX]{x1D700}_{1}$
smaller, we may assume that for every
![]() $q\in N\,\cap \,L_{i}$
we have
$q\in N\,\cap \,L_{i}$
we have
Corollary 4.5. Let
![]() $\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{1}$
. Let
$\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{1}$
. Let
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
![]() $\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
$\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
![]() $i=0,1$
. Suppose
$i=0,1$
. Suppose
![]() $p\in L_{0}\,\cap \,L_{1}$
such that
$p\in L_{0}\,\cap \,L_{1}$
such that
Then there exists
![]() $v_{\unicode[STIX]{x1D6FE}}$
as in Theorem 4.1(a) with
$v_{\unicode[STIX]{x1D6FE}}$
as in Theorem 4.1(a) with
![]() $v_{\unicode[STIX]{x1D6FE}}(0)=p$
.
$v_{\unicode[STIX]{x1D6FE}}(0)=p$
.
Proof. For
![]() $i=0,1$
, let
$i=0,1$
, let
![]() $\unicode[STIX]{x1D6FD}_{i}:[0,1]\rightarrow L_{i}$
be a path with
$\unicode[STIX]{x1D6FD}_{i}:[0,1]\rightarrow L_{i}$
be a path with
![]() $\unicode[STIX]{x1D6FD}_{i}(0)=p$
and
$\unicode[STIX]{x1D6FD}_{i}(0)=p$
and
![]() $\unicode[STIX]{x1D6FD}_{i}(1)=\unicode[STIX]{x1D6FE}(i)$
and
$\unicode[STIX]{x1D6FD}_{i}(1)=\unicode[STIX]{x1D6FE}(i)$
and
![]() $\unicode[STIX]{x1D6FD}_{i}([0,1])\subset B_{(2\unicode[STIX]{x1D700})/9}(p)$
. Such
$\unicode[STIX]{x1D6FD}_{i}([0,1])\subset B_{(2\unicode[STIX]{x1D700})/9}(p)$
. Such
![]() $\unicode[STIX]{x1D6FD}_{i}$
exist because by (10) with
$\unicode[STIX]{x1D6FD}_{i}$
exist because by (10) with
![]() $r=(2\unicode[STIX]{x1D700})/9$
, we have
$r=(2\unicode[STIX]{x1D700})/9$
, we have
![]() $\unicode[STIX]{x1D6FE}(i)\subset B_{(2\unicode[STIX]{x1D700})/9}(p,L_{i})$
, and
$\unicode[STIX]{x1D6FE}(i)\subset B_{(2\unicode[STIX]{x1D700})/9}(p,L_{i})$
, and
![]() $(2\unicode[STIX]{x1D700})/9$
is less than the injectivity radius of
$(2\unicode[STIX]{x1D700})/9$
is less than the injectivity radius of
![]() $L_{i}$
. It follows that
$L_{i}$
. It follows that
![]() $\unicode[STIX]{x1D6FD}_{i}([0,1])\subset B_{\unicode[STIX]{x1D700}/3}(\unicode[STIX]{x1D6FE}(0))$
. Apply Lemma 4.4 with
$\unicode[STIX]{x1D6FD}_{i}([0,1])\subset B_{\unicode[STIX]{x1D700}/3}(\unicode[STIX]{x1D6FE}(0))$
. Apply Lemma 4.4 with
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FE}$
.◻
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FE}$
.◻
Lemma 4.6. For
![]() $r>0$
there exists
$r>0$
there exists
![]() $\unicode[STIX]{x1D6FF}(r)>0$
with the following significance. If
$\unicode[STIX]{x1D6FF}(r)>0$
with the following significance. If
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
![]() $\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
$\unicode[STIX]{x1D6FE}(i)\in L_{i}$
for
![]() $i=0,1$
, and
$i=0,1$
, and
![]() $\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}(r)$
, then there exists
$\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}(r)$
, then there exists
![]() $p\in L_{0}\,\cap \,L_{1}$
such that
$p\in L_{0}\,\cap \,L_{1}$
such that
Proof. Take
Since
either
![]() $\unicode[STIX]{x1D6FE}(0)\in U_{r/2}$
or
$\unicode[STIX]{x1D6FE}(0)\in U_{r/2}$
or
![]() $\unicode[STIX]{x1D6FE}(1)\in U_{r/2}$
. So, there exists
$\unicode[STIX]{x1D6FE}(1)\in U_{r/2}$
. So, there exists
![]() $p\in L_{0}\,\cap \,L_{1}$
such that either
$p\in L_{0}\,\cap \,L_{1}$
such that either
![]() $\unicode[STIX]{x1D6FE}(0)\in B_{r/2}(p)$
or
$\unicode[STIX]{x1D6FE}(0)\in B_{r/2}(p)$
or
![]() $\unicode[STIX]{x1D6FE}(1)\in B_{r/2}(p)$
. Since
$\unicode[STIX]{x1D6FE}(1)\in B_{r/2}(p)$
. Since
![]() $\ell _{g}(\unicode[STIX]{x1D6FE})<r/2$
, inclusion (11) follows.◻
$\ell _{g}(\unicode[STIX]{x1D6FE})<r/2$
, inclusion (11) follows.◻
Theorem 4.1 is an immediate consequence of the following more precise statement.
Theorem 4.7. Let
![]() $\unicode[STIX]{x1D700}_{0}>0$
satisfy
$\unicode[STIX]{x1D700}_{0}>0$
satisfy
and with
![]() $\unicode[STIX]{x1D708},C$
, as in Corollary 4.3,
$\unicode[STIX]{x1D708},C$
, as in Corollary 4.3,
For
![]() $\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0}]$
, with
$\unicode[STIX]{x1D700}\in (0,\unicode[STIX]{x1D700}_{0}]$
, with
![]() $\unicode[STIX]{x1D6FF}$
as in Lemma 4.6, take
$\unicode[STIX]{x1D6FF}$
as in Lemma 4.6, take
Then Theorem 4.1 holds.

Figure 1. (Colour online) A situation in which the path
![]() $\unicode[STIX]{x1D6FC}$
must pass through a singularity of
$\unicode[STIX]{x1D6FC}$
must pass through a singularity of
![]() $L_{0}\,\cap \,L_{1}$
. Nonetheless, its length is controlled by Whitney regularity.
$L_{0}\,\cap \,L_{1}$
. Nonetheless, its length is controlled by Whitney regularity.
Proof. Inequality (12), Lemma 4.6 and Corollary 4.5 give (a).
It remains to prove (b). Suppose
![]() $v_{\unicode[STIX]{x1D6FE}}^{j}:H\rightarrow B_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FE}(0))$
for
$v_{\unicode[STIX]{x1D6FE}}^{j}:H\rightarrow B_{\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D6FE}(0))$
for
![]() $j=0,1$
, are two maps satisfying the conditions of (a). In particular,
$j=0,1$
, are two maps satisfying the conditions of (a). In particular,
It follows from inequality (13) that
![]() $v_{\unicode[STIX]{x1D6FE}}^{0}(0)$
and
$v_{\unicode[STIX]{x1D6FE}}^{0}(0)$
and
![]() $v_{\unicode[STIX]{x1D6FE}}^{1}(0)$
belong to the same component of
$v_{\unicode[STIX]{x1D6FE}}^{1}(0)$
belong to the same component of
![]() $L_{0}\,\cap \,L_{1}$
. By Corollary 4.3 and inequality (14), choose a piecewise smooth
$L_{0}\,\cap \,L_{1}$
. By Corollary 4.3 and inequality (14), choose a piecewise smooth
![]() $\unicode[STIX]{x1D6FC}:[0,1]\rightarrow L_{0}\,\cap \,L_{1}\subset M$
such that
$\unicode[STIX]{x1D6FC}:[0,1]\rightarrow L_{0}\,\cap \,L_{1}\subset M$
such that
![]() $\unicode[STIX]{x1D6FC}(0)=v_{\unicode[STIX]{x1D6FE}}^{0}(0)$
and
$\unicode[STIX]{x1D6FC}(0)=v_{\unicode[STIX]{x1D6FE}}^{0}(0)$
and
![]() $\unicode[STIX]{x1D6FC}(1)=v_{\unicode[STIX]{x1D6FE}}^{1}(0)$
and
$\unicode[STIX]{x1D6FC}(1)=v_{\unicode[STIX]{x1D6FE}}^{1}(0)$
and
See Figure 1. By inclusion (10), we have
By inequality (12), we may replace
![]() $4\unicode[STIX]{x1D700}$
by
$4\unicode[STIX]{x1D700}$
by
![]() $2\unicode[STIX]{x1D700}_{1}/9$
. Moreover, by (16) we have
$2\unicode[STIX]{x1D700}_{1}/9$
. Moreover, by (16) we have
For
![]() $i=0,1$
, apply Lemma 4.4 with
$i=0,1$
, apply Lemma 4.4 with
 $$\begin{eqnarray}\displaystyle & \displaystyle X=L_{i},\quad \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D700}_{1}/3,\quad \unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{j}(x)=\left\{\begin{array}{@{}ll@{}}v_{\unicode[STIX]{x1D6FE}}^{j}(1-x)\quad & i=0,\\ v_{\unicode[STIX]{x1D6FE}}^{j}(x-1)\quad & i=1\end{array}\right.\quad x\in [0,1] & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X=L_{i},\quad \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D700}_{1}/3,\quad \unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{j}(x)=\left\{\begin{array}{@{}ll@{}}v_{\unicode[STIX]{x1D6FE}}^{j}(1-x)\quad & i=0,\\ v_{\unicode[STIX]{x1D6FE}}^{j}(x-1)\quad & i=1\end{array}\right.\quad x\in [0,1] & \displaystyle \nonumber\end{eqnarray}$$
to obtain
such that for
![]() $x\in [0,1]$
$x\in [0,1]$
and
By the Poincaré lemma,
![]() $\unicode[STIX]{x1D714}|_{B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}(0))}$
is exact. Since
$\unicode[STIX]{x1D714}|_{B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}(0))}$
is exact. Since
![]() $\unicode[STIX]{x1D70E}_{i},v_{\unicode[STIX]{x1D6FE}}^{j}$
all map into
$\unicode[STIX]{x1D70E}_{i},v_{\unicode[STIX]{x1D6FE}}^{j}$
all map into
![]() $B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}(0))$
, Stokes’ theorem implies
$B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}(0))$
, Stokes’ theorem implies
On the other hand, since
![]() $\unicode[STIX]{x1D70E}_{j}$
maps into the Lagrangian
$\unicode[STIX]{x1D70E}_{j}$
maps into the Lagrangian
![]() $L_{j}$
, we have
$L_{j}$
, we have
![]() $\unicode[STIX]{x1D70E}_{j}^{\ast }\unicode[STIX]{x1D714}=0$
.◻
$\unicode[STIX]{x1D70E}_{j}^{\ast }\unicode[STIX]{x1D714}=0$
.◻
We will also need the following proposition, which is based on Theorem 4.7. Let
For
![]() $s\in [a,b]$
, define
$s\in [a,b]$
, define
![]() $\unicode[STIX]{x1D705}_{s}:[0,1]\rightarrow M$
by
$\unicode[STIX]{x1D705}_{s}:[0,1]\rightarrow M$
by
![]() $\unicode[STIX]{x1D705}_{s}(t)=\unicode[STIX]{x1D705}(s,t)$
.
$\unicode[STIX]{x1D705}_{s}(t)=\unicode[STIX]{x1D705}(s,t)$
.
Proposition 4.8. Let
![]() $\unicode[STIX]{x1D700}_{0},\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}_{0})$
, be as in Theorem 4.7. Suppose that for all
$\unicode[STIX]{x1D700}_{0},\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}_{0})$
, be as in Theorem 4.7. Suppose that for all
![]() $s\in [a,b]$
, either
$s\in [a,b]$
, either
or there exists
![]() $p(s)\in L_{0}\,\cap \,L_{1}$
such that
$p(s)\in L_{0}\,\cap \,L_{1}$
such that
Then
Proof. Equation (15) and Lemma 4.6 imply that for all
![]() $s\in [0,1]$
there exists
$s\in [0,1]$
there exists
![]() $p(s)$
such that inclusion (17) holds. A compactness argument yields
$p(s)$
such that inclusion (17) holds. A compactness argument yields
![]() $a\leqslant s_{0}<s_{1}<\cdots <s_{N}\leqslant b$
and
$a\leqslant s_{0}<s_{1}<\cdots <s_{N}\leqslant b$
and
![]() $\unicode[STIX]{x1D717}_{i}>0$
for
$\unicode[STIX]{x1D717}_{i}>0$
for
![]() $i=0,\ldots ,N$
, such that
$i=0,\ldots ,N$
, such that
 $$\begin{eqnarray}\displaystyle & \displaystyle [a,b]\subset \mathop{\bigcup }_{i=1}^{N}(s_{i}-\unicode[STIX]{x1D717}_{i},s_{i}+\unicode[STIX]{x1D717}_{i}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D705}_{s}([0,1])\subset B_{\unicode[STIX]{x1D700}_{0}/9}(p(s_{i})),\quad s\in (s_{i}-\unicode[STIX]{x1D717}_{i},s_{i}+\unicode[STIX]{x1D717}_{i}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle [a,b]\subset \mathop{\bigcup }_{i=1}^{N}(s_{i}-\unicode[STIX]{x1D717}_{i},s_{i}+\unicode[STIX]{x1D717}_{i}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D705}_{s}([0,1])\subset B_{\unicode[STIX]{x1D700}_{0}/9}(p(s_{i})),\quad s\in (s_{i}-\unicode[STIX]{x1D717}_{i},s_{i}+\unicode[STIX]{x1D717}_{i}). & \displaystyle\end{eqnarray}$$
Without loss of generality, we may assume
![]() $s_{i}-\unicode[STIX]{x1D717}_{i}<s_{i-1}+\unicode[STIX]{x1D717}_{i-1}$
and choose
$s_{i}-\unicode[STIX]{x1D717}_{i}<s_{i-1}+\unicode[STIX]{x1D717}_{i-1}$
and choose
![]() $\unicode[STIX]{x1D70D}_{i}\in (s_{i}-\unicode[STIX]{x1D717}_{i},s_{i-1}+\unicode[STIX]{x1D717}_{i-1})$
for
$\unicode[STIX]{x1D70D}_{i}\in (s_{i}-\unicode[STIX]{x1D717}_{i},s_{i-1}+\unicode[STIX]{x1D717}_{i-1})$
for
![]() $i=1,\ldots ,N$
, such that
$i=1,\ldots ,N$
, such that
![]() $\unicode[STIX]{x1D70D}_{1}<\cdots <\unicode[STIX]{x1D70D}_{N}$
. Write also
$\unicode[STIX]{x1D70D}_{1}<\cdots <\unicode[STIX]{x1D70D}_{N}$
. Write also
![]() $\unicode[STIX]{x1D70D}_{0}=0$
and
$\unicode[STIX]{x1D70D}_{0}=0$
and
![]() $\unicode[STIX]{x1D70D}_{N+1}=1$
. We show that
$\unicode[STIX]{x1D70D}_{N+1}=1$
. We show that
for
![]() $i=0,\ldots ,N$
.
$i=0,\ldots ,N$
.
Indeed, for
![]() $k=0,1$
, abbreviate
$k=0,1$
, abbreviate
![]() $\unicode[STIX]{x1D705}_{i}^{k}=\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70D}_{i+k}}$
. By inclusion (18), apply Corollary 4.5 with
$\unicode[STIX]{x1D705}_{i}^{k}=\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70D}_{i+k}}$
. By inclusion (18), apply Corollary 4.5 with
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}_{i}^{k}$
, and
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D705}_{i}^{k}$
, and
![]() $p=p(s_{i})$
to obtain
$p=p(s_{i})$
to obtain
with
![]() $v_{i}^{k}(0)=p(s_{i})$
. See Figure 2.
$v_{i}^{k}(0)=p(s_{i})$
. See Figure 2.

Figure 2. (Colour online) Breaking a long strip into short strips.
Furthermore, for
![]() $j=0,1$
, let
$j=0,1$
, let
be given by
By inclusions (18) and (10), we have
By inequality (12), we have
![]() $4\unicode[STIX]{x1D700}_{0}\leqslant 2\unicode[STIX]{x1D700}_{1}/9$
. For
$4\unicode[STIX]{x1D700}_{0}\leqslant 2\unicode[STIX]{x1D700}_{1}/9$
. For
![]() $j=0,1$
, apply Lemma 4.4 with
$j=0,1$
, apply Lemma 4.4 with
 $$\begin{eqnarray}\displaystyle & \displaystyle X=L_{j},\quad \unicode[STIX]{x1D6FF}=2\unicode[STIX]{x1D700}_{1}/9,\quad \unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FC}_{i}^{j}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{k}(x)=\left\{\begin{array}{@{}ll@{}}v_{i}^{k}(x)\quad & i=0,\\ v_{i}^{k}(-x)\quad & i=1\end{array}\right.\quad x\in [0,1] & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X=L_{j},\quad \unicode[STIX]{x1D6FF}=2\unicode[STIX]{x1D700}_{1}/9,\quad \unicode[STIX]{x1D712}=\unicode[STIX]{x1D6FC}_{i}^{j}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{k}(x)=\left\{\begin{array}{@{}ll@{}}v_{i}^{k}(x)\quad & i=0,\\ v_{i}^{k}(-x)\quad & i=1\end{array}\right.\quad x\in [0,1] & \displaystyle \nonumber\end{eqnarray}$$
to obtain
such that for
![]() $x\in [0,1]$
,
$x\in [0,1]$
,
and
Inclusion (18) implies that
![]() $\unicode[STIX]{x1D705}([\unicode[STIX]{x1D70D}_{i},\unicode[STIX]{x1D70D}_{i+1}]\times [0,1])$
and, in particular,
$\unicode[STIX]{x1D705}([\unicode[STIX]{x1D70D}_{i},\unicode[STIX]{x1D70D}_{i+1}]\times [0,1])$
and, in particular,
![]() $\unicode[STIX]{x1D705}_{i}^{1}(0)$
and
$\unicode[STIX]{x1D705}_{i}^{1}(0)$
and
![]() $\unicode[STIX]{x1D705}_{i}^{0}(1)=\unicode[STIX]{x1D6FC}_{i}^{1}(0)$
, are all contained in the
$\unicode[STIX]{x1D705}_{i}^{0}(1)=\unicode[STIX]{x1D6FC}_{i}^{1}(0)$
, are all contained in the
![]() $(2\unicode[STIX]{x1D700}_{0})/9$
ball centered at
$(2\unicode[STIX]{x1D700}_{0})/9$
ball centered at
![]() $\unicode[STIX]{x1D705}_{i}^{0}(0)=\unicode[STIX]{x1D6FC}_{i}^{0}(0)$
. It follows from inequality (12) that
$\unicode[STIX]{x1D705}_{i}^{0}(0)=\unicode[STIX]{x1D6FC}_{i}^{0}(0)$
. It follows from inequality (12) that
![]() $\unicode[STIX]{x1D70E}_{i}^{j},v_{i}^{k}$
, and
$\unicode[STIX]{x1D70E}_{i}^{j},v_{i}^{k}$
, and
![]() $\unicode[STIX]{x1D705}|_{[\unicode[STIX]{x1D70D}_{i},\unicode[STIX]{x1D70D}_{i+1}]\times [0,1]}$
, all map into
$\unicode[STIX]{x1D705}|_{[\unicode[STIX]{x1D70D}_{i},\unicode[STIX]{x1D70D}_{i+1}]\times [0,1]}$
, all map into
![]() $B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}_{i}^{0}(0))$
. By the Poincaré lemma,
$B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}_{i}^{0}(0))$
. By the Poincaré lemma,
![]() $\unicode[STIX]{x1D714}|_{B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}_{i}^{0}(0))}$
is exact. So, Stokes’ theorem implies
$\unicode[STIX]{x1D714}|_{B_{\unicode[STIX]{x1D700}_{1}}(\unicode[STIX]{x1D6FC}_{i}^{0}(0))}$
is exact. So, Stokes’ theorem implies
On the other hand, since
![]() $\unicode[STIX]{x1D70E}_{j}$
maps into the Lagrangian
$\unicode[STIX]{x1D70E}_{j}$
maps into the Lagrangian
![]() $L_{j}$
, we have
$L_{j}$
, we have
![]() $\unicode[STIX]{x1D70E}_{j}^{\ast }\unicode[STIX]{x1D714}=0$
. Moreover, by definition,
$\unicode[STIX]{x1D70E}_{j}^{\ast }\unicode[STIX]{x1D714}=0$
. Moreover, by definition,
Equation (19) follows. Finally, by (19) we have
5 Łojasiewicz isoperimetric inequality
We continue with the assumptions and notation at the beginning of § 4. The main result of this section is the following isoperimetric inequality for the local symplectic action.
Theorem 5.1. There exist constants
![]() $\unicode[STIX]{x1D6FF}_{1}>0$
and
$\unicode[STIX]{x1D6FF}_{1}>0$
and
![]() $\unicode[STIX]{x1D6FD}>1$
such that for all
$\unicode[STIX]{x1D6FD}>1$
such that for all
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
![]() $\unicode[STIX]{x1D6FE}(0)\in L_{0},\unicode[STIX]{x1D6FE}(1)\in L_{1}$
and
$\unicode[STIX]{x1D6FE}(0)\in L_{0},\unicode[STIX]{x1D6FE}(1)\in L_{1}$
and
![]() $\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{1}$
, the local symplectic action
$\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{1}$
, the local symplectic action
![]() $a(\unicode[STIX]{x1D6FE})$
is well defined and
$a(\unicode[STIX]{x1D6FE})$
is well defined and
The proof of Theorem 5.1 is given below. A key ingredient is Łojasiewicz’s gradient inequality [Reference ŁojasiewiczŁoj65].
Theorem 5.2 (Łojasiewicz).
Let
![]() $f$
be an analytic function on a neighborhood of
$f$
be an analytic function on a neighborhood of
![]() $0\in \mathbb{R}^{n}$
. Then there exists
$0\in \mathbb{R}^{n}$
. Then there exists
![]() $\unicode[STIX]{x1D703}\in (0,1)$
and a possibly smaller neighborhood
$\unicode[STIX]{x1D703}\in (0,1)$
and a possibly smaller neighborhood
![]() $U$
of
$U$
of
![]() $0$
such that
$0$
such that
The proof of Theorem 5.2 uses the theory of semi-analytic sets. A nice exposition is given in [Reference Bierstone and MilmanBM98, Proposition 6.8].
Let
![]() $z_{i}=x_{i}+\sqrt{-1}y_{i}$
denote the standard coordinates of
$z_{i}=x_{i}+\sqrt{-1}y_{i}$
denote the standard coordinates of
![]() $\mathbb{C}^{n}$
. Let
$\mathbb{C}^{n}$
. Let
denote the standard symplectic structure on
![]() $\mathbb{C}^{n}$
and let
$\mathbb{C}^{n}$
and let
![]() $g_{0}$
denote the Euclidean metric. Given an open subset
$g_{0}$
denote the Euclidean metric. Given an open subset
![]() $U\subset \mathbb{R}^{n}$
and
$U\subset \mathbb{R}^{n}$
and
![]() $f:U\rightarrow \mathbb{R}$
, write
$f:U\rightarrow \mathbb{R}$
, write
So,
![]() $\operatorname{graph}(\unicode[STIX]{x1D6FB}f)\subset \mathbb{C}^{n}$
is a Lagrangian submanifold.
$\operatorname{graph}(\unicode[STIX]{x1D6FB}f)\subset \mathbb{C}^{n}$
is a Lagrangian submanifold.
Lemma 5.3. Let
![]() $W\subset \mathbb{C}^{n}$
be an open set containing the origin, and let
$W\subset \mathbb{C}^{n}$
be an open set containing the origin, and let
![]() $f$
be a real analytic function defined on a neighborhood of the origin in
$f$
be a real analytic function defined on a neighborhood of the origin in
![]() $\mathbb{R}^{n}$
with
$\mathbb{R}^{n}$
with
![]() $\unicode[STIX]{x1D6FB}f(0)=0$
. Let
$\unicode[STIX]{x1D6FB}f(0)=0$
. Let
There exist
![]() $\unicode[STIX]{x1D6FD}>1$
and
$\unicode[STIX]{x1D6FD}>1$
and
![]() $\unicode[STIX]{x1D700}>0$
with the following significance. Suppose
$\unicode[STIX]{x1D700}>0$
with the following significance. Suppose
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow B_{\unicode[STIX]{x1D700}}(0)\subset \mathbb{C}^{n}$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow B_{\unicode[STIX]{x1D700}}(0)\subset \mathbb{C}^{n}$
with
![]() $\unicode[STIX]{x1D6FE}(i)\in Q_{i}$
for
$\unicode[STIX]{x1D6FE}(i)\in Q_{i}$
for
![]() $i=0,1$
, and
$i=0,1$
, and
![]() $\ell _{g_{0}}(\unicode[STIX]{x1D6FE})<1$
. Let
$\ell _{g_{0}}(\unicode[STIX]{x1D6FE})<1$
. Let
![]() $v_{\unicode[STIX]{x1D6FE}}:H\rightarrow B_{\unicode[STIX]{x1D700}}(0)$
with
$v_{\unicode[STIX]{x1D6FE}}:H\rightarrow B_{\unicode[STIX]{x1D700}}(0)$
with
Then
Proof. Apply Theorem 5.2 to
![]() $f$
to obtain
$f$
to obtain
![]() $\unicode[STIX]{x1D700}>0$
such that the gradient inequality (21) holds for all
$\unicode[STIX]{x1D700}>0$
such that the gradient inequality (21) holds for all
![]() $y\in B_{\unicode[STIX]{x1D700}}(0)\subset \mathbb{R}^{n}$
. Take
$y\in B_{\unicode[STIX]{x1D700}}(0)\subset \mathbb{R}^{n}$
. Take
![]() $\unicode[STIX]{x1D6FD}=1/\unicode[STIX]{x1D703}$
. Write
$\unicode[STIX]{x1D6FD}=1/\unicode[STIX]{x1D703}$
. Write
so
![]() $d\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D714}_{0}$
. Let
$d\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D714}_{0}$
. Let
![]() $c:[0,1]\rightarrow Q_{1}$
be given by
$c:[0,1]\rightarrow Q_{1}$
be given by
![]() $c(x)=v_{\unicode[STIX]{x1D6FE}}(-x)$
. So,
$c(x)=v_{\unicode[STIX]{x1D6FE}}(-x)$
. So,
![]() $c(0)\in Q_{0}\,\cap \,Q_{1}$
and
$c(0)\in Q_{0}\,\cap \,Q_{1}$
and
![]() $c(1)=\unicode[STIX]{x1D6FE}(1)$
. Since
$c(1)=\unicode[STIX]{x1D6FE}(1)$
. Since
![]() $\unicode[STIX]{x1D706}_{0}|_{Q_{0}}=0$
, Stokes’ theorem gives
$\unicode[STIX]{x1D706}_{0}|_{Q_{0}}=0$
, Stokes’ theorem gives
Write
![]() $\unicode[STIX]{x1D6FE}(t)=k(t)+\sqrt{-1}h(t)$
with
$\unicode[STIX]{x1D6FE}(t)=k(t)+\sqrt{-1}h(t)$
with
![]() $k,h:[0,1]\rightarrow \mathbb{R}^{n}$
. Since
$k,h:[0,1]\rightarrow \mathbb{R}^{n}$
. Since
![]() $\unicode[STIX]{x1D6FE}(0)\in Q_{0}$
, we have
$\unicode[STIX]{x1D6FE}(0)\in Q_{0}$
, we have
![]() $h(0)=0$
and thus
$h(0)=0$
and thus
Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{C}^{n}\rightarrow \mathbb{R}^{n}$
denote the projection given by
$\unicode[STIX]{x1D70B}:\mathbb{C}^{n}\rightarrow \mathbb{R}^{n}$
denote the projection given by
![]() $\unicode[STIX]{x1D70B}(x+\sqrt{-1}y)=x$
. So,
$\unicode[STIX]{x1D70B}(x+\sqrt{-1}y)=x$
. So,
and consequently
Since
![]() $c(0)\in Q_{0}\,\cap \,Q_{1}$
, we have
$c(0)\in Q_{0}\,\cap \,Q_{1}$
, we have
![]() $\unicode[STIX]{x1D70B}(c(0))=c(0)$
and
$\unicode[STIX]{x1D70B}(c(0))=c(0)$
and
![]() $\unicode[STIX]{x1D6FB}f(c(0))=0$
. So, the gradient inequality (21) implies
$\unicode[STIX]{x1D6FB}f(c(0))=0$
. So, the gradient inequality (21) implies
![]() $f(c(0))=f(0)$
. Furthermore, the gradient inequality gives
$f(c(0))=f(0)$
. Furthermore, the gradient inequality gives
Since
![]() $c(1)=\unicode[STIX]{x1D6FE}(1)$
, we have
$c(1)=\unicode[STIX]{x1D6FE}(1)$
, we have
![]() $\unicode[STIX]{x1D70B}(c(1))=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FE}(1))=k(1)$
. Moreover,
$\unicode[STIX]{x1D70B}(c(1))=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FE}(1))=k(1)$
. Moreover,
![]() $\unicode[STIX]{x1D6FE}(1)\in Q_{1}$
implies
$\unicode[STIX]{x1D6FE}(1)\in Q_{1}$
implies
![]() $h(1)=\unicode[STIX]{x1D6FB}f(k(1))$
. So, using inequality (23), we obtain
$h(1)=\unicode[STIX]{x1D6FB}f(k(1))$
. So, using inequality (23), we obtain
Combining inequalities (24) and (25) we conclude
On the other hand, to calculate
![]() $\int _{0}^{1}\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D706}_{0}$
we may assume without loss of generality that
$\int _{0}^{1}\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D706}_{0}$
we may assume without loss of generality that
![]() $\unicode[STIX]{x1D6FE}$
is parameterized by arc-length, so
$\unicode[STIX]{x1D6FE}$
is parameterized by arc-length, so
![]() $|\dot{\unicode[STIX]{x1D6FE}}(t)|=\ell _{g_{0}}(\unicode[STIX]{x1D6FE})$
. Thus, inequality (23) gives
$|\dot{\unicode[STIX]{x1D6FE}}(t)|=\ell _{g_{0}}(\unicode[STIX]{x1D6FE})$
. Thus, inequality (23) gives
Combining (22), (26) and (27), we obtain the desired bound. ◻
Proof of Theorem 5.1.
Equip
![]() $\mathbb{C}^{n}$
with the standard symplectic structure
$\mathbb{C}^{n}$
with the standard symplectic structure
![]() $\unicode[STIX]{x1D714}_{0}$
and the Euclidean metric
$\unicode[STIX]{x1D714}_{0}$
and the Euclidean metric
![]() $g_{0}$
. By Darboux’ theorem, for each point
$g_{0}$
. By Darboux’ theorem, for each point
![]() $p\in L_{0}\,\cap \,L_{1}$
, choose an open set
$p\in L_{0}\,\cap \,L_{1}$
, choose an open set
![]() $\widetilde{V}_{p}\subset M$
with
$\widetilde{V}_{p}\subset M$
with
![]() $p\in \widetilde{V}_{p}$
, an open set
$p\in \widetilde{V}_{p}$
, an open set
![]() $\widetilde{W}_{p}\subset \mathbb{C}^{n}$
with
$\widetilde{W}_{p}\subset \mathbb{C}^{n}$
with
![]() $0\in \widetilde{W}_{p}$
and a real analytic Lipschitz symplectomorphism
$0\in \widetilde{W}_{p}$
and a real analytic Lipschitz symplectomorphism
![]() $\unicode[STIX]{x1D711}_{p}:\widetilde{V}_{p}\rightarrow \widetilde{W}_{p}$
with
$\unicode[STIX]{x1D711}_{p}:\widetilde{V}_{p}\rightarrow \widetilde{W}_{p}$
with
![]() $\unicode[STIX]{x1D711}_{p}(p)=0$
. After possibly modifying
$\unicode[STIX]{x1D711}_{p}(p)=0$
. After possibly modifying
![]() $\unicode[STIX]{x1D711}_{p}$
and shrinking
$\unicode[STIX]{x1D711}_{p}$
and shrinking
![]() $\widetilde{V}_{p},\widetilde{W}_{p}$
, we may assume that
$\widetilde{V}_{p},\widetilde{W}_{p}$
, we may assume that
![]() $\unicode[STIX]{x1D711}_{p}(L_{0})=\mathbb{R}^{n}\,\cap \,\widetilde{W}_{p}$
and
$\unicode[STIX]{x1D711}_{p}(L_{0})=\mathbb{R}^{n}\,\cap \,\widetilde{W}_{p}$
and
where
![]() $f_{p}$
is analytic function defined on a neighborhood of
$f_{p}$
is analytic function defined on a neighborhood of
![]() $0$
in
$0$
in
![]() $\mathbb{R}^{n}$
. Let
$\mathbb{R}^{n}$
. Let
![]() $\unicode[STIX]{x1D6FD}_{p}>1$
and
$\unicode[STIX]{x1D6FD}_{p}>1$
and
![]() $\unicode[STIX]{x1D700}_{p}>0$
be the constants obtained from Lemma 5.3 with
$\unicode[STIX]{x1D700}_{p}>0$
be the constants obtained from Lemma 5.3 with
Write
![]() $W_{p}=B_{\unicode[STIX]{x1D700}_{p}}(0)\,\cap \,\widetilde{W}_{p}$
and
$W_{p}=B_{\unicode[STIX]{x1D700}_{p}}(0)\,\cap \,\widetilde{W}_{p}$
and
![]() $V_{p}=\unicode[STIX]{x1D711}_{p}^{-1}(W_{p})$
.
$V_{p}=\unicode[STIX]{x1D711}_{p}^{-1}(W_{p})$
.
By compactness of
![]() $L_{0}\,\cap \,L_{1}$
, choose a finite collection of points
$L_{0}\,\cap \,L_{1}$
, choose a finite collection of points
such that
![]() $L_{0}\,\cap \,L_{1}\subset \bigcup _{i=1}^{N}V_{p_{i}}$
. Let
$L_{0}\,\cap \,L_{1}\subset \bigcup _{i=1}^{N}V_{p_{i}}$
. Let
![]() $U_{r}$
denote the metric
$U_{r}$
denote the metric
![]() $r$
-neighborhood of
$r$
-neighborhood of
![]() $L_{0}\,\cap \,L_{1}$
with respect to
$L_{0}\,\cap \,L_{1}$
with respect to
![]() $g$
. Choose
$g$
. Choose
![]() $r_{0}>0$
small enough that
$r_{0}>0$
small enough that
Let
![]() $\unicode[STIX]{x1D700}_{2}$
be a Lebesgue number for the cover
$\unicode[STIX]{x1D700}_{2}$
be a Lebesgue number for the cover
![]() $\{V_{p_{i}}\,\cap \,\overline{U}_{r_{0}}\}_{i=1}^{N}$
of
$\{V_{p_{i}}\,\cap \,\overline{U}_{r_{0}}\}_{i=1}^{N}$
of
![]() $\overline{U}_{r_{0}}$
. Let
$\overline{U}_{r_{0}}$
. Let
![]() $\unicode[STIX]{x1D700}_{0}$
be as in Theorem 4.1 and let
$\unicode[STIX]{x1D700}_{0}$
be as in Theorem 4.1 and let
Let
![]() $\unicode[STIX]{x1D6FF}_{1}=\min \{\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}),1\}$
, and choose
$\unicode[STIX]{x1D6FF}_{1}=\min \{\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}),1\}$
, and choose
![]() $\unicode[STIX]{x1D6FD}$
such that
$\unicode[STIX]{x1D6FD}$
such that
For any path
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
with
![]() $\unicode[STIX]{x1D6FE}(i)\in L_{i}$
, for
$\unicode[STIX]{x1D6FE}(i)\in L_{i}$
, for
![]() $i=0,1$
, and
$i=0,1$
, and
![]() $\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{1}$
, there exists
$\ell _{g}(\unicode[STIX]{x1D6FE})<\unicode[STIX]{x1D6FF}_{1}$
, there exists
![]() $v_{\unicode[STIX]{x1D6FE}}$
as in Theorem 4.1(a). Since
$v_{\unicode[STIX]{x1D6FE}}$
as in Theorem 4.1(a). Since
![]() $v_{\unicode[STIX]{x1D6FE}}(0)\in L_{0}\,\cap \,L_{1}$
and
$v_{\unicode[STIX]{x1D6FE}}(0)\in L_{0}\,\cap \,L_{1}$
and
![]() $\unicode[STIX]{x1D700}\leqslant r_{0}/2$
, it follows that
$\unicode[STIX]{x1D700}\leqslant r_{0}/2$
, it follows that
![]() $v_{\unicode[STIX]{x1D6FE}}(H)\subset U_{r_{0}}$
. Since
$v_{\unicode[STIX]{x1D6FE}}(H)\subset U_{r_{0}}$
. Since
![]() $\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{2}$
, it follows that
$\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{2}$
, it follows that
![]() $v_{\unicode[STIX]{x1D6FE}}(H)\subset V_{p_{i}}$
for some
$v_{\unicode[STIX]{x1D6FE}}(H)\subset V_{p_{i}}$
for some
![]() $i$
. Therefore,
$i$
. Therefore,
where
![]() $C$
depends only on the Lipschitz constants of
$C$
depends only on the Lipschitz constants of
![]() $\unicode[STIX]{x1D711}_{p_{i}}$
. Possibly making
$\unicode[STIX]{x1D711}_{p_{i}}$
. Possibly making
![]() $\unicode[STIX]{x1D6FF}_{1}$
smaller, we eliminate the constant
$\unicode[STIX]{x1D6FF}_{1}$
smaller, we eliminate the constant
![]() $C$
and obtain the desired inequality.◻
$C$
and obtain the desired inequality.◻
6 Continuous extension
We continue with the assumptions and notation at the beginning of § 4. The main result of this section is the following theorem. Its proof and the resulting proof of Theorem 1.9 are given at the end of the section.
Theorem 6.1. Let
![]() $u:H\setminus \{0\}\rightarrow M$
be a
$u:H\setminus \{0\}\rightarrow M$
be a
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map with
$\unicode[STIX]{x1D6E9}$
-holomorphic map with
![]() $u([-1,0))\subset L_{1}$
and
$u([-1,0))\subset L_{1}$
and
![]() $u((0,1])\subset L_{0}$
. If
$u((0,1])\subset L_{0}$
. If
![]() $E_{g}(u)<\infty$
, then
$E_{g}(u)<\infty$
, then
![]() $u$
extends to a continuous map
$u$
extends to a continuous map
![]() $\overline{u}:H\rightarrow M$
. Moreover, there exist constants
$\overline{u}:H\rightarrow M$
. Moreover, there exist constants
![]() $c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that
$c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that
The proof of Theorem 6.1 relies on the following discussion and will be given at the end of the section. It combines ideas in the proof of [Reference McDuff and SalamonMS12, Theorem 4.1.2] with results from §§ 4 and 5.
The almost complex structure
![]() $\unicode[STIX]{x1D6E9}$
is called
$\unicode[STIX]{x1D6E9}$
is called
![]() $\unicode[STIX]{x1D714}$
-compatible if for all tangent vectors
$\unicode[STIX]{x1D714}$
-compatible if for all tangent vectors
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}\in T_{p}M$
we have
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}\in T_{p}M$
we have
![]() $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D709},\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D702})=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. The following lemma is of fundamental importance in Gromov’s theory of
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D709},\unicode[STIX]{x1D6E9}\unicode[STIX]{x1D702})=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
. The following lemma is of fundamental importance in Gromov’s theory of
![]() $J$
-holomorphic curves [Reference GromovGro85]. See [Reference McDuff and SalamonMS12, Lemma 2.2.1].
$J$
-holomorphic curves [Reference GromovGro85]. See [Reference McDuff and SalamonMS12, Lemma 2.2.1].
Lemma 6.2. Let
![]() $\unicode[STIX]{x1D6F4}$
be a Riemann surface. Every
$\unicode[STIX]{x1D6F4}$
be a Riemann surface. Every
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map
$\unicode[STIX]{x1D6E9}$
-holomorphic map
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
satisfies
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
satisfies
If
![]() $\unicode[STIX]{x1D6E9}$
is
$\unicode[STIX]{x1D6E9}$
is
![]() $\unicode[STIX]{x1D714}$
-compatible, then for any smooth map
$\unicode[STIX]{x1D714}$
-compatible, then for any smooth map
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
, we have
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
, we have
In fact, this follows from a pointwise equality of the integrands.
Let
denote the disk of radius
![]() $r$
and the upper half-disk of radius
$r$
and the upper half-disk of radius
![]() $r$
respectively. When it does not cause confusion, we abbreviate
$r$
respectively. When it does not cause confusion, we abbreviate
![]() $|\cdot |=|\cdot |_{g}$
. When not indicated otherwise, integrals over subsets of
$|\cdot |=|\cdot |_{g}$
. When not indicated otherwise, integrals over subsets of
![]() $\mathbb{C}$
are with respect to the volume form of the Euclidean metric on
$\mathbb{C}$
are with respect to the volume form of the Euclidean metric on
![]() $\mathbb{C}$
. We will use the following mean value inequality from [Reference McDuff and SalamonMS12, Lemma 4.3.1].
$\mathbb{C}$
. We will use the following mean value inequality from [Reference McDuff and SalamonMS12, Lemma 4.3.1].
Lemma 6.3. Let
![]() $L\subset M$
be a totally real submanifold with respect to
$L\subset M$
be a totally real submanifold with respect to
![]() $\unicode[STIX]{x1D6E9}$
. There are constants
$\unicode[STIX]{x1D6E9}$
. There are constants
![]() $c_{0},\unicode[STIX]{x1D6FF}_{2}>0$
such that the following holds. If
$c_{0},\unicode[STIX]{x1D6FF}_{2}>0$
such that the following holds. If
![]() $r>0$
and
$r>0$
and
![]() $u:(H_{2r},H_{2r}\,\cap \,\mathbb{R})\rightarrow (M,L)$
is
$u:(H_{2r},H_{2r}\,\cap \,\mathbb{R})\rightarrow (M,L)$
is
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic, then
$\unicode[STIX]{x1D6E9}$
-holomorphic, then
For
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
, abbreviate
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
, abbreviate
In the following lemmas, we consider a
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic map
$\unicode[STIX]{x1D6E9}$
-holomorphic map
with
We abbreviate
![]() $v(x,y)=v(x+\sqrt{-1}y)$
. For
$v(x,y)=v(x+\sqrt{-1}y)$
. For
![]() $x\in (-\infty ,0]$
, let
$x\in (-\infty ,0]$
, let
![]() $v_{x}:[0,1]\rightarrow M$
denote the path given by
$v_{x}:[0,1]\rightarrow M$
denote the path given by
Define
![]() $\mathbf{e}:(-\infty ,0]\rightarrow \mathbb{R}_{{\geqslant}0}$
by
$\mathbf{e}:(-\infty ,0]\rightarrow \mathbb{R}_{{\geqslant}0}$
by
The proof of the following lemma uses ideas from [Reference McDuff and SalamonMS12, Lemma 4.5.1].
Lemma 6.4. Let
![]() $\unicode[STIX]{x1D6FD}$
be as in Theorem 5.1 and let
$\unicode[STIX]{x1D6FD}$
be as in Theorem 5.1 and let
![]() $\unicode[STIX]{x1D6FF}_{2}$
be as in Lemma 6.3. There exists
$\unicode[STIX]{x1D6FF}_{2}$
be as in Lemma 6.3. There exists
![]() $\unicode[STIX]{x1D70F}_{0}\in (-\infty ,0]$
such that
$\unicode[STIX]{x1D70F}_{0}\in (-\infty ,0]$
such that
Proof. Let
![]() $\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}_{0})$
be as in Proposition 4.8, let
$\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D700}_{0})$
be as in Proposition 4.8, let
![]() $\unicode[STIX]{x1D6FF}_{1}$
be as in Theorem 5.1 and let
$\unicode[STIX]{x1D6FF}_{1}$
be as in Theorem 5.1 and let
![]() $\unicode[STIX]{x1D6FF}_{2},c_{0}$
, be as in Lemma 6.3. Abbreviate
$\unicode[STIX]{x1D6FF}_{2},c_{0}$
, be as in Lemma 6.3. Abbreviate
and let
![]() $\unicode[STIX]{x1D6FF}$
satisfy
$\unicode[STIX]{x1D6FF}$
satisfy
Observe that
![]() $\mathbf{e}$
is a continuous function with
$\mathbf{e}$
is a continuous function with
So, choose
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}$
such that for
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}$
such that for
![]() $\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}+1$
we have
$\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}+1$
we have
Lemma 6.3 with
![]() $r=\frac{1}{2}$
gives
$r=\frac{1}{2}$
gives
Since
![]() $v$
is
$v$
is
![]() $\unicode[STIX]{x1D6E9}$
holomorphic, it follows that
$\unicode[STIX]{x1D6E9}$
holomorphic, it follows that
and consequently
Let
![]() $\unicode[STIX]{x1D70F}_{0}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}_{3}}$
and let
$\unicode[STIX]{x1D70F}_{0}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}_{3}}$
and let
![]() $\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{0}$
. Then, Lemma 6.2, Proposition 4.8 with
$\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{0}$
. Then, Lemma 6.2, Proposition 4.8 with
![]() $\unicode[STIX]{x1D705}=v|_{[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}},\unicode[STIX]{x1D70F}]}$
and Theorem 5.1, give
$\unicode[STIX]{x1D705}=v|_{[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}},\unicode[STIX]{x1D70F}]}$
and Theorem 5.1, give
Since
![]() $\unicode[STIX]{x1D6FF}$
can be taken arbitrarily small, and we may assume without loss of generality that
$\unicode[STIX]{x1D6FF}$
can be taken arbitrarily small, and we may assume without loss of generality that
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}\rightarrow -\infty$
as
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}\rightarrow -\infty$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, the lemma follows.◻
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, the lemma follows.◻
For a smooth path
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
, the energy is given by
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
, the energy is given by
Lemma 6.5. We have
Proof. Using the fact that
![]() $v$
is
$v$
is
![]() $\unicode[STIX]{x1D6E9}$
holomorphic and Fubini’s theorem, we obtain
$\unicode[STIX]{x1D6E9}$
holomorphic and Fubini’s theorem, we obtain
The proof of the following lemma uses ideas from [Reference McDuff and SalamonMS12, Theorem 4.1.2].
Lemma 6.6. With
![]() $\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4, there exist constants
$\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4, there exist constants
![]() $c_{1},\unicode[STIX]{x1D6FC}_{1}>0$
such that
$c_{1},\unicode[STIX]{x1D6FC}_{1}>0$
such that
Proof. Write
![]() $\unicode[STIX]{x1D703}=1/\unicode[STIX]{x1D6FD}$
and let
$\unicode[STIX]{x1D703}=1/\unicode[STIX]{x1D6FD}$
and let
![]() $\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{0}$
. Without loss of generality, we may assume that
$\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{0}$
. Without loss of generality, we may assume that
![]() $\unicode[STIX]{x1D703}>\frac{1}{2}$
. By Lemma 6.4, Holder’s inequality and Lemma 6.5, we obtain
$\unicode[STIX]{x1D703}>\frac{1}{2}$
. By Lemma 6.4, Holder’s inequality and Lemma 6.5, we obtain
Integrating this differential inequality from
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() $\unicode[STIX]{x1D70F}_{0}$
gives
$\unicode[STIX]{x1D70F}_{0}$
gives
So,
and consequently
with
![]() $c_{1}=(2\unicode[STIX]{x1D703}-1)^{-1/(2\unicode[STIX]{x1D703}-1)}$
.◻
$c_{1}=(2\unicode[STIX]{x1D703}-1)^{-1/(2\unicode[STIX]{x1D703}-1)}$
.◻
Corollary 6.7. With
![]() $\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4 and
$\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4 and
![]() $\unicode[STIX]{x1D6FC}_{1}$
as in Lemma 6.6, there exists a constant
$\unicode[STIX]{x1D6FC}_{1}$
as in Lemma 6.6, there exists a constant
![]() $c_{2}>0$
such that
$c_{2}>0$
such that
Moreover,
Proof. Let
![]() $t\in (\infty ,\unicode[STIX]{x1D70F}_{0}-1]$
. Lemma 6.3 with
$t\in (\infty ,\unicode[STIX]{x1D70F}_{0}-1]$
. Lemma 6.3 with
![]() $r=\frac{1}{2}$
and Lemma 6.6 imply that
$r=\frac{1}{2}$
and Lemma 6.6 imply that
Since
![]() $|\dot{v}_{\unicode[STIX]{x1D70F}}(t)|=(1/\sqrt{2})|\,dv(\unicode[STIX]{x1D70F},t)|$
, we obtain
$|\dot{v}_{\unicode[STIX]{x1D70F}}(t)|=(1/\sqrt{2})|\,dv(\unicode[STIX]{x1D70F},t)|$
, we obtain
The following lemma uses an idea of [Reference ŁojasiewiczŁoj84]. See also [Reference Kurdyka, Mostowski and ParusińskiKMP00].
Lemma 6.8. With
![]() $\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4, there exists
$\unicode[STIX]{x1D70F}_{0}$
as in Lemma 6.4, there exists
![]() $p\in L_{0}\,\cap \,L_{1}$
and constants
$p\in L_{0}\,\cap \,L_{1}$
and constants
![]() $c_{3},\unicode[STIX]{x1D6FC}_{2}>0$
such that
$c_{3},\unicode[STIX]{x1D6FC}_{2}>0$
such that
Proof. Set
![]() $\unicode[STIX]{x1D703}=1/\unicode[STIX]{x1D6FD}$
and let
$\unicode[STIX]{x1D703}=1/\unicode[STIX]{x1D6FD}$
and let
![]() $\unicode[STIX]{x1D70F}\in (-\infty ,\unicode[STIX]{x1D70F}_{0}-1]$
. By Lemma 6.4 we have
$\unicode[STIX]{x1D70F}\in (-\infty ,\unicode[STIX]{x1D70F}_{0}-1]$
. By Lemma 6.4 we have
Thus, by Lemma 6.5 and Holder’s inequality, we obtain
Let
![]() $\unicode[STIX]{x1D70F}^{\prime }\in (-\infty ,\unicode[STIX]{x1D70F}]$
. Inequality (29), the fact that
$\unicode[STIX]{x1D70F}^{\prime }\in (-\infty ,\unicode[STIX]{x1D70F}]$
. Inequality (29), the fact that
![]() $v$
is
$v$
is
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic, and Tonelli’s theorem give
$\unicode[STIX]{x1D6E9}$
-holomorphic, and Tonelli’s theorem give
 $$\begin{eqnarray}\displaystyle \mathbf{e}(\unicode[STIX]{x1D70F})^{1-\unicode[STIX]{x1D703}}-\mathbf{e}(\unicode[STIX]{x1D70F}^{\prime })^{1-\unicode[STIX]{x1D703}}\geqslant \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\ell _{g}(v_{x})\,dx & = & \displaystyle \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl(\int _{0}^{1}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}(x,y)\biggr|\,dy\biggr)\,dx\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl(\int _{0}^{1}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}(x,y)\biggr|\,dy\biggr)\,dx=\int _{0}^{1}\biggl(\int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}(x,y)\biggr|\,dx\biggr)\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{e}(\unicode[STIX]{x1D70F})^{1-\unicode[STIX]{x1D703}}-\mathbf{e}(\unicode[STIX]{x1D70F}^{\prime })^{1-\unicode[STIX]{x1D703}}\geqslant \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\ell _{g}(v_{x})\,dx & = & \displaystyle \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl(\int _{0}^{1}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}(x,y)\biggr|\,dy\biggr)\,dx\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl(\int _{0}^{1}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}(x,y)\biggr|\,dy\biggr)\,dx=\int _{0}^{1}\biggl(\int _{\unicode[STIX]{x1D70F}^{\prime }}^{\unicode[STIX]{x1D70F}}\biggl|\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}(x,y)\biggr|\,dx\biggr)\,dy.\nonumber\end{eqnarray}$$
It follows that there exists
![]() $y\in [0,1]$
such that
$y\in [0,1]$
such that
So, with
![]() $\unicode[STIX]{x1D6FC}_{2}=(1-\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FC}_{1}$
, Lemma 6.6 implies
$\unicode[STIX]{x1D6FC}_{2}=(1-\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FC}_{1}$
, Lemma 6.6 implies
Finally, for arbitrary
![]() $t,t^{\prime }\in [0,1]$
, Corollary 6.7 gives
$t,t^{\prime }\in [0,1]$
, Corollary 6.7 gives
 $$\begin{eqnarray}\displaystyle d_{g}(v(\unicode[STIX]{x1D70F},t),v(\unicode[STIX]{x1D70F}^{\prime },t^{\prime })) & {\leqslant} & \displaystyle \ell _{g}(v_{\unicode[STIX]{x1D70F}})+d_{g}(v(\unicode[STIX]{x1D70F},y),v(\unicode[STIX]{x1D70F}^{\prime },y))+\ell _{g}(v_{\unicode[STIX]{x1D70F}^{\prime }})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (c_{1}^{(1-\unicode[STIX]{x1D703})}+c_{2})\biggl(\frac{1}{(\unicode[STIX]{x1D70F}_{0}-\unicode[STIX]{x1D70F}-1)^{\unicode[STIX]{x1D6FC}_{2}}}-\frac{1}{(\unicode[STIX]{x1D70F}_{0}-\unicode[STIX]{x1D70F}^{\prime }-1)^{\unicode[STIX]{x1D6FC}_{2}}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{g}(v(\unicode[STIX]{x1D70F},t),v(\unicode[STIX]{x1D70F}^{\prime },t^{\prime })) & {\leqslant} & \displaystyle \ell _{g}(v_{\unicode[STIX]{x1D70F}})+d_{g}(v(\unicode[STIX]{x1D70F},y),v(\unicode[STIX]{x1D70F}^{\prime },y))+\ell _{g}(v_{\unicode[STIX]{x1D70F}^{\prime }})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (c_{1}^{(1-\unicode[STIX]{x1D703})}+c_{2})\biggl(\frac{1}{(\unicode[STIX]{x1D70F}_{0}-\unicode[STIX]{x1D70F}-1)^{\unicode[STIX]{x1D6FC}_{2}}}-\frac{1}{(\unicode[STIX]{x1D70F}_{0}-\unicode[STIX]{x1D70F}^{\prime }-1)^{\unicode[STIX]{x1D6FC}_{2}}}\biggr).\end{eqnarray}$$
Let
![]() $(\unicode[STIX]{x1D70F}_{i},t_{i})\in S_{0}$
with
$(\unicode[STIX]{x1D70F}_{i},t_{i})\in S_{0}$
with
![]() $\lim _{i\rightarrow \infty }\unicode[STIX]{x1D70F}_{i}=-\infty$
. Inequality (30) implies that
$\lim _{i\rightarrow \infty }\unicode[STIX]{x1D70F}_{i}=-\infty$
. Inequality (30) implies that
![]() $v(\unicode[STIX]{x1D70F}_{i},t_{i})$
is a Cauchy sequence. Let
$v(\unicode[STIX]{x1D70F}_{i},t_{i})$
is a Cauchy sequence. Let
Set
![]() $(\unicode[STIX]{x1D70F}^{\prime },t^{\prime })=(\unicode[STIX]{x1D70F}_{i},t_{i})$
in inequality (30) and take the limit as
$(\unicode[STIX]{x1D70F}^{\prime },t^{\prime })=(\unicode[STIX]{x1D70F}_{i},t_{i})$
in inequality (30) and take the limit as
![]() $i\rightarrow \infty$
to obtain the desired inequality.◻
$i\rightarrow \infty$
to obtain the desired inequality.◻
Proof of Theorem 6.1.
Define
![]() $v:S_{0}\rightarrow M$
by
$v:S_{0}\rightarrow M$
by
![]() $v(z)=u(e^{\unicode[STIX]{x1D70B}z})$
. With
$v(z)=u(e^{\unicode[STIX]{x1D70B}z})$
. With
![]() $p$
as in Lemma 6.8, define
$p$
as in Lemma 6.8, define
![]() $\overline{u}(0)=p$
. Estimate (28) follows from Corollary 6.7.◻
$\overline{u}(0)=p$
. Estimate (28) follows from Corollary 6.7.◻
Proof of Theorem 1.9.
For each point
![]() $p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
, choose a map
$p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
, choose a map
with
![]() $\unicode[STIX]{x1D711}(0)=p$
and
$\unicode[STIX]{x1D711}(0)=p$
and
![]() $\unicode[STIX]{x1D711}$
a biholomorphism onto its image. Apply Theorem 6.1 to the map
$\unicode[STIX]{x1D711}$
a biholomorphism onto its image. Apply Theorem 6.1 to the map
![]() $u\circ \unicode[STIX]{x1D711}:H\setminus \{0\}\rightarrow M$
.◻
$u\circ \unicode[STIX]{x1D711}:H\setminus \{0\}\rightarrow M$
.◻
7 Homotopy classes
For the proof of Theorem 1.6, we need a couple more lemmas of a topological nature, which are the subject of the present section. Consider a nice Riemann surface
![]() $\unicode[STIX]{x1D6F4}$
as well as a symplectic manifold
$\unicode[STIX]{x1D6F4}$
as well as a symplectic manifold
![]() $(M,\unicode[STIX]{x1D714})$
and a collection
$(M,\unicode[STIX]{x1D714})$
and a collection
![]() ${\mathcal{L}}$
of Lagrangian submanifolds
${\mathcal{L}}$
of Lagrangian submanifolds
![]() $L_{i}\subset M,i\in A$
, all as in § 1. Let
$L_{i}\subset M,i\in A$
, all as in § 1. Let
![]() $l$
be an
$l$
be an
![]() $A$
-labeling of
$A$
-labeling of
![]() $\unicode[STIX]{x1D6F4}$
. Assume, moreover, that
$\unicode[STIX]{x1D6F4}$
. Assume, moreover, that
![]() $M,\unicode[STIX]{x1D714}$
and the Lagrangian submanifolds
$M,\unicode[STIX]{x1D714}$
and the Lagrangian submanifolds
![]() $L_{i}$
are real analytic. Let
$L_{i}$
are real analytic. Let
![]() $\operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
denote the space of continuous maps
$\operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
denote the space of continuous maps
![]() $f:\overline{\unicode[STIX]{x1D6F4}}\rightarrow M$
such that
$f:\overline{\unicode[STIX]{x1D6F4}}\rightarrow M$
such that
![]() $f(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
, endowed with the compact open topology. Let
$f(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
, endowed with the compact open topology. Let
![]() $[\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
denote the set of homotopy classes of such maps, that is, the set of path connected components of
$[\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
denote the set of homotopy classes of such maps, that is, the set of path connected components of
![]() $\operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
. For
$\operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
. For
![]() $n\in \mathbb{N}$
, abbreviate
$n\in \mathbb{N}$
, abbreviate
![]() $[n]:=\{1,\ldots ,n\}$
.
$[n]:=\{1,\ldots ,n\}$
.
Lemma 7.1. The set
![]() $[\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
is countable.
$[\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
is countable.
Proof. By Łojasiewicz’s triangulation theorem [Reference ŁojasiewiczŁoj64], choose a countable simultaneous triangulation of
![]() $M$
and
$M$
and
![]() $L_{l(i)}$
for
$L_{l(i)}$
for
![]() $i\in [b(\unicode[STIX]{x1D6F4})]$
. Choose also a finite simultaneous triangulation of
$i\in [b(\unicode[STIX]{x1D6F4})]$
. Choose also a finite simultaneous triangulation of
![]() $\overline{\unicode[STIX]{x1D6F4}}$
and
$\overline{\unicode[STIX]{x1D6F4}}$
and
![]() $\overline{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i}}$
for
$\overline{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i}}$
for
![]() $i\in [b(\unicode[STIX]{x1D6F4})]$
. Let
$i\in [b(\unicode[STIX]{x1D6F4})]$
. Let
![]() $f\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
. By [Reference SpanierSpa95, Theorem 3.4.8 and Corollary 3.4.4], after possible iterated barycentric subdivision of the triangulation of
$f\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
. By [Reference SpanierSpa95, Theorem 3.4.8 and Corollary 3.4.4], after possible iterated barycentric subdivision of the triangulation of
![]() $\overline{\unicode[STIX]{x1D6F4}}$
, there exists a simplicial approximation
$\overline{\unicode[STIX]{x1D6F4}}$
, there exists a simplicial approximation
![]() $g\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
of
$g\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
of
![]() $f$
. Examining [Reference SpanierSpa95, proof of Lemma 3.4.2], we see that
$f$
. Examining [Reference SpanierSpa95, proof of Lemma 3.4.2], we see that
Since the set of simplicial maps from an iterated barycentric subdivision of a fixed finite simplicial complex to a fixed countable simplicial complex is countable, the lemma follows. ◻
In the following,
![]() $g=g_{\unicode[STIX]{x1D6E9}}$
for
$g=g_{\unicode[STIX]{x1D6E9}}$
for
![]() $\unicode[STIX]{x1D6E9}$
an
$\unicode[STIX]{x1D6E9}$
an
![]() $\unicode[STIX]{x1D714}$
-compatible complex structure, and
$\unicode[STIX]{x1D714}$
-compatible complex structure, and
![]() $h$
is a Hermitian metric on
$h$
is a Hermitian metric on
![]() $\overline{\unicode[STIX]{x1D6F4}}$
.
$\overline{\unicode[STIX]{x1D6F4}}$
.
Definition 7.2. We say a continuous map
![]() $f\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
is almost smooth if
$f\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
is almost smooth if
![]() $\hat{f}:=f|_{\unicode[STIX]{x1D6F4}}$
is smooth, the energy
$\hat{f}:=f|_{\unicode[STIX]{x1D6F4}}$
is smooth, the energy
![]() $E_{g}(\hat{f})$
is finite, and there exist constants
$E_{g}(\hat{f})$
is finite, and there exist constants
![]() $c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that
$c,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D700}>0$
such that
Let
![]() $[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}\subset [\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
denote the set of homotopy classes that admit an almost smooth representative.
$[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}\subset [\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
denote the set of homotopy classes that admit an almost smooth representative.
Lemma 7.3. There is a well-defined map
given by
for
![]() $f$
an almost smooth representative.
$f$
an almost smooth representative.
Proof. By Lemma 6.2, the integral
![]() $\int _{\unicode[STIX]{x1D6F4}}\hat{f}^{\ast }\unicode[STIX]{x1D714}$
is well defined and finite. We must show that if
$\int _{\unicode[STIX]{x1D6F4}}\hat{f}^{\ast }\unicode[STIX]{x1D714}$
is well defined and finite. We must show that if
![]() $f_{j}\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
for
$f_{j}\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
for
![]() $j=0,1$
, are almost smooth and
$j=0,1$
, are almost smooth and
![]() $[f_{0}]=[f_{1}]\in [\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
, then
$[f_{0}]=[f_{1}]\in [\overline{\unicode[STIX]{x1D6F4}},(M,l)]$
, then
By assumption we have a continuous map
such that
If
![]() $F$
were smooth, the lemma would follow immediately from Stokes’ theorem. However, since there is no assumption on how the Lagrangian submanifolds
$F$
were smooth, the lemma would follow immediately from Stokes’ theorem. However, since there is no assumption on how the Lagrangian submanifolds
![]() $L_{i}$
intersect each other, it appears unreasonable to expect to find a homotopy
$L_{i}$
intersect each other, it appears unreasonable to expect to find a homotopy
![]() $F$
that is smooth on the whole domain
$F$
that is smooth on the whole domain
![]() $\overline{\unicode[STIX]{x1D6F4}}\times [0,1]$
. Rather we approximate
$\overline{\unicode[STIX]{x1D6F4}}\times [0,1]$
. Rather we approximate
![]() $F$
by a smooth map on
$F$
by a smooth map on
![]() $\unicode[STIX]{x1D6F4}\times [0,1]$
and use Proposition 4.8 together with the continuity of
$\unicode[STIX]{x1D6F4}\times [0,1]$
and use Proposition 4.8 together with the continuity of
![]() $F$
to work around the possible wild behavior of the approximation near points in
$F$
to work around the possible wild behavior of the approximation near points in
![]() $\overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
.
$\overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
.
Indeed, let
![]() $\unicode[STIX]{x1D700}_{0}$
be as in Theorem 4.7, let
$\unicode[STIX]{x1D700}_{0}$
be as in Theorem 4.7, let
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}_{1}$
be as in Theorem 5.1, and let
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}_{1}$
be as in Theorem 5.1, and let
![]() $\unicode[STIX]{x1D71A}>0$
be arbitrary. Using the techniques of [Reference HirschHir97, ch. 2], one can show there exists a smooth map
$\unicode[STIX]{x1D71A}>0$
be arbitrary. Using the techniques of [Reference HirschHir97, ch. 2], one can show there exists a smooth map
such that
and
For each
![]() $p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
, choose a neighborhood
$p\in \overline{\unicode[STIX]{x1D6F4}}\setminus \unicode[STIX]{x1D6F4}$
, choose a neighborhood
![]() $U_{p}$
biholomorphic to
$U_{p}$
biholomorphic to
![]() $H$
such that
$H$
such that
![]() $U_{p}\,\cap \,U_{q}=\emptyset$
for
$U_{p}\,\cap \,U_{q}=\emptyset$
for
![]() $p\neq q$
, so
$p\neq q$
, so
is a Riemann surface with corners. Let
![]() $I_{p}\subset \unicode[STIX]{x1D6F4}$
denote the topological boundary of
$I_{p}\subset \unicode[STIX]{x1D6F4}$
denote the topological boundary of
![]() $U_{p}$
, that is, the points in
$U_{p}$
, that is, the points in
![]() $U_{p}$
corresponding to the semi-circle in the boundary of
$U_{p}$
corresponding to the semi-circle in the boundary of
![]() $H$
. Thus,
$H$
. Thus,
![]() $I_{p}$
is diffeomorphic to a closed interval. It follows from condition (31) that by choosing
$I_{p}$
is diffeomorphic to a closed interval. It follows from condition (31) that by choosing
![]() $U_{p}$
sufficiently small, we may assume that
$U_{p}$
sufficiently small, we may assume that
Since
![]() $E_{g}(\hat{f}_{j})<\infty$
, we may choose
$E_{g}(\hat{f}_{j})<\infty$
, we may choose
![]() $U_{p}$
small enough that
$U_{p}$
small enough that
Furthermore, by continuity of
![]() $F$
, choosing
$F$
, choosing
![]() $U_{p}$
sufficiently small, we may assume that
$U_{p}$
sufficiently small, we may assume that
Stokes’ theorem and the Lagrangian boundary conditions (34) give
By inequalities (35) and (38), Proposition 4.8 with
![]() $\unicode[STIX]{x1D705}=F|_{[0,1]\times I_{p}}$
gives
$\unicode[STIX]{x1D705}=F|_{[0,1]\times I_{p}}$
gives
It then follows from Theorem 5.1 and the inequalities (36) that
Equation (39) and inequality (40) imply that
On the other hand, by inequality (37), for
![]() $j=0,1$
, we have
$j=0,1$
, we have
Combining inequalities (41) and (42), we obtain
Since
![]() $\unicode[STIX]{x1D71A}>0$
was arbitrary, the lemma follows.◻
$\unicode[STIX]{x1D71A}>0$
was arbitrary, the lemma follows.◻
8 Proofs of main theorems
We continue using the notation in the beginning of § 7, and we write
![]() $[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}$
for the set of almost smooth homotopy classes of maps as in Definition 7.2.
$[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}$
for the set of almost smooth homotopy classes of maps as in Definition 7.2.
Proof of Theorem 1.6.
Let
![]() $\unicode[STIX]{x1D6F4}$
be a nice Riemann surface and let
$\unicode[STIX]{x1D6F4}$
be a nice Riemann surface and let
![]() $l$
be an
$l$
be an
![]() $A$
-labeling of
$A$
-labeling of
![]() $\unicode[STIX]{x1D6F4}$
. For
$\unicode[STIX]{x1D6F4}$
. For
![]() $\unicode[STIX]{x1D6E9}=xJ+yK\in R_{I}$
, write
$\unicode[STIX]{x1D6E9}=xJ+yK\in R_{I}$
, write
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}=x\unicode[STIX]{x1D714}_{J}+y\unicode[STIX]{x1D714}_{K}$
, and let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}=x\unicode[STIX]{x1D714}_{J}+y\unicode[STIX]{x1D714}_{K}$
, and let
![]() $I_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}}:[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}\rightarrow \mathbb{R}$
be as in Lemma 7.3. For
$I_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}}}:[\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}\rightarrow \mathbb{R}$
be as in Lemma 7.3. For
define
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}:R_{I}\rightarrow \mathbb{R}$
by
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}:R_{I}\rightarrow \mathbb{R}$
by
Let
![]() $V$
be the vector space consisting of real linear combinations of
$V$
be the vector space consisting of real linear combinations of
![]() $\unicode[STIX]{x1D714}_{J}$
and
$\unicode[STIX]{x1D714}_{J}$
and
![]() $\unicode[STIX]{x1D714}_{K}$
. Define
$\unicode[STIX]{x1D714}_{K}$
. Define
by
![]() $\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}(p\unicode[STIX]{x1D714}_{J}+q\unicode[STIX]{x1D714}_{K})=pI_{\unicode[STIX]{x1D714}_{K}}(h)+qI_{\unicode[STIX]{x1D714}_{J}}(h)$
. Since
$\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}(p\unicode[STIX]{x1D714}_{J}+q\unicode[STIX]{x1D714}_{K})=pI_{\unicode[STIX]{x1D714}_{K}}(h)+qI_{\unicode[STIX]{x1D714}_{J}}(h)$
. Since
![]() $\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}$
is linear on
$\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}$
is linear on
![]() $V$
, the restriction of
$V$
, the restriction of
![]() $\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}$
to the circle
$\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}$
to the circle
![]() $\widetilde{R}_{I}=\{p\unicode[STIX]{x1D714}_{J}+q\unicode[STIX]{x1D714}_{K}|p^{2}+q^{2}=1\}$
is either identically zero or has a unique maximum. Since
$\widetilde{R}_{I}=\{p\unicode[STIX]{x1D714}_{J}+q\unicode[STIX]{x1D714}_{K}|p^{2}+q^{2}=1\}$
is either identically zero or has a unique maximum. Since
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}(\unicode[STIX]{x1D6E9})=\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}})$
, the same holds for
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}(\unicode[STIX]{x1D6E9})=\widetilde{\unicode[STIX]{x1D711}}_{h,\unicode[STIX]{x1D6F4}}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E9}})$
, the same holds for
![]() $\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
. Let
$\unicode[STIX]{x1D711}_{h,\unicode[STIX]{x1D6F4}}$
. Let
![]() $P\subset R_{I}$
be the set of
$P\subset R_{I}$
be the set of
![]() $\unicode[STIX]{x1D6E9}$
such that
$\unicode[STIX]{x1D6E9}$
such that
for some nice
![]() $\unicode[STIX]{x1D6F4}$
, some
$\unicode[STIX]{x1D6F4}$
, some
![]() $A$
-labeling
$A$
-labeling
![]() $l$
and some almost smooth homotopy class
$l$
and some almost smooth homotopy class
![]() $h\in [\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}$
. Since the set of topological types of
$h\in [\overline{\unicode[STIX]{x1D6F4}},(M,l)]^{\text{as}}$
. Since the set of topological types of
![]() $\unicode[STIX]{x1D6F4}$
and choices of
$\unicode[STIX]{x1D6F4}$
and choices of
![]() $l$
is countable, Lemma 7.1 implies
$l$
is countable, Lemma 7.1 implies
![]() $P$
is countable.
$P$
is countable.
Let
![]() $\unicode[STIX]{x1D6E9}_{0}\in R_{I}\setminus P$
, let
$\unicode[STIX]{x1D6E9}_{0}\in R_{I}\setminus P$
, let
![]() $\unicode[STIX]{x1D6F4}$
be a nice Riemann surface, and let
$\unicode[STIX]{x1D6F4}$
be a nice Riemann surface, and let
![]() $l$
be an
$l$
be an
![]() $A$
-labeling. Let
$A$
-labeling. Let
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow M$
be
$u:\unicode[STIX]{x1D6F4}\rightarrow M$
be
![]() $\unicode[STIX]{x1D6E9}_{0}$
-holomorphic with
$\unicode[STIX]{x1D6E9}_{0}$
-holomorphic with
![]() $u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
$u(\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}_{i})\subset L_{l(i)}$
and
![]() $E_{g}(u)<\infty$
. We prove that
$E_{g}(u)<\infty$
. We prove that
![]() $u$
is constant. Indeed, the condition
$u$
is constant. Indeed, the condition
![]() $E_{g}(u)<\infty$
and Theorem 1.9 imply that
$E_{g}(u)<\infty$
and Theorem 1.9 imply that
![]() $u$
extends to a continuous map
$u$
extends to a continuous map
![]() $\overline{u}\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
that is almost smooth. Let
$\overline{u}\in \operatorname{Map}(\overline{\unicode[STIX]{x1D6F4}},(M,l))$
that is almost smooth. Let
be the homotopy class represented by
![]() $\overline{u}$
. By Lemma 6.2,
$\overline{u}$
. By Lemma 6.2,
with equality if and only if
![]() $u$
is
$u$
is
![]() $\unicode[STIX]{x1D6E9}$
-holomorphic, that is,
$\unicode[STIX]{x1D6E9}$
-holomorphic, that is,
![]() $\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}_{0}$
. So,
$\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}_{0}$
. So,
![]() $\unicode[STIX]{x1D711}_{h_{u},\unicode[STIX]{x1D6F4}}$
achieves its maximum at
$\unicode[STIX]{x1D711}_{h_{u},\unicode[STIX]{x1D6F4}}$
achieves its maximum at
![]() $\unicode[STIX]{x1D6E9}_{0}$
. Since
$\unicode[STIX]{x1D6E9}_{0}$
. Since
![]() $\unicode[STIX]{x1D6E9}_{0}\notin P$
, it follows that
$\unicode[STIX]{x1D6E9}_{0}\notin P$
, it follows that
So,
![]() $u$
must be constant.◻
$u$
must be constant.◻
Proof of Theorem 1.7.
Let
![]() $\unicode[STIX]{x1D6E9}\in (R_{I}\setminus P)\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. If Theorem 1.7 were false, we could find a sequence of nice Riemann surfaces
$\unicode[STIX]{x1D6E9}\in (R_{I}\setminus P)\,\cap \,{\mathcal{J}}_{\unicode[STIX]{x1D714}}$
. If Theorem 1.7 were false, we could find a sequence of nice Riemann surfaces
![]() $\unicode[STIX]{x1D6F4}^{j}$
with
$\unicode[STIX]{x1D6F4}^{j}$
with
![]() $A_{0}$
-labelings
$A_{0}$
-labelings
![]() $l_{j}$
and
$l_{j}$
and
such that
By Gromov compactness, we would have the following:
(a) a real number
 $E_{\infty }\in [0,E_{0}]$
and an integer
$E_{\infty }\in [0,E_{0}]$
and an integer
 $\unicode[STIX]{x1D712}_{\infty }\geqslant \unicode[STIX]{x1D712}_{0}$
;
$\unicode[STIX]{x1D712}_{\infty }\geqslant \unicode[STIX]{x1D712}_{0}$
;(b) a labeled graph
 $\unicode[STIX]{x1D6E4}$
consisting of the following data:
$\unicode[STIX]{x1D6E4}$
consisting of the following data:– a finite set of vertices
 $V$
;
$V$
;– a finite set of half-edges
 $H$
;
$H$
;– a fixed point free involution
 $\unicode[STIX]{x1D70E}:H\rightarrow H$
(the set of orbits of
$\unicode[STIX]{x1D70E}:H\rightarrow H$
(the set of orbits of
 $\unicode[STIX]{x1D70E}$
, denoted by
$\unicode[STIX]{x1D70E}$
, denoted by
 $E$
, is called the set of edges of
$E$
, is called the set of edges of
 $\unicode[STIX]{x1D6E4}$
);
$\unicode[STIX]{x1D6E4}$
);– a map
 $\unicode[STIX]{x1D708}:H\rightarrow V$
sending each half-edge to the vertex to which it is attached;
$\unicode[STIX]{x1D708}:H\rightarrow V$
sending each half-edge to the vertex to which it is attached;– distinguished vertices
 $v_{0},v_{\infty }\in V$
;
$v_{0},v_{\infty }\in V$
;– a map
 $E:V\rightarrow \mathbb{R}_{{\geqslant}0}$
such that
$E:V\rightarrow \mathbb{R}_{{\geqslant}0}$
such that
 $\sum _{v\in V}E(v)=E_{\infty }$
;
$\sum _{v\in V}E(v)=E_{\infty }$
;– a map
 $\unicode[STIX]{x1D712}:V\rightarrow \mathbb{Z}$
such that
$\unicode[STIX]{x1D712}:V\rightarrow \mathbb{Z}$
such that
 $\sum _{v\in V}\unicode[STIX]{x1D712}(v)=\unicode[STIX]{x1D712}_{\infty }$
;
$\sum _{v\in V}\unicode[STIX]{x1D712}(v)=\unicode[STIX]{x1D712}_{\infty }$
;
(c) for each
 $v\in V\setminus \{v_{0}\}$
, a connected closed Riemann surface
$v\in V\setminus \{v_{0}\}$
, a connected closed Riemann surface
 $\unicode[STIX]{x1D6F4}^{v}$
and a
$\unicode[STIX]{x1D6F4}^{v}$
and a
 $\unicode[STIX]{x1D6E9}$
-holomorphic map with
$\unicode[STIX]{x1D6E9}$
-holomorphic map with $$\begin{eqnarray}u_{v}:\unicode[STIX]{x1D6F4}^{v}\rightarrow M\end{eqnarray}$$
$$\begin{eqnarray}u_{v}:\unicode[STIX]{x1D6F4}^{v}\rightarrow M\end{eqnarray}$$
 $E_{g}(u_{v})=E(v)$
and
$E_{g}(u_{v})=E(v)$
and
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6F4}^{v})-|\unicode[STIX]{x1D708}^{-1}(v)|=\unicode[STIX]{x1D712}(v)$
;
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6F4}^{v})-|\unicode[STIX]{x1D708}^{-1}(v)|=\unicode[STIX]{x1D712}(v)$
;(d) a nice Riemann surface
 $\unicode[STIX]{x1D6F4}^{v_{0}}$
with
$\unicode[STIX]{x1D6F4}^{v_{0}}$
with
 $\unicode[STIX]{x1D712}_{c}(\unicode[STIX]{x1D6F4}^{v_{0}})-|\unicode[STIX]{x1D708}^{-1}(v_{0})|=\unicode[STIX]{x1D712}(v_{0})$
and an
$\unicode[STIX]{x1D712}_{c}(\unicode[STIX]{x1D6F4}^{v_{0}})-|\unicode[STIX]{x1D708}^{-1}(v_{0})|=\unicode[STIX]{x1D712}(v_{0})$
and an
 $A_{0}$
-labeling
$A_{0}$
-labeling
 $l_{\infty }$
;
$l_{\infty }$
;(e) a
 $\unicode[STIX]{x1D6E9}$
-holomorphic map
$\unicode[STIX]{x1D6E9}$
-holomorphic map
 $u_{v_{0}}:\unicode[STIX]{x1D6F4}^{v_{0}}\rightarrow M$
with and
$u_{v_{0}}:\unicode[STIX]{x1D6F4}^{v_{0}}\rightarrow M$
with and $$\begin{eqnarray}u_{v_{0}}((\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}^{v_{0}})_{i})\subset L_{l_{\infty }(i)}\end{eqnarray}$$
$$\begin{eqnarray}u_{v_{0}}((\unicode[STIX]{x2202}\unicode[STIX]{x1D6F4}^{v_{0}})_{i})\subset L_{l_{\infty }(i)}\end{eqnarray}$$
 $E_{g}(u_{v_{0}})=E(v_{0})$
;
$E_{g}(u_{v_{0}})=E(v_{0})$
;(f) for each
 $h\in H$
, a point
$h\in H$
, a point
 $w_{h}\in \unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D708}(h)}$
such that for each edge
$w_{h}\in \unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D708}(h)}$
such that for each edge
 $e=\{h,h^{\prime }\}\in E$
, we have
$e=\{h,h^{\prime }\}\in E$
, we have
 $u_{\unicode[STIX]{x1D708}(h)}(w_{h})=u_{\unicode[STIX]{x1D708}(h^{\prime })}(w_{h^{\prime }})$
;
$u_{\unicode[STIX]{x1D708}(h)}(w_{h})=u_{\unicode[STIX]{x1D708}(h^{\prime })}(w_{h^{\prime }})$
;(g) a point
 $w_{\infty }\in \unicode[STIX]{x1D6F4}^{v_{\infty }}$
such that
$w_{\infty }\in \unicode[STIX]{x1D6F4}^{v_{\infty }}$
such that
 $u_{v_{\infty }}(w_{\infty })\in M\setminus V$
.
$u_{v_{\infty }}(w_{\infty })\in M\setminus V$
.
On the other hand, Theorem 1.6 asserts that
![]() $u_{v}$
is constant for all
$u_{v}$
is constant for all
![]() $v\in V$
, so
$v\in V$
, so
which is a contradiction. ◻
Remark 8.1. The proof of Theorem 1.7 uses a partial version of Gromov compactness that keeps track of only one of the components with boundary of the limiting stable map. Full Gromov compactness that keeps track of all components with boundary of the limiting stable map would be preferable. Indeed, if the topological type of
![]() $\unicode[STIX]{x1D6F4}$
and the labeling
$\unicode[STIX]{x1D6F4}$
and the labeling
![]() $l$
were fixed, full compactness would allow us to replace the hypothesis
$l$
were fixed, full compactness would allow us to replace the hypothesis
with the weaker hypothesis
Full compactness should indeed be true if we assume the Hamiltonian flows
![]() $\unicode[STIX]{x1D711}_{i,t}$
are real analytic. The proof would use an argument similar to the proof of Theorem 1.9 to control the behavior of low energy holomorphic strips and thus show that components with boundary connect. We leave this for future work.
$\unicode[STIX]{x1D711}_{i,t}$
are real analytic. The proof would use an argument similar to the proof of Theorem 1.9 to control the behavior of low energy holomorphic strips and thus show that components with boundary connect. We leave this for future work.
Acknowledgements
We are grateful to M. Abouzaid, S. Galkin, P. Seidel, I. Smith and G. Tian, for helpful discussions.