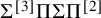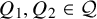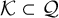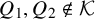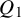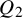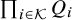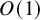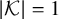A generalized Sylvester–Gallai-type theorem for quadratic polynomials

Abstract

In this work, we prove a version of the Sylvester–Gallai theorem for quadratic polynomials that takes us one step closer to obtaining a deterministic polynomial time algorithm for testing zeroness of $\Sigma ^{[3]}\Pi \Sigma \Pi ^{[2]}$ circuits. Specifically, we prove that, if a finite set of irreducible quadratic polynomials ${\mathcal {Q}}$ satisfies that for every two polynomials $Q_1,Q_2\in {\mathcal {Q}}$ there is a subset ${\mathcal {K}}\subset {\mathcal {Q}}$ such that $Q_1,Q_2 \notin {\mathcal {K}}$ and whenever $Q_1$ and $Q_2$ vanish, then $\prod _{i\in {\mathcal {K}}} Q_i$ vanishes, then the linear span of the polynomials in ${\mathcal {Q}}$ has dimension $O(1)$ . This extends the earlier result [21] that holds for the case $|{\mathcal {K}}| = 1$ .

1 Introduction

This paper studies a problem at the intersection of algebraic complexity, algebraic geometry and combinatorics that is motivated by the polynomial identity testing problem (PIT for short) for depth $4$ circuits. The question can also be regarded as an algebraic generalization and extension of the famous Sylvester–Gallai theorem from discrete geometry. We next describe the Sylvester–Gallai theorem and some of its many extensions and generalizations. For the relation to the PIT problem, see e.g. [20].

Sylvester–Gallai-type theorems:

The Sylvester–Gallai theorem asserts that, if a finite set of points in $\mathbb {R}^n$ has the property that every line passing through any two points in the set also contains a third point in the set, then all the points in the set are colinear [16, 10]. Kelly extended the theorem to points in $\mathbb {C}^n$ and proved that, if a finite set of points satisfy the Sylvester–Gallai condition, then the points in the set are coplanar. Many variants of this theorem were studied: extensions to higher dimensions, colored versions, robust versions and many more. For more on the Sylvester–Gallai theorem and some of its variants, see [4, 1, 8].

There are two extensions that are highly relevant to this work: The colored version, proved by Edelstein and Kelly, states that, if three finite sets of points satisfy that every line passing through points from two different sets also contain a point from the third set, then all the points belong to a low-dimensional space. This result was further extended to any constant number of sets. The robust version, obtained in [1, 8], states that, if a finite set of points satisfy that, for every point p in the set, a $\delta $ fraction of the other points satisfy that the line passing through each of them and p spans a third point in the set, then the set is contained in an $O(1/\delta )$ -dimensional space.

Although the Sylvester–Gallai theorem is formulated as a geometric question, it can be stated in algebraic terms: If a finite set of pairwise linearly independent vectors, ${\mathcal {S}} \subset \mathbb {C}^n$ , has the property that every two vectors span a third vector in the set, then the dimension of ${\mathcal {S}}$ is at most $3$ . It is not very hard to see that, if we pick a subspace H, of codimension $1$ , which is in general position with respect to the vectors in the set, then the intersection points $p_i = H \cap \operatorname {span}\{{s_i}\}$ , for $s_i\in {\mathcal {S}}$ satisfy the Sylvester–Gallai condition. Therefore, $\dim (S) \leq 3$ . Another formulation is the following: If a finite set of pairwise linearly independent linear forms, ${\mathcal {L}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ , has the property that, for every two forms $\ell _i,\ell _j \in {\mathcal {L}}$ , there is a third form $\ell _k \in {\mathcal {L}}$ , so that, whenever $\ell _i$ and $\ell _j$ vanish, then so does $\ell _k$ , then the linear dimension of ${\mathcal {L}}$ is at most $3$ . To see this, note that it must be the case that $\ell _k \in \operatorname {span}\{{\ell _i,\ell _j}\}$ and thus the coefficient vectors of the forms in the set satisfy the condition of the (vector version of the) Sylvester–Gallai theorem, and the bound on the dimension follows.

The last formulation can now be extended to higher-degree polynomials. In particular, the following question was asked by Gupta [12].

Problem 1.1 (Restatement of Conjecture 2 of [12]).

Can we bound the linear dimension or algebraic rank of a finite set ${\mathcal {P}}$ of pairwise linearly independent, irreducible, homogeneous polynomials of degree at most r in $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ that has the following property: For any two distinct polynomials $P_1,P_2 \in {\mathcal {P}}$ there is a third polynomial $P_3 \in {\mathcal {P}}$ such that, whenever $P_1,P_2$ vanish, then so does $P_3$ .

A robust or colored version of this problem can also be formulated. As we have seen, the case $r=1$ , that is, when all the polynomials are linear forms, follows from the Sylvester–Gallai theorem. For the case of quadratic polynomials, that is, $r=2$ , [20] gave a bound on the linear dimension for both the noncolored and colored versions. Recently, Oliveira and Sengupta solved the case $r=3$ [7]. In [18, 11] a bound for the robust version for $r=2$ was proved. For degrees, $r \geq 4$ , the problem is still open. Gupta [12] also raised more general questions of a similar form. As Gupta’s general question is for a colored version of the problem, we state a version of his Conjecture 32 that is in the spirit of this work and that is still open for degrees $r\geq 3$ .

Problem 1.2. Can we bound the linear dimension or algebraic rank of a finite set ${\mathcal {P}}$ of pairwise linearly independent irreducible polynomials of degree at most r in $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ that has the following property: For any two distinct polynomials $P_1,P_2 \in {\mathcal {P}}$ , there is a subset ${\mathcal {I}} \subset {\mathcal {P}}$ such that $P_1,P_2 \notin {\mathcal {I}}$ and whenever $P_1,P_2$ vanish, then so does $\prod _{P_i\in {\mathcal {I}}} P_i$ ?

As before, this problem can also be extended to robust and colored versions. In the case of linear forms, the bound for Theorem 1.1 carries over to Theorem 1.2 as well. This follows from the fact that the ideal generated by linear forms is prime (see section 2 for definitions). In the case of higher-degree polynomials, there is no clear reduction. For example, let $r=2$ and

$$ \begin{align*} P_1 = xy+zw \quad,\quad P_2 = xy-zw \quad,\quad P_3 = xw \quad,\quad P_4 = yz. \end{align*} $$

It is not hard to verify that whenever $P_1$ and $P_2$ vanish, then so does $P_3 \cdot P_4$ , but neither $P_3$ nor $P_4$ always vanishes when $P_1$ and $P_2$ do. The reason is that the radical of the ideal generated by $P_1$ and $P_2$ is not prime. Thus, it is not clear whether a bound for Theorem 1.1 would imply a bound for Theorem 1.2. The latter problem was open, prior to this work, for any degree $r> 1$ .

The Sylvester–Gallai theorem has important consequences for locally decodable and locally correctable codes [1, 8], for reconstruction of certain depth- $3$ circuits [19, 14, 21] and for the polynomial identity testing (PIT for short) problem, which was the main motivation for Gupta [12]. While a solution to Problem 1.1 would not yield new PIT algorithms, the following ‘colored’ version of it would [2, 12].

Conjecture 1.3 (Conjecture 30 of [12]).

There is a function $\lambda :\mathbb {N}\to \mathbb {N}$ such that the following holds for every $r,n\in \mathbb {N}$ . Let $R, B, G$ be finite disjoint sets of pairwise linearly independent, irreducible, homogeneous polynomials in $\mathbb {C}[x_1,\ldots ,x_n]$ of degree $\leq r$ such that for every pair $Q_1,Q_2$ from distinct sets it holds that, whenever both $Q_1$ and $Q_2$ vanish, then so does the product of all the polynomials in the third set. Then, the algebraic rank of $(R \cup B \cup G)$ is at most $\lambda (r)$ .

1.1 Subsequent work

In [17], we gave a positive answer to Conjecture 1.3 for the case of degree- $2$ polynomials ( $r=2$ ). This implied the first polynomial time PIT algorithm for depth- $4$ circuits with quadratic polynomials at the bottom (see [17] for a definition). While we do not know whether Conjecture 1.3 or Problem 1.1 imply the other, the proof technique in [17] is greatly influenced by the proof in this paper, and in particular, Theorem 1.5 played an important role in [17].

In [18, 11] a robust version of [20] was obtained, that is, a robust version of Theorem 1.1 for the case $r=2$ was proved.

1.2 Our result

Our main result gives a bound on the linear dimension of homogeneous polynomials satisfying the conditions of Theorem 1.2 when all the polynomials are irreducible of degree at most $2$ . Specifically, we prove the following theorem.

Theorem 1.4. There exists a universal constant c such that the following holds. Let ${{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$ be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every $Q_i\in {{\mathcal {Q}}}$ is either irreducible or a square of a linear form. Assume that, for every $i\neq j$ , whenever $Q_i$ and $Q_j$ vanish, then so does $\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$ . Then, $\dim (\operatorname {span}\{{{{\mathcal {Q}}}}\})\leq c$ .

An interesting aspect of our result is that, while the conjectures of [2, 12] speak about the algebraic rank, we prove a stronger result that bounds the linear dimension (the linear rank is an upper bound on the algebraic rank). As our proof is quite technical, it is an interesting question whether one could simplify our arguments by arguing directly about the algebraic rank.

An important algebraic tool in the proof of Theorem 1.4 is the following result characterizing the different cases in which a product of quadratic polynomials vanishes whenever two other quadratics vanish.

Theorem 1.5. Let $\{Q_k\}_{k\in {\mathcal {K}}},A$ and B be n-variate, homogeneous, quadratic polynomials, over $\mathbb {C}$ , satisfying that, whenever A and B vanish, then so does $\prod _{k\in {\mathcal {K}}} Q_k$ . Then, one of the following cases must hold:

• (prime-case): There is $k\in {\mathcal {K}}$ such that $Q_k$ is in the linear span of A and B.

• (product-case): There exists a nontrivial linear combination of the form $\alpha A+\beta B = ab$ , where a and b are linear forms.

• (linear-case): There exist two linear forms a and b such that when setting $a=b=0$ we get that A and B vanish.

The statement of the result is quite similar to Theorem 1.8 of [20] that proved a similar result when $|{\mathcal {K}}|=1$ . Specifically, in [20] the second item reads ‘There exists a non trivial linear combination of the form $\alpha A+\beta B = a^2$ , where a is a linear form.’ This difference in the statements (which is necessary) is also responsible for the harder work we do in the paper.

It was pointed out by Rafael Mendes de Oliveira and by one of the reviewers that a more general statement of Theorem 1.5 was obtained in [5, Section 1] and [13, Chapter XIII]. We discuss the similarities and differences from our theorem in subsection 1.5.

1.3 Proof idea

Our proof has a similar structure to the proofs in [20], but it does not rely on any of the results proved there.

Our starting point is the observation that Theorem 1.5 guarantees that unless one of $\{Q_k\}$ is in the linear span of A and B then A and B must satisfy a very strong property, namely, they must span a reducible quadratic or they have a very low rank (as quadratic polynomials). The proof of this theorem is based on analyzing the resultant of A and B with respect to some variable. We now explain how this theorem can be used to prove Theorem 1.4.

Consider a set of polynomials ${\mathcal {Q}}=\{{Q}_1,\ldots , {Q}_{m}\}$ satisfying the condition of Theorem 1.4. First, consider the case in which for every $Q\in {\mathcal {Q}}$ , at least, say, $(1/100)\cdot m$ of the polynomials $Q_i\in {\mathcal {Q}}$ , satisfy that there is another polynomial in ${\mathcal {Q}}$ in $\operatorname {span}\{{Q,Q_i}\}$ . In this case, we can use the robust version of the Sylvester–Gallai theorem [1, 8] (see Theorem 2.7) to deduce that the linear dimension of ${\mathcal {Q}}$ is small.

The second case we consider is when every polynomial $Q\in {\mathcal {Q}}$ that did not satisfy the first case now satisfies that for at least, say, $(1/100)\cdot m$ of the polynomials $Q_i\in {\mathcal {Q}}$ , there are linear forms $a_i$ and $b_i$ such that $Q,Q_i \in \left \langle {a_i,b_i}\right \rangle $ . We prove that, if this is the case, then there is a bounded dimensional linear space of linear forms, V such that all the polynomials in ${\mathcal {Q}}$ that are of rank $2$ are in $\left \langle {V}\right \rangle $ . Then we argue that the polynomials that are not in $\left \langle {V}\right \rangle $ satisfy the robust version of the Sylvester–Gallai theorem (Theorem 2.7). Finally, we bound the dimension of ${\mathcal {Q}} \cap \left \langle {V}\right \rangle $ .

Most of the work, however, (section 5) goes into studying what happens in the remaining case when there is some polynomial $Q_o\in {\mathcal {Q}}$ for which at least $0.98m$ of the other polynomials in ${\mathcal {Q}}$ satisfy Theorem 1.5(product-case) with $Q_o$ . This puts a strong restriction on the structure of these $0.98m$ polynomials. Specifically, each of them is of the form $Q_i = Q_o+a_ib_i$ , where $a_i$ and $b_i$ are linear forms. The idea in this case is to show that the set $\{a_i,b_i\}$ is of low dimension. This is done by again studying the consequences of Theorem 1.5 for pairs of polynomials $Q_o+a_ib_i,Q_o+a_jb_j\in {\mathcal {Q}}$ . After bounding the dimension of these $0.98m$ polynomials, we bound the dimension of all the polynomials in ${\mathcal {Q}}$ . The proof of this case is more involved than the cases described earlier. An outline of the proof is described in section 5.

1.4 On the relation to the proof of [20]

In [20], the following theorem was proved.

Theorem 1.6 (Theorem 1.7 of [20]).

Let $\{Q_i\}_{i\in [m]}$ be homogeneous quadratic polynomials over $\mathbb {C}$ such that each $Q_i$ is either irreducible or a square of a linear function. Assume further that for every $i\neq j$ there exists $k\not \in \{i,j\}$ such that whenever $Q_i$ and $Q_j$ vanish $Q_k$ vanishes as well. Then the linear span of the $Q_i$ ’s has dimension $O(1)$ .

As mentioned earlier, the steps in our proof are similar to the proof of Theorem 1.7 in [20]. Specifically, [20] also relies on an analog of Theorem 1.5 and divides the proof according to whether all polynomials satisfy the first case above (in our terminology, the prime case) or not. However, the fact that Theorem 1.5(product-case) is different than the corresponding case in the statement of Theorem 1.8 of [20] makes our proof significantly more difficult. The reason for this is that, while in [20] we could always pinpoint which polynomial vanishes when $Q_i$ and $Q_j$ vanish, here, we only know that this polynomial belongs to a small set of polynomials. This leads to a richer structure in Theorem 1.5 and consequently to a considerably more complicated proof. To understand the effect of this on our proof, we note that the case corresponding to Theorem 1.5(product-case) was the simpler case to analyze in the proof of [20]. The fact that $a_i=b_i$ when $|{\mathcal {K}}|=1$ almost immediately implied that the dimension of the span of the $a_i$ s is constant (see Claim 5.2 in [20]). In our case, however, this is the bulk of the proof, and section 5 is devoted to handling this case.

In addition to being technically more challenging, our proof gives new insights that may be extended to higher-degree polynomials. The first is Theorem 1.5, which extends a similar theorem that was proved for the simpler setting of [20]. Our second contribution is that we show (more or less) that either the polynomials in our set satisfy the robust version of the Sylvester–Gallai theorem (Theorem 2.6) or the linear functions composing the polynomials satisfy the theorem. Potentially, this may be extended to higher-degree polynomials.

1.5 The structure theorem

As mentioned above, Rafael Mendes de Oliveira and an anonymous referee turned our attention to [5, Section 1] and [13, Chapter XIII]. Both classify ideals generated by two quadratics, a result that is more general than what we prove in Theorem 1.5. Nevertheless, Theorem 1.5 is enough for us to obtain our results, and it has the added advantage that its proof is elementary.

Specifically, [5, Lemma 1.3] corresponds to the case where the ideal $\left \langle {A,B}\right \rangle $ is prime, which is covered in our Theorem 1.5(prime-case).

Theorem 1.5(product-case) was studied in Lemmata 1.6, 1.7 and 1.10 in [5]. For example, the subspace $H_1,H_2$ in Lemma 1.6 is the set of zeros of a and b from Theorem 1.5(product-case) and the rank- $2$ form of Lemma 1.7 is $ab$ . Lemma 1.10 covers the case $a=b$ .

Lemmata 1.2 and 1.4 in [5] correspond to the case where the ideal is contained in a linear subspace of codimension $2$ , which is covered in our Theorem 1.5(linear-case).

The proofs in [5] rely on cycle decomposition of the variety $\{{\boldsymbol {\alpha }}\in \mathbb {C}^n \mid A({\boldsymbol {\alpha }})=B({\boldsymbol {\alpha }})=0\}$ , while our proof only relies on simple properties of the resultant.

1.6 Organization

The paper is organized as follows. section 2 contains basic facts regarding the resultant and some other tools and notation used in this work. section 3 contains the proof of our structure theorem (Theorem 1.5). In section 4, we give the proof of Theorem 1.4. This proof uses a main theorem which will be proved in section 5. Finally, in section 6, we discuss further directions and open problems.

2 Preliminaries

In this section, we explain our notation and present some basic algebraic preliminaries.

We will use the following notation. Greek letters $\alpha , \beta ,\ldots $ denote scalars from $\mathbb {C}$ . Noncapitalized letters $a,b,c,\ldots $ denote linear forms and $x,y,z$ denote variables (which are also linear forms). Bold-faced letters denote vectors, for example, ${\mathbf {x}} = (x_1,\ldots ,x_n)$ denotes a vector of variables, ${\boldsymbol {\alpha }}=(\alpha _1,\ldots ,\alpha _n)$ is a vector of scalars and ${\mathbf {0}} = (0,\ldots ,0)$ the zero vector. We sometimes do not use a boldface notation for a point in a vector space if we do not use its structure as a vector. Capital letters such as $A,Q,P$ denote quadratic polynomials whereas $V,U,W$ denote linear spaces. Calligraphic letters $\cal I,J,F,Q,T$ denote sets. For a positive integer n, we denote $[n]=\{1,2,\ldots ,n\}$ . For a matrix X, we denote by $|X|$ the determinant of X.

A commutative ring is a ring in which the multiplication operation is commutative. We mainly use the multivariate polynomial ring, $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ . An Ideal $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ is an additive subgroup that is closed under multiplication by ring elements. For ${\mathcal {S}} \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ , we denote with $\left \langle {{\mathcal {S}}}\right \rangle $ the ideal generated by ${\mathcal {S}}$ , that is, the smallest ideal that contains ${\mathcal {S}}$ . For example, for two polynomials $Q_1$ and $Q_2$ , the ideal $\left \langle {Q_1,Q_2}\right \rangle $ is the set $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_1 + \mathbb {C}[ {x}_1,\ldots , {x}_{n}]Q_2$ . For a linear subspace V, we have that $\left \langle {V}\right \rangle $ is the ideal generated by any basis of V. The radical of an ideal I, denoted by $\sqrt {I}$ , is the set of all ring elements, r, satisfying that for some natural number m (that may depend on r), $r^m \in I$ . Hilbert’s Nullstellensatz implies that, in $\mathbb {C}[x_1,\ldots ,x_n]$ , if a polynomial Q vanishes whenever $Q_1$ and $Q_2$ vanish, then $Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$ (see, e.g., [6]). We shall often use the notation $Q\in \sqrt {\left \langle {Q_1,Q_2}\right \rangle }$ to denote this vanishing condition. For an ideal $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ , we denote by $\mathbb {C}[ {x}_1,\ldots , {x}_{n}] /I$ the quotient ring, that is, the ring whose elements are the cosets of I in $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ with the proper multiplication and addition operations. For an ideal $I\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ , we denote the set of all common zeros of elements of I by $Z(I)$ .

For $V_1,\ldots ,V_k$ linear spaces, we use $\sum _{i=1}^k V_i$ to denote the linear space $V_1 + \ldots + V_k$ . For two nonzero polynomials A and B, we denote $A\sim B$ if $B \in \operatorname {span}\{{A}\}$ . For a space of linear forms ${V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}}$ , we say that a polynomial $P \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ depends only on V if the value of P is determined by the values of the linear forms $v_1,\ldots ,v_{\Delta }$ . More formally, we say that P depends only on V if there is a $\Delta $ -variate polynomial $\tilde {P}$ such that $P \equiv \tilde {P}(v_1,\ldots ,v_{\Delta })$ . We denote by $\mathbb {C}[V]=\mathbb {C}[ {v}_1,\ldots , {v}_{\Delta }]\subseteq \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ the subring of polynomials that depend only on V.

Another notation that we will use throughout the proof is congruence modulo linear forms.

Definition 2.1. Let $V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be a space of linear forms, and $P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ . We say that $P\equiv _V Q$ if $P-Q \in \left \langle {V}\right \rangle $ .

Fact 2.2. Let $V\subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be a space of linear forms and $P,Q\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ . If $P = \prod _{k=1}^t P_k$ and $Q = \prod _{k=1}^t Q_k$ satisfy that, for all k, $P_k$ and $Q_k$ are irreducible in $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$ , and $P \equiv _V Q \not \equiv _V 0$ , then, up to a permutation of the indices and multiplication by scalars, $P_k\equiv _V Q_k$ for all $k\in [t]$ .

This follows from the fact that the quotient ring $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]/{\langle V\rangle }$ is a unique factorization domain.

2.1 Sylvester–Gallai theorem and some of its variants

In this section, we present the formal statement of the Sylvester–Gallai theorem and the extensions that we use in this work.

Definition 2.3. Given a set of points, $v_1,\ldots ,v_m$ , we call a line that passes through exactly two of the points of the set an ordinary line.

Theorem 2.4 (Sylvester–Gallai theorem [16, 10]).

If m distinct points $v_1,\ldots ,v_m$ in $\mathbb {R}^n$ are not colinear, then they define at least one ordinary line.

Theorem 2.5 (Kelly’s theorem [15]).

If m distinct points $v_1,\ldots ,v_m$ in $\mathbb {C}^n$ are not coplanar, then they define at least one ordinary line.

The robust version of the theorem was stated and proved in [1, 8].

Definition 2.6. We say that a finite set of points $\{v_1,\ldots ,v_m\}\subset \mathbb {C}^n$ is an $\delta $ -SG configuration if for every $i\in [m]$ there exists at least $\delta m$ values of $j \in [m]$ such that the line through $v_i,v_j$ is not ordinary.

Theorem 2.7 (Robust Sylvester–Gallai theorem, Theorem $1.9$ of [8]).

Let $V = \lbrace v_1,\ldots ,v_m\rbrace \subset \mathbb {C}^n$ be a $\delta $ -SG configuration. Then $\dim (\operatorname {span}\{{v_1,\ldots ,v_m}\}) \leq \frac {12}{\delta }+1$ .

The following is the colored version of the Sylvester–Gallai theorem.

Theorem 2.8 (Theorem $3$ of [9]).

Let ${\mathcal {T}}_i$ , for $i\in [3]$ , be disjoint finite subsets of $\mathbb {C}^n$ such that for every $i\neq j$ and any two points $p_1\in {\mathcal {T}}_i$ and $p_2 \in {\mathcal {T}}_j$ there exists a point $p_3$ in the third set that lies on the line passing through $p_1$ and $p_2$ . Then, any such $\{{\mathcal {T}}_i\}$ satisfy that $\dim (\operatorname {span}\{{\cup _i {\mathcal {T}}_i}\})\leq 3$ .

We also state the equivalent algebraic versions of the Sylvester–Gallai theorem.

Theorem 2.9. Let ${\mathcal {S}} = \lbrace {\mathbf {s}}_1,\ldots ,{\mathbf {s}}_m\rbrace \subset \mathbb {C}^n$ be a set of pairwise linearly independent vectors such that for every $i\neq j\in [m]$ there is a distinct $k \in [m]$ for which ${\mathbf {s}}_k \in \operatorname {span}\{{{\mathbf {s}}_i,{\mathbf {s}}_j}\}$ . Then $\dim ({\mathcal {S}}) \leq 3$ .

Theorem 2.10. Let ${\mathcal {P}} = \lbrace \ell _1,\ldots ,\ell _m\rbrace \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be a set of pairwise linearly independent linear forms such that for every $i\neq j\in [m]$ there is a distinct $k \in [m]$ for which whenever $\ell _i, \ell _j$ vanish so does $\ell _k$ . Then $\dim ({\mathcal {P}}) \leq 3$ .

In this paper, we refer to each of Theorem 2.5, Theorem 2.9 and Theorem 2.10 as the Sylvester–Gallai theorem. We shall also refer to sets of points/vectors/linear forms that satisfy the conditions of the relevant theorem as satisfying the condition of the Sylvester–Gallai theorem.

2.2 Resultant

A tool that will play an important role in the proof of Theorem 1.5 is the resultant of two polynomials. We will only define the resultant of a quadratic polynomial and a linear polynomial as this is the case relevant to our work. ¹ Let $A,B\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ . View A and B as polynomials in $x_1$ over $\mathbb {C}[x_2,\ldots ,x_n]$ , and assume that $\deg _{x_1}(A) = 2 $ and $\deg _{x_1}(B) = 1 $ , namely,

$$ \begin{align*} A = \alpha x_1^2 + ax_1 + A_0\quad \text{and}\quad B = b x_1 + B_0 . \end{align*} $$

Then, the resultant of A and B with respect to $x_1$ is the determinant of their Sylvester matrix

$$ \begin{align*} \mathrm{Res}_{x_1}(A,B) := \left| \begin{bmatrix} A_0 & B_0 & 0 \\ a & b & B_0 \\ \alpha & 0 & b \\ \end{bmatrix}\right| . \end{align*} $$

A useful fact is that, if the resultant of A and B vanishes, then they share a common factor.

Theorem 2.11 (See, for example, Proposition 8 in $5 of Chapter 3 in [6]).

Given $F,G\in \mathbb {F}[{x}_1,\ldots , {x}_{n}]$ of positive degree in $x_1$ , the resultant $\mathrm {Res}_{x_1}(F,G)$ is an integer polynomial in the coefficients of F and G. Furthermore, F and G have a common factor in $\mathbb {F}[{x}_1,\ldots , {x}_{n}]$ if and only if $\mathrm {Res}_{x_1}(F,G) = 0$ .

2.3 Rank of quadratic polynomials

In this section, we define the rank of a quadratic polynomial and present some of its useful properties.

Definition 2.12. For a homogeneous quadratic polynomial Q, we denote with $\operatorname {\mathrm {rank}}_{\text {s}}(Q)$ the minimal r such that there are $2r$ linear forms $\{a_k\}_{k=1}^{2r}$ satisfying $Q=\sum _{k=1}^r a_{2k}\cdot a_{2k-1}$ . We call such representation a minimal representation of Q.

This is a slightly different definition than the usual way one defines rank of quadratic forms, ² but it is more suitable for our needs. We note that a quadratic Q is irreducible if and only if $\operatorname {\mathrm {rank}}_{\text {s}}(Q)>1$ . The next claim shows that a minimal representation is unique in the sense that the space spanned by the linear forms in it is unique.

Claim 2.13. Let Q be a homogeneous quadratic polynomial, and let $Q=\sum _{i=1}^{r}a_{2i-1}\cdot a_{2i}$ and $Q = \sum _{i=1}^{r}b_{2i-1}\cdot b_{2i}$ be two different minimal representations of Q. Then $\operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\} =\operatorname {span}\{{{b}_1,\ldots , {b}_{2r}}\}$ .

Proof. Note that, if the statement does not hold, then, without loss of generality, $a_1$ is not contained in the span of the $b_i$ ’s. This means that when setting $a_1=0$ the $b_i$ ’s are not affected on the one hand, thus Q remains the same function of the $b_i$ ’s, and in particular $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r$ , but on the other hand, $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{a_1=0})=r-1$ (when considering its representation with the $a_i$ ’s), in contradiction.

This claim allows us to define the notion of minimal space of a quadratic polynomial Q, which we shall denote $\text {Lin}(Q)$ .

Definition 2.14. Let Q be a quadratic polynomial such that $\operatorname {\mathrm {rank}}_{\text {s}}(Q) = r$ , and let $Q = \sum \limits _{i=1}^r a_{2i-1}\cdot a_{2i}$ be some minimal representation of Q. Define $\text {Lin}(Q):= \operatorname {span}\{{{a}_1,\ldots , {a}_{2r}}\}$ , and also denote $\text {Lin}({Q}_1,\ldots , {Q}_{k}) = \sum \limits _{i=1}^k \text {Lin}(Q_i)$ .

Theorem 2.13 shows that the minimal space is well defined. The following fact is easy to verify.

Fact 2.15. Let $Q=\sum _{i=1}^{m}a_{2i-1}\cdot a_{2i}$ be a homogeneous quadratic polynomial, then $\text {Lin}(Q)\subseteq \operatorname {span}\{{{a}_1,\ldots , {a}_{2m}}\}$ .

We now give some basic claims regarding $\operatorname {\mathrm {rank}}_{\text {s}}$ .

Claim 2.16. Let Q be a homogeneous quadratic polynomial with $\operatorname {\mathrm {rank}}_{\text {s}}(Q)=r$ , and let $V \subset \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be a linear space of linear forms such that $\dim (V)=\Delta $ . Then $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0})\geq r-\Delta $ .

Proof. Assume without loss of generality $V = \operatorname {span}\{{{x}_1,\ldots , {x}_{\Delta }}\}$ , and consider $Q\in \mathbb {C}[x_{\Delta +1},\ldots ,x_n][{x}_1,\ldots , {x}_{\Delta }]$ . There are ${a}_1,\ldots , {a}_{\Delta } \in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ and $Q' \in \mathbb {C}[x_{\Delta +1},\ldots ,x_n]$ such that $Q = \sum _{i=1}^{\Delta } a_ix_i + Q'$ , where $Q|_{V=0} = Q'$ . As $\operatorname {\mathrm {rank}}_{\text {s}}(\sum _{i=1}^{\Delta } a_ix_i ) \leq \Delta $ , it must be that $\operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq r-\Delta $ .

Claim 2.17. Let $P_1\in \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$ , and $P_2 = y_1y_2\in \mathbb {C}[y_1,y_2]$ . Then $ \operatorname {\mathrm {rank}}_{\text {s}} (P_1+P_2) = \operatorname {\mathrm {rank}}_{\text {s}}(P_1) + 1$ . Moreover, $y_1,y_2 \in \text {Lin}(P_1+P_2).$

Proof. Denote $\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$ , and assume towards a contradiction that there are ${a}_1,\ldots , {a}_{2r}$ linear forms in $\mathbb {C}[x_1,\dots ,x_k,y_1,y_2]$ such that $P_1+P_2 = \sum \limits _{i=1}^{r}a_{2i-1}a_{2i}$ . Clearly, $\sum \limits _{i=1}^{r}a_{2i-1}a_{2i} \equiv _{y_1} P_1$ . As $\operatorname {\mathrm {rank}}_{\text {s}}(P_1) = r$ , this is a minimal representation of $P_1$ . Hence, for every i, $a_i|_{y_1=0} \in \text {Lin}(P_1)\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$ . Moreover, from the minimality of r, $a_i|_{y_1=0} \neq 0$ . Therefore, as $y_1$ and $y_2$ are linearly independent, we deduce that all the coefficients of $y_2$ in all the $a_i$ ’s are 0. By reversing the roles of $y_1$ and $y_2$ , we can conclude that ${a}_1,\ldots , {a}_{2r}\subset \mathbb {C}[ {x}_1,\ldots , {x}_{k}]$ which means that $P_1+P_2$ does not depend on $y_1$ nor on $y_2$ , in contradiction. Consider a minimal representation $P_1 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}$ , from the fact that $\operatorname {\mathrm {rank}}_{\text {s}}(P_1+P_2) = r+1$ it follows that $P_1+P_2 = \sum _{i=1}^{2r} b_{2i-1}b_{2i}+y_1y_2$ is a minimal representation of $P_1+P_2$ and thus $\text {Lin}(P_1+P_2) =\text {Lin}(P_1) + \operatorname {span}\{{y_1,y_2}\}$ .

Corollary 2.18. Let a and b be linearly independent linear forms. Then, if $c,d,e$ and f are linear forms such that $ab+cd=ef$ , then $\dim (\operatorname {span}\{{a,b}\}\cap \operatorname {span}\{{c,d}\})\geq 1$ .

Corollary 2.19. Let $a,b,c$ and d be linear forms such that a and b are linearly independent, and V be a linear space of linear forms. Assume $\{0\} \neq \text {Lin}(ab-cd) \subseteq V$ then $\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$ .

Proof. Let $ Q\in \mathbb {C}[V]$ be such that $ab-cd=Q$ . As $\operatorname {\mathrm {rank}}_{\text {s}}(Q-ab)=\operatorname {\mathrm {rank}}_{\text {s}}(-cd)=1$ , Theorem 2.17 implies that $\operatorname {span}\{{a,b}\} \cap V\neq \{0\}$ .

Lemma 2.20. Let $P_V\in \mathbb {C}[V]$ be a polynomial defined over a linear space of linear forms V, and let $c_1,c_2$ satisfy $ c_1 \notin V$ and $c_2 \notin \operatorname {span}\{{c_1 ,V}\}$ . If there are linear forms $e,f$ such that

$$ \begin{align*} c_1(\varepsilon_1 c_1 + v_1) + c_2(\varepsilon_2 c_2 + v_2) + ef = P_V, \end{align*} $$

then, without loss of generality, $e \in \operatorname {span}\{{c_1,c_2,V}\}$ and $e \notin \operatorname {span}\{{c_1,V}\}\cup \operatorname {span}\{{c_2,V}\}$ .

Proof. First, note that $e\not \in V$ as otherwise we would have that $c_1\equiv _V c_2$ , in contradiction.

By our assumption, $ef =P_V$ modulo $c_1,c_2$ . We can therefore assume without loss of generality that $e \in \operatorname {span}\{{c_1,c_2,V}\}$ . Assume towards a contradiction and without loss of generality that $e = \lambda c_1 + v_e$ , where $\lambda \neq 0$ and $v_e\in V$ . Consider the equation $c_1(\varepsilon _1 c_1 + v_1) + c_2(\varepsilon _2 c_2 + v_2) + ef = P_V$ modulo $c_1$ . We have that $c_2(\varepsilon _2 c_2 + v_2) + v_e f \equiv _{c_1} P_V$ which implies that $\varepsilon _2=0$ . Consequently, we also have that $f = \mu c_2 + \eta c_1 + v_f$ , for some $\mu \neq 0$ and $v_f \in V$ . We now observe that the product $c_1c_2$ has a nonzero coefficient $\lambda \mu $ in $ef$ and a zero coefficient in $P_V - c_2(\varepsilon _2 c_2 + v_2) + c_1(\varepsilon _1 c_1 + v_1) $ , in contradiction.

2.4 Linear algebra facts

Claim 2.21. Let $V = \sum _{i=1}^m V_i$ where $V_i$ are linear subspaces, and for every i, $\dim (V_i) = 2$ . If for every $i\neq j \in [m]$ , $\dim (V_i\cap V_j) = 1$ , then either $\dim (\bigcap _{i=1}^m V_i) = 1$ or $\dim (V)=3$ .

Proof. Let $w \in V_1\cap V_2$ . Complete it to basis of $V_1$ and $V_2$ : $V_1 = \operatorname {span}\{{u_1,w}\}$ and $V_2 = \operatorname {span}\{{u_2,w}\}$ . Assume that $\dim (\bigcap _{i=1}^m V_i) = 0$ . Then, there is some i for which $w \notin V_i$ . Let $x_1 \in V_i\cap V_1$ , and so $x_1 = \alpha _1 u_1 + \beta _1 w$ , where $\alpha _1 \neq 0$ . Similarly, let $x_2 \in V_i\cap V_2$ . Since $w \notin V_i$ , $x_2 = \alpha _2 u_2 + \beta _2 w$ , where $\alpha _2 \neq 0$ . Note that $x_1 \notin \operatorname {span}\{{ x_2}\}$ , as $\dim (V_1\cap V_2) = 1$ , and w is already in their intersection. Thus, we have $V_i = \operatorname {span}\{{x_1,x_2}\} \subset \operatorname {span}\{{w, u_1, u_2}\}$ .

Now, consider any other $j \in [m]$ . If $V_j$ does not contain w, we can apply the same argument as we did for $V_i$ and conclude that $V_j \subset \operatorname {span}\{{w,u_1,u_2}\}$ . On the other hand, if $w \in V_j$ , then let $x_j \in V_i\cap V_j$ . It is easy to see that $x_j, w$ are linearly independent and so $V_j = \operatorname {span}\{{w,x_j}\} \subset \operatorname {span}\{{w,V_i}\} \subseteq \operatorname {span}\{{w, u_1,u_2}\}$ . Thus, in any case $V_j \subset \operatorname {span}\{{w, u_1,u_2}\}$ . In particular, $\sum _j V_j \subseteq \operatorname {span}\{{w, u_1,u_2}\}$ as claimed.

Lemma 2.22. Let V be a linear space of dimension $\leq 4$ , and let $V_1,V_2,V_3 \subset V$ each of dimension $\geq 2$ such that $V_1\not \subseteq V_2$ and $V_3\not \subseteq V_2 + V_1$ then $V = V_1+V_2+V_3$ .

Proof. As $V_1\not \subseteq V_2$ , we have that $\dim (V_1+V_2)\geq 3$ . Similarly, we get $4\leq \dim (V_1+V_2+V_3)\leq \dim (V)=4$ .

The following corollary is an easy consequence of Theorem 2.22.

Corollary 2.23. Let Q be an irreducible quadratic polynomial. Let $\{P_i\}_{i=1}^{k}$ be irreducible quadratic polynomials such that $\dim (\text {Lin}(Q)) \leq 4$ , and for every $i\in [k]$ , $\dim (\text {Lin}(Q)\cap \text {Lin}(P_i)) \geq 2$ . Assume further that $\text {Lin}(P_1)\not \subset \text {Lin}(Q)$ , $\text {Lin}(P_2)\not \subset \text {Lin}(Q)+\text {Lin}(P_1) , \ldots , \text {Lin}(P_k)\not \subset \text {Lin}(Q)+\text {Lin}(P_1)+\ldots +\text {Lin}(P_{k-1})$ . Then, $k\leq 3$ .

2.5 Projection mappings

In this section, we present and apply a new technique which allows us to simplify the structure of quadratic polynomials. Naively, when we want to simplify a polynomial equation, we can project it on a subset of the variables. Unfortunately, this projection does not necessarily preserve pairwise linear independence, which is a crucial property in our proofs. To remedy this fact, we present a set of mappings, which are somewhat similar to projections but do preserve pairwise linear independence among polynomials that are not in $\mathbb {C}[V]$ , where V is the space being projected.

Definition 2.24. Let $V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$ be a $\Delta $ -dimensional linear space of linear forms, and let $\{{u}_1,\ldots , {u}_{{n-\Delta }}\}$ be a basis for $V^{\perp }$ . For ${\boldsymbol {\alpha }} = ({\alpha }_1,\ldots , {\alpha }_{\Delta })\in \mathbb {C}^{\Delta }$ , we define $T_{{\boldsymbol {\alpha }}, V} : \mathbb {C}[ {x}_1,\ldots , {x}_{n}] \mapsto \mathbb {C}[{x}_1,\ldots , {x}_{n},z]$ , where z is a new variable, to be the linear map given by the following action on the basis vectors: $T_{{\boldsymbol {\alpha }}, V}(v_i) = \alpha _i z$ and $T_{{\boldsymbol {\alpha }}, V}(u_i)=u_i$ .

Observation 2.25. $T_{{\boldsymbol {\alpha }}, V}$ is a linear transformation and is also a ring homomorphism. This follows from the fact that a basis for $\operatorname {span}\{{{x}_1,\ldots , {x}_{n}}\}$ is a basis for $\mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ as a $\mathbb {C}$ -algebra.

In the remaining claims in this section, we shall always assume that $V = \operatorname {span}\{{{v}_1,\ldots , {v}_{\Delta }}\}\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$ is a a $\Delta $ -dimensional linear space of linear forms. We define $T_{{\boldsymbol {\alpha }}, V}$ with respect to this basis.

Claim 2.26. Let $V\subseteq \operatorname {span}\{{x_1,\ldots ,x_n}\}$ be a $\Delta $ -dimensional linear space of linear forms. Let F and G be two polynomials that share no common irreducible factor. Then, with probability $1$ over the choice of ${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$ (say, according to the uniform distribution), $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ do not share a common factor that is not a polynomial in z.

Proof. Let $\lbrace {u}_1,\ldots , {u}_{{n-\Delta }}\rbrace $ be a basis for $V^{\perp }$ . We think of F and G as polynomials in $\mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }]$ . As $T_{{\boldsymbol {\alpha }},V}: \mathbb {C}[{v}_1,\ldots , {v}_{\Delta }, {u}_1,\ldots , {u}_{n-\Delta }] \rightarrow \mathbb {C}[z, {u}_1,\ldots , {u}_{n-\Delta }]$ , Theorem 2.11 implies that, if $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ share a common factor that is not a polynomial in z, then, without loss of generality, their resultant with respect to $u_1$ is zero. Theorem 2.11 also implies that the resultant of F and G with respect to $u_1$ is not zero. Observe that, with probability $1$ over the choice of ${\boldsymbol {\alpha }}$ , we have that $\deg _{u_1}(F) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(F))$ and $\deg _{u_1}(G) = \deg _{u_1}(T_{{\boldsymbol {\alpha }}, V}(G))$ . As $T_{{\boldsymbol {\alpha }}, V}$ is a ring homomorphism, this implies that $\mathrm {Res}_{u_1}(T_{{\boldsymbol {\alpha }}, V}(G), T_{{\boldsymbol {\alpha }}, V}(F)) = T_{{\boldsymbol {\alpha }}, V}(\mathrm {Res}_{u_1}(G, F))$ . The Schwartz–Zippel–DeMillo–Lipton lemma now implies that sending each basis element of V to a random multiple of z, chosen uniformly from $(0,1)$ , will keep the resultant nonzero with probability $1$ . This also means that $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ share no common factor.

Corollary 2.27. Let V be a $\Delta $ -dimensional linear space of linear forms. Let F and G be two linearly independent, irreducible quadratics such that $\text {Lin}(F),\text {Lin}(G)\not \subseteq V$ . Then, with probability $1$ over the choice of ${\boldsymbol {\alpha }} \in [0,1]^{\Delta }$ (say, according to the uniform distribution), $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ are linearly independent.

Proof. As F and G are irreducible they share no common factors. Theorem 2.26 implies that $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ do not share a common factor that is not a polynomial in z. The Schwartz–Zippel–DeMillo–Lipton lemma implies that, with probability $1$ , $T_{{\boldsymbol {\alpha }}, V}(F)$ and $T_{{\boldsymbol {\alpha }}, V}(G)$ are not polynomials in z, and therefore, they are linearly independent.

Claim 2.28. Let Q be an irreducible quadratic polynomial and V a $\Delta $ -dimensional linear space. Then for every ${\boldsymbol {\alpha }} \in \mathbb {C}^{\Delta }$ , $\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $ .

Proof. $\operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)) \geq \operatorname {\mathrm {rank}}_{\text {s}}(T_{{\boldsymbol {\alpha }}, V}(Q)|_{z=0}) = \operatorname {\mathrm {rank}}_{\text {s}}(Q|_{V=0}) \geq \operatorname {\mathrm {rank}}_{\text {s}}(Q)-\Delta $ , where the last inequality follows from Theorem 2.16.

Claim 2.29. Let ${\mathcal {Q}}$ be a set of quadratics and V be a $\Delta $ -dimensional linear space. Then, if there are linearly independent vectors, $\{{\boldsymbol {\alpha }}^1,\dots , {\boldsymbol {\alpha }}^{\Delta } \}\subset \mathbb {C}^{\Delta }$ such that, for every i, ³ $\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $ , then $\dim (\text {Lin}({\mathcal {Q}}))\leq (\sigma +1) \Delta $ .

Proof. As $\dim (\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})))\leq \sigma $ , there are ${u^i}_1,\ldots , {u^i}_{\sigma } \subset V^{\perp }$ such that $\text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}({\mathcal {Q}})) \subseteq \operatorname {span}\{{z,{u^i}_1,\ldots , {u^i}_{\sigma } }\}$ . We will show that $\text {Lin}({\mathcal {Q}}) \subset V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$ , which is of dimension at most $\Delta + \sigma \Delta $ .

Let $P \in {\mathcal {Q}}$ , then there are linear forms, ${a}_1,\ldots , {a}_{\Delta } \subset V^{\perp }$ and polynomials $P_{V} \in \mathbb {C}[V]$ and $P'\in \mathbb {C}[V^{\perp }]$ such that

$$ \begin{align*} P = P_{V} + \sum\limits_{j=1}^{\Delta} a_jv_j + P'. \end{align*} $$

Therefore, after taking the projection for a specific $T_{{\boldsymbol {\alpha }}^i, V}$ , for some $\gamma \in \mathbb {C}$ ,

$$ \begin{align*} T_{{\boldsymbol{\alpha}}^i,V}(P) = \gamma z^2 + \left(\sum\limits_{j=1}^{\Delta} \alpha^i_ja_j\right) z + P'. \end{align*} $$

Denote $b_{P,i} = \sum \limits _{j=1}^{\Delta } \alpha ^i_ja_j$ . By Theorem 2.27, if ${a}_1,\ldots , {a}_{\Delta }$ are not all zeros, then, with probability $1$ , $b_{P,i} \neq {\mathbf {0}}$ .

If $b_{P,i}\notin \text {Lin}(P')$ , then from Theorem 2.17 it follows that $\lbrace z, b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$ . If, on the other hand, $b_{P,i} \in \text {Lin}(P')$ , then clearly $\lbrace b_{P,i}, \text {Lin}(P')\rbrace \subseteq \operatorname {span}\{{ z, \text {Lin}(T_{{\boldsymbol {\alpha }}^i,V}(P))}\}$ . To conclude, in either case, $\{b_{P,i},\text {Lin}(P')\} \subseteq \operatorname {span}\{{z, {u^i}_1,\ldots , {u^i}_{\sigma }}\}.$

Applying the analysis above to $T_{{\boldsymbol {\alpha }}^1,V},\dots ,T_{{\boldsymbol {\alpha }}^{\Delta },V}$ , we obtain that $\operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}\subseteq \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$ . As ${\boldsymbol {\alpha }}^1,\dots {\boldsymbol {\alpha }}^{\Delta }$ are linearly independent, we have that $\{{{a}_1,\ldots , {a}_{\Delta }}\} \subset \operatorname {span}\{{b_{P,1}, \cdots b_{P,\Delta }}\}$ , and thus $\text {Lin}(P) \subseteq V + \lbrace {a}_1,\ldots , {a}_{\Delta }\rbrace + \text {Lin}(P') \subseteq V + \operatorname {span}\{{\{{u^i}_1,\ldots , {u^i}_{\sigma }\}_{i=1}^{\Delta }}\}$ .

3 Structure theorem for quadratics satisfying $ \prod _i Q_i \in \sqrt {(A,B)}$

An important tool in the proofs of our main results is Theorem 1.5 that classifies all the possible cases in which a product of quadratic polynomials $Q_1\cdot Q_2\cdot \ldots \cdot Q_k$ is in the radical of two other quadratics, $\sqrt {\left \langle {A,B}\right \rangle }$ . To ease the reading, we repeat the statement of the theorem here, albeit with slightly different notation.

Theorem 3.1. Let $\{Q_k\}_{k\in {\mathcal {K}}},A,B$ be homogeneous polynomials of degree $2$ such that $\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A,B}\right \rangle }$ . Then one of the following cases hold:

• (prime-case): There is $k\in {\mathcal {K}}$ such that $Q_k$ is in the linear span of $A,B$ .

• (product-case): There exists a nontrivial linear combination of the form $\alpha A+\beta B = c\cdot d$ , where c and d are linear forms.

• (linear-case): There exist two linear forms c and d such that when setting $c=d=0$ we get that $A,B$ and one of $\{Q_k\}_{k\in {\mathcal {K}}}$ vanish.

The following claim of [12] shows that we can assume $|{\mathcal {K}}| = 4$ in the statement of Theorem 3.1.

Claim 3.2 (Claim 11 in [12]).

Let ${P}_1,\ldots , {P}_{d},{Q}_1,\ldots , {Q}_{k}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be homogeneous and the degree of each $P_i$ is at most r. Then,

$$ \begin{align*} \prod_{i=1}^k Q_i \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} \Rightarrow \exists \lbrace {i}_1,\ldots, {i}_{r^d} \rbrace \subset [k] \; \text{ such that} \quad \prod_{j=1}^{r^d} Q_{i_j} \in \sqrt{\left \langle{{P}_1,\ldots, {P}_{d}}\right \rangle} . \end{align*} $$

Thus, for $r=d=2$ it follow that there are at most four polynomials among the $Q_i$ s whose product is in $\sqrt {\left \langle {A,B}\right \rangle }$ .

Before proving Theorem 3.1, we explain the intuition behind the different cases in the theorem. Clearly, if one of $Q_1,\ldots ,Q_4$ is a linear combination of $A,B$ , then it is in their radical (and in fact, in their linear span). If A and B span a product of the form $ab$ , then, say, $(A+ac)(A+bd)$ is in their radical. Indeed, $\sqrt {\left \langle {A,B}\right \rangle } = \sqrt {\left \langle {A,ab}\right \rangle }$ . This case is clearly different than the linear span case. Finally, we note that, if $A=ac+bd$ and $B=ae+bf$ , then the product $a\cdot b\cdot (cf-de)$ is in $\sqrt {\left \langle {A,B}\right \rangle }$ . ⁴ This case is different than the other two cases as A and B do not span any linear form (or any reducible quadratic) non trivially.

Thus, all the three cases are distinct and can happen. What Theorem 3.1 shows is that, essentially, these are the only possible cases.

Proof of Theorem 3.1.

Following Theorem 3.2, we shall assume in the proof that $|{\mathcal {K}}|=4$ . By applying a suitable linear transformation, we can assume that for some $r\geq 1$

$$ \begin{align*} A = \sum_{i=1}^{r} x_i^2. \end{align*} $$

We can also assume without loss of generality that $x_1^2$ appears only in A as we can replace B with any polynomial of the form $B'=B - \alpha A$ without affecting the result as $\left \langle {A,B}\right \rangle = \left \langle {A,B'}\right \rangle $ . Furthermore, all cases in the theorem remain the same if we replace B with $B'$ and vice versa.

In a similar fashion, we can replace $Q_1$ with $Q_1'=Q_1-\alpha A$ to get rid of the term $x_1^2$ in $Q_1$ . We can do the same for the other $Q_i$ s. Thus, without loss of generality, the situation is

(3.1) $$ \begin{align} \begin{aligned} A &= x_1^2 - A' \\ B &= x_1\cdot b - B' \ \\ Q_i &= x_1 \cdot b_i - Q^{\prime}_i \quad \text{for} \quad i\in\{1,2,3,4\}, \end{aligned} \end{align} $$

where $A',b,B',Q^{\prime }_i,b_i$ are homogeneous polynomials that do not depend on $x_1$ , the polynomials $A',B',Q'$ have degree $\leq 2$ and $b,b_i$ are linear forms. The analysis shall deal with two cases according to whether B depends on $x_1$ or not, as we only consider the resultant of A and B with respect to $x_1$ when it appears in both polynomials.

Case $\boldsymbol{b \not \equiv 0}$ :

Consider the resultant of A and B with respect to $x_1$ . It is easy to see that

$$ \begin{align*} \mathrm{Res}_{x_1}(A,B) = {B'}^2 - b^2 \cdot A'. \end{align*} $$

We first prove that, if the resultant is irreducible, then Case (prime-case) of Theorem 3.1 holds. For this, we shall need the following claim.

Claim 3.3. Whenever $\mathrm {Res}_{x_1}(A,B) =0$ , it holds that $\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) =0$ .

Proof. Let ${\boldsymbol {\alpha }} \in \mathbb {C}^{n-1}$ be such that $\mathrm {Res}_{x_1}(A,B)({\boldsymbol {\alpha }})=0$ then either $b({\boldsymbol {\alpha }})=0$ , which also implies $B'({\boldsymbol {\alpha }})=0$ and in this case the claim clearly holds, or $b({\boldsymbol {\alpha }})\neq 0$ . Consider the case $b({\boldsymbol {\alpha }})\neq 0$ , and set $x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})$ (we are free to select a value for $x_1$ as $\mathrm {Res}_{x_1}(A,B)$ does not involve $x_1$ ). Notice that for this substitution we have that $B({\boldsymbol {\alpha }})=0$ and that

$$ \begin{align*} A|_{x_1=B'({\boldsymbol{\alpha}})/b({\boldsymbol{\alpha}})} = (B'({\boldsymbol{\alpha}})/b({\boldsymbol{\alpha}}))^2 - A'({\boldsymbol{\alpha}}) = \mathrm{Res}_{x_1}(A,B)({\boldsymbol{\alpha}})/b({\boldsymbol{\alpha}})^2=0. \end{align*} $$

Hence, we also have $\prod _{i=1}^{4}Q_i |_{x_1=B'({\boldsymbol {\alpha }})/b({\boldsymbol {\alpha }})} = 0$ . In other words that

$$ \begin{align*} \left(\frac{1}{b^4}\prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i)\right)({\boldsymbol{\alpha}})=0 .\\[-49pt] \end{align*} $$

It follows that

$$ \begin{align*} \prod_{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime}_i) \in \sqrt{\mathrm{Res}_{x_1}(A,B)} . \end{align*} $$

In other words, for some positive integer k we have that $\mathrm {Res}_{x_1}(A,B)$ divides $\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$ . As every irreducible factor of $\left (\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i)\right )^k$ is of degree $3$ or less, we get that, if the resultant is irreducible, then one of the multiplicands must be identically zero. Assume without loss of generality that $B'b_1-bB^{\prime }_1=0$ . It is not hard to verify that in this case either $Q_1$ is a scalar multiple of B and then Theorem 3.1(prime-case) holds, or that $B'$ is divisible by b. However, in the latter case it also holds that b divides the resultant, contradicting the assumption that it is irreducible.

From now on we assume that $\mathrm {Res}_{x_1}(A,B)$ is reducible. We consider two possibilities. Either $\mathrm {Res}_{x_1}(A,B)$ has a linear factor or it can be written as

$$ \begin{align*} \mathrm{Res}_{x_1}(Q_1,Q_2)=C\cdot D, \end{align*} $$

for irreducible quadratic polynomials C and D.

Consider the case where the resultant has a linear factor. If that linear factor is b, then b also divides B and Theorem 3.1(product-case) holds. Otherwise, if it is a different linear form $\ell $ , then when setting $\ell =0$ we get that the resultant of $A|_{\ell =0}$ and $B|_{\ell =0}$ is zero, and hence, either $B|_{\ell =0}$ is identically zero and Theorem 3.1(product-case) holds or they share a common factor (see Theorem 2.11). It is not hard to see that, if that common factor is of degree $2$ , then Theorem 3.1(product-case) holds, and if it is a linear factor, then Theorem 3.1(linear-case) holds.

Thus, the only case left to handle (when $b\not \equiv 0$ ) is when there are two irreducible quadratic polynomials, C and D, such that $CD=\mathrm {Res}_{x_1}(A,B)$ . As C and D divide two multiplicands in $\prod _{i=1}^{4}(B'\cdot b_i - b\cdot Q^{\prime }_i) $ , we can assume, without loss of generality, that $(B'\cdot b_3 - b\cdot Q^{\prime }_3)\cdot (B'\cdot b_4 - b\cdot Q^{\prime }_4) \in \sqrt {\left \langle {\mathrm {Res}_{x_1}(A,B)}\right \rangle } $ . Next, we express $A',B',C$ and D as quadratics over b. That is,

(3.2) $$ \begin{align} A' &= \alpha b^2 + a_1 b + A" \\ B' &= \beta b^2 + a_2 b + B"\nonumber \\ C &= \gamma b^2 + a_3 b + C" \nonumber \\ D &= \delta b^2 + a_4 b + D",\nonumber \end{align} $$

where $a_1,\ldots ,D"$ do not involve b (nor $x_1$ ). We have the following two representations of the resultant:

(3.3) $$ \begin{align} \mathrm{Res}_{x_1}(A,B)&= {B'}^2 - b^2 \cdot A' \\ &= \beta^2\cdot b^4 + 2\beta a_2 \cdot b^3 + (2\beta B" + a_2^2) \cdot b^2 + 2a_2B" \cdot b + {B"}^2 - \alpha b^4- a_1 b^3 - A" b^2 \nonumber \\ &= (\beta^2-\alpha)b^4 + (2\beta a_2 - a_1)\cdot b^3 + (2\beta B" + a_2^2- A") \cdot b^2 + 2a_2B" \cdot b + {B"}^2 \nonumber \end{align} $$

and

(3.4) $$ \begin{align} \mathrm{Res}_{x_1}(Q_1,Q_2)&=CD \\ &= (\gamma b^2 + a_3 b + C")\cdot (\delta b^2 + a_4 b + D")\nonumber \\ &= \gamma\delta b^4 + (\gamma a_4 + \delta a_3)b^3 + (\gamma D" + a_3 a_4 + \delta C")b^2 + (a_3D" + a_4C")b + C"D" .\nonumber \end{align} $$

Comparing the different coefficients of b in the two representations in equations (3.3) and (3.4), we obtain the following equalities:

(3.5) $$ \begin{align} &\!\kern-1pt{B"}^2 = C"D"\quad\quad \end{align} $$

(3.6) $$ \begin{align} 2a_2B" &= a_3D" + a_{4} C". \end{align} $$

We now consider the two possible cases giving equation (3.5).

1. 1. Case 1 explaining equation (3.5): After rescaling C and D, we have that ${B"}=C"=D"$ . Equation (3.2) implies that for some linear form $u,v$ we have that

   $$ \begin{align*} C = bv + B' \quad \text{and} \quad D = bu+B'. \end{align*} $$

   We now expand the resultant again:

   $$ \begin{align*} {B'}^2 + b(v+u)B' + b^2 vu=(bv + B')\cdot ( bu+B') &= CD \\ &= \mathrm{Res}_{x_1}(A,B)= {B'}^2 - b^2 A'. \end{align*} $$

   Hence,

   (3.7) $$ \begin{align} (v+u)B' + b vu=- b A' . \end{align} $$

   Thus, either b divides $B'$ in which case we get that b divides B and we are done as Theorem 3.1 (product-case) holds, or b divides $u+v$ . That is,

   (3.8) $$ \begin{align} u+v = \varepsilon b \end{align} $$

   for some constant $\varepsilon \in \mathbb {C}$ . Plugging this back into equation (3.7), we get

   $$ \begin{align*} \varepsilon b B' + b vu=- b A' . \end{align*} $$

   In other words,

   $$ \begin{align*} \varepsilon B' + vu= - A' . \end{align*} $$

   Consider the linear combination $Q=A + \varepsilon B$ . We get that

   (3.9) $$ \begin{align} Q=A + \varepsilon B &= (x_1^2 - A') + \varepsilon (x_1 b-B') \nonumber \\ &= x_1^2 + \varepsilon x_1 b + vu \nonumber \\ &= x_1^2 + x_1(u+v)+uv \nonumber\\ &= (x_1+u)(x_1+v), \end{align} $$

   where the equality in the third line follows from equation (3.8). Thus, equation (3.9) shows that some linear combination of A and B is reducible which implies that Theorem 3.1(product-case) holds.

2. 2. Case 2 explaining equation (3.5): ${B"} = u\cdot v$ and we have that, without loss of generality, $C"=u^2$ and $D"=v^2$ (where $u,v$ are linear forms). Consider equation (3.6). We have that v divides $2a_2B" - a_3D"$ . It follows that v is also a factor of $ a_4C" $ . Thus, either u is a multiple of v and we are back in the case where $C"$ and $D"$ are multiples of each other, or $a_4$ is a multiple of v. In this case, we get from equation (3.2) that for some constant $\delta '$ ,

   $$ \begin{align*} D = \delta b^2 + a_4 b + D" = \delta b^2 +\delta' v b + v^2. \end{align*} $$

   Thus, D is a homogeneous polynomial in two linear forms. Hence, D is reducible, in contradiction.

This concludes the proof of Theorem 3.1 for the case $b\not \equiv 0$ .

Case $\boldsymbol{b \equiv 0}$ :

To ease notation, let use denote $x=x_1$ . We have that $A = x^2 - A' $ and that x does not appear in $A',B$ . Let y be some variable such that $B=y^2-B'$ , and $B'$ does not involve y (we can always assume this is the case without loss of generality). As before, we can subtract a multiple of B from A so that the term $y^2$ does not appear in A. If A still involves y, then we are back in the previous case (treating y as the variable according to which we take the resultant). Thus, the only case left to study is when there are two variables x and y such that

$$ \begin{align*} A = x^2 - A' \quad \text{and} \quad B= y^2 - B' \;, \end{align*} $$

where neither $A'$ nor $B'$ involve either x or y. To ease notation, denote the rest of the variables as ${\mathbf {z}}$ . Thus, $A'=A'({\mathbf {z}})$ and $B'=B'({\mathbf {z}})$ . It is immediate that for any assignment to ${\mathbf {z}}$ there is an assignment to $x,y$ that yields a common zero of $A,B$ .

By subtracting linear combinations of A and B from the $Q_i$ s, we can assume that for every $i\in [4]$

$$ \begin{align*} Q_i = \alpha_i xy + a_i({\mathbf{z}}) x + b_i({\mathbf{z}}) y + Q^{\prime}_i({\mathbf{z}}) . \end{align*} $$

We next show that, under the assumptions in the theorem’s statement, it must be the case that either $A'$ or $B'$ is a perfect square or that $A'\sim B'$ . In either situation, we have that Theorem 3.1(product-case) holds. We first show that, if $A'$ and $B'$ are linearly independent, then this implies that at least one of $A',B'$ is a perfect square.

Let $Z(A,B)$ be the set of common zeros of A and B, and denote by $\pi _{{\mathbf {z}}}: Z(A,B) \rightarrow \mathbb {C}^{n-2}$ , the projection on the ${\mathbf {z}}$ coordinates. Note that $\pi _{{\mathbf {z}}}$ is surjective; as for any assignment to ${\mathbf {z}}$ , there is an assignment to $x,y$ that yields a common zero of $A,B$ .

Claim 3.4. Let $Z(A,B) = \bigcup _{i=1}^k X_k$ be the decomposition of $Z(A,B)$ to irreducible components. Then there exists $i\in [k]$ such that $\pi _{{\mathbf {z}}}(X_i)$ is dense in $\mathbb {C}^{n-2}$ .

Proof. $\bigcup _{i=1}^k \pi _{{\mathbf {z}}}( X_i) = \pi _{{\mathbf {z}}}(Z(A,B)) = \mathbb {C}^{n-2}$ , as $\pi _{{\mathbf {z}}}$ is a surjection, it holds that $\bigcup _{i=1}^k \overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$ . We also know that $\mathbb {C}^{n-2}$ is irreducible, and thus, there is $i\in [k]$ such that $\overline {\pi _{{\mathbf {z}}}( X_i)} = \mathbb {C}^{n-2}$ , which implies that ${\pi _{{\mathbf {z}}}( X_i)} $ is dense.

Assume, without loss of generality, that $\pi _{{\mathbf {z}}}( X_1)$ is dense. We know that $X_1 \subseteq Z(\prod _{i=1}^{4}Q_i)$ , so we can assume, without loss of generality, that $X_1 \subseteq Z(Q_1)$ . Observe that this implies that $Q_1$ must depend on at least one of $x,y$ . Indeed, if $Q_1$ depends on neither, then it is a polynomial in ${\mathbf {z}}$ , and hence, its set of zeros cannot be dense.

Every point $\boldsymbol {\xi } \in X_1$ is of the form $\boldsymbol {\xi } = (\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }})$ , for some ${\boldsymbol {\beta }} \in \mathbb {C}^{n-2}$ , $\delta _1,\delta _2 \in \{\pm 1\}$ ( $ \delta _1,\delta _2$ may be functions of ${\boldsymbol {\beta }}$ ). Thus, $Q_1(\boldsymbol {\xi }) = Q_1(\delta _1\sqrt {A'({\boldsymbol {\beta }})},\delta _2\sqrt {B'({\boldsymbol {\beta }})},{\boldsymbol {\beta }}) =0$ , and we obtain that

(3.10) $$ \begin{align} \alpha_1 \delta_1\delta_2\sqrt{A'({\boldsymbol{\beta}}')}\cdot \sqrt{B'({\boldsymbol{\beta}}')} + a_1({\boldsymbol{\beta}}') \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}') \delta_2\sqrt{B'({\boldsymbol{\beta}}')} + Q^{\prime}_1({\boldsymbol{\beta}}')=0. \end{align} $$

As we assumed that $Q_1$ depends on at least one of $x,y$ , let us assume without loss of generality that either $\alpha _1$ or $a_1$ are nonzero. The next argument is similar to the proof that $\sqrt {2}$ is irrational. Note that we use the fact that $\delta _1^2=\delta _2^2=1$ .

(3.11) $$ \begin{align} (3.10) \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1 \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}') \right)^2 = \left( Q^{\prime}_1({\boldsymbol{\beta}}') +a_1({\boldsymbol{\beta}}') \delta_1 \sqrt{A'({\boldsymbol{\beta}}')} \right)^2 \nonumber \\ \implies & B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} +2\delta_1\alpha_1 b_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right) = \nonumber \\ & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 + 2\delta_1 a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \sqrt{A'({\boldsymbol{\beta}}')} + a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} \nonumber \\ \implies &\delta_1 \sqrt{A'({\boldsymbol{\beta}}')}\left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right) = \end{align} $$

(3.12) $$ \begin{align} & \quad\quad\quad Q^{\prime}_1({\boldsymbol{\beta}}')^2 +a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} -B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right)\nonumber \\ \qquad\ \!\implies & A'({\boldsymbol{\beta}}') \left( 2\alpha_1 b_1({\boldsymbol{\beta}}') B'({\boldsymbol{\beta}}') - 2a_1({\boldsymbol{\beta}}')Q^{\prime}_1({\boldsymbol{\beta}}') \right)^2 = \end{align} $$

$$\begin{align*}& \quad\quad\quad \left(Q^{\prime}_1({\boldsymbol{\beta}}')^2 +a_1({\boldsymbol{\beta}}')^2 {A'({\boldsymbol{\beta}}')} -B'({\boldsymbol{\beta}}')\left( \alpha_1^2 {A'({\boldsymbol{\beta}}')} + b_1({\boldsymbol{\beta}}')^2 \right)\right)^2 \nonumber . \end{align*}$$

This equality holds for every ${\boldsymbol {\beta }} \in \pi _{{\mathbf {z}}}(X_1)$ , which is a dense set, and hence holds as a polynomial identity. Thus, either $A'({\mathbf {z}})$ is a square, in which case we are done or it must be the case that the following identities hold

(3.13) $$ \begin{align} Q^{\prime}_1({\mathbf{z}})^2 +a_1({\mathbf{z}})^2 {A'({\mathbf{z}})} -B'({\mathbf{z}})\left( \alpha_1^2 {A'({\mathbf{z}})} + b_1({\mathbf{z}})^2 \right) = 0 \end{align} $$

and

(3.14) $$ \begin{align} \alpha_1 b_1({\mathbf{z}}) B'({\mathbf{z}}) - a_1({\mathbf{z}})Q^{\prime}_1({\mathbf{z}}) =0 . \end{align} $$

By symmetry, if $B'({\mathbf {z}})$ is not a square (as otherwise we are done), we get that

(3.15) $$ \begin{align} \alpha_1 a_1({\mathbf{z}}) A'({\mathbf{z}}) - b_1({\mathbf{z}})Q^{\prime}_1({\mathbf{z}}) =0 . \end{align} $$

If $\alpha _1=0$ , then we get from (3.14) that $Q^{\prime }_1\equiv 0$ . Hence, by (3.13),

$$ \begin{align*} a_1({\mathbf{z}})^2 {A'({\mathbf{z}})} = B'({\mathbf{z}})b_1({\mathbf{z}})^2. \end{align*} $$

Since we assumed that $A'$ and $B'$ are independent, this implies that $A'$ and $B'$ are both squares. If $Q^{\prime }_1\not \equiv 0$ (and in particular, $\alpha _1\neq 0$ ), then either $a_1({\mathbf {z}})=b_1({\mathbf {z}})\equiv 0$ , in which case Equation (3.13) implies that $Q^{\prime }_1({\mathbf {z}})^2 =\alpha _1^2 A'({\mathbf {z}})B'({\mathbf {z}})$ , and we are done (as either both $A'$ and $B'$ are squares or they are both multiples of $Q^{\prime }_1$ ), or equations (3.14) and (3.15) imply that $\alpha _1^2 A'({\mathbf {z}}) B'({\mathbf {z}}) = Q^{\prime }_1({\mathbf {z}})^2$ which again implies the claim.

This concludes the proof of Theorem 3.1 for the case $b\equiv 0$ and thus the proof of the theorem.

4 Sylvester–Gallai theorem for quadratic polynomials

In this section, we prove Theorem 1.4. For convenience, we repeat the statement of the theorem.

Theorem 1.4. There exists a universal constant c such that the following holds. Let $\tilde {{\mathcal {Q}}} = \{Q_i\}_{i\in \{1,\ldots ,m\}}\subset \mathbb {C}[x_1,\ldots ,x_n]$ be a finite set of pairwise linearly independent homogeneous quadratic polynomials such that every $Q_i\in \tilde {{\mathcal {Q}}}$ is either irreducible or a square of a linear form. Assume that, for every $i\neq j$ , whenever $Q_i$ and $Q_j$ vanish, then so does $\prod _{k\in \{1,\ldots ,m\} \setminus \{i,j\}} Q_k$ . Then, $\dim (\operatorname {span}\{{{\mathcal {Q}}}\})\leq c$ .

Remark 4.1. The requirement that the polynomials are homogeneous is not essential as homogenization does not affect the property $Q_k\in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$ .

Remark 4.2. Note that we no longer demand that the polynomials are irreducible but rather allow some of them to be squares of linear forms, but now we restrict all polynomials to be of degree exactly $2$ . Note that both versions of the theorem are equivalent as this modification does not affect the vanishing condition.

Remark 4.3. Note that from Theorem 3.2 it follows that for every $i\neq j$ there exists a subset ${\mathcal {K}} \subseteq [m]\setminus \{i,j\}$ such that $|{\mathcal {K}}|\leq 4$ , and whenever $Q_i$ and $Q_j$ vanish, then so does $\prod _{k\in {\mathcal {K}}} Q_k$ .

In what follows, we shall use the following terminology. Whenever we say that two quadratics $Q_1,Q_2\in \tilde {\mathcal {Q}}$ satisfy Theorem 3.1(prime-case), we mean that there is a polynomial $Q_3\in \tilde {\mathcal {Q}}\setminus \{Q_1,Q_2\}$ in their linear span. Similarly, when we say that they satisfy Theorem 3.1(product-case) (Theorem 3.1(linear-case)), we mean that there is a reducible quadratic in their linear span (they belong to $\left \langle {a_1,a_2}\right \rangle $ for linear forms $a_1,a_2$ ).

Proof of Theorem 1.4.

Partition the polynomials to two sets. Let ${\mathcal {L}}$ be the set of all squares, and let ${\mathcal {Q}}$ be the subset of irreducible quadratics, thus $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$ . Denote $|{\mathcal {Q}}| = m$ , $|{\mathcal {L}}| = r$ . Let $\delta =\frac {1}{100}$ , and denote

• • ${\mathcal {P}}_{\text {prime}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(prime-case) but not Theorem~3.1(product-case) with each of them} \}$ .

• • ${\mathcal {P}}_{\text {linear}} = \{P\in {\mathcal {Q}} \mid \text {There are at least } \delta m \text { polynomials in } {\mathcal {Q}} \text { such that } P \text { satisfies} \text {Theorem~3.1(linear-case) with each of them} \}$ .

The proof first deals with the case where ${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ . We then handle the case that there is $Q \in {\mathcal {Q}} \setminus ({\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}})$ .

4.1 The case ${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ .

Assume that ${\mathcal {Q}} = {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ . For our purposes, we may further assume that ${\mathcal {P}}_{\text {prime}}\cap {\mathcal {P}}_{\text {linear}} = \emptyset $ by letting ${\mathcal {P}}_{\text {prime}} = {\mathcal {P}}_{\text {prime}} \setminus {\mathcal {P}}_{\text {linear}}$ .

This is the simplest case in the analysis. The next claim shows that there is a small-dimensional linear space V such that ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $ . The intuition is based on the following simple observation.

Observation 4.4. If $Q_1,Q_2 \in {\mathcal {Q}}$ satisfy Theorem 3.1(linear-case), then $\dim (\text {Lin}(Q_1)), \dim (\text {Lin}(Q_2)) \leq 4$ and $\dim (\text {Lin}(Q_1)\cap \text {Lin}(Q_2)) \geq 2$ .

The observation shows that if $Q \in {\mathcal {P}}_{\text {linear}}$ and we add to V a basis for $\text {Lin}(Q)$ , then any P that satisfies Theorem 3.1(linear-case) with Q now belongs to $\left \langle {V}\right \rangle $ . Choosing several such Q’s cleverly, we manage to cover all of ${\mathcal {P}}_{\text {linear}} $ .

Claim 4.5. There exists a linear space of linear forms, V, such that $\dim (V)=O(1)$ and ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $ .

Thus, we have many small-dimensional spaces that have large pairwise intersections, and we can therefore expect that such a V may exist.

Proof. We prove the existence of V by explicitly constructing it. Repeat the following process: Set $V = \{{\mathbf {0}}\}$ , and ${\mathcal {P}}'=\emptyset $ . At each step, consider any $Q \in {\mathcal {P}}_{\text {linear}}$ such that $Q\notin \left \langle {V}\right \rangle $ , and set $V =\text {Lin}(Q) + V$ , and ${\mathcal {P}}'={\mathcal {P}}' \cup \{Q\}$ . Repeat this process as long as possible, that is, as long as ${\mathcal {P}}_{\text {linear}} \not \subseteq \left \langle {V}\right \rangle $ . We show next that this process must end after at most $\frac {3}{\delta }$ steps. Namely, $|{\mathcal {P}}'| \leq \frac {3}{\delta }$ . It is clear that at the end of the process it holds that ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $ .

Let $Q\in {\mathcal {Q}}$ and ${\mathcal {B}}\subseteq {\mathcal {P}}'$ be the subset of all polynomials in ${\mathcal {P}}'$ that satisfy Theorem 3.1(linear-case) with Q. Observe that, if $P_1,\ldots ,P_k$ are the first k elements of ${\mathcal {B}}$ that were added to ${\mathcal {P}}'$ , then $Q,P_1,\ldots ,P_k$ satisfy the conditions of Theorem 2.23. In particular, this implies that $|{\mathcal {B}}| \leq 3$ .

For $Q_i \in {\mathcal {P}}'$ , define $T_i =\{Q\in {\mathcal {Q}} \mid Q,Q_i \text { satisfy Theorem~3.1(linear-case)}\}$ . Since $|T_{i}|\geq \delta m$ and as by the discussion above each $Q\in {\mathcal {Q}}$ belongs to at most $3$ different sets, it follows by double counting that $|{\mathcal {P}}'|\leq 3/\delta $ . As in each step we add at most $4$ linearly independent linear forms to V, we obtain $\dim (V)\leq \frac {12}{\delta }$ .

This completes the proof of Theorem 4.5.

So far V satisfies that ${\mathcal {P}}_{\text {linear}} \subset \left \langle {V}\right \rangle $ . Next, we find a small set of polynomials ${\mathcal {I}}$ such that ${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$ . The construction of ${\mathcal {I}}$ is quite simple. Roughly, we iteratively add to ${\mathcal {I}}$ any $P \in {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$ . This is done in Theorem 4.6. We then show in Theorem 4.7 that each such polynomial P spans many other polynomials in $ {\mathcal {P}}_{\text {prime}}\setminus \{ \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}\}$ , and hence, this process terminates after a few steps. Interestingly, this may not cover all polynomials in ${\mathcal {Q}}$ . We show however, that the remaining polynomials satisfy the conditions of the robust Sylvester–Gallai theorem and hence are contained themselves in a low-dimensional space. Theorem 4.8 is where we the complete proof.

Construction 4.6. Set ${\mathcal {I}}= \emptyset $ and ${\mathcal {B}}={\mathcal {P}}_{\text {linear}}$ . First, add to ${\mathcal {B}}$ any polynomial from ${\mathcal {P}}_{\text {prime}}$ that is in $\left \langle {V}\right \rangle $ . Observe that at this point we have that ${\mathcal {B}}\subset {\mathcal {Q}}\cap \left \langle {V}\right \rangle $ . Consider the following process: At each step, pick any $P \in {\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$ such that P satisfies Theorem 3.1(prime-case), but not Theorem 3.1(product-case), ⁵ with at least $\frac {\delta }{3}m$ polynomials in ${\mathcal {B}}$ , and add it to both ${\mathcal {I}}$ and to ${\mathcal {B}}$ . Then, we add to ${\mathcal {B}}$ all the polynomials $P'\in {\mathcal {P}}_{\text {prime}}$ that satisfy $P' \in \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$ . Note that we always maintain that ${\mathcal {B}} \subset \operatorname {span}\{{({\mathcal {Q}} \cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$ . We continue this process as long as we can.

Next, we prove that at the end of the process we have that $|{\mathcal {I}}| \leq 3/\delta $ .

Claim 4.7. In each step, we added to ${\mathcal {B}}$ at least $\frac {\delta }{3}m$ new polynomials from ${\mathcal {P}}_{\text {prime}}$ . In particular, $|{\mathcal {I}}| \leq 3/\delta $ .

Proof. Consider what happens when we add some polynomial P to ${\mathcal {I}}$ . By the description of our process, P satisfies Theorem 3.1(prime-case) with at least $\frac {\delta }{3}m$ polynomials in ${\mathcal {B}}$ . Any $Q\in {\mathcal {B}}$ that satisfies Theorem 3.1(prime-case) with P must span with P a polynomial $P'\in \tilde {{\mathcal {Q}}}$ . Observe that $P' \notin {\mathcal {L}}$ as $Q,P$ do not satisfy Theorem 3.1(product-case), and thus, $P'\in {\mathcal {Q}}$ . It follows that $P'\in {\mathcal {P}}_{\text {prime}}$ since otherwise we would have that $P\in \operatorname {span}\{{{\mathcal {B}}}\}\subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$ , which implies $P\in {\mathcal {B}}$ in contradiction to the way that we defined the process. Furthermore, for each such $Q\in {\mathcal {B}}$ the polynomial $P'$ is unique. Indeed, if there was a $P\neq P'\in {\mathcal {P}}_{\text {prime}}$ and $Q_1,Q_2\in {\mathcal {B}}$ such that $P'\in \operatorname {span}\{{Q_1,P}\}\cap \operatorname {span}\{{Q_2,P}\}$ , then by pairwise independence we would conclude that $P\in \operatorname {span}\{{Q_1,Q_2}\}\subset \operatorname {span}\{{{\mathcal {B}}}\}$ , which, as we already showed, implies $P\in {\mathcal {B}}$ in contradiction. Thus, when we add P to ${\mathcal {I}}$ we add at least $\frac {\delta }{3}m$ polynomials to ${\mathcal {B}}$ . In particular, the process terminates after at most $3/\delta $ steps and thus $|{\mathcal {I}}|\leq 3/\delta $ .

We are now ready to complete the construction of ${\mathcal {I}}$ .

Claim 4.8. There exists a set ${\mathcal {I}}\subset {\mathcal {Q}}$ such that ${\mathcal {Q}} \subset \left \langle {V}\right \rangle +\operatorname {span}\{{{\mathcal {I}}}\}$ and $|{\mathcal {I}}|= O(1/\delta ) $ .

Proof. Let ${\mathcal {I}}$ and ${\mathcal {B}}$ be as above. Consider the polynomials left in ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$ . As they ‘survived’ the process, each of them satisfies the condition in the definition of ${\mathcal {P}}_{\text {prime}}$ with at most $\frac {\delta }{3}m$ polynomials in ${\mathcal {B}}$ . From the fact that ${\mathcal {P}}_{\text {linear}}\subseteq {\mathcal {B}}$ and the uniqueness property we obtained in the proof of Theorem 4.7, we get that ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$ satisfies the conditions of Theorem 2.6 with parameter $\delta /3$ , and thus, Theorem 2.7 implies that $\dim ({\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}})\leq O(1/\delta )$ . Adding a basis of ${\mathcal {P}}_{\text {prime}}\setminus {\mathcal {B}}$ to ${\mathcal {I}}$ , we get that $|{\mathcal {I}}| = O(1/\delta )$ and every polynomial in ${\mathcal {Q}}$ is in $\operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$ .

We are not done yet as the dimension of $\left \langle {V}\right \rangle $ , as a vector space, is not a constant. Nevertheless, we next show how to use Theorem 2.10 to bound the dimension of ${\mathcal {Q}}$ , given that ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$ . To achieve this, we introduce yet another iterative process: For each $P\in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $ , if there is quadratic L, with $\operatorname {\mathrm {rank}}_{\text {s}}(L) \leq 2$ , such that $P + L \in \left \langle {V}\right \rangle $ , then we set $V = V+\text {Lin}(L)$ (this increases the dimension of V by at most $4$ ). Since this operation increases $\dim \left ( \left \langle {V}\right \rangle \cap {\mathcal {Q}} \right )$ , we can remove one polynomial from ${\mathcal {I}}$ , and thus decrease its size by $1$ , and still maintain the property that ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$ . We repeat this process until either ${\mathcal {I}}$ is empty, or none of the polynomials in ${\mathcal {I}}$ satisfy the condition of the process. By the upper bound on $|{\mathcal {I}}|$ , the dimension of V grew by at most $4|{\mathcal {I}}|= O( 1/{\delta })$ , and thus, it remains of dimension $O( 1/{\delta })=O(1)$ . At the end of the process, we have that ${\mathcal {Q}} \subset \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle )\cup {\mathcal {I}}}\}$ and that every polynomial in $P \in {\mathcal {Q}}\setminus \left \langle {V}\right \rangle $ has $\operatorname {\mathrm {rank}}_{\text {s}}(P)> 2$ , even if we set all linear forms in V to zero.

Consider the map $T_{{\boldsymbol {\alpha }},V}$ as given in Theorem 2.24, for a randomly chosen ${\boldsymbol {\alpha }}\in [0,1]^{\dim (V)}$ . Each polynomial in ${\mathcal {Q}}\cap \left \langle {V}\right \rangle $ is mapped to a polynomial of the form $zb$ , for some linear form b. From Theorem 2.16, it follows that every polynomial in ${\mathcal {Q}}\setminus \left \langle {V}\right \rangle $ still has rank larger than $2$ after the mapping. Let

$$ \begin{align*} {\mathcal{A}}= \{b \mid \text{ some polynomial in } {\mathcal{Q}}\cap \left \langle{V}\right \rangle \text{ was mapped to } zb\} \cup T_{{\boldsymbol{\alpha}},V}({\mathcal{L}}) . \end{align*} $$

We now show that, modulo z, ${\mathcal {A}}$ satisfies the conditions of Theorem 2.10. Let $b_1,b_2\in {\mathcal {A}}$ such that $b_1 \not \in \operatorname {span}\{{z}\}$ and $b_2 \not \in \operatorname {span}\{{z,b_1}\}$ . As $\tilde {\mathcal {Q}}$ satisfies the conditions of Theorem 1.4, we get that there are polynomials $Q_1,\ldots ,Q_4 \in \tilde {\mathcal {Q}}$ such that $\prod _{i=1}^{4}T_{{\boldsymbol {\alpha }},V}(Q_i) \in \sqrt {\left \langle {b_1,b_2}\right \rangle }=\left \langle {b_1,b_2}\right \rangle $ , where the equality holds as $\left \langle {b_1,b_2}\right \rangle $ is a prime ideal. This fact also implies that, without loss of generality, $T_{{\boldsymbol {\alpha }},V}(Q_4)\in \left \langle {b_1,b_2}\right \rangle $ . Thus, $T_{{\boldsymbol {\alpha }},V}(Q_4)$ has rank at most $2$ and therefore $Q_4\in {\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) $ . Hence, $T_{{\boldsymbol {\alpha }},V}(Q_4)$ was mapped to $zb_4$ or to $b_4^2$ . In particular, $b_4\in {\mathcal {A}}$ . Theorem 2.26 and Theorem 2.27 imply that $b_4$ is neither a multiple of $b_1$ nor a multiple of $b_2$ , so it must hold that $b_4$ depends nontrivially on both $b_1$ and $b_2$ . Thus, ${\mathcal {A}}$ satisfies the conditions of Theorem 2.10 modulo z. It follows that $\dim ({\mathcal {A}})\leq 4$ .

The argument above shows that the dimension of $T_{{\boldsymbol {\alpha }},V}({\mathcal {L}}\cup ({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) ) =O(1)$ . Theorem 2.29 implies that if we denote $U = \operatorname {span}\{{{\mathcal {L}} \cup \text {Lin}({\mathcal {Q}}\cap \left \langle {V}\right \rangle )}\}$ then $\dim (U )$ is $(4+1)\cdot \dim (V)=O(1/\delta )$ . As ${\mathcal {Q}} \subseteq \operatorname {span}\{{({\mathcal {Q}}\cap \left \langle {V}\right \rangle ) \cup {\mathcal {I}}}\}$ , we obtain that $\dim (\tilde {\mathcal {Q}})=\dim ({\mathcal {L}}\cup {\mathcal {Q}}) = O(1/\delta )=O(1)$ , as we wanted to show.

This completes the proof of Theorem 1.4 for the case ${\mathcal {Q}}={\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ .

4.2 The case ${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ .

In this case, there is some polynomial $Q_o \in {\mathcal {Q}} \setminus ({{\mathcal {P}}}_1\cup {{\mathcal {P}}}_3)$ . In particular, $Q_o$ satisfies Theorem 3.1(product-case) with at least $(1-2\delta )m$ of the polynomials in ${\mathcal {Q}}$ ; of the remaining polynomials, at most $\delta m$ satisfy Theorem 3.1(prime-case) with $Q_o$ ; similarly, at most $\delta m$ polynomials satisfy Theorem 3.1(linear-case) with $Q_o$ . Let

• • ${\mathcal {Q}}_{\text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { satisfy Theorem}~{3.1}\text{(product-case) }\} \cup \{Q_o\}$

• • ${\mathcal {Q}}_{\neg \text {prod}} = \{P \in {\mathcal {Q}} \mid P,Q_o \text { do not satisfy Theorem}~{3.1}\text{(product-case)}\}$

• • $m_1+1 = |{\mathcal {Q}}_{\text {prod}}|$ , $m_2 = |{\mathcal {Q}}_{\neg \text {prod}}|$ .

As $Q_o \notin {\mathcal {P}}_{\text {prime}} \cup {\mathcal {P}}_{\text {linear}}$ , we have that $m_2 \leq 2\delta m$ and $m_1 \geq (1-2\delta )m$ . These properties of $Q_o$ and ${\mathcal {Q}}$ are captured by the following definition.

Definition 4.9. Let ${\mathcal {Q}}_{\text {prod}} = \{Q_o,Q_1,\ldots ,Q_{m_1}\hspace{-0.5pt}\}$ and ${\mathcal {Q}}_{\neg \text {prod}} = \{{P}_1,\ldots , {P}_{m_2}\}$ be sets of irreducible homogeneous quadratic polynomials. Let ${\mathcal {L}} = \{a_{m_1+1}^2,\ldots ,a_{m_1+r}^2\}$ be a set of squares of homogeneous linear forms. We say that $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$ , where ${\mathcal {Q}}={\mathcal {Q}}_{\text {prod}}\cup {\mathcal {Q}}_{\neg \text {prod}}$ is a $(Q_o,m_1,m_2)$ -set if it satisfies the following:

1. 1. $\tilde {{\mathcal {Q}}}$ satisfy the conditions in the statement of Theorem 1.4.

2. 2. $m_1> 5m_2+2$ .

3. 3. For every $j\in [m_1]$ , there are linear forms $a_j,b_j$ such that $Q_j = Q_o + a_j b_j$ .

4. 4. For every $i\in [m_2]$ , every nontrivial linear combination of $P_i$ and $Q_o$ has rank at least $2$ .

5. 5. At most $m_2$ of the polynomials in ${\mathcal {Q}}$ satisfy Theorem 3.1(linear-case) with $Q_o$ .

By the discussion above, the following theorem is what we need in order to complete the proof for the case ${\mathcal {Q}}\neq {\mathcal {P}}_{\text {prime}}\cup {\mathcal {P}}_{\text {linear}}$ .

Theorem 4.10. Let $\tilde {{\mathcal {Q}}}$ satisfy the conditions of Theorem 4.9, then $\dim {\tilde {{\mathcal {Q}}}} = O(1)$ .

We prove this theorem in section 5 to conclude the proof of Theorem 2.11. $\Box $

5 Proof of Theorem 4.10

Using the notation of Theorem 4.9, we denote, for $Q_i=Q_o+a_ib_i\in {\mathcal {Q}}_{\text {prod}}$ , $V_i := \operatorname {span}\{{a_i,b_i}\}$ , and for $Q_k=a_k^2 \in {\mathcal {L}}$ , we let $V_i=\operatorname {span}\{{a_k}\}$ . ⁶

The main idea is (roughly) proving that ${\mathcal {L}}\cup \bigcup V_i$ satisfies the conditions of the Sylvester–Gallai theorem (or its robust version). To this end, we first show, in subsection 5.1, that the different spaces $V_i$ satisfy some nontrivial intersection properties (Theorem 5.2). We then show in subsection 5.2 that there is a small-dimensional V that contains ‘most’ of the $\{a_i,b_i\}$ when ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ (Theorem 5.4). Then in subsection 5.3, we prove that there exists a constant-dimensional linear space of linear forms V (if ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ , then this is the V that we found in subsection 5.2) such that, for some $\alpha \in \{0,1\}$ , every polynomial $F\in \tilde {{\mathcal {Q}}}$ (more or less) has the form $F = \alpha Q_o +F' + c(\varepsilon c + v )$ , where c is a linear form, $\varepsilon \in \mathbb {C}$ , $v\in V$ and $F'\in \mathbb {C}[V]$ (Theorem 5.6). This structure is already very close to the claim of Theorem 4.10, and we conclude the proof in subsection 5.4 by showing that the different linear functions c satisfy the robust Sylvester–Gallai theorem (Claims 5.7 and 5.9). One case that we omitted from the description above is that, when the rank of $Q_o$ is small, We can also have $F\in \left \langle {V}\right \rangle $ . In the proof of Theorem 5.9, we handle this case using projection mappings (recall subsection 2.5).

5.1 Intersection properties of the $V_i$ s

We start by proving that the spaces $V_i$ s that were defined above intersect nontrivially under some mild condition. The proof follows almost immediately from Theorem 3.1.

Claim 5.1. Let $\tilde {{\mathcal {Q}}} = {\mathcal {Q}} \cup {\mathcal {L}}$ be a $(Q_o,m_1,m_2)\text{-}{set}$ , and let $Q_i=Q_o+a_ib_i$ and $Q_j= Q_o+a_jb_j$ be polynomials in ${\mathcal {Q}}_{\text {prod}}$ such that for every $\alpha \neq 0$ , $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$ .

1. 1. If there exists $k\in [m_1+r]\setminus \{i,j\}$ such that $Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$ , then, for some $\alpha ,\beta \in \mathbb {C}\setminus \{0\}$

   (5.1) $$ \begin{align} \alpha a_ib_i + \beta a_jb_j = a_k b_k. \end{align} $$

2. 2. If $Q_i$ and $Q_j$ satisfy Theorem 3.1(product-case), then there exist two linear forms c and d such that

   (5.2) $$ \begin{align} a_ib_i - a_jb_j = cd. \end{align} $$

3. 3. $Q_i$ and $Q_j$ do not satisfy Theorem 3.1(linear-case).

Note that the guarantee of this claim is not sufficient to conclude that the dimension of ${a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}$ is bounded. The reason is that c and d are not necessarily in the union of $V_i$ s (or in ${\mathcal {L}}$ ). For example, if for every i, $a_ib_i = x_i^2 - x_1^2$ , then every pair, $Q_i, Q_j$ satisfies Theorem 3.1(product-case), but the dimension of $\{{a}_1,\ldots , {a}_{m_1}, {b}_1,\ldots , {b}_{m_1}\}$ is unbounded.

Proof of Theorem 5.1.

If, for $k \in [m_1+r]\setminus \{i,j\}$ , $Q_k\in \operatorname {span}\{{Q_i,Q_j}\}$ , then there are constants $\alpha , \beta \in \mathbb {C}$ such that $\alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = \alpha Q_i+\beta Q_j = Q_k = \alpha _k Q_o+a_kb_k$ . ⁷ Rearranging, we get that

$$\begin{align*}\beta a_jb_j -a_kb_k = (\alpha_k-(\alpha+\beta))Q_o-\alpha a_ib_i.\end{align*}$$

As $\alpha \neq 0$ (since $Q_j \not \sim Q_k$ ), $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$ , which implies that $\alpha _k-(\alpha +\beta ) = 0$ . Hence,

(5.3) $$ \begin{align} \alpha a_ib_i + \beta a_jb_j = a_kb_k \end{align} $$

and equation (5.1) holds. As before, $\alpha , \beta \neq 0$ since otherwise we will have two linearly dependent polynomials in ${\mathcal {Q}}$ .

If $Q_i,Q_j$ satisfy Theorem 3.1(product-case), then there are $\alpha , \beta \in \mathbb {C}$ and two linear forms c and d such that $ \alpha (Q_o+a_ib_i) + \beta ( Q_o+a_jb_j) = cd$ , and again, by the same argument, we get that $\beta = -\alpha $ , and that, without loss of generality,

$$ \begin{align*} a_ib_i -a_jb_j = cd. \end{align*} $$

As $\operatorname {\mathrm {rank}}_{\text {s}}(Q_i)\geq 3$ they cannot satisfy Theorem 3.1(linear-case).

Corollary 5.2. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)\text{-}{set}$ . If for some $i\in [m_1]$ we have that $\dim (V_i)=2$ and $Q_i$ satisfies that for every $\alpha \neq 0$ , $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o + \alpha a_ib_i)\geq 3$ , then for every $j \in [m_1]$ it holds that $\dim (V_j\cap V_i) \geq 1$ . In particular, it follows that, if $dim(V_j)=1$ , then $V_j\varsubsetneq V_i$ .

Proof. This follows immediately from Theorem 5.1 and Theorem 2.18.

5.2 Constructing V using ${\mathcal {Q}}_{\neg \text {prod}}$

In this section, we show that, if ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ , then we can use any polynomial in it to define a linear space of linear forms V that contains many of the $V_i$ s. We first prove a simple claim showing that every polynomial in ${\mathcal {Q}_{\neg \text {prod}}}$ is a linear combination of $Q_o$ and a quadratic polynomial of rank $2$ .

Claim 5.3. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)\text{-}{set}$ . Then for every $i\in [m_2]$ , there exists $ \gamma _i\in \mathbb {C}$ such that $\operatorname {\mathrm {rank}}_{\text {s}}(P_i-\gamma _i Q_o) = 2$ .

Proof. Consider any $P_i$ for $i\in [m_2]$ . We shall analyze, for each $j \in [m_1]$ , which case of Theorem 3.1 $Q_j$ and $P_i$ satisfy.

If $P_i$ satisfies Theorem 3.1(linear-case) with any $Q_j\in {\mathcal {Q}}_{\text {prod}}$ , then the claim holds with $\gamma _i=0$ . If $P_i$ satisfies Theorem 3.1(product-case) with any $Q_j\in {\mathcal {Q}}$ , then there exist linear forms c and d and nonzero $\alpha , \beta \in \mathbb {C}$ such that

(5.4) $$ \begin{align} P_i = \frac{1}{\alpha}\left(cd - \beta \left(Q_o+a_j b_j\right)\right) = \frac{-\beta}{\alpha}Q_o + \left(\frac{1}{\alpha} cd - \frac{\beta}{\alpha} a_j b_j\right) . \end{align} $$

Observe that the rank of $cd - \beta a_j b_j$ cannot be $1$ by Theorem 4.9. Hence, the statement holds with $\gamma _i = -\frac {\beta }{\alpha }$ .

Thus, the only case left to consider is when $P_i$ satisfies Theorem 3.1(prime-case) with all the $Q_j$ ’s in ${\mathcal {Q}}_{\text {prod}}$ . We next show that in this case there must exist $j\neq j' \in [m_1]$ such that $Q_{j'}\in \operatorname {span}\{{Q_j,P_i}\}$ . Observe that this would imply that there are $\alpha , \beta \in \mathbb {C}\setminus \{0\}$ , for which $P_i =\alpha Q_j + \beta Q_{j'}$ and then

$$\begin{align*}P_i = (\alpha + \beta)Q_o + \alpha a_j b_j + \beta a_{j'} b_{j'}, \end{align*}$$

and the statement holds with $\gamma _i = \beta + \alpha $ , where we know by Theorem 4.9 that $\operatorname {\mathrm {rank}}_{\text {s}}(\alpha a_j b_j + \beta a_{j'} b_{j'})=2$ .

So, let us assume that, for every $j \in [m_1]$ , there is $t_j \in [m_2]$ such that $P_{t_j} \in \operatorname {span}\{{Q_j,P_i}\}$ . As $5m_2+2<m_1$ , there must be $j'\neq j" \in [m_1]$ and $t'\in [m_2]$ such that $P_{t'} \in \operatorname {span}\{{Q_{j'}, P_i}\}$ and $ P_{t'} \in \operatorname {span}\{{Q_{j"}, P_i}\}$ . Since $\mathcal {Q}$ is a set of pairwise linearly independent polynomials, we can deduce that $\operatorname {span}\{{P_i, P_{t'}}\} = \operatorname {span}\{{Q_{j'}, Q_{j"}}\}$ . In particular, there exist $\alpha , \beta \in \mathbb {C}$ , for which $P_i =\alpha Q_j + \beta Q_{j'}$ , which, as we already showed, implies what we wanted to prove.

For simplicity, rescale $P_i$ so that $P_i = \gamma _i Q_o+L_i$ with $\operatorname {\mathrm {rank}}_{\text {s}}(L_i)=2$ and $\gamma _i \in \{0,1\}$ . Clearly, ${\mathcal {Q}}$ still satisfies the conditions of Theorem 4.9 after this rescaling as it does not affect the vanishing conditions or linear independence.

Claim 5.4. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)\text{-}set$ , where ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ . Let $P=\gamma Q_o + L\in {\mathcal {Q}_{\neg \text {prod}}}$ . Let V be defined as

• • If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then $V=\text {Lin}(L)$ and in particular $\dim (V)\leq 4$ .

• • If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$ , then $V=\text {Lin}(Q_o)+\text {Lin}(L)$ , so $\dim (V)\leq 202$ .

Then, for at least $m_1-2m_2 $ indices $j\in [m_1]$ it holds that $a_j,b_j \in V $ . Furthermore, for $Q_i=\alpha _iQ_o+a_ib_i \in {\mathcal {Q}}_{\text {prod}}$ the only cases in which $\{a_i,b_i\}\not \subseteq V$ are

1. 1. If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then it must be the case that $Q_i$ and P span a polynomial $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$ .

2. 2. If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ , then either $Q_i$ and P span a polynomial $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$ or there are two linear functions $c,d$ such that $P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $ .

Remark 5.5. When $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , we actually get the result for $m_1-m_2$ many indices.

The idea of the proof is to study for each $Q_j\in {\mathcal {Q}}_{\text {prod}}\cup {\mathcal {L}}$ what case of Theorem 3.1 it satisfies with some $P\in {\mathcal {Q}_{\neg \text {prod}}}$ . If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$ is high, then $Q_o$ must ‘disappear’ from the equations and we trivially get $a_j,b_j\in V=\text {Lin}(P)$ . When the rank of $Q_o$ is low, the argument is slightly different. In this case, we let V also contain $\text {Lin}(Q_o)$ , and using this, we show $a_j,b_j\in V$ .

Proof. Let $P = \gamma Q_o+L\in {\mathcal {Q}_{\neg \text {prod}}}$ , where $\operatorname {\mathrm {rank}}_{\text {s}}(L) =2$ . Let V be defined as in the statement of the theorem: We set $V = \text {Lin}(L)$ when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ and $V =\text {Lin}(Q_o)+\text {Lin}(L)$ otherwise.

Let $Q_j=\alpha _j Q_o +a_j b_j\in {\mathcal {Q}}_{\text {prod}}$ . We consider which case of Theorem 3.1 P and $Q_j$ satisfy.

P and $Q_j$ satisfy Theorem 3.1(product-case):

In this case, there are two linear forms c and d, and nonzero $\alpha , \beta \in \mathbb {C}$ , such that $\alpha P + \beta Q_j = cd$ . Hence,

$$ \begin{align*} \beta\alpha_j Q_o+\alpha P= - \beta a_jb_j +cd.\\[-24pt] \end{align*} $$

As $\beta \alpha _j Q_o+\alpha P$ is a nontrivial linear combination of $Q_o$ and P, we get from property 4 of Theorem 4.9 that $2 \leq \operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma +\beta \alpha _j)Q_o+\alpha L)$ . It follows that

$$ \begin{align*} 2\leq \operatorname{\mathrm{rank}}_{\text{s}}((\alpha\gamma+\beta\alpha_j)Q_o+\alpha L)= \operatorname{\mathrm{rank}}_{\text{s}}(- \beta a_jb_j +cd)\leq 2. \end{align*} $$

If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then $\alpha \gamma +\beta \alpha _j=0$ . Thus, regardless of $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)$ , we get from Theorem 2.15 that

$$ \begin{align*} \{a_j,b_j,c,d\}\subseteq \text{Lin}(-\beta a_jb_j +cd)= \text{Lin}((\alpha\gamma+\beta)Q_o+\alpha L)\subseteq V, \end{align*} $$

and in particular $a_j,b_j\in V$ .

P and $Q_j$ satisfy Theorem 3.1(linear-case):

If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then it must hold that $\alpha _j = 0$ and $Q_j =a_j^2$ . By the rank condition on $Q_o$ , it also follows that $\gamma = 0$ , and therefore, $a_j \in \text {Lin}(L) = V$ .

Consider the case $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ . There are two linear forms c and d such that $Q_j,P\in \sqrt {\left \langle {c,d}\right \rangle }$ . This implies that $\operatorname {span}\{{c,d}\} \subseteq \text {Lin}(P) \subseteq V$ .

If $Q_o$ is zero modulo c and d, then $Q_{j},Q_o$ satisfy Theorem 3.1(linear-case), and from property 5 of Theorem 4.9, we know that there are at most $m_2$ such $Q_j$ ’s. Furthermore, as $c,d\in \text {Lin}(Q_o) \subset V$ , we obtain that $Q_j \in \left \langle {V}\right \rangle $ . Denote by ${\mathcal {K}}$ the set of all $Q_j$ that satisfy Theorem 3.1(linear-case) with $Q_o$ , and recall that $|{\mathcal {K}}|\leq m_2$ .

If $Q_o=Q_j-a_j b_j$ is not zero modulo ${c,d}$ , then we obtain that $Q_o\equiv _{c,d} -a_j b_j$ . Thus, there are linear forms $v_1,v_2\in \text {Lin}(Q_o)$ such that $a_j \equiv _{c,d} v_1$ and $b_j \equiv _{c,d} v_2$ . In particular, as $\text {Lin}(Q_o)\cup \{c,d\}\subseteq V$ , it follows that $a_j,b_j\in V$ .

P and $Q_j$ satisfy Theorem 3.1(prime-case):

Let P and $Q_j$ satisfy Theorem 3.1(prime-case) but not Theorem 3.1(product-case) (as we already handled this case), that is, they span another polynomial in $\tilde {{\mathcal {Q}}}\setminus {\mathcal {L}}$ . If this polynomial is in ${\mathcal {Q}}_{\text {prod}}$ , then there exists $j' \in [m_1]$ such that $Q_{j'}\in \operatorname {span}\{{P,Q_j}\}$ . In this case, $P = \alpha Q_j + \beta Q_{j'}$ , and as before, we conclude that $a_{j'} ,b_{j'}, a_{j}, b_{j} \in V$ .

All that is left is to bound the number of $j\in [m_1]$ so that P and $Q_j$ span a polynomial in ${\mathcal {Q}}_{\neg \text {prod}}$ . If there are more than $m_2$ such indices j, then, by the pigeonhole principle, for two of them, say $j,j'$ , it must be the case that there is some $i \in [m_2]$ such that $P_{i}\in \operatorname {span}\{{P,Q_j}\}$ and $P_{i}\in \operatorname {span}\{{P,Q_{j'}}\}$ . As our polynomials are pairwise independent, this implies that $P \in \operatorname {span}\{{Q_j,Q_{j'}}\}$ , and as before, we get that $a_{j'},b_{j'}, a_{j},b_{j}\in V$ .

It follows that the only case where $a_j,b_j\not \in V$ and P and $Q_j$ satisfy Theorem 3.1(prime-case) is when $Q_j$ and P span a polynomial in ${\mathcal {Q}}_{\neg \text {prod}}$ , and no other $Q_{j'}$ spans this polynomial with P. Therefore, there are at most $m_2$ such ‘bad’ j’s.

To conclude, the only j’s for which $a_j,b_j\not \in V$ can come from $Q_j\in {\mathcal {K}}$ (when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ ) and P and $Q_j$ satisfy Theorem 3.1(linear-case)), or it is one of the bad $Q_j$ when P and $Q_j$ satisfy Theorem 3.1(prime-case), so in total there are at most $2m_2$ bad indices. This also shows the ‘furthermore’ part of the claim.

5.3 Global structure

Our goal in this subsection is proving that there exists a constant-dimensional linear space of linear forms V such that, for some $\alpha \in \{0,1\}$ , every polynomial $F\in \tilde {{\mathcal {Q}}}$ (more or less) has the form $F = \alpha Q_o +F' + c(\varepsilon c + v )$ , where c is a linear form, $\varepsilon \in \mathbb {C}$ , $v\in V$ and $F'\in \mathbb {C}[V]$ .

We remark that $\alpha =1$ if $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ and $\alpha =0$ otherwise (as in the low-rank case we construct V so that $\text {Lin}(Q_o)\subseteq V$ ).

Formally, we prove the following claim.

Claim 5.6. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)\text{-}{set}$ . There exists a linear space of linear forms V such that

• • If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then $\dim (V)=4$ , and

• • If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$ , then $\dim (V)\leq 202$ ,

and the following hold: Every polynomial $F\in \tilde {{\mathcal {Q}}}$ satisfies at least one of the following:

1. 1. $F\in \mathbb {C}[V]$ , or

2. 2. $F = c^2$ , for a linear form c, or

3. 3. $F\in \left \langle {V}\right \rangle $ (only when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$ ), or

4. 4. $F = \alpha Q_o +F' + c(\varepsilon c + v )$ , where c is a linear form, $\varepsilon \in \mathbb {C}$ , $v\in V$ and $F'\in \mathbb {C}[V]$ . Furthermore, $\alpha =1$ if $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ and $\alpha =0$ otherwise.

The proof of the claim depends on the rank of $Q_o$ (we use different arguments in the high-rank case and in the low-rank case) and on whether ${\mathcal {Q}}_{\neg \text {prod}}$ is empty or not. When ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ , we show that the space V that we constructed in Theorem 5.4 is the required space. The idea is that V already ‘explains’ so much of the structure of $\tilde {{\mathcal {Q}}}$ that we can expand it to all polynomials in $\tilde {{\mathcal {Q}}}$ . When ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $ , the argument is different and does not rely on Theorem 5.4. Here, since all polynomials are of the form $Q_o + a_jb_j$ (ignoring squares of linear functions), using the conclusion of Theorem 5.1 that the $V_i$ s intersect nontrivially, and Theorem 2.21 we easily get the claimed structure.

Proof. We analyze two cases: when ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $ and the case ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ .

The case ${\mathcal {Q}_{\neg \text {prod}}}=\emptyset $ :

Let

$$ \begin{align*} {\mathcal{I}}=\{i\in[m_1] \mid \dim(V_i)=2 \text{ and for every } \alpha\neq 0,\; \operatorname{\mathrm{rank}}_{\text{s}}(Q_o + \alpha a_ib_i)\geq 3\}. \end{align*} $$

Observe that, if $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then ${\mathcal {I}}$ simply contains all $V_i$ s of dimension $2$ .

If ${\mathcal {I}}=\emptyset $ , then we can take $V=\{0\}$ when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ or $V=\text {Lin}(Q_o)$ in the case $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)< 100$ . Indeed, Theorem 2.18 implies that in this case every polynomial is of the form $F = \alpha Q_o +F' + c^2$ , with $\alpha =\mathbb {1}_{\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100}$ .

Assume then that ${\mathcal {I}}\neq \emptyset $ . Combining Theorem 5.2 and Theorem 2.21, we get that either $\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$ or $\dim (\bigcap _{i\in {\mathcal {I}}} V_i) =1$ .

If $\dim (\bigcup _{i\in {\mathcal {I}}} V_i) \leq 3$ , then we define $V'=\bigcup _{i\in {\mathcal {I}}} V_i$ . If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$ , then we let $V=V'+\text {Lin}(Q_o)$ so that $\dim (V)\leq 201$ , and when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)\geq 100$ , we let $V=V'$ and $\dim (V)=3$ . It is clear that V satisfies the requirement when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ . So assume $\operatorname {\mathrm {rank}}_{\text {s}}(Q_0)<100$ . Clearly, every $Q_i$ such that $i\in {\mathcal {I}}$ has the claimed structure as $\text {Lin}(Q_i)\subseteq V$ . Consider any polynomial $Q_i=Q_o+a_ib_i\in {\mathcal {Q}_{\text {prod}}}$ such that $i\not \in {\mathcal {I}}$ . As $i\not \in {\mathcal {I}}$ , we either have that $\dim (V_i)=1$ , in which case $Q_i$ has the claimed form, or for some nonzero $\beta $ , $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o +\beta a_i b_i)<3$ . In the later case, as $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 2$ , Theorem 2.17 implies that $\operatorname {span}\{{a_i,b_i}\}\cap \text {Lin}(Q_o)\neq \{0\}$ and in particular $\operatorname {span}\{{a_i,b_i}\}\cap V\neq \{0\}$ . Thus, in any of these cases, V has the required property.

Consider now the case $\dim (\bigcap _{i=1}^m V_i) =1$ . Let w be such that $\operatorname {span}\{{w}\} = \dim (\bigcap _{i=1}^m V_i)$ . As before, it is not hard to see that, if we define V as $V=\operatorname {span}\{{w}\}$ in the high rank case and $V=\operatorname {span}\{{w}\}+\text {Lin}(Q_o)$ in the low rank case, then V has the required property.

The case ${\mathcal {Q}_{\neg \text {prod}}}\neq \emptyset $ :

Let $P=\gamma Q+L\in {\mathcal {Q}_{\neg \text {prod}}}$ and V be as in the statement of Theorem 5.4. We next show that V satisfies the claim. Let ${\mathcal {J}} = \lbrace Q_j\mid j\in [m_1]\text { and }a_j,b_j \in V\rbrace $ . Theorem 5.4 implies that $|{\mathcal {J}}|\geq m_1-2m_2$ (and if $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , then $|{\mathcal {J}}|\geq m_1-m_2$ ).

We first note that every $P_i \in {\mathcal {J}}$ satisfies the claim with $P^{\prime }_i = a_ib_i$ and $v_i=c_i =0$ , and clearly the claim trivially holds for $Q_i \in {\mathcal {L}}$ .

Consider $Q_i \in {\mathcal {Q}}_{\text {prod}} \setminus {\mathcal {J}}$ . By the ‘furthermore’ part of Theorem 5.4 one of two cases must happen: Either $Q_i$ and P span a polynomial $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$ or, when $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ , there are two linear functions $c,d$ such that $P,Q_o,Q_j\in \left \langle {c,d}\right \rangle $ . Observe that, in the latter case, as $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ , we have that $\operatorname {span}\{{c,d}\}\subseteq \text {Lin}(Q_o)\subseteq V$ . In particular, $Q_i\in \left \langle {V}\right \rangle $ , and the claim follows. So assume that $Q_i$ and P span a polynomial $P_j \in {\mathcal {Q}}_{\neg \text {prod}}$ . Namely, there are $\alpha ,\beta \in \mathbb {C}\setminus \{0\}$ such that $P_j = \alpha P + \beta Q_i$ . Theorem 5.3 implies that $P_j = \gamma _j Q_o + L_j$ , where $\operatorname {\mathrm {rank}}_{\text {s}}(L_j)=2$ , and thus,

$$\begin{align*}(\alpha \gamma-\beta-\gamma_j )Q_o + \alpha L + \beta a_ib_i = L_j .\end{align*}$$

From property 4 of Theorem 4.9, we conclude that $\operatorname {\mathrm {rank}}_{\text {s}}((\alpha \gamma -\beta -\gamma _j )Q_o + \alpha L)\geq 2=\operatorname {\mathrm {rank}}_{\text {s}}(L_j)$ . Theorem 2.17 implies that $\operatorname {span}\{{a_i,b_i}\} \cap V \neq \{{\mathbf {0}}\}$ , and therefore, there is $v_i\in V$ such that, without loss of generality, $b_i = \varepsilon _i a_i + v_i$ , for some constant $\varepsilon _i$ . Thus, the claimed statement holds for $Q_i$ with $c_i = a_i$ and $Q^{\prime }_i = 0$ . That is, $Q_i = Q_o + 0+ a_i(\varepsilon _i a_i + v_i )$ .

Consider a polynomial $P_i=\gamma _iQ_o+L_i\in {\mathcal {Q}}_{\neg \text {prod}}$ . It is clear that, if $P_i$ satisfies Theorem 3.1(linear-case) with any polynomial in ${\mathcal {J}}$ , then $P\in \left \langle {V}\right \rangle $ (observe that in this case we must have $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ ).

Next, assume that $P_i$ satisfies Theorem 3.1(product-case) with at least $2$ polynomials whose indices are in ${\mathcal {J}}$ . Let $Q_j,Q_{j'}$ be two such polynomials. There are four linear forms, $c,d,e$ and f and scalars $\varepsilon _j, \varepsilon _{j'}$ such that

$$ \begin{align*} P_i + \varepsilon_j Q_j = cd \quad\quad \text{and}\quad\quad P_i + \varepsilon_{j'} Q_{j'} = ef . \end{align*} $$

Therefore,

(5.5) $$ \begin{align} (\varepsilon_j -\varepsilon_{j'}) Q_{0} +(\varepsilon_j a_jb_j-\varepsilon_{j'}a_{j'}b_{j'}) = \varepsilon_j Q_j -\varepsilon_{j'} Q_{j'} = cd -ef . \end{align} $$

As $\varepsilon _j a_jb_j-\varepsilon _{j'}a_{j'}b_{j'}\in \mathbb {C}[V]$ , rank arguments imply that $\text {Lin}(cd -ef)\subseteq V$ . From Theorem 2.19 and equation (5.5), we get that, without loss of generality, $d = \varepsilon c + v$ for some $v \in V$ and $\varepsilon \in \mathbb {C}$ . Thus, $P_i = cd -\varepsilon _j Q_j = c(\varepsilon c+v) -\varepsilon _jQ_o -\varepsilon _j a_j b_j$ , and it is clear that it has the required structure.

The only case left is when $P_i$ satisfies Theorem 3.1(prime-case) with all (except possibly one of the) polynomials whose indices are in ${\mathcal {J}}$ .

If $P_i$ and $Q_j$ , for $j\in {\mathcal {J}}$ span another polynomial $Q_{j'}$ such that $j'\in {\mathcal {J}}$ , then, as before, $\text {Lin}(P)\subseteq V$ . Similarly, if P and $Q_j$ span a polynomial $Q_{j'}\in {\mathcal {L}}$ , then $P = \alpha Q_j + \beta a_{j'}^2$ , and hence, it also satisfies the claim.

Hence, for P to fail to satisfy the claim, it must be the case that every polynomial $Q_j$ , for $j\in {\mathcal {J}}$ , that satisfies Theorem 3.1(prime-case) with P, does not span with P any polynomial in $\{Q_j \mid j\in {\mathcal {J}}\} \cup {\mathcal {L}}$ . Thus, it must span with P a polynomial in $\{Q_j \mid j\in [m_1]\setminus {\mathcal {J}}\} \cup {\mathcal {Q}}_{\neg \text {prod}}$ . Observe that by pairwise linear independence, if two polynomials from ${\mathcal {J}}$ span the same polynomial with P, then P is in their span, and we are done. However, notice that

$$ \begin{align*} \left|\{Q_j \mid j\in [m_1]\setminus {\mathcal{J}}\} \cup {\mathcal{Q}}_{\neg\text{prod}}\right| \leq \left(m_1 - |{\mathcal{J}}| \right) + m_2 \leq 3m_2 < m_1 -2m_2 -2 \leq |{\mathcal{J}}| -2. \end{align*} $$

As $P_i$ satisfies Theorem 3.1(prime-case) with at least $|{\mathcal {J}}|-1$ polynomials whose indices are in ${\mathcal {J}}$ , we get from the pigeonhole principle that there is some polynomial $F\in \tilde {Q}$ and two indices $j,j'\in {\mathcal {J}}$ such that $F\in \operatorname {span}\{{P_i,Q_j}\}\cap \operatorname {span}\{{P_i,Q_{j'}}\}$ . As before, pairwise linear independence implies that $P_i\in \operatorname {span}\{{Q_j,Q_{j'}}\}$ , and we are done.

5.4 Completing the proof

Now that we know that all polynomials in $\tilde {Q}$ satisfy the structure of Theorem 5.6, we can finish the proof of Theorem 4.10.

The main remaining step is proving that all linear polynomials c appearing in the statement of Theorem 4.10 form a Sylvester–Gallai configuration, and we will be done.

There is a small issue though. When the rank of $Q_o$ is small, some polynomials can belong to $\left \langle {V}\right \rangle $ and are not captured by the outlined approach. This difference requires us to handle the low- and high-rank cases separately.

Theorem 4.10 follows from Corollaries 5.8 and 5.10 below.

5.4.1 The case $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$

Consider the representation guaranteed in Theorem 4.10, and let

$$\begin{align*}\begin{aligned} {\mathcal{S}} = \lbrace c_i \mid \text{there is } P_i\in\tilde{{\mathcal{Q}}} \text{ such that either } P_i = c_i^2 \text{ or, for some } P^{\prime}_i \text{ defined over } V, \\ P_i= Q_o +P^{\prime}_i + c_i(\varepsilon_i c_i + v_i) \rbrace . \end{aligned} \end{align*}$$

Clearly, in order to bound the dimension of $\tilde {{\mathcal {Q}}}$ , it is enough to bound the dimension of ${\mathcal {S}}$ . We do so by proving that ${\mathcal {S}}$ satisfies the conditions of Sylvester–Gallai theorem modulo V and thus have dimension at most $3+\dim (V)=7$ .

Claim 5.7. Assume that $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , and let ${\mathcal {S}}$ be defined as above. Let $c_i, c_j \in {\mathcal {S}}$ be such that $c_i \notin V$ and $c_j \notin \operatorname {span}\{{c_i,V}\}$ . Then, there is $c_k \in {\mathcal {S}}$ such that $c_k \in \operatorname {span}\{{c_i,c_j,V}\}$ and $c_k \notin \operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\}$ .

Proof. Following the notation of Theorem 5.6, we either have $Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$ , for $Q^{\prime }_i\in \mathbb {C}[V]$ , or $Q_i = c_i^2$ . We consider which case of Theorem 3.1 $Q_i$ and $Q_j$ satisfy and what structure they have.

Assume $Q_i = Q_o + Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i )$ and $Q_j = Q_o + Q^{\prime }_j + c_j(\varepsilon _jc_j + v_j )$ . As argued before, since the rank of $Q_o$ is large, they cannot satisfy Theorem 3.1(linear-case). We consider the remaining cases:

• • $Q_i,Q_j$ satisfy Theorem 3.1(prime-case): There is $Q_k \in \tilde {{\mathcal {Q}}}$ such that $Q_k \in \operatorname {span}\{{Q_i,Q_j}\}$ .By assumption, for some scalars $\alpha ,\beta $ we have that

  (5.6) $$ \begin{align} Q_k = \alpha(Q_o + Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) + \beta(Q_o + Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)) . \end{align} $$
  If $Q_k$ depends only on V, then we would get a contradiction to the choice of $c_i,c_j$ . Indeed, in this case, we have that
  $$ \begin{align*} (\alpha+\beta)Q_o = Q_k - \alpha( Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i )) - \beta( Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j)). \end{align*} $$
  Rank arguments imply that $\alpha +\beta =0$ , and therefore,
  $$ \begin{align*} \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) = Q_k - \alpha Q^{\prime}_i - \beta Q^{\prime}_j \in\mathbb{C}[V], \end{align*} $$
  which implies that $c_i$ and $c_j$ are linearly dependent modulo V in contradiction.

  If $Q_k = c_k^2$ , then Theorem 2.20 implies that $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$ .

  We therefore assume that $Q_k$ is not a function of V alone, and it is not a square of a linear function. Denote $Q_k = \gamma _k Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$ . Equation 5.6 implies that

  $$ \begin{align*} (\gamma_k - \alpha-\beta)Q_o = \alpha Q^{\prime}_i + \beta Q^{\prime}_j - Q^{\prime}_k + \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k). \end{align*} $$
  As $\alpha Q^{\prime }_i + \beta Q^{\prime }_j - Q^{\prime }_k$ is a polynomial defined over V, its rank is smaller than $4$ , and thus, combined with the fact that $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o) \geq 100$ , we get that $ (\gamma _k - \alpha -\beta ) = 0$ and
  $$\begin{align*}Q^{\prime}_k -\alpha Q^{\prime}_i - \beta Q^{\prime}_j = \alpha c_i(\varepsilon_i c_i + v_i ) + \beta c_j(\varepsilon_j c_j + v_j) - c_k(\varepsilon_k c_k + v_k) .\end{align*}$$
  We conclude again from Theorem 2.20 that $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$ .

• • $Q_i,Q_j$ satisfy Theorem 3.1(product-case): There are linear forms $e,f$ such that for nonzero scalars $\alpha ,\beta $ , $\alpha Q_i + \beta Q_j = ef$ . In particular,

  $$\begin{align*}(\alpha + \beta ) Q_o = ef - \alpha Q^{\prime}_i - \beta Q^{\prime}_j - \alpha c_i(\varepsilon_i c_i + v_i ) - \beta c_j(\varepsilon_j c_j + v_j).\end{align*}$$
  From rank argument, we get that $\alpha + \beta = 0$ , and from Theorem 2.20, we conclude that, without loss of generality, $e = \mu c_i + \eta c_j +v_e$ , where $\mu , \eta \neq 0$ . We also assume without loss of generality that $Q_i=Q_j+ef$ .

  Since $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ , it follows that $Q_j$ is irreducible even after setting $e=0$ . It follows that, if a product of irreducible quadratics satisfy

  $$ \begin{align*} \prod_k A_k \in \sqrt{\left \langle{Q_i,Q_j}\right \rangle} = \sqrt{\left \langle{ef,Q_j}\right \rangle}, \end{align*} $$
  then, after setting $e=0$ , some $A_k$ is divisible by ${Q_j}|_{e=0}$ . Thus, there is a multiplicand that is equal to $ \gamma Q_j + ed$ for some linear form d and scalar $\gamma $ . In particular, there must be a polynomial $Q_k \in \tilde {\mathcal {Q}}\setminus \{Q_i,Q_j\}$ such that $Q_k = \gamma Q_j + ed$ . If $\gamma = 0$ , then it must hold that $Q_k = a_k^2 = ed$ and thus $a_k \sim e$ , and the statement holds. If $\gamma = 1$ , then we can assume without loss of generality that $Q_k = Q_j + ed$ . Thus,
  $$ \begin{align*} Q_o + Q^{\prime}_k + c_k(\varepsilon_k c_k + v_k) = Q_k = Q_j + ed = Q_o+ Q^{\prime}_j + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
  Rearranging, we get
  $$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_j(\varepsilon_j c_j + v_j) + (\mu c_i + \eta c_j + v_e)d . \end{align*} $$
  As the right-hand side vanishes modulo $\operatorname {span}\{{c_i,c_j,V}\}$ , it follows that $c_k\in \operatorname {span}\{{c_i,c_j,V}\}$ . Observe that, if $c_k\in \operatorname {span}\{{c_j,V}\}$ , then this implies that
  $$ \begin{align*} (\mu c_i + \eta c_j + v_e)d\in\mathbb{C}[V,c_j]. \end{align*} $$
  However, since $d\neq 0$ (as otherwise we would have $Q_k\sim Q_j$ ), this stands in contradiction to the fact that $\mu \neq 0$ and $c_i\not \in \operatorname {span}\{{c_j,V}\}$ . As $Q_i=Q_j+ef$ , we get that
  $$ \begin{align*} c_k(\varepsilon_k c_k + v_k) = (Q^{\prime}_j-Q^{\prime}_k) + c_i(\varepsilon_i c_i + v_i) + (\mu c_i + \eta c_j + v_e)(d-f) . \end{align*} $$
  We cannot have $d=f$ as this would give $Q_i=Q_k$ . Thus, a similar argument implies that $c_k\not \in \operatorname {span}\{{c_i,V}\}$ . In conclusion, $c_k\in \operatorname {span}\{{c_i,c_j,V}\}\setminus (\operatorname {span}\{{c_i,V}\}\cup \operatorname {span}\{{c_j,V}\})$ as claimed.

Now, let us consider the case where without loss of generality, $Q_i = Q_o +Q^{\prime }_i + c_i(\varepsilon _i c_i + v_i)$ and $Q_j = c_j^2$ . In this case, the polynomials satisfy Theorem 3.1(product-case) as $0 \cdot Q_i + Q_j = c_j^2$ . Similarly to the previous argument, it holds that there is $Q_k$ such that $Q_k = \gamma Q_i + c_j e$ . If $\gamma =0$ , then $Q_k$ is reducible and therefore a square of a linear form which is a multiple of $c_j$ , in contradiction to pairwise linear independence. Hence, we have that $\gamma \neq 0$ . If $Q_k$ is defined only on the linear functions in V, then it is of rank smaller than $\dim (V) \leq 4$ , which will result in a contradiction to the rank assumption on $Q_o$ . Thus, $Q_k = Q_o + Q^{\prime }_k + c_k(\varepsilon _k c_k + v_k)$ and $\gamma = 1$ . It follows that

$$\begin{align*}Q_o + Q^{\prime}_k + c_k(\varepsilon_k c_k + v_k) = Q_k = Q_i + c_j e\; = Q_o + Q^{\prime}_i + c_i(\varepsilon_i c_i + v_i)+ c_j e. \end{align*}$$

Hence,

$$\begin{align*}Q^{\prime}_k - Q^{\prime}_i -c_i(\varepsilon_i c_i + v_i) - c_je= -c_k(\varepsilon_k c_k + v_k). \end{align*}$$

An argument similar to the last one shows that $c_k \in \operatorname {span}\{{V, c_i, c_j}\}$ and that $c_k \notin \operatorname {span}\{{V, c_j}\}\cup \operatorname {span}\{{V, c_i}\}$ , as we wanted to show.

The last structure we have to consider is the case where $Q_i = c_i^2, Q_j = c_j^2$ . In this case, the ideal $\sqrt {\left \langle {c_i^2,c_j^2}\right \rangle } = \left \langle {c_i,c_j}\right \rangle $ is prime, and therefore, there is $Q_k \in \left \langle {c_i,c_j}\right \rangle $ . This means that $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) \leq 2$ . If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 1$ , then $Q_k = c_k^2$ and the statement holds. If $\operatorname {\mathrm {rank}}_{\text {s}}(Q_k) = 2$ , then Theorem 5.6 implies that $Q_k$ is in $\mathbb {C}[V]$ , from which we get that $c_i,c_j \in V$ in contradiction to our assumptions.

Corollary 5.8. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)\text{-}\mathrm{set}$ , where $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)\geq 100$ . Then $\dim (\tilde {{\mathcal {Q}}}) \leq 29$ .

Proof. Observe that definition of ${\mathcal {S}}$ and Theorem 5.6 imply that $\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 1+{\dim (\operatorname {span}\{{V+{\mathcal {S}}}\})+1 \choose 2}$ . As Theorem 5.7 implies that $\dim ({\mathcal {S}}+V)\leq 7$ , we get that $\dim \left ( \tilde {{\mathcal {Q}}}\right )\leq 29$ .

5.4.2 The case $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$

Observe that Theorem 5.6 implies that when $\operatorname {rank}(Q_o)<100$ then $\text {Lin}(Q_o)\subseteq V$ , and thus, any polynomial $Q_i \in \tilde {{\mathcal {Q}}}$ satisfies that either $Q_i \in \left \langle {V}\right \rangle $ or there is a linear form $a_i$ such that $\text {Lin}(Q_i) \subseteq \operatorname {span}\{{V,a_i}\}$ .

Let $\Delta =\dim (V)\leq 202$ . Fix some basis of V, $V=\operatorname {span}\{{v_1,\ldots ,v_{\Delta }}\}$ . Let ${\boldsymbol {\alpha }}\in \mathbb {C}^{\Delta }$ (recall Theorem 2.24) be such that, if two polynomials in $T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$ share a common factor, then it is a polynomial in z. Note that by Theorem 2.26 such ${\boldsymbol {\alpha }}$ exists. Thus, each $P\in \tilde {{\mathcal {Q}}}$ , satisfies that either $T_{{\boldsymbol {\alpha }}, V}(P)=\alpha _P z^2$ or $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(P))\subseteq \operatorname {span}\{{z,a_P}\}$ , for some linear form $a_P$ independent of z. It follows that every polynomial in $T_{{\boldsymbol {\alpha }}, V}(\tilde {{\mathcal {Q}}})$ is reducible. We next show that ${\mathcal {S}} = \{a_P \mid P\in \tilde {\mathcal {Q}}\}$ satisfies the conditions of Sylvester–Gallai theorem modulo z.

Claim 5.9. Let ${\mathcal {S}}$ be defined as above. Let $a_1, a_2 \in {\mathcal {S}}$ such that $a_1\not \in \operatorname {span}\{{z}\}$ and $a_2 \notin \operatorname {span}\{{z,a_1}\}$ . Then, there is $a_3\in {\mathcal {S}}$ such that $a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$ .

Proof. Let $Q_1$ be such that $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \subseteq \operatorname {span}\{{z,a_1}\}$ yet $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_1)) \not \subseteq \operatorname {span}\{{z}\}$ . Similarly, let $Q_2$ be such that $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \subseteq \operatorname {span}\{{z,a_2}\}$ and $\text {Lin}(T_{{\boldsymbol {\alpha }}, V}(Q_2)) \not \subseteq \operatorname {span}\{{z}\}$ . As $a_1,a_2\in {\mathcal {S}}$ , there must be such $Q_1,Q_2$ . By choice of $Q_1$ , there is a factor of $T_{{\boldsymbol {\alpha }},V}(Q_1)$ of the form $\gamma _1 z + \delta _1 a_1$ , where $\delta _1\neq 0$ . Similarly there is a factor of $T_{{\boldsymbol {\alpha }},V}(Q_2)$ of the form $\gamma _2 z + \delta _2 a_2$ , where $\delta _2\neq 0$ . It follows that $\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $ . Indeed, it is clear that, for $i\in \{1,2\}$ , ${T_{{\boldsymbol {\alpha }},V}(Q_i)}\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $ . Hence, $\sqrt {\left \langle {T_{{\boldsymbol {\alpha }},V}(Q_1), T_{{\boldsymbol {\alpha }},V}(Q_2)}\right \rangle } \subseteq \sqrt {\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle }=\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $ , where equality holds since $\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $ is a prime ideal.

We know that there are $Q_3,Q_4,Q_5,Q_6\in {\mathcal {Q}}$ such that

$$\begin{align*}Q_3\cdot Q_4\cdot Q_5\cdot Q_6 \in \sqrt{\left \langle{Q_1,Q_2}\right \rangle}. \end{align*}$$

As $T_{{\boldsymbol {\alpha }},V}$ is a ring homomorphism, it follows that

$$\begin{align*}T_{{\boldsymbol{\alpha}},V}(Q_3)\cdot T_{{\boldsymbol{\alpha}},V}(Q_4)\cdot T_{{\boldsymbol{\alpha}},V}(Q_5)\cdot T_{{\boldsymbol{\alpha}},V}(Q_6)\in \sqrt{\left \langle{T_{{\boldsymbol{\alpha}},V}(Q_1),T_{{\boldsymbol{\alpha}},V}(Q_2)}\right \rangle} \subseteq \left \langle{\gamma_1 z + \delta_1 a_1, \gamma_2 z + \delta_2 a_2}\right \rangle. \end{align*}$$

Primality of $\left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $ implies that, without loss of generality, $T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _1 z + \delta _1 a_1, \gamma _2 z + \delta _2 a_2}\right \rangle $ . It cannot be the case that $T_{{\boldsymbol {\alpha }},V}(Q_3)\in \left \langle {\gamma _i z + \delta _i a_i}\right \rangle $ for any $i \in \{1,2\}$ because otherwise this will imply that $T_{{\boldsymbol {\alpha }},V}(Q_3)$ and $T_{{\boldsymbol {\alpha }},V}(Q_i)$ share a common factor that is not a polynomial in z, in contradiction to our choice of $T_{{\boldsymbol {\alpha }}, V}$ . This means that there is a factor of $T_{{\boldsymbol {\alpha }},V}(Q_3)$ that is in $\operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$ . Consequently, $a_3 \in \operatorname {span}\{{a_1,a_2,z}\} \setminus \left (\operatorname {span}\{{a_1,z}\}\cup \operatorname {span}\{{a_2,z}\}\right )$ as we wanted to prove.

Corollary 5.10. Let $\tilde {{\mathcal {Q}}}$ be a $(Q_o,m_1,m_2)$ -set, where $\operatorname {\mathrm {rank}}_{\text {s}}(Q_o)<100$ . Then $\dim (\tilde {{\mathcal {Q}}}) \leq 8\dim (V)^2$ , where V is as in Theorem 5.6.

Proof. Theorem 5.9 shows that ${\mathcal {S}}$ satisfies the conditions of Theorem 2.10, and therefore, $\dim ({\mathcal {S}})\leq 3$ . Repeating the analysis of the claim for linearly independent ${{\boldsymbol {\alpha }}}_1,\ldots , {{\boldsymbol {\alpha }}}_{\Delta }$ , we conclude from Theorem 2.29 that $\dim (\text {Lin}(\tilde {\mathcal {Q}})) \leq (3+1)\Delta $ , and thus $\dim (\tilde {{\mathcal {Q}}}) \leq {4\Delta \choose 2}+\Delta \leq 8\Delta ^2$ .

6 Conclusions and future research

In this work, we solved Theorem 1.2 in the case where all the polynomials are irreducible and of degree at most $2$ . This result directly relates to the problem of obtaining deterministic algorithms for testing identities of $\Sigma ^{[3]}\Pi ^{[d]}\Sigma \Pi ^{[2]}$ circuits. As mentioned in section 1, to get a PIT algorithm a colored version of this result is required. Such a result was obtained in [17].

Our proof of Theorem 1.4 used the robust version of the Sylvester–Gallai theorem of [1, 8] (Theorem 2.7). We believe that in order to extend our results to higher degrees a similar robust version for quadratic polynomials may be useful.

Problem 6.1. Let $\delta \in (0,1]$ . Can we bound the linear dimension (as a function of $\delta $ ) of a set of polynomials $Q_1,\ldots ,Q_m\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ that satisfy the following property: For every $i\in [m]$ , there exist at least $\delta m$ values of $j \in [m]$ such that for each such j there is ${\mathcal {K}}_j \subset [m]$ , where $i,j \notin {\mathcal {K}}_j$ and $\prod _{k\in {\mathcal {K}}_j} Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$ ?

In subsequent work [18, 11], the following simpler version of Problem 6.1 was proved.

Theorem 6.2. Let $\delta \in (0,1]$ . Let ${\mathcal {Q}}=\{Q_1,\ldots ,Q_m\}\in \mathbb {C}[ {x}_1,\ldots , {x}_{n}]$ be irreducible polynomials of degree at most $2$ satisfying the following property: For every $i\in [m]$ , there exist at least $\delta m$ values of $j \in [m]$ such that for each such j there is $k\in [m]\setminus \{i,j\}$ with $Q_k \in \sqrt {\left \langle {Q_i,Q_j}\right \rangle }$ . Then, $\dim (\operatorname {span}\{{{\mathcal {Q}}}\})=O(1/\delta ^{16})$ .

Another interesting question is giving a tight bound in Theorem 1.4. A careful analysis of the proof shows that we can bound the dimension of the set ${\mathcal {T}}$ satisfying the conditions in Theorem 1.4 by $c\leq 20,000$ . This is a very loose bound, and we believe that it can be improved. It is also an interesting task to present examples with as large dimension as possible.

In our opinion, the most interesting problem is extending our result to higher degrees. Another important problem is to extend Theorem 3.1 to the case where $\prod _{k\in {\mathcal {K}}}Q_k \in \sqrt {\left \langle {A_1,\ldots ,A_e}\right \rangle }$ , for a constant $e>2$ .

In this paper, we only considered polynomials over the complex numbers. However, we believe (though we did not check the details) that a similar approach should work over positive characteristic as well. Observe that over positive characteristic we expect the dimension of the set to scale like $O(\log |{\mathcal {Q}}|)$ , as for such fields a weaker version of Sylvester–Gallai theorem holds.

Theorem 6.3 (Corollary $1.3$ in [3]).

Let $V=\lbrace {{\mathbf {v}}}_1,\ldots , {{\mathbf {v}}}_{m}\rbrace \subset \mathbb {F}_p^d$ be a set of m vectors, no two of which are linearly dependent. Suppose that, for every $i,j\in [m]$ , there exists $k\in [m]$ such that ${\mathbf {v}}_i,{\mathbf {v}}_j,{\mathbf {v}}_k$ are linearly dependent. Then, for every $\varepsilon>0$

$$\begin{align*}\dim(V)\leq\mathrm{poly}(p/\varepsilon)+(4+\varepsilon)\log_{p}m .\end{align*}$$