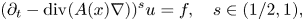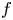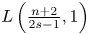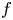1. Introduction and the statement of the main result
In this article we prove gradient continuity for the following nonlocal operators $(\partial _t - \operatorname {div}( A(x) \nabla ))^{s}$![]() which are modelled on the fractional heat operator $(\partial _t - \Delta )^{s}$
which are modelled on the fractional heat operator $(\partial _t - \Delta )^{s}$![]() with critical scalar perturbations. To provide some context to our work, we note that the study of the fractional heat operator $(\partial _t - \Delta )^{s}$
with critical scalar perturbations. To provide some context to our work, we note that the study of the fractional heat operator $(\partial _t - \Delta )^{s}$![]() was first proposed in M. Riesz’ visionary papers [Reference Riesz37] and [Reference Riesz38]. This nonlocal operator represents a basic model of the continuous time random walk (CTRW) introduced by Montroll and Weiss in [Reference Montroll and Weiss33]. We recall that a CTRW is a generalization of a random walk where the wandering particle waits for a random time between jumps. It is a stochastic jump process with arbitrary distributions of jump lengths and waiting times. In [Reference Metzler and Klafter32], Klafter and Metzler describe such processes by means of the nonlocal equation both in space and time
was first proposed in M. Riesz’ visionary papers [Reference Riesz37] and [Reference Riesz38]. This nonlocal operator represents a basic model of the continuous time random walk (CTRW) introduced by Montroll and Weiss in [Reference Montroll and Weiss33]. We recall that a CTRW is a generalization of a random walk where the wandering particle waits for a random time between jumps. It is a stochastic jump process with arbitrary distributions of jump lengths and waiting times. In [Reference Metzler and Klafter32], Klafter and Metzler describe such processes by means of the nonlocal equation both in space and time
which is an example of a master equation. Such equations were introduced in 1973 by Kenkre, Montroll and Shlesinger in [Reference Kenkre, Montroll and Shlesinger24], and they are presently receiving increasing attention by mathematicians also thanks to the work [Reference Caffarelli and Silvestre16] of Caffarelli and Silvestre in which the authors establish the Hölder continuity of viscosity solutions of generalized master equations
On the kernel $K$![]() they assume that there exist $0< s<1$
they assume that there exist $0< s<1$![]() and $\beta >2s$
and $\beta >2s$![]() such that for $0< c_1< c_2$
such that for $0< c_1< c_2$![]() one can find $0<\lambda \le \Lambda$
one can find $0<\lambda \le \Lambda$![]() for which for a.e. $(t,x)\in \mathbb {R}\times \mathbb {R}^{n}$
for which for a.e. $(t,x)\in \mathbb {R}\times \mathbb {R}^{n}$![]() one has
one has

The pseudo-differential operator $(\partial _t - \Delta )^{s}$![]() which is defined via the Bochner's subordination principle in the following way ( see for instance [Reference Balakrishnan5, Reference Banerjee and Garofalo8, Reference Stinga and Torrea40]),
which is defined via the Bochner's subordination principle in the following way ( see for instance [Reference Balakrishnan5, Reference Banerjee and Garofalo8, Reference Stinga and Torrea40]),

where $G(\tau,z) = (4\pi \tau )^{-\frac n2}\,{\rm e}^{-\frac {|z|^{2}}{4\tau }}$![]() is the standard heat kernel and $\Gamma (z)$
is the standard heat kernel and $\Gamma (z)$![]() indicates Euler gamma function, is seen to be a special case of the master equation. We mention that recently Nyström and Sande [Reference Nyström and Sande35] and Stinga and Torrea [Reference Stinga and Torrea40] have independently adapted to the fractional heat operator of the celebrated extension procedure of Caffarelli and Silvestre in [Reference Caffarelli and Silvestre15] which can be described as follows.
indicates Euler gamma function, is seen to be a special case of the master equation. We mention that recently Nyström and Sande [Reference Nyström and Sande35] and Stinga and Torrea [Reference Stinga and Torrea40] have independently adapted to the fractional heat operator of the celebrated extension procedure of Caffarelli and Silvestre in [Reference Caffarelli and Silvestre15] which can be described as follows.
Given $s\in (0,1)$![]() we introduce the parameter
we introduce the parameter
and indicate with $U = U(t,X),$![]() where $X=(x,y)$
where $X=(x,y)$![]() is a point in $\mathbb {R}^{n}\times (0, \infty )$
is a point in $\mathbb {R}^{n}\times (0, \infty )$![]() , the solution to the following extension problem
, the solution to the following extension problem

Using an appropriate Poisson representation of the extension problem it was proved in [Reference Nyström and Sande35, Reference Stinga and Torrea40], see also § 3 in [Reference Banerjee and Garofalo8] for details, that one has in $L^{2}(\mathbb {R} \times \mathbb {R}^{n})$![]()
Such an extension problem has been generalized for fractional powers of variable coefficient operators such as $(\partial _t - \operatorname {div} ((A(x) \nabla ))^{s}$![]() in [Reference Biswas, De Leon-Contreras and Stinga11, Reference Biswas and Stinga12]. We also refer to [Reference Banerjee, Garofalo, Munive and Nhieu9] for a generalization of the extension problem in the subelliptic situation. We would like to mention that the study of the fractional heat type operators as well as the related extension problem has received a lot of attention in recent times, see for instance [Reference Athanasopoulos, Caffarelli and Milakis2–Reference Audrito4, Reference Banerjee, Danielli, Garofalo and Petrosyan6–Reference Banerjee and Garofalo8, Reference Biswas and Stinga12, Reference Dong and Phan19, Reference Lai, Lin and Ruland29, Reference Litsgard and Nystrom30]. We would also like to mention that extension problem is prototype of the equations with general $A_2$
in [Reference Biswas, De Leon-Contreras and Stinga11, Reference Biswas and Stinga12]. We also refer to [Reference Banerjee, Garofalo, Munive and Nhieu9] for a generalization of the extension problem in the subelliptic situation. We would like to mention that the study of the fractional heat type operators as well as the related extension problem has received a lot of attention in recent times, see for instance [Reference Athanasopoulos, Caffarelli and Milakis2–Reference Audrito4, Reference Banerjee, Danielli, Garofalo and Petrosyan6–Reference Banerjee and Garofalo8, Reference Biswas and Stinga12, Reference Dong and Phan19, Reference Lai, Lin and Ruland29, Reference Litsgard and Nystrom30]. We would also like to mention that extension problem is prototype of the equations with general $A_2$![]() weight studied by Chiarenza and Serapioni in [Reference Chiarenza and Serapioni17].
weight studied by Chiarenza and Serapioni in [Reference Chiarenza and Serapioni17].
Now we will state our main result: Consider the following problem

where $a=1-2s;$![]() for $1/2< s<1$
for $1/2< s<1$![]() ,
,
and $A$![]() is a uniformly elliptic matrix with Dini modulus of continuity $\omega _A$
is a uniformly elliptic matrix with Dini modulus of continuity $\omega _A$![]() and $f$
and $f$![]() belongs to the scaling critical function space $L\left (\frac {n+2}{2s-1},1\right ).$
belongs to the scaling critical function space $L\left (\frac {n+2}{2s-1},1\right ).$![]()
Theorem 1.1 Let $U$![]() be a weak solution of (1.6) in $Q_1 \times (0,1)$
be a weak solution of (1.6) in $Q_1 \times (0,1)$![]() . Then there exist modulus of continuity $K$
. Then there exist modulus of continuity $K$![]() depending on ellipticity, $\omega _A,$
depending on ellipticity, $\omega _A,$![]() $n,$
$n,$![]() $s$
$s$![]() and $f$
and $f$![]() such that for all $(t_1,x_1,y_1),(t_2,x_2,y_2) \in Q_{\frac 12} \times (0,1/2)$
such that for all $(t_1,x_1,y_1),(t_2,x_2,y_2) \in Q_{\frac 12} \times (0,1/2)$![]()
and
where $C^{2}=\int _{Q_1}U(t,x,0)^{2}\,{\rm d}t\,{\rm d}x + \int _{Q_1 \times (0,1)}U(t,x,y)^{2}y^{a}\,{\rm d}t\,{\rm d}x\,{\rm d}y.$![]()
In view of the extension problem for $(\partial _t - \operatorname {div}(A(x) \nabla ))^{s}$![]() in [Reference Biswas and Stinga12] (see § 2 for relevant details), we obtain consequently that the following regularity result holds for the nonlocal fractional heat type problem.
in [Reference Biswas and Stinga12] (see § 2 for relevant details), we obtain consequently that the following regularity result holds for the nonlocal fractional heat type problem.
Theorem 1.2 Let $s \in (1/2, 1)$![]() and let $u$
and let $u$![]() solve weakly to $(\partial _t - \operatorname {div}(A(x) \nabla ))^{s}u =f$
solve weakly to $(\partial _t - \operatorname {div}(A(x) \nabla ))^{s}u =f$![]() where $A(x)$
where $A(x)$![]() is uniformly elliptic with Dini coefficients and $f \in L\left (\frac {n+2}{2s-1},1\right ).$
is uniformly elliptic with Dini coefficients and $f \in L\left (\frac {n+2}{2s-1},1\right ).$![]() Then $\nabla _x u$
Then $\nabla _x u$![]() is continuous.
is continuous.
Now to put our results in the right historical perspective, we note that in 1981, E. Stein in his work [Reference Stein39] showed the following ‘limiting’ case of Sobolev embedding theorem.
Theorem 1.3 Let $L(n,1)$![]() denote the standard Lorentz space, then the following implication holds$:$
denote the standard Lorentz space, then the following implication holds$:$![]()
The Lorentz space $L(n,1)$![]() appearing in theorem 1.3 consists of those measurable functions $g$
appearing in theorem 1.3 consists of those measurable functions $g$![]() satisfying the condition
satisfying the condition
Theorem 1.3 can be regarded as the limiting case of Sobolev–Morrey embedding that asserts
Note that indeed $L^{n+\varepsilon } \subset L(n, 1) \subset L^{n}$![]() for any $\varepsilon >0$
for any $\varepsilon >0$![]() with all the inclusions being strict. Now theorem 1.3 coupled with the standard Calderon–Zygmund theory has the following interesting consequence.
with all the inclusions being strict. Now theorem 1.3 coupled with the standard Calderon–Zygmund theory has the following interesting consequence.
Theorem 1.4 If $\Delta u \in L(n,1)$![]() then this implies $\nabla u$
then this implies $\nabla u$![]() is continuous.
is continuous.
Similar result holds in the parabolic situation for more general variable coefficient operators when $f \in L(n+2, 1)$![]() . The analogue of theorem 1.4 for general nonlinear and possibly degenerate elliptic and parabolic equations became accessible not so long ago through a rather sophisticated and powerful nonlinear potential theory (see for instance [Reference Duzaar and Mingione21, Reference Kuusi and Mingione25, Reference Kuusi and Mingione27] and the references therein). The first breakthrough in this direction came up in the work of Kuusi and Mingione in [Reference Kuusi and Mingione26] where they showed that the analogue of theorem 1.4 holds for operators modelled after the variational $p$
. The analogue of theorem 1.4 for general nonlinear and possibly degenerate elliptic and parabolic equations became accessible not so long ago through a rather sophisticated and powerful nonlinear potential theory (see for instance [Reference Duzaar and Mingione21, Reference Kuusi and Mingione25, Reference Kuusi and Mingione27] and the references therein). The first breakthrough in this direction came up in the work of Kuusi and Mingione in [Reference Kuusi and Mingione26] where they showed that the analogue of theorem 1.4 holds for operators modelled after the variational $p$![]() -Laplacian. Such a result was subsequently generalized to $p$
-Laplacian. Such a result was subsequently generalized to $p$![]() -Laplacian type systems by the same authors in [Reference Kuusi and Mingione28].
-Laplacian type systems by the same authors in [Reference Kuusi and Mingione28].
Since then, there has been several generalizations of theorem 1.4 to operators with other kinds of nonlinearities and in context of fully nonlinear elliptic equations, the analogue of theorem 1.4 has been established by Daskalopoulos–Kuusi–Mingione in [Reference Daskalopoulos, Kuusi and Mingione18]. We also refer to [Reference Adimurthi and Banerjee1] for the corresponding boundary regularity result and also to [Reference Banerjee and Munive10] for a similar result in the context of the game theoretic normalized $p-$![]() Laplacian operator. Our main result theorem 1.2 can thus be thought of as a nonlocal generalization of the Stein's theorem in the sense that $s \to 1$
Laplacian operator. Our main result theorem 1.2 can thus be thought of as a nonlocal generalization of the Stein's theorem in the sense that $s \to 1$![]() , it exactly reproduces the result theorem 1.3 for time-independent $f$
, it exactly reproduces the result theorem 1.3 for time-independent $f$![]() . Moreover, theorem 1.2 is also seen to be the limiting case of theorem 1.2 (ii) in [Reference Biswas and Stinga12] which instead deals gradient Hölder continuity in case of subcritical scalar perturbations when $f \in L^{p}$
. Moreover, theorem 1.2 is also seen to be the limiting case of theorem 1.2 (ii) in [Reference Biswas and Stinga12] which instead deals gradient Hölder continuity in case of subcritical scalar perturbations when $f \in L^{p}$![]() for $p > \frac {n+2}{2s-1}$
for $p > \frac {n+2}{2s-1}$![]() . As the reader will see, our proof is based on a somewhat delicate adaptation of the Caffarelli style compactness arguments in [Reference Adimurthi and Banerjee1] to the degenerate Neumann problem in (1.6).
. As the reader will see, our proof is based on a somewhat delicate adaptation of the Caffarelli style compactness arguments in [Reference Adimurthi and Banerjee1] to the degenerate Neumann problem in (1.6).
The paper is organized as follows. In § 2, we introduce some basic notations and gather some preliminary results. In § 3, we prove our main result. Finally in the appendix, we give a self-contained proof of a basic existence result, used in our approximation lemma 3.1, and a self-contained proof of Companato type characterization, theorem 2.12.
2. Notations and preliminaries
We will denote generic point of thick space $\mathbb {R} \times \mathbb {R}^{n} \times \mathbb {R}$![]() by $(t,X)=(t,x,y).$
by $(t,X)=(t,x,y).$![]() In general we will identify thin space $\mathbb {R} \times \mathbb {R}^{n} \times \{0\}$
In general we will identify thin space $\mathbb {R} \times \mathbb {R}^{n} \times \{0\}$![]() by $\mathbb {R} \times \mathbb {R}^{n}$
by $\mathbb {R} \times \mathbb {R}^{n}$![]() and its generic point will be denoted by $(t,x).$
and its generic point will be denoted by $(t,x).$![]() We will define cubes and balls in thin and thick space as following:
We will define cubes and balls in thin and thick space as following:

Similary we define $B_r$![]() , $B^{*}_r$
, $B^{*}_r$![]() and $\textbf {B}_r.$
and $\textbf {B}_r.$![]() For $(t_1,X_1)$
For $(t_1,X_1)$![]() and $(t_2,X_2),$
and $(t_2,X_2),$![]() we let
we let
where $||X_1-X_2||$![]() denotes Euclidean norm. We denote $Q_{\rho }(0,0)$
denotes Euclidean norm. We denote $Q_{\rho }(0,0)$![]() by $Q_{\rho }$
by $Q_{\rho }$![]() etc. For $((t_1,t_2)\times \Omega ) \subset \mathbb {R} \times \mathbb {R}^{n+1}$
etc. For $((t_1,t_2)\times \Omega ) \subset \mathbb {R} \times \mathbb {R}^{n+1}$![]() , $\partial _p ((t_1,t_2)\times \Omega )$
, $\partial _p ((t_1,t_2)\times \Omega )$![]() will denote the parabolic boundary of $(t_1,t_2)\times \Omega$
will denote the parabolic boundary of $(t_1,t_2)\times \Omega$![]() and defined as:
and defined as:
We will denote $L^{2}(Q_1^{*})$![]() with measure $y^{a}dtdX$
with measure $y^{a}dtdX$![]() by $L^{2}_a(Q_1^{*}).$
by $L^{2}_a(Q_1^{*}).$![]() Similarly we define $H^{1}_a(Q_1^{*})$
Similarly we define $H^{1}_a(Q_1^{*})$![]() or $H^{1}_{0,a}(Q_1^{*}).$
or $H^{1}_{0,a}(Q_1^{*}).$![]() Sometimes we will denote $C([-1,1];L^{2}_a(B_1^{*}))$
Sometimes we will denote $C([-1,1];L^{2}_a(B_1^{*}))$![]() by $C(-1,1;L^{2}_a(B_1^{*}))$
by $C(-1,1;L^{2}_a(B_1^{*}))$![]() and other spaces in similar fashion. Let $F=F(t,x)=(F_1,\ldots,F_n,F_{n+1})$
and other spaces in similar fashion. Let $F=F(t,x)=(F_1,\ldots,F_n,F_{n+1})$![]() be an $\mathbb {R}^{n+1}$
be an $\mathbb {R}^{n+1}$![]() -valued vector field defined on $Q^{*}_1$
-valued vector field defined on $Q^{*}_1$![]() such that
such that
We now recall the definition of the operator $(\partial _t-\operatorname {div}(A(x)\nabla ))^{s}$![]() from [Reference Biswas, De Leon-Contreras and Stinga11, Reference Biswas and Stinga12].
from [Reference Biswas, De Leon-Contreras and Stinga11, Reference Biswas and Stinga12].
Let $\Omega \subset \mathbb {R}^{n}$![]() be a bounded Lipschitz domain. Define $L= -\operatorname {div}(A(x)\nabla u).$
be a bounded Lipschitz domain. Define $L= -\operatorname {div}(A(x)\nabla u).$![]() Then $L$
Then $L$![]() has a discrete Dirichlet spectrum, that is L has a countable family of non-negative eigenvalues and eigenfunctions $(\lambda _k, \phi _k)$
has a discrete Dirichlet spectrum, that is L has a countable family of non-negative eigenvalues and eigenfunctions $(\lambda _k, \phi _k)$![]() for $k=0,1,2\ldots$
for $k=0,1,2\ldots$![]() such that the set $\{\phi _k\}$
such that the set $\{\phi _k\}$![]() forms an orthonormal basis for $L^{2}(\Omega ).$
forms an orthonormal basis for $L^{2}(\Omega ).$![]() Hence $u(t,x) \in L^{2}(\mathbb {R} \times \Omega )$
Hence $u(t,x) \in L^{2}(\mathbb {R} \times \Omega )$![]() can be written as
can be written as

where for almost every $t \in \mathbb {R},$![]()
and $\widehat {u_k}(\rho )$![]() is the Fourier transform of $u_k(t)$
is the Fourier transform of $u_k(t)$![]() in $t$
in $t$![]() variable. We define the domain of the operator $(\partial _t-\operatorname {div}(A(x)\nabla ))^{s}$
variable. We define the domain of the operator $(\partial _t-\operatorname {div}(A(x)\nabla ))^{s}$![]() , $0\le s\le 1$
, $0\le s\le 1$![]() , as following:
, as following:

Given $u \in \operatorname {Dom}(H^{s})$![]() , we define $H^{s}u=(\partial _t-\operatorname {div}(A(x)\nabla ))^{s}u$
, we define $H^{s}u=(\partial _t-\operatorname {div}(A(x)\nabla ))^{s}u$![]() as a bounded linear functional on $\operatorname {Dom}(H^{s})$
as a bounded linear functional on $\operatorname {Dom}(H^{s})$![]() that acts on $v \in \operatorname {Dom}(H^{s})$
that acts on $v \in \operatorname {Dom}(H^{s})$![]() by the following formula
by the following formula

with the understanding that we have chosen the principal branch of the complex function $z \rightarrow z^{s}$![]() and $\overline {\widehat {v_k}(\rho )}$
and $\overline {\widehat {v_k}(\rho )}$![]() denotes the complex conjugate of $\widehat {v_k}(\rho ).$
denotes the complex conjugate of $\widehat {v_k}(\rho ).$![]()
Since the set $\{\phi _k\}$![]() is an orthonormal basis of $L^{2}(\Omega ),$
is an orthonormal basis of $L^{2}(\Omega ),$![]() we can write the semigroup $\{{\rm e}^{-\tau L}\}_{\tau \ge 0}$
we can write the semigroup $\{{\rm e}^{-\tau L}\}_{\tau \ge 0}$![]() generated by $L$
generated by $L$![]() as
as

for any $\varphi, \psi \in L^{2}(\Omega )$![]() , where $\varphi _k= \int _{\Omega }\varphi \phi _kdx$
, where $\varphi _k= \int _{\Omega }\varphi \phi _kdx$![]() and $\psi _k=\int _{\Omega }\psi \phi _kdx.$
and $\psi _k=\int _{\Omega }\psi \phi _kdx.$![]() Given $u \in L^{2} (\mathbb {R}\times \Omega )$
Given $u \in L^{2} (\mathbb {R}\times \Omega )$![]() , we define ${\rm e}^{-\tau H}u$
, we define ${\rm e}^{-\tau H}u$![]()
in the sense that for any $v \in L^{2}(\mathbb {R}),$![]()

The following is theorem 1.6 from [Reference Biswas, De Leon-Contreras and Stinga11].
Theorem 2.1 Let $u \in \operatorname {Dom}(H^{s}).$![]() For $(t,x) \in \mathbb {R} \times \Omega$
For $(t,x) \in \mathbb {R} \times \Omega$![]() and $y>0$
and $y>0$![]() , we define
, we define
Then,
is a weak solution to the following problem

We now recall the proposition 3.6 from [Reference Biswas and Stinga12].
Proposition 2.2 Let $U$![]() be as defined in (2.2) and assume that $f\mathop {=}\limits ^{def} H^{s}u \in L^{2} (\mathbb {R} \times \Omega )$
be as defined in (2.2) and assume that $f\mathop {=}\limits ^{def} H^{s}u \in L^{2} (\mathbb {R} \times \Omega )$![]() . Then $U_t\in L^{2}(\mathbb {R};(H^{1}_a(\Omega \times (0,\infty ))^{*} ),$
. Then $U_t\in L^{2}(\mathbb {R};(H^{1}_a(\Omega \times (0,\infty ))^{*} ),$![]() where $(H^{1}_a(\Omega \times (0,\infty ))^{*}$
where $(H^{1}_a(\Omega \times (0,\infty ))^{*}$![]() is the dual space of $H^{1}_a(\Omega \times (0,\infty ).$
is the dual space of $H^{1}_a(\Omega \times (0,\infty ).$![]() In particular, we have
In particular, we have
Moreover $U$![]() satisfies
satisfies

$a.e.$![]() $-1< t_1< t_2<1$
$-1< t_1< t_2<1$![]() and for all $\phi \in H^{1}([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$
and for all $\phi \in H^{1}([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$![]() such that $\phi =0$
such that $\phi =0$![]() on $\partial _pQ_1^{*}\setminus (Q_1 \times \{0\}).$
on $\partial _pQ_1^{*}\setminus (Q_1 \times \{0\}).$![]()
Now consider the following local problem

We say that $U \in C([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$![]() is a weak solution to (2.5) if for every $-1< t_1< t_2<1$
is a weak solution to (2.5) if for every $-1< t_1< t_2<1$![]()

holds for all $\phi \in H^{1}([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$![]() such that $\phi =0$
such that $\phi =0$![]() on $\partial _pQ_1^{*}\setminus (Q_1 \times \{0\}).$
on $\partial _pQ_1^{*}\setminus (Q_1 \times \{0\}).$![]() Before proceeding further, we make the following discursive remark.
Before proceeding further, we make the following discursive remark.
Remark 2.3 We say a constant to be universal if it depends only on ellipticity, $n,$![]() $s,$
$s,$![]() $L\left (\frac {n+2}{2s-1},1\right )$
$L\left (\frac {n+2}{2s-1},1\right )$![]() norm of $f$
norm of $f$![]() and the Dini character of $\omega _A$
and the Dini character of $\omega _A$![]() .
.
We will need the following lemmas from [Reference Biswas and Stinga12].
Lemma 2.4 Assume that $U$![]() is a weak solution to (2.5) with $F$
is a weak solution to (2.5) with $F$![]() as described above. Then, for each $\varphi \in C^{\infty }_c(Q_1\times [0,1))$
as described above. Then, for each $\varphi \in C^{\infty }_c(Q_1\times [0,1))$![]() and for each $t_1,t_2 \in (-1,1)$
and for each $t_1,t_2 \in (-1,1)$![]() with $t_1 < t_2$
with $t_1 < t_2$![]() ,
,

where $C = C(n, s, \mathrm {ellipticity})>0$![]() .
.
Lemma 2.5 Let $W$![]() be a weak solution to
be a weak solution to
Then we have the following estimates:
(i) For $k \in \mathbb {N} \cup \{0\}$
 , multi-index $\alpha$
, multi-index $\alpha$ and $Q_r(t_0,x_0)\subset Q_1,$
and $Q_r(t_0,x_0)\subset Q_1,$ we have
\[ \sup_{Q_{\frac{r}{2}}^{*}(t_0,x_0,0) } \left|\partial^{k}_t D^{\alpha}_x W\right| \leq \frac{C(n,s)}{r^{k+|\alpha|}} \text{osc}_{Q_{r}^{*}(t_0,x_0,0)} W. \]
we have
\[ \sup_{Q_{\frac{r}{2}}^{*}(t_0,x_0,0) } \left|\partial^{k}_t D^{\alpha}_x W\right| \leq \frac{C(n,s)}{r^{k+|\alpha|}} \text{osc}_{Q_{r}^{*}(t_0,x_0,0)} W. \]
(ii) For $Q_r(t_0,x_0) \subset Q_1$
 ,
\[ \max_{Q_{\frac{r}{2}^{*}}(t_0,x_0,0) } \big|W\big| \leq C(r,n,s)\|W\|_{L^{2}_a(Q_r^{*}(t_0,x_0,0))}. \]
,
\[ \max_{Q_{\frac{r}{2}^{*}}(t_0,x_0,0) } \big|W\big| \leq C(r,n,s)\|W\|_{L^{2}_a(Q_r^{*}(t_0,x_0,0))}. \]
(iii) For all $0\leq y<\frac {1}{2}$
 ,
\[ \sup_{(t,x)\in Q_{\frac{1}{2}}} \big|W_y(t,x,y)\big| \leq C(n,s)\|W\|_{L^{2}_a(Q_1^{*})}y. \]
,
\[ \sup_{(t,x)\in Q_{\frac{1}{2}}} \big|W_y(t,x,y)\big| \leq C(n,s)\|W\|_{L^{2}_a(Q_1^{*})}y. \]
Theorem 2.6 For every $f \in L^{2}(Q_1)$![]() and $F \in L^{2}(Q_1^{*})$
and $F \in L^{2}(Q_1^{*})$![]() , there exists a $u \in C(-1,1;V(B_1^{*}))$
, there exists a $u \in C(-1,1;V(B_1^{*}))$![]() unique weak solution to
unique weak solution to

where $V(B_1^{*})=\left \{v\in H_a^{1}(B_1^{*}):\;v=0\;\text {on}\;\partial B_1^{*}\setminus \{y=0\}\right \}.$![]()
We now recall the definition of modulus of continuity and provide a brief collection of basic results concerning to the modulus of continuity functions.
Definition 2.7 Modulus of continuity
A function
is said to be a modulus of continuity if the following conditions are satisfied$:$![]()
(i) $\Psi (s) \rightarrow 0$
 as $s \searrow 0$
as $s \searrow 0$ .
.(ii) $\Psi (s)$
 is increasing as a function of $s$
is increasing as a function of $s$ .
.(iii) $\Psi (s_1 + s_2) \leq \Psi (s_1) + \Psi (s_2),\ \forall \ s_1,\; s_2 \in [0,\;1].$

(iv) $\Psi (s)$
 is continuous.
is continuous.
We now define the notion of $\mathrm {Dini}$![]() -continuity:
-continuity:
Definition 2.8 $\mathrm {Dini}$ -continuity
-continuity
Let $f : \mathbb {R}^{n} \rightarrow \mathbb {R}$![]() be a function. Define the following modulus of continuity:
be a function. Define the following modulus of continuity:
We then say $f$![]() is $\mathrm {Dini}$
is $\mathrm {Dini}$![]() -continuous if
-continuous if
We now recall the following result proved in [Reference Lorentz31, theorem 8]:
Theorem 2.9 For each modulus of continuity $\psi (s)$![]() defined on $[0,1]$
defined on $[0,1]$![]() , there is a concave modulus of continuity $\tilde {\Psi }(s)$
, there is a concave modulus of continuity $\tilde {\Psi }(s)$![]() satisfying
satisfying
We will also need the following definition which captures a certain monotonicity property of the modulus of continuity.
Definition 2.10 Given $\eta \in (0,1]$![]() , we say that
, we say that
is $\eta$![]() -decreasing if the following condition holds:
-decreasing if the following condition holds:
Remark 2.11 From [Reference Lorentz31, page 44], we have that any continuous, increasing function
with $\Psi (0)=0$![]() is a modulus of continuity if it is concave. More generally, it suffices to assume that $\frac {\Psi (s)}{s}$
is a modulus of continuity if it is concave. More generally, it suffices to assume that $\frac {\Psi (s)}{s}$![]() is decreasing instead of concavity for $\Psi$
is decreasing instead of concavity for $\Psi$![]() .
.
Finally, we recall the Campanato type characterization.
Theorem 2.12 Suppose $u \in L^{2}(Q_2)$![]() satisfies that for every $(t_0,x_0) \in Q_1$
satisfies that for every $(t_0,x_0) \in Q_1$![]() there exists an affine function $\ell _{(t_0,x_0)}(x)=a + b\cdot x$
there exists an affine function $\ell _{(t_0,x_0)}(x)=a + b\cdot x$![]() such that
such that
where $K$![]() is a modulus of continuity. Then $\nabla u$
is a modulus of continuity. Then $\nabla u$![]() exists with $\nabla u(t_0,x_0)=\nabla \ell _{(t_0,x_0)}$
exists with $\nabla u(t_0,x_0)=\nabla \ell _{(t_0,x_0)}$![]() and there exists $C=C(n)$
and there exists $C=C(n)$![]() such that
such that
and
We give a self-contained proof of theorem 2.12 in the appendix A. In the case when $K(r)= r^{\alpha }$![]() , we refer the reader to [Reference Biswas and Stinga12].
, we refer the reader to [Reference Biswas and Stinga12].
3. Proof of main theorem
Our proof is based on an appropriate adaptation of compactness arguments, which has its roots in a fundamental work of Caffarelli in [Reference Caffarelli13]. This section is organized as follows. In § 3.1, we prove some real analysis estimates which are fractional analogues of the estimates in [Reference Daskalopoulos, Kuusi and Mingione18]. In § 3.2, we establish regularity at the boundary, i.e. at $\{y=0\}$![]() . In § 3.3, we prove the required scaled version of the interior estimates. With such ingredients in hand, we finally give the proof of theorem 1.1.
. In § 3.3, we prove the required scaled version of the interior estimates. With such ingredients in hand, we finally give the proof of theorem 1.1.
3.1 Some real analysis estimates
We first introduce some notations. We define

Given a positive function $g,$![]() we denote $g^{*}: [0,\infty ) \rightarrow [0, \infty )$
we denote $g^{*}: [0,\infty ) \rightarrow [0, \infty )$![]() by the non-increasing rearrangement of g, that is $g^{*}(s) :=\text { sup} \{\tau \ge 0 : |\{(t,x) \in \mathbb {R}^{n+1} : |g(t,x)| > \tau \} | > s\}.$
by the non-increasing rearrangement of g, that is $g^{*}(s) :=\text { sup} \{\tau \ge 0 : |\{(t,x) \in \mathbb {R}^{n+1} : |g(t,x)| > \tau \} | > s\}.$![]()
The following estimate is a fractional analogue of [Reference Daskalopoulos, Kuusi and Mingione18, equation (3.4)].
Estimate 1: Let $r>0$![]() . For given $0<\sigma <1$
. For given $0<\sigma <1$![]() , define
, define
for $i=0,1,2,3,\ldots$![]() . We have
. We have

for some $c$![]() depends on $s$
depends on $s$![]() , $\sigma$
, $\sigma$![]() and $n$
and $n$![]() .
.
Proof. In this proof we will denote $Q_{r_i}(x_0,t_0)$![]() by $Q_i$
by $Q_i$![]() . We will assume $|Q_1|=1.$
. We will assume $|Q_1|=1.$![]()

Estimate 2: We have the following estimate which is a fractional analogue of [Reference Daskalopoulos, Kuusi and Mingione18, equation (3.13)],

where $0< r<1/2$![]() , $g=|f|^{2},$
, $g=|f|^{2},$![]() $g^{**}(\rho ):=\frac {1}{\rho }\int _{0}^{\rho }g^{*}(s)ds$
$g^{**}(\rho ):=\frac {1}{\rho }\int _{0}^{\rho }g^{*}(s)ds$![]() and $C_{n+1}$
and $C_{n+1}$![]() denotes measure of $Q_1$
denotes measure of $Q_1$![]() in $\mathbb {R}^{n+1}.$
in $\mathbb {R}^{n+1}.$![]()
Proof. From Hardy–Littlewood inequality [Reference Hardy, Littlewood and Pólya23], we have

Multiply (3.3) with $\rho ^{2s - 2}$![]() and integrate with respect to $\rho$
and integrate with respect to $\rho$![]() in $(0,r)$
in $(0,r)$![]() to get
to get
Now by changing variables we get (3.2).
3.2 Regularity estimates at the boundary
We will begin by proving the relevant closeness lemma.
Lemma 3.1 Let $U$![]() be a weak solution of (2.5) with
be a weak solution of (2.5) with
Then, given any $\epsilon >0$![]() , there exists a $\delta =\delta (\epsilon,n,s,ellipticity)>0$
, there exists a $\delta =\delta (\epsilon,n,s,ellipticity)>0$![]() such that if
such that if
then there exists $V$![]() which solves weakly
which solves weakly
such that

Proof. Consider the following problem:

Note that from theorem 2.6, we have the unique solution, which we will denote by $V$![]() , of (3.6). Now using the regularity of $V$
, of (3.6). Now using the regularity of $V$![]() (lemma 2.5) and the properties of Steklov average, we have, the Steklov average of $V,$
(lemma 2.5) and the properties of Steklov average, we have, the Steklov average of $V,$![]() i.e., $V_h(t,x,y)={\unicode{x2A0F}} _t^{t+h}V(\tau,x,y)\,d\tau,$
i.e., $V_h(t,x,y)={\unicode{x2A0F}} _t^{t+h}V(\tau,x,y)\,d\tau,$![]() $h<1/4,$
$h<1/4,$![]() solves
solves

where $U_h(t,x,y)={\unicode{x2A0F}} _t^{t+h}U(\tau,x,y)\,{\rm d}\tau,$![]() $h<1/4$
$h<1/4$![]() , is the Steklov average of $U.$
, is the Steklov average of $U.$![]() Now, we multiply (3.7) by $(U_h - V_h)$
Now, we multiply (3.7) by $(U_h - V_h)$![]() and integrate by parts to get
and integrate by parts to get

By standard arguments, we know $U$![]() can be replaced by $U_h$
can be replaced by $U_h$![]() in (2.6). Also $V_h$
in (2.6). Also $V_h$![]() solves (3.7) so we can put $\phi = (U_h - V_h)\eta (t) \in H^{1}([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$
solves (3.7) so we can put $\phi = (U_h - V_h)\eta (t) \in H^{1}([-1,1];L^{2}_a(B_1^{*})) \cap L^{2}([-1,1];H^{1}_a(B_1^{*}))$![]() in (2.6), where $\eta (t)$
in (2.6), where $\eta (t)$![]() is chosen such that $\eta (t)=1$
is chosen such that $\eta (t)=1$![]() in $(-1/2,1/2)$
in $(-1/2,1/2)$![]() and compactly supported in $(-5/8,5/8)$
and compactly supported in $(-5/8,5/8)$![]() . Hence, after integrating by parts in (2.6) with respect to $t$
. Hence, after integrating by parts in (2.6) with respect to $t$![]() we get
we get

where $f_h$![]() and $F_h$
and $F_h$![]() denote the Steklov average of $f$
denote the Steklov average of $f$![]() and $F$
and $F$![]() respectively. On adding (3.8) and (3.9), we get
respectively. On adding (3.8) and (3.9), we get

Using Fundamental theorem of calculus in $t$![]() -variable and the Young's inequality with $\varepsilon$
-variable and the Young's inequality with $\varepsilon$![]() we get,
we get,

where $I_h(0)=\int _{B^{*}_{1/2}} y^{a} (U_h - V_h)(0)\,{\rm d}X.$![]() We rewrite above equation as
We rewrite above equation as

Note that we can make third and fourth term small by taking $\delta$![]() small enough. For the first term, take $\varphi$
small enough. For the first term, take $\varphi$![]() compactly supported in ${Q^{*}_{3/4}}$
compactly supported in ${Q^{*}_{3/4}}$![]() such that $\varphi =1$
such that $\varphi =1$![]() in ${Q^{*}_{1/2}}$
in ${Q^{*}_{1/2}}$![]() and use lemma 2.4 to get
and use lemma 2.4 to get

where $C=C(n,s, \text {ellipticity})>0.$![]() Also by trace theorem [Reference Nekvinda34], we have
Also by trace theorem [Reference Nekvinda34], we have

where $C_T(n,s)$![]() is constant from trace theorem. Hence, (3.12) becomes
is constant from trace theorem. Hence, (3.12) becomes

Also, for each time label we will apply the Poincarè inequality [Reference Fabes, Kenig and Serapioni22] to get

where $C_P(n,s)$![]() is constant in the Poincarè inequality.
is constant in the Poincarè inequality.
Now, first choose $\varepsilon >0$![]() small enough such that $((1/4-\varepsilon C_T)C_P -\varepsilon C_T) >0$
small enough such that $((1/4-\varepsilon C_T)C_P -\varepsilon C_T) >0$![]() then choose $\delta$
then choose $\delta$![]() to get
to get

Also, from (3.13) and (3.14) we have
where $M$![]() is a universal constant. Since $U \in C([-1,1],L_a^{2}(B_1^{*})) \cap L^{2}([-1,1],H_a^{1}(B_1^{*}))$
is a universal constant. Since $U \in C([-1,1],L_a^{2}(B_1^{*})) \cap L^{2}([-1,1],H_a^{1}(B_1^{*}))$![]() , $U_h-V_h \rightarrow U-V$
, $U_h-V_h \rightarrow U-V$![]() , $\nabla (U_h-V_h) \rightarrow \nabla (U-V)$
, $\nabla (U_h-V_h) \rightarrow \nabla (U-V)$![]() in $L^{2}_a(Q_{1/2}^{*})$
in $L^{2}_a(Q_{1/2}^{*})$![]() and using (3.6), we have $I_h(0) \rightarrow 0$
and using (3.6), we have $I_h(0) \rightarrow 0$![]() . Hence by trace theorem $(U_h-V_h)(t,x,0) \rightarrow (U-V)(t,x,0)$
. Hence by trace theorem $(U_h-V_h)(t,x,0) \rightarrow (U-V)(t,x,0)$![]() in $L^{2}(Q_{1/2}).$
in $L^{2}(Q_{1/2}).$![]() This completes the proof of the lemma.
This completes the proof of the lemma.
We now prove the closeness of solution $U$![]() to (2.5) by an affine function at some fixed scale.
to (2.5) by an affine function at some fixed scale.
Lemma 3.2 There exist $0< \delta, \lambda <1$![]() $($
$($![]() depending on $n$
depending on $n$![]() , $s$
, $s$![]() and ellipticity$)$
and ellipticity$)$![]() , a linear function $\ell (x) =\mathcal {A} + \mathcal {B} \cdot x$
, a linear function $\ell (x) =\mathcal {A} + \mathcal {B} \cdot x$![]() and constant $C =C(n,s)>0$
and constant $C =C(n,s)>0$![]() such that for any solution $U$
such that for any solution $U$![]() of (2.5) which satisfies (3.4) and (3.5),
of (2.5) which satisfies (3.4) and (3.5),
and $|\mathcal {A}| + |\mathcal {B}| \leq C$![]() .
.
Proof. Let $0<\epsilon <1$![]() be any real number. From lemma 3.1, there exists a $\delta (\epsilon ) >0$
be any real number. From lemma 3.1, there exists a $\delta (\epsilon ) >0$![]() and a solution $V$
and a solution $V$![]() to (3.6) such that if (3.5) holds, then
to (3.6) such that if (3.5) holds, then

where $V$![]() solves (3.6). Now by lemma 2.5, $V$
solves (3.6). Now by lemma 2.5, $V$![]() is smooth, we define
is smooth, we define
Also by lemma 2.5, there exists a constant $\tilde {C}=\tilde {C}(n,s)$![]() such that
such that
Now, using triangle inequality, $(a+b)^{2} \leq 2a^{2} +2b^{2}$![]() , (3.15) and (3.4), we get
, (3.15) and (3.4), we get

Hence we get
where $C=4 \tilde {C}$![]() .
.
Using triangle inequality, we get

For any $(t,x,y) \in Q^{*}_{1/4}$![]() , using Mean value theorem, Taylor's theorem and lemma 2.5, we have a universal constant $D$
, using Mean value theorem, Taylor's theorem and lemma 2.5, we have a universal constant $D$![]() such that
such that

Hence, using (3.15) we get

Now first choose $0<\lambda <1/4$![]() small enough such that
small enough such that
then take $\epsilon$![]() such that
such that
which in turn fixes $\delta$![]() .
.
Now we will define some functions as in [Reference Adimurthi and Banerjee1]:
• Define
\[ \tilde{\omega}_1(r):=\text{max}\{\omega_{A}(\gamma r)/\tilde{\delta},r\}, \]where $\gamma$
 and $\tilde {\delta }$
and $\tilde {\delta }$ will be fixed later. By theorem 2.9, we can assume that $\tilde {\omega }_1$
will be fixed later. By theorem 2.9, we can assume that $\tilde {\omega }_1$ is concave. Without loss of generality we can assume $\tilde {\omega }_1(1)=1$
is concave. Without loss of generality we can assume $\tilde {\omega }_1(1)=1$ . Finally we define
\[ \omega_1(r):=\tilde{\omega}_1(\sqrt{r}). \]Then, $\omega _1(r)$
. Finally we define
\[ \omega_1(r):=\tilde{\omega}_1(\sqrt{r}). \]Then, $\omega _1(r)$
 is $1/2$
is $1/2$ -decreasing function in the sense of definition 2.10. Also, by application of change of variables we have $\omega _1(r)$
-decreasing function in the sense of definition 2.10. Also, by application of change of variables we have $\omega _1(r)$ is Dini continuous.
is Dini continuous.• We define
\[ \omega_2(r):=\operatorname{max}\left\{\gamma I(\gamma r)/\tilde{\delta},r\right\}, \]where $I(r):= r^{2s-1}({\unicode{x2A0F}} _{Q_r} |f(x,t)|^{2} dt dx)^{1/2}.$

• We define
\[ \omega_3(\lambda^{k}):=\sum_{i=0}^{k}\omega_1(\lambda^{k-i})\omega_2(\lambda^{i}), \]where $\lambda$
 is from lemma 3.2.
is from lemma 3.2.• Finally, we define
\[ \omega(\lambda^{k})=\operatorname{max}\left\{\omega_3(\lambda^{k}),\lambda^{k/2}\right\}. \]
Lemma 3.3 There exists a universal constant $C_{sum}$![]() such that
such that

Proof. From the definition of $\omega$![]() , we have
, we have

An application of Fubini's theorem and reindexing gives $\sum _{i=0}^{\infty }\omega _3(\lambda ^{i}) \le \sum _{i=0}^{\infty }\omega _1(\lambda ^{i})\sum _{i=0}^{\infty }\omega _2(\lambda ^{i}).$![]() Consequently, we have
Consequently, we have

Using the Dini continuity, increasing nature of $\omega _A$![]() and change of variables, we have
and change of variables, we have

Choose $\gamma < \tilde {\delta }$![]() such that
such that

Note that from (3.1), we have

Using (3.2) we have

where $g=f^{2}$![]() . We have given that $f \in L\left (\frac {n+2}{2s-1},1\right )$
. We have given that $f \in L\left (\frac {n+2}{2s-1},1\right )$![]() , which gives us $g \in L\left (\frac {n+2}{2(2s-1)},\frac {1}{2}\right )$
, which gives us $g \in L\left (\frac {n+2}{2(2s-1)},\frac {1}{2}\right )$![]() . Since $2(2s-1) < n+2$
. Since $2(2s-1) < n+2$![]() , therefore from [Reference O'Neil36, equation (6.8)], we get
, therefore from [Reference O'Neil36, equation (6.8)], we get
Hence we get a universal bound on $\sum _{i=0}^{\infty }\omega _2(\lambda ^{i})$![]() as $\lambda$
as $\lambda$![]() is a universal constant. This completes the proof of the lemma.
is a universal constant. This completes the proof of the lemma.
We now prove the closeness of solution $U$![]() to (2.5) by affine function at each dyadic scale and closeness of affine functions as well. Given the solution $U(t,X)$
to (2.5) by affine function at each dyadic scale and closeness of affine functions as well. Given the solution $U(t,X)$![]() of (2.5), we define
of (2.5), we define

Then $U_{\gamma }$![]() solves (2.5) with modulus of continuity for $A$
solves (2.5) with modulus of continuity for $A$![]() is $\omega _A(\gamma r),$
is $\omega _A(\gamma r),$![]()
and $r^{2s-1}({\unicode{x2A0F}} _{Q_r} |f(x,t)|^{2}\,{\rm d}t\,{\rm d}x)^{1/2}\le \gamma I(\gamma r)$![]() .
.
Lemma 3.4 There exist a sequence of linear functions $\ell _{k}(x) =a_k + b_k \cdot x$![]() and a constant $C=C(n,s)>0$
and a constant $C=C(n,s)>0$![]() such that for any solution $U$
such that for any solution $U$![]() of (2.5) satisfies
of (2.5) satisfies

Proof. For notational ease we shall denote $U_{\gamma }(t,X)$![]() by $U(t,X)$
by $U(t,X)$![]() , $\omega _A(\gamma r)$
, $\omega _A(\gamma r)$![]() by $\omega _A(r)$
by $\omega _A(r)$![]() and $\gamma I(\gamma r)$
and $\gamma I(\gamma r)$![]() by $I(r)$
by $I(r)$![]() . We will prove the lemma by induction on $k$
. We will prove the lemma by induction on $k$![]() . For $k=0$
. For $k=0$![]() , take $\ell _{k}(x)=0$
, take $\ell _{k}(x)=0$![]() and we get
and we get
Thus we are done for $k=0$![]() . Let us assume result is true for $k=0,1,\ldots,i$
. Let us assume result is true for $k=0,1,\ldots,i$![]() . We will prove it for $k=i+1$
. We will prove it for $k=i+1$![]() . Define
. Define
then $\tilde {U}$![]() is a weak solution to
is a weak solution to

where $\tilde {f}(t,x)=\frac {\lambda ^{-ia}}{{\omega }(\lambda ^{i})}f(\lambda ^{2i} t, \lambda ^{i} x)$![]() and the vector field $F$
and the vector field $F$![]() is given by ${\lambda ^{i}{\omega }(\lambda ^{i})} F= ((I-A(\lambda ^{i} x))\nabla _x \ell (\lambda ^{i} x), 0 )$
is given by ${\lambda ^{i}{\omega }(\lambda ^{i})} F= ((I-A(\lambda ^{i} x))\nabla _x \ell (\lambda ^{i} x), 0 )$![]() . Now we estimate the following:
. Now we estimate the following:
Bound for $f$![]() :
:

Bound for $F$![]() : Note that by induction hypothesis
: Note that by induction hypothesis

Now
We now integrate in $y$![]() -variable and then use change of variable to obtain
-variable and then use change of variable to obtain

Also, note that
Choose $\tilde {\delta }<\delta$![]() such that $2C^{2}_1\tilde {\delta }^{2}<\delta ^{2}$
such that $2C^{2}_1\tilde {\delta }^{2}<\delta ^{2}$![]() . We rewrite (3.16) for $k=i$
. We rewrite (3.16) for $k=i$![]() as
as

Now after changing the variables, we get
By lemma 3.2 there exists a $l(x)=a+b\cdot x$![]() such that
such that
and $|a| + |b| \leq C.$![]() After putting the value of $\tilde {U}$
After putting the value of $\tilde {U}$![]() and changing the variables, we get
and changing the variables, we get

where $\ell _{i+1}(x)=\ell _i(x)+\lambda ^{i}\omega (\lambda ^{i})l(\lambda ^{-i}x)$![]() . By putting $x=0$
. By putting $x=0$![]() we get $|a_{i+1}-a_i| \leq C \lambda ^{i}\omega (\lambda ^{i})$
we get $|a_{i+1}-a_i| \leq C \lambda ^{i}\omega (\lambda ^{i})$![]() . Take gradient to get $|b_{i+1}-b_i| \leq C \omega (\lambda ^{i})$
. Take gradient to get $|b_{i+1}-b_i| \leq C \omega (\lambda ^{i})$![]() .
.
With lemmas 3.3 and 3.4 in hand, we get the approximation of $U$![]() by an affine function.
by an affine function.
Lemma 3.5 There exists a linear function $\ell _{t_0,x_0}(x)=a_{\infty }+b_{\infty }\cdot x$![]() such that for any solution $U$
such that for any solution $U$![]() of (2.5) with (3.4) satisfies
of (2.5) with (3.4) satisfies
for all $0< r<1/2$![]() , where $C_l$
, where $C_l$![]() is a universal constant and $K$
is a universal constant and $K$![]() is $1/2-$
is $1/2-$![]() decreasing concave modulus of continuity.
decreasing concave modulus of continuity.
Proof. Without loss of generality we will assume that $(t_0,x_0)=(0,0).$![]() First we will estimate for $U_{\gamma }$
First we will estimate for $U_{\gamma }$![]() with small $r$
with small $r$![]() then will do it for $U.$
then will do it for $U.$![]() Note that $a_k$
Note that $a_k$![]() and $b_k$
and $b_k$![]() are convergent as
are convergent as

We define $a_{\infty }$![]() and $b_{\infty }$
and $b_{\infty }$![]() as limit of $a_k$
as limit of $a_k$![]() and $b_k$
and $b_k$![]() respectively. We will denote $\ell _{(0,0)}$
respectively. We will denote $\ell _{(0,0)}$![]() by $\ell _0$
by $\ell _0$![]() . Take $r$
. Take $r$![]() such that $\lambda ^{k+1} \leq r \leq \lambda ^{k}$
such that $\lambda ^{k+1} \leq r \leq \lambda ^{k}$![]() for some $k \in \mathbb {N}.$
for some $k \in \mathbb {N}.$![]() Now using triangle inequality, (3.16) and (3.17) we have
Now using triangle inequality, (3.16) and (3.17) we have

Note that from lemma 3.2, $\lambda$![]() depends only on $n,s$
depends only on $n,s$![]() , ellipticity therefore $(2\lambda ^{-n-2}+8C)$
, ellipticity therefore $(2\lambda ^{-n-2}+8C)$![]() is a universal constant. We now follow the same lines of proof as in [Reference Adimurthi and Banerjee1] from (4.30) to (4.35) to get
is a universal constant. We now follow the same lines of proof as in [Reference Adimurthi and Banerjee1] from (4.30) to (4.35) to get
where $K=K_1(r)+K_2(r)+K_3(r)$![]() and
and

Now put the value of $U_{\gamma }$![]() and do change of variables to get
and do change of variables to get

Call $K(r/{\gamma })$![]() by $K(r)$
by $K(r)$![]() , $\ell _{0}(\gamma ^{-1}x)$
, $\ell _{0}(\gamma ^{-1}x)$![]() by $\ell _{0}(x)$
by $\ell _{0}(x)$![]() and use the fact $\gamma$
and use the fact $\gamma$![]() is a universal constant to get
is a universal constant to get
for $0< r< \gamma \lambda.$![]() For $\gamma \lambda < r<1/2,$
For $\gamma \lambda < r<1/2,$![]() it will be done by replacing $\tilde {C_l}$
it will be done by replacing $\tilde {C_l}$![]() to $C\tilde {C_l}/(\gamma ^{n+6}\lambda K(\gamma \lambda )),$
to $C\tilde {C_l}/(\gamma ^{n+6}\lambda K(\gamma \lambda )),$![]() call it again by $C_l$
call it again by $C_l$![]() .
.
Lemma 3.6 There exists a universal constant $C_{bdr}$![]() such that
such that
and
for $(t_i,x_i) \in Q_{1/2}$![]() , where $\ell _{(t_i,x_i)}$
, where $\ell _{(t_i,x_i)}$![]() denotes the linear function constructed in lemma 3.5.
denotes the linear function constructed in lemma 3.5.
Proof. After proceeding as in the proof of lemma 3.5 we get a linear function $\ell _{t_0,x_0}(x)=a_{\infty }+b_{\infty }\cdot x$![]() such that
such that
Now apply theorem 2.12 (Companato type characterization) to get the result with modulus of continuity $K(2r)$![]() , which we again call as $K(r).$
, which we again call as $K(r).$![]()
3.3 Interior estimate
To prove theorem 1.1, we have to combine the above boundary estimates with known interior estimates in [Reference Caffarelli and Kenig14]. In order to do this we need the following rescaled version of interior estimate.
Theorem 3.7 Let $u$![]() be a weak solution of
be a weak solution of
with $||u||_{L^{2}(Q_1)} \le 1,$![]() where $B,$
where $B,$![]() $g$
$g$![]() are Dini continuous with modulus of continuity $\Psi _B$
are Dini continuous with modulus of continuity $\Psi _B$![]() and $\Psi _g$
and $\Psi _g$![]() respectively and $b$
respectively and $b$![]() is smooth. Then there exists a constant $C_{ir}>0$
is smooth. Then there exists a constant $C_{ir}>0$![]() depending on $n$
depending on $n$![]() , ellipticity, $||b||_1$
, ellipticity, $||b||_1$![]() ($C^{1}$
($C^{1}$![]() -norm of $b$
-norm of $b$![]() ), $||g||_{\infty },$
), $||g||_{\infty },$![]() and $\int _{0}^{1}\frac {\Psi _B(t)}{t}$
and $\int _{0}^{1}\frac {\Psi _B(t)}{t}$![]() , $\int _{0}^{1}\frac {\Psi _g(t)}{t}$
, $\int _{0}^{1}\frac {\Psi _g(t)}{t}$![]() such that for all $(t_1,x_1),(t_2,x_2) \in Q_{1/2},$
such that for all $(t_1,x_1),(t_2,x_2) \in Q_{1/2},$![]() we have
we have
where
and
Furthermore for all $(t,x) \in Q_{1/2},$![]()
The proof of the theorem 3.7 will be done by compactness method. We will sketch it as most of the details are similar to boundary estimate. We need the following lemmas.
Lemma 3.8 Let $u$![]() be a weak solution of (3.21) with $||u||_{L^{2}(Q_1)} \le 1.$
be a weak solution of (3.21) with $||u||_{L^{2}(Q_1)} \le 1.$![]() Then, given any $\epsilon >0$
Then, given any $\epsilon >0$![]() , there exists a $\delta =\delta (\epsilon, n, \text {ellipticity},||b||_1,||g||_{\infty } ) >0$
, there exists a $\delta =\delta (\epsilon, n, \text {ellipticity},||b||_1,||g||_{\infty } ) >0$![]() such that if
such that if
then there exists $v$![]() which solves weakly
which solves weakly
such that
Proof. We have existence of solution of (3.24) by remark A.1. We now proceed along the similar lines as in the proof of lemma 3.1. Also, for the required energy estimate, we refer to lemma 1.2.3 ([Reference Caffarelli and Kenig14]).
Lemma 3.9 There exist $0< \delta _{int}, \lambda _{int} <1$![]() $($
$($![]() depending on $n$
depending on $n$![]() , ellipticity, $||b||_1)$
, ellipticity, $||b||_1)$![]() , a linear function $\ell (x) =\mathcal {A}_{int} + \mathcal {B}_{int} \cdot x$
, a linear function $\ell (x) =\mathcal {A}_{int} + \mathcal {B}_{int} \cdot x$![]() and constant $C_{int} =C(n,||b||_1)>0$
and constant $C_{int} =C(n,||b||_1)>0$![]() such that for any solution $u$
such that for any solution $u$![]() of (3.21) with $||u||_{L^{2}(Q_1)}$
of (3.21) with $||u||_{L^{2}(Q_1)}$![]() and satisfies (3.23),
and satisfies (3.23),
and $|\mathcal {A}_{int}| + |\mathcal {B}_{int}| \leq C_{int}.$![]()
Proof. Since $v$![]() , solution of (3.24), is smooth therefore we can proceed like the proof of the lemma 3.2.
, solution of (3.24), is smooth therefore we can proceed like the proof of the lemma 3.2.
Lemma 3.10 There exist a sequence of linear functions $\ell ^{k}_{int}(x) =a^{k}_{int} + b^{k}_{int} \cdot x$![]() and a constant $C_{int}=C(n,||b||_1)>0$
and a constant $C_{int}=C(n,||b||_1)>0$![]() such that for any weak solution $u$
such that for any weak solution $u$![]() of (3.21) with $||u||_{L^{2}(Q_1)}$
of (3.21) with $||u||_{L^{2}(Q_1)}$![]() ,
,

and
Proof. Note that $u_{\gamma }(t,x)=u(\gamma ^{2} t, \gamma x)$![]() will satisfy (3.21) with $\Psi _B(\gamma r)$
will satisfy (3.21) with $\Psi _B(\gamma r)$![]() and $\gamma g(\gamma x)$
and $\gamma g(\gamma x)$![]() . Now we will define some functions:
. Now we will define some functions:
Define
where $\gamma _{int}$![]() and $\tilde {\delta }_{int}$
and $\tilde {\delta }_{int}$![]() will be fixed later. By theorem 2.9, we can assume $\tilde {\Psi }_1$
will be fixed later. By theorem 2.9, we can assume $\tilde {\Psi }_1$![]() is concave. Without loss of generality we can assume $\tilde {\Psi }_1(1)=1$
is concave. Without loss of generality we can assume $\tilde {\Psi }_1(1)=1$![]() . Finally we define
. Finally we define
Then, $\psi _1(r)$![]() is $1/2$
is $1/2$![]() -decreasing function. Also, using change of variables we have $\psi _1(r)$
-decreasing function. Also, using change of variables we have $\psi _1(r)$![]() is Dini continuous. Similarly, define $\psi _2(r)$
is Dini continuous. Similarly, define $\psi _2(r)$![]() corresponding to Dini continuity of $g$
corresponding to Dini continuity of $g$![]() , i.e., $\omega _g.$
, i.e., $\omega _g.$![]() Finally define
Finally define
where $\psi _3(\lambda ^{k}):=\sum _{i=0}^{k} \psi _1(\lambda ^{k-i})\psi _2(\lambda ^{i})$![]() . Now proceed as in the proof of lemma 3.4.
. Now proceed as in the proof of lemma 3.4.
Proof. Sketch of proof of theorem 3.7
First we will get the estimate as in lemma 3.5 and then use theorem 2.12 (Companato type characterization) to get the implications of the theorem.
Proof of theorem 1.1 Let $(t_1,x_1,y_1)$![]() and $(t_2,x_2,y_2)$
and $(t_2,x_2,y_2)$![]() be in $Q^{*}_{1/2}.$
be in $Q^{*}_{1/2}.$![]() Without loss of generality we shall assume $y_1 \leq y_2.$
Without loss of generality we shall assume $y_1 \leq y_2.$![]() We will do proof in two cases:
We will do proof in two cases:
(i) $|(t_1,X_1)-(t_2,X_2)| \leq \frac {y_1}{4}$

(ii) $|(t_1,X_1)-(t_2,X_2)| \geq \frac {y_1}{4}$
 .
.
In the first case, on using lemma 3.5 for $r=y_1/2$![]() , we have
, we have

where $C_n=2^{n+5+a}.$![]() Consider
Consider
Now observe that the following rescaled function
solves
in $\textbf {Q}_{1/2}(0,0,1)$![]() and
and
Note that for $g=(B(y_1X)-I )\cdot \nabla \ell /\sqrt {C_nC_l}K(y_1)$![]() , we have $\int _{0}^{1}\frac {\Psi _g(t)}{t}dt$
, we have $\int _{0}^{1}\frac {\Psi _g(t)}{t}dt$![]() and $||g||_{\infty }$
and $||g||_{\infty }$![]() is bounded by a universal constant. We now apply theorem 3.7 to get
is bounded by a universal constant. We now apply theorem 3.7 to get

for all $(t,X) \in \textbf {Q}_{1/2}(0,0,1)$![]() . Note that condition of case(i) implies that
. Note that condition of case(i) implies that
Therefore we put $(\tilde {t},\tilde {X})$![]() in (3.27). Subsequently, we use $\ell _{(t_1,x_1)}$
in (3.27). Subsequently, we use $\ell _{(t_1,x_1)}$![]() is linear and re-scale back to find
is linear and re-scale back to find

Since $K$![]() is $1/2$
is $1/2$![]() -decreasing, we obtain
-decreasing, we obtain
Similary, we get
This proves the first case.
To prove the case(ii) first note that using triangle inequality we get

Use lemma 3.6 and (3.22) of theorem 3.7 to get the following estimate

Now we will get estimate for continuity in $t$![]() variable:
variable:

where $\xi _1,\xi _2$![]() lies between $0$
lies between $0$![]() and $y.$
and $y.$![]() Since $\xi _1,\xi _2$
Since $\xi _1,\xi _2$![]() lies between $0$
lies between $0$![]() and $y$
and $y$![]() therefore $|(t_1,x,\xi _1)-(t_1,x,\xi _2)| \le y$
therefore $|(t_1,x,\xi _1)-(t_1,x,\xi _2)| \le y$![]() . We now use the condition of case(ii) to find $|(t_1,x,\xi _1)-(t_1,x,\xi _2)| \le 4|(t_1,X)-(t_2,X)|.$
. We now use the condition of case(ii) to find $|(t_1,x,\xi _1)-(t_1,x,\xi _2)| \le 4|(t_1,X)-(t_2,X)|.$![]() Hence we get
Hence we get
This completes the proof of case(ii).
Acknowledgments
We are thankful to Agnid Banerjee for various helpful discussions and suggestions. We would also like to thank the editor for the kind handling of our paper and the reviewer for various comments and suggestions which helped in improving the presentation of the manuscript.
Appendix A. Appendix
Proof of theorem 2.6. Consider $f \in L^{2}(Q_1)$![]() and $F \in L^{2}_a(Q_1^{*}).$
and $F \in L^{2}_a(Q_1^{*}).$![]() Now, using the density of smooth function, we have $f_k \in C^{\infty }_c(Q_1)$
Now, using the density of smooth function, we have $f_k \in C^{\infty }_c(Q_1)$![]() and $F_k \in C^{\infty }_c(Q_1^{*})$
and $F_k \in C^{\infty }_c(Q_1^{*})$![]() such that $f_k \rightarrow f$
such that $f_k \rightarrow f$![]() in $L^{2}(Q_1)$
in $L^{2}(Q_1)$![]() and $F_k\rightarrow F$
and $F_k\rightarrow F$![]() in $L^{2}_a(Q_1^{*}).$
in $L^{2}_a(Q_1^{*}).$![]() Let $V^{*}$
Let $V^{*}$![]() be the dual space of $V$
be the dual space of $V$![]() . Define $g_k:[-1,1]\rightarrow V^{*}$
. Define $g_k:[-1,1]\rightarrow V^{*}$![]() as following: Fix t, for $v \in V$
as following: Fix t, for $v \in V$![]() ,
,
Using triangle inequality, Cauchy–Schwarz inequality and trace theorem (in the first term), we have $g_k(t) \in V^{*}$![]() with
with

Use $f_k \in L^{2}(Q_1)$![]() and $F_k \in L^{2}_a(Q_1^{*})$
and $F_k \in L^{2}_a(Q_1^{*})$![]() to get $g_k \in L^{2}(-1,1;V^{*}).$
to get $g_k \in L^{2}(-1,1;V^{*}).$![]() Also, define $\tilde {g_k}:[-1,1]\rightarrow V^{*}$
Also, define $\tilde {g_k}:[-1,1]\rightarrow V^{*}$![]() as following: Fix t, for $v \in V,$
as following: Fix t, for $v \in V,$![]()
then $g_k'=\tilde {g_k} \in L^{2}(-1,1;V^{*}).$![]() For $u,v \in V,$
For $u,v \in V,$![]() define
define
Note that by Poincarè inequality, for all $u \in V$![]() we have
we have
Thus we have verified conditions of theorem 5.1 of [Reference Duvaut and Lions20] for $u_0=0$![]() and $\chi =0$
and $\chi =0$![]() . Hence we get $u_k \in L^{2}(-1,1;V)$
. Hence we get $u_k \in L^{2}(-1,1;V)$![]() and $(u_k)_t \in L^{2}(-1,1;V)$
and $(u_k)_t \in L^{2}(-1,1;V)$![]() such that for almost all $t$
such that for almost all $t$![]() and for all $v \in V$
and for all $v \in V$![]() we have
we have

Put $v=u_k(t)$![]() in (A.1) and integrate with respect to $t$
in (A.1) and integrate with respect to $t$![]() to get
to get

Since $t \rightarrow ||u_k(t)||_{V}$![]() is a absolutely continuous function, we get
is a absolutely continuous function, we get

On applying Hölder's inequality, trace theorem and AM-GM inequality in the first term of right-hand side and Hölder's inequality and AM-GM inequality in the second term we get

Now write (A.1) as

After applying Hölder's inequality and trace theorem in first term of right-hand side and Hölder's inequality in second term and third term of right-hand side we get, for almost all $t$![]()

After squaring both side and applying AM-GM inequality we get

Using (A.2) and boundedness of $||f_k||_{L^{2}}$![]() and $||F_k||_{L_a^{2}}$
and $||F_k||_{L_a^{2}}$![]() , we get $u_k$
, we get $u_k$![]() and $(u_k)_t$
and $(u_k)_t$![]() is bounded in $L^{2}(-1,1;V)$
is bounded in $L^{2}(-1,1;V)$![]() and $L^{2}(-1,1;V^{*})$
and $L^{2}(-1,1;V^{*})$![]() respectively. Hence we will get a weak convergent subsequence $u_k$
respectively. Hence we will get a weak convergent subsequence $u_k$![]() such that $u_k \rightharpoonup u$
such that $u_k \rightharpoonup u$![]() in $L^{2}(-1,1;V)$
in $L^{2}(-1,1;V)$![]() and $(u_k)_t \rightharpoonup u_t$
and $(u_k)_t \rightharpoonup u_t$![]() in $L^{2}(-1,1;V^{*}).$
in $L^{2}(-1,1;V^{*}).$![]() Hence, for all $\phi \in H^{1}_0(-1,1;V)$
Hence, for all $\phi \in H^{1}_0(-1,1;V)$![]() we have
we have

Also $u \in L^{2}(-1,1;V)$![]() and $u_t \in L^{2}(-1,1;V^{*})$
and $u_t \in L^{2}(-1,1;V^{*})$![]() implies $u \in C(-1,1;V).$
implies $u \in C(-1,1;V).$![]() Since $u_k(0)=0$
Since $u_k(0)=0$![]() for all $k$
for all $k$![]() , $u(0)=0.$
, $u(0)=0.$![]() Note that (A.4) is equivalent to following: for all $-1 < t_1 < t_2 <1$
Note that (A.4) is equivalent to following: for all $-1 < t_1 < t_2 <1$![]() and $\phi \in H^{1}(-1,1;V)$
and $\phi \in H^{1}(-1,1;V)$![]() we have
we have

Now we will prove uniqueness. Assume there are two solutions $u_1$![]() and $u_2$
and $u_2$![]() in $C(-1,1;V) \cap L^{2}(-1,1;V)$
in $C(-1,1;V) \cap L^{2}(-1,1;V)$![]() . By standard argument Steklov average of $u^{i}$
. By standard argument Steklov average of $u^{i}$![]() , $u^{i}_h$
, $u^{i}_h$![]() belongs to $H^{1}(-1,1;V)$
belongs to $H^{1}(-1,1;V)$![]() and satisfy
and satisfy

On putting $\phi =u^{2}_h-u^{1}_h$![]() and subtracting two equations we get
and subtracting two equations we get

On passing limit as $h \rightarrow 0$![]() we get
we get
Take $t_1 \rightarrow -1$![]() and conclude $u^{2}=u^{1}.$
and conclude $u^{2}=u^{1}.$![]() This completes the proof of uniqueness.
This completes the proof of uniqueness.
Remark A.1 For every $F \in L^{2}(Q_1)$![]() , there exists a unique weak solution $U \in C(-1,1;V (B_1))$
, there exists a unique weak solution $U \in C(-1,1;V (B_1))$![]() to
to

This can be obtained by taking $V=H^{1}_{0}(B_1)$![]() and measure $dxdt$
and measure $dxdt$![]() instead of $y^{a}dXdt.$
instead of $y^{a}dXdt.$![]()
Proof of theorem 2.12. We first prove the existence of $\nabla u.$![]() Observe that the Lebesgue differentiation theorem gives $u(t_0,x_0)=\ell _{(t_0,x_0)}(x_0)$
Observe that the Lebesgue differentiation theorem gives $u(t_0,x_0)=\ell _{(t_0,x_0)}(x_0)$![]() . Consequently, we have
. Consequently, we have

where $e_i \in \mathbb {R}^{n}$![]() denote the usual $i^{th}$
denote the usual $i^{th}$![]() basis element. Since $\ell _{(t_0,x_0)}(x_0+e_ir)=\ell _{(t_0,x_0)}(x_0)+r e_i \cdot \nabla \ell _{(t_0,x_0)},$
basis element. Since $\ell _{(t_0,x_0)}(x_0+e_ir)=\ell _{(t_0,x_0)}(x_0)+r e_i \cdot \nabla \ell _{(t_0,x_0)},$![]() therefore we get
therefore we get

Now we use $\int _{Q_r(x_0+re_i)}(x-x_0-re_i)\,{\rm d}x=0$![]() to obtain
to obtain

here for simplicity we have assumed $|Q_1|=1.$![]() We now add and subtract $u(t,x)$
We now add and subtract $u(t,x)$![]() and use (A.6) to find
and use (A.6) to find

It is easy to see for $r<1/2$![]() , $Q_r(t_0,x_0+re_i) \subset Q_{2r}(t_0,x_0).$
, $Q_r(t_0,x_0+re_i) \subset Q_{2r}(t_0,x_0).$![]() Hence using (2.9) we get
Hence using (2.9) we get
Now take $r \rightarrow 0$![]() to obtain $\partial _{x_i}u(t_0,x_0)=e_i \cdot \nabla \ell _{(t_0,x_0)}$
to obtain $\partial _{x_i}u(t_0,x_0)=e_i \cdot \nabla \ell _{(t_0,x_0)}$![]() . This proves the existence of $\nabla u.$
. This proves the existence of $\nabla u.$![]()
We now prove the continuity of $\nabla u$![]() . Let $(t_1,x_1), (t_2,x_2) \in Q_{1}$
. Let $(t_1,x_1), (t_2,x_2) \in Q_{1}$![]() with $r=|(t_1,x_1)-(t_2,x_2)|$
with $r=|(t_1,x_1)-(t_2,x_2)|$![]() . Since $\int _{Q_r}x_idx=0$
. Since $\int _{Q_r}x_idx=0$![]() for all $i$
for all $i$![]() and for $i \neq j$
and for $i \neq j$![]() we have $\int _{Q_r}(e_i\cdot x)(e_j\cdot x) =0$
we have $\int _{Q_r}(e_i\cdot x)(e_j\cdot x) =0$![]() . Therefore, we find
. Therefore, we find

where we have used $Q_r(t_1,x_1) \subset Q_{2r}(t_2,x_2)$![]() . Hence using (2.9) we obtain
. Hence using (2.9) we obtain
This completes the proof of continuity of $\nabla u.$![]()
We now prove continuity in $t$![]() -variable. Let $(t_1,x_0)$
-variable. Let $(t_1,x_0)$![]() and $(t_2,x_0)$
and $(t_2,x_0)$![]() with $r^{2}=|t_1-t_2|$
with $r^{2}=|t_1-t_2|$![]() . Using $u(t,x)=\ell _{(t,x)}(x)$
. Using $u(t,x)=\ell _{(t,x)}(x)$![]() we get
we get
On using $\int _{Q_r(t_1,x_0)}(x-x_0)=0$![]() , we find
, we find

where last inequality is a consequence of $Q_r(t_1,x_0) \subset Q_{2r}(t_2,x_0)$![]() . We now use (2.9) to get
. We now use (2.9) to get
This completes the proof of the lemma.