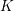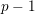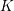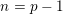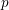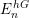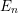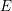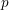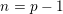1 Introduction
1.1 Picard groups in stable homotopy theory
Let
 $({\mathcal{C}},\otimes ,\mathbf{1})$
be any symmetric monoidal category. Recall that an object
$({\mathcal{C}},\otimes ,\mathbf{1})$
be any symmetric monoidal category. Recall that an object
![]() $X\in {\mathcal{C}}$
is called invertible if there exists an object
$X\in {\mathcal{C}}$
is called invertible if there exists an object
 $X^{-1}\in {\mathcal{C}}$
such that
$X^{-1}\in {\mathcal{C}}$
such that
 $X\otimes X^{-1}\simeq \mathbf{1}$
. We let
$X\otimes X^{-1}\simeq \mathbf{1}$
. We let
![]() $\operatorname{Pic}({\mathcal{C}})$
denote the group of isomorphism classes of invertible objects. For example, if
$\operatorname{Pic}({\mathcal{C}})$
denote the group of isomorphism classes of invertible objects. For example, if
 ${\mathcal{C}}=\operatorname{Mod}_{R}^{\text{cl}}$
is the category of (classical)
${\mathcal{C}}=\operatorname{Mod}_{R}^{\text{cl}}$
is the category of (classical)
![]() $R$
-modules, for
$R$
-modules, for
![]() $R$
a commutative ring, then this recovers the classical notion of the Picard group of a ring. As another example, it is not hard to show that the Picard group of the stable homotopy category is
$R$
a commutative ring, then this recovers the classical notion of the Picard group of a ring. As another example, it is not hard to show that the Picard group of the stable homotopy category is
![]() $\mathbb{Z}$
, generated by
$\mathbb{Z}$
, generated by
![]() $S^{1}$
. Our goal is to develop tools based on descent theory for determining the Picard groups of module categories in stable homotopy theory, i.e. module spectra over an
$S^{1}$
. Our goal is to develop tools based on descent theory for determining the Picard groups of module categories in stable homotopy theory, i.e. module spectra over an
![]() $\mathbf{E}_{\infty }$
-ring spectrum, and to apply them to a specific case of interest in chromatic homotopy theory.
$\mathbf{E}_{\infty }$
-ring spectrum, and to apply them to a specific case of interest in chromatic homotopy theory.
Let
![]() $R$
be an
$R$
be an
![]() $\mathbf{E}_{\infty }$
-ring spectrum, and let
$\mathbf{E}_{\infty }$
-ring spectrum, and let
![]() $\operatorname{Mod}_{R}$
denote its symmetric monoidal
$\operatorname{Mod}_{R}$
denote its symmetric monoidal
![]() $\infty$
-category of modules (i.e. module spectra). We are interested in the Picard group of
$\infty$
-category of modules (i.e. module spectra). We are interested in the Picard group of
![]() $\operatorname{Mod}_{R}$
(or, equivalently, of its homotopy category). When the homotopy groups of
$\operatorname{Mod}_{R}$
(or, equivalently, of its homotopy category). When the homotopy groups of
![]() $R$
are a regular ring, it is often possible to reduce this problem to pure algebra (i.e. the Picard group of the graded ring
$R$
are a regular ring, it is often possible to reduce this problem to pure algebra (i.e. the Picard group of the graded ring
![]() $\unicode[STIX]{x1D70B}_{\ast }(R)$
), cf. [Reference Baker and RichterBR05], [Reference Mathew and StojanoskaMS16, Theorem 2.4.6], and [Reference Hill and MeierHM15, Theorem 6.4] for the most general statement. However, in general, the determination of the Picard group is a subtle and complicated problem.
$\unicode[STIX]{x1D70B}_{\ast }(R)$
), cf. [Reference Baker and RichterBR05], [Reference Mathew and StojanoskaMS16, Theorem 2.4.6], and [Reference Hill and MeierHM15, Theorem 6.4] for the most general statement. However, in general, the determination of the Picard group is a subtle and complicated problem.
Our basic setup is that we will be working with ring spectra which themselves do not have regular homotopy groups, but are nonetheless closely related to ring spectra that do and whose Picard groups can be easily determined. We refer to [Reference Mathew and StojanoskaMS16] for a more detailed introduction to these types of questions.
Basic problem.
Consider an
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $B$
such that
$B$
such that
![]() $\unicode[STIX]{x1D70B}_{\ast }(B)$
is regular, together with an action of a finite group
$\unicode[STIX]{x1D70B}_{\ast }(B)$
is regular, together with an action of a finite group
![]() $G$
on
$G$
on
![]() $B$
as an
$B$
as an
![]() $\mathbf{E}_{\infty }$
-ring. From this, we can build a new
$\mathbf{E}_{\infty }$
-ring. From this, we can build a new
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
 $A=B^{hG}$
as the homotopy fixed points of the
$A=B^{hG}$
as the homotopy fixed points of the
![]() $G$
-action. As
$G$
-action. As
![]() $\unicode[STIX]{x1D70B}_{\ast }(B)$
was assumed regular, the Picard group of
$\unicode[STIX]{x1D70B}_{\ast }(B)$
was assumed regular, the Picard group of
![]() $B$
is the Picard group of the graded ring
$B$
is the Picard group of the graded ring
![]() $\unicode[STIX]{x1D70B}_{\ast }(B)$
. However, in general
$\unicode[STIX]{x1D70B}_{\ast }(B)$
. However, in general
![]() $\unicode[STIX]{x1D70B}_{\ast }(A)$
will be very far from regular, so one expects the determination of the Picard group of
$\unicode[STIX]{x1D70B}_{\ast }(A)$
will be very far from regular, so one expects the determination of the Picard group of
![]() $A$
to be an interesting homotopical problem.
$A$
to be an interesting homotopical problem.
We will primarily be interested in the case where
![]() $A\rightarrow B$
is a
$A\rightarrow B$
is a
![]() $G$
-Galois extension of
$G$
-Galois extension of
![]() $\mathbf{E}_{\infty }$
-ring spectra in the sense of Rognes [Reference RognesRog08]. That is, we assume there exists a
$\mathbf{E}_{\infty }$
-ring spectra in the sense of Rognes [Reference RognesRog08]. That is, we assume there exists a
![]() $G$
-action on
$G$
-action on
![]() $B$
as an
$B$
as an
![]() $\mathbf{E}_{\infty }$
-
$\mathbf{E}_{\infty }$
-
![]() $A$
-algebra such that
$A$
-algebra such that
 $A\simeq B^{hG}$
and the natural map
$A\simeq B^{hG}$
and the natural map
 $B\,\otimes _{A}B\rightarrow F(G_{+},B)$
is an equivalence. We additionally assume that the extension is faithful, i.e. that for each
$B\,\otimes _{A}B\rightarrow F(G_{+},B)$
is an equivalence. We additionally assume that the extension is faithful, i.e. that for each
![]() $A$
-module
$A$
-module
![]() $N$
with
$N$
with
 $N\otimes _{A}B\simeq \ast$
, we have
$N\otimes _{A}B\simeq \ast$
, we have
![]() $N\simeq \ast$
. In this case, work of Gepner and Lawson [Reference Gepner and LawsonGL16] gives a powerful tool for computing the Picard group of
$N\simeq \ast$
. In this case, work of Gepner and Lawson [Reference Gepner and LawsonGL16] gives a powerful tool for computing the Picard group of
![]() $A$
via a derived form of Galois descent. For another account of this, the reader is referred to [Reference Mathew and StojanoskaMS16]. In this paper, we use related techniques to show that in a certain class of examples, one does not obtain new ‘exotic’ classes in
$A$
via a derived form of Galois descent. For another account of this, the reader is referred to [Reference Mathew and StojanoskaMS16]. In this paper, we use related techniques to show that in a certain class of examples, one does not obtain new ‘exotic’ classes in
![]() $\operatorname{Pic}(A)$
.
$\operatorname{Pic}(A)$
.
1.2 The descent spectral sequence
To describe the Gepner–Lawson method, we will need to use higher homotopy coherences which we now review (again, see [Reference Mathew and StojanoskaMS16] for a more detailed exposition). Let
 $({\mathcal{C}},\otimes ,\mathbf{1})$
be a symmetric monoidal
$({\mathcal{C}},\otimes ,\mathbf{1})$
be a symmetric monoidal
![]() $\infty$
-category. Keeping track of all higher isomorphisms, we obtain a Picard
$\infty$
-category. Keeping track of all higher isomorphisms, we obtain a Picard
![]() $\infty$
-groupoid (or Picard space),
$\infty$
-groupoid (or Picard space),
![]() ${\mathcal{P}}ic({\mathcal{C}})$
of invertible objects in
${\mathcal{P}}ic({\mathcal{C}})$
of invertible objects in
![]() ${\mathcal{C}}$
, whose connected components give the Picard group of
${\mathcal{C}}$
, whose connected components give the Picard group of
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Thanks to the symmetric monoidal product
![]() $\otimes$
,
$\otimes$
,
![]() ${\mathcal{P}}ic({\mathcal{C}})$
is a grouplike
${\mathcal{P}}ic({\mathcal{C}})$
is a grouplike
![]() $\mathbf{E}_{\infty }$
-space, and so is the delooping of a connective spectrum
$\mathbf{E}_{\infty }$
-space, and so is the delooping of a connective spectrum
![]() $\mathfrak{pic}({\mathcal{C}})$
called the Picard spectrum. We have identifications
$\mathfrak{pic}({\mathcal{C}})$
called the Picard spectrum. We have identifications
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{0}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle \operatorname{Pic}({\mathcal{C}}),\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{1}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle (\unicode[STIX]{x1D70B}_{0}\operatorname{End}(\mathbf{1}))^{\times },\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{k}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle \unicode[STIX]{x1D70B}_{k-1}\operatorname{End}(\mathbf{1})\quad \text{for}~k>1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{0}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle \operatorname{Pic}({\mathcal{C}}),\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{1}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle (\unicode[STIX]{x1D70B}_{0}\operatorname{End}(\mathbf{1}))^{\times },\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{k}\,{\mathcal{P}}ic({\mathcal{C}}) & \simeq & \displaystyle \unicode[STIX]{x1D70B}_{k-1}\operatorname{End}(\mathbf{1})\quad \text{for}~k>1.\nonumber\end{eqnarray}$$
Example 1.1. Suppose that
 ${\mathcal{C}}=\operatorname{Mod}_{R}^{\text{cl}}$
is the symmetric monoidal category of (discrete) modules over a commutative ring
${\mathcal{C}}=\operatorname{Mod}_{R}^{\text{cl}}$
is the symmetric monoidal category of (discrete) modules over a commutative ring
![]() $R$
. Then
$R$
. Then
 ${\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}})$
is a space with
${\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}})$
is a space with
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{0}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & \simeq & \displaystyle \operatorname{Pic}(R),\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{1}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & \simeq & \displaystyle R^{\times },\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{k}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & = & \displaystyle 0\quad \text{for}~k>1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{0}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & \simeq & \displaystyle \operatorname{Pic}(R),\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{1}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & \simeq & \displaystyle R^{\times },\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{k}\,{\mathcal{P}}ic(\operatorname{Mod}_{R}^{\text{cl}}) & = & \displaystyle 0\quad \text{for}~k>1.\nonumber\end{eqnarray}$$
Let
![]() $R$
be an
$R$
be an
![]() $\mathbf{E}_{\infty }$
-ring. We write
$\mathbf{E}_{\infty }$
-ring. We write
![]() ${\mathcal{P}}ic(R)$
and
${\mathcal{P}}ic(R)$
and
![]() $\mathfrak{pic}(R)$
for
$\mathfrak{pic}(R)$
for
 ${\mathcal{P}}ic(\operatorname{Mod}_{R})$
and
${\mathcal{P}}ic(\operatorname{Mod}_{R})$
and
 $\mathfrak{pic}(\operatorname{Mod}_{R})$
, respectively. The space
$\mathfrak{pic}(\operatorname{Mod}_{R})$
, respectively. The space
![]() ${\mathcal{P}}ic(R)$
(or the spectrum
${\mathcal{P}}ic(R)$
(or the spectrum
![]() $\mathfrak{pic}(R)$
) provides a means of capturing the higher homotopy coherences that appear in descent processes. In particular, we have the following basic descent result due to Gepner and Lawson [Reference Gepner and LawsonGL16].
$\mathfrak{pic}(R)$
) provides a means of capturing the higher homotopy coherences that appear in descent processes. In particular, we have the following basic descent result due to Gepner and Lawson [Reference Gepner and LawsonGL16].
Theorem 1.2 (Cf. [Reference Gepner and LawsonGL16, Theorem 6.15] and [Reference Mathew and StojanoskaMS16, § 3.3]).
Suppose that
![]() $A\rightarrow B$
is a faithful
$A\rightarrow B$
is a faithful
![]() $G$
-Galois extension of
$G$
-Galois extension of
![]() $\mathbf{E}_{\infty }$
-rings. Then there is an equivalence of connective spectra
$\mathbf{E}_{\infty }$
-rings. Then there is an equivalence of connective spectra
 $$\begin{eqnarray}\mathfrak{pic}(A)\simeq \unicode[STIX]{x1D70F}_{{\geqslant}0}\,\mathfrak{pic}(B)^{hG}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{pic}(A)\simeq \unicode[STIX]{x1D70F}_{{\geqslant}0}\,\mathfrak{pic}(B)^{hG}.\end{eqnarray}$$
In the associated homotopy fixed-point spectral sequence (HFPSS)
 $$\begin{eqnarray}H^{s}(G,\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(B))\Rightarrow \unicode[STIX]{x1D70B}_{t-s}(\mathfrak{pic}\,B)^{hG},\end{eqnarray}$$
$$\begin{eqnarray}H^{s}(G,\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(B))\Rightarrow \unicode[STIX]{x1D70B}_{t-s}(\mathfrak{pic}\,B)^{hG},\end{eqnarray}$$
the abutment for
![]() $t=s$
is the Picard group
$t=s$
is the Picard group
![]() $\operatorname{Pic}(A)$
.
$\operatorname{Pic}(A)$
.
Gepner and Lawson [Reference Gepner and LawsonGL16, § 7.2] have completely calculated this spectral sequence in the fundamental example of the
![]() $C_{2}$
-Galois extension
$C_{2}$
-Galois extension
 $KO\rightarrow KU$
, and have shown that
$KO\rightarrow KU$
, and have shown that
 $\operatorname{Pic}(KO)\simeq \mathbb{Z}/8$
, generated by
$\operatorname{Pic}(KO)\simeq \mathbb{Z}/8$
, generated by
![]() $\unicode[STIX]{x1D6F4}KO$
. This calculation, via a slightly different method, is originally due to Hopkins (unpublished). We refer also to [Reference Mathew and StojanoskaMS16] for an account of the calculation of this spectral sequence. In practice, the hope in applying Theorem 1.2 above is that
$\unicode[STIX]{x1D6F4}KO$
. This calculation, via a slightly different method, is originally due to Hopkins (unpublished). We refer also to [Reference Mathew and StojanoskaMS16] for an account of the calculation of this spectral sequence. In practice, the hope in applying Theorem 1.2 above is that
![]() $\operatorname{Pic}(B)$
is easy to determine because the homotopy groups
$\operatorname{Pic}(B)$
is easy to determine because the homotopy groups
![]() $\unicode[STIX]{x1D70B}_{\ast }(B)$
are somehow simpler, and so the problem revolves around determining the behavior of the spectral sequence.
$\unicode[STIX]{x1D70B}_{\ast }(B)$
are somehow simpler, and so the problem revolves around determining the behavior of the spectral sequence.
In fact, the above spectral sequence (1.1) turns out to be very calculable in specific instances by comparing with the additive spectral sequence
 $$\begin{eqnarray}E_{2}^{s,t}=H^{s}(G,\unicode[STIX]{x1D70B}_{t}B)\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}A,\end{eqnarray}$$
$$\begin{eqnarray}E_{2}^{s,t}=H^{s}(G,\unicode[STIX]{x1D70B}_{t}B)\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}A,\end{eqnarray}$$
arising from the equivalence
 $A\simeq B^{hG}$
. In practice, one already knows the behavior of the additive spectral sequence in computing
$A\simeq B^{hG}$
. In practice, one already knows the behavior of the additive spectral sequence in computing
![]() $\unicode[STIX]{x1D70B}_{\ast }(A)$
. Since for
$\unicode[STIX]{x1D70B}_{\ast }(A)$
. Since for
![]() $k>1$
there is a
$k>1$
there is a
![]() $G$
-equivariant isomorphism
$G$
-equivariant isomorphism
 $\unicode[STIX]{x1D70B}_{k}(\mathfrak{pic}(B))\simeq \unicode[STIX]{x1D70B}_{k-1}B$
, one might hope that there is a relationship between differentials in the HFPSSs for
$\unicode[STIX]{x1D70B}_{k}(\mathfrak{pic}(B))\simeq \unicode[STIX]{x1D70B}_{k-1}B$
, one might hope that there is a relationship between differentials in the HFPSSs for
 $\unicode[STIX]{x1D70B}_{\ast }(B^{hG})$
and for
$\unicode[STIX]{x1D70B}_{\ast }(B^{hG})$
and for
 $\unicode[STIX]{x1D70B}_{\ast }(\mathfrak{pic}(B)^{hG})$
. To this effect, the following comparison result is proved in [Reference Mathew and StojanoskaMS16, § 5].
$\unicode[STIX]{x1D70B}_{\ast }(\mathfrak{pic}(B)^{hG})$
. To this effect, the following comparison result is proved in [Reference Mathew and StojanoskaMS16, § 5].
Lemma 1.3 (Comparison tool 5.2.4 of [Reference Mathew and StojanoskaMS16]).
Suppose that
![]() $A\rightarrow B$
is a faithful
$A\rightarrow B$
is a faithful
![]() $G$
-Galois extension. Whenever
$G$
-Galois extension. Whenever
 $2\leqslant r\leqslant t-1$
, there is an equality of differentials
$2\leqslant r\leqslant t-1$
, there is an equality of differentials
 $d_{r}^{s,t}(\mathfrak{pic}\,B)=d_{r}^{s,t-1}(B)$
in the Picard and additive descent spectral sequences. Here
$d_{r}^{s,t}(\mathfrak{pic}\,B)=d_{r}^{s,t-1}(B)$
in the Picard and additive descent spectral sequences. Here
![]() $d_{r}^{s,t}$
denotes the differential
$d_{r}^{s,t}$
denotes the differential
 $E_{r}^{s,t}\rightarrow E_{r}^{s+r,t+r-1}$
in the associated spectral sequences.
$E_{r}^{s,t}\rightarrow E_{r}^{s+r,t+r-1}$
in the associated spectral sequences.
The above result arises from the fact that there is a canonical identification of truncated spectra
 $$\begin{eqnarray}(\unicode[STIX]{x1D6F4}^{-1}\mathfrak{pic}(R))_{[n,2n-1]}\simeq R_{[n,2n-1]}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6F4}^{-1}\mathfrak{pic}(R))_{[n,2n-1]}\simeq R_{[n,2n-1]}\end{eqnarray}$$
for any
![]() $n>0$
. The existence of the equivalence (1.3) is a consequence of the Freudenthal suspension theorem. Of course, the main case of interest for these questions is when
$n>0$
. The existence of the equivalence (1.3) is a consequence of the Freudenthal suspension theorem. Of course, the main case of interest for these questions is when
![]() $s=t$
.
$s=t$
.
Our main technical advance in this paper is a strengthening of this comparison result when certain primes are inverted in
![]() $\unicode[STIX]{x1D70B}_{0}A$
. Motivated by the ‘truncated’ logarithm in algebra, we obtain the following expanded range of comparison of spectral sequences.
$\unicode[STIX]{x1D70B}_{0}A$
. Motivated by the ‘truncated’ logarithm in algebra, we obtain the following expanded range of comparison of spectral sequences.
Theorem 1.4. Suppose that
![]() $A\rightarrow B$
is a faithful
$A\rightarrow B$
is a faithful
![]() $G$
-Galois extension and
$G$
-Galois extension and
![]() $(p-1)!$
is invertible in
$(p-1)!$
is invertible in
![]() $\unicode[STIX]{x1D70B}_{0}A$
. Whenever
$\unicode[STIX]{x1D70B}_{0}A$
. Whenever
 $2\leqslant r\leqslant (p-1)(t-1)$
, there is an equality of differentials
$2\leqslant r\leqslant (p-1)(t-1)$
, there is an equality of differentials
 $d_{r}^{t,t}(\mathfrak{pic}\,B)=d_{r}^{t,t-1}(B)$
in the Picard and additive descent spectral sequences.
$d_{r}^{t,t}(\mathfrak{pic}\,B)=d_{r}^{t,t-1}(B)$
in the Picard and additive descent spectral sequences.
We also obtain a formula (in Theorem 7.1) for the first differential outside the above range in terms of power operations.
1.3 Higher real
 $K$
-theories
$K$
-theories
The primary application of these methods in the present paper will be to the higher real
![]() $K$
-theory spectra of Hopkins–Miller. In particular, we are interested in the case where
$K$
-theory spectra of Hopkins–Miller. In particular, we are interested in the case where
 $B=E_{n}$
, the
$B=E_{n}$
, the
![]() $n$
th Morava
$n$
th Morava
![]() $E$
-theory, the Landweber-exact ring spectrum with
$E$
-theory, the Landweber-exact ring spectrum with
 $$\begin{eqnarray}(E_{n})_{\ast }\simeq \mathbb{W}(\mathbb{F}_{p^{n}})[\![u_{1},\ldots ,u_{n-1}]\!][u^{\pm 1}],\end{eqnarray}$$
$$\begin{eqnarray}(E_{n})_{\ast }\simeq \mathbb{W}(\mathbb{F}_{p^{n}})[\![u_{1},\ldots ,u_{n-1}]\!][u^{\pm 1}],\end{eqnarray}$$
where
![]() $\mathbb{W}(\mathbb{F}_{p^{n}})$
denotes the Witt vectors over
$\mathbb{W}(\mathbb{F}_{p^{n}})$
denotes the Witt vectors over
![]() $\mathbb{F}_{p^{n}}$
, described in more detail in Example 3.2. Here the
$\mathbb{F}_{p^{n}}$
, described in more detail in Example 3.2. Here the
![]() $u_{i}$
have degree 0, while
$u_{i}$
have degree 0, while
![]() $u$
has degree
$u$
has degree
![]() $-2$
. This is an
$-2$
. This is an
![]() $\mathbf{E}_{\infty }$
-ring spectrum [Reference RezkRez98, Reference Goerss and HopkinsGH04] with an action through
$\mathbf{E}_{\infty }$
-ring spectrum [Reference RezkRez98, Reference Goerss and HopkinsGH04] with an action through
![]() $\mathbf{E}_{\infty }$
-ring maps by a profinite group,
$\mathbf{E}_{\infty }$
-ring maps by a profinite group,
 $\mathbb{G}_{n}=\mathbb{S}_{n}\rtimes \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
, the (extended) Morava stabilizer group. Here
$\mathbb{G}_{n}=\mathbb{S}_{n}\rtimes \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
, the (extended) Morava stabilizer group. Here
![]() $\mathbb{S}_{n}$
is the automorphism group of the Honda formal group law over
$\mathbb{S}_{n}$
is the automorphism group of the Honda formal group law over
![]() $\mathbb{F}_{p^{n}}$
.
$\mathbb{F}_{p^{n}}$
.
Following the work of Devinatz and Hopkins [Reference Devinatz and HopkinsDH04], for any closed subgroup
 $G\subset \mathbb{G}_{n}$
there is an associated
$G\subset \mathbb{G}_{n}$
there is an associated
![]() $\mathbf{E}_{\infty }$
-ring spectrum
$\mathbf{E}_{\infty }$
-ring spectrum
![]() $E_{n}^{G}$
, which acts like a homotopy fixed-point spectrum and, indeed, agrees with the usual construction when
$E_{n}^{G}$
, which acts like a homotopy fixed-point spectrum and, indeed, agrees with the usual construction when
![]() $G$
is finite. For
$G$
is finite. For
![]() $G$
a maximal finite subgroup of
$G$
a maximal finite subgroup of
![]() $\mathbb{G}_{n}$
, these sometimes are called higher real
$\mathbb{G}_{n}$
, these sometimes are called higher real
![]() $K$
-theory spectra; the nomenclature is inspired by the fact that when
$K$
-theory spectra; the nomenclature is inspired by the fact that when
![]() $n=1$
and
$n=1$
and
![]() $p=2$
, the maximal finite subgroup of
$p=2$
, the maximal finite subgroup of
 $\mathbb{G}_{1}\simeq \mathbb{Z}_{2}^{\times }$
is
$\mathbb{G}_{1}\simeq \mathbb{Z}_{2}^{\times }$
is
 $C_{2}\simeq \{\pm 1\}$
and
$C_{2}\simeq \{\pm 1\}$
and
![]() $E_{1}^{hC_{2}}$
is nothing other than 2-complete real
$E_{1}^{hC_{2}}$
is nothing other than 2-complete real
![]() $K$
-theory.
$K$
-theory.
Consider now the case of
 $G\subset \mathbb{G}_{n}$
a finite subgroup. Then, the natural map
$G\subset \mathbb{G}_{n}$
a finite subgroup. Then, the natural map
 $E_{n}^{G}=E_{n}^{hG}\rightarrow E_{n}$
is a
$E_{n}^{G}=E_{n}^{hG}\rightarrow E_{n}$
is a
![]() $K(n)$
-local
$K(n)$
-local
![]() $G$
-Galois extension by [Reference RognesRog08, Theorem 5.4.4] (see also § 3.1 below), so the Galois descent methods and the spectral sequence of (1.1) are applicable. Using our general tools and the Gepner–Lawson spectral sequence, we prove the following main result.
$G$
-Galois extension by [Reference RognesRog08, Theorem 5.4.4] (see also § 3.1 below), so the Galois descent methods and the spectral sequence of (1.1) are applicable. Using our general tools and the Gepner–Lawson spectral sequence, we prove the following main result.
Theorem 1.5. Let
![]() $p$
be an odd prime and
$p$
be an odd prime and
 $G\subset \mathbb{G}_{p-1}$
any finite subgroup. Then, the Picard group
$G\subset \mathbb{G}_{p-1}$
any finite subgroup. Then, the Picard group
 $\operatorname{Pic}(E_{p-1}^{hG})$
is cyclic, generated by
$\operatorname{Pic}(E_{p-1}^{hG})$
is cyclic, generated by
![]() $\unicode[STIX]{x1D6F4}E_{p-1}^{hG}$
.
$\unicode[STIX]{x1D6F4}E_{p-1}^{hG}$
.
Remark 1.6. The theorem is also true when
![]() $n=1$
,
$n=1$
,
![]() $p=2$
, as can be shown using the same argument as given for
$p=2$
, as can be shown using the same argument as given for
 $\operatorname{Pic}(KO)$
in [Reference Mathew and StojanoskaMS16].
$\operatorname{Pic}(KO)$
in [Reference Mathew and StojanoskaMS16].
When
 $G\subset \mathbb{G}_{p-1}$
is a maximal finite subgroup, the above result is due to Hopkins in unpublished work. In this case, the result can be proved without the new technical tools we develop in the paper. However, when (for example)
$G\subset \mathbb{G}_{p-1}$
is a maximal finite subgroup, the above result is due to Hopkins in unpublished work. In this case, the result can be proved without the new technical tools we develop in the paper. However, when (for example)
 $G=C_{p}\subset \mathbb{G}_{p-1}$
, our formula for the first differential is actually necessary to give an upper bound to the order of the Picard group of
$G=C_{p}\subset \mathbb{G}_{p-1}$
, our formula for the first differential is actually necessary to give an upper bound to the order of the Picard group of
![]() $E_{n}^{hG}$
. We note that Hopkins has informally observed that in most known examples, the Picard groups of these types of constructions tend to be cyclic. Thus, our main result can be viewed as a further example of Hopkins’s observation.
$E_{n}^{hG}$
. We note that Hopkins has informally observed that in most known examples, the Picard groups of these types of constructions tend to be cyclic. Thus, our main result can be viewed as a further example of Hopkins’s observation.
1.4 Connections with chromatic homotopy
Let
![]() $K(n)$
be the
$K(n)$
be the
![]() $n$
th Morava
$n$
th Morava
![]() $K$
-theory at an implicit prime
$K$
-theory at an implicit prime
![]() $p$
; it is a complex orientable spectrum with homotopy groups
$p$
; it is a complex orientable spectrum with homotopy groups
 $\unicode[STIX]{x1D70B}_{\ast }K(n)=\mathbb{F}_{p}[v_{n}^{\pm 1}]$
(where
$\unicode[STIX]{x1D70B}_{\ast }K(n)=\mathbb{F}_{p}[v_{n}^{\pm 1}]$
(where
 $|v_{n}|=2(p^{n}-1)$
), and its associated formal group law is the Honda formal group law. It is an insight of Hopkins [Reference Hopkins, Mahowald and SadofskyHMS94] that the Picard group
$|v_{n}|=2(p^{n}-1)$
), and its associated formal group law is the Honda formal group law. It is an insight of Hopkins [Reference Hopkins, Mahowald and SadofskyHMS94] that the Picard group
![]() $\operatorname{Pic}_{n}$
of the
$\operatorname{Pic}_{n}$
of the
![]() $K(n)$
-local category itself is quite large and interesting to study.
$K(n)$
-local category itself is quite large and interesting to study.
Here the calculation of
![]() $\operatorname{Pic}_{n}$
essentially breaks into two parts (which arise via the
$\operatorname{Pic}_{n}$
essentially breaks into two parts (which arise via the
![]() $K(n)$
-local profinite Galois extension
$K(n)$
-local profinite Galois extension
 $E_{n}^{\mathbb{G}_{n}}\rightarrow E_{n}$
); there is an algebraic part, which can be detected by cohomological methods, and an exotic part
$E_{n}^{\mathbb{G}_{n}}\rightarrow E_{n}$
); there is an algebraic part, which can be detected by cohomological methods, and an exotic part
![]() $\unicode[STIX]{x1D705}_{n}$
. The latter consists of the
$\unicode[STIX]{x1D705}_{n}$
. The latter consists of the
![]() $K(n)$
-local spectra such that the completed
$K(n)$
-local spectra such that the completed
![]() $E_{n}$
-homology of
$E_{n}$
-homology of
![]() $X$
,
$X$
,
 $(E_{n})_{\ast }^{\vee }X=\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge X)$
is isomorphic to
$(E_{n})_{\ast }^{\vee }X=\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge X)$
is isomorphic to
![]() $(E_{n})_{\ast }$
as Morava modules, i.e. as complete
$(E_{n})_{\ast }$
as Morava modules, i.e. as complete
![]() $(E_{n})_{\ast }$
-modules with a compatible action of
$(E_{n})_{\ast }$
-modules with a compatible action of
![]() $\mathbb{G}_{n}$
(see [Reference Goerss, Henn, Mahowald and RezkGHMR05, § 2]). This latter part always vanishes when
$\mathbb{G}_{n}$
(see [Reference Goerss, Henn, Mahowald and RezkGHMR05, § 2]). This latter part always vanishes when
![]() $p\gg n$
, but can be highly non-trivial otherwise.
$p\gg n$
, but can be highly non-trivial otherwise.
Let us write
![]() $\operatorname{Pic}_{n}^{\text{alg}}$
for the algebraic part (i.e. the Picard group of
$\operatorname{Pic}_{n}^{\text{alg}}$
for the algebraic part (i.e. the Picard group of
![]() $\mathbb{G}_{n}$
-equivariant
$\mathbb{G}_{n}$
-equivariant
![]() $(E_{n})_{\ast }$
-modules) and
$(E_{n})_{\ast }$
-modules) and
![]() $\unicode[STIX]{x1D705}_{n}$
for the exotic part. In all known cases the map
$\unicode[STIX]{x1D705}_{n}$
for the exotic part. In all known cases the map
 $\operatorname{Pic}_{n}\rightarrow \operatorname{Pic}_{n}^{\text{alg}}$
is surjective (although it is not known whether this is true in general), and there is a short exact sequence
$\operatorname{Pic}_{n}\rightarrow \operatorname{Pic}_{n}^{\text{alg}}$
is surjective (although it is not known whether this is true in general), and there is a short exact sequence
 $$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D705}_{n}\rightarrow \operatorname{Pic}_{n}\rightarrow \operatorname{Pic}_{n}^{\text{alg}}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D705}_{n}\rightarrow \operatorname{Pic}_{n}\rightarrow \operatorname{Pic}_{n}^{\text{alg}}\rightarrow 1.\end{eqnarray}$$
Moreover, the generators of
![]() $\unicode[STIX]{x1D705}_{n}$
and
$\unicode[STIX]{x1D705}_{n}$
and
![]() $\operatorname{Pic}_{n}^{\text{alg}}$
are understood well enough to determine the extension problem, so that the following results completely determine
$\operatorname{Pic}_{n}^{\text{alg}}$
are understood well enough to determine the extension problem, so that the following results completely determine
![]() $\operatorname{Pic}_{n}$
. However, the list of known cases is not very long, and consists of the following. The height 1 case is due to Hopkins et al. [Reference Hopkins, Mahowald and SadofskyHMS94], and the height 2 case has many contributions from a number of people: Hopkins for
$\operatorname{Pic}_{n}$
. However, the list of known cases is not very long, and consists of the following. The height 1 case is due to Hopkins et al. [Reference Hopkins, Mahowald and SadofskyHMS94], and the height 2 case has many contributions from a number of people: Hopkins for
![]() $p>3$
(unpublished, but see [Reference BehrensBeh12, Reference LaderLad13]), Goerss et al. [Reference Goerss, Henn, Mahowald and RezkGHMR15] for
$p>3$
(unpublished, but see [Reference BehrensBeh12, Reference LaderLad13]), Goerss et al. [Reference Goerss, Henn, Mahowald and RezkGHMR15] for
![]() $\unicode[STIX]{x1D705}_{2}$
at
$\unicode[STIX]{x1D705}_{2}$
at
![]() $p=3$
, and Karamanov [Reference KaramanovKar10] for the algebraic Picard group
$p=3$
, and Karamanov [Reference KaramanovKar10] for the algebraic Picard group
![]() $\operatorname{Pic}_{2}^{\text{alg}}$
at
$\operatorname{Pic}_{2}^{\text{alg}}$
at
![]() $p=3$
. The height 2 case for
$p=3$
. The height 2 case for
![]() $p=2$
is the subject of ongoing work of Beaudry–Bobkova–Goerss–Henn.
$p=2$
is the subject of ongoing work of Beaudry–Bobkova–Goerss–Henn.
Theorem 1.7. The Picard group of the
![]() $K(n)$
-local category is given by
$K(n)$
-local category is given by
 $$\begin{eqnarray}\displaystyle \operatorname{Pic}_{1}^{\text{alg}} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\mathbb{Z}_{2}\times \mathbb{Z}/2\times \mathbb{Z}/2\quad & p=2,\\ \mathbb{Z}_{p}\times \mathbb{Z}/2(p-1)\quad & p>2,\end{array}\right.\quad \unicode[STIX]{x1D705}_{1}=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}/2\quad & p=2,\\ 0\quad & p>2,\end{array}\right.\nonumber\\ \displaystyle \operatorname{Pic}_{2}^{\text{alg}} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}?\quad & p=2,\\ \mathbb{Z}_{3}^{2}\times \mathbb{Z}/16\quad & p=3,\\ \mathbb{Z}_{p}^{2}\times \mathbb{Z}/2(p^{2}-1)\quad & p>3,\end{array}\right.\quad \unicode[STIX]{x1D705}_{2}=\left\{\begin{array}{@{}ll@{}}?\quad & p=2,\\ \mathbb{Z}/3\times \mathbb{Z}/3\quad & p=3,\\ 0\quad & p>3.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Pic}_{1}^{\text{alg}} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\mathbb{Z}_{2}\times \mathbb{Z}/2\times \mathbb{Z}/2\quad & p=2,\\ \mathbb{Z}_{p}\times \mathbb{Z}/2(p-1)\quad & p>2,\end{array}\right.\quad \unicode[STIX]{x1D705}_{1}=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}/2\quad & p=2,\\ 0\quad & p>2,\end{array}\right.\nonumber\\ \displaystyle \operatorname{Pic}_{2}^{\text{alg}} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}?\quad & p=2,\\ \mathbb{Z}_{3}^{2}\times \mathbb{Z}/16\quad & p=3,\\ \mathbb{Z}_{p}^{2}\times \mathbb{Z}/2(p^{2}-1)\quad & p>3,\end{array}\right.\quad \unicode[STIX]{x1D705}_{2}=\left\{\begin{array}{@{}ll@{}}?\quad & p=2,\\ \mathbb{Z}/3\times \mathbb{Z}/3\quad & p=3,\\ 0\quad & p>3.\end{array}\right.\nonumber\end{eqnarray}$$
It is known that
![]() $\mathbb{Z}_{p}$
always injects into
$\mathbb{Z}_{p}$
always injects into
![]() $\operatorname{Pic}_{n}$
. However, apart from the vanishing of
$\operatorname{Pic}_{n}$
. However, apart from the vanishing of
![]() $\unicode[STIX]{x1D705}_{n}$
for large primes, essentially nothing is known above height 2. However, the program of Henn and collaborators [Reference HennHen07, Reference Goerss, Henn, Mahowald and RezkGHMR05, Reference BeaudryBea15, Reference BobkovaBob14] entails studying the
$\unicode[STIX]{x1D705}_{n}$
for large primes, essentially nothing is known above height 2. However, the program of Henn and collaborators [Reference HennHen07, Reference Goerss, Henn, Mahowald and RezkGHMR05, Reference BeaudryBea15, Reference BobkovaBob14] entails studying the
![]() $K(n)$
-local sphere
$K(n)$
-local sphere
 $S_{K(n)}=E_{n}^{\mathbb{G}_{n}}$
via finite resolutions by simpler homotopy fixed point spectra, namely
$S_{K(n)}=E_{n}^{\mathbb{G}_{n}}$
via finite resolutions by simpler homotopy fixed point spectra, namely
![]() $E_{n}^{hG}$
with
$E_{n}^{hG}$
with
![]() $G$
a finite subgroup of
$G$
a finite subgroup of
![]() $\mathbb{G}_{n}$
. Once such a resolution of the
$\mathbb{G}_{n}$
. Once such a resolution of the
![]() $K(n)$
-local sphere is understood, one can, in principle, build resolutions of any element of
$K(n)$
-local sphere is understood, one can, in principle, build resolutions of any element of
![]() $\unicode[STIX]{x1D705}_{n}$
by modifying the attaching maps in the resolution of the sphere [Reference Goerss, Henn, Mahowald and RezkGHMR15]. To proceed with this program, a first step is to understand the basic building blocks, i.e.
$\unicode[STIX]{x1D705}_{n}$
by modifying the attaching maps in the resolution of the sphere [Reference Goerss, Henn, Mahowald and RezkGHMR15]. To proceed with this program, a first step is to understand the basic building blocks, i.e.
 $\operatorname{Pic}(E_{n}^{hG})$
.
$\operatorname{Pic}(E_{n}^{hG})$
.
Let
 $\unicode[STIX]{x1D705}_{p-1}(G)$
denote the elements of
$\unicode[STIX]{x1D705}_{p-1}(G)$
denote the elements of
 $\operatorname{Pic}(E_{p-1}^{hG})$
that are detected in filtration at least
$\operatorname{Pic}(E_{p-1}^{hG})$
that are detected in filtration at least
![]() $2$
in the Picard spectral sequence (1.1) (in fact, we will see that, by sparsity, such classes will only be in filtration at least
$2$
in the Picard spectral sequence (1.1) (in fact, we will see that, by sparsity, such classes will only be in filtration at least
![]() $2p-1$
). Our calculations show that
$2p-1$
). Our calculations show that
 $\unicode[STIX]{x1D705}_{p-1}(G)\cong \mathbb{Z}/p$
, whenever
$\unicode[STIX]{x1D705}_{p-1}(G)\cong \mathbb{Z}/p$
, whenever
![]() $G$
contains an element of order
$G$
contains an element of order
![]() $p$
. One can check that base-change gives a well-defined morphism
$p$
. One can check that base-change gives a well-defined morphism
 $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D705}_{p-1}\rightarrow \unicode[STIX]{x1D705}_{p-1}(G)$
which, in the cases of
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D705}_{p-1}\rightarrow \unicode[STIX]{x1D705}_{p-1}(G)$
which, in the cases of
![]() $n=1$
,
$n=1$
,
![]() $p=2$
and
$p=2$
and
![]() $n=2$
,
$n=2$
,
![]() $p=3$
, and
$p=3$
, and
![]() $G$
the maximal finite subgroup, is known to be split surjective, cf. [Reference Mathew and StojanoskaMS16, § 8.5] and [Reference Goerss, Henn, Mahowald and RezkGHMR15, Example 5.1 and Theorem 5.5]. This leads to the following question.
$G$
the maximal finite subgroup, is known to be split surjective, cf. [Reference Mathew and StojanoskaMS16, § 8.5] and [Reference Goerss, Henn, Mahowald and RezkGHMR15, Example 5.1 and Theorem 5.5]. This leads to the following question.
Question 1.8. Is the map
 $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D705}_{p-1}\rightarrow \unicode[STIX]{x1D705}_{p-1}(G)\simeq \mathbb{Z}/p$
non-zero for any
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D705}_{p-1}\rightarrow \unicode[STIX]{x1D705}_{p-1}(G)\simeq \mathbb{Z}/p$
non-zero for any
![]() $G$
containing an element of order
$G$
containing an element of order
![]() $p$
?
$p$
?
1.5 Organization
The paper is arranged as follows. In the next section we review the basic properties of Morava
![]() $E$
-theory, the classification of the maximal finite subgroups of
$E$
-theory, the classification of the maximal finite subgroups of
![]() $\mathbb{G}_{n}$
, and recall some information about the action of these finite subgroups on
$\mathbb{G}_{n}$
, and recall some information about the action of these finite subgroups on
 $(E_{p-1})_{\ast }$
. In § 3 we prove some reduction results at general height, in particular showing that one can reduce the proof of cyclicity of
$(E_{p-1})_{\ast }$
. In § 3 we prove some reduction results at general height, in particular showing that one can reduce the proof of cyclicity of
 $\operatorname{Pic}(E_{n}^{hG})$
to that of
$\operatorname{Pic}(E_{n}^{hG})$
to that of
 $\operatorname{Pic}(E_{n}^{hG^{\prime }})$
, where
$\operatorname{Pic}(E_{n}^{hG^{\prime }})$
, where
![]() $G^{\prime }$
is the maximal
$G^{\prime }$
is the maximal
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $G$
; we then perform the main computation of this paper in § 4. This will rely on general techniques for comparing differentials in the additive and multiplicative algebraic and topological spectral sequences, which are described in the second part of the paper. More precisely, in § 5, we analyze truncated logarithms to give comparison results and a universal formula for the differentials in the Picard spectral sequence, and in § 6 we use the techniques of § 5 to determine the algebraic Picard group
$G$
; we then perform the main computation of this paper in § 4. This will rely on general techniques for comparing differentials in the additive and multiplicative algebraic and topological spectral sequences, which are described in the second part of the paper. More precisely, in § 5, we analyze truncated logarithms to give comparison results and a universal formula for the differentials in the Picard spectral sequence, and in § 6 we use the techniques of § 5 to determine the algebraic Picard group
 $H^{1}(C_{p},(E_{p-1})_{0}^{\times })$
.
$H^{1}(C_{p},(E_{p-1})_{0}^{\times })$
.
Part I. Generalities and computations
2 Finite subgroups of
 $\mathbb{G}_{n}$
and the additive spectral sequence
$\mathbb{G}_{n}$
and the additive spectral sequence
In this section, we recall the necessary information about the action of finite subgroups of
![]() $\mathbb{G}_{n}$
on
$\mathbb{G}_{n}$
on
![]() $E_{n}$
, particularly in the case
$E_{n}$
, particularly in the case
 $n=p-1$
. We will, in particular, recall the computation of the associated HFPSS for the homotopy of the higher real
$n=p-1$
. We will, in particular, recall the computation of the associated HFPSS for the homotopy of the higher real
![]() $K$
-theories and their variants for non-maximal subgroups. In the following, only the result of the computation for the group
$K$
-theories and their variants for non-maximal subgroups. In the following, only the result of the computation for the group
![]() $C_{p}$
will be used.
$C_{p}$
will be used.
2.1 The Morava stabilizer group
We start this section by reviewing more thoroughly the Morava stabilizer group
![]() $\mathbb{S}_{n}$
, as well as the extended Morava stabilizer group
$\mathbb{S}_{n}$
, as well as the extended Morava stabilizer group
![]() $\mathbb{G}_{n}$
. We use [Reference FröhlichFrö68, ch. III] as a general reference. Recall from the introduction that
$\mathbb{G}_{n}$
. We use [Reference FröhlichFrö68, ch. III] as a general reference. Recall from the introduction that
![]() $\mathbb{S}_{n}$
is the automorphism group of the height
$\mathbb{S}_{n}$
is the automorphism group of the height
![]() $n$
Honda formal group law
$n$
Honda formal group law
![]() $\unicode[STIX]{x1D6E4}_{n}$
over
$\unicode[STIX]{x1D6E4}_{n}$
over
![]() $\mathbb{F}_{p^{n}}$
; this is the formal group law
$\mathbb{F}_{p^{n}}$
; this is the formal group law
 $F_{\unicode[STIX]{x1D6E4}_{n}}(X,Y)\in \mathbb{F}_{p^{n}}[\![X,Y]\!]$
with
$F_{\unicode[STIX]{x1D6E4}_{n}}(X,Y)\in \mathbb{F}_{p^{n}}[\![X,Y]\!]$
with
![]() $p$
-series
$p$
-series
 $[p]_{\unicode[STIX]{x1D6E4}_{n}}(X)=X^{p^{n}}$
.
$[p]_{\unicode[STIX]{x1D6E4}_{n}}(X)=X^{p^{n}}$
.
Definition 2.1. The group
![]() $\mathbb{S}_{n}$
of automorphisms is given by those power series
$\mathbb{S}_{n}$
of automorphisms is given by those power series
 $f(X)\in \mathbb{F}_{p^{n}}[\![X]\!]$
such that:
$f(X)\in \mathbb{F}_{p^{n}}[\![X]\!]$
such that:
-
(i)
 $f(0)=0$
(i.e.
$f(0)=0$
(i.e.
 $f$
has no constant term);
$f$
has no constant term); -
(ii)
 $f^{\prime }(0)\neq 0\in \mathbb{F}_{p^{n}}$
;
$f^{\prime }(0)\neq 0\in \mathbb{F}_{p^{n}}$
; -
(iii)
 $F_{\unicode[STIX]{x1D6E4}_{n}}(f(X),f(Y))=f(F_{\unicode[STIX]{x1D6E4}_{n}}(X,Y))$
.
$F_{\unicode[STIX]{x1D6E4}_{n}}(f(X),f(Y))=f(F_{\unicode[STIX]{x1D6E4}_{n}}(X,Y))$
.
Observe that the group structure of
![]() $\mathbb{S}_{n}$
is given by composition of power series. The group
$\mathbb{S}_{n}$
is given by composition of power series. The group
![]() $\mathbb{S}_{n}$
has a topology induced from the
$\mathbb{S}_{n}$
has a topology induced from the
![]() $X$
-adic topology, and is a profinite group with respect to this topology.
$X$
-adic topology, and is a profinite group with respect to this topology.
We have a homomorphism
 $$\begin{eqnarray}\mathbb{S}_{n}\rightarrow \mathbb{F}_{p^{n}}^{\times },\quad f(X)\mapsto f^{\prime }(0).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{S}_{n}\rightarrow \mathbb{F}_{p^{n}}^{\times },\quad f(X)\mapsto f^{\prime }(0).\end{eqnarray}$$
More invariantly, this homomorphism sends an automorphism
![]() $f$
of the formal group
$f$
of the formal group
![]() $F$
to its action on the tangent space of
$F$
to its action on the tangent space of
![]() $F$
(dual to the Lie algebra). This homomorphism is surjective, and its kernel (which consists of automorphisms that are congruent to the identity modulo
$F$
(dual to the Lie algebra). This homomorphism is surjective, and its kernel (which consists of automorphisms that are congruent to the identity modulo
![]() $X^{2}$
) is a pro-
$X^{2}$
) is a pro-
![]() $p$
-group.
$p$
-group.
The group
![]() $\mathbb{S}_{n}$
can be described as the units in the maximal order
$\mathbb{S}_{n}$
can be described as the units in the maximal order
![]() ${\mathcal{O}}_{n}$
of the central division algebra
${\mathcal{O}}_{n}$
of the central division algebra
![]() $\mathbb{D}_{n}$
of Hasse invariant
$\mathbb{D}_{n}$
of Hasse invariant
![]() $1/n$
over
$1/n$
over
![]() $\mathbb{Q}_{p}$
. More explicitly, we have that
$\mathbb{Q}_{p}$
. More explicitly, we have that
![]() ${\mathcal{O}}_{n}$
is the non-commutative ring
${\mathcal{O}}_{n}$
is the non-commutative ring
 $$\begin{eqnarray}{\mathcal{O}}_{n}=\mathbb{W}(\mathbb{F}_{p^{n}})\langle S\rangle /(S^{n}=p,Sw=w^{\unicode[STIX]{x1D719}}S),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{n}=\mathbb{W}(\mathbb{F}_{p^{n}})\langle S\rangle /(S^{n}=p,Sw=w^{\unicode[STIX]{x1D719}}S),\end{eqnarray}$$
where
 $w\in \mathbb{W}(\mathbb{F}_{p^{n}})$
and
$w\in \mathbb{W}(\mathbb{F}_{p^{n}})$
and
![]() $\unicode[STIX]{x1D719}$
is a lift of the Frobenius to
$\unicode[STIX]{x1D719}$
is a lift of the Frobenius to
![]() $\mathbb{W}(\mathbb{F}_{p^{n}})$
. Then
$\mathbb{W}(\mathbb{F}_{p^{n}})$
. Then
![]() ${\mathcal{O}}_{n}$
is the endomorphism ring of the formal group
${\mathcal{O}}_{n}$
is the endomorphism ring of the formal group
![]() $\unicode[STIX]{x1D6E4}_{n}$
, and
$\unicode[STIX]{x1D6E4}_{n}$
, and
 $\mathbb{S}_{n}={\mathcal{O}}_{n}^{\times }$
.
$\mathbb{S}_{n}={\mathcal{O}}_{n}^{\times }$
.
Finally, because
![]() $\unicode[STIX]{x1D6E4}_{n}$
is already defined over
$\unicode[STIX]{x1D6E4}_{n}$
is already defined over
![]() $\mathbb{F}_{p}$
, the Galois group
$\mathbb{F}_{p}$
, the Galois group
 $\operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
acts on
$\operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
acts on
![]() $\mathbb{S}_{n}$
, and we define the extended Morava stabilizer group (which we will often just call the Morava stabilizer group) as the semidirect product
$\mathbb{S}_{n}$
, and we define the extended Morava stabilizer group (which we will often just call the Morava stabilizer group) as the semidirect product
 $\mathbb{S}_{n}\rtimes \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
, i.e. there is a split extension
$\mathbb{S}_{n}\rtimes \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
, i.e. there is a split extension
 $$\begin{eqnarray}1\rightarrow \mathbb{S}_{n}\rightarrow \mathbb{G}_{n}\rightarrow \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \mathbb{S}_{n}\rightarrow \mathbb{G}_{n}\rightarrow \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\rightarrow 1.\end{eqnarray}$$
2.2 The finite subgroups of
 $\mathbb{G}_{n}$
$\mathbb{G}_{n}$
Before proceeding with the calculations, let us recall the classification of the maximal finite subgroups of
![]() $\mathbb{G}_{n}$
, as well as their action on the coefficients of
$\mathbb{G}_{n}$
, as well as their action on the coefficients of
![]() $E_{n}$
. Bujard and Hewett [Reference HewettHew95, Reference BujardBuj12] have determined the maximal finite subgroups of
$E_{n}$
. Bujard and Hewett [Reference HewettHew95, Reference BujardBuj12] have determined the maximal finite subgroups of
 $\mathbb{S}_{n}\subset \mathbb{G}_{n}$
. Specifically, let
$\mathbb{S}_{n}\subset \mathbb{G}_{n}$
. Specifically, let
![]() $p>2$
and
$p>2$
and
 $n=(p-1)p^{k-1}m$
for
$n=(p-1)p^{k-1}m$
for
![]() $m$
prime to
$m$
prime to
![]() $p$
, and denote by
$p$
, and denote by
![]() $n_{\unicode[STIX]{x1D6FC}}$
the quotient
$n_{\unicode[STIX]{x1D6FC}}$
the quotient
 $n/\unicode[STIX]{x1D719}(p^{\unicode[STIX]{x1D6FC}})$
, where
$n/\unicode[STIX]{x1D719}(p^{\unicode[STIX]{x1D6FC}})$
, where
![]() $\unicode[STIX]{x1D719}$
is Euler’s totient function. There are exactly
$\unicode[STIX]{x1D719}$
is Euler’s totient function. There are exactly
![]() $k+1$
conjugacy classes of maximal finite subgroups of
$k+1$
conjugacy classes of maximal finite subgroups of
![]() $\mathbb{S}_{n}$
, represented by
$\mathbb{S}_{n}$
, represented by
 $$\begin{eqnarray}G_{0}=C_{p^{n}-1}\quad \text{and}\quad G_{\unicode[STIX]{x1D6FC}}=C_{p^{\unicode[STIX]{x1D6FC}}}\rtimes C_{(p^{n_{\unicode[STIX]{x1D6FC}}}-1)(p-1)}\quad \text{for}~1\leqslant \unicode[STIX]{x1D6FC}\leqslant k.\end{eqnarray}$$
$$\begin{eqnarray}G_{0}=C_{p^{n}-1}\quad \text{and}\quad G_{\unicode[STIX]{x1D6FC}}=C_{p^{\unicode[STIX]{x1D6FC}}}\rtimes C_{(p^{n_{\unicode[STIX]{x1D6FC}}}-1)(p-1)}\quad \text{for}~1\leqslant \unicode[STIX]{x1D6FC}\leqslant k.\end{eqnarray}$$
When
![]() $p-1$
does not divide
$p-1$
does not divide
![]() $n$
, the only class of maximal finite subgroups is that of
$n$
, the only class of maximal finite subgroups is that of
![]() $G_{0}$
, so, in particular, there are no finite subgroups of order divisible by
$G_{0}$
, so, in particular, there are no finite subgroups of order divisible by
![]() $p$
.
$p$
.
Remark 2.2. Given the description of
![]() $\mathbb{S}_{n}$
in § 2.1, we note that an element of order dividing
$\mathbb{S}_{n}$
in § 2.1, we note that an element of order dividing
![]() $p^{n}-1$
is always easy to describe: it is given by a Teichmüller lift
$p^{n}-1$
is always easy to describe: it is given by a Teichmüller lift
![]() $\unicode[STIX]{x1D702}$
of a primitive
$\unicode[STIX]{x1D702}$
of a primitive
 $(p^{n}-1)$
st root of unity,
$(p^{n}-1)$
st root of unity,
 $\unicode[STIX]{x1D702}\in \mathbb{W}(\mathbb{F}_{p^{n}})^{\times }\subset \mathbb{S}_{n}$
.
$\unicode[STIX]{x1D702}\in \mathbb{W}(\mathbb{F}_{p^{n}})^{\times }\subset \mathbb{S}_{n}$
.
Consider now the special case when
 $n=p-1$
. For convenience, we drop the subscripts after
$n=p-1$
. For convenience, we drop the subscripts after
![]() $\mathbb{G},\mathbb{S}$
. In this situation, there are two conjugacy classes of maximal finite subgroups of
$\mathbb{G},\mathbb{S}$
. In this situation, there are two conjugacy classes of maximal finite subgroups of
![]() $\mathbb{S}$
.
$\mathbb{S}$
.
-
(i) One of order not divisible by
 $p$
, namely the cyclic group
$p$
, namely the cyclic group
 $C_{p^{n}-1}$
.
$C_{p^{n}-1}$
. -
(ii) One of order divisible by
 $p$
, namely the semi-direct product
$p$
, namely the semi-direct product
 $F=C_{p}\rtimes C_{(p-1)^{2}}$
. In the latter case, the action of
$F=C_{p}\rtimes C_{(p-1)^{2}}$
. In the latter case, the action of
 $C_{(p-1)^{2}}$
on
$C_{(p-1)^{2}}$
on
 $C_{p}$
is given by a projection
$C_{p}$
is given by a projection  $$\begin{eqnarray}C_{(p-1)^{2}}\rightarrow C_{p-1}\simeq \text{Aut}(C_{p}).\end{eqnarray}$$
$$\begin{eqnarray}C_{(p-1)^{2}}\rightarrow C_{p-1}\simeq \text{Aut}(C_{p}).\end{eqnarray}$$
Remark 2.3. Using the description of
![]() $\mathbb{S}_{n}$
in § 2.1, we can give an explicit equation of an order
$\mathbb{S}_{n}$
in § 2.1, we can give an explicit equation of an order
![]() $p$
element when
$p$
element when
![]() $p=3$
. Let
$p=3$
. Let
![]() $\unicode[STIX]{x1D714}$
be a primitive eighth root of unity in
$\unicode[STIX]{x1D714}$
be a primitive eighth root of unity in
![]() $\mathbb{W}(\mathbb{F}_{9})$
, then we can take
$\mathbb{W}(\mathbb{F}_{9})$
, then we can take
 $-\frac{1}{2}(1+\unicode[STIX]{x1D714}S)$
. In general, however, it is difficult or impossible to give a similar expression with rational coefficients for an element of order
$-\frac{1}{2}(1+\unicode[STIX]{x1D714}S)$
. In general, however, it is difficult or impossible to give a similar expression with rational coefficients for an element of order
![]() $p$
when
$p$
when
![]() $n>2$
, see [Reference Gorbounov, Mahowald and SymondsGMS98, Remark 5.3].
$n>2$
, see [Reference Gorbounov, Mahowald and SymondsGMS98, Remark 5.3].
Finally, we recall from (2.2) that the extended Morava stabilizer group
![]() $\mathbb{G}$
sits in a split extension
$\mathbb{G}$
sits in a split extension
 $$\begin{eqnarray}1\rightarrow \mathbb{S}\rightarrow \mathbb{G}\rightarrow \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \mathbb{S}\rightarrow \mathbb{G}\rightarrow \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\rightarrow 1,\end{eqnarray}$$
and, therefore, any finite subgroup
![]() $G$
of
$G$
of
![]() $\mathbb{G}$
sits in a (not necessarily split) extension
$\mathbb{G}$
sits in a (not necessarily split) extension
 $$\begin{eqnarray}1\rightarrow G_{\mathbb{S}}\rightarrow G\rightarrow G_{\operatorname{Gal}}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow G_{\mathbb{S}}\rightarrow G\rightarrow G_{\operatorname{Gal}}\rightarrow 1,\end{eqnarray}$$
where
 $G_{\mathbb{S}}=G\cap \mathbb{S}$
, and
$G_{\mathbb{S}}=G\cap \mathbb{S}$
, and
![]() $G_{\operatorname{Gal}}$
is a subgroup of
$G_{\operatorname{Gal}}$
is a subgroup of
 $\operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\cong C_{n}$
.
$\operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})\cong C_{n}$
.
In the case when
![]() $G_{\mathbb{S}}$
is a maximal abelian subgroup of
$G_{\mathbb{S}}$
is a maximal abelian subgroup of
![]() $\mathbb{S}$
, Bujard [Reference BujardBuj12, Theorem 4.13] has determined that
$\mathbb{S}$
, Bujard [Reference BujardBuj12, Theorem 4.13] has determined that
![]() $G_{\operatorname{Gal}}$
can be maximally large, i.e. it is always possible that
$G_{\operatorname{Gal}}$
can be maximally large, i.e. it is always possible that
 $G_{\operatorname{Gal}}\cong \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
. This is also known to be true when
$G_{\operatorname{Gal}}\cong \operatorname{Gal}(\mathbb{F}_{p^{n}}/\mathbb{F}_{p})$
. This is also known to be true when
![]() $G_{\mathbb{S}}$
is a maximal finite subgroup of
$G_{\mathbb{S}}$
is a maximal finite subgroup of
![]() $\mathbb{S}$
, cf. [Reference HennHen07, Proposition 20].
$\mathbb{S}$
, cf. [Reference HennHen07, Proposition 20].
The proof of Theorem 1.5 for
![]() $G$
will consist of a reduction first from
$G$
will consist of a reduction first from
![]() $G$
to its subgroup
$G$
to its subgroup
![]() $G_{\mathbb{S}}$
, and then further to the
$G_{\mathbb{S}}$
, and then further to the
![]() $p$
-Sylow subgroup of
$p$
-Sylow subgroup of
![]() $G_{\mathbb{S}}$
.
$G_{\mathbb{S}}$
.
2.3 The action on
 $E_{\ast }$
$E_{\ast }$
The first explicit description of the action of
![]() $\mathbb{G}$
on
$\mathbb{G}$
on
![]() $E_{\ast }$
appears in unpublished work of Hopkins and Miller. The general situation for
$E_{\ast }$
appears in unpublished work of Hopkins and Miller. The general situation for
![]() $\mathbb{G}$
acting on
$\mathbb{G}$
acting on
![]() $E_{\ast }$
is determined by Devinatz and Hopkins [Reference Devinatz and HopkinsDH95].Footnote
1
We focus on the action of
$E_{\ast }$
is determined by Devinatz and Hopkins [Reference Devinatz and HopkinsDH95].Footnote
1
We focus on the action of
![]() $\mathbb{S}$
. For our purposes, a nice summary of what we need can be found in the work of Nave [Reference NaveNav10, § 2].
$\mathbb{S}$
. For our purposes, a nice summary of what we need can be found in the work of Nave [Reference NaveNav10, § 2].
Write an element
![]() $g\in \mathbb{S}$
as
$g\in \mathbb{S}$
as
 $g=\sum _{j=0}^{n-1}a_{j}S^{j}$
, where
$g=\sum _{j=0}^{n-1}a_{j}S^{j}$
, where
 $a_{j}\in \mathbb{W}(\mathbb{F}_{p^{n}})$
and
$a_{j}\in \mathbb{W}(\mathbb{F}_{p^{n}})$
and
![]() $a_{0}$
is a unit. Recall that
$a_{0}$
is a unit. Recall that
 $u\in \unicode[STIX]{x1D70B}_{-2}E_{n}$
is a generator. The next result follows from [Reference Devinatz and HopkinsDH95, Proposition 3.3 and Theorem 4.4].
$u\in \unicode[STIX]{x1D70B}_{-2}E_{n}$
is a generator. The next result follows from [Reference Devinatz and HopkinsDH95, Proposition 3.3 and Theorem 4.4].
Theorem 2.4. Let
![]() $\unicode[STIX]{x1D719}$
denote the lift of the Frobenius to
$\unicode[STIX]{x1D719}$
denote the lift of the Frobenius to
![]() $\mathbb{W}(\mathbb{F}_{p^{n}})$
. Then if
$\mathbb{W}(\mathbb{F}_{p^{n}})$
. Then if
 $g=\sum _{j=0}^{n-1}a_{j}S^{j}$
as above, we have
$g=\sum _{j=0}^{n-1}a_{j}S^{j}$
as above, we have
 $$\begin{eqnarray}\displaystyle g_{\ast }(u) & \equiv & \displaystyle a_{0}u+a_{n-1}^{\unicode[STIX]{x1D719}}uu_{1}+\cdots +a_{1}^{\unicode[STIX]{x1D719}^{n-1}}uu_{n-1}\quad \text{mod}~(p,\mathfrak{m}^{2})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{\ast }(u) & \equiv & \displaystyle a_{0}u+a_{n-1}^{\unicode[STIX]{x1D719}}uu_{1}+\cdots +a_{1}^{\unicode[STIX]{x1D719}^{n-1}}uu_{n-1}\quad \text{mod}~(p,\mathfrak{m}^{2})\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle g_{\ast }(uu_{i}) & \equiv & \displaystyle a_{0}^{\unicode[STIX]{x1D719}^{i}}uu_{i}+\cdots +a_{i-1}^{\unicode[STIX]{x1D719}}uu_{1}\quad \text{mod}~(p,\mathfrak{m}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{\ast }(uu_{i}) & \equiv & \displaystyle a_{0}^{\unicode[STIX]{x1D719}^{i}}uu_{i}+\cdots +a_{i-1}^{\unicode[STIX]{x1D719}}uu_{1}\quad \text{mod}~(p,\mathfrak{m}^{2}).\end{eqnarray}$$
In the case of elements
![]() $g$
of finite order, we can be much more explicit. By the classification of finite subgroups of
$g$
of finite order, we can be much more explicit. By the classification of finite subgroups of
![]() $\mathbb{S}$
, such a
$\mathbb{S}$
, such a
![]() $g$
either has order equal to
$g$
either has order equal to
![]() $p$
, or prime to
$p$
, or prime to
![]() $p$
:
$p$
:
-
(i) if
 $g$
has order
$g$
has order
 $p$
, it is known [Reference NaveNav10, Lemma 2.2] that
$p$
, it is known [Reference NaveNav10, Lemma 2.2] that
 $a_{0}\equiv 1~\text{mod}~(p)$
and
$a_{0}\equiv 1~\text{mod}~(p)$
and
 $a_{1}$
is a unit;
$a_{1}$
is a unit; -
(ii) If
 $g$
has order prime to
$g$
has order prime to
 $p$
, then
$p$
, then
 $g$
is a Teichmuller lift of
$g$
is a Teichmuller lift of
 $a$
, and it follows from [Reference HennHen07] that the induced map of rings
$a$
, and it follows from [Reference HennHen07] that the induced map of rings
 $g_{\ast }:E_{\ast }\rightarrow E_{\ast }$
is given by (2.6)
$g_{\ast }:E_{\ast }\rightarrow E_{\ast }$
is given by (2.6) $$\begin{eqnarray}g_{\ast }(u)=au\quad \text{and}\quad g_{\ast }(u_{i})=a^{p^{i}-1}u_{i}.\end{eqnarray}$$
$$\begin{eqnarray}g_{\ast }(u)=au\quad \text{and}\quad g_{\ast }(u_{i})=a^{p^{i}-1}u_{i}.\end{eqnarray}$$
2.4 The HFPSS
Because the action of finite subgroups on
![]() $E_{\ast }$
is well understood in our case of
$E_{\ast }$
is well understood in our case of
 $n=p-1$
(which we implicitly assume in this subsection), so is the computation of the associated group cohomology. In fact, the differentials in the HFPSS are also known. The calculations are due to Hopkins and Miller, although their work has not appeared in print. Published references include the thesis and subsequent paper of Nave [Reference NaveNav99, Reference NaveNav10], or for a detailed computation at
$n=p-1$
(which we implicitly assume in this subsection), so is the computation of the associated group cohomology. In fact, the differentials in the HFPSS are also known. The calculations are due to Hopkins and Miller, although their work has not appeared in print. Published references include the thesis and subsequent paper of Nave [Reference NaveNav99, Reference NaveNav10], or for a detailed computation at
![]() $n=2$
,
$n=2$
,
![]() $p=3$
, the work of Goerss et al. [Reference Goerss, Henn and MahowaldGHM04, Reference Goerss, Henn, Mahowald and RezkGHMR05].
$p=3$
, the work of Goerss et al. [Reference Goerss, Henn and MahowaldGHM04, Reference Goerss, Henn, Mahowald and RezkGHMR05].
We start by considering the prime-to-
![]() $p$
case.
$p$
case.
Example 2.5. If
![]() $p$
does not divide the order of
$p$
does not divide the order of
![]() $G$
, then the higher cohomology of
$G$
, then the higher cohomology of
![]() $G$
with coefficients in
$G$
with coefficients in
![]() $E_{\ast }$
vanishes, giving that
$E_{\ast }$
vanishes, giving that
 $$\begin{eqnarray}(E^{hG})_{\ast }=(E_{\ast })^{G}.\end{eqnarray}$$
$$\begin{eqnarray}(E^{hG})_{\ast }=(E_{\ast })^{G}.\end{eqnarray}$$
Using (2.6), we can (at least, in principle) determine these invariants. In particular, we see that if
![]() $m$
is the order of
$m$
is the order of
![]() $G_{\mathbb{S}}$
, then
$G_{\mathbb{S}}$
, then
![]() $u^{m}$
is
$u^{m}$
is
![]() $G_{\mathbb{S}}$
-invariant and is a minimal periodicity element of
$G_{\mathbb{S}}$
-invariant and is a minimal periodicity element of
![]() $(E_{\ast })^{G_{\mathbb{S}}}$
. However, this element is also fixed under the Galois quotient of
$(E_{\ast })^{G_{\mathbb{S}}}$
. However, this element is also fixed under the Galois quotient of
![]() $G$
, so
$G$
, so
![]() $E^{hG}$
has periodicity
$E^{hG}$
has periodicity
 $2m=2|G_{\mathbb{S}}|$
.
$2m=2|G_{\mathbb{S}}|$
.
The most interesting case for us is when
![]() $G=C_{p}$
. In this case, one has the following calculation of the
$G=C_{p}$
. In this case, one has the following calculation of the
![]() $E_{2}$
-page modulo transfers.
$E_{2}$
-page modulo transfers.
Proposition 2.6 (Hopkins–Miller).
There is an exact sequence
 $$\begin{eqnarray}E_{\ast }\xrightarrow[{}]{\text{tr}}H^{\ast }(C_{p},E_{\ast })\rightarrow \mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}E_{\ast }\xrightarrow[{}]{\text{tr}}H^{\ast }(C_{p},E_{\ast })\rightarrow \mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2})\rightarrow 0,\end{eqnarray}$$
of graded groups, where the
![]() $(s,t)$
-bidegrees are
$(s,t)$
-bidegrees are
 $|\unicode[STIX]{x1D6FC}|=(1,2n)$
,
$|\unicode[STIX]{x1D6FC}|=(1,2n)$
,
 $|\unicode[STIX]{x1D6FD}|=(2,2pn)$
, and
$|\unicode[STIX]{x1D6FD}|=(2,2pn)$
, and
 $|\unicode[STIX]{x1D6FF}|=(0,2p)$
.
$|\unicode[STIX]{x1D6FF}|=(0,2p)$
.
We note that because we have not taken Galois invariants anywhere, we see copies of
![]() $\mathbb{F}_{p^{n}}$
(rather than
$\mathbb{F}_{p^{n}}$
(rather than
![]() $\mathbb{F}_{p}$
) in the above spectral sequence. The passage to
$\mathbb{F}_{p}$
) in the above spectral sequence. The passage to
![]() $\mathbb{F}_{p}$
can be achieved by adding in the Galois group. For example, we also state the following result of Hopkins–Miller.
$\mathbb{F}_{p}$
can be achieved by adding in the Galois group. For example, we also state the following result of Hopkins–Miller.
Proposition 2.7 (Hopkins–Miller).
When
![]() $G\subset \mathbb{G}$
is a maximal finite subgroup containing
$G\subset \mathbb{G}$
is a maximal finite subgroup containing
![]() $p$
-torsion, then there is an exact sequence
$p$
-torsion, then there is an exact sequence
 $$\begin{eqnarray}E_{\ast }\xrightarrow[{}]{\text{tr}}H^{\ast }(G,E_{\ast })\rightarrow \mathbb{F}_{p}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6E5}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
$$\begin{eqnarray}E_{\ast }\xrightarrow[{}]{\text{tr}}H^{\ast }(G,E_{\ast })\rightarrow \mathbb{F}_{p}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6E5}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
with
 $|\unicode[STIX]{x1D6E5}|=(0,2pn^{2})$
and
$|\unicode[STIX]{x1D6E5}|=(0,2pn^{2})$
and
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
as above.
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
as above.
The above determines the
![]() $E_{2}$
-page of the HFPSS for
$E_{2}$
-page of the HFPSS for
 $\unicode[STIX]{x1D70B}_{\ast }(E^{hG})$
in two important cases. The differentials in the HFPSS are also well known. For any finite subgroup
$\unicode[STIX]{x1D70B}_{\ast }(E^{hG})$
in two important cases. The differentials in the HFPSS are also well known. For any finite subgroup
![]() $G\subset \mathbb{G}$
, there are maps
$G\subset \mathbb{G}$
, there are maps
 $$\begin{eqnarray}\operatorname{Ext}_{BP_{\ast }BP}(BP_{\ast },BP_{\ast })\rightarrow H^{\ast }(\mathbb{G},E_{\ast })\rightarrow H^{\ast }(G,E_{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{BP_{\ast }BP}(BP_{\ast },BP_{\ast })\rightarrow H^{\ast }(\mathbb{G},E_{\ast })\rightarrow H^{\ast }(G,E_{\ast }).\end{eqnarray}$$
If
![]() $G$
contains an element of order
$G$
contains an element of order
![]() $p$
, then, by [Reference RavenelRav78], the composite sends
$p$
, then, by [Reference RavenelRav78], the composite sends
![]() $\unicode[STIX]{x1D6FC}_{1}$
to
$\unicode[STIX]{x1D6FC}_{1}$
to
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}_{1}$
to
$\unicode[STIX]{x1D6FD}_{1}$
to
![]() $\unicode[STIX]{x1D6FD}$
, at least up to a non-zero scalar.
$\unicode[STIX]{x1D6FD}$
, at least up to a non-zero scalar.
One can also show this directly using the functoriality of the Greek letter construction, as in [Reference Goerss, Henn and MahowaldGHM04, Proposition 7]. For this, recall that there is a class
 $v_{1}\in \operatorname{Ext}_{BP_{\ast }BP}^{0,2(p-1)}(BP_{\ast },BP_{\ast }/(p))$
which defines a permanent cycle in the Adams–Novikov spectral sequence for the mod-
$v_{1}\in \operatorname{Ext}_{BP_{\ast }BP}^{0,2(p-1)}(BP_{\ast },BP_{\ast }/(p))$
which defines a permanent cycle in the Adams–Novikov spectral sequence for the mod-
![]() $p$
Moore spectrum
$p$
Moore spectrum
![]() $V(0)$
. Via the Greek letter construction,
$V(0)$
. Via the Greek letter construction,
![]() $v_{1}$
gives rise to an element
$v_{1}$
gives rise to an element
 $\unicode[STIX]{x1D6FC}_{1}\in \unicode[STIX]{x1D70B}_{2p-3}S_{(p)}^{0}\simeq \mathbb{Z}/p$
detected by a class, which we also denote by
$\unicode[STIX]{x1D6FC}_{1}\in \unicode[STIX]{x1D70B}_{2p-3}S_{(p)}^{0}\simeq \mathbb{Z}/p$
detected by a class, which we also denote by
![]() $\unicode[STIX]{x1D6FC}_{1}$
, in
$\unicode[STIX]{x1D6FC}_{1}$
, in
 $\operatorname{Ext}_{BP_{\ast }BP}^{1,2p-2}(BP_{\ast },BP_{\ast })$
. Recalling that
$\operatorname{Ext}_{BP_{\ast }BP}^{1,2p-2}(BP_{\ast },BP_{\ast })$
. Recalling that
![]() $v_{1}$
is sent to
$v_{1}$
is sent to
![]() $u_{1}u^{1-p}$
under the orientation map
$u_{1}u^{1-p}$
under the orientation map
 $BP\rightarrow E$
, one can check that the image of
$BP\rightarrow E$
, one can check that the image of
![]() $v_{1}$
defines a non-trivial element in
$v_{1}$
defines a non-trivial element in
 $H^{0}(G,E_{\ast }/(p))$
. Using the short exact sequence
$H^{0}(G,E_{\ast }/(p))$
. Using the short exact sequence
 $$\begin{eqnarray}0\rightarrow E_{\ast }\rightarrow E_{\ast }\rightarrow E_{\ast }/(p)\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow E_{\ast }\rightarrow E_{\ast }\rightarrow E_{\ast }/(p)\rightarrow 0,\end{eqnarray}$$
one can see that this class has non-trivial image in
 $\unicode[STIX]{x1D6FF}^{0}(v_{1})\in H^{1}(G,E_{2p-2})$
(which, if
$\unicode[STIX]{x1D6FF}^{0}(v_{1})\in H^{1}(G,E_{2p-2})$
(which, if
![]() $G$
is maximal, is
$G$
is maximal, is
![]() $\mathbb{F}_{p}$
). The result follows since this latter group is generated by
$\mathbb{F}_{p}$
). The result follows since this latter group is generated by
![]() $\unicode[STIX]{x1D6FC}$
. One can make a similar argument for
$\unicode[STIX]{x1D6FC}$
. One can make a similar argument for
![]() $\unicode[STIX]{x1D6FD}$
, and since
$\unicode[STIX]{x1D6FD}$
, and since
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{1}$
are permanent cycles, so are
$\unicode[STIX]{x1D6FD}_{1}$
are permanent cycles, so are
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. We also know via the calculations of Toda [Reference TodaTod67, Reference TodaTod68] that
$\unicode[STIX]{x1D6FD}$
. We also know via the calculations of Toda [Reference TodaTod67, Reference TodaTod68] that
 $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1}^{p}=0$
and
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1}^{p}=0$
and
 $\unicode[STIX]{x1D6FD}_{1}^{pn+1}=0$
in
$\unicode[STIX]{x1D6FD}_{1}^{pn+1}=0$
in
![]() $\unicode[STIX]{x1D70B}_{\ast }S^{0}$
. Sparsity in the HFPSS, as well as the multiplicative structure, then allow the complete determination of the differentials.
$\unicode[STIX]{x1D70B}_{\ast }S^{0}$
. Sparsity in the HFPSS, as well as the multiplicative structure, then allow the complete determination of the differentials.
In the following we use the notation
![]() $\stackrel{\cdot }{=}$
to denote an equality that holds up to multiplication by a non-zero scalar.
$\stackrel{\cdot }{=}$
to denote an equality that holds up to multiplication by a non-zero scalar.
Lemma 2.8. In the spectral sequence for
![]() $\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
, there are differentials
$\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
, there are differentials
 $$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6FF})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{p-1}\unicode[STIX]{x1D6FF}^{1-n^{2}}\quad \text{and}\quad d_{2n^{2}+1}(\unicode[STIX]{x1D6FF}^{n^{3}}\unicode[STIX]{x1D6FC})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6FF})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{p-1}\unicode[STIX]{x1D6FF}^{1-n^{2}}\quad \text{and}\quad d_{2n^{2}+1}(\unicode[STIX]{x1D6FF}^{n^{3}}\unicode[STIX]{x1D6FC})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1}.\end{eqnarray}$$
If
![]() $G$
is a maximal finite subgroup, then in the spectral sequence for
$G$
is a maximal finite subgroup, then in the spectral sequence for
![]() $\unicode[STIX]{x1D70B}_{\ast }E^{hG}$
, there are differentials
$\unicode[STIX]{x1D70B}_{\ast }E^{hG}$
, there are differentials
 $$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6E5})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{p-1}\quad \text{and}\quad d_{2n^{2}+1}(\unicode[STIX]{x1D6E5}^{n}\unicode[STIX]{x1D6FC})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6E5})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{p-1}\quad \text{and}\quad d_{2n^{2}+1}(\unicode[STIX]{x1D6E5}^{n}\unicode[STIX]{x1D6FC})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1}.\end{eqnarray}$$
These differentials determine all others by multiplicativity. More precisely, in the
![]() $C_{p}$
-HFPSS, the shorter differential
$C_{p}$
-HFPSS, the shorter differential
![]() $d_{2p-1}$
is non-zero on all
$d_{2p-1}$
is non-zero on all
![]() $\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
with
$\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
with
 $d\not \equiv 0~\text{mod}~p$
, and classes of form
$d\not \equiv 0~\text{mod}~p$
, and classes of form
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
are hit whenever
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
are hit whenever
 $b\geqslant p-1$
and
$b\geqslant p-1$
and
 $d\not \equiv -1~\text{mod}~p$
. Now consider a monomial
$d\not \equiv -1~\text{mod}~p$
. Now consider a monomial
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
that survives to the
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d}$
that survives to the
 $E_{2p}=E_{2n^{2}+1}$
-page; in particular,
$E_{2p}=E_{2n^{2}+1}$
-page; in particular,
 $d\equiv -1~\text{mod}~p$
or
$d\equiv -1~\text{mod}~p$
or
 $b<p-1$
. If
$b<p-1$
. If
 $d\not \equiv -1~\text{mod}~p$
(so we would have that
$d\not \equiv -1~\text{mod}~p$
(so we would have that
 $b<p-1$
), the potential elements for
$b<p-1$
), the potential elements for
 $d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d})$
(which are multiples of
$d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d})$
(which are multiples of
 $\unicode[STIX]{x1D6FD}^{n^{2}+b+1}\unicode[STIX]{x1D6FF}^{d-n^{3}}$
) have already been wiped out by
$\unicode[STIX]{x1D6FD}^{n^{2}+b+1}\unicode[STIX]{x1D6FF}^{d-n^{3}}$
) have already been wiped out by
![]() $d_{2p-1}$
. When
$d_{2p-1}$
. When
 $d\equiv -1~\text{mod}~p$
, the potential targets are still there, and Lemma 2.8 implies that indeed
$d\equiv -1~\text{mod}~p$
, the potential targets are still there, and Lemma 2.8 implies that indeed
 $d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+b+1}\unicode[STIX]{x1D6FF}^{d-n^{3}}$
.
$d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{b}\unicode[STIX]{x1D6FF}^{d})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+b+1}\unicode[STIX]{x1D6FF}^{d-n^{3}}$
.
As a specific example, note that
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}$
is a permanent cycle, but
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}$
is a permanent cycle, but
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}^{-1}$
is not.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}^{-1}$
is not.
Remark 2.9. This implies the following:
-
– the homotopy groups
 $\unicode[STIX]{x1D70B}_{\ast }E_{p-1}^{hC_{p}}$
are
$\unicode[STIX]{x1D70B}_{\ast }E_{p-1}^{hC_{p}}$
are
 $2p^{2}$
-periodic, with periodicity generator
$2p^{2}$
-periodic, with periodicity generator
 $\unicode[STIX]{x1D6FF}^{p}$
; and
$\unicode[STIX]{x1D6FF}^{p}$
; and -
– the homotopy groups
 $\unicode[STIX]{x1D70B}_{\ast }E_{p-1}^{hG}$
are
$\unicode[STIX]{x1D70B}_{\ast }E_{p-1}^{hG}$
are
 $2p^{2}n^{2}$
-periodic, with periodicity generator
$2p^{2}n^{2}$
-periodic, with periodicity generator
 $\unicode[STIX]{x1D6E5}^{p}$
.
$\unicode[STIX]{x1D6E5}^{p}$
.
We demonstrate the computation (modulo some elements on the 0-line) of
![]() $\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
for
$\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
for
 $n=2,p=3$
in Figure 1.
$n=2,p=3$
in Figure 1.

Figure 1. The HFPSS for
![]() $\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
in the case
$\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
in the case
![]() $n=2$
,
$n=2$
,
![]() $p=3$
. Circled dots refer to copies of
$p=3$
. Circled dots refer to copies of
![]() $\mathbb{F}_{9}$
, and the square represents a copy of
$\mathbb{F}_{9}$
, and the square represents a copy of
![]() $\mathbb{W}(\mathbb{F}_{9})$
. The dotted lines represent multiplication by
$\mathbb{W}(\mathbb{F}_{9})$
. The dotted lines represent multiplication by
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
3 General reduction steps
In this section, we prove some general results about the action of finite subgroups
 $G\subset \mathbb{G}_{n}$
on
$G\subset \mathbb{G}_{n}$
on
![]() $E_{n}$
that will be needed for the computation of the Picard group of
$E_{n}$
that will be needed for the computation of the Picard group of
![]() $E_{n}^{hG}$
(i.e. the proof that it is cyclic). First, we will give a detailed proof of the Devinatz–Hopkins–Rognes result (Proposition 3.6) that
$E_{n}^{hG}$
(i.e. the proof that it is cyclic). First, we will give a detailed proof of the Devinatz–Hopkins–Rognes result (Proposition 3.6) that
 $E_{n}^{hG}\rightarrow E_{n}$
is a faithful
$E_{n}^{hG}\rightarrow E_{n}$
is a faithful
![]() $G$
-Galois extension in the sense of Rognes [Reference RognesRog08], based on the affineness machinery of [Reference Mathew and MeierMM15] (where the proof is sketched). In particular, we obtain the descent spectral sequence for Picard groups that is our main tool.
$G$
-Galois extension in the sense of Rognes [Reference RognesRog08], based on the affineness machinery of [Reference Mathew and MeierMM15] (where the proof is sketched). In particular, we obtain the descent spectral sequence for Picard groups that is our main tool.
We then make two basic reductions for proving the cyclicity of the Picard group, which show that it suffices to do the calculation in a single case: when
![]() $G$
is a finite
$G$
is a finite
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $\mathbb{S}_{n}$
. The analysis of the descent spectral sequence in this case (in our special case of interest,
$\mathbb{S}_{n}$
. The analysis of the descent spectral sequence in this case (in our special case of interest,
 $n=p-1$
,
$n=p-1$
,
![]() $G$
will then be
$G$
will then be
![]() $C_{p}$
) will be carried out in the following section, using the technology developed in the second part of this paper.
$C_{p}$
) will be carried out in the following section, using the technology developed in the second part of this paper.
We emphasize that
![]() $n$
and
$n$
and
![]() $p$
are arbitrary in this section.
$p$
are arbitrary in this section.
3.1 The Galois property of the Hopkins–Miller spectra
In this subsection, we show that for any finite subgroup
 $G\subset \mathbb{G}_{n}$
, the extension
$G\subset \mathbb{G}_{n}$
, the extension
 $E_{n}^{hG}\rightarrow E_{n}$
is a faithful
$E_{n}^{hG}\rightarrow E_{n}$
is a faithful
![]() $G$
-Galois extension of ring spectra. This result is essentially due (at least in the
$G$
-Galois extension of ring spectra. This result is essentially due (at least in the
![]() $K(n)$
-local case) to Devinatz and Hopkins [Reference Devinatz and HopkinsDH04] and Rognes [Reference RognesRog08]. We note also that, for
$K(n)$
-local case) to Devinatz and Hopkins [Reference Devinatz and HopkinsDH04] and Rognes [Reference RognesRog08]. We note also that, for
 $n=p-1$
(the case in which we are primarily interested here), the first author in [Reference HeardHea15] has given a computational proof of the vanishing of the Tate construction, which is a key component of the result.
$n=p-1$
(the case in which we are primarily interested here), the first author in [Reference HeardHea15] has given a computational proof of the vanishing of the Tate construction, which is a key component of the result.
Using the results of [Reference Mathew and MeierMM15], it will suffice to show that the stack
 $(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G$
is affine over the moduli stack
$(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G$
is affine over the moduli stack
![]() $M_{FG}$
of formal groups. This is easy to check at the closed point, and follows in general by a formal argument that we describe here, involving ‘free actions’.
$M_{FG}$
of formal groups. This is easy to check at the closed point, and follows in general by a formal argument that we describe here, involving ‘free actions’.
We need to recall the following classical definition.
Definition 3.1. Let
![]() $A$
be a commutative ring with an action of a finite group
$A$
be a commutative ring with an action of a finite group
![]() $G$
. Then
$G$
. Then
![]() $G$
is said to act freely on
$G$
is said to act freely on
![]() $A$
if for every non-zero commutative ring
$A$
if for every non-zero commutative ring
![]() $A^{\prime }$
(it suffices to take
$A^{\prime }$
(it suffices to take
![]() $A^{\prime }$
to be a field), the
$A^{\prime }$
to be a field), the
![]() $G$
-action on the set
$G$
-action on the set
 $\operatorname{Hom}(A,A^{\prime })$
of ring-homomorphisms
$\operatorname{Hom}(A,A^{\prime })$
of ring-homomorphisms
 $A\rightarrow A^{\prime }$
is free. Equivalently, for every prime ideal
$A\rightarrow A^{\prime }$
is free. Equivalently, for every prime ideal
![]() $\mathfrak{p}\subset A$
, the subgroup
$\mathfrak{p}\subset A$
, the subgroup
 $G_{\mathfrak{p}}\subset G$
stabilizing
$G_{\mathfrak{p}}\subset G$
stabilizing
![]() $\mathfrak{p}$
acts faithfully on the residue field
$\mathfrak{p}$
acts faithfully on the residue field
![]() $k(\mathfrak{p})$
. In this case, the inclusion of rings
$k(\mathfrak{p})$
. In this case, the inclusion of rings
 $A^{G}\rightarrow A$
induces a
$A^{G}\rightarrow A$
induces a
![]() $G$
-torsor
$G$
-torsor
 $\operatorname{Spec}A\rightarrow \operatorname{Spec}A^{G}$
, and
$\operatorname{Spec}A\rightarrow \operatorname{Spec}A^{G}$
, and
 $\operatorname{Spec}A^{G}\simeq (\operatorname{Spec}A)/G$
in the category of stacks.
$\operatorname{Spec}A^{G}\simeq (\operatorname{Spec}A)/G$
in the category of stacks.
We refer to [Reference Grothendieck and RaynaudSGA1, Exp. V] for a detailed treatment and to [Reference LurieLur11, § 4] for a discussion with a view towards ring spectra. The following is an important example.
Example 3.2. We let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p$
. We recall (cf. [Reference SerreSer79, ch. II, §§ 5–6]) some properties of the functorial (in
$p$
. We recall (cf. [Reference SerreSer79, ch. II, §§ 5–6]) some properties of the functorial (in
![]() $k$
) construction of the
$k$
) construction of the
![]() $p$
-complete ring
$p$
-complete ring
![]() $\mathbb{W}(k)$
of
$\mathbb{W}(k)$
of
![]() $p$
-typical Witt vectors, which is uniquely determined by the condition that
$p$
-typical Witt vectors, which is uniquely determined by the condition that
![]() $\mathbb{W}(k)$
should be torsion-free and
$\mathbb{W}(k)$
should be torsion-free and
 $\mathbb{W}(k)/p\simeq k$
. The ring
$\mathbb{W}(k)/p\simeq k$
. The ring
![]() $\mathbb{W}(k)$
has the following universal property for
$\mathbb{W}(k)$
has the following universal property for
![]() $p$
-complete rings: given any
$p$
-complete rings: given any
![]() $p$
-complete ring
$p$
-complete ring
![]() $A_{0}$
, to give a map
$A_{0}$
, to give a map
 $\mathbb{W}(k)\rightarrow A_{0}$
is equivalent to giving a map of
$\mathbb{W}(k)\rightarrow A_{0}$
is equivalent to giving a map of
![]() $\mathbb{F}_{p}$
-algebras
$\mathbb{F}_{p}$
-algebras
 $k\rightarrow A_{0}/p$
.
$k\rightarrow A_{0}/p$
.
We will need the following basic fact about Witt vectors. Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p$
and let
$p$
and let
![]() $G$
be any finite subgroup of
$G$
be any finite subgroup of
![]() $\text{Aut}(k)$
. Then, the
$\text{Aut}(k)$
. Then, the
![]() $G$
-action on
$G$
-action on
![]() $\mathbb{W}(k)$
is free. In particular, the extension
$\mathbb{W}(k)$
is free. In particular, the extension
 $\mathbb{W}(k^{G})\rightarrow \mathbb{W}(k)$
is a
$\mathbb{W}(k^{G})\rightarrow \mathbb{W}(k)$
is a
![]() $G$
-Galois extension of commutative rings (cf. [Reference Grothendieck and RaynaudSGA1, Exp. I, Theorem 6.1]).
$G$
-Galois extension of commutative rings (cf. [Reference Grothendieck and RaynaudSGA1, Exp. I, Theorem 6.1]).
We now specialize to the case of interest in this subsection.
Construction 3.3. We consider the category consisting of pairs
![]() $(B,\unicode[STIX]{x1D6E4})$
where
$(B,\unicode[STIX]{x1D6E4})$
where
![]() $B$
is a commutative ring and
$B$
is a commutative ring and
![]() $\unicode[STIX]{x1D6E4}$
is a formal group over
$\unicode[STIX]{x1D6E4}$
is a formal group over
![]() $B$
. A morphism
$B$
. A morphism
 $(B,\unicode[STIX]{x1D6E4})\rightarrow (B^{\prime },\unicode[STIX]{x1D6E4}^{\prime })$
consists of a morphism of commutative rings
$(B,\unicode[STIX]{x1D6E4})\rightarrow (B^{\prime },\unicode[STIX]{x1D6E4}^{\prime })$
consists of a morphism of commutative rings
 $f:B\rightarrow B^{\prime }$
and an isomorphism of formal groups
$f:B\rightarrow B^{\prime }$
and an isomorphism of formal groups
 $f_{\ast }\unicode[STIX]{x1D6E4}\simeq \unicode[STIX]{x1D6E4}^{\prime }$
. This category is cofibered in groupoids over the category of commutative rings, and is encoded in the moduli stack of formal groups
$f_{\ast }\unicode[STIX]{x1D6E4}\simeq \unicode[STIX]{x1D6E4}^{\prime }$
. This category is cofibered in groupoids over the category of commutative rings, and is encoded in the moduli stack of formal groups
![]() $M_{FG}$
: that is, it is (by definition) the category of maps
$M_{FG}$
: that is, it is (by definition) the category of maps
 $\operatorname{Spec}B\rightarrow M_{FG}$
from affine schemes to
$\operatorname{Spec}B\rightarrow M_{FG}$
from affine schemes to
![]() $M_{FG}$
.
$M_{FG}$
.
We will consider group actions in this category, or equivalently morphisms of algebraic stacks of the form
 $(\operatorname{Spec}B)/G\rightarrow M_{FG}$
. In particular, giving a
$(\operatorname{Spec}B)/G\rightarrow M_{FG}$
. In particular, giving a
![]() $G$
-action on a pair
$G$
-action on a pair
![]() $(B,\unicode[STIX]{x1D6E4})$
yields for each
$(B,\unicode[STIX]{x1D6E4})$
yields for each
![]() $\unicode[STIX]{x1D70E}\in B$
the data of an automorphism
$\unicode[STIX]{x1D70E}\in B$
the data of an automorphism
 $\unicode[STIX]{x1D70E}:B\simeq B$
and an isomorphism of formal groups
$\unicode[STIX]{x1D70E}:B\simeq B$
and an isomorphism of formal groups
 $f_{\unicode[STIX]{x1D70E}}:\unicode[STIX]{x1D70E}_{\ast }\unicode[STIX]{x1D6E4}\simeq \unicode[STIX]{x1D6E4}$
which satisfy a homomorphism and cocycle condition, respectively. We will represent
$f_{\unicode[STIX]{x1D70E}}:\unicode[STIX]{x1D70E}_{\ast }\unicode[STIX]{x1D6E4}\simeq \unicode[STIX]{x1D6E4}$
which satisfy a homomorphism and cocycle condition, respectively. We will represent
![]() $\unicode[STIX]{x1D6E4}$
by a formal group law over
$\unicode[STIX]{x1D6E4}$
by a formal group law over
![]() $B$
given by a power series
$B$
given by a power series
 $F(X,Y)\in B[\![X,Y]\!]$
. In this case,
$F(X,Y)\in B[\![X,Y]\!]$
. In this case,
 $f_{\unicode[STIX]{x1D70E}}=f_{\unicode[STIX]{x1D70E}}(X)$
is a power series in
$f_{\unicode[STIX]{x1D70E}}=f_{\unicode[STIX]{x1D70E}}(X)$
is a power series in
![]() $B[\![X]\!]$
such that
$B[\![X]\!]$
such that
 $$\begin{eqnarray}F(f_{\unicode[STIX]{x1D70E}}(X),f_{\unicode[STIX]{x1D70E}}(Y))=f_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D70E}_{\ast }F(X,Y)).\end{eqnarray}$$
$$\begin{eqnarray}F(f_{\unicode[STIX]{x1D70E}}(X),f_{\unicode[STIX]{x1D70E}}(Y))=f_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D70E}_{\ast }F(X,Y)).\end{eqnarray}$$
We will need a general criterion to show that a map of the form
 $(\operatorname{Spec}B)/G\rightarrow M_{FG}$
is affine. For this, it will suffice to consider (for various
$(\operatorname{Spec}B)/G\rightarrow M_{FG}$
is affine. For this, it will suffice to consider (for various
![]() $n$
) the faithfully flat cover
$n$
) the faithfully flat cover
 $M_{FG}^{(n)}\rightarrow M_{FG}$
where
$M_{FG}^{(n)}\rightarrow M_{FG}$
where
![]() $M_{FG}^{(n)}$
is the moduli stack of formal groups together with a coordinate modulo degrees at least
$M_{FG}^{(n)}$
is the moduli stack of formal groups together with a coordinate modulo degrees at least
![]() $n+1$
.
$n+1$
.
Proposition 3.4. Suppose
![]() $G$
acts on the pair
$G$
acts on the pair
![]() $(B,\unicode[STIX]{x1D6E4})$
where
$(B,\unicode[STIX]{x1D6E4})$
where
![]() $\unicode[STIX]{x1D6E4}$
is a formal group over the commutative ring
$\unicode[STIX]{x1D6E4}$
is a formal group over the commutative ring
![]() $B$
with the above notation. For any prime ideal
$B$
with the above notation. For any prime ideal
![]() $\mathfrak{p}\subset B$
, we let
$\mathfrak{p}\subset B$
, we let
![]() $I_{\mathfrak{p}}\subset G$
be the subgroup of elements
$I_{\mathfrak{p}}\subset G$
be the subgroup of elements
![]() $\unicode[STIX]{x1D70E}\in G$
such that
$\unicode[STIX]{x1D70E}\in G$
such that
 $\unicode[STIX]{x1D70E}(\mathfrak{p})=\mathfrak{p}$
and
$\unicode[STIX]{x1D70E}(\mathfrak{p})=\mathfrak{p}$
and
![]() $\unicode[STIX]{x1D70E}$
induces the identity automorphism of
$\unicode[STIX]{x1D70E}$
induces the identity automorphism of
![]() $k(\mathfrak{p})$
.
$k(\mathfrak{p})$
.
Fix
![]() $n$
, and suppose that if
$n$
, and suppose that if
![]() $\mathfrak{p}$
is any prime ideal and
$\mathfrak{p}$
is any prime ideal and
![]() $\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
, then at least one of the first
$\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
, then at least one of the first
![]() $n$
coefficients of
$n$
coefficients of
 $f_{\unicode[STIX]{x1D70E}}(X)-X\in B[\![X]\!]$
has non-zero image in
$f_{\unicode[STIX]{x1D70E}}(X)-X\in B[\![X]\!]$
has non-zero image in
![]() $k(\mathfrak{p})$
. Then the
$k(\mathfrak{p})$
. Then the
![]() $G$
-action on the scheme
$G$
-action on the scheme
 $\operatorname{Spec}B\times _{M_{FG}}M_{FG}^{(n)}$
is free, so that
$\operatorname{Spec}B\times _{M_{FG}}M_{FG}^{(n)}$
is free, so that
 $(\operatorname{Spec}B/G)\times _{M_{FG}}M_{FG}^{(n)}$
is representable by an affine scheme.
$(\operatorname{Spec}B/G)\times _{M_{FG}}M_{FG}^{(n)}$
is representable by an affine scheme.
Proof. Let
![]() $B^{\prime }$
be the
$B^{\prime }$
be the
![]() $B$
-algebra which classifies coordinates modulo degrees at least
$B$
-algebra which classifies coordinates modulo degrees at least
![]() $n+1$
on the formal group
$n+1$
on the formal group
![]() $\unicode[STIX]{x1D6E4}$
. Abstractly,
$\unicode[STIX]{x1D6E4}$
. Abstractly,
 $B^{\prime }\simeq B[x_{1}^{\pm 1},x_{2},\ldots ,x_{n}]$
. The
$B^{\prime }\simeq B[x_{1}^{\pm 1},x_{2},\ldots ,x_{n}]$
. The
![]() $G$
-action on
$G$
-action on
![]() $(B,\unicode[STIX]{x1D6E4})$
induces a
$(B,\unicode[STIX]{x1D6E4})$
induces a
![]() $G$
-action on
$G$
-action on
![]() $(B^{\prime },\unicode[STIX]{x1D6E4}^{\prime })$
, where
$(B^{\prime },\unicode[STIX]{x1D6E4}^{\prime })$
, where
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
is the extension of scalars of
$\unicode[STIX]{x1D6E4}^{\prime }$
is the extension of scalars of
![]() $\unicode[STIX]{x1D6E4}$
to
$\unicode[STIX]{x1D6E4}$
to
![]() $B^{\prime }$
.
$B^{\prime }$
.
We need to show that
![]() $G$
acts freely on
$G$
acts freely on
 $\operatorname{Hom}(B^{\prime },k)$
for any field
$\operatorname{Hom}(B^{\prime },k)$
for any field
![]() $k$
. Let
$k$
. Let
 $\unicode[STIX]{x1D70E}\in G\setminus \{1\}$
fix an element of
$\unicode[STIX]{x1D70E}\in G\setminus \{1\}$
fix an element of
 $\operatorname{Hom}(B^{\prime },k)$
given by a map
$\operatorname{Hom}(B^{\prime },k)$
given by a map
 $\unicode[STIX]{x1D719}:B^{\prime }\rightarrow k$
. We get that
$\unicode[STIX]{x1D719}:B^{\prime }\rightarrow k$
. We get that
![]() $\unicode[STIX]{x1D70E}$
fixes the restriction
$\unicode[STIX]{x1D70E}$
fixes the restriction
 $\unicode[STIX]{x1D719}|_{B}:B\rightarrow k$
, which means that the prime ideal
$\unicode[STIX]{x1D719}|_{B}:B\rightarrow k$
, which means that the prime ideal
 $\mathfrak{p}=\text{ker}(\unicode[STIX]{x1D719}|_{B})$
is fixed by
$\mathfrak{p}=\text{ker}(\unicode[STIX]{x1D719}|_{B})$
is fixed by
![]() $\unicode[STIX]{x1D70E}$
, and that
$\unicode[STIX]{x1D70E}$
, and that
![]() $\unicode[STIX]{x1D70E}$
acts trivially on the residue field
$\unicode[STIX]{x1D70E}$
acts trivially on the residue field
![]() $k(\mathfrak{p})$
, so that
$k(\mathfrak{p})$
, so that
![]() $\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
. Note that the fiber above
$\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
. Note that the fiber above
![]() $\unicode[STIX]{x1D719}|_{B}$
of the map (which is preserved by
$\unicode[STIX]{x1D719}|_{B}$
of the map (which is preserved by
![]() $\unicode[STIX]{x1D70E}$
)
$\unicode[STIX]{x1D70E}$
)
 $$\begin{eqnarray}\operatorname{Hom}(B^{\prime },k)\rightarrow \operatorname{Hom}(B,k)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}(B^{\prime },k)\rightarrow \operatorname{Hom}(B,k)\end{eqnarray}$$
is given by the set of coordinates to degree
![]() $n$
on the formal group
$n$
on the formal group
 $(\unicode[STIX]{x1D719}|_{B})_{\ast }(\unicode[STIX]{x1D6E4})$
, and the action of
$(\unicode[STIX]{x1D719}|_{B})_{\ast }(\unicode[STIX]{x1D6E4})$
, and the action of
![]() $\unicode[STIX]{x1D70E}$
on this set of coordinates is given by composing with the image of
$\unicode[STIX]{x1D70E}$
on this set of coordinates is given by composing with the image of
![]() $f_{\unicode[STIX]{x1D70E}}$
. However, since the image of
$f_{\unicode[STIX]{x1D70E}}$
. However, since the image of
 $f_{\unicode[STIX]{x1D70E}}\in k[\![X]\!]$
is not the identity, it acts freely on the above set of coordinates up to degree
$f_{\unicode[STIX]{x1D70E}}\in k[\![X]\!]$
is not the identity, it acts freely on the above set of coordinates up to degree
![]() $n$
. In particular, the action of
$n$
. In particular, the action of
![]() $\unicode[STIX]{x1D70E}$
on the fiber of (3.1) above
$\unicode[STIX]{x1D70E}$
on the fiber of (3.1) above
![]() $\unicode[STIX]{x1D719}|_{B}$
has no fixed points, which is a contradiction and which completes the proof.◻
$\unicode[STIX]{x1D719}|_{B}$
has no fixed points, which is a contradiction and which completes the proof.◻
Lemma 3.5. Suppose
![]() $(R,\mathfrak{m})$
is a complete local ring with perfect residue field
$(R,\mathfrak{m})$
is a complete local ring with perfect residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\unicode[STIX]{x1D6E4}$
be a formal group over
$\unicode[STIX]{x1D6E4}$
be a formal group over
![]() $R$
. Let a finite group
$R$
. Let a finite group
![]() $G$
act on the pair
$G$
act on the pair
![]() $(R,\unicode[STIX]{x1D6E4})$
. Let
$(R,\unicode[STIX]{x1D6E4})$
. Let
![]() $S\subset G$
be the subgroup that acts trivially on the residue field. Suppose that every element
$S\subset G$
be the subgroup that acts trivially on the residue field. Suppose that every element
 $\unicode[STIX]{x1D70E}\in S\setminus \{1\}$
induces a non-trivial automorphism of the reduction of
$\unicode[STIX]{x1D70E}\in S\setminus \{1\}$
induces a non-trivial automorphism of the reduction of
![]() $\unicode[STIX]{x1D6E4}$
modulo
$\unicode[STIX]{x1D6E4}$
modulo
![]() $\mathfrak{m}$
. Then the morphism
$\mathfrak{m}$
. Then the morphism
 $(\operatorname{Spec}R)/G\rightarrow M_{FG}$
is affine.
$(\operatorname{Spec}R)/G\rightarrow M_{FG}$
is affine.
Proof. We will apply Proposition 3.4. Fix a prime ideal
![]() $\mathfrak{p}\subset R$
and
$\mathfrak{p}\subset R$
and
![]() $\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
. The first claim is that
$\unicode[STIX]{x1D70E}\in I_{\mathfrak{p}}$
. The first claim is that
![]() $\unicode[STIX]{x1D70E}\in S$
. In fact, this follows from the surjection
$\unicode[STIX]{x1D70E}\in S$
. In fact, this follows from the surjection
 $R/\mathfrak{p}\rightarrow R/\mathfrak{m}=k$
. Since
$R/\mathfrak{p}\rightarrow R/\mathfrak{m}=k$
. Since
![]() $\unicode[STIX]{x1D70E}$
acts trivially on
$\unicode[STIX]{x1D70E}$
acts trivially on
![]() $R/\mathfrak{p}$
, it must act trivially on
$R/\mathfrak{p}$
, it must act trivially on
![]() $k$
.
$k$
.
In applying Proposition 3.4, it suffices to consider the inertia subgroups
![]() $I_{\mathfrak{p}}$
; since these are contained in
$I_{\mathfrak{p}}$
; since these are contained in
![]() $S$
, we conclude that it suffices to consider the case when
$S$
, we conclude that it suffices to consider the case when
![]() $G$
itself acts trivially on the residue field. Choose
$G$
itself acts trivially on the residue field. Choose
![]() $n$
large enough such that each power series
$n$
large enough such that each power series
 $f_{\unicode[STIX]{x1D70E}}(X)\in R[\![X]\!]$
for
$f_{\unicode[STIX]{x1D70E}}(X)\in R[\![X]\!]$
for
![]() $\unicode[STIX]{x1D70E}\neq 1$
has a coefficient in degrees at most
$\unicode[STIX]{x1D70E}\neq 1$
has a coefficient in degrees at most
![]() $n$
different modulo
$n$
different modulo
![]() $\mathfrak{m}$
from
$\mathfrak{m}$
from
![]() $X$
. The claim is that
$X$
. The claim is that
 $(\operatorname{Spec}R)/G\times _{M_{FG}}M_{FG}^{(n)}$
is representable by an affine scheme. This now follows from Proposition 3.4 because each
$(\operatorname{Spec}R)/G\times _{M_{FG}}M_{FG}^{(n)}$
is representable by an affine scheme. This now follows from Proposition 3.4 because each
 $f_{\unicode[STIX]{x1D70E}}(X)-X$
for
$f_{\unicode[STIX]{x1D70E}}(X)-X$
for
![]() $\unicode[STIX]{x1D70E}\neq 1$
has a coefficient which is a unit in some degree at most
$\unicode[STIX]{x1D70E}\neq 1$
has a coefficient which is a unit in some degree at most
![]() $n$
.◻
$n$
.◻
Proposition 3.6. For any finite subgroup
 $G\subset \mathbb{G}_{n}$
, the natural map
$G\subset \mathbb{G}_{n}$
, the natural map
 $E_{n}^{hG}\rightarrow E_{n}$
exhibits the target as a faithful
$E_{n}^{hG}\rightarrow E_{n}$
exhibits the target as a faithful
![]() $G$
-Galois extension of the source.
$G$
-Galois extension of the source.
Proof. By [Reference Mathew and MeierMM15, Theorem 5.8], it suffices to show that
 $(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G\rightarrow M_{FG}$
is an affine morphism of stacks. However, this follows from Lemma 3.5 (with
$(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G\rightarrow M_{FG}$
is an affine morphism of stacks. However, this follows from Lemma 3.5 (with
 $S=G_{\mathbb{S}}=G\cap \mathbb{S}$
) because
$S=G_{\mathbb{S}}=G\cap \mathbb{S}$
) because
![]() $\mathbb{S}_{n}$
is defined as a subgroup of automorphisms of the Honda formal group over
$\mathbb{S}_{n}$
is defined as a subgroup of automorphisms of the Honda formal group over
![]() $\mathbb{F}_{p^{n}}$
. The above reasoning shows that there exists
$\mathbb{F}_{p^{n}}$
. The above reasoning shows that there exists
![]() $m$
such that
$m$
such that
 $(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G\times _{M_{FG}}M_{FG}^{(m)}$
is affine.◻
$(\operatorname{Spec}\unicode[STIX]{x1D70B}_{0}E_{n})/G\times _{M_{FG}}M_{FG}^{(m)}$
is affine.◻
It follows, in particular, that there is a descent spectral sequence for computing
 $\operatorname{Pic}(E_{n}^{hG})$
(for any finite subgroup
$\operatorname{Pic}(E_{n}^{hG})$
(for any finite subgroup
 $G\subset \mathbb{G}_{n}$
) based on the equivalence of spectra
$G\subset \mathbb{G}_{n}$
) based on the equivalence of spectra
 $$\begin{eqnarray}\mathfrak{pic}(E_{n}^{hG})\simeq \unicode[STIX]{x1D70F}_{{\geqslant}0}\,\mathfrak{pic}(E_{n})^{hG}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{pic}(E_{n}^{hG})\simeq \unicode[STIX]{x1D70F}_{{\geqslant}0}\,\mathfrak{pic}(E_{n})^{hG}.\end{eqnarray}$$
We know that
 $\operatorname{Pic}(E_{n})$
is cyclic (by regularity, cf. [Reference Baker and RichterBR05]), and we want to prove that
$\operatorname{Pic}(E_{n})$
is cyclic (by regularity, cf. [Reference Baker and RichterBR05]), and we want to prove that
 $\operatorname{Pic}(E_{n}^{hG})$
is also cyclic. In the rest of this section, we will reduce the analysis of this spectral sequence to the case where
$\operatorname{Pic}(E_{n}^{hG})$
is also cyclic. In the rest of this section, we will reduce the analysis of this spectral sequence to the case where
![]() $G$
is a
$G$
is a
![]() $p$
-subgroup of
$p$
-subgroup of
![]() $\mathbb{S}_{n}$
.
$\mathbb{S}_{n}$
.
Remark 3.7. As a consequence, we can prove that the two possible notions of Picard group that one might be interested in here are equivalent. Recall that if
![]() $R$
is a
$R$
is a
![]() $K(n)$
-local
$K(n)$
-local
![]() $\mathbf{E}_{\infty }$
-ring, one can consider two different Picard groups (cf. [Reference Hopkins, Mahowald and SadofskyHMS94]):
$\mathbf{E}_{\infty }$
-ring, one can consider two different Picard groups (cf. [Reference Hopkins, Mahowald and SadofskyHMS94]):
-
(i) the (usual) Picard group
 $\operatorname{Pic}(R)$
of all
$\operatorname{Pic}(R)$
of all
 $R$
-modules;
$R$
-modules; -
(ii) the Picard group
 $\operatorname{Pic}_{K(n)}(R)$
of the
$\operatorname{Pic}_{K(n)}(R)$
of the
 $\infty$
-category
$\infty$
-category
 $L_{K(n)}\operatorname{Mod}(R)$
of
$L_{K(n)}\operatorname{Mod}(R)$
of
 $K(n)$
-local
$K(n)$
-local
 $R$
-modules (with the
$R$
-modules (with the
 $K(n)$
-localized smash product).
$K(n)$
-localized smash product).
The first group
![]() $\operatorname{Pic}(R)$
is always a subgroup of
$\operatorname{Pic}(R)$
is always a subgroup of
 $\operatorname{Pic}_{K(n)}(R)$
, because any invertible
$\operatorname{Pic}_{K(n)}(R)$
, because any invertible
![]() $R$
-module is automatically perfect, hence
$R$
-module is automatically perfect, hence
![]() $K(n)$
-local itself and is easily seen to be
$K(n)$
-local itself and is easily seen to be
![]() $K(n)$
-locally invertible too. Given an element of
$K(n)$
-locally invertible too. Given an element of
 $\operatorname{Pic}_{K(n)}(R)$
, represented by a
$\operatorname{Pic}_{K(n)}(R)$
, represented by a
![]() $K(n)$
-local
$K(n)$
-local
![]() $R$
-module
$R$
-module
![]() $M$
, it belongs to the first group if and only if
$M$
, it belongs to the first group if and only if
![]() $M$
is perfect as an
$M$
is perfect as an
![]() $R$
-module.
$R$
-module.
We claim that if
 $R=E_{n}^{hG}$
for any finite
$R=E_{n}^{hG}$
for any finite
 $G\subset \mathbb{G}_{n}$
, the two notions coincide. Equivalently, if
$G\subset \mathbb{G}_{n}$
, the two notions coincide. Equivalently, if
![]() $M$
is a
$M$
is a
![]() $K(n)$
-local
$K(n)$
-local
![]() $R$
-module which is
$R$
-module which is
![]() $K(n)$
-locally invertible, then
$K(n)$
-locally invertible, then
![]() $M$
is invertible as an
$M$
is invertible as an
![]() $R$
-module to begin with.
$R$
-module to begin with.
To see this, we consider the faithful
![]() $G$
-Galois extension
$G$
-Galois extension
 $R\rightarrow E_{n}$
. Then
$R\rightarrow E_{n}$
. Then
![]() $E_{n}$
is a perfect
$E_{n}$
is a perfect
![]() $R$
-module by [Reference RognesRog08, Proposition 6.2.1]. Observe that the
$R$
-module by [Reference RognesRog08, Proposition 6.2.1]. Observe that the
![]() $E_{n}$
-module
$E_{n}$
-module
 $E_{n}\otimes _{R}M$
is still
$E_{n}\otimes _{R}M$
is still
![]() $K(n)$
-local as a result, and it is
$K(n)$
-local as a result, and it is
![]() $K(n)$
-locally invertible. This implies that
$K(n)$
-locally invertible. This implies that
 $E_{n}\otimes _{R}M$
belongs to
$E_{n}\otimes _{R}M$
belongs to
 $\operatorname{Pic}_{K(n)}(E_{n})$
. However,
$\operatorname{Pic}_{K(n)}(E_{n})$
. However,
 $\operatorname{Pic}_{K(n)}(E_{n})=\operatorname{Pic}(E_{n})=\mathbb{Z}/2$
(by [Reference Baker and RichterBR05]); in particular,
$\operatorname{Pic}_{K(n)}(E_{n})=\operatorname{Pic}(E_{n})=\mathbb{Z}/2$
(by [Reference Baker and RichterBR05]); in particular,
 $E_{n}\otimes _{R}M$
is a perfect
$E_{n}\otimes _{R}M$
is a perfect
![]() $E_{n}$
-module, and by descent (cf. [Reference MathewMat16, Proposition 3.27])
$E_{n}$
-module, and by descent (cf. [Reference MathewMat16, Proposition 3.27])
![]() $M$
is a perfect
$M$
is a perfect
![]() $R$
-module.
$R$
-module.
3.2 Elimination of the Galois piece
In this subsection, we make a basic reduction that enables us to eliminate the Galois piece. In other words, we reduce to proving cyclicity of the Picard group of
![]() $E_{n}^{hG}$
when
$E_{n}^{hG}$
when
![]() $G\subset \mathbb{S}_{n}$
.
$G\subset \mathbb{S}_{n}$
.
We will need a few basic properties of
![]() $\mathbb{W}(k)$
. Most of them can be encapsulated appropriately in the notion of ‘formal étaleness’, but we will spell out some details for the convenience of the reader.
$\mathbb{W}(k)$
. Most of them can be encapsulated appropriately in the notion of ‘formal étaleness’, but we will spell out some details for the convenience of the reader.
Let
 $f:A_{0}\rightarrow A_{0}^{\prime }$
be a morphism of
$f:A_{0}\rightarrow A_{0}^{\prime }$
be a morphism of
![]() $p$
-local commutative rings. We say that
$p$
-local commutative rings. We say that
![]() $f$
is a uniform
$f$
is a uniform
![]() ${\mathcal{F}}_{p}$
-isomorphism if there exists
${\mathcal{F}}_{p}$
-isomorphism if there exists
![]() $N>0$
such that:
$N>0$
such that:
-
(i)
 $\text{ker}(f)^{N}=0$
;
$\text{ker}(f)^{N}=0$
; -
(ii) given
 $x\in A_{0}^{\prime }$
,
$x\in A_{0}^{\prime }$
,
 $x^{p^{N}}\in \text{im}(f)$
.
$x^{p^{N}}\in \text{im}(f)$
.
Lemma 3.8. Let
 $f:A_{0}\rightarrow A_{0}^{\prime }$
be a uniform
$f:A_{0}\rightarrow A_{0}^{\prime }$
be a uniform
![]() ${\mathcal{F}}_{p}$
-isomorphism of
${\mathcal{F}}_{p}$
-isomorphism of
![]() $p$
-complete rings. Then given any perfect field
$p$
-complete rings. Then given any perfect field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
, any map of commutative rings
$p$
, any map of commutative rings
 $\mathbb{W}(k)\rightarrow A_{0}^{\prime }$
lifts uniquely to a map
$\mathbb{W}(k)\rightarrow A_{0}^{\prime }$
lifts uniquely to a map
 $\mathbb{W}(k)\rightarrow A_{0}$
.
$\mathbb{W}(k)\rightarrow A_{0}$
.
Proof. It is a straightforward calculation (cf. [Reference Mathew, Naumann and NoelMNN15, Proposition 3.26]) that
 $f\otimes _{\mathbb{Z}_{p}}\mathbb{F}_{p}$
is also a uniform
$f\otimes _{\mathbb{Z}_{p}}\mathbb{F}_{p}$
is also a uniform
![]() ${\mathcal{F}}_{p}$
-isomorphism, so that we may assume that
${\mathcal{F}}_{p}$
-isomorphism, so that we may assume that
![]() $A_{0}$
and
$A_{0}$
and
![]() $A_{0}^{\prime }$
are
$A_{0}^{\prime }$
are
![]() $\mathbb{F}_{p}$
-algebras by the universal property of the Witt vectors. It suffices to show that
$\mathbb{F}_{p}$
-algebras by the universal property of the Witt vectors. It suffices to show that
 $\operatorname{Hom}(k,A_{0})\simeq \operatorname{Hom}(k,A_{0}^{\prime })$
.
$\operatorname{Hom}(k,A_{0})\simeq \operatorname{Hom}(k,A_{0}^{\prime })$
.
Recall that an
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $C_{0}$
is said to be perfect if the Frobenius
$C_{0}$
is said to be perfect if the Frobenius
 $F:C_{0}\rightarrow C_{0}$
is an isomorphism. The inclusion of perfect
$F:C_{0}\rightarrow C_{0}$
is an isomorphism. The inclusion of perfect
![]() $\mathbb{F}_{p}$
-algebras into all
$\mathbb{F}_{p}$
-algebras into all
![]() $\mathbb{F}_{p}$
-algebras has a right adjoint, called the inverse limit perfection, which sends an
$\mathbb{F}_{p}$
-algebras has a right adjoint, called the inverse limit perfection, which sends an
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $C_{0}$
to the inverse limit of the Frobenius system
$C_{0}$
to the inverse limit of the Frobenius system
 $\cdots \rightarrow C_{0}\stackrel{F}{\rightarrow }C_{0}$
. Since
$\cdots \rightarrow C_{0}\stackrel{F}{\rightarrow }C_{0}$
. Since
![]() $k$
is perfect, and since the uniform
$k$
is perfect, and since the uniform
![]() ${\mathcal{F}}_{p}$
-isomorphism condition guarantees that
${\mathcal{F}}_{p}$
-isomorphism condition guarantees that
 $A_{0}\rightarrow A_{0}^{\prime }$
induces an isomorphism on inverse limit perfections, an adjunction argument now gives the desired claim.◻
$A_{0}\rightarrow A_{0}^{\prime }$
induces an isomorphism on inverse limit perfections, an adjunction argument now gives the desired claim.◻
Lemma 3.9. Let
![]() $\tilde{G}$
be a finite group acting on a
$\tilde{G}$
be a finite group acting on a
![]() $p$
-complete
$p$
-complete
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R$
in such a way that
$R$
in such a way that
 $R^{h\tilde{G}}\rightarrow R$
is a faithful
$R^{h\tilde{G}}\rightarrow R$
is a faithful
![]() $\tilde{G}$
-Galois extension. Let
$\tilde{G}$
-Galois extension. Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p$
. Then any map of commutative rings
$p$
. Then any map of commutative rings
 $\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
lifts uniquely to a map
$\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
lifts uniquely to a map
 $\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})$
.
$\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})$
.
Proof. By the previous lemma, it suffices to show that the reduction map
 $\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
is a uniform
$\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
is a uniform
![]() ${\mathcal{F}}_{p}$
-isomorphism. This follows as in [Reference MathewMat15, § 4] from the fact that the HFPSS for the
${\mathcal{F}}_{p}$
-isomorphism. This follows as in [Reference MathewMat15, § 4] from the fact that the HFPSS for the
![]() $\tilde{G}$
-action on
$\tilde{G}$
-action on
![]() $R$
has a horizontal vanishing line at a finite stage by the theory of ‘descendability’ (cf. [Reference MathewMat16, §§ 3–4]) and the fact that everything in positive filtration at
$R$
has a horizontal vanishing line at a finite stage by the theory of ‘descendability’ (cf. [Reference MathewMat16, §§ 3–4]) and the fact that everything in positive filtration at
![]() $E_{2}$
is annihilated by the
$E_{2}$
is annihilated by the
![]() $p$
-part of
$p$
-part of
![]() $|\tilde{G}|$
.◻
$|\tilde{G}|$
.◻
Proposition 3.10. Let
![]() $G$
be a finite group acting on an even-periodic
$G$
be a finite group acting on an even-periodic
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R$
. Suppose that:
$R$
. Suppose that:
-
(i)
 $\unicode[STIX]{x1D70B}_{0}R$
is a complete local ring with perfect residue field
$\unicode[STIX]{x1D70B}_{0}R$
is a complete local ring with perfect residue field
 $k$
of characteristic
$k$
of characteristic
 $p>0$
; let
$p>0$
; let
 $\tilde{G}\subseteq G$
be the subgroup that acts trivially on
$\tilde{G}\subseteq G$
be the subgroup that acts trivially on
 $k$
;
$k$
; -
(ii) the morphism of
 $\mathbf{E}_{\infty }$
-rings
$\mathbf{E}_{\infty }$
-rings
 $R^{hG}\rightarrow R$
is a faithful
$R^{hG}\rightarrow R$
is a faithful
 $G$
-Galois extension;
$G$
-Galois extension; -
(iii) the Picard group of the
 $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
 $R^{h\tilde{G}}$
is cyclic and generated by the suspension
$R^{h\tilde{G}}$
is cyclic and generated by the suspension
 $\unicode[STIX]{x1D6F4}R^{h\tilde{G}}$
.
$\unicode[STIX]{x1D6F4}R^{h\tilde{G}}$
.
Then the Picard group of
![]() $R^{hG}$
is cyclic and generated by the suspension
$R^{hG}$
is cyclic and generated by the suspension
![]() $\unicode[STIX]{x1D6F4}R^{hG}$
.
$\unicode[STIX]{x1D6F4}R^{hG}$
.
Proof. Let
 $\unicode[STIX]{x1D6E4}=G/\tilde{G}$
be the quotient group, so that by the Galois correspondence, the morphism of
$\unicode[STIX]{x1D6E4}=G/\tilde{G}$
be the quotient group, so that by the Galois correspondence, the morphism of
![]() $\mathbf{E}_{\infty }$
-rings
$\mathbf{E}_{\infty }$
-rings
 $A=R^{hG}\rightarrow B=R^{h\tilde{G}}$
is a faithful
$A=R^{hG}\rightarrow B=R^{h\tilde{G}}$
is a faithful
![]() $\unicode[STIX]{x1D6E4}$
-Galois extension. We claim first that it is actually a Galois extension on homotopy groups, i.e.
$\unicode[STIX]{x1D6E4}$
-Galois extension. We claim first that it is actually a Galois extension on homotopy groups, i.e.
![]() $A\rightarrow B$
is étale, in the sense that
$A\rightarrow B$
is étale, in the sense that
 $\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is étale and the natural map
$\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is étale and the natural map
 $\unicode[STIX]{x1D70B}_{\ast }A\otimes _{\unicode[STIX]{x1D70B}_{0}A}\unicode[STIX]{x1D70B}_{0}B\rightarrow \unicode[STIX]{x1D70B}_{\ast }B$
is an isomorphism; this will enable us to make the desired conclusion. We refer to [Reference Baker and RichterBR07] for the relationship between Galois extensions on homotopy and Galois extensions in the sense of Rognes [Reference RognesRog08], and to [Reference LurieLur11, § 4] as a convenient reference for some of the facts we need.
$\unicode[STIX]{x1D70B}_{\ast }A\otimes _{\unicode[STIX]{x1D70B}_{0}A}\unicode[STIX]{x1D70B}_{0}B\rightarrow \unicode[STIX]{x1D70B}_{\ast }B$
is an isomorphism; this will enable us to make the desired conclusion. We refer to [Reference Baker and RichterBR07] for the relationship between Galois extensions on homotopy and Galois extensions in the sense of Rognes [Reference RognesRog08], and to [Reference LurieLur11, § 4] as a convenient reference for some of the facts we need.
In particular, by [Reference LurieLur11, Corollary 4.15], we need to show that
![]() $\unicode[STIX]{x1D6E4}$
acts freely on
$\unicode[STIX]{x1D6E4}$
acts freely on
![]() $\unicode[STIX]{x1D70B}_{0}(B)$
. We will do this by functoriality. By the universal property of the (
$\unicode[STIX]{x1D70B}_{0}(B)$
. We will do this by functoriality. By the universal property of the (
![]() $p$
-typical) Witt vectors, we obtain a
$p$
-typical) Witt vectors, we obtain a
![]() $G$
-equivariant map
$G$
-equivariant map
 $$\begin{eqnarray}\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R),\end{eqnarray}$$
where
![]() $G$
acts on
$G$
acts on
![]() $\mathbb{W}(k)$
via the induced action on
$\mathbb{W}(k)$
via the induced action on
![]() $k$
. Of course, the
$k$
. Of course, the
![]() $G$
-action on
$G$
-action on
![]() $\mathbb{W}(k)$
factors through
$\mathbb{W}(k)$
factors through
 $\unicode[STIX]{x1D6E4}=G/\tilde{G}$
, and we claim that this lifts to a
$\unicode[STIX]{x1D6E4}=G/\tilde{G}$
, and we claim that this lifts to a
![]() $\unicode[STIX]{x1D6E4}$
-equivariant map
$\unicode[STIX]{x1D6E4}$
-equivariant map
 $$\begin{eqnarray}\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)=\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)=\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}}).\end{eqnarray}$$
The equivariance alone gives the
![]() $\unicode[STIX]{x1D6E4}$
-equivariant lift
$\unicode[STIX]{x1D6E4}$
-equivariant lift
 $\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
, which of course receives a map from
$\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\tilde{G}}$
, which of course receives a map from
 $\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})$
. Using Lemma 3.9, we can upgrade it to the claimed
$\unicode[STIX]{x1D70B}_{0}(R^{h\tilde{G}})$
. Using Lemma 3.9, we can upgrade it to the claimed
![]() $\unicode[STIX]{x1D6E4}$
-equivariant map
$\unicode[STIX]{x1D6E4}$
-equivariant map
 $\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
.
$\mathbb{W}(k)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
.
The
![]() $\unicode[STIX]{x1D6E4}$
-action on
$\unicode[STIX]{x1D6E4}$
-action on
![]() $W(k)$
is free (Example 3.2). It follows that the
$W(k)$
is free (Example 3.2). It follows that the
![]() $\unicode[STIX]{x1D6E4}$
-action on
$\unicode[STIX]{x1D6E4}$
-action on
![]() $\unicode[STIX]{x1D70B}_{0}(B)$
is free. Applying [Reference LurieLur11, Corollary 4.15], we conclude that
$\unicode[STIX]{x1D70B}_{0}(B)$
is free. Applying [Reference LurieLur11, Corollary 4.15], we conclude that
![]() $A\rightarrow B$
is an algebraic
$A\rightarrow B$
is an algebraic
![]() $\unicode[STIX]{x1D6E4}$
-Galois extension in that
$\unicode[STIX]{x1D6E4}$
-Galois extension in that
 $\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is one, and
$\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is one, and
 $\unicode[STIX]{x1D70B}_{\ast }(A)\otimes _{\unicode[STIX]{x1D70B}_{0}(A)}\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{\ast }(B)$
is an isomorphism.
$\unicode[STIX]{x1D70B}_{\ast }(A)\otimes _{\unicode[STIX]{x1D70B}_{0}(A)}\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{\ast }(B)$
is an isomorphism.
Finally, we prove the result about the Picard group. Let
![]() $M$
be an invertible
$M$
be an invertible
![]() $A$
-module. By assumption,
$A$
-module. By assumption,
 $M\otimes _{A}B$
is a suspension of a free
$M\otimes _{A}B$
is a suspension of a free
![]() $B$
-module of rank one; by desuspending
$B$
-module of rank one; by desuspending
![]() $M$
appropriately, we may assume that
$M$
appropriately, we may assume that
 $M\otimes _{A}B\simeq B$
. We would like to see that
$M\otimes _{A}B\simeq B$
. We would like to see that
![]() $M\simeq A$
. Since
$M\simeq A$
. Since
![]() $B$
is faithfully flat over
$B$
is faithfully flat over
![]() $A$
, we can conclude that
$A$
, we can conclude that
![]() $\unicode[STIX]{x1D70B}_{0}(M)$
is an invertible
$\unicode[STIX]{x1D70B}_{0}(M)$
is an invertible
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
-module and that the map
$\unicode[STIX]{x1D70B}_{0}(A)$
-module and that the map
 $\unicode[STIX]{x1D70B}_{0}(M)\otimes _{\unicode[STIX]{x1D70B}_{0}(A)}\unicode[STIX]{x1D70B}_{\ast }(A)\rightarrow \unicode[STIX]{x1D70B}_{\ast }(M)$
is an isomorphism (because this happens after base-change to
$\unicode[STIX]{x1D70B}_{0}(M)\otimes _{\unicode[STIX]{x1D70B}_{0}(A)}\unicode[STIX]{x1D70B}_{\ast }(A)\rightarrow \unicode[STIX]{x1D70B}_{\ast }(M)$
is an isomorphism (because this happens after base-change to
![]() $B$
). In particular,
$B$
). In particular,
![]() $M$
simply arises from an invertible module over
$M$
simply arises from an invertible module over
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
.
$\unicode[STIX]{x1D70B}_{0}(A)$
.
Therefore, it suffices to show that the Picard group of the (ordinary) commutative ring
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
is trivial. This will follow if we can show that
$\unicode[STIX]{x1D70B}_{0}(A)$
is trivial. This will follow if we can show that
![]() $\unicode[STIX]{x1D70B}_{0}(A)$
is a (possibly non-noetherian) local ring. Since
$\unicode[STIX]{x1D70B}_{0}(A)$
is a (possibly non-noetherian) local ring. Since
 $\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is finite étale, it suffices to show that
$\unicode[STIX]{x1D70B}_{0}(A)\rightarrow \unicode[STIX]{x1D70B}_{0}(B)$
is finite étale, it suffices to show that
![]() $\unicode[STIX]{x1D70B}_{0}(B)$
is a local ring, i.e. that its spectrum has a unique closed point. However,
$\unicode[STIX]{x1D70B}_{0}(B)$
is a local ring, i.e. that its spectrum has a unique closed point. However,
 $\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\widetilde{G}}$
is an
$\unicode[STIX]{x1D70B}_{0}(B)\rightarrow \unicode[STIX]{x1D70B}_{0}(R)^{\widetilde{G}}$
is an
![]() ${\mathcal{F}}_{p}$
-isomorphism as above, so that it induces an isomorphism on Zariski spectra. Therefore, the fact that
${\mathcal{F}}_{p}$
-isomorphism as above, so that it induces an isomorphism on Zariski spectra. Therefore, the fact that
![]() $\unicode[STIX]{x1D70B}_{0}(R)^{\widetilde{G}}$
is a local ring forces
$\unicode[STIX]{x1D70B}_{0}(R)^{\widetilde{G}}$
is a local ring forces
![]() $\unicode[STIX]{x1D70B}_{0}(B)$
to be one, and completes the proof.◻
$\unicode[STIX]{x1D70B}_{0}(B)$
to be one, and completes the proof.◻
In our example of interest,
![]() $R$
will be
$R$
will be
![]() $E_{n}$
,
$E_{n}$
,
![]() $G$
will be a finite subgroup of the extended Morava stabilizer group, and
$G$
will be a finite subgroup of the extended Morava stabilizer group, and
 $\tilde{G}=G_{\mathbb{S}}$
, as in (2.3).
$\tilde{G}=G_{\mathbb{S}}$
, as in (2.3).
3.3 Reduction to the
 $p$
-Sylow
$p$
-Sylow
Here, we will use basic facts about the structure of
![]() $\mathbb{S}_{n}$
, for which we refer the reader to § 2.1.
$\mathbb{S}_{n}$
, for which we refer the reader to § 2.1.
Proposition 3.11. Let
![]() $G$
be a finite subgroup of
$G$
be a finite subgroup of
![]() $\mathbb{S}_{n}$
at some height
$\mathbb{S}_{n}$
at some height
![]() $n$
and at the implicit prime
$n$
and at the implicit prime
![]() $p$
. Let
$p$
. Let
 $G_{p}\subseteq G$
be a
$G_{p}\subseteq G$
be a
![]() $p$
-Sylow subgroup. Suppose the Picard group of the
$p$
-Sylow subgroup. Suppose the Picard group of the
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $E_{n}^{hG_{p}}$
is cyclic, generated by the suspension. Then the Picard group of
$E_{n}^{hG_{p}}$
is cyclic, generated by the suspension. Then the Picard group of
![]() $E_{n}^{hG}$
is also cyclic, generated by the suspension.
$E_{n}^{hG}$
is also cyclic, generated by the suspension.
Proof. Observe first that
 $\operatorname{Pic}(E_{n}^{hG})=\unicode[STIX]{x1D70B}_{0}(\mathfrak{pic}(E_{n})^{hG})$
is a torsion group (cf. [Reference Mathew and StojanoskaMS16, § 5.3]), so it suffices to show that the suspension generates the
$\operatorname{Pic}(E_{n}^{hG})=\unicode[STIX]{x1D70B}_{0}(\mathfrak{pic}(E_{n})^{hG})$
is a torsion group (cf. [Reference Mathew and StojanoskaMS16, § 5.3]), so it suffices to show that the suspension generates the
![]() $q$
-part
$q$
-part
 $\operatorname{Pic}(E_{n}^{hG})_{q}$
of
$\operatorname{Pic}(E_{n}^{hG})_{q}$
of
 $\operatorname{Pic}(E_{n}^{hG})$
for any prime number
$\operatorname{Pic}(E_{n}^{hG})$
for any prime number
![]() $q$
. We consider two cases.
$q$
. We consider two cases.
(i)
![]() $q=p$
. In this case, the map
$q=p$
. In this case, the map
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{p}:\operatorname{Pic}(E_{n}^{hG})_{p}\rightarrow \operatorname{Pic}(E_{n}^{hG_{p}})_{p}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{p}:\operatorname{Pic}(E_{n}^{hG})_{p}\rightarrow \operatorname{Pic}(E_{n}^{hG_{p}})_{p}\end{eqnarray}$$
(induced by base-change along
 $E_{n}^{hG}\rightarrow E_{n}^{hG_{p}}$
) is injective thanks to the transfer map
$E_{n}^{hG}\rightarrow E_{n}^{hG_{p}}$
) is injective thanks to the transfer map
 $$\begin{eqnarray}\operatorname{Pic}(E_{n}^{hG_{p}})_{p}\simeq \unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG_{p}}\rightarrow \operatorname{Pic}(E_{n}^{hG})_{p}\simeq \unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Pic}(E_{n}^{hG_{p}})_{p}\simeq \unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG_{p}}\rightarrow \operatorname{Pic}(E_{n}^{hG})_{p}\simeq \unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG}.\end{eqnarray}$$
Namely, recall that if
![]() $X$
is a
$X$
is a
![]() $p$
-local spectrum with a
$p$
-local spectrum with a
![]() $G$
-action, the composite map
$G$
-action, the composite map
 $X^{hG}\rightarrow X^{hG_{p}}\stackrel{\text{tr}}{\rightarrow }X^{hG}$
is an equivalence. Since the map
$X^{hG}\rightarrow X^{hG_{p}}\stackrel{\text{tr}}{\rightarrow }X^{hG}$
is an equivalence. Since the map
![]() $\unicode[STIX]{x1D719}_{p}$
carries the suspension of the unit to itself, the fact that this class generates the target implies that it must generate the source.
$\unicode[STIX]{x1D719}_{p}$
carries the suspension of the unit to itself, the fact that this class generates the target implies that it must generate the source.
(ii)
![]() $q\neq p$
. Let
$q\neq p$
. Let
 $G_{q}\subseteq G$
be a
$G_{q}\subseteq G$
be a
![]() $q$
-Sylow subgroup. As above, we observe that the map
$q$
-Sylow subgroup. As above, we observe that the map
![]() $\unicode[STIX]{x1D719}_{q}$
defined via
$\unicode[STIX]{x1D719}_{q}$
defined via
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{q}:\operatorname{Pic}(E_{n}^{hG})_{q}\rightarrow \operatorname{Pic}(E_{n}^{hG_{q}})_{q}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{q}:\operatorname{Pic}(E_{n}^{hG})_{q}\rightarrow \operatorname{Pic}(E_{n}^{hG_{q}})_{q}\end{eqnarray}$$
is injective. So, it suffices to consider the case where
![]() $G$
is itself a
$G$
is itself a
![]() $q$
-group.
$q$
-group.
We consider the HFPSS converging to
 $\operatorname{Pic}(E_{n}^{hG})=\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG}$
. In this case, since
$\operatorname{Pic}(E_{n}^{hG})=\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E_{n})^{hG}$
. In this case, since
![]() $G$
is a
$G$
is a
![]() $q$
-group, we observe that the only contributions come from
$q$
-group, we observe that the only contributions come from
 $H^{0}(G,\mathbb{Z}/2)$
(which is
$H^{0}(G,\mathbb{Z}/2)$
(which is
![]() $\mathbb{Z}/2$
, generated by the suspension) and
$\mathbb{Z}/2$
, generated by the suspension) and
 $H^{1}(G,(E_{n})_{0}^{\times })\simeq H^{1}(G,(\mathbb{F}_{p^{n}})^{\times })$
via the Teichmüller lift. In other words, we need to show (to prove cyclicity of the Picard group in this case) that the group
$H^{1}(G,(E_{n})_{0}^{\times })\simeq H^{1}(G,(\mathbb{F}_{p^{n}})^{\times })$
via the Teichmüller lift. In other words, we need to show (to prove cyclicity of the Picard group in this case) that the group
 $H^{1}(G,(\mathbb{F}_{p^{n}})^{\times })=\operatorname{Hom}(G,\mathbb{F}_{p^{n}}^{\times })$
is generated by the class
$H^{1}(G,(\mathbb{F}_{p^{n}})^{\times })=\operatorname{Hom}(G,\mathbb{F}_{p^{n}}^{\times })$
is generated by the class
![]() $\unicode[STIX]{x1D713}$
corresponding to the
$\unicode[STIX]{x1D713}$
corresponding to the
![]() $G$
-action on
$G$
-action on
 $\unicode[STIX]{x1D70B}_{-2}(E_{n})\otimes _{(E_{n})_{0}}\mathbb{F}_{p^{n}}$
. (This will give the order of the Picard group as well as solve the extension problem.) However, we know (by general facts about even-periodic ring spectra) that this is simply the action on the Lie algebra, i.e. the homomorphism of (2.1). However, as we remarked before, the kernel of (2.1) is pro-
$\unicode[STIX]{x1D70B}_{-2}(E_{n})\otimes _{(E_{n})_{0}}\mathbb{F}_{p^{n}}$
. (This will give the order of the Picard group as well as solve the extension problem.) However, we know (by general facts about even-periodic ring spectra) that this is simply the action on the Lie algebra, i.e. the homomorphism of (2.1). However, as we remarked before, the kernel of (2.1) is pro-
![]() $p$
, so its restriction to
$p$
, so its restriction to
![]() $G$
must be injective. Hence,
$G$
must be injective. Hence,
![]() $G$
injects into
$G$
injects into
![]() $\mathbb{F}_{p^{n}}^{\times }$
, which forces
$\mathbb{F}_{p^{n}}^{\times }$
, which forces
 $H^{1}(G,\mathbb{F}_{p^{n}}^{\times })$
to be generated by the class of the injection.◻
$H^{1}(G,\mathbb{F}_{p^{n}}^{\times })$
to be generated by the class of the injection.◻
4 Cyclicity of the Picard group
We now fix an odd prime
![]() $p$
, and work at height
$p$
, and work at height
 $n=p-1$
; we will omit subscripts from our notation. In this section, we will use the HFPSS to compute
$n=p-1$
; we will omit subscripts from our notation. In this section, we will use the HFPSS to compute
 $\operatorname{Pic}(E^{hG})$
for all finite subgroups
$\operatorname{Pic}(E^{hG})$
for all finite subgroups
![]() $G\subset \mathbb{G}$
, referring to future sections of the document for some technical results required. We will use the results of the previous section to reduce to the case where
$G\subset \mathbb{G}$
, referring to future sections of the document for some technical results required. We will use the results of the previous section to reduce to the case where
 $G=C_{p}$
is the
$G=C_{p}$
is the
![]() $p$
-Sylow subgroup of a maximal finite subgroup of
$p$
-Sylow subgroup of a maximal finite subgroup of
![]() $\mathbb{S}$
. We also sketch a direct proof when
$\mathbb{S}$
. We also sketch a direct proof when
![]() $G$
is a maximal finite subgroup of
$G$
is a maximal finite subgroup of
![]() $\mathbb{G}$
with
$\mathbb{G}$
with
![]() $p$
-torsion, to illustrate to the reader that taking Galois invariants simplifies the calculation somewhat.
$p$
-torsion, to illustrate to the reader that taking Galois invariants simplifies the calculation somewhat.
4.1 The general case
Our goal in this subsection is to prove the main result of this paper, namely the following theorem.
Theorem 4.1. Let
![]() $G\subset \mathbb{G}$
be a finite subgroup. Then
$G\subset \mathbb{G}$
be a finite subgroup. Then
 $\operatorname{Pic}(E^{hG})$
is cyclic, generated by
$\operatorname{Pic}(E^{hG})$
is cyclic, generated by
![]() $\unicode[STIX]{x1D6F4}E^{hG}$
.
$\unicode[STIX]{x1D6F4}E^{hG}$
.
By combining Propositions 3.10, and 3.11, it is enough to prove the result when
![]() $G=C_{p}$
. To handle this case, we start by recalling from Proposition 2.6 that, modulo the image of the transfer,
$G=C_{p}$
. To handle this case, we start by recalling from Proposition 2.6 that, modulo the image of the transfer,
 $$\begin{eqnarray}H^{\ast }(C_{p},E_{\ast })/\text{transfers}\simeq \mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(C_{p},E_{\ast })/\text{transfers}\simeq \mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
where
 $|\unicode[STIX]{x1D6FC}|=(1,2n)$
,
$|\unicode[STIX]{x1D6FC}|=(1,2n)$
,
 $|\unicode[STIX]{x1D6FD}|=(2,2pn),$
and
$|\unicode[STIX]{x1D6FD}|=(2,2pn),$
and
 $|\unicode[STIX]{x1D6FF}|=(0,2p)$
. Recall also that the homotopy groups
$|\unicode[STIX]{x1D6FF}|=(0,2p)$
. Recall also that the homotopy groups
 $\unicode[STIX]{x1D70B}_{\ast }(E^{hC_{p}})$
are
$\unicode[STIX]{x1D70B}_{\ast }(E^{hC_{p}})$
are
![]() $2p^{2}$
-periodic; this sets
$2p^{2}$
-periodic; this sets
 $\mathbb{Z}/(2p^{2})$
as a lower bound on the order of the Picard group. We will use the Picard spectral sequence to determine an upper bound. Since we will be comparing the Picard spectral sequence with the additive one (for computing
$\mathbb{Z}/(2p^{2})$
as a lower bound on the order of the Picard group. We will use the Picard spectral sequence to determine an upper bound. Since we will be comparing the Picard spectral sequence with the additive one (for computing
![]() $\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
), we will write
$\unicode[STIX]{x1D70B}_{\ast }E^{hC_{p}}$
), we will write
![]() $d_{k,\times }$
for the Picard differentials and
$d_{k,\times }$
for the Picard differentials and
![]() $d_{k}$
for the additive ones.
$d_{k}$
for the additive ones.
Our first task is to work out the
![]() $E_{2}$
-term
$E_{2}$
-term
 $H^{s}(C_{p},\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E))$
, and we are interested in the abutment for
$H^{s}(C_{p},\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E))$
, and we are interested in the abutment for
 $t-s=0$
. In the range where
$t-s=0$
. In the range where
![]() $t\geqslant 2$
, this follows immediately from (4.1). Namely, we have
$t\geqslant 2$
, this follows immediately from (4.1). Namely, we have
 $$\begin{eqnarray}H^{s}(C_{p},\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E))=(\mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}))^{s,t-1}\quad \text{when}~t\geqslant 2,s\geqslant 1\end{eqnarray}$$
$$\begin{eqnarray}H^{s}(C_{p},\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E))=(\mathbb{F}_{p^{n}}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}))^{s,t-1}\quad \text{when}~t\geqslant 2,s\geqslant 1\end{eqnarray}$$
since in this case
 $\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E)=\unicode[STIX]{x1D70B}_{t-1}E$
, equivariantly. (The superscript notation on the right-hand side designates the bidegree.)
$\unicode[STIX]{x1D70B}_{t}\,\mathfrak{pic}(E)=\unicode[STIX]{x1D70B}_{t-1}E$
, equivariantly. (The superscript notation on the right-hand side designates the bidegree.)
Let us single out the classes in the
 $t-s=0$
column, i.e. those with potential contribution to the Picard group of
$t-s=0$
column, i.e. those with potential contribution to the Picard group of
![]() $E^{hC_{p}}$
, that come from the additive spectral sequence (so,
$E^{hC_{p}}$
, that come from the additive spectral sequence (so,
![]() $s>1$
). They are
$s>1$
). They are
 $$\begin{eqnarray}e_{c}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{pc-1}\unicode[STIX]{x1D6FF}^{n-1-c(pn-1)},\end{eqnarray}$$
$$\begin{eqnarray}e_{c}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{pc-1}\unicode[STIX]{x1D6FF}^{n-1-c(pn-1)},\end{eqnarray}$$
indexed by integers
![]() $c\geqslant 1$
, and have cohomological degree
$c\geqslant 1$
, and have cohomological degree
 $s(e_{c})=2pc-1$
.
$s(e_{c})=2pc-1$
.
Lemma 4.2. The classes
![]() $e_{c}$
for
$e_{c}$
for
![]() $c\neq 1$
do not survive the Picard spectral sequence.
$c\neq 1$
do not survive the Picard spectral sequence.
Proof. In the additive spectral sequence, by Lemma 2.8, the classes
![]() $e_{c}$
are never the source of a
$e_{c}$
are never the source of a
![]() $d_{2p-1}$
differential, but can be the target. In particular, there are additive differentials
$d_{2p-1}$
differential, but can be the target. In particular, there are additive differentials
 $$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6FD}^{a}\unicode[STIX]{x1D6FF}^{b})\stackrel{\cdot }{=}b\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{a+p-1}\unicode[STIX]{x1D6FF}^{b-n^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2p-1}(\unicode[STIX]{x1D6FD}^{a}\unicode[STIX]{x1D6FF}^{b})\stackrel{\cdot }{=}b\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{a+p-1}\unicode[STIX]{x1D6FF}^{b-n^{2}}.\end{eqnarray}$$
For this image to be (a multiple of)
![]() $e_{c}$
, we must have
$e_{c}$
, we must have
 $b=n^{2}+n-1-c(pn-1)\equiv c-1~\text{mod}~p$
.
$b=n^{2}+n-1-c(pn-1)\equiv c-1~\text{mod}~p$
.
-
– If
 $c\not \equiv 1~\text{mod}~p$
, then
$c\not \equiv 1~\text{mod}~p$
, then
 $e_{c}$
is the target of
$e_{c}$
is the target of
 $d_{2p-1}$
on an element with
$d_{2p-1}$
on an element with
 $t=2p(c-1)$
. Since such
$t=2p(c-1)$
. Since such
 $c\geqslant 2$
, we have that
$c\geqslant 2$
, we have that
 $t\geqslant 2p>2p-1$
, so that Theorem 1.4 implies that this differential can be imported in the Picard spectral sequence. Hence,
$t\geqslant 2p>2p-1$
, so that Theorem 1.4 implies that this differential can be imported in the Picard spectral sequence. Hence,
 $e_{c}$
itself is killed.
$e_{c}$
itself is killed. -
– If
 $c\equiv 1~\text{mod}~p$
, this differential is zero (as then
$c\equiv 1~\text{mod}~p$
, this differential is zero (as then
 $b\equiv 0~\text{mod}~p$
), so
$b\equiv 0~\text{mod}~p$
), so
 $e_{c}$
survives the
$e_{c}$
survives the
 $d_{2p-1}$
.
$d_{2p-1}$
.
The next and only possible additive differential is a
![]() $d_{2n^{2}+1}$
. We have
$d_{2n^{2}+1}$
. We have
 $$\begin{eqnarray}d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}^{n^{3}})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1},\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}^{n^{3}})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{n^{2}+1},\end{eqnarray}$$
which determines the rest. Namely, we have, for all
 $a,b\in \mathbb{Z}$
,
$a,b\in \mathbb{Z}$
,
![]() $a\geqslant 0$
,
$a\geqslant 0$
,
 $$\begin{eqnarray}d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{a}\unicode[STIX]{x1D6FF}^{bp-1})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{a+n^{2}+1}\unicode[STIX]{x1D6FF}^{pb-n^{3}-1}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{a}\unicode[STIX]{x1D6FF}^{bp-1})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{a+n^{2}+1}\unicode[STIX]{x1D6FF}^{pb-n^{3}-1}.\end{eqnarray}$$
When
 $c\equiv 1~\text{mod}~(p)$
, we have that
$c\equiv 1~\text{mod}~(p)$
, we have that
 $n-1-c(pn-1)\equiv -1~\text{mod}~p$
, hence
$n-1-c(pn-1)\equiv -1~\text{mod}~p$
, hence
 $$\begin{eqnarray}d_{2n^{2}+1}(e_{c})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{pc+n^{2}}\unicode[STIX]{x1D6FF}^{c(1-pn)+n-n^{3}-1}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1}(e_{c})\stackrel{\cdot }{=}\unicode[STIX]{x1D6FD}^{pc+n^{2}}\unicode[STIX]{x1D6FF}^{c(1-pn)+n-n^{3}-1}.\end{eqnarray}$$
To import this differential to the Picard spectral sequence, we need to have that
 $$\begin{eqnarray}2n^{2}+1\leqslant t(e_{c})=2pc-2.\end{eqnarray}$$
$$\begin{eqnarray}2n^{2}+1\leqslant t(e_{c})=2pc-2.\end{eqnarray}$$
This holds whenever
 $$\begin{eqnarray}p-2+\frac{5}{2p}\leqslant c\quad \Leftrightarrow \quad c\geqslant p-1.\end{eqnarray}$$
$$\begin{eqnarray}p-2+\frac{5}{2p}\leqslant c\quad \Leftrightarrow \quad c\geqslant p-1.\end{eqnarray}$$
Since
 $c\equiv 1~\text{mod}~(p)$
, we see we can import all differentials except that involving
$c\equiv 1~\text{mod}~(p)$
, we see we can import all differentials except that involving
![]() $e_{1}$
, and the result follows.◻
$e_{1}$
, and the result follows.◻
Remark 4.3. This lemma says nothing about the fate of
![]() $e_{1}$
; it does not survive in the additive spectral sequence, but we shall see later that it must survive in the multiplicative case.
$e_{1}$
; it does not survive in the additive spectral sequence, but we shall see later that it must survive in the multiplicative case.
We can now prove our main result.
Proof of Theorem 4.1.
We have seen that in the range
![]() $t\geqslant 2$
of the HFPSS for
$t\geqslant 2$
of the HFPSS for
 $\unicode[STIX]{x1D70B}_{t-s}\,\mathfrak{pic}(E^{hC_{p}})$
, we only have a single possible contribution to the 0-stem, namely a group of order at most
$\unicode[STIX]{x1D70B}_{t-s}\,\mathfrak{pic}(E^{hC_{p}})$
, we only have a single possible contribution to the 0-stem, namely a group of order at most
![]() $p^{n}$
, arising from the class
$p^{n}$
, arising from the class
![]() $e_{1}$
. This class has bidegree
$e_{1}$
. This class has bidegree
 $(2p-1,2p-1)$
, and it follows from Theorem 7.1 that there is a differential
$(2p-1,2p-1)$
, and it follows from Theorem 7.1 that there is a differential
 $$\begin{eqnarray}d_{2n^{2}+1,\times }(e_{1})\stackrel{\cdot }{=}d_{2n^{2}+1}(e_{1})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1}),\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1,\times }(e_{1})\stackrel{\cdot }{=}d_{2n^{2}+1}(e_{1})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1}),\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D701}\in \mathbb{F}_{p}^{\times }$
. Let
$\unicode[STIX]{x1D701}\in \mathbb{F}_{p}^{\times }$
. Let
 $f_{t}=\unicode[STIX]{x1D6FD}^{n^{2}+n+1}\unicode[STIX]{x1D6FF}^{-n^{2}(n+1)}$
so that we have (in the additive spectral sequence)
$f_{t}=\unicode[STIX]{x1D6FD}^{n^{2}+n+1}\unicode[STIX]{x1D6FF}^{-n^{2}(n+1)}$
so that we have (in the additive spectral sequence)
 $$\begin{eqnarray}d_{2n^{2}+1}(e_{1})\stackrel{\cdot }{=}f_{t}.\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1}(e_{1})\stackrel{\cdot }{=}f_{t}.\end{eqnarray}$$
While it is possible to work out exactly what
 $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})$
is, we will not need to be so precise. Instead we claim that the group
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})$
is, we will not need to be so precise. Instead we claim that the group
![]() $\mathbb{F}_{p^{n}}e_{1}$
on the
$\mathbb{F}_{p^{n}}e_{1}$
on the
![]() $E_{2}$
-page can contribute at most an element of order
$E_{2}$
-page can contribute at most an element of order
![]() $p$
to Picard group.
$p$
to Picard group.
Choose
 $\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
such that
$\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
such that
 $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})=\unicode[STIX]{x1D709}^{\prime }f_{t}$
. Then we have
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})=\unicode[STIX]{x1D709}^{\prime }f_{t}$
. Then we have
 $$\begin{eqnarray}d_{2n^{2}+1}(e_{1})=\unicode[STIX]{x1D709}f_{t}\quad \text{and}\quad \unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})=\unicode[STIX]{x1D709}^{\prime }f_{t},\end{eqnarray}$$
$$\begin{eqnarray}d_{2n^{2}+1}(e_{1})=\unicode[STIX]{x1D709}f_{t}\quad \text{and}\quad \unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})=\unicode[STIX]{x1D709}^{\prime }f_{t},\end{eqnarray}$$
for
 $\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
and
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
and
![]() $\unicode[STIX]{x1D709}\neq 0$
. It follows from (4.2) that, for any
$\unicode[STIX]{x1D709}\neq 0$
. It follows from (4.2) that, for any
![]() $a\in \mathbb{F}_{p^{n}}$
, we have
$a\in \mathbb{F}_{p^{n}}$
, we have
 $$\begin{eqnarray}\displaystyle d_{2n^{2}+1,\times }(ae_{1}) & = & \displaystyle d_{2n^{2}+1}(ae_{1})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(ae_{1})\nonumber\\ \displaystyle & = & \displaystyle a\unicode[STIX]{x1D709}f_{t}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})\nonumber\\ \displaystyle & = & \displaystyle a\unicode[STIX]{x1D709}f_{t}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}^{\prime }f_{t}\nonumber\\ \displaystyle & = & \displaystyle (a\unicode[STIX]{x1D709}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}^{\prime })f_{t}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{2n^{2}+1,\times }(ae_{1}) & = & \displaystyle d_{2n^{2}+1}(ae_{1})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(ae_{1})\nonumber\\ \displaystyle & = & \displaystyle a\unicode[STIX]{x1D709}f_{t}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{n/2}(e_{1})\nonumber\\ \displaystyle & = & \displaystyle a\unicode[STIX]{x1D709}f_{t}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}^{\prime }f_{t}\nonumber\\ \displaystyle & = & \displaystyle (a\unicode[STIX]{x1D709}+a^{p}\unicode[STIX]{x1D701}\unicode[STIX]{x1D709}^{\prime })f_{t}.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D709}\neq 0$
, there are at most
$\unicode[STIX]{x1D709}\neq 0$
, there are at most
![]() $p$
choices of
$p$
choices of
![]() $a$
that make the above vanish, and so we do indeed have an upper bound of
$a$
that make the above vanish, and so we do indeed have an upper bound of
![]() $\mathbb{Z}/p$
for the contribution of
$\mathbb{Z}/p$
for the contribution of
![]() $e_{1}$
in
$e_{1}$
in
 $\operatorname{Pic}(E^{hC_{p}})$
.
$\operatorname{Pic}(E^{hC_{p}})$
.
Finally, we know from Proposition 6.5 that
 $H^{1}(C_{p},\unicode[STIX]{x1D70B}_{1}\,\mathfrak{pic}(E))\simeq \mathbb{Z}/p$
, while as usual it follows from [Reference Baker and RichterBR05] that the invariants
$H^{1}(C_{p},\unicode[STIX]{x1D70B}_{1}\,\mathfrak{pic}(E))\simeq \mathbb{Z}/p$
, while as usual it follows from [Reference Baker and RichterBR05] that the invariants
 $H^{0}(C_{p},\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E))$
are
$H^{0}(C_{p},\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E))$
are
![]() $\mathbb{Z}/2$
. Thus, we have the following in the 0-stem of the Picard spectral sequence:
$\mathbb{Z}/2$
. Thus, we have the following in the 0-stem of the Picard spectral sequence:
-
– a group of order at most
 $2$
in
$2$
in
 $t=s=0$
;
$t=s=0$
; -
– a group of order at most
 $p$
in
$p$
in
 $t=s=1$
; and
$t=s=1$
; and -
– a group of order at most
 $p$
in
$p$
in
 $t=s=2p-1$
.
$t=s=2p-1$
.
This gives an upper bound of
![]() $2p^{2}$
for the order of the Picard group, but as noted previously this is also a lower bound, and the result follows. A picture of the Picard spectral sequence for
$2p^{2}$
for the order of the Picard group, but as noted previously this is also a lower bound, and the result follows. A picture of the Picard spectral sequence for
![]() $n=2$
,
$n=2$
,
![]() $p=3$
and
$p=3$
and
 $G=C_{3}$
is shown in Figure 2.◻
$G=C_{3}$
is shown in Figure 2.◻

Figure 2. The HFPSS for
 $\unicode[STIX]{x1D70B}_{\ast }\,\mathfrak{pic}\,E_{p-1}^{hC_{p}}$
in the case
$\unicode[STIX]{x1D70B}_{\ast }\,\mathfrak{pic}\,E_{p-1}^{hC_{p}}$
in the case
![]() $n=2$
,
$n=2$
,
![]() $p=3$
. The differential out of
$p=3$
. The differential out of
![]() $(0,5)$
has kernel
$(0,5)$
has kernel
![]() $\mathbb{Z}/3$
. (Here
$\mathbb{Z}/3$
. (Here
![]() $\bullet$
denotes
$\bullet$
denotes
![]() $\mathbb{Z}/3$
,
$\mathbb{Z}/3$
,
4.2 The maximal finite subgroup
In this short section we sketch a direct proof in the case that
![]() $G$
is a maximal finite subgroup of
$G$
is a maximal finite subgroup of
![]() $\mathbb{G}_{n}$
with
$\mathbb{G}_{n}$
with
![]() $p$
-torsion. We include this to show that after taking Galois invariants the calculation is slightly easier; in particular, we do not need to use Theorem 7.1. The calculation of
$p$
-torsion. We include this to show that after taking Galois invariants the calculation is slightly easier; in particular, we do not need to use Theorem 7.1. The calculation of
 $\operatorname{Pic}(E_{n}^{hG})$
in this case was previously known to Hopkins.
$\operatorname{Pic}(E_{n}^{hG})$
in this case was previously known to Hopkins.
We start by recalling that, modulo the image of the transfer, we have
 $$\begin{eqnarray}H^{\ast }(G,E_{\ast })/\text{transfers}\simeq \mathbb{F}_{p}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6E5}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(G,E_{\ast })/\text{transfers}\simeq \mathbb{F}_{p}[\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6E5}^{\pm 1}]/(\unicode[STIX]{x1D6FC}^{2}),\end{eqnarray}$$
where
 $|\unicode[STIX]{x1D6E5}|=(0,2pn^{2})$
, and that the homotopy groups
$|\unicode[STIX]{x1D6E5}|=(0,2pn^{2})$
, and that the homotopy groups
 $\unicode[STIX]{x1D70B}_{\ast }(E^{hG})$
are
$\unicode[STIX]{x1D70B}_{\ast }(E^{hG})$
are
![]() $2p^{2}n^{2}$
periodic; this sets
$2p^{2}n^{2}$
periodic; this sets
 $\mathbb{Z}/(2p^{2}n^{2})$
as a lower bound on the order of the Picard group. As usual, we will use the Picard spectral sequence to determine an upper bound.
$\mathbb{Z}/(2p^{2}n^{2})$
as a lower bound on the order of the Picard group. As usual, we will use the Picard spectral sequence to determine an upper bound.
In the range
![]() $t\geqslant 2$
we have classes
$t\geqslant 2$
we have classes
 $$\begin{eqnarray}e_{c}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{pc-1}\unicode[STIX]{x1D6E5}^{(c(1-pn)+n-1)/n^{2}},\end{eqnarray}$$
$$\begin{eqnarray}e_{c}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{pc-1}\unicode[STIX]{x1D6E5}^{(c(1-pn)+n-1)/n^{2}},\end{eqnarray}$$
in the 0-stem, indexed by integers
![]() $c\geqslant 1$
, which have cohomological degree
$c\geqslant 1$
, which have cohomological degree
 $s(e_{c})=2pc-1$
. Once again, one can check that the classes
$s(e_{c})=2pc-1$
. Once again, one can check that the classes
![]() $e_{c}$
for
$e_{c}$
for
![]() $c\neq 1$
do not survive the Picard spectral sequence. One key difference to the case of
$c\neq 1$
do not survive the Picard spectral sequence. One key difference to the case of
![]() $C_{p}$
is that we see immediately that
$C_{p}$
is that we see immediately that
![]() $e_{1}$
can contribute a group of at most order
$e_{1}$
can contribute a group of at most order
![]() $p$
to
$p$
to
 $\operatorname{Pic}(E^{hG})$
, thus avoiding the use of Theorem 7.1.
$\operatorname{Pic}(E^{hG})$
, thus avoiding the use of Theorem 7.1.
We are then left with calculating the contributions from
![]() $t=0$
and
$t=0$
and
![]() $t=1$
. It follows from [Reference Baker and RichterBR05] that
$t=1$
. It follows from [Reference Baker and RichterBR05] that
 $H^{0}(G,\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E))\simeq H^{0}(G,\mathbb{Z}/2)\simeq \mathbb{Z}/2$
, and so we are left to determine
$H^{0}(G,\unicode[STIX]{x1D70B}_{0}\,\mathfrak{pic}(E))\simeq H^{0}(G,\mathbb{Z}/2)\simeq \mathbb{Z}/2$
, and so we are left to determine
 $H^{1}(G,\unicode[STIX]{x1D70B}_{1}\,\mathfrak{pic}(E))\simeq H^{1}(G,E_{0}^{\times })$
. This can be done in at least a couple of different ways; for example, as in Proposition 6.5, or using an exponential map and several Bockstein spectral sequences as in [Reference KaramanovKar10]. In any case, the result is a group of order
$H^{1}(G,\unicode[STIX]{x1D70B}_{1}\,\mathfrak{pic}(E))\simeq H^{1}(G,E_{0}^{\times })$
. This can be done in at least a couple of different ways; for example, as in Proposition 6.5, or using an exponential map and several Bockstein spectral sequences as in [Reference KaramanovKar10]. In any case, the result is a group of order
![]() $pn^{2}$
.
$pn^{2}$
.

Figure 3. The HFPSS for
 $\unicode[STIX]{x1D70B}_{\ast }\,\mathfrak{pic}\,E^{hG}$
in the case
$\unicode[STIX]{x1D70B}_{\ast }\,\mathfrak{pic}\,E^{hG}$
in the case
![]() $n=2$
,
$n=2$
,
![]() $p=3$
for
$p=3$
for
![]() $G\subset \mathbb{G}$
a maximal finite subgroup whose order is divisible by
$G\subset \mathbb{G}$
a maximal finite subgroup whose order is divisible by
![]() $p$
. (Here
$p$
. (Here
![]() $\Box$
denotes
$\Box$
denotes
![]() $\mathbb{Z}/4$
,
$\mathbb{Z}/4$
,
![]() $\bullet$
denotes
$\bullet$
denotes
![]() $\mathbb{Z}/3$
, and
$\mathbb{Z}/3$
, and
![]() $\times$
denotes
$\times$
denotes
![]() $\mathbb{Z}/2$
.)
$\mathbb{Z}/2$
.)
Putting all of this together, we obtain an upper bound
 $2\cdot pn^{2}\cdot p$
for the abutment, i.e. for the Picard group of
$2\cdot pn^{2}\cdot p$
for the abutment, i.e. for the Picard group of
![]() $E^{hG}$
. However, by Remark 2.9 we know the Picard group contains a cyclic group of order
$E^{hG}$
. However, by Remark 2.9 we know the Picard group contains a cyclic group of order
![]() $2p^{2}n^{2}$
, and so it follows that
$2p^{2}n^{2}$
, and so it follows that
 $\operatorname{Pic}(E^{hG})$
is indeed cyclic of order
$\operatorname{Pic}(E^{hG})$
is indeed cyclic of order
![]() $2p^{2}n^{2}$
. We illustrate this for
$2p^{2}n^{2}$
. We illustrate this for
![]() $n=2$
,
$n=2$
,
![]() $p=3$
in Figure 3.
$p=3$
in Figure 3.
Part II. Computational tools
5 Truncated logarithms and differentials in the algebraic setting
5.1 Overview
In this section, we describe a tool for working with the following general situation. Let
![]() $R$
be a complete noetherian local ring with maximal ideal
$R$
be a complete noetherian local ring with maximal ideal
![]() $\mathfrak{m}\subset R$
such that the residue field
$\mathfrak{m}\subset R$
such that the residue field
![]() $R/\mathfrak{m}$
has characteristic
$R/\mathfrak{m}$
has characteristic
![]() $p$
. Suppose
$p$
. Suppose
![]() $G$
is a finite group acting on
$G$
is a finite group acting on
![]() $R$
. Our goal is to calculate the cohomology groups
$R$
. Our goal is to calculate the cohomology groups
 $H^{i}(G,R^{\times })$
. We assume that the additive analog, the cohomology groups
$H^{i}(G,R^{\times })$
. We assume that the additive analog, the cohomology groups
 $H^{i}(G,R)$
, are understood by other means.
$H^{i}(G,R)$
, are understood by other means.
One approach towards
 $H^{i}(G,R^{\times })$
is to consider the
$H^{i}(G,R^{\times })$
is to consider the
![]() $\mathfrak{m}$
-adic filtration on
$\mathfrak{m}$
-adic filtration on
![]() $R$
. It induces a
$R$
. It induces a
![]() $G$
-stable filtration on
$G$
-stable filtration on
![]() $R^{\times }$
,
$R^{\times }$
,
 $$\begin{eqnarray}R^{\times }\supset 1+\mathfrak{m}\supset 1+\mathfrak{m}^{2}\supset \cdots ,\end{eqnarray}$$
$$\begin{eqnarray}R^{\times }\supset 1+\mathfrak{m}\supset 1+\mathfrak{m}^{2}\supset \cdots ,\end{eqnarray}$$
which leads to a spectral sequence
 $$\begin{eqnarray}E_{1}^{i,j}=H^{i}(G,(1+\mathfrak{m}^{j})/(1+\mathfrak{m}^{j+1}))\;\Longrightarrow \;H^{i}(G,R^{\times }).\end{eqnarray}$$
$$\begin{eqnarray}E_{1}^{i,j}=H^{i}(G,(1+\mathfrak{m}^{j})/(1+\mathfrak{m}^{j+1}))\;\Longrightarrow \;H^{i}(G,R^{\times }).\end{eqnarray}$$
Here the differentials run
 $d_{k}:E_{k}^{i,j}\rightarrow E_{k}^{i+1,j+k}$
. For
$d_{k}:E_{k}^{i,j}\rightarrow E_{k}^{i+1,j+k}$
. For
![]() $j>0$
, there is a
$j>0$
, there is a
![]() $G$
-equivariant isomorphism (sending
$G$
-equivariant isomorphism (sending
 $1+x\mapsto x$
)
$1+x\mapsto x$
)
 $$\begin{eqnarray}(1+\mathfrak{m}^{j})/(1+\mathfrak{m}^{j+1})\simeq \mathfrak{m}^{j}/\mathfrak{m}^{j+1}\end{eqnarray}$$
$$\begin{eqnarray}(1+\mathfrak{m}^{j})/(1+\mathfrak{m}^{j+1})\simeq \mathfrak{m}^{j}/\mathfrak{m}^{j+1}\end{eqnarray}$$
between the associated graded module of the filtration (5.1) and the
![]() $\mathfrak{m}$
-adic filtration on
$\mathfrak{m}$
-adic filtration on
![]() $R$
itself. The latter, of course, leads to a spectral sequence (indexed similarly)
$R$
itself. The latter, of course, leads to a spectral sequence (indexed similarly)
 $$\begin{eqnarray}E_{1}^{i,j}=H^{i}(G,\mathfrak{m}^{j}/\mathfrak{m}^{j+1})\;\Longrightarrow \;H^{i}(G,R).\end{eqnarray}$$
$$\begin{eqnarray}E_{1}^{i,j}=H^{i}(G,\mathfrak{m}^{j}/\mathfrak{m}^{j+1})\;\Longrightarrow \;H^{i}(G,R).\end{eqnarray}$$
In practice, one may (and is likely to) understand the additive spectral sequence (5.3) concretely in specific instances, for instance, because of the additional tools provided by multiplicativity. The additive and the multiplicative spectral sequences have almost the same
![]() $E_{1}$
pages, and in this section we will give a tool for comparing differentials in a range of dimensions.
$E_{1}$
pages, and in this section we will give a tool for comparing differentials in a range of dimensions.
5.2 The
 $p$
-truncated exponential
$p$
-truncated exponential
Let
![]() $R$
be a commutative ring and let
$R$
be a commutative ring and let
![]() $I\subset R$
be an ideal such that
$I\subset R$
be an ideal such that
![]() $I^{2}=0$
. Then there is an isomorphism of groups
$I^{2}=0$
. Then there is an isomorphism of groups
 $$\begin{eqnarray}I\simeq 1+I\subset R^{\times },\quad x\mapsto 1+x.\end{eqnarray}$$
$$\begin{eqnarray}I\simeq 1+I\subset R^{\times },\quad x\mapsto 1+x.\end{eqnarray}$$
We now review a crucial and elementary piece of algebra that will enable generalizations of this fact when certain primes are inverted in
![]() $R$
.
$R$
.
Definition 5.1. Let
![]() $R$
be a
$R$
be a
 $\mathbb{Z}[1/(p-1)!]$
-algebra. We define a function
$\mathbb{Z}[1/(p-1)!]$
-algebra. We define a function
 $$\begin{eqnarray}\exp _{p}:R\rightarrow R,\quad \exp _{p}(x)=1+x+\frac{x^{2}}{2!}+\cdots +\frac{x^{p-1}}{(p-1)!},\end{eqnarray}$$
$$\begin{eqnarray}\exp _{p}:R\rightarrow R,\quad \exp _{p}(x)=1+x+\frac{x^{2}}{2!}+\cdots +\frac{x^{p-1}}{(p-1)!},\end{eqnarray}$$
called the
![]() $p$
-truncated exponential, and a function
$p$
-truncated exponential, and a function
 $$\begin{eqnarray}\log _{p}:R\rightarrow R,\quad \log _{p}(x)=\mathop{\sum }_{n=1}^{p-1}(-1)^{n-1}\frac{(x-1)^{n}}{n},\end{eqnarray}$$
$$\begin{eqnarray}\log _{p}:R\rightarrow R,\quad \log _{p}(x)=\mathop{\sum }_{n=1}^{p-1}(-1)^{n-1}\frac{(x-1)^{n}}{n},\end{eqnarray}$$
called the
![]() $p$
-truncated logarithm.
$p$
-truncated logarithm.
The significance arises from the following well-known application.
Lemma 5.2. If
![]() $I\subset R$
is an ideal with
$I\subset R$
is an ideal with
![]() $I^{p}=0$
and
$I^{p}=0$
and
![]() $R$
is a
$R$
is a
 $\mathbb{Z}[1/(p-1)!]$
-algebra, then the map
$\mathbb{Z}[1/(p-1)!]$
-algebra, then the map
 $$\begin{eqnarray}\exp _{p}:I\rightarrow 1+I\subset R^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\exp _{p}:I\rightarrow 1+I\subset R^{\times }\end{eqnarray}$$
is a group isomorphism (whose inverse is given by the truncated logarithm).
We note that the inverse isomorphisms
 $\exp _{p},\log _{p}$
between
$\exp _{p},\log _{p}$
between
![]() $I$
and
$I$
and
![]() $1+I$
are compatible with the
$1+I$
are compatible with the
![]() $I$
-adic filtration, and with the isomorphisms on associated graded modules
$I$
-adic filtration, and with the isomorphisms on associated graded modules
 $I^{k}/I^{k+1}\simeq (1+I^{k})/(1+I^{k+1})$
given by
$I^{k}/I^{k+1}\simeq (1+I^{k})/(1+I^{k+1})$
given by
 $1+x\mapsto x$
.
$1+x\mapsto x$
.
Example 5.3. Suppose
![]() $(A,\mathfrak{m})$
is a local ring whose residue field is of characteristic
$(A,\mathfrak{m})$
is a local ring whose residue field is of characteristic
![]() $p$
, a prime larger than
$p$
, a prime larger than
![]() $p$
, or zero. Then for each
$p$
, or zero. Then for each
![]() $k>0$
, we have a functorial isomorphism of groups
$k>0$
, we have a functorial isomorphism of groups
 $$\begin{eqnarray}(1+\mathfrak{m}^{k})/(1+\mathfrak{m}^{pk})\simeq \mathfrak{m}^{k}/\mathfrak{m}^{pk},\end{eqnarray}$$
$$\begin{eqnarray}(1+\mathfrak{m}^{k})/(1+\mathfrak{m}^{pk})\simeq \mathfrak{m}^{k}/\mathfrak{m}^{pk},\end{eqnarray}$$
given by the truncated logarithm. This leads to an identification of the spectral sequences (5.3) and (5.2) in a ‘stable’ range of dimensions (which we will make more precise below).
We will actually need a slight generalization of this fact (which measures the first-order failure of
![]() $\exp _{p}$
to be a homomorphism in general).
$\exp _{p}$
to be a homomorphism in general).
Definition 5.4. Given
 $x_{1},\ldots ,x_{k}\in R$
, we define
$x_{1},\ldots ,x_{k}\in R$
, we define
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\stackrel{\text{def}}{=}\frac{(\mathop{\sum }_{i}x_{i})^{p}-\mathop{\sum }_{i}x_{i}^{p}}{p!}=\mathop{\sum }_{\substack{ j_{1},\ldots ,j_{k}\in [0,p-1] \\ j_{1}+\cdots +j_{k}=p}}^{p-1}\frac{x_{1}^{j_{1}}x_{2}^{j_{2}}\ldots x_{k}^{j_{k}}}{j_{1}!\ldots j_{k}!},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\stackrel{\text{def}}{=}\frac{(\mathop{\sum }_{i}x_{i})^{p}-\mathop{\sum }_{i}x_{i}^{p}}{p!}=\mathop{\sum }_{\substack{ j_{1},\ldots ,j_{k}\in [0,p-1] \\ j_{1}+\cdots +j_{k}=p}}^{p-1}\frac{x_{1}^{j_{1}}x_{2}^{j_{2}}\ldots x_{k}^{j_{k}}}{j_{1}!\ldots j_{k}!},\end{eqnarray}$$
so that we obtain a function
 $\unicode[STIX]{x1D70E}_{p}(\cdot ,\ldots ,\cdot ):R^{k}\rightarrow R$
. If
$\unicode[STIX]{x1D70E}_{p}(\cdot ,\ldots ,\cdot ):R^{k}\rightarrow R$
. If
![]() $M$
is a
$M$
is a
 $\mathbb{Z}[1/(p-1)!]$
-module, we will also use
$\mathbb{Z}[1/(p-1)!]$
-module, we will also use
![]() $\unicode[STIX]{x1D70E}_{p}$
to denote the induced function
$\unicode[STIX]{x1D70E}_{p}$
to denote the induced function
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{p}:M^{k}\rightarrow \operatorname{Sym}^{p}M,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{p}:M^{k}\rightarrow \operatorname{Sym}^{p}M,\end{eqnarray}$$
defined by the same formula.
Proposition 5.5. Let
![]() $R$
be a
$R$
be a
 $\mathbb{Z}[1/(p-1)!]$
-algebra. Suppose that
$\mathbb{Z}[1/(p-1)!]$
-algebra. Suppose that
 $x_{1},\ldots ,x_{k}\in R$
and let
$x_{1},\ldots ,x_{k}\in R$
and let
 $I=(x_{1},\ldots ,x_{k})\subset R$
. Then
$I=(x_{1},\ldots ,x_{k})\subset R$
. Then
 $$\begin{eqnarray}\prod \exp _{p}(x_{i})-\exp _{p}\Bigl(\sum x_{i}\Bigr)\equiv \unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
$$\begin{eqnarray}\prod \exp _{p}(x_{i})-\exp _{p}\Bigl(\sum x_{i}\Bigr)\equiv \unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
Proof. This follows by a straightforward computation. ◻
With notation as above, observe that
 $\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\in I^{p}$
and that
$\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\in I^{p}$
and that
 $\exp _{p}(x)\in 1+I$
for
$\exp _{p}(x)\in 1+I$
for
![]() $x\in I$
. As a result, we also find that, if
$x\in I$
. As a result, we also find that, if
![]() $I$
is contained in the Jacobson radical of
$I$
is contained in the Jacobson radical of
![]() $R$
, then we have the formula
$R$
, then we have the formula
 $$\begin{eqnarray}\frac{\exp _{p}(\sum x_{i})}{\prod \exp _{p}(x_{i})}\equiv 1-\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\exp _{p}(\sum x_{i})}{\prod \exp _{p}(x_{i})}\equiv 1-\unicode[STIX]{x1D70E}_{p}(x_{1},\ldots ,x_{k})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
For example, taking
![]() $k=2$
and taking
$k=2$
and taking
 $x_{1}=y,x_{2}=-y$
, we find
$x_{1}=y,x_{2}=-y$
, we find
 $$\begin{eqnarray}\exp _{p}(y)\exp _{p}(-y)\equiv 1+\unicode[STIX]{x1D70E}_{p}(y,-y)\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
$$\begin{eqnarray}\exp _{p}(y)\exp _{p}(-y)\equiv 1+\unicode[STIX]{x1D70E}_{p}(y,-y)\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
Note, in addition, that
 $\unicode[STIX]{x1D70E}_{p}(y,-y)=y^{p}\unicode[STIX]{x1D70E}_{p}(1,-1)$
.
$\unicode[STIX]{x1D70E}_{p}(y,-y)=y^{p}\unicode[STIX]{x1D70E}_{p}(1,-1)$
.
Corollary 5.6. If
 $y_{0},\ldots ,y_{n}\in I$
and
$y_{0},\ldots ,y_{n}\in I$
and
![]() $I$
is contained in the radical of
$I$
is contained in the radical of
![]() $R$
, then
$R$
, then
 $$\begin{eqnarray}\frac{\exp _{p}(\mathop{\sum }_{i=0}^{n}(-1)^{i}y_{i})}{\mathop{\prod }_{i=0}^{n}\exp _{p}(y_{i})^{(-1)^{i}}}\equiv 1-\unicode[STIX]{x1D70E}_{p}(y_{0},-y_{1},\ldots ,(-1)^{n}y_{n})+\mathop{\sum }_{i~\text{odd}}\unicode[STIX]{x1D70E}_{p}(y_{i},-y_{i})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\exp _{p}(\mathop{\sum }_{i=0}^{n}(-1)^{i}y_{i})}{\mathop{\prod }_{i=0}^{n}\exp _{p}(y_{i})^{(-1)^{i}}}\equiv 1-\unicode[STIX]{x1D70E}_{p}(y_{0},-y_{1},\ldots ,(-1)^{n}y_{n})+\mathop{\sum }_{i~\text{odd}}\unicode[STIX]{x1D70E}_{p}(y_{i},-y_{i})\quad \text{mod}~I^{p+1}.\end{eqnarray}$$
Proof. This follows from (5.8) taking
 $x_{i}=(-1)^{i}y_{i}$
. We multiply it by
$x_{i}=(-1)^{i}y_{i}$
. We multiply it by
 $\prod _{i~\text{odd}}(\exp _{p}(-y_{i})/\exp _{p}(y_{i})^{-1})$
and invoke (5.9).◻
$\prod _{i~\text{odd}}(\exp _{p}(-y_{i})/\exp _{p}(y_{i})^{-1})$
and invoke (5.9).◻
We give a name to the discrepancy term; given
 $y_{0},\ldots ,y_{n}$
, we set
$y_{0},\ldots ,y_{n}$
, we set
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{p}(y_{0},\ldots ,y_{n})\stackrel{\text{def}}{=}\unicode[STIX]{x1D70E}_{p}(y_{0},-y_{1},\ldots ,(-1)^{n}y_{n})-\mathop{\sum }_{i~\text{odd}}\unicode[STIX]{x1D70E}_{p}(y_{i},-y_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{p}(y_{0},\ldots ,y_{n})\stackrel{\text{def}}{=}\unicode[STIX]{x1D70E}_{p}(y_{0},-y_{1},\ldots ,(-1)^{n}y_{n})-\mathop{\sum }_{i~\text{odd}}\unicode[STIX]{x1D70E}_{p}(y_{i},-y_{i}).\end{eqnarray}$$
5.3 The stable range and first differential
We begin by describing a version of the general setup of comparison of spectral sequences from the introduction to this section.
Proposition 5.7. Let
![]() $G$
be a finite group acting on a local noetherian ring
$G$
be a finite group acting on a local noetherian ring
![]() $(R,\mathfrak{n})$
with
$(R,\mathfrak{n})$
with
![]() $(p-1)!$
invertible. Consider the two
$(p-1)!$
invertible. Consider the two
 $\text{truncated}$
spectral sequences
$\text{truncated}$
spectral sequences
 $$\begin{eqnarray}\displaystyle E_{1}^{s,t} & = & \displaystyle H^{s}(G,\mathfrak{n}^{t}/\mathfrak{n}^{t+1})\;\Longrightarrow \;H^{i}(G,\mathfrak{n}^{k}/\mathfrak{n}^{pk}),\nonumber\\ \displaystyle E_{1}^{s,t} & = & \displaystyle H^{i}(G,\mathfrak{n}^{t}/\mathfrak{n}^{t+1})\;\Longrightarrow \;H^{i}(G,(1+\mathfrak{n}^{k})/(1+\mathfrak{n}^{pk})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}^{s,t} & = & \displaystyle H^{s}(G,\mathfrak{n}^{t}/\mathfrak{n}^{t+1})\;\Longrightarrow \;H^{i}(G,\mathfrak{n}^{k}/\mathfrak{n}^{pk}),\nonumber\\ \displaystyle E_{1}^{s,t} & = & \displaystyle H^{i}(G,\mathfrak{n}^{t}/\mathfrak{n}^{t+1})\;\Longrightarrow \;H^{i}(G,(1+\mathfrak{n}^{k})/(1+\mathfrak{n}^{pk})),\nonumber\end{eqnarray}$$
where
 $t\in [k,pk-1]$
. Then the natural identification of
$t\in [k,pk-1]$
. Then the natural identification of
![]() $E_{1}$
-terms extends to an isomorphism of spectral sequences given by the
$E_{1}$
-terms extends to an isomorphism of spectral sequences given by the
![]() $p$
-truncated exponential.
$p$
-truncated exponential.
We now describe the setup that will enable us to ultimately give a formula for the first unequal differential. For convenience, we will work with nonunital commutative rings here. If
![]() $A$
is a nonunital commutative ring, we define an abelian monoid
$A$
is a nonunital commutative ring, we define an abelian monoid
![]() $1+A$
consisting of formal elements
$1+A$
consisting of formal elements
 $1+x,x\in A$
with the obvious multiplication rule.
$1+x,x\in A$
with the obvious multiplication rule.
Construction 5.8. Suppose
![]() $\mathfrak{m}^{\bullet }$
is a nonunital cosimplicial commutative
$\mathfrak{m}^{\bullet }$
is a nonunital cosimplicial commutative
 $\mathbb{Z}[1/(p-1)!]$
-algebra such that
$\mathbb{Z}[1/(p-1)!]$
-algebra such that
 $\mathfrak{m}^{\bullet ,p+1}=0$
.Footnote
2
We have a descending multiplicative filtration by powers
$\mathfrak{m}^{\bullet ,p+1}=0$
.Footnote
2
We have a descending multiplicative filtration by powers
 $$\begin{eqnarray}\mathfrak{m}^{\bullet }\supset \mathfrak{m}^{\bullet ,2}\supset \cdots .\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}^{\bullet }\supset \mathfrak{m}^{\bullet ,2}\supset \cdots .\end{eqnarray}$$
Consider also the cosimplicial abelian group
![]() $1+\mathfrak{m}^{\bullet }$
.Footnote
3
We also have a filtration of cosimplicial abelian groups
$1+\mathfrak{m}^{\bullet }$
.Footnote
3
We also have a filtration of cosimplicial abelian groups
 $$\begin{eqnarray}1+\mathfrak{m}^{\bullet }\supset 1+\mathfrak{m}^{\bullet ,2}\supset \cdots ,\end{eqnarray}$$
$$\begin{eqnarray}1+\mathfrak{m}^{\bullet }\supset 1+\mathfrak{m}^{\bullet ,2}\supset \cdots ,\end{eqnarray}$$
and the successive quotients are isomorphic to those of the additive one.
Both lead to spectral sequences starting from the associated graded modules
 $\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1}$
(for
$\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1}$
(for
 $1\leqslant j\leqslant p$
) converging to the cohomology of
$1\leqslant j\leqslant p$
) converging to the cohomology of
![]() $\mathfrak{m}^{\bullet }$
(respectively
$\mathfrak{m}^{\bullet }$
(respectively
![]() $1+\mathfrak{m}^{\bullet }$
), i.e. the
$1+\mathfrak{m}^{\bullet }$
), i.e. the
![]() $E_{1}$
-pages are identified. We have spectral sequences
$E_{1}$
-pages are identified. We have spectral sequences
 $$\begin{eqnarray}\displaystyle E_{1}^{i,j} & = & \displaystyle H^{i}(\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1})\;\Longrightarrow \;H^{i}(\mathfrak{m}^{\bullet })\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}^{i,j} & = & \displaystyle H^{i}(\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1})\;\Longrightarrow \;H^{i}(\mathfrak{m}^{\bullet })\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle E_{1}^{i,j,\times } & = & \displaystyle H^{i}(\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1})\;\Longrightarrow \;H^{i}(1+\mathfrak{m}^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{1}^{i,j,\times } & = & \displaystyle H^{i}(\mathfrak{m}^{\bullet ,j}/\mathfrak{m}^{\bullet ,j+1})\;\Longrightarrow \;H^{i}(1+\mathfrak{m}^{\bullet }).\end{eqnarray}$$
The
![]() $E_{1}$
-terms are identified. We will denote the differentials at the
$E_{1}$
-terms are identified. We will denote the differentials at the
![]() $k$
th page by
$k$
th page by
![]() $d_{k}$
and
$d_{k}$
and
![]() $d_{k}^{\times }$
, respectively.
$d_{k}^{\times }$
, respectively.
Using the truncated exponential, we obtain isomorphisms of filtered cosimplicial abelian groups
 $$\begin{eqnarray}\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}\simeq (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p}),\quad \mathfrak{m}^{\bullet ,2}\simeq 1+\mathfrak{m}^{\bullet ,2}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}\simeq (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p}),\quad \mathfrak{m}^{\bullet ,2}\simeq 1+\mathfrak{m}^{\bullet ,2}\end{eqnarray}$$
inducing the above isomorphism on the associated graded modules.
The above construction yields the following result.
Proposition 5.9 (Spectral sequence comparison result, stable range).
In the spectral sequences
![]() $E_{k}^{\ast ,\ast }$
and
$E_{k}^{\ast ,\ast }$
and
![]() $E_{k}^{\ast ,\ast ,\times }$
above, we have isomorphisms
$E_{k}^{\ast ,\ast ,\times }$
above, we have isomorphisms
 $E_{k}^{\ast ,\ast }\simeq E_{k}^{\ast ,\ast ,\times }$
for
$E_{k}^{\ast ,\ast }\simeq E_{k}^{\ast ,\ast ,\times }$
for
 $k\leqslant p-1$
. This identification is compatible with the above identification at
$k\leqslant p-1$
. This identification is compatible with the above identification at
![]() $k=1$
and is compatible with the differentials
$k=1$
and is compatible with the differentials
![]() $d_{k}$
for
$d_{k}$
for
 $k<p-1$
.
$k<p-1$
.
The most important goal is to obtain a description of the first ‘unstable’ differential
![]() $d_{p-1}$
(in the present setup of nonunital algebras with
$d_{p-1}$
(in the present setup of nonunital algebras with
![]() $(p+1)$
-fold products zero, it is also the last differential in the spectral sequence).
$(p+1)$
-fold products zero, it is also the last differential in the spectral sequence).
Let
![]() $P^{\bullet }$
be a cosimplicial
$P^{\bullet }$
be a cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-module. Then we can consider the cosimplicial
$\mathbb{Z}[1/(p-1)!]$
-module. Then we can consider the cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-module
$\mathbb{Z}[1/(p-1)!]$
-module
 $\operatorname{Sym}^{p}P^{\bullet }$
obtained by applying the
$\operatorname{Sym}^{p}P^{\bullet }$
obtained by applying the
![]() $p$
th symmetric power levelwise. We construct an operation
$p$
th symmetric power levelwise. We construct an operation
 $$\begin{eqnarray}H^{i}(P^{\bullet })\rightarrow H^{i+1}(\operatorname{Sym}^{p}P^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(P^{\bullet })\rightarrow H^{i+1}(\operatorname{Sym}^{p}P^{\bullet }).\end{eqnarray}$$
Construction 5.10. Let
![]() $x\in P^{i}$
. We define
$x\in P^{i}$
. We define
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x)\stackrel{\text{def}}{=}\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x,\unicode[STIX]{x2202}^{1}x,\unicode[STIX]{x2202}^{2}x,\ldots ,\unicode[STIX]{x2202}^{i}x)\in \operatorname{Sym}^{p}P^{i+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x)\stackrel{\text{def}}{=}\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x,\unicode[STIX]{x2202}^{1}x,\unicode[STIX]{x2202}^{2}x,\ldots ,\unicode[STIX]{x2202}^{i}x)\in \operatorname{Sym}^{p}P^{i+1}.\end{eqnarray}$$
Here the
![]() $\unicode[STIX]{x2202}^{k}$
are the cosimplicial operators. We claim that:
$\unicode[STIX]{x2202}^{k}$
are the cosimplicial operators. We claim that:
-
(i) if
 $x$
is a cocycle in
$x$
is a cocycle in
 $P^{i}$
, then
$P^{i}$
, then
 $\unicode[STIX]{x1D719}(x)$
is a cocycle in
$\unicode[STIX]{x1D719}(x)$
is a cocycle in
 $\operatorname{Sym}^{p}P^{i+1}$
;
$\operatorname{Sym}^{p}P^{i+1}$
; -
(ii) if
 $x,y\in P^{i}$
are cohomologous cocycles, then
$x,y\in P^{i}$
are cohomologous cocycles, then
 $\unicode[STIX]{x1D719}(x)$
and
$\unicode[STIX]{x1D719}(x)$
and
 $\unicode[STIX]{x1D719}(y)$
are cohomologous in
$\unicode[STIX]{x1D719}(y)$
are cohomologous in
 $\operatorname{Sym}^{p}P^{i+1}$
.
$\operatorname{Sym}^{p}P^{i+1}$
.
The proofs of both these claims will be contained in Proposition 5.11 below. As a result, we will also abuse notation and use
![]() $\unicode[STIX]{x1D719}$
to denote the induced map in cohomology.
$\unicode[STIX]{x1D719}$
to denote the induced map in cohomology.
Return to the previous spectral sequences for computing the cohomology of the cosimplicial abelian groups
![]() $\mathfrak{m}^{\bullet }$
and
$\mathfrak{m}^{\bullet }$
and
![]() $1+\mathfrak{m}^{\bullet }$
. The
$1+\mathfrak{m}^{\bullet }$
. The
![]() $(p-1)$
th differential in each spectral sequence, namely
$(p-1)$
th differential in each spectral sequence, namely
![]() $d_{p-1}$
or
$d_{p-1}$
or
![]() $d_{p-1,\times }$
, runs from a sub-object of
$d_{p-1,\times }$
, runs from a sub-object of
 $H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
to a quotient of
$H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
to a quotient of
 $H^{i+1}(\mathfrak{m}^{\bullet ,p})$
.
$H^{i+1}(\mathfrak{m}^{\bullet ,p})$
.
Proposition 5.11 (First unstable differential).
The operator
![]() $\unicode[STIX]{x1D719}$
satisfies the claimed properties (i) and (ii) above, and we have
$\unicode[STIX]{x1D719}$
satisfies the claimed properties (i) and (ii) above, and we have
 $d_{p-1,\times }=d_{p-1}+\unicode[STIX]{x1D719}$
.
$d_{p-1,\times }=d_{p-1}+\unicode[STIX]{x1D719}$
.
Let us explain this formula. We have a natural (multiplication) morphism of cosimplicial abelian groups
 $\operatorname{Sym}^{p}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})\rightarrow \mathfrak{m}^{\bullet ,p}$
. The operator
$\operatorname{Sym}^{p}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})\rightarrow \mathfrak{m}^{\bullet ,p}$
. The operator
![]() $\unicode[STIX]{x1D719}$
gives us a natural map from
$\unicode[STIX]{x1D719}$
gives us a natural map from
 $H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
to
$H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
to
 $H^{i+1}(\operatorname{Sym}^{p}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2}))$
and we compose that with the multiplication map.
$H^{i+1}(\operatorname{Sym}^{p}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2}))$
and we compose that with the multiplication map.
Proof. We unwind the definitions. A class
 $x\in H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
that has survived to the
$x\in H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2})$
that has survived to the
![]() $E_{p-1}$
stage of the spectral sequence, by definition, lifts to a class in
$E_{p-1}$
stage of the spectral sequence, by definition, lifts to a class in
 $H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p})$
, which we represent by a degree
$H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p})$
, which we represent by a degree
![]() $i$
cycle
$i$
cycle
![]() $\widetilde{x}$
. The short exact sequence of cosimplicial abelian groups
$\widetilde{x}$
. The short exact sequence of cosimplicial abelian groups
 $$\begin{eqnarray}0\rightarrow \mathfrak{m}^{\bullet ,p}\rightarrow \mathfrak{m}^{\bullet }\rightarrow \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathfrak{m}^{\bullet ,p}\rightarrow \mathfrak{m}^{\bullet }\rightarrow \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}\rightarrow 0,\end{eqnarray}$$
leads to a connecting homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}:H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p})\rightarrow H^{i+1}(\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}:H^{i}(\mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p})\rightarrow H^{i+1}(\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
The differential
 $d_{p-1}(x)$
is given by the image of
$d_{p-1}(x)$
is given by the image of
![]() $\unicode[STIX]{x1D6FF}(\widetilde{x})$
.
$\unicode[STIX]{x1D6FF}(\widetilde{x})$
.
In the multiplicative setting, we know that the cycle
 $\exp _{p}(\widetilde{x})\in (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p})$
lifts the image of
$\exp _{p}(\widetilde{x})\in (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p})$
lifts the image of
![]() $x$
(or rather,
$x$
(or rather,
![]() $1+x$
) in the
$1+x$
) in the
![]() $E_{1}$
-page of the multiplicative spectral sequence. Now
$E_{1}$
-page of the multiplicative spectral sequence. Now
 $d_{p-1,\times }(x)$
is given as follows: one considers the short exact sequence of cosimplicial abelian groups
$d_{p-1,\times }(x)$
is given as follows: one considers the short exact sequence of cosimplicial abelian groups
 $$\begin{eqnarray}0\rightarrow (1+\mathfrak{m}^{\bullet ,p})\rightarrow (1+\mathfrak{m}^{\bullet })\rightarrow (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow (1+\mathfrak{m}^{\bullet ,p})\rightarrow (1+\mathfrak{m}^{\bullet })\rightarrow (1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p})\rightarrow 0,\end{eqnarray}$$
and the induced connecting homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }:H^{i}((1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p}))\rightarrow H^{i+1}(1+\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }:H^{i}((1+\mathfrak{m}^{\bullet })/(1+\mathfrak{m}^{\bullet ,p}))\rightarrow H^{i+1}(1+\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
Unwinding the definitions, the multiplicative differential
 $d_{p-1,\times }(x)$
is given by
$d_{p-1,\times }(x)$
is given by
 $$\begin{eqnarray}d_{p-1,\times }(x)=\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))\in H^{i+1}(1+\mathfrak{m}^{\bullet ,p})\simeq H^{i+1}(\mathfrak{m}^{\bullet ,p}),\end{eqnarray}$$
$$\begin{eqnarray}d_{p-1,\times }(x)=\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))\in H^{i+1}(1+\mathfrak{m}^{\bullet ,p})\simeq H^{i+1}(\mathfrak{m}^{\bullet ,p}),\end{eqnarray}$$
or rather the image in the quotient of this at the
![]() $E_{p-1}$
-page.
$E_{p-1}$
-page.
It follows now that we need to compare the additive and the multiplicative boundary maps
![]() $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\times }$
. Given a cycle
$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\times }$
. Given a cycle
 $\widetilde{x}\in \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}$
in degree
$\widetilde{x}\in \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,p}$
in degree
![]() $i$
, projecting to a cycle and induced cohomology class
$i$
, projecting to a cycle and induced cohomology class
 $x\in \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2}$
, we claim that
$x\in \mathfrak{m}^{\bullet }/\mathfrak{m}^{\bullet ,2}$
, we claim that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))=1+\unicode[STIX]{x1D6FF}(\widetilde{x})+\unicode[STIX]{x1D719}(\widetilde{x})\in H^{i+1}(1+\mathfrak{m}^{\bullet ,p})\simeq H^{i+1}(\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))=1+\unicode[STIX]{x1D6FF}(\widetilde{x})+\unicode[STIX]{x1D719}(\widetilde{x})\in H^{i+1}(1+\mathfrak{m}^{\bullet ,p})\simeq H^{i+1}(\mathfrak{m}^{\bullet ,p}).\end{eqnarray}$$
To prove this, we unwind the definitions again. Lift
![]() $\widetilde{x}$
to a chain
$\widetilde{x}$
to a chain
 $x^{\prime }\in \mathfrak{m}^{\bullet }$
(in degree
$x^{\prime }\in \mathfrak{m}^{\bullet }$
(in degree
![]() $i$
). The additive connecting homomorphism
$i$
). The additive connecting homomorphism
![]() $\unicode[STIX]{x1D6FF}(\widetilde{x})$
is obtained by considering the image in cohomology of the alternating sum
$\unicode[STIX]{x1D6FF}(\widetilde{x})$
is obtained by considering the image in cohomology of the alternating sum
 $y^{\prime }=\sum _{k}(-1)^{k}\unicode[STIX]{x2202}^{k}x^{\prime }$
, which is an
$y^{\prime }=\sum _{k}(-1)^{k}\unicode[STIX]{x2202}^{k}x^{\prime }$
, which is an
![]() $(i+1)$
-cocycle in
$(i+1)$
-cocycle in
![]() $\mathfrak{m}^{\bullet ,p}$
. For the multiplicative version, we have to consider the cocycle
$\mathfrak{m}^{\bullet ,p}$
. For the multiplicative version, we have to consider the cocycle
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))=\mathop{\prod }_{k}(\unicode[STIX]{x2202}^{k}\exp _{p}(x^{\prime }))^{(-1)^{k}}=\mathop{\prod }_{k}\exp _{p}(\unicode[STIX]{x2202}^{k}x^{\prime })^{(-1)^{k}}\in 1+\mathfrak{m}^{\bullet ,p+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x}))=\mathop{\prod }_{k}(\unicode[STIX]{x2202}^{k}\exp _{p}(x^{\prime }))^{(-1)^{k}}=\mathop{\prod }_{k}\exp _{p}(\unicode[STIX]{x2202}^{k}x^{\prime })^{(-1)^{k}}\in 1+\mathfrak{m}^{\bullet ,p+1}.\end{eqnarray}$$
Now we use (5.10), which gives us
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x})) & = & \displaystyle \exp _{p}\Bigl(\sum (-1)^{k}\unicode[STIX]{x2202}^{k}x^{\prime }\Bigr)+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \exp _{p}(y^{\prime })+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 1+y^{\prime }+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\times }(\exp _{p}(\widetilde{x})) & = & \displaystyle \exp _{p}\Bigl(\sum (-1)^{k}\unicode[STIX]{x2202}^{k}x^{\prime }\Bigr)+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \exp _{p}(y^{\prime })+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime })\nonumber\\ \displaystyle & = & \displaystyle 1+y^{\prime }+\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x2202}^{0}x^{\prime },\unicode[STIX]{x2202}^{1}x^{\prime },\ldots ,\unicode[STIX]{x2202}^{i}x^{\prime }).\nonumber\end{eqnarray}$$
In cohomology, this is the desired claim, provided we can justify the claims about
![]() $\unicode[STIX]{x1D719}$
made in Construction 5.10.
$\unicode[STIX]{x1D719}$
made in Construction 5.10.
The justification of Construction 5.10 now follows from reversing the above argument. Keep the notation from there. We consider the commutative nonunital cosimplicial algebra
 $$\begin{eqnarray}A^{\bullet }=\bigoplus _{0<k\leqslant p}\operatorname{Sym}^{k}P^{\bullet }\end{eqnarray}$$
$$\begin{eqnarray}A^{\bullet }=\bigoplus _{0<k\leqslant p}\operatorname{Sym}^{k}P^{\bullet }\end{eqnarray}$$
and its quotient
 $\overline{A}^{\bullet }=\bigoplus _{0<k<p}\operatorname{Sym}^{k}P^{\bullet }$
. Choose a cycle
$\overline{A}^{\bullet }=\bigoplus _{0<k<p}\operatorname{Sym}^{k}P^{\bullet }$
. Choose a cycle
 $x\in P^{\bullet }\subset \overline{A}^{\bullet }$
, which clearly extends to a cycle in
$x\in P^{\bullet }\subset \overline{A}^{\bullet }$
, which clearly extends to a cycle in
![]() $A^{\bullet }$
. Then
$A^{\bullet }$
. Then
 $\exp _{p}(x)$
is a cycle in
$\exp _{p}(x)$
is a cycle in
![]() $1+\overline{A}^{\bullet }$
. The coboundary of this class in
$1+\overline{A}^{\bullet }$
. The coboundary of this class in
 $\operatorname{Sym}^{p}P^{\bullet }\simeq 1+\operatorname{Sym}^{p}P^{\bullet }\subset 1+A^{\bullet }$
is given by
$\operatorname{Sym}^{p}P^{\bullet }\simeq 1+\operatorname{Sym}^{p}P^{\bullet }\subset 1+A^{\bullet }$
is given by
![]() $\unicode[STIX]{x1D719}(x)$
by the above analysis. This shows that
$\unicode[STIX]{x1D719}(x)$
by the above analysis. This shows that
![]() $\unicode[STIX]{x1D719}(x)$
is a cycle and that its cohomology class depends only on that of
$\unicode[STIX]{x1D719}(x)$
is a cycle and that its cohomology class depends only on that of
![]() $x$
.◻
$x$
.◻
5.4 Identification with
 $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
Let
![]() $P^{\bullet }$
be a cosimplicial
$P^{\bullet }$
be a cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-module. In the previous subsection, we described a natural operation (based on a formula)
$\mathbb{Z}[1/(p-1)!]$
-module. In the previous subsection, we described a natural operation (based on a formula)
 $$\begin{eqnarray}\unicode[STIX]{x1D719}:H^{i}(P^{\bullet })\rightarrow H^{i+1}(\operatorname{Sym}^{p}P^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}:H^{i}(P^{\bullet })\rightarrow H^{i+1}(\operatorname{Sym}^{p}P^{\bullet }).\end{eqnarray}$$
Suppose
![]() $i>0$
.Footnote
4
In the setting of cosimplicial
$i>0$
.Footnote
4
In the setting of cosimplicial
![]() $\mathbb{F}_{p}$
-vector spaces, the work of Priddy [Reference PriddyPri73] has classified all such operations, which amount to determining the cohomology of the symmetric powers of a cosimplicial vector space (one reduces to an Eilenberg–MacLane complex). In particular, for cosimplicial
$\mathbb{F}_{p}$
-vector spaces, the work of Priddy [Reference PriddyPri73] has classified all such operations, which amount to determining the cohomology of the symmetric powers of a cosimplicial vector space (one reduces to an Eilenberg–MacLane complex). In particular, for cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-modules, the only such natural operations are the scalar multiples of a single operation called
$\mathbb{Z}[1/(p-1)!]$
-modules, the only such natural operations are the scalar multiples of a single operation called
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
, as one sees from Priddy’s work (and the Bockstein spectral sequence). In other words, in the ‘universal’ case when
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
, as one sees from Priddy’s work (and the Bockstein spectral sequence). In other words, in the ‘universal’ case when
 $H^{\ast }(P^{\bullet })$
is a
$H^{\ast }(P^{\bullet })$
is a
 $\mathbb{Z}[1/(p-1)!]$
(generated by
$\mathbb{Z}[1/(p-1)!]$
(generated by
![]() $\unicode[STIX]{x1D704}$
) concentrated in degree
$\unicode[STIX]{x1D704}$
) concentrated in degree
![]() $i$
, we have
$i$
, we have
 $H^{i+1}(\operatorname{Sym}^{p}P^{\bullet })\simeq \mathbb{Z}/p$
, generated by the class
$H^{i+1}(\operatorname{Sym}^{p}P^{\bullet })\simeq \mathbb{Z}/p$
, generated by the class
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}\unicode[STIX]{x1D704}$
.
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}\unicode[STIX]{x1D704}$
.
Given a cosimplicial
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
![]() $P^{\bullet }$
, the cosimplicial commutative ring
$P^{\bullet }$
, the cosimplicial commutative ring
 $\operatorname{Sym}^{\ast }P^{\bullet }$
yields (upon taking the totalization) an
$\operatorname{Sym}^{\ast }P^{\bullet }$
yields (upon taking the totalization) an
![]() $\mathbf{E}_{\infty }$
-algebra over
$\mathbf{E}_{\infty }$
-algebra over
![]() $\mathbb{F}_{p}$
. Then
$\mathbb{F}_{p}$
. Then
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
is identified with the power operation on
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
is identified with the power operation on
![]() $\mathbf{E}_{\infty }$
-algebras over
$\mathbf{E}_{\infty }$
-algebras over
![]() $\mathbb{F}_{p}$
with the same name.
$\mathbb{F}_{p}$
with the same name.
In this section, we will prove the following proposition.
Proposition 5.12. For cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-modules, we have
$\mathbb{Z}[1/(p-1)!]$
-modules, we have
 $\unicode[STIX]{x1D719}=-\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
. As a result, in the situation of Proposition 5.11, we have
$\unicode[STIX]{x1D719}=-\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
. As a result, in the situation of Proposition 5.11, we have
 $$\begin{eqnarray}d_{p-1,\times \!}=d_{p-1}-\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}.\end{eqnarray}$$
$$\begin{eqnarray}d_{p-1,\times \!}=d_{p-1}-\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}.\end{eqnarray}$$
While one can compare explicit formulas, we will approach the determination of the operator
![]() $\unicode[STIX]{x1D719}$
by considering examples. We note that this formula will not be used in the following. Rather, it will suffice to know that
$\unicode[STIX]{x1D719}$
by considering examples. We note that this formula will not be used in the following. Rather, it will suffice to know that
![]() $\unicode[STIX]{x1D719}$
is Frobenius-semilinear.
$\unicode[STIX]{x1D719}$
is Frobenius-semilinear.
First of all, we give an example to show that
![]() $\unicode[STIX]{x1D719}$
is not identically zero, i.e. that the additive and multiplicative versions of
$\unicode[STIX]{x1D719}$
is not identically zero, i.e. that the additive and multiplicative versions of
![]() $d_{p-1}$
can, in fact, differ.
$d_{p-1}$
can, in fact, differ.
Example 5.13. Consider the commutative algebra
 $\mathbb{F}_{p}[x]/x^{p+1}$
and the ideal
$\mathbb{F}_{p}[x]/x^{p+1}$
and the ideal
 $\mathfrak{m}=(x)$
, so that
$\mathfrak{m}=(x)$
, so that
 $\mathfrak{m}^{p+1}=0$
. We then have an isomorphism
$\mathfrak{m}^{p+1}=0$
. We then have an isomorphism
 $$\begin{eqnarray}(1+\mathfrak{m})/(1+\mathfrak{m}^{p})\simeq (\mathbb{Z}/p)^{p-1},\end{eqnarray}$$
$$\begin{eqnarray}(1+\mathfrak{m})/(1+\mathfrak{m}^{p})\simeq (\mathbb{Z}/p)^{p-1},\end{eqnarray}$$
as one sees via the truncated exponential and logarithm. However, we also have
 $$\begin{eqnarray}1+\mathfrak{m}\simeq \mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}.\end{eqnarray}$$
$$\begin{eqnarray}1+\mathfrak{m}\simeq \mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}.\end{eqnarray}$$
In fact, the unit
 $1+x\in 1+\mathfrak{m}$
has order exactly
$1+x\in 1+\mathfrak{m}$
has order exactly
![]() $p^{2}$
. Meanwhile,
$p^{2}$
. Meanwhile,
 $\exp _{p}(x^{2}),\ldots ,\exp _{p}(x^{p-1})$
each have order
$\exp _{p}(x^{2}),\ldots ,\exp _{p}(x^{p-1})$
each have order
![]() $p$
(one could also take
$p$
(one could also take
 $1+x^{2},\ldots ,1+x^{p-1}$
). One sees that the map
$1+x^{2},\ldots ,1+x^{p-1}$
). One sees that the map
 $$\begin{eqnarray}1+\mathfrak{m}\rightarrow (1+\mathfrak{m})/(1+\mathfrak{m}^{p})\end{eqnarray}$$
$$\begin{eqnarray}1+\mathfrak{m}\rightarrow (1+\mathfrak{m})/(1+\mathfrak{m}^{p})\end{eqnarray}$$
can be identified with the direct sum of the reduction map
 $\mathbb{Z}/p^{2}\rightarrow \mathbb{Z}/p$
and the identity
$\mathbb{Z}/p^{2}\rightarrow \mathbb{Z}/p$
and the identity
 $(\mathbb{Z}/p)^{p-2}\rightarrow (\mathbb{Z}/p)^{p-2}$
.
$(\mathbb{Z}/p)^{p-2}\rightarrow (\mathbb{Z}/p)^{p-2}$
.
Now let
![]() $X_{\bullet }$
be a simplicial set and suppose that there exists a class in
$X_{\bullet }$
be a simplicial set and suppose that there exists a class in
 $H^{n}(X_{\bullet },\mathbb{Z}/p)$
which does not lift to
$H^{n}(X_{\bullet },\mathbb{Z}/p)$
which does not lift to
 $H^{n}(X_{\bullet },\mathbb{Z}/p^{2})$
. Form the nonunital cosimplicial commutative algebra
$H^{n}(X_{\bullet },\mathbb{Z}/p^{2})$
. Form the nonunital cosimplicial commutative algebra
 $F(X_{\bullet },\mathfrak{m})=\mathfrak{m}^{X_{\bullet }}$
, whose group of units is
$F(X_{\bullet },\mathfrak{m})=\mathfrak{m}^{X_{\bullet }}$
, whose group of units is
 $F(X_{\bullet },1+\mathfrak{m})$
. We can apply the machinery of the previous subsection to this example, where the filtration in question is the
$F(X_{\bullet },1+\mathfrak{m})$
. We can apply the machinery of the previous subsection to this example, where the filtration in question is the
![]() $\mathfrak{m}$
-adic filtration.
$\mathfrak{m}$
-adic filtration.
The additive spectral sequence converges to the cohomology of
![]() $X_{\bullet }$
with coefficients in
$X_{\bullet }$
with coefficients in
![]() $(\mathbb{Z}/p)^{p}$
and the multiplicative spectral sequence converges to the cohomology with coefficients in
$(\mathbb{Z}/p)^{p}$
and the multiplicative spectral sequence converges to the cohomology with coefficients in
 $\mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}$
. We see in particular that, while there are no differentials additively (the filtration splits), there is necessarily a
$\mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}$
. We see in particular that, while there are no differentials additively (the filtration splits), there is necessarily a
![]() $d_{p-1,\times }$
since there are cohomology classes in
$d_{p-1,\times }$
since there are cohomology classes in
 $H^{n}(X_{\bullet },\mathbb{Z}/p)$
which do not lift to
$H^{n}(X_{\bullet },\mathbb{Z}/p)$
which do not lift to
 $H^{n}(X_{\bullet },\mathbb{Z}/p^{2})$
.
$H^{n}(X_{\bullet },\mathbb{Z}/p^{2})$
.
We now describe an example where the additive spectral sequence supports a differential but the multiplicative spectral sequence does not.
Example 5.14. Consider the complete local ring
 $R=\mathbb{Z}_{p}[\unicode[STIX]{x1D701}_{p}]$
and the maximal ideal
$R=\mathbb{Z}_{p}[\unicode[STIX]{x1D701}_{p}]$
and the maximal ideal
 $\mathfrak{m}=(1-\unicode[STIX]{x1D701}_{p})$
. We consider the quotient
$\mathfrak{m}=(1-\unicode[STIX]{x1D701}_{p})$
. We consider the quotient
 $\overline{R}=R/\mathfrak{m}^{p+1}$
and the image
$\overline{R}=R/\mathfrak{m}^{p+1}$
and the image
![]() $\overline{\mathfrak{m}}$
of
$\overline{\mathfrak{m}}$
of
![]() $\mathfrak{m}$
. We have:
$\mathfrak{m}$
. We have:
-
(i)
 $(1+\overline{\mathfrak{m}})/(1+\overline{\mathfrak{m}}^{p})\simeq \overline{\mathfrak{m}}/\overline{\mathfrak{m}^{p}}\simeq (\mathbb{Z}/p)^{p-1}$
(note here that
$(1+\overline{\mathfrak{m}})/(1+\overline{\mathfrak{m}}^{p})\simeq \overline{\mathfrak{m}}/\overline{\mathfrak{m}^{p}}\simeq (\mathbb{Z}/p)^{p-1}$
(note here that
 $p\in \mathfrak{m}^{p-1}\setminus \mathfrak{m}^{p}$
);
$p\in \mathfrak{m}^{p-1}\setminus \mathfrak{m}^{p}$
); -
(ii)
 $\overline{\mathfrak{m}}\simeq \mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}$
; the generator of the
$\overline{\mathfrak{m}}\simeq \mathbb{Z}/p^{2}\oplus (\mathbb{Z}/p)^{p-2}$
; the generator of the
 $\mathbb{Z}/p^{2}$
is
$\mathbb{Z}/p^{2}$
is
 $(1-\unicode[STIX]{x1D701}_{p})$
and the generators of the remaining terms are
$(1-\unicode[STIX]{x1D701}_{p})$
and the generators of the remaining terms are
 $(1-\unicode[STIX]{x1D701}_{p})^{i},i=2,\ldots ,p-1$
; the map
$(1-\unicode[STIX]{x1D701}_{p})^{i},i=2,\ldots ,p-1$
; the map
 $\overline{\mathfrak{m}}\rightarrow \overline{\mathfrak{m}}/\overline{\mathfrak{m}^{p}}$
is a direct sum of the reduction
$\overline{\mathfrak{m}}\rightarrow \overline{\mathfrak{m}}/\overline{\mathfrak{m}^{p}}$
is a direct sum of the reduction
 $\mathbb{Z}/p^{2}{\twoheadrightarrow}\mathbb{Z}/p$
and the identity
$\mathbb{Z}/p^{2}{\twoheadrightarrow}\mathbb{Z}/p$
and the identity
 $(\mathbb{Z}/p)^{p-2}\rightarrow (\mathbb{Z}/p)^{p-2}$
;
$(\mathbb{Z}/p)^{p-2}\rightarrow (\mathbb{Z}/p)^{p-2}$
; -
(iii)
 $1+\overline{\mathfrak{m}}\simeq (\mathbb{Z}/p)^{p}$
. In fact, one sees that every element has order
$1+\overline{\mathfrak{m}}\simeq (\mathbb{Z}/p)^{p}$
. In fact, one sees that every element has order
 $p$
here (since
$p$
here (since
 $\unicode[STIX]{x1D701}_{p}$
does); the map
$\unicode[STIX]{x1D701}_{p}$
does); the map
 $1+\overline{\mathfrak{m}}\rightarrow (1+\overline{\mathfrak{m}})/(1+\overline{\mathfrak{m}}^{p})$
is a surjection
$1+\overline{\mathfrak{m}}\rightarrow (1+\overline{\mathfrak{m}})/(1+\overline{\mathfrak{m}}^{p})$
is a surjection
 $(\mathbb{Z}/p)^{p}\rightarrow (\mathbb{Z}/p)^{p-1}$
.
$(\mathbb{Z}/p)^{p}\rightarrow (\mathbb{Z}/p)^{p-1}$
.
Let
![]() $X_{\bullet }$
be a simplicial set as in the previous example. In this case, reasoning analogously, we find that the additive spectral sequence for
$X_{\bullet }$
be a simplicial set as in the previous example. In this case, reasoning analogously, we find that the additive spectral sequence for
 $F(X_{\bullet },\overline{\mathfrak{m}})$
must support a
$F(X_{\bullet },\overline{\mathfrak{m}})$
must support a
![]() $d_{p-1}$
but the multiplicative spectral sequence does not.
$d_{p-1}$
but the multiplicative spectral sequence does not.
Proof of Proposition 5.12.
We will analyze the last example more carefully to determine the precise multiple.Footnote
5
Note that
 $\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{2}\simeq \mathbb{F}_{p}$
(generated by the image of
$\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{2}\simeq \mathbb{F}_{p}$
(generated by the image of
![]() $1-\unicode[STIX]{x1D701}_{p}$
) and
$1-\unicode[STIX]{x1D701}_{p}$
) and
 $\overline{\mathfrak{m}}^{p}\simeq \mathbb{F}_{p}$
(generated by the image of
$\overline{\mathfrak{m}}^{p}\simeq \mathbb{F}_{p}$
(generated by the image of
 $(1-\unicode[STIX]{x1D701}_{p})^{p}$
). The (additive) differential
$(1-\unicode[STIX]{x1D701}_{p})^{p}$
). The (additive) differential
![]() $d_{p-1}$
comes from the short exact sequence
$d_{p-1}$
comes from the short exact sequence
 $$\begin{eqnarray}0\rightarrow \overline{\mathfrak{m}}^{p}\rightarrow \overline{\mathfrak{m}}\rightarrow \overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \overline{\mathfrak{m}}^{p}\rightarrow \overline{\mathfrak{m}}\rightarrow \overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\rightarrow 0,\end{eqnarray}$$
and we have the following commutative diagram of short exact sequences.

Here the map
 $\mathbb{Z}/p^{2}\rightarrow \overline{\mathfrak{m}}$
carries
$\mathbb{Z}/p^{2}\rightarrow \overline{\mathfrak{m}}$
carries
 $1\mapsto 1-\unicode[STIX]{x1D701}_{p}$
. Note that
$1\mapsto 1-\unicode[STIX]{x1D701}_{p}$
. Note that
 $p(1-\unicode[STIX]{x1D701}_{p})\equiv (1-\unicode[STIX]{x1D701}_{p})^{p}$
in
$p(1-\unicode[STIX]{x1D701}_{p})\equiv (1-\unicode[STIX]{x1D701}_{p})^{p}$
in
![]() $\overline{\mathfrak{m}}$
as one sees from the expression
$\overline{\mathfrak{m}}$
as one sees from the expression
 $\prod _{i=1}^{p-1}(T-\unicode[STIX]{x1D701}_{p}^{i})=T^{p-1}+T^{p-2}+\cdots +1$
with
$\prod _{i=1}^{p-1}(T-\unicode[STIX]{x1D701}_{p}^{i})=T^{p-1}+T^{p-2}+\cdots +1$
with
![]() $T=1$
.
$T=1$
.
Take
 $X_{\bullet }=K(\mathbb{Z}/p,n)$
, so that
$X_{\bullet }=K(\mathbb{Z}/p,n)$
, so that
 $H^{n}(X_{\bullet },\mathbb{F}_{p})=H^{n+1}(X_{\bullet },\mathbb{F}_{p})=\mathbb{F}_{p}$
. We let
$H^{n}(X_{\bullet },\mathbb{F}_{p})=H^{n+1}(X_{\bullet },\mathbb{F}_{p})=\mathbb{F}_{p}$
. We let
![]() $\unicode[STIX]{x1D704}$
be a generator of the former, so that
$\unicode[STIX]{x1D704}$
be a generator of the former, so that
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}$
is a generator of the latter for
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}$
is a generator of the latter for
![]() $\unicode[STIX]{x1D6FD}$
the Bockstein. Again, this analysis is based on the cosimplicial commutative ring
$\unicode[STIX]{x1D6FD}$
the Bockstein. Again, this analysis is based on the cosimplicial commutative ring
![]() $\overline{\mathfrak{m}}^{X_{\bullet }}$
.
$\overline{\mathfrak{m}}^{X_{\bullet }}$
.
-
(i) Note that
 $H^{n}(X_{\bullet },\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p})\simeq H^{n}(X_{\bullet },\mathbb{F}_{p})\otimes _{\mathbb{F}_{p}}\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\simeq \overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\unicode[STIX]{x1D704}$
and similarly for
$H^{n}(X_{\bullet },\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p})\simeq H^{n}(X_{\bullet },\mathbb{F}_{p})\otimes _{\mathbb{F}_{p}}\overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\simeq \overline{\mathfrak{m}}/\overline{\mathfrak{m}}^{p}\unicode[STIX]{x1D704}$
and similarly for
 $H^{n+1}(X_{\bullet },\overline{\mathfrak{m}}^{p})$
. The differential in question comes from the connecting homomorphism in the short exact sequence (5.17), so that by naturality of (5.18), it carries
$H^{n+1}(X_{\bullet },\overline{\mathfrak{m}}^{p})$
. The differential in question comes from the connecting homomorphism in the short exact sequence (5.17), so that by naturality of (5.18), it carries
 $(1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704}$
to
$(1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704}$
to
 $(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}\in H^{n+1}(X_{\bullet },\overline{\mathfrak{m}^{p}})$
.
$(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}\in H^{n+1}(X_{\bullet },\overline{\mathfrak{m}^{p}})$
. -
(ii) The associated graded module of
 $\overline{\mathfrak{m}}$
comes from the reduction of a
$\overline{\mathfrak{m}}$
comes from the reduction of a
 $\mathbb{Z}$
-algebra, so
$\mathbb{Z}$
-algebra, so
 $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
is the composite of the Bockstein and
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{0}$
is the composite of the Bockstein and
 ${\mathcal{P}}^{0}$
. Now
${\mathcal{P}}^{0}$
. Now
 ${\mathcal{P}}^{0}((1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704})=(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D704}\in H^{n}(X,\overline{\mathfrak{m}}^{p})$
since
${\mathcal{P}}^{0}((1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704})=(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D704}\in H^{n}(X,\overline{\mathfrak{m}}^{p})$
since
 ${\mathcal{P}}^{0}$
is the Frobenius on underlying rings. Applying
${\mathcal{P}}^{0}$
is the Frobenius on underlying rings. Applying
 $\unicode[STIX]{x1D6FD}$
to that, we obtain
$\unicode[STIX]{x1D6FD}$
to that, we obtain
 $(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}$
.
$(1-\unicode[STIX]{x1D701}_{p})^{p}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D704}$
.
Putting these together, it follows that if the class corresponding to
 $(1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704}$
is to survive in the multiplicative spectral sequence (as it must), the formula must be as desired.◻
$(1-\unicode[STIX]{x1D701}_{p})\unicode[STIX]{x1D704}$
is to survive in the multiplicative spectral sequence (as it must), the formula must be as desired.◻
We refer to [Reference MumfordMum66, Lecture 27] for an instance of the appearance of these Bockstein operators in the deformation theory of the Picard scheme in characteristic
![]() $p$
. In that case, there are no algebraic obstructions, but the multiplicative operations are controlled by the Bocksteins.
$p$
. In that case, there are no algebraic obstructions, but the multiplicative operations are controlled by the Bocksteins.
6 The algebraic Picard group for the
 $C_{p}$
-action on
$C_{p}$
-action on
 $E_{n}$
$E_{n}$
We keep the previous notation and fix a prime number
![]() $p$
, setting
$p$
, setting
 $n=p-1$
. Let
$n=p-1$
. Let
 $C_{p}\subset \mathbb{G}$
be a maximal finite
$C_{p}\subset \mathbb{G}$
be a maximal finite
![]() $p$
-subgroup. Recall that
$p$
-subgroup. Recall that
 $(E_{n})_{0}\simeq \mathbb{W}(\mathbb{F}_{p^{n}})[\![u_{1},\ldots ,u_{n-1}]\!]$
is a complete local ring; we denote the maximal ideal by
$(E_{n})_{0}\simeq \mathbb{W}(\mathbb{F}_{p^{n}})[\![u_{1},\ldots ,u_{n-1}]\!]$
is a complete local ring; we denote the maximal ideal by
![]() $\mathfrak{m}$
. It acquires a
$\mathfrak{m}$
. It acquires a
![]() $C_{p}$
-action by restriction.
$C_{p}$
-action by restriction.
In this section, we apply the tools of the preceding section and calculate the algebraic Picard group
 $H^{1}(C_{p},(E_{n})_{0}^{\times })$
, showing that it is cyclic of order
$H^{1}(C_{p},(E_{n})_{0}^{\times })$
, showing that it is cyclic of order
![]() $p$
. This will be a key input into the topological descent spectral sequence for Picard groups. The approach will be to use the
$p$
. This will be a key input into the topological descent spectral sequence for Picard groups. The approach will be to use the
![]() $\mathfrak{m}$
-adic filtration on
$\mathfrak{m}$
-adic filtration on
![]() $(E_{n})_{0}^{\times }$
.
$(E_{n})_{0}^{\times }$
.
6.1 The additive spectral sequence
The associated graded module of the
![]() $\mathfrak{m}$
-adic filtration of
$\mathfrak{m}$
-adic filtration of
![]() $(E_{n})_{0}$
has been determined in unpublished work of Hopkins and Miller and studied additionally in work of Hill [Reference HillHil06].
$(E_{n})_{0}$
has been determined in unpublished work of Hopkins and Miller and studied additionally in work of Hill [Reference HillHil06].
Since
![]() $(E_{n})_{0}$
is a regular local ring, one has canonical and
$(E_{n})_{0}$
is a regular local ring, one has canonical and
![]() $C_{p}$
-equivariant isomorphisms
$C_{p}$
-equivariant isomorphisms
 $$\begin{eqnarray}\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\simeq \operatorname{Sym}^{i}(\mathfrak{m}/\mathfrak{m}^{2}),\quad i\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\simeq \operatorname{Sym}^{i}(\mathfrak{m}/\mathfrak{m}^{2}),\quad i\geqslant 0,\end{eqnarray}$$
where the symmetric powers are taken over the residue field
![]() $\mathbb{F}_{p^{n}}$
(upon which the group
$\mathbb{F}_{p^{n}}$
(upon which the group
![]() $C_{p}$
acts trivially). The first main result is the following, which is a consequence of the coordinates given on [Reference NaveNav10, p. 497].
$C_{p}$
acts trivially). The first main result is the following, which is a consequence of the coordinates given on [Reference NaveNav10, p. 497].
Proposition 6.1 (Hopkins–Miller).
As a
![]() $C_{p}$
-representation,
$C_{p}$
-representation,
![]() $\mathfrak{m}/\mathfrak{m}^{2}$
is the reduced regular representation
$\mathfrak{m}/\mathfrak{m}^{2}$
is the reduced regular representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
over
$\overline{\unicode[STIX]{x1D70C}}$
over
![]() $\mathbb{F}_{p^{n}}$
.
$\mathbb{F}_{p^{n}}$
.
Recall that the reduced regular representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
of
$\overline{\unicode[STIX]{x1D70C}}$
of
![]() $C_{p}$
over a field
$C_{p}$
over a field
![]() $k$
is the quotient of the regular representation
$k$
is the quotient of the regular representation
![]() $k[C_{p}]$
by the trivial subrepresentation. As a corollary, we find that the associated graded module of
$k[C_{p}]$
by the trivial subrepresentation. As a corollary, we find that the associated graded module of
![]() $(E_{n})_{0}$
, as a
$(E_{n})_{0}$
, as a
![]() $C_{p}$
-representation and algebra, is the symmetric algebra
$C_{p}$
-representation and algebra, is the symmetric algebra
 $$\begin{eqnarray}\text{gr}(E_{n})_{0}\simeq \operatorname{Sym}^{\ast }\overline{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
$$\begin{eqnarray}\text{gr}(E_{n})_{0}\simeq \operatorname{Sym}^{\ast }\overline{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
of the reduced regular representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
.
$\overline{\unicode[STIX]{x1D70C}}$
.
Over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
, the decomposition of the symmetric powers of
$p$
, the decomposition of the symmetric powers of
![]() $\overline{\unicode[STIX]{x1D70C}}$
as
$\overline{\unicode[STIX]{x1D70C}}$
as
![]() $C_{p}$
-representations up to free summands is calculated in work of Almkvist and Fossum (and was done by Hopkins and Miller). We will let
$C_{p}$
-representations up to free summands is calculated in work of Almkvist and Fossum (and was done by Hopkins and Miller). We will let
![]() $\mathbf{1}$
denote the trivial representation.
$\mathbf{1}$
denote the trivial representation.
Proposition 6.2 (Almkvist–Fossum [Reference Almkvist and FossumAF78, ch. 3, Propositions 3.4–3.6]).
The
![]() $C_{p}$
-representation
$C_{p}$
-representation
![]() $\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}$
decomposes as follows:
$\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}$
decomposes as follows:
-
(i) if
 $i\equiv 0~\text{mod}~p$
, then
$i\equiv 0~\text{mod}~p$
, then
 $\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}\simeq \mathbf{1}\oplus \text{free}$
;
$\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}\simeq \mathbf{1}\oplus \text{free}$
; -
(ii) if
 $i\equiv 1~\text{mod}~p$
, then
$i\equiv 1~\text{mod}~p$
, then
 $\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}\simeq \overline{\unicode[STIX]{x1D70C}}\oplus \text{free}$
;
$\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}\simeq \overline{\unicode[STIX]{x1D70C}}\oplus \text{free}$
; -
(iii) if
 $i\not \equiv 0,1~\text{mod}~p$
, then
$i\not \equiv 0,1~\text{mod}~p$
, then
 $\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}$
is a free
$\operatorname{Sym}^{i}\overline{\unicode[STIX]{x1D70C}}$
is a free
 $k[C_{p}]$
-module.
$k[C_{p}]$
-module.
The invariant element of
![]() $\operatorname{Sym}^{p}\overline{\unicode[STIX]{x1D70C}}$
that generates the
$\operatorname{Sym}^{p}\overline{\unicode[STIX]{x1D70C}}$
that generates the
![]() $\mathbf{1}$
summand is given as follows. The representation
$\mathbf{1}$
summand is given as follows. The representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
is generated by elements
$\overline{\unicode[STIX]{x1D70C}}$
is generated by elements
 $\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{p}$
with
$\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{p}$
with
 $\unicode[STIX]{x1D716}_{1}+\cdots +\unicode[STIX]{x1D716}_{p}=0$
and with
$\unicode[STIX]{x1D716}_{1}+\cdots +\unicode[STIX]{x1D716}_{p}=0$
and with
![]() $C_{p}$
acting on the
$C_{p}$
acting on the
![]() $\unicode[STIX]{x1D716}_{i}$
via the natural permutation action. Then the (norm) product
$\unicode[STIX]{x1D716}_{i}$
via the natural permutation action. Then the (norm) product
 $\unicode[STIX]{x1D716}_{1}\ldots \unicode[STIX]{x1D716}_{p}\in \operatorname{Sym}^{p}\overline{\unicode[STIX]{x1D70C}}$
is
$\unicode[STIX]{x1D716}_{1}\ldots \unicode[STIX]{x1D716}_{p}\in \operatorname{Sym}^{p}\overline{\unicode[STIX]{x1D70C}}$
is
![]() $C_{p}$
-invariant and generates the desired summand. The analogous invariant elements in
$C_{p}$
-invariant and generates the desired summand. The analogous invariant elements in
 $\operatorname{Sym}^{pk}\overline{\unicode[STIX]{x1D70C}}$
are the powers of this norm product.
$\operatorname{Sym}^{pk}\overline{\unicode[STIX]{x1D70C}}$
are the powers of this norm product.
We now describe the cohomology of the associated graded module of
![]() $(E_{n})_{0}$
. Recall that
$(E_{n})_{0}$
. Recall that
 $$\begin{eqnarray}H^{\ast }(C_{p},\mathbb{F}_{p^{n}})\simeq \mathbb{F}_{p^{n}}[a,b]/a^{2},\quad |a|=1,|b|=2,\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(C_{p},\mathbb{F}_{p^{n}})\simeq \mathbb{F}_{p^{n}}[a,b]/a^{2},\quad |a|=1,|b|=2,\end{eqnarray}$$
is the tensor product on an exterior algebra on a class in degree one and a polynomial algebra on a class in degree two, both over
![]() $\mathbb{F}_{p^{n}}$
. Recall also that the cohomology of
$\mathbb{F}_{p^{n}}$
. Recall also that the cohomology of
![]() $\overline{\unicode[STIX]{x1D70C}}$
as a graded module is given by
$\overline{\unicode[STIX]{x1D70C}}$
as a graded module is given by
 $$\begin{eqnarray}H^{\ast }(C_{p},\overline{\unicode[STIX]{x1D70C}})\simeq H^{\ast }(C_{p},\mathbb{F}_{p^{n}})\{u_{0},u_{1}\}/(au_{0}=0,bu_{0}=au_{1}),\quad |u_{0}|=0,|u_{1}|=1.\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(C_{p},\overline{\unicode[STIX]{x1D70C}})\simeq H^{\ast }(C_{p},\mathbb{F}_{p^{n}})\{u_{0},u_{1}\}/(au_{0}=0,bu_{0}=au_{1}),\quad |u_{0}|=0,|u_{1}|=1.\end{eqnarray}$$
As a result, we can completely determine the cohomology modulo transfers (which only appear in
![]() $H^{0}$
).
$H^{0}$
).
Corollary 6.3. The cohomology
 $H^{\ast }(C_{p},\text{gr}(E_{n})_{0})$
modulo transfers is given by
$H^{\ast }(C_{p},\text{gr}(E_{n})_{0})$
modulo transfers is given by
 $$\begin{eqnarray}H^{\ast }(C_{p},\mathbb{F}_{p^{n}})[u,v,v^{\prime }]/(v^{2}={v^{\prime }}^{2}=0,av=0,bv=av^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(C_{p},\mathbb{F}_{p^{n}})[u,v,v^{\prime }]/(v^{2}={v^{\prime }}^{2}=0,av=0,bv=av^{\prime }).\end{eqnarray}$$
The internal grading of
![]() $u$
is
$u$
is
![]() $p$
and that of
$p$
and that of
![]() $v,v^{\prime }$
is
$v,v^{\prime }$
is
![]() $1$
. Moreover,
$1$
. Moreover,
![]() $u,v$
are in cohomological degree zero and
$u,v$
are in cohomological degree zero and
![]() $v^{\prime }$
is in
$v^{\prime }$
is in
![]() $H^{1}$
.
$H^{1}$
.
We display in Figure 4 the
![]() $E_{1}$
-page of the spectral sequence
$E_{1}$
-page of the spectral sequence
 $$\begin{eqnarray}H^{i}(C_{p},\text{gr}^{j}((E_{n})_{0}))\;\Longrightarrow \;H^{i}(C_{p},(E_{n})_{0})\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(C_{p},\text{gr}^{j}((E_{n})_{0}))\;\Longrightarrow \;H^{i}(C_{p},(E_{n})_{0})\end{eqnarray}$$
when
![]() $p=3$
.
$p=3$
.

Figure 4. The spectral sequence for
 $H^{\ast }(C_{p},(E_{n})_{0})$
for
$H^{\ast }(C_{p},(E_{n})_{0})$
for
![]() $p=3$
.
$p=3$
.
We note that none of the transfers support differentials in the spectral sequence thanks to the norm map. Moreover, this holds in the topological spectral sequence for the same reason.
It remains to determine the differentials. We do this by reverse-engineering the output of the Hopkins–Miller calculation.
Proposition 6.4. The spectral sequence (6.1) collapses at the
![]() $p$
th page. The differentials are (up to non-zero scalars) determined by
$p$
th page. The differentials are (up to non-zero scalars) determined by
 $d_{1}(a)\stackrel{\cdot }{=}bv$
and
$d_{1}(a)\stackrel{\cdot }{=}bv$
and
 $d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu$
. The classes
$d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu$
. The classes
![]() $u,b,v$
are permanent cycles.
$u,b,v$
are permanent cycles.
Proof. We start by describing the permanent cycles. First, the class
![]() $u$
in degree
$u$
in degree
![]() $p$
is constructed as a multiplicative norm. This construction can be carried out in
$p$
is constructed as a multiplicative norm. This construction can be carried out in
![]() $(E_{n})_{0}$
, so
$(E_{n})_{0}$
, so
![]() $u$
is necessarily a permanent cycle. The class
$u$
is necessarily a permanent cycle. The class
![]() $b$
comes from
$b$
comes from
 $H^{\ast }(C_{p},\mathbb{Z})$
and is also therefore a permanent cycle. The invariant class
$H^{\ast }(C_{p},\mathbb{Z})$
and is also therefore a permanent cycle. The invariant class
![]() $v$
in
$v$
in
 $H^{0}(C_{p},\overline{\unicode[STIX]{x1D70C}})$
is represented by the image of
$H^{0}(C_{p},\overline{\unicode[STIX]{x1D70C}})$
is represented by the image of
![]() $p$
in
$p$
in
![]() $\mathfrak{m}/\mathfrak{m}^{2}$
. Since this is invariant in
$\mathfrak{m}/\mathfrak{m}^{2}$
. Since this is invariant in
![]() $(E_{n})_{0}$
, it is also a permanent cycle.
$(E_{n})_{0}$
, it is also a permanent cycle.
Next, we describe the first differential
![]() $d_{1}$
. We claim that, up to unit scalars,
$d_{1}$
. We claim that, up to unit scalars,
 $d_{1}(a)=bv=av^{\prime }$
. One sees this by naturality with the filtration (by powers of the maximal ideal) on
$d_{1}(a)=bv=av^{\prime }$
. One sees this by naturality with the filtration (by powers of the maximal ideal) on
![]() $\mathbb{W}(\mathbb{F}_{p^{n}})$
. We have a
$\mathbb{W}(\mathbb{F}_{p^{n}})$
. We have a
![]() $C_{p}$
-equivariant, filtration-preserving map
$C_{p}$
-equivariant, filtration-preserving map
 $\mathbb{W}(\mathbb{F}_{p^{n}})\rightarrow (E_{n})_{0}$
, where the domain has trivial action. One easily computes the
$\mathbb{W}(\mathbb{F}_{p^{n}})\rightarrow (E_{n})_{0}$
, where the domain has trivial action. One easily computes the
![]() $d_{1}$
in the spectral sequence for
$d_{1}$
in the spectral sequence for
![]() $\mathbb{W}(\mathbb{F}_{p^{n}})$
(as a Bockstein), and uses the fact that the unique non-trivial map of
$\mathbb{W}(\mathbb{F}_{p^{n}})$
(as a Bockstein), and uses the fact that the unique non-trivial map of
![]() $C_{p}$
-representations
$C_{p}$
-representations
![]() $\mathbf{1}\rightarrow \overline{\unicode[STIX]{x1D70C}}$
induces an isomorphism on
$\mathbf{1}\rightarrow \overline{\unicode[STIX]{x1D70C}}$
induces an isomorphism on
![]() $H^{2}$
. By naturality, this determines the
$H^{2}$
. By naturality, this determines the
![]() $d_{1}$
in our spectral sequence.
$d_{1}$
in our spectral sequence.
Finally, we claim that
 $d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu$
as desired. We know that this differential must happen, because otherwise
$d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu$
as desired. We know that this differential must happen, because otherwise
 $H^{2}(C_{p},(E_{n})_{0})$
would have cardinality at least
$H^{2}(C_{p},(E_{n})_{0})$
would have cardinality at least
![]() $p^{2n}$
, whereas it has cardinality
$p^{2n}$
, whereas it has cardinality
![]() $p^{n}$
by the Hopkins–Miller calculations (Proposition 2.6).◻
$p^{n}$
by the Hopkins–Miller calculations (Proposition 2.6).◻
6.2 The multiplicative spectral sequence
We now describe the modifications to the above spectral sequence that occur for the multiplicative case, and determine the algebraic Picard group for the group
![]() $C_{p}$
.
$C_{p}$
.
The following is our main result. As before, we let
 $\mathfrak{m}\subset (E_{n})_{0}$
be the maximal ideal, with the induced
$\mathfrak{m}\subset (E_{n})_{0}$
be the maximal ideal, with the induced
![]() $C_{p}$
-action, and let
$C_{p}$
-action, and let
![]() $\unicode[STIX]{x1D714}$
denote
$\unicode[STIX]{x1D714}$
denote
![]() $\unicode[STIX]{x1D70B}_{2}E_{n}$
as an (invertible) equivariant
$\unicode[STIX]{x1D70B}_{2}E_{n}$
as an (invertible) equivariant
![]() $(E_{n})_{0}$
-module.
$(E_{n})_{0}$
-module.
Proposition 6.5. We have
 $H^{1}(C_{p},1+\mathfrak{m})\simeq H^{1}(C_{p},(E_{n})_{0}^{\times })\simeq \mathbb{Z}/p$
, generated by the class of
$H^{1}(C_{p},1+\mathfrak{m})\simeq H^{1}(C_{p},(E_{n})_{0}^{\times })\simeq \mathbb{Z}/p$
, generated by the class of
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.
Proof. We use the
![]() $\mathfrak{m}$
-adic filtration on
$\mathfrak{m}$
-adic filtration on
![]() $1+\mathfrak{m}$
, which leads to a spectral sequence whose
$1+\mathfrak{m}$
, which leads to a spectral sequence whose
![]() $E_{1}$
-page is identified with (6.1) with the bottom row removed, converging to
$E_{1}$
-page is identified with (6.1) with the bottom row removed, converging to
 $H^{\ast }(C_{p},1+\mathfrak{m})$
. We will denote the differentials by
$H^{\ast }(C_{p},1+\mathfrak{m})$
. We will denote the differentials by
![]() $d_{k,\times }$
.
$d_{k,\times }$
.
In the algebraic spectral sequence, we saw in Proposition 6.4 that everything that can contribute to the cohomological degree 1 abutment supports either a
![]() $d_{1}$
or a
$d_{1}$
or a
![]() $d_{p-1}$
. In filtration at least
$d_{p-1}$
. In filtration at least
![]() $2$
, we can import these differentials thanks to the truncated exponential and logarithm (Proposition 5.7). However, we cannot import the formula
$2$
, we can import these differentials thanks to the truncated exponential and logarithm (Proposition 5.7). However, we cannot import the formula
 $$\begin{eqnarray}d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu,\end{eqnarray}$$
$$\begin{eqnarray}d_{p-1}(v^{\prime })\stackrel{\cdot }{=}bu,\end{eqnarray}$$
into the multiplicative spectral sequence. Instead, we use the formula of Proposition 5.12, which gives the differential in the multiplicative spectral sequence. Suppose
 $d_{p-1}(v^{\prime })=\unicode[STIX]{x1D709}bu,\unicode[STIX]{x1D6FD}P^{0}(v^{\prime })=\unicode[STIX]{x1D709}^{\prime }bu$
for some
$d_{p-1}(v^{\prime })=\unicode[STIX]{x1D709}bu,\unicode[STIX]{x1D6FD}P^{0}(v^{\prime })=\unicode[STIX]{x1D709}^{\prime }bu$
for some
 $\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
. For any
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in \mathbb{F}_{p^{n}}$
. For any
![]() $e\in \mathbb{F}_{p^{n}}$
, one obtains:
$e\in \mathbb{F}_{p^{n}}$
, one obtains:
 $$\begin{eqnarray}\displaystyle d_{p-1,\times }(ev^{\prime }) & = & \displaystyle d_{p-1}(ev^{\prime })-\unicode[STIX]{x1D6FD}P^{0}(ev^{\prime })\nonumber\\ \displaystyle & = & \displaystyle e\unicode[STIX]{x1D709}bu-e^{p}\unicode[STIX]{x1D6FD}P^{0}(v^{\prime })\nonumber\\ \displaystyle & = & \displaystyle e\unicode[STIX]{x1D709}bu-e^{p}\unicode[STIX]{x1D709}^{\prime }bu=(e\unicode[STIX]{x1D709}-e^{p}\unicode[STIX]{x1D709}^{\prime })bu.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p-1,\times }(ev^{\prime }) & = & \displaystyle d_{p-1}(ev^{\prime })-\unicode[STIX]{x1D6FD}P^{0}(ev^{\prime })\nonumber\\ \displaystyle & = & \displaystyle e\unicode[STIX]{x1D709}bu-e^{p}\unicode[STIX]{x1D6FD}P^{0}(v^{\prime })\nonumber\\ \displaystyle & = & \displaystyle e\unicode[STIX]{x1D709}bu-e^{p}\unicode[STIX]{x1D709}^{\prime }bu=(e\unicode[STIX]{x1D709}-e^{p}\unicode[STIX]{x1D709}^{\prime })bu.\nonumber\end{eqnarray}$$
Now we know that
![]() $\unicode[STIX]{x1D709}\neq 0$
, so regardless of the value of
$\unicode[STIX]{x1D709}\neq 0$
, so regardless of the value of
![]() $\unicode[STIX]{x1D709}^{\prime }$
, there will be at most
$\unicode[STIX]{x1D709}^{\prime }$
, there will be at most
![]() $p$
choices of
$p$
choices of
![]() $e$
that make the above vanish. This gives an upper bound of
$e$
that make the above vanish. This gives an upper bound of
![]() $\mathbb{Z}/p$
for the
$\mathbb{Z}/p$
for the
![]() $H^{1}$
.
$H^{1}$
.
However, the Hopkins–Miller calculations (Proposition 2.6) also give a lower bound of
![]() $\mathbb{Z}/p$
for the Picard group: in fact, it shows that
$\mathbb{Z}/p$
for the Picard group: in fact, it shows that
 $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}_{2}E_{n}$
has order
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}_{2}E_{n}$
has order
![]() $p$
in the algebraic Picard group as
$p$
in the algebraic Picard group as
 $H^{\ast }(C_{p},\unicode[STIX]{x1D714}^{\otimes j})\neq H^{\ast }(C_{p},(E_{n})_{0})$
for
$H^{\ast }(C_{p},\unicode[STIX]{x1D714}^{\otimes j})\neq H^{\ast }(C_{p},(E_{n})_{0})$
for
![]() $j<p$
. This completes the proof.◻
$j<p$
. This completes the proof.◻
We emphasize that, in the above proof, the additive differentials were
![]() $\mathbb{F}_{p^{n}}$
-linear, but the multiplicative differentials were not. This enables us to reduce a group that was a priori
$\mathbb{F}_{p^{n}}$
-linear, but the multiplicative differentials were not. This enables us to reduce a group that was a priori
![]() $\mathbb{F}_{p^{n}}$
to a
$\mathbb{F}_{p^{n}}$
to a
![]() $\mathbb{Z}/p$
. Also, one can directly show that
$\mathbb{Z}/p$
. Also, one can directly show that
![]() $\unicode[STIX]{x1D709}^{\prime }\neq 0$
, although we do not need to do so here. The fact that the difference between the additive and multiplicative differentials is Frobenius-semilinear is all that was used, not any of the explicit formulas.
$\unicode[STIX]{x1D709}^{\prime }\neq 0$
, although we do not need to do so here. The fact that the difference between the additive and multiplicative differentials is Frobenius-semilinear is all that was used, not any of the explicit formulas.
7 The topological comparison of differentials
7.1 Context
We begin by reviewing the context from [Reference Mathew and StojanoskaMS16, §§ 5 and 6]. Let
![]() $R^{\bullet }$
be a cosimplicial
$R^{\bullet }$
be a cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring. In this case, there is a Bousfield–Kan spectral sequence (BKSS)
$\mathbf{E}_{\infty }$
-ring. In this case, there is a Bousfield–Kan spectral sequence (BKSS)
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{s}\unicode[STIX]{x1D70B}_{t}R^{\bullet }\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}\,\text{Tot}\,R^{\bullet }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{s}\unicode[STIX]{x1D70B}_{t}R^{\bullet }\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}\,\text{Tot}\,R^{\bullet }.\end{eqnarray}$$
Applying the functor
![]() $\mathfrak{gl}_{1}$
, one also obtains a BKSS
$\mathfrak{gl}_{1}$
, one also obtains a BKSS
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{s}\unicode[STIX]{x1D70B}_{t}\mathfrak{gl}_{1}(R^{\bullet })\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}\,\text{Tot}(\mathfrak{gl}_{1}(R^{\bullet })).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{s}\unicode[STIX]{x1D70B}_{t}\mathfrak{gl}_{1}(R^{\bullet })\;\Longrightarrow \;\unicode[STIX]{x1D70B}_{t-s}\,\text{Tot}(\mathfrak{gl}_{1}(R^{\bullet })).\end{eqnarray}$$
The latter spectral sequence is relevant to Picard group computations via descent theory, but the former spectral sequence (7.1) is usually better understood (e.g. because of the multiplicative structure).
For
 $t-s>0$
, these homotopy groups are determined by the BKSSs for the spaces
$t-s>0$
, these homotopy groups are determined by the BKSSs for the spaces
![]() $\unicode[STIX]{x1D6FA}^{\infty }R^{\bullet }$
and
$\unicode[STIX]{x1D6FA}^{\infty }R^{\bullet }$
and
 $\unicode[STIX]{x1D6FA}^{\infty }\mathfrak{gl}_{1}(R^{\bullet })$
, which have isomorphic connected components. As a result, the spectral sequences (7.1) and (7.2) can be compared in this range. However, it is the
$\unicode[STIX]{x1D6FA}^{\infty }\mathfrak{gl}_{1}(R^{\bullet })$
, which have isomorphic connected components. As a result, the spectral sequences (7.1) and (7.2) can be compared in this range. However, it is the
 $t-s=-1$
component of (7.2) that is relevant to the Picard group calculations. Although at
$t-s=-1$
component of (7.2) that is relevant to the Picard group calculations. Although at
![]() $E_{2}$
both spectral sequences (except for
$E_{2}$
both spectral sequences (except for
![]() $s=0,1$
) are the same in this column, the differentials vary. Nonetheless, in [Reference Mathew and StojanoskaMS16], the second and third authors showed that there is a stable range in which differentials can be compared, even for
$s=0,1$
) are the same in this column, the differentials vary. Nonetheless, in [Reference Mathew and StojanoskaMS16], the second and third authors showed that there is a stable range in which differentials can be compared, even for
 $t-s=-1$
, and the first differential beyond the stable range can be computed. In particular, one observes that in any range
$t-s=-1$
, and the first differential beyond the stable range can be computed. In particular, one observes that in any range
 $[n,2n-1]$
, there is a functorial equivalence of spectra
$[n,2n-1]$
, there is a functorial equivalence of spectra
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{[n,2n-1]}R\simeq \unicode[STIX]{x1D70F}_{[n,2n-1]}\mathfrak{gl}_{1}(R),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{[n,2n-1]}R\simeq \unicode[STIX]{x1D70F}_{[n,2n-1]}\mathfrak{gl}_{1}(R),\end{eqnarray}$$
for an
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R$
. This gives the stable range, and the first differential beyond this range can be computed via reduction to a universal example.
$R$
. This gives the stable range, and the first differential beyond this range can be computed via reduction to a universal example.
In this section, we will prove that after arithmetic localization there is a larger range in which one can compare differentials in the two spectral sequences, analogous to the range that one obtains in algebra using the truncated logarithm (cf. § 5). It is possible to prove an analog of (7.3) in this context (and construct a ‘spectral’ truncated logarithm); this will be explored in forthcoming work by Clausen, Heuts, Mathew and Stojanoska.
Let
![]() $R^{\bullet }$
be a cosimplicial
$R^{\bullet }$
be a cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring whose members are all
$\mathbf{E}_{\infty }$
-ring whose members are all
 $\mathbb{Z}[1/(p-1)!]$
-local. Our main goal is to demonstrate the following.
$\mathbb{Z}[1/(p-1)!]$
-local. Our main goal is to demonstrate the following.
Theorem 7.1. Suppose
![]() $R^{\bullet }$
is a cosimplicial
$R^{\bullet }$
is a cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-local
$\mathbb{Z}[1/(p-1)!]$
-local
![]() $\mathbf{E}_{\infty }$
-ring. Denote by
$\mathbf{E}_{\infty }$
-ring. Denote by
![]() $E_{\ast }^{s,t}$
and
$E_{\ast }^{s,t}$
and
![]() $E_{\ast ,\times }^{s,t}$
the associated spectral sequences (7.1) and (7.2) above. Suppose given
$E_{\ast ,\times }^{s,t}$
the associated spectral sequences (7.1) and (7.2) above. Suppose given
![]() $t\geqslant 2$
and an element
$t\geqslant 2$
and an element
 $x\in E_{2}^{t+1,t}$
such that
$x\in E_{2}^{t+1,t}$
such that
![]() $x$
survives to the
$x$
survives to the
![]() $E_{k}$
-page. Then:
$E_{k}$
-page. Then:
-
(i) if
 $k\leqslant (p-1)t$
, then
$k\leqslant (p-1)t$
, then
 $x$
survives to
$x$
survives to
 $E_{k,\times }$
in the
$E_{k,\times }$
in the
 $\mathfrak{gl}_{1}$
spectral sequence and
$\mathfrak{gl}_{1}$
spectral sequence and
 $d_{k,\times }(x)=d_{k}(x)$
;
$d_{k,\times }(x)=d_{k}(x)$
; -
(ii) if
 $t$
is even and
$t$
is even and
 $k=(p-1)t+1$
, then
$k=(p-1)t+1$
, then
 $d_{k,\times }(x)=d_{k}(x)+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}(x)$
for some
$d_{k,\times }(x)=d_{k}(x)+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}(x)$
for some
 $\unicode[STIX]{x1D701}\in \mathbb{F}_{p}^{\times }$
(independent of
$\unicode[STIX]{x1D701}\in \mathbb{F}_{p}^{\times }$
(independent of
 $R^{\bullet }$
).
$R^{\bullet }$
).
We will discuss the universal operation
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}$
as well: it arises from the right derived functors of the symmetric algebra functor in the sense of Priddy [Reference PriddyPri73], or as a power operation for
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}$
as well: it arises from the right derived functors of the symmetric algebra functor in the sense of Priddy [Reference PriddyPri73], or as a power operation for
![]() $\mathbf{E}_{\infty }$
-ring spectra over
$\mathbf{E}_{\infty }$
-ring spectra over
 $\mathbb{Z}[1/(p-1)!]$
. Again, the only fact we will need about it is its Frobenius-semilinearity property, and we will not try to determine the constant
$\mathbb{Z}[1/(p-1)!]$
. Again, the only fact we will need about it is its Frobenius-semilinearity property, and we will not try to determine the constant
![]() $\unicode[STIX]{x1D701}$
. When
$\unicode[STIX]{x1D701}$
. When
![]() $p=2$
, this recovers the comparison results of [Reference Mathew and StojanoskaMS16, §§ 5 and 6]. In particular, we shall assume throughout that
$p=2$
, this recovers the comparison results of [Reference Mathew and StojanoskaMS16, §§ 5 and 6]. In particular, we shall assume throughout that
![]() $p>2$
. Unlike in [Reference Mathew and StojanoskaMS16], we will use the same notation for elements of the multiplicative and additive spectral sequences.
$p>2$
. Unlike in [Reference Mathew and StojanoskaMS16], we will use the same notation for elements of the multiplicative and additive spectral sequences.
7.2 Proofs
Theorem 7.1 is proved using the same strategy as in [Reference Mathew and StojanoskaMS16, § 6], although we will not try to determine
![]() $\unicode[STIX]{x1D701}$
. Namely, we consider the ‘universal’ example of a cosimplicial
$\unicode[STIX]{x1D701}$
. Namely, we consider the ‘universal’ example of a cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R^{\bullet }$
(with
$R^{\bullet }$
(with
![]() $(p-1)!$
inverted) together with a class in
$(p-1)!$
inverted) together with a class in
![]() $E_{k}^{t+1,t}$
and prove the desired claims here, where it will follow by a sparsity argument. We need to look for the cosimplicial
$E_{k}^{t+1,t}$
and prove the desired claims here, where it will follow by a sparsity argument. We need to look for the cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring (which is
$\mathbf{E}_{\infty }$
-ring (which is
 $\mathbb{Z}[1/(p-1)!]$
-local) which corepresents the functor
$\mathbb{Z}[1/(p-1)!]$
-local) which corepresents the functor
 $$\begin{eqnarray}X^{\bullet }\mapsto \unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6F4}^{-1}\,\text{fib}(\text{Tot}_{t+k}(X^{\bullet })\rightarrow \text{Tot}_{t}(X^{\bullet }))),\end{eqnarray}$$
$$\begin{eqnarray}X^{\bullet }\mapsto \unicode[STIX]{x1D6FA}^{\infty }(\unicode[STIX]{x1D6F4}^{-1}\,\text{fib}(\text{Tot}_{t+k}(X^{\bullet })\rightarrow \text{Tot}_{t}(X^{\bullet }))),\end{eqnarray}$$
since a class in
![]() $E_{k}^{t+1,t}$
represents a class in
$E_{k}^{t+1,t}$
represents a class in
 $\unicode[STIX]{x1D70B}_{-1}\,\text{Tot}_{t+k}(X^{\bullet })$
trivialized in
$\unicode[STIX]{x1D70B}_{-1}\,\text{Tot}_{t+k}(X^{\bullet })$
trivialized in
 $\text{Tot}_{t}(X^{\bullet })$
.
$\text{Tot}_{t}(X^{\bullet })$
.
In this subsection, everything will be
 $\mathbb{Z}[1/(p-1)!]$
-localized.
$\mathbb{Z}[1/(p-1)!]$
-localized.
Construction 7.2. To construct this universal cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R^{\bullet }$
, we let
$R^{\bullet }$
, we let
![]() $\operatorname{Lan}$
denote the functor of left Kan extension. We define the pointed cosimplicial space
$\operatorname{Lan}$
denote the functor of left Kan extension. We define the pointed cosimplicial space
![]() ${\mathcal{F}}^{\bullet }$
via the homotopy pushout
${\mathcal{F}}^{\bullet }$
via the homotopy pushout

The cosimplicial
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $R^{\bullet }$
is defined via
$R^{\bullet }$
is defined via
 $$\begin{eqnarray}R^{\bullet }=\text{Free}(\unicode[STIX]{x1D6F4}^{-1}\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet })[1/(p-1)!].\end{eqnarray}$$
$$\begin{eqnarray}R^{\bullet }=\text{Free}(\unicode[STIX]{x1D6F4}^{-1}\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet })[1/(p-1)!].\end{eqnarray}$$
We write
![]() ${\mathcal{G}}^{\bullet }$
for the cosimplicial spectrum
${\mathcal{G}}^{\bullet }$
for the cosimplicial spectrum
 $\unicode[STIX]{x1D6F4}^{-1}\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }[1/(p-1)!]$
, so that
$\unicode[STIX]{x1D6F4}^{-1}\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }[1/(p-1)!]$
, so that
 $$\begin{eqnarray}R^{\bullet }=\text{Free}({\mathcal{G}}^{\bullet })[1/(p-1)!].\end{eqnarray}$$
$$\begin{eqnarray}R^{\bullet }=\text{Free}({\mathcal{G}}^{\bullet })[1/(p-1)!].\end{eqnarray}$$
Pointwise, the left Kan extensions have the homotopy types of wedges of spheres. As in [Reference Mathew and StojanoskaMS16, § 6.2], we find the following properties of the pointed cosimplicial space
 ${\mathcal{F}}^{\bullet }:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{S}}_{\ast }$
:
${\mathcal{F}}^{\bullet }:\unicode[STIX]{x1D6E5}\rightarrow {\mathcal{S}}_{\ast }$
:
-
(i)
 ${\mathcal{F}}(T)$
(for
${\mathcal{F}}(T)$
(for
 $T\in \unicode[STIX]{x1D6E5}$
) is a wedge of
$T\in \unicode[STIX]{x1D6E5}$
) is a wedge of
 $S^{t+1}$
and
$S^{t+1}$
and
 $S^{t+k}$
;
$S^{t+k}$
; -
(ii)
 ${\mathcal{F}}^{\bullet }|_{\unicode[STIX]{x1D6E5}^{{\leqslant}t}}$
is contractible; for any
${\mathcal{F}}^{\bullet }|_{\unicode[STIX]{x1D6E5}^{{\leqslant}t}}$
is contractible; for any
 $T\in \unicode[STIX]{x1D6E5}^{{\leqslant}t+k}$
,
$T\in \unicode[STIX]{x1D6E5}^{{\leqslant}t+k}$
,
 ${\mathcal{F}}(T)$
is a wedge of copies of
${\mathcal{F}}(T)$
is a wedge of copies of
 $S^{t+1}$
.
$S^{t+1}$
.
By desuspending, this of course determines the pointwise homotopy type of
![]() ${\mathcal{G}}(T)$
for any
${\mathcal{G}}(T)$
for any
![]() $T\in \unicode[STIX]{x1D6E5}$
.
$T\in \unicode[STIX]{x1D6E5}$
.
The BKSS for the cosimplicial spectrum
![]() $\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }$
is determined as in [Reference Mathew and StojanoskaMS16, § 6.4] (cf. [Reference Mathew and StojanoskaMS16, proof of Proposition 6.3.1]), and in particular follows from the calculation there of the BKSS for the cosimplicial spectrum
$\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }$
is determined as in [Reference Mathew and StojanoskaMS16, § 6.4] (cf. [Reference Mathew and StojanoskaMS16, proof of Proposition 6.3.1]), and in particular follows from the calculation there of the BKSS for the cosimplicial spectrum
 $\unicode[STIX]{x1D6F4}_{+}^{\infty }\text{Lan}_{\unicode[STIX]{x1D6E5}^{{\leqslant}t}\rightarrow \unicode[STIX]{x1D6E5}}(\ast )$
. The BKSS for
$\unicode[STIX]{x1D6F4}_{+}^{\infty }\text{Lan}_{\unicode[STIX]{x1D6E5}^{{\leqslant}t}\rightarrow \unicode[STIX]{x1D6E5}}(\ast )$
. The BKSS for
![]() ${\mathcal{G}}^{\bullet }$
is a shift by one of that of
${\mathcal{G}}^{\bullet }$
is a shift by one of that of
 $\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }[1/(p-1)!]$
, and we describe it next. For the reader’s convenience, we also include an example in Figure 5 below.
$\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{F}}^{\bullet }[1/(p-1)!]$
, and we describe it next. For the reader’s convenience, we also include an example in Figure 5 below.

Figure 5. The BKSS for
![]() ${\mathcal{G}}^{\bullet }$
for
${\mathcal{G}}^{\bullet }$
for
![]() $t=1$
,
$t=1$
,
![]() $k=4$
.
$k=4$
.
Proposition 7.3.
-
(i) As graded modules over
 $\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
, we have
$\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
, we have  $$\begin{eqnarray}H^{s}(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}})^{\bullet })\simeq \left\{\begin{array}{@{}ll@{}}0\quad & s\neq t+1,t+k+1,\\ \unicode[STIX]{x1D70B}_{\ast }(S^{t})[1/(p-1)!]\quad & s=t+1,\\ \unicode[STIX]{x1D70B}_{\ast }(S^{t+k-1})[1/(p-1)!]\quad & s=t+k+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}H^{s}(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}})^{\bullet })\simeq \left\{\begin{array}{@{}ll@{}}0\quad & s\neq t+1,t+k+1,\\ \unicode[STIX]{x1D70B}_{\ast }(S^{t})[1/(p-1)!]\quad & s=t+1,\\ \unicode[STIX]{x1D70B}_{\ast }(S^{t+k-1})[1/(p-1)!]\quad & s=t+k+1.\end{array}\right.\end{eqnarray}$$
-
(ii) We let
 $\unicode[STIX]{x1D704}\in E_{2}^{t+1,t}$
be the fundamental generating class. There is a
$\unicode[STIX]{x1D704}\in E_{2}^{t+1,t}$
be the fundamental generating class. There is a
 $d_{k}$
in the BKSS, which carries
$d_{k}$
in the BKSS, which carries
 $\unicode[STIX]{x1D704}$
to a generator in
$\unicode[STIX]{x1D704}$
to a generator in
 $E_{2}^{t+k+1,t+k-1}\simeq \unicode[STIX]{x1D70B}_{t+k-1}(S^{t+k-1})[1/(p-1)!]$
.
$E_{2}^{t+k+1,t+k-1}\simeq \unicode[STIX]{x1D70B}_{t+k-1}(S^{t+k-1})[1/(p-1)!]$
.
Now we consider the BKSS for
![]() $R^{\bullet }$
in the desired range, which depends only on the Postnikov section
$R^{\bullet }$
in the desired range, which depends only on the Postnikov section
![]() $\unicode[STIX]{x1D70F}_{{\leqslant}pt}R^{\bullet }$
. We observe that there is an equivalence of cosimplicial spectra
$\unicode[STIX]{x1D70F}_{{\leqslant}pt}R^{\bullet }$
. We observe that there is an equivalence of cosimplicial spectra
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\leqslant}pt}R^{\bullet }\simeq S^{0}[1/(p-1)!]\vee {\mathcal{G}}^{\bullet }\vee {\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{2}}^{\bullet \wedge 2}\vee \cdots \vee {\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\leqslant}pt}R^{\bullet }\simeq S^{0}[1/(p-1)!]\vee {\mathcal{G}}^{\bullet }\vee {\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{2}}^{\bullet \wedge 2}\vee \cdots \vee {\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}.\end{eqnarray}$$
We claim that in the range of concern, none of the terms besides
![]() ${\mathcal{G}}^{\bullet }$
and
${\mathcal{G}}^{\bullet }$
and
![]() ${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}$
can contribute; this follows from the next lemma.
${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}$
can contribute; this follows from the next lemma.
Lemma 7.4. For any
 $2\leqslant u\leqslant p-1$
, the BKSS for
$2\leqslant u\leqslant p-1$
, the BKSS for
 $({\mathcal{G}}^{\bullet \wedge u})_{h\unicode[STIX]{x1D6F4}_{u}}$
is zero at
$({\mathcal{G}}^{\bullet \wedge u})_{h\unicode[STIX]{x1D6F4}_{u}}$
is zero at
![]() $E_{2}$
in cohomological degrees below
$E_{2}$
in cohomological degrees below
 $(u-1)(t+1)+(t+k+1)$
.
$(u-1)(t+1)+(t+k+1)$
.
Proof. Consider the cosimplicial
 $\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
-module
$\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
-module
 $M^{\bullet }=\unicode[STIX]{x1D70B}_{\ast }{\mathcal{G}}^{\bullet }$
, which is levelwise free. The cosimplicial module
$M^{\bullet }=\unicode[STIX]{x1D70B}_{\ast }{\mathcal{G}}^{\bullet }$
, which is levelwise free. The cosimplicial module
 $\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{u}}^{\bullet \wedge u})$
is obtained as
$\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{u}}^{\bullet \wedge u})$
is obtained as
 $(M^{\otimes u})_{\unicode[STIX]{x1D6F4}_{u}}$
where the tensor product is taken over
$(M^{\otimes u})_{\unicode[STIX]{x1D6F4}_{u}}$
where the tensor product is taken over
![]() $\unicode[STIX]{x1D70B}_{\ast }(S^{0})$
, and where
$\unicode[STIX]{x1D70B}_{\ast }(S^{0})$
, and where
![]() $\unicode[STIX]{x1D6F4}_{u}$
acts by permuting the factors with appropriate signs. Since the order of
$\unicode[STIX]{x1D6F4}_{u}$
acts by permuting the factors with appropriate signs. Since the order of
![]() $\unicode[STIX]{x1D6F4}_{u}$
is invertible, the operation of taking coinvariants is well-behaved (and comes from the induced operation on cohomology); we obtain that
$\unicode[STIX]{x1D6F4}_{u}$
is invertible, the operation of taking coinvariants is well-behaved (and comes from the induced operation on cohomology); we obtain that
 $$\begin{eqnarray}H^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{u}}^{\bullet \wedge u}))\simeq (H^{\ast }(M^{\bullet })^{\otimes u})_{\unicode[STIX]{x1D6F4}_{u}}.\end{eqnarray}$$
$$\begin{eqnarray}H^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{u}}^{\bullet \wedge u}))\simeq (H^{\ast }(M^{\bullet })^{\otimes u})_{\unicode[STIX]{x1D6F4}_{u}}.\end{eqnarray}$$
For
 $s\leqslant (u-1)(t+1)+(t+k+1)$
, the only contribution to
$s\leqslant (u-1)(t+1)+(t+k+1)$
, the only contribution to
 $H^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}^{\bullet \wedge u}))$
is in cohomological degree
$H^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{G}}^{\bullet \wedge u}))$
is in cohomological degree
 $u(t+1)$
and is a free module of rank one over
$u(t+1)$
and is a free module of rank one over
 $\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
. However, the
$\unicode[STIX]{x1D70B}_{\ast }(S^{0})[1/(p-1)!]$
. However, the
![]() $\unicode[STIX]{x1D6F4}_{u}$
action is by the sign representation which annihilates this upon passage to the coinvariants.◻
$\unicode[STIX]{x1D6F4}_{u}$
action is by the sign representation which annihilates this upon passage to the coinvariants.◻
Finally, we need to determine the contribution of
![]() ${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}$
in case
${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge p}$
in case
 $k=(p-1)t+1$
. Here we assume that
$k=(p-1)t+1$
. Here we assume that
![]() $t$
is even. In the range in question, this only contributes via its
$t$
is even. In the range in question, this only contributes via its
![]() $\unicode[STIX]{x1D70B}_{pt}$
, given by
$\unicode[STIX]{x1D70B}_{pt}$
, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{pt}({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge pt})\simeq \text{Sym}^{p}\unicode[STIX]{x1D70B}_{t}{\mathcal{G}}^{\bullet }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{pt}({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge pt})\simeq \text{Sym}^{p}\unicode[STIX]{x1D70B}_{t}{\mathcal{G}}^{\bullet }.\end{eqnarray}$$
Proof of Theorem 7.1.
Following the outline of [Reference Mathew and StojanoskaMS16], it suffices to determine the behavior of the tautological class in the BKSS for
![]() $\mathfrak{gl}_{1}(R^{\bullet })$
. In the BKSS for
$\mathfrak{gl}_{1}(R^{\bullet })$
. In the BKSS for
![]() $R^{\bullet }$
, the tautological class supports a
$R^{\bullet }$
, the tautological class supports a
![]() $d_{k}$
as in Proposition 7.3 (by naturality for the map
$d_{k}$
as in Proposition 7.3 (by naturality for the map
 ${\mathcal{G}}^{\bullet }\rightarrow R^{\bullet }$
). We observe that the tautological class in the multiplicative spectral sequence cannot support a differential
${\mathcal{G}}^{\bullet }\rightarrow R^{\bullet }$
). We observe that the tautological class in the multiplicative spectral sequence cannot support a differential
![]() $d_{i,\times }$
for
$d_{i,\times }$
for
![]() $i<k$
as there is no suitable target in the spectral sequence. Indeed, for connectivity reasons, there are only the terms
$i<k$
as there is no suitable target in the spectral sequence. Indeed, for connectivity reasons, there are only the terms
![]() ${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{i}}^{\bullet \wedge i}$
for
${\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{i}}^{\bullet \wedge i}$
for
![]() $i<p$
that can contribute here, and these do nothing thanks to Lemma 7.4.
$i<p$
that can contribute here, and these do nothing thanks to Lemma 7.4.
If
 $k\leqslant (p-1)t$
, we find that the target for a
$k\leqslant (p-1)t$
, we find that the target for a
![]() $d_{k,\times }$
in the
$d_{k,\times }$
in the
![]() $\mathfrak{gl}_{1}$
spectral sequence is simply a
$\mathfrak{gl}_{1}$
spectral sequence is simply a
 $\mathbb{Z}[1/(p-1)!]$
; there are no additional contributions. As in [Reference Mathew and StojanoskaMS16], we conclude (by comparing with square-zero extensions) that we can identify the differentials
$\mathbb{Z}[1/(p-1)!]$
; there are no additional contributions. As in [Reference Mathew and StojanoskaMS16], we conclude (by comparing with square-zero extensions) that we can identify the differentials
![]() $d_{k}$
and
$d_{k}$
and
![]() $d_{k,\times }$
.
$d_{k,\times }$
.
Consider, finally, the case
 $k=(p-1)t+1$
and
$k=(p-1)t+1$
and
![]() $t$
even. In this case, the target of the differential
$t$
even. In this case, the target of the differential
![]() $d_{k,\times }$
still contains
$d_{k,\times }$
still contains
 $\mathbb{Z}[1/(p-1)!]d_{k}\unicode[STIX]{x1D704}$
, but also has another factor as
$\mathbb{Z}[1/(p-1)!]d_{k}\unicode[STIX]{x1D704}$
, but also has another factor as
 $H^{pt+2}(\unicode[STIX]{x1D70B}_{pt}R^{\bullet })$
, which we need to determine.
$H^{pt+2}(\unicode[STIX]{x1D70B}_{pt}R^{\bullet })$
, which we need to determine.
Here we will need to use some of the theory of right derived functors of symmetric powers [Reference PriddyPri73]. They determine the cohomology of the symmetric powers of a cosimplicial object. The next proposition follows from [Reference PriddyPri73, §§ 3 and 4], and in particular [Reference PriddyPri73, Theorem 4.0.1], by running a Bockstein spectral sequence. We note also that the work of Kraines [Reference KrainesKra66] relates these operations to
![]() $p$
-fold Massey powers.
$p$
-fold Massey powers.
Proposition 7.5. Let
![]() $X^{\bullet }$
be a cosimplicial
$X^{\bullet }$
be a cosimplicial
 $\mathbb{Z}[1/(p-1)!]$
-module which is levelwise free. Suppose
$\mathbb{Z}[1/(p-1)!]$
-module which is levelwise free. Suppose
 $H^{\ast }(X^{\bullet })$
is concentrated in degree
$H^{\ast }(X^{\bullet })$
is concentrated in degree
![]() $k$
,
$k$
,
![]() $k$
odd, and
$k$
odd, and
 $H^{k}(X^{\bullet })\simeq \mathbb{Z}[1/(p-1)!]$
generated by a tautological class
$H^{k}(X^{\bullet })\simeq \mathbb{Z}[1/(p-1)!]$
generated by a tautological class
![]() $\unicode[STIX]{x1D704}$
. Then for each
$\unicode[STIX]{x1D704}$
. Then for each
 $i\leqslant (k-1)/2$
, we have
$i\leqslant (k-1)/2$
, we have
 $H^{k+2i(p-1)+1}(\operatorname{Sym}^{p}X^{\bullet })\simeq \mathbb{Z}/p$
generated by a class
$H^{k+2i(p-1)+1}(\operatorname{Sym}^{p}X^{\bullet })\simeq \mathbb{Z}/p$
generated by a class
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{i}\unicode[STIX]{x1D704}$
.
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{i}\unicode[STIX]{x1D704}$
.
Now we take
 $k=t+1$
in the above. It follows that
$k=t+1$
in the above. It follows that
 $H^{pt+2}(\unicode[STIX]{x1D70B}_{pt}({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge pt}))\simeq \mathbb{Z}/p$
, generated by
$H^{pt+2}(\unicode[STIX]{x1D70B}_{pt}({\mathcal{G}}_{h\unicode[STIX]{x1D6F4}_{p}}^{\bullet \wedge pt}))\simeq \mathbb{Z}/p$
, generated by
![]() $\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}\unicode[STIX]{x1D704}$
. It follows that we must have a ‘universal’ formula
$\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}\unicode[STIX]{x1D704}$
. It follows that we must have a ‘universal’ formula
 $$\begin{eqnarray}d_{k,\times }(\unicode[STIX]{x1D704})=d_{k}(\unicode[STIX]{x1D704})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}\unicode[STIX]{x1D704},\end{eqnarray}$$
$$\begin{eqnarray}d_{k,\times }(\unicode[STIX]{x1D704})=d_{k}(\unicode[STIX]{x1D704})+\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}{\mathcal{P}}^{t/2}\unicode[STIX]{x1D704},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D701}\in \mathbb{F}_{p}$
. We note that the coefficient of
$\unicode[STIX]{x1D701}\in \mathbb{F}_{p}$
. We note that the coefficient of
![]() $d_{k}(\unicode[STIX]{x1D704})$
is argued to be one similarly as in [Reference Mathew and StojanoskaMS16].
$d_{k}(\unicode[STIX]{x1D704})$
is argued to be one similarly as in [Reference Mathew and StojanoskaMS16].
To complete the argument, we need to argue that
![]() $\unicode[STIX]{x1D701}\neq 0$
. To do this, we consider (for any even
$\unicode[STIX]{x1D701}\neq 0$
. To do this, we consider (for any even
![]() $t$
) an
$t$
) an
![]() $\mathbf{E}_{\infty }$
-ring
$\mathbf{E}_{\infty }$
-ring
![]() $A$
under
$A$
under
![]() $\mathbb{F}_{p}$
such that
$\mathbb{F}_{p}$
such that
 $\unicode[STIX]{x1D70B}_{\ast }(A)\simeq \mathbb{F}_{p}[u]/(u^{p+1})$
for
$\unicode[STIX]{x1D70B}_{\ast }(A)\simeq \mathbb{F}_{p}[u]/(u^{p+1})$
for
![]() $|u|=t$
. We can construct
$|u|=t$
. We can construct
![]() $A$
by taking the free
$A$
by taking the free
![]() $\mathbf{E}_{\infty }$
-ring over
$\mathbf{E}_{\infty }$
-ring over
![]() $\mathbb{F}_{p}$
on a class in degree
$\mathbb{F}_{p}$
on a class in degree
![]() $t$
and truncating at
$t$
and truncating at
![]() $pt$
, i.e.
$pt$
, i.e.
 $$\begin{eqnarray}A=\unicode[STIX]{x1D70F}_{{\leqslant}pt}\,\text{Free}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D6F4}^{t}\mathbb{F}_{p}),\end{eqnarray}$$
$$\begin{eqnarray}A=\unicode[STIX]{x1D70F}_{{\leqslant}pt}\,\text{Free}_{\mathbb{F}_{p}}(\unicode[STIX]{x1D6F4}^{t}\mathbb{F}_{p}),\end{eqnarray}$$
where
![]() $\text{Free}_{\mathbb{F}_{p}}$
denotes the free
$\text{Free}_{\mathbb{F}_{p}}$
denotes the free
![]() $\mathbf{E}_{\infty }$
-algebra functor over
$\mathbf{E}_{\infty }$
-algebra functor over
![]() $\mathbb{F}_{p}$
. In Lemma 7.6 below, we will show that the natural map
$\mathbb{F}_{p}$
. In Lemma 7.6 below, we will show that the natural map
 $$\begin{eqnarray}K(\mathbb{F}_{p},t)\rightarrow \operatorname{GL}_{1}(A),\end{eqnarray}$$
$$\begin{eqnarray}K(\mathbb{F}_{p},t)\rightarrow \operatorname{GL}_{1}(A),\end{eqnarray}$$
inducing an isomorphism on
![]() $\unicode[STIX]{x1D70B}_{t}$
, does not deloop. Of course, the analogous map
$\unicode[STIX]{x1D70B}_{t}$
, does not deloop. Of course, the analogous map
 $K(\mathbb{F}_{p},t)\rightarrow \unicode[STIX]{x1D6FA}^{\infty }A$
does deloop. Equivalently, the associated (Atiyah–Hirzebruch) spectral sequence (AHSS) for
$K(\mathbb{F}_{p},t)\rightarrow \unicode[STIX]{x1D6FA}^{\infty }A$
does deloop. Equivalently, the associated (Atiyah–Hirzebruch) spectral sequence (AHSS) for
 $\mathfrak{gl}_{1}(A)^{K(\mathbb{F}_{p},t+1)}$
admits a differential on the tautological class in
$\mathfrak{gl}_{1}(A)^{K(\mathbb{F}_{p},t+1)}$
admits a differential on the tautological class in
 $H^{t+1}(K(\mathbb{F}_{p},t+1),\unicode[STIX]{x1D70B}_{t}A)$
. By interpreting the AHSS as a BKSS, we find that there must be a non-zero
$H^{t+1}(K(\mathbb{F}_{p},t+1),\unicode[STIX]{x1D70B}_{t}A)$
. By interpreting the AHSS as a BKSS, we find that there must be a non-zero
![]() $d_{k,\times }$
and therefore
$d_{k,\times }$
and therefore
![]() $\unicode[STIX]{x1D701}\neq 0$
.◻
$\unicode[STIX]{x1D701}\neq 0$
.◻
Lemma 7.6. The map (7.5) does not deloop to a map
 $K(\mathbb{F}_{p},t+1)\rightarrow \operatorname{BGL}_{1}(A)$
.
$K(\mathbb{F}_{p},t+1)\rightarrow \operatorname{BGL}_{1}(A)$
.
Proof. To see that (7.5) is not a loop map, we use the universal properties of
![]() $\operatorname{GL}_{1}$
(cf. [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14, § 3]). If (7.5) were a loop map, we would have a morphism of associative ring spectra over
$\operatorname{GL}_{1}$
(cf. [Reference Ando, Blumberg, Gepner, Hopkins and RezkABGHR14, § 3]). If (7.5) were a loop map, we would have a morphism of associative ring spectra over
![]() $\mathbb{F}_{p}$
$\mathbb{F}_{p}$
 $$\begin{eqnarray}\mathbb{F}_{p}\wedge \unicode[STIX]{x1D6F4}_{+}^{\infty }K(\mathbb{F}_{p},t)\rightarrow A,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}_{p}\wedge \unicode[STIX]{x1D6F4}_{+}^{\infty }K(\mathbb{F}_{p},t)\rightarrow A,\end{eqnarray}$$
inducing an isomorphism on
![]() $\unicode[STIX]{x1D70B}_{t}$
. However, the class in
$\unicode[STIX]{x1D70B}_{t}$
. However, the class in
![]() $\unicode[STIX]{x1D70B}_{t}A$
has non-zero
$\unicode[STIX]{x1D70B}_{t}A$
has non-zero
![]() $p$
th power, while the
$p$
th power, while the
![]() $p$
th power of the tautological class in
$p$
th power of the tautological class in
 $\mathbb{F}_{p}\wedge \unicode[STIX]{x1D6F4}_{+}^{\infty }K(\mathbb{F}_{p},t)$
vanishes by [Reference Cohen, Lada and MayCLM76, Lemma 6.1].Footnote
6
◻
$\mathbb{F}_{p}\wedge \unicode[STIX]{x1D6F4}_{+}^{\infty }K(\mathbb{F}_{p},t)$
vanishes by [Reference Cohen, Lada and MayCLM76, Lemma 6.1].Footnote
6
◻
Acknowledgements
We are grateful to Paul Goerss, Hans-Werner Henn, and Mike Hill for extremely helpful discussions.