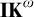ON ZARDINI’S RULES FOR MULTIPLICATIVE QUANTIFICATION AS THE SOURCE OF CONTRA(DI)CTIONS

Abstract

Certain instances of contraction are provable in Zardini’s system $\mathbf {IK}^\omega $ which causes triviality once a truth predicate and suitable fixed points are available.

1 Introduction

Zardini [11] introduces forms of quantification which are intended to generalize $\otimes $ -conjunction and $\oplus $ -disjunction in the way that usual quantification generalizes $\land $ -conjunction and $\lor $ -disjunction. In view of $\otimes $ -conjunction being called multiplicative this label then extends to the new form of quantification. Moreover it is intended to preserve tenets of contraction-free logic so as to avoid trouble with (semantic) paradoxes.

The aim of the present paper is to show that the rules for multiplicative quantification proposed by Zardini allow the derivation of a limited form of contraction which lends itself to proving triviality given an appropriate fixed point for the truth predicate.

My focus is on the formal logical side of proving a triviality result for Zardini’s system $\mathbf {IKT}^\omega $ augmented with specific fixed points. This means, in particular, that I do not engage with Zardini’s motivation for restricting contraction as based on what he calls “the metaphysical picture of the states-of-affairs expressed by paradoxical sentences as being distinctly ‘unstable’.” In view of the results to be presented here, this metaphysical picture is obviously not effective as a safeguard against a form of contraction sneaking into the system and thus as a protection against paradoxes from self-reference. On the one hand Zardini sets out to “show that ridding truth of contraction suffices for ridding it of contradiction” [11, p. 500] but on the other he introduces rules for multiplicative quantification which allow the derivation of a limited form of contraction.

As a consequence of this it is clear that Zardini’s original venture of adding his infinitary rules for multiplicative quantification to a contraction-free logic and still being able to keep the paradoxes of the truth predicate at bay cannot be upheld. It also suggests that the cut elimination proof proposed in [11] is unsound and that beyond the qualms raised by Fjellstad [4].

2 Rules for multiplicative generalization

Zardini assumes a “standard first order language $ \mathcal {L}^1$ without identity” but with “paradoxical sentences in the language” [11, p. 506]. He also speaks of providing a “syntax of a language capable of a minimum of self-reference” (p. 501). It may be a matter of contention what that “minimum” includes, but certainly one of the anonymous referees of the present paper took $\mathbf {IKT}^\omega $ as containing fixed points of the kind employed in this paper, and that on the basis of Zardini’s “metalinguistic coding scheme, however it works.” In view of this I just take the liberty to assume that the fixed point fp provided by Definition 4.6(2) belongs to that minimum.

The systems $\mathbf {IK}^\omega $ and $\mathbf {IKT}^\omega $ are formulated in sequential style with multisets instead of sequents of formulas. The main difference to standard formulations of sequential systems is that Zardini’s rules for multiplicative quantification are formulated by way of employing rules with infinitely many premisses, i.e., a semi-formal system in the sense of Schütte [8, p. 174]. For further details regarding Zardini’s system I refer interested readers to [4, Section 2]. Very little indeed is needed to prove the main results of the present paper and I want to keep the focus clearly on that.

In what follows I shall only deal with multiplicative generalization. Existentialization can be treated analogously, respectively defined in the usual way in terms of generalization and negation.

The rules for $\otimes $ -conjunction to be generalized are

Zardini’s rules for the multiplicative $\forall $ -quantifier are designed as straightforward extrapolations of these rules by allowing infinitely many premisses (upper sequents) and infinitely long sequents.

Following Zardini’s paper, $ \varGamma $ and $ \varDelta $ (possibly with numerical subscripts) stand for multisets.

I use nominal forms in the sense of Schütte [8, p. 14], ¹ which will be communicated by the Gothic letters $ \mathfrak {F} $ and $ \mathfrak {C} $ . Furthermore, it is assumed that there is a designated complete enumeration of the set of closed terms of the language in question the elements of which are communicated by $ t_i $ for $ 0 \leq i < \omega $ .

Definition 2.1. (1) Rules for $\forall $ .

(∀-R)

and

(∀-L)

(2) The system $ \mathbf {IK}^\omega $ is obtained from the contraction-free sequential propositional calculus restricted to $ \neg $ and $ \to $ with the forgoing rules for $\forall $ added. ²

(3) $\, {A \oplus B :\equiv \neg A \to B} $ , $\, {A \otimes B :\equiv \neg (\neg A \oplus \neg B)}$ , and $\, {\exists x \, \mathfrak {F}[x] :\equiv \neg \forall x \, \neg \, \mathfrak {F}[x]} $ .

Remark 2.2. (1) For convenience I shall employ the rules for $ \otimes $ mentioned in the introduction but in view of the foregoing definition it should be clear that they can be cashed out in terms of $\neg $ and $\to $ .

(2) As has been observed in [2] it is possible with the rules $\forall $ -R and $\forall $ -L to prove

$$ \begin{align*} (A \to \exists x \, \mathfrak{F}[x]) \to \exists x (A \to \mathfrak{F}[x]) \, , \end{align*} $$

or, correspondingly, in terms of $\ \forall $ and $ \otimes $ :

$$ \begin{align*} \forall x (A \otimes \mathfrak{F}[x]) \to (A \otimes \forall x \, \mathfrak{F}[x]) \,. \end{align*} $$

That the provability of these wffs is the source of trouble as soon as a certain amount of arithmetic is available has been discussed in [1], for instance, in the context of Łukasiwicz’ infinitely valued logic, and then in [2] in the context of Zardini’s system. Both focus on an extrapolation of a result by Shaw-Kwei [9] which yields $\omega $ -inconsistency, given a suitable fixed point, and extends to full-fledged inconsistency with the help of induction (or equally $\forall $ -R). According to the authors of Da Ré and Rosenblatt [2] a referee of their paper suggested that the provability of these wffs might indicate the presence of some contraction absorbing rule which would render the inconsistency result less surprising, a view, however, the authors regarded as “too hasty.” The present note can be seen as a confirmation of the referee’s suggestion by showing that $\forall $ -R and $\forall $ -L do indeed provide for certain instances of contraction.

(3) There is no provision in either usual formulations of a logical language or Zardini’s paper that would rule out vacuous quantification, but my impression is that some people, at least, feel uneasy about it. Apart from that, Zardini’s rules for multiplicative quantification seem to be inseparable from non-vacuous quantification, so I decided to use the good old device of adding (by way of $\otimes $ -conjunction) a provable wff which provides a variable to quantify over and only use vacuous quantification for the purpose of illustrating a proof structure as in Remark 4.9(2).

Convention 2.3. Let $ \mathcal {C}[s] $ be an $\mathbf {IK}^\omega $ -provable wff for every term $ s $ . Depending on the availability of a one-place predicate constant $ R^1 $ (such as $ tru $ later), this can be simply $ R^1(s) \to R^1(s) $ . ³

Labels for inferences are taken from [11, p. 508].

3 Proving instances of contraction in $\mathbf {IK}^\omega $

Proposition 3.4. Inferences according to the following schemata are $\mathbf {IK}^\omega $ -derivable for arbitrary wffs A:

(1a)

(1b)

(1c)

Proof. As regards 1a it is sufficient to show

$$\begin{align*}\mathbf{IK}^\omega \vdash \ \forall x (A \otimes \mathcal{C} [x]) \Rightarrow \forall x (A \otimes \mathcal{C} [x]) \otimes \forall x (A \otimes \mathcal{C} [x]), \end{align*}$$

which can be done as follows employing $\forall $ -R.

Due to the constraints of space on a page, the premisses for the derivation below are established separately beforehand:

and:

These two can now be employed to continue as follows:

Analogously for 1b.

As regards 1c it is sufficient to show

$$\begin{align*}\mathbf{IK}^\omega \vdash \forall x (A \otimes \mathcal{C} [x]) \Rightarrow A \otimes \forall x (A \otimes \mathcal{C} [x]) \, , \end{align*}$$

which can be seen as follows:

Remark 3.5. The foregoing proofs make use firstly of the fact that $ {\mathcal {C}[t_j] \leftrightarrow \mathcal {C}[t_k]} $ is trivially provable for all j and $ {k \in \mathbb {N}} $ and secondly of the possibility of rearranging the natural numbers according to different order types. In the specific case of the proofs of 1a and 1b the latter comes down to the possibility of separately enumerating terms according to whether their index number is even or odd, while that of 1c only requires the possibility of separating a single element from $ \mathbb {N}$ while the rest still suffices to carry out a $\forall $ -R inference.

4 Proving triviality by means of a truth predicate in conjunction with fixed points

In view of the provable instances of contraction established in the foregoing section it is not surprising that there are fixed points which give rise to triviality when added to $\mathbf {IK}^\omega $ augmented with a truth-predicate.

For a supply of self-referential sentences I adopt Zardini’s approach and simply assume that we “have paradoxical sentences in the language.” ⁴ Nothing much hinges on the way fixed points are introduced, and I wish to avoid the impression that arithmetic would play a crucial role in the triviality proof for $\mathbf {IKT}^\omega $ .

Definition 4.6. (1) Rules for the truth-predicate $tru$ :

(2) Rules for the fixed point fp:

(3) The system $\mathbf {IKT}^\omega $ is $\mathbf {IK}^\omega $ endorsed with the primitive symbols $tru$ and $ \ulcorner \: \urcorner $ plus the rules for the truth predicate $tru$ and the rules for the fixed point fp. ⁵

Remark 4.7. Of course, there are other fixed points which would do as well, such as $ {F \leftrightarrow \forall x \neg (tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x])} $ and $ {F \leftrightarrow \neg \forall x (tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x])} $ , but in the interest of keeping things simple I prefer to focus on just one.

Theorem 4.8. $\mathbf {IKT}^\omega $ is trivial.

Proof. Take the fixed point $ \,{F \leftrightarrow \forall x (\neg tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x]) }\, $ provided by fp. I present two ways of arriving at a contradiction, one using 3.4.1c, i.e., a form of contraction, and another one that doesn’t, i.e., where the contraction is hidden in the working of the $ \forall $ -rules (as essentially used in the proof of 3.4.1c.

Proof 1.

We thus have established a contradiction for the wff $ \,\forall x (\neg tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x]) $ .

2. Without the use of 3.4.1c. The first inference is one according to $\forall $ -R:

The remainder as for Proof 1.

Remark 4.9. (1) The first of the above proofs shows how the contraction established in 3.4.1c is used and I thus take it to render the inconsistency result less surprising.

(2) Zardini says nothing about vacuous quantification but for those who are prepared to deal with it there is the option of taking the fixed point $ \,{F \leftrightarrow \forall \neg \, tru (\ulcorner F \urcorner ))}\, $ which, in view of the truth of the equivalence $ \,{F \leftrightarrow tru (\ulcorner F \urcorner )}\, $ can be shortened to $ \,{F \leftrightarrow \forall \neg F}\, $ . In this way the triviality proof becomes particularly conspicuous (with fp1 properly adjusted, of course): ⁶

What I take to be the crucial point in this proof is the possibility of keeping the assumptions (antecedent) “open” until after a generalization on the right has been carried out and its result added to the assumptions. $ \ddagger $ is thus not indicating an inference but just expressing that the new occurrence of $ \neg F $ can be absorbed in the $ \,{ {\textstyle \bigsqcup } \neg F}\, $ without any further ado.

(3) There is nothing specifically semantic about the paradoxes that have been considered here; corresponding fixed points can be obtained with unrestricted abstraction as in [6, p. 382] (without arithmetization) and the proof goes through with the fp-inferences replaced by a fixed point derived by -inferences as formulated in [6, p. 367]. If the term Z is defined as , then the fixed point provided by does the job: $ \,{F \leftrightarrow \forall x \neg (F \otimes \mathcal {C} [x])}\, $ . This can equally be obtained from $ F \leftrightarrow \forall x \neg (tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x])\, $ with the help of $ F \leftrightarrow tru (\ulcorner F \urcorner ) $ . ⁷

5 On the relevance for cut elimination

In [3, 4] it was pointed out that Zardini’s cut elimination proof for $\mathbf {IKT}^\omega $ is not conclusive. ⁸ As Fjellstad emphasizes, however, this does not foreclose the possibility that cuts in $\mathbf {IKT}^\omega $ can still be eliminated by an alternative strategy.

Obviously, cut cannot be eliminable in $\mathbf {IKT}^\omega $ if it includes a fixed point like fp and it is instructive to look at what happens to the cut yielding the empty sequent with the cut formula $ \forall x (\neg tru (\ulcorner F \urcorner ) \otimes \mathcal {C} [x]) $ in the first proof of Theorem 4.8, when the usual strategy of reducing a cut after a contraction is applied. I replace $ \neg tru (F) $ by A to simplify the presentation.

Of course, this cut is not suitable for elimination, but it is nevertheless instructive to try the usual reduction steps on it. ⁹ This would amount to the following:

Now a single cut has been replaced by two cuts, and while the first one can be justified as usual by a reduced complexity of its derivation, the second would have to rely on something like the complexity of the cut formula which is not necessarily reduced in the presence of self-reference.

The point of a cut elimination proof that secures the consistency of a truth predicate in the face of self-reference would be that no reduction of this kind is required, i.e., no cut the justification of which is based on the complexity of the cut formula.

Systems which are truly contraction-free are not confronted with this problem; in fact I am inclined to take that as a criterion for a (sequential) system $ \Sigma $ to be “truly contraction free”: there is a cut elimination proof for $ \Sigma $ that does not require an induction on the complexity of the cut formula. As was pointed out in [6, p. 374]: “in the absence of contraction, normalization and cut elimination can be proved without a recourse to the length of the formula in question (maximum or cut formula). It is this that makes logic without contraction so safe against all antinomies arising from abstraction.” The problem is that despite the absence of explicit rules of contraction, there are still many ways of smuggling in some form of contraction through new constants. Zardini’s multiplicative quantification is an example.

But what does that mean for the possibility of obtaining a cut elimination proof for $\mathbf {IK}^\omega $ , i.e., a system which has neither a truth predicate nor self-reference? Just as classical logic on its own allows cut elimination, even if it becomes inconsistent when a truth predicate and self-reference are added, $\mathbf {IK}^\omega $ on its own may allow cut elimination.

Given the provability of a reduced form of contraction in $\mathbf {IK}^\omega $ it will not come as a surprise that the familiar procedure of shifting a cut “upwards” in a deduction as part of proving a cut elimination theorem runs into complications well-known from classical and intuitionistic systems, i.e., systems which have contraction as a basic rule.

Take a cut of the following form:

which is just the situation we are confronted with in view of the proof of 1c. The usual strategy for reducing a cut of this kind as exemplified in [10, p. 334], and expressly isolated as a separate case in [7, p. 423] under the label “bifurcation step,” and pp. 432 f (Remark 37.17), would amount to the following derivation:

where a further step would have to accommodate $ \Gamma _k $ in $ \bigsqcup _{0 \leq i < \omega } (\Gamma _i) $ and it might look like we are facing trouble. This, however, can be easily dealt with in the foregoing case by applying the strategy from the proof of 3.4.1c: change the enumeration of the antecedents of the premisses of the $\forall $ -R inference and construct the following derivation:

It is open, however, if this can be turned into a general strategy that can be employed in a cut elimination proof for $\mathbf {IK}^\omega $ . Even if it can, this will not provide a consistency proof for $\mathbf {IKT}^\omega $ because of the problem of assigning a measure of complexity to the cut formula of the second cut.