Statistical analysis of genetic interactions

Summary

Many common human diseases and complex traits are highly heritable and influenced by multiple genetic and environmental factors. Although genome-wide association studies (GWAS) have successfully identified many disease-associated variants, these genetic variants explain only a small proportion of the heritability of most complex diseases. Genetic interactions (gene–gene and gene–environment) substantially contribute to complex traits and diseases and could be one of the main sources of the missing heritability. This paper provides an overview of the available statistical methods and related computer software for identifying genetic interactions in animal and plant experimental crosses and human genetic association studies. The main discussion falls under the three broad issues in statistical analysis of genetic interactions: the definition, detection and interpretation of genetic interactions. Recently developed methods based on modern techniques for high-dimensional data are reviewed, including penalized likelihood approaches and hierarchical models; the relationships between these methods are also discussed. I conclude this review by highlighting some areas of future research.

1. Introduction

Many common human diseases and complex traits are highly heritable and are believed to be influenced by multiple genetic and environmental factors. A central goal of genetics, evolutionary biology and epidemiology is to identify genetic and environmental factors that influence complex traits and diseases, and to characterize the effects of these factors and their interactions (Lynch & Walsh, 1998; Thomas, 2004). Genetic interactions (gene–gene and gene–environment interactions) have long been recognized as an important component of the genetic architecture of complex traits and diseases and are fundamentally important for understanding the genetics of complex traits and diseases (Mackay, 2001; Moore, 2003; Flint & Mackay, 2009; Mackay et al., 2009).

There is a long history of the examination of genetic interactions in inbred plant and animal experimental crosses (Carlborg & Haley, 2004) and human populations (Cordell, 2009; Thomas, 2010). Recent advances in genome-wide association studies (GWAS) have provided unparalleled opportunities for studying the genetic architecture of complex diseases (Hardy & Singleton, 2009). In the past few years, these studies have identified many genetic variants associated with complex diseases (WTCCC, 2007; Hindorff et al., 2009). However, the main effects of the identified variants explain only a small proportion of the heritability of most complex diseases, motivating research interest in finding the remaining ‘missing’ heritability (Manolio et al., 2009). Since GWAS have not fully investigated interactions, it has been speculated that gene–gene and gene–environment interactions could be one of the potential sources of the missing heritability; this further boosts the investigation of genetic interactions (Cordell, 2009; Manolio et al., 2009; Cantor et al., 2010; Eichler et al., 2010; Thomas, 2010).

Here, I review the statistical methods and related computer software that are currently being used for identifying genetic interactions for complex traits in animal and plant experimental crosses and human population-based association studies. The discussion covers the three broad issues in statistical analysis of genetic interactions, namely, the definition, the detection and the interpretation of genetic interactions. Significant advances in all the three related topics have been made in the past decades (Cordell, 2009; Thomas, 2010), and many of these are reviewed. All the methods discussed can be used in targeted genetic studies with moderate numbers of variants (for example, from hypothesis-driven candidate-genes or pathway-based studies), and some can be applied to large-scale genetic studies with large numbers of variants (for example, from GWAS).

One of the challenges in statistical analysis of genetic interactions is that genetic interaction is not uniquely defined. I first describe the general definition and meaning of interaction and then introduce the commonly used models that define an interaction term as a product of main-effect variables. I also discuss the issue that any statement about interaction is necessarily scale and model dependent, and outline the general principles for analysing interactions. The detection of genetic interactions involves two issues, modelling and computational methods, and can be viewed as a problem of high-dimensional data analysis. The development of statistical methods for high-dimensional data analysis has recently become one of the most important and active areas in statistics (Hesterberg et al., 2008). Recently developed methods based on modern statistical techniques are mainly explored, including penalized likelihood approaches and hierarchical models, and the relationships among these methods are also discussed. The interpretation of genetic interactions has not been extensively discussed in the literature. The discussion is confined to key interpretations. Finally, I highlight some emerging directions and needs for making further progress.

2. Notation and challenges in analysing genetic interactions

We consider quantitative trait locus (QTL) mapping in experimental crosses from inbred animals or plants and population-based genetic association studies in humans. These two types of studies have the same observed data structure, and thus statistical methods can be fairly similar, while each has special problems. For each individual in the sample, observed data consist of a complex trait Y, a number of genetic markers G=(g ₁, g ₂, …, g_m) and some environmental factors E=(z ₁, z ₂, …, z_k), where m and k represent the numbers of makers and environmental factors, respectively. The trait phenotype Y can be continuous (e.g. body weight) or discrete (e.g. a binary disease indicator, counts). We consider experimental crosses (e.g. F₂ intercross) or markers (e.g. single-nucleotide polymorphisms (SNPs)) that segregate three distinct genotypes. Therefore, each genotype variable g_s is a three-level factor, indicating homozygous for the more common allele, heterozygous and homozygous for the minor allele, respectively. The genotyped markers can be densely distributed either across the entire genome or within some candidate genes, and for each case the number of markers can be large.

Our goal is to identify genomic loci that are associated with the complex trait, and to characterize their genetic effects. Since most complex traits and diseases are caused by interacting networks of multiple genetic and environmental factors, it is desirable to simultaneously consider multiple loci and environmental factors, and include gene–gene (epistatic) and gene–environment interactions in the model. Such joint analyses would improve the power for the detection of causal effects and hence lead to increased understanding about the genetic architecture of diseases. There are considerable challenges, however, to perform statistical analysis of genetic interactions:

• • One has limited understanding of what the word ‘interaction’ means because it has no unique and explicit definition. Different definitions have different properties and lead to different statistical models and interpretations.

• • With multiple genetic and environmental factors, there are many possible main effects and interactions, most of which are likely to be zero or at least negligible, leading to high-dimensional models and overfitting problems.

• • There are many more potential interactions than main effects, which would require different modelling for main effects and interactions.

• • Due to linkage disequilibrium, many genetic factors are highly correlated and nearly collinear, creating the difficulty of distinguishing disease-associated variants from others.

• • Frequencies of multi-locus genotypes that define interactions can be very low, which creates variables with near-zero variance and thus requires special parameterization.

• • The discreteness of genotype data can cause a separate identifiability problem, called separation, for discrete traits. Separation arises when a predictor or a linear combination of predictors is completely aligned with the outcome and can yield non-identified models (that is, have parameters that cannot be estimated).

These problems necessitate sophisticated techniques in all the steps of modelling, computation and interpretation for analysing genetic interactions. Some methods have been developed recently to overcome these problems and will be discussed in the following sections.

3. Definition of genetic interaction

The term ‘interaction’ generally refers to a phenomenon whereby two or more variables jointly affect the outcome response. In order to analyse and interpret interactions, it is important to understand how interactions are defined. In this section, I first discuss the general definition and meaning of statistical interactions, and then show how they can be made more concrete in the case of genetic analysis. We return to the issue of biological interpretation of statistical interaction later in the article.

(i) General definition of statistical interaction

As introduced earlier, the goal of QTL and association analysis is to investigate the relationship between the complex trait Y and the genetic and environmental factors, G=(g ₁, g ₂, …, g_m) and E=(z ₁, z ₂, …, z_k). For a normally distributed trait, this can be expressed as a statistical model

(1)

with the normal distribution assumption about the response variable Y, where E(·) is the expectation and η(·) represents a generally unknown function that relates the genetic and environmental factors to the expectation of Y.

With multiple genetic and environmental factors, even if we restrict our attention for simplicity to two-factor interactions, three different kinds have to be considered: (a) gene×gene (G×G), (b) gene×environment (G×E), (c) environment×environment (E×E). We do not discuss E×E interactions because they can be included in the model as covariates. While the formal definitions of G×G and G×E interactions are similar, their interpretations are rather different. I will briefly discuss their differences below.

With just two genetic factors g ₁ and g ₂, if the function of two factors η(g ₁, g ₂) can be replaced by the simpler form of two functions of one variable, i.e.

(2)

then there is no interaction between g ₁ and g ₂ (Cox, 1984). This implies that the genotypic effect of locus g ₁ (g ₂) does not depend on the genotypes of g ₂ (g ₁). Therefore, these two genetic factors act in a way that appears causally independent. For G×E interactions, the condition of independence, η(g ₁, z ₁)=η₁(g ₁)+f ₁(z ₁), appears identical to the above-mentioned one, but the interpretation is quite different. Here, the concern is with regard to the stability of the genotypic effect of g ₁ as the environmental condition z ₁ varies. In genetic mapping, the environmental effect f ₁(z ₁) itself is of no direct interest, but can be an important component in controlling the potential confounding effect.

The converse conclusion that condition (2) is not satisfied is an indication of interaction between the two factors. In that case a change in the response due to a change in g ₁ (g ₂) does depend on the level of g ₂ (g ₁). However, any deviation from the independence condition (2) could be specified in various ways, leading to different types of interaction that may require different methods to identify. I here discuss the most commonly used method that considers the interaction as a product term of the main-effect variables. Because the genetic factors g ₁ and g ₂ are three-level factors, we naturally start with a two-way factorial model:

(3)

where i=1, 2, 3; j=1, 2, 3; g _1i represents the main effect of factor g ₁ at level i; g _2j represents the main effect of factor g ₂ at level j; and δ_ij represents the interaction effect for factors g ₁ and g ₂ at levels i and j, respectively. With this model, the overall effect of factor g ₁ at level i (i.e. genotypic effects) equals μ+g _1i+δ_ij that does depend on the levels of g ₂.

(ii) Cockerham model and alternatives

With no constraints on the parameters, model (3) is non-identifiable. In model (3), genotype factors g ₁ and g ₂ take on three values and therefore each has three main effects. However, the classical regression framework can estimate only two parameters – if all three were included, they would be collinear with the constant term and thus cannot be estimated uniquely (i.e. the model is non-identifiable).

One of the commonly used constraints on the parameters is to exclude the first level of each genotype factor from the model. The level that is excluded from the model is known as the reference or baseline condition. With this constraint, the number of main effects of each genotype factor and interactions between two factors reduces to two and four, respectively. Model (3) can be re-parameterized as

(4)

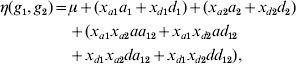
with x_ak=1 if g_k=2, x_ak=0 otherwise, and x_dk=1 if g_k=3, x_dk=0 otherwise, where a_k and d_k represent two main effects, and aa ₁₂, ad ₁₂, da ₁₂ and dd ₁₂ represent four interaction effects. In human genetic association studies, this model is called a co-dominant model (Thomas, 2004).

There are other options to construct constraints. The most widely used method is the Cockerham model (Cordell, 2002; Kao & Zeng, 2002; Zeng et al., 2005; Wang & Zeng, 2006, 2009; Cordell, 2009), which defines the main-effect variables as

(5)

For the Cockerham model, a_k and d_k correspond to the additive and dominance effects, respectively, and aa ₁₂, ad ₁₂, da ₁₂ and dd ₁₂ are interaction effects, called the additive×additive, additive×dominance, dominance×additive and dominance×dominance interactions, respectively. The Cockerham model can be easily understood by introducing the paternal and maternal indicators of the minor allele, ξ^p and ξ^m, centring by subtracting a conventional point 0·5. The indicator ξ^p (ξ^m) equals 1 if the paternal (maternal) allele is the minor allele and 0 otherwise. Therefore, the additive-effect variable can be expressed as x_ak=(ξ^p−0·5)+(ξ^m−0·5). This can be explained because a genotype consists of two alleles inherited from father and mother, respectively, and the paternal and maternal allelic effects are assumed to be identical. The dominance-effect variable can be expressed as x_dk=−2(ξ^p−0·5)(ξ^m−0·5), representing the interaction between paternal and maternal alleles. The Cockerham model can be modified by centring the indicators ξ^p and ξ^m by subtracting their mean p (i.e. the allelic frequency) (Wang & Zeng, 2006, 2009). Therefore, we have x_ak=(ξ^p−p)+(ξ^m−p) and x_dk=−2(ξ^p−p)(ξ^m−p).

The co-dominant and Cockerham models can be extended to include multiple genetic loci, environmental factors and their interactions:

(6)

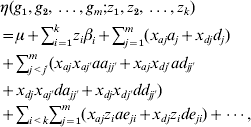
which consists of 2 m main effects and 2 m(m−1) two-way epistatic interactions. This model can be further extended to include higher-order interactions. We can see that even with a moderate number of factors m, the interaction model can include a huge number of parameters.

(iii) Generalized linear models

Generalized linear models have been widely used to analyse various types of non-normal complex traits (Yi & Banerjee, 2009; Li et al., 2010). A generalized linear model consists of three components: the linear predictor, the link function and the distribution of the outcome variable (McCullagh & Nelder, 1989; Gelman et al., 2003). The linear predictor is the same as that in the normal linear models described above. The link function h() is invertible and relates the mean of the outcome variable Y to the linear predictor:

(7)

or equivalently,

(8)

which obviously reduces to the normal linear model if h() is the identity function. The distribution of Y can take various forms, including normal, Gamma, binomial and Poisson distributions. Common forms of the link function for different assumed distributions of the outcome variable are h(η)=log (η) for Poisson treatment of counts, and logit=log (η/(1−η)), probit=Φ⁻¹(η), or cloglog=log (−log(1−η)) for binary and binomial data. Therefore, generalized linear modelling provides a unified framework for statistical analysis; by choosing appropriate link functions and data distributions, some commonly used models, e.g. normal linear, logistic, probit and Poisson regressions, become special cases.

Interaction effects are more complicated in generalized linear models due to the link function between the linear predictor and the outcome variable:

• • It is obvious from model (7) that the genetic effects correspond to a transformation of the mean of the outcome variable, h[E(Y)], rather than directly to the mean of the outcome variable E(Y) as in normal linear models. In a logistic regression, for example, genetic effects are defined on the scale of the log odds of a success outcome (i.e. Y=1), i.e. logit[Pr(Y=1)]=log[Pr(Y=1)/1−Pr(Y=1)].

• • Some generalized linear models (for example, logistic and probit regressions) can be expressed as a normal linear model with an unobserved or latent outcome variable. For example, the logistic regression logit[Pr(Y=1)]=η(g ₁,g ₂, …,g_m; z ₁,z ₂, …,z_k) is equivalent to the latent normal linear model, u~N(η(g ₁,g ₂, …,g_m; z ₁,z ₂, …,z_k), 1.6²), Y=1 if u>0 and Y=0 if u<0. Therefore, genetic effects in a logistic model actually correspond to the scale of a latent normally distributed outcome. The formulation of latent variables not only provides a computational trick but also a way to interpret the generalized linear models.

• • Because genetic effects depend on the link function, it is possible that interaction effects on a link function may be removed by changing the link function. This is similar to the phenomenon for continuous responses that interaction on one scale may possibly be removed by a non-linear transformation of the scale (e.g. logarithmic and simple powers) (Cox, 1984; Berrington & Cox, 2007). We may call an interaction removable if a transformation of the outcome scale can be found that induces additivity. I shall return to this issue later.

• • Even with no multiplicative interaction terms in a generalized linear model, it is possible that the effects of a factor on the mean of the observed outcome E(Y) may depend on the levels of other factors in the model, because of the non-linear transformation h ⁻¹() (Gill, 2001). Therefore, interaction effects are automatically introduced into all generalized linear models by a link function. However, these interactions do not affect the transformation of the observed data h[E(Y)]. Multiplicative interaction terms such as x_{a 1}x_{a 2}aa ₁₁ are called the ‘variable-specific’ interaction terms, which are different from the ‘automatic’ interaction. If specifying these variable-specific terms in the model leads to improved fit, then we have successfully captured through parameterization at least some of the necessarily existent interaction between variables by the model specification.

(iv) Principles for analysing interactions

The widely used genetic interaction models define an interaction term as a product of main-effect variables, following the general definition of interaction (Cox, 1984). For conventional models, guiding principles have been established for efficiently studying interactions. These principles could be more crucial for our problems because of the high-dimensional and correlated structure of genetic data. If appropriately applied, these principles can improve the analysis of genetic interactions (Kooperberg et al., 2009).

1. 1. The basic strategy for identifying interactions is to start from a simpler model involving only main effects, and then to introduce interaction effects when they improve the model fit to the data. The final interpretation of conclusions will be based on some simpler specification, for example, one involving some strong interaction terms (Cox, 1984).

2. 2. We prefer simultaneously fitting as many predictors as possible and introducing some hierarchical structure into the model (Gelman et al., 2003). This would allow us to take into account the correlation among the predictors. Applied to interaction analysis, therefore, it would be desirable to simultaneously include many correlated main effects and interactions.

3. 3. Inputs with large main effects are more likely to have appreciable interactions with other inputs, although small main effects do not preclude the possibility of large interactions (Cox, 1984; Gelman & Hill, 2007). Also, the interactions corresponding to larger main effects may be in some sense of more practical importance. This principle, sometimes referred to as ‘effect heredity’, has been used to build on interaction models (Hamada & Wu, 1992; Nelder, 1994; Chipman, 1996).

4. 4. When an interaction of multiple factors is in the model, the lower-order variables comprising the interaction should also be present (Nelder, 1994). This is called the ‘effect hierarchy principle’. The reason for this is that if some contrast interacts with, say, z, and is therefore non-zero at some levels of z, it would normally be very artificial to suppose that the value averaged out exactly to zero over the levels of z involved in defining the ‘main effect’ for the contrast (Cox, 1984). Applied to genetic interactions, genetic variants that have an interaction effect typically will also show some modest main effects (Kooperberg et al., 2009). This could be used to explore interactions more efficiently.

4. Detection of genetic interaction

The detection of genetic interactions involves issues of statistical modelling and computing. A variety of methods for detecting gene–gene and gene–environment interactions have been proposed in the past decade (Musani et al., 2007; Cordell, 2009; Kooperberg et al., 2009; Thomas, 2010), and it is impossible to discuss all the available methods in this review. I focus on the most commonly used approaches: penalized likelihood regressions and hierarchical models. These two approaches are based on modern statistical techniques for high-dimensional data analysis and are powerful to handle the challenges in statistical analysis of genetic interactions, although alternative methods, including simple exhaustive searches (Marchini et al., 2005), Bayesian partitioning algorithms (Zhang & Liu, 2007), non-parametric Bayesian methods (Zou et al., 2010) and various machine learning techniques (Ritchie et al., 2001; Chen et al., 2007; Lou et al., 2007), have their own advantages.

(i) Penalized likelihood approach

In the classical framework, parameter estimation is obtained by maximizing the likelihood function. A linear model with either many coefficients or highly correlated variables can be non-identifiable. A standard approach to overcome the problem of non-identifiability is to add a penalty to the likelihood function, yielding the penalized likelihood function:

(9)

where β represents all effects and φ represents other parameters (e.g. residual variance). The logarithm of the likelihood function log f(y|β,φ) is a standard statistical summary of model fit; larger likelihood means better fit to data. For classical models, adding a parameter to a model is expected to improve the fit, even if the new parameter represents pure noise (Gelman & Hill, 2007). Therefore, the penalty term p(β) serves to control the complexity of the model and place some constraints or prior information on the parameters. Maximization of the penalized likelihood results in a penalized likelihood estimator.

The penalized likelihood function not only stabilizes parameter estimation but also provides criteria for model selection and comparison. The form of the penalty p(β) determines the general behaviour of the penalized likelihood approach. Small penalties would lead to large models with limited bias, but potentially high variance; larger penalties lead to the selection of models with fewer predictors, but with less variance. A traditional approach is to specify a penalty on the number of coefficients in the model, p(β)=λ |M|, where λ is a penalty parameter and |M| is the size of a model M. Many classical criteria have this form, including the Akaike information criterion (AIC) (λ=1) (Akaike, 1969) and the Bayesian information criterion (BIC) (λ=log(sample size)/2) (Schwartz, 1978). These criteria have been widely used in earlier methods of multiple QTL mapping (Kao et al., 1999; Zeng et al., 1999). However, Broman & Speed (2002) showed that the original AIC and BIC tend to include many spurious QTLs and thus are not appropriate for model selection in QTL mapping, due to the large numbers of potential variables. Therefore, a variety of modifications to these classical criteria have been proposed, all seeking to control the false positive rate by using stronger penalty (Broman & Speed, 2002; Bogdan et al., 2004; Baierl et al., 2006).

For epistatic models, using a single penalty to control the overall complexity of the model would not be appropriate, because there are many more potential interactions than main effects. Therefore, two separate penalties should be used for main effects and pairwise epistatic interactions (Bogdan et al., 2004; Baierl et al., 2006; Manichaikul et al., 2009):

(10)

where λ_m and λ_i are the penalties on main effects and pairwise epistatic interactions, respectively, and |M|_m and |M|_i are the numbers of main effects and pairwise epistatic interactions. Bogdan et al. (2004) and Baierl et al. (2006) suggested incorporating prior numbers of main effects and interactions to specify the penalty parameters λ_m and λ_i. Manichaikul et al. (2009) used the null distribution of the genomewide maximum LOD score to derive the penalty on main effects and the results of a two-dimensional, two-QTL scan to derive the penalty for the interaction terms. These methods employed forward and stepwise procedures to select main effects and interactions based on the corresponding penalized likelihoods. Manichaikul et al. (2009) further imposed an effect hierarchy principle, with the inclusion of a pairwise interaction requiring the inclusion of both corresponding main effects, and always included both additive and dominance terms for a QTL and all four epistatic effects for a pair of interacting QTLs. The method of Manichaikul et al. (2009) has been implemented in the freely available software R/qtl. R/qtl is an extensible, interactive environment for mapping QTLs in experimental populations derived from inbred lines (Broman et al., 2003).

The above penalty is called the L ₀-penalty, which only involves the number of parameters and ignores the sizes of individual coefficients. Other penalty functions depend on the sizes of individual coefficients and can be more flexible. A popular method of this form uses an L ₂-penalty (quadratic penalty) on all coefficients (excluding the intercept), corresponding to ridge regression (Hoerl & Kennard, 1970):

(11)

which is equivalent to maximizing the likelihood function subject to a size constraint on the sum of the squared coefficients, . The penalty parameter is predetermined usually by cross-validation.

Ridge regression can handle the problem of collinearity and thus can simultaneously fit highly correlated variables. Malo et al. (2008) applied ridge regression to fit all SNPs in a genomic region in genetic association studies and showed that such multiple-SNP analyses accommodate linkage disequilibrium among SNPs and have the potential to distinguish causative from non-causative variants. Park & Hastie (2008) proposed a logistic regression with L ₂-penalty to fit genetic interactions in population-based case-control studies. They showed that the penalized logistic regression has a number of attractive properties for detecting genetic interactions. First, the L ₂-penalty can deal with perfectly collinear variables (they sum to 1), and thus makes it possible to code each level of a factor by a dummy variable, yielding coefficients with direct interpretations (see eqn 3). As described earlier, this coding method cannot be applied to classical regression. Secondly, the L ₂-penalty automatically assigns zero to the coefficients of zero columns and hence gracefully handles interaction models that consist of variables with near-zero variance. Thirdly, the quadratic penalty enables us to simultaneously fit a large number of factors and interactions in a stable fashion. Although the L ₂-penalty has the above advantages, it cannot shrink any coefficients directly to zero and thus does not automatically remove variables from the model. Park & Hastie (2008) proposed a forward stepwise method based on the penalized likelihood to perform variable selection. Their algorithm obeys the effect hierarchy principle and also provides the option to accept an interaction even with no corresponding main effects in the model.

Another widely used penalized likelihood approach uses an L ₁-penalty, leading to the lasso (least absolute shrinkage and selection operator) introduced by Tibshirani (Tibshirani, 1996). The lasso estimator is obtained by maximizing the likelihood function subject to a constraint on the sum of absolute values of the regression coefficients . This is equivalent to maximizing the following penalized likelihood function:

(12)

Compared to the ridge regression, a remarkable property of the lasso is that the L ₁-penalty can shrink some coefficients exactly to zero and therefore automatically achieve variable selection. This can be intuitively explained by the fact that |β_j| is much larger than |β_j|² for small β_j and thus the constraint forces some β_js exactly to zero. Various optimization algorithms have been proposed to obtain the lasso estimator (Hesterberg et al., 2008); Notably, the least angle regression (Efron et al., 2004) and the co-ordinate descent algorithm (Wu & Lange, 2008; Friedman et al., 2010) are the most computationally efficient.

The feature of continuous shrinkage and variable selection along with the fast algorithms makes the lasso an effective method for genome-wide analysis of interacting genes. Tanck et al. (2006) applied lasso penalized regression to detect epistatic interactions in association studies, with L ₂-penalty on main effects and L ₁-penalty on epistatic effects. Therefore, all main effects are always included in the model, while irrelevant interactions can be removed. Wu et al. (2009) developed a lasso penalized logistic regression for genome-wide association analysis in case-control studies. Their approach always selects a fixed number of predictors from all potential predictors. This yields a more efficient way of determining the penalty parameter. This novel strategy is similar to the composite model space approach that places an upper bound on the number of effects included in the model (Yi, 2004; Yi et al., 2005). For a given value of the penalty parameter, Wu et al. (2009) applied the co-ordinate descent algorithm to fit the lasso penalized logistic regression. Wu et al. (2009) handled interactions in two stages. In the first stage, the most important main effects of the predetermined number are identified; in the second stage, the two-way or higher-order interactions among the selected SNPs are examined. The method of Wu et al. (2009) has been implemented in the freely available software Mendel 9.0 at the UCLA Human Genetics web site.

(ii) Hierarchical models

Hierarchical modelling is an important tool in the analysis of complex and high-dimensional data and has been increasingly applied to QTL and association studies. Hierarchical models use a population distribution to structure some dependence into the parameters, thereby enabling to fit a large number of predictor variables. In contrast, non-hierarchical models generally cannot handle many variables simultaneously, because they are numerically unstable or tend to overfit data (i.e. fit the existing data well but lead to inferior prediction for new data). Hierarchical models are more easily interpreted and handled in the Bayesian framework. In Bayesian models, the population distribution of the parameters is often referred to as the prior distribution, and statistical inference is based on the posterior distribution that is proportional to the product of the likelihood function f(y|β,φ) and the prior distribution π(β,φ):

(13)

The posterior distribution contains all the current information about the parameters. Ideally one might fully explore the entire posterior distribution by sampling from the distribution p(β,φ|y) using Markov chain Monte Carlo (MCMC) algorithms (Gelman et al., 2003). For practical and computational purposes, however, it is desirable to have a fast algorithm that returns a point estimate of the parameters and standard errors. A commonly used point estimate is the posterior mode, that is, the single most likely value, which can be obtained by maximizing the posterior density p(β,φ|y), or equivalently its logarithm:

(14)

Compared with the penalized likelihood function (9), we can see that the posterior mode estimator is equivalent to the penalized estimator, with the logarithm of the prior density log π(β,φ) as the penalty. Therefore, with particular priors, hierarchical models can lead to the penalized likelihood approaches discussed above.

(a) Shrinkage priors

The prior distribution π(β,φ) plays an important role on the hierarchical modelling approach. A variety of priors have been proposed (Griffin & Brown, 2007), some of which have been adopted in QTL mapping and association analysis (Yi & Xu, 2008; Yi & Banerjee, 2009; Mutshinda & Sillanpää, 2010; Sun et al., 2010). For models with a large number of potential variables, it is reasonable to assume that most of the variables have no or weak effects on the phenotype, whereas only a few have noticeable effects. Therefore, we can set up a prior distribution that gives each effect β_j a high probability of being near zero. Such priors are often referred to as ‘shrinkage’ priors. In the following discussion, the prior distribution of φ is assumed to be non-informative and independent of β.

A class of shrinkage priors uses continuous distributions. A commonly used continuous shrinkage prior is the double exponential (also called Laplace) distribution (Tibshirani, 1996; Park & Casella, 2008; Yi & Xu, 2008), , where λ is a shrinkage parameter and controls the amount of shrinkage; larger λ forces more coefficients near zero. With this prior, the log posterior density can be expressed as . Therefore, the posterior mode estimate of the coefficients β is the lasso penalized estimate (Park & Casella, 2008).

Another widely used continuous shrinkage distribution is the well-known Student's t-distribution, , where the hyperparameters μ_j, ν_j>0 and s_j>0 are the location, the degrees of freedom and the scale parameters, respectively (Gelman et al., 2003). The location μ_j is usually set to zero. The hyperparameters ν_j and s_j control the global amount of shrinkage in the effect estimates; larger ν_j and smaller s _j² induce stronger shrinkage and force more effects to be near zero. The family of the Student's t-distributions includes various distributions as special cases. At s_j=∞, the t prior approaches a flat distribution, i.e. π(β_j)∝1. Placing flat priors on all β_j corresponds to a classical model, which usually fails in our problem as illustrated earlier. At ν_j=∞ and s_j=s, the t prior is equivalent to a normal distribution β_j~N(0,s ²), and thus the log posterior density can be expressed as . Therefore, the posterior mode estimate of the coefficients β is the ridge penalized estimate.

Both the double exponential distribution and the Student's t-distribution can be presented as a two-level hierarchical model (Griffin & Brown, 2007; Yi & Xu, 2008). The first level assumes that the coefficients β_j's follow independent normal distributions with mean zero and unknown variances τ_j ², and the second level assumes that the variances τ_j ² follow some specified independent prior distributions:

(15)

where θ_j represent hyperparameters. The above two-level priors result in a scale mixture of normal distributions for the coefficients: . For the double exponential prior, π(τ_j ²|θ_j) is an exponential distribution Expon(λ_j ²/2) or equivalently a gamma distribution Gamma(1,λ_j²/2). For the Student-t prior, π(τ_j ²|θ_j) is a scaled inverse-χ² distribution Inv-χ²(ν_j,s_j ²) or equivalently an inverse gamma distribution Inv-gamma (,).

The two-level hierarchical formulation has several advantages. First, it allows easy and efficient computation; conditional on the variances τ_j ² the coefficients β_j can be easily estimated and for some distributions π(τ_j ²|θ_j) (for example, the exponential and the inverse-χ² distributions) the variances τ_j ² also can be easily estimated. Secondly, it offers easy interpretation of the model; the coefficient-specific variances τ_j ² result in different shrinkage amounts for different coefficients. Thirdly, it is flexible enough to encompass most versions of the penalized regression procedures and also lead to new hierarchical models by using new priors for the variances τ_j ² or further modelling the hyperparameters θ_j (Griffin & Brown, 2007; Hoggart et al., 2008; Kyung et al., 2010; Sun et al., 2010).

The second class of shrinkage priors assumes a discrete, two-component mixture distribution for each genetic effect, a normal distribution, and a point mass at zero (Yi et al., 2005, 2007b; Yi & Shriner, 2008):

(16)

where I ₀ is a point mass at 0 and γ_j is a binary variable indicating the absence (γ_j=0) or presence (γ_j=1) of the effect β_j. The variance τ_j ² can be predetermined or treated as a random variable with an inverse-χ² hyper-prior distribution: τ_j ²~Inv-χ²(ν_j,s_j ²). The sparseness in the fitted model is controlled by the values of (ν_j,s_j ²) and the prior inclusion probability p(γ_j=1) for each effect. The values of (ν_j,s_j ²) can be chosen to control the prior expected mean and the prior confidence region of the proportion of the phenotypic variance explained by β_j. Yi et al. (2005) proposed a method to choose the prior inclusion probabilities p(γ_j=1) for main effects and the G×G and G×E interactions (Yi et al., 2007b; Yi & Shriner, 2008). These discrete ‘spike and slab’ priors lead to various Bayesian variable selection methods (Yi & Shriner, 2008).

(b) Estimating posterior modes

The continuous shrinkage priors result in continuous posterior distributions, allowing us to develop deterministic algorithms to quickly estimate the posterior mode. A variety of methods for computing the posterior mode have been developed for hierarchical models with continuous shrinkage priors, using the EM (expectation–maximization) algorithms by taking advantage of the two-level hierarchical formulation (Figueiredo, 2003; Gelman et al., 2008; Armagan & Zaretzki, 2010) or other optimization algorithms (Genkin et al., 2007). These algorithms have been adapted to multiple QTL mapping and genetic association analysis (Zhang & Xu, 2005; Xu, 2007, 2010; Hoggart et al., 2008; Yi & Banerjee, 2009; Sun et al., 2010; Yi et al., 2010). Among these developments, Yi & Banerjee (2009) and Yi et al. (2010) have attractive features and will be discussed below. The method of Yi & Banerjee (2009) has been implemented in the freely available software R/qtlbim (Yandell et al., 2007). R/qtlbim is an extensible, interactive environment for the Bayesian Interval Mapping of QTL, built on top of R/qtl (Broman et al., 2003), providing Bayesian analysis of multiple interacting QTL models for continuous, binary and ordinal traits in experimental crosses.

Yi & Banerjee (2009) and Yi et al. (2010) developed hierarchical generalized linear models with Student-t prior distributions on the coefficients for multiple interacting QTL mapping and genetic association studies. Yi & Banerjee (2009) discussed the choice of the shrinkage parameters ν_j and s_j to favour sparseness in the fitted model. Yi et al. (2010) further proposed different scales s_j for different types of effects (i.e. main effects, G×G and G×E interactions); this specification applies stronger shrinkage for interactions and thus allows more reliably a joint estimation of main effects and interactions. They used the EM algorithm to fit the model by estimating the marginal posterior modes of the coefficients β_js. The algorithm uses the two-level expression of the t prior distribution, treats the unknown variances τ_j ² as missing data and replaces them by their conditional expectations at each E-step. The conditional expectations of τ_j ² are independent of the response data, and thus the E-step is the same for different types of phenotypes. Given the variances τ_j ², the prior distributions β_j|τ_j ²~N(0,τ_j ²) can be included as additional ‘data points’ in the normal approximation of the generalized likelihood. Therefore, the coefficients β_j can be estimated using the standard iterative weighted least squares (IWLS) for fitting classical generalized linear models. Yi & Banerjee (2009) incorporated the above EM algorithm into the standard package glm in R for fitting classical generalized linear models. This computational strategy takes advantage of the standard algorithm and software, and thus leads to a stable, flexible and easily used computational tool.

The above approach is built upon the generalized linear model framework, and therefore can deal with various types of continuous and discrete phenotypes and any models as implemented in the R package glm (e.g. normal linear, gamma, logistic, Poisson, etc.). This flexibility allows us to conveniently analyse data in different ways. As described earlier, interactions are defined relative to particular models and thus can be affected by a change in the model (Cordell, 2002; Berrington & Cox, 2007). The above approach would allow us to investigate whether an interaction can be removed by a transformation of the scale and to detect interactions that are only present in a particular model. The hierarchieal generalized linear models with Student-t priors on the coefficients includes various methods as special cases that have been designed to handle problems encountered in interacting QTL and association studies (Yi et al., 2010). In addition, the above EM algorithm takes advantage of the two-level formulation of the t distribution and hence can be easily applied to other shrinkage priors (e.g. the double exponential distribution) with only modification on the conditional expectations of τ_j ².

The hierarchical models can simultaneously analyse many covariates, main effects of numerous loci, epistatic and G×E interactions. For large-scale genetic data, however, we recommend performing a preliminary analysis to weed out unnecessary variables, or use a variable selection procedure to build a parsimonious model that only includes the most important predictors. The above algorithm can be incorporated into various variable selection procedures. Following the general principle for analysing interactions discussed earlier, Yi & Banerjee (2009) proposed a useful model search strategy, beginning with a model with no genetic effect but relevant covariates if any, and then gradually adding main effects and interactions into the model. This procedure differs from most variable selection methods by simultaneously adding or deleting many correlated variables.

(c) Sampling from the continuous posterior distribution

In Bayesian inference, it is more comprehensive to fully explore the posterior distribution than merely calculate the posterior mode. For the hierarchical models described above, this requires MCMC algorithms to generate samples from the posterior density. Various MCMC algorithms have been developed for hierarchical models with the continuous shrinkage priors discussed above (Bae & Mallick, 2004; Park & Hastie, 2008; Hans, 2009; Kyung et al., 2010), most taking advantage of the hierarchical formulation of the priors. These algorithms have recently been adapted to multiple QTL mapping and genetic association analysis (Xu, 2003; Yi & Xu, 2008; Sun et al., 2010), although they consider only main effects.

For hierarchical models with shrinkage priors that can be expressed as a mixture of normal distributions, it is easy to construct MCMC algorithms. Yi & Xu (2008) and Sun et al. (2010) developed MCMC algorithms for mapping multiple QTLs using the hierarchical formulation of the double exponential and the Student-t priors. Since all priors for regression coefficients are conditionally Gaussian, a simple and unified scheme can be developed to update the coefficients β_j regardless of the specific prior distributions on the variances τ_j ². For the Student-t and double exponential priors, the conditional posterior distributions of the variances τ_j ² have the standard form and thus can be easily sampled. Since the variances are separated from the data by the regression coefficients, the conditional distributions of the variances are independent of the response data. Therefore, the same updating scheme can be used to update the variances regardless of the response distribution. The advantage of MCMC samplers for hierarchical priors becomes more obvious when dealing with hyperparameters λ in the double-exponential prior and (ν, s) in the Student-t prior. The penalized likelihood approaches predetermine the penalty parameter using cross-validation, and the mode-finding algorithms usually preset the hyperparameters. In the fully Bayesian framework, however, the hyperparameters can be assigned appropriate hyperpriors and are updated along with other parameters (Park & Casella, 2008; Yi & Xu, 2008; Kyung et al., 2010; Sun et al., 2010) or are estimated based on empirical Bayes using marginal maximum likelihood (Park & Casella, 2008; Yi & Xu, 2008; Kyung et al., 2010; Sun et al., 2010); this procedure obviates the choice of the hyperparameters and automatically accounts for the uncertainty in its selection that affects the estimates of the regression coefficients.

The disadvantage of the above fully Bayesian approach is the intensive computation. This may restrict its application in genetic interaction analysis of large-scale data. However, these methods can provide richer information on the posterior of a regression coefficient and adequately reflect the uncertainty in estimating a parameter to be close to zero (Park & Casella, 2008; Kyung et al., 2010). The fully Bayesian analysis can return not only point estimates but also interval estimates of all parameters, and offers a natural means of assessing model uncertainty. As the mode-finding algorithms, the fully Bayesian methods can simultaneously fit many correlated variables and can distinguish important effects from a large number of correlated variables (Yi & Xu, 2008; Sun et al., 2010).

(d) Bayesian variable selection using discrete priors

The hierarchical models with a discrete prior (16) are usually fitted using MCMC algorithms. A variety of algorithms have been proposed, some of which have been adapted to multiple interacting QTL mapping and genetic association analysis. Yi & Shriner (2008) provide a comprehensive review on these methods. In this section, I describe the Bayesian multiple interacting QTL mapping methods that have been implemented in the freely available software R/qtlbim (Yi et al., 2005; Yandell et al., 2007; Yi et al., 2007a, b).

Yi et al. (2005) developed a Bayesian model selection method for mapping epistatic QTL in experimental crosses for complex traits, based on the discrete priors described above and the composite model space approach of Yi (2004). The key idea of this approach is to place an upper bound on the number of QTLs included in the model. Yi et al. (2005) set up the upper bound based on the Poisson prior on the number of QTLs with the prior mean determined by any initial analyses. Given the upper bound, Yi et al. (2005) used a vector γ of binary (0 or 1) variables indicating the absence or presence of the corresponding effects, equivalent to assuming the discrete prior (16). The vector γ determines the number of included QTLs and the activity of the associated genetic effects. The use of the upper bound and the indicator variables avoids the need to explicitly model the number of QTLs as in the previous Bayesian methods, allowing us to fit models of different dimensions, e.g. one versus two QTLs, without resorting to complicated reversible jump MCMC (Yi, 2004). It also largely reduces the model space and provides an efficient way to walk through the space of models, spending more time at ‘good’ models.

Yi et al. (2005) developed an MCMC algorithm to generate samples from the posterior distribution and extended (2007b) the above method to include arbitrary environmental effects and G×E interactions, and to map interacting QTL for binary and ordinal traits based on the generalized probit models (2007a). The posterior samples can be used to summarize the genetic architecture and search for models with high posterior probabilities. Larger effects should appear more often, making them easier to identify. We use all the saved iterations of the Markov chain, corresponding to model averaging, which assesses characteristics of the genetic architecture by averaging over possible models weighted by their posterior probability. Various methods have been developed to graphically and numerically summarize and interpret the posterior samples (Yi et al., 2005; Yandell et al., 2007).

5. Interpretation of genetic interaction

In QTL and genetic association analysis, there are many options available when modelling the data and computing the model. Once multiple QTLs are detected and a model with main effects and interactions are established, it is important to assess the fit of the model to the data and to our substantive (biological) knowledge, and to interpret the fitted models. Assessment and interpretation of interaction models have not been extensively discussed in the literature, possibly because identifying genetic interactions is a challenge and researchers are often so relieved to have detected interactions that there is a temptation to stop and rest rather than interpret the fitted model. Here, we discuss some methods for interpreting genetic interactions, including the issues of model checking, removable or non-removable interactions, average predictive genotypic effects and biological interactions.

(i) Model checking and assessment

A flexible method for model checking and assessment is posterior predictive checking that can be applied to complex genetic models and can assess the fit of the model to various aspects of the data. Posterior predictive checking proceeds by generating replicated data sets from the fitted model and then comparing these replicated data sets to the observed data set with respect to any features of interest. Assume that our data analysis has generated a set of simulations of the parameters, θ^(s)=(β^(s), φ^(s)), s=1, …, n _sim. For each of these draws, we simulate a replicated data set y ^rep(s) from the predictive distribution of the data, p(y ^rep|β^(s), φ^(s)). We check the model by means of discrepancy measures (test quantities) T(y, θ); several discrepancy measures can be chosen to reveal interesting features of the data or discrepancies between the model and the data. For each discrepancy variable, each simulated realized value T(y, θ^(s)) is compared with the corresponding simulated replicated value T(y ^rep(s), θ^(s)). Large and systematic differences between realized and replicated values indicate a misfit of the model to the data. In some cases, differences are apparent visually; otherwise, it can be useful to compute the p-value, p=Pr(T(y ^rep,θ)>T(y,θ)|y), to see whether the difference could plausibly have arisen by chance under the model. Although the posterior predictive model checking method is very flexible and quite simple, an important issue is how to choose the discrepancy quantities; this deserves future research.

A related approach to model checking is cross-validation, in which observed data are partitioned, with each part of the data compared with its predictions conditional on the model and the rest of the data. Cross-validation has been considered as a standard method for the expected predictive fit to new data. But it is computationally intensive and cannot be widely applied to Bayesian model assessment. For hierarchical models, however, the posterior predictive checking can produce results close to cross-validation if higher-level parameters are also simulated from the posterior (Green et al., 2009). Another approach is the deviance information criterion (DIC), which is a mixed analytical/computational approximation to an estimated predictive error (Spiegelhalter et al., 2002).

(ii) Removable or non-removable interactions

Statistical interactions are defined relative to particular models and thus can be affected by a change of modelling or outcome scale (Cordell, 2002; Berrington & Cox, 2007; Cordell, 2009; Thomas, 2010). We call an interaction ‘removable’ if a transformation of the outcome scale can be found to induce additivity (Berrington & Cox, 2007). Removable interactions are sometimes referred to as quantitative, whereas non-removable interactions are referred to as qualitative interactions. It may be important to investigate whether the detected interactions are removable or non-removable. If the interactions can be removed, the resulting interpretation may be improved and easily understood by a reasonable and interpretable model simplification.

For a continuous positive outcome, the Box-Cox technique (Box & Cox, 1964) can be used to find a non-linear transformation of the outcome that optimally fits the data (Cox, 1984; Berrington & Cox, 2007). The Box-Cox transformations include commonly used logarithmic and simple powers as special cases. For binary data, the logistic or probit or complementary log scale may be effective (Berrington & Cox, 2007). The hierarchical generalized linear model approach of Yi & Banerjee (2009) and Yi et al. (2010) can deal with various types of continuous and discrete phenotypes and any generalized linear models, and allows us to conveniently analyse data using different models, providing a flexible way to investigate the nature of interactions.

(iii) Average predictive genotypic effects

Once we detect multiple QTLs with main effects and interactions, one of our interests is to infer which genotypes of these QTLs are associated with increased phenotypic value or disease risk, and to describe how a gene is associated with a trait or disease in combination with another gene or an environmental factor. This can be derived from the fitted models. However, challenges remain. First, single coefficients in an interaction model are less informative. In the presence of appreciable interaction, for example, main effects are rarely of direct concern because they represent effects among individuals with other variables equalling zero. Therefore, the genetic effects should always be interpreted jointly. Secondly, the predictors in genetic models are usually coded as functions of the genotypes, rather than the genotypes themselves, leading to further difficulty in interpreting the coefficients. Thirdly, for generalized linear models of interacting genes, the genetic effects are related to a non-linear transformation (i.e. the link function) of the observed data, and thus cannot be directly interpreted on the scale of the data.

One way to understand models with multiple interactions is to calculate the average predictive comparison of each of the inputs. The average predictive comparison is defined as the expected change in the outcome variable corresponding to a specified change in the input of interest averaging over some specified distribution of all other inputs and parameters (Gill, 2001; Gelman & Hill, 2007). Yi et al. (2010) extend the average predictive comparison method to interpret genetic interaction models in case-control studies by presenting the average predictive probability of case for each of the SNPs and each pair of SNPs (or an SNP and a covariate) that significantly interact.

The method of Yi et al. (2010) can be extended to any genetic interaction model. Suppose that an interaction model has already been established. Generally, we define the marginal expectation E(y|g_s=k) as the average predictive effect of the genotype g_s=k of QTL s, and E(y|g_s=k, g_{s ′}=k′) as the average predictive effect of the two-locus genotype (g_s, g_{s ′})= (k, k′) of QTL s and s′. For a binary trait, these expectations equal the average predictive probabilities as defined by Yi et al. (2010). These average predictive effects can be compared with each other, e.g. E(y|g_s=k)−E(y|g_s=k′), or with the overall mean E(y). Thus, the average predictive effects clearly show which genotypes of the detected QTL and their combinations are associated with increased or decreased phenotypic value or disease risk. Yi et al. (2010) developed a simple method to calculate the average predictive probability and graphically display the results. Their method can be extended to calculate the average predictive effects based on any generalized linear models.

(iv) Biological relevance of statistical interactions

The term ‘epistasis’ or ‘gene×gene interaction’ was originally used to describe instances in which the effect of a particular genetic variant was masked by a variant at another locus so that variation of phenotype with genotype at one locus was only apparent among those with certain genotypes at the second locus (Cordell, 2009; VanderWeele, 2010). This original concept of epistasis is different from the definitions of statistical interactions that are usually used in statistical analysis of complex traits. Phillips (2008) recently discussed the ambiguity in the term ‘epistasis’ and defines three distinct forms of epistasis: statistical epistasis, compositional epistasis and functional epistasis. Phillips (2008) defined ‘statistical epistasis’ as a departure from marginal effects in a statistical model, much closer to the statistical interaction described earlier. The term ‘compositional epistasis’ refers to epistasis in Bateson's original sense of the term, while the term ‘functional epistasis’ describes the physical molecular interactions between various proteins (and other genetic elements) (Phillips, 2008). Compositional epistasis is a more biological form of interaction than the commonly used statistical epistasis, but does not necessarily imply functional epistasis. These distinct concepts of epistasis can be also applied to gene–environment interactions (Thomas, 2010; VanderWeele, 2010).

Most statistical methods for analysing genetic interactions actually test statistical interactions. However, the extent to which statistical interaction implies biological or functional interaction has been extensively debated in both the genetics and epidemiological literature. A prevailing opinion is that statistical tests for interactions are of limited use for elucidating epistasis in the biological sense of the term (Cordell, 2009). However, VanderWeele recently showed some relationship between statistical interaction and compositional epistasis, and derived conditions under which statistical interactions correspond to compositional epistasis (VanderWeele, 2010; Vanderweele & Laird, 2010). These empirical conditions are quite strong, but the procedures proposed may provide a useful strategy to study biological interactions.

6. Needs for further progress

(i) Gene or pathway level information

Candidate gene studies usually consist of data at different levels, i.e. genetic variants (e.g. haplotype-tagging SNPs) within multiple candidate genes which may be functionally related or from different pathways. Most of the statistical methods that are recently being used consider only individual-level predictors (i.e. SNPs and covariates) and ignore the hierarchical structure of the data and gene or pathway-level information. It is biologically expected that genetic variants within a gene would influence the phenotype more similarly than those in different genes (Hung et al., 2004). Often, rich gene or pathway-level information is available (Rebbeck et al., 2004), including simple pathway indicator variables, genomic annotation or pathway ontologies, functional assays, in silico predictions of function or evolutionary conservation or simulation of pathway kinetics (Thomas et al., 2009). Therefore, there is a growing need to develop sophisticated approaches that model the multilevel variation simultaneously and incorporate gene or pathway-level data into the model (Dunson et al., 2008; Thomas, 2010).

Hierarchical models provide a natural and efficient way of incorporating the external information about candidate genes into the analysis. One way of including the gene-level information in the hierarchical models is to model the prior means in the prior distributions of coefficients β_j using gene-level predictors. This approach allows us to pool the information in the same genes and thus would provide more effective inference about the genetic effects. Recent developments of penalized regressions for high-dimensional data may provide alternative improved ways to deal with specific structures in candidate genes. It is well known that the original lasso regression does not effectively account for the relationship among a group of correlated predictors and tends to select individual variables from the grouped variables. The elastic net (Zou & Hastie, 2005) is a generalization of the lasso regression, which introduces an additional penalty or prior to incorporate the correlation of predictors into the model (Kyung et al., 2010). The elastic net can be implemented in a hierarchical fashion combining variable selection at lower levels (e.g. among SNPs within a pathway) and shrinkage at higher levels (e.g. between genes within a pathway or between pathways).

(ii) Modelling genetic interactions hierarchically

The effect heredity and hierarchy are two important principles for the statistical analysis of interaction (Chipman, 1996; Hamada & Wu, 1992; Nelder, 1994). These principles pose certain dependence of interactions on their main effects. Since with many predictors there are a huge number of potential interactions, a simple inclusion of interactions can degrade the model fit and thus preclude effective estimation of main effects and interactions. Although these two principles have been noticed in some of the previous methods of genetic interactions, there is a clear need for further studies in the future. Recently, the lasso penalized regression has been extended to incorporate the effect heredity and hierarchy principles (Yuan et al., 2007; Zhao et al., 2009; Choi et al., 2010). Theoretical and empirical results have showed that these extensions outperform the previous methods for detecting interactions. These new developments should be adapted to the statistical analysis of genetic interactions. Another promising approach could be modelling interactions in a structured way, for example, with larger variances for interactions whose main effects are large. This type of priors can incorporate the effect heredity principle in a more continuous form.

(iii) Next-generation sequencing and rare variants in genetic interactions

The genetic aetiology of common (or complex) human diseases is determined by both common and rare genetic variants (Bodmer & Bonilla, 2008; Schork et al., 2009). Since GWAS have so far focused on common variants (with minor allele frequency (MAF)≳5%) in the human genome, it has been speculated that rare variants might account for at least some of the heritability that GWAS have missed (Manolio et al., 2009; Cirulli & Goldstein, 2010; Eichler et al., 2010). Several studies have already shown that rare variants play an important role in genetic determination for some diseases (Cohen et al., 2004, 2006; Ahituv et al., 2007; Romeo et al., 2007, 2009; Azzopardi et al., 2008; Ji et al., 2008; Nejentsev et al., 2009). Recent advances in next-generation sequencing technologies facilitate the detection of rare variants, making it possible to uncover the roles of rare variants in complex diseases.

As a single rare variant contains little variation owing to low MAF (<0·5 or 1%), statistical methods that test variants individually provide insufficient power to detect causal rare variants. Therefore, association analysis of rare variants requires sophisticated methods that can effectively combine the information across variants and test for their overall effect (Manolio et al., 2009). Several approaches have been developed to analyse rare variants, including the Collapsing, Simple-Sum and Weighted-Sum methods (Li & Leal, 2008; Madsen & Browning, 2009; Morris & Zeggini, 2010; Price et al., 2010). These methods summarize multiple rare variants by weighting them equally (Li & Leal, 2008; Morris & Zeggini, 2010) or on the basis of estimated standard deviation (Madsen & Browning, 2009) or functional prediction (Price et al., 2010). Recently, penalized likelihood approach and hierarchical models have been applied to rare variants analysis (Zhou et al., 2010; Yi & Zhi, 2010). These methods have focused on rare variants in a gene or region, and exclude genetic interactions in the analysis. Since complex diseases are usually influenced by multiple genes and environmental factors and their interactions, it would be important to develop sophisticated methods for jointly analysing all rare variants in multiple genes and gene–environment and gene–gene interactions.

(iv) Using interaction models for risk prediction

GWAS have raised expectations for predicting individual susceptibility to common diseases using genetic variants (Wray et al., 2008; Kraft et al., 2009). Previous methods using only a limited number of significant variants have typically failed to achieve satisfactory prediction performance (Jakobsdottir et al., 2009; Kraft & Hunter, 2009). Recent studies show that joint analysis of a large number of genetic variants can improve the risk prediction performance (Meuwissen et al., 2001; Lee et al., 2008; de los Campos et al., 2009; Wei et al., 2009; Hayashi & Iwata, 2010; Yang et al., 2010). However, the previous studies have not included interactions into the predictive models. If G×G and G×E interactions are present, adding these interactions to a predictive model should increase the accuracy of prediction. Therefore, jointly modelling genetic, environmental factors and their interactions has important implications for disease risk prediction and personalized medicine (Clark, 2000; Moore & Williams, 2009). Because frequencies of multi-locus genotypes that define interactions are usually low, inclusion of interactions may not largely improve the overall prediction in the entire population based on the commonly used receiver operating characteristic (ROC) curve (Bjørnvold et al., 2008; Clayton, 2009). However, the interaction models can identify combinations of multiple susceptibility loci that confer very high or low risk, and hence can be highly predictive for subsets that carry certain combinations of interacting variants (Yi et al., 2010). Unfortunately, most of the genetic association studies have so far not addressed G×G and G×E interactions, and thus the translation of scientific understanding about G×G and G×E interactions into risk assessment and genomic profiling has been limited.

7. Conclusions

Genetic interactions are worth studying for many reasons (Cordell, 2009; Thomas, 2010). First, modelling G×G and G×E interactions can increase the power to detect additional variants or genes and more accurately characterize the genetic effects, Secondly, detection and characterization of genetic interactions will help elucidate the biological and biochemical pathways that underpin disease. Finally, including significant interactions in risk prediction models can have important implications for disease risk prediction and personalized medicine. Recent advances in GWAS have provided unparalleled opportunities for investigating the genetic architecture of complex diseases. However, most of these studies have used a single-locus analysis strategy and thus ignored interactions. Therefore, the follow-up studies should focus on investigating genetic interactions and other complexities (Manolio et al., 2009; Cantor et al., 2010). However, this requires sophisticated statistical methods. As discussed in this article, there are a variety of approaches that can be used to analyse genetic interactions. The integration of the modern high-dimensional statistical methods and the specific form of genetic data and external biological knowledge will further improve the power to detect complex interactions.