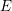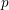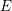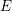1 Introduction
Many important cohomology theories
![]() $E$
are constructed from complex cobordism
$E$
are constructed from complex cobordism
![]() $\mathit{MU}$
or Brown–Peterson cohomology
$\mathit{MU}$
or Brown–Peterson cohomology
![]() $\mathit{BP}$
via Landweber’s exact functor theorem. Viewing this process as a simplification, one might wonder what kind of information about
$\mathit{BP}$
via Landweber’s exact functor theorem. Viewing this process as a simplification, one might wonder what kind of information about
 $\mathit{BP}^{\ast }(X)$
is retained in
$\mathit{BP}^{\ast }(X)$
is retained in
![]() $E^{\ast }(X)$
, for
$E^{\ast }(X)$
, for
![]() $X$
a space or a spectrum. Motivated by this question, the goal of this paper is two-fold: in the first part, we show that many properties of the
$X$
a space or a spectrum. Motivated by this question, the goal of this paper is two-fold: in the first part, we show that many properties of the
![]() $\mathit{BP}$
-cohomology of a spectrum are determined by the collection of its Morava
$\mathit{BP}$
-cohomology of a spectrum are determined by the collection of its Morava
![]() $K$
-theories
$K$
-theories
 $K(n)^{\ast }(X)$
. In the second part, transchromatic character theory is used to factor the rationalized
$K(n)^{\ast }(X)$
. In the second part, transchromatic character theory is used to factor the rationalized
![]() $\mathit{BP}$
-cohomology of classifying spaces of certain finite groups by establishing height-independent bounds on the torsion in Morava
$\mathit{BP}$
-cohomology of classifying spaces of certain finite groups by establishing height-independent bounds on the torsion in Morava
![]() $E$
-theory. This has the curious consequence that the
$E$
-theory. This has the curious consequence that the
![]() $\mathit{BP}$
-cohomology of finite groups behaves more algebro-geometrically than one might expect.
$\mathit{BP}$
-cohomology of finite groups behaves more algebro-geometrically than one might expect.
Let
![]() $E_{n}$
denote Morava
$E_{n}$
denote Morava
![]() $E$
-theory of height
$E$
-theory of height
![]() $n$
, which is a Landweber exact
$n$
, which is a Landweber exact
![]() $E_{\infty }$
-ring spectrum with coefficients
$E_{\infty }$
-ring spectrum with coefficients
 $E_{n}^{\ast }=W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u^{\pm 1}]$
. The key observation of this paper is a natural extension of a theorem due to Hovey [Reference HoveyHov95, Theorem 3.1], realizing
$E_{n}^{\ast }=W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u^{\pm 1}]$
. The key observation of this paper is a natural extension of a theorem due to Hovey [Reference HoveyHov95, Theorem 3.1], realizing
![]() $\mathit{BP}$
as a summand in a product of simpler cohomology theories.
$\mathit{BP}$
as a summand in a product of simpler cohomology theories.
Theorem.
The
![]() $p$
-completed Brown–Peterson spectrum
$p$
-completed Brown–Peterson spectrum
![]() $\mathit{BP}_{\!p}$
is a retract of
$\mathit{BP}_{\!p}$
is a retract of
 $\prod _{n>0}E_{n}$
, the product over all Morava
$\prod _{n>0}E_{n}$
, the product over all Morava
![]() $E$
-theories
$E$
-theories
![]() $E_{n}$
.
$E_{n}$
.
The general idea is as follows: the behavior of Morava
![]() $E$
-theory at height
$E$
-theory at height
![]() $n$
is closely connected to the behavior of Morava
$n$
is closely connected to the behavior of Morava
![]() $K$
-theory
$K$
-theory
![]() $K(n)$
at the same height, and these cohomology theories determine each other in many cases. Starting from knowledge about the Morava
$K(n)$
at the same height, and these cohomology theories determine each other in many cases. Starting from knowledge about the Morava
![]() $K$
-theories
$K$
-theories
 $K(n)^{\ast }(X)$
of a spectrum
$K(n)^{\ast }(X)$
of a spectrum
![]() $X$
, we can then deduce properties of
$X$
, we can then deduce properties of
![]() $E_{n}^{\ast }(X)$
, which collectively control
$E_{n}^{\ast }(X)$
, which collectively control
 $\mathit{BP}_{\!p}^{\ast }(X)$
by the above splitting. Conversely, the
$\mathit{BP}_{\!p}^{\ast }(X)$
by the above splitting. Conversely, the
![]() $\mathit{BP}$
-cohomology of spaces determines their Morava
$\mathit{BP}$
-cohomology of spaces determines their Morava
![]() $K$
-theory.
$K$
-theory.
The class of spectra amenable to such comparison results consists of those with evenly concentrated Morava
![]() $K$
-theory for all heights or, more generally, those with Landweber flat
$K$
-theory for all heights or, more generally, those with Landweber flat
![]() $\mathit{BP}$
-cohomology; examples abound. Using the previous theorem and certain base change formulas, we then obtain generalizations of the main structural results of [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] to spectra.
$\mathit{BP}$
-cohomology; examples abound. Using the previous theorem and certain base change formulas, we then obtain generalizations of the main structural results of [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] to spectra.
Theorem.
Let
![]() $X$
be a spectrum. If
$X$
be a spectrum. If
 $K(n)^{\ast }X$
is even for all
$K(n)^{\ast }X$
is even for all
![]() $n>0$
, then
$n>0$
, then
![]() $\mathit{BP}_{\!p}^{\ast }X$
is even and Landweber flat. Moreover, for a map
$\mathit{BP}_{\!p}^{\ast }X$
is even and Landweber flat. Moreover, for a map
 $f:X\overset{}{\longrightarrow }Y$
between spectra with even Morava
$f:X\overset{}{\longrightarrow }Y$
between spectra with even Morava
![]() $K$
-theories,
$K$
-theories,
![]() $\mathit{BP}_{\!p}^{\ast }(f)$
is injective or surjective if
$\mathit{BP}_{\!p}^{\ast }(f)$
is injective or surjective if
 $K(n)^{\ast }(f)$
is injective or surjective for all
$K(n)^{\ast }(f)$
is injective or surjective for all
![]() $n$
.
$n$
.
Moreover, we give conditions on a spectrum
![]() $X$
which imply that
$X$
which imply that
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is Landweber flat, where
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is Landweber flat, where
![]() $\mathbb{P}X$
denotes the free commutative algebra spectrum on
$\mathbb{P}X$
denotes the free commutative algebra spectrum on
![]() $X$
. Combining the retract theorem with work of Rezk [Reference RezkRez09] as well as work of the first author and Frankland [Reference Barthel and FranklandBF15], we construct a functor
$X$
. Combining the retract theorem with work of Rezk [Reference RezkRez09] as well as work of the first author and Frankland [Reference Barthel and FranklandBF15], we construct a functor
 $$\begin{eqnarray}\mathbb{T}^{\mathit{BP}}:\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}\longrightarrow \text{Mod}_{\mathit{BP}_{\!p}^{\ast }}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{T}^{\mathit{BP}}:\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}\longrightarrow \text{Mod}_{\mathit{BP}_{\!p}^{\ast }}.\end{eqnarray}$$
For a large class of spaces, which includes spheres and higher Eilenberg–MacLane spaces, we then show that
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is functorially determined by
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is functorially determined by
 $\mathit{BP}_{\!p}^{\ast }(X)$
.
$\mathit{BP}_{\!p}^{\ast }(X)$
.
Theorem.
There exists a functor
![]() $\mathbb{T}^{\mathit{BP}}$
on the category
$\mathbb{T}^{\mathit{BP}}$
on the category
 $\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}$
of (topological)
$\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}$
of (topological)
![]() $\mathit{BP}_{\!p}^{\ast }$
-modules such that, for
$\mathit{BP}_{\!p}^{\ast }$
-modules such that, for
![]() $X$
a space with
$X$
a space with
 $K(n)_{\ast }(X)$
even and degreewise finite for all
$K(n)_{\ast }(X)$
even and degreewise finite for all
![]() $n>0$
, there is a natural isomorphism
$n>0$
, there is a natural isomorphism

of
![]() $\mathit{BP}_{\!p}^{\ast }$
-modules.
$\mathit{BP}_{\!p}^{\ast }$
-modules.
Roughly speaking, this result says that the structure of the corresponding Künneth and homotopy orbit spectral sequences for
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is completely controlled by the topological module
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is completely controlled by the topological module
 $\mathit{BP}_{\!p}^{\ast }(X)$
.
$\mathit{BP}_{\!p}^{\ast }(X)$
.
As another consequence of our results, we deduce that various notions of good groups coincide and are controlled by the
![]() $\mathit{BP}$
-cohomology of the group. This motivates the second part of the paper, where we take the above ideas one step further. Transchromatic character theory establishes a link between Morava
$\mathit{BP}$
-cohomology of the group. This motivates the second part of the paper, where we take the above ideas one step further. Transchromatic character theory establishes a link between Morava
![]() $E$
-theories of different heights, leading to the question of which properties of
$E$
-theories of different heights, leading to the question of which properties of
![]() $E_{n}^{\ast }(X)$
and
$E_{n}^{\ast }(X)$
and
 $\mathit{BP}^{\ast }(X)$
are detected by height 1 and height 0, i.e. by topological
$\mathit{BP}^{\ast }(X)$
are detected by height 1 and height 0, i.e. by topological
![]() $K$
-theory and rational cohomology. It turns out that the connection is surprisingly strong, an observation that has already been exploited in [Reference Schlank and StapletonSS15, Reference Barthel and StapletonBS16].
$K$
-theory and rational cohomology. It turns out that the connection is surprisingly strong, an observation that has already been exploited in [Reference Schlank and StapletonSS15, Reference Barthel and StapletonBS16].
The second part of the paper focuses on the rationalization of the retract theorem. We apply the resulting map to classifying spaces of finite groups. Algebro-geometrically,
 $E_{n}^{\ast }(BA)$
for a finite abelian group
$E_{n}^{\ast }(BA)$
for a finite abelian group
![]() $A$
corepresents the scheme
$A$
corepresents the scheme
 $\text{Hom}(A^{\ast },\mathbb{G}_{E_{n}})$
that parametrizes maps from the Pontryagin dual of
$\text{Hom}(A^{\ast },\mathbb{G}_{E_{n}})$
that parametrizes maps from the Pontryagin dual of
![]() $A$
to the formal group
$A$
to the formal group
![]() $\mathbb{G}_{E_{n}}$
associated to Morava
$\mathbb{G}_{E_{n}}$
associated to Morava
![]() $E$
-theory. Rationally, there is then a decomposition into schemes classifying level structures
$E$
-theory. Rationally, there is then a decomposition into schemes classifying level structures
 $$\begin{eqnarray}\text{Hom}(A^{\ast },\mathbb{G}_{E_{n}}){\cong _{\mathbb{Q}}\coprod }_{H\subseteq A}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(A^{\ast },\mathbb{G}_{E_{n}}){\cong _{\mathbb{Q}}\coprod }_{H\subseteq A}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}),\end{eqnarray}$$
where
![]() $H$
runs through the subgroups of
$H$
runs through the subgroups of
![]() $A$
; see [Reference StricklandStr97]. Up to torsion, the scheme of level structures
$A$
; see [Reference StricklandStr97]. Up to torsion, the scheme of level structures
 $\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
is corepresented by
$\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
is corepresented by
 $E_{n}^{\ast }(BH)/I$
, where
$E_{n}^{\ast }(BH)/I$
, where
![]() $I$
is the transfer ideal, i.e. the ideal generated by transfers from the maximal subgroups of
$I$
is the transfer ideal, i.e. the ideal generated by transfers from the maximal subgroups of
![]() $H$
. We show that this statement holds integrally up to bounded integral torsion, where the exponent of the torsion is in fact independent of the height we work at. This uses a result about level structures proven by Jeremy Hahn, which is presented in the appendix to this paper.
$H$
. We show that this statement holds integrally up to bounded integral torsion, where the exponent of the torsion is in fact independent of the height we work at. This uses a result about level structures proven by Jeremy Hahn, which is presented in the appendix to this paper.
Theorem.
Let
![]() $A$
be a finite abelian group; then the exponent of the torsion in the cokernel of the natural map
$A$
be a finite abelian group; then the exponent of the torsion in the cokernel of the natural map
 $$\begin{eqnarray}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
is bounded independently of the height
![]() $n$
.
$n$
.
In order to prove this, we construct a variant of the transchromatic character maps of [Reference StapletonSta13, Reference Barthel and StapletonBS16] from
![]() $E$
-theory at height
$E$
-theory at height
![]() $n$
to height 1, which enables tight control over the torsion. Since products of torsion abelian groups with a common torsion exponent are torsion as well, it follows that the natural map
$n$
to height 1, which enables tight control over the torsion. Since products of torsion abelian groups with a common torsion exponent are torsion as well, it follows that the natural map
 $$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
is a rational isomorphism. It is possible to apply the retract theorem to immediately deduce a similar decomposition for the
![]() $\mathit{BP}$
-cohomology of finite abelian groups.
$\mathit{BP}$
-cohomology of finite abelian groups.
Corollary.
Let
![]() $A$
be a finite abelian group and let
$A$
be a finite abelian group and let
![]() $I$
denote the transfer ideal; then the natural map
$I$
denote the transfer ideal; then the natural map
 $$\begin{eqnarray}\mathit{BP}_{\!p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\mathit{BP}_{\!p}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}_{\!p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\mathit{BP}_{\!p}^{\ast }(BH)/I\end{eqnarray}$$
is a rational isomorphism.
Similarly, the scheme corepresented by
 $E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
decomposes rationally into a product of subgroup schemes
$E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
decomposes rationally into a product of subgroup schemes
 $\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})$
, indexed by partitions
$\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})$
, indexed by partitions
![]() $\unicode[STIX]{x1D706}\vdash m$
of
$\unicode[STIX]{x1D706}\vdash m$
of
![]() $m$
. Again, we prove that this statement holds integrally up to globally bounded integral torsion.
$m$
. Again, we prove that this statement holds integrally up to globally bounded integral torsion.
Theorem.
The exponent of the torsion in the cokernel of the natural map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
is bounded independently of the height
![]() $n$
. Consequently, there is a rational isomorphism
$n$
. Consequently, there is a rational isomorphism
 $$\begin{eqnarray}\mathit{BP}_{\!p}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }(\mathit{BP}_{\!p}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}},\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}_{\!p}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }(\mathit{BP}_{\!p}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}},\end{eqnarray}$$
where
![]() $I_{\unicode[STIX]{x1D706}}$
is a certain transfer ideal.
$I_{\unicode[STIX]{x1D706}}$
is a certain transfer ideal.
Finally, we give a further illustration of the methods of the paper by proving a well-known version of Artin induction for the
![]() $\mathit{BP}$
-cohomology of good groups.
$\mathit{BP}$
-cohomology of good groups.
1.1 Relation to the literature
The question of when and how
![]() $E^{\ast }(X)$
can be computed algebraically from
$E^{\ast }(X)$
can be computed algebraically from
 $\mathit{BP}^{\ast }(X)$
or, conversely, what kind of information about
$\mathit{BP}^{\ast }(X)$
or, conversely, what kind of information about
 $\mathit{BP}^{\ast }(X)$
is retained in
$\mathit{BP}^{\ast }(X)$
is retained in
![]() $E^{\ast }(X)$
has a long history. After the pioneering work of Johnson and Wilson [Reference Johnson and WilsonJW73, Reference Johnson and WilsonJW75] and Landweber [Reference LandweberLan76], these problems were studied systematically in a series of papers by Ravenel, Wilson and Yagita [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] and Kashiwabara [Reference KashiwabaraKas98, Reference KashiwabaraKas01]. Their methods are based on a careful study of the associated Atiyah–Hirzebruch spectral sequences. As a consequence, the results contained in these papers are unstable, i.e. they are valid only for spaces rather than for arbitrary spectra.
$E^{\ast }(X)$
has a long history. After the pioneering work of Johnson and Wilson [Reference Johnson and WilsonJW73, Reference Johnson and WilsonJW75] and Landweber [Reference LandweberLan76], these problems were studied systematically in a series of papers by Ravenel, Wilson and Yagita [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] and Kashiwabara [Reference KashiwabaraKas98, Reference KashiwabaraKas01]. Their methods are based on a careful study of the associated Atiyah–Hirzebruch spectral sequences. As a consequence, the results contained in these papers are unstable, i.e. they are valid only for spaces rather than for arbitrary spectra.
The results of our paper generalize the main structural theorems of [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] from spaces to spectra, by replacing the Atiyah–Hirzebruch spectral sequence arguments with the above retract result. This is remarkable, as such extensions had previously seemed impossible; see the remark following Theorem 1.8 in [Reference Ravenel, Wilson and YagitaRWY98, p. 2]. Furthermore, the retract result has the pleasant side effect of simplifying many of the proofs, at the cost of losing control over any explicit generators and relations descriptions. In particular, we are unable to recover the computations for spheres, Eilenberg–MacLane spaces, and other spaces appearing in certain
![]() $\unicode[STIX]{x1D6FA}$
-spectra given in the aforementioned papers.
$\unicode[STIX]{x1D6FA}$
-spectra given in the aforementioned papers.
In contrast to this, passing from
 $\mathit{BP}^{\ast }(X)$
to
$\mathit{BP}^{\ast }(X)$
to
 $K(n)^{\ast }(X)$
is more subtle, due to the existence of counterexamples to the generalizations of certain base change formulas to arbitrary spectra. Here, our results do not improve upon the results in [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99].
$K(n)^{\ast }(X)$
is more subtle, due to the existence of counterexamples to the generalizations of certain base change formulas to arbitrary spectra. Here, our results do not improve upon the results in [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99].
In [Reference KashiwabaraKas01], Kashiwabara studied the following question: when
![]() $X$
is a space, to what extent does
$X$
is a space, to what extent does
 $\mathit{BP}_{\!p}^{\ast }(X)$
control
$\mathit{BP}_{\!p}^{\ast }(X)$
control
 $\mathit{BP}_{\!p}^{\ast }(QX)$
? He showed that
$\mathit{BP}_{\!p}^{\ast }(QX)$
? He showed that
 $\mathit{BP}_{\!p}^{\ast }(QX)$
inherits Landweber flatness from
$\mathit{BP}_{\!p}^{\ast }(QX)$
inherits Landweber flatness from
 $\mathit{BP}_{\!p}^{\ast }(X)$
and constructed a functor
$\mathit{BP}_{\!p}^{\ast }(X)$
and constructed a functor
![]() ${\mathcal{D}}$
such that
${\mathcal{D}}$
such that

is an isomorphism under certain algebraic conditions on
![]() $X$
. Our description of
$X$
. Our description of
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is related to Kashiwabara’s result via the Snaith splitting; the precise relation between Kashiwabara’s theorem and ours is, however, not completely clear at the moment. It should nevertheless be noted that his functor allows for explicit calculations, whereas
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is related to Kashiwabara’s result via the Snaith splitting; the precise relation between Kashiwabara’s theorem and ours is, however, not completely clear at the moment. It should nevertheless be noted that his functor allows for explicit calculations, whereas
![]() $\mathbb{T}^{\mathit{BP}}$
involves the idempotent given by the retract and is thus much less computable.
$\mathbb{T}^{\mathit{BP}}$
involves the idempotent given by the retract and is thus much less computable.
1.2 Outline
We begin in § 2 by recalling the cohomology theories and basic concepts that will be used in this paper. These theories are related to each other by various base change formulas, most of which are collected from the literature. The first goal of § 3 is to prove the result which the rest of our paper is based on, namely that
![]() $\mathit{BP}_{\!p}$
is a retract of a product of Morava
$\mathit{BP}_{\!p}$
is a retract of a product of Morava
![]() $E$
-theories. We then deduce our main theorems about the structure of the
$E$
-theories. We then deduce our main theorems about the structure of the
![]() $\mathit{BP}$
-cohomology of spectra with even Morava
$\mathit{BP}$
-cohomology of spectra with even Morava
![]() $K$
-theory. Moreover, we discuss the
$K$
-theory. Moreover, we discuss the
![]() $\mathit{BP}$
-cohomology of free commutative algebras and show that various notions of good groups are equivalent.
$\mathit{BP}$
-cohomology of free commutative algebras and show that various notions of good groups are equivalent.
The second part of the paper starts in § 4 with a toy example, obtaining the existence of a height-independent torsion exponent in the case of finite cyclic groups and
![]() $\unicode[STIX]{x1D6F4}_{p}$
by an explicit calculation. A number of auxiliary commutative algebra results are proven before introducing a variant of the transchromatic character map. The rest of the section contains the proofs of the main theorems for Morava
$\unicode[STIX]{x1D6F4}_{p}$
by an explicit calculation. A number of auxiliary commutative algebra results are proven before introducing a variant of the transchromatic character map. The rest of the section contains the proofs of the main theorems for Morava
![]() $E$
-theory and their consequences for the rational
$E$
-theory and their consequences for the rational
![]() $\mathit{BP}$
-cohomology of abelian and symmetric groups. A key result for the case of abelian groups is deferred to an appendix, written by Jeremy Hahn.
$\mathit{BP}$
-cohomology of abelian and symmetric groups. A key result for the case of abelian groups is deferred to an appendix, written by Jeremy Hahn.
1.3 Notation and conventions
Throughout this paper we fix a prime
![]() $p$
and work in the category
$p$
and work in the category
![]() $\text{Sp}$
of
$\text{Sp}$
of
![]() $p$
-local spectra. By space we shall always mean a CW complex of finite type viewed as a suspension spectrum. The results in the first part of the paper are formulated and proven more generally for the theories
$p$
-local spectra. By space we shall always mean a CW complex of finite type viewed as a suspension spectrum. The results in the first part of the paper are formulated and proven more generally for the theories
![]() $P(m)$
, but the reader not familiar with these might want to specialize to
$P(m)$
, but the reader not familiar with these might want to specialize to
 $P(0)=\mathit{BP}_{\!p}$
. We will also always write
$P(0)=\mathit{BP}_{\!p}$
. We will also always write
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
for
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
for
 $(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{})^{n}$
.
$(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{})^{n}$
.
2 The Brown–Peterson spectrum and related cohomology theories
After introducing the complex oriented ring spectra that will be used throughout the paper, we recall the notion of Landweber flatness relative to the theory
![]() $P(m)$
and prove that Landweber flat modules are closed under products. We then give base change formulas relating these cohomology theories. Although most of these results are well known, we hope the reader will find it helpful to see them collected in one place.
$P(m)$
and prove that Landweber flat modules are closed under products. We then give base change formulas relating these cohomology theories. Although most of these results are well known, we hope the reader will find it helpful to see them collected in one place.
2.1 Preliminaries
We recall some basic terminology and facts that will be used in this paper; for more details, see for example [Reference Ravenel, Wilson and YagitaRWY98]. Let
![]() $\mathit{BP}$
be the Brown–Peterson spectrum with coefficients
$\mathit{BP}$
be the Brown–Peterson spectrum with coefficients
 $\mathit{BP}^{\ast }=\mathbb{Z}_{(p)}[v_{1},v_{2},\ldots ]$
, where the
$\mathit{BP}^{\ast }=\mathbb{Z}_{(p)}[v_{1},v_{2},\ldots ]$
, where the
![]() $v_{i}$
are Hazewinkel generators of degree
$v_{i}$
are Hazewinkel generators of degree
 $|v_{i}|=-2(p^{i}-1)$
with
$|v_{i}|=-2(p^{i}-1)$
with
![]() $v_{0}=p$
; as usual, none of the constructions or results in this paper depend on this choice of generators. By [Reference LandweberLan73], the invariant prime ideals in
$v_{0}=p$
; as usual, none of the constructions or results in this paper depend on this choice of generators. By [Reference LandweberLan73], the invariant prime ideals in
![]() $\mathit{BP}^{\ast }$
are given by
$\mathit{BP}^{\ast }$
are given by
 $I_{n}=(p,v_{1},\ldots ,v_{n-1})$
for
$I_{n}=(p,v_{1},\ldots ,v_{n-1})$
for
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
Recall that
![]() $P(m)$
denotes the
$P(m)$
denotes the
![]() $\mathit{BP}$
-module spectrum with coefficients
$\mathit{BP}$
-module spectrum with coefficients
 $$\begin{eqnarray}P(m)^{\ast }=\mathit{BP}^{\ast }/I_{m},\end{eqnarray}$$
$$\begin{eqnarray}P(m)^{\ast }=\mathit{BP}^{\ast }/I_{m},\end{eqnarray}$$
which can be constructed using the Baas–Sullivan theory of singularities or the methods of [Reference Elmendorf, Kriz, Mandell and MayEKMM97]. We set
 $P(0)=\mathit{BP}_{\!p}$
, the
$P(0)=\mathit{BP}_{\!p}$
, the
![]() $p$
-completion of
$p$
-completion of
![]() $\mathit{BP}$
. The ideals
$\mathit{BP}$
. The ideals
 $I_{m,n}=(v_{m},\ldots ,v_{n-1})$
for
$I_{m,n}=(v_{m},\ldots ,v_{n-1})$
for
![]() $n\geqslant m$
are then precisely the invariant prime ideals of
$n\geqslant m$
are then precisely the invariant prime ideals of
![]() $P(m)^{\ast }$
.
$P(m)^{\ast }$
.
The Landweber filtration theorem [Reference LandweberLan76] for
 $\mathit{BP}_{\ast }\mathit{BP}$
-comodules that are finitely presented as
$\mathit{BP}_{\ast }\mathit{BP}$
-comodules that are finitely presented as
![]() $\mathit{BP}_{\ast }$
-modules admits the following generalization to
$\mathit{BP}_{\ast }$
-modules admits the following generalization to
![]() $P(m)$
, due independently to Yagita and Yoshimura.
$P(m)$
, due independently to Yagita and Yoshimura.
Theorem 2.1 [Reference YagitaYag76, Reference YosimuraYos76].
Suppose that
![]() $M$
is a
$M$
is a
 $P(m)^{\ast }P(m)$
-module which is finitely presented as a
$P(m)^{\ast }P(m)$
-module which is finitely presented as a
![]() $P(m)^{\ast }$
-module. Then there exists a finite filtration of
$P(m)^{\ast }$
-module. Then there exists a finite filtration of
![]() $M$
by
$M$
by
 $P(m)^{\ast }P(m)$
-modules,
$P(m)^{\ast }P(m)$
-modules,
 $$\begin{eqnarray}0=M_{0}\subseteq M_{1}\subseteq \cdots \subseteq M_{s}=M,\end{eqnarray}$$
$$\begin{eqnarray}0=M_{0}\subseteq M_{1}\subseteq \cdots \subseteq M_{s}=M,\end{eqnarray}$$
with filtration quotients
 $M_{i+1}/M_{i}\cong P(m)^{\ast }/I_{m,n_{i}}$
up to a shift and for some
$M_{i+1}/M_{i}\cong P(m)^{\ast }/I_{m,n_{i}}$
up to a shift and for some
![]() $n_{i}\geqslant m$
.
$n_{i}\geqslant m$
.
Remark 2.2. The classical Landweber filtration theorem is usually stated for
![]() $\mathit{BP}$
, not for
$\mathit{BP}$
, not for
 $P(0)=\mathit{BP}_{\!p}$
. However, this will not affect any of the arguments or statements appearing later in this paper.
$P(0)=\mathit{BP}_{\!p}$
. However, this will not affect any of the arguments or statements appearing later in this paper.
From
![]() $P(m)$
we can construct, for
$P(m)$
we can construct, for
![]() $n\geqslant m$
, spectra
$n\geqslant m$
, spectra
 $E(m,n)$
by taking the quotient by the ideals
$E(m,n)$
by taking the quotient by the ideals
 $(v_{n+1},v_{n+2},\ldots )$
and then inverting
$(v_{n+1},v_{n+2},\ldots )$
and then inverting
![]() $v_{n}$
; that is,
$v_{n}$
; that is,
 $$\begin{eqnarray}E(m,n)^{\ast }=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}_{p}[v_{1},\ldots ,v_{n}][v_{n}^{-1}]\quad & \text{if}~m=0,\\ \mathbb{F}_{p}[v_{m},\ldots ,v_{n}][v_{n}^{-1}]\quad & \text{if}~m>0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}E(m,n)^{\ast }=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}_{p}[v_{1},\ldots ,v_{n}][v_{n}^{-1}]\quad & \text{if}~m=0,\\ \mathbb{F}_{p}[v_{m},\ldots ,v_{n}][v_{n}^{-1}]\quad & \text{if}~m>0.\end{array}\right.\end{eqnarray}$$
In particular, if
![]() $m=n$
, then
$m=n$
, then
 $E(m,m)=K(m)$
is Morava
$E(m,m)=K(m)$
is Morava
![]() $K$
-theory; and if
$K$
-theory; and if
![]() $m=0$
, then
$m=0$
, then
 $E(0,n)=E(n)$
is
$E(0,n)=E(n)$
is
![]() $p$
-complete Johnson–Wilson theory. Moreover, we define
$p$
-complete Johnson–Wilson theory. Moreover, we define
 $\hat{E}(m,n)$
to be the
$\hat{E}(m,n)$
to be the
![]() $K(n)$
-localization of
$K(n)$
-localization of
 $E(m,n)$
,
$E(m,n)$
,
 $$\begin{eqnarray}\hat{E}(m,n)=L_{K(n)}E(m,n),\end{eqnarray}$$
$$\begin{eqnarray}\hat{E}(m,n)=L_{K(n)}E(m,n),\end{eqnarray}$$
where
![]() $L_{K(n)}$
denotes Bousfield localization with respect to
$L_{K(n)}$
denotes Bousfield localization with respect to
![]() $K(n)$
. Finally, we let
$K(n)$
. Finally, we let
![]() $E_{n}$
denote height
$E_{n}$
denote height
![]() $n$
Morava
$n$
Morava
![]() $E$
-theory, which is a 2-periodic finite free extension of
$E$
-theory, which is a 2-periodic finite free extension of
![]() $\hat{E}(0,n)$
given by adjoining an element
$\hat{E}(0,n)$
given by adjoining an element
![]() $u$
of degree 2 with
$u$
of degree 2 with
 $u^{1-p^{n}}=v_{n}$
and extending coefficients to the ring
$u^{1-p^{n}}=v_{n}$
and extending coefficients to the ring
![]() $W(\unicode[STIX]{x1D705})$
of Witt vectors over a perfect field
$W(\unicode[STIX]{x1D705})$
of Witt vectors over a perfect field
![]() $\unicode[STIX]{x1D705}$
of characteristic
$\unicode[STIX]{x1D705}$
of characteristic
![]() $p$
.
$p$
.
2.2 Landweber flatness
Recall the following definition from [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99].
Definition 2.3. A module
 $M\in \text{Mod}_{P(m)^{\ast }}$
is said to be Landweber flat if it is a flat module for the category of
$M\in \text{Mod}_{P(m)^{\ast }}$
is said to be Landweber flat if it is a flat module for the category of
 $P(m)^{\ast }P(m)$
-modules which are finitely presented as
$P(m)^{\ast }P(m)$
-modules which are finitely presented as
![]() $P(m)^{\ast }$
-modules, i.e. if the functor
$P(m)^{\ast }$
-modules, i.e. if the functor

is exact.
The Landweber filtration theorem for
![]() $P(m)$
easily implies the following characterization of Landweber flatness; see for example [Reference Ravenel, Wilson and YagitaRWY98, Theorem 3.9].
$P(m)$
easily implies the following characterization of Landweber flatness; see for example [Reference Ravenel, Wilson and YagitaRWY98, Theorem 3.9].
Proposition 2.4. A
![]() $P(m)^{\ast }$
-module
$P(m)^{\ast }$
-module
![]() $M$
is Landweber flat if and only if
$M$
is Landweber flat if and only if
 $$\begin{eqnarray}v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}M\longrightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}M\end{eqnarray}$$
$$\begin{eqnarray}v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}M\longrightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}M\end{eqnarray}$$
is injective for all
![]() $n\geqslant m$
.
$n\geqslant m$
.
In the next section, we need a closure property for the collection of Landweber flat modules. Since we do not know of a published reference for this fact, we include the proof.
Lemma 2.5. The collection of Landweber flat
![]() $P(m)^{\ast }$
-modules is closed under products.
$P(m)^{\ast }$
-modules is closed under products.
Proof. Suppose that
![]() $(M_{i})_{i}$
is a collection of Landweber flat
$(M_{i})_{i}$
is a collection of Landweber flat
![]() $\mathit{BP}^{\ast }$
-modules and let
$\mathit{BP}^{\ast }$
-modules and let
![]() $n\geqslant m$
. By Proposition 2.4, it suffices to show that the top map in the commutative diagram
$n\geqslant m$
. By Proposition 2.4, it suffices to show that the top map in the commutative diagram

is injective. Since
 $P(m)^{\ast }/I_{m,n}$
is a finitely presented
$P(m)^{\ast }/I_{m,n}$
is a finitely presented
![]() $P(m)^{\ast }$
-module, the vertical maps
$P(m)^{\ast }$
-module, the vertical maps
![]() $\unicode[STIX]{x1D716}_{m}$
are isomorphisms. But, by assumption, the bottom map is injective, hence so is the top map.◻
$\unicode[STIX]{x1D716}_{m}$
are isomorphisms. But, by assumption, the bottom map is injective, hence so is the top map.◻
Remark 2.6. This result should be compared to a theorem of Chase: for
![]() $R$
a (not necessarily commutative) ring, the collection of flat
$R$
a (not necessarily commutative) ring, the collection of flat
![]() $R$
-modules is closed under arbitrary products if and only if
$R$
-modules is closed under arbitrary products if and only if
![]() $R$
is left coherent. For a discussion of products of flat modules and a proof of Chase’s theorem, see [Reference LamLam99].
$R$
is left coherent. For a discussion of products of flat modules and a proof of Chase’s theorem, see [Reference LamLam99].
2.3 Base change formulas
This section collects a number of base change formulas for the cohomology theories we use in this paper. While most of the results are well known, it is not always easy to locate references in the published literature.
Lemma 2.7. Suppose
![]() $n\geqslant m$
and let
$n\geqslant m$
and let
![]() $X$
be a spectrum such that
$X$
be a spectrum such that
 $\hat{E}(m,n)^{\ast }(X)$
is evenly concentrated and flat as an
$\hat{E}(m,n)^{\ast }(X)$
is evenly concentrated and flat as an
 $\hat{E}(m,n)^{\ast }$
-module. Then
$\hat{E}(m,n)^{\ast }$
-module. Then
 $$\begin{eqnarray}K(n)^{\ast }(X)\cong \hat{E}(m,n)^{\ast }(X)\otimes _{\hat{E}(m,n)^{\ast }}K(n)^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}K(n)^{\ast }(X)\cong \hat{E}(m,n)^{\ast }(X)\otimes _{\hat{E}(m,n)^{\ast }}K(n)^{\ast },\end{eqnarray}$$
which is even as well. Conversely, if
 $K(n)^{\ast }(X)$
is even, then
$K(n)^{\ast }(X)$
is even, then
 $\hat{E}(m,n)^{\ast }(X)$
is even and flat as an
$\hat{E}(m,n)^{\ast }(X)$
is even and flat as an
 $\hat{E}(m,n)^{\ast }$
-module.
$\hat{E}(m,n)^{\ast }$
-module.
Proof. We give the proof for
![]() $m=0$
and Morava
$m=0$
and Morava
![]() $E$
-theory
$E$
-theory
![]() $E_{n}$
; the argument and referenced results generalize easily to the
$E_{n}$
; the argument and referenced results generalize easily to the
![]() $m>0$
case. First note that
$m>0$
case. First note that
![]() $E_{n}^{\ast }(X)$
is automatically complete with respect to the maximal ideal of
$E_{n}^{\ast }(X)$
is automatically complete with respect to the maximal ideal of
![]() $E_{n}^{\ast }$
, because the function spectrum
$E_{n}^{\ast }$
, because the function spectrum
 $F(X,E_{n})$
is
$F(X,E_{n})$
is
![]() $K(n)$
-local. By [Reference Barthel and FranklandBF15, Proposition A.15], this means that
$K(n)$
-local. By [Reference Barthel and FranklandBF15, Proposition A.15], this means that
![]() $E_{n}^{\ast }(X)$
is flat as an
$E_{n}^{\ast }(X)$
is flat as an
![]() $E_{n}^{\ast }$
-module if and only if it is pro-free, i.e. if it is the completion of some free
$E_{n}^{\ast }$
-module if and only if it is pro-free, i.e. if it is the completion of some free
![]() $E_{n}^{\ast }$
-module. This reduces the claim to [Reference Hovey and StricklandHS99b, Proposition 2.5].◻
$E_{n}^{\ast }$
-module. This reduces the claim to [Reference Hovey and StricklandHS99b, Proposition 2.5].◻
In order to relate
 $E(m,n)$
-cohomology to
$E(m,n)$
-cohomology to
![]() $P(m)$
-cohomology, we need to recall the construction of the completed tensor product; see for example [Reference Kono and YagitaKY93].
$P(m)$
-cohomology, we need to recall the construction of the completed tensor product; see for example [Reference Kono and YagitaKY93].
Definition 2.8. Let
![]() $k$
be a cohomology theory and consider two complete topological algebras
$k$
be a cohomology theory and consider two complete topological algebras
![]() $A$
and
$A$
and
![]() $B$
over
$B$
over
![]() $k^{\ast }$
, with filtrations given by systems of opens
$k^{\ast }$
, with filtrations given by systems of opens
![]() $\{A_{r}\}$
and
$\{A_{r}\}$
and
![]() $\{B_{r}\}$
, respectively. The completed tensor product of
$\{B_{r}\}$
, respectively. The completed tensor product of
![]() $A$
and
$A$
and
![]() $B$
over
$B$
over
![]() $k^{\ast }$
is then defined as
$k^{\ast }$
is then defined as
 $$\begin{eqnarray}A\,\,\hat{\otimes }_{k^{\ast }}\,B=\lim _{r}(A\otimes _{k^{\ast }}B)/J_{r},\end{eqnarray}$$
$$\begin{eqnarray}A\,\,\hat{\otimes }_{k^{\ast }}\,B=\lim _{r}(A\otimes _{k^{\ast }}B)/J_{r},\end{eqnarray}$$
where
![]() $J_{r}$
is the ideal spanned by
$J_{r}$
is the ideal spanned by
 $A_{r}\otimes _{k^{\ast }}B+A\otimes _{k^{\ast }}B_{r}$
.
$A_{r}\otimes _{k^{\ast }}B+A\otimes _{k^{\ast }}B_{r}$
.
If
![]() $X$
is space with skeletal filtration
$X$
is space with skeletal filtration
![]() $\{\text{sk}_{r}X\}$
, then its cohomology
$\{\text{sk}_{r}X\}$
, then its cohomology
![]() $k^{\ast }(X)$
can be topologized using the system of fundamental neighborhoods of 0 given by
$k^{\ast }(X)$
can be topologized using the system of fundamental neighborhoods of 0 given by
 $F_{r}(X)=\ker (k^{\ast }(X)\rightarrow k^{\ast }(\text{sk}_{r}X))$
. In the following, we will always consider this topology when working with completed tensor products.
$F_{r}(X)=\ker (k^{\ast }(X)\rightarrow k^{\ast }(\text{sk}_{r}X))$
. In the following, we will always consider this topology when working with completed tensor products.
Remark 2.9. In particular, note that the completed tensor product of even cohomology groups is also concentrated in even degrees.
The next result is known as Morava’s little structure theorem; a proof in the generality we need is given in [Reference WilsonWil99, Proposition 1.9]; see also [Reference StricklandStr99].
Proposition 2.10. If
![]() $X$
is a space, then
$X$
is a space, then
 $$\begin{eqnarray}E(m,n)^{\ast }(X)\cong P(m)^{\ast }(X)\,\,\hat{\otimes }_{P(m)^{\ast }}\,E(m,n)^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}E(m,n)^{\ast }(X)\cong P(m)^{\ast }(X)\,\,\hat{\otimes }_{P(m)^{\ast }}\,E(m,n)^{\ast }\end{eqnarray}$$
for all
 $n\geqslant m>0$
or for
$n\geqslant m>0$
or for
![]() $m=0$
and all
$m=0$
and all
![]() $n>0$
, and similarly for the completed theories
$n>0$
, and similarly for the completed theories
 $\hat{E}(m,n)$
. Moreover, if
$\hat{E}(m,n)$
. Moreover, if
 $P(m)^{\ast }(X)$
is Landweber flat, then
$P(m)^{\ast }(X)$
is Landweber flat, then
 $\hat{E}(m,n)^{\ast }(X)$
is flat over
$\hat{E}(m,n)^{\ast }(X)$
is flat over
 $\hat{E}(m,n)^{\ast }$
for all
$\hat{E}(m,n)^{\ast }$
for all
 $n\geqslant m>0$
.
$n\geqslant m>0$
.
Proof. The base change formula for both
 $E(m,n)$
and
$E(m,n)$
and
 $\hat{E}(m,n)$
is contained in the aforementioned references; see for example [Reference StricklandStr99, Corollary 8.24]. To show the second part of the claim, observe that, by [Reference WilsonWil99, Proposition 2.1], the assumption implies that the ideal
$\hat{E}(m,n)$
is contained in the aforementioned references; see for example [Reference StricklandStr99, Corollary 8.24]. To show the second part of the claim, observe that, by [Reference WilsonWil99, Proposition 2.1], the assumption implies that the ideal
![]() $I_{m,n}$
acts regularly on
$I_{m,n}$
acts regularly on
 $\hat{E}(m,n)^{\ast }(X)$
. Then the obvious extension of [Reference Hovey and StricklandHS99b, Theorem A.9] from
$\hat{E}(m,n)^{\ast }(X)$
. Then the obvious extension of [Reference Hovey and StricklandHS99b, Theorem A.9] from
![]() $E_{n}$
to arbitrary
$E_{n}$
to arbitrary
 $\hat{E}(m,n)$
gives flatness.◻
$\hat{E}(m,n)$
gives flatness.◻
Example 2.11. This result does not hold for arbitrary spectra instead of spaces. As a counterexample, consider the connective Morava
![]() $K$
-theory spectrum
$K$
-theory spectrum
![]() $k(n)$
. While
$k(n)$
. While
 $K(n)^{\ast }k(n)\neq 0$
, it can be shown [Reference Ravenel, Wilson and YagitaRWY98, Remark 4.9] that
$K(n)^{\ast }k(n)\neq 0$
, it can be shown [Reference Ravenel, Wilson and YagitaRWY98, Remark 4.9] that
 $P(n)^{\ast }k(n)=0$
; hence the result fails for
$P(n)^{\ast }k(n)=0$
; hence the result fails for
![]() $m=n$
.
$m=n$
.
Lemma 2.12. For any spectrum
![]() $X$
with
$X$
with
 $P(m)^{\ast }(X)$
Landweber flat and
$P(m)^{\ast }(X)$
Landweber flat and
![]() $n\geqslant m$
, there is a natural isomorphism
$n\geqslant m$
, there is a natural isomorphism
 $$\begin{eqnarray}P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X).\end{eqnarray}$$
$$\begin{eqnarray}P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X).\end{eqnarray}$$
Proof. We prove this by induction on
![]() $n\geqslant m$
, the statement for
$n\geqslant m$
, the statement for
![]() $n=m$
being trivial. Now let
$n=m$
being trivial. Now let
![]() $n\geqslant m$
and recall that Proposition 2.4 shows that
$n\geqslant m$
and recall that Proposition 2.4 shows that
 $P(m)^{\ast }(X)$
being Landweber flat implies that
$P(m)^{\ast }(X)$
being Landweber flat implies that
 $$\begin{eqnarray}v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\longrightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\end{eqnarray}$$
$$\begin{eqnarray}v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\longrightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\end{eqnarray}$$
is injective for all
![]() $n\geqslant m$
. By construction of
$n\geqslant m$
. By construction of
 $P(n+1)$
, there is an exact triangle
$P(n+1)$
, there is an exact triangle

where the dashed arrow is the connecting homomorphism of degree 1. Since
 $P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)}P(m)^{\ast }(X)$
by the induction hypothesis, our assumption combined with (2.1) shows that
$P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)}P(m)^{\ast }(X)$
by the induction hypothesis, our assumption combined with (2.1) shows that
![]() $\unicode[STIX]{x1D70C}_{n}$
is surjective and that
$\unicode[STIX]{x1D70C}_{n}$
is surjective and that
 $$\begin{eqnarray}\displaystyle P(n+1)^{\ast }(X) & \cong & \displaystyle \text{coker}(v_{n}:P(n)^{\ast }(X)\rightarrow P(n)^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle \text{coker}(v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\rightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle P(n+1)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(n+1)^{\ast }(X) & \cong & \displaystyle \text{coker}(v_{n}:P(n)^{\ast }(X)\rightarrow P(n)^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle \text{coker}(v_{n}:P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\rightarrow P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle P(n+1)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X),\nonumber\end{eqnarray}$$
thereby proving the claim. ◻
Corollary 2.13. If
![]() $X$
is a space with Landweber flat
$X$
is a space with Landweber flat
![]() $P(m)$
-cohomology, then
$P(m)$
-cohomology, then
 $$\begin{eqnarray}K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(n)^{\ast }}\,(P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X))\end{eqnarray}$$
$$\begin{eqnarray}K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(n)^{\ast }}\,(P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X))\end{eqnarray}$$
for all
 $n\geqslant m>0$
or for
$n\geqslant m>0$
or for
![]() $m=0$
and all
$m=0$
and all
![]() $n>0$
. In particular, under the same assumptions, if
$n>0$
. In particular, under the same assumptions, if
 $P(m)^{\ast }(X)$
is even, then
$P(m)^{\ast }(X)$
is even, then
 $K(n)^{\ast }(X)$
is even as well.
$K(n)^{\ast }(X)$
is even as well.
Proof. Let
![]() $X$
be a space such that
$X$
be a space such that
 $P(m)^{\ast }(X)$
is Landweber flat. From the previous lemma we get
$P(m)^{\ast }(X)$
is Landweber flat. From the previous lemma we get
 $$\begin{eqnarray}P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\end{eqnarray}$$
$$\begin{eqnarray}P(n)^{\ast }(X)\cong P(n)^{\ast }\otimes _{P(m)^{\ast }}P(m)^{\ast }(X)\end{eqnarray}$$
for all
![]() $n\geqslant m$
. But Proposition 2.10 with
$n\geqslant m$
. But Proposition 2.10 with
![]() $m=n$
shows that
$m=n$
shows that
 $$\begin{eqnarray}K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(n)^{\ast }}\,P(n)^{\ast }(X),\end{eqnarray}$$
$$\begin{eqnarray}K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(n)^{\ast }}\,P(n)^{\ast }(X),\end{eqnarray}$$
which together with (2.3) yields the claim.◻
Remark 2.14. In [Reference Kono and YagitaKY93, equation (1.8)], Kono and Yagita showed that
 $K(n)^{\ast }(X)$
is isomorphic to
$K(n)^{\ast }(X)$
is isomorphic to
 $K(n)^{\ast }\,\,\hat{\otimes }_{P(m)^{\ast }}\,P(m)^{\ast }(X)$
for a space
$K(n)^{\ast }\,\,\hat{\otimes }_{P(m)^{\ast }}\,P(m)^{\ast }(X)$
for a space
![]() $X$
with
$X$
with
 $\mathit{BP}^{\ast }(X)$
Landweber flat. We do not know whether their methods generalize to imply that
$\mathit{BP}^{\ast }(X)$
Landweber flat. We do not know whether their methods generalize to imply that
 $K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(m)^{\ast }}\,P(m)^{\ast }(X)$
in the situation of Corollary 2.13.
$K(n)^{\ast }(X)\cong K(n)^{\ast }\,\,\hat{\otimes }_{P(m)^{\ast }}\,P(m)^{\ast }(X)$
in the situation of Corollary 2.13.
3 The splitting and some consequences
In this section, we first prove that
![]() $P(m)$
is a retract of an infinite product of
$P(m)$
is a retract of an infinite product of
![]() $E$
-theories, following closely the argument given in [Reference HoveyHov95, Theorem 3.1]. Combined with the base change results of the previous section, this allows us to generalize the main structural results of [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] from spaces to spectra. Since we do not require any analysis of the Atiyah–Hirzebruch spectral sequence for this, our arguments are rather short in comparison. In § 3.3, we construct an analogue of Rezk’s algebraic approximation functor
$E$
-theories, following closely the argument given in [Reference HoveyHov95, Theorem 3.1]. Combined with the base change results of the previous section, this allows us to generalize the main structural results of [Reference Ravenel, Wilson and YagitaRWY98, Reference WilsonWil99] from spaces to spectra. Since we do not require any analysis of the Atiyah–Hirzebruch spectral sequence for this, our arguments are rather short in comparison. In § 3.3, we construct an analogue of Rezk’s algebraic approximation functor
![]() $\mathbb{T}^{E_{n}}$
for
$\mathbb{T}^{E_{n}}$
for
![]() $\mathit{BP}_{\!p}$
. These functors are then used to prove a version of Kashiwabara’s main result [Reference KashiwabaraKas01] about the
$\mathit{BP}_{\!p}$
. These functors are then used to prove a version of Kashiwabara’s main result [Reference KashiwabaraKas01] about the
![]() $\mathit{BP}_{\!p}$
-cohomology of free commutative algebras. Finally, we give several equivalent characterizations of good groups, thereby showing that this notion is really a global one.
$\mathit{BP}_{\!p}$
-cohomology of free commutative algebras. Finally, we give several equivalent characterizations of good groups, thereby showing that this notion is really a global one.
3.1
 $\mathit{BP}$
as a retract of a product of Morava
$\mathit{BP}$
as a retract of a product of Morava
 $E$
-theories
$E$
-theories
Let
 $I:\text{Sp}\rightarrow \text{Sp}$
denote Brown–Comenetz duality, which is a lift of Pontryagin duality for abelian groups to the category of spectra. To be precise, if
$I:\text{Sp}\rightarrow \text{Sp}$
denote Brown–Comenetz duality, which is a lift of Pontryagin duality for abelian groups to the category of spectra. To be precise, if
![]() $X$
is a spectrum, then
$X$
is a spectrum, then
![]() $I$
represents the functor
$I$
represents the functor
 $$\begin{eqnarray}X\mapsto \text{Hom}(\unicode[STIX]{x1D70B}_{0}X,\mathbb{Q}/\mathbb{Z}_{(p)})\end{eqnarray}$$
$$\begin{eqnarray}X\mapsto \text{Hom}(\unicode[STIX]{x1D70B}_{0}X,\mathbb{Q}/\mathbb{Z}_{(p)})\end{eqnarray}$$
and we set
 $IX=F(X,I)$
. In [Reference MargolisMar83, Proposition 5.2], Margolis proves a non-existence result for
$IX=F(X,I)$
. In [Reference MargolisMar83, Proposition 5.2], Margolis proves a non-existence result for
![]() $f$
-phantom maps with target of the form
$f$
-phantom maps with target of the form
![]() $IX$
; recall that a map
$IX$
; recall that a map
 $Y\rightarrow X$
of spectra is said to be
$Y\rightarrow X$
of spectra is said to be
![]() $f$
-phantom if
$f$
-phantom if
 $Z\overset{}{\longrightarrow }Y\overset{}{\longrightarrow }X$
is null for all finite spectra
$Z\overset{}{\longrightarrow }Y\overset{}{\longrightarrow }X$
is null for all finite spectra
![]() $Z$
.
$Z$
.
Lemma 3.1 (Margolis).
Any
![]() $f$
-phantom map with target
$f$
-phantom map with target
![]() $IX$
must be null.
$IX$
must be null.
The next result is a natural generalization of [Reference HoveyHov95, Theorem 3.1].
Theorem 3.2. Suppose that
![]() $D$
is a
$D$
is a
![]() $p$
-complete Landweber flat
$p$
-complete Landweber flat
![]() $P(m)$
-module spectrum. If there is a morphism
$P(m)$
-module spectrum. If there is a morphism
 $f:P(m)\overset{}{\longrightarrow }D$
such that the induced maps
$f:P(m)\overset{}{\longrightarrow }D$
such that the induced maps

are injective for all
![]() $n>m$
, then
$n>m$
, then
![]() $f$
is a split inclusion of spectra.
$f$
is a split inclusion of spectra.
Proof. We will prove the result for
![]() $m=0$
using the classical Landweber filtration theorem. The argument in the
$m=0$
using the classical Landweber filtration theorem. The argument in the
![]() $m>0$
case uses Theorem 2.1, but is easier as
$m>0$
case uses Theorem 2.1, but is easier as
![]() $P(m)$
is already
$P(m)$
is already
![]() $p$
-complete. Let
$p$
-complete. Let
![]() $F$
be the fiber of the map
$F$
be the fiber of the map
 $\mathit{BP}_{\!p}\rightarrow D$
and let
$\mathit{BP}_{\!p}\rightarrow D$
and let
 $$\begin{eqnarray}F^{\prime }=\text{fib}(\mathit{BP}\overset{}{\longrightarrow }D);\end{eqnarray}$$
$$\begin{eqnarray}F^{\prime }=\text{fib}(\mathit{BP}\overset{}{\longrightarrow }D);\end{eqnarray}$$
we need to check that
 $F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is null. Since
$F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is null. Since
![]() $\mathit{BP}$
has degreewise finitely generated homotopy groups,
$\mathit{BP}$
has degreewise finitely generated homotopy groups,
 $\mathit{BP}_{\!p}=I^{2}\mathit{BP}$
. In order to show the claim, it thus suffices by Lemma 3.1 to check that
$\mathit{BP}_{\!p}=I^{2}\mathit{BP}$
. In order to show the claim, it thus suffices by Lemma 3.1 to check that
 $F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is
$F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is
![]() $f$
-phantom. There is a commutative diagram
$f$
-phantom. There is a commutative diagram

with all rows and columns being cofiber sequences. Since
![]() $D$
is
$D$
is
![]() $p$
-complete, we get
$p$
-complete, we get
![]() $C_{3}=0$
and hence that the top row in the diagram
$C_{3}=0$
and hence that the top row in the diagram

is a cofiber sequence. If we can show that
 $F^{\prime }\overset{}{\longrightarrow }\mathit{BP}$
is
$F^{\prime }\overset{}{\longrightarrow }\mathit{BP}$
is
![]() $f$
-phantom, then the composite
$f$
-phantom, then the composite
 $F^{\prime }\overset{}{\longrightarrow }\mathit{BP}\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is also
$F^{\prime }\overset{}{\longrightarrow }\mathit{BP}\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
is also
![]() $f$
-phantom, and hence is null by Lemma 3.1, so the indicated factorization in the right triangle exists. Because
$f$
-phantom, and hence is null by Lemma 3.1, so the indicated factorization in the right triangle exists. Because
 $\text{cof}(\mathit{BP}\overset{}{\longrightarrow }\mathit{BP}_{\!p})$
is acyclic with respect to the mod-
$\text{cof}(\mathit{BP}\overset{}{\longrightarrow }\mathit{BP}_{\!p})$
is acyclic with respect to the mod-
![]() $p$
Moore spectrum
$p$
Moore spectrum
![]() $M(p)$
and
$M(p)$
and
![]() $\mathit{BP}_{\!p}$
is
$\mathit{BP}_{\!p}$
is
![]() $M(p)$
-local, the dashed map must be null; hence so is
$M(p)$
-local, the dashed map must be null; hence so is
 $F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
.
$F\overset{}{\longrightarrow }\mathit{BP}_{\!p}$
.
Therefore, Spanier–Whitehead duality reduces the claim to proving that if
![]() $X$
is a finite spectrum, the induced map
$X$
is a finite spectrum, the induced map

is injective. By the Landweber filtration theorem, the
 $\mathit{BP}_{\ast }\mathit{BP}$
-comodule
$\mathit{BP}_{\ast }\mathit{BP}$
-comodule
 $\mathit{BP}_{\ast }(X)$
admits a finite filtration by comodules
$\mathit{BP}_{\ast }(X)$
admits a finite filtration by comodules
![]() $F_{i}$
with filtration quotients
$F_{i}$
with filtration quotients
 $F_{i+1}/F_{i}\cong \mathit{BP}_{\ast }/I_{n_{i}}$
(up to suspensions). Since
$F_{i+1}/F_{i}\cong \mathit{BP}_{\ast }/I_{n_{i}}$
(up to suspensions). Since
 $\mathit{BP}_{\ast }/I_{n_{i}}\overset{}{\longrightarrow }D_{\ast }/I_{n_{i}}$
is injective by assumption, Landweber exactness of
$\mathit{BP}_{\ast }/I_{n_{i}}\overset{}{\longrightarrow }D_{\ast }/I_{n_{i}}$
is injective by assumption, Landweber exactness of
![]() $D$
and the snake lemma applied to the commutative diagram
$D$
and the snake lemma applied to the commutative diagram

gives the claim inductively. ◻
Remark 3.3. Note that the splitting constructed above is only additive, and is not a map of ring spectra.
Corollary 3.4. The natural diagonal map

is a split inclusion for any infinite set
![]() $I$
of integers greater than
$I$
of integers greater than
![]() $m$
. In particular,
$m$
. In particular,
![]() $\mathit{BP}_{\!p}$
is a retract of
$\mathit{BP}_{\!p}$
is a retract of
 $\prod _{n>0}E_{n}$
.
$\prod _{n>0}E_{n}$
.
Proof. It suffices to check that
 $D_{I}=\prod _{n\in I}\hat{E}(m,n)$
satisfies the conditions of Theorem 3.2. The spectra
$D_{I}=\prod _{n\in I}\hat{E}(m,n)$
satisfies the conditions of Theorem 3.2. The spectra
 $\hat{E}(m,n)$
are Landweber exact and
$\hat{E}(m,n)$
are Landweber exact and
![]() $K(n)$
-local, hence
$K(n)$
-local, hence
![]() $p$
-complete. By Lemma 2.5,
$p$
-complete. By Lemma 2.5,
![]() $D_{I}$
is also Landweber flat, and because products of local objects are local, it is also
$D_{I}$
is also Landweber flat, and because products of local objects are local, it is also
![]() $p$
-complete. Since the standard maps
$p$
-complete. Since the standard maps
 $P(m)\overset{}{\longrightarrow }\hat{E}(m,n)$
clearly make
$P(m)\overset{}{\longrightarrow }\hat{E}(m,n)$
clearly make

injective for all
![]() $k\geqslant m$
, the claim follows.◻
$k\geqslant m$
, the claim follows.◻
Remark 3.5. The infinite product in Corollary 3.4 cannot be replaced by a coproduct. In fact, every map

is null, for any
![]() $m\geqslant 0$
. To see this, note that
$m\geqslant 0$
. To see this, note that
![]() $P(m)$
is
$P(m)$
is
![]() $H\mathbb{F}_{p}$
-local, while
$H\mathbb{F}_{p}$
-local, while
![]() $E_{n}$
is
$E_{n}$
is
![]() $H\mathbb{F}_{p}$
-acyclic for all
$H\mathbb{F}_{p}$
-acyclic for all
![]() $n$
because the Morava
$n$
because the Morava
![]() $K$
-theories are; hence
$K$
-theories are; hence
![]() $f$
must be null.
$f$
must be null.
Remark 3.6. Combining [Reference HoveyHov95, Theorem 3.1] with [Reference Hovey and SadofskyHS99a, Theorem B] yields a splitting similar to Corollary 3.4: the map

is a split inclusion, where the
![]() $S(n)$
are explicit indexing sets of even integers. The spectrum on the right-hand side is, however, much bigger than
$S(n)$
are explicit indexing sets of even integers. The spectrum on the right-hand side is, however, much bigger than
 $\prod _{n>0}E_{n}$
and less convenient for taking cohomology due to the infinite wedge. In some sense, our splitting is as small as possible when using these techniques, but structural properties of
$\prod _{n>0}E_{n}$
and less convenient for taking cohomology due to the infinite wedge. In some sense, our splitting is as small as possible when using these techniques, but structural properties of
![]() $\mathit{BP}_{\!p}$
could also be deduced from the spectrum in (3.1).
$\mathit{BP}_{\!p}$
could also be deduced from the spectrum in (3.1).
Furthermore, since
![]() $\mathit{MU}$
splits
$\mathit{MU}$
splits
![]() $p$
-locally into a wedge of even suspensions of
$p$
-locally into a wedge of even suspensions of
![]() $\mathit{BP}$
, there are similar results for
$\mathit{BP}$
, there are similar results for
![]() $\mathit{MU}_{(p)}$
.
$\mathit{MU}_{(p)}$
.
3.2 Brown–Peterson cohomology and Morava
 $K$
-theory
$K$
-theory
In this section, we draw some inferences from Corollary 3.4 on the kind of information that the Morava
![]() $K$
-theories detect about the
$K$
-theories detect about the
![]() $P(m)$
-cohomology of spectra. These results generalize the main structural theorems of [Reference Ravenel, Wilson and YagitaRWY98] from spaces to spectra.
$P(m)$
-cohomology of spectra. These results generalize the main structural theorems of [Reference Ravenel, Wilson and YagitaRWY98] from spaces to spectra.
Remark 3.7. While the authors remark in [Reference Ravenel, Wilson and YagitaRWY98, p. 2] that their results are strictly unstable, their counterexample refers to Example 2.11 and hence only affects Proposition 2.10, which is not needed in our approach.
We start with a lemma that allows us to pass between ordinary and
![]() $p$
-complete Brown–Peterson cohomology.
$p$
-complete Brown–Peterson cohomology.
Lemma 3.8. Suppose that
![]() $X$
is a spectrum of finite type which is bounded below and such that either:
$X$
is a spectrum of finite type which is bounded below and such that either:
-
(i)
 $X$
is a suspension spectrum which is rationally equivalent to
$X$
is a suspension spectrum which is rationally equivalent to
 $S^{0}$
; or
$S^{0}$
; or -
(ii)
 $X$
is a spectrum which is rationally acyclic;
$X$
is a spectrum which is rationally acyclic;
then
 $\mathit{BP}^{\ast }(X)$
is even and Landweber flat if and only if
$\mathit{BP}^{\ast }(X)$
is even and Landweber flat if and only if
 $\mathit{BP}_{\!p}^{\ast }(X)$
is.
$\mathit{BP}_{\!p}^{\ast }(X)$
is.
Proof. Since
![]() $\mathit{BP}$
is connective,
$\mathit{BP}$
is connective,
![]() $\mathit{BP}_{\!p}$
is the Bousfield localization of
$\mathit{BP}_{\!p}$
is the Bousfield localization of
![]() $\mathit{BP}$
with respect to the mod-
$\mathit{BP}$
with respect to the mod-
![]() $p$
Moore spectrum
$p$
Moore spectrum
![]() $M(p)$
, and we get a fiber sequence
$M(p)$
, and we get a fiber sequence

where
 $C_{M(p)}\mathit{BP}$
is rational and concentrated in odd degrees. On the one hand, if
$C_{M(p)}\mathit{BP}$
is rational and concentrated in odd degrees. On the one hand, if
![]() $X$
is a rationally acyclic spectrum, then
$X$
is a rationally acyclic spectrum, then
 $C_{M(p)}\mathit{BP}^{\ast }(X)=0$
. On the other hand, if
$C_{M(p)}\mathit{BP}^{\ast }(X)=0$
. On the other hand, if
![]() $X$
is a space that is rationally equivalent to the sphere, then
$X$
is a space that is rationally equivalent to the sphere, then
 $C_{M(p)}\mathit{BP}^{\ast }(X)\cong C_{M(p)}\mathit{BP}^{\ast }(S^{0})$
is concentrated in odd degrees. Moreover, the connecting homomorphism
$C_{M(p)}\mathit{BP}^{\ast }(X)\cong C_{M(p)}\mathit{BP}^{\ast }(S^{0})$
is concentrated in odd degrees. Moreover, the connecting homomorphism
![]() $\unicode[STIX]{x1D6FF}$
fitting in the commutative diagram
$\unicode[STIX]{x1D6FF}$
fitting in the commutative diagram

is surjective. Therefore, in either case the long exact sequence associated to (3.2) yields isomorphisms

and a short exact sequence

This implies the claim about evenness. To see that
 $\mathit{BP}^{\ast }(X)$
is Landweber flat if and only if
$\mathit{BP}^{\ast }(X)$
is Landweber flat if and only if
 $\mathit{BP}_{p}^{\ast }(X)$
is Landweber flat, note that the finite type condition together with the Atiyah–Hirzebruch spectral sequence show that
$\mathit{BP}_{p}^{\ast }(X)$
is Landweber flat, note that the finite type condition together with the Atiyah–Hirzebruch spectral sequence show that
 $\mathit{BP}^{\ast }(X)$
is finitely generated in each degree. By [Reference BousfieldBou79, Proposition 2.5], we thus get an isomorphism
$\mathit{BP}^{\ast }(X)$
is finitely generated in each degree. By [Reference BousfieldBou79, Proposition 2.5], we thus get an isomorphism

so the claim follows from Proposition 2.4 by using flatness of
![]() $\mathbb{Z}_{p}$
and naturality.◻
$\mathbb{Z}_{p}$
and naturality.◻
In particular, this applies to finite spectra of type at least 1 and classifying spaces of finite groups. It will be used implicitly from now on, so whenever the assumptions are satisfied,
![]() $\mathit{BP}$
refers to the
$\mathit{BP}$
refers to the
![]() $p$
-complete Brown–Peterson spectrum
$p$
-complete Brown–Peterson spectrum
![]() $\mathit{BP}_{\!p}$
. The following theorem was proven for spaces in [Reference Ravenel, Wilson and YagitaRWY98, Theorems 1.8 and 1.9].
$\mathit{BP}_{\!p}$
. The following theorem was proven for spaces in [Reference Ravenel, Wilson and YagitaRWY98, Theorems 1.8 and 1.9].
Theorem 3.9. Let
![]() $X$
be a spectrum. If
$X$
be a spectrum. If
 $K(n)^{\ast }(X)$
is even for infinitely many
$K(n)^{\ast }(X)$
is even for infinitely many
![]() $n$
, then
$n$
, then
 $P(m)^{\ast }(X)$
is even and Landweber flat for all
$P(m)^{\ast }(X)$
is even and Landweber flat for all
![]() $m$
. In particular, (2.1) gives short exact sequences
$m$
. In particular, (2.1) gives short exact sequences

Proof. Let
![]() $I$
be the infinite set of natural numbers
$I$
be the infinite set of natural numbers
![]() $n$
such that
$n$
such that
 $K(n)^{\ast }(X)$
is even and
$K(n)^{\ast }(X)$
is even and
![]() $n\geqslant m$
. By Lemma 2.7, the assumption implies that
$n\geqslant m$
. By Lemma 2.7, the assumption implies that
 $\hat{E}(m,n)^{\ast }(X)$
is even and flat over
$\hat{E}(m,n)^{\ast }(X)$
is even and flat over
 $\hat{E}(m,n)^{\ast }$
. Since the
$\hat{E}(m,n)^{\ast }$
. Since the
![]() $P(m)^{\ast }$
-module
$P(m)^{\ast }$
-module
 $\hat{E}(m,n)^{\ast }$
is Landweber flat, so is
$\hat{E}(m,n)^{\ast }$
is Landweber flat, so is
 $\hat{E}(m,n)^{\ast }(X)$
for all
$\hat{E}(m,n)^{\ast }(X)$
for all
![]() $n\in I$
. It follows from Lemma 2.5 that
$n\in I$
. It follows from Lemma 2.5 that
 $\prod _{n\in I}\hat{E}(m,n)^{\ast }(X)$
is Landweber flat as well. Since Landweber flat modules are clearly closed under retracts, the claim now follows from Corollary 3.4.◻
$\prod _{n\in I}\hat{E}(m,n)^{\ast }(X)$
is Landweber flat as well. Since Landweber flat modules are clearly closed under retracts, the claim now follows from Corollary 3.4.◻
Remark 3.10. More generally, the same proof shows that any spectrum
![]() $X$
with
$X$
with
 $K(n)^{\ast }(X)$
concentrated in degrees divisible by a fixed integer
$K(n)^{\ast }(X)$
concentrated in degrees divisible by a fixed integer
![]() $d$
for infinitely many
$d$
for infinitely many
![]() $n$
has
$n$
has
 $P(m)^{\ast }X$
also concentrated in degrees divisible by
$P(m)^{\ast }X$
also concentrated in degrees divisible by
![]() $d$
for all
$d$
for all
![]() $m$
. Similar observations apply to the next corollary; this should be compared to [Reference MinamiMin02].
$m$
. Similar observations apply to the next corollary; this should be compared to [Reference MinamiMin02].
As an immediate consequence, we recover [Reference Ravenel, Wilson and YagitaRWY98, Theorem 1.2], which complements Theorem 3.9 for spaces. By Example 2.11, this result does not generalize to arbitrary spectra.
Corollary 3.11. If
![]() $X$
is a space with
$X$
is a space with
 $K(n)^{\ast }(X)$
even for infinitely many
$K(n)^{\ast }(X)$
even for infinitely many
![]() $n$
, then
$n$
, then
 $K(m)^{\ast }(X)$
is even for all
$K(m)^{\ast }(X)$
is even for all
![]() $m>0$
.
$m>0$
.
Proof. By Theorem 3.9 with
![]() $m=0$
,
$m=0$
,
 $P(0)^{\ast }(X)$
is even, and hence so is
$P(0)^{\ast }(X)$
is even, and hence so is
 $K(m)^{\ast }(X)$
for all
$K(m)^{\ast }(X)$
for all
![]() $m>0$
by Corollary 2.13.◻
$m>0$
by Corollary 2.13.◻
Example 3.12. The spectrum
![]() $\unicode[STIX]{x1D6F4}H\mathbb{Q}$
has trivial Morava
$\unicode[STIX]{x1D6F4}H\mathbb{Q}$
has trivial Morava
![]() $K$
-theory for all heights
$K$
-theory for all heights
![]() $n>0$
, but
$n>0$
, but
 $K(0)^{1}\unicode[STIX]{x1D6F4}H\mathbb{Q}\neq 0$
. For a more interesting example, let
$K(0)^{1}\unicode[STIX]{x1D6F4}H\mathbb{Q}\neq 0$
. For a more interesting example, let
 $X=K(\mathbb{Z},3)$
; then the rational cohomology
$X=K(\mathbb{Z},3)$
; then the rational cohomology
 $K(0)^{\ast }(X)\cong \mathbb{Q}[x]/x^{2}$
with
$K(0)^{\ast }(X)\cong \mathbb{Q}[x]/x^{2}$
with
![]() $x$
in degree 3, but
$x$
in degree 3, but
 $K(n)^{\ast }(X)$
is even and non-trivial for all
$K(n)^{\ast }(X)$
is even and non-trivial for all
![]() $n\geqslant 2$
by [Reference Ravenel and WilsonRW80]. Therefore, the conclusion of the corollary cannot be extended to
$n\geqslant 2$
by [Reference Ravenel and WilsonRW80]. Therefore, the conclusion of the corollary cannot be extended to
![]() $m=0$
.
$m=0$
.
Corollary 3.13. If
![]() $X$
is a space such that
$X$
is a space such that
 $P(m)^{\ast }(X)$
is even for some
$P(m)^{\ast }(X)$
is even for some
![]() $m\geqslant 0$
, then
$m\geqslant 0$
, then
 $K(n)^{\ast }(X)$
is even for all
$K(n)^{\ast }(X)$
is even for all
![]() $n>0$
.
$n>0$
.
Proof. If
 $P(m)^{\ast }(X)$
is even, then it is also Landweber flat as the connecting homomorphism in (2.1) must be zero for degree reasons. Therefore, Corollary 2.13 shows that
$P(m)^{\ast }(X)$
is even, then it is also Landweber flat as the connecting homomorphism in (2.1) must be zero for degree reasons. Therefore, Corollary 2.13 shows that
 $K(n)^{\ast }(X)$
is even for all
$K(n)^{\ast }(X)$
is even for all
 $n\geqslant m+1$
, so Corollary 3.11 applies.◻
$n\geqslant m+1$
, so Corollary 3.11 applies.◻
We will need the following lemma about maps of complete modules; a proof in the case of
![]() $m=n$
can be found in Hovey’s unpublished notes [Reference HoveyHov04b] or [Reference Barthel and FranklandBF15], and it requires only minor modifications for the general case.
$m=n$
can be found in Hovey’s unpublished notes [Reference HoveyHov04b] or [Reference Barthel and FranklandBF15], and it requires only minor modifications for the general case.
Lemma 3.14. Suppose that
![]() $M$
and
$M$
and
![]() $N$
are flat
$N$
are flat
 $\hat{E}(m,n)^{\ast }$
-modules which are complete with respect to the maximal ideal
$\hat{E}(m,n)^{\ast }$
-modules which are complete with respect to the maximal ideal
![]() $I_{m,n}$
of
$I_{m,n}$
of
 $\hat{E}(m,n)^{\ast }$
. A map
$\hat{E}(m,n)^{\ast }$
. A map
 $f:M\overset{}{\longrightarrow }N$
is injective or surjective if and only if
$f:M\overset{}{\longrightarrow }N$
is injective or surjective if and only if
 $f\otimes _{\hat{E}(m,n)^{\ast }}K(n)^{\ast }$
is injective or surjective, respectively.
$f\otimes _{\hat{E}(m,n)^{\ast }}K(n)^{\ast }$
is injective or surjective, respectively.
The next theorem generalizes [Reference Ravenel, Wilson and YagitaRWY98, Theorems 1.17 and 1.18] to all spectra.
Theorem 3.15. Let
 $f:X\overset{}{\longrightarrow }Y$
be a map of spectra such that both
$f:X\overset{}{\longrightarrow }Y$
be a map of spectra such that both
 $K(n)^{\ast }(X)$
and
$K(n)^{\ast }(X)$
and
 $K(n)^{\ast }(Y)$
are even for
$K(n)^{\ast }(Y)$
are even for
![]() $n\in I$
with
$n\in I$
with
![]() $I\subset \mathbb{N}$
infinite.
$I\subset \mathbb{N}$
infinite.
-
(i) If
 $f^{\ast }:K(n)^{\ast }(Y)\overset{}{\longrightarrow }K(n)^{\ast }(X)$
is injective (surjective) for all
$f^{\ast }:K(n)^{\ast }(Y)\overset{}{\longrightarrow }K(n)^{\ast }(X)$
is injective (surjective) for all
 $n\in I$
, then so is for all
$n\in I$
, then so is for all $$\begin{eqnarray}f^{\ast }:P(m)^{\ast }(Y)\overset{}{\longrightarrow }P(m)^{\ast }(X)\end{eqnarray}$$
$$\begin{eqnarray}f^{\ast }:P(m)^{\ast }(Y)\overset{}{\longrightarrow }P(m)^{\ast }(X)\end{eqnarray}$$
 $m$
.
$m$
.
-
(ii) Suppose that
 $g:Y\overset{}{\longrightarrow }Z$
is another map with
$g:Y\overset{}{\longrightarrow }Z$
is another map with
 $K(n)^{\ast }(Z)$
even for all
$K(n)^{\ast }(Z)$
even for all
 $n\in I$
and such that
$n\in I$
and such that
 $g\circ f\simeq 0$
. Ifis an exact sequence for all
$g\circ f\simeq 0$
. Ifis an exact sequence for all
 $n\in I$
, then so isfor all
$n\in I$
, then so isfor all
 $m\geqslant 0$
.
$m\geqslant 0$
.
Proof. Fix some integer
![]() $m\geqslant 0$
. We will prove the surjectivity statement; the argument for injectivity is analogous. By assumption and Lemma 2.7, there is a commutative diagram
$m\geqslant 0$
. We will prove the surjectivity statement; the argument for injectivity is analogous. By assumption and Lemma 2.7, there is a commutative diagram

Since
 $K(n)^{\ast }f$
is surjective, Lemma 3.14 implies that
$K(n)^{\ast }f$
is surjective, Lemma 3.14 implies that
 $\hat{E}(m,n)^{\ast }f$
is surjective for
$\hat{E}(m,n)^{\ast }f$
is surjective for
![]() $n\in I$
as well. Products in the category of modules are exact, so the bottom map in the commutative square is also surjective:
$n\in I$
as well. Products in the category of modules are exact, so the bottom map in the commutative square is also surjective:

Retracts of surjective maps are surjective, hence Corollary 3.4 yields the claim.
Assertion (ii) follows formally from (i) as in the proof of [Reference Ravenel, Wilson and YagitaRWY98, Theorem 1.18]. ◻
3.3 Applications to the cohomology of free commutative algebras
In [Reference KashiwabaraKas98, Reference KashiwabaraKas01], Kashiwabara studied the question of when and how
 $\mathit{BP}_{\!p}^{\ast }(\unicode[STIX]{x1D6FA}^{\infty }X)$
is determined by
$\mathit{BP}_{\!p}^{\ast }(\unicode[STIX]{x1D6FA}^{\infty }X)$
is determined by
 $\mathit{BP}_{\!p}^{\ast }(X)$
for
$\mathit{BP}_{\!p}^{\ast }(X)$
for
![]() $X$
a space or spectrum. In particular, he considered two variants
$X$
a space or spectrum. In particular, he considered two variants
![]() ${\mathcal{K}}_{0\mathit{BP}}^{\prime }$
and
${\mathcal{K}}_{0\mathit{BP}}^{\prime }$
and
![]() ${\mathcal{M}}_{\mathit{BP}}^{\prime }$
of the category of augmented unstable
${\mathcal{M}}_{\mathit{BP}}^{\prime }$
of the category of augmented unstable
![]() $\mathit{BP}$
-cohomology algebras and the category of stable
$\mathit{BP}$
-cohomology algebras and the category of stable
![]() $\mathit{BP}_{\!p}$
-cohomology algebras, respectively, and showed that there is a left adjoint
$\mathit{BP}_{\!p}$
-cohomology algebras, respectively, and showed that there is a left adjoint

to the augmention ideal functor
![]() ${\mathcal{I}}$
. This adjunction should be thought of as being analogous to the adjunction
${\mathcal{I}}$
. This adjunction should be thought of as being analogous to the adjunction
 $(\unicode[STIX]{x1D6F4}^{\infty }\dashv \unicode[STIX]{x1D6FA}^{\infty })$
between spaces and spectra. Kashiwabara then showed in [Reference KashiwabaraKas01, Theorem 0.11] that if
$(\unicode[STIX]{x1D6F4}^{\infty }\dashv \unicode[STIX]{x1D6FA}^{\infty })$
between spaces and spectra. Kashiwabara then showed in [Reference KashiwabaraKas01, Theorem 0.11] that if
![]() $X$
is a space,
$X$
is a space,
 $\mathit{BP}_{\!p}^{\ast }(QX)$
inherits Landweber flatness from
$\mathit{BP}_{\!p}^{\ast }(QX)$
inherits Landweber flatness from
 $\mathit{BP}_{\!p}^{\ast }(X)$
. Furthermore, if
$\mathit{BP}_{\!p}^{\ast }(X)$
. Furthermore, if
![]() $X$
is a connected space satisfying certain conditions, there is a natural isomorphism
$X$
is a connected space satisfying certain conditions, there is a natural isomorphism

see [Reference KashiwabaraKas01, Theorem 0.12].
In this section, we will prove some extensions and variants of Kashiwabara’s results. To this end, recall that if
![]() $X$
is a connected space, the Snaith splitting provides an equivalence
$X$
is a connected space, the Snaith splitting provides an equivalence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\infty }QX\simeq \mathbb{P}\unicode[STIX]{x1D6F4}_{+}^{\infty }X,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\infty }QX\simeq \mathbb{P}\unicode[STIX]{x1D6F4}_{+}^{\infty }X,\end{eqnarray}$$
where
![]() $\mathbb{P}Y$
denotes the free commutative algebra on a spectrum
$\mathbb{P}Y$
denotes the free commutative algebra on a spectrum
![]() $Y$
. Thus our results, which are formulated in terms of
$Y$
. Thus our results, which are formulated in terms of
![]() $\mathbb{P}$
, are readily translated and compared to Kashiwabara’s.
$\mathbb{P}$
, are readily translated and compared to Kashiwabara’s.
Fix a height
![]() $n$
and recall the completed algebraic approximation functor of [Reference RezkRez09, Reference Barthel and FranklandBF15]: this is an endofunctor
$n$
and recall the completed algebraic approximation functor of [Reference RezkRez09, Reference Barthel and FranklandBF15]: this is an endofunctor
![]() $\mathbb{T}^{E_{n}}$
on the category of complete
$\mathbb{T}^{E_{n}}$
on the category of complete
![]() $E_{n}^{\ast }$
-modules together with a natural comparison map
$E_{n}^{\ast }$
-modules together with a natural comparison map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{n}(M):\mathbb{T}^{E_{n}}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}M\overset{}{\longrightarrow }\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}^{E_{n}}M,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{n}(M):\mathbb{T}^{E_{n}}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}M\overset{}{\longrightarrow }\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}^{E_{n}}M,\end{eqnarray}$$
where
![]() $M$
is an
$M$
is an
![]() $E_{n}$
-module and
$E_{n}$
-module and
![]() $\mathbb{P}^{E_{n}}$
denotes the free commutative
$\mathbb{P}^{E_{n}}$
denotes the free commutative
![]() $E_{n}$
-algebra functor. By [Reference RezkRez09, Proposition 4.9],
$E_{n}$
-algebra functor. By [Reference RezkRez09, Proposition 4.9],
![]() $\unicode[STIX]{x1D6FC}_{n}(M)$
is an isomorphism whenever
$\unicode[STIX]{x1D6FC}_{n}(M)$
is an isomorphism whenever
![]() $M^{\ast }$
is flat over
$M^{\ast }$
is flat over
![]() $E_{n}^{\ast }$
. By [Reference Barthel and FranklandBF15, Propositions 3.9 and A.15],
$E_{n}^{\ast }$
. By [Reference Barthel and FranklandBF15, Propositions 3.9 and A.15],
![]() $\mathbb{T}^{E_{n}}$
preserves the category of flat
$\mathbb{T}^{E_{n}}$
preserves the category of flat
![]() $E_{n}^{\ast }$
-modules, and it also preserves evenness; see [Reference RezkRez12, 3.2(7)]. Moreover, there is natural decomposition of functors
$E_{n}^{\ast }$
-modules, and it also preserves evenness; see [Reference RezkRez12, 3.2(7)]. Moreover, there is natural decomposition of functors
 $$\begin{eqnarray}\mathbb{T}^{E_{n}}\cong \mathop{\vee }_{d\geqslant 0}\mathbb{T}_{d}^{E_{n}},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{T}^{E_{n}}\cong \mathop{\vee }_{d\geqslant 0}\mathbb{T}_{d}^{E_{n}},\end{eqnarray}$$
corresponding to the analogous decomposition of
![]() $\mathbb{P}^{E_{n}}$
.
$\mathbb{P}^{E_{n}}$
.
We are now in a position to prove a generalization of [Reference KashiwabaraKas01, Theorem 0.11] to spectra. Note, however, that Kashiwabara assumes that
 $\mathit{BP}_{\!p}^{\ast }(X)$
is Landweber flat (without evenness) to deduce that
$\mathit{BP}_{\!p}^{\ast }(X)$
is Landweber flat (without evenness) to deduce that
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is also Landweber flat, so our result is only a partial generalization.
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is also Landweber flat, so our result is only a partial generalization.
Proposition 3.16. If
![]() $X$
is a spectrum with even Morava
$X$
is a spectrum with even Morava
![]() $K$
-theory for infinitely many
$K$
-theory for infinitely many
![]() $n$
, then
$n$
, then
 $\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is even and Landweber flat.
$\mathit{BP}_{\!p}^{\ast }(\mathbb{P}X)$
is even and Landweber flat.
Proof. Let
![]() $n>0$
be such that
$n>0$
be such that
 $K(n)_{\ast }(X)$
is even. Recall that the completed
$K(n)_{\ast }(X)$
is even. Recall that the completed
![]() $E$
-homology of
$E$
-homology of
![]() $X$
is defined as
$X$
is defined as
 $E_{n,\ast }^{\vee }(X)=\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge X)$
. The assumption on
$E_{n,\ast }^{\vee }(X)=\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge X)$
. The assumption on
![]() $X$
implies that
$X$
implies that
 $E_{n,\ast }^{\vee }(X)$
is flat and even by the homological version of Lemma 2.7 (see [Reference Hovey and StricklandHS99b, Proposition 8.4(f)]), and so the previous discussion gives an isomorphism
$E_{n,\ast }^{\vee }(X)$
is flat and even by the homological version of Lemma 2.7 (see [Reference Hovey and StricklandHS99b, Proposition 8.4(f)]), and so the previous discussion gives an isomorphism

of flat and evenly concentrated
![]() $E_{n}^{\ast }$
-modules, using the equivalence
$E_{n}^{\ast }$
-modules, using the equivalence
 $E_{n}\wedge \mathbb{P}X\simeq \mathbb{P}^{E_{n}}(E_{n}\wedge X)$
. It follows from Lemma 2.7 that
$E_{n}\wedge \mathbb{P}X\simeq \mathbb{P}^{E_{n}}(E_{n}\wedge X)$
. It follows from Lemma 2.7 that
 $K(n)^{\ast }(\mathbb{P}X)$
is even as well, so Theorem 3.9 finishes the proof.◻
$K(n)^{\ast }(\mathbb{P}X)$
is even as well, so Theorem 3.9 finishes the proof.◻
Denote by
 $$\begin{eqnarray}\unicode[STIX]{x1D716}:\underset{n>0}{\prod }E_{n}\rightarrow \underset{n>0}{\prod }E_{n}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}:\underset{n>0}{\prod }E_{n}\rightarrow \underset{n>0}{\prod }E_{n}\end{eqnarray}$$
the idempotent given by Corollary 3.4; note that
![]() $\unicode[STIX]{x1D716}$
is not necessarily unique, but we will fix a particular one throughout this section.
$\unicode[STIX]{x1D716}$
is not necessarily unique, but we will fix a particular one throughout this section.
Definition 3.17. The
![]() $\mathit{BP}$
-based algebraic approximation functor
$\mathit{BP}$
-based algebraic approximation functor
![]() $\mathbb{T}_{d}^{\mathit{BP}}$
of degree
$\mathbb{T}_{d}^{\mathit{BP}}$
of degree
![]() $d\geqslant 0$
is constructed as the functor
$d\geqslant 0$
is constructed as the functor
 $$\begin{eqnarray}\mathbb{T}_{d}^{\mathit{BP}}:=\unicode[STIX]{x1D716}\mathop{\prod }_{n>0}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }\,\,\hat{\otimes }_{\mathit{BP}_{\!p}^{\ast }}\,-):\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}\longrightarrow \text{Mod}_{\mathit{BP}_{\!p}^{\ast }}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{T}_{d}^{\mathit{BP}}:=\unicode[STIX]{x1D716}\mathop{\prod }_{n>0}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }\,\,\hat{\otimes }_{\mathit{BP}_{\!p}^{\ast }}\,-):\text{Mod}_{\mathit{BP}_{\!p}^{\ast }}^{c}\longrightarrow \text{Mod}_{\mathit{BP}_{\!p}^{\ast }}\end{eqnarray}$$
on the category of
![]() $\mathit{BP}_{\!p}^{\ast }$
-modules equipped with a complete topology as in Definition 2.8. We then define the total algebraic approximation functor as
$\mathit{BP}_{\!p}^{\ast }$
-modules equipped with a complete topology as in Definition 2.8. We then define the total algebraic approximation functor as
 $\mathbb{T}^{\mathit{BP}}=\prod _{d\geqslant 0}\mathbb{T}_{d}^{\mathit{BP}}$
.
$\mathbb{T}^{\mathit{BP}}=\prod _{d\geqslant 0}\mathbb{T}_{d}^{\mathit{BP}}$
.
This allows us to prove an analogue of Kashiwabara’s result [Reference KashiwabaraKas01, Theorem 0.12] exhibiting a class of spaces
![]() $X$
for which the
$X$
for which the
![]() $\mathit{BP}_{\!p}^{\ast }$
-cohomology of
$\mathit{BP}_{\!p}^{\ast }$
-cohomology of
![]() $\mathbb{P}X$
is functorially determined by the topological module
$\mathbb{P}X$
is functorially determined by the topological module
 $\mathit{BP}_{\!p}^{\ast }(X)$
.
$\mathit{BP}_{\!p}^{\ast }(X)$
.
Theorem 3.18. Let
![]() $X$
be a space with
$X$
be a space with
 $K(n)_{\ast }(X)$
even and degreewise finite for infinitely many
$K(n)_{\ast }(X)$
even and degreewise finite for infinitely many
![]() $n$
; then there exists a natural isomorphism
$n$
; then there exists a natural isomorphism

of
![]() $\mathit{BP}_{\!p}^{\ast }$
-modules.
$\mathit{BP}_{\!p}^{\ast }$
-modules.
Proof. Let
![]() $S$
be the set of natural numbers
$S$
be the set of natural numbers
![]() $n$
such that
$n$
such that
 $K(n)_{\ast }(X)$
is even and degreewise finite. The free commutative algebra functor decomposes into its degree-
$K(n)_{\ast }(X)$
is even and degreewise finite. The free commutative algebra functor decomposes into its degree-
![]() $d$
constituents,
$d$
constituents,
 $$\begin{eqnarray}\mathbb{P}(-)\simeq \mathop{\vee }_{d\geqslant 0}\mathbb{P}_{d}(-)\simeq \mathop{\vee }_{d\geqslant 0}(-)_{h\unicode[STIX]{x1D6F4}_{d}}^{\wedge d},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(-)\simeq \mathop{\vee }_{d\geqslant 0}\mathbb{P}_{d}(-)\simeq \mathop{\vee }_{d\geqslant 0}(-)_{h\unicode[STIX]{x1D6F4}_{d}}^{\wedge d},\end{eqnarray}$$
so we obtain a natural commutative diagram

for any spectrum
![]() $X$
. Since
$X$
. Since
![]() $\mathbb{T}^{\mathit{BP}}$
is compatible with this decomposition, we can reduce to a fixed degree
$\mathbb{T}^{\mathit{BP}}$
is compatible with this decomposition, we can reduce to a fixed degree
![]() $d\geqslant 0$
.
$d\geqslant 0$
.
There are natural isomorphisms
 $$\begin{eqnarray}\displaystyle \mathbb{T}_{d}^{\mathit{BP}}\mathit{BP}_{\!p}^{\ast }(X) & = & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }\,\hat{\otimes }_{\mathit{BP}_{\!p}^{\ast }}\mathit{BP}_{\!p}^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }(X))\quad \text{by Proposition 2.10}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}\unicode[STIX]{x1D70B}_{\ast }E_{n}^{X}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}\quad \text{via}~\mathop{\prod }_{n\in S}\unicode[STIX]{x1D6FC}_{n}(E_{n}^{X}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{T}_{d}^{\mathit{BP}}\mathit{BP}_{\!p}^{\ast }(X) & = & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }\,\hat{\otimes }_{\mathit{BP}_{\!p}^{\ast }}\mathit{BP}_{\!p}^{\ast }(X))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}(E_{n}^{\ast }(X))\quad \text{by Proposition 2.10}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\mathbb{T}_{d}^{E_{n}}\unicode[STIX]{x1D70B}_{\ast }E_{n}^{X}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}\quad \text{via}~\mathop{\prod }_{n\in S}\unicode[STIX]{x1D6FC}_{n}(E_{n}^{X}),\nonumber\end{eqnarray}$$
so it is enough to understand
 $\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}$
in terms of
$\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}$
in terms of
 $E_{n}^{\ast }(\mathbb{P}_{d}X)$
. By [Reference Hovey and StricklandHS99b, Theorem 8.6], a spectrum
$E_{n}^{\ast }(\mathbb{P}_{d}X)$
. By [Reference Hovey and StricklandHS99b, Theorem 8.6], a spectrum
![]() $X$
has degreewise finite
$X$
has degreewise finite
 $K(n)_{\ast }(X)$
if and only if
$K(n)_{\ast }(X)$
if and only if
![]() $X$
is dualizable in the
$X$
is dualizable in the
![]() $K(n)$
-local category; we write
$K(n)$
-local category; we write
![]() $D_{K(n)}$
for
$D_{K(n)}$
for
![]() $K(n)$
-local duality. Therefore, we obtain
$K(n)$
-local duality. Therefore, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X} & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}(E_{n}\wedge D_{K(n)}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge \mathbb{P}_{d}D_{K(n)}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge D_{K(n)}\mathbb{P}_{d}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}E_{n}^{\mathbb{P}_{d}X}\nonumber\\ \displaystyle & \cong & \displaystyle E_{n}^{\ast }(\mathbb{P}_{d}X).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X} & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}(E_{n}\wedge D_{K(n)}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge \mathbb{P}_{d}D_{K(n)}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}(E_{n}\wedge D_{K(n)}\mathbb{P}_{d}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{\ast }L_{K(n)}E_{n}^{\mathbb{P}_{d}X}\nonumber\\ \displaystyle & \cong & \displaystyle E_{n}^{\ast }(\mathbb{P}_{d}X).\nonumber\end{eqnarray}$$
Here, the third isomorphism uses the fact [Reference Greenlees and SadofskyGS96] that homotopy orbits agree with homotopy fixed points with respect to a finite group
![]() $G$
in the
$G$
in the
![]() $K(n)$
-local category, i.e.
$K(n)$
-local category, i.e.
 $Y_{hG}\overset{\simeq }{\longrightarrow }Y^{hG}$
$Y_{hG}\overset{\simeq }{\longrightarrow }Y^{hG}$
![]() $K(n)$
-locally. Moreover, the fourth isomorphism can be understood as follows: because
$K(n)$
-locally. Moreover, the fourth isomorphism can be understood as follows: because
![]() $X$
is dualizable,
$X$
is dualizable,
 $K(n)_{\ast }(X)$
is degreewise finite, and hence so is
$K(n)_{\ast }(X)$
is degreewise finite, and hence so is
 $K(n)_{\ast }(\mathbb{P}_{d}X)$
as
$K(n)_{\ast }(\mathbb{P}_{d}X)$
as
 $K(n)_{\ast }(B\unicode[STIX]{x1D6F4}_{d})$
is degreewise finite; using [Reference Hovey and StricklandHS99b, Theorem 8.6] again, we see that
$K(n)_{\ast }(B\unicode[STIX]{x1D6F4}_{d})$
is degreewise finite; using [Reference Hovey and StricklandHS99b, Theorem 8.6] again, we see that
![]() $\mathbb{P}_{d}X$
is also
$\mathbb{P}_{d}X$
is also
![]() $K(n)$
-locally dualizable, giving the fourth isomorphism above.
$K(n)$
-locally dualizable, giving the fourth isomorphism above.
Putting the pieces together, we obtain
 $$\begin{eqnarray}\displaystyle \mathbb{T}_{d}^{\mathit{BP}}\mathit{BP}_{\!p}^{\ast }(X) & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}E_{n}^{\ast }(\mathbb{P}_{d}X)\nonumber\\ \displaystyle & \cong & \displaystyle \mathit{BP}_{\!p}^{\ast }(\mathbb{P}_{d}X),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{T}_{d}^{\mathit{BP}}\mathit{BP}_{\!p}^{\ast }(X) & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}\unicode[STIX]{x1D70B}_{\ast }L_{K(n)}\mathbb{P}_{d}^{E_{n}}E_{n}^{X}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D716}\mathop{\prod }_{n\in S}E_{n}^{\ast }(\mathbb{P}_{d}X)\nonumber\\ \displaystyle & \cong & \displaystyle \mathit{BP}_{\!p}^{\ast }(\mathbb{P}_{d}X),\nonumber\end{eqnarray}$$
hence the claim. ◻
Note that having degreewise finite Morava
![]() $K$
-theory is less restrictive than one might think. For example, all finite CW complexes satisfy this condition. For a different class of examples that includes classifying spaces of finite groups and Eilenberg–MacLane spaces
$K$
-theory is less restrictive than one might think. For example, all finite CW complexes satisfy this condition. For a different class of examples that includes classifying spaces of finite groups and Eilenberg–MacLane spaces
 $K(\mathbb{Z}/p,l)$
, recall that a
$K(\mathbb{Z}/p,l)$
, recall that a
![]() $\unicode[STIX]{x1D70B}$
-finite space is a space with only finitely many non-zero homotopy groups which are all finite. By [Reference Hovey and StricklandHS99b, Corollary 8.8],
$\unicode[STIX]{x1D70B}$
-finite space is a space with only finitely many non-zero homotopy groups which are all finite. By [Reference Hovey and StricklandHS99b, Corollary 8.8],
![]() $\unicode[STIX]{x1D70B}$
-finite spaces are
$\unicode[STIX]{x1D70B}$
-finite spaces are
![]() $K(n)$
-locally dualizable and hence have degreewise finite Morava
$K(n)$
-locally dualizable and hence have degreewise finite Morava
![]() $K$
-theory as well. Finite CW complexes with even cells and many
$K$
-theory as well. Finite CW complexes with even cells and many
![]() $\unicode[STIX]{x1D70B}$
-finite spaces satisfy the evenness condition as well.
$\unicode[STIX]{x1D70B}$
-finite spaces satisfy the evenness condition as well.
We should, however, mention that we do not know the precise relation between our condition and Kashiwabara’s assumption of well-generated
![]() $\mathit{BP}_{\!p}$
-cohomology. In fact, Kashiwabara’s result is somewhat sharper, in that his functor
$\mathit{BP}_{\!p}$
-cohomology. In fact, Kashiwabara’s result is somewhat sharper, in that his functor
![]() ${\mathcal{D}}$
is computable in an entirely algebraic fashion, as demonstrated in [Reference KashiwabaraKas01].
${\mathcal{D}}$
is computable in an entirely algebraic fashion, as demonstrated in [Reference KashiwabaraKas01].
Remark 3.19. The hypotheses in Theorem 3.18 can be weakened if one is willing to work with a version of
![]() $\mathbb{T}^{\mathit{BP}}$
that incorporates a continuous dual. To be more precise, Hovey [Reference HoveyHov04a, Theorem 5.1] showed that for spectra
$\mathbb{T}^{\mathit{BP}}$
that incorporates a continuous dual. To be more precise, Hovey [Reference HoveyHov04a, Theorem 5.1] showed that for spectra
![]() $X$
with flat completed
$X$
with flat completed
![]() $E_{n}$
-homology
$E_{n}$
-homology
 $E_{\ast ,n}^{\vee }(X)$
, there is a natural isomorphism
$E_{\ast ,n}^{\vee }(X)$
, there is a natural isomorphism

Passing from cohomology to homology is more subtle, however, and requires that we take into account the topology on
![]() $E_{n}^{\ast }(X)$
coming from the skeletal filtration on a CW spectrum
$E_{n}^{\ast }(X)$
coming from the skeletal filtration on a CW spectrum
![]() $X$
. In [Reference StricklandStr, § 7], Strickland proved that
$X$
. In [Reference StricklandStr, § 7], Strickland proved that

when
![]() $X$
is a CW spectrum with free
$X$
is a CW spectrum with free
![]() $E_{\ast }(X)$
, where
$E_{\ast }(X)$
, where
![]() $\text{Hom}^{c}$
denotes the module of continuous homomorphisms. Together, these two isomorphisms can be used to translate the statement into one about completed homology, to which the algebraic approximation functor
$\text{Hom}^{c}$
denotes the module of continuous homomorphisms. Together, these two isomorphisms can be used to translate the statement into one about completed homology, to which the algebraic approximation functor
![]() $\mathbb{T}^{E_{n}}$
applies directly.
$\mathbb{T}^{E_{n}}$
applies directly.
We end this section by giving a different criterion for when
 $P(m)^{\ast }(X)$
is even and Landweber flat. Let
$P(m)^{\ast }(X)$
is even and Landweber flat. Let
 $\unicode[STIX]{x1D6F7}_{n}:\text{Top}\overset{}{\longrightarrow }\text{Sp}$
be the Bousfield–Kuhn functor, which was constructed in [Reference BousfieldBou87] for
$\unicode[STIX]{x1D6F7}_{n}:\text{Top}\overset{}{\longrightarrow }\text{Sp}$
be the Bousfield–Kuhn functor, which was constructed in [Reference BousfieldBou87] for
![]() $n=1$
and in [Reference KuhnKuh89] for arbitrary
$n=1$
and in [Reference KuhnKuh89] for arbitrary
![]() $n$
by using the periodicity theorem [Reference Devinatz, Hopkins and SmithDHS88, Reference Hopkins and SmithHS98]. This functor gives a factorization
$n$
by using the periodicity theorem [Reference Devinatz, Hopkins and SmithDHS88, Reference Hopkins and SmithHS98]. This functor gives a factorization
 $$\begin{eqnarray}L_{K(n)}X\simeq \unicode[STIX]{x1D6F7}_{n}\unicode[STIX]{x1D6FA}^{\infty }X\end{eqnarray}$$
$$\begin{eqnarray}L_{K(n)}X\simeq \unicode[STIX]{x1D6F7}_{n}\unicode[STIX]{x1D6FA}^{\infty }X\end{eqnarray}$$
for any spectrum
![]() $X$
; in fact, this can be improved so as to factor the telescopic localization in an analogous way, but we will not need this here. For
$X$
; in fact, this can be improved so as to factor the telescopic localization in an analogous way, but we will not need this here. For
![]() $X\in \text{Sp}$
, Kuhn [Reference KuhnKuh06] used
$X\in \text{Sp}$
, Kuhn [Reference KuhnKuh06] used
![]() $\unicode[STIX]{x1D6F7}_{n}$
to produce a (weak) map
$\unicode[STIX]{x1D6F7}_{n}$
to produce a (weak) map
 $$\begin{eqnarray}s_{n}(X):L_{K(n)}\mathbb{P}X\overset{}{\longrightarrow }L_{K(n)}\unicode[STIX]{x1D6F4}_{+}^{\infty }\unicode[STIX]{x1D6FA}^{\infty }X\end{eqnarray}$$
$$\begin{eqnarray}s_{n}(X):L_{K(n)}\mathbb{P}X\overset{}{\longrightarrow }L_{K(n)}\unicode[STIX]{x1D6F4}_{+}^{\infty }\unicode[STIX]{x1D6FA}^{\infty }X\end{eqnarray}$$
which induces a natural monomorphism
 $$\begin{eqnarray}s_{n}(X)_{\ast }:K(n)_{\ast }(\mathbb{P}X)\overset{}{\longrightarrow }K(n)_{\ast }(\unicode[STIX]{x1D6FA}^{\infty }X).\end{eqnarray}$$
$$\begin{eqnarray}s_{n}(X)_{\ast }:K(n)_{\ast }(\mathbb{P}X)\overset{}{\longrightarrow }K(n)_{\ast }(\unicode[STIX]{x1D6FA}^{\infty }X).\end{eqnarray}$$
As an easy consequence, we get the following result.
Proposition 3.20. Let
![]() $X$
be a spectrum such that
$X$
be a spectrum such that
 $K(n)_{\ast }\unicode[STIX]{x1D6FA}^{\infty }X$
is even for infinitely many
$K(n)_{\ast }\unicode[STIX]{x1D6FA}^{\infty }X$
is even for infinitely many
![]() $n$
; then
$n$
; then
 $P(m)^{\ast }(\mathbb{P}X)$
is even and Landweber flat for all
$P(m)^{\ast }(\mathbb{P}X)$
is even and Landweber flat for all
![]() $m$
.
$m$
.
Proof. By assumption, Kuhn’s map
![]() $s_{n}(X)_{\ast }$
shows that
$s_{n}(X)_{\ast }$
shows that
 $K(n)_{\ast }(\mathbb{P}X)$
is even, so Theorem 3.9 applies.◻
$K(n)_{\ast }(\mathbb{P}X)$
is even, so Theorem 3.9 applies.◻
3.4 Equivalent characterizations of good groups
Now let
![]() $G$
be a finite group. For the purposes of this paper, a group
$G$
be a finite group. For the purposes of this paper, a group
![]() $G$
is said to be good if the Morava
$G$
is said to be good if the Morava
![]() $K$
-theories
$K$
-theories
 $K(n)^{\ast }(BG)$
are even for all
$K(n)^{\ast }(BG)$
are even for all
![]() $n\geqslant 0$
. Note that this notion of good is a priori weaker than the one given in [Reference Hopkins, Kuhn and RavenelHKR00], but is conjectured to be equivalent. The following definition first appeared in [Reference Schuster and YagitaSY01] for
$n\geqslant 0$
. Note that this notion of good is a priori weaker than the one given in [Reference Hopkins, Kuhn and RavenelHKR00], but is conjectured to be equivalent. The following definition first appeared in [Reference Schuster and YagitaSY01] for
![]() $m=0$
.
$m=0$
.
Definition 3.21. A finite group
![]() $G$
is said to be
$G$
is said to be
![]() $P(m)$
-good if the
$P(m)$
-good if the
![]() $P(m)$
-cohomology of its classifying space
$P(m)$
-cohomology of its classifying space
![]() $BG$
is concentrated in even degrees and Landweber flat.
$BG$
is concentrated in even degrees and Landweber flat.
Note that it follows from Lemma 3.8 that a group is
![]() $P(0)$
-good if and only if
$P(0)$
-good if and only if
 $\mathit{BP}^{\ast }(BG)$
is even and Landweber flat. We now see that the various notions of good groups coincide, thereby revealing the global nature of goodness for finite groups.
$\mathit{BP}^{\ast }(BG)$
is even and Landweber flat. We now see that the various notions of good groups coincide, thereby revealing the global nature of goodness for finite groups.
Proposition 3.22. For a finite group
![]() $G$
, the following conditions are equivalent:
$G$
, the following conditions are equivalent:
-
(i)
 $G$
is good;
$G$
is good; -
(ii)
 $K(n)^{\ast }(BG)$
is even for infinitely many
$K(n)^{\ast }(BG)$
is even for infinitely many
 $n\geqslant 0$
;
$n\geqslant 0$
; -
(iii)
 $G$
is
$G$
is
 $\mathit{BP}_{\!p}$
-good;
$\mathit{BP}_{\!p}$
-good; -
(iv)
 $G$
is
$G$
is
 $P(m)$
-good for some
$P(m)$
-good for some
 $m\geqslant 0$
.
$m\geqslant 0$
.
Proof. The implications
 $(1)\;\Longrightarrow \;(2)$
and
$(1)\;\Longrightarrow \;(2)$
and
 $(3)\;\Longrightarrow \;(4)$
are trivial. Theorem 3.9 gives
$(3)\;\Longrightarrow \;(4)$
are trivial. Theorem 3.9 gives
 $(2)\;\Longrightarrow \;(3)$
, while
$(2)\;\Longrightarrow \;(3)$
, while
 $(4)\;\Longrightarrow \;(1)$
follows from Corollary 3.13.◻
$(4)\;\Longrightarrow \;(1)$
follows from Corollary 3.13.◻
This result generalizes work of Kono and Yagita in [Reference Kono and YagitaKY93] for finite groups.
4 Bounded torsion results for the Morava
 $E$
-cohomology of finite groups
$E$
-cohomology of finite groups
In this section we study the rationalization of the
![]() $\mathit{BP}$
-cohomology of certain finite groups by working with the rationalization of the split inclusion of Corollary 3.4:
$\mathit{BP}$
-cohomology of certain finite groups by working with the rationalization of the split inclusion of Corollary 3.4:
 $$\begin{eqnarray}\mathbb{Q}\otimes \mathit{BP}_{\!p}^{\ast }(X)\overset{}{\longrightarrow }\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }(X).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes \mathit{BP}_{\!p}^{\ast }(X)\overset{}{\longrightarrow }\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }(X).\end{eqnarray}$$
There is a close analogy to number theory. The right-hand side is a kind of
![]() $p$
-local adeles in the stable homotopy category. Just as in number theory, we use these
$p$
-local adeles in the stable homotopy category. Just as in number theory, we use these
![]() $p$
-local adeles to study more global phenomena (the left-hand side). The purpose of this section is to produce a factorization of
$p$
-local adeles to study more global phenomena (the left-hand side). The purpose of this section is to produce a factorization of
 $\mathbb{Q}\otimes \mathit{BP}_{\!p}^{\ast }(X)$
when
$\mathbb{Q}\otimes \mathit{BP}_{\!p}^{\ast }(X)$
when
 $X=BA$
or
$X=BA$
or
 $X=B\unicode[STIX]{x1D6F4}_{m}$
by lifting a factorization of
$X=B\unicode[STIX]{x1D6F4}_{m}$
by lifting a factorization of
 $\mathbb{Q}\otimes \prod _{n}E_{n}^{\ast }(X)$
. For instance, in the case where
$\mathbb{Q}\otimes \prod _{n}E_{n}^{\ast }(X)$
. For instance, in the case where
 $X=BA$
, we factor
$X=BA$
, we factor
 $\mathbb{Q}\otimes \prod _{n}E_{n}^{\ast }(BA)$
by proving that the cokernel of the canonical map
$\mathbb{Q}\otimes \prod _{n}E_{n}^{\ast }(BA)$
by proving that the cokernel of the canonical map
 $$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
has bounded torsion, where
![]() $I$
is the image of a transfer map. In this section, we will always work with the
$I$
is the image of a transfer map. In this section, we will always work with the
![]() $p$
-complete version of the Brown–Peterson spectrum; for simplicity we shall write
$p$
-complete version of the Brown–Peterson spectrum; for simplicity we shall write
 $\mathit{BP}=\mathit{BP}_{\!p}$
for this spectrum.
$\mathit{BP}=\mathit{BP}_{\!p}$
for this spectrum.
4.1 Cyclic groups and
 $\unicode[STIX]{x1D6F4}_{p}$
: a toy case
$\unicode[STIX]{x1D6F4}_{p}$
: a toy case
In this subsection we present some elementary observations that provide evidence for general bounded torsion results. Therefore, this subsection works backwards from the subsections that follow it. It uses
![]() $\mathit{BP}$
-cohomology to give bounded torsion results for Morava
$\mathit{BP}$
-cohomology to give bounded torsion results for Morava
![]() $E$
-theory.
$E$
-theory.
Recall that, after choosing a coordinate, there is an isomorphism
 $$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\cong \mathit{BP}^{\ast }[\![x]\!]/[p^{k}](x),\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\cong \mathit{BP}^{\ast }[\![x]\!]/[p^{k}](x),\end{eqnarray}$$
where
![]() $[p^{k}](x)$
is the
$[p^{k}](x)$
is the
![]() $p^{k}$
-series for the formal group law associated to
$p^{k}$
-series for the formal group law associated to
![]() $\mathit{BP}$
.
$\mathit{BP}$
.
For any formal group law, it is standard to set
 $$\begin{eqnarray}\langle p^{k}\rangle (x)=[p^{k}](x)/[p^{k-1}](x)=\langle p\rangle ([p^{k-1}](x))\end{eqnarray}$$
$$\begin{eqnarray}\langle p^{k}\rangle (x)=[p^{k}](x)/[p^{k-1}](x)=\langle p\rangle ([p^{k-1}](x))\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})/I\cong \mathit{BP}^{\ast }[\![x]\!]/\langle p^{k}\rangle (x),\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})/I\cong \mathit{BP}^{\ast }[\![x]\!]/\langle p^{k}\rangle (x),\end{eqnarray}$$
where
 $I\subset \mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})$
is the image of the transfer along
$I\subset \mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})$
is the image of the transfer along
 $\mathbb{Z}/p^{k-1}\subset \mathbb{Z}/p^{k}$
. This fact is a consequence of Quillen’s result in [Reference QuillenQui71, Proposition 4.2]. There is a canonical map
$\mathbb{Z}/p^{k-1}\subset \mathbb{Z}/p^{k}$
. This fact is a consequence of Quillen’s result in [Reference QuillenQui71, Proposition 4.2]. There is a canonical map
 $$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\overset{}{\longrightarrow }\underset{0\leqslant j\leqslant k}{\prod }\mathit{BP}^{\ast }(B\mathbb{Z}/p^{j})/I\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\overset{}{\longrightarrow }\underset{0\leqslant j\leqslant k}{\prod }\mathit{BP}^{\ast }(B\mathbb{Z}/p^{j})/I\end{eqnarray}$$
given by sending
![]() $1$
to
$1$
to
 $(1,\ldots ,1)$
and
$(1,\ldots ,1)$
and
![]() $x$
to
$x$
to
 $(0,x,x,\ldots ,x)$
.
$(0,x,x,\ldots ,x)$
.
The following proposition is well known.
Proposition 4.1. There is an isomorphism
 $$\begin{eqnarray}\mathbb{Q}\otimes \mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{0\leqslant j\leqslant k}{\prod }\mathit{BP}^{\ast }(B\mathbb{Z}/p^{j})/I.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes \mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{0\leqslant j\leqslant k}{\prod }\mathit{BP}^{\ast }(B\mathbb{Z}/p^{j})/I.\end{eqnarray}$$
Proof. For any formal group law there is a factorization
 $$\begin{eqnarray}[p^{k}](x)=\underset{0\leqslant j\leqslant k}{\prod }\langle p^{j}\rangle (x).\end{eqnarray}$$
$$\begin{eqnarray}[p^{k}](x)=\underset{0\leqslant j\leqslant k}{\prod }\langle p^{j}\rangle (x).\end{eqnarray}$$
We will show that the factors are coprime in the rationalization; the Chinese remainder theorem will then imply the claim. We may write
 $\langle p\rangle (x)=p+f(x)$
for some power series
$\langle p\rangle (x)=p+f(x)$
for some power series
![]() $f(x)$
with
$f(x)$
with
![]() $x|f(x)$
. This implies that
$x|f(x)$
. This implies that
 $$\begin{eqnarray}[p^{j}](x)=[p^{j-1}](x)(p+f([p^{j-1}](x)))\end{eqnarray}$$
$$\begin{eqnarray}[p^{j}](x)=[p^{j-1}](x)(p+f([p^{j-1}](x)))\end{eqnarray}$$
and hence
 $$\begin{eqnarray}\langle p^{j}\rangle (x)=p+f([p^{j-1}](x)).\end{eqnarray}$$
$$\begin{eqnarray}\langle p^{j}\rangle (x)=p+f([p^{j-1}](x)).\end{eqnarray}$$
But now if
![]() $t<j$
, we have
$t<j$
, we have
 $\langle p^{t}\rangle (x)|[p^{j-1}](x)$
by definition, so that
$\langle p^{t}\rangle (x)|[p^{j-1}](x)$
by definition, so that
 $$\begin{eqnarray}\langle p^{t}\rangle (x)|f([p^{j-1}](x)),\end{eqnarray}$$
$$\begin{eqnarray}\langle p^{t}\rangle (x)|f([p^{j-1}](x)),\end{eqnarray}$$
and using (4.2) then gives
 $$\begin{eqnarray}p=\langle p^{j}\rangle (x)-\langle p^{t}\rangle (x)\frac{f([p^{j-1}](x))}{\langle p^{t}\rangle (x)}.\Box\end{eqnarray}$$
$$\begin{eqnarray}p=\langle p^{j}\rangle (x)-\langle p^{t}\rangle (x)\frac{f([p^{j-1}](x))}{\langle p^{t}\rangle (x)}.\Box\end{eqnarray}$$
The Morava
![]() $E$
-cohomology of
$E$
-cohomology of
![]() $B\mathbb{Z}/p^{k}$
satisfies an isomorphism as in (4.1). Let
$B\mathbb{Z}/p^{k}$
satisfies an isomorphism as in (4.1). Let
![]() $\mathbb{G}_{E_{n}}$
be the formal group associated to
$\mathbb{G}_{E_{n}}$
be the formal group associated to
![]() $E_{n}$
. Given a coordinate
$E_{n}$
. Given a coordinate
![]() $x$
on
$x$
on
![]() $\mathbb{G}_{E_{n}}$
, there is an isomorphism
$\mathbb{G}_{E_{n}}$
, there is an isomorphism
 $$\begin{eqnarray}E_{n}^{\ast }(B\mathbb{Z}/p^{k})\cong E_{n}^{\ast }[\![x]\!]/[p^{k}](x),\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\mathbb{Z}/p^{k})\cong E_{n}^{\ast }[\![x]\!]/[p^{k}](x),\end{eqnarray}$$
where
![]() $[p^{k}](x)$
is the
$[p^{k}](x)$
is the
![]() $p^{k}$
-series for the formal group law
$p^{k}$
-series for the formal group law
 $x+_{\mathbb{G}_{E_{n}}}y$
induced by the coordinate. It is worth noting that the Weierstrass preparation theorem implies that this ring is a free
$x+_{\mathbb{G}_{E_{n}}}y$
induced by the coordinate. It is worth noting that the Weierstrass preparation theorem implies that this ring is a free
![]() $E_{n}^{\ast }$
-module of rank
$E_{n}^{\ast }$
-module of rank
![]() $p^{kn}$
. This is very different from
$p^{kn}$
. This is very different from
 $\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})$
, which is infinitely generated as a
$\mathit{BP}^{\ast }(B\mathbb{Z}/p^{k})$
, which is infinitely generated as a
![]() $\mathit{BP}^{\ast }$
-module.
$\mathit{BP}^{\ast }$
-module.
Corollary 4.2. There is an isomorphism
 $$\begin{eqnarray}\mathbb{Q}\otimes \underset{n>0}{\prod }E_{n}^{\ast }(B\mathbb{Z}/p^{k})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{n>0}{\prod }\,\underset{0\leqslant j\leqslant k}{\prod }E_{n}^{\ast }[\![x]\!]/\langle p^{j}\rangle (x).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes \underset{n>0}{\prod }E_{n}^{\ast }(B\mathbb{Z}/p^{k})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{n>0}{\prod }\,\underset{0\leqslant j\leqslant k}{\prod }E_{n}^{\ast }[\![x]\!]/\langle p^{j}\rangle (x).\end{eqnarray}$$
Proof. We will prove the easiest case for clarity. Fix a height
![]() $n$
and let
$n$
and let
![]() $k=1$
; then with a coordinate this is the map
$k=1$
; then with a coordinate this is the map
 $$\begin{eqnarray}E_{n}^{\ast }[\![x]\!]/[p](x)\overset{}{\longrightarrow }E_{n}^{\ast }\times E_{n}^{\ast }[\![x]\!]/\langle p\rangle (x)\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }[\![x]\!]/[p](x)\overset{}{\longrightarrow }E_{n}^{\ast }\times E_{n}^{\ast }[\![x]\!]/\langle p\rangle (x)\end{eqnarray}$$
sending
 $x\mapsto (0,x)$
and where
$x\mapsto (0,x)$
and where
![]() $[p](x)$
now indicates the
$[p](x)$
now indicates the
![]() $p$
-series for the formal group law associated to
$p$
-series for the formal group law associated to
![]() $E_{n}$
. We may write down a basis for each side. For the left-hand side we have the basis
$E_{n}$
. We may write down a basis for each side. For the left-hand side we have the basis
 $\{1,x,\ldots ,x^{p^{n}-1}\}$
, and for the right-hand side we can take the basis
$\{1,x,\ldots ,x^{p^{n}-1}\}$
, and for the right-hand side we can take the basis
 $$\begin{eqnarray}\{(1,1),(0,1),(0,x),\ldots ,(0,x^{p^{n}-2})\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(1,1),(0,1),(0,x),\ldots ,(0,x^{p^{n}-2})\}.\end{eqnarray}$$
It is clear that the basis elements
 $\{(1,1),(0,x),\ldots ,(0,x^{p^{n}-2})\}$
are hit under this map. Dividing by a power of
$\{(1,1),(0,x),\ldots ,(0,x^{p^{n}-2})\}$
are hit under this map. Dividing by a power of
![]() $p$
is required to hit the basis element
$p$
is required to hit the basis element
![]() $(0,1)$
. But
$(0,1)$
. But
![]() $\mathit{BP}$
provides a global element that hits
$\mathit{BP}$
provides a global element that hits
![]() $(0,1)$
at each height
$(0,1)$
at each height
![]() $n$
. It is the element (using the notation of the proof of the previous proposition)
$n$
. It is the element (using the notation of the proof of the previous proposition)
 $$\begin{eqnarray}-f(x)/p.\end{eqnarray}$$
$$\begin{eqnarray}-f(x)/p.\end{eqnarray}$$
Thus we see that we only need to divide by
![]() $p$
once in order to establish an isomorphism for all
$p$
once in order to establish an isomorphism for all
![]() $n$
. For
$n$
. For
![]() $k>1$
the proof is similar, but we need to divide by
$k>1$
the proof is similar, but we need to divide by
![]() $p^{k}$
. For instance, when
$p^{k}$
. For instance, when
![]() $k=2$
,
$k=2$
,
 $$\begin{eqnarray}\displaystyle -f([p](x)) & \mapsto & \displaystyle (0,0,p),\nonumber\\ \displaystyle -f(x) & \mapsto & \displaystyle (0,p,g(x)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -f([p](x)) & \mapsto & \displaystyle (0,0,p),\nonumber\\ \displaystyle -f(x) & \mapsto & \displaystyle (0,p,g(x)),\nonumber\end{eqnarray}$$
where
![]() $g(x)$
is some polynomial. This implies that
$g(x)$
is some polynomial. This implies that
 $$\begin{eqnarray}-\frac{f(x)}{p}+\frac{f([p](x))g(x)}{p^{2}}\mapsto (0,1,0).\end{eqnarray}$$
$$\begin{eqnarray}-\frac{f(x)}{p}+\frac{f([p](x))g(x)}{p^{2}}\mapsto (0,1,0).\end{eqnarray}$$
Finally, we see that the cokernel of the map
 $$\begin{eqnarray}\underset{n>0}{\prod }E_{n}^{\ast }(B\mathbb{Z}/p^{k})\overset{}{\longrightarrow }\underset{n>0}{\prod }\,\underset{0\leqslant j\leqslant k}{\prod }E_{n}^{\ast }[\![x]\!]/\langle p^{j}\rangle (x)\end{eqnarray}$$
$$\begin{eqnarray}\underset{n>0}{\prod }E_{n}^{\ast }(B\mathbb{Z}/p^{k})\overset{}{\longrightarrow }\underset{n>0}{\prod }\,\underset{0\leqslant j\leqslant k}{\prod }E_{n}^{\ast }[\![x]\!]/\langle p^{j}\rangle (x)\end{eqnarray}$$
is all
![]() $p^{k}$
-torsion independently of the height. Thus the map is a rational isomorphism.◻
$p^{k}$
-torsion independently of the height. Thus the map is a rational isomorphism.◻
To prove a similar result for
![]() $\unicode[STIX]{x1D6F4}_{p}$
, we need to recall a few basic facts regarding
$\unicode[STIX]{x1D6F4}_{p}$
, we need to recall a few basic facts regarding
 $E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})$
. Let
$E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})$
. Let
 $I\subset E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})$
be the image of the transfer along
$I\subset E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})$
be the image of the transfer along
![]() $e\subset \unicode[STIX]{x1D6F4}_{p}$
. For each
$e\subset \unicode[STIX]{x1D6F4}_{p}$
. For each
![]() $n\in \mathbb{N}$
, the natural map
$n\in \mathbb{N}$
, the natural map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{}{\longrightarrow }E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{}{\longrightarrow }E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I\end{eqnarray}$$
is injective and induces an isomorphism
 $$\begin{eqnarray}\mathbb{Q}\otimes E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes (E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes (E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I).\end{eqnarray}$$
Injectivity can be seen by considering Rezk’s pullback square [Reference RezkRez09, Proposition 10.5]

and the isomorphism follows by applying
![]() $\mathbb{Q}\otimes -$
to the pullback square above using the fact that
$\mathbb{Q}\otimes -$
to the pullback square above using the fact that
![]() $\mathbb{Q}$
is a flat
$\mathbb{Q}$
is a flat
![]() $\mathbb{Z}$
-module.
$\mathbb{Z}$
-module.
By considering the homotopy pullback of
 $Be\subset B\unicode[STIX]{x1D6F4}_{p}$
along
$Be\subset B\unicode[STIX]{x1D6F4}_{p}$
along
 $B\mathbb{Z}/p\rightarrow B\unicode[STIX]{x1D6F4}_{p}$
(the key point is that
$B\mathbb{Z}/p\rightarrow B\unicode[STIX]{x1D6F4}_{p}$
(the key point is that
 $|\unicode[STIX]{x1D6F4}_{p}/(\mathbb{Z}/p)|$
is coprime to
$|\unicode[STIX]{x1D6F4}_{p}/(\mathbb{Z}/p)|$
is coprime to
![]() $p$
), one can see that there is a canonical map
$p$
), one can see that there is a canonical map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I\rightarrow E_{n}^{\ast }(B\mathbb{Z}/p)/I.\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I\rightarrow E_{n}^{\ast }(B\mathbb{Z}/p)/I.\end{eqnarray}$$
Lemma 4.3. There is an isomorphism
 $$\begin{eqnarray}\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})\overset{\cong }{\longrightarrow }\mathbb{Q}\otimes \underset{n}{\prod }E_{n}^{\ast }\times E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{p})/I,\end{eqnarray}$$
where
![]() $I$
is the ideal generated by the transfer from the trivial group.
$I$
is the ideal generated by the transfer from the trivial group.
Proof. Let
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
be the cokernel
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
be the cokernel

We will show that
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
is all
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
is all
![]() $p$
-torsion with exponent
$p$
-torsion with exponent
![]() $1$
, i.e. that it is annihilated by multiplication by
$1$
, i.e. that it is annihilated by multiplication by
![]() $p$
.
$p$
.
There is a stable splitting
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{+}^{\infty }B\mathbb{Z}/p\simeq \unicode[STIX]{x1D6F4}_{+}^{\infty }B\unicode[STIX]{x1D6F4}_{p}\times Y\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{+}^{\infty }B\mathbb{Z}/p\simeq \unicode[STIX]{x1D6F4}_{+}^{\infty }B\unicode[STIX]{x1D6F4}_{p}\times Y\end{eqnarray}$$
where
![]() $Y$
is some spectrum. Applying
$Y$
is some spectrum. Applying
![]() $E$
-theory to this yields a commutative diagram
$E$
-theory to this yields a commutative diagram

in which the first vertical map
![]() $i$
is split injective (by the stable splitting above). Since
$i$
is split injective (by the stable splitting above). Since
 $E_{n}^{\ast }B\mathbb{Z}/p$
is free, the cokernel of
$E_{n}^{\ast }B\mathbb{Z}/p$
is free, the cokernel of
![]() $i$
is projective and hence
$i$
is projective and hence
![]() $p$
-torsion free. Since
$p$
-torsion free. Since
 $\mathbb{Q}\otimes \text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})=0$
, the kernel of the map
$\mathbb{Q}\otimes \text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})=0$
, the kernel of the map
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})\rightarrow \text{Cok}_{E_{n}}(\mathbb{Z}/p)$
must be torsion. Therefore the snake lemma implies that the kernel of the right vertical map
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})\rightarrow \text{Cok}_{E_{n}}(\mathbb{Z}/p)$
must be torsion. Therefore the snake lemma implies that the kernel of the right vertical map
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})\rightarrow \text{Cok}_{E_{n}}(\mathbb{Z}/p)$
must be a torsion subgroup of a torsion-free module and hence is zero. Thus
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})\rightarrow \text{Cok}_{E_{n}}(\mathbb{Z}/p)$
must be a torsion subgroup of a torsion-free module and hence is zero. Thus
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
is a subgroup of
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{p})$
is a subgroup of
 $\text{Cok}_{E_{n}}(\mathbb{Z}/p)$
. The claim now follows from Corollary 4.2.◻
$\text{Cok}_{E_{n}}(\mathbb{Z}/p)$
. The claim now follows from Corollary 4.2.◻
4.2 Commutative algebra
In this subsection we prove some basic facts about integer torsion in modules.
The following lemma is part of a well-known collection of facts that go under the title ‘fracture squares’.
Lemma 4.4. Let
 $R=L_{K(t)}E_{n}^{0}\cong W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u_{t}^{-1}]_{I_{t}}^{\wedge }$
for
$R=L_{K(t)}E_{n}^{0}\cong W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u_{t}^{-1}]_{I_{t}}^{\wedge }$
for
![]() $t>0$
and let
$t>0$
and let
![]() $S$
be a subset of
$S$
be a subset of
 $R-(p)$
; then there is a pullback square of commutative rings
$R-(p)$
; then there is a pullback square of commutative rings

Moreover, for any finitely generated free
![]() $R$
-module
$R$
-module
![]() $M$
there is a similar square given by tensoring the pullback square with
$M$
there is a similar square given by tensoring the pullback square with
![]() $M$
.
$M$
.
Proof. The square in the proposition is the composite of two squares:

The right-hand square is an ‘arithmetic square’. It is a pullback square by applying [Reference Dwyer and GreenleesDG02, 4.12 and 4.13]. In [Reference Dwyer and GreenleesDG02] it is shown that the derived functors of localization and completion fit into a homotopy pullback square. The result we want is recovered by noticing that
![]() $S^{-1}R$
is free as an
$S^{-1}R$
is free as an
![]() $S^{-1}R$
-module so that
$S^{-1}R$
-module so that
 $H_{0}(S^{-1}R)=S^{-1}R$
, and that the derived completion and ordinary completion agree because
$H_{0}(S^{-1}R)=S^{-1}R$
, and that the derived completion and ordinary completion agree because
![]() $S^{-1}R$
is Noetherian.
$S^{-1}R$
is Noetherian.
The left-hand square is a pullback by direct computation. Let
 $r/s^{k}\in S^{-1}R$
and
$r/s^{k}\in S^{-1}R$
and
 $r^{\prime }/p^{l}\in \mathbb{Q}\otimes R$
such that
$r^{\prime }/p^{l}\in \mathbb{Q}\otimes R$
such that
 $$\begin{eqnarray}\frac{r}{s^{k}}=\frac{r^{\prime }}{p^{l}}\in \mathbb{Q}\otimes S^{-1}R\end{eqnarray}$$
$$\begin{eqnarray}\frac{r}{s^{k}}=\frac{r^{\prime }}{p^{l}}\in \mathbb{Q}\otimes S^{-1}R\end{eqnarray}$$
where
 $r,r^{\prime }\in R$
. Thus
$r,r^{\prime }\in R$
. Thus
 $s^{k}r^{\prime }=p^{l}r$
and
$s^{k}r^{\prime }=p^{l}r$
and
 $$\begin{eqnarray}r\mapsto \frac{s^{k}r^{\prime }}{p^{l}}\in \mathbb{Q}\otimes R.\end{eqnarray}$$
$$\begin{eqnarray}r\mapsto \frac{s^{k}r^{\prime }}{p^{l}}\in \mathbb{Q}\otimes R.\end{eqnarray}$$
But this implies that
 $s^{k}r^{\prime }/p^{l}\in R$
, since the map is an inclusion. Since
$s^{k}r^{\prime }/p^{l}\in R$
, since the map is an inclusion. Since
![]() $R$
is an integral domain and
$R$
is an integral domain and
![]() $s$
is, by definition, not in the ideal generated by
$s$
is, by definition, not in the ideal generated by
![]() $p$
, we have
$p$
, we have
 $$\begin{eqnarray}p^{l}|r^{\prime }\in R.\end{eqnarray}$$
$$\begin{eqnarray}p^{l}|r^{\prime }\in R.\end{eqnarray}$$
Now
![]() $r^{\prime }/p^{l}$
is the pullback.◻
$r^{\prime }/p^{l}$
is the pullback.◻
Lemma 4.5. Let
 $M\overset{f}{\longrightarrow }N$
be an injective map of finitely generated free
$M\overset{f}{\longrightarrow }N$
be an injective map of finitely generated free
![]() $R$
-modules. If
$R$
-modules. If
![]() $x\in N$
has the property that
$x\in N$
has the property that
 $p^{l}x\in \text{im}\,f$
and
$p^{l}x\in \text{im}\,f$
and
 $s^{k}x\in \text{im}\,f$
for
$s^{k}x\in \text{im}\,f$
for
![]() $s\in S$
, then
$s\in S$
, then
 $x\in \text{im}\,f$
.
$x\in \text{im}\,f$
.
Proof. It suffices to set
 $k=l=1$
. We will use Lemma 4.4. There are
$k=l=1$
. We will use Lemma 4.4. There are
 $m_{1},m_{2}\in M$
such that
$m_{1},m_{2}\in M$
such that
 $m_{1}/s\in S^{-1}M_{p}^{\wedge }$
maps to
$m_{1}/s\in S^{-1}M_{p}^{\wedge }$
maps to
![]() $x$
and
$x$
and
 $m_{2}/p\in p^{-1}M$
maps to
$m_{2}/p\in p^{-1}M$
maps to
![]() $x$
. Now consider the commutative cube
$x$
. Now consider the commutative cube

The front and back faces are pullback squares. The elements
![]() $m_{1}/s$
and
$m_{1}/s$
and
![]() $m_{2}/p$
must agree in
$m_{2}/p$
must agree in
 $p^{-1}(S^{-1}M_{p}^{\wedge })$
, and thus there is an element
$p^{-1}(S^{-1}M_{p}^{\wedge })$
, and thus there is an element
![]() $m\in M$
that maps to both of these. By commutativity we must have
$m\in M$
that maps to both of these. By commutativity we must have
 $f(m)=x$
.◻
$f(m)=x$
.◻
By the torsion of an
![]() $R$
-module
$R$
-module
![]() $M$
we will always mean the set of elements
$M$
we will always mean the set of elements
![]() $x\in M$
such that
$x\in M$
such that
![]() $nx=0$
for some non-zero
$nx=0$
for some non-zero
![]() $n\in \mathbb{N}$
.
$n\in \mathbb{N}$
.
Definition 4.6. For an abelian group
![]() $M$
let
$M$
let
![]() $e(M)$
be the exponent of the torsion in
$e(M)$
be the exponent of the torsion in
![]() $M$
. That is, let
$M$
. That is, let
![]() $K$
be the kernel of
$K$
be the kernel of
 $M\overset{}{\longrightarrow }\mathbb{Q}\otimes M$
, and then
$M\overset{}{\longrightarrow }\mathbb{Q}\otimes M$
, and then
![]() $e(M)$
is the minimum number
$e(M)$
is the minimum number
 $n\in \mathbb{N}\cup \{\infty \}$
such that
$n\in \mathbb{N}\cup \{\infty \}$
such that
 $nK=0$
.
$nK=0$
.
Proposition 4.7. Let
![]() $R$
be a Noetherian ring and
$R$
be a Noetherian ring and
![]() $M$
a finitely generated
$M$
a finitely generated
![]() $R$
-module. Then the torsion in
$R$
-module. Then the torsion in
![]() $M$
is bounded.
$M$
is bounded.
Proof. Let
![]() $K$
be the kernel
$K$
be the kernel
 $$\begin{eqnarray}0\overset{}{\longrightarrow }K\overset{}{\longrightarrow }M\overset{}{\longrightarrow }\mathbb{Q}\otimes M=(\mathbb{Q}\otimes R)\otimes _{R}M.\end{eqnarray}$$
$$\begin{eqnarray}0\overset{}{\longrightarrow }K\overset{}{\longrightarrow }M\overset{}{\longrightarrow }\mathbb{Q}\otimes M=(\mathbb{Q}\otimes R)\otimes _{R}M.\end{eqnarray}$$
The
![]() $R$
-module
$R$
-module
![]() $K$
is finitely generated since
$K$
is finitely generated since
![]() $R$
is Noetherian and
$R$
is Noetherian and
![]() $M$
is finitely generated. Choose generators
$M$
is finitely generated. Choose generators
 $k_{1},\ldots ,k_{m}$
of
$k_{1},\ldots ,k_{m}$
of
![]() $K$
; then there exists an
$K$
; then there exists an
![]() $n$
such that
$n$
such that
![]() $nk_{i}=0$
for all
$nk_{i}=0$
for all
![]() $i$
. Now any element of
$i$
. Now any element of
![]() $K$
is of the form
$K$
is of the form
![]() $\sum r_{i}k_{i}$
, and this is also killed by
$\sum r_{i}k_{i}$
, and this is also killed by
![]() $n$
.◻
$n$
.◻
Proposition 4.8. Let
![]() $R$
be a torsion-free Noetherian ring. Let
$R$
be a torsion-free Noetherian ring. Let
 $f:N{\hookrightarrow}M$
be an injection of finitely generated free
$f:N{\hookrightarrow}M$
be an injection of finitely generated free
![]() $R$
-modules and let
$R$
-modules and let
 $\unicode[STIX]{x1D6E5}:M{\hookrightarrow}M\times M$
be the diagonal. Then
$\unicode[STIX]{x1D6E5}:M{\hookrightarrow}M\times M$
be the diagonal. Then
 $e(\text{Cok}(f))=e(\text{Cok}(\unicode[STIX]{x1D6E5}f))$
.
$e(\text{Cok}(f))=e(\text{Cok}(\unicode[STIX]{x1D6E5}f))$
.
Proof. Consider the map of short exact sequences

The diagonal
![]() $\unicode[STIX]{x1D6E5}$
is a section of the projection onto a factor and the left vertical arrow is an equality, so
$\unicode[STIX]{x1D6E5}$
is a section of the projection onto a factor and the left vertical arrow is an equality, so
![]() $g$
is an injection. Thus there is an induced map
$g$
is an injection. Thus there is an induced map
 $\text{Cok}(\unicode[STIX]{x1D6E5}f)\overset{r}{\longrightarrow }\text{Cok}(f)$
such that
$\text{Cok}(\unicode[STIX]{x1D6E5}f)\overset{r}{\longrightarrow }\text{Cok}(f)$
such that
![]() $rg=1$
. Since integer torsion is sent to integer torsion, this implies that the map induced by
$rg=1$
. Since integer torsion is sent to integer torsion, this implies that the map induced by
![]() $g$
on integer torsion is a split injection. It is an isomorphism since a torsion element must be of the form
$g$
on integer torsion is a split injection. It is an isomorphism since a torsion element must be of the form
 $(m,m)\in M\times M$
with
$(m,m)\in M\times M$
with
 $(nm,nm)\in \unicode[STIX]{x1D6E5}fN$
, and so the kernel of
$(nm,nm)\in \unicode[STIX]{x1D6E5}fN$
, and so the kernel of
![]() $r$
is trivial.◻
$r$
is trivial.◻
Proposition 4.9. Let
![]() $R$
be Noetherian and torsion free. For a flat
$R$
be Noetherian and torsion free. For a flat
![]() $R$
-algebra
$R$
-algebra
![]() $T$
and a finitely generated
$T$
and a finitely generated
![]() $R$
-module
$R$
-module
![]() $M$
,
$M$
,
 $e(M)\geqslant e(T\otimes _{R}M)$
. If
$e(M)\geqslant e(T\otimes _{R}M)$
. If
![]() $T$
is a faithfully flat
$T$
is a faithfully flat
![]() $R$
-algebra, then equality holds, i.e.
$R$
-algebra, then equality holds, i.e.
 $e(M)=e(T\otimes _{R}M)$
.
$e(M)=e(T\otimes _{R}M)$
.
Proof. Assume that
 $e(M)=n$
and let
$e(M)=n$
and let
 $[n]:M\overset{}{\longrightarrow }M$
be the multiplication-by-
$[n]:M\overset{}{\longrightarrow }M$
be the multiplication-by-
![]() $n$
map. Consider the exact sequence
$n$
map. Consider the exact sequence
 $$\begin{eqnarray}0\overset{}{\longrightarrow }K\overset{}{\longrightarrow }M\overset{[n]}{\longrightarrow }\text{im}[n]\overset{}{\longrightarrow }0,\end{eqnarray}$$
$$\begin{eqnarray}0\overset{}{\longrightarrow }K\overset{}{\longrightarrow }M\overset{[n]}{\longrightarrow }\text{im}[n]\overset{}{\longrightarrow }0,\end{eqnarray}$$
where
![]() $K$
is the torsion in
$K$
is the torsion in
![]() $M$
. Base change to
$M$
. Base change to
![]() $T$
gives a short exact sequence and
$T$
gives a short exact sequence and
 $T\otimes _{R}\text{im}[n]$
is necessarily torsion free; thus
$T\otimes _{R}\text{im}[n]$
is necessarily torsion free; thus
 $$\begin{eqnarray}e(T\otimes _{R}K)=e(T\otimes _{R}M)\leqslant n.\end{eqnarray}$$
$$\begin{eqnarray}e(T\otimes _{R}K)=e(T\otimes _{R}M)\leqslant n.\end{eqnarray}$$
If
![]() $T$
is faithfully flat, then
$T$
is faithfully flat, then
 $K\overset{}{\longrightarrow }T\otimes _{R}K$
is injective [Reference LamLam99, 4.74 and 4.83], so
$K\overset{}{\longrightarrow }T\otimes _{R}K$
is injective [Reference LamLam99, 4.74 and 4.83], so
 $e(T\otimes _{R}M)=e(M)$
.◻
$e(T\otimes _{R}M)=e(M)$
.◻
Corollary 4.10. Let
![]() $R$
be as in Lemma 4.4, let
$R$
be as in Lemma 4.4, let
![]() $T$
be a faithfully flat
$T$
be a faithfully flat
 $(S^{-1}R)_{p}^{\wedge }$
-algebra, and let
$(S^{-1}R)_{p}^{\wedge }$
-algebra, and let
 $M\overset{f}{\longrightarrow }N$
be a map of finitely generated free
$M\overset{f}{\longrightarrow }N$
be a map of finitely generated free
![]() $R$
-modules; then
$R$
-modules; then
 $$\begin{eqnarray}e(N/\text{im}\,f)=e(T\otimes _{R}(N/\text{im}\,f)).\end{eqnarray}$$
$$\begin{eqnarray}e(N/\text{im}\,f)=e(T\otimes _{R}(N/\text{im}\,f)).\end{eqnarray}$$
Proof. By Lemma 4.5, the torsion in
![]() $N/\text{im}\,f$
is contained in the torsion of
$N/\text{im}\,f$
is contained in the torsion of
 $(S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f$
, so
$(S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f$
, so
 $$\begin{eqnarray}e(N/\text{im}\,f)\leqslant e((S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f).\end{eqnarray}$$
$$\begin{eqnarray}e(N/\text{im}\,f)\leqslant e((S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f).\end{eqnarray}$$
Also,
 $(S^{-1}R)_{p}^{\wedge }$
is a flat extension of
$(S^{-1}R)_{p}^{\wedge }$
is a flat extension of
![]() $R$
, and this gives the reverse inequality. Since
$R$
, and this gives the reverse inequality. Since
![]() $T$
is faithfully flat, base change to
$T$
is faithfully flat, base change to
![]() $T$
is injective. Thus we have have equalities
$T$
is injective. Thus we have have equalities
 $$\begin{eqnarray}e(N/\text{im}\,f)=e((S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f)=e(T\otimes _{R}(N/\text{im}\,f))\end{eqnarray}$$
$$\begin{eqnarray}e(N/\text{im}\,f)=e((S^{-1}R)_{p}^{\wedge }\otimes _{R}N/\text{im}\,f)=e(T\otimes _{R}(N/\text{im}\,f))\end{eqnarray}$$
by Proposition 4.9. ◻
4.3 A few hand-crafted cohomology theories
In order to prove the bounded torsion results for
![]() $E$
-theory we make use of several
$E$
-theory we make use of several
![]() $E_{n}$
-algebras. In this section we construct the
$E_{n}$
-algebras. In this section we construct the
![]() $E_{n}$
-algebras that we need and prove or recall some basic properties of them. We rely heavily on ideas from [Reference Barthel and StapletonBS16].
$E_{n}$
-algebras that we need and prove or recall some basic properties of them. We rely heavily on ideas from [Reference Barthel and StapletonBS16].
Let
 $L_{1}=L_{K(1)}E_{n}$
(it does depend on
$L_{1}=L_{K(1)}E_{n}$
(it does depend on
![]() $n$
) and recall from [Reference HoveyHov97, Corollary 1.5.5] that
$n$
) and recall from [Reference HoveyHov97, Corollary 1.5.5] that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}L_{1}=W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u_{1}^{-1}]_{p}^{\wedge }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}L_{1}=W(\unicode[STIX]{x1D705})[\![u_{1},\ldots ,u_{n-1}]\!][u_{1}^{-1}]_{p}^{\wedge }.\end{eqnarray}$$
This is a flat
![]() $E_{n}^{0}$
-algebra. Recall that we may localize an
$E_{n}^{0}$
-algebra. Recall that we may localize an
![]() $E_{\infty }$
-ring spectrum
$E_{\infty }$
-ring spectrum
![]() $R$
at a prime ideal
$R$
at a prime ideal
 $\mathfrak{p}\subseteq \unicode[STIX]{x1D70B}_{0}R$
by inverting every element in
$\mathfrak{p}\subseteq \unicode[STIX]{x1D70B}_{0}R$
by inverting every element in
 $\unicode[STIX]{x1D70B}_{0}R-\mathfrak{p}$
; we write
$\unicode[STIX]{x1D70B}_{0}R-\mathfrak{p}$
; we write
![]() $R_{\mathfrak{p}}$
for the localized ring spectrum. Define
$R_{\mathfrak{p}}$
for the localized ring spectrum. Define
 $$\begin{eqnarray}F_{1}=L_{K(1)}((E_{n})_{(p)})\end{eqnarray}$$
$$\begin{eqnarray}F_{1}=L_{K(1)}((E_{n})_{(p)})\end{eqnarray}$$
by inverting all of the elements away from
![]() $\mathfrak{p}=(p)$
and then
$\mathfrak{p}=(p)$
and then
![]() $K(1)$
-localizing the resulting spectrum. Note that this inverts
$K(1)$
-localizing the resulting spectrum. Note that this inverts
 $u_{1},\ldots ,u_{n-1}$
. The ring spectrum
$u_{1},\ldots ,u_{n-1}$
. The ring spectrum
![]() $F_{1}$
is an even-periodic Landweber-exact
$F_{1}$
is an even-periodic Landweber-exact
![]() $E_{\infty }$
-ring such that
$E_{\infty }$
-ring such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}F_{1}=F_{1}^{0}=((E_{n}^{0})_{(p)})_{p}^{\wedge }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{0}F_{1}=F_{1}^{0}=((E_{n}^{0})_{(p)})_{p}^{\wedge }.\end{eqnarray}$$
Since
![]() $F_{1}$
is
$F_{1}$
is
![]() $K(1)$
-local, there is a canonical map
$K(1)$
-local, there is a canonical map
 $$\begin{eqnarray}L_{1}\overset{}{\longrightarrow }F_{1}\end{eqnarray}$$
$$\begin{eqnarray}L_{1}\overset{}{\longrightarrow }F_{1}\end{eqnarray}$$
inducing the obvious map on coefficients. This suggests another construction of
![]() $F_{1}$
. It is clear that
$F_{1}$
. It is clear that
 $$\begin{eqnarray}((L_{1})_{(p)})_{p}^{\wedge }\overset{\cong }{\longrightarrow }F_{1},\end{eqnarray}$$
$$\begin{eqnarray}((L_{1})_{(p)})_{p}^{\wedge }\overset{\cong }{\longrightarrow }F_{1},\end{eqnarray}$$
by considering the quotient of this ring by powers of
![]() $p$
. This allows Corollary 4.10 to be used with
$p$
. This allows Corollary 4.10 to be used with
 $(R,S)=(E_{n}^{\ast },E_{n}^{\ast }-(p))$
or
$(R,S)=(E_{n}^{\ast },E_{n}^{\ast }-(p))$
or
 $(R,S)=(L_{1}^{\ast },L_{1}^{\ast }-(p))$
.
$(R,S)=(L_{1}^{\ast },L_{1}^{\ast }-(p))$
.
Now let
![]() $G$
be a finite group.
$G$
be a finite group.
Proposition 4.11. The canonical map
 $$\begin{eqnarray}F_{1}\wedge _{L_{1}}L_{1}^{BG}\overset{\simeq }{\longrightarrow }F_{1}^{BG}\end{eqnarray}$$
$$\begin{eqnarray}F_{1}\wedge _{L_{1}}L_{1}^{BG}\overset{\simeq }{\longrightarrow }F_{1}^{BG}\end{eqnarray}$$
is an equivalence that is natural in
![]() $G$
.
$G$
.
Proof. The proof follows the proof of Proposition 6.2 in [Reference Barthel and StapletonBS16]. It is clear that the map is natural. To prove that it is an equivalence, the main idea is to note that the smash product on the left is
![]() $K(1)$
-local and then use the
$K(1)$
-local and then use the
![]() $K(1)$
-local self-duality of classifying spaces of finite groups.◻
$K(1)$
-local self-duality of classifying spaces of finite groups.◻
Following ideas in [Reference Barthel and StapletonBS16] based on work of Hopkins in [Reference HopkinsHop], we further define
 $$\begin{eqnarray}\bar{F}_{1}=L_{K(1)}(F_{1}\wedge K_{p}),\end{eqnarray}$$
$$\begin{eqnarray}\bar{F}_{1}=L_{K(1)}(F_{1}\wedge K_{p}),\end{eqnarray}$$
where
![]() $K_{p}$
is
$K_{p}$
is
![]() $p$
-adic
$p$
-adic
![]() $K$
-theory. We do not have much control over the coefficients of this ring spectrum. However, following [Reference Barthel and StapletonBS16, Proposition 5.8],
$K$
-theory. We do not have much control over the coefficients of this ring spectrum. However, following [Reference Barthel and StapletonBS16, Proposition 5.8],
![]() $\bar{F}_{1}$
does have a very desirable property as follows.
$\bar{F}_{1}$
does have a very desirable property as follows.
Proposition 4.12. The ring of coefficients of
![]() $\bar{F}_{1}$
is faithfully flat as a
$\bar{F}_{1}$
is faithfully flat as a
![]() $K_{p}^{\ast }$
-module and as an
$K_{p}^{\ast }$
-module and as an
![]() $F_{1}^{\ast }$
-module.
$F_{1}^{\ast }$
-module.
Proof. This follows from the proof of Proposition 5.8 in [Reference Barthel and StapletonBS16], which relies on the important (and somewhat surprising) Proposition 3.13 that extends an argument of Hovey’s in [Reference HoveyHov04b]. Both module structures are faithfully flat because
![]() $K_{p}^{\ast }$
and
$K_{p}^{\ast }$
and
![]() $F_{1}^{\ast }$
are both complete local Noetherian.◻
$F_{1}^{\ast }$
are both complete local Noetherian.◻
Proposition 4.13. For a finite group
![]() $G$
, there are natural equivalences
$G$
, there are natural equivalences
 $$\begin{eqnarray}\bar{F}_{1}\wedge _{F_{1}}F_{1}^{BG}\overset{\simeq }{\longrightarrow }\bar{F}_{1}^{BG}\overset{\simeq }{\longleftarrow }\bar{F}_{1}\wedge _{K_{p}}K_{p}^{BG}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{F}_{1}\wedge _{F_{1}}F_{1}^{BG}\overset{\simeq }{\longrightarrow }\bar{F}_{1}^{BG}\overset{\simeq }{\longleftarrow }\bar{F}_{1}\wedge _{K_{p}}K_{p}^{BG}.\end{eqnarray}$$
Proof. This also follows the proof of Proposition 6.2 in [Reference Barthel and StapletonBS16], using Proposition 4.12 above. ◻
Now let
![]() $H\subset G$
so that we have a transfer map
$H\subset G$
so that we have a transfer map
 $E^{BH}\overset{\text{Tr}}{\longrightarrow }E^{BG}$
for any cohomology theory
$E^{BH}\overset{\text{Tr}}{\longrightarrow }E^{BG}$
for any cohomology theory
![]() $E$
.
$E$
.
Proposition 4.14. Let
![]() $E$
and
$E$
and
![]() $F$
be
$F$
be
![]() $E_{\infty }$
-rings and let
$E_{\infty }$
-rings and let
![]() $F$
be an
$F$
be an
![]() $E$
-algebra. There is a commutative square
$E$
-algebra. There is a commutative square

Proof. The map of
![]() $E_{\infty }$
-rings
$E_{\infty }$
-rings
 $E\overset{}{\longrightarrow }F$
and the transfer map
$E\overset{}{\longrightarrow }F$
and the transfer map
 $\unicode[STIX]{x1D6F4}_{+}^{\infty }BH\overset{}{\longrightarrow }\unicode[STIX]{x1D6F4}_{+}^{\infty }BG$
induce a commutative square of function spectra
$\unicode[STIX]{x1D6F4}_{+}^{\infty }BH\overset{}{\longrightarrow }\unicode[STIX]{x1D6F4}_{+}^{\infty }BG$
induce a commutative square of function spectra

and we can now base change the left-hand side to
![]() $F$
over
$F$
over
![]() $E$
.◻
$E$
.◻
Let
![]() $E$
be any cohomology theory, let
$E$
be any cohomology theory, let
 $H_{1},\ldots ,H_{m}\subset G$
, and let
$H_{1},\ldots ,H_{m}\subset G$
, and let
 $I\subset E^{\ast }(BG)$
be the ideal generated by the image of the transfers
$I\subset E^{\ast }(BG)$
be the ideal generated by the image of the transfers
 $E^{\ast }(BH_{i})\overset{\text{Tr}}{\longrightarrow }E^{\ast }(BG)$
. This is the image of the map
$E^{\ast }(BH_{i})\overset{\text{Tr}}{\longrightarrow }E^{\ast }(BG)$
. This is the image of the map
 $$\begin{eqnarray}\underset{i}{\bigoplus }E^{\ast }(BH_{i})\overset{\oplus \text{Tr}}{\longrightarrow }E^{\ast }(BG).\end{eqnarray}$$
$$\begin{eqnarray}\underset{i}{\bigoplus }E^{\ast }(BH_{i})\overset{\oplus \text{Tr}}{\longrightarrow }E^{\ast }(BG).\end{eqnarray}$$
Proposition 4.15. Let
 $E=K_{p},L_{1},F_{1}$
or
$E=K_{p},L_{1},F_{1}$
or
![]() $\bar{F}_{1}$
, let
$\bar{F}_{1}$
, let
 $H_{1},\ldots ,H_{m}\subset G$
, and let
$H_{1},\ldots ,H_{m}\subset G$
, and let
 $I\subset E^{\ast }(BG)$
be the associated transfer ideal. There are isomorphisms
$I\subset E^{\ast }(BG)$
be the associated transfer ideal. There are isomorphisms
 $$\begin{eqnarray}F_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }(BG)/I\overset{\cong }{\longrightarrow }F_{1}^{\ast }(BG)/I\end{eqnarray}$$
$$\begin{eqnarray}F_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }(BG)/I\overset{\cong }{\longrightarrow }F_{1}^{\ast }(BG)/I\end{eqnarray}$$
and
 $$\begin{eqnarray}\bar{F}_{1}^{\ast }\otimes _{F_{1}^{\ast }}F_{1}^{\ast }(BG)/I\overset{\cong }{\longrightarrow }\bar{F}_{1}^{\ast }(BG)/I\overset{\cong }{\longleftarrow }\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}K_{p}^{\ast }(BG)/I.\end{eqnarray}$$
$$\begin{eqnarray}\bar{F}_{1}^{\ast }\otimes _{F_{1}^{\ast }}F_{1}^{\ast }(BG)/I\overset{\cong }{\longrightarrow }\bar{F}_{1}^{\ast }(BG)/I\overset{\cong }{\longleftarrow }\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}K_{p}^{\ast }(BG)/I.\end{eqnarray}$$
Proof. The first isomorphism follows from the previous proposition and Proposition 4.11, and the second isomorphism follows from the previous proposition and Proposition 4.13. ◻
In the next section we will make use of character theory for Morava
![]() $E$
-theory. This will involve two more
$E$
-theory. This will involve two more
![]() $E_{n}$
-algebras. The first was introduced in [Reference Hopkins, Kuhn and RavenelHKR00] and the second was introduced in [Reference StapletonSta13].
$E_{n}$
-algebras. The first was introduced in [Reference Hopkins, Kuhn and RavenelHKR00] and the second was introduced in [Reference StapletonSta13].
Let
 $\unicode[STIX]{x1D6EC}_{k,n}=(\mathbb{Z}/p^{k})^{n}$
. The
$\unicode[STIX]{x1D6EC}_{k,n}=(\mathbb{Z}/p^{k})^{n}$
. The
![]() $E_{n}$
-algebra
$E_{n}$
-algebra
![]() $C_{0}$
is constructed in [Reference Hopkins, Kuhn and RavenelHKR00, § 6.2]. It is a
$C_{0}$
is constructed in [Reference Hopkins, Kuhn and RavenelHKR00, § 6.2]. It is a
![]() $p^{-1}E_{n}$
-algebra and may be constructed as an
$p^{-1}E_{n}$
-algebra and may be constructed as an
![]() $E_{n}$
-algebra as a localization of the colimit
$E_{n}$
-algebra as a localization of the colimit
 $$\begin{eqnarray}\underset{k}{\text{colim}}\,E_{n}^{B\unicode[STIX]{x1D6EC}_{k,n}}.\end{eqnarray}$$
$$\begin{eqnarray}\underset{k}{\text{colim}}\,E_{n}^{B\unicode[STIX]{x1D6EC}_{k,n}}.\end{eqnarray}$$
The commutative ring
![]() $C_{0}^{\ast }$
is faithfully flat as a
$C_{0}^{\ast }$
is faithfully flat as a
![]() $\mathbb{Q}\otimes E_{n}^{\ast }$
-algebra. The point of the construction (and this is [Reference Hopkins, Kuhn and RavenelHKR00, Theorem C]) is that for any finite group
$\mathbb{Q}\otimes E_{n}^{\ast }$
-algebra. The point of the construction (and this is [Reference Hopkins, Kuhn and RavenelHKR00, Theorem C]) is that for any finite group
![]() $G$
, there is a canonical equivalence
$G$
, there is a canonical equivalence
 $$\begin{eqnarray}C_{0}\wedge _{E_{n}}E_{n}^{BG}\overset{{\sim}}{\longrightarrow }C_{0}\wedge _{p^{-1}E_{n}}(p^{-1}E_{n})^{{\mathcal{L}}^{n}BG},\end{eqnarray}$$
$$\begin{eqnarray}C_{0}\wedge _{E_{n}}E_{n}^{BG}\overset{{\sim}}{\longrightarrow }C_{0}\wedge _{p^{-1}E_{n}}(p^{-1}E_{n})^{{\mathcal{L}}^{n}BG},\end{eqnarray}$$
where
 ${\mathcal{L}}(-)=\hom (B\mathbb{Z}_{p},-)$
is the
${\mathcal{L}}(-)=\hom (B\mathbb{Z}_{p},-)$
is the
![]() $p$
-adic free loop space functor. Since
$p$
-adic free loop space functor. Since
![]() $p^{-1}E_{n}$
is rational and
$p^{-1}E_{n}$
is rational and
![]() $C_{0}^{\ast }$
is faithfully flat as a
$C_{0}^{\ast }$
is faithfully flat as a
![]() $p^{-1}E_{n}^{\ast }$
-algebra, the target is equivalent to
$p^{-1}E_{n}^{\ast }$
-algebra, the target is equivalent to
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D70B}_{0}{\mathcal{L}}^{n}BG}{\prod }C_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D70B}_{0}{\mathcal{L}}^{n}BG}{\prod }C_{0}.\end{eqnarray}$$
The
![]() $E_{n}$
-algebra
$E_{n}$
-algebra
![]() $C_{1}$
is constructed (as a commutative ring) in [Reference StapletonSta13] and as an
$C_{1}$
is constructed (as a commutative ring) in [Reference StapletonSta13] and as an
![]() $E_{n}$
-algebra in [Reference Barthel and StapletonBS16]. It is a
$E_{n}$
-algebra in [Reference Barthel and StapletonBS16]. It is a
![]() $K(1)$
-local
$K(1)$
-local
![]() $L_{1}$
-algebra which is given as the
$L_{1}$
-algebra which is given as the
![]() $p$
-completion of a localization of the colimit
$p$
-completion of a localization of the colimit
 $$\begin{eqnarray}\underset{k}{\text{colim}}\,L_{1}\wedge _{E_{n}}E_{n}^{B\unicode[STIX]{x1D6EC}_{k,n-1}}.\end{eqnarray}$$
$$\begin{eqnarray}\underset{k}{\text{colim}}\,L_{1}\wedge _{E_{n}}E_{n}^{B\unicode[STIX]{x1D6EC}_{k,n-1}}.\end{eqnarray}$$
The point of the construction (and this is a special case of the main theorem of [Reference StapletonSta13]) is that there is an equivalence
 $$\begin{eqnarray}C_{1}\wedge _{E_{n}}E_{n}^{BG}\overset{{\sim}}{\longrightarrow }C_{1}\wedge _{L_{1}}L_{1}^{{\mathcal{L}}^{n-1}BG}.\end{eqnarray}$$
$$\begin{eqnarray}C_{1}\wedge _{E_{n}}E_{n}^{BG}\overset{{\sim}}{\longrightarrow }C_{1}\wedge _{L_{1}}L_{1}^{{\mathcal{L}}^{n-1}BG}.\end{eqnarray}$$
Since
![]() $C_{1}^{\ast }$
is flat as an
$C_{1}^{\ast }$
is flat as an
![]() $E_{n}^{\ast }$
-algebra and faithfully flat as an
$E_{n}^{\ast }$
-algebra and faithfully flat as an
![]() $L_{1}^{\ast }$
-algebra, applying
$L_{1}^{\ast }$
-algebra, applying
![]() $\unicode[STIX]{x1D70B}_{\ast }$
to this equivalence gives the isomorphism
$\unicode[STIX]{x1D70B}_{\ast }$
to this equivalence gives the isomorphism
 $$\begin{eqnarray}C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BG)\overset{\cong }{\longrightarrow }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BG).\end{eqnarray}$$
$$\begin{eqnarray}C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BG)\overset{\cong }{\longrightarrow }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BG).\end{eqnarray}$$
The iterated
![]() $p$
-adic free loop space of
$p$
-adic free loop space of
![]() $BG$
is a disjoint union of classifying spaces of certain centralizer subgroups of
$BG$
is a disjoint union of classifying spaces of certain centralizer subgroups of
![]() $G$
, and this is how the codomain is most easily understood explicitly. Let
$G$
, and this is how the codomain is most easily understood explicitly. Let
 $$\begin{eqnarray}\hom (\mathbb{Z}_{p}^{l},G)/\sim\end{eqnarray}$$
$$\begin{eqnarray}\hom (\mathbb{Z}_{p}^{l},G)/\sim\end{eqnarray}$$
be conjugacy classes of continuous maps from
![]() $\mathbb{Z}_{p}^{l}$
to
$\mathbb{Z}_{p}^{l}$
to
![]() $G$
; then
$G$
; then
 $$\begin{eqnarray}C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BG)\cong \underset{[\unicode[STIX]{x1D6FC}]\in \hom (\mathbb{Z}_{p}^{n-1},G)/\sim }{\prod }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BC(\text{im}\,\unicode[STIX]{x1D6FC})),\end{eqnarray}$$
$$\begin{eqnarray}C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BG)\cong \underset{[\unicode[STIX]{x1D6FC}]\in \hom (\mathbb{Z}_{p}^{n-1},G)/\sim }{\prod }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }({\mathcal{L}}^{n-1}BC(\text{im}\,\unicode[STIX]{x1D6FC})),\end{eqnarray}$$
where
 $C(\text{im}\,\unicode[STIX]{x1D6FC})$
is the centralizer of the image of a choice
$C(\text{im}\,\unicode[STIX]{x1D6FC})$
is the centralizer of the image of a choice
![]() $\unicode[STIX]{x1D6FC}\in [\unicode[STIX]{x1D6FC}]$
.
$\unicode[STIX]{x1D6FC}\in [\unicode[STIX]{x1D6FC}]$
.
The equivalences above behave well with respect to transfers. Formulas can be found in [Reference Hopkins, Kuhn and RavenelHKR00, Theorem D] and [Reference StapletonSta15, Theorems 2.18 and 3.11].
4.4 Bounded torsion in
 $E$
-theory
$E$
-theory
In this subsection we prove that rational factorizations of the Morava
![]() $E$
-cohomology of finite abelian groups and symmetric groups hold integrally up to a torsion cokernel with a height-independent bounded exponent. We do this by putting together the tools developed in the preceding two subsections.
$E$
-cohomology of finite abelian groups and symmetric groups hold integrally up to a torsion cokernel with a height-independent bounded exponent. We do this by putting together the tools developed in the preceding two subsections.
When we write
 $I\subset E^{\ast }(BA)$
for an abelian group
$I\subset E^{\ast }(BA)$
for an abelian group
![]() $A$
we will always mean the ideal generated by the image of the transfer along proper subgroups of
$A$
we will always mean the ideal generated by the image of the transfer along proper subgroups of
![]() $A$
. When we write
$A$
. When we write
 $I\subset E^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
we will always mean the ideal generated by the image of the transfer along the proper partition subgroups
$I\subset E^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
we will always mean the ideal generated by the image of the transfer along the proper partition subgroups
 $\unicode[STIX]{x1D6F4}_{i}\times \unicode[STIX]{x1D6F4}_{j}\overset{}{\longrightarrow }\unicode[STIX]{x1D6F4}_{m}$
, where
$\unicode[STIX]{x1D6F4}_{i}\times \unicode[STIX]{x1D6F4}_{j}\overset{}{\longrightarrow }\unicode[STIX]{x1D6F4}_{m}$
, where
 $i+j=m$
with
$i+j=m$
with
![]() $i,j>0$
.
$i,j>0$
.
We will begin with symmetric groups. First we will set up the algebro-geometric objects that witness the rational factorization.
Let
![]() $\unicode[STIX]{x1D706}\vdash m$
be a partition of
$\unicode[STIX]{x1D706}\vdash m$
be a partition of
![]() $m$
. We write
$m$
. We write
 $$\begin{eqnarray}\unicode[STIX]{x1D706}=a_{1}\unicode[STIX]{x1D706}_{1}+a_{2}\unicode[STIX]{x1D706}_{2}+\cdots +a_{k}\unicode[STIX]{x1D706}_{k},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}=a_{1}\unicode[STIX]{x1D706}_{1}+a_{2}\unicode[STIX]{x1D706}_{2}+\cdots +a_{k}\unicode[STIX]{x1D706}_{k},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D706}_{j}$
when
$\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D706}_{j}$
when
![]() $i<j$
,
$i<j$
,
![]() $a_{i}\in \mathbb{N}$
, and the value of the sum is
$a_{i}\in \mathbb{N}$
, and the value of the sum is
![]() $m$
. To simplify the notation, we write
$m$
. To simplify the notation, we write
 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{1}}^{\times a_{1}}\times \cdots \times \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{k}}^{\times a_{k}}$
and
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{1}}^{\times a_{1}}\times \cdots \times \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{k}}^{\times a_{k}}$
and
 $\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}=\unicode[STIX]{x1D6F4}_{a_{1}}\times \cdots \times \unicode[STIX]{x1D6F4}_{a_{k}}$
. Furthermore, let
$\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}=\unicode[STIX]{x1D6F4}_{a_{1}}\times \cdots \times \unicode[STIX]{x1D6F4}_{a_{k}}$
. Furthermore, let
![]() $I_{\unicode[STIX]{x1D706}}$
be the ideal in
$I_{\unicode[STIX]{x1D706}}$
be the ideal in
 $E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})$
generated by the individual transfer ideals
$E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})$
generated by the individual transfer ideals
 $I\subset E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})$
; that is,
$I\subset E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})$
; that is,
![]() $I_{\unicode[STIX]{x1D706}}$
has the property that
$I_{\unicode[STIX]{x1D706}}$
has the property that
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}}\cong \underset{i}{\bigotimes }(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}}\cong \underset{i}{\bigotimes }(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}}.\end{eqnarray}$$
Furthermore, there is an action of
![]() $\unicode[STIX]{x1D6F4}_{a_{i}}$
on the tensor power
$\unicode[STIX]{x1D6F4}_{a_{i}}$
on the tensor power
 $$\begin{eqnarray}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}}.\end{eqnarray}$$
For each tensor factor, we will take the fixed points by this action and denote the result by
 $$\begin{eqnarray}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}}=\underset{i}{\bigotimes }((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}})^{\unicode[STIX]{x1D6F4}_{a_{i}}}.\end{eqnarray}$$
$$\begin{eqnarray}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}}=\underset{i}{\bigotimes }((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}})^{\unicode[STIX]{x1D6F4}_{a_{i}}}.\end{eqnarray}$$
This commutative ring can be understood algebro-geometrically by a theorem of Strickland’s. In [Reference StricklandStr97], Strickland proved that
 $E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})/I$
is a finitely generated free
$E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})/I$
is a finitely generated free
![]() $E_{n}^{\ast }$
-module and produces a canonical isomorphism
$E_{n}^{\ast }$
-module and produces a canonical isomorphism
 $$\begin{eqnarray}\text{Spf}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})/I)\cong \text{Sub}_{m}(\mathbb{G}_{E_{n}}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Spf}(E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})/I)\cong \text{Sub}_{m}(\mathbb{G}_{E_{n}}),\end{eqnarray}$$
where
 $\text{Sub}_{m}(\mathbb{G}_{E_{n}})$
is the scheme classifying subgroup schemes of order
$\text{Sub}_{m}(\mathbb{G}_{E_{n}})$
is the scheme classifying subgroup schemes of order
![]() $m$
in
$m$
in
![]() $\mathbb{G}_{E_{n}}$
. It is worth noting that this is the empty scheme if
$\mathbb{G}_{E_{n}}$
. It is worth noting that this is the empty scheme if
![]() $m$
is coprime to
$m$
is coprime to
![]() $p$
. The scheme associated to the ring that we are interested in is built out of
$p$
. The scheme associated to the ring that we are interested in is built out of
 $\text{Sub}_{m}(\mathbb{G}_{E_{n}})$
. Thus we may define
$\text{Sub}_{m}(\mathbb{G}_{E_{n}})$
. Thus we may define
 $$\begin{eqnarray}\displaystyle \text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}}) & = & \displaystyle \text{Spec}((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}})\nonumber\\ \displaystyle & \cong & \displaystyle \underset{i}{\prod }\text{Spec}(((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}})^{\unicode[STIX]{x1D6F4}_{a_{i}}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}}) & = & \displaystyle \text{Spec}((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}})\nonumber\\ \displaystyle & \cong & \displaystyle \underset{i}{\prod }\text{Spec}(((E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}})/I)^{\otimes a_{i}})^{\unicode[STIX]{x1D6F4}_{a_{i}}}).\nonumber\end{eqnarray}$$
The point of the notation
 $\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})$
is that this scheme represents unordered sets of
$\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})$
is that this scheme represents unordered sets of
![]() $\sum _{i}a_{i}$
subgroups of
$\sum _{i}a_{i}$
subgroups of
![]() $\mathbb{G}_{E_{n}}$
in which
$\mathbb{G}_{E_{n}}$
in which
![]() $a_{i}$
of the subgroups have order
$a_{i}$
of the subgroups have order
![]() $\unicode[STIX]{x1D706}_{i}$
. This scheme-theoretic description is not essential to the proof of the result. However, one of the goals of decomposing
$\unicode[STIX]{x1D706}_{i}$
. This scheme-theoretic description is not essential to the proof of the result. However, one of the goals of decomposing
 $\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
rationally is to suggest that it may have a tractable algebro-geometric description.
$\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})$
rationally is to suggest that it may have a tractable algebro-geometric description.
Let
![]() $\unicode[STIX]{x1D6E4}(-)$
be the functor that takes a scheme to the ring of functions on the scheme. There is a canonical map
$\unicode[STIX]{x1D6E4}(-)$
be the functor that takes a scheme to the ring of functions on the scheme. There is a canonical map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
induced by restriction. The only part to check here is that it actually lands in the fixed points, but this is clear as there is an inner automorphism of
![]() $\unicode[STIX]{x1D6F4}_{m}$
that permutes the
$\unicode[STIX]{x1D6F4}_{m}$
that permutes the
![]() $a_{i}$
groups of the form
$a_{i}$
groups of the form
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}}$
sitting inside
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}_{i}}$
sitting inside
![]() $\unicode[STIX]{x1D6F4}_{m}$
.
$\unicode[STIX]{x1D6F4}_{m}$
.
Proposition 4.16. The canonical map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
is injective and a rational isomorphism.
Proof. This is a basic application of HKR-character theory [Reference Hopkins, Kuhn and RavenelHKR00]. It is clear that the map is an isomorphism after base change to
![]() $C_{0}^{\ast }$
. The resulting ring is the ring of
$C_{0}^{\ast }$
. The resulting ring is the ring of
![]() $C_{0}^{\ast }$
-valued functions on the set
$C_{0}^{\ast }$
-valued functions on the set
 $$\begin{eqnarray}\text{Sum}_{m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})=\underset{\unicode[STIX]{x1D706}\vdash m}{\coprod }\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Sum}_{m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})=\underset{\unicode[STIX]{x1D706}\vdash m}{\coprod }\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}).\end{eqnarray}$$
But
![]() $C_{0}^{\ast }$
is a faithfully flat
$C_{0}^{\ast }$
is a faithfully flat
![]() $p^{-1}E_{n}^{\ast }$
-algebra, so the map is a rational isomorphism.◻
$p^{-1}E_{n}^{\ast }$
-algebra, so the map is a rational isomorphism.◻
Most of the results in §§ 4.2 and 4.3 will go into the proof of the next theorem. We will use the method of the proof twice more in Theorem 4.18 and Proposition 4.24. The idea of the proof is the following. We begin with a short exact sequence with a torsion cokernel. We will apply character theory to height 1 and use faithful flatness to get a short exact sequence in
![]() $L_{1}$
-cohomology. In this case, the cokernel will be a product of cokernels of maps. The sorts of maps that can occur are bounded by the number of centralizers of tuples of commuting elements in
$L_{1}$
-cohomology. In this case, the cokernel will be a product of cokernels of maps. The sorts of maps that can occur are bounded by the number of centralizers of tuples of commuting elements in
![]() $\unicode[STIX]{x1D6F4}_{m}$
. However,
$\unicode[STIX]{x1D6F4}_{m}$
. However,
![]() $F_{1}$
depends on
$F_{1}$
depends on
![]() $n$
, so we do not have complete control over the cokernel as
$n$
, so we do not have complete control over the cokernel as
![]() $n$
varies. We will extend to
$n$
varies. We will extend to
![]() $\bar{F}_{1}$
and then use faithful flatness to change the product of maps to a product of maps in
$\bar{F}_{1}$
and then use faithful flatness to change the product of maps to a product of maps in
![]() $K_{p}$
-cohomology. Now we are in a situation that is height independent, the number of maps that can appear in the product is bounded, and the cokernel of each map is bounded torsion.
$K_{p}$
-cohomology. Now we are in a situation that is height independent, the number of maps that can appear in the product is bounded, and the cokernel of each map is bounded torsion.
Theorem 4.17. The cokernel of the map
 $$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\end{eqnarray}$$
is torsion with exponent bounded independently of the height
![]() $n$
.
$n$
.
Proof. Note that both the source and the target are finitely generated free
![]() $E_{n}^{\ast }$
-modules and the map is an injection. The cokernel
$E_{n}^{\ast }$
-modules and the map is an injection. The cokernel
 $\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m})$
is a torsion
$\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m})$
is a torsion
![]() $E_{n}^{\ast }$
-module. We will repeatedly base change the short exact sequence
$E_{n}^{\ast }$
-module. We will repeatedly base change the short exact sequence
 $$\begin{eqnarray}0\overset{}{\longrightarrow }E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\overset{}{\longrightarrow }\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }0\end{eqnarray}$$
$$\begin{eqnarray}0\overset{}{\longrightarrow }E_{n}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{E_{n}})\overset{}{\longrightarrow }\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }0\end{eqnarray}$$
to prove the result. Base change to
![]() $C_{1}^{\ast }$
(a flat
$C_{1}^{\ast }$
(a flat
![]() $E_{n}^{\ast }$
-algebra) and (4.3) give the short exact sequence
$E_{n}^{\ast }$
-algebra) and (4.3) give the short exact sequence
 $$\begin{eqnarray}\displaystyle \underset{[\unicode[STIX]{x1D6FD}]\in \text{Hom}(\mathbb{Z}_{p}^{n-1},\unicode[STIX]{x1D6F4}_{m})/\sim }{\prod }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD})) & \overset{}{\longrightarrow } & \displaystyle \underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{C_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\nonumber\\ \displaystyle & \overset{}{\longrightarrow } & \displaystyle C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underset{[\unicode[STIX]{x1D6FD}]\in \text{Hom}(\mathbb{Z}_{p}^{n-1},\unicode[STIX]{x1D6F4}_{m})/\sim }{\prod }C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD})) & \overset{}{\longrightarrow } & \displaystyle \underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{C_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\nonumber\\ \displaystyle & \overset{}{\longrightarrow } & \displaystyle C_{1}^{\ast }\otimes _{L_{1}^{\ast }}L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\nonumber\end{eqnarray}$$
Here we have used the fact that the scheme classifying subgroups behaves well under base change ([Reference StapletonSta15, Theorem 3.11] is particularly relevant). Corollary 4.10 implies that the exponent of the torsion cannot have changed. By faithful flatness (Proposition 4.9), we may remove the
![]() $C_{1}^{\ast }$
without changing the exponent of the torsion. Thus we arrive at the short exact sequence
$C_{1}^{\ast }$
without changing the exponent of the torsion. Thus we arrive at the short exact sequence
 $$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }L_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{L_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }L_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{L_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
Because the first and second terms are finitely generated and free, we may apply Corollary 4.10 to base change (4.4) to
![]() $F_{1}^{\ast }$
without changing the exponent of
$F_{1}^{\ast }$
without changing the exponent of
 $L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(A)$
. We may then further base change to
$L_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(A)$
. We may then further base change to
![]() $\bar{F}_{1}^{\ast }$
(which is faithfully flat over
$\bar{F}_{1}^{\ast }$
(which is faithfully flat over
![]() $F_{1}^{\ast }$
by Proposition 4.12), obtaining
$F_{1}^{\ast }$
by Proposition 4.12), obtaining
 $$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }\bar{F}_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{\bar{F}_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }\bar{F}_{1}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{\bar{F}_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
Now Proposition 4.13 gives the short exact sequence
 $$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{\bar{F}_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{\bar{F}_{1}}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
By the naturality of the equivalence, the first map in the sequence is induced by restriction maps. Let
 $$\begin{eqnarray}M_{A,n}=\text{Cok}\biggl(\underset{[\unicode[STIX]{x1D6FD}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\biggr);\end{eqnarray}$$
$$\begin{eqnarray}M_{A,n}=\text{Cok}\biggl(\underset{[\unicode[STIX]{x1D6FD}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\biggr);\end{eqnarray}$$
then
 $$\begin{eqnarray}\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}M_{A,n}\cong \bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\bar{F}_{1}^{\ast }\otimes _{K_{p}^{\ast }}M_{A,n}\cong \bar{F}_{1}^{\ast }\otimes _{E_{n}^{\ast }}\text{Cok}_{E_{n}}(\unicode[STIX]{x1D6F4}_{m}).\end{eqnarray}$$
By Proposition 4.9, it suffices to show that the torsion in
![]() $M_{A,n}$
is independent of
$M_{A,n}$
is independent of
![]() $n$
. The map
$n$
. The map
 $$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\end{eqnarray}$$
$$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FD}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FD}))\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }\unicode[STIX]{x1D6E4}\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\end{eqnarray}$$
is the ring of functions on the canonical map
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D706}\vdash m}{\coprod }\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{f}{\longrightarrow }\text{Spec}(K_{p}^{\ast }({\mathcal{L}}^{n-1}B\unicode[STIX]{x1D6F4}_{m})).\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D706}\vdash m}{\coprod }\,\text{Sub}_{\unicode[STIX]{x1D706}\vdash m}(\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{f}{\longrightarrow }\text{Spec}(K_{p}^{\ast }({\mathcal{L}}^{n-1}B\unicode[STIX]{x1D6F4}_{m})).\end{eqnarray}$$
There is a commutative triangle

where
 $$\begin{eqnarray}\text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})=\biggl\{\bigoplus _{i}H_{i}\;\biggm\vert\;H_{i}\subset \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}~\text{and}~\mathop{\sum }_{i}|H_{i}|\leqslant m\biggr\}\end{eqnarray}$$
$$\begin{eqnarray}\text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})=\biggl\{\bigoplus _{i}H_{i}\;\biggm\vert\;H_{i}\subset \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}~\text{and}~\mathop{\sum }_{i}|H_{i}|\leqslant m\biggr\}\end{eqnarray}$$
is the set of formal sums of subgroups in
 $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
with order no greater than
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
with order no greater than
![]() $m$
. For each element
$m$
. For each element
 $\unicode[STIX]{x1D6FC}\in \text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
, the map that lives over
$\unicode[STIX]{x1D6FC}\in \text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
, the map that lives over
![]() $\unicode[STIX]{x1D6FC}$
is a rational isomorphism (and an injection after applying
$\unicode[STIX]{x1D6FC}$
is a rational isomorphism (and an injection after applying
![]() $\unicode[STIX]{x1D6E4}(-)$
). Thus it suffices to prove that, regardless of the choice of
$\unicode[STIX]{x1D6E4}(-)$
). Thus it suffices to prove that, regardless of the choice of
![]() $n$
, there are only finitely many different maps that can appear as fibers. This is essentially a consequence of the fact that there are only finitely many groups that are centralizers of
$n$
, there are only finitely many different maps that can appear as fibers. This is essentially a consequence of the fact that there are only finitely many groups that are centralizers of
![]() $\unicode[STIX]{x1D6F4}_{m}$
.
$\unicode[STIX]{x1D6F4}_{m}$
.
To make this precise, note that there is an action of
 $\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
on the triangle. This action must send the map over
$\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
on the triangle. This action must send the map over
 $\unicode[STIX]{x1D6FC}\in \text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
to a map with the same exponent of the torsion in the cokernel. The action of
$\unicode[STIX]{x1D6FC}\in \text{Sum}_{{\leqslant}m}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
to a map with the same exponent of the torsion in the cokernel. The action of
 $\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
is compatible with the inclusion of triangles induced by the inclusion of
$\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
is compatible with the inclusion of triangles induced by the inclusion of
 $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}\overset{}{\longrightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
as the first
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}\overset{}{\longrightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
as the first
![]() $n-1$
summands. For
$n-1$
summands. For
![]() $n$
large enough, any sum of subgroups of size less than or equal to
$n$
large enough, any sum of subgroups of size less than or equal to
![]() $m$
in
$m$
in
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
is isomorphic to a sum of subgroups in
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n}$
is isomorphic to a sum of subgroups in
 $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
under this action, and this finishes the proof.◻
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
under this action, and this finishes the proof.◻
It is worth noting that this could probably be factored further using Strickland’s schemes called
![]() $\text{Type}$
and [Reference StricklandStr97, Theorem 12.4].
$\text{Type}$
and [Reference StricklandStr97, Theorem 12.4].
Now we turn our attention to an analogous theorem for level structures. The theory of level structures for a formal group is developed in [Reference StricklandStr97]. We make use of it now because there is a close relationship between
 $E_{n}^{\ast }(BH)/I$
and
$E_{n}^{\ast }(BH)/I$
and
 $\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
, where
$\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
, where
![]() $H^{\ast }$
is the Pontryagin dual of
$H^{\ast }$
is the Pontryagin dual of
![]() $H$
. In [Reference Ando, Hopkins and StricklandAHS04], it is proved that the image of
$H$
. In [Reference Ando, Hopkins and StricklandAHS04], it is proved that the image of
 $E_{n}^{\ast }(BH)/I$
in
$E_{n}^{\ast }(BH)/I$
in
 $\mathbb{Q}\otimes E_{n}^{\ast }(BH)/I$
is canonically isomorphic to
$\mathbb{Q}\otimes E_{n}^{\ast }(BH)/I$
is canonically isomorphic to
 $\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
.
$\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
.
Theorem 4.18. For
![]() $A$
a finite abelian group, the cokernel of the map
$A$
a finite abelian group, the cokernel of the map
 $$\begin{eqnarray}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})\end{eqnarray}$$
is torsion with exponent bounded independently of the height
![]() $n$
.
$n$
.
Proof. Since the argument is similar to the proof of Theorem 4.17, we only point out the differences. We can again reduce to showing that the torsion in
 $$\begin{eqnarray}M_{A,n}=\text{Cok}\biggl(\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\biggr)\end{eqnarray}$$
$$\begin{eqnarray}M_{A,n}=\text{Cok}\biggl(\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\biggr)\end{eqnarray}$$
has exponent independent of
![]() $n$
. To this end, note that the map
$n$
. To this end, note that the map
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\end{eqnarray}$$
is obtained by taking global sections of the canonical map
 $$\begin{eqnarray}\underset{H\subset A}{\coprod }\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{f}{\longrightarrow }\text{Hom}(A^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}).\end{eqnarray}$$
$$\begin{eqnarray}\underset{H\subset A}{\coprod }\text{Level}(H^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{f}{\longrightarrow }\text{Hom}(A^{\ast },\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}).\end{eqnarray}$$
It is a product of ring maps since we have the commutative triangle

and
 $\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\cong \text{Hom}(\mathbb{Z}_{p}^{n-1},A)$
is a set and thus disconnects the horizontal map. The diagonal arrow sends a level structure
$\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\cong \text{Hom}(\mathbb{Z}_{p}^{n-1},A)$
is a set and thus disconnects the horizontal map. The diagonal arrow sends a level structure
 $H^{\ast }{\hookrightarrow}\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
to the composite
$H^{\ast }{\hookrightarrow}\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}$
to the composite
 $$\begin{eqnarray}A^{\ast }{\twoheadrightarrow}H^{\ast }{\hookrightarrow}\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}{\twoheadrightarrow}\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}A^{\ast }{\twoheadrightarrow}H^{\ast }{\hookrightarrow}\mathbb{G}_{m}\oplus \mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}{\twoheadrightarrow}\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1}.\end{eqnarray}$$
Let
![]() $f_{\unicode[STIX]{x1D6FD}}$
be the fiber over
$f_{\unicode[STIX]{x1D6FD}}$
be the fiber over
![]() $\unicode[STIX]{x1D6FD}$
. It is a map of schemes. It is clear that there is an action of
$\unicode[STIX]{x1D6FD}$
. It is a map of schemes. It is clear that there is an action of
 $\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
on the triangle above. This implies that the fibers over maps
$\text{Aut}(\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
on the triangle above. This implies that the fibers over maps
 $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in \text{Hom}(\mathbb{Z}_{p}^{n-1},A)$
with
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in \text{Hom}(\mathbb{Z}_{p}^{n-1},A)$
with
 $\text{im}\,\unicode[STIX]{x1D6FD}=\text{im}\,\unicode[STIX]{x1D6FD}^{\prime }$
are isomorphic. Hence the exponent of the cokernel of
$\text{im}\,\unicode[STIX]{x1D6FD}=\text{im}\,\unicode[STIX]{x1D6FD}^{\prime }$
are isomorphic. Hence the exponent of the cokernel of
![]() $\unicode[STIX]{x1D6E4}(f_{\unicode[STIX]{x1D6FD}})$
equals the exponent of the cokernel of
$\unicode[STIX]{x1D6E4}(f_{\unicode[STIX]{x1D6FD}})$
equals the exponent of the cokernel of
![]() $\unicode[STIX]{x1D6E4}(f_{\unicode[STIX]{x1D6FD}^{\prime }})$
. Adding another
$\unicode[STIX]{x1D6E4}(f_{\unicode[STIX]{x1D6FD}^{\prime }})$
. Adding another
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}^{}$
to the constant étale part does not affect this in the sense that the induced inclusion
$\mathbb{Q}_{p}/\mathbb{Z}_{p}^{}$
to the constant étale part does not affect this in the sense that the induced inclusion
 $$\begin{eqnarray}\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})\overset{}{\longrightarrow }\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})\end{eqnarray}$$
lifts to an inclusion of triangles. As
![]() $n$
increases above the number of generators of
$n$
increases above the number of generators of
![]() $A$
,
$A$
,
 $e(M_{A,n})$
remains constant. The fibers over all of the maps in
$e(M_{A,n})$
remains constant. The fibers over all of the maps in
 $\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})$
are isomorphic to the fibers over maps that were already there in
$\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n})$
are isomorphic to the fibers over maps that were already there in
 $\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
. Thus the exponent of the torsion in
$\text{Hom}(A^{\ast },\mathbb{Q}_{p}/\mathbb{Z}_{p}^{n-1})$
. Thus the exponent of the torsion in
![]() $M_{A,n}$
is bounded independently of
$M_{A,n}$
is bounded independently of
![]() $n$
.◻
$n$
.◻
The proof of the following result, due to Jeremy Hahn, is given in the appendix.
Proposition 4.19. Let
![]() $H$
be a finite abelian group. The exponent of the torsion in
$H$
be a finite abelian group. The exponent of the torsion in
 $$\begin{eqnarray}E_{n}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(BH)/I\end{eqnarray}$$
is bounded independently of the height
![]() $n$
.
$n$
.
Corollary 4.20. If
![]() $A$
is a finite abelian group, then the map
$A$
is a finite abelian group, then the map
 $$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\end{eqnarray}$$
is a rational isomorphism.
Proof. Consider the composite
 $$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}).\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BA)\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }E_{n}^{\ast }(BH)/I\overset{}{\longrightarrow }\underset{n}{\prod }\underset{H\subseteq A}{\prod }\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}).\end{eqnarray}$$
By Proposition 4.19 the second map is a rational isomorphism, and by Theorem 4.18 the composite is a rational isomorphism. Thus the first map is a rational isomorphism. ◻
4.5
 $\mathit{BP}$
-cohomology of abelian and symmetric groups
$\mathit{BP}$
-cohomology of abelian and symmetric groups
We show that the rational decomposition of Theorem 4.17 extends to a rational decomposition of
![]() $\mathit{BP}$
-cohomology.
$\mathit{BP}$
-cohomology.
Lemma 4.21. Let
![]() $G$
be a finite group and let
$G$
be a finite group and let
 $H_{1},\ldots ,H_{m}\subset G$
be subgroups. Let
$H_{1},\ldots ,H_{m}\subset G$
be subgroups. Let
![]() $I$
be the ideal generated by the image of the transfer maps along the inclusions
$I$
be the ideal generated by the image of the transfer maps along the inclusions
 $H_{i}\subset G$
. There is a split inclusion
$H_{i}\subset G$
. There is a split inclusion

which is compatible with the map of Corollary 3.4.
Proof. Let
 $H_{1},\ldots ,H_{m}\subseteq G$
be subgroups and consider the commutative diagram
$H_{1},\ldots ,H_{m}\subseteq G$
be subgroups and consider the commutative diagram

where
![]() $I$
denotes the transfer ideal generated by
$I$
denotes the transfer ideal generated by
 $H_{1},\ldots ,H_{m}$
. The dashed arrows are the retracts which exist by Corollary 3.4, and the transfers make the left square commute by naturality and the fact that the splitting exists on the level of spectra. Therefore, the maps between the quotients exist and the resulting retract is compatible with the rest of the diagram. ◻
$H_{1},\ldots ,H_{m}$
. The dashed arrows are the retracts which exist by Corollary 3.4, and the transfers make the left square commute by naturality and the fact that the splitting exists on the level of spectra. Therefore, the maps between the quotients exist and the resulting retract is compatible with the rest of the diagram. ◻
Consequently, for any symmetric group
![]() $\unicode[STIX]{x1D6F4}_{m}$
, we have a commutative diagram
$\unicode[STIX]{x1D6F4}_{m}$
, we have a commutative diagram

In Theorem 4.17 we showed that the middle horizontal map is an isomorphism. Now it is an easy consequence that the top map is an isomorphism, stated in the next corollary.
Corollary 4.22. There is a rational isomorphism
 $$\begin{eqnarray}\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }(\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{m})\overset{}{\longrightarrow }\underset{\unicode[STIX]{x1D706}\vdash m}{\prod }(\mathit{BP}^{\ast }(B\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}})/I_{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6F4}_{\text{}\underline{a}}}.\end{eqnarray}$$
Corollary 4.23. There is a rational isomorphism
 $$\begin{eqnarray}\mathit{BP}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\mathit{BP}^{\ast }(BH)/I.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(BA)\overset{}{\longrightarrow }\underset{H\subseteq A}{\prod }\mathit{BP}^{\ast }(BH)/I.\end{eqnarray}$$
Proof. The argument is similar to the proof of Corollary 4.22. ◻
4.6 Artin induction for
 $\mathit{BP}$
$\mathit{BP}$
It is not hard to use the methods of the previous subsections to prove an Artin induction theorem for
![]() $\mathit{BP}$
. We do this by transferring the result for
$\mathit{BP}$
. We do this by transferring the result for
![]() $E_{n}$
(due to [Reference Hopkins, Kuhn and RavenelHKR00]) to
$E_{n}$
(due to [Reference Hopkins, Kuhn and RavenelHKR00]) to
![]() $\mathit{BP}$
. Stronger results than this have been known for some time (e.g. [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A] applies to all complex oriented theories).
$\mathit{BP}$
. Stronger results than this have been known for some time (e.g. [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A] applies to all complex oriented theories).
Let
![]() ${\mathcal{A}}(G)$
be the full subcategory of the orbit category of
${\mathcal{A}}(G)$
be the full subcategory of the orbit category of
![]() $G$
consisting of quotients of the form
$G$
consisting of quotients of the form
![]() $G/A$
, where
$G/A$
, where
![]() $A$
is an abelian
$A$
is an abelian
![]() $p$
-group.
$p$
-group.
Proposition 4.24. If
![]() $G$
is a good group, the canonical map
$G$
is a good group, the canonical map
 $$\begin{eqnarray}\mathit{BP}^{\ast }(BG)\overset{}{\longrightarrow }\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(BG)\overset{}{\longrightarrow }\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\end{eqnarray}$$
is a rational isomorphism.
Proof. Because
![]() $G$
is good there is no integral torsion in
$G$
is good there is no integral torsion in
 $\mathit{BP}^{\ast }(BG)$
. This follows immediately from the injection
$\mathit{BP}^{\ast }(BG)$
. This follows immediately from the injection
 $$\begin{eqnarray}\mathit{BP}^{\ast }(BG){\hookrightarrow}\underset{n}{\prod }E_{n}^{\ast }(BG).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(BG){\hookrightarrow}\underset{n}{\prod }E_{n}^{\ast }(BG).\end{eqnarray}$$
Character theory for good groups [Reference Hopkins, Kuhn and RavenelHKR00] implies that the natural map
 $$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BG)\overset{}{\longrightarrow }\mathop{\prod }_{n>0}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}E_{n}^{\ast }(BA)\end{eqnarray}$$
$$\begin{eqnarray}\underset{n}{\prod }E_{n}^{\ast }(BG)\overset{}{\longrightarrow }\mathop{\prod }_{n>0}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}E_{n}^{\ast }(BA)\end{eqnarray}$$
is injective and, since limits of split injections are split injections, the canonical map
 $$\begin{eqnarray}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\overset{}{\longrightarrow }\mathop{\prod }_{n>0}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}E_{n}^{\ast }(BA)\end{eqnarray}$$
$$\begin{eqnarray}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\overset{}{\longrightarrow }\mathop{\prod }_{n>0}\lim _{A\in {\mathcal{A}}({\mathcal{G}})}E_{n}^{\ast }(BA)\end{eqnarray}$$
is injective.
We are interested in the commutative diagram

Since the left vertical arrow is injective and the second horizontal arrow on the bottom is injective, the natural map
 $$\begin{eqnarray}\mathit{BP}^{\ast }(BG)\overset{}{\longrightarrow }\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\end{eqnarray}$$
$$\begin{eqnarray}\mathit{BP}^{\ast }(BG)\overset{}{\longrightarrow }\lim _{A\in {\mathcal{A}}({\mathcal{G}})}\mathit{BP}^{\ast }(BA)\end{eqnarray}$$
is injective. This implies that the top sequence of maps is short exact. Therefore it suffices to prove that
![]() $C_{\mathit{BP}}$
is torsion.
$C_{\mathit{BP}}$
is torsion.
This means that it suffices to show that
![]() $C_{E_{n}}$
has exponent bounded independently of the height
$C_{E_{n}}$
has exponent bounded independently of the height
![]() $n$
. By [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A], the abelian group
$n$
. By [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A], the abelian group
![]() $C_{E_{n}}$
is torsion.
$C_{E_{n}}$
is torsion.
Note the map of short exact sequences

where
![]() $D_{E_{n}}$
is the cokernel. The first two vertical arrows are injections (the first is an equality), so the right vertical arrow is an injection. Therefore it suffices to show that the exponent of the torsion in
$D_{E_{n}}$
is the cokernel. The first two vertical arrows are injections (the first is an equality), so the right vertical arrow is an injection. Therefore it suffices to show that the exponent of the torsion in
![]() $D_{E_{n}}$
is bounded independently of
$D_{E_{n}}$
is bounded independently of
![]() $n$
.
$n$
.
To bound the torsion, we apply character theory to height 1. Since
![]() $C_{1}^{\ast }$
is a flat
$C_{1}^{\ast }$
is a flat
![]() $E_{n}^{\ast }$
-module, we get a short exact sequence
$E_{n}^{\ast }$
-module, we get a short exact sequence
 $$\begin{eqnarray}C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BG){\hookrightarrow}\underset{A\subset G}{\prod }C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }C_{1}^{\ast }\otimes _{E_{n}^{\ast }}D_{E_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BG){\hookrightarrow}\underset{A\subset G}{\prod }C_{1}^{\ast }\otimes _{E_{n}^{\ast }}E_{n}^{\ast }(BA)\overset{}{\longrightarrow }C_{1}^{\ast }\otimes _{E_{n}^{\ast }}D_{E_{n}}.\end{eqnarray}$$
Now we can follow the argument in Theorem 4.18 to reduce to
![]() $p$
-adic
$p$
-adic
![]() $K$
-theory. This leads to considering the cokernel of the injection
$K$
-theory. This leads to considering the cokernel of the injection
 $$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FC}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC})){\hookrightarrow}\underset{A\subset G}{\prod }\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA).\end{eqnarray}$$
$$\begin{eqnarray}\underset{[\unicode[STIX]{x1D6FC}]}{\prod }K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC})){\hookrightarrow}\underset{A\subset G}{\prod }\underset{\unicode[STIX]{x1D6FD}}{\prod }K_{p}^{\ast }(BA).\end{eqnarray}$$
If we fix a conjugacy class
 $[\unicode[STIX]{x1D6FC}:\mathbb{Z}_{p}^{n-1}\rightarrow G]$
, then there is a map
$[\unicode[STIX]{x1D6FC}:\mathbb{Z}_{p}^{n-1}\rightarrow G]$
, then there is a map
 $K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC}))\overset{}{\longrightarrow }K_{p}^{\ast }(BA)$
when the composite
$K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC}))\overset{}{\longrightarrow }K_{p}^{\ast }(BA)$
when the composite
 $$\begin{eqnarray}\mathbb{Z}_{p}^{n-1}\overset{\unicode[STIX]{x1D6FD}}{\longrightarrow }A\subset G\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}_{p}^{n-1}\overset{\unicode[STIX]{x1D6FD}}{\longrightarrow }A\subset G\end{eqnarray}$$
is conjugate to
![]() $\unicode[STIX]{x1D6FC}$
. In that case
$\unicode[STIX]{x1D6FC}$
. In that case
 $A\subset C(\text{im}\,\unicode[STIX]{x1D6FC})$
. Let
$A\subset C(\text{im}\,\unicode[STIX]{x1D6FC})$
. Let
 $i_{H}:A\subset G$
be the inclusion. The map out of the factor corresponding to
$i_{H}:A\subset G$
be the inclusion. The map out of the factor corresponding to
![]() $[\unicode[STIX]{x1D6FC}]$
is
$[\unicode[STIX]{x1D6FC}]$
is
 $$\begin{eqnarray}K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC}))\overset{}{\longrightarrow }\underset{A\subset G}{\prod }\biggl(\,\underset{\{\unicode[STIX]{x1D6FD}|[i_{H}\unicode[STIX]{x1D6FD}]=[\unicode[STIX]{x1D6FC}]\}}{\prod }K_{p}^{\ast }(BA)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}K_{p}^{\ast }(BC(\text{im}\,\unicode[STIX]{x1D6FC}))\overset{}{\longrightarrow }\underset{A\subset G}{\prod }\biggl(\,\underset{\{\unicode[STIX]{x1D6FD}|[i_{H}\unicode[STIX]{x1D6FD}]=[\unicode[STIX]{x1D6FC}]\}}{\prod }K_{p}^{\ast }(BA)\biggr).\end{eqnarray}$$
This map is an injection, although it may not be the case that every abelian subgroup of
 $C(\text{im}\,\unicode[STIX]{x1D6FC})$
is represented in the codomain. Abelian subgroups of
$C(\text{im}\,\unicode[STIX]{x1D6FC})$
is represented in the codomain. Abelian subgroups of
![]() $G$
that are conjugate to abelian subgroups of
$G$
that are conjugate to abelian subgroups of
 $C(\text{im}\,\unicode[STIX]{x1D6FC})$
may appear as well. Also, subgroups may appear multiple times. However, Proposition 4.8 implies that repeat subgroups do not contribute to the exponent of the torsion in the cokernel. Finally, since there are only a finite number of abelian subgroups of
$C(\text{im}\,\unicode[STIX]{x1D6FC})$
may appear as well. Also, subgroups may appear multiple times. However, Proposition 4.8 implies that repeat subgroups do not contribute to the exponent of the torsion in the cokernel. Finally, since there are only a finite number of abelian subgroups of
 $C(\text{im}\,\unicode[STIX]{x1D6FC})$
(or abelian subgroups of
$C(\text{im}\,\unicode[STIX]{x1D6FC})$
(or abelian subgroups of
![]() $G$
that may be conjugated into
$G$
that may be conjugated into
 $C(\text{im}\,\unicode[STIX]{x1D6FC})$
), the exponent of the torsion in the cokernel must be bounded by the maximal exponent of this finite number of options.◻
$C(\text{im}\,\unicode[STIX]{x1D6FC})$
), the exponent of the torsion in the cokernel must be bounded by the maximal exponent of this finite number of options.◻
This subsection is not just an exercise. Artin induction for
![]() $E_{n}$
can be proved independently of [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A] by using character theory. The retract theorem now allows us to bootstrap to
$E_{n}$
can be proved independently of [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A] by using character theory. The retract theorem now allows us to bootstrap to
![]() $\mathit{BP}$
. It is not hard to imagine moving from there to any Landweber flat (or perhaps complex oriented) theory. One might hope that this could provide an independent proof of [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A], at least when
$\mathit{BP}$
. It is not hard to imagine moving from there to any Landweber flat (or perhaps complex oriented) theory. One might hope that this could provide an independent proof of [Reference Hopkins, Kuhn and RavenelHKR00, Theorem A], at least when
![]() $G$
is good and
$G$
is good and
![]() $X=\ast$
.
$X=\ast$
.
Acknowledgements
We would like to thank Tyler Lawson, Eric Peterson, Charles Rezk, Tomer Schlank and Neil Strickland for helpful conversations, and the Max Planck Institute for Mathematics for its hospitality. Jeremy Hahn thanks Danny Shi and Mike Hopkins for instilling him with enough practical knowledge of level structures to contribute to this project.
Appendix A Proof of Proposition 4.19
Jeremy Hahn
We recall our notational conventions. Let
![]() $H$
be a finite abelian group,
$H$
be a finite abelian group,
![]() $n$
a positive integer, and
$n$
a positive integer, and
![]() $E_{n}$
a height
$E_{n}$
a height
![]() $n$
Morava
$n$
Morava
![]() $E$
-theory at the prime
$E$
-theory at the prime
![]() $p$
. We use
$p$
. We use
![]() $H^{\ast }$
to denote the Pontryagin dual group
$H^{\ast }$
to denote the Pontryagin dual group
 $\text{Hom}(H,S^{1})$
. In the ring
$\text{Hom}(H,S^{1})$
. In the ring
 $E_{n}^{\ast }(BH)$
, denote by
$E_{n}^{\ast }(BH)$
, denote by
![]() $I$
the ideal generated by the images of transfers from proper subgroups of
$I$
the ideal generated by the images of transfers from proper subgroups of
![]() $H$
. We let
$H$
. We let
![]() $R_{n}$
denote the quotient ring
$R_{n}$
denote the quotient ring
 $E_{n}^{\ast }(BH)/I$
.
$E_{n}^{\ast }(BH)/I$
.
Algebro-geometrically,
 $E_{n}^{\ast }(BH)$
may be interpreted as global sections of the affine formal scheme
$E_{n}^{\ast }(BH)$
may be interpreted as global sections of the affine formal scheme
 $\text{Hom}(H^{\ast },\mathbb{G}_{E_{n}})$
. The closed subscheme with global sections
$\text{Hom}(H^{\ast },\mathbb{G}_{E_{n}})$
. The closed subscheme with global sections
 $R_{n}=E_{n}^{\ast }(BH)/I$
is not as well behaved as one might hope. In particular, for almost no values of
$R_{n}=E_{n}^{\ast }(BH)/I$
is not as well behaved as one might hope. In particular, for almost no values of
![]() $H$
and
$H$
and
![]() $n$
is
$n$
is
![]() $R_{n}$
an integral domain. Let
$R_{n}$
an integral domain. Let
![]() $T_{n}$
denote the ideal of
$T_{n}$
denote the ideal of
![]() $p$
-power torsion in
$p$
-power torsion in
![]() $R_{n}$
(i.e.
$R_{n}$
(i.e.
![]() $x\in T_{n}$
if and only if
$x\in T_{n}$
if and only if
 $p^{a}x=0$
for some positive integer
$p^{a}x=0$
for some positive integer
![]() $a$
). In [Reference Ando, Hopkins and StricklandAHS04], Ando et al. identified the further quotient
$a$
). In [Reference Ando, Hopkins and StricklandAHS04], Ando et al. identified the further quotient
![]() $R_{n}/T_{n}$
with an object of algebro-geometric significance, namely the global sections of the formal scheme of Drinfeld level structures
$R_{n}/T_{n}$
with an object of algebro-geometric significance, namely the global sections of the formal scheme of Drinfeld level structures
 $\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
. In [Reference DrinfeldDri74], Drinfeld proved that
$\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
. In [Reference DrinfeldDri74], Drinfeld proved that
 $\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
is a regular local ring, so
$\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
is a regular local ring, so
![]() $R_{n}/T_{n}$
is in fact very well behaved.
$R_{n}/T_{n}$
is in fact very well behaved.
The Ando–Hopkins–Strickland result allows one to identify
 $\mathbb{Q}\otimes E_{n}^{\ast }(BH)/I$
with
$\mathbb{Q}\otimes E_{n}^{\ast }(BH)/I$
with
 $\mathbb{Q}\otimes \unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
. In this appendix, our goal is to extend this to an isomorphism
$\mathbb{Q}\otimes \unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}})$
. In this appendix, our goal is to extend this to an isomorphism
 $$\begin{eqnarray}\mathbb{Q}\otimes \mathop{\prod }_{n>0}E_{n}^{\ast }(BH)/I\cong \mathbb{Q}\otimes \mathop{\prod }_{n>0}\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}\otimes \mathop{\prod }_{n>0}E_{n}^{\ast }(BH)/I\cong \mathbb{Q}\otimes \mathop{\prod }_{n>0}\unicode[STIX]{x1D6E4}\text{Level}(H^{\ast },\mathbb{G}_{E_{n}}).\end{eqnarray}$$
The isomorphism follows immediately from the following proposition, whose proof occupies the remainder of the appendix.
Proposition A.1. There is a positive integer
![]() $k$
, depending on
$k$
, depending on
![]() $H$
but not depending on
$H$
but not depending on
![]() $n$
, such that
$n$
, such that
 $p^{k}T_{n}=0\subset R_{n}$
.
$p^{k}T_{n}=0\subset R_{n}$
.
In other words, we claim that the exponent of the
![]() $p$
-power torsion in
$p$
-power torsion in
 $E_{n}^{\ast }(BH)/I_{n}$
may be bounded independently of the height
$E_{n}^{\ast }(BH)/I_{n}$
may be bounded independently of the height
![]() $n$
.
$n$
.
We can make two immediate reductions. First, note that
![]() $H$
may be written as a direct sum of a
$H$
may be written as a direct sum of a
![]() $p$
-group and a group of order prime to
$p$
-group and a group of order prime to
![]() $p$
, the prime-to-
$p$
, the prime-to-
![]() $p$
part having no contribution to
$p$
part having no contribution to
![]() $E$
-theory. Furthermore, since
$E$
-theory. Furthermore, since
 $E_{n}^{\ast }(BH)$
is Noetherian, the exponent of the
$E_{n}^{\ast }(BH)$
is Noetherian, the exponent of the
![]() $p$
-power torsion in
$p$
-power torsion in
![]() $R_{n}$
is bounded for any fixed
$R_{n}$
is bounded for any fixed
![]() $n$
. In light of these facts, for the remainder of the appendix we assume that
$n$
. In light of these facts, for the remainder of the appendix we assume that
![]() $H$
is a
$H$
is a
![]() $p$
-group and study
$p$
-group and study
 $E_{n}^{\ast }(BH)$
for
$E_{n}^{\ast }(BH)$
for
![]() $n$
larger than the
$n$
larger than the
![]() $p$
-rank of
$p$
-rank of
![]() $H$
.
$H$
.
Since
 $E_{n}^{\ast }(BH)\cong \unicode[STIX]{x1D6E4}\text{Hom}(H^{\ast },\mathbb{G}_{E_{n}})$
, there is a natural inclusion of
$E_{n}^{\ast }(BH)\cong \unicode[STIX]{x1D6E4}\text{Hom}(H^{\ast },\mathbb{G}_{E_{n}})$
, there is a natural inclusion of
![]() $H^{\ast }$
into
$H^{\ast }$
into
 $E_{n}^{\ast }(BH)$
. This is the map that takes a character
$E_{n}^{\ast }(BH)$
. This is the map that takes a character
 $\unicode[STIX]{x1D712}:H\rightarrow S^{1}$
to the first Chern class of the induced map
$\unicode[STIX]{x1D712}:H\rightarrow S^{1}$
to the first Chern class of the induced map
 $BH\rightarrow BS^{1}$
. Composing with the projection
$BH\rightarrow BS^{1}$
. Composing with the projection
 $E_{n}^{\ast }(BH)\rightarrow R_{n}$
, we obtain a map
$E_{n}^{\ast }(BH)\rightarrow R_{n}$
, we obtain a map
 $\unicode[STIX]{x1D719}:H^{\ast }\rightarrow R_{n}$
.
$\unicode[STIX]{x1D719}:H^{\ast }\rightarrow R_{n}$
.
Lemma A.2. For each non-zero
![]() $\unicode[STIX]{x1D712}\in H^{\ast }$
,
$\unicode[STIX]{x1D712}\in H^{\ast }$
,
![]() $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
divides
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
divides
![]() $p$
in
$p$
in
![]() $R_{n}$
.
$R_{n}$
.
Proof. Suppose that
 $\unicode[STIX]{x1D712}:H\rightarrow S^{1}$
has kernel
$\unicode[STIX]{x1D712}:H\rightarrow S^{1}$
has kernel
![]() $A\subset H$
. The quotient
$A\subset H$
. The quotient
![]() $H/A$
is isomorphic to a non-trivial subgroup of
$H/A$
is isomorphic to a non-trivial subgroup of
![]() $S^{1}$
. Assume that
$S^{1}$
. Assume that
![]() $H/A$
is cyclic of order
$H/A$
is cyclic of order
![]() $p^{k}$
. It follows that the kernel of
$p^{k}$
. It follows that the kernel of
![]() $p^{k-1}\unicode[STIX]{x1D712}$
is an index-
$p^{k-1}\unicode[STIX]{x1D712}$
is an index-
![]() $p$
subgroup
$p$
subgroup
![]() $A^{\prime }$
of
$A^{\prime }$
of
![]() $H$
containing
$H$
containing
![]() $A$
. The composite of the transfer and projection
$A$
. The composite of the transfer and projection
 $$\begin{eqnarray}E_{n}^{\ast }(BA^{\prime })\rightarrow E_{n}^{\ast }(BH)\rightarrow R_{n}\end{eqnarray}$$
$$\begin{eqnarray}E_{n}^{\ast }(BA^{\prime })\rightarrow E_{n}^{\ast }(BH)\rightarrow R_{n}\end{eqnarray}$$
then sends 1 to
 $$\begin{eqnarray}\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))=\frac{[p^{k}](\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))}{[p^{k-1}](\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))},\end{eqnarray}$$
$$\begin{eqnarray}\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))=\frac{[p^{k}](\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))}{[p^{k-1}](\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))},\end{eqnarray}$$
by the corresponding formula for the transfer
 $e\subset \mathbb{Z}/p$
and the naturality of transfer. In particular,
$e\subset \mathbb{Z}/p$
and the naturality of transfer. In particular,
 $\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))=0$
in
$\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))=0$
in
![]() $R_{n}$
. But
$R_{n}$
. But
 $\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))$
is a power series in
$\langle p^{k}\rangle (\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}))$
is a power series in
![]() $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
with constant term
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
with constant term
![]() $p$
, so it follows that
$p$
, so it follows that
![]() $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
divides
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712})$
divides
![]() $p$
.◻
$p$
.◻
Suppose now that
 $$\begin{eqnarray}H\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}\times \mathbb{Z}/p^{m_{2}}\mathbb{Z}\times \cdots \times \mathbb{Z}/p^{m_{\ell }}\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}H\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}\times \mathbb{Z}/p^{m_{2}}\mathbb{Z}\times \cdots \times \mathbb{Z}/p^{m_{\ell }}\mathbb{Z},\end{eqnarray}$$
where
 $m_{1}\geqslant m_{2}\geqslant \cdots \geqslant m_{\ell }$
. We proceed to prove Proposition A.1 by induction on
$m_{1}\geqslant m_{2}\geqslant \cdots \geqslant m_{\ell }$
. We proceed to prove Proposition A.1 by induction on
![]() $\ell$
.
$\ell$
.
If
![]() $\ell =1$
, then
$\ell =1$
, then
 $H\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}$
. This case is covered in § 4.1 of this paper, but see also [Reference Ando, Hopkins and StricklandAHS04, Example 9.22].
$H\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}$
. This case is covered in § 4.1 of this paper, but see also [Reference Ando, Hopkins and StricklandAHS04, Example 9.22].
For
![]() $\ell >1$
, consider
$\ell >1$
, consider
 $$\begin{eqnarray}H^{\prime }\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}\times \mathbb{Z}/p^{m_{2}}\mathbb{Z}\times \cdots \times \mathbb{Z}/p^{m_{\ell -1}}\mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}H^{\prime }\cong \mathbb{Z}/p^{m_{1}}\mathbb{Z}\times \mathbb{Z}/p^{m_{2}}\mathbb{Z}\times \cdots \times \mathbb{Z}/p^{m_{\ell -1}}\mathbb{Z}\end{eqnarray}$$
equipped with the natural inclusion
 $H^{\prime }\subset H$
. Let
$H^{\prime }\subset H$
. Let
![]() $R_{n}^{\prime }$
denote
$R_{n}^{\prime }$
denote
 $E_{n}^{\ast }(BH^{\prime })$
modulo its ideal of transfers, and let
$E_{n}^{\ast }(BH^{\prime })$
modulo its ideal of transfers, and let
![]() $T_{n}^{\prime }$
denote the ideal of
$T_{n}^{\prime }$
denote the ideal of
![]() $p$
-power torsion in
$p$
-power torsion in
![]() $R_{n}^{\prime }$
. Finally, we use the notation
$R_{n}^{\prime }$
. Finally, we use the notation
 $\unicode[STIX]{x1D719}^{\prime }:(H^{\prime })^{\ast }\rightarrow R_{n}^{\prime }$
to denote the obvious analogue of
$\unicode[STIX]{x1D719}^{\prime }:(H^{\prime })^{\ast }\rightarrow R_{n}^{\prime }$
to denote the obvious analogue of
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
The power series ring
![]() $(R_{n}^{\prime })[\![z]\!]$
is an
$(R_{n}^{\prime })[\![z]\!]$
is an
![]() $E_{n}^{\ast }$
-algebra, so one may consider the element
$E_{n}^{\ast }$
-algebra, so one may consider the element
 $[p^{m_{\ell }}](z)$
, which we denote by
$[p^{m_{\ell }}](z)$
, which we denote by
![]() $q(z)$
. We use
$q(z)$
. We use
![]() $\bar{q}(z)$
to denote projection of
$\bar{q}(z)$
to denote projection of
![]() $q(z)$
to
$q(z)$
to
 $(R_{n}^{\prime }/T_{n}^{\prime })[\![z]\!]$
. For each
$(R_{n}^{\prime }/T_{n}^{\prime })[\![z]\!]$
. For each
 $\unicode[STIX]{x1D712}\in (H^{\prime })^{\ast }$
of order at most
$\unicode[STIX]{x1D712}\in (H^{\prime })^{\ast }$
of order at most
![]() $p^{m_{\ell }}$
, one has that
$p^{m_{\ell }}$
, one has that
 $[p^{m_{\ell }}](\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))=0$
. Since
$[p^{m_{\ell }}](\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))=0$
. Since
![]() $R_{n}^{\prime }/T_{n}^{\prime }$
is a regular local ring, and since
$R_{n}^{\prime }/T_{n}^{\prime }$
is a regular local ring, and since
![]() $n$
is larger than the rank of
$n$
is larger than the rank of
![]() $H$
, it follows that
$H$
, it follows that
![]() $\bar{q}(z)$
is divisible by
$\bar{q}(z)$
is divisible by
 $$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712})),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712})),\end{eqnarray}$$
where the product runs across all
 $\unicode[STIX]{x1D712}\in (H^{\prime })^{\ast }$
of order at most
$\unicode[STIX]{x1D712}\in (H^{\prime })^{\ast }$
of order at most
![]() $p^{m_{\ell }}$
. The quotient of
$p^{m_{\ell }}$
. The quotient of
![]() $\bar{q}(z)$
by this product may, by the Weierstrass preparation theorem, be written as a unit times a monic polynomial
$\bar{q}(z)$
by this product may, by the Weierstrass preparation theorem, be written as a unit times a monic polynomial
![]() $g(z)$
.
$g(z)$
.
The following key lemma was proved by Drinfeld [Reference DrinfeldDri74, proof of Proposition 4.3] and was realized in topology by Strickland (see [Reference StricklandStr, § 26] and [Reference StricklandStr97, § 7]).
Lemma A.3 (Drinfeld).
There is an isomorphism
 $R_{n}/T_{n}\cong (R_{n}^{\prime }/T_{n}^{\prime })[z]/g(z)$
.
$R_{n}/T_{n}\cong (R_{n}^{\prime }/T_{n}^{\prime })[z]/g(z)$
.
The coefficients of
![]() $g(z)$
lie in
$g(z)$
lie in
![]() $R_{n}^{\prime }/T_{n}^{\prime }$
and may be lifted arbitrarily to elements of
$R_{n}^{\prime }/T_{n}^{\prime }$
and may be lifted arbitrarily to elements of
![]() $R_{n}^{\prime }$
. This defines a non-canonical lift
$R_{n}^{\prime }$
. This defines a non-canonical lift
 $\tilde{g}(z)\in R_{n}^{\prime }[z]$
of
$\tilde{g}(z)\in R_{n}^{\prime }[z]$
of
![]() $g(z)$
. Lemma A.3 then implies that
$g(z)$
. Lemma A.3 then implies that
![]() $R_{n}/T_{n}$
is isomorphic to the quotient of
$R_{n}/T_{n}$
is isomorphic to the quotient of
![]() $R_{n}^{\prime }[z]$
by the ideal
$R_{n}^{\prime }[z]$
by the ideal
 $(\tilde{g}(z),T_{n}^{\prime })$
generated by
$(\tilde{g}(z),T_{n}^{\prime })$
generated by
![]() $\tilde{g}(z)$
and the elements of
$\tilde{g}(z)$
and the elements of
![]() $T_{n}^{\prime }$
. Note that
$T_{n}^{\prime }$
. Note that
![]() $R_{n}$
is already a quotient of
$R_{n}$
is already a quotient of
![]() $R_{n}^{\prime }[z]$
by the Künneth isomorphism applied to
$R_{n}^{\prime }[z]$
by the Künneth isomorphism applied to
 $E_{n}^{\ast }(BH)\cong E_{n}^{\ast }(BH^{\prime }\times B\mathbb{Z}/p^{m_{\ell }}\mathbb{Z})$
and elementary properties of transfers.
$E_{n}^{\ast }(BH)\cong E_{n}^{\ast }(BH^{\prime }\times B\mathbb{Z}/p^{m_{\ell }}\mathbb{Z})$
and elementary properties of transfers.
Example A.4. Suppose that
![]() $H$
is the group
$H$
is the group
 $\mathbb{Z}/2\times \mathbb{Z}/2\times \mathbb{Z}/2$
. Then, for sufficiently large
$\mathbb{Z}/2\times \mathbb{Z}/2\times \mathbb{Z}/2$
. Then, for sufficiently large
![]() $n$
, Lemma A.3 implies that
$n$
, Lemma A.3 implies that
 $$\begin{eqnarray}R_{n}/T_{n}\cong E_{n}^{\ast }[\![x,y,z]\!]/(\tilde{g}_{1},\tilde{g}_{2},\tilde{g}_{3}),\end{eqnarray}$$
$$\begin{eqnarray}R_{n}/T_{n}\cong E_{n}^{\ast }[\![x,y,z]\!]/(\tilde{g}_{1},\tilde{g}_{2},\tilde{g}_{3}),\end{eqnarray}$$
where:
-
–
 $\tilde{g}_{1}=[2](x)/x$
is an element defined in
$\tilde{g}_{1}=[2](x)/x$
is an element defined in
 $E_{n}^{\ast }[\![x]\!]$
;
$E_{n}^{\ast }[\![x]\!]$
; -
–
 $\tilde{g}_{2}=[2](y)/(y(y-x))$
is a lift of an element uniquely defined in
$\tilde{g}_{2}=[2](y)/(y(y-x))$
is a lift of an element uniquely defined in
 $E_{n}^{\ast }[\![x,y]\!]/\tilde{g}_{1}$
; and
$E_{n}^{\ast }[\![x,y]\!]/\tilde{g}_{1}$
; and -
–
 $\tilde{g}_{3}=[2](z)/(z(z-x)(z-y)(z-(x+\mathbb{G}y)))$
is a lift of an element defined in
$\tilde{g}_{3}=[2](z)/(z(z-x)(z-y)(z-(x+\mathbb{G}y)))$
is a lift of an element defined in
 $E_{n}^{\ast }[\![x,y,z]\!]/(\tilde{g}_{1},\tilde{g}_{2})$
.
$E_{n}^{\ast }[\![x,y,z]\!]/(\tilde{g}_{1},\tilde{g}_{2})$
.
It follows that if
![]() $w\in T_{n}$
, then
$w\in T_{n}$
, then
 $w=a_{1}\tilde{g}_{1}+a_{2}\tilde{g}_{2}+a_{3}\tilde{g}_{3}$
for some
$w=a_{1}\tilde{g}_{1}+a_{2}\tilde{g}_{2}+a_{3}\tilde{g}_{3}$
for some
 $a_{1},a_{2},a_{3}\in R_{n}$
. The arguments below will show that, regardless of the height
$a_{1},a_{2},a_{3}\in R_{n}$
. The arguments below will show that, regardless of the height
![]() $n$
,
$n$
,
 $16\tilde{g}_{1}=16\tilde{g}_{2}=16\tilde{g}_{3}=0$
, and so
$16\tilde{g}_{1}=16\tilde{g}_{2}=16\tilde{g}_{3}=0$
, and so
 $16w=0$
.
$16w=0$
.
Remark A.5. The reader familiar with [Reference Ando, Hopkins and StricklandAHS04] should be wary of a small typo in the statement of Proposition 9.15. The correct statement appears at the end of the proof of Proposition 9.15 on p. 29 of that paper. The difference between the stated and proved versions of [Reference Ando, Hopkins and StricklandAHS04, Proposition 9.15] is elucidated by the existence of elements such as
![]() $\tilde{g}_{2}$
in the above example, which annihilates
$\tilde{g}_{2}$
in the above example, which annihilates
 $y-_{\mathbb{G}_{E_{n}}}x$
in
$y-_{\mathbb{G}_{E_{n}}}x$
in
 $E^{\ast }(BH)/(\text{ann}(x),\text{ann(y)})$
but is not defined in
$E^{\ast }(BH)/(\text{ann}(x),\text{ann(y)})$
but is not defined in
 $E_{n}^{\ast }(BH)$
itself.
$E_{n}^{\ast }(BH)$
itself.
By the inductive assumption, there is an integer
![]() $k^{\prime }$
such that
$k^{\prime }$
such that
 $p^{k^{\prime }}T_{n}^{\prime }=0\subset R_{n}^{\prime }$
. As a corollary of the comments preceding Example A.4, we see that the complete proof of Proposition A.1 rests only on the following lemma.
$p^{k^{\prime }}T_{n}^{\prime }=0\subset R_{n}^{\prime }$
. As a corollary of the comments preceding Example A.4, we see that the complete proof of Proposition A.1 rests only on the following lemma.
Lemma A.6. Let
![]() $h$
denote the image of
$h$
denote the image of
![]() $\tilde{g}(z)$
under the projection
$\tilde{g}(z)$
under the projection
 $\unicode[STIX]{x1D70B}:R_{n}^{\prime }[z]\rightarrow R_{n}$
. Then there is a positive integer
$\unicode[STIX]{x1D70B}:R_{n}^{\prime }[z]\rightarrow R_{n}$
. Then there is a positive integer
![]() $r$
, independent of
$r$
, independent of
![]() $n$
, such that
$n$
, such that
 $p^{r}h=0$
.
$p^{r}h=0$
.
Proof. Let
 $\unicode[STIX]{x1D712}:H^{\prime }\rightarrow S^{1}$
denote any element of
$\unicode[STIX]{x1D712}:H^{\prime }\rightarrow S^{1}$
denote any element of
![]() $(H^{\prime })^{\ast }$
. We first claim that
$(H^{\prime })^{\ast }$
. We first claim that
 $\unicode[STIX]{x1D70B}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
divides
$\unicode[STIX]{x1D70B}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
divides
![]() $p$
in
$p$
in
![]() $R_{n}$
.
$R_{n}$
.
-
– Let
 $\unicode[STIX]{x1D712}_{1}:H\rightarrow S^{1}$
denote the composite of the projection
$\unicode[STIX]{x1D712}_{1}:H\rightarrow S^{1}$
denote the composite of the projection
 $H\rightarrow \mathbb{Z}/p^{m_{\ell }}$
with the inclusion
$H\rightarrow \mathbb{Z}/p^{m_{\ell }}$
with the inclusion
 $\mathbb{Z}/p^{m_{\ell }}\rightarrow S^{1}$
. Note that
$\mathbb{Z}/p^{m_{\ell }}\rightarrow S^{1}$
. Note that
 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1})=\unicode[STIX]{x1D70B}(z)$
.
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1})=\unicode[STIX]{x1D70B}(z)$
. -
– Let
 $\unicode[STIX]{x1D712}_{2}:H\rightarrow S^{1}$
denote the composite of the projection
$\unicode[STIX]{x1D712}_{2}:H\rightarrow S^{1}$
denote the composite of the projection
 $H\rightarrow H^{\prime }$
with
$H\rightarrow H^{\prime }$
with
 $\unicode[STIX]{x1D712}$
. Note that
$\unicode[STIX]{x1D712}$
. Note that
 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{2})=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
.
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{2})=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
.
Now
 $(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
is a unit times
$(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
is a unit times
 $z-_{\mathbb{G}_{E_{n}}}\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712})$
. Furthermore,
$z-_{\mathbb{G}_{E_{n}}}\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712})$
. Furthermore,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(z-_{\mathbb{G}_{E_{n}}}\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1})-\mathbb{G}_{E_{n}}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{2})=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(z-_{\mathbb{G}_{E_{n}}}\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1})-\mathbb{G}_{E_{n}}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{2})=\unicode[STIX]{x1D719}(\unicode[STIX]{x1D712}_{1}-\unicode[STIX]{x1D712}_{2}),\end{eqnarray}$$
and by Lemma A.2 the claim follows.
Turning to the proof of the lemma, recall that by definition
 $\tilde{g}(z)\prod _{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
has coefficients in
$\tilde{g}(z)\prod _{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))$
has coefficients in
![]() $T_{n}^{\prime }$
, where the product ranges over all
$T_{n}^{\prime }$
, where the product ranges over all
 $\unicode[STIX]{x1D712}:H^{\prime }\rightarrow S^{1}$
of order at most
$\unicode[STIX]{x1D712}:H^{\prime }\rightarrow S^{1}$
of order at most
![]() $p^{m_{\ell }}$
. It follows that
$p^{m_{\ell }}$
. It follows that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}\biggl(p^{k^{\prime }}\tilde{g}(z)\mathop{\prod }_{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))\biggr)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}\biggl(p^{k^{\prime }}\tilde{g}(z)\mathop{\prod }_{\unicode[STIX]{x1D712}}(z-\unicode[STIX]{x1D719}^{\prime }(\unicode[STIX]{x1D712}))\biggr)=0\end{eqnarray}$$
in
![]() $R_{n}$
. Then, by the claim,
$R_{n}$
. Then, by the claim,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}\biggl(p^{k^{\prime }}\tilde{g}(z)\mathop{\prod }_{\unicode[STIX]{x1D712}}p\biggr)=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}\biggl(p^{k^{\prime }}\tilde{g}(z)\mathop{\prod }_{\unicode[STIX]{x1D712}}p\biggr)=0,\end{eqnarray}$$
and so we may take
![]() $r$
to be the sum of
$r$
to be the sum of
![]() $k^{\prime }$
and the number of
$k^{\prime }$
and the number of
![]() $\unicode[STIX]{x1D712}$
appearing in the product.◻
$\unicode[STIX]{x1D712}$
appearing in the product.◻