Female education, marital assortative mating, and dowry: Theory and evidence from districts of India

Abstract

We study marital assortative mating in education and its relation to dowry in India. There are four main results and contributions of this paper. First, instrumental variable estimates using Indian Human Development Survey-II data suggest existence of positive assortative mating in education levels of husband and wife. Second, this association is weaker in dowry-prominent districts suggesting that in districts with strong patriarchal norms, high dowry transfers could substitute for lower bride's education. Third, we study the independent effect of husband's and wife's education and its interaction on dowry. Estimates suggest that dowry rises with the groom's education and falls with the bride's schooling years. However, the joint effect of husband-and-wife education on dowry is negative, implying that though dowry rises with groom's education, the rate of increase is smaller the more educated the bride is. Finally, to explain the empirical results, we propose a theoretical model of assortative mating in the presence of dowry.

1. Introduction

We examine the association between the education levels of husband and wife, or marital assortative mating in education, and the role of dowry in India in determining this relation. Historically, marriages in India are arranged by the families of the bride and groom, and caste and religion have been important determinants of match selection. Lin et al. (2020) argue that partner pools may be more restricted for Indian women because of the prevalence of arranged marriages resulting in a greater emphasis on ascribed characteristics such as caste and kinship. At the same time, with economic and social development, achieved attributes such as education, wages, and occupation should increasingly become important in the marriage market [Qian and Litcher (2007); Blossfeld (2009)].

Education is widely discussed in the literature to be an important determinant of assortative matching. In Becker's theory of marriage (1974, 1981), positive assortative mating in education exists if both husband and wife's years of schooling offer increasing returns in the labor market and thus education is a complementary characteristic. However, whether or not positive assortative mating in education exists in the marriage market is debatable. Pencavel (1998) finds that in the U.S.A., husbands and wives had similar schooling backgrounds and the trends increased post-1960s. Similar conclusions were made by Mare (1991). Greenwood et al. (2014) also find analogous results where correlation between the education of husband and wife increased between 1960 and 2005. On the contrary, Gihleb and Lang (2016) find that assortative mating in education has not increased in recent years.

Marriage markets in developing countries differ from those in the developed world in many ways [Anukriti and Dasgupta (2017)]. The Indian marriage market is unique due to at least three reasons; the presence of patriarchal social norms, the substantial non-market benefits of female education combined with low female labor force participation rates and the existence of dowry.

Gender inequality is striking in India, a country with rigid patriarchal social norms. Sons are traditionally considered as the main income earners while daughters carry the burden of dowry [Barua et al. (2017)]. These rigid cultural norms have led to gender gaps in sex ratio, marriageable age, education, and labor force participation [Klasen and Pieters (2015); Afridi et al. (2018); Dhar et al. (2019)].

Moreover, a consequence of the patriarchal norms is that there are significant non-market benefits of female education such as their contribution towards raising and educating children, investment in child health and sanitation, support for household financial and social decisions. In recent years, there has been a fall in rural employment among married women while at the same time their participation in domestic work and their average level of education is increasing [Anukriti and Dasgupta (2017); Afridi et al. (2018)]. This suggests that positive assortative mating in education in the Indian context can also be explained by the non-market benefits of female education.

Finally, Indian marriage market is characterized by dowry, the direct transfers from the bride's family to the groom's family, to compensate for the differences in the characteristics of the bride and the groom [Anderson (2007)].

These socio-cultural features of Indian marriages imply that it is difficult to study positive assortative mating for education through the lens of traditional theories in the literature. To study marital assortative mating in education in the Indian context, one has to identify and factor in the role of patriarchal norms, the non-market benefits of education, and the role of dowry.

The first aim of this paper is to empirically test the association between education levels of husband and wife. Using data from the Indian Human Development Survey (IHDS-II, 2011) and an instrumental variable (IV) strategy to deal with the endogeneity of education levels, we find that there exists assortative mating in the Indian marriage market.

Second, we study if assortative mating in education differs between districts with and without the prominence of dowry. Districts with patriarchal norms, where dowry is more predominant, may view bride education and dowry income as substitutes, such that high dowry transfers could substitute for lower bride's schooling years. Consistent with this, we find that marital assortative mating outcomes are weaker in districts with higher dowry deaths (our measure of dowry prominence).

Third, we study if dowry transfers from the bride's family to the groom can have potentially offsetting effects on assortative mating in education. To the best of our knowledge, existing studies have not looked at the impact of female education on marital sorting due to changes in relative bargaining powers of potential grooms and brides reflected in average dowry exchanges. If parents of an educated bride are willing to pay a higher dowry for an educated son-in-law, there would exist complementarities in the education levels of the bride and groom, and this relation would be increasing in dowry transfers. However, if the bride's family is less willing to pay a dowry because the daughter is educated or the groom's family is willing to accept a lower dowry for an educated bride, husband and wife schooling years are substitutes in dowry. In this case, the marginal increase in dowry transfers with groom's education would fall with increase in education of the wife. Our empirical results suggest that dowry rises with the groom's education level and falls with the bride's schooling years. However, the joint effect of husband-and-wife schooling years on dowry is negative, which suggests that although dowry rises with groom's education, the rate of increase is smaller, the more educated the bride is.

Finally, to explain the empirical results, we propose a theoretical model of assortative mating in the presence of dowry and low female labor force participation. We model assortative mating in education as a net effect of increased female productivity at home due to increased female education and reduced dowry transfers in the groom's household production. Dowry may compensate for lower education levels of the potential bride. In the presence of low labor market returns to female education and substitutability between dowry and years of schooling, negative assortative mating in years of schooling may be an ideal outcome for the households. However, in the presence of non-monetary human capital endowments, positive assortative mating may be optimal if the cost reducing effect is stronger than the substitution effect between female education and dowry.

Our results are important for policy as they suggest that in the Indian marriage market, dowry is a function of the relative schooling years of the potential bride and groom. Increasing education levels of girls will act as a deterrent toward dowry when norms are gender neutral or in favor of women. But, in regions with gender-biased norms and stereotypes, high dowry transfers would act as a substitute for lower bridal education. Hence, policies that aim to raise education levels of girls may by itself not be enough to counter dowry unless accompanied by interventions targeted at raising female bargaining power in the household (e.g., through increased economic opportunities). For instance, Qian (2008) finds that as women's share of household income increased in rural China, they gained bargaining power in their families. Since women had weaker son preference than men, this translated to gender balance in sex ratio and educational outcomes in the next generation. Similarly, Carranza (2014) finds that in India, regions with lower female labor force participation rates also witnessed a more male skewed sex ratio, consistent with the theory of weaker bargaining power of women.

The rest of the paper is structured as follows. Section 2 discusses the literature pertaining to marital assortative mating and the role of dowry as an equilibrating mechanism in the marriage market. This section also discusses the institutional background in India that is relevant for the analysis. In section 3, we discuss the data used in the study. Section 4 presents the empirical framework and identification strategy. Section 5 shows the main results from the empirical analysis whereas section 6 explains these results with a theoretical model of assortative mating, education and dowry. Finally, we conclude and discuss policy implications of our study in section 7.

2. Literature and institutional background

Our paper contributes to at least two strands of literature. The first deals with the literature on marital assortative matching. Second, we contribute to the literature on the role played by dowry as an equilibrating mechanism to compensate for the differences in the characteristics of the bride and the groom. Below we discuss the contributions of this study in the context of these two strands of literature.

There is divided opinion among economists regarding the existence of positive assortative mating in education in the marriage market. Dalmia and Lawrence (2001) find that similarity in education is the second most important predictor of marital matchmaking in India after age. Deolalikar and Rao (1992) find a positive association between the traits of bride and groom in characteristics such as height, age at marriage, and schooling in rural south-central India. Lin et al. (2020) on the contrary find evidence of a decline in education hypergamy in India, women marrying men with higher education, and a rise in hypogamy, women married to men with fewer years of schooling.

Studies of education-based assortative matching in India are both unique and complex since marriages and spouse selection are governed by two important elements of the marriage market. First, most marriages are arranged by the families of the bride and groom and are governed by strong social and cultural norms [Schwartz (2013)]. These norms, and the resulting son preference, guide human capital investments with persistent gaps in the literacy levels of boys and girls in all age groups. Girls are more likely to drop out of schools to take care of younger children in the family, to support household work, or due to financial constraints [White et al. (2016)]. The socio-economic status of women in India has remained persistently poor relative to men, and women are less likely to participate in the wage market, own assets, migrate for work, or take part in decision-making within or outside the family [Agarwal Goel (2021)].

Thus, contrary to the evidence from developed countries that explicitly attributes the rise in assortative mating in education to rise in wages and female work productivity, similar conclusions are hard to draw for India. Women are engaged in low productivity and low-paying jobs and there exists a significant gender wage gap in the labor market [Duraisamy and Duraisamy (2016)]. Grossbard-Schectman (2019) suggest that changes in market-determined wages or quasi-wages for spousal work relative to market wages for labor work can alter decisions regarding labor supply by women. In this paper, we argue that gender-segregated roles and non-monetary benefits of education offer an alternative explanation for the existence of assortative mating in India.

Second, dowry transfers from the bride to the groom's family are common across Indian states [Anderson (2003, 2007)]. Such inter-household transfers act as income insurance in low-income countries [Rosenzweig and Stark (1989)]. In economic theory, dowry in the marriage market is perceived as an equilibrating mechanism to compensate for the differences in the characteristics of the bride and the groom [Anderson (2007)]. Larger is the difference in the distribution of traits of the groom relative to the bride, greater is the dowry that is exchanged as a compensation. In India, girls are usually married up, with grooms likely to be taller, better educated, and with higher earnings. Rao (1993) in estimating the rising groom prices in South-Central India shows that dowry transfers rise with the widening gap in bride and groom characteristics such as height, land ownership, and years of schooling. A positive shift in the potential brides' ability distribution and rise in female education should raise female bargaining in the marriage market [Sweeney and Cancian (2004); Anderson (2007)]. However, Edlund (2000) suggests that attributes do not influence dowry symmetrically, i.e., dowry should be regressed on individual traits instead of differences in traits.

We contribute to the literature on assortative matching in education by studying, empirically and theoretically, assortative mating decisions in the presence of strong patriarchal social norms, low female labor force participation rates, and the institutional practice of dowry.

Empirically, we draw four important conclusions. First, there exists positive assortative matching in education levels of husbands and wives in India. Second, this association is weaker in dowry-prominent districts. This suggests that assortative mating in education is weakened by the existence of dowry and the groom's family is willing to substitute lower bride's education in return for higher dowry. Third, we directly test for the independent effects of gender-specific education levels and the joint effect of male and female education on dowry. The estimates show that dowry payments rise with additional years of male education but falls with female education. Fourth, we find that, the joint effect of male and female education on dowry is negative, indicating that dowry increases with male education but at a decreasing rate in response to rise in female education. Finally, we explain the heterogeneity in the empirical results as a trade-off between marginal benefits and costs associated with female education and dowry using a simple theoretical framework.

3. Data

The empirical analysis uses household level data drawn from the India Human Development Survey (IHDS-II), 2011. IHDS-II is a nationally representative, multi-topic survey of 42,152 households across India for 2011–12. The survey gathers household and individual level details on variables related to health, education, employment status, marriage, and other components that are important indicators of economic and social well-being.

For our analysis, we map data at the level of household, individual (belonging to the given household), and eligible women¹ (of the household). The data set on eligible women provides variables on education of the married woman and the husband, mother-in-law's education, age, expectation of expenses borne during the marriage by the groom side and the bride side and other forms of gifts received from the community in marriage. These variables are used to study assortative mating in education and its relation to dowry. Factors such as household income and average education level in the household are mapped from the household data of IHDS-II. These variables are used as controls since they may play an important role in selection of bride. For example, a household with high average education would prefer educated brides. Further religious affiliation and caste categories are also taken from the household data.

Marriage expenditure net of expenses by the bride and groom's family provides for a close proxy for dowry. Marital expenditure by the groom's family was based on the following question from the head of the household, “At the time of the boy's marriage, how much money is usually spent by the boy's family?” Similarly, expenditure by the bride's family was based on the following question, “At the time of the girl's marriage, how much money is usually spent by the girl's family?” Dowry was calculated as the difference in average expenditure incurred by the bride and the groom's family. To avoid measurement bias due to differences in cost of living across states, the calculated dowry was weighted by consumer price index of each state in the year 2011.

We include dowry prominence status of a district as an explanatory variable to examine marital assortative mating. Marital expenditure however may not be a good measure for dowry prominence in a district. Marriage expenditure may be determined by other factors also such as ability to pay and preferences of individuals, besides the cultural norms regarding marital transfers. To compute a measure of dowry predominance in a district, we used the proportionate number of dowry deaths in a district in 2011 based on data provided by National Crime Records Bureau (NCRB). Dowry deaths provide a good proxy for the prominence of dowry in a district, since it is likely to be reported with a high probability and with greater accuracy. A district is defined as more tolerant toward the practice of dowry if the percentage of dowry deaths exceeds 1.5 (average percentage of dowry deaths).² Finally, data for 10–16 age-specific sex ratio (males per 1000 females) at the district level is taken from the Indian Decennial Census 2011 and data for the number of high schools in a district is sourced from the Department of School Education and Literacy Statistics Division, MHRD, Government of India.

The descriptive statistics for the variables from IHDS-II, NCRB, and Census 2011 are presented in Table A.1 in Appendix A.3. The descriptive statistics suggest that, on average, husbands are more educated than the wives. The net expenses borne on wedding by the bride's family are positive, indicating positive groom price and marital transfers from the bride to the groom's family. The statistics are representative of sex ratio biased toward males, showing 1098 males as compared to females in the age group of 10–16 years old across India. Dowry deaths as a percentage of married females in a district range from 0 to 8.4%. On average, the districts in India witness approximately 1.5% of dowry deaths as a proportion of married girls.

Scatter plots of the education level of husband and wife in Figure 1 show a strong positive association between the two variables. Potential grooms and brides are likely to choose from their own education (ability) distribution.

Figure 1. Scatter plot for association between the education level of husband and wife in a household (IHDS-II).

Figure 2 provides an overview of state-wise average net expenditure incurred by the bride's family. The figure suggests large regional variation in the net marital expenditures borne by the bride side of the family. A closer look at the numbers is indicative of least dowry transfers in the north-eastern states of India including Nagaland, Assam, Mizoram, and Meghalaya. These states are also known for an above average level of women representation and independence. On the contrary, states from southern India such as Kerala, Tamil Nadu, and Karnataka, although possess highest standards of women literacy levels and women workforce participation, rank highest in dowry payments.

Figure 2. Average dowry expenditure across states of India (IHDS-II).

Region-wise and state-wise dot plot in Figure 3 provides an overview of the association between average dowry payments and years of schooling of the husband and wife. Dowry payments are seen to be higher in states with higher levels of husband's education and lower levels of wife's education.

Figure 3. Region-wise dot plot of average dowry across states and average schooling years of husband and wife.

4. Identification strategy

To study the association between female education, marital sorting, and dowry prominence, we estimate the following specification for individual i in household h of district d:

(1)$$ \eqalign{ Edu\_Wife_{ihd} = \alpha & + \beta _1Edu\_Husband_{ihd} + \beta _2Dowry\_District_d \cr & + \beta _3Educ\_Husband_{ihd} \times Dowry\_District_d + \gamma _hX_h + \delta _{rh} + \delta _{ch} + \delta _s \cr & + \varepsilon _{ih}}$$

where $Edu\_Husband_{ihd}$ denotes the education level of husband (of the surveyed married female i) in household h of district d. A positive estimate of β ₁ would indicate positive assortative mating where a household finds it optimal to marry potential grooms and brides with similar education levels. β ₂ measures the difference in the education level of brides in districts with greater prominence of dowry.

β ₃ estimates the differential outcome on marital assortative decision of male education in districts with greater dowry prominence. This could be either positive or negative. Districts strongly driven by norms of dowry may exhibit a positive β ₃ that would suggest stronger assortative mating in marriage market in dowry prevalent districts. In this case, dowry and female education are complements, such that higher dowry is paid to seek a better educated groom for a bride with higher education. If dowry and female education are substitutes, β ₃ would be negative that indicates males with higher education find it desirable to substitute education of potential bride in compensation of dowry.

X _h includes household level controls for income, age difference between husband and wife, average education level of the household, and the urban or rural status of residence of the household. δ _rh, δ _ch, and δ _s are the fixed effect controls for religion and caste of a household³ and state fixed effects, respectively.

Ordinary least squares (OLS) estimates may pose potential endogeneity bias due to omitted unobserved factors that may together determine the education levels of husband and wife. To circumvent this problem, we use the IV strategy and instrument husband's years of schooling with the mother-in-laws years of schooling. Existing studies show that the education level of mothers is positively and significantly associated with the education level of children [Rihani (2006); De Coulon et al. (2008)]. Mother-in-laws schooling is derived from the “Eligible Woman” questionnaire for married females in the age group of 15–49 years. An eligible woman's response to mother-in-law's education is recorded from the question that asks, “How many standards/class your husband's parents completed?” (The response is recorded for mother and father separately.)

As discussed before, dowry transfers from the bride's family to the groom can have potentially offsetting effects on education homogamy. To examine this hypothesis, we estimate in equation (2) the direct relation between dowry and education levels of husband and wife, independently, and the joint effects of husband-and-wife education on dowry. The coefficient b ₃ in equation (2) directly tests for the joint association between husband-and-wife female education and the dowry exchanged:

(2)$$Log( {Dowry} ) _{ihd} = a + b_1Edu\_Husband_{ihd} + b_2Edu\_Wife_{ihd} + b_3Edu\_Husband_{ihd} \times Edu\_Wife_{ihd} + \gamma _hX_h + \gamma _dX_d + \delta _{rh} + \delta _{ch} + \delta _s + \varepsilon _{ih}$$

Here, b ₁ is expected to be positive as higher education of potential grooms would reflect greater ability and hence be more valued in the marriage market. b ₂, on the contrary, is expected to be negative. A rise in the education level of potential bride would raise her bargaining power in the marriage market and hence would lead to a fall in the transfers made to the groom's family at the time of marriage. b ₃ directly tests for whether dowry changes with an additional year of education of both the groom-and-bride. A positive estimate of b ₃ would suggest complementarity in education levels for dowry, such that the bride's parents are willing to pay a higher dowry to seek a better ability husband for their daughters with higher education. If b ₃ is negative, education levels of husband and wife are substitutes in dowry. With a positive b ₁, although dowry may rise with male education, but the marginal increase is smaller with rise in female education with a negative b ₃. The household is willing to substitute dowry for a bride with higher education. The conceptual framework shown in section 6 mathematically shows these relations in further details.

X _h includes household level controls for income, age difference between husband and wife, and urban or rural status of residence of the household. X _d includes district level control for sex ratio. δ _rh, δ _ch, and δ _s are the fixed effect controls for religion and caste of a household and state fixed effects, respectively.

However, OLS estimates may be biased due to unobserved factors that may simultaneously affect the education levels and dowry. The endogenous variables in this specification are: education level of husband and wife, and the interaction. Following Currie and Moretti (2003) who use availability of colleges in a woman's county as an instrument for maternal education, years of schooling of the wife is instrumented with the number of high schools in the district. The number of schools in a district is unlikely to be correlated with dowry exchanged in the household. Unlike in equation (1), we cannot use mother-in-law's education as an instrument for husband's education due to the potential failure of the exclusion restriction. Jeyaseelan et al. (2015) show that the socio-economic status of the mother-in-law affects dowry and dowry-inflicted violence on the bride. Instead, we proxy husband's education with that of his mother and instrument for female education with the number of high schools in a district as shown in equation (2a):

(2a)$$Log( {Dowry} ) _{ihd} = \mu + \psi _1Edu\_Husband\_Mother_{ihd} + \psi _2\widehat{{Edu\_Wife_{ihd}}} + \psi _3Edu\_Husband\_Mother_{ihd} \times \widehat{{Edu\_Wife}}_{ihd} + \gamma _hX_h + \gamma _dX_d + \delta _{rh} + \delta _{ch} + \delta _s + \varepsilon _{ih}$$

where $\widehat{{Edu\_Wife_{ihd}}}$ is the predicted education of wife from the first stage when instrumented with the number of high schools in the district.

5. Empirical assessment

Table 1 shows results for equation (1). Columns 1–3 show the OLS estimates. All regressions control for district and household-specific characteristics that may be correlated with the education level of the husband and the wife.

Table 1. Marital assortative mating in years of schooling and difference in dowry-prominent districts

Includes controls for urban/rural residence of the household, average education of the household, difference in age of the husband and wife, household income, religion, and caste.

Robust standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

The OLS estimates are directionally consistent. The results suggest that there exists a positive association between the education levels of husband and wife which indicates positive assortative mating in education.

These results are consistent with the findings of Mare (1991) and Mancuso (1997) who show that it is unlikely for individuals with higher education levels to marry someone with a lower education. Similarly, Qian (1998) found that females with higher education were less likely to marry men with a lower education level.

In column 3, we include as an additional regressor the interaction variable between the dowry district and husband's education. Although the estimates suggest a positive and significant association between the education level of the husband and the wife, this association is weaker in the dowry prevalent districts as indicated by the negative significant effect of the interaction variable. The groom's family is willing to accept a bride with lower education for higher dowry. There exists substitution between bride's schooling years and dowry exchanged. Potential brides with lower education are able to secure a better educated groom by paying higher dowry and vice-versa.

As discussed in the empirical strategy, IV estimation addresses any potential endogeneity arising due to reverse causality or omitted variable. A female with higher education may choose to marry a male who is better educated and thus the causality may run in the reverse direction. Alternatively, husband and wife's education levels may be determined simultaneously by factors such as cultural norms, preferences, attitude, and perception of individuals toward education. Wu–Hausman's F-statistic to test for the endogeneity of education level of husband is 685.43 and rejects the null of the variable being exogenous. To address this, bride's mother-in-law's education is used as an IV for the years of schooling of the husband.

Table 2 shows the first-stage estimates. The estimates suggest that men with mothers of higher education have higher years of schooling. Husband's mother's education is significantly and positively associated with husband's education level and the overall model is significant with a high F-statistic.⁴

Table 2. First stage: husband's mother's years of schooling as IV for husband's years of schooling

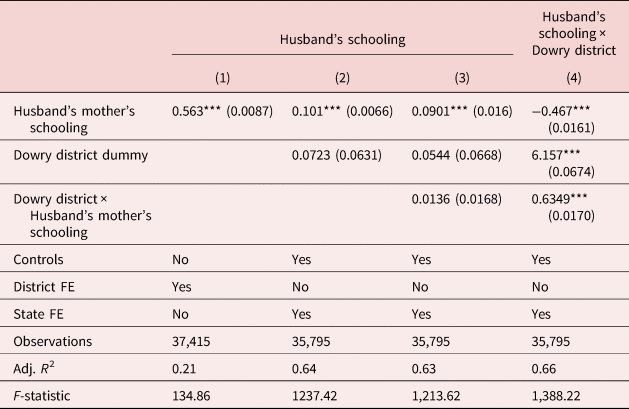
Includes controls for urban/rural residence of the household, average education of the household, difference in age of the husband and wife, household income, religion, and caste.

Robust standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

In Table 1, columns 4–6 show the estimates with IV estimation. Comparing the OLS to IV estimates in Table 1, we find that OLS estimates are downward biased suggesting that omitted variables such as cultural beliefs that encourage investment in education of men may also discourage schooling among women.

A threat to the exclusion restriction is that the mother-in-law's socio-economic status, in particular education level, may be correlated with the bride's schooling level. For instance, more educated mother-in-law may have greater bargaining power in the household and consequentially in deciding the characteristics of potential brides including age at marriage and education. In our study, there is some survey evidence that this may not be the case. As part of the IHDS survey, ever-married women between the ages of 15 and 49 were asked a series of five questions about decision-making in the household. The respondent reported whether she, her husband, a senior male, a senior female, or someone else had a say in that decision. One of the questions asked was: “Please tell me who in your family decides: To whom your children should marry?”. Survey data revealed that in 74% of the cases, the decision is made mostly by the husband. The respondent herself has a larger role only in 11% of the cases. Since women are less likely to make a decision on the marital choices for their children, it would be valid to assume that husband's mother's education is exogenous to the years of schooling of wife.

However, survey data responses could be influenced by the experimenter demand effect. Thus, we conduct additional robustness checks to test for the validity of the instrument. We first estimate the model again by excluding from the sample households with a female household head who may be more likely to make marriage-related decisions.

The results in Table 3 in column 1 show that the findings on positive assortative mating in education are robust to exclusion of such households, where mother-in-law could have a significant role in determining the education levels of the bride. In columns 2 and 3, we exclude females “who have ever worked for pay/wages” and those with years of schooling more than 10 years, respectively. By restricting the sample to women who either do not have sufficient education levels or have never been employed, we focus on the sub-sample where female education offers pure non-monetary benefits to the household. The estimates are consistent with the main specification, which suggests positive marital assortative mating in education, with results being weaker in districts with greater dowry prominence.

Table 3. Validity of mother-in-laws schooling as an IV for husband's years of schooling

Robust standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

Next, we study the association between dowry on the one hand and husband and wife's education level and their interaction on the other hand. OLS estimates in Table 4, columns 1 and 2, show a positive and significant relationship between education levels of both husband and wife and the amount of dowry exchanged. However, OLS estimates may be biased due to unobserved factors that may simultaneously affect the education levels and dowry. As discussed in the empirical strategy, in this case, we are wary of using mother-in-law's education as an instrument for husband's education due to the potential failure of the exclusion restriction. Instead, we proxy husband's education with that of his mother and instrument for female education with the number of high schools in a district.

Table 4. Association between dowry and years of schooling

Includes controls for urban/rural residence of the household, difference in age of the husband and wife, household income, religion, caste, and district sex ratio.

Standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

First-stage estimates are presented in Table 5. The estimates show a strong positive association between the number of high schools in the district and wife's years of schooling. In case of higher district sex ratio with a greater number of males, females achieve fewer years of schooling. Estimates suggest that in households with urban residence and higher income, wives have higher education levels. Higher age difference between husband and wife is negatively correlated with wives' education level.⁵ The overall F-statistic of first-stage model is 210.92 for wife's schooling and indicates the overall model being significant.

Table 5. First stage: number of high schools in the district as IV for wife's years of schooling

Standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

In column 4 of Table 6, IV estimates suggest that an additional year of husband's schooling is associated with a rise in dowry by 1%. A rise in wife's schooling year on the contrary shows a fall in dowry by 0.21%. The estimates thus suggest that son's education offers positive returns to the household in terms of a higher dowry, whereas bride's education is associated with lower dowry exchanged. The coefficient for interaction between education levels of husband-and-wife tests for the joint marginal effect of additional years of schooling of the bride and groom on dowry. A negative estimate for the interaction term suggests that the marginal rise in dowry with male education is smaller with a rise in female years of schooling. Thus, there exists substitution between the education levels of bride and the dowry exchanged.

Table 6. Robustness validation IV estimates for the association between dowry payments and years of schooling

Robust standard errors in parentheses.

***p < 0.01, **p < 0.05, *p < 0.1.

These results provide credence to the assortative mating estimates in Table 1 that show that positive assortative mating result is weaker in dowry-prominent districts. Education of husband-and-wife is substitutes in dowry. Dowry falls with the education level of the bride for a given level of groom's education, and rises if the bride is less educated. In India, therefore, both education and transfers at the time of marriage are significant determinants of marital assortative mating.

It may be argued that the IV estimates derived in Table 4, that estimate the joint association of husband-and-wife's years of schooling on dowry, may be driven by certain factors specific to individuals, household, or the districts themselves. Validation tests are presented in Table 6. Models 1 and 2 exclude women from analysis who belonged to a different town or city before marriage. Since we use the “number of high schools in the district” as an instrument for wife's education level, this robustness check ensures that we have correctly mapped high-school data to each eligible woman. The IHDS-II data do not provide information on the district of residence of females before marriage, therefore we are assuming here that the spouses belong to the same district. But, the survey asks the eligible women “What is your childhood place of residence.” There are approximately 2,000 observations where the natal district of the wife is not same as the husband's. Our results are robust to excluding these observations.

Models 3 and 4 exclude the outlier districts in dowry deaths to ensure that the results are not driven by extreme values. Excluding the districts that either have a history of almost negligible dowry deaths or a large percentage of dowry deaths, we exclude any biasedness in the results that may be caused due to strong cultural norms or social beliefs. The estimates from the validation tests are consistent, significant, and close to the main model.

6. Model to explain empirical findings

Our empirical results suggest that there exists education homogamy in India; however, this association is weaker in dowry-prominent districts. This section explains the empirical findings through a theoretical model of household utility maximization based on Becker's (1991) “Assortative Marriage Market” model. We derive and discuss the conditions under which positive or negative assortative mating would be optimal in education levels. Dowry is considered to be a one-time income augmenting transfer payment from the bride's family to the groom's family. Since dowry is an equilibrating factor for the differences in the traits of the husband and wife, we model dowry to be a function of education levels of groom and bride [Anderson (2007)].

The household utility function of the groom is a function of m market goods and services x _i, and leisure t _j for each male j. We assume that only males participate in the wage market so that there is no division of time by females between leisure and labor work. This assumption is driven by the data that indicate low female participation in the labor market in India.

Household production function:

(3)$$Z = f( {x_1, \;\ldots , \;x_m; \;t_1, \;\ldots , \;t_j} ) $$

where x _i is the market goods and services i = 1…..m and t _j is the leisure hours of male members j = 1…..n.

Budget constraint: The household budget constraint ensures that the total expenditure on consumption goods and services, x _i, with price vector p cannot exceed the sum of income from labor l _j at a wage rate w _j for each male individual j in the household; property income v (given and constant); and dowry, D. Dowry is assumed to be a one-time inter-household transfer and adds to the income of the post marital household (groom's household). Dowry is a function of male and female education in the post-marital household, S _m and S _f respectively⁶ (Goli et al., 2013). In the marriage market, households choose a bride with a given level of education among potential brides (with different education levels). We assume that further investment in the education of girl after marriage is not taken into consideration at the time of match making or for fixing the dowry amount:

(4)$$\mathop \sum \limits_{i = 1}^m p_ix_i = \mathop \sum \limits_{\,j = 1}^n w_jl_j + v + D( {S_m, \;S_f} ) ; \;\;\;\;\;\;\;\;\;\;\;\;$$

where p _i is the price of market goods and services; w _j is the wages of male j; l _j is the work hours of male j; v is the property income; D is the dowry; S _f is the education of female, bride; and S _m is the education of male, groom

Time constraint:

(5)$$l_j + t_j = T, \;\;\;\;\;\;\;\forall j$$

Substituting equation (5) in (4), the goods market and time constraints can be represented as a full income constraint:

(6)$$\mathop \sum \limits_{i = 1}^m p_ix_i + \sum w_jt_j = \sum w_jT + v + D( {S_m, \;S_f} ) = I$$

where I stands for full income achievable with w _j as given in a perfectly competitive labor market.

In developing nations characterized by low female workforce participation and poor returns to female education, there exists division of work roles between males and females. Males take up larger roles in the labor market and females in household activities. We thus assume that S _m increases both monetary and non-monetary returns in the household production and males face competitive wages across labor markets such that, w _j = w. Female education, S _f, on the other hand, is a non-monetary trait. This is consistent with Afridi et al. (2018) who find evidence of declining labor force participation in rural India among married and educated women. They further argue that relatively higher returns from education from engaging in domestic work, than from labor force, may explain the declining trends.

6.1 Household cost of production

Household production necessitates the employment of inputs in the production process. The household output is the amount of goods and services it could consume, assets it could raise, and the quality of children it could rear. Children are considered consumption goods that generate positive utility with inputs required in terms of time and effort. Costs would involve time, effort, and human capital required in the process of production. Cost of household production is a function of prices of consumption goods and education levels of household members. Rise in prices makes consumption expensive, raising the opportunity cost of leisure, and cost of household production:

(7)$$C = C( {\,p, \;S_m, \;\;S_f} ) $$

Researchers have shown that the children of better educated mothers spend more time studying and exhibit better health outcomes compared to mothers with lower schooling [Glewwe (1999); Cui et al. (2019)]. Thus, education raises individual efficiency through increased marginal productivity in production and affects outcomes such as health and child education positively leading to lower costs of household production. Due to improved efficiency with education, marginal cost of the household is assumed to be decreasing in the education of both male and female such that:

$$\displaystyle{{\partial C} \over {\partial S_m}}\equiv C_m < 0$$

$$\displaystyle{{\partial C} \over {\partial S_f}}\equiv C_f < 0$$

The household production could be represented as a proportion of household production to costs:

$$\eqalign{Z = & \displaystyle{{Full\;Income} \over {Average\;Cost\;of\;Production}} = \displaystyle{{\sum w_jT + v + D( {S_m, \;S_f} ) } \over {C( {\;p, \;S_m, \;\;S_f} ) }} \cr = & \;\displaystyle{I \over {C( {\;p, \;S_m, \;\;S_f} ) }}} $$

As is evident from the household income per unit of cost, the education of the potential groom (S _m) and bride (S _f) impacts household production function both via a change in dowry income and a fall in the cost of household production.

A rise in male education raises the groom-price in the market with a corresponding increase in dowry transfers. Higher male education simultaneously brings down the cost of household production. The total effect of increase in male education is thus positive on household production per unit of cost. However, a rise in female education increases bargaining power in the marriage market and leads to fall in dowry transfers. This causes countering effects on the production to cost ratio. On the one hand, the groom's household would see a fall in dowry with rise in female education, reducing the post-marital income. On the other hand, an educated bride would lead to a fall in cost. The net effect of female education on household production per unit of cost is thus ambiguous. Mathematical explanations for the same are provided in the following sub-sections and Appendix A.1 shows the derivations.

6.2 First-order partial derivatives: the impact of education on total output

We discuss the effect of education levels of bride and groom on household production per unit of cost through the first order partial derivatives, ∂Z/∂S _m and ∂Z/∂S _f (derived in Appendix A.1).

Dowry is an equilibrating factor for the differences in the relative traits of the groom and the bride, we assume therefore D _m > 0 and D _f < 0, marital transfers rise with groom's education and falls with rise in bride's schooling years. The empirical analysis confirms this as we find a positive association between dowry and education levels of the groom and negative association between dowry and the bride's schooling years. Furthermore, dowry, that is the net transfer from bride's family to groom's family, is positive such that D(S _m, S _f) > 0. An increase in human capital investment by the groom unambiguously leads to an increase in household production, both through an increase in dowry that adds to the income of the groom's household and a decrease in the cost of household production. However, given the assumption (and empirical evidence) that D _f < 0, total output of the household would increase with female education, if the proportionate fall in household costs is greater than the proportionate fall in dowry. Bride schooling years cause countering effects with a negative impact on dowry income and positive on cost reduction. Thus, there exists a trade-off in decisions on the education level of potential brides. A household would prefer a bride with higher education if the efficiency gains in cost outweigh the loss in the dowry component.

6.3 Second-order partial derivatives: assortative mating

We observe that the household production is monotonic and increasing in male schooling. However, assortative mating, i.e., who marries whom is based on the second-order conditions, i.e., the joint marginal effects of education of groom-and-bride on household production. Empirical estimates from IHDS-II data provide suggestive evidence of positive assortative mating in education in India. The association however is found to be weaker in dowry-prominent districts. This can be explained in our model through the joint marginal effects of schooling years of husband-and-wife on the overall household production, Z. Mathematically, positive assortative mating in education, mating of likes (where males and females seek potential partners from similar ability distribution) is desirable if ∂²Z(S _m, S _f)/∂S _mS _f > 0. And negative assortative mating of un-likes is desired if ∂²Z(S _m, S _f)∂S _mS _f < 0. A household would gain from positive assortative mating if the education levels of husband and wife are complementary while negative sorting would be optimal if education of husband and wife are substitutes and generate offsetting effects in household production.⁷

We further study the disaggregated joint marginal effects of education on the cost of household production and dowry. The disaggregated analysis not only helps explain the heterogeneity in results for dowry districts, but also derives the conditions under which positive or negative assortative mating in education would be an optimal strategy. As shown in Appendix A.2, the sign of the cross-partial derivative of Z with respect to S _m and S _f would depend upon the relative magnitude and signs of D _m.f (cross-marginal effects on dowry) and C _m.f (cross-marginal effects on costs), given the assumptions of C ⁻¹ > 0, D _m > 0, D _f < 0, C _m < 0, and C _f < 0.

Education may have either reinforcing or offsetting effects on household cost of production and dowry exchanged. The cost effects are reinforcing if the education of male and female act as complements, such that C _m.f < 0. However, such costs could be offsetting if C _m.f > 0, when education of husband and wife are substitutes. The costs though would fall due to the individual effect of female education (C _f < 0), but the rate of fall would be smaller.

Under the assumption of dowry as an equilibrating factor in the marriage market, and as suggested by the empirical analysis, the magnitude of dowry falls with the rise in female education, i.e., D _f < 0. However, the sign of the joint marginal effect on dowry of male and female education is less obvious. If male and female education are substitutes, education would have offsetting effects such that D _m.f < 0. However, if the two are complements, the market would witness an increase in dowry with the education level of the groom and the bride. Although on average, dowry may fall with the education level of the female, yet an educated female may be willing to pay a higher dowry for a better educated male. Female education may therefore generate complementarities in the marriage market for dowry such that D _m.f > 0.

6.4 Model propositions

In the given framework, there exists four conditions/propositions under which positive or negative assortative mating in education may be optimal.

Proposition 1: Reinforcing household cost and offsetting dowry in education of husband-and-wife, such that C _m.f < 0 and D _m.f < 0 .

For positive assortative mating to be an optimal outcome, the decline in costs −both direct (C _m and C _f) and joint (C _m.f) −should be stronger to overcome the fall in dowry with a rise in female education (D _f) and the corresponding offsetting effects (D _m.f).

Proposition 2: Offsetting effects on household cost and dowry in education of husband-and-wife, C _m.f > 0 and D _m.f < 0.

In this case, the marriage market can still achieve positive sorting where the likes get sorted in equilibrium if the direct effects of fall in cost and rise in dowry with male education are stronger than the offsetting effects. This would be true if the individual efficiencies in cost achieved with higher education are stronger than the offsetting effects on both cost and dowry. If the bride individually is able to bring down the household costs to an extent that it compensates both for the loss in dowry and any substitutions in the cost reductions, positive assortative mating would be ideal even with offsetting education effects on costs and dowry.

Proposition 3: Offsetting household costs and reinforcing dowry effects in education of male and female, C _m.f > 0 and D _m.f > 0.

The result on positive assortative mating gets strengthened, in comparison with proposition 2. Dowry effect may be reinforcing, i.e., dowry increases with the education of husband-and-wife together, with the willingness to marry an educated daughter to a higher educated groom. The household would achieve higher output with an increase in education levels of both the groom-and-bride if the individual cost reducing effects and reinforcing dowry effects are stronger than the joint offsetting cost effects.

Proposition 4: Reinforcing effects of education of husband-and-wife together in both household costs and dowry, C _m.f < 0 and D _m.f > 0.

With reinforcing dowry effects, the parents of the bride may be willing to pay a higher dowry for a better, higher educated groom. Bride with higher education would thus add to the groom's household production, both by reduction in cost and a rise in dowry. This would make positive assortative mating an optimal outcome.

6.5 How does the model explain the empirical results?

There are three main results in the empirical estimation that can now be explained within the framework of the above model.

First, we find a positive association in the education levels of husband-and-wife in India. The empirical findings on positive assortative mating in education suggest that schooling years of husband-and-wife generate complementarities such that ∂²Z(S _m, S _f)/∂S _mS _f > 0.

Second, the results further suggest that though there exists positive assortative mating in education, the association is weaker in dowry-prominent districts. This is an important result, since it provides suggestive evidence of substitution between dowry and bride's education. Groom's family is seen to substitute bride's schooling years in exchange for higher dowry. This substitution effect is however not large enough to reverse the result of positive assortative mating. These findings may be explained by the strong reinforcing cost effects of husband and wife’ s education, C _m.f < 0. There is suggestive evidence that the joint marginal effects of bride and groom's schooling years on fall in household cost of production are stronger than the substitution effects between dowry and bride's schooling.

Third, the estimates for the direct association between dowry and joint marginal effects of husband and wife's schooling years is found to be negative, that is D _m.f < 0. Education of husband and wife has offsetting effects on dowry transfers. The results suggest that although dowry rises with groom's schooling, D _m > 0, the rate of increase in dowry falls with bride's education, conditional on the education years of the groom. Thus, even though the marriage market tags a higher price to the schooling years of groom, but it also offers a positive return for bride's education, by substituting for dowry payments. This is an important result, since it suggests that investment in girl's education may reduce the magnitude of dowry transfers.

7. Conclusion

Using data from India, we find a significant positive association between the education levels of husband and wife suggesting that positive assortative mating exists in Indian marriage markets. This association however is found to be weaker in dowry-prominent districts with harmful social norms and gender stereotypes. We argue that, this is because, in regions with strong patriarchal norms, households may view bridal education, and dowry income as substitutes, such that high dowry transfers could compensate for lower bride's schooling years. Consistent with this, we find that although dowry rises with groom's education, the rate of increase is smaller, the more educated the bride is.

To support the empirical results, we propose a model of assortative mating in the presence of dowry. The model suggests that a rise in female education would have countering effects on the household production. On the one hand, higher education level of the bride would be associated with smaller dowry transfers to the groom's family reducing the post-marital family income and household utility of the groom. On the other hand, higher education of the bride would cause a reduction in household cost of production. At the same time, the education level of the groom unambiguously leads to a rise in dowry and a fall in household production cost. Marital assortative matching decisions on education would be determined by the cross-marginal effects of education on household production. Positive assortative mating would be desirable for a household if the efficiencies achieved in cost are greater than the loss in dowry with rise in female education. The model also suggests conditions under which positive or negative assortative matching in the marriage market are optimal.

The expectations of future dowry payments restrict investment in girls' education and health [Bhalotra et al. (2020)]. This could be a potential reason for the widening gender wage gap, poor health, and education outcomes among girls, domestic violence and a rise in crime rates against women in India. The government of India has framed various policies to constrain dowry. Dowry Prohibition Act (1961) made payment of goods, property, or money by either party to the marriage a criminal offense. Protection of women from Domestic Violence Act (2005) added another layer of protection to the Dowry Act. These laws, however, have not been effective at curbing the exchange of dowry or dowry-related violence in India. According to the NCRB data, on average there are 8000 deaths annually in India related to dowry.

Our empirical results are important for policy as they suggest that in the Indian marriage market, although dowry exists as a cultural norm, yet it is a function of the relative schooling years of the potential brides and groom. The substitution between dowry and education years of bride, as found in our paper, may offer girl child education to be a strong policy measure against dowry in districts where gender norms are neutral or in favor of women. However, in districts where dowry is prevalent and gender norms are distorted, the groom's family is willing to substitute higher levels of dowry for lower levels of bridal education. This substitution effect may, in fact, encourage lower investment in girl's education since her parents would have to save for marriage expenses in expectation of higher future dowry payments. Therefore, in these regions, policy intervention that increase education levels will have to be accompanied with interventions aimed at increasing female bargaining power.