Configuration selection for tip-over stability of a modular reconfigurable mobile manipulator under various application situations

Abstract

A method is presented for configuration selection to obtain the best tip-over stability of a modular reconfigurable mobile manipulator (MRMM) under various application situations. The said MRMM consists of a modular reconfigurable robot (MRR) mounted on a mobile platform. The MRR in different configurations creates different wrenches onto the mobile platform, leading to different tip-over moments of the MRMM, even though the joint speeds or tip speeds remain the same. The underlying problem pertains to selecting one configuration of MRR for reconfiguration that would obtain the best tip-over stability under a given application. First, all the permissible configurations are identified through an enumeration method. Then, the feasible configurations are determined based on application-oriented workspace classifications. At last, two workspace indices, vertical reach and horizontal reach, are used to select an optimal configuration. The tip-over stability analysis and evaluation of MRMM are carried out for verification for three cases including vertical, horizontal, and general 3D space applications. The results demonstrate the effectiveness of the proposed method.

1. Introduction

A mobile manipulator combines a mobile platform with a manipulator and offers dexterous manipulability as well as open mobility for a variety of applications [1]. In ref. [2], a wheeled mobile manipulator was developed for aircraft manufacturing, such as fuselage drilling or riveting. A baseline drawing mobile manipulator was developed for interior decoration [2]. In ref. [3], a mobile manipulator was developed for concrete 3D printing on construction sites [3]. In ref. [4], a mobile manipulator was developed for upper limb rehabilitation with interactive force and torque for patients. As one kind of mobile manipulator, a modular reconfigurable mobile manipulator (MRMM) integrates a modular reconfigurable robot (MRR) with a mobile platform [5]. Since the MRR can form a new system enabling new functionalities by disconnecting and reconnecting modules in different configurations, the MRMM inherits this feature to adapt to a new application instead of resorting to a new manipulator [6]. In the past few decades, a plethora of research has been carried out, including kinematics and dynamics analysis [7], tip-over stability analysis [8, 9], control method [10], path or trajectory planning [11, 12], configuration optimization [13], structural design [14], and updating method [15].

For traditional mobile manipulators, the tip-over instability can be analyzed by the reaction wrench transferred from the manipulator to the mobile platform. The instability problem caused by this wrench poses a great concern for the safety of robot operation. The issue of tip-over stability has been studied for decades with many criteria proposed to measure the stability margin of a mobile system, for example, center of gravity, static stability margin, zero moment point (ZMP), longitudinal stability margin [16], dynamic stability margin [17], tumble stability judgment [18], leg-end supporting moment [19], force-angle stability (FA) [20], foot-rotation indicator (FRI) [21], moment-height stability [22], stability pyramid, and tip-over moment (TOM) [13, 23, 24]. With these criteria, several path planning and guidance control methods were proposed. Qiang et al. proposed a path planning method using a stability potential field to maintain the stability of the system moving along a given trajectory [25]. Hatanol et al. studied the ZMP-based stability of a mobile manipulator in transient states [26]. Lee et al. proposed an online compensation scheme for rollover prevention of mobile manipulators based on the invariance control framework with the gradient of ZMP [27]. Peters et al. presented a method to control the Sample Return Rover’s reconfigurability to enhance system tip-over stability with the FA criterion [28]. Talke et al. developed an autonomous tip-over prevention behavior for a mobile robot using a FA stability measure [29]. Choi et al. provided an asymptotically stabilizing controller that integrates fully actuated and underactuated phases of walking with the FRI criterion [30].

For reconfigurable manipulator, many researchers have focused on configuration optimization. Jason et al. presented a task-based optimization method to maximize the number of attractive regions and minimize the number of repellent regions [31]. Jan et al. proposed an optimization method of reconfiguration planning of handling systems. With this method, a fixed number of configurations is optimally selected from the entire configuration space and simultaneously allocated to a set of handling tasks in the most energy-efficient way [32]. Bo et al. proposed a task-oriented configuration optimization method to obtain a lattice distorted reconfigurable robot that has enough workspace reachability and structural strength to perform a specific task [33]. Liu proposed a novel configuration optimization method for reconfigurable manipulators using genetic algorithms and Dijkstra algorithms. This method combines a minimum task execution time with minimum energy consumption [34]. Saleh et al. proposed a memetic algorithm approach to optimize a serial modular and reconfigurable robot that can generate multiple solutions to the inverse kinematics problem for any given spatial task [13].

So far, the configuration selection to obtain the best tip-over stability for MRMM has not been fully studied, especially considering the reachability of the system under various applications. In this paper, one methodology is presented to study this problem.

2. Problem formulation

The MRR under this study is mounted on a mobile platform. The MRR consists of several joint modules and link modules. Each joint module can be manually reconfigured to provide the rotation about one of three axes of the module’s body coordinates system. Successive modules are connected by attaching one end of the link module to one of the flat faces of the previous joint module to form a serial manipulator. Figure 1(a) and (b) show one configuration with three revolute joint modules and three link modules.

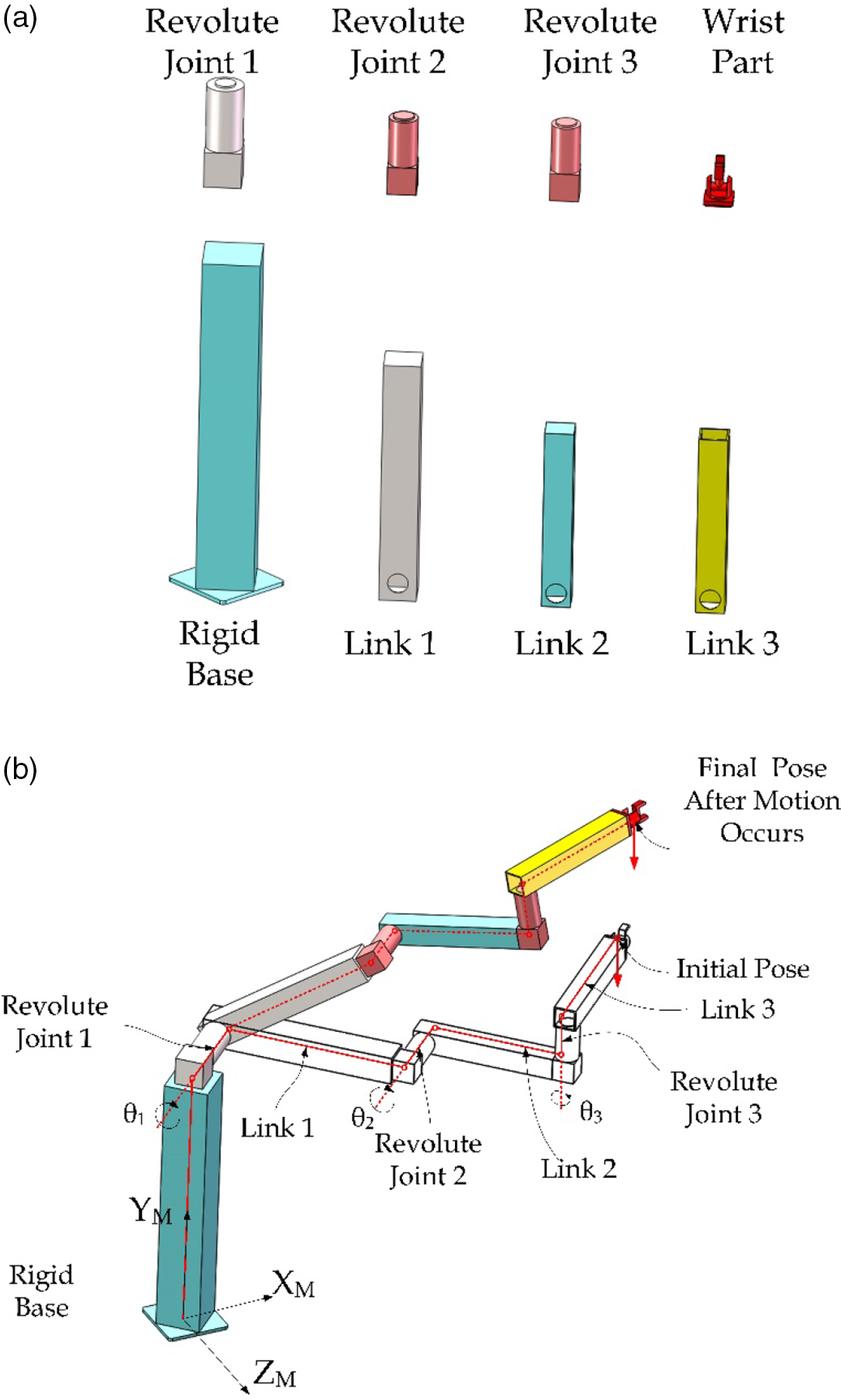
Figure 1. (a) Joint and link modules, (b) assembled MRR.

Figure 2. The configuration selection process to improve MRMM’s tip-over stability.

This research is to select an optimal configuration that can improve MRMM’s stability under a given application situation. In Fig. 2, the selection method is proposed as follows:

1. 1. For given joint modules and link modules, all the permissible configurations (PCs) of an MRR will be found using an enumeration algorithm [6]. These PCs contain all the possibilities but eliminate the duplicate configurations.

2. 2. For all PCs, the feasible configurations (FCs) will be identified by application-oriented workspace classifications, that is, for a specific application, the chosen FCs should meet the requirement of its workspace.

3. 3. For all FCs, the objective configuration will be determined based on the workspace indices. After this step, the selected one is supposed to improve the MRMM’s tip-over stability.

3. Methodology

3.1. MRR modeling

Kinematically, MRR can be modeled as [13]:

(1) \begin{equation}\mathbf{X}=\mathrm{f}\!\left(\mathbf{q}, {}^{\textrm{C}}{\mathbf{g}}{}\right), \mathbf{q}_{\mathbf{i}}=\left({\unicode[Times]{x03B8}}_{\mathrm{i}},\mathrm{s}_{\mathrm{i}}\right), {}^{\textrm{C}}{\mathbf{g}_{\mathrm{i}}}{}=({\mathrm{x}_{\mathrm{i}}},{\mathrm{y}_{\mathrm{i}}},{\mathrm{z}_{\mathrm{i}}},{{\unicode[Times]{x03B1}}_{\mathrm{i}}},{{\unicode[Times]{x03B2}}_{\mathrm{i}}},{{\unicode[Times]{x03B3}}_{\mathrm{i}}})^{\mathrm{T}},\mathrm{i}=1,\ldots,\mathrm{n}\end{equation}

where $\mathbf{X}$ is a vector representing the MRR’s pose, that is, $\mathbf{X}=(\mathrm{x},\mathrm{y},\mathrm{z},{\unicode[Times]{x03B1}},{\unicode[Times]{x03B2}},{\unicode[Times]{x03B3}})^{\mathrm{T}}$ with the first three components representing the end-effector’s position and the last three ones representing the pitch, roll, and yaw (PRY) angles of the end-effector; $\mathbf{q}_{\mathrm{i}}$ is the joint variable for the ith joint with ${\unicode[Times]{x03B8}}_{\mathrm{i}}$ for a revolute joint and $\mathrm{s}_{\mathrm{i}}$ for a prismatic joint; ${}^{\textrm{C}}{\mathbf{g}_{\mathrm{i}}}{}$ is a set of kinematic parameters for setting up a joint-link module at an initial configuration, with $({\mathrm{x}_{\mathrm{i}}},{\mathrm{y}_{\mathrm{i}}},{\mathrm{z}_{\mathrm{i}}})^{\mathrm{T}}$ representing its position and $({{\unicode[Times]{x03B1}}_{\mathrm{i}}},{{\unicode[Times]{x03B2}}_{\mathrm{i}}},{{\unicode[Times]{x03B3}}_{\mathrm{i}}})^{\mathrm{T}}$ for its orientation with respect to the global coordinates. Superscript C is a configuration index and subscript i is a joint-link module index. By selecting the configurations of these modules, the overall structure of the MRR is reconfigured.

For reconfiguration purpose, the initial configuration set-up (ICSU) is defined for an MRR by including a static rotation matrix ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{si}}}{}$ and a static body vector ${}^{\textrm{C}}{\mathbf{b}_{\mathrm{si}}}{}$ , which can be obtained from ${}^{\textrm{C}}{\mathbf{g}_{\mathrm{i}}}{}$ ,

(2) \begin{equation}\text{ICSU}_{\mathrm{i}}=\left({}^{\textrm{C}}{\mathbf{b}_{\mathrm{si}}}{},{}^{\textrm{C}}{\mathbf{R}_{\mathrm{si}}}{}\right)=\mathrm{f}'\!\left({}^{\textrm{C}}{\mathbf{g}_{\mathrm{i}}}{}\right)\end{equation}

where

(3) \begin{equation}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{si}}}{}=\mathbf{R}_{\mathrm{x}}\!\left({\unicode[Times]{x03B1}}_{\mathrm{i}}\right)\mathbf{R}_{\mathrm{y}}\!\left({\unicode[Times]{x03B2}}_{\mathrm{i}}\right)\mathbf{R}_{\mathrm{z}}\!\left({\unicode[Times]{x03B3}}_{\mathrm{i}}\right)\end{equation}

(4) \begin{equation}{}^{\textrm{C}}{\mathbf{b}_{\mathrm{si}}}{}=\mathrm{x}_{\mathrm{i}}\vec {\mathbf{X'}_{\!\!\mathrm{i}}}+\mathrm{y}_{\mathrm{i}}\vec {\mathbf{Y'}_{\!\!\mathrm{i}}}+\mathrm{z}_{\mathrm{i}}\vec {\mathbf{Z'}_{\!\!\mathrm{i}}}\end{equation}

Where $\mathbf{R}_{\mathrm{x}}({\unicode[Times]{x03B1}}_{\mathrm{i}})$ , $\mathbf{R}_{\mathrm{y}}({\unicode[Times]{x03B2}}_{\mathrm{i}})$ , and $\mathbf{R}_{\mathrm{z}}({\unicode[Times]{x03B3}}_{\mathrm{i}})$ are the rotation matrices according to the PRY angles, respectively, and $\vec {\mathbf{X'}_{\!\!\mathrm{i}}}$ , $\vec {\mathbf{Y'}_{\!\!\mathrm{i}}}$ , and $\vec {\mathbf{Z'}_{\!\!\mathrm{i}}}$ are the three unit-vectors of the local frame attached to the ith joint. A conventional robot manipulator usually has its fixed ICSU, while an MRR’s ICSU changes each time after reconfiguration. Based on ref. [13], the kinematic formulation involves a static part and a motion part. As shown in Fig. 3, the static part ( ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}(\mathrm{i}-1)\mathrm{i}}}{}, {}^{\textbf{C}}{\mathbf{b}_{\mathrm{si}}}{}$ ) is defined according to the ICSU as indicated in Eq. (2), and the motion part ( $\mathbf{R}_{\mathrm{mi}}$ , $\mathbf{b}_{\mathrm{mi}}$ ) represents the movement of either joint or link $\mathbf{q}_{\mathrm{i}}$ . The total translation $\mathbf{b'}_{\!\!\mathrm{i}}$ and rotation $\mathbf{R}_{(\mathrm{i}-1)\mathrm{i}}$ of the ith link can be given as

(5) \begin{equation}{}^{\textrm{C}}{\mathbf{R}_{(\mathrm{i}-1)\mathrm{i}}}{}={}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}\left(\mathrm{i}-1\right)\mathrm{i}}}{}\mathbf{R}_{\mathrm{mi}}\end{equation}

(6) \begin{equation}{}^{\textrm{C}}{\mathbf{b'}_{\!\!\mathrm{i}}}{}={}^{\textbf{C}}{\mathbf{b}_{\mathrm{si}}}{}+\mathbf{b}_{\mathrm{mi}}\end{equation}

where $\mathbf{R}_{\mathrm{mi}}$ and $\mathbf{b}_{\mathrm{mi}}$ are the rotation matrices and body vectors, respectively, which are functions of the joint variables $\mathbf{q}_{\mathrm{i}}$ in Eq.(1), and their calculations are equivalent to Eqs. (3) and (4). The end-effector’s pose can be expressed with respect to the global reference frame by

(7) \begin{equation}{}^{\textrm{C}}{\mathbf{p}_{\mathrm{n}+1}}{}=\sum _{\mathrm{i}=0}^{\mathrm{n}}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{oi}}}{}{}^{\textrm{C}}{\mathbf{b'}_{\!\!\mathrm{i}}}{}\end{equation}

(8) \begin{equation}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{on}}}{}=\prod _{\mathrm{i}=1}^{\mathrm{n}}{}^{\textrm{C}}{\mathbf{R}_{(\mathrm{i}-1)\mathrm{i}}}{}\end{equation}

where ${}^{\textrm{C}}{\mathbf{b'}_{\!\!\mathrm{i}}}{}$ is the link body vector in the local frames, which is transformed to the global frame by multiplying the orientation matrix ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{oi}}}{}$ and then summed to obtain the position of the end effector, as given in Eq. (7); ${}^{\textrm{C}}{\mathbf{R}_{(\mathrm{i}-1)\mathrm{i}}}{}$ represents the rotation matrix between two adjacent link body frames, which is sequentially multiplied together to determine the orientation of the end-effector, as given in Eq. (8).

Figure 3. Manipulator kinematic modeling with static and motion parts.

The separation of the static part and dynamic part of the rotation matrix in Eq. (5) allows the use of the zero reference plane (ZRP) [35]. Under ZRP, all modules can be set up uniformly with respect to the global coordinates for each configuration, that is, previously mentioned ICSU. This would alleviate some burdens when required to re-generate the robot kinematics and dynamics equations after reconfiguration. The following can be obtained at ZRP, meaning that no joint motion is applied.

(9) \begin{equation}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0\mathrm{i}}}{}={}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0(\mathrm{i}-1)}}{}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}(\mathrm{i}-1)\mathrm{i}}}{}\end{equation}

where ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0\mathrm{i}}}{}$ is the static rotation matrix of the ith module that is set up with respect to the global frame at ZRP; ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0(\mathrm{i}-1)}}{}$ is the static rotation matrix of the (i-1)th module with respect to the global frame at ZRP. Then, ${}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}(\mathrm{i}-1)\mathrm{i}}}{}$ needed for Eq. (5) can be derived as

(10) \begin{equation}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}(\mathrm{i}-1)\mathrm{i}}}{}={}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0(\mathrm{i}-1)}^{\mathrm{T}}}{}{}^{\textrm{C}}{\mathbf{R}_{\mathrm{s}0\mathrm{i}}}{}\end{equation}

Eq. (10) is the basic formulation for the robot kinematics and dynamics based on ZRP.

3.2. Configurations enumeration

Configuration space is referred to as the number of PCs that can be realized using the robot modules of an MRR without violating physical constraints. The basic structure of the MRR under study follows that of a traditional industrial robot manipulator. The first three joint-link modules form the main body for positioning and the last three joints form a wrist for orientation. This study focuses on the first three modules because the last three joints contribute little to the stability. Based on the joint-link modules shown in Fig. 1, the total number of FCs for them would be $6^{6}=46656$ . However, through isomorphism analysis, deletion of collinear modules, and consideration of physical limits, a three DOFs MRR yields 14 PCs for spatial motions, as listed in Table I. All these PCs and their workspaces are shown in Appendix as well. In Table I, these axes are the initial axes set up according to the global frame at ZRP. It is noted that Conf. 11 is the configuration of PUMA 560.

Table I. Permissible configurations and axes arrangement.

3.3. Application-oriented workspace classifications

To obtain FCs in PCs, three general applications are considered. The first one is that the tip of MRMM works in a vertical plane like drilling or riveting of flat or curved panels, such as aircraft fuselage. The second one is that the tip works in a horizontal plane. These applications include grinding, welding, and painting of large components, such as train roofs. The third one is that the tip works in a general 3D space, just like part handling or assembling.

For all PCs, their workspace shapes are listed in the appendix and can be classified into three classes. The first one is a vertical doughnut shape which is suited for the vertical plane application. The second one is a horizontal doughnut shape which is suited for the horizontal plane application. The last one is a hemisphere or hemi-ellipsoid shape which is suited for the 3D space application.

The first class includes Conf. 1 and Conf. 4. For these two configurations, the axes of adjacent joint 1 and 2 are all along the same direction, that is, Joints 1 and 2 in Conf. 1 are both along the x-direction, while Joints 1 and 2 in Conf. 4 are both along the z-direction. Since these axes are not in parallel with the horizontal direction, their workspaces are of doughnut shape in the vertical direction. The second class is similar to the first class which includes Conf. 9 and Conf. 12. The axes of Joints 1 and 2 of these two configurations are both along the y-direction, that is, along the vertical direction. Their workspaces are of doughnut shape in the horizontal direction. The last class includes all the rest, that is, Conf. 2, 3, 5, 6, 7, 8, 10, 11, 13, and 14. For those, the axes of Joints 1 and 2 are not along the same direction, making their workspaces like a hemisphere or hemi-ellipsoid shape.

3.4. Selection based on workspace indices

Since the workspace of MRR is the main performance index that is closely related to the tip-over problem, two indices describing the workspace characteristics are introduced. Taking Conf. 1 shown in Fig. 4 as an example, one important index is vertical reach (VR), that is, the highest position that the manipulator can reach. The other one is horizontal reach (HR), that is, the farthest position that the manipulator can reach. VR and HR of all FCs are listed in Table II. These two indices play a key role in selecting an optimal configuration for a given task. If these two indices are longer, it means the workspace is bigger. Based on the former research [13], for the static case, long HR may mean more TOMs if the manipulator tip moves to the outside of the mobile platform. For the dynamic case, long HR or VR may mean less tip-over stability with the same joint speed and acceleration. For the tip payload case, long HR or VR means a long arm of force, which may lead to less tip-over stability. The method proposed here is configuration selection with these two workspace indices. After application-oriented workspace classifications, the configuration corresponding to the short HR and VR combination will be assigned as an optimal one. The short HR and VR will also result in a small workspace, which will reduce reachability. This problem can be solved with a linear guide rail module between the mobile platform and MRR.

Figure 4. VR and HR.

Table II. Workspace Classifications and Indices.

4. Tip-over stability verification

4.1. Tip-over stability modeling

For the tip-over analysis of a traditional mobile manipulator, two criteria are used: $\mathrm{TOM}$ and stable region ratio ( $\mathrm{SRR}$ ) [13, 23, 24]. This method is based on the dynamic interaction of the manipulator with the mobile platform. These criteria are now applied to MRMM as well.

Figure 5 depicts the underlying problem. In this figure, the ellipse represents a mobile platform on which the afore-mentioned MRR is mounted. A local coordinate frame $\{\mathrm{X}_{\mathrm{P}},\mathrm{Y}_{\mathrm{P}},\mathrm{Z}_{\mathrm{P}}\}$ is attached to the center of gravity of the platform at point $\mathrm{O}_{\mathrm{P}}$ . $\mathbf{g}_{\mathrm{P}}$ is the vector of the gravitational force of the mobile platform and $\mathrm{m}_{\mathrm{P}}$ is its mass. The mass of the MRR is $\mathrm{m}_{\mathrm{r}}$ . It is mounted at point M to which the MRR’s base coordinate frame $\{\mathrm{X}_{\mathrm{M}},\mathrm{Y}_{\mathrm{M}},\mathrm{Z}_{\mathrm{M}}\}$ is attached. The reaction wrench, denoted by $-{}^{\textrm{C}}{\mathbf{w}_{1}}{},$ is acting on point M from the MRR onto the mobile platform. This wrench has three force components ${}^{\textrm{C}}{\mathbf{f}_{\mathrm{M}}}{}=[{\mathrm{f}_{1\mathrm{X}}}, {\mathrm{f}_{1\mathrm{Y}}}, {\mathrm{f}_{1\mathrm{Z}}}]^{\mathrm{T}}$ and three moment components ${}^{\textrm{C}}{\mathbf{m}_{\mathrm{M}}}{}=[{\mathrm{m}_{1\mathrm{X}}}, {\mathrm{m}_{1\mathrm{Y}}}, {\mathrm{m}_{1\mathrm{Z}}}]^{\mathrm{T}}$ , that is, $-{}^{\textrm{C}}{\mathbf{w}_{1}}{}=[{}^{\textrm{C}}{{\mathbf{f}_{\mathrm{M}}}^{\mathrm{T}}}{}, {}^{\textrm{C}}{{\mathbf{m}_{\mathrm{M}}}^{\mathrm{T}}}{}]^{\mathrm{T}}$ .

Figure 5. Forces and moments on a mobile platform.

When tip-over occurs, the mobile platform rolls about a tip-over axis formed by two adjacent wheels. Two vectors ${}^{\textrm{n}}{\mathbf{p}_{\mathrm{j}}}{}$ and ${}^{\textrm{n}}{\mathbf{p}_{\mathrm{j}+1}}{}$ represent two adjacent wheels of the mobile platform, forming a tip-over axis $\mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}$ . $\mathbf{d}_{\mathrm{M}}$ is the vector from the origin $\mathrm{O}_{\mathrm{P}}$ to point M, representing the mounting position of the MRR. $\mathbf{d}_{\mathrm{j}(\mathrm{j}+1)}$ is a vector from point $\mathrm{M}$ to the tip-over axis $\mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}$ , while $\mathbf{l}_{\mathrm{j}(\mathrm{j}+1)}$ is a vector from $\mathrm{O}_{\mathrm{P}}$ to the tip-over axis $\mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}$ . TOM about the tip-over axis $\mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}$ can be derived considering all the afore-mentioned forces and moments as [13]

(11) \begin{equation}{}^{\textrm{C}}{\mathrm{TOM}_{\mathrm{j}(\mathrm{j}+1)}}{}={}^{\textrm{C}}{\mathbf{m}_{\mathrm{M}}}{}\cdot \mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}+\left({}^{\textrm{C}}{\mathbf{f}_{\mathrm{M}}}{}\times \mathbf{d}_{\mathrm{j}(\mathrm{j}+1)}\right)\cdot \mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}+\left(\mathbf{g}_{\mathrm{P}}\times \mathbf{l}_{\mathrm{j}(\mathrm{j}+1)}\right)\cdot \mathbf{e}_{\mathrm{j}(\mathrm{j}+1)}\end{equation}

Based on Eq. (11), it can be seen that the size of the mobile platform, the number of wheels, the size of the mobile platform, the mass of the mobile platform, the placement of the manipulator, and accessory will affect the tip-over stability. These factors have already been discussed in refs. [13, 23, 24]. Generally, for an $\mathrm{n}$ -wheel mobile manipulator, there are $\mathrm{n}$ tip-over axes, that is, $\mathrm{n}{}^{\textrm{C}}{\mathrm{TOM}_{\mathrm{i}(\mathrm{i}+1)}}{}$ values. The maximum ${}^{\textrm{C}}{\mathrm{TOM}_{\mathrm{i}(\mathrm{i}+1)}}{}$ value represents the largest TOM that the system has around the axis $\mathbf{e}_{\mathrm{i}(\mathrm{i}+1)}$ . If this maximum ${}^{\textrm{C}}{\mathrm{TOM}_{\mathrm{i}(\mathrm{i}+1)}}{}$ is positive, the system will tip over. If this maximum one is negative, the system is stable with a TOM margin of $|{}^{\textrm{C}}{\mathrm{TOM}_{\mathrm{i}(\mathrm{i}+1)}}{}|$ . As mentioned before, except these factors, the configuration of MRR affects the tip-over stability as well. For this reason, our study is to find one configuration that has the maximum TOM margin or minimum TOM for a set of given tasks.

For a selected configuration of MRR, the actual workspace volume can be obtained after mounting the MRR on the mobile platform. The obtained workspace is denoted by ${}^{\textrm{C}}{\mathrm{v}_{\mathrm{W}}}{}$ , and the tip-over stability region is denoted by ${}^{\textrm{C}}{\mathrm{v}_{\mathrm{S}}}{}$ . A stable region ratio ( ${}^{\textrm{C}}{\mathrm{SRR}}{}$ ) is introduced as ${}^{\textrm{C}}{\mathrm{SRR}}{}= {}^{\textrm{C}}{\mathrm{v}_{\mathrm{S}}}{}/{}^{\textrm{C}}{\mathrm{v}_{\mathrm{W}}}{}$ , which normalizes ${}^{\textrm{C}}{\mathrm{v}_{\mathrm{S}}}{}$ against ${}^{\textrm{C}}{\mathrm{v}_{\mathrm{W}}}{}$ . The second objective of this study is to identify a configuration that has the maximum SRR with which the system can remain stable as much in workspace as possible.

The search method proposed in Fig. 2 is implemented using a workspace-based approach to select an optimal configuration. For simplicity, the mobile platform, joint modules, link modules, and payload are set the same for all PCs, so are the motion parameters including joint ranges, speeds, and accelerations. In this case, the study of tip-over stability of the MRMM is bounded to the configuration of MRR.

As mentioned above, searching over all PCs would be time consuming. An effective approach would be application-oriented workspace classifications. The first step is to classify the FCs into three classes according to the workspaces. Secondl, the two workspace indices, VR and HR, are used to further narrow down the selected classes. As analyzed in the previous research [13], the tip-over mostly occurs when the manipulator reaches the workspace boundary. Based on this, the selected configurations can be further sorted out from the FCs. Finally, an optimal configuration will be identified from the selected configuration space by the two criteria: $\mathrm{TOM}$ and $\mathrm{SRR}$ .

In this section, the proposed method is applied for three applications, vertical, horizontal, and 3D, respectively. For the first two applications, three cases are simulated: static, dynamic, and tip force cases. For the last application, two situations are simulated: the static and dynamic cases.

In the static case, all joints’ speed and acceleration are equal to 0. In the dynamic case, based on the conclusions in ref. [13], TOM and SRR will be computed as follows: the joint speeds of all revolute joints are set at $175^{\circ}/\mathrm{s}$ in two directions, and the joint accelerations are also set at $200^{\circ}/\mathrm{s}^{2}$ in two directions. In this case, a 5 kg payload at the tip is also included. In the tip force case, the force vector will be chosen based on workspace and application. For example, the horizontal tip force will be introduced into simulation if an MRMM works on a vertical plane, with applications including drilling or riveting of the fuselage. The vertical tip force will be introduced if an MRMM works on a horizontal plane, with applications including grinding and welding. TOM and SRR of all configurations will be computed and compared to obtain the most stable configuration.

4.2. Vertical plane application

As shown in Fig. 6, this mobile manipulator can drill or rivet on an aircraft fuselage. Under normal conditions, the fuselage to be machined is a cylindrical shape with a radius usually about 2-3 m. It can be considered a vertical plane application. As shown in Fig. 7, the baseline drawing mobile manipulator’s end-effector always moves in a vertical plane as well. The vertical plane is the building’s blank wall (the glass screen wall shown in the figure instead for the experiment). For these vertical plane applications, through the above analysis, the selected class only includes Conf. 1 and 4. Comparing the workspace indices listed in Table II, HR and VR of Conf. 4 are shorter than those of Conf. 1. With the method given in Section 3.2, it can be predicted that the MRMM system in Conf. 4 has a higher tip-over stability margin. For validation, the dynamics simulation is carried out.

Figure 6. Fuselage drilling or riveting with mobile manipulator for aircraft manufacturing.

Figure 7. Baseline drawing with mobile manipulator for interior decoration.

The simulation results of these two configurations in three cases are listed in Tables III and IV. In the static case, the MRMM system is stable with a certain TOM margin in these two configurations, and SRR results are both 100%. In the dynamic case, the TOM results show that the MRMM systems in two configurations are unstable but the one in Conf. 4 is more stable than the one in Conf. 1. SRR results are consistent with TOM. Conf. 1’s SRR is smaller than Conf. 4’s which means that the MRMM with MRR in Conf. 4 is more stable than the one in Conf. 1. In the tip force case, the TOM and SRR results show that the system in Conf. 4 is more stable than the one in Conf. 1 as well.

Table III. TOM and SRR results of the static and dynamic cases for a vertical plane application.

Table IV. TOM and SRR results of tip force case for a vertical plane application.

As the figures listed in the Appendix shown, it can be found that Conf. 1’s axes of Joint 1 and 2 are in the same direction, while Conf. 4’s axes of Joint 1 and 2 are in the opposite direction. With the offset caused by motor length, it leads to that the tip and link CG positions of Conf. 1 are a little further than that of Conf. 4 from the origin point under the same joint angles. Based on ref. [13], in the static case, the conclusion has already been obtained that tip-over instability correlates with the horizontal positions of link CGs and the manipulator’s tip. Given this, the system with MRR in Conf. 4 is more stable than the one in Conf. 1 in the static case. In the dynamic case, the tip and link CG position difference also makes Conf. 1’s linear velocity and acceleration bigger than Conf. 4’s under the same joint speeds and accelerations, which in turn makes the system with MRR in Conf. 4 more stable than the one in Conf. 1. In the tip-force case, this difference means that a long arm of force for Conf. 1 would cause a bigger TOM.

Given this, the conclusions can be drawn. For the vertical plane application, the MRMM system with MRR in Conf. 4 is optimal. The result of dynamics calculation is in coordination with the result obtained with the proposed method. Since SRR of Conf. 4 is not equal to 100% in the dynamic case, for tip-over safety, the system should decrease joint speeds and accelerations.

4.3. Horizontal plane application

As shown in Fig. 8, the mobile manipulator is developed for concrete 3D printing. 3D printing can be directly used to construct complex buildings through computer-aided design models without the aid of additional tools and fixtures, and it is a process from deposition of materials layer-by-layer to products. In this application, the end-effector moved in a horizontal plane in a layer. The height difference between different layers can be made up by the reach of the manipulator or an additional longitudinal seventh axis. For the horizontal plane application, through the above analysis, the selected class only contains Conf. 9 and 12. Comparing the data as shown in Table II, the HR and VR of Conf. 12 are shorter than those of Conf. 9 simultaneously. With the method proposed, it can be predicted that the MRMM system in Conf. 12 has a higher tip-over stability margin.

Figure 8. Concrete 3D printing with mobile manipulator for intelligent construction.

The simulation results of these two configurations are listed in Tables V and VI. It can be found that, in the static and tip-force cases, the systems are both stable. As shown in Table II, the difference between these two configurations is the direction of joint 2’s axis. The one of Conf. 9’s is along the positive direction, while the one of Conf. 12’s is along the minus direction. This difference makes the workspace of Conf. 9 stand higher than that of Conf. 12, but this difference does not affect the horizontal positions of the tip or CG, that is, not affect the tip-over stability of the system in static or tip-force cases.

In the dynamic case, the horizontal components of force caused by joint speeds and act the tip-ccelerations are the same. Since Conf. 9’s arm of force in the vertical direction is longer, the TOM is bigger. It should be noted that, in real applications, the vertical height of the system is fixed according to the workpiece, so the height difference between Conf. 9 and 12 will be made up by an extra linear lifting platform. The aforementioned difference will no longer exist. In other words, the stability of MRMM in Conf. 9 and 12 is nearly the same.

Given this, the conclusions can be drawn. For a horizontal plane application, the stability of the MRMM system with MRR in Conf. 12 has better tip-over stability than the one in Conf. 9. The result of dynamics calculation is in correlation with the result obtained with the proposed method. To improve the stability, the operation height should be kept as low as possible.

4.4. 3D space application

As shown in Fig. 9, one mobile manipulator is used for upper limb rehabilitation or bedside rehabilitation. The system can be easily moved to the bedside or treatment room due to the mobility of this system. The manipulator can offer interaction force and torque for patients which can be used as the auxiliary force, or the gravity reduction force. In this application, the end effector moves in a 3D space, to match the motion space of the human upper limbs. For this 3D space application, the selected class includes the rest ten configurations. The VR of Conf. 7 is the smallest, but its HR of Conf. 7 is the biggest. It means that the workspace of Conf. 7 is short in the vertical direction but long in the horizontal direction. The second smallest VR is Conf. 14, and its HR is the second smallest as well. The smallest HR is Conf. 8, while its VR is the third smallest. Overall, Conf. 14 may have the highest tip-over stability, since the distances in both directions are smaller.

The simulation results are listed in Table VII. In the static and dynamic cases, it can be found that the tip-over stability difference of these ten configurations is very small. In the static case, the horizontal position change of different configurations’ CG is small which makes tip-over stability nearly the same. It can be obtained from Table II that Conf. 14’s VR and HR are shorter than most of the others. MRR in Conf. 14 cannot reach far positions in the either vertical or horizontal direction, and this will decrease TOM. It improves the stability of the system.

Table V. ${TOM}$ and ${SRR}$ results of the static and dynamic cases for a horizontal plane application.

Table VI. ${TOM}$ and ${SRR}$ results of tip force case for a horizontal plane application.

Figure 9. Upper limb rehabilitation with mobile manipulator.

Given this, a conclusion can be drawn. For a 3D space application, the stability of the MRMM system with MRR in Conf. 14 is optimal. The result of dynamics calculation is in correlation with the result obtained with the proposed method.

5. Conclusions

In this paper, a method for selecting the configuration of MRR is proposed for an MRMM to obtain the best tip-over stability. The proposed method is of three steps. First, the PCs are found using an enumeration algorithm. An application-oriented workspace classification is carried out to obtain FCs for different applications. At last, two workspace indices, VR and HR, are used for configuration selection. The optimal configuration improves the tip-over stability of MRMM. With the proposed method, three cases including the vertical/horizontal plane and 3D space applications are investigated. It is found that for vertical and horizontal plane applications, Conf. 4 and 12 are the selected ones, respectively, and for 3D space applications, Conf. 14 is the selected configuration. Simulations on different cases are carried out for method validation. The results show that the proposed method can obtain a selected configuration for MRMM for a given application that improves tip-over stability under various application situations.

Table VII. TOM and SRR results of the static and dynamic cases for a horizontal plane application.