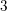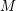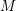When trying to distinguish two compact
![]() $3$
-manifolds
$3$
-manifolds
![]() $M,N$
, in practice the easiest method is often to compute some finite quotients of their fundamental groups, and notice that there is a finite group
$M,N$
, in practice the easiest method is often to compute some finite quotients of their fundamental groups, and notice that there is a finite group
![]() $Q$
which is a quotient of
$Q$
which is a quotient of
![]() $\unicode[STIX]{x1D70B}_{1}M$
, say, but not of
$\unicode[STIX]{x1D70B}_{1}M$
, say, but not of
![]() $\unicode[STIX]{x1D70B}_{1}N$
. It would be very useful, both theoretically and in practice, to know that this method always works. The set of finite quotients of a group
$\unicode[STIX]{x1D70B}_{1}N$
. It would be very useful, both theoretically and in practice, to know that this method always works. The set of finite quotients of a group
![]() $\unicode[STIX]{x1D6E4}$
is encoded by the profinite completion
$\unicode[STIX]{x1D6E4}$
is encoded by the profinite completion
![]() $\widehat{\unicode[STIX]{x1D6E4}}$
(the inverse limit of the system of finite quotient groups), and so one is naturally led to the following question.
$\widehat{\unicode[STIX]{x1D6E4}}$
(the inverse limit of the system of finite quotient groups), and so one is naturally led to the following question.
Question 0.1. Let
![]() $M$
be a compact, orientable
$M$
be a compact, orientable
![]() $3$
-manifold. To what extent is
$3$
-manifold. To what extent is
![]() $\unicode[STIX]{x1D70B}_{1}M$
determined by its profinite completion?
$\unicode[STIX]{x1D70B}_{1}M$
determined by its profinite completion?
In particular, if
![]() $M$
is determined among all compact, orientable
$M$
is determined among all compact, orientable
![]() $3$
-manifolds by
$3$
-manifolds by
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
, then
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
, then
![]() $M$
is said to be profinitely rigid. If there are at most finitely many compact, orientable
$M$
is said to be profinitely rigid. If there are at most finitely many compact, orientable
![]() $3$
-manifolds
$3$
-manifolds
![]() $N$
with
$N$
with
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
, then
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
, then
![]() $M$
is said to have finite genus. More precise versions of Question 0.1 ask which
$M$
is said to have finite genus. More precise versions of Question 0.1 ask which
![]() $3$
-manifolds are profinitely rigid, which have finite genus and whether various properties of
$3$
-manifolds are profinitely rigid, which have finite genus and whether various properties of
![]() $M$
are determined by
$M$
are determined by
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
.
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
.
The results of this paper show that the profinite completion
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines both the Kneser–Milnor and the Jaco–Shalen–Johannson (JSJ) decompositions of
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines both the Kneser–Milnor and the Jaco–Shalen–Johannson (JSJ) decompositions of
![]() $M$
. This complements our previous results showing that
$M$
. This complements our previous results showing that
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines the geometry of
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines the geometry of
![]() $M$
[Reference Wilton and ZalesskiiWZ17]. The first theorem concerns the Kneser–Milnor decomposition.
$M$
[Reference Wilton and ZalesskiiWZ17]. The first theorem concerns the Kneser–Milnor decomposition.
Theorem A. Let
![]() $M,N$
be closed, orientable
$M,N$
be closed, orientable
![]() $3$
-manifolds with Kneser–Milnor decompositions
$3$
-manifolds with Kneser–Milnor decompositions
![]() $M\cong M_{1}\#\cdots \#M_{m}\#r(S_{1}\times S_{2})$
and
$M\cong M_{1}\#\cdots \#M_{m}\#r(S_{1}\times S_{2})$
and
![]() $N\cong N_{1}\#\cdots \#N_{n}\#s(S_{1}\times S_{2})$
. If
$N\cong N_{1}\#\cdots \#N_{n}\#s(S_{1}\times S_{2})$
. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
then
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
then
![]() $m=n$
,
$m=n$
,
![]() $r=s$
, and, up to re-indexing, the image of
$r=s$
, and, up to re-indexing, the image of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}_{i}$
is conjugate to
$\widehat{\unicode[STIX]{x1D70B}_{1}M}_{i}$
is conjugate to
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}_{i}$
for each
$\widehat{\unicode[STIX]{x1D70B}_{1}N}_{i}$
for each
![]() $i$
.
$i$
.
In particular,
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines whether or not
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
determines whether or not
![]() $M$
is irreducible. While this work was in progress we discovered that a similar result has also been proved in the pro-
$M$
is irreducible. While this work was in progress we discovered that a similar result has also been proved in the pro-
![]() $p$
setting by Wilkes, using
$p$
setting by Wilkes, using
![]() $l^{2}$
-cohomology [Reference WilkesWil17a, Proposition 6.2.4]. Our proof is different, using the continuous cohomology of the profinite completion, and naturally generalizes to our next theorem, which shows that the profinite completion determines the JSJ decomposition of
$l^{2}$
-cohomology [Reference WilkesWil17a, Proposition 6.2.4]. Our proof is different, using the continuous cohomology of the profinite completion, and naturally generalizes to our next theorem, which shows that the profinite completion determines the JSJ decomposition of
![]() $M$
.
$M$
.
Theorem B. Let
![]() $M$
and
$M$
and
![]() $N$
be closed, orientable, irreducible
$N$
be closed, orientable, irreducible
![]() $3$
-manifolds, and suppose
$3$
-manifolds, and suppose
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
. Then the underlying graphs of the JSJ decompositions of
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
. Then the underlying graphs of the JSJ decompositions of
![]() $\unicode[STIX]{x1D70B}_{1}M,\unicode[STIX]{x1D70B}_{1}N$
are isomorphic, and corresponding vertex groups have isomorphic profinite completions.
$\unicode[STIX]{x1D70B}_{1}M,\unicode[STIX]{x1D70B}_{1}N$
are isomorphic, and corresponding vertex groups have isomorphic profinite completions.
See Theorem 4.3 for a more precise statement, phrased in terms of profinite Bass–Serre trees. Partial results along the lines of Theorem B have also been obtained by Wilkes [Reference WilkesWil17a, Theorem I].
In [Reference Wilton and ZalesskiiWZ17, Theorem 8.4], it was shown that the profinite completion of the fundamental group of a closed, orientable
![]() $3$
-manifold
$3$
-manifold
![]() $M$
determines the geometry of
$M$
determines the geometry of
![]() $M$
. As an immediate consequence of Theorem B, we can extend this result to the case with toral boundary. Recall that
$M$
. As an immediate consequence of Theorem B, we can extend this result to the case with toral boundary. Recall that
![]() $\overline{H}$
denotes the closure of a subgroup
$\overline{H}$
denotes the closure of a subgroup
![]() $H$
in the profinite completion
$H$
in the profinite completion
![]() $\overline{G}$
.
$\overline{G}$
.
Corollary C. Let
![]() $M,N$
be compact, orientable, irreducible
$M,N$
be compact, orientable, irreducible
![]() $3$
-manifolds with non-empty toral boundaries; let
$3$
-manifolds with non-empty toral boundaries; let
![]() $\{P_{1},\ldots ,P_{m}\}$
and
$\{P_{1},\ldots ,P_{m}\}$
and
![]() $\{Q_{1},\ldots ,Q_{n}\}$
be conjugacy representatives for the boundary subgroups of
$\{Q_{1},\ldots ,Q_{n}\}$
be conjugacy representatives for the boundary subgroups of
![]() $\unicode[STIX]{x1D70B}_{1}M$
and
$\unicode[STIX]{x1D70B}_{1}M$
and
![]() $\unicode[STIX]{x1D70B}_{1}N$
, respectively. Suppose that
$\unicode[STIX]{x1D70B}_{1}N$
, respectively. Suppose that
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
, that
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}N}$
, that
![]() $m=n$
, and that the isomorphism takes
$m=n$
, and that the isomorphism takes
![]() $\overline{P}_{i}$
to
$\overline{P}_{i}$
to
![]() $\overline{Q}_{i}$
for each
$\overline{Q}_{i}$
for each
![]() $i$
. If
$i$
. If
![]() $M$
is geometric then
$M$
is geometric then
![]() $N$
is also geometric, with the same geometry. In particular,
$N$
is also geometric, with the same geometry. In particular,
![]() $M$
is Seifert fibred if and only if
$M$
is Seifert fibred if and only if
![]() $N$
is Seifert fibred.
$N$
is Seifert fibred.
Proof. Let
![]() $D$
be the double of
$D$
be the double of
![]() $M$
and
$M$
and
![]() $E$
be the double of
$E$
be the double of
![]() $N$
. Note that
$N$
. Note that
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}D}\cong \widehat{\unicode[STIX]{x1D70B}_{1}E}$
, and also that the isomorphism respects the profinite completions of the boundary subgroups of
$\widehat{\unicode[STIX]{x1D70B}_{1}D}\cong \widehat{\unicode[STIX]{x1D70B}_{1}E}$
, and also that the isomorphism respects the profinite completions of the boundary subgroups of
![]() $\unicode[STIX]{x1D70B}_{1}M$
and
$\unicode[STIX]{x1D70B}_{1}M$
and
![]() $\unicode[STIX]{x1D70B}_{1}N$
. The result follows from the observation that the geometry of
$\unicode[STIX]{x1D70B}_{1}N$
. The result follows from the observation that the geometry of
![]() $M$
is reflected in properties of the double
$M$
is reflected in properties of the double
![]() $D$
.
$D$
.
Indeed, if
![]() $M$
is Seifert fibred then so is
$M$
is Seifert fibred then so is
![]() $D$
. In this case, if
$D$
. In this case, if
![]() $M$
is homeomorphic to an interval bundle over the torus then
$M$
is homeomorphic to an interval bundle over the torus then
![]() $D$
has Euclidean geometry; otherwise,
$D$
has Euclidean geometry; otherwise,
![]() $M$
and
$M$
and
![]() $D$
both have
$D$
both have
![]() $\mathbb{H}^{2}\times \mathbb{R}$
geometry. Finally,
$\mathbb{H}^{2}\times \mathbb{R}$
geometry. Finally,
![]() $M$
is hyperbolic if and only if
$M$
is hyperbolic if and only if
![]() $D$
has non-trivial JSJ decomposition, and the boundary tori of
$D$
has non-trivial JSJ decomposition, and the boundary tori of
![]() $M$
are the only JSJ tori of
$M$
are the only JSJ tori of
![]() $D$
. Combining these facts with Theorem B and [Reference Wilton and ZalesskiiWZ17, Theorem 8.4], the result follows.◻
$D$
. Combining these facts with Theorem B and [Reference Wilton and ZalesskiiWZ17, Theorem 8.4], the result follows.◻
In light of Theorem B, the next step in addressing Question 0.1 is to consider the pieces of the JSJ decomposition. The Seifert fibred case has been resolved by Wilkes [Reference WilkesWil17b], building on work of Hempel [Reference HempelHem14]: Seifert fibred
![]() $3$
-manifolds are not profinitely rigid, but do have finite genus, and Wilkes was able to give a complete description of when two such
$3$
-manifolds are not profinitely rigid, but do have finite genus, and Wilkes was able to give a complete description of when two such
![]() $3$
-manifold groups have isomorphic profinite completions; he was subsequently able to extend this to a complete answer to Question 0.1 for graph manifolds [Reference WilkesWil18a, Theorem 10.9]. In that paper, Sol-manifolds were not included in the class of graph manifolds. Nevertheless, Sol-manifolds are also well understood: they are not profinitely rigid [Reference FunarFun13], but do have finite genus [Reference Grunewald, Pickel and SegalGPS80]. A definitive treatment of the case of Sol-manifolds would be a valuable addition to the literature.
$3$
-manifold groups have isomorphic profinite completions; he was subsequently able to extend this to a complete answer to Question 0.1 for graph manifolds [Reference WilkesWil18a, Theorem 10.9]. In that paper, Sol-manifolds were not included in the class of graph manifolds. Nevertheless, Sol-manifolds are also well understood: they are not profinitely rigid [Reference FunarFun13], but do have finite genus [Reference Grunewald, Pickel and SegalGPS80]. A definitive treatment of the case of Sol-manifolds would be a valuable addition to the literature.
The case of hyperbolic
![]() $3$
-manifolds remains an important open problem. The complement of the figure-eight knot was shown to be profinitely rigid by Boileau and Friedl [Reference Boileau and FriedlBF15] and by Bridson and Reid [Reference Bridson and ReidBR15]; see also [Reference Bridson, Conder and ReidBCR16] for analogous results for Fuchsian groups and [Reference Bridson, Reid and WiltonBRW17] for once-punctured-torus bundles.
$3$
-manifolds remains an important open problem. The complement of the figure-eight knot was shown to be profinitely rigid by Boileau and Friedl [Reference Boileau and FriedlBF15] and by Bridson and Reid [Reference Bridson and ReidBR15]; see also [Reference Bridson, Conder and ReidBCR16] for analogous results for Fuchsian groups and [Reference Bridson, Reid and WiltonBRW17] for once-punctured-torus bundles.
Both [Reference Boileau and FriedlBF15, Reference Bridson and ReidBR15], as well as [Reference Bridson, Reid and WiltonBRW17], rely on results showing that fibredness is a profinite invariant in certain contexts. This has recently been proved in full generality by Jaikin-Zapirain [Reference Jaikin-ZapirainJai17]. Ueki also recently showed that the profinite completion of a knot group determines the Alexander polynomial of the knot [Reference UekiUek18].
The results of this paper are proved by considering profinite Poincaré duality groups. The main difficulty in the above theorems is to show that profinite completions of
![]() $3$
-manifold groups do not admit unexpected splittings which are not induced by splittings of the underlying group. It is well known that non-splitting theorems for discrete Poincaré duality groups follow from the Mayer–Vietoris sequence. As a result of the work of Agol, Wise and others on the virtual Haken conjecture [Reference AgolAgo13, Reference WiseWis12],
$3$
-manifold groups do not admit unexpected splittings which are not induced by splittings of the underlying group. It is well known that non-splitting theorems for discrete Poincaré duality groups follow from the Mayer–Vietoris sequence. As a result of the work of Agol, Wise and others on the virtual Haken conjecture [Reference AgolAgo13, Reference WiseWis12],
![]() $3$
-manifold groups are known to be good in the sense of Serre, meaning that the cohomology of the profinite completion is isomorphic to the ordinary cohomology (with coefficients in finite modules). Furthermore, a version of the Mayer–Vietoris sequence is known for efficient decompositions of profinite completions. The main idea of the proofs of Theorems A and B is to prove the analogues for profinite completions of the non-splitting theorems from the discrete case.
$3$
-manifold groups are known to be good in the sense of Serre, meaning that the cohomology of the profinite completion is isomorphic to the ordinary cohomology (with coefficients in finite modules). Furthermore, a version of the Mayer–Vietoris sequence is known for efficient decompositions of profinite completions. The main idea of the proofs of Theorems A and B is to prove the analogues for profinite completions of the non-splitting theorems from the discrete case.
1 Preliminaries on profinite groups
1.1 Profinite trees
A graph
![]() $\unicode[STIX]{x1D6E4}$
is a disjoint union
$\unicode[STIX]{x1D6E4}$
is a disjoint union
![]() $E(\unicode[STIX]{x1D6E4})\cup V(\unicode[STIX]{x1D6E4})$
of sets, with two maps
$E(\unicode[STIX]{x1D6E4})\cup V(\unicode[STIX]{x1D6E4})$
of sets, with two maps
![]() $d_{0},d_{1}:\unicode[STIX]{x1D6E4}\rightarrow V(\unicode[STIX]{x1D6E4})$
that are the identity on the set of vertices
$d_{0},d_{1}:\unicode[STIX]{x1D6E4}\rightarrow V(\unicode[STIX]{x1D6E4})$
that are the identity on the set of vertices
![]() $V(\unicode[STIX]{x1D6E4})$
. For an element
$V(\unicode[STIX]{x1D6E4})$
. For an element
![]() $e$
of the set of edges
$e$
of the set of edges
![]() $E(\unicode[STIX]{x1D6E4})$
,
$E(\unicode[STIX]{x1D6E4})$
,
![]() $d_{0}(e)$
is called the initial and
$d_{0}(e)$
is called the initial and
![]() $d_{1}(e)$
the terminal vertex of
$d_{1}(e)$
the terminal vertex of
![]() $e$
.
$e$
.
Definition 1.1. A profinite graph
![]() $\unicode[STIX]{x1D6E4}$
is a graph such that:
$\unicode[STIX]{x1D6E4}$
is a graph such that:
(i)
 $\unicode[STIX]{x1D6E4}$
is a profinite space (i.e. an inverse limit of finite discrete spaces);
$\unicode[STIX]{x1D6E4}$
is a profinite space (i.e. an inverse limit of finite discrete spaces);(ii)
 $V(\unicode[STIX]{x1D6E4})$
is closed; and
$V(\unicode[STIX]{x1D6E4})$
is closed; and(iii) the maps
 $d_{0}$
and
$d_{0}$
and
 $d_{1}$
are continuous.
$d_{1}$
are continuous.
Note that
![]() $E(\unicode[STIX]{x1D6E4})$
is not necessary closed.
$E(\unicode[STIX]{x1D6E4})$
is not necessary closed.
A morphism
![]() $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6E4}\longrightarrow \unicode[STIX]{x1D6E5}$
of profinite graphs is a continuous map with
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6E4}\longrightarrow \unicode[STIX]{x1D6E5}$
of profinite graphs is a continuous map with
![]() $\unicode[STIX]{x1D6FC}d_{i}=d_{i}\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}d_{i}=d_{i}\unicode[STIX]{x1D6FC}$
for
![]() $i=0,1$
.
$i=0,1$
.
By [Reference Zalesskii and Mel’nikovZM88, Proposition 1.7] or [Reference RibesRib17, Proposition 2.1.4] every profinite graph
![]() $\unicode[STIX]{x1D6E4}$
is an inverse limit of finite quotient graphs of
$\unicode[STIX]{x1D6E4}$
is an inverse limit of finite quotient graphs of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
For a profinite space
![]() $X$
that is the inverse limit of finite discrete spaces
$X$
that is the inverse limit of finite discrete spaces
![]() $X_{j}$
,
$X_{j}$
,
![]() $[[\widehat{\mathbb{Z}}X]]$
is defined to be the inverse limit of
$[[\widehat{\mathbb{Z}}X]]$
is defined to be the inverse limit of
![]() $[\widehat{\mathbb{Z}}X_{j}]$
, where
$[\widehat{\mathbb{Z}}X_{j}]$
, where
![]() $[\widehat{\mathbb{Z}}X_{j}]$
is the free
$[\widehat{\mathbb{Z}}X_{j}]$
is the free
![]() $\widehat{\mathbb{Z}}$
-module with basis
$\widehat{\mathbb{Z}}$
-module with basis
![]() $X_{j}$
. For a pointed profinite space
$X_{j}$
. For a pointed profinite space
![]() $(X,\ast )$
that is the inverse limit of pointed finite discrete spaces
$(X,\ast )$
that is the inverse limit of pointed finite discrete spaces
![]() $(X_{j},\ast )$
,
$(X_{j},\ast )$
,
![]() $[[\widehat{\mathbb{Z}}(X,\ast )]]$
is the inverse limit of
$[[\widehat{\mathbb{Z}}(X,\ast )]]$
is the inverse limit of
![]() $[\widehat{\mathbb{Z}}(X_{j},\ast )]$
, where
$[\widehat{\mathbb{Z}}(X_{j},\ast )]$
, where
![]() $[\widehat{\mathbb{Z}}(X_{j},\ast )]$
is the free
$[\widehat{\mathbb{Z}}(X_{j},\ast )]$
is the free
![]() $\widehat{\mathbb{Z}}$
-module with basis
$\widehat{\mathbb{Z}}$
-module with basis
![]() $X_{j}\setminus \{\ast \}$
[Reference Ribes and ZalesskiiRZ10, ch. 5.2].
$X_{j}\setminus \{\ast \}$
[Reference Ribes and ZalesskiiRZ10, ch. 5.2].
For a profinite graph
![]() $\unicode[STIX]{x1D6E4}$
, define the pointed space
$\unicode[STIX]{x1D6E4}$
, define the pointed space
![]() $(E^{\ast }(\unicode[STIX]{x1D6E4}),\ast )$
as
$(E^{\ast }(\unicode[STIX]{x1D6E4}),\ast )$
as
![]() $\unicode[STIX]{x1D6E4}/V(\unicode[STIX]{x1D6E4})$
with the image of
$\unicode[STIX]{x1D6E4}/V(\unicode[STIX]{x1D6E4})$
with the image of
![]() $V(\unicode[STIX]{x1D6E4})$
as a distinguished point
$V(\unicode[STIX]{x1D6E4})$
as a distinguished point
![]() $\ast$
, and denote the image of
$\ast$
, and denote the image of
![]() $e\in E(\unicode[STIX]{x1D6E4})$
by
$e\in E(\unicode[STIX]{x1D6E4})$
by
![]() $\bar{e}$
.
$\bar{e}$
.
Definition 1.2. A profinite tree
![]() $\unicode[STIX]{x1D6E4}$
is a profinite graph such that the sequence
$\unicode[STIX]{x1D6E4}$
is a profinite graph such that the sequence
is exact, where
![]() $\unicode[STIX]{x1D6FF}(\bar{e})=d_{1}(e)-d_{0}(e)$
for every
$\unicode[STIX]{x1D6FF}(\bar{e})=d_{1}(e)-d_{0}(e)$
for every
![]() $e\in E(\unicode[STIX]{x1D6E4})$
and
$e\in E(\unicode[STIX]{x1D6E4})$
and
![]() $\unicode[STIX]{x1D716}(v)=1$
for every
$\unicode[STIX]{x1D716}(v)=1$
for every
![]() $v\in V(\unicode[STIX]{x1D6E4})$
.
$v\in V(\unicode[STIX]{x1D6E4})$
.
If
![]() $v$
and
$v$
and
![]() $w$
are elements of a profinite tree
$w$
are elements of a profinite tree
![]() $T$
, we denote by
$T$
, we denote by
![]() $[v,w]$
the smallest profinite subtree of
$[v,w]$
the smallest profinite subtree of
![]() $T$
containing
$T$
containing
![]() $v$
and
$v$
and
![]() $w$
and call it a geodesic (cf. [Reference Zalesskii and Mel’nikovZM88, 1.19] or [Reference RibesRib17, Proposition 2.4.9]).
$w$
and call it a geodesic (cf. [Reference Zalesskii and Mel’nikovZM88, 1.19] or [Reference RibesRib17, Proposition 2.4.9]).
By definition a profinite group
![]() $G$
acts on a profinite graph
$G$
acts on a profinite graph
![]() $\unicode[STIX]{x1D6E4}$
if we have a continuous action of
$\unicode[STIX]{x1D6E4}$
if we have a continuous action of
![]() $G$
on the profinite space
$G$
on the profinite space
![]() $\unicode[STIX]{x1D6E4}$
that commutes with the maps
$\unicode[STIX]{x1D6E4}$
that commutes with the maps
![]() $d_{0}$
and
$d_{0}$
and
![]() $d_{1}$
.
$d_{1}$
.
We shall need the following lemma; its proof is contained in the first eight lines of the proof of [Reference ZalesskiiZal90, Lemma 2.3].
Lemma 1.3. Suppose that a profinite group
![]() $G$
acts on a profinite tree
$G$
acts on a profinite tree
![]() $T$
and does not fix any vertex. Then there exists an open normal subgroup
$T$
and does not fix any vertex. Then there exists an open normal subgroup
![]() $U$
of
$U$
of
![]() $G$
that is not generated by its vertex stabilizers.
$G$
that is not generated by its vertex stabilizers.
When we say that
![]() ${\mathcal{G}}$
is a finite graph of profinite groups we mean that
${\mathcal{G}}$
is a finite graph of profinite groups we mean that
![]() ${\mathcal{G}}$
contains the data of the underlying finite graph, the edge profinite groups, the vertex profinite groups and the attaching continuous maps. More precisely, let
${\mathcal{G}}$
contains the data of the underlying finite graph, the edge profinite groups, the vertex profinite groups and the attaching continuous maps. More precisely, let
![]() $\unicode[STIX]{x1D6E5}$
be a connected finite graph. The data of a graph of profinite groups
$\unicode[STIX]{x1D6E5}$
be a connected finite graph. The data of a graph of profinite groups
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E5})$
over
$({\mathcal{G}},\unicode[STIX]{x1D6E5})$
over
![]() $\unicode[STIX]{x1D6E5}$
consists of a profinite group
$\unicode[STIX]{x1D6E5}$
consists of a profinite group
![]() ${\mathcal{G}}(m)$
for each
${\mathcal{G}}(m)$
for each
![]() $m\in \unicode[STIX]{x1D6E5}$
, and continuous monomorphisms
$m\in \unicode[STIX]{x1D6E5}$
, and continuous monomorphisms
![]() $\unicode[STIX]{x2202}_{i}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{i}(e))$
for each edge
$\unicode[STIX]{x2202}_{i}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{i}(e))$
for each edge
![]() $e\in E(\unicode[STIX]{x1D6E5})$
.
$e\in E(\unicode[STIX]{x1D6E5})$
.
The definition of the profinite fundamental group of a connected profinite graph of profinite groups is quite involved (see [Reference Zalesskii and Mel’nikovZM89] or [Reference RibesRib17, ch. 6]). However, the profinite fundamental group
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
of a finite graph of finitely generated profinite groups
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
of a finite graph of finitely generated profinite groups
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
can be defined as the profinite completion of the abstract (usual) fundamental group
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
can be defined as the profinite completion of the abstract (usual) fundamental group
![]() $\unicode[STIX]{x1D6F1}_{1}^{\text{abs}}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
(using here the fact that every subgroup of finite index in a finitely generated profinite group is open [Reference Nikolov and SegalNS07, Theorem 1.1]). The fundamental profinite group
$\unicode[STIX]{x1D6F1}_{1}^{\text{abs}}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
(using here the fact that every subgroup of finite index in a finitely generated profinite group is open [Reference Nikolov and SegalNS07, Theorem 1.1]). The fundamental profinite group
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
has the following presentation:
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
has the following presentation:
where
![]() $T$
is a maximal subtree of
$T$
is a maximal subtree of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x2202}_{0}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{0}(e)),~\unicode[STIX]{x2202}_{1}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{1}(e))$
are monomorphisms.
$\unicode[STIX]{x2202}_{0}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{0}(e)),~\unicode[STIX]{x2202}_{1}:{\mathcal{G}}(e)\longrightarrow {\mathcal{G}}(d_{1}(e))$
are monomorphisms.
In contrast to the abstract case, the vertex groups of
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
do not always embed in
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
do not always embed in
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
. If they do embed,
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
. If they do embed,
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is called injective. If
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is called injective. If
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is not injective the edge and vertex groups can be replaced by their images in
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is not injective the edge and vertex groups can be replaced by their images in
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
, and after this replacement
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
, and after this replacement
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
becomes injective (see [Reference RibesRib17, § 6.4]).
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
becomes injective (see [Reference RibesRib17, § 6.4]).
The profinite fundamental group
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
acts on the standard profinite tree
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
acts on the standard profinite tree
![]() $T$
(defined analogously to the abstract Bass–Serre tree) associated to it, with vertex and edge stabilizers being conjugates of vertex and edge groups, and such that
$T$
(defined analogously to the abstract Bass–Serre tree) associated to it, with vertex and edge stabilizers being conjugates of vertex and edge groups, and such that
![]() $\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})\backslash T=\unicode[STIX]{x1D6E4}$
[Reference Zalesskii and Mel’nikovZM88, Proposition 3.8] or [Reference RibesRib17, Theorem 6.3.5]. In particular, this applies to the cases of an amalgamated free product
$\unicode[STIX]{x1D6F1}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})\backslash T=\unicode[STIX]{x1D6E4}$
[Reference Zalesskii and Mel’nikovZM88, Proposition 3.8] or [Reference RibesRib17, Theorem 6.3.5]. In particular, this applies to the cases of an amalgamated free product
![]() $G={G_{1}\amalg }_{H}G_{2}$
(
$G={G_{1}\amalg }_{H}G_{2}$
(
![]() $\unicode[STIX]{x1D6E4}$
is an edge with two vertices) and an HNN extension
$\unicode[STIX]{x1D6E4}$
is an edge with two vertices) and an HNN extension
![]() $G={G_{1}\amalg }_{H}$
(
$G={G_{1}\amalg }_{H}$
(
![]() $\unicode[STIX]{x1D6E4}$
is a loop); if
$\unicode[STIX]{x1D6E4}$
is a loop); if
![]() $({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is injective and, in the case of an amalgamated free product,
$({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is injective and, in the case of an amalgamated free product,
![]() $G_{1}\neq H\neq G_{2}$
, we say that
$G_{1}\neq H\neq G_{2}$
, we say that
![]() $G$
splits over
$G$
splits over
![]() $H$
.
$H$
.
Example 1.4. If
![]() $G=\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is the fundamental group of a finite graph of (abstract) groups then one has the induced graph of profinite completions of edge and vertex groups
$G=\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is the fundamental group of a finite graph of (abstract) groups then one has the induced graph of profinite completions of edge and vertex groups
![]() $(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
and a natural homomorphism
$(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
and a natural homomorphism
![]() $G=\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})\longrightarrow \unicode[STIX]{x1D6F1}_{1}(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
. It is an embedding if
$G=\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})\longrightarrow \unicode[STIX]{x1D6F1}_{1}(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
. It is an embedding if
![]() $\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is residually finite. In this case
$\unicode[STIX]{x1D70B}_{1}({\mathcal{G}},\unicode[STIX]{x1D6E4})$
is residually finite. In this case
![]() $\unicode[STIX]{x1D6F1}_{1}(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
is simply the profinite completion
$\unicode[STIX]{x1D6F1}_{1}(\widehat{{\mathcal{G}}},\unicode[STIX]{x1D6E4})$
is simply the profinite completion
![]() $\widehat{G}$
. Moreover, if the edge groups
$\widehat{G}$
. Moreover, if the edge groups
![]() ${\mathcal{G}}(e)$
are separable in
${\mathcal{G}}(e)$
are separable in
![]() $G$
then the standard tree
$G$
then the standard tree
![]() $T_{G}$
naturally embeds in the standard profinite tree
$T_{G}$
naturally embeds in the standard profinite tree
![]() $\widehat{T}_{G}$
(see [Reference Cotton-BarrattCot13, Proposition 2.5]). In particular, this is the case if edge groups are finitely generated and
$\widehat{T}_{G}$
(see [Reference Cotton-BarrattCot13, Proposition 2.5]). In particular, this is the case if edge groups are finitely generated and
![]() $G$
is subgroup separable.
$G$
is subgroup separable.
1.2 Profinite Poincaré duality groups
In this section we collect the facts about profinite groups that we will need. The following results are all profinite analogues of well-known results in the setting of discrete groups. Let
![]() $\mathbb{Z}_{p}$
denote the ring of
$\mathbb{Z}_{p}$
denote the ring of
![]() $p$
-adic integers.
$p$
-adic integers.
Definition 1.5 [Reference Symonds and WeigelSW00].
Let
![]() $p$
be a prime. A profinite group
$p$
be a prime. A profinite group
![]() $G$
of type
$G$
of type
![]() $p$
-
$p$
-
![]() $FP_{\infty }$
is called a Poincaré duality group at
$FP_{\infty }$
is called a Poincaré duality group at
![]() $p$
of dimension
$p$
of dimension
![]() $n$
if
$n$
if
![]() $cd_{p}(G)=n$
and
$cd_{p}(G)=n$
and
We say that such a group
![]() $G$
is a profinite
$G$
is a profinite
![]() $PD^{n}$
-group at
$PD^{n}$
-group at
![]() $p$
.
$p$
.
If
![]() $G$
is a profinite group with
$G$
is a profinite group with
![]() $cd_{p}(G)<\infty$
and
$cd_{p}(G)<\infty$
and
![]() $U$
is an open subgroup of
$U$
is an open subgroup of
![]() $G$
, then
$G$
, then
![]() $G$
is a profinite
$G$
is a profinite
![]() $PD^{n}$
-group at
$PD^{n}$
-group at
![]() $p$
if and only if
$p$
if and only if
![]() $U$
is a profinite
$U$
is a profinite
![]() $PD^{n}$
-group at
$PD^{n}$
-group at
![]() $p$
(see [Reference Symonds and WeigelSW00, Remark 4.2.9]).
$p$
(see [Reference Symonds and WeigelSW00, Remark 4.2.9]).
The proofs of our main results rely on the following lemma. In the discrete case, the corresponding result is Strebel’s theorem [Reference StrebelStr77]. In the profinite case, this is from [Reference SerreSer97, Exercise 5(b) on p. 44]. The reader is referred to [Reference Ribes and ZalesskiiRZ10, § 2.3] for the definition of supernatural numbers.
Lemma 1.6. Let
![]() $G$
be a profinite
$G$
be a profinite
![]() $PD^{n}$
group at
$PD^{n}$
group at
![]() $p$
and
$p$
and
![]() $H$
a closed subgroup of
$H$
a closed subgroup of
![]() $G$
such that the supernatural number
$G$
such that the supernatural number
![]() $p^{\infty }$
divides
$p^{\infty }$
divides
![]() $[G:H]$
. Then
$[G:H]$
. Then
![]() $cd_{p}(H)<n$
.
$cd_{p}(H)<n$
.
The following theorem is the profinite analogue of the well-known fact in the discrete setting that
![]() $PD^{n}$
groups cannot split over groups of much smaller cohomological dimension [Reference Dicks and DunwoodyDD89, Proposition V.7.4].
$PD^{n}$
groups cannot split over groups of much smaller cohomological dimension [Reference Dicks and DunwoodyDD89, Proposition V.7.4].
Theorem 1.7. Suppose that
![]() $G$
is a profinite
$G$
is a profinite
![]() $PD^{n}$
group at every prime
$PD^{n}$
group at every prime
![]() $p$
. If
$p$
. If
![]() $G$
acts on a profinite tree
$G$
acts on a profinite tree
![]() $T$
with edge stabilizers of
$T$
with edge stabilizers of
![]() $cd(G_{e})<n-1$
, then
$cd(G_{e})<n-1$
, then
![]() $G$
fixes a vertex.
$G$
fixes a vertex.
Proof. By [Reference Zalesskii and Mel’nikovZM88, paragraph 2.7],
Suppose that
![]() $G$
acts on
$G$
acts on
![]() $T$
without fixing a vertex. We now argue that there exists
$T$
without fixing a vertex. We now argue that there exists
![]() $p$
such that the supernatural number
$p$
such that the supernatural number
![]() $p^{\infty }$
divides
$p^{\infty }$
divides
![]() $[G:G_{v}]$
for every
$[G:G_{v}]$
for every
![]() $v\in V(\unicode[STIX]{x1D6E4})$
, and deduce a contradiction from Lemma 1.6.
$v\in V(\unicode[STIX]{x1D6E4})$
, and deduce a contradiction from Lemma 1.6.
By [Reference ZalesskiiZal90, Lemma 1.5] or [Reference RibesRib17, Proposition 2.4.12] we may assume that the action of
![]() $G$
on
$G$
on
![]() $T$
is irreducible (i.e. does not contain proper
$T$
is irreducible (i.e. does not contain proper
![]() $G$
-invariant subtrees). If
$G$
-invariant subtrees). If
![]() $K$
is the kernel of the action then
$K$
is the kernel of the action then
![]() $G/K$
acts faithfully on
$G/K$
acts faithfully on
![]() $T$
. Hence by [Reference ZalesskiiZal90, Proposition 2.10 and Lemma 2.7] or [Reference RibesRib17, Theorem 4.2.10]
$T$
. Hence by [Reference ZalesskiiZal90, Proposition 2.10 and Lemma 2.7] or [Reference RibesRib17, Theorem 4.2.10]
![]() $G/K$
contains a free pro-
$G/K$
contains a free pro-
![]() $p$
subgroup acting freely on
$p$
subgroup acting freely on
![]() $T$
and therefore so does
$T$
and therefore so does
![]() $G$
, whence
$G$
, whence
![]() $p^{\infty }\mid [G:G_{v}]$
as claimed.◻
$p^{\infty }\mid [G:G_{v}]$
as claimed.◻
We will apply these results to discrete groups
![]() $\unicode[STIX]{x1D6E4}$
such that the cohomology of
$\unicode[STIX]{x1D6E4}$
such that the cohomology of
![]() $\unicode[STIX]{x1D6E4}$
is closely intertwined with the cohomology of the profinite completion
$\unicode[STIX]{x1D6E4}$
is closely intertwined with the cohomology of the profinite completion
![]() $\widehat{\unicode[STIX]{x1D6E4}}$
. Serre called such groups ‘good’ [Reference SerreSer97, I.2.6].
$\widehat{\unicode[STIX]{x1D6E4}}$
. Serre called such groups ‘good’ [Reference SerreSer97, I.2.6].
Definition 1.8. A discrete group
![]() $\unicode[STIX]{x1D6E4}$
is good (in the sense of Serre) if, for any finite
$\unicode[STIX]{x1D6E4}$
is good (in the sense of Serre) if, for any finite
![]() $\unicode[STIX]{x1D6E4}$
-module
$\unicode[STIX]{x1D6E4}$
-module
![]() $M$
, the natural map to the profinite completion
$M$
, the natural map to the profinite completion
![]() $\unicode[STIX]{x1D6E4}\rightarrow \widehat{\unicode[STIX]{x1D6E4}}$
induces an isomorphism
$\unicode[STIX]{x1D6E4}\rightarrow \widehat{\unicode[STIX]{x1D6E4}}$
induces an isomorphism
![]() $H^{\ast }(\unicode[STIX]{x1D6E4},M)\cong$
$H^{\ast }(\unicode[STIX]{x1D6E4},M)\cong$
![]() $H^{\ast }(\widehat{\unicode[STIX]{x1D6E4}},M)$
(where the cohomology of the profinite group
$H^{\ast }(\widehat{\unicode[STIX]{x1D6E4}},M)$
(where the cohomology of the profinite group
![]() $\widehat{\unicode[STIX]{x1D6E4}}$
is defined using the continuous
$\widehat{\unicode[STIX]{x1D6E4}}$
is defined using the continuous
![]() $\text{Hom}$
functor).
$\text{Hom}$
functor).
It has been noticed in various places (e.g. [Reference CavendishCav12, Reference Aschenbrenner, Friedl and WiltonAFW15]; cf. [Reference Grunewald, Jaikin-Zapirain and ZalesskiiGJZ08]) that
![]() $3$
-manifold groups are good. For convenience, we record the result here.
$3$
-manifold groups are good. For convenience, we record the result here.
Theorem 1.9. If
![]() $M$
is a closed
$M$
is a closed
![]() $3$
-manifold then
$3$
-manifold then
![]() $\unicode[STIX]{x1D70B}_{1}M$
is good.
$\unicode[STIX]{x1D70B}_{1}M$
is good.
Proof. Since goodness passes to finite extensions, we may assume that
![]() $M$
is orientable. By [Reference Wilton and ZalesskiiWZ10, Proposition 4.3] and the usual Kneser–Milnor and JSJ decompositions, it suffices to prove that Seifert fibred and hyperbolic
$M$
is orientable. By [Reference Wilton and ZalesskiiWZ10, Proposition 4.3] and the usual Kneser–Milnor and JSJ decompositions, it suffices to prove that Seifert fibred and hyperbolic
![]() $3$
-manifold groups are good. The Seifert fibred case is [Reference Wilton and ZalesskiiWZ10, Proposition 4.2], and the case of closed hyperbolic
$3$
-manifold groups are good. The Seifert fibred case is [Reference Wilton and ZalesskiiWZ10, Proposition 4.2], and the case of closed hyperbolic
![]() $3$
-manifolds follows from the virtually fibred theorem [Reference AgolAgo13], by [Reference Grunewald, Jaikin-Zapirain and ZalesskiiGJZ08, Lemmas 3.2 and 3.3].◻
$3$
-manifolds follows from the virtually fibred theorem [Reference AgolAgo13], by [Reference Grunewald, Jaikin-Zapirain and ZalesskiiGJZ08, Lemmas 3.2 and 3.3].◻
The next result is the subject of [Reference Kochloukova and ZalesskiiKZ08, Theorem 4.1] for
![]() $PD^{3}$
-groups, and for general
$PD^{3}$
-groups, and for general
![]() $n$
the proof can be repeated replacing
$n$
the proof can be repeated replacing
![]() $3$
by
$3$
by
![]() $n$
.
$n$
.
Theorem 1.10. If
![]() $\unicode[STIX]{x1D6E4}$
is a good
$\unicode[STIX]{x1D6E4}$
is a good
![]() $PD^{n}$
group, then
$PD^{n}$
group, then
![]() $\widehat{\unicode[STIX]{x1D6E4}}$
is
$\widehat{\unicode[STIX]{x1D6E4}}$
is
![]() $PD^{n}$
at every
$PD^{n}$
at every
![]() $p$
.
$p$
.
We immediately obtain a profinite non-splitting result for good Poincaré duality groups.
Corollary 1.11. Let
![]() $G$
be
$G$
be
![]() $PD^{n}$
group which is good in the sense of Serre. Then any action of
$PD^{n}$
group which is good in the sense of Serre. Then any action of
![]() $\widehat{G}$
on a profinite tree with edge stabilizers of cohomological dimension
$\widehat{G}$
on a profinite tree with edge stabilizers of cohomological dimension
![]() $n-2$
has a global fixed point.
$n-2$
has a global fixed point.
Proof. Since
![]() $G$
is good,
$G$
is good,
![]() $\widehat{G}$
is a profinite
$\widehat{G}$
is a profinite
![]() $PD^{n}$
group at
$PD^{n}$
group at
![]() $p$
for every
$p$
for every
![]() $p$
by Theorem 1.10, so the result follows from Theorem 1.7.◻
$p$
by Theorem 1.10, so the result follows from Theorem 1.7.◻
Remark 1.12. The combined hypotheses of goodness and
![]() $PD^{n}$
apply to many examples in dimensions 2 and 3, but are restrictive in higher dimensions.
$PD^{n}$
apply to many examples in dimensions 2 and 3, but are restrictive in higher dimensions.
Combining all of the above results, we obtain the following fact, which will be extremely useful to us in what follows.
Corollary 1.13. If
![]() $M$
is a closed, orientable, irreducible
$M$
is a closed, orientable, irreducible
![]() $3$
-manifold then any action of
$3$
-manifold then any action of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on a profinite tree with procyclic edge stabilizers has a global fixed point.
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on a profinite tree with procyclic edge stabilizers has a global fixed point.
Proof. By the sphere theorem, irreducible
![]() $3$
-manifolds either have finite fundamental group or are aspherical (see, for instance, [Reference Aschenbrenner, Friedl and WiltonAFW15, (C.1)]). In the first case
$3$
-manifolds either have finite fundamental group or are aspherical (see, for instance, [Reference Aschenbrenner, Friedl and WiltonAFW15, (C.1)]). In the first case
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
is finite, and the result follows from [Reference Zalesskii and Mel’nikovZM88, Theorem 2.10] or [Reference RibesRib17, Theorem 4.1.8]. In the second case,
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
is finite, and the result follows from [Reference Zalesskii and Mel’nikovZM88, Theorem 2.10] or [Reference RibesRib17, Theorem 4.1.8]. In the second case,
![]() $\unicode[STIX]{x1D70B}_{1}M$
is
$\unicode[STIX]{x1D70B}_{1}M$
is
![]() $PD^{3}$
, and the result follows from Theorem 1.9 and Corollary 1.11.◻
$PD^{3}$
, and the result follows from Theorem 1.9 and Corollary 1.11.◻
2 The Kneser–Milnor decomposition
As a warm-up, we show that the profinite completion of a
![]() $3$
-manifold group determines its Kneser–Milnor decomposition. As noted above, this result can also be obtained using methods from
$3$
-manifold group determines its Kneser–Milnor decomposition. As noted above, this result can also be obtained using methods from
![]() $l^{2}$
-cohomology [Reference WilkesWil17a]. Recall that a closed
$l^{2}$
-cohomology [Reference WilkesWil17a]. Recall that a closed
![]() $3$
-manifold
$3$
-manifold
![]() $M$
is irreducible if every embedded
$M$
is irreducible if every embedded
![]() $2$
-sphere bounds a
$2$
-sphere bounds a
![]() $3$
-ball; equivalently,
$3$
-ball; equivalently,
![]() $\unicode[STIX]{x1D70B}_{1}M$
does not admit a non-trivial splitting over the trivial subgroup.
$\unicode[STIX]{x1D70B}_{1}M$
does not admit a non-trivial splitting over the trivial subgroup.
Proposition 2.1. Suppose that
![]() $M_{1},M_{2}$
are closed, orientable
$M_{1},M_{2}$
are closed, orientable
![]() $3$
-manifolds. If
$3$
-manifolds. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}_{1}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M}_{2}$
and
$\widehat{\unicode[STIX]{x1D70B}_{1}M}_{1}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M}_{2}$
and
![]() $M_{1}$
is irreducible then so is
$M_{1}$
is irreducible then so is
![]() $M_{2}$
.
$M_{2}$
.
Proof. If
![]() $M_{2}$
were reducible then
$M_{2}$
were reducible then
![]() $\unicode[STIX]{x1D70B}_{1}M_{2}$
would act on a tree with trivial edge stabilizers and without a global fixed point, and
$\unicode[STIX]{x1D70B}_{1}M_{2}$
would act on a tree with trivial edge stabilizers and without a global fixed point, and
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}_{1}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M}_{2}$
would act on a profinite tree with trivial edge stabilizers and without a global fixed point. This contradicts Corollary 1.13.◻
$\widehat{\unicode[STIX]{x1D70B}_{1}M}_{1}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M}_{2}$
would act on a profinite tree with trivial edge stabilizers and without a global fixed point. This contradicts Corollary 1.13.◻
Non-irreducible
![]() $3$
-manifolds admit non-trivial Kneser–Milnor decompositions. If
$3$
-manifolds admit non-trivial Kneser–Milnor decompositions. If
![]() $M$
is a closed, oriented
$M$
is a closed, oriented
![]() $3$
-manifold then the Kneser–Milnor decomposition decomposes
$3$
-manifold then the Kneser–Milnor decomposition decomposes
![]() $M$
as a connect sum
$M$
as a connect sum
where each
![]() $N_{i}$
is irreducible and
$N_{i}$
is irreducible and
![]() $F_{r}$
is a connect sum of copies of
$F_{r}$
is a connect sum of copies of
![]() $S^{1}\times S^{2}$
. The
$S^{1}\times S^{2}$
. The
![]() $N_{i}$
are uniquely determined, in an appropriate sense. In particular, the conjugacy classes of the subgroups
$N_{i}$
are uniquely determined, in an appropriate sense. In particular, the conjugacy classes of the subgroups
![]() $\unicode[STIX]{x1D70B}_{1}N_{i}$
are unique up to reordering, and the integer
$\unicode[STIX]{x1D70B}_{1}N_{i}$
are unique up to reordering, and the integer
![]() $r$
is also unique. The reader is referred to [Reference Aschenbrenner, Friedl and WiltonAFW15, Theorem 1.2.1] for details.
$r$
is also unique. The reader is referred to [Reference Aschenbrenner, Friedl and WiltonAFW15, Theorem 1.2.1] for details.
Theorem 2.2 (Profinite Kneser–Milnor).
Consider closed, orientable
![]() $3$
-manifolds with Kneser–Milnor decompositions
$3$
-manifolds with Kneser–Milnor decompositions
![]() $M=N_{1}\#\cdots \#N_{m}\#F_{r}$
and
$M=N_{1}\#\cdots \#N_{m}\#F_{r}$
and
![]() $M^{\prime }=N_{1}^{\prime }\#\cdots \#N_{m^{\prime }}^{\prime }\#F_{r^{\prime }}$
, where each
$M^{\prime }=N_{1}^{\prime }\#\cdots \#N_{m^{\prime }}^{\prime }\#F_{r^{\prime }}$
, where each
![]() $N_{i}$
and
$N_{i}$
and
![]() $N_{j}^{\prime }$
is irreducible and
$N_{j}^{\prime }$
is irreducible and
![]() $F_{r}$
and
$F_{r}$
and
![]() $F_{r^{\prime }}$
are connect sums of
$F_{r^{\prime }}$
are connect sums of
![]() $S^{1}\times S^{2}$
. If
$S^{1}\times S^{2}$
. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}$
then
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\cong \widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}$
then
![]() $m=m^{\prime }$
,
$m=m^{\prime }$
,
![]() $r=r^{\prime }$
, and, up to reordering,
$r=r^{\prime }$
, and, up to reordering,
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}}$
is conjugate to
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}}$
is conjugate to
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}^{\prime }}$
for each
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}^{\prime }}$
for each
![]() $i$
.
$i$
.
Proof. Let
![]() $S$
be the Bass–Serre tree of the corresponding decomposition of
$S$
be the Bass–Serre tree of the corresponding decomposition of
![]() $\unicode[STIX]{x1D70B}_{1}M$
, and let
$\unicode[STIX]{x1D70B}_{1}M$
, and let
![]() $\widehat{S}$
be the corresponding profinite tree for
$\widehat{S}$
be the corresponding profinite tree for
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on which
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on which
![]() $\unicode[STIX]{x1D70B}_{1}M$
acts with trivial edge stabilizers. By Corollary 1.13, each profinite completion
$\unicode[STIX]{x1D70B}_{1}M$
acts with trivial edge stabilizers. By Corollary 1.13, each profinite completion
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}^{\prime }}$
fixes a vertex of
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}^{\prime }}$
fixes a vertex of
![]() $\widehat{S}$
, and hence is conjugate into some
$\widehat{S}$
, and hence is conjugate into some
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{j}}$
. By symmetry, each
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{j}}$
. By symmetry, each
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}}$
is conjugate into some
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{i}}$
is conjugate into some
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N_{j}^{\prime }}$
. Profinite subgroups cannot be conjugate to proper subgroups of themselves, as it would imply the same for some finite image, and for a finite group it is clearly impossible. Therefore, it follows that
$\widehat{\unicode[STIX]{x1D70B}_{1}N_{j}^{\prime }}$
. Profinite subgroups cannot be conjugate to proper subgroups of themselves, as it would imply the same for some finite image, and for a finite group it is clearly impossible. Therefore, it follows that
![]() $m=m^{\prime }$
and the profinite completions of the vertex groups are conjugate. Factoring the normal closures of these subgroups out, we see that
$m=m^{\prime }$
and the profinite completions of the vertex groups are conjugate. Factoring the normal closures of these subgroups out, we see that
![]() $\widehat{F}_{r}\cong \widehat{F}_{r^{\prime }}$
and hence
$\widehat{F}_{r}\cong \widehat{F}_{r^{\prime }}$
and hence
![]() $r=r^{\prime }$
as claimed.◻
$r=r^{\prime }$
as claimed.◻
3 Cusped hyperbolic
 $3$
-manifolds
$3$
-manifolds
An immediate consequence of Corollary 1.11 is that, for a closed
![]() $3$
-manifold
$3$
-manifold
![]() $M$
,
$M$
,
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
does not split over a subgroup of cohomological dimension 0 or 1 (e.g. a profinite free group). In this section we prove some profinite non-splitting results for hyperbolic manifolds with toral boundary. In the hyperbolic case, we will need a fact from [Reference Wilton and ZalesskiiWZ17], describing the non-procyclic abelian subgroups of
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
does not split over a subgroup of cohomological dimension 0 or 1 (e.g. a profinite free group). In this section we prove some profinite non-splitting results for hyperbolic manifolds with toral boundary. In the hyperbolic case, we will need a fact from [Reference Wilton and ZalesskiiWZ17], describing the non-procyclic abelian subgroups of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
.
Proposition 3.1. Let
![]() $N$
be a finite-volume hyperbolic
$N$
be a finite-volume hyperbolic
![]() $3$
-manifold and
$3$
-manifold and
![]() $A$
a closed abelian subgroup of
$A$
a closed abelian subgroup of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
. If
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
. If
![]() $A$
is not procyclic then
$A$
is not procyclic then
![]() $A$
is in the closure of a peripheral subgroup of
$A$
is in the closure of a peripheral subgroup of
![]() $\unicode[STIX]{x1D70B}_{1}N$
, and this peripheral subgroup is unique up to conjugacy.
$\unicode[STIX]{x1D70B}_{1}N$
, and this peripheral subgroup is unique up to conjugacy.
Proof. By [Reference Wilton and ZalesskiiWZ17, Theorem 9.3],
![]() $A$
is conjugate into the closure of a peripheral subgroup, and by [Reference Wilton and ZalesskiiWZ17, Lemma 4.5], the conjugacy class of the cusp subgroup is unique.◻
$A$
is conjugate into the closure of a peripheral subgroup, and by [Reference Wilton and ZalesskiiWZ17, Lemma 4.5], the conjugacy class of the cusp subgroup is unique.◻
In the classical
![]() $PD^{n}$
setting, one handles manifolds with boundary using the theory of
$PD^{n}$
setting, one handles manifolds with boundary using the theory of
![]() $PD^{n}$
pairs [Reference DicksDic80]. One of the upshots of this theory is that the fundamental group of an aspherical manifold with aspherical boundary cannot split over a boundary subgroup, relative to the collection of boundary subgroups. (This can be deduced from the results of [Reference Kropholler and RollerKR88].) No doubt the profinite analogue of this statement can be proved by developing the theory of profinite
$PD^{n}$
pairs [Reference DicksDic80]. One of the upshots of this theory is that the fundamental group of an aspherical manifold with aspherical boundary cannot split over a boundary subgroup, relative to the collection of boundary subgroups. (This can be deduced from the results of [Reference Kropholler and RollerKR88].) No doubt the profinite analogue of this statement can be proved by developing the theory of profinite
![]() $PD^{n}$
pairs.Footnote
1
We take a quicker route here: we prove the result in the cusped hyperbolic case, using Dehn filling. First, we need to recall the definition of an acylindrical splitting.
$PD^{n}$
pairs.Footnote
1
We take a quicker route here: we prove the result in the cusped hyperbolic case, using Dehn filling. First, we need to recall the definition of an acylindrical splitting.
Definition 3.2. An action of a group
![]() $\unicode[STIX]{x1D6E4}$
on a tree
$\unicode[STIX]{x1D6E4}$
on a tree
![]() $T$
is
$T$
is
![]() $k$
-acylindrical (for an integer
$k$
-acylindrical (for an integer
![]() $k$
) if, for every
$k$
) if, for every
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}\smallsetminus 1$
, the subtree fixed by
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}\smallsetminus 1$
, the subtree fixed by
![]() $\unicode[STIX]{x1D6FE}$
is either empty or of diameter at most
$\unicode[STIX]{x1D6FE}$
is either empty or of diameter at most
![]() $k$
. Likewise, an action of a profinite group
$k$
. Likewise, an action of a profinite group
![]() $G$
on a profinite tree
$G$
on a profinite tree
![]() $\widehat{T}$
is
$\widehat{T}$
is
![]() $k$
-acylindrical if the subtree fixed by
$k$
-acylindrical if the subtree fixed by
![]() $\hat{\unicode[STIX]{x1D6FE}}$
is either empty or of diameter at most
$\hat{\unicode[STIX]{x1D6FE}}$
is either empty or of diameter at most
![]() $k$
, for every
$k$
, for every
![]() $\hat{\unicode[STIX]{x1D6FE}}\in G$
. Such an action is called acylindrical if it is
$\hat{\unicode[STIX]{x1D6FE}}\in G$
. Such an action is called acylindrical if it is
![]() $k$
-acylindrical for some
$k$
-acylindrical for some
![]() $k$
.
$k$
.
Acylindricity gives useful control over non-cyclic abelian subgroups, via the following lemma. This was proved in [Reference Wilton and ZalesskiiWZ17, Theorem 5.2]. (The discrete version of this fact is left as an instructive exercise to the reader.)
Lemma 3.3. If
![]() $A$
is an abelian, profinite, non-procyclic group, and
$A$
is an abelian, profinite, non-procyclic group, and
![]() $A$
acts acylindrically on a profinite tree
$A$
acts acylindrically on a profinite tree
![]() $T$
, then
$T$
, then
![]() $A$
fixes a vertex.
$A$
fixes a vertex.
We are now ready to prove the non-splitting result for hyperbolic manifolds with cusps.
Lemma 3.4. If
![]() $N$
is a compact, orientable, hyperbolic
$N$
is a compact, orientable, hyperbolic
![]() $3$
-manifold with toral boundary and
$3$
-manifold with toral boundary and
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts on a profinite tree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts on a profinite tree
![]() $T$
with each edge stabilizer either procyclic or conjugate into a peripheral subgroup, then
$T$
with each edge stabilizer either procyclic or conjugate into a peripheral subgroup, then
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex.
Proof. First, note that if
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts on
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts on
![]() $T$
without fixed points then, by Lemma 1.3, after passing to a proper open subgroup we may assume that
$T$
without fixed points then, by Lemma 1.3, after passing to a proper open subgroup we may assume that
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is not generated by vertex stabilizers.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is not generated by vertex stabilizers.
Let the family of peripheral subgroups of
![]() $\unicode[STIX]{x1D70B}_{1}N$
be
$\unicode[STIX]{x1D70B}_{1}N$
be
![]() $P_{1},\ldots ,P_{n}$
. By Thurston’s hyperbolic Dehn filling theorem (see, for instance, [Reference AgolAgo10, Reference Lackenby and MeyerhoffLM13] for modern improvements), we may choose slopes
$P_{1},\ldots ,P_{n}$
. By Thurston’s hyperbolic Dehn filling theorem (see, for instance, [Reference AgolAgo10, Reference Lackenby and MeyerhoffLM13] for modern improvements), we may choose slopes
![]() $c_{i}\in P_{i}$
so that the resulting Dehn filled manifold
$c_{i}\in P_{i}$
so that the resulting Dehn filled manifold
![]() $N(c_{1},\ldots ,c_{n})$
is a closed, hyperbolic (in particular, aspherical) manifold. Therefore,
$N(c_{1},\ldots ,c_{n})$
is a closed, hyperbolic (in particular, aspherical) manifold. Therefore,
is a profinite
![]() $PD^{3}$
group. Since
$PD^{3}$
group. Since
![]() $\overline{\langle \langle c_{1},\ldots ,c_{n}\rangle \rangle }$
is generated by vertex stabilizers,
$\overline{\langle \langle c_{1},\ldots ,c_{n}\rangle \rangle }$
is generated by vertex stabilizers,
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}(c_{1},\ldots ,c_{n})$
acts on a profinite tree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}(c_{1},\ldots ,c_{n})$
acts on a profinite tree
![]() $\overline{\langle \langle c_{1},\ldots ,c_{n}\rangle \rangle }\backslash T$
(see [Reference Zalesskii and Mel’nikovZM88, Proposition 2.5] or [Reference RibesRib17, Proposition 4.1.1]) and still does not fix a vertex. The edge stabilizers of the latter action are procyclic. This contradicts Corollary 1.11.◻
$\overline{\langle \langle c_{1},\ldots ,c_{n}\rangle \rangle }\backslash T$
(see [Reference Zalesskii and Mel’nikovZM88, Proposition 2.5] or [Reference RibesRib17, Proposition 4.1.1]) and still does not fix a vertex. The edge stabilizers of the latter action are procyclic. This contradicts Corollary 1.11.◻
4 The JSJ decomposition
In this section we show that, as well as the Kneser–Milnor decomposition, the JSJ decomposition is also determined by the profinite completion. In order to avoid ambiguity, we start by stating the form of the JSJ decomposition we consider. In a nutshell, it is the minimal decomposition along tori such that the complementary pieces are geometric.
Definition 4.1. Let
![]() $M$
be a closed, orientable, irreducible
$M$
be a closed, orientable, irreducible
![]() $3$
-manifold which is not a torus bundle over the circle. Let
$3$
-manifold which is not a torus bundle over the circle. Let
![]() ${\mathcal{T}}\subseteq M$
be an embedded disjoint union of essential tori such that the connected components of
${\mathcal{T}}\subseteq M$
be an embedded disjoint union of essential tori such that the connected components of
![]() $M\smallsetminus {\mathcal{T}}$
are each geometric – that is, either Seifert fibred or admitting hyperbolic or Sol-geometry. Such a union
$M\smallsetminus {\mathcal{T}}$
are each geometric – that is, either Seifert fibred or admitting hyperbolic or Sol-geometry. Such a union
![]() ${\mathcal{T}}$
with the smallest number of connected components is called the JSJ decomposition of
${\mathcal{T}}$
with the smallest number of connected components is called the JSJ decomposition of
![]() $M$
.
$M$
.
The existence of the JSJ decomposition follows from the work of Jaco, Shalen and Johannson together with Perelman’s proof of the geometrization conjecture; see [Reference Aschenbrenner, Friedl and WiltonAFW15, § 1.6, § 1.7] for details. The tori are unique up to isotopy. We follow Wilkes’s elegant terminology [Reference WilkesWil18a], and use the term minor to denote those components of
![]() $M\smallsetminus {\mathcal{T}}$
that are homeomorphic to the twisted interval bundle over the Klein bottle; the remaining components we call major. If two minor components are adjacent then their union is virtually a torus bundle over a circle, and so admits either Euclidean, Nil- or Sol-geometry, which contradicts the hypothesis that
$M\smallsetminus {\mathcal{T}}$
that are homeomorphic to the twisted interval bundle over the Klein bottle; the remaining components we call major. If two minor components are adjacent then their union is virtually a torus bundle over a circle, and so admits either Euclidean, Nil- or Sol-geometry, which contradicts the hypothesis that
![]() ${\mathcal{T}}$
was minimal. Therefore, every edge adjoins at least one major vertex.
${\mathcal{T}}$
was minimal. Therefore, every edge adjoins at least one major vertex.
The submanifold
![]() ${\mathcal{T}}$
induces a graph-of-spaces decomposition of
${\mathcal{T}}$
induces a graph-of-spaces decomposition of
![]() $M$
, and hence a graph-of-groups decomposition of
$M$
, and hence a graph-of-groups decomposition of
![]() $\unicode[STIX]{x1D70B}_{1}M$
and a profinite graph-of-groups decomposition of
$\unicode[STIX]{x1D70B}_{1}M$
and a profinite graph-of-groups decomposition of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
(see Example 1.4). The Bass–Serre trees of the latter are denoted by
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
(see Example 1.4). The Bass–Serre trees of the latter are denoted by
![]() $T_{M}$
and
$T_{M}$
and
![]() $\widehat{T}_{M}$
, respectively. Crucially, these trees turn out to be acylindrical, in the sense of Definition 3.2.
$\widehat{T}_{M}$
, respectively. Crucially, these trees turn out to be acylindrical, in the sense of Definition 3.2.
Proposition 4.2. For
![]() $M$
a closed, orientable, irreducible
$M$
a closed, orientable, irreducible
![]() $3$
-manifold, the JSJ tree
$3$
-manifold, the JSJ tree
![]() $T_{M}$
and the profinite JSJ tree
$T_{M}$
and the profinite JSJ tree
![]() $\widehat{T}_{M}$
are both
$\widehat{T}_{M}$
are both
![]() $4$
-acylindrical.
$4$
-acylindrical.
Proof. In [Reference Wilton and ZalesskiiWZ10] the authors showed that the corresponding decomposition of
![]() $\unicode[STIX]{x1D70B}_{1}M$
is
$\unicode[STIX]{x1D70B}_{1}M$
is
![]() $4$
-acylindrical and fits into Example 1.4. In [Reference Hamilton, Wilton and ZalesskiiHWZ13], the authors showed with Hamilton that the corresponding profinite decomposition of
$4$
-acylindrical and fits into Example 1.4. In [Reference Hamilton, Wilton and ZalesskiiHWZ13], the authors showed with Hamilton that the corresponding profinite decomposition of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
is a
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
is a
![]() $4$
-acylindrical injective graph of profinite groups (see also [Reference Wilton and ZalesskiiWZ17, Lemma 4.5]).◻
$4$
-acylindrical injective graph of profinite groups (see also [Reference Wilton and ZalesskiiWZ17, Lemma 4.5]).◻
We are now ready to state our main theorem.
Theorem 4.3. If
![]() $M,M^{\prime }$
are closed, orientable, irreducible
$M,M^{\prime }$
are closed, orientable, irreducible
![]() $3$
-manifolds and
$3$
-manifolds and
is an isomorphism, then there is an
![]() $f$
-equivariant isomorphism
$f$
-equivariant isomorphism
of the corresponding profinite Bass–Serre trees. In particular, the underlying graphs of the JSJ decompositions of
![]() $M$
and
$M$
and
![]() $M^{\prime }$
are isomorphic, as are the profinite completions of the fundamental groups of the corresponding pieces.
$M^{\prime }$
are isomorphic, as are the profinite completions of the fundamental groups of the corresponding pieces.
Consider a vertex space
![]() $N$
of
$N$
of
![]() $M$
. The next three lemmas show that
$M$
. The next three lemmas show that
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
must act with a fixed point on
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
must act with a fixed point on
![]() $\widehat{T}_{M^{\prime }}$
. We start with the hyperbolic case.
$\widehat{T}_{M^{\prime }}$
. We start with the hyperbolic case.
Lemma 4.4. Consider
![]() $N$
a compact, hyperbolic
$N$
a compact, hyperbolic
![]() $3$
-manifold with (possibly empty) toral boundary. If
$3$
-manifold with (possibly empty) toral boundary. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
![]() $\widehat{S}$
with abelian edge stabilizers then
$\widehat{S}$
with abelian edge stabilizers then
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
Proof. If
![]() $N$
is closed then every abelian subgroup of
$N$
is closed then every abelian subgroup of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is procyclic [Reference Wilton and ZalesskiiWZ17, Theorem D] and the result follows from Corollary 1.13.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is procyclic [Reference Wilton and ZalesskiiWZ17, Theorem D] and the result follows from Corollary 1.13.
Suppose therefore that
![]() $N$
has non-empty toroidal boundary. By Proposition 3.1 every edge stabilizer is either procyclic or conjugate into a peripheral subgroup, and therefore
$N$
has non-empty toroidal boundary. By Proposition 3.1 every edge stabilizer is either procyclic or conjugate into a peripheral subgroup, and therefore
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex by Lemma 3.4.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex by Lemma 3.4.
Uniqueness follows from [Reference Zalesskii and Mel’nikovZM88, Corollary 2.9] or [Reference RibesRib17, Corollary 4.1.6], since
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is non-abelian and edge stabilizers are abelian.◻
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
is non-abelian and edge stabilizers are abelian.◻
We move on to the major Seifert fibred case.
Lemma 4.5. Consider
![]() $N$
a compact, major Seifert fibred
$N$
a compact, major Seifert fibred
![]() $3$
-manifold with (possibly empty) toral boundary. If
$3$
-manifold with (possibly empty) toral boundary. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
![]() $\widehat{S}$
with abelian edge groups then
$\widehat{S}$
with abelian edge groups then
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
Proof. The subgroups of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
which are isomorphic to
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
which are isomorphic to
![]() $\widehat{\mathbb{Z}}^{2}$
each fix a vertex by Lemma 3.3. Thus the maximal procyclic normal subgroup
$\widehat{\mathbb{Z}}^{2}$
each fix a vertex by Lemma 3.3. Thus the maximal procyclic normal subgroup
![]() $C$
of
$C$
of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a vertex.
Suppose to the contrary
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
does not fix a vertex. By [Reference ZalesskiiZal90, Lemma 1.5] or [Reference RibesRib17, Proposition 2.4.12], there exists a unique minimal
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
does not fix a vertex. By [Reference ZalesskiiZal90, Lemma 1.5] or [Reference RibesRib17, Proposition 2.4.12], there exists a unique minimal
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
-invariant subtree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
-invariant subtree
![]() $\widehat{D}$
of
$\widehat{D}$
of
![]() $\widehat{S}$
, which is infinite. Now by [Reference Zalesskii and Mel’nikovZM88, Theorem 2.12] or [Reference RibesRib17, Proposition 4.2.2],
$\widehat{S}$
, which is infinite. Now by [Reference Zalesskii and Mel’nikovZM88, Theorem 2.12] or [Reference RibesRib17, Proposition 4.2.2],
![]() $C$
acts trivially on
$C$
acts trivially on
![]() $\widehat{D}$
, which contradicts the acylindricity of the action.
$\widehat{D}$
, which contradicts the acylindricity of the action.
Uniqueness again follows from [Reference Zalesskii and Mel’nikovZM88, Corollary 2.9] or [Reference RibesRib17, Corollary 4.1.6]. ◻
The case of minor Seifert fibred vertex follows immediately from [Reference Wilton and ZalesskiiWZ17, Theorem 5.2] and [Reference Zalesskii and Mel’nikovZM88, Corollary 2.9] or [Reference RibesRib17, Corollary 4.1.6].
Lemma 4.6. Consider
![]() $N$
a minor Seifert fibred
$N$
a minor Seifert fibred
![]() $3$
-manifold. If
$3$
-manifold. If
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
acts acylindrically on a profinite tree
![]() $\widehat{S}$
with abelian edge groups then
$\widehat{S}$
with abelian edge groups then
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
fixes a unique vertex.
We next classify the fixed point sets of
![]() $\widehat{\mathbb{Z}}^{2}$
subgroups of
$\widehat{\mathbb{Z}}^{2}$
subgroups of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
. First, we need an analysis of their normalizers in vertex stabilizers. We start with the hyperbolic case, in which case normalizers coincide with centralizers.
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
. First, we need an analysis of their normalizers in vertex stabilizers. We start with the hyperbolic case, in which case normalizers coincide with centralizers.
Lemma 4.7. Let
![]() $N$
be a compact, orientable, hyperbolic
$N$
be a compact, orientable, hyperbolic
![]() $3$
-manifold with toral boundary, and
$3$
-manifold with toral boundary, and
![]() $H\cong \widehat{\mathbb{Z}}^{2}$
a subgroup of
$H\cong \widehat{\mathbb{Z}}^{2}$
a subgroup of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
. Then
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
. Then
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
.
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
.
Proof. By [Reference Wilton and ZalesskiiWZ17, Theorem 9.3],
![]() $H$
is conjugate into the closure of a cusp subgroup, and by [Reference Wilton and ZalesskiiWZ17, Lemma 4.5], that cusp subgroup is malnormal. The result follows.◻
$H$
is conjugate into the closure of a cusp subgroup, and by [Reference Wilton and ZalesskiiWZ17, Lemma 4.5], that cusp subgroup is malnormal. The result follows.◻
We next treat the case of a major Seifert fibred manifold.
Lemma 4.8. Let
![]() $N$
be a compact, orientable, major Seifert fibred
$N$
be a compact, orientable, major Seifert fibred
![]() $3$
-manifold with toral boundary, and
$3$
-manifold with toral boundary, and
![]() $H\cong \widehat{\mathbb{Z}}^{2}$
a subgroup of
$H\cong \widehat{\mathbb{Z}}^{2}$
a subgroup of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}N}$
conjugate to the closure of the fundamental group of a boundary component. Then
$\widehat{\unicode[STIX]{x1D70B}_{1}N}$
conjugate to the closure of the fundamental group of a boundary component. Then
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
.
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
.
Proof. The fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}N$
is torsion-free of the form
$\unicode[STIX]{x1D70B}_{1}N$
is torsion-free of the form
where
![]() $\unicode[STIX]{x1D70B}_{1}O$
is a Fuchsian group and
$\unicode[STIX]{x1D70B}_{1}O$
is a Fuchsian group and
![]() $Z$
is infinite cyclic (and not necessarily central). Since Seifert fibred
$Z$
is infinite cyclic (and not necessarily central). Since Seifert fibred
![]() $3$
-manifold groups are LERF [Reference ScottSco78, Reference ScottSco85] we have a corresponding short exact sequence of profinite completions,
$3$
-manifold groups are LERF [Reference ScottSco78, Reference ScottSco85] we have a corresponding short exact sequence of profinite completions,
Then
![]() $C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
contains
$C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H)$
contains
![]() $\widehat{Z}$
and centralizes it. So
$\widehat{Z}$
and centralizes it. So
![]() $f(C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H))=C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
and
$f(C_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H))=C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
and
![]() $f(N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
. Hence it suffices to show that
$f(N_{\widehat{\unicode[STIX]{x1D70B}_{1}N}}(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
. Hence it suffices to show that
![]() $C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
. We may assume that
$C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
. We may assume that
![]() $H$
is the closure of the fundamental group of a boundary component; then
$H$
is the closure of the fundamental group of a boundary component; then
![]() $f(H)$
is the closure of a peripheral infinite-cyclic subgroup
$f(H)$
is the closure of a peripheral infinite-cyclic subgroup
![]() $C$
of
$C$
of
![]() $\unicode[STIX]{x1D70B}_{1}O$
. Since Fuchsian groups are conjugacy separable [Reference Fine and RosenbergerFR90] we deduce that every-finite index subgroup of
$\unicode[STIX]{x1D70B}_{1}O$
. Since Fuchsian groups are conjugacy separable [Reference Fine and RosenbergerFR90] we deduce that every-finite index subgroup of
![]() $\unicode[STIX]{x1D70B}_{1}O$
is conjugacy separable. Then
$\unicode[STIX]{x1D70B}_{1}O$
is conjugacy separable. Then
![]() $\overline{C_{\unicode[STIX]{x1D70B}_{1}O}(C)}=C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
by [Reference MinasyanMin12, Corollary 12.3], and
$\overline{C_{\unicode[STIX]{x1D70B}_{1}O}(C)}=C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
by [Reference MinasyanMin12, Corollary 12.3], and
![]() $\overline{N_{\unicode[STIX]{x1D70B}_{1}O}(C)}=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
by [Reference Chagas and ZalesskiiCZ13, Lemma 2.3 combined with Theorem 2.14]. But
$\overline{N_{\unicode[STIX]{x1D70B}_{1}O}(C)}=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
by [Reference Chagas and ZalesskiiCZ13, Lemma 2.3 combined with Theorem 2.14]. But
![]() $N_{\unicode[STIX]{x1D70B}_{1}O}(C)=C_{\unicode[STIX]{x1D70B}_{1}O}(C)$
, so
$N_{\unicode[STIX]{x1D70B}_{1}O}(C)=C_{\unicode[STIX]{x1D70B}_{1}O}(C)$
, so
![]() $C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
as required.◻
$C_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))=N_{\widehat{\unicode[STIX]{x1D70B}_{1}O}}(f(H))$
as required.◻
Next, we classify the possible fixed subtrees for
![]() $\widehat{\mathbb{Z}}^{2}$
subgroups of
$\widehat{\mathbb{Z}}^{2}$
subgroups of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
.
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
.
Lemma 4.9. Let
![]() $M$
be a closed, orientable, irreducible
$M$
be a closed, orientable, irreducible
![]() $3$
-manifold. Consider the action of a subgroup
$3$
-manifold. Consider the action of a subgroup
![]() $H\cong \widehat{\mathbb{Z}}^{2}$
of
$H\cong \widehat{\mathbb{Z}}^{2}$
of
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on
$\widehat{\unicode[STIX]{x1D70B}_{1}M}$
on
![]() $\widehat{T}_{M}$
. One of the following holds.
$\widehat{T}_{M}$
. One of the following holds.
(i) The fixed point set of
 $H$
is a vertex with Seifert fibred stabilizer.
$H$
is a vertex with Seifert fibred stabilizer.(ii) The fixed point set of
 $H$
consists of exactly one edge.
$H$
consists of exactly one edge.(iii) The fixed subtree of
 $H$
consists of exactly two edges; the central vertex has a minor Seifert fibred stabilizer, and the other two vertices are major.
$H$
consists of exactly two edges; the central vertex has a minor Seifert fibred stabilizer, and the other two vertices are major.
Furthermore, if the centralizer
![]() $C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
is properly contained in the normalizer
$C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
is properly contained in the normalizer
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
, then we are in case (i) or case (iii).
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
, then we are in case (i) or case (iii).
Proof. By Lemma 3.3 and Proposition 4.2,
![]() $H$
fixes a non-empty subtree. Recall that every edge of
$H$
fixes a non-empty subtree. Recall that every edge of
![]() $\widehat{T}_{M}$
adjoins a major vertex, and that every minor vertex of
$\widehat{T}_{M}$
adjoins a major vertex, and that every minor vertex of
![]() $\widehat{T}_{M}$
adjoins exactly two edges. If
$\widehat{T}_{M}$
adjoins exactly two edges. If
![]() $H$
stabilizes an edge
$H$
stabilizes an edge
![]() $e$
and an adjacent major vertex
$e$
and an adjacent major vertex
![]() $v$
then, by Lemmas 4.7 and 4.8,
$v$
then, by Lemmas 4.7 and 4.8,
![]() $e$
is the unique edge incident at
$e$
is the unique edge incident at
![]() $v$
stabilized by
$v$
stabilized by
![]() $H$
. It follows that the fixed tree of
$H$
. It follows that the fixed tree of
![]() $H$
is of one of the three claimed forms.
$H$
is of one of the three claimed forms.
We now prove that, in case (ii),
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
. Indeed,
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
. Indeed,
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
preserves the fixed subtree of
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
preserves the fixed subtree of
![]() $C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
, and so if
$C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
, and so if
![]() $H$
fixes a unique edge,
$H$
fixes a unique edge,
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
is contained in an edge stabilizer, hence is abelian, and so
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
is contained in an edge stabilizer, hence is abelian, and so
![]() $N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
.◻
$N_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)=C_{\widehat{\unicode[STIX]{x1D70B}_{1}M}}(H)$
.◻
We now have enough information to construct a map
![]() $\unicode[STIX]{x1D719}$
. To start with, it will only be a map of abstract, unoriented graphs.
$\unicode[STIX]{x1D719}$
. To start with, it will only be a map of abstract, unoriented graphs.
Lemma 4.10. Consider closed, orientable, irreducible
![]() $3$
-manifolds
$3$
-manifolds
![]() $M,M^{\prime }$
, and let
$M,M^{\prime }$
, and let
![]() $f:\widehat{\unicode[STIX]{x1D70B}_{1}M}\rightarrow \widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}$
be an isomorphism. Then there exists an
$f:\widehat{\unicode[STIX]{x1D70B}_{1}M}\rightarrow \widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}$
be an isomorphism. Then there exists an
![]() $f$
-equivariant morphism of graphs
$f$
-equivariant morphism of graphs
Note that, here, we only claim that
![]() $\unicode[STIX]{x1D719}$
is a map of abstract, non-oriented graphs. This map may in principle send edges to either edges or vertices.
$\unicode[STIX]{x1D719}$
is a map of abstract, non-oriented graphs. This map may in principle send edges to either edges or vertices.
Proof. For brevity, we write
![]() $G=\widehat{\unicode[STIX]{x1D70B}_{1}M}$
and
$G=\widehat{\unicode[STIX]{x1D70B}_{1}M}$
and
![]() $\widehat{S}=\widehat{T}_{M^{\prime }}$
, and let
$\widehat{S}=\widehat{T}_{M^{\prime }}$
, and let
![]() $G$
act on
$G$
act on
![]() $\widehat{S}$
via
$\widehat{S}$
via
![]() $f$
. Let
$f$
. Let
![]() $e$
be an edge of
$e$
be an edge of
![]() $\widehat{T}_{M}$
with stabilizer
$\widehat{T}_{M}$
with stabilizer
![]() $G_{e}\cong \widehat{\mathbb{Z}}^{2}$
. Let
$G_{e}\cong \widehat{\mathbb{Z}}^{2}$
. Let
![]() $u_{1},u_{2}$
be the adjacent vertices of
$u_{1},u_{2}$
be the adjacent vertices of
![]() $\widehat{T}_{M}$
. Lemmas 4.4–4.6 together guarantee the existence of unique vertices
$\widehat{T}_{M}$
. Lemmas 4.4–4.6 together guarantee the existence of unique vertices
![]() $v_{1},v_{2}$
of
$v_{1},v_{2}$
of
![]() $\widehat{S}$
such that
$\widehat{S}$
such that
![]() $G_{u_{i}}\subseteq G_{v_{i}}$
for both
$G_{u_{i}}\subseteq G_{v_{i}}$
for both
![]() $i$
.
$i$
.
We claim that
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
are either equal or adjacent. Suppose therefore that
$v_{2}$
are either equal or adjacent. Suppose therefore that
![]() $v_{1},v_{2}$
are at distance greater than
$v_{1},v_{2}$
are at distance greater than
![]() $2$
(possibly infinite). Then
$2$
(possibly infinite). Then
![]() $G_{e}$
stabilizes the geodesic
$G_{e}$
stabilizes the geodesic
![]() $[v_{1},v_{2}]$
(see [Reference Zalesskii and Mel’nikovZM88, Corollary 2.9] or [Reference RibesRib17, Corollary 4.1.6]) and therefore, by Lemma 4.9,
$[v_{1},v_{2}]$
(see [Reference Zalesskii and Mel’nikovZM88, Corollary 2.9] or [Reference RibesRib17, Corollary 4.1.6]) and therefore, by Lemma 4.9,
![]() $v_{1},v_{2}$
are at distance precisely
$v_{1},v_{2}$
are at distance precisely
![]() $2$
, are both adjacent to a minor vertex
$2$
, are both adjacent to a minor vertex
![]() $w$
, and
$w$
, and
![]() $C_{G}(G_{e})$
is properly contained in
$C_{G}(G_{e})$
is properly contained in
![]() $N_{G}(G_{e})$
. Therefore, by Lemma 4.9,
$N_{G}(G_{e})$
. Therefore, by Lemma 4.9,
![]() $e$
is adjacent to a minor vertex; without loss of generality, we may assume that
$e$
is adjacent to a minor vertex; without loss of generality, we may assume that
![]() $u_{1}$
is major,
$u_{1}$
is major,
![]() $G_{u_{1}}\subseteq G_{v_{1}}$
, and that
$G_{u_{1}}\subseteq G_{v_{1}}$
, and that
![]() $u_{2}$
is minor and
$u_{2}$
is minor and
![]() $G_{u_{2}}\subseteq G_{v_{2}}$
. But
$G_{u_{2}}\subseteq G_{v_{2}}$
. But
![]() $G_{w}$
also normalizes
$G_{w}$
also normalizes
![]() $G_{e}$
, so
$G_{e}$
, so
![]() $G_{w}\subseteq G_{u_{2}}\subseteq G_{v_{2}}$
. This implies that
$G_{w}\subseteq G_{u_{2}}\subseteq G_{v_{2}}$
. This implies that
![]() $G_{w}$
stabilizes an edge, which is absurd because edge stabilizers are abelian. Therefore,
$G_{w}$
stabilizes an edge, which is absurd because edge stabilizers are abelian. Therefore,
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
are either equal or adjacent. If they are equal to a vertex
$v_{2}$
are either equal or adjacent. If they are equal to a vertex
![]() $v$
, we set
$v$
, we set
![]() $\unicode[STIX]{x1D719}(e)=v$
. If they are adjacent, we set
$\unicode[STIX]{x1D719}(e)=v$
. If they are adjacent, we set
![]() $\unicode[STIX]{x1D719}(e)$
to be the image of the unique edge joining them. This completes the construction of the map
$\unicode[STIX]{x1D719}(e)$
to be the image of the unique edge joining them. This completes the construction of the map
![]() $\unicode[STIX]{x1D719}:\widehat{T}_{M}\rightarrow \widehat{S}$
, which is equivariant by construction.◻
$\unicode[STIX]{x1D719}:\widehat{T}_{M}\rightarrow \widehat{S}$
, which is equivariant by construction.◻
We are now ready to complete the proof of the main theorem.
Proof of Theorem 4.3.
Applying Lemma 4.10 twice, we obtain maps of graphs
where
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $f$
-equivariant and
$f$
-equivariant and
![]() $\unicode[STIX]{x1D713}$
is
$\unicode[STIX]{x1D713}$
is
![]() $f^{-1}$
-equivariant. Equivariance implies that
$f^{-1}$
-equivariant. Equivariance implies that
for all
![]() $g\in \widehat{\unicode[STIX]{x1D70B}_{1}M}$
and
$g\in \widehat{\unicode[STIX]{x1D70B}_{1}M}$
and
![]() $x\in \widehat{T}_{M}$
, whence the stabilizer of
$x\in \widehat{T}_{M}$
, whence the stabilizer of
![]() $x$
is contained in the stabilizer of
$x$
is contained in the stabilizer of
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}(x)$
. Since vertex stabilizers stabilize unique vertices, it follows that
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}(x)$
. Since vertex stabilizers stabilize unique vertices, it follows that
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}$
is equal to the identity on vertices, and hence on the whole of
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D719}$
is equal to the identity on vertices, and hence on the whole of
![]() $\widehat{T}_{M}$
. In particular,
$\widehat{T}_{M}$
. In particular,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
induce isomorphisms of the finite quotient graphs
$\unicode[STIX]{x1D713}$
induce isomorphisms of the finite quotient graphs
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M}\backslash \widehat{T}_{M}$
and
$\widehat{\unicode[STIX]{x1D70B}_{1}M}\backslash \widehat{T}_{M}$
and
![]() $\widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}\backslash \widehat{T}_{M}^{\prime }$
; we may therefore choose consistent orientations on these graphs, which lift to equivariant orientations on the profinite trees
$\widehat{\unicode[STIX]{x1D70B}_{1}M^{\prime }}\backslash \widehat{T}_{M}^{\prime }$
; we may therefore choose consistent orientations on these graphs, which lift to equivariant orientations on the profinite trees
![]() $\widehat{T}_{M}$
and
$\widehat{T}_{M}$
and
![]() $\widehat{T}_{M^{\prime }}$
, which are respected by
$\widehat{T}_{M^{\prime }}$
, which are respected by
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
; this also implies continuity of
$\unicode[STIX]{x1D713}$
; this also implies continuity of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
. ◻
$\unicode[STIX]{x1D713}$
. ◻
Acknowledgements
The authors are grateful to Peter Kropholler for explaining the results of [Reference Kropholler and RollerKR88], and to Michel Boileau and Stefan Friedl for pointing out Corollary C. This work was completed while the first author was a participant in the Non-positive curvature, group actions and cohomology programme at the Isaac Newton Institute, funded by the EPSRC grant no. EP/K032208/1. The first author is also supported by an EPSRC standard grant no. EP/L026481/1. The second author was supported by CAPES as part of the ‘Estagio Senior’ programme, and thanks Trinity College and the Department of Pure Mathematics and Mathematical Statistics at the University of Cambridge for their hospitality.