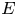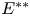1. Introduction
The second adjoint $u^{**}$![]() of a linear operator $u$
of a linear operator $u$![]() , which is a bidual extension of $u$
, which is a bidual extension of $u$![]() , is a powerful tool in several areas of mathematics. For multilinear operators, this role has been played by Arens extensions. This has been extensively studied over the past 70 years since its introduction by Arens in his seminal paper, [Reference Arens3]. In order to state the two recent results that have motivated our work, let us fix some notation. By $E^\sim$
, is a powerful tool in several areas of mathematics. For multilinear operators, this role has been played by Arens extensions. This has been extensively studied over the past 70 years since its introduction by Arens in his seminal paper, [Reference Arens3]. In order to state the two recent results that have motivated our work, let us fix some notation. By $E^\sim$![]() we denote the order dual of a Riesz space $E$
we denote the order dual of a Riesz space $E$![]() , hence $E^{\sim \sim } = (E^\sim )^\sim$
, hence $E^{\sim \sim } = (E^\sim )^\sim$![]() denotes its second order dual. For a Banach lattice $E$
denotes its second order dual. For a Banach lattice $E$![]() , $E^*$
, $E^*$![]() denotes its topological dual, hence $E^{**}$
denotes its topological dual, hence $E^{**}$![]() stands for its bidual. The symbols $(E^\sim )_n^{\sim }$
stands for its bidual. The symbols $(E^\sim )_n^{\sim }$![]() and $(E^*)_n^{*}$
and $(E^*)_n^{*}$![]() stand for the corresponding subspaces formed by the order continuous functionals. The results that motivated our research are the following:
stand for the corresponding subspaces formed by the order continuous functionals. The results that motivated our research are the following:
• Buskes and Roberts (2019) [Reference Buskes and Roberts10, Theorem 3.4]: If $A \colon E_1 \times \cdots \times E_m \longrightarrow F$
 is an $m$
is an $m$ -linear operator of order bounded variation between Riesz spaces, then its Arens extension $A^{\ast [m+1]} \colon E_1^{\sim \sim } \times \cdots \times E_m^{\sim \sim } \longrightarrow F^{\sim \sim }$
-linear operator of order bounded variation between Riesz spaces, then its Arens extension $A^{\ast [m+1]} \colon E_1^{\sim \sim } \times \cdots \times E_m^{\sim \sim } \longrightarrow F^{\sim \sim }$ is separately order continuous on $(E_1^\sim )_n^{\sim } \times \cdots \times (E_m^\sim )_n^{\sim }.$
is separately order continuous on $(E_1^\sim )_n^{\sim } \times \cdots \times (E_m^\sim )_n^{\sim }.$
• Boyd, Ryan and Snigireva (2021) [Reference Boyd, Ryan and Snigireva7, Theorem 1]: If $A \colon E_1 \times \cdots \times E_m \longrightarrow F$
 is a regular $m$
is a regular $m$ -linear operator between Banach lattices, with $F$
-linear operator between Banach lattices, with $F$ Dedekind complete, then its Arens extension $A^{\ast [m+1]}\colon E_1^{**} \times \cdots \times E_m^{**} \longrightarrow F^{**}$
Dedekind complete, then its Arens extension $A^{\ast [m+1]}\colon E_1^{**} \times \cdots \times E_m^{**} \longrightarrow F^{**}$ is separately order continuous on $(E_1^*)_n^{*} \times \cdots \times (E_m^*)_n^{*}.$
is separately order continuous on $(E_1^*)_n^{*} \times \cdots \times (E_m^*)_n^{*}.$
The obvious question is whether or not these results can be improved to get order continuity on $E_1^{\sim \sim } \times \cdots \times E_m^{\sim \sim }$![]() and $E_1^{**} \times \cdots \times E_m^{**}$
and $E_1^{**} \times \cdots \times E_m^{**}$![]() , respectively. By means of a simple but efficient counterexample we show that this is not the case (cf. Section 3). Actually the counterexample, which is the bilinear form $A$
, respectively. By means of a simple but efficient counterexample we show that this is not the case (cf. Section 3). Actually the counterexample, which is the bilinear form $A$![]() on $\ell _1 \times c_0$
on $\ell _1 \times c_0$![]() given by the duality $c_0^* = \ell _1$
given by the duality $c_0^* = \ell _1$![]() , discloses an interesting phenomenon: its Arens extension $A^{***}$
, discloses an interesting phenomenon: its Arens extension $A^{***}$![]() is not separately order continuous on $\ell _1^{**} \times c_0^{**}$
is not separately order continuous on $\ell _1^{**} \times c_0^{**}$![]() (more precisely, it is order continuous in the first variable but not in the second one), while the other Arens extension of $A$
(more precisely, it is order continuous in the first variable but not in the second one), while the other Arens extension of $A$![]() is. We then proceed to find conditions on the operator and/or on the underlying spaces so that all Arens extensions are separately order continuous on the product of the whole of the biduals. In § 4 we prove that this holds for finite sums of multiplicative operators from Riesz spaces to Archimedean $f$
is. We then proceed to find conditions on the operator and/or on the underlying spaces so that all Arens extensions are separately order continuous on the product of the whole of the biduals. In § 4 we prove that this holds for finite sums of multiplicative operators from Riesz spaces to Archimedean $f$![]() -algebras, in particular for operators of finite type between arbitrary Riesz spaces. The main result of § 4 (Theorem 4.6): (i) implies that all Arens extensions of any regular multilinear operator between Riesz spaces are order continuous in at least one variable, (ii) implies that all Arens extensions of a regular homogeneous polynomial from the Riesz space $E$
-algebras, in particular for operators of finite type between arbitrary Riesz spaces. The main result of § 4 (Theorem 4.6): (i) implies that all Arens extensions of any regular multilinear operator between Riesz spaces are order continuous in at least one variable, (ii) implies that all Arens extensions of a regular homogeneous polynomial from the Riesz space $E$![]() to a Riesz space $F$
to a Riesz space $F$![]() are order continuous at the origin on $E^{\sim \sim }$
are order continuous at the origin on $E^{\sim \sim }$![]() , (iii) improves the results of Boyd, Ryan and Snigireva and of Buskes and Roberts for regular operators (see Remark 4.7). In the final § 5 we give sufficient conditions on the Banach lattices $E_1,\, \ldots,\, E_m$
, (iii) improves the results of Boyd, Ryan and Snigireva and of Buskes and Roberts for regular operators (see Remark 4.7). In the final § 5 we give sufficient conditions on the Banach lattices $E_1,\, \ldots,\, E_m$![]() so that Arens extensions of any regular $m$
so that Arens extensions of any regular $m$![]() -linear operator from $E_1 \times \cdots \times E_m$
-linear operator from $E_1 \times \cdots \times E_m$![]() to an arbitrary Banach lattice $F$
to an arbitrary Banach lattice $F$![]() are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$
are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$![]() ; and conditions so that Arens extensions of regular homogeneous polynomials on a Banach lattice $E$
; and conditions so that Arens extensions of regular homogeneous polynomials on a Banach lattice $E$![]() are order continuous on $E^{**}$
are order continuous on $E^{**}$![]() .
.
In § 2 we discuss briefly the notion of order continuity of linear operators and recall the characterization of the Arens extensions of regular multilinear operators between Riesz spaces that shall fit our purposes. Although these extensions are usually called Aron-Berner extensions in the case of operators between Banach spaces (see [Reference Aron and Berner4, Reference Dineen13]), for simplicity we shall refer to Arens extensions even for operators between Banach lattices.
2. Background
Our references to Riesz spaces, Banach lattices and regular linear operators are the canonical ones [Reference Aliprantis and Burkinshaw2, Reference Meyer–Nieberg17, Reference Schaefer19].
The following three definitions of order convergence can be found in the literature (see [Reference Abramovich and Sirotkin1]). A net $(x_{\alpha })_{\alpha \in \Omega }$![]() in a Riesz space $E$
in a Riesz space $E$![]() is said to be:
is said to be:
• order convergent to $x\in E$
 if there is a net $(y_{\alpha })_{\alpha \in \Omega }$
if there is a net $(y_{\alpha })_{\alpha \in \Omega }$ in $E$
in $E$ such that $y_{\alpha }\downarrow 0$
such that $y_{\alpha }\downarrow 0$ and $|x_{\alpha }-x|\leq y_{\alpha }$
and $|x_{\alpha }-x|\leq y_{\alpha }$ for every $\alpha \in \Omega$
for every $\alpha \in \Omega$ .
.• 1-convergent to $x\in E$
 if there are a net $(y_{\alpha })_{\alpha \in \Omega }$
if there are a net $(y_{\alpha })_{\alpha \in \Omega }$ in $E$
in $E$ and $\alpha _{0}\in \Omega$
and $\alpha _{0}\in \Omega$ such that $y_{\alpha }\downarrow 0$
such that $y_{\alpha }\downarrow 0$ and $|x_{\alpha }-x|\leq y_{\alpha }$
and $|x_{\alpha }-x|\leq y_{\alpha }$ for every $\alpha \geq \alpha _{0}$
for every $\alpha \geq \alpha _{0}$ .
.• 2-convergent to $x\in E$
 is there are a net $(y_{\beta })_{\beta \in \Gamma }$
is there are a net $(y_{\beta })_{\beta \in \Gamma }$ in $E$
in $E$ such that $y_{\beta }\downarrow 0$
such that $y_{\beta }\downarrow 0$ and for every $\beta \in \Gamma$
and for every $\beta \in \Gamma$ there exists $\alpha _{0}\in \Omega$
there exists $\alpha _{0}\in \Omega$ such that $|x_{\alpha }-x|\leq y_{\beta }$
such that $|x_{\alpha }-x|\leq y_{\beta }$ for any $\alpha \geq \alpha _{0}$
for any $\alpha \geq \alpha _{0}$ .
.
If $E$![]() is Dedekind complete, then the notions of 1-convergence and 2-convergence coincide [Reference Abramovich and Sirotkin1], but otherwise they may be different (see [Reference Abramovich and Sirotkin1, Example 1.4]).
is Dedekind complete, then the notions of 1-convergence and 2-convergence coincide [Reference Abramovich and Sirotkin1], but otherwise they may be different (see [Reference Abramovich and Sirotkin1, Example 1.4]).
Order continuity can be considered with respect to any of these three notions of order convergence: a linear operator $T \colon E \longrightarrow F$![]() between Riesz spaces is said to be order continuous (1-order continuous, 2-order continuous, respectively) if $(T(x_{\alpha }))_{\alpha \in \Omega }$
between Riesz spaces is said to be order continuous (1-order continuous, 2-order continuous, respectively) if $(T(x_{\alpha }))_{\alpha \in \Omega }$![]() is order convergent (1-convergent, 2-convergent, respectively) to zero in $F$
is order convergent (1-convergent, 2-convergent, respectively) to zero in $F$![]() whenever $(x_{\alpha })_{\alpha \in \Omega }$
whenever $(x_{\alpha })_{\alpha \in \Omega }$![]() is order convergent (1-convergent, 2-convergent, respectively) to zero in $E$
is order convergent (1-convergent, 2-convergent, respectively) to zero in $E$![]() .
.
The following coincidences are known (see [Reference Aliprantis and Burkinshaw2, Theorem 1.56] or [Reference Meyer–Nieberg17, Proposition 1.3.9]):
• If $F$
 is Dedekind complete, then $T$
is Dedekind complete, then $T$ is order continuous if and only if $T$
is order continuous if and only if $T$ is 1-order continuous.
is 1-order continuous.• If $E$
 and $F$
and $F$ are Dedekind complete, then $T$
are Dedekind complete, then $T$ is order continuous if and only if $T$
is order continuous if and only if $T$ is 1-order continuous if and only if $T$
is 1-order continuous if and only if $T$ is 2-order continuous.
is 2-order continuous.
In most cases in this paper we will investigate the order continuity of regular linear operators from $E^{\sim \sim }$![]() to $F^{\sim \sim }$
to $F^{\sim \sim }$![]() , where $E$
, where $E$![]() and $F$
and $F$![]() are Riesz spaces, or from $E^{**}$
are Riesz spaces, or from $E^{**}$![]() to $F^{**}$
to $F^{**}$![]() , where $E$
, where $E$![]() and $F$
and $F$![]() are Banach lattices. Since all these spaces are Dedekind complete, we are free to use any of the three notions of order continuity. We shall denote the order convergence by $x_\alpha \stackrel {o}{\longrightarrow } x$
are Banach lattices. Since all these spaces are Dedekind complete, we are free to use any of the three notions of order continuity. We shall denote the order convergence by $x_\alpha \stackrel {o}{\longrightarrow } x$![]() .
.
For the theory of regular multilinear operators and regular homogeneous polynomials we refer to [Reference Bu and Buskes9, Reference Buskes and Roberts10, Reference Loane16]. An $m$![]() -linear operator $A \colon E_1 \times \cdots \times E_m \longrightarrow F$
-linear operator $A \colon E_1 \times \cdots \times E_m \longrightarrow F$![]() is separately order continuous (separately 1-order continuous, separately 2-order continuous) if for all $j \in \{1,\, \ldots,\, m\}$
is separately order continuous (separately 1-order continuous, separately 2-order continuous) if for all $j \in \{1,\, \ldots,\, m\}$![]() and $x_k \in E_k,\, k = 1,\,\ldots,\, m,\, k\neq j$
and $x_k \in E_k,\, k = 1,\,\ldots,\, m,\, k\neq j$![]() , the linear operator
, the linear operator
is order continuous (1-order continuous, 2-order continuous). For the definition of joint order continuity see [Reference Boyd, Ryan and Snigireva7, p. 234]. If $A$![]() is a regular operator between Banach lattices with $F$
is a regular operator between Banach lattices with $F$![]() Dedekind complete, then $A$
Dedekind complete, then $A$![]() is separately order continuous if and only if $A$
is separately order continuous if and only if $A$![]() is jointly order continuous [Reference Boyd, Ryan and Snigireva7, Theorem 2].
is jointly order continuous [Reference Boyd, Ryan and Snigireva7, Theorem 2].
Now we recall the description of the Arens extensions of regular multilinear operators between Riesz spaces as presented in [Reference Botelho and Garcia6]. By $J_E \colon E \longrightarrow E^{\sim \sim }$![]() we denote the canonical operator ($J_E(x)(x'') = x''(x)$
we denote the canonical operator ($J_E(x)(x'') = x''(x)$![]() ), which happens to be a Riesz homomorphism.
), which happens to be a Riesz homomorphism.
Given Riesz spaces $E_1,\, \ldots,\, E_m,\,F$![]() , the space of regular $m$
, the space of regular $m$![]() -linear operators from $E_1 \times \cdots \times E_m$
-linear operators from $E_1 \times \cdots \times E_m$![]() to $F$
to $F$![]() is denoted by ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m;F)$
is denoted by ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m;F)$![]() . When $F$
. When $F$![]() is the scalar field we write ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$
is the scalar field we write ${\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$![]() . We use $S_m$
. We use $S_m$![]() to denote the set of permutations of $\{1,\, \ldots,\, m\}$
to denote the set of permutations of $\{1,\, \ldots,\, m\}$![]() .
.
Let $m\in \mathbb {N}$![]() and $\rho \in S_{m}$
and $\rho \in S_{m}$![]() be given. For an $m$
be given. For an $m$![]() -linear form $C\colon E_{1}\times \cdots \times E_{m}\longrightarrow \mathbb {R}$
-linear form $C\colon E_{1}\times \cdots \times E_{m}\longrightarrow \mathbb {R}$![]() , define the $m$
, define the $m$![]() -linear form
-linear form
where $x_{j}\in E_{\rho (j)},\, j=1,\,\ldots,\,m$![]() . Furthermore, for each $i=1,\,\ldots,\,m-1$
. Furthermore, for each $i=1,\,\ldots,\,m-1$![]() , and $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim }$
, and $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim }$![]() , consider the regular linear operator
, consider the regular linear operator
where $B^{i}\colon E_{\rho (i+1)}\times \cdots \times E_{\rho (m)}\longrightarrow E_{\rho (i)}^{\sim }$![]() is given by
is given by
In the case $i=m$![]() we define $\overline {x_{\rho (m)}^{\prime \prime }}\colon E_{\rho (m)}^{\sim }\longrightarrow \mathbb {R}$
we define $\overline {x_{\rho (m)}^{\prime \prime }}\colon E_{\rho (m)}^{\sim }\longrightarrow \mathbb {R}$![]() by $\overline {x_{\rho (m)}^{\prime \prime }}(x_{\rho (m)})=x_{\rho (m)}^{\prime \prime }(x_{\rho (m)})$
by $\overline {x_{\rho (m)}^{\prime \prime }}(x_{\rho (m)})=x_{\rho (m)}^{\prime \prime }(x_{\rho (m)})$![]() .
.
The Arens extension of the regular $m$![]() -linear operator $A\colon E_{1}\times \cdots \times E_{m}\longrightarrow F$
-linear operator $A\colon E_{1}\times \cdots \times E_{m}\longrightarrow F$![]() is the regular $m$
is the regular $m$![]() -linear operator $AR_{m}^{\rho }(A)\colon E_{1}^{\sim \sim }\times \cdots \times E_{m}^{\sim \sim }\longrightarrow F^{\sim \sim }$
-linear operator $AR_{m}^{\rho }(A)\colon E_{1}^{\sim \sim }\times \cdots \times E_{m}^{\sim \sim }\longrightarrow F^{\sim \sim }$![]() given by
given by
for all $x_{1}^{\prime \prime }\in E_{1}^{\sim \sim },\,\ldots,\,x_{m}^{\prime \prime }\in E_{m}^{\sim \sim }$![]() and every $y^{\prime }\in F^{\sim }$
and every $y^{\prime }\in F^{\sim }$![]() . Although the notation is a bit different, these are exactly the Arens extensions studied in [Reference Botelho and Garcia6].
. Although the notation is a bit different, these are exactly the Arens extensions studied in [Reference Botelho and Garcia6].
According to [Reference Botelho and Garcia6, Theorem 2.2], $AR_{m}^{\rho }(A)$![]() is a regular $m$
is a regular $m$![]() -linear operator that extends $A$
-linear operator that extends $A$![]() in the sense that $AR_{m}^{\rho }(A)\circ (J_{E_{1}},\,\ldots,\,J_{E_{m}})=J_{F}\circ A.$
in the sense that $AR_{m}^{\rho }(A)\circ (J_{E_{1}},\,\ldots,\,J_{E_{m}})=J_{F}\circ A.$![]() Moreover, $AR_{m}^{\rho }(A)$
Moreover, $AR_{m}^{\rho }(A)$![]() is positive for positive $A$
is positive for positive $A$![]() .
.
The extension $A^{\ast [m+1]}$![]() from [Reference Boyd, Ryan and Snigireva7, Reference Buskes and Roberts10] is recovered by considering the permutation $\theta (m) = 1,\, \theta (m-1) = 2,\, \ldots,\,\theta (2) = m-1,\, \theta (1) = m$
from [Reference Boyd, Ryan and Snigireva7, Reference Buskes and Roberts10] is recovered by considering the permutation $\theta (m) = 1,\, \theta (m-1) = 2,\, \ldots,\,\theta (2) = m-1,\, \theta (1) = m$![]() , that is, $AR_m^\theta (A) = A^{*[m+1]}$
, that is, $AR_m^\theta (A) = A^{*[m+1]}$![]() . In particular, $AR_2^\theta (A) = A^{***}$
. In particular, $AR_2^\theta (A) = A^{***}$![]() in the bilinear case $m = 2$
in the bilinear case $m = 2$![]() .
.
3. The counterexample
Consider the positive bilinear form given by the duality bracket $(c_0,\,\ell _1)$![]() :
:

The two Arens extensions of $A$![]() shall be denoted by $A^{***} =AR_2^\theta (A)$
shall be denoted by $A^{***} =AR_2^\theta (A)$![]() and $AR_2^{\rm id}(A)$
and $AR_2^{\rm id}(A)$![]() , where id is the identity permutation. As announced, we shall prove that $AR_2^{\rm id}(A)$
, where id is the identity permutation. As announced, we shall prove that $AR_2^{\rm id}(A)$![]() is separately order continuous on $\ell _1^{**} \times c_0^{**}$
is separately order continuous on $\ell _1^{**} \times c_0^{**}$![]() and that $A^{***}$
and that $A^{***}$![]() is order continuous in the first variable but not in the second one. Although everything can be proved directly to this bilinear form, to avoid unnecessary repetitions we shall apply some results that will be proved later.
is order continuous in the first variable but not in the second one. Although everything can be proved directly to this bilinear form, to avoid unnecessary repetitions we shall apply some results that will be proved later.
From Theorem 4.6 we know that $A^{***} \colon \ell _{1}^{\ast \ast }\times c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$![]() is order continuous in the first variable. Suppose that $A^{***}$
is order continuous in the first variable. Suppose that $A^{***}$![]() is order continuous in the second variable, that is, for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$
is order continuous in the second variable, that is, for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$![]() , the linear functional $A^{***}(x^{\ast \ast },\,\bullet )\colon c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$
, the linear functional $A^{***}(x^{\ast \ast },\,\bullet )\colon c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$![]() , defined by $A^{***}(x^{\ast \ast },\,\bullet )(y^{**}) = A^{***}(x^{**},\, y^{**})$
, defined by $A^{***}(x^{\ast \ast },\,\bullet )(y^{**}) = A^{***}(x^{**},\, y^{**})$![]() , is order continuous. Denoting by $\psi \colon \ell _{1}\longrightarrow c_{0}^{*}$
, is order continuous. Denoting by $\psi \colon \ell _{1}\longrightarrow c_{0}^{*}$![]() the canonical isometric isomorphism, note that $\psi$
the canonical isometric isomorphism, note that $\psi$![]() and $\psi ^{-1}\colon c_{0}^{\ast }\longrightarrow \ell _{1}$
and $\psi ^{-1}\colon c_{0}^{\ast }\longrightarrow \ell _{1}$![]() , $\psi ^{-1}(\varphi )=(\varphi (e_{n}))_{n=1}^{\infty }$
, $\psi ^{-1}(\varphi )=(\varphi (e_{n}))_{n=1}^{\infty }$![]() , are positive operators, hence $\psi$
, are positive operators, hence $\psi$![]() is a Riesz homomorphism [Reference Aliprantis and Burkinshaw2, Theorem 2.15]. Moreover, $\psi (x)=A_\theta (\bullet,\, x)$
is a Riesz homomorphism [Reference Aliprantis and Burkinshaw2, Theorem 2.15]. Moreover, $\psi (x)=A_\theta (\bullet,\, x)$![]() for every $x\in \ell _{1}$
for every $x\in \ell _{1}$![]() , where $A_{\theta }(\bullet,\,x)\colon c_{0}\longrightarrow \mathbb {R}$
, where $A_{\theta }(\bullet,\,x)\colon c_{0}\longrightarrow \mathbb {R}$![]() is given by $A_{\theta }(\bullet,\,x)(y)=A_{\theta }(y,\,x)$
is given by $A_{\theta }(\bullet,\,x)(y)=A_{\theta }(y,\,x)$![]() .
.
Claim 1. $\psi ^{\ast \ast }(x^{\ast \ast })=A^{***}(x^{\ast \ast },\,\bullet )$![]() for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$
for every $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$![]() .
.
Indeed, given $y^{\ast \ast }\in c_{0}^{\ast \ast }$![]() and $x\in \ell _{1}$
and $x\in \ell _{1}$![]() , noting that $A_{\theta }^{1}\colon \ell _{1}\longrightarrow c_{0}^{\ast }$
, noting that $A_{\theta }^{1}\colon \ell _{1}\longrightarrow c_{0}^{\ast }$![]() is given by $A_{\theta }^{1}(x)(y)=A_{\theta }(y,\,x)$
is given by $A_{\theta }^{1}(x)(y)=A_{\theta }(y,\,x)$![]() , we have $A_{\theta }^{1}(x)=A_{\theta }(\bullet,\,x)$
, we have $A_{\theta }^{1}(x)=A_{\theta }(\bullet,\,x)$![]() , hence
, hence

proving that $\psi ^{\ast }(y^{\ast \ast })=\overline {y^{\ast \ast }}(A_{\theta })$![]() . Therefore, for $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$
. Therefore, for $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$![]() and $y^{\ast \ast }\in c_{0}^{\ast \ast }$
and $y^{\ast \ast }\in c_{0}^{\ast \ast }$![]() , bearing in mind that $A^{***} =AR_2^\theta (A)$
, bearing in mind that $A^{***} =AR_2^\theta (A)$![]() ,
,

Claim 2. $x^{**}\in \ell _{1}^{\ast \ast }$![]() is order continuous on $\ell _1^*$
is order continuous on $\ell _1^*$![]() if and only if $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$
if and only if $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$![]() is order continuous on $c_0^{**}$
is order continuous on $c_0^{**}$![]() .
.
Let $x^{**}\in \ell _{1}^{\ast \ast }$![]() be such that $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$
be such that $\psi ^{\ast \ast }(x^{\ast \ast })\in c_{0}^{\ast \ast \ast }$![]() is order continuous on $c_0^{**}$
is order continuous on $c_0^{**}$![]() . Supposing that $x^{\ast \ast }$
. Supposing that $x^{\ast \ast }$![]() fails to be order continuous on $\ell _1^*$
fails to be order continuous on $\ell _1^*$![]() , the positive functional $|x^{\ast \ast }|\in \ell _{1}^{\ast \ast }$
, the positive functional $|x^{\ast \ast }|\in \ell _{1}^{\ast \ast }$![]() is not order continuous on $\ell _1^*$
is not order continuous on $\ell _1^*$![]() either [Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Then there is a net $(x_{\alpha }^{\ast })_{\alpha \in \Omega }$
either [Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Then there is a net $(x_{\alpha }^{\ast })_{\alpha \in \Omega }$![]() in $\ell _{1}^{\ast }$
in $\ell _{1}^{\ast }$![]() such that $x_{\alpha }^{\ast }\downarrow 0$
such that $x_{\alpha }^{\ast }\downarrow 0$![]() but $\displaystyle \inf _{\alpha \in \Omega }|x^{\ast \ast }|(x_{\alpha }^{\ast })> 0$
but $\displaystyle \inf _{\alpha \in \Omega }|x^{\ast \ast }|(x_{\alpha }^{\ast })> 0$![]() . For each $\alpha \in \Omega$
. For each $\alpha \in \Omega$![]() let $y_{\alpha }^{\ast \ast }\in c_{0}^{\ast \ast }$
let $y_{\alpha }^{\ast \ast }\in c_{0}^{\ast \ast }$![]() be such that $\psi ^{\ast }(y_{\alpha }^{\ast \ast })=x_{\alpha }^{\ast }$
be such that $\psi ^{\ast }(y_{\alpha }^{\ast \ast })=x_{\alpha }^{\ast }$![]() . Thus
. Thus
because $(\psi ^{-1})^{\ast }$![]() is positive and order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73]. By assumption $\psi ^{\ast \ast }(x^{\ast \ast })$
is positive and order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73]. By assumption $\psi ^{\ast \ast }(x^{\ast \ast })$![]() is order continuous on $c_0^{**}$
is order continuous on $c_0^{**}$![]() , so is $|\psi ^{\ast \ast }(x^{\ast \ast })|$
, so is $|\psi ^{\ast \ast }(x^{\ast \ast })|$![]() [Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Since $\psi$
[Reference Aliprantis and Burkinshaw2, Theorem 1.56]. Since $\psi$![]() is a Riesz homomorphism, $\psi ^{\ast \ast }$
is a Riesz homomorphism, $\psi ^{\ast \ast }$![]() is as well, so $\psi ^{\ast \ast }(|x^{\ast \ast }|)(y_{\alpha }^{\ast \ast })=|\psi ^{\ast \ast }(x^{\ast \ast })|(y_{\alpha }^{\ast \ast })\downarrow 0$
is as well, so $\psi ^{\ast \ast }(|x^{\ast \ast }|)(y_{\alpha }^{\ast \ast })=|\psi ^{\ast \ast }(x^{\ast \ast })|(y_{\alpha }^{\ast \ast })\downarrow 0$![]() , from which it follows that
, from which it follows that
This contradiction proves that $x^{\ast \ast }\in \ell _{1}^{\ast \ast }$![]() is order continuous on $\ell _1^*$
is order continuous on $\ell _1^*$![]() . The reverse implication if straightforward.
. The reverse implication if straightforward.
Claim 3. $\ell _{1}^{\ast \ast }$![]() contains a functional that fails to be order continuous on $\ell _1^*$
contains a functional that fails to be order continuous on $\ell _1^*$![]() .
.
Let $c$![]() be the space of convergent real sequences and consider the positive linear functional $\varphi \in c^*$
be the space of convergent real sequences and consider the positive linear functional $\varphi \in c^*$![]() given by $\varphi ((x_{n})_{n=1}^{\infty })=\displaystyle \lim _{n\rightarrow \infty }x_{n}$
given by $\varphi ((x_{n})_{n=1}^{\infty })=\displaystyle \lim _{n\rightarrow \infty }x_{n}$![]() . Since $c$
. Since $c$![]() is a majorizing subspace of $\ell _{\infty }$
is a majorizing subspace of $\ell _{\infty }$![]() , $\varphi$
, $\varphi$![]() admits a positive extension $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$
admits a positive extension $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$![]() [Reference Aliprantis and Burkinshaw2, Theorem 1.32]. Suppose that $\widetilde {\varphi }$
[Reference Aliprantis and Burkinshaw2, Theorem 1.32]. Suppose that $\widetilde {\varphi }$![]() is $\sigma$
is $\sigma$![]() -order continuous on $\ell _\infty$
-order continuous on $\ell _\infty$![]() . For each $n\in \mathbb {N}$
. For each $n\in \mathbb {N}$![]() let $x_{n}=(1,\,\ldots,\,1,\,0,\,\ldots ) = e_1 + \cdots + e_n\in c$
let $x_{n}=(1,\,\ldots,\,1,\,0,\,\ldots ) = e_1 + \cdots + e_n\in c$![]() and $y=(1,\,1,\,\ldots )\in c$
and $y=(1,\,1,\,\ldots )\in c$![]() . Note that $0\leq x_{n}\uparrow y$
. Note that $0\leq x_{n}\uparrow y$![]() and, since $\widetilde {\varphi }$
and, since $\widetilde {\varphi }$![]() is a positive $\sigma$
is a positive $\sigma$![]() -order continuous operator, $0\leq \widetilde {\varphi }(x_{n})\uparrow \widetilde {\varphi }(y)$
-order continuous operator, $0\leq \widetilde {\varphi }(x_{n})\uparrow \widetilde {\varphi }(y)$![]() (see [Reference Aliprantis and Burkinshaw2, p. 46]). So,
(see [Reference Aliprantis and Burkinshaw2, p. 46]). So,
which proves that $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$![]() is not $\sigma$
is not $\sigma$![]() -order continuous on $\ell _\infty$
-order continuous on $\ell _\infty$![]() . Considering the canonical Riesz isomorphism $\phi \colon \ell _{\infty }\longrightarrow \ell _{1}^{\ast }$
. Considering the canonical Riesz isomorphism $\phi \colon \ell _{\infty }\longrightarrow \ell _{1}^{\ast }$![]() , there is $z^{\ast \ast }\in \ell _{1}^{\ast \ast }$
, there is $z^{\ast \ast }\in \ell _{1}^{\ast \ast }$![]() such that $\phi ^{\ast }(z^{\ast \ast })=\widetilde {\varphi }$
such that $\phi ^{\ast }(z^{\ast \ast })=\widetilde {\varphi }$![]() . Since $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$
. Since $\widetilde {\varphi }\in \ell _{\infty }^{\ast }$![]() fails to be $\sigma$
fails to be $\sigma$![]() -order continuous, there is a sequence $(z_{n})_{n=1}^{\infty }$
-order continuous, there is a sequence $(z_{n})_{n=1}^{\infty }$![]() in $\ell _{\infty }$
in $\ell _{\infty }$![]() such that $z_{n}\downarrow 0$
such that $z_{n}\downarrow 0$![]() and $\displaystyle \inf _{n\in \mathbb {N}}\widetilde {\varphi }(z_{n})>0$
and $\displaystyle \inf _{n\in \mathbb {N}}\widetilde {\varphi }(z_{n})>0$![]() . Furthermore, for each $n \in \mathbb {N}$
. Furthermore, for each $n \in \mathbb {N}$![]() there is $y_{n}^{\ast }\in \ell _{1}^{\ast }$
there is $y_{n}^{\ast }\in \ell _{1}^{\ast }$![]() such that $\phi ^{-1}(y_{n}^{\ast })=z_{n}$
such that $\phi ^{-1}(y_{n}^{\ast })=z_{n}$![]() , hence $y_{n}^{\ast }=\phi (z_{n})\downarrow$
, hence $y_{n}^{\ast }=\phi (z_{n})\downarrow$![]() because $\phi$
because $\phi$![]() is positive, so $0\leq y_{n}^{\ast }\downarrow$
is positive, so $0\leq y_{n}^{\ast }\downarrow$![]() . Suppose that there exists $y^{\ast }\in \ell _{1}^{\ast }$
. Suppose that there exists $y^{\ast }\in \ell _{1}^{\ast }$![]() such that $0< y^{\ast }\leq y_{n}^{\ast }$
such that $0< y^{\ast }\leq y_{n}^{\ast }$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() . On the one hand, as $\phi ^{-1}$
. On the one hand, as $\phi ^{-1}$![]() is positive,
is positive,
from which we conclude that $\phi ^{-1}(y^{\ast })=0$![]() , and so $y^{\ast }=0$
, and so $y^{\ast }=0$![]() because $\phi ^{-1}$
because $\phi ^{-1}$![]() is injective. This shows that $y_{n}^{\ast }\downarrow 0$
is injective. This shows that $y_{n}^{\ast }\downarrow 0$![]() in $\ell _{1}^{\ast }$
in $\ell _{1}^{\ast }$![]() . On the other hand,
. On the other hand,

proving that $z^{\ast \ast }$![]() is not order continuous on $\ell _\infty$
is not order continuous on $\ell _\infty$![]() , as claimed.
, as claimed.
Finally, combining claims 1 and 2 we have that $A^{***}(z^{**},\, \bullet )= \psi ^{**}(z^{**})$![]() is not order continuous on $c_0^{**}$
is not order continuous on $c_0^{**}$![]() . We have established that $A^{***}$
. We have established that $A^{***}$![]() is order continuous in the first variable and fails to be order continuous in the second variable.
is order continuous in the first variable and fails to be order continuous in the second variable.
As to the other Arens extension of $A$![]() , namely $AR_{2}^{\rm id}(A)\colon \ell _{1}^{\ast \ast }\times c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$
, namely $AR_{2}^{\rm id}(A)\colon \ell _{1}^{\ast \ast }\times c_{0}^{\ast \ast }\longrightarrow \mathbb {R}$![]() , since $c_{0}^{\ast } = \ell _{1}$
, since $c_{0}^{\ast } = \ell _{1}$![]() has order continuous norm, Corollary 5.1 guarantees that $AR_{2}^{id}(A)$
has order continuous norm, Corollary 5.1 guarantees that $AR_{2}^{id}(A)$![]() is separately order continuous, hence jointly order continuous by [Reference Boyd, Ryan and Snigireva7, Theorem 2].
is separately order continuous, hence jointly order continuous by [Reference Boyd, Ryan and Snigireva7, Theorem 2].
Since the bilinear form $A$![]() is regular and of bounded order variation, this example shows that the results of Buskes and Roberts and of Boyd, Ryan and Snigireva quoted in the introduction cannot be improved to get separate order continuity on the product of the whole biduals.
is regular and of bounded order variation, this example shows that the results of Buskes and Roberts and of Boyd, Ryan and Snigireva quoted in the introduction cannot be improved to get separate order continuity on the product of the whole biduals.
4. Operators between Riesz spaces
In this section we present our results on order continuity to the whole of the bidual of Arens extensions of multilinear operators on Riesz spaces. The main result of the section, namely Theorem 4.6, is a multipurpose result: in this section it will be used to prove that Arens extensions of regular homogeneous polynomials are always order continuous at the origin on the whole of the bidual of the domain space, to extend [Reference Boyd, Ryan and Snigireva7, Theorem 1] and to show that Arens extensions are always order continuous in at least one variable. Furthermore, Theorem 4.6 will be helpful a couple of times in the next section.
Recall that a Riesz algebra $\mathcal {A}$![]() is a Riesz space which is an associative algebra with respect to a product $\ast$
is a Riesz space which is an associative algebra with respect to a product $\ast$![]() such that $x\ast y\geq 0$
such that $x\ast y\geq 0$![]() for all $x,\,y\in \mathcal {A}^{+}$
for all $x,\,y\in \mathcal {A}^{+}$![]() . And that a Riesz algebra $(\mathcal {A},\,\ast )$
. And that a Riesz algebra $(\mathcal {A},\,\ast )$![]() is an $f$
is an $f$![]() -algebra if $x\wedge y=0$
-algebra if $x\wedge y=0$![]() in $\mathcal {A}$
in $\mathcal {A}$![]() implies that $(x\ast z)\wedge y=(z\ast x)\wedge y=0$
implies that $(x\ast z)\wedge y=(z\ast x)\wedge y=0$![]() for every $z\in \mathcal {A}^{+}.$
for every $z\in \mathcal {A}^{+}.$![]() The following Riesz spaces are $f$
The following Riesz spaces are $f$![]() –algebras: $\mathbb {R}$
–algebras: $\mathbb {R}$![]() , $C(X)$
, $C(X)$![]() and $C_{b}(X)$
and $C_{b}(X)$![]() -spaces, where $X$
-spaces, where $X$![]() is a topological space, $\ell _{\infty }(X)$
is a topological space, $\ell _{\infty }(X)$![]() and $\mathbb {R}^{X}$
and $\mathbb {R}^{X}$![]() -spaces, where $X$
-spaces, where $X$![]() is a nonempty set, $L_{\infty }(\mu )$
is a nonempty set, $L_{\infty }(\mu )$![]() -spaces, and spaces of measurable functions on measure spaces (see [Reference Aliprantis and Burkinshaw2, p. 126]). If $(\mathcal {A},\,\ast )$
-spaces, and spaces of measurable functions on measure spaces (see [Reference Aliprantis and Burkinshaw2, p. 126]). If $(\mathcal {A},\,\ast )$![]() is an $f$
is an $f$![]() -algebra, then the Arens product $\odot$
-algebra, then the Arens product $\odot$![]() , defined as follows, makes ${\mathcal {A}}^{\sim \sim }$
, defined as follows, makes ${\mathcal {A}}^{\sim \sim }$![]() an $f$
an $f$![]() -algebra [Reference Yilmaz20]: for $x\in \mathcal {A}$
-algebra [Reference Yilmaz20]: for $x\in \mathcal {A}$![]() , $y^{\prime }\in \mathcal {A}^{\sim }$
, $y^{\prime }\in \mathcal {A}^{\sim }$![]() and $x^{\prime \prime },\, y^{\prime \prime }\in \mathcal {A}^{\sim \sim }$
and $x^{\prime \prime },\, y^{\prime \prime }\in \mathcal {A}^{\sim \sim }$![]() ,
,

An operator $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$![]() is multiplicative if there are regular linear operators $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$
is multiplicative if there are regular linear operators $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$![]() , such that $A(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$
, such that $A(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$![]() for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$
for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$![]() .
.
Since Arens extensions $AR_{m}^{\rho }(A)$![]() of multilinear operators $A$
of multilinear operators $A$![]() are mappings between Dedekind complete spaces, we can use any of the three notions of order continuous linear operators to investigate the separate order continuity of $AR_{m}^{\rho }(A)$
are mappings between Dedekind complete spaces, we can use any of the three notions of order continuous linear operators to investigate the separate order continuity of $AR_{m}^{\rho }(A)$![]() .
.
Proposition 4.1 Let $E_{1},\,\ldots,\,E_{m}$![]() be Riesz spaces and $(\mathcal {A},\,\ast )$
be Riesz spaces and $(\mathcal {A},\,\ast )$![]() be an Archimedean $f$
be an Archimedean $f$![]() -algebra. If $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$
-algebra. If $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$![]() is a finite sum of multiplicative operators, then all Arens extensions of $A$
is a finite sum of multiplicative operators, then all Arens extensions of $A$![]() , $AR_{m}^{\rho }(A)$
, $AR_{m}^{\rho }(A)$![]() , $\rho \in S_{m}$
, $\rho \in S_{m}$![]() , coincide and are separately order continuous.
, coincide and are separately order continuous.
Proof. Given a multiplicative operator $B\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};\mathcal {A})$![]() , let $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$
, let $T_{i}\colon E_{i}\longrightarrow \mathcal {A},\, i=1,\,\ldots,\,m$![]() , be such that $B(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$
, be such that $B(x_{1},\,\ldots,\,x_{m})=T_{1}(x_{1})\ast \cdots \ast T_{m}(x_{m})$![]() for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$
for all $x_{1}\in E_{1},\,\ldots,\,x_{m}\in E_{m}$![]() . By [Reference Botelho and Garcia6, Remark 3.3 and the proof of Theorem 3.2] we have that, for each $\rho \in S_{m}$
. By [Reference Botelho and Garcia6, Remark 3.3 and the proof of Theorem 3.2] we have that, for each $\rho \in S_{m}$![]() and all $x_{1}^{\prime \prime }\in E_{1}^{\sim \sim },\,\ldots,\,x_{m}^{\prime \prime }\in E_{m}^{\sim \sim }$
and all $x_{1}^{\prime \prime }\in E_{1}^{\sim \sim },\,\ldots,\,x_{m}^{\prime \prime }\in E_{m}^{\sim \sim }$![]() ,
,
The Arens product $\odot$![]() makes $\mathcal {A}^{\sim \sim }$
makes $\mathcal {A}^{\sim \sim }$![]() a Dedekind complete, hence Archimedean, commutative $f$
a Dedekind complete, hence Archimedean, commutative $f$![]() -algebra [Reference Yilmaz20, Corollaries 3.5 and 3.6], so
-algebra [Reference Yilmaz20, Corollaries 3.5 and 3.6], so
which gives, in particular, that all Arens extensions of $A$![]() coincide. In order to check that $AR_{m}^{\rho }(B)$
coincide. In order to check that $AR_{m}^{\rho }(B)$![]() is separately order continuous, let $j\in \{1,\,\ldots.m\}$
is separately order continuous, let $j\in \{1,\,\ldots.m\}$![]() , $x_{i}^{\prime \prime }\in E_{i}^{\sim \sim },\, i=1,\,\ldots,\,m$
, $x_{i}^{\prime \prime }\in E_{i}^{\sim \sim },\, i=1,\,\ldots,\,m$![]() , with $i\neq j$
, with $i\neq j$![]() be given and let $(x_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$
be given and let $(x_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$![]() be a net in $E_{j}^{\sim \sim }$
be a net in $E_{j}^{\sim \sim }$![]() such that $x_{\alpha _{j}}^{\prime \prime } \xrightarrow {\, o \,} 0$
such that $x_{\alpha _{j}}^{\prime \prime } \xrightarrow {\, o \,} 0$![]() . There exists a net $(z_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$
. There exists a net $(z_{\alpha _{j}}^{\prime \prime })_{\alpha _{j}\in \Omega _{j}}$![]() such that $z_{\alpha _{j}}^{\prime \prime } \downarrow 0$
such that $z_{\alpha _{j}}^{\prime \prime } \downarrow 0$![]() and $|x_{\alpha _{j}}^{\prime \prime }|\leq z_{\alpha _{j}}^{\prime \prime }$
and $|x_{\alpha _{j}}^{\prime \prime }|\leq z_{\alpha _{j}}^{\prime \prime }$![]() for every $\alpha _{j}\in \Omega _{j}$
for every $\alpha _{j}\in \Omega _{j}$![]() . The functional
. The functional
is positive. Using again that the product $\odot$![]() is commutative and [Reference Aliprantis and Burkinshaw2, Exercise 12, p. 131],
is commutative and [Reference Aliprantis and Burkinshaw2, Exercise 12, p. 131],

Now it is enough to prove that $|T_{j}^{\prime \prime }|(z_{\alpha _{j}}^{\prime \prime })\odot \varphi \downarrow 0$![]() . Let $0\leq y^{\prime }\in \mathcal {A}^{\sim }$
. Let $0\leq y^{\prime }\in \mathcal {A}^{\sim }$![]() be given. Then $\varphi \diamond y^{\prime }$
be given. Then $\varphi \diamond y^{\prime }$![]() is positive and, since $|T_{j}^{\prime \prime }|$
is positive and, since $|T_{j}^{\prime \prime }|$![]() is order continuous and positive [Reference Aliprantis and Burkinshaw2, Theorems 1.56 and 1.73],
is order continuous and positive [Reference Aliprantis and Burkinshaw2, Theorems 1.56 and 1.73],
from which it follows that $(|T_{j}^{\prime \prime }|(z_{\alpha _{j}}^{\prime \prime })\odot \varphi )\downarrow 0$![]() [Reference Aliprantis and Burkinshaw2, Theorem 1.18] and gives the separate order continuity of $AR_{m}^{\rho }(B)$
[Reference Aliprantis and Burkinshaw2, Theorem 1.18] and gives the separate order continuity of $AR_{m}^{\rho }(B)$![]() .
.
The linearity of the correspondence $A \mapsto AR_{m}^{\rho }(A)$![]() gives the result for finite sums of multiplicative operators.
gives the result for finite sums of multiplicative operators.
Since scalar-valued Riesz multimorphisms are multiplicative [Reference Kusraev and Kusraeva14, Theorem 6], Proposition 4.1 yields the following.
Corollary 4.2 All Arens extensions of a finite sum of scalar-valued Riesz multimorphisms coincide and are separately order continuous.
An operator $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m;F)$![]() is of finite type if there are $n\in \mathbb {N}$
is of finite type if there are $n\in \mathbb {N}$![]() , functionals $\varphi _{j}^{i}\in E_{i}^{\sim }$
, functionals $\varphi _{j}^{i}\in E_{i}^{\sim }$![]() and vectors $y_{j}\in F$
and vectors $y_{j}\in F$![]() , $j=1,\,\ldots,\,n$
, $j=1,\,\ldots,\,n$![]() , $i=1,\,\ldots,\,m$
, $i=1,\,\ldots,\,m$![]() , such that
, such that

Corollary 4.3 All Arens extensions of a multilinear operator of finite type coincide, are of finite type and are separately order continuous.
Proof. It is not difficult to check that if $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$![]() is separately order continuous and $y \in F$
is separately order continuous and $y \in F$![]() , then the operator
, then the operator
is separately order continuous as well. Now the result follows from Proposition 4.1 and from its proof.
To proceed to the main results of the section we need some preparation.
Lemma 4.4 Let $E_{1},\,\ldots,\,E_{m},\, F$![]() be Riesz spaces with $F$
be Riesz spaces with $F$![]() Dedekind complete and $(B_{\alpha })_\alpha$
Dedekind complete and $(B_{\alpha })_\alpha$![]() be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m}; F)$
be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m}; F)$![]() . Then $B_{\alpha }\downarrow 0$
. Then $B_{\alpha }\downarrow 0$![]() if and only if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$
if and only if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$![]() in $F$
in $F$![]() for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$
for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$![]() .
.
Proof. It is straightforward that $B_{\alpha }\downarrow 0$![]() if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$
if $B_{\alpha }(x_{1},\,\ldots,\,x_{m})\downarrow 0$![]() in $F$
in $F$![]() for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$
for all $x_{1}\in E_{1}^{+},\,\ldots,\, x_{m}\in E_{m}^{+}$![]() . We prove the other implication by induction on $m$
. We prove the other implication by induction on $m$![]() . The case $m=1$
. The case $m=1$![]() follows from the Riesz-Kantorovich theorem [Reference Aliprantis and Burkinshaw2, Theorem 1.18]. Assume that the result holds for $n$
follows from the Riesz-Kantorovich theorem [Reference Aliprantis and Burkinshaw2, Theorem 1.18]. Assume that the result holds for $n$![]() and let $(B_{\alpha })_\alpha$
and let $(B_{\alpha })_\alpha$![]() be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1}; F)$
be a net in $\mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1}; F)$![]() such that $B_{\alpha }\downarrow 0$
such that $B_{\alpha }\downarrow 0$![]() . Consider the canonical Riesz isomorphism
. Consider the canonical Riesz isomorphism
We have $0\leq \psi (B_{\alpha })\downarrow$![]() because $\psi$
because $\psi$![]() is positive. Let $T \in \mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$
is positive. Let $T \in \mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$![]() be such that $0\leq T\leq \psi (B_{\alpha })$
be such that $0\leq T\leq \psi (B_{\alpha })$![]() for every $\alpha$
for every $\alpha$![]() . Since $\psi ^{-1}$
. Since $\psi ^{-1}$![]() is positive, $0 \leq \psi ^{-1}(T)\leq B_{\alpha }\downarrow 0$
is positive, $0 \leq \psi ^{-1}(T)\leq B_{\alpha }\downarrow 0$![]() , hence $0\leq \psi ^{-1}(T)\leq 0$
, hence $0\leq \psi ^{-1}(T)\leq 0$![]() , which proves that $\psi (B_{\alpha })\downarrow 0$
, which proves that $\psi (B_{\alpha })\downarrow 0$![]() in $\mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$
in $\mathcal {L}_{r}(E_{1};\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F))$![]() . The linear case of the result gives that $\psi (B_{\alpha })(x_{1})\downarrow 0$
. The linear case of the result gives that $\psi (B_{\alpha })(x_{1})\downarrow 0$![]() in $\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F)$
in $\mathcal {L}_{r}(E_{2}\ldots,\,E_{n+1}; F)$![]() for every $x_{1}\in E_{1}^{+}$
for every $x_{1}\in E_{1}^{+}$![]() . The induction hypothesis gives that, regardless of the $x_{2}\in E_{2}^{+},\,\ldots,\,x_{n+1}\in E_{n+1}^{+}$
. The induction hypothesis gives that, regardless of the $x_{2}\in E_{2}^{+},\,\ldots,\,x_{n+1}\in E_{n+1}^{+}$![]() ,
,
completing the proof.
Lemma 4.5 Let $E_{1},\,\ldots,\,E_{m}$![]() be Riesz spaces, $\rho \in S_{m}$
be Riesz spaces, $\rho \in S_{m}$![]() , $k \in \{1,\,\ldots,\,m-1\}$
, $k \in \{1,\,\ldots,\,m-1\}$![]() and $x_{\rho (k)}^{\prime \prime }\in (E_{\rho (k)}^{\sim })_{n}^{\sim }$
and $x_{\rho (k)}^{\prime \prime }\in (E_{\rho (k)}^{\sim })_{n}^{\sim }$![]() . Then the operator
. Then the operator
defined in (2.1), is order continuous.
Proof. We already know that $\overline {x_{\rho (k)}^{\prime \prime }}$![]() is a regular linear operator, $\big |\overline {x_{\rho (k)}^{\prime \prime }} \big |\leq \overline {|x_{\rho (k)}^{\prime \prime }|}$
is a regular linear operator, $\big |\overline {x_{\rho (k)}^{\prime \prime }} \big |\leq \overline {|x_{\rho (k)}^{\prime \prime }|}$![]() because $B^{k}$
because $B^{k}$![]() is positive for every positive $B\in \mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$
is positive for every positive $B\in \mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$![]() , so
, so
Let $(A_{\alpha })_{\alpha \in \Omega }$![]() be a net in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$
be a net in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$![]() such that $A_{\alpha }\xrightarrow {\, o\, } 0$
such that $A_{\alpha }\xrightarrow {\, o\, } 0$![]() . Then there are a net $(B_{\alpha })_{\alpha \in \Omega }$
. Then there are a net $(B_{\alpha })_{\alpha \in \Omega }$![]() in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$
in $\mathcal {L}_{r}(E_{\rho (k)},\,\ldots,\,E_{\rho (m)})$![]() and $\alpha _{0}\in \Omega$
and $\alpha _{0}\in \Omega$![]() such that $B_{\alpha }\downarrow 0$
such that $B_{\alpha }\downarrow 0$![]() and $|A_{\alpha }|\leq B_{\alpha }$
and $|A_{\alpha }|\leq B_{\alpha }$![]() for every $\alpha \geq \alpha _{0}$
for every $\alpha \geq \alpha _{0}$![]() . Thus,
. Thus,
For $x_{i}\in E_{\rho (i)}^{+}$![]() , $i\in \{k,\,\ldots,\,m\}$
, $i\in \{k,\,\ldots,\,m\}$![]() , Lemma 4.4 gives
, Lemma 4.4 gives
By [Reference Aliprantis and Burkinshaw2, Theorem 1.18] it follows that $B_{\alpha }^{k}(x_{k+1},\,\ldots,\,x_{m})\downarrow 0$![]() . Since $x_{\rho (k)}^{\prime \prime }$
. Since $x_{\rho (k)}^{\prime \prime }$![]() is an order continuous functional, $|x_{\rho (k)}^{\prime \prime }|$
is an order continuous functional, $|x_{\rho (k)}^{\prime \prime }|$![]() is a positive order continuous operator [Reference Aliprantis and Burkinshaw2, Theorem 1.56], so $|x_{\rho (k)}^{\prime \prime }|(B_{\alpha }^{k}(x_{k+1},\,\ldots,\,x_{m}))\downarrow 0$
is a positive order continuous operator [Reference Aliprantis and Burkinshaw2, Theorem 1.56], so $|x_{\rho (k)}^{\prime \prime }|(B_{\alpha }^{k}(x_{k+1},\,\ldots,\,x_{m}))\downarrow 0$![]() , that is, $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })(x_{k+1},\,\ldots,\,x_{m})\downarrow 0.$
, that is, $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })(x_{k+1},\,\ldots,\,x_{m})\downarrow 0.$![]() Calling on Lemma 4.4 once again it follows that $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })\downarrow 0$
Calling on Lemma 4.4 once again it follows that $\overline {|x_{\rho (k)}^{\prime \prime }|}(B_{\alpha })\downarrow 0$![]() , proving that $\overline {x_{\rho (k)}^{\prime \prime }}$
, proving that $\overline {x_{\rho (k)}^{\prime \prime }}$![]() is order continuous.
is order continuous.
Theorem 4.6 Let $E_{1},\,\ldots,\,E_{m},\, F$![]() be Riesz spaces, $\rho \in S_{m}$
be Riesz spaces, $\rho \in S_{m}$![]() and $A\in \mathcal {L}_{r}(E_{1},\,\ldots, \,E_{m};F)$
and $A\in \mathcal {L}_{r}(E_{1},\,\ldots, \,E_{m};F)$![]() .
.
(a) For all $j\in \{1,\,\ldots,\,m\}$
 , $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$
, $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$ , and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$
, and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$ , the operator
(4.1)\begin{equation} x''_{\rho(j)} \in E_{\rho(j)}^{{\sim}{\sim}} \mapsto AR_{m}^{\rho}(A)(x_{1}^{\prime\prime},\ldots,x_{{\rho(j)}}^{\prime\prime},\ldots,x_{m}^{\prime\prime}) \in F^{{\sim}{\sim}} \end{equation}is order continuous on $E_{\rho (j)}^{\sim \sim }$
, the operator
(4.1)\begin{equation} x''_{\rho(j)} \in E_{\rho(j)}^{{\sim}{\sim}} \mapsto AR_{m}^{\rho}(A)(x_{1}^{\prime\prime},\ldots,x_{{\rho(j)}}^{\prime\prime},\ldots,x_{m}^{\prime\prime}) \in F^{{\sim}{\sim}} \end{equation}is order continuous on $E_{\rho (j)}^{\sim \sim }$
 .
.(b) $AR_{m}^{\rho }(A)$
 is separately order continuous on $(E_{1}^{\sim })_{n}^{\sim }\times \cdots \times (E_{m}^{\sim })_{n}^{\sim }$
is separately order continuous on $(E_{1}^{\sim })_{n}^{\sim }\times \cdots \times (E_{m}^{\sim })_{n}^{\sim }$ .
.(c) $AR_{m}^{\rho }(A)$
 is order continuous in the $\rho (m)$
is order continuous in the $\rho (m)$ -th variable on the whole of $E_{\rho (m)}^{\sim \sim }$
-th variable on the whole of $E_{\rho (m)}^{\sim \sim }$ .
.
Proof. It is clear that (b) and (c) follow from (a) (for (c) just take $j = m$![]() in (a)). To prove (a), take $j\in \{1,\,\ldots,\,m\}$
in (a)). To prove (a), take $j\in \{1,\,\ldots,\,m\}$![]() , $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$
, $x_{\rho (i)}^{\prime \prime }\in E_{\rho (i)}^{\sim \sim },\, i=1,\,\ldots,\,j-1$![]() , and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$
, and $x_{\rho (i)}^{\prime \prime }\in (E_{\rho (i)}^{\sim })_{n}^{\sim },\, i=j+1,\,\ldots,\,m$![]() . Given a net $(x_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$
. Given a net $(x_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$![]() in $E_{\rho (j)}^{\sim \sim }$
in $E_{\rho (j)}^{\sim \sim }$![]() such that $x_{\alpha _{\rho (j)}}^{\prime \prime } \xrightarrow {\, o \, } 0$
such that $x_{\alpha _{\rho (j)}}^{\prime \prime } \xrightarrow {\, o \, } 0$![]() , there is a net $(z_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$
, there is a net $(z_{\alpha _{\rho (j)}}^{\prime \prime })_{\alpha _{\rho (j)}\in \Omega _{\rho (j)}}$![]() in $E_{\rho (j)}^{\sim \sim }$
in $E_{\rho (j)}^{\sim \sim }$![]() and $\alpha _{\rho (j)_{0}}$
and $\alpha _{\rho (j)_{0}}$![]() such that $z_{\alpha _{\rho (j)}}^{\prime \prime }\downarrow 0$
such that $z_{\alpha _{\rho (j)}}^{\prime \prime }\downarrow 0$![]() and $|x_{\alpha _{\rho (j)}}^{\prime \prime }|\leq z_{\alpha _{\rho (j)}}^{\prime \prime }$
and $|x_{\alpha _{\rho (j)}}^{\prime \prime }|\leq z_{\alpha _{\rho (j)}}^{\prime \prime }$![]() for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$
for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$![]() . Let $A_{1},\, A_{2}\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$
. Let $A_{1},\, A_{2}\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$![]() be positive operators such that $A=A_{1}-A_{2}$
be positive operators such that $A=A_{1}-A_{2}$![]() and put $B:=A_{1}+A_{2}$
and put $B:=A_{1}+A_{2}$![]() . Of course $B$
. Of course $B$![]() is positive. Denoting the operator in (4.1) by $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$
is positive. Denoting the operator in (4.1) by $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$![]() , for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$
, for every $\alpha _{\rho (j)}\geq \alpha _{\rho (j)_{0}}$![]() ,
,

As Arens extensions of positive operators are positive, it follows that
Setting $T:=\overline {|x_{\rho (m)}^{\prime \prime }|}\circ \cdots \circ \overline {|x_{\rho (j+1)}^{\prime \prime }|}$![]() , since each $|x_{\rho (i)}^{\prime \prime }|,\, i=j+1,\,\ldots,\,m$
, since each $|x_{\rho (i)}^{\prime \prime }|,\, i=j+1,\,\ldots,\,m$![]() , is order continuous, by Lemma 4.5 it follows that $\overline {|x_{\rho (i)}^{\prime \prime }|}$
, is order continuous, by Lemma 4.5 it follows that $\overline {|x_{\rho (i)}^{\prime \prime }|}$![]() is order continuous, so $T$
is order continuous, so $T$![]() is order continuous and positive. On the other hand, it is clear that, for every positive $y^{\prime }\in F^{\sim }$
is order continuous and positive. On the other hand, it is clear that, for every positive $y^{\prime }\in F^{\sim }$![]() ,
,
is positive. From $z_{\alpha _{\rho (j)}}^{\prime \prime }\downarrow 0$![]() we conclude that $\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S)\downarrow 0$
we conclude that $\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S)\downarrow 0$![]() , therefore $T(\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S))\downarrow 0$
, therefore $T(\overline {z_{\alpha _{\rho (j)}}^{\prime \prime }}(S))\downarrow 0$![]() . It follows that, for every positive $y^{\prime }\in F^{\sim }$
. It follows that, for every positive $y^{\prime }\in F^{\sim }$![]() ,
,

Lemma 4.4 gives that $AR_{m}^{\rho }(B)_{|x_{\rho (1)}^{\prime \prime }|,\,\ldots,\,|x_{\rho (j-1)}^{\prime \prime }|,\,|x_{\rho (j+1)}^{\prime \prime }|,\,\ldots,\,|x_{\rho (m)}^{\prime \prime }|}(z_{\alpha _{\rho (j)}}^{\prime \prime })\downarrow 0$![]() , and this allows us to conclude that $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$
, and this allows us to conclude that $AR_{m}^{\rho }(A)_{x_{\rho (1)}^{\prime \prime },\,\ldots,\,x_{\rho (j-1)}^{\prime \prime },\,x_{\rho (j+1)}^{\prime \prime },\,\ldots,\,x_{\rho (m)}^{\prime \prime }}$![]() is order continuous.
is order continuous.
Remark 4.7 Theorem 4.6 improves [Reference Boyd, Ryan and Snigireva7, Theorem 1] in the sense that it holds for all Arens extensions, it holds for operators between Riesz spaces, it drops the assumption of $F$![]() being Dedekind complete and it assures the order continuity on the whole bidual in one of the variables. For regular operators, it improves [Reference Buskes and Roberts10, Theorem 3.4] by taking into account all Arens extensions and by assuring the order continuity on the whole bidual in one of the variables. In particular, Theorem 4.6(b) provides an alternative proof of [Reference Boyd, Ryan and Snigireva7, Theorem 1] and of [Reference Buskes and Roberts10, Theorem 3.4] for regular operators between Riesz spaces and (c) shows that $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$
being Dedekind complete and it assures the order continuity on the whole bidual in one of the variables. For regular operators, it improves [Reference Buskes and Roberts10, Theorem 3.4] by taking into account all Arens extensions and by assuring the order continuity on the whole bidual in one of the variables. In particular, Theorem 4.6(b) provides an alternative proof of [Reference Boyd, Ryan and Snigireva7, Theorem 1] and of [Reference Buskes and Roberts10, Theorem 3.4] for regular operators between Riesz spaces and (c) shows that $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$![]() is order continuous in the first variable on the whole of $E_1^{\sim \sim }$
is order continuous in the first variable on the whole of $E_1^{\sim \sim }$![]() .
.
Recall that an $m$![]() -homogeneous polynomial $P \colon E \longrightarrow F$
-homogeneous polynomial $P \colon E \longrightarrow F$![]() between Riesz spaces is positive if the corresponding symmetric $m$
between Riesz spaces is positive if the corresponding symmetric $m$![]() -linear operator $\check P$
-linear operator $\check P$![]() is positive, and that $P$
is positive, and that $P$![]() is regular, in symbols $P \in {\mathcal {P}}_r(^mE;F)$
is regular, in symbols $P \in {\mathcal {P}}_r(^mE;F)$![]() , if $P$
, if $P$![]() can be written as the difference of two positive polynomials.
can be written as the difference of two positive polynomials.
The Arens extensions of a regular polynomial $P \in {\mathcal {P}}_r(^mE;F)$![]() are the polynomials associated to the Arens extensions of $\check P$
are the polynomials associated to the Arens extensions of $\check P$![]() , that is: for $\rho \in S_m$
, that is: for $\rho \in S_m$![]() , the Arens extension of $P$
, the Arens extension of $P$![]() with respect to $\rho$
with respect to $\rho$![]() is the polynomial
is the polynomial
In [Reference Buskes and Roberts10, Theorem 3.5] it is proved that $AR_m^\theta (P)$![]() is order continuous on $(E^\sim )_n^{\sim }$
is order continuous on $(E^\sim )_n^{\sim }$![]() . We can go a bit further at the origin:
. We can go a bit further at the origin:
Proposition 4.8 All Arens extensions of a polynomial $P \in {\mathcal {P}}_r(^mE;F)$![]() are order continuous at the origin on $E^{\sim \sim }$
are order continuous at the origin on $E^{\sim \sim }$![]() , meaning that $AR_m^\rho (P)(x_{\alpha }^{\prime \prime })\xrightarrow {\, o\,} 0$
, meaning that $AR_m^\rho (P)(x_{\alpha }^{\prime \prime })\xrightarrow {\, o\,} 0$![]() in $F^{\sim \sim }$
in $F^{\sim \sim }$![]() for every $\rho \in S_m$
for every $\rho \in S_m$![]() and any $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$
and any $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$![]() in $E^{\sim \sim }$
in $E^{\sim \sim }$![]() such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$
such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$![]() in $E^{\sim \sim }$
in $E^{\sim \sim }$![]() .
.
Proof. Write $P=P_{1}-P_{2}$![]() , where $P_1$
, where $P_1$![]() and $P_2$
and $P_2$![]() are positive $m$
are positive $m$![]() -homogeneous polynomials, and let $\check {P}_{1},\, \check {P}_{2}\colon E^{m}\longrightarrow F$
-homogeneous polynomials, and let $\check {P}_{1},\, \check {P}_{2}\colon E^{m}\longrightarrow F$![]() be the positive symmetric $m$
be the positive symmetric $m$![]() -linear operators associated to $P_1$
-linear operators associated to $P_1$![]() and $P_2$
and $P_2$![]() , respectively. Let $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$
, respectively. Let $(x_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$![]() be a net in $E^{\sim \sim }$
be a net in $E^{\sim \sim }$![]() such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$
such that $x_{\alpha }^{\prime \prime }\xrightarrow {\, o \,} 0$![]() . There are a net $(z_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$
. There are a net $(z_{\alpha }^{\prime \prime })_{\alpha \in \Omega }$![]() in $E^{\sim \sim }$
in $E^{\sim \sim }$![]() and $\alpha _{0}\in \Omega$
and $\alpha _{0}\in \Omega$![]() such that $z_{\alpha }^{\prime \prime }\downarrow 0$
such that $z_{\alpha }^{\prime \prime }\downarrow 0$![]() and $|x_{\alpha }^{\prime \prime }|\leq z_{\alpha }^{\prime \prime }$
and $|x_{\alpha }^{\prime \prime }|\leq z_{\alpha }^{\prime \prime }$![]() for every $\alpha \geq \alpha _{0}$
for every $\alpha \geq \alpha _{0}$![]() . For a permutation $\rho \in S_m$
. For a permutation $\rho \in S_m$![]() , we know from Theorem 4.6 that the operator
, we know from Theorem 4.6 that the operator
where $x''$![]() is placed at the $\rho (m)$
is placed at the $\rho (m)$![]() -th coordinate, is order continuous. For $\alpha \geq \alpha _{0}$
-th coordinate, is order continuous. For $\alpha \geq \alpha _{0}$![]() we have $z_{\alpha }^{\prime \prime }\leq z_{\alpha _{0}}^{\prime \prime }$
we have $z_{\alpha }^{\prime \prime }\leq z_{\alpha _{0}}^{\prime \prime }$![]() , so, using that $AR_m^{\rho }(\check {P}_1 + \check {P}_2)$
, so, using that $AR_m^{\rho }(\check {P}_1 + \check {P}_2)$![]() is positive,
is positive,

This proves that $AR_m^\rho (P)(x_{\alpha }^{\prime \prime })\xrightarrow {\, o\,} 0$![]() .
.
In [Reference Boyd, Ryan and Snigireva8] it is proved that, for a regular homogeneous polynomial, order continuity at one point does not imply order continuity at every point in general. The result above shall be useful later.
5. Operators between Banach lattices
In this section we give conditions on the Banach lattices $E_1,\, \ldots,\, E_m$![]() so that, for every Banach lattice $F$
so that, for every Banach lattice $F$![]() , all Arens extensions of any regular $m$
, all Arens extensions of any regular $m$![]() -linear operator from $E_1 \times \cdots \times E_m$
-linear operator from $E_1 \times \cdots \times E_m$![]() to $F$
to $F$![]() are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$
are separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$![]() . Consequences on order continuity of extensions of regular homogeneous polynomials shall also be obtained.
. Consequences on order continuity of extensions of regular homogeneous polynomials shall also be obtained.
If the dual $E^{\ast }$![]() of a Banach lattice $E$
of a Banach lattice $E$![]() has order continuous norm, then $E^{\ast \ast }=(E^{\ast })_{n}^{\ast }$
has order continuous norm, then $E^{\ast \ast }=(E^{\ast })_{n}^{\ast }$![]() [Reference Meyer–Nieberg17, Theorem 2.4.2]. So, the following is immediate from Theorem 4.6 .
[Reference Meyer–Nieberg17, Theorem 2.4.2]. So, the following is immediate from Theorem 4.6 .
Corollary 5.1 Let $E_{1},\,\ldots,\, E_{m},\, F$![]() be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$
be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$![]() and $\rho \in S_{m}$
and $\rho \in S_{m}$![]() . If $E_{j}^{\ast }$
. If $E_{j}^{\ast }$![]() has order continuous norm for $j=1,\,\ldots,\,m$
has order continuous norm for $j=1,\,\ldots,\,m$![]() , $j\neq \rho (1)$
, $j\neq \rho (1)$![]() , then the Arens extension $AR_{m}^{\rho }(A)$
, then the Arens extension $AR_{m}^{\rho }(A)$![]() of $A$
of $A$![]() is separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$
is separately order continuous on $E_1^{**} \times \cdots \times E_m^{**}$![]() .
.
The next result makes clear what type of condition should be asked to get order continuity of Arens extensions on the product of the whole of the biduals.
Proposition 5.2 Let $m \geq 2$![]() and $E_{1},\, \ldots,\,E_{m}$
and $E_{1},\, \ldots,\,E_{m}$![]() be Banach lattices such that the Arens extension $A^{\ast [m+1]}$
be Banach lattices such that the Arens extension $A^{\ast [m+1]}$![]() of any form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$
of any form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$![]() is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$
is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$![]() . Then, for every operator $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast }),\,\ i,\,j=1,\,\ldots,\,m$
. Then, for every operator $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast }),\,\ i,\,j=1,\,\ldots,\,m$![]() , $i\neq j$
, $i\neq j$![]() , the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$
, the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$![]() is order continuous on $E_{j}^{\ast \ast }$
is order continuous on $E_{j}^{\ast \ast }$![]() for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$
for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$![]() .
.
Proof. Let $i,\,j=1,\,\ldots,\,m,\, i\neq j$![]() , and $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast })$
, and $T\in \mathcal {L}_{r}(E_{i};E_{j}^{\ast })$![]() be given. For $k=1,\,\ldots,\,m,\, i \neq k\neq j$
be given. For $k=1,\,\ldots,\,m,\, i \neq k\neq j$![]() , choose $0 \neq \varphi _{k}\in E_{k}^{\ast }$
, choose $0 \neq \varphi _{k}\in E_{k}^{\ast }$![]() and consider the regular $m$
and consider the regular $m$![]() -linear form
-linear form

Of course we can assume $i< j$![]() . Using the Davie–Gamelin description of the Arens extensions [Reference Davie and Gamelin12], for $x_l^{**} \in E_l^{**}$
. Using the Davie–Gamelin description of the Arens extensions [Reference Davie and Gamelin12], for $x_l^{**} \in E_l^{**}$![]() and nets $(x_{\alpha _{l}})_{\alpha _{l}\in \Omega _{l}}$
and nets $(x_{\alpha _{l}})_{\alpha _{l}\in \Omega _{l}}$![]() in $E_{l}$
in $E_{l}$![]() such that $x_{l}^{\ast \ast }=\omega ^{\ast }-\displaystyle \lim _{\alpha _{l}}J_{E_{l}}(x_{\alpha _{l}}),\, l=1,\,\ldots,\,m$
such that $x_{l}^{\ast \ast }=\omega ^{\ast }-\displaystyle \lim _{\alpha _{l}}J_{E_{l}}(x_{\alpha _{l}}),\, l=1,\,\ldots,\,m$![]() , we have
, we have

Choosing $x_{k}\in E_{k}$![]() so that $\varphi _k(x_{k})=1$
so that $\varphi _k(x_{k})=1$![]() , $i \neq k \neq j$
, $i \neq k \neq j$![]() , we get
, we get
Since $A^{\ast [m+1]}$![]() is separately order continuous by assumption, the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$
is separately order continuous by assumption, the functional $T^{\ast \ast }(x_{i}^{\ast \ast })$![]() is order continuous for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$
is order continuous for every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$![]() .
.
Although the next results hold, with the obvious modifications, for all Arens extensions $AR_{m}^{\rho }(A)$![]() of a regular $m$
of a regular $m$![]() -linear operator $A$
-linear operator $A$![]() , to make the proofs more readable we shall restrict ourselves to the extension $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$
, to make the proofs more readable we shall restrict ourselves to the extension $A^{\ast [m+1]}=AR_{m}^{\theta }(A)$![]() .
.
Lemma 5.3 Let $E_{1},\, \ldots,\,E_{m}$![]() be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$
be Banach lattices, $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$![]() and $i\in \{1,\,\ldots,\,m\}$
and $i\in \{1,\,\ldots,\,m\}$![]() . If $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$
. If $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$![]() , and $x_{i+1}^{\ast \ast }\in E_{i+1}^{\ast \ast },\,\ldots,\,x_{m}^{\ast \ast }\in E_{m}^{\ast \ast }$
, and $x_{i+1}^{\ast \ast }\in E_{i+1}^{\ast \ast },\,\ldots,\,x_{m}^{\ast \ast }\in E_{m}^{\ast \ast }$![]() , then the operator
, then the operator
is $\omega ^{\ast }$![]() -continuous and
-continuous and

Proof. Let $(x_{\alpha _{i}}^{\ast \ast })_{\alpha _{i}\in \Omega _{i}}$![]() be a net in $E_{i}^{\ast \ast }$
be a net in $E_{i}^{\ast \ast }$![]() such that $x_{\alpha _{i}}^{\ast \ast }\xrightarrow {\, \omega ^{\ast } \,} x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$
such that $x_{\alpha _{i}}^{\ast \ast }\xrightarrow {\, \omega ^{\ast } \,} x_{i}^{\ast \ast }\in E_{i}^{\ast \ast }$![]() . For every $x_{i}^{\ast }\in E_{i}^{\ast }$
. For every $x_{i}^{\ast }\in E_{i}^{\ast }$![]() we have $x_{i}^{\ast \ast }(x_{i}^{\ast })=\displaystyle \lim _{\alpha _{i}}x_{\alpha _{i}}^{\ast \ast }(x_{i}^{\ast })$
we have $x_{i}^{\ast \ast }(x_{i}^{\ast })=\displaystyle \lim _{\alpha _{i}}x_{\alpha _{i}}^{\ast \ast }(x_{i}^{\ast })$![]() . Given $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$
. Given $x_{1}\in E_{1},\,\ldots,\,x_{i-1}\in E_{i-1}$![]() and $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast },\, j=i+1,\,\ldots,\,m$
and $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast },\, j=i+1,\,\ldots,\,m$![]() ,
,

where, in $(\Delta )$![]() , we used that $((\overline {x_{i+1}^{\ast \ast }}\circ \cdots \circ \overline {x_{m}^{\ast \ast }})(A_{\theta }))^{m-i+1}(x_{i-1},\,\ldots,\,x_{1})\in E_{i}^{\ast }$
, we used that $((\overline {x_{i+1}^{\ast \ast }}\circ \cdots \circ \overline {x_{m}^{\ast \ast }})(A_{\theta }))^{m-i+1}(x_{i-1},\,\ldots,\,x_{1})\in E_{i}^{\ast }$![]() .
.
Definition 5.4 Let $\mathcal {P}$![]() be a property of linear functionals on Banach lattices. We say that:
be a property of linear functionals on Banach lattices. We say that:
• A form $A\colon E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast } \longrightarrow \mathbb {R}$
 , where $E_1,\, \ldots,\, E_m$
, where $E_1,\, \ldots,\, E_m$ are Banach lattices, has $\mathcal {P}$
are Banach lattices, has $\mathcal {P}$ -separately if for all $j \in \{1,\, \ldots,\, m\}$
-separately if for all $j \in \{1,\, \ldots,\, m\}$ and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$
and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$ , $i\neq j$
, $i\neq j$ , the functional
\[ A_{x_{1}^{{\ast}{\ast}},\ldots, x_{j-1}^{{\ast}{\ast}},x_{j+1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}}}\colon E_{j}^{{\ast}{\ast}}\longrightarrow \mathbb{R},~x_j^{**} \mapsto A(x_1^{**}, \ldots, x_m^{**}), \]has property $\mathcal {P}$
, the functional
\[ A_{x_{1}^{{\ast}{\ast}},\ldots, x_{j-1}^{{\ast}{\ast}},x_{j+1}^{{\ast}{\ast}},\ldots,x_{m}^{{\ast}{\ast}}}\colon E_{j}^{{\ast}{\ast}}\longrightarrow \mathbb{R},~x_j^{**} \mapsto A(x_1^{**}, \ldots, x_m^{**}), \]has property $\mathcal {P}$
 .
.• $\mathcal {P}$
 is an Arens property if, regardless of positive $m \geq 2$
is an Arens property if, regardless of positive $m \geq 2$ , the Banach lattices $E_1,\, \ldots,\, E_m$
, the Banach lattices $E_1,\, \ldots,\, E_m$ and the form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$
and the form $A \in {\mathcal {L}}_r(E_1,\, \ldots,\, E_m)$ , the Arens extension $A^{\ast [m+1]}$
, the Arens extension $A^{\ast [m+1]}$ of $A$
of $A$ has $\mathcal {P}$
has $\mathcal {P}$ in the first variable, in the sense that the operator $A^{\ast [m+1]}_{x_{2}^{\ast \ast },\, \ldots,\,x_{m}^{\ast \ast }}\colon E_{1}^{\ast \ast }\longrightarrow \mathbb {R}$
in the first variable, in the sense that the operator $A^{\ast [m+1]}_{x_{2}^{\ast \ast },\, \ldots,\,x_{m}^{\ast \ast }}\colon E_{1}^{\ast \ast }\longrightarrow \mathbb {R}$ has $\mathcal {P}$
has $\mathcal {P}$ for all $x_2^{\ast \ast } \in E_2^{**},\, \ldots,\, x_m^{\ast \ast } \in E_m^{**}$
for all $x_2^{\ast \ast } \in E_2^{**},\, \ldots,\, x_m^{\ast \ast } \in E_m^{**}$ .
.
Example 5.5 Order continuity (Theorem 4.6(c)) and $\omega ^*$![]() -continuity [Reference Dineen13, p. 413] are Arens properties.
-continuity [Reference Dineen13, p. 413] are Arens properties.
Theorem 5.6 Let $\mathcal {P}$![]() be an Arens property, $m \geq 2$
be an Arens property, $m \geq 2$![]() and $E_{1},\, \ldots,\,E_{m}$
and $E_{1},\, \ldots,\,E_{m}$![]() be Banach lattices. Suppose that:
be Banach lattices. Suppose that:
(a) For $j=2,\,\ldots,\,m-1,$
 and $i=1,\,\ldots,\,m-j$
and $i=1,\,\ldots,\,m-j$ , every regular linear operator from $E_{j}$
, every regular linear operator from $E_{j}$ to $E_{j+i}^{\ast }$
to $E_{j+i}^{\ast }$ is weakly compact;
is weakly compact;(b) For all $k=2,\,\ldots,\,m$
 , $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$
, $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$ and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$
and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$ , the functional $T^{\ast \ast }(x_{1}^{\ast \ast })\in E_{k}^{\ast \ast \ast }$
, the functional $T^{\ast \ast }(x_{1}^{\ast \ast })\in E_{k}^{\ast \ast \ast }$ has property $\mathcal {P}$
has property $\mathcal {P}$ .
.
Then, for every form $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$![]() , the Arens extension $A^{\ast [m+1]} \colon E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast } \longrightarrow \mathbb {R}$
, the Arens extension $A^{\ast [m+1]} \colon E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast } \longrightarrow \mathbb {R}$![]() has $\mathcal {P}$
has $\mathcal {P}$![]() -separately.
-separately.
Proof. We shall proceed by induction on $m$![]() . Given $A\in \mathcal {L}_{r}(E_{1},\,E_{2})$
. Given $A\in \mathcal {L}_{r}(E_{1},\,E_{2})$![]() , $A^{***}$
, $A^{***}$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() in the first variable because $\mathcal {P}$
in the first variable because $\mathcal {P}$![]() is an Arens property. Let us prove that, for every $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$
is an Arens property. Let us prove that, for every $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$![]() , $A^{***}(x_{1}^{\ast \ast },\,\bullet )\in E_{2}^{\ast \ast \ast }$
, $A^{***}(x_{1}^{\ast \ast },\,\bullet )\in E_{2}^{\ast \ast \ast }$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() . Recall that $A_{\theta }\colon E_{2}\times E_{1}\longrightarrow \mathbb {R}$
. Recall that $A_{\theta }\colon E_{2}\times E_{1}\longrightarrow \mathbb {R}$![]() and consider the regular linear operator $T:=A_{\theta }^{1}\colon E_{1}\longrightarrow E_{2}^{\ast }$
and consider the regular linear operator $T:=A_{\theta }^{1}\colon E_{1}\longrightarrow E_{2}^{\ast }$![]() , $T(x_{2})(x_{1})=A_{\theta }(x_{1},\,x_{2})$
, $T(x_{2})(x_{1})=A_{\theta }(x_{1},\,x_{2})$![]() . For all $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$
. For all $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$![]() and $x_{2}\in E_{1}$
and $x_{2}\in E_{1}$![]() ,
,
that is, $T^{\ast }(x_{2}^{\ast \ast })=\overline {x_{2}^{\ast \ast }}(A_{\theta }).$![]() So, for all $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast },\, x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$
So, for all $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast },\, x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$![]() ,
,
Since $T^{\ast \ast }(x_{1}^{\ast \ast })$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() by assumption, it follows that $A^{***}(x_{1}^{\ast \ast },\,\bullet )$
by assumption, it follows that $A^{***}(x_{1}^{\ast \ast },\,\bullet )$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() . This shows that the result holds for $m=2$
. This shows that the result holds for $m=2$![]() .
.
Assume now that the result holds for $n$![]() and let us prove it holds for $n+1$
and let us prove it holds for $n+1$![]() . To do so we suppose that conditions (a) and (b) hold for $n+1$
. To do so we suppose that conditions (a) and (b) hold for $n+1$![]() . Let $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1})$
. Let $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{n+1})$![]() be given. For every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=2,\,\ldots,\,n+1$
be given. For every $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=2,\,\ldots,\,n+1$![]() , we have
, we have
where $B^{i}\colon E_{n-i+1}\times \cdots \times E_{1}\longrightarrow E_{n-i+2}^{\ast },\, B^{i}(x_{i+1},\,\ldots,\,x_{n+1})(x_{i})=B(x_{i},\,x_{i+1}, \ldots,\,x_{n+1})$![]() . And for each $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$
. And for each $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$![]() , the functional $\overline {x_{1}^{\ast \ast }}\colon E_{1}^{\ast }\longrightarrow \mathbb {R}$
, the functional $\overline {x_{1}^{\ast \ast }}\colon E_{1}^{\ast }\longrightarrow \mathbb {R}$![]() is given by $\overline {x_{1}^{\ast \ast }}=x_{1}^{\ast \ast }$
is given by $\overline {x_{1}^{\ast \ast }}=x_{1}^{\ast \ast }$![]() . Moreover,
. Moreover,

Since $\overline {x_{n+1}^{\ast \ast }}(A_{\theta })\in \mathcal {L}_{r}(E_{n},\,\ldots,\,E_{1})$![]() , by the induction hypothesis we have that $(\overline {x_{n+1}^{\ast \ast }}(A_{\theta }))^{\ast [n+1]}$
, by the induction hypothesis we have that $(\overline {x_{n+1}^{\ast \ast }}(A_{\theta }))^{\ast [n+1]}$![]() has $\mathcal {P}$
has $\mathcal {P}$![]() -separately, so $A^{\ast [n+2]}$
-separately, so $A^{\ast [n+2]}$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() in the first $n$
in the first $n$![]() variables. To prove that $A^{\ast [n+2]}$
variables. To prove that $A^{\ast [n+2]}$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() in the $(n+1)$
in the $(n+1)$![]() -th variable, let $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,n$
-th variable, let $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,n$![]() , be given. Our job is to show that $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )\colon E_{n+1}^{\ast \ast }\longrightarrow \mathbb {R}$
, be given. Our job is to show that $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )\colon E_{n+1}^{\ast \ast }\longrightarrow \mathbb {R}$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() . Recall that $A_{\theta }\colon E_{n+1}\times \cdots \times E_{1}\longrightarrow \mathbb {R}$
. Recall that $A_{\theta }\colon E_{n+1}\times \cdots \times E_{1}\longrightarrow \mathbb {R}$![]() is given by $A_{\theta }(x_{1},\,\ldots,\,x_{n+1})=A(x_{n+1},\,\ldots,\,x_{1})$
is given by $A_{\theta }(x_{1},\,\ldots,\,x_{n+1})=A(x_{n+1},\,\ldots,\,x_{1})$![]() and $A_{\theta }^{1}\colon E_{n}\times \cdots \times E_{1}\longrightarrow E_{n+1}^{\ast },\, A_{\theta }^{1}(x_{2},\,\ldots,\,x_{n+1})(x_{1})=A_{\theta }(x_{1},\,x_{2},\,\ldots,\,x_{n+1})$
and $A_{\theta }^{1}\colon E_{n}\times \cdots \times E_{1}\longrightarrow E_{n+1}^{\ast },\, A_{\theta }^{1}(x_{2},\,\ldots,\,x_{n+1})(x_{1})=A_{\theta }(x_{1},\,x_{2},\,\ldots,\,x_{n+1})$![]() . Given $x_{3}\in E_{n-1},\,\ldots,\,x_{n+1}\in E_{1}$
. Given $x_{3}\in E_{n-1},\,\ldots,\,x_{n+1}\in E_{1}$![]() , consider the regular linear operator
, consider the regular linear operator
Given $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$![]() , take a net $(x_{\alpha _2})_{\alpha _2}$
, take a net $(x_{\alpha _2})_{\alpha _2}$![]() in $E_{n}$
in $E_{n}$![]() such that $J_{E_{n}}(x_{\alpha _2}) \stackrel {\omega ^*} \longrightarrow x_{n}^{\ast \ast }$
such that $J_{E_{n}}(x_{\alpha _2}) \stackrel {\omega ^*} \longrightarrow x_{n}^{\ast \ast }$![]() and apply the $\omega ^{\ast }$
and apply the $\omega ^{\ast }$![]() -$\omega ^{\ast }$
-$\omega ^{\ast }$![]() -continuity of $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }$
-continuity of $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }$![]() and Lemma 5.3 for $i=n+1$
and Lemma 5.3 for $i=n+1$![]() and $i=n$
and $i=n$![]() to obtain
to obtain

For $x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$![]() and $x_{4}\in E_{n-2},\,\ldots,\,x_{n+1}\in E_{1}$
and $x_{4}\in E_{n-2},\,\ldots,\,x_{n+1}\in E_{1}$![]() , consider the regular linear operator $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}\colon$
, consider the regular linear operator $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}\colon$![]() $E_{n-1}\longrightarrow E_{n+1}^{\ast }$
$E_{n-1}\longrightarrow E_{n+1}^{\ast }$![]() given by
given by
On the one hand, for every $x_{3}\in E_{n-1}$![]() the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})]^{\ast \ast }$
the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})]^{\ast \ast }$![]() is a $\omega ^{\ast }$
is a $\omega ^{\ast }$![]() -continuous extension of $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})$
-continuous extension of $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}(x_{3})$![]() . On the other hand, since $A_{x_3, \ldots, x_{n+1}}$
. On the other hand, since $A_{x_3, \ldots, x_{n+1}}$![]() is weakly compact by assumption, for every $x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$
is weakly compact by assumption, for every $x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$![]() the functional $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }(x_{n}^{\ast \ast })$
the functional $[A_{x_{3},\,\ldots,\,x_{n+1}}]^{\ast \ast }(x_{n}^{\ast \ast })$![]() is $\omega ^{\ast }$
is $\omega ^{\ast }$![]() -continuous. Taking a net $(x_{\alpha _{1}})_{\alpha _{1}}$
-continuous. Taking a net $(x_{\alpha _{1}})_{\alpha _{1}}$![]() in $E_{n+1}$
in $E_{n+1}$![]() such that $J_{E_{n+1}}(x_{\alpha _{1}}) \stackrel {\omega ^*} \longrightarrow x_{n+1}^{\ast \ast }$
such that $J_{E_{n+1}}(x_{\alpha _{1}}) \stackrel {\omega ^*} \longrightarrow x_{n+1}^{\ast \ast }$![]() ,
,

Take a net $(x_{\alpha _{3}})_{\alpha _{3}}$![]() in $E_{n-1}$
in $E_{n-1}$![]() such that $J_{E_{n-1}}(x_{\alpha _{3}}) \stackrel {\omega ^*} \longrightarrow x_{n-1}^{\ast \ast }$
such that $J_{E_{n-1}}(x_{\alpha _{3}}) \stackrel {\omega ^*} \longrightarrow x_{n-1}^{\ast \ast }$![]() . Using that $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }$
. Using that $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }$![]() is $\omega ^{\ast }$
is $\omega ^{\ast }$![]() -$\omega ^{\ast }$
-$\omega ^{\ast }$![]() -continuous and calling on Lemma 5.3 for $i = n-1$
-continuous and calling on Lemma 5.3 for $i = n-1$![]() , for each $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$
, for each $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$![]() we have
we have

For $x_{n-1}^{\ast \ast }\in E_{n-1}^{\ast \ast },\, x_{n}^{\ast \ast }\in E_{n}^{\ast \ast }$![]() and $x_{5}\in E_{n-3},\,\ldots,\,x_{n+1}\in E_{1}$
and $x_{5}\in E_{n-3},\,\ldots,\,x_{n+1}\in E_{1}$![]() , consider the regular linear operator $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}\colon E_{n-2}\longrightarrow E_{n+1}^{\ast }$
, consider the regular linear operator $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}\colon E_{n-2}\longrightarrow E_{n+1}^{\ast }$![]() given by
given by

For every $x_{4}\in E_{n-2}$![]() the functional $[A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})]^{\ast \ast }$
the functional $[A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})]^{\ast \ast }$![]() is a $\omega ^{\ast }$
is a $\omega ^{\ast }$![]() -continuous extension of $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})$
-continuous extension of $A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}(x_{4})$![]() . On the other hand, since $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{**}}$
. On the other hand, since $A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{**}}$![]() is weakly compact by assumption, for every $x_{n-1}^{\ast \ast }\in E_{n-1}^{\ast \ast }$
is weakly compact by assumption, for every $x_{n-1}^{\ast \ast }\in E_{n-1}^{\ast \ast }$![]() the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{n-1}^{\ast \ast })$
the functional $[A_{x_{4},\,\ldots,\,x_{n+1},\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{n-1}^{\ast \ast })$![]() is $\omega ^{\ast }$
is $\omega ^{\ast }$![]() -continuous on $E_{n-2}$
-continuous on $E_{n-2}$![]() . So, repeating the procedure using (5.3) we get
. So, repeating the procedure using (5.3) we get

Since the operator $[A_{x_{5},\,\ldots,\,x_{n+1},\,x_{n-1}^{\ast \ast },\,x_{n}^{\ast \ast }}]^{\ast \ast }$![]() is $\omega ^{\ast }$
is $\omega ^{\ast }$![]() -$\omega ^{\ast }$
-$\omega ^{\ast }$![]() -continuous, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$
-continuous, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$![]() , taking a net $(x_{\alpha _{4}})_{\alpha _{4}}$
, taking a net $(x_{\alpha _{4}})_{\alpha _{4}}$![]() in $E_{n-2}$
in $E_{n-2}$![]() such that $J_{E_{n-2}}(x_{\alpha _{4}}) \stackrel {\omega ^*} \longrightarrow x_{n-2}^{\ast \ast }$
such that $J_{E_{n-2}}(x_{\alpha _{4}}) \stackrel {\omega ^*} \longrightarrow x_{n-2}^{\ast \ast }$![]() , using Lemma 5.3 for $i = n-2$
, using Lemma 5.3 for $i = n-2$![]() and ( 5.4) we have
and ( 5.4) we have

Repeating the procedure $(n-3)$![]() times, we end up with
times, we end up with
for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$![]() , where, for each $x_{n+1}\in E_{1}$
, where, for each $x_{n+1}\in E_{1}$![]() and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=3,\,\ldots,\,n$
and $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=3,\,\ldots,\,n$![]() , $A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon$
, $A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon$![]() $E_{2}\longrightarrow E_{n+1}^{\ast }$
$E_{2}\longrightarrow E_{n+1}^{\ast }$![]() is the regular linear operator given by
is the regular linear operator given by
Finally, given $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=2,\,\ldots,\,n$![]() , the regular linear operator $A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon E_{1} \longrightarrow E_{n+1}^{\ast }$
, the regular linear operator $A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}\colon E_{1} \longrightarrow E_{n+1}^{\ast }$![]() defined by
defined by
is weakly compact by condition (ii) for $n+1$![]() . So, for every $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$
. So, for every $x_{2}^{\ast \ast }\in E_{2}^{\ast \ast }$![]() , $[A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{2}^{\ast \ast })$
, $[A_{x_{n+1},\,x_{3}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{2}^{\ast \ast })$![]() is $\omega ^{\ast }$
is $\omega ^{\ast }$![]() -continuous, therefore
-continuous, therefore

For the final time, taking a net $(x_{\alpha _{n+1}})_{\alpha _{n+1}}$![]() in $E_{1}$
in $E_{1}$![]() such that $J_{E_{1}}(x_{\alpha _{n+1}}) \stackrel {\omega ^*} \longrightarrow x_{1}^{\ast \ast }$
such that $J_{E_{1}}(x_{\alpha _{n+1}}) \stackrel {\omega ^*} \longrightarrow x_{1}^{\ast \ast }$![]() , the $\omega ^{\ast }$
, the $\omega ^{\ast }$![]() -$\omega ^{\ast }$
-$\omega ^{\ast }$![]() continuity of $[A_{x_{2}^{\ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }$
continuity of $[A_{x_{2}^{\ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }$![]() and Lemma 5.3 for $i = 1$
and Lemma 5.3 for $i = 1$![]() give, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$
give, for every $x_{n+1}^{\ast \ast }\in E_{n+1}^{\ast \ast }$![]() ,
,

This proves that $[A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{1}^{\ast \ast }) = A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )$![]() . By condition (b) for $n+1$
. By condition (b) for $n+1$![]() we know that $[A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{1}^{\ast \ast })$
we know that $[A_{x_{2}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast }}]^{\ast \ast }(x_{1}^{\ast \ast })$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() , so $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )$
, so $A^{\ast [n+2]}(x_{1}^{\ast \ast },\,\ldots,\,x_{n}^{\ast \ast },\,\bullet )$![]() has property $\mathcal {P}$
has property $\mathcal {P}$![]() , which completes the proof.
, which completes the proof.
Theorem 5.6 gives sufficient conditions for Arens extensions of regular multilinear forms to be separately order continuous on the product of the whole of the biduals. Now we derive the case of vector-valued regular multilinear operators.
Theorem 5.7 Let $m \geq 2$![]() and $E_{1},\, \ldots,\,E_{m}$
and $E_{1},\, \ldots,\,E_{m}$![]() be Banach lattices such that:
be Banach lattices such that:
(a) For $j=2,\,\ldots,\,m-1,$
 and $i=1,\,\ldots,\,m-j$
and $i=1,\,\ldots,\,m-j$ , every regular linear operator from $E_{j}$
, every regular linear operator from $E_{j}$ to $E_{j+i}^{\ast }$
to $E_{j+i}^{\ast }$ is weakly compact;
is weakly compact;(b) For all $k=2,\,\ldots,\,m$
 , $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$
, $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$ and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$
and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$ , the functional $T^{\ast \ast }(x_{1}^{\ast \ast })$
, the functional $T^{\ast \ast }(x_{1}^{\ast \ast })$ is order continuous on $E_{k}^{\ast \ast \ast }$
is order continuous on $E_{k}^{\ast \ast \ast }$ .
.
Then, for every Banach lattice $F$![]() and any $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$
and any $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$![]() , the Arens extension $A^{\ast [m+1]}$
, the Arens extension $A^{\ast [m+1]}$![]() is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$
is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$![]() .
.
Proof. Let $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$![]() and $y^{\ast }\in F^{\ast }$
and $y^{\ast }\in F^{\ast }$![]() be given. Since $y^{\ast }\circ A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$
be given. Since $y^{\ast }\circ A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m})$![]() and order continuity is an Arens property, by Theorem 5.6 the extension $(y^* \circ A)^{\ast [m+1]}$
and order continuity is an Arens property, by Theorem 5.6 the extension $(y^* \circ A)^{\ast [m+1]}$![]() is separately order continuous. For all $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$
is separately order continuous. For all $x_{i}^{\ast \ast }\in E_{i}^{\ast \ast },\, i=1,\,\ldots,\,m$![]() ,
,
For each $j\in \{1,\,\ldots,\,m\}$![]() let $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast }$
let $x_{j}^{\ast \ast }\in E_{j}^{\ast \ast }$![]() and let $(x_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$
and let $(x_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$![]() be a net $E_{j}^{\ast \ast }$
be a net $E_{j}^{\ast \ast }$![]() such that $x_{\alpha _{j}}^{\ast \ast } \xrightarrow {\, o \, } 0$
such that $x_{\alpha _{j}}^{\ast \ast } \xrightarrow {\, o \, } 0$![]() . There exists a net $(y_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$
. There exists a net $(y_{\alpha _{j}}^{\ast \ast })_{\alpha _{j}\in \Omega _{j}}$![]() in $E_{j}^{\ast \ast }$
in $E_{j}^{\ast \ast }$![]() and $\alpha _{j_{0}}\in \Omega _{j}$
and $\alpha _{j_{0}}\in \Omega _{j}$![]() so that $y_{\alpha _{j}}^{\ast \ast }\downarrow 0$
so that $y_{\alpha _{j}}^{\ast \ast }\downarrow 0$![]() and $|x_{\alpha _{j}}^{\ast \ast }|\leq y_{\alpha _{j}}^{\ast \ast }$
and $|x_{\alpha _{j}}^{\ast \ast }|\leq y_{\alpha _{j}}^{\ast \ast }$![]() for every $\alpha _{j}\geq \alpha _{j_{0}}$
for every $\alpha _{j}\geq \alpha _{j_{0}}$![]() . Without loss of generality, assume that $A$
. Without loss of generality, assume that $A$![]() and $y^{\ast }$
and $y^{\ast }$![]() are positive. Since $(y^{\ast }\circ A)^{*[m+1]}(|x_{1}^{\ast \ast }|,\,\ldots,\,\bullet,\,\ldots,\,|x_{m}^{\ast \ast }|)\colon E_{j}^{\ast \ast }\longrightarrow \mathbb {R}$
are positive. Since $(y^{\ast }\circ A)^{*[m+1]}(|x_{1}^{\ast \ast }|,\,\ldots,\,\bullet,\,\ldots,\,|x_{m}^{\ast \ast }|)\colon E_{j}^{\ast \ast }\longrightarrow \mathbb {R}$![]() is positive and order continuous,
is positive and order continuous,

It follows that $A^{*[m+1]}(|x_{1}^{\ast \ast }|,\,\ldots,\,y_{\alpha _{j}}^{\ast \ast },\,\ldots,\,|x_{m}^{\ast \ast }|) \downarrow 0$![]() [Reference Aliprantis and Burkinshaw2, Theorem 1.18] and, for every $\alpha _{j}\geq \alpha _{j_{0}}$
[Reference Aliprantis and Burkinshaw2, Theorem 1.18] and, for every $\alpha _{j}\geq \alpha _{j_{0}}$![]() ,
,

This shows that $A^{*[m+1]}(x_{1}^{\ast \ast },\,\ldots,\,x_{\alpha _{j}}^{\ast \ast },\,\ldots,\,x_{m}^{\ast \ast }) \xrightarrow {\, o \, } 0$![]() and proves that $A^{*[m+1]}$
and proves that $A^{*[m+1]}$![]() is separately order continuous.
is separately order continuous.
Recall that a Banach lattice $E$![]() is said to be a Kantorovich-Banach space (or briefly a KB-space) if increasing positive bounded sequences of $E$
is said to be a Kantorovich-Banach space (or briefly a KB-space) if increasing positive bounded sequences of $E$![]() are norm convergent.
are norm convergent.
Example 5.8 As to condition (a) above, we have the following examples between nonreflexive Banach lattices:
(a) Every operator from $c_0$
 to $c_0^*=\ell _1$
to $c_0^*=\ell _1$ is compact, hence weakly compact (this is Pitt's theorem).
is compact, hence weakly compact (this is Pitt's theorem).(b) Every operator from $C(K)$
 , where $K$
, where $K$ is a compact Hausdorff space, to a KB-space is weakly compact. Just recall that KB-spaces do not contain a copy of $c_0$
is a compact Hausdorff space, to a KB-space is weakly compact. Just recall that KB-spaces do not contain a copy of $c_0$ [Reference Aliprantis and Burkinshaw2, Theorem 4.60] and apply [Reference Pełczyński18, Theorem 5].
[Reference Aliprantis and Burkinshaw2, Theorem 4.60] and apply [Reference Pełczyński18, Theorem 5].(c) Since any AM-space with order unity is order isometric to a $C(K)$
 -space [Reference Aliprantis and Burkinshaw2, Theorem 4.29], from (b) it follows that every operator from an AM-space with order unity to a KB-space is weakly compact. And since the dual of an AM-space is a KB-space, every operator from an AM-space with order unity to its dual is weakly compact. In particular, every operator from $\ell _\infty$
-space [Reference Aliprantis and Burkinshaw2, Theorem 4.29], from (b) it follows that every operator from an AM-space with order unity to a KB-space is weakly compact. And since the dual of an AM-space is a KB-space, every operator from an AM-space with order unity to its dual is weakly compact. In particular, every operator from $\ell _\infty$ to $\ell _\infty ^*$
to $\ell _\infty ^*$ is weakly compact.
is weakly compact.
Corollary 5.9 Let $m\geq 2$![]() and $E_{1},\, \ldots,\,E_{m},\, F$
and $E_{1},\, \ldots,\,E_{m},\, F$![]() be Banach lattices such that every regular operator from $E_{j}$
be Banach lattices such that every regular operator from $E_{j}$![]() to $E_{j+i}^{\ast }$
to $E_{j+i}^{\ast }$![]() is weakly compact, $j=2,\,\ldots,\,m-1,\, i=1,\,\ldots,\,m-j$
is weakly compact, $j=2,\,\ldots,\,m-1,\, i=1,\,\ldots,\,m-j$![]() . If $E_{1}^{\ast }$
. If $E_{1}^{\ast }$![]() has order continuous norm, then the Arens extension $A^{\ast [m+1]}$
has order continuous norm, then the Arens extension $A^{\ast [m+1]}$![]() of any operator $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$
of any operator $A\in \mathcal {L}_{r}(E_{1},\,\ldots,\,E_{m};F)$![]() is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$
is separately order continuous on $E_{1}^{\ast \ast }\times \cdots \times E_{m}^{\ast \ast }$![]() .
.
Proof. Condition (a) of Theorem 5.7 is given by assumption. For $x_{1}^{\ast \ast }\in E_{1}^{\ast \ast }$![]() and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$
and $T\in \mathcal {L}_{r}(E_{1};E_{k}^{\ast })$![]() , $x_{1}^{\ast \ast }$
, $x_{1}^{\ast \ast }$![]() is order continuous because the norm of $E_{1}^{\ast }$
is order continuous because the norm of $E_{1}^{\ast }$![]() is order continuous [Reference Meyer–Nieberg17, Theorem 2.4.2]. Since $T^*$
is order continuous [Reference Meyer–Nieberg17, Theorem 2.4.2]. Since $T^*$![]() is order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73], $T^{**}(x_1^{**}) = x_1^{**} \circ T^*$
is order continuous [Reference Aliprantis and Burkinshaw2, Theorem 1.73], $T^{**}(x_1^{**}) = x_1^{**} \circ T^*$![]() is order continuous as well, so condition (b) is fulfilled too.
is order continuous as well, so condition (b) is fulfilled too.
Recall that a Banach space $E$![]() is Arens regular if every bounded linear operator from $E$
is Arens regular if every bounded linear operator from $E$![]() to $E^*$
to $E^*$![]() is weakly compact (see, e.g., [Reference Dineen13]). The Banach lattices $c_0,\, \ell _\infty$
is weakly compact (see, e.g., [Reference Dineen13]). The Banach lattices $c_0,\, \ell _\infty$![]() and $C(K)$
and $C(K)$![]() , where $K$
, where $K$![]() is a compact Hausdorff space, in particular AM-spaces with order unit, are Arens regular (cf. Example 5.8).
is a compact Hausdorff space, in particular AM-spaces with order unit, are Arens regular (cf. Example 5.8).
Corollary 5.10 Let $E$![]() be an Arens regular Banach lattice. Then, for every Banach lattice $F$
be an Arens regular Banach lattice. Then, for every Banach lattice $F$![]() , the Arens extension $A^{\ast [m+1]}$
, the Arens extension $A^{\ast [m+1]}$![]() of any regular $m$
of any regular $m$![]() -linear operator $A \colon E^m \longrightarrow F$
-linear operator $A \colon E^m \longrightarrow F$![]() is separately order continuous on $(E^{**})^m$
is separately order continuous on $(E^{**})^m$![]() .
.
Proof. The Arens regularity of $E$![]() immediately gives condition (a) of Theorem 5.7 and implies that, for every $T\in \mathcal {L}_{r}(E;E^{\ast })$
immediately gives condition (a) of Theorem 5.7 and implies that, for every $T\in \mathcal {L}_{r}(E;E^{\ast })$![]() , $T^{**}(E^{**}) \subseteq J_{E^*}(E^*) \subseteq (E^{**})^*_n$
, $T^{**}(E^{**}) \subseteq J_{E^*}(E^*) \subseteq (E^{**})^*_n$![]() , which gives condition (b).
, which gives condition (b).
We conclude this paper with one more result on order continuity of Arens extensions of homogeneous polynomials. For a polynomial $P \in {\mathcal {P}}_r(^mE;F)$![]() , we write $P^{*[m+1]} := AR_m^{\theta }(P)$
, we write $P^{*[m+1]} := AR_m^{\theta }(P)$![]() . Recall that $P$
. Recall that $P$![]() is orthogonally additive if $P(x+y) = P(x) + P(y)$
is orthogonally additive if $P(x+y) = P(x) + P(y)$![]() whenever $x$
whenever $x$![]() and $y$
and $y$![]() are disjoint. The literature on orthogonally additive polynomials is extensive.
are disjoint. The literature on orthogonally additive polynomials is extensive.
A linear operator $u\colon E \longrightarrow E^*$![]() is symmetric if $u(x)(y) = u(y)(x)$
is symmetric if $u(x)(y) = u(y)(x)$![]() for all $x,\,y \in E$
for all $x,\,y \in E$![]() . A Banach space $E$
. A Banach space $E$![]() is symetrically Arens regular if every symmetric operator from $E$
is symetrically Arens regular if every symmetric operator from $E$![]() to $E^*$
to $E^*$![]() is weakly compact. Of course, Arens regular spaces are symmetrically Arens regular, but there are symmetrically Arens regular spaces that fail to be Arens regular [Reference Leung15].
is weakly compact. Of course, Arens regular spaces are symmetrically Arens regular, but there are symmetrically Arens regular spaces that fail to be Arens regular [Reference Leung15].
Proposition 5.11 Let $E,\,F$![]() be Banach lattices and $P \in {\mathcal {P}}_r(^mE;F)$
be Banach lattices and $P \in {\mathcal {P}}_r(^mE;F)$![]() . If either $P$
. If either $P$![]() is orthogonally additive and $F = \mathbb {R}$
is orthogonally additive and $F = \mathbb {R}$![]() or $E$
or $E$![]() is symmetrically Arens regular, then the Arens extension $P^{\ast [m+1]} \colon E^{**} \longrightarrow F^{**}$
is symmetrically Arens regular, then the Arens extension $P^{\ast [m+1]} \colon E^{**} \longrightarrow F^{**}$![]() of $P$
of $P$![]() is order continuous on $E^{**}$
is order continuous on $E^{**}$![]() .
.
Proof. Assume first that $P$![]() is orthogonally additive and $F = \mathbb {R}$
is orthogonally additive and $F = \mathbb {R}$![]() . By Proposition 4.8 we know that $P^{\ast [m+1]}$
. By Proposition 4.8 we know that $P^{\ast [m+1]}$![]() is order continuous at the origin on $E^{**}$
is order continuous at the origin on $E^{**}$![]() , therefore it is order continuous at every point of $E^{**}$
, therefore it is order continuous at every point of $E^{**}$![]() by [Reference Boyd, Ryan and Snigireva8, Proposition 8].
by [Reference Boyd, Ryan and Snigireva8, Proposition 8].
Suppose now that $E$![]() is symmetrically Arens regular. It is clear that we can assume that $P$
is symmetrically Arens regular. It is clear that we can assume that $P$![]() is positive. We know that $(\check {P})^{\ast [m+1]}$
is positive. We know that $(\check {P})^{\ast [m+1]}$![]() is order continuous in the first variable on $E^{**}$
is order continuous in the first variable on $E^{**}$![]() (Theorem 4.6) and positive because $\check {P}$
(Theorem 4.6) and positive because $\check {P}$![]() is positive. In order to check that it is symmetric, let $\rho \in S_m$
is positive. In order to check that it is symmetric, let $\rho \in S_m$![]() be given. For every $\varphi \in F^*$
be given. For every $\varphi \in F^*$![]() , since $E$
, since $E$![]() is symmetrically Arens regular and $\varphi \circ \check {P}$
is symmetrically Arens regular and $\varphi \circ \check {P}$![]() is symmetric, by [Reference Aron, Cole and Gamelin5, Theorem 8.3] (or [Reference Cabello Sánchez, García and Villanueva11, Corollary 6]) we know that $AR_m^{\theta }(\varphi \circ \check {P})$
is symmetric, by [Reference Aron, Cole and Gamelin5, Theorem 8.3] (or [Reference Cabello Sánchez, García and Villanueva11, Corollary 6]) we know that $AR_m^{\theta }(\varphi \circ \check {P})$![]() is symmetric as well. So, for $x_1^{**},\, \ldots,\, x_m^{**} \in E^{**}$
is symmetric as well. So, for $x_1^{**},\, \ldots,\, x_m^{**} \in E^{**}$![]() ,
,

proving that $(\check {P})^{\ast [m+1]}$![]() is symmetric. The order continuity in the first variable and the symmetry yield that the positive $m$
is symmetric. The order continuity in the first variable and the symmetry yield that the positive $m$![]() -linear operator $(\check {P})^{\ast [m+1]}$
-linear operator $(\check {P})^{\ast [m+1]}$![]() is separately order continuous on $(E^{**})^m$
is separately order continuous on $(E^{**})^m$![]() . By [Reference Buskes and Roberts10, Lemma 2.6] it follows that $(\check {P})^{\ast [m+1]}$
. By [Reference Buskes and Roberts10, Lemma 2.6] it follows that $(\check {P})^{\ast [m+1]}$![]() is jointly order continuous on $(E^{**})^m$
is jointly order continuous on $(E^{**})^m$![]() . So, if $x_{\alpha }^{**}\xrightarrow {\, o \,} x^{**}$
. So, if $x_{\alpha }^{**}\xrightarrow {\, o \,} x^{**}$![]() in $E^{**}$
in $E^{**}$![]() , then
, then

Acknowledgements
The authors thank the reviewer for the invaluable comments and suggestions that improved the final presentation of the paper. We are also grateful to R. Ryan for his helpful suggestions and for drawing our attention to [Reference Boyd, Ryan and Snigireva8].